how hypothesis testing works

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
Duis aute irure dolor in reprehenderit in voluptate
Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

S.3 hypothesis testing.

In reviewing hypothesis tests, we start first with the general idea. Then, we keep returning to the basic procedures of hypothesis testing, each time adding a little more detail.

The general idea of hypothesis testing involves:

Making an initial assumption.
Collecting evidence (data).
Based on the available evidence (data), deciding whether to reject or not reject the initial assumption.

Every hypothesis test — regardless of the population parameter involved — requires the above three steps.

Example S.3.1

Is normal body temperature really 98.6 degrees f section .

Consider the population of many, many adults. A researcher hypothesized that the average adult body temperature is lower than the often-advertised 98.6 degrees F. That is, the researcher wants an answer to the question: "Is the average adult body temperature 98.6 degrees? Or is it lower?" To answer his research question, the researcher starts by assuming that the average adult body temperature was 98.6 degrees F.

Then, the researcher went out and tried to find evidence that refutes his initial assumption. In doing so, he selects a random sample of 130 adults. The average body temperature of the 130 sampled adults is 98.25 degrees.

Then, the researcher uses the data he collected to make a decision about his initial assumption. It is either likely or unlikely that the researcher would collect the evidence he did given his initial assumption that the average adult body temperature is 98.6 degrees:

If it is likely , then the researcher does not reject his initial assumption that the average adult body temperature is 98.6 degrees. There is not enough evidence to do otherwise.
either the researcher's initial assumption is correct and he experienced a very unusual event;
or the researcher's initial assumption is incorrect.

In statistics, we generally don't make claims that require us to believe that a very unusual event happened. That is, in the practice of statistics, if the evidence (data) we collected is unlikely in light of the initial assumption, then we reject our initial assumption.

Example S.3.2

Criminal trial analogy section .

One place where you can consistently see the general idea of hypothesis testing in action is in criminal trials held in the United States. Our criminal justice system assumes "the defendant is innocent until proven guilty." That is, our initial assumption is that the defendant is innocent.

In the practice of statistics, we make our initial assumption when we state our two competing hypotheses -- the null hypothesis ( H 0 ) and the alternative hypothesis ( H A ). Here, our hypotheses are:

H 0 : Defendant is not guilty (innocent)
H A : Defendant is guilty

In statistics, we always assume the null hypothesis is true . That is, the null hypothesis is always our initial assumption.

The prosecution team then collects evidence — such as finger prints, blood spots, hair samples, carpet fibers, shoe prints, ransom notes, and handwriting samples — with the hopes of finding "sufficient evidence" to make the assumption of innocence refutable.

In statistics, the data are the evidence.

The jury then makes a decision based on the available evidence:

If the jury finds sufficient evidence — beyond a reasonable doubt — to make the assumption of innocence refutable, the jury rejects the null hypothesis and deems the defendant guilty. We behave as if the defendant is guilty.
If there is insufficient evidence, then the jury does not reject the null hypothesis . We behave as if the defendant is innocent.

In statistics, we always make one of two decisions. We either "reject the null hypothesis" or we "fail to reject the null hypothesis."

Errors in Hypothesis Testing Section

Did you notice the use of the phrase "behave as if" in the previous discussion? We "behave as if" the defendant is guilty; we do not "prove" that the defendant is guilty. And, we "behave as if" the defendant is innocent; we do not "prove" that the defendant is innocent.

This is a very important distinction! We make our decision based on evidence not on 100% guaranteed proof. Again:

If we reject the null hypothesis, we do not prove that the alternative hypothesis is true.
If we do not reject the null hypothesis, we do not prove that the null hypothesis is true.

We merely state that there is enough evidence to behave one way or the other. This is always true in statistics! Because of this, whatever the decision, there is always a chance that we made an error .

Let's review the two types of errors that can be made in criminal trials:

Table S.3.2 shows how this corresponds to the two types of errors in hypothesis testing.

Note that, in statistics, we call the two types of errors by two different names -- one is called a "Type I error," and the other is called a "Type II error." Here are the formal definitions of the two types of errors:

There is always a chance of making one of these errors. But, a good scientific study will minimize the chance of doing so!

Making the Decision Section

Recall that it is either likely or unlikely that we would observe the evidence we did given our initial assumption. If it is likely , we do not reject the null hypothesis. If it is unlikely , then we reject the null hypothesis in favor of the alternative hypothesis. Effectively, then, making the decision reduces to determining "likely" or "unlikely."

In statistics, there are two ways to determine whether the evidence is likely or unlikely given the initial assumption:

We could take the " critical value approach " (favored in many of the older textbooks).
Or, we could take the " P -value approach " (what is used most often in research, journal articles, and statistical software).

In the next two sections, we review the procedures behind each of these two approaches. To make our review concrete, let's imagine that μ is the average grade point average of all American students who major in mathematics. We first review the critical value approach for conducting each of the following three hypothesis tests about the population mean $\mu$:

In Practice

We would want to conduct the first hypothesis test if we were interested in concluding that the average grade point average of the group is more than 3.
We would want to conduct the second hypothesis test if we were interested in concluding that the average grade point average of the group is less than 3.
And, we would want to conduct the third hypothesis test if we were only interested in concluding that the average grade point average of the group differs from 3 (without caring whether it is more or less than 3).

Upon completing the review of the critical value approach, we review the P -value approach for conducting each of the above three hypothesis tests about the population mean $\mu$. The procedures that we review here for both approaches easily extend to hypothesis tests about any other population parameter.

school Campus Bookshelves
menu_book Bookshelves
perm_media Learning Objects
login Login
how_to_reg Request Instructor Account
hub Instructor Commons

Margin Size

Download Page (PDF)
Download Full Book (PDF)
Periodic Table
Physics Constants
Scientific Calculator
Reference & Cite
Tools expand_more
Readability

selected template will load here

This action is not available.

7.1: Basics of Hypothesis Testing

Last updated
Save as PDF
Page ID 16360

Kathryn Kozak
Coconino Community College

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

To understand the process of a hypothesis tests, you need to first have an understanding of what a hypothesis is, which is an educated guess about a parameter. Once you have the hypothesis, you collect data and use the data to make a determination to see if there is enough evidence to show that the hypothesis is true. However, in hypothesis testing you actually assume something else is true, and then you look at your data to see how likely it is to get an event that your data demonstrates with that assumption. If the event is very unusual, then you might think that your assumption is actually false. If you are able to say this assumption is false, then your hypothesis must be true. This is known as a proof by contradiction. You assume the opposite of your hypothesis is true and show that it can’t be true. If this happens, then your hypothesis must be true. All hypothesis tests go through the same process. Once you have the process down, then the concept is much easier. It is easier to see the process by looking at an example. Concepts that are needed will be detailed in this example.

Example $\PageIndex{1}$ basics of hypothesis testing

Suppose a manufacturer of the XJ35 battery claims the mean life of the battery is 500 days with a standard deviation of 25 days. You are the buyer of this battery and you think this claim is inflated. You would like to test your belief because without a good reason you can’t get out of your contract.

What do you do?

Well first, you should know what you are trying to measure. Define the random variable.

Let x = life of a XJ35 battery

Now you are not just trying to find different x values. You are trying to find what the true mean is. Since you are trying to find it, it must be unknown. You don’t think it is 500 days. If you did, you wouldn’t be doing any testing. The true mean, $\mu$, is unknown. That means you should define that too.

Let $\mu$= mean life of a XJ35 battery

You may want to collect a sample. What kind of sample?

You could ask the manufacturers to give you batteries, but there is a chance that there could be some bias in the batteries they pick. To reduce the chance of bias, it is best to take a random sample.

How big should the sample be?

A sample of size 30 or more means that you can use the central limit theorem. Pick a sample of size 30.

Example $\PageIndex{1}$ contains the data for the sample you collected:

Now what should you do? Looking at the data set, you see some of the times are above 500 and some are below. But looking at all of the numbers is too difficult. It might be helpful to calculate the mean for this sample.

The sample mean is $\overline{x} = 490$ days. Looking at the sample mean, one might think that you are right. However, the standard deviation and the sample size also plays a role, so maybe you are wrong.

Before going any farther, it is time to formalize a few definitions.

You have a guess that the mean life of a battery is less than 500 days. This is opposed to what the manufacturer claims. There really are two hypotheses, which are just guesses here – the one that the manufacturer claims and the one that you believe. It is helpful to have names for them.

Definition $\PageIndex{1}$

Null Hypothesis : historical value, claim, or product specification. The symbol used is $H_{o}$.

Definition $\PageIndex{2}$

Alternate Hypothesis : what you want to prove. This is what you want to accept as true when you reject the null hypothesis. There are two symbols that are commonly used for the alternative hypothesis: $H_{A}$ or $H_{I}$. The symbol $H_{A}$ will be used in this book.

In general, the hypotheses look something like this:

$H_{o} : \mu=\mu_{o}$

$H_{A} : \mu<\mu_{o}$

where $\mu_{o}$ just represents the value that the claim says the population mean is actually equal to.

Also, $H_{A}$ can be less than, greater than, or not equal to.

For this problem:

$H_{o} : \mu=500$ days, since the manufacturer says the mean life of a battery is 500 days.

$H_{A} : \mu<500$ days, since you believe that the mean life of the battery is less than 500 days.

Now back to the mean. You have a sample mean of 490 days. Is this small enough to believe that you are right and the manufacturer is wrong? How small does it have to be?

If you calculated a sample mean of 235, you would definitely believe the population mean is less than 500. But even if you had a sample mean of 435 you would probably believe that the true mean was less than 500. What about 475? Or 483? There is some point where you would stop being so sure that the population mean is less than 500. That point separates the values of where you are sure or pretty sure that the mean is less than 500 from the area where you are not so sure. How do you find that point?

Well it depends on how much error you want to make. Of course you don’t want to make any errors, but unfortunately that is unavoidable in statistics. You need to figure out how much error you made with your sample. Take the sample mean, and find the probability of getting another sample mean less than it, assuming for the moment that the manufacturer is right. The idea behind this is that you want to know what is the chance that you could have come up with your sample mean even if the population mean really is 500 days.

You want to find $P\left(\overline{x}<490 | H_{o} \text { is true }\right)=P(\overline{x}<490 | \mu=500)$

To compute this probability, you need to know how the sample mean is distributed. Since the sample size is at least 30, then you know the sample mean is approximately normally distributed. Remember $\mu_{\overline{x}}=\mu$ and $\sigma_{\overline{x}}=\dfrac{\sigma}{\sqrt{n}}$

A picture is always useful.

Before calculating the probability, it is useful to see how many standard deviations away from the mean the sample mean is. Using the formula for the z-score from chapter 6, you find

$z=\dfrac{\overline{x}-\mu_{o}}{\sigma / \sqrt{n}}=\dfrac{490-500}{25 / \sqrt{30}}=-2.19$

This sample mean is more than two standard deviations away from the mean. That seems pretty far, but you should look at the probability too.

On TI-83/84:

$P(\overline{x}<490 | \mu=500)=\text { normalcdf }(-1 E 99,490,500,25 \div \sqrt{30}) \approx 0.0142$

$P(\overline{x}<490 \mu=500)=\text { pnorm }(490,500,25 / \operatorname{sqrt}(30)) \approx 0.0142$

There is a 1.42% chance that you could find a sample mean less than 490 when the population mean is 500 days. This is really small, so the chances are that the assumption that the population mean is 500 days is wrong, and you can reject the manufacturer’s claim. But how do you quantify really small? Is 5% or 10% or 15% really small? How do you decide?

Before you answer that question, a couple more definitions are needed.

Definition $\PageIndex{3}$

Test Statistic : $z=\dfrac{\overline{x}-\mu_{o}}{\sigma / \sqrt{n}}$ since it is calculated as part of the testing of the hypothesis.

Definition $\PageIndex{4}$

p – value : probability that the test statistic will take on more extreme values than the observed test statistic, given that the null hypothesis is true. It is the probability that was calculated above.

Now, how small is small enough? To answer that, you really want to know the types of errors you can make.

There are actually only two errors that can be made. The first error is if you say that $H_{o}$ is false, when in fact it is true. This means you reject $H_{o}$ when $H_{o}$ was true. The second error is if you say that $H_{o}$ is true, when in fact it is false. This means you fail to reject $H_{o}$ when $H_{o}$ is false. The following table organizes this for you:

Type of errors:

Definition $\PageIndex{5}$

Type I Error is rejecting $H_{o}$ when $H_{o}$ is true, and

Definition $\PageIndex{6}$

Type II Error is failing to reject $H_{o}$ when $H_{o}$ is false.

Since these are the errors, then one can define the probabilities attached to each error.

Definition $\PageIndex{7}$

$\alpha$ = P(type I error) = P(rejecting $H_{o} / H_{o}$ is true)

Definition $\PageIndex{8}$

$\beta$ = P(type II error) = P(failing to reject $H_{o} / H_{o}$ is false)

$\alpha$ is also called the level of significance .

Another common concept that is used is Power = $1-\beta $.

Now there is a relationship between $\alpha$ and $\beta$. They are not complements of each other. How are they related?

If $\alpha$ increases that means the chances of making a type I error will increase. It is more likely that a type I error will occur. It makes sense that you are less likely to make type II errors, only because you will be rejecting $H_{o}$ more often. You will be failing to reject $H_{o}$ less, and therefore, the chance of making a type II error will decrease. Thus, as $\alpha$ increases, $\beta$ will decrease, and vice versa. That makes them seem like complements, but they aren’t complements. What gives? Consider one more factor – sample size.

Consider if you have a larger sample that is representative of the population, then it makes sense that you have more accuracy then with a smaller sample. Think of it this way, which would you trust more, a sample mean of 490 if you had a sample size of 35 or sample size of 350 (assuming a representative sample)? Of course the 350 because there are more data points and so more accuracy. If you are more accurate, then there is less chance that you will make any error. By increasing the sample size of a representative sample, you decrease both $\alpha$ and $\beta$.

Summary of all of this:

For a certain sample size, n , if $\alpha$ increases, $\beta$ decreases.
For a certain level of significance, $\alpha$, if n increases, $\beta$ decreases.

Now how do you find $\alpha$ and $\beta$? Well $\alpha$ is actually chosen. There are only three values that are usually picked for $\alpha$: 0.01, 0.05, and 0.10. $\beta$ is very difficult to find, so usually it isn’t found. If you want to make sure it is small you take as large of a sample as you can afford provided it is a representative sample. This is one use of the Power. You want $\beta$ to be small and the Power of the test is large. The Power word sounds good.

Which pick of $\alpha$ do you pick? Well that depends on what you are working on. Remember in this example you are the buyer who is trying to get out of a contract to buy these batteries. If you create a type I error, you said that the batteries are bad when they aren’t, most likely the manufacturer will sue you. You want to avoid this. You might pick $\alpha$ to be 0.01. This way you have a small chance of making a type I error. Of course this means you have more of a chance of making a type II error. No big deal right? What if the batteries are used in pacemakers and you tell the person that their pacemaker’s batteries are good for 500 days when they actually last less, that might be bad. If you make a type II error, you say that the batteries do last 500 days when they last less, then you have the possibility of killing someone. You certainly do not want to do this. In this case you might want to pick $\alpha$ as 0.10. If both errors are equally bad, then pick $\alpha$ as 0.05.

The above discussion is why the choice of $\alpha$ depends on what you are researching. As the researcher, you are the one that needs to decide what $\alpha$ level to use based on your analysis of the consequences of making each error is.

If a type I error is really bad, then pick $\alpha$ = 0.01.

If a type II error is really bad, then pick $\alpha$ = 0.10

If neither error is bad, or both are equally bad, then pick $\alpha$ = 0.05

The main thing is to always pick the $\alpha$ before you collect the data and start the test.

The above discussion was long, but it is really important information. If you don’t know what the errors of the test are about, then there really is no point in making conclusions with the tests. Make sure you understand what the two errors are and what the probabilities are for them.

Now it is time to go back to the example and put this all together. This is the basic structure of testing a hypothesis, usually called a hypothesis test. Since this one has a test statistic involving z, it is also called a z-test. And since there is only one sample, it is usually called a one-sample z-test.

Example $\PageIndex{2}$ battery example revisited

State the random variable and the parameter in words.
State the null and alternative hypothesis and the level of significance.
A random sample of size n is taken.
The population standard derivation is known.
The sample size is at least 30 or the population of the random variable is normally distributed.
Find the sample statistic, test statistic, and p-value.
Interpretation

1. x = life of battery

$\mu$ = mean life of a XJ35 battery

2. $H_{o} : \mu=500$ days

$H_{A} : \mu<500$ days

$\alpha = 0.10$ (from above discussion about consequences)

3. Every hypothesis has some assumptions that be met to make sure that the results of the hypothesis are valid. The assumptions are different for each test. This test has the following assumptions.

This occurred in this example, since it was stated that a random sample of 30 battery lives were taken.
This is true, since it was given in the problem.
The sample size was 30, so this condition is met.

4. The test statistic depends on how many samples there are, what parameter you are testing, and assumptions that need to be checked. In this case, there is one sample and you are testing the mean. The assumptions were checked above.

Sample statistic:

$\overline{x} = 490$

Test statistic:

Using TI-83/84:

$P(\overline{x}<490 | \mu=500)=\text { normalcdf }(-1 \mathrm{E} 99,490,500,25 / \sqrt{30}) \approx 0.0142$

$P(\overline{x}<490 | \mu=500)=\operatorname{pnorm}(490,500,25 / \operatorname{sqrt}(30)) \approx 0.0142$

5. Now what? Well, this p-value is 0.0142. This is a lot smaller than the amount of error you would accept in the problem -$\alpha$ = 0.10. That means that finding a sample mean less than 490 days is unusual to happen if $H_{o}$ is true. This should make you think that $H_{o}$ is not true. You should reject $H_{o}$.

In fact, in general:

Reject $H_{o}$ if the p-value < $\alpha$ and

Fail to reject $H_{o}$ if the p-value $\geq \alpha$.

6. Since you rejected $H_{o}$, what does this mean in the real world? That is what goes in the interpretation. Since you rejected the claim by the manufacturer that the mean life of the batteries is 500 days, then you now can believe that your hypothesis was correct. In other words, there is enough evidence to show that the mean life of the battery is less than 500 days.

Now that you know that the batteries last less than 500 days, should you cancel the contract? Statistically, there is evidence that the batteries do not last as long as the manufacturer says they should. However, based on this sample there are only ten days less on average that the batteries last. There may not be practical significance in this case. Ten days do not seem like a large difference. In reality, if the batteries are used in pacemakers, then you would probably tell the patient to have the batteries replaced every year. You have a large buffer whether the batteries last 490 days or 500 days. It seems that it might not be worth it to break the contract over ten days. What if the 10 days was practically significant? Are there any other things you should consider? You might look at the business relationship with the manufacturer. You might also look at how much it would cost to find a new manufacturer. These are also questions to consider before making any changes. What this discussion should show you is that just because a hypothesis has statistical significance does not mean it has practical significance. The hypothesis test is just one part of a research process. There are other pieces that you need to consider.

That’s it. That is what a hypothesis test looks like. All hypothesis tests are done with the same six steps. Those general six steps are outlined below.

State the random variable and the parameter in words. This is where you are defining what the unknowns are in this problem. x = random variable $\mu$ = mean of random variable, if the parameter of interest is the mean. There are other parameters you can test, and you would use the appropriate symbol for that parameter.
State the null and alternative hypotheses and the level of significance $H_{o} : \mu=\mu_{o}$, where $\mu_{o}$ is the known mean $H_{A} : \mu<\mu_{o}$ $H_{A} : \mu>\mu_{o}$, use the appropriate one for your problem $H_{A} : \mu \neq \mu_{o}$ Also, state your $\alpha$ level here.
State and check the assumptions for a hypothesis test. Each hypothesis test has its own assumptions. They will be stated when the different hypothesis tests are discussed.
Find the sample statistic, test statistic, and p-value. This depends on what parameter you are working with, how many samples, and the assumptions of the test. The p-value depends on your $H_{A}$. If you are doing the $H_{A}$ with the less than, then it is a left-tailed test, and you find the probability of being in that left tail. If you are doing the $H_{A}$ with the greater than, then it is a right-tailed test, and you find the probability of being in the right tail. If you are doing the $H_{A}$ with the not equal to, then you are doing a two-tail test, and you find the probability of being in both tails. Because of symmetry, you could find the probability in one tail and double this value to find the probability in both tails.
Conclusion This is where you write reject $H_{o}$ or fail to reject $H_{o}$. The rule is: if the p-value < $\alpha$, then reject $H_{o}$. If the p-value $\geq \alpha$, then fail to reject $H_{o}$.
Interpretation This is where you interpret in real world terms the conclusion to the test. The conclusion for a hypothesis test is that you either have enough evidence to show $H_{A}$ is true, or you do not have enough evidence to show $H_{A}$ is true.

Sorry, one more concept about the conclusion and interpretation. First, the conclusion is that you reject $H_{o}$ or you fail to reject $H_{o}$. Why was it said like this? It is because you never accept the null hypothesis. If you wanted to accept the null hypothesis, then why do the test in the first place? In the interpretation, you either have enough evidence to show $H_{A}$ is true, or you do not have enough evidence to show $H_{A}$ is true. You wouldn’t want to go to all this work and then find out you wanted to accept the claim. Why go through the trouble? You always want to show that the alternative hypothesis is true. Sometimes you can do that and sometimes you can’t. It doesn’t mean you proved the null hypothesis; it just means you can’t prove the alternative hypothesis. Here is an example to demonstrate this.

Example $\PageIndex{3}$ conclusion in hypothesis tests

In the U.S. court system a jury trial could be set up as a hypothesis test. To really help you see how this works, let’s use OJ Simpson as an example. In the court system, a person is presumed innocent until he/she is proven guilty, and this is your null hypothesis. OJ Simpson was a football player in the 1970s. In 1994 his ex-wife and her friend were killed. OJ Simpson was accused of the crime, and in 1995 the case was tried. The prosecutors wanted to prove OJ was guilty of killing his wife and her friend, and that is the alternative hypothesis

$H_{0}$: OJ is innocent of killing his wife and her friend

$H_{A}$: OJ is guilty of killing his wife and her friend

In this case, a verdict of not guilty was given. That does not mean that he is innocent of this crime. It means there was not enough evidence to prove he was guilty. Many people believe that OJ was guilty of this crime, but the jury did not feel that the evidence presented was enough to show there was guilt. The verdict in a jury trial is always guilty or not guilty!

The same is true in a hypothesis test. There is either enough or not enough evidence to show that alternative hypothesis. It is not that you proved the null hypothesis true.

When identifying hypothesis, it is important to state your random variable and the appropriate parameter you want to make a decision about. If count something, then the random variable is the number of whatever you counted. The parameter is the proportion of what you counted. If the random variable is something you measured, then the parameter is the mean of what you measured. (Note: there are other parameters you can calculate, and some analysis of those will be presented in later chapters.)

Example $\PageIndex{4}$ stating hypotheses

Identify the hypotheses necessary to test the following statements:

The average salary of a teacher is more than $30,000.
The proportion of students who like math is less than 10%.
The average age of students in this class differs from 21.

a. x = salary of teacher

$\mu$ = mean salary of teacher

The guess is that $\mu>\$ 30,000$ and that is the alternative hypothesis.

The null hypothesis has the same parameter and number with an equal sign.

$\begin{array}{l}{H_{0} : \mu=\$ 30,000} \\ {H_{A} : \mu>\$ 30,000}\end{array}$

b. x = number od students who like math

p = proportion of students who like math

The guess is that p < 0.10 and that is the alternative hypothesis.

$\begin{array}{l}{H_{0} : p=0.10} \\ {H_{A} : p<0.10}\end{array}$

c. x = age of students in this class

$\mu$ = mean age of students in this class

The guess is that $\mu \neq 21$ and that is the alternative hypothesis.

$\begin{array}{c}{H_{0} : \mu=21} \\ {H_{A} : \mu \neq 21}\end{array}$

Example $\PageIndex{5}$ Stating Type I and II Errors and Picking Level of Significance

The plant-breeding department at a major university developed a new hybrid raspberry plant called YumYum Berry. Based on research data, the claim is made that from the time shoots are planted 90 days on average are required to obtain the first berry with a standard deviation of 9.2 days. A corporation that is interested in marketing the product tests 60 shoots by planting them and recording the number of days before each plant produces its first berry. The sample mean is 92.3 days. The corporation wants to know if the mean number of days is more than the 90 days claimed. State the type I and type II errors in terms of this problem, consequences of each error, and state which level of significance to use.
A concern was raised in Australia that the percentage of deaths of Aboriginal prisoners was higher than the percent of deaths of non-indigenous prisoners, which is 0.27%. State the type I and type II errors in terms of this problem, consequences of each error, and state which level of significance to use.

a. x = time to first berry for YumYum Berry plant

$\mu$ = mean time to first berry for YumYum Berry plant

$\begin{array}{l}{H_{0} : \mu=90} \\ {H_{A} : \mu>90}\end{array}$

Type I Error: If the corporation does a type I error, then they will say that the plants take longer to produce than 90 days when they don’t. They probably will not want to market the plants if they think they will take longer. They will not market them even though in reality the plants do produce in 90 days. They may have loss of future earnings, but that is all.

Type II error: The corporation do not say that the plants take longer then 90 days to produce when they do take longer. Most likely they will market the plants. The plants will take longer, and so customers might get upset and then the company would get a bad reputation. This would be really bad for the company.

Level of significance: It appears that the corporation would not want to make a type II error. Pick a 10% level of significance, $\alpha = 0.10$.

b. x = number of Aboriginal prisoners who have died

p = proportion of Aboriginal prisoners who have died

$\begin{array}{l}{H_{o} : p=0.27 \%} \\ {H_{A} : p>0.27 \%}\end{array}$

Type I error: Rejecting that the proportion of Aboriginal prisoners who died was 0.27%, when in fact it was 0.27%. This would mean you would say there is a problem when there isn’t one. You could anger the Aboriginal community, and spend time and energy researching something that isn’t a problem.

Type II error: Failing to reject that the proportion of Aboriginal prisoners who died was 0.27%, when in fact it is higher than 0.27%. This would mean that you wouldn’t think there was a problem with Aboriginal prisoners dying when there really is a problem. You risk causing deaths when there could be a way to avoid them.

Level of significance: It appears that both errors may be issues in this case. You wouldn’t want to anger the Aboriginal community when there isn’t an issue, and you wouldn’t want people to die when there may be a way to stop it. It may be best to pick a 5% level of significance, $\alpha = 0.05$.

Hypothesis testing is really easy if you follow the same recipe every time. The only differences in the various problems are the assumptions of the test and the test statistic you calculate so you can find the p-value. Do the same steps, in the same order, with the same words, every time and these problems become very easy.

Exercise $\PageIndex{1}$

For the problems in this section, a question is being asked. This is to help you understand what the hypotheses are. You are not to run any hypothesis tests and come up with any conclusions in this section.

Eyeglassomatic manufactures eyeglasses for different retailers. They test to see how many defective lenses they made in a given time period and found that 11% of all lenses had defects of some type. Looking at the type of defects, they found in a three-month time period that out of 34,641 defective lenses, 5865 were due to scratches. Are there more defects from scratches than from all other causes? State the random variable, population parameter, and hypotheses.
According to the February 2008 Federal Trade Commission report on consumer fraud and identity theft, 23% of all complaints in 2007 were for identity theft. In that year, Alaska had 321 complaints of identity theft out of 1,432 consumer complaints ("Consumer fraud and," 2008). Does this data provide enough evidence to show that Alaska had a lower proportion of identity theft than 23%? State the random variable, population parameter, and hypotheses.
The Kyoto Protocol was signed in 1997, and required countries to start reducing their carbon emissions. The protocol became enforceable in February 2005. In 2004, the mean CO2 emission was 4.87 metric tons per capita. Is there enough evidence to show that the mean CO2 emission is lower in 2010 than in 2004? State the random variable, population parameter, and hypotheses.
The FDA regulates that fish that is consumed is allowed to contain 1.0 mg/kg of mercury. In Florida, bass fish were collected in 53 different lakes to measure the amount of mercury in the fish. The data for the average amount of mercury in each lake is in Example $\PageIndex{5}$ ("Multi-disciplinary niser activity," 2013). Do the data provide enough evidence to show that the fish in Florida lakes has more mercury than the allowable amount? State the random variable, population parameter, and hypotheses.
Eyeglassomatic manufactures eyeglasses for different retailers. They test to see how many defective lenses they made in a given time period and found that 11% of all lenses had defects of some type. Looking at the type of defects, they found in a three-month time period that out of 34,641 defective lenses, 5865 were due to scratches. Are there more defects from scratches than from all other causes? State the type I and type II errors in this case, consequences of each error type for this situation from the perspective of the manufacturer, and the appropriate alpha level to use. State why you picked this alpha level.
According to the February 2008 Federal Trade Commission report on consumer fraud and identity theft, 23% of all complaints in 2007 were for identity theft. In that year, Alaska had 321 complaints of identity theft out of 1,432 consumer complaints ("Consumer fraud and," 2008). Does this data provide enough evidence to show that Alaska had a lower proportion of identity theft than 23%? State the type I and type II errors in this case, consequences of each error type for this situation from the perspective of the state of Arizona, and the appropriate alpha level to use. State why you picked this alpha level.
The Kyoto Protocol was signed in 1997, and required countries to start reducing their carbon emissions. The protocol became enforceable in February 2005. In 2004, the mean CO2 emission was 4.87 metric tons per capita. Is there enough evidence to show that the mean CO2 emission is lower in 2010 than in 2004? State the type I and type II errors in this case, consequences of each error type for this situation from the perspective of the agency overseeing the protocol, and the appropriate alpha level to use. State why you picked this alpha level.
The FDA regulates that fish that is consumed is allowed to contain 1.0 mg/kg of mercury. In Florida, bass fish were collected in 53 different lakes to measure the amount of mercury in the fish. The data for the average amount of mercury in each lake is in Example $\PageIndex{5}$ ("Multi-disciplinary niser activity," 2013). Do the data provide enough evidence to show that the fish in Florida lakes has more mercury than the allowable amount? State the type I and type II errors in this case, consequences of each error type for this situation from the perspective of the FDA, and the appropriate alpha level to use. State why you picked this alpha level.

1. $H_{o} : p=0.11, H_{A} : p>0.11$

3. $H_{o} : \mu=4.87 \text { metric tons per capita, } H_{A} : \mu<4.87 \text { metric tons per capita }$

5. See solutions

7. See solutions

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Unit 12: Significance tests (hypothesis testing)

About this unit.

Significance tests give us a formal process for using sample data to evaluate the likelihood of some claim about a population value. Learn how to conduct significance tests and calculate p-values to see how likely a sample result is to occur by random chance. You'll also see how we use p-values to make conclusions about hypotheses.

The idea of significance tests

Simple hypothesis testing (Opens a modal)
Idea behind hypothesis testing (Opens a modal)
Examples of null and alternative hypotheses (Opens a modal)
P-values and significance tests (Opens a modal)
Comparing P-values to different significance levels (Opens a modal)
Estimating a P-value from a simulation (Opens a modal)
Using P-values to make conclusions (Opens a modal)
Simple hypothesis testing Get 3 of 4 questions to level up!
Writing null and alternative hypotheses Get 3 of 4 questions to level up!
Estimating P-values from simulations Get 3 of 4 questions to level up!

Error probabilities and power

Introduction to Type I and Type II errors (Opens a modal)
Type 1 errors (Opens a modal)
Examples identifying Type I and Type II errors (Opens a modal)
Introduction to power in significance tests (Opens a modal)
Examples thinking about power in significance tests (Opens a modal)
Consequences of errors and significance (Opens a modal)
Type I vs Type II error Get 3 of 4 questions to level up!
Error probabilities and power Get 3 of 4 questions to level up!

Tests about a population proportion

Constructing hypotheses for a significance test about a proportion (Opens a modal)
Conditions for a z test about a proportion (Opens a modal)
Reference: Conditions for inference on a proportion (Opens a modal)
Calculating a z statistic in a test about a proportion (Opens a modal)
Calculating a P-value given a z statistic (Opens a modal)
Making conclusions in a test about a proportion (Opens a modal)
Writing hypotheses for a test about a proportion Get 3 of 4 questions to level up!
Conditions for a z test about a proportion Get 3 of 4 questions to level up!
Calculating the test statistic in a z test for a proportion Get 3 of 4 questions to level up!
Calculating the P-value in a z test for a proportion Get 3 of 4 questions to level up!
Making conclusions in a z test for a proportion Get 3 of 4 questions to level up!

Tests about a population mean

Writing hypotheses for a significance test about a mean (Opens a modal)
Conditions for a t test about a mean (Opens a modal)
Reference: Conditions for inference on a mean (Opens a modal)
When to use z or t statistics in significance tests (Opens a modal)
Example calculating t statistic for a test about a mean (Opens a modal)
Using TI calculator for P-value from t statistic (Opens a modal)
Using a table to estimate P-value from t statistic (Opens a modal)
Comparing P-value from t statistic to significance level (Opens a modal)
Free response example: Significance test for a mean (Opens a modal)
Writing hypotheses for a test about a mean Get 3 of 4 questions to level up!
Conditions for a t test about a mean Get 3 of 4 questions to level up!
Calculating the test statistic in a t test for a mean Get 3 of 4 questions to level up!
Calculating the P-value in a t test for a mean Get 3 of 4 questions to level up!
Making conclusions in a t test for a mean Get 3 of 4 questions to level up!

Hypothesis Testing

Already have an account? Log in here.

A hypothesis test is a statistical inference method used to test the significance of a proposed (hypothesized) relation between population statistics (parameters) and their corresponding sample estimators . In other words, hypothesis tests are used to determine if there is enough evidence in a sample to prove a hypothesis true for the entire population.

The test considers two hypotheses: the null hypothesis , which is a statement meant to be tested, usually something like "there is no effect" with the intention of proving this false, and the alternate hypothesis , which is the statement meant to stand after the test is performed. The two hypotheses must be mutually exclusive ; moreover, in most applications, the two are complementary (one being the negation of the other). The test works by comparing the $p$-value to the level of significance (a chosen target). If the $p$-value is less than or equal to the level of significance, then the null hypothesis is rejected.

When analyzing data, only samples of a certain size might be manageable as efficient computations. In some situations the error terms follow a continuous or infinite distribution, hence the use of samples to suggest accuracy of the chosen test statistics. The method of hypothesis testing gives an advantage over guessing what distribution or which parameters the data follows.

Definitions and Methodology

Hypothesis test and confidence intervals.

In statistical inference, properties (parameters) of a population are analyzed by sampling data sets. Given assumptions on the distribution, i.e. a statistical model of the data, certain hypotheses can be deduced from the known behavior of the model. These hypotheses must be tested against sampled data from the population.

The null hypothesis $($denoted $H_0)$ is a statement that is assumed to be true. If the null hypothesis is rejected, then there is enough evidence (statistical significance) to accept the alternate hypothesis $($denoted $H_1).$ Before doing any test for significance, both hypotheses must be clearly stated and non-conflictive, i.e. mutually exclusive, statements. Rejecting the null hypothesis, given that it is true, is called a type I error and it is denoted $\alpha$, which is also its probability of occurrence. Failing to reject the null hypothesis, given that it is false, is called a type II error and it is denoted $\beta$, which is also its probability of occurrence. Also, $\alpha$ is known as the significance level , and $1-\beta$ is known as the power of the test. $H_0$ $\textbf{is true}$$\hspace{15mm}$ $H_0$ $\textbf{is false}$ $\textbf{Reject}$ $H_0$$\hspace{10mm}$ Type I error Correct Decision $\textbf{Reject}$ $H_1$ Correct Decision Type II error The test statistic is the standardized value following the sampled data under the assumption that the null hypothesis is true, and a chosen particular test. These tests depend on the statistic to be studied and the assumed distribution it follows, e.g. the population mean following a normal distribution. The $p$-value is the probability of observing an extreme test statistic in the direction of the alternate hypothesis, given that the null hypothesis is true. The critical value is the value of the assumed distribution of the test statistic such that the probability of making a type I error is small.

Methodologies: Given an estimator $\hat \theta$ of a population statistic $\theta$, following a probability distribution $P(T)$, computed from a sample $\mathcal{S},$ and given a significance level $\alpha$ and test statistic $t^*,$ define $H_0$ and $H_1;$ compute the test statistic $t^*.$ $p$-value Approach (most prevalent): Find the $p$-value using $t^*$ (right-tailed). If the $p$-value is at most $\alpha,$ reject $H_0$. Otherwise, reject $H_1$. Critical Value Approach: Find the critical value solving the equation $P(T\geq t_\alpha)=\alpha$ (right-tailed). If $t^*>t_\alpha$, reject $H_0$. Otherwise, reject $H_1$. Note: Failing to reject $H_0$ only means inability to accept $H_1$, and it does not mean to accept $H_0$.

Assume a normally distributed population has recorded cholesterol levels with various statistics computed. From a sample of 100 subjects in the population, the sample mean was 214.12 mg/dL (milligrams per deciliter), with a sample standard deviation of 45.71 mg/dL. Perform a hypothesis test, with significance level 0.05, to test if there is enough evidence to conclude that the population mean is larger than 200 mg/dL. Hypothesis Test We will perform a hypothesis test using the $p$-value approach with significance level $\alpha=0.05:$ Define $H_0$: $\mu=200$. Define $H_1$: $\mu>200$. Since our values are normally distributed, the test statistic is $z^*=\frac{\bar X - \mu_0}{\frac{s}{\sqrt{n}}}=\frac{214.12 - 200}{\frac{45.71}{\sqrt{100}}}\approx 3.09$. Using a standard normal distribution, we find that our $p$-value is approximately $0.001$. Since the $p$-value is at most $\alpha=0.05,$ we reject $H_0$. Therefore, we can conclude that the test shows sufficient evidence to support the claim that $\mu$ is larger than $200$ mg/dL.

If the sample size was smaller, the normal and $t$-distributions behave differently. Also, the question itself must be managed by a double-tail test instead.

Assume a population's cholesterol levels are recorded and various statistics are computed. From a sample of 25 subjects, the sample mean was 214.12 mg/dL (milligrams per deciliter), with a sample standard deviation of 45.71 mg/dL. Perform a hypothesis test, with significance level 0.05, to test if there is enough evidence to conclude that the population mean is not equal to 200 mg/dL. Hypothesis Test We will perform a hypothesis test using the $p$-value approach with significance level $\alpha=0.05$ and the $t$-distribution with 24 degrees of freedom: Define $H_0$: $\mu=200$. Define $H_1$: $\mu\neq 200$. Using the $t$-distribution, the test statistic is $t^*=\frac{\bar X - \mu_0}{\frac{s}{\sqrt{n}}}=\frac{214.12 - 200}{\frac{45.71}{\sqrt{25}}}\approx 1.54$. Using a $t$-distribution with 24 degrees of freedom, we find that our $p$-value is approximately $2(0.068)=0.136$. We have multiplied by two since this is a two-tailed argument, i.e. the mean can be smaller than or larger than. Since the $p$-value is larger than $\alpha=0.05,$ we fail to reject $H_0$. Therefore, the test does not show sufficient evidence to support the claim that $\mu$ is not equal to $200$ mg/dL.

The complement of the rejection on a two-tailed hypothesis test (with significance level $\alpha$) for a population parameter $\theta$ is equivalent to finding a confidence interval $($with confidence level $1-\alpha)$ for the population parameter $\theta$. If the assumption on the parameter $\theta$ falls inside the confidence interval, then the test has failed to reject the null hypothesis $($with $p$-value greater than $\alpha).$ Otherwise, if $\theta$ does not fall in the confidence interval, then the null hypothesis is rejected in favor of the alternate $($with $p$-value at most $\alpha).$

Statistics (Estimation)
Normal Distribution
Correlation
Confidence Intervals

Problem Loading...

Note Loading...

Set Loading...

Comprehensive Learning Paths
150+ Hours of Videos
Complete Access to Jupyter notebooks, Datasets, References.

Hypothesis Testing – A Deep Dive into Hypothesis Testing, The Backbone of Statistical Inference

September 21, 2023

Explore the intricacies of hypothesis testing, a cornerstone of statistical analysis. Dive into methods, interpretations, and applications for making data-driven decisions.

In this Blog post we will learn:

What is Hypothesis Testing?
Steps in Hypothesis Testing 2.1. Set up Hypotheses: Null and Alternative 2.2. Choose a Significance Level (α) 2.3. Calculate a test statistic and P-Value 2.4. Make a Decision
Example : Testing a new drug.
Example in python

1. What is Hypothesis Testing?

In simple terms, hypothesis testing is a method used to make decisions or inferences about population parameters based on sample data. Imagine being handed a dice and asked if it’s biased. By rolling it a few times and analyzing the outcomes, you’d be engaging in the essence of hypothesis testing.

Think of hypothesis testing as the scientific method of the statistics world. Suppose you hear claims like “This new drug works wonders!” or “Our new website design boosts sales.” How do you know if these statements hold water? Enter hypothesis testing.

2. Steps in Hypothesis Testing

Set up Hypotheses : Begin with a null hypothesis (H0) and an alternative hypothesis (Ha).
Choose a Significance Level (α) : Typically 0.05, this is the probability of rejecting the null hypothesis when it’s actually true. Think of it as the chance of accusing an innocent person.
Calculate Test statistic and P-Value : Gather evidence (data) and calculate a test statistic.
p-value : This is the probability of observing the data, given that the null hypothesis is true. A small p-value (typically ≤ 0.05) suggests the data is inconsistent with the null hypothesis.
Decision Rule : If the p-value is less than or equal to α, you reject the null hypothesis in favor of the alternative.

2.1. Set up Hypotheses: Null and Alternative

Before diving into testing, we must formulate hypotheses. The null hypothesis (H0) represents the default assumption, while the alternative hypothesis (H1) challenges it.

For instance, in drug testing, H0 : “The new drug is no better than the existing one,” H1 : “The new drug is superior .”

2.2. Choose a Significance Level (α)

When You collect and analyze data to test H0 and H1 hypotheses. Based on your analysis, you decide whether to reject the null hypothesis in favor of the alternative, or fail to reject / Accept the null hypothesis.

The significance level, often denoted by $α$, represents the probability of rejecting the null hypothesis when it is actually true.

In other words, it’s the risk you’re willing to take of making a Type I error (false positive).

Type I Error (False Positive) :

Symbolized by the Greek letter alpha (α).
Occurs when you incorrectly reject a true null hypothesis . In other words, you conclude that there is an effect or difference when, in reality, there isn’t.
The probability of making a Type I error is denoted by the significance level of a test. Commonly, tests are conducted at the 0.05 significance level , which means there’s a 5% chance of making a Type I error .
Commonly used significance levels are 0.01, 0.05, and 0.10, but the choice depends on the context of the study and the level of risk one is willing to accept.

Example : If a drug is not effective (truth), but a clinical trial incorrectly concludes that it is effective (based on the sample data), then a Type I error has occurred.

Type II Error (False Negative) :

Symbolized by the Greek letter beta (β).
Occurs when you accept a false null hypothesis . This means you conclude there is no effect or difference when, in reality, there is.
The probability of making a Type II error is denoted by β. The power of a test (1 – β) represents the probability of correctly rejecting a false null hypothesis.

Example : If a drug is effective (truth), but a clinical trial incorrectly concludes that it is not effective (based on the sample data), then a Type II error has occurred.

Balancing the Errors :

In practice, there’s a trade-off between Type I and Type II errors. Reducing the risk of one typically increases the risk of the other. For example, if you want to decrease the probability of a Type I error (by setting a lower significance level), you might increase the probability of a Type II error unless you compensate by collecting more data or making other adjustments.

It’s essential to understand the consequences of both types of errors in any given context. In some situations, a Type I error might be more severe, while in others, a Type II error might be of greater concern. This understanding guides researchers in designing their experiments and choosing appropriate significance levels.

2.3. Calculate a test statistic and P-Value

Test statistic : A test statistic is a single number that helps us understand how far our sample data is from what we’d expect under a null hypothesis (a basic assumption we’re trying to test against). Generally, the larger the test statistic, the more evidence we have against our null hypothesis. It helps us decide whether the differences we observe in our data are due to random chance or if there’s an actual effect.

P-value : The P-value tells us how likely we would get our observed results (or something more extreme) if the null hypothesis were true. It’s a value between 0 and 1. – A smaller P-value (typically below 0.05) means that the observation is rare under the null hypothesis, so we might reject the null hypothesis. – A larger P-value suggests that what we observed could easily happen by random chance, so we might not reject the null hypothesis.

2.4. Make a Decision

Relationship between $α$ and P-Value

When conducting a hypothesis test:

We then calculate the p-value from our sample data and the test statistic.

Finally, we compare the p-value to our chosen $α$:

If $p−value≤α$: We reject the null hypothesis in favor of the alternative hypothesis. The result is said to be statistically significant.
If $p−value>α$: We fail to reject the null hypothesis. There isn’t enough statistical evidence to support the alternative hypothesis.

3. Example : Testing a new drug.

Imagine we are investigating whether a new drug is effective at treating headaches faster than drug B.

Setting Up the Experiment : You gather 100 people who suffer from headaches. Half of them (50 people) are given the new drug (let’s call this the ‘Drug Group’), and the other half are given a sugar pill, which doesn’t contain any medication.

Set up Hypotheses : Before starting, you make a prediction:
Null Hypothesis (H0): The new drug has no effect. Any difference in healing time between the two groups is just due to random chance.
Alternative Hypothesis (H1): The new drug does have an effect. The difference in healing time between the two groups is significant and not just by chance.

Calculate Test statistic and P-Value : After the experiment, you analyze the data. The “test statistic” is a number that helps you understand the difference between the two groups in terms of standard units.

For instance, let’s say:

The average healing time in the Drug Group is 2 hours.
The average healing time in the Placebo Group is 3 hours.

The test statistic helps you understand how significant this 1-hour difference is. If the groups are large and the spread of healing times in each group is small, then this difference might be significant. But if there’s a huge variation in healing times, the 1-hour difference might not be so special.

Imagine the P-value as answering this question: “If the new drug had NO real effect, what’s the probability that I’d see a difference as extreme (or more extreme) as the one I found, just by random chance?”

For instance:

P-value of 0.01 means there’s a 1% chance that the observed difference (or a more extreme difference) would occur if the drug had no effect. That’s pretty rare, so we might consider the drug effective.
P-value of 0.5 means there’s a 50% chance you’d see this difference just by chance. That’s pretty high, so we might not be convinced the drug is doing much.
If the P-value is less than ($α$) 0.05: the results are “statistically significant,” and they might reject the null hypothesis , believing the new drug has an effect.
If the P-value is greater than ($α$) 0.05: the results are not statistically significant, and they don’t reject the null hypothesis , remaining unsure if the drug has a genuine effect.

4. Example in python

For simplicity, let’s say we’re using a t-test (common for comparing means). Let’s dive into Python:

Making a Decision : “The results are statistically significant! p-value < 0.05 , The drug seems to have an effect!” If not, we’d say, “Looks like the drug isn’t as miraculous as we thought.”

5. Conclusion

Hypothesis testing is an indispensable tool in data science, allowing us to make data-driven decisions with confidence. By understanding its principles, conducting tests properly, and considering real-world applications, you can harness the power of hypothesis testing to unlock valuable insights from your data.

Correlation – connecting the dots, the role of correlation in data analysis, sampling and sampling distributions – a comprehensive guide on sampling and sampling distributions, law of large numbers – a deep dive into the world of statistics, central limit theorem – a deep dive into central limit theorem and its significance in statistics, skewness and kurtosis – peaks and tails, understanding data through skewness and kurtosis”, similar articles, complete introduction to linear regression in r, how to implement common statistical significance tests and find the p value, logistic regression – a complete tutorial with examples in r.

Subscribe to Machine Learning Plus for high value data science content

Machine Learning A-Z™: Hands-On Python & R In Data Science

Free sample videos:.

An official website of the United States government

The .gov means it's official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you're on a federal government site.

The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Publications
Account settings
Browse Titles

NCBI Bookshelf. A service of the National Library of Medicine, National Institutes of Health.

StatPearls [Internet]. Treasure Island (FL): StatPearls Publishing; 2024 Jan-.

StatPearls [Internet].

Hypothesis testing, p values, confidence intervals, and significance.

Jacob Shreffler ; Martin R. Huecker .

Affiliations

Last Update: March 13, 2023 .

Definition/Introduction

Medical providers often rely on evidence-based medicine to guide decision-making in practice. Often a research hypothesis is tested with results provided, typically with p values, confidence intervals, or both. Additionally, statistical or research significance is estimated or determined by the investigators. Unfortunately, healthcare providers may have different comfort levels in interpreting these findings, which may affect the adequate application of the data.

Issues of Concern

Without a foundational understanding of hypothesis testing, p values, confidence intervals, and the difference between statistical and clinical significance, it may affect healthcare providers' ability to make clinical decisions without relying purely on the research investigators deemed level of significance. Therefore, an overview of these concepts is provided to allow medical professionals to use their expertise to determine if results are reported sufficiently and if the study outcomes are clinically appropriate to be applied in healthcare practice.

Hypothesis Testing

Investigators conducting studies need research questions and hypotheses to guide analyses. Starting with broad research questions (RQs), investigators then identify a gap in current clinical practice or research. Any research problem or statement is grounded in a better understanding of relationships between two or more variables. For this article, we will use the following research question example:

Research Question: Is Drug 23 an effective treatment for Disease A?

Research questions do not directly imply specific guesses or predictions; we must formulate research hypotheses. A hypothesis is a predetermined declaration regarding the research question in which the investigator(s) makes a precise, educated guess about a study outcome. This is sometimes called the alternative hypothesis and ultimately allows the researcher to take a stance based on experience or insight from medical literature. An example of a hypothesis is below.

Research Hypothesis: Drug 23 will significantly reduce symptoms associated with Disease A compared to Drug 22.

The null hypothesis states that there is no statistical difference between groups based on the stated research hypothesis.

Researchers should be aware of journal recommendations when considering how to report p values, and manuscripts should remain internally consistent.

Regarding p values, as the number of individuals enrolled in a study (the sample size) increases, the likelihood of finding a statistically significant effect increases. With very large sample sizes, the p-value can be very low significant differences in the reduction of symptoms for Disease A between Drug 23 and Drug 22. The null hypothesis is deemed true until a study presents significant data to support rejecting the null hypothesis. Based on the results, the investigators will either reject the null hypothesis (if they found significant differences or associations) or fail to reject the null hypothesis (they could not provide proof that there were significant differences or associations).

To test a hypothesis, researchers obtain data on a representative sample to determine whether to reject or fail to reject a null hypothesis. In most research studies, it is not feasible to obtain data for an entire population. Using a sampling procedure allows for statistical inference, though this involves a certain possibility of error. [1] When determining whether to reject or fail to reject the null hypothesis, mistakes can be made: Type I and Type II errors. Though it is impossible to ensure that these errors have not occurred, researchers should limit the possibilities of these faults. [2]

Significance

Significance is a term to describe the substantive importance of medical research. Statistical significance is the likelihood of results due to chance. [3] Healthcare providers should always delineate statistical significance from clinical significance, a common error when reviewing biomedical research. [4] When conceptualizing findings reported as either significant or not significant, healthcare providers should not simply accept researchers' results or conclusions without considering the clinical significance. Healthcare professionals should consider the clinical importance of findings and understand both p values and confidence intervals so they do not have to rely on the researchers to determine the level of significance. [5] One criterion often used to determine statistical significance is the utilization of p values.

P values are used in research to determine whether the sample estimate is significantly different from a hypothesized value. The p-value is the probability that the observed effect within the study would have occurred by chance if, in reality, there was no true effect. Conventionally, data yielding a p<0.05 or p<0.01 is considered statistically significant. While some have debated that the 0.05 level should be lowered, it is still universally practiced. [6] Hypothesis testing allows us to determine the size of the effect.

An example of findings reported with p values are below:

Statement: Drug 23 reduced patients' symptoms compared to Drug 22. Patients who received Drug 23 (n=100) were 2.1 times less likely than patients who received Drug 22 (n = 100) to experience symptoms of Disease A, p<0.05.

Statement:Individuals who were prescribed Drug 23 experienced fewer symptoms (M = 1.3, SD = 0.7) compared to individuals who were prescribed Drug 22 (M = 5.3, SD = 1.9). This finding was statistically significant, p= 0.02.

For either statement, if the threshold had been set at 0.05, the null hypothesis (that there was no relationship) should be rejected, and we should conclude significant differences. Noticeably, as can be seen in the two statements above, some researchers will report findings with < or > and others will provide an exact p-value (0.000001) but never zero [6] . When examining research, readers should understand how p values are reported. The best practice is to report all p values for all variables within a study design, rather than only providing p values for variables with significant findings. [7] The inclusion of all p values provides evidence for study validity and limits suspicion for selective reporting/data mining.

While researchers have historically used p values, experts who find p values problematic encourage the use of confidence intervals. [8] . P-values alone do not allow us to understand the size or the extent of the differences or associations. [3] In March 2016, the American Statistical Association (ASA) released a statement on p values, noting that scientific decision-making and conclusions should not be based on a fixed p-value threshold (e.g., 0.05). They recommend focusing on the significance of results in the context of study design, quality of measurements, and validity of data. Ultimately, the ASA statement noted that in isolation, a p-value does not provide strong evidence. [9]

When conceptualizing clinical work, healthcare professionals should consider p values with a concurrent appraisal study design validity. For example, a p-value from a double-blinded randomized clinical trial (designed to minimize bias) should be weighted higher than one from a retrospective observational study [7] . The p-value debate has smoldered since the 1950s [10] , and replacement with confidence intervals has been suggested since the 1980s. [11]

Confidence Intervals

A confidence interval provides a range of values within given confidence (e.g., 95%), including the accurate value of the statistical constraint within a targeted population. [12] Most research uses a 95% CI, but investigators can set any level (e.g., 90% CI, 99% CI). [13] A CI provides a range with the lower bound and upper bound limits of a difference or association that would be plausible for a population. [14] Therefore, a CI of 95% indicates that if a study were to be carried out 100 times, the range would contain the true value in 95, [15] confidence intervals provide more evidence regarding the precision of an estimate compared to p-values. [6]

In consideration of the similar research example provided above, one could make the following statement with 95% CI:

Statement: Individuals who were prescribed Drug 23 had no symptoms after three days, which was significantly faster than those prescribed Drug 22; there was a mean difference between the two groups of days to the recovery of 4.2 days (95% CI: 1.9 – 7.8).

It is important to note that the width of the CI is affected by the standard error and the sample size; reducing a study sample number will result in less precision of the CI (increase the width). [14] A larger width indicates a smaller sample size or a larger variability. [16] A researcher would want to increase the precision of the CI. For example, a 95% CI of 1.43 – 1.47 is much more precise than the one provided in the example above. In research and clinical practice, CIs provide valuable information on whether the interval includes or excludes any clinically significant values. [14]

Null values are sometimes used for differences with CI (zero for differential comparisons and 1 for ratios). However, CIs provide more information than that. [15] Consider this example: A hospital implements a new protocol that reduced wait time for patients in the emergency department by an average of 25 minutes (95% CI: -2.5 – 41 minutes). Because the range crosses zero, implementing this protocol in different populations could result in longer wait times; however, the range is much higher on the positive side. Thus, while the p-value used to detect statistical significance for this may result in "not significant" findings, individuals should examine this range, consider the study design, and weigh whether or not it is still worth piloting in their workplace.

Similarly to p-values, 95% CIs cannot control for researchers' errors (e.g., study bias or improper data analysis). [14] In consideration of whether to report p-values or CIs, researchers should examine journal preferences. When in doubt, reporting both may be beneficial. [13] An example is below:

Reporting both: Individuals who were prescribed Drug 23 had no symptoms after three days, which was significantly faster than those prescribed Drug 22, p = 0.009. There was a mean difference between the two groups of days to the recovery of 4.2 days (95% CI: 1.9 – 7.8).

Clinical Significance

Recall that clinical significance and statistical significance are two different concepts. Healthcare providers should remember that a study with statistically significant differences and large sample size may be of no interest to clinicians, whereas a study with smaller sample size and statistically non-significant results could impact clinical practice. [14] Additionally, as previously mentioned, a non-significant finding may reflect the study design itself rather than relationships between variables.

Healthcare providers using evidence-based medicine to inform practice should use clinical judgment to determine the practical importance of studies through careful evaluation of the design, sample size, power, likelihood of type I and type II errors, data analysis, and reporting of statistical findings (p values, 95% CI or both). [4] Interestingly, some experts have called for "statistically significant" or "not significant" to be excluded from work as statistical significance never has and will never be equivalent to clinical significance. [17]

The decision on what is clinically significant can be challenging, depending on the providers' experience and especially the severity of the disease. Providers should use their knowledge and experiences to determine the meaningfulness of study results and make inferences based not only on significant or insignificant results by researchers but through their understanding of study limitations and practical implications.

Nursing, Allied Health, and Interprofessional Team Interventions

All physicians, nurses, pharmacists, and other healthcare professionals should strive to understand the concepts in this chapter. These individuals should maintain the ability to review and incorporate new literature for evidence-based and safe care.

Review Questions
Access free multiple choice questions on this topic.
Comment on this article.

Disclosure: Jacob Shreffler declares no relevant financial relationships with ineligible companies.

Disclosure: Martin Huecker declares no relevant financial relationships with ineligible companies.

This book is distributed under the terms of the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International (CC BY-NC-ND 4.0) ( http://creativecommons.org/licenses/by-nc-nd/4.0/ ), which permits others to distribute the work, provided that the article is not altered or used commercially. You are not required to obtain permission to distribute this article, provided that you credit the author and journal.

Cite this Page Shreffler J, Huecker MR. Hypothesis Testing, P Values, Confidence Intervals, and Significance. [Updated 2023 Mar 13]. In: StatPearls [Internet]. Treasure Island (FL): StatPearls Publishing; 2024 Jan-.

In this Page

Bulk download.

Bulk download StatPearls data from FTP

Related information

PMC PubMed Central citations
PubMed Links to PubMed

Recent Activity

Hypothesis Testing, P Values, Confidence Intervals, and Significance - StatPearl... Hypothesis Testing, P Values, Confidence Intervals, and Significance - StatPearls

Your browsing activity is empty.

Activity recording is turned off.

Turn recording back on

Connect with NLM

National Library of Medicine 8600 Rockville Pike Bethesda, MD 20894

Web Policies FOIA HHS Vulnerability Disclosure

Help Accessibility Careers

Statistics Made Easy

Introduction to Hypothesis Testing

A statistical hypothesis is an assumption about a population parameter .

For example, we may assume that the mean height of a male in the U.S. is 70 inches.

The assumption about the height is the statistical hypothesis and the true mean height of a male in the U.S. is the population parameter .

A hypothesis test is a formal statistical test we use to reject or fail to reject a statistical hypothesis.

The Two Types of Statistical Hypotheses

To test whether a statistical hypothesis about a population parameter is true, we obtain a random sample from the population and perform a hypothesis test on the sample data.

There are two types of statistical hypotheses:

The null hypothesis , denoted as H 0 , is the hypothesis that the sample data occurs purely from chance.

The alternative hypothesis , denoted as H 1 or H a , is the hypothesis that the sample data is influenced by some non-random cause.

Hypothesis Tests

A hypothesis test consists of five steps:

1. State the hypotheses.

State the null and alternative hypotheses. These two hypotheses need to be mutually exclusive, so if one is true then the other must be false.

2. Determine a significance level to use for the hypothesis.

Decide on a significance level. Common choices are .01, .05, and .1.

3. Find the test statistic.

Find the test statistic and the corresponding p-value. Often we are analyzing a population mean or proportion and the general formula to find the test statistic is: (sample statistic – population parameter) / (standard deviation of statistic)

4. Reject or fail to reject the null hypothesis.

Using the test statistic or the p-value, determine if you can reject or fail to reject the null hypothesis based on the significance level.

The p-value tells us the strength of evidence in support of a null hypothesis. If the p-value is less than the significance level, we reject the null hypothesis.

5. Interpret the results.

Interpret the results of the hypothesis test in the context of the question being asked.

The Two Types of Decision Errors

There are two types of decision errors that one can make when doing a hypothesis test:

Type I error: You reject the null hypothesis when it is actually true. The probability of committing a Type I error is equal to the significance level, often called alpha , and denoted as α.

Type II error: You fail to reject the null hypothesis when it is actually false. The probability of committing a Type II error is called the Power of the test or Beta , denoted as β.

One-Tailed and Two-Tailed Tests

A statistical hypothesis can be one-tailed or two-tailed.

A one-tailed hypothesis involves making a “greater than” or “less than ” statement.

For example, suppose we assume the mean height of a male in the U.S. is greater than or equal to 70 inches. The null hypothesis would be H0: µ ≥ 70 inches and the alternative hypothesis would be Ha: µ < 70 inches.

A two-tailed hypothesis involves making an “equal to” or “not equal to” statement.

For example, suppose we assume the mean height of a male in the U.S. is equal to 70 inches. The null hypothesis would be H0: µ = 70 inches and the alternative hypothesis would be Ha: µ ≠ 70 inches.

Note: The “equal” sign is always included in the null hypothesis, whether it is =, ≥, or ≤.

Related: What is a Directional Hypothesis?

Types of Hypothesis Tests

There are many different types of hypothesis tests you can perform depending on the type of data you’re working with and the goal of your analysis.

The following tutorials provide an explanation of the most common types of hypothesis tests:

Introduction to the One Sample t-test Introduction to the Two Sample t-test Introduction to the Paired Samples t-test Introduction to the One Proportion Z-Test Introduction to the Two Proportion Z-Test

Featured Posts

5 Regularization Techniques You Should Know

Hey there. My name is Zach Bobbitt. I have a Masters of Science degree in Applied Statistics and I’ve worked on machine learning algorithms for professional businesses in both healthcare and retail. I’m passionate about statistics, machine learning, and data visualization and I created Statology to be a resource for both students and teachers alike. My goal with this site is to help you learn statistics through using simple terms, plenty of real-world examples, and helpful illustrations.

Join the Statology Community

Sign up to receive Statology's exclusive study resource: 100 practice problems with step-by-step solutions. Plus, get our latest insights, tutorials, and data analysis tips straight to your inbox!

By subscribing you accept Statology's Privacy Policy.

How Does Statistical Hypothesis Testing Work?

These terms are not only commonly used in statistics but also have made their way into the vernacular. Making sense of most scientific publications, which can have practical, significant effects on public policy and your life, means understanding a core framework with which we derive much knowledge. That framework is called hypothesis testing , or more formally, Null Hypothesis Significance Testing (NHST).

When comparing two measurements, whether they be completion rates, ease scores, or even the effectiveness of different vaccines, a hypothesis test’s primary goal is to make a binary classification decision: is the difference statistically significant or not? Yes or no.

The yes or no output from a hypothesis test looks simple, indistinguishable from a guess or a coin flip. It’s the process of getting to yes or no that’s different in NHST.

While we certainly want to make the right decision, we can never be correct 100% of the time. There will always be mistakes; there will always be errors. It’s through the framework of hypothesis testing that we can control the frequency of errors over time.

Hypothesis testing can be a confusing concept, so we’ve broken it into steps with examples. In a follow-up article, we’ll discuss how things can go wrong in hypothesis testing and some criticisms of the framework.

Step 1: Define the Null Hypothesis

Statistical hypothesis testing starts with something called the Null Hypothesis. Null means none or no difference. A few ways to think of the Null Hypothesis are as the no-difference hypothesis or as the hypothesis that we want to nullify (disprove).

Mathematicians love using symbols, and that applies to hypothesis testing. The Null Hypothesis is represented as H 0 . H stands for hypothesis, and the 0—that’s a zero in the subscript, not the letter O—reminds us it’s the hypothesis of 0 (no, null) difference.

We start with the Null Hypothesis because it’s easier to disprove something than to prove something. If we disprove the Null Hypothesis (reject the null), then we know there’s at least some relationship between the variables we’re measuring (e.g., different websites and ease scores).

Here are four examples of Null Hypotheses (H 0 ) from studies we’ll refer to throughout this article.

Rental Cars Ease : There’s no difference in System Usability Scale ( SUS ) scores between two rental car websites.
Flight Booking Friction : There’s no difference in perceived ease ratings ( SEQ ) when booking a flight on two airline websites.
CRM Ease : There’s no difference in System Usability Scale (SUS) scores between two Customer Relationship Management (CRM) apps.
Numbers and Emojis : There’s no difference in mean ratings on the UMUX-Lite when using numbers and face emojis as response options in its agreement scales.

Step 2: Collect Data and Compute the Difference

You need data to make decisions. Use methods such as surveys, experiments, and observations to collect data, and then calculate the differences observed. Data can be collected using either a between-subjects (different people in each condition) or within-subjects (same people in both) approach .

Building on the examples from Step 1,

Rental Cars Ease : 14 users attempted five tasks on two rental car websites. The average SUS scores were 80.4 (sd = 11) for rental website A and 63.5 (sd = 15) for rental website B. The observed difference was 16.9 points (the SUS can range from 0 to 100).
Flight Booking Friction : 10 users booked a flight on airline site A and 13 on airline site B. The average SEQ score for Airline A was 6.1 (sd = .83) and for Airline B, it was 5.1 (sd = 1.5). The observed difference was 1 point (the SEQ can range from 1 to 7).
CRM Ease : 11 users attempted tasks on Product A, and 12 users attempted the same tasks on Product B. Product A had a mean SUS score of 51.6 (sd = 4.07) and Product B had a mean SUS score of 49.6 (sd = 4.63). The observed difference was 2 points.
Numbers and Emojis : 240 respondents used two versions of the UMUX-Lite, one with a standard numeric format and the other using face emojis in place of numbers . The mean UMUX-Lite rating with the numeric format was 85.9 (sd = 17.5), and for the face emojis version, the score was 85.4 (sd = 17.1). That’s a difference of .5 points on a 0-100–point scale.

Table 1 summarizes the four examples (metrics and observed differences).

Table 1: Descriptive statistics (mean, standard deviation, and sample size) and differences for the four examples.

Step 3: Compute the p-value

With these differences computed, we want to know how likely it is they could have happened by chance. To do so, we use the probability value—the p-value.

Books are written on the p-value. Statisticians love to argue over its technical definition (similar to how UX practitioners and researchers argue over the definition of UX). In short, p-value is the probability of getting the differences we found in Step 2 if there really are no differences .

This often gets simplified as the probability that the difference is due to chance. Technically, that’s not quite correct , but it’s conceptually close enough for practical purposes (just watch whom you say it to).

We explain how to compute the p-value by hand for many common statistical tests in Chapter 5 of Quantifying the User Experience . But you’ll usually use statistical software such as SPSS or R to compute the p-value. (p-values are computed automatically in our MUIQ platform , as shown in Figure 1.)

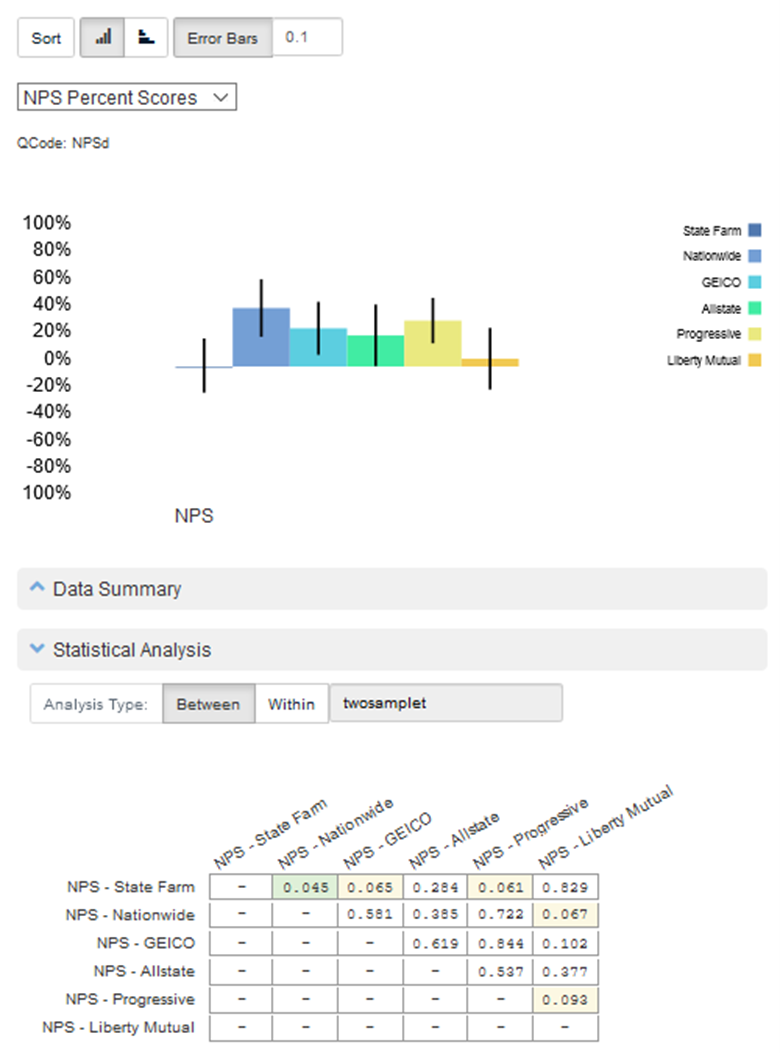
Figure 1: MUIQ output that compares the Net Promoter Scores for six auto insurance websites ; the statistical analysis table shows the p-values for all the possible comparisons, with green highlights for p < .05 and yellow highlights for .05 < p < .10.

Rental Cars Ease : Used a paired t-test to assess the difference of 16.9 points (t(13) = 3.48; p = .004).
Flight Booking Friction: The observed SEQ difference was 1 point, assessed with an independent groups t-test (t(20) = 2.1; p = .0499).
CRM Ease: An independent groups t-test on the difference of 2 points found t(20) = 1.1; p = .28.
Numbers and Emojis : A dependent-groups t-test on the difference of .5 points found t(239 = .88; p = .38.

The lower the p-value, the less credible the Null Hypothesis is (or as is often interpreted, it’s less likely the difference is due to chance). But how low is low enough?

Step 4: Compare p-value to Alpha to Determine Statistical Significance

The p-value is compared to a criterion called the alpha error (α). If p is less than the criterion, then you can declare statistical significance (sort of like Michael Scott from The Office—Figure 2). When p is below alpha, we reject the Null Hypothesis.

Figure 2: Declaring statistical significance with a meme.

The most common criterion is .05 (the basis for saying that p < .05 indicates statistical significance). It doesn’t always have to be .05, but that’s what most scientific journals have adopted. We’ll cover how that threshold became the default in another article.

When something is statistically significant, it doesn’t mean it’s different. It just means we wouldn’t expect to see a difference that large if there really was no difference. Or if the null hypothesis is true, we would not expect to see the difference very often.

Let’s compare the p-values to the typical alpha criterion of .05 for our sample data to see whether there are any statistically significant differences:

Rental Cars Ease : The 16.9 difference has a p-value of .004. We’d expect a difference this large or larger only about 4/1000 times if there is no difference. p is less than .05. Statistically significant.
Flight Booking Friction : The observed difference of 1 point generated a p-value of .0499. We’d expect to see this difference just under 5% of the time if there was no difference. p is less than .05. Statistically significant.
CRM Ease : The 2-point difference generated a p-value of .28. A difference this large or larger could happen 28% of the time if there is no difference. p is greater than .05. NOT significant.
Numbers and Emojis : The .5-point UMUX-Lite difference generated a p-value of .38. If there is no difference, you’d expect to see a p-value this large 38% of the time. p is greater than .05. NOT significant.

Table 2 shows the four examples, the observed differences, resulting p-values, and conclusions.

Table 2: Observed differences, resulting p-values, and conclusions for the four examples.

The Path to Statistical Significance

We have visualized these steps in a flowchart (Figure 3).

When the difference is statistically significant (p < alpha) you reject the Null hypothesis (H 0 ). If p > alpha you can say something is not statistically significant, so you do not reject the Null Hypothesis. But, more importantly, you also do not accept it. There might be no difference, but it’s also possible that there is a real difference. The difference might be too small to detect with the given sample size and variability of measurement, making the outcome ambiguous. Strictly speaking, you fail to reject the Null Hypothesis (H 0 ). The language is subtle: the important point is you never accept the Null Hypothesis as true; you can only reject it (p < alpha) or fail to reject it (p > alpha).

In a future article, we’ll discuss other aspects of hypothesis testing, including the specification of an alternative hypothesis and how that expands the framework of NHST to define the two ways decisions can be right and the two ways they can be wrong.

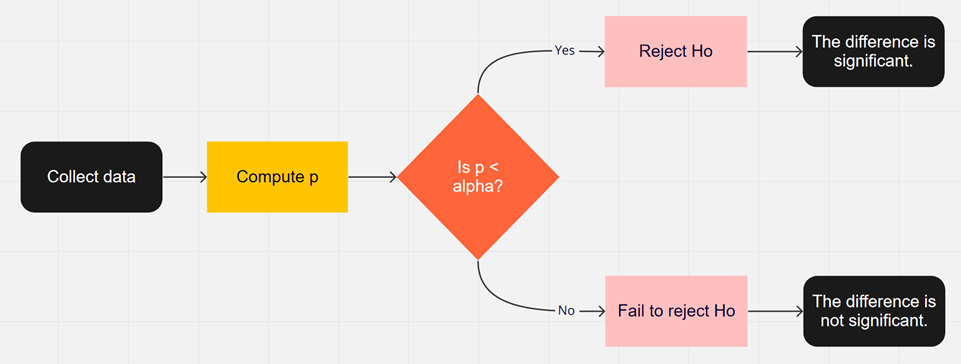
Figure 3: High-level flowchart of statistical hypothesis testing.

When making decisions in research, business, or even medicine, we can’t be correct 100% of the time. There will always be mistakes; there will always be errors. Through the framework of hypothesis testing, we can measure and reduce the frequency of errors over time. To use hypothesis testing when making comparisons, follow these four steps:

Define the Null Hypothesis. If we can rule out no difference, then we can conclude there’s at least some difference between the variables.
Collect data and compute the difference. Just because you observe a difference doesn’t mean it’s greater than what you’d see from sampling error or random fluctuation.
Compute the p-value. The probability value (p-value) is the probability of observing that difference or a larger one if there really is no difference.
Compare the p-value to alpha to determine statistical significance. If the p-value is less than the alpha criterion (typically .05), we conclude the difference is statistically significant. Otherwise, we withhold final judgment and can only say we failed to reject the Null Hypothesis.

You might also be interested in

Tutorial Playlist

Statistics tutorial, everything you need to know about the probability density function in statistics, the best guide to understand central limit theorem, an in-depth guide to measures of central tendency : mean, median and mode, the ultimate guide to understand conditional probability.

A Comprehensive Look at Percentile in Statistics

The Best Guide to Understand Bayes Theorem

Everything you need to know about the normal distribution, an in-depth explanation of cumulative distribution function, a complete guide to chi-square test, a complete guide on hypothesis testing in statistics, understanding the fundamentals of arithmetic and geometric progression, the definitive guide to understand spearman’s rank correlation, a comprehensive guide to understand mean squared error, all you need to know about the empirical rule in statistics, the complete guide to skewness and kurtosis, a holistic look at bernoulli distribution.

All You Need to Know About Bias in Statistics

A Complete Guide to Get a Grasp of Time Series Analysis

The Key Differences Between Z-Test Vs. T-Test

The Complete Guide to Understand Pearson's Correlation

A complete guide on the types of statistical studies, everything you need to know about poisson distribution, your best guide to understand correlation vs. regression, the most comprehensive guide for beginners on what is correlation, what is hypothesis testing in statistics types and examples.

Lesson 10 of 24 By Avijeet Biswal

A Complete Guide on Hypothesis Testing in Statistics

In today’s data-driven world , decisions are based on data all the time. Hypothesis plays a crucial role in that process, whether it may be making business decisions, in the health sector, academia, or in quality improvement. Without hypothesis & hypothesis tests, you risk drawing the wrong conclusions and making bad decisions. In this tutorial, you will look at Hypothesis Testing in Statistics.

What Is Hypothesis Testing in Statistics?

Hypothesis Testing is a type of statistical analysis in which you put your assumptions about a population parameter to the test. It is used to estimate the relationship between 2 statistical variables.

Let's discuss few examples of statistical hypothesis from real-life -

A teacher assumes that 60% of his college's students come from lower-middle-class families.
A doctor believes that 3D (Diet, Dose, and Discipline) is 90% effective for diabetic patients.

Now that you know about hypothesis testing, look at the two types of hypothesis testing in statistics.

Hypothesis Testing Formula

Z = ( x̅ – μ0 ) / (σ /√n)

Here, x̅ is the sample mean,
μ0 is the population mean,
σ is the standard deviation,
n is the sample size.

How Hypothesis Testing Works?

An analyst performs hypothesis testing on a statistical sample to present evidence of the plausibility of the null hypothesis. Measurements and analyses are conducted on a random sample of the population to test a theory. Analysts use a random population sample to test two hypotheses: the null and alternative hypotheses.

The null hypothesis is typically an equality hypothesis between population parameters; for example, a null hypothesis may claim that the population means return equals zero. The alternate hypothesis is essentially the inverse of the null hypothesis (e.g., the population means the return is not equal to zero). As a result, they are mutually exclusive, and only one can be correct. One of the two possibilities, however, will always be correct.

Your Dream Career is Just Around The Corner!

Null Hypothesis and Alternate Hypothesis

The Null Hypothesis is the assumption that the event will not occur. A null hypothesis has no bearing on the study's outcome unless it is rejected.

H0 is the symbol for it, and it is pronounced H-naught.

The Alternate Hypothesis is the logical opposite of the null hypothesis. The acceptance of the alternative hypothesis follows the rejection of the null hypothesis. H1 is the symbol for it.

Let's understand this with an example.

A sanitizer manufacturer claims that its product kills 95 percent of germs on average.

To put this company's claim to the test, create a null and alternate hypothesis.

H0 (Null Hypothesis): Average = 95%.

Alternative Hypothesis (H1): The average is less than 95%.

Another straightforward example to understand this concept is determining whether or not a coin is fair and balanced. The null hypothesis states that the probability of a show of heads is equal to the likelihood of a show of tails. In contrast, the alternate theory states that the probability of a show of heads and tails would be very different.

Become a Data Scientist with Hands-on Training!

Hypothesis Testing Calculation With Examples

Let's consider a hypothesis test for the average height of women in the United States. Suppose our null hypothesis is that the average height is 5'4". We gather a sample of 100 women and determine that their average height is 5'5". The standard deviation of population is 2.

To calculate the z-score, we would use the following formula:

z = ( x̅ – μ0 ) / (σ /√n)

z = (5'5" - 5'4") / (2" / √100)

z = 0.5 / (0.045)

We will reject the null hypothesis as the z-score of 11.11 is very large and conclude that there is evidence to suggest that the average height of women in the US is greater than 5'4".

Steps of Hypothesis Testing

Step 1: specify your null and alternate hypotheses.

It is critical to rephrase your original research hypothesis (the prediction that you wish to study) as a null (Ho) and alternative (Ha) hypothesis so that you can test it quantitatively. Your first hypothesis, which predicts a link between variables, is generally your alternate hypothesis. The null hypothesis predicts no link between the variables of interest.

Step 2: Gather Data

For a statistical test to be legitimate, sampling and data collection must be done in a way that is meant to test your hypothesis. You cannot draw statistical conclusions about the population you are interested in if your data is not representative.

Step 3: Conduct a Statistical Test

Other statistical tests are available, but they all compare within-group variance (how to spread out the data inside a category) against between-group variance (how different the categories are from one another). If the between-group variation is big enough that there is little or no overlap between groups, your statistical test will display a low p-value to represent this. This suggests that the disparities between these groups are unlikely to have occurred by accident. Alternatively, if there is a large within-group variance and a low between-group variance, your statistical test will show a high p-value. Any difference you find across groups is most likely attributable to chance. The variety of variables and the level of measurement of your obtained data will influence your statistical test selection.

Step 4: Determine Rejection Of Your Null Hypothesis

Your statistical test results must determine whether your null hypothesis should be rejected or not. In most circumstances, you will base your judgment on the p-value provided by the statistical test. In most circumstances, your preset level of significance for rejecting the null hypothesis will be 0.05 - that is, when there is less than a 5% likelihood that these data would be seen if the null hypothesis were true. In other circumstances, researchers use a lower level of significance, such as 0.01 (1%). This reduces the possibility of wrongly rejecting the null hypothesis.

Step 5: Present Your Results

The findings of hypothesis testing will be discussed in the results and discussion portions of your research paper, dissertation, or thesis. You should include a concise overview of the data and a summary of the findings of your statistical test in the results section. You can talk about whether your results confirmed your initial hypothesis or not in the conversation. Rejecting or failing to reject the null hypothesis is a formal term used in hypothesis testing. This is likely a must for your statistics assignments.

Types of Hypothesis Testing

To determine whether a discovery or relationship is statistically significant, hypothesis testing uses a z-test. It usually checks to see if two means are the same (the null hypothesis). Only when the population standard deviation is known and the sample size is 30 data points or more, can a z-test be applied.

A statistical test called a t-test is employed to compare the means of two groups. To determine whether two groups differ or if a procedure or treatment affects the population of interest, it is frequently used in hypothesis testing.

Chi-Square

You utilize a Chi-square test for hypothesis testing concerning whether your data is as predicted. To determine if the expected and observed results are well-fitted, the Chi-square test analyzes the differences between categorical variables from a random sample. The test's fundamental premise is that the observed values in your data should be compared to the predicted values that would be present if the null hypothesis were true.

Hypothesis Testing and Confidence Intervals

Both confidence intervals and hypothesis tests are inferential techniques that depend on approximating the sample distribution. Data from a sample is used to estimate a population parameter using confidence intervals. Data from a sample is used in hypothesis testing to examine a given hypothesis. We must have a postulated parameter to conduct hypothesis testing.

Bootstrap distributions and randomization distributions are created using comparable simulation techniques. The observed sample statistic is the focal point of a bootstrap distribution, whereas the null hypothesis value is the focal point of a randomization distribution.

A variety of feasible population parameter estimates are included in confidence ranges. In this lesson, we created just two-tailed confidence intervals. There is a direct connection between these two-tail confidence intervals and these two-tail hypothesis tests. The results of a two-tailed hypothesis test and two-tailed confidence intervals typically provide the same results. In other words, a hypothesis test at the 0.05 level will virtually always fail to reject the null hypothesis if the 95% confidence interval contains the predicted value. A hypothesis test at the 0.05 level will nearly certainly reject the null hypothesis if the 95% confidence interval does not include the hypothesized parameter.

Simple and Composite Hypothesis Testing

Depending on the population distribution, you can classify the statistical hypothesis into two types.

Simple Hypothesis: A simple hypothesis specifies an exact value for the parameter.

Composite Hypothesis: A composite hypothesis specifies a range of values.

A company is claiming that their average sales for this quarter are 1000 units. This is an example of a simple hypothesis.

Suppose the company claims that the sales are in the range of 900 to 1000 units. Then this is a case of a composite hypothesis.

One-Tailed and Two-Tailed Hypothesis Testing

The One-Tailed test, also called a directional test, considers a critical region of data that would result in the null hypothesis being rejected if the test sample falls into it, inevitably meaning the acceptance of the alternate hypothesis.

In a one-tailed test, the critical distribution area is one-sided, meaning the test sample is either greater or lesser than a specific value.

In two tails, the test sample is checked to be greater or less than a range of values in a Two-Tailed test, implying that the critical distribution area is two-sided.

If the sample falls within this range, the alternate hypothesis will be accepted, and the null hypothesis will be rejected.

Become a Data Scientist With Real-World Experience

Right Tailed Hypothesis Testing

If the larger than (>) sign appears in your hypothesis statement, you are using a right-tailed test, also known as an upper test. Or, to put it another way, the disparity is to the right. For instance, you can contrast the battery life before and after a change in production. Your hypothesis statements can be the following if you want to know if the battery life is longer than the original (let's say 90 hours):

The null hypothesis is (H0 <= 90) or less change.
A possibility is that battery life has risen (H1) > 90.

The crucial point in this situation is that the alternate hypothesis (H1), not the null hypothesis, decides whether you get a right-tailed test.

Left Tailed Hypothesis Testing

Alternative hypotheses that assert the true value of a parameter is lower than the null hypothesis are tested with a left-tailed test; they are indicated by the asterisk "<".

Suppose H0: mean = 50 and H1: mean not equal to 50

According to the H1, the mean can be greater than or less than 50. This is an example of a Two-tailed test.

In a similar manner, if H0: mean >=50, then H1: mean <50

Here the mean is less than 50. It is called a One-tailed test.

Type 1 and Type 2 Error

A hypothesis test can result in two types of errors.

Type 1 Error: A Type-I error occurs when sample results reject the null hypothesis despite being true.

Type 2 Error: A Type-II error occurs when the null hypothesis is not rejected when it is false, unlike a Type-I error.

Suppose a teacher evaluates the examination paper to decide whether a student passes or fails.

H0: Student has passed

H1: Student has failed

Type I error will be the teacher failing the student [rejects H0] although the student scored the passing marks [H0 was true].

Type II error will be the case where the teacher passes the student [do not reject H0] although the student did not score the passing marks [H1 is true].

Level of Significance

The alpha value is a criterion for determining whether a test statistic is statistically significant. In a statistical test, Alpha represents an acceptable probability of a Type I error. Because alpha is a probability, it can be anywhere between 0 and 1. In practice, the most commonly used alpha values are 0.01, 0.05, and 0.1, which represent a 1%, 5%, and 10% chance of a Type I error, respectively (i.e. rejecting the null hypothesis when it is in fact correct).

Future-Proof Your AI/ML Career: Top Dos and Don'ts

A p-value is a metric that expresses the likelihood that an observed difference could have occurred by chance. As the p-value decreases the statistical significance of the observed difference increases. If the p-value is too low, you reject the null hypothesis.

Here you have taken an example in which you are trying to test whether the new advertising campaign has increased the product's sales. The p-value is the likelihood that the null hypothesis, which states that there is no change in the sales due to the new advertising campaign, is true. If the p-value is .30, then there is a 30% chance that there is no increase or decrease in the product's sales. If the p-value is 0.03, then there is a 3% probability that there is no increase or decrease in the sales value due to the new advertising campaign. As you can see, the lower the p-value, the chances of the alternate hypothesis being true increases, which means that the new advertising campaign causes an increase or decrease in sales.

Why is Hypothesis Testing Important in Research Methodology?

Hypothesis testing is crucial in research methodology for several reasons:

Provides evidence-based conclusions: It allows researchers to make objective conclusions based on empirical data, providing evidence to support or refute their research hypotheses.
Supports decision-making: It helps make informed decisions, such as accepting or rejecting a new treatment, implementing policy changes, or adopting new practices.
Adds rigor and validity: It adds scientific rigor to research using statistical methods to analyze data, ensuring that conclusions are based on sound statistical evidence.
Contributes to the advancement of knowledge: By testing hypotheses, researchers contribute to the growth of knowledge in their respective fields by confirming existing theories or discovering new patterns and relationships.

Limitations of Hypothesis Testing

Hypothesis testing has some limitations that researchers should be aware of:

It cannot prove or establish the truth: Hypothesis testing provides evidence to support or reject a hypothesis, but it cannot confirm the absolute truth of the research question.
Results are sample-specific: Hypothesis testing is based on analyzing a sample from a population, and the conclusions drawn are specific to that particular sample.
Possible errors: During hypothesis testing, there is a chance of committing type I error (rejecting a true null hypothesis) or type II error (failing to reject a false null hypothesis).
Assumptions and requirements: Different tests have specific assumptions and requirements that must be met to accurately interpret results.

After reading this tutorial, you would have a much better understanding of hypothesis testing, one of the most important concepts in the field of Data Science . The majority of hypotheses are based on speculation about observed behavior, natural phenomena, or established theories.

If you are interested in statistics of data science and skills needed for such a career, you ought to explore Simplilearn’s Post Graduate Program in Data Science.

If you have any questions regarding this ‘Hypothesis Testing In Statistics’ tutorial, do share them in the comment section. Our subject matter expert will respond to your queries. Happy learning!

1. What is hypothesis testing in statistics with example?

Hypothesis testing is a statistical method used to determine if there is enough evidence in a sample data to draw conclusions about a population. It involves formulating two competing hypotheses, the null hypothesis (H0) and the alternative hypothesis (Ha), and then collecting data to assess the evidence. An example: testing if a new drug improves patient recovery (Ha) compared to the standard treatment (H0) based on collected patient data.

2. What is hypothesis testing and its types?

Hypothesis testing is a statistical method used to make inferences about a population based on sample data. It involves formulating two hypotheses: the null hypothesis (H0), which represents the default assumption, and the alternative hypothesis (Ha), which contradicts H0. The goal is to assess the evidence and determine whether there is enough statistical significance to reject the null hypothesis in favor of the alternative hypothesis.

Types of hypothesis testing:

One-sample test: Used to compare a sample to a known value or a hypothesized value.
Two-sample test: Compares two independent samples to assess if there is a significant difference between their means or distributions.
Paired-sample test: Compares two related samples, such as pre-test and post-test data, to evaluate changes within the same subjects over time or under different conditions.
Chi-square test: Used to analyze categorical data and determine if there is a significant association between variables.
ANOVA (Analysis of Variance): Compares means across multiple groups to check if there is a significant difference between them.

3. What are the steps of hypothesis testing?

The steps of hypothesis testing are as follows:

Formulate the hypotheses: State the null hypothesis (H0) and the alternative hypothesis (Ha) based on the research question.
Set the significance level: Determine the acceptable level of error (alpha) for making a decision.
Collect and analyze data: Gather and process the sample data.
Compute test statistic: Calculate the appropriate statistical test to assess the evidence.
Make a decision: Compare the test statistic with critical values or p-values and determine whether to reject H0 in favor of Ha or not.
Draw conclusions: Interpret the results and communicate the findings in the context of the research question.

4. What are the 2 types of hypothesis testing?

One-tailed (or one-sided) test: Tests for the significance of an effect in only one direction, either positive or negative.
Two-tailed (or two-sided) test: Tests for the significance of an effect in both directions, allowing for the possibility of a positive or negative effect.

The choice between one-tailed and two-tailed tests depends on the specific research question and the directionality of the expected effect.

5. What are the 3 major types of hypothesis?

The three major types of hypotheses are:

Null Hypothesis (H0): Represents the default assumption, stating that there is no significant effect or relationship in the data.
Alternative Hypothesis (Ha): Contradicts the null hypothesis and proposes a specific effect or relationship that researchers want to investigate.
Nondirectional Hypothesis: An alternative hypothesis that doesn't specify the direction of the effect, leaving it open for both positive and negative possibilities.

Find our Data Analyst Online Bootcamp in top cities:

About the author.

Avijeet is a Senior Research Analyst at Simplilearn. Passionate about Data Analytics, Machine Learning, and Deep Learning, Avijeet is also interested in politics, cricket, and football.

Recommended Resources

Free eBook: Top Programming Languages For A Data Scientist

Normality Test in Minitab: Minitab with Statistics

Machine Learning Career Guide: A Playbook to Becoming a Machine Learning Engineer

PMP, PMI, PMBOK, CAPM, PgMP, PfMP, ACP, PBA, RMP, SP, and OPM3 are registered marks of the Project Management Institute, Inc.

Search Search Please fill out this field.

What Is Hypothesis Testing?

How It Works

4 Step Process

The bottom line.

Fundamental Analysis

Hypothesis Testing: 4 Steps and Example

Hypothesis testing, sometimes called significance testing, is an act in statistics whereby an analyst tests an assumption regarding a population parameter. The methodology employed by the analyst depends on the nature of the data used and the reason for the analysis.

Hypothesis testing is used to assess the plausibility of a hypothesis by using sample data. Such data may come from a larger population or a data-generating process. The word "population" will be used for both of these cases in the following descriptions.

Key Takeaways

Hypothesis testing is used to assess the plausibility of a hypothesis by using sample data.
The test provides evidence concerning the plausibility of the hypothesis, given the data.
Statistical analysts test a hypothesis by measuring and examining a random sample of the population being analyzed.
The four steps of hypothesis testing include stating the hypotheses, formulating an analysis plan, analyzing the sample data, and analyzing the result.

How Hypothesis Testing Works

In hypothesis testing, an analyst tests a statistical sample, intending to provide evidence on the plausibility of the null hypothesis. Statistical analysts measure and examine a random sample of the population being analyzed. All analysts use a random population sample to test two different hypotheses: the null hypothesis and the alternative hypothesis.

The null hypothesis is usually a hypothesis of equality between population parameters; e.g., a null hypothesis may state that the population mean return is equal to zero. The alternative hypothesis is effectively the opposite of a null hypothesis. Thus, they are mutually exclusive , and only one can be true. However, one of the two hypotheses will always be true.

The null hypothesis is a statement about a population parameter, such as the population mean, that is assumed to be true.

State the hypotheses.
Formulate an analysis plan, which outlines how the data will be evaluated.
Carry out the plan and analyze the sample data.
Analyze the results and either reject the null hypothesis, or state that the null hypothesis is plausible, given the data.

Example of Hypothesis Testing

If an individual wants to test that a penny has exactly a 50% chance of landing on heads, the null hypothesis would be that 50% is correct, and the alternative hypothesis would be that 50% is not correct. Mathematically, the null hypothesis is represented as Ho: P = 0.5. The alternative hypothesis is shown as "Ha" and is identical to the null hypothesis, except with the equal sign struck-through, meaning that it does not equal 50%.

A random sample of 100 coin flips is taken, and the null hypothesis is tested. If it is found that the 100 coin flips were distributed as 40 heads and 60 tails, the analyst would assume that a penny does not have a 50% chance of landing on heads and would reject the null hypothesis and accept the alternative hypothesis.

If there were 48 heads and 52 tails, then it is plausible that the coin could be fair and still produce such a result. In cases such as this where the null hypothesis is "accepted," the analyst states that the difference between the expected results (50 heads and 50 tails) and the observed results (48 heads and 52 tails) is "explainable by chance alone."

When Did Hypothesis Testing Begin?

Some statisticians attribute the first hypothesis tests to satirical writer John Arbuthnot in 1710, who studied male and female births in England after observing that in nearly every year, male births exceeded female births by a slight proportion. Arbuthnot calculated that the probability of this happening by chance was small, and therefore it was due to “divine providence.”

What are the Benefits of Hypothesis Testing?

Hypothesis testing helps assess the accuracy of new ideas or theories by testing them against data. This allows researchers to determine whether the evidence supports their hypothesis, helping to avoid false claims and conclusions. Hypothesis testing also provides a framework for decision-making based on data rather than personal opinions or biases. By relying on statistical analysis, hypothesis testing helps to reduce the effects of chance and confounding variables, providing a robust framework for making informed conclusions.

What are the Limitations of Hypothesis Testing?

Hypothesis testing relies exclusively on data and doesn’t provide a comprehensive understanding of the subject being studied. Additionally, the accuracy of the results depends on the quality of the available data and the statistical methods used. Inaccurate data or inappropriate hypothesis formulation may lead to incorrect conclusions or failed tests. Hypothesis testing can also lead to errors, such as analysts either accepting or rejecting a null hypothesis when they shouldn’t have. These errors may result in false conclusions or missed opportunities to identify significant patterns or relationships in the data.

Hypothesis testing refers to a statistical process that helps researchers determine the reliability of a study. By using a well-formulated hypothesis and set of statistical tests, individuals or businesses can make inferences about the population that they are studying and draw conclusions based on the data presented. All hypothesis testing methods have the same four-step process, which includes stating the hypotheses, formulating an analysis plan, analyzing the sample data, and analyzing the result.

Sage. " Introduction to Hypothesis Testing ," Page 4.

Elder Research. " Who Invented the Null Hypothesis? "

Formplus. " Hypothesis Testing: Definition, Uses, Limitations and Examples ."

Terms of Service
Editorial Policy
Privacy Policy
Your Privacy Choices

Hypothesis Testing: Definition, Uses, Limitations + Examples

Hypothesis testing is as old as the scientific method and is at the heart of the research process.

Research exists to validate or disprove assumptions about various phenomena. The process of validation involves testing and it is in this context that we will explore hypothesis testing.

What is a Hypothesis?

A hypothesis is a calculated prediction or assumption about a population parameter based on limited evidence. The whole idea behind hypothesis formulation is testing—this means the researcher subjects his or her calculated assumption to a series of evaluations to know whether they are true or false.

Typically, every research starts with a hypothesis—the investigator makes a claim and experiments to prove that this claim is true or false . For instance, if you predict that students who drink milk before class perform better than those who don’t, then this becomes a hypothesis that can be confirmed or refuted using an experiment.

Read: What is Empirical Research Study? [Examples & Method]

What are the Types of Hypotheses?

1. simple hypothesis.

Also known as a basic hypothesis, a simple hypothesis suggests that an independent variable is responsible for a corresponding dependent variable. In other words, an occurrence of the independent variable inevitably leads to an occurrence of the dependent variable.

Typically, simple hypotheses are considered as generally true, and they establish a causal relationship between two variables.

Examples of Simple Hypothesis

Drinking soda and other sugary drinks can cause obesity.
Smoking cigarettes daily leads to lung cancer.

2. Complex Hypothesis

A complex hypothesis is also known as a modal. It accounts for the causal relationship between two independent variables and the resulting dependent variables. This means that the combination of the independent variables leads to the occurrence of the dependent variables .

Examples of Complex Hypotheses

Adults who do not smoke and drink are less likely to develop liver-related conditions.
Global warming causes icebergs to melt which in turn causes major changes in weather patterns.

3. Null Hypothesis

As the name suggests, a null hypothesis is formed when a researcher suspects that there’s no relationship between the variables in an observation. In this case, the purpose of the research is to approve or disapprove this assumption.

Examples of Null Hypothesis

This is no significant change in a student’s performance if they drink coffee or tea before classes.
There’s no significant change in the growth of a plant if one uses distilled water only or vitamin-rich water.

Read: Research Report: Definition, Types + [Writing Guide]

4. Alternative Hypothesis

To disapprove a null hypothesis, the researcher has to come up with an opposite assumption—this assumption is known as the alternative hypothesis. This means if the null hypothesis says that A is false, the alternative hypothesis assumes that A is true.

An alternative hypothesis can be directional or non-directional depending on the direction of the difference. A directional alternative hypothesis specifies the direction of the tested relationship, stating that one variable is predicted to be larger or smaller than the null value while a non-directional hypothesis only validates the existence of a difference without stating its direction.

Examples of Alternative Hypotheses

Starting your day with a cup of tea instead of a cup of coffee can make you more alert in the morning.
The growth of a plant improves significantly when it receives distilled water instead of vitamin-rich water.

5. Logical Hypothesis

Logical hypotheses are some of the most common types of calculated assumptions in systematic investigations. It is an attempt to use your reasoning to connect different pieces in research and build a theory using little evidence. In this case, the researcher uses any data available to him, to form a plausible assumption that can be tested.

Examples of Logical Hypothesis

Waking up early helps you to have a more productive day.
Beings from Mars would not be able to breathe the air in the atmosphere of the Earth.

6. Empirical Hypothesis

After forming a logical hypothesis, the next step is to create an empirical or working hypothesis. At this stage, your logical hypothesis undergoes systematic testing to prove or disprove the assumption. An empirical hypothesis is subject to several variables that can trigger changes and lead to specific outcomes.

Examples of Empirical Testing

People who eat more fish run faster than people who eat meat.
Women taking vitamin E grow hair faster than those taking vitamin K.

7. Statistical Hypothesis

When forming a statistical hypothesis, the researcher examines the portion of a population of interest and makes a calculated assumption based on the data from this sample. A statistical hypothesis is most common with systematic investigations involving a large target audience. Here, it’s impossible to collect responses from every member of the population so you have to depend on data from your sample and extrapolate the results to the wider population.

Examples of Statistical Hypothesis

45% of students in Louisiana have middle-income parents.
80% of the UK’s population gets a divorce because of irreconcilable differences.

What is Hypothesis Testing?

Hypothesis testing is an assessment method that allows researchers to determine the plausibility of a hypothesis. It involves testing an assumption about a specific population parameter to know whether it’s true or false. These population parameters include variance, standard deviation, and median.

Typically, hypothesis testing starts with developing a null hypothesis and then performing several tests that support or reject the null hypothesis. The researcher uses test statistics to compare the association or relationship between two or more variables.

Explore: Research Bias: Definition, Types + Examples

Researchers also use hypothesis testing to calculate the coefficient of variation and determine if the regression relationship and the correlation coefficient are statistically significant.

How Hypothesis Testing Works

The basis of hypothesis testing is to examine and analyze the null hypothesis and alternative hypothesis to know which one is the most plausible assumption. Since both assumptions are mutually exclusive, only one can be true. In other words, the occurrence of a null hypothesis destroys the chances of the alternative coming to life, and vice-versa.

Interesting: 21 Chrome Extensions for Academic Researchers in 2021

What Are The Stages of Hypothesis Testing?

To successfully confirm or refute an assumption, the researcher goes through five (5) stages of hypothesis testing;

Determine the null hypothesis
Specify the alternative hypothesis
Set the significance level
Calculate the test statistics and corresponding P-value
Draw your conclusion
Determine the Null Hypothesis

Like we mentioned earlier, hypothesis testing starts with creating a null hypothesis which stands as an assumption that a certain statement is false or implausible. For example, the null hypothesis (H0) could suggest that different subgroups in the research population react to a variable in the same way.

Specify the Alternative Hypothesis

Once you know the variables for the null hypothesis, the next step is to determine the alternative hypothesis. The alternative hypothesis counters the null assumption by suggesting the statement or assertion is true. Depending on the purpose of your research, the alternative hypothesis can be one-sided or two-sided.

Using the example we established earlier, the alternative hypothesis may argue that the different sub-groups react differently to the same variable based on several internal and external factors.

Set the Significance Level

Many researchers create a 5% allowance for accepting the value of an alternative hypothesis, even if the value is untrue. This means that there is a 0.05 chance that one would go with the value of the alternative hypothesis, despite the truth of the null hypothesis.

Something to note here is that the smaller the significance level, the greater the burden of proof needed to reject the null hypothesis and support the alternative hypothesis.

Explore: What is Data Interpretation? + [Types, Method & Tools]

Calculate the Test Statistics and Corresponding P-Value

Test statistics in hypothesis testing allow you to compare different groups between variables while the p-value accounts for the probability of obtaining sample statistics if your null hypothesis is true. In this case, your test statistics can be the mean, median and similar parameters.

If your p-value is 0.65, for example, then it means that the variable in your hypothesis will happen 65 in100 times by pure chance. Use this formula to determine the p-value for your data:

Draw Your Conclusions

After conducting a series of tests, you should be able to agree or refute the hypothesis based on feedback and insights from your sample data.

Applications of Hypothesis Testing in Research

Hypothesis testing isn’t only confined to numbers and calculations; it also has several real-life applications in business, manufacturing, advertising, and medicine.

In a factory or other manufacturing plants, hypothesis testing is an important part of quality and production control before the final products are approved and sent out to the consumer.

During ideation and strategy development, C-level executives use hypothesis testing to evaluate their theories and assumptions before any form of implementation. For example, they could leverage hypothesis testing to determine whether or not some new advertising campaign, marketing technique, etc. causes increased sales.

In addition, hypothesis testing is used during clinical trials to prove the efficacy of a drug or new medical method before its approval for widespread human usage.

What is an Example of Hypothesis Testing?

An employer claims that her workers are of above-average intelligence. She takes a random sample of 20 of them and gets the following results:

Mean IQ Scores: 110

Standard Deviation: 15

Mean Population IQ: 100

Step 1: Using the value of the mean population IQ, we establish the null hypothesis as 100.

Step 2: State that the alternative hypothesis is greater than 100.

Step 3: State the alpha level as 0.05 or 5%

Step 4: Find the rejection region area (given by your alpha level above) from the z-table. An area of .05 is equal to a z-score of 1.645.

Step 5: Calculate the test statistics using this formula

Z = (110–100) ÷ (15÷√20)

10 ÷ 3.35 = 2.99

If the value of the test statistics is higher than the value of the rejection region, then you should reject the null hypothesis. If it is less, then you cannot reject the null.

In this case, 2.99 > 1.645 so we reject the null.

Importance/Benefits of Hypothesis Testing

The most significant benefit of hypothesis testing is it allows you to evaluate the strength of your claim or assumption before implementing it in your data set. Also, hypothesis testing is the only valid method to prove that something “is or is not”. Other benefits include:

Hypothesis testing provides a reliable framework for making any data decisions for your population of interest.
It helps the researcher to successfully extrapolate data from the sample to the larger population.
Hypothesis testing allows the researcher to determine whether the data from the sample is statistically significant.
Hypothesis testing is one of the most important processes for measuring the validity and reliability of outcomes in any systematic investigation.
It helps to provide links to the underlying theory and specific research questions.

Criticism and Limitations of Hypothesis Testing

Several limitations of hypothesis testing can affect the quality of data you get from this process. Some of these limitations include:

The interpretation of a p-value for observation depends on the stopping rule and definition of multiple comparisons. This makes it difficult to calculate since the stopping rule is subject to numerous interpretations, plus “multiple comparisons” are unavoidably ambiguous.
Conceptual issues often arise in hypothesis testing, especially if the researcher merges Fisher and Neyman-Pearson’s methods which are conceptually distinct.
In an attempt to focus on the statistical significance of the data, the researcher might ignore the estimation and confirmation by repeated experiments.
Hypothesis testing can trigger publication bias, especially when it requires statistical significance as a criterion for publication.
When used to detect whether a difference exists between groups, hypothesis testing can trigger absurd assumptions that affect the reliability of your observation.

Connect to Formplus, Get Started Now - It's Free!

alternative hypothesis
alternative vs null hypothesis
complex hypothesis
empirical hypothesis
hypothesis testing
logical hypothesis
simple hypothesis
statistical hypothesis
busayo.longe

What is Pure or Basic Research? + [Examples & Method]

Simple guide on pure or basic research, its methods, characteristics, advantages, and examples in science, medicine, education and psychology

Internal Validity in Research: Definition, Threats, Examples

In this article, we will discuss the concept of internal validity, some clear examples, its importance, and how to test it.

Alternative vs Null Hypothesis: Pros, Cons, Uses & Examples

We are going to discuss alternative hypotheses and null hypotheses in this post and how they work in research.

Type I vs Type II Errors: Causes, Examples & Prevention

This article will discuss the two different types of errors in hypothesis testing and how you can prevent them from occurring in your research

Formplus - For Seamless Data Collection

Collect data the right way with a versatile data collection tool. try formplus and transform your work productivity today..

What is Hypothesis Testing in Statistics? Types and Examples

Varun Saharawat is a seasoned professional in the fields of SEO and content writing. With a profound knowledge of the intricate aspects of these disciplines, Varun has established himself as a valuable asset in the world of digital marketing and online content creation.

Hypothesis testing in statistics involves testing an assumption about a population parameter using sample data. Learners can download Hypothesis Testing PDF to get instant access to all information!

What exactly is hypothesis testing, and how does it work in statistics? Can I find practical examples and understand the different types from this blog?

Hypothesis Testing : Ever wonder how researchers determine if a new medicine actually works or if a new marketing campaign effectively drives sales? They use hypothesis testing! It is at the core of how scientific studies, business experiments and surveys determine if their results are statistically significant or just due to chance.

Hypothesis testing allows us to make evidence-based decisions by quantifying uncertainty and providing a structured process to make data-driven conclusions rather than guessing. In this post, we will discuss hypothesis testing types, examples, and processes!

Table of Contents

Hypothesis Testing

Hypothesis testing is a statistical method used to evaluate the validity of a hypothesis using sample data. It involves assessing whether observed data provide enough evidence to reject a specific hypothesis about a population parameter.

Hypothesis Testing in Data Science

Hypothesis testing in data science is a statistical method used to evaluate two mutually exclusive population statements based on sample data. The primary goal is to determine which statement is more supported by the observed data.

Hypothesis testing assists in supporting the certainty of findings in research and data science projects. This statistical inference aids in making decisions about population parameters using sample data. For those who are looking to deepen their knowledge in data science and expand their skillset, we highly recommend checking out Master Generative AI: Data Science Course by Physics Wallah .

Also Read: What is Encapsulation Explain in Details

What is the Hypothesis Testing Procedure in Data Science?

The hypothesis testing procedure in data science involves a structured approach to evaluating hypotheses using statistical methods. Here’s a step-by-step breakdown of the typical procedure:

1) State the Hypotheses:

Null Hypothesis (H0): This is the default assumption or a statement of no effect or difference. It represents what you aim to test against.
Alternative Hypothesis (Ha): This is the opposite of the null hypothesis and represents what you want to prove.

2) Choose a Significance Level (α):

Decide on a threshold (commonly 0.05) beyond which you will reject the null hypothesis. This is your significance level.

3) Select the Appropriate Test:

Depending on your data type (e.g., continuous, categorical) and the nature of your research question, choose the appropriate statistical test (e.g., t-test, chi-square test, ANOVA, etc.).

4) Collect Data:

Gather data from your sample or population, ensuring that it’s representative and sufficiently large (or as per your experimental design).

5)Compute the Test Statistic:

Using your data and the chosen statistical test, compute the test statistic that summarizes the evidence against the null hypothesis.

6) Determine the Critical Value or P-value:

Based on your significance level and the test statistic’s distribution, determine the critical value from a statistical table or compute the p-value.

7) Make a Decision:

If the p-value is less than α: Reject the null hypothesis.
If the p-value is greater than or equal to α: Fail to reject the null hypothesis.

8) Draw Conclusions:

Based on your decision, draw conclusions about your research question or hypothesis. Remember, failing to reject the null hypothesis doesn’t prove it true; it merely suggests that you don’t have sufficient evidence to reject it.

9) Report Findings:

Document your findings, including the test statistic, p-value, conclusion, and any other relevant details. Ensure clarity so that others can understand and potentially replicate your analysis.

How Hypothesis Testing Works?

Hypothesis testing is a fundamental concept in statistics that aids analysts in making informed decisions based on sample data about a larger population. The process involves setting up two contrasting hypotheses, the null hypothesis and the alternative hypothesis, and then using statistical methods to determine which hypothesis provides a more plausible explanation for the observed data.

The Core Principles:

The Null Hypothesis (H0): This serves as the default assumption or status quo. Typically, it posits that there is no effect or no difference, often represented by an equality statement regarding population parameters. For instance, it might state that a new drug’s effect is no different from a placebo.
The Alternative Hypothesis (H1 or Ha): This is the counter assumption or what researchers aim to prove. It’s the opposite of the null hypothesis, indicating that there is an effect, a change, or a difference in the population parameters. Using the drug example, the alternative hypothesis would suggest that the new drug has a different effect than the placebo.

Testing the Hypotheses:

Once these hypotheses are established, analysts gather data from a sample and conduct statistical tests. The objective is to determine whether the observed results are statistically significant enough to reject the null hypothesis in favor of the alternative.

Examples to Clarify the Concept:

Null Hypothesis (H0): The sanitizer’s average efficacy is 95%.
By conducting tests, if evidence suggests that the sanitizer’s efficacy is significantly less than 95%, we reject the null hypothesis.
Null Hypothesis (H0): The coin is fair, meaning the probability of heads and tails is equal.
Through experimental trials, if results consistently show a skewed outcome, indicating a significantly different probability for heads and tails, the null hypothesis might be rejected.

What are the 3 types of Hypothesis Test?

Hypothesis testing is a cornerstone in statistical analysis, providing a framework to evaluate the validity of assumptions or claims made about a population based on sample data. Within this framework, several specific tests are utilized based on the nature of the data and the question at hand. Here’s a closer look at the three fundamental types of hypothesis tests:

The z-test is a statistical method primarily employed when comparing means from two datasets, particularly when the population standard deviation is known. Its main objective is to ascertain if the means are statistically equivalent.

A crucial prerequisite for the z-test is that the sample size should be relatively large, typically 30 data points or more. This test aids researchers and analysts in determining the significance of a relationship or discovery, especially in scenarios where the data’s characteristics align with the assumptions of the z-test.

The t-test is a versatile statistical tool used extensively in research and various fields to compare means between two groups. It’s particularly valuable when the population standard deviation is unknown or when dealing with smaller sample sizes.

By evaluating the means of two groups, the t-test helps ascertain if a particular treatment, intervention, or variable significantly impacts the population under study. Its flexibility and robustness make it a go-to method in scenarios ranging from medical research to business analytics.

3. Chi-Square Test:

The Chi-Square test stands distinct from the previous tests, primarily focusing on categorical data rather than means. This statistical test is instrumental when analyzing categorical variables to determine if observed data aligns with expected outcomes as posited by the null hypothesis.

By assessing the differences between observed and expected frequencies within categorical data, the Chi-Square test offers insights into whether discrepancies are statistically significant. Whether used in social sciences to evaluate survey responses or in quality control to assess product defects, the Chi-Square test remains pivotal for hypothesis testing in diverse scenarios.

Also Read: Python vs Java: Which is Best for Machine learning algorithm

Hypothesis Testing in Statistics

Hypothesis testing is a fundamental concept in statistics used to make decisions or inferences about a population based on a sample of data. The process involves setting up two competing hypotheses, the null hypothesis H 0 and the alternative hypothesis H 1.

Through various statistical tests, such as the t-test, z-test, or Chi-square test, analysts evaluate sample data to determine whether there’s enough evidence to reject the null hypothesis in favor of the alternative. The aim is to draw conclusions about population parameters or to test theories, claims, or hypotheses.

Hypothesis Testing in Research

In research, hypothesis testing serves as a structured approach to validate or refute theories or claims. Researchers formulate a clear hypothesis based on existing literature or preliminary observations. They then collect data through experiments, surveys, or observational studies.

Using statistical methods, researchers analyze this data to determine if there’s sufficient evidence to reject the null hypothesis. By doing so, they can draw meaningful conclusions, make predictions, or recommend actions based on empirical evidence rather than mere speculation.

Hypothesis Testing in R

R, a powerful programming language and environment for statistical computing and graphics, offers a wide array of functions and packages specifically designed for hypothesis testing. Here’s how hypothesis testing is conducted in R:

Data Collection : Before conducting any test, you need to gather your data and ensure it’s appropriately structured in R.
Choose the Right Test : Depending on your research question and data type, select the appropriate hypothesis test. For instance, use the t.test() function for a t-test or chisq.test() for a Chi-square test.
Set Hypotheses : Define your null and alternative hypotheses. Using R’s syntax, you can specify these hypotheses and run the corresponding test.
Execute the Test : Utilize built-in functions in R to perform the hypothesis test on your data. For instance, if you want to compare two means, you can use the t.test() function, providing the necessary arguments like the data vectors and type of t-test (one-sample, two-sample, paired, etc.).
Interpret Results : Once the test is executed, R will provide output, including test statistics, p-values, and confidence intervals. Based on these results and a predetermined significance level (often 0.05), you can decide whether to reject the null hypothesis.
Visualization : R’s graphical capabilities allow users to visualize data distributions, confidence intervals, or test statistics, aiding in the interpretation and presentation of results.

Hypothesis testing is an integral part of statistics and research, offering a systematic approach to validate hypotheses. Leveraging R’s capabilities, researchers and analysts can efficiently conduct and interpret various hypothesis tests, ensuring robust and reliable conclusions from their data.

Do Data Scientists do Hypothesis Testing?

Yes, data scientists frequently engage in hypothesis testing as part of their analytical toolkit. Hypothesis testing is a foundational statistical technique used to make data-driven decisions, validate assumptions, and draw conclusions from data. Here’s how data scientists utilize hypothesis testing:

Validating Assumptions : Before diving into complex analyses or building predictive models, data scientists often need to verify certain assumptions about the data. Hypothesis testing provides a structured approach to test these assumptions, ensuring that subsequent analyses or models are valid.
Feature Selection : In machine learning and predictive modeling, data scientists use hypothesis tests to determine which features (or variables) are most relevant or significant in predicting a particular outcome. By testing hypotheses related to feature importance or correlation, they can streamline the modeling process and enhance prediction accuracy.
A/B Testing : A/B testing is a common technique in marketing, product development, and user experience design. Data scientists employ hypothesis testing to compare two versions (A and B) of a product, feature, or marketing strategy to determine which performs better in terms of a specified metric (e.g., conversion rate, user engagement).
Research and Exploration : In exploratory data analysis (EDA) or when investigating specific research questions, data scientists formulate hypotheses to test certain relationships or patterns within the data. By conducting hypothesis tests, they can validate these relationships, uncover insights, and drive data-driven decision-making.
Model Evaluation : After building machine learning or statistical models, data scientists use hypothesis testing to evaluate the model’s performance, assess its predictive power, or compare different models. For instance, hypothesis tests like the t-test or F-test can help determine if a new model significantly outperforms an existing one based on certain metrics.
Business Decision-making : Beyond technical analyses, data scientists employ hypothesis testing to support business decisions. Whether it’s evaluating the effectiveness of a marketing campaign, assessing customer preferences, or optimizing operational processes, hypothesis testing provides a rigorous framework to validate assumptions and guide strategic initiatives.

Hypothesis Testing Examples and Solutions

Let’s delve into some common examples of hypothesis testing and provide solutions or interpretations for each scenario.

Example: Testing the Mean

Scenario : A coffee shop owner believes that the average waiting time for customers during peak hours is 5 minutes. To test this, the owner takes a random sample of 30 customer waiting times and wants to determine if the average waiting time is indeed 5 minutes.

Hypotheses :

H 0 (Null Hypothesis): 5 μ =5 minutes (The average waiting time is 5 minutes)
H 1 (Alternative Hypothesis): 5 μ =5 minutes (The average waiting time is not 5 minutes)

Solution : Using a t-test (assuming population variance is unknown), calculate the t-statistic based on the sample mean, sample standard deviation, and sample size. Then, determine the p-value and compare it with a significance level (e.g., 0.05) to decide whether to reject the null hypothesis.

Example: A/B Testing in Marketing

Scenario : An e-commerce company wants to determine if changing the color of a “Buy Now” button from blue to green increases the conversion rate.

H 0: Changing the button color does not affect the conversion rate.
H 1: Changing the button color affects the conversion rate.

Solution : Split website visitors into two groups: one sees the blue button (control group), and the other sees the green button (test group). Track the conversion rates for both groups over a specified period. Then, use a chi-square test or z-test (for large sample sizes) to determine if there’s a statistically significant difference in conversion rates between the two groups.

Hypothesis Testing Formula

The formula for hypothesis testing typically depends on the type of test (e.g., z-test, t-test, chi-square test) and the nature of the data (e.g., mean, proportion, variance). Below are the basic formulas for some common hypothesis tests:

Z-Test for Population Mean :

Z=(σ/n)(xˉ−μ0)

ˉ x ˉ = Sample mean
0 μ 0 = Population mean under the null hypothesis
σ = Population standard deviation
n = Sample size

T-Test for Population Mean :

t= (s/ n ) ( x ˉ −μ 0 )

s = Sample standard deviation

Chi-Square Test for Goodness of Fit :

χ2=∑Ei(Oi−Ei)2

Oi = Observed frequency
Ei = Expected frequency

Hypothesis Testing Calculator

While you can perform hypothesis testing manually using the above formulas and statistical tables, many online tools and software packages simplify this process. Here’s how you might use a calculator or software:

Z-Test and T-Test Calculators : These tools typically require you to input sample statistics (like sample mean, population mean, standard deviation, and sample size). Once you input these values, the calculator will provide you with the test statistic (Z or t) and a p-value.
Chi-Square Calculator : For chi-square tests, you’d input observed and expected frequencies for different categories or groups. The calculator then computes the chi-square statistic and provides a p-value.
Software Packages (e.g., R, Python with libraries like scipy, or statistical software like SPSS) : These platforms offer more comprehensive tools for hypothesis testing. You can run various tests, get detailed outputs, and even perform advanced analyses, including regression models, ANOVA, and more.

When using any calculator or software, always ensure you understand the underlying assumptions of the test, interpret the results correctly, and consider the broader context of your research or analysis.

Hypothesis Testing FAQs

What are the key components of a hypothesis test.

The key components include: Null Hypothesis (H0): A statement of no effect or no difference. Alternative Hypothesis (H1 or Ha): A statement that contradicts the null hypothesis. Test Statistic: A value computed from the sample data to test the null hypothesis. Significance Level (α): The threshold for rejecting the null hypothesis. P-value: The probability of observing the given data, assuming the null hypothesis is true.

What is the significance level in hypothesis testing?

The significance level (often denoted as α) is the probability threshold used to determine whether to reject the null hypothesis. Commonly used values for α include 0.05, 0.01, and 0.10, representing a 5%, 1%, or 10% chance of rejecting the null hypothesis when it's actually true.

How do I choose between a one-tailed and two-tailed test?

The choice between one-tailed and two-tailed tests depends on your research question and hypothesis. Use a one-tailed test when you're specifically interested in one direction of an effect (e.g., greater than or less than). Use a two-tailed test when you want to determine if there's a significant difference in either direction.

What is a p-value, and how is it interpreted?

The p-value is a probability value that helps determine the strength of evidence against the null hypothesis. A low p-value (typically ≤ 0.05) suggests that the observed data is inconsistent with the null hypothesis, leading to its rejection. Conversely, a high p-value suggests that the data is consistent with the null hypothesis, leading to no rejection.

Can hypothesis testing prove a hypothesis true?

No, hypothesis testing cannot prove a hypothesis true. Instead, it helps assess the likelihood of observing a given set of data under the assumption that the null hypothesis is true. Based on this assessment, you either reject or fail to reject the null hypothesis.

Predictive Modeling: Revolutionizing Decision-Making with AI

Predictive modeling is like using math and computer smarts to guess what might happen in the future. We look at…

Top 10 Online Coding Competitions in 2024?

“PW Skills will conduct a national-level coding competition on December 21, 2023. The winners and top rankers will get many…

Top 30 Excel Formulas And Functions You Should Know

Microsoft Excel is the most common instrument for working with data and their structures. A handful of people probably haven’t…

School Guide
Mathematics
Number System and Arithmetic
Trigonometry
Probability
Mensuration
Maths Formulas
Class 8 Maths Notes
Class 9 Maths Notes
Class 10 Maths Notes
Class 11 Maths Notes
Class 12 Maths Notes
Data Analysis with Python

Introduction to Data Analysis

What is Data Analysis?
Data Analytics and its type
How to Install Numpy on Windows?
How to Install Pandas in Python?
How to Install Matplotlib on python?
How to Install Python Tensorflow in Windows?

Data Analysis Libraries

Pandas Tutorial
NumPy Tutorial - Python Library
Data Analysis with SciPy
Introduction to TensorFlow

Data Visulization Libraries

Matplotlib Tutorial
Python Seaborn Tutorial
Plotly tutorial
Introduction to Bokeh in Python

Exploratory Data Analysis (EDA)

Univariate, Bivariate and Multivariate data and its analysis
Measures of Central Tendency in Statistics
Measures of spread - Range, Variance, and Standard Deviation
Interquartile Range and Quartile Deviation using NumPy and SciPy
Anova Formula
Skewness of Statistical Data
How to Calculate Skewness and Kurtosis in Python?
Difference Between Skewness and Kurtosis
Histogram | Meaning, Example, Types and Steps to Draw
Interpretations of Histogram
Quantile Quantile plots
What is Univariate, Bivariate & Multivariate Analysis in Data Visualisation?
Using pandas crosstab to create a bar plot
Exploring Correlation in Python
Mathematics | Covariance and Correlation
Factor Analysis | Data Analysis
Data Mining - Cluster Analysis
MANOVA Test in R Programming
Python - Central Limit Theorem
Probability Distribution Function
Probability Density Estimation & Maximum Likelihood Estimation
Exponential Distribution in R Programming - dexp(), pexp(), qexp(), and rexp() Functions
Mathematics | Probability Distributions Set 4 (Binomial Distribution)
Poisson Distribution - Definition, Formula, Table and Examples
P-Value: Comprehensive Guide to Understand, Apply, and Interpret
Z-Score in Statistics
How to Calculate Point Estimates in R?
Confidence Interval
Chi-square test in Machine Learning

Understanding Hypothesis Testing

Data preprocessing.

ML | Data Preprocessing in Python
ML | Overview of Data Cleaning
ML | Handling Missing Values
Detect and Remove the Outliers using Python

Data Transformation

Data Normalization Machine Learning
Sampling distribution Using Python

Time Series Data Analysis

Data Mining - Time-Series, Symbolic and Biological Sequences Data
Basic DateTime Operations in Python
Time Series Analysis & Visualization in Python
How to deal with missing values in a Timeseries in Python?
How to calculate MOVING AVERAGE in a Pandas DataFrame?
What is a trend in time series?
How to Perform an Augmented Dickey-Fuller Test in R
AutoCorrelation

Case Studies and Projects

Top 8 Free Dataset Sources to Use for Data Science Projects
Step by Step Predictive Analysis - Machine Learning
6 Tips for Creating Effective Data Visualizations

Hypothesis testing involves formulating assumptions about population parameters based on sample statistics and rigorously evaluating these assumptions against empirical evidence. This article sheds light on the significance of hypothesis testing and the critical steps involved in the process.

What is Hypothesis Testing?

Hypothesis testing is a statistical method that is used to make a statistical decision using experimental data. Hypothesis testing is basically an assumption that we make about a population parameter. It evaluates two mutually exclusive statements about a population to determine which statement is best supported by the sample data.

Example: You say an average height in the class is 30 or a boy is taller than a girl. All of these is an assumption that we are assuming, and we need some statistical way to prove these. We need some mathematical conclusion whatever we are assuming is true.

Defining Hypotheses

$\mu$

Key Terms of Hypothesis Testing

$\alpha$

P-value: The P value , or calculated probability, is the probability of finding the observed/extreme results when the null hypothesis(H0) of a study-given problem is true. If your P-value is less than the chosen significance level then you reject the null hypothesis i.e. accept that your sample claims to support the alternative hypothesis.
Test Statistic: The test statistic is a numerical value calculated from sample data during a hypothesis test, used to determine whether to reject the null hypothesis. It is compared to a critical value or p-value to make decisions about the statistical significance of the observed results.
Critical value : The critical value in statistics is a threshold or cutoff point used to determine whether to reject the null hypothesis in a hypothesis test.
Degrees of freedom: Degrees of freedom are associated with the variability or freedom one has in estimating a parameter. The degrees of freedom are related to the sample size and determine the shape.

Why do we use Hypothesis Testing?

Hypothesis testing is an important procedure in statistics. Hypothesis testing evaluates two mutually exclusive population statements to determine which statement is most supported by sample data. When we say that the findings are statistically significant, thanks to hypothesis testing.

One-Tailed and Two-Tailed Test

One tailed test focuses on one direction, either greater than or less than a specified value. We use a one-tailed test when there is a clear directional expectation based on prior knowledge or theory. The critical region is located on only one side of the distribution curve. If the sample falls into this critical region, the null hypothesis is rejected in favor of the alternative hypothesis.

One-Tailed Test

There are two types of one-tailed test:

$\mu \geq 50$

Two-Tailed Test

A two-tailed test considers both directions, greater than and less than a specified value.We use a two-tailed test when there is no specific directional expectation, and want to detect any significant difference.

$\mu =$

What are Type 1 and Type 2 errors in Hypothesis Testing?

In hypothesis testing, Type I and Type II errors are two possible errors that researchers can make when drawing conclusions about a population based on a sample of data. These errors are associated with the decisions made regarding the null hypothesis and the alternative hypothesis.

$\alpha$

How does Hypothesis Testing work?

Step 1: define null and alternative hypothesis.

We first identify the problem about which we want to make an assumption keeping in mind that our assumption should be contradictory to one another, assuming Normally distributed data.

Step 2 – Choose significance level

$\alpha$

Step 3 – Collect and Analyze data.

Gather relevant data through observation or experimentation. Analyze the data using appropriate statistical methods to obtain a test statistic.

Step 4-Calculate Test Statistic

The data for the tests are evaluated in this step we look for various scores based on the characteristics of data. The choice of the test statistic depends on the type of hypothesis test being conducted.

There are various hypothesis tests, each appropriate for various goal to calculate our test. This could be a Z-test , Chi-square , T-test , and so on.

Z-test : If population means and standard deviations are known. Z-statistic is commonly used.
t-test : If population standard deviations are unknown. and sample size is small than t-test statistic is more appropriate.
Chi-square test : Chi-square test is used for categorical data or for testing independence in contingency tables
F-test : F-test is often used in analysis of variance (ANOVA) to compare variances or test the equality of means across multiple groups.

We have a smaller dataset, So, T-test is more appropriate to test our hypothesis.

T-statistic is a measure of the difference between the means of two groups relative to the variability within each group. It is calculated as the difference between the sample means divided by the standard error of the difference. It is also known as the t-value or t-score.

Step 5 – Comparing Test Statistic:

In this stage, we decide where we should accept the null hypothesis or reject the null hypothesis. There are two ways to decide where we should accept or reject the null hypothesis.

Method A: Using Crtical values

Comparing the test statistic and tabulated critical value we have,

If Test Statistic>Critical Value: Reject the null hypothesis.
If Test Statistic≤Critical Value: Fail to reject the null hypothesis.

Note: Critical values are predetermined threshold values that are used to make a decision in hypothesis testing. To determine critical values for hypothesis testing, we typically refer to a statistical distribution table , such as the normal distribution or t-distribution tables based on.

Method B: Using P-values

We can also come to an conclusion using the p-value,

$p\leq\alpha$

Note : The p-value is the probability of obtaining a test statistic as extreme as, or more extreme than, the one observed in the sample, assuming the null hypothesis is true. To determine p-value for hypothesis testing, we typically refer to a statistical distribution table , such as the normal distribution or t-distribution tables based on.

Step 7- Interpret the Results

At last, we can conclude our experiment using method A or B.

Calculating test statistic

To validate our hypothesis about a population parameter we use statistical functions . We use the z-score, p-value, and level of significance(alpha) to make evidence for our hypothesis for normally distributed data .

1. Z-statistics:

When population means and standard deviations are known.

$z = \frac{\bar{x} - \mu}{\frac{\sigma}{\sqrt{n}}}$

μ represents the population mean,
σ is the standard deviation
and n is the size of the sample.

2. T-Statistics

T test is used when n<30,

t-statistic calculation is given by:

$t=\frac{x̄-μ}{s/\sqrt{n}}$

t = t-score,
x̄ = sample mean
μ = population mean,
s = standard deviation of the sample,
n = sample size

3. Chi-Square Test

Chi-Square Test for Independence categorical Data (Non-normally distributed) using:

$\chi^2 = \sum \frac{(O_{ij} - E_{ij})^2}{E_{ij}}$

i,j are the rows and columns index respectively.

$E_{ij}$

Real life Hypothesis Testing example

Let’s examine hypothesis testing using two real life situations,

Case A: D oes a New Drug Affect Blood Pressure?

Imagine a pharmaceutical company has developed a new drug that they believe can effectively lower blood pressure in patients with hypertension. Before bringing the drug to market, they need to conduct a study to assess its impact on blood pressure.

Before Treatment: 120, 122, 118, 130, 125, 128, 115, 121, 123, 119
After Treatment: 115, 120, 112, 128, 122, 125, 110, 117, 119, 114

Step 1 : Define the Hypothesis

Null Hypothesis : (H 0 )The new drug has no effect on blood pressure.
Alternate Hypothesis : (H 1 )The new drug has an effect on blood pressure.

Step 2: Define the Significance level

Let’s consider the Significance level at 0.05, indicating rejection of the null hypothesis.

If the evidence suggests less than a 5% chance of observing the results due to random variation.

Step 3 : Compute the test statistic

Using paired T-test analyze the data to obtain a test statistic and a p-value.

The test statistic (e.g., T-statistic) is calculated based on the differences between blood pressure measurements before and after treatment.

t = m/(s/√n)

m = mean of the difference i.e X after, X before
s = standard deviation of the difference (d) i.e d i = X after, i − X before,
n = sample size,

then, m= -3.9, s= 1.8 and n= 10

we, calculate the , T-statistic = -9 based on the formula for paired t test

Step 4: Find the p-value

The calculated t-statistic is -9 and degrees of freedom df = 9, you can find the p-value using statistical software or a t-distribution table.

thus, p-value = 8.538051223166285e-06

Step 5: Result

If the p-value is less than or equal to 0.05, the researchers reject the null hypothesis.
If the p-value is greater than 0.05, they fail to reject the null hypothesis.

Conclusion: Since the p-value (8.538051223166285e-06) is less than the significance level (0.05), the researchers reject the null hypothesis. There is statistically significant evidence that the average blood pressure before and after treatment with the new drug is different.

Python Implementation of Hypothesis Testing

Let’s create hypothesis testing with python, where we are testing whether a new drug affects blood pressure. For this example, we will use a paired T-test. We’ll use the scipy.stats library for the T-test.

Scipy is a mathematical library in Python that is mostly used for mathematical equations and computations.

We will implement our first real life problem via python,

In the above example, given the T-statistic of approximately -9 and an extremely small p-value, the results indicate a strong case to reject the null hypothesis at a significance level of 0.05.

The results suggest that the new drug, treatment, or intervention has a significant effect on lowering blood pressure.
The negative T-statistic indicates that the mean blood pressure after treatment is significantly lower than the assumed population mean before treatment.

Case B : Cholesterol level in a population

Data: A sample of 25 individuals is taken, and their cholesterol levels are measured.

Cholesterol Levels (mg/dL): 205, 198, 210, 190, 215, 205, 200, 192, 198, 205, 198, 202, 208, 200, 205, 198, 205, 210, 192, 205, 198, 205, 210, 192, 205.

Populations Mean = 200

Population Standard Deviation (σ): 5 mg/dL(given for this problem)

Step 1: Define the Hypothesis

Null Hypothesis (H 0 ): The average cholesterol level in a population is 200 mg/dL.
Alternate Hypothesis (H 1 ): The average cholesterol level in a population is different from 200 mg/dL.

As the direction of deviation is not given , we assume a two-tailed test, and based on a normal distribution table, the critical values for a significance level of 0.05 (two-tailed) can be calculated through the z-table and are approximately -1.96 and 1.96.

$(203.8 - 200) / (5 \div \sqrt{25})$

Step 4: Result

Since the absolute value of the test statistic (2.04) is greater than the critical value (1.96), we reject the null hypothesis. And conclude that, there is statistically significant evidence that the average cholesterol level in the population is different from 200 mg/dL

Limitations of Hypothesis Testing

Although a useful technique, hypothesis testing does not offer a comprehensive grasp of the topic being studied. Without fully reflecting the intricacy or whole context of the phenomena, it concentrates on certain hypotheses and statistical significance.
The accuracy of hypothesis testing results is contingent on the quality of available data and the appropriateness of statistical methods used. Inaccurate data or poorly formulated hypotheses can lead to incorrect conclusions.
Relying solely on hypothesis testing may cause analysts to overlook significant patterns or relationships in the data that are not captured by the specific hypotheses being tested. This limitation underscores the importance of complimenting hypothesis testing with other analytical approaches.

Hypothesis testing stands as a cornerstone in statistical analysis, enabling data scientists to navigate uncertainties and draw credible inferences from sample data. By systematically defining null and alternative hypotheses, choosing significance levels, and leveraging statistical tests, researchers can assess the validity of their assumptions. The article also elucidates the critical distinction between Type I and Type II errors, providing a comprehensive understanding of the nuanced decision-making process inherent in hypothesis testing. The real-life example of testing a new drug’s effect on blood pressure using a paired T-test showcases the practical application of these principles, underscoring the importance of statistical rigor in data-driven decision-making.

Frequently Asked Questions (FAQs)

1. what are the 3 types of hypothesis test.

There are three types of hypothesis tests: right-tailed, left-tailed, and two-tailed. Right-tailed tests assess if a parameter is greater, left-tailed if lesser. Two-tailed tests check for non-directional differences, greater or lesser.

2.What are the 4 components of hypothesis testing?

Null Hypothesis ( ): No effect or difference exists. Alternative Hypothesis ( ): An effect or difference exists. Significance Level ( ): Risk of rejecting null hypothesis when it’s true (Type I error). Test Statistic: Numerical value representing observed evidence against null hypothesis.

3.What is hypothesis testing in ML?

Statistical method to evaluate the performance and validity of machine learning models. Tests specific hypotheses about model behavior, like whether features influence predictions or if a model generalizes well to unseen data.

4.What is the difference between Pytest and hypothesis in Python?

Pytest purposes general testing framework for Python code while Hypothesis is a Property-based testing framework for Python, focusing on generating test cases based on specified properties of the code.

Please Login to comment...

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

IMAGES

Hypothesis Testing Steps & Real Life Examples
Hypothesis Testing: Significance Level and Rejection Region
Hypothesis Testing Solved Problems
Hypothesis testing Basic Intuition
What is Hypothesis Testing? Types and Methods
Hypothesis Testing Solved Examples(Questions and Solutions)

VIDEO

Hypothesis Testing of Normal Variables- examples
Hypothesis Testing based on Proportion(s)
Introduction to Hypothesis Testing Part 1
Hypothesis testing
What Is A Hypothesis?
Principles of Hypothesis Testing Part 2

COMMENTS

Hypothesis Testing
Present the findings in your results and discussion section. Though the specific details might vary, the procedure you will use when testing a hypothesis will always follow some version of these steps. Table of contents. Step 1: State your null and alternate hypothesis. Step 2: Collect data. Step 3: Perform a statistical test.
Hypothesis Testing
Statistical hypothesis testing is defined as: Assessing evidence provided by the data against the null claim (the claim which is to be assumed true unless enough evidence exists to reject it). Here is how the process of statistical hypothesis testing works: We have two claims about what is going on in the population.
S.3 Hypothesis Testing
hypothesis testing. S.3 Hypothesis Testing. In reviewing hypothesis tests, we start first with the general idea. Then, we keep returning to the basic procedures of hypothesis testing, each time adding a little more detail. The general idea of hypothesis testing involves: Making an initial assumption. Collecting evidence (data).
9.1: Introduction to Hypothesis Testing
In hypothesis testing, the goal is to see if there is sufficient statistical evidence to reject a presumed null hypothesis in favor of a conjectured alternative hypothesis.The null hypothesis is usually denoted $H_0$ while the alternative hypothesis is usually denoted $H_1$. An hypothesis test is a statistical decision; the conclusion will either be to reject the null hypothesis in favor ...
7.1: Basics of Hypothesis Testing
Test Statistic: z = x¯¯¯ −μo σ/ n−−√ z = x ¯ − μ o σ / n since it is calculated as part of the testing of the hypothesis. Definition 7.1.4 7.1. 4. p - value: probability that the test statistic will take on more extreme values than the observed test statistic, given that the null hypothesis is true.
Statistical Hypothesis Testing Overview
Hypothesis testing is a crucial procedure to perform when you want to make inferences about a population using a random sample. These inferences include estimating population properties such as the mean, differences between means, proportions, and the relationships between variables. This post provides an overview of statistical hypothesis testing.
Significance tests (hypothesis testing)
Unit test. Significance tests give us a formal process for using sample data to evaluate the likelihood of some claim about a population value. Learn how to conduct significance tests and calculate p-values to see how likely a sample result is to occur by random chance. You'll also see how we use p-values to make conclusions about hypotheses.
How Hypothesis Tests Work: Significance Levels (Alpha) and P values
And it gets to how these tests work. The hypothesis test that I'm illustrating here is the one-sample t-test. And this graph illustrates the sampling distribution for the t-test. T-tests use the t-distribution to determine the sampling distribution. For the t-distribution, you need to specify the degrees of freedom, which entirely defines the ...
Hypothesis Testing
A hypothesis test is a statistical inference method used to test the significance of a proposed (hypothesized) relation between population statistics (parameters) and their corresponding sample estimators. In other words, hypothesis tests are used to determine if there is enough evidence in a sample to prove a hypothesis true for the entire population. The test considers two hypotheses: the ...
A Complete Guide to Hypothesis Testing
Hypothesis testing is a method of statistical inference that considers the null hypothesis H ₀ vs. the alternative hypothesis H a, where we are typically looking to assess evidence against H ₀. Such a test is used to compare data sets against one another, or compare a data set against some external standard. The former being a two sample ...
Statistical hypothesis test
The above image shows a table with some of the most common test statistics and their corresponding tests or models.. A statistical hypothesis test is a method of statistical inference used to decide whether the data sufficiently support a particular hypothesis. A statistical hypothesis test typically involves a calculation of a test statistic.Then a decision is made, either by comparing the ...
Hypothesis Testing
It is the total probability of achieving a value so rare and even rarer. It is the area under the normal curve beyond the P-Value mark. This P-Value is calculated using the Z score we just found. Each Z-score has a corresponding P-Value. This can be found using any statistical software like R or even from the Z-Table.
Hypothesis Testing
Hypothesis testing is an indispensable tool in data science, allowing us to make data-driven decisions with confidence. By understanding its principles, conducting tests properly, and considering real-world applications, you can harness the power of hypothesis testing to unlock valuable insights from your data.
Understanding Hypothesis Testing
Hypothesis testing is a statistical method to determine whether a hypothesis that you have holds true or not. The hypothesis can be with respect to two variables within a dataset, an association between two groups or a situation. ... That's why it's always better to work with the p-value in hypothesis testing. Despite the above mentioned ...
Hypothesis Testing, P Values, Confidence Intervals, and Significance
Medical providers often rely on evidence-based medicine to guide decision-making in practice. Often a research hypothesis is tested with results provided, typically with p values, confidence intervals, or both. Additionally, statistical or research significance is estimated or determined by the investigators. Unfortunately, healthcare providers may have different comfort levels in interpreting ...
Introduction to Hypothesis Testing
A hypothesis test consists of five steps: 1. State the hypotheses. State the null and alternative hypotheses. These two hypotheses need to be mutually exclusive, so if one is true then the other must be false. 2. Determine a significance level to use for the hypothesis. Decide on a significance level.
How Does Statistical Hypothesis Testing Work?
Step 1: Define the Null Hypothesis. Statistical hypothesis testing starts with something called the Null Hypothesis. Null means none or no difference. A few ways to think of the Null Hypothesis are as the no-difference hypothesis or as the hypothesis that we want to nullify (disprove).
What is Hypothesis Testing in Statistics? Types and Examples
How Hypothesis Testing Works? An analyst performs hypothesis testing on a statistical sample to present evidence of the plausibility of the null hypothesis. Measurements and analyses are conducted on a random sample of the population to test a theory. Analysts use a random population sample to test two hypotheses: the null and alternative ...
Hypothesis Testing
Step 2: State the Alternate Hypothesis. The claim is that the students have above average IQ scores, so: H 1: μ > 100. The fact that we are looking for scores "greater than" a certain point means that this is a one-tailed test. Step 3: Draw a picture to help you visualize the problem. Step 4: State the alpha level.
Hypothesis Testing: 4 Steps and Example
Hypothesis testing is an act in statistics whereby an analyst tests an assumption regarding a population parameter. The methodology employed by the analyst depends on the nature of the data used ...
Hypothesis Testing: Definition, Uses, Limitations + Examples
How Hypothesis Testing Works. The basis of hypothesis testing is to examine and analyze the null hypothesis and alternative hypothesis to know which one is the most plausible assumption. Since both assumptions are mutually exclusive, only one can be true. In other words, the occurrence of a null hypothesis destroys the chances of the ...
Hypothesis Testing Explained (How I Wish It Was Explained to Me)
The curse of hypothesis testing is that we will never know if we are dealing with a True or a False Positive (Negative). All we can do is fill the confusion matrix with probabilities that are acceptable given our application. To be able to do that, we must start from a hypothesis. Step 1. Defining the hypothesis
What is Hypothesis Testing in Statistics? Types and Examples
How Hypothesis Testing Works? Hypothesis testing is a fundamental concept in statistics that aids analysts in making informed decisions based on sample data about a larger population. The process involves setting up two contrasting hypotheses, the null hypothesis and the alternative hypothesis, and then using statistical methods to determine ...
Understanding Hypothesis Testing
How does Hypothesis Testing work? Step 1: Define Null and Alternative Hypothesis. State the null hypothesis (), representing no effect, and the alternative hypothesis ( ), suggesting an effect or difference.We first identify the problem about which we want to make an assumption keeping in mind that our assumption should be contradictory to one another, assuming Normally distributed data.
The impact of fast spectrum graphite moderated systems on thermal
Understanding the nuclear data used in predictive modeling and simulation of advanced reactors is vital for their development, licensing, and deployment. In this paper, we use the Kairos gFHR and the X-Energy Xe-100 as demonstration examples to test the scientific hypothesis that the resonance physics of n+ 12 C allows for integral experiments with fast-neutron-spectra to be useful in helping ...

User Preferences

Keyboard Shortcuts

Example S.3.1

Example S.3.2

Errors in Hypothesis Testing Section

Making the Decision Section

In Practice

Margin Size

7.1: Basics of Hypothesis Testing

Unit 12: Significance tests (hypothesis testing)

The idea of significance tests

Error probabilities and power

Tests about a population proportion

Tests about a population mean

More significance testing videos

Hypothesis Testing

Definitions and Methodology

Hypothesis Testing – A Deep Dive into Hypothesis Testing, The Backbone of Statistical Inference

1. What is Hypothesis Testing?

2. Steps in Hypothesis Testing

2.1. Set up Hypotheses: Null and Alternative

2.2. Choose a Significance Level (α)

2.3. Calculate a test statistic and P-Value

2.4. Make a Decision

3. Example : Testing a new drug.

4. Example in python

5. Conclusion

More Articles

Machine Learning A-Z™: Hands-On Python & R In Data Science

StatPearls [Internet].

Affiliations

In this Page

Related information

Similar articles in PubMed

Recent Activity

Introduction to Hypothesis Testing

The Two Types of Statistical Hypotheses

Hypothesis Tests

The Two Types of Decision Errors

One-Tailed and Two-Tailed Tests

Types of Hypothesis Tests

Featured Posts

Leave a Reply Cancel reply

Join the Statology Community

How Does Statistical Hypothesis Testing Work?

Step 1: Define the Null Hypothesis

Step 2: Collect Data and Compute the Difference

Step 3: Compute the p-value

Step 4: Compare p-value to Alpha to Determine Statistical Significance

The Path to Statistical Significance

You might also be interested in

Tutorial Playlist

The Best Guide to Understand Bayes Theorem

A Complete Guide to Get a Grasp of Time Series Analysis

The Complete Guide to Understand Pearson's Correlation

Table of Contents

What Is Hypothesis Testing in Statistics?

Hypothesis Testing Formula

How Hypothesis Testing Works?

Your Dream Career is Just Around The Corner!

Null Hypothesis and Alternate Hypothesis

Become a Data Scientist with Hands-on Training!

Hypothesis Testing Calculation With Examples

Steps of Hypothesis Testing

Step 2: Gather Data

Step 3: Conduct a Statistical Test

Step 4: Determine Rejection Of Your Null Hypothesis

Step 5: Present Your Results

Types of Hypothesis Testing

Chi-Square

Hypothesis Testing and Confidence Intervals

Simple and Composite Hypothesis Testing

One-Tailed and Two-Tailed Hypothesis Testing

Become a Data Scientist With Real-World Experience

Right Tailed Hypothesis Testing

Left Tailed Hypothesis Testing

Type 1 and Type 2 Error

Level of Significance

Future-Proof Your AI/ML Career: Top Dos and Don'ts

Why is Hypothesis Testing Important in Research Methodology?