assignment problem in linear programming with example

• MapReduce Algorithm
• Linear Programming using Pyomo
• Networking and Professional Development for Machine Learning Careers in the USA
• Predicting Employee Churn in Python
• Airflow Operators

Solving Assignment Problem using Linear Programming in Python

Learn how to use Python PuLP to solve Assignment problems using Linear Programming.

In earlier articles, we have seen various applications of Linear programming such as transportation, transshipment problem, Cargo Loading problem, and shift-scheduling problem. Now In this tutorial, we will focus on another model that comes under the class of linear programming model known as the Assignment problem. Its objective function is similar to transportation problems. Here we minimize the objective function time or cost of manufacturing the products by allocating one job to one machine.

If we want to solve the maximization problem assignment problem then we subtract all the elements of the matrix from the highest element in the matrix or multiply the entire matrix by –1 and continue with the procedure. For solving the assignment problem, we use the Assignment technique or Hungarian method, or Flood’s technique.

The transportation problem is a special case of the linear programming model and the assignment problem is a special case of transportation problem, therefore it is also a special case of the linear programming problem.

In this tutorial, we are going to cover the following topics:

Assignment Problem

A problem that requires pairing two sets of items given a set of paired costs or profit in such a way that the total cost of the pairings is minimized or maximized. The assignment problem is a special case of linear programming.

For example, an operation manager needs to assign four jobs to four machines. The project manager needs to assign four projects to four staff members. Similarly, the marketing manager needs to assign the 4 salespersons to 4 territories. The manager’s goal is to minimize the total time or cost.

Problem Formulation

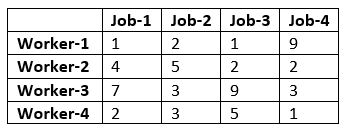
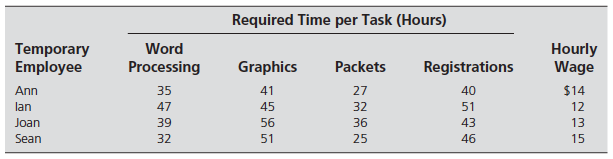
A manager has prepared a table that shows the cost of performing each of four jobs by each of four employees. The manager has stated his goal is to develop a set of job assignments that will minimize the total cost of getting all 4 jobs.  

Initialize LP Model

In this step, we will import all the classes and functions of pulp module and create a Minimization LP problem using LpProblem class.

Define Decision Variable

In this step, we will define the decision variables. In our problem, we have two variable lists: workers and jobs. Let’s create them using  LpVariable.dicts()  class.  LpVariable.dicts()  used with Python’s list comprehension.  LpVariable.dicts()  will take the following four values:

• First, prefix name of what this variable represents.
• Second is the list of all the variables.
• Third is the lower bound on this variable.
• Fourth variable is the upper bound.
• Fourth is essentially the type of data (discrete or continuous). The options for the fourth parameter are  LpContinuous  or  LpInteger .

Let’s first create a list route for the route between warehouse and project site and create the decision variables using LpVariable.dicts() the method.

Define Objective Function

In this step, we will define the minimum objective function by adding it to the LpProblem  object. lpSum(vector)is used here to define multiple linear expressions. It also used list comprehension to add multiple variables.

Define the Constraints

Here, we are adding two types of constraints: Each job can be assigned to only one employee constraint and Each employee can be assigned to only one job. We have added the 2 constraints defined in the problem by adding them to the LpProblem  object.

Solve Model

In this step, we will solve the LP problem by calling solve() method. We can print the final value by using the following for loop.

From the above results, we can infer that Worker-1 will be assigned to Job-1, Worker-2 will be assigned to job-3, Worker-3 will be assigned to Job-2, and Worker-4 will assign with job-4.

In this article, we have learned about Assignment problems, Problem Formulation, and implementation using the python PuLp library. We have solved the Assignment problem using a Linear programming problem in Python. Of course, this is just a simple case study, we can add more constraints to it and make it more complicated. You can also run other case studies on Cargo Loading problems , Staff scheduling problems . In upcoming articles, we will write more on different optimization problems such as transshipment problem, balanced diet problem. You can revise the basics of mathematical concepts in  this article  and learn about Linear Programming  in this article .

• Solving Blending Problem in Python using Gurobi
• Transshipment Problem in Python Using PuLP

You May Also Like

Text Analytics for Beginner using Python TextBlob

Spectral Clustering

Solving Balanced Diet Problem in Python using PuLP

All The Dots Are Connected / It's Not Rocket Science

Transportation and assignment problems with r.

In the previous post “ Linear Programming with R ” we examined the approach to solve general linear programming problems with “Rglpk” and “lpSolve” packages. Today, let’s explore “lpSolve” package in depth with two specific problems of linear programming: transportation and assignment.

1. Transportation problem

Code & Output:

The solution is shown as lptrans$solution and the total cost is 20500 as lptrans$objval.

2. Assignment problem

Similarly, the solution and the total cost are shown as lpassign$solution and lpassign$objval respectively.

This article was really helpful, but I am facing issue while solving unbalanced transportation problem when there is excess demand. Could you please guide me on what has to be done in this case.

Hello sir, this article was really helpful. But, I am facing issue while solving unbalanced transportation problem when there is excess demand, it gives solution as no feasible solution. works perfectly fine for balanced and excess supply problems. Could you please guide me on why this issue is occurring and a possible solution for the same. Thank you.

• Maths Notes Class 12
• NCERT Solutions Class 12
• RD Sharma Solutions Class 12
• Maths Formulas Class 12
• Maths Previous Year Paper Class 12
• Class 12 Syllabus
• Class 12 Revision Notes
• Physics Notes Class 12
• Chemistry Notes Class 12
• Biology Notes Class 12
• CBSE Class 12 Maths Notes: Chapter Wise Notes 2024

Chapter 1: Relations and Functions

• Types of Functions
• Composite functions - Relations and functions
• Invertible Functions
• Composition of Functions
• Inverse Functions
• Verifying Inverse Functions by Composition

Chapter 2: Inverse Trigonometric Functions

• Inverse Trigonometric Functions
• Graphs of Inverse Trigonometric Functions - Trigonometry | Class 12 Maths
• Properties of Inverse Trigonometric Functions
• Inverse Trigonometric Identities

Chapter 3: Matrices

• Types of Matrices
• Matrix Operations
• Matrix Addition
• Matrix Multiplication
• Transpose of a Matrix
• Symmetric and Skew Symmetric Matrices
• Elementary Operations on Matrices
• Inverse of a Matrix by Elementary Operations - Matrices | Class 12 Maths
• Invertible Matrix

Chapter 4: Determinants

• Determinant of a Matrix with Solved Examples
• Properties of Determinants
• Area of a Triangle using Determinants
• Minors and Cofactors
• Adjoint of a Matrix
• Applications of Matrices and Determinants

Chapter 5: Continuity and Differentiability

• Continuity and Discontinuity in Calculus - Class 12 CBSE
• Differentiability of a Function | Class 12 Maths
• Derivatives of Inverse Functions
• Derivatives of Implicit Functions - Continuity and Differentiability | Class 12 Maths
• Derivatives of Composite Functions
• Derivatives of Inverse Trigonometric Functions | Class 12 Maths
• Derivative of Exponential Functions
• Logarithmic Differentiation - Continuity and Differentiability
• Proofs for the derivatives of eˣ and ln(x) - Advanced differentiation
• Rolle's Theorem and Lagrange's Mean Value Theorem
• Derivative of Functions in Parametric Forms
• Second Order Derivatives in Continuity and Differentiability | Class 12 Maths
• Mean Value Theorem
• Algebra of Continuous Functions - Continuity and Differentiability | Class 12 Maths

Chapter 6: Applications of Derivatives

• Critical Points
• Derivatives as Rate of Change
• Increasing and Decreasing Functions
• Increasing and Decreasing Intervals
• Tangents and Normals
• Equation of Tangents and Normals
• Relative Minima and Maxima
• Absolute Minima and Maxima
• Concave Function
• Inflection Point
• Curve Sketching
• Approximations & Maxima and Minima - Application of Derivatives | Class 12 Maths
• Higher Order Derivatives

Chapter 7: Integrals

• Integration by Substitution
• Integration by Partial Fractions
• Integration by Parts
• Integration of Trigonometric Functions
• Functions Defined by Integrals
• Definite Integral
• Computing Definite Integrals
• Fundamental Theorem of Calculus
• Finding Derivative with Fundamental Theorem of Calculus
• Evaluating Definite Integrals
• Properties of Definite Integrals
• Definite Integrals of Piecewise Functions
• Improper Integrals
• Riemann Sum
• Riemann Sums in Summation Notation
• Trapezoidal Rule
• Definite Integral as the Limit of a Riemann Sum
• Antiderivatives
• Indefinite Integrals
• Particular Solutions to Differential Equations
• Integration by U-substitution
• Reverse Chain Rule
• Partial Fraction Expansion
• Trigonometric Substitution

Chapter 8: Applications of Integrals

• Area under Simple Curves
• Area Between Two Curves - Calculus
• Area between Polar Curves
• Area as Definite Integral

Chapter 9: Differential Equations

• Differential Equations
• Homogeneous Differential Equations
• Separable Differential Equations
• Exact Equations and Integrating Factors
• Implicit Differentiation
• Implicit differentiation - Advanced Examples
• Advanced Differentiation
• Disguised Derivatives - Advanced differentiation | Class 12 Maths
• Derivative of Inverse Trig Functions
• Logarithmic Differentiation

Chapter 10: Vector Algebra

• Vector Algebra
• Dot and Cross Products on Vectors
• How to Find the Angle Between Two Vectors?
• Section Formula - Vector Algebra

Chapter 11: Three-dimensional Geometry

• Direction Cosines and Direction Ratios
• Equation of a Line in 3D
• Angles Between two Lines in 3D Space
• Shortest Distance Between Two Lines in 3D Space | Class 12 Maths
• Points, Lines and Planes

Chapter 12: Linear Programming

Linear programming.

• Graphical Solution of Linear Programming Problems

Chapter 13: Probability

• Conditional Probability and Independence - Probability | Class 12 Maths
• Multiplication Theorem
• Dependent and Independent Events
• Bayes' Theorem
• Probability Distribution
• Binomial Distribution in Probability
• Binomial Mean and Standard Deviation - Probability | Class 12 Maths
• Bernoulli Trials and Binomial Distribution
• Discrete Random Variable
• Expected Value
• NCERT Solutions for Class 12 Maths -Chapter Wise with PDF
• RD Sharma Class 12 Solutions for Maths

Linear programming is a mathematical concept that is used to find the optimal solution of the linear function. This method uses simple assumptions for optimizing the given function. Linear Programming has a huge real-world application and it is used to solve various types of problems.

Linear programming is used in various industries such as shipping industries, manufacturing industries, transportation industries, telecommunications, and others.

Term “linear programming” consists of two words linear and programming, the word linear tells the relation between various types of variables of degree one used in a problem and the word programming tells us the step-by-step procedure to solve these problems.

In this article, we will learn about linear programming, its examples, formulas, and other concepts in detail.

Table of Content

What is Linear Programming? 

Components of linear programming, linear programming examples, linear programming problems, types of linear programming problems, linear programming formula, how to solve linear programming problems, linear programming methods, linear programming simplex method, linear programming graphical method, linear programming applications, importance of linear programming, up-to-date applications of linear programming, linear programming in operations research, simplex method.

Linear programming or Linear optimization is a technique that helps us to find the optimum solution for a given problem, an optimum solution is a solution that is the best possible outcome of a given particular problem.

In simple terms, it is the method to find out how to do something in the best possible way. With limited resources, you need to do the optimum utilization of resources and achieve the best possible result in a particular objective such as least cost, highest margin, or least time. 

The situation that requires a search for the best values of the variables subject to certain constraints is where we use linear programming problems. These situations cannot be handled by the usual calculus and numerical techniques.

Linear Programming Definition

Linear programming is the technique used for optimizing a particular scenario. Using linear programming provides us with the best possible outcome in a given situation. It uses all the available resources in a manner such that they produce the optimum result.

The basic components of a linear programming(LP) problem are:

• Decision Variables: Variables you want to determine to achieve the optimal solution.
• Objective Function: M athematical equation that represents the goal you want to achieve
• Constraints: Limitations or restrictions that your decision variables must follow.
• Non-Negativity Restrictions: In some real-world scenarios, decision variables cannot be negative

Additional Characteristics of Linear Programming

• Finiteness: The number of decision variables and constraints in an LP problem are finite.
• Linearity: The objective function and all constraints must be linear functions of the decision variables . It means the degree of variables should be one.

We can understand the situations in which Linear programming is applied with the help of the example discussed below,

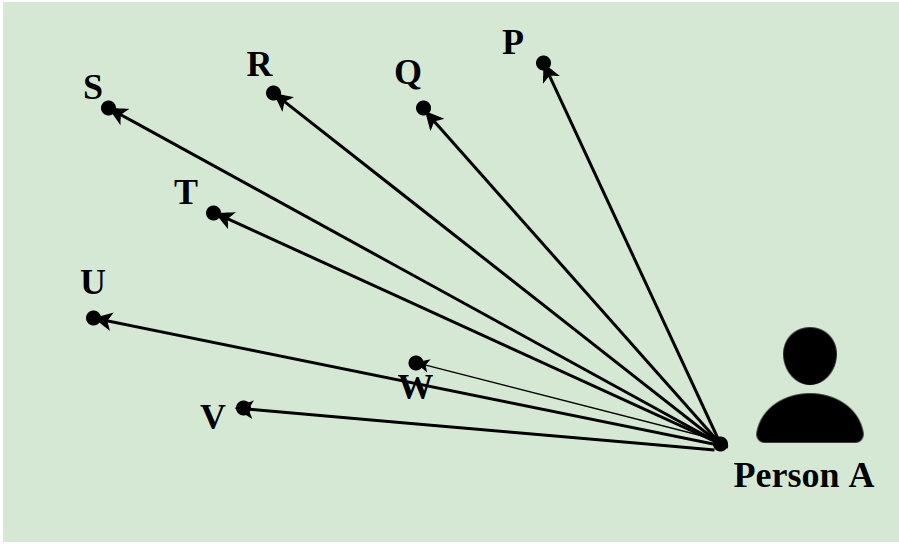
Suppose a delivery man has to deliver 8 packets in a day to the different locations of a city. He has to pick all the packets from A and has to deliver them to points P, Q, R, S, T, U, V, and W. The distance between them is indicated using the lines as shown in the image below. The shortest path followed by the delivery man is calculated using the concept of Linear Programming.

Linear Programming Problems (LPP) involve optimizing a linear function to find the optimal value solution for the function. The optimal value can be either the maximum value or the minimum value.

In LPP, the linear functions are called objective functions. An objective function can have multiple variables, which are subjected to conditions and have to satisfy the linear constraints .

There are many different linear programming problems(LPP) but we will deal with three major linear programming problems in this article.

Manufacturing Problems

Manufacturing problems are a problem that deals with the number of units that should be produced or sold to maximize profits when each product requires fixed manpower, machine hours, and raw materials.

Diet Problems

It is used to calculate the number of different kinds of constituents to be included in the diet to get the minimum cost, subject to the availability of food and their prices.

Transportation Problems

It is used to determine the transportation schedule to find the cheapest way of transporting a product from plants /factories situated at different locations to different markets.

A linear programming problem consists of,

• Decision variables
• Objective function
• Constraints
• Non-Negative restrictions

Decision variables are the variables x, and y, which decide the output of the linear programming problem and represent the final solution. 

The objective function , generally represented by Z, is the linear function that needs to be optimized according to the given condition to get the final solution. 

The restrictions imposed on decision variables that limit their values are called constraints.

Now, the general formula of a linear programming problem is,

Objective Function : Z = ax + by

Constraints: cx + dy ≥ e, px + qy ≤ r

Non-Negative restrictions: x ≥ 0, y ≥ 0

In the above condition x, and y are the decision variables.

Before solving the linear programming problems first we have to formulate the problems according to the standard parameters. The steps for solving linear programming problems are,

Step 1: Mark the decision variables in the problem. Step 2: Build the objective function of the problem and check if the function needs to be minimized or maximized. Step 3: Write down all the constraints of the linear problems. Step 4: Ensure non-negative restrictions of the decision variables. Step 5: Now solve the linear programming problem using any method generally we use either the simplex or graphical method.

We use various methods for solving linear programming problems. The two most common methods used are,

• Graphical Method

Let’s learn about these two methods in detail in this article,

One of the most common methods to solve the linear programming problem is the simplex method. In this method, we repeat a specific condition ‘n’ a number of times until an optimum solution is achieved.

The steps required to solve linear programming problems using the simplex method are,

Step 1: Formulate the linear programming problems based on the given constraints. Step 2: Convert all the given inequalities to equations or equalities of the linear programming problems by adding the slack variable to each inequality where ever required. Step 3: Construct the initial simplex table. By representing each constraint equation in a row and writing the objective function at the bottom row. The table so obtained is called the Simplex table. Step 4: Identify the greatest negative entry in the bottom row the column of the element with the highest negative entry is called the pivot column Step 5: Divide the entries of the right-most column with the entries of the respective pivot column, excluding the entries of the bottommost row. Now the row containing the least entry is called the pivot row. The pivot element is obtained by the intersection of the pivot row and the pivot column. Step 6: Using matrix operation and with the help of the pivot element make all the entries in the pivot column to be zero. Step 7: Check for the non-negative entries in the bottommost row if there are no negative entries in the bottom row, end the process else start the process again from step 4. Step 8: The final simplex table so obtained gives the solution to our problem.

Graphical Method is another method than the Simplex method which is used to solve linear programming problems. As the name suggests this method uses graphs to solve the given linear programming problems. This is the best method to solve linear programming problems and requires less effort than the simplex method. 

While using this method we plot all the inequalities that are subjected to constraints in the given linear programming problems. As soon as all the inequalities of the given LPP are plotted in the XY graph the common region of all the inequalities gives the optimum solution. All the corner points of the feasible region are calculated and the value of the objective function at all those points is calculated then comparing these values we get the optimum solution of the LPP.

Example: Find the maximal and minimal value of z = 6x + 9y when the constraint conditions are,

• 2x + 3y ≤ 12
• x and y ≥ 0

Step 1 : First convert the inequations into normal equations. Hence the equations will be 2x+3y = 0, x = 0, y = 0 and x + y = 5. Step 2 : Find the points at which 2x + 3y and x + y = 5 cut the x-axis and y-axis. To find the point of intersection of the x-axis put y = 0 in the respective equation and find the point. Similarly for y-axis intersection points put x = 0 in the respective equation. Step 3 : Draw the two lines cutting the x-axis and y-axis. We find that the two axes cut each other at (3,2). Step 4 : For x ≥ 0 and y ≥ 0, we find that both inequations are followed. Hence the region will include an area region enclosed by two axes and both lines including the origin. The plotted region is shown below in the figure. Step 5 : Find Z for each point and maxima and minima. Coordinates Z = 6x + 9y (0,5) Z = 45 (0,4) Z = 36 (5,0) Z = 30 (6,0) Z = 36 (3,2) Z = 36 Hence, we find that Z = 6x + 9y is maximum at (0,5) and minimum at (5,0).

Linear Programming has applications in various fields. It is used to find the minimum cost of a process when all the constraints of the problems are given. It is used to optimize the transportation cost of the vehicle, etc. Various applications of Linear Programming are

Engineering Industries

Engineering Industries use linear programming to solve design and manufacturing problems and to get the maximum output from a given condition.

Manufacturing Industries

Manufacturing Industries use linear programming to maximize the profit of the companies and to reduce the manufacturing cost.

Energy Industries

Energy companies use linear programming to optimize their production output.

Transportation Industries

Linear programming is also used in transportation industries to find the path to minimize the cost of transportation.

Linear Programming has huge importance in various industries it maximizes the output value while minimizing the input values according to various constraints.

LP is highly applicable when we have multiple conditions while solving a problem and we have to optimize the output of the problem i.e. either we have to find the minimum or the maximum value according to a given condition.

Linear Inequalities Algebraic Solution of Linear Inequalities

Problem 1: A company manufactures and sells two types of products and the cost of production of each unit a and b is rupees 200 and 150 respectively each unit of product yields a profit of 20 rupees and each unit of product b yields a profit of 15 rupees on selling. The company estimates the monthly demand of A and B to be at a maximum of the harvested unit in all the production budget for the month is set at rupees 50000. How many units should the company manufacture to earn maximum profit from its monthly sales from a and b?

Let x = number of units of type A y = Number of units of type B Maximize Z = 40x + 50y Subject to the constraints 3x + y ≤ 9 x + 2y ≤ 8 and x, y ≥ 0 Consider the equation, 3x + y = 9 x = 3 y = 0 and x + 2y = 8 x = 8 y = 0 Now, we can determine the maximum value of Z by evaluating the value of Z at the four points (vertices) is shown below Vertices Z = 40x + 50y (0, 0) Z = 40 × 0 + 50 × 0 = Rs. 0 (3, 0) Z = 40 × 3 + 50 × 0 = Rs. 120 (0, 4)  Z = 40 × 0 + 50 × 4 = Rs. 200 (2, 3) Z = 40 × 2 + 50 × 3 = Rs. 230 Maximum profit, Z = Rs. 230 ∴ Number of units of type A is 2 and the number of units of type B is 3.

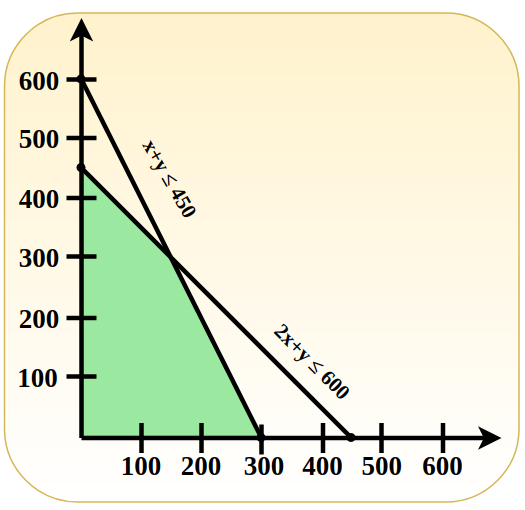
Problem 2: Maximize Z = 3x + 4y.

Subject to constraints , x + y ≤ 450, 2x + y ≤ 600 and x, y ≤ 0.

We have from the given Constraints (1) X + Y = 450 Putting x = 0, ⇒ 0 + y = 450 ⇒ y = 450 Putting y = 0, ⇒ x + 0 = 450 ⇒ x = 450 From, Constraints (2) 2x + y = 600 Putting x = 0, ⇒ 0 + y = 600 ⇒ y = 600 Putting  y = 0, ⇒ 2x + 0 = 600 ⇒ x = 300 Now, we have the points co-ordinate Z = 3x + 4y

Therefore, the optimal solution maximum Z = 1800 at co-ordinate x = 0 and y = 450. The graph is given below.

Linear programming, a powerful mathematical technique, is used to solve optimization problems in various industries. Here are some modern applications:

• Supply Chain Optimization : Linear programming helps companies minimize costs and maximize efficiency in their supply chains. It’s used for determining the most cost-effective transportation routes, warehouse operations, and inventory management strategies.
• Energy Management : In the energy sector, linear programming is utilized to optimize the mix of energy production methods. This includes balancing traditional energy sources with renewable ones to reduce costs and environmental impact while meeting demand.
• Telecommunications Network Design : Linear programming aids in designing efficient telecommunications networks. It helps in allocating bandwidth, designing network layouts, and optimizing the flow of data to ensure high-speed communication at lower costs.
• Financial Planning : Businesses and financial analysts use linear programming for portfolio optimization, risk management, and capital budgeting. It helps in making investment decisions that maximize returns while minimizing risk.
• Healthcare Logistics : In healthcare, linear programming is applied to optimize the allocation of resources, such as hospital beds, medical staff, and equipment. It’s crucial for improving patient care, reducing wait times, and managing costs effectively.
• Manufacturing Process Optimization : Linear programming is used to determine the optimal production levels for multiple products within a manufacturing facility, considering constraints like labor, materials, and machine availability.
• Agricultural Planning : Farmers and agricultural planners use linear programming to decide on crop selection, land use, and resource allocation to maximize yields and profits while conserving resources.
• Airline Crew Scheduling : Airlines employ linear programming to schedule crews efficiently, ensuring that flights are staffed in compliance with regulations and minimizing operational costs.

These applications demonstrate the versatility and power of linear programming in solving complex optimization problems across various sectors, showcasing its relevance in today’s data-driven world.

• Core Tool : Linear programming is a foundational tool in operations research for optimizing resources.
• Decision Making : Helps in making the best decisions regarding resource allocation, maximizing profits, or minimizing costs.
• Wide Applications : Used in various fields such as logistics, manufacturing, finance, and healthcare for solving complex problems.
• Modeling Real-World Problems : Transforms real-world problems into mathematical models to find the most efficient solutions.
• Optimization Algorithm : The Simplex Method is a powerful algorithm used in linear programming to find the optimal solution to linear inequalities.
• Step-by-Step Approach : It iteratively moves towards the best solution by navigating the edges of the feasible region defined by constraints.
• Efficiency : Known for its efficiency in solving large-scale linear programming problems.
• Versatility : Applicable in various domains like diet planning, network flows, production scheduling, and more, showcasing its versatility.

Linear Programming – FAQs

What is linear programming.

Linear programming is a mathematical concept which is used to optimize a given linear problem which has a variety of constraints. Using linear programming we the optimum output of the given problem

What are Linear Programming Problems?

Linear Programming Problems (LPP) are the problems which give the optimum solution to the given conditions.

What is Linear Programming Formula?

General Linear Programming Formulas are, Objective Function: Z = ax + by Constraints: px + qy ≤ r, sx + ty ≤ u Non-Negative Restrictions: x ≥ 0, y ≥ 0

What are the different types of Linear Programming?

Different types of linear programming methods are, Linear Programming by Simplex Method Linear Programming by R Method Linear Programming by Graphical Method

What are requirements of Linear Programming?

Various requirements of linear programming problems are, Linearity Objective Function Constraints Non-negativity

What are the advantages of Linear Programming?

Various advantages of linear programming are, It provides the optimal solution to any given linear problem. It is easy to use and always gives consistent results It helps to maximize profits and to reduce the input cost.

Please Login to comment...

• Math-Concepts
• Maths-Class-12
• Technical Scripter 2020
• Mathematics
• School Learning
• Technical Scripter
• 10 Best Todoist Alternatives in 2024 (Free)
• How to Get Spotify Premium Free Forever on iOS/Android
• Yahoo Acquires Instagram Co-Founders' AI News Platform Artifact
• OpenAI Introduces DALL-E Editor Interface
• Top 10 R Project Ideas for Beginners in 2024

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

Assignment Problem: Linear Programming

The assignment problem is a special type of transportation problem , where the objective is to minimize the cost or time of completing a number of jobs by a number of persons.

In other words, when the problem involves the allocation of n different facilities to n different tasks, it is often termed as an assignment problem.

The model's primary usefulness is for planning. The assignment problem also encompasses an important sub-class of so-called shortest- (or longest-) route models. The assignment model is useful in solving problems such as, assignment of machines to jobs, assignment of salesmen to sales territories, travelling salesman problem, etc.

It may be noted that with n facilities and n jobs, there are n! possible assignments. One way of finding an optimal assignment is to write all the n! possible arrangements, evaluate their total cost, and select the assignment with minimum cost. But, due to heavy computational burden this method is not suitable. This chapter concentrates on an efficient method for solving assignment problems that was developed by a Hungarian mathematician D.Konig.

"A mathematician is a device for turning coffee into theorems." -Paul Erdos

Formulation of an assignment problem

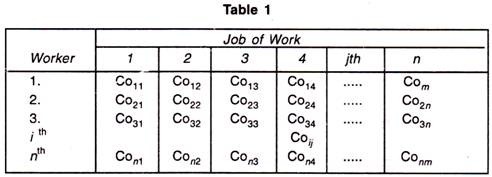
Suppose a company has n persons of different capacities available for performing each different job in the concern, and there are the same number of jobs of different types. One person can be given one and only one job. The objective of this assignment problem is to assign n persons to n jobs, so as to minimize the total assignment cost. The cost matrix for this problem is given below:

The structure of an assignment problem is identical to that of a transportation problem.

To formulate the assignment problem in mathematical programming terms , we define the activity variables as

for i = 1, 2, ..., n and j = 1, 2, ..., n

In the above table, c ij is the cost of performing jth job by ith worker.

Generalized Form of an Assignment Problem

The optimization model is

Minimize c 11 x 11 + c 12 x 12 + ------- + c nn x nn

subject to x i1 + x i2 +..........+ x in = 1          i = 1, 2,......., n x 1j + x 2j +..........+ x nj = 1          j = 1, 2,......., n

x ij = 0 or 1

In Σ Sigma notation

x ij = 0 or 1 for all i and j

An assignment problem can be solved by transportation methods, but due to high degree of degeneracy the usual computational techniques of a transportation problem become very inefficient. Therefore, a special method is available for solving such type of problems in a more efficient way.

Assumptions in Assignment Problem

• Number of jobs is equal to the number of machines or persons.
• Each man or machine is assigned only one job.
• Each man or machine is independently capable of handling any job to be done.
• Assigning criteria is clearly specified (minimizing cost or maximizing profit).

Share this article with your friends

Operations Research Simplified Back Next

Goal programming Linear programming Simplex Method Transportation Problem

Quantitative Techniques: Theory and Problems by P. C. Tulsian, Vishal Pandey

Get full access to Quantitative Techniques: Theory and Problems and 60K+ other titles, with a free 10-day trial of O'Reilly.

There are also live events, courses curated by job role, and more.

WHAT IS ASSIGNMENT PROBLEM

Assignment Problem is a special type of linear programming problem where the objective is to minimise the cost or time of completing a number of jobs by a number of persons.

The assignment problem in the general form can be stated as follows:

“Given n facilities, n jobs and the effectiveness of each facility for each job, the problem is to assign each facility to one and only one job in such a way that the measure of effectiveness is optimised (Maximised or Minimised).”

Several problems of management has a structure identical with the assignment problem.

Example I A manager has four persons (i.e. facilities) available for four separate jobs (i.e. jobs) and the cost of assigning (i.e. effectiveness) each job to each ...

Get Quantitative Techniques: Theory and Problems now with the O’Reilly learning platform.

O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

Don’t leave empty-handed

Get Mark Richards’s Software Architecture Patterns ebook to better understand how to design components—and how they should interact.

It’s yours, free.

Check it out now on O’Reilly

Dive in for free with a 10-day trial of the O’Reilly learning platform—then explore all the other resources our members count on to build skills and solve problems every day.

Your Article Library

Assignment problem in linear programming : introduction and assignment model.

ADVERTISEMENTS:

Assignment problem is a special type of linear programming problem which deals with the allocation of the various resources to the various activities on one to one basis. It does it in such a way that the cost or time involved in the process is minimum and profit or sale is maximum. Though there problems can be solved by simplex method or by transportation method but assignment model gives a simpler approach for these problems.

In a factory, a supervisor may have six workers available and six jobs to fire. He will have to take decision regarding which job should be given to which worker. Problem forms one to one basis. This is an assignment problem.

1. Assignment Model :

Suppose there are n facilitates and n jobs it is clear that in this case, there will be n assignments. Each facility or say worker can perform each job, one at a time. But there should be certain procedure by which assignment should be made so that the profit is maximized or the cost or time is minimized.

In the table, Co ij is defined as the cost when j th job is assigned to i th worker. It maybe noted here that this is a special case of transportation problem when the number of rows is equal to number of columns.

Mathematical Formulation:

Any basic feasible solution of an Assignment problem consists (2n – 1) variables of which the (n – 1) variables are zero, n is number of jobs or number of facilities. Due to this high degeneracy, if we solve the problem by usual transportation method, it will be a complex and time consuming work. Thus a separate technique is derived for it. Before going to the absolute method it is very important to formulate the problem.

Suppose x jj is a variable which is defined as

1 if the i th job is assigned to j th machine or facility

0 if the i th job is not assigned to j th machine or facility.

Now as the problem forms one to one basis or one job is to be assigned to one facility or machine.

The total assignment cost will be given by

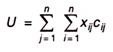
The above definition can be developed into mathematical model as follows:

Determine x ij > 0 (i, j = 1,2, 3…n) in order to

Subjected to constraints

and x ij is either zero or one.

Method to solve Problem (Hungarian Technique):

Consider the objective function of minimization type. Following steps are involved in solving this Assignment problem,

1. Locate the smallest cost element in each row of the given cost table starting with the first row. Now, this smallest element is subtracted form each element of that row. So, we will be getting at least one zero in each row of this new table.

2. Having constructed the table (as by step-1) take the columns of the table. Starting from first column locate the smallest cost element in each column. Now subtract this smallest element from each element of that column. Having performed the step 1 and step 2, we will be getting at least one zero in each column in the reduced cost table.

3. Now, the assignments are made for the reduced table in following manner.

(i) Rows are examined successively, until the row with exactly single (one) zero is found. Assignment is made to this single zero by putting square □ around it and in the corresponding column, all other zeros are crossed out (x) because these will not be used to make any other assignment in this column. Step is conducted for each row.

(ii) Step 3 (i) in now performed on the columns as follow:- columns are examined successively till a column with exactly one zero is found. Now , assignment is made to this single zero by putting the square around it and at the same time, all other zeros in the corresponding rows are crossed out (x) step is conducted for each column.

(iii) Step 3, (i) and 3 (ii) are repeated till all the zeros are either marked or crossed out. Now, if the number of marked zeros or the assignments made are equal to number of rows or columns, optimum solution has been achieved. There will be exactly single assignment in each or columns without any assignment. In this case, we will go to step 4.

4. At this stage, draw the minimum number of lines (horizontal and vertical) necessary to cover all zeros in the matrix obtained in step 3, Following procedure is adopted:

(iii) Now tick mark all the rows that are not already marked and that have assignment in the marked columns.

(iv) All the steps i.e. (4(i), 4(ii), 4(iii) are repeated until no more rows or columns can be marked.

(v) Now draw straight lines which pass through all the un marked rows and marked columns. It can also be noticed that in an n x n matrix, always less than ‘n’ lines will cover all the zeros if there is no solution among them.

5. In step 4, if the number of lines drawn are equal to n or the number of rows, then it is the optimum solution if not, then go to step 6.

6. Select the smallest element among all the uncovered elements. Now, this element is subtracted from all the uncovered elements and added to the element which lies at the intersection of two lines. This is the matrix for fresh assignments.

7. Repeat the procedure from step (3) until the number of assignments becomes equal to the number of rows or number of columns.

Related Articles:

• Two Phase Methods of Problem Solving in Linear Programming: First and Second Phase
• Linear Programming: Applications, Definitions and Problems

No comments yet.

Leave a reply click here to cancel reply..

You must be logged in to post a comment.

• Google OR-Tools
• Español – América Latina
• Português – Brasil
• Tiếng Việt

Solving an Assignment Problem

This section presents an example that shows how to solve an assignment problem using both the MIP solver and the CP-SAT solver.

In the example there are five workers (numbered 0-4) and four tasks (numbered 0-3). Note that there is one more worker than in the example in the Overview .

The costs of assigning workers to tasks are shown in the following table.

The problem is to assign each worker to at most one task, with no two workers performing the same task, while minimizing the total cost. Since there are more workers than tasks, one worker will not be assigned a task.

MIP solution

The following sections describe how to solve the problem using the MPSolver wrapper .

Import the libraries

The following code imports the required libraries.

Create the data

The following code creates the data for the problem.

The costs array corresponds to the table of costs for assigning workers to tasks, shown above.

Declare the MIP solver

The following code declares the MIP solver.

Create the variables

The following code creates binary integer variables for the problem.

Create the constraints

Create the objective function.

The following code creates the objective function for the problem.

The value of the objective function is the total cost over all variables that are assigned the value 1 by the solver.

Invoke the solver

The following code invokes the solver.

Print the solution

The following code prints the solution to the problem.

Here is the output of the program.

Complete programs

Here are the complete programs for the MIP solution.

CP SAT solution

The following sections describe how to solve the problem using the CP-SAT solver.

Declare the model

The following code declares the CP-SAT model.

The following code sets up the data for the problem.

The following code creates the constraints for the problem.

Here are the complete programs for the CP-SAT solution.

Except as otherwise noted, the content of this page is licensed under the Creative Commons Attribution 4.0 License , and code samples are licensed under the Apache 2.0 License . For details, see the Google Developers Site Policies . Java is a registered trademark of Oracle and/or its affiliates.

Last updated 2023-01-02 UTC.

Linear Programming Problems, Solutions & Applications [With Example]

 Data science encompasses numerous applications, with optimization being one of the most prominent. We’re always striving to optimize various aspects to achieve the best possible outcomes with the resources at our disposal. There are diverse problems within optimization, ranging from simple to highly complex.    

 Despite these, linear programming problems have a distinct place. In this article, I have delved into these issues and how professionals can tackle them effectively. Aspiring data scientists should familiarize themselves with linear programming problems they commonly encounter in real-world scenarios and mastering them can significantly enhance one’s analytical capabilities in data science.   

Suppose you’re a fruit seller who can either buy oranges or apples or a certain combination of them both. However you only have a budget of INR 5,000 and you can only store 30 bags of them. Now, you have to buy them in the way that yields you the highest profit.

Now one bag of oranges costs you INR 500 while a bag of apples costs you INR 750. You can make INR 100 from the sale of one bag of oranges and INR 200 from the sale of one bag of apples. 

This problem has various possibilities. You might choose to only buy oranges but then, you’d only have 10 bags in your storage and your profit would be INR 1000. Similarly, you might choose to only buy apples and make INR 1500 as profit. You can also buy a combination of the two. 

Such problems are called linear programming problems and we’ll discuss them in detail. Let’s get started:

What is Linear Programming?

Linear programming is a method of depicting complex relationships by using linear functions. Our aim with linear programming is to find the most suitable solutions for those functions. The real relationship between two points can be highly complex, but we can use linear programming to depict them with simplicity. Linear programming finds applications in many industries. 

Check out our data science online courses to upskill yourself

Basics of Linear Programming

Here are some fundamental terms of linear programming:

The limitations (or restrictions) of your decision variables are called constraints. Most of the time constraints are the limitations you have on your resources for solving a problem. 

Decision Variable

These variables define your output. Your result depends on these variables, that’s why we call them ‘decision variables’. 

Non-negativity Restriction

The decision variables of a linear programming problem can only have non-negative value. It means the values for your decision variables can be equal to or greater than zero only. 

Objective Function

The objective function is the objective of making your decision. In simple terms it is the final result of your linear programming problem. For example, when you’re finding the maximum profit you can make with a given set of resources, the maximum profit is the objective function.

Formulating Linear Programming Problems

You should know how to formulate a linear programming to apply it in real-life. Suppose you are a manufacturer of toys and you only produce two toys: A and B. Roughly speaking, your toys require two resources X and Y to manufacture. Here are the requirements of your toys:

• One unit of toy A requires you one unit of resource X and three units of resource Y
• One unit of toy B requires one unit of resource X and two units of resource Y

You have five units of resource X and 12 units of resource Y. Your profit margins on the sale of these toys are:

• INR 6 on each sold unit of toy A
• INR 5 on each sold unit of toy B

How many units of each toy would you produce to get the maximum profit?

The Solution

Let’s represent our linear programming problem in an equation:

Z = 6a + 5b

Here, z stands for the total profit, a stands for the total number of toy A units and b stands for total number to B units. Our aim is to maximize the value of Z (the profit). 

Now, your company would want to produce as many units of these toys as possible, but you have limited resources. The limitations on our resources are the constraints of this problem. We only have a total of

Now every unit of toy A and B requires 3 and 2 units of resource Y respectively. And we only have a total of 12 units of resource Y so mathematically, it would look like this:

Remember that the values for the units of toy A can be in integers only. This means we also have the constraints of a->0 and b<-0. 

So, now you have a proper linear programming problem. You can formulate other linear programming problems by following this example. While this example was quite simple, LP problems can become highly complicated. 

Read: Linear Programming Project Ideas & Topics

upGrad’s Exclusive Data Science Webinar for you –

ODE Thought Leadership Presentation

Explore our Popular Data Science Online Courses

Types of Linear Programming Problems        

• Maximization Problems: These involve maximizing an objective function subject to linear constraints. The goal is to find the optimal values of decision variables that maximize the objective function.   
• Minimization Problems: Unlike maximization problems, minimization problems seek to minimize an objective function while satisfying linear constraints. The objective is to identify the optimal values of decision variables that minimize the objective function.   
• Feasibility Problems: Feasibility problems focus on determining whether a feasible solution exists within the given constraints. The aim is to ascertain if any possible solutions satisfy all constraints without optimizing an objective function.   
• Unboundedness Problems: Arise when the feasible region is unbounded, leading to infinitely many solutions. The objective function can either be maximized or minimized without reaching an optimal solution due to the unbounded nature of the feasible region.     

Steps of Formulating Linear Programming Problems

To formulate a linear programming problem, follow these steps:

• Find the decision variables
• Find the objective function
• Identify the constraints
• Remember the non-negativity restriction

If a problem meets the above criteria, it is a linear programming problem. It’s best practice to keep this criterion in mind when you’re working on identifying the type of the problem. 

Solving Linear Programming Problems with R

If you’re using R, solving linear programming problems becomes much simpler. That’s because R has the lpsolve package which comes with various functions specifically designed for solving such problems. It’s highly probable that you’ll be using R very frequently to solve LP problems as a data scientist. That’s why we’ve shared two distinct examples to help you understand its implementation better:

Let’s start with a basic problem. An organization has two products with selling prices of INR 25 and INR 20 and are called product A and B respectively. Every day, they have 1800 units of resources to produce these products. Product A requires 20 resources units and B requires 12 resources units. The production time for both of these products is four minutes and the organization gets a total of eight working hours every day. The problem is, what should be the production quantity for each of these products to maximize the company’s profits?

We’ll start solving this problem by defining its objective function:

max(Sales) = max( 25 y 1 + 20 y 2 )

Here, 25 and 20 are the prices of product A and B respectively, y1 is the total units of product A produced and y2 is the total units of product B produced. Our decision variables are y1 and y2. 

Top Data Science Skills to Learn to upskill

We’ll now set the constraints for our problem:

Resource constraint:

20 y 1 + 12 y 2 1800

Time constraint:

4 y 1 + 4 y 2 8*60

We aim to find the correct number of products we have to manufacture to get the maximum profit. 

Using R to Solve the Problem:

We’ll use lpsolve to solve this LP problem and start with setting the objective function:

> require(lpSolve)

Loading required package: lpSolve

> objective.in  <- c(25, 20)

> objective.in

Then we’ll build a matrix for the constraints:

> const <- matrix(c(20,  12, 4, 4), nrow=2, byrow=TRUE)

     [,1] [,2]

[1,]   20 12

[2,]    4 4

> time_constraints <- (8*60)

> resource_constraints <- 1800

> time_constraints

> resource_constraints

Let’s now create the already-defined equations:

> rhs <- c(resource_constraints, time_constraints)

[1] 1800  480

> direction  <- c(“<=”, “<=”)

> direction

[1] “<=” “<=”

Once all the necessary information is added, we can start finding the optimal answer. The syntax for our package is:

lp( direction, objective, const.mat, const.dir, const.rhs )

> optimum <-  lp(direction=”max”,  objective.in, const, direction,  rhs)

> optimum

Success: the objective function is 2625

> summary(optimum)

                 Length Class Mode     

direction        1 -none- numeric  

x.count          1 -none- numeric  

objective        2 -none- numeric  

const.count      1 -none- numeric  

constraints      8 -none- numeric  

int.count        1 -none- numeric  

int.vec          1 -none- numeric  

bin.count        1 -none- numeric  

binary.vec       1 -none- numeric  

num.bin.solns    1 -none- numeric  

objval           1 -none- numeric  

solution         2 -none- numeric  

presolve         1 -none- numeric  

compute.sens     1 -none- numeric  

sens.coef.from   1 -none- numeric  

sens.coef.to     1 -none- numeric  

duals            1 -none- numeric  

duals.from       1 -none- numeric  

duals.to         1 -none- numeric  

scale            1 -none- numeric  

use.dense        1 -none- numeric  

dense.col        1 -none- numeric  

dense.val        1 -none- numeric  

dense.const.nrow 1      -none- numeric 

dense.ctr        1 -none- numeric  

use.rw           1 -none- numeric  

tmp              1 -none- character

status           1 -none- numeric

After running the code above, you can get the desired solutions for our problem.

The optimum values for y1 and y2:

Remember that y1 and y2 were the units of product A and product B we had to produce:

> optimum$solution

The optimum sales figure:

The maximum profit we can generate with the obtained values of y1 and y2 is:

> optimum$objval

Also Read:  Linear Algebra For Machine Learning

Read our popular Data Science Articles

Uses of linear programming.

As we mentioned before, linear programming finds applications in many industries. Here are some areas where we use it:

• With the rising popularity of delivery services, linear programming has become one of the most favoured methods of finding the optimum routes. When you take an Ola or Uber, the software would use linear programming to find the best route. Delivery companies like Amazon and FedEx also use it to determine the best routes for their delivery men. They focus on reducing the delivery time and cost. 
• Machine learning’s supervised learning works on the fundamental concepts of linear programming. In supervised learning, you have to find the optimal mathematical model to predict the output according to the provided input data.
• The retail sector uses linear programming for optimizing shelf space. With so many brands and products available, determining where to place them in the store is a very rigorous task. The placement of a product in the store can affect its sales greatly. Major retail chains such as Big Bazaar, Reliance, Walmart, etc. use linear programming for determining product placement. They have to keep the consumers’ interest in mind while ensuring the best product placement to yield maximum profit. 
• Companies use linear programming to improve their supply chains. The efficiency of a supply chain depends on many factors such as the chosen routes, timings, etc. By using linear programming, they can find the best routes, timings, and other allocations of resources to optimize their efficiency. 

Learn More about Linear Programming and Data Science

Linear programming is one of the most vital concepts of data science. It is also a fundamental topic that you should know about to become a proficient data scientist. As we discussed, there are many applications for this concept and you can find its use cases in your daily life. 

You can learn more about data science and its related concepts, by going to our blog. We have many valuable resources to help you learn more. Here are some for your further reading:

• Top Reasons to become a Data Scientist
• The Algorithms Every Data Scientist Should Know
• How to Become a Data Scientist

On the other hand, you can get a data science course to learn from industry experts. You’ll get to learn interactively through videos, quizzes, and projects. Taking a course will help you learn the necessary skills to become a professional data scientist. Check out IIIT-B & upGrad’s  PG Diploma in Data Science  which is created for working professionals and offers 10+ case studies & projects, practical hands-on workshops, mentorship with industry experts, 1-on-1 with industry mentors, 400+ hours of learning and job assistance with top firms.

Conclusion:   

In summary, linear programming problems systematically optimize resources and achieve desired outcomes across various industries. Understanding the basics and steps in formulating these problems is crucial for mid-career professionals seeking to enhance their analytical skills and decision-making abilities. Through real-world examples and applications, we’ve explored the versatility and effectiveness of linear programming in solving complex optimization challenges.   

 Aspiring data scientists and professionals can benefit from delving deeper into linear programming problems, leveraging tools like R to implement solutions and drive impactful results in their respective fields. Continuously expanding our knowledge in linear programming and data science opens doors to new opportunities and advancements in our careers.  

Rohit Sharma

Something went wrong

Our Popular Data Science Course

Data Science Skills to Master

• Data Analysis Courses
• Inferential Statistics Courses
• Hypothesis Testing Courses
• Logistic Regression Courses
• Linear Regression Courses
• Linear Algebra for Analysis Courses

Our Trending Data Science Courses

• Data Science for Managers from IIM Kozhikode - Duration 8 Months
• Executive PG Program in Data Science from IIIT-B - Duration 12 Months
• Master of Science in Data Science from LJMU - Duration 18 Months
• Executive Post Graduate Program in Data Science and Machine LEarning - Duration 12 Months
• Master of Science in Data Science from University of Arizona - Duration 24 Months

Frequently Asked Questions (FAQs)

Optimization is a way of life for many people. Everything utilizes optimization, from how you spend your time to how you solve supply chain issues for your organization. It's a very fascinating and relevant issue in data science. Linear Programming is one of the most effective methods for doing optimization. It aids in the solution of specific extremely complicated optimization problems by making more easy assumptions. As an analyst, you will undoubtedly come across applications and situations that need Linear Programming. Machine Learning takes advantage of optimizations as well. Supervised learning builds on the foundations of Linear Programming. A system is trained to fit a mathematical model of a function using labeled input data to predict values from unknown test data.

Linear programming is a necessary skill for anyone interested in machine learning/data science. Everything in machine learning and deep learning is about optimization. Convex or nonconvex optimization is used in ML algorithms. The key difference between the two categories is that there can only be one optimal solution in convex optimization, which is globally optimal, or you can prove that there is no feasible solution to the problem. In contrast, in nonconvex optimization, there can be multiple locally optimal points. It can take a long time to determine whether the problem has no solution or if the answer is global.

Professionals can use linear programming in a wide range of disciplines of study. It is often used in mathematics and to a lesser extent in business, economics, and some engineering difficulties. Transportation, energy, telecommunications, and manufacturing are among the industries that employ linear programming methods. It is beneficial in simulating a wide range of problems in planning, routing, scheduling, assignment, and design. Certain specific instances of linear programming, such as network flow issues and multicommodity flow problems, are deemed significant enough to warrant extensive study on specialized methods to solve them. To stabilize YouTube videos, Google employs linear programming.

Related Programs View All

View Program

Executive PG Program

Complimentary Python Bootcamp

Master's Degree

Live Case Studies and Projects

8+ Case Studies & Assignments

Certification

Live Sessions by Industry Experts

ChatGPT Powered Interview Prep

Top US University

120+ years Rich Legacy

Based in the Silicon Valley

Case based pedagogy

High Impact Online Learning

Mentorship & Career Assistance

AACSB accredited

Placement Assistance

Earn upto 8LPA

Interview Opportunity

8-8.5 Months

Exclusive Job Portal

Learn Generative AI Developement

Explore Free Courses

Learn more about the education system, top universities, entrance tests, course information, and employment opportunities in Canada through this course.

Advance your career in the field of marketing with Industry relevant free courses

Build your foundation in one of the hottest industry of the 21st century

Master industry-relevant skills that are required to become a leader and drive organizational success

Build essential technical skills to move forward in your career in these evolving times

Get insights from industry leaders and career counselors and learn how to stay ahead in your career

Kickstart your career in law by building a solid foundation with these relevant free courses.

Stay ahead of the curve and upskill yourself on Generative AI and ChatGPT

Build your confidence by learning essential soft skills to help you become an Industry ready professional.

Learn more about the education system, top universities, entrance tests, course information, and employment opportunities in USA through this course.

Suggested Blogs

by Rohit Sharma

05 Mar 2024

by Harish K

28 Feb 2024

by Rohan Vats

27 Feb 2024

19 Feb 2024

Quadratic assignment problem

Author: Thomas Kueny, Eric Miller, Natasha Rice, Joseph Szczerba, David Wittmann (SysEn 5800 Fall 2020)

• 1 Introduction
• 2.1 Koopmans-Beckman Mathematical Formulation
• 2.2.1 Parameters
• 2.3.1 Optimization Problem
• 2.4 Computational Complexity
• 2.5 Algorithmic Discussions
• 2.6 Branch and Bound Procedures
• 2.7 Linearizations
• 3.1 QAP with 3 Facilities
• 4.1 Inter-plant Transportation Problem
• 4.2 The Backboard Wiring Problem
• 4.3 Hospital Layout
• 4.4 Exam Scheduling System
• 5 Conclusion
• 6 References

Introduction

The Quadratic Assignment Problem (QAP), discovered by Koopmans and Beckmann in 1957 [1] , is a mathematical optimization module created to describe the location of invisible economic activities. An NP-Complete problem, this model can be applied to many other optimization problems outside of the field of economics. It has been used to optimize backboards, inter-plant transportation, hospital transportation, exam scheduling, along with many other applications not described within this page.

Theory, Methodology, and/or Algorithmic Discussions

Koopmans-beckman mathematical formulation.

Economists Koopmans and Beckman began their investigation of the QAP to ascertain the optimal method of locating important economic resources in a given area. The Koopmans-Beckman formulation of the QAP aims to achieve the objective of assigning facilities to locations in order to minimize the overall cost. Below is the Koopmans-Beckman formulation of the QAP as described by neos-guide.org.

Quadratic Assignment Problem Formulation

Inner Product

Note: The true objective cost function only requires summing entries above the diagonal in the matrix comprised of elements

Since this matrix is symmetric with zeroes on the diagonal, dividing by 2 removes the double count of each element to give the correct cost value. See the Numerical Example section for an example of this note.

Optimization Problem

With all of this information, the QAP can be summarized as:

Computational Complexity

QAP belongs to the classification of problems known as NP-complete, thus being a computationally complex problem. QAP’s NP-completeness was proven by Sahni and Gonzalez in 1976, who states that of all combinatorial optimization problems, QAP is the “hardest of the hard”. [2]

Algorithmic Discussions

While an algorithm that can solve QAP in polynomial time is unlikely to exist, there are three primary methods for acquiring the optimal solution to a QAP problem:

• Dynamic Program
• Cutting Plane

Branch and Bound Procedures

The third method has been proven to be the most effective in solving QAP, although when n > 15, QAP begins to become virtually unsolvable.

The Branch and Bound method was first proposed by Ailsa Land and Alison Doig in 1960 and is the most commonly used tool for solving NP-hard optimization problems.

A branch-and-bound algorithm consists of a systematic enumeration of candidate solutions by means of state space search: the set of candidate solutions is thought of as forming a rooted tree with the full set at the root. The algorithm explores branches of this tree, which represent subsets of the solution set. Before one lists all of the candidate solutions of a branch, the branch is checked against upper and lower estimated bounds on the optimal solution, and the branch is eliminated if it cannot produce a better solution than the best one found so far by the algorithm.

Linearizations

The first attempts to solve the QAP eliminated the quadratic term in the objective function of

in order to transform the problem into a (mixed) 0-1 linear program. The objective function is usually linearized by introducing new variables and new linear (and binary) constraints. Then existing methods for (mixed) linear integer programming (MILP) can be applied. The very large number of new variables and constraints, however, usually poses an obstacle for efficiently solving the resulting linear integer programs. MILP formulations provide LP relaxations of the problem which can be used to compute lower bounds.

Numerical Example

Qap with 3 facilities.

Applications

Inter-plant transportation problem.

The QAP was first introduced by Koopmans and Beckmann to address how economic decisions could be made to optimize the transportation costs of goods between both manufacturing plants and locations. [1] Factoring in the location of each of the manufacturing plants as well as the volume of goods between locations to maximize revenue is what distinguishes this from other linear programming assignment problems like the Knapsack Problem.

The Backboard Wiring Problem

As the QAP is focused on minimizing the cost of traveling from one location to another, it is an ideal approach to determining the placement of components in many modern electronics. Leon Steinberg proposed a QAP solution to optimize the layout of elements on a blackboard by minimizing the total amount of wiring required. [4]

When defining the problem Steinberg states that we have a set of n elements

as well as a set of r points

In his paper he derives the below formula:

In his paper Steinberg a backboard with a 9 by 4 array, allowing for 36 potential positions for the 34 components that needed to be placed on the backboard. For the calculation, he selected a random initial placement of s1 and chose a random family of 25 unconnected sets.

The initial placement of components is shown below:

After the initial placement of elements, it took an additional 35 iterations to get us to our final optimized backboard layout. Leading to a total of 59 iterations and a final wire length of 4,969.440.

Hospital Layout

Building new hospitals was a common event in 1977 when Alealid N Elshafei wrote his paper on "Hospital Layouts as a Quadratic Assignment Problem". [5] With the high initial cost to construct the hospital and to staff it, it is important to ensure that it is operating as efficiently as possible. Elshafei's paper was commissioned to create an optimization formula to locate clinics within a building in such a way that minimizes the total distance that a patient travels within the hospital throughout the year. When doing a study of a major hospital in Cairo he determined that the Outpatient ward was acting as a bottleneck in the hospital and focused his efforts on optimizing the 17 departments there.

Elshafei identified the following QAP to determine where clinics should be placed:

For the Cairo hospital with 17 clinics, and one receiving and recording room bringing us to a total of 18 facilities. By running the above optimization Elshafei was able to get the total distance per year down to 11,281,887 from a distance of 13,973,298 based on the original hospital layout.

Exam Scheduling System

The scheduling system uses matrices for Exams, Time Slots, and Rooms with the goal of reducing the rate of schedule conflicts. To accomplish this goal, the “examination with the highest cross faculty student is been prioritized in the schedule after which the examination with the highest number of cross-program is considered and finally with the highest number of repeating student, at each stage group with the highest number of student are prioritized.” [6]

• ↑ 1.0 1.1 1.2 Koopmans, T., & Beckmann, M. (1957). Assignment Problems and the Location of Economic Activities. Econometrica, 25(1), 53-76. doi:10.2307/1907742
• ↑ 2.0 2.1 Quadratic Assignment Problem. (2020). Retrieved December 14, 2020, from https://neos-guide.org/content/quadratic-assignment-problem
• ↑ 3.0 3.1 3.2 Burkard, R. E., Çela, E., Pardalos, P. M., & Pitsoulis, L. S. (2013). The Quadratic Assignment Problem. https://www.opt.math.tugraz.at/~cela/papers/qap_bericht.pdf .
• ↑ 4.0 4.1 Leon Steinberg. The Backboard Wiring Problem: A Placement Algorithm. SIAM Review . 1961;3(1):37.
• ↑ 5.0 5.1 Alwalid N. Elshafei. Hospital Layout as a Quadratic Assignment Problem. Operational Research Quarterly (1970-1977) . 1977;28(1):167. doi:10.2307/300878
• ↑ 6.0 6.1 Muktar, D., & Ahmad, Z.M. (2014). Examination Scheduling System Based On Quadratic Assignment.

Navigation menu

Problems Solvable Using Linear Programming

• First Online: 13 April 2021

Cite this chapter

• Josef Kallrath 5  

Part of the book series: International Series in Operations Research & Management Science ((ISOR,volume 307))

1091 Accesses

In this chapter a number of standard LP problems will be formulated. These are problems that occur frequently and may provide ways of formulating parts of the users’ problems, to which other conditions, e.g., integrality conditions or nonlinear terms, will be added, and secondly they will give an indication as to the ease or difficulty of solving a particular problem when it becomes apparent that it is similar to some standard problem. For some of the problem types a case study is also provided and a model relating to the case is supplied with the software included with the book.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

• Available as PDF
• Read on any device
• Instant download
• Own it forever
• Available as EPUB and PDF
• Compact, lightweight edition
• Dispatched in 3 to 5 business days
• Free shipping worldwide - see info
• Durable hardcover edition

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

See Sect. 4.5 for further details.

Appa, G.M.: The transportation problem and its variants. Oper. Res. Quart. 24 , 79–99 (1973)

Article   Google Scholar  

Baston, V.J.D., Rahmouni, M.K., Williams, H.P.: The practical conversion of linear programmes to network flow models. Eur. J. Oper. Res. 50 , 325–334 (1991)

Bazaraa, M.S., Jarvis, J.J., Sherali, D.: Linear Programming and Network Flows, 4th edn. Wiley, New York (2010)

Google Scholar  

Bixby, R.E., Cunningham, W.H.: Converting linear programs to network problems. Math. Oper. Res. 5 , 321–357 (1980)

Blais, J.Y., Lamont, J., Rousseau, J.M.: The HASTUS vehicle and manpower scheduling system at Societeè de Transport de la Communantè Urbaine de Montrèal. Interfaces 20 (1), 26–42 (1990)

Bradley, G., Brown, G.H., Graves, G.W.: Design and implementation of large-scale primal transshipment algorithms. Manage. Sci. 24 (1), 1–34 (1977)

Burkhard, R.E., Derigs, U.: Assignment and Matching Problems: Solution Methods with Fortran-Programs. Springer, Berlin (1980)

Book   Google Scholar  

Carpaneto, G., Martello, S., Toth, P.: Algorithms and codes for the assignment problem. Ann. Oper. Res. 13 , 193–223 (1988)

Charnes, A., Cooper, W.W.: The stepping-stone method of explaining linear programming calculations in transportation problems. Manage. Sci. 1 , 49–69 (1954)

Dantzig, G.B.: Application of the simplex method to a transportation problem. In: T.C. Koopmans (ed.) Activity Analysis of Production and Allocation, pp. 359–373. Wiley, New York (1951)

Dennis, J.B.: A high-speed computer technique for the transportation problem. J. Assoc. Comput. Mach. 5 , 132–153 (1958)

Dyson, R.G., Gregory, A.S.: The cutting stock problem in the glass industry. Oper. Res. Quart. 25 , 41–54 (1974)

Farley, A.A.: Planning the cutting of photographic color paper rolls for Kodak (Australasia) Pty. Ltd. Interfaces 21 (1), 96–106 (1991)

Gilmore, P.C., Gomory, R.E.: A linear programming approach to the cutting stock problem. Oper. Res. 9 , 849–859 (1961)

Glover, F., Klingman, D., Philips, N.: Netform modeling and applications. Interfaces 20 (4), 7–27 (1990)

Hitchcock, F.L.: The distribution of a product from several sources to numerous localities. J. Math. Phys. 20 , 224–230 (1941)

Hung, M.S., Rom, W.O.: Solving the assignment problem by relaxation. Oper. Res. 28 , 969–982 (1980)

Jonker, R., Volgenat, T.: Improving the Hungarian assignment algorithm. Oper. Res. Lett. 5 , 171–175 (1986)

Jungnickel, D.: Graphs, Networks and Algorithms, 4th edn. Springer, Berlin (2012)

Kallrath, J., Rebennack, S., Kallrath, J., Kusche, R.: Solving real-world cutting stock-problems in the paper industry: mathematical approaches, experience and challenges. Eur. J. Oper. Res. 238 , 374–389 (2014)

Kantorovich, L.V.: Mathematical methods in the organization and planning of production. Transl. Manage. Sci. 6 , 366–422 (1960 (1939))

Koopmans, T.C.: Optimum utilization of the transport systems. Econometr. Suppl. 17 , 136–145 (1947)

Kuhn, H.W.: The Hungarian method for the assignment problem. Naval Res. Logist. Quart. 2 , 83–97 (1955)

Letchford, A.: Allocation of school bus contracts using integer programming. J. Oper. Res. Soc. 47 , 369–372 (1996)

Mulvey, J.M.: Testing of a large-scale network optimization program. Math. Program. 15 , 291–315 (1978)

Nemhauser, G.L., Wolsey, L.A.: Integer and Combinatorial Optimization. Wiley, New York (1988)

Reinfeld, N.V., Vogel, W.R.: Mathematical Programming. Prentice-Hall International, Englewood Cliffs, NJ (1958)

Vajda, S.: Mathematical Programming. Adison-Wesley, Reading, MA (1961)

Williams, H.P., Redwood, A.C.: A structured linear programming model in the food industry. Oper. Res. Quart. 25 , 517–528 (1974)

Wilson, E.J.G., Willis, R.G.: Scheduling of telephone betting operators - a case study. J. Oper. Res. Soc. 33 , 991–998 (1983)

Wright, M.M.: Speeding up the Hungarian algorithm. Comput. Oper. Res. 17 , 95–96 (1990)

Download references

Author information

Authors and affiliations.

Department of Astronomy, University of Florida, Gainesville, FL, USA

Josef Kallrath

You can also search for this author in PubMed   Google Scholar

4.1 Electronic Supplementary Material

Chapter 4(zip 15kb), rights and permissions.

Reprints and permissions

Copyright information

© 2021 Springer Nature Switzerland AG

About this chapter

Kallrath, J. (2021). Problems Solvable Using Linear Programming. In: Business Optimization Using Mathematical Programming. International Series in Operations Research & Management Science, vol 307. Springer, Cham. https://doi.org/10.1007/978-3-030-73237-0_4

Download citation

DOI : https://doi.org/10.1007/978-3-030-73237-0_4

Published : 13 April 2021

Publisher Name : Springer, Cham

Print ISBN : 978-3-030-73236-3

Online ISBN : 978-3-030-73237-0

eBook Packages : Business and Management Business and Management (R0)

Share this chapter

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Publish with us

Policies and ethics

• Find a journal
• Track your research

Free Mathematics Tutorials

Linear Programming Problems and Questions

How are linear programming problems and word problems solved? Below are links to many examples on how to formulate and solve optimization problems in linear programming.

• Solve Inequalities with Two Variables .
• Solve Systems of Inequalities with Two Variables .
• Linear Programming and Optimization .
• Linear Programming: Word Problems and Applications .

Popular Pages

• Solve Inequalities with Two Variables
• Trigonometry Problems and Questions with Solutions - Grade 10
• Algebra Questions with Answers for Grade 10
• High School Math (Grades 10, 11 and 12) - Free Questions and Problems With Answers
• Geometry Problems with Answers and Solutions - Grade 10

Stay In Touch

• Privacy Policy