unit 5 trigonometric functions answer key homework 2

• Skip to main content

PAYMENT PLANS ARE NOW AVAILABLE! • VISIT THE SHOP TO LEARN MORE!

All Things Algebra®

Pre-Calculus Unit 5: Trigonometric Functions

This unit includes 93 pages of guided notes, homework assignments, four quizzes, a study guide, and a unit test that cover the topics listed in the description below.

• Description
• Additional Information
• What Educators Are Saying

This unit contains the following topics:

• Angles in Standard Position • Degrees and Radians • Coterminal Angles • Degree-Minute-Second (DMS) Form • Arc Lengths • Area of Sectors • Circular Motion: Linear Speed and Angular Speed • Six Trigonometric Functions (Sine, Cosine, Tangent, Cosecant, Secant, Cotangent) • Trigonometric Functions Values in Special Right Triangles • Finding Sides and Angles in Right Triangles • Solving Right Triangles • Right Triangle Applications (Angle of Elevation and Angle of Depression) • Trigonometric Functions of Angle Angle • Reference Angles • The Unit Circle • Law of Sines • Law of Cosines • Applications of Law of Sines and Law of Cosines • Area of Triangles and Heron’s Formula • Graphing Sine, Cosine, and Tangent Functions • Translating Trigonometric Functions (Vertical and Horizontal Phase Shifts) • Graphing Reciprocal Functions (with and without translations) • Evaluating Inverse Trigonometric Functions • Graphing Inverse Trigonometric Functions • Compositions of Trigonometric Functions

This unit does not contain activities.

This is the guided notes, homework assignments, quizzes, study guide, and unit test only.  For suggested activities to go with this unit, check out the ATA Activity Alignment Guides .

This resource is included in the following bundle(s):

Pre-Calculus Curriculum

License Terms:

This purchase includes a single non-transferable license, meaning it is for one teacher only for personal use in their classroom and can not be passed from one teacher to another.  No part of this resource is to be shared with colleagues or used by an entire grade level, school, or district without purchasing the proper number of licenses.  A t ransferable license is not available for this resource.

Copyright Terms:

No part of this resource may be uploaded to the internet in any form, including classroom/personal websites or network drives, unless the site is password protected and can only be accessed by students.

What standards is this curriculum aligned to?

What format are the files in, will i have access to materials if they are updated, are answer keys included, are videos included.

Excellent Resource as always! Students understand the material, are engaged, and retain the information for a long time. Logically presented and easy to follow!

Excellent resource! Very helpful in filling in the gaps - a lifesaver for me, saving me hours of writing my own!!

I love using Gina Wilson's materials. They are easy for my students to follow, and I like that they are designed with the Cornell Notetaking method in mind. It allows for the teacher to decide if more practice is needed after teaching the concepts.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

5.4: Right Triangle Trigonometry

• Last updated
• Save as PDF
• Page ID 1363

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Objectives

• Use right triangles to evaluate trigonometric functions.
• Find function values for 30°(\(\dfrac{\pi}{6}\)),45°(\(\dfrac{\pi}{4}\)),and 60°(\(\dfrac{\pi}{3}\)).
• Use equal cofunctions of complementary angles.
• Use the definitions of trigonometric functions of any angle.
• Use right-triangle trigonometry to solve applied problems.

Mt. Everest, which straddles the border between China and Nepal, is the tallest mountain in the world. Measuring its height is no easy task and, in fact, the actual measurement has been a source of controversy for hundreds of years. The measurement process involves the use of triangles and a branch of mathematics known as trigonometry. In this section, we will define a new group of functions known as trigonometric functions, and find out how they can be used to measure heights, such as those of the tallest mountains.

We have previously defined the sine and cosine of an angle in terms of the coordinates of a point on the unit circle intersected by the terminal side of the angle:

\[ \begin{align*} \cos t &= x \\ \sin t &=y \end{align*} \]

In this section, we will see another way to define trigonometric functions using properties of right triangles .

Using Right Triangles to Evaluate Trigonometric Functions

In earlier sections, we used a unit circle to define the trigonometric functions . In this section, we will extend those definitions so that we can apply them to right triangles. The value of the sine or cosine function of \(t\) is its value at \(t\) radians. First, we need to create our right triangle. Figure \(\PageIndex{1}\) shows a point on a unit circle of radius 1. If we drop a vertical line segment from the point \((x,y)\) to the x -axis, we have a right triangle whose vertical side has length \(y\) and whose horizontal side has length \(x\). We can use this right triangle to redefine sine, cosine, and the other trigonometric functions as ratios of the sides of a right triangle.

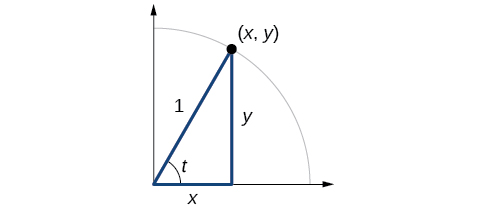
\[ \cos t= \frac{x}{1}=x \]

Likewise, we know

\[ \sin t= \frac{y}{1}=y \]

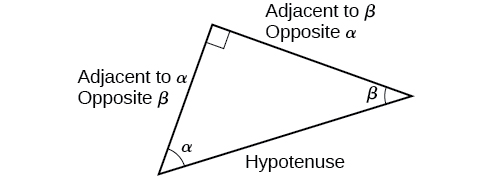
These ratios still apply to the sides of a right triangle when no unit circle is involved and when the triangle is not in standard position and is not being graphed using \((x,y)\) coordinates. To be able to use these ratios freely, we will give the sides more general names: Instead of \(x\),we will call the side between the given angle and the right angle the adjacent side to angle \(t\). (Adjacent means “next to.”) Instead of \(y\),we will call the side most distant from the given angle the opposite side from angle \(t\). And instead of \(1\),we will call the side of a right triangle opposite the right angle the hypotenuse . These sides are labeled in Figure \(\PageIndex{2}\).

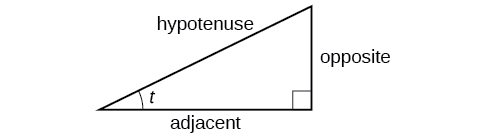
Understanding Right Triangle Relationships

Given a right triangle with an acute angle of \(t\),

\[\begin{align} \sin (t) &= \dfrac{\text{opposite}}{\text{hypotenuse}} \label{sindef}\\ \cos (t) &= \dfrac{\text{adjacent}}{\text{hypotenuse}} \label{cosdef}\\ \tan (t) &= \dfrac{\text{opposite}}{\text{adjacent}} \label{tandef}\end{align}\]

A common mnemonic for remembering these relationships is SohCahToa, formed from the first letters of “ S ine is o pposite over h ypotenuse, C osine is a djacent over h ypotenuse, T angent is o pposite over a djacent.”

how to: Given the side lengths of a right triangle and one of the acute angles, find the sine, cosine, and tangent of that angle

• Find the sine as the ratio of the opposite side to the hypotenuse.
• Find the cosine as the ratio of the adjacent side to the hypotenuse.
• Find the tangent is the ratio of the opposite side to the adjacent side.

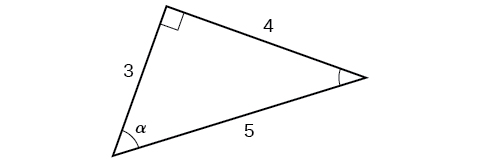
Example \(\PageIndex{1}\): Evaluating a Trigonometric Function of a Right Triangle

Given the triangle shown in Figure \(\PageIndex{3}\), find the value of \(\cos α\).

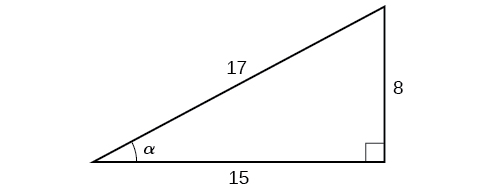
The side adjacent to the angle is 15, and the hypotenuse of the triangle is 17, so via Equation \ref{cosdef}:

\[\begin{align*} \cos (α) &= \dfrac{\text{adjacent}}{\text{hypotenuse}} \\[4pt] &= \dfrac{15}{17} \end{align*}\]

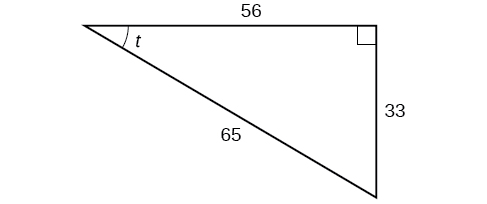
Exercise \(\PageIndex{1}\)

Given the triangle shown in Figure \(\PageIndex{4}\), find the value of \(\sin t\).

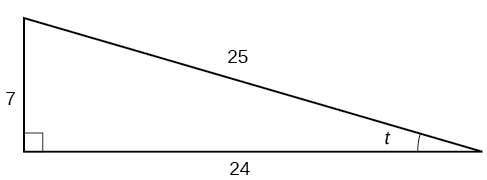
\(\frac{7}{25}\)

Relating Angles and Their Functions

When working with right triangles, the same rules apply regardless of the orientation of the triangle. In fact, we can evaluate the six trigonometric functions of either of the two acute angles in the triangle in Figure \(\PageIndex{5}\). The side opposite one acute angle is the side adjacent to the other acute angle, and vice versa.

We will be asked to find all six trigonometric functions for a given angle in a triangle. Our strategy is to find the sine, cosine, and tangent of the angles first. Then, we can find the other trigonometric functions easily because we know that the reciprocal of sine is cosecant, the reciprocal of cosine is secant, and the reciprocal of tangent is cotangent.

how to: Given the side lengths of a right triangle, evaluate the six trigonometric functions of one of the acute angles

• If needed, draw the right triangle and label the angle provided.
• Identify the angle, the adjacent side, the side opposite the angle, and the hypotenuse of the right triangle.
• sine as the ratio of the opposite side to the hypotenuse
• cosine as the ratio of the adjacent side to the hypotenuse
• tangent as the ratio of the opposite side to the adjacent side
• secant as the ratio of the hypotenuse to the adjacent side
• cosecant as the ratio of the hypotenuse to the opposite side
• cotangent as the ratio of the adjacent side to the opposite side

Example \(\PageIndex{2}\): Evaluating Trigonometric Functions of Angles Not in Standard Position

Using the triangle shown in Figure \(\PageIndex{6}\), evaluate \( \sin α, \cos α, \tan α, \sec α, \csc α,\) and \( \cot α\).

\[ \begin{align*} \sin α &= \dfrac{\text{opposite } α}{\text{hypotenuse}} = \dfrac{4}{5} \\ \cos α &= \dfrac{\text{adjacent to }α}{\text{hypotenuse}}=\dfrac{3}{5} \\ \tan α &= \dfrac{\text{opposite }α}{\text{adjacent to }α}=\dfrac{4}{3} \\ \sec α &= \dfrac{\text{hypotenuse}}{\text{adjacent to }α}= \dfrac{5}{3} \\ \csc α &= \dfrac{\text{hypotenuse}}{\text{opposite }α}=\dfrac{5}{4} \\ \cot α &= \dfrac{\text{adjacent to }α}{\text{opposite }α}=\dfrac{3}{4} \end{align*}\]

Exercise \(\PageIndex{2}\)

Using the triangle shown in Figure \(\PageIndex{7}\), evaluate \( \sin t, \cos t,\tan t, \sec t, \csc t,\) and \(\cot t\).

\[\begin{align*} \sin t &= \frac{33}{65}, \cos t= \frac{56}{65},\tan t= \frac{33}{56}, \\ \\ \sec t &= \frac{65}{56},\csc t= \frac{65}{33},\cot t= \frac{56}{33} \end{align*}\]

Finding Trigonometric Functions of Special Angles Using Side Lengths

We have already discussed the trigonometric functions as they relate to the special angles on the unit circle. Now, we can use those relationships to evaluate triangles that contain those special angles. We do this because when we evaluate the special angles in trigonometric functions, they have relatively friendly values, values that contain either no or just one square root in the ratio. Therefore, these are the angles often used in math and science problems. We will use multiples of \(30°, 60°,\) and \(45°\), however, remember that when dealing with right triangles, we are limited to angles between \(0° \text{ and } 90°\).

Suppose we have a \(30°,60°,90°\) triangle, which can also be described as a \(\frac{π}{6}, \frac{π}{3},\frac{π}{2}\) triangle. The sides have lengths in the relation \(s,\sqrt{3}s,2s.\) The sides of a \(45°,45°,90° \)triangle, which can also be described as a \(\frac{π}{4},\frac{π}{4},\frac{π}{2}\) triangle, have lengths in the relation \(s,s,\sqrt{2}s.\) These relations are shown in Figure \(\PageIndex{8}\).

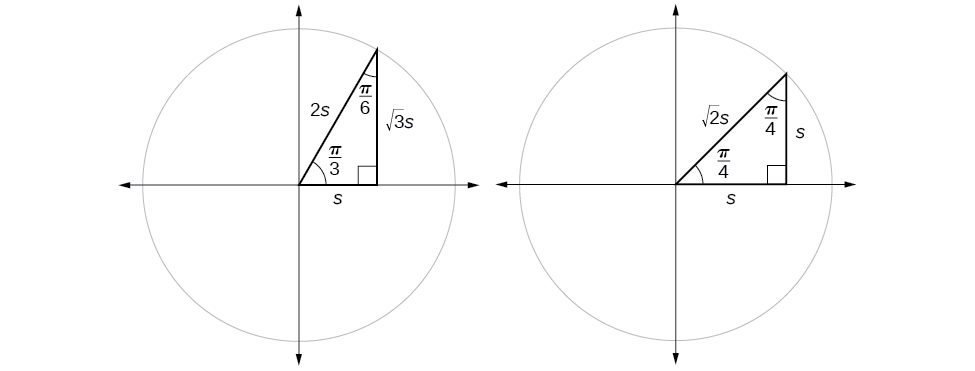
We can then use the ratios of the side lengths to evaluate trigonometric functions of special angles.

Given trigonometric functions of a special angle, evaluate using side lengths.

• Use the side lengths shown in Figure \(\PageIndex{8}\) for the special angle you wish to evaluate.
• Use the ratio of side lengths appropriate to the function you wish to evaluate.

Example \(\PageIndex{3}\): Evaluating Trigonometric Functions of Special Angles Using Side Lengths

Find the exact value of the trigonometric functions of \(\frac{π}{3}\), using side lengths.

\[\begin{align*} \sin (\dfrac{π}{3}) &= \dfrac{\text{opp}}{\text{hyp}}=\dfrac{\sqrt{3}s}{2s}=\dfrac{\sqrt{3}}{2} \\ \cos (\dfrac{π}{3}) &= \dfrac{\text{adj}}{\text{hyp}}=\dfrac{s}{2s}=\dfrac{1}{2} \\ \tan (\dfrac{π}{3}) &= \dfrac{\text{opp}}{\text{adj}} =\dfrac{\sqrt{3}s}{s}=\sqrt{3} \\ \sec (\dfrac{π}{3}) &= \dfrac{\text{hyp}}{\text{adj}} = \dfrac{2s}{s}=2 \\ \csc (\dfrac{π}{3}) &= \dfrac{\text{hyp}}{\text{opp}} =\dfrac{2s}{\sqrt{3}s}=\dfrac{2}{\sqrt{3}}=\dfrac{2\sqrt{3}}{3} \\ \cot (\dfrac{π}{3}) &= \dfrac{\text{adj}}{\text{opp}}=\dfrac{s}{\sqrt{3}s}=\dfrac{1}{\sqrt{3}}=\dfrac{\sqrt{3}}{3} \end{align*}\]

Exercise \(\PageIndex{3}\)

Find the exact value of the trigonometric functions of \(\frac{π}{4}\) using side lengths.

\( \sin (\frac{π}{4})=\frac{\sqrt{2}}{2}, \cos (\frac{π}{4})=\frac{\sqrt{2}}{2}, \tan (\frac{π}{4})=1,\)

\( \sec (\frac{π}{4})=\sqrt{2}, \csc (\frac{π}{4})=\sqrt{2}, \cot (\frac{π}{4}) =1 \)

Using Equal Cofunction of Complements

If we look more closely at the relationship between the sine and cosine of the special angles relative to the unit circle, we will notice a pattern. In a right triangle with angles of \(\frac{π}{6}\) and \(\frac{π}{3}\), we see that the sine of \(\frac{π}{3}\), namely \(\frac{\sqrt{3}}{2}\), is also the cosine of \(\frac{π}{6}\), while the sine of \(\frac{π}{6}\), namely \(\frac{1}{2},\) is also the cosine of \(\frac{π}{3}\) (Figure \(\PageIndex{9}\)).

\[\begin{align*} \sin \frac{π}{3} &= \cos \frac{π}{6}=\frac{\sqrt{3}s}{2s}=\frac{\sqrt{3}}{2} \\ \sin \frac{π}{6} &= \cos \frac{π}{3}=\frac{s}{2s}=\frac{1}{2} \end{align*}\]

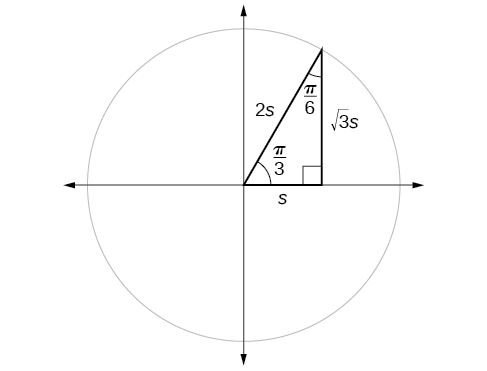
This result should not be surprising because, as we see from Figure \(\PageIndex{9}\), the side opposite the angle of \(\frac{π}{3}\) is also the side adjacent to \(\frac{π}{6}\), so \(\sin (\frac{π}{3})\) and \(\cos (\frac{π}{6})\) are exactly the same ratio of the same two sides, \(\sqrt{3} s\) and \(2s.\) Similarly, \( \cos (\frac{π}{3})\) and \( \sin (\frac{π}{6})\) are also the same ratio using the same two sides, \(s\) and \(2s\).

The interrelationship between the sines and cosines of \(\frac{π}{6}\) and \(\frac{π}{3}\) also holds for the two acute angles in any right triangle, since in every case, the ratio of the same two sides would constitute the sine of one angle and the cosine of the other. Since the three angles of a triangle add to π, and the right angle is \(\frac{π}{2}\), the remaining two angles must also add up to \(\frac{π}{2}\). That means that a right triangle can be formed with any two angles that add to \(\frac{π}{2}\)—in other words, any two complementary angles. So we may state a cofunction identity : If any two angles are complementary, the sine of one is the cosine of the other, and vice versa. This identity is illustrated in Figure \(\PageIndex{10}\).

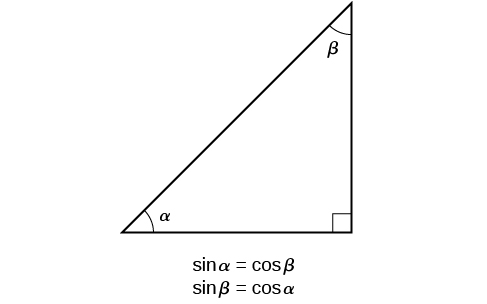
Using this identity, we can state without calculating, for instance, that the sine of \(\frac{π}{12}\) equals the cosine of \(\frac{5π}{12}\), and that the sine of \(\frac{5π}{12}\) equals the cosine of \(\frac{π}{12}\). We can also state that if, for a certain angle \(t, \cos t= \frac{5}{13},\) then \( \sin (\frac{π}{2}−t)=\frac{5}{13}\) as well.

COFUNCTION IDENTITIES

The cofunction identities in radians are listed in Table \(\PageIndex{1}\).

how to: Given the sine and cosine of an angle, find the sine or cosine of its complement.

• To find the sine of the complementary angle, find the cosine of the original angle.
• To find the cosine of the complementary angle, find the sine of the original angle.

Example \(\PageIndex{4}\): Using Cofunction Identities

If \( \sin t = \frac{5}{12},\) find \(( \cos \frac{π}{2}−t)\).

According to the cofunction identities for sine and cosine,

\[ \sin t= \cos (\dfrac{π}{2}−t). \nonumber\]

\[ \cos (\dfrac{π}{2}−t)= \dfrac{5}{12}. \nonumber\]

Exercise \(\PageIndex{4}\)

If \(\csc (\frac{π}{6})=2,\) find \( \sec (\frac{π}{3}).\)

Using Trigonometric Functions

In previous examples, we evaluated the sine and cosine in triangles where we knew all three sides. But the real power of right-triangle trigonometry emerges when we look at triangles in which we know an angle but do not know all the sides.

how to: Given a right triangle, the length of one side, and the measure of one acute angle, find the remaining sides

• For each side, select the trigonometric function that has the unknown side as either the numerator or the denominator. The known side will in turn be the denominator or the numerator.
• Write an equation setting the function value of the known angle equal to the ratio of the corresponding sides.
• Using the value of the trigonometric function and the known side length, solve for the missing side length.

Example \(\PageIndex{5}\): Finding Missing Side Lengths Using Trigonometric Ratios

Find the unknown sides of the triangle in Figure \(\PageIndex{11}\).

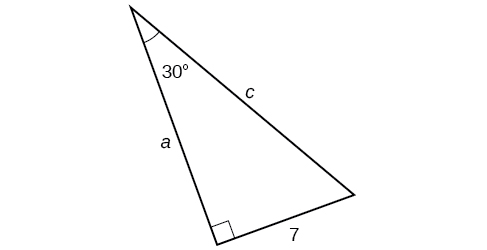
We know the angle and the opposite side, so we can use the tangent to find the adjacent side.

\[ \tan (30°)= \dfrac{7}{a} \nonumber\]

We rearrange to solve for \(a\).

\[\begin{align} a &=\dfrac{7}{ \tan (30°)} \\ & =12.1 \end{align} \nonumber\]

We can use the sine to find the hypotenuse.

\[ \sin (30°)= \dfrac{7}{c} \nonumber\]

Again, we rearrange to solve for \(c\).

\[\begin{align*} c &= \dfrac{7}{\sin (30°)} =14 \end{align*}\]

Exercise \(\PageIndex{5}\):

A right triangle has one angle of \(\frac{π}{3}\) and a hypotenuse of 20. Find the unknown sides and angle of the triangle.

\(\mathrm{adjacent=10; opposite=10 \sqrt{3}; }\) missing angle is \(\frac{π}{6}\)

Using Right Triangle Trigonometry to Solve Applied Problems

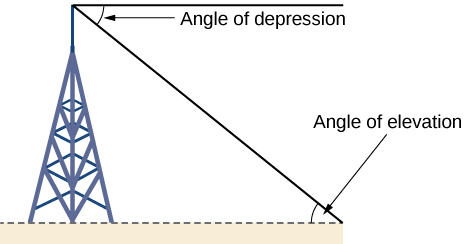
Right-triangle trigonometry has many practical applications. For example, the ability to compute the lengths of sides of a triangle makes it possible to find the height of a tall object without climbing to the top or having to extend a tape measure along its height. We do so by measuring a distance from the base of the object to a point on the ground some distance away, where we can look up to the top of the tall object at an angle. The angle of elevation of an object above an observer relative to the observer is the angle between the horizontal and the line from the object to the observer's eye. The right triangle this position creates has sides that represent the unknown height, the measured distance from the base, and the angled line of sight from the ground to the top of the object. Knowing the measured distance to the base of the object and the angle of the line of sight, we can use trigonometric functions to calculate the unknown height. Similarly, we can form a triangle from the top of a tall object by looking downward. The angle of depression of an object below an observer relative to the observer is the angle between the horizontal and the line from the object to the observer's eye. See Figure \(\PageIndex{12}\).

how to: Given a tall object, measure its height indirectly

• Make a sketch of the problem situation to keep track of known and unknown information.
• Lay out a measured distance from the base of the object to a point where the top of the object is clearly visible.
• At the other end of the measured distance, look up to the top of the object. Measure the angle the line of sight makes with the horizontal.
• Write an equation relating the unknown height, the measured distance, and the tangent of the angle of the line of sight.
• Solve the equation for the unknown height.

Example \(\PageIndex{6}\): Measuring a Distance Indirectly

To find the height of a tree, a person walks to a point 30 feet from the base of the tree. She measures an angle of 57° 57° between a line of sight to the top of the tree and the ground, as shown in Figure \(\PageIndex{13}\). Find the height of the tree.

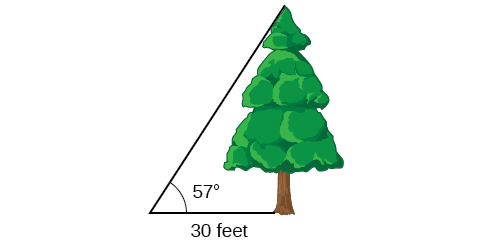
We know that the angle of elevation is \(57°\) and the adjacent side is 30 ft long. The opposite side is the unknown height.

The trigonometric function relating the side opposite to an angle and the side adjacent to the angle is the tangent. So we will state our information in terms of the tangent of \(57°\), letting \(h\) be the unknown height.

\[\begin{array}{cl} \tan θ = \dfrac{\text{opposite}}{\text{adjacent}} & \text{} \\ \tan (57°) = \dfrac{h}{30} & \text{Solve for }h. \\ h=30 \tan (57°) & \text{Multiply.} \\ h≈46.2 & \text{Use a calculator.} \end{array} \]

The tree is approximately 46 feet tall.

Exercise \(\PageIndex{6}\):

How long a ladder is needed to reach a windowsill 50 feet above the ground if the ladder rests against the building making an angle of \(\frac{5π}{12}\) with the ground? Round to the nearest foot.

About 52 ft

Access these online resources for additional instruction and practice with right triangle trigonometry.

• Finding Trig Functions on Calculator
• Finding Trig Functions Using a Right Triangle
• Relate Trig Functions to Sides of a Right Triangle
• Determine Six Trig Functions from a Triangle
• Determine Length of Right Triangle Side

Visit this website for additional practice questions from Learningpod.

Key Equations

Cofunction Identities

\[\begin{align*} \cos t &= \sin ( \frac{π}{2}−t) \\ \sin t &= \cos (\frac{π}{2}−t) \\ \tan t &= \cot (\frac{π}{2}−t) \\ \cot t &= \tan (\frac{π}{2}−t) \\ \sec t &= \csc (\frac{π}{2}−t) \\ \csc t &= \sec (\frac{π}{2}−t) \end{align*}\]

Key Concepts

• We can define trigonometric functions as ratios of the side lengths of a right triangle. See Example .
• The same side lengths can be used to evaluate the trigonometric functions of either acute angle in a right triangle. See Example .
• We can evaluate the trigonometric functions of special angles, knowing the side lengths of the triangles in which they occur. See Example .
• Any two complementary angles could be the two acute angles of a right triangle.
• If two angles are complementary, the cofunction identities state that the sine of one equals the cosine of the other and vice versa. See Example .
• We can use trigonometric functions of an angle to find unknown side lengths.
• Select the trigonometric function representing the ratio of the unknown side to the known side. See Example .
• Right-triangle trigonometry permits the measurement of inaccessible heights and distances.
• The unknown height or distance can be found by creating a right triangle in which the unknown height or distance is one of the sides, and another side and angle are known. See Example .

Chapter 5: Equations and Identities

Exercises: Chapter 5 Review Problems

Suggested problems.

Exercises for Chapter 5 Review

Exercise group.

For Problems 1–4, evaluate the expressions for [latex]x = 120°,~ y = 225°,[/latex] and [latex]z = 90°{.}[/latex] Give exact values for your answers.

[latex]\sin^2 x \cos y[/latex]

[latex]\sin z - \dfrac{1}{2} \sin y[/latex]

[latex]\tan (z - x) \cos (y - z)[/latex]

[latex]\dfrac{\tan^2 x}{2 \cos y}[/latex]

For Problems 5–8, evaluate the expressions using a calculator. Are they equal?

• [latex]\sin (20° + 40°)[/latex]
• [latex]\sin 20° + \sin 40°[/latex]
• [latex]\cos^2 70° - \sin^2 70°[/latex]
• [latex]\cos (2\cdot 70°)[/latex]
• [latex]\dfrac{\sin 55°}{\cos 55°}[/latex]
• [latex]\tan 55°[/latex]
• [latex]\tan 80° - \tan 10°[/latex]
• [latex]\tan (80° - 10°)[/latex]

For Problems 9–12, simplify the expression.

[latex]3\sin x - 2\sin x \cos y + 2\sin x - \cos y[/latex]

[latex]\cos t + 3\cos 3t - 3\cos t - 2\cos 3t[/latex]

[latex]6 \tan^2 \theta + 2\tan \theta - (4\tan \theta )^2[/latex]

[latex]\sin \theta (2\cos \theta - 2) + \sin \theta (1 - \sin \theta)[/latex]

For Problems 13–16, decide whether or not the expressions are equivalent. Explain.

[latex]\cos \theta + \cos 2\theta;~~\cos 3\theta[/latex]

[latex]1 + \sin^2 x;~~(1 + \sin x)^2[/latex]

[latex]3\tan^2 t - \tan^2 t;~~2\tan^2 t[/latex]

[latex]\cos 4\theta;~~2\cos 2\theta[/latex]

For Problems 17–20, multiply or expand.

[latex](\cos \alpha + 2)(2\cos \alpha - 3)[/latex]

[latex](1 - 3\tan \beta)^2[/latex]

[latex](\tan \phi - \cos \phi)^2 = 0[/latex]

[latex](\sin \rho - 2\cos \rho)(\sin \rho + \cos \rho)[/latex]

For Problems 21–24, factor the expression.

[latex]12\sin 3x - 6\sin 2x[/latex]

[latex]2\cos^2 \beta + \cos \beta[/latex]

[latex]1 - 9\tan^2 \theta[/latex]

[latex]\sin^2 \phi - \sin \phi \tan \phi - 2\tan^2 \phi[/latex]

For Problems 25–30, reduce the fraction.

[latex]\dfrac{\cos^2 \alpha - \sin^2 \alpha}{\cos \alpha - \sin \alpha}[/latex]

[latex]\dfrac{1 - \tan^2 \theta}{1 - \tan \theta}[/latex]

[latex]\dfrac{3\cos x + 9}{2\cos x + 6}[/latex]

[latex]\dfrac{5\sin \theta - 10}{\sin^2 \theta - 4}[/latex]

[latex]\dfrac{3\tan^2 C - 12}{\tan^2 C - 4\tan C + 4}[/latex]

[latex]\dfrac{\tan^2 \beta - \tan \beta - 6}{\tan \beta - 3}[/latex]

For Problems 31–32, use a graph to solve the equation for [latex]0° \le x \lt 360°{.}[/latex] Check your solutions by substitution.

[latex]8\cos x - 3 = 2[/latex]

[latex]6\tan x - 2 = 8[/latex]

For Problems 33–40, find all solutions between [latex]0°[/latex] and [latex]360°{.}[/latex] Give exact answers.

[latex]2\cos^2 \theta + \cos \theta = 0[/latex]

[latex]\sin^2 \alpha - \sin \alpha = 0[/latex]

[latex]2\sin^2 x - \sin x - 1 = 0[/latex]

[latex]\cos^2 B + 2\cos B + 1 = 0[/latex]

[latex]\tan^2 x = \dfrac{1}{3}[/latex]

[latex]\tan^2 t - \tan t = 0[/latex]

[latex]6\cos^2 \alpha - 3\cos \alpha - 3 = 0[/latex]

[latex]2\sin^2 \theta + 4\sin \theta + 2 = 0[/latex]

For Problems 41–44, solve the equation for [latex]0° \le x \lt 360°{.}[/latex] Round your answers to two decimal places.

[latex]2 - 5\tan \theta = -6[/latex]

[latex]3 + 5\cos \theta = 4[/latex]

[latex]3\cos^2 x + 7\cos x = 0[/latex]

[latex]8 - 9\sin^2 x = 0[/latex]

A light ray passes from glass to water, with a [latex]37°[/latex] angle of incidence. What is the angle of refraction? The index of refraction from water to glass is 1.1.

A light ray passes from glass to water, with a [latex]76°[/latex] angle of incidence. What is the angle of refraction? The index of refraction from water to glass is 1.1.

For Problems 47–50, decide which of the following equations are identities. Explain your reasoning.

[latex]\cos x\tan x = \sin x[/latex]

[latex]\sin \theta = 1 - \cos \theta[/latex]

[latex]\tan \phi + \tan \phi = \tan 2\phi[/latex]

[latex]\tan^2 x = \dfrac{\sin^2 x}{1 - \sin^2 x}[/latex]

For Problems 51–54, use graphs to decide which of the following equations are identities.

[latex]\cos 2\theta = 2 \cos \theta[/latex]

[latex]\cos (x - 90°) = \sin x[/latex]

[latex]\sin 2x = 2\sin x \cos x[/latex]

[latex]\cos (\theta + 90°) = \cos \theta - 1[/latex]

For Problems 55–58, show that the equation is an identity by transforming the left side into the right side.

[latex]\dfrac{1 - \cos^2 \alpha}{\tan \alpha} = \sin \alpha \cos \alpha[/latex]

[latex]\cos^2 \beta \tan^2 \beta + \cos^2 \beta = 1[/latex]

[latex]\dfrac{\tan \theta - \sin \theta \cos \theta}{\sin \theta \cos \theta} = \sin \theta[/latex]

[latex]\tan \phi - \dfrac{\sin^2 \phi}{\tan \phi} = \tan \phi \sin^2 \phi[/latex]

For Problems 59–62, simplify, using identities as necessary.

[latex]\tan \theta + \dfrac{\cos \theta}{\sin \theta}[/latex]

[latex]\dfrac{1 - 2\cos^2 \beta}{\sin \beta \cos \beta} + \dfrac{\cos \beta}{\sin \beta}[/latex]

[latex]\dfrac{1}{1 - \sin^2 v} - \tan^2 v[/latex]

[latex]\cos u + (\sin u)(\tan u)[/latex]

For Problems 63–66, evaluate the expressions without using a calculator.

[latex]\sin 137° - \tan 137° \cdot \cos 137°[/latex]

[latex]\cos^2 8° + \cos 8° \cdot \tan 8° \cdot \sin 8°[/latex]

[latex]\dfrac{1}{\cos^2 54°} - \tan^2 54°[/latex]

[latex]\dfrac{2}{\cos^2 7°} - 2\tan^2 7°[/latex]

For Problems 67–70, use identities to rewrite each expression.

Write [latex]\tan^2 \beta + 1[/latex] in terms of [latex]\cos^2 \beta{.}[/latex]

Write [latex]2\sin^2 t + \cos t[/latex] in terms of [latex]\cos t{.}[/latex]

Write [latex]\dfrac{\cos x}{\tan x}[/latex] in terms of [latex]\sin x{.}[/latex]

For Problems 71–74, find the values of the three trigonometric functions.

[latex]7\tan \beta - 4 = 2, ~~ 180° \lt \beta \lt 270°[/latex]

[latex]3\tan C + 5 = 3, ~~-90° \lt C \lt 0°[/latex]

[latex]5\cos \alpha + 3 = 1, ~~ 90° \lt \alpha \lt 180°[/latex]

[latex]3\sin \theta + 2 = 4, ~~ 90° \lt \beta \lt 180°[/latex]

For Problems 75–82, solve the equation for [latex]0° \le x \lt 360°{.}[/latex] Round angles to three decimal places if necessary.

[latex]\sin w + 1 = \cos^2 w[/latex]

[latex]\cos^2 \phi - \cos \phi - \sin^2 \phi = 0[/latex]

[latex]\cos x + \sin x = 0[/latex]

[latex]3\sin \theta = \sqrt{3} \cos \theta[/latex]

[latex]2\sin \beta - \tan \beta = 0[/latex]

[latex]6\tan \theta \cos \theta + 6 = 0[/latex]

[latex]\cos^2 t - \sin^2 t = 1[/latex]

[latex]5\cos^2 \beta - 5\sin^2 \beta = -5[/latex]

Trigonometry Copyright © 2024 by Bimal Kunwor; Donna Densmore; Jared Eusea; and Yi Zhen. All Rights Reserved.

Share This Book

Trigonometric Functions (PreCalculus Curriculum Unit 5) | All Things Algebra®

• Google Apps™

What educators are saying

Also included in.

Description

This Trigonometric Functions Unit Bundle includes guided notes, homework assignments, four quizzes, a study guide, and a unit test that cover the following topics:

• Angles in Standard Position

• Degrees and Radians

• Coterminal Angles

• Degree-Minute-Second (DMS) Form

• Arc Lengths

• Area of Sectors

• Circular Motion: Linear Speed and Angular Speed

• Six Trigonometric Functions (Sine, Cosine, Tangent, Cosecant, Secant, Cotangent)

• Trigonometric Functions Values in Special Right Triangles

• Finding Sides and Angles in Right Triangles

• Solving Right Triangles

• Right Triangle Applications (Angle of Elevation and Angle of Depression)

• Trigonometric Functions of Angle Angle

• Reference Angles

• The Unit Circle

• Law of Sines

• Law of Cosines

• Applications of Law of Sines and Law of Cosines

• Area of Triangles and Heron's Formula

• Graphing Sine, Cosine, and Tangent Functions

• Translating Trigonometric Functions (Vertical and Horizontal Phase Shifts)

• Graphing Reciprocal Functions (with and without translations)

• Evaluating Inverse Trigonometric Functions

• Graphing Inverse Trigonometric Functions

• Compositions of Trigonometric Functions

ADDITIONAL COMPONENTS INCLUDED:

(1) Links to Instructional Videos: Links to videos of each lesson in the unit are included. Videos were created by fellow teachers for their students using the guided notes and shared in March 2020 when schools closed with no notice.  Please watch through first before sharing with your students. Many teachers still use these in emergency substitute situations. (2) Editable Assessments: Editable versions of each quiz and the unit test are included. PowerPoint is required to edit these files. Individual problems can be changed to create multiple versions of the assessment. The layout of the assessment itself is not editable. If your Equation Editor is incompatible with mine (I use MathType), simply delete my equation and insert your own.

(3) Google Slides Version of the PDF: The second page of the Video links document contains a link to a Google Slides version of the PDF. Each page is set to the background in Google Slides. There are no text boxes;  this is the PDF in Google Slides.  I am unable to do text boxes at this time but hope this saves you a step if you wish to use it in Slides instead! 

This resource is included in the following bundle(s):

Pre-Calculus Curriculum

More Pre-Calculus Units:

Unit 1 – Fundamental Skills

Unit 2 – Functions and Their Graphs

Unit 3 – Polynomial and Rational Functions

Unit 4 – Exponential and Logarithmic Functions

Unit 6 – Trigonometric Identities and Equations

Unit 7 – Polar and Parametric Equations

Unit 8 – Vectors

Unit 9 – Conic Sections Unit 10 – Systems of Equations and Matrices Unit 11 – Sequences and Series

Unit 12 – Introduction to Calculus

LICENSING TERMS: This purchase includes a license for one teacher only for personal use in their classroom. Licenses are non-transferable , meaning they can not be passed from one teacher to another. No part of this resource is to be shared with colleagues or used by an entire grade level, school, or district without purchasing the proper number of licenses. If you are a coach, principal, or district interested in transferable licenses to accommodate yearly staff changes, please contact me for a quote at [email protected].

COPYRIGHT TERMS: This resource may not be uploaded to the internet in any form, including classroom/personal websites or network drives, unless the site is password protected and can only be accessed by students.

© All Things Algebra (Gina Wilson), 2012-present

Questions & Answers

All things algebra.

• We're hiring
• Help & FAQ
• Privacy policy
• Student privacy
• Terms of service
• Tell us what you think

Math 112 (Online) Walkthrough Text

Walkthrough of unit 5: inverse trig functions and solving trig equations, learning outcomes.

• Understand and use the inverse sine, cosine, and tangent functions.
• Find the exact value of expressions involving the inverse sine, cosine, and tangent functions.
• Use a calculator to evaluate inverse trigonometric functions.
• Use inverse trigonometric functions to solve right triangles.
• Find exact values of composite functions with inverse trigonometric functions.

Understanding and Using the Inverse Sine, Cosine, and Tangent Functions

In order to use inverse trigonometric functions, we need to understand that an inverse trigonometric function “undoes” what the original trigonometric function “does,” as is the case with any other function and its inverse. In other words, the domain of the inverse function is the range of the original function, and vice versa, as summarized in Figure 1.

For example, if [latex]f(x)=\sin x[/latex], then we would write [latex]f^{1}(x)={\sin}^{-1}{x}[/latex]. Be aware that [latex]{\sin}^{-1}x[/latex] does not mean [latex]\frac{1}{\sin{x}}[/latex]. The following examples illustrate the inverse trigonometric functions:

• Since [latex]\sin\left(\frac{\pi}{6}\right)=\frac{1}{2}[/latex], then [latex]\frac{\pi}{6}=\sin^{−1}(\frac{1}{2})[/latex].
• Since [latex]\cos(\pi)=−1[/latex], then [latex]\pi=\cos^{−1}(−1)[/latex].
• Since [latex]\tan\left(\frac{\pi}{4}\right)=1[/latex], then [latex]\frac{\pi}{4}=\tan^{−1}(1)[/latex].

In previous sections, we evaluated the trigonometric functions at various angles, but at times we need to know what angle would yield a specific sine, cosine, or tangent value. For this, we need inverse functions. Recall that, for a one-to-one function , if [latex]f(a)=b[/latex], then an inverse function would satisfy [latex]f^{−1}(b)=a[/latex].

Bear in mind that the sine, cosine, and tangent functions are not one-to-one functions. The graph of each function would fail the horizontal line test. In fact, no periodic function can be one-to-one because each output in its range corresponds to at least one input in every period, and there are an infinite number of periods. As with other functions that are not one-to-one, we will need to restrict the domain of each function to yield a new function that is one-to-one. We choose a domain for each function that includes the number 0. Figure 2 shows the graph of the sine function limited to [latex]\left[\frac{−\pi}{2}\text{, }\frac{\pi}{2}\right][/latex] and the graph of the cosine function limited to [0, π].

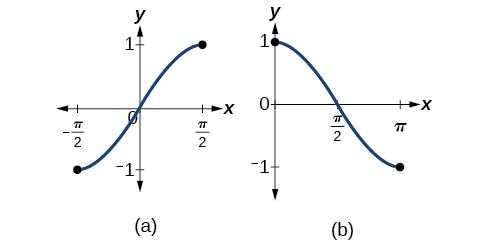
Figure 2. (a) Sine function on a restricted domain of [latex]\left[−\frac{\pi}{2}\text{, }\frac{\pi}{2}\right][/latex]; (b) Cosine function on a restricted domain of [0, π]

Figure 3 shows the graph of the tangent function limited to [latex]\left(−\frac{\pi}{2}\text{, }\frac{\pi}{2}\right)[/latex].

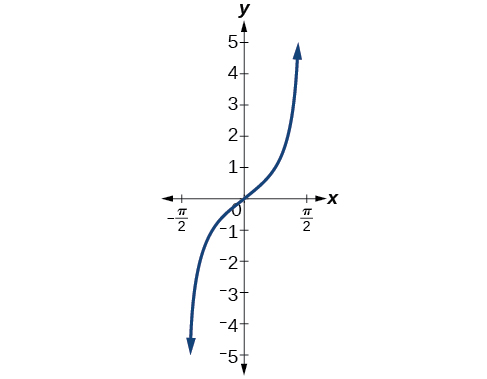
Figure 3.  Tangent function on a restricted domain of [latex]\left(−\frac{\pi}{2}\text{, }\frac{\pi}{2}\right)[/latex]

These conventional choices for the restricted domain are somewhat arbitrary, but they have important, helpful characteristics. Each domain includes the origin and some positive values, and most importantly, each results in a one-to-one function that is invertible. The conventional choice for the restricted domain of the tangent function also has the useful property that it extends from one vertical asymptote to the next instead of being divided into two parts by an asymptote.

On these restricted domains, we can define the inverse trigonometric functions .

• The inverse sine function  [latex]y=\sin^{−1}x[/latex] means [latex]x=\sin y[/latex]. The inverse sine function is sometimes called the arcsine function, and notated arcsin x . [latex]y=\sin^{−1}x[/latex] has domain [−1, 1] and range [latex]\left[−\frac{\pi}{2}\text{, }\frac{\pi}{2}\right][/latex]
• The inverse cosine function  [latex]y=\cos^{−1}x[/latex] means [latex]x=\cos y[/latex]. The inverse cosine function is sometimes called the arccosine function, and notated arccos x . [latex]y=\cos^{−1}x[/latex] has domain [−1, 1] and range [0, π]
• The inverse tangent function  [latex]y=\tan^{−1}x[/latex] means [latex]x=\tan y[/latex]. The inverse tangent function is sometimes called the arctangent function, and notated arctan x . [latex]y=\tan^{−1}x[/latex] has domain (−∞, ∞) and range [latex]\left(−\frac{\pi}{2}\text{, }\frac{\pi}{2}\right)[/latex]

The graphs of the inverse functions are shown in Figure 4, Figure 5, and Figure 6. Notice that the output of each of these inverse functions is a number, an angle in radian measure. We see that [latex]\sin^{−1}x[/latex] has domain [−1, 1] and range [latex]\left[−\frac{\pi}{2}\text{, }\frac{\pi}{2}\right][/latex], [latex]\cos^{−1}x[/latex] has domain [−1, 1] and range [0, π], and [latex]\tan^{−1}x[/latex] has domain of all real numbers and range [latex]\left(−\frac{\pi}{2}\text{, }\frac{\pi}{2}\right)[/latex]. To find the domain and range of inverse trigonometric functions, switch the domain and range of the original functions. Each graph of the inverse trigonometric function is a reflection of the graph of the original function about the line [latex]y=x[/latex].

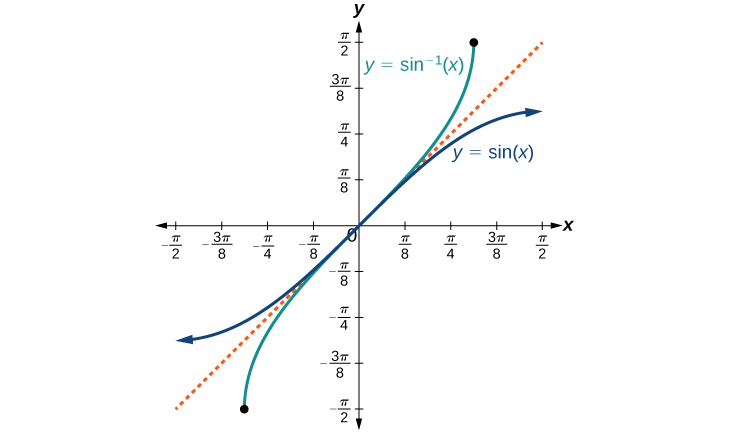
Figure 4.  The sine function and inverse sine (or arcsine) function

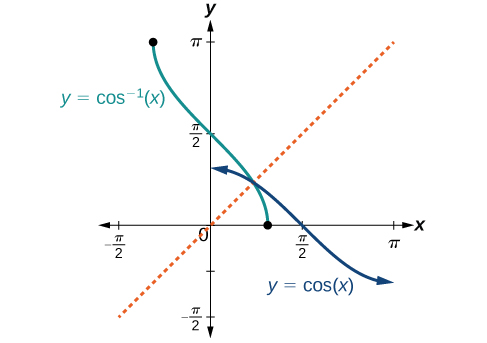
Figure 5. The cosine function and inverse cosine (or arccosine) function

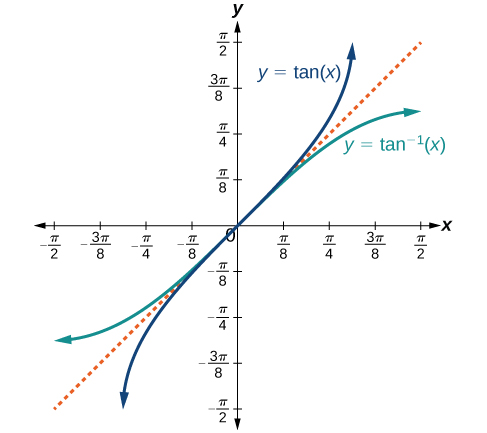
Figure 6. The tangent function and inverse tangent (or arctangent) function

A General Note: Relations for Inverse Sine, Cosine, and Tangent Functions

For angles in the interval [latex]\left[−\frac{\pi}{2}\text{, }\frac{\pi}{2}\right][/latex], if [latex]\sin y=x[/latex], then [latex]\sin^{−1}x=y[/latex].

For angles in the interval [0, π], if [latex]\cos y=x[/latex], then [latex]\cos^{−1}x=y[/latex].

For angles in the interval [latex]\left(−\frac{\pi}{2}\text{, }\frac{\pi}{2}\right)[/latex], if [latex]\tan y=x[/latex], then [latex]\tan^{−1}x=y[/latex].

Example 1: Writing a Relation for an Inverse Function

Given [latex]\sin\left(\frac{5\pi}{12}\right)\approx 0.96593[/latex], write a relation involving the inverse sine.

Use the relation for the inverse sine. If [latex]\sin y=x[/latex], then [latex]\sin^{−1}x=y[/latex].

In this problem, [latex]x=0.96593[/latex], and [latex]y=\frac{5\pi}{12}[/latex].

[latex]\sin^{−1}(0.96593)\approx \frac{5\pi}{12}[/latex]

Given [latex]\cos(0.5)\approx 0.8776[/latex], write a relation involving the inverse cosine.

[latex]\arccos(0.8776)\approx0.5[/latex]

Finding the Exact Value of Expressions Involving the Inverse Sine, Cosine, and Tangent Functions

Now that we can identify inverse functions, we will learn to evaluate them. For most values in their domains, we must evaluate the inverse trigonometric functions by using a calculator, interpolating from a table, or using some other numerical technique. Just as we did with the original trigonometric functions, we can give exact values for the inverse functions when we are using the special angles, specifically [latex]\frac{\pi}{ 6} (30^\circ)\text{, }\frac{\pi}{ 4} (45^\circ),\text{ and } \frac{\pi}{ 3} (60^\circ)[/latex], and their reflections into other quadrants.

How To: Given a “special” input value, evaluate an inverse trigonometric function.

• Find angle  x  for which the original trigonometric function has an output equal to the given input for the inverse trigonometric function.
• If  x  is not in the defined range of the inverse, find another angle  y  that is in the defined range and has the same sine, cosine, or tangent as  x , depending on which corresponds to the given inverse function.

Example 2: Evaluating Inverse Trigonometric Functions for Special Input Values

Evaluate each of the following.

a. [latex]\sin−1\left(\frac{1}{2}\right)[/latex]

b. [latex]\sin−1\left(−\frac{2}{\sqrt{2}}\right)[/latex]

c. [latex]\cos−1\left(−\frac{3}{\sqrt{2}}\right)[/latex]

d. [latex]\tan^{− 1}(1)[/latex]

a. Evaluating [latex]\sin^{−1}(\frac{1}{2})[/latex] is the same as determining the angle that would have a sine value of [latex]\frac{1}{2}[/latex]. In other words, what angle x would satisfy [latex]\sin(x)=\frac{1}{2}[/latex]? There are multiple values that would satisfy this relationship, such as [latex]\frac{\pi}{6}[/latex] and [latex]\frac{5\pi}{6}[/latex], but we know we need the angle in the interval [latex]\left[−\frac{\pi}{2}\text{, }\frac{\pi}{2}\right][/latex], so the answer will be [latex]\sin^{−1}(\frac{1}{2})=\frac{\pi}{6}[/latex]. Remember that the inverse is a function, so for each input, we will get exactly one output.

b. To evaluate [latex]\sin^{−1}\left(−\frac{\sqrt{2}}{2}\right)[/latex], we know that [latex]\frac{5\pi}{4}[/latex] and [latex]\frac{7\pi}{4}[/latex] both have a sine value of [latex]−\frac{\sqrt{2}}{2}[/latex], but neither is in the interval [latex]\left[−\frac{\pi}{2}\text{, }\frac{\pi}{2}\right][/latex]. For that, we need the negative angle coterminal with [latex]\frac{7\pi}{4}:\sin^{−1}\left(−\frac{\sqrt{2}}{2}\right)=−\frac{\pi}{4}[/latex].

c. To evaluate [latex]\cos^{−1}\left(−\frac{\sqrt{3}}{2}\right)[/latex], we are looking for an angle in the interval [0,π] with a cosine value of [latex]−\frac{\sqrt{3}}{2}[/latex]. The angle that satisfies this is [latex]\cos^{−1}\left(−\frac{\sqrt{3}}{2}\right)=\frac{5\pi}{6}[/latex].

d. Evaluating [latex]\tan^{−1}(1)[/latex], we are looking for an angle in the interval [latex](−\frac{\pi}{2}\text{, }\frac{\pi}{2})[/latex] with a tangent value of 1. The correct angle is [latex]\tan^{−1}(1)=\frac{\pi}{4}[/latex].

• [latex]\sin^{−1}(−1)[/latex]
• [latex]\tan^{−1}(−1)[/latex]
• [latex]\cos^{−1}(−1)[/latex]
• [latex]\cos^{−1}(\frac{1}{2})[/latex]

1. [latex]−\frac{\pi}{2}[/latex];

2. [latex]−\frac{\pi}{4}[/latex]

3. [latex]\pi[/latex]

4. [latex]\frac{\pi}{3}[/latex]

Using a Calculator to Evaluate Inverse Trigonometric Functions

To evaluate inverse trigonometric functions that do not involve the special angles discussed previously, we will need to use a calculator or other type of technology. Most scientific calculators and calculator-emulating applications have specific keys or buttons for the inverse sine, cosine, and tangent functions. These may be labeled, for example, SIN-1, ARCSIN, or ASIN.

In the previous chapter, we worked with trigonometry on a right triangle to solve for the sides of a triangle given one side and an additional angle. Using the inverse trigonometric functions, we can solve for the angles of a right triangle given two sides, and we can use a calculator to find the values to several decimal places.

In these examples and exercises, the answers will be interpreted as angles and we will use θ as the independent variable. The value displayed on the calculator may be in degrees or radians, so be sure to set the mode appropriate to the application.

Example 3: Evaluating the Inverse Sine on a Calculator

Evaluate [latex]\sin^{−1}(0.97)[/latex] using a calculator.

Because the output of the inverse function is an angle, the calculator will give us a degree value if in degree mode and a radian value if in radian mode. Calculators also use the same domain restrictions on the angles as we are using.

In radian mode, [latex]\sin^{−1}(0.97)\approx1.3252[/latex]. In degree mode, [latex]\sin^{−1}(0.97)\approx75.93^{\circ}[/latex]. Note that in calculus and beyond we will use radians in almost all cases.

Evaluate [latex]\cos^{−1}(−0.4)[/latex] using a calculator.

1.9823 or 113.578°

How To: Given two sides of a right triangle like the one shown in Figure 7, find an angle.

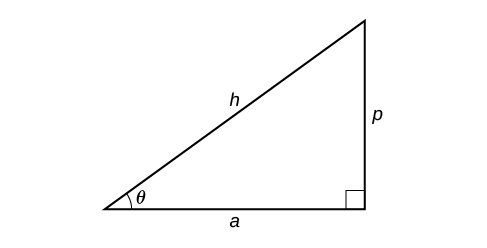
• If one given side is the hypotenuse of length h and the side of length a adjacent to the desired angle is given, use the equation [latex]\theta=\cos^{−1}\left(\frac{a}{h}\right)[/latex].
• If one given side is the hypotenuse of length h and the side of length p opposite to the desired angle is given, use the equation [latex]\theta=\sin^{−1}\left(\frac{p}{h}\right)[/latex].
• If the two legs (the sides adjacent to the right angle) are given, then use the equation [latex]\theta=\tan^{−1}\left(\frac{p}{a}\right)[/latex].

Example 4: Applying the Inverse Cosine to a Right Triangle

Solve the triangle in Figure 8 for the angle θ.

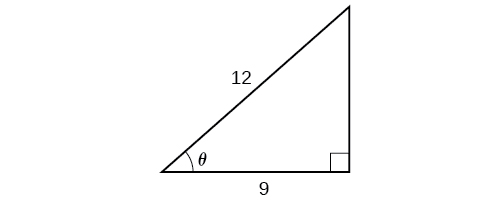
Because we know the hypotenuse and the side adjacent to the angle, it makes sense for us to use the cosine function.

[latex]\begin{align}&\cos\theta=\frac{9}{12}\\ &\theta=\cos^{−1}\left(\frac{9}{12}\right) && \text{Apply definition of the inverse.} \\ &\theta\approx0.7227\text{ or about }41.4096^{\circ} && \text{Evaluate.} \end{align}[/latex]

Solve the triangle in Figure 9 for the angle θ.

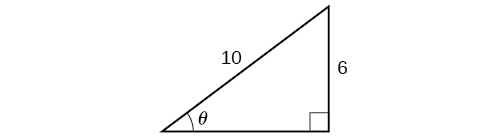
[latex]\sin^{−1}(0.6)=36.87^{\circ}=0.6435[/latex] radians

Finding Exact Values of Composite Functions with Inverse Trigonometric Functions

There are times when we need to compose a trigonometric function with an inverse trigonometric function. In these cases, we can usually find exact values for the resulting expressions without resorting to a calculator. Even when the input to the composite function is a variable or an expression, we can often find an expression for the output. To help sort out different cases, let f ( x ) and g ( x ) be two different trigonometric functions belonging to the set {sin( x ), cos( x ), tan( x )} and let [latex]f^{−1}(y)[/latex] and [latex]g^{−1}(y)[/latex] be their inverses.

Evaluating Compositions of the Form [latex]f\left(f^{−1}(y)\right)[/latex] and [latex]f^{−1}(f(x))[/latex]

For any trigonometric function, [latex]f(f^{−1}(y))=y[/latex] for all y in the proper domain for the given function. This follows from the definition of the inverse and from the fact that the range of f was defined to be identical to the domain of [latex]f^{−1}[/latex]. However, we have to be a little more careful with expressions of the form [latex]f^{−1}(f(x))[/latex].

A General Note: Compositions of a trigonometric function and its inverse

[latex]\begin{align} &\sin(\sin^{−1}x)=x\text{ for }−1\leq x\leq1\\ &\cos(\cos^{−1}x)=x\text{ for }−\infty\leq x\leq1 \\ &\tan(\tan^{−1}x)=x\text{ for }−\infty\text{ < }x\text{ < }\infty \end{align}[/latex]

[latex]\begin{align} \hfill &\sin^{−1}(\sin x)=x\text{ only for }−\frac{\pi}{2} \leq x \leq \frac{\pi}{2} \hfill \\ &\cos^{−1}(\cos x)=x\text{ only for }0\leq x\leq\pi \hfill \\ &\tan^{−1}(\tan x)=x\text{ only for }−\frac{\pi}{2}\text{ < }x\text{ < }\frac{\pi}{2} \end{align}[/latex]

Is it correct that [latex]\sin^{−1}(\sin x)=x[/latex]?

No. This equation is correct if x belongs to the restricted domain [latex]\left[−\frac{\pi}{2},\frac{\pi}{2}\right][/latex], but sine is defined for all real input values, and for x outside the restricted interval, the equation is not correct because its inverse always returns a value in  [latex]\left[−\frac{\pi}{2},\frac{\pi}{2}\right][\latex] . The situation is similar for cosine and tangent and their inverses. For example, [latex]\sin^{−1}\left(\sin\left(\frac{3\pi}{4}\right)\right)=\frac{\pi}{4}[/latex].

Given an expression of the form [latex]f^{−1}(f(\theta))[/latex] where [latex]f(\theta)=\sin\theta\text{, }\cos\theta\text{, or }\tan\theta[/latex], evaluate.

• If θ is in the restricted domain of f , then [latex]f^{−1}(f(\theta))=\theta[/latex].
• If not, then find an angle ϕ within the restricted domain of f such that [latex]f(\phi)=f(\theta)[/latex]. Then [latex]f^{−1}(f(\theta))=\phi[/latex].

Example 5: Using Inverse Trigonometric Functions

Evaluate the following:

• [latex]\sin^{−1}(\sin(\frac{\pi}{3}))[/latex]
• [latex]\sin^{−1}(\sin(\frac{2\pi}{3}))[/latex]
• [latex]\cos^{−1}(\cos(\frac{2\pi}{3}))[/latex]
• [latex]\cos^{−1}(\cos(−\frac{\pi}{3}))[/latex]
• [latex]\frac{\pi}{3}[/latex] is in [latex]\left[−\frac{\pi}{2}\text{, }\frac{\pi}{2}\right][/latex], so [latex]\sin^{−1}(\sin(\frac{\pi}{3}))=\frac{\pi}{3}[/latex].
• [latex]\frac{2\pi}{3}[/latex] is not in [latex]\left[−\frac{\pi}{2}\text{, }\frac{\pi}{2}\right][/latex], but [latex]\sin\left(\frac{2\pi}{3}\right)=\sin\left(\frac{\pi}{3}\right)[/latex], so [latex]\sin^{−1}\left(\sin\left(\frac{2\pi}{3}\right)\right)=\frac{\pi}{3}[/latex].
• [latex]\frac{2\pi}{3}[/latex] is in [0,π], so [latex]\cos^{−1}\left(\cos\left(\frac{2\pi}{3}\right)\right)=\frac{2\pi}{3}[/latex].
• [latex]−\frac{\pi}{3}[/latex] is not in [0,π], but [latex]\cos(−\frac{\pi}{3})=\cos\left(\frac{\pi}{3}\right)[/latex] because cosine is an even function.

Evaluate [latex]\tan^{−1}\left(\tan\left(\frac{\pi}{8}\right)\right)[/latex] and [latex]\tan^{−1}\left(\tan\left(\frac{11\pi}{9}\right)\right)[/latex].

[latex]\frac{\pi}{8}\text{; }\frac{2\pi}{9}[/latex]

Evaluating Compositions of the Form [latex]f^{−1}(g(x))[/latex]

Now that we can compose a trigonometric function with its inverse, we can explore how to evaluate a composition of a trigonometric function and the inverse of another trigonometric function. We will begin with compositions of the form [latex]f^{−1}(g(x))[/latex]. For special values of x , we can exactly evaluate the inner function and then the outer, inverse function. However, we can find a more general approach by considering the relation between the two acute angles of a right triangle where one is θ, making the other [latex]\frac{\pi}{2}−\theta[/latex]. Consider the sine and cosine of each angle of the right triangle in Figure 10.

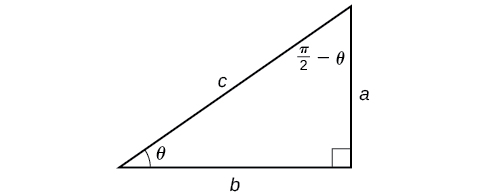
Figure 10. Right triangle illustrating the cofunction relationships

Because [latex]\cos\theta=\frac{b}{c}=\sin\left(\frac{\pi}{2}−\theta\right)[/latex], we have [latex]\sin^{−1}(\cos\theta)=\frac{\pi}{2}−\theta\text{ if }0\leq\theta\leq\pi[/latex]. If θ is not in this domain, then we need to find another angle that has the same cosine as θ and does belong to the restricted domain; we then subtract this angle from [latex]\frac{\pi}{2}[/latex]. Similarly, [latex]\sin\theta=\frac{a}{c}=\cos\left(\frac{\pi}{2}−\theta\right)[/latex], so [latex]\cos^{−1}(\sin\theta)=\frac{\pi}{2}−\theta\text{ if }−\frac{\pi}{2}\leq\theta\leq\frac{\pi}{2}[/latex]. These are just the function-cofunction relationships presented in another way.

How To: Given functions of the form [latex]\sin^{−1}(\cos x)\text{ and }\cos^{−1}(\sin x)[/latex], evaluate them.

• If x  is in [0,π], then [latex]\sin^{−1}(\cos x)=\frac{\pi}{2}−x[/latex].
• If x  is not in [0,π], then find another angle y  in [0,π] such that [latex]\cos y=\cos x[/latex]. [latex]\sin^{−1}(\cos x)=\frac{\pi}{2}−y[/latex]
• If x  is in [latex]\left[−\frac{\pi}{2},\frac{\pi}{2}\right][/latex], then [latex]\cos^{−1}(\sin x)=\frac{\pi}{2}−x[/latex].
• If x  is not in [latex]\left[−\frac{\pi}{2},\frac{\pi}{2}\right][/latex], then find another angle y  in [latex]\left[−\frac{\pi}{2}\text{, }\frac{\pi}{2}\right][/latex] such that [latex]\sin y=\sin x[/latex]. [latex]\cos^{−1}(\sin x)=\frac{\pi}{2}−y[/latex]

Example 6: Evaluating the Composition of an Inverse Sine with a Cosine

Evaluate [latex]\sin^{−1}(\cos(\frac{13\pi}{6}))[/latex]

• by direct evaluation.
• by the method described previously.

Now, we can evaluate the inverse function as we did earlier.

• We have [latex]x=\frac{13\pi}{6}[/latex], [latex]y=\frac{\pi}{6}[/latex], and [latex]\begin{align}\sin^{−1}\left(\cos\left(\frac{13\pi}{6}\right)\right)=\frac{\pi}{2}−\frac{\pi}{6} =\frac{\pi}{3} \end{align}[/latex]

Evaluate [latex]\cos^{−1}(\sin(−\frac{11\pi}{4}))[/latex].

[latex]\frac{3\pi}{4}[/latex]

Evaluating Compositions of the Form [latex]f(g^{−1}(x))[/latex]

To evaluate compositions of the form [latex]f(g^{−1}(x))[/latex], where f and g are any two of the functions sine, cosine, or tangent and x is any input in the domain of [latex]g−1[/latex], we have exact formulas, such as [latex]\sin\left({\cos}^{−1}x\right)=\sqrt{1−{x}^{2}}[/latex]. When we need to use them, we can derive these formulas by using the trigonometric relations between the angles and sides of a right triangle, together with the use of Pythagoras’s relation between the lengths of the sides. We can use the Pythagorean identity, [latex]\sin^{2}x+cos^{2}x=1[/latex], to solve for one when given the other. We can also use the inverse trigonometric functions to find compositions involving algebraic expressions.

Example 7: Evaluating the Composition of a Sine with an Inverse Cosine

Find an exact value for [latex]\sin\left(\cos^{−1}\left(\frac{4}{5}\right)\right)[/latex].

Beginning with the inside, we can say there is some angle such that [latex]\theta=\cos^{−1}(\frac{4}{5})[/latex], which means [latex]\cos\theta=\frac{4}{5}[/latex], and we are looking for [latex]\sin\theta[/latex]. We can use the Pythagorean identity to do this.

[latex]\begin{align} &\sin^{2}\theta+\cos^{2}\theta=1 && \text{Use our known value for cosine.} \\ &\sin^{2}\theta+\left(\frac{4}{5}\right)^{2}=1 && \text{Solve for sine.} \\ &\sin^{2}\theta=1−\frac{16}{25} \\ &\sin\theta=\pm\sqrt{\frac{9}{25}}=\pm\frac{3}{5} \end{align}[/latex]

Since [latex]\theta=\cos^{−1}(\frac{4}{5})[/latex] is in quadrant I, [latex]\sin{\theta}[/latex] must be positive, so the solution is [latex]\frac{3}{5}[/latex]. See Figure 11.

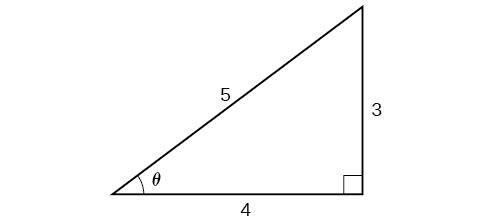
Figure 11. Right triangle illustrating that if [latex]\cos\theta=\frac{4}{5}[/latex], then [latex]\sin\theta=\frac{3}{5}[/latex]

We know that the inverse cosine always gives an angle on the interval [0, π], so we know that the sine of that angle must be positive; therefore [latex]\sin\left(\cos^{−1}\left(\frac{4}{5}\right)\right)=\sin\theta=\frac{3}{5}[/latex].

Evaluate [latex]\cos(\tan^{−1}(\frac{5}{12}))[/latex].

[latex]\frac{12}{13}[/latex]

Example 8: Evaluating the Composition of a Sine with an Inverse Tangent

Find an exact value for [latex]\sin\left(\tan^{−1}\left(\frac{7}{4}\right)\right)[/latex].

While we could use a similar technique as in Example 6, we will demonstrate a different technique here. From the inside, we know there is an angle such that [latex]\tan\theta=\frac{7}{4}[/latex]. We can envision this as the opposite and adjacent sides on a right triangle, as shown in Figure 12.

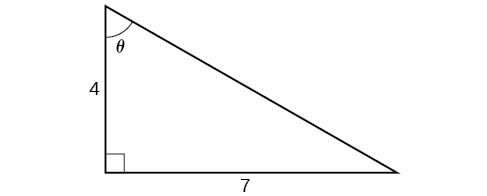
Figure 12. A right triangle with two sides known

Using the Pythagorean Theorem, we can find the hypotenuse of this triangle.

[latex]\begin{gathered}4^{2}+7^{2}=\text{hypotenuse}^{2} \\ \text{hypotenuse}=\sqrt{65} \end{gathered}[/latex]

Evaluate [latex]\cos(\sin^{−1}(\frac{7}{9}))[/latex].

[latex]\frac{4\sqrt{2}}{9}[/latex]

Example 9: Finding the Cosine of the Inverse Sine of an Algebraic Expression

Find a simplified expression for [latex]\cos\left(\sin^{−1}\left(\frac{x}{3}\right)\right)[/latex] for [latex]−3\leq x\leq3[/latex].

We know there is an angle θ such that [latex]\sin\theta=\frac{x}{3}\\[/latex]

[latex]\begin{align}&\sin^{2}\theta+\cos^{2}\theta=1 7&& \text{Use the Pythagorean Theorem.} \\ &\left(\frac{x}{3}\right)^{2}+\cos^{2}+\cos^2\theta=1 && \text{Solve for cosine.} \\ &\cos^{2}\theta=1−\frac{x^{2}}{9} \\ &\cos\theta=\pm\sqrt{\frac{9−x^{2}}{9}}=\pm\frac{\sqrt{9−x^{2}}}{3} \end{align}[/latex]

Because we know that the inverse sine must give an angle on the interval [latex]\left[−\frac{\pi}{2}\text{, }\frac{\pi}{2}\right][/latex], we can deduce that the cosine of that angle must be positive.

[latex]\cos\left(\sin^{−1}\left(\frac{x}{3}\right)\right)=\frac{\sqrt{9−x^{2}}}{3}[/latex]

Find a simplified expression for [latex]\sin\left(\tan^{−1}\left(4x\right)\right)\\[/latex] for [latex]−\frac{1}{4}\leq x \leq\frac{1}{4}[/latex].

[latex]\frac{4x}{\sqrt{16x^{2}+1}}[/latex]

Solving Linear Trigonometric Equations in Sine and Cosine

Trigonometric equations are, as the name implies, equations that involve trigonometric functions. Similar in many ways to solving polynomial equations or rational equations, only specific values of the variable will be solutions, if there are solutions at all. Often we will solve a trigonometric equation over a specified interval. However, just as often, we will be asked to find all possible solutions, and as trigonometric functions are periodic, solutions are repeated within each period. In other words, trigonometric equations may have an infinite number of solutions. Additionally, like rational equations, the domain of the function must be considered before we assume that any solution is valid. The period of both the sine function and the cosine function is [latex]2\pi [/latex]. In other words, every [latex]2\pi [/latex] units, the y- values repeat. If we need to find all possible solutions, then we must add [latex]2\pi k[/latex], where [latex]k[/latex] is an integer, to the initial solution. Recall the rule that gives the format for stating all possible solutions for a function where the period is [latex]2\pi :[/latex]

There are similar rules for indicating all possible solutions for the other trigonometric functions. Solving trigonometric equations requires the same techniques as solving algebraic equations. We read the equation from left to right, horizontally, like a sentence. We look for known patterns, factor, find common denominators, and substitute certain expressions with a variable to make solving a more straightforward process. However, with trigonometric equations, we also have the advantage of using the identities we developed in the previous sections.

Example 10: Solving a Linear Trigonometric Equation Involving the Cosine Function

Find all possible exact solutions for the equation [latex]\cos \theta =\frac{1}{2}[/latex].

From the unit circle , we know that

[latex]\begin{gathered}\cos \theta =\frac{1}{2} \\ \theta =\frac{\pi }{3},\frac{5\pi }{3} \end{gathered}[/latex]

These are the solutions in the interval [latex]\left[0,2\pi \right][/latex]. All possible solutions are given by

[latex]\theta =\frac{\pi }{3}\pm 2k\pi \text{ and }\theta =\frac{5\pi }{3}\pm 2k\pi [/latex]

where [latex]k[/latex] is an integer.

Example 11: Solving a Linear Equation Involving the Sine Function

Find all possible exact solutions for the equation [latex]\sin t=\frac{1}{2}[/latex].

Solving for all possible values of t means that solutions include angles beyond the period of [latex]2\pi [/latex]. From the unit circle, we can see that the solutions are [latex]t=\frac{\pi }{6}[/latex] and [latex]t=\frac{5\pi }{6}[/latex]. But the problem is asking for all possible values that solve the equation. Therefore, the answer is

[latex]t=\frac{\pi }{6}\pm 2\pi k\text{ and }t=\frac{5\pi }{6}\pm 2\pi k[/latex]

How To: Given a trigonometric equation, solve using algebra.

• Look for a pattern that suggests an algebraic property, such as the difference of squares or a factoring opportunity.
• Substitute the trigonometric expression with a single variable, such as [latex]x[/latex] or [latex]u[/latex].
• Solve the equation the same way an algebraic equation would be solved.
• Substitute the trigonometric expression back in for the variable in the resulting expressions.
• Solve for the angle.

Example 12: Solve the Trigonometric Equation in Linear Form

Solve the equation exactly: [latex]2\cos \theta -3=-5,0\le \theta <2\pi [/latex].

[latex]\begin{gathered}2\cos \theta -3=-5 \\ \cos \theta =-2 \\ \cos \theta =-1 \\ \theta =\pi \end{gathered}[/latex]

Solve exactly the following linear equation on the interval [latex]\left[0,2\pi \right):2\sin x+1=0[/latex].

[latex]x=\frac{7\pi }{6},\frac{11\pi }{6}[/latex]

Solve Trigonometric Equations Using a Calculator

Not all functions can be solved exactly using only the unit circle. When we must solve an equation involving an angle other than one of the special angles, we will need to use a calculator. Make sure it is set to the proper mode, either degrees or radians, depending on the criteria of the given problem.

Example 13: Using a Calculator to Solve a Trigonometric Equation Involving Sine

Use a calculator to solve the equation [latex]\sin \theta =0.8[/latex], where [latex]\theta [/latex] is in radians.

Make sure mode is set to radians. To find [latex]\theta [/latex], use the inverse sine function. On most calculators, you will need to push the 2 ND button and then the SIN button to bring up the [latex]{\sin }^{-1}[/latex] function. What is shown on the screen is [latex]{\sin}^{-1}[/latex](. The calculator is ready for the input within the parentheses. For this problem, we enter [latex]{\sin }^{-1}\left(0.8\right)[/latex], and press ENTER. Thus, to four decimals places,

[latex]{\sin }^{-1}\left(0.8\right)\approx 0.9273[/latex]

This is the solution in quadrant I. There is also a solution in quadrant II. To find this we subtract [latex]/pi - 0.9273 \approx 2.2143 [/latex]

The general solution is

[latex]\theta \approx 0.9273\pm 2\pi k \text{ and } \theta \approx 2.2143 \pm 2\pi k[/latex]

The angle measurement in degrees is

[latex]\begin{align} \theta &\approx {53.1}^{\circ } \\ \theta &\approx {180}^{\circ }-{53.1}^{\circ } \\ &\approx {126.9}^{\circ } \end{align}[/latex]

Analysis of the Solution

Note that a calculator will only return an angle in quadrants I or IV for the sine function, since that is the range of the inverse sine. The other angle is obtained by using [latex]\pi -\theta [/latex].

Example 14: Using a Calculator to Solve a Trigonometric Equation Involving Secant

Use a calculator to solve the equation [latex]\sec \theta =-4[/latex], giving your answer in radians.

We can begin with some algebra.

[latex]\begin{gathered}\sec \theta =-4\\ \frac{1}{\cos \theta }=-4\\ \cos \theta =-\frac{1}{4}\end{gathered}[/latex]

Check that the MODE is in radians. Now use the inverse cosine function.

[latex]\begin{gathered}{\cos }^{-1}\left(-\frac{1}{4}\right)\approx 1.8235 \\ \theta \approx 1.8235+2\pi k \end{gathered}[/latex]

Since [latex]\frac{\pi }{2}\approx 1.57[/latex] and [latex]\pi \approx 3.14[/latex], 1.8235 is between these two numbers, thus [latex]\theta \approx \text{1}\text{.8235}[/latex] is in quadrant II. Cosine is also negative in quadrant III. Note that a calculator will only return an angle in quadrants I or II for the cosine function, since that is the range of the inverse cosine.

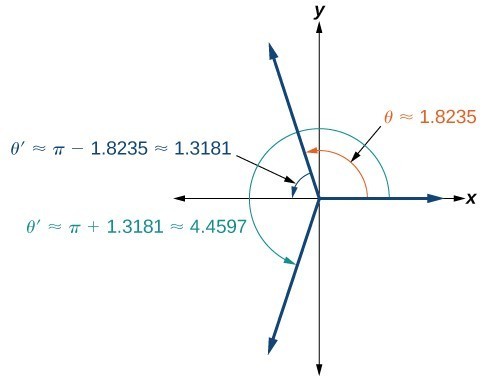
So, we also need to find the measure of the angle in quadrant III. In quadrant III, the reference angle is [latex]\theta \text{ }\text{ }\text{‘}\approx \pi -\text{1}\text{.8235}\approx \text{1}\text{.3181}\text{.}[/latex] The other solution in quadrant III is [latex]\theta \text{ }\text{ }\text{‘}\approx \pi +\text{1}\text{.3181}\approx \text{4}\text{.4597}\text{.}[/latex]

The solutions are [latex]\theta \approx 1.8235\pm 2\pi k[/latex] and [latex]\theta \approx 4.4597\pm 2\pi k[/latex].

Solve [latex]\cos \theta =-0.2[/latex].

[latex]\theta \approx 1.7722\pm 2\pi k[/latex] and [latex]\theta \approx 4.5110\pm 2\pi k[/latex]

Solving Equations Involving a Single Trigonometric Function

When we are given equations that involve only one of the six trigonometric functions, their solutions involve using algebraic techniques and the unit circle. We need to make several considerations when the equation involves trigonometric functions other than sine and cosine. Problems involving the reciprocals of the primary trigonometric functions need to be viewed from an algebraic perspective. In other words, we will write the reciprocal function, and solve for the angles using the function. Also, an equation involving the tangent function is slightly different from one containing a sine or cosine function. First, as we know, the period of tangent is [latex]\pi [/latex], not [latex]2\pi [/latex]. Further, the domain of tangent is all real numbers with the exception of odd integer multiples of [latex]\frac{\pi }{2}[/latex], unless, of course, a problem places its own restrictions on the domain.

Example 15: Solving a Problem Involving a Single Trigonometric Function

Solve the problem exactly: [latex]2{\sin }^{2}\theta -1=0,0\le \theta <2\pi [/latex].

As this problem is not easily factored, we will solve using the square root property. First, we use algebra to isolate [latex]\sin \theta [/latex]. Then we will find the angles.

[latex]\begin{gathered}2{\sin }^{2}\theta -1=0 \\ 2{\sin }^{2}\theta =1 \\ {\sin }^{2}\theta =\frac{1}{2} \\ \sqrt{{\sin }^{2}\theta }=\pm \sqrt{\frac{1}{2}} \\ \sin \theta =\pm \frac{1}{\sqrt{2}}=\pm \frac{\sqrt{2}}{2} \\ \theta =\frac{\pi }{4},\frac{3\pi }{4},\frac{5\pi }{4},\frac{7\pi }{4} \end{gathered}[/latex]

Example 16: Solving a Trigonometric Equation Involving Cosecant

Solve the following equation exactly: [latex]\csc \theta =-2,0\le \theta <4\pi [/latex].

We want all values of [latex]\theta [/latex] for which [latex]\csc \theta =-2[/latex] over the interval [latex]0\le \theta <4\pi [/latex].

[latex]\begin{gathered}\csc \theta =-2 \\ \frac{1}{\sin \theta }=-2 \\ \sin \theta =-\frac{1}{2} \\ \theta =\frac{7\pi }{6},\frac{11\pi }{6},\frac{19\pi }{6},\frac{23\pi }{6} \end{gathered}[/latex]

As [latex]\sin \theta =-\frac{1}{2}[/latex], notice that all four solutions are in the third and fourth quadrants.

Example 17: Solving an Equation Involving Tangent

Solve the equation exactly: [latex]\tan \left(\theta -\frac{\pi }{2}\right)=1,0\le \theta <2\pi [/latex].

Recall that the tangent function has a period of [latex]\pi [/latex]. On the interval [latex]\left[0,\pi \right)[/latex], and at the angle of [latex]\frac{\pi }{4}[/latex], the tangent has a value of 1. However, the angle we want is [latex]\left(\theta -\frac{\pi }{2}\right)[/latex]. Thus, if [latex]\tan \left(\frac{\pi }{4}\right)=1[/latex], then

[latex]\begin{gathered}\theta -\frac{\pi }{2}=\frac{\pi }{4}\\ \theta =\frac{3\pi }{4}\pm k\pi \end{gathered}[/latex]

Over the interval [latex]\left[0,2\pi \right)[/latex], we have two solutions:

[latex]\theta =\frac{3\pi }{4}\text{ and }\theta =\frac{3\pi }{4}+\pi =\frac{7\pi }{4}[/latex]

Find all solutions for [latex]\tan x=\sqrt{3}[/latex].

[latex]\frac{\pi }{3}\pm \pi k[/latex]

Example 18: Identify all Solutions to the Equation Involving Tangent

Identify all exact solutions to the equation [latex]2\left(\tan x+3\right)=5+\tan x,0\le x<2\pi [/latex].

We can solve this equation using only algebra. Isolate the expression [latex]\tan x[/latex] on the left side of the equals sign.

[latex]\begin{gathered} 2\left(\tan x\right)+2\left(3\right) =5+\tan x \\ 2\tan x+6 =5+\tan x \\ 2\tan x-\tan x =5 - 6 \\ \tan x =-1\end{gathered}[/latex]

There are two angles on the unit circle that have a tangent value of [latex]-1:\theta =\frac{3\pi }{4}[/latex] and [latex]\theta =\frac{7\pi }{4}[/latex].

Solving Trigonometric Equations in Quadratic Form

Solving a quadratic equation may be more complicated, but once again, we can use algebra as we would for any quadratic equation. Look at the pattern of the equation. Is there more than one trigonometric function in the equation, or is there only one? Which trigonometric function is squared? If there is only one function represented and one of the terms is squared, think about the standard form of a quadratic. Replace the trigonometric function with a variable such as [latex]x[/latex] or [latex]u[/latex]. If substitution makes the equation look like a quadratic equation, then we can use the same methods for solving quadratics to solve the trigonometric equations.

Example 19: Solving a Trigonometric Equation in Quadratic Form

Solve the equation exactly: [latex]{\cos }^{2}\theta +3\cos \theta -1=0,0\le \theta <2\pi[/latex].

We begin by using substitution and replacing cos [latex]\theta[/latex] with [latex]x[/latex]. It is not necessary to use substitution, but it may make the problem easier to solve visually. Let [latex]\cos \theta =x[/latex]. We have

[latex]{x}^{2}+3x - 1=0[/latex]

The equation cannot be factored, so we will use the quadratic formula [latex]x=\frac{-b\pm \sqrt{{b}^{2}-4ac}}{2a}[/latex].

[latex]\begin{align} x&=\frac{-3\pm \sqrt{{\left(-3\right)}^{2}-4\left(1\right)\left(-1\right)}}{2}&=\frac{-3\pm \sqrt{13}}{2} \end{align}[/latex]

Replace [latex]x[/latex] with [latex]\cos \theta[/latex], and solve. Thus,

[latex]\begin{gathered} \cos \theta =\frac{-3\pm \sqrt{13}}{2}\theta ={\cos }^{-1}\left(\frac{-3+\sqrt{13}}{2}\right)\end{gathered}[/latex]

Note that only the + sign is used. This is because we get an error when we solve [latex]\theta ={\cos }^{-1}\left(\frac{-3-\sqrt{13}}{2}\right)[/latex] on a calculator, since the domain of the inverse cosine function is [latex]\left[-1,1\right][/latex]. However, there is a second solution:

[latex]\begin{align}\theta &={\cos }^{-1}\left(\frac{-3+\sqrt{13}}{2}\right) \\ &\approx 1.26 \end{align}[/latex]

This terminal side of the angle lies in quadrant I. Since cosine is also positive in quadrant IV, the second solution is

[latex]\begin{align}\theta &=2\pi -{\cos }^{-1}\left(\frac{-3+\sqrt{13}}{2}\right) \\ &\approx 5.02 \end{align}[/latex]

Example 20: Solving a Trigonometric Equation in Quadratic Form by Factoring

Solve the equation exactly: [latex]2{\sin }^{2}\theta -5\sin \theta +3=0,0\le \theta \le 2\pi[/latex].

Using grouping, this quadratic can be factored. Either make the real substitution, [latex]\sin \theta =u[/latex], or imagine it, as we factor:

[latex]\begin{gathered}2{\sin }^{2}\theta -5\sin \theta +3=0 \\ \left(2\sin \theta -3\right)\left(\sin \theta -1\right)=0 \end{gathered}[/latex]

Now set each factor equal to zero.

[latex]\begin{gathered}2\sin \theta -3=0 \\ 2\sin \theta =3 \\ \sin \theta =\frac{3}{2} \\ \text{ } \\ \sin \theta -1=0 \\ \sin \theta =1 \end{gathered}[/latex]

Next solve for [latex]\theta :\sin \theta \ne \frac{3}{2}[/latex], as the range of the sine function is [latex]\left[-1,1\right][/latex]. However, [latex]\sin \theta =1[/latex], giving the solution [latex]\theta =\frac{\pi }{2}[/latex].

Make sure to check all solutions on the given domain as some factors have no solution.

Solve [latex]{\sin }^{2}\theta =2\cos \theta +2,0\le \theta \le 2\pi[/latex]. [Hint: Make a substitution to express the equation only in terms of cosine.]

[latex]\cos \theta =-1,\theta =\pi [/latex]

Example 21: Solving a Trigonometric Equation Using Algebra

Solve exactly:

[latex]2{\sin }^{2}\theta +\sin \theta =0;0\le \theta <2\pi[/latex]

This problem should appear familiar as it is similar to a quadratic. Let [latex]\sin \theta =x[/latex]. The equation becomes [latex]2{x}^{2}+x=0[/latex]. We begin by factoring:

[latex]\begin{gathered}2{x}^{2}+x=0\\ x\left(2x+1\right)=0\end{gathered}[/latex]

Set each factor equal to zero.

[latex]\begin{gathered}x=0 \\ 2x+1=0 \\ x=-\frac{1}{2} \end{gathered}[/latex]

Then, substitute back into the equation the original expression [latex]\sin \theta[/latex] for [latex]x[/latex]. Thus,

[latex]\begin{gathered}\sin \theta =0 \\ \theta =0,\pi \\ \text{ } \\ \sin \theta =-\frac{1}{2} \\ \theta =\frac{7\pi }{6},\frac{11\pi }{6} \end{gathered}[/latex]

The solutions within the domain [latex]0\le \theta <2\pi[/latex] are [latex]\theta =0,\pi ,\frac{7\pi }{6},\frac{11\pi }{6}[/latex].

If we prefer not to substitute, we can solve the equation by following the same pattern of factoring and setting each factor equal to zero.

[latex]\begin{gathered}2{\sin }^{2}\theta +\sin \theta =0 \\ \sin \theta \left(2\sin \theta +1\right)=0 \\ \sin \theta =0 \\ \theta =0,\pi \\ \text{ } \\ 2\sin \theta +1=0 \\ 2\sin \theta =-1 \\ \sin \theta =-\frac{1}{2} \\ \theta =\frac{7\pi }{6},\frac{11\pi }{6} \end{gathered}[/latex]

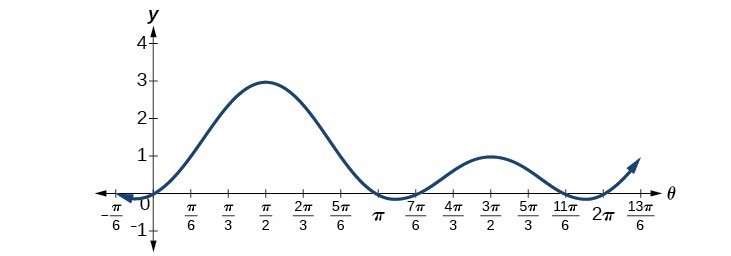
We can see the solutions on the graph in Figure 3. On the interval [latex]0\le \theta <2\pi[/latex], the graph crosses the x- axis four times, at the solutions noted. Notice that trigonometric equations that are in quadratic form can yield up to four solutions instead of the expected two that are found with quadratic equations. In this example, each solution (angle) corresponding to a positive sine value will yield two angles that would result in that value.

We can verify the solutions on the unit circle in Sum and Difference Identities as well.

Example 22: Solving a Trigonometric Equation Quadratic in Form

Solve the equation quadratic in form exactly: [latex]2{\sin }^{2}\theta -3\sin \theta +1=0,0\le \theta <2\pi[/latex].

We can factor using grouping. Solution values of [latex]\theta[/latex] can be found on the unit circle:

[latex]\begin{gathered}\left(2\sin \theta -1\right)\left(\sin \theta -1\right)=0 \\ 2\sin \theta -1=0 \\ \sin \theta =\frac{1}{2} \\ \theta =\frac{\pi }{6},\frac{5\pi }{6} \\ \text{ } \\ \sin \theta =1 \\ \theta =\frac{\pi }{2} \end{gathered}[/latex]

Solve the quadratic equation [latex]2{\cos }^{2}\theta +\cos \theta =0[/latex].

[latex]\frac{\pi }{2},\frac{2\pi }{3},\frac{4\pi }{3},\frac{3\pi }{2}[/latex]

Key Concepts

• An inverse function is one that “undoes” another function. The domain of an inverse function is the range of the original function and the range of an inverse function is the domain of the original function.
• Because the trigonometric functions are not one-to-one on their natural domains, inverse trigonometric functions are defined for restricted domains.
• For any trigonometric function [latex]f(x)[/latex], if [latex]x=f^{−1}(y)[/latex], then [latex]f(x)=y[/latex]. However, [latex]f(x)=y[/latex] only implies [latex]x=f^{−1}(y)[/latex] if x is in the restricted domain of f .
• Special angles are the outputs of inverse trigonometric functions for special input values; for example, [latex]\frac{\pi}{4}=\tan^{−1}( 1 )\text{ and }\frac{\pi}{6}=\sin^{−1}(\frac{1}{2})[/latex].
• A calculator will return an angle within the restricted domain of the original trigonometric function.
• Inverse functions allow us to find an angle when given two sides of a right triangle.
• In function composition, if the inside function is an inverse trigonometric function, then there are exact expressions; for example, [latex]\sin\left(\cos^{−1}\left(x\right)\right)=\sqrt{1−x^{2}}[/latex].
• If the inside function is a trigonometric function, then the only possible combinations are [latex]\sin^{−1}\left(\cos x\right)=\frac{\pi}{2}−x[/latex] if [latex]0\leq x\leq\pi[/latex] and [latex]\cos^{−1}\left(\sin x\right)=\frac{\pi}{2}−x[/latex] if [latex]−\frac{\pi}{2}\leq x \leq\frac{\pi}{2}[/latex].
• When evaluating the composition of a trigonometric function with an inverse trigonometric function, draw a reference triangle to assist in determining the ratio of sides that represents the output of the trigonometric function.
• When evaluating the composition of a trigonometric function with an inverse trigonometric function, you may use trig identities to assist in determining the ratio of sides.
• When solving linear trigonometric equations, we can use algebraic techniques just as we do solving algebraic equations. Look for patterns, like the difference of squares, quadratic form, or an expression that lends itself well to substitution.
• Equations involving a single trigonometric function can be solved or verified using the unit circle.
• We can also solve trigonometric equations using a graphing calculator.
• Many equations appear quadratic in form. We can use substitution to make the equation appear simpler, and then use the same techniques we use solving an algebraic quadratic: factoring, the quadratic formula, etc.
• Precalculus. Authored by : OpenStax College. Provided by : OpenStax. Located at : http://cnx.org/contents/[email protected]:1/Preface . License : CC BY: Attribution

2.1 The Rectangular Coordinate Systems and Graphs

x -intercept is ( 4 , 0 ) ; ( 4 , 0 ) ; y- intercept is ( 0 , 3 ) . ( 0 , 3 ) .

125 = 5 5 125 = 5 5

( − 5 , 5 2 ) ( − 5 , 5 2 )

2.2 Linear Equations in One Variable

x = −5 x = −5

x = −3 x = −3

x = 10 3 x = 10 3

x = 1 x = 1

x = − 7 17 . x = − 7 17 . Excluded values are x = − 1 2 x = − 1 2 and x = − 1 3 . x = − 1 3 .

x = 1 3 x = 1 3

m = − 2 3 m = − 2 3

y = 4 x −3 y = 4 x −3

x + 3 y = 2 x + 3 y = 2

Horizontal line: y = 2 y = 2

Parallel lines: equations are written in slope-intercept form.

y = 5 x + 3 y = 5 x + 3

2.3 Models and Applications

C = 2.5 x + 3 , 650 C = 2.5 x + 3 , 650

L = 37 L = 37 cm, W = 18 W = 18 cm

2.4 Complex Numbers

−24 = 0 + 2 i 6 −24 = 0 + 2 i 6

( 3 −4 i ) − ( 2 + 5 i ) = 1 −9 i ( 3 −4 i ) − ( 2 + 5 i ) = 1 −9 i

5 2 − i 5 2 − i

18 + i 18 + i

−3 −4 i −3 −4 i

2.5 Quadratic Equations

( x − 6 ) ( x + 1 ) = 0 ; x = 6 , x = − 1 ( x − 6 ) ( x + 1 ) = 0 ; x = 6 , x = − 1

( x −7 ) ( x + 3 ) = 0 , ( x −7 ) ( x + 3 ) = 0 , x = 7 , x = 7 , x = −3. x = −3.

( x + 5 ) ( x −5 ) = 0 , ( x + 5 ) ( x −5 ) = 0 , x = −5 , x = −5 , x = 5. x = 5.

( 3 x + 2 ) ( 4 x + 1 ) = 0 , ( 3 x + 2 ) ( 4 x + 1 ) = 0 , x = − 2 3 , x = − 2 3 , x = − 1 4 x = − 1 4

x = 0 , x = −10 , x = −1 x = 0 , x = −10 , x = −1

x = 4 ± 5 x = 4 ± 5

x = 3 ± 22 x = 3 ± 22

x = − 2 3 , x = − 2 3 , x = 1 3 x = 1 3

2.6 Other Types of Equations

{ −1 } { −1 }

0 , 0 , 1 2 , 1 2 , − 1 2 − 1 2

1 ; 1 ; extraneous solution − 2 9 − 2 9

−2 ; −2 ; extraneous solution −1 −1

−1 , −1 , 3 2 3 2

−3 , 3 , − i , i −3 , 3 , − i , i

2 , 12 2 , 12

−1 , −1 , 0 0 is not a solution.

2.7 Linear Inequalities and Absolute Value Inequalities

[ −3 , 5 ] [ −3 , 5 ]

( − ∞ , −2 ) ∪ [ 3 , ∞ ) ( − ∞ , −2 ) ∪ [ 3 , ∞ )

x < 1 x < 1

x ≥ −5 x ≥ −5

( 2 , ∞ ) ( 2 , ∞ )

[ − 3 14 , ∞ ) [ − 3 14 , ∞ )

6 < x ≤ 9 ​ or ( 6 , 9 ] 6 < x ≤ 9 ​ or ( 6 , 9 ]

( − 1 8 , 1 2 ) ( − 1 8 , 1 2 )

| x −2 | ≤ 3 | x −2 | ≤ 3

k ≤ 1 k ≤ 1 or k ≥ 7 ; k ≥ 7 ; in interval notation, this would be ( − ∞ , 1 ] ∪ [ 7 , ∞ ) . ( − ∞ , 1 ] ∪ [ 7 , ∞ ) .

2.1 Section Exercises

Answers may vary. Yes. It is possible for a point to be on the x -axis or on the y -axis and therefore is considered to NOT be in one of the quadrants.

The y -intercept is the point where the graph crosses the y -axis.

The x- intercept is ( 2 , 0 ) ( 2 , 0 ) and the y -intercept is ( 0 , 6 ) . ( 0 , 6 ) .

The x- intercept is ( 2 , 0 ) ( 2 , 0 ) and the y -intercept is ( 0 , −3 ) . ( 0 , −3 ) .

The x- intercept is ( 3 , 0 ) ( 3 , 0 ) and the y -intercept is ( 0 , 9 8 ) . ( 0 , 9 8 ) .

y = 4 − 2 x y = 4 − 2 x

y = 5 − 2 x 3 y = 5 − 2 x 3

y = 2 x − 4 5 y = 2 x − 4 5

d = 74 d = 74

d = 36 = 6 d = 36 = 6

d ≈ 62.97 d ≈ 62.97

( 3 , − 3 2 ) ( 3 , − 3 2 )

( 2 , −1 ) ( 2 , −1 )

( 0 , 0 ) ( 0 , 0 )

y = 0 y = 0

not collinear

A: ( −3 , 2 ) , B: ( 1 , 3 ) , C: ( 4 , 0 ) A: ( −3 , 2 ) , B: ( 1 , 3 ) , C: ( 4 , 0 )

d = 8.246 d = 8.246

d = 5 d = 5

( −3 , 4 ) ( −3 , 4 )

x = 0          y = −2 x = 0          y = −2

x = 0.75 y = 0 x = 0.75 y = 0

x = − 1.667 y = 0 x = − 1.667 y = 0

15 − 11.2 = 3.8 mi 15 − 11.2 = 3.8 mi shorter

6 .0 42 6 .0 42

Midpoint of each diagonal is the same point ( 2 , –2 ) ( 2 , –2 ) . Note this is a characteristic of rectangles, but not other quadrilaterals.

2.2 Section Exercises

It means they have the same slope.

The exponent of the x x variable is 1. It is called a first-degree equation.

If we insert either value into the equation, they make an expression in the equation undefined (zero in the denominator).

x = 2 x = 2

x = 2 7 x = 2 7

x = 6 x = 6

x = 3 x = 3

x = −14 x = −14

x ≠ −4 ; x ≠ −4 ; x = −3 x = −3

x ≠ 1 ; x ≠ 1 ; when we solve this we get x = 1 , x = 1 , which is excluded, therefore NO solution

x ≠ 0 ; x ≠ 0 ; x = − 5 2 x = − 5 2

y = − 4 5 x + 14 5 y = − 4 5 x + 14 5

y = − 3 4 x + 2 y = − 3 4 x + 2

y = 1 2 x + 5 2 y = 1 2 x + 5 2

y = −3 x − 5 y = −3 x − 5

y = 7 y = 7

y = −4 y = −4

8 x + 5 y = 7 8 x + 5 y = 7

Perpendicular

m = − 9 7 m = − 9 7

m = 3 2 m = 3 2

m 1 = − 1 3 ,   m 2 = 3 ;   Perpendicular . m 1 = − 1 3 ,   m 2 = 3 ;   Perpendicular .

y = 0.245 x − 45.662. y = 0.245 x − 45.662. Answers may vary. y min = −50 , y max = −40 y min = −50 , y max = −40

y = − 2.333 x + 6.667. y = − 2.333 x + 6.667. Answers may vary. y min = −10 ,   y max = 10 y min = −10 ,   y max = 10

y = − A B x + C B y = − A B x + C B

The slope for  ( −1 , 1 ) to  ( 0 , 4 ) is  3. The slope for  ( −1 , 1 ) to  ( 2 , 0 ) is  − 1 3 . The slope for  ( 2 , 0 ) to  ( 3 , 3 ) is  3. The slope for  ( 0 , 4 ) to  ( 3 , 3 ) is  − 1 3 . The slope for  ( −1 , 1 ) to  ( 0 , 4 ) is  3. The slope for  ( −1 , 1 ) to  ( 2 , 0 ) is  − 1 3 . The slope for  ( 2 , 0 ) to  ( 3 , 3 ) is  3. The slope for  ( 0 , 4 ) to  ( 3 , 3 ) is  − 1 3 .

Yes they are perpendicular.

2.3 Section Exercises

Answers may vary. Possible answers: We should define in words what our variable is representing. We should declare the variable. A heading.

2 , 000 − x 2 , 000 − x

v + 10 v + 10

Ann: 23 ; 23 ; Beth: 46 46

20 + 0.05 m 20 + 0.05 m

90 + 40 P 90 + 40 P

50 , 000 − x 50 , 000 − x

She traveled for 2 h at 20 mi/h, or 40 miles.

$5,000 at 8% and $15,000 at 12%

B = 100 + .05 x B = 100 + .05 x

R = 9 R = 9

r = 4 5 r = 4 5 or 0.8

W = P − 2 L 2 = 58 − 2 ( 15 ) 2 = 14 W = P − 2 L 2 = 58 − 2 ( 15 ) 2 = 14

f = p q p + q = 8 ( 13 ) 8 + 13 = 104 21 f = p q p + q = 8 ( 13 ) 8 + 13 = 104 21

m = − 5 4 m = − 5 4

h = 2 A b 1 + b 2 h = 2 A b 1 + b 2

length = 360 ft; width = 160 ft

A = 88 in . 2 A = 88 in . 2

h = V π r 2 h = V π r 2

r = V π h r = V π h

C = 12 π C = 12 π

2.4 Section Exercises

Add the real parts together and the imaginary parts together.

Possible answer: i i times i i equals -1, which is not imaginary.

−8 + 2 i −8 + 2 i

14 + 7 i 14 + 7 i

− 23 29 + 15 29 i − 23 29 + 15 29 i

8 − i 8 − i

−11 + 4 i −11 + 4 i

2 −5 i 2 −5 i

6 + 15 i 6 + 15 i

−16 + 32 i −16 + 32 i

−4 −7 i −4 −7 i

2 − 2 3 i 2 − 2 3 i

4 − 6 i 4 − 6 i

2 5 + 11 5 i 2 5 + 11 5 i

1 + i 3 1 + i 3

( 3 2 + 1 2 i ) 6 = −1 ( 3 2 + 1 2 i ) 6 = −1

5 −5 i 5 −5 i

9 2 − 9 2 i 9 2 − 9 2 i

2.5 Section Exercises

It is a second-degree equation (the highest variable exponent is 2).

We want to take advantage of the zero property of multiplication in the fact that if a ⋅ b = 0 a ⋅ b = 0 then it must follow that each factor separately offers a solution to the product being zero: a = 0 o r b = 0. a = 0 o r b = 0.

One, when no linear term is present (no x term), such as x 2 = 16. x 2 = 16. Two, when the equation is already in the form ( a x + b ) 2 = d . ( a x + b ) 2 = d .

x = 6 , x = 6 , x = 3 x = 3

x = − 5 2 , x = − 5 2 , x = − 1 3 x = − 1 3

x = 5 , x = 5 , x = −5 x = −5

x = − 3 2 , x = − 3 2 , x = 3 2 x = 3 2

x = −2 , 3 x = −2 , 3

x = 0 , x = 0 , x = − 3 7 x = − 3 7

x = −6 , x = −6 , x = 6 x = 6

x = 6 , x = 6 , x = −4 x = −4

x = 1 , x = 1 , x = −2 x = −2

x = −2 , x = −2 , x = 11 x = 11

z = 2 3 , z = 2 3 , z = − 1 2 z = − 1 2

x = 3 ± 17 4 x = 3 ± 17 4

One rational

Two real; rational

x = − 1 ± 17 2 x = − 1 ± 17 2

x = 5 ± 13 6 x = 5 ± 13 6

x = − 1 ± 17 8 x = − 1 ± 17 8

x ≈ 0.131 x ≈ 0.131 and x ≈ 2.535 x ≈ 2.535

x ≈ − 6.7 x ≈ − 6.7 and x ≈ 1.7 x ≈ 1.7

a x 2 + b x + c = 0 x 2 + b a x = − c a x 2 + b a x + b 2 4 a 2 = − c a + b 4 a 2 ( x + b 2 a ) 2 = b 2 − 4 a c 4 a 2 x + b 2 a = ± b 2 − 4 a c 4 a 2 x = − b ± b 2 − 4 a c 2 a a x 2 + b x + c = 0 x 2 + b a x = − c a x 2 + b a x + b 2 4 a 2 = − c a + b 4 a 2 ( x + b 2 a ) 2 = b 2 − 4 a c 4 a 2 x + b 2 a = ± b 2 − 4 a c 4 a 2 x = − b ± b 2 − 4 a c 2 a

x ( x + 10 ) = 119 ; x ( x + 10 ) = 119 ; 7 ft. and 17 ft.

maximum at x = 70 x = 70

The quadratic equation would be ( 100 x −0.5 x 2 ) − ( 60 x + 300 ) = 300. ( 100 x −0.5 x 2 ) − ( 60 x + 300 ) = 300. The two values of x x are 20 and 60.

2.6 Section Exercises

This is not a solution to the radical equation, it is a value obtained from squaring both sides and thus changing the signs of an equation which has caused it not to be a solution in the original equation.

He or she is probably trying to enter negative 9, but taking the square root of −9 −9 is not a real number. The negative sign is in front of this, so your friend should be taking the square root of 9, cubing it, and then putting the negative sign in front, resulting in −27. −27.

A rational exponent is a fraction: the denominator of the fraction is the root or index number and the numerator is the power to which it is raised.

x = 81 x = 81

x = 17 x = 17

x = 8 ,     x = 27 x = 8 ,     x = 27

x = −2 , 1 , −1 x = −2 , 1 , −1

y = 0 ,     3 2 ,     − 3 2 y = 0 ,     3 2 ,     − 3 2

m = 1 , −1 m = 1 , −1

x = 2 5 , ±3 i x = 2 5 , ±3 i

x = 32 x = 32

t = 44 3 t = 44 3

x = −2 x = −2

x = 4 , −4 3 x = 4 , −4 3

x = − 5 4 , 7 4 x = − 5 4 , 7 4

x = 3 , −2 x = 3 , −2

x = 1 , −1 , 3 , -3 x = 1 , −1 , 3 , -3

x = 2 , −2 x = 2 , −2

x = 1 , 5 x = 1 , 5

x ≥ 0 x ≥ 0

x = 4 , 6 , −6 , −8 x = 4 , 6 , −6 , −8

2.7 Section Exercises

When we divide both sides by a negative it changes the sign of both sides so the sense of the inequality sign changes.

( − ∞ , ∞ ) ( − ∞ , ∞ )

We start by finding the x -intercept, or where the function = 0. Once we have that point, which is ( 3 , 0 ) , ( 3 , 0 ) , we graph to the right the straight line graph y = x −3 , y = x −3 , and then when we draw it to the left we plot positive y values, taking the absolute value of them.

( − ∞ , 3 4 ] ( − ∞ , 3 4 ]

[ − 13 2 , ∞ ) [ − 13 2 , ∞ )

( − ∞ , 3 ) ( − ∞ , 3 )

( − ∞ , − 37 3 ] ( − ∞ , − 37 3 ]

All real numbers ( − ∞ , ∞ ) ( − ∞ , ∞ )

( − ∞ , − 10 3 ) ∪ ( 4 , ∞ ) ( − ∞ , − 10 3 ) ∪ ( 4 , ∞ )

( − ∞ , −4 ] ∪ [ 8 , + ∞ ) ( − ∞ , −4 ] ∪ [ 8 , + ∞ )

No solution

( −5 , 11 ) ( −5 , 11 )

[ 6 , 12 ] [ 6 , 12 ]

[ −10 , 12 ] [ −10 , 12 ]

x > − 6 and x > − 2 Take the intersection of two sets . x > − 2 ,   ( − 2 , + ∞ ) x > − 6 and x > − 2 Take the intersection of two sets . x > − 2 ,   ( − 2 , + ∞ )

x < − 3   or   x ≥ 1 Take the union of the two sets . ( − ∞ , − 3 ) ∪ ​ ​ [ 1 , ∞ ) x < − 3   or   x ≥ 1 Take the union of the two sets . ( − ∞ , − 3 ) ∪ ​ ​ [ 1 , ∞ )

( − ∞ , −1 ) ∪ ( 3 , ∞ ) ( − ∞ , −1 ) ∪ ( 3 , ∞ )

[ −11 , −3 ] [ −11 , −3 ]

It is never less than zero. No solution.

Where the blue line is above the orange line; point of intersection is x = − 3. x = − 3.

( − ∞ , −3 ) ( − ∞ , −3 )

Where the blue line is above the orange line; always. All real numbers.

( − ∞ , − ∞ ) ( − ∞ , − ∞ )

( −1 , 3 ) ( −1 , 3 )

( − ∞ , 4 ) ( − ∞ , 4 )

{ x | x < 6 } { x | x < 6 }

{ x | −3 ≤ x < 5 } { x | −3 ≤ x < 5 }

( −2 , 1 ] ( −2 , 1 ]

( − ∞ , 4 ] ( − ∞ , 4 ]

Where the blue is below the orange; always. All real numbers. ( − ∞ , + ∞ ) . ( − ∞ , + ∞ ) .

Where the blue is below the orange; ( 1 , 7 ) . ( 1 , 7 ) .

x = 2 , − 4 5 x = 2 , − 4 5

( −7 , 5 ] ( −7 , 5 ]

80 ≤ T ≤ 120 1 , 600 ≤ 20 T ≤ 2 , 400 80 ≤ T ≤ 120 1 , 600 ≤ 20 T ≤ 2 , 400

[ 1 , 600 , 2 , 400 ] [ 1 , 600 , 2 , 400 ]

Review Exercises

x -intercept: ( 3 , 0 ) ; ( 3 , 0 ) ; y -intercept: ( 0 , −4 ) ( 0 , −4 )

y = 5 3 x + 4 y = 5 3 x + 4

72 = 6 2 72 = 6 2

620.097 620.097

midpoint is ( 2 , 23 2 ) ( 2 , 23 2 )

x = 4 x = 4

x = 12 7 x = 12 7

y = 1 6 x + 4 3 y = 1 6 x + 4 3

y = 2 3 x + 6 y = 2 3 x + 6

females 17, males 56

x = − 3 4 ± i 47 4 x = − 3 4 ± i 47 4

horizontal component −2 ; −2 ; vertical component −1 −1

7 + 11 i 7 + 11 i

−16 − 30 i −16 − 30 i

−4 − i 10 −4 − i 10

x = 7 − 3 i x = 7 − 3 i

x = −1 , −5 x = −1 , −5

x = 0 , 9 7 x = 0 , 9 7

x = 10 , −2 x = 10 , −2

x = − 1 ± 5 4 x = − 1 ± 5 4

x = 2 5 , − 1 3 x = 2 5 , − 1 3

x = 5 ± 2 7 x = 5 ± 2 7

x = 0 , 256 x = 0 , 256

x = 0 , ± 2 x = 0 , ± 2

x = 11 2 , −17 2 x = 11 2 , −17 2

[ − 10 3 , 2 ] [ − 10 3 , 2 ]

( − 4 3 , 1 5 ) ( − 4 3 , 1 5 )

Where the blue is below the orange line; point of intersection is x = 3.5. x = 3.5.

( 3.5 , ∞ ) ( 3.5 , ∞ )

Practice Test

y = 3 2 x + 2 y = 3 2 x + 2

( 0 , −3 ) ( 0 , −3 ) ( 4 , 0 ) ( 4 , 0 )

( − ∞ , 9 ] ( − ∞ , 9 ]

x = −15 x = −15

x ≠ −4 , 2 ; x ≠ −4 , 2 ; x = − 5 2 , 1 x = − 5 2 , 1

x = 3 ± 3 2 x = 3 ± 3 2

( −4 , 1 ) ( −4 , 1 )

y = −5 9 x − 2 9 y = −5 9 x − 2 9

y = 5 2 x − 4 y = 5 2 x − 4

5 13 − 14 13 i 5 13 − 14 13 i

x = 2 , − 4 3 x = 2 , − 4 3

x = 1 2 ± 2 2 x = 1 2 ± 2 2

x = 1 2 , 2 , −2 x = 1 2 , 2 , −2

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/algebra-and-trigonometry/pages/1-introduction-to-prerequisites

• Authors: Jay Abramson
• Publisher/website: OpenStax
• Book title: Algebra and Trigonometry
• Publication date: Feb 13, 2015
• Location: Houston, Texas
• Book URL: https://openstax.org/books/algebra-and-trigonometry/pages/1-introduction-to-prerequisites
• Section URL: https://openstax.org/books/algebra-and-trigonometry/pages/chapter-2

© Dec 8, 2021 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.