research projects for math

12 Math Project Ideas for Middle and High School Students

By János Perczel

Co-founder of Polygence, PhD from MIT

6 minute read

Mathematics serves as the foundation for most fields of science, such as physics, engineering, computer science, and economics. It equips you with critical problem-solving skills and the ability to break down complex problems into smaller, more manageable parts. It helps you avoid ambiguity and communicate in what is often called “the universal language,” so-called because its principles and concepts are the same worldwide. Beyond the fact that studying math can open up many career opportunities, some mathematicians also simply find beauty in the equations and proofs themselves.

In this post, we’ll give you ideas for different math research and passion projects and talk about how you can showcase your project.

Finding Your Math Passion Project Focus

Because math is so foundational in the sciences, there are many different directions you can take with your math passion project. Decide which topics within mathematics most speak to you. Maybe you’re more interested in how math is used in sports statistics, how you can harness math to solve global problems, or perhaps you’re curious about how math manifests itself in the physical realm. Once you find a topic that interests you, then you can begin to dive deeper. 

Keep in mind that some passion projects may require more technical skills, such as computer programming, whereas others may just explore theoretical concepts. The route you take is totally up to you and what you feel comfortable with, but don’t be afraid to pursue a project if you don’t currently have the technical skills for it. You can view it as an opportunity to learn new skills while also exploring a topic you’re excited about.

Do your own research through polygence

Polygence pairs you with an expert mentor in your area of passion. Together, you work to create a high quality research project that is uniquely your own.

12 Math Research and Passion Project Ideas

1. the mathematical properties of elections.

In recent years, there has been a lot of discussion about which election mechanism is most effective at achieving various goals. Proposed mechanisms in United States elections include majority elections, the electoral college, approval voting, and ranked-choice voting. All of these mechanisms have benefits and drawbacks, and it turns out that no perfect election mechanism exists. Look at the work being done by mathematicians to understand when elections fail, and what can be done to improve them. Choose the strongest mechanism and use evidence to support your claim.

Idea by math research mentor Grayson

2. Knot theory

A knot is simply a closed loop of string. Explore how mathematicians represent knots on a page. Learn how knots can be combined, and how to find knots that can't be created by combining other knots. You can learn techniques for determining whether or not two knots are distinct, in the sense that neither can be deformed to match the other. You can also study related objects, such as links and braids, and research the application of knots in the physical sciences.

Idea by math research mentor Alex

3. Bayesian basketball win prediction system

The Bayes’ Rule is crucial to modern statistics (as well as data science and machine learning). Using a Bayesian model to predict the probability distribution of basketball performance statistics, you can attempt to predict a team’s win and loss rate versus another team by drawing samples from these distributions and computing correlation to win or loss. Your project could be as simple or as complicated as you want. Based on your interest and comfort level, you could use simple normal models, mixture models, Gibbs sampling , and hidden Markov models. You can also learn how to code a fairly simple simulation in R or Python. Then, you’ll need to learn how to interpret the significance of statistical results and adjust results over time based on the success/failure of your model over time.

Idea by math research mentor Ari

4. Finding value in Major League Baseball free agency

Here’s another sports-related project idea. Every offseason, there are hundreds of professional baseball players who become free agents and can be signed by any team. This project involves determining which players might be a good "value" by deciding which statistics are most important to helping a team win relative to how players are generally paid. After deciding which stats are the most important, a ranked list of "value" can be produced based on expected salaries.

Idea by math research mentor Dante

5. Impact of climate change on drought risk

Are you interested in environmental economics, risk analysis, or water resource economics?

You can use historical data on precipitation, temperature, soil moisture, drought indicators, and meteorological models that simulate atmospheric conditions to train a machine-learning model that can assess the likelihood and intensity of droughts in different regions under different climate scenarios. You can also explore your assessments' potential adaptation strategies and policy implications. This project would require some skills in data processing, machine learning, and meteorological modeling.

Idea by math research mentor Jameson

Go beyond crunching numbers

Interested in Math? We'll match you with an expert mentor who will help you explore your next project.

6. Making machines make art 

You can program a computer to create an infinite number of images, music, video game levels, 3D objects, or text using techniques like neural style transfer, genetic algorithms, rejection sampling, Perlin noise , or Voronoi tessellation . Your challenge then is to create a functioning content generator that you could then showcase on a website, research conference, or even in a gallery exhibition.

Idea by math research mentor Sam

7. Measuring income inequality and social mobility

If you’re interested in the intersection of mathematics and public policy, here’s an idea. Use data from the World Bank, the Organization for Economic Co-operation and Development (OECD), and other sources to calculate the Gini coefficient and the intergenerational elasticity of income for different countries and regions over time. Explore the factors that influence these measures and their implications for economic development and social justice. You will need to have some skills in data collection, analysis, and visualization.

8. Rocket (fuel) science

Rockets are mainly made out of fuel. When the fuel burns, it gets heated and expelled out, producing thrust. Fuel is heavy and, for long-range space missions, we need to carry around the fuel for the rest of the mission the whole way. It is important that the fuel gives us the most bang for our buck (i.e., the most acceleration per unit of fuel). Compare the amount of fuel (weight) required to get to various celestial objects and back using current electric and chemical propulsion technologies . Then do a cost analysis and compare how long it would take.

Idea by math research mentor Derek

9. COVID-19 and the global financial crisis

It is shocking how the economic effects of COVID-19 have far outweighed the ones from the Global Financial Crisis in 2007-08 . How much is the difference in terms of employment? Production? Let's go to the data!

Idea by math research mentor Alberto

10. Modeling polarization in social networks

We've all seen or heard about nasty political arguments and echo chambers on social media, but how and why do these happen? To try and find out, construct a mathematical and/or computational model of how people with different opinions interact in a social network. When do people come to a consensus, and when do they become more strongly divided? How can we design social networks with these ideas in mind?

Idea by math research mentor Emily

11. The world of mathematics

The history of mathematics dates all the way back to the very first civilizations and followed throughout history all over the globe. This development leads us to our way of living and thinking today. Rarely taught in math courses, the origins of math can provide clear insight into the necessities of learning math and the broad applications that math has in the world. Conduct research on a chosen time period, location, or figure in mathematics and describe the impacts this innovation or innovator had on the development of math as we know it today.

Idea by math research mentor Shae

12. Simulating the stock market

Here’s an idea for a beginner-to-intermediate statistics and programming project centered around Monte Carlo simulations. Monte Carlo simulations are random methods for modeling the outcome of a complicated process. These methods are used in finance all the time. How could you code a program that uses the Monte Carlo technique to "simulate" the stock market? You will need some familiarity with statistics, basic finance, and basic programming in any language to complete this project.

Idea by math research mentor Sahil

Showcasing Your Math Passion Project

After you’ve done the hard work of completing your mathematics passion project, it’s also equally important to showcase your accomplishments . You can see that in many of the project ideas above, there is a clear topic, but how you want to present the project is open-ended. You could try to publish a research paper , create a podcast or infographic, or even create a visual representation of your concept. You’ll find that although many project ideas can simply be summarized in a paper, projects can also be showcased in other creative ways.

Polygence Scholars Are Also Passionate About

Examples of math passion projects completed by polygence students.

There are several examples of math projects Polygence students have completed through enrolling in our programs; we’ll highlight two here.

Ahmet's mathematical passion project offers detailed breakdowns of the first introduced quantum algorithm Deutsch-Jozsa, and the first quantum algorithm proven to be faster than classical algorithms, Grover’s Algorithm. It also includes a side-by-side comparison of the quantum algorithms and their classical counterparts. He uploaded his paper on Github and plans to submit it to an official publication soon.

Anna’s finance project provides an overview of topics related to personal finance, covering tax and benefits, tax-deferred savings, interest rates, cost of living, investing, insurance, and housing to help young adults manage their savings. To further her understanding of how different areas of finance influence one's life consumption, she created a life consumption plan for a hypothetical person and produced a paper. 

Getting Guidance and Support on Your Math Project

In this post, we covered how to find the right mathematics project for you, shared a dozen ideas for physics passion projects, and discussed how to showcase your project.

If you have a passion for math–or are generally curious about exploring mathematical concepts–and are interested in pursuing a passion project, Polygence’s programs are a great place to start. You’ll be paired with a mathematics research mentor with whom you’ll be able to meet one-on-one. Through these virtual mentorship sessions, your mentor can help you learn new concepts, troubleshoot issues you encounter along the way to bringing your math project to completion, and brainstorm with you on how to showcase your passion project .

Related Content

Math Competitions for High School Students

Why Research Mentorship is Critical for High School Students

Get an Edge in College Admissions Through Doing a Research Project

What Sets Polygence Apart from Other Research Programs for Middle and High School Students

More Than Just a Number: Showcasing Your Research on College Applications

How I Advocated for Students as an Admission Officer When They Wrote About Passion Projects

• Contact Info

DEPARTMENT OF MATHEMATICS

• Undergraduate

Undergraduate Research Projects

Northwestern undergraduates have opportunities to explore mathematics beyond our undergraduate curriculum by enrolling in math 399-0 independent study, working on a summer project, or writing a senior thesis under the supervision of a faculty member. below are descriptions of projects that our faculty have proposed.  students interested in one of these projects should contact the project adviser. this should not be taken to be an exhaustive list of all projects that are availalbe, nor as a list of the only faculty open to supervising such projects. contact the director of undergraduate studies  for additional guidance. these projects are only available to northwestern undergraduates., combinatorial structures in symplectic topology, eric zaslow, symplectic and contact geometry describe the mathematics of phase space for particles and light, respectively.  they therefore are the mathematical home for dynamical systems arising from physics.  a noteworthy structure within contact geometry is that of a legendrian surface, closely related to the wavefront of propagating light.  these subspaces sometimes have combinatorial descriptions via graphs.  the project explores how well the combinatorial descriptions can distinguish legendrian surfaces, just as in knot theory one might explore whether the jones polynomial can distinguish different knots. , prerequisites:  math 330-1 or math 331-1, math 342-0. recommended: math 308-0., complexity and periodicity, the simplest bi-infinite sequences in $\{0, 1\}^{\mathbb z}$ are the periodic sequences, where a single pattern is concatenated with itself infinitely often. at the opposite extreme are bi-infinite sequences containing every possible configuration of $0$'s and $1$'s. for periodic sequences, the number of substrings of length $n$ is bounded, while in the second case, all substrings appear and so there are $2^n$ substrings of length $n$. the growth rate of the possible patterns is a measurement of the complexity of the sequence, giving information about the sequence itself and describing objects encoded by the sequence. symbolic dynamics is the study of such sequences, associated dynamical systems, and their properties. an old theorem of morse and hedlund gives a simple relation between this measurement of complexity and periodicity: a bi-infinite sequence with entries in a finite alphabet $\mathcal a$ is periodic if and only if there exists some $n\in\mathbb n$ such that the sequence contains at most $n$ words of length $n$. however, as soon as we turn to higher dimensions, meaning a sequence in $\mathcal a^{\mathbb z^d}$ for some $d\geq 2$ rather than $d=1$, the relation between complexity and periodicity is no longer clear.  even defining what is meant by low complexity or periodicity is not clear.  this project will cover what is known in one dimension and then turn to understanding how to generalize these phenomena to higher dimensions.   prerequisite: math 320-3 or math 321-3., finite simple groups, ezra getzler, finite simple groups are the building blocks of finite groups. for any finite group $g$, there is a normal subgroup $h$ such that $g/h$ is a simple group: the simple groups are those groups with no nontrivial normal subgroups.  the abelian finite simple groups are the cyclic groups of prime order; in this sense, finite simple groups generalize the prime numbers.  one of the beautiful theorems of algebra is that the alternating groups $a_n$ (subgroups of the symmetric groups $s_n$) are simple for $n\geq 5$. in fact, $a_5$ is the smallest non-abelian finite simple group (its order is $60$). another series of finite simple groups was discovered by galois. let $\mathbb f$ be a field.  the group $sl_2(\mathbb f)$ is the group of all $2\times2$ matrices of determinant $1$. if we take $\mathbb f$ to be a finite field, we get a finite group; for example, we can take $\mathbb f=\mathbb f_p$, the field with $p$ elements. it is a nice exercise to check that $sl_2(\mathbb f_p)$ has $p^3-p$ elements. the center $z(sl_2(\mathbb f_p))$ of $sl_2(\mathbb f_p)$ is the set of matrices $\pm i$; this has two elements unless $p=2$. the group $psl_2(\mathbb f)$ is the quotient of $sl_2(\mathbb f)$ by its center $z(sl_2(\mathbb f))$: we see that $psl_2(\mathbb f_p)$ has order $(p^3-p)/2$ unless $p=2$. it turns out that $psl_2(\mathbb f_2)$ and $psl_2(\mathbb f_3)$ are isomorphic to $s_3$ and $a_4$, which are not simple, but $psl_2(\mathbb f_5)$ is isomorphic to $a_5$, the smallest nonabelian finite simple group, and $psl_2(\mathbb f_7)$, of order $168$, is the second smallest nonabelian finite simple group. (when $\mathbb f$ is the field of complex numbers, the group $psl_2(\mathbb c)$ is also very interesting, though of course it is not finite: it is isomorphic to the lorentz group of special relativity.)  the goal of this project is to learn about generalizations of this construction, which together with the alternating groups yield all but a finite number of the finite simple groups. (there are 26 missing ones called the sporadic simple groups that cannot be obtained in this way.) this mysterious link between geometry and algebra is hard to explain, but very important: much of what we know about the finite simple groups comes from the study of matrix groups over the complex numbers. prerequisite: math 330-3 or math 331-3., fourier series and representation theory, fourier series allow you to write a periodic function in terms of a basis of sines and cosines.  one way to think of this is to understand sines and cosines as the eigenfunctions of the second derivative operator – so fourier series generalize the spectral theorem of linear algebra in this sense.  there is another viewpoint that is useful:  periodic functions can be thought of as functions defined on a circle, which is itself a group.  the connection between group theory and fourier series runs deeper, and this is the subject of this project. moving up a dimension, functions on a sphere can be described in terms of spherical harmonics.  while the sphere is not a group, it is the orbit space of the unit vector in the vertical direction.  thus it can be constructed as a homogeneous space:  it is the group of rotations modulo the group of rotations around the vertical axis.  we can therefore access functions on the sphere via functions on the group of rotations.  the peter-weyl theorem describes the vector space of functions on the group in terms of its representation theory.  (a representation of a group is a vector space on which group elements act as linear transformations [e.g., matrices], consistent with their relations.)  the entries of matrix elements of the irreducible representations of the group play the role that sines and cosines did above.  indeed, we can combine sines and cosines into complex exponentials and these are the sole entries of the one-by-one matrices (characters) representing the abelian circle group.  finally, we will connect spherical harmonics to polynomial functions relevant to geometric structures described in the borel-weyl-bott theorem.  students will explore many examples along with learning the foundations of the theory. prerequisites:  math 351-0 or math 381-0., linear poisson geometry, santiago cañez , a poisson bracket is a type of operation which takes as input two functions and outputs some expression obtained by multiplying their derivatives, subject to some constraints. for instance, the standard poisson bracket of two functions $f,g$ on $\mathbb r^2$ is defined by $\{f,g\} =\frac{\partial f}{\partial x} \frac{\partial g}{\partial y} - \frac{\partial f}{\partial y} \frac{\partial g}{\partial x}$. such objects first arose in physics in order to describe the time evolution of mechanical systems, but have now found other uses as well. in particular, a linear poisson bracket on a vector space turns out to encode the same data as that of a lie algebra, another type of algebraic object which is ubiquitous in mathematics. this relation between linear poisson brackets and lie algebra structures allows one to study the same object from different perspectives; in particular, this allows one to better understand the notion of coadjoint orbits and the hidden structure within them., the goal of this project is to understand the relation between linear poisson brackets and lie algebras, and to use this relation to elucidate properties of coadjoint orbits. all of these structures are heavily used in physics, and gaining a deep understanding as to why depends on the relation described above. moreover, this project will bring in topics from many different areas of mathematics – analysis, group theory, and linear algebra – to touch on areas of modern research., prerequisites: math 320-1 or math 321-1, math 330-1 or math 331-1, math 334-0 or math 291-2., noncommutative topology, given a space $x$, one can consider various types of functions defined on $x$, say for instance continuous functions from $x$ to $\mathbb c$. the set $c(x)$ of all such functions often comes equipped with some additional structure itself, which allows for the study of various geometric or topological properties of $x$ in terms of the set of functions $c(x)$ instead. in particular, when $x$ is a compact hausdorff space, the set $c(x)$ of complex-valued continuous functions on $x$ has the structure of what is known as a commutative $c^*$-algebra, and the gelfand-naimark theorem asserts that all knowledge about $x$ can be recovered from that of $c(x)$. this then suggests that arbitrary non-commutative $c^*$-algebras can be viewed as describing functions on "noncommutative spaces," of the type which arise in various formulations of quantum mechanics. the goal of this project is to understand the relation between compact hausdorff spaces and commutative $c^*$-algebras, and see how the topological information encoded within $x$ is reflected in the algebraic  information encoded within $c(x)$. this duality between topological and algebraic data is at the core of many aspects of modern mathematics, and beautifully blends together concepts from analysis, algebra, and topology. the ultimate aim in this area is to see how much geometry and topology one can carry out using only algebraic means. prerequisites: math 330-2 or math 331-2, math 344-1., simple lie algebras, a lie algebra is a vector space equipped with a certain type of algebraic operation known as a lie bracket, which gives a way to measure how close two elements are to commuting with one another. for instance, the most basic example is that of the space of all $n \times n$ matrices, where the "bracket" operation takes two $n \times n$ matrices $a$ and $b$ and outputs the difference $ab-ba$; in this case the lie bracket of $a$ and $b$ is zero if and only if $a$ and $b$ commute in the usual sense. lie algebras arise in various contexts, and in particular are used to describe "infinitesimal symmetries" of physical systems. among all lie algebras are those referred to as being simple, which in a sense are the lie algebras from which all other lie algebras can be built. it turns out that one can encode the structure of a simple lie algebra in terms of purely combinatorial data, and that in particular one can classify simple lie algebras in terms of certain pictures known as dynkin diagrams. the goal of this project is to understand the classification of simple lie algebras in terms of dynkin diagrams. there are four main families of such lie algebras which describe matrices with special properties, as well as a few so-called exceptional lie algebras whose existence seems to come out of nowhere. such structures are now commonplace in modern physics, and their study continues to shed new light on various phenomena. prerequisites: math 330-2 or math 331-2, math 334-0 or math 291-2., the spectral theory of polygons, jared wunsch, we can study, for any domain the plane, the eigenfunctions of the laplace-operator (with boundary conditions) on this domain: these are the natural frequencies of vibration of this drum head. students might want to read mark kac's famous paper "can you hear the shape of a drum" as part of this project, and there is lots of fun mathematics associated to this classical question and its negative answer by gordon-webb-wolpert.   an ambitious direction that this could possibly head in would be the theory of diffraction of waves on surfaces. in the plane, this is a classical theory, going back to work of sommerfeld in the 1890's, but there's still a remarkable amount that we don't know.  the mathematical story is more or less as follows: a wave (i.e. a solution to the wave equation, which could be a sound or electromagnetic wave, or, with a slight change of point of view, the wavefunction of a quantum particle) is known to reflect nicely off a straight interface.  at a corner, however, something quite interesting happens, which is that the tip of the corner acts as a new point source of waves.  this is the phenomenon of diffraction, and is responsible for many fascinating effects in mathematical physics.  the student could learn the classical theory in the 2d context, starting with flat surfaces and possibly (if there is sufficient geometric background) curved ones, and then work on a novel project in one of a number of directions, which would touch current research in the field., prerequisites: math 320-1 or math 321-1, math 325-0 or math 382-0. more ambitious parts of this project might require math 410-1,2,3..

• Chair's Welcome
• General Information
• Strategic Plan
• MathJobs Postings
• Photo Album
• Make a Gift
• Department's History
• People Search
• Administration
• Retired Professors
• Postdocs/Res. Associates
• Instructors
• Graduate Students
• Research Interests
• Seminars & Colloquia
• Porcelli Lecture Series
• Federal Grants
• Undergraduate Program
• Placement and Credit
• Degree Requirements
• Contact an Advisor
• Programs and Clubs
• Scholarships and Awards
• Careers in Math
• Undergraduate Research
• Welcome & News
• Graduate Degrees
• Courses and Research
• 7000 Courses by Semester
• Prospective Students
• Teaching Assistantships
• GEAUX Orientation Program
• Advising and Registration
• Exam & Graduation Instructions
• Travel Funding
• Activities and Organizations
• Graduate Student Awards
• PhD Graduates
• High School Math Contest
• Math Circle Competition Team
• Math Circle Summer Camp
• Dual Enrollment
• Capstone Course
• Actuarial Club
• Assoc. for Women in Math
• LSU Math Club
• Student Colloquium
• Computing & IT
• Files To Geaux
• Journals (MathSciNet)
• Virtual Lab
• Emergency Information

Undergraduate Mathematics Projects

Undergraduate menu.

This page describes projects in the LSU Department of Mathematics in which undergraduate students are involved. Some of them may be seeking undergraduate participants. Return to the main page for undergraduate research .

Active Projects

Van kampen's obstruction and graph planarity, stochastic marine robotic control systems, bayesian machine learning, fourier analysis on finite fields, laplacian on periodic discrete graphs, modeling, analysis, and simulation of liquid crystals with applications in material science and biology.

• Mottram, N. J. & Newton, C. J. P., “Introduction to Q-tensor theory,” arXiv e-prints, 2014.
• Virga, E. G., “Variational Theories for Liquid Crystals,” Chapman and Hall, London, 1994, 8, 376.
• Ball, J. M., “Mathematics and liquid crystals,” Molecular Crystals and Liquid Crystals, Taylor & Francis, 2017, 647, 1-27.
• de Gennes, P. G. & Prost, J., “The Physics of Liquid Crystals,” Oxford Science Publication, 1995, 83.
• Lagerwall, J. P. & Scalia, G., “A new era for liquid crystal research: Applications of liquid crystals in soft matter nano-, bio- and microtechnology,” Current Applied Physics, 2012, 12, 1387-1412.

Flow Semigroups: Global Linearization of Nonlinear Problems

Nodal sets of eigenfunctions in balls, bethe equations for the gaudin model and wronskian relations, flat connections on riemann surfaces, control of dynamical systems with engineering applications.

Also see the Senior Design Project that Dr. Malisoff jointly advises.

Control of Marine Robots

Stochastic algorithms, a viral topology course, an online graphical user interface for electromagnetic waves in layered media, schrödinger operators on graphs, wave scattering by periodic structures: surface modes and resonance, math consultation clinic (mcc), past projects, explicit time-integration of a nonlinear string model, visualizing trends in teacher production using title ii data, how to design an automobile insurance product for autonomous vehicles, informetric indicators for citation networks, a variation of the stable marriage problem, quantitative nevanlinna-pick interpolation, predicting outcomes in college football using machine learning, local langlands correspondence for sl 2.

• Printable View

Undergraduate Research

Where to start:.

A good starting point is the Harvard College Undergraduate Research and Fellowships page. The Office of Undergraduate Research and Fellowships administers research programs for Harvard College undergraduates. Check out the website . Another resource is OCS , the Harvard Office of Career Services. It offers help on preparing a CV or cover letters and gives advice on how to network, interview, etc. Their website is here . Other Sources that can provide additional information on Scholarships, awards, and other grants:

• Committee on General Scholarships: more …
• Office of International Programs: more …
• Student Employment Office: more …

Independent study in Mathematics

Students who would like to do some independent study or a reading class please read the pamphlet page . about Math 91r.

THE ANNUAL OCS SUMMER OPPORTUNITIES FAIR

The Office of Career Services hosts summer programs to help you begin your summer search. Programs are both Harvard affiliated and public or private sector and include internships, public service, funding, travel, and research (URAF staff will be there to answer your questions!). Check out the website.

Harvard-Amgen Scholars program in Biotechnology

Check out the Harvard-Amgen Scholars Program Learn about Harvard’s Amgen 10-week intensive summer research program, one of ten Amgen U.S. programs that support research in biotechnology. The Harvard program includes faculty projects in FAS science departments, SEAS, the Wyss Institute for Biologically-inspired Engineering, and the School of Medicine, open to rising juniors and seniors in biotechnology-related fields.

PRIMO program

The Program for research in Markets and Organizations (PRIMO) is a 10-week program for Harvard undergraduates who wish to work closely with Harvard Business School faculty on research projects.

Harvard Undergraduate Research Events

• Wednesday, October 10, 12:00-1: 20 PM – Fall Undergraduate Research Spotlight. Come and meet Harvard undergraduate peers who will showcase their research projects and share their experiences conducting research at Harvard and abroad, followed by reception and deserts. Event program and list of presentations can be found here: here (pizza and desserts while supplies last). Free for Harvard students. Cabot Library 1st floor Discovery Bar.
• Wednesday, October 17, 12:00-1: 00 PM – Undergraduate Science Research Workshop. Workshop facilitators Dr. Margaret A. Lynch, (Assoc. Director of Science #Education) and Dr. Anna Babakhanyan, (Undergraduate Research Advisor) will help Harvard students learn about science research landscape at Harvard. You will learn about what kind of research (basic science vs. clinical, various research areas) is available at Harvard, where you can conduct research, the types of undergraduate research appointments, how to find a lab that fits, interviewing and more. In addition, the workshop will provide strategies for students to prepare for the Annual HUROS Fair, see below. No registration is required for this event (pizza while supplies last). Free for all Harvard students. Cabot Library first floor Discover Bar. More.

Outside Programs

Caltech always announces two summer research opportunities available to continuing undergraduate students. Examples: WAVE Student-Faculty Programs The WAVE Fellows program provides support for talented undergraduates intent on pursuing a Ph.D. to conduct a 10-week summer research project at Caltech. And then there is the AMGEN Scholars program. See the website for more details.

Johns Hopkins Summer 2018 Opportunities

The Johns Hopkins University Center for Talented Youth (CTY) is seeking instructors and teaching assistants for our summer programs. CTY offers challenging academic programs for highly talented elementary, middle, and high school students from across the country and around the world. Positions are available at residential and day sites at colleges, universities, and schools on the East and West coasts, as well as internationally in Hong Kong. Website

Math REU list from AMS

Mellon Mays opportunities awareness

The Mellon Mays Undergraduate Fellowship Program ( MMUF ) selects ten students in their sophomore year to join a tightly-knit research community during junior and senior years to conduct independent research in close collaboration with a faculty mentor. Join us at this information session to find out more about the program. MMUF exists to counter the under-representation of minority groups on college and university faculties nationwide through activities designed to encourage the pursuit of the Ph.D. in the humanities and core sciences.

MIT Amgen and UROP

You may be familiar with the Amgen Scholars Program, a summer research program in science and biotechnology. The Massachusetts Institute of Technology is a participant in the Amgen-UROP Scholars Program for a ninth year. UROP is MIT’s Undergraduate Research Opportunities Program. The mission of the Amgen-UROP Scholars Program is to provide students with a strong science research experience that may be pivotal in their undergraduate career, cultivate a passion for science, encourage the pursuit of graduate studies in the sciences, and stimulate interest in research and scientific careers. MIT is delighted to invite undergraduate students from other colleges and universities to join our research enterprise. We value the knowledge, experience, and enthusiasm these young scholars will bring to our campus and appreciate this opportunity to build a relationship with your faculty and campus.

More REU's, not only math

The National Science Foundation Research Experiences for Undergraduates (REU) NSF funds a large number of research opportunities for undergraduate students through its REU Sites program. An REU Site consists of a group of ten or so undergraduates who work in the research programs of the host institution. Each student is associated with a specific research project, where he/she works closely with the faculty and other researchers. Students are granted stipends and, in many cases, assistance with housing and travel. Undergraduate students supported with NSF funds must be citizens or permanent residents of the United States or its possessions. An REU Site may be at either the US or foreign location. By using the web page , search for an REU Site, you may examine opportunities in the subject areas supported by various NSF units. Also, you may search by keywords to identify sites in particular research areas or with certain features, such as a particular location. Students must contact the individual sites for information and application materials. NSF does not have application materials and does not select student participants. A contact person and contact information are listed for each site.

Here is a link with more information about summer programs for undergraduates at NSA: NSA The most math-related one is DSP, but those students who are more interested in computer science could also look at, say, CES SP. They are all paid with benefits and housing is covered. Note that application deadlines are pretty early (usually mid-October). The application process will involve usually a few interviews and a trip down to DC.

NSF Graduate Research Fellowships

US citizens and permanent residents who are planning to enter graduate school in the fall of 2019 are eligible (as are those in the first two years of such a graduate program, or who are returning to graduate school after being out for two or more years). The program solicitation contains full details. Information about the NSF Graduate Research Fellowship Program (GRFP) is here . The GRFP supports outstanding graduate students in NSF-supported science, technology, engineering, and mathematics disciplines who are pursuing research-based Masters and doctoral degrees at accredited United States institutions. The program provides up to three years of graduate education support, including an annual, 000 stipend. Applications for Mathematical Sciences topics are due October 26, 2018.

Pathway to Science

summer research listings from pathways to science.

Perimeter Institute

Applications are now being accepted for Perimeter Institute’s Undergraduate Theoretical Physics Summer Program. The program consists of two parts:

• Fully-Funded Two Week Summer School (May 27 to June 7, 2019) Students are immersed in Perimeter’s dynamic research environment — attending courses on cutting-edge topics in physics, learning new techniques to solve interesting problems, working on group research projects, and potentially even publishing their work. All meals, accommodation, and transportation provided
• Paid Research Internship (May 1 to August 30, 2019, negotiable) Students will work on projects alongside Perimeter researchers. Students will have the opportunity to develop their research skills and absorb the rich variety of talks, conferences, and events at the Perimeter Institute. Applicants can apply for the two-week summer school or for both the summer school and the research internship. Summer school and internship positions will be awarded by February 28, 2019. Selected interns will be contacted with the research projects topics. All research interns must complete the two-week summer school.

Apply online at perimeterinstitute.ca/undergrad

Stanford resident counselors

Stanford Pre-Collegiate Institutes is hiring Residential Counselors for the summer to work with the following courses:

• Cryptography (grades 9-10)
• Knot Theory (grades 10-11)
• Logic and Problem Solving (grades 8-9)
• Number Theory (grades 9-11)
• Excursions in Probability (grades 8-9)
• Discrete Mathematics (grades 9-10)
• The Mathematics of Symmetry (grades 10-11)
• Mathematical Puzzles and Games (grades 8-9)

Stanford Pre-Collegiate Institutes offers three-week sessions for academically talented high school students during June and July. Interested candidates can learn more about our positions and apply by visiting our employment website .

Summer Research 2019 at Nebraska

We are now accepting applications for the University of Nebraska’s 2019 Summer Research Program, and we’d like to encourage your students to apply. Details.

• Undergraduate Research

Undergraduate Research Projects

• Student intranet /
• Staff intranet

Department of Mathematics

Research projects

Find a postgraduate research project in your area of interest by exploring the research projects we offer in the Department of Mathematics.

Programme directors

If you are not sure which supervisors are the best match for your interests, contact the postgraduate programme directors:

• Sean Holman  (applied mathematics and numerical analysis)
• Olatunji Johnson (probability, statistics and financial mathematics)
• Marcus Tressl  (pure mathematics)

You can also get in touch with the postgraduate research leads through our  research themes  page.

Opportunities within the department are advertised by supervisors as either:

• Specific, well-defined individual projects : which you can apply for directly after contacting the named supervisor
• Research fields with suggestions for possible projects : where you can discuss a range of potential projects available in a specific area with the supervisor.

Choosing the right PhD project depends on matching your interests to those of your supervisor.

Our  research themes  page gives an overview of the research taking place in the Department and contacts for each area. Potential supervisors can also be contacted directly through the academic staff list . They will be able to tell you more about the type of projects they offer and/or you can suggest a research project yourself.

Please note that all PhD projects are eligible for funding via a variety of scholarships from the Department, the Faculty of Science and Engineering and/or the University; see our  funding page  for further details. All scholarships are awarded competitively by the relevant postgraduate funding committees.

Academics regularly apply for research grants and may therefore be able to offer funding for specific projects without requiring approval from these committees. Some specific funded projects are listed below, but many of our students instead arrive at a project through discussion with potential supervisors.

Specific, individual projects

Browse all of our specific, individual projects listed on FindAPhD:

Research field projects

In addition to individual projects listed on FindAPhD, we are also looking for postgraduate researchers for potential projects within a number of other research fields.

Browse these fields below and get in contact with the named supervisor to find out more..

Applied Mathematics and Numerical Analysis

Adaptive finite element approximation strategies.

Theme: Numerical analytics and scientific computing | Supervisor: David Silvester

I would be happy to supervise projects in the general area of efficient solution of elliptic and parabolic partial differential equations using finite elements. PhD projects would involve a mix of theoretical analysis and the development of proof-of-concept software written in MATLAB or Python. The design of robust and efficient error estimators is an open problem in computational fluid dynamics. Recent papers on this topic include Alex Bespalov, Leonardo Rocchi and David Silvester, T--IFISS: a toolbox for adaptive FEM computation, Computers and Mathematics with Applications, 81: 373--390, 2021. https://doi.org/10.1016/j.camwa.2020.03.005 Arbaz Khan, Catherine Powell and David Silvester, Robust a posteriori error estimators for mixed approximation of nearly incompressible elasticity, International Journal for Numerical Methods in Engineering, 119: 1--20, 2019. https://doi.org/10.1002/nme.6040 John Pearson, Jen Pestana and David Silvester, Refined saddle-point preconditioners for discretized Stokes problems, Numerische Mathematik, 138: 331--363, 2018. https://doi.org/10.1007/s00211-017-0908-4

Bayesian and machine learning methods for statistical inverse problems

Theme: Statistics, inverse problems, uncertainty quantification and data science | Supervisor: Simon Cotter

A range of projects are available on the topic of statistical inverse problems, in particular with application to problems in applied mathematics. Our aim is to construct new methods for the solution of statistical inverse problems, and to apply them to real problems from science, biology, engineering, etc. These may be more traditional Markov chain Monte Carlo (MCMC) methods, Piecewise-deterministic Markov processes (PDMPs), gradient flows (e.g. Stein gradient descent), or entirely new families of methods. Where possible the methods will be flexible and widely applicable, which will enable us to also apply them to real problems and datasets. Some recent applications involve cell matching in biology, and characterisation of physical properties of materials, for example the thermal properties of a manmade material, or the Young's modulus of a tendon or artery. The project will require the candidate to be proficient in a modern programming language (e.g. Python).

Complex deformations of biological soft tissues

Theme: Continuum mechanics | Supervisor: Tom Shearer , Andrew Hazel

The answers to many open questions in medicine depend on understanding the mechanical behaviour of biological soft tissues. For example, which tendon is most appropriate to replace the anterior cruciate ligament in reconstruction surgery? what causes the onset of aneurysms in the aorta? and how does the mechanics of the bladder wall affect afferent nerve firing? Current work at The University of Manchester seeks to understand how the microstructure of a biological soft tissue affects its macroscale mechanical properties. We have previously focused on developing non-linear elastic models of tendons and are now seeking to incorporate more complex physics such as viscoelasticity, and to consider other biological soft tissues, using our “in house” finite element software oomph-lib. The work will require development and implementation of novel constitutive equations as well as formulation of non-standard problems in solid mechanics. The project is likely to appeal to students with an interest in continuum mechanics, computational mathematics and interdisciplinary science.

Efficient solution for PDEs with random data

I would be happy to supervise projects in the general area of efficient solution of elliptic and parabolic partial differential equations with random data. PhD projects would involve a mix of theoretical analysis and the development of proof-of-concept software written in MATLAB or Python. The design of robust and efficient error estimators for stochastic collocation approximation methods is an active area of research within the uncertainty quantification community. Recent papers on this topic include Alex Bespalov, David Silvester and Feng Xu. Error estimation and adaptivity for stochastic collocation finite elements Part I: single-level approximation, SIAM J. Scientific Computing, 44: A3393--A3412, 2022. {\tt https://doi.org/10.1137/21M1446745} Arbaz Khan, Alex Bespalov, Catherine Powell and David Silvester, Robust a posteriori error estimators for stochastic Galerkin formulations of parameter-dependent linear elasticity equations, Mathematics of Computation, 90: 613--636, 2021. https://doi.org/10.1090/mcom/3572 Jens Lang, Rob Scheichl and David Silvester, A fully adaptive multilevel collocation strategy for solving elliptic PDEs with random data, J. Computational Physics, 419, 109692, 2020. https://doi.org/10.1016/j.jcp.2020.109692

Fluid flow, interfaces, bifurcations, continuation and control

Theme: Continuum mechanics | Supervisor: Alice Thompson

My research interests are in fluid dynamical systems with deformable interfaces, for example bubbles in very viscous fluid, or inkjet printed droplets. The deformability of the interface can lead to complex nonlinear behaviour, and often occurs in configurations where full numerical simulation of the three-dimensional system is computationally impossible. This computational difficulty leaves an important role for mathematical modelling, in using asymptotic or physical arguments to devise simpler models which can help us understand underlying physical mechanisms, make testable predictions, and to directly access control problems for active (feedback) or passive control mechanisms. Most recently I am interested in how different modelling methodologies affect whether models are robust in the forward or control problems. I am also interested in how control-based continuation methods can be used in continuum mechanics to directly observe unstable dynamical behaviour in experiments, even without access to a physical model. This research combines fluid dynamics, mathematical modelling, computational methods (e.g. with the finite-element library oomph-lib), experiments conducted in the Manchester Centre for Nonlinear Dynamics, control theory and nonlinear dynamics. I would not expect any student to have experience in all these areas and there is scope to shape any project to your interests.

Granular materials in industry and nature

Theme: Continuum mechanics | Supervisor: Chris Johnson

The field of granular materials encompasses a vast range of materials and processes, from the formation of sand dunes on a beach and snow avalanches in the mountains, to the roasting of coffee beans and the manufacture of pharmaceutical tablets. The science of granular materials is still in its relative infancy, and many aspects of flowing grains cannot yet be predicted with a continuum rheology. Insights into granular material behaviour come from a range of methods, and my research therefore combines mathematical modelling, computation, and laboratory experiments, undertaken at the Manchester Centre for Nonlinear Dynamics laboratories. Some example areas of work suitable for a PhD project include: - Debris flows and their deposits Debris flows are rapid avalanches of rock and water, which are triggered on mountainsides when erodible sediment is destabilised by heavy rainfall or snowmelt. These flows cause loss of life and infrastructure across the world, but many of the physical mechanisms underlying their motion remain poorly understood. Because it is difficult to predict where and when a debris flow will occur, scientific observations are rarely made on an active flow. More often, all we have to work from is the deposit left behind, and some detective work is required to infer properties of the flow (such as its speed and composition) from this deposit. This project focuses on developing theoretical models for debris flows that predict both a debris flow and its deposit -- in particular the way in which grains of different sizes are distributed throughout the deposit. The aim is then to invert such models, allowing observations of a deposit, when combined with model simulations, to constrain what must have happened during the flow. - Modelling polydispersity Much of the current theory of granular materials has been formulated with the assumption of a single type of grain. When grains vary in size, shape or density, it opens up the possibility that such grains with different properties separate from one another, a process called segregation. A fundamental question in this area is predicting the rate of segregation from a description of a granular material, such as the distribution of particle sizes. Thanks to some recent developments, we are approaching a point where this can be done for very simple granular materials (in particular those containing only two, similar, sizes sizes of grain), but many practical granular materials are much more complex. For example, it is common for mixtures of grains used in industry to vary in diameter by a factor of more than 100, and the complex segregation that can occur in these mixtures is poorly understood. This project will make measurements of the segregation behaviour of such mixtures and use these to put together a theoretical framework for describing segregation in complex granular materials.

Machine learning with partial differential equations

Theme: Statistics, inverse problems, uncertainty quantification and data science | Supervisor: Jonas Latz

Machine learning and artificial intelligence play a major part in our everyday life. Self-driving cars, automatic diagnoses from medical images, face recognition, or fraud detection, all profit especially from the universal applicability of deep neural networks. Their use in safety critical applications, however, is problematic: no interpretability, missing mathematical guarantees for network or learning process, and no quantification of the uncertainties in the neural network output. Recently, models that are based on partial differential equations (PDEs) have gained popularity in machine learning. In a classification problem, for instance, a PDE is constructed whose solution correctly classifies the training data and gives a suitable model to classify unlabelled feature vectors. In practice, feature vectors tend to be high dimensional and the natural space on which they live tends to have a complicated geometry. Therefore, partial differential equations on graphs are particularly suitable and popular. The resulting models are interpretable, mathematically well-understood, and uncertainty quantification is possible. In addition, they can be employed in a semi-supervised fashion, making them highly applicable in small data settings. I am interested in various mathematical, statistical, and computational aspects of PDE-based machine learning. Many of those aspects translate easily into PhD projects; examples are - Efficient algorithms for p-Laplacian-based regression and clustering - Bayesian identification of graphs from flow data - PDEs on random graphs - Deeply learned PDEs in data science Depending on the project, applicants should be familiar with at least one of: (a) numerical analysis and numerical linear algebra; (b) probability theory and statistics; (c) machine learning and deep learning.

Mathematical modelling of nano-reinforced foams

Theme: Maths: Continuum mechanics | Supervisor: William Parnell

Complex materials are important in almost every aspect of our lives, whether that is using a cell phone, insulating a house, ensuring that transport is environmentally friendly or that packaging is sustainable. An important facet of this is to ensure that materials are optimal in some sense. This could be an optimal stiffness for a given weight or an optimal conductivity for a given stiffness. Foams are an important class of material that are lightweight but also have the potential for unprecedented mechanical properties by adding nano-reinforcements (graphene flakes or carbon nanotubes) into the background or matrix material from which the foam is fabricated. When coupled with experimentation such as imaging and mechanical testing, mathematical models allow us to understand how to improve the design and properties of such foams. A number of projects are available in this broad area and interested parties can discuss these by making contact with the supervisor.

Multiscale modelling of structure-function relationships in biological tissues

Theme: Maths: Mathematics in the life sciences | Supervisor: Oliver Jensen

Biological tissues have an intrinsically multiscale structure. They contain components that range in size from individual molecules to the scale of whole organs. The organisation of individual components of a tissue, which often has a stochastic component, is intimately connected to biological function. Examples include exchange organs such as the lung and placenta, and developing multicellular tissues where mechanical forces play an crucial role in growth. To describe such materials mathematically, new multiscale approaches are needed that retain essential elements of tissue organisation at small scales, while providing tractable descriptions of function at larger scales. Projects are available in these areas that offer opportunities to collaborate with life scientists while developing original mathematical models relating tissue structure to its biological function.

Wave manipulation using metamaterials

The ability to control electromagnetic waves, sound, vibration has been of practical interest for decades. Over the last century a number of materials have been designed to assist with the attenuation of unwanted noise and vibration. However, recently there has been an explosion of interest in the topic of metamaterials and metasurfaces. Such media have special microstructures, designed to provide overall (dynamic) material properties that natural materials can never hope to attain and lead to the potential of negative refraction, wave redirection and the holy grail of cloaking. Many of the mechanisms to create these artificial materials rely on low frequency resonance. Frequently we are interested in the notion of homogenisation of these microstructures and this requires a mathematical framework. A number of projects are available in this broad area and interested parties can discuss these by making contact with the supervisor.

Pure Mathematics and Logic

Algebraic differential equations and model theory.

Theme: Algebra, logic and number theory | Supervisor: Omar Leon sanchez

Differential rings and algebraic differential equations have been a crucial source of examples for model theory (more specifically, geometric stability theory), and have had numerous application in number theory, algebraic geometry, and combinatorics (to name a few). In this project we propose to establish and analyse deep structural results on the model theory of (partial) differential fields. In particular, in the setup of differentially large fields. There are interesting questions around inverse problems in differential Galois theory that can be address as part of this project. On the other hand, there are (still open) questions related to the different notions of rank in differentially closed fields; for instance: are there infinite dimensional types that are also strongly minimal? This is somewhat related to the understanding of regular types, which interestingly are quite far from being fully classified. A weak version of Zilber's dichotomy have been established for such types, but is the full dichotomy true?

Algebraic invariants of abelian varieties

Theme: Algebra, logic and number theory | Supervisor: Martin Orr

Project: Algebraic invariants of abelian varieties Abelian varieties are higher-dimensional generalisations of elliptic curves, objects of algebraic geometry which are of great interest to number theorists. There are various open questions about how properties of abelian varieties vary across a families of abelian varieties. The aim of this project is to study the variation of algebraic objects attached to abelian varieties, such as endomorphism algebras, Mumford-Tate groups or isogenies. These algebraic objects control much of the behaviour of the abelian variety. We aim to bound their complexity in terms of the equations defining the abelian variety. Potential specific projects include: (1) Constructing "relations between periods" from the Mumford-Tate group. This involves concrete calculations of polynomials, similar in style to classical invariant theory of reductive groups. (2) Understanding the interactions between isogenies and polarisations of abelian varieties. This involves calculations with fundamental sets for arithmetic group actions, generalising reduction theory for quadratic forms. A key tool is the theory of reductive groups and their finite-dimensional representations (roots and weights).

Algebraic Model Theory of Fields with Operators

Model theory is a branch of Mathematical Logic that has had several remarkable applications with other areas of mathematics, such as Combinatorics, Algebraic Geometry, Number Theory, Arithmetic Geometry, Complex and Real Analysis, Functional Analysis, and Algebra (to name a few). Some of these applications have come from the study of model-theoretic properties of fields equipped with a family of operators. For instance, this includes differential/difference fields. In this project, we look at the model theory of fields equipped with general classes of operators and also within certain natural classes of arithmetic fields (such as large fields). Several foundational questions remain open around what is called "model-companion", "elimination of imaginaries", and the "trichotomy", this is a small sample of the problems that can be tackled.

Homeomorphism groups from a geometric viewpoint

Theme: Algebra, logic and number theory | Supervisor: Richard Webb

A powerful technique for studying groups is to use their actions by isometries on metric spaces. Properties of the action can be translated into algebraic properties of the group, and vice versa. This is called geometric group theory, and has played a key role in different fields of mathematics e.g. random groups, mapping class groups of surfaces, fundamental groups of 3-manifolds, the Cremona group. In this project we will study the homeomorphisms of a surface by using geometric group theoretic techniques recently introduced by Bowden, Hensel, and myself. This is a new research initiative at the frontier between dynamics, topology, and geometric group theory, and there are many questions waiting to be explored using these tools. These range from new questions on the relationship between the topology/dynamics of homeomorphisms and their action on metric spaces, to older questions regarding the algebraic structure of the homeomorphism group.

The Existential Closedness problem for exponential and automorphic functions

Theme: Maths: Algebra, logic and number theory | Supervisor: Vahagn Aslanyan

The Existential Closedness problem asks when systems of equations involving field operations and certain classical functions of a complex variable, such as exponential and modular functions, have solutions in the complex numbers. There are conjectures predicting when such systems should have solutions. The general philosophy is that when a system is not "overdetermined" (e.g. more equations than variables) then it should have a solution. The notion of an overdetermined system of equations is related to Schanuel's conjecture and its analogues and is captured by some purely algebraic conditions. The aim of this project is to make progress towards the Existential Closedness conjectures (EC for short) for exponential and automorphic functions (and the derivatives of automorphic functions). These include the usual complex exponential function, as well as the exponential functions of semi-abelian varieties, and modular functions such as the j-invariant. Significant progress has been made towards EC in recent years, but the full conjectures are open. There are many special cases which are within reach and could be tackled as part of a PhD project. Methods used to approach EC come from complex analysis and geometry, differential algebra, model theory (including o-minimality), tropical geometry. Potential specific projects are: (1) proving EC in low dimensions (e.g. for 2 or 3 variables), (2) proving EC for certain relations defined in terms of the function under consideration, e.g. establishing new EC results for "blurred" exponential and/or modular functions, (3) proving EC under additional geometric assumptions on the system of equations, (4) using EC to study the model-theoretic properties of exponential and automorphic functions.

Statistics and Probability

Distributional approximation by stein's method theme.

Theme: Probability, financial mathematics and actuarial science | Supervisor: Robert Gaunt

Stein's method is a powerful (and elegant) technique for deriving bounds on the distance between two probability distributions with respect to a probability metric. Such bounds are of interest, for example, in statistical inference when samples sizes are small; indeed, obtaining bounds on the rate of convergence of the central limit theorem was one of the most important problems in probability theory in the first half of the 20th century. The method is based on differential or difference equations that in a sense characterise the limit distribution and coupling techniques that allow one to derive approximations whilst retaining the probabilistic intuition. There is an active area of research concerning the development of Stein's method as a probabilistic tool and its application in areas as diverse as random graph theory, statistical mechanics and queuing theory. There is an excellent survey of Stein's method (see below) and, given a strong background in probability, the basic method can be learnt quite quickly, so it would be possible for the interested student to make progress on new problems relatively shortly into their PhD. Possible directions for research (although not limited) include: extend Stein's method to new limit distributions; generalisations of the central limit theorem; investigate `faster than would be expected' convergence rates and establish necessary and sufficient conditions under which they occur; applications of Stein's method to problems from, for example, statistical inference. Literature: Ross, N. Fundamentals of Stein's method. Probability Surveys 8 (2011), pp. 210-293.

Long-term behaviour of Markov Chains

Theme: Probability, financial mathematics and actuarial science | Supervisor: Malwina Luczak

Several projects are available, studying idealised Markovian models of epidemic, population and network processes. The emphasis will mostly be on theoretical aspects of the models, involving advanced probability theory. For instance, there are a number of stochastic models of epidemics where the course of the epidemic is known to follow the solution of a differential equation over short time intervals, but where little or nothing has been proved about the long-term behaviour of the stochastic process. Techniques have been developed for studying such problems, and a project might involve adapting these methods to new settings. Depending on the preference of the candidate, a project might involve a substantial computational component, gaining insights into the behaviour of a model, via simulations, ahead of proving rigorous theoretical results.

Mathematical Epidemiology

Theme: Mathematics in the life sciences | Supervisor: Thomas House

Understanding patterns of disease at the population level - Epidemiology - is inherently a quantitative problem, and increasingly involves sophisticated research-level mathematics and statistics in both infectious and chronic diseases. The details of which diseases and mathematics offer the best PhD directions are likely to vary over time, but this broad area is available for PhD research.

Spatial and temporal modelling for crime

Theme: Maths: Statistics, inverse problems, uncertainty quantification and data science | Supervisor: Ines Henriques-Cadby , Olatunji Johnson

A range of projects are available on the topic of statistical spatial and temporal modelling for crime. These projects will focus on developing novel methods for modelling crime related events in space and time, and applying these to real world datasets, mostly within the UK, but with the possibility to use international datasets. Some examples of recent applications include spatio-temporal modelling of drug overdoses and related crime. These projects will aim to use statistical spatio-temporalpoint processes methods, Bayesian methods, and machine learning methods. The project will require the candidate to be proficient in a modern programming language (e.g., R or Python). Applicants should have achieved a first-class degree in Statistics or Mathematics, with a significant component of Statistics, and be proficient in a statistical programming language (e.g., R, Python, Stata, S). We strongly recommend that you contact the supervisor(s) for this project before you apply. Please send your CV and a brief cover letter to [email protected] before you apply. At Manchester we offer a range of scholarships, studentships and awards at university, faculty and department level, to support both UK and overseas postgraduate researchers. For more information, visit our funding page or search our funding database for specific scholarships, studentships and awards you may be eligible for.

• Weekly Bulletin
• Ph.D. Programs
• M.S. Programs
• M.S. in Mathematics
• M.S. in Scientific Computing
• M.S. in Mathematics in Finance
• M.S. in Data Science
• Undergraduate Program
• Postdoc and Visitor Programs
• Committees & Leadership
• Useful Links
• Job Openings

Research projects suitable for undergraduates

What follows is a sample, provided by members of the faculty, of mathematical research projects where undergraduate students in the honors program in mathematics could participate. Interested students should contact either the faculty members directly, one of the honors advisors: professors Al Novikoff or Steve Childress .

A joint research project of Helmut Hofer and Esteban Tabak studies the behavior of Hamiltonian flows on a prescribed energy surface. Computer experiments using symplectic integrators could give some new insight. Such a project would be ideal for a team of an undergraduate and a graduate student. Codes would be developed and experiments would be conducted, shedding new light on the intriguing dynamics of these flows.

Charles Newman has recently studied zero-temperature stochastic dynamics of Ising models with a quenched (i.e., random) initial configuration. When the Ising models are disordered (e.g., a spin glass), there are a host of open problems in statistical physics which could be profitably investigated via Monte Carlo simulations by students (graduate and undergraduate) without an extensive background in the field. For example, on a two-dimensional square lattice, in the +/- J spin glass model, it is known that some sites flip forever and some don't; what happens in dimension three?

Current experiments in the Applied Mathematics Laboratory (WetLab/VisLab) include one project on dynamics of friction, and another involving the interaction of fluid flow with deformable bodies. Gathering data, mathematical modeling, and data analysis all provide excellent opportunities for undergraduate research experiences. In the friction experiment of Steve Childress, for example, the formulation and numerical solution of simplified models of stick/slip dynamics gives exposure to modern concepts of dynamical systems, computer graphics and analysis, and the mathematics of numerical analysis.

Marco Avellaneda's current research in mathematical finance demands econometric data to establish a basis for mathematical modeling and computation. The collection and analysis of such data could be done by undergraduates. The idea is to get comprehensive historical price data from several sources and perform empirical analysis of the correlation matrices between different price shocks in the same economy. The goal of the project is to map the ``principal components'' of the major markets.

Joel Spencer is studying the enumeration of connected graphs with given numbers of vertices and edges. The approach turns asymptotically into certain questions about Brownian motion. Much of the asymptotic calculation is suitable for undergraduates, while the subtleties of going to the Brownian limit would need a more advanced student.

A joint project of David McLaughlin, Michael Shelley, and Robert Shapley (Professor, Center for Neural Science, NYU) is developing a computer model of the area V1 of the monkey's primary visual cortex. Simplifications of this complex network model can provide projects for advanced undergraduate students, giving excellent exposure to mathematical and computational modeling, as well as to biological experiment and observation.

Peter Lax has carried out many numerical experiments with dispersive systems, and with systems modeling shock waves. The basic theory of these equations is well within the grasp of interested undergraduates, and calculations can reveal new phenomena.

A joint research project of David Holland and Esteban Tabak investigates ocean circulation at regional, basinal and global scales. Their approach is based on a combination of numerical and analytical techniques. There is an opportunity within this framework for undergraduate and graduate students to work together to further develop the simplified analytical and numerical models so as to gain insight into various mechanisms underlying and controlling ocean circulation.

Aspects of Lai-Sang Young's work in dynamical systems, chaos, and fractal geometry are suitable for undergraduate research projects. Simple analytic tools for iterations are accessible to students. Research in this area brings together material the undergraduate student has just learned from his or her classes. With proper guidance, this can be a meaningful scientific experience with the possibility of new discoveries.

David McLaughlin and Jalal Shatah's work on dynamical systems provides opportunities for undergraduate research experiences. For instance, the study of normal forms and resonances can be simplified to require only calculus and linear algebra. Thus undergraduate students can study analytically what is resonant in a given physical system, as well as its concrete consequences on qualitative behavior.

Leslie Greengard and Marsha Berger's work on adaptive computational methods plays an increasingly critical role in scientific computing and simulation. There are a number of opportunities for undergraduate involvement in this research. These range from designing algorithms for parallel computing to using large-scale simulation for the investigation of basic questions in fluid mechanics and materials science.

© NEW YORK UNIVERSITY

Purdue REU Opportunities

Vertically Integrated Projects (VIP) are research projects in directed by faculty and aimed at providing research opportunities in mathematics for undergraduate students at all levels. Below are a list of projects that are currently accepting applications from students. Students who are interested in one of the projects below should send an e-mail to the professor supervising the project  with a resume, a list of courses taken (or transcript), and a personal statement explaining their reason for wanting to participate in the project.

• Project:  Exceptional Affine Standard Lyndon Words Through Coding Project available Fall 2023
• Project: 2-Parameter BCD-Type Quantum Affine Algebras Project available Fall 2023
• Project: Polyhedral Development and Polygon Foldng Project available Spring 2024
• Faculty Research Areas
• Center for Computational & Applied Mathematics
• Funding Opportunities
• Research at Purdue
• Undergraduate Research

Department of Mathematics, Purdue University, 150 N. University Street, West Lafayette, IN 47907-2067

Phone: (765) 494-1901 - FAX: (765) 494-0548   Contact Us

© 2024 Purdue University | An equal access/equal opportunity university | Copyright Complaints

Trouble with this page? Disability-related accessibility issue ? Please contact the College of Science .

Maintained by Science IT

• Request info
• Majors & Degrees
• Prospective Students
• Current Undergraduate Students
• Current Graduate Students
• Online Students
• Alumni and Friends
• Faculty and Staff

School of Mathematics and Natural Sciences

Sample Undergraduate Research Projects

Page content.

Here is a list of recent undergraduate research projects. When available, we have added images that give you a flavor of some of the topics studied. If the student wrote a thesis, you can look it up at USM's library .

• Samuel Dent , "Applications of the Sierpiński Triangle to Musical Composition", Honors Thesis 
• Brandon Hollingsworth, "A time integration method for nonlinear ordinary differential equations", undergraduate research thesis.
• Haley Dozier, "Ideal Nim", undergraduate research project.
• Sean Patterson, "Generalizing the Relation between the 2-Domination and Annihilation Number of a Graph", Honors Thesis.
• Elyse Garon, "Modeling the Diffusion of Heat Energy within Composites of Homogeneous Materials Using the Uncertainty Principle", Honors Thesis.
• Brandi Moore, "Magic Surfaces", Mathematics Undergraduate Thesis.
• Amber Robertson, "Chebyshev Polynomial Approximation to Solutions of Ordinary Differential Equations", Mathematics Undergraduate Thesis
• Kinsey Ann Zarske, " Surfaces of Revolution with Constant Mean Curvature H=c in Hyperbolic 3-Space H 3 (- c 2 )", Undergraduate Student Paper Competition, 2013 meeting of the LA/MS Section of the MAA.
• Benjamin Benson, "Special Matrices, the Centrosymmetric Matrices", Undergraduate Thesis, 2010.
• Christopher R. Mills, "Method of approximate fundamental solutions for ill-posed elliptic boundary value problems", Honors Thesis, 2009.
• Ashley Sanders, "Problems in the College Math Journal", Undergraduate Project, 2009.

430 Chain Tech. (TEC)

Hattiesburg Campus

Email Theofanis.KitsopoulosFREEMississippi

Phone 601.266.4934

Quick Links +

Research projects.

Undergraduate Research is an great opportunity to get more involved in the Math Department while working directly with faculty to expand the bounds of existing knowledge. In this page, you will find both Quarterly and Summer Research Projects.

Quarterly Research Projects

Please note that this is a dynamic list each quarter. Check back regularly to see if new research positions have been added.

If you are interested in working on an area of research not represented on this list below, you are encouraged to contact faculty directly who are doing work in that area. A list of math faculty, including their research areas, is available here .

For more information about research units and the benefits of research, please visit the Math Undergraduate Research homepage .

Summer Research Projects

Summer undergraduate research positions provide a unique opportunity to join an active research group in the department and work on a project. In some cases this may lead to employment as an Undergraduate Research Assistant during the Academic Year and/or the following summer.

Every year there are a limited number of paid summer research positions. Please note that if you are planning to do a senior thesis, the optimal time to start is the summer of your sophomore or junior year.

As projects come to be known in the department, they will be posted here. In addition, feel free to reach out to faculty directly and/or the undergraduate research coordinator for further information on undergraduate reseach.

High School Research

Advanced high school math students interested in research and mathematics can undertake research projects during the academic year as well as the summer. The two programs available to high school students are:

• RSI - Research Science Institute
• PRIMES - Program for Research In Mathematics, Engineering, and Science

Please visit each section for more information.

251+ Math Research Topics [2024 Updated]

Mathematics, often dubbed as the language of the universe, holds immense significance in shaping our understanding of the world around us. It’s not just about crunching numbers or solving equations; it’s about unraveling mysteries, making predictions, and creating innovative solutions to complex problems. In this blog, we embark on a journey into the realm of math research topics, exploring various branches of mathematics and their real-world applications.

How Do You Write A Math Research Topic?

Writing a math research topic involves several steps to ensure clarity, relevance, and feasibility. Here’s a guide to help you craft a compelling math research topic:

• Identify Your Interests: Start by exploring areas of mathematics that interest you. Whether it’s pure mathematics, applied mathematics, or interdisciplinary topics, choose a field that aligns with your passion and expertise.
• Narrow Down Your Focus: Mathematics is a broad field, so it’s essential to narrow down your focus to a specific area or problem. Consider the scope of your research and choose a topic that is manageable within your resources and time frame.
• Review Existing Literature: Conduct a thorough literature review to understand the current state of research in your chosen area. Identify gaps, controversies, or unanswered questions that could form the basis of your research topic.
• Formulate a Research Question: Based on your exploration and literature review, formulate a clear and concise research question. Your research question should be specific, measurable, achievable, relevant, and time-bound (SMART).
• Consider Feasibility: Assess the feasibility of your research topic in terms of available resources, data availability, and research methodologies. Ensure that your topic is realistic and achievable within the constraints of your project.
• Consult with Experts: Seek feedback from mentors, advisors, or experts in the field to validate your research topic and refine your ideas. Their insights can help you identify potential challenges and opportunities for improvement.
• Refine and Iterate: Refine your research topic based on feedback and further reflection. Iterate on your ideas to ensure clarity, coherence, and relevance to the broader context of mathematics research.
• Craft a Title: Once you have finalized your research topic, craft a compelling title that succinctly summarizes the essence of your research. Your title should be descriptive, engaging, and reflective of the key themes of your study.
• Write a Research Proposal: Develop a comprehensive research proposal outlining the background, objectives, methodology, and expected outcomes of your research. Your research proposal should provide a clear roadmap for your study and justify the significance of your research topic.

By following these steps, you can effectively write a math research topic that is well-defined, relevant, and poised to make a meaningful contribution to the field of mathematics.

251+ Math Research Topics: Beginners To Advanced

• Prime Number Distribution in Arithmetic Progressions
• Diophantine Equations and their Solutions
• Applications of Modular Arithmetic in Cryptography
• The Riemann Hypothesis and its Implications
• Graph Theory: Exploring Connectivity and Coloring Problems
• Knot Theory: Unraveling the Mathematics of Knots and Links
• Fractal Geometry: Understanding Self-Similarity and Dimensionality
• Differential Equations: Modeling Physical Phenomena and Dynamical Systems
• Chaos Theory: Investigating Deterministic Chaos and Strange Attractors
• Combinatorial Optimization: Algorithms for Solving Optimization Problems
• Computational Complexity: Analyzing the Complexity of Algorithms
• Game Theory: Mathematical Models of Strategic Interactions
• Number Theory: Exploring Properties of Integers and Primes
• Algebraic Topology: Studying Topological Invariants and Homotopy Theory
• Analytic Number Theory: Investigating Properties of Prime Numbers
• Algebraic Geometry: Geometry Arising from Algebraic Equations
• Galois Theory: Understanding Field Extensions and Solvability of Equations
• Representation Theory: Studying Symmetry in Linear Spaces
• Harmonic Analysis: Analyzing Functions on Groups and Manifolds
• Mathematical Logic: Foundations of Mathematics and Formal Systems
• Set Theory: Exploring Infinite Sets and Cardinal Numbers
• Real Analysis: Rigorous Study of Real Numbers and Functions
• Complex Analysis: Analytic Functions and Complex Integration
• Measure Theory: Foundations of Lebesgue Integration and Probability
• Topological Groups: Investigating Topological Structures on Groups
• Lie Groups and Lie Algebras: Geometry of Continuous Symmetry
• Differential Geometry: Curvature and Topology of Smooth Manifolds
• Algebraic Combinatorics: Enumerative and Algebraic Aspects of Combinatorics
• Ramsey Theory: Investigating Structure in Large Discrete Structures
• Analytic Geometry: Studying Geometry Using Analytic Methods
• Hyperbolic Geometry: Non-Euclidean Geometry of Curved Spaces
• Nonlinear Dynamics: Chaos, Bifurcations, and Strange Attractors
• Homological Algebra: Studying Homology and Cohomology of Algebraic Structures
• Topological Vector Spaces: Vector Spaces with Topological Structure
• Representation Theory of Finite Groups: Decomposition of Group Representations
• Category Theory: Abstract Structures and Universal Properties
• Operator Theory: Spectral Theory and Functional Analysis of Operators
• Algebraic Number Theory: Study of Algebraic Structures in Number Fields
• Cryptanalysis: Breaking Cryptographic Systems Using Mathematical Methods
• Discrete Mathematics: Combinatorics, Graph Theory, and Number Theory
• Mathematical Biology: Modeling Biological Systems Using Mathematical Tools
• Population Dynamics: Mathematical Models of Population Growth and Interaction
• Epidemiology: Mathematical Modeling of Disease Spread and Control
• Mathematical Ecology: Dynamics of Ecological Systems and Food Webs
• Evolutionary Game Theory: Evolutionary Dynamics and Strategic Behavior
• Mathematical Neuroscience: Modeling Brain Dynamics and Neural Networks
• Mathematical Physics: Mathematical Models in Physical Sciences
• Quantum Mechanics: Foundations and Applications of Quantum Theory
• Statistical Mechanics: Statistical Methods in Physics and Thermodynamics
• Fluid Dynamics: Modeling Flow of Fluids Using Partial Differential Equations
• Mathematical Finance: Stochastic Models in Finance and Risk Management
• Option Pricing Models: Black-Scholes Model and Beyond
• Portfolio Optimization: Maximizing Returns and Minimizing Risk
• Stochastic Calculus: Calculus of Stochastic Processes and Itô Calculus
• Financial Time Series Analysis: Modeling and Forecasting Financial Data
• Operations Research: Optimization of Decision-Making Processes
• Linear Programming: Optimization Problems with Linear Constraints
• Integer Programming: Optimization Problems with Integer Solutions
• Network Flow Optimization: Modeling and Solving Flow Network Problems
• Combinatorial Game Theory: Analysis of Games with Perfect Information
• Algorithmic Game Theory: Computational Aspects of Game-Theoretic Problems
• Fair Division: Methods for Fairly Allocating Resources Among Parties
• Auction Theory: Modeling Auction Mechanisms and Bidding Strategies
• Voting Theory: Mathematical Models of Voting Systems and Social Choice
• Social Network Analysis: Mathematical Analysis of Social Networks
• Algorithm Analysis: Complexity Analysis of Algorithms and Data Structures
• Machine Learning: Statistical Learning Algorithms and Data Mining
• Deep Learning: Neural Network Models with Multiple Layers
• Reinforcement Learning: Learning by Interaction and Feedback
• Natural Language Processing: Statistical and Computational Analysis of Language
• Computer Vision: Mathematical Models for Image Analysis and Recognition
• Computational Geometry: Algorithms for Geometric Problems
• Symbolic Computation: Manipulation of Mathematical Expressions
• Numerical Analysis: Algorithms for Solving Numerical Problems
• Finite Element Method: Numerical Solution of Partial Differential Equations
• Monte Carlo Methods: Statistical Simulation Techniques
• High-Performance Computing: Parallel and Distributed Computing Techniques
• Quantum Computing: Quantum Algorithms and Quantum Information Theory
• Quantum Information Theory: Study of Quantum Communication and Computation
• Quantum Error Correction: Methods for Protecting Quantum Information from Errors
• Topological Quantum Computing: Using Topological Properties for Quantum Computation
• Quantum Algorithms: Efficient Algorithms for Quantum Computers
• Quantum Cryptography: Secure Communication Using Quantum Key Distribution
• Topological Data Analysis: Analyzing Shape and Structure of Data Sets
• Persistent Homology: Topological Invariants for Data Analysis
• Mapper Algorithm: Method for Visualization and Analysis of High-Dimensional Data
• Algebraic Statistics: Statistical Methods Based on Algebraic Geometry
• Tropical Geometry: Geometric Methods for Studying Polynomial Equations
• Model Theory: Study of Mathematical Structures and Their Interpretations
• Descriptive Set Theory: Study of Borel and Analytic Sets
• Ergodic Theory: Study of Measure-Preserving Transformations
• Combinatorial Number Theory: Intersection of Combinatorics and Number Theory
• Additive Combinatorics: Study of Additive Properties of Sets
• Arithmetic Geometry: Interplay Between Number Theory and Algebraic Geometry
• Proof Theory: Study of Formal Proofs and Logical Inference
• Reverse Mathematics: Study of Logical Strength of Mathematical Theorems
• Nonstandard Analysis: Alternative Approach to Analysis Using Infinitesimals
• Computable Analysis: Study of Computable Functions and Real Numbers
• Graph Theory: Study of Graphs and Networks
• Random Graphs: Probabilistic Models of Graphs and Connectivity
• Spectral Graph Theory: Analysis of Graphs Using Eigenvalues and Eigenvectors
• Algebraic Graph Theory: Study of Algebraic Structures in Graphs
• Metric Geometry: Study of Geometric Structures Using Metrics
• Geometric Measure Theory: Study of Measures on Geometric Spaces
• Discrete Differential Geometry: Study of Differential Geometry on Discrete Spaces
• Algebraic Coding Theory: Study of Error-Correcting Codes
• Information Theory: Study of Information and Communication
• Coding Theory: Study of Error-Correcting Codes
• Cryptography: Study of Secure Communication and Encryption
• Finite Fields: Study of Fields with Finite Number of Elements
• Elliptic Curves: Study of Curves Defined by Cubic Equations
• Hyperelliptic Curves: Study of Curves Defined by Higher-Degree Equations
• Modular Forms: Analytic Functions with Certain Transformation Properties
• L-functions: Analytic Functions Associated with Number Theory
• Zeta Functions: Analytic Functions with Special Properties
• Analytic Number Theory: Study of Number Theoretic Functions Using Analysis
• Dirichlet Series: Analytic Functions Represented by Infinite Series
• Euler Products: Product Representations of Analytic Functions
• Arithmetic Dynamics: Study of Iterative Processes on Algebraic Structures
• Dynamics of Rational Maps: Study of Dynamical Systems Defined by Rational Functions
• Julia Sets: Fractal Sets Associated with Dynamical Systems
• Mandelbrot Set: Fractal Set Associated with Iterations of Complex Quadratic Polynomials
• Arithmetic Geometry: Study of Algebraic Geometry Over Number Fields
• Diophantine Geometry: Study of Solutions of Diophantine Equations Using Geometry
• Arithmetic of Elliptic Curves: Study of Elliptic Curves Over Number Fields
• Rational Points on Curves: Study of Rational Solutions of Algebraic Equations
• Galois Representations: Study of Representations of Galois Groups
• Automorphic Forms: Analytic Functions with Certain Transformation Properties
• L-functions: Analytic Functions Associated with Automorphic Forms
• Selberg Trace Formula: Tool for Studying Spectral Theory and Automorphic Forms
• Langlands Program: Program to Unify Number Theory and Representation Theory
• Hodge Theory: Study of Harmonic Forms on Complex Manifolds
• Riemann Surfaces: One-dimensional Complex Manifolds
• Shimura Varieties: Algebraic Varieties Associated with Automorphic Forms
• Modular Curves: Algebraic Curves Associated with Modular Forms
• Hyperbolic Manifolds: Manifolds with Constant Negative Curvature
• Teichmüller Theory: Study of Moduli Spaces of Riemann Surfaces
• Mirror Symmetry: Duality Between Calabi-Yau Manifolds
• Kähler Geometry: Study of Hermitian Manifolds with Special Symmetries
• Algebraic Groups: Linear Algebraic Groups and Their Representations
• Lie Algebras: Study of Algebraic Structures Arising from Lie Groups
• Representation Theory of Lie Algebras: Study of Representations of Lie Algebras
• Quantum Groups: Deformation of Lie Groups and Lie Algebras
• Algebraic Topology: Study of Topological Spaces Using Algebraic Methods
• Homotopy Theory: Study of Continuous Deformations of Spaces
• Homology Theory: Study of Algebraic Invariants of Topological Spaces
• Cohomology Theory: Study of Dual Concepts to Homology Theory
• Singular Homology: Homology Theory Defined Using Simplicial Complexes
• Sheaf Theory: Study of Sheaves and Their Cohomology
• Differential Forms: Study of Multilinear Differential Forms
• De Rham Cohomology: Cohomology Theory Defined Using Differential Forms
• Morse Theory: Study of Critical Points of Smooth Functions
• Symplectic Geometry: Study of Symplectic Manifolds and Their Geometry
• Floer Homology: Study of Symplectic Manifolds Using Pseudoholomorphic Curves
• Gromov-Witten Invariants: Invariants of Symplectic Manifolds Associated with Pseudoholomorphic Curves
• Mirror Symmetry: Duality Between Symplectic and Complex Geometry
• Calabi-Yau Manifolds: Ricci-Flat Complex Manifolds
• Moduli Spaces: Spaces Parameterizing Geometric Objects
• Donaldson-Thomas Invariants: Invariants Counting Sheaves on Calabi-Yau Manifolds
• Algebraic K-Theory: Study of Algebraic Invariants of Rings and Modules
• Homological Algebra: Study of Homology and Cohomology of Algebraic Structures
• Derived Categories: Categories Arising from Homological Algebra
• Stable Homotopy Theory: Homotopy Theory with Stable Homotopy Groups
• Model Categories: Categories with Certain Homotopical Properties
• Higher Category Theory: Study of Higher Categories and Homotopy Theory
• Higher Topos Theory: Study of Higher Categorical Structures
• Higher Algebra: Study of Higher Categorical Structures in Algebra
• Higher Algebraic Geometry: Study of Higher Categorical Structures in Algebraic Geometry
• Higher Representation Theory: Study of Higher Categorical Structures in Representation Theory
• Higher Category Theory: Study of Higher Categorical Structures
• Homotopical Algebra: Study of Algebraic Structures in Homotopy Theory
• Homotopical Groups: Study of Groups with Homotopical Structure
• Homotopical Categories: Study of Categories with Homotopical Structure
• Homotopy Groups: Algebraic Invariants of Topological Spaces
• Homotopy Type Theory: Study of Foundations of Mathematics Using Homotopy Theory

In conclusion, the world of mathematics is vast and multifaceted, offering endless opportunities for exploration and discovery. Whether delving into the abstract realms of pure mathematics or applying mathematical principles to solve real-world problems, mathematicians play a vital role in advancing human knowledge and shaping the future of our world.

By embracing diverse math research topics and interdisciplinary collaborations, we can unlock new possibilities and harness the power of mathematics to address the challenges of today and tomorrow. So, let’s embark on this journey together as we unravel the mysteries of numbers and explore the boundless horizons of mathematical inquiry.

Related Posts

Step by Step Guide on The Best Way to Finance Car

The Best Way on How to Get Fund For Business to Grow it Efficiently

Leave a comment cancel reply.

Your email address will not be published. Required fields are marked *

Independent Research with a Faculty Mentor in Mathematics

Interested in pursuing an individual research project in mathematics? We encourage you to pursue independent research under the supervision of a faculty mentor. Student research activities include:

• Honors theses
• Inter- or intradisciplinary collaborative research on cutting-edge problems from a specific field of computer science
• Reading courses on advanced topics
• Qualified self-designed projects

Below, check out some of mathematics students’ most recent independent research projects.

Mathematics Student Projects

Our universe as a manifold.

Mateo Gomez (now a 3-2 combined plan student at Columbia University), Sherman-Fairchild Fellow; summer research 2017 Mentor: Prof. Amir Aazami

This research project gave a rigorous introduction to understanding spaces that locally look just like our familiar space, but globally may be curved. The perfect example of this is earth: locally it looks flat, but globally it is a sphere. In fact, our very universe itself is assumed to have this local/global property, but being four-dimensional — three dimensions of space and one of time — we cannot “see” this as we can with Earth. Such spaces are called manifolds. The key question is: how does one do calculus on manifolds? How does one study their geometry, their curvature? E.g., the shortest distance between two points on earth can no longer be a straight line, because earth is curved, so how does one answer such questions now? The difficult task is that, given the “local/global” relationship that manifolds possess, one cannot rely solely on coordinates: one must think, so to speak, coordinate-independently. In fact, everything from the ground up has to be re-formulated: differentiability, vectors, the gradient, the Jacobian of a function, etc. All this needs to be understood before one can even begin to talk about geometry, or curvature, or gravity, or the universe and Einstein’s equations.

Designing New Evolutionary Algorithms for Parameter Estimation

Mike Gaiewski (now a Ph.D. student in Applied Math at UConn), Sherman-Fairchild Fellow; summer research 2017 and 2018 Mentor: Prof. Jacqueline Dresch

One of the most important steps in mathematical modeling of a biological system is fitting the parameters of your model to experimental data. There is an extremely large number of different parameter estimation algorithms available, and an important question to ask is: what parameter estimation method should be used on my particular problem? In an attempt to answer this question in the context of modeling gene regulation, Michael developed and implemented novel parameter estimation algorithms based on the principles of evolution.

Topics in Functional Analysis

Andrew Mezzi , Sherman-Fairchild Fellow; summer research 2018 Mentor : Prof. Gideon Maschler

Andrew worked on a project that encompassed many different topics from functional analysis: infinite-dimensional linear algebra, operators, and applications of solutions to ordinary differential equations.

During the summer, Andrew was also exposed to a variety of internet resources and professional tools of the working mathematician, including the arXiv, MathSciNet, LaTeX and TeX-related editors, as well as the MathOverflow and StackExchange websites.

Topics in Differential Geometry

Emma Kirkman-Davis , summer reading course 2017 Tenzing Gurung , summer reading course 2017 Wenwen Shen , honors thesis 2016 Mentor: Prof. Gideon Maschler

Emma, Tenzing, and Wenwen all worked on topics in differential geometry. Their work focused on curves and surfaces, lengths on these, intrinsic and extrinsic curvature, and the relation between curvature and topology (i.e., global geometry, the Gauss-Bonnet Theorem).

Bioinformatic Analysis of Transcription Factor Binding Sites

Navid Al Hossain , Sherman-Fairchild Fellow; summer research 2016 and 2017 Regan Conrad , Sherman-Fairchild Fellow; summer research 2017 and 2018 Mentor: Prof. Jacqueline Dresch

Predicting the location of protein binding sites within a genome is a difficult task, but is an integral part of furthering our understanding of gene regulation. Traditional methods involve PWMs (position weight matrices), which rely on the underlying assumption that each nucleotide within a TF binding site is independent of the other nucleotides. More recently, models have been implemented which relax this assumption to include dependence on neighboring nucleotides (i.e. a string of contiguous nucleotides).

Navid’s project focused on analyzing the correlation between the frequency of binding sites within raw sequence data and the bioinformatically predicted ‘strength’ of these binding sites. His work has been instrumental in the experimental design and continued collaboration between the Dresch group in the Mathematics and Computer Science Department, the Drewell lab in Biology, and the Spratt lab in Chemistry.

Regan’s project focused on analyzing bioinformatic predictions of binding sites within core promoter regions from Drosophila melanogaster to investigate potential nucleotide dependencies and improve the predictive power of these algorithms.

Image Processing and Drosophila Embryos

Logan Bishop-Van Horn , directed study, spring 2016 Teodor Nicola-Antoniu , summer research 2016 Mentor: Prof. Jacqueline Dresch

Using raw data from microscope images in modeling gene expression levels presents the researcher with many challenges; one must be able to remove any extraneous information from the image and be able to compare images prepared and taken from different embryos on different days. For this reason, Logan and Teodor’s projects focused on creating a pipeline for processing these images, including noise and background subtraction, normalization, spatial registration, and extraction of quantitative levels of gene expression.

Counting Complicated Combinatorial Sets using Markov Chain Monte-Carlo Algorithms

Trung Ngo (now an application developer at Morgan Stanley), honors thesis 2018 Mentor: Prof. Michael Satz

Can you imagine a set that is finite but impossible to practically count even with a supercomputer? One way to build such a set is to define it as a subset all permutations of the integers 1 through N. For example, our hard-to-count set may be all such permutations satisfying some constraint involving these integers and the position they’re in. Depending on the constraint, the hard-to-count set may not be particularly large, but the parent set (which has N! elements) may well be too large for an exhaustive check-and-count approach. Monte-Carlo Markov chain methods introduce randomness to estimate the sizes and other features of such complicated combinatorial sets. Trung Ngo applied four algorithms to one such counting problem. The algorithms were implemented in Python and tested and analyzed for performance, convergence, and accuracy.

Differential Geometry and Brain Images

Franklin Feingold (now a project manager at Stanford University), honors thesis 2015 Mentor: Prof. Gideon Maschler

In recent years, there have been multiple studies that use techniques in differential geometry to analyze brain MRIs. Franklin’s project focused on exploring some of the methods used and understanding how differential geometry can be used in modern-day medicine.

Mathematics behind Plasmas

First-year students in the Diving into Research course,  2014-15 Mentor: Prof. Natalia Sternberg

Plasma televisions, plasma lights, the heat around the space shuttle and communication blackout caused by plasma, laser treatments in medicine, and production of microchips for computers are just a few applications of plasmas that became a big part of our lives. Students will learn about plasmas by developing and studying mathematical models that explain the experiments and help to obtain plasmas with certain prope rties.   

Diving into Research

In addition to independent research projects, our department periodically provides opportunities for first-year and upper-class students to work in groups with faculty members on research projects through the course Diving into Research (MATH110, MATH 111). MATH110 Diving into Research is a year-long opportunity for first-year students to work in groups with faculty members on research projects.

Recent topics have included:

• Modeling re-entry communication blackout on the space shuttle caused by plasma
• Modeling gene regulation in a developing fruit fly embryo

Groups are limited to eight students. Students earn 0.5 credits each semester, and the full year is necessary to obtain credit. May be repeated as MATH111. Note: Neither MATH 110 nor MATH 111 count as credit towards the Math major.

A Sampling of Course Descriptions for Diving into Research

Mathematics behind plasmas.

Plasma televisions, plasma lights, the heat around the space shuttle and communication blackout caused by plasma, laser treatments in medicine, and production of microchips for computers are just a few applications of plasmas that became a big part of our lives. Students will learn about plasmas by developing and studying mathematical models that explain the experiments and help to obtain plasmas with certain properties. (Instructor: N.Sternberg)

The Mathematics Behind Gene Regulation

This course will introduce the idea of mathematically modeling gene regulation in a developing organism. Students will learn how mathematicians work with biologists to design simple experiments and derive equations to model gene expression. We will also explore some of the computational approaches currently being implemented in modern biology, including bioinformatics, data processing, and parameter estimation. This one-year course will be an interactive experience for students interested in learning more about the interface of mathematics, computer science, and molecular biology. (Instructor: J.Dresch)

Geometry is a branch of mathematics which closely relies on visual intuition. As such, parts of it are accessible even without obtaining extensive preliminary background, while still being deep and thought-provoking. In this seminar-style class, we explore the subject from a number of different perspectives, thus demonstrating its richness. Among the possible topics chosen are Projective and Differential Geometry, and symmetries and their relation to the mathematical concept of a group. Our guiding principle for these choices will be their accessibility to direct geometric intuition and imagination. The need for prior mathematical background will be kept at a minimum level. We will also be employing computer graphics and related software for visual exploration. The main purpose is to have fun while appreciating geometry. (Instructor: G.Maschler)

Working Together to Build Solutions

Mathematics

Bio-Physics (BP) Building, Room 327 950 Main Street Worcester, MA 01610

• 1-508-793-7343
• mathcs[at]clarku[dot]edu
• Faculty Directory
• Staff Directory
• Follow Us on Facebook

The Math and Numeracy Lab

Institute of Child Development

Research Projects

Please select from the links below or to the left to learn more about current and completed projects in the Math and Numeracy lab:

Ongoing Projects

Numbers in context.

The principal theme across our major research projects is numbers in context. We study numerical processing and the role context plays in concurrent attention to numerosity in children and adults, children’s  interpretation of number words, and obligatory arithmetic  processing. These basic science questions are a major focus of our work. 

Attention to Numerosity : This project seeks to determine what physical features may help direct children’s attention to numerical information, which may inform the design and implementation of educational materials.

Storybooks Project : Do counting books and other storybooks align with what we know about how children develop an understanding of number? Our research suggests this is not always the case, and that specific features of books may support or interfere with children’s learning to map numerosities onto number words.

Numerical Ambiguity : Number words usually refer to magnitude or ordinal properties of number, but not always. We study whether individual differences in children’s and adults’ sensitivity to numerical vs non-numerical contexts influence how and when an individual interprets number words.

Development and Research in Early Mathematics Education (DREME)

The DREME Network is a collaborative effort funded by the Heising-Simons Foundation. This work included an emphasis on applied research and the development of materials for early childhood educators, parents, and parent support professionals.  The DREME Network Project has ended. Current efforts are limited to dissemination.  Our lab was  involved in several DREME supported projects:

Making More of Mathematics

The Preschool Mathematics and Executive Function project is a DREME Network Collaboration funded by the Heising-Simons Foundation. This project was focused on enriching children’s exposure to early mathematics activities in PreK settings, and determining how and if high quality mathematics activities enhance the development of early math and EF skills. Through this project we contributed to developing materials for teachers that focus on strengthening children’s mathematical and executive function skills. For example, we wrote a set of articles that described the ways in which EF skills are related to doing and learning mathematics. For more information, see https://preschoolmath.stanford.edu/

Supporting Family Support Professionals as a Means to Promote Family Engagement in Early Mathematics  

A principal emphasis of the DREME Network was to develop resources to promote early mathematics. The UMN team developed a set of modules suitable for asynchronous online professional development for parent educators, home visitors, librarians, and other family support professionals (FSPs) who work with parents and caregivers of young children (0 to 5+ years). Through three modules, these materials were designed to introduce family support professionals to early mathematics, by addressing ways to (a) foster healthy dispositions towards mathematics, (b) recognize developmentally appropriate early mathematics interactions with young children, and (c) explore ways to integrate meaningful mathematical thinking in everyday interactions, including playful interactions. 

Through this project, we developed activities for family support professionals to use with caregivers, including materials to share with families. 

Completed Projects

The math skills development project (msdp).

The MSDP is a completed, in-depth, 13 year longitudinal study of mathematical thinking from Kindergarten to Grade 12 (Funded primarily but not exclusively by the NIH). There are multiple opportunities for secondary analyses of existing data from this project. These data focus on cognitive correlates of early mathematics, select experimental measures of mathematical thinking, and early indicators of persistent mathematics learning difficulties.  The study was designed to explore math learning difficulties from the perspective of individual differences in cognitive and related skills. 

Neurogenetic Syndrome Phenotypes: Model Pathways to Mathematics Learning Disabilities

This was a primary component of the completed MSDP, and an extension of this work was focused on Turner syndrome in one component of the Numbers in Context research.

GopherMath was a collaborative endeavor initiated in Fall 2016 by faculty in the UMN STEM Center. It involved faculty in Educational Psychology (Dr Robin Codding and Keisha Varma), Curriculum and Instruction (Dr. Kathy Cramer and Erin Baldinger) Child Development (Michele Mazzocco), and Educational Psychology Graduate Student Stacey Brandjord.

The overarching goal of the study was to improve children’s rational number concept development through teacher professional development, parent engagement, and strengthening whole number skills and concepts. The contribution of the Mazzocco Math and Numeracy Lab to this study was to study the foundational role of whole number concepts in rational number learning.

This research was a partnership with the Minneapolis Public Schools, and is supported by General Next and the University of Minnesota.

Parents and Caregivers’ Roles in Early Mathematical Thinking and Development

“Parents and Caregivers’ Roles in Early Mathematical Thinking and Development: The Role of Counting and Number Books in Early Number Concepts” is a collaborative, cross-institutional research project that was launched in 2015 at the Minnesota State Fair University of Minnesota Driven to Discover Research Pavilion.

This project involves several separate studies, including the Math and Numeracy Lab’s work on counting books, shared reading, parent-child interactions related to mathematical thinking, family child care setting learning environments, and developing parent-educator workshops.

This work is funded in part by the University of Minnesota and by the Heising-Simons Foundation.

Make Math Instruction Better: 3 Tips on How From Researchers

• Share article

Education Week reporter and data journalist Sarah D. Sparks attended the American Educational Research Association’s annual conference in Philadelphia earlier this month. Here, she shares three of the key takeaways she heard from researchers studying some of the key challenges around math instruction.

Sign Up for EdWeek Update

Edweek top school jobs.

Sign Up & Sign In

Math Projects : 20 Simple and Interesting Ideas

Table of Contents

23 January 2021

Reading Time: 7 minutes

Mathematics is not about understanding different things and concepts; it is about getting used to them by applying the concepts in everyday tasks.

What could be a better way to learn these applications other than interesting maths projects which facilitate both creativity and knowledge.

These projects on mathematics give an understanding of how mathematics works. Mathematics is in and around you everywhere in the form of numbers, shapes, sizes, volume, weight, etc.

Our task is to figure out and identify these numerous situations and things around us to play with numbers and concepts. 

• Fun Math activities for Class 3

Math projects  

Here is a downloadable PDF that consists of Math projects for Grades 6-10. Click on the download button to explore them. Understanding and grasping the ideas of mathematics in a better way.

These maths projects help in developing very important mathematical skills like:-

Correlating the concepts taught in the classes with the practical applications of those concepts

Proving a hand on experience to the children 

Fostering teamwork, coordination, and communication along with creativity and knowledge

Understanding and grasping the ideas of mathematics in a better way

Visualizing the concepts in the form of diagrams, graphs, and images facilitates a better understanding

Improving their problem-solving skills, reasoning, and planning skills, etc.

Making real-life decisions that leads to a holistic approach to learning.

In this article, we have brought for you 20 topics for maths projects which will help you develop simple maths projects.

Maths project ideas for Class 6

Some of the ideas for simple maths projects for class 6 are:

Number System Tree

The number system is one of the most basic concepts in mathematics. It is very important to understand the different types of numbers (order and even numbers, fractions and decimals, natural numbers, whole numbers, positive and negative numbers, etc.) and the different properties of numbers. A project for the same will help the student understand and correlate the relations between different types of numbers.

Shapes and Figures

Shapes, figures, and sizes are a very important concept of geometry. A student must understand the different properties of different geometrical figures. It starts from class 6 but has various applications in higher-level education. Therefore it is very important to have a proper foundation that is only possible through a project on the same.

Practical examples of different chapters

From class six onwards, students start getting exposed to different topics that have a number of practical applications like percentages, profit, and loss, interest, etc. Students can be asked to make their own problem statements by practicing creative problems with respect to the same chapters. This will help them to correlate the concepts with the practical world.

History of maths and different topics

It is very important to understand the history or the background of a subject or a topic before starting to learn more about it. But, because of the curriculum norms, this very important aspect is skipped from the school syllabus. Projects can be a great way to help students do research about it. This will facilitate better knowledge and understanding.

Conversions

There can be a project work that is specifically dedicated to conversions of different things like fractions to decimals or vice versa, negative to positive or vice versa, etc. These are very simple concepts but students often tend to make mistakes because of a lack of clear understanding. Good, detailed project work will help them develop a base.

Ideas for Maths Project for Class 7

Some of the ideas for the projects on mathematics for class 7 are:

Practical Applications of different chapters

As stated above, maths is a practical subject and it is very important to understand the concepts. The best way to do this will be to allow students to undergo practical examples related to different chapters and come up with creative problem statements, ideas, and solutions. For example, the student can find out the average amount spent on the purchase of different items, or he/she can find out the profit or the loss of the shopkeeper, etc.

Formula lists

Making a formula list will be a great project work because it will not only help the student in the short run but also facilitate his/her learning before the exams and in the case of higher education. This will serve both as a research and as a document of reference.

Puzzles and brain teasers projects

Puzzles and brain teasers are a very dynamic way of inculcating knowledge, fostering creativity, and facilitating practical viewpoints. This helps a student to think and come up with answers along with reasons to support it. It helps them in a better decision making process.

Algebraic expressions 

Students are exposed to a new field of mathematics in class 7 which is algebra. Good project work can help a student to develop a strong base in understanding different algebraic equations and expressions. This project work can include a number of numerical, interesting problem statements, and mental math calculations.

Sets and Venn diagrams

This is a very interesting concept but can be a confusing one if not understood properly because the concepts are somewhat overlapping with each other. There are very minute differences in this particular topic. Detailed project work can actually help a student clear all their doubts and develop a strong base for higher education.

Topics for Maths Project for Class 8

Some of the ideas for interesting maths projects for class 8 are:

Construction in Geometry

A very important part of geometry is to learn constructions of different shapes and figures of different types. Learning and building the basics of construction in geometry is very important to understand various higher-level educational studies like physics and architecture. 

This project work is actually never-ending. Students don't learn all the concepts in a single standard. They continue learning various different concepts in different chapters that have different practical applications. Slowly, the level of difficulty keeps on increasing. Therefore it is very important to stay updated and improvise the skills through project works which allow us to correlate the concepts of the chapters with practical examples.

Mensuration of figures

For the first time in class VIII, a student gets exposed to the chapter on menstruation. This chapter facilitates measurements of different things. It may include length, perimeter, area, etc. There are a number of concepts and a number of formulas that are related to this particular topic. Therefore giving good project work that helps students to understand these concepts by applying the given formulas and correlating them with the practical ships will foster growth and development in knowledge.

Mirror symmetry and Reflection

Symmetry and reflection are one of the easiest concepts of mathematics. This could be a very fun and interesting project for a student wherein he will understand the difference between symmetrical and asymmetrical figures and will also develop a base for higher-level education.

Making practical models for different topics

Project works can be done in two ways - (1) As mentioned above, using pen and paper by drawing various diagrams and graphs; (2) Making practical models explain different concepts. These practical models help a student to develop the power of visualization and foster teamwork and creativity. This will be a little difficult because it will require the culmination of different ideas from other subjects also. But, if done successfully, this can be a great learning experience.

Maths project ideas for Class 9-10

Some of the ideas for maths projects for class 9-10 are:

Heights and Distances

A student gets exposed to the concept of trigonometry for the first time in class 9-10. This concept is very widely used to understand heights and distances which plays a very important role in practical life. This also develops a base for various higher-level studies. Students can be asked to draw diagrams and graphs and correlate the concepts with the same to develop a better understanding.

Statistics and graphs

It is in class 9 that a very new dimension of mathematics opens up for the students which are known as statistics. A very important part of statistics is graphical representations that have their application in almost every sphere of knowledge. Therefore, it becomes very important to understand the basics of these concepts and good project work on this topic will definitely foster good learning.

Making and understanding 3D figures

There are various 3-D figures which a student must understand, like cubes and cuboid being the basics. The calculations for these 3-D figures are not as easy as the 2-D figures. Therefore, good project work will facilitate the visualization of 3-D figures and also help students to understand the various formulas and calculations related to it.

Similarity and Congruency

Another very important concept of geometry that pops up in class 9-10 is the similarity and congruency of triangles. Students often face a lot of difficulty in understanding these concepts. Therefore, a project work that has a good amount of research work with a number of assignments and questions to solve will definitely help a student to learn the concept of similarity incongruency.

Mensuration and Volume

The concepts of mensuration take a whole new level in class 9-10. It brings in new concepts like surface area, volume, etc., and also brings in new figures like a cylinder, circle, cone, etc. It is equally important to understand these concepts and shapes also. Good project work will definitely foster a good knowledge of these concepts.

These were some of the most interesting lists of maths project topics that we have curated for you through this article. We hope this article was useful and will help the readers to choose some of the most interesting topics out there to learn, grow and develop. These topics are proven to be the most beneficial for students. Choose from the best, the ones which suit you the best.

About Cuemath

Cuemath, a student-friendly mathematics and coding platform, conducts regular  Online Classes  for academics and skill-development, and their Mental Math App, on both  iOS  and  Android , is a one-stop solution for kids to develop multiple skills. Understand the Cuemath Fee structure and sign up for a free trial. 

Frequently Asked Questions (FAQs)

What are the mathematical tools which are essential in building projects.

• Chart Paper (For creating shapes etc.)
• Set Squares

What are different types of graphs which can be used to describe data?

• Bar Graph - For Discrete Numerical Data
• Pie Chart - For Percentage Data
• Histograms - For Continuous Numerical Data
• Line Chart - For Discrete Numerical Data (used for showing the comparison between the values)

What are different examples of Symmetrical shapes? ​​​​​

• Equilateral Triangle
• Cardioid (Heart Shape)
• Letter 'A'
• Letter 'U'

Accessibility Tools

Highlight links, change contrast, increase text size, increase letter spacing, readability bar, dyslexia friendly font, increase cursor size, research projects.

The math ed faculty and doctoral students at MSU are active researchers. Please click on research projects to the right to see a sample of their activity.

Make Math Instruction Better: 3 Tips on How From Researchers

• Share article

Education Week reporter and data journalist Sarah D. Sparks attended the American Educational Research Association’s annual conference in Philadelphia earlier this month. Here, she shares three of the key takeaways she heard from researchers studying some of the key challenges around math instruction.

Sign Up for EdWeek Update

Edweek top school jobs.

Sign Up & Sign In

Your browser is unsupported

We recommend using the latest version of IE11, Edge, Chrome, Firefox or Safari.

MSCS Undergraduate Research Laboratory

Mathematics, statistics and computer science college of liberal arts and sciences.

Fall 2024 Projects

Machine learning, chess and mathematics Heading link Copy link

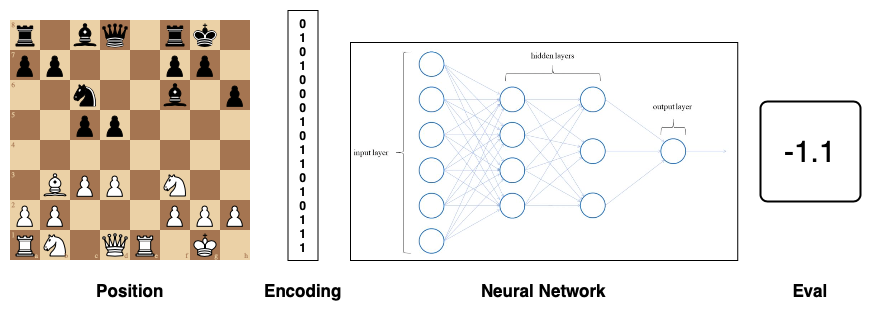
Project Supervisors: Drew Shulman and Evangelos Kobotis

Neural networks have been developed to recognize handwritten text, predict housing prices, improve autonomous driving systems, and even play games like chess and Go.  A neural network is an example of a **machine learning algorithm**.  In this project, we will explore machine learning algorithms and apply them to chess.  Our goal is  to introduce the student to the mathematical treatment of chess and to also write concrete programs that will implement relevant algorithms. Chess and neural networks are two vast fields of study and we  would like to explore different directions, depending on the students’ preferences, and our hope is to make this a fun project that will serve as an introduction to some modern techniques in computer programming.

The quest for prime numbers Heading link Copy link

Project Supervisor: Evangelos Kobotis

The purpose of this exciting project is to acquaint the student with the mysteries of prime numbers and explore the numerical techniques that allow us to explore them. Our main goal will be to become acquainted with the different primality tests and use them in practice in order to see what it takes to find never-seen-before prime numbers. All theory will be explained in detail.

Prerequisites: An interest in prime numbers. All background material and programming techniques will be covered from scratch.

Distribution of sequences modulo 1 Heading link Copy link

Project Supervisor: Daniel Ingebretson

Any real number $ x $ can be written as its integer part $ \lfloor x \rfloor \in \mathbb{Z} $ plus its fractional part $ \{ x \} \in (0,1) $. How is the sequence $ \{ \sqrt{2} \}, \{ 2 \sqrt{2} \}, \{ 3 \sqrt{2} \}, \ldots, $ distributed in the interval $ [0,1] $? How about the sequence $ \{ \pi \}, \{ \pi^2 \}, \{ \pi^3 \}, \ldots $? The answer to the first question is a well-known theorem of Weyl, and the second is a difficult open problem.

In this project we will study distribution of sequences of this form in the interval, using tools from real analysis, with applications to numerical integration and discrepancy.

Time permitting, we will explore connections with diophantine approximation, dynamics, and ergodic theory.

Prerequisites: Math 215. Some knowledge of real analysis will be helpful but not required.

Conflicts of physics laws and mathematical theory Heading link Copy link

Project supervisor: Mimi Dai

Prerequisites: Math 210, Math 220.

Turning handwriting into digital information – the magic of neural networks Heading link Copy link

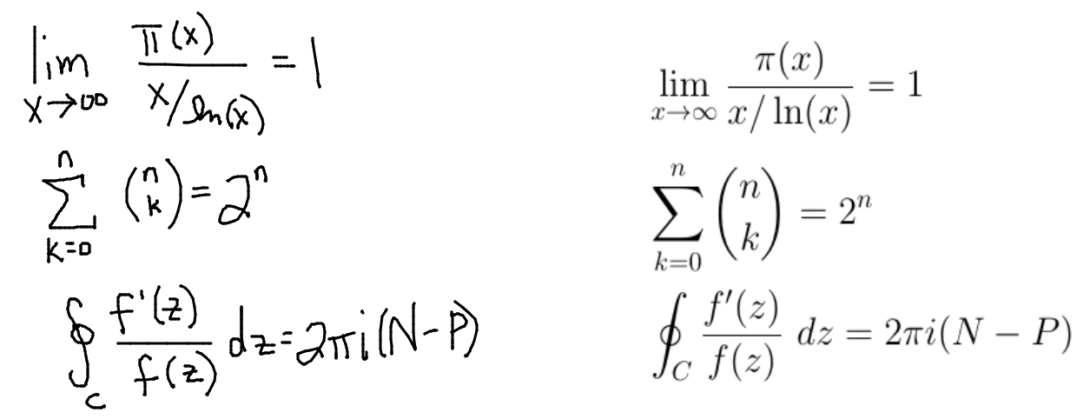
The purpose of this project is to introduce students to Neural Networks in the context of dynamic optical character recognition related to mathematical writing. We will explore how neural networks allow us to recognize handwritten text and turn it into digital text that can be further processed and typeset. We will also try to explore the dynamic side of things with the goal of producing software that will turn mathematical writing dynamically into digital content. The first part of the project will focus on the basics of Neural Networks and mathematical typesetting, whereas the latter and most important part will focus on linking these two items.

Prerequisites: none

Rational points on elliptic curves Heading link Copy link

The purpose of this project is to introduce the student to the magical work of elliptic curves and one of the fascinating problems of their theory. An elliptic curve amounts to considering an equation as simple as $y^2=x^3+ax+b$, with $a$ and $b$ integer numbers. One wants to find all the pairs of rational numbers $(x,y)$ that satisfy this equation. It turns out that one can add such points and generate a group law that in some sense gives a measure of the complexity of the underlying elliptic curves. The understanding of this group of rational points has been an important problem for many years that branches off to all sorts of interesting questions. Our interest will lie in understanding as much as possible about this group and in particular about its rank. No initial knowledge of the field or of programming is required.

Shape-constrained statistical inference in functional data analysis Heading link Copy link

Project Supervisor: Kyunghee Han

The statistical analysis of random objects has become an important class of research framework in modern statistics and machine learning literature. In response to new challenges with the surge of data complexity in data science, data sets that consist of random objects like curves, images, and manifolds are frequently involved. The standard methods in functional data analysis usually assume random objects are fully observed. However, it is more common in practice that responses are partially observed and irregularly collected at subject-dependent times. This often leads to an irregular density of observations, which makes statistical inferences on functional shapes inconsistent per the domain of interest. In this project, shape-constrained functional data analysis will be introduced, and students will have experience in statistical analysis of real data.

Prerequisite: Probability, statistics, and programming experience

Chromatic Symmetric Functions of Graphs Heading link Copy link

Project Supervisor: Victor Protsak

The idea of coloring is quite old, and also very natural: given a set of objects, some of which are said to be adjacent, assign to each of them a label, or color, in a such a way that adjacent objects are colored differently. One can ask whether colorings exist and how to count them. This has been applied to planar maps, where two regions are adjacent if they share a piece of boundary (Four-Color Problem), and to abstract mathematical graphs, where two vertices are adjacent if they are connected by an edge (chromatic polynomial). In 1995, Richard Stanley has encapsulated all colorings of a finite graph G in its chromatic symmetric function X(G). In spite of extensive research, many fundamental questions remain unsolved (for example, which functions are possible?). The aim of this project is to explore X(G)’s from theoretical and computational perspectives.

Prerequisites: Interest in algebra and combinatorics, Math 215 and CS 151 (or equivalent).  Programming experience with algebraic structures (e.g. in SAGE) would be helpful.

Skip to Content

Regents approve plans for new chemistry and applied mathematics facility

• Share via Twitter
• Share via Facebook
• Share via LinkedIn
• Share via E-mail

Rendering of the newly approved chemistry and applied mathematics facility. This is a draft rendering, subject to change.

The University of Colorado Board of Regents today approved plans to construct a new academic and research facility aimed at advancing research and educational opportunities in the fields of chemistry and applied mathematics. The proposed facility, spanning approximately 79,200 square feet, will be situated on the southeast side of Business Field on Main Campus.

The project, with an estimated cost of $175.43 million, will be funded primarily through a combination of campus cash reserves and debt.

Key features

• Shelled space for future specialized quantum research laboratories and offices.
• A nuclear magnetic resonance (NMR) spectroscopic core facility
• Modern classroom, office, meeting and research lab space
• A centrally scheduled 200-seat auditorium
• Student study areas
• Upper-level roof terrace

Academic goals

• The facility will provide modern research laboratories to promote the Department of Chemistry ’s research mission, improve recruitment and strengthen retention. Foundational and interdisciplinary research fields include: analytical spectroscopy, environmental chemistry, experimental and theoretical physical/ biophysical chemistry, inorganic and materials chemistry, synthetic and physical organic/bio-organic chemistry.
• The facility will support the Department of Applied Mathematics ’ efforts to continue to provide a major research presence in computational and physical/biological mathematics and the statistical sciences, enhancing the department’s effort to be a leading program of applied mathematics in the United States.
• The facility will provide shelled spaces to be completed in the future for the growing field of quantum-chemistry research.
• It will serve as a central hub for cutting-edge research, student learning outcomes and sustainable innovation, and it will foster interdisciplinary collaboration among students and researchers.
• It will provide training opportunities for students and researchers, fostering interdisciplinary collaboration and innovation.

Sustainability considerations

• The chemistry and applied math building seeks to be one of the most energy-efficient research buildings in the history of CU Boulder by achieving an Energy Use Intensity (EUI) of approximately 100 kilo British thermal units (kBtu) per gross square feet of the building (kBtu/ft2), according to current modeling.
• Construction will follow Buy Clean Colorado Act guidelines, using eligible materials that do not exceed the maximum allowable global warming potential limit in each construction category. 
• The building’s mechanical system is being designed to use low-temperature hot water in preparation for the eventual connection to a future district energy loop heated by electricity, in support of the university’s overarching decarbonization plans.
• It will be the first building on campus to implement the use of cross-laminated timber (CLT) construction. The project will use CLT instead of concrete for the structure in non-research areas of the building. This will reduce the carbon impact of the structure.

What they’re saying

“The approval of the new chemistry and applied mathematics facility marks a significant milestone for our campus,” CU Boulder Chancellor Phil DiStefano said.

“This project underscores our commitment to advancing research and fostering interdisciplinary collaboration. It will not only provide state-of-the-art resources for our scholars but also pave the way for groundbreaking discoveries that will benefit both our campus community and society at large."

What’s next

Construction is slated to begin in October, with occupancy planned for late 2026/early 2027.

Vacated spaces within Cristol Chemistry & Biochemistry are anticipated to be assigned to the College of Media, Communications and Information (CMCI), while spaces vacated by Applied Mathematics within the Engineering Center will benefit the College of Engineering and Applied Science.

• Administration

Campus Community

Related articles.

Final Climate Action Plan released

CMCI and ENVD integration advances as first milestone approaches

Regents consider tuition, compensation, concealed carry policies and more

News headlines.

• Arts & Humanities
• Business & Entrepreneurship
• Climate & Environment
• Education & Outreach
• Health & Society
• Law & Politics
• Science & Technology
• Announcements & Deadlines
• Career Development
• Getting Involved
• Mind & Body

Events & Exhibits

• Arts & Culture
• Conferences
• Lectures & Presentations
• Performances & Concerts
• Sports & Recreation
• Workshops & Seminars

Subscribe to CUBT

Sign up for Alerts

Administrative eMemos

Buff Bulletin Board

Events Calendar

Inside the CIA’s Clandestine Mission to Turn Psychics Into Government Spies

During the height of the Cold War, the CIA ran tests on people with paranormal abilities in an effort to unlock top-secret intel on foreign targets.

As Harold Puthoff, a physicist with the Stanford Research Institute, witnessed the output from his magnetometer changing, he was mind-blown. There was no physical explanation for the reading changing the way it did. And as soon as Puthoff asked Swann to stop thinking about the apparatus, the unexplained changes in the magnetic field abruptly stopped.

“These phenomena are real. Psychic phenomena are real,” Dean Radin , Ph.D., chief scientist at the California-based nonprofit Institute of Noetic Sciences, tells Popular Mechanics . He’s been examining parapsychology, or the study of psychic events, for the past four decades.

And in the early 1970s—in the midst of the Cold War—the U.S. government agreed.

By the time Puthoff and his colleague Russel Targ, another physicist at the Stanford Research Institute (now known as SRI International), presented their results at an international meeting on quantum physics and parapsychology, the CIA had already begun working with SRI to perform top-secret research on paranormal phenomena—primarily “remote viewing” for intelligence collection. Remote viewing refers to a type of extra-sensorial perception that involves using the mind to “see” or manipulate distant objects, people, events, or other information that are hidden from physical view.

By the mid-1980s, the Defense Intelligence Agency (DIA) took the program over, calling it “Stargate.” DIA had three main goals for its research:

• Determine how to apply remote viewing to intelligence gathering against foreign targets;
• Figure out how other countries could be doing the same thing and using it against the U.S.; and
• Perform laboratory experiments to find ways to improve remote viewing for use in the intelligence field

The program was about as clandestine as it gets. Radin, who served as a visiting scientist on the Stargate program, says security personnel would brief him and his colleagues about the incredible sensitivity of their highly classified work every two weeks, and ask them if they had any reason to believe that anyone outside of the project knew anything about it.

“You had to become a professional paranoid, essentially. It was very uncomfortable for me,” Radin says.

He remembers asking one of his supervisors what would happen if they had a breakthrough—say, coming up with a drug to make someone super psychic. The response was immediate. “It would disappear and you would never be able to talk about it again,” Radin recalls, “which is antithetical to the whole scientific process, but I also understood why.” Any weapon or intelligence tool developed under Stargate would have presumably been too valuable and too dangerous for public release.

The DIA continued the project until the mid-1990s, when the CIA began declassifying its documents on remote viewing research to facilitate an external review of the project, and the DIA quickly followed suit. In June 1995, the CIA asked The American Institutes for Research (AIR)—an Arlington, Virginia-based nonprofit tasked with evaluating and providing technical assistance in behavioral and social science research—to conduct an external review of the Stargate program .

To present a balanced review of the scientific credibility of the program, AIR asked two researchers with opposing perspectives on parapsychology to write the report: Jessica Utts , Ph.D., an accomplished statistician and now professor emerita at the University of California, Irvine, who views parapsychology as a promising science; and Ray Hyman , Ph.D., a renowned psychologist and now professor emeritus at the University of Oregon, who is a noted skeptic and critic of parapsychology.

.css-2l0eat{font-family:UnitedSans,UnitedSans-roboto,UnitedSans-local,Helvetica,Arial,Sans-serif;font-size:1.625rem;line-height:1.2;margin:0rem;padding:0.9rem 1rem 1rem;}@media(max-width: 48rem){.css-2l0eat{font-size:1.75rem;line-height:1;}}@media(min-width: 48rem){.css-2l0eat{font-size:1.875rem;line-height:1;}}@media(min-width: 64rem){.css-2l0eat{font-size:2.25rem;line-height:1;}}.css-2l0eat b,.css-2l0eat strong{font-family:inherit;font-weight:bold;}.css-2l0eat em,.css-2l0eat i{font-style:italic;font-family:inherit;} “These phenomena are real. Psychic phenomena are real.”

“They sent us these boxes full of reports and papers and told us we had one summer to write this report,” Utts tells Popular Mechanics . She and Hyman separately reviewed dozens of Stargate experiments while also taking into account data from the broader scientific community at the time.

The reviewers’ individual conclusions were as expected. Utts found the statistics compelling, and believed the studies provided strong evidence that remote viewing is a human capability. One of the things she found most convincing was that the results seen across studies in different laboratories were all very similar. “And it was all statistically significant,” she says, “so that’s really hard to explain by chance, or cheating, or coincidence, or fluke.”

To that extent, Hyman agreed with Utts, but it wasn’t enough to convince him that remote viewing is real. He found what he considered to be potential flaws in the experimental methods, such as using the same person to judge psychic ability in each trial, and determined that the experimental results were not consistent enough with experiments outside the program. Nonetheless, he wrote in the final report: “The case for psychic functioning seems better than it ever has been. The contemporary findings along with the output of the [Stargate] program do seem to indicate that something beyond odd statistical hiccups is taking place.”

Despite what may be viewed as an optimistic review, the Stargate program no longer exists, and as far as we know, the U.S. government hasn’t continued such research. “I’m sorry it ended, because I really do think that there’s much more to be discovered there,” Utts says.

But maybe it hasn’t ended. Maybe it’s just top secret. Only a true psychic would know.

Kimberly is a freelance science writer with a degree in marine biology from Texas A&M University, a master's degree in biology from Southeastern Louisiana University and a graduate certificate in science communication from the University of California, Santa Cruz. Her work has been published by NBC, Science, Live Science, Space.com and many others. Her favorite stories are about health, animals and obscurities.  

.css-cuqpxl:before{padding-right:0.3125rem;content:'//';display:inline;} Pop Mech Pro: Science .css-xtujxj:before{padding-left:0.3125rem;content:'//';display:inline;}

Immortality Is Impossible Until We Beat Physics

How Vacuum Energy Could Help Us Reach Light Speed

Could the Chair You Sit on Have a Soul?

Here’s How We Could Live in Trees

The Engine Driving Our Oceans Could Die by 2100

Can AI Help Solve Math’s Thorniest Mysteries?

You Can Give Your Body Back to Nature When You Die

How Does UFO Footage Play Tricks on Your Mind?

Why Doesn’t the Living Human Body ‘Go Bad’?

Is the Room-Temperature Superconductor Back?

What 9 Months on a Cruise Ship Can Do to You