random assignment matlab

Help Center Help Center

• Help Center
• Trial Software
• Product Updates
• Documentation

Random Number Generation

Statistics and Machine Learning Toolbox™ supports the generation of random numbers from various distributions. Each random number generator (RNG) represents a parametric family of distributions. RNGs return random numbers from the specified distribution in an array of the specified dimensions.

Other random number generation functions which do not support specific distributions include:

cvpartition

hmmgenerate

slicesample

RNGs in Statistics and Machine Learning Toolbox software depend on the default random number stream of MATLAB ® via the rand and randn functions. Each RNG uses one of the techniques discussed in Common Pseudorandom Number Generation Methods to generate random numbers from a given distribution.

By controlling the default random number stream and its state, you can control how the RNGs in Statistics and Machine Learning Toolbox software generate random values. For example, to reproduce the same sequence of values from an RNG, you can save and restore the default stream's state, or reset the default stream. For details on managing the default random number stream, see Managing the Global Stream Using RandStream .

MATLAB initializes the default random number stream to the same state each time it starts up. Thus, RNGs in Statistics and Machine Learning Toolbox software will generate the same sequence of values for each MATLAB session unless you modify that state at startup. One simple way to do that is to add commands to startup.m such as

that initialize the default random number stream to a different state for each session.

The following table lists the supported distributions and their respective random number generation functions.

Related Topics

• Generate Random Numbers Using the Triangular Distribution
• Generate Random Numbers Using Uniform Distribution Inversion
• Generating Pseudorandom Numbers
• Generating Quasi-Random Numbers
• Working with Probability Distributions
• Supported Distributions

MATLAB Command

You clicked a link that corresponds to this MATLAB command:

Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site

Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .

• Switzerland (English)
• Switzerland (Deutsch)
• Switzerland (Français)
• 中国 (English)

You can also select a web site from the following list:

How to Get Best Site Performance

Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.

• América Latina (Español)
• Canada (English)
• United States (English)
• Belgium (English)
• Denmark (English)
• Deutschland (Deutsch)
• España (Español)
• Finland (English)
• France (Français)
• Ireland (English)
• Italia (Italiano)
• Luxembourg (English)
• Netherlands (English)
• Norway (English)
• Österreich (Deutsch)
• Portugal (English)
• Sweden (English)
• United Kingdom (English)

Asia Pacific

• Australia (English)
• India (English)
• New Zealand (English)

Contact your local office

Matlab and Simulink Tutorials

Matlab Simulink Examples

Generating Random Numbers and Data in Matlab

Are you intrigued by the power and versatility of Matlab for generating random numbers and data? Look no further, as we delve into the various ways to generate random numbers and data in Matlab. With subheadings such as “Generating random numbers in Matlab,” “Creating arrays of random numbers,” “Generating random data with specified characteristics,” “Generating random numbers within a specific range,” and “Random sampling from a dataset in Matlab,” this blog post will be your comprehensive guide to mastering the art of randomness in Matlab. Whether you’re a beginner looking to understand the basics or an experienced user hoping to explore advanced techniques, this post will equip you with the knowledge and skills to confidently generate and manipulate random numbers and data in Matlab. Let’s unlock the potential of randomness and data generation in Matlab together!

Generating random numbers in Matlab

When working with data analysis or simulations in Matlab, it is often necessary to generate random numbers. This can be done using the built-in functions for random number generation in Matlab.

One way to generate random numbers in Matlab is by using the rand function, which creates an array of random numbers between 0 and 1. For example, you can generate a 1×5 array of random numbers using the command rand(1,5) .

If you need random numbers with specific characteristics, you can use the randn function to generate numbers from a normal distribution with a specified mean and standard deviation.

Another option for generating random numbers within a specific range is using the randi function, which generates random integers within a specified range. For example, you can create a 1×5 array of random integers between 1 and 10 using the command randi([1, 10], 1, 5) .

Creating arrays of random numbers

When working in Matlab, it is often necessary to generate arrays of random numbers for various applications. One way to do this is by using the rand function, which creates an array of random numbers from a uniform distribution between 0 and 1. For example, the code x = rand(1, 10) would generate an array x containing 10 random numbers. This can be helpful in simulations, testing, and other mathematical operations.

Another useful function for creating arrays of random numbers is randi , which generates random integer values within a specified range. For instance, the code y = randi([1, 100], 1, 10) would produce an array y containing 10 random integers between 1 and 100. This is particularly advantageous when needing to work with discrete values rather than continuous ones.

It is worth noting that both the rand and randi functions can take additional arguments to create multidimensional arrays or arrays with specific characteristics. These can include specifying the size of the array, setting the random number generator seed, or controlling the distribution of the generated values. This flexibility allows for tailored random number arrays to be generated to suit the needs of the user.

In conclusion, Matlab provides powerful tools for creating arrays of random numbers, enabling users to easily generate and manipulate random data for a wide range of applications. Whether working with continuous or discrete values, the rand and randi functions offer a versatile and customizable approach to meeting the demands of various projects and tasks.

Generating random data with specified characteristics

When working with data analysis and simulation in Matlab, it is often necessary to generate random data with specific characteristics. This could include generating data with a certain distribution, mean, variance, or correlation structure. Fortunately, Matlab provides several functions and tools to assist in generating such random data.

The randn function in Matlab is often used to generate random data with a normal distribution. This function returns an array of random numbers from the standard normal distribution with a mean of 0 and standard deviation of 1. By using appropriate scaling and shifting, it is possible to generate random data with a normal distribution having the desired mean and variance.

For generating random data with other distributions such as uniform, exponential, or Poisson, Matlab provides the rand , exprnd , and poissrnd functions respectively. These functions allow the user to specify the desired characteristics of the random data to be generated, such as the mean, standard deviation, rate, or shape parameter.

In addition to generating univariate random data, Matlab also provides functions for generating multivariate random data with specified correlation structures. The mvnrnd function, for example, can be used to generate multivariate normal random data with a specified mean vector and covariance matrix, allowing for the generation of data that exhibits specific correlations between variables.

Generating random numbers within a specific range

When working with random number generation in Matlab, there may be times when you need to generate numbers within a specific range. Fortunately, Matlab provides easy-to-use functions for achieving this, allowing you to specify the minimum and maximum values for the range.

The randi function is one such tool that generates random integers within a specified range. By using this function, you can easily generate random numbers that fall within the range you desire. For example, if you want to generate random integers between 1 and 100, you would use the command randi([1, 100]) .

In addition to randi, Matlab also offers the unifrnd function, which allows you to generate random numbers from a uniform distribution within a specific range. This can be useful for scenarios where you need random decimal numbers within a defined interval.

By utilizing these built-in functions, you can efficiently generate random numbers within a specific range in Matlab, catering to your specific requirements for data analysis or simulation.

Random sampling from a dataset in Matlab

When working with large datasets in Matlab, it can be useful to take a random sample of the data for analysis. Random sampling allows you to ensure that your sample is representative of the larger population, and can be an important tool in statistical analysis.

One way to generate a random sample from a dataset in Matlab is to use the datasample function. This function allows you to specify the size of the sample you want to take, as well as whether or not you want to sample with or without replacement. For example, if you have a dataset stored in a variable called data and you want to take a sample of size 100 without replacement, you could use the following code:

sample = datasample(data, 100, ‘Replace’, false)

This would give you a random sample of 100 observations from the dataset data, without allowing for duplicates.

You may also like...

Introduction to Parallel Computing in Matlab

January 16, 2024

 by Matlab · Published January 16, 2024

Signal Processing in Matlab

January 17, 2024

 by Matlab · Published January 17, 2024

Creating Interactive Plots in Matlab

January 22, 2024

 by Matlab · Published January 22, 2024

• Next story  Creating Simulink Simulations for Control Systems
• Previous story  Working with RF Toolbox for Matlab

Privacy Overview

Help Center Help Center

• Help Center
• Trial Software
• Product Updates
• Documentation

Controlling Random Number Generation

This example shows how to use the rng function, which provides control over random number generation.

(Pseudo)Random numbers in MATLAB® come from the rand , randi , and randn functions. Many other functions call those three, but those are the fundamental building blocks. All three depend on a single shared random number generator that you can control using rng .

It's important to realize that "random" numbers in MATLAB are not unpredictable at all, but are generated by a deterministic algorithm. The algorithm is designed to be sufficiently complicated so that its output appears to be an independent random sequence to someone who does not know the algorithm, and can pass various statistical tests of randomness. The function that is introduced here provides ways to take advantage of the determinism to

repeat calculations that involve random numbers, and get the same results, or

guarantee that different random numbers are used in repeated calculations

and to take advantage of the apparent randomness to justify combining results from separate calculations.

"Starting Over"

If you look at the output from rand , randi , or randn in a new MATLAB session, you'll notice that they return the same sequences of numbers each time you restart MATLAB. It's often useful to be able to reset the random number generator to that startup state, without actually restarting MATLAB. For example, you might want to repeat a calculation that involves random numbers, and get the same result.

When you first start a MATLAB session or call rng("default") , MATLAB initializes the random number generator using the default algorithm and seed. Starting in R2023b, you can set the default algorithm and seed in MATLAB preferences. If you do not change these preferences, then rng uses the factory value of "twister" for the Mersenne Twister generator with seed 0, as in previous releases. For more information, see Default Settings for Random Number Generator and Reproducibility for Random Number Generator .

rng("default") provides a very simple way to put the random number generator back to its default settings.

What are the "default" random number settings that MATLAB starts up with, or that rng("default") gives you? Before R2023b, if you call rng with no inputs, you can see that it is the Mersenne Twister generator algorithm, seeded with 0.

You'll see in more detail below how to use the above output, including the State field, to control and change how MATLAB generates random numbers. For now, it serves as a way to see what generator rand , randi , and randn are currently using.

Non-Repeatability

Each time you call rand , randi , or randn , they draw a new value from their shared random number generator, and successive values can be treated as statistically independent. But as mentioned above, each time you restart MATLAB those functions are reset and return the same sequences of numbers. Obviously, calculations that use the same "random" numbers cannot be thought of as statistically independent. So when it's necessary to combine calculations done in two or more MATLAB sessions as if they were statistically independent, you cannot use the default generator settings.

One simple way to avoid repeating the same random numbers in a new MATLAB session is to choose a different seed for the random number generator. rng gives you an easy way to do that, by creating a seed based on the current time.

Each time you use "shuffle" , it reseeds the generator with a different seed. You can call rng with no inputs to see what seed it actually used.

"shuffle" is a very easy way to reseed the random number generator. You might think that it's a good idea, or even necessary, to use it to get "true" randomness in MATLAB. For most purposes, though, it is not necessary to use "shuffle" at all . Choosing a seed based on the current time does not improve the statistical properties of the values you'll get from rand , randi , and randn , and does not make them "more random" in any real sense. While it is perfectly fine to reseed the generator each time you start up MATLAB, or before you run some kind of large calculation involving random numbers, it is actually not a good idea to reseed the generator too frequently within a session, because this can affect the statistical properties of your random numbers.

What "shuffle" does provide is a way to avoid repeating the same sequences of values. Sometimes that is critical, sometimes it's just "nice", but often it is not important at all. Bear in mind that if you use "shuffle" , you may want to save the seed that rng created so that you can repeat your calculations later on. You'll see how to do that below.

More Control over Repeatability and Non-Repeatability

So far, you've seen how to reset the random number generator to its default settings, and reseed it using a seed that is created using the current time. rng also provides a way to reseed it using a specific seed.

You can use the same seed several times, to repeat the same calculations. For example, if you run this code twice ...

... you get exactly the same results. You might do this to recreate x after having cleared it, so that you can repeat what happens in subsequent calculations that depend on x , using those specific values.

On the other hand, you might want to choose different seeds to ensure that you don't repeat the same calculations. For example, if you run this code in one MATLAB session ...

and this code in another ...

... you could combine the two results and be confident that they are not simply the same results repeated twice.

As with " shuffle" there is a caveat when reseeding MATLAB's random number generator, because it affects all subsequent output from rand , randi , and randn . Unless you need repeatability or uniqueness, it is usually advisable to simply generate random values without reseeding the generator. If you do need to reseed the generator, that is usually best done at the command line, or in a spot in your code that is not easily overlooked.

Choosing a Generator Type

Not only can you reseed the random number generator as shown above, you can also choose the type of random number generator that you want to use. Different generator types produce different sequences of random numbers, and you might, for example, choose a specific type because of its statistical properties. Or you might need to recreate results from an older version of MATLAB that used a different default generator type.

One other common reason for choosing the generator type is that you are writing a validation test that generates "random" input data, and you need to guarantee that your test can always expect exactly the same predictable result. If you call rng with a seed before creating the input data, it reseeds the random number generator. But if the generator type has been changed for some reason, then the output from rand , randi , and randn will not be what you expect from that seed. Therefore, to be 100% certain of repeatability, you can also specify a generator type.

For example,

causes rand , randi , and randn to use the Mersenne Twister generator algorithm, after seeding it with 0.

Using "combRecursive"

selects the Combined Multiple Recursive generator algorithm, which supports some parallel features that the Mersenne Twister does not.

This command

selects the generator algorithm that was the default in MATLAB 4.0.

And of course, this command returns the random number generator to its default settings.

However, because the default random number generator settings may change between MATLAB releases, using "default" does not guarantee predictable results over the long-term. "default" is a convenient way to reset the random number generator, but for even more predictability, specify a generator type and a seed.

On the other hand, when you are working interactively and need repeatability, it is simpler, and usually sufficient, to call rng with just a seed.

Saving and Restoring Random Number Generator Settings

Calling rng with no inputs returns a scalar structure with fields that contain two pieces of information described already: the generator type, and the integer with which the generator was last reseeded.

The third field, State , contains a copy of the generator's current state vector. This state vector is the information that the generator maintains internally in order to generate the next value in its sequence of random numbers. Each time you call rand , randi , or randn , the generator that they share updates its internal state. Thus, the state vector in the settings structure returned by rng contains the information necessary to repeat the sequence, beginning from the point at which the state was captured.

While just being able to see this output is informative, rng also accepts a settings structure as an input , so that you can save the settings, including the state vector, and restore them later to repeat calculations. Because the settings contain the generator type, you'll know exactly what you're getting, and so "later" might mean anything from moments later in the same MATLAB session, to years (and multiple MATLAB releases) later. You can repeat results from any point in the random number sequence at which you saved the generator settings. For example

Notice that while reseeding provides only a coarse reinitialization, saving and restoring the generator state using the settings structure allows you to repeat any part of the random number sequence.

The most common way to use a settings structure is to restore the generator state. However, because the structure contains not only the state, but also the generator type and seed, it's also a convenient way to temporarily switch generator types. For example, if you need to create values using one of the legacy generators from MATLAB 5.0, you can save the current settings at the same time that you switch to use the old generator.

You can then restore the original settings later.

You should not modify the contents of any of the fields in a settings structure. In particular, you should not construct your own state vector, or even depend on the format of the generator state.

Writing Simpler, More Flexible, Code

rng allows you to either

reseed the random number generator, or

save and restore random number generator settings

without having to know what type it is. You can also return the random number generator to its default settings without having to know what those settings are. While there are situations when you might want to specify a generator type, rng affords you the simplicity of not having to specify it.

If you are able to avoid specifying a generator type, your code will automatically adapt to cases where a different generator needs to be used, and will automatically benefit from improved properties in a new default random number generator type.

rng and RandStream

rng provides a convenient way to control random number generation in MATLAB for the most common needs. However, more complicated situations involving multiple random number streams and parallel random number generation require a more complicated tool. The RandStream class is that tool, and it provides the most powerful way to control random number generation. The two tools are complementary, with rng providing a much simpler and concise syntax that is built on top of the flexibility of RandStream .

MATLAB Command

You clicked a link that corresponds to this MATLAB command:

Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site

Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .

• Switzerland (English)
• Switzerland (Deutsch)
• Switzerland (Français)
• 中国 (English)

You can also select a web site from the following list:

How to Get Best Site Performance

Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.

• América Latina (Español)
• Canada (English)
• United States (English)
• Belgium (English)
• Denmark (English)
• Deutschland (Deutsch)
• España (Español)
• Finland (English)
• France (Français)
• Ireland (English)
• Italia (Italiano)
• Luxembourg (English)
• Netherlands (English)
• Norway (English)
• Österreich (Deutsch)
• Portugal (English)
• Sweden (English)
• United Kingdom (English)

Asia Pacific

• Australia (English)
• India (English)
• New Zealand (English)

Contact your local office

Help Center Help Center

• Help Center
• Trial Software
• Product Updates
• Documentation

Creating and Controlling a Random Number Stream

The RandStream class allows you to create a random number stream. This is useful for several reasons:

You can generate random values without affecting the state of the global stream.

You can separate sources of randomness in a simulation.

You can use a generator that is configured differently than the one MATLAB ® software uses at startup.

With a RandStream object, you can create your own stream, set the writable properties, and use the stream to generate random numbers. You can control the stream you create the same way you control the global stream. You can even replace the global stream with the stream you create.

To create a stream, use the RandStream function.

The random stream myStream acts separately from the global stream. If you call the rand , randn , randi , and randperm functions with myStream as the first argument, they draw from the stream you created. If you call rand , randn , randi , and randperm without myStream , they draw from the global stream.

You can make myStream the global stream using the RandStream.setGlobalStream method.

You can use substreams to get different results that are statistically independent from a stream. Unlike seeds, where the locations along the sequence of random numbers are not exactly known, the spacing between substreams is known, so any chance of overlap can be eliminated. In short, substreams are a more-controlled way to do many of the same things that seeds have traditionally been used for. Substreams are also a more lightweight solution than parallel streams.

Substreams provide a quick and easy way to ensure that you get different results from the same code at different times. To use the Substream property of a RandStream object, create a stream using a generator that supports substreams. For a list of generator algorithms that support substreams and their properties, see the table in the next section. For example, generate several random numbers in a loop.

In another loop, you can generate random values that are independent from the first set of 5 iterations.

Substreams are useful in serial computation. Substreams can recreate all or part of a simulation by returning to a particular checkpoint in stream. For example, you can return to the 6th substream in the loop. The result contains the same values as the 6th output above.

Choosing a Random Number Generator

MATLAB offers several generator algorithm options. The table summarizes the key properties of the available generator algorithms and the keywords used to create them. To return a list of all the available generator algorithms, use the RandStream.list method.

The generators mcg16807 , shr3cong , and swb2712 provide for backwards compatibility with earlier versions of MATLAB. mt19937ar and dsfmt19937 are designed primarily for sequential applications. The remaining generators provide explicit support for parallel random number generation.

Depending on the application, some generators might be faster or return values with more precision. All pseudorandom number generators are based on deterministic algorithms, and all generators pass a sufficiently specific statistical test for randomness. One way to check the results of a Monte Carlo simulation is to rerun the simulation with two or more different generator algorithms, and the choice of generators in MATLAB provides you with the means to do that. Although it is unlikely that your results will differ by more than the Monte Carlo sampling error when using different generators, there are examples in the literature where this kind of validation has turned up flaws in a particular generator algorithm. (See [13] for an example.)

Generator Algorithms

The Mersenne Twister, as described in [11] , has period 2 19937 − 1 and each U(0,1) value is created using two 32-bit integers. The possible values are multiples of 2 − 53 in the interval (0, 1). This generator does not support multiple streams or substreams. The randn algorithm used by default for mt19937ar streams is the ziggurat algorithm [7] , but with the mt19937ar generator underneath.

This generator is identical to the one used by the rand function beginning in MATLAB Version 7, activated by rand('twister',s) .

The double precision SIMD-oriented Fast Mersenne Twister, as described in [12] , is a faster implementation of the Mersenne Twister algorithm. The period is 2 19937 − 1 and the possible values are multiples of 2 − 52 in the interval (0, 1). The generator produces double precision values in [1, 2) natively, which are transformed to create U(0,1) values. This generator does not support multiple streams or substreams.

A 32-bit multiplicative congruential generator, as described in [14] , with multiplier a = 7 5 , modulo m = 2 31 − 1 . This generator has a period of 2 31 − 2 and does not support multiple streams or substreams. Each U(0,1) value is created using a single 32-bit integer from the generator; the possible values are all multiples of ( 2 31 − 1 ) − 1 strictly within the interval (0, 1). For mcg16807 streams, the default algorithm used by randn is the polar algorithm (described in [1] ).

This generator is identical to the one used beginning in MATLAB Version 4 by both the rand and randn functions, activated using rand('seed',s) or randn('seed',s) .

A 64-bit multiplicative lagged Fibonacci generator, as described in [10] , with lags l = 63 , k = 31 . This generator is similar to the MLFG implemented in the SPRNG library. It has a period of approximately 2 124 . It supports up to 2 61 parallel streams, via parameterization, and 2 51 substreams each of length 2 72 . Each U(0,1) value is created using one 64-bit integer from the generator; the possible values are all multiples of 2 − 64 strictly within the interval (0, 1). The randn algorithm used by default for mlfg6331_64 streams is the ziggurat algorithm [7] , but with the mlfg6331_64 generator underneath.

A 32-bit combined multiple recursive generator, as described in [2] . This generator is similar to the CMRG implemented in the RngStreams package in C. It has a period of 2 191 and supports up to 2 63 parallel streams through sequence splitting, each of length 2 127 . It also supports 2 51 substreams, each of length 2 76 . Each U(0,1) value is created using two 32-bit integers from the generator; the possible values are multiples of 2 − 53 strictly within the interval (0, 1). The randn algorithm used by default for mrg32k3a streams is the ziggurat algorithm [7] , but with the mrg32k3a generator underneath.

A 4x32 generator with 10 rounds as described in [15] . This generator uses a Feistel network and integer multiplication. The generator is specifically designed for high performance in highly parallel systems such as GPUs. It has a period of 2 193 (2 64 streams of length 2 129 ).

A 4x64 generator with 20 rounds as described in [15] . This generator is a non-cryptographic adaptation of the Threefish block cipher from the Skein Hash Function. It has a period of 2 514 (2 256 streams of length 2 258 ).

Marsaglia's SHR3 shift-register generator summed with a linear congruential generator with multiplier a = 69069 , addend b = 1234567 , and modulus 2 − 32 . SHR3 is a 3-shift-register generator defined as u = u ( I + L 13 ) ( I + R 17 ) ( I + L 5 ) , where I is the identity operator, L is the left shift operator, and R is the right shift operator. The combined generator (the SHR3 part is described in [7] ) has a period of approximately 2 64 . This generator does not support multiple streams or substreams. Each U(0,1) value is created using one 32-bit integer from the generator; the possible values are all multiples of 2 − 32 strictly within the interval (0, 1). The randn algorithm used by default for shr3cong streams is the earlier form of the ziggurat algorithm [9] , but with the shr3cong generator underneath. This generator is identical to the one used by the randn function beginning in MATLAB Version 5, activated using randn('state',s) .

The SHR3 generator used in [6] (1999) differs from the one used in [7] (2000). MATLAB uses the most recent version of the generator, presented in [7] .

A modified Subtract-with-Borrow generator, as described in [8] . This generator is similar to an additive lagged Fibonacci generator with lags 27 and 12, but it is modified to have a much longer period of approximately 2 1492 . The generator works natively in double precision to create U(0,1) values, and all values in the open interval (0, 1) are possible. The randn algorithm used by default for swb2712 streams is the ziggurat algorithm [7] , but with the swb2712 generator underneath.

This generator is identical to the one used by the rand function beginning in MATLAB Version 5, activated using rand('state',s) .

Transformation Algorithms

Computes a normal random variate by applying the standard normal inverse cumulative distribution function to a uniform random variate. Exactly one uniform value is consumed per normal value.

The polar rejection algorithm, as described in [1] . Approximately 1.27 uniform values are consumed per normal value, on average.

The ziggurat algorithm, as described in [7] . Approximately 2.02 uniform values are consumed per normal value, on average.

Configuring a Stream

A random number stream s has properties that control its behavior. To access or change a property, use the syntax p = s.Property and s.Property = p .

For example, you can configure the transformation algorithm to generate normally distributed pseudorandom values when using randn . Generate normally distributed pseudorandom values using the default Ziggurat transformation algorithm.

Configure the stream to use the Polar transformation algorithm to generate normally distributed pseudorandom values.

When generating random numbers with uniform distribution using rand , you can also configure the stream to generate antithetic pseudorandom values, that is, the usual values subtracted from 1 for uniform values.

Create 6 random numbers with uniform distribution from the stream s.

Restore the initial state of the stream. Create another 6 random numbers with the Antithetic property set to true. Check that these 6 random numbers are equal to the previously generated random numbers subtracted from 1.

Instead of setting the properties of a stream one-by-one, you can save and restore all properties of a stream s by using A = get(s) and set(s,A) , respectively. For example, configure all properties of the stream s2 to be the same as the stream s1 .

The get and set functions enable you to save and restore a stream's entire configuration so that results are exactly reproducible later on.

Restore State of Random Number Generator to Reproduce Output

The State property is the internal state of the random number generator. You can save the state of the global stream at a certain point in your simulation when generating random numbers to reproduce the results later on.

Use RandStream.getGlobalStream to return a handle to the global stream, that is, the current global stream that rand generates random numbers from. Save the state of the global stream.

Using myState , you can restore the state of globalStream and reproduce previous results. A = rand(1,100); globalStream.State = myState; B = rand(1,100); isequal(A,B) ans = logical 1

rand , randi , randn , and randperm access the global stream. Since all of these functions access the same underlying stream, a call to one affects the values produced by the others at subsequent calls.

You can also reset a stream to its initial settings using the reset function. reset(globalStream) A = rand(1,100); reset(globalStream) B = rand(1,100); isequal(A,B) ans = logical 1

[1] Devroye, L. Non-Uniform Random Variate Generation , Springer-Verlag, 1986.

[2] L’Ecuyer, P. “Good Parameter Sets for Combined Multiple Recursive Random Number Generators”, Operations Research , 47(1): 159–164. 1999.

[3] L'Ecuyer, P. and S. Côté. “Implementing A Random Number Package with Splitting Facilities”, ACM Transactions on Mathematical Software , 17: 98–111. 1991.

[4] L'Ecuyer, P. and R. Simard. “TestU01: A C Library for Empirical Testing of Random Number Generators,” ACM Transactions on Mathematical Software , 33(4): Article 22. 2007.

[5] L'Ecuyer, P., R. Simard, E. J. Chen, and W. D. Kelton. “An Objected-Oriented Random-Number Package with Many Long Streams and Substreams.” Operations Research , 50(6):1073–1075. 2002.

[6] Marsaglia, G. “Random numbers for C: The END?” Usenet posting to sci.stat.math. 1999. Available online at https://groups.google.com/group/sci.crypt/browse_thread/ thread/ca8682a4658a124d/ .

[7] Marsaglia G., and W. W. Tsang. “The ziggurat method for generating random variables.” Journal of Statistical Software , 5:1–7. 2000. Available online at https://www.jstatsoft.org/v05/i08 .

[8] Marsaglia, G., and A. Zaman. “A new class of random number generators.” Annals of Applied Probability 1(3):462–480. 1991.

[9] Marsaglia, G., and W. W. Tsang. “A fast, easily implemented method for sampling from decreasing or symmetric unimodal density functions.” SIAM J. Sci. Stat. Comput . 5(2):349–359. 1984.

[10] Mascagni, M., and A. Srinivasan. “Parameterizing Parallel Multiplicative Lagged-Fibonacci Generators.” Parallel Computing , 30: 899–916. 2004.

[11] Matsumoto, M., and T. Nishimura.“Mersenne Twister: A 623-Dimensionally Equidistributed Uniform Pseudorandom Number Generator.” ACM Transactions on Modeling and Computer Simulation , 8(1):3–30. 1998.

[12] Matsumoto, M., and M. Saito.“A PRNG Specialized in Double Precision Floating Point Numbers Using an Affine Transition.” Monte Carlo and Quasi-Monte Carlo Methods 2008 , 10.1007/978-3-642-04107-5_38. 2009.

[13] Moler, C.B. Numerical Computing with MATLAB . SIAM, 2004. Available online at https://www.mathworks.com/moler

[14] Park, S.K., and K.W. Miller. “Random Number Generators: Good Ones Are Hard to Find.” Communications of the ACM , 31(10):1192–1201. 1998.

[15] Salmon, J. K., M. A. Moraes, R. O. Dror, and D. E. Shaw. "Parallel Random Numbers: As Easy As 1, 2, 3." In Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis (SC11) . New York, NY: ACM, 2011.

rng | RandStream

Related Topics

• Managing the Global Stream Using RandStream
• Multiple Streams
• Controlling Random Number Generation
• Create Arrays of Random Numbers

MATLAB Command

You clicked a link that corresponds to this MATLAB command:

Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site

Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .

• Switzerland (English)
• Switzerland (Deutsch)
• Switzerland (Français)
• 中国 (English)

You can also select a web site from the following list:

How to Get Best Site Performance

Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.

• América Latina (Español)
• Canada (English)
• United States (English)
• Belgium (English)
• Denmark (English)
• Deutschland (Deutsch)
• España (Español)
• Finland (English)
• France (Français)
• Ireland (English)
• Italia (Italiano)
• Luxembourg (English)
• Netherlands (English)
• Norway (English)
• Österreich (Deutsch)
• Portugal (English)
• Sweden (English)
• United Kingdom (English)

Asia Pacific

• Australia (English)
• India (English)
• New Zealand (English)

Contact your local office

• Trending Now
• Foundational Courses
• Data Science
• Practice Problem
• Machine Learning
• System Design
• DevOps Tutorial

Random Numbers in MATLAB

• Generate a Random Float Number in C++
• Generate Random Double Numbers in C++
• Random Numbers in Python
• Generating random numbers in Java
• Generating Random Numbers in Golang
• Generate N Random Hexadecimal Numbers
• Random Package in R
• Online Random Number Generator
• numpy.random.laplace() in Python
• Random vs Secure Random numbers in Java
• PostgreSQL - Random Number Generation
• Pseudo Random Number Generator (PRNG)
• Java Math random() Method
• C# | Random.NextDouble() Method
• How to generate Random Numbers in PHP?
• numpy matrix operations | rand() function
• C# | Random.Next() Method
• C++ program to generate random number
• numpy matrix operations | randn() function

Random numbers, as the name suggests, are numbers chosen randomly from a set of numbers. In practical application, classical computers cannot create truly random numbers as they are developed on binary logic thus, they require some sort of algorithm to generate random numbers, this type of random number is called a pseudorandom number. They are random numbers generated by an algorithm in the core of a given programming language by using some variable such as system time, which will never be the same, as a seed to produce different numbers every time.

In MATLAB, there are plenty of options to generate random numbers of different types. This article will discuss how to generate random numbers with various options available in MATLAB.

Generating Random Numbers:

The rand function in MATLAB generates random numbers in MATLAB. 

num = rand(<optional parameters>)

The rand function generates uniformly distributed random numbers (real numbers) in the range of (0,1).

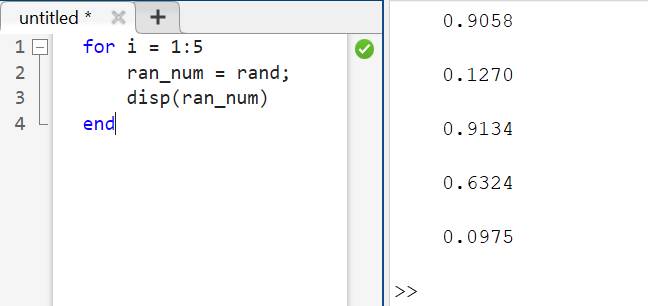
The above code generates 5 random numbers and displays them using the disp() function.

Square Matrix of Random Numbers:

To generate an n-order matrix of random numbers in the range (0,1), we use the following method.

mat = rand(n)

where n is the order of required matrix.

This will generate a 3 by 3 matrix of random numbers in the range of (0,1).

Generating an Array of Random Numbers of Any Size:

MATLAB provides the option to generate an array of any size and shape by using the same rand() function and passing the size of the array as a row vector to it.

arr = rand([<size of required array>])

We will create an array of 4-by-3-by-2 sizes and display it.

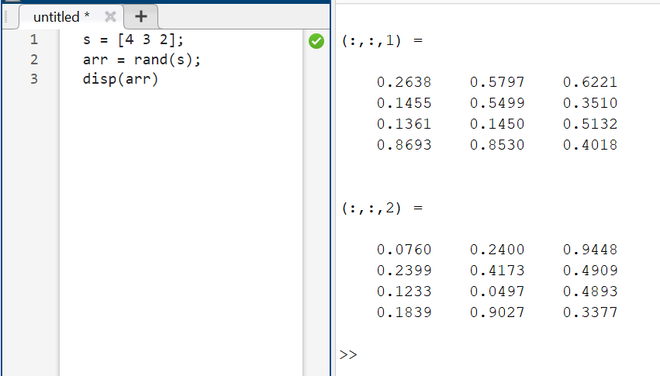
Generating Random Numbers in Any Range (min, max):

We can create random numbers in any range of real numbers (min, max) using the standard formula:

min + (max-min)*rand

The following code creates a 3-order matrix in the range (-2.3, 2.3).

Please Login to comment...

Similar reads.

• MATLAB-Maths
• Technical Scripter 2022
• Technical Scripter

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

• Random Number Generation in MATLAB: Probability Distributions

How to Generate Random Numbers for Different Probability Distributions in MATLAB

Random numbers are a fundamental component of various scientific and engineering applications, including statistical simulations, data analysis, and experimental research. MATLAB, a powerful computational tool widely used in universities, offers several functions to generate random numbers and samples from various probability distributions. In this blog post, we will delve into the concept of random number generation in MATLAB and provide a comprehensive understanding of how to generate samples from different probability distributions using MATLAB functions. This theoretical discussion aims to assist university students in tackling assignments related to random number generation and probability distribution sampling without getting into complex code or intricate mathematical formulas. If you need help to complete your Probability Distributions assignment using MATLAB , this post can serve as a valuable resource.

Concept of Random Number Generation

Random numbers play a crucial role in many areas of science and engineering. They are used to simulate uncertain or stochastic processes, conduct statistical experiments, and solve various computational problems. In MATLAB, random numbers are generated using pseudo-random number generators (PRNGs). These PRNGs produce sequences of numbers that appear random but are determined by an initial seed value. Understanding the concept of random number generation involves grasping the following key points:

Pseudo-Random Number Generators (PRNGs)

Pseudo-random number generators (PRNGs) are algorithms used to generate sequences of numbers that appear to be random but are, in fact, deterministic. These algorithms mimic true randomness by starting with an initial value known as the seed. Once the seed is set, the PRNG follows a predefined set of mathematical operations to produce a sequence of numbers that seems unpredictable.

• Deterministic Nature: PRNGs are deterministic because they produce the same sequence of numbers when initialized with the same seed value. This determinism is advantageous for debugging and reproducibility in research because it ensures that the same set of random numbers can be generated consistently.
• Applications: PRNGs have widespread applications in various fields, including computer science, statistics, and simulations. They are used for tasks such as Monte Carlo simulations, random sampling, cryptography, and procedural content generation in video games.
• MATLAB PRNGs: MATLAB employs various PRNG algorithms to generate random numbers. These algorithms have different properties and characteristics, so students should be aware of which PRNG they are using for their assignments. Two common PRNGs in MATLAB are the Mersenne Twister and the default MATLAB generator. Each has its strengths and limitations, making them suitable for different types of applications.

The seed value is a critical parameter in PRNGs. It serves as the starting point for the PRNG algorithm to generate the sequence of numbers. When you provide a specific seed value to a PRNG, it ensures that the sequence of random numbers generated is reproducible. In other words, using the same seed value will yield the same sequence of random numbers every time the PRNG is initialized.

• Reproducibility: The ability to reproduce the same sequence of random numbers is crucial in research, debugging, and sharing results with others. It ensures that experiments and simulations can be precisely replicated, leading to more reliable and verifiable outcomes.
• Random-Looking Variability: Despite being deterministic, PRNGs create sequences that appear to exhibit the unpredictability and randomness associated with true random processes. This makes them suitable for a wide range of applications where random inputs are required.

Uniform Random Numbers

In MATLAB, by default, random numbers are generated from a uniform distribution in the range [0, 1]. This means that any number within this interval has an equal chance of being generated. Uniform random numbers are evenly distributed across the specified range and are commonly used in various applications.

• Equal Probability: One of the key characteristics of uniform random numbers is that each value within the specified range has an equal probability of being chosen. This property makes them ideal for simulating events where all outcomes are equally likely.
• Applications: Uniform random numbers are employed in statistical simulations, random sampling, Monte Carlo methods, and modeling scenarios where random events are involved. They provide a basis for generating random inputs in a wide range of computational and mathematical applications.

Understanding PRNGs, seed values, and uniform random numbers is fundamental in MATLAB for tasks involving random number generation. PRNGs enable the generation of seemingly random sequences, while seed values ensure reproducibility. Meanwhile, uniform random numbers, generated by default in MATLAB, offer a reliable and evenly distributed source of randomness, suitable for various scientific and engineering simulations and experiments. This knowledge equips university students with the foundational concepts needed to work with random numbers in MATLAB effectively.

Generating Uniform Random Numbers

Uniform random numbers are those that can take any value within a specified range, and each value within that range has an equal likelihood of being chosen. In MATLAB, you can generate such numbers using the rand function. This function produces floating-point numbers that are uniformly distributed between 0 and 1 by default.

To control the size and shape of the random number array, you can specify the dimensions as arguments to the rand function. For example, if you need a 3x4 matrix of random numbers, you would use rand(3, 4).

This capability to generate uniform random numbers is valuable in various applications, such as statistical simulations, where you need random inputs with equal probability across a defined range.

Generating Random Integers

In some situations, you may require random integers rather than floating-point numbers. MATLAB offers the randi function for this purpose. The randi function allows you to specify both the range and the size of the random integers you want to generate.

Here's how it works: Let's say you need random integers between 1 and 100. You can achieve this by using the randi function with the range specified as [1, 100]. Additionally, you can control the dimensions of the resulting array, just like with the rand function. For example, randi([1, 100], 3, 4) would generate a 3x4 matrix of random integers between 1 and 100. Generating random integers is particularly useful in scenarios like modeling discrete events or selecting random samples from a finite set of values.

MATLAB provides convenient tools for generating random numbers and random integers. The rand function generates uniform random numbers that can be used in various applications, while the randi function allows you to produce random integers within specified ranges and dimensions. These capabilities are foundational in statistical simulations, data analysis, and many other fields where randomness is a crucial component of the analysis or modeling process.

Generating Samples from Probability Distributions

In addition to generating uniform random numbers, MATLAB offers functions to sample from various probability distributions, which are essential for statistical analysis and modeling. Let's explore how to generate samples from common probability distributions:

Normal Distribution

The normal distribution, also known as the Gaussian distribution, is one of the most common probability distributions encountered in statistics. It is characterized by its bell-shaped curve and is widely used to model natural phenomena and many real-world data sets. In MATLAB, you can generate random numbers following a normal distribution using the randn function.

Key Points:

• Mean and Standard Deviation: The normal distribution is defined by two parameters: the mean (μ) and the standard deviation (σ). The mean represents the center of the distribution, while the standard deviation controls the spread or dispersion of the data. By default, randn generates random numbers from a standard normal distribution with μ = 0 and σ = 1.
• Adjusting Parameters: MATLAB allows you to adjust the mean and standard deviation as needed for your specific application. For example, if you want to generate random numbers from a normal distribution with μ = 5 and σ = 2, you can use mu + sigma * randn(size) where mu is 5, sigma is 2, and size specifies the dimensions of the random number array.

Uniform Distribution

The uniform distribution is one of the simplest probability distributions, and it is often used when all outcomes within a given range are equally likely. In MATLAB, you can generate random numbers following a uniform distribution using the rand function.

• Lower and Upper Bounds: To generate random numbers from a uniform distribution, you need to specify the lower and upper bounds of the range within which the random numbers should fall. For example, rand(1, 100) generates random numbers between 1 and 100.
• Uniformity: Each value within the specified range has an equal probability of being generated, making this distribution useful for simulating events with equal likelihood.

Exponential Distribution

The exponential distribution is commonly used to model the time between events in a Poisson process, where events occur at a constant average rate over time. It is characterized by its memoryless property, which means that the probability of an event occurring in the next time interval does not depend on how much time has already passed. In MATLAB, you can generate random numbers following an exponential distribution using the exprnd function.

• Rate Parameter: The exponential distribution is determined by a single parameter known as the rate parameter (λ). This parameter controls the average rate of events. The larger the λ, the shorter the expected time between events.
• Applications: The exponential distribution is commonly used in reliability engineering, queuing theory, and survival analysis, where modeling the time to failure or the time between events is crucial.

Poisson Distribution

The Poisson distribution is used to model the number of events occurring in a fixed interval of time or space, given that events occur at a constant average rate. It is particularly useful for counting the occurrences of rare events. In MATLAB, you can generate random numbers following a Poisson distribution using the poissrnd function.

• Mean Parameter: The Poisson distribution is characterized by a single parameter, often denoted as λ, which represents the average rate of events occurring in the given interval. The distribution is discrete, and random values generated from it represent counts of events.
• Applications: The Poisson distribution finds applications in various fields, including epidemiology, physics, and telecommunications, where the counting of rare events is essential.

Custom Distributions

Sometimes, real-world scenarios require modeling with probability distributions that are not standard, such as specific types of non-parametric distributions or custom distributions tailored to your research needs. MATLAB provides the flexibility to define and work with custom probability distribution functions using the makedist and random functions.

• Customization: With makedist, you can create a custom probability distribution object by specifying the probability density function (PDF) or probability mass function (PMF) of your distribution. This allows you to tailor the distribution to your data.
• Sampling: After creating a custom distribution object, you can use the random function to sample random numbers from your custom distribution. This enables you to work with specialized distributions that are not part of MATLAB's built-in functions.

MATLAB offers a versatile set of tools for generating random numbers from various probability distributions, from the commonly used normal and uniform distributions to more specialized distributions like exponential and Poisson. Additionally, MATLAB's flexibility allows researchers and students to work with custom distributions, empowering them to model and analyze data that may not fit standard distributions. Understanding these concepts and functions is invaluable for university students working on assignments involving statistical simulations and data analysis.

In conclusion, understanding random number generation in MATLAB is essential for university students working on assignments involving probability simulations and statistical analysis. In this theoretical discussion, we explored the concept of random number generation using pseudo-random number generators and seed values. We also covered the generation of uniform random numbers and random integers in MATLAB.

Furthermore, we discussed how to generate samples from various probability distributions, including the normal, uniform, exponential, and Poisson distributions. MATLAB's built-in functions simplify the process of sampling from these distributions, making it easier for students to apply statistical concepts to real-world problems.

By mastering these fundamentals, university students can confidently tackle assignments that involve random number generation and probability distribution sampling in MATLAB, enhancing their analytical and computational skills in various academic disciplines.

Post a comment...

Random number generation in matlab: probability distributions submit your assignment, attached files.

Help Center Help Center

• Hilfe-Center
• Produkt-Updates
• Documentation

Uniformly distributed random numbers

Description

X = rand returns a random scalar drawn from the uniform distribution in the interval (0,1).

X = rand( n ) returns an n -by- n matrix of uniformly distributed random numbers.

X = rand( sz1,...,szN ) returns an sz1 -by-...-by- szN array of random numbers where sz1,...,szN indicate the size of each dimension. For example, rand(3,4) returns a 3-by-4 matrix.

X = rand( sz ) returns an array of random numbers where size vector sz defines size(X) . For example, rand([3 4]) returns a 3-by-4 matrix.

X = rand( ___ , typename ) returns an array of random numbers of data type typename . The typename input can be either "single" or "double" . You can use any of the input arguments in the previous syntaxes.

X = rand( ___ ,"like", p ) returns an array of random numbers like p ; that is, of the same data type and complexity (real or complex) as p . You can specify either typename or "like" , but not both.

X = rand( s , ___ ) generates numbers from random number stream s instead of the default global stream. To create a stream, use RandStream . You can specify s followed by any of the input argument combinations in previous syntaxes.

collapse all

Matrix of Random Numbers

Generate a 5-by-5 matrix of uniformly distributed random numbers between 0 and 1.

Random Numbers Within Specified Interval

Generate a 10-by-1 column vector of uniformly distributed numbers in the interval (-5,5).

In general, you can generate N random numbers in the interval (a,b) with the formula r = a + (b-a).*rand(N,1) .

Random Integers

Use the randi function (instead of rand ) to generate 5 random integers from the uniform distribution between 10 and 50.

Reset Random Number Generator

Save the current state of the random number generator and create a 1-by-5 vector of random numbers.

Restore the state of the random number generator to s , and then create a new 1-by-5 vector of random numbers. The values are the same as before.

3-D Array of Random Numbers

Create a 3-by-2-by-3 array of random numbers.

Specify Data Type of Random Numbers

Create a 1-by-4 vector of random numbers whose elements are single precision.

Size Defined by Existing Array

Create a matrix of uniformly distributed random numbers with the same size as an existing array.

It is a common pattern to combine the previous two lines of code into a single line:

Size and Data Type Defined by Existing Array

Create a 2-by-2 matrix of single-precision random numbers.

Create an array of random numbers that is the same size and data type as p .

Random Complex Numbers

Generate 10 random complex numbers from the uniform distribution over a square domain with real and imaginary parts in the interval (0,1).

Input Arguments

N — size of square matrix integer value.

Size of square matrix, specified as an integer value.

If n is 0 , then X is an empty matrix.

If n is negative, then it is treated as 0 .

Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64

sz1,...,szN — Size of each dimension (as separate arguments) integer values

Size of each dimension, specified as separate arguments of integer values.

If the size of any dimension is 0 , then X is an empty array.

If the size of any dimension is negative, then it is treated as 0 .

Beyond the second dimension, rand ignores trailing dimensions with a size of 1. For example, rand(3,1,1,1) produces a 3-by-1 vector of random numbers.

sz — Size of each dimension (as a row vector) integer values

Size of each dimension, specified as a row vector of integer values. Each element of this vector indicates the size of the corresponding dimension:

Beyond the second dimension, rand ignores trailing dimensions with a size of 1. For example, rand([3 1 1 1]) produces a 3-by-1 vector of random numbers.

Example: sz = [2 3 4] creates a 2-by-3-by-4 array.

typename — Data type (class) to create "double" (default) | "single"

Data type (class) to create, specified as "double" , "single" , or the name of another class that provides rand support.

Example: rand(5,"single")

p — Prototype of array to create numeric array

Prototype of array to create, specified as a numeric array.

Example: rand(5,"like",p)

Data Types: single | double Complex Number Support: Yes

s — Random number stream RandStream object

Random number stream, specified as a RandStream object.

Example: s = RandStream("dsfmt19937"); rand(s,[3 1])

The sequence of numbers produced by rand is determined by the internal settings of the uniform pseudorandom number generator that underlies rand , randi , and randn . You can control that shared random number generator using rng .

Extended Capabilities

C/c++ code generation generate c and c++ code using matlab® coder™..

Usage notes and limitations:

The data type (class) must be a built-in MATLAB ® numeric type. For other classes, the static rand method is not invoked. For example, rand(sz,'myclass') does not invoke myclass.rand(sz) .

Size arguments must have a fixed size.

See Variable-Sizing Restrictions for Code Generation of Toolbox Functions (MATLAB Coder) .

If extrinsic calls are enabled and rand is not called from inside a parfor loop, generated MEX files use the same random number state as MATLAB in serial code. Otherwise, the generated MEX code and standalone code maintain their own random number state that is initialized to the same state as MATLAB.

Thread-Based Environment Run code in the background using MATLAB® backgroundPool or accelerate code with Parallel Computing Toolbox™ ThreadPool .

This function fully supports thread-based environments. For more information, see Run MATLAB Functions in Thread-Based Environment .

GPU Arrays Accelerate code by running on a graphics processing unit (GPU) using Parallel Computing Toolbox™.

The stream syntax rand( s ,___) is not supported on a GPU.

You can specify typename as 'gpuArray' . If you specify typename as 'gpuArray' , the default underlying type of the array is double .

To create a GPU array with underlying type datatype , specify the underlying type as an additional argument before typename . For example, X = rand(3,datatype,'gpuArray') creates a 3-by-3 GPU array of random numbers with underlying type datatype .

You can specify the underlying type datatype as one of these options:

You can also specify the numeric variable p as a gpuArray .

If you specify p as a gpuArray , the underlying type of the returned array is the same as p .

For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox) .

Distributed Arrays Partition large arrays across the combined memory of your cluster using Parallel Computing Toolbox™.

The stream syntax rand( s ,___) is not supported for codistributed or distributed arrays.

You can specify typename as 'codistributed' or 'distributed' . If you specify typename as 'codistributed' or 'distributed' , the default underlying type of the returned array is double .

To create a distributed or codistributed array with underlying type datatype , specify the underlying type as an additional argument before typename . For example, X = rand(3,datatype,'distributed') creates a 3-by-3 distributed matrix of random numbers with underlying type datatype .

You can also specify p as a codistributed or distributed array.

If you specify p as a codistributed or distributed array, the underlying type of the returned array is the same as p .

For additional codistributed syntaxes, see rand (codistributed) (Parallel Computing Toolbox) .

For more information, see Run MATLAB Functions with Distributed Arrays (Parallel Computing Toolbox) .

Version History

R2022a: match complexity with "like" , and use "like" with randstream object.

The "like" input supports both real and complex prototype arrays. For example: r = rand(2,2,"like",1i) r = 0.8147 + 0.9058i 0.6324 + 0.0975i 0.1270 + 0.9134i 0.2785 + 0.5469i

All syntaxes support this feature. Also, you can now use "like" with a RandStream object as the first input of rand .

R2014a: Match data type of an existing variable with 'like'

To generate random numbers with the same data type as an existing variable, use the syntax rand(__,'like',p) . For example: A = single(pi); r = rand(4,4,'like',A); class(r) ans = single This feature is not available when passing a RandStream object as the first input to rand .

R2013b: Non-integer size inputs are not supported

Specifying a dimension that is not an integer causes an error. Use floor to convert non-integer size inputs to integers.

R2008b: 'seed' , 'state' , and 'twister' inputs are not recommended

There are no plans to remove these inputs, which control the random number generator that underlies rand , randi and randn . However, the rng function is recommended instead for these reasons:

The 'seed' and 'state' generators are flawed.

The terms 'seed' and 'state' are misleading names for the generators. 'seed' refers to the MATLAB v4 generator, not the seed initialization value. 'state' refers to the v5 generators, not the internal state of the generator.

These three inputs unnecessarily use different generators for rand and randn .

For information on updating your code, see Replace Discouraged Syntaxes of rand and randn .

randi | randn | rng | RandStream | sprand | sprandn | randperm

• Create Arrays of Random Numbers
• Generate Random Numbers That Are Repeatable
• Generate Random Numbers That Are Different
• Random Numbers Within a Specific Range
• Random Numbers Within a Sphere
• Creating and Controlling a Random Number Stream
• Class Support for Array-Creation Functions
• Replace Discouraged Syntaxes of rand and randn
• Why Do Random Numbers Repeat After Startup?

MATLAB-Befehl

Sie haben auf einen Link geklickt, der diesem MATLAB-Befehl entspricht:

Führen Sie den Befehl durch Eingabe in das MATLAB-Befehlsfenster aus. Webbrowser unterstützen keine MATLAB-Befehle.

Select a Web Site

Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .

• Switzerland (English)
• Switzerland (Deutsch)
• Switzerland (Français)
• 中国 (English)

You can also select a web site from the following list:

How to Get Best Site Performance

Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.

• América Latina (Español)
• Canada (English)
• United States (English)
• Belgium (English)
• Denmark (English)
• Deutschland (Deutsch)
• España (Español)
• Finland (English)
• France (Français)
• Ireland (English)
• Italia (Italiano)
• Luxembourg (English)
• Netherlands (English)
• Norway (English)
• Österreich (Deutsch)
• Portugal (English)
• Sweden (English)
• United Kingdom (English)

Asia Pacific

• Australia (English)
• India (English)
• New Zealand (English)

Contact your local office

Browse Course Material

Course info.

• Yossi Farjoun

Departments

• Mathematics

As Taught In

• Programming Languages
• Computational Modeling and Simulation
• Applied Mathematics

Learning Resource Types

Introduction to matlab programming, unit 1 the basics.

Exercise 1 (PDF)

Exercise 2 (PDF)

Exercise 3 (PDF)

Unit 2 Root-Finding

Exercise 4 (PDF)

Exercise 5 (PDF)

Exercise 6 (PDF)

Exercise 7 (PDF)

Exercise 8 (PDF)

Exercise 9 (PDF)

Unit 3 Basic Plotting

Exercise 10 (PDF)

Exercise 11 (PDF)

Unit 4 Vectorization

Exercise 12 (PDF)

Exercise 13 (PDF)

Exercise 14 (PDF)

Exercise 15 (PDF)

Unit 5 Fractals and Chaos

Exercise 16 (PDF)

Exercise 17 (PDF)

Exercise 18 (PDF)

Exercise 19 (PDF)

Unit 6 Debugging

Unit 7 conway game of life.

Exercise 20 (PDF)

Exercise 21 (PDF)

You are leaving MIT OpenCourseWare

When randomisation is not good enough: Matching groups in intervention studies

• Brief Report
• Open access
• Published: 09 July 2021
• Volume 28 , pages 2085–2093, ( 2021 )

Cite this article

You have full access to this open access article

• Francesco Sella 1 ,
• Gal Raz 2 &
• Roi Cohen Kadosh 2  

12k Accesses

10 Citations

3 Altmetric

Explore all metrics

Randomised assignment of individuals to treatment and controls groups is often considered the gold standard to draw valid conclusions about the efficacy of an intervention. In practice, randomisation can lead to accidental differences due to chance. Researchers have offered alternatives to reduce such differences, but these methods are not used frequently due to the requirement of advanced statistical methods. Here, we recommend a simple assignment procedure based on variance minimisation (VM), which assigns incoming participants automatically to the condition that minimises differences between groups in relevant measures. As an example of its application in the research context, we simulated an intervention study whereby a researcher used the VM procedure on a covariate to assign participants to a control and intervention group rather than controlling for the covariate at the analysis stage. Among other features of the simulated study, such as effect size and sample size, we manipulated the correlation between the matching covariate and the outcome variable and the presence of imbalance between groups in the covariate. Our results highlighted the advantages of VM over prevalent random assignment procedure in terms of reducing the Type I error rate and providing accurate estimates of the effect of the group on the outcome variable. The VM procedure is valuable in situations whereby the intervention to an individual begins before the recruitment of the entire sample size is completed. We provide an Excel spreadsheet, as well as scripts in R, MATLAB, and Python to ease and foster the implementation of the VM procedure.

Similar content being viewed by others

Qualitative Research: Ethical Considerations

How to use and assess qualitative research methods

Sampling Techniques for Quantitative Research

Avoid common mistakes on your manuscript.

Introduction

Randomisation in controlled trials.

A common problem in intervention studies is comparing the effect of intervention while minimising the influence of confounding factors. In the pre-treatment assessment, a researcher usually measures the characteristics that the treatment aims to modify (i.e., outcome measures) as well as other variables that can exert an influence on the treatment (i.e., covariates). Then, the researcher will randomly assign individuals to the treatment and the control condition. In the ideal scenario, the control condition matches the treatment condition except for that specific feature of the treatment that the researcher considers to be crucial for causing a change in the outcome measures (e.g., placebo vs the active molecule in pharmacological studies). If the treatment is effective, the treatment group should improve in the outcome measures compared to the control group.

In the case of randomisation with large sample size, the statistical test for a difference at baseline or in other covariates becomes irrelevant as occurring significant differences reflect Type I error (de Boer et al., 2015 ; Roberts & Torgerson, 1999 ), which more likely arises when several covariates are considered (Austin et al., 2010 ). However, large sample sizes are difficult to achieve. Many researchers, especially in the clinical sciences, rely on small naturally occurring samples composed of individuals who voluntarily join the study when they wish to. In this scenario, the sampling is suboptimal as participants are not randomly sampled from the population, but they take part in the study based on convenience and opportunity. Although the assignment to different treatment conditions can be random, differences at baseline are more likely to emerge in small compared to large trials (Bruhn & Mckenzie, 2009 ; Chia, 2000 ; Nguyen & Collins, 2017 ; Saint-mont, 2015 ). Unfortunately, there is no statistical way to control for these differences between groups at pre-test (Miller & Chapman, 2001 ; Van Breukelen, 2006 ). Therefore, the imbalance in the pre-treatment scores can compromise the evaluation of the treatment efficacy, and seriously harm the interpretability of the results. To correct for this, the researcher may choose to allocate individuals to a condition based on previously collected pre-treatment scores and match the groups on these scores. However, this procedure requires the researcher to complete the pre-treatment assessment of all participants before the beginning of the treatment. The whole process may take several months, increase the attrition rate before the treatment begins and cannot account for unwanted changes in the measures of interest. Furthermore, the immediate implementation of the treatment is frequently necessary, especially in a clinical setting, where the treatment must begin in a critical phase of the patients’ clinical condition.

Minimising group differences

One solution is the use of covariate-adaptive randomisation procedures (Chen & Lee, 2011 ; Dragalin et al., 2003 ; Endo et al., 2006 ; Scott et al., 2002 ), which allocate participants to the different conditions as they join the study and, at the same time, reduce the difference between groups on predefined critical variables. There are three commonly used types of covariate-adaptive randomisation methods: stratified randomisation, dynamic hierarchical randomisation, and minimisation (Lin et al., 2015 ). Differences at baseline can be reduced by using stratified randomisation, whereby specific (prognostic) variables are divided into strata and participants are randomly selected from each stratum. However, stratified randomisation becomes difficult to implement as the factors to control for increase (Therneau, 1993 ). In dynamic hierarchical randomisation, covariates are ranked in order of importance and participants are assigned to conditions via biased coin allocation when thresholds of imbalance are exceeded in selected covariates (Signorini et al., 1993 ). A minimisation procedure, the focus of this paper, calculates the level of imbalance in covariates that assigning a participant to each condition would cause, then allocates with high probability (to maintain a degree of randomness) the current participant to the condition that minimises the imbalance.

In this vein, the use of covariate-adaptive randomisation procedures not only matches groups on covariates, but also implicitly forces researchers to state in advance those critical covariates related to the treatment rather than controlling for their effect at a later stage, when running statistical analyses (Simmons et al., 2011 ). A covariate-adaptive randomisation procedure attempts to reduce the unwanted differences at baseline that inadvertently emerge from a random assignment. However, it is worth highlighting that the covariate-adaptive randomisation procedures aim to solve the imbalances at pre-test that might emerge from the random assignment of participants, rather than issues related to non-random selection of participants from naturally occurring samples.

Despite a variety of covariate-adaptive randomisation procedures at disposal, researchers conducting training/treatment studies, including randomised control trials (RCTs), seldom implement these methods (Ciolino et al., 2019 ; Lin et al., 2015 ; Taves, 2010 ). The lack of popularity of these procedures might be due to multiple factors. Researchers may feel more comfortable in implementing more traditional and easier to understand stratified/block randomisation. In this vein, an efficient implementation of covariate-adaptive procedures would require the consultancy of an expert statistician for the entire duration of the trial; an extra cost that principal investigators may prefer to avoid (Ciolino et al., 2019 ). Finally, the lack of free, easy-to-use, computerised functions to automatically implement covariate-adaptive procedures may have contributed to their still limited dissemination (Treasure & Farewell, 2012 ; Treasure & MacRae, 1998 ).

Here, we provide a procedure based on variance minimisation (VM; Frane, 1998 ; Pocock & Simon, 1975 ; Scott et al., 2002 ; Treasure & MacRae, 1998 ), which assigns the next incoming participant to the condition that minimises differences between groups in the chosen measures. Our procedure brings the benefit of using multiple covariates without creating strata in advance, as done in the stratified randomisation, and it is relatively easy to implement compared with the more complex dynamic hierarchical randomisation. The logic and the calculation behind the procedure are simple and easy-to-grasp also from an audience of non-experts. We provided ready-to-use code to implement the procedure using different (also free) software along with step-by-step written instructions, thereby reducing any costs associated with product licenses or consultancy from expert statisticians.

Description of the VM procedure

The goal of the VM procedure is to find the best group assignment for participants prior to an intervention, such that the groups are matched in terms of the scores that the researcher suspects might cause random differences in post-intervention outcomes. The VM procedure requires the researcher to define the number of groups to which participants can be assigned and to collect individual scores for each variable on which groups are matched. These variables can be continuous or binary, where nominal variables with more than two categories can be transformed into multiple dummy variables (as in regression analysis) before being passed to the VM procedure (see section Using VM Procedure on Non-Dichotomous Nominal Variables, in the Supplementary Materials ). The procedure particularly suits those studies in which proper matching is essential, but the assignment to groups needs to occur while the recruitment is still ongoing. It works as follows.

The first participants joining the study are sequentially assigned one to each group. For example, in case of three different groups (i.e., A, B, C), the first participant is assigned to Group A, the second participant to Group B, and the third participant to Group C. Then the fourth participant is added temporarily to each group, and for each temporary group assignment, the algorithm checks which group assignment for this participant would minimize the between-group variance (i.e., V in Fig. 1 ) of the measures of interest and assigns the participant to that group. The next (fifth) participant undergoes the same procedure, but the algorithm will not assign the present participant to the group of the previous participant in order to ensure a balanced distribution of participants in each condition. The same procedure goes on until there is only one group remaining, which in the case of three groups would be for the sixth participant. The sixth participant would be automatically assigned to the remaining group, such that each group would now have two participants assigned to them. Then, the entire procedure starts again with the possibility for the next participant to be assigned to all available groups (for a formal description of the variance minimisation procedure, see section Details of the Minimisation Procedure, in the Supplementary Materials ).

Comparison of assignment to groups using ( a ) variance minimisation and ( b ) random assignment. When a new participant joins a study, variance minimisation assigns the participant to the group that minimises the variance between groups along with the pre-defined variables (i.e., V ); in this case intelligence (IQ), executive functions (EFs), attentional performance (AP), and gender, while keeping the number of participants in each group balanced. Random assignment, on the other hand, assigns the participant to every group with equal probability and does not match the groups

To avoid predictable group assignments due to this shrinking set of available groups, the user can also specify a small probability of random assignment over the VM procedure (see section Discontinuous Implementation of the VM Procedure: The Parameter pRand, in the Supplementary Materials ). This random component makes the assignment unpredictable even if the researcher has access to previous group allocations.

Simulations

We present multiple simulations to illustrate how the VM procedure can be implemented in different scenarios and the advantages it provides.

In the first simulation, we implemented the VM procedure to assign participants to three experimental groups based on three continuous and one dichotomous variable. We compared the matching obtained from the VM procedure with random assignment. In the second simulation, we showed that the VM procedure better detects group differences and provides better estimates of effects compared with the attempt to control for the effect of covariates. In the supplementary materials , we demonstrate how to incorporate a random component in the VM procedure to ensure a non-deterministic assignment of participants to conditions (section Discontinuous Implementation of the VM Procedure: The Parameter pRand ) and how the VM can match participants also on non-dichotomous nominal variables (section Using VM Procedure on Non-Dichotomous Nominal Variables ). We briefly discuss the results of these two additional simulations in the Discussion section.

The functions to implement the VM procedure in Excel, MATLAB, Python, and R along with tutorials, as well as the R code of the simulation, can be found at the Open Science Framework ( https://osf.io/6jfvk/?view_only=8d405f7b794d4e3bbff7e345e6ef4eed ).

VM procedure outperforms random assignment in matching groups on continuous and dichotomous variables

In the first fictional example, a researcher wants to evaluate whether the combination of cognitive training of executive functions and brain stimulation improves the clinical symptoms of ADHD. The study design comprises three groups: the first group receives brain stimulation and the executive functions training; the second group receives sham stimulation and the training; the third group receives neither training nor stimulation (passive control group). The researcher aims to match the three groups on intelligence, executive functions performance, attentional performance, and gender. Figure 1 illustrates how VM assigns incoming participants compared with a traditional random assignment.

We simulated 1,000 data sets whereby we randomly drew the scores for IQ, executive functions, and attentional performance from a normal distribution, with a mean of 100 and a standard deviation of 15. Participants’ gender came from a binomial distribution with the same probability for a participant to be male or female. The simulated values for the matching variables were randomly generated, therefore there were no real differences between groups. We varied the sample size to be very small ( n = 36), small ( n = 66), medium ( n = 159), and large ( n = 969), reflecting the researcher’s intention to evaluate the possible presence of an extremely large ( f = 0.55), large ( f = 0.40), medium ( f = 0.25), and small ( f = 0.10) effect size, respectively, while keeping the alpha at .05 and power at 80% (Faul et al., 2009 ). We assigned participants to the three groups randomly or by using the VM procedure.

We ran univariate analyses of variance (ANOVAs) with IQ, executive functions, and attentional performance as dependent variables and group as factor whereas differences in gender distribution across groups were analysed using χ 2 tests. In Fig. 2 , we show the distributions of F , p , and η 2 values from ANOVAs on IQ, executive functions, and attentional performance (top panel), whereas in the case of gender, we presented the distribution and χ 2 , p , and Cramer’s V values (bottom panel) separately for the random assignment and the VM procedure across different sample sizes. Compared with random assignment, the VM procedure yielded smaller F , η 2 , χ 2 , and Cramer’s V values and the distribution of p -values was skewed toward 1, rather than uniform. The VM procedure demonstrated an efficient matching between groups starting from a very small sample size while keeping the number of participants in each group balanced. Moreover, both the VM procedure and the random assignment violated ANOVA assumptions on the normality of residuals and homogeneity of variance between groups with a similar rate (see Supplementary Materials, Fig. S1 ).

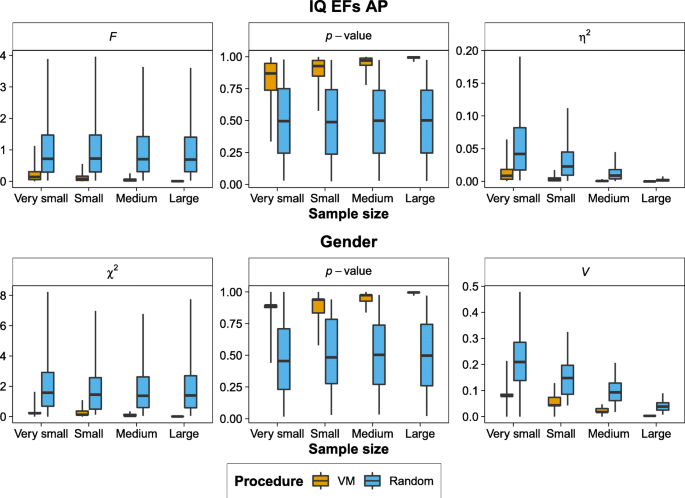
A comparison of the VM procedure and random assignment based on simulated data. Top panel: Distributions of F -values, p -values, and η 2 values from ANOVAs comparing groups on intelligence (IQ), executive functions (EFs), and attentional performance (AP) separately for the VM procedure (orange boxplots) and the random assignment (blue boxplots). Bottom panel: Distributions of χ 2 , p -values, and Cramer’s V values comparing groups on gender separately for the VM procedure (orange boxplots) and the random assignment (blue boxplots). The boxplots represent the quartiles whereas the whiskers represent the 95% limits of the distribution. (Colour figure online)

Matching groups on a covariate versus controlling for a covariate with imbalance

We simulated an intervention study to display the advantages that the minimisation procedure provides in terms of detecting group differences and better estimates of effects compared with the attempt to control for the effect of covariates in the statistical analysis after the intervention was completed. A researcher evaluates the effect of an intervention on a dependent variable Y while controlling for the possible confounding effect of a covariate A, which positively correlates with Y, and a covariate B that correlates with covariate A (i.e., pattern correlation 1), or Y (i.e., pattern correlation 2), or neither of them (i.e., pattern correlation 3). In this vein, the covariate A represents a variable that the researchers ought to control for, given its known relation with the dependent variable Y, whereas the covariate B represents a non-matching variable that is still inserted into the model as it might have a real or spurious correlation with the covariate A and the dependent variable Y. We simulated a small, medium, and large effect of the intervention (i.e., Cohen’s d = 0.2; d = 0.5; d = 0.8) and, accordingly, we varied the total sample size to be 788, 128, and 52 to achieve a power of 80% while keeping the alpha at .05 (Faul et al., 2009 ). For comparison, we used the same sample sizes, 788, 128, and 52, when simulating the absence of an intervention effect (i.e., Cohen’s d = 0). Crucially, we compared the scenario whereby the researcher matches participants on the covariate A (i.e., VM on CovA) before implementing the intervention or randomly assigns participants to the control and training group and then attempts to control for the effect of covariate after the intervention (i.e., Control for CovA). The subsequent inclusion of the covariate A in the analysis, especially in the case of imbalance between groups in the covariate A, would bias the effect of the group on Y when the difference between groups in the covariate A is larger in the direction of the intervention effect. Conversely, the minimisation procedure reduces the difference between groups on the covariate A and the inclusion of the covariate A into the analysis (i.e., analysis of covariance; ANCOVA) would not cause biases in the estimation of the effect of the group on Y.

In the case of the control for covariate approach, we generated the scores of the covariate A by taking them from a standard normal distribution ( M = 0, SD = 1) and we randomly assigned participants to the control and training group. We generated an imbalance in the covariate A by calculating the standard error of the mean and multiplying it for the standard normal deviates ±1.28, ±1.64, ±1.96 corresponding to the 20%, 10%, and 5% probabilities respectively of the standard normal distribution. The use of the standard error allowed to keep the imbalance proportionate to the sample size. The obtained imbalance was added to the scores of the covariate A only for the training group, thereby generating a difference in covariate A that went in the same or in the opposite direction with respect to the intervention effect (i.e., larger scores on the dependent variable only for the training group; Egbewale et al., 2014 ). We also included the case of absent imbalance for reference. In the case of the VM procedure, we took the previously generated scores of the covariate A with the imbalance, and we assigned participants to the control or training group using the VM procedure. Then, we generated the scores of Y that were correlated with the covariate A according to four correlations, that were, 0, 0.5, 0.7, and 0.9. Finally, we added 0, 0.2, 0.5, 0.8 to the Y scores of the training group to simulate an absent, small, medium, and large effect of the intervention.

In both the random assignment and the VM procedure, the covariate B was generated to alternatively have a correlation of 0.5 ( SD = 0.1) with the covariate A (i.e., Pattern 1), Y (i.e., Pattern 2), or no correlation with these two variables (i.e., Pattern 3). We randomly selected the correlation from a normal distribution with an average 0.5 and standard deviation of 0.1 to add some noise to the correlation while maintaining it positive and centred on 0.5.

Overall, we varied multiple experimental conditions in 504 scenarios (for a similar approach, see Egbewale et al., 2014 ):

seven imbalances on the covariate A: −1.96, −1.64, −1.28, 0, 1.28, 1.64, 1.96;

four correlations between covariates A and Y: 0, 0.5, 0.7, 0.9;

six treatment effects: 0 (×3 as the absence of the effect was tested with three sample sizes, that were, 52, 128, 788), 0.2, 0.5, 0.8;

three patterns of correlation between the covariate B, covariate A, and Y.

We simulated each scenario 1,000 times.

As expected, the correlations between the covariate B and the other two variables varied according to the pre-specified patterns of correlations, which were practically identical in the VM and control for covariate approach (see Table S1 in the Supplementary Materials).

We ran a series of ANCOVAs with Y as the dependent variable, the covariates A and B, and group [Training, Control] as independent variables. We used a regression approach as the variable group was converted to a dichotomous numerical variable (i.e., control = 0, training = 1) to directly use the regression coefficients as estimates for the effect of each variable on Y. Both the VM procedure and the control for the covariate approach display a similar rate in violating ANCOVA assumptions of the normality of residuals and homogeneity of variance between groups (see Supplementary Materials; Fig. S2 ).

In this fictitious scenario, the researcher would be interested in evaluating the effect of the group on Y while controlling for covariates. Therefore, we reported the proportion of significant results ( p < .05; Fig. 3 ) and the estimated effect (i.e., coefficient of the regression; Fig. 4 ) for the effect of group on Y depending on the imbalance in the covariate A, the effect size of the intervention, and the degree of correlation between the covariate A and Y. For simplicity, in Figs. 3 and 4 , we reported only the simulation with a large sample size (i.e., n = 788) when the effect of the intervention was absent (i.e., d =0). The pattern of results remained stable across the patterns of correlations of the covariate B. Therefore, we reported the proportion of significant results and estimated effects for the group, covariate A, and covariate B across the patterns correlation of the covariate B in the Supplementary Materials (Figs. S5 – S22 ).

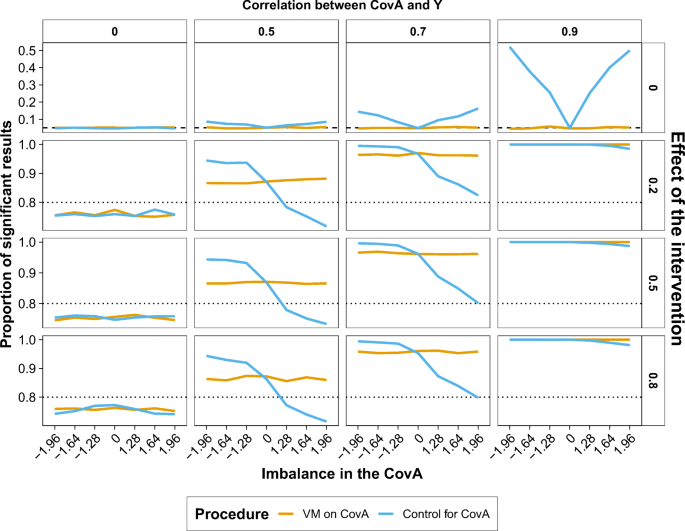
Proportion of significant results ( y -axis) for the effect of group in the ANCOVA (Y ~ CovA + CovB + Group) separately for the VM procedure (orange lines) and control for CovA approach (blue lines) across imbalances of the covariate A ( x -axis) when the sample size varied according to the effect size to be detected (rows; absent = 0, n = 788; small = 0.2, n = 788; medium = 0.5, n = 128; large = 0.8, n = 52) and the correlation between the covariate A and the dependent variable Y ranged between 0 and 0.9 (columns). The black dotted line represents alpha (i.e., 0.05) and the dashed black line represents the expected power (i.e., 0.8). (Colour figure online)

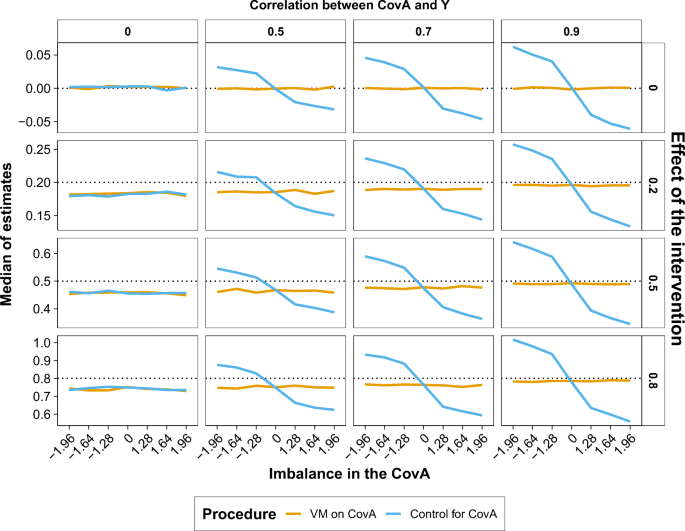
Median of estimates ( y -axis; regression coefficients) for the effect of group in the ANCOVA (Y ~ CovA + CovB + Group) separately for the VM procedure (orange lines) and control for CovA approach (blue lines) across imbalances of the covariate A ( x -axis) when the sample size varied according to the effect size to be detected (rows; absent = 0, n = 788; small = 0.2, n = 788; medium = 0.5, n = 128; large = 0.8, n = 52) and the correlation between the covariate A and the dependent variable Y ranged between 0 and 0.9 (columns). The black dotted line represents the expected regression coefficients (i.e., 0, 0.2, 0.5, 0.8). (Colour figure online)

When the effect of the intervention was present (second to fourth rows in Fig. 3 ), the VM procedure showed a more stable detection of significant results also in the presence of serious imbalances in the covariate A. This stability became clearer as the correlation between the covariate A and Y increased. When the effect of the intervention was absent (first row in Fig. 3 ), the VM procedure always kept the Type I error around 0.05 while the control covariate approach inflated Type I error rate in the case of strong imbalance in the covariate A when it was highly correlated (i.e., 0.7, 0.9) with the outcome variable Y.

A similar pattern of results emerged when we compared the estimates of the effect of the group (i.e., regression coefficients) yielded by the VM procedure and the control for covariate approach. The VM procedure always provided accurate estimates of the effect of the group. Conversely, the control for covariate approach returned biased estimates with large imbalances in the covariate A and when its correlation with the outcome variable Y was high (i.e., 0.7, 0.9; Fig. 4 ).

In treatment studies, groups should be as similar as possible in all the variables of interest before the beginning of the treatment. An optimal matching can ensure that the effect of the treatment is not related to the pre-treatment characteristics of the groups and can, therefore, be extended to the general population. In contrast, the random assignment can yield relevant, and even statistically significant, differences between the groups before the treatment (Treasure & MacRae, 1998 ).

The proposed VM procedure constitutes a quick and useful tool to match groups before treatment on both continuous and categorical covariates (Pocock & Simon, 1975 ; Scott et al., 2002 ; Treasure & MacRae, 1998 ). The latter, though, need to be transformed into dummy variables to be passed to the minimisation algorithm (for a minimisation procedure that directly handles nominal covariates see Colavincenzo, 2013 ). We simulated an intervention study whereby a researcher used the VM procedure on a covariate to assign participants to a control and intervention group rather than controlling for the covariate at the analysis stage. Among other features of the simulated study, we manipulated the correlation between the matching covariate and the outcome variable and the presence of imbalance between groups in the covariate. Controlling for covariates post hoc inflated Type I error rate and yielded biased estimates of the effect of the group on the outcome variable when the imbalance between groups in the covariate increased and the correlation between the covariate and the outcome variable was high. Conversely, the use of VM on the covariate did not inflate Type I error rate and provided accurate estimates of the effect of the group on the outcome variable.

The progressive shrinking of available conditions when using the VM procedure ensures a perfect balance in the number of participants across conditions while still minimising covariate imbalance. However, some participants will be forcefully assigned to a given condition irrespective of their scores in the covariates. Therefore, in some instances, the researcher will know in advance the condition the participants will be assigned to and not all participants will have the chance to be assigned to each of the available conditions. This restriction might be relevant for clinical trials where one of the conditions is potentially beneficial (i.e., the treatment group). In this case, the researcher can insert a random component into the VM procedure by defining the probability to implement a random assignment. The random component prevents the researcher from being sure about the condition some participants will be assigned to and gives all participants the possibility, in principle, to be assigned to one of the conditions. Using a small amount of randomness (e.g., pRand = 0.1) provides a good balance between matching groups on covariates while avoiding predictable allocation (see section Discontinuous Implementation of the VM Procedure: The Parameter pRand, in the Supplementary Materials ).

Despite the benefits of the minimisation procedure, limitations must be carefully considered. First, the application of the VM procedure on small sample sizes does not prevent the treatment effect from being influenced by the unequal distribution of unobserved confounding variables, whose equal distribution is most likely achieved with large sample sizes. This limitation related to small sample sizes affects both the VM procedure and random assignment. Nevertheless, the selection of matching covariates for the minimisation procedure encourages researchers to carefully think in advance about possible confounding variables and match participants on them. Secondly, we showed that the VM is beneficial in simple ANOVA/ANCOVA simulations. In the case of more complex models (e.g., with an interaction), the researcher should carefully consider whether the minimisation procedure constitutes an advantage to the design. We recommend running simulations tailored to specific research designs to ensure that the VM procedure adequately matches participants across conditions.

Third, the minimisation procedure considers all covariates equally important without giving the user the possibility to allow more imbalance in some covariates compared to others (for a minimisation procedure that allows weighting see Saghaei, 2011 ). It is therefore paramount that the researchers will carefully consider the covariates they wish to match the groups on.

Overall, our minimisation procedure, even after considering the above-mentioned limitations, provides important advantages over the randomisation procedure that is used frequently. Its relative simplicity encourages researchers to use covariate-adaptive matching procedures (Ciolino et al., 2019 ; Lin et al., 2015 ). To allow the requested shift from the randomisation procedure, we provide scripts, written using popular software (i.e., R, Python, MATLAB, and Excel), which allow a fast and easy implementation of the VM procedure and integration with other stimulus presentation and analysis scripts. In this light, the treatment can start in the same session in which pre-treatment measures are acquired, thereby reducing the total number of sessions and, consequently, the overall costs. The immediate application of the treatment also excludes the possibility that pre-treatment measures change between the period of the initial recruitment and the actual implementation of the treatment. We strongly recommend using the VM procedure in these studies to yield more effective and valid RCTs.

Austin, P. C., Manca, A., Zwarenstein, M., Juurlink, D. N., & Stanbrook, M. B. (2010). Baseline comparisons in randomized controlled trials. Journal of Clinical Epidemiology , 63 (8), 940–942. https://doi.org/10.1016/j.jclinepi.2010.03.009

Article   Google Scholar  

Bruhn, M., & Mckenzie, D. (2009). In pursuit of balance: Randomization in practice in development field experiments. American Economic Journal: Applied Economics, 4 (1), 200–232. https://www.jstor.org/stable/25760187

Google Scholar  

Chen, L. H., & Lee, W. C. (2011). Two-way minimization: A novel treatment allocation method for small trials. PLOS ONE , 6 (12), 1–8. https://doi.org/10.1371/journal.pone.0028604

Chia, K. S. (2000). Randomisation: Magical cure for bias? Annals of the Academy of Medicine, Singapore, 29 (5), 563–564.

Ciolino, J. D., Palac, H. L., Yang, A., Vaca, M., & Belli, H. M. (2019). Ideal vs. real: A systematic review on handling covariates in randomized controlled trials. BMC Medical Research Methodology, 19 (1), 136. https://doi.org/10.1186/s12874-019-0787-8

Colavincenzo, J. (2013). Doctoring your clinical trial with adaptive randomization: SAS® Macros to perform adaptive randomization. Proceedings of the SAS® Global Forum 2013 Conference [Internet]. Cary (NC): SAS Institute Inc. https://support.sas.com/resources/papers/proceedings13/181-2013.pdf

de Boer, M. R., Waterlander, W. E., Kuijper, L. D. J., Steenhuis, I. H. M., & Twisk, J. W. R. (2015). Testing for baseline differences in randomized controlled trials: An unhealthy research behavior that is hard to eradicate. International Journal of Behavioral Nutrition and Physical Activity , 12 (1), 1–8. https://doi.org/10.1186/s12966-015-0162-z

Dragalin, V., Fedorov, V., Patterson, S., & Jones, B. (2003). Kullback-Leibler divergence for evaluating bioequivalence. Statistics in Medicine , 22 (6), 913–930. https://doi.org/10.1002/sim.1451

Article   PubMed   Google Scholar  

Egbewale, B. E., Lewis, M. & Sim, J. (2014). Bias, precision and statistical power of analysis of covariance in the analysis of randomized trials with baseline imbalance: a simulation study. BMC Med Res Methodol, 14 , 49. https://doi.org/10.1186/1471-2288-14-49

Endo, A., Nagatani, F., Hamada, C., & Yoshimura, I. (2006). Minimization method for balancing continuous prognostic variables between treatment and control groups using Kullback-Leibler divergence. Contemporary Clinical Trials , 27 (5), 420–431. https://doi.org/10.1016/j.cct.2006.05.002

Faul, F., Erdfelder, E., Buchner, A., & Lang, A.-G. (2009). Statistical power analyses using G*Power 3.1: tests for correlation and regression analyses. Behavior Research Methods , 41 (4), 1149–1160. https://doi.org/10.3758/BRM.41.4.1149

Frane, J. W. (1998). A method of biased coin randomisation, its implementation and its validation. Drug Information Journal , 32 , 423–432.

Lin, Y., Zhu, M., & Su, Z. (2015). The pursuit of balance: An overview of covariate-adaptive randomization techniques in clinical trials. Contemporary Clinical Trials, 45, 21–25. https://doi.org/10.1016/j.cct.2015.07.011

Miller, G. A., & Chapman, J. P. (2001). Misunderstanding analysis of covariance. Journal of Abnormal Psychology , 110 (1), 40–48.

Nguyen, T., & Collins, G. S. (2017). Simple randomization did not protect against bias in smaller trials, 84 , 105–113. https://doi.org/10.1016/j.jclinepi.2017.02.010

Pocock, S. J., & Simon, R. (1975). Sequential treatment assignment with balancing for prognostic factors in the controlled clinical trial. Biometrics , 31 (1), 103. https://doi.org/10.2307/2529712

Roberts, C., & Torgerson, D. J. (1999). Understanding controlled trials: Baseline imbalance in randomised controlled trials. BMJ , 319 (7203), 185–185. https://doi.org/10.1136/bmj.319.7203.185

Article   PubMed   PubMed Central   Google Scholar  

Saghaei, M. (2011). An overview of randomization and minimization programs for randomized clinical trials. Journal of Medical Signals and Sensors, 1 (1), 55.

Saint-mont, U. (2015). Randomization does not help much, comparability does. PLOS ONE, 10 (7), Article e0132102. https://doi.org/10.1371/journal.pone.0132102

Scott, N. W., McPherson, G. C., Ramsay, C. R., & Campbell, M. K. (2002). The method of minimization for allocation to clinical trials: A review. Controlled Clinical Trials , 23 (6), 662–674. https://doi.org/10.1016/S0197-2456(02)00242-8

Signorini, D. F., Leung, O., Simes, R. J., Beller, E., Gebski, V. J., & Callaghan, T. (1993). Dynamic balanced randomization for clinical trials. Statistics in Medicine, 12 (24), 2343–2350.

Simmons, J. P., Nelson, L. D., & Simonsohn, U. (2011). False-positive psychology: Undisclosed flexibility in data collection and analysis allows presenting anything as significant. Psychological Science , 22 (11), 1359–1366. https://doi.org/10.1177/0956797611417632

Taves, D. R. (2010). The use of minimization in clinical trials. Contemporary Clinical Trials , 31 (2), 180–184. https://doi.org/10.1016/j.cct.2009.12.005

Therneau, T. M. (1993). How many stratification factors are “too many” to use in a randomization plan? Controlled Clinical Trials , 14(2), 98–108. https://doi.org/10.1016/0197-2456(93)90013-4

Treasure, T., & Farewell, V. (2012). Minimization in interventional trials : great value but residual vulnerability. Journal of Clinical Epidemiology , 65 (1), 7–9. https://doi.org/10.1016/j.jclinepi.2011.07.005

Treasure, T., & MacRae, K. D. (1998). Minimisation: The platinum standard for trials? BMJ (Clinical Research Ed.) , 317 (7155), 362–363. https://doi.org/10.1136/bmj.317.7155.362

Van Breukelen, G. J. P. (2006). ANCOVA versus change from baseline had more power in randomized studies and more bias in nonrandomized studies. Journal of Clinical Epidemiology , 59 (9), 920–925. https://doi.org/10.1016/j.jclinepi.2006.02.007

Download references

Acknowledgements

This study was supported by the European Research Council (Learning&Achievement 338065).

Author information

Authors and affiliations.

Centre for Mathematical Cognition, Loughborough University, Loughborough, UK

Francesco Sella

Department of Experimental Psychology, University of Oxford, Oxford, UK

Gal Raz & Roi Cohen Kadosh

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Francesco Sella .

Additional information

Open practices statement

The R code of the analyses is available at https://osf.io/6jfvk/?view_only=8d405f7b794d4e3bbff7e345e6ef4eed

Publisher’s note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary Information

(DOCX 2855 kb)

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ .

Reprints and permissions

About this article

Sella, F., Raz, G. & Cohen Kadosh, R. When randomisation is not good enough: Matching groups in intervention studies. Psychon Bull Rev 28 , 2085–2093 (2021). https://doi.org/10.3758/s13423-021-01970-5

Download citation

Accepted : 03 June 2021

Published : 09 July 2021

Issue Date : December 2021

DOI : https://doi.org/10.3758/s13423-021-01970-5

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Variance minimisation
• Randomised controlled trial
• Research design
• Clinical trials
• Allocation methods
• Find a journal
• Publish with us
• Track your research

• MATLAB Answers
• File Exchange
• AI Chat Playground
• Discussions
• Communities
• Treasure Hunt
• Community Advisors
• Virtual Badges
• Trial software

You are now following this question

• You will see updates in your followed content feed .
• You may receive emails, depending on your communication preferences .

Random assignments through the use of a MatLab programmed Calender

Direct link to this question

https://ch.mathworks.com/matlabcentral/answers/472420-random-assignments-through-the-use-of-a-matlab-programmed-calender

   0 Comments Show -2 older comments Hide -2 older comments

Sign in to comment.

Sign in to answer this question.

Answers (2)

Direct link to this answer

https://ch.mathworks.com/matlabcentral/answers/472420-random-assignments-through-the-use-of-a-matlab-programmed-calender#answer_383846

https://ch.mathworks.com/matlabcentral/answers/472420-random-assignments-through-the-use-of-a-matlab-programmed-calender#answer_383858

• random assignments
• assignments

Community Treasure Hunt

Find the treasures in MATLAB Central and discover how the community can help you!

An Error Occurred

Unable to complete the action because of changes made to the page. Reload the page to see its updated state.

Select a Web Site

Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .

You can also select a web site from the following list

How to Get Best Site Performance

Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.

• América Latina (Español)
• Canada (English)
• United States (English)
• Belgium (English)
• Denmark (English)
• Deutschland (Deutsch)
• España (Español)
• Finland (English)
• France (Français)
• Ireland (English)
• Italia (Italiano)
• Luxembourg (English)
• Netherlands (English)
• Norway (English)
• Österreich (Deutsch)
• Portugal (English)
• Sweden (English)
• United Kingdom (English)

Asia Pacific

• Australia (English)
• India (English)
• New Zealand (English)
• 简体中文 Chinese
• 日本 Japanese (日本語)
• 한국 Korean (한국어)

Contact your local office

• Ablebits blog
• Random data

RANDARRAY function - quick way to generate random numbers in Excel

The tutorial shows how to generate random numbers, randomly sort a list, get random selection and randomly assign data to groups. All with a new dynamic array function - RANDARRAY.

As you probably know, Microsoft Excel already has a couple of randomizing functions - RAND and RANDBETWEEN . What is the sense in introducing another one? In a nutshell, because it's far more powerful and can replace both older functions. Apart from setting up your own maximum and minimum values, it lets you specify how many rows and columns to fill and whether to produce random decimals or integers. Used together with other functions, RANDARRAY can even shuffle data and pick a random sample.

Excel RANDARRAY function

• Basic RANDARRAY formula

Generate random numbers between two numbers

Generate random date between two dates.

• Create random workdays in Excel
• Generate random numbers without duplicates
• Random sort in Excel
• Get a random sample
• Select random rows
• Random assignment in Excel
• Randomly assign data to groups

Excel RANDARRAY function not working

The RANDARRAY function in Excel returns an array of random numbers between any two numbers that you specify.

It is one of six new dynamic array functions introduced in Microsoft Excel 365. The result is a dynamic array that spills into the specified number of rows and columns automatically.

The function has the following syntax. Please notice that all the arguments are optional:

Rows (optional) - defines how many rows to fill. If omitted, defaults to 1 row.

Columns (optional) - defines how many columns to fill. If omitted, defaults to 1 column.

Min (optional) - the smallest random number to produce. If not specified, the default 0 value is used.

Max (optional) - the largest random number to create. If not specified, the default 1 value is used.

Whole_number (optional) - determines what kind of values to return:

• TRUE - whole numbers
• FALSE or omitted (default) - decimal numbers

RANDARRAY function - things to remember

To efficiently generate random numbers in your Excel worksheets, there are 6 important points to take notice of:

• The RANDARRAY function is only available in Excel for Microsoft 365 and Excel 2021. In Excel 2019, Excel 2016 and earlier versions the RANDARRAY function is not available.
• If the array returned by RANDARRAY is the final result (output in a cell and not passed to another function), Excel automatically creates a dynamic spill range and populates it with the random numbers. So, be sure you have enough empty cells down and/or to the right of the cell where you enter the formula, otherwise a #SPILL error will occur.
• If none of the arguments is specified, a RANDARRAY() formula returns a single decimal number between 0 and 1.
• If the rows or/and columns arguments are represented by decimal numbers, they will be truncated to the whole integer before the decimal point (e.g. 5.9 will be treated as 5).
• If the min or max argument is not defined, RANDARRAY defaults to 0 and 1, respectively.
• Like other random functions, Excel RANDARRAY is volatile , meaning it generates a new list of random values every time the worksheet is calculated. To prevent this from happening, you can replace formulas with values by using Excel's Paste Special > Values feature.

Basic Excel RANDARRAY formula

And now, let me show you a random Excel formula in its simplest form.

Supposing you want to fill a range consisting of 5 rows and 3 columns with any random numbers. To have it done, set up the first two arguments this way:

• Rows is 5 since we want the results in 5 rows.
• Columns is 3 as we want the results in 3 columns.

All of the other arguments we leave to their default values and get the following formula:

=RANDARRAY(5, 3)

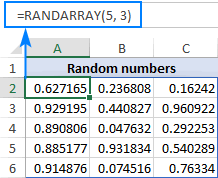
How to randomize in Excel - RANDARRAY formula examples

Below you will find a few advanced formulas that cover typical randomizing scenarios in Excel.

To create a list of random numbers within a specific range, supply the minimum value in the 3 rd argument and the maximum number in the 4 th argument. Depending on whether you need integers or decimals, set the 5 th argument to TRUE or FALSE, respectively.

As an example, let's populate a range of 6 rows and 4 columns with random integers from 1 to 100. For this, we set up the following arguments of the RANDARRAY function:

• Rows is 6 since we want the results in 6 rows.
• Columns is 4 as we want the results in 4 columns.
• Min is 1, which is the minimum value we wish to have.
• Max is 100, which is the maximum value to be generated.
• Whole_number is TRUE because we need integers.

Putting the arguments together, we get this formula:

=RANDARRAY(6, 4, 1, 100, TRUE)

Looking for a random date generator in Excel? The RANDARRAY function is an easy solution! All you have to do is input the earlier date (date 1) and later date (date 2) in predefined cells, and then reference those cells in your formula:

For this example, we have created a list of random dates between the dates in D1 and D2 with this formula:

Of course, nothing prevents you from supplying the min and max dates directly in the formula if you wish to. Just be sure you enter them in the format that Excel can understand:

=RANDARRAY(10, 1, "1/1/2020", "12/31/2020", TRUE)

To prevent mistakes, you can use the DATE function for entering dates:

=RANDARRAY(10, 1, DATE(2020,1,1), DATE(2020,12,31), TRUE)

Generate random workdays in Excel

To produce random working days, embed the RANDARRAY function in the first argument of WORKDAY like this:

RANDARRAY will create an array of random start dates, to which the WORKDAY function will add 1 workday and ensure that all the returned dates are working days.

With date 1 in D1 and date 2 in D2, here's the formula to produce a list of 10 weekdays:

How to generate random numbers without duplicates

Though modern Excel offers 6 new dynamic array functions, unfortunately, there is still no inbuilt function to return random numbers without duplicates.

To build your own unique random number generator in Excel, you will need to chain several functions together like shown below.

Random integers :

Random decimals :

• N is how many values you wish to generate.
• Min is the lowest value.
• Max is the highest value.

For example, to produce 10 random whole numbers with no duplicates, use this formula:

To create a list of 10 unique random decimal numbers , change TRUE to FALSE in the last argument of the RANDARRAY function or simply omit this argument:

Tips and notes:

• The detailed explanation of the formula can be found in How to generate random numbers in Excel without duplicates .
• In Excel 2019 and earlier, the RANDARRAY function is not available. Instead, please check out this solution .

How to randomly sort in Excel

To shuffle data in Excel, use RANDARRAY for the "sort by" array ( by_array argument) of the SORTBY function . The ROWS function will count the number of rows in your data set, indicating how many random numbers to generate:

With this approach, you can randomly sort a list in Excel, whether it contains numbers, dates or text entries:

Also, you can also shuffle rows without mixing your data:

How to get a random selection in Excel

To extract a random sample from a list, here's a generic formula to use:

Where n is the number of random entries you wish to extract.

For example, to randomly select 3 names from the list in A2:A10, use this formula:

=INDEX(A2:A10, RANDARRAY(3, 1, 1, ROWS(A2:A10), TRUE))

Or input the desired sample size in some cell, say C2, and reference that cell:

How this formula works:

At the core of this formula is the RANDARRAY function that creates a random array of integers, with the value in C2 defining how many values to generate. The minimal number is hardcoded (1) and the maximum number corresponds to the number of rows in your data set, which is returned by the ROWS function.

The array of random integers goes directly to the row_num argument of the INDEX function, specifying the positions of the items to return. For the sample in the screenshot above, it is:

=INDEX(A2:A10, {8;7;4})

How to select random rows in Excel

If your data set contains more than one column, then specify which columns to include in the sample. For this, supply an array constant for the last argument ( column_num ) of the INDEX function, like this:

=INDEX(A2:B10, RANDARRAY(D2, 1, 1, ROWS(A2:A10), TRUE), {1,2})

Where A2:B10 is the source data and D2 is the sample size.

How to randomly assign numbers and text in Excel

To do random assignment in Excel, use RANDBETWEEN together with the CHOOSE function in this way:

• Data is a range of your source data to which you want to assign random values.
• N is the total number of values to assign.
• Value1 , value2 , value3 , etc. are the values to be assigned randomly.

For example, to assign numbers from 1 to 3 to participants in A2:A13, use this formula:

For convenience, you can enter the values to assign in separate cells, say from D2 to D4, and reference those cells in your formula (individually, not as a range):

=CHOOSE(RANDARRAY(ROWS(A2:A13), 1, 1, 3, TRUE), D2, D3, D4)

How this formula works

At the heart of this solution is again the RANDARRAY function that produces an array of random integers based on the min and max numbers that you specify (from 1 to 3 in our case). The ROWS function tells RANDARRAY how many random numbers to generate. This array goes to the index_num argument of the CHOOSE function . For example:

=CHOOSE({1;2;1;2;3;2;3;3;1;3;1;2}, D2, D3, D4)

How to randomly assign data to groups

When your task is to randomly assign participants to groups, the above formula may not be suitable because it does not control how many times a given group is chosen. For example, 5 persons could be assigned to group A while only 2 persons to group C. To do random assignment evenly , so that each group has the same number of participants, you need a different solution.

First, you generate a list of random numbers by using this formula:

=RANDARRAY(ROWS(A2:A13))

And then, you assign groups (or anything else) by using this generic formula:

Where n is the group size, i.e. the number of times each value should be assigned.

For example, to randomly assign people to the groups listed in E2:E5, so that each group has 3 participants, use this formula:

=INDEX($E$2:$E$5, ROUNDUP(RANK(B2,$B$2:$B$13)/3,0))

Please notice that it's a regular formula (not a dynamic array formula!), so you need to lock the ranges with absolute references like in the above formula.

Please remember that the RANDARRAY function is volatile. To prevent generating new random values every time you change something in the worksheet, replace formulas with their values by using the Paste Special feature.

The RANDARRAY formula in the helper column is very simple and hardly requires explanation, so let us focus on the formula in column C.

The RANK function ranks the value in B2 against the array of random numbers in B2:B13. The result is a number between 1 and the total number of participants (12 in our case).

The rank is divided by the group size, (3 in our example), and the ROUNDUP function rounds it up to the nearest integer. The result of this operation is a number between 1 and the total number of groups (4 in this example).

When your RANDARRAY formula returns an error, these are the most obvious reasons to check:

#SPILL error

#value error.

A #VALUE! error may occur in these circumstances:

• If a max value is less than a min value.
• If any of the arguments is non-numeric.

#NAME error

In most cases, a #NAME! error indicates one of the following:

• The function's name is misspelled.
• The function is not available in your Excel version.

#CALC! error

That's how to build a random number generator in Excel with the new RANDARRAY function. I thank you for reading and hope to see you on our blog next week!

Practice workbook for download

You may also be interested in.

• How to select random sample in Excel
• How to sort randomly in Excel
• How to generate random numbers in Excel with no repeats
• Flash Fill in Excel with examples

Table of contents

S. No Date Time Shift Day Subject Session Group

S.No Date Time Shift Day Subject Session Group

Formula in excel

Hi! We have a special tutorial that can help to solve your problem: How to convert rows to columns in Excel (transpose data) .

how to random array with the total of each row is 100?

I think you can try to use the custom functions and macros described in this article to create a random array with a specific sum in a row: How to find all combinations of numbers that equal given sum in Excel .

I always get a #name error

Hi, This error most often appears if you specified the function name incorrectly.

Post a comment

Help Center Help Center

• Help Center
• Trial Software
• Product Updates
• Documentation

Generate Random Numbers That Are Repeatable

Specify the generator algorithm and seed.

This example shows how to repeat arrays of random numbers by specifying the generator algorithm and seed first. Every time you initialize the generator using the same algorithm and seed, you always get the same result.

First, initialize the random number generator to make the results in this example repeatable. For example, the following code sets the seed to 1 and the generator algorithm to Mersenne Twister.

Next, create an array of random numbers.

Repeat the same command.

The first call to rand changed the state of the generator, so the second result is different.

Now, reinitialize the generator using the same seed and algorithm as before. Then reproduce the first matrix, A .

Set the seed and generator type together when you want to:

Ensure that the behavior of code you write today returns the same results when you run that code in a future MATLAB ® release.

Ensure that the behavior of code you wrote in a previous MATLAB release returns the same results using the current release.

Repeat random numbers in your code after running someone else’s random number code.

See the rng reference page for a list of available generators.

When you first start a MATLAB session or call rng("default") , MATLAB initializes the random number generator using the default algorithm and seed. You can set the default algorithm and seed in MATLAB preferences (since R2023b) . If you do not change these preferences, then rng uses the factory value of "twister" for the Mersenne Twister generator with seed 0, as in previous releases. For more information, see Default Settings for Random Number Generator and Reproducibility for Random Number Generator .

Save and Restore the Generator Settings

This example shows how to create repeatable arrays of random numbers by saving and restoring the generator settings. The most common reason to save and restore generator settings is to reproduce the random numbers generated at a specific point in an algorithm or iteration. For example, you can use the generator settings as an aid in debugging. Unlike reseeding, which reinitializes the generator, this approach allows you to save and restore the generator settings at any point.

First, initialize the random number generator to make the results in this example repeatable.

Create an array of random integer values between 1 and 10.

The first call to randi changed the state of the generator. Save the generator settings after the first call to randi in a structure s .

Create another array of random integer values between 1 and 10.

Now, return the generator to the previous state stored in s and reproduce the second array A .

Related Topics

• Generate Random Numbers That Are Different
• Controlling Random Number Generation

MATLAB Command

You clicked a link that corresponds to this MATLAB command:

Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site

Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .

• Switzerland (English)
• Switzerland (Deutsch)
• Switzerland (Français)
• 中国 (English)

You can also select a web site from the following list:

How to Get Best Site Performance

Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.

• América Latina (Español)
• Canada (English)
• United States (English)
• Belgium (English)
• Denmark (English)
• Deutschland (Deutsch)
• España (Español)
• Finland (English)
• France (Français)
• Ireland (English)
• Italia (Italiano)
• Luxembourg (English)
• Netherlands (English)
• Norway (English)
• Österreich (Deutsch)
• Portugal (English)
• Sweden (English)
• United Kingdom (English)

Asia Pacific

• Australia (English)
• India (English)
• New Zealand (English)

Contact your local office