identify a hypothesis and conclusion of each conditional

Conditional Statement – Definition, Truth Table, Examples, FAQs

What is a conditional statement, how to write a conditional statement, what is a biconditional statement, solved examples on conditional statements, practice problems on conditional statements, frequently asked questions about conditional statements.

A conditional statement is a statement that is written in the “If p, then q” format. Here, the statement p is called the hypothesis and q is called the conclusion. It is a fundamental concept in logic and mathematics. 

Conditional statement symbol :  p → q

A conditional statement consists of two parts.

• The “if” clause, which presents a condition or hypothesis.
• The “then” clause, which indicates the consequence or result that follows if the condition is true. 

Example : If you brush your teeth, then you won’t get cavities.

Hypothesis (Condition): If you brush your teeth

Conclusion (Consequence): then you won’t get cavities 

Conditional Statement: Definition

A conditional statement is characterized by the presence of “if” as an antecedent and “then” as a consequent. A conditional statement, also known as an “if-then” statement consists of two parts:

• The “if” clause (hypothesis): This part presents a condition, situation, or assertion. It is the initial condition that is being considered.
• The “then” clause (conclusion): This part indicates the consequence, result, or action that will occur if the condition presented in the “if” clause is true or satisfied. 

Related Worksheets

Representation of Conditional Statement

The conditional statement of the form ‘If p, then q” is represented as p → q. 

It is pronounced as “p implies q.”

Different ways to express a conditional statement are:

• p implies q
• p is sufficient for q
• q is necessary for p

Parts of a Conditional Statement

There are two parts of conditional statements, hypothesis and conclusion. The hypothesis or condition will begin with the “if” part, and the conclusion or action will begin with the “then” part. A conditional statement is also called “implication.”

Conditional Statements Examples:

Example 1: If it is Sunday, then you can go to play. 

Hypothesis: If it is Sunday

Conclusion: then you can go to play. 

Example 2: If you eat all vegetables, then you can have the dessert.

Condition: If you eat all vegetables

Conclusion: then you can have the dessert 

To form a conditional statement, follow these concise steps:

Step 1 : Identify the condition (antecedent or “if” part) and the consequence (consequent or “then” part) of the statement.

Step 2 : Use the “if… then…” structure to connect the condition and consequence.

Step 3 : Ensure the statement expresses a logical relationship where the condition leads to the consequence.

Example 1 : “If you study (condition), then you will pass the exam (consequence).” 

This conditional statement asserts that studying leads to passing the exam. If you study (condition is true), then you will pass the exam (consequence is also true).

Example 2 : If you arrange the numbers from smallest to largest, then you will have an ascending order.

Hypothesis: If you arrange the numbers from smallest to largest

Conclusion: then you will have an ascending order

Truth Table for Conditional Statement

The truth table for a conditional statement is a table used in logic to explore the relationship between the truth values of two statements. It lists all possible combinations of truth values for “p” and “q” and determines whether the conditional statement is true or false for each combination. 

The truth value of p → q is false only when p is true and q is False. 

If the condition is false, the consequence doesn’t affect the truth of the conditional; it’s always true.

In all the other cases, it is true.

The truth table is helpful in the analysis of possible combinations of truth values for hypothesis or condition and conclusion or action. It is useful to understand the presence of truth or false statements. 

Converse, Inverse, and Contrapositive

The converse, inverse, and contrapositive are three related conditional statements that are derived from an original conditional statement “p → q.” 

Consider a conditional statement: If I run, then I feel great.

• Converse: 

The converse of “p → q” is “q → p.” It reverses the order of the original statement. While the original statement says “if p, then q,” the converse says “if q, then p.” 

Converse: If I feel great, then I run.

• Inverse: 

The inverse of “p → q” is “~p → ~q,” where “” denotes negation (opposite). It negates both the antecedent (p) and the consequent (q). So, if the original statement says “if p, then q,” the inverse says “if not p, then not q.”

Inverse : If I don’t run, then I don’t feel great.

• Contrapositive: 

The contrapositive of “p → q” is “~q → ~p.” It reverses the order and also negates both the statements. So, if the original statement says “if p, then q,” the contrapositive says “if not q, then not p.”

Contrapositive: If I don’t feel great, then I don’t run.

A biconditional statement is a type of compound statement in logic that expresses a bidirectional or two-way relationship between two statements. It asserts that “p” is true if and only if “q” is true, and vice versa. In symbolic notation, a biconditional statement is represented as “p ⟺ q.”

In simpler terms, a biconditional statement means that the truth of “p” and “q” are interdependent. 

If “p” is true, then “q” must also be true, and if “q” is true, then “p” must be true. Conversely, if “p” is false, then “q” must be false, and if “q” is false, then “p” must be false. 

Biconditional statements are often used to express equality, equivalence, or conditions where two statements are mutually dependent for their truth values. 

Examples : 

• I will stop my bike if and only if the traffic light is red.  
• I will stay if and only if you play my favorite song.

Facts about Conditional Statements

• The negation of a conditional statement “p → q” is expressed as “p and not q.” It is denoted as “𝑝 ∧ ∼𝑞.” 
• The conditional statement is not logically equivalent to its converse and inverse.
• The conditional statement is logically equivalent to its contrapositive. 
• Thus, we can write p → q ∼q → ∼p

In this article, we learned about the fundamentals of conditional statements in mathematical logic, including their structure, parts, truth tables, conditional logic examples, and various related concepts. Understanding conditional statements is key to logical reasoning and problem-solving. Now, let’s solve a few examples and practice MCQs for better comprehension.

Example 1: Identify the hypothesis and conclusion. 

If you sing, then I will dance.

Solution : 

Given statement: If you sing, then I will dance.

Here, the antecedent or the hypothesis is “if you sing.”

The conclusion is “then I will dance.”

Example 2: State the converse of the statement: “If the switch is off, then the machine won’t work.” 

Here, p: The switch is off

q: The machine won’t work.

The conditional statement can be denoted as p → q.

Converse of p → q is written by reversing the order of p and q in the original statement.

Converse of  p → q is q → p.

Converse of  p → q: q → p: If the machine won’t work, then the switch is off.

Example 3: What is the truth value of the given conditional statement? 

If 2+2=5 , then pigs can fly.

Solution:  

q: Pigs can fly.

The statement p is false. Now regardless of the truth value of statement q, the overall statement will be true. 

F → F = T

Hence, the truth value of the statement is true. 

Conditional Statement - Definition, Truth Table, Examples, FAQs

Attend this quiz & Test your knowledge.

What is the antecedent in the given conditional statement? If it’s sunny, then I’ll go to the beach.

A conditional statement can be expressed as, what is the converse of “a → b”, when the antecedent is true and the consequent is false, the conditional statement is.

What is the meaning of conditional statements?

Conditional statements, also known as “if-then” statements, express a cause-and-effect or logical relationship between two propositions.

When does the truth value of a conditional statement is F?

A conditional statement is considered false when the antecedent is true and the consequent is false.

What is the contrapositive of a conditional statement?

The contrapositive reverses the order of the statements and also negates both the statements. It is equivalent in truth value to the original statement.

RELATED POSTS

• Ordering Decimals: Definition, Types, Examples
• Decimal to Octal: Steps, Methods, Conversion Table
• Lattice Multiplication – Definition, Method, Examples, Facts, FAQs
• X Intercept – Definition, Formula, Graph, Examples
• Lateral Face – Definition With Examples

Math & ELA | PreK To Grade 5

Kids see fun., you see real learning outcomes..

Make study-time fun with 14,000+ games & activities, 450+ lesson plans, and more—free forever.

Parents, Try for Free Teachers, Use for Free

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

2.11: If Then Statements

• Last updated
• Save as PDF
• Page ID 2144

Hypothesis followed by a conclusion in a conditional statement.

Conditional Statements

A conditional statement (also called an if-then statement ) is a statement with a hypothesis followed by a conclusion . The hypothesis is the first, or “if,” part of a conditional statement. The conclusion is the second, or “then,” part of a conditional statement. The conclusion is the result of a hypothesis.

If-then statements might not always be written in the “if-then” form. Here are some examples of conditional statements:

• Statement 1: If you work overtime, then you’ll be paid time-and-a-half.
• Statement 2: I’ll wash the car if the weather is nice.
• Statement 3: If 2 divides evenly into \(x\), then \(x\) is an even number.
• Statement 4: I’ll be a millionaire when I win the lottery.
• Statement 5: All equiangular triangles are equilateral.

Statements 1 and 3 are written in the “if-then” form. The hypothesis of Statement 1 is “you work overtime.” The conclusion is “you’ll be paid time-and-a-half.” Statement 2 has the hypothesis after the conclusion. If the word “if” is in the middle of the statement, then the hypothesis is after it. The statement can be rewritten: If the weather is nice, then I will wash the car. Statement 4 uses the word “when” instead of “if” and is like Statement 2. It can be written: If I win the lottery, then I will be a millionaire. Statement 5 “if” and “then” are not there. It can be rewritten: If a triangle is equiangular, then it is equilateral.

What if you were given a statement like "All squares are rectangles"? How could you determine the hypothesis and conclusion of this statement?

Example \(\PageIndex{1}\)

Determine the hypothesis and conclusion: I'll bring an umbrella if it rains.

Hypothesis: "It rains." Conclusion: "I'll bring an umbrella."

Example \(\PageIndex{2}\)

Determine the hypothesis and conclusion: All right angles are \(90^{\circ}\).

Hypothesis: "An angle is right." Conclusion: "It is \(90^{\circ}\)."

Example \(\PageIndex{3}\)

Use the statement: I will graduate when I pass Calculus.

Rewrite in if-then form and determine the hypothesis and conclusion.

This statement can be rewritten as If I pass Calculus, then I will graduate. The hypothesis is “I pass Calculus,” and the conclusion is “I will graduate.”

Example \(\PageIndex{4}\)

Use the statement: All prime numbers are odd.

Rewrite in if-then form, determine the hypothesis and conclusion, and determine whether this is a true statement.

This statement can be rewritten as If a number is prime, then it is odd. The hypothesis is "a number is prime" and the conclusion is "it is odd". This is not a true statement (remember that not all conditional statements will be true!) since 2 is a prime number but it is not odd.

Example \(\PageIndex{5}\)

Determine the hypothesis and conclusion: Sarah will go to the store if Riley does the laundry.

The statement can be rewritten as "If Riley does the laundry then Sarah will go to the store." The hypothesis is "Riley does the laundry" and the conclusion is "Sarah will go to the store."

Determine the hypothesis and the conclusion for each statement.

• If 5 divides evenly into \(x\), then \(x\) ends in 0 or 5.
• If a triangle has three congruent sides, it is an equilateral triangle.
• Three points are coplanar if they all lie in the same plane.
• If \(x=3\), then \(x^2=9\).
• If you take yoga, then you are relaxed.
• All baseball players wear hats.
• I'll learn how to drive when I am 16 years old.
• If you do your homework, then you can watch TV.
• Alternate interior angles are congruent if lines are parallel.
• All kids like ice cream.

Additional Resources

Video: If-Then Statements Principles - Basic

Activities: If-Then Statements Discussion Questions

Study Aids: Conditional Statements Study Guide

Practice: If Then Statements

Real World: If Then Statements

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

3.3: Truth Tables- Conditional, Biconditional

• Last updated
• Save as PDF
• Page ID 52962

• David Lippman
• Pierce College via The OpenTextBookStore

Conditional

A conditional is a logical compound statement in which a statement \(p\), called the hypothesis, implies a statement \(q\), called the conclusion.

A conditional is written as \(p \rightarrow q\) and is translated as "if \(p\), then \(q\)".

The English statement “If it is raining, then there are clouds is the sky” is a conditional statement. It makes sense because if the hypothesis “it is raining” is true, then the conclusion “there are clouds in the sky” must also be true.

Notice that the statement tells us nothing of what to expect if it is not raining; there might be clouds in the sky, or there might not. If the hypothesis is false, then the conclusion becomes irrelevant.

Suppose you order a team jersey online on Tuesday and want to receive it by Friday so you can wear it to Saturday’s game. The website says that if you pay for expedited shipping, you will receive the jersey by Friday. In what situation is the website telling a lie?

There are four possible outcomes:

• You pay for expedited shipping and receive the jersey by Friday
• You pay for expedited shipping and don’t receive the jersey by Friday
• You don’t pay for expedited shipping and receive the jersey by Friday
• You don’t pay for expedited shipping and don’t receive the jersey by Friday

Only one of these outcomes proves that the website was lying: the second outcome in which you pay for expedited shipping but don’t receive the jersey by Friday. The first outcome is exactly what was promised, so there’s no problem with that. The third outcome is not a lie because the website never said what would happen if you didn’t pay for expedited shipping; maybe the jersey would arrive by Friday whether you paid for expedited shipping or not. The fourth outcome is not a lie because, again, the website didn’t make any promises about when the jersey would arrive if you didn’t pay for expedited shipping.

It may seem strange that the third outcome in the previous example, in which the first part is false but the second part is true, is not a lie. Remember, though, that if the hypothesis is false, we cannot make any judgment about the conclusion. The website never said that paying for expedited shipping was the only way to receive the jersey by Friday.

A friend tells you “If you upload that picture to Facebook, you’ll lose your job.” Under what conditions can you say that your friend was wrong?

• You upload the picture and lose your job
• You upload the picture and don’t lose your job
• You don’t upload the picture and lose your job
• You don’t upload the picture and don’t lose your job

There is only one possible case in which you can say your friend was wrong: the second outcome in which you upload the picture but still keep your job. In the last two cases, your friend didn’t say anything about what would happen if you didn’t upload the picture, so you can’t say that their statement was wrong. Even if you didn’t upload the picture and lost your job anyway, your friend never said that you were guaranteed to keep your job if you didn’t upload the picture; you might lose your job for missing a shift or punching your boss instead.

Truth Table for the Conditional

\(\begin{array}{|c|c|c|} \hline p & q & p \rightarrow q \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{T} \\ \hline \end{array}\)

Again, if the hypothesis \(p\) is false, we cannot prove that the statement is a lie, so the result of the third and fourth rows is true.

Construct a truth table for the statement \((m \wedge \sim p) \rightarrow r\)

We start by constructing a truth table with 8 rows to cover all possible scenarios. Next, we can focus on the hypothesis, \(m \wedge \sim p\).

\(\begin{array}{|c|c|c|} \hline m & p & r \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{F} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{F} \\ \hline \end{array}\)

\(\begin{array}{|c|c|c|c|} \hline m & p & r & \sim p \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{F} \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{F} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{F} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{T} \\ \hline \end{array}\)

\(\begin{array}{|c|c|c|c|c|} \hline m & p & r & \sim p & m \wedge \sim p \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{F} \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{F} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{F} \\ \hline \end{array}\)

Now we can create a column for the conditional. Because it can be confusing to keep track of all the Ts and \(\mathrm{Fs}\), why don't we copy the column for \(r\) to the right of the column for \(m \wedge \sim p\) ? This makes it a lot easier to read the conditional from left to right.

\(\begin{array}{|c|c|c|c|c|c|c|} \hline m & p & r & \sim p & m \wedge \sim p & r & (m \wedge \sim p) \rightarrow r \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{T} \\ \hline \end{array}\)

When \(m\) is true, \(p\) is false, and \(r\) is false- -the fourth row of the table-then the hypothesis \(m \wedge \sim p\) will be true but the conclusion false, resulting in an invalid conditional; every other case gives a valid conditional.

If you want a real-life situation that could be modeled by \((m \wedge \sim p) \rightarrow r\), consider this: let \(m=\) we order meatballs, \(p=\) we order pasta, and \(r=\) Rob is happy. The statement \((m \wedge \sim p) \rightarrow r\) is "if we order meatballs and don't order pasta, then Rob is happy". If \(m\) is true (we order meatballs), \(p\) is false (we don't order pasta), and \(r\) is false (Rob is not happy), then the statement is false, because we satisfied the hypothesis but Rob did not satisfy the conclusion.

For any conditional, there are three related statements, the converse, the inverse, and the contrapositive.

Derived Forms of a Conditional

The original conditional is \(\quad\) "if \(p,\) then \(q^{\prime \prime} \quad p \rightarrow q\)

The converse is \(\quad\) "if \(q,\) then \(p^{\prime \prime} \quad q \rightarrow p\)

The inverse is \(\quad\) "if not \(p,\) then not \(q^{\prime \prime} \quad \sim p \rightarrow \sim q\)

The contrapositive is "if not \(q,\) then not \(p^{\prime \prime} \quad \sim q \rightarrow \sim p\)

Consider again the conditional “If it is raining, then there are clouds in the sky.” It seems reasonable to assume that this is true.

The converse would be “If there are clouds in the sky, then it is raining.” This is not always true.

The inverse would be “If it is not raining, then there are not clouds in the sky.” Likewise, this is not always true.

The contrapositive would be “If there are not clouds in the sky, then it is not raining.” This statement is true, and is equivalent to the original conditional.

Looking at truth tables, we can see that the original conditional and the contrapositive are logically equivalent, and that the converse and inverse are logically equivalent.

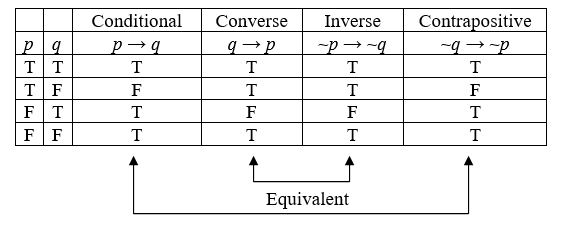
Equivalence

A conditional statement and its contrapositive are logically equivalent.

The converse and inverse of a conditional statement are logically equivalent.

In other words, the original statement and the contrapositive must agree with each other; they must both be true, or they must both be false. Similarly, the converse and the inverse must agree with each other; they must both be true, or they must both be false.

We typically represent the conditional using the words, "if ..., then ...," but there are other ways this logical connective can be represented in English. Consider the conditional from Example 5: "If it is raining, then there are clouds in the sky." We could equivalently write, "It is raining only if there are clouds in the sky." You can probably imagine how these two statements are saying the same thing - whenever it's raining outside, it is a safe conclusion there are clouds in the sky as well. Some other wordings that communicate the same information use either "sufficient" or "necessary." For example, "Raining is a sufficient condition for it to be cloudy," and "Being cloudy is a necessary condition for it to be raining." Here is a table summarizing the different wordings.

Different Wordings of the Conditional

The following statements are equivalent:

• If \(p\), then \(q\).
• \(q\) only if \(p\).
• \(p\) is sufficient for \(q\).
• \(q\) is necessary for \(p\).

In everyday life, we often have a stronger meaning in mind when we use a conditional statement. Consider “If you submit your hours today, then you will be paid next Friday.” What the payroll rep really means is “If you submit your hours today, then you will be paid next Friday, and if you don’t submit your hours today, then you won’t be paid next Friday.” The conditional statement if t , then p also includes the inverse of the statement: if not t , then not p . A more compact way to express this statement is “You will be paid next Friday if and only if you submit your timesheet today.” A statement of this form is called a biconditional .

Biconditional

A biconditional is a logical conditional statement in which the hypothesis and conclusion are interchangeable.

A biconditional is written as \(p \leftrightarrow q\) and is translated as " \(p\) if and only if \(q^{\prime \prime}\).

Because a biconditional statement \(p \leftrightarrow q\) is equivalent to \((p \rightarrow q) \wedge(q \rightarrow p),\) we may think of it as a conditional statement combined with its converse: if \(p\), then \(q\) and if \(q\), then \(p\). The double-headed arrow shows that the conditional statement goes from left to right and from right to left. A biconditional is considered true as long as the hypothesis and the conclusion have the same truth value; that is, they are either both true or both false.

Truth Table for the Biconditional

\(\begin{array}{|c|c|c|} \hline p & q & p \leftrightarrow q \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{T} \\ \hline \end{array}\)

Notice that the fourth row, where both components are false, is true; if you don’t submit your timesheet and you don’t get paid, the person from payroll told you the truth.

Suppose this statement is true: “The garbage truck comes down my street if and only if it is Thursday morning.” Which of the following statements could be true?

• It is noon on Thursday and the garbage truck did not come down my street this morning.
• It is Monday and the garbage truck is coming down my street.
• It is Wednesday at 11:59PM and the garbage truck did not come down my street today.
• This cannot be true. This is like the second row of the truth table; it is true that I just experienced Thursday morning, but it is false that the garbage truck came.
• This cannot be true. This is like the third row of the truth table; it is false that it is Thursday, but it is true that the garbage truck came.
• This could be true. This is like the fourth row of the truth table; it is false that it is Thursday, but it is also false that the garbage truck came, so everything worked out like it should.

Try it Now 1

Suppose this statement is true: “I wear my running shoes if and only if I am exercising.” Determine whether each of the following statements must be true or false.

• I am exercising and I am not wearing my running shoes.
• I am wearing my running shoes and I am not exercising.
• I am not exercising and I am not wearing my running shoes.

Choices a & b are false; c is true.

Create a truth table for the statement \((A \vee B) \leftrightarrow \sim C\)

Whenever we have three component statements, we start by listing all the possible truth value combinations for \(A, B,\) and \(C .\) After creating those three columns, we can create a fourth column for the hypothesis, \(A \vee B\). Now we will temporarily ignore the column for \(C\) and focus on \(A\) and \(B\), writing the truth values for \(A \vee B\).

\(\begin{array}{|c|c|c|} \hline A & B & C \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{F} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{F} \\ \hline \end{array}\)

\(\begin{array}{|c|c|c|c|} \hline A & B & C & A \vee B \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{F} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{F} \\ \hline \end{array}\)

Next we can create a column for the negation of \(C\). (Ignore the \(A \vee B\) column and simply negate the values in the \(C\) column.)

\(\begin{array}{|c|c|c|c|c|} \hline A & B & C & A \vee B & \sim C \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{F} \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{F} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{F} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{T} \\ \hline \end{array}\)

Finally, we find the truth values of \((A \vee B) \leftrightarrow \sim C\). Remember, a biconditional is true when the truth value of the two parts match, but it is false when the truth values do not match.

\(\begin{array}{|c|c|c|c|c|c|} \hline A & B & C & A \vee B & \sim C & (A \vee B) \leftrightarrow \sim C \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{F} \\ \hline \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{F} \\ \hline \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{F} \\ \hline \mathrm{F} & \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{T} \\ \hline \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{F} \\ \hline \end{array}\)

To illustrate this situation, suppose your boss needs you to do either project \(A\) or project \(B\) (or both, if you have the time). If you do one of the projects, you will not get a crummy review ( \(C\) is for crummy). So \((A \vee B) \leftrightarrow \sim C\) means "You will not get a crummy review if and only if you do project \(A\) or project \(B\)." Looking at a few of the rows of the truth table, we can see how this works out. In the first row, \(A, B,\) and \(C\) are all true: you did both projects and got a crummy review, which is not what your boss told you would happen! That is why the final result of the first row is false. In the fourth row, \(A\) is true, \(B\) is false, and \(C\) is false: you did project \(A\) and did not get a crummy review. This is what your boss said would happen, so the final result of this row is true. And in the eighth row, \(A, B\), and \(C\) are all false: you didn't do either project and did not get a crummy review. This is not what your boss said would happen, so the final result of this row is false. (Even though you may be happy that your boss didn't follow through on the threat, the truth table shows that your boss lied about what would happen.)

Identify the hypothesis and the conclusion of each conditional statement.

Nov 19, 2014

260 likes | 495 Views

Identify the hypothesis and the conclusion of each conditional statement. 1. If x > 10, then x > 5. 2. If you live in Milwaukee, then you live in Wisconsin. Write each statement as a conditional. 3. Squares have four sides. 4. All butterflies have wings.

Share Presentation

• conditional
• conditional statement
• good definition
• conditional statements
• true conditional statement
• good definitions avoid words

Presentation Transcript

Identify the hypothesis and the conclusion of each conditional statement. 1. If x > 10, then x > 5. 2. If you live in Milwaukee, then you live in Wisconsin. Write each statement as a conditional. 3. Squares have four sides. 4. All butterflies have wings. Write the converse of each statement. 5. If the sun shines, then we go on a picnic. 6. If two lines are skew, then they do not intersect. 7. If x = –3, then x3 = –27. 2-2

Biconditionals and Definitions Section 2-2

Objectives • To write biconditionals. • To recognize good definitions.

A ______________ is the combination of a conditional statement and its converse. A biconditional contains the words “___________________.” In symbols, we write this as:

Consider the true conditional statement. Write its converse. If the converse is also true, combine the statements as a biconditional. 1. Conditional: If two angles have the same measure, then the angles are congruent.

Consider the true conditional statement. Write its converse. If the converse is also true, combine the statements as a biconditional. 2. Conditional: If three points are collinear, then they lie on the same line.

Consider the true conditional statement. Write its converse. If the converse is also true, combine the statements as a biconditional. 3. Conditional: If two segments have the same length, then they are congruent.

Consider the true conditional statement. Write its converse. If the converse is also true, combine the statements as a biconditional. 4. Conditional: If x = 12, then 2x – 5 = 19.

Separating a Biconditional into Parts Write the two (conditional) statements that form the biconditional. 1. A number is divisible by three if and only if the sum of its digits is divisible by three.

Separating a Biconditional into Parts Write the two (conditional) statements that form the biconditional. 2. A number is prime if and only if it has two distinct factors, 1 and itself.

Separating a Biconditional into Parts Write the two (conditional) statements that form the biconditional. 3. A line bisects a segment if and only if the line intersects the segment only at its midpoint.

Separating a Biconditional into Parts Write the two (conditional) statements that form the biconditional. 4. An integer is divisible by 100 if and only if its last two digits are zeros.

Recognizing a Good Definition Use the examples to identify the figures above that are polyglobs. Write a definition of a polyglob by describing what a polyglob is.

A good definition is a statement that can help you to ____________ or ___________ an object.

A good definition: • Uses clearly understood terms. The terms should be commonly understood or already defined. • Is precise. Good definitions avoid words such as large, sort of, and some. • Is reversible. That means that you can write a good definition as a true biconditional.

Show that the definition is reversible. Then write it as a true biconditional. 1. Definition: Perpendicular lines are two lines that intersect to form right angles.

Show that the definition is reversible. Then write it as a true biconditional. 2. Definition: A right angle is an angle whose measure is 90 (degrees).

Show that the definition is reversible. Then write it as a true biconditional. 3. Definition: Parallel planes are planes that do not intersect.

Show that the definition is reversible. Then write it as a true biconditional. 4. Definition: A rectangle is a four-sided figure with at least one right angle.

Is the given statement a good definition? Explain. • An airplane is a vehicle that flies. • A triangle has sharp corners. • A square is a figure with four right angles.

Write your own good definition.

Homework: Pg 78 #1-23 odd

1. Write the converse of the statement. If it rains, then the car gets wet. 2. Write the statement above and its converse as a biconditional. 3. Write the two conditional statements that make up the biconditional. Lines are skew if and only if they are noncoplanar. Is each statement a good definition? If not, find a counterexample. 4. The midpoint of a line segment is the point that divides the segment into two congruent segments. 5. A line segment is a part of a line.

• More by User

Statement of the Hypothesis

Statement of the Hypothesis. H R 1 Planned outdoor learning experiences, twice a week for 4 weeks, will lead to increased gains in the science learning of 25 fourth graders at P.S. X, as measured by pre and post learning experiences questionnaires. . Method. Participants

218 views • 6 slides

Part 2 Module 2 The Conditional Statement

Part 2 Module 2 The Conditional Statement. The Conditional Statement. A conditional statement is a statement of the form "If p, then q," denoted p  q. Conditional statements. EXAMPLE Let p represent: "You drink Pepsi." Let q represent: "You are happy."

544 views • 27 slides

Conditional Statement Book

Conditional Statement Book. Mr. Sheldon Ms. Lytle. What is that????. A conditional statement is an if and then statement. If A, then B A is the antecedent or cause B is the conclusion. Raining Example and Non-example. Which is a true statement?

175 views • 10 slides

Hypothesis & Conclusion Writing

Hypothesis & Conclusion Writing. Hypothesis Writing. What is a hypothesis?. A hypothesis is an “if” and “then” statement at the beginning of the lab stating the question the lab is designed to answer. Example: If I eat lots of chocolate , then I will get zits.

701 views • 12 slides

Warm Up Write a conditional statement from each of the following.

Warm Up Write a conditional statement from each of the following. 1. The intersection of two lines is a point. 2. An odd number is one more than a multiple of 2. 3. Write the converse of the conditional “If Pedro lives in Chicago, then he lives in Illinois.” Find its truth value.

428 views • 18 slides

Question Hypothesis Data analysis conclusion

1. Jennifer wants to know which of three light bulbs lasts the longest. In her lab journal she writes: “The light bulb with the lowest wattage will last the longest.” Which part of the investigation has she written?. Question Hypothesis Data analysis conclusion. 29.

208 views • 10 slides

Identify the goals of each of the following leaders:

Identify the goals of each of the following leaders:. Hitler (Germany) Mussolini (Italy) Tojo (Japan) Roosevelt (U.S.) Churchill (Great Britain) Stalin (Russia). Axis Powers. Hitler (Germany) - Dominate Europe and eliminate “inferior” peoples. Mussolini (Italy) -

738 views • 53 slides

Identify the Property which supports each Conclusion

Identify the Property which supports each Conclusion. IF then . Symmetric Property of Congruence. Reflexive Property of Congruence. IF and then . Transitive Property of Congruence. If. and. then. Substitution Property of Equality. IF AB = CD Then

706 views • 56 slides

Statement/hypothesis _______________________________________________________

Question 5. Statement/hypothesis _______________________________________________________ Debate _______________________________V.___________________________________. s trongly disagrees. p artially disagrees. s trongly agrees. p artially agrees. a grees. disagrees. Source

184 views • 8 slides

Identify the direct and/or indirect object in each.

Identify the direct and/or indirect object in each. Drought destroyed the crops. The journalist interviewed the astronauts before and after their flight. Ms. Cruz showed our class a video about Moorish architecture. The animal trainer fed the bears fish. Conventions. Standards: * ELA10W1,4.f

337 views • 25 slides

Problem: Identify the oxidizing and reducing agent in each of the Rx:

Problem: Identify the oxidizing and reducing agent in each of the Rx: a) Zn( s ) + 2 HCl( aq ) ZnCl 2 ( aq ) + H 2 ( g ) b) S 8 ( s ) + 12 O 2 ( g ) 8 SO 3 ( g ) c) NiO( s ) + CO( g ) Ni( s ) + CO 2 ( g ).

712 views • 47 slides

Warm Up Identify the hypothesis and conclusion of each conditional.

Warm Up Identify the hypothesis and conclusion of each conditional. 1. A mapping that is a reflection is a type of transformation. 2. The quotient of two negative numbers is positive.

180 views • 2 slides

Do Now Identify each of the cells in the diagram and indicate the

Do Now Identify each of the cells in the diagram and indicate the Human chromosome number of each. Sperm (23). Egg (23). Zygote (46). How do we go from a zygote (a single cell) to a multicellular organism? (hint: think about a process used to increase cell#).

359 views • 15 slides

Conditional Statement

Conditional Statement. Conditional Statements. Allow different sets of instructions to be executed depending on truth or falsity of a logical condition Also called Branching How do we specify conditions? Using expressions non-zero value means condition is true

445 views • 30 slides

Warm Up Underline the hypothesis and circle the conclusion of each conditional.

2.3 Logic Laws. Warm Up Underline the hypothesis and circle the conclusion of each conditional. 1. A mapping that is a reflection is a type of transformation. 2. The quotient of two negative numbers is positive. 3. Determine if the conditional “If x is a number then | x | > 0” is true.

272 views • 15 slides

275 views • 27 slides

Pre-assessment Questions Identify the correct statement.

Pre-assessment Questions Identify the correct statement. a) The Request Dispatcher object can only be used to include the output of another document. b) The Request Dispatcher object can only be used to forward the request to another document.

431 views • 40 slides

Identify, write, and analyze the truth value of conditional statements.

Objectives. Identify, write, and analyze the truth value of conditional statements. Write the inverse, converse, and contrapositive of a conditional statement. By phrasing a conjecture as an if-then statement, you can quickly identify its hypothesis and conclusion.

212 views • 21 slides

468 views • 45 slides

Pre assessment Questions Identify the correct statement.

Pre assessment Questions Identify the correct statement. a) Cookies are created on the server and stored by the browser on the client machine. b) Cookies are created and stored on the server. c) Cookies are created by the browser and stored by the server on the client machine.

304 views • 30 slides

conditional statement hypothesis/conclusion truth value/table negation converse inverse

2-1 Vocabulary. conditional statement hypothesis/conclusion truth value/table negation converse inverse contrapostive logically equivalent statements biconditional statements (iff, if and only if).

234 views • 22 slides

Python conditional statement

Conditional statements are used to control the flow of the program. Conditional Statement in Python perform different computations or actions depending on whether a specific Boolean constraint evaluates to true or false.

182 views • 16 slides

Snapsolve any problem by taking a picture. Try it in the Numerade app?