example of research using chi square

Statistics Made Easy

4 Examples of Using Chi-Square Tests in Real Life

In statistics, there are two different types of Chi-Square tests:

1. The Chi-Square Goodness of Fit Test – Used to determine whether or not a categorical variable follows a hypothesized distribution.

2. The Chi-Square Test of Independence – Used to determine whether or not there is a significant association between two categorical variables.

In this article, we share several examples of how each of these types of Chi-Square tests are used in real-life situations.

Example 1: Chi-Square Goodness of Fit Test

Suppose a shop owner claims that an equal number of customers come into his shop each weekday.

To test this hypothesis, he records the number of customers that come into the shop on a given week and finds the following:

• Monday:  50 customers
• Tuesday:  60 customers
• Wednesday:  40 customers
• Thursday:  47 customers
• Friday:  53 customers

He can use a Chi-Square Goodness of Fit Test to determine if the distribution of the customers that come in each day is consistent with his hypothesized distribution.

Using the Chi-Square Goodness of Fit Test Calculator , he can find that the p-value of the test is 0.359 .

Since this p-value is not less than .05, there is not sufficient evidence to say that the true distribution of customers is different from the distribution that the shop owner claimed.

Example 2: Chi-Square Goodness of Fit Test

Suppose a biologist claims that an equal number of four different species of deer enter a certain wooded area in a forest each week.

To test this hypothesis, she records the number of each species of deer that enter the wooded area over the course of one week:

• Species #1: 22 
• Species #2: 20
• Species #3: 23
• Species #4: 35

She can use a Chi-Square Goodness of Fit Test to determine if the distribution of the deer species that enter the wooded area in the forest each week is consistent with his hypothesized distribution.

Using the Chi-Square Goodness of Fit Test Calculator , she can find that the p-value of the test is 0.137 .

Since this p-value is not less than .05, there is not sufficient evidence to say that the true distribution of deer is different from the distribution that the biologist claimed.

Example 3: Chi-Square Test of Independence

Suppose a policy maker in a certain town wants to know whether or not gender is associated with political party preference.

He decides to take a simple random sample of 500 voters and survey them on their political party preference. The following table shows the results of the survey:

He can use a Chi-Square Test of Independence to determine if there is a statistically significant association between the two variables.

Using the Chi-Square Test of Independence Calculator , he can find that the p-value of the test is 0.649 .

Since the p-value is not less than .05, there is not sufficient evidence to say that there is an association between gender and political party preference.

Example 4: Chi-Square Test of Independence

Suppose a researcher wants to know whether or not marital status is associated with education level.

He decides to take a simple random sample of 300 individuals and obtains the following results:

Using the Chi-Square Test of Independence Calculator , he can find that the p-value of the test is 0.000011 .

Since the p-value is less than .05, there is sufficient evidence to say that there is an association between marital status and education level.

Additional Resources

The following tutorials provide an introduction to the different types of Chi-Square Tests:

• Chi-Square Test of Independence
• Chi-Square Goodness of Fit Test

The following tutorials explain the difference between Chi-Square tests and other statistical tests:

• Chi-Square Test vs. T-Test
• Chi-Square Test vs. ANOVA

Published by Zach

Leave a reply cancel reply.

Your email address will not be published. Required fields are marked *

• Search Search Please fill out this field.

What Is a Chi-Square Statistic?

• What Does It Tell You?

When to Use a Chi-Square Test

• How to Perform It
• Limitations

The Bottom Line

• Business Leaders
• Math and Statistics

Chi-Square (χ2) Statistic: What It Is, Examples, How and When to Use the Test

Adam Hayes, Ph.D., CFA, is a financial writer with 15+ years Wall Street experience as a derivatives trader. Besides his extensive derivative trading expertise, Adam is an expert in economics and behavioral finance. Adam received his master's in economics from The New School for Social Research and his Ph.D. from the University of Wisconsin-Madison in sociology. He is a CFA charterholder as well as holding FINRA Series 7, 55 & 63 licenses. He currently researches and teaches economic sociology and the social studies of finance at the Hebrew University in Jerusalem.

Investopedia / Paige McLaughlin

A chi-square ( χ 2 ) statistic is a test that measures how a model compares to actual observed data. The data used in calculating a chi-square statistic must be random, raw, mutually exclusive , drawn from independent variables, and drawn from a large enough sample. For example, the results of tossing a fair coin meet these criteria.

Chi-square tests are often used to test hypotheses . The chi-square statistic compares the size of any discrepancies between the expected results and the actual results, given the size of the sample and the number of variables in the relationship.

For these tests, degrees of freedom are used to determine if a certain  null hypothesis  can be rejected based on the total number of variables and samples within the experiment. As with any statistic, the larger the sample size, the more reliable the results.

Key Takeaways

• A chi-square ( χ 2 ) statistic is a measure of the difference between the observed and expected frequencies of the outcomes of a set of events or variables.
• Chi-square is useful for analyzing such differences in categorical variables, especially those nominal in nature.
• χ 2 depends on the size of the difference between actual and observed values, the degrees of freedom, and the sample size.
• χ 2 can be used to test whether two variables are related or independent of each other.
• It can also be used to test the goodness of fit between an observed distribution and a theoretical distribution of frequencies.

Formula for Chi-Square

 χ c 2 = ∑ ( O i − E i ) 2 E i where: c = Degrees of freedom O = Observed value(s) \begin{aligned}&\chi^2_c = \sum \frac{(O_i - E_i)^2}{E_i} \\&\textbf{where:}\\&c=\text{Degrees of freedom}\\&O=\text{Observed value(s)}\\&E=\text{Expected value(s)}\end{aligned} ​ χ c 2 ​ = ∑ E i ​ ( O i ​ − E i ​ ) 2 ​ where: c = Degrees of freedom O = Observed value(s) ​ 

What Does a Chi-Square Statistic Tell You?

There are two main kinds of chi-square tests: the test of independence, which asks a question of relationship, such as, "Is there a relationship between student gender and course choice?"; and the  goodness-of-fit test , which asks something like "How well does the coin in my hand match a theoretically fair coin?"

Chi-square analysis is applied to categorical variables and is especially useful when those variables are nominal (where order doesn't matter, like marital status or gender).

Independence

When considering student gender and course choice, a χ 2 test for independence could be used. To do this test, the researcher would collect data on the two chosen variables (gender and courses picked) and then compare the frequencies at which male and female students select among the offered classes using the formula given above and a χ 2 statistical table.

If there is no relationship between gender and course selection (that is if they are independent), then the actual frequencies at which male and female students select each offered course should be expected to be approximately equal, or conversely, the proportion of male and female students in any selected course should be approximately equal to the proportion of male and female students in the sample.

A χ 2 test for independence can tell us how likely it is that random chance can explain any observed difference between the actual frequencies in the data and these theoretical expectations.

Goodness-of-Fit

χ 2 provides a way to test how well a sample of data matches the (known or assumed) characteristics of the larger population that the sample is intended to represent. This is known as goodness of fit.

If the sample data do not fit the expected properties of the population that we are interested in, then we would not want to use this sample to draw conclusions about the larger population.

For example, consider an imaginary coin with exactly a 50/50 chance of landing heads or tails and a real coin that you toss 100 times. If this coin is fair, then it will also have an equal probability of landing on either side, and the expected result of tossing the coin 100 times is that heads will come up 50 times and tails will come up 50 times.

In this case, χ 2 can tell us how well the actual results of 100 coin flips compare to the theoretical model that a fair coin will give 50/50 results. The actual toss could come up 50/50, or 60/40, or even 90/10. The farther away the actual results of the 100 tosses are from 50/50, the less good the fit of this set of tosses is to the theoretical expectation of 50/50, and the more likely we might conclude that this coin is not actually a fair coin.

A chi-square test is used to help determine if observed results are in line with expected results and to rule out that observations are due to chance.

A chi-square test is appropriate for this when the data being analyzed are from a random sample , and when the variable in question is a categorical variable. A categorical variable consists of selections such as type of car, race, educational attainment, male or female, or how much somebody likes a political candidate (from very much to very little).

These types of data are often collected via survey responses or questionnaires. Therefore, chi-square analysis is often most useful in analyzing this type of data.

How to Perform a Chi-Square Test

These are the basic steps whether you are performing a goodness of fit test or a test of independence:

• Create a table of the observed and expected frequencies;
• Use the formula to calculate the chi-square value;
• Find the critical chi-square value using a chi-square value table or statistical software;
• Determine whether the chi-square value or the critical value is the larger of the two;
• Reject or accept the null hypothesis.

Limitations of the Chi-Square Test

The chi-square test is sensitive to sample size. Relationships may appear to be significant when they aren't simply because a very large sample is used.

In addition, the chi-square test cannot establish whether one variable has a causal relationship with another. It can only establish whether two variables are related.

What Is a Chi-square Test Used for?

Chi-square is a statistical test used to examine the differences between categorical variables from a random sample in order to judge the goodness of fit between expected and observed results. 

Who Uses Chi-Square Analysis?

Since chi-square applies to categorical variables, it is most used by researchers who are studying survey response data. This type of research can range from demography to consumer and marketing research to political science and economics.

Is Chi-Square Analysis Used When the Independent Variable Is Nominal or Ordinal?

A nominal variable is a categorical variable that differs by quality, but whose numerical order could be irrelevant. For instance, asking somebody their favorite color would produce a nominal variable. Asking somebody's age, on the other hand, would produce an ordinal set of data. Chi-square can be best applied to nominal data.

There are two types of chi-square tests: the test of independence and the test of goodness of fit. Both are used to determine the validity of a hypothesis or an assumption. The result is a piece of evidence that can be used to make a decision. For example:

In a test of independence, a company may want to evaluate whether its new product, an herbal supplement that promises to give people an energy boost, is reaching the people who are most likely to be interested. It is being advertised on websites related to sports and fitness, on the assumption that active and health-conscious people are most likely to buy it. It does an extensive poll that is intended to evaluate interest in the product by demographic group. The poll suggests no correlation between interest in this product and the most health-conscious people.

In a test of goodness of fit, a marketing professional is considering launching a new product that the company believes will be irresistible to women over 45. The company has conducted product testing panels of 500 potential buyers of the product. The marketing professional has information about the age and gender of the test panels, This allows the construction of a chi-square test showing the distribution by age and gender of the people who said they would buy the product. The result will show whether or not the likeliest buyer is a woman over 45. If the test shows that men over 45 or women between 18 and 44 are just as likely to buy the product, the marketing professional will revise the advertising, promotion, and placement of the product to appeal to this wider group of customers.

The Open University. " Chi Square Analysis ," Page 2.

Kent State University, University Libraries. " SPSS Tutorials: Chi-Square Test of Independence ."

The Open University. " Chi Square Analysis ," Page 3.

The Open University. " Chi Square Analysis ," Pages 3-5.

Scribbr. " Chi-Square Tests, Types, Formula & Examples ."

• Terms of Service
• Editorial Policy
• Privacy Policy
• Your Privacy Choices

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

• Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
• Duis aute irure dolor in reprehenderit in voluptate
• Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

S.4 chi-square tests, chi-square test of independence section  .

Do you remember how to test the independence of two categorical variables? This test is performed by using a Chi-square test of independence.

Recall that we can summarize two categorical variables within a two-way table, also called an r × c contingency table, where r = number of rows, c = number of columns. Our question of interest is “Are the two variables independent?” This question is set up using the following hypothesis statements:

 \[E=\frac{\text{row total}\times\text{column total}}{\text{sample size}}\]

We will compare the value of the test statistic to the critical value of \(\chi_{\alpha}^2\) with the degree of freedom = ( r - 1) ( c - 1), and reject the null hypothesis if \(\chi^2 \gt \chi_{\alpha}^2\).

Example S.4.1 Section  

Is gender independent of education level? A random sample of 395 people was surveyed and each person was asked to report the highest education level they obtained. The data that resulted from the survey are summarized in the following table:

Question : Are gender and education level dependent at a 5% level of significance? In other words, given the data collected above, is there a relationship between the gender of an individual and the level of education that they have obtained?

Here's the table of expected counts:

So, working this out, \(\chi^2= \dfrac{(60−50.886)^2}{50.886} + \cdots + \dfrac{(57 − 48.132)^2}{48.132} = 8.006\)

The critical value of \(\chi^2\) with 3 degrees of freedom is 7.815. Since 8.006 > 7.815, we reject the null hypothesis and conclude that the education level depends on gender at a 5% level of significance.

An official website of the United States government

The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

• Publications
• Account settings

Preview improvements coming to the PMC website in October 2024. Learn More or Try it out now .

• Advanced Search
• Journal List
• Biochem Med (Zagreb)
• v.23(2); 2013 Jun

The Chi-square test of independence

The Chi-square statistic is a non-parametric (distribution free) tool designed to analyze group differences when the dependent variable is measured at a nominal level. Like all non-parametric statistics, the Chi-square is robust with respect to the distribution of the data. Specifically, it does not require equality of variances among the study groups or homoscedasticity in the data. It permits evaluation of both dichotomous independent variables, and of multiple group studies. Unlike many other non-parametric and some parametric statistics, the calculations needed to compute the Chi-square provide considerable information about how each of the groups performed in the study. This richness of detail allows the researcher to understand the results and thus to derive more detailed information from this statistic than from many others.

The Chi-square is a significance statistic, and should be followed with a strength statistic. The Cramer’s V is the most common strength test used to test the data when a significant Chi-square result has been obtained. Advantages of the Chi-square include its robustness with respect to distribution of the data, its ease of computation, the detailed information that can be derived from the test, its use in studies for which parametric assumptions cannot be met, and its flexibility in handling data from both two group and multiple group studies. Limitations include its sample size requirements, difficulty of interpretation when there are large numbers of categories (20 or more) in the independent or dependent variables, and tendency of the Cramer’s V to produce relative low correlation measures, even for highly significant results.

Introduction

The Chi-square test of independence (also known as the Pearson Chi-square test, or simply the Chi-square) is one of the most useful statistics for testing hypotheses when the variables are nominal, as often happens in clinical research. Unlike most statistics, the Chi-square (χ 2 ) can provide information not only on the significance of any observed differences, but also provides detailed information on exactly which categories account for any differences found. Thus, the amount and detail of information this statistic can provide renders it one of the most useful tools in the researcher’s array of available analysis tools. As with any statistic, there are requirements for its appropriate use, which are called “assumptions” of the statistic. Additionally, the χ 2 is a significance test, and should always be coupled with an appropriate test of strength.

The Chi-square test is a non-parametric statistic, also called a distribution free test. Non-parametric tests should be used when any one of the following conditions pertains to the data:

• The level of measurement of all the variables is nominal or ordinal.
• The sample sizes of the study groups are unequal; for the χ 2 the groups may be of equal size or unequal size whereas some parametric tests require groups of equal or approximately equal size.
• The distribution of the data was seriously skewed or kurtotic (parametric tests assume approximately normal distribution of the dependent variable), and thus the researcher must use a distribution free statistic rather than a parametric statistic.
• The data violate the assumptions of equal variance or homoscedasticity.
• For any of a number of reasons ( 1 ), the continuous data were collapsed into a small number of categories, and thus the data are no longer interval or ratio.

Assumptions of the Chi-square

As with parametric tests, the non-parametric tests, including the χ 2 assume the data were obtained through random selection. However, it is not uncommon to find inferential statistics used when data are from convenience samples rather than random samples. (To have confidence in the results when the random sampling assumption is violated, several replication studies should be performed with essentially the same result obtained). Each non-parametric test has its own specific assumptions as well. The assumptions of the Chi-square include:

• The data in the cells should be frequencies, or counts of cases rather than percentages or some other transformation of the data.
• The levels (or categories) of the variables are mutually exclusive. That is, a particular subject fits into one and only one level of each of the variables.
• Each subject may contribute data to one and only one cell in the χ 2 . If, for example, the same subjects are tested over time such that the comparisons are of the same subjects at Time 1, Time 2, Time 3, etc., then χ 2 may not be used.
• The study groups must be independent. This means that a different test must be used if the two groups are related. For example, a different test must be used if the researcher’s data consists of paired samples, such as in studies in which a parent is paired with his or her child.
• There are 2 variables, and both are measured as categories, usually at the nominal level. However, data may be ordinal data. Interval or ratio data that have been collapsed into ordinal categories may also be used. While Chi-square has no rule about limiting the number of cells (by limiting the number of categories for each variable), a very large number of cells (over 20) can make it difficult to meet assumption #6 below, and to interpret the meaning of the results.
• The value of the cell expecteds should be 5 or more in at least 80% of the cells, and no cell should have an expected of less than one ( 3 ). This assumption is most likely to be met if the sample size equals at least the number of cells multiplied by 5. Essentially, this assumption specifies the number of cases (sample size) needed to use the χ 2 for any number of cells in that χ 2 . This requirement will be fully explained in the example of the calculation of the statistic in the case study example.

To illustrate the calculation and interpretation of the χ 2 statistic, the following case example will be used:

The owner of a laboratory wants to keep sick leave as low as possible by keeping employees healthy through disease prevention programs. Many employees have contracted pneumonia leading to productivity problems due to sick leave from the disease. There is a vaccine for pneumococcal pneumonia, and the owner believes that it is important to get as many employees vaccinated as possible. Due to a production problem at the company that produces the vaccine, there is only enough vaccine for half the employees. In effect, there are two groups; employees who received the vaccine and employees who did not receive the vaccine. The company sent a nurse to every employee who contracted pneumonia to provide home health care and to take a sputum sample for culture to determine the causative agent. They kept track of the number of employees who contracted pneumonia and which type of pneumonia each had. The data were organized as follows:

• Group 1: Not provided with the vaccine (unvaccinated control group, N = 92)
• Group 2: Provided with the vaccine (vaccinated experimental group, N = 92)

In this case, the independent variable is vaccination status (vaccinated versus unvaccinated). The dependent variable is health outcome with three levels:

• contracted pneumoccal pneumonia;
• contracted another type of pneumonia; and
• did not contract pneumonia.

The company wanted to know if providing the vaccine made a difference. To answer this question, they must choose a statistic that can test for differences when all the variables are nominal. The χ 2 statistic was used to test the question, “Was there a difference in incidence of pneumonia between the two groups?” At the end of the winter, Table 1 was constructed to illustrate the occurrence of pneumonia among the employees.

Results of the vaccination program.

Calculating Chi-square

With the data in table form, the researcher can proceed with calculating the χ 2 statistic to find out if the vaccination program made any difference in the health outcomes of the employees. The formula for calculating a Chi-Square is:

The first step in calculating a χ 2 is to calculate the sum of each row, and the sum of each column. These sums are called the “marginals” and there are row marginal values and column marginal values. The marginal values for the case study data are presented in Table 2 .

Calculation of marginals.

The second step is to calculate the expected values for each cell. In the Chi-square statistic, the “expected” values represent an estimate of how the cases would be distributed if there were NO vaccine effect. Expected values must reflect both the incidence of cases in each category and the unbiased distribution of cases if there is no vaccine effect. This means the statistic cannot just count the total N and divide by 6 for the expected number in each cell. That would not take account of the fact that more subjects stayed healthy regardless of whether they were vaccinated or not. Chi-Square expecteds are calculated as follows:

Specifically, for each cell, its row marginal is multiplied by its column marginal, and that product is divided by the sample size. For Cell 1, the math is as follows: (28 × 92)/184 = 13.92. Table 3 provides the results of this calculation for each cell. Once the expected values have been calculated, the cell χ 2 values are calculated with the following formula:

The cell χ 2 for the first cell in the case study data is calculated as follows: (23−13.93) 2 /13.93 = 5.92. The cell χ 2 value for each cellis the value in parentheses in each of the cells in Table 3 .

Cell expected values and (cell Chi-square values).

Once the cell χ 2 values have been calculated, they are summed to obtain the χ 2 statistic for the table. In this case, the χ 2 is 12.35 (rounded). The Chi-square table requires the table’s degrees of freedom (df) in order to determine the significance level of the statistic. The degrees of freedom for a χ 2 table are calculated with the formula:

For example, a 2 × 2 table has 1 df. (2−1) × (2−1) = 1. A 3 × 3 table has (3−1) × (3−1) = 4 df. A 4 × 5 table has (4−1) × (5−1) = 3 × 4 = 12 df. Assuming a χ 2 value of 12.35 with each of these different df levels (1, 4, and 12), the significance levels from a table of χ 2 values, the significance levels are: df = 1, P < 0.001, df = 4, P < 0.025, and df = 12, P > 0.10. Note, as degrees of freedom increase, the P-level becomes less significant, until the χ 2 value of 12.35 is no longer statistically significant at the 0.05 level, because P was greater than 0.10.

For the sample table with 3 rows and 2 columns, df = (3−1) × (2−1) = 2 × 1 = 2. A Chi-square table of significances is available in many elementary statistics texts and on many Internet sites. Using a χ 2 table, the significance of a Chi-square value of 12.35 with 2 df equals P < 0.005. This value may be rounded to P < 0.01 for convenience. The exact significance when the Chi-square is calculated through a statistical program is found to be P = 0.0011.

As the P-value of the table is less than P < 0.05, the researcher rejects the null hypothesis and accepts the alternate hypothesis: “There is a difference in occurrence of pneumococcal pneumonia between the vaccinated and unvaccinated groups.” However, this result does not specify what that difference might be. To fully interpret the result, it is useful to look at the cell χ 2 values.

Interpreting cell χ 2 values

It can be seen in Table 3 that the largest cell χ 2 value of 5.92 occurs in Cell 1. This is a result of the observed value being 23 while only 13.92 were expected. Therefore, this cell has a much larger number of observed cases than would be expected by chance. Cell 1 reflects the number of unvaccinated employees who contracted pneumococcal pneumonia. This means that the number of unvaccinated people who contracted pneumococcal pneumonia was significantly greater than expected. The second largest cell χ 2 value of 4.56 is located in Cell 2. However, in this cell we discover that the number of observed cases was much lower than expected (Observed = 5, Expected = 12.57). This means that a significantly lower number of vaccinated subjects contracted pneumococcal pneumonia than would be expected if the vaccine had no effect. No other cell has a cell χ 2 value greater than 0.99.

A cell χ 2 value less than 1.0 should be interpreted as the number of observed cases being approximately equal to the number of expected cases, meaning there is no vaccination effect on any of the other cells. In the case study example, all other cells produced cell χ 2 values below 1.0. Therefore the company can conclude that there was no difference between the two groups for incidence of non-pneumococcal pneumonia. It can be seen that for both groups, the majority of employees stayed healthy. The meaningful result was that there were significantly fewer cases of pneumococcal pneumonia among the vaccinated employees and significantly more cases among the unvaccinated employees. As a result, the company should conclude that the vaccination program did reduce the incidence of pneumoccal pneumonia.

Very few statistical programs provide tables of cell expecteds and cell χ 2 values as part of the default output. Some programs will produce those tables as an option, and that option should be used to examine the cell χ 2 values. If the program provides an option to print out only the cell χ 2 value (but not cell expecteds), the direction of the χ 2 value provides information. A positive cell χ 2 value means that the observed value is higher than the expected value, and a negative cell χ 2 value (e.g. −12.45) means the observed cases are less than the expected number of cases. When the program does not provide either option, all the researcher can conclude is this: The overall table provides evidence that the two groups are independent (significantly different because P < 0.05), or are not independent (P > 0.05). Most researchers inspect the table to estimate which cells are overrepresented with a large number of cases versus those which have a small number of cases. However, without access to cell expecteds or cell χ 2 values, the interpretation of the direction of the group differences is less precise. Given the ease of calculating the cell expecteds and χ 2 values, researchers may want to hand calculate those values to enhance interpretation.

Chi-square and closely related tests

One might ask if, in this case, the Chi-square was the best or only test the researcher could have used. Nominal variables require the use of non-parametric tests, and there are three commonly used significance tests that can be used for this type of nominal data. The first and most commonly used is the Chi-square. The second is the Fisher’s exact test, which is a bit more precise than the Chi-square, but it is used only for 2 × 2 Tables ( 4 ). For example, if the only options in the case study were pneumonia versus no pneumonia, the table would have 2 rows and 2 columns and the correct test would be the Fisher’s exact. The case study example requires a 2 × 3 table and thus the data are not suitable for the Fisher’s exact test.

The third test is the maximum likelihood ratio Chi-square test which is most often used when the data set is too small to meet the sample size assumption of the Chi-square test. As exhibited by the table of expected values for the case study, the cell expected requirements of the Chi-square were met by the data in the example. Specifically, there are 6 cells in the table. To meet the requirement that 80% of the cells have expected values of 5 or more, this table must have 6 × 0.8 = 4.8 rounded to 5. This table meets the requirement that at least 5 of the 6 cells must have cell expected of 5 or more, and so there is no need to use the maximum likelihood ratio chi-square. Suppose the sample size were much smaller. Suppose the sample size was smaller and the table had the data in Table 4 .

Example of a table that violates cell expected values.

Sample raw data presented first, sample expected values in parentheses, and cell follow the slash.

Although the total sample size of 39 exceeds the value of 5 cases × 6 cells = 30, the very low distribution of cases in 4 of the cells is of concern. When the cell expecteds are calculated, it can be seen that 4 of the 6 cells have expecteds below 5, and thus this table violates the χ 2 test assumption. This table should be tested with a maximum likelihood ratio Chi-square test.

When researchers use the Chi-square test in violation of one or more assumptions, the result may or may not be reliable. In this author’s experience of having output from both the appropriate and inappropriate tests on the same data, one of three outcomes are possible:

First, the appropriate and the inappropriate test may give the same results.

Second, the appropriate test may produce a significant result while the inappropriate test provides a result that is not statistically significant, which is a Type II error.

Third, the appropriate test may provide a non-significant result while the inappropriate test may provide a significant result, which is a Type I error.

Strength test for the Chi-square

The researcher’s work is not quite done yet. Finding a significant difference merely means that the differences between the vaccinated and unvaccinated groups have less than 1.1 in a thousand chances of being in error (P = 0.0011). That is, there are 1.1 in one thousand chances that there really is no difference between the two groups for contracting pneumococcal pneumonia, and that the researcher made a Type I error. That is a sufficiently remote probability of error that in this case, the company can be confident that the vaccination made a difference. While useful, this is not complete information. It is necessary to know the strength of the association as well as the significance.

Statistical significance does not necessarily imply clinical importance. Clinical significance is usually a function of how much improvement is produced by the treatment. For example, if there was a significant difference, but the vaccine only reduced pneumonias by two cases, it might not be worth the company’s money to vaccinate 184 people (at a cost of $20 per person) to eliminate only two cases. In this case study, the vaccinated group experienced only 5 cases out of 92 employees (a rate of 5%) while the unvaccinated group experienced 23 cases out of 92 employees (a rate of 25%). While it is always a matter of judgment as to whether the results are worth the investment, many employers would view 25% of their workforce becoming ill with a preventable infectious illness as an undesirable outcome. There is, however, a more standardized strength test for the Chi-Square.

Statistical strength tests are correlation measures. For the Chi-square, the most commonly used strength test is the Cramer’s V test. It is easily calculated with the following formula:

Where n is the number of rows or number of columns, whichever is less. For the example, the V is 0.259 or rounded, 0.26 as calculated below.

The Cramer’s V is a form of a correlation and is interpreted exactly the same. For any correlation, a value of 0.26 is a weak correlation. It should be noted that a relatively weak correlation is all that can be expected when a phenomena is only partially dependent on the independent variable.

In the case study, five vaccinated people did contract pneumococcal pneumonia, but vaccinated or not, the majority of employees remained healthy. Clearly, most employees will not get pneumonia. This fact alone makes it difficult to obtain a moderate or high correlation coefficient. The amount of change the treatment (vaccine) can produce is limited by the relatively low rate of disease in the population of employees. While the correlation value is low, it is statistically significant, and the clinical importance of reducing a rate of 25% incidence to 5% incidence of the disease would appear to be clinically worthwhile. These are the factors the researcher should take into account when interpreting this statistical result.

Summary and conclusions

The Chi-square is a valuable analysis tool that provides considerable information about the nature of research data. It is a powerful statistic that enables researchers to test hypotheses about variables measured at the nominal level. As with all inferential statistics, the results are most reliable when the data are collected from randomly selected subjects, and when sample sizes are sufficiently large that they produce appropriate statistical power. The Chi-square is also an excellent tool to use when violations of assumptions of equal variances and homoscedascity are violated and parametric statistics such as the t-test and ANOVA cannot provide reliable results. As the Chi-Square and its strength test, the Cramer’s V are both simple to compute, it is an especially convenient tool for researchers in the field where statistical programs may not be easily accessed. However, most statistical programs provide not only the Chi-square and Cramer’s V, but also a variety of other non-parametric tools for both significance and strength testing.

Potential conflict of interest

None declared.

Chi-Square (Χ²) Test & How To Calculate Formula Equation

Benjamin Frimodig

Science Expert

B.A., History and Science, Harvard University

Ben Frimodig is a 2021 graduate of Harvard College, where he studied the History of Science.

Learn about our Editorial Process

Saul Mcleod, PhD

Editor-in-Chief for Simply Psychology

BSc (Hons) Psychology, MRes, PhD, University of Manchester

Saul Mcleod, PhD., is a qualified psychology teacher with over 18 years of experience in further and higher education. He has been published in peer-reviewed journals, including the Journal of Clinical Psychology.

On This Page:

Chi-square (χ2) is used to test hypotheses about the distribution of observations into categories with no inherent ranking.

What Is a Chi-Square Statistic?

The Chi-square test (pronounced Kai) looks at the pattern of observations and will tell us if certain combinations of the categories occur more frequently than we would expect by chance, given the total number of times each category occurred.

It looks for an association between the variables. We cannot use a correlation coefficient to look for the patterns in this data because the categories often do not form a continuum.

There are three main types of Chi-square tests, tests of goodness of fit, the test of independence, and the test for homogeneity. All three tests rely on the same formula to compute a test statistic.

These tests function by deciphering relationships between observed sets of data and theoretical or “expected” sets of data that align with the null hypothesis.

What is a Contingency Table?

Contingency tables (also known as two-way tables) are grids in which Chi-square data is organized and displayed. They provide a basic picture of the interrelation between two variables and can help find interactions between them.

In contingency tables, one variable and each of its categories are listed vertically, and the other variable and each of its categories are listed horizontally.

Additionally, including column and row totals, also known as “marginal frequencies,” will help facilitate the Chi-square testing process.

In order for the Chi-square test to be considered trustworthy, each cell of your expected contingency table must have a value of at least five.

Each Chi-square test will have one contingency table representing observed counts (see Fig. 1) and one contingency table representing expected counts (see Fig. 2).

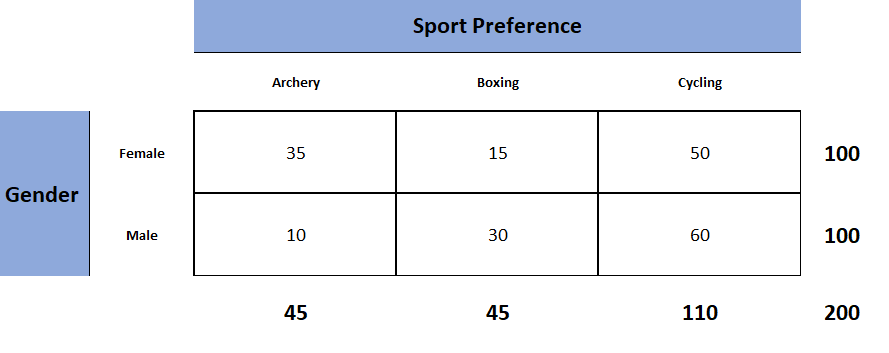
Figure 1. Observed table (which contains the observed counts).

To obtain the expected frequencies for any cell in any cross-tabulation in which the two variables are assumed independent, multiply the row and column totals for that cell and divide the product by the total number of cases in the table.

Figure 2. Expected table (what we expect the two-way table to look like if the two categorical variables are independent).

To decide if our calculated value for χ2 is significant, we also need to work out the degrees of freedom for our contingency table using the following formula: df= (rows – 1) x (columns – 1).

Formula Calculation

Calculate the chi-square statistic (χ2) by completing the following steps:

• Calculate the expected frequencies and the observed frequencies.
• For each observed number in the table, subtract the corresponding expected number (O — E).
• Square the difference (O —E)².
• Divide the squares obtained for each cell in the table by the expected number for that cell (O – E)² / E.
• Sum all the values for (O – E)² / E. This is the chi-square statistic.
• Calculate the degrees of freedom for the contingency table using the following formula; df= (rows – 1) x (columns – 1).

Once we have calculated the degrees of freedom (df) and the chi-squared value (χ2), we can use the χ2 table (often at the back of a statistics book) to check if our value for χ2 is higher than the critical value given in the table. If it is, then our result is significant at the level given.

Interpretation

The chi-square statistic tells you how much difference exists between the observed count in each table cell to the counts you would expect if there were no relationship at all in the population.

Small Chi-Square Statistic: If the chi-square statistic is small and the p-value is large (usually greater than 0.05), this often indicates that the observed frequencies in the sample are close to what would be expected under the null hypothesis.

The null hypothesis usually states no association between the variables being studied or that the observed distribution fits the expected distribution.

In theory, if the observed and expected values were equal (no difference), then the chi-square statistic would be zero — but this is unlikely to happen in real life.

Large Chi-Square Statistic : If the chi-square statistic is large and the p-value is small (usually less than 0.05), then the conclusion is often that the data does not fit the model well, i.e., the observed and expected values are significantly different. This often leads to the rejection of the null hypothesis.

How to Report

To report a chi-square output in an APA-style results section, always rely on the following template:

χ2 ( degrees of freedom , N = sample size ) = chi-square statistic value , p = p value .

In the case of the above example, the results would be written as follows:

A chi-square test of independence showed that there was a significant association between gender and post-graduation education plans, χ2 (4, N = 101) = 54.50, p < .001.

APA Style Rules

• Do not use a zero before a decimal when the statistic cannot be greater than 1 (proportion, correlation, level of statistical significance).
• Report exact p values to two or three decimals (e.g., p = .006, p = .03).
• However, report p values less than .001 as “ p < .001.”
• Put a space before and after a mathematical operator (e.g., minus, plus, greater than, less than, equals sign).
• Do not repeat statistics in both the text and a table or figure.

p -value Interpretation

You test whether a given χ2 is statistically significant by testing it against a table of chi-square distributions , according to the number of degrees of freedom for your sample, which is the number of categories minus 1. The chi-square assumes that you have at least 5 observations per category.

If you are using SPSS then you will have an expected p -value.

For a chi-square test, a p-value that is less than or equal to the .05 significance level indicates that the observed values are different to the expected values.

Thus, low p-values (p< .05) indicate a likely difference between the theoretical population and the collected sample. You can conclude that a relationship exists between the categorical variables.

Remember that p -values do not indicate the odds that the null hypothesis is true but rather provide the probability that one would obtain the sample distribution observed (or a more extreme distribution) if the null hypothesis was true.

A level of confidence necessary to accept the null hypothesis can never be reached. Therefore, conclusions must choose to either fail to reject the null or accept the alternative hypothesis, depending on the calculated p-value.

The four steps below show you how to analyze your data using a chi-square goodness-of-fit test in SPSS (when you have hypothesized that you have equal expected proportions).

Step 1 : Analyze > Nonparametric Tests > Legacy Dialogs > Chi-square… on the top menu as shown below:

Step 2 : Move the variable indicating categories into the “Test Variable List:” box.

Step 3 : If you want to test the hypothesis that all categories are equally likely, click “OK.”

Step 4 : Specify the expected count for each category by first clicking the “Values” button under “Expected Values.”

Step 5 : Then, in the box to the right of “Values,” enter the expected count for category one and click the “Add” button. Now enter the expected count for category two and click “Add.” Continue in this way until all expected counts have been entered.

Step 6 : Then click “OK.”

The four steps below show you how to analyze your data using a chi-square test of independence in SPSS Statistics.

Step 1 : Open the Crosstabs dialog (Analyze > Descriptive Statistics > Crosstabs).

Step 2 : Select the variables you want to compare using the chi-square test. Click one variable in the left window and then click the arrow at the top to move the variable. Select the row variable and the column variable.

Step 3 : Click Statistics (a new pop-up window will appear). Check Chi-square, then click Continue.

Step 4 : (Optional) Check the box for Display clustered bar charts.

Step 5 : Click OK.

Goodness-of-Fit Test

The Chi-square goodness of fit test is used to compare a randomly collected sample containing a single, categorical variable to a larger population.

This test is most commonly used to compare a random sample to the population from which it was potentially collected.

The test begins with the creation of a null and alternative hypothesis. In this case, the hypotheses are as follows:

Null Hypothesis (Ho) : The null hypothesis (Ho) is that the observed frequencies are the same (except for chance variation) as the expected frequencies. The collected data is consistent with the population distribution.

Alternative Hypothesis (Ha) : The collected data is not consistent with the population distribution.

The next step is to create a contingency table that represents how the data would be distributed if the null hypothesis were exactly correct.

The sample’s overall deviation from this theoretical/expected data will allow us to draw a conclusion, with a more severe deviation resulting in smaller p-values.

Test for Independence

The Chi-square test for independence looks for an association between two categorical variables within the same population.

Unlike the goodness of fit test, the test for independence does not compare a single observed variable to a theoretical population but rather two variables within a sample set to one another.

The hypotheses for a Chi-square test of independence are as follows:

Null Hypothesis (Ho) : There is no association between the two categorical variables in the population of interest.

Alternative Hypothesis (Ha) : There is no association between the two categorical variables in the population of interest.

The next step is to create a contingency table of expected values that reflects how a data set that perfectly aligns the null hypothesis would appear.

The simplest way to do this is to calculate the marginal frequencies of each row and column; the expected frequency of each cell is equal to the marginal frequency of the row and column that corresponds to a given cell in the observed contingency table divided by the total sample size.

Test for Homogeneity

The Chi-square test for homogeneity is organized and executed exactly the same as the test for independence.

The main difference to remember between the two is that the test for independence looks for an association between two categorical variables within the same population, while the test for homogeneity determines if the distribution of a variable is the same in each of several populations (thus allocating population itself as the second categorical variable).

Null Hypothesis (Ho) : There is no difference in the distribution of a categorical variable for several populations or treatments.

Alternative Hypothesis (Ha) : There is a difference in the distribution of a categorical variable for several populations or treatments.

The difference between these two tests can be a bit tricky to determine, especially in the practical applications of a Chi-square test. A reliable rule of thumb is to determine how the data was collected.

If the data consists of only one random sample with the observations classified according to two categorical variables, it is a test for independence. If the data consists of more than one independent random sample, it is a test for homogeneity.

What is the chi-square test?

The Chi-square test is a non-parametric statistical test used to determine if there’s a significant association between two or more categorical variables in a sample.

It works by comparing the observed frequencies in each category of a cross-tabulation with the frequencies expected under the null hypothesis, which assumes there is no relationship between the variables.

This test is often used in fields like biology, marketing, sociology, and psychology for hypothesis testing.

What does chi-square tell you?

The Chi-square test informs whether there is a significant association between two categorical variables. Suppose the calculated Chi-square value is above the critical value from the Chi-square distribution.

In that case, it suggests a significant relationship between the variables, rejecting the null hypothesis of no association.

How to calculate chi-square?

To calculate the Chi-square statistic, follow these steps:

1. Create a contingency table of observed frequencies for each category.

2. Calculate expected frequencies for each category under the null hypothesis.

3. Compute the Chi-square statistic using the formula: Χ² = Σ [ (O_i – E_i)² / E_i ], where O_i is the observed frequency and E_i is the expected frequency.

4. Compare the calculated statistic with the critical value from the Chi-square distribution to draw a conclusion.

A Handy Workbook for Research Methods & Statistics

4 one-sample chi-square, 4.1 the worked example.

Here is our data:

And if we add on a column showing the total number of participants, adding all the numbers in the different conditions together, (i.e. 4 + 5 + 8 + 15 = 32), then we get:

Now the formula for the chi-square is:

\[\chi^2 = \sum\frac{(Observed - Expected)^2}{Expected}\]

The Expected values for each condition, in a one-sample chi-square assuming a uniform (equal) distribution is calculated by \(N \times \frac{1}{k}\) where \(k\) is the number of conditions and \(N\) is the total number of participants. This can also be written more straightforward as \(N/k\) . That means that in our example the expected value in each condition would be:

\[Expected = \frac{N}{k} = \frac{32}{4} = 8\]

Let's now add those Expected values to our table which looks like:

We now have our data, let's start putting it into the formula, which we said was:

Which really means:

\[\chi^2 = \frac{(Observed_{A} - Expected_{A})^2}{Expected_{A}} + \frac{(Observed_{B} - Expected_{B})^2}{Expected_{B}} + \frac{(Observed_{C} - Expected_{C})^2}{Expected_{C}} + \\ \frac{(Observed_{D} - Expected_{D})^2}{Expected_{D}}\]

\[\chi^2 = \frac{(4 - 8)^2}{8}+\frac{(5 - 8)^2}{8}+\frac{(8 - 8)^2}{8}+\frac{(15 - 8)^2}{8}\]

Which becomes:

\[\chi^2 = \frac{(-4)^2}{8} + \frac{(-3)^2}{8} + \frac{(0)^2}{8} + \frac{(7)^2}{8}\]

And if we now square the top halves (the numerators):

\[\chi^2 = \frac{16}{8} + \frac{9}{8} + \frac{0}{8} + \frac{49}{8}\]

Then divide the top half by the bottom half for each condition:

\[\chi^2 = {2}+{1.125}+{0}+{6.125}\] And finally add them altogether

\[\chi^2 = 9.25\]

So we find that \(\chi^2 = 9.25\)

The degrees of freedom in this test is \(k - 1\) and given that we have 4 conditions:

\[df = k - 1\] \[df = 4 - 1\] \[df = 3\]

The effect size

A common effect size for the one-sample chi-square test is \(\phi\) (pronounced "ph-aye" and can be written as "phi"). The formula for \(\phi\) is:

\[\phi = \sqrt\frac{\chi^2}{N}\]

And if we know that \(\chi^2 =9.25\) and that \(N = 32\) , then putting them into the formula we get:

\[\phi = \sqrt\frac{9.25}{32}\]

\[\phi = 0.5376453\]

The write-up

If we were to look at a critical value look-up table, we would see that the critical value associated with a \(df = 3\) at \(\alpha = .05\) , to three decimal places, is \(\chi^2_{crit} = 7.815\) . As the chi-square value of this test (i.e. \(\chi^2 = 9.25\) ) is larger than \(\chi^2_{crit}\) then we can say that our test is significant, and as such would be written up as \(\chi^2(df = 3, N = 32) = 9.25,p < .05\) .

Finally, if our test was significant then all we need to do is state the condition with the highest frequency (i.e. the mode), which in this case is Condition D

4.2 Test Yourself

4.2.1 dataset 1.

And if we add on a column showing the total number of participants, adding all the numbers in the different conditions together, (i.e. 6 + 0 + 1 + 11 = 18), then we get:

\[Expected = \frac{N}{k} = \frac{18}{4} = 4.5\]

\[\chi^2 = \frac{(6 - 4.5)^2}{4.5}+\frac{(0 - 4.5)^2}{4.5}+\frac{(1 - 4.5)^2}{4.5}+\frac{(11 - 4.5)^2}{4.5}\]

\[\chi^2 = \frac{(1.5)^2}{4.5} + \frac{(-4.5)^2}{4.5} + \frac{(-3.5)^2}{4.5} + \frac{(6.5)^2}{4.5}\]

\[\chi^2 = \frac{2.25}{4.5} + \frac{20.25}{4.5} + \frac{12.25}{4.5} + \frac{42.25}{4.5}\]

\[\chi^2 = {0.5}+{4.5}+{2.7222222}+{9.3888889}\] And finally add them altogether

\[\chi^2 = 17.1111111\]

So we find that \(\chi^2 = 17.1111111\)

And if we know that \(\chi^2 =17.1111111\) and that \(N = 18\) , then putting them into the formula we get:

\[\phi = \sqrt\frac{17.1111111}{18}\]

\[\phi = 0.974996\]

If we were to look at a critical value look-up table, we would see that the critical value associated with a \(df = 3\) at \(\alpha = .05\) , to three decimal places, is \(\chi^2_{crit} = 7.815\) . As the chi-square value of this test (i.e. \(\chi^2 = 17.1111111\) ) is larger than \(\chi^2_{crit}\) then we can say that our test is significant, and as such would be written up as \(\chi^2(df = 3, N = 18) = 17.1111111,p < .05\) .

4.2.2 DataSet 2

And if we add on a column showing the total number of participants, adding all the numbers in the different conditions together, (i.e. 12 + 16 + 11 + 14 = 53), then we get:

\[Expected = \frac{N}{k} = \frac{53}{4} = 13.25\]

\[\chi^2 = \frac{(12 - 13.25)^2}{13.25}+\frac{(16 - 13.25)^2}{13.25}+\frac{(11 - 13.25)^2}{13.25}+\frac{(14 - 13.25)^2}{13.25}\]

\[\chi^2 = \frac{(-1.25)^2}{13.25} + \frac{(2.75)^2}{13.25} + \frac{(-2.25)^2}{13.25} + \frac{(0.75)^2}{13.25}\]

\[\chi^2 = \frac{1.5625}{13.25} + \frac{7.5625}{13.25} + \frac{5.0625}{13.25} + \frac{0.5625}{13.25}\]

\[\chi^2 = {0.1179245}+{0.5707547}+{0.3820755}+{0.0424528}\] And finally add them altogether

\[\chi^2 = 1.1132075\]

So we find that \(\chi^2 = 1.1132075\)

And if we know that \(\chi^2 =1.1132075\) and that \(N = 53\) , then putting them into the formula we get:

\[\phi = \sqrt\frac{1.1132075}{53}\]

\[\phi = 0.1449273\]

If we were to look at a critical value look-up table, we would see that the critical value associated with a \(df = 3\) at \(\alpha = .05\) , to three decimal places, is \(\chi^2_{crit} = 7.815\) . As the chi-square value of this test (i.e. \(\chi^2 = 1.1132075\) ) is smaller than \(\chi^2_{crit}\) then we can say that our test is non-significant, and as such would be written up as \(\chi^2(df = 3, N = 53) = 1.1132075,p > .05\) .

Finally, if our test was significant then all we need to do is state the condition with the highest frequency (i.e. the mode), which in this case is Condition B

4.2.3 DataSet 3

And if we add on a column showing the total number of participants, adding all the numbers in the different conditions together, (i.e. 20 + 9 + 19 + 1 = 49), then we get:

\[Expected = \frac{N}{k} = \frac{49}{4} = 12.25\]

\[\chi^2 = \frac{(20 - 12.25)^2}{12.25}+\frac{(9 - 12.25)^2}{12.25}+\frac{(19 - 12.25)^2}{12.25}+\frac{(1 - 12.25)^2}{12.25}\]

\[\chi^2 = \frac{(7.75)^2}{12.25} + \frac{(-3.25)^2}{12.25} + \frac{(6.75)^2}{12.25} + \frac{(-11.25)^2}{12.25}\]

\[\chi^2 = \frac{60.0625}{12.25} + \frac{10.5625}{12.25} + \frac{45.5625}{12.25} + \frac{126.5625}{12.25}\]

\[\chi^2 = {4.9030612}+{0.8622449}+{3.7193878}+{10.3316327}\] And finally add them altogether

\[\chi^2 = 19.8163265\]

So we find that \(\chi^2 = 19.8163265\)

And if we know that \(\chi^2 =19.8163265\) and that \(N = 49\) , then putting them into the formula we get:

\[\phi = \sqrt\frac{19.8163265}{49}\]

\[\phi = 0.6359362\]

If we were to look at a critical value look-up table, we would see that the critical value associated with a \(df = 3\) at \(\alpha = .05\) , to three decimal places, is \(\chi^2_{crit} = 7.815\) . As the chi-square value of this test (i.e. \(\chi^2 = 19.8163265\) ) is larger than \(\chi^2_{crit}\) then we can say that our test is significant, and as such would be written up as \(\chi^2(df = 3, N = 49) = 19.8163265,p < .05\) .

Finally, if our test was significant then all we need to do is state the condition with the highest frequency (i.e. the mode), which in this case is Condition A

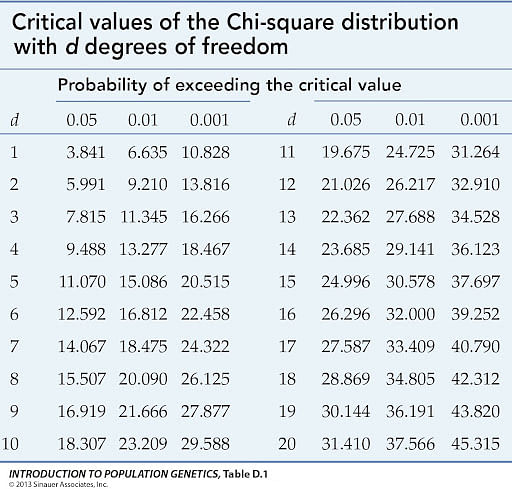
4.3 Chi-Square ( \(\chi^2\) ) Look-up Table

• 1-800-609-6480

• Your Audience
• Your Industry
• Customer Stories
• Case Studies
• Alchemer Survey
• Alchemer Survey is the industry leader in flexibility, ease of use, and fastest implementation. Learn More
• Alchemer Workflow
• Alchemer Workflow is the fastest, easiest, and most effective way to close the loop with customers. Learn More
• Alchemer Digital
• Alchemer Digital drives omni-channel customer engagement across Mobile and Web digital properties. Learn More
• Additional Products
• Alchemer Mobile
• Alchemer Web
• Email and SMS Distribution
• Integrations
• Panel Services
• Website Intercept
• Onboarding Services
• Business Labs
• Basic Training
• Alchemer University
• Our full-service team will help you find the audience you need. Learn More
• Professional Services
• Specialists will custom-fit Alchemer Survey and Workflow to your business. Learn More
• Mobile Executive Reports
• Get help gaining insights into mobile customer feedback tailored to your requirements. Learn More
• Self-Service Survey Pricing
• News & Press
• Help Center
• Mobile Developer Guides
• Resource Library
• Close the Loop
• Security & Privacy

An Introduction to the Chi-Square Test & When to Use It

• Share this post:

Alchemer is a powerful online survey and data collection platform that allows you to perform very advanced analysis, such as the Chi-Square test. Being able to investigate whether the data from two questions are correlated helps market researchers better understand context in their findings.

What is the Chi-Square Test?

The Chi-Square test is a statistical procedure used by researchers to examine the differences between categorical variables in the same population. 

For example, imagine that a research group is interested in whether or not education level and marital status are related for all people in the U.S. 

After collecting a simple random sample of 500 U.S. citizens, and administering a survey to this sample, the researchers could first manually observe the frequency distribution of marital status and education category within their sample. 

The researchers could then perform a Chi-Square test to validate or provide additional context for these observed frequencies.

Chi-Square calculation formula is as follows:

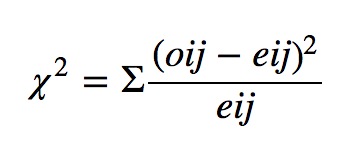
When is the Chi-Square Test Used in Market Research?

Market researchers use the Chi-Square test when they find themselves in one of the following situations:

• They need to estimate how closely an observed distribution matches an expected distribution. This is referred to as a “goodness-of-fit” test.
• They need to estimate whether two random variables are independent.

When to Use the Chi-Square Test on Survey Results

The Chi-Square test is most useful when analyzing cross tabulations of survey response data. 

Because cross tabulations reveal the frequency and percentage of responses to questions by various segments or categories of respondents (gender, profession, education level, etc.), the Chi-Square test informs researchers about whether or not there is a statistically significant difference between how the various segments or categories answered a given question.

Important things to note when considering using the Chi-Square test

First, Chi-Square only tests whether two individual variables are independent in a binary, “yes” or “no” format.

Chi-Square testing does not provide any insight into the degree of difference between the respondent categories, meaning that researchers are not able to tell which statistic (result of the Chi-Square test) is greater or less than the other.

Second, Chi-Square requires researchers to use numerical values, also known as frequency counts, instead of using percentages or ratios. This can limit the flexibility that researchers have in terms of the processes that they use.

What Software is Needed to Run a Chi-Square Test?

Chi-Square tests can be run in either Microsoft Excel or Google Sheets, however, there are more intuitive statistical software packages available to researchers, such as SPSS, Stata, and SAS. 

Check out this article on Exporting Your Survey Data with SPSS to learn how to get started today!

• Get Your Free Demo Today Get Demo
• See How Easy Alchemer Is to Use See Help Docs

Start making smarter decisions

Related posts, playing with logic to collect better feedback.

• January 12, 2024
• 4 minute read

Combining Reports – An Answer to One of Your NPS Questions 

• October 27, 2022
• 2 minute read

Survey Templates – An Answer to One of Your NPS Questions

• October 11, 2022
• 3 minute read

See it in Action

Request a demo.

• Privacy Overview
• Strictly Necessary Cookies
• 3rd Party Cookies

This website uses cookies so that we can provide you with the best user experience possible. Cookie information is stored in your browser and performs functions such as recognising you when you return to our website and helping our team to understand which sections of the website you find most interesting and useful.

Strictly Necessary Cookie should be enabled at all times so that we can save your preferences for cookie settings.

If you disable this cookie, we will not be able to save your preferences. This means that every time you visit this website you will need to enable or disable cookies again.

This website uses Google Analytics to collect anonymous information such as the number of visitors to the site, and the most popular pages.

Keeping this cookie enabled helps us to improve our website.

Please enable Strictly Necessary Cookies first so that we can save your preferences!

Tutorial Playlist

Statistics tutorial, everything you need to know about the probability density function in statistics, the best guide to understand central limit theorem, an in-depth guide to measures of central tendency : mean, median and mode, the ultimate guide to understand conditional probability, a comprehensive look at percentile in statistics, the best guide to understand bayes theorem, everything you need to know about the normal distribution, an in-depth explanation of cumulative distribution function, a complete guide to chi-square test.

A Complete Guide on Hypothesis Testing in Statistics

Understanding the Fundamentals of Arithmetic and Geometric Progression

The definitive guide to understand spearman’s rank correlation, a comprehensive guide to understand mean squared error, all you need to know about the empirical rule in statistics, the complete guide to skewness and kurtosis, a holistic look at bernoulli distribution, all you need to know about bias in statistics, a complete guide to get a grasp of time series analysis.

The Key Differences Between Z-Test Vs. T-Test

The Complete Guide to Understand Pearson's Correlation

A complete guide on the types of statistical studies, everything you need to know about poisson distribution, your best guide to understand correlation vs. regression, the most comprehensive guide for beginners on what is correlation, what is a chi-square test formula, examples & application.

Lesson 9 of 24 By Avijeet Biswal

Table of Contents

The world is constantly curious about the Chi-Square test's application in machine learning and how it makes a difference. Feature selection is a critical topic in machine learning , as you will have multiple features in line and must choose the best ones to build the model. By examining the relationship between the elements, the chi-square test aids in the solution of feature selection problems. In this tutorial, you will learn about the chi-square test and its application.

What Is a Chi-Square Test?

The Chi-Square test is a statistical procedure for determining the difference between observed and expected data. This test can also be used to determine whether it correlates to the categorical variables in our data. It helps to find out whether a difference between two categorical variables is due to chance or a relationship between them.

Chi-Square Test Definition

A chi-square test is a statistical test that is used to compare observed and expected results. The goal of this test is to identify whether a disparity between actual and predicted data is due to chance or to a link between the variables under consideration. As a result, the chi-square test is an ideal choice for aiding in our understanding and interpretation of the connection between our two categorical variables.

A chi-square test or comparable nonparametric test is required to test a hypothesis regarding the distribution of a categorical variable. Categorical variables, which indicate categories such as animals or countries, can be nominal or ordinal. They cannot have a normal distribution since they can only have a few particular values.

For example, a meal delivery firm in India wants to investigate the link between gender, geography, and people's food preferences.

It is used to calculate the difference between two categorical variables, which are:

• As a result of chance or
• Because of the relationship

Your Data Analytics Career is Around The Corner!

Formula For Chi-Square Test

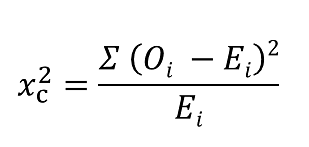
c = Degrees of freedom

O = Observed Value

E = Expected Value

The degrees of freedom in a statistical calculation represent the number of variables that can vary in a calculation. The degrees of freedom can be calculated to ensure that chi-square tests are statistically valid. These tests are frequently used to compare observed data with data that would be expected to be obtained if a particular hypothesis were true.

The Observed values are those you gather yourselves.

The expected values are the frequencies expected, based on the null hypothesis. 

Fundamentals of Hypothesis Testing

Hypothesis testing is a technique for interpreting and drawing inferences about a population based on sample data. It aids in determining which sample data best support mutually exclusive population claims.

Null Hypothesis (H0) - The Null Hypothesis is the assumption that the event will not occur. A null hypothesis has no bearing on the study's outcome unless it is rejected.

H0 is the symbol for it, and it is pronounced H-naught.

Alternate Hypothesis(H1 or Ha) - The Alternate Hypothesis is the logical opposite of the null hypothesis. The acceptance of the alternative hypothesis follows the rejection of the null hypothesis. H1 is the symbol for it.

Become a Data Science Expert & Get Your Dream Job

What Are Categorical Variables?

Categorical variables belong to a subset of variables that can be divided into discrete categories. Names or labels are the most common categories. These variables are also known as qualitative variables because they depict the variable's quality or characteristics.

Categorical variables can be divided into two categories:

• Nominal Variable: A nominal variable's categories have no natural ordering. Example: Gender, Blood groups
• Ordinal Variable: A variable that allows the categories to be sorted is ordinal variables. Customer satisfaction (Excellent, Very Good, Good, Average, Bad, and so on) is an example.

Why Do You Use the Chi-Square Test?

Chi-square is a statistical test that examines the differences between categorical variables from a random sample in order to determine whether the expected and observed results are well-fitting.

Here are some of the uses of the Chi-Squared test:

• The Chi-squared test can be used to see if your data follows a well-known theoretical probability distribution like the Normal or Poisson distribution.
• The Chi-squared test allows you to assess your trained regression model's goodness of fit on the training, validation, and test data sets.

Become an Expert in Data Analytics!

What Does A Chi-Square Statistic Test Tell You?

A Chi-Square test ( symbolically represented as  2 ) is fundamentally a data analysis based on the observations of a random set of variables. It computes how a model equates to actual observed data. A Chi-Square statistic test is calculated based on the data, which must be raw, random, drawn from independent variables, drawn from a wide-ranging sample and mutually exclusive. In simple terms, two sets of statistical data are compared -for instance, the results of tossing a fair coin. Karl Pearson introduced this test in 1900 for categorical data analysis and distribution. This test is also known as ‘Pearson’s Chi-Squared Test’. 

Chi-Squared Tests are most commonly used in hypothesis testing. A hypothesis is an assumption that any given condition might be true, which can be tested afterwards. The Chi-Square test estimates the size of inconsistency between the expected results and the actual results when the size of the sample and the number of variables in the relationship is mentioned. 

These tests use degrees of freedom to determine if a particular null hypothesis can be rejected based on the total number of observations made in the experiments. Larger the sample size, more reliable is the result.

There are two main types of Chi-Square tests namely -

Independence 

• Goodness-of-Fit 

The Chi-Square Test of Independence is a derivable ( also known as inferential ) statistical test which examines whether the two sets of variables are likely to be related with each other or not. This test is used when we have counts of values for two nominal or categorical variables and is considered as non-parametric test. A relatively large sample size and independence of obseravations are the required criteria for conducting this test.

For Example- 

In a movie theatre, suppose we made a list of movie genres. Let us consider this as the first variable. The second variable is whether or not the people who came to watch those genres of movies have bought snacks at the theatre. Here the null hypothesis is that th genre of the film and whether people bought snacks or not are unrelatable. If this is true, the movie genres don’t impact snack sales. 

Future-Proof Your AI/ML Career: Top Dos and Don'ts

Goodness-Of-Fit

In statistical hypothesis testing, the Chi-Square Goodness-of-Fit test determines whether a variable is likely to come from a given distribution or not. We must have a set of data values and the idea of the distribution of this data. We can use this test when we have value counts for categorical variables. This test demonstrates a way of deciding if the data values have a “ good enough” fit for our idea or if it is a representative sample data of the entire population. 

Suppose we have bags of balls with five different colours in each bag. The given condition is that the bag should contain an equal number of balls of each colour. The idea we would like to test here is that the proportions of the five colours of balls in each bag must be exact. 

Who Uses Chi-Square Analysis?

Chi-square is most commonly used by researchers who are studying survey response data because it applies to categorical variables. Demography, consumer and marketing research, political science, and economics are all examples of this type of research.

Let's say you want to know if gender has anything to do with political party preference. You poll 440 voters in a simple random sample to find out which political party they prefer. The results of the survey are shown in the table below:

To see if gender is linked to political party preference, perform a Chi-Square test of independence using the steps below.

Step 1: Define the Hypothesis

H0: There is no link between gender and political party preference.

H1: There is a link between gender and political party preference.

Step 2: Calculate the Expected Values

Now you will calculate the expected frequency.

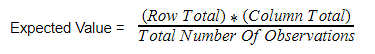
For example, the expected value for Male Republicans is: 

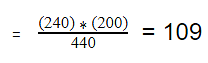
Similarly, you can calculate the expected value for each of the cells.

Step 3: Calculate (O-E)2 / E for Each Cell in the Table

Now you will calculate the (O - E)2 / E for each cell in the table.

Step 4: Calculate the Test Statistic X2

X2  is the sum of all the values in the last table

 =  0.743 + 2.05 + 2.33 + 3.33 + 0.384 + 1

Before you can conclude, you must first determine the critical statistic, which requires determining our degrees of freedom. The degrees of freedom in this case are equal to the table's number of columns minus one multiplied by the table's number of rows minus one, or (r-1) (c-1). We have (3-1)(2-1) = 2.

Finally, you compare our obtained statistic to the critical statistic found in the chi-square table. As you can see, for an alpha level of 0.05 and two degrees of freedom, the critical statistic is 5.991, which is less than our obtained statistic of 9.83. You can reject our null hypothesis because the critical statistic is higher than your obtained statistic.

This means you have sufficient evidence to say that there is an association between gender and political party preference.

When to Use a Chi-Square Test?

A Chi-Square Test is used to examine whether the observed results are in order with the expected values. When the data to be analysed is from a random sample, and when the variable is the question is a categorical variable, then Chi-Square proves the most appropriate test for the same. A categorical variable consists of selections such as breeds of dogs, types of cars, genres of movies, educational attainment, male v/s female etc. Survey responses and questionnaires are the primary sources of these types of data. The Chi-square test is most commonly used for analysing this kind of data. This type of analysis is helpful for researchers who are studying survey response data. The research can range from customer and marketing research to political sciences and economics. 

The Ultimate Ticket to Top Data Science Job Roles

Chi-Square Distribution 

Chi-square distributions (X2) are a type of continuous probability distribution. They're commonly utilized in hypothesis testing, such as the chi-square goodness of fit and independence tests. The parameter k, which represents the degrees of freedom, determines the shape of a chi-square distribution.

A chi-square distribution is followed by very few real-world observations. The objective of chi-square distributions is to test hypotheses, not to describe real-world distributions. In contrast, most other commonly used distributions, such as normal and Poisson distributions, may explain important things like baby birth weights or illness cases per year.

Because of its close resemblance to the conventional normal distribution, chi-square distributions are excellent for hypothesis testing. Many essential statistical tests rely on the conventional normal distribution.

In statistical analysis , the Chi-Square distribution is used in many hypothesis tests and is determined by the parameter k degree of freedoms. It belongs to the family of continuous probability distributions . The Sum of the squares of the k independent standard random variables is called the Chi-Squared distribution. Pearson’s Chi-Square Test formula is - 

Where X^2 is the Chi-Square test symbol

Σ is the summation of observations

O is the observed results

E is the expected results 

The shape of the distribution graph changes with the increase in the value of k, i.e. degree of freedoms. 

When k is 1 or 2, the Chi-square distribution curve is shaped like a backwards ‘J’. It means there is a high chance that X^2 becomes close to zero. 

Courtesy: Scribbr

When k is greater than 2, the shape of the distribution curve looks like a hump and has a low probability that X^2 is very near to 0 or very far from 0. The distribution occurs much longer on the right-hand side and shorter on the left-hand side. The probable value of X^2 is (X^2 - 2).

When k is greater than ninety, a normal distribution is seen, approximating the Chi-square distribution.

Become a Data Scientist With Real-World Experience

Chi-Square P-Values

Here P denotes the probability; hence for the calculation of p-values, the Chi-Square test comes into the picture. The different p-values indicate different types of hypothesis interpretations. 

• P <= 0.05 (Hypothesis interpretations are rejected)
• P>= 0.05 (Hypothesis interpretations are accepted) 

The concepts of probability and statistics are entangled with Chi-Square Test. Probability is the estimation of something that is most likely to happen. Simply put, it is the possibility of an event or outcome of the sample. Probability can understandably represent bulky or complicated data. And statistics involves collecting and organising, analysing, interpreting and presenting the data. 

Finding P-Value

When you run all of the Chi-square tests, you'll get a test statistic called X2. You have two options for determining whether this test statistic is statistically significant at some alpha level:

• Compare the test statistic X2 to a critical value from the Chi-square distribution table.
• Compare the p-value of the test statistic X2 to a chosen alpha level.

Test statistics are calculated by taking into account the sampling distribution of the test statistic under the null hypothesis, the sample data, and the approach which is chosen for performing the test. 

The p-value will be as mentioned in the following cases.

• A lower-tailed test is specified by: P(TS ts | H0 is true) p-value = cdf (ts)
• Lower-tailed tests have the following definition: P(TS ts | H0 is true) p-value = cdf (ts)
• A two-sided test is defined as follows, if we assume that the test static distribution  of H0 is symmetric about 0. 2 * P(TS |ts| | H0 is true) = 2 * (1 - cdf(|ts|))

P: probability Event

TS: Test statistic is computed observed value of the test statistic from your sample cdf(): Cumulative distribution function of the test statistic's distribution (TS)

Types of Chi-square Tests

Pearson's chi-square tests are classified into two types:

• Chi-square goodness-of-fit analysis
• Chi-square independence test

These are, mathematically, the same exam. However, because they are utilized for distinct goals, we generally conceive of them as separate tests.

The chi-square test has the following significant properties:

• If you multiply the number of degrees of freedom by two, you will receive an answer that is equal to the variance.
• The chi-square distribution curve approaches the data is normally distributed as the degree of freedom increases.
• The mean distribution is equal to the number of degrees of freedom.

Properties of Chi-Square Test 

• Variance is double the times the number of degrees of freedom.
• Mean distribution is equal to the number of degrees of freedom.
• When the degree of freedom increases, the Chi-Square distribution curve becomes normal.

Limitations of Chi-Square Test

There are two limitations to using the chi-square test that you should be aware of. 

• The chi-square test, for starters, is extremely sensitive to sample size. Even insignificant relationships can appear statistically significant when a large enough sample is used. Keep in mind that "statistically significant" does not always imply "meaningful" when using the chi-square test.
• Be mindful that the chi-square can only determine whether two variables are related. It does not necessarily follow that one variable has a causal relationship with the other. It would require a more detailed analysis to establish causality.

Get In-Demand Skills to Launch Your Data Career

Chi-Square Goodness of Fit Test

When there is only one categorical variable, the chi-square goodness of fit test can be used. The frequency distribution of the categorical variable is evaluated for determining whether it differs significantly from what you expected. The idea is that the categories will have equal proportions, however, this is not always the case.

When you want to see if there is a link between two categorical variables, you perform the chi-square test. To acquire the test statistic and its related p-value in SPSS, use the chisq option on the statistics subcommand of the crosstabs command. Remember that the chi-square test implies that each cell's anticipated value is five or greater.

In this tutorial titled ‘The Complete Guide to Chi-square test’, you explored the concept of Chi-square distribution and how to find the related values. You also take a look at how the critical value and chi-square value is related to each other.

If you want to gain more insight and get a work-ready understanding in statistical concepts and learn how to use them to get into a career in Data Analytics , our Post Graduate Program in Data Analytics in partnership with Purdue University should be your next stop. A comprehensive program with training from top practitioners and in collaboration with IBM, this will be all that you need to kickstart your career in the field. 

Was this tutorial on the Chi-square test useful to you? Do you have any doubts or questions for us? Mention them in this article's comments section, and we'll have our experts answer them for you at the earliest!

1) What is the chi-square test used for? 

The chi-square test is a statistical method used to determine if there is a significant association between two categorical variables. It helps researchers understand whether the observed distribution of data differs from the expected distribution, allowing them to assess whether any relationship exists between the variables being studied.

2) What is the chi-square test and its types? 

The chi-square test is a statistical test used to analyze categorical data and assess the independence or association between variables. There are two main types of chi-square tests: a) Chi-square test of independence: This test determines whether there is a significant association between two categorical variables. b) Chi-square goodness-of-fit test: This test compares the observed data to the expected data to assess how well the observed data fit the expected distribution.

3) What is the chi-square test easily explained? 

The chi-square test is a statistical tool used to check if two categorical variables are related or independent. It helps us understand if the observed data differs significantly from the expected data. By comparing the two datasets, we can draw conclusions about whether the variables have a meaningful association.

4) What is the difference between t-test and chi-square? 

The t-test and the chi-square test are two different statistical tests used for different types of data. The t-test is used to compare the means of two groups and is suitable for continuous numerical data. On the other hand, the chi-square test is used to examine the association between two categorical variables. It is applicable to discrete, categorical data. So, the choice between the t-test and chi-square test depends on the nature of the data being analyzed.

5) What are the characteristics of chi-square? 

The chi-square test has several key characteristics:

1) It is non-parametric, meaning it does not assume a specific probability distribution for the data.

2) It is sensitive to sample size; larger samples can result in more significant outcomes.

3) It works with categorical data and is used for hypothesis testing and analyzing associations.

4) The test output provides a p-value, which indicates the level of significance for the observed relationship between variables.

5)It can be used with different levels of significance (e.g., 0.05 or 0.01) to determine statistical significance.

Find our Data Analyst Online Bootcamp in top cities:

About the author.

Avijeet is a Senior Research Analyst at Simplilearn. Passionate about Data Analytics, Machine Learning, and Deep Learning, Avijeet is also interested in politics, cricket, and football.

Recommended Resources

Getting Started with Google Display Network: The Ultimate Beginner’s Guide

Sanity Testing Vs Smoke Testing: Know the Differences, Applications, and Benefits Of Each

Fundamentals of Software Testing

The Building Blocks of API Development

• PMP, PMI, PMBOK, CAPM, PgMP, PfMP, ACP, PBA, RMP, SP, and OPM3 are registered marks of the Project Management Institute, Inc.

Chi-square statistics in research for data analysis

In this blog, I will explain you what is a chi-square test in a more clear way and how it can be used for data analysis.

Chi-Square Test

Things don’t generally turn out the way in which you expect in statistical insights. There might be a shrouded predisposition in the decisions individuals make or possibly the information are not made equally. We use a unique statistical test called a Chi-Square Test to address the expected vs the unexpected. It is a unique sort of test that manages frequency of data rather than means as in other statistical tests. Chi-square test is often determines whether to retain the null hypothesis or the problem of the study. If you have two categorical variables in your data and you want to test the relationship between the two, then chi-square test serves the purpose. For any data analysis, the important thing is to formulate the research plan (test statistic, significance level). It should describe how to use the data to accept or reject the null. Suppose, if you wish to conduct a chi-square testing problem to check the independence of two categorical variables, then the following are the main requirements for the analysis:

• Degrees of freedom
•  Expected frequencies
• Test statistic

Let me explain you what exactly the chi-square does and how it can be used for data analysis by means of an example.

I love to watch horror movies. With lot of curiosity, I once inquired some of my classmates if they like to watch horror movies too. So, I gathered the data so that I could investigate it and identify some patterns. And the data I got is:

By looking at the data, it would seem that both men and women watch horror movies in equal proportion. However, if you look closely, it is not! This is the place where bias places a significant role. This situation lead me to analyse the data or Data Analysis for statistical significance. In this case, there are no mean values to work with! Well, the data is purely categorical in nature, so I should use a test which deals with count data instead of mean values. In order to test the statistical significance for this situation, I would adapt the most widely used chi-square test like other test like t-test and F-test for means. The problem of claim or the problem statement is: Null Hypothesis: There is no significant difference between the movie preferences and gender. Alternative hypothesis: There is a significant difference between the movie preference and gender. And from Agresti (2002), the chi-square test statistic can be represented as

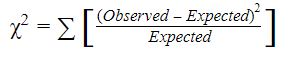
Now comes a question! What is the expected mean here? How do you calculate? Before that, we need to frame the null hypothesis stating that the participants who love to watch horror movie are independent of gender. Let us calculate the expected frequencies for the computation purpose. The chance of a woman who likes to watch horror movie (Women-yes) is (70/112) * (62/112) = 38.75. Likewise, other expected frequencies are calculated and found to be Women-no = 31.25, Men-yes = 23.25, and Men-no = 18.75. Thus, the chi-square value will be 7.02 based on the formula. Next, we have to take a decision whether it is statistically significant or not. For this, we need to compare the value with the critical value of the distribution with the corresponding degrees of freedom. Degrees of freedom is calculated as (no.of rows -1) * (no.of columns -1). If the calculated value exceed the critical, then we conclude there is a lack of independence. Thus, for this horror movies example, our calculated value is higher than the critical value with 1 degrees of freedom with 5% level of significance, leading us to reject the null hypothesis (i.e) Horror movie liking is not independent of gender.

Main use of the chi-square statistic is to test the statistical significance between the observed and the expected frequencies and it is applicable only when the data is nominal in nature. Chi-Square test is similar to the non-parametric Kolmogorov test. Apart from this, chi-square test have certain limitations: If the expected values is less an 5, then chi-square test may lead to invalid results. In addition, if there is a small sample size, chi-square test will not provide reasonable results.

Uses of chi-square test for data analysis:

Let’s look at situations where the Chi-Square Test is useful for Data Analysis .

• A marketing company wants to identify the relationship between the customer’s geographical location and their brand preferences. In such case, chi-square plays an important role and based on the value of the statistic, the company will develop its marketing strategy to different locations to make profits.
• The Chi-square test will be helpful for data analysis to test the homogeneity or independence between the categorical variables, or to test the goodness-of-fit of the model considered.
• It has the flexibility in handling two or more groups of variables. And it is used in various fields such as research field, marketing, Finance, and Economics, Psychology, Medicine, etc.
• It is a distribution-free test or simply it is a non-parametric test used for categorical data and it is more robust with respect to the distribution of the data.
• It doesn’t require mean or variance like in other test statistics such as t-test, F-test, ANOVA, etc.
• It is easy to compute and a detailed information can be obtained with this test and it is easily carried out in software like R, SAS, SPSS, etc.

The main application of the chi-square statistic could be found in the medicine field. If the researcher wants to identify the performance of a drug with control group, then the chi-square test will satisfies the needs. Likewise, there are many areas still utilizing the omnibus test statistic chi-square for identifying the relationship between two categorical outcomes.

• Agresti, A. (2002). Categorical Data Analysis (Second Edition). Wiley, New York.
• Kateri, M. (2014). Contingency Table Analysis. Springer.
• Voinov, V, Nikulin M, Balakrishnan N (2013). Chi-squared Goodness-of-fit Tests with Applications, Elseiver.
• chi-square analysis
• chi-square distribution
• chi-square formula
• chi-square test
• chi-square test in r
• Data Analysis Services
• Data Collection services
• Data Mining services
• Statistical Data Analysis
• Statistics Services

• A global market analysis (1)
• Academic (22)
• Algorithms (1)
• Big Data Analytics (4)
• Bio Statistics (3)
• Clinical Prediction Model (1)
• Corporate (9)
• Corporate statistics service (1)
• Data Analyses (23)
• Data collection (11)
• Genomics & Bioinformatics (1)
• Guidelines (2)
• Machine Learning – Blogs (1)
• Meta-analysis service (2)
• Network Analysis (1)
• Predictive analyses (2)
• Qualitative (1)
• Quantitaive (2)
• Quantitative Data analysis service (1)
• Research (59)
• Shipping & Logistics (1)
• Statistical analysis service (7)
• Statistical models (1)
• Statistical Report Writing (1)
• Statistical Software (10)
• Statistics (64)
• Survey & Interview from Statswork (1)
• Uncategorized (1)

Recent Posts

• Top 10 Machine Learning Algorithms Expected to Shape the Future of AI
• Data-Driven Governance: Revolutionizing State Youth Policies through Web Scraping
• The Future is Now: The Potential of Predictive Analytics Models and Algorithms
• 2024 Vision: Exploring the Impact and Evolution of Advanced Analytics Tools
• Application of machine learning in marketing

Statswork is a pioneer statistical consulting company providing full assistance to researchers and scholars. Statswork offers expert consulting assistance and enhancing researchers by our distinct statistical process and communication throughout the research process with us.

Functional Area

– Research Planning – Tool Development – Data Mining – Data Collection – Statistics Coursework – Research Methodology – Meta Analysis – Data Analysis

• – Corporate
• – Statistical Software
• – Statistics

Corporate Office

#10, Kutty Street, Nungambakkam, Chennai, Tamil Nadu – 600034, India No : +91 4433182000, UK No : +44-1223926607 , US No : +1-9725029262 Email: [email protected]

Website: www.statswork.com

© 2024 Statswork. All Rights Reserved

Have a language expert improve your writing

Run a free plagiarism check in 10 minutes, generate accurate citations for free.

• Knowledge Base
• Chi-Square Goodness of Fit Test | Formula, Guide & Examples

Chi-Square Goodness of Fit Test | Formula, Guide & Examples

Published on May 24, 2022 by Shaun Turney . Revised on June 22, 2023.

A chi-square (Χ 2 ) goodness of fit test is a type of Pearson’s chi-square test . You can use it to test whether the observed distribution of a categorical variable differs from your expectations.

You recruit a random sample of 75 dogs and offer each dog a choice between the three flavors by placing bowls in front of them. You expect that the flavors will be equally popular among the dogs, with about 25 dogs choosing each flavor.

The chi-square goodness of fit test tells you how well a statistical model fits a set of observations. It’s often used to analyze genetic crosses .

Table of contents

What is the chi-square goodness of fit test, chi-square goodness of fit test hypotheses, when to use the chi-square goodness of fit test, how to calculate the test statistic (formula), how to perform the chi-square goodness of fit test, when to use a different test, practice questions and examples, other interesting articles, frequently asked questions about the chi-square goodness of fit test.

A chi-square (Χ 2 ) goodness of fit test is a goodness of fit test for a categorical variable . Goodness of fit is a measure of how well a statistical model fits a set of observations.

• When goodness of fit is high , the values expected based on the model are close to the observed values.
• When goodness of fit is low , the values expected based on the model are far from the observed values.

The statistical models that are analyzed by chi-square goodness of fit tests are distributions . They can be any distribution, from as simple as equal probability for all groups, to as complex as a probability distribution with many parameters.

• Hypothesis testing

The chi-square goodness of fit test is a hypothesis test . It allows you to draw conclusions about the distribution of a population based on a sample. Using the chi-square goodness of fit test, you can test whether the goodness of fit is “good enough” to conclude that the population follows the distribution.

With the chi-square goodness of fit test, you can ask questions such as: Was this sample drawn from a population that has…

• Equal proportions of male and female turtles?
• Equal proportions of red, blue, yellow, green, and purple jelly beans?
• 90% right-handed and 10% left-handed people?
• Offspring with an equal probability of inheriting all possible genotypic combinations (i.e., unlinked genes)?
• A Poisson distribution of floods per year?
• A normal distribution of bread prices?

To help visualize the differences between your observed and expected frequencies, you also create a bar graph:

The president of the dog food company looks at your graph and declares that they should eliminate the Garlic Blast and Minty Munch flavors to focus on Blueberry Delight. “Not so fast!” you tell him.

You explain that your observations were a bit different from what you expected, but the differences aren’t dramatic. They could be the result of a real flavor preference or they could be due to chance.

Here's why students love Scribbr's proofreading services

Discover proofreading & editing

Like all hypothesis tests, a chi-square goodness of fit test evaluates two hypotheses: the null and alternative hypotheses. They’re two competing answers to the question “Was the sample drawn from a population that follows the specified distribution?”

• Null hypothesis ( H 0 ): The population follows the specified distribution.
• Alternative hypothesis ( H a ):   The population does not follow the specified distribution.

These are general hypotheses that apply to all chi-square goodness of fit tests. You should make your hypotheses more specific by describing the “specified distribution.” You can name the probability distribution (e.g., Poisson distribution) or give the expected proportions of each group.

• Null hypothesis ( H 0 ): The dog population chooses the three flavors in equal proportions ( p 1 = p 2 = p 3 ).
• Alternative hypothesis ( H a ): The dog population does not choose the three flavors in equal proportions.

The following conditions are necessary if you want to perform a chi-square goodness of fit test:

• You want to test a hypothesis about the distribution of one categorical variable . If your variable is continuous , you can convert it to a categorical variable by separating the observations into intervals. This process is known as data binning.
• The sample was randomly selected from the population .
• There are a minimum of five observations expected in each group.
• You want to test a hypothesis about the distribution of one categorical variable. The categorical variable is the dog food flavors.
• You recruited a random sample of 75 dogs.
• There were a minimum of five observations expected in each group. For all three dog food flavors, you expected 25 observations of dogs choosing the flavor.

The test statistic for the chi-square (Χ 2 ) goodness of fit test is Pearson’s chi-square:

The larger the difference between the observations and the expectations ( O − E in the equation), the bigger the chi-square will be.

To use the formula, follow these five steps:

Step 1: Create a table

Create a table with the observed and expected frequencies in two columns.

Step 2: Calculate O − E

Add a new column called “ O −  E ”. Subtract the expected frequencies from the observed frequency.

Step 3: Calculate ( O − E ) 2

Add a new column called “( O −  E ) 2 ”. Square the values in the previous column.

Step 4: Calculate ( O − E ) 2 / E

Add a final column called “( O − E )² /  E “. Divide the previous column by the expected frequencies.

Step 5: Calculate Χ 2

Add up the values of the previous column. This is the chi-square test statistic (Χ 2 ).

Prevent plagiarism. Run a free check.

The chi-square statistic is a measure of goodness of fit, but on its own it doesn’t tell you much. For example, is Χ 2 = 1.52 a low or high goodness of fit?

To interpret the chi-square goodness of fit, you need to compare it to something. That’s what a chi-square test is: comparing the chi-square value to the appropriate chi-square distribution to decide whether to reject the null hypothesis .

To perform a chi-square goodness of fit test, follow these five steps (the first two steps have already been completed for the dog food example):

Step 1: Calculate the expected frequencies

Sometimes, calculating the expected frequencies is the most difficult step. Think carefully about which expected values are most appropriate for your null hypothesis .

In general, you’ll need to multiply each group’s expected proportion by the total number of observations to get the expected frequencies.

Step 2: Calculate chi-square

Calculate the chi-square value from your observed and expected frequencies using the chi-square formula.

Step 3: Find the critical chi-square value

Find the critical chi-square value in a chi-square critical value table or using statistical software. The critical value is calculated from a chi-square distribution. To find the critical chi-square value, you’ll need to know two things:

• The degrees of freedom ( df ): For chi-square goodness of fit tests, the df is the number of groups minus one.
• Significance level (α): By convention, the significance level is usually .05.

Step 4: Compare the chi-square value to the critical value

Compare the chi-square value to the critical value to determine which is larger.

Critical value = 5.99

Step 5: Decide whether the reject the null hypothesis

• The data allows you to reject the null hypothesis and provides support for the alternative hypothesis.
• The data doesn’t allow you to reject the null hypothesis and doesn’t provide support for the alternative hypothesis.

Whether you use the chi-square goodness of fit test or a related test depends on what hypothesis you want to test and what type of variable you have.

When to use the chi-square test of independence

There’s another type of chi-square test, called the chi-square test of independence .

• Use the chi-square goodness of fit test when you have one categorical variable and you want to test a hypothesis about its distribution .
• Use the chi-square test of independence when you have two categorical variables and you want to test a hypothesis about their relationship .

When to use a different goodness of fit test

The Anderson–Darling and Kolmogorov–Smirnov goodness of fit tests are two other common goodness of fit tests for distributions.

• Use the Anderson–Darling or the Kolmogorov–Smirnov goodness of fit test when you have a continuous variable (that you don’t want to bin).
• Use the chi-square goodness of fit test when you have a categorical variable (or a continuous variable that you want to bin).

Do you want to test your knowledge about the chi-square goodness of fit test? Download our practice questions and examples with the buttons below.

Download Word doc Download Google doc

If you want to know more about statistics , methodology , or research bias , make sure to check out some of our other articles with explanations and examples.

• Chi square test of independence
• Statistical power
• Descriptive statistics
• Degrees of freedom
• Pearson correlation
• Null hypothesis

Methodology

• Double-blind study
• Case-control study
• Research ethics
• Data collection
• Structured interviews

Research bias

• Hawthorne effect
• Unconscious bias
• Recall bias
• Halo effect
• Self-serving bias
• Information bias

You can use the CHISQ.TEST() function to perform a chi-square goodness of fit test in Excel. It takes two arguments, CHISQ.TEST(observed_range, expected_range), and returns the p value .

You can use the chisq.test() function to perform a chi-square goodness of fit test in R. Give the observed values in the “x” argument, give the expected values in the “p” argument, and set “rescale.p” to true. For example:

chisq.test(x = c(22,30,23), p = c(25,25,25), rescale.p = TRUE)

Chi-square goodness of fit tests are often used in genetics. One common application is to check if two genes are linked (i.e., if the assortment is independent). When genes are linked, the allele inherited for one gene affects the allele inherited for another gene.

Suppose that you want to know if the genes for pea texture (R = round, r = wrinkled) and color (Y = yellow, y = green) are linked. You perform a dihybrid cross between two heterozygous ( RY / ry ) pea plants. The hypotheses you’re testing with your experiment are:

• This would suggest that the genes are unlinked.
• This would suggest that the genes are linked.

You observe 100 peas:

• 78 round and yellow peas
• 6 round and green peas
• 4 wrinkled and yellow peas
• 12 wrinkled and green peas

To calculate the expected values, you can make a Punnett square. If the two genes are unlinked, the probability of each genotypic combination is equal.

The expected phenotypic ratios are therefore 9 round and yellow: 3 round and green: 3 wrinkled and yellow: 1 wrinkled and green.

From this, you can calculate the expected phenotypic frequencies for 100 peas:

Χ 2 = 8.41 + 8.67 + 11.6 + 5.4 = 34.08

Since there are four groups (round and yellow, round and green, wrinkled and yellow, wrinkled and green), there are three degrees of freedom .

For a test of significance at α = .05 and df = 3, the Χ 2 critical value is 7.82.

Χ 2 = 34.08

Critical value = 7.82

The Χ 2 value is greater than the critical value .

The Χ 2 value is greater than the critical value, so we reject the null hypothesis that the population of offspring have an equal probability of inheriting all possible genotypic combinations. There is a significant difference between the observed and expected genotypic frequencies ( p < .05).

The data supports the alternative hypothesis that the offspring do not have an equal probability of inheriting all possible genotypic combinations, which suggests that the genes are linked

The two main chi-square tests are the chi-square goodness of fit test and the chi-square test of independence .

A chi-square distribution is a continuous probability distribution . The shape of a chi-square distribution depends on its degrees of freedom , k . The mean of a chi-square distribution is equal to its degrees of freedom ( k ) and the variance is 2 k . The range is 0 to ∞.

Cite this Scribbr article

If you want to cite this source, you can copy and paste the citation or click the “Cite this Scribbr article” button to automatically add the citation to our free Citation Generator.

Turney, S. (2023, June 22). Chi-Square Goodness of Fit Test | Formula, Guide & Examples. Scribbr. Retrieved April 9, 2024, from https://www.scribbr.com/statistics/chi-square-goodness-of-fit/

Is this article helpful?

Shaun Turney

Other students also liked, chi-square (χ²) tests | types, formula & examples, chi-square (χ²) distributions | definition & examples, chi-square test of independence | formula, guide & examples, what is your plagiarism score.

LEARN STATISTICS EASILY

Learn Data Analysis Now!

How to Report Chi-Square Test Results in APA Style: A Step-By-Step Guide

In this article, we guide you through reporting Chi-Square Test results, including essential components like the Chi-Square statistic (χ²), degrees of freedom (df), p-value, and Effect Size , aligning with established guidelines for clarity and reproducibility.

Introduction

The Chi-Square Test of Independence serves as a cornerstone in the field of statistical analysis, mainly when researchers aim to examine associations between categorical variables. For instance, in healthcare research, it could be employed to determine whether smoking status is independent of lung cancer incidence within a particular demographic. This statistical technique can decipher the intricacies of frequencies or proportions across different categories, thereby providing robust conclusions on the presence or absence of significant associations.

Conforming to the American Psychological Association (APA) guidelines for statistical reporting not only bolsters the credibility of your findings but also facilitates comprehension among a diversified audience, which may include scholars, healthcare professionals, and policy-makers. Adherence to the APA style is imperative for ensuring that the statistical rigor and the nuances of the Chi-Square Test are communicated effectively and unequivocally.

• A p-value under 0.05 signifies statistical significance.
• The Chi-Square Test evaluates relationships between categorical variables.
• Cramer’s V and Phi measure effect size and direction.
• For tables larger than 2×2, use adjusted residuals; 5% thresholds are -1.96 and +1.96.
• Detailed reporting of Chi-Square, p-value, and df enhances scientific rigor.

Ad description. Lorem ipsum dolor sit amet, consectetur adipiscing elit.

Guide to Reporting Chi-Square Test Results

1. state the chi-square test purpose.

Before you delve into the specifics of the Chi-Square Test, clearly outline the research question you aim to answer. The research question will guide your analysis, and it generally revolves around investigating how certain categorical variables might be related to one another.

Once you have a well-framed research question, you must state your hypothesis clearly . The hypothesis will predict what you expect to find in your study. The researcher needs to have a clear understanding of both the null and alternative hypotheses. These hypotheses function as the backbone of the statistical analysis, providing the framework for evaluating the data.

2. Report Sample Size and Characteristics

The sample size is pivotal for the reliability of your results. Indicate how many subjects or items were part of your study and describe the method used for sample size determination.

Offer any relevant demographic information, such as age, gender, socioeconomic status, or other categorical variables that could impact the results. Providing these details will enhance the clarity and comprehensibility of your report.

3. Present Observed Frequencies

For each category or class under investigation, present the observed frequencies . These are the actual counts of subjects or items in each category collected through your research.

The expected frequencies are what you would anticipate if the null hypothesis is true, suggesting no association between the variables. If you prefer, you can also present these expected frequencies in your report to provide additional context for interpretation.

4. Report the Chi-Square Statistic and Degrees of Freedom

Clearly state the Chi-Square value that you calculated during the test. This is often denoted as χ² . It is the test statistic that you’ll compare to a critical value to decide whether to reject the null hypothesis.

In statistical parlance, degrees of freedom refer to the number of values in a study that are free to vary. When reporting your Chi-Square Test results, it is vital to mention the degrees of freedom, typically denoted as “ df .”

5. Indicate the p-value

The p-value is a critical component in statistical hypothesis testing, representing the probability that the observed data would occur if the null hypothesis were true. It quantifies the evidence against the null hypothesis.

Values below 0.05 are commonly considered indicators of statistical significance. This suggests that there is less than a 5% probability of observing a test statistic at least as extreme as the one observed, assuming that the null hypothesis is true. It implies that the association between the variables under study is unlikely to have occurred by random chance alone.

6. Report Effect Size

While a statistically significant p-value can inform you of an association between variables, it does not indicate the strength or magnitude of the relationship. This is where effect size comes into play. Effect size measures such as Cramer’s V or Phi coefficient offer a quantifiable method to determine how strong the association is.

Cramer’s V and Phi coefficient are the most commonly used effect size measures in Chi-Square Tests. Cramer’s V is beneficial for tables larger than 2×2, whereas Phi is generally used for 2×2 tables. Both are derived from the Chi-Square statistic and help compare results across different studies or datasets.

Effect sizes are generally categorized as small (0.1), medium (0.3), or large (0.5). These categories help the audience in making practical interpretations of the study findings.

7. Interpret the Results

Based on the Chi-Square statistic, degrees of freedom, p-value, and effect size, you need to synthesize all this data into coherent and clear conclusions. Here, you must state whether your results support the null hypothesis or suggest that it should be rejected.

Interpreting the results also involves detailing the real-world relevance or practical implications of the findings. For instance, if a Chi-Square Test in a medical study finds a significant association between a particular treatment and patient recovery rates, the practical implication could be that the treatment is effective and should be considered in clinical guidelines.

8. Additional Information

When working with contingency tables larger than 2×2, analyzing the adjusted residuals for each combination of categories between the two nominal qualitative variables becomes necessary. Suppose the significance level is set at 5%. In that case, adjusted residuals with values less than -1.96 or greater than +1.96 indicate an association in the analyzed combination. Similarly, at a 1% significance level, adjusted residuals with values less than -2.576 or greater than +2.576 indicate an association.

Charts , graphs , or tables can be included as supplementary material to represent the statistical data visually. This helps the reader grasp the details and implications of the study more effectively.

Vaccine Efficacy in Two Age Groups

Suppose a study aims to assess whether a new vaccine is equally effective across different age groups: those aged 18-40 and those aged 41-60. A sample of 200 people is randomly chosen, half from each age group. After administering the vaccine, it is observed whether or not the individuals contracted the disease within a specified timeframe.

Observed Frequencies

• Contracted Disease: 12
• Did Not Contract Disease: 88
• Contracted Disease: 28
• Did Not Contract Disease: 72

Expected Frequencies

If there were no association between age group and vaccine efficacy, we would expect an equal proportion of individuals in each group to contract the disease. The expected frequencies would then be:

• Contracted Disease: (12+28)/2 = 20
• Did Not Contract Disease: (88+72)/2 = 80
• Contracted Disease: 20
• Did Not Contract Disease: 80

Chi-Square Test Results

• Chi-Square Statistic (χ²) : 10.8
• Degrees of Freedom (df) : 1
• p-value : 0.001
• Effect Size (Cramer’s V) : 0.23

Interpretation

• Statistical Significance : The p-value being less than 0.05 indicates a statistically significant association between age group and vaccine efficacy.
• Effect Size : The effect size of 0.23, although statistically significant, is on the smaller side, suggesting that while age does have an impact on vaccine efficacy, the practical significance is moderate.
• Practical Implications : Given the significant but moderate association, healthcare providers may consider additional protective measures for the older age group but do not necessarily need to rethink the vaccine’s distribution strategy entirely.

Results Presentation

To evaluate the effectiveness of the vaccine across two different age groups, a Chi-Square Test of Independence was executed. The observed frequencies revealed that among those aged 18-40, 12 contracted the disease, while 88 did not. Conversely, in the 41-60 age group, 28 contracted the disease, and 72 did not. Under the assumption that there was no association between age group and vaccine efficacy, the expected frequencies were calculated to be 20 contracting the disease and 80 not contracting the disease for both age groups. The analysis resulted in a Chi-Square statistic (χ²) of 10.8, with 1 degree of freedom. The associated p-value was 0.001, below the alpha level of 0.05, suggesting a statistically significant association between age group and vaccine efficacy. Additionally, an effect size was calculated using Cramer’s V, which was found to be 0.23. While this effect size is statistically significant, it is moderate in magnitude.

Alternative Results Presentation

To assess the vaccine’s effectiveness across different age demographics, we performed a Chi-Square Test of Independence. In the age bracket of 18-40, observed frequencies indicated that 12 individuals contracted the disease, in contrast to 88 who did not (Expected frequencies: Contracted = 20, Not Contracted = 80). Similarly, for the 41-60 age group, 28 individuals contracted the disease, while 72 did not (Expected frequencies: Contracted = 20, Not Contracted = 80). The Chi-Square Test yielded significant results (χ²(1) = 10.8, p = .001, V = .23). These results imply a statistically significant, albeit moderately sized, association between age group and vaccine efficacy.

Reporting Chi-Square Test results in APA style involves multiple layers of detail. From stating the test’s purpose, presenting sample size, and explaining the observed and expected frequencies to elucidating the Chi-Square statistic, p-value, and effect size, each component serves a unique role in building a compelling narrative around your research findings.

By diligently following this comprehensive guide, you empower your audience to gain a nuanced understanding of your research. This not only enhances the validity and impact of your study but also contributes to the collective scientific endeavor of advancing knowledge.

Recommended Articles

Interested in learning more about statistical analysis and its vital role in scientific research? Explore our blog for more insights and discussions on relevant topics.

Mastering the Chi-Square Test: A Comprehensive Guide

• What is the Difference Between the T-Test vs. Chi-Square Test?
• Understanding the Null Hypothesis in Chi-Square
• Effect Size for Chi-Square Tests: Unveiling its Significance
• Understanding the Assumptions for Chi-Square Test of Independence

Applied Statistics: Data Analysis

Frequently Asked Questions (FAQs)

Q1: What is a Chi-Square Test of Independence?  The Chi-Square Test of Independence is a statistical method used to evaluate the relationship between two or more categorical variables. It is commonly employed in various research fields to determine if there are significant associations between variables.

Q2: When should I use a Chi-Square Test?  Use a Chi-Square Test to examine the relationship between two or more categorical variables. This test is often applied in healthcare, social sciences, and marketing research, among other disciplines.

Q3: What is the p-value in a Chi-Square Test?  The p-value represents the probability that the observed data occurred by chance if the null hypothesis is true. A p-value less than 0.05 generally indicates a statistically significant relationship between the variables being studied.

Q4: How do I report the results in APA style?  To report the results in APA style, state the purpose, sample size, observed frequencies, Chi-Square statistic, degrees of freedom, p-value, effect size, and interpretation of the findings. Additional information, such as adjusted residuals and graphical representations, may also be included.

Q5: What is the effect size in a Chi-Square Test?  Effect size measures like Cramer’s V or Phi coefficient quantify the strength and direction of the relationship between variables. Effect sizes are categorized as small (0.1), medium (0.3), or large (0.5).

Q6: How do I interpret the effect size?  Interpret the effect size in terms of its practical implications. For example, a small effect size, although statistically significant, might not be practically important. Conversely, a large effect size would likely have significant real-world implications.

Q7: What are adjusted residuals?  In contingency tables larger than 2×2, adjusted residuals are calculated to identify which specific combinations of categories are driving the observed associations. Thresholds commonly used are -1.96 and +1.96 at a 5% significance level.

Q8: Can I use Chi-Square Tests for small samples?  Chi-square tests are more reliable with larger sample sizes. For small sample sizes, it is advisable to use an alternative test like Fisher’s Exact Test.

Q9: What is the difference between a Chi-Square Test and a t-test?  While a t-test is used to compare the means of two groups, a Chi-Square Test is used to examine the relationship between two or more categorical variables. Both tests provide different types of information and are used under other conditions.

Q10: Are there any alternatives to the Chi-Square Test?  Yes, options like the Fisher’s Exact Test for small samples and the Kruskal-Wallis test for ordinal data are available. These are used when the assumptions for a Chi-Square Test cannot be met.

Similar Posts

How to Report Cohen’s d in APA Style

How to report Cohen’s d in APA format? Understand the concept of Cohen’s d, and master the steps for reporting it in APA style.

Fisher’s Exact Test: A Comprehensive Guide

Master Fisher’s Exact Test with our comprehensive guide, elevating your statistical analysis and research insights.

Uncover the workings, assumptions, and limitations of the Chi-Square Test — a vital tool for analyzing categorical data.

How to Report Pearson Correlation Results in APA Style

Learn how to report correlation in APA style, mastering the key steps and considerations for clearly communicating research findings.

How to Report Results of Multiple Linear Regression in APA Style

Master how to report results of multiple linear regression in APA style, covering coefficients, model fit, and diagnostics.

How to Report Simple Linear Regression Results in APA Style

Discover key steps for APA-style reporting on simple linear regression. Ensure accurate, credible research results.

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Save my name, email, and website in this browser for the next time I comment.