the pythagorean theorem and its converse assignment answers

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Unit 9: Pythagorean theorem

About this unit.

The Pythagorean theorem describes a special relationship between the sides of a right triangle. Even the ancients knew of this relationship. In this topic, we’ll figure out how to use the Pythagorean theorem and prove why it works.

Pythagorean theorem

• Intro to the Pythagorean theorem (Opens a modal)
• Pythagorean theorem example (Opens a modal)
• Pythagorean theorem intro problems (Opens a modal)
• Use Pythagorean theorem to find right triangle side lengths 7 questions Practice
• Use Pythagorean theorem to find isosceles triangle side lengths 7 questions Practice
• Right triangle side lengths 4 questions Practice
• Use area of squares to visualize Pythagorean theorem 4 questions Practice

Pythagorean theorem application

• Pythagorean theorem word problem: carpet (Opens a modal)
• Pythagorean theorem word problem: fishing boat (Opens a modal)
• Pythagorean theorem in 3D (Opens a modal)
• Use Pythagorean theorem to find perimeter 4 questions Practice
• Pythagorean theorem word problems 4 questions Practice
• Pythagorean theorem in 3D 4 questions Practice
• Pythagorean theorem challenge 4 questions Practice

Pythagorean theorem and distance between points

• Distance formula (Opens a modal)
• Distance formula review (Opens a modal)
• Distance between two points 7 questions Practice

Pythagorean theorem proofs

• Garfield's proof of the Pythagorean theorem (Opens a modal)
• Bhaskara's proof of the Pythagorean theorem (Opens a modal)
• Pythagorean theorem proof using similarity (Opens a modal)
• Another Pythagorean theorem proof (Opens a modal)

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

4.33: Pythagorean Theorem and its Converse

• Last updated
• Save as PDF
• Page ID 4965

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Use a-squared + b-squared = c-squared to prove triangles are right triangles.

Suppose you're pitching a tent, and an 8-foot pole makes a right angle with the ground. If a rope goes from the top of the pole to a point on the ground 12 feet away from the base of the pole, how long is the rope? How would you calculate its length?

Pythagorean Theorem and its Converse

The pythagorean theorem.

One of the most important theorems in mathematics and science is Pythagorean’s Theorem. Simply put, it states, “The sum of the square of each leg of a right triangle is equal to the square of the hypotenuse .”

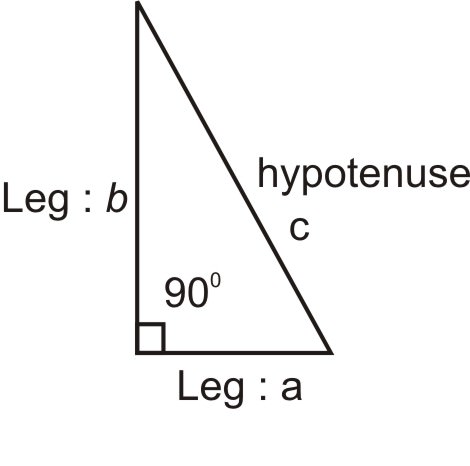
A right triangle is a triangle with a right angle. Let’s review basic right triangle anatomy.

The two segments forming the right angle (\(90^{\circ}\)) are called the legs of the right triangle. The segment opposite the right angle is called the hypotenuse.

The Pythagorean Theorem states, \((leg_1)^2+(leg_2)^2=(hypotenuse)^2\):

\(a^2+b^2=c^2\)

Or, to find the hypotenuse, \(c=\sqrt{a^2+b^2}\).

Notice this relationship is only true for right triangles. In later courses, you will learn how to determine relationships with non-right triangles.

Although we usually refer to the Pythagorean Theorem when determining side lengths of a right triangle, the theorem originally made a statement about areas. If we build squares on each side of a right triangle, the Pythagorean Theorem says that the area of the square whose side is the hypotenuse is equal to the sum of the areas of the squares formed by the legs of the triangle.

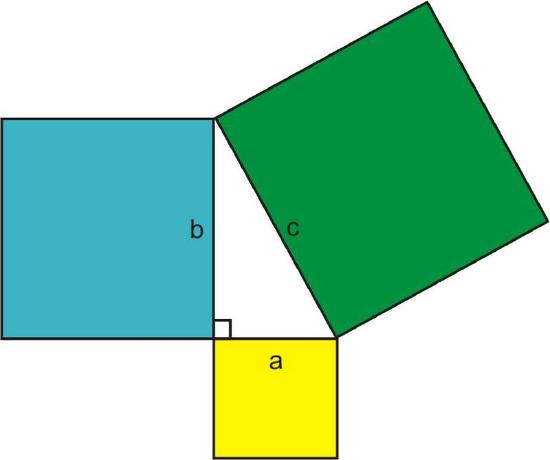
The Converse of the Pythagorean Theorem

The Converse of the Pythagorean Theorem is also true. That is, if the lengths of three sides of a triangle make the equation \(a^2+b^2=c^2\) true, then they represent the sides of a right triangle.

With this converse, you can use the Pythagorean Theorem to prove that a triangle is a right triangle, even if you do not know any of the triangle’s angle measurements.

Let's complete the following problems involving right triangles and the Pythagorean Theorem:

• Does the triangle below contain a right angle?

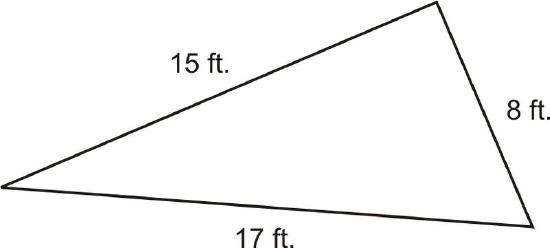
This triangle does not have any right angle marks or measured angles, so you cannot assume you know whether the triangle is acute, right, or obtuse just by looking at it. Take a moment to analyze the side lengths and see how they are related. Two of the sides, 15 and 17, are relatively close in length. The third side, 8, is about half the length of the two longer sides.

To see if the triangle might be right, try substituting the side lengths into the Pythagorean Theorem to see if they make the equation true. The hypotenuse is always the longest side, so 17 should be substituted for c. The other two values can represent a and b and the order is not important.

\(\begin{align*} a^2+b^2&=c^2 \\ 8^2+15^2&=17^2 \\ 64+225&=289 \\ 289&=289\end{align*}\)

Since both sides of the equation are equal, these values satisfy the Pythagorean Theorem. Therefore, the triangle described in the problem is a right triangle.

• One leg of a right triangle is 5 more than the other leg. The hypotenuse is one more than twice the size of the short leg. Find the dimensions of the triangle.

Let x= length of the short leg. Then, \(x+5= length\:of \:the \:long \:leg\) and \(2x+1= length \:of \:the \:hypotenuse\).

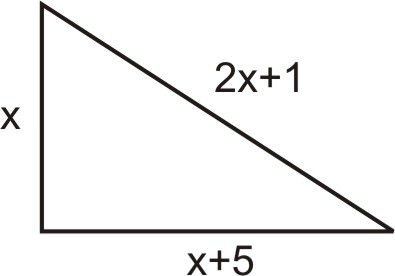
The sides of the triangle must satisfy the Pythagorean Theorem.

\(\begin{align*} & & x^2+(x+5)^2 &=(2x+1) \\ &Eliminate \:the \:parentheses. &\qquad x^2+x^2+10x+25 &=4x^2+4x+1 \\ &Move \:all \:terms \:to \:the \:right \:hand \:side \:of \:the \:equation. &\qquad 0 &=2x^2−6x−24 \\ &Divide \:all \:terms \:by \:2. &\qquad 0 &=x^2−3x−12 \\ &Solve \:using \:the \:quadratic \:formula. &\qquad x &=\dfrac{3 \pm \sqrt{9+48}}{2}=\dfrac{3 \pm \sqrt{57}}{2} \\ & & x &\neq 5.27 \:or \:x\neq −2.27 \end{align*}\)

The negative solution does not make sense in the context of this problem. So, use \(x=5.27\) and we get

\(short\:−leg=5.27,\: long\:−leg=10.27\) and

\(hypotenuse=11.54\).

• Find the area of the shaded region in the following diagram.

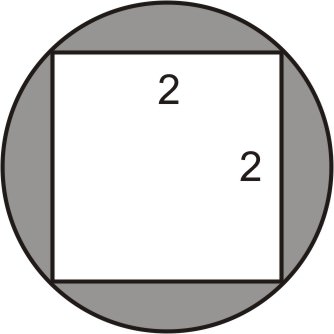
Draw the diagonal of the square on the figure.

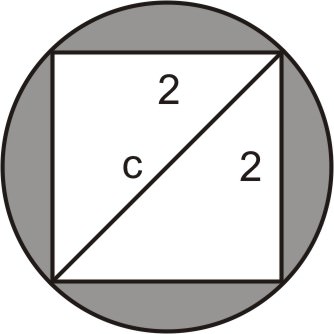
Notice that the diagonal of the square is also the diameter of the circle.

Define variables. Let \(c= diameter\: of\: the\: circle\).

\(\begin{align*} & & 2^2+2^2 &= c^2 \\ & & 4+4 &=c^2 \\ &Write\: the \:formula \:and \:solve. \: & c^2 & = 8\Rightarrow c=\sqrt{8}\Rightarrow c=2\sqrt{2}\end{align*}\)

The diameter of the circle is \(2\sqrt{2}\). Therefore, the radius is \(r=\sqrt{2}\).

The area of a circle is \(A=\pi r^2=\pi (\sqrt{2} )^2=2\pi\).

The area of the shaded region is, therefore, 2\pi −4\neq 2.28\).

Example \(\PageIndex{1}\)

Earlier, you were asked to find the length of a rope you used to pitch a tent. You know that the rope goes from the top of an 8 foot pole to a point on the ground 12 feet away from the base.

This situation can be represented by a right triangle.

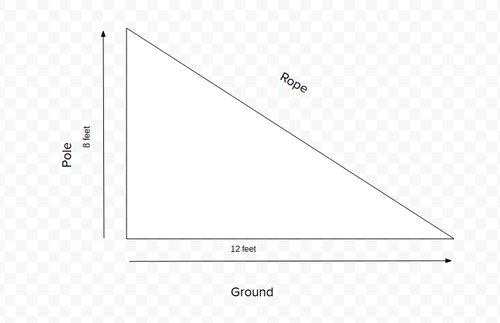
Assuming that the angle between the ground and the pole is 90 degrees, we can use the Pythagorean Theorem to solve for the length of the rope.

Let \(a= 8 \:feet (length of the pole), \(b= 12\:feet\) (the distance from the pole to the rope on the ground), and \(c= the\:length \:of \:the \:rope\).

\(\begin{align*}a^2+b^2&=c^2 \\ 8^2+12^2&=c^2 \\ 208&=c^2 \\ c&=\sqrt{208} \\ c&=\sqrt{16}\sqrt{13} \\ c&=4\sqrt{13}\:feet \end{align*}\)

The rope is \(4\sqrt{13} \) feet long.

Example \(\PageIndex{2}\)

Determine whether or not a triangle with sides of lengths 5, 6 and 8 forms a right triangle.

Use the Converse of the Pythagorean Theorem:

\(\begin{align*} Start \:with \:the \:Pythagorean \:equation.&\qquad a^2+b^2 &=c^2 \\ Substitute \:in \:the \:values \:of \:the\: sides. &\qquad 5^2+6^2&\stackrel{?}{=}8^2 \\ Simplify. &\qquad 25+36 &\stackrel{?}{=}64 \\ Check. &\qquad 61 &\neq 64\end{align*} \)

Since these lengths of sides do not satisfy the equation of the Pythagorean Theorem, the triangle is not a right triangle.

Verify that each triangle is a right triangle.

• \(a=12, \:b=9,\:c=15\)
• \(a=6, \:b=6, \:c=6\sqrt{2}\)
• \(a=8, \:b=8\sqrt{3}, \:c=16\)

Find the missing length of each right triangle.

• \(a=12,\: b=16, \:c=?\)
• \(a=?, \:b=20, \:c=30\)
• \(a=4, \:b=?, \:c=11\)

• One leg of a right triangle is 4 feet less than the hypotenuse. The other leg is 12 feet. Find the lengths of the three sides of the triangle.
• One leg of a right triangle is 3 more than twice the length of the other. The hypotenuse is 3 times the length of the short leg. Find the lengths of the three legs of the triangle.
• A regulation baseball diamond is a square with 90 feet between bases. How far is second base from home plate?
• Emanuel has a cardboard box that measures \(20\: cm\times 10\: cm\times 8\: cm\)(\(length\times width\times height\)). What is the length of the diagonal from a bottom corner to the opposite top corner?
• Samuel places a ladder against his house. The base of the ladder is 6 feet from the house and the ladder is 10 feet long. How high above the ground does the ladder touch the wall of the house?

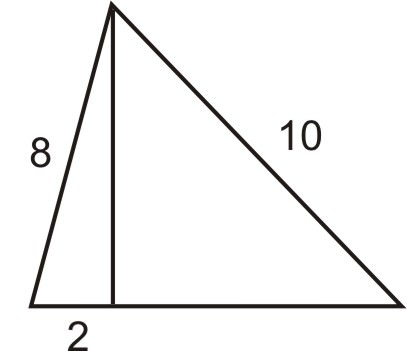
• Instead of walking along the two sides of a rectangular field, Mario decided to cut across the diagonal. He saves a distance that is half of the long side of the field. Find the length of the long side of the field given that the short side is 123 feet.
• Marcus sails due north and Sandra sails due east from the same starting point. In two hours, Marcus’s boat is 35 miles from the starting point and Sandra’s boat is 28 miles from the starting point. How far are the boats from each other?

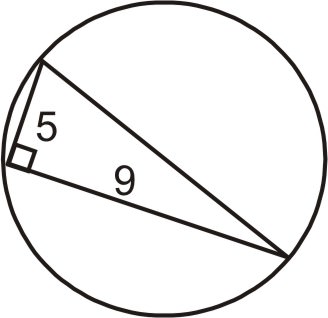
• In a right triangle, one leg is twice as long as the other and the perimeter is 28. What are the measures of the sides of the triangle?
• Maria has a rectangular cookie sheet that measures \(10\:inches\times 14\:inches\). Find the length of the diagonal of the cookie sheet.
• Mike is loading a moving van by walking up a ramp. The ramp is 10 feet long and the bed of the van is 2.5 feet above the ground. How far does the ramp extend past the back of the van?
• Identify the origin of \(h(x)=\sqrt{x−2}+5\), and then graph the function.
• Simplify \(6\sqrt[3]{2}\) by rationalizing the denominator.
• Simplify: \(\sqrt[4]{−32}\). If the answer is not possible, explain why.
• What is an extraneous solution? In what situations do such solutions occur?
• Can sides with lengths of 3, 4, and 6 form a right triangle?
• Solve \(5=y+\sqrt[3]{y+6}\).

Additional Resources

Interactive Element

Video: Pythagorean Theorem - Overview

Activities: Pythagorean Theorem and its Converse Discussion Questions

Practice: Pythagorean Theorem and its Converse

Real World: SF Map - PythThm

• Math Article
• Converse Of Pythagoras Theorem

Converse of Pythagoras Theorem

The converse of Pythagoras theorem  states that “If the square of a side is equal to the sum of the square of the other two sides, then triangle must be right angle triangle”. Whereas Pythagorean theorem states that the sum of the square of two sides (legs) is equal to the square of the hypotenuse of a right-angle triangle. But, in the reverse of the Pythagorean theorem, it is said that if this relation satisfies, then triangle must be right angle triangle. So, if the sides of a triangle have length, a, b and c and satisfy given condition a 2 + b 2 = c 2 , then the triangle is a right-angle triangle.

Let us see the proof of this theorem along with examples.

Converse of Pythagoras Theorem Proof

Statement: If the length of a triangle is a, b and c and c 2 = a 2 + b 2 , then the triangle is a right-angle triangle.

Proof: Construct another triangle, △EGF, such as AC = EG = b and BC = FG = a.

In △EGF, by Pythagoras Theorem:

EF 2 = EG 2 + FG 2 = b 2 + a 2 …………(1)

In △ABC, by Pythagoras Theorem:

AB 2 = AC 2 + BC 2 = b 2 + a 2 …………(2)

From equation (1) and (2), we have;

EF 2 = AB 2

⇒ △ ACB ≅ △EGF (By SSS postulate)

⇒ ∠G is right angle

Thus, △EGF is a right triangle.

Hence, we can say that the converse of Pythagorean theorem also holds.

Hence Proved.

As per the converse of the Pythagorean theorem, the formula for a right-angled triangle is given by:

Where a, b and c are the sides of a triangle.

Applications

Basically, the converse of the Pythagoras theorem is used to find whether the measurements of a given triangle belong to the right triangle or not. If we come to know that the given sides belong to a right-angled triangle, it helps in the construction of such a triangle. Using the concept of the converse of Pythagoras theorem, one can determine if the given three sides form a Pythagorean triplet.

Converse of Pythagoras Theorem Examples

Question 1: The sides of a triangle are 5, 12 and 13. Check whether the given triangle is a right triangle or not?

Solution: Given,

By using the converse of Pythagorean Theorem,

a 2 +b 2 = c 2

c 2 = a 2 +b 2

Substitute the given values in the above equation,

13 2 = 5 2 +12 2

169 = 25 + 144

So, the given lengths are does not satisfy the above condition.

Therefore, the given triangle is a right triangle.

Question 2: The sides of a triangle are 7, 11 and 13. Check whether the given triangle is a right triangle or not?

Solution: Given;

Substitute the given values in the the above equation,

13 2 = 7 2 + 11 2

169 = 49 + 121

So, it is not satisfied with the above condition.

Therefore, the given triangle is not a right triangle.

Question 3: The sides of a triangle are 4,6 and 8. Say whether the given triangle is a right triangle or not.

Solution: Given: a = 4, b = 6, c = 8

By the converse of Pythagoras theorem

8 2 = 4 2 + 6 2

64 = 16 + 36

The sides of the given triangle do not satisfy the condition a 2 +b 2 = c 2 .

• Share Share

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

Converse of Pythagoras Theorem

The converse of Pythagoras theorem is the reverse of the Pythagoras theorem and it helps in determining if a triangle is acute, right, or obtuse if the sum of the squares of two sides of a triangle is compared to the square of its third side. The Pythagorean theorem is the most used in trigonometry. Let us learn more about the converse of the Pythagoras theorem, the proof, and solve a few examples.

What is the Converse of Pythagoras Theorem?

The converse of Pythagoras theorem states that if the square of the length of the longest side of a triangle is equal to the sum of the squares of the other two sides, then the triangle is a right triangle. The converse is the complete reverse of the Pythagoras theorem. The main application of the converse of the Pythagorean theorem is that the measurements help in determining the type of triangle - right, acute, or obtuse. Once the triangle is identified, constructing that triangle becomes simple. There are three cases that occur:

1. If the sum of the squares of two sides of a triangle is considered equivalent to the square of the hypotenuse, the triangle is a right triangle .

2. If the sum of the squares of two sides of a triangle is less than the square of the hypotenuse, the triangle is an obtuse triangle .

3. If the sum of the squares of two sides of a triangle is greater than the square of the hypotenuse, the triangle is an acute triangle .

Pythagoras Theorem

The Pythagoras theorem states that if a triangle is right-angled (90 degrees), then the square of the hypotenuse is equal to the sum of the squares of the other two sides. In the given triangle ABC, we have BC 2 = AB 2 + AC 2 ​​. Here, ​​​​AB is the base, AC is the altitude or the height, and BC is the hypotenuse. In other words, we can say, in a right triangle, (Opposite) 2 + (Adjacent) 2 = (Hypotenuse) 2 ​​​​​​.

Proof of Converse of Pythagoras Theorem

Statement: In a triangle, if the square of one side is equal to the sum of the squares of the other two sides, then the angle opposite the first side is a right angle.

Proof: Here, we are given a triangle ABC in which AC 2 = AB 2 + BC 2 . We need to prove that ∠B = 90°.

To start with, we construct a ΔPQR right-angled at Q such that PQ = AB and QR = BC.

Now, from Δ PQR, we have:

PR 2 = PQ 2 + QR 2 (Pythagoras Theorem, as ∠Q=90°)

or PR 2 = AB 2 + BC 2 (By construction)........ (1)

But AC 2 = AB 2 + BC 2 (Given).......... (2)

So, AC = PR (From (1) and (2)).............. (3)

Now, in ΔABC and ΔPQR,

AB = PQ (By construction)

BC = QR (By construction)

AC = PR (Proved in (3))

So, ΔABC ≃ ΔPQR (According to the SSS congruence)

∠B = ∠Q (Corresponding angles of congruent triangles)

∠Q = 90° (By construction)

So ∠B = 90°.

Hence, the converse of the Pythagoras theorem is proved.

Converse of Pythagoras Theorem Formula

The converse of Pythagoras theorem formula is c 2 = a 2 + b 2 , where a, b, and c are the sides of the triangle.

Related Topics

Listed below are a few topics related to the converse of the Pythagoras theorem, take a look.

• Right Triangle Formulas
• Hypotenuse Leg Theorem
• What is Similarity
• Similarity in Triangles

Examples on Converse of Pythagoras Theorem

Example 1: The side of the triangle is of length 8 units, 10 units, and 6 units. Is this triangle a right triangle? If so, which side is the hypotenuse?

We know that the hypotenuse is the longest side in a triangle. The side or lengths is given as 8 units, 10 units, and 6 units. Therefore, 10 units is the hypotenuse.

Using the converse of Pythagoras theorem, we get,

(10) 2 = (8) 2 + (6) 2

100 = 64 + 36

Since both sides are equal, the triangle is a right triangle.

Example 2: Check if the triangle is acute, right, or an obtuse triangle with side lengths as 6, 8, and 11 units.

Solution: According to the length, we know that 11 units are the longest side.

Compare the square lengths of both the sides in the equation c 2 = a 2 + b 2 .

(11) 2 = (6) 2 + (8) 2

121 = 36 + 64

Hence, (11) 2 > (6) 2 + (8) 2

Therefore, according to the application of converse of Pythagoras theorem (If the sum of the squares of two sides of a triangle is less than the square of the hypotenuse, the triangle is an obtuse triangle), the triangle is an obtuse triangle.

go to slide go to slide

Book a Free Trial Class

Practice Questions on Converse of Pythagoras Theorem

Faqs on converse of pythagoras theorem.

The coverse of the Pythagoras theore m states that, in a triangle, if the square of one side is equal to the sum of the squares of the other two sides, then the angle opposite the first side is a right angle.

What is the Formula for Converse of Pythagoras Theorem?

The converse of Pythagoras theorem formula is c 2 = a 2 + b 2 , where a, b, and c are the sides of the triangle .

How Do You Prove the Converse of Pythagoras Theorem?

The converse of the Pythagoras theorem states that if the square of the length of the longest side of a triangle is equal to the sum of the squares of the other two sides, then the triangle is a right triangle. If we consider two triangles ΔABC and ΔPQR where c 2 = a 2 + b 2 then we can say ∠C is a right triangle.

What is the Converse of the Pythagoras Theorem Useful For?

The converse of the Pythagoras theorem is useful in determining if a triangle is a right triangle or not. Whereas, a Pythagorean theorem helps in determining the length of the missing side of a right triangle.

What is the Application of the Converse of Pythagoras Theorem?

The application of the converse of the Pythagoras theorem is that the measurements help in determining what type of a triangle it is. There are three scenarios that we can determine, they are:

• If the sum of the squares of two sides of a triangle is considered equivalent to the square of the hypotenuse, the triangle is a right triangle.
• If the sum of the squares of two sides of a triangle is less than the square of the hypotenuse, the triangle is an obtuse triangle.
• If the sum of the squares of two sides of a triangle is greater than the square of the hypotenuse, the triangle is an acute triangle.

What is the Pythagorean Theorem?

The Pythagoras theorem states that if a triangle is right-angled (90 degrees), then the square of the hypotenuse is equal to the sum of the squares of the other two sides. We can say, (Opposite) 2 + (Adjacent) 2 = (Hypotenuse) 2 ​​​​​​.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

9.1: The Pythagorean Theorem

• Last updated
• Save as PDF
• Page ID 35449

• David Arnold
• College of the Redwoods

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Pythagoras was a Greek mathematician and philosopher, born on the island of Samos (ca. 582 BC). He founded a number of schools, one in particular in a town in southern Italy called Crotone, whose members eventually became known as the Pythagoreans. The inner circle at the school, the Mathematikoi, lived at the school, rid themselves of all personal possessions, were vegetarians, and observed a strict vow of silence. They studied mathematics, philosophy, and music, and held the belief that numbers constitute the true nature of things, giving numbers a mystical or even spiritual quality.

Today, nothing is known of Pythagoras’s writings, perhaps due to the secrecy and silence of the Pythagorean society. However, one of the most famous theorems in all of mathematics does bear his name, the Pythagorean Theorem.

Prior to revealing the contents of the Pythagorean Theorem, we pause to provide the definition of a right triangle and its constituent parts.

Right Triangle

A triangle with one right angle (90 ◦ ) is called a right triangle . In the figure below, the right angle is marked with a little square.

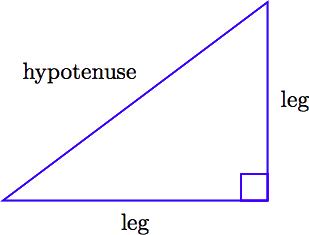
The side of the triangle that is directly opposite the right angle is called the hypotenuse . The sides of the triangle that include the right angle are called the legs of the right triangle.

Now we can state one of the most ancient theorems of mathematics, the Pythagorean Theorem .

Pythagorean Theorem

Let \(c\) represent the length of the hypotenuse of a right triangle, and let a and b represent the lengths of its legs, as pictured in the image that follows.

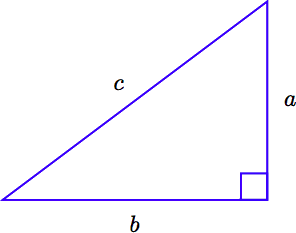
The relationship involving the legs and hypotenuse of the right triangle, given by

\[a^2 + b^2 = c^2,\nonumber \]

is called the Pythagorean Theorem .

Here are two important observations.

Observations Regarding the Hypotenuse

Two important facts regarding the hypotenuse of the right triangle are:

• The hypotenuse is the longest side of the triangle and lies directly opposite the right angle.
• In the Pythagorean equation \(a^2 + b^2 = c^2\), the hypotenuse lies by itself on one side of the equation.

The Pythagorean Theorem can only be applied to right triangles.

Let’s look at a simple application of the Pythagorean Theorem.

The legs of a right triangle measure 3 and 4 meters, respectively. Find the length of the hypotenuse.

Let’s follow the Requirements for Word Problem Solutions .

1. Set up a Variable Dictionary . Let c represent the length of the hypotenuse, as pictured in the following sketch.

2. Set up an Equation . The Pythagorean Theorem says that

\[a^2 + b^2 = c^2.\nonumber \]

In this example, the legs are known. Substitute 4 for a and 3 for b (3 for a and 4 for b works equally well) into the Pythagorean equation.

\[4^2 + 3^2 = c^2\nonumber \]

3. Solve the Equation .

\[ \begin{aligned} 4^2 + 3^2 = c^2 ~ & \textcolor{red}{ \text{ The Pythagorean equation.}} \\ 16 + 9 = c^2 ~ & \textcolor{red}{ \text{ Exponents first: } 4^2 = 16 \text{ and } 3^2 = 9.} \\ 25 = c^2 ~ & \textcolor{red}{ \text{ Add: } 16+9=25.} \\ 5 = c~ & \textcolor{red}{ \text{ Take the nonnegative square root.}} \end{aligned}\nonumber \]

Technically, there are two answers to c 2 = 25, i.e., c = −5 or c = 5. However, c represents the hypotenuse of the right triangle and must be nonnegative. Hence, we must choose c = 5.

4. Answer the Question . The hypotenuse has length 5 meters.

5. Look Back . Do the numbers satisfy the Pythagorean Theorem? The sum of the squares of the legs should equal the square of the hypotenuse. Let’s check.

\[\begin{aligned} 4^2 + 3^2 = 5^2 \\ 16 + 9 = 25 \\ 25 = 25 \end{aligned}\nonumber \]

All is well!

The legs of a right triangle measure 5 and 12 feet, respectively. Find the length of the hypotenuse.

Given the following right triangle, find the length of the missing side.

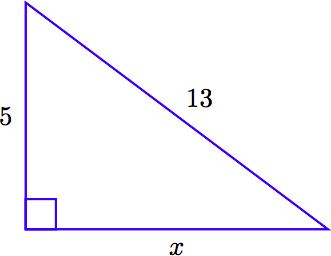
Note that the hypotenuse (across from the right angle) has length 13. This quantity should lie on one side of the Pythagorean equation all by itself. The sum of the squares of the legs go on the other side. Hence,

\[5^2 + x^2 = 13^2\nonumber \]

Solve the equation for x .

\[ \begin{aligned} 25+x^2 = 169 ~ & \textcolor{red}{ \text{ Exponents first: } 5^2 = 25 \text{ and } 13^2 = 169.} \\ 25 + x^2 -25 = 169 - 25 ~ & \textcolor{red}{ \text{ Subtract 25 from both sides.}} \\ x^2 = 144 ~ & \textcolor{red}{ \text{ Simplify both sides.}} \\ x= 12 ~ & \textcolor{red}{ \text{ Take the nonnegative square root of 144.}} \end{aligned}\nonumber \]

The hypotenuse of a right triangle measures 25 centimeters. One leg of the right triangle measures 24 centimeters. Find the length of the remaining leg.

7 centimeters

Perfect squares are nice, but not required.

Given the following right triangle, find the exact length of the missing side.

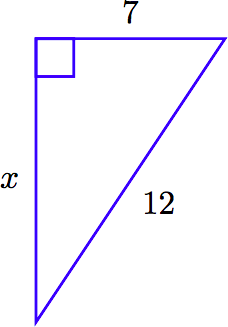
Note that the hypotenuse (across from the right angle) has length 12. This quantity should lie on one side of the Pythagorean equation all by itself. The sum of the squares of the legs go on the other side. Hence,

\[x^2 + 7^2 = 12^2\nonumber \]

\[ \begin{aligned} x^2 + 49 = 144 ~ & \textcolor{red}{ \text{ Exponents first: } 7^2 = 49 \text{ and } 12^2 = 144.} \\ x^2 + 49-49 = 144 - 49 ~ & \textcolor{red}{ \text{ Subtract 49 from both sides.}} \\ x^2 = 95 ~ & \textcolor{red}{ \text{ Simplify both sides.}} \\ x = \sqrt{95} ~ & \textcolor{red}{ \text{ Take the nonnegative square root of 95.}} \end{aligned}\nonumber \]

Hence, the exact length of the missing side is \(\sqrt{95}\).

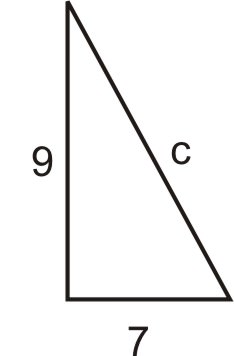
The hypotenuse and one leg of a right triangle measure 9 and 7 inches, respectively. Find the length of the remaining leg.

Add texts here. Do not delete this text first.

Important Observation

Any attempt to use your calculator to approximate 95 in Example 3 would be an error as the instructions asked for an exact answer.

Sometimes an approximate answer is desired, particularly in applications.

Ginny want to create a vegetable garden in the corner of her yard in the shape of a right triangle. She cuts two boards of length 8 feet which will form the legs of her garden. Find the length of board she should cut to form the hypotenuse of her garden, correct to the nearest tenth of a foot.

We follow the Requirements for Word Problem Solutions .

1. Set up a Variable Dictionary . We begin with a labeled sketch. Let x represent the length of the unknown hypotenuse.

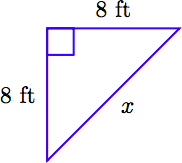
2. Set Up an Equation . The hypotenuse is isolated on one side of the Pythagorean equation.

\[x^2 = 8^2 + 8^2\nonumber \]

\[ \begin{aligned} x^2 = 8^2 + 8^2 ~ & \textcolor{red}{ \text{ The Pythagorean equation.}} \\ x^2 = 64 + 64 ~ & \textcolor{red}{ \text{ Exponents first: } 8^2 = 64 \text{ and } 8^2 = 64.} \\ x^2 = 128 ~ & \textcolor{red}{ \text{ Add: } 64 + 64 = 128.} \\ x = \sqrt{128} ~ & \textcolor{red}{ \text{ Take the nonnegative square root.}} \end{aligned}\nonumber \]

4. Answer the Question . The exact length of the hypotenuse is \(\sqrt{128}\) feet, but we’re asked to find the hypotenuse to the nearest tenth of a foot. Using a calculator, we find an approximation for \(\sqrt{128}\).

\[\sqrt{128} \approx 11.313708499\nonumber \]

To round to the nearest tenth, first identify the rounding and test digits.

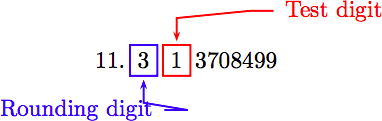
The test digit is less than five. So we leave the rounding digit alone and truncate. Therefore, correct to the nearest tenth of a foot, the length of the hypotenuse is approximately 11.3 feet.

5. Look Back . The sum of the squares of the legs is

\[ \begin{aligned} 8^2 + 8^2 = 64 + 64 \\ = 128. \end{aligned}\nonumber \]

The square of the hypotenuse is

\[(11.3)^2 = 127.69\nonumber \]

These are almost the same, the discrepancy due to the fact that we rounded to find an approximation for the hypotenuse.

A 15 foot ladder leans against the wall of a building. The base of the ladder lies 5 feet from the base of the wall. How high up the wall does the top of the ladder reach? Round your answer to the nearest tenth of a foot.

In Exercises 1-16, your solutions should include a well-labeled sketch.

1. The length of one leg of a right triangle is 15 meters, and the length of the hypotenuse is 25 meters. Find the exact length of the other leg.

2. The length of one leg of a right triangle is 7 meters, and the length of the hypotenuse is 25 meters. Find the exact length of the other leg.

3. The lengths of two legs of a right triangle are 12 meters and 16 meters. Find the exact length of the hypotenuse.

4. The lengths of two legs of a right triangle are 9 meters and 12 meters. Find the exact length of the hypotenuse.

5. The length of one leg of a right triangle is 13 meters, and the length of the hypotenuse is 22 meters. Find the exact length of the other leg.

6. The length of one leg of a right triangle is 6 meters, and the length of the hypotenuse is 15 meters. Find the exact length of the other leg.

7. The lengths of two legs of a right triangle are 2 meters and 21 meters. Find the exact length of the hypotenuse.

8. The lengths of two legs of a right triangle are 7 meters and 8 meters. Find the exact length of the hypotenuse.

9. The length of one leg of a right triangle is 12 meters, and the length of the hypotenuse is 19 meters. Find the exact length of the other leg.

10. The length of one leg of a right triangle is 5 meters, and the length of the hypotenuse is 10 meters. Find the exact length of the other leg.

11. The lengths of two legs of a right triangle are 6 meters and 8 meters. Find the exact length of the hypotenuse.

12. The lengths of two legs of a right triangle are 5 meters and 12 meters. Find the exact length of the hypotenuse.

13. The length of one leg of a right triangle is 6 meters, and the length of the hypotenuse is 10 meters. Find the exact length of the other leg.

14. The length of one leg of a right triangle is 9 meters, and the length of the hypotenuse is 15 meters. Find the exact length of the other leg.

15. The lengths of two legs of a right triangle are 6 meters and 22 meters. Find the exact length of the hypotenuse.

16. The lengths of two legs of a right triangle are 9 meters and 19 meters. Find the exact length of the hypotenuse.

In Exercises 17-24, your solutions should include a well-labeled sketch.

17. The lengths of two legs of a right triangle are 3 meters and 18 meters. Find the length of the hypotenuse. Round your answer to the nearest hundredth.

18. The lengths of two legs of a right triangle are 10 feet and 16 feet. Find the length of the hypotenuse. Round your answer to the nearest tenth.

19. The length of one leg of a right triangle is 2 meters, and the length of the hypotenuse is 17 meters. Find the length of the other leg. Round your answer to the nearest tenth.

20. The length of one leg of a right triangle is 4 meters, and the length of the hypotenuse is 12 meters. Find the length of the other leg. Round your answer to the nearest hundredth.

21. The lengths of two legs of a right triangle are 15 feet and 18 feet. Find the length of the hypotenuse. Round your answer to the nearest hundredth.

22. The lengths of two legs of a right triangle are 6 feet and 13 feet. Find the length of the hypotenuse. Round your answer to the nearest tenth.

23. The length of one leg of a right triangle is 4 meters, and the length of the hypotenuse is 8 meters. Find the length of the other leg. Round your answer to the nearest hundredth.

24. The length of one leg of a right triangle is 3 meters, and the length of the hypotenuse is 15 meters. Find the length of the other leg. Round your answer to the nearest tenth.

25. Greta and Fritz are planting a 13-meter by 18-meter rectangular garden, and are laying it out using string. They would like to know the length of a diagonal to make sure that right angles are formed. Find the length of a diagonal. Round your answer to the nearest hundredth. Your solution should include a well-labeled sketch.

26. Markos and Angelina are planting an 11- meter by 19-meter rectangular garden, and are laying it out using string. They would like to know the length of a diagonal to make sure that right angles are formed. Find the length of a diagonal. Round your answer to the nearest tenth. Your solution should include a well-labeled sketch.

27. The base of a 24-meter long guy wire is located 10 meters from the base of the telephone pole that it is anchoring. How high up the pole does the guy wire reach? Round your answer to the nearest hundredth. Your solution should include a well-labeled sketch.

28. The base of a 30-foot long guy wire is located 9 feet from the base of the telephone pole that it is anchoring. How high up the pole does the guy wire reach? Round your answer to the nearest hundredth. Your solution should include a well-labeled sketch.

29. Hiking Trail. A hiking trail runs due south for 8 kilometers, then turns west for about 15 kilometers, and then heads northeast on a direct path to the starting point. How long is the entire trail?

30. Animal Trail. An animal trail runs due east from a watering hole for 12 kilometers, then goes north for 5 kilometers. Then the trail turns southwest on a direct path back to the watering hole. How long is the entire trail?

31. Upper Window. A 10-foot ladder leans against the wall of a house. How close to the wall must the bottom of the ladder be in order to reach a window 8 feet above the ground?

32. How high? A 10-foot ladder leans against the wall of a house. How high will the ladder be if the bottom of the ladder is 4 feet from the wall? Round your answer to the nearest tenth.

1. 20 meters

3. 20 meters

5. √315 meters

7. \(\sqrt{445}\) meters

9. \(\sqrt{217}\) meters

11. 10 meters

13. 8 meters

15. \(\sqrt{520}\) meters

17. 18.25 meters

19. 16.9 meters

21. 23.43 feet

23. 6.93 meters

25. 22.20 meters

27. 21.82 meters

29. 40 kilometers