solving rational equations homework answers

Study Guides > College Algebra CoRequisite Course

Solve rational equations, learning outcomes.

• Solve rational equations by clearing denominators
• Identify extraneous solutions in a rational equation

[latex]\begin{array}{c}\frac{1}{2}x-3=2-\frac{3}{4}x\\ 4\left(\frac{1}{2}x-3\right)=4\left(2-\frac{3}{4}x\right)\\\text{}\\\,\,\,\,4\left(\frac{1}{2}x\right)-4\left(3\right)=4\left(2\right)+4\left(-\frac{3}{4}x\right)\\2x-12=8-3x\\\underline{+3x}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\underline{+3x}\\5x-12=8\,\,\,\,\,\,\,\,\\\,\,\,\,\,\,\,\underline{+12}\,\,\,\,\underline{+12} \\5x=20\\x=4\end{array}[/latex]

[latex]\begin{array}{r}8\cdot \frac{x+5}{8}=\frac{7}{4}\cdot 8\,\,\,\,\,\,\,\\\\\frac{8(x+5)}{8}=\frac{7(8)}{4}\,\,\,\,\,\,\\\\\frac{8}{8}\cdot (x+5)=\frac{7(4\cdot 2)}{4}\\\\\frac{8}{8}\cdot (x+5)=7\cdot 2\cdot \frac{4}{4}\\\\1\cdot (x+5)=14\cdot 1\,\,\,\end{array}[/latex]

[latex]\begin{array}{r}x+5=14\\x=9\,\,\,\end{array}[/latex]

[latex]\begin{array}{r}\frac{x+5}{8}=\frac{7}{4}\\\\\frac{9+5}{8}=\frac{7}{4}\\\\\frac{14}{8}=\frac{7}{4}\\\\\frac{7}{4}=\frac{7}{4}\end{array}[/latex]

[latex]\begin{array}{c}3\left(x+1\right)\left(\frac{8}{x+1}\right)=3\left(x+1\right)\left(\frac{4}{3}\right)\end{array}[/latex]

Simplify common factors.

[latex]\begin{array}{c}3\cancel{\left(x+1\right)}\left(\frac{8}{\cancel{x+1}}\right)=\cancel{3}\left(x+1\right)\left(\frac{4}{\cancel{3}}\right)\\24=4\left(x+1\right)\\24=4x+4\end{array}[/latex]

Now this looks like a linear equation, and we can use the addition and multiplication properties of equality to solve it.

[latex]\begin{array}{c}24=4x+4\\\underline{-4}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\underline{-4}\\20=4x\,\,\,\,\,\,\,\,\\\\x=5\,\,\,\,\,\,\,\,\,\end{array}[/latex]

[latex]\begin{array}{r}\,\,\,\,\,\frac{8}{\left(x+1\right)}=\frac{4}{3}\\\\\frac{8}{\left(5+1\right)}=\frac{4}{3}\\\\\frac{8}{6}=\frac{4}{3}\\\frac{4}{3}=\frac{4}{3}\end{array}[/latex]

[latex] 3\left( \frac{x}{3}+1 \right)=3\left( \frac{4}{3} \right)[/latex]

[latex]\begin{array}{r}3\left( \frac{x}{3} \right)+3\left( 1 \right)=3\left( \frac{4}{3} \right)\\\\\cancel{3}\left( \frac{x}{\cancel{3}} \right)+3\left( 1 \right)=\cancel{3}\left( \frac{4}{\cancel{3}} \right)\\\\ x+3=4\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\underline{-3}\,\,\,\,\,\underline{-3}\\\\x=1\end{array}[/latex]

Excluded Values and Extraneous Solutions

[latex] \frac{2x-5}{x-5}=\frac{15}{x-5}[/latex]

[latex]\begin{array}{r}2x-5=15\\2x=20\\x=10\end{array}[/latex]

[latex]\begin{array}{r}\frac{2x-5}{x-5}=\frac{15}{x-5}\,\,\\\\\frac{2(10)-5}{10-5}=\frac{15}{10-5}\\\\\frac{20-5}{10-5}=\frac{15}{10-5}\\\\\frac{15}{5}=\frac{15}{5}\,\,\,\,\,\,\,\,\,\end{array}[/latex]

[latex]\begin{array}{l}16=m^{2}\\\,\,\,0={{m}^{2}}-16\\\,\,\,0=\left( m+4 \right)\left( m-4 \right)\end{array}[/latex]

[latex]\begin{array}{c}0=m+4\,\,\,\,\,\,\text{or}\,\,\,\,\,\,0=m-4\\m=-4\,\,\,\,\,\,\text{or}\,\,\,\,\,\,m=4\\m=4,-4\end{array}[/latex]

[latex]\begin{array}{c}\frac{16}{m+4}=\frac{{{m}^{2}}}{m+4}\\\\\frac{16}{-4+4}=\frac{{{(-4)}^{2}}}{-4+4}\\\\\frac{16}{0}=\frac{16}{0}\end{array}[/latex]

[latex]\begin{array}{c}\frac{16}{4+4}=\frac{{{(4)}^{2}}}{4+4}\\\\\frac{16}{8}=\frac{16}{8}\end{array}[/latex]

Licenses & Attributions

Cc licensed content, original.

• Revision and Adaptation. Provided by: Lumen Learning License: CC BY: Attribution .
• Solve Basic Rational Equations. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution .
• Solve Rational Equations with Like Denominators. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution .

CC licensed content, Shared previously

• Unit 15: Rational Expressions, from Developmental Math: An Open Program. Provided by: Monterey Institute of Technology and Education License: CC BY: Attribution .
• Ex 2: Solve a Literal Equation for a Variable. Authored by: James Sousa (Mathispower4u.com). License: CC BY: Attribution .

Please add a message.

Message received. Thanks for the feedback.

Solving Rational Equations · Examples

Listen up, fraction fans! In today’s lesson, you will learn and practice solving rational equations. As you will see, these are any equation involving a fraction, also known as a rational number in math talk!

By the end, you will know the difference between rational and irrational numbers and have two tricks for solving rational equations.

You could even tackle one of the tricky challenges to form a rational equation using the Pythagorean theorem , or to simplify an expression involving some radicals!

What is a Rational Equation? How to Solve Rational Equations Step 1: Eliminate the Denominators Step 2: Simplify the Equation Step 3: Solve the Equation Step 4: Check Solutions Practice & Challenges Question 1 Question 2 Challenge 1 Challenge 2 Worksheet To Sum Up (Pun Intended!)

What is a Rational Equation?

A rational equation is simply an equation involving a rational number.

A ratio -nal number can be written as a ratio of two integers – an irratio -nal number cannot.

Most of the numbers you know and love such as \(\Large\frac{2}{7}\), \(\Large\frac{1}{2}\) and \(-\Large\frac{20817}{43}\) are rational. Some common irrational numbers are π, \(\sqrt{2}\) and Euler’s number, e. These cannot be written as a fraction of integers.

Numberphile has an interesting video about All the Numbers , which categorizes number types, including rational and irrational numbers .

Technically speaking, basic equations like x+2=5 are rational because each term is a rational number. However, the rational equations you will solve today won’t be so easy!

An example of what you will more likely see in an exam is something like this:

Each term is shown as a fraction.

Rational equations can also include radicals:

Or other operations such as division:

Luckily, the technique you learn now will work for every type of rational equation!

How to Solve Rational Equations

The method to solve these equations is pretty much the same for every type of rational equation. You’ll see questions of varying difficulty in this lesson; don’t be afraid to tackle the challenges later on!

Step 1: The Denominator Elimination Round!

First, you need to deal with the elephant in the room: what should you do with the denominators!?

Solving rational equations is just like solving any other equation once you complete this step.

If it’s a simple case, where you have one fraction being equal to one other fraction, you can cross multiply .

Multiply both sides by the values of both denominators. In this example, both sides are multiplied by 3, then 5.

The 3 cancels with the left denominator and the 5 cancels with the right denominator, leaving you with 5(x+4)=3×2.

See why it’s called cross multiplying?

The product of the left denominator and right numerator equals the product of the right denominator and left numerator !

The more general way to deal with the denominators is to find their lowest common multiple (LCM) . This is the smallest number which all denominators divide neatly, leaving no remainder.

If you cannot find the LCM by inspection – if you cannot “just see it” – you need to factor every denominator like you would with a polynomial.

If you have more than one constant term, you may need to find their prime factors.

The LCM is the smallest combination of each denominator’s factors.

You’ll now see a worked example to illustrate!

Remember, you can only cross multiply when each side has only one fraction, so in this case, your first step is to find the LCM.

The only factors of 3x you know for certain are 3 and x. The only factor you know of x is just x, and 4 is a constant so you can use it as it is.

Write down each denominator’s polynomial factors into rows, with similar terms lined up in the same column.

You need to include both 3 and 4 because neither is a factor of the other. You don’t need both copies of x because x is a factor of itself! So the LCM is 12x.

You might find another example of finding the LCM with the same technique helpful.

You’re now ready to eliminate the denominators by multiplying both sides by the LCM.

Step 2: Simplify the Equation

Multiply each term by the LCM. Continuing from the last example, you have:

You now have a regular equation with no fractions, which should be familiar ground!

Step 3: Solve the Equation

Solving rational equations usually produces a simple polynomial equation. Hopefully, you’ve solved lots of these before!

You could complete the square, factor the terms by inspection, or use the quadratic formula.

This example can be solved by factoring the polynomial, having found that x+2 and x+4 are factors.

You could also solve the equation by completing the square:

Or by using the quadratic formula with a=1, b=6 and c=8:

Each way of solving the simplified rational equation is valid, but you will find that some are quicker than others!

Step 4: Check Every Solution

It is important to check that your solutions are complete, meaning you’ve found all of them and that they don’t give any weird numbers when substituted into the original equation.

In the worked example, you were left with a quadratic equation and found two distinct roots.

Quadratic equations either have two distinct solutions, one repeated solution, or no real solution so the solution x=-2 or x=-4 is complete.

You must be careful that none of the rational terms in the original equation have a zero in the denominator.

Do this by going back to the beginning and substituting your answers into the denominators!

The denominators in the worked example are 3x, x, and 4. Replacing x with -2 or -4 doesn’t give you zero in any of them, so you’re safe here!

A solution that gives a zero-denominator is not allowed. That’s because dividing by zero is “illegal” in math!

Any number divided by zero gives an error on a calculator. Ever wondered why that is?

This is your time to shine – try solving rational equations for yourself and, if you’re feeling confident, tackle the challenges too.

As they say, practice makes perfect! Use the worked example for guidance if you get stuck.

Find x in the following rational equation:

The equation is two equal fractions so you can cross-multiply. You could also simplify \(\Large\frac{15}{3}\normalsize\) to 5, but this does not change the final answer.

Each term is divisible by 9. Simplify the equation by dividing both sides by 9:

This form is called the difference of two squares because it can be factored like this:

So the solution is x=±3.

These must be all the solutions because quadratic equations have a maximum of two distinct real roots.

Neither denominator in the original rational equation has an x term, so substituting any value for x makes no difference to their values – there is no chance of them being zero!

This means the solutions x=3 and x=-3 are valid.

Solve the following rational equation:

There are three fractions so you cannot cross-multiply.

See that the second denominator is the difference of two squares?

Multiply each term by the LCM and simplify.

So its solution is -5, right?… STOP RIGHT THERE! Don’t forget, we can’t divide by zero!

If you put x=±5 into the original equation, at least one of the denominators is always zero, so the original equation has no solutions.

Challenge 1

Can you spot the mistake in the following example? Hint: there has been some cheating with radicals!

If you need a refresher on radicals , check out our lesson on multiplying them. That will get you on the right track!

The mistake is that radicals cannot be subtracted like normal terms.

Instead, you must square both sides of the equation to remove the radical. Similar terms can then be combined as usual.

Still confused? You can find lots of interactive questions on Lumen Learning . Radicals often pop up in rational equations, so getting comfortable with radicals is super helpful for exam success!

Challenge 2

Find the value of x, by using the Pythagorean theorem on the following right-angled triangle:

If you need a refresher on the Pythagorean theorem or are interested in the man himself, check out our lesson. Do the worksheets and you’ll be acing triangle questions in no time !

The Pythagorean theorem states that:

Where c is the length of the hypotenuse, and a and b are the other side lengths.

This gives the rational equation:

Simplifying, you find:

The LCM is 36 so the denominators are removed by dividing each term by this:

It’s always fun when different areas of math link together!

To Sum Up (Pun Intended!)

In today’s lesson on solving rational equations, you first saw the difference between rational and irrational numbers.

Rational numbers are “nice” because they can be written as a fraction of integers. Remember that all integers are rational because they can be written with a denominator of 1!

Irrational numbers are a little more abstract. They include weird but incredibly beautiful numbers like π and e, which cannot be written as a fraction of integers.

Rational equations are solved by eliminating the denominator in every term, then simplifying and solving as normal.

Denominators can be removed by cross-multiplication if there is only one fraction on either side or by finding the LCM if the equation is more complicated.

Don’t be shy, leave a comment below if you have any questions or need help!

Still curious about rational numbers, or eager for an extra challenge? Check out our lesson on the rational root theorem , which combines algebra and equation solving.

Leave a Comment Cancel Reply

Your email address will not be published. Required fields are marked *

Save my name, email, and website in this browser for the next time I comment.

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Course: Algebra 2   >   Unit 10

Rational equations intro.

• Equations with rational expressions
• Equations with rational expressions (example 2)
• Rational equations
• Finding inverses of rational functions
• Find inverses of rational functions

Want to join the conversation?

• Upvote Button navigates to signup page
• Downvote Button navigates to signup page
• Flag Button navigates to signup page

Video transcript

• Math Lessons Online

Lesson 3 Homework Practice Solve Equations with Rational Coefficients

You’re now diving into Lesson 3 , where your mission will be to tackle equations with rational coefficients. The term ‘rational coefficients’ is intimidating. But don’t worry! We’re here to break it down. A rational coefficient is a fancy term for a number that can be formulated as a ratio of two integers. It provides a logical framework to tackle complex equations.

Overview of solving equations with rational coefficients

First up, let’s take a clear look at equations. You can think about equations like balanced see-saws. Whatever you do on one side has to be balanced out on the other side. Equations with rational coefficients can be easily simplified by manipulating the fractional coefficients to isolate the variable.

Step 1:  Identify the rational coefficient. The fraction in the equation is multiplied by the variable (e.g., 2/3x = 4).

Step 2:  To isolate your variable, you will perform the inverse operation to eliminate the rational coefficient. You’ll multiply both sides of your equation by the reciprocal of your rational coefficient.

Example:  Let’s use the equation above. If we multiply both sides of 2/3x = 4 by 3/2 (the reciprocal of 2/3), we get 1x = 6. And voila, you have your solution.

In just a few steps, you’ve tackled equations with rational coefficients. Don’t let challenges discourage you in mathematics. It involves estimation, trial and error, and practice. But you can master it. Keep practicing, be persistent, and continue to hone your problem-solving skills . Remember, every mathematician learns at their own pace. You got this!

Practice is the key here, so nail down these steps and tackle additional problems independently. Happy solving!

The Concept of Rational Coefficients

You’ve made it to Lesson 3 , where you’ll tackle problems including rational coefficients. It might seem daunting at first, but with a systematic approach and a little practice, you’ll quickly learn how to navigate this mathematical territory.

Explanation of rational coefficients and their role in equations

In algebra, a rational coefficient is a ratio of two integers with a zero denominator. It is important to remember that these coefficients, just like any number in an algebraic equation, can be manipulated through the usual multiplication, division, addition, and subtraction.

Now, you ask, how do rational coefficients affect the equation? These coefficients play a pivotal role in determining the solution to the equation.

Here is how you can approach it:

Step 1:  Simplify the equation. If you have fractions in the equation, sometimes called rational numbers , making them whole numbers is easier. You can multiply every term with the least common denominator (LCD).

Step 2:  The next step is to use simple math techniques to find the variable. It is fundamentally the same as solving any basic algebraic equation –addition, subtraction, multiplication, and division are your friends.

Step 3:  Remember to check if your solution is correct. Substitute the solution into the original equation and see if both sides balance.

Remember:  The key to mastering equations with rational coefficients is understanding and accurately manipulating these coefficients to find your solution.

Remember, the key to success is consistent practice. Each equation you tackle improves your skill and confidence. Solving equations with rational coefficients will be easy. Good luck!

Let’s recap:

Techniques for Solving Equations with Rational Coefficients

As an aspiring mathematician or someone trying to polish their math skills , navigating the world of equations with rational coefficients can sometimes seem daunting. Worry not! Let’s simplify the process into two easy-to-follow steps: clearing fractions and cross-multiplication.

Step-by-step methods for solving equations with rational coefficients

Step 1:  Identify the equation with a rational coefficient. Rational coefficients are fractions expressed as a ratio of two integers.

Step 2:  Apply one of the strategies below to solve the equation.

• Method 1: Clearing Fractions

Wherever you see fractions, simplify them!

Step 1:  Multiply each term in the equation by the fraction’s denominator to clear the fractions.

Step 2:  Carry out the arithmetic operations and solve the equation.

Step 3:  Check your work by substituting the solution into the original equation. If it makes the equation true, then your solution is correct.

• Method 2: Cross-Multiplication

When your solution is a proportion, this method works well.

Step 1:  Use cross-multiplication if two fractions are set equal.

Step 2:  Multiply the terms diagonally and set the products equal.

Step 3:  Solve for the variable.

Step 4:  Verify your solution by plugging it into the original equation.

Please make no mistake: the key to mastering mathematical equations is through practice, and lots of it. Please don’t avoid making mistakes; use them to strengthen your understanding and sharpen your skills. Get your homework and apply the strategies you learned. You can solve these problems if you keep practicing. With unwavering dedication and practice, you can conquer any equation that comes your way.

Examples and Practice Problems

You’ll come across equations with rational terms as you learn math. At first, it might seem challenging, but after reading this blog, you can do it like a pro!

Solving equations with rational coefficients through examples and practice problems

As you embark on your mathematical journey, you are bound to encounter equations with rational coefficients. By the end of this guide, you will be a pro at solving these types of equations.

• Example 1: Clearing fractions and solving for the variable

Take this equation:  3/4x = 6. First, clear out the fraction by multiplying both sides of the equation by 4. You’ll get 3x = 24. Now, try solving for ‘x’ by dividing 24 by 3. Your answer will be x = 8.

Now let’s practice:

• Try solving 2/7y = 6.
• Keep in mind the steps followed in the example.
• Clear the fraction, isolate the variable, and solve for ‘y’.
• Example 2: Cross-multiplication to solve for the variable

Here’s our equation:  4/5 = x/10. Cross-multiplication involves multiplying the fraction’s numerator on the left by the fraction’s denominator on the right and vice versa. This gives us 4 10 = 5 x, which simplifies to 40 = 5x.

Proceed with the operation:  Solve for ‘x’ by dividing both sides by 5, which leaves us with x = 8.

Time to practice:  Try the same steps with the equation 3/4 = y/12. Follow this example above, and you can solve this equation effectively.

In both types of equations, remember always to check your answers. Substituting your calculated value into the original equation should give you a true statement. These tutorials can guide you in solving complex equations and hone your skills.

• Grade 1 Lessons
• Grade 2 Lessons
• Grade 3 Lessons
• Grade 4 Lessons
• Grade 5 Lessons
• Grade 6 Lessons
• Grade 7 Lessons
• Grade 8 Lessons
• Kindergarten
• Math Activities
• Math Tutorial
• Multiplication
• Subtraction
• #basic mathematic
• #Basic Mathematical Operation
• #best math online math tutor
• #Best Math OnlineTutor
• #dividing fractions
• #effective teaching
• #grade 8 math lessons
• #linear equation
• #Math Online Blog
• #mathematical rule
• #mutiplying fractions
• #odd and even numbers
• #Online Math Tutor
• #online teaching
• #order of math operations
• #pemdas rule
• #Point-Slope Form
• #Precalculus
• #Slope-Intercept Form
• #Tutoring Kids

Thank you for signing up!

GET IN TOUCH WITH US

Rational Equations: Solving

This packet helps students understand how to solve rational equations. Each page starts with easier problems that get more difficult as students work through the packet. After doing all 30 problems, students should be more comfortable doing these problems and have a clear understanding of how to solve them. 

Solve for the variable.   

$\dfrac{2}{x} + \dfrac{2}{3} = \dfrac{1}{x}$ 

$\dfrac{4}{x-3} - \dfrac{x}{x+3} = 1$

Practice problems require knowledge of addition, subtraction, mutliplication, and division of fractions.

Solving Rational Equations (Proportions)

Solving Rational Equations (with addition or subtraction)

Video provided by Khan Academy ( www.khanacademy.org ).

Ed Boost  - 3300 Overland Avenue, #202, Los Angeles, CA 90034 - Phone: 310.559.1991 - Fax: 323.345.6473 - edboost at edboost dot org

Smarter Kids, Better world

Copyright© 2024,

Game Central

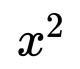
Get step-by-step explanations

Graph your math problems

Practice, practice, practice

Get math help in your language

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

7.4: Solve Rational Equations

• Last updated
• Save as PDF
• Page ID 51477

Learning Objectives

• Solve rational equations by clearing denominators
• Identify extraneous solutions in a rational equation
• Solve for a variable in a rational formula
• Identify the components of a work equation
• Solve a work equation
• Define and write a proportion
• Solve proportional problems involving scale drawings
• Define direct variation, and solve problems involving direct variation
• Define inverse variation and solve problems involving inverse variation
• Define joint variation and solve problems involving joint variation

Equations that contain rational expressions are called rational equations . For example, \(\frac{2x+1}{4}=\frac{x}{3}\) is a rational equation. Rational equations can be useful for representing real-life situations and for finding answers to real problems. In particular, they are quite good for describing a variety of proportional relationships.

One of the most straightforward ways to solve a rational equation is to eliminate denominators with the common denominator, then use properties of equality to isolate the variable. This method is often used to solve linear equations that involve fractions as in the following example:

Solve \(\frac{1}{2}x-3=2-\frac{3}{4}x\) by clearing the fractions in the equation first.

Multiply both sides of the equation by 4, the common denominator of the fractional coefficients.

\(\begin{array}{c}\frac{1}{2}x-3=2-\frac{3}{4}x\\ 4\left(\frac{1}{2}x-3\right)=4\left(2-\frac{3}{4}x\right)\\\text{}\\\,\,\,\,4\left(\frac{1}{2}x\right)-4\left(3\right)=4\left(2\right)+4\left(-\frac{3}{4}x\right)\\2x-12=8-3x\\\underline{+3x}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\underline{+3x}\\5x-12=8\,\,\,\,\,\,\,\,\\\,\,\,\,\,\,\,\underline{+12}\,\,\,\,\underline{+12} \\5x=20\\x=4\end{array}\)

We could have found a common denominator and worked with fractions, but that often leads to more mistakes. We can apply the same idea to solving rational equations. The difference between a linear equation and a rational equation is that rational equations can have polynomials in the numerator and denominator of the fractions. This means that clearing the denominator may sometimes mean multiplying the whole rational equation by a polynomial. In the next example, we will clear the denominators of a rational equation with a terms that has a polynomial in the numerator.

Solve the equation \(2\cdot2\cdot2\), or 8, will be the LCM.

\(\begin{array}{l}4=2\cdot2\\8=2\cdot2\cdot2\cdot2\\\text{LCM}=2\cdot2\cdot2\\\text{LCM}=8\end{array}\)

The LCM of 4 and 8 is also the lowest common denominator for the two fractions.

Multiply both sides of the equation by the common denominator, 8, to keep the equation balanced and to eliminate the denominators.

\(\begin{array}{r}8\cdot \frac{x+5}{8}=\frac{7}{4}\cdot 8\,\,\,\,\,\,\,\\\\\frac{8(x+5)}{8}=\frac{7(8)}{4}\,\,\,\,\,\,\\\\\frac{8}{8}\cdot (x+5)=\frac{7(4\cdot 2)}{4}\\\\\frac{8}{8}\cdot (x+5)=7\cdot 2\cdot \frac{4}{4}\\\\1\cdot (x+5)=14\cdot 1\,\,\,\end{array}\)

Simplify and solve for x .

\(\begin{array}{r}x+5=14\\x=9\,\,\,\end{array}\)

Check the solution by substituting 9 for x in the original equation.

\(\begin{array}{r}\frac{x+5}{8}=\frac{7}{4}\\\\\frac{9+5}{8}=\frac{7}{4}\\\\\frac{14}{8}=\frac{7}{4}\\\\\frac{7}{4}=\frac{7}{4}\end{array}\)

[/hidden-answer]

In the next example, we show how to solve a rational equation with a binomial in the denominator of one term. We will use the common denominator to eliminate the denominators from both fractions. Note that the LCD is the product of both denominators because they don’t share any common factors.

Solve the equation \(\frac{8}{x+1}=\frac{4}{3}\).

[reveal-answer q=”331190″]Show Solution[/reveal-answer] [hidden-answer a=”331190″]Clear the denominators by multiplying each side by the common denominator. The common denominator is \(3\text{ and }x+1\) don’t have any common factors.

\(\begin{array}{c}3\left(x+1\right)\left(\frac{8}{x+1}\right)=3\left(x+1\right)\left(\frac{4}{3}\right)\end{array}\)

Simplify common factors.

\(\begin{array}{c}3\cancel{\left(x+1\right)}\left(\frac{8}{\cancel{x+1}}\right)=\cancel{3}\left(x+1\right)\left(\frac{4}{\cancel{3}}\right)\\24=4\left(x+1\right)\\24=4x+4\end{array}\)

Now this looks like a linear equation, and we can use the addition and multiplication properties of equality to solve it.

\(\begin{array}{c}24=4x+4\\\underline{-4}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\underline{-4}\\20=4x\,\,\,\,\,\,\,\,\\\\x=5\,\,\,\,\,\,\,\,\,\end{array}\)

Check the solution in the original equation.

\(\begin{array}{r}\,\,\,\,\,\frac{8}{\left(x+1\right)}=\frac{4}{3}\\\\\frac{8}{\left(5+1\right)}=\frac{4}{3}\\\\\frac{8}{6}=\frac{4}{3}\end{array}\)

Reduce the fraction \(\frac{8}{6}\) by simplifying the common factor of 2:

\(\large\frac{\cancel{2}\cdot4}{\cancel{2}\cdot3}\normalsize=\large\frac{4}{3}\)

You could also solve this problem by multiplying each term in the equation by 3 to eliminate the fractions altogether. Here is how it would look.

Solve the equation \(\frac{x}{3}+1=\frac{4}{3}\).

[reveal-answer q=”950823″]Show Solution[/reveal-answer] [hidden-answer a=”950823″]Both fractions in the equation have a denominator of 3. Multiply both sides of the equation (not just the fractions!) by 3 to eliminate the denominators.

\(3\left( \frac{x}{3}+1 \right)=3\left( \frac{4}{3} \right)\)

Apply the distributive property and multiply 3 by each term within the parentheses. Then simplify and solve for x .

\(\begin{array}{r}3\left( \frac{x}{3} \right)+3\left( 1 \right)=3\left( \frac{4}{3} \right)\\\\\cancel{3}\left( \frac{x}{\cancel{3}} \right)+3\left( 1 \right)=\cancel{3}\left( \frac{4}{\cancel{3}} \right)\\\\ x+3=4\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\underline{-3}\,\,\,\,\,\underline{-3}\\\\x=1\end{array}\)

In the video that follows we present two ways to solve rational equations with both integer and variable denominators.

A YouTube element has been excluded from this version of the text. You can view it online here: pb.libretexts.org/ba/?p=132

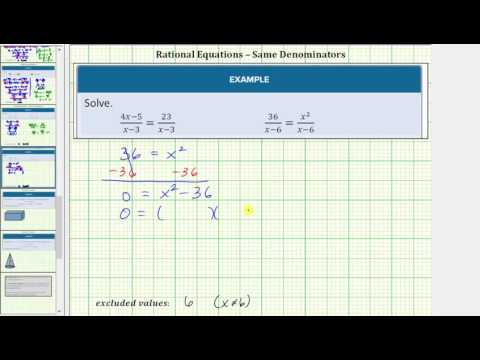
Excluded Values and Extraneous Solutions

Some rational expressions have a variable in the denominator. When this is the case, there is an extra step in solving them. Since division by 0 is undefined, you must exclude values of the variable that would result in a denominator of 0. These values are called excluded values . Let’s look at an example.

Solve the equation \(\frac{2x-5}{x-5}=\frac{15}{x-5}\).

[reveal-answer q=”266674″]Show Solution[/reveal-answer] [hidden-answer a=”266674″]Determine any values for x that would make the denominator 0.

\(\frac{2x-5}{x-5}=\frac{15}{x-5}\)

5 is an excluded value because it makes the denominator \(x-5\) equal to 0.

Since the denominator of each expression in the equation is the same, the numerators must be equal. Set the numerators equal to one another and solve for x.

\(\begin{array}{r}2x-5=15\\2x=20\\x=10\end{array}\)

\(\begin{array}{r}\frac{2x-5}{x-5}=\frac{15}{x-5}\,\,\\\\\frac{2(10)-5}{10-5}=\frac{15}{10-5}\\\\\frac{20-5}{10-5}=\frac{15}{10-5}\\\\\frac{15}{5}=\frac{15}{5}\,\,\,\,\,\,\,\,\,\end{array}\)

In the following video we present an example of solving a rational equation with variables in the denominator.

You’ve seen that there is more than one way to solve rational equations. Because both of these techniques manipulate and rewrite terms, sometimes they can produce solutions that don’t work in the original form of the equation. These types of answers are called extraneous solutions . That’s why it is always important to check all solutions in the original equations—you may find that they yield untrue statements or produce undefined expressions.

Solve the equation \(\frac{16}{m+4}=\frac ParseError: colon expected (click for details) Callstack: at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/07:_Rational_Expressions_and_Equations/7.04:_Solve_Rational_Equations), /content/body/div[5]/div[2]/p[1]/span, line 1, column 3 {m+4}\).

[reveal-answer q=”450589″]Show Solution[/reveal-answer] [hidden-answer a=”450589″]Determine any values for m that would make the denominator 0. \(m+4\) equal to 0.

Since the denominator of each expression in the equation is the same, the numerators must be equal. Set the numerators equal to one another and solve for m.

\(\begin{array}{l}16=m^{2}\\\,\,\,0= ParseError: EOF expected (click for details) Callstack: at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/07:_Rational_Expressions_and_Equations/7.04:_Solve_Rational_Equations), /content/body/div[5]/div[2]/p[4]/span, line 1, column 2 -16\\\,\,\,0=\left( m+4 \right)\left( m-4 \right)\end{array}\)

\(\begin{array}{c}0=m+4\,\,\,\,\,\,\text{or}\,\,\,\,\,\,0=m-4\\m=-4\,\,\,\,\,\,\text{or}\,\,\,\,\,\,m=4\\m=4,-4\end{array}\)

Check the solutions in the original equation.

Since \(m=−4\) leads to division by 0, it is an extraneous solution.

\(\begin{array}{c}\frac{16}{m+4}=\frac ParseError: colon expected (click for details) Callstack: at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/07:_Rational_Expressions_and_Equations/7.04:_Solve_Rational_Equations), /content/body/div[5]/div[2]/p[8]/span[1], line 1, column 3 {m+4}\\\\\frac{16}{-4+4}=\frac ParseError: colon expected (click for details) Callstack: at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/07:_Rational_Expressions_and_Equations/7.04:_Solve_Rational_Equations), /content/body/div[5]/div[2]/p[8]/span[2], line 1, column 6 {-4+4}\\\\\frac{16}{0}=\frac{16}{0}\end{array}\)

\(-4\) is excluded because it leads to division by 0.

\(\begin{array}{c}\frac{16}{4+4}=\frac ParseError: colon expected (click for details) Callstack: at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/07:_Rational_Expressions_and_Equations/7.04:_Solve_Rational_Equations), /content/body/div[5]/div[2]/p[10]/span, line 1, column 5 {4+4}\\\\\frac{16}{8}=\frac{16}{8}\end{array}\)

Rational formulas

Rational formulas can be useful tools for representing real-life situations and for finding answers to real problems. Equations representing direct, inverse, and joint variation are examples of rational formulas that can model many real-life situations. As you will see, if you can find a formula, you can usually make sense of a situation.

When solving problems using rational formulas, it is often helpful to first solve the formula for the specified variable. For example, work problems ask you to calculate how long it will take different people working at different speeds to finish a task. The algebraic models of such situations often involve rational equations derived from the work formula, \(W=rt\). The amount of work done ( W ) is the product of the rate of work ( r ) and the time spent working ( t ). Using algebra, you can write the work formula 3 ways:

Find the time (t): \(t=\frac{W}{r}\) (divide both sides by r)

Find the rate (r): \(r=\frac{W}{t}\) (divide both sides by t)

The formula for finding the density of an object is \(D=\frac{m}{v}\), where D is the density, m is the mass of the object and v is the volume of the object. Rearrange the formula to solve for the mass ( m ) and then for the volume ( v ).

[reveal-answer q=”537110″]Show Solution[/reveal-answer] [hidden-answer a=”537110″]Start with the formula for density.

\(D=\frac{m}{v}\)

Multiply both side of the equation by v to isolate m.

\(v\cdot D=\frac{m}{v}\cdot v\)

Simplify and rewrite the equation, solving for m .

\(\begin{array}{l}v\cdot D=m\cdot \frac{v}{v}\\v\cdot D=m\cdot 1\\v\cdot D=m\end{array}\)

To solve the equation \(D=\frac{m}{v}\) in terms of v , you will need do the same steps to this point, and then divide both sides by D .

\(\begin{array}{r}\frac{v\cdot D}{D}=\frac{m}{D}\\\\\frac{D}{D}\cdot v=\frac{m}{D}\\\\1\cdot v=\frac{m}{D}\\\\v=\frac{m}{D}\end{array}\)

\(v=\frac{m}{D}\)

Now let’s look at an example using the formula for the volume of a cylinder.

The formula for finding the volume of a cylinder is \(V=\pi{r^{2}}h\), where V is the volume, r is the radius and h is the height of the cylinder. Rearrange the formula to solve for the height ( h ).

[reveal-answer q=”644317″]Show Solution[/reveal-answer] [hidden-answer a=”644317″]Start with the formula for the volume of a cylinder.

\(V=\pi ParseError: EOF expected (click for details) Callstack: at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/07:_Rational_Expressions_and_Equations/7.04:_Solve_Rational_Equations), /content/body/div[6]/div[2]/p[3]/span, line 1, column 2 h\)

Divide both sides by \(\pi ParseError: EOF expected (click for details) Callstack: at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/07:_Rational_Expressions_and_Equations/7.04:_Solve_Rational_Equations), /content/body/div[6]/div[2]/p[4]/span, line 1, column 2 \) to isolate h.

\(\frac{V}{\pi ParseError: EOF expected (click for details) Callstack: at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/07:_Rational_Expressions_and_Equations/7.04:_Solve_Rational_Equations), /content/body/div[6]/div[2]/p[5]/span[1], line 1, column 2 }=\frac{\pi ParseError: EOF expected (click for details) Callstack: at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/07:_Rational_Expressions_and_Equations/7.04:_Solve_Rational_Equations), /content/body/div[6]/div[2]/p[5]/span[2], line 1, column 2 h}{\pi ParseError: EOF expected (click for details) Callstack: at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/07:_Rational_Expressions_and_Equations/7.04:_Solve_Rational_Equations), /content/body/div[6]/div[2]/p[5]/span[3], line 1, column 2 }\)

Simplify. You find the height, h , is equal to \(\frac{V}{\pi ParseError: EOF expected (click for details) Callstack: at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/07:_Rational_Expressions_and_Equations/7.04:_Solve_Rational_Equations), /content/body/div[6]/div[2]/p[6]/span, line 1, column 2 }\).

\(\frac{V}{\pi ParseError: EOF expected (click for details) Callstack: at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/07:_Rational_Expressions_and_Equations/7.04:_Solve_Rational_Equations), /content/body/div[6]/div[2]/p[7]/span, line 1, column 2 }=h\)

\(h=\frac{V}{\pi ParseError: EOF expected (click for details) Callstack: at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/07:_Rational_Expressions_and_Equations/7.04:_Solve_Rational_Equations), /content/body/div[6]/div[2]/div/p[1]/span, line 1, column 2 }\)

In the following video we give another example of solving for a variable in a formula, or as they are also called, a literal equation.

Applications of Rational Equations

Rational equations can be used to solve a variety of problems that involve rates, times and work. Using rational expressions and equations can help you answer questions about how to combine workers or machines to complete a job on schedule.

A “work problem” is an example of a real life situation that can be modeled and solved using a rational equation. Work problems often ask you to calculate how long it will take different people working at different speeds to finish a task. The algebraic models of such situations often involve rational equations derived from the work formula, \(d=rt\).) The amount of work done ( W ) is the product of the rate of work ( r ) and the time spent working ( t ). The work formula has 3 versions.

\(\begin{array}{l}W=rt\\\\\,\,\,\,\,t=\frac{W}{r}\\\\\,\,\,\,\,r=\frac{W}{t}\end{array}\)

Some work problems include multiple machines or people working on a project together for the same amount of time but at different rates. In that case, you can add their individual work rates together to get a total work rate. Let’s look at an example.

Myra takes 2 hours to plant 50 flower bulbs. Francis takes 3 hours to plant 45 flower bulbs. Working together, how long should it take them to plant 150 bulbs?

[reveal-answer q=”550322″]Show Solution[/reveal-answer] [hidden-answer a=”550322″]Think about how many bulbs each person can plant in one hour. This is their planting rate.

Myra: \(\frac{25\,\,\text{bulbs}}{1\,\,\text{hour}}\)

Francis: \(\frac{15\,\,\text{bulbs}}{1\,\,\text{hour}}\)

Combine their hourly rates to determine the rate they work together.

Myra and Francis together:

\(\frac{25\,\,\text{bulbs}}{1\,\,\text{hour}}+\frac{15\,\,\text{bulbs}}{1\,\,\text{hour}}=\frac{40\,\,\text{bulbs}}{1\,\,\text{hour}}\)

Use one of the work formulas to write a rational equation, for example \(r=\frac{W}{t}\). You know r , the combined work rate, and you know W , the amount of work that must be done. What you don’t know is how much time it will take to do the required work at the designated rate.

\(\frac{40}{1}=\frac{150}{t}\)

Solve the equation by multiplying both sides by the common denominator, then isolating t .

\(\begin{array}{c}\frac{40}{1}\cdot 1t=\frac{150}{t}\cdot 1t\\\\40t=150\\\\t=\frac{150}{40}=\frac{15}{4}\\\\t=3\frac{3}{4}\text{hours}\end{array}\)

It should take 3 hours 45 minutes for Myra and Francis to plant 150 bulbs together.

Other work problems go the other way. You can calculate how long it will take one person to do a job alone when you know how long it takes people working together to complete the job.

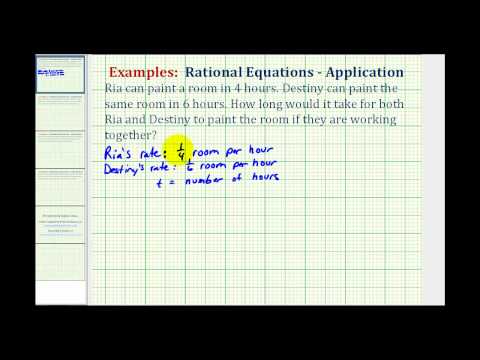
Joe and John are planning to paint a house together. John thinks that if he worked alone, it would take him 3 times as long as it would take Joe to paint the entire house. Working together, they can complete the job in 24 hours. How long would it take each of them, working alone, to complete the job?

[reveal-answer q=”593775″]Show Solution[/reveal-answer] [hidden-answer a=”593775″]Choose variables to represent the unknowns. Since it takes John 3 times as long as Joe to paint the house, his time is represented as 3 x .

Let x = time it takes Joe to complete the job

3 x = time it takes John to complete the job

The work is painting 1 house or 1. Write an expression to represent each person’s rate using the formula \(r=\frac{W}{t}\) .

Joe’s rate: \(\frac{1}{x}\)

John’s rate: \(\frac{1}{3x}\)

Their combined rate is the sum of their individual rates. Use this rate to write a new equation using the formula \(W=rt\).

combined rate: \(\frac{1}{x}+\frac{1}{3x}\)

The problem states that it takes them 24 hours together to paint a house, so if you multiply their combined hourly rate \(\left( \frac{1}{x}+\frac{1}{3x} \right)\) by 24, you will get 1, which is the number of houses they can paint in 24 hours.

\(\begin{array}{l}1=\left( \frac{1}{x}+\frac{1}{3x} \right)24\\\\1=\frac{24}{x}+\frac{24}{3x}\end{array}\)

Now solve the equation for x . (Remember that x represents the number of hours it will take Joe to finish the job.)

\(\begin{array}{l}\,\,\,1=\frac{3}{3}\cdot \frac{24}{x}+\frac{24}{3x}\\\\\,\,\,1=\frac{3\cdot 24}{3x}+\frac{24}{3x}\\\\\,\,\,1=\frac{72}{3x}+\frac{24}{3x}\\\\\,\,\,1=\frac{72+24}{3x}\\\\\,\,\,1=\frac{96}{3x}\\\\3x=96\\\\\,\,\,x=32\end{array}\)

\(\begin{array}{l}1=\left( \frac{1}{x}+\frac{1}{3x} \right)24\\\\1=\left[ \frac{\text{1}}{\text{32}}+\frac{1}{3\text{(32})} \right]24\\\\1=\frac{24}{\text{32}}+\frac{24}{3\text{(32})}\\\\1=\frac{24}{\text{32}}+\frac{24}{96}\\\\1=\frac{3}{3}\cdot \frac{24}{\text{32}}+\frac{24}{96}\\\\1=\frac{72}{96}+\frac{24}{96}[\end{array}\)

The solution checks. Since \(x=32\), it takes Joe 32 hours to paint the house by himself. John’s time is 3 x , so it would take him 96 hours to do the same amount of work.

It takes 32 hours for Joe to paint the house by himself and 96 hours for John the paint the house himself.

In the video that follows, we show another example of finding one person’s work rate given a combined work rate.

As shown above, many work problems can be represented by the equation \(\frac{t}{a}+\frac{t}{b}=1\), where t is the time to do the job together, a is the time it takes person A to do the job, and b is the time it takes person B to do the job. The 1 refers to the total work done—in this case, the work was to paint 1 house.

The key idea here is to figure out each worker’s individual rate of work. Then, once those rates are identified, add them together, multiply by the time t , set it equal to the amount of work done, and solve the rational equation.

We present another example of two people painting at different rates in the following video.

Proportions

A proportion is a statement that two ratios are equal to each other. There are many things that can be represented with ratios, including the actual distance on the earth that is represented on a map. In fact, you probably use proportional reasoning on a regular basis and don’t realize it. For example, say you have volunteered to provide drinks for a community event. You are asked to bring enough drinks for 35-40 people. At the store you see that drinks come in packages of 12. You multiply 12 by 3 and get 36 – this may not be enough if 40 people show up, so you decide to buy 4 packages of drinks just to be sure.

This process can also be expressed as a proportional equation and solved using mathematical principles. First, we can express the number of drinks in a package as a ratio:

\(\frac{12\text{ drinks }}{1\text{ package }}\)

Then we express the number of people who we are buying drinks for as a ratio with the unknown number of packages we need. We will use the maximum so we have enough.

\(\frac{40\text{ people }}{x\text{ packages }}\)

We can find out how many packages to purchase by setting the expressions equal to each other:

\(\frac{12\text{ drinks }}{1\text{ package }}=\frac{40\text{ people }}{x\text{ packages }}\)

To solve for x, we can use techniques for solving linear equations, or we can cross multiply as a shortcut.

\(\begin{array}{l}\,\,\,\,\,\,\,\frac{12\text{ drinks }}{1\text{ package }}=\frac{40\text{ people }}{x\text{ packages }}\\\text{}\\x\cdot\frac{12\text{ drinks }}{1\text{ package }}=\frac{40\text{ people }}{x\text{ packages }}\cdot{x}\\\text{}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,12x=40\\\text{}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x=\frac{40}{12}=\frac{10}{3}=3.33\end{array}\)

We can round up to 4 since it doesn’t make sense to by 0.33 of a package of drinks. Of course, you don’t write out your thinking this way when you are in the grocery store, but doing so helps you to be able to apply the concepts to less obvious problems. In the following example we will show how to use a proportion to find the number of people on teh planet who don’t have access to a toilet.

As of March, 2016 the world’s population was estimated at 7.4 billion. [1] . According to water.org , 1 out of every 3 people on the planet lives without access to a toilet. Find the number of people on the planet that do not have access to a toilet. [reveal-answer q=”54118″]Show Solution[/reveal-answer] [hidden-answer a=”54118″]

Read and Understand: We can use a proportion to find the unknown number of people who live without a toilet since we are given that 1 in 3 don’t have access, and we are given the population of the planet.

Define and Translate: We know that 1 out of every 3 people don’t have access, so we can write that as a ratio (fraction)

\(\frac{1\text{ doesn't }}{3\text{ do }}\).

Let the number of people without access to a toilet be x. The ratio of people with and without toilets is then

\(\frac{x\text{ don't }}{7.4\text{ billion do}}\)

Notice how it helps to use descriptions or units to know where to place the given numbers in the proportion.

Write and Solve: Equate the two ratios since they are representing the same fractional amount of the population.

\(\frac{1}{3}=\frac{x}{7.4\text{ billion }}\)

\(\begin{array}{l}\frac{1}{3}=\frac{x}{7.4}\\\text{}\\7.4\cdot\frac{1}{3}=\frac{x}{7.4}\cdot{7.4}\\\text{}\\2.46=x\end{array}\)

Interpret: The original units were billions of people, so our answer is \(2.46\) billion people don’t have access to a toilet. Wow, that’s a lot of people.

2.46 billion people don’t have access to a toilet.

In the next example, we will use the length of a person’t femur to estimate their height. This process is used in forensic science and anthropology, and has been found in many scientific studies to be a very good estimate.

It has been shown that a person’s height is proportional to the length of their femur [2] . Given that a person who is 71 inches tall has a femur length of 17.75 inches, how tall is someone with a femur length of 16 inches? [reveal-answer q=”987898″]Show Solution[/reveal-answer] [hidden-answer a=”987898″]

Read and Understand: Height and femur length are proportional for everyone, so we can define a ratio with the given height and femur length. We can then use this to write a proportion to find the unknown height.

Define and Translate: Let x be the unknown height. Define the ratio of femur length and height for both people using the given measurements.

Person 1: \(\frac{\text{femur length}}{\text{height}}=\frac{17.75\text{inches}}{71\text{inches}}\)

Person 2: \(\frac{\text{femur length}}{\text{height}}=\frac{16\text{inches}}{x\text{inches}}\)

Write and Solve: Equate the ratios, since we are assuming height and femur length are proportional for everyone.

\(\frac{17.75\text{inches}}{71\text{inches}}=\frac{16\text{inches}}{x\text{inches}}\)

Solve by using the common denominator to clear fractions. The common denominator is \(71x\)

\(\begin{array}{c}\frac{17.75}{71}=\frac{16}{x}\\\\71x\cdot\frac{17.75}{71}=\frac{16}{x}\cdot{71x}\\\\17.75\cdot{x}=16\cdot{71}\\\\x=\frac{16\cdot{71}}{17.75}=64\end{array}\)

Interpret: The unknown height of person 2 is 64 inches. In general, we can reduce the fraction \(\frac{17.75}{71}=0.25=\frac{1}{4}\) to find a general rule for everyone. This would translate to saying for every one femur length, a person’s height is 4 times that length.

Another way to describe the ratio of femur length to height that we found in the last example is to say there’s a 1:4 ratio between femur length and height, or 1 to 4.

Ratios are also used in scale drawings. Scale drawings are enlarged or reduced drawings of objects, buildings, roads, and maps. Maps are smaller than what they represent and a drawing of dendritic cells in your brain is most likely larger than what it represents. The scale of the drawing is a ratio that represents a comparison of the length of the actual object and it’s representation in the drawing. The image below shows a map of the us with a scale of 1 inch representing 557 miles. We could write the scale factor as a fraction \(\frac{1}{557}\) or as we did with the femur-height relationship, 1:557.

In the next example we will use the scale factor given in the image above to find the distance between Seattle Washington and San Jose California.

Given a scale factor of 1:557 on a map of the US, if the distance from Seattle, WA to San Jose, CA is 1.5 inches on the map, define a proportion to find the actual distance between them. [reveal-answer q=”936583″]Show Solution[/reveal-answer] [hidden-answer a=”936583″]

Read and Understand: We need to define a proportion to solve for the unknown distance between Seattle and San Jose.

Define and Translate: T he scale factor is 1:557, and we will call the unknown distance x. The ratio of inches to miles is \(\frac{1}{557}\).

We know inches between the two cities, but we don’t know miles, so the ratio that describes the distance between them is \(\frac{1.5}{x}\).

Write and Solve: The proportion that will help us solve this problem is \(\frac{1}{557}=\frac{1.5}{x}\).

Solve using the common denominator \(557x\) to clear fractions.

\(\begin{array}{c}\frac{1}{557}=\frac{1.5}{x}\\\\557x\cdot\frac{1}{557}=\frac{1.5}{x}\cdot{557x}\\\\x=1.5\cdot{557}=835.5\)

Interpret: We used the scale factor 1:557 to find an unknown distance between Seattle and San Jose. We also check our answer of 835.5 miles with Google maps, and found that the distance is 839.9 miles, so we did pretty well!

In the next example, we will find a scale factor given the length between two cities on a map, and their actual distance from each other.

Two cities are 2.5 inches apart on a map. Their actual distance from each other is 325 miles. Write a proportion to represent and solve for the scale factor for one inch of the map. [reveal-answer q=”151234″]Show Solution[/reveal-answer] [hidden-answer a=”151234″]

Read and Understand: We know that for each 2.5 inches on the map, it represents 325 actual miles. We are looking for the scale factor for one inch of the map.

Define and Translate: The ratio we want is \(\frac{2.5}{325}\)

Write and Solve: We can use a proportion to equate the two ratios and solve for the unknown distance.

\(\begin{array}{c}\frac{1}{x}=\frac{2.5}{325}\\\\325x\cdot\frac{1}{x}=\frac{2.5}{325}\cdot{325x}\\\\325=2.5x\\\\x=130\)

Interpret: The scale factor for one inch on the map is 1:130, or for every inch of map there are 130 actual miles.

The video that follows show another example of finding an actual distance using the scale factor from a map.

In the video that follows, we present an example of using proportions to obtain the correct amount of medication for a patient, as well as finding a desired mixture of coffees.

Direct Variation

Variation equations are examples of rational formulas and are used to describe the relationship between variables. For example, imagine a parking lot filled with cars. The total number of tires in the parking lot is dependent on the total number of cars. Algebraically, you can represent this relationship with an equation.

\(\text{number of tires}=4\cdot\text{number of cars}\)

The number 4 tells you the rate at which cars and tires are related. You call the rate the constant of variation . It’s a constant because this number does not change. Because the number of cars and the number of tires are linked by a constant, changes in the number of cars cause the number of tires to change in a proportional, steady way. This is an example of direct variation , where the number of tires varies directly with the number of cars.

You can use the car and tire equation as the basis for writing a general algebraic equation that will work for all examples of direct variation. In the example, the number of tires is the output, 4 is the constant, and the number of cars is the input. Let’s enter those generic terms into the equation. You get \(y=kx\). That’s the formula for all direct variation equations.

\(\text{number of tires}=4\cdot\text{number of cars}\\\text{output}=\text{constant}\cdot\text{input}\)

Solve for k , the constant of variation, in a direct variation problem where \(x=10\).

[reveal-answer q=”714779″]Show Solution[/reveal-answer] [hidden-answer a=”714779″]Write the formula for a direct variation relationship.

Substitute known values into the equation.

\(300=k\left(10\right)\)

Solve for k by dividing both sides of the equation by 10.

\(\begin{array}{l}\frac{300}{10}=\frac{10k}{10}\\\\\,\,\,\,30=k\end{array}\)

The constant of variation, k , is 30.

In the video that follows, we present an example of solving a direct variation equation.

Inverse Variation

Another kind of variation is called inverse variation . In these equations, the output equals a constant divided by the input variable that is changing. In symbolic form, this is the equation \(y=\frac{k}{x}\).

One example of an inverse variation is the speed required to travel between two cities in a given amount of time.

Let’s say you need to drive from Boston to Chicago, which is about 1,000 miles. The more time you have, the slower you can go. If you want to get there in 20 hours, you need to go 50 miles per hour (assuming you don’t stop driving!), because \(\frac{1,000}{40}=25\).

The equation for figuring out how fast to travel from the amount of time you have is \(d=rt\). If you solve \(r=\frac{d}{t}\), or \(speed=\frac{miles}{time}\).

In the case of the Boston to Chicago trip, you can write \(y=\frac{k}{x}\).

Solve for k , the constant of variation, in an inverse variation problem where \(y=25\).

[reveal-answer q=”752007″]Show Solution[/reveal-answer] [hidden-answer a=”752007″]Write the formula for an inverse variation relationship.

\(y=\frac{k}{x}\)

\(25=\frac{k}{5}\)

Solve for k by multiplying both sides of the equation by 5.

\(\begin{array}{c}5\cdot 25=\frac{k}{5}\cdot 5\\\\125=\frac{5k}{5}\\\\125=k\,\,\,\end{array}\)

The constant of variation, k , is 125.

In the next example, we will find the water temperature in the ocean at a depth of 500 meters. Water temperature is inversely proportional to depth in the ocean.

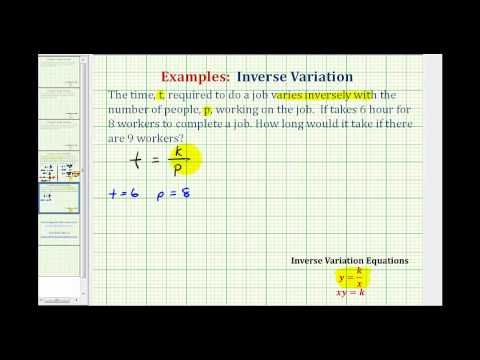
The water temperature in the ocean varies inversely with the depth of the water. The deeper a person dives, the colder the water becomes. At a depth of 1,000 meters, the water temperature is 5º Celsius. What is the water temperature at a depth of 500 meters?

[reveal-answer q=”700119″]Show Solution[/reveal-answer] [hidden-answer a=”700119″]You are told that this is an inverse relationship, and that the water temperature ( y ) varies inversely with the depth of the water ( x ).

\(\begin{array}{l}\,\,\,\,\,\,\,\,\,\,y=\frac{k}{x}\\\\temp=\frac{k}{depth}\end{array}\)

\(5=\frac{k}{1,000}\)

Solve for k .

\(\begin{array}{l}1,000\cdot5=\frac{k}{1,000}\cdot 1,000\\\\\,\,\,\,\,\,\,\,5,000=\frac{1,000k}{1,000}\\\\\,\,\,\,\,\,\,\,5,000=k\end{array}\)

Now that k , the constant of variation is known, use that information to solve the problem: find the water temperature at 500 meters.

\(\begin{array}{l}temp=\frac{k}{depth}\\\\temp=\frac{5,000}{500}\\\\temp=10\end{array}\)

At 500 meters, the water temperature is 10º C.

In the video that follows, we present an example of inverse variation.

Joint Variation

A third type of variation is called joint variation . Joint variation is the same as direct variation except there are two or more quantities. For example, the area of a rectangle can be found using the formula \(A=lw\), where l is the length of the rectangle and w is the width of the rectangle. If you change the width of the rectangle, then the area changes and similarly if you change the length of the rectangle then the area will also change. You can say that the area of the rectangle “varies jointly with the length and the width of the rectangle.”

The formula for the volume of a cylinder, \(\pi\).

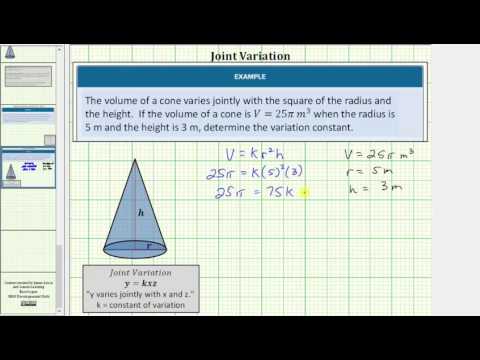
The area of a triangle varies jointly with the lengths of its base and height. If the area of a triangle is 30 inches\(^{2}\) when the base is 10 inches and the height is 6 inches, find the variation constant and the area of a triangle whose base is 15 inches and height is 20 inches.

[reveal-answer q=”264626″]Show Solution[/reveal-answer] [hidden-answer a=”264626″]You are told that this is a joint variation relationship, and that the area of a triangle ( A ) varies jointly with the lengths of the base ( b ) and height ( h ).

\(\begin{array}{l}\,\,\,\,\,\,\,\,\,\,y=kxz\\Area=k(base)(height)\end{array}\)

Substitute known values into the equation, and solve for k .

\(30=k\left(10\right)\left(6\right)\\30=60k\\\\\frac{30}{60}=\frac{60k}{60}\\\\\frac{1}{2}=k\)

Now that k is known, solve for the area of a triangle whose base is 15 inches and height is 20 inches.

\(\begin{array}{l}Area=k(base)(height)\\\\Area=(15)(20)(\frac{1}{2})\\\\Area=\frac{300}{2}\\\\Area=150\,\,\text{square inches}\end{array}\)

The constant of variation, k , is \(\frac{1}{2}\), and the area of the triangle is 150 square inches.

Finding k to be \(A=\frac{1}{2}bh\). The \(\frac{1}{2}\) that you calculated in this example!

In the following video, we show an example of finding the constant of variation for a jointly varying relation.

Direct, Joint, and Inverse Variation

k is the constant of variation. In all cases, \(k\neq0\).

• Direct variation: \(y=kx\)
• Inverse variation: \(y=\frac{k}{x}\)
• Joint variation: \(y=kxz\)

Rational formulas can be used to solve a variety of problems that involve rates, times, and work. Direct, inverse, and joint variation equations are examples of rational formulas. In direct variation, the variables have a direct relationship—as one quantity increases, the other quantity will also increase. As one quantity decreases, the other quantity decreases. In inverse variation, the variables have an inverse relationship—as one variable increases, the other variable decreases, and vice versa. Joint variation is the same as direct variation except there are two or more variables.

You can solve rational equations by finding a common denominator. By rewriting the equation so that all terms have the common denominator, you can solve for the variable using just the numerators. Or, you can multiply both sides of the equation by the least common multiple of the denominators so that all terms become polynomials instead of rational expressions.

An important step in solving rational equations is to reject any extraneous solutions from the final answer. Extraneous solutions are solutions that don’t satisfy the original form of the equation because they produce untrue statements or are excluded values that make a denominator equal to 0.

• "Current World Population." World Population Clock: 7.4 Billion People (2016). Accessed June 21, 2016. http://www.worldometers.info/world-population/ . "Current World Population." World Population Clock: 7.4 Billion People (2016). Accessed June 21, 2016. http://www.worldometers.info/world-population/ . "Current World Population." World Population Clock: 7.4 Billion People (2016). Accessed June 21, 2016. http://www.worldometers.info/world-population/ . ↵
• Obialor, Ambrose, Churchill Ihentuge, and Frank Akapuaka. "Determination of Height Using Femur Length in Adult Population of Oguta Local Government Area of Imo State Nigeria." Federation of American Societies for Experimental Biology, April 2015. Accessed June 22, 2016. www.fasebj.org/content/29/1_Supplement/LB19.short. ↵
• Revision and Adaptation. Provided by : Lumen Learning. License : CC BY: Attribution
• Solve Basic Rational Equations. Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/R9y2D9VFw0I . License : CC BY: Attribution
• Solve Rational Equations with Like Denominators. Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/gGA-dF_aQQQ . License : CC BY: Attribution
• Screenshot: A Good Day's Work. Provided by : Lumen Learning. License : CC BY: Attribution
• Screenshot: Matroyshka, or nesting dolls.. Provided by : Lumen Learning. License : CC BY: Attribution
• Screenshot: map with scale factor. Provided by : Lumen Learning. License : CC BY: Attribution
• Proportion Applications: Map Scale Factor (Clear Fractions, No Cross Products). Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/id3sp4wvmVg . License : CC BY: Attribution
• Screenshot: so many cars, so many tires. Provided by : Lumen Learning. License : CC BY: Attribution
• Screenshot: Water temperature in the ocean varies inversely with depth. Provided by : Lumen Learning. License : CC BY: Attribution
• Joint Variation: Determine the Variation Constant (Volume of a Cone). Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/JREPATMScbM . License : CC BY: Attribution
• Unit 15: Rational Expressions, from Developmental Math: An Open Program. Provided by : Monterey Institute of Technology and Education. License : CC BY: Attribution
• Ex 2: Solve a Literal Equation for a Variable. Authored by : James Sousa (Mathispower4u.com). Located at : https://www.youtube.com/watch?v=ecEUUbRLDQs&feature=youtu.be . License : CC BY: Attribution
• Ex 1: Rational Equation Application - Painting Together. Authored by : James Sousa (Mathispower4u.com) . Located at : https://youtu.be/SzSasnDF7Ms . License : CC BY: Attribution
• Ex: Rational Equation App - Find Individual Working Time Given Time Working Together. Authored by : James Sousa (Mathispower4u.com) . Located at : https://www.youtube.com/watch?v=kbRSYb8UYqU&feature=youtu.be . License : CC BY: Attribution
• Ex: Proportion Applications - Mixtures . Authored by : James Sousa (Mathispower4u.com) . Located at : https://youtu.be/yGid1a_x38g . License : CC BY: Attribution
• Ex: Direct Variation Application - Aluminum Can Usage. Authored by : James Sousa (Mathispower4u.com) . Located at : https://youtu.be/DLPKiMD_ZZw . License : CC BY: Attribution
• Ex: Inverse Variation Application - Number of Workers and Job Time. Authored by : James Sousa (Mathispower4u.com). Located at : https://youtu.be/y9wqI6Uo6_M . License : CC BY: Attribution