quartile problem solving examples

Quartiles are the values that divide a list of numbers into quarters:

• Put the list of numbers in order
• Then cut the list into four equal parts
• The Quartiles are at the "cuts"

Example: 5, 7, 4, 4, 6, 2, 8

Put them in order: 2, 4, 4, 5, 6, 7, 8

Cut the list into quarters:

And the result is:

• Quartile 1 (Q1) = 4
• Quartile 2 (Q2), which is also the Median , = 5
• Quartile 3 (Q3) = 7

Sometimes a "cut" is between two numbers ... the Quartile is the average of the two numbers.

Example: 1, 3, 3, 4, 5, 6, 6, 7, 8, 8

The numbers are already in order

In this case Quartile 2 is half way between 5 and 6:

Q2 = (5+6)/2 = 5.5

• Quartile 1 (Q1) = 3
• Quartile 2 (Q2) = 5.5

Interquartile Range

The "Interquartile Range" is from Q1 to Q3:

To calculate it: subtract Quartile 1 from Quartile 3 , like this:

The Interquartile Range is:

Q3 − Q1 = 7 − 4 = 3

Box and Whisker Plot

We can show all the important values in a "Box and Whisker Plot", like this:

A final example covering everything:

Example: Box and Whisker Plot and Interquartile Range for

4, 17, 7, 14, 18, 12, 3, 16, 10, 4, 4, 11

Put them in order:

3, 4, 4, 4, 7, 10, 11, 12, 14, 16, 17, 18

Cut it into quarters:

3, 4, 4 | 4, 7, 10 | 11, 12, 14 | 16, 17, 18

In this case all the quartiles are between numbers:

• Quartile 1 (Q1) = (4+4)/2 = 4
• Quartile 2 (Q2) = (10+11)/2 = 10.5
• Quartile 3 (Q3) = (14+16)/2 = 15
• The Lowest Value is 3 ,
• The Highest Value is 18

So now we have enough data for the Box and Whisker Plot :

And the Interquartile Range is:

Q3 − Q1 = 15 − 4 = 11

Definition, Formula, Solved Example Problems - Quartiles | 11th Statistics : Chapter 5 : Measures of Central Tendency

Chapter: 11th statistics : chapter 5 : measures of central tendency.

There are three quartiles denoted by  Q 1 ,  Q 2  and  Q 3  divides the frequency distribution in to four equal parts

That is 25 percent of data will lie below  Q 1 , 50 percent of data below  Q 2  and 75 percent below  Q 3 . Here  Q 2  is called the Median. Quartiles are obtained in almost the same way as median

Quartiles for Raw or Ungrouped data:

If the data set consist of n items and arranged in ascending order then

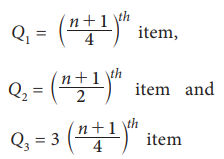
Example 5.30

Compute  Q 1  and  Q 3  for the data relating to the marks of 8 students in an examination given below 25, 48, 32, 52, 21, 64, 29, 57  

  n = 8

 Arrange the values in ascending order

 21, 25, 29, 32, 48, 52, 57, 64 we have

Quartiles for Discrete Series (grouped data)

Step 1:  Find cumulative frequencies

Step 2  : Find ((N+1)/ 4)

Step 3  : See in the cumulative frequencies, the value just greater than ((N+1)/ 4) the corresponding value of  x  is  Q 1

Step 4  : Find 3((N+1)/ 4)

Step 5  : See in the cumulative frequencies, the value just greater than 3((N+1)/ 4) then the corresponding value of  x  is  Q3 .

Example 5.31

Compute  Q 1  and  Q 3  for the data relating to age in years of 543 members in a village

Quartiles for Continuous series (grouped data)

Step 2  : Find (N/4)

Step 3  :  Q 1   class is the class interval corresponding to the value of the cumulative frequency just greater than (N/4)

Step 4  : Q3 class is the class interval corresponding to the value of the cumulative frequency just greater than 3 (N/4)

Example 5.32

Calculate the quartiles  Q 1  and  Q 3  for wages of the labours given below

Related Topics

Privacy Policy , Terms and Conditions , DMCA Policy and Compliant

Copyright © 2018-2024 BrainKart.com; All Rights Reserved. Developed by Therithal info, Chennai.

Median, Quartiles And Percentiles (Ungrouped Data)

In these lessons, we will learn how to find the median, quartiles and percentiles of ungrouped data (discrete data).

Related Pages Frequency Table Cumulative Frequency Graph More Statistics Lessons

We have learned that the median is the middle value when a set of data is arranged in order of increasing magnitude. We will now consider lower quartiles and upper quartiles.

The median divides the data into a lower half and an upper half. The lower quartile is the middle value of the lower half. The upper quartile is the middle value of the upper half.

The following figure shows the median, quartiles and interquartile range. Scroll down the page for examples and solutions.

How To Find Median, Quartiles And Percentiles?

Example: Find the median, lower quartile and upper quartile of the following numbers. 12, 5, 22, 30, 7, 36, 14, 42, 15, 53, 25

Median (middle value) = 22

Lower quartile (middle value of the lower half) = 12

Upper quartile (middle value of the upper half) = 36

If there is an even number of data items, then we need to get the average of the middle numbers.

Example: Find the median, lower quartile, upper quartile, interquartile range and range of the following numbers. 12, 5, 22, 30, 7, 36, 14, 42, 15, 53, 25, 65

Interquartile range = Upper quartile – lower quartile = 39 – 13 = 26

Range = largest value – smallest value = 65 – 5 = 60

When evaluating the quartiles, always remember to first arrange the data in increasing order.

How to compute the interquartile range for a set of data? Remember to reorganize the data so that you can find the median values easier.

Median, Quartiles and Interquartile Range How to calculate median, quartiles and interquartile range for discrete data.

How to summarize data using quartiles and interquartile range?

How to Estimate Mean, Median and Quartiles from Continuous Grouped Data?

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

• Mathematicians
• Math Lessons
• Square Roots
• Math Calculators
• The Quartiles – Explanation & Examples

JUMP TO TOPIC

What are the quartiles in statistics?

– example 1 of an odd list, – example 2 of an odd list, – example 3 of an even list, – example 4 of an even list, practical questions, the quartiles – explanation & examples.

“The quartiles are values that divide your numerical data into four parts or quarters.”

In this topic, we will discuss the quartiles from the following aspects:

How to find quartiles?

• The role of quartiles.
• Practical questions.

The quartiles are values that divide your numerical data into four parts or quarters. The four parts may or may not be of equal size.

The three main quartiles are:

• The first or the lower quartile (denoted as Q1) is the value where 25% of the data points are less than that value.
• The second quartile or the median (denoted as Q2) is the value where 50% of the data points lie below this value.
• The third or the upper quartile (denoted as Q3) is the value where 75% of the data points are less than that value.

These quartiles divide the data into 4 quarters:

• The first quarter contains the data points from the smallest value (minimum) up to Q1.
• The second quarter includes data points from Q1 to the median.
• The third quarter includes data points from the median to Q3.
• The fourth quarter includes data points from Q3 to the highest data point or maximum.

The method will differ according to the presence of an odd or even list of numbers.

For the numbers (1,2,3,4,5), find Q1,Q2,Q3.

1. Order the data from smallest to largest.

Our data is already in order, 1,2,3,4,5.

2. Find the median or Q2.

The median is the central value of the odd list of ordered numbers.

The median or Q2 is 3 because there are 2 numbers below 3 (1,2) and two numbers above 3 (4,5).

If we have an even list of ordered numbers, the median value is the sum of the middle pair divided by two.

3. Find the first and third quartiles.

For an odd list of ordered numbers, the first quartile or Q1 is the median of the first half of data points including the median.

The third quartile or Q3 is the median of the second half of data points including the median.

The first half of the data including the median is 1,2,3.

The first quartile is 2 because 2 has 1 number before it (1) and 1 number after it (3).

The second half of the data including the median is 3,4,5.

The third quartile is 4 because 4 has 1 number before it (3) and 1 number after it (5).

We can plot this data as a box plot with the box showing 3 quartiles.

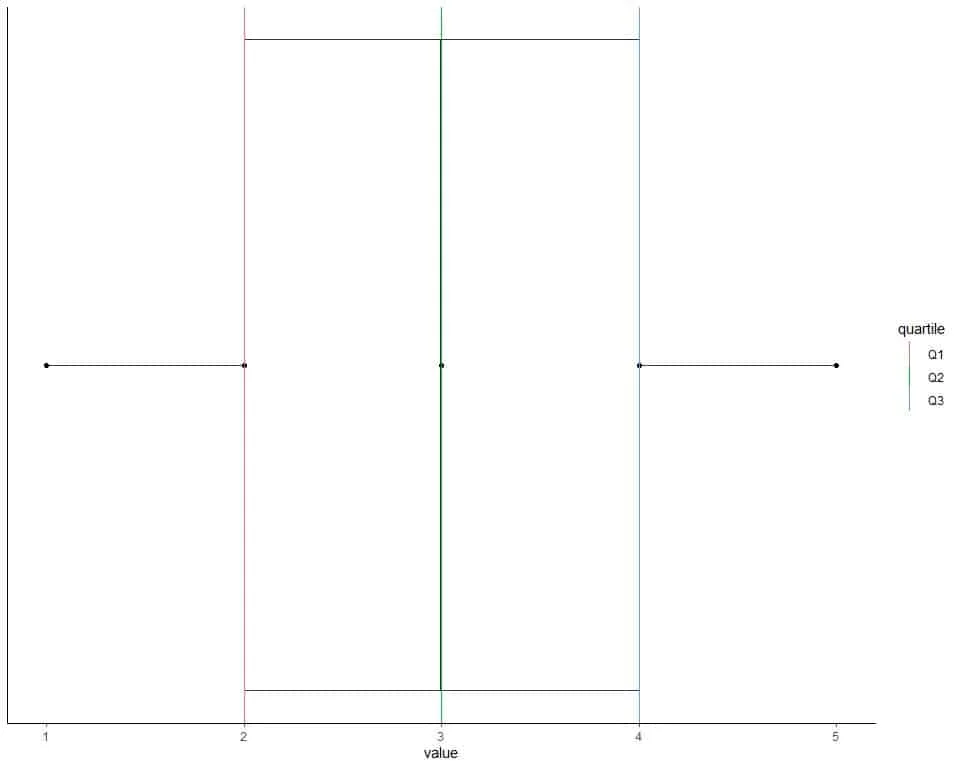
The data points are shown as black solid dots.

The first quartile is shown as a red line, the second quartile as a green line, and the third quartile as a blue line.

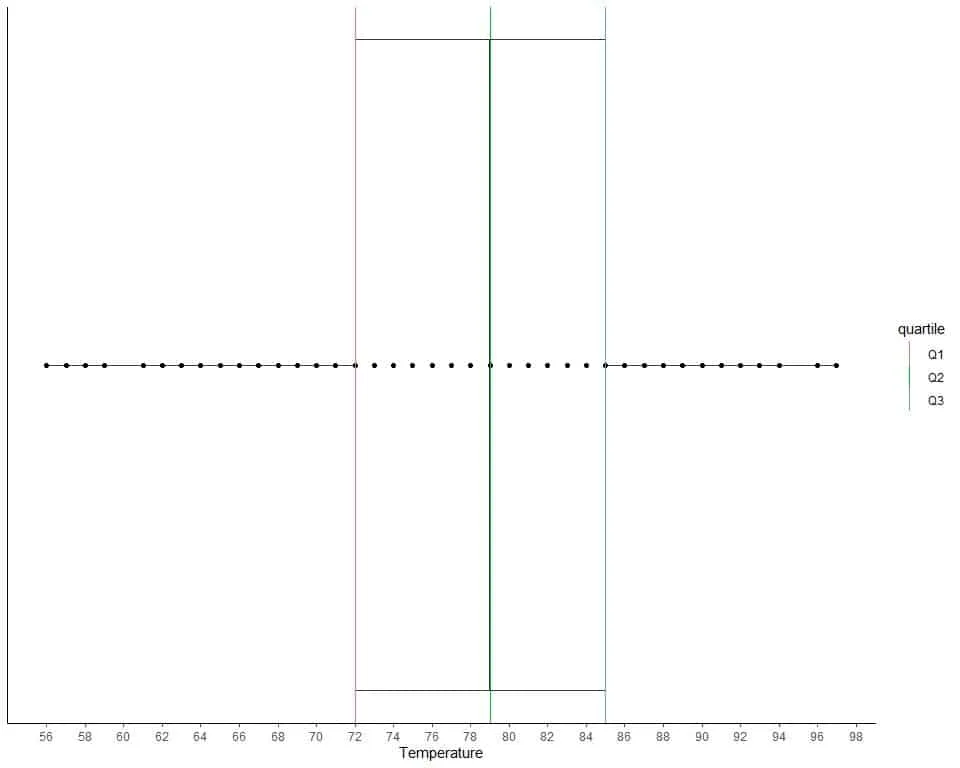
The following are 153 daily temperature measurements in New York, May to September 1973.

67 72 74 62 56 66 65 59 61 69 74 69 66 68 58 64 66 57 68 62 59 73 61 61 57 58 57 67 81 79 76 78 74 67 84 85 79 82 87 90 87 93 92 82 80 79 77 72 65 73 76 77 76 76 76 75 78 73 80 77 83 84 85 81 84 83 83 88 92 92 89 82 73 81 91 80 81 82 84 87 85 74 81 82 86 85 82 86 88 86 83 81 81 81 82 86 85 87 89 90 90 92 86 86 82 80 79 77 79 76 78 78 77 72 75 79 81 86 88 97 94 96 94 91 92 93 93 87 84 80 78 75 73 81 76 77 71 71 78 67 76 68 82 64 71 81 69 63 70 77 75 76 68.

find Q1, Q2, Q3.

56 57 57 57 58 58 59 59 61 61 61 62 62 63 64 64 65 65 66 66 66 67 67 67 67 68 68 68 68 69 69 69 70 71 71 71 72 72 72 73 73 73 73 73 74 74 74 74 75 75 75 75 76 76 76 76 76 76 76 76 76 77 77 77 77 77 77 77 78 78 78 78 78 78 79 79 79 79 79 79 80 80 80 80 80 81 81 81 81 81 81 81 81 81 81 81 82 82 82 82 82 82 82 82 82 83 83 83 83 84 84 84 84 84 85 85 85 85 85 86 86 86 86 86 86 86 87 87 87 87 87 88 88 88 89 89 90 90 90 91 91 92 92 92 92 92 93 93 93 94 94 96 97.

The median or Q2 is 79 because there are 76 numbers below 79 (56,57,……79) and 76 numbers above 79 (79,79,79,…..97).

The first half of data including the median is:

56 57 57 57 58 58 59 59 61 61 61 62 62 63 64 64 65 65 66 66 66 67 67 67 67 68 68 68 68 69 69 69 70 71 71 71 72 72 72 73 73 73 73 73 74 74 74 74 75 75 75 75 76 76 76 76 76 76 76 76 76 77 77 77 77 77 77 77 78 78 78 78 78 78 79 79 79.

The first quartile is 72 because 72 has 38 numbers before it (56,57,….72) and 38 numbers after it (73,73,….79).

The second half of data including the median is:

79 79 79 79 80 80 80 80 80 81 81 81 81 81 81 81 81 81 81 81 82 82 82 82 82 82 82 82 82 83 83 83 83 84 84 84 84 84 85 85 85 85 85 86 86 86 86 86 86 86 87 87 87 87 87 88 88 88 89 89 90 90 90 91 91 92 92 92 92 92 93 93 93 94 94 96 97.

The third quartile is 85 because 85 has 38 numbers before it (79,79,…84) and 38 numbers after it (85,85,….97).

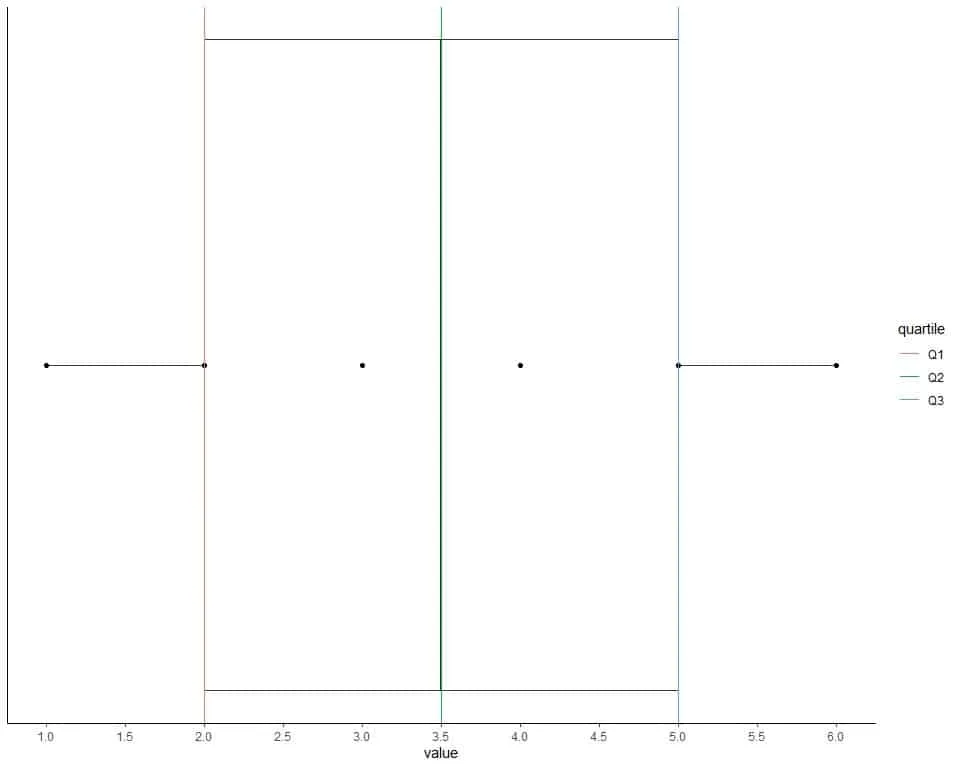
For the numbers (1,2,3,4,5,6), find Q1,Q2,Q3.

Our data is already in order, 1,2,3,4,5,6.

1,2,3,4,5,6.

The middle pair is (3,4) because it has 2 numbers below it (1,2) and 2 numbers above it (5,6).

The median or Q2 = (3+4)/2 = 3.5.

For an even list of ordered numbers, the first quartile is the median of the first half of data points and the third quartile is the median of the second half of data points. The first half of the data is 1,2,3.

The first quartile is 2 because 2 has 1 number before it (1) and 1 number after it (3). The second half of the data is 4,5,6.

The third quartile is 5 because 5 has 1 number before it (4) and 1 number after it (6).

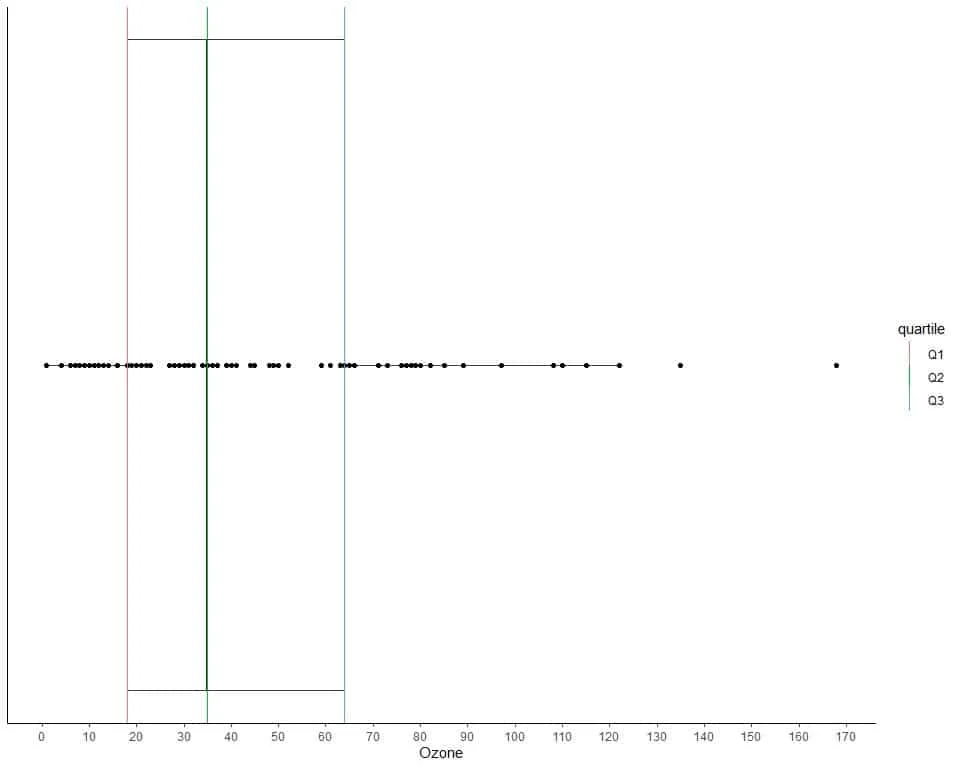
The following are 84 daily ozone measurements in New York, May to September 1973.

41 36 12 18 28 23 19 8 7 16 11 14 18 14 34 6 30 11 1 11 4 32 23 45 115 37 29 71 39 23 21 37 20 12 13 135 49 32 64 40 77 97 97 85 10 27 7 48 35 61 79 63 16 80 108 20 52 82 50 64 59 39 9 16 78 35 66 122 89 110 44 28 65 22 59 23 31 44 21 9 45 168 73 76.

Find Q1, Q2, Q3.

1 4 6 7 7 8 9 9 10 11 11 11 12 12 13 14 14 16 16 16 18 18 19 20 20 21 21 22 23 23 23 23 27 28 28 29 30 31 32 32 34 35 35 36 37 37 39 39 40 41 44 44 45 45 48 49 50 52 59 59 61 63 64 64 65 66 71 73 76 77 78 79 80 82 85 89 97 97 108 110 115 122 135 168.

The middle pair is (35,35) because it has 41 numbers below it (1,4,..,34) and 41 numbers above it (36,37,…,168).

The median or Q2 = (35+35)/2 = 35.

For an even list of ordered numbers, the first quartile is the median of the first half of data points and the third quartile is the median of the second half of data points.

The first half of data is another even list of numbers so we pick the middle pair to find median:

1 4 6 7 7 8 9 9 10 11 11 11 12 12 13 14 14 16 16 16 18 18 19 20 20 21 21 22 23 23 23 23 27 28 28 29 30 31 32 32 34 35.

The middle pair is (18,18) because it has 20 numbers below it (1,4,..,16) and 20 numbers above it (19,20,…,35).

The first quartile or Q1 = (18+18)/2 = 18.

The second half of data is another even list of numbers:

35 36 37 37 39 39 40 41 44 44 45 45 48 49 50 52 59 59 61 63 64 64 65 66 71 73 76 77 78 79 80 82 85 89 97 97 108 110 115 122 135 168.

The middle pair is (64,64) because it has 20 numbers below it (35,35,..,63) and 20 numbers above it (65,66,…,168).

The third quartile or Q3 = (64+64)/2 = 64.

The role of quartiles

The second quartile or the median (Q2) provides information about the data center.

The difference between the first and third quartiles (Q3-Q1) is called the interquartile range (IQR ) and provides information about the data spread.

If Q2 or median is more close to Q1 than Q3, this means that our data is right-skewed as we see in example 4. In other words, the upper half of the box plot is larger than the lower half.

If Q2 or median is more close to Q3 than Q1, this means that our data is left-skewed as we see in example 2. In other words, the upper half of the box plot is smaller than the lower half.

1. The following are the quartiles of prices for some fair and ideal cut diamonds.

Which cut is more spread in its prices?

Is the price data right or left-skewed?

2. The following are the quartiles of temperature for some months in New York, May to September 1973.

Which month is the least spread in its temperatures?

3. The following is the age in years of 10 participants from a certain survey.

26 48 67 39 25 25 36 44 44 47.

What is Q1, Q2, Q3 of this data?

4. The following is the age in years of 11 participants from a certain survey.

63 54 62 40 33 75 89 56 24 27 71.

5. The following are the box plots for different TV hours of different races from a certain survey.

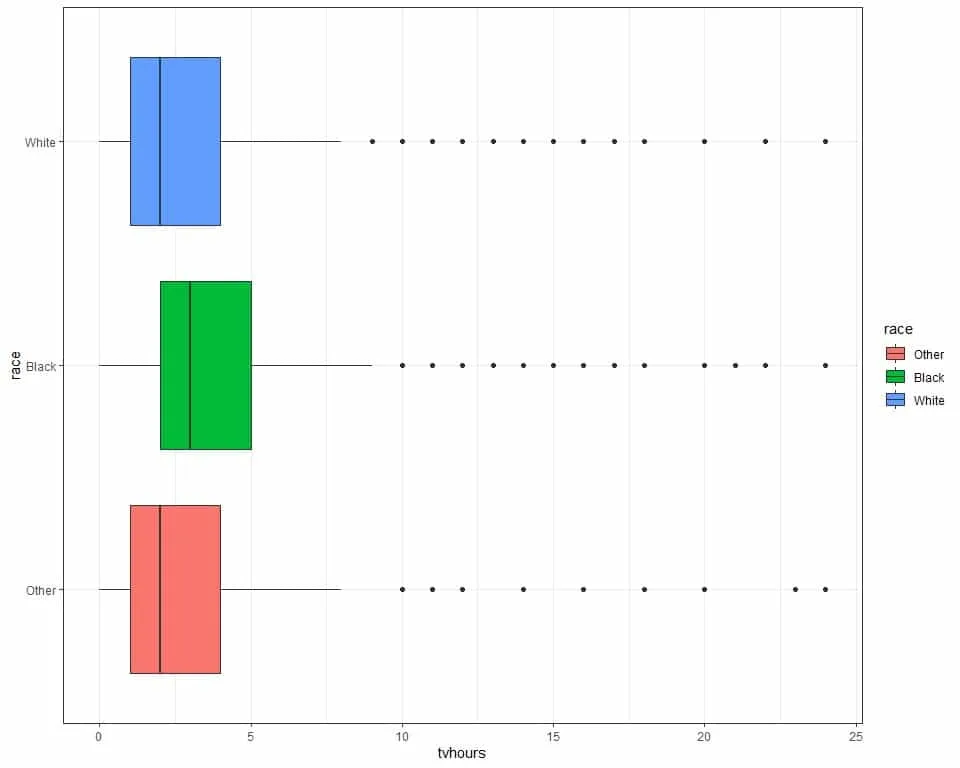
Is the TV hours right or left skewed?

1. Look at IQR = Q3-Q1 =, for fair cut, 3155.25.

For ideal cut, IQR = 3800.5. The ideal cut has a larger IQR so it is more spread in its prices.

In both cut types, the Q2 or median is more close to Q1 than Q3 which means that price data is right-skewed.

2. For month 5, IQR = 9.

For month 6, IQR = 6.75.

For month 7, IQR = 4.5.

For month 8, IQR =9.5.

For month 9, IQR =10.

The least spread is for month 7 or July.

3. 26 48 67 39 25 25 36 44 44 47 is an even list of numbers.

Following the above steps, Q2 = 41.5, Q1 = 26, Q3 = 47.

4. 63 54 62 40 33 75 89 56 24 27 71 is an odd list of numbers.

Following the above steps, Q2 = 56, Q1 = 36.5, Q3 = 67.

5. The black race has the highest Q3 at about 5 hours.

In all box plots, the Q2 or median is more close to Q1 than Q3 which means that TV hours are right-skewed.

Previous Lesson  |  Main Page | Next Lesson

Calculating Quartiles: A Step-by-Step Explanation

Quartiles are statistical objects that represent four equally divided intervals for data observations. These calculations are a useful way to compare different parts of the data such as maximum, minimum, median and outlier values. These statistical values are essential for comparing groups. For example, if we look at the quartiles in U.S. incomes in 2022 these values will be much more spread out than if we just consider incomes of oncologists in New York City because the range of all incomes in the first is much wider than the second. Quartiles would allow us to detect that an oncologist in New York making an annual salary of $50,000 would be an outlier. Even more, this salary may be so far off from the range of typical values, an analyst or data scientist may conclude that it is a bad value that may be the result of human input error. 

Although this example seems intuitive, calculating quartiles is a statistically rigorous way to measure and compare the spread of values in data. Given this rigor, quartiles have many industrial applications including comparing company compensation, performing customer segmentation, detecting fraud in financial markets, and comparing ticket sales in the entertainment industry. 

One of the most common ways to carry out such analysis is to use the quantile method in Pandas, which is useful because it can calculate any type of quantiles, such as median, tertiles (3 groups), quintiles (5 groups) and all the way up to percentiles (100 groups). Further, the Seaborn library is a Python visualization tool that allows you to visualize quartiles through boxplots. 

Another use of quartiles is in analyzing subgroups of data. The Pandas quantile method also makes analyzing quartiles in subgroups within your data straightforward. Consider customer billing data for a phone and internet service provider. This data may contain information such as customer tenure, gender and service type. Quartiles at varying levels can give insights into which factors most influence customer retention. Using quartiles, you can gain insights that can help answer a wide array of analytical questions. For example, quartiles can help us with all the following questions:

• Do customers with fiber optic internet service keep their service for longer than those with DSL? 
• How does gender correlate to length ofcustomer tenure?
• Are there significant differences in monthly charges for customers who stay versus those who leave?

Quartiles and their visualizations can help us tackle these questions in an analytically rigorous way. 

Here, we will be calculating and analyzing quartiles using the Telco churn data set . This data contains customer billing information for a fictional Telco company. It specifies whether a customer stopped or continued using the service, known as churning. The data is publicly available and is free to use, share and modify under the Apache 2.0 license . 

More From Sadrach Pierre Python Profiling Tools: A Tutorial

Reading in Data 

To start, let’s import the Python Pandas library:

Next, let’s read our data into a Pandas data frame:

Now, let’s print the first five rows with the head() method:

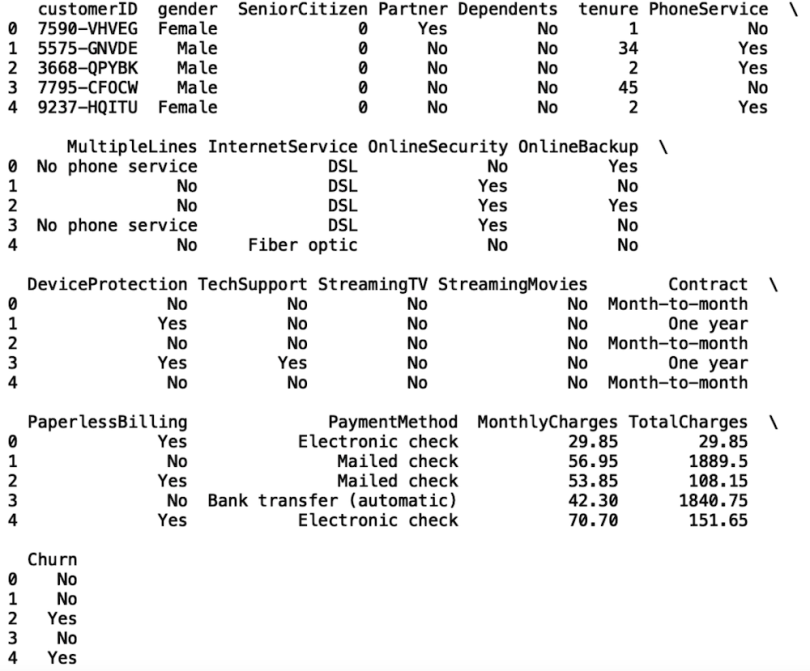
Quartiles correspond to data observations that have been divided into four intervals. They have the following definitions:

• First Quartile (Q1): This corresponds to the 25th percentile. This means that 25 percent of the data is lower than Q1 and 75 percent of the data is above Q1. 
• Second Quartile (Q2): This corresponds to the 50th percentile. This value is also called the median. This means that 50 percent of the data is lower than Q2 and 50 percent of the data is above Q2.
• Third Quartile (Q3): This corresponds to the 75th percentile. This means that 75 percent of the data is lower than Q2 and 25 percent of the data is above Q2.
• Fourth Quartile: This is just the maximum value in the data. 

Using Pandas to Generate Quartiles

Calculating quartiles with the Pandas library is straightforward. Let’s calculate the quartiles for the tenure column, which is shown in months, across the entire data set. To do this, we will use the quantile method on our Pandas data frame object. We pass in 0.25 as the argument for the quantile method. 

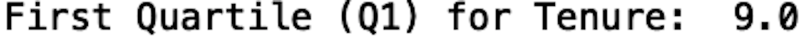
We see that the first quartile for tenure is nine months. This means that the 25th percentile for tenure is nine months, meaning 25 percent of customers stayed with the company for fewer than nine months.

Let’s calculate the second quartile. We do this by passing in 0.5 as the argument:

We see that the second quartile for tenure is 29 months. This means that the 50th percentile for tenure is 29 months, meaning 50 percent of customers stayed with the company for less than 29 months. 

Finally, let’s calculate the third quartile. Here we pass in 0.75 as thee argument in the quantile method:

Here, the third quartile for tenure is 55 months. This means that the 75th percentile for tenure is 55 months, meaning 75 percent of customers stayed with the company for less than 29 months. 

Using Pandas to Generate Quantiles

The quantile method’s name refers to a statistical quantity that is a generalization for dividing data observations into any number of intervals. With quartiles, we divide data observations into four intervals. But with the same method, we can just as easily divide the data into five intervals (quintiles), 10 intervals (deciles), or even 100 intervals (percentiles). The choice of how data observations are split depends on the application, which is why having a general method for performing these splits is useful. 

For example, to generate a decile, we simply pass arguments into the quantile method within the range 0.1 - 0.9. The value 0.1 corresponds to the 10th percentile (i.e., 10 percent of data observations fall below this value) and 0.9 corresponds to the 90th percentile (90 percent of data observations fall below this value). Let’s calculate the 9th decile, also called the 90th percentile, in tenure:

Quartiles and Quantiles for Data Subgroups 

Generating quartiles for subgroups is also useful. For example, maybe we’d like to compare the tenure of customers with fiber optic to the tenure of customers with DSL. Let’s calculate the quartiles for each of these subgroups. First, let’s filter our data frames on the internet service columns to create a data frame for customer with DSL and another for thosewith fiber optic:

Now, let’s look at the third quartile in tenure for DSL and fiber optic:

We see that Q3 values for DSL and fiber optic customers are the same; for both DSL and fiber optic, a tenure of 56 months is greater than 75 percent of customer tenure values in the data. 

We can also look at the ninth decile:

Here we see a small difference in the ninth decile for DSL and fiber optic. For DSL, 90 percent of customers stay with the company for less than 70 months. For fiber optic, 90 percent of customers stay with the company for less than 69 months. 

Since the data we are working with corresponds to customer churn, let’s see if there are any differences between those who leave and those who stay. Let’s check if there are any differences between monthly charges for customers who churn versus customers who stay. Let’s create filter data frames for each group:

Next, let’s calculate the third quartile in tenure:

We see that, for customers who churned, 75 percent stayed for fewer than 29 months. For those who stayed, 75 percent stayed with the company for less than 61 months. This illustrates what we already expect, which is that customers who leave have significantly lower values for tenure than those who stay. 

Let’s consider the monthly chargers column for customers who churn versus customers who stay:

Here, we see that Q3 for monthly charges for customers who churn is $94.20, while for those who stay, Q3 is $88.40. From this, we can conclude that 75 percent of customers who churn pay less than $94.20, while 75 percent of customers who stay pay less than $88.40. This may suggest that customers who end up leaving the service are being overcharged. 

Visualizing Quartiles with Boxplots

Oftentimes, generating visualizations that clearly represent statistical quantities that are of interest is useful. One good way to visually represent quartiles is through boxplots. The Seaborn Python visualization library makes generating these plots easy. Let’s start by importing the Matplotlib and Seaborn libraries:

Let’s generate a box plot for tenure across the entire data set:

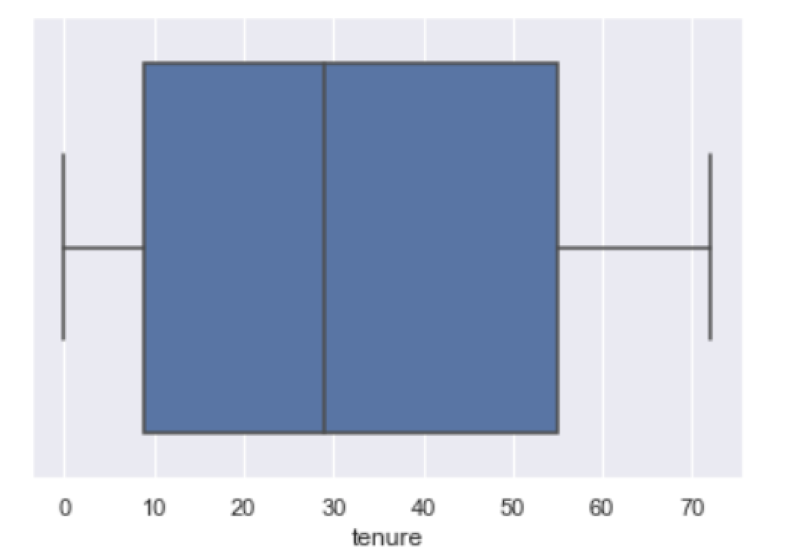
We can inspect the quartiles by looking at the blue box. The left side of the blue box corresponds to the first quartile (Q1), the black line in the middle is the second quartile (Q2, also called the median) and the right side of the blue box is the third quartile (Q3). 

Another thing we can do is define a function that allows us to compare quartiles across categories:

Let’s call this function with our full data frame, the churn column as the categorical column, and the tenure column as the numerical column. The limit for the number of categories displayed is set to five:

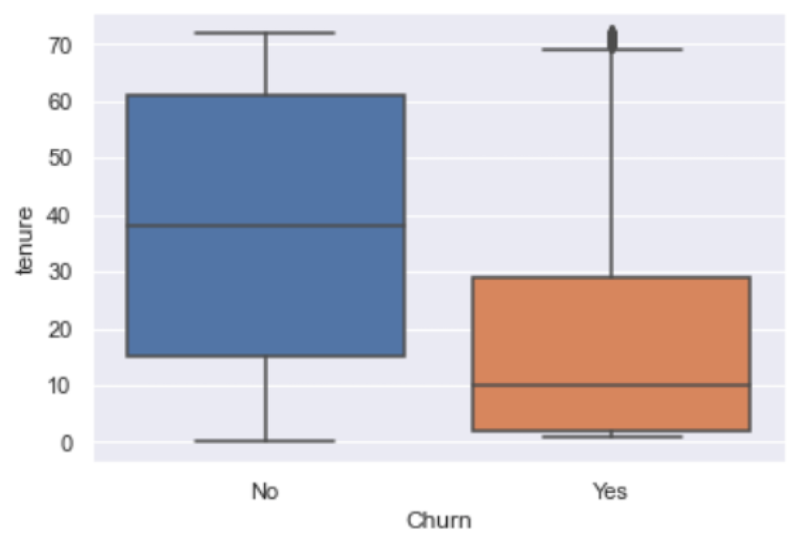
We see that the tenure values for Q1 and Q3 are greater for customers who stay than customers who churn, which we expect. Let’s generate this plot for monthly charges and churn:

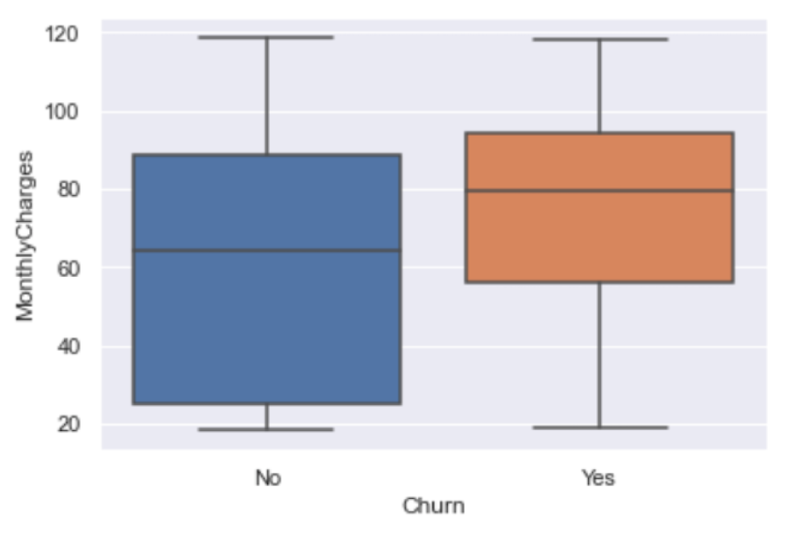
We see that Q1, Q2 and Q3 values for monthly charges are less for those who stay than those who churn. We also expect this because, as we saw earlier, customers who stay with the company are generally those who are paying less in monthly charges than those who leave. 

The code in this post is available on GitHub . 

More in Data Science How to Use Float in Python (With Sample Code!)

Calculate Quartiles Now

Quartiles and quantiles are useful for comparing groups within data. The spread in values can differ dramatically across groups and categories in data observations. Understanding how numerical values in data is distributed within groups can aid data scientists and analysts in understanding differences in customer demographics. This analysis can help companies identify high value customers who are more likely to continue purchasing services or products. Companies can use this information to continue to target high value customers while also targeting the casual or infrequent buyer with deals and promotions as a part of a robust customer retention program. 

Built In’s expert contributor network publishes thoughtful, solutions-oriented stories written by innovative tech professionals. It is the tech industry’s definitive destination for sharing compelling, first-person accounts of problem-solving on the road to innovation.

Great Companies Need Great People. That's Where We Come In.

In statistics, a quartile is an element in a data set, ordered from smallest to largest, that divides the set into four parts, or quarters. The four parts are more or less equal in size, but can vary slightly depending on the number of elements in the set. In the set below, 9, 28, and 47 are quartiles:

{3, 5, 9 , 10, 21, 28 , 32, 38, 47 , 58, 66}

In the above set, the quartiles divide the set into four equal parts, so each of the four parts contains 25% of the data. In cases where the data cannot be exactly divided into four equal parts, some parts will have more elements than others, but each part will still roughly comprise 25% of the data. The second quartile, referred to as Q2, is the median of the set. In this case Q2, or 28, is the median.

There are a number of different ways to refer to each of the quartiles, such as Q1, Q2, and Q3:

• Q1 - also referred to as the first quartile, lower quartile, or 25th percentile. Q1 separates the lowest 25% of data from the highest 75%.
• Q2 - also referred to as the second quartile, middle quartile, median, or 50th percentile. Q2 separates the lowest 50% of data from the highest 50%. In other words, it cuts the data in half.
• Q3 - also referred to as the third quartile, upper quartile, or 75th percentile. Q3 separates the highest 25% of data from the lowest 75%.

Quartiles can be depicted using a number of different graphical methods, such as a frequency distribution or a box plot.

Frequency distribution

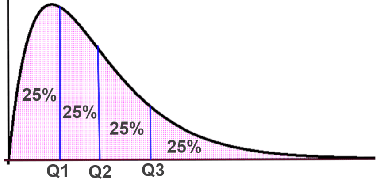
How to select quartile values

There is no one way to select quartile values that everyone agrees on, but there are some general guidelines for doing so. Before starting the process, the set of data must be arranged from smallest to largest:

{1, 4, 5, 6, 7, 10, 11, 13, 16, 18, 25}

• Use the median to divide the set into two halves. If there are an odd number of elements in the set, the middle value, or Q2, divides the set in half. If there are an even number of elements, take the average of the two elements closest to the middle. Q2 divides the set in half at this average value. In the example above, Q2 = 10.
• The lower quartile, Q1, is the median of the lower half of the data (from the first element to Q2).
• The upper quartile, Q3, is the median of the upper half of the data (from Q2 to the final element).

The following formulas can be used to determine the position of each quartile. They are particularly useful when working with larger data sets. Given that the set is ordered from smallest to largest,

Q1 = 0.25(n + 1)

Q2 = 0.50(n + 1)

Q2 = 0.75(n + 1)

where n is the number of elements in the set. Note that the formulas output the position of the quartile, not the actual value of the element. For example, using the data set above:

Q1 = 0.25(11 + 1) = 3

Thus, Q1 is the 3rd element (5) in the set. If there are an even number of elements in the set, the formulas yield a decimal number, which indicates that the quartile lies between the values of the two elements on either side of the element denoted by the decimal number. For example, if Q1 = 2.3, Q1 is determined by computing the average of elements 2 and 3 in the set. Using the above set, Q1 would be (4 + 5)/2 = 4.5.

Using quartiles to find the interquartile range

The interquartile range (IQR) is comprised of the range of values between the first and third quartiles, and is a measure of how spread out the middle 50% of the data is. 50% of the data is contained within this range:

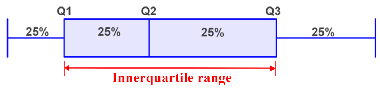
The interquartile range is found by subtracting Q1 from Q3:

IQR = Q3 - Q1

Using quartiles to find outliers

Quartiles can be used to find outliers (values in the set that lie significantly outside the expected value). Values that lie farther than 1.5 times the IQR away from either end of the IQR (Q1 or Q3) are considered outliers, as shown in the figure below:

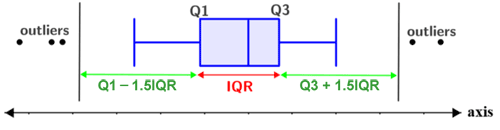
Thus, the expected range of values is:

[Q1 - 1.5(IQR), Q3 + 1.5(IQR)]

Anything outside the above range of values is an outlier.

• Mastering Quartiles: A Guide to Calculating Them Efficiently.

Welcome to Warren Institute, where we explore the fascinating world of Mathematics education. In this article, we will delve into the topic of calculating quartiles. Quartiles are essential statistical measures that divide a data set into four equal parts. Understanding quartiles is crucial for analyzing and interpreting data, making it an invaluable skill for students and professionals alike. Join us as we uncover the step-by-step process to calculate quartiles, discover their significance in data analysis, and explore real-world applications . Whether you're a student, teacher, or data enthusiast, this article will equip you with the knowledge and tools necessary to master quartiles. Let's get started!

Understanding Quartiles

Calculation methods for quartiles, interpreting quartiles, applications of quartiles in mathematics education, what is the formula to calculate quartiles in statistics, how do you find the lower quartile in a dataset, can you explain the concept of quartiles and their importance in data analysis, are quartiles only applicable in normal distributions or can they be used for any type of data distribution, what are some practical examples or real-life applications where quartiles are used in mathematics education.

Quartiles are statistical measures that divide a data set into four equal parts, each representing 25% of the total data. This subtitle delves into the concept of quartiles, explaining their significance and how they are calculated using different methods.

This section explores the three commonly used methods for calculating quartiles: the exclusive method, the inclusive method, and the nearest-rank method. Each method has its own approach to determining the values of quartiles, and this subtitle provides a detailed explanation of each technique.

Once quartiles are calculated, it is important to interpret their meaning in the context of the data set. This section discusses how quartiles can be used to understand the distribution, spread, and skewness of data, as well as their importance in making comparisons and identifying outliers.

Quartiles have various applications in mathematics education . This subtitle highlights how quartiles can be used to teach students about data analysis, probability, and descriptive statistics. It also showcases real-world examples where quartiles play a crucial role in understanding and interpreting data.

frequently asked questions

The formula to calculate quartiles in statistics is the interpolation formula . It involves finding the values that divide a dataset into four equal parts, with the first quartile (Q1) being the median of the lower half, the second quartile (Q2) being the overall median, and the third quartile (Q3) being the median of the upper half.

To find the lower quartile in a dataset, you need to sort the data in ascending order and then calculate the median of the lower half of the dataset. The lower quartile is the median of the first half of the data.

Quartiles are values that divide a data set into four equal parts. They are important in data analysis as they provide information about the distribution and spread of the data. The first quartile (Q1) represents the 25th percentile, while the third quartile (Q3) represents the 75th percentile. The second quartile, also known as the median, divides the data set into two equal halves. Quartiles help identify outliers, assess the skewness of the data, and compare different data sets.

Quartiles can be used for any type of data distribution, not just normal distributions. They are a useful tool for understanding the spread and distribution of data, regardless of its shape or characteristics.

Quartiles are commonly used in Mathematics education to analyze and interpret data. Some practical examples or real-life applications where quartiles are used include:

1. Data Analysis: Quartiles are used to divide a dataset into four equal parts, providing insights into the distribution and spread of the data. This helps students understand how to summarize and compare data sets.

2. Box-and-Whisker Plots: Quartiles play a key role in constructing box-and-whisker plots, which visually represent the distribution of a dataset. Students learn to identify the lower quartile, median, and upper quartile, allowing them to analyze the spread and skewness of the data.

3. Measures of Central Tendency: Quartiles are used in conjunction with other measures of central tendency, such as the mean and median, to provide a comprehensive understanding of a dataset. Students learn to calculate quartiles to assess the variability and central tendencies of the data.

Overall, understanding quartiles is essential for Mathematics education as it enables students to analyze, interpret, and communicate information effectively using real-life data.

In conclusion, understanding how to calculate quartiles is crucial in the field of Mathematics education. By knowing how to find the first, second, and third quartiles, educators can effectively analyze data sets and provide students with a deeper understanding of statistical measures. The ability to interpret quartiles allows for the identification of outliers, the determination of data distribution, and the comparison of different data sets. Moreover, being proficient in calculating quartiles enables educators to design appropriate lesson plans and exercises that enhance students' mathematical skills and critical thinking abilities. Therefore, it is essential for Mathematics educators to familiarize themselves with the concept of quartiles and incorporate its application into their teaching methodologies.

If you want to know other articles similar to Mastering Quartiles: A Guide to Calculating Them Efficiently. you can visit the category General Education .

Michaell Miller

Michael Miller is a passionate blog writer and advanced mathematics teacher with a deep understanding of mathematical physics. With years of teaching experience, Michael combines his love of mathematics with an exceptional ability to communicate complex concepts in an accessible way. His blog posts offer a unique and enriching perspective on mathematical and physical topics, making learning fascinating and understandable for all.

• Wave hello to electromagnetic wonders!
• Feet to miles, speed in style!

Unlock the Secrets: Methods of Science Crossword Puzzle Answer Key Revealed

Correct Statements About Temporary Tables: Which Holds True?

Countdown: Only 7 Days Until the Launch - Prepare for Liftoff!

Understanding the Implications of r2=1 in Regression and Correlation Analysis

Unlocking Safety: Data Table 2 Sodium Hypochlorite SDS Information

Unit 8 Right Triangles & Trigonometry Homework 2 Answers Key: Complete Guide

Solutions to Quartiles, Deciles and Percentiles Problems

Percentiles, quartiles and deciles, what are percentiles, example 1: finding the percentile value, what are deciles, problem 1: finding deciles and percentiles, solution to problem 1, what are quartiles.

If you’ve ever taken a standardized test, you will have used the word “percentile” before. It’s association with what many students consider the bane of their existence - official exams - isn’t doing the concept any favours. However, percentiles might be more important than many people realize - involved in everything from the apps on your phone to the algorithms that choose which songs you’re most likely to enjoy.

In this section, you’ll learn everything you need to know about what percentiles are, how to calculate them, and why they’re important in statistics.

The simple definition for a percentile is that it indicates the number at which a certain percentage of data falls below. As you learned in previous sections, there are two types of measurements in descriptive statistics: measures of central tendency and variability.

Percentiles are one version of measuring the variability within a data set. A percentile is an important measure because it can help you understand a certain data set better than simple means, modes or medians can.

The easiest way to understand why is to look at an example. You have a group of test scores out of 100 points from a class, following the table below.

You scored 50 points. At first glance, 50 out of 100 points may seem like a disappointing grade - for many classes, it would also be considered at the point of failure. However, calculating the percentile, you are at the 90th percentile. In other words, 90% of students scored lower than you did.

To calculate the percentile, your data should be ordered from least to greatest, similar to taking the median. Next, take the number for which you’d like to calculate the percentile for, in our case 50, and count what position its in.

You can be in a situation where you want to find the value corresponding to a certain percentile. Taking our example above, you want to find the 70th percentile, or the score at which 70% of students scored below.

To do this, we take

0.70*10 = 9

The index gives you the observation number for which your 70th percentile is located. If it has a decimal, round to the nearest whole number. Here, the index 7 means that the 7th observation in our data set is the score at the 70th percentile. Counting from the lowest to the highest score, we reach the 7th observed value: a score of 40, which is the 70th percentile for our data.

If we wanted to find the median , we can also use percentiles. For odd numbers, the median is:

\dfrac{n}{2} = index

In this case, since we have an even amount of numbers, we take the average of two indices,

index \thickspace 1 = \dfrac{n}{2}

index \thickspace 2 = \dfrac{n}{2}  + 1

Here, we get

\dfrac{10}{2} = 5

\dfrac{10}{2} + 1 = 6

Meaning the, the median is the average of the scores found at the fifth and sixth values in our ordered data set,

\dfrac{34+36}{2} = 34 \thickspace points

This means that 50% of students scored below 34 points and the other 50% of students scored above 34 points.

Deciles are a form of percentiles that split the data up into groups of 10%. Meaning, every decile contains 10% of the data. To find the decile, first order the data from least to greatest. Then, divide the data by 10. This indicates the number of observed values within each decile.

Using our previous example, we divide our data into 10 groups, each containing 10% of the data. This can be visualized in the data above. Because our n is equal to 10, each decile contains only 1 score.

The 1st decile = 15 . This score, at the 1st decile, is at the 10th percentile. Meaning, 10% of students scored below this number. This doesn’t really have much meaning here because there’s only 1 value at the 1st decile - however, it can be interpreted for data sets with larger sample sizes.

The 6th decile = 36 . This score, at the 6th decile, is at the 60th percentile, meaning that 60% of students scored below this number.

Using the first example, fill in the rest of the table with the corresponding deciles and percentiles.

You should obtain the following result:

Similar to deciles, quartiles are a form of percentiles. While deciles split the data into 10 “buckets,” quartiles split them into quarters . A good way of remembering this is that “deci” means a tenth, whereas quartile sounds similar to quarter, which is a fourth.

Splitting our data set into quarters, gives us the following.

Which is easier to understand when visualized:

From the image above, we can see that each quartile, or “bucket” contains 25% of our data. The score 24 is at the 25th percentile, which means that 25% of students scored below this score. The reason why this is at the 25th percentile and not the 30th percentile this time is because half of the score belongs to the first quartile and half belongs to the second.

The second quartile is also known as the median, which, as we calculated earlier, is 34 points. Quartile 3 is the 75th percentile, which means that at 41 points, 25% students scored above and 75% of students scored below this number.

The properties of quartiles are noted below.

Did you like this article? Rate it!

I am passionate about travelling and currently live and work in Paris. I like to spend my time reading, gardening, running, learning languages and exploring new places.

Frequency Distribution

Solutions to average deviation, variance and standard deviation problems, solutions to statistical measures problems, solutions to discrete and continuous variable problems, solutions to frequency distribution problems, solutions to bar chart problems, solutions to mode, median, mean, range, average deviation, variance and standard deviation problems, solutions to mean problems, solutions to coefficient of variation problems, solutions to pie chart and mean problems, solutions to median and quartile problems, standard deviation, mean, median and mode problem, solutions to categorical, discrete and continuous variable problems, solutions to histogram and cumulative frequency polygon problems, coefficient of variation, standard scores, solutions to histogram, mode and median problems, solutions to absolute cumulative frequency distribution problems, solutions to mean and standard deviation problems, solutions to categorical and quantitative variables problems, solutions to variance and standard deviation problems, solutions to mean, median and mode problems, solutions to median, mode, mean and quartiles problems, solutions to histogram and frequency polygon problems, solutions to frequency polygon and histogram problems, average deviation, standard score problem, solutions to standard score problems, solutions to mode, median, mean and variance problems, solutions to mean and variance problems, solutions to mean, median, standard deviation and percentile problems, solutions to statistical table problems, statistical variable, solutions to frequency distribution and bar chart problems, regression line , pmcc – scientific calculator., statistical formulas, descriptive statistical formulas, statistical word problems, variance problems, statistics problems, cancel reply.

Your comment

Current ye@r *

Leave this field empty

Can you help me answer my activities

HIGH SCHOOL

• ACT Tutoring
• SAT Tutoring
• PSAT Tutoring
• ASPIRE Tutoring
• SHSAT Tutoring
• STAAR Tutoring

GRADUATE SCHOOL

• MCAT Tutoring
• GRE Tutoring
• LSAT Tutoring
• GMAT Tutoring
• AIMS Tutoring
• HSPT Tutoring
• ISAT Tutoring
• SSAT Tutoring

Search 50+ Tests

Loading Page

math tutoring

• Elementary Math
• Pre-Calculus
• Trigonometry

science tutoring

Foreign languages.

• Mandarin Chinese

elementary tutoring

• Computer Science

Search 350+ Subjects

• Video Overview
• Tutor Selection Process
• Online Tutoring
• Mobile Tutoring
• Instant Tutoring
• How We Operate
• Our Guarantee
• Impact of Tutoring
• Reviews & Testimonials
• Media Coverage
• About Varsity Tutors

SAT II Math I : Quartiles and Interquartile Range

Study concepts, example questions & explanations for sat ii math i, all sat ii math i resources, example questions, example question #1 : quartiles and interquartile range.

What is the 3rd quartile of this set?

To find the 3rd quartile, you find the middle number of the set of numbers above the median.  

Example Question #1 : How To Find Interquartile Range

Given the following set of data, what is twice the interquartile range?

How do you find the interquartile range?

We can find the interquartile range or IQR in four simple steps:

•      Order the data from least to greatest
•      Find the median
•      Calculate the median of both the lower and upper half of the data
•      The IQR is the difference between the upper and lower medians

Step 1: Order the data

In order to calculate the IQR, we need to begin by ordering the values of the data set from the least to the greatest. Likewise, in order to calculate the median, we need to arrange the numbers in ascending order (i.e. from the least to the greatest).

Let's sort an example data set with an odd number of values into ascending order. 

Now, let's perform this task with another example data set that is comprised of an even number of values.

Rearrange into ascending order.

Step 2: Calculate the median

Next, we need to calculate the median. The median is the "center" of the data. If the data set has an odd number of data points, then the mean is the centermost number. On the other hand, if the data set has an even number of values, then we will need to take the arithmetic average of the two centermost values. We will calculate this average by adding the two numbers together and then dividing that number by two.

First, we will find the median of a set with an odd number of values. Cross out values until you find the centermost point

The median of the odd valued data set is four.

Now, let's find the mean of the data set with an even number of values. Cross out values until you find the two centermost points and then calculate the average the two values. 

Find the average of the two centermost values.

The median of the even valued set is four.

Step 3: Upper and lower medians

Once we have found the median of the entire set, we can find the medians of the upper and lower portions of the data. If the data set has an odd number of values, we will omit the median or centermost value of the set. Afterwards, we will find the individual medians for the upper and lower portions of the data.

Omit the centermost value.

Find the median of the lower portion.

Calculate the average of the two values.

Find the median of the upper portion.

If the data set has an even number of values, we will use the two values used to calculate the original median to divide the data set. These values are not omitted and become the largest value of the lower data set and the lowest values of the upper data set, respectively. Afterwards, we will calculate the medians of both the upper and lower portions.

The median of the lower portion is two.

Find the median of the upper portion.

The median of the upper portion is eight.

Step 4: Calculate the difference

Last, we need to calculate the difference of the upper and lower medians by subtracting the lower median from the upper median. This value equals the IQR.

Let's find the IQR of the odd data set. 

Finally, we will find the IQR of the even data set.

In order to better illustrate these values, their positions in a box plot have been labeled in the provided image.

Now that we have solved a few examples, let's use this knowledge to solve the given problem. 

First, we need to put the data in order from smallest to largest.

The median of the lower half falls between two values.

The median of the upper half falls between two values.

The interquartile range is the difference between the third and first quartiles.

Determine the interquartile range of the following numbers:

42, 51, 62, 47, 38, 50, 54, 43

None of these

First reorder the numbers in ascending order:

38, 42, 43, 47, 50, 51, 54, 62

Then divide the numbers into 2 groups, each containing an equal number of values:

(38, 42, 43, 47)(50, 51, 54, 62)

Q1 is the median of the group on the left, and Q3 is the median of the group on the right. Because there is an even number in each group, we'll need to find the average of the 2 middle numbers:

The interquartile range is the difference between Q3 and Q1:

Example Question #4 : How To Find Interquartile Range

The interquartile range is the difference in value between the upper quartile and lower quartile.

Find the interquartile range for the data set.

As always, rearranging the data set helps us immensely:

Find the interquartile range of the following data set:

The first step (as with most data set problems) is to rearrange the data set from least to greatest value:

Since our 3rd number is 2, and our 4th number is 3, we need to find 1/4 of the way between 2 and 3. We will use the equation

Using the data provided above, what is the interquartile range (IQR)? 

Using the data above, what is the interquartile range? 

In a previous problem, we placed the data pieces in numerical order: 

Example Question #2 : How To Find Interquartile Range

Using the data provided, find the Interquartile range, IQR. 

The data set provided is called a five number summary.

These data values allow us to find the median, IQR, and range.

Using the data above, find the interquartile range. 

For the upper quartile, if placed in numerical order 

we see that there is an even number, thus we must take the center two numbers and find the average to find the true center of this data set, giving us

We do the same for the lower quartile, giving us a 

Example Question #3 : How To Find Interquartile Range

Using the data above, find the IQR. (interquartile range) 

Report an issue with this question

If you've found an issue with this question, please let us know. With the help of the community we can continue to improve our educational resources.

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC 101 S. Hanley Rd, Suite 300 St. Louis, MO 63105

Or fill out the form below:

Contact Information

Complaint details.

Quartile Formula

Statistics is an important part of mathematics and is used extensively. The concept of quarters is a fundamental one in statistics. Let us learn more about quarters and the Quartile Formula.

Quartile, as it sounds phonetically, is a statistical term that divides the data into four quarters. It basically divides the data points into a data set in 4 quarters on the number line. One thing we need to keep in mind is that data points can be random and we have to put those numbers in line first on the number line in ascending order and then divide them into quartiles. It is basically an extended version of the median. Median divides the data into two equal parts which quartiles divide it into four parts. Once we divide the data, the four quartiles will be:

• 1 st  quartile also known as the lower quartile basically separates the lowest 25% of data from the highest 75%.
• 2 nd  quartile or the middle quartile also the same as the median it divides numbers into 2 equal parts.
• 3 rd  quartile or the upper quartile separates the highest 25% of data from the lowest 75%.

Quartile divides a set of observations into 4 equal parts. The first quartile is the value in the middle of the first term and the median. The median is the second quartile. The middle value between the median and the last term is the third quartile. Mathematically, they are represented as follows,

When the set of observations are arranged in ascending order the quartiles are represented as,

• First Quartile(Q 1) = (( n + 1)/ 4 ) t h   T e r m also known as the lower quartile.
• The second quartile or the 50th percentile or the Median is given as:   Second Quartile(Q 2) = (( n + 1)/ 2 ) t h   T e r m
• The third Quartile of the 75th Percentile (Q3) is given as:  Third Quartile(Q 3) = ( 3 ( n + 1 )/ 4 ) t h   T e r m also known as the upper quartile.
•  The interquartile range is calculated as: Upper Quartile – Lower Quartile.

Solved Example for Quartile Formula

Question:  Find the median, lower quartile, upper quartile and interquartile range of the following data set of values: 19, 21, 23, 20, 23, 27, 25, 24, 31?

Solution:  Firstly arrange the values in ascending order.

Plugging in the values in the formulas above we get,

Median(Q 2) = 5 t h  T e r m = 23

Lower Quartile ( Q 1)  = 2.5 th  Term = 11

Upper Quartile(Q3) = 7.5 th Term = 24.5

I Q R = U p p e r  Q u a r t i l e − L o w e r  Q u a r t i l e

IQR = 24.5 – 11

Question : Find the upper quartile for the following set of numbers: 27, 19, 5, 7, 6, 9, 15, 12, 18, 2, 1.

Solution:  The upper quartile formula is: Q3 = ¾(n + 1)th Term.

The formula doesn’t give you the value for the upper quartile, it gives you the place. For example, 5th place,  8th place etc.

So firstly we put your numbers in order: 1, 2, 5, 6, 7, 9, 12, 15, 18, 19, 27. Note that for very large data sets, you may want to use Excel to place your numbers in order. And then we work the formula. There are 11 numbers in the set, so:

Q3 = ¾(n + 1)th Term.

Q3 = ¾(12)th Term. = 9th Term.

In this set of numbers given, the upper quartile (18) is the 9th term or the 9th place from the left.

Customize your course in 30 seconds

Which class are you in.

Maths Formulas

• Hexagon Formula
• Integral Calculus Formulas
• Prime Number Formula
• Scalene Triangle Formula
• Geometric Sequence Formula
• Linear Interpolation Formula
• Calculus Formulas
• Sin 2x Formula
• Secant Formula
• Equation Formula

One response to “Equation Formula”

I get a different answer for first example. I got Q1 as 20.5 median 23 and Q3 26

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Download the App

[FREE] Fun Math Games & Activities Packs

Always on the lookout for fun math games and activities in the classroom? Try our ready-to-go printable packs for students to complete independently or with a partner!

In order to access this I need to be confident with:

Interq. range

Interquartile range

Here you will learn about interquartile range, including finding the interquartile range from the quartiles for a set of data, comparing data sets using the median and the interquartile range, and analyzing data using quartiles and the interquartile range.

Students will first learn about interquartile range as part of statistics and probability in 6 th grade.

What is interquartile range?

Interquartile range is the difference between the upper quartile (or third quartile) and the lower quartile (or first quartile) in an ordered data set.

Interquartile range \textbf{=} upper quartile \textbf{-} lower quartile

I Q R=U Q-L Q \, or \, I Q R=Q 3-Q 1

The set of numbers that make up the data set must be in ascending order (lowest value to highest value).

• The first quartile (Q1) is \cfrac{1}{4} of the way through the data – the lower quartile.
• The second quartile (M or Q2) is \cfrac{1}{2} of the way through the data – the median value.
• The third quartile (Q3) is \cfrac{3}{4} of the way through the data – the upper quartile.

You can also consider each quartile as a percentile where,

• The lower quartile (Q1) is the \bf{25} th percentile as 25 \% of the data lies below this value.
• The median (M or Q2) is the \bf{50} th percentile as 50 \% of the data lies below (or above) this value.
• The upper quartile (Q3) is the \bf{75} th percentile as 75 \% of the data lies below this value.

Note : the lower quartile is the median of the lower half of the data, the upper quartile is the median of the upper half of the data.

For example, find the interquartile range of the following data.

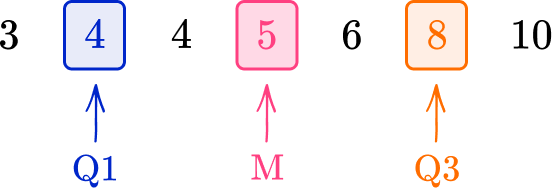
Here, IQR=Q3-Q1=8-4=4

The interquartile range (IQR) is a descriptive statistic and measures the variability or spread of the data.

The larger the interquartile range, the wider the spread of the central 50 \% of data.

The smaller the value for the interquartile range, the narrower the central 50 \% of data for the data set.

The IQR is far more representative of the spread of this data set than the range because it is not affected by extreme values.

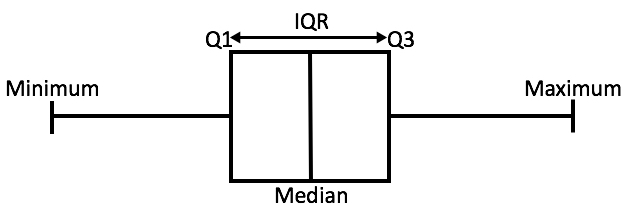
The median and lower and upper quartiles, along with the minimum value and the maximum value of the data set, form a five-number summary of descriptive statistics for the data set. This information can then be presented in a box plot (box and whisker plot or diagram) making it easy to compare with other sets of data.

The interquartile range is not part of this five-number summary, but is useful alongside it as a measure of dispersion or spread.

Common Core State Standards

How does this relate to 6 th grade math?

• Grade 6 – Statistics and Probability (6.SP.B.4) Display numerical data in plots on a number line, including dot plots, histograms, and box plots.

How to find the interquartile range

In order to find the interquartile range for a set of data:

Find the lower quartile \textbf{(Q1)}.

Find the upper quartile \textbf{(Q3)}.

Subtract the lower quartile from the upper quartile \textbf{(Q3 - Q1)}.

[FREE] Representing Data Check for Understanding (Grade 6 to 7)

Use this quiz to check your grade 6th to 7th students’ understanding of representing data. 10+ questions with answers covering a range of 6th and 7th grade representing data topics to identify areas of strength and support!

Interquartile range examples

Example 1: odd number of ordered data values.

Find the interquartile range for the following set of data.

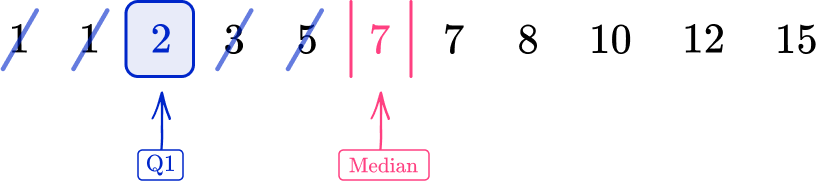
The median is the middle value, 7 , and so the lower quartile is the middle number in the lower half of the data, excluding the median.

2 Find the upper quartile \textbf{(Q3)}.

The upper quartile is the middle value in the upper half of the data, excluding the median value (7).

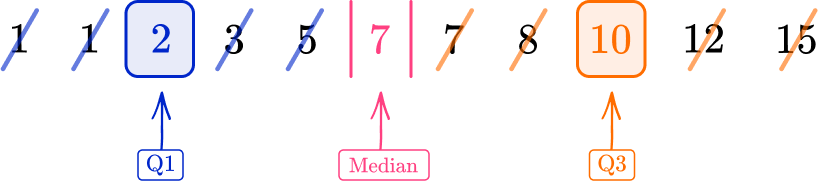
3 Subtract the lower quartile from the upper quartile \textbf{(Q3 - Q1)}.

As Q1=2 and Q3=10

IQR=Q3-Q1=10-2=8

Example 2: small continuous data set (even amount of data values)

The data below shows birth weights of 10 babies in kilograms.

Calculate the interquartile range for the data set.

The median for an even number of data values in a data set is the average of these two middle values. Here, the median is 3.4. The lower quartile is the middle of the lower half of the data.

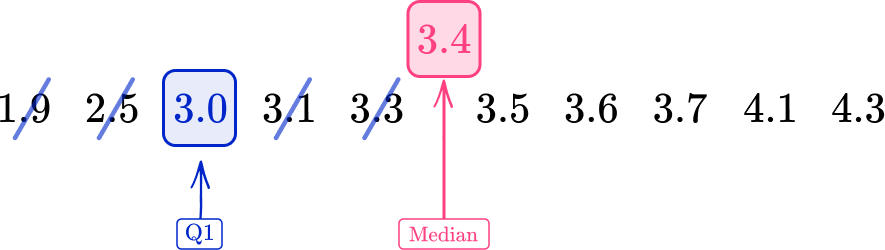
The upper quartile is the middle value of the upper half of the data set.

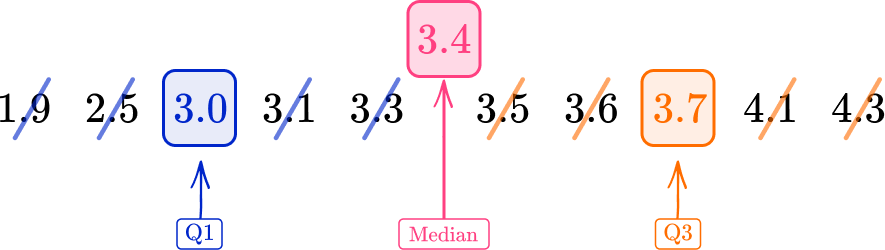
As Q1=3.0 and Q3=3.7

IQR=Q3-Q1=3.7-3.0=0.7 \, kg

Example 3: odd number of unordered data values

Find the interquartile range.

Using the ordered data set, you have

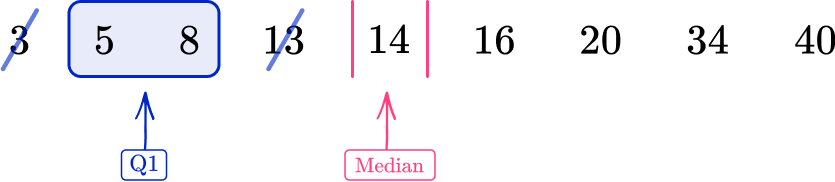
The midpoint of the two data values 5 and 8 is 6.5.

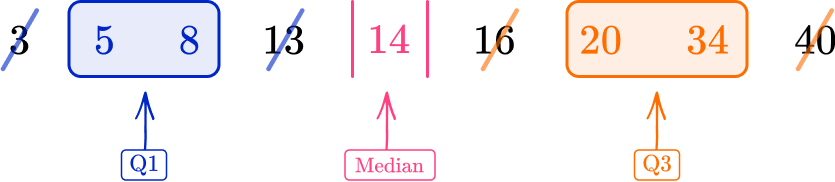
The midpoint of the two data values 20 and 34 is 27.

As Q1=6.5 and Q3=27

IQR=Q3-Q1=27-6.5=21.5

Example 4: IQR from a stem and leaf diagram

Find the interquartile range from the data in the stem and leaf diagram.

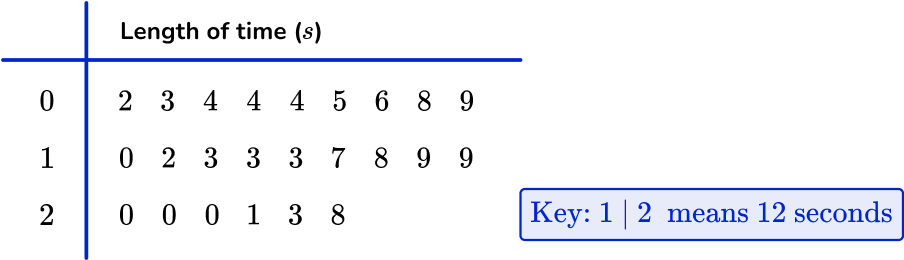
n is the number of values in the data set; here n=24.

As you have an even number of values in the data set, you use the formula \cfrac{n+1}{4} with n=24 to give

\cfrac{24+1}{4}=\cfrac{25}{4}=6.25

So the lower quartile lies between the 6 th and 7 th data point. You can use the midpoint of these two values.

Using the stem and leaf diagram, you have

After using the key, the 6 th and 7 th of values are 5 and 6. The midpoint of these is 5.5, so the lower quartile is 5.5.

You can use the formula 3 \times \, \cfrac{n+1}{4} with n=24 to give

3 \times \cfrac{24+1}{4}=3 \times \cfrac{25}{4}=3 \times 6.25=18.75

Note that if you’ve already found that the lower quartile is the 6.25 th value, you can simply multiply 6.25 by 3 to get 18.75.

So the upper quartile lies between the 18 th and 19 th data point, and you use the midpoint of these values.

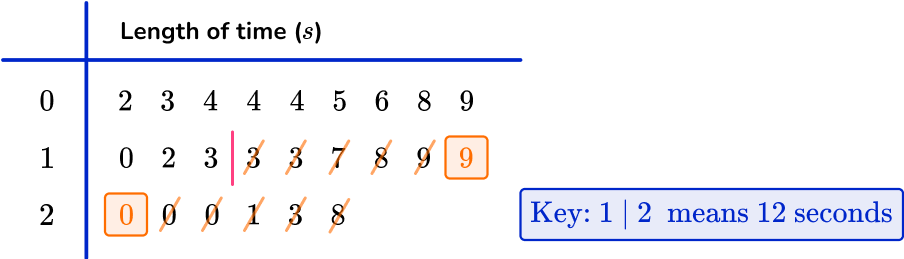
Using the key, the 18 th and 19 th values are 19 and 20 respectively. The midpoint of these is 19.5, so the upper quartile is 19.5.

As Q1=5.5 and Q3=19.5

IQR=Q3-Q1=19.5-5.5=14

Example 5: IQR from a five-number summary

Below is a table showing a summary of statistical values for a plant growth experiment.

Determine the interquartile range of reaction times.

The lower quartile is the value Q1. Here Q1=5.4 \, cm.

The upper quartile is the value Q3. Here Q3=9.1 \, cm.

IQR=Q3-Q1=9.1-5.4=3.7 \, cm

Example 6: IQR from a box plot

The box plot below shows the distribution of the age of trees in a woodland.

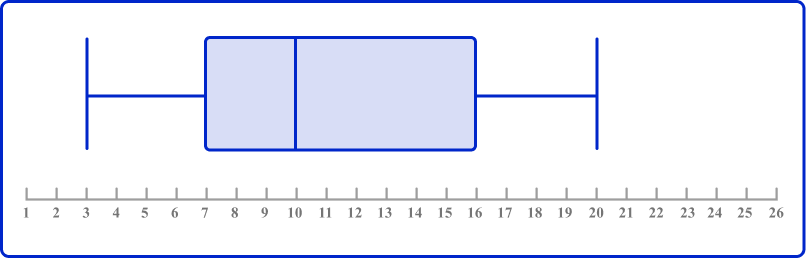
Calculate the interquartile range of ages of trees.

The lower quartile of a box plot is the left edge of the box within the box plot. This line is positioned above the value 7 on the scale and so,

The upper quartile of a box plot is the right edge of the box within the box plot. This line is positioned above the value 16 on the scale and so,

As Q3=16 and Q1=7,

IQR=Q3-Q1=16-7=9

Teaching tips for interquartile range

• Begin by explaining the basics of data and its representation using measures like mean, median, and range (each being a measure of central tendency). Then, introduce the interquartile range as a measure of variability that focuses on the middle 50 \% of the data.
• Provide ample opportunities for students to practice calculating interquartile range. Start with simple examples and gradually increase the complexity of the data sets as well as the number of data points as their proficiency improves.
• Incorporate technology tools such as spreadsheet software or online graphing calculators to facilitate data analysis and calculate the interquartile range. Students can even use an online interquartile range calculator. These tools can help students visualize and manipulate data more efficiently.

Easy mistakes to make

• Forgetting to order the data set before finding the median or quartiles The list/data set must be in order from lowest value to highest value before you start finding the key values.
• Stating the quartile value as the number given by the formula, rather than counting and finding that value in the data For example, for the data set 3, 4, 6, 7, 10, the formula for the lower quartile gives \cfrac{5+1}{4}=\cfrac{6}{4}=1.5. This tells you which data values to select (in this case, the midpoint of the 1 st and 2 nd values); do not just write Q1=1.5.
• The range is calculated instead of the interquartile range The range is the smallest value subtracted from the largest value whereas the interquartile range is the lower quartile subtracted from the upper quartile.

Related representing data lessons

• Representing data
• Stem and leaf plot
• Scatterplot
• Two way tables
• Time series graph

Practice interquartile range questions

1. Calculate the interquartile range for the following list of values.

Find the lower quartile (Q1) and the upper quartile (Q3). Then subtract the lower quartile from the upper quartile to get the IQR.

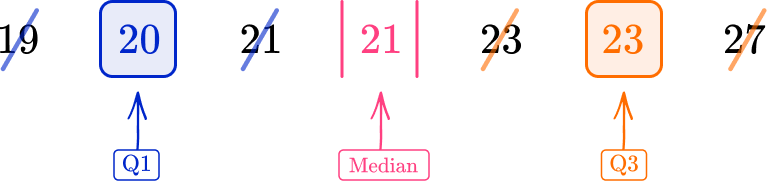
Q1=20, \, Q3=23

IQR=Q3-Q1=23-20=3

2. Find the interquartile range for the data set.

Q1=4, \, Q3=13.5

IQR=Q3-Q1=13.5-4=9.5

3. Find the interquartile range.

First, you need to order the data from lowest value to highest value:

6, 12, 14, 15, 19, 21, 23, 33, 45

Then, find the lower quartile (Q1) and the upper quartile (Q3). Finally, subtract the lower quartile from the upper quartile to get the IQR.

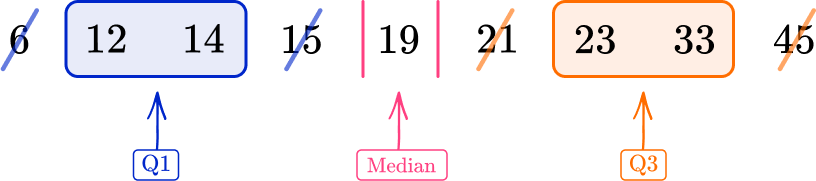
Q1=13, \, Q3=28

IQR=Q3-Q1=28-13=15

4. This table shows the shoe sizes of 18 boys. Calculate the interquartile range for the data.

Q1=6, \, Q3=10

IQR=Q3-Q1=10-6=4

5. This table shows the five-number summary for a set of data.

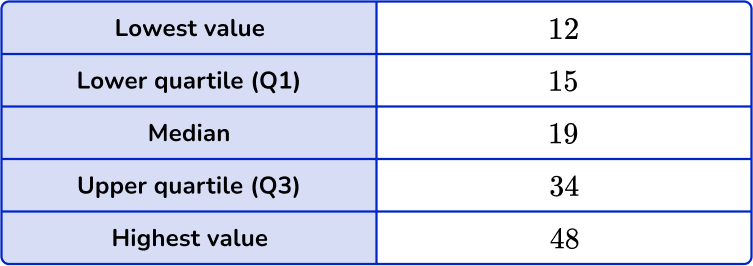
Calculate the interquartile range.

Q1=15, \, Q3=34 and then 34-15=19

6. This table shows some descriptive statistics for a set of data.

Calculate the value for the upper quartile, x.

Q1=12 and IQR=43.

To calculate the Q3, you add the interquartile range to the value for the lower quartile:

x=Q1+IQR=12+43=55.

7. Data was collected about the circumference of apples in an orchard. The data was sorted into the stem and leaf diagram below.

Calculate the interquartile range of circumferences of apples within the orchard.

There are 25 apples in the data set.

The median for an odd number of data values is found in the position \cfrac{n+1}{2}. 

As n=25, the median is in the 13 th position and so the value for the median is 29.2 \, cm.

The lower quartile is the middle value of the lower half of the data, excluding the median value (29.2 \, cm). Here, the lower quartile is between the two values 28.0 \, cm and 28.0 \, cm and so the lower quartile is 28.0 \, cm.

The upper quartile is the middle of the upper half of the data, excluding the median. Here the upper quartile is halfway between 30.0 \, cm and 30.1 \, cm which is equal to 30.05 \, cm.

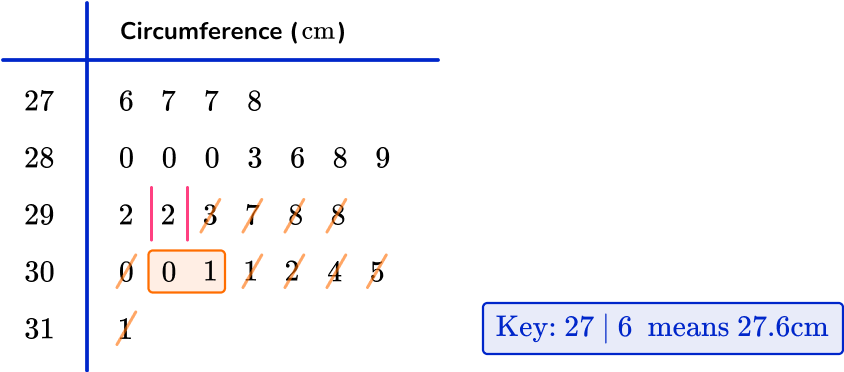
As IQR=Q3-Q1,

IQR=30.05-28.0=2.05 \, cm.

Interquartile range FAQs

The interquartile range (IQR) is a measure of the spread or range of values in a dataset. It represents the difference between the upper quartile ( 75 th percentile) and the lower quartile ( 25 th percentile). It shows the range of values that fall within the middle 50 \% of the data.

To find the interquartile range (IQR) of a data set, subtract the lower quartile (Q1) from the upper quartile (Q3).

Outliers can change the interquartile range (IQR) by making it larger or smaller. This happens because outliers can shift the upper and lower quartiles, which are used to calculate the IQR. However, the IQR is less affected by outliers compared to other measures of spread.

The next lessons are

• Frequency table
• Frequency graph
• Sampling methods
• Ratio and proportion
• Represent and interpret data

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs .

[FREE] Common Core Practice Tests (Grades 3 to 6)

Prepare for math tests in your state with these Grade 3 to Grade 6 practice assessments for Common Core and state equivalents.

40 multiple choice questions and detailed answers to support test prep, created by US math experts covering a range of topics!

Privacy Overview

How to Calculate Quartiles for Grouped Data

Quartiles are values that split up a dataset into four equal parts.

You can use the following formula to calculate quartiles for grouped data:

• Q i = L + (C/F) * (iN/4 – M)

L : The lower bound of the interval that contains the i th quartile

C : The class width

F : The frequency of the interval that contains the i th quartile

N : The total frequency

M : The cumulative frequency leading up to the interval that contains the i th quartile

The following example shows how to use this formula in practice.

Example: Calculate Quartiles for Grouped Data

Suppose we have the following frequency distribution:

Now suppose we’d like to calculate the value at the third quartile (Q 3 ) of this distribution.

The value at the third quartile will be located at position (iN/4) in the distribution.

Thus, (iN/4) = (3*92/4) = 69.

The interval that contains the third quartile will be the 21-25 interval since 69 is between the cumulative frequencies of 58 and 70.

Knowing this, we can find each of the values necessary to plug into our formula:

• The lower bound of the interval is 21 .
• The class width is calculated as 25 – 21 = 4 .
• The frequency of the 21-25 class is 12
• The total cumulative frequency in the table is 92 .
• The cumulative frequency leading up to the 21-25 class is 58 .

We can then plug in all of these values into the formula from earlier to find the value at the third quartile:

• Q 3 = 21 + (4/12) * ((3)(92)/4 – 58)
• Q 3 = 24.67

The value at the third quartile is 24.67 .

You can use a similar approach to calculate the values for the first and second quartiles.

Additional Resources

The following tutorials provide additional information for working with grouped data:

How to Find Mean & Standard Deviation of Grouped Data How to Find the Mode of Grouped Data How to Find the Median of Grouped Data Grouped vs. Ungrouped Frequency Distributions

How to Perform a One Sample T-Test in R

How to add & subtract hours from time in excel, related posts, how to normalize data between -1 and 1, vba: how to check if string contains another..., how to interpret f-values in a two-way anova, how to create a vector of ones in..., how to find the mode of a histogram..., how to find quartiles in even and odd..., how to determine if a probability distribution is..., what is a symmetric histogram (definition & examples), how to calculate sxy in statistics (with example), how to calculate sxx in statistics (with example).

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

3.3: Measures of Position

• Last updated
• Save as PDF
• Page ID 10928

The common measures of location are quartiles and percentiles. Quartiles are special percentiles. The first quartile, Q 1 , is the same as the 25 th percentile, and the third quartile, Q 3 , is the same as the 75 th percentile. The median, M , is called both the second quartile and the 50 th percentile.

To calculate quartiles and percentiles, the data must be ordered from smallest to largest. Quartiles divide ordered data into quarters. Percentiles divide ordered data into hundredths. To score in the 90 th percentile of an exam does not mean, necessarily, that you received 90% on a test. It means that 90% of test scores are the same or less than your score and 10% of the test scores are the same or greater than your test score.

Percentiles are useful for comparing values. For this reason, universities and colleges use percentiles extensively. One instance in which colleges and universities use percentiles is when SAT results are used to determine a minimum testing score that will be used as an acceptance factor. For example, suppose Duke accepts SAT scores at or above the 75 th percentile. That translates into a score of at least 1220.

Percentiles are mostly used with very large populations. Therefore, if you were to say that 90% of the test scores are less (and not the same or less) than your score, it would be acceptable because removing one particular data value is not significant.

The median is a number that measures the "center" of the data. You can think of the median as the "middle value," but it does not actually have to be one of the observed values. It is a number that separates ordered data into halves. Half the values are the same number or smaller than the median, and half the values are the same number or larger. For example, consider the following data.

1; 11.5; 6; 7.2; 4; 8; 9; 10; 6.8; 8.3; 2; 2; 10; 1

Ordered from smallest to largest:

1; 1; 2; 2; 4; 6; 6.8; 7.2; 8; 8.3; 9; 10; 10; 11.5

Since there are 14 observations, the median is between the seventh value, 6.8, and the eighth value, 7.2. To find the median, add the two values together and divide by two.

The median is seven. Half of the values are smaller than seven and half of the values are larger than seven.

Quartiles are numbers that separate the data into quarters. Quartiles may or may not be part of the data. To find the quartiles, first find the median or second quartile. The first quartile, Q 1 , is the middle value of the lower half of the data, and the third quartile, Q 3 , is the middle value, or median, of the upper half of the data. To get the idea, consider the same data set:

The median or second quartile is seven. The lower half of the data are 1, 1, 2, 2, 4, 6, 6.8. The middle value of the lower half is two.

1; 1; 2; 2; 4; 6; 6.8

The number two, which is part of the data, is the first quartile . One-fourth of the entire sets of values are the same as or less than two and three-fourths of the values are more than two.

The upper half of the data is 7.2, 8, 8.3, 9, 10, 10, 11.5. The middle value of the upper half is nine.

The third quartile , Q 3, is nine. Three-fourths (75%) of the ordered data set are less than nine. One-fourth (25%) of the ordered data set are greater than nine. The third quartile is part of the data set in this example.

The interquartile range is a number that indicates the spread of the middle half or the middle 50% of the data. It is the difference between the third quartile ( Q 3 ) and the first quartile ( Q 1 ).

\[IQR = Q_3 – Q_1 \tag{2.4.1}\]

The IQR can help to determine potential outliers . A value is suspected to be a potential outlier if it is less than (1.5)( IQR ) below the first quartile or more than (1.5)( IQR ) above the third quartile . Potential outliers always require further investigation.

Definition: Outliers

A potential outlier is a data point that is significantly different from the other data points. These special data points may be errors or some kind of abnormality or they may be a key to understanding the data.

Example 2.4.1

For the following 13 real estate prices, calculate the IQR and determine if any prices are potential outliers. Prices are in dollars.

389,950; 230,500; 158,000; 479,000; 639,000; 114,950; 5,500,000; 387,000; 659,000; 529,000; 575,000; 488,800; 1,095,000

• Order the data from smallest to largest.

114,950; 158,000; 230,500; 387,000; 389,950; 479,000; 488,800; 529,000; 575,000; 639,000; 659,000; 1,095,000; 5,500,000

\[M = 488,800 \nonumber\]

\[Q_{1} = \dfrac{230,500 + 387,000}{2} = 308,750\nonumber\]

\[Q_{3} = \dfrac{639,000 + 659,000}{2} = 649,000\nonumber\]

\[IQR = 649,000 - 308,750 = 340,250\nonumber\]

\[(1.5)(IQR) = (1.5)(340,250) = 510,375\nonumber\]

\[Q_{1} - (1.5)(IQR) = 308,750 - 510,375 = –201,625\nonumber\]

\[Q_{3} + (1.5)(IQR) = 649,000 + 510,375 = 1,159,375\nonumber\]

No house price is less than –201,625. However, 5,500,000 is more than 1,159,375. Therefore, 5,500,000 is a potential outlier .

Exercise \(\PageIndex{1}\)

For the following 11 salaries, calculate the IQR and determine if any salaries are outliers. The salaries are in dollars.

$33,000; $64,500; $28,000; $54,000; $72,000; $68,500; $69,000; $42,000; $54,000; $120,000; $40,500

$28,000; $33,000; $40,500; $42,000; $54,000; $54,000; $64,500; $68,500; $69,000; $72,000; $120,000

Median = $54,000

\[Q_{1} = $40,500\nonumber\]

\[Q_{3} = $69,000\nonumber\]

\[IQR = $69,000 - $40,500 = $28,500\nonumber\]

\[(1.5)(IQR) = (1.5)($28,500) = $42,750\nonumber\]

\[Q_{1} - (1.5)(IQR) = $40,500 - $42,750 = -$2,250\nonumber\]

\[Q_{3} + (1.5)(IQR) = $69,000 + $42,750 = $111,750\nonumber\]

No salary is less than –$2,250. However, $120,000 is more than $11,750, so $120,000 is a potential outlier.

Example 2.4.2

For the two data sets in the test scores example , find the following:

• The interquartile range. Compare the two interquartile ranges.
• Any outliers in either set.

The five number summary for the day and night classes is

The IQR for the night group is \(Q_{3} - Q_{1} = 89 - 78 = 11\)

The interquartile range (the spread or variability) for the day class is larger than the night class IQR . This suggests more variation will be found in the day class’s class test scores.

• \(Q_{1} - IQR(1.5) = 56 – 26.5(1.5) = 16.25\)
• \(Q_{3} + IQR(1.5) = 82.5 + 26.5(1.5) = 122.25\)

Since the minimum and maximum values for the day class are greater than 16.25 and less than 122.25, there are no outliers.

Night class outliers are calculated as:

• \(Q_{1} - IQR (1.5) = 78 – 11(1.5) = 61.5\)
• \(Q_{3} + IQR(1.5) = 89 + 11(1.5) = 105.5\)

For this class, any test score less than 61.5 is an outlier. Therefore, the scores of 45 and 25.5 are outliers. Since no test score is greater than 105.5, there is no upper end outlier.

Exercise \(\PageIndex{2}\)

Find the interquartile range for the following two data sets and compare them.

Test Scores for Class A

69; 96; 81; 79; 65; 76; 83; 99; 89; 67; 90; 77; 85; 98; 66; 91; 77; 69; 80; 94

Test Scores for Class B

90; 72; 80; 92; 90; 97; 92; 75; 79; 68; 70; 80; 99; 95; 78; 73; 71; 68; 95; 100

65; 66; 67; 69; 69; 76; 77; 77; 79; 80; 81; 83; 85; 89; 90; 91; 94; 96; 98; 99

\(Median = \dfrac{80 + 81}{2}\) = 80.5

\(Q_{1} = \dfrac{69 + 76}{2} = 72.5\)

\(Q_{3} = \dfrac{90 + 91}{2} = 90.5\)

\(IQR = 90.5 - 72.5 = 18\)

68; 68; 70; 71; 72; 73; 75; 78; 79; 80; 80; 90; 90; 92; 92; 95; 95; 97; 99; 100

\(Median = \dfrac{80 + 80}{2} = 80\)

\(Q_{1} = \dfrac{72 + 73}{2} = 72.5\)

\(Q_{3} = \dfrac{92 + 95}{2} = 93.5\)

\(IQR = 93.5 - 72.5 = 21\)

The data for Class B has a larger IQR , so the scores between Q 3 and Q 1 (middle 50%) for the data for Class B are more spread out and not clustered about the median.

Example \(\PageIndex{3}\)

Fifty statistics students were asked how much sleep they get per school night (rounded to the nearest hour). The results were:

Find the 28 th percentile . Notice the 0.28 in the "cumulative relative frequency" column. Twenty-eight percent of 50 data values is 14 values. There are 14 values less than the 28 th percentile. They include the two 4s, the five 5s, and the seven 6s. The 28 th percentile is between the last six and the first seven. The 28 th percentile is 6.5.

Find the median . Look again at the "cumulative relative frequency" column and find 0.52. The median is the 50 th percentile or the second quartile. 50% of 50 is 25. There are 25 values less than the median. They include the two 4s, the five 5s, the seven 6s, and eleven of the 7s. The median or 50 th percentile is between the 25 th , or seven, and 26 th , or seven, values. The median is seven.

Find the third quartile . The third quartile is the same as the 75 th percentile. You can "eyeball" this answer. If you look at the "cumulative relative frequency" column, you find 0.52 and 0.80. When you have all the fours, fives, sixes and sevens, you have 52% of the data. When you include all the 8s, you have 80% of the data. The 75 th percentile, then, must be an eight . Another way to look at the problem is to find 75% of 50, which is 37.5, and round up to 38. The third quartile, Q 3 , is the 38 th value, which is an eight. You can check this answer by counting the values. (There are 37 values below the third quartile and 12 values above.)

Exercise \(\PageIndex{3}\)

Forty bus drivers were asked how many hours they spend each day running their routes (rounded to the nearest hour). Find the 65 th percentile.

The 65 th percentile is between the last three and the first four.

The 65 th percentile is 3.5.

Example 2.4.4

Using the table above in Example \(\PageIndex{3}\)

• Find the 80 th percentile.
• Find the 90 th percentile.
• Find the first quartile. What is another name for the first quartile?

Using the data from the frequency table, we have:

• The 80 th percentile is between the last eight and the first nine in the table (between the 40 th and 41 st values). Therefore, we need to take the mean of the 40 th an 41 st values. The 80 th percentile \(= \dfrac{8+9}{2} = 8.5\)
• The 90 th percentile will be the 45 th data value (location is \(0.90(50) = 45\)) and the 45 th data value is nine.
• Q 1 is also the 25 th percentile. The 25 th percentile location calculation: \(P_{25} = 0.25(50) = 12.5 \approx 13\) the 13 th data value. Thus, the 25 th percentile is six.

Exercise \(\PageIndex{4}\)

Refer to the table above in Exercise \(\PageIndex{3}\) . Find the third quartile. What is another name for the third quartile?

The third quartile is the 75 th percentile, which is four. The 65 th percentile is between three and four, and the 90 th percentile is between four and 5.75. The third quartile is between 65 and 90, so it must be four.

COLLABORATIVE STATISTICS

Your instructor or a member of the class will ask everyone in class how many sweaters they own. Answer the following questions:

• How many students were surveyed?
• What kind of sampling did you do?
• Construct two different histograms. For each, starting value = _____ ending value = ____.
• Find the median, first quartile, and third quartile.
• the 10 th percentile
• the 70 th percentile
• the percent of students who own less than four sweaters

A Formula for Finding the k th Percentile

If you were to do a little research, you would find several formulas for calculating the kth percentile. Here is one of them.

• \(k =\) the kth percentile. It may or may not be part of the data.
• \(i =\) the index (ranking or position of a data value)
• \(n =\) the total number of data

Calculate \(i = \dfrac{k}{100}(n + 1)\)

If \(i\) is an integer, then the \(k^{th}\) percentile is the data value in the \(i^{th}\) position in the ordered set of data.

If \(i\) is not an integer, then round \(i\) up and round \(i\) down to the nearest integers. Average the two data values in these two positions in the ordered data set. This is easier to understand in an example.

Example 2.4.5

Listed are 29 ages for Academy Award winning best actors in order from smallest to largest.

• Find the 70 th percentile.
• Find the 83 rd percentile.
• \(i\) = the index
• \(k\) = 83 rd percentile
• \(i \)= the index

Exercise \(\PageIndex{5}\)

18; 21; 22; 25; 26; 27; 29; 30; 31; 33; 36; 37; 41; 42; 47; 52; 55; 57; 58; 62; 64; 67; 69; 71; 72; 73; 74; 76; 77

Calculate the 20 th percentile and the 55 th percentile.

\(k = 20\). Index \(= i = \dfrac{k}{100}(n+1) = \dfrac{20}{100}(29 + 1) = 6\). The age in the sixth position is 27. The 20 th percentile is 27 years.

\(k = 55\). Index \(= i = \dfrac{k}{100}(n+1) = \dfrac{55}{100}(29 + 1) = 16.5\). Round down to 16 and up to 17. The age in the 16 th position is 52 and the age in the 17 th position is 55. The average of 52 and 55 is 53.5. The 55 th percentile is 53.5 years.

You can calculate percentiles using calculators and computers. There are a variety of online calculators.

A Formula for Finding the Percentile of a Value in a Data Set

• \(x =\) the number of data values counting from the bottom of the data list up to but not including the data value for which you want to find the percentile.
• \(y =\) the number of data values equal to the data value for which you want to find the percentile.
• \(n =\) the total number of data.
• Calculate \(\dfrac{x + 0.5y}{n}(100)\). Then round to the nearest integer.

Example 2.4.6

• Find the percentile for 58.
• Find the percentile for 25.

\(x = 18\) and \(y = 1\). \(\dfrac{x + 0.5y}{n}(100) = \dfrac{18 + 0.5(1)}{29}(100) = 63.80\). 58 is the 64 th percentile.

\(x = 3\) and \(y = 1\). \(\dfrac{x + 0.5y}{n}(100) = \dfrac{3 + 0.5(1)}{29}(100) = 12.07\). Twenty-five is the 12 th percentile.

Exercise \(\PageIndex{6}\)

Listed are 30 ages for Academy Award winning best actors in order from smallest to largest.

18; 21; 22; 25; 26; 27; 29; 30; 31, 31; 33; 36; 37; 41; 42; 47; 52; 55; 57; 58; 62; 64; 67; 69; 71; 72; 73; 74; 76; 77

Find the percentiles for 47 and 31.

Percentile for 47: Counting from the bottom of the list, there are 15 data values less than 47. There is one value of 47.

\(x = 15\) and \(y = 1\). \(\dfrac{x + 0.5y}{n}(100) = \dfrac{15 + 0.5(1)}{30}(100) = 51.67\). 47 is the 52 nd percentile.

Percentile for 31: Counting from the bottom of the list, there are eight data values less than 31. There are two values of 31.

\(x = 8\) and \(y = 2\). \(\dfrac{x + 0.5y}{n}(100) = \dfrac{8 + 0.5(2)}{30}(100) = 30\). 31 is the 30 th percentile.

Interpreting Percentiles, Quartiles, and Median

A percentile indicates the relative standing of a data value when data are sorted into numerical order from smallest to largest. Percentages of data values are less than or equal to the p th percentile. For example, 15% of data values are less than or equal to the 15 th percentile.

• Low percentiles always correspond to lower data values.
• High percentiles always correspond to higher data values.

A percentile may or may not correspond to a value judgment about whether it is "good" or "bad." The interpretation of whether a certain percentile is "good" or "bad" depends on the context of the situation to which the data applies. In some situations, a low percentile would be considered "good;" in other contexts a high percentile might be considered "good". In many situations, there is no value judgment that applies.

Understanding how to interpret percentiles properly is important not only when describing data, but also when calculating probabilities in later chapters of this text.

When writing the interpretation of a percentile in the context of the given data, the sentence should contain the following information.

• information about the context of the situation being considered
• the data value (value of the variable) that represents the percentile
• the percent of individuals or items with data values below the percentile
• the percent of individuals or items with data values above the percentile.

Example 2.4.7

On a timed math test, the first quartile for time it took to finish the exam was 35 minutes. Interpret the first quartile in the context of this situation.

• Twenty-five percent of students finished the exam in 35 minutes or less.
• Seventy-five percent of students finished the exam in 35 minutes or more.
• A low percentile could be considered good, as finishing more quickly on a timed exam is desirable. (If you take too long, you might not be able to finish.)

Exercise \(\PageIndex{7}\)

For the 100-meter dash, the third quartile for times for finishing the race was 11.5 seconds. Interpret the third quartile in the context of the situation.

Twenty-five percent of runners finished the race in 11.5 seconds or more. Seventy-five percent of runners finished the race in 11.5 seconds or less. A lower percentile is good because finishing a race more quickly is desirable.

Example 2.4.8

On a 20 question math test, the 70 th percentile for number of correct answers was 16. Interpret the 70 th percentile in the context of this situation.

• Seventy percent of students answered 16 or fewer questions correctly.
• Thirty percent of students answered 16 or more questions correctly.
• A higher percentile could be considered good, as answering more questions correctly is desirable.

Exercise \(\PageIndex{8}\)

On a 60 point written assignment, the 80 th percentile for the number of points earned was 49. Interpret the 80 th percentile in the context of this situation.

Eighty percent of students earned 49 points or fewer. Twenty percent of students earned 49 or more points. A higher percentile is good because getting more points on an assignment is desirable.

Example 2.4.9

At a community college, it was found that the 30 th percentile of credit units that students are enrolled for is seven units. Interpret the 30 th percentile in the context of this situation.

• Thirty percent of students are enrolled in seven or fewer credit units.
• Seventy percent of students are enrolled in seven or more credit units.
• In this example, there is no "good" or "bad" value judgment associated with a higher or lower percentile. Students attend community college for varied reasons and needs, and their course load varies according to their needs.

Exercise \(\PageIndex{9}\)

During a season, the 40 th percentile for points scored per player in a game is eight. Interpret the 40 th percentile in the context of this situation.

Forty percent of players scored eight points or fewer. Sixty percent of players scored eight points or more. A higher percentile is good because getting more points in a basketball game is desirable.

Example 2.4.10

Sharpe Middle School is applying for a grant that will be used to add fitness equipment to the gym. The principal surveyed 15 anonymous students to determine how many minutes a day the students spend exercising. The results from the 15 anonymous students are shown.

0 minutes; 40 minutes; 60 minutes; 30 minutes; 60 minutes

10 minutes; 45 minutes; 30 minutes; 300 minutes; 90 minutes;

30 minutes; 120 minutes; 60 minutes; 0 minutes; 20 minutes

Determine the following five values.

If you were the principal, would you be justified in purchasing new fitness equipment? Since 75% of the students exercise for 60 minutes or less daily, and since the IQR is 40 minutes (60 – 20 = 40), we know that half of the students surveyed exercise between 20 minutes and 60 minutes daily. This seems a reasonable amount of time spent exercising, so the principal would be justified in purchasing the new equipment.

However, the principal needs to be careful. The value 300 appears to be a potential outlier.

\[Q_{3} + 1.5(IQR) = 60 + (1.5)(40) = 120\].

The value 300 is greater than 120 so it is a potential outlier. If we delete it and calculate the five values, we get the following values:

We still have 75% of the students exercising for 60 minutes or less daily and half of the students exercising between 20 and 60 minutes a day. However, 15 students is a small sample and the principal should survey more students to be sure of his survey results.

• Cauchon, Dennis, Paul Overberg. “Census data shows minorities now a majority of U.S. births.” USA Today, 2012. Available online at usatoday30.usatoday.com/news/...sus/55029100/1 (accessed April 3, 2013).
• Data from the United States Department of Commerce: United States Census Bureau. Available online at http://www.census.gov/ (accessed April 3, 2013).
• “1990 Census.” United States Department of Commerce: United States Census Bureau. Available online at http://www.census.gov/main/www/cen1990.html (accessed April 3, 2013).
• Data from San Jose Mercury News .
• Data from Time Magazine ; survey by Yankelovich Partners, Inc.

The values that divide a rank-ordered set of data into 100 equal parts are called percentiles. Percentiles are used to compare and interpret data. For example, an observation at the 50 th percentile would be greater than 50 percent of the other obeservations in the set. Quartiles divide data into quarters. The first quartile ( Q 1 ) is the 25 th percentile,the second quartile ( Q 2 or median) is 50 th percentile, and the third quartile ( Q 3 ) is the the 75 th percentile. The interquartile range, or IQR , is the range of the middle 50 percent of the data values. The IQR is found by subtracting Q 1 from Q 3 , and can help determine outliers by using the following two expressions.

• \(Q_{3} + IQR(1.5)\)
• \(Q_{1} - IQR(1.5)\)

Formula Review

\[i = \dfrac{k}{100}(n+1) \nonumber\]

where \(i\) = the ranking or position of a data value,

• \(k\) = the k th percentile,
• \(n\) = total number of data.

Expression for finding the percentile of a data value: \(\left(\dfrac{x + 0.5y}{n}\right)(100)\)

where \(x =\) the number of values counting from the bottom of the data list up to but not including the data value for which you want to find the percentile,

\(y =\) the number of data values equal to the data value for which you want to find the percentile,

\(n =\) total number of data

Save 10% on All AnalystPrep 2024 Study Packages with Coupon Code BLOG10 .

• Payment Plans
• Product List
• Partnerships

• Try Free Trial
• Study Packages
• Levels I, II & III Lifetime Package
• Video Lessons
• Study Notes
• Practice Questions
• Levels II & III Lifetime Package
• About the Exam
• About your Instructor
• Part I Study Packages
• Part I & Part II Lifetime Package
• Part II Study Packages
• Exams P & FM Lifetime Package
• Quantitative Questions
• Verbal Questions
• Data Insight Questions
• Live Tutoring
• About your Instructors
• EA Practice Questions
• Data Sufficiency Questions
• Integrated Reasoning Questions

Calculating and Interpreting Quartiles, Quintiles, Deciles and Percentiles

Quartiles, quintiles, deciles, and percentiles are values or cut points that partition a finite number of observations into nearly equal-sized subsets. The number of partitions depends on the type of cut point involved.

They divide data into four parts. The first quartile, Q 1 , is referred to as the lower quartile, and the last quartile, Q 4 , is known as the upper quartile. Q 1 splits the data into the lower 25% of the values and the upper 75%. Similarly, the upper quartile subdivides the data into the lower 75% of the values and the upper 25%. The difference between the upper quartile and the lower quartile is known as the interquartile range , which indicates the spread of the middle 50% of the data.

Though rarely used in practice, quintiles split a set of data into five equal parts, i.e., fifths. Therefore, the second quintile splits the data into the lower 40% of the values and the upper 60%.

Deciles subdivide data into ten equal parts. There are 10 deciles in any data set. For example, the fourth decile splits data into the lower 40% of the values and the upper 60%.

Percentiles

Percentiles split data into 100 equal parts, i.e., hundredths. So, for instance, the 77 th percentile splits data into the lower 77% of the values and the upper 23%.

Financial analysts commonly use the four types of subdivisions to rank investment performance. You should note that quartiles, quintiles, and deciles can all be expressed as percentiles. For instance, the first quartile is just the 25 th percentile. Similarly, the fourth decile is simply the 40 th percentile. This enables the application of the formula below.

$$ \text{Position of percentile}, \text{denoted } p_y =\cfrac {(n + 1) y}{100} $$

Where n is the number of observations and y is the percentile.

Note: you must always order the data set, usually in ascending order, before calculating any of these values.

Example: Quartiles

Given the following distribution of returns, determine the lower quartile:

{10%   23%   12%   21%   14%   17%   16%   11%   15%   19%}

First, we have to arrange the values in ascending order:

{10%   11%   12%   14%   15%   16%   17%   19%    21%   23%}

Next, we establish the position of the first quartile. This is simply the 25 th percentile. Therefore:

$$ \begin{align*} P_{25} & =\cfrac {(10 + 1)25}{100} \\ & = 2.75^{\text{th}} \text{ value}\\ \end{align*} $$

Since the value is not straightforward, we have to extrapolate between the 2 nd and the 3 rd data points. The 25 th percentile is three-fourth (0.75) of the way from the 2 nd data point (11%) to the 3 rd data point (12%):

$$ \begin{align*} & 11\% + 0.75 * (12 – 11) \\ & = 11.75\% \end{align*} $$

Question A mutual fund achieved the following rates of growth over an 11-month period: {3%   2%   7%   8%   2%   4%   3%   7.5%   7.2%   2.7%   2.09%} Determine the 5 th decile from the data. A. 4% B. 3% C. 2% Solution The correct answer is B. First, you should re-arrange the data in ascending order: {2%   2%   2.7%   2.09%   3%   3%   4%   7%   7.2%   7.5%   8%} Secondly, you should establish the 5 th decile. This is simply the 50 th percentile and is actually the median : $$ \begin{align*} P_{50} & =\cfrac {(1 + 11) 50}{100} \\ & = 12 * 0.5 \\ & = 6 \text{ i}.\text{e}. \text{ the }6^{\text{th}} \text{ data point}. \\ \end{align*} $$ Therefore, $$ \text{the } 5^{\text{th}} \text{ decile} = 50^{\text{th}} \text { percentile} = \text{median} = 3\% $$

Offered by AnalystPrep

The Short-run and Long-run Aggregate Supply Curve

Sampling considerations and 5 common biases in sampling, simple random sampling and sampling di ....

Simple Random Sampling Simple random sampling, also called chance selection, refers to a... Read More

Analysis of Variance (ANOVA)

The sum of squares of a regression model is usually represented in the... Read More

Considerations and Biases in Sampling

Understanding test statistics.

A test statistic is a standardized value computed from sample information when testing... Read More