illustrative mathematics homework

IM 6–12 Math: Grading and Homework Policies and Practices

By Jennifer Willson,  Director, 6–12 Professional Learning Design

In my role at IM, working with teachers and administrators, I am asked to help with the challenges of implementing an IM curriculum. One of the most common challenges is: how can we best align these materials to our homework and grading practices? This question is a bit different from “How should we assess student learning?” or “How should we use assessment to inform instruction?” 

When we created the curriculum, we chose not to prescribe homework assignments or decide which student work should count as a graded event. This was deliberate—homework policies and grading practices are highly variable, localized, and values-driven shared understandings that evolve over time. For example, the curriculum needed to work for schools where nightly, graded assignments are expected; schools where no work done outside of class is graded; and schools who take a feedback-only approach for any formative work.

IM 6–8 Math was released in 2017, and IM Algebra 1, Geometry, and Algebra 2 in 2019. In that time, I’ve been able to observe some patterns in the ways schools and teachers align the materials to their local practices. So, while we’re still not going to tell you what to do, we’re now in a position to describe some trends and common ways in which schools and districts make use of the materials to meet their local constraints. Over the past four years, I have heard ideas from teachers, administrators, and IM certified facilitators. In December, I invited our IM community to respond to a survey to share grading and homework policies and practices. In this post I am sharing a compilation of results from the 31 teachers who responded to the survey, as well as ideas from conversations with teachers and IMCFs. We hope that you find some ideas here to inform and inspire your classroom.

How do teachers collect student responses?

Most teachers who responded to the survey collect student work for assessments in a digital platform such as LearnZillion, McGraw-Hill, ASSISTments, Edulastic, Desmos, etc. Others have students upload their work (photo, PDF, etc.) to a learning management system such as Canvas or Google classroom. Even fewer ask students to respond digitally to questions in their learning management system.

How do teachers tend to score each type of assessment, and how is feedback given?

The table shows a summary of how teachers who responded to the survey most often provide feedback for the types of assessments included in the curriculum.

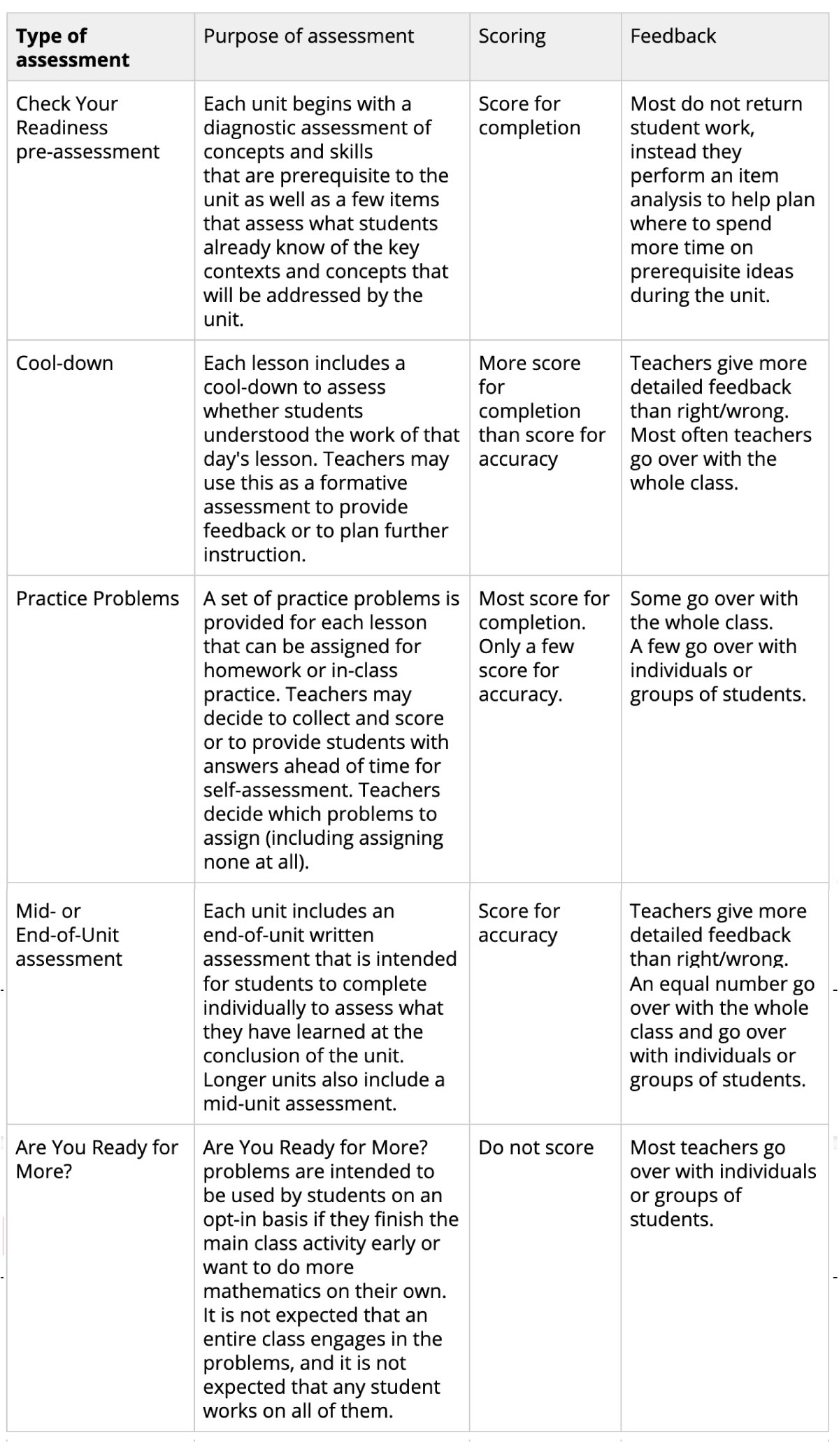
How are practice problems used?

Every lesson in the curriculum (with a very small number of exceptions) includes a short set of cumulative practice problems. Each set could be used as an assignment done in class after the lesson or worked on outside of class, but teachers make use of these items in a variety of ways to meet their students’ learning needs.

While some teachers use the practice problems that are attached to each lesson as homework, others do not assign work outside of class. Here are some other purposes for which teachers use the practice problems:

• extra practice
• student reflection
• as examples to discuss in class or use for a mini-lesson
• as a warm-up question to begin class
• as group work during class

How do teachers structure time and communication to “go over” practice problems?

It’s common practice to assemble practice problems into assignments that are worked on outside of class meeting time. Figuring out what works best for students to get feedback on practice problems while continuing to move students forward in their learning and work through the next lesson can be challenging. 

Here are some ways teachers describe how they approach this need:

• We don’t have time to go over homework every day, but I do build in one class period per section to pause and look at some common errors in cool-downs and invite students to do some revisions where necessary, then I also invite students to look at select practice problems. I collect some practice problems along with cool-downs and use that data to inform what, if anything, I address with the whole class or with a small group.
• Students vote for one practice problem that they thought was challenging, and we spend less than five minutes to get them started. We don’t necessarily work through the whole problem.
• I post solutions to practice problems, sometimes with a video of my solution strategy, so that students can check their work.
• I assign practice problems, post answers, invite students to ask questions (they email me or let me know during the warm-up), and then give section quizzes that are closely aligned to the practice problems, which is teaching my students that asking questions is important.
• I invite students to vote on the most challenging problem and then rather than go over the practice problem I weave it into the current day’s lesson so that students recognize “that’s just like that practice problem!” What I find important is moving students to take responsibility to evaluate their own understanding of the practice problems and not depend on me (the teacher) or someone else to check them. Because my district requires evidence of a quiz and grade each week and I preferred to use my cool-downs formatively, I placed the four most highly requested class practice problems from the previous week on the quiz which I substituted for that day’s cool-down. That saved me quiz design time, there were no surprises for the students, and after about four weeks of consistency with this norm, the students quickly learned that they should not pass up their opportunity to study for the quiz by not only completing the 4–5 practice problems nightly during the week, but again, by reflecting on their own depth of understanding and being ready to give me focused feedback about their greatest struggle on a daily basis.
• I see the practice problems as an opportunity to allow students to go at different paces. It’s more work, but I include extension problems and answers to each practice problem with different strategies and misconceptions underneath. When students are in-person for class, they work independently or in pairs moving to the printed answer keys posted around the room for each problem. They initial under different prompts on the answer key (tried more than one strategy, used a DNL, used a table, made a mistake, used accurate units, used a strategy that’s not on here…) It gives the students and I more feedback when I collect the responses later and allows me to be more present with smaller groups while students take responsibility for checking their work. It also gets students up and moving around the room and normalizes multiple approaches as well as making mistakes as part of the problem solving process.

Quizzes—How often, and how are they made?

Most of the teachers give quizzes—a short graded assessment completed individually under more controlled conditions than other assignments. How often is as varied as the number of teachers who responded: one per unit, twice per unit, once a week, two times per week, 2–3 times per quarter.

If teachers don’t write quiz items themselves or with their team, the quiz items come from practice problems, activities, and adapted cool-downs.

When and how do students revise their work?

Policies for revising work are also as varied as the number of teachers who responded. 

Here are some examples:

• Students are given feedback as they complete activities and revise based on their feedback.
• Students revise cool-downs and practice problems.
• Students can revise end-of-unit assessments and cool-downs.
• Students can meet with me at any time to increase a score on previous work.
• Students revise cool-downs if incorrect, and they are encouraged to ask for help if they can’t figure out their own error.
• Students can revise graded assignments during office hours to ensure successful completion of learning goals.
• Students are given a chance to redo assignments after I work with them individually.
• Students can review and revise their Desmos activities until they are graded.
• We make our own retake versions of the assessments.
• Students can do error logs and retakes on summative assessments.
• We complete the student facing tasks together as a whole class on Zoom in ASSISTments. If a student needs to revise the answers they notify me during the session.

Other advice and words of wisdom

I also asked survey participants for any other strategies that both have and haven’t worked in their classrooms. Here are some responses.

What have you tried that has not worked?

• Going over practice problems with the whole class every day. The ones who need it most often don’t benefit from the whole-class instruction, and the ones who don’t need it distract those who do. 
• Grading work on the tasks within the lessons for accuracy
• Leaving assignments open for the length of the semester so that students can always see unfinished work
• Going through problems on the board with the whole class does not correct student errors
• Most students don’t check feedback comments unless you look at them together
• Grading images of student work on the classroom activity tasks uploaded by students in our learning management systems
• Providing individual feedback on google classroom assignments was time consuming and inefficient
• Allowing students to submit late and missing work with no penalty
• Trying to grade everything
• Below grade 9, homework really does not work.
• Going over every practice problem communicates that students do not really think about the practice problems on their own. 

What else have you tried that has worked well?

• My students do best when I consistently assign practice problems. I have tried giving them an assignment once a week but most students lose track. It is better to give 2–3 problems or reflective prompts after every class, which also helps me get ahead of misconceptions.
• I don’t grade homework since I am unsure who completes it with or for the students.
• A minimum score of 50% on assignments, which allows students the opportunity to recover, in terms of their grade in the class
• Time constraints imposed during remote learning impact the amount and type of homework I give as well as what I grade
• Give fewer problems than normal on second chance assignments
• I have used platforms such as Kahoot to engage students in IM material. I also build Google Forms to administer the Check Your Readiness pre-assessment and End-of-Unit assessments, but I may start using ASSISTments for this in the future.
• The value of homework in high school is okay, but personally I skip good for great.
• Students are able to go back and revise their independent practice work upon recognizing their mistakes and learning further about how to solve the problems.
• Sometimes I select only one or two slides to grade instead of the whole set when I use Desmos activities.
• Allow for flexibility in timing. Give students opportunities for revision.
• Frequent short assessments are better than longer tests, and they allow students to focus on specific skills and get feedback more frequently.
• Especially during the pandemic, many of my students are overwhelmed and underachieving. I am focusing on the core content.
• Homework assignments consist of completing Desmos activities students began in class. Additional slides contain IM practice problems.
• I am only grading the summative assessment for accuracy and all else for completion. I want the students to know that they have the room to learn, try new strategies and be wrong while working on formative assessments.

What grading and homework policies have worked for you and your students that aren’t listed? Share your ideas in the comments so that we can all learn from your experience.

What would you like to learn more about? Let us know in the comments, and it will help us design future efforts like this one so that we can all learn more in a future blog post.

We are grateful to the teachers and facilitators who took the time to share their learning with us.

to the IM Blog and Newsletter

RECENT POSTS

• Leveraging PLCs to Maintain the Magic in Math Communities Throughout the Entire Year April 4, 2024
• Elements of Problem-Based Teaching and Learning February 28, 2024
• Inviting Students to the Math Party: Creating an Inclusive and Engaging Math Community February 6, 2024
• Visualizing IM K-5 Math in Specialized Academic Settings: Part 2 January 18, 2024
• IM Kickoff Message for 2024 January 4, 2024
• Back to School (3)
• Grades 3–5 (105)
• Grades 6–8 (116)
• Grades 9–12 (92)
• Grades K–2 (86)
• Grades K–5 (53)
• Partners (4)
• Professional Learning (74)
• Recent Blog Posts (7)
• Uncategorized (2)

Popular Tags

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

7th grade (Illustrative Mathematics)

Unit 1: scale drawings, unit 2: introducing proportional relationships, unit 3: measuring circles, unit 4: proportional relationships and percentages, unit 5: rational number arithmetic, unit 6: expressions, equations, and inequalities, unit 7: angles, triangles, and prisms, unit 8: probability and sampling.

• Math Curriculum
• Professional Learning

Free Resources to Support Your Use of IM K–12 TM Math

You are now in the im resource hub, where you can explore a variety of useful documents, on-demand videos, and presentations that are useful to the im community. to get started, click below or browse the top navigation toolbar to find the resources you need..

• Follow on Facebook
• Follow on Twitter
• Follow on Pinterest
• Follow on LinkedIn
• Follow our Feed
• Subscribe to our blog and newsletter
• Illustrative Mathematics PO Box 69822 Oro Valley AZ 85737
• 855.741.6284
• Get in Touch
• Practice Standards
• Content Standards
• Our Purpose
• IM Certified Facilitators
• IM Certified Partners
• Presentations
• Privacy Policy

All products and services are offered throughout the United States. Content on this page is licensed. © copyright 2021, Illustrative Mathematics, all rights reserved.

Factors and Multiples

• Understand Factors and Multiples
• Find Factor Pairs and Multiples

Fraction Equivalence and Comparison

• Size and Location of Fractions
• Equivalent Fractions
• Fraction Comparison

Extending Operations to Fractions

• Equal Groups of Fractions
• Addition and Subtraction of Fractions
• Addition of Tenths and Hundredths

From Hundredths to Hundred-thousands

• Decimals with Tenths and Hundredths
• Place-value Relationships through 1,000,000
• Compare, Order, and Round
• Add and Subtract

Multiplicative Comparison and Measurement

• Multiplicative Comparison
• Measurement Conversion
• Let’s Put it to Work

Multiplying and Dividing Multi-digit Numbers

• Features of Patterns
• Multi-digit Multiplication
• Multi-digit Division
• Let’s Put It to Work: Problem Solving with Large Numbers

Angles and Angle Measurement

• Points, Lines, Segments, Rays, and Angles
• The Size of Angles
• Angle Analysis

Properties of Two-dimensional Shapes

• Side Lengths, Angles, and Lines of Symmetry
• Reason about Attributes to Solve Problems

Putting It All Together

• Reason with Fractions
• Whole-number Operations
• Solve Problems with Multiplication and Division
• Creation and Design

• Illustrative Tutor
• 6th Grade IM Math Playlists
• 7th Grade Im Math Playlists
• 8th Grade IM Math Playlist
• Supplemental Math Videos

Support for Open Up Resources - Illustrative Mathematics Practice Lessons

• Like my videos
• Comment on my videos
• Share my videos on Facebook and other social media platforms
• Subscribe to my channel

How to Calculate G.P.A.

How Grades Work

Tips for Parents and Students Staring the Distance Learning School Year

Using Google Slides with an iPad

How to Turn in Assignments in Google Classroom Using an iPad

Use Google to Check Your Math Homework!

How to Split Screens Using an iPad

Open Up Resources - Illustrative Mathematics Tutorial and Supplemental Videos ​

Scaling and Area

6.1: Scaling a Pattern Block (10 minutes)

CCSS Standards

Building Towards

By now, students understand that lengths in a scaled copy are related to the original lengths by the scale factor. Here they see that the area of a scaled copy is related to the original area by the square of the scale factor.

Students build scaled copies of a single pattern block, using blocks of the same shape to do so. They determine how many blocks are needed to create a copy at each specified scale factor. Each pattern block serves as an informal unit of area. Because each original shape has an area of 1 block, the \(\text{(scale factor)}^2\) pattern for the area of a scaled copy is easier to recognize.

Students use the same set of scale factors to build copies of three different shapes (a rhombus, a triangle, and a hexagon). They notice regularity in their repeated reasoning and use their observations to predict the number of blocks needed to build other scaled copies (MP8).

Arrange students in groups of 3–4. Distribute pattern blocks and ask students to use them to build scaled copies of each shape as described in the task. Each group would need at most 16 blocks each of the green triangle, the blue rhombus, and the red trapezoid. If there are not enough for each group to have a full set with 16 each of the green, blue, and red blocks, consider rotating the blocks of each color through the groups, or having students start with 10 blocks of each and ask for more as needed.

Give students 6–7 minutes to collaborate on the task and follow with a whole-class discussion. Make sure all students understand that “twice as long” means “2 times as long.”

Using real pattern blocks is preferred, but the Digital Activity can replace the manipulatives if they are unavailable.

Student Facing

Use the applets to explore the pattern blocks. Work with your group to build the scaled copies described in each question.

Where each side is twice as long?

Where each side is 3 times as long?

Where each side is 4 times as long?

Using a scale factor of 4?

Using a scale factor of 2?

Using a scale factor of 3?

• Make a prediction: How many blocks would it take to build scaled copies of these shapes using a scale factor of 5? Using a scale factor of 6? Be prepared to explain your reasoning.

Student Response

For access, consult one of our IM Certified Partners .

Your teacher will give you some pattern blocks. Work with your group to build the scaled copies described in each question.

How many blue rhombus blocks does it take to build a scaled copy of Figure A:

How many green triangle blocks does it take to build a scaled copy of Figure B:

How many red trapezoid blocks does it take to build a scaled copy of Figure C:

Anticipated Misconceptions

Some students may come up with one of these arrangements for the first question, because they assume the answer will take 2 blocks to build:

You could use one pattern block to demonstrate measuring the lengths of the sides of their shape, to show them which side they have not doubled.

Students may also come up with:

for tripling the trapezoid, because they triple the height of the scaled copy but they do not triple the length. You could use the process described above to show that not all side lengths have tripled.

Activity Synthesis

Display a table with only the column headings filled in. For the first four rows, ask different students to share how many blocks it took them to build each shape and record their answers in the table.

To help student notice, extend, and generalize the pattern in the table, guide a discussion using questions such as these: 

• In the table, how is the number of blocks related to the scale factor? Is there a pattern?
• How many blocks are needed to build scaled copies using scale factors of 5 or 10? How do you know?
• How many blocks are needed to build a scaled copy using any scale factor \(s\) ? 
• If we want a scaled copy where each side is half as long, how much of a block would it take? How do you know? Does the same rule still apply?

If not brought up by students, highlight the fact that the number of blocks it took to build each scaled shape equals the scale factor times itself, regardless of the shape (look at the table row for  \(s\) ). This rule applies to any factor, including those that are less than 1.

6.2: Scaling More Pattern Blocks (10 minutes)

Routines and Materials

Instructional Routines

• Anticipate, Monitor, Select, Sequence, Connect
• MLR8: Discussion Supports

Required Materials

• Pattern blocks

Optional activity

This activity extends the conceptual work of the previous one by adding a layer of complexity. Here, the original shapes are comprised of more than 1 block, so the number of blocks needed to build their scaled copies is not simply \(\text{(scale factor)}^2\) , but rather \(n \times \text{(scale factor)}^2\) , where \(n\) is the number of blocks in the original shape. Students begin to think about how the scaled area relates to the original area, which is no longer 1 area unit. They notice that the pattern \(\text{(scale factor)}^2\) presents itself in the factor by which the original number of blocks has changed, rather than in the total number of blocks in the copy.

As in the previous task, students observe regularity in repeated reasoning (MP8), noticing that regardless of the shapes, starting with \(n\) pattern blocks and scaling by \(s\) uses  \(ns^2\) pattern blocks.

Also as in the previous task, the shape composed of trapezoids might be more challenging to scale than those composed of rhombuses and triangles. Prepare to support students scaling the red shape by offering some direction or additional time, if feasible. 

As students work, monitor for groups who notice that the pattern of squared scale factors still occurs here, and that it is apparent if the original number of blocks is taken into account. Select them to share during class discussion.  

Keep students in the same groups, or form combined groups if there are not enough blocks. Assign one shape for each group to build (or let groups choose a shape, as long as all 3 shapes are equally represented). To build a copy of each given shape using a scale factor of 2, groups will need 12 blue rhombuses, 8 red trapezoids, or 16 green triangles. To completely build a copy of each given shape with a scale factor of 3, they would need 27 blue rhombuses, 18 red trapezoids, and 36 green triangles; however, the task prompts them to stop building when they know what the answer will be. 

Give students 6–7 minutes to build their shapes and complete the task. Remind them to use the same blocks as those in the original shape and to check the side lengths of each built shape to make sure they are properly scaled.

Your teacher will assign your group one of these figures, each made with original-size blocks.

Description: <p>3 shapes composed of pattern blocks. First shape, labeled figure D composed of 3 blue rhombuses. Second, labeled figure E composed of 2 red trapezoids. Third, labeled figure F composed of 4 green triangles.</p>

In the applet, move the slider to see a scaled copy of your assigned shape, using a scale factor of 2. Use the original-size blocks to build a figure to match it. How many blocks did it take?

Your classmate thinks that the scaled copies in the previous problem will each take 4 blocks to build. Do you agree or disagree? Explain you reasoning.

Move the slider to see a scaled copy of your assigned shape using a scale factor of 3. Start building a figure with the original-size blocks to match it. Stop when you can tell for sure how many blocks it would take. Record your answer.

Predict: How many blocks would it take to build scaled copies using scale factors 4, 5, and 6? Explain or show your reasoning.

How is the pattern in this activity the same as the pattern you saw in the previous activity? How is it different?

Your teacher will assign your group one of these figures.

Build a scaled copy of your assigned shape using a scale factor of 2. Use the same shape blocks as in the original figure. How many blocks did it take?

Your classmate thinks that the scaled copies in the previous problem will each take 4 blocks to build. Do you agree or disagree? Explain you reasoning.

Start building a scaled copy of your assigned figure using a scale factor of 3. Stop when you can tell for sure how many blocks it would take. Record your answer.

How many blocks would it take to build scaled copies of your figure using scale factors 4, 5, and 6? Explain or show your reasoning.

Are you ready for more?

How many blocks do you think it would take to build a scaled copy of one yellow hexagon where each side is twice as long? Three times as long?

Figure out a way to build these scaled copies. 

Do you see a pattern for the number of blocks used to build these scaled copies? Explain your reasoning.

Students may forget to check that the lengths of all sides of their shape have been scaled and end with an inaccurate count of the pattern blocks. Remind them that all segments must be scaled by the same factor.

The goal of this discussion is to ensure that students understand that the pattern for the number of blocks in the scaled copies depends both on the scale factor and on the number of blocks in the pattern.

Display a table with only the column headings filled in. Poll the class on how many blocks it took them to build each scaled copy using the factors of 2 and 3. Record their answers in the table.

Consider displaying the built shapes or pictures of them for all to see. 

Invite selected students to share the pattern that their groups noticed and used to predict the number of blocks needed for copies with scale factors 4, 5, and 6. Record their predictions in the table. Discuss:

• How does the pattern for the number of blocks in this activity compare to the pattern in the previous activity? Are they related? How?
• For each figure, how many blocks does it take to build a copy using any scale factor \(s\) ?

6.3: Area of Scaled Parallelograms and Triangles (15 minutes)

Building On

• MLR7: Compare and Connect
• Think Pair Share
• Geometry toolkits
• Pre-printed slips, cut from copies of the blackline master

In this activity, students transfer what they learned with the pattern blocks to calculate the area of other scaled shapes (MP8). In groups of 2, students draw scaled copies of either a parallelogram or a triangle and calculate the areas. Then, each group compares their results with those of a group that worked on the other shape. They find that the scaled areas of two shapes are the same (even though the starting shapes are different and have different measurements) and attribute this to the fact that the two shapes had the same original area and were scaled using the same scale factors.

Description: <p>Two blue shapes. One parallelogram base 5, height 2. One triangle base 4, height 5.</p>

While students are not asked to reason about scaled areas by tiling (as they had done in the previous activities), each scaled copy can be tiled to illustrate how length measurements have scaled and how the original area has changed. Some students may choose to draw scaled copies and think about scaled areas this way.

As students find the areas of copies with scale factors 5 and \(\frac35\) without drawing (for the last question), monitor for these methods, depending on their understanding of or comfort with the \(\text{(scale factor)}^2\) pattern:

• Scaling the original base and height and then multiplying to find the area
• Multiplying the original area by the square of the scale factor

Select students using each approach. Invite them to share their reasoning, sequenced in this order, during the discussion.

You will need the Area of Scaled Parallelograms and Triangles blackline master for this activity.

Arrange students in groups of 2. Provide access to geometry toolkits.

Distribute slips showing the parallelogram to half the groups and the triangle to the others. Give students 1 minute of quiet work time for the first question, and then time to complete the rest of the task with their partner.

• Your teacher will give you a figure with measurements in centimeters. What is the area of your figure? How do you know?
• Compare your results with a group that worked with a different figure. What is the same about your answers? What is different?

Students may not remember how to calculate the area of parallelograms and triangles. Make sure that they have the correct area of 10 square units for their original shape before they calculate the area of their scaled copies.

When drawing their scaled copies, some students might not focus on making corresponding angles equal. As long as they scale the base and height of their polygon correctly, this will not impact their area calculations. If time permits, however, prompt them to check their angles using tracing paper or a protractor.

Some students might focus unnecessarily on measuring other side lengths of their polygon, instead of attending only to base and height. If time is limited, encourage them to scale the base and height carefully and check or measure the angles instead. 

Invite selected students to share their solutions. Then focus class discussion on two themes: how the values in the tables for the two shapes compare, and how students determined the scaled areas for the scale factors 5 and \(\frac35\) . Ask questions such as: 

• What did you notice when you compared your answerswithanother group that worked with the other figure? (When the scale factors are the same, the scaled areas are the same, though the bases and heights are different.)
• How did you find the scaled areas for scale factors of 5 and \(\frac35\) ? (By scaling the original base and height and multiplying the scaled measurements; by multiplying the original area by  \(\text{(scale factor)}^2\) .)
• How is the process for finding scaled area here the same as and different than that in the previous activities with pattern blocks? (The area units are different; the pattern of squaring the scale factor is the same.)

Highlight the connection between the two ways of finding scaled areas. Point out that when we multiply the base and height each by the scale factor and then multiply the results, we are essentially multiplying the original lengths by the scale factor two times. The effect of this process is the same as multiplying the original area by  \(\text{(scale factor)}^2\) .

Lesson Synthesis

• Why not? (Both the length and the width get multiplied by 2, so the area gets multiplied by 4.)
• If the scale factor is 5, how many times larger will the scaled copy’s area be? (25 times larger)

6.4: Cool-down - Enlarged Areas (5 minutes)

Student lesson summary.

Scaling affects lengths and areas differently. When we make a scaled copy, all original lengths are multiplied by the scale factor. If we make a copy of a rectangle with side lengths 2 units and 4 units using a scale factor of 3, the side lengths of the copy will be 6 units and 12 units, because \(2\boldcdot 3 = 6\) and \(4\boldcdot 3 = 12\) .

The area of the copy, however, changes by a factor of (scale factor) 2 . If each side length of the copy is 3 times longer than the original side length, then the area of the copy will be 9 times the area of the original, because \(3\boldcdot 3\) , or  \(3^2\) , equals 9.

Description: <p>Two rectangles. The first rectangle has the vertical side labeled 2 and the horizontal side labeled 4. The second rectangle has the vertical side labeled 6 and the horizontal side labeled 12. Two horizontal dashed lines and 2 vertical dashed lines are drawn in the second rectangle dividing it into 9 identical smaller rectangles.</p>

In this example, the area of the original rectangle is 8 units 2 and the area of the scaled copy is 72 units 2 , because \(9\boldcdot 8 = 72\) . We can see that the large rectangle is covered by 9 copies of the small rectangle, without gaps or overlaps. We can also verify this by multiplying the side lengths of the large rectangle: \(6\boldcdot 12=72\) .

Lengths are one-dimensional, so in a scaled copy, they change by the scale factor. Area is two-dimensional, so it changes by the square of the scale factor. We can see this is true for a rectangle with length \(l\) and width \(w\) . If we scale the rectangle by a scale factor of \(s\) , we get a rectangle with length \(s\boldcdot l\) and width \(s\boldcdot w\) . The area of the scaled rectangle is  \(A = (s\boldcdot l) \boldcdot (s\boldcdot w)\) , so  \(A= (s^2) \boldcdot (l \boldcdot w)\) . The fact that the area is multiplied by the square of the scale factor is true for scaled copies of other two-dimensional figures too, not just for rectangles.

Video Summary

Engage your students with effective distance learning resources. ACCESS RESOURCES>>

Math homework problems.

Over a two week period, Jenna had the following number of math homework problems given each day:$$20,\,0,\,7,\,10,\,1,\,11,\,0,\,25,\,15,\,1.$$

• What is the mean number of homework problems Jenna had?
• What is the Mean Absolute Deviation for the number of homework problems?
• What do the mean and Mean Absolute Deviation tell you about the number of homework problems Jenna had over these two weeks?

IM Commentary

The goal of this task is to calculate and interpret the Mean Absolute Deviation in a context. It is intended to be an introductory task but can readily be adapted for a more in depth study. The teacher may wish to have students make a dot plot of the data or analyze the quartiles and create a box plot. The data set is peculiar in that it roughly divides into three separate parts: the days (4) when there is little or no homework, the days (3) when there is a moderate number of homework problems, and the days (3) when the assignment is relatively large. Teachers may wish to have students discuss  why  homework assignments might have this structure: for example, the assignments with only one question are likely challenging problems, perhaps involving modeling or work outside of class. Or there may be an upcoming exam so students are given more time to prepare. The large assignments are likely more routine problems while the days when no homework is assigned the class is probably wrapping up previous material. 

Teachers may prefer to substitute actual data from their own class. Alternatively, they could examine and compare data from different math classes. A follow-up challenging question would be: how much flexibility is there in the data if the mean is 8 and the Mean Absolute Deviation is 7.2? In other words, how much information do these statistics tell us about the actual data?

• To calculate the mean, we first find the total number of homework problems assigned: $$20 + 0 + 7 + 10 + 1 + 11 + 0 + 25 + 15 + 1 = 90.$$ There were 10 homework assignments so the mean number of homework problems is 90 $\div$ 10 = 9.

If we add the numbers in the last column we get 72. There are 10 assignments so the Mean Absolute Deviation is 72 $\div$ 10 = 7.2.

The mean is 9 and the Mean Absolute Deviation is 7.2. The mean tells us the average number of homework problems Jenna had each day. The Mean Absolute Deviation is almost as large as the mean so this tells us that there is substantial variation in the number of homework problems assigned each day: some days there are a lot more than the mean of 9 and some days there are a lot less.  

Problem-Based Learning with Imagine Learning Illustrative Mathematics

The instructional design of imagine learning illustrative mathematics supports k–12 learners through dynamic, engaging instructional experiences. students develop deep conceptual understanding through a coherent progression of the mathematics based on standards and research-based learning trajectories..

"Imagine Learning offers a digital experience that makes teachers’ lives easier and supports student engagement with enhancement features like Student Spotlight videos and digital centers."

Focus, rigor, and coherence across units, lessons, and activities.

Instructional Design

Overall dna of the instructional design.

• Teachers can provide timely feedback through assignable items and better inform instruction.
• Students have tools that promote ownership and accountability for learning.
• Assessments are available in print and digital formats for equity and access in all instructional models.

"I'm excited about the tools that we're developing that really put students at the center of the curriculum—tools that help them not only collaborate with their peers and with their teachers but really express their thinking."

Ready to start creating change together?

Illustrative Math Homework and Assessments Unit 1

What educators are saying

Also included in.

Description

The Illustrative Mathematics unit is for extra practice / homework and is carefully designed to be Illustrative Math friendly. 3 assessments have been included with a made-to match format found in this unit.

Extra Practice / Homework and 3 Assessments: (See every page in the preview)

• 1 extra practice page per lesson
• 14 lessons included in the resource
• Supports vocabulary
• Lesson format is extended here
• Supports game-play
• Can be sent home as homework or used in class
• Can also be used as a quiz
• Can be used outside of the IM program as standards-based math practice.

Are there assessments included?

• I have updated Unit 1 to include assessments
• There are 3 assessments
• Section A Counting, Expressions / Adding, Making 10, Subtracting
• Section B Sorting and naming categories
• Section C Answering questions about a graph

Will you be making other units?

• I need this extra practice as much as you do!
• I plan to post a unit every few weeks.

What Units are available?

• ⭐ Unit 1 Posted August 25th
• ⭐ Unit 2 Posted Sep 7
• ⭐ Unit 3 Posted Sep 18th
• ⭐ Unit 4 Posted October 1
• ⭐ Unit 5 Posted October 9
• ⭐ Unit 6 Posted October 30
• ⭐ Unit 7 Posted Dec 6
• ⭐ Unit 8 Wahooooo!

Will you bundle?

• ⭐ Unit 1-8 Bundle is posted!

Teachers Like You Are Saying:

• ⭐⭐⭐⭐⭐ Alexis C: Katie once again is a lifesaver! If you are a teacher using IM this is the resource you need especially for unit 1 no questions asked. Primary friendly and incredibly useful!!!
• ⭐⭐⭐⭐⭐ Amanda M: I am a first grade teacher. I have used Envision Math in the past. This year, our district adopted Illustrative Math. I am so very glad I now have this wonderful product to use with my first graders. It helps make the Math engaging and comprehensible. This product has helped relieve a lot of my stress with implementing a new and very different curriculum. My students love doing these math activities! I know this will build a better understanding of the concepts. Thank you so much for the creation of this Math!!!
• ⭐⭐⭐⭐⭐ Traci D: I absolutely LOVE this resource! I have been searching for something to supplement our new math program. This resource has been a blessing. My kids and I are thrilled.
• ⭐⭐⭐⭐⭐ Celeste says : This math from Teacher to the Core is everything Illustrative Math is not. It’s engaging, it’s cute, and the kids actually want to do it and I want to teach it! I will be buying more units!
• ⭐⭐⭐⭐⭐ Whitney R: This resource has been very helpful for my students! It provides all the extra practice and support we need with our curriculum in a way that is fun and engaging for students.

Questions & Answers

Teacher to the core.

• We're hiring
• Help & FAQ
• Privacy policy
• Student privacy
• Terms of service
• Tell us what you think