How to Find if Triangles are Similar
Two triangles are similar if they have:
- all their angles equal
- corresponding sides are in the same ratio
But we don't need to know all three sides and all three angles ... two or three out of the six is usually enough.
There are three ways to find if two triangles are similar: AA , SAS and SSS :
AA stands for "angle, angle" and means that the triangles have two of their angles equal.
If two triangles have two of their angles equal, the triangles are similar.

Example: these two triangles are similar:
If two of their angles are equal, then the third angle must also be equal, because angles of a triangle always add to make 180° .
In this case the missing angle is 180° − (72° + 35°) = 73°
So AA could also be called AAA (because when two angles are equal, all three angles must be equal).
SAS stands for "side, angle, side" and means that we have two triangles where:
- the ratio between two sides is the same as the ratio between another two sides
- and we we also know the included angles are equal.
If two triangles have two pairs of sides in the same ratio and the included angles are also equal, then the triangles are similar.
In this example we can see that:
- one pair of sides is in the ratio of 21 : 14 = 3 : 2
- another pair of sides is in the ratio of 15 : 10 = 3 : 2
- there is a matching angle of 75° in between them
So there is enough information to tell us that the two triangles are similar .
Using Trigonometry
We could also use Trigonometry to calculate the other two sides using the Law of Cosines :
Example Continued
In Triangle ABC:
- a 2 = b 2 + c 2 - 2bc cos A
- a 2 = 21 2 + 15 2 - 2 × 21 × 15 × Cos75°
- a 2 = 441 + 225 - 630 × 0.2588...
- a 2 = 666 - 163.055...
- a 2 = 502.944...
- So a = √502.94 = 22.426...
In Triangle XYZ:
- x 2 = y 2 + z 2 - 2yz cos X
- x 2 = 14 2 + 10 2 - 2 × 14 × 10 × Cos75°
- x 2 = 196 + 100 - 280 × 0.2588...
- x 2 = 296 - 72.469...
- x 2 = 223.530...
- So x = √223.530... = 14.950...
Now let us check the ratio of those two sides:
a : x = 22.426... : 14.950... = 3 : 2
the same ratio as before!
Note: we can also use the Law of Sines to show that the other two angles are equal.
SSS stands for "side, side, side" and means that we have two triangles with all three pairs of corresponding sides in the same ratio.
If two triangles have three pairs of sides in the same ratio, then the triangles are similar.
In this example, the ratios of sides are:
- a : x = 6 : 7.5 = 12 : 15 = 4 : 5
- b : y = 8 : 10 = 4 : 5
- c : z = 4 : 5
These ratios are all equal, so the two triangles are similar.
Using Trigonometry we can show that the two triangles have equal angles by using the Law of Cosines in each triangle:
- cos A = (b 2 + c 2 - a 2 )/2bc
- cos A = (8 2 + 4 2 - 6 2 )/(2× 8 × 4)
- cos A = (64 + 16 - 36)/64
- cos A = 44/64
- cos A = 0.6875
- So Angle A = 46.6°
- cos X = (y 2 + z 2 - x 2 )/2yz
- cos X = (10 2 + 5 2 - 7.5 2 )/(2× 10 × 5)
- cos X = (100 + 25 - 56.25)/100
- cos X = 68.75/100
- cos X = 0.6875
- So Angle X = 46.6°
So angles A and X are equal!
Similarly we can show that angles B and Y are equal, and angles C and Z are equal.
9.3 Use Properties of Angles, Triangles, and the Pythagorean Theorem
Learning objectives.
By the end of this section, you will be able to:
- Use the properties of angles
- Use the properties of triangles
Use the Pythagorean Theorem
Be Prepared 9.7
Before you get started, take this readiness quiz.
Solve: x + 3 + 6 = 11 . x + 3 + 6 = 11 . If you missed this problem, review Example 8.6 .
Be Prepared 9.8
Solve: a 45 = 4 3 . a 45 = 4 3 . If you missed this problem, review Example 6.42 .
Be Prepared 9.9
Simplify: 36 + 64 . 36 + 64 . If you missed this problem, review Example 5.72 .
So far in this chapter, we have focused on solving word problems, which are similar to many real-world applications of algebra. In the next few sections, we will apply our problem-solving strategies to some common geometry problems.
Use the Properties of Angles
Are you familiar with the phrase ‘do a 180 ’? 180 ’? It means to turn so that you face the opposite direction. It comes from the fact that the measure of an angle that makes a straight line is 180 180 degrees. See Figure 9.5 .
An angle is formed by two rays that share a common endpoint. Each ray is called a side of the angle and the common endpoint is called the vertex . An angle is named by its vertex. In Figure 9.6 , ∠ A ∠ A is the angle with vertex at point A . A . The measure of ∠ A ∠ A is written m ∠ A . m ∠ A .
We measure angles in degrees, and use the symbol ° ° to represent degrees. We use the abbreviation m m for the measure of an angle. So if ∠ A ∠ A is 27° , 27° , we would write m ∠ A = 27 . m ∠ A = 27 .
If the sum of the measures of two angles is 180° , 180° , then they are called supplementary angles . In Figure 9.7 , each pair of angles is supplementary because their measures add to 180° . 180° . Each angle is the supplement of the other.
If the sum of the measures of two angles is 90° , 90° , then the angles are complementary angles . In Figure 9.8 , each pair of angles is complementary, because their measures add to 90° . 90° . Each angle is the complement of the other.
Supplementary and Complementary Angles
If the sum of the measures of two angles is 180° , 180° , then the angles are supplementary.
If ∠ A ∠ A and ∠ B ∠ B are supplementary, then m ∠ A + m ∠ B = 180°. m ∠ A + m ∠ B = 180°.
If the sum of the measures of two angles is 90° , 90° , then the angles are complementary.
If ∠ A ∠ A and ∠ B ∠ B are complementary, then m ∠ A + m ∠ B = 90°. m ∠ A + m ∠ B = 90°.
In this section and the next, you will be introduced to some common geometry formulas. We will adapt our Problem Solving Strategy for Geometry Applications. The geometry formula will name the variables and give us the equation to solve.
In addition, since these applications will all involve geometric shapes, it will be helpful to draw a figure and then label it with the information from the problem. We will include this step in the Problem Solving Strategy for Geometry Applications.
Use a Problem Solving Strategy for Geometry Applications.
- Step 1. Read the problem and make sure you understand all the words and ideas. Draw a figure and label it with the given information.
- Step 2. Identify what you are looking for.
- Step 3. Name what you are looking for and choose a variable to represent it.
- Step 4. Translate into an equation by writing the appropriate formula or model for the situation. Substitute in the given information.
- Step 5. Solve the equation using good algebra techniques.
- Step 6. Check the answer in the problem and make sure it makes sense.
- Step 7. Answer the question with a complete sentence.
The next example will show how you can use the Problem Solving Strategy for Geometry Applications to answer questions about supplementary and complementary angles.
Example 9.16
An angle measures 40° . 40° . Find ⓐ its supplement, and ⓑ its complement.
Try It 9.31
An angle measures 25° . 25° . Find its: ⓐ supplement ⓑ complement.
Try It 9.32
An angle measures 77° . 77° . Find its: ⓐ supplement ⓑ complement.
Did you notice that the words complementary and supplementary are in alphabetical order just like 90 90 and 180 180 are in numerical order?
Example 9.17
Two angles are supplementary. The larger angle is 30° 30° more than the smaller angle. Find the measure of both angles.
Try It 9.33
Two angles are supplementary. The larger angle is 100° 100° more than the smaller angle. Find the measures of both angles.
Try It 9.34
Two angles are complementary. The larger angle is 40° 40° more than the smaller angle. Find the measures of both angles.
Use the Properties of Triangles
What do you already know about triangles? Triangle have three sides and three angles. Triangles are named by their vertices. The triangle in Figure 9.9 is called Δ A B C , Δ A B C , read ‘triangle ABC ABC ’. We label each side with a lower case letter to match the upper case letter of the opposite vertex.
The three angles of a triangle are related in a special way. The sum of their measures is 180° . 180° .
Sum of the Measures of the Angles of a Triangle
For any Δ A B C , Δ A B C , the sum of the measures of the angles is 180° . 180° .
Example 9.18
The measures of two angles of a triangle are 55° 55° and 82° . 82° . Find the measure of the third angle.
Try It 9.35
The measures of two angles of a triangle are 31° 31° and 128° . 128° . Find the measure of the third angle.
Try It 9.36
A triangle has angles of 49° 49° and 75° . 75° . Find the measure of the third angle.
Right Triangles
Some triangles have special names. We will look first at the right triangle . A right triangle has one 90° 90° angle, which is often marked with the symbol shown in Figure 9.10 .
If we know that a triangle is a right triangle, we know that one angle measures 90° 90° so we only need the measure of one of the other angles in order to determine the measure of the third angle.
Example 9.19
One angle of a right triangle measures 28° . 28° . What is the measure of the third angle?
Try It 9.37
One angle of a right triangle measures 56° . 56° . What is the measure of the other angle?
Try It 9.38
One angle of a right triangle measures 45° . 45° . What is the measure of the other angle?
In the examples so far, we could draw a figure and label it directly after reading the problem. In the next example, we will have to define one angle in terms of another. So we will wait to draw the figure until we write expressions for all the angles we are looking for.
Example 9.20
The measure of one angle of a right triangle is 20° 20° more than the measure of the smallest angle. Find the measures of all three angles.
Try It 9.39
The measure of one angle of a right triangle is 50° 50° more than the measure of the smallest angle. Find the measures of all three angles.
Try It 9.40
The measure of one angle of a right triangle is 30° 30° more than the measure of the smallest angle. Find the measures of all three angles.
Similar Triangles
When we use a map to plan a trip, a sketch to build a bookcase, or a pattern to sew a dress, we are working with similar figures. In geometry, if two figures have exactly the same shape but different sizes, we say they are similar figures . One is a scale model of the other. The corresponding sides of the two figures have the same ratio, and all their corresponding angles have the same measures.
The two triangles in Figure 9.11 are similar. Each side of Δ A B C Δ A B C is four times the length of the corresponding side of Δ X Y Z Δ X Y Z and their corresponding angles have equal measures.
Properties of Similar Triangles
If two triangles are similar, then their corresponding angle measures are equal and their corresponding side lengths are in the same ratio.
The length of a side of a triangle may be referred to by its endpoints, two vertices of the triangle. For example, in Δ A B C : Δ A B C :
the length a can also be written B C the length b can also be written A C the length c can also be written A B the length a can also be written B C the length b can also be written A C the length c can also be written A B
We will often use this notation when we solve similar triangles because it will help us match up the corresponding side lengths.
Example 9.21
Δ A B C Δ A B C and Δ X Y Z Δ X Y Z are similar triangles. The lengths of two sides of each triangle are shown. Find the lengths of the third side of each triangle.
Try It 9.41
Δ A B C Δ A B C is similar to Δ X Y Z . Δ X Y Z . Find a . a .
Try It 9.42
Δ A B C Δ A B C is similar to Δ X Y Z . Δ X Y Z . Find y . y .
The Pythagorean Theorem is a special property of right triangles that has been used since ancient times. It is named after the Greek philosopher and mathematician Pythagoras who lived around 500 500 BCE.
Remember that a right triangle has a 90° 90° angle, which we usually mark with a small square in the corner. The side of the triangle opposite the 90° 90° angle is called the hypotenuse , and the other two sides are called the legs . See Figure 9.12 .
The Pythagorean Theorem tells how the lengths of the three sides of a right triangle relate to each other. It states that in any right triangle, the sum of the squares of the two legs equals the square of the hypotenuse.
The Pythagorean Theorem
In any right triangle Δ A B C , Δ A B C ,
where c c is the length of the hypotenuse a a and b b are the lengths of the legs.
To solve problems that use the Pythagorean Theorem, we will need to find square roots. In Simplify and Use Square Roots we introduced the notation m m and defined it in this way:
For example, we found that 25 25 is 5 5 because 5 2 = 25 . 5 2 = 25 .
We will use this definition of square roots to solve for the length of a side in a right triangle.
Example 9.22
Use the Pythagorean Theorem to find the length of the hypotenuse.
Try It 9.43
Try it 9.44, example 9.23.
Use the Pythagorean Theorem to find the length of the longer leg.
Try It 9.45
Use the Pythagorean Theorem to find the length of the leg.
Try It 9.46
Example 9.24.
Kelvin is building a gazebo and wants to brace each corner by placing a 10-inch 10-inch wooden bracket diagonally as shown. How far below the corner should he fasten the bracket if he wants the distances from the corner to each end of the bracket to be equal? Approximate to the nearest tenth of an inch.

Try It 9.47
John puts the base of a 13-ft 13-ft ladder 5 5 feet from the wall of his house. How far up the wall does the ladder reach?
Try It 9.48
Randy wants to attach a 17-ft 17-ft string of lights to the top of the 15-ft 15-ft mast of his sailboat. How far from the base of the mast should he attach the end of the light string?
ACCESS ADDITIONAL ONLINE RESOURCES
- Animation: The Sum of the Interior Angles of a Triangle
- Similar Polygons
- Example: Determine the Length of the Hypotenuse of a Right Triangle
Section 9.3 Exercises
Practice makes perfect.
In the following exercises, find ⓐ the supplement and ⓑ the complement of the given angle.
In the following exercises, use the properties of angles to solve.
Find the supplement of a 135° 135° angle.
Find the complement of a 38° 38° angle.
Find the complement of a 27.5° 27.5° angle.
Find the supplement of a 109.5° 109.5° angle.
Two angles are supplementary. The larger angle is 56° 56° more than the smaller angle. Find the measures of both angles.
Two angles are supplementary. The smaller angle is 36° 36° less than the larger angle. Find the measures of both angles.
Two angles are complementary. The smaller angle is 34° 34° less than the larger angle. Find the measures of both angles.
Two angles are complementary. The larger angle is 52° 52° more than the smaller angle. Find the measures of both angles.
In the following exercises, solve using properties of triangles.
The measures of two angles of a triangle are 26° 26° and 98° . 98° . Find the measure of the third angle.
The measures of two angles of a triangle are 61° 61° and 84° . 84° . Find the measure of the third angle.
The measures of two angles of a triangle are 105° 105° and 31° . 31° . Find the measure of the third angle.
The measures of two angles of a triangle are 47° 47° and 72° . 72° . Find the measure of the third angle.
One angle of a right triangle measures 33° . 33° . What is the measure of the other angle?
One angle of a right triangle measures 51° . 51° . What is the measure of the other angle?
One angle of a right triangle measures 22.5 ° . 22.5 ° . What is the measure of the other angle?
One angle of a right triangle measures 36.5 ° . 36.5 ° . What is the measure of the other angle?
The two smaller angles of a right triangle have equal measures. Find the measures of all three angles.
The measure of the smallest angle of a right triangle is 20° 20° less than the measure of the other small angle. Find the measures of all three angles.
The angles in a triangle are such that the measure of one angle is twice the measure of the smallest angle, while the measure of the third angle is three times the measure of the smallest angle. Find the measures of all three angles.
The angles in a triangle are such that the measure of one angle is 20° 20° more than the measure of the smallest angle, while the measure of the third angle is three times the measure of the smallest angle. Find the measures of all three angles.
Find the Length of the Missing Side
In the following exercises, Δ A B C Δ A B C is similar to Δ X Y Z . Δ X Y Z . Find the length of the indicated side.
On a map, San Francisco, Las Vegas, and Los Angeles form a triangle whose sides are shown in the figure below. The actual distance from Los Angeles to Las Vegas is 270 270 miles.
Find the distance from Los Angeles to San Francisco.
Find the distance from San Francisco to Las Vegas.
In the following exercises, use the Pythagorean Theorem to find the length of the hypotenuse.
In the following exercises, use the Pythagorean Theorem to find the length of the missing side. Round to the nearest tenth, if necessary.
In the following exercises, solve. Approximate to the nearest tenth, if necessary.
A 13-foot 13-foot string of lights will be attached to the top of a 12-foot 12-foot pole for a holiday display. How far from the base of the pole should the end of the string of lights be anchored?
Pam wants to put a banner across her garage door to congratulate her son on his college graduation. The garage door is 12 12 feet high and 16 16 feet wide. How long should the banner be to fit the garage door?
Chi is planning to put a path of paving stones through her flower garden. The flower garden is a square with sides of 10 10 feet. What will the length of the path be?
Brian borrowed a 20-foot 20-foot extension ladder to paint his house. If he sets the base of the ladder 6 6 feet from the house, how far up will the top of the ladder reach?
Everyday Math
Building a scale model Joe wants to build a doll house for his daughter. He wants the doll house to look just like his house. His house is 30 30 feet wide and 35 35 feet tall at the highest point of the roof. If the dollhouse will be 2.5 2.5 feet wide, how tall will its highest point be?
Measurement A city engineer plans to build a footbridge across a lake from point X X to point Y , Y , as shown in the picture below. To find the length of the footbridge, she draws a right triangle XYZ , XYZ , with right angle at X . X . She measures the distance from X X to Z , 800 Z , 800 feet, and from Y Y to Z , 1,000 Z , 1,000 feet. How long will the bridge be?
Writing Exercises
Write three of the properties of triangles from this section and then explain each in your own words.
Explain how the figure below illustrates the Pythagorean Theorem for a triangle with legs of length 3 3 and 4 . 4 .
ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
ⓑ What does this checklist tell you about your mastery of this section? What steps will you take to improve?
As an Amazon Associate we earn from qualifying purchases.
This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.
Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.
Access for free at https://openstax.org/books/prealgebra-2e/pages/1-introduction
- Authors: Lynn Marecek, MaryAnne Anthony-Smith, Andrea Honeycutt Mathis
- Publisher/website: OpenStax
- Book title: Prealgebra 2e
- Publication date: Mar 11, 2020
- Location: Houston, Texas
- Book URL: https://openstax.org/books/prealgebra-2e/pages/1-introduction
- Section URL: https://openstax.org/books/prealgebra-2e/pages/9-3-use-properties-of-angles-triangles-and-the-pythagorean-theorem
© Jan 23, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Chapter 1: Triangles and Circles
Exercises: 1.1 Triangles and Angles
Practice each skill in the Homework Problems listed.
- Sketch a triangle with given properties #1–6
- Find an unknown angle in a triangle #7–12, 17–20
- Find angles formed by parallel lines and a transversal #13–16, 35–44
- Find exterior angles of a triangle #21–24
- Find angles in isosceles, equilateral, and right triangles #25–34
- State reasons for conclusions #45–48
Suggested Problems
Exercises for 1.1 Triangles and Angles
Exercise group, 1. an isosceles triangle with a vertex angle [latex]306^{\circ}[/latex], 2. a scalene triangle with one obtuse angle ( scalene means three unequal sides.), 3. a right triangle with legs [latex]4[/latex] and [latex]7[/latex], 4. an isosceles right triangle, 5. an isosceles triangle with one obtuse angle, 6. a right triangle with one angle [latex]20°[/latex].
In parts (a) and (b), find the exterior angle [latex]\phi[/latex].
- Use your answer to part (c) to write a rule for finding an exterior angle of a triangle.
In Problems 25 and 26, the figures inscribed are regular polygons , which means that all their sides are the same length, and all the angles have the same measure. Find the angles [latex]\theta[/latex] and [latex]\phi[/latex].
In problems 27 and 28, triangle ABC is equilateral. Find the unknown angles.
a. [latex]2\theta + 2\phi =[/latex]
b. [latex]\theta + \phi =[/latex]
c. [latex]\triangle ABC[/latex] is
Find [latex]\alpha[/latex] and [latex]\beta[/latex]
- Explain why [latex]\angle OAB[/latex] and [latex]\angle ABO[/latex] are equal in measure.
- Explain why [latex]\angle OBC[/latex] and [latex]\angle BCO[/latex] are equal in measure.
- Explain why [latex]\angle ABC[/latex] is a right angle. (Hint: Use Problem 29.)
- Compare [latex]\theta[/latex] with [latex]\alpha + \beta[/latex] (Hint: What do you know about supplementary angles and the sum of angles in a triangle?)
- Compare [latex]\alpha[/latex] and [latex]\beta[/latex]
- Explain why the inscribed angle [latex]\angle BAO[/latex] is half the size of the central angle [latex]\angle BOD[/latex]
Find [latex]\alpha[/latex] and [latex]\beta[/latex]
- [latex]\angle 4 + \angle 2 + \angle 5 =[/latex]
- Use parts (a) and (b) to explain why the sum of the angles of a triangle is [latex]180^{\circ}[/latex]
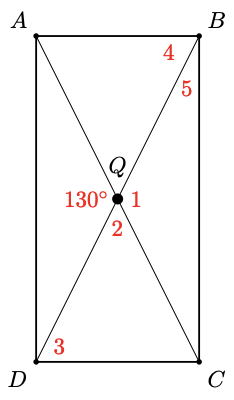
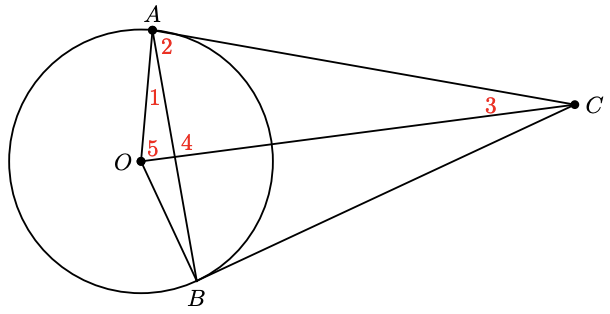
ABCD is a rectangle. The diagonals of a rectangle bisect each other. In the figure, [latex]\angle AQD = 130^{\circ}[/latex]. Find the angles labeled 1 through 5 in order, and give a reason for each answer.
A tangent meets the radius of a circle at a right angle. In the figure, [latex]\angle AOB = 140^{\circ}[/latex]. Find the angles labeled 1 through 5 in order, and give a reason for each answer.
Trigonometry Copyright © 2024 by Bimal Kunwor; Donna Densmore; Jared Eusea; and Yi Zhen. All Rights Reserved.
Share This Book

- school Campus Bookshelves
- menu_book Bookshelves
- perm_media Learning Objects
- login Login
- how_to_reg Request Instructor Account
- hub Instructor Commons
- Download Page (PDF)
- Download Full Book (PDF)
- Periodic Table
- Physics Constants
- Scientific Calculator
- Reference & Cite
- Tools expand_more
- Readability
selected template will load here
This action is not available.

1.0: Angles and Triangles
- Last updated
- Save as PDF
- Page ID 112400

- Katherine Yoshiwara
- Los Angeles Pierce College
Historically, trigonometry began as the study of triangles and their properties. Let’s review some definitions and facts from geometry.
- We measure angles in degrees.
- One full rotation is \(360^{\circ}\), as shown below.
- Half a full rotation is \(180^{\circ}\) and is called a straight angle .
- One quarter of a full rotation is \(90^{\circ}\) and is called a right angle .
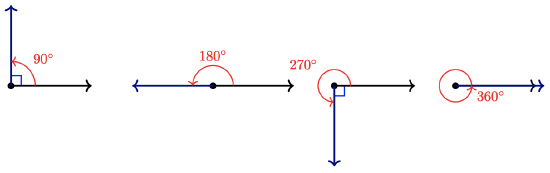
If you tear off the corners of any triangle and line them up, as shown below, they will always form a straight angle.
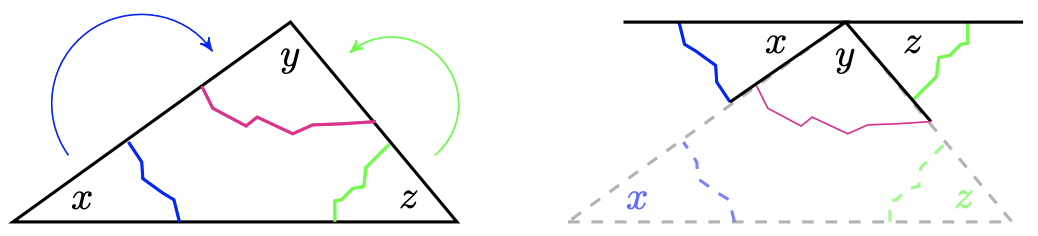
Sum of angles in a triangle.
1. The sum of the angles in a triangle is \(180^{\circ}\).
Example 1.1
Two of the angles in the triangle at right are \(25^{\circ}\) and \(115^{\circ}\). Find the third angle.
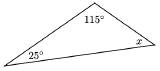
To find the third angle, we write an equation.
\begin{aligned} x+25+115 &=180 \quad \quad &&\text{Simplify the left side.} \\ x+140 &=180 \quad \quad &&\text{Subtract 140 from both sides.}\\ x &=40 \end{aligned}
The third angle is \(40^{\circ}\).
Checkpoint 1.2
Find each of the angles in the triangle at right.
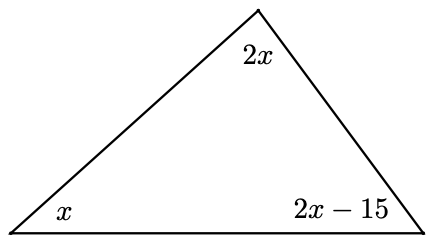
\(x = 39^{\circ}, 2x = 78^{\circ}, 2x-15 = 63^{\circ}\)
Some special categories of triangles are particularly useful. Most important of these are the right triangles .
Right triangle.
2. A right triangle has one angle of \(90^{\circ}\).
Example 1.3
One of the smaller angles of a right triangle is \(34^{\circ}\). What is the third angle?
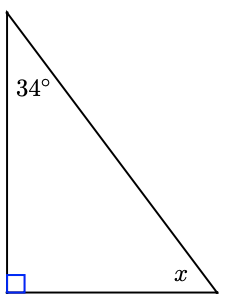
The sum of the two smaller angles in a right triangle is \(90^{\circ}\). So
\begin{aligned} x+34 &=90 \quad \quad \text{Subtract 34 from both sides} \\ x &=56 \end{aligned}
The unknown angle must be \(56^{\circ}\).
Checkpoint 1.4
Two angles of a triangle are \(35^{\circ}\) and \(45^{\circ}\). Can it be a right triangle?
An equilateral triangle has all three sides the same length.
Angles of equilateral triangle.
3. All of the angles of an equilateral triangle are equal.
Example 1.5
All three sides of a triangle are 4 feet long. Find the angles.
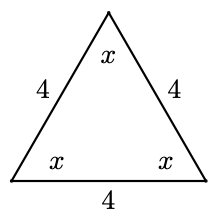
The triangle is equilateral, so all of its angles are equal. Thus
\begin{aligned} 3 x &=180 \quad \quad \quad \text{Divide both sides by 3.}\\ x &=60 \end{aligned}
Each of the angles is \(60^{\circ}\).
Checkpoint 1.6
Find \(x, y\), and \(z\) in the triangle at right.
\(x=60^{\circ}, y=8, z=8\)
An isosceles triangle has two sides of equal length. The angle between the equal sides is the vertex angle . The other two angles are the base angles.
Base angles of an isoceles triangle.
4. The base angles of an isosceles triangle are equal.
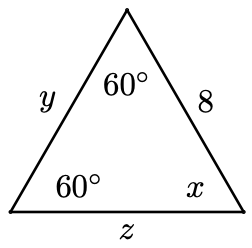
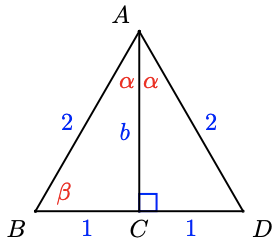
Example 1.7
Find \(x\) and \(y\) in the triangle at right.
The triangle is isosceles, so the base angles are equal. Therefore, \(y=38^{\circ}\). To find the vertex angle, we solve
\begin{aligned} x+38+38 &=180 \\ x+76 &=180 \quad \quad \quad \text{Subtract 76 from both sides.}\\ x &=104 \end{aligned}
The vertex angle is \(104^{\circ}\).
Checkpoint 1.8
Find \(x\) and \(y\) in the figure at right.
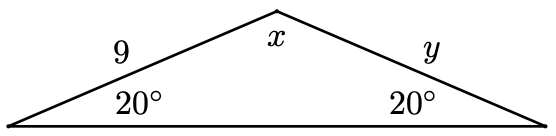
\(x=140^{\circ}, y=9\)
In addition to the facts about triangles reviewed above, there are several useful properties of angles.
- Two angles that add to \(180^{\circ}\) are called supplementary .
- Two angles that add to \(90^{\circ}\) are called complementary .
- Angles between \(0^{\circ}\) and \(90^{\circ}\) are called acute .
- Angles between \(90^{\circ}\) and \(180^{\circ}\) are called obtuse .

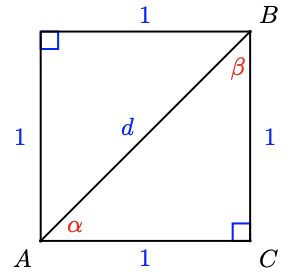
Example 1.9
In the figure at right,
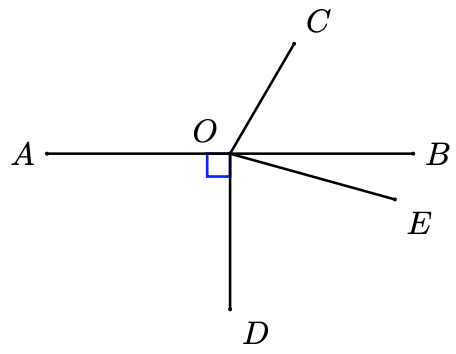
- \(\angle A O C\) and \(\angle B O C\) are supplementary.
- \(\angle D O E\) and \(\angle B O E\) are complementary.
- \(\angle A O C\) is obtuse,
- and \(\angle B O C\) is acute.
In trigonometry we often use lower-case Greek letters to represent unknown angles (or, more specifically, the measure of the angle in degrees). In the next Exercise, we use the Greek letters \(\alpha\) (alpha), \(\beta\) (beta), and \(\gamma\) (gamma).
Checkpoint 1.10
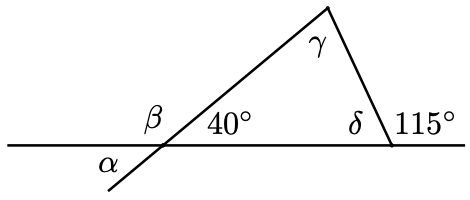
In the figure, \(\alpha, \beta\), and \(\gamma\) denote the measures of the angles in degrees.
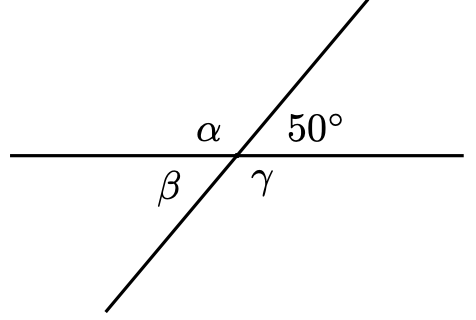
a. Find the measure of angle \(\alpha\). b. Find the measure of angle \(\beta\). c. Find the measure of angle \(\gamma\). d. What do you notice about the measures of the angles?
\(\quad \alpha=130^{\circ}, \beta=50^{\circ}, \gamma=130^{\circ}\). The non-adjacent angles are equal.
Non-adjacent angles formed by the intersection of two straight lines are called vertical angles . In the previous exercise, the angles labeled \(\alpha\) and \(\gamma\) are vertical angles, as are the angles labeled \(\beta\) and \(50^{\circ}\).
Vertical Angles.
5. Vertical angles are equal.
Example 1.11
Explain why \(\alpha=\beta\) in the triangle at right.
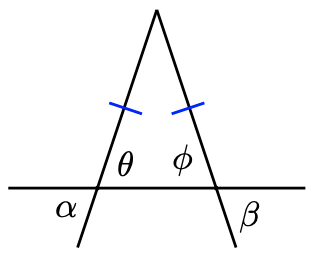
Because they are the base angles of an isosceles triangle, \(\theta\) (theta) and \(\phi(\mathrm{phi})\) are equal. Also, \(\alpha=\theta\) because they are vertical angles, and similarly \(\beta=\phi\). Therefore, \(\alpha=\beta\) because they are equal to equal quantities.
Checkpoint 1.12
Find all the unknown angles in the figure at right. (You will find a list of all the Greek letters and their names at the end of this section.)
\(\alpha=40^{\circ}, \beta=140^{\circ}, \gamma=75^{\circ}, \delta=65^{\circ}\)
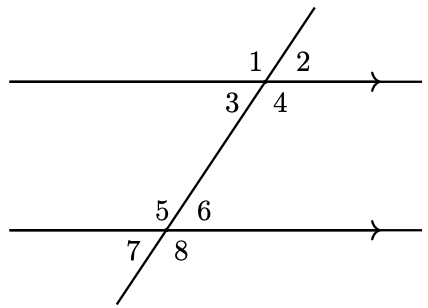
A line that intersects two parallel lines forms eight angles, as shown in the figure below. There are four pairs of vertical angles, and four pairs of corresponding angles , or angles in the same position relative to the transversal on each of the parallel lines.
For example, the angles labeled 1 and 5 are corresponding angles, as are the angles labeled 4 and 8. Finally, angles 3 and 6 are called alternate interior angles , and so are angles 4 and 5.
Parallel lines cut by a transversal.
6. If parallel lines are intersected by a transversal, the alternate interior angles are equal. Corresponding angles are also equal.
Example 1.13
The parallelogram \(A B C D\) shown at right is formed by the intersection of two sets of parallel lines. Show that the opposite angles of the parallelogram are equal.
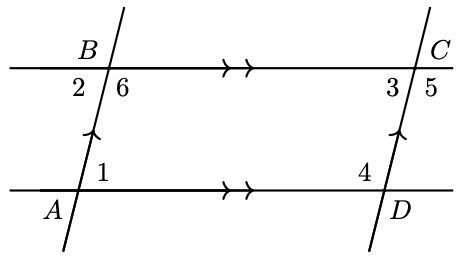
Angles 1 and 2 are equal because they are alternate interior angles, and angles 2 and 3 are equal because they are corresponding angles. Therefore angles 1 and 3 , the opposite angles of the parallelogram, are equal. Similarly, you can show that angles 4,5 , and 6 are equal.
Checkpoint 1.14
Show that the adjacent angles of a parallelogram are supplementary. (You can use angles 1 and 4 in the parallelogram of the previous example.)
Note that angles 2 and 6 are supplementary because they form a straight angle. Angle 1 equals angle 2 because they are alternate interior angles, and similarly angle 4 equals angle 5. Angle 5 equals angle 6 because they are corresponding angles. Thus, angle 4 equals angle 6, and angle 1 equals angle 2. So angles 4 and 1 are supplementary because 2 and 6 are.
Note 1.15 In the Section 1.1 Summary, you will find a list of vocabulary words and a summary of the facts from geometry that we reviewed in this section. You will also find a set of study questions to test your understanding, and a list of skills to practice in the homework problems.
Table 1.16 Lower Case Letters in the Greek Alphabet
\begin{aligned} &\quad \quad \quad \quad \quad \text { Greek Alphabet }\\ &\begin{array}{cc|cc|cc|} \hline \alpha & \text { alpha } & \beta & \text { beta } & \gamma & \text { gamma } \\ \hline \delta & \text { delta } & \epsilon & \text { epsilon } & \gamma & \text { gamma } \\ \hline \eta & \text { eta } & \theta & \text { theta } & \iota & \text { iota } \\ \hline \kappa & \text { kappa } & \lambda & \text { lambda } & \mu & \text { mu } \\ \hline \nu & \text { nu } & \xi & \text { xi } & o & \text { omicron } \\ \hline \pi & \text { pi } & \rho & \text { rho } & \sigma & \text { sigma } \\ \hline \tau & \text { tau } & v & \text { upsilon } & \phi & \text { phi } \\ \hline \chi & \text { chi } & \psi & \text { psi } & \omega & \text { omega } \\ \hline \end{array} \end{aligned}
Review the following skills you will need for this section.
Algebra Refresher 1.2
Solve the equation.
1. \(x-8=19-2 x\) 2. \(2 x-9=12-x\) 3. \(13 x+5=2 x-28\) 4. \(4+9 x=-7+x\)
Solve the system.
5. \(5x - 2y = -13\)
\(2x + 3y = -9\)
6. \(4x + 3y = 9\)
\(3x + 2y = 8\)
5. \(x=-3,y=-1\)
6. \(x=6,y=-5\)
Section 1.1 Summary
• Right angle
• Straight angle
• Right triangle
• Equilateral triangle
• Isosceles triangle
• Vertex angle
• Base angle
• Supplementary
• Complementary
• Acute
• Obtuse
• Vertical angles
• Transversal
• Corresponding angles
• Alternate interior angles
Facts from Geometry.
1. The sum of the angles in a triangle is \(180^{\circ}\). 2. A right triangle has one angle of \(90^{\circ}\). 3. All of the angles of an equilateral triangle are equal. 4. The base angles of an isosceles triangle are equal. 5. Vertical angles are equal. 6. If parallel lines are intersected by a transversal, the alternate interior angles are equal.
Corresponding angles are also equal.
Study Questions
1. Is it possible to have more than one obtuse angle in a triangle? Why or why not?
2. Draw any quadrilateral (a four-sided polygon) and divide it into two triangles by connecting two opposite vertices by a diagonal. What is the sum of the angles in your quadrilateral?
3. What is the difference between a vertex angle and vertical angles?
4. Can two acute angles be supplementary?
5. Choose any two of the eight angles formed by a pair of parallel lines cut by a transversal. Those two angles are either equal or _______ .
Practice each skill in the Homework Problems listed.
1. Sketch a triangle with given properties #1–6
2. Find an unknown angle in a triangle #7–12, 17–20
3. Find angles formed by parallel lines and a transversal #13–16, 35–44
4. Find exterior angles of a triangle #21–24
5. Find angles in isosceles, equilateral, and right triangles #25–34
6. State reasons for conclusions #45–48
Homework 1.1
For Problems 1–6, sketch and label a triangle with the given properties.
1. An isosceles triangle with vertex angle \(30^{\circ}\) 2. A scalene triangle with one obtuse angle ( Scalene means three unequal sides.) 3. A right triangle with \(\operatorname{legs} 4\) and 7 4. An isosceles right triangle 5. An isosceles triangle with one obtuse angle 6. A right triangle with one angle \(20^{\circ}\)
For Problems 7–20, find each unknown angle.
In Problems 21 and 22, the angle labeled \(\phi\) is called an exterior angle of the triangle, formed by one side and the extension of an adjacent side. Find \(\phi\).
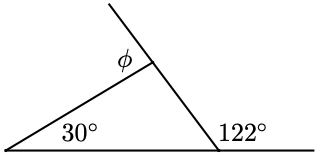
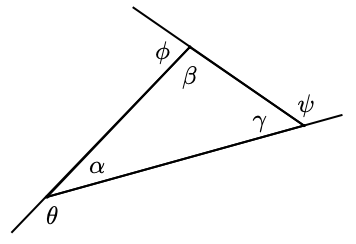
23. In parts (a) and (b), find the exterior angle \(\phi\).
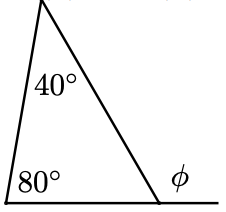
c. Find an algebraic expression for \(\phi\).
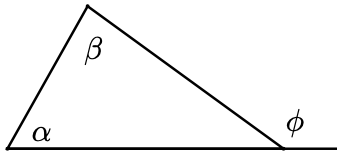
d Use your answer to part (c) to write a rule for finding an exterior angle of a triangle.
a Find the three exterior angles of the triangle. What is the sum of the exterior angles?
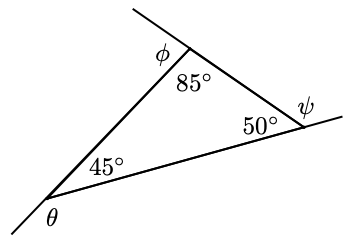
b Write an algebraic expression for each exterior angle in terms of one of the angles of the triangle. What is the sum of the exterior angles?
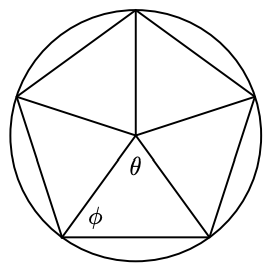
In Problems 25 and 26, the figures inscribed are regular polygons , which means that all their sides are the same length, and all the angles have the same measure. Find the angles \(\theta\) and \(\phi\).
In problems 27 and 28, \(\Delta ABC\) is equilateral. Find the unknown angles
a \(2\theta + 2\phi = ________\)
b \(\theta + \phi = ________\)
c \(\Delta ABC\) is ________
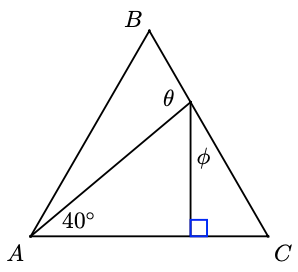
30. Find \(\alpha\) and \(\beta\).
a Explain why \(\angle O A B\) and \(\angle A B O\) are equal in measure.
b Explain why \(\angle O B C\) and \(\angle B C O\) are equal in measure.
c Explain why \(\angle A B C\) is a right angle. (Hint: Use Problem 29.)
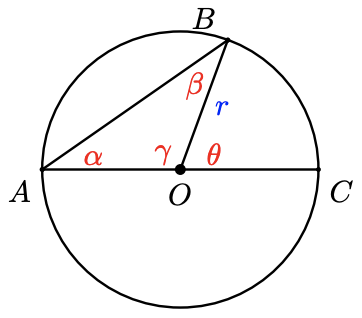
a Compare \(\theta\) with \(\alpha+\beta\). (Hint: What do you know about supplementary angles and the sum of angles in a triangle?
b Compare \(\alpha\) and \(\beta\).
c Explain why the inscribed angle \(\angle B A O\) is half the size of the central angle \(\angle B O D\).
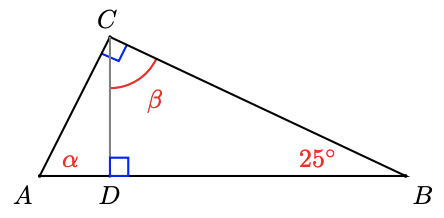
33. Find \(\alpha\) and \(\beta\).
34. Find \(\alpha\) and \(\beta\).
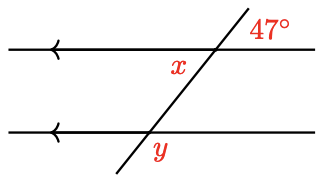
In Problems 35–44, arrows on a pair of lines indicate that they are parallel. Find \(x\) and \(y\).
a Among the angles labeled 1 through 5 in the figure at right, find two pairs of equal angles.
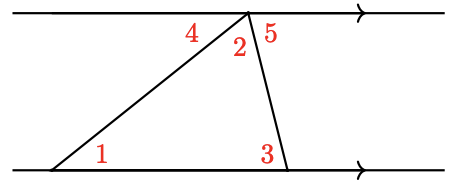
b \(\angle 4+\angle 2+\angle 5= _________\)
c Use parts (a) and (b) to explain why the sum of the angles of a triangle is \(180^{\circ}\)
a In the figure below, find \(\theta\), and justify your answer.
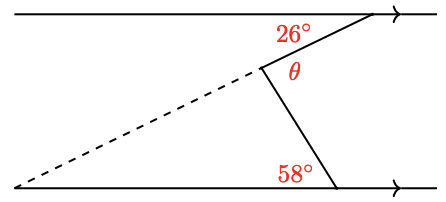
b Write an algebraic expression for \(\theta\) in the figure below.
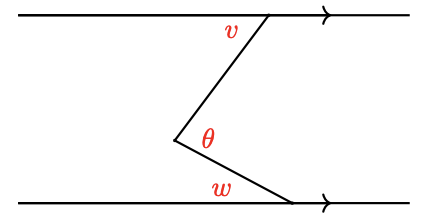
47. \(A B C D\) is a rectangle. The diagonals of a rectangle bisect each other. In the figure, \(\angle A Q D=130^{\circ}\). Find the angles labeled 1 through 5 in order, and give a reason for each answer.
48. A tangent meets the radius of a circle at a right angle. In the figure, \(\angle AOB = 140^{\circ}\). Find the angles labeled 1 through 5 in order, and give a reason for each answer.

Snapsolve any problem by taking a picture. Try it in the Numerade app?

IMAGES
VIDEO
COMMENTS
14/20 = x/100. Then multiply the numerator of the first fraction by the denominator of the second fraction: 1400 =. Then, multiply the denominator of the first fraction by the numerator of the second, and you will get: 1400 = 20x. Solve by dividing both sides by 20. The answer is 70.
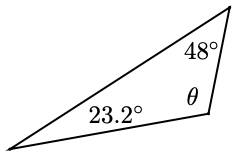
The third angle in both triangles is \(80^{\circ}\), so the triangles are similar because their corresponding angles are equal. Note 1.23 In part (b) of the previous exercise, note that the third angle in each triangle must be \(80^{\circ}\), because the sum of the angles is \(180^{\circ}\).
No, there is not a similarity criterion using only angles for quadrilaterals. This is because some figures can have all corresponding pairs of angles congruent and still not be similar. For example, all angles in a rectangle are 90 degrees, but a 3-by-4 rectangle is not similar to a 3-by-5 rectangle. Feel free to give me any feedback or critiques!
Lesson: Similar Triangles Just as congruence introduced us to new notation, similarity will have its own set of notation. ... 3. Triangle MNO and PQR are similar a. List corresponding angles b. List the ratios of corresponding sides. Warm Up 1. Triangles ABC and DEF are similar. ... Homework- Similar Triangles For questions 1 ...
Angles of Triangles. Section 4-3: Congruent Triangles. Section 4-4: Proving Congruence: SSS, SAS ... Similar Triangles. Section 7-4: Parallel Lines and Proportional Parts. Section 7-5: Parts of Similar Triangles ... Our resource for Geometry: Homework Practice Workbook includes answers to chapter exercises, as well as detailed information to ...
Practice each skill in the Homework Problems listed. Identify congruent triangles and find unknown parts #1-6. Identify similar triangles #7-10. Find unknown parts of similar triangles #11-20. Solve problems using proportions and similar triangles #21-26. Use proportions to relate sides of similar triangles #27-38. Suggested Problems.
Example: these two triangles are similar: If two of their angles are equal, then the third angle must also be equal, because angles of a triangle always add to make 180°. In this case the missing angle is 180° − (72° + 35°) = 73°. So AA could also be called AAA (because when two angles are equal, all three angles must be equal).
Which triangles are similar to A B C ? Choose 1 answer: Q R S only. A. Q R S only. T U V only. B. T U V only. Both.
Watch this segment after you've completed Problem B1. Think about why in this situation having the same angle measurement is enough to make two triangles similar. You can find this segment on the session video approximately 11 minutes and 27 seconds after the Annenberg Media logo. To further explore similar triangles, go to Learning Math ...
Homework 5 Mini-Quiz 2 Review Test ©Maneuvering the Middle LLC, 2017 . o th GRADE Unit: Angle Re ationships Homework 2 Name Date ... DAY 5 Angles in Similar Triangles Student Handout 5 Homework 5 Mini-Quiz 2 ©Maneuvering the Middle LLC, 2017 DAY 3 Interior Angles of Triangles Mini-Quiz 1 Student Handout 3
with an acute angle of measure 30°. 5. Consider the triangles shown below. M N E B A T a) Name the similar triangles. b) Write an extended proportion that is true for these triangles. c) If t = 2, a = 3, and n = 6, find e. 6. Consider the triangles shown below. G R E T A a) Name the similar triangles. b) Write an extended proportion that is ...
XZ Y in. 1 23456789 10 11 206 Chapter 5 Angles and Similarity STATE STANDARDS MA.8.G.2.1 S 5.4 Using Similar Triangles Which properties of triangles make them special among all other types of polygons? You already know that two triangles are similar if and only if the ratios of their corresponding side lengths are equal.
Figure 9.6 ∠ A is the angle with vertex at point A. We measure angles in degrees, and use the symbol ° to represent degrees. We use the abbreviation m for the measure of an angle. So if ∠ A is 27°, we would write m ∠ A = 27. If the sum of the measures of two angles is 180°, then they are called supplementary angles.
A comparison of three or more quantities written as a:b:c or a to b to c. Proportion. An equation stating that two ratios are equal. Similar polygons. Two polygons whose corresponding angles are congruent and whose corresponding sides are proportional. Scale factor. The ratio of corresponding side lengths of similar figures.
The value of x in all the options can be determined by using the arithmetic operations. The calculations are given below. 1) Given : Two side lengths of a triangle are (x + 32) and 33. According to the similar triangles property: SImplify the above expression in order to determine the value of 'x'. 768 + 24x = 1056. 24x = 288.
The Angle-Angle Similarity Theorem states that if two angles in one triangle are equal to two angles in another triangle, then the triangles are similar. Use the Angle-Angle Similarity Theorem to confirm that the triangles in the interactive below are similar. Allow students time to complete questions.
AB 24. mZQSP CD mZQSR O Gina Wilson (All Things Algebra), 2014. Name: Date: Unit 5: Relationships in Triangles Homæork 7: Triangle Inequalities & Algebra ** This is a 2-page documenU ** Directions: If the sidæ of a triangle have the following lewths, find a rangeof Sible values for x. 1. PO=7x+ 13, 101-2, PR = x + 27 Range of Values: x + 40 ...
For Problems 1-6, sketch and label a triangle with the given properties. 1. An isosceles triangle with a vertex angle 306∘ 306 ∘. 2. A scalene triangle with one obtuse angle ( Scalene means three unequal sides.) 3. A right triangle with legs 4 4 and 7 7. 4. An isosceles right triangle.
Since the sum of the interior angles in a triangle is always 180 ∘ , we can use an equation to find the measure of a missing angle. Example: Find the value of x in the triangle shown below. 106 ∘ x ∘ 42 ∘. We can use the following equation to represent the triangle: x ∘ + 42 ∘ + 106 ∘ = 180 ∘. The missing angle is 180 ∘ minus ...
Sketch a triangle with given properties #1-6. 2. Find an unknown angle in a triangle #7-12, 17-20. 3. Find angles formed by parallel lines and a transversal #13-16, 35-44. 4. Find exterior angles of a triangle #21-24. 5. Find angles in isosceles, equilateral, and right triangles #25-34.
Similar triangles are triangles that have the same shape but may have different sizes. In other words, the corresponding angles of similar triangles are equal, and the corresponding sides are in proportion. This means that if we know the ratio of the sides of one triangle, we can find the corresponding sides of the other triangle.
Step 1/5. Step 1: Identify the given information in the problem. Determine which sides and angles are given, and which ones you need to find. Step 2/5. Step 2: Determine which trigonometric function (sine, cosine, or tangent) to use based on the given information. Remember the acronym SOHCAHTOA to help you decide which function to use: - Sine ...
Corresponding angles are congruent in similar triangles. Corresponding sides: Sides that are in the same relative position in each of the similar triangles. The ratio of the lengths of corresponding sides is constant in similar triangles and is called the scale factor. Perimeter: The perimeter of a similar triangle is proportional to the scale ...