9.1 Null and Alternative Hypotheses
The actual test begins by considering two hypotheses . They are called the null hypothesis and the alternative hypothesis . These hypotheses contain opposing viewpoints.
H 0 , the — null hypothesis: a statement of no difference between sample means or proportions or no difference between a sample mean or proportion and a population mean or proportion. In other words, the difference equals 0.
H a —, the alternative hypothesis: a claim about the population that is contradictory to H 0 and what we conclude when we reject H 0 .
Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample data.
After you have determined which hypothesis the sample supports, you make a decision. There are two options for a decision. They are reject H 0 if the sample information favors the alternative hypothesis or do not reject H 0 or decline to reject H 0 if the sample information is insufficient to reject the null hypothesis.
Mathematical Symbols Used in H 0 and H a :
H 0 always has a symbol with an equal in it. H a never has a symbol with an equal in it. The choice of symbol depends on the wording of the hypothesis test. However, be aware that many researchers use = in the null hypothesis, even with > or < as the symbol in the alternative hypothesis. This practice is acceptable because we only make the decision to reject or not reject the null hypothesis.

Example 9.1
H 0 : No more than 30 percent of the registered voters in Santa Clara County voted in the primary election. p ≤ 30 H a : More than 30 percent of the registered voters in Santa Clara County voted in the primary election. p > 30
A medical trial is conducted to test whether or not a new medicine reduces cholesterol by 25 percent. State the null and alternative hypotheses.
Example 9.2
We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). The null and alternative hypotheses are the following: H 0 : μ = 2.0 H a : μ ≠ 2.0
We want to test whether the mean height of eighth graders is 66 inches. State the null and alternative hypotheses. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.
- H 0 : μ __ 66
- H a : μ __ 66
Example 9.3
We want to test if college students take fewer than five years to graduate from college, on the average. The null and alternative hypotheses are the following: H 0 : μ ≥ 5 H a : μ < 5
We want to test if it takes fewer than 45 minutes to teach a lesson plan. State the null and alternative hypotheses. Fill in the correct symbol ( =, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.
- H 0 : μ __ 45
- H a : μ __ 45
Example 9.4
An article on school standards stated that about half of all students in France, Germany, and Israel take advanced placement exams and a third of the students pass. The same article stated that 6.6 percent of U.S. students take advanced placement exams and 4.4 percent pass. Test if the percentage of U.S. students who take advanced placement exams is more than 6.6 percent. State the null and alternative hypotheses. H 0 : p ≤ 0.066 H a : p > 0.066
On a state driver’s test, about 40 percent pass the test on the first try. We want to test if more than 40 percent pass on the first try. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.
- H 0 : p __ 0.40
- H a : p __ 0.40
Collaborative Exercise
Bring to class a newspaper, some news magazines, and some internet articles. In groups, find articles from which your group can write null and alternative hypotheses. Discuss your hypotheses with the rest of the class.
This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.
Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute Texas Education Agency (TEA). The original material is available at: https://www.texasgateway.org/book/tea-statistics . Changes were made to the original material, including updates to art, structure, and other content updates.
Access for free at https://openstax.org/books/statistics/pages/1-introduction
- Authors: Barbara Illowsky, Susan Dean
- Publisher/website: OpenStax
- Book title: Statistics
- Publication date: Mar 27, 2020
- Location: Houston, Texas
- Book URL: https://openstax.org/books/statistics/pages/1-introduction
- Section URL: https://openstax.org/books/statistics/pages/9-1-null-and-alternative-hypotheses
© Apr 16, 2024 Texas Education Agency (TEA). The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.
Have a thesis expert improve your writing
Check your thesis for plagiarism in 10 minutes, generate your apa citations for free.
- Knowledge Base
- Null and Alternative Hypotheses | Definitions & Examples
Null and Alternative Hypotheses | Definitions & Examples
Published on 5 October 2022 by Shaun Turney . Revised on 6 December 2022.
The null and alternative hypotheses are two competing claims that researchers weigh evidence for and against using a statistical test :
- Null hypothesis (H 0 ): There’s no effect in the population .
- Alternative hypothesis (H A ): There’s an effect in the population.
The effect is usually the effect of the independent variable on the dependent variable .
Table of contents
Answering your research question with hypotheses, what is a null hypothesis, what is an alternative hypothesis, differences between null and alternative hypotheses, how to write null and alternative hypotheses, frequently asked questions about null and alternative hypotheses.
The null and alternative hypotheses offer competing answers to your research question . When the research question asks “Does the independent variable affect the dependent variable?”, the null hypothesis (H 0 ) answers “No, there’s no effect in the population.” On the other hand, the alternative hypothesis (H A ) answers “Yes, there is an effect in the population.”
The null and alternative are always claims about the population. That’s because the goal of hypothesis testing is to make inferences about a population based on a sample . Often, we infer whether there’s an effect in the population by looking at differences between groups or relationships between variables in the sample.
You can use a statistical test to decide whether the evidence favors the null or alternative hypothesis. Each type of statistical test comes with a specific way of phrasing the null and alternative hypothesis. However, the hypotheses can also be phrased in a general way that applies to any test.
The null hypothesis is the claim that there’s no effect in the population.
If the sample provides enough evidence against the claim that there’s no effect in the population ( p ≤ α), then we can reject the null hypothesis . Otherwise, we fail to reject the null hypothesis.
Although “fail to reject” may sound awkward, it’s the only wording that statisticians accept. Be careful not to say you “prove” or “accept” the null hypothesis.
Null hypotheses often include phrases such as “no effect”, “no difference”, or “no relationship”. When written in mathematical terms, they always include an equality (usually =, but sometimes ≥ or ≤).
Examples of null hypotheses
The table below gives examples of research questions and null hypotheses. There’s always more than one way to answer a research question, but these null hypotheses can help you get started.
*Note that some researchers prefer to always write the null hypothesis in terms of “no effect” and “=”. It would be fine to say that daily meditation has no effect on the incidence of depression and p 1 = p 2 .
The alternative hypothesis (H A ) is the other answer to your research question . It claims that there’s an effect in the population.
Often, your alternative hypothesis is the same as your research hypothesis. In other words, it’s the claim that you expect or hope will be true.
The alternative hypothesis is the complement to the null hypothesis. Null and alternative hypotheses are exhaustive, meaning that together they cover every possible outcome. They are also mutually exclusive, meaning that only one can be true at a time.
Alternative hypotheses often include phrases such as “an effect”, “a difference”, or “a relationship”. When alternative hypotheses are written in mathematical terms, they always include an inequality (usually ≠, but sometimes > or <). As with null hypotheses, there are many acceptable ways to phrase an alternative hypothesis.
Examples of alternative hypotheses
The table below gives examples of research questions and alternative hypotheses to help you get started with formulating your own.
Null and alternative hypotheses are similar in some ways:
- They’re both answers to the research question
- They both make claims about the population
- They’re both evaluated by statistical tests.
However, there are important differences between the two types of hypotheses, summarized in the following table.
To help you write your hypotheses, you can use the template sentences below. If you know which statistical test you’re going to use, you can use the test-specific template sentences. Otherwise, you can use the general template sentences.
The only thing you need to know to use these general template sentences are your dependent and independent variables. To write your research question, null hypothesis, and alternative hypothesis, fill in the following sentences with your variables:
Does independent variable affect dependent variable ?
- Null hypothesis (H 0 ): Independent variable does not affect dependent variable .
- Alternative hypothesis (H A ): Independent variable affects dependent variable .
Test-specific
Once you know the statistical test you’ll be using, you can write your hypotheses in a more precise and mathematical way specific to the test you chose. The table below provides template sentences for common statistical tests.
Note: The template sentences above assume that you’re performing one-tailed tests . One-tailed tests are appropriate for most studies.
The null hypothesis is often abbreviated as H 0 . When the null hypothesis is written using mathematical symbols, it always includes an equality symbol (usually =, but sometimes ≥ or ≤).
The alternative hypothesis is often abbreviated as H a or H 1 . When the alternative hypothesis is written using mathematical symbols, it always includes an inequality symbol (usually ≠, but sometimes < or >).
A research hypothesis is your proposed answer to your research question. The research hypothesis usually includes an explanation (‘ x affects y because …’).
A statistical hypothesis, on the other hand, is a mathematical statement about a population parameter. Statistical hypotheses always come in pairs: the null and alternative hypotheses. In a well-designed study , the statistical hypotheses correspond logically to the research hypothesis.
Cite this Scribbr article
If you want to cite this source, you can copy and paste the citation or click the ‘Cite this Scribbr article’ button to automatically add the citation to our free Reference Generator.
Turney, S. (2022, December 06). Null and Alternative Hypotheses | Definitions & Examples. Scribbr. Retrieved 21 October 2024, from https://www.scribbr.co.uk/stats/null-and-alternative-hypothesis/
Is this article helpful?

Shaun Turney
Other students also liked, levels of measurement: nominal, ordinal, interval, ratio, the standard normal distribution | calculator, examples & uses, types of variables in research | definitions & examples.
All Subjects
study guides for every class
That actually explain what's on your next test, alternative hypothesis, from class:, probability and statistics.
The alternative hypothesis is a statement that suggests a potential outcome or effect in a statistical test, contrasting with the null hypothesis. It represents what researchers aim to support through evidence gathered from data analysis, indicating that there is a significant difference or relationship that exists within the context of the data being studied.
congrats on reading the definition of Alternative Hypothesis . now let's actually learn it.
5 Must Know Facts For Your Next Test
- The alternative hypothesis can be directional (one-tailed) if it specifies the direction of the effect or non-directional (two-tailed) if it only indicates that an effect exists without specifying a direction.
- In hypothesis testing, if evidence strongly contradicts the null hypothesis, researchers will reject it in favor of the alternative hypothesis.
- The strength of the alternative hypothesis is evaluated using statistical tests such as t-tests or ANOVA to determine if the data support it over the null hypothesis.
- Establishing an alternative hypothesis is crucial for framing research questions and guiding statistical analysis, as it provides a clear focus for what is being tested.
- In Bayesian statistics, the alternative hypothesis plays a role in updating beliefs based on prior knowledge and new evidence, contrasting with traditional frequentist approaches.
Review Questions
- The alternative hypothesis directly contrasts with the null hypothesis, which posits that there is no effect or difference. In statistical testing, researchers seek evidence to support the alternative hypothesis by gathering data that may suggest a significant relationship or outcome exists. If enough evidence is found to refute the null hypothesis, researchers will accept the alternative hypothesis as a plausible explanation for their findings.
- Statistical tests assess whether sample data provides enough evidence to reject the null hypothesis in favor of the alternative hypothesis. This process typically involves calculating a test statistic and comparing it to critical values determined by significance levels. If the p-value associated with the test statistic falls below this threshold, it indicates sufficient evidence to support the alternative hypothesis, leading researchers to reject the null hypothesis.
- Choosing between a directional and non-directional alternative hypothesis can significantly impact the outcomes and interpretations of statistical tests. A directional hypothesis focuses on a specific effect direction, which can increase power to detect that effect if it exists. Conversely, a non-directional hypothesis accounts for effects in either direction but may require larger sample sizes to achieve statistical significance. Researchers must carefully consider their research objectives when selecting which type of alternative hypothesis to adopt, as it shapes both their testing strategy and conclusions drawn from data.
Related terms
The null hypothesis is a statement asserting that there is no effect or difference, serving as the default position in hypothesis testing.
Statistical Significance : Statistical significance measures whether the results observed in data are likely due to chance or reflect a real effect, often evaluated against a predetermined significance level.
P-value : The p-value is a probability that indicates the strength of evidence against the null hypothesis, helping to determine whether to reject or fail to reject it in favor of the alternative hypothesis.
" Alternative Hypothesis " also found in:
Subjects ( 75 ).
- AP Psychology
- AP Statistics
- Advanced Communication Research Methods
- Advanced Design Strategy and Software
- Advanced quantitative methods
- Analytical Chemistry
- Bayesian Statistics
- Big Data Analytics and Visualization
- Biostatistics
- Business Analytics
- Business Anthropology
- Business Decision Making
- Causal Inference
- College Introductory Statistics
- Communication Research Methods
- Communication in Healthcare
- Computational Chemistry
- Covering Politics
- Data Journalism
- Data Visualization for Business
- Data, Inference, and Decisions
- Documentary Forms
- Engineering Applications of Statistics
- Engineering Probability
- Epidemiology
- Experimental Design
- Financial Mathematics
- Foundations of Data Science
- Fundamentals of Ecology
- Fundamentals of Mechanical Prototyping
- Healthcare Quality and Outcomes
- History of Mathematics
- Honors Statistics
- Intro to Business Statistics
- Introduction to Advanced Programming in R
- Introduction to Biostatistics
- Introduction to Business Analytics
- Introduction to Econometrics
- Introduction to Environmental Science
- Introduction to Mathematical Economics
- Introduction to Political Research
- Introduction to Probabilistic Methods in Mathematics and the Sciences
- Introduction to Probability
- Introduction to Programming in R
- Introduction to Public Health
- Introductory Probability and Statistics for Business
- Linear Modeling: Theory and Applications
- Machine Learning Engineering
- Market Research: Tools and Techniques for Data Collection and Analysis
- Marketing Research
- Marketing Strategy
- Mathematical Modeling
- Mathematical Probability Theory
- Mathematical and Computational Methods in Molecular Biology
- Media Effects
- Methods for Public Health Practice
- Methods of Mathematics: Calculus, Statistics, and Combinatorics
- Philosophy of Science
- Predictive Analytics in Business
- Preparatory Statistics
- Principles & Techniques of Data Science
- Principles of Finance
- Probabilistic & Statistical Decision-Making for Management
- Probability and Mathematical Statistics in Data Science
- Professionalism and Research in Nursing
- Public Health Policy and Administration
- Public Policy Analysis
- Reproducible and Collaborative Statistical Data Science
- Risk Management and Insurance
- Sampling Surveys
- Statistical Inference
- Statistical Methods for Data Science
- Structural Health Monitoring
- Theoretical Statistics
- Thinking Like a Mathematician
© 2024 Fiveable Inc. All rights reserved.
Ap® and sat® are trademarks registered by the college board, which is not affiliated with, and does not endorse this website..
Alternative hypothesis
by Marco Taboga , PhD
In a statistical test, observed data is used to decide whether or not to reject a restriction on the data-generating probability distribution.
The assumption that the restriction is true is called null hypothesis , while the statement that the restriction is not true is called alternative hypothesis.
A correct specification of the alternative hypothesis is essential to decide between one-tailed and two-tailed tests.
Table of contents
Mathematical setting
Choice between one-tailed and two-tailed tests, the critical region, the interpretation of the rejection, the interpretation must be coherent with the alternative hypothesis.
- Power function
Accepting the alternative
More details, keep reading the glossary.
In order to fully understand the concept of alternative hypothesis, we need to remember the essential elements of a statistical inference problem:
we observe a sample drawn from an unknown probability distribution;
in principle, any valid probability distribution could have generated the sample;
however, we usually place some a priori restrictions on the set of possible data-generating distributions;
A couple of simple examples follow.
When we conduct a statistical test, we formulate a null hypothesis as a restriction on the statistical model.
The alternative hypothesis is
The alternative hypothesis is used to decide whether a test should be one-tailed or two-tailed.
The null hypothesis is rejected if the test statistic falls within a critical region that has been chosen by the statistician.
The critical region is a set of values that may comprise:
only the left tail of the distribution or only the right tail (one-tailed test);
both the left and the right tail (two-tailed test).
The choice of the critical region depends on the alternative hypothesis. Let us see why.
The interpretation is different depending on the tail of the distribution in which the test statistic falls.
![def of alternative hypothesis [eq7]](https://www.statlect.com/images/alternative-hypothesis__27.png)
The choice between a one-tailed or a two-tailed test needs to be done in such a way that the interpretation of a rejection is always coherent with the alternative hypothesis.
When we deal with the power function of a test, the term "alternative hypothesis" has a special meaning.
We conclude with a caveat about the interpretation of the outcome of a test of hypothesis.
The interpretation of a rejection of the null is controversial.
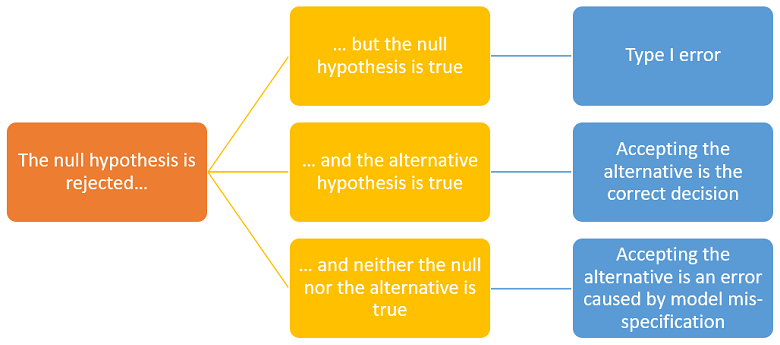
According to some statisticians, rejecting the null is equivalent to accepting the alternative.
However, others deem that rejecting the null does not necessarily imply accepting the alternative. In fact, it is possible to think of situations in which both hypotheses can be rejected. Let us see why.
According to the conceptual framework illustrated by the images above, there are three possibilities:
the null is true;
the alternative is true;
neither the null nor the alternative is true because the true data-generating distribution has been excluded from the statistical model (we say that the model is mis-specified).
If we are in case 3, accepting the alternative after a rejection of the null is an incorrect decision. Moreover, a second test in which the alternative becomes the new null may lead us to another rejection.
You can find more details about the alternative hypothesis in the lecture on Hypothesis testing .
Previous entry: Almost sure
Next entry: Binomial coefficient
How to cite
Please cite as:
Taboga, Marco (2021). "Alternative hypothesis", Lectures on probability theory and mathematical statistics. Kindle Direct Publishing. Online appendix. https://www.statlect.com/glossary/alternative-hypothesis.
Most of the learning materials found on this website are now available in a traditional textbook format.
- Maximum likelihood
- Binomial distribution
- Beta distribution
- Convergence in probability
- Delta method
- Exponential distribution
- Chi-square distribution
- Set estimation
- Wishart distribution
- Mathematical tools
- Fundamentals of probability
- Probability distributions
- Asymptotic theory
- Fundamentals of statistics
- About Statlect
- Cookies, privacy and terms of use
- Precision matrix
- Loss function
- Integrable variable
- Critical value
- To enhance your privacy,
- we removed the social buttons,
- but don't forget to share .
Module 9: Hypothesis Testing With One Sample
Null and alternative hypotheses, learning outcomes.
- Describe hypothesis testing in general and in practice
The actual test begins by considering two hypotheses . They are called the null hypothesis and the alternative hypothesis . These hypotheses contain opposing viewpoints.
H 0 : The null hypothesis: It is a statement about the population that either is believed to be true or is used to put forth an argument unless it can be shown to be incorrect beyond a reasonable doubt.
H a : The alternative hypothesis : It is a claim about the population that is contradictory to H 0 and what we conclude when we reject H 0 .
Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample data.
After you have determined which hypothesis the sample supports, you make adecision. There are two options for a decision . They are “reject H 0 ” if the sample information favors the alternative hypothesis or “do not reject H 0 ” or “decline to reject H 0 ” if the sample information is insufficient to reject the null hypothesis.
Mathematical Symbols Used in H 0 and H a :
H 0 always has a symbol with an equal in it. H a never has a symbol with an equal in it. The choice of symbol depends on the wording of the hypothesis test. However, be aware that many researchers (including one of the co-authors in research work) use = in the null hypothesis, even with > or < as the symbol in the alternative hypothesis. This practice is acceptable because we only make the decision to reject or not reject the null hypothesis.
H 0 : No more than 30% of the registered voters in Santa Clara County voted in the primary election. p ≤ 30
H a : More than 30% of the registered voters in Santa Clara County voted in the primary election. p > 30
A medical trial is conducted to test whether or not a new medicine reduces cholesterol by 25%. State the null and alternative hypotheses.
H 0 : The drug reduces cholesterol by 25%. p = 0.25
H a : The drug does not reduce cholesterol by 25%. p ≠ 0.25
We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). The null and alternative hypotheses are:
H 0 : μ = 2.0
H a : μ ≠ 2.0
We want to test whether the mean height of eighth graders is 66 inches. State the null and alternative hypotheses. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses. H 0 : μ __ 66 H a : μ __ 66
- H 0 : μ = 66
- H a : μ ≠ 66
We want to test if college students take less than five years to graduate from college, on the average. The null and alternative hypotheses are:
H 0 : μ ≥ 5
H a : μ < 5
We want to test if it takes fewer than 45 minutes to teach a lesson plan. State the null and alternative hypotheses. Fill in the correct symbol ( =, ≠, ≥, <, ≤, >) for the null and alternative hypotheses. H 0 : μ __ 45 H a : μ __ 45
- H 0 : μ ≥ 45
- H a : μ < 45
In an issue of U.S. News and World Report , an article on school standards stated that about half of all students in France, Germany, and Israel take advanced placement exams and a third pass. The same article stated that 6.6% of U.S. students take advanced placement exams and 4.4% pass. Test if the percentage of U.S. students who take advanced placement exams is more than 6.6%. State the null and alternative hypotheses.
H 0 : p ≤ 0.066
H a : p > 0.066
On a state driver’s test, about 40% pass the test on the first try. We want to test if more than 40% pass on the first try. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses. H 0 : p __ 0.40 H a : p __ 0.40
- H 0 : p = 0.40
- H a : p > 0.40
Concept Review
In a hypothesis test , sample data is evaluated in order to arrive at a decision about some type of claim. If certain conditions about the sample are satisfied, then the claim can be evaluated for a population. In a hypothesis test, we: Evaluate the null hypothesis , typically denoted with H 0 . The null is not rejected unless the hypothesis test shows otherwise. The null statement must always contain some form of equality (=, ≤ or ≥) Always write the alternative hypothesis , typically denoted with H a or H 1 , using less than, greater than, or not equals symbols, i.e., (≠, >, or <). If we reject the null hypothesis, then we can assume there is enough evidence to support the alternative hypothesis. Never state that a claim is proven true or false. Keep in mind the underlying fact that hypothesis testing is based on probability laws; therefore, we can talk only in terms of non-absolute certainties.

Formula Review
H 0 and H a are contradictory.
- OpenStax, Statistics, Null and Alternative Hypotheses. Provided by : OpenStax. Located at : http://cnx.org/contents/[email protected]:58/Introductory_Statistics . License : CC BY: Attribution
- Introductory Statistics . Authored by : Barbara Illowski, Susan Dean. Provided by : Open Stax. Located at : http://cnx.org/contents/[email protected] . License : CC BY: Attribution . License Terms : Download for free at http://cnx.org/contents/[email protected]
- Simple hypothesis testing | Probability and Statistics | Khan Academy. Authored by : Khan Academy. Located at : https://youtu.be/5D1gV37bKXY . License : All Rights Reserved . License Terms : Standard YouTube License
- Science, Tech, Math ›
- Statistics ›
- Inferential Statistics ›
Null Hypothesis and Alternative Hypothesis
- Inferential Statistics
- Statistics Tutorials
- Probability & Games
- Descriptive Statistics
- Applications Of Statistics
- Math Tutorials
- Pre Algebra & Algebra
- Exponential Decay
- Worksheets By Grade
- Ph.D., Mathematics, Purdue University
- M.S., Mathematics, Purdue University
- B.A., Mathematics, Physics, and Chemistry, Anderson University
Hypothesis testing involves the careful construction of two statements: the null hypothesis and the alternative hypothesis. These hypotheses can look very similar but are actually different.
How do we know which hypothesis is the null and which one is the alternative? We will see that there are a few ways to tell the difference.
The Null Hypothesis
The null hypothesis reflects that there will be no observed effect in our experiment. In a mathematical formulation of the null hypothesis, there will typically be an equal sign. This hypothesis is denoted by H 0 .
The null hypothesis is what we attempt to find evidence against in our hypothesis test. We hope to obtain a small enough p-value that it is lower than our level of significance alpha and we are justified in rejecting the null hypothesis. If our p-value is greater than alpha, then we fail to reject the null hypothesis.
If the null hypothesis is not rejected, then we must be careful to say what this means. The thinking on this is similar to a legal verdict. Just because a person has been declared "not guilty", it does not mean that he is innocent. In the same way, just because we failed to reject a null hypothesis it does not mean that the statement is true.
For example, we may want to investigate the claim that despite what convention has told us, the mean adult body temperature is not the accepted value of 98.6 degrees Fahrenheit . The null hypothesis for an experiment to investigate this is “The mean adult body temperature for healthy individuals is 98.6 degrees Fahrenheit.” If we fail to reject the null hypothesis, then our working hypothesis remains that the average adult who is healthy has a temperature of 98.6 degrees. We do not prove that this is true.
If we are studying a new treatment, the null hypothesis is that our treatment will not change our subjects in any meaningful way. In other words, the treatment will not produce any effect in our subjects.
The Alternative Hypothesis
The alternative or experimental hypothesis reflects that there will be an observed effect for our experiment. In a mathematical formulation of the alternative hypothesis, there will typically be an inequality, or not equal to symbol. This hypothesis is denoted by either H a or by H 1 .
The alternative hypothesis is what we are attempting to demonstrate in an indirect way by the use of our hypothesis test. If the null hypothesis is rejected, then we accept the alternative hypothesis. If the null hypothesis is not rejected, then we do not accept the alternative hypothesis. Going back to the above example of mean human body temperature, the alternative hypothesis is “The average adult human body temperature is not 98.6 degrees Fahrenheit.”
If we are studying a new treatment, then the alternative hypothesis is that our treatment does, in fact, change our subjects in a meaningful and measurable way.
The following set of negations may help when you are forming your null and alternative hypotheses. Most technical papers rely on just the first formulation, even though you may see some of the others in a statistics textbook.
- Null hypothesis: “ x is equal to y .” Alternative hypothesis “ x is not equal to y .”
- Null hypothesis: “ x is at least y .” Alternative hypothesis “ x is less than y .”
- Null hypothesis: “ x is at most y .” Alternative hypothesis “ x is greater than y .”
- What 'Fail to Reject' Means in a Hypothesis Test
- Type I and Type II Errors in Statistics
- An Example of a Hypothesis Test
- The Runs Test for Random Sequences
- An Example of Chi-Square Test for a Multinomial Experiment
- The Difference Between Type I and Type II Errors in Hypothesis Testing
- What Level of Alpha Determines Statistical Significance?
- What Is the Difference Between Alpha and P-Values?
- What Is ANOVA?
- How to Find Critical Values with a Chi-Square Table
- Example of a Permutation Test
- Degrees of Freedom for Independence of Variables in Two-Way Table
- Example of an ANOVA Calculation
- How to Find Degrees of Freedom in Statistics
- How to Construct a Confidence Interval for a Population Proportion
- Degrees of Freedom in Statistics and Mathematics
Research Hypothesis In Psychology: Types, & Examples
Saul McLeod, PhD
Editor-in-Chief for Simply Psychology
BSc (Hons) Psychology, MRes, PhD, University of Manchester
Saul McLeod, PhD., is a qualified psychology teacher with over 18 years of experience in further and higher education. He has been published in peer-reviewed journals, including the Journal of Clinical Psychology.
Learn about our Editorial Process
Olivia Guy-Evans, MSc
Associate Editor for Simply Psychology
BSc (Hons) Psychology, MSc Psychology of Education
Olivia Guy-Evans is a writer and associate editor for Simply Psychology. She has previously worked in healthcare and educational sectors.
On This Page:
A research hypothesis, in its plural form “hypotheses,” is a specific, testable prediction about the anticipated results of a study, established at its outset. It is a key component of the scientific method .
Hypotheses connect theory to data and guide the research process towards expanding scientific understanding
Some key points about hypotheses:
- A hypothesis expresses an expected pattern or relationship. It connects the variables under investigation.
- It is stated in clear, precise terms before any data collection or analysis occurs. This makes the hypothesis testable.
- A hypothesis must be falsifiable. It should be possible, even if unlikely in practice, to collect data that disconfirms rather than supports the hypothesis.
- Hypotheses guide research. Scientists design studies to explicitly evaluate hypotheses about how nature works.
- For a hypothesis to be valid, it must be testable against empirical evidence. The evidence can then confirm or disprove the testable predictions.
- Hypotheses are informed by background knowledge and observation, but go beyond what is already known to propose an explanation of how or why something occurs.
Predictions typically arise from a thorough knowledge of the research literature, curiosity about real-world problems or implications, and integrating this to advance theory. They build on existing literature while providing new insight.
Types of Research Hypotheses
Alternative hypothesis.
The research hypothesis is often called the alternative or experimental hypothesis in experimental research.
It typically suggests a potential relationship between two key variables: the independent variable, which the researcher manipulates, and the dependent variable, which is measured based on those changes.
The alternative hypothesis states a relationship exists between the two variables being studied (one variable affects the other).
A hypothesis is a testable statement or prediction about the relationship between two or more variables. It is a key component of the scientific method. Some key points about hypotheses:
- Important hypotheses lead to predictions that can be tested empirically. The evidence can then confirm or disprove the testable predictions.
In summary, a hypothesis is a precise, testable statement of what researchers expect to happen in a study and why. Hypotheses connect theory to data and guide the research process towards expanding scientific understanding.
An experimental hypothesis predicts what change(s) will occur in the dependent variable when the independent variable is manipulated.
It states that the results are not due to chance and are significant in supporting the theory being investigated.
The alternative hypothesis can be directional, indicating a specific direction of the effect, or non-directional, suggesting a difference without specifying its nature. It’s what researchers aim to support or demonstrate through their study.
Null Hypothesis
The null hypothesis states no relationship exists between the two variables being studied (one variable does not affect the other). There will be no changes in the dependent variable due to manipulating the independent variable.
It states results are due to chance and are not significant in supporting the idea being investigated.
The null hypothesis, positing no effect or relationship, is a foundational contrast to the research hypothesis in scientific inquiry. It establishes a baseline for statistical testing, promoting objectivity by initiating research from a neutral stance.
Many statistical methods are tailored to test the null hypothesis, determining the likelihood of observed results if no true effect exists.
This dual-hypothesis approach provides clarity, ensuring that research intentions are explicit, and fosters consistency across scientific studies, enhancing the standardization and interpretability of research outcomes.
Nondirectional Hypothesis
A non-directional hypothesis, also known as a two-tailed hypothesis, predicts that there is a difference or relationship between two variables but does not specify the direction of this relationship.
It merely indicates that a change or effect will occur without predicting which group will have higher or lower values.
For example, “There is a difference in performance between Group A and Group B” is a non-directional hypothesis.
Directional Hypothesis
A directional (one-tailed) hypothesis predicts the nature of the effect of the independent variable on the dependent variable. It predicts in which direction the change will take place. (i.e., greater, smaller, less, more)
It specifies whether one variable is greater, lesser, or different from another, rather than just indicating that there’s a difference without specifying its nature.
For example, “Exercise increases weight loss” is a directional hypothesis.

Falsifiability
The Falsification Principle, proposed by Karl Popper , is a way of demarcating science from non-science. It suggests that for a theory or hypothesis to be considered scientific, it must be testable and irrefutable.
Falsifiability emphasizes that scientific claims shouldn’t just be confirmable but should also have the potential to be proven wrong.
It means that there should exist some potential evidence or experiment that could prove the proposition false.
However many confirming instances exist for a theory, it only takes one counter observation to falsify it. For example, the hypothesis that “all swans are white,” can be falsified by observing a black swan.
For Popper, science should attempt to disprove a theory rather than attempt to continually provide evidence to support a research hypothesis.
Can a Hypothesis be Proven?
Hypotheses make probabilistic predictions. They state the expected outcome if a particular relationship exists. However, a study result supporting a hypothesis does not definitively prove it is true.
All studies have limitations. There may be unknown confounding factors or issues that limit the certainty of conclusions. Additional studies may yield different results.
In science, hypotheses can realistically only be supported with some degree of confidence, not proven. The process of science is to incrementally accumulate evidence for and against hypothesized relationships in an ongoing pursuit of better models and explanations that best fit the empirical data. But hypotheses remain open to revision and rejection if that is where the evidence leads.
- Disproving a hypothesis is definitive. Solid disconfirmatory evidence will falsify a hypothesis and require altering or discarding it based on the evidence.
- However, confirming evidence is always open to revision. Other explanations may account for the same results, and additional or contradictory evidence may emerge over time.
We can never 100% prove the alternative hypothesis. Instead, we see if we can disprove, or reject the null hypothesis.
If we reject the null hypothesis, this doesn’t mean that our alternative hypothesis is correct but does support the alternative/experimental hypothesis.
Upon analysis of the results, an alternative hypothesis can be rejected or supported, but it can never be proven to be correct. We must avoid any reference to results proving a theory as this implies 100% certainty, and there is always a chance that evidence may exist which could refute a theory.
How to Write a Hypothesis
- Identify variables . The researcher manipulates the independent variable and the dependent variable is the measured outcome.
- Operationalized the variables being investigated . Operationalization of a hypothesis refers to the process of making the variables physically measurable or testable, e.g. if you are about to study aggression, you might count the number of punches given by participants.
- Decide on a direction for your prediction . If there is evidence in the literature to support a specific effect of the independent variable on the dependent variable, write a directional (one-tailed) hypothesis. If there are limited or ambiguous findings in the literature regarding the effect of the independent variable on the dependent variable, write a non-directional (two-tailed) hypothesis.
- Make it Testable : Ensure your hypothesis can be tested through experimentation or observation. It should be possible to prove it false (principle of falsifiability).
- Clear & concise language . A strong hypothesis is concise (typically one to two sentences long), and formulated using clear and straightforward language, ensuring it’s easily understood and testable.
Consider a hypothesis many teachers might subscribe to: students work better on Monday morning than on Friday afternoon (IV=Day, DV= Standard of work).
Now, if we decide to study this by giving the same group of students a lesson on a Monday morning and a Friday afternoon and then measuring their immediate recall of the material covered in each session, we would end up with the following:
- The alternative hypothesis states that students will recall significantly more information on a Monday morning than on a Friday afternoon.
- The null hypothesis states that there will be no significant difference in the amount recalled on a Monday morning compared to a Friday afternoon. Any difference will be due to chance or confounding factors.
More Examples
- Memory : Participants exposed to classical music during study sessions will recall more items from a list than those who studied in silence.
- Social Psychology : Individuals who frequently engage in social media use will report higher levels of perceived social isolation compared to those who use it infrequently.
- Developmental Psychology : Children who engage in regular imaginative play have better problem-solving skills than those who don’t.
- Clinical Psychology : Cognitive-behavioral therapy will be more effective in reducing symptoms of anxiety over a 6-month period compared to traditional talk therapy.
- Cognitive Psychology : Individuals who multitask between various electronic devices will have shorter attention spans on focused tasks than those who single-task.
- Health Psychology : Patients who practice mindfulness meditation will experience lower levels of chronic pain compared to those who don’t meditate.
- Organizational Psychology : Employees in open-plan offices will report higher levels of stress than those in private offices.
- Behavioral Psychology : Rats rewarded with food after pressing a lever will press it more frequently than rats who receive no reward.
- Math Article
Alternative Hypothesis

Alternative hypothesis defines there is a statistically important relationship between two variables. Whereas null hypothesis states there is no statistical relationship between the two variables. In statistics, we usually come across various kinds of hypotheses. A statistical hypothesis is supposed to be a working statement which is assumed to be logical with given data. It should be noticed that a hypothesis is neither considered true nor false.
The alternative hypothesis is a statement used in statistical inference experiment. It is contradictory to the null hypothesis and denoted by H a or H 1 . We can also say that it is simply an alternative to the null. In hypothesis testing, an alternative theory is a statement which a researcher is testing. This statement is true from the researcher’s point of view and ultimately proves to reject the null to replace it with an alternative assumption. In this hypothesis, the difference between two or more variables is predicted by the researchers, such that the pattern of data observed in the test is not due to chance.
To check the water quality of a river for one year, the researchers are doing the observation. As per the null hypothesis, there is no change in water quality in the first half of the year as compared to the second half. But in the alternative hypothesis, the quality of water is poor in the second half when observed.
Difference Between Null and Alternative Hypothesis
Basically, there are three types of the alternative hypothesis, they are;
Left-Tailed : Here, it is expected that the sample proportion (π) is less than a specified value which is denoted by π 0 , such that;
H 1 : π < π 0
Right-Tailed: It represents that the sample proportion (π) is greater than some value, denoted by π 0 .
H 1 : π > π 0
Two-Tailed: According to this hypothesis, the sample proportion (denoted by π) is not equal to a specific value which is represented by π 0 .
H 1 : π ≠ π 0
Note: The null hypothesis for all the three alternative hypotheses, would be H 1 : π = π 0 .
Register with BYJU'S & Download Free PDFs
Register with byju's & watch live videos.
- Mathematics
- Number System and Arithmetic
- Trigonometry
- Probability
- Mensuration
- Maths Formulas
- Class 8 Maths Notes
- Class 9 Maths Notes
- Class 10 Maths Notes
- Class 11 Maths Notes
- Class 12 Maths Notes
Alternative Hypothesis: Definition, Types and Examples
In statistical hypothesis testing, the alternative hypothesis is an important proposition in the hypothesis test. The goal of the hypothesis test is to demonstrate that in the given condition, there is sufficient evidence supporting the credibility of the alternative hypothesis instead of the default assumption made by the null hypothesis.

Both hypotheses include statements with the same purpose of providing the researcher with a basic guideline. The researcher uses the statement from each hypothesis to guide their research. In statistics, alternative hypothesis is often denoted as H a or H 1 .
Table of Content
What is a Hypothesis?
Alternative hypothesis, types of alternative hypothesis, difference between null and alternative hypothesis, formulating an alternative hypothesis, example of alternative hypothesis, application of alternative hypothesis.
"A hypothesis is a statement of a relationship between two or more variables." It is a working statement or theory that is based on insufficient evidence.
While experimenting, researchers often make a claim, that they can test. These claims are often based on the relationship between two or more variables. "What causes what?" and "Up to what extent?" are a few of the questions that a hypothesis focuses on answering. The hypothesis can be true or false, based on complete evidence.
While there are different hypotheses, we discuss only null and alternate hypotheses. The null hypothesis, denoted H o , is the default position where variables do not have a relation with each other. That means the null hypothesis is assumed true until evidence indicates otherwise. The alternative hypothesis, denoted H 1 , on the other hand, opposes the null hypothesis. It assumes a relation between the variables and serves as evidence to reject the null hypothesis.
Example of Hypothesis:
Mean age of all college students is 20.4 years. (simple hypothesis).
An Alternative Hypothesis is a claim or a complement to the null hypothesis. If the null hypothesis predicts a statement to be true, the Alternative Hypothesis predicts it to be false. Let's say the null hypothesis states there is no difference between height and shoe size then the alternative hypothesis will oppose the claim by stating that there is a relation.
We see that the null hypothesis assumes no relationship between the variables whereas an alternative hypothesis proposes a significant relation between variables. An alternative theory is the one tested by the researcher and if the researcher gathers enough data to support it, then the alternative hypothesis replaces the null hypothesis.
Null and alternative hypotheses are exhaustive, meaning that together they cover every possible outcome. They are also mutually exclusive, meaning that only one can be true at a time.
There are a few types of alternative hypothesis that we will see:
1. One-tailed test H 1 : A one-tailed alternative hypothesis focuses on only one region of rejection of the sampling distribution. The region of rejection can be upper or lower.
- Upper-tailed test H 1 : Population characteristic > Hypothesized value
- Lower-tailed test H 1 : Population characteristic < Hypothesized value
2. Two-tailed test H 1 : A two-tailed alternative hypothesis is concerned with both regions of rejection of the sampling distribution.
3. Non-directional test H 1 : A non-directional alternative hypothesis is not concerned with either region of rejection; rather, it is only concerned that null hypothesis is not true.
4. Point test H 1 : Point alternative hypotheses occur when the hypothesis test is framed so that the population distribution under the alternative hypothesis is a fully defined distribution, with no unknown parameters; such hypotheses are usually of no practical interest but are fundamental to theoretical considerations of statistical inference and are the basis of the Neyman–Pearson lemma.
the differences between Null Hypothesis and Alternative Hypothesis is explained in the table below:
Formulating an alternative hypothesis means identifying the relationships, effects or condition being studied. Based on the data we conclude that there is a different inference from the null-hypothesis being considered.
- Understand the null hypothesis.
- Consider the alternate hypothesis
- Choose the type of alternate hypothesis (one-tailed or two-tailed)
Alternative hypothesis must be true when the null hypothesis is false. When trying to identify the information need for alternate hypothesis statement, look for the following phrases:
- "Is it reasonable to conclude..."
- "Is there enough evidence to substantiate..."
- "Does the evidence suggest..."
- "Has there been a significant..."
When alternative hypotheses in mathematical terms, they always include an inequality ( usually ≠, but sometimes < or >) . When writing the alternate hypothesis, make sure it never includes an "=" symbol.
To help you write your hypotheses, you can use the template sentences below.
Does independent variable affect dependent variable?
- Null Hypothesis (H 0 ): Independent variable does not affect dependent variable.
- Alternative Hypothesis (H a ): Independent variable affects dependent variable.
Various examples of Alternative Hypothesis includes:
Two-Tailed Example
- Research Question : Do home games affect a team's performance?
- Null-Hypothesis: Home games do not affect a team's performance.
- Alternative Hypothesis: Home games have an effect on team's performance.
- Research Question: Does sleeping less lead to depression?
- Null-Hypothesis: Sleeping less does not have an effect on depression.
- Alternative Hypothesis : Sleeping less has an effect on depression.
One-Tailed Example
- Research Question: Are candidates with experience likely to get a job?
- Null-Hypothesis: Experience does not matter in getting a job.
- Alternative Hypothesis: Candidates with work experience are more likely to receive an interview.
- Alternative Hypothesis : Teams with home advantage are more likely to win a match.
Some applications of Alternative Hypothesis includes:
- Rejecting Null-Hypothesis : A researcher performs additional research to find flaws in the null hypothesis. Following the research, which uses the alternative hypothesis as a guide, they may decide whether they have enough evidence to reject the null hypothesis.
- Guideline for Research : An alternative and null hypothesis include statements with the same purpose of providing the researcher with a basic guideline. The researcher uses the statement from each hypothesis to guide their research.
- New Theories : Alternative hypotheses can provide the opportunity to discover new theories that a researcher can use to disprove an existing theory that may not have been backed up by evidence.
We defined the relationship that exist between null-hypothesis and alternative hypothesis. While the null hypothesis is always a default assumption about our test data, the alternative hypothesis puts in all the effort to make sure the null hypothesis is disproved.
Null-hypothesis always explores new relationships between the independent variables to find potential outcomes from our test data. We should note that for every null hypothesis, one or more alternate hypotheses can be developed.
Also Check:
Mathematics Maths Formulas Branches of Mathematics
FAQs on Alternative Hypothesis
What is hypothesis.
A hypothesis is a statement of a relationship between two or more variables." It is a working statement or theory that is based on insufficient evidence.
What is an Alternative Hypothesis?
Alternative hypothesis, denoted by H 1 , opposes the null-hypothesis. It assumes a relation between the variables and serves as an evidence to reject the null-hypothesis.
What is the Difference between Null-Hypothesis and Alternative Hypothesis?
Null hypothesis is the default claim that assumes no relationship between variables while alternative hypothesis is the opposite claim which considers statistical significance between the variables.
What is Alternative and Experimental Hypothesis?
Null hypothesis (H 0 ) states there is no effect or difference, while the alternative hypothesis (H 1 or H a ) asserts the presence of an effect, difference, or relationship between variables. In hypothesis testing, we seek evidence to either reject the null hypothesis in favor of the alternative hypothesis or fail to do so.
Similar Reads
- School Learning
- Math-Statistics
Please Login to comment...
Improve your coding skills with practice.
What kind of Experience do you want to share?

IMAGES
VIDEO
COMMENTS
The null hypothesis (H0) answers "No, there's no effect in the population.". The alternative hypothesis (Ha) answers "Yes, there is an effect in the population.". The null and alternative are always claims about the population. That's because the goal of hypothesis testing is to make inferences about a population based on a sample.
Null hypothesis: µ ≥ 70 inches. Alternative hypothesis: µ < 70 inches. A two-tailed hypothesis involves making an "equal to" or "not equal to" statement. For example, suppose we assume the mean height of a male in the U.S. is equal to 70 inches. The null and alternative hypotheses in this case would be: Null hypothesis: µ = 70 inches.
The actual test begins by considering two hypotheses.They are called the null hypothesis and the alternative hypothesis.These hypotheses contain opposing viewpoints. H 0, the —null hypothesis: a statement of no difference between sample means or proportions or no difference between a sample mean or proportion and a population mean or proportion. In other words, the difference equals 0.
Basic definition. The alternative hypothesis and null hypothesis are types of conjectures used in statistical tests, which are formal methods of reaching conclusions or making judgments on the basis of data. In statistical hypothesis testing, the null hypothesis and alternative hypothesis are two mutually exclusive statements.
The actual test begins by considering two hypotheses.They are called the null hypothesis and the alternative hypothesis.These hypotheses contain opposing viewpoints. \(H_0\): The null hypothesis: It is a statement of no difference between the variables—they are not related. This can often be considered the status quo and as a result if you cannot accept the null it requires some action.
The null and alternative hypotheses are two competing claims that researchers weigh evidence for and against using a statistical test: Null hypothesis (H0): There's no effect in the population. Alternative hypothesis (HA): There's an effect in the population. The effect is usually the effect of the independent variable on the dependent ...
Definition. The alternative hypothesis is a statement that suggests a potential outcome or effect in a statistical test, contrasting with the null hypothesis. It represents what researchers aim to support through evidence gathered from data analysis, indicating that there is a significant difference or relationship that exists within the ...
Example Consider a test of hypothesis for the mean of a normal distribution, where we test . The test statistic is the z-statistic where is the sample mean, is the variance of the distribution and is the sample size. If we run a two-tailed test with critical value , the critical region is the union of the right and left tails of the ...
Thus, our alternative hypothesis is the mathematical way of stating our research question. If we expect our obtained sample mean to be above or below the null hypothesis value, which we call a directional hypothesis, then our alternative hypothesis takes the form: HA: μ> 7.47 or HA: μ <7.47 H A: μ> 7.47 or H A: μ <7.47.
The alternative hypothesis is one of two mutually exclusive hypotheses in a hypothesis test. The alternative hypothesis states that a population parameter does not equal a specified value. Typically, this value is the null hypothesis value associated with no effect, such as zero.If your sample contains sufficient evidence, you can reject the null hypothesis and favor the alternative hypothesis.
H0: The null hypothesis: It is a statement about the population that either is believed to be true or is used to put forth an argument unless it can be shown to be incorrect beyond a reasonable doubt. Ha: The alternative hypothesis: It is a claim about the population that is contradictory to H0 and what we conclude when we reject H0. Since the ...
With the null hypothesis, you get what you expect, from a historical point of view. In hypothesis-testing, there are always two competing hypotheses under consideration [1]: The status quo (null) hypothesis (H 0), The research (alternate) hypothesis (H a or H 1). You can think of the alternate hypothesis as just an alternative to the null. For ...
Most technical papers rely on just the first formulation, even though you may see some of the others in a statistics textbook. Null hypothesis: " x is equal to y.". Alternative hypothesis " x is not equal to y.". Null hypothesis: " x is at least y.". Alternative hypothesis " x is less than y.". Null hypothesis: " x is at most ...
Examples. A research hypothesis, in its plural form "hypotheses," is a specific, testable prediction about the anticipated results of a study, established at its outset. It is a key component of the scientific method. Hypotheses connect theory to data and guide the research process towards expanding scientific understanding.
A research hypothesis is your proposed answer to your research question. The research hypothesis usually includes an explanation ("x affects y because …"). A statistical hypothesis, on the other hand, is a mathematical statement about a population parameter. Statistical hypotheses always come in pairs: the null and alternative hypotheses.
The definition of alternative hypothesis with examples. An alternative hypothesis is a hypothesis that there is a relationship between variables. This includes any hypothesis that predicts positive correlation, negative correlation, non-directional correlation or causation.The only hypothesis that isn't an alternative hypothesis is a null hypothesis that predicts no relationship between ...
The alternative hypothesis is a hypothesis used in significance testing which contains a strict inequality. A test of significance will result in either rejecting the null hypothesis (indicating ...
Definition. The alternative hypothesis is a statement used in statistical inference experiment. It is contradictory to the null hypothesis and denoted by H a or H 1. We can also say that it is simply an alternative to the null. In hypothesis testing, an alternative theory is a statement which a researcher is testing.
a statement that is contrasted with or contradicts the null hypothesis as an explanation for observed data. Generally, it is a scientific prediction of significant results in hypothesis testing; that is, an alternative hypothesis posits meaningful differences or relationships between the variables under investigation.
There are a few types of alternative hypothesis that we will see: 1. One-tailed test H1: A one-tailed alternative hypothesis focuses on only one region of rejection of the sampling distribution. The region of rejection can be upper or lower. Upper-tailed test H1: Population characteristic > Hypothesized value.