logistic regression and null hypothesis

Logistic Regression – Simple Introduction

• Logistic Regression Equation

Logistic Regression Example Curves

Logistic regression - b-coefficients.

• Logistic Regression - Effect Size

Logistic Regression Assumptions

Logistic regression is a technique for predicting a dichotomous outcome variable from 1+ predictors. Example: how likely are people to die before 2020, given their age in 2015? Note that “die” is a dichotomous variable because it has only 2 possible outcomes (yes or no). This analysis is also known as binary logistic regression or simply “logistic regression”. A related technique is multinomial logistic regression which predicts outcome variables with 3+ categories.

Logistic Regression - Simple Example

A nursing home has data on N = 284 clients’ sex, age on 1 January 2015 and whether the client passed away before 1 January 2020. The raw data are in this Googlesheet , partly shown below.

Let's first just focus on age: can we predict death before 2020 from age in 2015? And -if so- precisely how ? And to what extent? A good first step is inspecting a scatterplot like the one shown below.

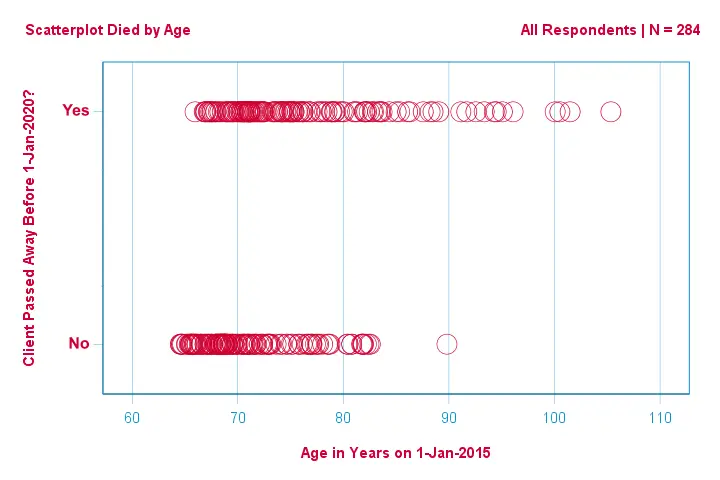
A few things we see in this scatterplot are that

• all but one client over 83 years of age died within the next 5 years;
• the standard deviation of age is much larger for clients who died than for clients who survived;
• age has a considerable positive skewness , especially for the clients who died.

But how can we predict whether a client died, given his age? We'll do just that by fitting a logistic curve.

Simple Logistic Regression Equation

Simple logistic regression computes the probability of some outcome given a single predictor variable as

$$P(Y_i) = \frac{1}{1 + e^{\,-\,(b_0\,+\,b_1X_{1i})}}$$

• \(P(Y_i)\) is the predicted probability that \(Y\) is true for case \(i\);
• \(e\) is a mathematical constant of roughly 2.72;
• \(b_0\) is a constant estimated from the data;
• \(b_1\) is a b-coefficient estimated from the data;
• \(X_i\) is the observed score on variable \(X\) for case \(i\).

The very essence of logistic regression is estimating \(b_0\) and \(b_1\). These 2 numbers allow us to compute the probability of a client dying given any observed age. We'll illustrate this with some example curves that we added to the previous scatterplot.

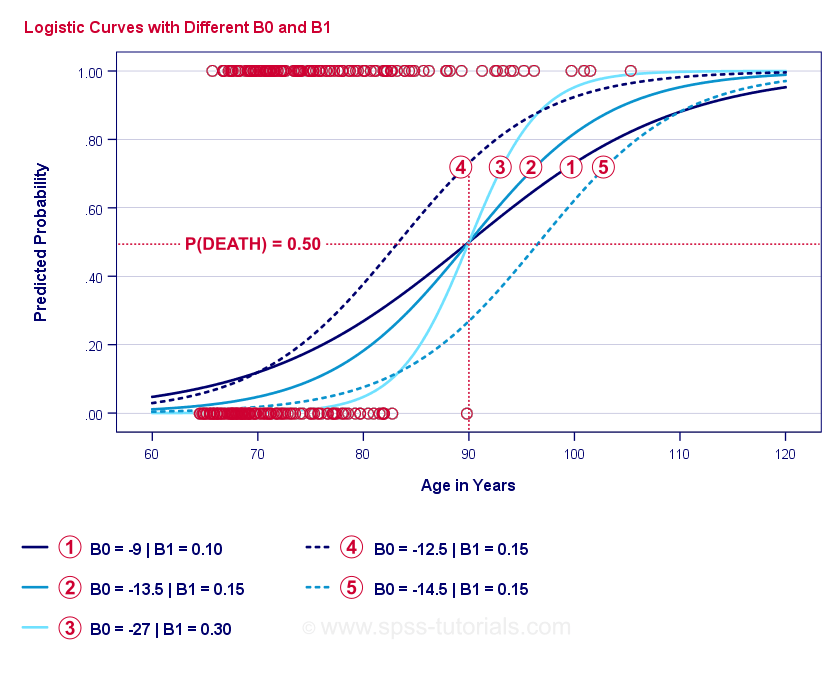
If you take a minute to compare these curves, you may see the following:

For now, we've one question left: how do we find the “best” \(b_0\) and \(b_1\)?

Logistic Regression - Log Likelihood

For each respondent, a logistic regression model estimates the probability that some event \(Y_i\) occurred. Obviously, these probabilities should be high if the event actually occurred and reversely. One way to summarize how well some model performs for all respondents is the log-likelihood \(LL\):

$$LL = \sum_{i = 1}^N Y_i \cdot ln(P(Y_i)) + (1 - Y_i) \cdot ln(1 - P(Y_i))$$

• \(Y_i\) is 1 if the event occurred and 0 if it didn't;
• \(ln\) denotes the natural logarithm: to what power must you raise \(e\) to obtain a given number?

Now let's say our model predicted a 0.95 probability for somebody who did actually die. For this person,

$$LL_i = 1 \cdot ln(0.95) + (1 - 1) \cdot ln(1 - 0.95) =$$

$$LL_i = 1 \cdot -0.051 + 0 \cdot -2.996 =$$

\(LL\) is a goodness-of-fit measure: everything else equal, a logistic regression model fits the data better insofar as \(LL\) is larger . Somewhat confusingly, \(LL\) is always negative. So we want to find the \(b_0\) and \(b_1\) for which \(LL\) is as close to zero as possible.

Maximum Likelihood Estimation

In contrast to linear regression, logistic regression can't readily compute the optimal values for \(b_0\) and \(b_1\). Instead, we need to try different numbers until \(LL\) does not increase any further. Each such attempt is known as an iteration. The process of finding optimal values through such iterations is known as maximum likelihood estimation .

So that's basically how statistical software -such as SPSS , Stata or SAS - obtain logistic regression results. Fortunately, they're amazingly good at it. But instead of reporting \(LL\), these packages report \(-2LL\). \(-2LL\) is a “badness-of-fit” measure which follows a chi-square-distribution. This makes \(-2LL\) useful for comparing different models as we'll see shortly. \(-2LL\) is denoted as -2 Log likelihood in the output shown below.

The footnote here tells us that the maximum likelihood estimation needed only 5 iterations for finding the optimal b-coefficients \(b_0\) and \(b_1\). So let's look into those now.

The most important output for any logistic regression analysis are the b-coefficients. The figure below shows them for our example data.

Before going into details, this output briefly shows

The b-coefficients complete our logistic regression model, which is now

$$P(death_i) = \frac{1}{1 + e^{\,-\,(-9.079\,+\,0.124\, \cdot\, age_i)}}$$

For a 75-year-old client, the probability of passing away within 5 years is

$$P(death_i) = \frac{1}{1 + e^{\,-\,(-9.079\,+\,0.124\, \cdot\, 75)}}=$$

$$P(death_i) = \frac{1}{1 + e^{\,-\,0.249}}=$$

$$P(death_i) = \frac{1}{1 + 0.780}=$$

$$P(death_i) \approx 0.562$$

So now we know how to predict death within 5 years given somebody’s age. But how good is this prediction? There's several approaches. Let's start off with model comparisons.

Logistic Regression - Baseline Model

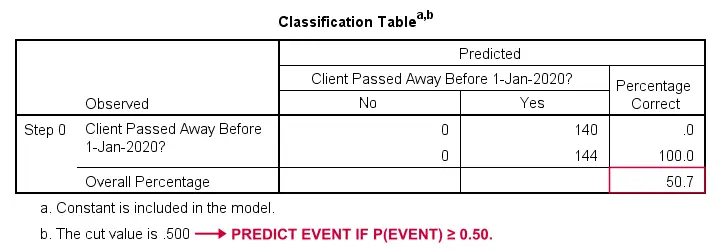
How could we predict who passed away if we didn't have any other information? Well, 50.7% of our sample passed away. So the predicted probability would simply be 0.507 for everybody .

For classification purposes, we usually predict that an event occurs if p(event) ≥ 0.50. Since p(died) = 0.507 for everybody, we simply predict that everybody passed away. This prediction is correct for the 50.7% of our sample that died.

Logistic Regression - Likelihood Ratio

Now, from these predicted probabilities and the observed outcomes we can compute our badness-of-fit measure: -2LL = 393.65. Our actual model -predicting death from age- comes up with -2LL = 354.20. The difference between these numbers is known as the likelihood ratio \(LR\):

$$LR = (-2LL_{baseline}) - (-2LL_{model})$$

Importantly, \(LR\) follows a chi-square distribution with \(df\) degrees of freedom, computed as

$$df = k_{model} - k_{baseline}$$

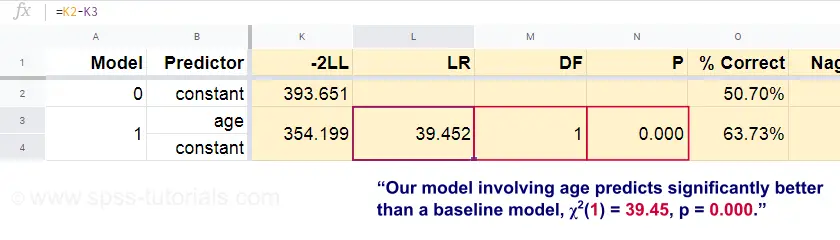
The null hypothesis here is that some model predicts equally poorly as the baseline model in some population. Since p = 0.000, we reject this: our model (predicting death from age) performs significantly better than a baseline model without any predictors. But precisely how much better? This is answered by its effect size.

Logistic Regression - Model Effect Size

A good way to evaluate how well our model performs is from an effect size measure . One option is the Cox & Snell R 2 or \(R^2_{CS}\) computed as

$$R^2_{CS} = 1 - e^{\frac{(-2LL_{model})\,-\,(-2LL_{baseline})}{n}}$$

Sadly, \(R^2_{CS}\) never reaches its theoretical maximum of 1. Therefore, an adjusted version known as Nagelkerke R 2 or \(R^2_{N}\) is often preferred:

$$R^2_{N} = \frac{R^2_{CS}}{1 - e^{-\frac{-2LL_{baseline}}{n}}}$$

For our example data, \(R^2_{CS}\) = 0.130 which indicates a medium effect size. \(R^2_{N}\) = 0.173, slightly larger than medium.

Last, \(R^2_{CS}\) and \(R^2_{N}\) are technically completely different from r-square as computed in linear regression. However, they do attempt to fulfill the same role. Both measures are therefore known as pseudo r-square measures.

Logistic Regression - Predictor Effect Size

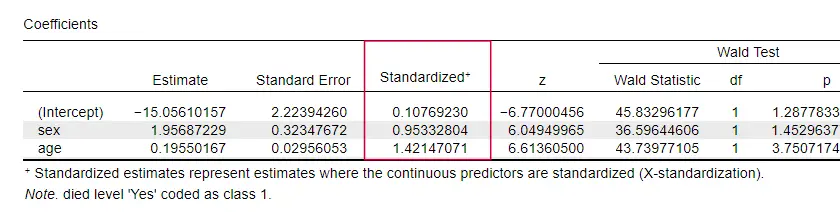
Oddly, very few textbooks mention any effect size for individual predictors. Perhaps that's because these are completely absent from SPSS. The reason we do need them is that b-coeffients depend on the (arbitrary) scales of our predictors: if we'd enter age in days instead of years, its b-coeffient would shrink tremendously. This obviously renders b-coefficients unsuitable for comparing predictors within or across different models. JASP includes partially standardized b-coefficients : quantitative predictors -but not the outcome variable- are entered as z-scores as shown below.

Logistic regression analysis requires the following assumptions:

• independent observations;
• correct model specification;
• errorless measurement of outcome variable and all predictors;
• linearity: each predictor is related linearly to \(e^B\) (the odds ratio).

Assumption 4 is somewhat disputable and omitted by many textbooks 1 , 6 . It can be evaluated with the Box-Tidwell test as discussed by Field 4 . This basically comes down to testing if there's any interaction effects between each predictor and its natural logarithm or \(LN\).

Multiple Logistic Regression

Thus far, our discussion was limited to simple logistic regression which uses only one predictor. The model is easily extended with additional predictors, resulting in multiple logistic regression:

$$P(Y_i) = \frac{1}{1 + e^{\,-\,(b_0\,+\,b_1X_{1i}+\,b_2X_{2i}+\,...+\,b_kX_{ki})}}$$

• \(b_1\), \(b_2\), ... ,\(b_k\) are the b-coefficient for predictors 1, 2, ... ,\(k\);
• \(X_{1i}\), \(X_{2i}\), ... ,\(X_{ki}\) are observed scores on predictors \(X_1\), \(X_2\), ... ,\(X_k\) for case \(i\).

Multiple logistic regression often involves model selection and checking for multicollinearity. Other than that, it's a fairly straightforward extension of simple logistic regression.

Logistic Regression - Next Steps

This basic introduction was limited to the essentials of logistic regression. If you'd like to learn more, you may want to read up on some of the topics we omitted:

• multiple logistic regression involves
• odds ratios -computed as \(e^B\) in logistic regression- express how probabilities change depending on predictor scores ;
• the Box-Tidwell test examines if the relations between the aforementioned odds ratios and predictor scores are linear;
• the Hosmer and Lemeshow test is an alternative goodness-of-fit test for an entire logistic regression model.

Thanks for reading!

• Warner, R.M. (2013). Applied Statistics (2nd. Edition) . Thousand Oaks, CA: SAGE.
• Agresti, A. & Franklin, C. (2014). Statistics. The Art & Science of Learning from Data. Essex: Pearson Education Limited.
• Hair, J.F., Black, W.C., Babin, B.J. et al (2006). Multivariate Data Analysis. New Jersey: Pearson Prentice Hall.
• Field, A. (2013). Discovering Statistics with IBM SPSS Statistics . Newbury Park, CA: Sage.
• Howell, D.C. (2002). Statistical Methods for Psychology (5th ed.). Pacific Grove CA: Duxbury.
• Pituch, K.A. & Stevens, J.P. (2016). Applied Multivariate Statistics for the Social Sciences (6th. Edition) . New York: Routledge.

Tell us what you think!

This tutorial has 23 comments:.

By Ruben Geert van den Berg on February 12th, 2023

This is very probably due to a human error or inaccuracies.

Make sure you

-minimize rounding of all numbers involved -compare the exact same models -use the exact same variables -treat missing values similarly as SPSS

and you should be able to replicate SPSS' results.

Hope that helps!

SPSS tutorials

By Donald W. Buckwalter on September 6th, 2023

Thanks! This is clearly written and presented--appropriate to my level of comprehension.

By Neal Bliven on October 25th, 2023

Nicely worded and logically presented.

Privacy Overview

Logistic Regression and Survival Analysis

•   1  
• |   2  
• |   3  
• |   4  
• Contributing Authors:
• Learning Objectives
• Logistic Regression
• Why use logistic regression?
• Overview of Logistic Regression

Logistic Regression in R

• Survival Analysis
• Why use survival analysis?
• Overview of Survival Analysis
• Things we did not cover (or only touched on)

To perform logistic regression in R, you need to use the glm() function.  Here, glm stands for "general linear model." Suppose we want to run the above logistic regression model in R, we use the following command:

> summary( glm( vomiting ~ age, family = binomial(link = logit) ) )

glm(formula = vomiting ~ age, family = binomial(link = logit))

Deviance Residuals:

    Min       1Q   Median       3Q      Max 

-1.0671  -1.0174  -0.9365   1.3395   1.9196 

Coefficients:

             Estimate Std. Error z value Pr(>|z|)   

(Intercept) -0.141729   0.106206  -1.334    0.182   

age         -0.015437   0.003965  -3.893 9.89e-05 ***

Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for binomial family taken to be 1)

Null deviance: 1452.3   on 1093  degrees of freedom

Residual deviance: 1433.9 on 1092  degrees of freedom

AIC: 1437.9

Number of Fisher Scoring iterations: 4

To get the significance for the overall model we use the following command:

> 1-pchisq(1452.3-1433.9, 1093-1092)

 [1] 1.79058e-05

The input to this test is:

• deviance of "null" model minus deviance of current model (can be thought of as "likelihood")
• degrees of freedom of the null model minus df of current model

This is analogous to the global F test for the overall significance of the model that comes automatically when we run the lm() command. This is testing the null hypothesis that the model is no better (in terms of likelihood) than a model fit with only the intercept term, i.e. that all beta terms are 0.

Thus the logistic model for these data is:

E[ odds(vomiting) ] = -0.14 – 0.02*age

This means that for a one-unit increase in age there is a 0.02 decrease in the log odds of vomiting. This can be translated to e -0.02 =  0.98. Groups of people in an age group one unit higher than a reference group have, on average, 0.98 times the odds of vomiting.

How do we test the association between vomiting and age?

• H 0 : There is no association between vomiting and age (the odds ratio is equal to 1).
• H a : There is an association between vomiting and age (the odds ratio is not equal to 1).

When testing the null hypothesis that there is no association between vomiting and age we reject the null hypothesis at the 0.05 alpha level ( z = -3.89, p-value = 9.89e-05).

On average, the odds of vomiting is 0.98 times that of identical subjects in an age group one unit smaller.

Finally, when we are looking at whether we should include a particular variable in our model (maybe it's a confounder), we can include it based on the "10% rule," where if the change in our estimate of interest changes more than 10% when we include the new covariate in the model, then we that new covariate in our model. When we do this in logistic regression, we compare the exponential of the betas, not the untransformed betas themselves!

return to top | previous page | next page

Logistic Regression

Regression with binary factor variable, regression with a continuous variable, regression with multiple variables, deviance and mcfadden’s pseudo r 2.

Last week, we introduced the concept of maximum likelihood and applied it to box models and simple logistic regression. To recap, we consider a binary variable \(y\) that takes the values of 0 and 1. We want to use the maximum likelihood method to estimate the parameters \(\{ p(x) \}\) . These are the fractions, or equivalently the probabilities, of the \(y=1\) outcome as a function of another variable \(x\) . In the box models, \(x\) is categorical. In simple logistic regression, \(x\) can be a continuous variable (as well as discrete categorical variable, as will be seen below). The maximum likelihood estimate for \(\{ p(x) \}\) is to find the parameters to maximize the log-likelihood function \[\ln L(\{ p(x) \}) = \sum_{i=1}^N \{ y_i \ln p(x_i) + (1-y_i) \ln [1-p(x_i)] \}\] In a k-box models, \(x\) is a factor variable with k levels, \(\{ p(x) \}\) contains k values corresponding to the k parameters \(p_1, p_2,\cdots,p_k\) . If \(x\) is a continuous variable, \(\{ p(x) \}\) in principle has infinite possible values and we have to use another approach: specify a functional form for \(p(x)\) containing a few parameters. In (one-variable) logistic regression, we specify the function having the form \[p(x) = p(x; \beta_0,\beta_1) = \frac{e^{\beta_0 + \beta_1 x}}{1+e^{\beta_0+\beta_1 x}} = \frac{1}{1+e^{-\beta_0-\beta_1 x}}\] The logistic function is constructed so that the log odds, \(\ln [p/(1-p)]\) , is a linear function of \(x\) : \[\ln \frac{p}{1-p} = \beta_0 + \beta_1 x\] The two parameters \(\beta_0\) and \(\beta_1\) are determined by maximizing the log-likelihood function \[\ln L(\beta_0,\beta_1) = \sum_{i=1}^N \{ y_i \ln p(x_i; \beta_0,\beta_1) + (1-y_i) \ln [1-p(x_i;\beta_0,\beta_1)] \}\]

The logistic regression is a probability model that is more general than the box model. Setting ln(odds) = β 0 + β 1 x is just the simplest model. We can consider a model in which ln(odds) depends on multiple variables \(X_1\) , \(X_2\) , …, \(X_k\) : \[\ln \frac{p}{1-p} = \beta_0 + \beta_1 X_1 + \beta_2 X_2 + \cdots + \beta_p X_k\] The probability can then be written as \[p(X_1, X_2, \cdots, X_k; \beta_0, \beta_0, \beta_1,\cdots , \beta_k) = \frac{e^{\beta_0 + \beta_1 X_1 + \beta_2 X_2 + \cdots + \beta_k X_k}}{1+e^{\beta_0 + \beta_1 X_1 + \beta_2 X_2 + \cdots + \beta_k X_k}} = \frac{1}{1+e^{-\beta_0 - \beta_1 X_1 - \beta_2 X_2 - \cdots - \beta_k X_k}}\] The parameters \(\beta_0\) , \(\beta_1\) , …, \(\beta_k\) are determined by maximizing the corresponding log-likelihood function.

Note that in general the variables \(X_1\) , \(X_2\) , …, \(X_k\) are not restricted to be continuous variables. Some of them can be continuous variables and some of them can be discrete categorical variables. We can also make ln(odds) depend nonlinearly on a variable \(x\) . For example, we can consider a model where \[\ln\frac{p}{1-p} = \beta_0 + \beta_1 x + \beta_2 x^2\] The ln(odds) is still linear in the fitting parameters \(\beta_0\) , \(\beta_1\) , \(\beta_2\) . We can set \(X_1=x\) and \(X_2=x^2\) and the ln(odds) equation becomes \[\ln\frac{p}{1-p} = \beta_0 + \beta_1 X_1 + \beta_2 X_2\] Thus we can still use R’s glm() function to fit this model.

In the special case where \(\ln[p/(1-p)]=\beta_0+\beta_1 x\) and \(x\) is a factor variable with k levels, \(p(x)\) has only k values and it can be shown that the logistic regression model reduces to the k-box model. Therefore, the k-box model is a special case of a logistic regression model.

Another special case is to assume \(\ln[p/(1-p)]=\beta_0\) , or \(p=e^{\beta_0}/(1+e^{\beta_0})\) . In this model, the probability \(p\) is independent of any other variable and is the same for all data points. This is equivalent to the one-box model we considered last week. This is also called the null model . The probability \(p\) in the null model is equal to the value of \(y\) averaged over all data points.

In the following, we use the credit card data considered last week to demonstrate how to use R to fit various logistic regression models.

Logistic Regression Examples

Recall that the credit card data is a simulated data set freely available from the ISLR package for the book An Introduction to Statistical Learning . The data have been uploaded to our website and can be loaded to R directly using the command

The data contain 10,000 observations and 4 columns. The first column, default , is a two-level (No/Yes) factor variable indicating whether the customer defaulted on their debt. The second column, student , is also a two-level (No/Yes) factor variable indicating whether the customer is a student. The third column, balance , is the average balance that the customer has remaining on their credit card after making their monthly payment. The last column, income , lists the income of the customer.

For convenience of later calculations, we create a new column named y . We set y to 1 for defaulted customers and 0 for undefaulted customers. This can be achieved by the command

As stated in last week’s note, R’s glm() function can be used to fit families of generalized linear models. The logistic regression model belongs to the ‘binomial’ family of generalized linear models. The syntax of glm() for logistic regression is very similar to the lm() function:

Like lm() in linear regression, the formula syntax can take variety of forms. The simplest form is y ~ x, but it can also be y ~ x1 + x2 + x3 for multiple variables.

The simplest model is the null model, where we only fit one parameter:

Just like linear regression, we can see the coefficient by typing fit0 or summary(fit0) .

The output is also similar to linear regression. We only have one parameter: the intercept. The fitted equation is \(\ln[p/(1-p)]=-3.36833\) or \(p = e^{-3.36833}/(1+e^{-3.36833})=0.0333\) . This means that 3.3% of the customs defaulted, the same result as the one-box model we considered last week. If we don’t have any other information about a customer, we can only predict that the probability for this customer to default is 3.3%.

The column named student is a No/Yes binary factor variable, with the reference level set to “No” by default since “N” precedes “Y” in alphabetical order. We can fit a logistic regression model predicting y from student using the command

Since student is a two-level factor variable, glm() creates a binary variable studentYes , which is equal to 1 for the value “Yes” in ‘student’ and 0 for the value “No” in student . The intercept and slope are the coefficients for ln(odds). So the fitted equation is \[\ln \frac{p}{1-p} = -3.50413 + 0.40489 S \] or \[ p = \frac{e^{-3.50413+0.40489S}}{1+e^{-3.50413+0.40489S}}\] where we use \(S\) to denote the binary variable studentYes for simplicity. We see that the slope is positive. This means that ln(odds) is larger for a student, which also translates to the statement that a student has a higher probability to default than a non-student. summary(fit1) also provides the information of the standard errors, z-values and p-values of the fitted coefficients. These parameters are analogous to the standard errors, t-values and p-values in linear regression. The small p-value for the slope indicates that there is a significant difference in ln(odds) between students and non-students.

For non-students, \(S=0\) . So ln(odds) = -3.50413 and p(non-students) = 0.02919. For students, \(S=1\) . So ln(odds)=-3.50413+0.40489=-3.09924 and p(students) = 0.04314. This means that about 2.9% of non-students defaulted and 4.3% of students defaulted. These numbers are exactly the same as the two-box model we considered last week. This is not a coincidence. It can be shown that a logistic regression on a factor variable produces the same result as a box model.

Recall that the predict() function can be used to predict the outcome of new data. In our example, there are only two possible values for student : “No” and “Yes” and we can obtain the predicted values using the command

The function returns the values of ln(odds) by default. If we want the values of probability, we use the option type="response" :

At the end of last week’s note, we fit a logistic regression model predicting y from balance , which is a continuous variable.

The slope is positive, indicating that the fraction of defaults increases with increasing values of balance . The fitted values of the probability of the data are stored in the vector fit2$fitted.values . The name can be abbreviated. Here is a plot of the fitted probabilities:

To calculate the probability of default for a given value of balance , we can use the fitted coefficients to calculate ln(odds) and then use it to calculate the probability. Alternative, we can use the predict() function as shown above. For example, to calculate the probability of default for balance = 1850, we use the command

Hence the probability that the customer will default is 38.3% if the credit balance is $1850.

Since we find that the probability of default depends on balance as well as whether or not the customer is a student, we can use these two variables to fit a model predicting y from both balance and student :

This model has three parameters: one intercept and two slopes. The ln(odds) equation is \[\ln \frac{p}{1-p} = -10.75 -0.7149 S + 0.005738 B\] For simplicity, we use the symbol \(S\) for studentYes and \(B\) for balance . Here we find something interesting. Previously, when we fit \(y\) with \(S\) alone, the slope for \(S\) is positive, meaning that students are more likely to default compared to non-students. Now when we fit \(y\) with both \(S\) and \(B\) , the slope for \(S\) is negative, meaning that for a fixed value of balance , students are less likely to default compared to non-students. This is Simpson’s paradox.

To understand the discrepancy, we plot the probability as a function of balance for both students and non-students. Setting \(S=0\) in the ln(odds) equation, we obtain the ln(odds) equation for non-students: \[\ln \frac{p}{1-p} = -10.75 + 0.005738 B \ \ \ \mbox{(non-students)}\] Setting \(S=1\) we obtain the ln(odds) equation for students: \[\ln \frac{p}{1-p} = -11.46 + 0.005738 B \ \ \ \mbox{(students)}\] The curves for students and non-students can be plotted using the curve() function. 1

In this plot, black solid line is the probability of default for non-students versus balance; red solid line is the probability of default for students versus balance; black horizontal line is the probability of default for non-students (0.0292) averaged over all values of balance ; red horizontal line is the probability of default for students (0.0431) averaged over all values of balance . The plot clearly shows that at every value of balance ,the student default rate is at or below that of the non-student default rate. The reason why the overall default rate for students is higher must be due to the fact that students tend to have higher levels of balance . This can be seen from the following box plots.

This explains the paradox. Students tend to have a higher level of credit balance, which is associated with higher default rates. Therefore, even though at a given balance students are less likely to default compared to non-students, the overall default rate for students is still higher. This is an important information for a credit card company. A student is riskier than a non-student if no information about the student’s credit card balance is available. However, a student is less risky than a non-student with the same credit card balance!

The credit card data has a column named income . We can include it in the model in addition to balance and student :

We see that the p-value of the slope for income is large, suggesting that y is not dependent on the income variable. Including income in the model may not improve the accuracy of the model substantially. This raises the question: how do we know if a model is better than another? In linear regression, both R 2 and the residual standard error can be used to judge the “goodness of fit”. Are there similar quantities in logistic regression?

Recall that in logistic regression the coefficients are determined by maximizing the log-likelihood function. Thus a good model should produce a large log-likelihood. Recall that the likelihood is a joint probability, and probability is a number between 0 and 1. Also recall that ln(x) is negative if x is between 0 and 1. It follows that log-likelihood is a negative number, so larger log-likelihood means the number is less negative. Dealing with negative numbers is inconvenient. There is a quantity called deviance , which is defined to be -2 times the log-likelihood: \[{\rm Deviance} = -2 \ln ({\rm likelihood})\] Since log-likelihood is negative, deviance is positive. Maximizing log-likelihood is the same as minimizing the deviance.

In glm() , two deviances are calculated: the residual deviance and null deviance. The residual deviance is the value of deviance for the fitted model, whereas null deviance is the value of the deviance for the null model, i.e. the model with only the intercept and the probability \(P(y=1)\) is the same for all data points and is equal to the average of \(y\) . Hence the null deviance \(D_{\rm null}\) is given by the formula \[D_{\rm null} = -2\ln L_{\rm null} = -2 \sum_{i=1}^n [y_i \ln \bar{y} + (1-y_i) \ln (1-\bar{y})]\] From summary output of the models above, we see that the deviance of the null model is 2920.6. 2

The difference between the null deviance and residual deviance provides some information on the “goodness of fit” of the model. From the summary output of the models considered above, we see that residual deviance for fit1 (predicting P(y=1) from student ) is 2908.7. This is only slightly smaller than the null deviance. For fit2 (predicting P(y=1) from balance ), the residual deviance is 1596.5, substantially smaller than fit1 . For fit3 (predicting P(y=1) from balance and student ), the residual deviance is 1571.7, slightly better than fit2 . For fit4 (predicting P(y=1) from balance , student and income ), the residual deviance is 1571.5, almost the same as fit3 . We therefore conclude that adding income to the model does not substantially improve the model’s accuracy.

The null deviance in logistic regression plays a similar role as SST in linear regression, whereas residual deviance plays a similar role as SSE in linear regression. In linear regression, R 2 can be written as \[R^2 = \frac{SSM}{SST} = \frac{SST-SSE}{SST}=1-\frac{SSE}{SST}\] Similarly, in logistic regression, one can define a quantity similar to R 2 as \[R_{MF}^2 = 1-\frac{D_{\rm residual}}{D_{\rm null}}\] This is called McFadden’s R 2 or pseudo R 2 . McFadden’s R-squared also takes a value between 0 and 1. The larger the \(R_{MF}^2\) , the better the model fits the data. It can be used as an indicator for the “goodness of fit” of a model. For the model fit3 , we have \[R_{MF}^2=1-\frac{1571.7}{2920.6}=0.46\] The R returned by the logistic regression in our data program is the square root of McFadden’s R-squared. The data program also provides a \(\chi^2\) , which is analogous to the F-value in linear regression. It can be used to calculate a p-value from which we can determine if at least one of the slopes is significant. The returned \(\chi^2\) is simply the difference between the null deviance and residual deviance. It can be shown that for a model with \(p\) parameters and the number of data is sufficiently large, \(D_{\rm null}-D_{\rm residual}\) follows a \(\chi^2\) distribution with \(p\) degrees of freedom under the null hypothesis that all slopes are equal to 0.

There is another method to make the same plot. We can use the predict() function to generate two vectors for the predicted values of probability for both students and non-students. Then we make the plot using plot() and lines() as shown below.

We can also calculate the null and residual deviance directly and compare them with the results of the glm() function. We first write a function to compute the deviance. Recall that deviance is defined as -2 times the log-likelihood. Explicitly, \[D = -2 \ln L = -2 \sum_{i=1}^N [y_i \ln p_i + (1-y_i)\ln(1-p_i)]\] In R, the above formula can be vectorized for any given vectors y and p:

For null deviance, \(p_i=\bar{y}\) is the same for all data points. For the credit card data, the null deviance is

We see that we get the same number as in the summary output of the glm() function (type, e.g., summary(fit3)$null.deviance to extract the null deviance directly from the summary output). To compute the residual deviance of e.g. the model fit3 , we need to know the fitted values of the probability \(p_i\) for all data points. These values are stored in the vector fit3$fitted.values , so we can simple pass it to the deviance() function:

Again, we obtain the same number as in the output of summary(fit3) (type summary(fit3)$deviance to extract the residual deviance directly). ↩

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

5.6: Simple Logistic Regression

• Last updated
• Save as PDF
• Page ID 1751

• John H. McDonald
• University of Delaware

Learning Objectives

• To use simple logistic regression when you have one nominal variable and one measurement variable, and you want to know whether variation in the measurement variable causes variation in the nominal variable.

When to use it

Use simple logistic regression when you have one nominal variable with two values (male/female, dead/alive, etc.) and one measurement variable. The nominal variable is the dependent variable, and the measurement variable is the independent variable.

I'm separating simple logistic regression, with only one independent variable, from multiple logistic regression, which has more than one independent variable. Many people lump all logistic regression together, but I think it's useful to treat simple logistic regression separately, because it's simpler.

Simple logistic regression is analogous to linear regression, except that the dependent variable is nominal, not a measurement. One goal is to see whether the probability of getting a particular value of the nominal variable is associated with the measurement variable; the other goal is to predict the probability of getting a particular value of the nominal variable, given the measurement variable.

As an example of simple logistic regression, Suzuki et al. (2006) measured sand grain size on \(28\) beaches in Japan and observed the presence or absence of the burrowing wolf spider Lycosa ishikariana on each beach. Sand grain size is a measurement variable, and spider presence or absence is a nominal variable. Spider presence or absence is the dependent variable; if there is a relationship between the two variables, it would be sand grain size affecting spiders, not the presence of spiders affecting the sand.

One goal of this study would be to determine whether there was a relationship between sand grain size and the presence or absence of the species, in hopes of understanding more about the biology of the spiders. Because this species is endangered, another goal would be to find an equation that would predict the probability of a wolf spider population surviving on a beach with a particular sand grain size, to help determine which beaches to reintroduce the spider to.

You can also analyze data with one nominal and one measurement variable using a one-way anova or a Student's t –test, and the distinction can be subtle. One clue is that logistic regression allows you to predict the probability of the nominal variable. For example, imagine that you had measured the cholesterol level in the blood of a large number of \(55\)-year-old women, then followed up ten years later to see who had had a heart attack. You could do a two-sample \(t\)–test, comparing the cholesterol levels of the women who did have heart attacks vs. those who didn't, and that would be a perfectly reasonable way to test the null hypothesis that cholesterol level is not associated with heart attacks; if the hypothesis test was all you were interested in, the \(t\)–test would probably be better than the less-familiar logistic regression. However, if you wanted to predict the probability that a \(55\)-year-old woman with a particular cholesterol level would have a heart attack in the next ten years, so that doctors could tell their patients "If you reduce your cholesterol by \(40\) points, you'll reduce your risk of heart attack by \(X\%\)," you would have to use logistic regression.

Another situation that calls for logistic regression, rather than an anova or \(t\)–test, is when you determine the values of the measurement variable, while the values of the nominal variable are free to vary. For example, let's say you are studying the effect of incubation temperature on sex determination in Komodo dragons. You raise \(10\) eggs at \(30^{\circ}C\), \(30\) eggs at \(32^{\circ}C\), \(12\) eggs at \(34^{\circ}C\), etc., then determine the sex of the hatchlings. It would be silly to compare the mean incubation temperatures between male and female hatchlings, and test the difference using an anova or \(t\)–test, because the incubation temperature does not depend on the sex of the offspring; you've set the incubation temperature, and if there is a relationship, it's that the sex of the offspring depends on the temperature.

When there are multiple observations of the nominal variable for each value of the measurement variable, as in the Komodo dragon example, you'll often sees the data analyzed using linear regression, with the proportions treated as a second measurement variable. Often the proportions are arc-sine transformed, because that makes the distributions of proportions more normal. This is not horrible, but it's not strictly correct. One problem is that linear regression treats all of the proportions equally, even if they are based on much different sample sizes. If \(6\) out of \(10\) Komodo dragon eggs raised at \(30^{\circ}C\) were female, and \(15\) out of \(30\) eggs raised at \(32^{\circ}C\) were female, the \(60\%\) female at \(30^{\circ}C\) and \(50\%\) at \(32^{\circ}C\) would get equal weight in a linear regression, which is inappropriate. Logistic regression analyzes each observation (in this example, the sex of each Komodo dragon) separately, so the \(30\) dragons at \(32^{\circ}C\) would have \(3\) times the weight of the \(10\) dragons at \(30^{\circ}C\).

While logistic regression with two values of the nominal variable (binary logistic regression) is by far the most common, you can also do logistic regression with more than two values of the nominal variable, called multinomial logistic regression. I'm not going to cover it here at all. Sorry.

You can also do simple logistic regression with nominal variables for both the independent and dependent variables, but to be honest, I don't understand the advantage of this over a chi-squared or G –test of independence.

Null hypothesis

The statistical null hypothesis is that the probability of a particular value of the nominal variable is not associated with the value of the measurement variable; in other words, the line describing the relationship between the measurement variable and the probability of the nominal variable has a slope of zero.

How the test works

Simple logistic regression finds the equation that best predicts the value of the \(Y\) variable for each value of the \(X\) variable. What makes logistic regression different from linear regression is that you do not measure the \(Y\) variable directly; it is instead the probability of obtaining a particular value of a nominal variable. For the spider example, the values of the nominal variable are "spiders present" and "spiders absent." The \(Y\) variable used in logistic regression would then be the probability of spiders being present on a beach. This probability could take values from \(0\) to \(1\). The limited range of this probability would present problems if used directly in a regression, so the odds, \(Y/(1-Y)\), is used instead. (If the probability of spiders on a beach is \(0.25\), the odds of having spiders are \(0.25/(1-0.25)=1/3\). In gambling terms, this would be expressed as "\(3\) to \(1\) odds against having spiders on a beach.") Taking the natural log of the odds makes the variable more suitable for a regression, so the result of a logistic regression is an equation that looks like this:

\[ln\left [ \frac{Y}{(1-Y)}\right ]=a+bX\]

You find the slope (\(b\)) and intercept (\(a\)) of the best-fitting equation in a logistic regression using the maximum-likelihood method, rather than the least-squares method you use for linear regression. Maximum likelihood is a computer-intensive technique; the basic idea is that it finds the values of the parameters under which you would be most likely to get the observed results.

For the spider example, the equation is:

\[ln\left [ \frac{Y}{(1-Y)}\right ]=-1.6476+5.1215(\text{grain size})\]

Rearranging to solve for \(Y\) (the probability of spiders on a beach) yields:

\[Y=\frac{e^{-1.6476+5.1215(\text{grain size})}}{(1+e^{-1.6476+5.1215(\text{grain size}))}}\]

where \(e\) is the root of natural logs. So if you went to a beach and wanted to predict the probability that spiders would live there, you could measure the sand grain size, plug it into the equation, and get an estimate of \(Y\), the probability of spiders being on the beach.

There are several different ways of estimating the \(P\) value. The Wald chi-square is fairly popular, but it may yield inaccurate results with small sample sizes. The likelihood ratio method may be better. It uses the difference between the probability of obtaining the observed results under the logistic model and the probability of obtaining the observed results in a model with no relationship between the independent and dependent variables. I recommend you use the likelihood-ratio method; be sure to specify which method you've used when you report your results.

For the spider example, the \(P\) value using the likelihood ratio method is \(0.033\), so you would reject the null hypothesis. The \(P\) value for the Wald method is \(0.088\), which is not quite significant.

Assumptions

Simple logistic regression assumes that the observations are independent; in other words, that one observation does not affect another. In the Komodo dragon example, if all the eggs at \(30^{\circ}C\) were laid by one mother, and all the eggs at \(32^{\circ}C\) were laid by a different mother, that would make the observations non-independent. If you design your experiment well, you won't have a problem with this assumption.

Simple logistic regression assumes that the relationship between the natural log of the odds ratio and the measurement variable is linear. You might be able to fix this with a transformation of your measurement variable, but if the relationship looks like a \(U\) or upside-down \(U\), a transformation won't work. For example, Suzuki et al. (2006) found an increasing probability of spiders with increasing grain size, but I'm sure that if they looked at beaches with even larger sand (in other words, gravel), the probability of spiders would go back down. In that case you couldn't do simple logistic regression; you'd probably want to do multiple logistic regression with an equation including both \(X\) and \(X^2\) terms, instead.

Simple logistic regression does not assume that the measurement variable is normally distributed.

McDonald (1985) counted allele frequencies at the mannose-6-phosphate isomerase ( Mpi ) locus in the amphipod crustacean Megalorchestia californiana, which lives on sandy beaches of the Pacific coast of North America. There were two common alleles, Mpi 90 and Mpi 100 . The latitude of each collection location, the count of each of the alleles, and the proportion of the Mpi 100 allele, are shown here:

Allele ( Mpi 90 or Mpi 100 ) is the nominal variable, and latitude is the measurement variable. If the biological question were "Do different locations have different allele frequencies?", you would ignore latitude and do a chi-square or G –test of independence; here the biological question is "Are allele frequencies associated with latitude?"

Note that although the proportion of the Mpi 100 allele seems to increase with increasing latitude, the sample sizes for the northern and southern areas are pretty small; doing a linear regression of allele frequency vs. latitude would give them equal weight to the much larger samples from Oregon, which would be inappropriate. Doing a logistic regression, the result is \(chi 2 =83.3,\; 1 d.f.,\; P=7\times 10^{-20}\). The equation of the relationship is:

\[ln\left [ \frac{Y}{(1-Y)}\right ]=-7.6469+0.1786(latitude)\]

where \(Y\) is the predicted probability of getting an Mpi 100 allele. Solving this for \(Y\) gives:

\[Y=\frac{e^{-7.6469+0.1786(latitude)}}{1+e^{-7.6469+0.1786(latitude)}}\]

This logistic regression line is shown on the graph; note that it has a gentle \(S\)-shape. All logistic regression equations have an \(S\)-shape, although it may not be obvious if you look over a narrow range of values.

Graphing the results

If you have multiple observations for each value of the measurement variable, as in the amphipod example above, you can plot a scattergraph with the measurement variable on the \(X\) axis and the proportions on the \(Y\) axis. You might want to put 95% confidence intervals on the points; this gives a visual indication of which points contribute more to the regression (the ones with larger sample sizes have smaller confidence intervals).

There's no automatic way in spreadsheets to add the logistic regression line. Here's how I got it onto the graph of the amphipod data. First, I put the latitudes in column \(A\) and the proportions in column \(B\). Then, using the Fill: Series command, I added numbers \(30,\; 30.1,\; 30.2,...50\) to cells \(A10\) through \(A210\). In column \(C\) I entered the equation for the logistic regression line; in Excel format, it's

\(=exp(-7.6469+0.1786*(A10))/(1+exp(-7.6469+0.1786*(A10)))\)

for row \(10\). I copied this into cells \(C11\) through \(C210\). Then when I drew a graph of the numbers in columns \(A,\; B,\; \text{and}\; C\), I gave the numbers in column B symbols but no line, and the numbers in column \(C\) got a line but no symbols.

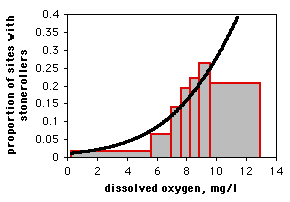
If you only have one observation of the nominal variable for each value of the measurement variable, as in the spider example, it would be silly to draw a scattergraph, as each point on the graph would be at either \(0\) or \(1\) on the \(Y\) axis. If you have lots of data points, you can divide the measurement values into intervals and plot the proportion for each interval on a bar graph. Here is data from the Maryland Biological Stream Survey on \(2180\) sampling sites in Maryland streams. The measurement variable is dissolved oxygen concentration, and the nominal variable is the presence or absence of the central stoneroller, Campostoma anomalum . If you use a bar graph to illustrate a logistic regression, you should explain that the grouping was for heuristic purposes only, and the logistic regression was done on the raw, ungrouped data.

Similar tests

You can do logistic regression with a dependent variable that has more than two values, known as multinomial, polytomous, or polychotomous logistic regression. I don't cover this here.

Use multiple logistic regression when the dependent variable is nominal and there is more than one independent variable. It is analogous to multiple linear regression, and all of the same caveats apply.

Use linear regression when the \(Y\) variable is a measurement variable.

When there is just one measurement variable and one nominal variable, you could use one-way anova or a t –test to compare the means of the measurement variable between the two groups. Conceptually, the difference is whether you think variation in the nominal variable causes variation in the measurement variable (use a \(t\)–test) or variation in the measurement variable causes variation in the probability of the nominal variable (use logistic regression). You should also consider who you are presenting your results to, and how they are going to use the information. For example, Tallamy et al. (2003) examined mating behavior in spotted cucumber beetles ( Diabrotica undecimpunctata ). Male beetles stroke the female with their antenna, and Tallamy et al. wanted to know whether faster-stroking males had better mating success. They compared the mean stroking rate of \(21\) successful males (\(50.9\) strokes per minute) and \(16\) unsuccessful males (\(33.8\) strokes per minute) with a two-sample \(t\)–test, and found a significant result (\(P<0.0001\)). This is a simple and clear result, and it answers the question, "Are female spotted cucumber beetles more likely to mate with males who stroke faster?" Tallamy et al. (2003) could have analyzed these data using logistic regression; it is a more difficult and less familiar statistical technique that might confuse some of their readers, but in addition to answering the yes/no question about whether stroking speed is related to mating success, they could have used the logistic regression to predict how much increase in mating success a beetle would get as it increased its stroking speed. This could be useful additional information (especially if you're a male cucumber beetle).

How to do the test

Spreadsheet.

I have written a spreadsheet to do simple logistic regression logistic.xls. You can enter the data either in summarized form (for example, saying that at \(30^{\circ}C\) there were \(7\) male and \(3\) female Komodo dragons) or non-summarized form (for example, entering each Komodo dragon separately, with "\(0\)" for a male and "\(1\)" for a female). It uses the likelihood-ratio method for calculating the \(P\) value. The spreadsheet makes use of the "Solver" tool in Excel. If you don't see Solver listed in the Tools menu, go to Add-Ins in the Tools menu and install Solver.

The spreadsheet is fun to play with, but I'm not confident enough in it to recommend that you use it for publishable results.

There is a very nice web page that will do logistic regression, with the likelihood-ratio chi-square. You can enter the data either in summarized form or non-summarized form, with the values separated by tabs (which you'll get if you copy and paste from a spreadsheet) or commas. You would enter the amphipod data like this:

48.1,47,139 45.2,177,241 44.0,1087,1183 43.7,187,175 43.5,397,671 37.8,40,14 36.6,39,17 34.3,30,0

Salvatore Mangiafico's \(R\) Companion has a sample R program for simple logistic regression.

Use PROC LOGISTIC for simple logistic regression. There are two forms of the MODEL statement. When you have multiple observations for each value of the measurement variable, your data set can have the measurement variable, the number of "successes" (this can be either value of the nominal variable), and the total (which you may need to create a new variable for, as shown here). Here is an example using the amphipod data:

DATA amphipods; INPUT location $ latitude mpi90 mpi100; total=mpi90+mpi100; DATALINES; Port_Townsend,_WA 48.1 47 139 Neskowin,_OR 45.2 177 241 Siuslaw_R.,_OR 44.0 1087 1183 Umpqua_R.,_OR 43.7 187 175 Coos_Bay,_OR 43.5 397 671 San_Francisco,_CA 37.8 40 14 Carmel,_CA 36.6 39 17 Santa_Barbara,_CA 34.3 30 0 ; PROC LOGISTIC DATA=amphipods; MODEL mpi100/total=latitude; RUN;

Note that you create the new variable TOTAL in the DATA step by adding the number of Mpi90 and Mpi100 alleles. The MODEL statement uses the number of Mpi100 alleles out of the total as the dependent variable. The \(P\) value would be the same if you used Mpi90; the equation parameters would be different.

There is a lot of output from PROC LOGISTIC that you don't need. The program gives you three different \(P\) values; the likelihood ratio \(P\) value is the most commonly used:

Testing Global Null Hypothesis: BETA=0 Test Chi-Square DF Pr > ChiSq Likelihood Ratio 83.3007 1 <.0001 P value Score 80.5733 1 <.0001 Wald 72.0755 1 <.0001

The coefficients of the logistic equation are given under "estimate":

Analysis of Maximum Likelihood Estimates Standard Wald Parameter DF Estimate Error Chi-Square Pr > ChiSq Intercept 1 -7.6469 0.9249 68.3605 <.0001 latitude 1 0.1786 0.0210 72.0755 <.0001

Using these coefficients, the maximum likelihood equation for the proportion of Mpi100 alleles at a particular latitude is:

It is also possible to use data in which each line is a single observation. In that case, you may use either words or numbers for the dependent variable. In this example, the data are height (in inches) of the \(2004\) students of my class, along with their favorite insect (grouped into beetles vs. everything else, where "everything else" includes spiders, which a biologist really should know are not insects):

DATA insect; INPUT height insect $ @@; DATALINES; 62 beetle 66 other 61 beetle 67 other 62 other 76 other 66 other 70 beetle 67 other 66 other 70 other 70 other 77 beetle 76 other 72 beetle 76 beetle 72 other 70 other 65 other 63 other 63 other 70 other 72 other 70 beetle 74 other ; PROC LOGISTIC DATA=insect; MODEL insect=height; RUN;

The format of the results is the same for either form of the MODEL statement. In this case, the model would be the probability of BEETLE, because it is alphabetically first; to model the probability of OTHER, you would add an EVENT after the nominal variable in the MODEL statement, making it "MODEL insect (EVENT='other')=height;"

Power analysis

You can use G*Power to estimate the sample size needed for a simple logistic regression. Choose "\(z\) tests" under Test family and "Logistic regression" under Statistical test. Set the number of tails (usually two), alpha (usually \(0.05\)), and power (often \(0.8\) or \(0.9\)). For simple logistic regression, set "X distribution" to Normal, "R 2 other X" to \(0\), "X parm μ" to \(0\), and "X parm σ" to \(1\).

The last thing to set is your effect size. This is the odds ratio of the difference you're hoping to find between the odds of \(Y\) when \(X\) is equal to the mean \(X\), and the odds of \(Y\) when \(X\) is equal to the mean \(X\) plus one standard deviation. You can click on the "Determine" button to calculate this.

For example, let's say you want to study the relationship between sand particle size and the presences or absence of tiger beetles. You set alpha to \(0.05\) and power to \(0.90\). You expect, based on previous research, that \(30\%\) of the beaches you'll look at will have tiger beetles, so you set "Pr(Y=1|X=1) H0" to \(0.30\). Also based on previous research, you expect a mean sand grain size of \(0.6 mm\) with a standard deviation of \(0.2 mm\). The effect size (the minimum deviation from the null hypothesis that you hope to see) is that as the sand grain size increases by one standard deviation, from \(0.6 mm\) to \(0.8 mm\), the proportion of beaches with tiger beetles will go from \(0.30\) to \(0.40\). You click on the "Determine" button and enter \(0.40\) for "Pr(Y=1|X=1) H1" and \(0.30\) for "Pr(Y=1|X=1) H0", then hit "Calculate and transfer to main window." It will fill in the odds ratio (\(1.555\) for our example) and the "Pr(Y=1|X=1) H0". The result in this case is \(206\), meaning your experiment is going to require that you travel to \(206\) warm, beautiful beaches.

Picture of amphipod from Vikram Iyengar's home page.

McDonald, J.H. 1985. Size-related and geographic variation at two enzyme loci in Megalorchestia californiana (Amphipoda: Talitridae). Heredity 54: 359-366.

Suzuki, S., N. Tsurusaki, and Y. Kodama. 2006. Distribution of an endangered burrowing spider Lycosa ishikariana in the San'in Coast of Honshu, Japan (Araneae: Lycosidae). Acta Arachnologica 55: 79-86.

Tallamy, D.W., M.B. Darlington, J.D. Pesek, and B.E. Powell. 2003. Copulatory courtship signals male genetic quality in cucumber beetles. Proceedings of the Royal Society of London B 270: 77-82.

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

• Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
• Duis aute irure dolor in reprehenderit in voluptate
• Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

6.2.3 - more on model-fitting.

Suppose two models are under consideration, where one model is a special case or "reduced" form of the other obtained by setting \(k\) of the regression coefficients (parameters) equal to zero. The larger model is considered the "full" model, and the hypotheses would be

\(H_0\): reduced model versus \(H_A\): full model

Equivalently, the null hypothesis can be stated as the \(k\) predictor terms associated with the omitted coefficients have no relationship with the response, given the remaining predictor terms are already in the model. If we fit both models, we can compute the likelihood-ratio test (LRT) statistic:

\(G^2 = −2 (\log L_0 - \log L_1)\)

where \(L_0\) and \(L_1\) are the max likelihood values for the reduced and full models, respectively. The degrees of freedom would be \(k\), the number of coefficients in question. The p-value is the area under the \(\chi^2_k\) curve to the right of \( G^2)\).

To perform the test in SAS, we can look at the "Model Fit Statistics" section and examine the value of "−2 Log L" for "Intercept and Covariates." Here, the reduced model is the "intercept-only" model (i.e., no predictors), and "intercept and covariates" is the full model. For our running example, this would be equivalent to testing "intercept-only" model vs. full (saturated) model (since we have only one predictor).

Larger differences in the "-2 Log L" values lead to smaller p-values more evidence against the reduced model in favor of the full model. For our example, \( G^2 = 5176.510 − 5147.390 = 29.1207\) with \(2 − 1 = 1\) degree of freedom. Notice that this matches the deviance we got in the earlier text above.

Also, notice that the \(G^2\) we calculated for this example is equal to 29.1207 with 1df and p-value <.0001 from "Testing Global Hypothesis: BETA=0" section (the next part of the output, see below).

Testing the Joint Significance of All Predictors Section  

Testing the null hypothesis that the set of coefficients is simultaneously zero. For example, consider the full model

\(\log\left(\dfrac{\pi}{1-\pi}\right)=\beta_0+\beta_1 x_1+\cdots+\beta_k x_k\)

and the null hypothesis \(H_0\colon \beta_1=\beta_2=\cdots=\beta_k=0\) versus the alternative that at least one of the coefficients is not zero. This is like the overall F−test in linear regression. In other words, this is testing the null hypothesis of the intercept-only model:

\(\log\left(\dfrac{\pi}{1-\pi}\right)=\beta_0\)

versus the alternative that the current (full) model is correct. This corresponds to the test in our example because we have only a single predictor term, and the reduced model that removes the coefficient for that predictor is the intercept-only model.

In the SAS output, three different chi-square statistics for this test are displayed in the section "Testing Global Null Hypothesis: Beta=0," corresponding to the likelihood ratio, score, and Wald tests. Recall our brief encounter with them in our discussion of binomial inference in Lesson 2.

Large chi-square statistics lead to small p-values and provide evidence against the intercept-only model in favor of the current model. The Wald test is based on asymptotic normality of ML estimates of \(\beta\)s. Rather than using the Wald, most statisticians would prefer the LR test. If these three tests agree, that is evidence that the large-sample approximations are working well and the results are trustworthy. If the results from the three tests disagree, most statisticians would tend to trust the likelihood-ratio test more than the other two.

In our example, the "intercept only" model or the null model says that student's smoking is unrelated to parents' smoking habits. Thus the test of the global null hypothesis \(\beta_1=0\) is equivalent to the usual test for independence in the \(2\times2\) table. We will see that the estimated coefficients and standard errors are as we predicted before, as well as the estimated odds and odds ratios.

Residual deviance is the difference between −2 logL for the saturated model and −2 logL for the currently fit model. The high residual deviance shows that the model cannot be accepted. The null deviance is the difference between −2 logL for the saturated model and −2 logL for the intercept-only model. The high residual deviance shows that the intercept-only model does not fit.

In our \(2\times2\) table smoking example, the residual deviance is almost 0 because the model we built is the saturated model. And notice that the degree of freedom is 0 too. Regarding the null deviance, we could see it equivalent to the section "Testing Global Null Hypothesis: Beta=0," by likelihood ratio in SAS output.

For our example, Null deviance = 29.1207 with df = 1. Notice that this matches the deviance we got in the earlier text above.

The Homer-Lemeshow Statistic Section  

An alternative statistic for measuring overall goodness-of-fit is the  Hosmer-Lemeshow statistic .

This is a Pearson-like chi-square statistic that is computed after the data are grouped by having similar predicted probabilities. It is more useful when there is more than one predictor and/or continuous predictors in the model too. We will see more on this later.

\(H_0\): the current model fits well \(H_A\): the current model does not fit well

To calculate this statistic:

• Group the observations according to model-predicted probabilities ( \(\hat{\pi}_i\))
• The number of groups is typically determined such that there is roughly an equal number of observations per group
• The Hosmer-Lemeshow (HL) statistic, a Pearson-like chi-square statistic, is computed on the grouped data but does NOT have a limiting chi-square distribution because the observations in groups are not from identical trials. Simulations have shown that this statistic can be approximated by a chi-squared distribution with \(g − 2\) degrees of freedom, where \(g\) is the number of groups.

Warning about the Hosmer-Lemeshow goodness-of-fit test:

• It is a conservative statistic, i.e., its value is smaller than what it should be, and therefore the rejection probability of the null hypothesis is smaller.
• It has low power in predicting certain types of lack of fit such as nonlinearity in explanatory variables.
• It is highly dependent on how the observations are grouped.
• If too few groups are used (e.g., 5 or less), it almost always fails to reject the current model fit. This means that it's usually not a good measure if only one or two categorical predictor variables are involved, and it's best used for continuous predictors.

In the model statement, the option lackfit tells SAS to compute the HL statistic and print the partitioning. For our example, because we have a small number of groups (i.e., 2), this statistic gives a perfect fit (HL = 0, p-value = 1). Instead of deriving the diagnostics, we will look at them from a purely applied viewpoint. Recall the definitions and introductions to the regression residuals and Pearson and Deviance residuals.

Residuals Section  

The Pearson residuals are defined as

\(r_i=\dfrac{y_i-\hat{\mu}_i}{\sqrt{\hat{V}(\hat{\mu}_i)}}=\dfrac{y_i-n_i\hat{\pi}_i}{\sqrt{n_i\hat{\pi}_i(1-\hat{\pi}_i)}}\)

The contribution of the \(i\)th row to the Pearson statistic is

\(\dfrac{(y_i-\hat{\mu}_i)^2}{\hat{\mu}_i}+\dfrac{((n_i-y_i)-(n_i-\hat{\mu}_i))^2}{n_i-\hat{\mu}_i}=r^2_i\)

and the Pearson goodness-of fit statistic is

\(X^2=\sum\limits_{i=1}^N r^2_i\)

which we would compare to a \(\chi^2_{N-p}\) distribution. The deviance test statistic is

\(G^2=2\sum\limits_{i=1}^N \left\{ y_i\text{log}\left(\dfrac{y_i}{\hat{\mu}_i}\right)+(n_i-y_i)\text{log}\left(\dfrac{n_i-y_i}{n_i-\hat{\mu}_i}\right)\right\}\)

which we would again compare to \(\chi^2_{N-p}\), and the contribution of the \(i\)th row to the deviance is

\(2\left\{ y_i\log\left(\dfrac{y_i}{\hat{\mu}_i}\right)+(n_i-y_i)\log\left(\dfrac{n_i-y_i}{n_i-\hat{\mu}_i}\right)\right\}\)

We will note how these quantities are derived through appropriate software and how they provide useful information to understand and interpret the models.

Companion to BER 642: Advanced Regression Methods

Chapter 11 multinomial logistic regression, 11.1 introduction to multinomial logistic regression.

Logistic regression is a technique used when the dependent variable is categorical (or nominal). For Binary logistic regression the number of dependent variables is two, whereas the number of dependent variables for multinomial logistic regression is more than two.

Examples: Consumers make a decision to buy or not to buy, a product may pass or fail quality control, there are good or poor credit risks, and employee may be promoted or not.

11.2 Equation

In logistic regression, a logistic transformation of the odds (referred to as logit) serves as the depending variable:

\[\log (o d d s)=\operatorname{logit}(P)=\ln \left(\frac{P}{1-P}\right)=a+b_{1} x_{1}+b_{2} x_{2}+b_{3} x_{3}+\ldots\]

\[p=\frac{\exp \left(a+b_{1} X_{1}+b_{2} X_{2}+b_{3} X_{3}+\ldots\right)}{1+\exp \left(a+b_{1} X_{1}+b_{2} X_{2}+b_{3} X_{3}+\ldots\right)}\] > Where:

p = the probability that a case is in a particular category,

exp = the exponential (approx. 2.72),

a = the constant of the equation and,

b = the coefficient of the predictor or independent variables.

Logits or Log Odds

Odds value can range from 0 to infinity and tell you how much more likely it is that an observation is a member of the target group rather than a member of the other group.

• Odds = p/(1-p)

If the probability is 0.80, the odds are 4 to 1 or .80/.20; if the probability is 0.25, the odds are .33 (.25/.75).

The odds ratio (OR), estimates the change in the odds of membership in the target group for a one unit increase in the predictor. It is calculated by using the regression coefficient of the predictor as the exponent or exp.

Assume in the example earlier where we were predicting accountancy success by a maths competency predictor that b = 2.69. Thus the odds ratio is exp(2.69) or 14.73. Therefore the odds of passing are 14.73 times greater for a student for example who had a pre-test score of 5 than for a student whose pre-test score was 4.

11.3 Hypothesis Test of Coefficients

In logistic regression, hypotheses are of interest:

The null hypothesis, which is when all the coefficients in the regression equation take the value zero, and

The alternate hypothesis that the model currently under consideration is accurate and differs significantly from the null of zero, i.e. gives significantly better than the chance or random prediction level of the null hypothesis.

Evaluation of Hypothesis

We then work out the likelihood of observing the data we actually did observe under each of these hypotheses. The result is usually a very small number, and to make it easier to handle, the natural logarithm is used, producing a log likelihood (LL) . Probabilities are always less than one, so LL’s are always negative. Log likelihood is the basis for tests of a logistic model.

11.4 Likelihood Ratio Test

The likelihood ratio test is based on -2LL ratio. It is a test of the significance of the difference between the likelihood ratio (-2LL) for the researcher’s model with predictors (called model chi square) minus the likelihood ratio for baseline model with only a constant in it.

Significance at the .05 level or lower means the researcher’s model with the predictors is significantly different from the one with the constant only (all ‘b’ coefficients being zero). It measures the improvement in fit that the explanatory variables make compared to the null model.

Chi square is used to assess significance of this ratio (see Model Fitting Information in SPSS output).

\(H_0\) : There is no difference between null model and final model.

\(H_1\) : There is difference between null model and final model.

11.5 Checking AssumptionL: Multicollinearity

Just run “linear regression” after assuming categorical dependent variable as continuous variable

If the largest VIF (Variance Inflation Factor) is greater than 10 then there is cause of concern (Bowerman & O’Connell, 1990)

Tolerance below 0.1 indicates a serious problem.

Tolerance below 0.2 indicates a potential problem (Menard,1995).

If the Condition index is greater than 15 then the multicollinearity is assumed.

11.6 Features of Multinomial logistic regression

Multinomial logistic regression to predict membership of more than two categories. It (basically) works in the same way as binary logistic regression. The analysis breaks the outcome variable down into a series of comparisons between two categories.

E.g., if you have three outcome categories (A, B and C), then the analysis will consist of two comparisons that you choose:

Compare everything against your first category (e.g. A vs. B and A vs. C),

Or your last category (e.g. A vs. C and B vs. C),

Or a custom category (e.g. B vs. A and B vs. C).

The important parts of the analysis and output are much the same as we have just seen for binary logistic regression.

11.7 R Labs: Running Multinomial Logistic Regression in R

11.7.1 understanding the data: choice of programs.

The data set(hsbdemo.sav) contains variables on 200 students. The outcome variable is prog, program type (1=general, 2=academic, and 3=vocational). The predictor variables are ses, social economic status (1=low, 2=middle, and 3=high), math, mathematics score, and science, science score: both are continuous variables.

(Research Question):When high school students choose the program (general, vocational, and academic programs), how do their math and science scores and their social economic status (SES) affect their decision?

11.7.2 Prepare and review the data

Now let’s do the descriptive analysis

11.7.3 Run the Multinomial Model using “nnet” package

Below we use the multinom function from the nnet package to estimate a multinomial logistic regression model. There are other functions in other R packages capable of multinomial regression. We chose the multinom function because it does not require the data to be reshaped (as the mlogit package does) and to mirror the example code found in Hilbe’s Logistic Regression Models.

First, we need to choose the level of our outcome that we wish to use as our baseline and specify this in the relevel function. Then, we run our model using multinom. The multinom package does not include p-value calculation for the regression coefficients, so we calculate p-values using Wald tests (here z-tests).

These are the logit coefficients relative to the reference category. For example,under ‘math’, the -0.185 suggests that for one unit increase in ‘science’ score, the logit coefficient for ‘low’ relative to ‘middle’ will go down by that amount, -0.185.

11.7.4 Check the model fit information

Interpretation of the Model Fit information

The log-likelihood is a measure of how much unexplained variability there is in the data. Therefore, the difference or change in log-likelihood indicates how much new variance has been explained by the model.

The chi-square test tests the decrease in unexplained variance from the baseline model (408.1933) to the final model (333.9036), which is a difference of 408.1933 - 333.9036 = 74.29. This change is significant, which means that our final model explains a significant amount of the original variability.

The likelihood ratio chi-square of 74.29 with a p-value < 0.001 tells us that our model as a whole fits significantly better than an empty or null model (i.e., a model with no predictors).

11.7.5 Calculate the Goodness of fit

11.7.6 calculate the pseudo r-square.

Interpretation of the R-Square:

These are three pseudo R squared values. Logistic regression does not have an equivalent to the R squared that is found in OLS regression; however, many people have tried to come up with one. These statistics do not mean exactly what R squared means in OLS regression (the proportion of variance of the response variable explained by the predictors), we suggest interpreting them with great caution.

Cox and Snell’s R-Square imitates multiple R-Square based on ‘likelihood’, but its maximum can be (and usually is) less than 1.0, making it difficult to interpret. Here it is indicating that there is the relationship of 31% between the dependent variable and the independent variables. Or it is indicating that 31% of the variation in the dependent variable is explained by the logistic model.

The Nagelkerke modification that does range from 0 to 1 is a more reliable measure of the relationship. Nagelkerke’s R2 will normally be higher than the Cox and Snell measure. In our case it is 0.357, indicating a relationship of 35.7% between the predictors and the prediction.

McFadden = {LL(null) – LL(full)} / LL(null). In our case it is 0.182, indicating a relationship of 18.2% between the predictors and the prediction.

11.7.7 Likelihood Ratio Tests

Interpretation of the Likelihood Ratio Tests

The results of the likelihood ratio tests can be used to ascertain the significance of predictors to the model. This table tells us that SES and math score had significant main effects on program selection, \(X^2\) (4) = 12.917, p = .012 for SES and \(X^2\) (2) = 10.613, p = .005 for SES.

These likelihood statistics can be seen as sorts of overall statistics that tell us which predictors significantly enable us to predict the outcome category, but they don’t really tell us specifically what the effect is. To see this we have to look at the individual parameter estimates.

11.7.8 Parameter Estimates

Note that the table is split into two rows. This is because these parameters compare pairs of outcome categories.

We specified the second category (2 = academic) as our reference category; therefore, the first row of the table labelled General is comparing this category against the ‘Academic’ category. the second row of the table labelled Vocational is also comparing this category against the ‘Academic’ category.

Because we are just comparing two categories the interpretation is the same as for binary logistic regression:

The relative log odds of being in general program versus in academic program will decrease by 1.125 if moving from the highest level of SES (SES = 3) to the lowest level of SES (SES = 1) , b = -1.125, Wald χ2(1) = -5.27, p <.001.

Exp(-1.1254491) = 0.3245067 means that when students move from the highest level of SES (SES = 3) to the lowest level of SES (1= SES) the odds ratio is 0.325 times as high and therefore students with the lowest level of SES tend to choose general program against academic program more than students with the highest level of SES.

The relative log odds of being in vocational program versus in academic program will decrease by 0.56 if moving from the highest level of SES (SES = 3) to the lowest level of SES (SES = 1) , b = -0.56, Wald χ2(1) = -2.82, p < 0.01.

Exp(-0.56) = 0.57 means that when students move from the highest level of SES (SES = 3) to the lowest level of SES (SES=1) the odds ratio is 0.57 times as high and therefore students with the lowest level of SES tend to choose vocational program against academic program more than students with the highest level of SES.

11.7.9 Interpretation of the Predictive Equation

Please check your slides for detailed information. You can find all the values on above R outcomes.

11.7.10 Build a classification table

11.8 supplementary learning materials.

Field, A (2013). Discovering statistics using IBM SPSS statistics (4th ed.). Los Angeles, CA: Sage Publications

Agresti, A. (1996). An introduction to categorical data analysis. New York, NY: Wiley & Sons.

IBM SPSS Regression 22.

• Skip to primary navigation
• Skip to main content
• Skip to primary sidebar

Institute for Digital Research and Education

Logistic Regression | SPSS Annotated Output

This page shows an example of logistic regression with footnotes explaining the output.  These data were collected on 200 high schools students and are scores on various tests, including science, math, reading and social studies ( socst ). The variable female is a dichotomous variable coded 1 if the student was female and 0 if male.

In the syntax below, the get file command is used to load the hsb2 data into SPSS.  In quotes, you need to specify where the data file is located on your computer.  Remember that you need to use the .sav extension and that you need to end the command with a period.  By default, SPSS does a listwise deletion of missing values.  This means that only cases with non-missing values for the dependent as well as all independent variables will be used in the analysis.

Because we do not have a suitable dichotomous variable to use as our dependent variable, we will create one (which we will call honcomp , for honors composition) based on the continuous variable write .  We do not advocate making dichotomous variables out of continuous variables; rather, we do this here only for purposes of this illustration.

Use the keyword with after the dependent variable to indicate all of the variables (both continuous and categorical) that you want included in the model.  If you have a categorical variable with more than two levels, for example, a three-level ses variable (low, medium and high), you can use the categorical subcommand to tell SPSS to create the dummy variables necessary to include the variable in the logistic regression, as shown below.  You can use the keyword by to create interaction terms.  For example, the command logistic regression honcomp with read female read by female. will create a model with the main effects of read and female , as well as the interaction of read by female .

We will start by showing the SPSS commands to open the data file, creating the dichotomous dependent variable, and then running the logistic regression. We will show the entire output, and then break up the output with explanation.

Logistic Regression

Block 0: Beginning Block

Block 1: Method = Enter

This part of the output tells you about the cases that were included and excluded from the analysis, the coding of the dependent variable, and coding of any categorical variables listed on the categorical subcommand.  (Note:  You will not get the third table (“Categorical Variable Codings”) if you do not specify the categorical subcommand.)

b.  N – This is the number of cases in each category (e.g., included in the analysis, missing, total).

c.  Percent – This is the percent of cases in each category (e.g., included in the analysis, missing, total).

d.  Included in Analysis – This row gives the number and percent of cases that were included in the analysis.  Because we have no missing data in our example data set, this also corresponds to the total number of cases.

e.  Missing Cases – This row give the number and percent of missing cases.  By default, SPSS logistic regression does a listwise deletion of missing data.  This means that if there is missing value for any variable in the model, the entire case will be excluded from the analysis.

f.  Total – This is the sum of the cases that were included in the analysis and the missing cases.  In our example, 200 + 0 = 200.

Unselected Cases – If the select subcommand is used and a logical condition is specified with a categorical variable in the dataset, then the number of unselected cases would be listed here.  Using the select subcommand is different from using the filter command.  When the select subcommand is used, diagnostic and residual values are computed for all cases in the data.  If the filter command is used to select cases to be used in the analysis, residual and diagnostic values are not computed for unselected cases.

This part of the output describes a “null model”, which is model with no predictors and just the intercept.  This is why you will see all of the variables that you put into the model in the table titled “Variables not in the Equation”.

c.  Step 0 – SPSS allows you to have different steps in your logistic regression model.  The difference between the steps is the predictors that are included.  This is similar to blocking variables into groups and then entering them into the equation one group at a time.  By default, SPSS logistic regression is run in two steps.  The first step, called Step 0, includes no predictors and just the intercept.  Often, this model is not interesting to researchers.

d.  Observed – This indicates the number of 0’s and 1’s that are observed in the dependent variable.

e.  Predicted – In this null model, SPSS has predicted that all cases are 0 on the dependent variable.

f.  Overall Percentage – This gives the percent of cases for which the dependent variables was correctly predicted given the model.  In this part of the output, this is the null model.  73.5 = 147/200.

g.  B – This is the coefficient for the constant (also called the “intercept”) in the null model.

h.  S.E. – This is the standard error around the coefficient for the constant.

i.  Wald and Sig . – This is the Wald chi-square test that tests the null hypothesis that the constant equals 0.  This hypothesis is rejected because the p-value (listed in the column called “Sig.”) is smaller than the critical p-value of .05 (or .01).  Hence, we conclude that the constant is not 0.  Usually, this finding is not of interest to researchers.

j.  df – This is the degrees of freedom for the Wald chi-square test.  There is only one degree of freedom because there is only one predictor in the model, namely the constant.

k.  Exp(B) – This is the exponentiation of the B coefficient, which is an odds ratio.  This value is given by default because odds ratios can be easier to interpret than the coefficient, which is in log-odds units. This is the odds:  53/147 = .361.

l.  Score and Sig. – This is a Score test that is used to predict whether or not an independent variable would be significant in the model. Looking at the p-values (located in the column labeled “Sig.”), we can see that each of the predictors would be statistically significant except the first dummy for ses .

m.  df – This column lists the degrees of freedom for each variable.  Each variable to be entered into the model, e.g., read , science , ses(1) and ses(2) , has one degree of freedom, which leads to the total of four shown at the bottom of the column.  The variable ses is listed here only to show that if the dummy variables that represent ses were tested simultaneously, the variable ses would be statistically significant.

n.  Overall Statistics – This shows the result of including all of the predictors into the model.

The section contains what is frequently the most interesting part of the output:  the overall test of the model (in the “Omnibus Tests of Model Coefficients” table) and the coefficients and odds ratios (in the “Variables in the Equation” table).

b.  Step 1 – This is the first step (or model) with predictors in it.  In this case, it is the full model that we specified in the logistic regression command.  You can have more steps if you do stepwise or use blocking of variables.

c.  Chi-square and Sig. – This is the chi-square statistic and its significance level.  In this example, the statistics for the Step, Model and Block are the same because we have not used stepwise logistic regression or blocking.  The value given in the Sig. column is the probability of obtaining the chi-square statistic given that the null hypothesis is true.  In other words, this is the probability of obtaining this chi-square statistic (65.588) if there is in fact no effect of the independent variables, taken together, on the dependent variable.  This is, of course, the p-value, which is compared to a critical value, perhaps .05 or .01 to determine if the overall model is statistically significant.  In this case, the model is statistically significant because the p-value is less than .000.

d.  df – This is the number of degrees of freedom for the model. There is one degree of freedom for each predictor in the model.  In this example, we have four predictors:  read , write and two dummies for ses (because there are three levels of ses ).

e.  -2 Log likelihood – This is the -2 log likelihood for the final model.  By itself, this number is not very informative. However, it can be used to compare nested (reduced) models.

f.  Cox & Snell R Square and Nagelkerke R Square – These are pseudo R-squares.  Logistic regression does not have an equivalent to the R-squared that is found in OLS regression; however, many people have tried to come up with one.  There are a wide variety of pseudo-R-square statistics (these are only two of them).  Because this statistic does not mean what R-squared means in OLS regression (the proportion of variance explained by the predictors), we suggest interpreting this statistic with great caution.

g.  Observed – This indicates the number of 0’s and 1’s that are observed in the dependent variable.

h.  Predicted – These are the predicted values of the dependent variable based on the full logistic regression model.  This table shows how many cases are correctly predicted (132 cases are observed to be 0 and are correctly predicted to be 0; 27 cases are observed to be 1 and are correctly predicted to be 1), and how many cases are not correctly predicted (15 cases are observed to be 0 but are predicted to be 1; 26 cases are observed to be 1 but are predicted to be 0).

i.  Overall Percentage – This gives the overall percent of cases that are correctly predicted by the model (in this case, the full model that we specified).  As you can see, this percentage has increased from 73.5 for the null model to 79.5 for the full model.

j.  B – These are the values for the logistic regression equation for predicting the dependent variable from the independent variable.  They are in log-odds units.  Similar to OLS regression, the prediction equation is

log(p/1-p) = b0 + b1*x1 + b2*x2 + b3*x3 + b3*x3+b4*x4

where p is the probability of being in honors composition.  Expressed in terms of the variables used in this example, the logistic regression equation is

log(p/1-p) = –9.561 + 0.098*read + 0.066*science + 0.058*ses(1) – 1.013*ses(2)

These estimates tell you about the relationship between the independent variables and the dependent variable, where the dependent variable is on the logit scale.  These estimates tell the amount of increase (or decrease, if the sign of the coefficient is negative) in the predicted log odds of honcomp = 1 that would be predicted by a 1 unit increase (or decrease) in the predictor, holding all other predictors constant.  Note: For the independent variables which are not significant, the coefficients are not significantly different from 0, which should be taken into account when interpreting the coefficients.  (See the columns labeled Wald and Sig. regarding testing whether the coefficients are statistically significant).  Because these coefficients are in log-odds units, they are often difficult to interpret, so they are often converted into odds ratios.  You can do this by hand by exponentiating the coefficient, or by looking at the right-most column in the Variables in the Equation table labeled “Exp(B)”. read – For every one-unit increase in reading score (so, for every additional point on the reading test), we expect a 0.098 increase in the log-odds of honcomp , holding all other independent variables constant. science – For every one-unit increase in science score, we expect a 0.066 increase in the log-odds of honcomp , holding all other independent variables constant. ses – This tells you if the overall variable ses is statistically significant.  There is no coefficient listed, because ses is not a variable in the model.  Rather, dummy variables which code for ses are in the equation, and those have coefficients.  However, as you can see in this example, the coefficient for one of the dummies is statistically significant while the other one is not.  The statistic given on this row tells you if the dummies that represent ses , taken together, are statistically significant.  Because there are two dummies, this test has two degrees of freedom.  This is equivalent to using the test statement in SAS or the test command is Stata. ses(1) – The reference group is level 3 (see the Categorical Variables Codings table above), so this coefficient represents the difference between level 1 of ses and level 3.  Note:  The number in the parentheses only indicate the number of the dummy variable; it does not tell you anything about which levels of the categorical variable are being compared. For example, if you changed the reference group from level 3 to level 1, the labeling of the dummy variables in the output would not change. ses(2) – The reference group is level 3 (see the Categorical Variables Codings table above), so this coefficient represents the difference between level 2 of ses and level 3.  Note:  The number in the parentheses only indicate the number of the dummy variable; it does not tell you anything about which levels of the categorical variable are being compared. For example, if you changed the reference group from level 3 to level 1, the labeling of the dummy variables in the output would not change. constant – This is the expected value of the log-odds of honcomp when all of the predictor variables equal zero.  In most cases, this is not interesting.  Also, oftentimes zero is not a realistic value for a variable to take.

k.  S.E. – These are the standard errors associated with the coefficients.  The standard error is used for testing whether the parameter is significantly different from 0; by dividing the parameter estimate by the standard error you obtain a t-value.  The standard errors can also be used to form a confidence interval for the parameter.

l.  Wald and Sig. – These columns provide the Wald chi-square value and 2-tailed p-value used in testing the null hypothesis that the coefficient (parameter) is 0.   If you use a 2-tailed test, then you would compare each p-value to your preselected value of alpha.  Coefficients having p-values less than alpha are statistically significant.  For example, if you chose alpha to be 0.05, coefficients having a p-value of 0.05 or less would be statistically significant (i.e., you can reject the null hypothesis and say that the coefficient is significantly different from 0).   If you use a 1-tailed test (i.e., you predict that the parameter will go in a particular direction), then you can divide the p-value by 2 before comparing it to your preselected alpha level. For the variable read , the p-value is .000, so the null hypothesis that the coefficient equals 0 would be rejected. For the variable science , the p-value is .015, so the null hypothesis that the coefficient equals 0 would be rejected. For the variable ses , the p-value is .035, so the null hypothesis that the coefficient equals 0 would be rejected.  Because the test of the overall variable is statistically significant, you can look at the one degree of freedom tests for the dummies ses(1) and ses(2).  The dummy ses(1) is not statistically significantly different from the dummy ses(3) (which is the omitted, or reference, category), but the dummy ses(2) is statistically significantly different from the dummy ses(3) with a p-value of .022.

m.  df – This column lists the degrees of freedom for each of the tests of the coefficients.

n.  Exp(B) – These are the odds ratios for the predictors. They are the exponentiation of the coefficients.  There is no odds ratio for the variable ses because ses (as a variable with 2 degrees of freedom) was not entered into the logistic regression equation.

Odds Ratios

In this next example, we will illustrate the interpretation of odds ratios.  In this example, we will simplify our model so that we have only one predictor, the binary variable female .  Before we run the logistic regression, we will use the crosstabs command to obtain a crosstab of the two variables.

If we divide the number of males who are in honors composition, 18, by the number of males who are not in honors composition, 73, we get the odds of being in honors composition for males, 18/73 = .246.  If we do the same thing for females, we get 35/74 = .472.  To get the odds ratio, which is the ratio of the two odds that we have just calculated, we get .472/.246 = 1.918.  As we can see in the output below, this is exactly the odds ratio we obtain from the logistic regression.  The thing to remember here is that you want the group coded as 1 over the group coded as 0, so honcomp=1/honcomp=0 for both males and females, and then the odds for females/odds for males, because the females are coded as 1.

You can get the odds ratio from the crosstabs command by using the /statistics risk subcommand, as shown below.

As you can see in the output below, we get the same odds ratio when we run the logistic regression. (NOTE: Although it is equivalent to the odds ratio estimated from the logistic regression, the odds ratio in the “Risk Estimate” table is calculated as the ratio of the odds of honcomp=0 for males over the odds of honcomp=0 for females, which explains the confusing row heading “Odds Ratio for female (.00/1.00)”). If we calculated a 95% confidence interval, we would not want this to include the value of 1.  When we were considering the coefficients, we did not want the confidence interval to include 0.  If we exponentiate 0, we get 1 (exp(0) = 1).  Hence, this is two ways of saying the same thing.  As you can see, the 95% confidence interval includes 1; hence, the odds ratio is not statistically significant.  Because the lower bound of the 95% confidence interval is so close to 1, the p-value is very close to .05.  We can use the /print = ic(95) subcommand to get the 95% confidence intervals included in our output.

There are a few other things to note about the output below.  The first is that although we have only one predictor variable, the test for the odds ratio does not match with the overall test of the model.  This is because the test of the coefficient is a Wald chi-square test, while the test of the overall model is a likelihood ratio chi-square test.  While these two types of chi-square tests are asymptotically equivalent, in small samples they can differ, as they do here.  Also, we have the unfortunate situation in which the results of the two tests give different conclusions.  This does not happen very often.  In a situation like this, it is difficult to know what to conclude.  One might consider the power, or one might decide if an odds ratio of this magnitude is important from a clinical or practical standpoint.

For more information on interpreting odds ratios, please see How do I interpret odds ratios in logistic regression? .  Although this FAQ uses Stata for purposes of illustration, the concepts and explanations are useful.

Your Name (required)

Your Email (must be a valid email for us to receive the report!)

Comment/Error Report (required)

How to cite this page

• © 2021 UC REGENTS

Please enable JavaScript to view this site.

• Statistics Guide
• Curve Fitting Guide
• Prism Guide
• Zoom Window Out
• Larger Text  |  Smaller Text
• Hide Page Header
• Show Expanding Text
• Printable Version
• Save Permalink URL

A reminder of how hypothesis tests work

Two hypothesis tests are offered by Prism for assessing how well a model fits the entered data. Like other hypothesis-based tests that you’ve likely encountered, these two tests start by defining a null hypothesis (H0). Each test then calculates a statistic and corresponding P value. The calculated P value represents the probability of obtaining a test statistic as large as the one calculated (or larger) if the null hypothesis were true . This test also requires that a threshold be set for how small a P value must be to make a decision about whether to reject the null hypothesis. This – admittedly arbitrary – threshold is typically set to 0.05, and is also referred to as the alpha (α) level. If the obtained P value is smaller than α, then we reject the null hypothesis.

Before reading about each of the tests below, it's also important to understand what is meant by the terms "specified model" and "intercept-only model". The specified model is simply the model that was fit to the data (the one that you defined on the Model tab of the analysis). It includes the effects of the predictor variables on the probability of observing a success. The intercept-only model is a model that assumes that the contributions from the predictor variables is zero. In other words, the intercept-only model assumes that none of the independent variables help predict the outcome.

Hosmer-Lemeshow (HL) Test

The Hosmer-Lemeshow test is a classic hypothesis test for logistic regression. The null hypothesis is that the specified model is correct (that it fits well). The way the test works is by first sorting the observations by their predicted probability, and splitting them into 10 groups of equal numbers of observations (N). For each group, the average predicted probability is calculated, and that average is multiplied by N to get an expected number of 1s for that group (and in turn the expected number of 0s for that group). It then calculates a Pearson goodness of fit statistic using the observed and expected numbers of 0s and 1s, and summing across all of the groups. It uses a chi-squared distribution to then calculate a P value.

As mentioned, the null hypothesis is that the specified model fits well, so contrary to many tests, a small P value indicates a poor fit of the model to the data. Another way to think about this is that a small P value indicates that there is more deviation from the expected number of 0s and 1s (given 10 bins) than you'd expect by chance. Thus, there may be some additional factor, interaction, or transform that is missing from the model.

This test has received criticism for the arbitrary number of bins (10), since it has been shown that changing this number can influence the result of the test. The test is included as an option in Prism so you can compare results obtained in Prism with results calculated elsewhere, even though this test is not recommended.

Log likelihood ratio test (LRT)

The log likelihood ratio test is also a classic test that compares how well the model selected fits compared to the intercept only model. In this case, the null hypothesis is that the intercept-only model fits best, so a small P value here indicates that you would reject this null hypothesis (or that the specified model outperforms the intercept only model). As the name implies, this test uses the log likelihood of the specified model and the intercept-only model to calculate the associated statistic and P value. Although this test specifically looks at the defined model and an intercept-only model, it is the same test that is provided on the Compare tab of the multiple logistic regression parameters dialog to compare any two nested models.

The likelihood ratio tells you how much more likely the data were to be generated by the fit model than by the intercept-only model. If the independent variables do a good job of predicting the outome, the likelihood ratio will be high and the corresponding P value will be small.

Note the different meaning of the P values

A small P value has opposite meanings with the two tests:

• A small P value from the Hosmer-Lemeshow test means that the specified model doesn't do a good  job of predicting the data. Consider whether you need additional independent variables or interactions included in the model.

• A small P value from the likelihood ratio test means that the intercept-only model doesn't do a good job of predicting the data. The specified independent variables and interactions improve the fit of the model to the data.

© 1995- 2019 GraphPad Software, LLC. All rights reserved.

Statistics Made Easy

Understanding the Null Hypothesis for Linear Regression

Linear regression is a technique we can use to understand the relationship between one or more predictor variables and a response variable .

If we only have one predictor variable and one response variable, we can use simple linear regression , which uses the following formula to estimate the relationship between the variables:

ŷ = β 0 + β 1 x

• ŷ: The estimated response value.
• β 0 : The average value of y when x is zero.
• β 1 : The average change in y associated with a one unit increase in x.
• x: The value of the predictor variable.

Simple linear regression uses the following null and alternative hypotheses:

• H 0 : β 1 = 0
• H A : β 1 ≠ 0

The null hypothesis states that the coefficient β 1 is equal to zero. In other words, there is no statistically significant relationship between the predictor variable, x, and the response variable, y.

The alternative hypothesis states that β 1 is not equal to zero. In other words, there is a statistically significant relationship between x and y.

If we have multiple predictor variables and one response variable, we can use multiple linear regression , which uses the following formula to estimate the relationship between the variables:

ŷ = β 0 + β 1 x 1 + β 2 x 2 + … + β k x k

• β 0 : The average value of y when all predictor variables are equal to zero.
• β i : The average change in y associated with a one unit increase in x i .
• x i : The value of the predictor variable x i .

Multiple linear regression uses the following null and alternative hypotheses:

• H 0 : β 1 = β 2 = … = β k = 0
• H A : β 1 = β 2 = … = β k ≠ 0

The null hypothesis states that all coefficients in the model are equal to zero. In other words, none of the predictor variables have a statistically significant relationship with the response variable, y.

The alternative hypothesis states that not every coefficient is simultaneously equal to zero.

The following examples show how to decide to reject or fail to reject the null hypothesis in both simple linear regression and multiple linear regression models.

Example 1: Simple Linear Regression

Suppose a professor would like to use the number of hours studied to predict the exam score that students will receive in his class. He collects data for 20 students and fits a simple linear regression model.

The following screenshot shows the output of the regression model:

The fitted simple linear regression model is:

Exam Score = 67.1617 + 5.2503*(hours studied)

To determine if there is a statistically significant relationship between hours studied and exam score, we need to analyze the overall F value of the model and the corresponding p-value:

• Overall F-Value:  47.9952
• P-value:  0.000

Since this p-value is less than .05, we can reject the null hypothesis. In other words, there is a statistically significant relationship between hours studied and exam score received.

Example 2: Multiple Linear Regression

Suppose a professor would like to use the number of hours studied and the number of prep exams taken to predict the exam score that students will receive in his class. He collects data for 20 students and fits a multiple linear regression model.

The fitted multiple linear regression model is:

Exam Score = 67.67 + 5.56*(hours studied) – 0.60*(prep exams taken)

To determine if there is a jointly statistically significant relationship between the two predictor variables and the response variable, we need to analyze the overall F value of the model and the corresponding p-value:

• Overall F-Value:  23.46
• P-value:  0.00

Since this p-value is less than .05, we can reject the null hypothesis. In other words, hours studied and prep exams taken have a jointly statistically significant relationship with exam score.

Note: Although the p-value for prep exams taken (p = 0.52) is not significant, prep exams combined with hours studied has a significant relationship with exam score.

Additional Resources

Understanding the F-Test of Overall Significance in Regression How to Read and Interpret a Regression Table How to Report Regression Results How to Perform Simple Linear Regression in Excel How to Perform Multiple Linear Regression in Excel

Published by Zach

Leave a reply cancel reply.

Your email address will not be published. Required fields are marked *