hypothesis testing for the mean calculator

Hypothesis Testing Calculator

Related: confidence interval calculator, type ii error.

The first step in hypothesis testing is to calculate the test statistic. The formula for the test statistic depends on whether the population standard deviation (σ) is known or unknown. If σ is known, our hypothesis test is known as a z test and we use the z distribution. If σ is unknown, our hypothesis test is known as a t test and we use the t distribution. Use of the t distribution relies on the degrees of freedom, which is equal to the sample size minus one. Furthermore, if the population standard deviation σ is unknown, the sample standard deviation s is used instead. To switch from σ known to σ unknown, click on $\boxed{\sigma}$ and select $\boxed{s}$ in the Hypothesis Testing Calculator.

Next, the test statistic is used to conduct the test using either the p-value approach or critical value approach. The particular steps taken in each approach largely depend on the form of the hypothesis test: lower tail, upper tail or two-tailed. The form can easily be identified by looking at the alternative hypothesis (H a ). If there is a less than sign in the alternative hypothesis then it is a lower tail test, greater than sign is an upper tail test and inequality is a two-tailed test. To switch from a lower tail test to an upper tail or two-tailed test, click on $\boxed{\geq}$ and select $\boxed{\leq}$ or $\boxed{=}$, respectively.

In the p-value approach, the test statistic is used to calculate a p-value. If the test is a lower tail test, the p-value is the probability of getting a value for the test statistic at least as small as the value from the sample. If the test is an upper tail test, the p-value is the probability of getting a value for the test statistic at least as large as the value from the sample. In a two-tailed test, the p-value is the probability of getting a value for the test statistic at least as unlikely as the value from the sample.

To test the hypothesis in the p-value approach, compare the p-value to the level of significance. If the p-value is less than or equal to the level of signifance, reject the null hypothesis. If the p-value is greater than the level of significance, do not reject the null hypothesis. This method remains unchanged regardless of whether it's a lower tail, upper tail or two-tailed test. To change the level of significance, click on $\boxed{.05}$. Note that if the test statistic is given, you can calculate the p-value from the test statistic by clicking on the switch symbol twice.

In the critical value approach, the level of significance ($\alpha$) is used to calculate the critical value. In a lower tail test, the critical value is the value of the test statistic providing an area of $\alpha$ in the lower tail of the sampling distribution of the test statistic. In an upper tail test, the critical value is the value of the test statistic providing an area of $\alpha$ in the upper tail of the sampling distribution of the test statistic. In a two-tailed test, the critical values are the values of the test statistic providing areas of $\alpha / 2$ in the lower and upper tail of the sampling distribution of the test statistic.

To test the hypothesis in the critical value approach, compare the critical value to the test statistic. Unlike the p-value approach, the method we use to decide whether to reject the null hypothesis depends on the form of the hypothesis test. In a lower tail test, if the test statistic is less than or equal to the critical value, reject the null hypothesis. In an upper tail test, if the test statistic is greater than or equal to the critical value, reject the null hypothesis. In a two-tailed test, if the test statistic is less than or equal the lower critical value or greater than or equal to the upper critical value, reject the null hypothesis.

When conducting a hypothesis test, there is always a chance that you come to the wrong conclusion. There are two types of errors you can make: Type I Error and Type II Error. A Type I Error is committed if you reject the null hypothesis when the null hypothesis is true. Ideally, we'd like to accept the null hypothesis when the null hypothesis is true. A Type II Error is committed if you accept the null hypothesis when the alternative hypothesis is true. Ideally, we'd like to reject the null hypothesis when the alternative hypothesis is true.

Hypothesis testing is closely related to the statistical area of confidence intervals. If the hypothesized value of the population mean is outside of the confidence interval, we can reject the null hypothesis. Confidence intervals can be found using the Confidence Interval Calculator . The calculator on this page does hypothesis tests for one population mean. Sometimes we're interest in hypothesis tests about two population means. These can be solved using the Two Population Calculator . The probability of a Type II Error can be calculated by clicking on the link at the bottom of the page.

Teach yourself statistics

Hypothesis Test for a Mean

This lesson explains how to conduct a hypothesis test of a mean, when the following conditions are met:

• The sampling method is simple random sampling .
• The sampling distribution is normal or nearly normal.

Generally, the sampling distribution will be approximately normally distributed if any of the following conditions apply.

• The population distribution is normal.
• The population distribution is symmetric , unimodal , without outliers , and the sample size is 15 or less.
• The population distribution is moderately skewed , unimodal, without outliers, and the sample size is between 16 and 40.
• The sample size is greater than 40, without outliers.

This approach consists of four steps: (1) state the hypotheses, (2) formulate an analysis plan, (3) analyze sample data, and (4) interpret results.

State the Hypotheses

Every hypothesis test requires the analyst to state a null hypothesis and an alternative hypothesis . The hypotheses are stated in such a way that they are mutually exclusive. That is, if one is true, the other must be false; and vice versa.

The table below shows three sets of hypotheses. Each makes a statement about how the population mean μ is related to a specified value M . (In the table, the symbol ≠ means " not equal to ".)

The first set of hypotheses (Set 1) is an example of a two-tailed test , since an extreme value on either side of the sampling distribution would cause a researcher to reject the null hypothesis. The other two sets of hypotheses (Sets 2 and 3) are one-tailed tests , since an extreme value on only one side of the sampling distribution would cause a researcher to reject the null hypothesis.

Formulate an Analysis Plan

The analysis plan describes how to use sample data to accept or reject the null hypothesis. It should specify the following elements.

• Significance level. Often, researchers choose significance levels equal to 0.01, 0.05, or 0.10; but any value between 0 and 1 can be used.
• Test method. Use the one-sample t-test to determine whether the hypothesized mean differs significantly from the observed sample mean.

Analyze Sample Data

Using sample data, conduct a one-sample t-test. This involves finding the standard error, degrees of freedom, test statistic, and the P-value associated with the test statistic.

SE = s * sqrt{ ( 1/n ) * [ ( N - n ) / ( N - 1 ) ] }

SE = s / sqrt( n )

• Degrees of freedom. The degrees of freedom (DF) is equal to the sample size (n) minus one. Thus, DF = n - 1.

t = ( x - μ) / SE

• P-value. The P-value is the probability of observing a sample statistic as extreme as the test statistic. Since the test statistic is a t statistic, use the t Distribution Calculator to assess the probability associated with the t statistic, given the degrees of freedom computed above. (See sample problems at the end of this lesson for examples of how this is done.)

Sample Size Calculator

As you probably noticed, the process of hypothesis testing can be complex. When you need to test a hypothesis about a mean score, consider using the Sample Size Calculator. The calculator is fairly easy to use, and it is free. You can find the Sample Size Calculator in Stat Trek's main menu under the Stat Tools tab. Or you can tap the button below.

Interpret Results

If the sample findings are unlikely, given the null hypothesis, the researcher rejects the null hypothesis. Typically, this involves comparing the P-value to the significance level , and rejecting the null hypothesis when the P-value is less than the significance level.

Test Your Understanding

In this section, two sample problems illustrate how to conduct a hypothesis test of a mean score. The first problem involves a two-tailed test; the second problem, a one-tailed test.

Problem 1: Two-Tailed Test

An inventor has developed a new, energy-efficient lawn mower engine. He claims that the engine will run continuously for 5 hours (300 minutes) on a single gallon of regular gasoline. From his stock of 2000 engines, the inventor selects a simple random sample of 50 engines for testing. The engines run for an average of 295 minutes, with a standard deviation of 20 minutes. Test the null hypothesis that the mean run time is 300 minutes against the alternative hypothesis that the mean run time is not 300 minutes. Use a 0.05 level of significance. (Assume that run times for the population of engines are normally distributed.)

Solution: The solution to this problem takes four steps: (1) state the hypotheses, (2) formulate an analysis plan, (3) analyze sample data, and (4) interpret results. We work through those steps below:

Null hypothesis: μ = 300

Alternative hypothesis: μ ≠ 300

• Formulate an analysis plan . For this analysis, the significance level is 0.05. The test method is a one-sample t-test .

SE = s / sqrt(n) = 20 / sqrt(50) = 20/7.07 = 2.83

DF = n - 1 = 50 - 1 = 49

t = ( x - μ) / SE = (295 - 300)/2.83 = -1.77

where s is the standard deviation of the sample, x is the sample mean, μ is the hypothesized population mean, and n is the sample size.

Since we have a two-tailed test , the P-value is the probability that the t statistic having 49 degrees of freedom is less than -1.77 or greater than 1.77. We use the t Distribution Calculator to find P(t < -1.77) is about 0.04.

• If you enter 1.77 as the sample mean in the t Distribution Calculator, you will find the that the P(t < 1.77) is about 0.04. Therefore, P(t >  1.77) is 1 minus 0.96 or 0.04. Thus, the P-value = 0.04 + 0.04 = 0.08.
• Interpret results . Since the P-value (0.08) is greater than the significance level (0.05), we cannot reject the null hypothesis.

Note: If you use this approach on an exam, you may also want to mention why this approach is appropriate. Specifically, the approach is appropriate because the sampling method was simple random sampling, the population was normally distributed, and the sample size was small relative to the population size (less than 5%).

Problem 2: One-Tailed Test

Bon Air Elementary School has 1000 students. The principal of the school thinks that the average IQ of students at Bon Air is at least 110. To prove her point, she administers an IQ test to 20 randomly selected students. Among the sampled students, the average IQ is 108 with a standard deviation of 10. Based on these results, should the principal accept or reject her original hypothesis? Assume a significance level of 0.01. (Assume that test scores in the population of engines are normally distributed.)

Null hypothesis: μ >= 110

Alternative hypothesis: μ < 110

• Formulate an analysis plan . For this analysis, the significance level is 0.01. The test method is a one-sample t-test .

SE = s / sqrt(n) = 10 / sqrt(20) = 10/4.472 = 2.236

DF = n - 1 = 20 - 1 = 19

t = ( x - μ) / SE = (108 - 110)/2.236 = -0.894

Here is the logic of the analysis: Given the alternative hypothesis (μ < 110), we want to know whether the observed sample mean is small enough to cause us to reject the null hypothesis.

The observed sample mean produced a t statistic test statistic of -0.894. We use the t Distribution Calculator to find P(t < -0.894) is about 0.19.

• This means we would expect to find a sample mean of 108 or smaller in 19 percent of our samples, if the true population IQ were 110. Thus the P-value in this analysis is 0.19.
• Interpret results . Since the P-value (0.19) is greater than the significance level (0.01), we cannot reject the null hypothesis.

Hypothesis Test for a Mean

Use the calculator below to analyze the results of a hypothesis test for a mean. Enter your null hypothesis's mean, sample mean, sample standard deviation, sample size, test type, and significance level to find your results.

You will find a description of how to conduct a hypothesis test of a mean below the calculator.

Define the t-test

Sample mean under the null distribution, conducting single mean hypothesis tests.

A hypothesis test of a sample mean can help you make inferences about the population from which you drew it. It is a tool to determine what is probably true about an event or phenomena.

Testing a Mean

For the results of a hypothesis test of a mean to be valid, you should follow these steps:

Check Your Conditions

State your hypothesis, determine your analysis plan, analyze your sample, interpret your results.

To use the testing procedure described below, you should check the following conditions:

• Simple Random Sampling - You should collect your sample with simple random sampling. This type of sampling requires that every occurrence of a value in a population has an equal chance of being selected when taking a sample.
• Normal Sampling Distribution -The sampling distribution should follow the Normal or a nearly Normal distribution. A sampling distribution will be nearly Normal when the samples are collected independently and when the population distribution is nearly Normal. Generally, the larger the sample size, the more normally distributed the sampling distribution. Additionally, outlier data points can make a distribution less Normal, so if your data contains many outliers, exercise caution when verifying this condition.

You must state a null hypothesis and an alternative hypothesis to conduct a hypothesis test for a mean.

The null hypothesis, is a skeptical claim that you would like to test. It is defined by the null hypothesis's mean, which is often labeled μ 0 .

The alternative hypothesis represents an alternative claim to the null hypothesis.

Your null hypothesis and alternative hypothesis should be stated in one of three mutually exclusive ways listed in the table below.

Before conducting a hypothesis test, you must determine a reasonable significance level, α, or the probability of rejecting the null hypothesis assuming it is true. The lower your significance level, the more confident you can be of the conclusion of your hypothesis test. Common significance levels are 10%, 5%, and 1%.

To evaluate your hypothesis test at the significance level that you set, consider if you are conducting a one or two tail test:

• Two-tail tests divide the rejection region, or critical region, evenly above and below the null distribution, i.e. to the tails of the null sampling distribution. For example, in a two-tail test with a 5% significance level, your rejection region would be the upper and lower 2.5% of the null distribution. An alternative hypothesis of μ ≠ μ 0 requires a two-tail test.
• One-tail tests place the rejection region entirely on one side of the distribution i.e. to the right or left tail of the null sampling distribution. For example, in a one-tail test evaluating if the sampling distribution is above the null sampling distribution with a 5% significance level, your rejection region would be the upper 5% of the null distribution. μ > μ 0 and μ 0 alternative hypotheses require one-tail tests.

The graphical results section of the calculator above shades rejection regions blue.

After checking your conditions, stating your hypothesis, determining your significance level, and collecting your sample, you are ready to analyze your hypothesis.

Sample means follow the Normal Distribution with the following parameters:

• The Population Mean, μ - The population mean is assumed to be the null hypothesis's mean in a single mean hypothesis test.
• The Standard Error, SE - For samples that are much smaller than the population, the standard error can be computed as follows: SE = s / sqrt(n), with s being the sample standard deviation and n being the sample size. It defines how sample means are expected to vary around the null hypothesis's mean given the sample size and under the assumption that the null hypothesis is true.
• Degrees of Freedom, DF - For hypothesis tests for a single mean, the degrees of freedom equals n – 1, with n being the sample size.

In a hypothesis test for a mean, we calculate the probability that we would observe the sample mean, x̄, assuming the null hypothesis is true, also known as the p-value . If the p-value is less than the significance level, then we can reject the null hypothesis.

You can determine a precise p-value using the calculator above, but we can find an estimate of the p-value manually by calculating the t-score, or t-statistic, as follows: t = (x̄ - μ 0 ) / SE

The t-score is a test statistic that tells us how far our observation is from the null hypothesis's mean under the null distribution. Using any t-score table, we can look up the probability of observing the results under the null distribution. You will need to look up the t-score for the type of test you are conducting, i.e. one or two tail. A hypothesis test for a mean is sometimes known as a t-test because of the use of a t-score in analyzing results.

If you find the probability is below the significance level, we reject the null hypothesis.

The conclusion of a hypothesis test for a mean is always either:

• Reject the null hypothesis
• Do not reject the null hypothesis

If you reject the null hypothesis, you cannot say that your sample mean is the true population mean. If you do not reject the null hypothesis, you cannot say that the null hypothesis is true.

A hypothesis test is simply a way to look at a sample and conclude if it provides sufficient evidence to reject the null hypothesis.

Example: Hypothesis Test for a Mean

Let’s say that you manage a clothing store with a historical average transaction amount of $53.24.

You believe the best way to improve your business is to increase your average sale amount. So, you have been working hard on training your sales staff on how sell more items to customers to increase sales.

To test if your sales training has increased your average sale amount, you decide to run a hypothesis test for a mean with a sample of 50 transactions to see if your average sale amount has increased.

• Check the conditions - You collect your sample using simple random sampling , and you know that historically your transactions are normally distributed about the average transaction. So, your conditions for running a hypothesis test for a mean are satisfied.
• State Your Hypothesis - Your null hypothesis is that your average transaction amount is the same or less than the historical average, formally stated μ ≤ $53.24. Your alternative hypothesis is that your average is greater than the historical average, formally stated μ > $53.24.
• Determine Your Analysis Plan - You believe that a 5% significance level is reasonable. As your test is one-tail test, you will evaluate if your sample mean would occur at the upper 5% of the null distribution.
• Analyze Your Sample - After collecting your sample (which you do after steps 1-3), you find that the sample mean, x̄, transaction amount is $61.02 with a standard deviation of $39.12. Using the calculator above, you find that a sample mean of $61.02 would results in a t-score of 1.41 under the null distribution, which translates to a p-value of 8.30%.
• Interpret Your Results - Since your p-value of 8.30% is greater than the significance level of 5%, you do not have sufficient evidence to reject the null hypothesis.

In this example, you found that you cannot reject the claim that your current transaction amount is less than or equal to your historical transaction amount of $53.24. Your results do not guarantee that your transaction amount is $53.24 or below, but they do indicate that your sales training has likely not had the effect that you wanted on your store's average sale amount.

Hypothesis Testing Calculator for Population Mean English Español

A free online hypothesis testing calculator for population mean to find the Hypothesis for the given population mean. Enter the sample mean, population mean, sample standard deviation, population size and the significance level to know the T score test value, P value and result of hypothesis.

Hypothesis Testing: Hypothesis Test, also known as Statistical Hypothesis Test is a method of statistical inference. Since it is a hypothesis that is testable on the basis of observing a process that is modeled via a set of random variables, it is also referred to as confirmatory data analysis. The hypothesis testing for population mean analyses the results of the null hypothesis and the alternative hypothesis of a population. Hypothesis testing is one of the final analysis of statistical data. Use this free sample and population statistics calculator to perform a statistical hypothesis test for the given population mean. This online hypothesis testing calculator for population mean helps you to perform the two-tailed and one-tailed statistical hypothesis testing.

If you are performing one-tailed test for the sample mean of 20, population mean of 15, the size of the population of 5, SD of 25 and the significance level of -10, then you will get the below values as result.

Solution 1 :

T-score is 0.44721

Solution 2 :

P-value is 0.6726

P-value > -10 ( Significance level). Hence, H0 is not rejected. H0 is Null Hypothesis.

Related Calculators:

• Standard Deviation Calculator
• Population Confidence Interval
• Sample Size Calculator
• Mean Squared Error, Sum Of Squared Error Calculator
• Hypothesis Test For Population Variance
• Probability (P) Value T Test Calculator
• Cumulative Sum Calculator

Calculators and Converters

• Calculators
• Sample And Population Statistics

Top Calculators

Popular calculators.

• Derivative Calculator
• Inverse of Matrix Calculator
• Compound Interest Calculator
• Pregnancy Calculator Online

Top Categories

Z-test for One Population Mean

Instructions: This calculator conducts a Z-test for one population mean (\(\mu\)), with known population standard deviation (\(\sigma\)). Please select the null and alternative hypotheses, type the hypothesized mean, the significance level, the sample mean, the population standard deviation, and the sample size, and the results of the z-test will be displayed for you:

How to Conduct a Z-Test for One Population Mean?

More about the z-test for one mean so you can better interpret the results obtained by this solver: A z-test for one mean is a hypothesis test that attempts to make a claim about the population mean (\(\mu\)).

The test has two non-overlapping hypotheses, the null and the alternative hypothesis. The null hypothesis is a statement about the population mean, under the assumption of no effect, and the alternative hypothesis is the complementary hypothesis to the null hypothesis. The main properties of a one sample z-test for one population mean are:

• Depending on our knowledge about the "no effect" situation, the z-test can be two-tailed, left-tailed or right-tailed
• The main principle of hypothesis testing is that the null hypothesis is rejected if the test statistic obtained is sufficiently unlikely under the assumption that the null hypothesis is true
• The p-value is the probability of obtaining sample results as extreme or more extreme than the sample results obtained, under the assumption that the null hypothesis is true
• In a hypothesis tests there are two types of errors. Type I error occurs when we reject a true null hypothesis, and the Type II error occurs when we fail to reject a false null hypothesis

Uses of this z-test calculator

What can you do with this z-test statistic calculator for hypothesis testing? The formula for a z-statistic is

The null hypothesis is rejected when the z-statistic lies on the rejection region, which is determined by the significance level (\(\alpha\)) and the type of tail (two-tailed, left-tailed or right-tailed).

What if the population standard deviation is not known?

It frequently happens that you don't actually know the population standard deviation, in which case you need to use a t-test for one mean calculator instead, which adjusts for that by using the sample standard deviation, by using a slightly different distribution (the t-distribution)

How to calculate p-value in the context of a z-test?

The answer depends on whether you are using a two-tailed, a left-tailed or a right-tailed test. Say you have the calculated z-statistic, \(Z_{obs}\).

• For a two-tailed test, the p-value is computed as: \(p = \Pr( Z > |Z_{obs}|) \)
• For a left-tailed test, the p-value is computed as: \(p = \Pr( Z < Z_{obs}) \)
• For a right-tailed test, the p-value is computed as: \(p = \Pr( Z > Z_{obs}) \)

where \(Z\) has a standard normal distribution.

Other types of Z-calculators

In case that you need to compare two population means, when you know the corresponding population standard deviations, you need to use this z-test for two means with known population standard deviations instead.

Outlier Detection

Don't forget to detect outliers before running a z-test for one mean. It is important that outliers are detected and removed before conducting the test, but the results of the test statistics may be slanted.

Example: Application of the Z-test calculator

Question : Assume that you want to test whether or not the population mean is 12.3. You collect a representative random sample of size n = 16, and you find that the sample mean is 11.3. Also, you know that the population is 2.3. Do the sample data provide enough evidence to reject the claim that the population mean is 12.3? Use a two-tailed test, with a significance level of 0.01.

The following information has been provided:

(1) Null and Alternative Hypotheses

The following null and alternative hypotheses need to be tested:

This corresponds to a two-tailed test, for which a z-test for one mean, with known population standard deviation will be used.

(2) Rejection Region

Based on the information provided, the significance level is \(\alpha = 0.01\), and the critical value for a two-tailed test is \(z_c = 2.58\).

The rejection region for this two-tailed test is \(R = \{z: |z| > 2.576\}\)

(3) Test Statistics

The z-statistic is computed as follows:

(4) Decision about the null hypothesis

Since it is observed that \(|z| = 1.739 \le z_c = 2.576\), it is then concluded that the null hypothesis is not rejected.

Using the P-value approach: The p-value is \(p = 0.082\), and since \(p = 0.082 \ge 0.01\), it is concluded that the null hypothesis is not rejected.

(5) Conclusion

It is concluded that the null hypothesis Ho is not rejected. Therefore, there is not enough evidence to claim that the population mean \(\mu\) is different than 12.3, at the \(\alpha = 0.01\) significance level.

Confidence Interval

The 99% confidence interval is \(9.819 < \mu < 12.781\).

Related Calculators

log in to your account

Reset password.

• FOR INSTRUCTOR
• FOR INSTRUCTORS

8.4.3 Hypothesis Testing for the Mean

$\quad$ $H_0$: $\mu=\mu_0$, $\quad$ $H_1$: $\mu \neq \mu_0$.

$\quad$ $H_0$: $\mu \leq \mu_0$, $\quad$ $H_1$: $\mu > \mu_0$.

$\quad$ $H_0$: $\mu \geq \mu_0$, $\quad$ $H_1$: $\mu \lt \mu_0$.

Two-sided Tests for the Mean:

Therefore, we can suggest the following test. Choose a threshold, and call it $c$. If $|W| \leq c$, accept $H_0$, and if $|W|>c$, accept $H_1$. How do we choose $c$? If $\alpha$ is the required significance level, we must have

• As discussed above, we let \begin{align}%\label{} W(X_1,X_2, \cdots,X_n)=\frac{\overline{X}-\mu_0}{\sigma / \sqrt{n}}. \end{align} Note that, assuming $H_0$, $W \sim N(0,1)$. We will choose a threshold, $c$. If $|W| \leq c$, we accept $H_0$, and if $|W|>c$, accept $H_1$. To choose $c$, we let \begin{align} P(|W| > c \; | \; H_0) =\alpha. \end{align} Since the standard normal PDF is symmetric around $0$, we have \begin{align} P(|W| > c \; | \; H_0) = 2 P(W>c | \; H_0). \end{align} Thus, we conclude $P(W>c | \; H_0)=\frac{\alpha}{2}$. Therefore, \begin{align} c=z_{\frac{\alpha}{2}}. \end{align} Therefore, we accept $H_0$ if \begin{align} \left|\frac{\overline{X}-\mu_0}{\sigma / \sqrt{n}} \right| \leq z_{\frac{\alpha}{2}}, \end{align} and reject it otherwise.
• We have \begin{align} \beta (\mu) &=P(\textrm{type II error}) = P(\textrm{accept }H_0 \; | \; \mu) \\ &= P\left(\left|\frac{\overline{X}-\mu_0}{\sigma / \sqrt{n}} \right| \lt z_{\frac{\alpha}{2}}\; | \; \mu \right). \end{align} If $X_i \sim N(\mu,\sigma^2)$, then $\overline{X} \sim N(\mu, \frac{\sigma^2}{n})$. Thus, \begin{align} \beta (\mu)&=P\left(\left|\frac{\overline{X}-\mu_0}{\sigma / \sqrt{n}} \right| \lt z_{\frac{\alpha}{2}}\; | \; \mu \right)\\ &=P\left(\mu_0- z_{\frac{\alpha}{2}} \frac{\sigma}{\sqrt{n}} \leq \overline{X} \leq \mu_0+ z_{\frac{\alpha}{2}} \frac{\sigma}{\sqrt{n}}\right)\\ &=\Phi\left(z_{\frac{\alpha}{2}}+\frac{\mu_0-\mu}{\sigma / \sqrt{n}}\right)-\Phi\left(-z_{\frac{\alpha}{2}}+\frac{\mu_0-\mu}{\sigma / \sqrt{n}}\right). \end{align}
• Let $S^2$ be the sample variance for this random sample. Then, the random variable $W$ defined as \begin{equation} W(X_1,X_2, \cdots, X_n)=\frac{\overline{X}-\mu_0}{S / \sqrt{n}} \end{equation} has a $t$-distribution with $n-1$ degrees of freedom, i.e., $W \sim T(n-1)$. Thus, we can repeat the analysis of Example 8.24 here. The only difference is that we need to replace $\sigma$ by $S$ and $z_{\frac{\alpha}{2}}$ by $t_{\frac{\alpha}{2},n-1}$. Therefore, we accept $H_0$ if \begin{align} |W| \leq t_{\frac{\alpha}{2},n-1}, \end{align} and reject it otherwise. Let us look at a numerical example of this case.

$\quad$ $H_0$: $\mu=170$, $\quad$ $H_1$: $\mu \neq 170$.

• Let's first compute the sample mean and the sample standard deviation. The sample mean is \begin{align}%\label{} \overline{X}&=\frac{X_1+X_2+X_3+X_4+X_5+X_6+X_7+X_8+X_9}{9}\\ &=165.8 \end{align} The sample variance is given by \begin{align}%\label{} {S}^2=\frac{1}{9-1} \sum_{k=1}^9 (X_k-\overline{X})^2&=68.01 \end{align} The sample standard deviation is given by \begin{align}%\label{} S&= \sqrt{S^2}=8.25 \end{align} The following MATLAB code can be used to obtain these values: x=[176.2,157.9,160.1,180.9,165.1,167.2,162.9,155.7,166.2]; m=mean(x); v=var(x); s=std(x); Now, our test statistic is \begin{align} W(X_1,X_2, \cdots, X_9)&=\frac{\overline{X}-\mu_0}{S / \sqrt{n}}\\ &=\frac{165.8-170}{8.25 / 3}=-1.52 \end{align} Thus, $|W|=1.52$. Also, we have \begin{align} t_{\frac{\alpha}{2},n-1} = t_{0.025,8} \approx 2.31 \end{align} The above value can be obtained in MATLAB using the command $\mathtt{tinv(0.975,8)}$. Thus, we conclude \begin{align} |W| \leq t_{\frac{\alpha}{2},n-1}. \end{align} Therefore, we accept $H_0$. In other words, we do not have enough evidence to conclude that the average height in the city is different from the average height in the country.

Let us summarize what we have obtained for the two-sided test for the mean.

One-sided Tests for the Mean:

• As before, we define the test statistic as \begin{align}%\label{} W(X_1,X_2, \cdots,X_n)=\frac{\overline{X}-\mu_0}{\sigma / \sqrt{n}}. \end{align} If $H_0$ is true (i.e., $\mu \leq \mu_0$), we expect $\overline{X}$ (and thus $W$) to be relatively small, while if $H_1$ is true, we expect $\overline{X}$ (and thus $W$) to be larger. This suggests the following test: Choose a threshold, and call it $c$. If $W \leq c$, accept $H_0$, and if $W>c$, accept $H_1$. How do we choose $c$? If $\alpha$ is the required significance level, we must have \begin{align} P(\textrm{type I error}) &= P(\textrm{Reject }H_0 \; | \; H_0) \\ &= P(W > c \; | \; \mu \leq \mu_0) \leq \alpha. \end{align} Here, the probability of type I error depends on $\mu$. More specifically, for any $\mu \leq \mu_0$, we can write \begin{align} P(\textrm{type I error} \; | \; \mu) &= P(\textrm{Reject }H_0 \; | \; \mu) \\ &= P(W > c \; | \; \mu)\\ &=P \left(\frac{\overline{X}-\mu_0}{\sigma / \sqrt{n}}> c \; | \; \mu\right)\\ &=P \left(\frac{\overline{X}-\mu}{\sigma / \sqrt{n}}+\frac{\mu-\mu_0}{\sigma / \sqrt{n}}> c \; | \; \mu\right)\\ &=P \left(\frac{\overline{X}-\mu}{\sigma / \sqrt{n}}> c+\frac{\mu_0-\mu}{\sigma / \sqrt{n}} \; | \; \mu\right)\\ &\leq P \left(\frac{\overline{X}-\mu}{\sigma / \sqrt{n}}> c \; | \; \mu\right) \quad (\textrm{ since }\mu \leq \mu_0)\\ &=1-\Phi(c) \quad \big(\textrm{ since given }\mu, \frac{\overline{X}-\mu}{\sigma / \sqrt{n}} \sim N(0,1) \big). \end{align} Thus, we can choose $\alpha=1-\Phi(c)$, which results in \begin{align} c=z_{\alpha}. \end{align} Therefore, we accept $H_0$ if \begin{align} \frac{\overline{X}-\mu_0}{\sigma / \sqrt{n}} \leq z_{\alpha}, \end{align} and reject it otherwise.

$\quad$ $H_0$: $\mu \geq \mu_0$, $\quad$ $H_1$: $\mu \lt \mu_0$,

Hypothesis Testing Calculator Online

Hypothesis testing is a foundational method used in statistics to infer the validity of a hypothesis about a population parameter. The Hypothesis Testing Calculator facilitates this process by automating the computations necessary for the t-test , a method used to compare sample means against a hypothesized mean or against each other. Let’s delve into the formulas this calculator uses to execute one-sample and two-sample t-tests.

One-Sample t-Test

This test is used to determine if the mean (x̄) of your sample is statistically different from a hypothesized population mean (μ₀).

• t is the test statistic
• x̄ is the sample mean
• μ₀ is the hypothesized population mean
• s is the sample standard deviation
• n is the sample size (number of observations)

Two-Sample t-Test

This formula compares the means of two independent groups (x̄₁ and x̄₂), with variations for equal and unequal variances.

Equal Variances:

• x̄₁ and x̄₂ are the means of the first and second sample, respectively
• s pooled is the pooled standard deviation (calculated from both samples)
• n₁ and n₂ are the sizes of the first and second sample, respectively

Unequal Variances (Welch’s t-Test):

t = (x̄₁ – x̄₂) / (√((s₁² / n₁) + (s₂² / n₂)))

• x̄₁ is the mean of the first sample
• x̄₂ is the mean of the second sample
• s₁ and s₂ are the standard deviations of the first and second sample, respectively

Table of Critical t-Values

The following table provides critical t-values for different confidence levels and degrees of freedom which are typically use to determine the cutoff points at which the null hypothesis is reject.

These values are crucial in hypothesis testing as they help define the threshold for significance, assisting users of the calculator in interpreting their results accurately.

Consider a scenario where a school administrator wants to test if the average test score of the students this semester differs from a hypothesized mean of 70%. Using the one-sample t-test:

• Sample mean (x̄) = 74%
• Hypothesized mean (μ₀) = 70%
• Sample standard deviation (s) = 8%
• Sample size (n) = 36

Using the one-sample t-test formula:

t = (74 – 70) / (8 / √36) = (4 / 1.333) = 3.00

The calculated t-value is 3.00. Using the critical t-values table, at 95% confidence level and 35 degrees of freedom, the critical value is approximately 2.030. Since 3.00 > 2.030, the null hypothesis is reject, indicating a significant difference from the hypothesize mean.

Most Common FAQs

The p-value represents the probability of obtaining test results at least as extreme as the results observed, under the assumption that the null hypothesis is correct. A low p-value (typically below 0.05) indicates strong evidence against the null hypothesis, hence it is usually rejected.

Use a one-sample t-test when comparing the mean of a single sample to a known standard or hypothesized mean. Use a two-sample t-test when comparing the means of two independent groups to see if there is a statistically significant difference between them.

Yes, while the t-test is specifically design for means, the principles of hypothesis testing apply to other parameters such as proportions and variances. Which can also be tested using appropriate versions of hypothesis tests such as the z-test and F-test.

🚀 Upgrade Your Calculations with AI-Powered Precision!

Solve any problem in a snap with Calculatorshub Ai Calculator.

Related Calculators

Le Chatelier’s Principle Calculator Online

K and J Magnetics Calculator Online

Mass of Moon Calculator Online

Electrostatic Calculator Online

WKG Calculator Online

Richter Scale Calculator Online

Fick’s Calculator Online

Viscosity of Air Calculator Online

Young Modulus Calculator Online

Reduced Mass Calculator Online

Leave a Comment Cancel reply

Save my name, email, and website in this browser for the next time I comment.

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Unit 12: Significance tests (hypothesis testing)

About this unit.

Significance tests give us a formal process for using sample data to evaluate the likelihood of some claim about a population value. Learn how to conduct significance tests and calculate p-values to see how likely a sample result is to occur by random chance. You'll also see how we use p-values to make conclusions about hypotheses.

The idea of significance tests

• Simple hypothesis testing (Opens a modal)
• Idea behind hypothesis testing (Opens a modal)
• Examples of null and alternative hypotheses (Opens a modal)
• P-values and significance tests (Opens a modal)
• Comparing P-values to different significance levels (Opens a modal)
• Estimating a P-value from a simulation (Opens a modal)
• Using P-values to make conclusions (Opens a modal)
• Simple hypothesis testing Get 3 of 4 questions to level up!
• Writing null and alternative hypotheses Get 3 of 4 questions to level up!
• Estimating P-values from simulations Get 3 of 4 questions to level up!

Error probabilities and power

• Introduction to Type I and Type II errors (Opens a modal)
• Type 1 errors (Opens a modal)
• Examples identifying Type I and Type II errors (Opens a modal)
• Introduction to power in significance tests (Opens a modal)
• Examples thinking about power in significance tests (Opens a modal)
• Consequences of errors and significance (Opens a modal)
• Type I vs Type II error Get 3 of 4 questions to level up!
• Error probabilities and power Get 3 of 4 questions to level up!

Tests about a population proportion

• Constructing hypotheses for a significance test about a proportion (Opens a modal)
• Conditions for a z test about a proportion (Opens a modal)
• Reference: Conditions for inference on a proportion (Opens a modal)
• Calculating a z statistic in a test about a proportion (Opens a modal)
• Calculating a P-value given a z statistic (Opens a modal)
• Making conclusions in a test about a proportion (Opens a modal)
• Writing hypotheses for a test about a proportion Get 3 of 4 questions to level up!
• Conditions for a z test about a proportion Get 3 of 4 questions to level up!
• Calculating the test statistic in a z test for a proportion Get 3 of 4 questions to level up!
• Calculating the P-value in a z test for a proportion Get 3 of 4 questions to level up!
• Making conclusions in a z test for a proportion Get 3 of 4 questions to level up!

Tests about a population mean

• Writing hypotheses for a significance test about a mean (Opens a modal)
• Conditions for a t test about a mean (Opens a modal)
• Reference: Conditions for inference on a mean (Opens a modal)
• When to use z or t statistics in significance tests (Opens a modal)
• Example calculating t statistic for a test about a mean (Opens a modal)
• Using TI calculator for P-value from t statistic (Opens a modal)
• Using a table to estimate P-value from t statistic (Opens a modal)
• Comparing P-value from t statistic to significance level (Opens a modal)
• Free response example: Significance test for a mean (Opens a modal)
• Writing hypotheses for a test about a mean Get 3 of 4 questions to level up!
• Conditions for a t test about a mean Get 3 of 4 questions to level up!
• Calculating the test statistic in a t test for a mean Get 3 of 4 questions to level up!
• Calculating the P-value in a t test for a mean Get 3 of 4 questions to level up!
• Making conclusions in a t test for a mean Get 3 of 4 questions to level up!

More significance testing videos

• Hypothesis testing and p-values (Opens a modal)
• One-tailed and two-tailed tests (Opens a modal)
• Z-statistics vs. T-statistics (Opens a modal)
• Small sample hypothesis test (Opens a modal)
• Large sample proportion hypothesis testing (Opens a modal)

Other calculators ...

Free statistical calculators, test for one mean calculator, description, required input, computational notes.

This procedure calculates the difference of an observed mean with a hypothesized value. A significance value (P-value) and 95% Confidence Interval (CI) of the observed mean is reported. The P-value is the probability of obtaining the observed mean in the sample if the null hypothesis value were the true value.

The P-value is the area of the t distribution with n −1 degrees of freedom, that falls outside ± t (see Values of the t distribution table).

How to cite this page

“extremely user friendly”

“truly amazing!”

“so easy to use!”

Statistics Calculator

You want to analyze your data effortlessly? DATAtab makes it easy and online.

Online Statistics Calculator

What do you want to calculate online? The online statistics calculator is simple and uncomplicated! Here you can find a list of all implemented methods!

Create charts online with DATAtab

Create your charts for your data directly online and uncomplicated. To do this, insert your data into the table under Charts and select which chart you want.

The advantages of DATAtab

Statistics, as simple as never before..

DATAtab is a modern statistics software, with unique user-friendliness. Statistical analyses are done with just a few clicks, so DATAtab is perfect for statistics beginners and for professionals who want more flow in the user experience.

Directly in the browser, fully flexible.

Directly in the browser, fully flexible. DATAtab works directly in your web browser. You have no installation and maintenance effort whatsoever. Wherever and whenever you want to use DATAtab, just go to the website and get started.

All the statistical methods you need.

DATAtab offers you a wide range of statistical methods. We have selected the most central and best known statistical methods for you and do not overwhelm you with special cases.

Data security is a top priority.

All data that you insert and evaluate on DATAtab always remain on your end device. The data is not sent to any server or stored by us (not even temporarily). Furthermore, we do not pass on your data to third parties in order to analyze your user behavior.

Many tutorials with simple examples.

In order to facilitate the introduction, DATAtab offers a large number of free tutorials with focused explanations in simple language. We explain the statistical background of the methods and give step-by-step explanations for performing the analyses in the statistics calculator.

Practical Auto-Assistant.

DATAtab takes you by the hand in the world of statistics. When making statistical decisions, such as the choice of scale or measurement level or the selection of suitable methods, Auto-Assistants ensure that you get correct results quickly.

Charts, simple and clear.

With DATAtab data visualization is fun! Here you can easily create meaningful charts that optimally illustrate your results.

New in the world of statistics?

DATAtab was primarily designed for people for whom statistics is new territory. Beginners are not overwhelmed with a lot of complicated options and checkboxes, but are encouraged to perform their analyses step by step.

Online survey very simple.

DATAtab offers you the possibility to easily create an online survey, which you can then evaluate immediately with DATAtab.

Our references

Alternative to statistical software like SPSS and STATA

DATAtab was designed for ease of use and is a compelling alternative to statistical programs such as SPSS and STATA. On datatab.net, data can be statistically evaluated directly online and very easily (e.g. t-test, regression, correlation etc.). DATAtab's goal is to make the world of statistical data analysis as simple as possible, no installation and easy to use. Of course, we would also be pleased if you take a look at our second project Statisty .

Extensive tutorials

Descriptive statistics.

Here you can find out everything about location parameters and dispersion parameters and how you can describe and clearly present your data using characteristic values.

Hypothesis Test

Here you will find everything about hypothesis testing: One sample t-test , Unpaired t-test , Paired t-test and Chi-square test . You will also find tutorials for non-parametric statistical procedures such as the Mann-Whitney u-Test and Wilcoxon-Test . mann-whitney-u-test and the Wilcoxon test

The regression provides information about the influence of one or more independent variables on the dependent variable. Here are simple explanations of linear regression and logistic regression .

Correlation

Correlation analyses allow you to analyze the linear association between variables. Learn when to use Pearson correlation or Spearman rank correlation . With partial correlation , you can calculate the correlation between two variables to the exclusion of a third variable.

Partial Correlation

The partial correlation shows you the correlation between two variables to the exclusion of a third variable.

Levene Test

The Levene Test checks your data for variance equality. Thus, the levene test is used as a prerequisite test for many hypothesis tests .

The p-value is needed for every hypothesis test to be able to make a statement whether the null hypothesis is accepted or rejected.

Distributions

DATAtab provides you with tables with distributions and helpful explanations of the distribution functions. These include the Table of t-distribution and the Table of chi-squared distribution

Contingency table

With a contingency table you can get an overview of two categorical variables in the statistics.

Equivalence and non-inferiority

In an equivalence trial, the statistical test aims at showing that two treatments are not too different in characteristics and a non-inferiority trial wants to show that an experimental treatment is not worse than an established treatment.

If there is a clear cause-effect relationship between two variables, then we can speak of causality. Learn more about causality in our tutorial.

Multicollinearity

Multicollinearity is when two or more independent variables have a high correlation.

Effect size for independent t-test

Learn how to calculate the effect size for the t-test for independent samples.

Reliability analysis calculator

On DATAtab, Cohen's Kappa can be easily calculated online in the Cohen’s Kappa Calculator . there is also the Fleiss Kappa Calculator . Of course, the Cronbach's alpha can also be calculated in the Cronbach's Alpha Calculator .

Analysis of variance with repeated measurement

Repeated measures ANOVA tests whether there are statistically significant differences in three or more dependent samples.

Cite DATAtab: DATAtab Team (2024). DATAtab: Online Statistics Calculator. DATAtab e.U. Graz, Austria. URL https://datatab.net

One Sample T Test Calculator

Enter sample data, reporting results in apa style, one sample t-test, what is a one sample t-test, how to use the one sample t test calculator, calculators.

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

• Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
• Duis aute irure dolor in reprehenderit in voluptate
• Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

S.3.1 hypothesis testing (critical value approach).

The critical value approach involves determining "likely" or "unlikely" by determining whether or not the observed test statistic is more extreme than would be expected if the null hypothesis were true. That is, it entails comparing the observed test statistic to some cutoff value, called the " critical value ." If the test statistic is more extreme than the critical value, then the null hypothesis is rejected in favor of the alternative hypothesis. If the test statistic is not as extreme as the critical value, then the null hypothesis is not rejected.

Specifically, the four steps involved in using the critical value approach to conducting any hypothesis test are:

• Specify the null and alternative hypotheses.
• Using the sample data and assuming the null hypothesis is true, calculate the value of the test statistic. To conduct the hypothesis test for the population mean μ , we use the t -statistic \(t^*=\frac{\bar{x}-\mu}{s/\sqrt{n}}\) which follows a t -distribution with n - 1 degrees of freedom.
• Determine the critical value by finding the value of the known distribution of the test statistic such that the probability of making a Type I error — which is denoted \(\alpha\) (greek letter "alpha") and is called the " significance level of the test " — is small (typically 0.01, 0.05, or 0.10).
• Compare the test statistic to the critical value. If the test statistic is more extreme in the direction of the alternative than the critical value, reject the null hypothesis in favor of the alternative hypothesis. If the test statistic is less extreme than the critical value, do not reject the null hypothesis.

Example S.3.1.1

Mean gpa section  .

In our example concerning the mean grade point average, suppose we take a random sample of n = 15 students majoring in mathematics. Since n = 15, our test statistic t * has n - 1 = 14 degrees of freedom. Also, suppose we set our significance level α at 0.05 so that we have only a 5% chance of making a Type I error.

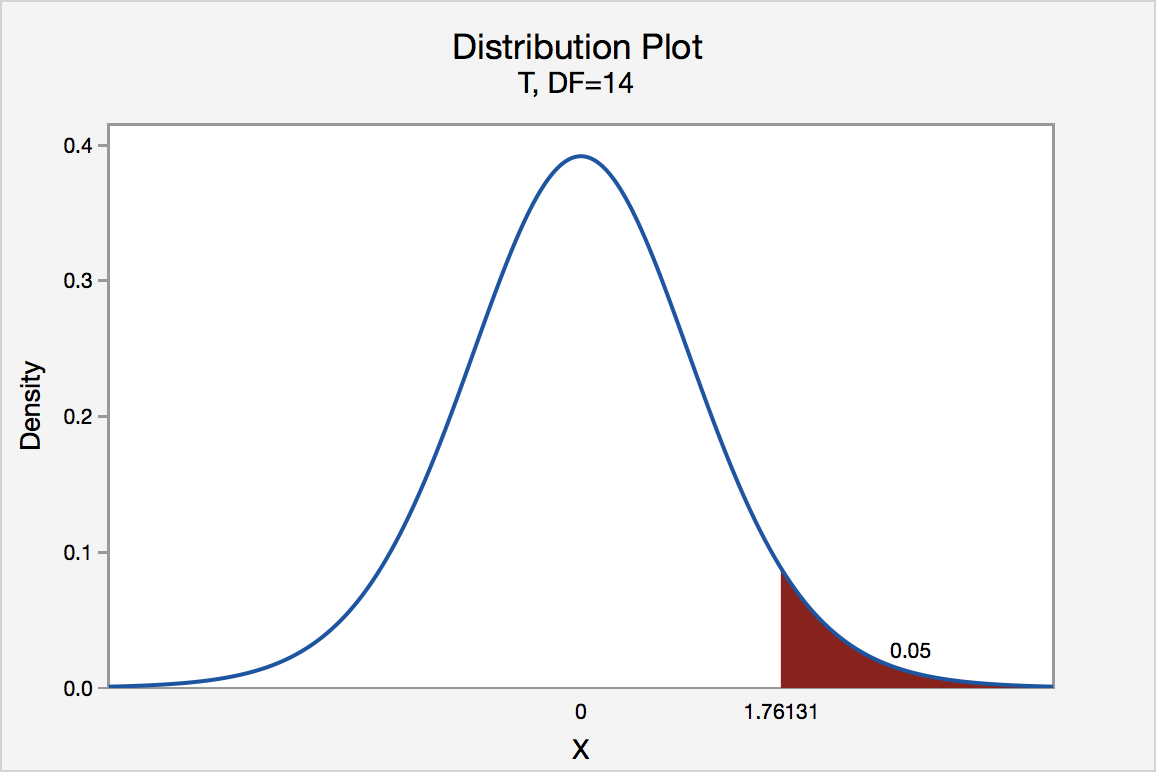
Right-Tailed

The critical value for conducting the right-tailed test H 0 : μ = 3 versus H A : μ > 3 is the t -value, denoted t \(\alpha\) , n - 1 , such that the probability to the right of it is \(\alpha\). It can be shown using either statistical software or a t -table that the critical value t 0.05,14 is 1.7613. That is, we would reject the null hypothesis H 0 : μ = 3 in favor of the alternative hypothesis H A : μ > 3 if the test statistic t * is greater than 1.7613. Visually, the rejection region is shaded red in the graph.

Left-Tailed

The critical value for conducting the left-tailed test H 0 : μ = 3 versus H A : μ < 3 is the t -value, denoted -t ( \(\alpha\) , n - 1) , such that the probability to the left of it is \(\alpha\). It can be shown using either statistical software or a t -table that the critical value -t 0.05,14 is -1.7613. That is, we would reject the null hypothesis H 0 : μ = 3 in favor of the alternative hypothesis H A : μ < 3 if the test statistic t * is less than -1.7613. Visually, the rejection region is shaded red in the graph.

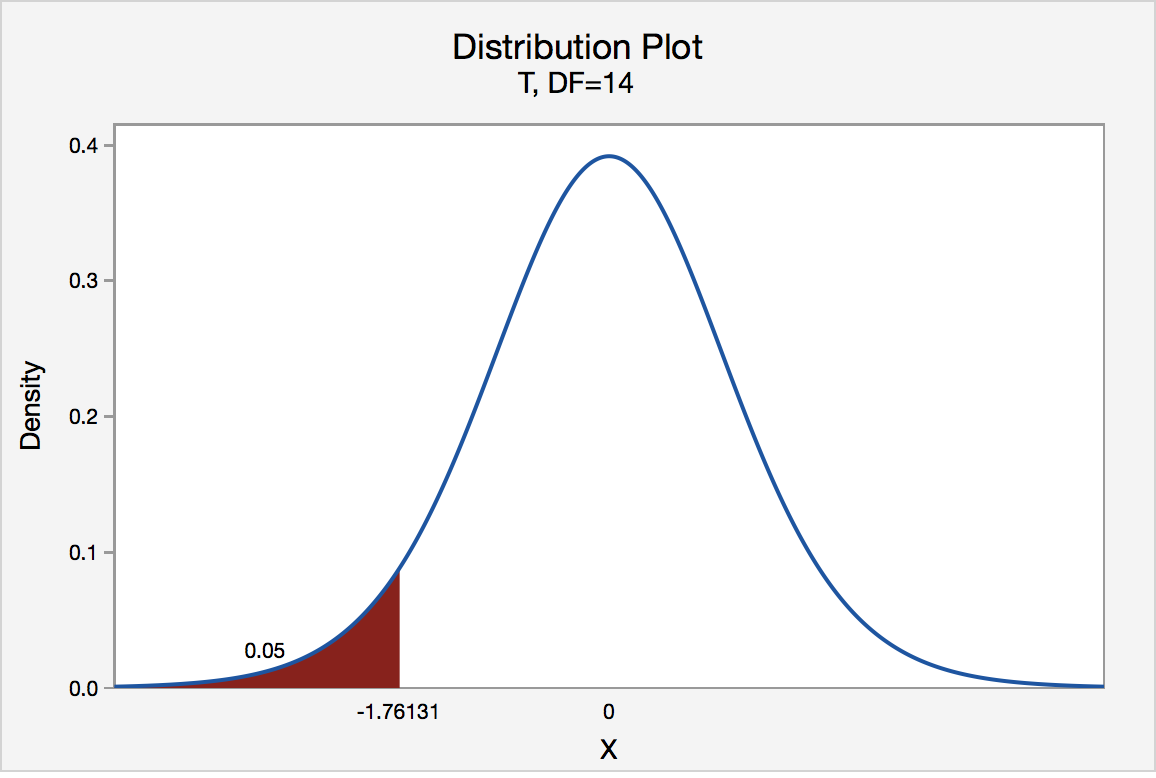
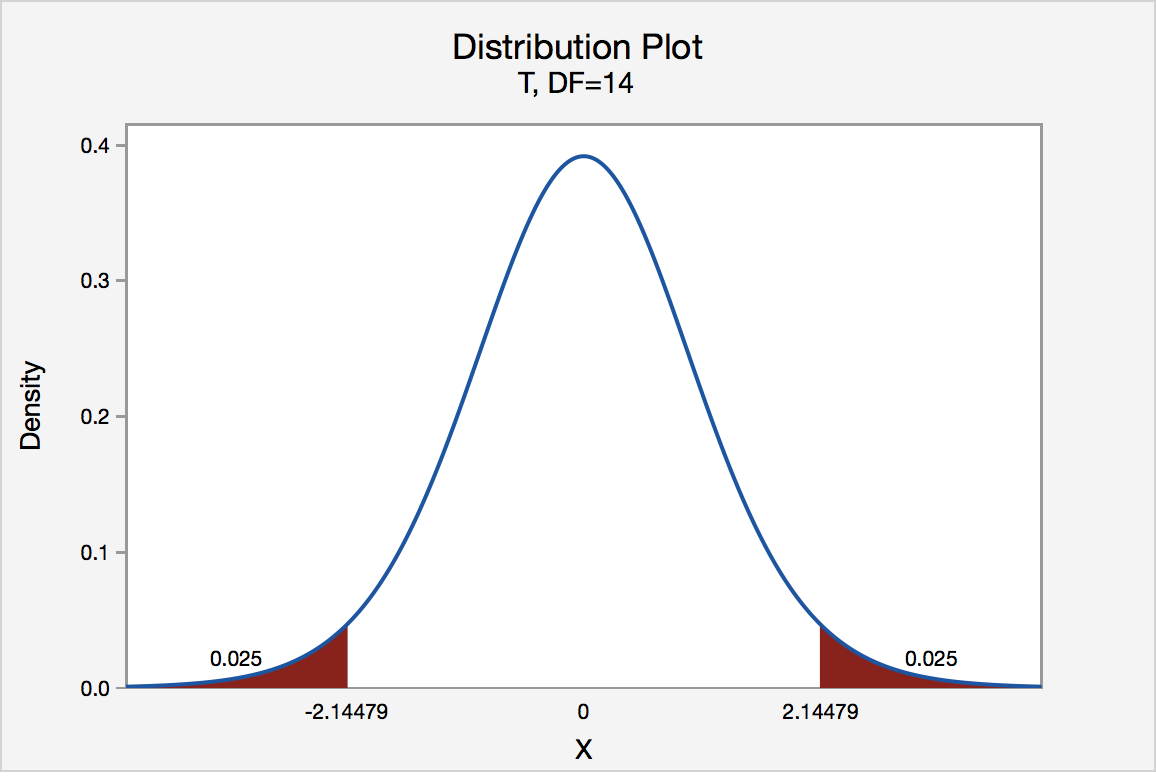
There are two critical values for the two-tailed test H 0 : μ = 3 versus H A : μ ≠ 3 — one for the left-tail denoted -t ( \(\alpha\) / 2, n - 1) and one for the right-tail denoted t ( \(\alpha\) / 2, n - 1) . The value - t ( \(\alpha\) /2, n - 1) is the t -value such that the probability to the left of it is \(\alpha\)/2, and the value t ( \(\alpha\) /2, n - 1) is the t -value such that the probability to the right of it is \(\alpha\)/2. It can be shown using either statistical software or a t -table that the critical value -t 0.025,14 is -2.1448 and the critical value t 0.025,14 is 2.1448. That is, we would reject the null hypothesis H 0 : μ = 3 in favor of the alternative hypothesis H A : μ ≠ 3 if the test statistic t * is less than -2.1448 or greater than 2.1448. Visually, the rejection region is shaded red in the graph.

• 1-800-234-2933
• [email protected]

Hypothesis testing for the mean Calculator

How does the Hypothesis testing for the mean Calculator work?

What 1 formula is used for the hypothesis testing for the mean calculator, what 7 concepts are covered in the hypothesis testing for the mean calculator.

An Automated Online Math Tutor serving 8.1 million parents and students in 235 countries and territories.

Our Services

• All Subjects
• A.I. Training Data and Analytics
• Get Paid as an Affiliate

Top Categories

• Trigonometry
• Pre-Algebra
• Pre-Calculus
• Post a Math Problem

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants

Scientific Calculator

• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

29: Hypothesis Test for a Population Proportion Calculator

• Last updated
• Save as PDF
• Page ID 8351

• Larry Green
• Lake Tahoe Community College

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

hypothesis test for a population Proportion calculator

Fill in the sample size, n, the number of successes, x, the hypothesized population proportion \(p_0\), and indicate if the test is left tailed, <, right tailed, >, or two tailed, \(\neq\).  Then hit "Calculate" and the test statistic and p-Value will be calculated for you.