heron's formula case study

CBSE Expert

CBSE Case Study Questions Class 9 Maths Chapter 12 Heron’s Formula PDF Download

CBSE Case Study Questions Class 9 Maths Chapter 12  are very important to solve for your exam. Class 9 Maths Chapter 12 Case Study Questions have been prepared for the latest exam pattern. You can check your knowledge by solving  case study-based   questions for Class 9 Maths Chapter 12  Heron’s Formula

Case Study Questions Class 9 Maths Chapter 12

Case Study 1: A group of students is learning about Heron’s Formula for finding the area of a triangle. They encountered the following scenario:

Rohan and Kavya came across a triangular field in their village. They made the following observations:

• The lengths of the three sides of the triangular field are 8 meters, 12 meters, and 15 meters.
• The perimeter of the triangular field is 35 meters.

Based on this information, the students were asked to apply Heron’s Formula to find the area of the triangular field. Let’s see if you can answer the questions correctly:

MCQ Questions:

Q1. The semiperimeter of the triangular field is: (a) 8 meters (b) 12 meters (c) 15 meters (d) 17.5 meters

Answer: (d) 17.5 meters

Q2. Using Heron’s Formula, the area of the triangular field is: (a) 24 square meters (b) 30 square meters (c) 36 square meters (d) 40 square meters

Answer: (b) 30 square meters

Q3. The type of triangle formed by the sides of the field is: (a) Equilateral (b) Isosceles (c) Scalene (d) Right-angled

Answer: (c) Scalene

Q4. The length of the altitude corresponding to the side of 15 meters is: (a) 2 meters (b) 4 meters (c) 6 meters (d) 8 meters

Answer: (c) 6 meters

Q5. The lengths of the altitudes corresponding to the sides of 8 meters and 12 meters are: (a) 4 meters and 6 meters (b) 6 meters and 8 meters (c) 8 meters and 10 meters (d) 10 meters and 12 meters

Answer: (a) 4 meters and 6 meters

Case Study 2: A group of students is studying Heron’s Formula for finding the area of a triangle. They encountered the following scenario:

Neha and Mohan went on a field trip to a riverbank. They noticed a triangular piece of land that they wanted to measure and calculate its area. They made the following observations:

• Neha measured the lengths of the three sides of the triangular piece of land as 7 meters, 9 meters, and 11 meters.
• Mohan measured the lengths of the three sides of the same triangular piece of land as 10 meters, 12 meters, and 15 meters.

Based on this information, the students were asked to apply Heron’s Formula to find the area of the triangular piece of land. Let’s see if you can answer the questions correctly:

Q1. Using Neha’s measurements, the semiperimeter of the triangular piece of land is: (a) 13 meters (b) 16 meters (c) 19 meters (d) 23 meters

Answer: (c) 19 meters

Q2. Using Neha’s measurements, the area of the triangular piece of land is: (a) 24 square meters (b) 26 square meters (c) 28 square meters (d) 30 square meters

Answer: (a) 24 square meters

Q3. Using Mohan’s measurements, the semiperimeter of the triangular piece of land is: (a) 16 meters (b) 18 meters (c) 21 meters (d) 25 meters

Answer: (c) 21 meters

Q4. Using Mohan’s measurements, the area of the triangular piece of land is: (a) 40 square meters (b) 42 square meters (c) 45 square meters (d) 48 square meters

Answer: (b) 42 square meters

Q5. The measurements taken by Neha represent a triangle that is: (a) Equilateral (b) Isosceles (c) Scalene (d) Right-angled

Hope the information shed above regarding Case Study and Passage Based Questions for Case Study Questions Class 9 Maths Chapter 12 Heron’s Formula with Answers Pdf free download has been useful to an extent. If you have any other queries about Case Study Questions Class 9 Maths Chapter 12 Heron’s Formula and Passage-Based Questions with Answers, feel free to comment below so that we can revert back to us at the earliest possible.

Leave a Comment Cancel reply

Save my name, email, and website in this browser for the next time I comment.

Download India's best Exam Preparation App Now.

Key Features

• Revision Notes
• Important Questions
• Previous Years Questions
• Case-Based Questions
• Assertion and Reason Questions

No thanks, I’m not interested!

Test: Heron`s Formula- Case Based Type Questions - Class 9 MCQ

10 questions mcq test - test: heron`s formula- case based type questions, direction: isosceles triangles were used to construct a bridge in which the base (unequal side) of an isosceles triangle is 4 cm and its perimeter is 20 cm. q. what is the length of equal sides.

So, x + x + 4 = 20

2x + 4 = 20

2x = 20 – 4

x = 16/2 = 8 cm.

Direction: Isosceles triangles were used to construct a bridge in which the base (unequal side) of an isosceles triangle is 4 cm and its perimeter is 20 cm. Q. If the sides of a triangle are in the ratio 3 : 5 : 7 and its perimeter is 300 m. Find its area.

100√2 m 2

500√2 m 2

1500√3 m 2

200√3 m 2

Let the sides of a triangle are a = 3x, b = 5x, c = 7x

Then a + b + c = 300

3x + 5x + 7x = 300

So, a = 60, b = 100, c = 140

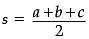
= 300/2 = 150

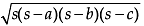
Direction: Isosceles triangles were used to construct a bridge in which the base (unequal side) of an isosceles triangle is 4 cm and its perimeter is 20 cm. Q. What is the Heron's formula for the area of?

{Area} = area

s = semi-perimeter

a = length of side a

b = length of side b

c = length of side c

Isosceles triangles were used to construct a bridge in which the base (unequal side) of an isosceles triangle is 4 cm and its perimeter is 20 cm. What is the semi perimeter of the Isosceles triangle?

Required semi perimeter = Perimeter/2 = 20/2 = 10 m.

Direction: Isosceles triangles were used to construct a bridge in which the base (unequal side) of an isosceles triangle is 4 cm and its perimeter is 20 cm.

Q. What is the area of highlighted triangle ?

Thus, area of the triangle

Direction: Shakshi prepared a Rangoli in triangular shape on Diwali. She makes a small triangle under a big triangle as shown in figure.

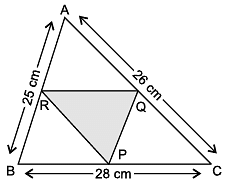
Sides of big triangle are 25 cm, 26 cm and 28 cm. Also, ΔPQR is formed by joining mid points of sides of ΔABC.

Use the above data to help her in resolving below doubts.

Q. What is the semi-perimeter of ΔABC?

= (25 + 26 + 28) cm = 79 cm

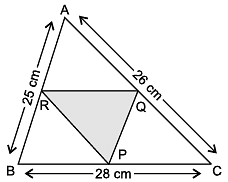
Q. Area of ΔPQR =

where s is the semi-perimeter of ΔPQR.

Q. ½ of AB =

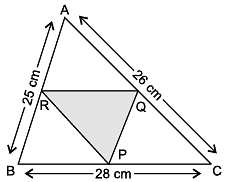
Q. What is the length of RQ?

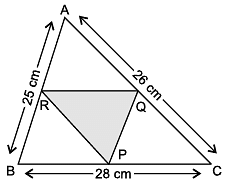
Q. If colourful rope is to be placed along the sides of small ΔPQR. What is the length of the rope?

= (12.5 + 13 + 14) cm

Top Courses for Class 9

Important Questions for Heron`s Formula- Case Based Type Questions

Heron`s formula- case based type questions mcqs with answers, online tests for heron`s formula- case based type questions, welcome back, create your account for free.

Forgot Password

Forgot password? New user? Sign up

Existing user? Log in

Heron's Formula

Already have an account? Log in here.

• Jubayer Nirjhor
• Mahindra Jain
• Syed Hamza Khalid
• Sravanth C.
• Sathvik Acharya
• A Former Brilliant Member

Proof of Heron's Formula

Additional problems.

Heron's formula is a formula that can be used to find the area of a triangle, when given its three side lengths. It can be applied to any shape of triangle, as long as we know its three side lengths. The formula is as follows:

The area of a triangle whose side lengths are \(a, b,\) and \(c\) is given by \[A=\sqrt{s(s-a)(s-b)(s-c)},\] where \(s=\dfrac{(\text{perimeter of the triangle})}{2}=\dfrac{a+b+c}{2}\), semi-perimeter of the triangle. Other useful forms are \[\begin{align} A&=\frac 1 4\sqrt{(a+b+c)(a+b-c)(a-b+c)(-a+b+c)}\\ \\ A&=\frac 1 4\sqrt{ \big[(a+b+c)(a+b-c) \big] \times \Big[\big(+(a-b)+c\big)\big(-(a-b)+c\big) \Big]}\\ A&=\frac 1 4\sqrt{\Big[(a+b)^2-c^2\Big] \times \ \Big[c^2-(a-b)^2\Big] }\\ \\ A&=\frac{1}{4}\sqrt{4a^2b^2-\big(a^2+b^2-c^2\big)^2}\\ A&=\frac{1}{4}\sqrt{2\left(a^2 b^2+a^2c^2+b^2c^2\right)-\left(a^4+b^4+c^4\right)} \\ A&=\frac{1}{4}\sqrt{\left(a^2+b^2+c^2\right)^2-2\left(a^4+b^4+c^4\right)}. \end{align}\]

Although this seems to be a bit tricky (in fact, it is), it might come in handy when we have to find the area of a triangle, and we have no other information other than its three side lengths.

This formula follows from the area formula \(A=\frac{1}{2}ab\sin C\). By the law of cosines , \(\cos C=\frac{a^2+b^2-c^2}{2ab}\). Substituting into the Pythagorean identity \(\sin C=\sqrt{1-\cos^2 C}\) yields Heron's formula (after a series of algebraic manipulations). \(_\square\)

Find the area of the triangle below. Imgur Since the three side lengths are all equal to 6, the semiperimeter is \(s=\frac{6+6+6}{2}=9\). Therefore the area of the triangle is \[A=\sqrt{9\times(9-6)\times(9-6)\times(9-6)}=9\sqrt{3}.\ _\square\]

Find the area of the triangle below. Imgur Since the three side lengths are 4, 5, and 7, the semiperimeter is \(s=\frac{4+5+7}{2}=8\). Therefore the area of the triangle is \[A=\sqrt{8\times(8-4)\times(8-5)\times(8-7)}=4\sqrt{6}.\ _\square\]

What is the area of a triangle with side lengths 13, 14, and 15? Since the three side lengths are 13, 14, and 15, the semiperimeter is \(s=\frac{13+14+15}{2}=21\). Therefore the area of the triangle is \[A=\sqrt{21\times(21-13)\times(21-14)\times(21-15)}=84.\ _\square\]

Find the area of the triangle below. Imgur Since the three side lengths are 6, 8, and 10, the semiperimeter is \(s=\frac{6+8+10}{2}=12\). Therefore the area of the triangle is \[A=\sqrt{12\times(12-6)\times(12-8)\times(12-10)}=24.\ _\square\]

Find the area of a triangle with side lengths \(4,13\) and \(15\). We have \(a=4, b=13, c=15\) and \(s=\frac{4+13+15}{2}=16\). Hence, \[A = \sqrt{16(16-4)(16-13)(16-15)} = 24. \ _\square\]

Find the area of the triangle outlined in black. Image We can use the Pythagorean theorem to find that the side lengths are \( 5, \sqrt{ 29}, 2 \sqrt{10} \). If we used the direct form of \( A = \sqrt{ s (s-a)(s-b)(s-c) } \), we will quickly get into a huge mess because these lengths are not integers. Instead, we will use an alternate form of Heron's formula: \[\begin{align} A & = \frac{1}{4}\sqrt{2\big(a^2 b^2+a^2c^2+b^2c^2\big)-\big(a^4+b^4+c^4\big)} \\ & = \frac{1}{4} \sqrt{ 2 ( 25 \times 29 + 25 \times 40 + 29 \times 40) - 25^2 - 29^2 - 40^2 } \\ & = \frac{1}{4} \sqrt{ 2704 } \\ & = 13. \ _\square \end{align}\] Note: This triangle appears in Composite Figures , which is an easier approach.

What is the area of a triangle with sides of length 13, 14, and 15?

If \(\triangle \text{JAY}\) has side lengths 10, 8, and 4, then the area of the triangle can be expressed as \(\sqrt{\, \overline{abc}\, }\), where \(\overline{abc}\) is a \(3\)-digit number. Find \(a+b+c\).

In the figure to the right, the areas of the squares \(A, B,\) and \(C\) are 388, 153, and 61, respectively.

Find the area of the blue triangle.

Problem Loading...

Note Loading...

Set Loading...

Heron's Formula

Heron's formula was first given by Heron of Alexandria. It is used to find the area of different types of triangles like equilateral, isosceles, and scalene triangles or quadrilaterals. We can use heron's formula to find the area of triangles when the sides of the triangle are given. We use the semi-perimeter of the triangle and the side lengths to find the area of the triangle using heron's formula.

In this lesson, we will find how to determine the value of the area of triangles or quadrilaterals using Heron's formula with the help of solved examples for a better understanding of the application of the formula.

What is Heron's Formula?

Heron's formula is used to determine the area of triangles when lengths of all their sides are given or to find the area of quadrilaterals . We also know it as Hero's formula. This formula for finding the area does not depend on the angles of a triangle. It solely depends on the lengths of all sides of triangles. It contains the term "s" which is known as semi-perimeter, which is obtained by halving the perimeter of a triangle. Similarly, this concept of finding the area is further extended to determine the area of quadrilaterals as well.

History of Heron's Formula

Heron's formula was written in 60 CE by Heron of Alexandria. He was a Greek Engineer and Mathematician who determined the value of the area of the triangle using only the lengths of its sides and further extended it to calculate areas of quadrilaterals. He used this formula to prove the trigonometric laws such as Laws of cosines or Laws of cotangents.

Heron's Formula Definition

Area of triangle ABC = √s(s-a)(s-b)(s-c), where s = Perimeter/2 = (a + b + c)/2

Example: Find the area of a triangle whose lengths are 5 units, 6 units, and 9 units respectively.

Solution: As we know, a = 5 units, b = 6 units and c = 9 units

Thus, Semi-perimeter, s = (a + b + c)/2 = (5 + 6 + 9)/2 = 10 units

Area of triangle = √(s(s-a)(s-b)(s-c)) = √(10(10-5)(10-6)(10-9))

⇒ Area of triangle = √(10 × 5 × 4 × 1) = √200 = 14.142 unit 2

∴ The area of the triangle is 14.142 unit 2

Heron's Formula for Area of Triangle Proof

We will use some Pythagoras theorem , area of a triangle formula, and algebraic identities to derive Heron's formula. Let us take a triangle having lengths of sides, a, b, and c. Let the semi-perimeter of the triangle ABC be "s", the perimeter of the triangle ABC is "P" and the area of triangle ABC is "A". Let us assume the side length b is divided into two parts p and q as a perpendicular(h) falls from the vertex B on the side AC at point M. Consider the triangle below:

As we know, the area of a triangle = (1/2) b × h where b is the base and h is the height of the triangle. Let us begin to calculate the value of h.

Thus, as per the image, b = p + q

⇒ q = b - p ....(1)

On squaring both sides we get,

⇒ q 2 = b 2 + p 2 - 2bp ....(2)

Adding h 2 on both sides we get,

q 2 + h 2 = b 2 + p 2 - 2bp + h 2 ....(3)

Applying Pythagoras Theorem in the triangle BCM we get,

h 2 + q 2 = a 2 ....(4)

Applying Pythagoras Theorem in the triangle MBA we get,

p 2 + h 2 = c 2 ....(5)

Substituting the value of (4) and (5) in (3) we get,

q 2 + h 2 = b 2 + p 2 - 2bp + h 2

⇒ a 2 = b 2 + c 2 - 2bp

⇒ p = (b 2 + c 2 - a 2 )/2b ....(6)

p 2 + h 2 = c 2

⇒ h 2 = c 2 - p 2 = (c + p) (c - p) ....(7) (As a 2 - b 2 = (a+b)(a-b))

Substituting (6) in (7) we get,

h 2 = (c + p) (c - p)

⇒ h 2 = (c + (b 2 + c 2 - a 2 )/2b) (c - (b 2 + c 2 - a 2 )/2b)

⇒ h 2 = ((2bc + b 2 + c 2 - a 2 )/2b) ((2bc - b 2 - c 2 + a 2 )/2b)

⇒ h 2 = ((b + c) 2 - a 2 )/2b) ((a 2 - (b - c) 2 )/2b)

⇒ h 2 = ((b + c + a)(b + c - a)(a + b - c)(a - b + c))/4b 2 ) ....(8) (As a 2 - b 2 = (a+b)(a-b))

As perimeter of triangle is P = a + b + c and P = 2s. (Here s = semi-perimeter and s = P/2)

∴ 2s = a + b + c ....(9)

Substituting (9) in (8) we get,

h 2 = ((b + c + a)(b + c - a)(a + b - c)(a - b + c))/4b 2 )

⇒ h 2 = (2s × (2s - 2a) × (2s - 2b) × (2s - 2c))/4b 2 )

⇒ h 2 = (2s × 2(s - a) × 2(s - b) × 2(s - c))/4b 2 )

⇒ h 2 = 16s(s - a)(s - b)(s - c)/4b 2

⇒ h = √(4s(s - a)(s - b)(s - c)/b 2 )

⇒ h = 2√(s(s - a)(s - b)(s - c))/b ....(10)

Area of triangle ABC, A = (1/2) × base × height

⇒ A = (1/2) × b × h

⇒ A = (1/2) × b × 2√(s(s - a)(s - b)(s - c))/b (From (10))

⇒ A = √(s(s - a)(s - b)(s - c))

∴ Area of the triangle ABC = √(s(s - a)(s - b)(s - c)) unit 2

Area of Triangle By Heron's Formula?

The steps to determine the area using Heron's formula are:

• Step 1: Find the perimeter of the given triangle.
• Step 2: Find the semi-perimeter by halving the perimeter.
• Step 3: Find the area of the triangle using Heron's formula √(s(s - a)(s - b)(s - c)).
• Step 4: Once the value is determined, write the unit at the end (For example, m 2 , cm 2 , or in 2 ).

Heron's Formula for Equilateral Triangle

An equilateral triangle has all sides of the same length. Thus, in this case, the lengths of all sides are equal. Let us assume the length of all sides is "a", semi-perimeter is "s" and the area of the equilateral triangle is "A". Thus, the semi-perimeter of the triangle is s = (a + a + a)/2 = 3a/2

Area of the equilateral triangle, A = √(s(s-a)(s-b)(s-c)) = √((3a/2)((3a/2)-a)((3a/2)-a)((3a/2)-a))

⇒ A = √((3a/2)(3a/2-a) 3 ) = √((3a/2)(a/2) 3 )

⇒ A = √((3a × a 3 )/2 × 8) = √(3a 4 /16) = (√3 × a 2 )/4

Heron's Formula for Scalene Triangle

A scalene triangle has all lengths of different sides. Let us assume the length of sides is a, b, c, semi-perimeter is "s" and the area of the scalene triangle is "A". Area of scalene triangle = √s(s-a)(s-b)(s-c), where s = (a + b + c)/2

Heron's Formula for Isosceles Triangle

An isosceles triangle has two sides of equal length. Let us assume the length of the two sides is a and one side is b, semi-perimeter is "s" and the area of the isosceles triangle is "A". Thus, the semi-perimeter of the triangle is s = (a + a + b)/2 = (a+b/2)

Area of the isosceles triangle, A = √(s(s-a)(s-b)(s-c)) = √(a+b/2)((a+b/2)-a)((a+b/2)-a)((a+b/2)-b))

⇒ A = √(a+b/2)((b/2)(b/2)(a-b/2))= √((a 2 - (b/2) 2 )(b/2) 2 )

⇒ A = √(a 2 - (b 2 /4))× (b 2 /4)) = (b/4)√(4a 2 - b 2 )

Heron's Formula for Area of Quadrilateral

We can use Heron's formula to determine the formula for the area of the quadrilateral by dividing it into two triangles. Let us say we have a quadrilateral ABCD with the length of its sides measuring a, b, c, and d. Let us say A and B are joined to show the diagonal of the quadrilateral having length e.

• The area of triangle ADC = √(s(s - a)(s - d)(s - e)), where s = (a + d + e)/2
• The area of triangle ABC = √(s'(s' - b)(s' - c)(s' - e)), where s' = (b + c + e)/2

Thus, area of quadrilateral ABCD = Area of triangle ADC + Area of triangle ABC

⇒ Area of quadrilateral ABCD = √(s(s - a)(s - d)(s - e)) + √(s'(s' - b)(s' - c)(s' - e))

Applications of Heron's Formula

Heron's formula has numerous applications. They are:

• It can be used to determine the area of different types of triangles if the lengths of their different sides are given.
• It can be used to find the area of the quadrilateral if the lengths of all its sides are given.

Application of Heron's Formula in Finding Area of Quadrilateral

The application of Heron's formula in finding the area of the quadrilateral is that it can be used to determine the area of any irregular quadrilateral by converting the quadrilateral into triangles.

Important Notes on Heron's Formula

• Heron's formula is used to find the area of a triangle when all its sides are given.
• We can use heron's formula to find the area of the quadrilateral by dividing it into two triangles.
• The formula uses the semi-perimeter and side of lengths of a triangle.

Related Articles

• Herons Formula Calculator
• Area of Triangle Calculator
• Area of Scalene Triangle
• Area of a Quadrilateral Calculator

Heron's Formula Examples

Example 1: If the length of the sides of a triangle ABC are 4 in, 3 in, and 5 in. Calculate its area using the heron's formula.

Solution: To find: Area of the triangle ABC.

Given that, AB = 4 in, BC = 3 in, AC = 5 in (let)

Using Heron's Formula,

A = √(s(s-a)(s-b)(s-c))

As, s = (a+b+c)/2 s = (4+3+5)/2 s = 6 units

Put the values, A = √(6(6-4)(6-3)(6-5)) ⇒ A = √(6(2)(3)(1)) ⇒ A = √(36) = 6 in 2

Answer: ∴ The area of the triangle is 6 in 2 .

Example 2: The area of an equilateral triangle is √3 squared units. Find the length of the sides of the triangle.

Solution: To find: The length of the sides of the triangle. Area = √3 unit 2 (given) Let the length of the triangle is "a" unit.

Using Heron's Formula, Area of equilateral triangle = (√3 × a 2 )/4 √3 = (√3 × a 2 )/4 ⇒ a 2 = 4 ⇒ a = √4 = 2 units

Answer: ∴ The length of the sides of the equilateral triangle is 2 units.

Example 3: Calculate the area of an isosceles triangle using Heron's formula if the lengths of its sides are 4 units, 8 units, and 8 units.

Solution: To find: Area of triangle Given the lengths of sides are 4 units, 8 units, and 8 units.

Using Heron's Formula, A = √(s(s-a)(s-b)(s-c))

As, s = (4 + 8 + 8)/2 = 10 units

A = √(10(10-4)(10-8)(10-8)) ⇒ A = √(10 × 6 × 2 × 2) ⇒ A = 15.491 unit 2

Answer: ∴ The area of the isosceles triangle is 15.491 unit 2 .

Example 4: What is the area of the quadrilateral ABCD shown in the figure below using Heron's formula?

Solution: Note that we have only been given the lengths of the four sides, but not the length of any diagonal. Fortunately, AB and AD are perpendiculars, which means that the Pythagoras theorem can be used to calculate BD:

In triangle ABD, Given a = 4 units, b = 5 units and c = 4 units s = (4 + 5 + 3)/2 = 6 units A = √(s(s-a)(s-b)(s-c)) = √(6(6-4)(6-5)(6-3)) = 6 unit 2

In triangle CDB, Given a = 3 units, b = 5 units and c = 5 units s = (3 + 5 + 5)/2 = 13/2 units A = √(s(s-a)(s-b)(s-c)) = √((13/2)((13/2)-3)((13/2)-5)((13/2)-5)) = 7.15 unit 2

Area of ABCD = Area of triangle ABD + Area of triangle CDB ⇒ Area of ABCD = (6 + 7.15) unit 2 = 13.15 unit 2

Answer: ∴ The area of the quadrilateral is 13.15 unit 2 .

go to slide go to slide go to slide go to slide

Book a Free Trial Class

Heron's Formula Questions

go to slide go to slide go to slide

FAQs on Heron's Formula

What is heron's formula for area of triangle.

Heron's formula is used to find the area of the triangle when the lengths of all triangles are given. It can be used to determine areas of different types of triangles, equilateral, isosceles, or scalene triangles. For a triangle having three sides, a, b, and c, semi-perimeter, s, and area of triangle A, the semi-perimeter and area of the triangle are given as (a + b + c)/2 and √s(s-a)(s-b)(s-c) respectively.

How Does Heron's Formula Work?

The heron's formula depends only on the semi-perimeter of a triangle and the length of its three sides. We first determine the value of the semi-perimeter using the lengths of three sides of the triangle. Once the value of the semi-perimeter is obtained we can find the area of the shape.

Who Discovered Heron's Formula?

Heron's Formula was discovered by Heron of Alexandria (also known as Hero of Alexandria) who was a Greek Engineer and Mathematician. He found the area of the triangle using only the lengths of its sides which made it possible to apply to any type of triangle be it, equilateral, isosceles, or scalene. This formula was further extended by him to calculate areas of quadrilaterals and proved the trigonometric laws such as Laws of cosines or Laws of cotangents.

What Does S Stand for in Heron's Formula?

S stands for semi-perimeter in Heron's formula. It is obtained by halving the value of the perimeter.

Can We Use Heron's Formula In Equilateral Triangle?

Yes, we can use Heron's formula in an equilateral triangle. The area of an equilateral triangle is given as (√3 × a 2 )/4 unit 2 .

How to Derive Heron's Formula?

We can derive Heron's formula by using the Pythagoras theorem, area of a triangle formula, and algebraic identities. We construct an altitude from the top vertex to the base of the triangle, which divides the triangle into 2 triangles. Thereby applying the Pythagoras theorem, on both triangles and substituting the values obtained we derive Heron's formula.

How to Find Area of Trapezium Using Heron's Formula?

We can find the area of the trapezium by drawing a perpendicular from one of the vertices at the top to the base. Once this is done we obtain one parallelogram and a triangle. In this case, the area of the trapezium can be found by adding the area of a parallelogram and a triangle. Now, the area of the parallelogram can be found by using the formula of the area of a parallelogram or by dividing the parallelogram into two parts by drawing a diagonal. In this case, we obtain three triangles. Thus, we calculate the area of all the 3 triangles using Heron's formula. In either case, area values are calculated individually and then are added to obtain the value of the area of trapezium .

Where is Heron's Formula Used?

Heron's formula is used to determine the value of the area of any type of triangle, area of quadrilaterals, and area of polygons when the lengths of their sides are given.

How to Find Height of a Triangle with Heron's Formula?

As Heron's formula gives the value of the area of the triangle, it is equal to the area of the triangle obtained by the formula (1/2) × base × height. Thus, we can obtain the value of the height of the triangle.

How to Solve Heron's Formula Questions?

We solve Heron's formula questions using the below steps:

• Step 1: First find the perimeter of the given triangle.
• Step 2: Now, divide the perimeter by 2 to obtain the semi-perimeter.
• Step 3: Use the semi-perimeter to find the area of the triangle using Heron's formula √(s(s - a)(s - b)(s - c)).
• Step 4: Write the unit at the end once the value of the area is obtained(For example, m 2 , cm 2 , or in 2 ).

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Course: Class 9   >   Unit 10

• Heron's formula
• Heron's Formula 10.1

Finding area of triangle using Heron's formula

• Your answer should be
• an integer, like 6 ‍  
• a simplified proper fraction, like 3 / 5 ‍  
• a simplified improper fraction, like 7 / 4 ‍  
• a mixed number, like 1   3 / 4 ‍  
• an exact decimal, like 0.75 ‍  

• School Guide
• Class 9 Syllabus
• Maths Notes Class 9
• Science Notes Class 9
• History Notes Class 9
• Geography Notes Class 9
• Political Science Notes Class 9
• NCERT Soln. Class 9 Maths
• RD Sharma Soln. Class 9
• Math Formulas Class 9
• CBSE Class 9 Maths Revision Notes

Chapter 1: Number System

• Number System in Maths
• Natural Numbers | Definition, Examples, Properties
• Whole Numbers | Definition, Properties and Examples
• Rational Number: Definition, Examples, Worksheet
• Irrational Numbers- Definition, Identification, Examples, Symbol, Properties
• Real Numbers
• Decimal Expansion of Real Numbers
• Decimal Expansions of Rational Numbers
• Representation of Rational Numbers on the Number Line | Class 8 Maths
• Represent √3 on the number line
• Operations on Real Numbers
• Rationalization of Denominators
• Laws of Exponents for Real Numbers

Chapter 2: Polynomials

• Polynomials in One Variable - Polynomials | Class 9 Maths
• Polynomial Formula
• Types of Polynomials
• Zeros of Polynomial
• Factorization of Polynomial
• Remainder Theorem
• Factor Theorem
• Algebraic Identities

Chapter 3: Coordinate Geometry

• Coordinate Geometry
• Cartesian Coordinate System in Maths
• Cartesian Plane

Chapter 4: Linear equations in two variables

• Linear Equations in One Variable
• Linear Equation in Two Variables
• Graph of Linear Equations in Two Variables
• Graphical Methods of Solving Pair of Linear Equations in Two Variables
• Equations of Lines Parallel to the x-axis and y-axis

Chapter 5: Introduction to Euclid's Geometry

• Euclidean Geometry
• Equivalent Version of Euclid’s Fifth Postulate

Chapter 6: Lines and Angles

• Lines and Angles
• Types of Angles
• Pairs of Angles - Lines & Angles
• Transversal Lines
• Angle Sum Property of a Triangle

Chapter 7: Triangles

• Triangles in Geometry
• Congruence of Triangles |SSS, SAS, ASA, and RHS Rules
• Theorem - Angle opposite to equal sides of an isosceles triangle are equal | Class 9 Maths
• Triangle Inequality

Chapter 8: Quadrilateral

• Angle Sum Property of a Quadrilateral
• Quadrilateral - Definition, Properties, Types, Formulas, Examples
• Introduction to Parallelogram: Properties, Types, and Theorem
• Rhombus: Definition, Properties, Formula, Examples
• Kite - Quadrilaterals
• Properties of Parallelograms
• Mid Point Theorem

Chapter 9: Areas of Parallelograms and Triangles

• Area of Triangle | Formula and Examples
• Area of Parallelogram
• Figures on the Same Base and between the Same Parallels

Chapter 10: Circles

• Circles in Maths
• Radius of Circle
• Tangent to a Circle
• What is the longest chord of a Circle?
• Circumference of Circle - Definition, Perimeter Formula, and Examples
• Angle subtended by an arc at the centre of a circle
• What is Cyclic Quadrilateral
• Theorem - The sum of opposite angles of a cyclic quadrilateral is 180° | Class 9 Maths

Chapter 11: Construction

• Basic Constructions - Angle Bisector, Perpendicular Bisector, Angle of 60°
• Construction of Triangles

Chapter 12: Heron's Formula

• Area of Equilateral Triangle
• Area of Isosceles Triangle
• Heron's Formula
• Applications of Heron's Formula
• Area of Quadrilateral
• Area of Polygons

Chapter 13: Surface Areas and Volumes

• Surface Area of Cuboid
• Volume of Cuboid | Formula and Examples
• Surface Area of Cube
• Volume of a Cube
• Surface Area of Cylinder (CSA and TSA) |Formula, Derivation, Examples
• Volume of Cylinder
• Surface Area of Cone
• Volume of Cone | Formula, Derivation and Examples
• Surface Area of Sphere | CSA, TSA, Formula and Derivation
• Volume of a Sphere
• Surface Area of a Hemisphere
• Volume of Hemisphere

Chapter 14: Statistics

• Collection and Presentation of Data
• Graphical Representation of Data
• Bar graphs and Histograms
• Central Tendency
• Mean, Median and Mode

Chapter 15: Probability

• Experimental Probability
• Empirical Probability
• CBSE Class 9 Maths Formulas
• NCERT Solutions for Class 9 Maths
• RD Sharma Class 9 Solutions

Applications of Heron’s Formula

While solving and finding the Area of a Triangle, Certain parameters are expected to be provided beforehand, for example, the height and the base of the triangle must be available Or in case of an Equilateral Triangle, the lengths of the side should be given.

Area of triangle is usually given by,

Where base and height are measured from the given triangle. But sometimes it might happen that we don’t have that information. Suppose we only have information about the length of the sides. Height is not known, how will the area be calculated then? 

The answer to this question is Heron’s formula. 

Heron was born in Egypt in about 10AD. He was a great mathematician, he worked in applied mathematics. His great deal of work revolved around squares, rectangles. This formula is also called “Hero’s Formula”. 

Heron’s Formula

Heron’s Formula is also known as Hero’s formula, it is named after a very famous engineer of Egypt, He was famous and known as the “Hero of Alexandria”, His famous works include Heron’s formula, Vending machine, etc. The best part about Heron’s formula was that it did not require any angle or distance prior to solving the area of any Triangle.

Let’s say we have a triangle ABC whose sides are of length “a”, “b” and “c”. 

Then the area of that triangle as given by Heron, 

Where a, b and c are the length of the sides and s = semi-perimeter (Half of the perimeter)

This formula allows us to calculate the area of the triangle where the length of the altitude is not given. 

Application of Heron’s Formula in Finding Area of Triangles

Heron’s Formula can be used to find areas of different types of triangles if the length of their sides is given,

Question: Find out the area of the triangle if its sides are 3, 5, 4. 

Solution: 

Area of this triangle can be calculated by Heron’s formula studied above,  Let’s calculate semi-perimeter first,  Plugging the values of s, a, b and c in the formula. Let’s calculate the area.  Thus, the area of the triangle is 6 square units. 

Application of Heron’s Formula in Finding Area of Quadrilaterals

We know how to calculate the area of standard quadrilaterals like rectangles, squares, and trapeziums. But sometimes it might happen that our quadrilaterals are not in any of these forms.

The quadrilateral given above doesn’t lie in any of these categories, so our standard formulas cannot be used. Heron’s formula helps us in such cases. We can join any two opposite vertices in the above figure and can form two triangles. Then the area can be calculated. Let’s see some examples regarding that. 

Question: Find the area of the given rhombus using Heron’s Formula. 

There are two triangles here, both of them are similar.  The length of sides of both triangles are 100, 100 and 120.  Thus, semi perimeter for both the triangles is,  Now, calculating the area of the triangle Thus, area of a single triangle is 4800. Since, there are two equal triangles. So, the total area is 9600 sq units.

Let’s see some sample problems on these concepts, 

Sample Problems based on Heron’s Formula

Question 1: There is concrete space in the shape of a triangle that needs to be tiled. The cost of tiling is Rs 20 per square unit. Find the total cost of tiling the area. 

Answer: 

The length of given sides are 10, 10 and 10. The semi-perimeter “s” = 15 We know the area of the triangle using Heron’s formula. Here, s = 15, a = b = c = 10.  The area of the triangle is 25√3 So, the cost of tiling the area = 25√3 x 20                                               = 500√3                                              = 500 (1.73)                                              = 866 (approx) Thus, cost of tiling the area is Rs. 866. 

Question 2: The length of sides of a triangle is in ratio 3:5:4 and the perimeter is 96m. Find the area of the triangle. 

The sides are in ratio of 3:5:4. Suppose the length of the sides is 3x,5x and 4x.  3x + 5x + 4x = 96  = 12x = 96 = x = 8.  Thus, the sides are 24, 40, 32. Now let’s calculate “s” and plug in the values in Heron’s formula. 

Question 3: Let’s say the sides of the triangle are given as 3y, 4y, and 5y. Find out the expression for the area of the triangle. 

Let’s find out the perimeter and semi perimeter so that we can plug in the values in Heron’s formula.  Plugging in the values in Heron’s Formula. 

Question 4: Find out the area of the quadrilateral given below:

The quadrilateral ABCD can be divided into two triangles whose area we can compute if we join A and C.  Now we have triangles ACD and ABC. Out of which ACD is a right-angled triangle.  AC 2 = AD 2 + DC 2   ⇒ AC 2 = 9 2 + 40 2 ⇒ AC 2 = 81 + 1600  ⇒ AC 2 = 1681  ⇒ AC = 41 Area of triangle ADC = Area of triangle ABC will be calculated using Heron’s Formula. The sides of the triangle are 28,15 and 41.  Area of triangle ABC = Area of quadrilateral = Area of triangle ADC + Area of triangle ABC                                  = 180 + 126                                   = 306 sq units. 

Question 5: Let’s assume a triangle whose sides are given as 2y, 2y + 2, and 4y – 2 and its area if given by y√10.  Find out the value of y. 

Let’s calculate “s”  Comparing both sides of the equation, 

Please Login to comment...

Similar reads.

• Mathematics
• School Learning
• How to Use ChatGPT with Bing for Free?
• 7 Best Movavi Video Editor Alternatives in 2024
• How to Edit Comment on Instagram
• 10 Best AI Grammar Checkers and Rewording Tools
• 30 OOPs Interview Questions and Answers (2024)

Improve your Coding Skills with Practice

What kind of Experience do you want to share?