z test for hypothesis testing calculator

Z-test Calculator

What is a z-test, when do i use z-tests, z-test formula, p-value from z-test, two-tailed z-test and one-tailed z-test, z-test critical values & critical regions, how to use the one-sample z-test calculator, z-test examples.

This Z-test calculator is a tool that helps you perform a one-sample Z-test on the population's mean . Two forms of this test - a two-tailed Z-test and a one-tailed Z-tests - exist, and can be used depending on your needs. You can also choose whether the calculator should determine the p-value from Z-test or you'd rather use the critical value approach!

Read on to learn more about Z-test in statistics, and, in particular, when to use Z-tests, what is the Z-test formula, and whether to use Z-test vs. t-test. As a bonus, we give some step-by-step examples of how to perform Z-tests!

Or you may also check our t-statistic calculator , where you can learn the concept of another essential statistic. If you are also interested in F-test, check our F-statistic calculator .

A one sample Z-test is one of the most popular location tests. The null hypothesis is that the population mean value is equal to a given number, μ 0 \mu_0 μ 0 ​ :

We perform a two-tailed Z-test if we want to test whether the population mean is not μ 0 \mu_0 μ 0 ​ :

and a one-tailed Z-test if we want to test whether the population mean is less/greater than μ 0 \mu_0 μ 0 ​ :

Let us now discuss the assumptions of a one-sample Z-test.

You may use a Z-test if your sample consists of independent data points and:

the data is normally distributed , and you know the population variance ;

the sample is large , and data follows a distribution which has a finite mean and variance. You don't need to know the population variance.

The reason these two possibilities exist is that we want the test statistics that follow the standard normal distribution N ( 0 , 1 ) \mathrm N(0, 1) N ( 0 , 1 ) . In the former case, it is an exact standard normal distribution, while in the latter, it is approximately so, thanks to the central limit theorem.

The question remains, "When is my sample considered large?" Well, there's no universal criterion. In general, the more data points you have, the better the approximation works. Statistics textbooks recommend having no fewer than 50 data points, while 30 is considered the bare minimum.

Let x 1 , . . . , x n x_1, ..., x_n x 1 ​ , ... , x n ​ be an independent sample following the normal distribution N ( μ , σ 2 ) \mathrm N(\mu, \sigma^2) N ( μ , σ 2 ) , i.e., with a mean equal to μ \mu μ , and variance equal to σ 2 \sigma ^2 σ 2 .

We pose the null hypothesis, H 0  ⁣  ⁣ :  ⁣  ⁣   μ = μ 0 \mathrm H_0 \!\!:\!\! \mu = \mu_0 H 0 ​ :   μ = μ 0 ​ .

We define the test statistic, Z , as:

x ˉ \bar x x ˉ is the sample mean, i.e., x ˉ = ( x 1 + . . . + x n ) / n \bar x = (x_1 + ... + x_n) / n x ˉ = ( x 1 ​ + ... + x n ​ ) / n ;

μ 0 \mu_0 μ 0 ​ is the mean postulated in H 0 \mathrm H_0 H 0 ​ ;

n n n is sample size; and

σ \sigma σ is the population standard deviation.

In what follows, the uppercase Z Z Z stands for the test statistic (treated as a random variable), while the lowercase z z z will denote an actual value of Z Z Z , computed for a given sample drawn from N(μ,σ²).

If H 0 \mathrm H_0 H 0 ​ holds, then the sum S n = x 1 + . . . + x n S_n = x_1 + ... + x_n S n ​ = x 1 ​ + ... + x n ​ follows the normal distribution, with mean n μ 0 n \mu_0 n μ 0 ​ and variance n 2 σ n^2 \sigma n 2 σ . As Z Z Z is the standardization (z-score) of S n / n S_n/n S n ​ / n , we can conclude that the test statistic Z Z Z follows the standard normal distribution N ( 0 , 1 ) \mathrm N(0, 1) N ( 0 , 1 ) , provided that H 0 \mathrm H_0 H 0 ​ is true. By the way, we have the z-score calculator if you want to focus on this value alone.

If our data does not follow a normal distribution, or if the population standard deviation is unknown (and thus in the formula for Z Z Z we substitute the population standard deviation σ \sigma σ with sample standard deviation), then the test statistics Z Z Z is not necessarily normal. However, if the sample is sufficiently large, then the central limit theorem guarantees that Z Z Z is approximately N ( 0 , 1 ) \mathrm N(0, 1) N ( 0 , 1 ) .

In the sections below, we will explain to you how to use the value of the test statistic, z z z , to make a decision , whether or not you should reject the null hypothesis . Two approaches can be used in order to arrive at that decision: the p-value approach, and critical value approach - and we cover both of them! Which one should you use? In the past, the critical value approach was more popular because it was difficult to calculate p-value from Z-test. However, with help of modern computers, we can do it fairly easily, and with decent precision. In general, you are strongly advised to report the p-value of your tests!

Formally, the p-value is the smallest level of significance at which the null hypothesis could be rejected. More intuitively, p-value answers the questions: provided that I live in a world where the null hypothesis holds, how probable is it that the value of the test statistic will be at least as extreme as the z z z - value I've got for my sample? Hence, a small p-value means that your result is very improbable under the null hypothesis, and so there is strong evidence against the null hypothesis - the smaller the p-value, the stronger the evidence.

To find the p-value, you have to calculate the probability that the test statistic, Z Z Z , is at least as extreme as the value we've actually observed, z z z , provided that the null hypothesis is true. (The probability of an event calculated under the assumption that H 0 \mathrm H_0 H 0 ​ is true will be denoted as P r ( event ∣ H 0 ) \small \mathrm{Pr}(\text{event} | \mathrm{H_0}) Pr ( event ∣ H 0 ​ ) .) It is the alternative hypothesis which determines what more extreme means :

• Two-tailed Z-test: extreme values are those whose absolute value exceeds ∣ z ∣ |z| ∣ z ∣ , so those smaller than − ∣ z ∣ -|z| − ∣ z ∣ or greater than ∣ z ∣ |z| ∣ z ∣ . Therefore, we have:

The symmetry of the normal distribution gives:

• Left-tailed Z-test: extreme values are those smaller than z z z , so
• Right-tailed Z-test: extreme values are those greater than z z z , so

To compute these probabilities, we can use the cumulative distribution function, (cdf) of N ( 0 , 1 ) \mathrm N(0, 1) N ( 0 , 1 ) , which for a real number, x x x , is defined as:

Also, p-values can be nicely depicted as the area under the probability density function (pdf) of N ( 0 , 1 ) \mathrm N(0, 1) N ( 0 , 1 ) , due to:

With all the knowledge you've got from the previous section, you're ready to learn about Z-tests.

• Two-tailed Z-test:

From the fact that Φ ( − z ) = 1 − Φ ( z ) \Phi(-z) = 1 - \Phi(z) Φ ( − z ) = 1 − Φ ( z ) , we deduce that

The p-value is the area under the probability distribution function (pdf) both to the left of − ∣ z ∣ -|z| − ∣ z ∣ , and to the right of ∣ z ∣ |z| ∣ z ∣ :

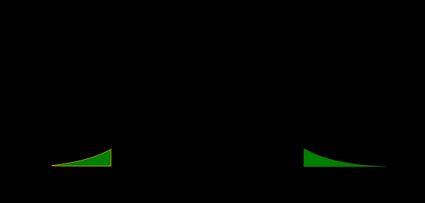
• Left-tailed Z-test:

The p-value is the area under the pdf to the left of our z z z :

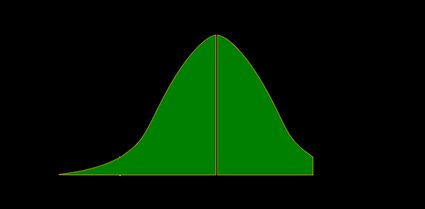
• Right-tailed Z-test:

The p-value is the area under the pdf to the right of z z z :

The decision as to whether or not you should reject the null hypothesis can be now made at any significance level, α \alpha α , you desire!

if the p-value is less than, or equal to, α \alpha α , the null hypothesis is rejected at this significance level; and

if the p-value is greater than α \alpha α , then there is not enough evidence to reject the null hypothesis at this significance level.

The critical value approach involves comparing the value of the test statistic obtained for our sample, z z z , to the so-called critical values . These values constitute the boundaries of regions where the test statistic is highly improbable to lie . Those regions are often referred to as the critical regions , or rejection regions . The decision of whether or not you should reject the null hypothesis is then based on whether or not our z z z belongs to the critical region.

The critical regions depend on a significance level, α \alpha α , of the test, and on the alternative hypothesis. The choice of α \alpha α is arbitrary; in practice, the values of 0.1, 0.05, or 0.01 are most commonly used as α \alpha α .

Once we agree on the value of α \alpha α , we can easily determine the critical regions of the Z-test:

To decide the fate of H 0 \mathrm H_0 H 0 ​ , check whether or not your z z z falls in the critical region:

If yes, then reject H 0 \mathrm H_0 H 0 ​ and accept H 1 \mathrm H_1 H 1 ​ ; and

If no, then there is not enough evidence to reject H 0 \mathrm H_0 H 0 ​ .

As you see, the formulae for the critical values of Z-tests involve the inverse, Φ − 1 \Phi^{-1} Φ − 1 , of the cumulative distribution function (cdf) of N ( 0 , 1 ) \mathrm N(0, 1) N ( 0 , 1 ) .

Our calculator reduces all the complicated steps:

Choose the alternative hypothesis: two-tailed or left/right-tailed.

In our Z-test calculator, you can decide whether to use the p-value or critical regions approach. In the latter case, set the significance level, α \alpha α .

Enter the value of the test statistic, z z z . If you don't know it, then you can enter some data that will allow us to calculate your z z z for you:

• sample mean x ˉ \bar x x ˉ (If you have raw data, go to the average calculator to determine the mean);
• tested mean μ 0 \mu_0 μ 0 ​ ;
• sample size n n n ; and
• population standard deviation σ \sigma σ (or sample standard deviation if your sample is large).

Results appear immediately below the calculator.

If you want to find z z z based on p-value , please remember that in the case of two-tailed tests there are two possible values of z z z : one positive and one negative, and they are opposite numbers. This Z-test calculator returns the positive value in such a case. In order to find the other possible value of z z z for a given p-value, just take the number opposite to the value of z z z displayed by the calculator.

To make sure that you've fully understood the essence of Z-test, let's go through some examples:

• A bottle filling machine follows a normal distribution. Its standard deviation, as declared by the manufacturer, is equal to 30 ml. A juice seller claims that the volume poured in each bottle is, on average, one liter, i.e., 1000 ml, but we suspect that in fact the average volume is smaller than that...

Formally, the hypotheses that we set are the following:

H 0  ⁣ :   μ = 1000  ml \mathrm H_0 \! : \mu = 1000 \text{ ml} H 0 ​ :   μ = 1000  ml

H 1  ⁣ :   μ < 1000  ml \mathrm H_1 \! : \mu \lt 1000 \text{ ml} H 1 ​ :   μ < 1000  ml

We went to a shop and bought a sample of 9 bottles. After carefully measuring the volume of juice in each bottle, we've obtained the following sample (in milliliters):

1020 , 970 , 1000 , 980 , 1010 , 930 , 950 , 980 , 980 \small 1020, 970, 1000, 980, 1010, 930, 950, 980, 980 1020 , 970 , 1000 , 980 , 1010 , 930 , 950 , 980 , 980 .

Sample size: n = 9 n = 9 n = 9 ;

Sample mean: x ˉ = 980   m l \bar x = 980 \ \mathrm{ml} x ˉ = 980   ml ;

Population standard deviation: σ = 30   m l \sigma = 30 \ \mathrm{ml} σ = 30   ml ;

And, therefore, p-value = Φ ( − 2 ) ≈ 0.0228 \text{p-value} = \Phi(-2) \approx 0.0228 p-value = Φ ( − 2 ) ≈ 0.0228 .

As 0.0228 < 0.05 0.0228 \lt 0.05 0.0228 < 0.05 , we conclude that our suspicions aren't groundless; at the most common significance level, 0.05, we would reject the producer's claim, H 0 \mathrm H_0 H 0 ​ , and accept the alternative hypothesis, H 1 \mathrm H_1 H 1 ​ .

We tossed a coin 50 times. We got 20 tails and 30 heads. Is there sufficient evidence to claim that the coin is biased?

Clearly, our data follows Bernoulli distribution, with some success probability p p p and variance σ 2 = p ( 1 − p ) \sigma^2 = p (1-p) σ 2 = p ( 1 − p ) . However, the sample is large, so we can safely perform a Z-test. We adopt the convention that getting tails is a success.

Let us state the null and alternative hypotheses:

H 0  ⁣ :   p = 0.5 \mathrm H_0 \! : p = 0.5 H 0 ​ :   p = 0.5 (the coin is fair - the probability of tails is 0.5 0.5 0.5 )

H 1  ⁣ :   p ≠ 0.5 \mathrm H_1 \! : p \ne 0.5 H 1 ​ :   p  = 0.5 (the coin is biased - the probability of tails differs from 0.5 0.5 0.5 )

In our sample we have 20 successes (denoted by ones) and 30 failures (denoted by zeros), so:

Sample size n = 50 n = 50 n = 50 ;

Sample mean x ˉ = 20 / 50 = 0.4 \bar x = 20/50 = 0.4 x ˉ = 20/50 = 0.4 ;

Population standard deviation is given by σ = 0.5 × 0.5 \sigma = \sqrt{0.5 \times 0.5} σ = 0.5 × 0.5 ​ (because 0.5 0.5 0.5 is the proportion p p p hypothesized in H 0 \mathrm H_0 H 0 ​ ). Hence, σ = 0.5 \sigma = 0.5 σ = 0.5 ;

• And, therefore

Since 0.1573 > 0.1 0.1573 \gt 0.1 0.1573 > 0.1 we don't have enough evidence to reject the claim that the coin is fair , even at such a large significance level as 0.1 0.1 0.1 . In that case, you may safely toss it to your Witcher or use the coin flip probability calculator to find your chances of getting, e.g., 10 heads in a row (which are extremely low!).

What is the difference between Z-test vs t-test?

We use a t-test for testing the population mean of a normally distributed dataset which had an unknown population standard deviation . We get this by replacing the population standard deviation in the Z-test statistic formula by the sample standard deviation, which means that this new test statistic follows (provided that H₀ holds) the t-Student distribution with n-1 degrees of freedom instead of N(0,1) .

When should I use t-test over the Z-test?

For large samples, the t-Student distribution with n degrees of freedom approaches the N(0,1). Hence, as long as there are a sufficient number of data points (at least 30), it does not really matter whether you use the Z-test or the t-test, since the results will be almost identical. However, for small samples with unknown variance, remember to use the t-test instead of Z-test .

How do I calculate the Z test statistic?

To calculate the Z test statistic:

• Compute the arithmetic mean of your sample .
• From this mean subtract the mean postulated in null hypothesis .
• Multiply by the square root of size sample .
• Divide by the population standard deviation .
• That's it, you've just computed the Z test statistic!

BMR - Harris-Benedict equation

Conditional probability, pie chart percentage.

• Biology (100)
• Chemistry (100)
• Construction (144)
• Conversion (295)
• Ecology (30)
• Everyday life (262)
• Finance (570)
• Health (440)
• Physics (510)
• Sports (105)
• Statistics (182)
• Other (182)
• Discover Omni (40)

Hypothesis Testing Calculator

Related: confidence interval calculator, type ii error.

The first step in hypothesis testing is to calculate the test statistic. The formula for the test statistic depends on whether the population standard deviation (σ) is known or unknown. If σ is known, our hypothesis test is known as a z test and we use the z distribution. If σ is unknown, our hypothesis test is known as a t test and we use the t distribution. Use of the t distribution relies on the degrees of freedom, which is equal to the sample size minus one. Furthermore, if the population standard deviation σ is unknown, the sample standard deviation s is used instead. To switch from σ known to σ unknown, click on $\boxed{\sigma}$ and select $\boxed{s}$ in the Hypothesis Testing Calculator.

Next, the test statistic is used to conduct the test using either the p-value approach or critical value approach. The particular steps taken in each approach largely depend on the form of the hypothesis test: lower tail, upper tail or two-tailed. The form can easily be identified by looking at the alternative hypothesis (H a ). If there is a less than sign in the alternative hypothesis then it is a lower tail test, greater than sign is an upper tail test and inequality is a two-tailed test. To switch from a lower tail test to an upper tail or two-tailed test, click on $\boxed{\geq}$ and select $\boxed{\leq}$ or $\boxed{=}$, respectively.

In the p-value approach, the test statistic is used to calculate a p-value. If the test is a lower tail test, the p-value is the probability of getting a value for the test statistic at least as small as the value from the sample. If the test is an upper tail test, the p-value is the probability of getting a value for the test statistic at least as large as the value from the sample. In a two-tailed test, the p-value is the probability of getting a value for the test statistic at least as unlikely as the value from the sample.

To test the hypothesis in the p-value approach, compare the p-value to the level of significance. If the p-value is less than or equal to the level of signifance, reject the null hypothesis. If the p-value is greater than the level of significance, do not reject the null hypothesis. This method remains unchanged regardless of whether it's a lower tail, upper tail or two-tailed test. To change the level of significance, click on $\boxed{.05}$. Note that if the test statistic is given, you can calculate the p-value from the test statistic by clicking on the switch symbol twice.

In the critical value approach, the level of significance ($\alpha$) is used to calculate the critical value. In a lower tail test, the critical value is the value of the test statistic providing an area of $\alpha$ in the lower tail of the sampling distribution of the test statistic. In an upper tail test, the critical value is the value of the test statistic providing an area of $\alpha$ in the upper tail of the sampling distribution of the test statistic. In a two-tailed test, the critical values are the values of the test statistic providing areas of $\alpha / 2$ in the lower and upper tail of the sampling distribution of the test statistic.

To test the hypothesis in the critical value approach, compare the critical value to the test statistic. Unlike the p-value approach, the method we use to decide whether to reject the null hypothesis depends on the form of the hypothesis test. In a lower tail test, if the test statistic is less than or equal to the critical value, reject the null hypothesis. In an upper tail test, if the test statistic is greater than or equal to the critical value, reject the null hypothesis. In a two-tailed test, if the test statistic is less than or equal the lower critical value or greater than or equal to the upper critical value, reject the null hypothesis.

When conducting a hypothesis test, there is always a chance that you come to the wrong conclusion. There are two types of errors you can make: Type I Error and Type II Error. A Type I Error is committed if you reject the null hypothesis when the null hypothesis is true. Ideally, we'd like to accept the null hypothesis when the null hypothesis is true. A Type II Error is committed if you accept the null hypothesis when the alternative hypothesis is true. Ideally, we'd like to reject the null hypothesis when the alternative hypothesis is true.

Hypothesis testing is closely related to the statistical area of confidence intervals. If the hypothesized value of the population mean is outside of the confidence interval, we can reject the null hypothesis. Confidence intervals can be found using the Confidence Interval Calculator . The calculator on this page does hypothesis tests for one population mean. Sometimes we're interest in hypothesis tests about two population means. These can be solved using the Two Population Calculator . The probability of a Type II Error can be calculated by clicking on the link at the bottom of the page.

• By IIT Bombay Learn HTML Java Tutorial Django Tutorial PHP Tutorial
• On-Demand (Videos) Core Python Certification Complete Python Certification Course Online Create Own Cryptocurrency C Programming Online
• Live Courses (1:1 Live Sesions) Coding For Kids Online C Programming Complete Python For Kids Online Essential Python For Kids Online Complete C++ Programming For Kids
• For Kids Coding For Kids Online C Programming Essential Python For Kids Online Complete Python For Kids Online C Programming For Kids Complete C++ Programming For Kids

EVM - Cryptocurrency

Cryptocurrency

Z-test Calculator

Streamline your statistical calculations with the z-test calculator by newtum.

Discover the power of our Z-test Calculator, expertly developed by Newtum. This essential tool simplifies statistical testing, making it accessible for professionals and students alike. Unveil the mysteries of z-scores and enhance your data analysis skills.

Understanding the Statistical Significance Tool

The Z-test Calculator is a statistical tool designed to determine if there is a significant difference between sample and population means. It's ideal for researchers and students engaged in hypothesis testing and data analysis.

Z-test Calculation Formula Explained

Learn the critical formula used in the Z-test Calculator and its significance in statistical analysis. Understanding this formula is vital for accurate hypothesis testing and research conclusions.

• Define the null and alternative hypotheses.
• Calculate the sample mean (x̄) and population mean (μ).
• Determine the standard deviation (σ) and the sample size (n).
• Compute the standard error of the mean (σ/√n).
• Use the formula Z = (x̄ - μ) / (σ/√n) to calculate the Z-score.

Step-by-Step Guide to Using the Z-test Calculator

Our Z-test Calculator is incredibly user-friendly. Just follow the simple instructions below, and you'll be on your way to obtaining quick and accurate z-score results.

• Enter the sample mean into the designated field.
• Input the population mean.
• Provide the standard deviation of the population.
• Specify the sample size.
• Click 'Calculate' to get your Z-score and p-value.

Discover the Superior Features of Our Z-test Calculator

• User-Friendly Interface: Navigate with ease.
• Instant Results: Get your answers without delays.
• Data Security: Your data remains on your device.
• Accessibility Across Devices: Use on any modern device.
• No Installation Needed: Access directly from your browser.
• Examples for Clarity: Understand with practical scenarios.
• Transparent Process: No hidden steps or calculations.
• Educational Resource: Enhance your statistical knowledge.
• Responsive Customer Support: We're here to assist you.
• Regular Updates: Benefit from the latest features.
• Privacy Assurance: Your data is safe with us.
• Efficient Age Retrieval: Quick and accurate.
• Language Accessibility: Use in your preferred language.
• Engaging and Informative Content: Learn while you use.
• Fun and Interactive Learning: Enjoy the process.
• Shareable Results: Easily export your findings.
• Responsive Design: Works flawlessly on any screen size.
• Educational Platform Integration: Perfect for e-learning environments.
• Comprehensive Documentation: All the information you need.

Applications and Use Cases for the Z-test Calculator

• Analyze the difference between sample means and population means.
• Validate research findings with statistical significance.
• Enhance academic projects with precise hypothesis testing.
• Apply in various scientific and market research studies.
• Utilize in quality control processes for product consistency.

Illustrating the Z-test Calculator with Practical Examples

Example 1: Suppose your sample mean (x) is 105, the population mean (y) is 100, the population standard deviation is 15, and the sample size is 30. Plugging these into the Z-test formula, we get a Z-score, which we then compare against the standard normal distribution.

Example 2: If your sample mean is 130, the population mean is 120, the standard deviation is 20, and the sample size is 50, the Z-test Calculator will give you a Z-score indicating the probability of this difference occurring by chance.

Ensuring Data Security with the Z-test Calculator

Our Z-test Calculator not only provides precise statistical analysis but also guarantees the utmost data security. As the calculations are performed entirely within your browser, your data never leaves your computer, ensuring complete confidentiality. This tool is a crucial asset for users who prioritize privacy while seeking reliable statistical solutions. Rest assured that with our Z-test Calculator, your data is processed securely without any risk of server-side exposure.

Frequently Asked Questions About Z-test Calculator

• What is a Z-test Calculator used for?
• How accurate is the Z-test Calculator?
• Can I use the Z-test Calculator for any sample size?
• Is there a cost associated with using the Z-test Calculator?
• How does the Z-test Calculator ensure the privacy of my data?

People also viewed

104, Building No. 5, Sector 3, Millennium Business Park, Mahape, Navi Mumbai - 400710

• Core Python Certification
• Create Own Cryptocurrency
• Python for Kids
• Learn HTML (IIT)
• Learn PHP(IIT)
• Java Tutorial (IIT)
• Django Tutorial (IIT)
• C Prog. for Kids
• Python For Kids Online
• C++ for Kids
• Verify Certificate
• Book Free Demo
• Online Compiler
• Generate Genesis Block

Copyright © 2024 Newtum. All Right Reserved.

• Privacy policy
• Terms & Conditions

• Insert this widget code anywhere inside the body tag
• Use the code as it is for proper working.
• Z-Test Calculator

Z-Test (Z 0 , Z e & H 0 ) Calculator

getcalc.com's Z-test calculator to estimate Z-statistic (Z 0 ), critical value (Z e ) from normal distribution table for given degrees of freedom (ν) & hypothesis test (H 0 ) to conduct the test of significance for mean, difference between two means , proportion & difference between two proportions for large sample mean, proportion or difference between two means or proportions in statistical surveys & experiments. In addition, users can generate the complete work with steps for any corresponding input values to solve grade school Z-test worksheet problems. Users also use the population standard deviation & sample mean calculators seperately to calculate the corresponding values.

Z-Test (Large Samples) & its Applications

Z-test is the statistical technique which represents how many standard deviation or standard error the sample mean or proportion (p value) is away from the population mean or success proportions (p value) to check if the test of hypothesis (significance) is accepted in statistical experiments. The Z-statistic (Z 0 ) value used to test the validity of assumptions in the test of significance. Here the difference between the hypothesized & actual value of the sample data is being analyzed to determine if the difference is significant or not. Z-statistic is applicable for the test of significance for proportion, difference between two proportions, mean or difference between two means. The probability is higher for the hypothesized value for mean or proportion to be correct, if the difference between the hypothesized & actual value is smaller. The probability is smaller for the hypothesized value for mean or proportion to be correct, if the difference between the hypothesized & actual value is higher. The sample values should be large enough or approximately equal to the population parameters and all the sampling distributions follow normal asymptotically to conduct the test of significance for large samples using z-test.

Test of Significance for Large Samples (Z 0 , Z e & H 0 ) & Formulas

Work with steps for Z-Test (Z 0 , Z e & H 0 )

This Z-test calculator for test of significance featured to generate the complete work with steps for any corresponding input values for test of significance for mean (using standard deviation), test of significance for difference between two means (using standard deviation), test of significance for proportion (using p value) and test of significance for difference between two proportions (using p value) to solve the grade school Z-statistic workout problems. Supply the input values, click on "CALCULATE" button and then "Generate Workout" to generate the complete work with steps for the input given to this calculator. The below is the solved examples for Z-statistic calculation by using standard deviation & without using standard deviation.

• Test of significance for sample mean
• Test of significance for 2 sample proportion with unknown P values
• Test of significance for difference between 2 proportions with known P values
• Z-test for difference between 2 proportions with unknown P Values
• Z-test example for difference between 2 samples with different σ 1 & σ 2
• Z-test example for difference between 2 samples with common σ
• More Expert Resources
• average of first 100 numbers
• 1/4 divided by 1/2
• 7C2: 7 choose 2
• 15 days after today
• LCM of 12 and 16
• Step-by-step Work
• 0.83 as a fraction
• 11/45 as a decimal
• 1/4 times 1/8
• 2/5 + 3/7 equals to
• 3/4 minus 1/2
• 15/75 simplified in lowest terms
• Explore More
• ideal weight of 165cm female
• ideal weight of 175cm male
• 0.67 as a fraction
• 0.24 as a fraction
• 2/3 times 4 equals to
• 3.16 as a fraction

• Basic Calculator
• Scientific Calculator
• Digital Numbers
• Algebraic Functions
• Statistics and Probability
• Finance Calculators
• Stock Market
• Geometry and Shapes
• General Purpose
• Health and Fitness
• Math Formulas
• Electrical Engineering
• Mechanical Engineering

Input 2 Proportions

Formula and output, when do you use z-test two independent sample means.

When performing a Z-test on two independent samples you want to sum the variances of the means and then take the square root to find the standard deviation of variance sum. In this example you are given the standard deviations for each sample thus you need to take the square of the standar deviations to find the variances: - Variance sample 1 = 0.26^2 = 0.0676 - Variance sample 2 = 0.22^2 = 0.0484 Now when you have the variances you use the formula for Z-test two independent samples or you can use the calculator provided. The Z-value is 3.648 which is above the critical value of 2.5758 (two tailed test), thus there is a significant difference between the soils.

• Calculators
• Descriptive Statistics
• Merchandise
• Which Statistics Test?

Z Score Calculator for 2 Population Proportions

This is a simple z score calculator that calculates the value of z (and associated p value) for two population proportions.

Further Information

The z score test for two population proportions is used when you want to know whether two populations or groups (e.g., males and females; theists and atheists) differ significantly on some single (categorical) characteristic - for example, whether they are vegetarians.

Requirements

• A random sample of each of the population groups to be compared.
• Categorial data

Null Hypothesis

H0: p1 - p2 = 0, where p1 is the proportion from the first population and p2 the proportion from the second.

As above, the null hypothesis tends to be that there is no difference between the two population proportions; or, more formally, that the difference is zero (so, for example, that there is no difference between the proportion of males who are vegetarian and the proportion of females who are vegetarian). 

Two Sample Z-Test Calculator

Enter sample data, z-test claculator, assumptions, required sample data, calculators.

Z-Test for Statistical Hypothesis Testing Explained

The Z-test is a statistical hypothesis test used to determine where the distribution of the test statistic we are measuring, like the mean , is part of the normal distribution .

There are multiple types of Z-tests, however, we’ll focus on the easiest and most well known one, the one sample mean test. This is used to determine if the difference between the mean of a sample and the mean of a population is statistically significant.

What Is a Z-Test?

A Z-test is a type of statistical hypothesis test where the test-statistic follows a normal distribution.  

The name Z-test comes from the Z-score of the normal distribution. This is a measure of how many standard deviations away a raw score or sample statistics is from the populations’ mean.

Z-tests are the most common statistical tests conducted in fields such as healthcare and data science . Therefore, it’s an essential concept to understand.

Requirements for a Z-Test

In order to conduct a Z-test, your statistics need to meet a few requirements, including:

• A Sample size that’s greater than 30. This is because we want to ensure our sample mean comes from a distribution that is normal. As stated by the c entral limit theorem , any distribution can be approximated as normally distributed if it contains more than 30 data points.
• The standard deviation and mean of the population is known .
• The sample data is collected/acquired randomly .

More on Data Science:   What Is Bootstrapping Statistics?

Z-Test Steps

There are four steps to complete a Z-test. Let’s examine each one.

4 Steps to a Z-Test

• State the null hypothesis.
• State the alternate hypothesis.
• Choose your critical value.
• Calculate your Z-test statistics. 

1. State the Null Hypothesis

The first step in a Z-test is to state the null hypothesis, H_0 . This what you believe to be true from the population, which could be the mean of the population, μ_0 :

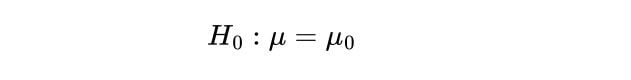
2. State the Alternate Hypothesis

Next, state the alternate hypothesis, H_1 . This is what you observe from your sample. If the sample mean is different from the population’s mean, then we say the mean is not equal to μ_0:

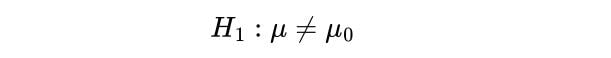
3. Choose Your Critical Value

Then, choose your critical value, α , which determines whether you accept or reject the null hypothesis. Typically for a Z-test we would use a statistical significance of 5 percent which is z = +/- 1.96 standard deviations from the population’s mean in the normal distribution:

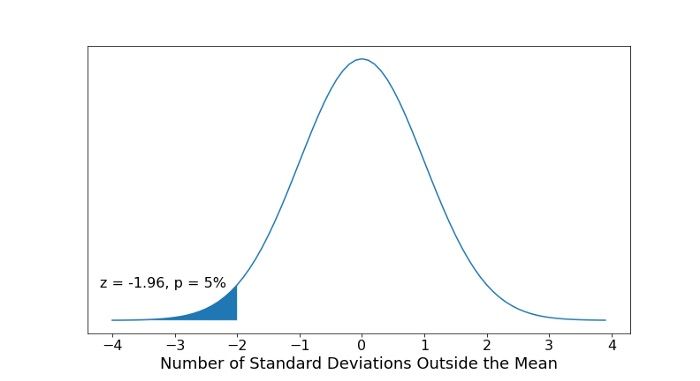
This critical value is based on confidence intervals.

4. Calculate Your Z-Test Statistic

Compute the Z-test Statistic using the sample mean, μ_1 , the population mean, μ_0 , the number of data points in the sample, n and the population’s standard deviation, σ :

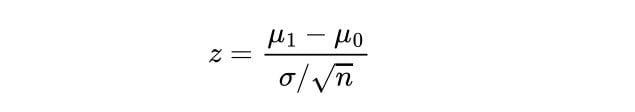
If the test statistic is greater (or lower depending on the test we are conducting) than the critical value, then the alternate hypothesis is true because the sample’s mean is statistically significant enough from the population mean.

Another way to think about this is if the sample mean is so far away from the population mean, the alternate hypothesis has to be true or the sample is a complete anomaly.

More on Data Science: Basic Probability Theory and Statistics Terms to Know

Z-Test Example

Let’s go through an example to fully understand the one-sample mean Z-test.

A school says that its pupils are, on average, smarter than other schools. It takes a sample of 50 students whose average IQ measures to be 110. The population, or the rest of the schools, has an average IQ of 100 and standard deviation of 20. Is the school’s claim correct?

The null and alternate hypotheses are:

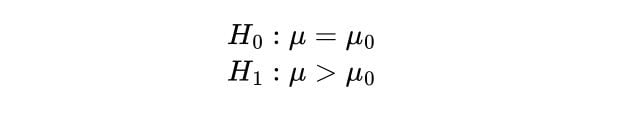
Where we are saying that our sample, the school, has a higher mean IQ than the population mean.

Now, this is what’s called a right-sided, one-tailed test as our sample mean is greater than the population’s mean. So, choosing a critical value of 5 percent, which equals a Z-score of 1.96 , we can only reject the null hypothesis if our Z-test statistic is greater than 1.96.

If the school claimed its students’ IQs were an average of 90, then we would use a left-tailed test, as shown in the figure above. We would then only reject the null hypothesis if our Z-test statistic is less than -1.96.

Computing our Z-test statistic, we see:

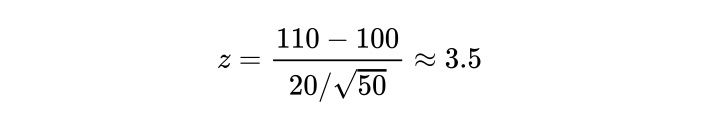
Therefore, we have sufficient evidence to reject the null hypothesis, and the school’s claim is right.

Hope you enjoyed this article on Z-tests. In this post, we only addressed the most simple case, the one-sample mean test. However, there are other types of tests, but they all follow the same process just with some small nuances.  

Built In’s expert contributor network publishes thoughtful, solutions-oriented stories written by innovative tech professionals. It is the tech industry’s definitive destination for sharing compelling, first-person accounts of problem-solving on the road to innovation.

Great Companies Need Great People. That's Where We Come In.

Z test is a statistical test that is conducted on data that approximately follows a normal distribution. The z test can be performed on one sample, two samples, or on proportions for hypothesis testing. It checks if the means of two large samples are different or not when the population variance is known.

A z test can further be classified into left-tailed, right-tailed, and two-tailed hypothesis tests depending upon the parameters of the data. In this article, we will learn more about the z test, its formula, the z test statistic, and how to perform the test for different types of data using examples.

What is Z Test?

A z test is a test that is used to check if the means of two populations are different or not provided the data follows a normal distribution. For this purpose, the null hypothesis and the alternative hypothesis must be set up and the value of the z test statistic must be calculated. The decision criterion is based on the z critical value.

Z Test Definition

A z test is conducted on a population that follows a normal distribution with independent data points and has a sample size that is greater than or equal to 30. It is used to check whether the means of two populations are equal to each other when the population variance is known. The null hypothesis of a z test can be rejected if the z test statistic is statistically significant when compared with the critical value.

Z Test Formula

The z test formula compares the z statistic with the z critical value to test whether there is a difference in the means of two populations. In hypothesis testing , the z critical value divides the distribution graph into the acceptance and the rejection regions. If the test statistic falls in the rejection region then the null hypothesis can be rejected otherwise it cannot be rejected. The z test formula to set up the required hypothesis tests for a one sample and a two-sample z test are given below.

One-Sample Z Test

A one-sample z test is used to check if there is a difference between the sample mean and the population mean when the population standard deviation is known. The formula for the z test statistic is given as follows:

z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\). \(\overline{x}\) is the sample mean, \(\mu\) is the population mean, \(\sigma\) is the population standard deviation and n is the sample size.

The algorithm to set a one sample z test based on the z test statistic is given as follows:

Left Tailed Test:

Null Hypothesis: \(H_{0}\) : \(\mu = \mu_{0}\)

Alternate Hypothesis: \(H_{1}\) : \(\mu < \mu_{0}\)

Decision Criteria: If the z statistic < z critical value then reject the null hypothesis.

Right Tailed Test:

Alternate Hypothesis: \(H_{1}\) : \(\mu > \mu_{0}\)

Decision Criteria: If the z statistic > z critical value then reject the null hypothesis.

Two Tailed Test:

Alternate Hypothesis: \(H_{1}\) : \(\mu \neq \mu_{0}\)

Two Sample Z Test

A two sample z test is used to check if there is a difference between the means of two samples. The z test statistic formula is given as follows:

z = \(\frac{(\overline{x_{1}}-\overline{x_{2}})-(\mu_{1}-\mu_{2})}{\sqrt{\frac{\sigma_{1}^{2}}{n_{1}}+\frac{\sigma_{2}^{2}}{n_{2}}}}\). \(\overline{x_{1}}\), \(\mu_{1}\), \(\sigma_{1}^{2}\) are the sample mean, population mean and population variance respectively for the first sample. \(\overline{x_{2}}\), \(\mu_{2}\), \(\sigma_{2}^{2}\) are the sample mean, population mean and population variance respectively for the second sample.

The two-sample z test can be set up in the same way as the one-sample test. However, this test will be used to compare the means of the two samples. For example, the null hypothesis is given as \(H_{0}\) : \(\mu_{1} = \mu_{2}\).

Z Test for Proportions

A z test for proportions is used to check the difference in proportions. A z test can either be used for one proportion or two proportions. The formulas are given as follows.

One Proportion Z Test

A one proportion z test is used when there are two groups and compares the value of an observed proportion to a theoretical one. The z test statistic for a one proportion z test is given as follows:

z = \(\frac{p-p_{0}}{\sqrt{\frac{p_{0}(1-p_{0})}{n}}}\). Here, p is the observed value of the proportion, \(p_{0}\) is the theoretical proportion value and n is the sample size.

The null hypothesis is that the two proportions are the same while the alternative hypothesis is that they are not the same.

Two Proportion Z Test

A two proportion z test is conducted on two proportions to check if they are the same or not. The test statistic formula is given as follows:

z =\(\frac{p_{1}-p_{2}-0}{\sqrt{p(1-p)\left ( \frac{1}{n_{1}} +\frac{1}{n_{2}}\right )}}\)

where p = \(\frac{x_{1}+x_{2}}{n_{1}+n_{2}}\)

\(p_{1}\) is the proportion of sample 1 with sample size \(n_{1}\) and \(x_{1}\) number of trials.

\(p_{2}\) is the proportion of sample 2 with sample size \(n_{2}\) and \(x_{2}\) number of trials.

How to Calculate Z Test Statistic?

The most important step in calculating the z test statistic is to interpret the problem correctly. It is necessary to determine which tailed test needs to be conducted and what type of test does the z statistic belong to. Suppose a teacher claims that his section's students will score higher than his colleague's section. The mean score is 22.1 for 60 students belonging to his section with a standard deviation of 4.8. For his colleague's section, the mean score is 18.8 for 40 students and the standard deviation is 8.1. Test his claim at \(\alpha\) = 0.05. The steps to calculate the z test statistic are as follows:

• Identify the type of test. In this example, the means of two populations have to be compared in one direction thus, the test is a right-tailed two-sample z test.
• Set up the hypotheses. \(H_{0}\): \(\mu_{1} = \mu_{2}\), \(H_{1}\): \(\mu_{1} > \mu_{2}\).
• Find the critical value at the given alpha level using the z table. The critical value is 1.645.
• Determine the z test statistic using the appropriate formula. This is given by z = \(\frac{(\overline{x_{1}}-\overline{x_{2}})-(\mu_{1}-\mu_{2})}{\sqrt{\frac{\sigma_{1}^{2}}{n_{1}}+\frac{\sigma_{2}^{2}}{n_{2}}}}\). Substitute values in this equation. \(\overline{x_{1}}\) = 22.1, \(\sigma_{1}\) = 4.8, \(n_{1}\) = 60, \(\overline{x_{2}}\) = 18.8, \(\sigma_{2}\) = 8.1, \(n_{2}\) = 40 and \(\mu_{1} - \mu_{2} = 0\). Thus, z = 2.32
• Compare the critical value and test statistic to arrive at a conclusion. As 2.32 > 1.645 thus, the null hypothesis can be rejected. It can be concluded that there is enough evidence to support the teacher's claim that the scores of students are better in his class.

Z Test vs T-Test

Both z test and t-test are univariate tests used on the means of two datasets. The differences between both tests are outlined in the table given below:

Related Articles:

• Probability and Statistics
• Data Handling
• Summary Statistics

Important Notes on Z Test

• Z test is a statistical test that is conducted on normally distributed data to check if there is a difference in means of two data sets.
• The sample size should be greater than 30 and the population variance must be known to perform a z test.
• The one-sample z test checks if there is a difference in the sample and population mean,
• The two sample z test checks if the means of two different groups are equal.

Examples on Z Test

Example 1: A teacher claims that the mean score of students in his class is greater than 82 with a standard deviation of 20. If a sample of 81 students was selected with a mean score of 90 then check if there is enough evidence to support this claim at a 0.05 significance level.

Solution: As the sample size is 81 and population standard deviation is known, this is an example of a right-tailed one-sample z test.

\(H_{0}\) : \(\mu = 82\)

\(H_{1}\) : \(\mu > 82\)

From the z table the critical value at \(\alpha\) = 1.645

z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\)

\(\overline{x}\) = 90, \(\mu\) = 82, n = 81, \(\sigma\) = 20

As 3.6 > 1.645 thus, the null hypothesis is rejected and it is concluded that there is enough evidence to support the teacher's claim.

Answer: Reject the null hypothesis

Example 2: An online medicine shop claims that the mean delivery time for medicines is less than 120 minutes with a standard deviation of 30 minutes. Is there enough evidence to support this claim at a 0.05 significance level if 49 orders were examined with a mean of 100 minutes?

Solution: As the sample size is 49 and population standard deviation is known, this is an example of a left-tailed one-sample z test.

\(H_{0}\) : \(\mu = 120\)

\(H_{1}\) : \(\mu < 120\)

From the z table the critical value at \(\alpha\) = -1.645. A negative sign is used as this is a left tailed test.

\(\overline{x}\) = 100, \(\mu\) = 120, n = 49, \(\sigma\) = 30

As -4.66 < -1.645 thus, the null hypothesis is rejected and it is concluded that there is enough evidence to support the medicine shop's claim.

Example 3: A company wants to improve the quality of products by reducing defects and monitoring the efficiency of assembly lines. In assembly line A, there were 18 defects reported out of 200 samples while in line B, 25 defects out of 600 samples were noted. Is there a difference in the procedures at a 0.05 alpha level?

Solution: This is an example of a two-tailed two proportion z test.

\(H_{0}\): The two proportions are the same.

\(H_{1}\): The two proportions are not the same.

As this is a two-tailed test the alpha level needs to be divided by 2 to get 0.025.

Using this, the critical value from the z table is 1.96.

\(n_{1}\) = 200, \(n_{2}\) = 600

\(p_{1}\) = 18 / 200 = 0.09

\(p_{2}\) = 25 / 600 = 0.0416

p = (18 + 25) / (200 + 600) = 0.0537

z =\(\frac{p_{1}-p_{2}-0}{\sqrt{p(1-p)\left ( \frac{1}{n_{1}} +\frac{1}{n_{2}}\right )}}\) = 2.62

As 2.62 > 1.96 thus, the null hypothesis is rejected and it is concluded that there is a significant difference between the two lines.

go to slide go to slide go to slide

Book a Free Trial Class

FAQs on Z Test

What is a z test in statistics.

A z test in statistics is conducted on data that is normally distributed to test if the means of two datasets are equal. It can be performed when the sample size is greater than 30 and the population variance is known.

What is a One-Sample Z Test?

A one-sample z test is used when the population standard deviation is known, to compare the sample mean and the population mean. The z test statistic is given by the formula \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\).

What is the Two-Sample Z Test Formula?

The two sample z test is used when the means of two populations have to be compared. The z test formula is given as \(\frac{(\overline{x_{1}}-\overline{x_{2}})-(\mu_{1}-\mu_{2})}{\sqrt{\frac{\sigma_{1}^{2}}{n_{1}}+\frac{\sigma_{2}^{2}}{n_{2}}}}\).

What is a One Proportion Z test?

A one proportion z test is used to check if the value of the observed proportion is different from the value of the theoretical proportion. The z statistic is given by \(\frac{p-p_{0}}{\sqrt{\frac{p_{0}(1-p_{0})}{n}}}\).

What is a Two Proportion Z Test?

When the proportions of two samples have to be compared then the two proportion z test is used. The formula is given by \(\frac{p_{1}-p_{2}-0}{\sqrt{p(1-p)\left ( \frac{1}{n_{1}} +\frac{1}{n_{2}}\right )}}\).

How Do You Find the Z Test?

The steps to perform the z test are as follows:

• Set up the null and alternative hypotheses.
• Find the critical value using the alpha level and z table.
• Calculate the z statistic.
• Compare the critical value and the test statistic to decide whether to reject or not to reject the null hypothesis.

What is the Difference Between the Z Test and the T-Test?

A z test is used on large samples n ≥ 30 and normally distributed data while a t-test is used on small samples (n < 30) following a student t distribution . Both tests are used to check if the means of two datasets are the same.

• Hypothesis Testing using the Z-Test on the TI-83 Plus, TI-84 Plus, TI-89, and Voyage 200

The TI-83 Plus and TI-84 Plus are optimized for performing many tasks in statistics, and one of their most powerful features is the ability to perform a variety of tests of statistical significance. With the statistics package installed, the TI-89, TI-92 Plus, and Voyage 200 also have much of this capability. This tutorial demonstrates how to use your graphing calculator to solve basic hypothesis testing problems such as the following using the Z-Test:

A researcher designs an experiment where a random sample of n = 50 high school seniors are given a pill to improve their concentration and problem solving skills. After being administered the pill, subjects take the SAT, and their scores on the SAT Math section are tabulated. The average score of student who took the pill is x̄ = 540. Given that the average score of all high school seniors on the SAT is μ = 510 with standard deviation σ = 100, is there statistically significant evidence that students who took the pill scored higher?

Before beginning the calculations, it is necessary to come up with specific hypotheses for the tests and choose a level of significance. In inferential statistics, there are two hypothesis, the null hypothesis, and the alternative hypothesis. The null hypothesis, denoted H₀, is always that the statistic measures of the treated group (in this case students given a pill) is the same as that for the general population. Since we are only interested in whether or not the pill has a positive effect, we are doing a one-tailed Z-Test, and our null hypothesis is:

H₀: μ <= μ₀

Where μ is the true mean (as opposed to sample mean) of scores of students in the treatment group. μ₀ refers to the known population mean, in this case 510. The alternative hypothesis H 1 is what we expect if the treatment does have an effect on the population, and is always the opposite of the alternative hypothesis. Our alternative hypothesis is:

H₁: μ > μ₀

Finally, we have to choose a level of significance (α) for our test. It is possible that even if the treatment has no effect, we could get a mean score of 540. This seems unlikely and the chances of this happening goes down with the more subjects in the study, but the purpose of hypothesis testing is first of all to avoid coming to the wrong conclusion. The level of significance is a threshold probability below which we say that we have found statistical evidence. It is considered good practice to choose this beforehand so that the statistician doesn’t change α after wards in order to “find” statistical evidence where there is none. For most problems, a level of significance is:

α = .05

This means that if we find there is less than a 5% chance that the sample mean is higher than 540 by chance alone, we will conclude statistical significance.

Performing a Z-Test on the TI-83 Plus and TI-84 Plus

From the home screen, press STAT ▶ ▶ to select the TESTS menu. “Z-Test” should already be selected, so press ENTER to be taken to the Z-Test menu.

Now select the desired settings and values. While it is possible to use a list to store a set of scores from which your calculator can determine the sample data, this problem doesn’t give individual scores, so make sure STATS is selected and press ENTER .

Enter the data given in the problem, μ₀ = 510, σ = 100, x̄ = 540, and n = 50. Finally, make sure to select >μ₀ for the alternative hypothesis.

There are now two options for the output of the Z-Test: “Calculate” displays the z-score (the number of standard deviations x̄ is above or below the mean) and then the corresponding p-value, the probability of getting such a sample by luck alone.

“Draw” draws a normal distribution graph and displays the z-score and p-value at the bottom of the screen.

We have z = 2.12 and p = .017 , which means that there is a 1.7% chance of seeing such a variation in sample mean by chance alone. Since p<α, we can conclude that there is significant evidence that the treatment group is different from the general population. Assuming good experimental practices, this implies (but does not prove) that taking the pill improves students' Math SAT scores. Note that this does not necessarily mean the pill improves concentration and problem solving skills as claimed-although these may be skills important for scoring higher on the Math SAT, this is a separate claim.

Performing a Z-Test on the TI-89, TI-92 Plus, and Voyage 200

Before you begin, it is necessary to have the proper software on your device. If you have a TI-89 Titanium or other newer calculator, then you should have a Stats/List Editor icon on your Apps screen. Otherwise, you should have a Stats/List Editor application in your Flash Apps folder. (Reached by pressing APPS then ENTER ). If you don’t have this software or you aren’t sure, you can download it here .

Once you are in the Stats/List Editor app, press 2nd F1 (F6) to enter the tests menu. Z-Test should already be selected, so press ENTER to confirm. You will be prompted for the data input method. Data uses a list containing the of scores from which your calculator can determine the sample data, this problem doesn’t give individual scores, so make sure STATS is selected and press ENTER .

Enter the data given in the problem, μ₀ = 510, σ = 100, x̄ = 540, and n = 50. Finally, make sure to select μ > μ₀ for the alternative hypothesis.

There are two options for the output of the Z-Test. Selecting “Results: Calculate” displays the z-score (the number of standard deviations x̄ is above or below the mean) and then the corresponding p-value, the probability of getting such a sample by luck alone.

“Results: Draw” draws a normal distribution graph and displays the z-score and p-value at the bottom of the screen.

We have z = 2.12 and p = .017 , which means that there is a 1.7% chance of seeing such a variation in sample mean by chance alone. Since p<α, we can conclude that there is significant evidence that the treatment group is different from the general population. As before, this implies (but does not prove) that taking the pill improves students' Math SAT scores.

You might also like:

• SAT Calculator Strategies - SAT Test Prep #5
• How to Enter Logarithms on Your Graphing Calculator
• Quick Tip: How to Clear Variables on the TI-89, TI-92 Plus, and Voyage 200

One Response to Hypothesis Testing using the Z-Test on the TI-83 Plus, TI-84 Plus, TI-89, and Voyage 200

Leave a reply cancel reply.

Your email address will not be published. Required fields are marked *

Save my name, email, and website in this browser for the next time I comment.

Notice: It seems you have Javascript disabled in your Browser. In order to submit a comment to this post, please copy this code and paste it along with your comment: 4ea202fb09a9e1194ec521116b85bc14_3a0

• Search for:

Calcblog Newswire

Recently popular.

• SAT Test Prep #1: Mean, Mode, and Median on the TI-83 Plus, TI-84 Plus, and TI-89
• Business and Finance Math #2: Calculating the Effective Annual Rate (EAR) on Your TI BA II Plus or HP 12c
• Sums and Sequences on the TI-83 Plus and TI-84 Plus
• Calculating Derivatives on the TI-83 Plus, TI-84 Plus, TI-89, TI-92 Plus, and Voyage 200

Calculators

• No categories

Visit Our Sponsors

© MMXIII | Legal | Sitemap

Z-test vs T-test: the differences and when to use each

What is hypothesis testing, what is a z-test, examples of a z-test, what is a t-test, examples of a t-test, how to know when to use z-test vs t-test, difference between z-test and t-test: a comparative table.

The EPAM Anywhere Editorial Team is an international collective of senior software engineers, managers and communications professionals who create, review and share their insights on technology, career, remote work, and the daily life here at Anywhere.

Testing is how you determine effectiveness. Whether you work as a data scientist , statistician, or software developer, to ensure quality, you must measure performance. Without tests, you could deploy flawed code, features, or data points.

With that in mind, the use cases of testing are endless. Machine learning models need statistical tests. Data analysis involves statistical tests to validate assumptions. Optimization of any kind requires evaluation. You even need to test the strength of your hypothesis before you begin an inquiry.

Let's explore two inferential statistics: the Z-test vs the T-test. That way you can understand their differences, their unique purposes, and when to use a Z-test vs T-test.

To start, imagine you have a good idea. At the moment of inception, you have no data to back up your idea. It is an unformed thought. But the idea is an excellent starting point that can launch a full investigation. We consider this starting point a hypothesis.

But what if your hypothesis is off-base? You don’t want to dive into a full-scale search if it is a pointless chase with no reward. That is a waste of resources. You need to determine if you have a workable hypothesis.

Enter hypothesis testing. It is a statistical act used to assess the viability of a hypothesis. The method discovers whether there is sufficient data to support your idea. If there is next to no significance, you do not have a very plausible hypothesis.

To confirm the validity of a hypothesis, you compare it against the status quo (also known as the null hypothesis). Your idea is something new, opposite from normal conditions (also known as the alternative hypothesis). It is zero sum: only one hypothesis between the null and alternate hypothesis can be true in a given set of parameters.

In such a comparison test, you can now determine validity. You can compare and contrast conditions to find meaningful conclusions. Whichever conditions become statistically apparent determines which hypothesis is plausible.

A Z-test is a test statistic. It works with two groups: the sample mean and the population mean. It will test whether these two groups are different.

With a Z-test, you know the population standard deviation. That is to ensure statistical accuracy as you compare one group (the sample mean) vs the second group (the population mean). In other words, you can minimize external confounding factors with a normal distribution. In addition, a defining characteristic of a Z-test is that it works with large sample sizes (typically more than 30, so we achieve normal distribution as defined by the central limit theorem). These are two crucial criteria for using a Z-test.

Within hypothesis testing, your null hypothesis states there is no difference between the two groups your Z-test will compare. Your alternative hypothesis will state there is a difference that your Z-test will expose.

How to perform a Z-test

A Z-test occurs in the following standard format:

• Formulate your hypothesis: First, define the parameters of your alternative and null hypothesis.
• Choose a critical value: Second, determine what you consider a viable difference between your two groups. This threshold determines when you can say the null hypothesis should be rejected. Common levels are 0.01 (1%) or 0.05 (5%) , values found to best balance Type I and Type II errors .
• Collect samples: Obtain the needed data. The data must be large enough and random.
• Calculate for a Z-score: Input your data into the standard Z-test statistics formula, shown below, where Z = standard score, x = observed value, mu = mean of the sample, sigma = standard deviation of the sample .
• Compare: If the statistical test is greater than the critical value, you have achieved statistical significance. The sample mean is so different so you can reject the null hypothesis. Your alternative hypothesis (something other than the status quo) is at work, and that's worth investigating.

There are different variations of a Z-test. Let's explore examples of one-sample and two-sample Z-tests.

One-sample Z-test

A one-sample Z-test looks for either an increase or a decrease. There is one sample group involved, taken from a population. We want to see if there is a difference between those two means.

For example, consider a school principal who believes their students' IQ is higher than the state average. The state average is 100 points (population mean), give or take 20 (the population standard deviation). To prove this hypothesis, the principal takes 50 students (the sample size) and finds their IQ scores. To their delight, they earn an average of 110.

But does the difference offer any statistical value? The principal then plugs the numbers into a Z-test. Any Z-score greater than the critical value would state there is sufficient significance. The claim that the students have an above-average IQ is valid.

Two-sample Z-test

A two-sample test involves comparing the average of two sample groups against the population means. It is to determine a difference between two independent samples.

For example, our principal wants to compare their students' IQ scores to the school across the street. They believe their students' average IQ is higher. They don’t need to know the exact numerical increase or decrease. All they want is proof that their student's average scores are higher than the other group.

To confirm the validity of this hypothesis, the principal will search for statistical significance. They can take a 50-student sample size from their school and a 50-student sample size from the rival school. Now in possession of both sample group's average IQ (and the sample standard deviation), they hope to find a number value that is not equal. And they need them to be unequal by a significant amount.

If the test statistic comes in less than the critical value, the differences are negligible. There is not enough evidence to say the hypothesis is worth exploring, the null hypothesis is maintained. He would not have enough proof that the IQ levels between the two schools are different.

Read full story

A T-test performs the same crucial function as a Z-test: determine if there is a difference between the means of two groups. If there is a significant difference, you have achieved statistical validity for your hypothesis.

However, a T-test involves a different set of factors. Most importantly, a T-test applies when you do not know the sample variance of your values. You must generalize the normal distribution (or T-distribution). Plus, there is an expectation that you do not possess all the data in a given scenario.

These conditions better match reality, as it is often hard to collect data from entire populations or always obtain a standard normal distribution. That is why T-tests are more widely applicable than Z-tests, though they operate with less precision.

How to perform a T-test

A T-test occurs in the following standard format:

• Formulate your hypothesis: First, define the parameters of your null and alternative hypothesis.
• Choose a critical value: Like a Z-test, determine what you consider a viable difference between your two groups.
• Collect data: Obtain the needed data. One of the key differences is degrees of freedom in the samples of a T-test, so try to define the typical values and range of values in each group.
• Calculate your T-score: Input your data into the T-test formula you chose. Here is a one-sample formula:
• Compare: If the statistical test is greater than the critical value, you have achieved statistical significance. The sample mean is so far from the population mean that you likely have a useful hypothesis.

There are several different kinds of T-tests as well. Let's go through the standard one-sample and two-sample T-tests.

One-sample T-test

A one-sample T-test looks for an increase or decrease compared to a population mean.

For example, your company just went through sales training. Now, the manager wants to know if the training helped improve sales.

Previous company sales data shows an average of $100 on each transaction from all workers. The null hypothesis would be no change. The alternative hypothesis (which you hope is significant), is that there is an improvement.

To test if there is significance, you take the sales average of 20 salesmen. That is the only available data, and you have no other data from nationwide stores. The average of that sample of salesmen in the past month is $130. We will also assume that the standard deviation is approximately equal .

With this set of factors, you can calculate your T-score with a T-test. You compare the sample result to the critical value. In addition, you assess it against the number of degrees of freedom. Since we know with smaller sample data sizes there is greater uncertainty, we allow more room for our data to vary.

After comparing, we may find a lot of significance. That means the data possesses enough strength to support our hypothesis that sales training likely impacted sales. Of course, this is an estimate, as we only assessed one factor with a small group. Sales could have risen for numerous other reasons. But with our set of assumptions, our hypothesis is valid.

Two-sample T-test

A two-sample T-test occurs the same as a two-sample Z-test and compares if two groups are equal when compared to a defined population parameter.

For example, consider English and non-native speakers. We want to see the effect of maternal language on test scores inside a country. To do that, we will offer both groups a reading test and compare those scores to the average.

Of course, finding the mean of an entire population of language speakers is impossible to procure. Still, we can make some assumptions and compare them with a smaller size. We take 15 English speakers and 15 non-native speakers and collect their results. We can decide on a critical score value on the reading test as well. If the average score on the test is not crucially different or outside the population standard deviation, our assumption failed. There is no significant difference between the groups, so the impact of maternal language is not worth investigating.

Both a Z-test and a T-test validate a hypothesis. Both are parametric tests that rely on assumptions. The key difference between Z-test and T-test is in their assumptions (e.g. population variance).

Key differences about the data used result in different applications. You want to use the appropriate tool, otherwise you won’t draw valid conclusions from your data.

So when should you use a Z-test vs a T-test? Here are some factors to consider:

• Sample size: If the available sample size is small, opt for a T-test. Small sample sizes are more variable, so the greater spread of distribution and estimation of error involved with T-tests is ideal.
• Knowledge of the population standard deviation: Z-tests are more precise and often simpler to execute. So if you know the standard deviation, use a Z-test.
• Test purpose: If you are assessing the validity of a mean, a T-test is the best choice. If you are working with a hypothesized population proportion, go for a Z-test.
• Assumption of normality: A Z-test assumes a normal distribution. This does not apply to all real-world scenarios. If you hope to validate a hypothesis that is not well-defined, opt for a T-test instead.
• Type of data: You can only work within the constraints of the available data. The more information the better, but that is often not possible given testing and collecting conditions. If you have limited data describing means between groups, opt for a T-test. If you have large data sets comparing means between populations, you can use a Z-test.

Knowing the key differences with each statistical test makes selecting the right tool far easier. Here is a table that can help you compare:

Statistical testing lets you determine the validity of a hypothesis. You discover validity by determining if there is a significant difference between your hypothesis and the status quo. If there is, you have a possible idea worth exploring.

That process has numerous applications in the field of computer science and data analysis . You might want to determine the performance of an app with an A/B test. Or you might need to test if an application fits within the defined limits and compare performance metrics. Z-tests and T-tests can depict whether there is significant evidence in each of these scenarios. With that information, you can take the appropriate measures to fix bugs or optimize processes.

Z-test and T-test are helpful tools, especially for hypothesis testing. For data engineers of the future, knowledge of statistical testing will only help your work and overall career trajectory.

Are you a data scientist looking for a job? Check out our remote data scientist jobs available .

Explore our Editorial Policy to learn more about our standards for content creation.

step-by-step guide to creating, building, and showcasing your data analyst portfolio projects

10 most popular programming languages for 2020 and beyond

what is .NET?

want to boost your growth as a software engineer? try coding stories

SDLC models: approach development the way that works for you

how quantitative usability testing improves digital products

C# introduction: basics, introduction, and beginner projects

computer science vs data science: unraveling the differences & similarities

rebase vs. merge: a comprehensive guide

the future of Agile: what to expect in 2024 and beyond

best react projects for a portfolio: from ideas to standout examples

Ruby on Rails interview questions

data scientist interview questions and answers

24 unique JavaScript projects for portfolio

top resume-boosting Java projects for your portfolio

network engineer interview questions

Z-test for Two Proportions

Instructions: This calculator conducts a Z-test for two population proportions (\(p_1\) and \(p_2\)), Please select the null and alternative hypotheses, type the significance level, the sample sizes, the number of favorable cases (or the sample proportions) and the results of the z-test will be displayed for you:

When Do You Use a Z-test for Two Proportions?

More about the z-test for two proportions so you can better understand the results yielded by this solver: A z-test for two proportions is a hypothesis test that attempts to make a claim about the population proportions p 1 and p 2 . Specifically, we are interested in assessing whether or not it is reasonable to claim that p 1 = p 2 , using sample information. The Z-test for two proportions has two non-overlapping hypotheses, the null and the alternative hypothesis.

What are the null and alternative hypotheses for the z-test for two proportions?

The null hypothesis is a statement about the population parameter which indicates no effect, and the alternative hypothesis is the complementary hypothesis to the null hypothesis. The main properties of a one sample z-test for two population proportions are:

• Depending on our knowledge about the "no effect" situation, the z-test can be two-tailed, left-tailed or right-tailed
• The main principle of hypothesis testing is that the null hypothesis is rejected if the test statistic obtained is sufficiently unlikely under the assumption that the null hypothesis is true
• The p-value is the probability of obtaining sample results as extreme or more extreme than the sample results obtained, under the assumption that the null hypothesis is true
• In a hypothesis tests there are two types of errors. Type I error occurs when we reject a true null hypothesis, and the Type II error occurs when we fail to reject a false null hypothesis

What is the z-test formula in this case?

The formula for a z-statistic for two population proportions is

where \(\bar p = \frac{X_1+X_2}{n_1+n_2}\) corresponds to the pooled proportion (Notice that in the above z test for proportions formula, we get in the denominator something like our "best guess" of what the population proportion is from information from the two samples, assuming that the null hypothesis of equality of proportions is true). The null hypothesis is rejected when the z-statistic lies on the rejection region, which is determined by the significance level (\(\alpha\)) and the type of tail (two-tailed, left-tailed or right-tailed).

The Case for one population proportion

In case you only have one sample proportion (so you are testing for one population proportion), you should use our z-test for one proportion calculator , which specifically addresses that case.

Related Calculators

log in to your account

Reset password.