theoretical probability assignment quizlet

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

4.2: Theoretical Probability

• Last updated
• Save as PDF
• Page ID 16346

• Kathryn Kozak
• Coconino Community College

It is not always feasible to conduct an experiment over and over again, so it would be better to be able to find the probabilities without conducting the experiment. These probabilities are called Theoretical Probabilities .

To be able to do theoretical probabilities, there is an assumption that you need to consider. It is that all of the outcomes in the sample space need to be equally likely outcomes . This means that every outcome of the experiment needs to have the same chance of happening.

Example \(\PageIndex{1}\) Equally likely outcomes

Which of the following experiments have equally likely outcomes?

• Rolling a fair die.
• Flip a coin that is weighted so one side comes up more often than the other.
• Pull a ball out of a can containing 6 red balls and 8 green balls. All balls are the same size.
• Picking a card from a deck.
• Rolling a die to see if it is fair.
• Since the die is fair, every side of the die has the same chance of coming up. The outcomes are the different sides, so each outcome is equally likely.
• Since the coin is weighted, one side is more likely to come up than the other side. The outcomes are the different sides, so each outcome is not equally likely.
• Since each ball is the same size, then each ball has the same chance of being chosen. The outcomes of this experiment are the individual balls, so each outcome is equally likely. Don’t assume that because the chances of pulling a red ball are less than pulling a green ball that the outcomes are not equally likely. The outcomes are the individual balls and they are equally likely.
• If you assume that the deck is fair, then each card has the same chance of being chosen. Thus the outcomes are equally likely outcomes. You do have to make this assumption. For many of the experiments you will do, you do have to make this kind of assumption.
• In this case you are not sure the die is fair. The only way to determine if it is fair is to actually conduct the experiment, since you don’t know if the outcomes are equally likely. If the experimental probabilities are fairly close to the theoretical probabilities, then the die is fair.

If the outcomes are not equally likely, then you must do experimental probabilities. If the outcomes are equally likely, then you can do theoretical probabilities.

Definition \(\PageIndex{1}\): Theoretical Probabilities

If the outcomes of an experiment are equally likely, then the probability of event A happening is

\(P(A)=\dfrac{\# \text { of outcomes in event space }}{\# \text { of outcomes in sample space }}\)

Example \(\PageIndex{2}\) calculating theoretical probabilities

Suppose you conduct an experiment where you flip a fair coin twice.

• What is the sample space?
• What is the probability of getting exactly one head?
• What is the probability of getting at least one head?
• What is the probability of getting a head and a tail?
• What is the probability of getting a head or a tail?
• What is the probability of getting a foot?
• What is the probability of each outcome? What is the sum of these probabilities?

a. There are several different sample spaces you can do. One is SS={0, 1, 2} where you are counting the number of heads. However, the outcomes are not equally likely since you can get one head by getting a head on the first flip and a tail on the second or a tail on the first flip and a head on the second. There are 2 ways to get that outcome and only one way to get the other outcomes. Instead it might be better to give the sample space as listing what can happen on each flip. Let H = head and T = tail, and list which can happen on each flip.

SS={HH, HT, TH, TT}

b. Let A = getting exactly one head. The event space is A = {HT, TH}. So

\(P(A)=\dfrac{2}{4} \text { or } \dfrac{1}{2}\)

It may not be advantageous to reduce the fractions to lowest terms, since it is easier to compare fractions if they have the same denominator.

c. Let B = getting at least one head. At least one head means get one or more. The event space is B = {HT, TH, HH} and

\(P(B)=\dfrac{3}{4}\)

Since P(B) is greater than the P(A), then event B is more likely to happen than event A.

d. Let C = getting a head and a tail = {HT, TH} and

\(P(C)=\dfrac{2}{4}\)

This is the same event space as event A, but it is a different event. Sometimes two different events can give the same event space.

e. Let D = getting a head or a tail. Since or means one or the other or both and it doesn’t specify the number of heads or tails, then D = {HH, HT, TH, TT} and

\(P(D)=\dfrac{4}{4}=1\)

f. Let E = getting a foot. Since you can’t get a foot, E = {} or the empty set and

\(P(E)=\dfrac{0}{4}=0\)

g. \(P(H H)=P(H T)=P(T H)=P(T T)=\dfrac{1}{4}\). If you add all of these probabilities together you get 1.

This example had some results in it that are important concepts. They are summarized below:

Probability Properties

• \(0 \leq P(\text { event }) \leq 1\)
• If the P(event)=1, then it will happen and is called the certain event.
• If the P(event)=0, then it cannot happen and is called the impossible event.
• \(\sum P(\text { outcome })=1\)

Example \(\PageIndex{3}\) calculating theoretical probabilities

Suppose you conduct an experiment where you pull a card from a standard deck.

• What is the probability of getting a Spade?
• What is the probability of getting a Jack?
• What is the probability of getting an Ace?
• What is the probability of not getting an Ace?
• What is the probability of getting a Spade and an Ace?
• What is the probability of getting a Spade or an Ace?
• What is the probability of getting a Jack and an Ace?
• What is the probability of getting a Jack or an Ace?

a. SS = {2S, 3S, 4S, 5S, 6S, 7S, 8S, 9S, 10S, JS, QS, KS, AS, 2C, 3C, 4C, 5C, 6C, 7C, 8C, 9C, 10C, JC, QC, KC, AC, 2D, 3D, 4D, 5D, 6D, 7D, 8D, 9D, 10D, JD, QD, KD, AD, 2H, 3H, 4H, 5H, 6H, 7H, 8H, 9H, 10H, JH, QH, KH, AH}

b. Let A = getting a spade = {2S, 3S, 4S, 5S, 6S, 7S, 8S, 9S, 10S, JS, QS, KS, AS} so

\(P(A)=\dfrac{13}{52}\)

c. Let B = getting a Jack = {JS, JC, JH, JD} so

\(P(B)=\dfrac{4}{52}\)

d. Let C = getting an Ace = {AS, AC, AH, AD} so

\(P(C)=\dfrac{4}{52}\)

e. Let D = not getting an Ace = {2S, 3S, 4S, 5S, 6S, 7S, 8S, 9S, 10S, JS, QS, KS, 2C, 3C, 4C, 5C, 6C, 7C, 8C, 9C, 10C, JC, QC, KC, 2D, 3D, 4D, 5D, 6D, 7D, 8D, 9D, 10D, JD, QD, KD, 2H, 3H, 4H, 5H, 6H, 7H, 8H, 9H, 10H, JH, QH, KH} so

\(P(D)=\dfrac{48}{52}\)

Notice, \(P(D)+P(C)=\dfrac{48}{52}+\dfrac{4}{52}=1\), so you could have found the probability of D by doing 1 minus the probability of C \(P(D)=1-P(C)=1-\dfrac{4}{52}=\dfrac{48}{52}\).

f. Let E = getting a Spade and an Ace = {AS} so

\(P(E)=\dfrac{1}{52}\)

g. Let F = getting a Spade and an Ace ={2S, 3S, 4S, 5S, 6S, 7S, 8S, 9S, 10S, JS, QS, KS, AS, AC, AD, AH} so

\(P(F)=\dfrac{16}{52}\)

h. Let G = getting a Jack and an Ace = { } since you can’t do that with one card. So

i. Let H = getting a Jack or an Ace = {JS, JC, JD, JH, AS, AC, AD, AH} so

\(P(H)=\dfrac{8}{52}\)

Example \(\PageIndex{4}\) calculating theoretical probabilities

Suppose you have an iPod Shuffle with the following songs on it: 5 Rolling Stones songs, 7 Beatles songs, 9 Bob Dylan songs, 4 Faith Hill songs, 2 Taylor Swift songs, 7 U2 songs, 4 Mariah Carey songs, 7 Bob Marley songs, 6 Bunny Wailer songs, 7 Elton John songs, 5 Led Zeppelin songs, and 4 Dave Mathews Band songs. The different genre that you have are rock from the 60s which includes Rolling Stones, Beatles, and Bob Dylan; country includes Faith Hill and Taylor Swift; rock of the 90s includes U2 and Mariah Carey; Reggae includes Bob Marley and Bunny Wailer; rock of the 70s includes Elton John and Led Zeppelin; and bluegrasss/rock includes Dave Mathews Band.

The way an iPod Shuffle works, is it randomly picks the next song so you have no idea what the next song will be. Now you would like to calculate the probability that you will hear the type of music or the artist that you are interested in. The sample set is too difficult to write out, but you can figure it from looking at the number in each set and the total number. The total number of songs you have is 67.

• What is the probability that you will hear a Faith Hill song?
• What is the probability that you will hear a Bunny Wailer song?
• What is the probability that you will hear a song from the 60s?
• What is the probability that you will hear a Reggae song?
• What is the probability that you will hear a song from the 90s or a bluegrass/rock song?
• What is the probability that you will hear an Elton John or a Taylor Swift song?
• What is the probability that you will hear a country song or a U2 song?

a. There are 4 Faith Hill songs out of the 67 songs, so

\(P(\text { Faith Hill song })=\dfrac{4}{67}\)

b. There are 6 Bunny Wailer songs, so

\(P(\text { Bunny Wailer })=\dfrac{6}{67}\)

c. There are 5, 7, and 9 songs that are classified as rock from the 60s, which is 21 total, so

\(P(\text { rock from the } 60 \mathrm{s})=\dfrac{21}{67}\)

d. There are 6 and 7 songs that are classified as Reggae, which is 13 total, so

\(P(\text { Reggae })=\dfrac{13}{67}\)

e. There are 7 and 4 songs that are songs from the 90s and 4 songs that are bluegrass/rock, for a total of 15, so

\(P(\text { rock from the } 90 \text { s or bluegrass/rock })=\dfrac{15}{67}\)

f. There are 7 Elton John songs and 2 Taylor Swift songs, for a total of 9, so

\(P(\text { Elton John or Taylor Swift song })=\dfrac{9}{67}\)

g. There are 6 country songs and 7 U2 songs, for a total of 13, so

\(P(\text { country or } \mathrm{U} 2 \text { song })=\dfrac{13}{67}\)

Of course you can do any other combinations you would like.

Notice in Example \(\PageIndex{3}\) part e, it was mentioned that the probability of event D plus the probability of event C was 1. This is because these two events have no outcomes in common, and together they make up the entire sample space. Events that have this property are called complementary events .

Definition \(\PageIndex{2}\): complementary events

If two events are complementary events then to find the probability of one just subtract the probability of the other from one. Notation used for complement of A is not A or \(A^{c}\).

\(P(A)+P\left(A^{c}\right)=1, \text { or } P(A)=1-P\left(A^{c}\right)\)

Example \(\PageIndex{5}\) complementary events

• Suppose you know that the probability of it raining today is 0.45. What is the probability of it not raining?
• Suppose you know the probability of not getting the flu is 0.24. What is the probability of getting the flu?
• In an experiment of picking a card from a deck, what is the probability of not getting a card that is a Queen?

a. Since not raining is the complement of raining, then

\(P(\text { not raining })=1-P(\text { raining })=1-0.45=0.55\)

b. Since getting the flu is the complement of not getting the flu, then

\(P(\text { getting the flu })=1-P(\text { not getting the flu })=1-0.24=0.76\)

c. You could do this problem by listing all the ways to not get a queen, but that set is fairly large. One advantage of the complement is that it reduces the workload. You use the complement in many situations to make the work shorter and easier. In this case it is easier to list all the ways to get a Queen, find the probability of the Queen, and then subtract from one. Queen = {QS, QC, QD, QH} so

\(P(\text { Queen })=\dfrac{4}{52}\) and

\(P(\text { not Queen })=1-P(\text { Queen })=1-\dfrac{4}{52}=\dfrac{48}{52}\)

The complement is useful when you are trying to find the probability of an event that involves the words at least or an event that involves the words at most. As an example of an at least event is suppose you want to find the probability of making at least $50,000 when you graduate from college. That means you want the probability of your salary being greater than or equal to $50,000. An example of an at most event is suppose you want to find the probability of rolling a die and getting at most a 4. That means that you want to get less than or equal to a 4 on the die. The reason to use the complement is that sometimes it is easier to find the probability of the complement and then subtract from 1. Example \(\PageIndex{6}\) demonstrates how to do this.

Example \(\PageIndex{6}\) using the complement to find probabilities

• In an experiment of rolling a fair die one time, find the probability of rolling at most a 4 on the die.
• In an experiment of pulling a card from a fair deck, find the probability of pulling at least a 5 (ace is a high card in this example).

a. The sample space for this experiment is {1, 2, 3, 4, 5, 6}. You want the event of getting at most a 4, which is the same as thinking of getting 4 or less. The event space is {1, 2, 3, 4}. The probability is

\(P(\text { at most } 4)=\dfrac{4}{6}\)

Or you could have used the complement. The complement of rolling at most a 4 would be rolling number bigger than 4. The event space for the complement is {5, 6}. The probability of the complement is \(\dfrac{2}{6}\). The probability of at most 4 would be

\(P(\text { at most } 4)=1-P(\text { more than } 4)=1-\dfrac{2}{6}=\dfrac{4}{6}\)

Notice you have the same answer, but the event space was easier to write out. On this example it probability wasn’t that useful, but in the future there will be events where it is much easier to use the complement.

b. The sample space for this experiment is

SS = {2S, 3S, 4S, 5S, 6S, 7S, 8S, 9S, 10S, JS, QS, KS, AS, 2C, 3C, 4C, 5C, 6C, 7C, 8C, 9C, 10C, JC, QC, KC, AC, 2D, 3D, 4D, 5D, 6D, 7D, 8D, 9D, 10D, JD, QD, KD, AD, 2H, 3H, 4H, 5H, 6H, 7H, 8H, 9H, 10H, JH, QH, KH, AH}

Pulling a card that is at least a 5 would involve listing all of the cards that are a 5 or more. It would be much easier to list the outcomes that make up the complement. The complement of at least a 5 is less than a 5. That would be the event of 4 or less. The event space for the complement would be {2S, 3S, 4S, 2C, 3C, 4C, 2D, 3D, 4D, 2H, 3H, 4H}. The probability of the complement would be \(\dfrac{12}{52}\). The probability of at least a 5 would be

\(P(\text { at least } \mathbf{a} 5)=1-P(4 \text { or less })=1-\dfrac{12}{52}=\dfrac{40}{52}\)

Another concept was show in Example \(\PageIndex{3}\) parts g and i. The problems were looking for the probability of one event or another. In part g, it was looking for the probability of getting a Spade or an Ace. That was equal to \(\dfrac{16}{52}\). In part i, it was looking for the probability of getting a Jack or an Ace. That was equal to \(\dfrac{8}{52}\). If you look back at the parts b, c, and d, you might notice the following result:

\(P(\text { Jack })+P(\text { Ace })=P(\text { Jack or Ace }) \text { but } P(\text { Spade })+P(\text { Ace }) \neq P(\text { Spade or } \text { Ace })\)

Why does adding two individual probabilities together work in one situation to give the probability of one or another event and not give the correct probability in the other?

The reason this is true in the case of the Jack and the Ace is that these two events cannot happen together. There is no overlap between the two events, and in fact the \(P(\text { Jack and } \mathrm{Acc})=0\). However, in the case of the Spade and Ace, they can happen together. There is overlap, mainly the ace of spades. The \(P(\text { Spade and } \mathrm{Ace}) \neq 0\).

When two events cannot happen at the same time, they are called mutually exclusive . In the above situation, the events Jack and Ace are mutually exclusive, while the events Spade and Ace are not mutually exclusive.

Addition Rules:

If two events A and B are mutually exclusive, then

\(P(A \text { or } B)=P(A)+P(B) \text { and } P(A \text { and } B)=0\)

If two events A and B are not mutually exclusive, then

\(P(A \text { or } B)=P(A)+P(B)-P(A \text { and } B)\)

Example \(\PageIndex{7}\) using addition rules

Suppose your experiment is to roll two fair dice.

• What is the probability of getting a sum of 5?
• What is the probability of getting the first die a 2?
• What is the probability of getting a sum of 7?
• What is the probability of getting a sum of 5 and the first die a 2?
• What is the probability of getting a sum of 5 or the first die a 2?
• What is the probability of getting a sum of 5 and sum of 7?
• What is the probability of getting a sum of 5 or sum of 7?

a. As with the other examples you need to come up with a sample space that has equally likely outcomes. One sample space is to list the sums possible on each roll. That sample space would look like: SS = {2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}. However, there are more ways to get a sum of 7 then there are to get a sum of 2, so these outcomes are not equally likely. Another thought is to list the possibilities on each roll. As an example you could roll the dice and on the first die you could get a 1. The other die could be any number between 1 and 6, but say it is a 1 also. Then this outcome would look like (1,1). Similarly, you could get (1, 2), (1, 3), (1,4), (1, 5), or (1, 6). Also, you could get a 2, 3, 4, 5, or 6 on the first die instead. Putting this all together, you get the sample space:

\(\begin{array}{r}{\mathrm{SS}=\{(1,1),(1,2),(1,3),(1,4),(1,5),(1,6)} \\ {(2,1),(2,2),(2,3),(2,4),(2,5),(2,6)} \\ {(3,1),(3,2),(3,3),(3,4),(3,5),(3,6)} \\ {(4,1),(4,2),(4,3),(4,4),(4,5),(4,6)} \\ {(5,1),(5,2),(5,3),(5,4),(5,5),(5,6)} \\ {(6,1),(6,2),(6,3),(6,4),(6,5),(6,6) \}}\end{array}\)

Notice that a (2,3) is different from a (3,2), since the order that you roll the die is important and you can tell the difference between these two outcomes. You don’t need any of the doubles twice, since these are not distinguishable from each other in either order. This will always be the sample space for rolling two dice.

b. Let A = getting a sum of 5 = {(4,1), (3,2), (2,3), (1,4)} so

\(P(A)=\dfrac{4}{36}\)

c. Let B = getting first die a 2 = {(2,1), (2,2), (2,3), (2,4), (2,5), (2,6)} so

\(P(B)=\dfrac{6}{36}\)

d. Let C = getting a sum of 7 = {(6,1), (5,2), (4,3), (3,4), (2,5), (1,6)} so

\(P(C)=\dfrac{6}{36}\)

e. This is events A and B which contains the outcome {(2,3)} so

\(P(A \text { and } B)=\dfrac{1}{36}\)

f. Notice from part e, that these two events are not mutually exclusive, so

\(=\dfrac{4}{36}+\dfrac{6}{36}-\dfrac{1}{36}\)

\(=\dfrac{9}{36}\)

g. These are the events A and C, which have no outcomes in common. Thus A and C = { } so

\(P(A \text { and } C)=0\)

h. From part g, these two events are mutually exclusive, so

\(P(A \text { or } C)=P(A)+P(C)\)

\(=\dfrac{4}{36}+\dfrac{6}{36}\)

\(=\dfrac{10}{36}\)

Many people like to talk about the odds of something happening or not happening. Mathematicians, statisticians, and scientists prefer to deal with probabilities since odds are difficult to work with, but gamblers prefer to work in odds for figuring out how much they are paid if they win.

Definition \(\PageIndex{3}\)

The actual odds against event A occurring are the ratio \(P\left(A^{c}\right) / P(A)\), usually expressed in the form a:b or a to b , where a and b are integers with no common factors.

Definition \(\PageIndex{4}\)

The actual odds in favor event A occurring are the ratio \(P(A) / P\left(A^{c}\right)\), which is the reciprocal of the odds against. If the odds against event A are a:b , then the odds in favor event A are b:a .

Definition \(\PageIndex{5}\)

The payoff odds against event A occurring are the ratio of the net profit (if you win) to the amount bet.

payoff odds against event A = (net profit) : (amount bet)

Example \(\PageIndex{8}\) odds against and payoff odds

In the game of Craps, if a shooter has a come-out roll of a 7 or an 11, it is called a natural and the pass line wins. The payoff odds are given by a casino as 1:1.

• Find the probability of a natural.
• Find the actual odds for a natural.
• Find the actual odds against a natural.
• If the casino pays 1:1, how much profit does the casino make on a $10 bet?

a. A natural is a 7 or 11. The sample space is

The event space is {(1,6), (2,5), (3,4), (4,3), (5,2), (6,1), (5,6), (6,5)}

So \(P(7 \text { or } 11)=\dfrac{8}{36}\)

odd for a natural \(=\dfrac{P(7 \text { or } 11)}{P(\text {not} 7 \text { or } 11)}\)

\(=\dfrac{8 / 36}{1-8 / 36}\)

\(=\dfrac{8 / 36}{28 / 36}\)

\(=\dfrac{8}{28}\)

\(=\dfrac{2}{7}\)

odds against a natural \(=\dfrac{P(\text { not } 7 \text { or } 11)}{P(7 \text { or } 11)}=\dfrac{28}{8}=\dfrac{7}{2}=\dfrac{3.5}{1}\)

d. The actual odds are 3.5 to 1 while the payoff odds are 1 to 1. The casino pays you $10 for your $10 bet. If the casino paid you the actual odds, they would pay $3.50 on every $1 bet, and on $10, they pay \(3.5 * \$ 10=\$ 35\). Their profit is \(\$ 35-\$ 10=\$ 25\).

Exercise \(\PageIndex{1}\)

Table \(\PageIndex{1}\) : M&M Distribution a. Find the probability of choosing a green or red M&M. b. Find the probability of choosing a blue, red, or yellow M&M. c. Find the probability of not choosing a brown M&M. d. Find the probability of not choosing a green M&M.

Table \(\PageIndex{2}\) : Number of Defective Lenses a. Find the probability of picking a lens that is scratched or flaked. b. Find the probability of picking a lens that is the wrong PD or was lost in lab. c. Find the probability of picking a lens that is not scratched. d. Find the probability of picking a lens that is not the wrong shape.

• State the sample space.
• Find the probability of getting exactly two heads. Make sure you state the event space.
• Find the probability of getting at least two heads. Make sure you state the event space.
• Find the probability of getting an odd number of heads. Make sure you state the event space.
• Find the probability of getting all heads or all tails. Make sure you state the event space.
• Find the probability of getting exactly two heads or exactly two tails.
• Find the probability of not getting an odd number of heads.
• Find the probability of getting a head. Make sure you state the event space.
• Find the probability of getting a 6. Make sure you state the event space.
• Find the probability of getting a 6 or a head.
• Find the probability of getting a 3 and a tail.
• Find the probability of getting a sum of 3. Make sure you state the event space.
• Find the probability of getting the first die is a 4. Make sure you state the event space.
• Find the probability of getting a sum of 8. Make sure you state the event space.
• Find the probability of getting a sum of 3 or sum of 8.
• Find the probability of getting a sum of 3 or the first die is a 4.
• Find the probability of getting a sum of 8 or the first die is a 4.
• Find the probability of not getting a sum of 8.
• Find the probability of getting a Ten. Make sure you state the event space.
• Find the probability of getting a Diamond. Make sure you state the event space.
• Find the probability of getting a Club. Make sure you state the event space.
• Find the probability of getting a Diamond or a Club.
• Find the probability of getting a Ten or a Diamond.
• Find the probability of getting a red ball.
• Find the probability of getting a blue ball.
• Find the odds for getting a red ball.
• Find the odds for getting a blue ball.
• Find the probability of winning if you pick the number 7 and it comes up on the wheel.
• Find the odds against winning if you pick the number 7.
• The casino will pay you $20 for every dollar you bet if your number comes up. How much profit is the casino making on the bet?

1. a. P(green or red) = 0.326, b. P(blue, red, or yellow) = 0.466, c. P(not brown) = 0.858, d. P(not green) = 0.816

3. a. See solutions, b. P(2 heads) = 0.375, c. P(at least 2 heads) = 0.50, d. P(odd number of heads) = 0.50, e. P(all heads or all tails) = 0.25, f. P(two heads or two tails) = 0.75, g. P(no an odd number of heads) = 0.50

5. a. See solutions, b. P(sum of 3) = 0.056, c. P(1st die a 4) = 0.167, d. P(sum of 8) = 0.139, e. P(sum of 3 or sum of 8) = 0.194, f. P(sum of 3 or 1st die a 4) = 0.222, g. P(sum of 8 or 1st die a 4) = 0.278, h. P(not getting a sum of 8) = 0.861

7. a. P(red ball) = 0.625, b. P(blue ball) = 0.375, c. 5 to 3 d. 3 to 5

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Statistics and probability

Course: statistics and probability   >   unit 7.

• Intro to theoretical probability

Probability: the basics

• Simple probability: yellow marble
• Simple probability: non-blue marble
• Simple probability
• Intuitive sense of probabilities
• Comparing probabilities
• The Monty Hall problem
• The probability of an event can only be between 0 and 1 and can also be written as a percentage.
• The probability of event A ‍   is often written as P ( A ) ‍   .
• If P ( A ) > P ( B ) ‍   , then event A ‍   has a higher chance of occurring than event B ‍   .
• If P ( A ) = P ( B ) ‍   , then events A ‍   and B ‍    are equally likely to occur.

Want to join the conversation?

• Upvote Button navigates to signup page
• Downvote Button navigates to signup page
• Flag Button navigates to signup page

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

7.6: Basic Concepts of Probability

• Last updated
• Save as PDF
• Page ID 129597

Learning Objectives

After completing this section, you should be able to:

• Define probability including impossible and certain events.
• Calculate basic theoretical probabilities.
• Calculate basic empirical probabilities.
• Distinguish among theoretical, empirical, and subjective probability.
• Calculate the probability of the complement of an event.

It all comes down to this. The game of Monopoly that started hours ago is in the home stretch. Your sister has the dice, and if she rolls a 4, 5, or 7 she’ll land on one of your best spaces and the game will be over. How likely is it that the game will end on the next turn? Is it more likely than not? How can we measure that likelihood? This section addresses this question by introducing a way to measure uncertainty.

Introducing Probability

Uncertainty is, almost by definition, a nebulous concept. In order to put enough constraints on it that we can mathematically study it, we will focus on uncertainty strictly in the context of experiments. Recall that experiments are processes whose outcomes are unknown; the sample space for the experiment is the collection of all those possible outcomes. When we want to talk about the likelihood of particular outcomes, we sometimes group outcomes together; for example, in the Monopoly example at the beginning of this section, we were interested in the roll of 2 dice that might fall as a 4, 5, or 7. A grouping of outcomes that we’re interested in is called an event . In other words, an event is a subset of the sample space of an experiment; it often consists of the outcomes of interest to the experimenter.

Once we have defined the event that interests us, we can try to assess the likelihood of that event. We do that by assigning a number to each event ( E E ) called the probability of that event ( P ( E ) P ( E ) ). The probability of an event is a number between 0 and 1 (inclusive). If the probability of an event is 0, then the event is impossible. On the other hand, an event with probability 1 is certain to occur. In general, the higher the probability of an event, the more likely it is that the event will occur.

Example 7.16

Determining certain and impossible events.

Consider an experiment that consists of rolling a single standard 6-sided die (with faces numbered 1-6). Decide if these probabilities are equal to zero, equal to one, or somewhere in between.

• P ( roll a 4 ) P ( roll a 4 )
• P ( roll a 7 ) P ( roll a 7 )
• P ( roll a positive number ) P ( roll a positive number )
• P ( roll a 1 3 ) P ( roll a 1 3 )
• P ( roll an even number ) P ( roll an even number )
• P ( roll a single-digit number ) P ( roll a single-digit number )

Let's start by identifying the sample space. For one roll of this die, the possible outcomes are {1, 2, 3, 4, 5,6}. We can use that to assess these probabilities:

• We see that 4 is in the sample space, so it’s possible that it will be the outcome. It’s not certain to be the outcome, though. So, 0 < P ( roll a 4 ) < 1 0 < P ( roll a 4 ) < 1 .
• Notice that 7 is not in the sample space. So, P ( roll a 7 ) = 0 P ( roll a 7 ) = 0 .
• Every outcome in the sample space is a positive number, so this event is certain. Thus, P ( roll a positive number ) = 1 P ( roll a positive number ) = 1 .
• Since 1 3 1 3 is not in the sample space, P ( roll a 1 3 ) = 0 P ( roll a 1 3 ) = 0 .
• Some outcomes in the sample space are even numbers (2, 4, and 6), but the others aren’t. So, 0 < P ( roll an even number ) < 1 0 < P ( roll an even number ) < 1 .
• Every outcome in the sample space is a single-digit number, so P ( roll a single-digit number ) = 1 P ( roll a single-digit number ) = 1 .

Your Turn 7.16

Three ways to assign probabilities.

The probabilities of events that are certain or impossible are easy to assign; they’re just 1 or 0, respectively. What do we do about those in-between cases, for events that might or might not occur? There are three methods to assign probabilities that we can choose from. We’ll discuss them here, in order of reliability.

Method 1: Theoretical Probability

The theoretical method gives the most reliable results, but it cannot always be used. If the sample space of an experiment consists of equally likely outcomes, then the theoretical probability of an event is defined to be the ratio of the number of outcomes in the event to the number of outcomes in the sample space.

For an experiment whose sample space S S consists of equally likely outcomes, the theoretical probability of the event E E is the ratio

P ( E ) = n ( E ) n ( S ) , P ( E ) = n ( E ) n ( S ) ,

where n ( E ) n ( E ) and n ( S ) n ( S ) denote the number of outcomes in the event and in the sample space, respectively.

Example 7.17

Computing theoretical probabilities.

Recall that a standard deck of cards consists of 52 unique cards which are labeled with a rank (the whole numbers from 2 to 10, plus J, Q, K, and A) and a suit ( ♣ ♣ , ♢ ♢ , ♡ ♡ , or ♠ ♠ ). A standard deck is thoroughly shuffled, and you draw one card at random (so every card has an equal chance of being drawn). Find the theoretical probability of each of these events:

• The card is 10 ♠ 10 ♠ .
• The card is a ♡ ♡ .
• The card is a king (K).

There are 52 cards in the deck, so the sample space for each of these experiments has 52 elements. That will be the denominator for each of our probabilities.

• There is only one 10 ♠ 10 ♠ in the deck, so this event only has one outcome in it. Thus, P ( 10 ♠ ) = 1 52 P ( 10 ♠ ) = 1 52 .
• There are 13 ♡ s ♡ s in the deck, so P ( ♡ ) = 13 52 = 1 4 P ( ♡ ) = 13 52 = 1 4 .
• There are 4 cards of each rank in the deck, so P ( K ) = 4 52 = 1 13 P ( K ) = 4 52 = 1 13 .

Your Turn 7.17

It is critical that you make sure that every outcome in a sample space is equally likely before you compute theoretical probabilities!

Example 7.18

Using tables to find theoretical probabilities.

In the Basic Concepts of Probability, we were considering a Monopoly game where, if your sister rolled a sum of 4, 5, or 7 with 2 standard dice, you would win the game. What is the probability of this event? Use tables to determine your answer.

We should think of this experiment as occurring in two stages: (1) one die roll, then (2) another die roll. Even though these two stages will usually occur simultaneously in practice, since they’re independent, it’s okay to treat them separately.

Step 1: Since we have two independent stages, let’s create a table (Figure 7.27), which is probably the most efficient method for determining the sample space.

Now, each of the 36 ordered pairs in the table represent an equally likely outcome.

Step 2: To make our analysis easier, let’s replace each ordered pair with the sum (Figure 7.28).

Step 3: Since the event we’re interested in is the one consisting of rolls of 4, 5, or 7. Let’s shade those in (Figure 7.29).

Our event contains 13 outcomes, so the probability that your sister rolls a losing number is 13 36 13 36 .

Your Turn 7.18

Example 7.19, using tree diagrams to compute theoretical probability.

If you flip a fair coin 3 times, what is the probability of each event? Use a tree diagram to determine your answer

• You flip exactly 2 heads.
• You flip 2 consecutive heads at some point in the 3 flips.
• All 3 flips show the same result.

Let’s build a tree to identify the sample space (Figure 7.30).

The sample space is {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}, which has 8 elements.

• Flipping exactly 2 heads occurs three times (HHT, HTH, THH), so the probability is 3 8 3 8 .
• Flipping 2 consecutive heads at some point in the experiment happens 3 times: HHH, HHT, THH. So, the probability is 3 8 3 8 .
• There are 2 outcomes that all show the same result: HHH and TTT. So, the probability is 2 8 = 1 4 2 8 = 1 4 .

Your Turn 7.19

People in mathematics, gerolamo cardano.

The first known text that provided a systematic approach to probabilities was written in 1564 by Gerolamo Cardano (1501–1576). Cardano was a physician whose illegitimate birth closed many doors that would have otherwise been open to someone with a medical degree in 16th-century Italy. As a result, Cardano often turned to gambling to help ends meet. He was a remarkable mathematician, and he used his knowledge to gain an edge when playing at cards or dice. His 1564 work, titled Liber de ludo aleae (which translates as Book on Games of Chance ), summarized everything he knew about probability. Of course, if that book fell into the hands of those he played against, his advantage would disappear. That’s why he never allowed it to be published in his lifetime (it was eventually published in 1663). Cardano made other contributions to mathematics; he was the first person to publish the third degree analogue of the Quadratic Formula (though he didn’t discover it himself), and he popularized the use of negative numbers.

Method 2: Empirical Probability

Theoretical probabilities are precise, but they can’t be found in every situation. If the outcomes in the sample space are not equally likely, then we’re out of luck. Suppose you’re watching a baseball game, and your favorite player is about to step up to the plate. What is the probability that he will get a hit?

In this case, the sample space is {hit, not a hit}. That doesn’t mean that the probability of a hit is 1 2 1 2 , since those outcomes aren’t equally likely. The theoretical method simply can’t be used in this situation. Instead, we might look at the player’s statistics up to this point in the season, and see that he has 122 hits in 531 opportunities. So, we might think that the probability of a hit in the next plate appearance would be about 122 531 ≈ 0.23 122 531 ≈ 0.23 . When we use the outcomes of previous replications of an experiment to assign a probability to the next replication, we’re defining an empirical probability . Empirical probability is assigned using the outcomes of previous replications of an experiment by finding the ratio of the number of times in the previous replications the event occurred to the total number of previous replications.

Empirical probabilities aren’t exact, but when the number of previous replications is large, we expect them to be close. Also, if the previous runs of the experiment are not conducted under the exact set of circumstances as the one we’re interested in, the empirical probability is less reliable. For instance, in the case of our favorite baseball player, we might try to get a better estimate of the probability of a hit by looking only at his history against left- or right-handed pitchers (depending on the handedness of the pitcher he’s about to face).

Probability and Statistics

One of the broad uses of statistics is called statistical inference, where statisticians use collected data to make a guess (or inference) about the population the data were collected from. Nearly every tool that statisticians use for inference is based on probability. Not only is the method we just described for finding empirical probabilities one type of statistical inference, but some more advanced techniques in the field will give us an idea of how close that empirical probability might be to the actual probability!

Example 7.20

Finding empirical probabilities.

Assign an empirical probability to the following events:

• Jose is on the basketball court practicing his shots from the free throw line. He made 47 out of his last 80 attempts. What is the probability he makes his next shot?
• Amy is about to begin her morning commute. Over her last 60 commutes, she arrived at work 12 times in under half an hour. What is the probability that she arrives at work in 30 minutes or less?
• Felix is playing Yahtzee with his sister. Felix won 14 of the last 20 games he played against her. How likely is he to win this game?
• Since Jose made 47 out of his last 80 attempts, assign this event an empirical probability of 47 80 ≈ 59 % 47 80 ≈ 59 % .
• Amy completed the commute in under 30 minutes in 12 of the last 60 commutes, so we can estimate her probability of making it in under 30 minutes this time at 12 60 = 20 % 12 60 = 20 % .
• Since Felix has won 14 of the last 20 games, assign a probability for a win this time of 14 20 = 70 % 14 20 = 70 % .

Your Turn 7.20

Work it out, buffon’s needle.

A famous early question about probability (posed by Georges-Louis Leclerc, Comte de Buffon in the 18th century) had to do with the probability that a needle dropped on a floor finished with wooden slats would lay across one of the seams. If the distance between the slats is exactly the same length as the needle, then it can be shown using calculus that the probability that the needle crosses a seam is 2 π 2 π . Using toothpicks or matchsticks (or other uniformly long and narrow objects), assign an empirical probability to this experiment by drawing parallel lines on a large sheet of paper where the distance between the lines is equal to the length of your dropping object, then repeatedly dropping the objects and noting whether the object touches one of the lines. Once you have your empirical probability, take its reciprocal and multiply by 2. Is the result close to π π ?

Method 3: Subjective Probability

In cases where theoretical probability can’t be used and we don’t have prior experience to inform an empirical probability, we’re left with one option: using our instincts to guess at a subjective probability . A subjective probability is an assignment of a probability to an event using only one’s instincts.

Subjective probabilities are used in cases where an experiment can only be run once, or it hasn’t been run before. Because subjective probabilities may vary widely from person to person and they’re not based on any mathematical theory, we won’t give any examples. However, it’s important that we be able to identify a subjective probability when we see it; they will in general be far less accurate than empirical or theoretical probabilities.

Example 7.21

Distinguishing among theoretical, empirical, and subjective probabilities.

Classify each of the following probabilities as theoretical, empirical, or subjective.

• An eccentric billionaire is testing a brand new rocket system. He says there is a 15% chance of failure.
• With 4 seconds to go in a close basketball playoff game, the home team need 3 points to tie up the game and send it to overtime. A TV commentator says that team captain should take the final 3-point shot, because he has a 38% chance of making it (greater than every other player on the team).
• Felix is losing his Yahtzee game against his sister. He has one more chance to roll 2 dice; he’ll win the game if they both come up 4. The probability of this is about 2.8%.
• This experiment has never been run before, so the given probability is subjective.
• Presumably, the commentator has access to each player’s performance statistics over the entire season. So, the given probability is likely empirical.
• Rolling 2 dice results in a sample space with equally likely outcomes. This probability is theoretical. (We’ll learn how to calculate that probability later in this chapter.)

Your Turn 7.21

Benford’s law.

In 1938, Frank Benford published a paper (“The law of anomalous numbers,” in Proceedings of the American Philosophical Society ) with a surprising result about probabilities. If you have a list of numbers that spans at least a couple of orders of magnitude (meaning that if you divide the largest by the smallest, the result is at least 100), then the digits 1–9 are not equally likely to appear as the first digit of those numbers, as you might expect. Benford arrived at this conclusion using empirical probabilities; he found that 1 was about 6 times as likely to be the initial digit as 9 was!

New Probabilities from Old: Complements

One of the goals of the rest of this chapter is learning how to break down complicated probability calculations into easier probability calculations. We’ll look at the first of the tools we can use to accomplish this goal in this section; the rest will come later.

Given an event E E , the complement of E E (denoted E ′ E ′ ) is the collection of all of the outcomes that are not in E E . (This is language that is taken from set theory, which you can learn more about elsewhere in this text.) Since every outcome in the sample space either is or is not in E E , it follows that n ( E ) + n ( E ′ ) = n ( S ) n ( E ) + n ( E ′ ) = n ( S ) . So, if the outcomes in S S are equally likely, we can compute theoretical probabilities P ( E ) = n ( E ) n ( S ) P ( E ) = n ( E ) n ( S ) and P ( E ′ ) = n ( E ′ ) n ( S ) P ( E ′ ) = n ( E ′ ) n ( S ) . Then, adding these last two equations, we get

P ( E ) + P ( E ′ ) = n ( E ) n ( S ) + n ( E ′ ) n ( S ) = n ( E ) + n ( E ′ ) n ( S ) = n ( S ) n ( S ) = 1 P ( E ) + P ( E ′ ) = n ( E ) n ( S ) + n ( E ′ ) n ( S ) = n ( E ) + n ( E ′ ) n ( S ) = n ( S ) n ( S ) = 1

Thus, if we subtract P ( E ′ ) P ( E ′ ) from both sides, we can conclude that P ( E ) = 1 − P ( E ′ ) P ( E ) = 1 − P ( E ′ ) . Though we performed this calculation under the assumption that the outcomes in S S are all equally likely, the last equation is true in every situation.

P ( E ) = 1 − P ( E ′ ) P ( E ) = 1 − P ( E ′ )

How is this helpful? Sometimes it is easier to compute the probability that an event won’t happen than it is to compute the probability that it will . To apply this principle, it’s helpful to review some tricks for dealing with inequalities. If an event is defined in terms of an inequality, the complement will be defined in terms of the opposite inequality: Both the direction and the inclusivity will be reversed, as shown in the table below.

Example 7.22

Using the formula for complements to compute probabilities.

• If you roll a standard 6-sided die, what is the probability that the result will be a number greater than one?
• If you roll two standard 6-sided dice, what is the probability that the sum will be 10 or less?
• If you flip a fair coin 3 times, what is the probability that at least one flip will come up tails?
• Here, the sample space is {1, 2, 3, 4, 5, 6}. It’s easy enough to see that the probability in question is 5 6 5 6 , because there are 5 outcomes that fall into the event “roll a number greater than 1.” Let’s also apply our new formula to find that probability. Since E E is defined using the inequality roll > 1 roll > 1 , then E ′ E ′ is defined using roll ≤ 1 roll ≤ 1 . Since there’s only one outcome (1) in E ′ E ′ , we have P ( E ′ ) = 1 6 P ( E ′ ) = 1 6 . Thus, P ( E ) = 1 − P ( E ′ ) = 5 6 P ( E ) = 1 − P ( E ′ ) = 5 6 .

Here, the event E E is defined by the inequality sum ≤ 10 sum ≤ 10 . Thus, E ′ E ′ is defined by sum > 10 sum > 10 . There are three outcomes in E ′ E ′ : two 11s and one 12. Thus, P ( E ) = 1 − P ( E ′ ) = 1 − 3 36 = 11 12 P ( E ) = 1 − P ( E ′ ) = 1 − 3 36 = 11 12 .

• In Example 7.15, we found the sample space for this experiment consisted of these equally likely outcomes: {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}. Our event E E is defined by T ≥ 1 T ≥ 1 , so E ′ E ′ is defined by T < 1 T < 1 . The only outcome in E ′ E ′ is the first one on the list, where zero tails are flipped. So, P ( E ) = 1 − P ( E ′ ) = 1 − 1 8 = 7 8 P ( E ) = 1 − P ( E ′ ) = 1 − 1 8 = 7 8 .

Your Turn 7.22

Check your understanding, section 7.5 exercises.

For the following exercises, use the following table of the top 15 players by number of plate appearances (PA) in the 2019 Major League Baseball season to assign empirical probabilities to the given events. A plate appearance is a batter’s opportunity to try to get a hit. The other columns are runs scored (R), hits (H), doubles (2B), triples (3B), home runs (HR), walks (BB), and strike outs (SO).

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

7.3: Theoretical and Experimental Spinners

• Last updated
• Save as PDF
• Page ID 5736

Theoretical and Experimental Spinners

The 2 types of probability are theoretical probability and experimental probability . Theoretical probability is defined as the number of desired outcomes divided by the total number of outcomes.

Theoretical Probability

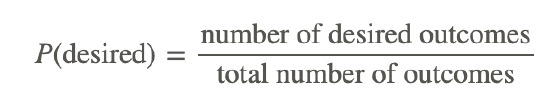
Experimental probability is, just as the name suggests, dependent on some form of data collection. To calculate the experimental probability, divide the number of times the desired outcome has occurred by the total number of trials.

Experimental Probability

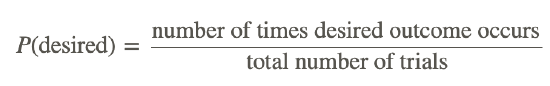
What is interesting about theoretical and experimental probabilities is that, in general, the more trials you do, the closer the experimental probability gets to the theoretical probability. We'll see this as we go through the examples.

Comparing Experimental and Theoretical Probability

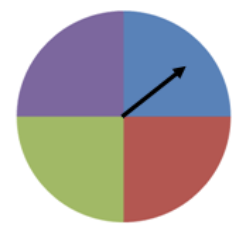
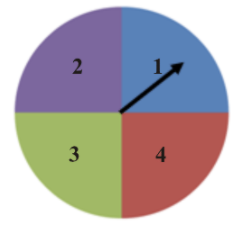
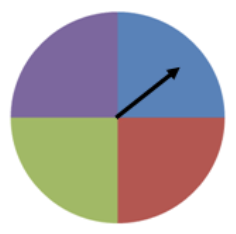
1. You are spinning a spinner like the one shown below 20 times. How many times does it land on blue? How does the experimental probability of landing on blue compare to the theoretical probability? Simulate the spinning of the spinner using technology.

On the TI-84 calculator, there are a number of possible simulations you can do. You can do a coin toss, spin a spinner, roll dice, pick marbles from a bag, or even draw cards from a deck.

After pressing ENTER, you will have the following screen appear.

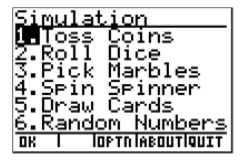
Since we're doing a spinner problem, choose Spin Spinner.

In Spin Spinner, a wheel with 4 possible outcomes is shown. You can adjust the number of spins, graph the frequency of each number, and use a table to see the number of spins for each number. We want to set this spinner to spin 20 times. Look at the keystrokes below and see how this is done.

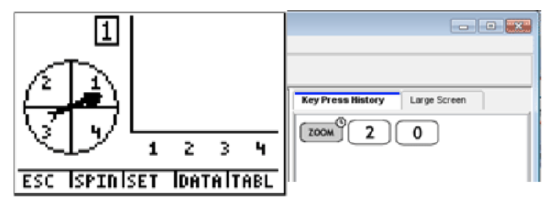
In order to match our color spinner with the one found in the calculator, you will see that we have added numbers to our spinner. This is not necessary, but it may help in the beginning to remember that 1 = blue (for this example).

Now that the spinner is set up for 20 trials, choose SPIN by pressing WINDOW

We can see the result of each trial by choosing TABL, or pressing GRAPH

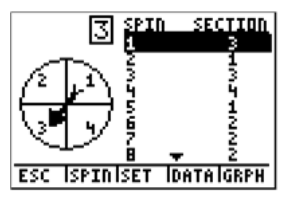
And we see the graph of the resulting table, or go back to the first screen, simply by choosing GRPH, or pressing GRAPH again.

Now, the question asks how many times we landed on blue (number 1). We can actually see how many times we landed on blue for these 20 spins. If you press the right arrow (▸), the frequency label will show you how many of the times the spinner landed on blue (number 1).

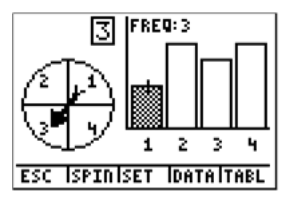
To go back to the question, how many times does the spinner land on blue if it is spun 20 times? The answer is 3. To calculate the experimental probability of landing on blue, we have to divide by the total number of spins.

P(blue)= 3 / 20 =0.15

Therefore, for this experiment, the experimental probability of landing on blue with 20 spins is 15%.

Now let's calculate the theoretical probability. We know that the spinner has 4 equal parts (blue, purple, green, and red). In a single trial, we can assume that:

P(blue)= 1 / 4 =0.25

Therefore, for our spinner example, the theoretical probability of landing on blue is 0.25. Finding the theoretical probability requires no collection of data.

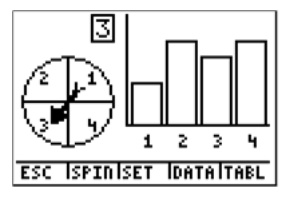
2. You are spinning a spinner like the one shown below 50 times. How many times does it land on blue? How about if you spin it 100 times? Does the experimental probability get closer to the theoretical probability? Simulate the spinning of the spinner using technology.

Set the spinner to spin 50 times and choose SPIN by pressing WINDOW

You can see the result of each trial by choosing TABL, or pressing GRAPH

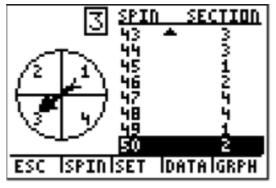
Again, we can see the graph of the resulting table, or go back to the first screen, simply by choosing GRAPH, or pressing GRAPH again.

The question asks how many times we landed on blue (number 1) for the 50 spins. Press the right arrow (▸), and the frequency label will show you how many of the times the spinner landed on blue (number 1).

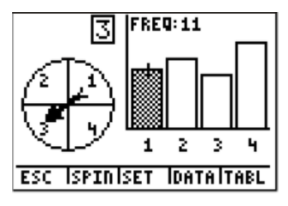
Now go back to the question. How many times does the spinner land on blue if it is spun 50 times? The answer is 11. To calculate the probability of landing on blue, we have to divide by the total number of spins.

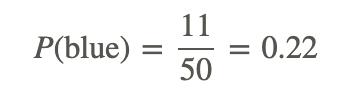
Therefore, for this experiment, the probability of landing on blue with 50 spins is 22%.

If we tried 100 trials, we would see something like the following:

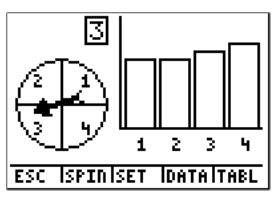
In this case, we see that the frequency of 1 is 23.

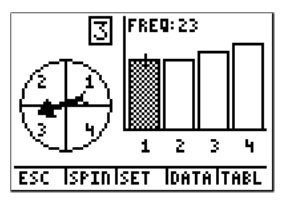
So how many times does the spinner land on blue if it is spun 100 times? The answer is 23. To calculate the probability of landing on blue in this case, we again have to divide by the total number of spins.

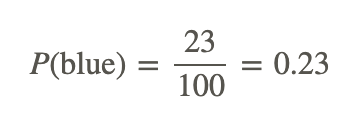
Therefore, for this experiment, the probability of landing on blue with 100 spins is 23%. You can see that as we perform more trials, we get closer to 25%, which is the theoretical probability.

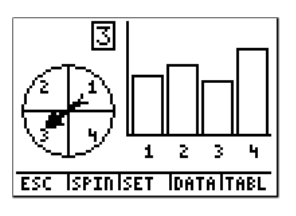
3. You are spinning a spinner like the one shown below 170 times. How many times does it land on blue? Does the experimental probability get closer to the theoretical probability? How many times do you predict we would have to spin the spinner to have the experimental probability equal the theoretical probability? Simulate the spinning of the spinner using technology.

With 170 spins, we get a frequency of 42 for blue.

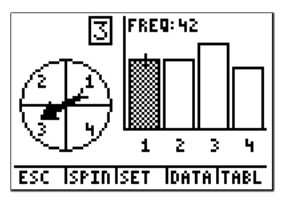
The experimental probability in this case can be calculated as follows

Therefore, the experimental probability is 24.7%, which is even closer to the theoretical probability of 25%. While we're getting closer to the theoretical probability, there is no number of trials that will guarantee that the experimental probability will exactly equal the theoretical probability.

You are spinning a spinner like the one shown below 500 times. How many times does it land on blue? How does the experimental probability of landing on blue compare to the theoretical probability? Simulate the spinning of the spinner using technology.

In the list of applications on the TI-84 calculator, choose Prob Sim.

In Spin Spinner, a wheel with 4 possible outcomes is shown. You can adjust the number of spins, graph the frequency of each number, and use a table to see the number of spins for each number. We want to set this spinner to spin 500 times. To do this, choose SET by pressing ZOOM, enter 500 after Trial Set, and choose OK by pressing GRAPH.

Remember that for this example, 1 = blue.

Now that the spinner is set up for 500 trials, choose SPIN by pressing WINDOW. Since we've chosen a large number of spins, the spinning may take a while!

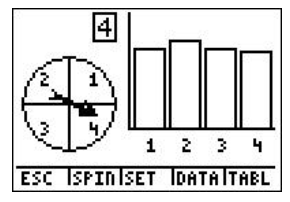
Now, the question asks how many times we landed on blue (number 1). We can actually see how many times we landed on blue for these 500 spins. If you press the right arrow (▸), the frequency label will show you how many of the times the spinner landed on blue (number 1).

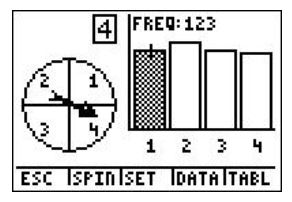
To go back to the question, how many times does the spinner land on blue if it is spun 500 times? The answer is 123. To calculate the experimental probability of landing on blue, we have to divide by the total number of spins.

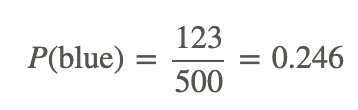
Therefore, for this experiment, the experimental probability of landing on blue with 500 spins is 24.6%.

Do you remember how to calculate the theoretical probability from Example A? We know that the spinner has 4 equal parts (blue, purple, green, and red). In a single trial, we can assume that:

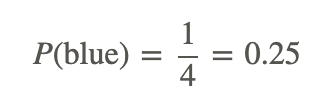
Therefore, for our spinner example, the theoretical probability of landing on blue is 0.25. As we pointed out in Example A, finding the theoretical probability requires no collection of data. It's also worth mentioning that our experimental probability was slightly farther away from the theoretical probability with 500 spins that it was with 170 spins in Example C. While, in general, increasing the number of spins will produce an experimental probability that is closer to the theoretical probability, as we've just seen, this is not always the case!

• Based on what you know about probabilities, write definitions for theoretical and experimental probability.
• What is the difference between theoretical and experimental probability?
• As you add more data, do your experimental probabilities get closer to or further away from your theoretical probabilities?
• Is spinning 1 spinner 100 times the same as spinning 100 spinners 1 time? Why or why not?

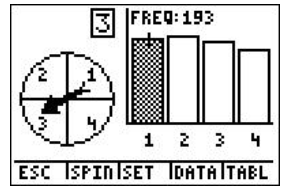
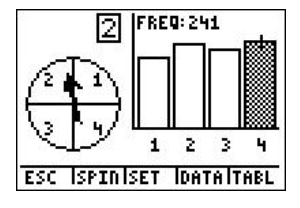
A spinner was spun 750 times using Spin Spinner on the TI-84 calculator, with 1 representing blue, 2 representing purple, 3 representing green, and 4 representing red as shown:

3. According to the following screen, what was the experimental probability of landing on blue?

4. According to the following screen, what was the experimental probability of landing on purple?

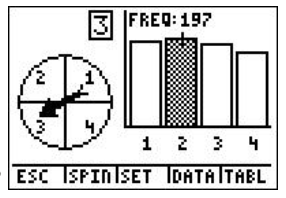
5. According to the following screen, what was the experimental probability of landing on green?

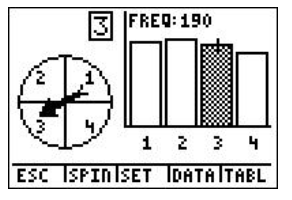
6. According to the following screen, what was the experimental probability of landing on red?

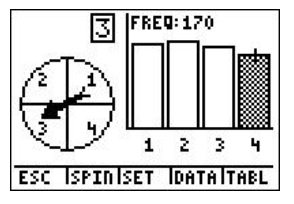
A spinner was spun 900 times using Spin Spinner on the TI-84 calculator, with 1 representing blue, 2 representing purple, 3 representing green, and 4 representing red as shown:

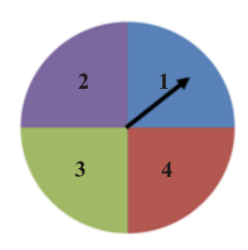
7. According to the following screen, what was the experimental probability of landing on blue?

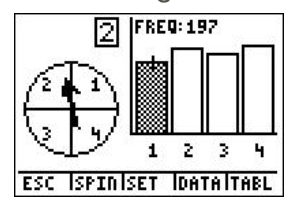
8. According to the following screen, what was the experimental probability of landing on purple?

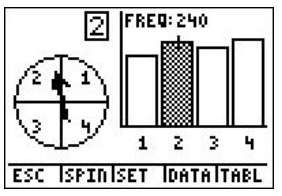
9. According to the following screen, what was the experimental probability of landing on green?

10. According to the following screen, what was the experimental probability of landing on red?

Review (Answers)

To view the Review answers, open this PDF file and look for section 3.5.

Additional Resources

Video: Theoretical and Experimental Spinners Principles

Activities: Theoretical and Experimental Coin Tosses Discussion Questions

Lesson Plans: Using Technology to Find Probability Distributions, Spinning a Spinner Lesson Plan

Practice: Theoretical and Experimental Spinners

Real World: Theoretical and Experimental Probability

Theoretical and Experimental Probability

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

Theoretical Probability

Theoretical probability as the name suggests is the theory behind probability. Theoretical probability gives the outcome of the occurrence of an event based on mathematics and reasoning. It tells us about what should happen in an ideal situation without conducting any experiments.

Theoretical probability is extremely useful in situations, such as in the launching of a satellite, where it is not feasible to conduct an actual experiment to arrive at a sound conclusion. In this article, we will learn more about the meaning of theoretical probability, the differences between the types of probabilities, and see some associated examples.

What is Theoretical Probability?

Theoretical probability is an approach in probability theory that is used to calculate the probability of an outcome of a specific event. Probability theory is a branch of mathematics that is concerned with finding the likelihood of occurrence of a random event. The probability that an event will occur lies between 0 and 1. If the probability is closer to 0 it implies that the event is less likely to take place. Similarly, if the probability is closer to 1 it denotes that the event has a higher chance of occurring.

Theoretical Probability Definition

Theoretical probability can be defined as the number of favorable outcomes divided by the total number of possible outcomes. To determine the theoretical probability there is no need to conduct an experiment. However, knowledge of the situation is required to find the probability of occurrence of that event. Theoretical probability predicts the probability of occurrence of an event by assuming that all events are equally likely to occur.

Theoretical Probability Example

Suppose there are a total of 5 cards and the probability of drawing 2 cards needs to be determined. Then by using the concept of theoretical probability, the number of favorable outcomes (2) is divided by the total possible outcomes (5) to get the probability as 0.4.

Theoretical Probability Formula

Theoretical probability can be calculated either by using logical reasoning or by using a simple formula. The result of such a type of probability is based on the number of possible outcomes. The theoretical probability formula is equal to the ratio of the number of favorable outcomes to the total number of probable outcomes. This formula is expressed as follows:

Theoretical Probability = Number of favorable outcomes / Number of possible outcomes.

How to Find Theoretical Probability?

Theoretical probability is used to express the likelihood of occurrence of an event without conducting any experiments. Suppose a person has 30 raffle tickets and, in total, 500 tickets were sold. The steps to calculate the theoretical probability of the person winning a prize are as follows:

• Step 1: Identify the number of favorable outcomes. As there are 30 raffle tickets thus, 30 will be the number of desired outcomes.
• Step 2: Determine the total possible outcomes. Since 500 total tickets were sold thus, 500 will be the number of total possible outcomes.
• Step 3: To calculate the theoretical probability divide the value from step 1 by step 2. Thus, 30 / 500 = 0.06. This shows that the probability of a person winning a raffle prize is 0.06.

Theoretical Probability vs Empirical Probability

Empirical probability is also known as experimental probability . Both theoretical probability and empirical probability are approaches to calculating the chance that a random event will occur. The difference between theoretical probability and empirical probability is given in the table below:

Related Articles:

• Probability Rules
• Probability and Statistics
• Poisson Distribution Formula
• Event Probability Calculator

Important Notes on Theoretical Probability

• Theoretical probability is used to calculate the probability of occurrence of an event without performing an experiment.
• Theoretical probability assumes that all events have an equal likelihood of occurrence.
• The theoretical probability formula is given as \(\frac{Number\: of\: favorable \:outcomes}{Number\: of \:possible \:outcomes}\).

Examples on Theoretical Probability

Example 1: If a bag contains 5 red and 7 blue balls then what is the probability of picking up a red ball?

Solution: To calculate the theoretical probability the following formula is used.

Number of favorable outcomes = 5

Number of possible outcomes = 5 + 7 = 12

P(red) = 5 / 12 = 0.4167

Answer: The probability of picking up a red ball is 0.4167.

Example 2: Find the probability of getting 3 on a fair die.

Solution: The possible outcomes of rolling a die are 1, 2, 3, 4, 5, 6.

In other words, the total number of outcomes = 6

As we want to calculate the probability of getting only number 3 thus, the number of favorable outcomes = 1

P(3) = 1 / 6 = 0.167

Answer: The probability of getting 3 on a fair die is 0.167.

Example 3: The letters of the word "MATHEMATICS" are placed in a bag. What is the probability of drawing the letter "T" from the bag?

Solution: The total number of letters = 11

As there are two T's placed in the bag thus, the number of favorable outcomes = 2.

P(T) = 2 / 11 = 0.182

Answer: The probability of drawing the letter "T" is 0.182

go to slide go to slide go to slide

Book a Free Trial Class

Practice Questions on Theoretical Probability

go to slide go to slide

FAQs on Theoretical Probability

What is theoretical probability in math.

Theoretical probability in math refers to the probability that is calculated without any experiment being performed. It can be defined as the ratio of the number of favorable outcomes to the total number of possible outcomes.

What is the Formula for Theoretical Probability?

The theoretical probability formula is given as follows:

Theoretical probability = \(\frac{Number\: of\: favorable \:outcomes}{Number\: of \:possible \:outcomes}\)

How Do You Calculate Theoretical Probability?

To calculate the theoretical probability the steps are as follows:

• Find the number of desired or favorable outcomes.
• Find the total number of outcomes.
• Divide the value obtained in step 1 by the value from step 2.

What is the Difference Between Theoretical Probability and Experimental Probability?

Theoretical probability is calculated when conducting an experiment is not possible. It gives a fair idea of the likelihood of occurrence of an outcome. In contrast, experimental probability is calculated based on experiments that have been conducted in the past.

Is Classical Probability the Same as Theoretical Probability?

Yes, theoretical probability is the same as classical probability. It is an approach used to calculate the outcome of an event based on the assumption that each outcome of the given event is equally likely to occur.

Why Do You Use Theoretical Probability?

Theoretical probability is required in situations where it is not possible to conduct repeated experiments due to its impracticality or lack of finance. For example, direct experiments cannot be performed when determining the various probabilities associated with subatomic particles. In such a case theoretical probability is used.

What is a Theoretical Probability Distribution?

Theoretical distributions that are designed based on certain assumptions are known as theoretical probability distributions. They are required for the quick analysis of the distribution of random variables. For example, Bernoulli distribution , normal distribution , binomial distribution , etc. are theoretical probability distributions.

Statistics Made Easy

Theoretical Probability: Definition + Examples

Probability is a topic in statistics that describes the likelihood of certain events happening. When we talk about probability, we’re often referring to one of two types:

1. Theoretical probability

Theoretical probability is the likelihood that an event will happen based on pure mathematics. The formula to calculate the theoretical probability of event  A  happening is:

P( A ) = number of desired outcomes / total number of possible outcomes

For example, the theoretical probability that a dice lands on “2” after one roll can be calculated as:

P( land on 2 ) = (only one way the dice can land on 2) / (six possible sides the dice can land on) = 1/6

2. Experimental probability

Experimental probability is the actual probability of an event occurring that you directly observe in an experiment. The formula to calculate the experimental probability of event  A  happening is:

P( A ) = number of times event occurs / total number of trials

For example, suppose we roll a dice 11 times and it lands on a “2” three times. The experimental probability for the dice landing on “2” can be calculated as:

P( land on 2 ) = (lands on 2 three times) / (rolled the dice 11 times) =  3/11

How to Remember the Difference

You can remember the difference between theoretical probability and experimental probability using the following trick:

• The theoretical probability of an event occurring can be calculated in theory using math.
• The experimental probability of an event occurring can be calculated by directly observing the results of an experiment .

The Benefit of Using Theoretical Probability

Statisticians often like to calculate the theoretical probability of events because it’s much easier and faster to calculate compared to actually conducting an experiment.

For example, suppose it’s known that 1 out of every 30 students at a particular school will need additional help with their math homework after school. Instead of waiting to see how many students show up for homework help after school, a school administrator could instead calculate the total number of students at the school (suppose it’s 300) and multiply by the theoretical probability (1/30) to know that he will likely need 10 people present to help each of the students one-on-one.

Examples of Theoretical Probability

Experimental probabilities are usually easier to calculate than theoretical probabilities because it just involves counting the number of times that a certain event actually occurred relative to the total number of trials.

Conversely, theoretical probabilities can be trickier to calculate. So, here are several examples of how to calculate theoretical probabilities to help you master the topic.

A bag contains the following:

• 3 red balls
• 4 green balls
• 2 purple balls

Question: If you close your eyes and randomly pull out one ball, what is the probability that it will be green?

Answer:  We can use the following formula to calculate the theoretical probability of pulling out a green ball:

P( green ) = (4 green balls) / (9 total balls) = 4/9

You own a 9-sided dice that contains the numbers 1 through 9 on the sides.

Question:  What is the probability that the dice lands on “7” if you were to roll it one time?

Answer:  We can use the following formula to calculate the theoretical probability that the dice lands on 7:

P( lands on 7 ) = (only one way the dice can land on 7) / (9 possible sides) =  1/9

A bag contains the name of 3 boys and 7 seven girls.

Question:  If you close your eyes and randomly pull one name out of the bag, what is the probability that you pull out a girl’s name?

Answer:  We can use the following formula to calculate the theoretical probability that you pull out a girl’s name:

P( girls name ) = (7 possible girl names) / (10 total names) =  7/10

Published by Zach

Leave a reply cancel reply.

Your email address will not be published. Required fields are marked *

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

• Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
• Duis aute irure dolor in reprehenderit in voluptate
• Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

2.4 - how to assign probability to events.

We know that probability is a number between 0 and 1. How does an event get assigned a particular probability value? Well, there are three ways of doing so:

• the personal opinion approach
• the relative frequency approach
• the classical approach

On this page, we'll take a look at each approach.

The Personal Opinion Approach Section  

This approach is the simplest in practice, but therefore it also the least reliable. You might think of it as the "whatever it is to you" approach. Here are some examples:

• "I think there is an 80% chance of rain today."
• "I think there is a 50% chance that the world's oil reserves will be depleted by the year 2100."
• "I think there is a 1% chance that the men's basketball team will end up in the Final Four sometime this decade."

Example 2-4 Section  

At which end of the probability scale would you put the probability that:

• one day you will die?
• you can swim around the world in 30 hours?
• you will win the lottery someday?
• a randomly selected student will get an A in this course?
• you will get an A in this course?

The Relative Frequency Approach Section  

The relative frequency approach involves taking the follow three steps in order to determine P ( A ), the probability of an event A :

• Perform an experiment a large number of times, n , say.
• Count the number of times the event A of interest occurs, call the number N ( A ), say.
• Then, the probability of event A equals:

\(P(A)=\dfrac{N(A)}{n}\)

The relative frequency approach is useful when the classical approach that is described next can't be used.

Example 2-5 Section  

When you toss a fair coin with one side designated as a "head" and the other side designated as a "tail", what is the probability of getting a head?

I think you all might instinctively reply \(\dfrac{1}{2}\). Of course, right? Well, there are three people who once felt compelled to determine the probability of getting a head using the relative frequency approach:

As you can see, the relative frequency approach yields a pretty good approximation to the 0.50 probability that we would all expect of a fair coin. Perhaps this example also illustrates the large number of times an experiment has to be conducted in order to get reliable results when using the relative frequency approach.

By the way, Count Buffon (1707-1788) was a French naturalist and mathematician who often pondered interesting probability problems. His most famous question

Suppose we have a floor made of parallel strips of wood, each the same width, and we drop a needle onto the floor. What is the probability that the needle will lie across a line between two strips?

came to be known as Buffon's needle problem. Karl Pearson (1857-1936) effectively established the field of mathematical statistics. And, once you hear John Kerrich's story, you might understand why he, of all people, carried out such a mind-numbing experiment. He was an English mathematician who was lecturing at the University of Copenhagen when World War II broke out. He was arrested by the Germans and spent the war interned in a prison camp in Denmark. To help pass the time he performed a number of probability experiments, such as this coin-tossing one.

Example 2-6 Section  

Some trees in a forest were showing signs of disease. A random sample of 200 trees of various sizes was examined yielding the following results:

What is the probability that one tree selected at random is large?

There are 68 large trees out of 200 total trees, so the relative frequency approach would tell us that the probability that a tree selected at random is large is 68/200 = 0.34.

What is the probability that one tree selected at random is diseased?

There are 37 diseased trees out of 200 total trees, so the relative frequency approach would tell us that the probability that a tree selected at random is diseased is 37/200 = 0.185.

What is the probability that one tree selected at random is both small and diseased?

There are 8 small, diseased trees out of 200 total trees, so the relative frequency approach would tell us that the probability that a tree selected at random is small and diseased is 8/200 = 0.04.

What is the probability that one tree selected at random is either small or disease-free?

There are 121 trees (35 + 46 + 24 + 8 + 8) out of 200 total trees that are either small or disease-free, so the relative frequency approach would tell us that the probability that a tree selected at random is either small or disease-free is 121/200 = 0.605.

What is the probability that one tree selected at random from the population of medium trees is doubtful of disease?

There are 92 medium trees in the sample. Of those 92 medium trees, 32 have been identified as being doubtful of disease. Therefore, the relative frequency approach would tell us that the probability that a medium tree selected at random is doubtful of disease is 32/92 = 0.348.

The Classical Approach Section  

The classical approach is the method that we will investigate quite extensively in the next lesson. As long as the outcomes in the sample space are equally likely (!!!), the probability of event \(A\) is:

\(P(A)=\dfrac{N(A)}{N(\mathbf{S})}\)

where \(N(A)\) is the number of elements in the event \(A\), and \(N(\mathbf{S})\) is the number of elements in the sample space \(\mathbf{S}\). Let's take a look at an example.

Example 2-7 Section  

Suppose you draw one card at random from a standard deck of 52 cards. Recall that a standard deck of cards contains 13 face values (Ace, 2, 3, 4, 5, 6, 7, 8, 9, 10, Jack, Queen, and King) in 4 different suits (Clubs, Diamonds, Hearts, and Spades) for a total of 52 cards. Assume the cards were manufactured to ensure that each outcome is equally likely with a probability of 1/52. Let \(A\) be the event that the card drawn is a 2, 3, or 7. Let \(B\) be the event that the card is a 2 of hearts (H), 3 of diamonds (D), 8 of spades (S) or king of clubs (C). That is:

• \(A= \{x: x \text{ is a }2, 3,\text{ or }7\}\)
• \(B = \{x: x\text{ is 2H, 3D, 8S, or KC}\}\)
• What is the probability that a 2, 3, or 7 is drawn?
• What is the probability that the card is a 2 of hearts, 3 of diamonds, 8 of spades or king of clubs?
• What is the probability that the card is either a 2, 3, or 7 or a 2 of hearts, 3 of diamonds, 8 of spades or king of clubs?
• What is \(P(A\cap B)\)?

7.5 Basic Concepts of Probability

Learning objectives.

After completing this section, you should be able to:

• Define probability including impossible and certain events.
• Calculate basic theoretical probabilities.
• Calculate basic empirical probabilities.
• Distinguish among theoretical, empirical, and subjective probability.
• Calculate the probability of the complement of an event.

It all comes down to this. The game of Monopoly that started hours ago is in the home stretch. Your sister has the dice, and if she rolls a 4, 5, or 7 she’ll land on one of your best spaces and the game will be over. How likely is it that the game will end on the next turn? Is it more likely than not? How can we measure that likelihood? This section addresses this question by introducing a way to measure uncertainty.

Introducing Probability

Uncertainty is, almost by definition, a nebulous concept. In order to put enough constraints on it that we can mathematically study it, we will focus on uncertainty strictly in the context of experiments. Recall that experiments are processes whose outcomes are unknown; the sample space for the experiment is the collection of all those possible outcomes. When we want to talk about the likelihood of particular outcomes, we sometimes group outcomes together; for example, in the Monopoly example at the beginning of this section, we were interested in the roll of 2 dice that might fall as a 4, 5, or 7. A grouping of outcomes that we’re interested in is called an event . In other words, an event is a subset of the sample space of an experiment; it often consists of the outcomes of interest to the experimenter.

Once we have defined the event that interests us, we can try to assess the likelihood of that event. We do that by assigning a number to each event ( E E ) called the probability of that event ( P ( E ) P ( E ) ). The probability of an event is a number between 0 and 1 (inclusive). If the probability of an event is 0, then the event is impossible. On the other hand, an event with probability 1 is certain to occur. In general, the higher the probability of an event, the more likely it is that the event will occur.

Example 7.16

Determining certain and impossible events.

Consider an experiment that consists of rolling a single standard 6-sided die (with faces numbered 1-6). Decide if these probabilities are equal to zero, equal to one, or somewhere in between.

• P ( roll a 4 ) P ( roll a 4 )
• P ( roll a 7 ) P ( roll a 7 )
• P ( roll a positive number ) P ( roll a positive number )
• P ( roll a 1 3 ) P ( roll a 1 3 )
• P ( roll an even number ) P ( roll an even number )
• P ( roll a single-digit number ) P ( roll a single-digit number )

Let's start by identifying the sample space. For one roll of this die, the possible outcomes are {1, 2, 3, 4, 5,6}. We can use that to assess these probabilities:

• We see that 4 is in the sample space, so it’s possible that it will be the outcome. It’s not certain to be the outcome, though. So, 0 < P ( roll a 4 ) < 1 0 < P ( roll a 4 ) < 1 .
• Notice that 7 is not in the sample space. So, P ( roll a 7 ) = 0 P ( roll a 7 ) = 0 .
• Every outcome in the sample space is a positive number, so this event is certain. Thus, P ( roll a positive number ) = 1 P ( roll a positive number ) = 1 .
• Since 1 3 1 3 is not in the sample space, P ( roll a 1 3 ) = 0 P ( roll a 1 3 ) = 0 .
• Some outcomes in the sample space are even numbers (2, 4, and 6), but the others aren’t. So, 0 < P ( roll an even number ) < 1 0 < P ( roll an even number ) < 1 .
• Every outcome in the sample space is a single-digit number, so P ( roll a single-digit number ) = 1 P ( roll a single-digit number ) = 1 .

Your Turn 7.16

Three ways to assign probabilities.

The probabilities of events that are certain or impossible are easy to assign; they’re just 1 or 0, respectively. What do we do about those in-between cases, for events that might or might not occur? There are three methods to assign probabilities that we can choose from. We’ll discuss them here, in order of reliability.

Method 1: Theoretical Probability

The theoretical method gives the most reliable results, but it cannot always be used. If the sample space of an experiment consists of equally likely outcomes, then the theoretical probability of an event is defined to be the ratio of the number of outcomes in the event to the number of outcomes in the sample space.

For an experiment whose sample space S S consists of equally likely outcomes, the theoretical probability of the event E E is the ratio

where n ( E ) n ( E ) and n ( S ) n ( S ) denote the number of outcomes in the event and in the sample space, respectively.

Example 7.17

Computing theoretical probabilities.

Recall that a standard deck of cards consists of 52 unique cards which are labeled with a rank (the whole numbers from 2 to 10, plus J, Q, K, and A) and a suit ( ♣ ♣ , ♢ ♢ , ♡ ♡ , or ♠ ♠ ). A standard deck is thoroughly shuffled, and you draw one card at random (so every card has an equal chance of being drawn). Find the theoretical probability of each of these events:

• The card is 10 ♠ 10 ♠ .
• The card is a ♡ ♡ .
• The card is a king (K).

There are 52 cards in the deck, so the sample space for each of these experiments has 52 elements. That will be the denominator for each of our probabilities.

• There is only one 10 ♠ 10 ♠ in the deck, so this event only has one outcome in it. Thus, P ( 10 ♠ ) = 1 52 P ( 10 ♠ ) = 1 52 .
• There are 13 ♡ s ♡ s in the deck, so P ( ♡ ) = 13 52 = 1 4 P ( ♡ ) = 13 52 = 1 4 .
• There are 4 cards of each rank in the deck, so P ( K ) = 4 52 = 1 13 P ( K ) = 4 52 = 1 13 .

Your Turn 7.17

It is critical that you make sure that every outcome in a sample space is equally likely before you compute theoretical probabilities!

Example 7.18

Using tables to find theoretical probabilities.

In the Basic Concepts of Probability , we were considering a Monopoly game where, if your sister rolled a sum of 4, 5, or 7 with 2 standard dice, you would win the game. What is the probability of this event? Use tables to determine your answer.

We should think of this experiment as occurring in two stages: (1) one die roll, then (2) another die roll. Even though these two stages will usually occur simultaneously in practice, since they’re independent, it’s okay to treat them separately.

Step 1: Since we have two independent stages, let’s create a table ( Figure 7.27 ), which is probably the most efficient method for determining the sample space.

Now, each of the 36 ordered pairs in the table represent an equally likely outcome.

Step 2: To make our analysis easier, let’s replace each ordered pair with the sum ( Figure 7.28 ).

Step 3: Since the event we’re interested in is the one consisting of rolls of 4, 5, or 7. Let’s shade those in ( Figure 7.29 ).

Our event contains 13 outcomes, so the probability that your sister rolls a losing number is 13 36 13 36 .

Your Turn 7.18

Example 7.19, using tree diagrams to compute theoretical probability.

If you flip a fair coin 3 times, what is the probability of each event? Use a tree diagram to determine your answer

• You flip exactly 2 heads.
• You flip 2 consecutive heads at some point in the 3 flips.
• All 3 flips show the same result.

Let’s build a tree to identify the sample space ( Figure 7.30 ).

The sample space is {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}, which has 8 elements.

• Flipping exactly 2 heads occurs three times (HHT, HTH, THH), so the probability is 3 8 3 8 .
• Flipping 2 consecutive heads at some point in the experiment happens 3 times: HHH, HHT, THH. So, the probability is 3 8 3 8 .
• There are 2 outcomes that all show the same result: HHH and TTT. So, the probability is 2 8 = 1 4 2 8 = 1 4 .

Your Turn 7.19

People in mathematics, gerolamo cardano.

The first known text that provided a systematic approach to probabilities was written in 1564 by Gerolamo Cardano (1501–1576). Cardano was a physician whose illegitimate birth closed many doors that would have otherwise been open to someone with a medical degree in 16th-century Italy. As a result, Cardano often turned to gambling to help ends meet. He was a remarkable mathematician, and he used his knowledge to gain an edge when playing at cards or dice. His 1564 work, titled Liber de ludo aleae (which translates as Book on Games of Chance ), summarized everything he knew about probability. Of course, if that book fell into the hands of those he played against, his advantage would disappear. That’s why he never allowed it to be published in his lifetime (it was eventually published in 1663). Cardano made other contributions to mathematics; he was the first person to publish the third degree analogue of the Quadratic Formula (though he didn’t discover it himself), and he popularized the use of negative numbers.

Method 2: Empirical Probability

Theoretical probabilities are precise, but they can’t be found in every situation. If the outcomes in the sample space are not equally likely, then we’re out of luck. Suppose you’re watching a baseball game, and your favorite player is about to step up to the plate. What is the probability that he will get a hit?

In this case, the sample space is {hit, not a hit}. That doesn’t mean that the probability of a hit is 1 2 1 2 , since those outcomes aren’t equally likely. The theoretical method simply can’t be used in this situation. Instead, we might look at the player’s statistics up to this point in the season, and see that he has 122 hits in 531 opportunities. So, we might think that the probability of a hit in the next plate appearance would be about 122 531 ≈ 0.23 122 531 ≈ 0.23 . When we use the outcomes of previous replications of an experiment to assign a probability to the next replication, we’re defining an empirical probability . Empirical probability is assigned using the outcomes of previous replications of an experiment by finding the ratio of the number of times in the previous replications the event occurred to the total number of previous replications.

Empirical probabilities aren’t exact, but when the number of previous replications is large, we expect them to be close. Also, if the previous runs of the experiment are not conducted under the exact set of circumstances as the one we’re interested in, the empirical probability is less reliable. For instance, in the case of our favorite baseball player, we might try to get a better estimate of the probability of a hit by looking only at his history against left- or right-handed pitchers (depending on the handedness of the pitcher he’s about to face).

Probability and Statistics

One of the broad uses of statistics is called statistical inference, where statisticians use collected data to make a guess (or inference) about the population the data were collected from. Nearly every tool that statisticians use for inference is based on probability. Not only is the method we just described for finding empirical probabilities one type of statistical inference, but some more advanced techniques in the field will give us an idea of how close that empirical probability might be to the actual probability!

Example 7.20

Finding empirical probabilities.

Assign an empirical probability to the following events:

• Jose is on the basketball court practicing his shots from the free throw line. He made 47 out of his last 80 attempts. What is the probability he makes his next shot?
• Amy is about to begin her morning commute. Over her last 60 commutes, she arrived at work 12 times in under half an hour. What is the probability that she arrives at work in 30 minutes or less?
• Felix is playing Yahtzee with his sister. Felix won 14 of the last 20 games he played against her. How likely is he to win this game?
• Since Jose made 47 out of his last 80 attempts, assign this event an empirical probability of 47 80 ≈ 59 % 47 80 ≈ 59 % .
• Amy completed the commute in under 30 minutes in 12 of the last 60 commutes, so we can estimate her probability of making it in under 30 minutes this time at 12 60 = 20 % 12 60 = 20 % .
• Since Felix has won 14 of the last 20 games, assign a probability for a win this time of 14 20 = 70 % 14 20 = 70 % .

Your Turn 7.20

Work it out, buffon’s needle.

A famous early question about probability (posed by Georges-Louis Leclerc, Comte de Buffon in the 18th century) had to do with the probability that a needle dropped on a floor finished with wooden slats would lay across one of the seams. If the distance between the slats is exactly the same length as the needle, then it can be shown using calculus that the probability that the needle crosses a seam is 2 π 2 π . Using toothpicks or matchsticks (or other uniformly long and narrow objects), assign an empirical probability to this experiment by drawing parallel lines on a large sheet of paper where the distance between the lines is equal to the length of your dropping object, then repeatedly dropping the objects and noting whether the object touches one of the lines. Once you have your empirical probability, take its reciprocal and multiply by 2. Is the result close to π π ?

Method 3: Subjective Probability

In cases where theoretical probability can’t be used and we don’t have prior experience to inform an empirical probability, we’re left with one option: using our instincts to guess at a subjective probability . A subjective probability is an assignment of a probability to an event using only one’s instincts.

Subjective probabilities are used in cases where an experiment can only be run once, or it hasn’t been run before. Because subjective probabilities may vary widely from person to person and they’re not based on any mathematical theory, we won’t give any examples. However, it’s important that we be able to identify a subjective probability when we see it; they will in general be far less accurate than empirical or theoretical probabilities.

Example 7.21

Distinguishing among theoretical, empirical, and subjective probabilities.

Classify each of the following probabilities as theoretical, empirical, or subjective.

• An eccentric billionaire is testing a brand new rocket system. He says there is a 15% chance of failure.
• With 4 seconds to go in a close basketball playoff game, the home team need 3 points to tie up the game and send it to overtime. A TV commentator says that team captain should take the final 3-point shot, because he has a 38% chance of making it (greater than every other player on the team).
• Felix is losing his Yahtzee game against his sister. He has one more chance to roll 2 dice; he’ll win the game if they both come up 4. The probability of this is about 2.8%.
• This experiment has never been run before, so the given probability is subjective.
• Presumably, the commentator has access to each player’s performance statistics over the entire season. So, the given probability is likely empirical.
• Rolling 2 dice results in a sample space with equally likely outcomes. This probability is theoretical. (We’ll learn how to calculate that probability later in this chapter.)

Your Turn 7.21

Benford’s law.

In 1938, Frank Benford published a paper (“The law of anomalous numbers,” in Proceedings of the American Philosophical Society ) with a surprising result about probabilities. If you have a list of numbers that spans at least a couple of orders of magnitude (meaning that if you divide the largest by the smallest, the result is at least 100), then the digits 1–9 are not equally likely to appear as the first digit of those numbers, as you might expect. Benford arrived at this conclusion using empirical probabilities; he found that 1 was about 6 times as likely to be the initial digit as 9 was!

New Probabilities from Old: Complements

One of the goals of the rest of this chapter is learning how to break down complicated probability calculations into easier probability calculations. We’ll look at the first of the tools we can use to accomplish this goal in this section; the rest will come later.

Given an event E E , the complement of E E (denoted E ′ E ′ ) is the collection of all of the outcomes that are not in E E . (This is language that is taken from set theory, which you can learn more about elsewhere in this text.) Since every outcome in the sample space either is or is not in E E , it follows that n ( E ) + n ( E ′ ) = n ( S ) n ( E ) + n ( E ′ ) = n ( S ) . So, if the outcomes in S S are equally likely, we can compute theoretical probabilities P ( E ) = n ( E ) n ( S ) P ( E ) = n ( E ) n ( S ) and P ( E ′ ) = n ( E ′ ) n ( S ) P ( E ′ ) = n ( E ′ ) n ( S ) . Then, adding these last two equations, we get

P ( E ) + P ( E ′ ) = n ( E ) n ( S ) + n ( E ′ ) n ( S ) = n ( E ) + n ( E ′ ) n ( S ) = n ( S ) n ( S ) = 1 P ( E ) + P ( E ′ ) = n ( E ) n ( S ) + n ( E ′ ) n ( S ) = n ( E ) + n ( E ′ ) n ( S ) = n ( S ) n ( S ) = 1

Thus, if we subtract P ( E ′ ) P ( E ′ ) from both sides, we can conclude that P ( E ) = 1 − P ( E ′ ) P ( E ) = 1 − P ( E ′ ) . Though we performed this calculation under the assumption that the outcomes in S S are all equally likely, the last equation is true in every situation.

P ( E ) = 1 − P ( E ′ ) P ( E ) = 1 − P ( E ′ )

How is this helpful? Sometimes it is easier to compute the probability that an event won’t happen than it is to compute the probability that it will . To apply this principle, it’s helpful to review some tricks for dealing with inequalities. If an event is defined in terms of an inequality, the complement will be defined in terms of the opposite inequality: Both the direction and the inclusivity will be reversed, as shown in the table below.

Example 7.22

Using the formula for complements to compute probabilities.

• If you roll a standard 6-sided die, what is the probability that the result will be a number greater than one?
• If you roll two standard 6-sided dice, what is the probability that the sum will be 10 or less?
• If you flip a fair coin 3 times, what is the probability that at least one flip will come up tails?
• Here, the sample space is {1, 2, 3, 4, 5, 6}. It’s easy enough to see that the probability in question is 5 6 5 6 , because there are 5 outcomes that fall into the event “roll a number greater than 1.” Let’s also apply our new formula to find that probability. Since E E is defined using the inequality roll > 1 roll > 1 , then E ′ E ′ is defined using roll ≤ 1 roll ≤ 1 . Since there’s only one outcome (1) in E ′ E ′ , we have P ( E ′ ) = 1 6 P ( E ′ ) = 1 6 . Thus, P ( E ) = 1 − P ( E ′ ) = 5 6 P ( E ) = 1 − P ( E ′ ) = 5 6 .

Here, the event E E is defined by the inequality sum ≤ 10 sum ≤ 10 . Thus, E ′ E ′ is defined by sum > 10 sum > 10 . There are three outcomes in E ′ E ′ : two 11s and one 12. Thus, P ( E ) = 1 − P ( E ′ ) = 1 − 3 36 = 11 12 P ( E ) = 1 − P ( E ′ ) = 1 − 3 36 = 11 12 .

• In Example 7.15 , we found the sample space for this experiment consisted of these equally likely outcomes: {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}. Our event E E is defined by T ≥ 1 T ≥ 1 , so E ′ E ′ is defined by T < 1 T < 1 . The only outcome in E ′ E ′ is the first one on the list, where zero tails are flipped. So, P ( E ) = 1 − P ( E ′ ) = 1 − 1 8 = 7 8 P ( E ) = 1 − P ( E ′ ) = 1 − 1 8 = 7 8 .

Your Turn 7.22

Check your understanding, section 7.5 exercises.

For the following exercises, use the following table of the top 15 players by number of plate appearances (PA) in the 2019 Major League Baseball season to assign empirical probabilities to the given events. A plate appearance is a batter’s opportunity to try to get a hit. The other columns are runs scored (R), hits (H), doubles (2B), triples (3B), home runs (HR), walks (BB), and strike outs (SO).

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/contemporary-mathematics/pages/1-introduction

• Authors: Donna Kirk
• Publisher/website: OpenStax
• Book title: Contemporary Mathematics
• Publication date: Mar 22, 2023
• Location: Houston, Texas
• Book URL: https://openstax.org/books/contemporary-mathematics/pages/1-introduction
• Section URL: https://openstax.org/books/contemporary-mathematics/pages/7-5-basic-concepts-of-probability

© Dec 21, 2023 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Theory of Probability

• First Online: 13 July 2022

Cite this chapter

• Massimiliano Bonamente 13  

Part of the book series: Graduate Texts in Physics ((GTP))

2039 Accesses

The theory of probability is the mathematical framework for the study of the probability of occurrence of events. The first step is to establish a method to assign the probability of an event, for example, the probability that a coin lands heads up after a toss. The frequentist or empirical approach, and the subjective or Bayesian approach, are two methods that can be used to calculate probabilities. Once a method for assigning probabilities is established, the Kolmogorov axioms are introduced as the “rules” required to manipulate probabilities. Fundamental results known as Bayes’ theorem and the theorem of total probability are used to define and interpret the concepts of statistical independence and of conditional probability, which play a central role in much of the material presented in this book.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

• Available as PDF
• Read on any device
• Instant download
• Own it forever
• Available as EPUB and PDF
• Durable hardcover edition
• Dispatched in 3 to 5 business days
• Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

In his book Foundations of the Theory of Probability [63], Kolmogorov lists a larger number of axioms, due to the need of ensuring certain mathematical properties of probability.

Author information

Authors and affiliations.

University of Alabama in Huntsville, Huntsville, AL, USA

Massimiliano Bonamente

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Massimiliano Bonamente .

1 Electronic supplementary material

Below is the link to the electronic supplementary material.

Supplementary material 1 (pdf 104 KB)

Rights and permissions.

Reprints and permissions

Copyright information

© 2022 The Author(s), under exclusive license to Springer Nature Singapore Pte Ltd.

About this chapter

Bonamente, M. (2022). Theory of Probability. In: Statistics and Analysis of Scientific Data. Graduate Texts in Physics. Springer, Singapore. https://doi.org/10.1007/978-981-19-0365-6_1

Download citation

DOI : https://doi.org/10.1007/978-981-19-0365-6_1

Published : 13 July 2022

Publisher Name : Springer, Singapore

Print ISBN : 978-981-19-0364-9

Online ISBN : 978-981-19-0365-6

eBook Packages : Physics and Astronomy Physics and Astronomy (R0)

Share this chapter

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Publish with us

Policies and ethics

• Find a journal
• Track your research