problem solver meaning in education

Center for Teaching

Teaching problem solving.

Print Version

Tips and Techniques

Expert vs. novice problem solvers, communicate.

• Have students  identify specific problems, difficulties, or confusions . Don’t waste time working through problems that students already understand.
• If students are unable to articulate their concerns, determine where they are having trouble by  asking them to identify the specific concepts or principles associated with the problem.
• In a one-on-one tutoring session, ask the student to  work his/her problem out loud . This slows down the thinking process, making it more accurate and allowing you to access understanding.
• When working with larger groups you can ask students to provide a written “two-column solution.” Have students write up their solution to a problem by putting all their calculations in one column and all of their reasoning (in complete sentences) in the other column. This helps them to think critically about their own problem solving and helps you to more easily identify where they may be having problems. Two-Column Solution (Math) Two-Column Solution (Physics)

Encourage Independence

• Model the problem solving process rather than just giving students the answer. As you work through the problem, consider how a novice might struggle with the concepts and make your thinking clear
• Have students work through problems on their own. Ask directing questions or give helpful suggestions, but  provide only minimal assistance and only when needed to overcome obstacles.
• Don’t fear  group work ! Students can frequently help each other, and talking about a problem helps them think more critically about the steps needed to solve the problem. Additionally, group work helps students realize that problems often have multiple solution strategies, some that might be more effective than others

Be sensitive

• Frequently, when working problems, students are unsure of themselves. This lack of confidence may hamper their learning. It is important to recognize this when students come to us for help, and to give each student some feeling of mastery. Do this by providing  positive reinforcement to let students know when they have mastered a new concept or skill.

Encourage Thoroughness and Patience

• Try to communicate that  the process is more important than the answer so that the student learns that it is OK to not have an instant solution. This is learned through your acceptance of his/her pace of doing things, through your refusal to let anxiety pressure you into giving the right answer, and through your example of problem solving through a step-by step process.

Experts (teachers) in a particular field are often so fluent in solving problems from that field that they can find it difficult to articulate the problem solving principles and strategies they use to novices (students) in their field because these principles and strategies are second nature to the expert. To teach students problem solving skills,  a teacher should be aware of principles and strategies of good problem solving in his or her discipline .

The mathematician George Polya captured the problem solving principles and strategies he used in his discipline in the book  How to Solve It: A New Aspect of Mathematical Method (Princeton University Press, 1957). The book includes  a summary of Polya’s problem solving heuristic as well as advice on the teaching of problem solving.

Teaching Guides

• Online Course Development Resources
• Principles & Frameworks
• Pedagogies & Strategies
• Reflecting & Assessing
• Challenges & Opportunities
• Populations & Contexts

Quick Links

• Services for Departments and Schools
• Examples of Online Instructional Modules

Why Every Educator Needs to Teach Problem-Solving Skills

Strong problem-solving skills will help students be more resilient and will increase their academic and career success .

Want to learn more about how to measure and teach students’ higher-order skills, including problem solving, critical thinking, and written communication?

Problem-solving skills are essential in school, careers, and life.

Problem-solving skills are important for every student to master. They help individuals navigate everyday life and find solutions to complex issues and challenges. These skills are especially valuable in the workplace, where employees are often required to solve problems and make decisions quickly and effectively.

Problem-solving skills are also needed for students’ personal growth and development because they help individuals overcome obstacles and achieve their goals. By developing strong problem-solving skills, students can improve their overall quality of life and become more successful in their personal and professional endeavors.

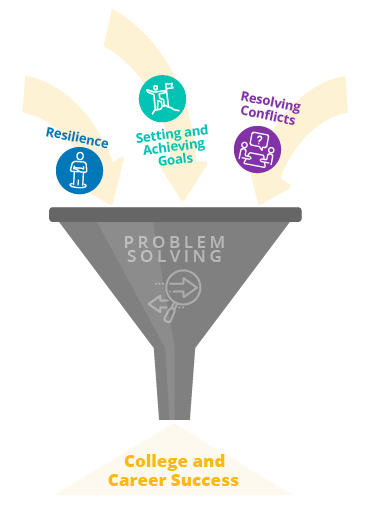
Problem-Solving Skills Help Students…

   develop resilience.

Problem-solving skills are an integral part of resilience and the ability to persevere through challenges and adversity. To effectively work through and solve a problem, students must be able to think critically and creatively. Critical and creative thinking help students approach a problem objectively, analyze its components, and determine different ways to go about finding a solution.  

This process in turn helps students build self-efficacy . When students are able to analyze and solve a problem, this increases their confidence, and they begin to realize the power they have to advocate for themselves and make meaningful change.

When students gain confidence in their ability to work through problems and attain their goals, they also begin to build a growth mindset . According to leading resilience researcher, Carol Dweck, “in a growth mindset, people believe that their most basic abilities can be developed through dedication and hard work—brains and talent are just the starting point. This view creates a love of learning and a resilience that is essential for great accomplishment.”

    Set and Achieve Goals

Students who possess strong problem-solving skills are better equipped to set and achieve their goals. By learning how to identify problems, think critically, and develop solutions, students can become more self-sufficient and confident in their ability to achieve their goals. Additionally, problem-solving skills are used in virtually all fields, disciplines, and career paths, which makes them important for everyone. Building strong problem-solving skills will help students enhance their academic and career performance and become more competitive as they begin to seek full-time employment after graduation or pursue additional education and training.

  Resolve Conflicts

In addition to increased social and emotional skills like self-efficacy and goal-setting, problem-solving skills teach students how to cooperate with others and work through disagreements and conflicts. Problem-solving promotes “thinking outside the box” and approaching a conflict by searching for different solutions. This is a very different (and more effective!) method than a more stagnant approach that focuses on placing blame or getting stuck on elements of a situation that can’t be changed.

While it’s natural to get frustrated or feel stuck when working through a conflict, students with strong problem-solving skills will be able to work through these obstacles, think more rationally, and address the situation with a more solution-oriented approach. These skills will be valuable for students in school, their careers, and throughout their lives.

    Achieve Success

We are all faced with problems every day. Problems arise in our personal lives, in school and in our jobs, and in our interactions with others. Employers especially are looking for candidates with strong problem-solving skills. In today’s job market, most jobs require the ability to analyze and effectively resolve complex issues. Students with strong problem-solving skills will stand out from other applicants and will have a more desirable skill set.

In a recent opinion piece published by The Hechinger Report , Virgel Hammonds, Chief Learning Officer at KnowledgeWorks, stated “Our world presents increasingly complex challenges. Education must adapt so that it nurtures problem solvers and critical thinkers.” Yet, the “traditional K–12 education system leaves little room for students to engage in real-world problem-solving scenarios.” This is the reason that a growing number of K–12 school districts and higher education institutions are transforming their instructional approach to personalized and competency-based learning, which encourage students to make decisions, problem solve and think critically as they take ownership of and direct their educational journey.

Problem-Solving Skills Can Be Measured and Taught

Research shows that problem-solving skills can be measured and taught. One effective method is through performance-based assessments which require students to demonstrate or apply their knowledge and higher-order skills to create a response or product or do a task.

What Are Performance-Based Assessments?

With the No Child Left Behind Act (2002), the use of standardized testing became the primary way to measure student learning in the U.S. The legislative requirements of this act shifted the emphasis to standardized testing, and this led to a  decline in nontraditional testing methods .

But   many educators, policy makers, and parents have concerns with standardized tests. Some of the top issues include that they don’t provide feedback on how students can perform better, they don’t value creativity, they are not representative of diverse populations, and they can be disadvantageous to lower-income students.

While standardized tests are still the norm, U.S. Secretary of Education Miguel Cardona is encouraging states and districts to move away from traditional multiple choice and short response tests and instead use performance-based assessment, competency-based assessments, and other more authentic methods of measuring students abilities and skills rather than rote learning. 

Performance-based assessments  measure whether students can apply the skills and knowledge learned from a unit of study. Typically, a performance task challenges students to use their higher-order skills to complete a project or process. Tasks can range from an essay to a complex proposal or design.

Preview a Performance-Based Assessment

Want a closer look at how performance-based assessments work?  Preview CAE’s K–12 and Higher Education assessments and see how CAE’s tools help students develop critical thinking, problem-solving, and written communication skills.

Performance-Based Assessments Help Students Build and Practice Problem-Solving Skills

In addition to effectively measuring students’ higher-order skills, including their problem-solving skills, performance-based assessments can help students practice and build these skills. Through the assessment process, students are given opportunities to practically apply their knowledge in real-world situations. By demonstrating their understanding of a topic, students are required to put what they’ve learned into practice through activities such as presentations, experiments, and simulations. 

This type of problem-solving assessment tool requires students to analyze information and choose how to approach the presented problems. This process enhances their critical thinking skills and creativity, as well as their problem-solving skills. Unlike traditional assessments based on memorization or reciting facts, performance-based assessments focus on the students’ decisions and solutions, and through these tasks students learn to bridge the gap between theory and practice.

Performance-based assessments like CAE’s College and Career Readiness Assessment (CRA+) and Collegiate Learning Assessment (CLA+) provide students with in-depth reports that show them which higher-order skills they are strongest in and which they should continue to develop. This feedback helps students and their teachers plan instruction and supports to deepen their learning and improve their mastery of critical skills.

Explore CAE’s Problem-Solving Assessments

CAE offers performance-based assessments that measure student proficiency in higher-order skills including problem solving, critical thinking, and written communication.

• College and Career Readiness Assessment (CCRA+) for secondary education and
• Collegiate Learning Assessment (CLA+) for higher education.

Our solution also includes instructional materials, practice models, and professional development.

We can help you create a program to build students’ problem-solving skills that includes:

• Measuring students’ problem-solving skills through a performance-based assessment    
• Using the problem-solving assessment data to inform instruction and tailor interventions
• Teaching students problem-solving skills and providing practice opportunities in real-life scenarios
• Supporting educators with quality professional development

Get started with our problem-solving assessment tools to measure and build students’ problem-solving skills today! These skills will be invaluable to students now and in the future.

Ready to Get Started?

Learn more about cae’s suite of products and let’s get started measuring and teaching students important higher-order skills like problem solving..

10 minute read

Problem Solving

Cognitive processing aimed at figuring out how to achieve a goal is called problem solving. In problem solving, the problem solver seeks to devise a method for transforming a problem from its current state into a desired state when a solution is not immediately obvious to the problem solver. Thus, the hallmark of problem solving is the invention of a new method for addressing a problem. This definition has three parts: (1) problem solving is cognitive –that is, it occurs internally in the mind (or cognitive system) and must be inferred indirectly from behavior; (2) problem solving is a process –it involves the manipulation of knowledge representations (or carrying out mental computations); and (3) problem solving is directed –it is guided by the goals of the problem solver.

The definition of problem solving covers a broad range of human cognitive activities, including educationally relevant cognition–figuring out how to manage one's time, writing an essay on a selected topic, summarizing the main point of a textbook section, solving an arithmetic word problem, or determining whether a scientific theory is valid by conducting experiments.

A problem occurs when a problem solver has a goal but initially does not know how to achieve the goal. This definition has three parts: (1) the current state –the problem begins in a given state; (2) the goal state –the problem solver wants the problem to be in a different state, and problem solving is required to transform the problem from the current (or given) state into the goal state, and (3) obstacles –the problem solver does not know the correct solution and an effective solution method is not obvious to the problem solver.

According to this definition a problem is personal, so that a situation that is a problem for one person might not be a problem for another person. For example, "3 + 5 = ___" might be a problem for a six-year-old child who reasons, "Let's see. I can take one from the 5 and give it to the 3. That makes 4 plus 4, and I know that 4 plus 4 is 8." However, this equation is not a problem for an adult who knows the correct answer.

Types of Problems

Routine and nonroutine problems. It is customary to distinguish between routine and nonroutine problems. In a routine problem, the problem solver knows a solution method and only needs to carry it out. For example, for most adults the problem "589 × 45 = ___" is a routine problem if they know the procedure for multicolumn multiplication. Routine problems are sometimes called exercises, and technically do not fit the definition of problem stated above. When the goal of an educational activity is to promote all the aspects of problem solving (including devising a solution plan), then nonroutine problems (or exercises) are appropriate.

In a nonroutine problem, the problem solver does not initially know a method for solving the problem. For example, the following problem (reported by Robert Sternberg and Janet Davidson) is nonroutine for most people: "Water lilies double in area every twenty-four hours. At the beginning of the summer, there is one water lily on the lake. It takes sixty days for the lake to be completely covered with water lilies. On what day is the lake half covered?" In this problem, the problem solver must invent a solution method based on working backwards from the last day. Based on this method, the problem solver can ask what the lake would look like on the day before the last day, and conclude that the lake is half covered on the fifty-ninth day.

Well-defined and ill-defined problems. It is also customary to distinguish between well-defined and ill-defined problems. In a well-defined problem, the given state of the problem, the goal state of the problem, and the allowable operators (or moves) are each clearly specified. For example, the following water-jar problem (adapted from Abrahama Luchins) is an example of a well defined problem: "I will give you three empty water jars; you can fill any jar with water and pour water from one jar into another (until the second jar is full or the first one is empty); you can fill and pour as many times as you like. Given water jars of size 21, 127, and 3 units and an unlimited supply of water, how can you obtain exactly 100 units of water?" This is a well-defined problem because the given state is clearly specified (you have empty jars of size 21, 127, and 3), the goal state is clearly specified (you want to get 100 units of water in one of the jars), and the allowable operators are clearly specified (you can fill and pour according to specific procedures). Well-defined problems may be either routine or nonroutine; if you do not have previous experience with water jar problems, then finding the solution (i.e., fill the 127, pour out 21 once, and pour out 3 twice) is a nonroutine problem.

In an ill-defined problem, the given state, goal state, and/or operations are not clearly specified. For example, in the problem, "Write a persuasive essay in favor of year-round schools," the goal state is not clear because the criteria for what constitutes a "persuasive essay" are vague and the allowable operators, such as how to access sources of information, are not clear. Only the given state is clear–a blank piece of paper. Ill-defined problems can be routine or nonroutine; if one has extensive experience in writing then writing a short essay like this one is a routine problem.

Processes in Problem Solving

The process of problem solving can be broken down into two major phases: problem representation, in which the problem solver builds a coherent mental representation of the problem, and problem solution, in which the problem solver devises and carries out a solution plan. Problem representation can be broken down further into problem translation, in which the problem solver translates each sentence (or picture) into an internal mental representation, and problem integration, in which the problem solver integrates the information into a coherent mental representation of the problem (i.e., a mental model of the situation described in the problem). Problem solution can be broken down further into solution planning, in which the problem solver devises a plan for how to solve the problem, and solution execution, in which the problem solver carries out the plan by engaging in solution behaviors. Although the four processes of problem solving are listed sequentially, they may occur in many different orderings and with many iterations in the course of solving a problem.

For example, consider the butter problem described by Mary Hegarty, Richard Mayer, and Christopher Monk: "At Lucky, butter costs 65 cents per stick. This is two cents less per stick than butter at Vons. If you need to buy 4 sticks of butter, how much will you pay at Vons?" In the problem translation phase, the problem solver may mentally represent the first sentence as "Lucky = 0.65," the second sentence as "Lucky = Vons - 0.02," and the third sentence as "4 × Vons = ___." In problem integration, the problem solver may construct a mental number line with Lucky at 0.65 and Vons to the right of Lucky (at 0.67); or the problem solver may mentally integrate the equations as "4 × (Lucky + 0.02) = ____." A key insight in problem integration is to recognize the proper relation between the cost of butter at Lucky and the cost of butter at Vons, namely that butter costs more at Vons (even though the keyword in the problem is "less"). In solution planning, the problem solver may break the problem into parts, such as: "First add 0.02 to 0.65, then multiply the result by 4." In solution executing, the problem solver carries out the plan: 0.02 + 0.65 =0.67, 0.67 × 4 = 2.68. In addition, the problem solver must monitor the problem-solving process and make adjustments as needed.

Teaching for Problem Solving

A challenge for educators is to teach in ways that foster meaningful learning rather than rote learning. Rote instructional methods promote retention (the ability to solve problems that are identical or highly similar to those presented in instruction), but not problem solving transfer (the ability to apply what was learned to novel problems). For example, in 1929, Alfred Whitehead used the term inert knowledge to refer to learning that cannot be used to solve novel problems. In contrast, meaningful instructional methods promote both retention and transfer.

In a classic example of the distinction between rote and meaningful learning, the psychologist Max Wertheimer (1959) described two ways of teaching students to compute the area of a parallelogram. In the rote method, students learn to measure the base, measure the height, and then multiply base times height. Students taught by the A = b × h method are able to find the area of parallelograms shaped like the ones given in instruction (a retention problem) but not unusual parallelograms or other shapes (a transfer problem). Wertheimer used the term reproductive thinking to refer to problem solving in which one blindly carries out a previously learned procedure. In contrast, in the meaningful method, students learn by cutting the triangle from one end of a cardboard parallelogram and attaching it to the other end to form a rectangle. Once students have the insight that a parallelogram is just a rectangle in disguise, they can compute the area because they already know the procedure for finding the area of a rectangle. Students taught by the insight method perform well on both retention and transfer problems. Wertheimer used the term productive thinking to refer to problem solving in which one invents a new approach to solving a novel problem.

Educationally Relevant Advances in Problem Solving

Recent advances in educational psychology point to the role of domain-specific knowledge in problem solving–such as knowledge of specific strategies or problem types that apply to a particular field. Three important advances have been: (1) the teaching of problem-solving processes, (2) the nature of expert problem solving, and (3) new conceptions of individual differences in problem-solving ability.

Teaching of problem-solving processes. An important advance in educational psychology is cognitive strategy instruction, which includes the teaching of problem-solving processes. For example, in Project Intelligence, elementary school children successfully learned the cognitive processes needed for solving problems similar to those found on intelligence tests. In Instrumental Enrichment, students who had been classified as mentally retarded learned cognitive processes that allowed them to show substantial improvements on intelligence tests.

Expert problem solving. Another important advance in educational psychology concerns differences between what experts and novices know in given fields, such as medicine, physics, and computer programming. For example, expert physicists tend to store their knowledge in large integrated chunks, whereas novices tend to store their knowledge as isolated fragments; expert physicists tend to focus on the underlying structural characteristics of physics word problems, whereas novices focus on the surface features; and expert physicists tend to work forward from the givens to the goal, whereas novices work backwards from the goal to the givens. Research on expertise has implications for professional education because it pinpoints the kinds of domain-specific knowledge that experts need to learn.

Individual differences in problem-solving ability. This third advance concerns new conceptions of intellectual ability based on differences in the way people process information. For example, people may differ in cognitive style–such as their preferences for visual versus verbal representations, or for impulsive versus reflective approaches to problem solving. Alternatively, people may differ in the speed and efficiency with which they carry out specific cognitive processes, such as making a mental comparison or retrieving a piece of information from memory. Instead of characterizing intellectual ability as a single, monolithic ability, recent conceptions of intellectual ability focus on the role of multiple differences in information processing.

See also: C REATIVITY ; L EARNING , subentry on A NALOGICAL R EASONING ; M ATHEMATICS L EARNING, subentry on C OMPLEX P ROBLEM S OLVING .

BIBLIOGRAPHY

C HI , M ICHELENE T. H.; G LASER , R OBERT ; and F ARR , M ARSHALL J., eds. 1988. The Nature of Expertise. Hillsdale, NJ: Erlbaum.

D UNKER , K ARL . 1945. On Problem Solving. Washington, DC: American Psychological Association.

F EUERSTEIN , R EUVEN . 1980. Instrumental Enrichment. Baltimore: University Park Press.

H EGARTY , M ARY ; M AYER , R ICHARD E.; and M ONK , C HRISTOPHER A. 1995. "Comprehension of Arithmetic Word Problems: Evidence from Students' Eye Fixations." Journal of Educational Psychology 84:76–84.

H UNT , E ARL ; L UNNEBORG , C LIFF ; and L EWIS , J. 1975. "What Does It Mean to Be High Verbal?" Cognitive Psychology 7:194–227.

L ARKIN , J ILL H.; M C D ERMOTT , J OHN ; S IMON , D OROTHEA P.; and S IMON , H ERBERT A. 1980. "Expert and Novice Performance in Solving Physics Problems." Science 208:1335–1342.

L UCHINS , A BRAHAMA S. 1942. Mechanization in Problem Solving: The Effect of Einstellung. Evanston, IL: American Psychological Association.

M AYER , R ICHARD E. 1992. Thinking, Problem Solving, Cognition, 2nd edition. New York: Freeman.

M AYER , R ICHARD E. 1999. The Promise of Educational Psychology. Upper Saddle River, NJ: Prentice-Hall.

N ICKERSON , R AYMOND S. 1995. "Project Intelligence." In Encyclopedia of Human Intelligence, ed. Robert J. Sternberg. New York: Macmillan.

P RESSLEY , M ICHAEL J., and W OLOSHYN , V ERA . 1995. Cognitive Strategy Instruction that Really Improves Children's Academic Performance. Cambridge, MA: Brookline Books.

S TERNBERG , R OBERT J., and D AVIDSON , J ANET E. 1982. "The Mind of the Puzzler." Psychology Today 16:37–44.

S TERNBERG , R OBERT J., and Z HANG , L I -F ANG , eds. 2001. Perspectives on Thinking, Learning, and Cognitive Styles. Mahwah, NJ: Erlbaum.

W ERTHEIMER , M AX . 1959. Productive Thinking. New York: Harper and Row.

W HITEHEAD , A LFRED N ORTH . 1929. The Aims of Education. New York: Macmillan.

R ICHARD E. M AYER

Additional topics

• Learning - Reasoning
• Learning - Perceptual Processes

Education - Free Encyclopedia Search Engine Education Encyclopedia Learning - Causal Reasoning, Conceptual Change, Knowledge Acquisition, Representation, And Organization, Neurological Foundation, Perceptual Processes - ANALOGICAL REASONING

Center for Teaching Innovation

Resource library.

• Establishing Community Agreements and Classroom Norms
• Sample group work rubric
• Problem-Based Learning Clearinghouse of Activities, University of Delaware

Problem-Based Learning

Problem-based learning  (PBL) is a student-centered approach in which students learn about a subject by working in groups to solve an open-ended problem. This problem is what drives the motivation and the learning. 

Why Use Problem-Based Learning?

Nilson (2010) lists the following learning outcomes that are associated with PBL. A well-designed PBL project provides students with the opportunity to develop skills related to:

• Working in teams.
• Managing projects and holding leadership roles.
• Oral and written communication.
• Self-awareness and evaluation of group processes.
• Working independently.
• Critical thinking and analysis.
• Explaining concepts.
• Self-directed learning.
• Applying course content to real-world examples.
• Researching and information literacy.
• Problem solving across disciplines.

Considerations for Using Problem-Based Learning

Rather than teaching relevant material and subsequently having students apply the knowledge to solve problems, the problem is presented first. PBL assignments can be short, or they can be more involved and take a whole semester. PBL is often group-oriented, so it is beneficial to set aside classroom time to prepare students to   work in groups  and to allow them to engage in their PBL project.

Students generally must:

• Examine and define the problem.
• Explore what they already know about underlying issues related to it.
• Determine what they need to learn and where they can acquire the information and tools necessary to solve the problem.
• Evaluate possible ways to solve the problem.
• Solve the problem.
• Report on their findings.

Getting Started with Problem-Based Learning

• Articulate the learning outcomes of the project. What do you want students to know or be able to do as a result of participating in the assignment?
• Create the problem. Ideally, this will be a real-world situation that resembles something students may encounter in their future careers or lives. Cases are often the basis of PBL activities. Previously developed PBL activities can be found online through the University of Delaware’s PBL Clearinghouse of Activities .
• Establish ground rules at the beginning to prepare students to work effectively in groups.
• Introduce students to group processes and do some warm up exercises to allow them to practice assessing both their own work and that of their peers.
• Consider having students take on different roles or divide up the work up amongst themselves. Alternatively, the project might require students to assume various perspectives, such as those of government officials, local business owners, etc.
• Establish how you will evaluate and assess the assignment. Consider making the self and peer assessments a part of the assignment grade.

Nilson, L. B. (2010).  Teaching at its best: A research-based resource for college instructors  (2nd ed.).  San Francisco, CA: Jossey-Bass. 

Chapter 9: Facilitating Complex Thinking

Problem-solving.

Somewhat less open-ended than creative thinking is problem solving , the analysis and solution of tasks or situations that are complex or ambiguous and that pose difficulties or obstacles of some kind (Mayer & Wittrock, 2006). Problem solving is needed, for example, when a physician analyzes a chest X-ray: a photograph of the chest is far from clear and requires skill, experience, and resourcefulness to decide which foggy-looking blobs to ignore, and which to interpret as real physical structures (and therefore real medical concerns). Problem solving is also needed when a grocery store manager has to decide how to improve the sales of a product: should she put it on sale at a lower price, or increase publicity for it, or both? Will these actions actually increase sales enough to pay for their costs?

Example 1: Problem Solving in the Classroom

Problem solving happens in classrooms when teachers present tasks or challenges that are deliberately complex and for which finding a solution is not straightforward or obvious. The responses of students to such problems, as well as the strategies for assisting them, show the key features of problem solving. Consider this example, and students’ responses to it. We have numbered and named the paragraphs to make it easier to comment about them individually:

Scene #1: A problem to be solved

A teacher gave these instructions: “Can you connect all of the dots below using only four straight lines?” She drew the following display on the chalkboard:

The problem itself and the procedure for solving it seemed very clear: simply experiment with different arrangements of four lines. But two volunteers tried doing it at the board, but were unsuccessful. Several others worked at it at their seats, but also without success.

Scene #2: Coaxing students to re-frame the problem

When no one seemed to be getting it, the teacher asked, “Think about how you’ve set up the problem in your mind—about what you believe the problem is about. For instance, have you made any assumptions about how long the lines ought to be? Don’t stay stuck on one approach if it’s not working!”

Scene #3: Alicia abandons a fixed response

After the teacher said this, Alicia indeed continued to think about how she saw the problem. “The lines need to be no longer than the distance across the square,” she said to herself. So she tried several more solutions, but none of them worked either.

The teacher walked by Alicia’s desk and saw what Alicia was doing. She repeated her earlier comment: “Have you assumed anything about how long the lines ought to be?”

Alicia stared at the teacher blankly, but then smiled and said, “Hmm! You didn’t actually say that the lines could be no longer than the matrix! Why not make them longer?” So she experimented again using oversized lines and soon discovered a solution:

Scene #4: Willem’s and Rachel’s alternative strategies

Meanwhile, Willem worked on the problem. As it happened, Willem loved puzzles of all kinds, and had ample experience with them. He had not, however, seen this particular problem. “It must be a trick,” he said to himself, because he knew from experience that problems posed in this way often were not what they first appeared to be. He mused to himself: “Think outside the box, they always tell you. . .” And that was just the hint he needed: he drew lines outside the box by making them longer than the matrix and soon came up with this solution:

When Rachel went to work, she took one look at the problem and knew the answer immediately: she had seen this problem before, though she could not remember where. She had also seen other drawing-related puzzles, and knew that their solution always depended on making the lines longer, shorter, or differently angled than first expected. After staring at the dots briefly, she drew a solution faster than Alicia or even Willem. Her solution looked exactly like Willem’s.

This story illustrates two common features of problem solving: the effect of degree of structure or constraint on problem solving, and the effect of mental obstacles to solving problems. The next sections discuss each of these features, and then looks at common techniques for solving problems.

The effect of constraints: well-structured versus ill-structured problems

Problems vary in how much information they provide for solving a problem, as well as in how many rules or procedures are needed for a solution. A well-structured problem provides much of the information needed and can in principle be solved using relatively few clearly understood rules. Classic examples are the word problems often taught in math lessons or classes: everything you need to know is contained within the stated problem and the solution procedures are relatively clear and precise. An ill-structured problem has the converse qualities: the information is not necessarily within the problem, solution procedures are potentially quite numerous, and a multiple solutions are likely (Voss, 2006). Extreme examples are problems like “How can the world achieve lasting peace?” or “How can teachers insure that students learn?”

By these definitions, the nine-dot problem is relatively well-structured—though not completely. Most of the information needed for a solution is provided in Scene #1: there are nine dots shown and instructions given to draw four lines. But not all necessary information was given: students needed to consider lines that were longer than implied in the original statement of the problem. Students had to “think outside the box,” as Willem said—in this case, literally.

When a problem is well-structured, so are its solution procedures likely to be as well. A well-defined procedure for solving a particular kind of problem is often called an algorithm ; examples are the procedures for multiplying or dividing two numbers or the instructions for using a computer (Leiserson, et al., 2001). Algorithms are only effective when a problem is very well-structured and there is no question about whether the algorithm is an appropriate choice for the problem. In that situation it pretty much guarantees a correct solution. They do not work well, however, with ill-structured problems, where they are ambiguities and questions about how to proceed or even about precisely what the problem is about. In those cases it is more effective to use heuristics , which are general strategies—“rules of thumb,” so to speak—that do not always work, but often do, or that provide at least partial solutions. When beginning research for a term paper, for example, a useful heuristic is to scan the library catalogue for titles that look relevant. There is no guarantee that this strategy will yield the books most needed for the paper, but the strategy works enough of the time to make it worth trying.

In the nine-dot problem, most students began in Scene #1 with a simple algorithm that can be stated like this: “Draw one line, then draw another, and another, and another.” Unfortunately this simple procedure did not produce a solution, so they had to find other strategies for a solution. Three alternatives are described in Scenes #3 (for Alicia) and 4 (for Willem and Rachel). Of these, Willem’s response resembled a heuristic the most: he knew from experience that a good general strategy that often worked for such problems was to suspect a deception or trick in how the problem was originally stated. So he set out to question what the teacher had meant by the word line , and came up with an acceptable solution as a result.

Common obstacles to solving problems

The example also illustrates two common problems that sometimes happen during problem solving. One of these is functional fixedness : a tendency to regard the functions of objects and ideas as fixed (German & Barrett, 2005). Over time, we get so used to one particular purpose for an object that we overlook other uses. We may think of a dictionary, for example, as necessarily something to verify spellings and definitions, but it also can function as a gift, a doorstop, or a footstool. For students working on the nine-dot matrix described in the last section, the notion of “drawing” a line was also initially fixed; they assumed it to be connecting dots but not extending lines beyond the dots. Functional fixedness sometimes is also called response set , the tendency for a person to frame or think about each problem in a series in the same way as the previous problem, even when doing so is not appropriate to later problems. In the example of the nine-dot matrix described above, students often tried one solution after another, but each solution was constrained by a set response not to extend any line beyond the matrix.

Functional fixedness and the response set are obstacles in problem representation , the way that a person understands and organizes information provided in a problem. If information is misunderstood or used inappropriately, then mistakes are likely—if indeed the problem can be solved at all. With the nine-dot matrix problem, for example, construing the instruction to draw four lines as meaning “draw four lines entirely within the matrix” means that the problem simply could not be solved. For another, consider this problem: “The number of water lilies on a lake doubles each day. Each water lily covers exactly one square foot. If it takes 100 days for the lilies to cover the lake exactly, how many days does it take for the lilies to cover exactly half of the lake?” If you think that the size of the lilies affects the solution to this problem, you have not represented the problem correctly. Information about lily size is not relevant to the solution, and only serves to distract from the truly crucial information, the fact that the lilies double their coverage each day. (The answer, incidentally, is that the lake is half covered in 99 days; can you think why?)

Strategies to assist problem solving

Just as there are cognitive obstacles to problem solving, there are also general strategies that help the process be successful, regardless of the specific content of a problem (Thagard, 2005). One helpful strategy is problem analysis —identifying the parts of the problem and working on each part separately. Analysis is especially useful when a problem is ill-structured. Consider this problem, for example: “Devise a plan to improve bicycle transportation in the city.” Solving this problem is easier if you identify its parts or component subproblems, such as (1) installing bicycle lanes on busy streets, (2) educating cyclists and motorists to ride safely, (3) fixing potholes on streets used by cyclists, and (4) revising traffic laws that interfere with cycling. Each separate subproblem is more manageable than the original, general problem. The solution of each subproblem contributes the solution of the whole, though of course is not equivalent to a whole solution.

Another helpful strategy is working backward from a final solution to the originally stated problem. This approach is especially helpful when a problem is well-structured but also has elements that are distracting or misleading when approached in a forward, normal direction. The water lily problem described above is a good example: starting with the day when all the lake is covered (Day 100), ask what day would it therefore be half covered (by the terms of the problem, it would have to be the day before, or Day 99). Working backward in this case encourages reframing the extra information in the problem (i. e. the size of each water lily) as merely distracting, not as crucial to a solution.

A third helpful strategy is analogical thinking —using knowledge or experiences with similar features or structures to help solve the problem at hand (Bassok, 2003). In devising a plan to improve bicycling in the city, for example, an analogy of cars with bicycles is helpful in thinking of solutions: improving conditions for both vehicles requires many of the same measures (improving the roadways, educating drivers). Even solving simpler, more basic problems is helped by considering analogies. A first grade student can partially decode unfamiliar printed words by analogy to words he or she has learned already. If the child cannot yet read the word screen , for example, he can note that part of this word looks similar to words he may already know, such as seen or green , and from this observation derive a clue about how to read the word screen . Teachers can assist this process, as you might expect, by suggesting reasonable, helpful analogies for students to consider.

Bassok, J. (2003). Analogical transfer in problem solving. In Davidson, J. & Sternberg, R. (Eds.). The psychology of problem solving. New York: Cambridge University Press.

German, T. & Barrett, H. (2005). Functional fixedness in a technologically sparse culture. Psychological Science, 16 (1), 1–5.

Leiserson, C., Rivest, R., Cormen, T., & Stein, C. (2001). Introduction to algorithms. Cambridge, MA: MIT Press.

Luchins, A. & Luchins, E. (1994). The water-jar experiment and Einstellung effects. Gestalt Theory: An International Interdisciplinary Journal, 16 (2), 101–121.

Mayer, R. & Wittrock, M. (2006). Problem-solving transfer. In D. Berliner & R. Calfee (Eds.), Handbook of Educational Psychology, pp. 47–62. Mahwah, NJ: Erlbaum.

Thagard, R. (2005). Mind: Introduction to Cognitive Science, 2nd edition. Cambridge, MA: MIT Press.

Voss, J. (2006). Toulmin’s model and the solving of ill-structured problems. Argumentation, 19 (3), 321–329.

• Educational Psychology. Authored by : Kelvin Seifert and Rosemary Sutton. Located at : https://open.umn.edu/opentextbooks/BookDetail.aspx?bookId=153 . License : CC BY: Attribution

  Problems and Problem Solving

What is a problem?

In common language, a problem is an unpleasant situation, a difficulty.

But in education the first definition in Webster's Dictionary — "a question raised for inquiry, consideration, or solution" — is a common meaning.

More generally in education, it's useful to define problem broadly — as any situation, in any area of life, where you have an opportunity to make a difference, to make things better — so problem solving is converting an actual current state into a desired future state that is better, so you have "made things better."  Whenever you are thinking creatively-and-critically about ways to increase the quality of life (or to avoid a decrease in quality) for yourself and/or for others, you are actively involved in problem solving.  Defined in this way, problem solving includes almost everything you do in life.

  Problem-Solving Skills  —  Creative and Critical

An important goal of education is helping students learn how to think more productively while solving problems, by combining creative thinking (to generate ideas) and critical thinking (to evaluate ideas) with accurate knowledge (about the truth of reality).  Both modes of thinking (creative & critical) are essential for a well-rounded productive thinker, according to experts in both fields:

Richard Paul (a prominent advocate of CRITICAL THINKING ) says, "Alternative solutions are often not given, they must be generated or thought-up.  Critical thinkers must be creative thinkers as well, generating possible solutions in order to find the best one.  Very often a problem persists, not because we can't tell which available solution is best, but because the best solution has not yet been made available — no one has thought of it yet."

Patrick Hillis & Gerard Puccio (who focus on CREATIVE THINKING ) describe the combining of creative generation with critical evaluation in a strategy of creative-and-critical Problem Solving that "contains many tools which can be used interchangeably within any of the stages.  These tools are selected according to the needs of the task and are either divergent (i.e., used to generate options) or convergent (i.e., used to evaluate options)."

Creative Thinking can be motivated and guided by Creative Thinking:   One of the interactions between creative thinking and critical thinking occurs when we use critical Evaluation to motivate and guide creative Generation in a critical - and - creative process of Guided Generation that is Guided Creativity .  In my links-page for CREATIVITY you can explore this process in three stages, to better understand how a process of Guided Creativity — explored & recognized by you in Part 1 and then described by me in Part 2 — could be used (as illustrated in Part 3 ) to improve “the party atmosphere” during a dinner you'll be hosting, by improving a relationship.

  Education for Problem Solving

By using broad definitions for problem solving and education, we can show students how they already are using productive thinking to solve problems many times every day, whenever they try to “make things better” in some way..

Problem Solving:   a problem is an opportunity , in any area of life, to make things better.   Whenever a decision-and-action helps you “ make it better ” — when you convert an actual state (in the past) into a more desirable actual state (in the present and/or future) — you are problem solving, and this includes almost everything you do in life, in all areas of life.      { You can make things better if you increase quality for any aspect of life, or you maintain quality by reducing a potential decrease of quality.   }     /     design thinking ( when it's broadly defined ) is the productive problem-solving thinking we use to solve problems.  We can design (i.e. find, invent, or improve ) a better product, activity, relationship, and/or strategy (in General Design ) and/or (in Science-Design ) explanatory theory.     {   The editor of this links-page ( Craig Rusbult ) describes problem solving in all areas of life .}

note:  To help you decide whether to click a link or avoid it, links highlighted with green or purple go to pages I've written, in my website about Education for Problem Solving or in this website for THINKING SKILLS ( CREATIVE and CRITICAL ) we use to SOLVE PROBLEMS .

Education:   In another broad definition, education is learning from life-experiences, learning how to improve, to become more effective in making things better.   For example, Maya Angelou – describing an essential difference between past and present – says "I did then what I knew how to do. Now that I know better, I do better, " where improved problem solving skills (when "do better" leads to being able to more effectively "make things better") has been a beneficial result of education, of "knowing better" due to learning from life-experiences.

Growth:   One of the best ways to learn more effectively is by developing-and-using a better growth mindset so — when you ask yourself “how well am I doing in this area of life?” and honestly self-answer “not well enough” — instead of thinking “not ever” you are thinking “not yet” because you know that your past performance isn't your future performance;  and you are confident that in this area of life (and in other areas) you can “grow” by improving your understandings-and-skills, when you invest intelligent effort in your self-education and self-improving.  And you can "be an educator" by supporting the self-improving of other people by helping them improve their own growth mindsets.    { resources for Growth Mindset }

Growth in Problem-Solving Skills:   A main goal of this page is to help educators help students improve their skill in solving problems — by improving their ability to think productively (to more effectively combine creative thinking with critical thinking and accurate knowledge ) — in all areas of their everyday living.    {resources: growth mindset for problem solving that is creative-and-critical }

How?   You can improve your Education for Problem Solving by creatively-and-critically using general principles & strategies (like those described above & below, and elsewhere) and adapting them to specific situations, customizing them for your students (for their ages, abilities, experiences,...) and teachers, for your community and educational goals.

Promote Productive Thinking:

Build Educational Bridges:

When we show students how they use a similar problem-solving process (with design thinking ) for almost everything they do in life , we can design a wide range of activities that let us build two-way educational bridges:

• from Life into School, building on the experiences of students, to improve confidence:   When we help students recognize how they have been using a problem-solving process of design thinking in a wide range of problem-solving situations,... then during a classroom design activity they can think “I have done this before (during design-in-life ) so I can do it again (for design-in-school )” to increase their confidence about learning.  They will become more confident that they can (and will) improve the design-thinking skills they have been using (and will be using) to solve problems in life and in school.

• from School into Life, appealing to the hopes of students, to improve motivation:   We can show each student how they will be using design thinking for "almost everything they do" in their future life (in their future whole-life, inside & outside school) so the design-thinking skills they are improving in school will transfer from school into life and will help them achieve their personal goals for life .  When students want to learn in school because they are learning for life, this will increase their motivations to learn.

Improve Educational Equity:

When we build these bridges (past-to-present from Life into School , and present-to-future from School into Life ) we can improve transfers of learning — in time (past-to-present & present-to-future) and between areas (in school-life & whole-life) for whole-person education — and transitions in attitudes to improve a student's confidence & motivations.  This will promote diversity and equity in education by increasing confidence & motivation for a wider range of students, and providing a wider variety of opportunities for learning in school, and for success in school.  We want to “open up the options” for all students, so they will say “yes, I can do this” for a wider variety of career-and-life options, in areas of STEM (Science, Technology, Engineering, Math) and non-STEM .

This will help us improve diversity-and-equity in education by increasing confidence & motivations for a wider range of students, and providing a wider variety of opportunities for learning in school, and success in school.

  Design Curriculum & Instruction:  

• DEFINE GOALS for desired outcomes, for ideas-and-skills we want students to learn,

• DESIGN INSTRUCTION with learning activities (and associated teaching activities ) that will provide opportunities for experience with these ideas & skills, and help students learn more from their experiences.     {more about Defining Goals and Designing Instruction }   {one valuable activity is using a process-of-inquiry to learn principles-for-inquiry }

  Problem-Solving Process for Science and Design

We'll look at problem-solving process for science (below) and design ( later ) separately, and for science-and-design together., problem-solving process for science, is there a “scientific method”      we have reasons to say....

    NO, because there is not a rigid sequence of steps that is used in the same way by all scientists, in all areas of science, at all times,  but also...

    YES, because expert scientists (and designers) tend to be more effective when they use flexible strategies — analogous to the flexible goal-directed improvising of a hockey player, but not the rigid choreography of a figure skater — to coordinate their thinking-and-actions in productive ways, so they can solve problems more effectively.

Below are some models that can help students understand and do the process of science.  We'll begin with simplicity, before moving on to models that are more complex so they can describe the process more completely-and-accurately.

A simple model of science is PHEOC (Problem, Hypothesis, Experiment, Observe, Conclude).  When PHEOC, or a similar model, is presented — or is misinterpreted — as a rigid sequence of fixed steps, this can lead to misunderstandings of science, because the real-world process of science is flexible.  An assumption that “model = rigidity” is a common criticism of all models-for-process, but this unfortunate stereotype of "rigidity" is not logically justifiable because all models emphasize the flexibility of problem-solving process in real life, and (ideally) in the classroom.  If a “step by step” model (like PHEOC or its variations) is interpreted properly and is used wisely, the model can be reasonably accurate and educationally useful.  For example,...

A model that is even simpler — the 3-step POE (Predict, Observe, Learn) — has the essentials of scientific logic, and is useful for classroom instruction.

Science Buddies has Steps of the Scientific Method with a flowchart showing options for flexibility of timing.  They say, "Even though we show the scientific method as a series of steps, keep in mind that new information or thinking might cause a scientist to back up and repeat steps at any point during the process.  A process like the scientific method that involves such backing up and repeating is called an iterative process."    And they compare Scientific Method with Engineering Design Process .

Lynn Fancher explains - in The Great SM - that "while science can be done (and often is) following different kinds of protocols, the [typical simplified] description of the scientific method includes some very important features that should lead to understanding some very basic aspects of all scientific practice," including Induction & Deduction and more.

From thoughtco.com, many thoughts to explore in a big website .

Other models for the problem solving process of science are more complex, so they can be more thorough — by including a wider range of factors that actually occur in real-life science, that influence the process of science when it's done by scientists who work as individuals and also as members of their research groups & larger communities — and thus more accurate.  For example,

Understanding Science (developed at U.C. Berkeley - about ) describes a broad range of science-influencers, * beyond the core of science: relating evidence and ideas .  Because "the process of science is exciting" they want to "give users an inside look at the general principles, methods, and motivations that underlie all of science."  You can begin learning in their homepage (with US 101, For Teachers, Resource Library,...) and an interactive flowchart for "How Science Works" that lets you explore with mouse-overs and clicking.

* These factors affect the process of science, and occasionally (at least in the short run) the results of science.  To learn more about science-influencers,...

    Knowledge Building (developed by Bereiter & Scardamalia, links - history ) describes a human process of socially constructing knowledge.

    The Ethics of Science by Henry Bauer — author of Scientific Literacy and the Myth of the Scientific Method (click "look inside") — examines The Knowledge Filter and a Puzzle and Filter Model of "how science really works."

[[ i.o.u. - soon, in mid-June 2021, I'll fix the links in this paragraph.]] Another model that includes a wide range of factors (empirical, social, conceptual) is Integrated Scientific Method by Craig Rusbult, editor of this links-page .  Part of my PhD work was developing this model of science, in a unifying synthesis of ideas from scholars in many fields, from scientists, philosophers, historians, sociologists, psychologists, educators, and myself.  The model is described in two brief outlines ( early & later ), more thoroughly, in a Basic Overview (with introduction, two visual/verbal representations, and summaries for 9 aspects of Science Process ) and a Detailed Overview (examining the 9 aspects more deeply, with illustrations from history & philosophy of science), and even more deeply in my PhD dissertation (with links to the full text, plus a “world record” Table of Contents, references, a visual history of my diagrams for Science Process & Design Process, and using my integrative model for [[ integrative analysis of instruction ).   /   Later, I developed a model for the basic logic-and-actions of Science Process in the context of a [[ more general Design Process .

Problem-Solving Process for Design

Because "designing" covers a wide range of activities, we'll look at three kinds of designing..

Engineering Design Process:   As with Scientific Method,

    a basic process of Engineering Design can be outlined in a brief models-with-steps  –  5   5 in cycle   7 in cycle   8   10   3 & 11 .     {these pages are produced by ==[later, I'll list their names]}

    and it can be examined in more depth:  here & here and in some of the models-with-steps (5... 3 & 11), and later .

Problem-Solving Process:   also has models-with-steps (  4   4   5   6   7  ) * and models-without-steps (like the editor's model for Design-Thinking Process ) to describe creative-and-critical thinking strategies that are similar to Engineering Design Process, and are used in a wider range of life — for all problem-solving situations (and these include almost everything we do in life) — not just for engineering.     { *  these pages are produced by ==}

Design-Thinking Process:   uses a similar creative-and-critical process, * but with a focus on human - centered problems & solutions & solving - process and a stronger emphasis on using empathy .  (and creativity )

* how similar?  This depends on whether we define Design Thinking in ways that are narrow or broad.   {the wide scope of problem-solving design thinking }  {why do I think broad definitions (for objectives & process) are educationally useful ?}

Education for Design Thinking (at Stanford's Design School and beyond)

  Problem Solving in Our Schools:

Improving education for problem solving, educators should want to design instruction that will help students improve their thinking skills.  an effective strategy for doing this is..., goal-directed designing of curriculum & instruction.

When we are trying to solve a problem (to “make things better”) by improving our education for problem solving, a useful two-part process is to...

    1.  Define GOALS for desired outcomes, for the ideas-and-skills we want students to learn;

    2.  Design INSTRUCTION with Learning Activities that will provide opportunities for experience with these ideas & skills, and will help students learn more from their experiences.

Basically, the first part ( Define Goals ) is deciding WHAT to Teach , and the second part ( Design Instruction ) is deciding HOW to Teach .

But before looking at WHAT and HOW   , here are some ways to combine them with...

Strategies for Goal-Directed Designing of WHAT-and-HOW.

Understanding by Design ( UbD ) is a team of experts in goal-directed designing,

as described in an overview of Understanding by Design from Vanderbilt U.

Wikipedia describes two key features of UbD:  "In backward design, the teacher starts with classroom outcomes [#1 in Goal-Directed Designing above ] and then [#2] plans the curriculum, * choosing activities and materials that help determine student ability and foster student learning," and  "The goal of Teaching for Understanding is to give students the tools to take what they know, and what they will eventually know, and make a mindful connection between the ideas. ...  Transferability of skills is at the heart of the technique.  Jay McTighe and Grant Wiggin's technique.  If a student is able to transfer the skills they learn in the classroom to unfamiliar situations, whether academic or non-academic, they are said to truly understand."

* UbD "offers a planning process and structure to guide curriculum, assessment, and instruction.  Its two key ideas are contained in the title:  1) focus on teaching and assessing for understanding and learning transfer, and   2) design curriculum “backward” from those ends."

ASCD – the Association for Supervision and Curriculum Development (specializing in educational leadership ) – has a resources-page for Understanding by Design that includes links to The UbD Framework and Teaching for Meaning and Understanding: A Summary of Underlying Theory and Research plus sections for online articles and books — like Understanding by Design ( by Grant Wiggins & Jay McTighe with free intro & U U ) and Upgrade Your Teaching: Understanding by Design Meets Neuroscience ( about How the Brain Learns Best by Jay McTighe & Judy Willis who did a fascinating ASCD Webinar ) and other books — plus DVDs and videos (e.g. overview - summary ) & more .

Other techniques include Integrative Analysis of Instruction and Goal-Directed Aesop's Activities .

In two steps for a goal-directed designing of education , you:

1)  Define GOALS (for WHAT you want students to improve) ;

2)  Design INSTRUCTION (for HOW to achieve these Goals) .

Although the sections below are mainly about 1. WHAT to Teach (by defining Goals ) and 2. HOW to Teach (by designing Instruction ) there is lots of overlapping, so you will find some "how" in the WHAT, and lots of "what" in the HOW.

P ERSONAL Skills   (for Thinking about Self)

A very useful personal skill is developing-and-using a...

Growth Mindset:  If self-education is broadly defined as learning from your experiences,   better self-education is learning more effectively by learning more from experience, and getting more experiences.   One of the best ways to learn more effectively is by developing a better growth mindset so — when you ask yourself “how well am I doing in this area of life?” and honestly answer “not well enough” — you are thinking “not yet” (instead of “not ever”) because you are confident that in this area of life (as in most areas, including those that are most important) you can “grow” by improving your skills, when you invest intelligent effort in your self-education.  And you can support the self-education of other people by helping them improve their own growth mindsets.     Carol Dweck Revisits the Growth Mindset and (also by Dweck) a video, Increasing Educational Equity and Opportunity .     3 Ways Educators Can Promote A Growth Mindset by Dan LaSalle, for Teach for America.     Growth Mindset: A Driving Philosophy, Not Just a Tool by David Hochheiser, for Edutopia.     Growth Mindset, Educational Equity, and Inclusive Excellence by Kris Slowinski who links to 5 videos .     What’s Missing from the Conversation: The Growth Mindset in Cultural Competency by Rosetta Lee.     YouTube video search-pages for [ growth mindset ] & [ mindset in education ] & [ educational equity mindset ].

also:  Growth Mindset for Creativity

Self-Perception -- [[a note to myself: accurate understanding/evaluation of self + confidence in ability to improve/grow ]]

M ETA C OGNITIVE Skills   (for Solving Problems)

What is metacognition?   Thinking is cognition.   When you observe your thinking and think about your thinking (maybe asking “how can I think more effectively?”) this is meta- cognition, which is cognition about cognition.  To learn more about metacognition — what it is, why it's valuable, and how to use it more effectively — some useful web-resources are:

a comprehensive introductory overview by Nancy Chick, for Vanderbilt U.

my links-section has descriptions of (and links to) pages by other authors: Jennifer Livingston, How People Learn, Marsha Lovett, Carleton College, Johan Lehrer, Rick Sheets, William Peirce, and Steven Shannon, plus links for Self-Efficacy with a Growth Mindset , and more about metacognition.

my summaries about the value of combining cognition-and-metacognition and regulating it for Thinking Strategies (of many kinds ) to improve Performing and/or Learning by Learning More from Experience with a process that is similar to...

the Strategies for Self-Regulated Learning developed by other educators.

videos — search youtube for [ metacognition ] and [ metacognitive strategies ] and [ metacognition in education ].

And in other parts of this links-page,

As one part of guiding students during an inquiry activity a teacher can stimulate their metacognition by helping them reflect on their experiences.

While solving problems, almost always it's useful to think with empathy and also with metacognitive self-empathy by asking “what do they want?” and “what do I want?” and aiming for a win-win solution.

P ROCESS -C OORDINATING Skills   (for Solving Problems)

THINKING SKILLS and THINKING PROCESS:  When educators develop strategies to improve the problem solving abilities of students, usually their focus is on thinking skills.   But thinking process is also important.

Therefore, it's useful to define thinking skills broadly, to include thinking that leads to decisions-about-actions, and actions:

        thinking  →  action-decisions  →  actions

[[ I.O.U. -- later, in mid-June 2021, the ideas below will be developed -- and i'll connect it with Metacognitive Skills because we use Metacognition to Coordinate Process.

[[ here are some ideas that eventually will be in this section:

Collaborative Problem Solving [[ this major new section will link to creative.htm# collaborative-creativity (with a brief summary of ideas from there) and expand these ideas to include general principles and "coordinating the collaboration" by deciding who will do what, when, with some individual "doing" and some together "doing" ]]

actions can be mental and/or physical (e.g. actualizing Experimental Design to do a Physical Experiment, or actualizing an Option-for-Action into actually doing the Action

[[a note to myself: educational goals:  we should help students improve their ability to combine their thinking skills — their creative Generating of Options and critical Generating of Options, plus using their Knowledge-of-Ideas that includes content-area knowledge plus the Empathy that is emphasized in Design Thinking — into an effective thinking process .

[[ Strategies for Coordinating:  students can do this by skillfully Coordinating their Problem-Solving Actions (by using their Conditional Knowledge ) into an effective Problem-Solving Process.

[[ During a process of design, you coordinate your thinking-and-actions by making action decisions about “what to do next.”  How?  When you are "skillfully Coordinating..." you combine cognitive/metacognitive awareness (of your current problem-solving process) with (by knowing, for each skill, what it lets you accomplish, and the conditions in which it will be useful).

[[ a little more about problem-solving process

[[ here are more ideas that might be used here:

Sometimes tenacious hard work is needed, and perseverance is rewarded.  Or it may be wise to be flexible – to recognize that what you've been doing may not be the best approach, so it's time to try something new – and when you dig in a new location your flexibility pays off.

Perseverance and flexibility are contrasting virtues.  When you aim for an optimal balancing of this complementary pair, self-awareness by “knowing yourself” is useful.  Have you noticed a personal tendency to err on the side of either too much perseverance or not enough?  Do you tend to be overly rigid, or too flexible?

Making a wise decision about perseverance — when you ask, “Do I want to continue in the same direction, or change course?” * — is more likely when you have an aware understanding of your situation, your actions, the results, and your goals.  Comparing results with goals is a Quality Check, providing valuable feedback that you can use as a “compass” to help you move in a useful direction.  When you look for signs of progress toward your goals in the direction you're moving, you may have a feeling, based on logic and experience, that your strategy for coordinating the process of problem solving isn't working well, and it probably never will.  Or you may feel that the goal is almost in sight and you'll soon reach it.

- How I didn't Learn to Ski (and then did) with Persevering plus Flexible Insight -

PRINCIPLES for PROBLEM SOLVING

Should we explicitly teach principles for thinking, can we use a process of inquiry to teach principles for inquiry, should we use a “model” for problem-solving process.

combining models?

What are the benefits of infusion and separate programs?  

Principles & Strategies & Models ?

Should we explicitly teach “principles” for thinking?

Using evidence and logic — based on what we know about the ways people think and learn — we should expect a well-designed combination of “experience + reflection + principles” to be more educationally effective than experience by itself, to help students improve their creative-and-critical thinking skills and whole-process skills in solving problems (for design-inquiry) and answering questions (for science-inquiry).

Can we use a process-of-inquiry to teach principles-for-inquiry?

*   In a typical sequence of ERP, students first get Experiences by doing a design activity.  During an activity and afterward, they can do Reflections (by thinking about their experiences) and this will help them recognize Principles for doing Design-Thinking Process that is Problem-Solving Process.     { design thinking is problem-solving thinking }

During reflections & discussions, typically students are not discovering new thoughts & actions.  Instead they are recognizing that during a process of design they are using skills they already know because they already have been using Design Thinking to do almost everything in their life .  A teacher can facilitate these recognitions by guiding students with questions about what they are doing now, and what they have done in the past, and how these experiences are similar, but also are different in some ways.  When students remember (their prior experience) and recognize (the process they did use, and are using), they can formulate principles for their process of design thinking.  But when they formulate principles for their process of problem solving, they are just making their own experience-based prior knowledge — of how they have been solving problems, and are now solving problems — more explicit and organized.

If we help students "make their own experience-based prior knowledge... more explicit and organized" by showing them how their knowledge can be organized into a model for problem-solving process, will this help them improve their problem-solving abilities?

IOU - This mega-section will continue being developed in mid-June 2021.

[[a note to myself: thinking skills and thinking process — What is the difference? - Experience + Reflection + Principles - coordination-decisions

[[are the following links specifically for this section about "experience + principles"? maybe not because these seem to be about principles, not whether to teach principles.]]

An excellent overview is Teaching Thinking Skills by Kathleen Cotton. (the second half of her page is a comprehensive bibliography)

This article is part of The School Improvement Research Series (available from Education Northwest and ERIC ) where you can find many useful articles about thinking skills & other topics, by Cotton & other authors.  [[a note to myself: it still is excellent, even though it's fairly old, written in 1991 -- soon, I will search to find more-recent overviews ]]

Another useful page — What Is a Thinking Curriculum ? (by Fennimore & Tinzmann) — begins with principles and then moves into applications in Language Arts, Mathematics, Sciences, and Social Sciences.

My links-page for Teaching-Strategies that promote Active Learning explores a variety of ideas about strategies for teaching (based on principles of constructivism, meaningful reception,...) in ways that are intended to stimulate active learning and improve thinking skills.   Later, a continuing exploration of the web will reveal more web-pages with useful “thinking skills & problem solving” ideas (especially for K-12 students & teachers) and I'll share these with you, here and in TEACHING ACTIVITIES .

Of course, thinking skills are not just for scholars and schoolwork, as emphasized in an ERIC Digest , Higher Order Thinking Skills in Vocational Education .  And you can get information about 23 ==Programs that Work from the U.S. Dept of Education. 

goals can include improving affective factors & character == e.g. helping students learn how to develop & use use non-violent solutions for social problems .

INFUSION and/or SEPARATE PROGRAMS?

In education for problem solving, one unresolved question is "What are the benefits of infusion, or separate programs? "  What is the difference?

With infusion , thinking skills are closely integrated with content instruction in a subject area, in a "regular" course.

In separate programs , independent from content-courses, the explicit focus of a course is to help students improve their thinking skills.

In her overview of the field, Kathleen Cotton says,

    Of the demonstrably effective programs, about half are of the infused variety, and the other half are taught separately from the regular curriculum. ...  The strong support that exists for both approaches... indicates that either approach can be effective.  Freseman represents what is perhaps a means of reconciling these differences [between enthusiastic advocates of each approach] when he writes, at the conclusion of his 1990 study: “Thinking skills need to be taught directly before they are applied to the content areas. ...  I consider the concept of teaching thinking skills directly to be of value especially when there follows an immediate application to the content area.”

For principles and examples of infusion , check the National Center for Teaching Thinking which lets you see == What is Infusion? (an introduction to the art of infusing thinking skills into content instruction), and == sample lessons (for different subjects, grade levels, and thinking skills). -- resources from teach-think-org -- [also, lessons designed to infuse Critical and Creative Thinking into content instruction]

Infusing Teaching Thinking Into Subject-Area Instruction (by Robert Swarz & David Perkins) - and more about the book

And we can help students improve their problem-solving skills with teaching strategies that provide structure for instruction and strategies for thinking . ==[use structure+strategies only in edu-section?

Adobe [in creative]

MORE about Teaching Principles for Problem Solving

[[ i.o.u. -- this section is an "overlap" between #1 (Goals) and #2 (Methods) so... maybe i'll put it in-between them? -- i'll decide soon, maybe during mid-June 2021 ]]

Two Kinds of Inquiry Activities  (for Science and Design )

To more effectively help students improve their problem-solving skills, teachers can provide opportunities for students to be actively involved in solving problems, with inquiry activities .  What happens during inquiry?  Opportunities for inquiry occur whenever a gap in knowledge — in conceptual knowledge (so students don't understand) or procedural knowledge (so they don't know what to do, or how) — stimulates action (mental and/or physical) and students are allowed to think-do-learn.

Students can be challenged to solve two kinds of problems during two kinds of inquiry activity:

    during Science-Inquiry they try to improve their understanding, by asking problem-questions and seeking answers.  During their process of solving problems, they are using Science-Design , aka Science , to design a better explanatory theory.

    during Design-Inquiry they try to improve some other aspect(s) of life, by defining problem-projects and seeking solutions.   During their process of solving problems, they are using General Design (which includes Engineering and more) to design a better product, activity, or strategy.

    But... whether the main objective is for Science-Design or General Design, a skilled designer will be flexible, will do whatever will help them solve the problem(s).  Therefore a “scientist” sometimes does engineering, and an “engineer” sometimes does science.  A teacher can help students recognize how-and-why they also do these “ crossover actions ” during an activity for Science Inquiry or Design Inquiry.  Due to these connections, we can build transfer-bridges between the two kinds of inquiry ,  and combine both to develop “hybrid activities” for Science-and-Design Inquiry.

Goal-Priorities:  There are two kinds of inquiry, so (re: Goals for What to Learn) what emphasis do we want to place on activities for Science -Inquiry and Design -Inquiry?  (in the limited amount of classroom time that teachers can use for Inquiry Activities)

Two Kinds of Improving  (for Performing and Learning )

Goal-Priorities:  There are two kinds of improving, so (re: Goals for What to Learn) what emphasis do we want to place on better Performing (now) and Learning (for later)?

When defining goals for education, we ask “How important is improving the quality of performing now, and (by learning now ) of performing later   ?”   For example, a basketball team (coach & players) will have a different emphasis in an early-season practice (when their main goal is learning well) and end-of-season championship game (when their main goal is performing well).     {we can try to optimize the “total value” of performing/learning/enjoying for short-term fun plus long-term satisfactions }

SCIENCE   (to use-learn-teach Skills for Problem Solving )

Problem-solving skills used for science.

This section supplements models for Scientific Method that "begin with simplicity, before moving on to models that are more complex so they can describe the process more completely-and-accurately. "  On the spectrum of simplicity → complexity , one of the simplest models is...

POE (Predict, Observe, Learn) to give students practice with the basic scientific logic we use to evaluate an explanatory theory about “what happens, how, and why.”  POE is often used for classroom instruction — with interactive lectures [iou - their website is temporarily being "restored"] & in other ways — and research has shown it to be effective.  A common goal of instruction-with-POE is to improve the conceptual knowledge of students, especially to promote conceptual change their alternative concepts to scientific concepts.  But students also improve their procedural knowledge for what the process of science is, and how to do the process.     { more – What's missing from POE ( experimental skills ) w hen students use it for evidence-based argumentation    and   Ecologies - Educational & Conceptual  }

Dany Adams (at Smith College) explicitly teaches critical thinking skills – and thus experiment-using skills – in the context of scientific method.

Science Buddies has models for Scientific Method (and for Engineering Design Process ) and offers Detailed Help that is useful for “thinking skills” education. ==[DetH]

Next Generation Science Standards ( NGSS ) emphasizes the importance of designing curriculum & instruction for Three Dimensional Learning with productive interactions between problem-solving Practices (for Science & Engineering ) and Crosscutting Concepts and Disciplinary Core Ideas.

Science: A Process Approach ( SAPA ) was a curriculum program earlier, beginning in the 1960s.  Michael Padilla explains how SAPA defined The Science Process Skills as "a set of broadly transferable abilities, appropriate to many science disciplines and reflective of the behavior of scientists.  SAPA categorized process skills into two types, basic and integrated.  The basic (simpler) process skills provide a foundation for learning the integrated (more complex) skills."   Also, What the Research Says About Science Process Skills by Karen Ostlund;  and Students' Understanding of the Procedures of Scientific Enquiry by Robin Millar, who examines several approaches and concludes (re: SAPA) that "The process approach is not, therefore, a sound basis for curriculum planning, nor does the analysis on which it is based provide a productive framework for research."  But I think parts of it can be used creatively for effective instruction.     { more about SAPA }

ENGINEERING   (to use-learn-teach Skills for Problem Solving )

Problem-solving skills used for engineering.

Engineering is Elementary ( E i E ) develops activities for students in grades K-8.  To get a feeling for the excitement they want to share with teachers & students, watch an "about EiE" video and explore their website .  To develop its curriculum products, EiE uses research-based Design Principles and works closely with teachers to get field-testing feedback, in a rigorous process of educational design .  During instruction, teachers use a simple 5-phase flexible model of engineering design process "to guide students through our engineering design challenges... using terms [ Ask, Imagine, Plan, Create, Improve ] children can understand."   {plus other websites about EiE }

Project Lead the Way ( PLTW ), another major developer of k-12 curriculum & instruction for engineering and other areas, has a website you can explore to learn about their educational philosophy & programs (at many schools ) & resources and more.  And you can web-search for other websites about PLTW.

Science Buddies , at level of k-12, has tips for science & engineering .

EPICS ( home - about ), at college level, is an engineering program using EPICS Design Process with a framework supplemented by sophisticated strategies from real-world engineering.  EPICS began at Purdue University and is now used at ( 29 schools) (and more with IUCCE ) including Purdue, Princeton, Notre Dame, Texas A&M, Arizona State, UC San Diego, Drexel, and Butler.

DESIGN THINKING   (to use-learn-teach Skills for Problem Solving )

Design Thinking emphasizes the importance of using empathy to solve human-centered problems.

Stanford Institute of Design ( d.school ) is an innovative pioneer in teaching a process of human-centered design thinking that is creative-and-critical with empathy .  In their Design Thinking Bootleg – that's an updated version of their Bootcamp Bootleg – they share a wide variety of attitudes & techniques — about brainstorming and much more — to stimulate productive design thinking with the objective of solving real-world problems.   {their first pioneer was David Kelley }

The d.school wants to "help prepare a generation of students to rise with the challenges of our times."  This goal is shared by many other educators, in k-12 and colleges, who are excited about design thinking.  Although d.school operates at college level, they (d.school + IDEO ) are active in K-12 education as in their website about Design Thinking in Schools ( FAQ - resources ) that "is a directory [with brief descriptions] of schools and programs that use design thinking in the curriculum for K12 students...  design thinking is a powerful way for today’s students to learn, and it’s being implemented by educators all around the world."     { more about Education for Design Thinking in California & Atlanta & Pittsburgh & elsewhere} [[a note to myself: @ ws and maybe my broad-definition page]]

On twitter, # DTk12 chat is an online community of enthusiastic educators who are excited about Design Thinking ( DT ) for K-12 Education, so they host a weekly twitter chat (W 9-10 ET) and are twitter-active informally 24/7.

PROBLEM-BASED LEARNING   (to use-learn-teach Skills for Problem Solving )

Problem-Based Learning ( PBL ? ) is a way to improve motivation, thinking, and learning.  You can learn more from:

overviews of PBL from U of WA & Learning-Theories.com ;

and (in ERIC Digests) using PBL for science & math plus a longer introduction - challenges for students & teachers (we never said it would be easy!) ;

a deeper examination by John Savery (in PDF & [without abstract] web-page );

Most Popular Papers from The Interdisciplinary Journal of Problem-based Learning ( about IJPBL ).

videos about PBL by Edutopia (9:26) and others ;

a search in ACSD for [problem-based learning] → a comprehensive links-page for Problem-Based Learning and an ACSD-book about...

Problems as Possibilities by Linda Torp and Sara Sage:  Table of Contents - Introduction (for 2nd Edition) - samples from the first & last chapters - PBL Resources (including WeSites in Part IV) .

PBL in Schools:

Samford University uses PBL (and other activities) for Transformational Learning that "emphasizes the whole person, ... helps students grow physically, mentally, and spiritually, and encourages them to value public service as well as personal gain."

In high school education, Problem-Based Learning Design Institute from Illinois Math & Science Academy ( about );  they used to have an impressive PBL Network ( sitemap & web-resources from 2013, and 9-23-2013 story about Kent, WA ) that has mysteriously disappeared. https://www.imsa.edu/academics/inquiry/resources/ research_ethics

Vanderbilt U has Service Learning thru Community Engagement with Challenges and Opportunities and tips for Teaching Step by Step & Best Practices and Resource-Links for many programs, organizations, articles, and more.

What is PBL?   The answer is " Problem-Based Learning and/or Project-Based Learning " because both meanings are commonly used.  Here are 3 pages (+ Wikipedia) that compare PBL with PBL, examine similarities & differences, consider definitions:

    John Larmer says "we [at Buck Institute for Education which uses Project Based Learning ] decided to call problem-based learning a subset of project-based learning [with these definitions, ProblemBL is a narrower category, so all ProblemBL is ProjectBL, but not vice versa] – that is, one of the ways a teacher could frame a project is to solve a problem, " and concludes that "the semantics aren't worth worrying about, at least not for very long.  The two PBLs are really two sides of the same coin. ...  The bottom line is the same:  both PBLs can powerfully engage and effectively teach your students!"     Chris Campbell concludes, "it is probably the importance of conducting active learning with students that is worthy and not the actual name of the task.  Both problem-based and project-based learning have their place in today’s classroom and can promote 21st Century learning."     Jan Schwartz says "there is admittedly a blurring of lines between these two approaches to education, but there are differences."     Wikipedia has Problem-Based Learning (with "both" in P5BL ) and Project-Based Learning .

i.o.u. - If you're wondering "What can I do in my classroom today ?", eventually (maybe in June 2021) there will be a section for "thinking skills activities" in this page, and in the area for TEACHING ACTIVITIES .

• Tools and Resources
• Customer Services
• Original Language Spotlight
• Alternative and Non-formal Education 
• Cognition, Emotion, and Learning
• Curriculum and Pedagogy
• Education and Society
• Education, Change, and Development
• Education, Cultures, and Ethnicities
• Education, Gender, and Sexualities
• Education, Health, and Social Services
• Educational Administration and Leadership
• Educational History
• Educational Politics and Policy
• Educational Purposes and Ideals
• Educational Systems
• Educational Theories and Philosophies
• Globalization, Economics, and Education
• Languages and Literacies
• Professional Learning and Development
• Research and Assessment Methods
• Technology and Education
• Share This Facebook LinkedIn Twitter

Article contents

Problem solving.

• Richard E. Mayer Richard E. Mayer University of California, Santa Barbara
• https://doi.org/10.1093/acrefore/9780190264093.013.860
• Published online: 30 October 2019

Problem solving refers to cognitive processing directed at achieving a goal when the problem solver does not initially know a solution method. A problem exists when someone has a goal but does not know how to achieve it. Problems can be classified as routine or non-routine, and as well-defined or ill-defined. The major cognitive processes in problem solving are representing, planning, executing, and monitoring. The major kinds of knowledge required for problem solving are facts, concepts, procedures, strategies, and beliefs. The theoretical approaches that have developed over the history of research on problem are associationism, Gestalt, and information processing. Each of these approaches involves fundamental issues in problem solving such as the nature of transfer, insight, and goal-directed heuristics, respectively. Some current research topics in problem solving include decision making, intelligence and creativity, teaching of thinking skills, expert problem solving, analogical reasoning, mathematical and scientific thinking, everyday thinking, and the cognitive neuroscience of problem solving. Common theme concerns the domain specificity of problem solving and a focus on problem solving in authentic contexts.

• problem solving
• decision making
• intelligence
• expert problem solving
• analogical reasoning
• mathematical thinking
• scientific thinking
• everyday thinking

You do not currently have access to this article

Please login to access the full content.

Access to the full content requires a subscription

Printed from Oxford Research Encyclopedias, Education. Under the terms of the licence agreement, an individual user may print out a single article for personal use (for details see Privacy Policy and Legal Notice).

date: 01 May 2024

• Cookie Policy
• Privacy Policy
• Legal Notice
• Accessibility
• [66.249.64.20|185.80.149.115]
• 185.80.149.115

Character limit 500 /500

Teaching Problem-Solving Skills

Many instructors design opportunities for students to solve “problems”. But are their students solving true problems or merely participating in practice exercises? The former stresses critical thinking and decision­ making skills whereas the latter requires only the application of previously learned procedures.

Problem solving is often broadly defined as "the ability to understand the environment, identify complex problems, review related information to develop, evaluate strategies and implement solutions to build the desired outcome" (Fissore, C. et al, 2021). True problem solving is the process of applying a method – not known in advance – to a problem that is subject to a specific set of conditions and that the problem solver has not seen before, in order to obtain a satisfactory solution.

Below you will find some basic principles for teaching problem solving and one model to implement in your classroom teaching.

Principles for teaching problem solving

• Model a useful problem-solving method . Problem solving can be difficult and sometimes tedious. Show students how to be patient and persistent, and how to follow a structured method, such as Woods’ model described below. Articulate your method as you use it so students see the connections.
• Teach within a specific context . Teach problem-solving skills in the context in which they will be used by students (e.g., mole fraction calculations in a chemistry course). Use real-life problems in explanations, examples, and exams. Do not teach problem solving as an independent, abstract skill.
• Help students understand the problem . In order to solve problems, students need to define the end goal. This step is crucial to successful learning of problem-solving skills. If you succeed at helping students answer the questions “what?” and “why?”, finding the answer to “how?” will be easier.
• Take enough time . When planning a lecture/tutorial, budget enough time for: understanding the problem and defining the goal (both individually and as a class); dealing with questions from you and your students; making, finding, and fixing mistakes; and solving entire problems in a single session.
• Ask questions and make suggestions . Ask students to predict “what would happen if …” or explain why something happened. This will help them to develop analytical and deductive thinking skills. Also, ask questions and make suggestions about strategies to encourage students to reflect on the problem-solving strategies that they use.
• Link errors to misconceptions . Use errors as evidence of misconceptions, not carelessness or random guessing. Make an effort to isolate the misconception and correct it, then teach students to do this by themselves. We can all learn from mistakes.

Woods’ problem-solving model

Define the problem.

• The system . Have students identify the system under study (e.g., a metal bridge subject to certain forces) by interpreting the information provided in the problem statement. Drawing a diagram is a great way to do this.
• Known(s) and concepts . List what is known about the problem, and identify the knowledge needed to understand (and eventually) solve it.
• Unknown(s) . Once you have a list of knowns, identifying the unknown(s) becomes simpler. One unknown is generally the answer to the problem, but there may be other unknowns. Be sure that students understand what they are expected to find.
• Units and symbols . One key aspect in problem solving is teaching students how to select, interpret, and use units and symbols. Emphasize the use of units whenever applicable. Develop a habit of using appropriate units and symbols yourself at all times.
• Constraints . All problems have some stated or implied constraints. Teach students to look for the words "only", "must", "neglect", or "assume" to help identify the constraints.
• Criteria for success . Help students consider, from the beginning, what a logical type of answer would be. What characteristics will it possess? For example, a quantitative problem will require an answer in some form of numerical units (e.g., $/kg product, square cm, etc.) while an optimization problem requires an answer in the form of either a numerical maximum or minimum.

Think about it

• “Let it simmer”.  Use this stage to ponder the problem. Ideally, students will develop a mental image of the problem at hand during this stage.
• Identify specific pieces of knowledge . Students need to determine by themselves the required background knowledge from illustrations, examples and problems covered in the course.
• Collect information . Encourage students to collect pertinent information such as conversion factors, constants, and tables needed to solve the problem.

Plan a solution

• Consider possible strategies . Often, the type of solution will be determined by the type of problem. Some common problem-solving strategies are: compute; simplify; use an equation; make a model, diagram, table, or chart; or work backwards.
• Choose the best strategy . Help students to choose the best strategy by reminding them again what they are required to find or calculate.

Carry out the plan

• Be patient . Most problems are not solved quickly or on the first attempt. In other cases, executing the solution may be the easiest step.
• Be persistent . If a plan does not work immediately, do not let students get discouraged. Encourage them to try a different strategy and keep trying.

Encourage students to reflect. Once a solution has been reached, students should ask themselves the following questions:

• Does the answer make sense?
• Does it fit with the criteria established in step 1?
• Did I answer the question(s)?
• What did I learn by doing this?
• Could I have done the problem another way?

If you would like support applying these tips to your own teaching, CTE staff members are here to help.  View the  CTE Support  page to find the most relevant staff member to contact. 

• Fissore, C., Marchisio, M., Roman, F., & Sacchet, M. (2021). Development of problem solving skills with Maple in higher education. In: Corless, R.M., Gerhard, J., Kotsireas, I.S. (eds) Maple in Mathematics Education and Research. MC 2020. Communications in Computer and Information Science, vol 1414. Springer, Cham. https://doi.org/10.1007/978-3-030-81698-8_15
• Foshay, R., & Kirkley, J. (1998). Principles for Teaching Problem Solving. TRO Learning Inc., Edina MN.  (PDF) Principles for Teaching Problem Solving (researchgate.net)
• Hayes, J.R. (1989). The Complete Problem Solver. 2nd Edition. Hillsdale, NJ: Lawrence Erlbaum Associates.
• Woods, D.R., Wright, J.D., Hoffman, T.W., Swartman, R.K., Doig, I.D. (1975). Teaching Problem solving Skills.
• Engineering Education. Vol 1, No. 1. p. 238. Washington, DC: The American Society for Engineering Education.

Catalog search

Teaching tip categories.

• Assessment and feedback
• Blended Learning and Educational Technologies
• Career Development
• Course Design
• Course Implementation
• Inclusive Teaching and Learning
• Learning activities
• Support for Student Learning
• Support for TAs
• Learning activities ,

• Bipolar Disorder
• Therapy Center
• When To See a Therapist
• Types of Therapy
• Best Online Therapy
• Best Couples Therapy
• Best Family Therapy
• Managing Stress
• Sleep and Dreaming
• Understanding Emotions
• Self-Improvement
• Healthy Relationships
• Student Resources
• Personality Types
• Guided Meditations
• Verywell Mind Insights
• 2024 Verywell Mind 25
• Mental Health in the Classroom
• Editorial Process
• Meet Our Review Board
• Crisis Support

Overview of the Problem-Solving Mental Process

Kendra Cherry, MS, is a psychosocial rehabilitation specialist, psychology educator, and author of the "Everything Psychology Book."

Rachel Goldman, PhD FTOS, is a licensed psychologist, clinical assistant professor, speaker, wellness expert specializing in eating behaviors, stress management, and health behavior change.

• Identify the Problem
• Define the Problem
• Form a Strategy
• Organize Information
• Allocate Resources
• Monitor Progress
• Evaluate the Results

Frequently Asked Questions

Problem-solving is a mental process that involves discovering, analyzing, and solving problems. The ultimate goal of problem-solving is to overcome obstacles and find a solution that best resolves the issue.

The best strategy for solving a problem depends largely on the unique situation. In some cases, people are better off learning everything they can about the issue and then using factual knowledge to come up with a solution. In other instances, creativity and insight are the best options.

It is not necessary to follow problem-solving steps sequentially, It is common to skip steps or even go back through steps multiple times until the desired solution is reached.

In order to correctly solve a problem, it is often important to follow a series of steps. Researchers sometimes refer to this as the problem-solving cycle. While this cycle is portrayed sequentially, people rarely follow a rigid series of steps to find a solution.

The following steps include developing strategies and organizing knowledge.

1. Identifying the Problem

While it may seem like an obvious step, identifying the problem is not always as simple as it sounds. In some cases, people might mistakenly identify the wrong source of a problem, which will make attempts to solve it inefficient or even useless.

Some strategies that you might use to figure out the source of a problem include :

• Asking questions about the problem
• Breaking the problem down into smaller pieces
• Looking at the problem from different perspectives
• Conducting research to figure out what relationships exist between different variables

2. Defining the Problem

After the problem has been identified, it is important to fully define the problem so that it can be solved. You can define a problem by operationally defining each aspect of the problem and setting goals for what aspects of the problem you will address

At this point, you should focus on figuring out which aspects of the problems are facts and which are opinions. State the problem clearly and identify the scope of the solution.

3. Forming a Strategy

After the problem has been identified, it is time to start brainstorming potential solutions. This step usually involves generating as many ideas as possible without judging their quality. Once several possibilities have been generated, they can be evaluated and narrowed down.

The next step is to develop a strategy to solve the problem. The approach used will vary depending upon the situation and the individual's unique preferences. Common problem-solving strategies include heuristics and algorithms.

• Heuristics are mental shortcuts that are often based on solutions that have worked in the past. They can work well if the problem is similar to something you have encountered before and are often the best choice if you need a fast solution.
• Algorithms are step-by-step strategies that are guaranteed to produce a correct result. While this approach is great for accuracy, it can also consume time and resources.

Heuristics are often best used when time is of the essence, while algorithms are a better choice when a decision needs to be as accurate as possible.

4. Organizing Information

Before coming up with a solution, you need to first organize the available information. What do you know about the problem? What do you not know? The more information that is available the better prepared you will be to come up with an accurate solution.

When approaching a problem, it is important to make sure that you have all the data you need. Making a decision without adequate information can lead to biased or inaccurate results.

5. Allocating Resources

Of course, we don't always have unlimited money, time, and other resources to solve a problem. Before you begin to solve a problem, you need to determine how high priority it is.

If it is an important problem, it is probably worth allocating more resources to solving it. If, however, it is a fairly unimportant problem, then you do not want to spend too much of your available resources on coming up with a solution.

At this stage, it is important to consider all of the factors that might affect the problem at hand. This includes looking at the available resources, deadlines that need to be met, and any possible risks involved in each solution. After careful evaluation, a decision can be made about which solution to pursue.

6. Monitoring Progress

After selecting a problem-solving strategy, it is time to put the plan into action and see if it works. This step might involve trying out different solutions to see which one is the most effective.

It is also important to monitor the situation after implementing a solution to ensure that the problem has been solved and that no new problems have arisen as a result of the proposed solution.

Effective problem-solvers tend to monitor their progress as they work towards a solution. If they are not making good progress toward reaching their goal, they will reevaluate their approach or look for new strategies .

7. Evaluating the Results

After a solution has been reached, it is important to evaluate the results to determine if it is the best possible solution to the problem. This evaluation might be immediate, such as checking the results of a math problem to ensure the answer is correct, or it can be delayed, such as evaluating the success of a therapy program after several months of treatment.

Once a problem has been solved, it is important to take some time to reflect on the process that was used and evaluate the results. This will help you to improve your problem-solving skills and become more efficient at solving future problems.

A Word From Verywell​

It is important to remember that there are many different problem-solving processes with different steps, and this is just one example. Problem-solving in real-world situations requires a great deal of resourcefulness, flexibility, resilience, and continuous interaction with the environment.

Get Advice From The Verywell Mind Podcast

Hosted by therapist Amy Morin, LCSW, this episode of The Verywell Mind Podcast shares how you can stop dwelling in a negative mindset.

Follow Now : Apple Podcasts / Spotify / Google Podcasts

You can become a better problem solving by:

• Practicing brainstorming and coming up with multiple potential solutions to problems
• Being open-minded and considering all possible options before making a decision
• Breaking down problems into smaller, more manageable pieces
• Asking for help when needed
• Researching different problem-solving techniques and trying out new ones
• Learning from mistakes and using them as opportunities to grow

It's important to communicate openly and honestly with your partner about what's going on. Try to see things from their perspective as well as your own. Work together to find a resolution that works for both of you. Be willing to compromise and accept that there may not be a perfect solution.

Take breaks if things are getting too heated, and come back to the problem when you feel calm and collected. Don't try to fix every problem on your own—consider asking a therapist or counselor for help and insight.

If you've tried everything and there doesn't seem to be a way to fix the problem, you may have to learn to accept it. This can be difficult, but try to focus on the positive aspects of your life and remember that every situation is temporary. Don't dwell on what's going wrong—instead, think about what's going right. Find support by talking to friends or family. Seek professional help if you're having trouble coping.

Davidson JE, Sternberg RJ, editors.  The Psychology of Problem Solving .  Cambridge University Press; 2003. doi:10.1017/CBO9780511615771

Sarathy V. Real world problem-solving .  Front Hum Neurosci . 2018;12:261. Published 2018 Jun 26. doi:10.3389/fnhum.2018.00261

By Kendra Cherry, MSEd Kendra Cherry, MS, is a psychosocial rehabilitation specialist, psychology educator, and author of the "Everything Psychology Book."

Problem Solving in Mathematics Education

• Open Access
• First Online: 28 June 2016

Cite this chapter

You have full access to this open access chapter

• Peter Liljedahl 6 ,
• Manuel Santos-Trigo 7 ,
• Uldarico Malaspina 8 &
• Regina Bruder 9  

Part of the book series: ICME-13 Topical Surveys ((ICME13TS))

90k Accesses

14 Citations

Problem solving in mathematics education has been a prominent research field that aims at understanding and relating the processes involved in solving problems to students’ development of mathematical knowledge and problem solving competencies. The accumulated knowledge and field developments include conceptual frameworks to characterize learners’ success in problem solving activities, cognitive, metacognitive, social and affective analysis, curriculum proposals, and ways to foster problem solving approaches. In the survey, four interrelated areas are reviewed: (i) the relevance of heuristics in problem solving approaches—why are they important and what research tells us about their use? (ii) the need to characterize and foster creative problem solving approaches—what type of heuristics helps learners think of and practice creative solutions? (iii) the importance for learners to formulate and pursue their own problems; and (iv) the role played by the use of both multiple purpose and ad hoc mathematical action types of technologies in problem solving activities—what ways of reasoning do learners construct when they rely on the use of digital technologies and how technology and technology approaches can be reconciled?

You have full access to this open access chapter,  Download chapter PDF

• Mathematical Problem
• Prospective Teacher
• Creative Process
• Digital Technology
• Mathematical Task

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

Mathematical problem solving has long been seen as an important aspect of mathematics, the teaching of mathematics, and the learning of mathematics. It has infused mathematics curricula around the world with calls for the teaching of problem solving as well as the teaching of mathematics through problem solving. And as such, it has been of interest to mathematics education researchers for as long as our field has existed. More relevant, mathematical problem solving has played a part in every ICME conference, from 1969 until the forthcoming meeting in Hamburg, wherein mathematical problem solving will reside most centrally within the work of Topic Study 19: Problem Solving in Mathematics Education. This booklet is being published on the occasion of this Topic Study Group.

To this end, we have assembled four summaries looking at four distinct, yet inter-related, dimensions of mathematical problem solving. The first summary, by Regina Bruder, is a nuanced look at heuristics for problem solving. This notion of heuristics is carried into Peter Liljedahl’s summary, which looks specifically at a progression of heuristics leading towards more and more creative aspects of problem solving. This is followed by Luz Manuel Santos Trigo’s summary introducing us to problem solving in and with digital technologies. The last summary, by Uldarico Malaspina Jurado, documents the rise of problem posing within the field of mathematics education in general and the problem solving literature in particular.

Each of these summaries references in some critical and central fashion the works of George Pólya or Alan Schoenfeld. To the initiated researchers, this is no surprise. The seminal work of these researchers lie at the roots of mathematical problem solving. What is interesting, though, is the diverse ways in which each of the four aforementioned contributions draw on, and position, these works so as to fit into the larger scheme of their respective summaries. This speaks to not only the depth and breadth of these influential works, but also the diversity with which they can be interpreted and utilized in extending our thinking about problem solving.

Taken together, what follows is a topical survey of ideas representing the diversity of views and tensions inherent in a field of research that is both a means to an end and an end onto itself and is unanimously seen as central to the activities of mathematics.

1 Survey on the State-of-the-Art

1.1 role of heuristics for problem solving—regina bruder.

The origin of the word heuristic dates back to the time of Archimedes and is said to have come out of one of the famous stories told about this great mathematician and inventor. The King of Syracuse asked Archimedes to check whether his new wreath was really made of pure gold. Archimedes struggled with this task and it was not until he was at the bathhouse that he came up with the solution. As he entered the tub he noticed that he had displaced a certain amount of water. Brilliant as he was, he transferred this insight to the issue with the wreath and knew he had solved the problem. According to the legend, he jumped out of the tub and ran from the bathhouse naked screaming, “Eureka, eureka!”. Eureka and heuristic have the same root in the ancient Greek language and so it has been claimed that this is how the academic discipline of “heuristics” dealing with effective approaches to problem solving (so-called heurisms) was given its name. Pólya ( 1964 ) describes this discipline as follows:

Heuristics deals with solving tasks. Its specific goals include highlighting in general terms the reasons for selecting those moments in a problem the examination of which could help us find a solution. (p. 5)

This discipline has grown, in part, from examining the approaches to certain problems more in detail and comparing them with each other in order to abstract similarities in approach, or so-called heurisms. Pólya ( 1949 ), but also, inter alia, Engel ( 1998 ), König ( 1984 ) and Sewerin ( 1979 ) have formulated such heurisms for mathematical problem tasks. The problem tasks examined by the authors mentioned are predominantly found in the area of talent programmes, that is, they often go back to mathematics competitions.

In 1983 Zimmermann provided an overview of heuristic approaches and tools in American literature which also offered suggestions for mathematics classes. In the German-speaking countries, an approach has established itself, going back to Sewerin ( 1979 ) and König ( 1984 ), which divides school-relevant heuristic procedures into heuristic tools, strategies and principles, see also Bruder and Collet ( 2011 ).

Below is a review of the conceptual background of heuristics, followed by a description of the effect mechanisms of heurisms in problem-solving processes.

1.1.1 Research Review on the Promotion of Problem Solving

In the 20th century, there has been an advancement of research on mathematical problem solving and findings about possibilities to promote problem solving with varying priorities (c.f. Pehkonen 1991 ). Based on a model by Pólya ( 1949 ), in a first phase of research on problem solving, particularly in the 1960s and the 1970s, a series of studies on problem-solving processes placing emphasis on the importance of heuristic strategies (heurisms) in problem solving has been carried out. It was assumed that teaching and learning heuristic strategies, principles and tools would provide students with an orientation in problem situations and that this could thus improve students’ problem-solving abilities (c.f. for instance, Schoenfeld 1979 ). This approach, mostly researched within the scope of talent programmes for problem solving, was rather successful (c.f. for instance, Sewerin 1979 ). In the 1980s, requests for promotional opportunities in everyday teaching were given more and more consideration: “ problem solving must be the focus of school mathematics in the 1980s ” (NCTM 1980 ). For the teaching and learning of problem solving in regular mathematics classes, the current view according to which cognitive, heuristic aspects were paramount, was expanded by certain student-specific aspects, such as attitudes, emotions and self-regulated behaviour (c.f. Kretschmer 1983 ; Schoenfeld 1985 , 1987 , 1992 ). Kilpatrick ( 1985 ) divided the promotional approaches described in the literature into five methods which can also be combined with each other.

Osmosis : action-oriented and implicit imparting of problem-solving techniques in a beneficial learning environment

Memorisation : formation of special techniques for particular types of problem and of the relevant questioning when problem solving

Imitation : acquisition of problem-solving abilities through imitation of an expert

Cooperation : cooperative learning of problem-solving abilities in small groups

Reflection : problem-solving abilities are acquired in an action-oriented manner and through reflection on approaches to problem solving.

Kilpatrick ( 1985 ) views as success when heuristic approaches are explained to students, clarified by means of examples and trained through the presentation of problems. The need of making students aware of heuristic approaches is by now largely accepted in didactic discussions. Differences in varying approaches to promoting problem-solving abilities rather refer to deciding which problem-solving strategies or heuristics are to imparted to students and in which way, and not whether these should be imparted at all or not.

1.1.2 Heurisms as an Expression of Mental Agility

The activity theory, particularly in its advancement by Lompscher ( 1975 , 1985 ), offers a well-suited and manageable model to describe learning activities and differences between learners with regard to processes and outcomes in problem solving (c.f. Perels et al. 2005 ). Mental activity starts with a goal and the motive of a person to perform such activity. Lompscher divides actual mental activity into content and process. Whilst the content in mathematical problem-solving consists of certain concepts, connections and procedures, the process describes the psychological processes that occur when solving a problem. This course of action is described in Lompscher by various qualities, such as systematic planning, independence, accuracy, activity and agility. Along with differences in motivation and the availability of expertise, it appears that intuitive problem solvers possess a particularly high mental agility, at least with regard to certain contents areas.

According to Lompscher, “flexibility of thought” expresses itself

… by the capacity to change more or less easily from one aspect of viewing to another one or to embed one circumstance or component into different correlations, to understand the relativity of circumstances and statements. It allows to reverse relations, to more or less easily or quickly attune to new conditions of mental activity or to simultaneously mind several objects or aspects of a given activity (Lompscher 1975 , p. 36).

These typical manifestations of mental agility can be focused on in problem solving by mathematical means and can be related to the heurisms known from the analyses of approaches by Pólya et al. (c.f. also Bruder 2000 ):

Reduction : Successful problem solvers will intuitively reduce a problem to its essentials in a sensible manner. To achieve such abstraction, they often use visualisation and structuring aids, such as informative figures, tables, solution graphs or even terms. These heuristic tools are also very well suited to document in retrospect the approach adopted by the intuitive problem solvers in a way that is comprehensible for all.

Reversibility : Successful problem solvers are able to reverse trains of thought or reproduce these in reverse. They will do this in appropriate situations automatically, for instance, when looking for a key they have mislaid. A corresponding general heuristic strategy is working in reverse.

Minding of aspects : Successful problem solvers will mind several aspects of a given problem at the same time or easily recognise any dependence on things and vary them in a targeted manner. Sometimes, this is also a matter of removing barriers in favour of an idea that appears to be sustainable, that is, by simply “hanging on” to a certain train of thought even against resistance. Corresponding heurisms are, for instance, the principle of invariance, the principle of symmetry (Engel 1998 ), the breaking down or complementing of geometric figures to calculate surface areas, or certain terms used in binomial formulas.

Change of aspects : Successful problem solvers will possibly change their assumptions, criteria or aspects minded in order to find a solution. Various aspects of a given problem will be considered intuitively or the problem be viewed from a different perspective, which will prevent “getting stuck” and allow for new insights and approaches. For instance, many elementary geometric propositions can also be proved in an elegant vectorial manner.

Transferring : Successful problem solvers will be able more easily than others to transfer a well-known procedure to another, sometimes even very different context. They recognise more easily the “framework” or pattern of a given task. Here, this is about own constructions of analogies and continual tracing back from the unknown to the known.

Intuitive, that is, untrained good problem solvers, are, however, often unable to access these flexibility qualities consciously. This is why they are also often unable to explain how they actually solved a given problem.

To be able to solve problems successfully, a certain mental agility is thus required. If this is less well pronounced in a certain area, learning how to solve problems means compensating by acquiring heurisms. In this case, insufficient mental agility is partly “offset” through the application of knowledge acquired by means of heurisms. Mathematical problem-solving competences are thus acquired through the promotion of manifestations of mental agility (reduction, reversibility, minding of aspects and change of aspects). This can be achieved by designing sub-actions of problem solving in connection with a (temporarily) conscious application of suitable heurisms. Empirical evidence for the success of the active principle of heurisms has been provided by Collet ( 2009 ).

Against such background, learning how to solve problems can be established as a long-term teaching and learning process which basically encompasses four phases (Bruder and Collet 2011 ):

Intuitive familiarisation with heuristic methods and techniques.

Making aware of special heurisms by means of prominent examples (explicit strategy acquisition).

Short conscious practice phase to use the newly acquired heurisms with differentiated task difficulties.

Expanding the context of the strategies applied.

In the first phase, students are familiarised with heurisms intuitively by means of targeted aid impulses and questions (what helped us solve this problem?) which in the following phase are substantiated on the basis of model tasks, are given names and are thus made aware of their existence. The third phase serves the purpose of a certain familiarisation with the new heurisms and the experience of competence through individualised practising at different requirement levels, including in the form of homework over longer periods. A fourth and delayed fourth phase aims at more flexibility through the transfer to other contents and contexts and the increasingly intuitive use of the newly acquired heurisms, so that students can enrich their own problem-solving models in a gradual manner. The second and third phases build upon each other in close chronological order, whilst the first phase should be used in class at all times.

All heurisms can basically be described in an action-oriented manner by means of asking the right questions. The way of asking questions can thus also establish a certain kind of personal relation. Even if the teacher presents and suggests the line of basic questions with a prototypical wording each time, students should always be given the opportunity to find “their” wording for the respective heurism and take a note of it for themselves. A possible key question for the use of a heuristic tool would be: How to illustrate and structure the problem or how to present it in a different way?

Unfortunately, for many students, applying heuristic approaches to problem solving will not ensue automatically but will require appropriate early and long-term promoting. The results of current studies, where promotion approaches to problem solving are connected with self-regulation and metacognitive aspects, demonstrate certain positive effects of such combination on students. This field of research includes, for instance, studies by Lester et al. ( 1989 ), Verschaffel et al. ( 1999 ), the studies on teaching method IMPROVE by Mevarech and Kramarski ( 1997 , 2003 ) and also the evaluation of a teaching concept on learning how to solve problems by the gradual conscious acquisition of heurisms by Collet and Bruder ( 2008 ).

1.2 Creative Problem Solving—Peter Liljedahl

There is a tension between the aforementioned story of Archimedes and the heuristics presented in the previous section. Archimedes, when submersing himself in the tub and suddenly seeing the solution to his problem, wasn’t relying on osmosis, memorisation, imitation, cooperation, or reflection (Kilpatrick 1985 ). He wasn’t drawing on reduction, reversibility, minding of aspects, change of aspect, or transfer (Bruder 2000 ). Archimedes was stuck and it was only, in fact, through insight and sudden illumination that he managed to solve his problem. In short, Archimedes was faced with a problem that the aforementioned heuristics, and their kind, would not help him to solve.

According to some, such a scenario is the definition of a problem. For example, Resnick and Glaser ( 1976 ) define a problem as being something that you do not have the experience to solve. Mathematicians, in general, agree with this (Liljedahl 2008 ).

Any problem in which you can see how to attack it by deliberate effort, is a routine problem, and cannot be an important discover. You must try and fail by deliberate efforts, and then rely on a sudden inspiration or intuition or if you prefer to call it luck. (Dan Kleitman, participant cited in Liljedahl 2008 , p. 19).

Problems, then, are tasks that cannot be solved by direct effort and will require some creative insight to solve (Liljedahl 2008 ; Mason et al. 1982 ; Pólya 1965 ).

1.2.1 A History of Creativity in Mathematics Education

In 1902, the first half of what eventually came to be a 30 question survey was published in the pages of L’Enseignement Mathématique , the journal of the French Mathematical Society. The authors, Édouard Claparède and Théodore Flournoy, were two Swiss psychologists who were deeply interested in the topics of mathematical discovery, creativity and invention. Their hope was that a widespread appeal to mathematicians at large would incite enough responses for them to begin to formulate some theories about this topic. The first half of the survey centered on the reasons for becoming a mathematician (family history, educational influences, social environment, etc.), attitudes about everyday life, and hobbies. This was eventually followed, in 1904, by the publication of the second half of the survey pertaining, in particular, to mental images during periods of creative work. The responses were sorted according to nationality and published in 1908.

During this same period Henri Poincaré (1854–1912), one of the most noteworthy mathematicians of the time, had already laid much of the groundwork for his own pursuit of this same topic and in 1908 gave a presentation to the French Psychological Society in Paris entitled L’Invention mathématique —often mistranslated to Mathematical Creativity Footnote 1 (c.f. Poincaré 1952 ). At the time of the presentation Poincaré stated that he was aware of Claparède and Flournoy’s work, as well as their results, but expressed that they would only confirm his own findings. Poincaré’s presentation, as well as the essay it spawned, stands to this day as one of the most insightful, and thorough treatments of the topic of mathematical discovery, creativity, and invention.

Just at this time, I left Caen, where I was living, to go on a geological excursion under the auspices of the School of Mines. The incident of the travel made me forget my mathematical work. Having reached Coutances, we entered an omnibus to go some place or other. At the moment when I put my foot on the step, the idea came to me, without anything in my former thoughts seeming to have paved the way for it, that the transformations I had used to define the Fuschian functions were identical with those of non-Euclidean geometry. I did not verify the idea; I should not have had the time, as, upon taking my seat in the omnibus, I went on with the conversation already commenced, but I felt a perfect certainty. On my return to Caen, for conscience’ sake, I verified the results at my leisure. (Poincaré 1952 , p. 53)

So powerful was his presentation, and so deep were his insights into his acts of invention and discovery that it could be said that he not so much described the characteristics of mathematical creativity, as defined them. From that point forth mathematical creativity, or even creativity in general, has not been discussed seriously without mention of Poincaré’s name.

Inspired by this presentation, Jacques Hadamard (1865–1963), a contemporary and a friend of Poincaré’s, began his own empirical investigation into this fascinating phenomenon. Hadamard had been critical of Claparède and Flournoy’s work in that they had not adequately treated the topic on two fronts. As exhaustive as the survey appeared to be, Hadamard felt that it failed to ask some key questions—the most important of which was with regard to the reason for failures in the creation of mathematics. This seemingly innocuous oversight, however, led directly to his second and “most important criticism” (Hadamard 1945 ). He felt that only “first-rate men would dare to speak of” (p. 10) such failures. So, inspired by his good friend Poincaré’s treatment of the subject Hadamard retooled the survey and gave it to friends of his for consideration—mathematicians such as Henri Poincaré and Albert Einstein, whose prominence were beyond reproach. Ironically, the new survey did not contain any questions that explicitly dealt with failure. In 1943 Hadamard gave a series of lectures on mathematical invention at the École Libre des Hautes Études in New York City. These talks were subsequently published as The Psychology of Mathematical Invention in the Mathematical Field (Hadameard 1945 ).

Hadamard’s classic work treats the subject of invention at the crossroads of mathematics and psychology. It provides not only an entertaining look at the eccentric nature of mathematicians and their rituals, but also outlines the beliefs of mid twentieth-century mathematicians about the means by which they arrive at new mathematics. It is an extensive exploration and extended argument for the existence of unconscious mental processes. In essence, Hadamard took the ideas that Poincaré had posed and, borrowing a conceptual framework for the characterization of the creative process from the Gestaltists of the time (Wallas 1926 ), turned them into a stage theory. This theory still stands as the most viable and reasonable description of the process of mathematical creativity.

1.2.2 Defining Mathematical Creativity

The phenomena of mathematical creativity, although marked by sudden illumination, actually consist of four separate stages stretched out over time, of which illumination is but one stage. These stages are initiation, incubation, illumination, and verification (Hadamard 1945 ). The first of these stages, the initiation phase, consists of deliberate and conscious work. This would constitute a person’s voluntary, and seemingly fruitless, engagement with a problem and be characterized by an attempt to solve the problem by trolling through a repertoire of past experiences. This is an important part of the inventive process because it creates the tension of unresolved effort that sets up the conditions necessary for the ensuing emotional release at the moment of illumination (Hadamard 1945 ; Poincaré 1952 ).

Following the initiation stage the solver, unable to come up with a solution stops working on the problem at a conscious level and begins to work on it at an unconscious level (Hadamard 1945 ; Poincaré 1952 ). This is referred to as the incubation stage of the inventive process and can last anywhere from several minutes to several years. After the period of incubation a rapid coming to mind of a solution, referred to as illumination , may occur. This is accompanied by a feeling of certainty and positive emotions (Poincaré 1952 ). Although the processes of incubation and illumination are shrouded behind the veil of the unconscious there are a number of things that can be deduced about them. First and foremost is the fact that unconscious work does, indeed, occur. Poincaré ( 1952 ), as well as Hadamard ( 1945 ), use the very real experience of illumination, a phenomenon that cannot be denied, as evidence of unconscious work, the fruits of which appear in the flash of illumination. No other theory seems viable in explaining the sudden appearance of solution during a walk, a shower, a conversation, upon waking, or at the instance of turning the conscious mind back to the problem after a period of rest (Poincaré 1952 ). Also deducible is that unconscious work is inextricably linked to the conscious and intentional effort that precedes it.

There is another remark to be made about the conditions of this unconscious work: it is possible, and of a certainty it is only fruitful, if it is on the one hand preceded and on the other hand followed by a period of conscious work. These sudden inspirations never happen except after some days of voluntary effort which has appeared absolutely fruitless and whence nothing good seems to have come … (Poincaré 1952 , p. 56)

Hence, the fruitless efforts of the initiation phase are only seemingly so. They not only set up the aforementioned tension responsible for the emotional release at the time of illumination, but also create the conditions necessary for the process to enter into the incubation phase.

Illumination is the manifestation of a bridging that occurs between the unconscious mind and the conscious mind (Poincaré 1952 ), a coming to (conscious) mind of an idea or solution. What brings the idea forward to consciousness is unclear, however. There are theories of the aesthetic qualities of the idea, effective surprise/shock of recognition, fluency of processing, or breaking functional fixedness. For reasons of brevity I will only expand on the first of these.

Poincaré proposed that ideas that were stimulated during initiation remained stimulated during incubation. However, freed from the constraints of conscious thought and deliberate calculation, these ideas would begin to come together in rapid and random unions so that “their mutual impacts may produce new combinations” (Poincaré 1952 ). These new combinations, or ideas, would then be evaluated for viability using an aesthetic sieve, which allows through to the conscious mind only the “right combinations” (Poincaré 1952 ). It is important to note, however, that good or aesthetic does not necessarily mean correct. Correctness is evaluated during the verification stage.

The purpose of verification is not only to check for correctness. It is also a method by which the solver re-engages with the problem at the level of details. That is, during the unconscious work the problem is engaged with at the level of ideas and concepts. During verification the solver can examine these ideas in closer details. Poincaré succinctly describes both of these purposes.

As for the calculations, themselves, they must be made in the second period of conscious work, that which follows the inspiration, that in which one verifies the results of this inspiration and deduces their consequences. (Poincaré 1952 , p. 62)

Aside from presenting this aforementioned theory on invention, Hadamard also engaged in a far-reaching discussion on a number of interesting, and sometimes quirky, aspects of invention and discovery that he had culled from the results of his empirical study, as well as from pertinent literature. This discussion was nicely summarized by Newman ( 2000 ) in his commentary on the elusiveness of invention.

The celebrated phrenologist Gall said mathematical ability showed itself in a bump on the head, the location of which he specified. The psychologist Souriau, we are told, maintained that invention occurs by “pure chance”, a valuable theory. It is often suggested that creative ideas are conjured up in “mathematical dreams”, but this attractive hypothesis has not been verified. Hadamard reports that mathematicians were asked whether “noises” or “meteorological circumstances” helped or hindered research [..] Claude Bernard, the great physiologist, said that in order to invent “one must think aside”. Hadamard says this is a profound insight; he also considers whether scientific invention may perhaps be improved by standing or sitting or by taking two baths in a row. Helmholtz and Poincaré worked sitting at a table; Hadamard’s practice is to pace the room (“Legs are the wheels of thought”, said Emile Angier); the chemist J. Teeple was the two-bath man. (p. 2039)

1.2.3 Discourses on Creativity

Creativity is a term that can be used both loosely and precisely. That is, while there exists a common usage of the term there also exists a tradition of academic discourse on the subject. A common usage of creative refers to a process or a person whose products are original, novel, unusual, or even abnormal (Csíkszentmihályi 1996 ). In such a usage, creativity is assessed on the basis of the external and observable products of the process, the process by which the product comes to be, or on the character traits of the person doing the ‘creating’. Each of these usages—product, process, person—is the roots of the discourses (Liljedahl and Allan 2014 ) that I summarize here, the first of which concerns products.

Consider a mother who states that her daughter is creative because she drew an original picture. The basis of such a statement can lie either in the fact that the picture is unlike any the mother has ever seen or unlike any her daughter has ever drawn before. This mother is assessing creativity on the basis of what her daughter has produced. However, the standards that form the basis of her assessment are neither consistent nor stringent. There does not exist a universal agreement as to what she is comparing the picture to (pictures by other children or other pictures by the same child). Likewise, there is no standard by which the actual quality of the picture is measured. The academic discourse that concerns assessment of products, on the other hand, is both consistent and stringent (Csíkszentmihályi 1996 ). This discourse concerns itself more with a fifth, and as yet unmentioned, stage of the creative process; elaboration . Elaboration is where inspiration becomes perspiration (Csíkszentmihályi 1996 ). It is the act of turning a good idea into a finished product, and the finished product is ultimately what determines the creativity of the process that spawned it—that is, it cannot be a creative process if nothing is created. In particular, this discourse demands that the product be assessed against other products within its field, by the members of that field, to determine if it is original AND useful (Csíkszentmihályi 1996 ; Bailin 1994 ). If it is, then the product is deemed to be creative. Note that such a use of assessment of end product pays very little attention to the actual process that brings this product forth.

The second discourse concerns the creative process. The literature pertaining to this can be separated into two categories—a prescriptive discussion of the creativity process and a descriptive discussion of the creativity process. Although both of these discussions have their roots in the four stages that Wallas ( 1926 ) proposed makes up the creative process, they make use of these stages in very different ways. The prescriptive discussion of the creative process is primarily focused on the first of the four stages, initiation , and is best summarized as a cause - and - effect discussion of creativity, where the thinking processes during the initiation stage are the cause and the creative outcome are the effects (Ghiselin 1952 ). Some of the literature claims that the seeds of creativity lie in being able to think about a problem or situation analogically. Other literature claims that utilizing specific thinking tools such as imagination, empathy, and embodiment will lead to creative products. In all of these cases, the underlying theory is that the eventual presentation of a creative idea will be precipitated by the conscious and deliberate efforts during the initiation stage. On the other hand, the literature pertaining to a descriptive discussion of the creative process is inclusive of all four stages (Kneller 1965 ; Koestler 1964 ). For example, Csíkszentmihályi ( 1996 ), in his work on flow attends to each of the stages, with much attention paid to the fluid area between conscious and unconscious work, or initiation and incubation. His claim is that the creative process is intimately connected to the enjoyment that exists during times of sincere and consuming engagement with a situation, the conditions of which he describes in great detail.

The third, and final, discourse on creativity pertains to the person. This discourse is space dominated by two distinct characteristics, habit and genius. Habit has to do with the personal habits as well as the habits of mind of people that have been deemed to be creative. However, creative people are most easily identified through their reputation for genius. Consequently, this discourse is often dominated by the analyses of the habits of geniuses as is seen in the work of Ghiselin ( 1952 ), Koestler ( 1964 ), and Kneller ( 1965 ) who draw on historical personalities such as Albert Einstein, Henri Poincaré, Vincent Van Gogh, D.H. Lawrence, Samuel Taylor Coleridge, Igor Stravinsky, and Wolfgang Amadeus Mozart to name a few. The result of this sort of treatment is that creative acts are viewed as rare mental feats, which are produced by extraordinary individuals who use extraordinary thought processes.

These different discourses on creativity can be summed up in a tension between absolutist and relativist perspectives on creativity (Liljedahl and Sriraman 2006 ). An absolutist perspective assumes that creative processes are the domain of genius and are present only as precursors to the creation of remarkably useful and universally novel products. The relativist perspective, on the other hand, allows for every individual to have moments of creativity that may, or may not, result in the creation of a product that may, or may not, be either useful or novel.

Between the work of a student who tries to solve a problem in geometry or algebra and a work of invention, one can say there is only a difference of degree. (Hadamard 1945 , p. 104).

Regardless of discourse, however, creativity is not “part of the theories of logical forms” (Dewey 1938 ). That is, creativity is not representative of the lock-step logic and deductive reasoning that mathematical problem solving is often presumed to embody (Bibby 2002 ; Burton 1999 ). Couple this with the aforementioned demanding constraints as to what constitutes a problem, where then does that leave problem solving heuristics? More specifically, are there creative problem solving heuristics that will allow us to resolve problems that require illumination to solve? The short answer to this question is yes—there does exist such problem solving heuristics. To understand these, however, we must first understand the routine problem solving heuristics they are built upon. In what follows, I walk through the work of key authors and researchers whose work offers us insights into progressively more creative problem solving heuristics for solving true problems.

1.2.4 Problem Solving by Design

In a general sense, design is defined as the algorithmic and deductive approach to solving a problem (Rusbult 2000 ). This process begins with a clearly defined goal or objective after which there is a great reliance on relevant past experience, referred to as repertoire (Bruner 1964 ; Schön 1987 ), to produce possible options that will lead towards a solution of the problem (Poincaré 1952 ). These options are then examined through a process of conscious evaluations (Dewey 1933 ) to determine their suitability for advancing the problem towards the final goal. In very simple terms, problem solving by design is the process of deducing the solution from that which is already known.

Mayer ( 1982 ), Schoenfeld ( 1982 ), and Silver ( 1982 ) state that prior knowledge is a key element in the problem solving process. Prior knowledge influences the problem solver’s understanding of the problem as well as the choice of strategies that will be called upon in trying to solve the problem. In fact, prior knowledge and prior experiences is all that a solver has to draw on when first attacking a problem. As a result, all problem solving heuristics incorporate this resource of past experiences and prior knowledge into their initial attack on a problem. Some heuristics refine these ideas, and some heuristics extend them (c.f. Kilpatrick 1985 ; Bruder 2000 ). Of the heuristics that refine, none is more influential than the one created by George Pólya (1887–1985).

1.2.5 George Pólya: How to Solve It

In his book How to Solve It (1949) Pólya lays out a problem solving heuristic that relies heavily on a repertoire of past experience. He summarizes the four-step process of his heuristic as follows:

Understanding the Problem

First. You have to understand the problem.

What is the unknown? What are the data? What is the condition?

Is it possible to satisfy the condition? Is the condition sufficient to determine the unknown? Or is it insufficient? Or redundant? Or contradictory?

Draw a figure. Introduce suitable notation.

Separate the various parts of the condition. Can you write them down?

Devising a Plan

Second. Find the connection between the data and the unknown. You may be obliged to consider auxiliary problems if an immediate connection cannot be found. You should obtain eventually a plan of the solution.

Have you seen it before? Or have you seen the same problem in a slightly different form?

Do you know a related problem? Do you know a theorem that could be useful?

Look at the unknown! And try to think of a familiar problem having the same or a similar unknown.

Here is a problem related to yours and solved before. Could you use it? Could you use its result? Could you use its method? Should you introduce some auxiliary element in order to make its use possible?

Could you restate the problem? Could you restate it still differently? Go back to definitions.

If you cannot solve the proposed problem try to solve first some related problem. Could you imagine a more accessible related problem? A more general problem? A more special problem? An analogous problem? Could you solve a part of the problem? Keep only a part of the condition, drop the other part; how far is the unknown then determined, how can it vary? Could you derive something useful from the data? Could you think of other data appropriate to determine the unknown? Could you change the unknown or data, or both if necessary, so that the new unknown and the new data are nearer to each other?

Did you use all the data? Did you use the whole condition? Have you taken into account all essential notions involved in the problem?

Carrying Out the Plan

Third. Carry out your plan.

Carrying out your plan of the solution, check each step. Can you see clearly that the step is correct? Can you prove that it is correct?

Looking Back

Fourth. Examine the solution obtained.

Can you check the result? Can you check the argument?

Can you derive the solution differently? Can you see it at a glance?

Can you use the result, or the method, for some other problem?

The emphasis on auxiliary problems, related problems, and analogous problems that are, in themselves, also familiar problems is an explicit manifestation of relying on a repertoire of past experience. This use of familiar problems also requires an ability to deduce from these related problems a recognizable and relevant attribute that will transfer to the problem at hand. The mechanism that allows for this transfer of knowledge between analogous problems is known as analogical reasoning (English 1997 , 1998 ; Novick 1988 , 1990 , 1995 ; Novick and Holyoak 1991 ) and has been shown to be an effective, but not always accessible, thinking strategy.

Step four in Pólya’s heuristic, looking back, is also a manifestation of utilizing prior knowledge to solve problems, albeit an implicit one. Looking back makes connections “in memory to previously acquired knowledge [..] and further establishes knowledge in long-term memory that may be elaborated in later problem-solving encounters” (Silver 1982 , p. 20). That is, looking back is a forward-looking investment into future problem solving encounters, it sets up connections that may later be needed.

Pólya’s heuristic is a refinement on the principles of problem solving by design. It not only makes explicit the focus on past experiences and prior knowledge, but also presents these ideas in a very succinct, digestible, and teachable manner. This heuristic has become a popular, if not the most popular, mechanism by which problem solving is taught and learned.

1.2.6 Alan Schoenfeld: Mathematical Problem Solving

The work of Alan Schoenfeld is also a refinement on the principles of problem solving by design. However, unlike Pólya ( 1949 ) who refined these principles at a theoretical level, Schoenfeld has refined them at a practical and empirical level. In addition to studying taught problem solving strategies he has also managed to identify and classify a variety of strategies, mostly ineffectual, that students invoke naturally (Schoenfeld 1985 , 1992 ). In so doing, he has created a better understanding of how students solve problems, as well as a better understanding of how problems should be solved and how problem solving should be taught.

For Schoenfeld, the problem solving process is ultimately a dialogue between the problem solver’s prior knowledge, his attempts, and his thoughts along the way (Schoenfeld 1982 ). As such, the solution path of a problem is an emerging and contextually dependent process. This is a departure from the predefined and contextually independent processes of Pólya’s ( 1949 ) heuristics. This can be seen in Schoenfeld’s ( 1982 ) description of a good problem solver.

To examine what accounts for expertise in problem solving, you would have to give the expert a problem for which he does not have access to a solution schema. His behavior in such circumstances is radically different from what you would see when he works on routine or familiar “non-routine” problems. On the surface his performance is no longer proficient; it may even seem clumsy. Without access to a solution schema, he has no clear indication of how to start. He may not fully understand the problem, and may simply “explore it for a while until he feels comfortable with it. He will probably try to “match” it to familiar problems, in the hope it can be transformed into a (nearly) schema-driven solution. He will bring up a variety of plausible things: related facts, related problems, tentative approaches, etc. All of these will have to be juggled and balanced. He may make an attempt solving it in a particular way, and then back off. He may try two or three things for a couple of minutes and then decide which to pursue. In the midst of pursuing one direction he may go back and say “that’s harder than it should be” and try something else. Or, after the comment, he may continue in the same direction. With luck, after some aborted attempts, he will solve the problem. (p. 32-33)

Aside from demonstrating the emergent nature of the problem solving process, this passage also brings forth two consequences of Schoenfeld’s work. The first of these is the existence of problems for which the solver does not have “access to a solution schema”. Unlike Pólya ( 1949 ), who’s heuristic is a ‘one size fits all (problems)’ heuristic, Schoenfeld acknowledges that problem solving heuristics are, in fact, personal entities that are dependent on the solver’s prior knowledge as well as their understanding of the problem at hand. Hence, the problems that a person can solve through his or her personal heuristic are finite and limited.

The second consequence that emerges from the above passage is that if a person lacks the solution schema to solve a given problem s/he may still solve the problem with the help of luck . This is an acknowledgement, if only indirectly so, of the difference between problem solving in an intentional and mechanical fashion verses problem solving in a more creative fashion, which is neither intentional nor mechanical (Pehkonen 1997 ).

1.2.7 David Perkins: Breakthrough Thinking

As mentioned, many consider a problem that can be solved by intentional and mechanical means to not be worthy of the title ‘problem’. As such, a repertoire of past experiences sufficient for dealing with such a ‘problem’ would disqualify it from the ranks of ‘problems’ and relegate it to that of ‘exercises’. For a problem to be classified as a ‘problem’, then, it must be ‘problematic’. Although such an argument is circular it is also effective in expressing the ontology of mathematical ‘problems’.

Perkins ( 2000 ) also requires problems to be problematic. His book Archimedes’ Bathtub: The Art and Logic of Breakthrough Thinking (2000) deals with situations in which the solver has gotten stuck and no amount of intentional or mechanical adherence to the principles of past experience and prior knowledge is going to get them unstuck. That is, he deals with problems that, by definition, cannot be solved through a process of design [or through the heuristics proposed by Pólya ( 1949 ) and Schoenfeld ( 1985 )]. Instead, the solver must rely on the extra-logical process of what Perkins ( 2000 ) calls breakthrough thinking .

Perkins ( 2000 ) begins by distinguishing between reasonable and unreasonable problems. Although both are solvable, only reasonable problems are solvable through reasoning. Unreasonable problems require a breakthrough in order to solve them. The problem, however, is itself inert. It is neither reasonable nor unreasonable. That quality is brought to the problem by the solver. That is, if a student cannot solve a problem by direct effort then that problem is deemed to be unreasonable for that student. Perkins ( 2000 ) also acknowledges that what is an unreasonable problem for one person is a perfectly reasonable problem for another person; reasonableness is dependent on the person.

This is not to say that, once found, the solution cannot be seen as accessible through reason. During the actual process of solving, however, direct and deductive reasoning does not work. Perkins ( 2000 ) uses several classic examples to demonstrate this, the most famous being the problem of connecting nine dots in a 3 × 3 array with four straight lines without removing pencil from paper, the solution to which is presented in Fig.  1 .

Nine dots—four lines problem and solution

To solve this problem, Perkins ( 2000 ) claims that the solver must recognize that the constraint of staying within the square created by the 3 × 3 array is a self-imposed constraint. He further claims that until this is recognized no amount of reasoning is going to solve the problem. That is, at this point in the problem solving process the problem is unreasonable. However, once this self-imposed constraint is recognized the problem, and the solution, are perfectly reasonable. Thus, the solution of an, initially, unreasonable problem is reasonable.

The problem solving heuristic that Perkins ( 2000 ) has constructed to deal with solvable, but unreasonable, problems revolves around the idea of breakthrough thinking and what he calls breakthrough problems . A breakthrough problem is a solvable problem in which the solver has gotten stuck and will require an AHA! to get unstuck and solve the problem. Perkins ( 2000 ) poses that there are only four types of solvable unreasonable problems, which he has named wilderness of possibilities , the clueless plateau , narrow canyon of exploration , and oasis of false promise . The names for the first three of these types of problems are related to the Klondike gold rush in Alaska, a time and place in which gold was found more by luck than by direct and systematic searching.

The wilderness of possibilities is a term given to a problem that has many tempting directions but few actual solutions. This is akin to a prospector searching for gold in the Klondike. There is a great wilderness in which to search, but very little gold to be found. The clueless plateau is given to problems that present the solver with few, if any, clues as to how to solve it. The narrow canyon of exploration is used to describe a problem that has become constrained in such a way that no solution now exists. The nine-dot problem presented above is such a problem. The imposed constraint that the lines must lie within the square created by the array makes a solution impossible. This is identical to the metaphor of a prospector searching for gold within a canyon where no gold exists. The final type of problem gets its name from the desert. An oasis of false promise is a problem that allows the solver to quickly get a solution that is close to the desired outcome; thereby tempting them to remain fixed on the strategy that they used to get this almost-answer. The problem is, that like the canyon, the solution does not exist at the oasis; the solution strategy that produced an almost-answer is incapable of producing a complete answer. Likewise, a desert oasis is a false promise in that it is only a reprieve from the desolation of the dessert and not a final destination.

Believing that there are only four ways to get stuck, Perkins ( 2000 ) has designed a problem solving heuristic that will “up the chances” of getting unstuck. This heuristic is based on what he refers to as “the logic of lucking out” (p. 44) and is built on the idea of introspection. By first recognizing that they are stuck, and then recognizing that the reason they are stuck can only be attributed to one of four reasons, the solver can access four strategies for getting unstuck, one each for the type of problem they are dealing with. If the reason they are stuck is because they are faced with a wilderness of possibilities they are to begin roaming far, wide, and systematically in the hope of reducing the possible solution space to one that is more manageable. If they find themselves on a clueless plateau they are to begin looking for clues, often in the wording of the problem. When stuck in a narrow canyon of possibilities they need to re-examine the problem and see if they have imposed any constraints. Finally, when in an oasis of false promise they need to re-attack the problem in such a way that they stay away from the oasis.

Of course, there are nuances and details associated with each of these types of problems and the strategies for dealing with them. However, nowhere within these details is there mention of the main difficulty inherent in introspection; that it is much easier for the solver to get stuck than it is for them to recognize that they are stuck. Once recognized, however, the details of Perkins’ ( 2000 ) heuristic offer the solver some ways for recognizing why they are stuck.

1.2.8 John Mason, Leone Burton, and Kaye Stacey: Thinking Mathematically

The work of Mason et al. in their book Thinking Mathematically ( 1982 ) also recognizes the fact that for each individual there exists problems that will not yield to their intentional and mechanical attack. The heuristic that they present for dealing with this has two main processes with a number of smaller phases, rubrics, and states. The main processes are what they refer to as specializing and generalizing. Specializing is the process of getting to know the problem and how it behaves through the examination of special instances of the problem. This process is synonymous with problem solving by design and involves the repeated oscillation between the entry and attack phases of Mason et al. ( 1982 ) heuristic. The entry phase is comprised of ‘getting started’ and ‘getting involved’ with the problem by using what is immediately known about it. Attacking the problem involves conjecturing and testing a number of hypotheses in an attempt to gain greater understanding of the problem and to move towards a solution.

At some point within this process of oscillating between entry and attack the solver will get stuck, which Mason et al. ( 1982 ) refer to as “an honourable and positive state, from which much can be learned” (p. 55). The authors dedicate an entire chapter to this state in which they acknowledge that getting stuck occurs long before an awareness of being stuck develops. They proposes that the first step to dealing with being stuck is the simple act of writing STUCK!

The act of expressing my feelings helps to distance me from my state of being stuck. It frees me from incapacitating emotions and reminds me of actions that I can take. (p. 56)

The next step is to reengage the problem by examining the details of what is known, what is wanted, what can be introduced into the problem, and what has been introduced into the problem (imposed assumptions). This process is engaged in until an AHA!, which advances the problem towards a solution, is encountered. If, at this point, the problem is not completely solved the oscillation is then resumed.

At some point in this process an attack on the problem will yield a solution and generalizing can begin. Generalizing is the process by which the specifics of a solution are examined and questions as to why it worked are investigated. This process is synonymous with the verification and elaboration stages of invention and creativity. Generalization may also include a phase of review that is similar to Pólya’s ( 1949 ) looking back.

1.2.9 Gestalt: The Psychology of Problem Solving

The Gestalt psychology of learning believes that all learning is based on insights (Koestler 1964 ). This psychology emerged as a response to behaviourism, which claimed that all learning was a response to external stimuli. Gestalt psychologists, on the other hand, believed that there was a cognitive process involved in learning as well. With regards to problem solving, the Gestalt school stands firm on the belief that problem solving, like learning, is a product of insight and as such, cannot be taught. In fact, the theory is that not only can problem solving not be taught, but also that attempting to adhere to any sort of heuristic will impede the working out of a correct solution (Krutestkii 1976 ). Thus, there exists no Gestalt problem solving heuristic. Instead, the practice is to focus on the problem and the solution rather than on the process of coming up with a solution. Problems are solved by turning them over and over in the mind until an insight, a viable avenue of attack, presents itself. At the same time, however, there is a great reliance on prior knowledge and past experiences. The Gestalt method of problem solving, then, is at the same time very different and very similar to the process of design.

Gestalt psychology has not fared well during the evolution of cognitive psychology. Although it honours the work of the unconscious mind it does so at the expense of practicality. If learning is, indeed, entirely based on insight then there is little point in continuing to study learning. “When one begins by assuming that the most important cognitive phenomena are inaccessible, there really is not much left to talk about” (Schoenfeld 1985 , p. 273). However, of interest here is the Gestalt psychologists’ claim that focus on problem solving methods creates functional fixedness (Ashcraft 1989 ). Mason et al. ( 1982 ), as well as Perkins ( 2000 ) deal with this in their work on getting unstuck.

1.2.10 Final Comments

Mathematics has often been characterized as the most precise of all sciences. Lost in such a misconception is the fact that mathematics often has its roots in the fires of creativity, being born of the extra-logical processes of illumination and intuition. Problem solving heuristics that are based solely on the processes of logical and deductive reasoning distort the true nature of problem solving. Certainly, there are problems in which logical deductive reasoning is sufficient for finding a solution. But these are not true problems. True problems need the extra-logical processes of creativity, insight, and illumination, in order to produce solutions.

Fortunately, as elusive as such processes are, there does exist problem solving heuristics that incorporate them into their strategies. Heuristics such as those by Perkins ( 2000 ) and Mason et al. ( 1982 ) have found a way of combining the intentional and mechanical processes of problem solving by design with the extra-logical processes of creativity, illumination, and the AHA!. Furthermore, they have managed to do so without having to fully comprehend the inner workings of this mysterious process.

1.3 Digital Technologies and Mathematical Problem Solving—Luz Manuel Santos-Trigo

Mathematical problem solving is a field of research that focuses on analysing the extent to which problem solving activities play a crucial role in learners’ understanding and use of mathematical knowledge. Mathematical problems are central in mathematical practice to develop the discipline and to foster students learning (Pólya 1945 ; Halmos 1994 ). Mason and Johnston-Wilder ( 2006 ) pointed out that “The purpose of a task is to initiate mathematically fruitful activity that leads to a transformation in what learners are sensitized to notice and competent to carry out” (p. 25). Tasks are essential for learners to elicit their ideas and to engage them in mathematical thinking. In a problem solving approach, what matters is the learners’ goals and ways to interact with the tasks. That is, even routine tasks can be a departure point for learners to extend initial conditions and transform them into some challenging activities.

Thus, analysing and characterizing ways in which mathematical problems are formulated (Singer et al. 2015 ) and the process involved in pursuing and solving those problems generate important information to frame and structure learning environments to guide and foster learners’ construction of mathematical concepts and problem solving competences (Santos-Trigo 2014 ). Furthermore, mathematicians or discipline practitioners have often been interested in unveiling and sharing their own experience while developing the discipline. As a results, they have provided valuable information to characterize mathematical practices and their relations to what learning processes of the discipline entails. It is recognized that the work of Pólya ( 1945 ) offered not only bases to launch several research programs in problem solving (Schoenfeld 1992 ; Mason et al. 1982 ); but also it became an essential resource for teachers to orient and structure their mathematical lessons (Krulik and Reys 1980 ).

1.3.1 Research Agenda

A salient feature of a problem solving approach to learn mathematics is that teachers and students develop and apply an enquiry or inquisitive method to delve into mathematical concepts and tasks. How are mathematical problems or concepts formulated? What types of problems are important for teachers/learners to discuss and engage in mathematical reasoning? What mathematical processes and ways of reasoning are involved in understanding mathematical concepts and solving problems? What are the features that distinguish an instructional environment that fosters problem-solving activities? How can learners’ problem solving competencies be assessed? How can learners’ problem solving competencies be characterized and explained? How can learners use digital technologies to understand mathematics and to develop problem-solving competencies? What ways of reasoning do learners construct when they use digital technologies in problem solving approaches? These types of questions have been important in the problem solving research agenda and delving into them has led researchers to generate information and results to support and frame curriculum proposals and learning scenarios. The purpose of this section is to present and discuss important themes that emerged in problem solving approaches that rely on the systematic use of several digital technologies.

In the last 40 years, the accumulated knowledge in the problem solving field has shed lights on both a characterization of what mathematical thinking involves and how learners can construct a robust knowledge in problem solving environments (Schoenfeld 1992 ). In this process, the field has contributed to identify what types of transformations traditional learning scenarios might consider when teachers and students incorporate the use of digital technologies in mathematical classrooms. In this context, it is important to briefly review what main themes and developments the field has addressed and achieved during the last 40 years.

1.3.2 Problem Solving Developments

There are traces of mathematical problems and solutions throughout the history of civilization that explain the humankind interest for identifying and exploring mathematical relations (Kline 1972 ). Pólya ( 1945 ) reflects on his own practice as a mathematician to characterize the process of solving mathematical problems through four main phases: Understanding the problem, devising a plan, carrying out the plan, and looking back. Likewise, Pólya ( 1945 ) presents and discusses the role played by heuristic methods throughout all problem solving phases. Schoenfeld ( 1985 ) presents a problem solving research program based on Pólya’s ( 1945 ) ideas to investigate the extent to which problem solving heuristics help university students to solve mathematical problems and to develop a way of thinking that shows consistently features of mathematical practices. As a result, he explains the learners’ success or failure in problem solving activities can be characterized in terms their mathematical resources and ways to access them, cognitive and metacognitive strategies used to represent and explore mathematical tasks, and systems of beliefs about mathematics and solving problems. In addition, Schoenfeld ( 1992 ) documented that heuristics methods as illustrated in Pólya’s ( 1945 ) book are ample and general and do not include clear information and directions about how learners could assimilate, learn, and use them in their problem solving experiences. He suggested that students need to discuss what it means, for example, to think of and examining special cases (one important heuristic) in finding a closed formula for series or sequences, analysing relationships of roots of polynomials, or focusing on regular polygons or equilateral/right triangles to find general relations about these figures. That is, learners need to work on examples that lead them to recognize that the use of a particular heuristic often involves thinking of different type of cases depending on the domain or content involved. Lester and Kehle ( 2003 ) summarize themes and methodological shifts in problem solving research up to 1995. Themes include what makes a problem difficult for students and what it means to be successful problem solvers; studying and contrasting experts and novices’ problem solving approaches; learners’ metacognitive, beliefs systems and the influence of affective behaviours; and the role of context; and social interactions in problem solving environments. Research methods in problem solving studies have gone from emphasizing quantitative or statistical design to the use of cases studies and ethnographic methods (Krutestkii ( 1976 ). Teaching strategies also evolved from being centred on teachers to the active students’ engagement and collaboration approaches (NCTM 2000 ). Lesh and Zawojewski ( 2007 ) propose to extend problem solving approaches beyond class setting and they introduce the construct “model eliciting activities” to delve into the learners’ ideas and thinking as a way to engage them in the development of problem solving experiences. To this end, learners develop and constantly refine problem-solving competencies as a part of a learning community that promotes and values modelling construction activities. Recently, English and Gainsburg ( 2016 ) have discussed the importance of modeling eliciting activities to prepare and develop students’ problem solving experiences for 21st Century challenges and demands.

Törner et al. ( 2007 ) invited mathematics educators worldwide to elaborate on the influence and developments of problem solving in their countries. Their contributions show a close relationship between countries mathematical education traditions and ways to frame and implement problem solving approaches. In Chinese classrooms, for example, three instructional strategies are used to structure problem solving lessons: one problem multiple solutions , multiple problems one solution , and one problem multiple changes . In the Netherlands, the realistic mathematical approach permeates the students’ development of problem solving competencies; while in France, problem solving activities are structured in terms of two influential frameworks: The theory of didactical situations and anthropological theory of didactics.

In general, problem solving frameworks and instructional approaches came from analysing students’ problem solving experiences that involve or rely mainly on the use of paper and pencil work. Thus, there is a need to re-examined principles and frameworks to explain what learners develop in learning environments that incorporate systematically the coordinated use of digital technologies (Hoyles and Lagrange 2010 ). In this perspective, it becomes important to briefly describe and identify what both multiple purpose and ad hoc technologies can offer to the students in terms of extending learning environments and representing and exploring mathematical tasks. Specifically, a task is used to identify features of mathematical reasoning that emerge through the use digital technologies that include both mathematical action and multiple purpose types of technologies.

1.3.3 Background

Digital technologies are omnipresent and their use permeates and shapes several social and academic events. Mobile devices such as tablets or smart phones are transforming the way people communicate, interact and carry out daily activities. Churchill et al. ( 2016 ) pointed out that mobile technologies provide a set of tools and affordances to structure and support learning environments in which learners continuously interact to construct knowledge and solve problems. The tools include resources or online materials, efficient connectivity to collaborate and discuss problems, ways to represent, explore and store information, and analytical and administration tools to management learning activities. Schmidt and Cohen ( 2013 ) stated that nowadays it is difficult to imagine a life without mobile devices, and communication technologies are playing a crucial role in generating both cultural and technical breakthroughs. In education, the use of mobile artefacts and computers offers learners the possibility of continuing and extending peers and groups’ mathematical discussions beyond formal settings. In this process, learners can also consult online materials and interact with experts, peers or more experienced students while working on mathematical tasks. In addition, dynamic geometry systems (GeoGebra) provide learners a set of affordances to represent and explore dynamically mathematical problems. Leung and Bolite-Frant ( 2015 ) pointed out that tools help activate an interactive environment in which teachers and students’ mathematical experiences get enriched. Thus, the digital age brings new challenges to the mathematics education community related to the changes that technologies produce to curriculum, learning scenarios, and ways to represent, explore mathematical situations. In particular, it is important to characterize the type of reasoning that learners can develop as a result of using digital technologies in their process of learning concepts and solving mathematical problems.

1.3.4 A Focus on Mathematical Tasks

Mathematical tasks are essential elements for engaging learners in mathematical reasoning which involves representing objects, identifying and exploring their properties in order to detect invariants or relationships and ways to support them. Watson and Ohtani ( 2015 ) stated that task design involves discussions about mathematical content and students’ learning (cognitive perspective), about the students’ experiences to understand the nature of mathematical activities; and about the role that tasks played in teaching practices. In this context, tasks are the vehicle to present and discuss theoretical frameworks for supporting the use of digital technology, to analyse the importance of using digital technologies in extending learners’ mathematical discussions beyond formal settings, and to design ways to foster and assess the use of technologies in learners’ problem solving environments. In addition, it is important to discuss contents, concepts, representations and strategies involved in the process of using digital technologies in approaching the tasks. Similarly, it becomes essential to discuss what types of activities students will do to learn and solve the problems in an environment where the use of technologies fosters and values the participation and collaboration of all students. What digital technologies are important to incorporate in problem solving approaches? Dynamic Geometry Systems can be considered as a milestone in the development of digital technologies. Objects or mathematical situations can be represented dynamically through the use of a Dynamic Geometry System and learners or problem solvers can identify and examine mathematical relations that emerge from moving objects within the dynamic model (Moreno-Armella and Santos-Trigo 2016 ).

Leung and Bolite-Frant ( 2015 ) stated that “dynamic geometry software can be used in task design to cover a large epistemic spectrum from drawing precise robust geometrical figures to exploration of new geometric theorems and development of argumentation discourse” (p. 195). As a result, learners not only need to develop skills and strategies to construct dynamic configuration of problems; but also ways of relying on the tool’s affordances (quantifying parameters or objects attributes, generating loci, graphing objects behaviours, using sliders, or dragging particular elements within the configuration) in order to identify and support mathematical relations. What does it mean to represent and explore an object or mathematical situation dynamically?

A simple task that involves a rhombus and its inscribed circle is used to illustrate how a dynamic representation of these objects and embedded elements can lead learners to identify and examine mathematical properties of those objects in the construction of the configuration. To this end, learners are encouraged to pose and pursue questions to explain the behaviours of parameters or attributes of the family of objects that is generated as a result of moving a particular element within the configuration.

1.3.5 A Task: A Dynamic Rhombus

Figure  2 represents a rhombus APDB and its inscribed circle (O is intersection of diagonals AD and BP and the radius of the inscribed circle is the perpendicular segment from any side of the rhombus to point O), vertex P lies on a circle c centred at point A. Circle c is only a heuristic to generate a family of rhombuses. Thus, point P can be moved along circle c to generate a family of rhombuses. Indeed, based on the symmetry of the circle it is sufficient to move P on the semicircle B’CA to draw such a family of rhombuses.

A dynamic construction of a rhombus

1.3.6 Posing Questions

A goal in constructing a dynamic model or configuration of problems is always to identify and explore mathematical properties and relations that might result from moving objects within the model. How do the areas of both the rhombus and the inscribed circle behave when point P is moved along the arc B’CB? At what position of point P does the area of the rhombus or inscribed circle reach the maximum value? The coordinates of points S and Q (Fig.  3 ) are the x -value of point P and as y -value the corresponding area values of rhombus ABDP and the inscribed circle respectively. Figure  2 shows the loci of points S and Q when point P is moved along arc B’CB. Here, finding the locus via the use of GeoGebra is another heuristic to graph the area behaviour without making explicit the algebraic model of the area.

Graphic representation of the area variation of the family of rhombuses and inscribed circles generated when P is moved through arc B’CB

The area graphs provide information to visualize that in that family of generated rhombuses the maximum area value of the inscribed circle and rhombus is reached when the rhombus becomes a square (Fig.  4 ). That is, the controlled movement of particular objects is an important strategy to analyse the area variation of the family of rhombuses and their inscribed circles.

Visualizing the rhombus and the inscribed circle with maximum area

It is important to observe the identification of points P and Q in terms of the position of point P and the corresponding areas and the movement of point P was sufficient to generate both area loci. That is, the graph representation of the areas is achieved without having an explicit algebraic expression of the area variation. Clearly, the graphic representations provide information regarding the increasing or decreasing interval of both areas; it is also important to explore what properties both graphic representations hold. The goal is to argue that the area variation of the rhombus represents an ellipse and the area of the inscribed circle represents a parabola. An initial argument might involve selecting five points on each locus and using the tool to draw the corresponding conic section (Fig.  5 ). In this case, the tool affordances play an important role in generating the graphic representation of the areas’ behaviours and in identifying properties of those representations. In this context, the use of the tool can offer learners the opportunity to problematize (Santos-Trigo 2007 ) a simple mathematical object (rhombus) as a means to search for mathematical relations and ways to support them.

Drawing the conic section that passes through five points

1.3.7 Looking for Different Solutions Methods

Another line of exploration might involve asking for ways to construct a rhombus and its inscribed circle: Suppose that the side of the rhombus and the circle are given, how can you construct the rhombus that has that circle inscribed? Figure  6 shows the given data, segment A 1 B 1 and circle centred at O and radius OD. The initial goal is to draw the circle tangent to the given segment. To this end, segment AB is congruent to segment A 1 B 1 and on this segment a point P is chosen and a perpendicular to segment AB that passes through point P is drawn. Point C is on this perpendicular and the centre of a circle with radius OD and h is the perpendicular to line PC that passes through point C. Angle ACB changes when point P is moved along segment AB and point E and F are the intersection of line h and the circle with centre M the midpoint of AB and radius MA (Fig.  6 ).

Drawing segment AB tangent to the given circle

Figure  7 a shows the right triangle AFB as the base to construct the rhombus and the inscribed circle and Fig.  7 b shows the second solution based on triangle AEB.

a Drawing the rhombus and the inscribed circle. b Drawing the second solution

Another approach might involve drawing the given circle centred at the origin and the segment as EF with point E on the y-axis. Line OC is perpendicular to segment EF and the locus of point C when point E moves along the y-axis intersects the given circle (Fig.  8 a, b). Both figures show two solutions to draw the rhombus that circumscribe the given circle.

a and b Another solution that involves finding a locus of point C

In this example, the GeoGebra affordances not only are important to construct a dynamic model of the task; but also offer learners and opportunity to explore relations that emerge from moving objects within the model. As a result, learners can rely on different concepts and strategies to solve the tasks. The idea in presenting this rhombus task is to illustrate that the use of a Dynamic Geometry System provides affordances for learners to construct dynamic representation of mathematical objects or problems, to move elements within the representation to pose questions or conjectures to explain invariants or patterns among involved parameters; to search for arguments to support emerging conjectures, and to develop a proper language to communicate results.

1.3.8 Looking Back

Conceptual frameworks used to explain learners’ construction of mathematical knowledge need to capture or take into account the different ways of reasoning that students might develop as a result of using a set of tools during the learning experiences. Figure  9 show some digital technologies that learners can use for specific purpose at the different stages of problem solving activities.

The coordinated use of digital tools to engage learners in problem solving experiences

The use of a dynamic system (GeoGebra) provides a set of affordances for learners to conceptualize and represent mathematical objects and tasks dynamically. In this process, affordances such as moving objects orderly (dragging), finding loci of objects, quantifying objects attributes (lengths, areas, angles, etc.), using sliders to vary parameters, and examining family of objects became important to look for invariance or objects relationships. Likewise, analysing the parameters or objects behaviours within the configuration might lead learners to identify properties to support emerging mathematical relations. Thus, with the use of the tool, learners might conceptualize mathematical tasks as an opportunity for them to engage in mathematical activities that include constructing dynamic models of tasks, formulating conjectures, and always looking for different arguments to support them. Similarly, learners can use an online platform to share their ideas, problem solutions or questions in a digital wall and others students can also share ideas or solution methods and engaged in mathematical discussions that extend mathematical classroom activities.

1.4 Problem Posing: An Overview for Further Progress—Uldarico Malaspina Jurado

Problem posing and problem solving are two essential aspects of the mathematical activity; however, researchers in mathematics education have not emphasized their attention on problem posing as much as problem solving. In that sense, due to its importance in the development of mathematical thinking in students since the first grades, we agree with Ellerton’s statement ( 2013 ): “for too long, successful problem solving has been lauded as the goal; the time has come for problem posing to be given a prominent but natural place in mathematics curricula and classrooms” (pp. 100–101); and due to its importance in teacher training, with Abu-Elwan’s statement ( 1999 ):

While teacher educators generally recognize that prospective teachers require guidance in mastering the ability to confront and solve problems, what is often overlooked is the critical fact that, as teachers, they must be able to go beyond the role as problem solvers. That is, in order to promote a classroom situation where creative problem solving is the central focus, the practitioner must become skillful in discovering and correctly posing problems that need solutions. (p. 1)

Scientists like Einstein and Infeld ( 1938 ), recognized not only for their notable contributions in the fields they worked, but also for their reflections on the scientific activity, pointed out the importance of problem posing; thus it is worthwhile to highlight their statement once again:

The formulation of a problem is often more essential than its solution, which may be merely a matter of mathematical or experimental skills. To raise new questions, new possibilities, to regard old questions from a new angle, requires creative imagination and marks real advance in science. (p. 92)

Certainly, it is also relevant to remember mathematician Halmos’s statement ( 1980 ): “I do believe that problems are the heart of mathematics, and I hope that as teachers (…) we will train our students to be better problem posers and problem solvers than we are” (p. 524).

An important number of researchers in mathematics education has focused on the importance of problem posing, and we currently have numerous, very important publications that deal with different aspects of problem posing related to the mathematics education of students in all educational levels and to teacher training.

1.4.1 A Retrospective Look

Kilpatrick ( 1987 ) marked a historical milestone in research related to problem posing and points out that “problem formulating should be viewed not only as a goal of instruction but also as a means of instruction” (Kilpatrick 1987 , p. 123); and he also emphasizes that, as part of students’ education, all of them should be given opportunities to live the experience of discovering and posing their own problems. Drawing attention to the few systematic studies on problem posing performed until then, Kilpatrick contributes defining some aspects that required studying and investigating as steps prior to a theoretical building, though he warns, “attempts to teach problem-formulating skills, of course, need not await a theory” (p. 124).

Kilpatrick refers to the “Source of problems” and points out how virtually all problems students solve have been posed by another person; however, in real life “many problems, if not most, must be created or discovered by the solver, who gives the problem an initial formulation” (p. 124). He also points out that problems are reformulated as they are being solved, and he relates this to investigation, reminding us what Davis ( 1985 ) states that, “what typically happens in a prolonged investigation is that problem formulation and problem solution go hand in hand, each eliciting the other as the investigation progresses” (p. 23). He also relates it to the experiences of software designers, who formulate an appropriate sequence of sub-problems to solve a problem. He poses that a subject to be examined by teachers and researchers “is whether, by drawing students’ attention to the reformulating process and given them practice in it, we can improve their problem solving performance” (p. 130). He also points out that problems may be a mathematical formulation as a result of exploring a situation and, in that sense, “school exercises in constructing mathematical models of a situation presented by the teacher are intended to provide students with experiences in formulating problems.” (p. 131).

Another important section of Kilpatrick’s work ( 1987 ) is Processes of Problem Formulating , in which he considers association, analogy, generalization and contradiction. He believes the use of concept maps to represent concept organization, as cognitive scientists Novak and Gowin suggest, might help to comprehend such concepts, stimulate creative thinking about them, and complement the ideas Brown and Walter ( 1983 ) give for problem posing by association. Further, in the section “Understanding and developing problem formulating abilities”, he poses several questions, which have not been completely answered yet, like “Perhaps the central issue from the point of view of cognitive science is what happens when someone formulates the problem? (…) What is the relation between problem formulating, problem solving and structured knowledge base? How rich a knowledge base is needed for problem formulating? (…) How does experience in problem formulating add to knowledge base? (…) What metacognitive processes are needed for problem formulating?”

It is interesting to realize that some of these questions are among the unanswered questions proposed and analyzed by Cai et al. ( 2015 ) in Chap. 1 of the book Mathematical Problem Posing (Singer et al. 2015 ). It is worth stressing the emphasis on the need to know the cognitive processes in problem posing, an aspect that Kilpatrick had already posed in 1987, as we just saw.

1.4.2 Researches and Didactic Experiences

Currently, there are a great number of publications related to problem posing, many of which are research and didactic experiences that gather the questions posed by Kilpatrick, which we just commented. Others came up naturally as reflections raised in the framework of problem solving, facing the natural requirement of having appropriate problems to use results and suggestions of researches on problem solving, or as a response to a thoughtful attitude not to resign to solving and asking students to solve problems that are always created by others. Why not learn and teach mathematics posing one’s own problems?

1.4.3 New Directions of Research

Singer et al. ( 2013 ) provides a broad view about problem posing that links problem posing experiences to general mathematics education; to the development of abilities, attitudes and creativity; and also to its interrelation with problem solving, and studies on when and how problem-solving sessions should take place. Likewise, it provides information about research done regarding ways to pose new problems and about the need for teachers to develop abilities to handle complex situations in problem posing contexts.

Singer et al. ( 2013 ) identify new directions in problem posing research that go from problem-posing task design to the development of problem-posing frameworks to structure and guide teachers and students’ problem posing experiences. In a chapter of this book, Leikin refers to three different types of problem posing activities, associated with school mathematics research: (a) problem posing through proving; (b) problem posing for investigation; and (c) problem posing through investigation. This classification becomes evident in the problems posed in a course for prospective secondary school mathematics teachers by using a dynamic geometry environment. Prospective teachers posed over 25 new problems, several of which are discussed in the article. The author considers that, by developing this type of problem posing activities, prospective mathematics teachers may pose different problems related to a geometric object, prepare more interesting lessons for their students, and thus gradually develop their mathematical competence and their creativity.

1.4.4 Final Comments

This overview, though incomplete, allows us to see a part of what problem posing experiences involve and the importance of this area in students mathematical learning. An important task is to continue reflecting on the questions posed by Kilpatrick ( 1987 ), as well as on the ones that come up in the different researches aforementioned. To continue progressing in research on problem posing and contribute to a greater consolidation of this research line, it will be really important that all mathematics educators pay more attention to problem posing, seek to integrate approaches and results, and promote joint and interdisciplinary works. As Singer et al. ( 2013 ) say, going back to Kilpatrick’s proposal ( 1987 ),

Problem posing is an old issue. What is new is the awareness that problem posing needs to pervade the education systems around the world, both as a means of instruction (…) and as an object of instruction (…) with important targets in real-life situations. (p. 5)

Although it can be argued that there is a difference between creativity, discovery, and invention (see Liljedahl and Allan 2014 ) for the purposes of this book these will be assumed to be interchangeable.

Abu-Elwan, R. (1999). The development of mathematical problem posing skills for prospective middle school teachers. In A. Rogerson (Ed.), Proceedings of the International Conference on Mathematical Education into the 21st century: Social Challenges, Issues and Approaches , (Vol. 2, pp. 1–8), Cairo, Egypt.

Google Scholar  

Ashcraft, M. (1989). Human memory and cognition . Glenview, Illinois: Scott, Foresman and Company.

Bailin, S. (1994). Achieving extraordinary ends: An essay on creativity . Norwood, NJ: Ablex Publishing Corporation.

Bibby, T. (2002). Creativity and logic in primary-school mathematics: A view from the classroom. For the Learning of Mathematics, 22 (3), 10–13.

Brown, S., & Walter, M. (1983). The art of problem posing . Philadelphia: Franklin Institute Press.

Bruder, R. (2000). Akzentuierte Aufgaben und heuristische Erfahrungen. In W. Herget & L. Flade (Eds.), Mathematik lehren und lernen nach TIMSS. Anregungen für die Sekundarstufen (pp. 69–78). Berlin: Volk und Wissen.

Bruder, R. (2005). Ein aufgabenbasiertes anwendungsorientiertes Konzept für einen nachhaltigen Mathematikunterricht—am Beispiel des Themas “Mittelwerte”. In G. Kaiser & H. W. Henn (Eds.), Mathematikunterricht im Spannungsfeld von Evolution und Evaluation (pp. 241–250). Hildesheim, Berlin: Franzbecker.

Bruder, R., & Collet, C. (2011). Problemlösen lernen im Mathematikunterricht . Berlin: CornelsenVerlag Scriptor.

Bruner, J. (1964). Bruner on knowing . Cambridge, MA: Harvard University Press.

Burton, L. (1999). Why is intuition so important to mathematicians but missing from mathematics education? For the Learning of Mathematics, 19 (3), 27–32.

Cai, J., Hwang, S., Jiang, C., & Silber, S. (2015). Problem posing research in mathematics: Some answered and unanswered questions. In F.M. Singer, N. Ellerton, & J. Cai (Eds.), Mathematical problem posing: From research to effective practice (pp.3–34). Springer.

Churchill, D., Fox, B., & King, M. (2016). Framework for designing mobile learning environments. In D. Churchill, J. Lu, T. K. F. Chiu, & B. Fox (Eds.), Mobile learning design (pp. 20–36)., lecture notes in educational technology NY: Springer.

Chapter   Google Scholar  

Collet, C. (2009). Problemlösekompetenzen in Verbindung mit Selbstregulation fördern. Wirkungsanalysen von Lehrerfortbildungen. In G. Krummheuer, & A. Heinze (Eds.), Empirische Studien zur Didaktik der Mathematik , Band 2, Münster: Waxmann.

Collet, C., & Bruder, R. (2008). Longterm-study of an intervention in the learning of problem-solving in connection with self-regulation. In O. Figueras, J. L. Cortina, S. Alatorre, T. Rojano, & A. Sepúlveda (Eds.), Proceedings of the Joint Meeting of PME 32 and PME-NA XXX, (Vol. 2, pp. 353–360).

Csíkszentmihályi, M. (1996). Creativity: Flow and the psychology of discovery and invention . New York: Harper Perennial.

Davis, P. J. (1985). What do I know? A study of mathematical self-awareness. College Mathematics Journal, 16 (1), 22–41.

Article   Google Scholar  

Dewey, J. (1933). How we think . Boston, MA: D.C. Heath and Company.

Dewey, J. (1938). Logic: The theory of inquiry . New York, NY: Henry Holt and Company.

Einstein, A., & Infeld, L. (1938). The evolution of physics . New York: Simon and Schuster.

Ellerton, N. (2013). Engaging pre-service middle-school teacher-education students in mathematical problem posing: Development of an active learning framework. Educational Studies in Math, 83 (1), 87–101.

Engel, A. (1998). Problem-solving strategies . New York, Berlin und Heidelberg: Springer.

English, L. (1997). Children’s reasoning processes in classifying and solving comparison word problems. In L. D. English (Ed.), Mathematical reasoning: Analogies, metaphors, and images (pp. 191–220). Mahwah, NJ: Lawrence Erlbaum Associates Inc.

English, L. (1998). Reasoning by analogy in solving comparison problems. Mathematical Cognition, 4 (2), 125–146.

English, L. D. & Gainsburg, J. (2016). Problem solving in a 21st- Century mathematics education. In L. D. English & D. Kirshner (Eds.), Handbook of international research in mathematics education (pp. 313–335). NY: Routledge.

Ghiselin, B. (1952). The creative process: Reflections on invention in the arts and sciences . Berkeley, CA: University of California Press.

Hadamard, J. (1945). The psychology of invention in the mathematical field . New York, NY: Dover Publications.

Halmos, P. (1980). The heart of mathematics. American Mathematical Monthly, 87 , 519–524.

Halmos, P. R. (1994). What is teaching? The American Mathematical Monthly, 101 (9), 848–854.

Hoyles, C., & Lagrange, J.-B. (Eds.). (2010). Mathematics education and technology–Rethinking the terrain. The 17th ICMI Study . NY: Springer.

Kilpatrick, J. (1985). A retrospective account of the past 25 years of research on teaching mathematical problem solving. In E. Silver (Ed.), Teaching and learning mathematical problem solving: Multiple research perspectives (pp. 1–15). Hillsdale, New Jersey: Lawrence Erlbaum.

Kilpatrick, J. (1987). Problem formulating: Where do good problem come from? In A. H. Schoenfeld (Ed.), Cognitive science and mathematics education (pp. 123–147). Hillsdale, NJ: Erlbaum.

Kline, M. (1972). Mathematical thought from ancient to modern times . NY: Oxford University Press.

Kneller, G. (1965). The art and science of creativity . New York, NY: Holt, Reinhart, and Winstone Inc.

Koestler, A. (1964). The act of creation . New York, NY: The Macmillan Company.

König, H. (1984). Heuristik beim Lösen problemhafter Aufgaben aus dem außerunterrichtlichen Bereich . Technische Hochschule Chemnitz, Sektion Mathematik.

Kretschmer, I. F. (1983). Problemlösendes Denken im Unterricht. Lehrmethoden und Lernerfolge . Dissertation. Frankfurt a. M.: Peter Lang.

Krulik, S. A., & Reys, R. E. (Eds.). (1980). Problem solving in school mathematics. Yearbook of the national council of teachers of mathematics . Reston VA: NCTM.

Krutestkii, V. A. (1976). The psychology of mathematical abilities in school children . University of Chicago Press.

Lesh, R., & Zawojewski, J. S. (2007). Problem solving and modeling. In F. K. Lester, Jr. (Ed.), The second handbook of research on mathematics teaching and learning (pp. 763–804). National Council of Teachers of Mathematics, Charlotte, NC: Information Age Publishing.  

Lester, F., & Kehle, P. E. (2003). From problem solving to modeling: The evolution of thinking about research on complex mathematical activity. In R. Lesh & H. Doerr (Eds.), Beyond constructivism: Models and modeling perspectives on mathematics problem solving, learning and teaching (pp. 501–518). Mahwah, NJ: Lawrence Erlbaum.

Lester, F. K., Garofalo, J., & Kroll, D. (1989). The role of metacognition in mathematical problem solving: A study of two grade seven classes. Final report to the National Science Foundation, NSF Project No. MDR 85-50346. Bloomington: Indiana University, Mathematics Education Development Center.

Leung, A., & Bolite-Frant, J. (2015). Designing mathematical tasks: The role of tools. In A. Watson & M. Ohtani (Eds.), Task design in mathematics education (pp. 191–225). New York: Springer.

Liljedahl, P. (2008). The AHA! experience: Mathematical contexts, pedagogical implications . Saarbrücken, Germany: VDM Verlag.

Liljedahl, P., & Allan, D. (2014). Mathematical discovery. In E. Carayannis (Ed.), Encyclopedia of creativity, invention, innovation, and entrepreneurship . New York, NY: Springer.

Liljedahl, P., & Sriraman, B. (2006). Musings on mathematical creativity. For the Learning of Mathematics, 26 (1), 20–23.

Lompscher, J. (1975). Theoretische und experimentelle Untersuchungen zur Entwicklung geistiger Fähigkeiten . Berlin: Volk und Wissen. 2. Auflage.

Lompscher, J. (1985). Die Lerntätigkeit als dominierende Tätigkeit des jüngeren Schulkindes. In L. Irrlitz, W. Jantos, E. Köster, H. Kühn, J. Lompscher, G. Matthes, & G. Witzlack (Eds.), Persönlichkeitsentwicklung in der Lerntätigkeit . Berlin: Volk und Wissen.

Mason, J., & Johnston-Wilder, S. (2006). Designing and using mathematical tasks . St. Albans: Tarquin Publications.

Mason, J., Burton, L., & Stacey, K. (1982). Thinking mathematically . Harlow: Pearson Prentice Hall.

Mayer, R. (1982). The psychology of mathematical problem solving. In F. K. Lester & J. Garofalo (Eds.), Mathematical problem solving: Issues in research (pp. 1–13). Philadelphia, PA: Franklin Institute Press.

Mevarech, Z. R., & Kramarski, B. (1997). IMPROVE: A multidimensional method for teaching mathematics in heterogeneous classrooms. American Educational Research Journal, 34 (2), 365–394.

Mevarech, Z. R., & Kramarski, B. (2003). The effects of metacognitive training versus worked-out examples on students’ mathematical reasoning. British Journal of Educational Psychology, 73 , 449–471.

Moreno-Armella, L., & Santos-Trigo, M. (2016). The use of digital technologies in mathematical practices: Reconciling traditional and emerging approaches. In L. English & D. Kirshner (Eds.), Handbook of international research in mathematics education (3rd ed., pp. 595–616). New York: Taylor and Francis.

National Council of Teachers of Mathematics (NCTM). (1980). An agenda for action . Reston, VA: NCTM.

National Council of Teachers of Mathematics (NCTM). (2000). Principles and standards for school mathematics . Reston, VA: National Council of Teachers of Mathematics.

Newman, J. (2000). The world of mathematics (Vol. 4). New York, NY: Dover Publishing.

Novick, L. (1988). Analogical transfer, problem similarity, and expertise. Journal of Educational Psychology: Learning, Memory, and Cognition, 14 (3), 510–520.

Novick, L. (1990). Representational transfer in problem solving. Psychological Science, 1 (2), 128–132.

Novick, L. (1995). Some determinants of successful analogical transfer in the solution of algebra word problems. Thinking & Reasoning, 1 (1), 5–30.

Novick, L., & Holyoak, K. (1991). Mathematical problem solving by analogy. Journal of Experimental Psychology, 17 (3), 398–415.

Pehkonen, E. K. (1991). Developments in the understanding of problem solving. ZDM—The International Journal on Mathematics Education, 23 (2), 46–50.

Pehkonen, E. (1997). The state-of-art in mathematical creativity. Analysis, 97 (3), 63–67.

Perels, F., Schmitz, B., & Bruder, R. (2005). Lernstrategien zur Förderung von mathematischer Problemlösekompetenz. In C. Artelt & B. Moschner (Eds.), Lernstrategien und Metakognition. Implikationen für Forschung und Praxis (pp. 153–174). Waxmann education.

Perkins, D. (2000). Archimedes’ bathtub: The art of breakthrough thinking . New York, NY: W.W. Norton and Company.

Poincaré, H. (1952). Science and method . New York, NY: Dover Publications Inc.

Pólya, G. (1945). How to solve It . Princeton NJ: Princeton University.

Pólya, G. (1949). How to solve It . Princeton NJ: Princeton University.

Pólya, G. (1954). Mathematics and plausible reasoning . Princeton: Princeton University Press.

Pólya, G. (1964). Die Heuristik. Versuch einer vernünftigen Zielsetzung. Der Mathematikunterricht , X (1), 5–15.

Pólya, G. (1965). Mathematical discovery: On understanding, learning and teaching problem solving (Vol. 2). New York, NY: Wiley.

Resnick, L., & Glaser, R. (1976). Problem solving and intelligence. In L. B. Resnick (Ed.), The nature of intelligence (pp. 230–295). Hillsdale, NJ: Lawrence Erlbaum Associates.

Rusbult, C. (2000). An introduction to design . http://www.asa3.org/ASA/education/think/intro.htm#process . Accessed January 10, 2016.

Santos-Trigo, M. (2007). Mathematical problem solving: An evolving research and practice domain. ZDM—The International Journal on Mathematics Education , 39 (5, 6): 523–536.

Santos-Trigo, M. (2014). Problem solving in mathematics education. In S. Lerman (Ed.), Encyclopedia of mathematics education (pp. 496–501). New York: Springer.

Schmidt, E., & Cohen, J. (2013). The new digital age. Reshaping the future of people nations and business . NY: Alfred A. Knopf.

Schoenfeld, A. H. (1979). Explicit heuristic training as a variable in problem-solving performance. Journal for Research in Mathematics Education, 10 , 173–187.

Schoenfeld, A. H. (1982). Some thoughts on problem-solving research and mathematics education. In F. K. Lester & J. Garofalo (Eds.), Mathematical problem solving: Issues in research (pp. 27–37). Philadelphia: Franklin Institute Press.

Schoenfeld, A. H. (1985). Mathematical problem solving . Orlando, Florida: Academic Press Inc.

Schoenfeld, A. H. (1987). What’s all the fuss about metacognition? In A. H. Schoenfeld (Ed.), Cognitive science and mathematics education (pp. 189–215). Hillsdale, NJ: Lawrence Erlbaum Associates.

Schoenfeld, A. H. (1992). Learning to think mathematically: Problem solving, metacognition, and sense making in mathematics. In D. A. Grouws (Ed.), Handbook of research on mathematics teaching and learning (pp. 334–370). New York, NY: Simon and Schuster.

Schön, D. (1987). Educating the reflective practitioner . San Fransisco, CA: Jossey-Bass Publishers.

Sewerin, H. (1979): Mathematische Schülerwettbewerbe: Beschreibungen, Analysen, Aufgaben, Trainingsmethoden mit Ergebnissen . Umfrage zum Bundeswettbewerb Mathematik. München: Manz.

Silver, E. (1982). Knowledge organization and mathematical problem solving. In F. K. Lester & J. Garofalo (Eds.), Mathematical problem solving: Issues in research (pp. 15–25). Philadelphia: Franklin Institute Press.

Singer, F., Ellerton, N., & Cai, J. (2013). Problem posing research in mathematics education: New questions and directions. Educational Studies in Mathematics, 83 (1), 9–26.

Singer, F. M., Ellerton, N. F., & Cai, J. (Eds.). (2015). Mathematical problem posing. From research to practice . NY: Springer.

Törner, G., Schoenfeld, A. H., & Reiss, K. M. (2007). Problem solving around the world: Summing up the state of the art. ZDM—The International Journal on Mathematics Education, 39 (1), 5–6.

Verschaffel, L., de Corte, E., Lasure, S., van Vaerenbergh, G., Bogaerts, H., & Ratinckx, E. (1999). Learning to solve mathematical application problems: A design experiment with fifth graders. Mathematical Thinking and Learning, 1 (3), 195–229.

Wallas, G. (1926). The art of thought . New York: Harcourt Brace.

Watson, A., & Ohtani, M. (2015). Themes and issues in mathematics education concerning task design: Editorial introduction. In A. Watson & M. Ohtani (Eds.), Task design in mathematics education, an ICMI Study 22 (pp. 3–15). NY: Springer.

Zimmermann, B. (1983). Problemlösen als eine Leitidee für den Mathematikunterricht. Ein Bericht über neuere amerikanische Beiträge. Der Mathematikunterricht, 3 (1), 5–45.

Further Reading

Boaler, J. (1997). Experiencing school mathematics: Teaching styles, sex, and setting . Buckingham, PA: Open University Press.

Borwein, P., Liljedahl, P., & Zhai, H. (2014). Mathematicians on creativity. Mathematical Association of America.

Burton, L. (1984). Thinking things through . London, UK: Simon & Schuster Education.

Feynman, R. (1999). The pleasure of finding things out . Cambridge, MA: Perseus Publishing.

Gardner, M. (1978). Aha! insight . New York, NY: W. H. Freeman and Company.

Gardner, M. (1982). Aha! gotcha: Paradoxes to puzzle and delight . New York, NY: W. H. Freeman and Company.

Gardner, H. (1993). Creating minds: An anatomy of creativity seen through the lives of Freud, Einstein, Picasso, Stravinsky, Eliot, Graham, and Ghandi . New York, NY: Basic Books.

Glas, E. (2002). Klein’s model of mathematical creativity. Science & Education, 11 (1), 95–104.

Hersh, D. (1997). What is mathematics, really? . New York, NY: Oxford University Press.

Root-Bernstein, R., & Root-Bernstein, M. (1999). Sparks of genius: The thirteen thinking tools of the world’s most creative people . Boston, MA: Houghton Mifflin Company.

Zeitz, P. (2006). The art and craft of problem solving . New York, NY: Willey.

Download references

Author information

Authors and affiliations.

Faculty of Education, Simon Fraser University, Burnaby, BC, Canada

Peter Liljedahl

Mathematics Education Department, Cinvestav-IPN, Centre for Research and Advanced Studies, Mexico City, Mexico

Manuel Santos-Trigo

Pontificia Universidad Católica del Perú, Lima, Peru

Uldarico Malaspina

Technical University Darmstadt, Darmstadt, Germany

Regina Bruder

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Peter Liljedahl .

Rights and permissions

Open Access This chapter is distributed under the terms of the Creative Commons Attribution 4.0 International License ( http://creativecommons.org/licenses/by/4.0/ ), which permits use, duplication, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, a link is provided to the Creative Commons license and any changes made are indicated.

The images or other third party material in this chapter are included in the work’s Creative Commons license, unless indicated otherwise in the credit line; if such material is not included in the work’s Creative Commons license and the respective action is not permitted by statutory regulation, users will need to obtain permission from the license holder to duplicate, adapt or reproduce the material.

Reprints and permissions

Copyright information

© 2016 The Author(s)

About this chapter

Liljedahl, P., Santos-Trigo, M., Malaspina, U., Bruder, R. (2016). Problem Solving in Mathematics Education. In: Problem Solving in Mathematics Education. ICME-13 Topical Surveys. Springer, Cham. https://doi.org/10.1007/978-3-319-40730-2_1

Download citation

DOI : https://doi.org/10.1007/978-3-319-40730-2_1

Published : 28 June 2016

Publisher Name : Springer, Cham

Print ISBN : 978-3-319-40729-6

Online ISBN : 978-3-319-40730-2

eBook Packages : Education Education (R0)

Share this chapter

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Publish with us

Policies and ethics

• Find a journal
• Track your research

Problem-Solving Model for Improving Student Achievement

Principal Leadership Magazine, Vol. 5, Number 4, December 2004

Counseling 101 column, a problem-solving model for improving student achievement.

Problem solving is an alternative to assessments and diagnostic categories as a means to identify students who need special services.

By Andrea Canter

Andrea Canter recently retired from Minneapolis Public Schools where she served as lead psychologist and helped implement a district-wide problem solving model. She currently is a consultant to the National Association of School Psychologists (NASP) and editor of its newspaper, Communiquè . “Counseling 101” is provided by NASP ( www.nasponline.org ).

The implementation of the No Child Left Behind Act (NCLB) has prompted renewed efforts to hold schools and students accountable for meeting high academic standards. At the same time, Congress has been debating the reauthorization of the Individuals With Disabilities Education Act (IDEA), which has heightened concerns that NCLB will indeed “leave behind” many students who have disabilities or other barriers to learning. This convergence of efforts to address the needs of at-risk students while simultaneously implementing high academic standards has focused attention on a number of proposals and pilot projects that are generally referred to as problem-solving models. A more specific approach to addressing academic difficulties, response to intervention (RTI), has often been proposed as a component of problem solving.

What Is Problem Solving?

A problem-solving model is a systematic approach that reviews student strengths and weaknesses, identifies evidence-based instructional interventions, frequently collects data to monitor student progress, and evaluates the effectiveness of interventions implemented with the student. Problem solving is a model that first solves student difficulties within general education classrooms. If problem-solving interventions are not successful in general education classrooms, the cycle of selecting intervention strategies and collecting data is repeated with the help of a building-level or grade-level intervention assistance or problem-solving team. Rather than relying primarily on test scores (e.g., from an IQ or math test), the student’s response to general education interventions becomes the primary determinant of his or her need for special education evaluation and services (Marston, 2002; Reschly & Tilly, 1999).

Why Is a New Approach Needed?

Although much of the early implementation of problem-solving models has involved elementary schools, problem solving also has significant potential to improve outcomes for secondary school students. Therefore, it is important for secondary school administrators to understand the basic concepts of problem solving and consider how components of this model could mesh with the needs of their schools and students. Because Congress will likely include RTI options in its reauthorization of special education law and regulations regarding learning disabilities, it is also important for school personnel to be familiar with the pros and cons of the problem-solving model.

Student outcomes. Regardless of state or federal mandates, schools need to change the way they address academic problems. More than 25 years of special education legislation and funding have failed to demonstrate either the cost effectiveness or the validity of aligning instruction to diagnostic classifications (Fletcher et al., 2002; Reschly & Tilly, 1999; Ysseldyke & Marston, 1999). Placement in special education programs has not guaranteed significant academic gains or better life outcomes for students with disabilities. Time-consuming assessments that are intended to differentiate students with disabilities from those with low achievement have not resulted in better instruction for struggling students.

READ MORE: Best Appetite Suppressant: 5 Hunger Control Supplements Complete Guide

Dilemma of learning disabilities. The learning disabilities (LD) classification has proven especially problematic. Researchers and policymakers representing diverse philosophies regarding disability are generally in agreement that the current process needs revision (Fletcher et al., 2002). Traditionally, if a student with LD is to be served in special education, an evaluation using individual intelligence tests and norm-referenced achievement tests is required to document an ability/achievement discrepancy. This model has been criticized for the following reasons:

• A reliance on intelligence tests in general and with students from ethnic and linguistic minority populations in particular
• A focus on within-child deficiencies that often ignore quality of instruction and environmental factors
• The limited applicability of norm-referenced information to actual classroom teaching
• The burgeoning identification of students as disabled
• The resulting allocation of personnel to responsibilities (classification) that are significantly removed from direct service to students (Ysseldyke & Marston, 1999).

Wait to fail. A major flaw in the current system of identifying student needs is what has been dubbed the wait to fail approach in which students are not considered eligible for support until their skills are widely discrepant from expectations. This runs counter to years of research demonstrating the importance of early intervention (President’s Commission on Excellence in Special Education, 2002). Thus, a number of students fail to receive any remedial services until they reach the intermediate grades or middle school, by which time they often exhibit motivational problems and behavioral problems as well as academic deficits.

For other students, although problems are noted when they are in the early grades, referral is delayed until they fail graduation or high school standards tests, increasing the probability that they will drop out. Their school records often indicate that teachers and parents expressed concern for these students in the early grades, which sometimes resulted in referral for assessments, but did not result in qualification for special education or other services.

Call for evidence-based programs. One of the major tenets of NCLB is the implementation of scientifically based interventions to improve student performance. The traditional models used by most schools today lack such scientifically based evidence. There are, however, many programs and instructional strategies that have demonstrated positive outcomes for diverse student populations and needs (National Reading Panel, 2000). It is clear that schools need systemic approaches to identify and resolve student achievement problems and access proven instructional strategies.

READ MORE: Red Boost Reviews – Ingredients, Benefits, Pros and Cons

How It Works

Although problem-solving steps can be described in several stages, the steps essentially reflect the scientific method of defining and describing a problem (e.g., Ted does not comprehend grade-level reading material); generating potential solutions (e.g., Ted might respond well to direct instruction in comprehension strategies); and implementing, monitoring, and evaluating the effectiveness of the selected intervention.

Problem-solving models have been implemented in many versions at local and state levels to reflect the unique features and needs of individual schools. However, all problem-solving models share the following components:

• Screening and assessment that is focused on student skills rather than classification
• Measuring response to instruction rather than relying on norm-referenced comparisons
• Using evidence-based strategies within general education classrooms
• Developing a collaborative partnership among general and special educators for consultation and team decision making.

Three-tiered model. One common problem-solving model is the three-tiered model. In this model, tier one includes problem-solving strategies directed by the teacher within the general education classrooms. Tier two includes problem-solving efforts at a team level in which grade-level staff members or a team of various school personnel collaborate to develop an intervention plan that is still within the general education curriculum. Tier three involves referral to a special education team for additional problem solving and, potentially, a special education assessment (Office of Special Education Programs, 2002).

Response to intervention. A growing body of research and public policy discussion has focused on problem-solving models that include evaluating a student’s RTI as an alternative to the IQ-achievement discrepancy approach to identifying learning disabilities (Gresham, 2002). RTI refers to specific procedures that align with the steps of problem solving:

• Implementing evidence-based interventions
• Frequently measuring a student’s progress to determine whether the intervention is effective
• Evaluating the quality of the instructional strategy
• Evaluating the fidelity of its implementation. (For example, did the intervention work? Was it scientifically based? Was it implemented as planned?)

Although there is considerable debate about replacing traditional eligibility procedures with RTI approaches (Vaughn & Fuchs, 2003), there is promising evidence that RTI can systematically improve the effectiveness of instruction for struggling students and provide school teams with evidence-based procedures that measures a student’s progress and his or her need for special services.

New roles for personnel. An important component of problem-solving models is the allocation (or realignment) of personnel who are knowledgeable about the applications of research to classroom practice. Whereas traditional models often limit the availability of certain personnel-for example, school psychologists-to prevention and early intervention activities (e.g., classroom consultation), problem-solving models generally enhance the roles of these service providers through a systemic process that is built upon general education consultation. Problem solving shifts the emphasis from identifying disabilities to implementing earlier interventions that have the potential to reduce referral and placement in special education.

Outcomes of Problem Solving and RTI

Anticipated benefits of problem-solving models, particularly those using RTI procedures, include emphasizing scientifically proven instructional methods, the early identification and remediation of achievement difficulties, more functional and frequent measurement of student progress, a reduction in inappropriate and disproportionate special education placements of students from diverse cultural and linguistic backgrounds, and a reallocation of instructional and behavior support personnel to better meet the needs of all students (Gresham, 2002; Ysseldyke & Marston, 1999). By using problem solving, some districts have reduced overall special education placements, increased individual and group performance on standards tests, and increased collaboration among special and general educators.

READ MORE: Exipure Review : Weight loss Pills Dosage, Works, Uses

The enhanced collaboration between general education teachers and support personnel is particularly important at the secondary level because staff members often have limited interaction with school personnel who are outside of their specialty area. Problem solving provides a vehicle to facilitate communication across disciplines to resolve student difficulties in the classroom. Secondary schools, however, face additional barriers to collaboration because each student may have five or more teachers. Special education is often even more separated from general education in secondary school settings. Secondary school teachers also have a greater tendency to see themselves as content specialists and may be less invested in addressing general learning problems, particularly when they teach five or six class periods (and 150 or more students) each day. The sheer size of the student body and the staff can create both funding and logistical difficulties for scheduling training and team meetings.

Is Problem Solving Worth the Effort?

Data from district-wide and state-level projects in rural, suburban, and urban communities around the country support the need to thoughtfully implement problem-solving models at all grade levels. There are several federally funded demonstration centers that systematically collect information about these approaches. Although national demonstration models may be a few years away, it seems likely that state and federal regulations under IDEA will include problem solving and RTI as accepted experimental options. Problem solving continues to offer much promise to secondary school administrators who are seeking to improve student performance through ongoing assessment and evidence-based instruction. PL

• Fletcher, J., Lyon, R., Barnes, M., Stuebing, K., Francis, D., Olson, R., Shaywitz, S., & Shaywitz, B. (2002). Classification of learning disabilities: An evidence-based evaluation. In R. Bradley, L. Donaldson, & D. Hallahan (Eds.), Identification of learning disabilities (pp. 185-250). Mahwah, NJ: Erlbaum.
• Gresham, F. (2002). Responsiveness to intervention: An alternative approach to the identification of learning disabilities. In R. Bradley, L. Donaldson, & D. Hallahan (Eds.), Identification of learning disabilities (pp. 467-519). Mahwah, NJ: Erlbaum.
• Marston, D. (2002). A functional and intervention-based assessment approach to establishing discrepancy for students with learning disabilities. In R. Bradley, L. Donaldson, & D. Hallahan (Eds.), Identification of learning disabilities (pp. 437-447). Mahwah, NJ: Erlbaum.
• National Reading Panel. (2000). Teaching children to read: An evidence-based assessment of the scientific literature on reading and its implications for reading instruction-Reports of the subgroups. Washington, DC: Author.
• Office of Special Education Programs, U.S. Department of Education. (2002). Specific learning disabilities: Finding common ground (Report of the Learning Disabilities Round Table). Washington, DC: Author.
• President’s Commission on Excellence in Special Education. (2002). A new era: Revitalizing special education for children and their families. Washington, DC: U.S. Department of Education.
• Reschly, D., & Tilly, W. D. III (1999). Reform trends and system design alternatives. In D. Reschly, W. D. Tilly III, & J. Grimes (Eds.), Special education in transition: Functional assessment and noncategorical programming (pp. 19-48). Longmont, CO: Sopris West.
• Vaughn, S., & Fuchs, L. (Eds.) (2003). Special issue: Response to intervention. Learning Disabilities Research & Practice, 18(3).
• Ysseldyke, J., & Marston, D. (1999). Origins of categorical special education services in schools and a rationale for changing them. In D. Reschly, W. D. Tilly III, & J. Grimes (Eds.), Special education in transition: Functional assessment and noncategorical programming (pp. 1-18). Longmont, CO: Sopris West.

Case Study: Optimizing Success Through Problem Solving

By Marcia Staum and Lourdes Ocampo

Milwaukee Public Schools, the largest school district in Wisconsin, is educating students with Optimizing Success Through Problem Solving (OSPS), a problem-solving initiative that uses a four-step, data-based, decision-making process to enhance school reform efforts. OSPS is patterned after best practices in the prevention literature and focuses on prevention, early intervention, and focused intervention levels.  Problem-solving facilitators provide staff members with the training, modeling, support, and tools they need to effectively use data to drive their instructional decision-making. The OSPS initiative began in the fall of 2000 with seven participating schools. Initially, elementary and middle level schools began to use OSPS, with an emphasis on problem solving for individual student issues. As the initiative matured, increased focus was placed on prevention and early intervention support in the schools. Today, 78 schools participate in the OSPS initiative and are serviced by a team of 18 problem-solving facilitators. 

OSPS in Action: Juneau High School

The administration of Juneau High School, a Milwaukee public charter school with 900 students, invited OSPS to become involved at Juneau for the 2003-2004 school year. Because at the time OSPS had limited involvement with high schools, two problem-solving facilitators were assigned to Juneau for one half-day each week. The problem-solving facilitators immediately joined the Juneau’s learning team, which is a small group of staff members and administrators who make educational decisions aimed at increasing student achievement.

When the problem-solving facilitators became involved with Juneau, the learning team was working to improve student participation on the Wisconsin Knowledge and Concepts Exam (WKCE). The previous year, Juneau’s 10th-grade participation on the exam had been very low. The learning team used OSPS’s four-step problem-solving process to develop and implement a plan that resulted in a 99% student participation rate on the WKCE. After this initial success, the problem-solving model was also used at Juneau to increase parent participation in parent-teacher conferences. According to Myron Cain, Juneau’s principal, “Problem solving has helped the learning team at Juneau go from dialogue into action. In addition, problem solving has supported the school within the Collaborative Support Team process and with teambuilding, which resulted in a better school climate.”

By starting at the prevention level, Juneau found that there was increased commitment from staff members. OSPS is now in the initial stages of working with Juneau to explore alternatives to suspension.  The goal is to create a working plan that will lead to creative ways of decreasing the number of suspensions at Juneau.

Marcia Staum is a school psychologist, and Lourdes Ocampo is a school social worker for Optimizing Success Through Problem Solving.

What Is Response to Intervention?

Many researchers have recommended that a student’s response to intervention or response to instruction (RTI) should be considered as an alternative or replacement to the traditional IQ-achievement discrepancy approach to identifying learning disabilities (Gresham, 2002; President’s Commission on Excellence in Special Education, 2002). Although there is considerable debate about replacing traditional eligibility procedures with RTI approaches (Vaughn & Fuchs, 2003), there is promising evidence that RTI can systematically improve the effectiveness of instruction for struggling students and provide school teams with evidence-based procedures to measure student progress and need for special services. In fact, Congress has proposed the use of research-based RTI methods (as part of a comprehensive evaluation process to reauthorize IDEA) as an allowable alternative to the use of an IQ-achievement discrepancy procedure in identifying learning disabilities.

RTI refers to specific procedures that align with the steps of problem solving. These steps include the implementation of evidence-based instructional strategies in the general education classroom and the frequent measurement of a student’s progress to determine if the intervention is effective. In settings where RTI is also a criteria for identification of disability, a student’s progress in response to intervention is an important determinant of the need and eligibility for special education services.

It is important for administrators to recognize that RTI can be implemented in various ways depending on a school’s overall service delivery model and state and federal mandates. An RTI approach benefits from the involvement of specially trained personnel, such as school psychologists and curriculum specialists, who have expertise in instructional consultation and evaluation.

• National Center on Student Progress Monitoring, www.studentprogress.org
• National Research Center on Learning Disabilities, www.nrcld.org

This article was adapted from a handout published in Helping Children at Home and School II: Handouts for Families and Educators (NASP, 2004). “Counseling 101” articles and related HCHS II handouts can be downloaded from www.naspcenter.org/principals .

You May Also Like

Collaborating with physicians: a guide for school leaders, psychological evaluations: what every principal should know.

the Kick-ass Multipurpose WordPress Theme

• Author Rights
• Diversity, Equity & Inclusion

• JOLE 2023 Special Issue
• Editorial Staff
• 20th Anniversary Issue
• The Development of Problem-Solving Skills for Aspiring Educational Leaders

Jeremy D. Visone 10.12806/V17/I4/R3

Introduction

Solving problems is a quintessential aspect of the role of an educational leader. In particular, building leaders, such as principals, assistant principals, and deans of students, are frequently beset by situations that are complex, unique, and open-ended. There are often many possible pathways to resolve the situations, and an astute educational leader needs to consider many factors and constituencies before determining a plan of action. The realm of problem solving might include student misconduct, personnel matters, parental complaints, school culture, instructional leadership, as well as many other aspects of educational administration. Much consideration has been given to the development of problem-solving skills for educational leaders. This study was designed to answer the following research question: “How do aspiring educational leaders’ problem solving skills, as well as perceptions of their problem-solving skills, develop during a year-long graduate course sequence focused on school-level leadership that includes the presentation of real-world scenarios?” This mixed-methods study extends research about the development of problem-solving skills conducted with acting administrators (Leithwood & Steinbach, 1992, 1995).

The Nature of Problems

Before examining how educational leaders can process and solve problems effectively, it is worth considering the nature of problems. Allison (1996) posited simply that problems are situations that require thought and/or actions. Further, there are different types of problems presented to educational leaders. First, there are  well-structured problems , which can be defined as those with clear goals and relatively prescribed resolution pathways, including an easy way of determining whether goals were met (Allison, 1996).

Conversely,  ill-structured problems  are those with more open-ended profiles, whereby the goals, resolution pathways, or evidence of success are not necessarily clear. These types of problems could also be considered  unstructured  (Leithwood & Steinbach, 1995) or  open-design  (Allison, 1996). Many of the problems presented to educational leaders are unstructured problems. For example, a principal must decide how to discipline children who misbehave, taking into consideration their disciplinary history, rules and protocols of the school, and other contextual factors; determine how best to raise student achievement (Duke, 2014); and resolve personnel disputes among staff members. None of these problems point to singular solutions that can be identified as “right” or “wrong.” Surely there are responses that are less desirable than others (i.e. suspension or recommendation for expulsion for minor infractions), but, with justification and context, many possible solutions exist.

Problem-Solving Perspectives and Models

Various authors have shared perspectives about effective problem solving. Marzano, Waters, and McNulty (2005) outlined the “21 Responsibilities of the School Leader.” These responsibilities are highly correlated with student achievement based upon the authors’ meta- analysis of 69 studies about leadership’s effect on student achievement. The most highly correlated of the responsibilities was  situational awareness , which refers to understanding the school deeply enough to anticipate what might go wrong from day-to-day, navigate the individuals and groups within the school, and recognize issues that might surface at a later time (Marzano et al., 2005). Though the authors discuss the utility of situational awareness for long- term, large-scale decision making, in order for an educational leader to effectively solve the daily problems that come her way, she must again have a sense of situational awareness, lest she make seemingly smaller-scale decisions that will lead to large-scale problems later.

Other authors have focused on problems that can be considered more aligned with the daily work of educational leaders. Considering the problem-type classification dichotomies of Allison (1996) and Leithwood and Steinbach (1995), problems that educational leaders face on a daily basis can be identified as either well-structured or unstructured. Various authors have developed problem-solving models focused on unstructured problems (Bolman & Deal, 2008; Leithwood & Steinbach, 1995; Simon, 1993), and these models will be explored next.

Simon (1993) outlined three phases of the decision-making process. The first is to find problems that need attention. Though many problems of educational leaders are presented directly to them via, for example, an adult referring a child for discipline, a parent registering a complaint about a staff member, or a staff member describing a grievance with a colleague, there is a corollary skill of identifying what problems—of the many that come across one’s desk— require immediate attention, or ultimately, any attention, at all. Second, Simon identified “designing possible courses of action” (p. 395). Finally, educational leaders must evaluate the quality of their decisions. From this point of having selected a viable and positively evaluated potential solution pathway, implementation takes place.

Bolman and Deal (2008) outlined a model of reframing problems using four different frames, through which problems of practice can be viewed. These frames provide leaders with a more complete set of perspectives than they would likely utilize on their own. The  structural frame  represents the procedural and systems-oriented aspects of an organization. Within this frame, a leader might ask whether there is a supervisory relationship involved in a problem, if a protocol exists to solve such a problem, or what efficiencies or logical processes can help steer a leader toward a resolution that meets organizational goals. The  human resource frame  refers to the needs of individuals within the organization. A leader might try to solve a problem of practice with the needs of constituents in mind, considering the development of employees and the balance between their satisfaction and intellectual stimulation and the organization’s needs. The  political frame  includes the often competing interests among individuals and groups within the organization, whereby alliances and negotiations are needed to navigate the potential minefield of many groups’ overlapping aims. From the political frame, a leader could consider what the interpersonal costs will be for the leader and organization among different constituent groups, based upon which alternatives are selected. Last, the  symbolic frame  includes elements of meaning within an organization, such as traditions, unspoken rules, and myths. A leader may need to consider this frame when proposing a solution that might interfere with a long-standing organizational tradition.

Bolman and Deal (2008) identified the political and symbolic frames as weaknesses in most leaders’ consideration of problems of practice, and the weakness in recognizing political aspects of decision making for educational leaders was corroborated by Johnson and Kruse (2009). An implication for leadership preparation is to instruct students in the considerations of these frames and promote their utility when examining problems.

Authors have noted that experts use different processes than novice problem solvers (Simon, 1993; VanLehn, 1991). An application of this would be Simon’s (1993) assertion that experts can rely on their extensive experience to remember solutions to many problems, without having to rely on an extensive analytical process. Further, they may not even consider a “problem” identified by a novice a problem, at all. With respect to educational leaders, Leithwood and Steinbach (1992, 1995) outlined a set of competencies possessed by expert principals, when compared to their typical counterparts. Expert principals were better at identifying the nature of problems; possessing a sense of priority, difficulty, how to proceed, and connectedness to prior situations; setting meaningful goals for problem solving, such as seeking goals that are student-centered and knowledge-focused; using guiding principles and long-term purposes when determining the best courses of action; seeing fewer obstacles and constraints when presented with problems; outlining detailed plans for action that include gathering extensive information to inform decisions along the plan’s pathway; and responding with confidence and calm to problem solving. Next, I will examine how problem-solving skills are developed.

Preparation for Educational Leadership Problem Solving

How can the preparation of leaders move candidates toward the competencies of expert principals? After all, leading a school has been shown to be a remarkably complex enterprise (Hallinger & McCary, 1990; Leithwood & Steinbach, 1992), especially if the school is one where student achievement is below expectations (Duke, 2014), and the framing of problems by educational leaders has been espoused as a critically important enterprise (Bolman & Deal, 2008; Dimmock, 1996; Johnson & Kruse, 2009; Leithwood & Steinbach, 1992, 1995; Myran & Sutherland, 2016). In other disciplines, such as business management, simulations and case studies are used to foster problem-solving skills for aspiring leaders (Rochford & Borchert, 2011; Salas, Wildman, & Piccolo, 2009), and attention to problem-solving skills has been identified as an essential curricular component in the training of journalism and mass communication students (Bronstein & Fitzpatrick, 2015). Could such real-world problem solving methodologies be effective in the preparation of educational leaders? In a seminal study about problem solving for educational leaders, Leithwood and Steinbach (1992, 1995) sought to determine if effective problem-solving expertise could be explicitly taught, and, if so, could teaching problem- processing expertise be helpful in moving novices toward expert competence? Over the course of four months and four separate learning sessions, participants in the control group were explicitly taught subskills within six problem-solving components: interpretation of the problem for priority, perceived difficulty, data needed for further action, and anecdotes of prior experience that can inform action; goals for solving the problem; large-scale principles that guide decision making; barriers or obstacles that need to be overcome; possible courses of action; and the confidence of the leader to solve the problem. The authors asserted that providing conditions to participants that included models of effective problem-solving, feedback, increasingly complex problem-solving demands, frequent opportunities for practice, group problem-solving, individual reflection, authentic problems, and help to stimulate metacognition and reflection would result in educational leaders improving their problem-solving skills.

The authors used two experts’ ratings of participants’ problem-solving for both process (their methods of attacking the problem) and product (their solutions) using a 0-3 scale in a pretest-posttest design. They found significant increases in some problem-solving skills (problem interpretation, goal setting, and identification of barriers or obstacles that need to be overcome) after explicit instruction (Leithwood & Steinbach, 1992, 1995). They recommended conducting more research on the preparation of educational leaders, with particular respect to approaches that would improve the aspiring leaders’ problem-solving skills.

Solving problems for practicing principals could be described as constructivist, since most principals do solve problems within a social context of other stakeholders, such as teachers, parents, and students (Leithwood & Steinbach, 1992). Thus, some authors have examined providing opportunities for novice or aspiring leaders to construct meaning from novel scenarios using the benefits of, for example, others’ point of view, expert modeling, simulations, and prior knowledge (Duke, 2014; Leithwood & Steinbach, 1992, 1995; Myran & Sutherland, 2016; Shapira-Lishchinsky, 2015). Such collaborative inquiry has been effective for teachers, as well (DeLuca, Bolden, & Chan, 2017). Such learning can be considered consistent with the ideas of other social constructivist theorists (Berger & Luckmann, 1966; Vygotsky, 1978) as well, since individuals are working together to construct meaning, and they are pushing into areas of uncertainty and lack of expertise.

Shapira-Lishchinsky (2015) added some intriguing findings and recommendations to those of Leithwood and Steinbach (1992, 1995). In this study, 50 teachers with various leadership roles in their schools were presented regularly with ethical dilemmas during their coursework. Participants either interacted with the dilemmas as members of a role play or by observing those chosen. When the role play was completed, the entire group debriefed and discussed the ethical dilemmas and role-playing participants’ treatment of the issues. This method was shown, through qualitative analysis of participants’ discussions during the simulations, to produce rich dialogue and allow for a safe and controlled treatment of difficult issues. As such, the use of simulations was presented as a viable means through which to prepare aspiring educational leaders. Further, the author suggested the use of further studies with simulation-based learning that seek to gain information about aspiring leaders’ self-efficacy and psychological empowerment. A notable example of project-based scenarios in a virtual collaboration environment to prepare educational leaders is the work of Howard, McClannon, and Wallace (2014). Shapira-Lishchinsky (2015) also recommended similar research in other developed countries to observe the utility of the approaches of simulation and social constructivism to examine them for a wider and diverse aspiring administrator candidate pool.

Further, in an extensive review of prior research studies on the subject, Hallinger and Bridges (2017) noted that Problem-Based Learning (PBL), though applied successfully in other professions and written about extensively (Hallinger & Bridges, 1993, 2017; Stentoft, 2017), was relatively unheralded in the preparation of educational leaders. According to the authors, characteristics of PBL included problems replacing theory as the organization of course content, student-led group work, creation of simulated products by students, increased student ownership over learning, and feedback along the way from professors. Their review noted that PBL had positive aspects for participants, such as increased motivation, real-world connections, and positive pressure that resulted from working with a team. However, participants also expressed concerns about time constraints, lack of structure, and interpersonal dynamics within their teams. There were positive effects found on aspiring leaders’ problem-solving skill development with PBL (Copland, 2000; Hallinger & Bridges, 2017). Though PBL is much more prescribed than the scenarios strategy described in the Methods section below, the applicability of real-world problems to the preparation of educational leaders is summarized well by Copland (2000):

[I]nstructional practices that activate prior knowledge and situate learning in contexts similar to those encountered in practice are associated with the development of students’ ability to understand and frame problems. Moreover, the incorporation of debriefing techniques that encourage students’ elaboration of knowledge and reflection on learning appear to help students solidify a way of thinking about problems. (p. 604)

This study involved a one-group pretest-posttest design. No control group was assigned, as the pedagogical strategy in question—the use of real-world scenarios to build problem-solving skill for aspiring educational leaders—is integral to the school’s curriculum that prepares leaders, and, therefore, it is unethical to deny to student participants (Gay & Airasian, 2003). Thus, all participants were provided instruction with the use of real-world scenarios.

Participants.  Graduate students at a regional, comprehensive public university in the Northeast obtaining a 6 th -year degree (equivalent to a second master’s degree) in educational leadership and preparing for certification as educational administrators served as participants. Specifically, students in three sections of the same full-year, two-course sequence, entitled “School Leadership I and II” were invited to participate. This particular course was selected from the degree course sequence, as it deals most directly with the problem-solving nature and daily work of school administrators. Some key outcomes of the course include students using data to drive school improvement action plans, communicating effectively with a variety of stakeholders, creating a safe and caring school climate, creating and maintaining a strategic and viable school budget, articulating all the steps in a hiring process for teachers and administrators, and leading with cultural proficiency.

The three sections were taught by two different professors. The professors used real- world scenarios in at least half of their class meetings throughout the year, or in approximately 15 classes throughout the year. During these classes, students were presented with realistic situations that have occurred, or could occur, in actual public schools. Students worked with their classmates to determine potential solutions to the problems and then discussed their responses as a whole class under the direction of their professor, a master practitioner. Both professors were active school administrators, with more than 25 years combined educational leadership experience in public schools. It should be noted that the scenario presentation and discussions took place during the class sessions, only. These were not presented for homework or in online forums.

Of the 44 students in these three sections, 37 volunteered to participate at some point in the data collection sequence, but not all students in the pretest session attended the posttest session months later and vice versa. As a result, only 20 students’ data were used for the matched pairs analysis. All 37 participants were certified professional educators in public schools in Connecticut. The participants’ professional roles varied and included classroom teachers, instructional coaches, related service personnel, unified arts teachers, as well as other non- administrative educational roles. Characteristics of participants in the overall and matched pairs groups can be found in Table 1.

Table 1 Participant Characteristics

Procedure.  Participants’ data were compared between a fall of 2016 baseline data collection period and a spring of 2017 posttest data collection period. During the fall data collection period, participants were randomly assigned one of two versions of a Google Forms survey. After items about participant characteristics, the survey consisted of 11 items designed to elicit quantitative and qualitative data about participants’ perceptions of their problem-solving abilities, as well as their ability to address real-world problems faced by educational leaders. The participants were asked to rate their perception of their situational awareness, flexibility, and problem solving ability on a 10-point (1-10) Likert scale, following operational definitions of the terms (Marzano, Waters, & McNulty, 2005; Winter, 1982). They were asked, for each construct, to write open-ended responses to justify their numerical rating. They were then asked to write what they perceived they still needed to improve their problem-solving skills. The final four items included two real-world, unstructured, problem-based scenarios for which participants were asked to create plans of action. They were also asked to rate their problem-solving confidence with respect to their proposed action plans for each scenario on a 4-point (0-3) Likert scale.

During the spring data collection period, participants accessed the opposite version of the Google Forms survey from the one they completed in the fall. All items were identical on the two survey versions, except the scenarios, which were different on each survey version. The use of two versions was to ensure that any differences in perceived or actual difficulty among the four scenarios provided would not alter results based upon the timing of participant access (Leithwood & Steinbach, 1995). In order to link participants’ fall and spring data in a confidential manner, participants created a unique, six-digit alphanumeric code.

A focus group interview followed each spring data collection session. The interviews were recorded to allow for accurate transcription. The list of standard interview questions can be found in Table 2. This interview protocol was designed to elicit qualitative data with respect to aspiring educational leaders’ perceptions about their developing problem-solving abilities.

Table 2 Focus Group Interview Questions ___________________________________________________________________________________________

Please describe the development of your problem-solving skills as an aspiring educational leader over the course of this school year. In what ways have you improved your skills? Be as specific as you can.

What has been helpful to you (i.e. coursework, readings, experiences, etc.) in this development of your problem-solving skills? Why?

What do you believe you still need for the development in your problem-solving skills as an aspiring educational leader?

Discuss your perception of your ability to problem solve as an aspiring educational leader. How has this changed from the beginning of this school year? Why?

Please add anything else you perceive is relevant to this conversation about the development of your problem-solving skills as an aspiring educational leader.

___________________________________________________________________________________________

Data Analysis.

Quantitative data .  Data were obtained from participants’ responses to Likert-scale items relating to their confidence levels with respect to aspects of problem solving, as well as from the rating of participants’ responses to the given scenarios  against a rubric. The educational leadership problem-solving rubric chosen (Leithwood & Steinbach, 1995) was used with permission, and it reflects the authors’ work with explicitly teaching practicing educational leaders components of problem solving. The adapted rubric can be found in Figure 1. Through the use of this rubric, each individual response by a participant to a presented scenario was assigned a score from 0-15. It should be noted that affect data (representing the final 3 possible points on the 18-point rubric) were obtained via participants’ self-reporting their confidence with respect to their proposed plans of action. To align with the rubric, participants self-assessed their confidence through this item with a 0-3 scale.

0 = No Use of the Subskill 1 = There is Some Indication of Use of the Subskill 2 = The Subskill is Present to Some Degree 3 = The Subskill is Present to a Marked Degree; This is a Fine Example of this Subskill

Figure 1.  Problem-solving model for unstructured problems. Adapted from “Expert Problem Solving: Evidence from School and District Leaders,” by K. Leithwood and R. Steinbach, pp. 284-285. Copyright 1995 by the State University of New York Press.

I compared Likert-scale items and rubric scores via descriptive statistics and rubric scores also via a paired sample  t -test and Cohen’s  d , all using the software program IBM SPSS. I did not compare the Likert-scale items about situational awareness, flexibility, and problem solving ability with  t -tests or Cohen’s  d , since these items did not represent a validated instrument. They were only single items based upon participants’ ratings compared to literature-based definitions. However, the value of the comparison of means from fall to spring was triangulated with qualitative results to provide meaning. For example, to say that participants’ self-assessment ratings for perceived problem-solving abilities increased, I examined both the mean difference for items from fall to spring and what participants shared throughout the qualitative survey items and focus group interviews.

Prior to scoring participants’ responses to the scenarios using the rubric, and in an effort to maximize the content validity of the rubric scores, I calibrated my use of the rubric with two experts from the field. Two celebrated principals, representing more than 45 combined years of experience in school-level administration, collaboratively and comparatively scored participant responses. Prior to scoring, the team worked collaboratively to construct appropriate and comprehensive exemplar responses to the four problem-solving scenarios. Then the team blindly scored fall pretest scenario responses using the Leithwood and Steinbach (1995) rubric, and upon comparing scores, the interrater reliability correlation coefficient was .941, indicating a high degree of agreement throughout the team.

Qualitative data.  These data were obtained from open-ended items on the survey, including participants’ responses to the given scenarios, as well as the focus group interview transcripts. I analyzed qualitative data consistent with the grounded theory principles of Strauss and Corbin (1998) and the constant comparative methods of Glaser (1965), including a period of open coding of results, leading to axial coding to determine the codes’ dimensions and relationships between categories and their subcategories, and selective coding to arrive at themes. Throughout the entire data analysis process, I repeatedly returned to raw data to determine the applicability of emergent codes to previously analyzed data. Some categorical codes based upon the review of literature were included in the initial coding process. These codes were derived from the existing theoretical problem-solving models of Bolman and Deal (2008) and Leithwood and Steinbach (1995). These codes included  modeling ,  relationships , and  best for kids . Open codes that emerged from the participants’ responses included  experience ,  personality traits ,  current job/role , and  team . Axial coding revealed, for example, that current jobs or roles cited, intuitively, provided both sufficient building-wide perspective and situational memory (i.e. for special education teachers and school counselors) and insufficient experiences (i.e. for classroom teachers) to solve the given problems with confidence. From such understandings of the codes, categories, and their dimensions, themes were developed.

Quantitative Results.   First, participants’ overall, aggregate responses (not matched pairs) were compared from the fall to spring, descriptively. These findings are outlined in Table  3. As is seen in the table, each item saw a modest increase over the course of the year. Participant perceptions of their problem-solving abilities across the three constructs presented (situational awareness, flexibility, and problem solving) did increase over the course of the year, as did the average group score for the problem-solving scenarios. However, due to participant differences in the two data collection periods, these aggregate averages do not represent a matched-pair dataset.

Table 3 Fall to Spring Comparison of Likert-Scale and Rubric-Scored Items

a  These problem-solving dimensions from literature were rated by participants on a scale from 1- 10. b  Participants received a rubric score for each scenario between 0-18. Participants’ two scenario scores for each data collection period (fall, spring) were averaged to arrive at the scores represented here.

In order to determine the statistical significance of the increase in participants’ problem- solving rubric scores, a paired-samples  t -test was applied to the fall ( M  = 9.15;  SD  = 2.1) and spring ( M  = 9.25;  SD  = 2.3) averages. Recall that 20 participants had valid surveys for both the fall and spring. The  t -test ( t  = -.153;  df  = 19;  p  = .880) revealed no statistically significant change from fall to spring, despite the minor increase (0.10). I applied Cohen’s  d  to calculate the effect size. The small sample size ( n  = 20) for the paired-sample  t -test may have contributed to the lack of statistical significance. However, standard deviations were also relatively small, so the question of effect size was of particular importance. Cohen’s  d  was 0.05, which is also very small, indicating that little change—really no improvement, from a statistical standpoint—in participants’ ability to create viable action plans to solve real-world problems occurred throughout the year. However, the participants’ perceptions of their problem-solving abilities did increase, as evidenced by the increases in the paired-samples perception means shown in Table 3, though these data were only examined descriptively (from a quantitative perspective) due to the fact that these questions were individual items that are not part of a validated instrument.

Qualitative Results.   Participant responses to open-ended items on the questionnaire, responses to the scenarios, and oral responses to focus group interview questions served as sources of qualitative data. Since the responses to the scenarios were focused on participant competence with problem solving, as measured by the aforementioned rubric (Leithwood &  Steinbach, 1995), these data were examined separately from data collected from the other two sources.

Responses to scenarios.  As noted, participants’ rubric ratings for the scenarios did not display a statistically significant increase from fall to spring. As such, this outline will not focus upon changes in responses from fall to spring. Rather, I examined the responses, overall, through the lens of the Leithwood and Steinbach (1995) problem-solving framework indicators against which they were rated. Participants typically had outlined reasonable, appropriate, and logical solution processes. For example, in a potential bullying case scenario, two different participants offered, “I would speak to the other [students] individually if they have said or done anything mean to other student [ sic ] and be clear that it is not tolerable and will result in major consequences” and “I would initiate an investigation into the situation beginning with [an] interview with the four girls.” These responses reflect actions that the consulted experts anticipated from participants and deemed as logical and needed interventions. However, these two participants omitted other needed steps, such as addressing the bullied student’s mental health needs, based upon her mother’s report of suicidal ideations. Accordingly, participants earned points for reasonable and logical responses very consistently, yet, few full-credit responses were observed.

Problem interpretation scores were much more varied. For this indicator, some participants were able to identify many, if not all, the major issues in the scenarios that needed attention. For example, for a scenario where two teachers were not interacting professionally toward each other, many participants correctly identified that this particular scenario could include elements of sexual harassment, professionalism, teaching competence, and personality conflict. However, many other participants missed at least two of these key elements of the problem, leaving their solution processes incomplete. The categories of (a) goals and (b) principles and values also displayed a similarly wide distribution of response ratings.

One category, constraints, presented consistent difficulty for the participants. Ratings were routinely 0 and 1. Participants could not consistently report what barriers or obstacles would need addressing prior to success with their proposed solutions. To be clear, it was not a matter of participants listing invalid or unrealistic barriers or obstacles; rather, the participants were typically omitting constraints altogether from their responses. For example, for a scenario involving staff members arriving late and unprepared to data team meetings, many participants did not identify that a school culture of not valuing data-driven decision making or lack of norms for data team work could be constraints that the principal could likely face prior to reaching a successful resolution.

Responses to open-ended items.  When asked for rationale regarding their ratings for situational awareness, flexibility, and problem solving, participants provided open-ended responses. These responses revealed patterns worth considering, and, again, this discussion will consider, in aggregate, responses made in both the pre- and post- data collection periods, again due to the similarities in responses between the two data collection periods. The most frequently observed code (112 incidences) was  experience . Closely related were the codes  current job/role  (50 incidences). Together, these codes typically represented a theme that participants were linking their confidence with respect to problem solving with their exposure (or lack thereof) in their professional work. For example, a participant reported, “As a school counselor, I have a lot of contact with many stakeholders in the school -admin [ sic ], parents, teachers, staff, etc. I feel that I have a pretty good handle on the systemic issues.” This example is one of many where individuals working in counseling, instructional coaching, special education, and other support roles expressed their advanced levels of perspective based upon their regular contact with many stakeholders, including administrators. Thus, they felt they had more prior knowledge and situational memory about problems in their schools.

However, this category of codes also included those, mostly classroom or unified arts teachers, who expressed that their relative lack of experiences outside their own classrooms limited their perspective for larger-scale problem solving. One teacher succinctly summarized this sentiment, “I have limited experience in being part of situations outside of my classroom.” Another focused on the general problem solving skill in her classroom not necessarily translating to confidence with problem solving at the school level: “I feel that I have a high situational awareness as a teacher in the classroom, but as I move through these leadership programs I find that I struggle to take the perspective of a leader.” These experiences were presented in opposition to their book learning or university training. There were a number of instances (65 combined) of references to the value of readings, class discussions, group work, scenarios presented, research, and coursework in the spring survey. When asked what the participants need more, again, experience was referenced often. One participant summarized this concept, “I think that I, personally, need more experience in the day-to-day . . . setting.” Another specifically separated experiences from scenario work, “[T]here is [ sic ] some things you can not [ sic ] learn from merely discussing a ‘what if” scenario. A seasoned administrator learns problem solving skills on the job.”

Another frequently cited code was  personality traits  (63 incidences), which involved participants linking elements of their own personalities to their perceived abilities to process problems, almost exclusively from an assets perspective. Examples of traits identified by participants as potentially helpful in problem solving included: open-mindedness, affinity for working with others, not being judgmental, approachability, listening skills, and flexibility. One teacher exemplified this general approach by indicating, “I feel that I am a good listener in regards to inviting opinions. I enjoy learning through cooperation and am always willing to adapt my teaching to fit needs of the learners.” However, rare statements of personality traits interfering with problem solving included, “I find it hard to trust others [ sic ] abilities” and “my personal thoughts and biases.”

Another important category of the participant responses involved connections with others. First, there were many references to  relationships  (27 incidences), mostly from the perspective that building positive relationships leads to greater problem-solving ability, as the aspiring leader knows stakeholders better and can rely on them due to the history of positive interactions. One participant framed this idea from a deficit perspective, “Not knowing all the outlying relationships among staff members makes situational awareness difficult.” Another identified that established positive relationships are already helpful to an aspiring leader, “I have strong rapport with fellow staff members and administrators in my building.” In a related way, many instances of the code  team  were identified (29). These references overwhelmingly identified that solving problems within a team context is helpful. One participant stated, “I often team with people to discuss possible solutions,” while another elaborated,

I recognize that sometimes problems may arise for which I am not the most qualified or may not have the best answer. I realize that I may need to rely on others or seek out help/opinions to ensure that I make the appropriate decision.

Overall, participants recognized that problem-solving for leaders does not typically occur in a vacuum.

Responses to focus group interview questions.  As with the open-ended responses, patterns were evident in the interview responses, and many of these findings were supportive of the aforementioned themes. First, participants frequently referenced the power of group work to help build their understanding about problems and possible solutions. One participant stated, “hearing other people talk and realizing other concerns that you may not have thought of . . . even as a teacher sometimes, you look at it this way, and someone else says to see it this way.” Another added, “seeing it from a variety of persons [ sic ] point of views. How one person was looking at it, and how another person was looking at it was really helpful.” Also, the participants noted the quality of the discussion was a direct result of “professors who have had real-life experience” as practicing educational leaders, so they could add more realistic feedback and insight to the discussions.

Perhaps most notable in the participant responses during the focus groups was the emphasis on the value of real-world scenarios for the students. These were referenced, without prompting, in all three focus groups by many participants. Answers to the question about what has been most helpful in the development of their problem-solving skills included, “I think the real-world application we are doing,” “I think being presented with all the scenarios,” and “[the professor] brought a lot of real situations.”

With respect to what participants believed they still needed to become better and more confident problem solvers, two patterns emerged. First, students recognized that they have much more to learn, especially with respect to policy and law. It is noteworthy that, with few exceptions, these students had not taken the policy or law courses in the program, and they had not yet completed their administrative internships. Some students actually reported rating themselves as less capable problem solvers in the spring because they now understood more clearly what they lacked in knowledge. One student exemplified this sentiment, “I might have graded myself higher in the fall than I did now . . . [I now can] self identify areas I could improve in that I was not as aware of.” Less confidence in the spring was a minority opinion, however. In a more typical response, another participant stated, “I feel much more prepared for that than I did at the beginning of the year.”

Overall, the most frequently discussed future need identified was experience, either through the administrative internship or work as a formal school administrator. Several students summarized this idea, “That real-world experience to have to deal with it without being able to talk to 8 other people before having to deal with it . . . until you are the person . . . you don’t know” and “They tell you all they want. You don’t know it until you are in it.” Overall, most participants perceived themselves to have grown as problem solvers, but they overwhelmingly recognized that they needed more learning and experience to become confident and effective problem solvers.

This study continues a research pathway about the development of problem-solving skills for administrators by focusing on their preparation. The participants did not see a significant increase in their problem-solving skills over the year-long course in educational leadership.

Whereas, this finding is not consistent with the findings of others who focused on the development of problem-solving skills for school leaders (Leithwood & Steinbach, 1995; Shapira-Lishchinsky, 2015), nor is it consistent with PBL research about the benefits of that approach for aspiring educational leaders (Copland, 2000; Hallinger & Bridges, 2017), it is important to note that the participants in this study were at a different point in their careers. First, they were aspirants, as opposed to practicing leaders. Also, the studied intervention (scenarios) was not the same or nearly as comprehensive as the prescriptive PBL approach. Further, unlike the participants in either the practicing leader or PBL studies, because these individuals had not yet had their internship experiences, they had no practical work as educational leaders. This theme of lacking practical experience was observed in both open-ended responses and focus group interviews, with participants pointing to their upcoming internship experiences, or even their eventual work as administrators, as a key missing piece of their preparation.

Despite the participants’ lack of real gains across the year of preparation in their problem- solving scores, the participants did, generally, report an increase in their confidence in problem solving, which they attributed to a number of factors. The first was the theme of real-world context. This finding was consistent with others who have advocated for teaching problem solving through real-world scenarios (Duke, 2014; Leithwood & Steinbach, 1992, 1995; Myran & Sutherland, 2016; Shapira-Lishchinsky, 2015). This study further adds to this conversation, not only a corroboration of the importance of this method (at least in aspiring leaders’ minds), but also that participants specifically recognized their professors’ experiences as school administrators as important for providing examples, context, and credibility to the work in the classroom.

In addition to the scenario approach, the participants also recognized the importance of learning from one another. In addition to the experiences of their practitioner-professors, many participants espoused the value of hearing the diverse perspectives of other students. The use of peer discussion was also an element of instruction in the referenced studies (Leithwood & Steinbach, 1995; Shapira-Lishchinsky, 2015), corroborating the power of aspiring leaders learning from one another and supporting existing literature about the social nature of problem solving (Berger & Luckmann, 1966; Leithwood & Steinbach, 1992; Vygotsky, 1978).

Finally, the ultimate theme identified through this study is the need for real-world experience in the field as an administrator or intern. It is simply not enough to learn about problem solving or learn the background knowledge needed to solve problems, even when the problems presented are real-world in nature. Scenarios are not enough for aspiring leaders to perceive their problem-solving abilities to be adequate or for their actual problem-solving abilities to improve. They need to be, as some of the participants reasoned, in positions of actual responsibility, where the weight of their decisions will have tangible impacts on stakeholders, including students.

The study of participants’ responses to the scenarios connected to the Four Frames model of Bolman and Deal (2008). The element for which participants received the consistently highest scores was identifying solution processes. This area might most logically be connected to the structural and human resource frames, as solutions typically involve working to meet individuals’ needs, as is necessary in the human resource frame, and attending to protocols and procedures, which is the essence of the structural frame. As identified above, the political and symbolic frames have been cited by the authors as the most underdeveloped by educational leaders, and this assertion is corroborated by the finding in this study that participants struggled the most with identifying constraints, which can sometimes arise from an understanding of the competing personal interests in an organization (political frame) and the underlying meaning behind aspects of an organization (symbolic frame), such as unspoken rules and traditions. The lack of success identifying constraints is also consistent with participants’ statements that they needed actual experiences in leadership roles, during which they would likely encounter, firsthand, the types of constraints they were unable to articulate for the given scenarios. Simply, they had not yet “lived” these types of obstacles.

The study includes several notable limitations. First, the study’s size is limited, particularly with only 20 participants’ data available for the matched pairs analysis. Further, this study was conducted at one university, within one particular certification program, and over three sections of one course, which represented about one-half of the time students spend in the program. It is likely that more gains in problem-solving ability and confidence would have been observed if this study was continued through the internship year. Also, the study did not include a control group. The lack of an experimental design limits the power of conclusions about causality. However, this limitation is mitigated by two factors. First, the results did not indicate a statistically significant improvement, so there is not a need to attribute a gain score to a particular variable (i.e. use of scenarios), anyway, and, second, the qualitative results did reveal the perceived value for participants in the use of scenarios, without any prompting of the researcher. Finally, the participant pool was not particularly diverse, though this fact is not particularly unusual for the selected university, in general, representing a contemporary challenge the university’s state is facing to educate its increasingly diverse student population, with a teaching and administrative workforce that is predominantly White.

The findings in this study invite further research. In addressing some of the limitations identified here, expanding this study to include aspiring administrators across other institutions representing different areas of the United States and other developed countries, would provide a more generalizable set of results. Further, studying the development of problem-solving skills during the administrative internship experience would also add to the work outlined here by considering the practical experience of participants.

In short, this study illustrates for those who prepare educational leaders the value of using scenarios in increasing aspiring leaders’ confidence and knowledge. However, intuitively, scenarios alone are not enough to engender significant change in their actual problem-solving abilities. Whereas, real-world context is important to the development of aspiring educational leaders’ problem-solving skills, the best context is likely to be the real work of administration.

Allison, D. J. (1996). Problem finding, classification and interpretation: In search of a theory of administrative problem processing. In K. Leithwood, J. Chapman, D. Corson, P. Hallinger, & A. Hart (Eds.),  International handbook of educational leadership and administration  (pp. 477–549). Norwell, MA: Kluwer Academic.

Berger, P. L., & Luckmann, T. (1966).  The social construction of reality . Garden City, NJ: Doubleday.

Bolman, L. G., & Deal, T. E. (2008).  Re-framing organizations: Artistry, choice and leadership  (4th ed.). San Francisco: Jossey Bass.

Bronstein, C., & Fitzpatrick, K. R. (2015). Preparing tomorrow’s leaders: Integrating leadership development in journalism and mass communication education.  Journalism & Mass Communication Educator, 70 (1), 75–88. https://doi.org/10.1177/1077695814566199

Copland, M. A. (2000). Problem-based learning and prospective principals’ problem-framing ability.  Educational Administration Quarterly ,  36 , 585–607.

Deluca, C., Bolden, B., & Chan, J. (2017). Systemic professional learning through collaborative inquiry: Examining teachers’ perspectives.  Teaching and Teacher Education ,  67 , 67–78. https://doi.org/10.1016/j.tate.2017.05.014

Dimmock, C. (1996). Dilemmas for school leaders and administrators in restructuring. In K. Leithwood, J. Chapman, D. Corson, P. Hallinger, & A. Hart (Eds.),  International Handbook of Educational Leadership and Administration  (pp. 135–170). Norwell, MA: Kluwer Academic.

Duke, D. L. (2014). A bold approach to developing leaders for low-performing schools. Management in Education, 28 (3), 80–85. https://doi.org/10.1177/0892020614537665

Gay, L. R., & Airasian, P. (2003).  Educational research: Competancies for analysis and applications  (7th ed.). Upper Saddle River, NJ: Pearson Education.

Glaser, B. G. (1965). The constant comparative method of qualitative analysis.  Social Problems, 12 (4), 436-445.

Hallinger, P., & Bridges, E. (1993). Problem-based learning in medical and managerial education. In P. Hallinger, K. Leithwood, & J. Murphy (Eds.),  Cognitive perspectives on educational leadership  (pp. 253–267). New York: Teachers’ College Press.

Hallinger, P., & Bridges, E. M. (2017). A systematic review of research on the use of problem- based learning in the preparation and development of school leaders.  Educational Administration Quarterly . 53(2), 255-288. https://doi.org/10.1177/0013161X16659347

Hallinger, P., & McCary, C. E. (1990). Developing the strategic thinking of instructional leaders. Elementary School Journal ,  91 (2), 89–108.

Howard, B. B., McClannon, T. W., & Wallace, P. R. (2014). Collaboration through role play among graduate students in educational leadership in distance learning.  American Journal of Distance Education ,  28 (1), 51–61. https://doi.org/10.1080/08923647.2014.868665

Johnson, B. L., & Kruse, S. D. (2009).  Decision making for educational leaders: Underexamined dimensions and issues . Albany, NY: State University of New York Press.

Leithwood, K., & Steinbach, R. (1992). Improving the problem-solving expertise of school administrators: Theory and practice.  Education and Urban Society ,  24 (3), 317–345. Retrieved from https://journals.sagepub.com.ccsu.idm.oclc.org/doi/pdf/10.1177/0013124592024003003

Leithwood, K., & Steinbach, R. (1995).  Expert problem solving: Evidence from school and district leaders . Albany, NY: State University of New York Press.

Marzano, R. J., Waters, T., & McNulty, B. A. (2005).  School leadership that works: From research to results . Denver, CO: ASCD.

Myran, S., & Sutherland, I. (2016). Problem posing in leadership education: Using case study to foster more effective problem solving.  Journal of Cases in Educational Leadership ,  19 (4), 57–71. https://doi.org/10.1177/1555458916664763

Rochford, L., & Borchert, P. S. (2011). Assessing higher level learning: Developing rubrics for case analysis.  Journal of Education for Business ,  86 , 258–265. https://doi.org/10.1080/08832323.2010.512319

Salas, E., Wildman, J. L., & Piccolo, R. F. (2009). Using simulation based training to enhance management education.  Academy of Management Learning & Education ,  8 (4), 559–573. https://doi.org/10.5465/AMLE.2009.47785474

Shapira-Lishchinsky, O. (2015). Simulation-based constructivist approach for education leaders. Educational Management Administration & Leadership ,  43 (6), 972–988. https://doi.org/10.1177/1741143214543203

Simon, H. A. (1993). Decision making: Rational, nonrational, and irrational.  Educational Administration Quarterly ,  29 (3), 392–411. https://doi.org/10.1177/0013161X93029003009

Stentoft, D. (2017). From saying to doing interdisciplinary learning: Is problem-based learning the answer?  Active Learning in Higher Education ,  18 (1), 51–61. https://doi.org/10.1177/1469787417693510

Strauss, A., & Corbin, J. (1998).  Basics of qualitative research  (2nd ed.). Thousand Oaks, CA: Sage.

VanLehn, K. (1991). Rule acquisition events in the discovery of problem-solving strategies. Cognitive Science ,  15 (1), 1–47. https://doi.org/10.1016/0364-0213(91)80012-T

Vygotsky, L. S. (1978).  Mind in society . Cambridge, MA: Harvard University Press.

Winter, R. (1982). Dilemma analysis: A contribution to methodology for action research. Cambridge Journal of Education, 12 (3), 166-173.

Author Biography

Dr. Jeremy Visone is an Assistant Professor of Educational Leadership, Policy, & Instructional Technology. Until 2016, he worked as an administrator at both the elementary and secondary levels, most recently at Anna Reynolds Elementary School, a National Blue Ribbon School in 2016. Dr. Visone can be reached at  [email protected] .

What Is Problem Solving?

You will often see beach clean-up drives being publicized in coastal cities. There are already dustbins available on the beaches,…

You will often see beach clean-up drives being publicized in coastal cities. There are already dustbins available on the beaches, so why do people need to organize these drives? It’s evident that despite advertising and posting anti-littering messages, some of us don’t follow the rules.

Temporary food stalls and shops make it even more difficult to keep the beaches clean. Since people can’t ask the shopkeepers to relocate or prevent every single person from littering, the clean-up drive is needed.  This is an ideal example of problem-solving psychology in humans. ( 230-fifth.com ) So, what is problem-solving? Let’s find out.

What Is Problem-Solving?

At its simplest, the meaning of problem-solving is the process of defining a problem, determining its cause, and implementing a solution. The definition of problem-solving is rooted in the fact that as humans, we exert control over our environment through solutions. We move forward in life when we solve problems and make decisions. 

We can better define the problem-solving process through a series of important steps.

Identify The Problem: 

This step isn’t as simple as it sounds. Most times, we mistakenly identify the consequences of a problem rather than the problem itself. It’s important that we’re careful to identify the actual problem and not just its symptoms. 

Define The Problem: 

Once the problem has been identified correctly, you should define it. This step can help clarify what needs to be addressed and for what purpose.

Form A Strategy: 

Develop a strategy to solve your problem. Defining an approach will provide direction and clarity on the next steps. 

Organize The Information:  

Organizing information systematically will help you determine whether something is missing. The more information you have, the easier it’ll become for you to arrive at a solution.  

Allocate Resources:  

We may not always be armed with the necessary resources to solve a problem. Before you commit to implementing a solution for a problem, you should determine the availability of different resources—money, time and other costs.

Track Progress: 

The true meaning of problem-solving is to work towards an objective. If you measure your progress, you can evaluate whether you’re on track. You could revise your strategies if you don’t notice the desired level of progress. 

Evaluate The Results:  

After you spot a solution, evaluate the results to determine whether it’s the best possible solution. For example, you can evaluate the success of a fitness routine after several weeks of exercise.

Meaning Of Problem-Solving Skill

Now that we’ve established the definition of problem-solving psychology in humans, let’s look at how we utilize our problem-solving skills.  These skills help you determine the source of a problem and how to effectively determine the solution. Problem-solving skills aren’t innate and can be mastered over time. Here are some important skills that are beneficial for finding solutions.

Communication

Communication is a critical skill when you have to work in teams.  If you and your colleagues have to work on a project together, you’ll have to collaborate with each other. In case of differences of opinion, you should be able to listen attentively and respond respectfully in order to successfully arrive at a solution.

As a problem-solver, you need to be able to research and identify underlying causes. You should never treat a problem lightly. In-depth study is imperative because often people identify only the symptoms and not the actual problem.

Once you have researched and identified the factors causing a problem, start working towards developing solutions. Your analytical skills can help you differentiate between effective and ineffective solutions.

Decision-Making

You’ll have to make a decision after you’ve identified the source and methods of solving a problem. If you’ve done your research and applied your analytical skills effectively, it’ll become easier for you to take a call or a decision.

Organizations really value decisive problem-solvers. Harappa Education’s   Defining Problems course will guide you on the path to developing a problem-solving mindset. Learn how to identify the different types of problems using the Types of Problems framework. Additionally, the SMART framework, which is a five-point tool, will teach you to create specific and actionable objectives to address problem statements and arrive at solutions. 

Explore topics & skills such as Problem Solving Skills , PICK Chart , How to Solve Problems & Barriers to Problem Solving from our Harappa Diaries blog section and develop your skills.

Problem-Solving Method in Teaching

The problem-solving method is a highly effective teaching strategy that is designed to help students develop critical thinking skills and problem-solving abilities . It involves providing students with real-world problems and challenges that require them to apply their knowledge, skills, and creativity to find solutions. This method encourages active learning, promotes collaboration, and allows students to take ownership of their learning.

Table of Contents

Definition of problem-solving method.

Problem-solving is a process of identifying, analyzing, and resolving problems. The problem-solving method in teaching involves providing students with real-world problems that they must solve through collaboration and critical thinking. This method encourages students to apply their knowledge and creativity to develop solutions that are effective and practical.

Meaning of Problem-Solving Method

The meaning and Definition of problem-solving are given by different Scholars. These are-

Woodworth and Marquis(1948) : Problem-solving behavior occurs in novel or difficult situations in which a solution is not obtainable by the habitual methods of applying concepts and principles derived from past experience in very similar situations.

Skinner (1968): Problem-solving is a process of overcoming difficulties that appear to interfere with the attainment of a goal. It is the procedure of making adjustments in spite of interference

Benefits of Problem-Solving Method

The problem-solving method has several benefits for both students and teachers. These benefits include:

• Encourages active learning: The problem-solving method encourages students to actively participate in their own learning by engaging them in real-world problems that require critical thinking and collaboration
• Promotes collaboration: Problem-solving requires students to work together to find solutions. This promotes teamwork, communication, and cooperation.
• Builds critical thinking skills: The problem-solving method helps students develop critical thinking skills by providing them with opportunities to analyze and evaluate problems
• Increases motivation: When students are engaged in solving real-world problems, they are more motivated to learn and apply their knowledge.
• Enhances creativity: The problem-solving method encourages students to be creative in finding solutions to problems.

Steps in Problem-Solving Method

The problem-solving method involves several steps that teachers can use to guide their students. These steps include

• Identifying the problem: The first step in problem-solving is identifying the problem that needs to be solved. Teachers can present students with a real-world problem or challenge that requires critical thinking and collaboration.
• Analyzing the problem: Once the problem is identified, students should analyze it to determine its scope and underlying causes.
• Generating solutions: After analyzing the problem, students should generate possible solutions. This step requires creativity and critical thinking.
• Evaluating solutions: The next step is to evaluate each solution based on its effectiveness and practicality
• Selecting the best solution: The final step is to select the best solution and implement it.

Verification of the concluded solution or Hypothesis

The solution arrived at or the conclusion drawn must be further verified by utilizing it in solving various other likewise problems. In case, the derived solution helps in solving these problems, then and only then if one is free to agree with his finding regarding the solution. The verified solution may then become a useful product of his problem-solving behavior that can be utilized in solving further problems. The above steps can be utilized in solving various problems thereby fostering creative thinking ability in an individual.

The problem-solving method is an effective teaching strategy that promotes critical thinking, creativity, and collaboration. It provides students with real-world problems that require them to apply their knowledge and skills to find solutions. By using the problem-solving method, teachers can help their students develop the skills they need to succeed in school and in life.

• Jonassen, D. (2011). Learning to solve problems: A handbook for designing problem-solving learning environments. Routledge.
• Hmelo-Silver, C. E. (2004). Problem-based learning: What and how do students learn? Educational Psychology Review, 16(3), 235-266.
• Mergendoller, J. R., Maxwell, N. L., & Bellisimo, Y. (2006). The effectiveness of problem-based instruction: A comparative study of instructional methods and student characteristics. Interdisciplinary Journal of Problem-based Learning, 1(2), 49-69.
• Richey, R. C., Klein, J. D., & Tracey, M. W. (2011). The instructional design knowledge base: Theory, research, and practice. Routledge.
• Savery, J. R., & Duffy, T. M. (2001). Problem-based learning: An instructional model and its constructivist framework. CRLT Technical Report No. 16-01, University of Michigan. Wojcikowski, J. (2013). Solving real-world problems through problem-based learning. College Teaching, 61(4), 153-156

Problem Solving in Education: A Global Imperative

Pedagogical Shifts

Essential lessons, leadership challenges and opportunities.

Jamaludin, A., & Hung, D. W. L. (2016). Digital "learning trails": Scaling technology-facilitated curricular innovation in schools with a rhizomatic lens. Journal of Educational Change , 17 (3), 355–377.

Kahneman, D. (2011). Thinking, fast and slow . New York: Farrar, Strauss, & Giroux.

National Academy of Sciences. (2010). Rising above the gathering storm, revisited: Rapidly approaching category 5. Washington, DC: National Academies Press.

McNeill, K. L., González-Howard, M., Katsh-Singer, R., & Loper, S. (2017). Moving beyond pseudoargumentation: Teachers' enactments of an educative science curriculum focused on argumentation. Science Education , 101 (3), 426–457.

Ng, P. T. (2017). Learning from Singapore: The power of paradoxes . New York: Routledge.

OECD. (2012). PISA 2012 results: Creative problem solving. Paris: OECD.

Patchen, A. K., Zhang, L., & Barnett, M. (2017). Growing plants and scientists: Fostering positive attitudes toward science among all participants in an afterschool hydroponics program. Journal of Science and Educational Technology , 26 (3), 279–294.

Prensky, M. R. (2012). From digital natives to digital wisdom: Hopeful essays for 21st century learning. Thousand Oaks, CA: Corwin.

Shirley, D. (2016). The new imperatives of educational change: Achievement with integrity . New York: Routledge.

• 1 Read more about the Jurong Secondary School project .

He has conducted in-depth studies about school innovations in England, Germany, Canada, and South Korea. Shirley has been a visiting professor at Harvard University in the United States, Venice International University in Italy, the National Institute of Education in Singapore, the University of Barcelona in Spain, and the University of Stavanger in Norway. He is a fellow of the Royal Society of Arts. Shirley’s previous book is The New Imperatives of Educational Change: Achievement with Integrity .

Pak Tee Ng is Associate Dean, Leadership Learning at the National Institute of Education of Nanyang Technological University in Singapore and the author of Learning from Singapore: The Power of Paradoxes (Routledge, 2017).

ASCD is a community dedicated to educators' professional growth and well-being.

Let us help you put your vision into action., related articles.

For STEM Education, the Time Is Now

How to Signal “STEM Is For You”?

STEM Doesn’t Have to Be Rocket Science

How to Start with STEM

Picture Books Aren’t Just for the Youngest Students

From our issue.

To process a transaction with a Purchase Order please send to [email protected]

Intervention based on science of reading, math boosts comprehension, word problem-solving skills

English learners with math difficulty showed improvement following culturally-responsive training.

New research from the University of Kansas has found an intervention based on the science of reading and math effectively helped English learners boost their comprehension, visualize and synthesize information, and make connections that significantly improved their math performance.

The intervention, performed for 30 minutes twice a week for 10 weeks with 66 third-grade English language learners who displayed math learning difficulties, improved students' performance when compared to students who received general instruction. That indicates emphasizing cognitive concepts involved in the science of reading and math are key to helping students improve, according to researchers.

"Word problem-solving is influenced by both the science of reading and the science of math. Key components include number sense, decoding, language comprehension and working memory. Utilizing direct and explicit teaching methods enhances understanding and enables students to effectively connect these skills to solve math problems. This integrated approach ensures that students are equipped with necessary tools to navigate both the linguistic and numerical demands of word problems," said Michael Orosco, professor of educational psychology at KU and lead author of the study.

The intervention incorporates comprehension strategy instruction in both reading and math, focusing and decoding, phonological awareness, vocabulary development, inferential thinking, contextualized learning and numeracy.

"It is proving to be one of the most effective evidence-based practices available for this growing population," Orosco said.

The study, co-written with Deborah Reed of the University of Tennessee, was published in the journal Learning Disabilities Research and Practice .

For the research, trained tutors developed the intervention, developed by Orosco and colleagues based on cognitive and culturally responsive research conducted over a span of 20 years. One example of an intervention session tested in the study included a script in which a tutor examined a word problem that explained a person made a quesadilla for his friend Mario, giving him one-fourth of it, then needed to students to determine how much remained.

The tutor first asked students if they remembered a class session in which they made quesadillas, what shape they were and demonstrated concepts by drawing a circle on the board, dividing it into four equal pieces, having students repeat terms like numerator and denominator, and explaining that when a question asks how much is left, subtraction is required. The students also collaborated with peers to practice using important vocabulary in sentences. The approach both helps students learn and understand mathematical concepts while being culturally responsive.

"Word problems are complex because they require translating words into mathematical equations, and this involves integrating the science of reading and math through language concepts and differentiated instruction," Orosco said. "We have not extensively tested these approaches with this group of children. However, we are establishing an evidence-based framework that aids them in developing background knowledge and connecting it to their cultural contexts."

Orosco, director of KU's Center for Culturally Responsive Educational Neuroscience, emphasized the critical role of language in word problems, highlighting the importance of using culturally familiar terms. For instance, substituting "pastry" for "quesadilla" could significantly affect comprehension for students from diverse backgrounds. Failure to grasp the initial scenario can impede subsequent problem-solving efforts.

The study proved effective in improving students' problem-solving abilities, despite covariates including an individual's basic calculation skills, fluid intelligence and reading comprehension scores. That finding is key as, while ideally all students would begin on equal footing and there were little variations in a classroom, in reality, covariates exist and are commonplace.

The study had trained tutors deliver the intervention, and its effectiveness should be further tested with working teachers, the authors wrote. Orosco said professional development to help teachers gain the skills is necessary, and it is vital for teacher preparation programs to train future teachers with such skills as well. And helping students at the elementary level is necessary to help ensure success in future higher-level math classes such as algebra.

The research builds on Orosco and colleagues' work in understanding and improving math instruction for English learners. Future work will continue to examine the role of cognitive functions such as working memory and brain science, as well as potential integration of artificial intelligence in teaching math.

"Comprehension strategy instruction helps students make connections, ask questions, visualize, synthesize and monitor their thinking about word problems," Orosco and Reed wrote. "Finally, applying comprehension strategy instruction supports ELs in integrating their reading, language and math cognition… Focusing on relevant language in word problems and providing collaborative support significantly improved students' solution accuracy."

• Learning Disorders
• K-12 Education
• Educational Psychology
• Intelligence
• Special education
• Problem solving
• Developmental psychology
• Child prodigy
• Intellectual giftedness
• Lateral thinking

Story Source:

Materials provided by University of Kansas . Original written by Mike Krings. Note: Content may be edited for style and length.

Journal Reference :

• Michael J. Orosco, Deborah K. Reed. Supplemental intervention for third-grade English learners with significant problem-solving challenges . Learning Disabilities Research & Practice , 2024; 39 (2): 60 DOI: 10.1177/09388982241229407

Cite This Page :

Explore More

• Climate Change and Mercury Through the Eons
• Iconic Horsehead Nebula
• Sustainable Jet Fuel from Landfill Emissions
• Bacterial Spores in Bioplastic Make It 'Green'
• Genetic Signals Linked to Blood Pressure
• Double-Fangs of Adolescence Saber-Toothed Cats
• Microarray Patches for Vaccinating Children
• Virus to Save Billions of Gallons of Wastewater
• Weather Report On Planet 280 Light-Years Away
• Trotting Robots and Animal Gait Transitions

Trending Topics

Strange & offbeat.