what is a parametric hypothesis distribution

• Machine Learning Tutorial
• Data Analysis Tutorial
• Python - Data visualization tutorial
• Machine Learning Projects
• Machine Learning Interview Questions
• Machine Learning Mathematics
• Deep Learning Tutorial
• Deep Learning Project
• Deep Learning Interview Questions
• Computer Vision Tutorial
• Computer Vision Projects
• NLP Project
• NLP Interview Questions
• Statistics with Python
• 100 Days of Machine Learning

Linear Algebra and Matrix

• Scalar and Vector
• Python Program to Add Two Matrices
• Python program to multiply two matrices
• Vector Operations
• Product of Vectors
• Scalar Product of Vectors
• Dot and Cross Products on Vectors
• Transpose a matrix in Single line in Python
• Transpose of a Matrix
• Adjoint and Inverse of a Matrix
• How to inverse a matrix using NumPy
• Determinant of a Matrix
• Program to find Normal and Trace of a matrix
• Data Science | Solving Linear Equations
• Data Science - Solving Linear Equations with Python
• System of Linear Equations
• System of Linear Equations in three variables using Cramer's Rule
• Eigenvalues
• Applications of Eigenvalues and Eigenvectors
• How to compute the eigenvalues and right eigenvectors of a given square array using NumPY?

Statistics for Machine Learning

• Descriptive Statistic
• Measures of Central Tendency
• Measures of Dispersion | Types, Formula and Examples
• Mean, Variance and Standard Deviation
• Calculate the average, variance and standard deviation in Python using NumPy
• Random Variables

Difference between Parametric and Non-Parametric Methods

• Probability Distribution
• Confidence Interval
• Mathematics | Covariance and Correlation
• Program to find correlation coefficient
• Robust Correlation
• Normal Probability Plot
• Quantile Quantile plots
• True Error vs Sample Error
• Bias-Variance Trade Off - Machine Learning
• Understanding Hypothesis Testing
• Paired T-Test - A Detailed Overview
• P-value in Machine Learning
• F-Test in Statistics
• Residual Leverage Plot (Regression Diagnostic)
• Difference between Null and Alternate Hypothesis
• Mann and Whitney U test
• Wilcoxon Signed Rank Test
• Kruskal Wallis Test
• Friedman Test
• Mathematics | Probability

Probability and Probability Distributions

• Mathematics - Law of Total Probability
• Bayes's Theorem for Conditional Probability
• Mathematics | Probability Distributions Set 1 (Uniform Distribution)
• Mathematics | Probability Distributions Set 4 (Binomial Distribution)
• Mathematics | Probability Distributions Set 5 (Poisson Distribution)
• Uniform Distribution Formula
• Mathematics | Probability Distributions Set 2 (Exponential Distribution)
• Mathematics | Probability Distributions Set 3 (Normal Distribution)
• Mathematics | Beta Distribution Model
• Gamma Distribution Model in Mathematics
• Chi-Square Test for Feature Selection - Mathematical Explanation
• Student's t-distribution in Statistics
• Python - Central Limit Theorem
• Mathematics | Limits, Continuity and Differentiability
• Implicit Differentiation

Calculus for Machine Learning

• Engineering Mathematics - Partial Derivatives
• Advanced Differentiation
• How to find Gradient of a Function using Python?
• Optimization techniques for Gradient Descent
• Higher Order Derivatives
• Taylor Series
• Application of Derivative - Maxima and Minima | Mathematics
• Absolute Minima and Maxima
• Optimization for Data Science
• Unconstrained Multivariate Optimization
• Lagrange Multipliers
• Lagrange's Interpolation
• Linear Regression in Machine learning
• Ordinary Least Squares (OLS) using statsmodels

Regression in Machine Learning

Statistical analysis plays a crucial role in understanding and interpreting data across various disciplines. Two prominent approaches in statistical analysis are Parametric and Non-Parametric Methods. While both aim to draw inferences from data, they differ in their assumptions and underlying principles. This article delves into the differences between these two methods, highlighting their respective strengths and weaknesses, and providing guidance on choosing the appropriate method for different scenarios.

Parametric Methods

Parametric methods are statistical techniques that rely on specific assumptions about the underlying distribution of the population being studied. These methods typically assume that the data follows a known Probability distribution, such as the normal distribution, and estimate the parameters of this distribution using the available data.

The basic idea behind the Parametric method is that there is a set of fixed parameters that are used to determine a probability model that is used in Machine Learning as well. Parametric methods are those methods for which we priory know that the population is normal, or if not then we can easily approximate it using a Normal Distribution which is possible by invoking the Central Limit Theorem.

Parameters for using the normal distribution are as follows: 

• Standard Deviation

Eventually, the classification of a method to be parametric completely depends on the presumptions that are made about a population.

Assumptions for Parametric Methods

Parametric methods require several assumptions about the data:

• Normality:  The data follows a normal (Gaussian) distribution.
• Homogeneity of variance:  The variance of the population is the same across all groups.
• Independence:  Observations are independent of each other.

What are Parametric Methods?

• t-test:  Tests for the difference between the means of two independent groups.
• ANOVA:  Tests for the difference between the means of three or more groups.
• F-test:  Compares the variances of two groups.
• Chi-square test:  Tests for relationships between categorical variables.
• Correlation analysis:  Measures the strength and direction of the linear relationship between two continuous variables.
• Linear regression:  Predicts a continuous outcome based on a linear relationship with one or more independent variables.
• Logistic regression:  Predicts a binary outcome (e.g., yes/no) based on a set of independent variables.
• Naive Bayes:  Classifies data points based on Bayes’ theorem and assuming independence between features.
• Hidden Markov Models:  Models sequential data with hidden states and observable outputs.

some more common parametric methods available some of them are:

• Confidence interval used for – population mean along with known standard deviation.
• The confidence interval is used for – population means along with the unknown standard deviation.
• The confidence interval for population variance.
• The confidence interval for the difference of two means, with unknown standard deviation.

Advantages of Parametric Methods

• More powerful:  When the assumptions are met, parametric tests are generally more powerful than non-parametric tests, meaning they are more likely to detect a real effect when it exists.
• More efficient:  Parametric tests require smaller sample sizes than non-parametric tests to achieve the same level of power.
• Provide estimates of population parameters:  Parametric methods provide estimates of the population mean, variance, and other parameters, which can be used for further analysis.

Disadvantages of Parametric Methods

• Sensitive to assumptions:  If the assumptions of normality, homogeneity of variance, and independence are not met, parametric tests can be invalid and produce misleading results.
• Limited flexibility:  Parametric methods are limited to the specific probability distribution they are based on.
• May not capture complex relationships:  Parametric methods are not well-suited for capturing complex non-linear relationships between variables.

Applications of Parametric Methods

Parametric methods are widely used in various fields, including:

• Biostatistics:  Comparing the effectiveness of different treatments.
• Social sciences:  Investigating relationships between variables.
• Finance:  Estimating risk and return of investments.
• Engineering:  Analyzing the performance of systems.

Nonparametric Methods

Non-parametric methods are statistical techniques that do not rely on specific assumptions about the underlying distribution of the population being studied. These methods are often referred to as “distribution-free” methods because they make no assumptions about the shape of the distribution.

The basic idea behind the parametric method is no need to make any assumption of parameters for the given population or the population we are studying. In fact, the methods don’t depend on the population. Here there is no fixed set of parameters are available, and also there is no distribution (normal distribution, etc.) of any kind is available for use. This is also the reason that nonparametric methods are also referred to as distribution-free methods. Nowadays Non-parametric methods are gaining popularity and an impact of influence some reasons behind this fame is:

• The main reason is that there is no need to be mannered while using parametric methods.
• The second important reason is that we do not need to make more and more assumptions about the population given (or taken) on which we are working on.
• Most of the nonparametric methods available are very easy to apply and to understand also i.e. the complexity is very low.

Assumptions of Non-Parametric Methods

Non Parametric methods require several assumptions about the data:

• Independence:  Data points are independent and not influenced by others.
• Random Sampling:  Data represents a random sample from the population.
• Homogeneity of Measurement:  Measurements are consistent across all data points.

What is Non-Parametric Methods?

• Mann-Whitney U test:  Tests for the difference between the medians of two independent groups.
• Kruskal-Wallis test:  Tests for the difference between the medians of three or more groups.
• Spearman’s rank correlation:  Measures the strength and direction of the monotonic relationship between two variables.
• Wilcoxon signed-rank test:  Tests for the difference between the medians of two paired samples.
• K-Nearest Neighbors (KNN):  Classifies data points based on the k nearest neighbors.
• Decision Trees:  Makes classifications based on a series of yes/no questions about the features.
• Support Vector Machines (SVM):  Creates a decision boundary that maximizes the margin between different classes.
• Neural networks:  Can be designed with specific architectures to handle non-parametric data, such as convolutional neural networks for image data and recurrent neural networks for sequential data.

Advantages of Non-Parametric Methods

• Robust to outliers:  Non-parametric methods are not affected by outliers in the data, making them more reliable in situations where the data is noisy.
• Widely applicable:  Non-parametric methods can be used with a variety of data types, including ordinal, nominal, and continuous data.
• Easy to implement:  Non-parametric methods are often computationally simple and easy to implement, making them suitable for a wide range of users.

Diadvantages of Non-Parametric Methods

• Less powerful:  When the assumptions of parametric methods are met, non-parametric tests are generally less powerful, meaning they are less likely to detect a real effect when it exists.
• May require larger sample sizes:  Non-parametric tests may require larger sample sizes than parametric tests to achieve the same level of power.
• Less information about the population:  Non-parametric methods provide less information about the population parameters than parametric methods.

Applications of Non-Parametric Methods

Non-parametric methods are widely used in various fields, including:

• Medicine:  Comparing the effectiveness of different treatments.
• Psychology:  Investigating relationships between variables.
• Ecology:  Analyzing environmental data.
• Computer science:  Developing machine learning algorithms.

Difference Between Parametric and Non-Parametric

There are several Difference between Parametric and Non-Parametric Methods are as follows:

Parametric and non-parametric methods offer distinct advantages and limitations. Understanding these differences is crucial for selecting the most suitable method for a specific analysis. Choosing the appropriate method ensures valid and reliable inferences, enabling researchers to draw insightful conclusions from their data. As statistical analysis continues to evolve, both parametric and non-parametric methods will play crucial roles in advancing knowledge across various fields.

Frequently Asked Question(FAQs)

Q. what are non-parametric methods.

Non-parametric methods do not make any assumptions about the underlying distribution of the data. Instead, they rely on the data itself to determine the relationship between variables. These methods are more flexible than parametric methods but can be less powerful.

Q. What are parametric methods?

Parametric methods are statistical techniques that make assumptions about the underlying distribution of the data. These methods typically use a pre-defined functional form for the relationship between variables, such as a linear or exponential model.

Q. What is the difference between non-parametric method and distribution free method?

Non-Parametric methods: No assumptions about the underlying distribution’s parameters:  This includes the mean, variance, or even the shape (e.g., normal, skewed) of the distribution. Estimates parameters:  However, the number and nature of these parameters are flexible and not predetermined. Examples:  Chi-square tests, Wilcoxon signed-rank test

Q. What are some common Non Parametric Methods?

Some common Non Parametric Methods: Chi-square test Wilcoxon signed-rank test Mann-Whitney U test Spearman’s rank correlation coefficient

Please Login to comment...

Similar reads.

• Machine Learning

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

Parametric vs. Non-Parametric Tests and When to Use Them

The fundamentals of data science include computer science, statistics and math. It’s very easy to get caught up in the latest and greatest, most powerful algorithms —  convolutional neural nets, reinforcement learning, etc.

As an ML/health researcher and algorithm developer, I often employ these techniques. However, something I have seen rife in the data science community after having trained ~10 years as an electrical engineer is that if all you have is a hammer, everything looks like a nail. Suffice it to say that while many of these exciting algorithms have immense applicability, too often the statistical underpinnings of the data science community are overlooked. 

What is the Difference Between Parametric and Non-Parametric Tests?

A parametric test makes assumptions about a population’s parameters, and a non-parametric test does not assume anything about the underlying distribution.

I’ve been lucky enough to have had both undergraduate and graduate courses dedicated solely to statistics , in addition to growing up with a statistician for a mother. So this article will share some basic statistical tests and when/where to use them.

A parametric test makes assumptions about a population’s parameters:

• Normality  : Data in each group should be normally distributed.
• Independence  : Data in each group should be sampled randomly and independently.
• No outliers  : No extreme outliers in the data.
• Equal Variance  : Data in each group should have approximately equal variance.

If possible, we should use a parametric test. However, a non-parametric test (sometimes referred to as a distribution free test ) does not assume anything about the underlying distribution (for example, that the data comes from a normal (parametric distribution).

We can assess normality visually using a Q-Q (quantile-quantile) plot. In these plots, the observed data is plotted against the expected quantile of a normal distribution . A demo code in Python is seen here, where a random normal distribution has been created. If the data are normal, it will appear as a straight line.

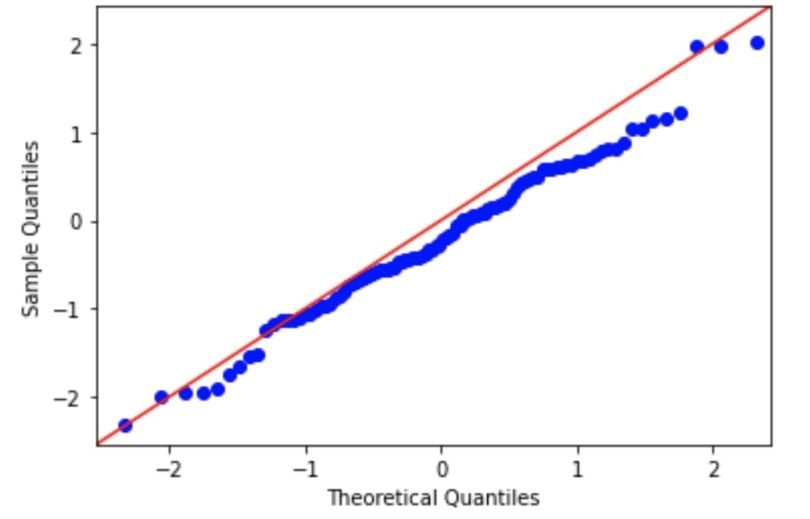
Read more about data science Random Forest Classifier: A Complete Guide to How It Works in Machine Learning

Tests to Check for Normality

• Shapiro-Wilk
• Kolmogorov-Smirnov

The null hypothesis of both of these tests is that the sample was sampled from a normal (or Gaussian) distribution. Therefore, if the p-value is significant, then the assumption of normality has been violated and the alternate hypothesis that the data must be non-normal is accepted as true.

Selecting the Right Test

You can refer to this table when dealing with interval level data for parametric and non-parametric tests.

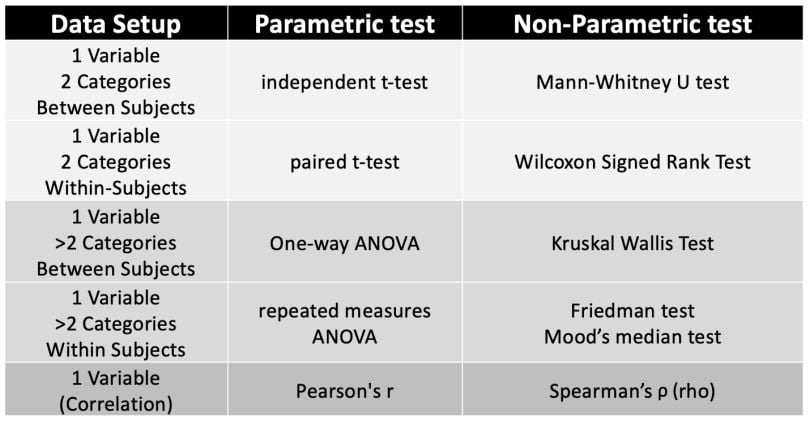
Read more about data science Statistical Tests: When to Use T-Test, Chi-Square and More

Advantages and Disadvantages

Non-parametric tests have several advantages, including:

• More statistical power when assumptions of parametric tests are violated.
• Assumption of normality does not apply.
• Small sample sizes are okay.
• They can be used for all data types, including ordinal, nominal and interval (continuous).
• Can be used with data that has outliers.

Disadvantages of non-parametric tests:

• Less powerful than parametric tests if assumptions haven’t been violated

[1] Kotz, S.; et al., eds. (2006), Encyclopedia of Statistical Sciences , Wiley.

[2] Lindstrom, D. (2010). Schaum’s Easy Outline of Statistics , Second Edition (Schaum’s Easy Outlines) 2nd Edition. McGraw-Hill Education

[3] Rumsey, D. J. (2003). Statistics for dummies, 18th edition  

Built In’s expert contributor network publishes thoughtful, solutions-oriented stories written by innovative tech professionals. It is the tech industry’s definitive destination for sharing compelling, first-person accounts of problem-solving on the road to innovation.

Great Companies Need Great People. That's Where We Come In.

What are statistics parametric tests and where to apply them?

This article will help you understand statistics parametric tests, their most common types, and also where and when to apply them.

Statistics parametric tests are a type of statistical analysis used to test hypotheses about the population mean and variance. These tests are based on the assumption that the underlying data follows a normal distribution and have several key properties, including robustness, reliability, and the ability to detect subtle differences in the data.

Parametric tests are often used in a variety of different applications, including medical research, market research, and social sciences. In these fields, researchers may use parametric tests to determine the significance of changes in population means or variances, or to determine if a particular treatment or intervention has had a significant impact on the data.

Most common types of statistics parametric tests

The t-test .

One of the most commonly used parametric tests is the t-test, which is used to compare the means of two populations. The t-test assumes that the underlying data is normally distributed and that the variances of the two populations are equal. The test statistic is calculated using the difference in the means of the two populations, divided by the standard error of the difference.

Another common parametric test is the analysis of variance (ANOVA), which is used to compare the means of three or more populations. The ANOVA test assumes that the underlying data is normally distributed and that the variances of all populations are equal. The test statistic is calculated using the ratio of the variance between the populations to the variance within the populations.

Other parametric tests

In addition to the t-test and ANOVA, there are several other statistics parametric tests that are used in different applications, including the paired t-test, the one-way ANOVA, the two-way ANOVA, the repeated measures ANOVA, and the mixed-design ANOVA. Each of these tests has different assumptions and test statistics, and is used to address different types of research questions.

One of the key benefits of parametric tests is that they are robust, meaning that they are not sensitive to the shape of the underlying data distribution. As long as the data is approximately normally distributed, parametric tests can provide accurate results.

Create amazing infographics in minutes

Mind the Graph is the perfect tool to bring your data together and present them visually. Use charts, tables and scientific illustrations to make your work easier to understand.

The reliability of statistics parametric tests

Another benefit of parametric tests is their reliability, as they are based on well-established statistical methods and assumptions. The results of parametric tests are highly repeatable and can be used to make valid inferences about the underlying population.

Despite their many benefits, parametric tests are not always the best choice for every data set. In some cases, the underlying data may not be normally distributed, or the variances of the populations may not be equal. In these cases, non-parametric tests may be more appropriate.

Parametric tests vs. Nonparametric tests

Non-parametric tests are a type of statistical analysis that do not make any assumptions about the underlying data distribution. Instead, they rely on the rank of the data to determine the significance of the results. Some common non-parametric tests include the Wilcoxon rank-sum test , the Kruskal-Wallis test , and the Mann-Whitney test .

When choosing between parametric and non-parametric tests, it is important to consider the nature of the data and the research question being addressed. In general, parametric tests are appropriate for data that is normally distributed and has equal variances, while non-parametric tests are appropriate for data that does not meet these assumptions.

Example of a statistics parametric test

Suppose a researcher is interested in testing whether there is a difference in the mean height of two groups of children – Group A and Group B. To do this, the researcher randomly selects 20 children from each group and measures their heights.

The researcher wants to know if the mean height of children in Group A is different from the mean height of children in Group B. To test this hypothesis, the researcher can use a two-sample t-test. The t-test assumes that the underlying data is normally distributed and that the variances of the two groups are equal.

The researcher calculates the mean height for each group and finds that the mean height for Group A is 150 cm and the mean height for Group B is 155 cm. The researcher then calculates the standard deviation for each group and finds that the standard deviation for Group A is 5 cm and the standard deviation for Group B is 4 cm.

Next, the researcher calculates the t-statistic using the difference in the means of the two groups, divided by the standard error of the difference. If the t-statistic is larger than a critical value determined by the level of significance and degrees of freedom, the researcher can conclude that there is a significant difference in the mean height of children in Group A and Group B.

This example demonstrates how a two-sample t-test can be used to test a hypothesis about the difference in means of two groups. The t-test is a powerful and widely used parametric test that provides a robust and reliable way to test hypotheses about the population mean.

Powerful tools for analyzing data

In conclusion, parametric tests are a powerful tool for statistical analysis, providing robust and reliable results for a wide range of applications. However, it is important to choose the appropriate test based on the nature of the data and the research question being addressed. Whether using parametric or non-parametric tests, the goal of statistical analysis is always to make valid inferences about the underlying population and to draw meaningful conclusions from the data.

Nothing can beat a flawless visual piece that delivers a complex message

Having difficulty communicating a large quantity of information? Use infographics and illustrations to make your work more understandable and accessible. Mind the Graph is an excellent tool for researchers who want to make their work more effective by using visually attractive infographics. 

Subscribe to our newsletter

Exclusive high quality content about effective visual communication in science.

Unlock Your Creativity

Create infographics, presentations and other scientifically-accurate designs without hassle — absolutely free for 7 days!

About Fabricio Pamplona

Fabricio Pamplona is the founder of Mind the Graph - a tool used by over 400K users in 60 countries. He has a Ph.D. and solid scientific background in Psychopharmacology and experience as a Guest Researcher at the Max Planck Institute of Psychiatry (Germany) and Researcher in D'Or Institute for Research and Education (IDOR, Brazil). Fabricio holds over 2500 citations in Google Scholar. He has 10 years of experience in small innovative businesses, with relevant experience in product design and innovation management. Connect with him on LinkedIn - Fabricio Pamplona .

Content tags

An official website of the United States government

The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

• Publications
• Account settings

Preview improvements coming to the PMC website in October 2024. Learn More or Try it out now .

• Advanced Search
• Journal List
• Invest Ophthalmol Vis Sci
• v.61(8); 2020 Jul

Parametric Statistical Inference for Comparing Means and Variances

Johannes ledolter.

1 Department of Business Analytics, Tippie College of Business, University of Iowa, Iowa City, Iowa, United States

2 Center for the Prevention and Treatment of Visual Loss, Iowa City VA Health Care System, Iowa City, Iowa, United States

Oliver W. Gramlich

3 Department of Ophthalmology and Visual Sciences, University of Iowa, Iowa City, Iowa, United States

Randy H. Kardon

Associated data.

The purpose of this tutorial is to provide visual scientists with various approaches for comparing two or more groups of data using parametric statistical tests, which require that the distribution of data within each group is normal (Gaussian). Non-parametric tests are used for inference when the sample data are not normally distributed or the sample is too small to assess its true distribution.

Methods are reviewed using retinal thickness, as measured by optical coherence tomography (OCT), as an example for comparing two or more group means. The following parametric statistical approaches are presented for different situations: two-sample t-test, Analysis of Variance (ANOVA), paired t-test, and the analysis of repeated measures data using a linear mixed-effects model approach.

Analyzing differences between means using various approaches is demonstrated, and follow-up procedures to analyze pairwise differences between means when there are more than two comparison groups are discussed. The assumption of equal variance between groups and methods to test for equal variances are examined. Examples of repeated measures analysis for right and left eyes on subjects, across spatial segments within the same eye (e.g. quadrants of each retina), and over time are given.

Conclusions

This tutorial outlines parametric inference tests for comparing means of two or more groups and discusses how to interpret the output from statistical software packages. Critical assumptions made by the tests and ways of checking these assumptions are discussed. Efficient study designs increase the likelihood of detecting differences between groups if such differences exist. Situations commonly encountered by vision scientists involve repeated measures from the same subject over time, measurements on both right and left eyes from the same subject, and measurements from different locations within the same eye. Repeated measurements are usually correlated, and the statistical analysis needs to account for the correlation. Doing this the right way helps to ensure rigor so that the results can be repeated and validated.

This tutorial deals with statistical parametric tests for inference, such as comparing the means of two or more groups. Parametric tests refer to those that make assumptions about the distribution of the data, most commonly assuming that observations follow normal (Gaussian) distributions or that observations can be mathematically transformed to a normal distribution (e.g., log transformation). Non-parametric tests are used for inference when the sample data are not normally distributed or the sample is too small to assess its true distribution and will be covered in a separate tutorial.

For this tutorial on parametric statistical inference, optical coherence tomography thickness measurements of the inner retinal layers recorded in eyes of control mice and mice with optic neuritis produced by experimental autoimmune encephalitis (EAE) serve as illustration. For brevity, we refer to the measured response as retinal thickness. We have explained the goals of this study in another tutorial on the display of data, 1 and they are summarized here. There are three treatment groups: control mice, diseased mice (EAE) with optic neuritis, and treated diseased mice (EAE + treatment). For the purpose of this tutorial, we consider only mice with measurements made on both eyes. This leaves us with 15, 12, and six subjects (mice) in the three groups, respectively. For the various statistical analyses in this tutorial, the variance ( s 2 ) is defined as the sum of the squared differences of each sample from their sample mean, which is then divided by the number of samples minus 1 (subtracting 1 corrects for the sample bias). The standard deviation is the square root of the variance. The software programs Prism 8 (GraphPad, San Diego, CA, USA) and Minitab (State College, PA, USA) were used to generate the graphs shown in this tutorial.

This tutorial analyzes the average inner retinal thickness of subjects by averaging the measurements on right and left eyes. It also analyzes the inner retinal thickness of eyes, but incorporates the correlation between right and left eye measurements on the same subject.

Analysis of the Average Retinal Thickness of Subjects After Combining Their Measurements on Right and Left Eyes

Comparing means of two treatment groups: two-sample t -test.

First we discuss whether there is a difference between the average retinal thickness of control and diseased mice after EAE-induced optic neuritis. We compare the two groups A = control and B = EAE. Measurements in these two groups are independent, as each group contains different mice. The two-sample t -test relates the difference of the sample means y ¯ A - y ¯ B to its estimated standard error, s e y ¯ A - y ¯ B = s A 2 n A + s B 2 n B . Here, n A , y ¯ A , s A and n B , y ¯ B , s B are the sample size, mean, and standard deviation for each of the two groups.

Under the null hypothesis of no difference between the two means, the ratio y ¯ A - y ¯ B s A 2 n A + s B 2 n B is well-approximated by a t -distribution, with its degrees of freedom [ ( s A 2 / n A ) + ( s B 2 / n B ) ] 2 ( s A 4 / n A 2 ( n A - 1 ) ) + ( s B 4 / n B 2 ( n B - 1 ) ) given from the Welch approximation. 2 Confidence intervals and probability values can be calculated. Small probability values (smaller than 0.05 or 0.10) indicate that the null hypothesis of no difference between the means can be rejected. Note that, although traditionally a probability of <0.05 has been considered significant, some groups favor an even more stringent criterion, but others feel that a less conservative criterion (e.g., P < 0.1) may still be meaningful, depending on the context of the study.

One can also use the standard error that uses the pooled standard deviation, s e y ¯ A - y ¯ B = s p o o l e d 1 n A + 1 n B = ( n A - 1 ) s A 2 + ( n B - 1 ) s B 2 n A + n B - 2 1 n A + 1 n B , and a t -distribution with n A − n B − 2 degrees of freedom. However, we prefer the first method, where the standard error of each group is calculated separately (not pooled), and the Welch approximation of the degrees of freedom, as it does not require that the two group variances be the same. The pooled version of the test assumes equal variances and can be misleading when they are not. 3 Both t -tests are robust to non-normality as long as the sample sizes are reasonably large (sample sizes of 30 or larger; robustness follows from the central limit effect).

The mean retinal thickness of the diseased mice (group B, EAE: mean = 59.81 µm; SD = 3.72 µm) is 6.40 microns smaller than that of the control group (group A, control: mean = 66.21 µm, SD = 3.39 µm). The P value (0.0001) shows that this difference is quite significant, leaving little doubt that the disease leads to thinning of the inner retinal layer ( Table 1 ).

Subject Average Retinal Thickness (in µm) for Control and Disease Groups: Two-Sample t -Test with Welch Correction Comparing Group A (Control) with Group B (EAE) *

Comparing Means of Two or More (Independent) Treatment Groups: One-Way ANOVA

The one-way analysis of variance can be used to compare two or more means. Assume that there are k groups (for our illustration, k = 3) with observations y ij for i = 1, 2, …, k and j = 1, 2, …, n i (number of observations in the i th group). The ANOVA table partitions the sum of squared deviations of the n = ∑ i = 1 k n i observations from their overall mean, y ¯ , into two components: the between-group (or treatment) sum of squares, S S B = ∑ i = 1 k n i ( y ¯ i - y ¯ ) 2 , expressing the variability of the group means y ¯ i from the overall mean y ¯ , and the within-group (or residual) sum of squares, S S W = ∑ i = 1 k { ∑ j = 1 n i ( y i j - y ¯ i ) 2 } = ∑ i = 1 k ( n i - 1 ) s i 2 , adding up all within-group variances, s i 2 . The ratio of the resulting mean squares (where mean squares are obtained by dividing sums of squares by their degrees of freedom), F = S S B / ( k - 1 ) S S W / ( n - k ) , serves as the statistic for testing the null hypothesis that all group means are equal. The probability value for testing this hypothesis can be obtained from the F -distribution. Small probability values (smaller than 0.05 or 0.10) indicate that the null hypothesis should be rejected.

The ANOVA assumes that all measurements are independent. This is the case here, as we have different subjects in the three groups. Note that independence could not be assumed if both right and left eyes were included, as right and left eye observations from the same subject are most likely correlated; we will discuss later how to handle this situation.

The ANOVA assumes that the variances of the treatment groups are the same. Its conclusions may be misleading if the variances are different. Box 3 showed that the F -test is sensitive to violations of the equal variance assumption, especially if the sample sizes in the groups are different. The F -test is less affected by unequal variances if the sample sizes are equal. Although the F -test assumes normality, it is robust to non-normality as long as the sample sizes are reasonably large (e.g., 30 samples per group).

For only two treatment groups, the ANOVA approach reduces to the two-sample t -test that uses the pooled variance. Earlier we had recommended the Welch approximation, which uses a different standard error calculation for the difference of two sample means, as it does not assume equal variances. Useful tests for the equality of variances are discussed later.

If the null hypothesis of equal group means is rejected when there are more than two treatment groups, then follow-up tests are needed to determine which of the treatment groups differ from the others using pairwise comparisons. For three groups, one calculates three pairwise (multiple) comparisons and three confidence intervals for each pairwise difference of two means. The significance level of individual pairwise tests needs to be adjusted for the number of comparisons being made. Under the null hypothesis of no treatment effects, we set the error that one or more of these multiple pairwise comparisons are falsely significant at a given significance level, such as α = 0.05. To achieve this, one must lengthen individual confidence intervals and increase individual probability values. This is exactly what the Tukey multiple comparison procedure 4 does ( Table 2 ,  Fig. 1 ). Many other multiple comparison procedures are available (Bonferroni, Scheffe, Sidak, Holm, Dunnett, Benjamini–Hochberg), but their discussion would go beyond this introduction. For a discussion of the general statistical theory of multiple comparisons, see Hsu. 5

Subject Average Retinal Thickness (in µm): One-Way ANOVA with Three Groups (Control, EAE, EAE + Treatment) and Tukey's Multiple Comparison Tests *

Subject average retinal thickness (in µm). Visualizations of results. ( A ) Plot of group means and their 95% confidence intervals. Confidence intervals are not adjusted for multiple comparisons. Analysis with Minitab. ( B ) Plot of pairwise differences and their Tukey-adjusted confidence intervals. Analysis with GraphPad Prism 8.

The ANOVA results in  Table 2 show that mean retinal thickness differs significantly across the three treatment groups ( P = 0.0001). Tukey pairwise comparisons show differences between the group means of thickness for control and EAE and for control and EAE + treatment. The means of EAE and EAE + treatment are not significantly different.

Comparing Variances of Two or More (Independent) Treatment Groups: Bartlett, Levine, and Brown–Forsythe Tests

As stated above, ANOVA testing assumes that the group variances are equal. How does one test for equal variances? Bartlett's test 6 (see Snedecor and Cochran 7 ) is employed for testing if two or more samples are from populations with equal variances. Equal variances across populations are referred to as homoscedasticity or homogeneity of variances. The Bartlett test compares each group variance with the pooled variance and is sensitive to departures from normality. The tests by Levene 8 and Brown and Forsythe 9 are good alternatives that are less sensitive to departures from normality. These tests make use of the results of a one-way ANOVA on the absolute value of the difference between measurements and their respective group mean (Levine test) or their group median (for the Brown–Forsythe test).

We apply these tests to the average retinal thickness data. We cannot reject the hypothesis that all three variances are the same, so we can be more confident in our interpretation of the ANOVA results, as the variances of the groups appear to be similar ( Table 3 ). If one of the tests shows unequal variance but the other test does not, then one needs to evaluate how significant the P value was in rejecting the null hypothesis of equal variance. If a fair amount of uncertainty remains, then alternative approaches are discussed in the next section.

Subject Average Thickness (in µm): Bartlett and Brown–Forsythe Tests for Equality of Group Variances *

Approaches to Take When Variances Are Different

A finding of unequal variances is not just a nuisance (because it puts into question the results from the ANOVA on means) but it also provides an opportunity to learn something more about the data. Discovering that particular groups have different variances gives valuable insights.

Transforming measurements usually helps to satisfy the requirement that variances are equal. Box and Cox 10 discussed transformations that stabilize the variability so that the variances in the groups are the same. A logarithmic transformation is indicated when the standard deviation in a group is proportional to the group mean; a square root transformation is indicated when the variance is proportional to the mean. Reciprocal transformations are useful if one studies the time from the onset of a disease (or of a treatment) to a certain failure event such as death or blindness. The reciprocal of time to death, which expresses the rate of dying, often stabilizes group variances. For details, see Box et al. 11

If one cannot find a variance-stabilizing transformation, one can proceed with the Welch approximation of pairwise two-sample comparisons. For nearly equal and moderately large sample sizes, the assumption of equal standard deviations is not a crucial assumption, and moderate violations of equal variances can be ignored. Another alternative would be to use nonparametric procedures (they are covered in a different tutorial).

Analysis of Retinal Thickness Using Both Right and Left Eye Measurements of Each Subject

Comparing means of two repeated measurements: paired t -test.

In the earlier two-sample comparison, different subjects were assigned to each of two treatment groups. Often it is more efficient to design the experiment such that a treatment (or induction of a disease phenotype, as in this example) is applied to the same subject. For our example, each mouse could be observed both under its initial healthy condition and after having been exposed to a multiple sclerosis phenotype EAE protocol. Measurements are then available on the same mouse under both conditions, and one can control for (remove) the subject effect that exists. A within-subject comparison of the effectiveness of a treatment or drug is subject to fewer interfering variables than a comparison across subjects. The same is true for the comparison of right and left eyes when both measurements come from the same subject and only one eye is treated, with the other eye acting as a within-subject control. The large subject effect that affects both eyes in a similar way can be removed, resulting in an increase of the precision of the comparison, potentially making it more sensitive to detecting an effect, if one exists.

The paired t -test considers treatment differences, d , on n different subjects and compares the sample mean ( d ¯ ) to its standard error, s e d ¯ = s d / n . Under the null hypothesis of no difference, the ratio (test statistic) d ¯ / s e d ¯ has a t -distribution with n – 1 degrees of freedom, and confidence intervals and probability values can be calculated. Small probability values (usually smaller than 0.05 or 0.10) would indicate that the null hypothesis should be rejected.

For illustration, we use the right eye (OD) and left eye (OS) retinal thickness measurements from the 15 mice of the control group. Figure 2 demonstrates considerable between-subject variability; the intercepts of the lines that connect measurements from the same subject differ considerably. Pairing the observations and working with changes on the same subject removes the subject variability and makes the analysis more precise.  Table 4 indicates that there is no difference in the average retinal thickness of right and left eyes. We had expected this result, as neither eye was treated. However, if one wanted to test a treatment that is given to just one eye without affecting the other, such a paired treatment comparison between the two eyes would be a desirable analysis plan.

Retinal Thickness (in µm) of OD and OS Eyes in the Control Group (15 Mice): Paired t -Test *

Retinal thickness (in µm) of OD and OS eyes in the control group (15 mice). OD and OS measurements from the same subject are connected. Analysis with Minitab.

Correlation Between Repeated Measurements on the Same Subject

The two-sample t -test in Table 1 and the ANOVA in Table 2 used subject averages of the thickness of the right and left eyes. Switching to eyes as the unit of observation, it is tempting to run the same tests with twice the number of observations in each group, as now each subject provides two observations. But, if eyes on the same subject are correlated (in our illustration with 33 subjects, the correlation between OD and OS retinal thickness is very large: r = 0.90), this amounts to “cheating,” as correlated observations carry less information than independent ones. By artificially inflating the number of observations and inappropriately reducing standard errors, the probability values appear more significant than they actually are.

Suppose that measurements on the right and left eye are perfectly correlated. Adding perfect replicates does not change the group means and the standard deviations that we obtained from the analysis of subject averages; however, with perfect replicates, the earlier standard error of the difference of the two group means gets divided by 2 , which increases the test statistic and makes the difference appear more significant than it actually is. The earlier ANOVA is equally affected. Adding replicates increases the between-group mean square by a factor of 2 but does not affect the within-group mean square, thus increasing the F -test statistic. This shows that a strategy of adding more and more perfect replicates to each observation makes even the smallest difference significant. One cannot ignore the correlation among measurements on the same subject! The following two sections show how this correlation can be incorporated into the analysis.

Analysis of Repeated Measures Data

Many studies involve repeated measurements on each subject. Here we have 15 healthy control mice, 12 diseased mice (EAE), and 6 treated diseased mice (EAE + treatment), and we have repeated measurements on each subject: measurements on the left and right eye. But, repeated measurements may also reflect measurements over time or across spatial segments (e.g., quadrants of each retina). The objective is to study the effects of the two factors, treatment and eye. Repeated measurements on the same subject can be expected to be dependent, as a subject that measures high on one eye tends to also measure high on the other. The correlation must be incorporated into the analysis. This makes the analysis different from that of a completely randomized two-factor experiment where all observations are assumed independent.

The model for data from such a repeated measures experiment represents the observation Y ijk on subject i in treatment group j and eye k according to

• • α is an intercept.
• • β j in this example represents (three) fixed differential treatment effects, with β 1 + β 2 + β 3 = 0. With this restriction, treatment effects are expressed as deviations from the average. An equivalent representation sets one of the three coefficients equal to zero, then the parameter of each included group represents the difference between the averages of the included group and the reference group for which the parameter has been omitted.
• • π i ( j ) represents random subject effects, represented by a normal distribution with mean 0 and variance σ π 2 . The subscript notation i ( j ) expresses the fact that subject i is nested within factor j ; that is, subject 1 in treatment group 1 is a different subject than subject 1 in treatment group 2. Each subject is observed under only a single treatment group. This is different from the “crossed” design where each subject is studied under all treatment groups.
• • γ k represents fixed eye (OD, OS) effects with coefficients adding to zero: γ 1 + γ 2 = 0.
• • βγ jk represents the interaction effects between the two fixed effects, treatment and eye, with row and column sums of the array βγ jk restricted to zero. There is no interaction when all βγ jk are zero; this makes effects easier to interpret, as the effects of one factor do not depend on the level of the other.
• • ε i ( j ) k represents random measurement errors, with a normal distribution, mean = 0, and variance = σ ɛ 2 . Measurement errors reflect the eye by subject (within treatment) interaction.

This model is known as a linear mixed-effects model as it involves fixed effects (here, treatment and eye and their interaction) and random effects (here, the subject effects and the measurement errors). Maximum likelihood or, preferably, restricted maximum likelihood methods are commonly used to obtain estimates of the fixed effects and the variances of the random effects; standard errors of the fixed effects can be calculated, as well. For detailed discussion, see Diggle et al. 12 and McCulloch et al. 13

Computer software for analyzing the data from such repeated measurement design is readily available. Minitab, SAS (SAS Institute, Cary, NC, USA), R (The R Foundation for Statistical Computing, Vienna, Austria), and GraphPad Prism all have tools for fitting the appropriate models. An important feature of these software packages is that they can handle missing data. It would be quite unusual if a study would not have any missing observations, and software that can handle only balanced datasets would be of little use. Without missing data (as is the case here), the computer output includes the repeated measures ANOVA table. The output from the mixed-effects analysis (which is used if observations are missing) is similar. Computer software also allows for very general correlation structure among repeated measures. The random subject representation discussed here implies compound symmetry with equal correlations among all repeated measures. With time as the repeated factor, other useful models include conditional autoregressive specifications that model the correlation of repeated measurements as a geometrically decreasing function of their time.

Results of the two-way repeated measures ANOVA for the thickness data are shown in  Table 5 . Estimates of the two error variances come into play differently when testing fixed effects. The variability between subjects is used when testing the treatment effect; the measurement (residual) variability is used in all tests that involve within-subject factors. See, for example, Winer. 14 These variabilities are estimated by the two mean square (MS) errors that are shown in  Table 5 with bold-face type.

Retinal Thickness (in µm) of OD and OS Eyes *

Shown is the GraphPad Prism8 ANOVA output of the two-factor repeated measures experiment with three treatment groups and the repeated factor eye. Sphericity assumes that variances of differences between all possible pairs of within-subject conditions are equal.

In  Table 5 , MS(Subject) = 23.45 is used to test the effect of treatment: F (Treatment) = 287.2/23.45 = 12.25. The treatment effect is significant at P = 0.0001. MS(Residual) = 2.192 is used in the test for subject effects and in tests of the main effect of eye and the eye × treatment interaction: F (Subject) = 23.45/2.192 = 10.70 (significant; P < 0.0001); F (Eye) = 1.351/2.192 = 0.6164 (not significant, P = 0.4385) and F (Eye × Treatment) = 0.298/2.192 = 0.1360 (not significant, P = 0.8734). In summary, the mean retinal thickness differs among the control, EAE, and EAE + treatment groups. Thickness varies widely among subjects, but difference in means between right and left eyes are not significant.

Assume that we ignore the correlation of repeated measures on the same subject and run a one-way ANOVA (with our three treatment groups) on individual eye measurements. The mean square error in that analysis is (1345.31 – 574.5)/(65 – 2) = 12.23, increasing the F -statistic to F = 287.2/12.23 = 23.47 which is highly significant. However, such incorrect analysis that does not account for the high correlation between measurements on right and left eyes leads to wrong probability values and wrong conclusions. It makes the treatment effect appear even more significant than it really is. In this example, the conclusions about the factors are not changed, but that is not true in general for all cases.

A standard two-way ANOVA on treatment (with three levels) and eye (with two levels) that does not account for repeated measurements also leads to incorrect results, as such analysis assumes that observations in the six groups are independent. This is not so, as observations in different groups come from the same subject.

More Complicated Repeated Measures Designs

Extensions of repeated measures designs are certainly possible. Here are two different illustrations for a potential third factor.

In the first model, the third factor is the (spatial) quadrant of the retina in which the measurement is taken. Measurements on the superior, inferior, nasal, and temporal quadrants are taken on each eye. The model includes random subject effects for the different mice in each of the three treatment groups (G1, G2, G3), with each mouse studied under all eight eye/quadrant combinations. The design layout is shown in  Table 6 .

Retinal Thickness (in µm) of OD and OS Eyes: MINITAB Output of the Repeated Measures Experiment with Three Factors: Treatment Group, Eye, and Quadrant *

The residual sum of squares pools the interaction sums of squares between subjects and the effects of eye, quadrant, and eye by quadrant interaction. The three-factor ANOVA in GraphPad Prism8 is quite limited (two of the three factors can only have two levels) and could not be used.

Data for the 15, 12, and six mice from the three treatment groups are analyzed. A total of 33 subjects × 8 regions (four quadrants for the right eye and four for the left eye) = 264 measurements is used to estimate this repeated measures model. Results are shown in  Table 6 . MS(Subject) = 93.80 is used for testing the treatment effect, F (Treatment) = 1148.93/93.80 = 12.25. MS(Residual) = 12.66 is used in all other tests (subject effects, main and interaction effects of eye and quadrant, and all of their interactions with treatment). Treatment and subject effects are highly significant, but all effects of eye and quadrant are insignificant, meaning that eyes and quadrants had no effect on retinal thickness.

In the second model, a third factor, type, represents two different genetic mouse strains. The experiment studies the effect of treatment on mice from either of two genetic strains (type 1 and type 2 below). Treatment and strain are crossed fixed effects, as every level of one factor is combined with every level of the other. Each mouse taken from one of the six groups has a measurement made at four different quadrants in one eye. This is a different repeated measures design, as now the mice are nested within the treatment–strain combinations. The design looks as follows:

The variability between subjects is used for testing main and interaction effects of treatment and strain. The measurement (residual) variability is used in the test for subject effects and the tests for the main effect of quadrant and its interactions with treatment and strain.

This tutorial outlines parametric inference tests for comparing means of two or more groups and how to interpret the output from statistical software packages. Critical assumptions made by the tests and ways of checking these assumptions are discussed.

Efficient study designs increase the likelihood of detecting differences among groups if such differences exist. Situations commonly encountered by vision scientists involve repeated measures from the same subject over time, on both right and left eyes from the same subject, and from different locations within the same eye. Repeated measures are usually correlated, and the statistical analysis must account for the correlation. Doing this the right way helps to ensure rigor so that the results can be repeated and validated with time. The data used in this review (in both Excel and Prism 8 format) are available in the Supplementary Materials.

Two Excel data files can be found under the Supplementary Materials: Supplementary Data S1 contains measurements on each eye as well as on each subject, whereas Supplementary Data S2 contains measurements for each quadrant of the retina. The two GraphPad Prism8 files under the Supplementary Materials illustrate the data analysis: Supplementary Material S3 on the analysis of subject averages, and Supplementary Material S4 on the analysis of individual eyes.

Supplementary Material

Acknowledgments.

Supported by a VA merit grant (C2978-R); by the Center for the Prevention and Treatment of Visual Loss, Iowa City VA Health Care Center (RR&D C9251-C, RX003002); and by an endowment from the Pomerantz Family Chair in Ophthalmology (RHK).

Disclosure: J. Ledolter , None; O.W. Gramlich , None; R.H. Kardon , None

What is Parametric Tests? Types: z-Test, t-Test, F-Test

• Post last modified: 3 September 2023
• Reading time: 9 mins read
• Post category: Research Methodology

What is Parametric Tests?

Parametric tests are statistical measures used in the analysis phase of research to draw inferences and conclusions to solve a research problem. There are various types of parametric tests, such as z-test, t-test and F-test. The selection of a particular test for research depends upon various factors, such as the type of population, sample size, Standard Deviation (SD) and variance of population. It is important for a researcher to identify the appropriate test to maintain the authenticity and validity of research results.

Table of Content

• 1 What is Parametric Tests?
• 2.1 Parametric Tests
• 2.2 Non-Parametric Tests
• 4 Assumptions of F-Test

Types of Hypothesis Tests

A hypothesis can be tested by using a large number of tests. Therefore, researchers have found it more convenient to categorise these tests on the basis of their similarities and differences. Hypothesis tests are divided into two types, as mentioned below:

Parametric Tests

In these tests, the researcher makes assumptions about the parameters of the population from which a sample is derived. An example of a parametric test is z-test.

Non-Parametric Tests

These are distribution-free tests of hypotheses. Here, the researcher does not make assumptions about the parameters of the population from which a sample is derived. An example of a non-parametric test is the Kruskal Wallis test.

Types of Parametric Tests

In parametric tests, researchers assume certain properties of the parent population from which samples are drawn. These assumptions include properties, such as the sample size, type of population, mean and variance of population and distribution of the variable. For example, t-test assumes that the variable under study in population is normally distributed.

Researchers calculate the parameters of population using various test statistics. Then, they test the hypothesis by comparing the calculated value of parameters with the benchmark value given in the problem. The scale used for dependent value in parametric tests is mostly the interval scale or ratio.

There are various types of parametric tests are:

This test is used to study the mean and proportion of samples having a sample size of more than 30. It involves comparison of means of two different and unrelated samples drawn from the same population whose variance in known. The z-value (test statistic) is calculated for the present data and compared with the z-value at that level of significance, which is decided earlier in the question/problem. After comparison, researcher may decide to reject or support null hypothesis.

The z-test is used in the following cases:

• To compare the mean of a sample with the mean of a hypothesised population when the sample size is large and the population variance is known
• To compare the significant difference between the means of two independent samples in the case of large samples or when the population variance is known
• To compare the proportion of a sample with the proportion of the population

This test is used to study the mean of samples when the sample size is less than 30 and/or the population variance is unknown. It is based on t-distribution. A t-distribution is a type of probability distribution that is appropriate for estimating the mean of a normally distributed population where the sample size is small and population variance is unknown.

The t-value (test statistic) is calculated for the present data and compared with the t-value at a specified level of significance for concerning degrees of freedom for accepting/rejecting the null hypothesis. The degree of freedom is calculated by subtracting one observation from the number of observations. It is used to check the t-value in the t-distribution table.

Sometimes, the t-test is used to compare the means of two related samples when the sample size is small and the population variance is unknown. In such a situation, it is known as the paired t-test.

This test is used to compare the ratio of variances of two samples under study. It involves comparing the ratio of two variances of two samples. The F-distribution is a right-skewed distribution that is used most common in Analysis of Variance (ANOVA). Here, the test statistic has an F-distribution. The F-value (test statistic) is calculated for the present data and compared with the F-value at that level of significance, which is decided earlier in the question/ problem.

In a F-test, these are two independent degrees of freedom in numerator and denominator respectively. The degrees of freedom (d.f.) of two samples are calculated separately by subtracting one from the number of observations. After that, the F-value is calculated from the F-distribution table.

Parametric tests are further divided into two parts – one-sample tests and two-sample tests. You will learn more about them in the next sections.

Assumptions of F-Test

F-distribution is usually asymmetric with minimum value of zero. However, the maximum value is infinity. Assumptions for using an F-test include:

• Both the samples come from normal distribution.
• Observations in each sample are selected randomly

F-statistic can never be negative as it is a ratio of two squared numbers. The degrees of freedom for different tests is calculated in different ways as follows:

Business Ethics

( Click on Topic to Read )

• What is Ethics?
• What is Business Ethics?
• Values, Norms, Beliefs and Standards in Business Ethics
• Indian Ethos in Management
• Ethical Issues in Marketing
• Ethical Issues in HRM
• Ethical Issues in IT
• Ethical Issues in Production and Operations Management
• Ethical Issues in Finance and Accounting
• What is Corporate Governance?
• What is Ownership Concentration?
• What is Ownership Composition?
• Types of Companies in India
• Internal Corporate Governance
• External Corporate Governance
• Corporate Governance in India
• What is Enterprise Risk Management (ERM)?
• What is Assessment of Risk?
• What is Risk Register?
• Risk Management Committee

Corporate social responsibility (CSR)

• Theories of CSR
• Arguments Against CSR
• Business Case for CSR
• Importance of CSR in India
• Drivers of Corporate Social Responsibility
• Developing a CSR Strategy
• Implement CSR Commitments
• CSR Marketplace
• CSR at Workplace
• Environmental CSR
• CSR with Communities and in Supply Chain
• Community Interventions
• CSR Monitoring
• CSR Reporting
• Voluntary Codes in CSR
• What is Corporate Ethics?

Lean Six Sigma

• What is Six Sigma?
• What is Lean Six Sigma?
• Value and Waste in Lean Six Sigma
• Six Sigma Team
• MAIC Six Sigma
• Six Sigma in Supply Chains
• What is Binomial, Poisson, Normal Distribution?
• What is Sigma Level?
• What is DMAIC in Six Sigma?
• What is DMADV in Six Sigma?
• Six Sigma Project Charter
• Project Decomposition in Six Sigma
• Critical to Quality (CTQ) Six Sigma
• Process Mapping Six Sigma
• Flowchart and SIPOC
• Gage Repeatability and Reproducibility
• Statistical Diagram
• Lean Techniques for Optimisation Flow
• Failure Modes and Effects Analysis (FMEA)
• What is Process Audits?
• Six Sigma Implementation at Ford
• IBM Uses Six Sigma to Drive Behaviour Change
• Research Methodology
• What is Research?
• What is Hypothesis?

Sampling Method

Research methods.

• Data Collection in Research
• Methods of Collecting Data
• Application of Business Research
• Levels of Measurement
• What is Sampling?
• Hypothesis Testing
• Research Report
• What is Management?
• Planning in Management
• Decision Making in Management
• What is Controlling?
• What is Coordination?
• What is Staffing?
• Organization Structure
• What is Departmentation?
• Span of Control
• What is Authority?
• Centralization vs Decentralization
• Organizing in Management
• Schools of Management Thought
• Classical Management Approach
• Is Management an Art or Science?
• Who is a Manager?

Operations Research

• What is Operations Research?
• Operation Research Models
• Linear Programming
• Linear Programming Graphic Solution
• Linear Programming Simplex Method
• Linear Programming Artificial Variable Technique
• Duality in Linear Programming
• Transportation Problem Initial Basic Feasible Solution
• Transportation Problem Finding Optimal Solution
• Project Network Analysis with Critical Path Method
• Project Network Analysis Methods
• Project Evaluation and Review Technique (PERT)
• Simulation in Operation Research
• Replacement Models in Operation Research

Operation Management

• What is Strategy?
• What is Operations Strategy?
• Operations Competitive Dimensions
• Operations Strategy Formulation Process
• What is Strategic Fit?
• Strategic Design Process
• Focused Operations Strategy
• Corporate Level Strategy
• Expansion Strategies
• Stability Strategies
• Retrenchment Strategies
• Competitive Advantage
• Strategic Choice and Strategic Alternatives
• What is Production Process?
• What is Process Technology?
• What is Process Improvement?
• Strategic Capacity Management
• Production and Logistics Strategy
• Taxonomy of Supply Chain Strategies
• Factors Considered in Supply Chain Planning
• Operational and Strategic Issues in Global Logistics
• Logistics Outsourcing Strategy
• What is Supply Chain Mapping?
• Supply Chain Process Restructuring
• Points of Differentiation
• Re-engineering Improvement in SCM
• What is Supply Chain Drivers?
• Supply Chain Operations Reference (SCOR) Model
• Customer Service and Cost Trade Off
• Internal and External Performance Measures
• Linking Supply Chain and Business Performance
• Netflix’s Niche Focused Strategy
• Disney and Pixar Merger
• Process Planning at Mcdonald’s

Service Operations Management

• What is Service?
• What is Service Operations Management?
• What is Service Design?
• Service Design Process
• Service Delivery
• What is Service Quality?
• Gap Model of Service Quality
• Juran Trilogy
• Service Performance Measurement
• Service Decoupling
• IT Service Operation
• Service Operations Management in Different Sector

Procurement Management

• What is Procurement Management?
• Procurement Negotiation
• Types of Requisition
• RFX in Procurement
• What is Purchasing Cycle?
• Vendor Managed Inventory
• Internal Conflict During Purchasing Operation
• Spend Analysis in Procurement
• Sourcing in Procurement
• Supplier Evaluation and Selection in Procurement
• Blacklisting of Suppliers in Procurement
• Total Cost of Ownership in Procurement
• Incoterms in Procurement
• Documents Used in International Procurement
• Transportation and Logistics Strategy
• What is Capital Equipment?
• Procurement Process of Capital Equipment
• Acquisition of Technology in Procurement
• What is E-Procurement?
• E-marketplace and Online Catalogues
• Fixed Price and Cost Reimbursement Contracts
• Contract Cancellation in Procurement
• Ethics in Procurement
• Legal Aspects of Procurement
• Global Sourcing in Procurement
• Intermediaries and Countertrade in Procurement

Strategic Management

• What is Strategic Management?
• What is Value Chain Analysis?
• Mission Statement
• Business Level Strategy
• What is SWOT Analysis?
• What is Competitive Advantage?
• What is Vision?
• What is Ansoff Matrix?
• Prahalad and Gary Hammel
• Strategic Management In Global Environment
• Competitor Analysis Framework
• Competitive Rivalry Analysis
• Competitive Dynamics
• What is Competitive Rivalry?
• Five Competitive Forces That Shape Strategy
• What is PESTLE Analysis?
• Fragmentation and Consolidation Of Industries
• What is Technology Life Cycle?
• What is Diversification Strategy?
• What is Corporate Restructuring Strategy?
• Resources and Capabilities of Organization
• Role of Leaders In Functional-Level Strategic Management
• Functional Structure In Functional Level Strategy Formulation
• Information And Control System
• What is Strategy Gap Analysis?
• Issues In Strategy Implementation
• Matrix Organizational Structure
• What is Strategic Management Process?

Supply Chain

• What is Supply Chain Management?
• Supply Chain Planning and Measuring Strategy Performance
• What is Warehousing?
• What is Packaging?
• What is Inventory Management?
• What is Material Handling?
• What is Order Picking?
• Receiving and Dispatch, Processes
• What is Warehouse Design?
• What is Warehousing Costs?

You Might Also Like

What is causal research advantages, disadvantages, how to perform, types of charts used in data analysis, what is questionnaire design characteristics, types, don’t, what is measure of central tendency, what is measurement scales, types, criteria and developing measurement tools, what is research types, purpose, characteristics, process, what is research problem components, identifying, formulating,, cross-sectional and longitudinal research, sampling process and characteristics of good sample design, what is hypothesis definition, meaning, characteristics, sources, leave a reply cancel reply.

You must be logged in to post a comment.

World's Best Online Courses at One Place

We’ve spent the time in finding, so you can spend your time in learning

Digital Marketing

Personal growth.

Development

Parametric Tests: Definition and Characteristics

Concept Building in Fisheries Data Analysis pp 59–80 Cite as

Basic Concept of Hypothesis Testing and Parametric Test

• Basant Kumar Das 7 ,
• Dharm Nath Jha 8 ,
• Sanjeev Kumar Sahu 9 ,
• Anil Kumar Yadav 10 ,
• Rohan Kumar Raman 11 &
• M. Kartikeyan 12  
• First Online: 12 October 2022

210 Accesses

Statistical analysis is done by many ways, but the majority of biologists use the ‘classical’ statistics which involves testing of null hypothesis using experimental data. In this process we estimate the probability that is obtained from the observed results or, something more extreme, if the null hypothesis is true. If the estimated probability (the p -value) is lesser than the significance value, we conclude that null hypothesis is unlikely true, and we reject the null hypothesis. So, hypothesis is defined as an assumption about a single population or about the relationship between two or more populations. It is testable and provides a possible explanation of a certain phenomenon or event. On the other hand, if a hypothesis is not testable, then it implies insufficient evidence to provide more than a tentative explanation, e.g. extinction of inland fishes. To test the new information or knowledge or belief about the populations against the existing one, two hypotheses are used, the null hypothesis ( H 0 ) and the alternative hypothesis ( H 1 ). Null hypothesis ( H 0 ) assumes that there is no difference between the new and existing populations. However there can be some indications that existing knowledge of beliefs may not be true. The null hypothesis ( H 0 ) is tested against the alternative hypothesis ( H 1 ). The alternative hypothesis states the statistical statement indicating the presence of an effect or a difference and sometimes known as ‘an intelligent guess’ based on limited information. It may so happen that the experimental results may match predictions, but it should be believed after proper testing and analysis of appropriate statistical tool(s), which includes designing an experiment or survey to generate or collect data/information (raw), exploratory data analysis and choosing an appropriate significance level or confidence limits (intervals).

Download chapter PDF

Importance of testing of hypothesis in fisheries

Concept of hypothesis testing for inference

One sample parametric test of significance

Two sample parametric test of significance

In the process of hypothesis testing, only null hypothesis is tested; based on the data outputs or results, it is either accepted or rejected, which is expressed as follows:

As the hypothesis is either accepted or rejected based on the numerical facts, only trustworthy data can be used for this purpose. Hypothesis testing therefore involves data collection using proper methods, compilation and securitization, use of appropriate tools for analysis and judicious decision, interpretation and explanation.

For an example, suppose a researcher is interested to conduct a study in which n samples of fishes are randomly selected from the fish population size N and their weight is measured. Now he/she is interested to test the mean weight of the fishes if 1000 g or not. The null and alternative hypothesis can be written as H 0 : μ = 1000 g and H 1 : μ ≠ 1000 g. Here null hypothesis shows that the mean weight of the population represented by the samples n is 1000 g, and the alternative hypothesis is that the mean of the population represented by the sample is not equal to 1000 g. In the above situation, the alternative hypothesis is non-directional, and it does not make a statement towards specific direction. The alternative hypothesis H 1 : μ ≠ 1000 g states only the fish population mean is not equal to 1000 g, but it does not state whether it will be less or greater than 1000 g. The directional alternative hypothesis can be represented in two directions (referred as one-tailed) H 1 : μ > 1000 g or H 1 : μ < 1000 g. The alternative hypothesis H 1 : μ > 1000 g states that the mean of the fish population represented by sample value is greater than 1000 g. If the directional alternative hypothesis H 1 : μ > 1000 g is employed, the null hypothesis can only be rejected if the data indicate that fish population mean is some value above 1000 g. The alternative hypothesis H 1 : μ < 1000 g states that

Note : In general, researcher selects the alternative hypothesis as non-directional when there is no expectation of the proposed research output and chooses directional alternative hypothesis if one have a definite expectation about output of the experiment. For non-directional alternative hypothesis, large effect or difference in sample data is obtained as compared to the directional alternative hypothesis.

4.1 Significance Level

The mean of the fish population represented by sample value is less than 1000 g. If the directional alternative hypothesis H 1 : μ < 1000 g is employed, the null hypothesis can only be rejected if the data indicate that fish population mean is some value less than 1000 g.

The term significance implies that the obtained results from an experiment(s) differ from the hypothesis due to chance or in reality. The decision on null hypothesis either to accept or reject is based on contrasting the observed outcome of an experiment with the outcome one can expect if, in fact, the null hypothesis is true. This decision is made by using the appropriate inferential statistical test. An inferential statistical test is designated as a test statistic which is evaluated in reference to a sampling distribution, which is a theoretical probability distribution of all the possible values the test statistic can assume if one were to conduct an infinite number of studies employing a sample size equal to that used in the study being evaluated. The probabilities in a sampling distribution are based on assumption that samples are randomly drawn from the representing population. Researcher’s decision to declare the difference is statistically significant is based on an analysis of sampling distribution of the test statistic. If the test statistic is found to be significant at the given level of significance, then the result is due to the effect of treatment in the experiment, not a chance. In relation to this, the most likely decision is to conclude that the difference is due to the experimental treatment and thus reject the null hypothesis. In general for scientific purpose, there should not be more than a 5% likelihood that the difference is due to chance. If one thinks that 5% is too high, one may choose to employ 1%, or an even lower minimum likelihood, before concluding that a difference is significant. If the p > 0 . 05 is observed which indicates that the result of an experiment is not significant. This notation indicates that there is greater than 5% likelihood that an observed difference or effect could be due to chance. On the other hand, the notation p < 0 . 05 indicates that the outcome of a study is significant at the 5% level. This indicates that there is less than a 5% likelihood that an obtained difference or effect can be due to chance. The notation p < 0 . 01 indicates a significant result at the 0 . 01 level (i.e. there is less than a 1% likelihood that the difference is due to chance). The value Z = 1 . 96 is referred to as the tabulated critical two-tailed 0 . 05 Z value. This value is employed since the total proportion of cases in the normal distribution that falls above Z = +1 . 96 or below Z = −1 . 96 is 0.05. The value Z = 2 . 58 is referred to as the tabled critical two-tailed Z value. This value is employed since the total proportion of cases in the normal distribution that falls above Z = +2 . 58 or below Z = −2 . 58 is 0.01. The value Z = 1 . 65 is referred to as the tabled critical one-tailed 0 . 05 Z value. This value is employed since the proportion of cases in the normal distribution that falls above Z = +1 . 65 or below Z = −1 . 65 in each tail of the distribution is 0.05. The value Z = 2 . 33 is referred to as the tabled critical one-tailed 0 . 01 Z value. This value is employed since the proportion of cases in the normal distribution that falls above Z = +2 . 33 or below Z = −2 . 33 in each tail of the distribution is 0.01. The probability value which identifies the level of significance is represented by the notation α which is the lowercase Greek letter alpha (Table 4.1 ).

4.2 Type of Errors

To design a research trial, a researcher has to make proper design or survey and to select suitable statistical tools while analysing data. Minimization of errors plays a crucial role. However, in reality errors occur quite often. In the framework of hypothesis testing, researcher commits two types of errors, Type I and Type II error. In Type I error, the null hypothesis is rejected when it is true (i.e. it is considered that false alternative hypothesis is true). The likelihood of committing a Type I error is specified by the α level when a researcher employs in evaluating an experiment. A Type II error occurs when a false null hypothesis is accepted (i.e. it is considered that a true alternative hypothesis is false). The likelihood of committing a Type II error is represented by β, which is the lowercase Greek letter beta. The likelihood of rejecting a false null hypothesis represents what is known as the power of a statistical test. Committing Type II error is more harmful than committing Type I error. So the test procedure is formulated in such a way that Type II error is minimized with fixed level of Type I error. This fixed level of Type I error is knows as level of significance ( α ). Table 4.2 shows the summary of the errors.

4.3 Power of Test

The power of a test is determined by subtracting the value of beta from 1 (i.e. power = 1 − β ). The likelihood of committing a Type II error is inversely related to the likelihood of committing a Type I error. In other words, as the likelihood of committing one type of error decreases, the likelihood of committing the other type of error increases. Thus, with respect to the alternative hypothesis one employs, there is a higher likelihood of committing a Type II error when alpha is set equal to 0.01 than when it is set equal to 0.05. The likelihood of committing a Type II error is also inversely related to the power of a statistical test. In other words, as the likelihood of committing a Type II error decreases, the power of the test increases. Consequently, the higher the alpha value (i.e. the higher the likelihood of committing a Type I error), the more powerful the test. In other words, the power of the test is the probability of making the right decision or detecting significant difference when it exists. Therefore, power analysis is important, especially when the results are non-significant. Power analysis can reveal whether the replication was adequate for any treatment to show its effects. A minimum of 80% (or β = 0.20) is considered acceptable statistical power (Searcy-Bernal 1994). The higher the value of power, the better the test.

Example 4.1: Illustration of type I and type II errors

The concept of Type I and Type II errors is illustrated here by a case study. An experimental trial was conducted to test the tilapia production of a new strain of tilapia in comparison to the local tilapia strain. A researcher states the null hypothesis and alternative hypothesis as H 0 : Local tilapia strain production = new tilapia strain production and as H 1 : new tilapia strain production >Local tilapia strain production. Now researcher ‘A’ (let) found that a new strain of tilapia gave higher production compared to the local strain (select alternative H 1 hypothesis) and recommended the farmers to grow a new one. But, researcher ‘B’ later used the same experimental protocols and did not actually find any statistical difference. In this situation researcher ‘A’ made a Type I error. In another trial with catfish, researcher ‘A’ did not see any difference between new and local strain and select null hypothesis that production of both strains is the same. But, later researcher ‘B’ found new strain could actually produce more and statistical difference was detected. Now researcher ‘A’ made a Type II error. Now by comparing the Type I error with Type II error, it was observed that Type I is more harmful than the Type II since in the case of tilapia, many farmers might have spent a lot to purchase the new strain as per recommendation to replace the existing stock and also change the existing practices and facilities, whereas in the case of catfish, farmers didn’t need to change anything—they just followed their existing protocols. This means that there was no additional cost involved. Although both of these errors are unwanted and should be avoided, the case of tilapia (Type I error) is more dangerous than the case of catfish (Type II error).

4.4 Confidence Level, Limits and Interval

The decision of hypothesis that either it is true or false is taken at a certain level of confidence. In statistical point of view, nothing is absolutely true or false that does not support 100% confidence. In social survey research, even 90% confidence level is enough, but in biological research 95% is considered as sufficient, but in medical research, confidence level is usually as high as 99%. Any mean (parameter in broad sense) has two confidence limits for the given level of confidence, i.e. lower confidence limit (LL) and the upper confidence limit (UL). The difference between these two is known as confidence interval (CI). The sample mean estimates the true mean, and standard error (SE) describes the variability of that estimation. The variability is expressed in terms of probabilities by calculating CIs.

Statistically, a confidence interval estimate of a parameter consists of an interval of numbers along with a probability that the interval contains the unknown parameter, and the level of confidence is a probability that represents the percentage of intervals that will contain if a large number of repeated samples are obtained. A 95% level of confidence means that if 100 confidence intervals were constructed, each based on a different sample from the same population, we would expect 95 of the intervals to contain the population mean. The three factors are needed to construct a confidence interval for the population mean (a) point estimate of population, (b) level of confidence and (c) standard deviation of the sample mean.

Suppose we obtain a simple random sample from a population. Provided that the population is normally distributed or the sample size is large, the distribution of the sample mean will be normal with mean ( μ ) and standard deviation \( \left(\upsigma /\sqrt{n}\right) \) , since here is normally distributed, we know that 95% sample means should lie within 1.96 standard deviations of the population mean μ and 2.5% will lie in each tail (see Fig. 4.1 ). Of all sample means, 95% are in the interval

and the probability of this interval is

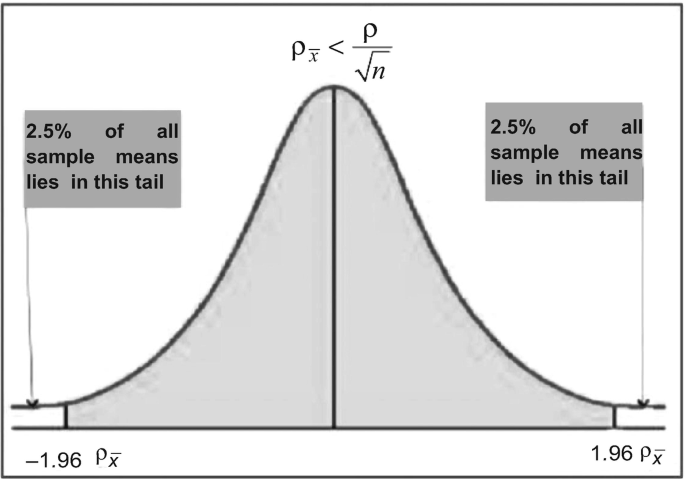
Normal plot with 95% confidence limit between −1 . 96 \( {\upsigma}_{\overline{x}} \) and 1 . 96 \( {\upsigma}_{\overline{x}} \)

4.4.1 Interpretation of Confidence Interval

A (1– α ) × 100% confidence interval means that if we obtain many simple random samples of size μ from the population mean, μ , which is unknown, then approximately (1– α ) × 100% of the intervals will contain μ. For constructing a (1– α ) × 100% confidence interval about l and o known, then the confidence limit is given by lower confidence limit (CL) as \( \overline{x}-{Z}_{\upalpha /2}\cdot \frac{\upsigma}{\sqrt{n}} \) and \( \overline{x}+{Z}_{\upalpha /2}\times \frac{\upsigma}{\sqrt{n}} \) upper limit (see Fig. 4.2 ). Here samples are drawn from the normal population.

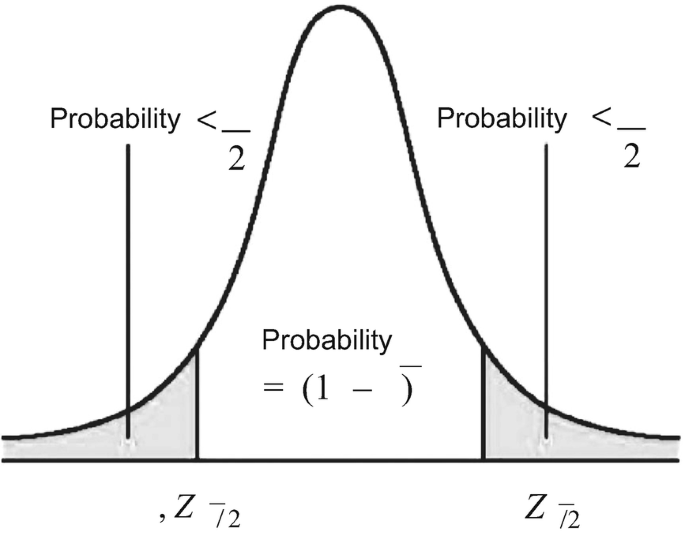
A generic (1– α ) × 100% confidence interval for the mean of a normally distributed population

Example 4.2

The following example shows that when the population variance is unknown, then using student’s t-statistic, we can compute 68%, 95% and 99% CIs. Suppose a sample of 40 fish was drawn from a pond containing 2,000 fish. If the computed mean is 500 g and standard deviation (SD) is 33 g, what are the LL and UL for 68%, 95% and 99% CIs?

For this, SE is computed as

The range mean ± 1 × SE covers 68% in the normal curve. Or by simply adding/subtracting 1 × SE to/from the mean, we can get the LL and UL for 68% CI:

To calculate the 95% and 99% CIs, SE has to be multiplied by t-statistics, which depend on the degree of freedom (df), before adding to or subtracting from the mean (the critical value for 39 df of the t-distribution): t-statistics for 95% CI = t (0 . 05 , 39) × SE for n –1 = 39 ; i.e. 2 . 023 × 5 . 16 = 10 . 43 g .

In this case, we can now say with 95% confidence that the true mean falls between these limits ( 489 . 56−510 . 43 ). Similarly, CI further increases as we want higher confidence, e.g. for 99%: t-statistics = mean ± (2 . 708 × 5 . 16) = 500 ± 13 . 97 g,

This above example shows that as CI increases, the confident level also increases. Wider range is necessary to be confident that the sample mean will fall within the range.

Statistical Significance and Biological Significance

Let us assume if a feed item vitamin C at 50 g kg −1 of feed is given to the fish and the survival is increased by 10%. This 10% survival that is claimed due to the use of vitamin C is substantial and has an economic value for farmers. However, an increase lower than this may be still statistically significant but may not be considered substantial.

4.5 Selection of Statistical Tools

The appropriate selection of statistical tools is necessary after carefully examining the conditions because even if the data have been generated perfectly and collected carefully, the misuse of statistical tools might result in wrong conclusions and provide bad recommendation. Researchers need to determine which distribution a particular data set follows: normal, binomial, Poisson or free of any distribution. The fundamental principle is that, if the data sets are normally distributed sample means, standard deviations represent the population but, if the data sets are distribution-free, then these parameters do not represent the population. Therefore, use of the mean values to represent and compare between/among them has no meaning. In such cases, non-parametric tests are used. These tests do not consider the actual figures and degree of deviations from central tendency but simply use ranks assigned to the data points. Whatever may be the tools selected for testing of hypothesis, the following objectives are set to perform any statistical test of significance:

State the null and alternative hypotheses.

Choose a level of significance and sample size n .

Determine the appropriate test statistic and sampling distribution.

Determine the critical values that divide the rejection and non-rejection regions.

Collect data and compute the value of the test statistic.

Make the statistical decision and state the conclusion.

4.5.1 One Sample Parametric Test

A test of significance allows us to draw conclusions or make decisions regarding population from sample data. When sample is drawn from single population to make inference on the population, we call it as a signal sample problem. Usually a population is characterized by some parameter. There are several parametric tests by which inference is made on the population parameter based on a random sample. In this section, we describe the most popular and widely used parametric test applied in one sample problem.

4.5.2 Large Sample Test of Significance for Population Parameter

For large (sample size), almost all the distributions can be approximated very closely by a normal distribution. Therefore the normal test of significance is used for large samples. If u is any statistic (function of sample values), then for large sample,

where E ( u ) = expectation of u and V ( u ) = variance of u and N (0, 1) = standard normal distribution, i.e. normal distribution with 0 mean and variance 1.

Thus if the discrepancy between the observed and the expected (hypothetical) values of a statistic is greater than Z α times the standard error (SE), the hypothesis is rejected at Z α level of significance. Similarly if

The deviation is not regarded significant at 5% level of significance. In other words, the deviation u − E( u ) could have arisen due to fluctuations of sampling, and the data do not provide any evidence against the null hypothesis which may therefore be accepted at a level of significance.

If | Z | ≤ 1 . 96, then the hypothesis H 0 is accepted at 5% level of significance. Thus the steps to be used in the normal test are as follows:

Compute the test statistic Z under H 0 .

If | Z | > 3, H 0 is always rejected.

If | Z | < 3, test its significance at certain level of significance. Table 4.3 provides some critical values of Z

Large Sample Test for Single Mean

A very important assumption underlying the tests of significance for variables is that the sample mean is asymptotically normally distributed even if the parent population from which the sample is drawn is not normal. If x i ( i = 1, 2, …, n ) is a random sample of size n from a normal population with mean μ and variance \( \frac{\upsigma^2}{n} \) the sample mean is distributed normally with mean μ and variance, i.e. \( \overline{x}\sim N\left(\upmu, \frac{\upsigma^2}{n}\right) \) . Thus to test the hypothesis, H 0 : μ = μ 0 against the alternative H 1 : μ ≠ μ 0 , the test statistic is as follows:

If σ 2 is unknown, then it is estimated by sample variance, i.e. σ 2 = s 2 (for large n ).

Example 4.3

A sample of 900 members has a mean of 3.4 cm and standard deviation (SD) 2.61 cm of certain attribute. Is the sample drawn from a large population of mean 3.25 cm?

Here a large sample has been drawn from the population with mean 3.25 cm. We set the null and alternative hypothesis as H 0 : μ = 3 . 25 and H 1 : μ ≠ 3 . 25 . The sample mean, \( \overline{x}=3.4\ cm \) , n = 900 , μ = 3 . 25 cm and σ = 2 . 61 .

So under H 0 ,

Since | Z | < 1 . 96 , we conclude that the data does not provide any evidence against the null hypothesis H 0 may therefore be accepted at 5% level of significance.

Large Sample Test for Single Proportion

Example 4.4

In a sample of 1000 people, 540 are fish eaters and the rest are meat eaters. Can we assume that both fish and meat are equally popular at 1% level of significance?

It is given that n = 1000 and x  =  the number of fish eaters  = 540 .

p = sample proportion of fish eaters \( =\frac{540}{100}=0.54 \)

P = Population proportion of fish eaters \( =\frac{1}{2}=0.50 \)

H 0 : Both fish and meat are equally popular, i.e. P = 0 . 50; H 1 : P ≠ 0 . 50

Since computed Z < 2 . 58 at 1% level of significance therefore fails to reject H 0 , we conclude that fish and meat are equally popular.

Small Sample Test of Significance for Single Mean

Suppose a random sample x 1 , …, x n of size ( n > 2) has been drawn from a normal population whose variance s 2 is unknown. On the basis of this random sample, the aim is to test

Test statistic \( =\frac{\overline{x}-{\upmu}_0}{\frac{s}{\sqrt{n}}}\sim {t}_{n-1} \) , where

The computed value of t is compared with the tabulated value at 5 or 1% levels of significance and at ( n − 1) degrees of freedom, and accordingly the null hypothesis is accepted or rejected.

Example 4.5

A farmer has stocked some quantity of seed of rohu ( Labeo rohita ) in a pond for its production. After 1 year he wants to know whether fishes have attained the weight of 800 g (as said by researched) or not? He wants to keep DO (dissolved oxygen) level more than 5 ppm during the period in his pond for proper growth. He collects water sample monthly to monitor the DO in the pond. After 1 year he caught 20 fishes as sample using a gill net to measure the weight of fishes. Weight of fishes and value of DO are given in Table 4.4 .

Solution for DO: Here the hypotheses to be tested are H 0 : mean DO is equal to 5 ppm against H 1 : mean DO is less than 5 ppm. Here,

\( \overline{x}=5.44 \) ; n = 12; μ 0 = 5; SD = 1 . 14.

The value of the t-statistic is

Table value of t at 5% level and 11 degree of freedom is 2.2009. Since calculated t-value is less than tabulated t-value, hence based on sample we fail to reject H 0 .

Therefore we can say that DO level in the pond during the year was almost 5 ppm or more.

Solution for weight : The hypotheses are H 0 : the mean weight of captured fish is equal to 800 g, i.e. μ = 800, and H 1 : the mean weight of captured fish is not equal to 800 g, i.e. H 0 ≠ 800. Here, sample mean = \( \overline{x}=812.8 \) ; n = 20; SD = 107.45.

Under H 0 ,

Table value of t at 5% level and 19 degree of freedom is 2.093. Since calculated t- value is less than tabulated t- value, hence based on sample we fail to reject H 0 . Therefore, we can say that weight of rohu in the pond after 1 year was almost 800 g.

4.5.3 Parametric Test of Significance Based on Two Samples

Suppose we want to evaluate the effect of supplementary stocking on the fish yield of floodplain wetlands (beels) of Assam. This could be evaluated in two different ways: (1) In a planned experiment, we select a group of subjects (i.e. beels) and record their fish yield. Then they must be subjected to supplementary stocking through in situ raising of fingerlings in pens for a period, after which we record their yield again. We compare the yield before and after the adoption of technology. (2) In a sample survey, we consider two groups of beels: one group of beels not practising supplementary stocking regularly and another group of beels practising. We compare the yield of the beels in the two groups. These two approaches illustrate the two main techniques of comparing the two sets of data. This section delineates three parametric tests of significance based on two samples, that is, paired t-test , unpaired t-test for means and F-test for equality of variances.

Paired t-Test for Comparing Two Dependent Samples

The paired sample t-test , sometimes called the dependent sample t-test , is a statistical procedure used to determine whether the mean difference between two sets of observations is zero. In a paired sample t-test , each subject or entity is measured twice, resulting in pairs of observations. Common applications of the paired sample t-test include case-control studies or repeated-measures designs. Suppose you are interested in evaluating the effectiveness of fish stock enhancement through adoption of pen aquaculture. One approach you might consider would be to record the fish yield of a sample of beels before and after adoption of technology and analyse the differences using a paired sample t-test .

Assumptions for Paired t-Test

In a paired sample t-test , the observations are defined as the differences between two sets of values, and each assumption refers to these differences, not the original data values. The paired sample t-test has four main assumptions:

The dependent variable must be continuous.

The observations are independent of one another.

The dependent variable should be approximately normally distributed.

The dependent variable should not contain any outliers.

H 0 : The true mean difference ( μ d ) is equal to zero, that is, μ d = 0.

H 1 : The true mean difference ( μ d ) is not equal to zero.

That is, μ d ≠ 0 (two-tailed) or μ d > 0 (right-tailed) or μ d < 0 (left-tailed).

Test Statistic

Let n be the size of each of the two samples and d i , i = 1, 2, …, n the difference between the corresponding members of the sample. Let \( \overline{d} \) denote the mean of differences and the SD standard deviation of these differences. The test statistic is given by

where, \( \overline{d}=\frac{1}{n}{\sum}_{i=1}^n{d}_i,{S}_d=\sqrt{\frac{\Sigma {\left({d}_i-\overline{d}\right)}^2}{n-1}} \)

Test Criterion : Null hypothesis ( H 0 ) is rejected at level α if t calculated > t ( n –1) .

Example 4.6

A study was conducted to determine if there is a significant effect of adoption of fish stock enhancement through pen aquaculture technology on fish yield of beels of Assam. MS Excel snip shown below represents yield of 22 beels of Assam before and after the adoption of technology. The normality test for the differences was examined by q-q plot and Shapiro–Wilk test statistic ( W = 0 . 961, p = 0 . 501). The p-value is not significant, and we conclude that differences ( di’s ) follow normal distribution. Therefore, we can apply paired t-test .

Step 1: State the null and research hypotheses.

H 0 : The mean yield of beels before and after the adoption of technology is the same, that is, μ 1 = μ 2 .

H 1 : The mean yield of beels before and after the adoption of technology is different, that is, μ 1 ≠ μ 2 .

Step 2: Compute the test statistic.

SPSS software has been used for analysing the above data. Feed the following data from Excel to SPSS. Go to Analyze → Compare Means → Paired Samples TTest.

Send variables after and before to the Variable 1 and Variable 2 under Paired Variables box by clicking the small arrow button. Finally, click OK. SPSS output obtained is shown in Table 4.5 and Figs. 4.3 , 4.4 , and 4.5 :

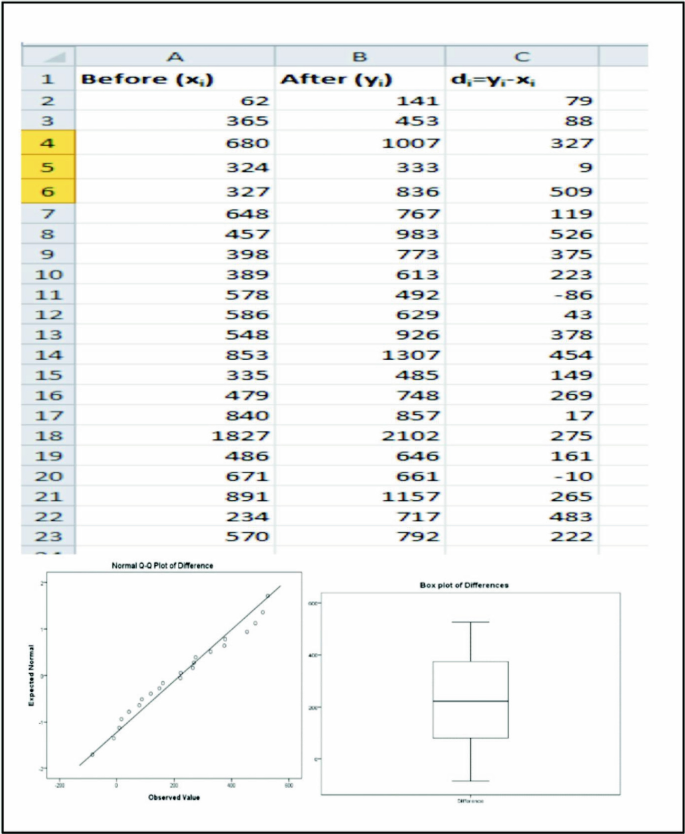
Screenshot results of paired t-test in SPSS package

Screenshot of paired t-test in SPSS package

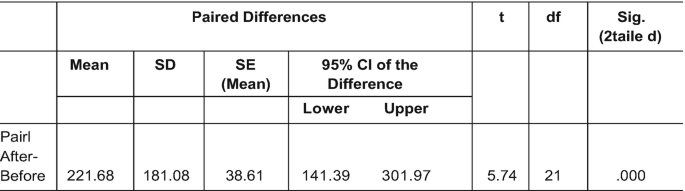
Step 3: Statistical decision.

Here, the calculated p-value of the statistic is 0.001 which is lower than the observed p-value (0 . 05). Hence, it is highly significant, and we reject the null hypothesis and conclude that there is significant difference in the yield of beels.

Step 4: Interpret the result.

The paired t-test was highly significant ( t = 5 . 742 , df = 21 , p = 0 . 001). We rejected the null hypothesis, suggesting that the fish mean yield of beels was significantly higher after (792.1 ± 394.1 kg/ha) intervention than that of before intervention (570.4 ± 348.1 kg/ha). The data shows that mean yield increased by 38.9% after intervention.

4.5.4 t-Test for Testing of Difference Between Two Means of Uncorrelated Observations

The independent sample student’s t- test (also known as Welch two sample test) consists of comparing two mean values of continuous-level (interval/ratio data), normally distributed data. It requires that samples are independent, of equal variance and normally distributed. It tells us whether the difference we see between the two independent samples is a true difference or whether it is just a random effect caused by skewed sampling. The Shapiro–Wilk test may be employed to check for normality prior to performing the comparison; Fisher’s F-test will help checking for equal variances and Levene’s test for equality of error variances.

Let \( \overline{x} \) and s 1 be the mean and standard deviation of a sample of size n 1 from a normal population with mean μ 1 and \( {\upsigma}_1^2 \) variance, and let \( \overline{y} \) and s 2 be the mean and standard deviation of another sample of size n 2 from a normal population with mean μ 2 and variance \( {\upsigma}_2^2 \) . We assume that \( {\upsigma}_1^2={\upsigma}_2^2={\upsigma}^2 \) . We want to test whether the population means differ significantly.

Hypothesis : H 0 : The mean difference is zero, that is, μ 1 = μ 2 . H 1 : The mean difference is significantly different from zero, that is, μ 1 ≠ μ 2 (two-tailed) or μ 1 > μ 2 (right tailed) or μ 1 ≤ μ 2 (left-tailed).

Test statistic : Under H 0 , the test statistic is given by

where \( \overline{x}=\frac{1}{n}{\sum}_{i=1}^n{x}_i,\overline{y}=\frac{1}{n}{\sum}_{i=1}^n{y}_i \) and \( S=\sqrt{\frac{\Sigma {\left(x-\overline{x}\right)}^2-{\left(y-\overline{y}\right)}^2}{n_1+{n}_2-2}} \)

Test criterion : Null hypothesis ( H 0 ) is rejected at the level α if \( {\mathrm{t}}_{\mathrm{calculated}}>{t}_{n_1+{n}_2-2} \) .

Example 4.7

In a wetland (beel) survey, the fish production (MT) of randomly selected beels was recorded as under. 1 stands for unstocked beels and 2 stands for stocked beels. Test whether there is significant difference in mean production of stocked and unstocked beels. Shapiro–Wilk test statistic ( W = 0 . 895 , p = 0 . 302) conducted for test of normality showed that data is normally distributed.

H 0 : In the general population, the mean production of stocked and unstocked beels is the same.

H 1 : In the general population, the mean production of stocked and unstocked beels is different.

Feed the data into SPSS as shown in Excel snip above.

Go to Analyse → Compare Means → Independent Samples T Test. Send variables production to the test variable(s) box by clicking the small arrow button. Click grouping variable. New window define groups open up. Enter 1 for Group 1 and 2 for Group 2. Click continue to return to independent samples T Test… window. Finally, click OK. SPSS output obtained is shown in Fig. 4.6 and Tables 4.6 , 4.7 , and 4.8 .

Screenshot of two sample t-test in SPSS package

Levene’s test for equality of variances shows that error variances are not equal. Here, the calculated p-value of the statistic is 0.03 (for both equal and unequal variances assumed) which is low than observed p- value (0.05). Hence, it is significant, and we reject the null hypothesis and conclude that there is significant difference between production of beels.

The independent sample t-test for unequal variances assumed was significant ( t = 2 . 55, df = 8, p = 0 . 03). We rejected the null hypothesis, suggesting that the production of stocked beels (2120 . 03 ± 921 . 3 MT) was significantly higher than unstocked beels (1153 . 8 ± 391 . 6 MT).

4.6 F-Test for Equality of Two Population Variances

F-test was first worked out by G.W. Snedecor. This test is referred to as variance ratio test. F-test is used to test whether two independent samples ( x i , i = 1, 2, . . . , n 1 ) and ( y j , j = 1, 2, . . . , n 2 ) have been drawn from the normal distributions with the same variance σ 2 . Alternatively, we can say that it is used to test whether the two independent estimates of the population variances are homogeneous. Let \( {s}_1^2 \) be the variance of a sample of size n 1 and \( {s}_2^2 \) be the variance of a sample of size n 2 .

H 0 : The population variances are equal \( {\upsigma}_1^2={\upsigma}_2^2={\upsigma}^2 \) .

H 1 : The population variances are not equal, that is, two-tailed or right-tailed or left-tailed.

Under H 0 , the test statistic is given by

where \( {S}_1^2=\frac{\sum {\left(x-\overline{x}\right)}^2}{\left({n}_1-1\right)} \) and \( {S}_2^2=\frac{\sum {\left(y-\overline{y}\right)}^2}{\left({n}_2-1\right)} \)

Note : The greater of the two variances is to be taken in the numerator.

Test Criterion

Null hypothesis is rejected at level α if \( {F}_{calculated}>{F}_{\left({n}_1-1\right),\left({n}_2-1\right)} \) .

Example 4.8

Data on daily fish landings recorded for 31 days in a landing centre showed variance of 60 kg 2 , whereas landings recorded for 25 days in another centre showed variance of 40 kg 2 . We want to test whether the variability of daily fish landings is the same in two landing centres.

H 0 : In the general population, there is no variability of daily fish landings in two landing centres.

H 1 : In the general population, there is a variability of daily fish landings in two landing centres.

The steps for computing the F-statistic is shown in the Excel snip given below (see Fig. 4.7 ).

Screenshot for F-test in excel

Step 3. Statistical decision.

The critical (tabulated) value for rejecting the null hypothesis is 1.94, and the obtained (calculated) value is 1.5. Here if the critical value is not less than or equal to the obtained value, we may accept the null hypothesis. This implies that there is no variability of daily fish landings in two landing centres.

The F-test was not significant ( F (19,24) = 1 . 5, p > 0 . 05). We may accept the null hypothesis and conclude that there is no variability of daily fish landings in two landing centres.

4.7 Conclusion

The researchers always make inferences on inland fisheries based on some representative sample data. This chapter provides a guideline on the basics of inferences by using a statistical test of significance. This chapter will help the reader to formulate the null and alternative hypothesis. The chapter guides the users to devise decision rule for accepting and rejecting the hypothesis along with the errors. The chapter describes only frequently used hypothesis testing. The example used will help the readers to devise their hypothesis formulation and their testing. The concept impregnated will help the readers in the prudent use of parametric tests, e.g. Z-test, t-test, paired t-test, χ 2 test, F-test, etc.

Further Reading

Anderson TW, Sclove SL (1974) Introductory statistical analysis. Houghton Mifflin Company, Boston

Google Scholar  

Bhujel RC (2008) Statistics for aquaculture, 1st edn. Wiley, Hoboken

Biradar RS (2002) Fisheries statistics, 2nd edn. Central Institute of Fisheries Education, Mumbai

Clarke GM, Cooke D (1998) A basic course in statistics. Arnold. Electronic Statistics Textbook. http://www.statsoftinc.com/textbook/stathome.html

Sheskin D (1997) Handbook of parametric and nonparametric statistical procedures. CRC Press, Boca Raton, p 719

Freund JE (2001) Modern elementary statistics. Prentice-Hall, Hoboken

Gupta SC, Kapoor VK (2006) Fundamentals of mathematical statistics. New Delhi, Sultan Chand & Sons, Educational Publishers

Johnson RA, Bhattacharyya GK (1992) Statistics: principles and methods, 2nd edn. Wiley, Hoboken

McDonald JH (2014) Handbook of biological statistics, 3rd edn. Sparky House Publishing, Baltimore

Mood AM, Graybill FA, Boes DC Introduction to the theory of statistics. Tata McGraw-Hill, New Delhi

Rohatgi VK, Saleh AK An introduction to probability and statistics. Wiley, New York

Roy AK, Sarangi N (2008) Applied bioinformatics, statistics & economics in fisheries research. New India Publishing Agency, New Delhi

Download references

Author information

Authors and affiliations.

ICAR, Central Inland Fisheries Research Institute, Barrackpore, West Bengal, India

Basant Kumar Das

Prayagraj Regional Centre, ICAR-CIFRI, Prayagraj, Uttar Pradesh, India

Dharm Nath Jha

Fisheries Resource Assessment & Informatics, ICAR-CIFRI, Barrackpore, West Bengal, India

Sanjeev Kumar Sahu

Guwahati Regional Centre, ICAR-CIFRI, Gowahati, Assam, India

Anil Kumar Yadav

Division of Socio Economics & Extension, ICAR Research Complex for Eastern Region, Patna, Bihar, India

Rohan Kumar Raman

Bengaluru Regional Centre, ICAR-CIFRI, Bangalore, Karnataka, India

M. Kartikeyan

You can also search for this author in PubMed   Google Scholar

A random sample of 30 fishes from a particular species showed an average length of 8.2 cm. Can you conclude that this has been drawn from a population with mean 8.1 cm and standard deviation 0.25 cm at 1% level of significance?

A total of 1250 fishes were taken at random from a pond, and their mean length was 9.95 cm with a standard deviation of 7.81 cm. Calculate an approximate 95% confidence interval for the mean length of the fishes.

In a particular water body, the long-term proportion of catla caught in the total catch is 51.46%. In a random sample of 5000 fishes caught from the same water body, the proportion of catla was 52.55%. Determine whether those two proportions differ significantly at 10% level or not.

The price of an aquarium fish feed at a national store is Rs. 179. A person has purchased the same feed at an online auction site for the following prices 155, 179, 175, 175 and 161 rupees. Determine (at 1% level of significance) whether the average price of the aquarium fish feed is than Rs. 179 if purchased at an online auction. Assume that the auction prices of fish feeds are normally distributed.

A group of 20 fishery graduate students were assessed by a test before and after a training programme. Their pre-test and post-test scores were recorded. The mean and standard deviation of the differences were 2.05 and 2.837, respectively. Assuming that the differences are normally distributed, can we conclude that the training improved the knowledge level of students.

A random sample of 15 fishes taken from a pond showed a mean length of 68.4 cm with a standard deviation of 16.47. A sample of 12 fishes taken from the same pond had a mean length of 83.42 cm and standard deviation of 17.63 cm. Can we conclude that there is no difference between the two means?

Failing to reject null hypothesis when it is false is

Type I error

Type II error

A ‘statistic’ is

A sample characteristic

A population characteristic

Normally distributed

What is ‘standard normal variate’?

What is the ‘power’ in hypothesis testing?

Rights and permissions

Reprints and permissions

Copyright information

© 2023 Narendra Publishing House

About this chapter

Cite this chapter.

Das, B.K., Jha, D.N., Sahu, S.K., Yadav, A.K., Raman, R.K., Kartikeyan, M. (2023). Basic Concept of Hypothesis Testing and Parametric Test. In: Concept Building in Fisheries Data Analysis. Springer, Singapore. https://doi.org/10.1007/978-981-19-4411-6_4

Download citation

DOI : https://doi.org/10.1007/978-981-19-4411-6_4

Published : 12 October 2022

Publisher Name : Springer, Singapore

Print ISBN : 978-981-19-4410-9

Online ISBN : 978-981-19-4411-6

eBook Packages : Biomedical and Life Sciences Biomedical and Life Sciences (R0)

Share this chapter

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Publish with us

Policies and ethics

• Find a journal
• Track your research

DSCI 551: Descriptive Statistics and Probability for Data Science

Lecture 2 parametric families.

September 11, 2019

2.1 Learning Objectives

• Identify probability as an expectation of a binary random variable.
• Calculate expectations of a linear combination of random variables.
• Match a physical process to a distribution family (Binomial, Geometric, Negative Binomial, Poisson, Bernoulli).
• Calculate probabilities, mean, and variance of a distribution belonging to a distribution family using either R or python.
• Distinguish between a family of distributions and a distribution.
• Identify whether a specification of parameters (such as mean and variance) is enough / too little / too much to specify a distribution from a family of distributions.

2.2 Properties of Distributions: Practice

Let’s practice some of the concepts from last time.

2.2.1 Demonstration: Example computation (8 min)

Let’s calculate the mean, variance, mode, and entropy of the following distribution (on the board).

2.2.2 Activity: Comparing Variance to Entropy (12 min)

True or false?

• Plot A has higher entropy than Plot B.
• Plot A has higher variance than Plot B.
• Plot C has the highest possible variance amongst distributions with support {0, 1, 2, 3}.
• Plot D has the highest possible entropy amongst distributions with support {0, 1, 2, 3}.

2.3 Expectations of Transformations

There are some properties of expectations that are particularly useful for some transformed random variables.

2.3.1 Linearity of Expectations (5 min)

Expectations can be calculated simply under linear transformations. If \(a\) is a constant and \(Y\) is another random variable, then:

• \(E[a X]=a E[X]\) (also true for standard deviation)
• \(E[X+Y]=E[X]+E[Y]\)

It does not mean \(E[XY]=E[X]E[Y]\) unless further assumptions are made; this is coming next week.

It also does not mean \(E(X^2)=E(X)^2\) , for instance.

Example 1 : The mean daily high temperature in Vancouver is 61 degrees Fahrenheit. What’s the mean temperature in Celcius? Remember, the conversion is \(C = 5/9(F − 32)\) .

Example 3 : You’ll see in DSCI 562 that sometimes it makes more sense to calculate the mean of a logarithm. Suppose \(E(\log(X)) = 1.5\) . Is it true that \(E(X) = \exp(1.5) \approx 4.48\) ?

2.3.2 Probability as an Expectation (3 min)

Machine learning techniques are typically built to calculate expectations. But what if you want to calculate a probability? Luckily, probability can be defined as an expectation! Specifically, if you want to find out the probability of some event \(A\) , this is simply the expectation of the following binary random variable: \[ X = \begin{cases} 0 \text{ if } A \text{ does not happen}, \\ 1 \text{ if } A \text{ does happen} \end{cases} \] That is, \[P(A) = E(X).\]

2.4 Distribution Families

So far in our discussion of distributions, we’ve been talking about properties of distributions in general. Again, this is important because a huge component of data science is in attempting to describe an uncertain outcome, like the number of ships that arrive to the port of Vancouver on a given day, or the identity of a rock.

There are some common processes that give rise to probability distributions having a very specific form, and these distributions are very useful in practice.

Let’s use the Binomial family of distributions as an example.

2.4.1 Binomial Distribution (8 min)

Process : Suppose you play a game, and win with probability \(p\) . Let \(X\) be the number of games you win after playing \(N\) games. \(X\) is said to have a Binomial distribution, written \(X \sim \text{Binomial} (N, p)\) .

Example : (Demonstration on the board) Let’s derive the probability of winning exactly two games out of three. That is, \(P(X=2)\) when \(N=3\) .

pmf : A binomial distribution is characterized by the following pmf: \[P(X=x) = {N \choose x} p^x (1-p)^{N-x}.\]

Remember, \(N \choose x\) is read as “N choose x”. You can think of it as the number of ways you can make a team of \(x\) people from a total of \(N\) people. You can calculate this in R with choose(N, x) , and its formula is \[{N \choose x} = \frac{N!}{x!(N-x)!}.\]

mean : \(Np\)

variance : \(Np(1-p)\)

Code : The pmf can be calculated in R with dbinom() ; in python, scipy.stats.binom .

Here is an example pmf for a Binomial(N = 5, p = 0.2) distribution:

2.4.2 Families vs. distributions (3 min)

Specifying a value for both \(p\) and \(N\) results in a unique Binomial distribution. For example, the Binomial(N = 5, p = 0.2) distribution is plotted above. It’s therefore helpful to remember that there are in fact many Binomial distributions (actually infinite), one for each choice of \(p\) and \(N\) . We refer to the entire set of probability distributions as the Binomial family of distributions.

This means that it doesn’t actually make sense to talk about “the” Binomial distribution! This is important to remember as we add on concepts throughout MDS, such as the maximum likelihood estimator that you’ll see in a future course.

2.4.3 Parameters (5 min)

True or false:

• For a distribution with possible values {0, 1, 2, 3, 4, 5}, five probabilities need to be specified in order to fully describe the distribution.
• For a Binomial distribution with \(N=5\) , five probabilities need to be specified in order to fully describe the distribution.

Knowing \(p\) and \(N\) is enough to know the entire distribution within the Binomial family. That is, no further information is needed – we know all \(N+1\) probabilities based on only two numbers! Since \(p\) and \(N\) fully specify a Binomial distribution, we call them parameters of the Binomial family, and we call the Binomial family a parametric family of distributions.

In general, a parameter is a variable whose specification narrows down the space of possible distributions (or to be even more general, the space of possible models).

2.4.4 Parameterization (8 min)

A Binomial distribution can be specified by knowing \(N\) and \(p\) , but there are other ways we can specify the distribution. For instance, specifying the mean and variance is enough to specify a Binomial distribution.

Demonstration: Which Binomial distribution has mean 2 and variance 1? (on the whiteboard)

Exactly which variables we decide to use to identify a distribution within a family is called the family’s parameterization . So, the Binomial distribution is usually parameterized according to \(N\) and \(p\) , but could also be parameterized in terms of the mean and variance. The “usual” parameterization of a distribution family is sometimes called the canonical parameterization.

In general, there are many ways in which a distribution family can be parameterized. The parameterization you use in practice will depend on the information you can more easily obtain.

2.4.5 Distribution Families in Practice

Why is it useful to know about distribution families?

In general when we’re modelling something, like river flow or next month’s net gains or the number of ships arriving at port tomorrow, you have the choice to make a distributional assumption or not. That is, do you want to declare the random variable of interest as belonging to a certain distribution family, or do you want to allow the random variable to have a fully general distribution? Both are good options depending on the scenario, and later in the program, we’ll explore the tradeoff with both options in more detail.

2.5 Common Distribution Families (12 min)

Aside from the Binomial family of distributions, there are many other families that come up in practice. Here are some of them. For a more complete list, check out Wikipedia’s list of probability distributions .

In practice, it’s rare to encounter situations that are exactly described by a distribution family, but distribution families still act as useful approximations.

Details about these distributions are specified abundantly online. My favourite resource is Wikipedia, which organizes a distribution family’s properties in a fairly consistent way – for example here is the page on the Binomial family. We won’t bother transcribing these details here, but instead focus on some highlights.

2.5.1 Geometric

Process : Suppose you play a game, and win with probability \(p\) . Let \(X\) be the number of attempts at playing the game before experiencing a win. Then \(X\) is said to have a Geometric distribution.

• Sometimes this family is defined so that \(X\) includes the winning attempt. The properties of the distribution differ, so be sure to be deliberate about which one you use.
• Since there’s only one parameter, this means that if you know the mean, you also know the variance!

Code : The pmf can be calculated in R with dgeom() ; in python, scipy.stats.geom .

2.5.2 Negative Binomial

Process : Suppose you play a game, and win with probability \(p\) . Let \(X\) be the number of attempts at playing the game before experiencing \(k\) wins. Then \(X\) is said to have a Negative Binomial distribution.

• Two parameters.
• The Geometric family results with \(k=1\) .

Code : The pmf can be calculated in R with dnb() ; in python, scipy.stats.nbinom .

2.5.3 Poisson

Process : Suppose customers independently arrive at a store at some average rate. The total number of customers having arrived after a pre-specified length of time follows a Poisson distribution, and can be parameterized by a single parameter, usually the mean \(\lambda\) .

A noteable property of this family is that the mean is equal to the variance.

Examples that are indicative of this process:

• The number of ships that arrive at the port of Vancouver in a given day.
• The number of emails you receive in a given day.

Code : The pmf can be calculated in R with dpois() ; in python, scipy.stats.poisson .

2.5.4 Bernoulli

• A random variable that is either \(1\) (with probability \(p\) ) or \(0\) (with probability \(1-p\) ).
• Parameterized by \(p\) .
• A special case of the Binomial family, with \(N=1\) .

Academia.edu no longer supports Internet Explorer.

To browse Academia.edu and the wider internet faster and more securely, please take a few seconds to  upgrade your browser .

Enter the email address you signed up with and we'll email you a reset link.

• We're Hiring!
• Help Center

APPLICATIONS AND LIMITATIONS OF PARAMETRIC TESTS IN HYPOTHESIS TESTING

The process of testing research hypothesis is important for researchers, academicians, statisticians, policy implementers among other users. It enables concerned individuals to deduce meaning as well as make decisions based on the outcomes of the tests (accepting or rejection of null hypothesis). A research hypothesis has been defined by statisticians who have also advanced various ways of testing a research hypothesis using statistical tests. The tests of hypothesis (tests of significance) include the parametric and non-parametric tests. The parametric tests are based on the assumption that the samples are drawn from a normal population and on interval scale measurement whereas non-parametric tests are based on nominal as well as ordinal data and it requires more observations than parametric tests. However, in this essay paper the parametric tests will be the centre of focus. In parametric tests, the common ones involves Normal (Z) tests, Student (t) tests, Fischer’s (F) tests, regression analysis, correlation analysis and the Chi-square (ᵡ2) test.

Related Papers

Dr. Ravindra Bhardwaj

siti nurhabibah hutagalung

The health sector data survey on data variables randomly for data greater than 100 was tested for several hypotheses with significant values. &gt;0.05, the effectiveness of using SPSS 17.00 and Microsoft Office on the feature settings used. The normality test on the data distribution is adjusted to the limit value for each test. The data input discrepancy is influenced by the significant value and the limit value. Hypothesis testing performs a comparison between the sample value and the proposed hypothesis value. The conclusions that can be drawn from hypothesis testing are rejecting the null hypothesis and failing to reject it. the value of = 0.05 (5%) for health/social research and = 0.01 (10%) for laboratory researc

Dr Yashpal D Netragaonkar

This article tries to explore the meaning of testing of hypothesis and find out its effect on research work. It aimed at to describe the process of different statistical test followed for the testing of hypothesis. Hypothesis is a most important tool of research. After formulation of hypo thesis the researcher g oes for its testing . For this purpose he goes step by step. First, he deduces its consequences, then conducts experiment or collect evidence to show that the consequences actually occur, and then tests, i.e., proves or disproves th e hypothesis by applying some statically test in case of experimental researcher us ing internal - external criticism, sa in case of historical research or critically analyzing the data in case of qualitative research.

International Research Journal of MMC

Dr. Lok Raj Sharma

This article provides a comprehensive overview of the most commonly used parametric tests, such as one sample t-test, dependent samples t-test, independent samples t-test, analysis of variance, and analysis of covariance. A parametric test is a statistical test that assumes the data being analyzed follows a certain probability distribution, typically a normal distribution. A statistical test is a procedure used in statistical analysis to make inferences about a population based on a sample of data. It covers the basics of statistical analysis, including the assumptions of parametric tests and how to check for these assumptions. It includes the access to use SPSS (Statistical Package for the Social Sciences) software to perform the tests, with detailed demonstration of outcomes and the ways of reporting them briefly. It is prepared on the basis of the secondary qualitative data garnered from journal articles, books, and web site materials. It is a valuable resource for researchers, s...

Joginder Kaur

This paper reviews the methods to select correct statistical tests for research projects or other investigations. Research is a scientific search on a particular topic including various steps in which formulating and testing of hypothesis is an important step. To test a hypothesis there are various tests like Student’s t-test, F test, Chi square test, ANOVA etc. and the conditions and methods to apply these tests are explained here. Only the correct use of these tests gives valid results about hypothesis testing.

International Journal of Research and Analytical Reviews

Anasuya Adhikari , Ramesh Chandra Mahato , Sourav Chandra Gorain , subir sen

The two testing in statistics are the Parametric and non-parametric techniques in inferential statistics. To define the probability distribution of variables and draw conclusions about the distribution's parameters, one uses a statistical technique known as parametric technique. Non-parametric approaches are used when the probability distribution cannot be defined. The present work deals with how the parametric test and non-parametric test can be used in educational research and the broad array of research area they produce.

Open Science Framework (OSF) Preprints

Loc Nguyen's Academic Network , Loc Nguyen

This report is the brief survey of nonparametric hypothesis testing. It includes four main sections about hypothesis testing, one additional section discussing goodness-of-fit and conclusion section. Sign test section gives an overview of nonparametric testing, which begins with the test on sample median without assumption of normal distribution. Signed-rank test section and rank-sum test section concern improvements of sign test. The prominence of signed-rank test is to be able to test sample mean based on the assumption about symmetric distribution. Rank-sum test discards the task of assigning and counting plus signs and so it is the most effective method among ranking test methods. Nonparametric ANOVA section discusses application of analysis of variance (ANOVA) in nonparametric model. ANOVA is useful to compare and evaluate various data samples at the same time. Nonparametric goodness-fit-test section, an additional section, focuses on different hypothesis, which measure the distribution similarity between two samples. It determines whether two samples have the same distribution without concerning how the form of distribution is. The last section is the conclusion. Note that in this report terms sample and data sample have the same meaning. A sample contains many data points. Each data point is also called an observation.

Xavier Gellynck

Often junior researchers face the challenge of inadequate knowledge and skills in statistical techniques because not all academic disciplines teach statistics. Although these researchers are supposed to conduct research as part of their academic award fulfilment, one wonders how to solve a given research problem statistically without introductory classes in the past. Thus, this article attempts to explain the primary scales of measurement for survey data. Furthermore, the paper differentiates between parametric and non-parametric test statistics by explaining distinctive statistical tests required for each type of measurement scale. A cross reference was used to synthesize relevant answers for the research question. As a topic of interest, frequently Journal reviewers and editors comment on the robustness of results based on the choice of measurement scale and the test statistics used. Therefore, the authors are motivated essentially to provide a comprehensive point of reference for...

BOHR Publishers

BOHR International Journal of Operations Management Research and Practices (BIJOMRP)

Many researchers and beginners in social research have several dilemmas and confusion in their mind about hypothesis statement and statistical testing of hypotheses. A distinction between the research hypothesis and statistical hypotheses, and understanding the limitations of the historically used null hypothesis statistical testing, is useful in clarifying these doubts. This article presents some data from the published research articles to support the view that the is format as well as the will format is appropriate to stating hypotheses. The article presents a social research framework to present the research hypothesis and statistical hypotheses is proper perspective.

Journal of emerging technologies and innovative research

Statistics is a branch of science that deals with the collection, organization, and analysis of data and drawing of inferences from the samples to the whole population. The subject Statistics is widely used in almost all fields like Biology, Botany, Commerce, Medicine, Education, Physics, Chemistry, Bio-Technology, Psychology, Zoology etc. While doing research in the above fields, the researchers should have some awareness in using the statistical tools which helps them in drawing rigorous and good conclusions. Major objectives of the present study was to know application of different statistical test in educational research, to identify basic statistical test used in educational research like t-test, z-test, ANOVA, MANOVA, ANCOVA, Chisquare test, Kolmogorov-Smirnov test, Mann-Whitney test, Wilcoxon signed rank sum test, Kruskal-Wallis test, Jonckheere test and Friedman test and to know the different statistical software used in educational research like Statistical Package for the ...

RELATED PAPERS

Wildlife Society Bulletin

Todd Fuller

Shehata E Abdel Raheem

Revista Conhecimento Online

The Science of Citizen Science

Marina Manzoni

Circular Economy and Sustainability

dorothee spuhler

billy nyagaya

John Channing

Nuntius Antiquus

Andressa De Sa Sousa

Eduardo Lozano Garcia

Epilepsy &amp; Behavior

Danielle Goldsmith

Physical Review D

Joanna Dzieńdziora

Juvenal Panesso Bermonth

Ger Bergkamp

Nasrullah Khan

Shadi Ansari

European Journal of Education Studies

Alhaji Alpha Kamara

Food Control

Aluck Thipayarat

Jack Parent

Jurnal Teknologi Rekayasa

Dede Irmayanti

Acta agriculturae Slovenica

Michael Okoth

Journal of Minimally Invasive Gynecology

Dra. Verónica Nicolalde

Covid-19 Litigation. The role of national and international courts in global health crises

Natalia Rueda

Journal of Agricultural and Food Chemistry

Elvis Leung

Advances in Science, Technology and Engineering Systems Journal

Sultana Parween

RELATED TOPICS

•   We're Hiring!
•   Help Center
• Find new research papers in:
• Health Sciences
• Earth Sciences
• Cognitive Science
• Mathematics
• Computer Science
• Academia ©2024

Parameter of a distribution

by Marco Taboga , PhD

A parameter of a distribution is a number or a vector of numbers describing some characteristic of that distribution.

Table of contents

Examples of scalar parameters

Examples of vector parameters, parametric families, mathematical definition of a parametric family, examples of parametric families, model parameters, difference between parametric family and statistical model, more details, keep reading the glossary.

Examples of distribution parameters are:

the expected value of a univariate probability distribution;

its standard deviation ;

its variance ;

one of its quantiles ;

one of its moments .

All of the above are scalar parameters, that is, single numbers. Instead, the following are examples of vector parameters:

the expected value of a multivariate probability distribution;

its covariance matrix (a matrix can be thought of as a vector whose entries have been written on multiple columns/rows);

a vector of cross-moments .

What does such a statement mean?

Some examples of parametric families are reported in the next table.

In statistical inference, we observe a sample of data and we make inferences about the probability distribution that generated the sample.

What we typically do is to set up a statistical model and carry out inferences (estimation, testing, etc.) about a model parameter.

What does it mean to set up a statistical model? It just means that we make some hypotheses about the probability distribution that generated the data, that is, we restrict our attention to a well-defined set of probability distributions (e.g., the set of all continuous distributions, the set of all multivariate normal distributions, the set of all distributions having finite mean and variance).

After setting up the model, we exploit the assumptions we have made to learn something about the distribution that generated the data.

For instance, if we have assumed that the data come from a normal distribution, we can use the observed data to estimate the distribution parameters (mean and variance) or to test the null hypothesis that one of them is equal to a specific value.

The concept of a statistical model is broader than the concept of a parametric family . They are both sets of probability distributions, but the members of a model need not be uniquely identified by a parameter.

For example, suppose that our model is the set of all distributions having finite mean, and the parameter of interest, which we want to estimate, is the mean.

Then, there are several distributions in the set having the same mean: the distributions are not uniquely identified by the parameter of interest.

Actually, there is no parameter (single number or finite-dimensional vector) that allows us to uniquely identify a member of the model.

In lecture entitled Statistical inference we define parameters, parametric families and inference in a formal manner.

You can also have a look at a related glossary entry: Parameter space .

Previous entry: Null hypothesis

Next entry: Parameter space

How to cite

Please cite as:

Taboga, Marco (2021). "Parameter of a distribution", Lectures on probability theory and mathematical statistics. Kindle Direct Publishing. Online appendix. https://www.statlect.com/glossary/parameter.

Most of the learning materials found on this website are now available in a traditional textbook format.

• Multinomial distribution
• Multivariate normal distribution
• Combinations
• Maximum likelihood
• Uniform distribution
• Gamma distribution
• Chi-square distribution
• Binomial distribution
• Mathematical tools
• Fundamentals of probability
• Probability distributions
• Asymptotic theory
• Fundamentals of statistics
• About Statlect
• Cookies, privacy and terms of use
• Probability density function
• Precision matrix
• Critical value
• Type II error
• Continuous mapping theorem
• To enhance your privacy,
• we removed the social buttons,
• but don't forget to share .

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

• View all journals
• My Account Login
• Explore content
• About the journal
• Publish with us
• Sign up for alerts
• Open access
• Published: 22 April 2024

Non-parametric quantile regression-based modelling of additive effects to solar irradiation in Southern Africa

• Amon Masache 1 ,
• Daniel Maposa 2   na1 ,
• Precious Mdlongwa 1   na1 &
• Caston Sigauke 3   na1  

Scientific Reports volume  14 , Article number:  9244 ( 2024 ) Cite this article

Metrics details

• Climate sciences
• Energy science and technology
• Mathematics and computing

Modelling of solar irradiation is paramount to renewable energy management. This warrants the inclusion of additive effects to predict solar irradiation. Modelling of additive effects to solar irradiation can improve the forecasting accuracy of prediction frameworks. To help develop the frameworks, this current study modelled the additive effects using non-parametric quantile regression (QR). The approach applies quantile splines to approximate non-parametric components when finding the best relationships between covariates and the response variable. However, some additive effects are perceived as linear. Thus, the study included the partial linearly additive quantile regression model (PLAQR) in the quest to find how best the additive effects can be modelled. As a result, a comparative investigation on the forecasting performances of the PLAQR, an additive quantile regression (AQR) model and the new quantile generalised additive model (QGAM) using out-of-sample and probabilistic forecasting metric evaluations was done. Forecasted density plots, Murphy diagrams and results from the Diebold–Mariano (DM) hypothesis test were also analysed. The density plot, the curves on the Murphy diagram and most metric scores computed for the QGAM were slightly better than for the PLAQR and AQR models. That is, even though the DM test indicates that the PLAQR and AQR models are less accurate than the QGAM, we could not conclude an outright greater forecasting performance of the QGAM than the PLAQR or AQR models. However, in situations of probabilistic forecasting metric preferences, each model can be prioritised to be applied to the metric where it performed slightly the best. The three models performed differently in different locations, but the location was not a significant factor in their performances. In contrast, forecasting horizon and sample size influenced model performance differently in the three additive models. The performance variations also depended on the metric being evaluated. Therefore, the study has established the best forecasting horizons and sample sizes for the different metrics. It was finally concluded that a 20% forecasting horizon and a minimum sample size of 10000 data points are ideal when modelling additive effects of solar irradiation using non-parametric QR.

Introduction

Literature reviews show that solar irradiation (SI) data in Southern Africa does not follow a normal distribution and sometimes contain outliers 1 , 2 , 3 , 4 . It is heavy-tailed to the right and platykurtic. These statistical characteristics can be attributed to the significant effects of heterogeneous meteorological features such as temperature and sunshine hours, which are characterised by rapidly fluctuating uncertainties and error distributions with infinite limits. Assuming linear effects only is an over-generalisation of SI behaviour. However, some covariates may have linear effects or even correlated, but deducing from their nature, they also have non-linear effects on SI without reasonable doubt. Thus, the structure of the relationship between SI and suspected covariates is not known. Consequently, modelling such data using parametric assumptions would not be significant and can lead to meaningless results. One of the most proper modelling approaches is non-parametric regression because here assumptions on parametric regression do not hold. Non-parametric regression is flexible, and robust and can be applied to qualitative data. Very few assumptions need to be valid and the response variable can be agnostic. After relaxing linearity assumptions, covariate effects are restricted to smooth and continuous functions. Therefore, non-parametric regression aims to have the best regression fitted function according to how the response is distributed 5 i.e. constructing a smooth curve as a geometric representation of the effects of the covariates on the response. A wide range of non-parametric approaches have been proposed to describe SI data. Still, the application of quantile regression (QR) has been found to outperform other methods in Southern Africa. Non-parametric estimation of families of conditional quantile functions models the full distribution of the response through conditional quantiles. Koenker 6 stipulated that quantile functional families expose systematic differences in dispersion, tail behaviour and other features concerning the covariates. QR generates the whole conditional distribution of all predicted values. Thus, a complete picture of how covariates affect the response at different quantile levels can be described. That is, QR is more generalised than conditional mean modelling 7 . Potentially different solutions at distinct quantiles can be interpreted as differences in the response to changes in covariates at various points in the conditional distribution. QR allows a more realistic interpretation of the sparsity of the covariates effects and it is naturally robust to outlier contamination associated with heavy-tailed errors 8 . However, in multivariate cases, QR lacks a description of the additive effects of the covariates. Instead, non-parametric QR additive models have been found to handle the curse of dimensionality quite well while retaining great flexibility 9 . Such additive models are flexible regression tools that manipulate linear as well as non-linear effects at the same time 10 . Reference 11 claimed that additive models provide programmatic approaches for nonparametric regression by restricting nonlinear covariate effects to be composed of low-dimensional additive pieces. The additive terms can be fixed, random or smooth effects. The modelling framework can be an application of non-parametric QR on additive effects or applying additive terms to non-parametric QR. The already existing modelling of SI lacks the application of non-parametric QR on additive effects to SI. Non-parametric quantile regression-based regression provides an attractive framework for parametric as well as nonparametric modelling of additive effects to the response characteristics beyond the conditional mean. The modelling of additive effects to SI using non-parametric QR may be better than the already existing additive modelling frameworks. Therefore, this current study explored non-parametric QR modelling frameworks when investigating additive effects on SI in Southern Africa.

Review of related literature

The earliest study according to the best of our knowledge to apply QR when modelling SI data from Southern Africa was done by 12 . They proposed a partial linearly additive quantile regression (PLAQR) to model data from the Tellerie radiometric station in South Africa. The modelling framework consists of a parametric linear component and a non-parametric additive component. This modelling structure may work effectively because some covariates are perceived to have linear effects on SI. The PLAQR model with pairwise hierarchical interactions outperformed both support vector regression (SVR) and stochastic gradient boosting models. We concur with the authors on the idea of including pairwise interaction effects because, in our yet-to-be-published paper, we discovered that a significant number of SI data sets from Southern Africa had covariates with significant multicollinearity. Although 2 did not apply QR in their study, their results also confirm that modelling SI with pairwise interactions included significantly improved forecasting model performances. Forecasts were further improved by extending the application of QR to combine forecasts through quantile regression averaging. Ranganai and Sigauke 13 modelled SI data from Cape Town, Pretoria and Ritchersveld used an additive quantile regression (AQR) model as a benchmark against three other SARIMA models. AQR modelling framework is an application of the additive modelling concept on QR introduced by 14 . Though SARIMA models are known to capture seasonal variations in any data more than any modelling framework, they were often outperformed by AQR on the metrics considered. The study demonstrated that whenever covariates to SI can be accessed then QR modelling is recommended because residual modelling is inferior. However, the authors recommended the application of the SARIMA models in cases of non-existent or scanty covariates. A separate study 15 demonstrated that AQR is also superior to extreme models in estimating extreme quantiles of SI data from Venda in South Africa except on the \(\tau = 0.9999\) quantile level. This shows that additive non-parametric QR is a very powerful modelling framework when forecasting the whole response distribution, and cyclical and seasonal variations in SI. A quantile generalised additive model (QGAM) is a new approach that was introduced by 16 where smooth effects estimated by a generalised additive model (GAM) are taken as inputs to a QR model. That is, performing QR on smooth function outputs from a GAM. The modelling framework is still very new in such a way that its literature is very limited. Among studies in Africa, we can only cite 17 who modelled the additive effects of fertility rate and birth rate on human live births. The QGAM was found to be a robust alternative to a GAM on most quantile levels although they had the same adjusted R-sqaure at the 50th quantile level. Recently, 18 studied spatially compounding climate extremes using QGAMs and they could predict the extremes more accurately than the conventional peak-over-threshold models. However, the outperformance was discovered in some regions, while it was inferior in other regions. This means that we can perceive that among other forecasting frameworks, QGAMs likewise perform differently in different geographical locations. QGAMs have not been used to forecast SI anywhere else except as a means of combining forecasts done by 1 , according to the best of our knowledge. However, the approach was inferior to other forecasts combining frameworks. As a result, it is not a good forecast combination method. We argue that the QGAM framework is better applied as a forecast-generating model rather than a forecast combination. It is a novel additive effect modelling in climate science applications and presents key advantages over residual modelling. QGAMs remove the need for direct identification and parameterisation since they model all quantiles of the distribution of interest. Thus, making use of all information available does not require any prior information about the relationships between the response variable and its covariates. Therefore, we propose to compare the predictive performance of QGAM against PLAQR and AQR using SI data from Southern Africa.

Contributions and research highlights

SI data is known to be skewed and plakurtic, and assumptions on parametric modelling do not hold well. As a result, non-parametric quantile regression, where normality assumptions are ignored can best model SI. Therefore, to the already existing work on QR modelling of SI data in Southern Africa, the main contribution of this study is to introduce the idea of predicting SI using a QGAM. In this modelling framework, a QR approach was applied to a generalised additive model. That is, hybridising a GAM with a QR model. This non-parametric modelling framework is new to SI data. Non-parametric QR-based models namely PLAQR and AQR have been used before to model SI in independent separate studies. However, they have not been compared in their forecasting performances. Although PLAQR and AQR were best in those separate studies, they have their weaknesses. As a result, the other contribution of this study is the comparison of predictive performances of the three non-parametric quantile regression-based models on different geographical locations. We perceive that probabilistic forecasting can be affected by the spatial distribution of data sources. Grid differences, location elevation, climatic conditions and their combinations may affect forecasting models. The last contribution of this study is to investigate separately how forecasting horizon and sample size affect the performance of the additive models. This helps identify the forecasting horizon up to which the QR-based models retain their predictive performances. It is generally perceived that the more data points we have the more a training model is effective. This is because more data points give more information to train. As a result, a supervised machine learning model like non-parametric QR-based can learn more about the data given. However, the question is, if the sample size is increased continuously then do QR-based models also continuously increase their performances? That is, we also established the smallest sample size that can be considered when training a non-parametric QR-based model.

In this research study, we applied Lasso via hierarchical interactions to select significant covariates and interaction effects from each location. We considered covariates recommended from our study that is still under review. PLAQR, AQR and QGAM models were trained on each set of locational selected covariates at all quantile levels. The residual mean square error (RMSE) validation metric was used to find the best quantile level for the three models. The best quantile level was then used for comparison investigations on the three models. Breusch–Godfrey and Box–Ljung tests were used to check on the assumption of residual serial autocorrelation. We also validated the models using the R-square as well as cross-validation correlations to check whether the models were overfitting the data or not. The accuracy of the additive models was compared using the mean absolute scaled error (MASE). MASE is one of the most appropriate accuracy metrics when the response has zero or near zero values. Since the main objective of QR is to minimise the pinball loss, then it became the priority performance evaluation metric in this study. Other probabilistic forecasting performance evaluation metrics namely the Winkler score, Coverage Probability (CP) and Continuous Rank Probability Score (CRPS) were used to compare the predictive performances of the models. The QGAM outperformed both the PLAQR and AQR models in most scenarios of forecasting performance evaluations. However, it was not superior at all when using the Winkler score. The performance evaluations were also done in different locations, increasing forecasting horizons and increasing sample sizes.

The study helps develop SI modelling frameworks that can be used to accurately forecast solar power. Accurate forecasts of solar power improve the stability of solar power generation and effective management of renewable resources. Exploration of multisite modelling captures variations in weather conditions in the region and allows the evaluation of data management systems at different ground-based radiometric stations. Evaluation of forecasting horizons and sample sizes helps inform the body of knowledge and the solar power generation industry of the forecasting horizons thresholds and minimum sample sizes to be considered when predicting solar irradiation.

Methodology

Non-parametric quantile regression concept.

The \(\tau \) th quantile is the minimiser of the expected loss \(\rho _{\tau }\) with respect to \(Q_{Y_i}(\tau |x_i)\) , where by definition

and F is the conditional cumulative distribution function (CDF) of Y . When approximating the quantile loss function (where y is the observation used for forecast evaluation and \(\tau _q\) is the q th quantile for \(q= 1,2,..., 99\) ) we obtain the quantile estimator

where \(g=\text{ inf }\left\{ y: \text{ F }(y|x)\ge \tau \right\} \) ,

\(\text{ F}_i\) should be continuous with continuous density \(f_i(\tau )=g(x_i,\beta (\tau ))\) uniformly bounded away from 0 and \(\infty \) at some points as a first regularity condition to the minimisation problem in Eq. ( 3 ). To ensure that the objective function of the problem has a unique minimum at \(\beta \) and is sufficiently smooth we consider the following assumptions from 11 .

there exist positive constants \(a_0\) and \(a_1\) such that,

and there also exist positive definite matrices \(\text{ M}_0\) and \(\text{ M}_1(\tau )\) such that:

\(\underbrace{{\text{ lim }}}_{n\rightarrow \infty }\frac{1}{n}\sum ^n_{i=1}{\dot{g}}_i{\dot{g}}^{T}_i=\text{ M}_0\) ,

\(\underbrace{{\text{ lim }}}_{n\rightarrow \infty }\frac{1}{n}\sum ^n_{i=1} f_i{\dot{g}}_i{\dot{g}}^{T}_i=\text{ M}_1(\tau )\) , and

\(\underbrace{{\text{ max }}}_{i=1,2, \ldots ,n} \frac{||{\dot{g}}_i||}{\sqrt{n}}\rightarrow 0, \)

where \({\dot{g}}=\frac{\partial g(x_i,\beta )}{\partial \beta }|_{\beta =\beta _0}.\)

A provision of uniform linear representation and convergence of the minimisation process is given by the following theorem.

Under the above assumptions 6

The minimiser of the problem in Eq. ( 3 ) by choice of a tuning parameter (or a penalty) satisfies the following :

The number of terms , \(n_-\) , with \(y_i<g(x_i,\beta )\) is bounded above by \(\tau n\) .

The number of terms , \(n_+\) , with \(y_i>g(x_i,\beta )\) is bounded above by \((1-\tau ) n\) .

For \(n\rightarrow \infty \) , the fraction \(\frac{n_-}{n}\) converges to \(\tau \) if Pr( y | x ) is completely continuous .

But Pr( y | x ) is not known, so it has been suggested by 19 to resort to minimising the regularised empirical risk

where \(R(f)=E_{\text{ Pr }(y|x)}[\rho _{\tau }(y-f(x))]\) is the empirical risk and \(||.||_H\) is the reproducing Kernel Hilbert space (RKHS) norm.

The minimiser of Eq . ( 6 ) when assuming that f contains an unregularised scalar term satisfies :

The number of terms , \(n_-\) , with \(y_i<f(x_i)\) is bounded above by \(\tau n\) .

The number of terms , \(n_+\) , with \(y_i>f(x_i)\) is bounded above by \((1-\tau ) n\) .

If ( x ,  y ) is drawn iid from a continuous distribution Pr( y | x ) and the expectation of the modulus of absolute continuity of its density satisfying the limit of \(E[\epsilon (\delta )]\) as \(\delta \rightarrow 0\) is equal to zero with probability one, then \(\frac{n_-}{n}\) converges to \(\tau \) asymptotically .

• Quantile splines

Now, the quantile function in Eq. ( 1 ) can be more generalised as

where m is much smaller than the covariate space dimension. The minimisation problem in Eq. ( 3 ) may involve additive models of the form

where \(\mu _{\tau }\) is an unknown constant and \(g_i\) is an additive term which is a function of a smooth function. We assume the quantile error term, \(e_{\tau }\) to be uncorrelated to include linear effects in all of the models when estimating the generalised quantile function. The additive form has easy interpretability and visualisation. Quite several local polynomial methods have been developed for estimating the additive models, but do not work well for QR applications. Instead, quantile smoothing has been traditionally done competitively between kernel and spline functions to model the non- linear effects. However, multicultural tendencies have weakened the competition with consideration of the two through penalty methods. Penalised quantile smoothing splines have been found to avoid the arbitrary choice of the number and positions of knots. That is, the non-parametric conditional quantile functions can now be estimated by solving the following problem:

where \(\textbf{S}\) is a Sobolev space of real-valued functions, \(x_i=(x_{i1},x_{i2}, \ldots ,x_{id},)\) is an element of d dimensional space of real numbers and P is the penalty term designed to control the roughness of the fitted function, \({\hat{g}}\) .

Now, any solution \({\hat{g}}\) must interpolate itself at the observed \(\left\{ x_i \right\} \) i.e. we have to find the smoothest interpolant of the points \(\left\{ (x_i,y_i),~i=1,2, \ldots ,n \right\} \) in the sense of solving

and the functions for which the infima are attained.

Let \(z_1,z_2, \ldots ,z_N~ (z_i \ne z_{i+1}, ~i=1,2, \ldots ,N-1)\) be given real fixed data, then for each \(t\in T_N\) set

where \(T_N=\left\{ t:t=(t_1,t_2, \ldots ,t_N),~0\le t_1\le t_2\le \ldots \le t_N \right\} \) and \(p\in (1,\infty )\) . Thus solving

\(\textbf{S}^d_p\) is the Sobolev space of real-valued functions with \(d-1\) absolutely continuous derivatives of which the d th derivative exist as a function in \(L_p[0,1]\) which means that

where \(a_i=\frac{g^{(d)}(0)}{i!},~i=0,1, \ldots ,d-1\) and \(h \equiv g^{(d)}\in L_p\) . If we assume the following facts;

\((z_i-z_{i-1})(z_{i+1}-z_i)<0,~i=1,2, \ldots ,N,\)

\(N>d\) and

\(t_1=0\) and \(t_N=1\) ,

then there exists a solution to the problem ( 11 ) \(g\in \textbf{S}^d_p\) which must be of a particular form and oscillate strictly between \((z_i)^N_1\) . This solution is a unique necessary and sufficient solution to problem ( 9 ).

Now, it means that solving the problem ( 10 ) is equivalent to solving

which can be shown that

is the unique solution to the problem, where \( B_{i,d}\) is a positive multiple of a B-spline of degree \(d-1\) with knots \(t_i,t_{i+1}, \ldots ,t_{i+d}\) . \(E_i=g[t_i,t_{i+1}, \ldots ,t_{i+d}]\) is obtained by applying the d th divided difference at the points \(t_i,t_{i+1}, \ldots ,t_{i+d}\) to \(g\in \textbf{S}^d_p(t,z)\) . This follows that

is a unique solution to the problem ( 10 ) when \((a_i)^{d-1}_0\) is uniquely determined so that \(g_p(t_i)=z_i,~i=1,2, \ldots ,d\) . Therefore,

Now, 20 expanded the original space of real functions to

and replaced the \(L_1\) penalty on the smooth effects with a total variation penalty on \(g'\) defined as \(V(g')=\int |g''(x)|dx\) to have the following theorem.

The function \(g\in W^2\) minimising

is a linear spline with knots at the points \(x_i,~i=1,2, \ldots ,d\) .

Therefore, we can deduce that \(g(x)=\sum ^n_{j=1}s_j(x)\) and the \(s_j's\) are the additive smooth effects. The smooth effects are defined in terms of spline basis as follows;

The first derivative of \(g~(g':R\rightarrow R)\) is continuous and if we denote \(\nabla ^2g(x)\) as a Hessian matrix of g and ||.|| as a Hilbert Schmidt norm for matrices then

That is, \(\lambda V(\nabla g)\) becomes the \(L_1\) form of the roughness penalty and is a linear spline.

Regression coefficients estimation

The estimation of regression coefficients heavily depends on how the additive effects are being modelled. When considering linear effects as well as additive effects a PLAQR model can be fitted while an AQR is fitted when considering a complete additive model. In our study, we propose fitting a QGAM which can be more efficient and accurate than an AQR.

Partial linearly additive quantile regression model

Notwithstanding that some of the covariates may have linear effects on SI then it is prudent to consider a non-parametric QR model that includes the linear effects. It may not be practical to assume that all covariates are non-linear. Such a model was introduced by 9 , which has a non-parametric component and an additive linear parametric component.

where \(\mu _{\tau }(t)\) is an unknown constant, \(x_{it}\in \textbf{X}_{m_1 \times 1}\) are continuous variables for \(i=1,2, \ldots ,m_1\) , \(s_{it,\tau }\in \textbf{S}\) are the smooth functions, \( {z_{jt}\in \textbf{Z}}_{m_2 \times 1}\) are the linear covariates for \(j=1,2, \ldots , m_2\) and \(e_{\tau }\) is the quantile error term such that

If we assume that \(\textbf{X}\) takes values in \(\chi \equiv [-1,1]^{m_1}\) and letting

then we can write the PLAQR model in matrix notation as follows.

where \(\textbf{X}=(x_{1t},(x_{2t}, \ldots ,x_{m_1t},)\in \chi .\) If we also let \(\lambda _i\) be a non-negative penalty then the quantile estimates of the PLAQR model can be found by minimising

where the \(\rho _{\tau }(u)=u(\tau -I(u<0))\) is the pinball loss function.

Additive quantile regression model

The AQR model proposed by 14 and algorithm further developed by 16 gives flexibility when modelling non-linear effects beyond the conditional mean. The non-parametric components are composed of low-dimensional additive quantile pieces. Thus, an application of additive modelling on QR. As a result, the Laplacean quantile fidelity replaces the Gaussian likelihood in conditional mean regression. \(L_1\) -norms replace \(L_2\) -norms as measures of roughness on fitted functions. A generic AQR model for non-linear and varying regression coefficient terms can be written as an extension of a linear predictor with a sum of nonlinear functions of continuous covariates 14 as follows:

Now, the following form of problem ( 9 ) is solved to estimate the continuous functions g and regression coefficients;

where the pinball loss function is defined as in PLAQR model fitting. Though the model can be estimated by linear programming algorithms as in linear QR, penalty methods are applied because the known selected basis functions can be included in the design matrices 14 . As a result, sparse algebra is the supplant basis expansion through either performance-oriented iteration for large data sets (PIRLS) or the Newton algorithm.

Quantile generalised additive model

Additive effects of the covariates are modelled by considering the smooth effects estimated by a GAM as inputs to a linear QR. That is, a conditional quantile is modelled as a sum of unknown smooth functions 18 . Fasiolo 21 developed a regression coefficient estimation process by introducing a learning rate \(\frac{1}{\sigma }>0\) and positive semidefinite matrices M to a penalised pinball loss as follows:

where \(\lambda _j\) are positive smoothing parameters. The learning rate determines the relative weight of the loss and penalty while the matrices penalise the wiggliness of the corresponding smoothing effect. The pinball loss function is replaced by a scaled pinball loss called the extended log-f (ELF) loss function;

The ordinary pinball loss function is piecewise linear and has discontinuous derivatives while the ELF loss leads to more accurate quantiles because it is an optimally smoothed version. Thus, it enables efficient model fitting through the use of smooth optimisation methods. Now, the regression coefficients being the solution to problem ( 26 ) are obtained as a vector of maximum a posteriori (MAP) estimator, \({\hat{\beta }}_{\tau }\) . A stable estimation can be done by exploiting orthogonal methods for solving least squares problems.

Performance evaluations

The main model forecasting performance evaluation metrics considered in this study are the pinball loss function, Winkler score, CP and CRPS. The pinball loss measures the sharpness of a QR model. It is a special case of an asymmetric piecewise linear loss function defined as follows:

where \({\hat{Q}}_{y_t}(q)\) is the predicted SI at the \(q^{th}\) quantile level and \(y_t\) is the actual SI.

CP runs numerous samples in which a wide range of possible outcomes is generated for each sample. Then, this range of possible outcomes can be compared to the actual value to see if they properly account for it in its range. That is, if, for example, a \(95\%\) prediction interval covers at least \(95\%\) of the observed then the model is reliable, well-calibrated or unbiased.

The Winkler score then becomes a trade-off between coverage and the prediction interval width (PIW). It is the length of the prediction interval plus a penalty if the observation is outside the interval. It is defined as,

where \([l_{\alpha ,t},u_{\alpha ,t}]\) is the \((100-\alpha )\%\) prediction interval at time t.

We evaluated how the models predicted the whole forecast distribution (rather than particular quantiles) by obtaining a CRPS by averaging quantile scores over all values of p . That is,

where \(\hat{F_{p}}\) is the predictive cumulative density function and 1 is an indicator.

Data analysis and results

Data sources.

Five among several other radiometric stations considered in this study are geographically located as shown in Fig. 1 and Table 1 . The stations were Namibia University of Science and Technology (NUST), University of Fort Hare (UFH), University of Kwazulu-Natal (UKZN) Howard College, University of Pretoria (UPR) and University of Venda (UNV). Data is uploaded from the stations by the Southern Africa Universities Radiometric Association Network (SAURAN) into their database and can be accessed through their website. The five stations shown in the map were the only ones that had consistent hourly data and manageable missing observations for the same period of March 2017 up to June 2019.

Map showing the geographic positions of the radiometric stations considered from Southern Africa: Source, 1 Edited.

Data exploration

Si distribution.

In this study, solar irradiation was measured as global horizontal irradiance (GHI). Distributions of GHI from the five locations had similar densities and Q–Q plots as those shown in Fig. 2 . The distribution exhibited in Fig. 2 shows the general curve of the density plots and pattern followed by the Q–Q plots. The two plots show that GHI does not follow a normal distribution. The data exhibited asymmetric distributions in all locations as shown by box plots in Fig. 3 . The box plots also show that GHI is skewed to the right-hand side and heavily tailed. A Jarque–Bera (JB) test was done on all locations to confirm the non-normality in the data. It is a goodness-of-fit test of whether sample data have the skewness and kurtosis matching a normal distribution. Among the most effective normality tests, the JB test is the most suitable test for large sample sizes. The parametric test presumes that the data originates from a particular distribution. Distributions of GHI from different locations were fitted in one of our studies 22 . Since all p-values were less than 0.05 (shown in Table 2 ) then the results confirmed that solar irradiation does not follow a normal distribution. The descriptive statistics in Table 2 also indicate that SI is positively skewed and platykurtic. These results are consistent with results from 22 and several other studies.

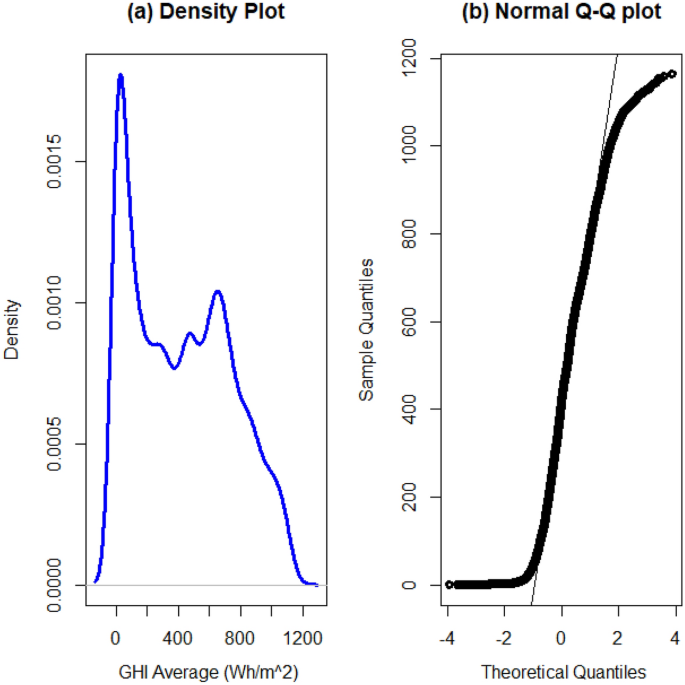
General pattern exhibited by the density and normal Q–Q plots constructed for GHI from Pretoria, Venda, Durban, Windhoek and Alice SI data sets.

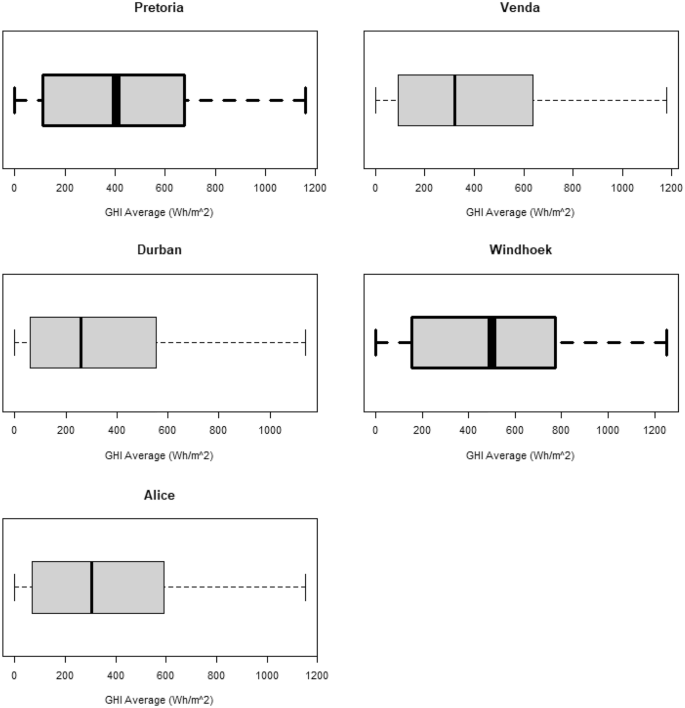
Box plots showing distributions of GHI from the five locations.

Variable selection

The following covariates; hour, temperature (Temp), relative humidity (RH), barometric pressure (BP), wind speed (WS) and wind direction (WD) were considered in this study. The descriptive statistics of the covariates are shown in Appendix A . One of the assumptions to hold valid when applying additive models to predict a response variable is that the covariates are stationary. As a result, the Kwiatkowski–Phillips–Schmidt–Shin (KPSS) test was done to check on the stationarity of the covariates. Among the most effective stationarity tests available the KPSS test is the most appropriate one for large samples. The KPSS test results in Table 3 indicate that all covariates were stationary except WD from Alice and WS from Durban (It does not matter to consider the stationarity of time, in this study time is measured in hours). On stationary covariates, the p-values were less than 0.05. That is, the null hypothesis that ‘The variable is not stationary’ was rejected and we conclude that there is enough evidence to support the assumption that the covariate is stationary. Non-stationary covariates were differenced to achieve stationarity. Lasso hierarchical pairwise interaction selections (using the ‘hierNet’ R package by 23 ) with Lag1 and Lag2 of GHI included to model trend in SI time series 12 . Hour, Temperature, RH, Lag1 and Lag2 had significant effects on GHI in all locations. However, BP had a significant effect on solar irradiance in Alice only while WD had a significant effect in Alice and Durban. WS was not significant in Alice and Venda.

Model validations

The best quantile level for each model was identified by comparing the root mean square error (RMSE) and \(\tau =0.5\) as the best quantile level for all models fitted at all locations. As a result, all models were trained and fitted at the 50th quantile level. The proposed QGAM was fitted using the ‘mgcViz’ package developed by 24 while the ‘plaqr‘ package by 25 and ‘quantreg‘ by 26 were used to fit the PLAQR and AQR models respectively. All three models were validated by checking whether the assumption of no residual serial autocorrelation was holding using the Breusch–Godfrey (BG) test and the Ljung Box test. The BG test requires the assumption of predeterminedness. The assumption was considered valid to proceed with the BG test because all covariates used were stationary. The Ljung Box requires the assumption of strict exogeneity. Since all covariates considered do not depend on solar irradiance but rather SI depends on meteorological features and the error terms of the models fitted. Both the BG test and the Ljung–Box test had p-values greater than 0.05 (Table 4 ) indicating that the null hypothesis, ’there is no residual serial autocorrelation’ could not be rejected. This meant that all models fitted had no serial autocorrelation of the errors.

While the Ljung Box test provides a suitably robust alternative when the distribution of the response variable is heavily tailed, the BG test is the most appropriate residual serial autocorrelation test in the presence of a lagged response. Therefore, all of the models were valid to fit all data sets used for training. In addition, all coefficients of determination were at least \(90\%\) . That is, more than \(90\%\) of the variations in the response were explained by the models. The very high R-square values indicate that all models learned the data very well and are very efficient in predicting solar irradiation. We note that QGAM had the highest R-square R-square values in bold) in all locations. The model explained variations in solar irradiation better than any of the models compared. Cross-validations results indicated that no model overfitted nor underfitted the data because the cross-validation correlations on the test data were all approximately equal to those on the training data (Table 4 ).

Forecasting results

General model performances.

All of Theil’s U statistics were less than one meaning that all models could fit the data better than corresponding naive models which could be fitted (Table 5 ). This means that all of the three non-parametric QR frameworks were suitable to model additive effects to SI. The QGAM model had the lowest AIC in all locations indicating that it fitted the data better than both the PLAQR and AQR models, though all of the AIC scores were approximately equal with regards to the locations. The RMSE values also confirm that the QGAM performed marginally the best in all locations because it had the lowest RMSE. However, the magnitudes of the RMSE scores were approximately the same.

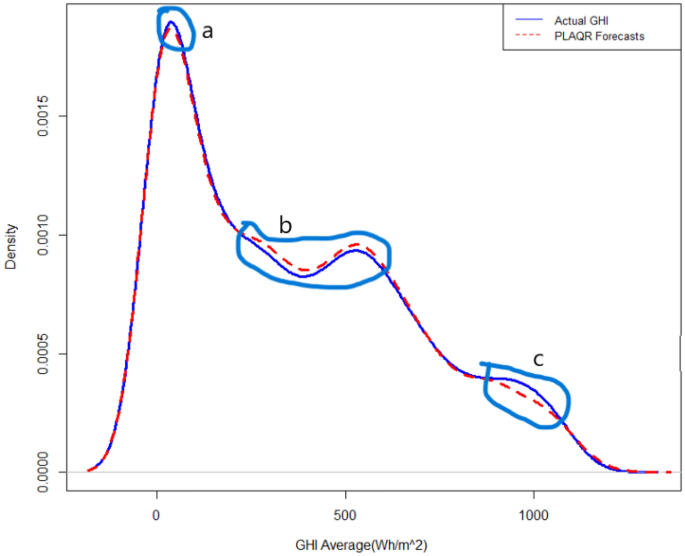
Forecasted density plot of GHI using the fitted PLAQR model.

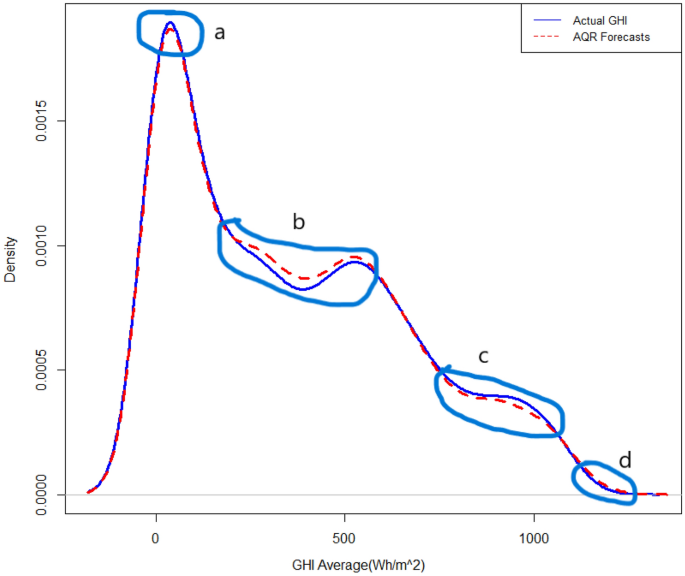
Forecasted density plot of GHI using the fitted AQR model.

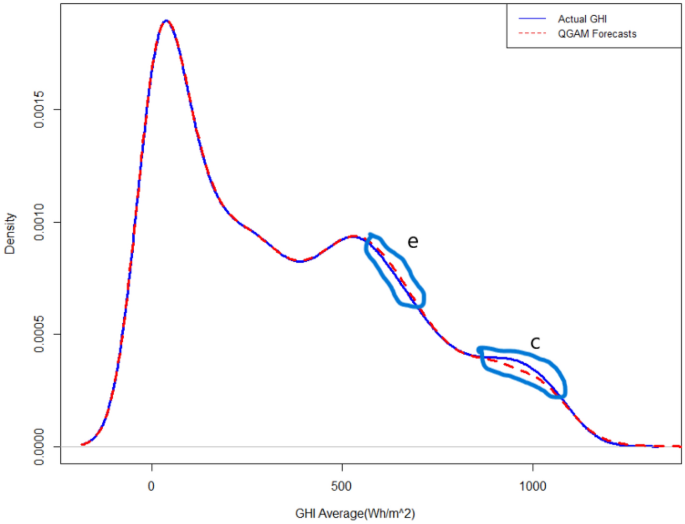
Forecasted density plot of GHI using the fitted QGAM model.

All mean absolute scaled error (MASE) scores were less than 1 meaning that all models performed better than a naïve benchmark. The MASE scores also demonstrate that QGAM predicted SI the most accurately by close margins because though the model had the lowest MASE in all locations the MASE scores were approximately equal. The MASE metric is one of the most appropriate metrics when the response has zero or near zero values like solar irradiation. The above three metric evaluations indicate that the three additive models have approximately the same out-of-sample forecasting performances. The forecasted density using the PLAQR is shown in Fig. 4 . The model underestimated slightly the SI density in part (a) and notable in part (c) of the density plot. There is also a notable overestimation of the forecasted density in part (b). On the other hand, the AQR model did not estimate the forecasted density accurately on four different parts of the density plot. The model underestimated and overestimated the forecasted density on the same parts as the PLAQR model and additionally, slightly overestimated part (d) as shown in Fig. 5 . Figure 6 for the QGAM exhibited the best-forecasted density because there are only two parts where the model did not estimate quite well the forecasted density. In the same part (c) as other models performed, the underestimation from QGAM was notable but slightly smaller than those from both the PLAQR and AQR models. However, the QGAM overestimated the forecasted density but on a different part (e) from the parts where the PLAQR and AQR models had overestimated. These results mean that the QGAM fitted the SI density a little closer to the actual density in all locations than the PLAQR and AQR models.

Sharpness and reliability analysis

Metric Evaluations: From Table 6 we can deduce that QGAM was the sharpest model and the most accurate on all locations because it had the lowest pinball loss in all locations. However, the pinball loss values from the QGAM were slightly smaller than those from the PLAQR and AQR models. We note that the pinball loss is an important metric when evaluating QR-based models. The lowest normalised Winkler scores were from the AQR model. Thus, AQR was the best model for the trade-off between coverage and prediction interval width but taking note of the slight differences in the normalised Winkler scores. The PLAQR was the most reliable except on Windhoek data because the model had the highest CP. However, results indicate that the CP values were slightly different and all models were reliable and unbiased because they had high CP values. The probabilistic metric evaluations demonstrate that the superiority in forecasting accuracy of the additive models depends on the metric but the models are generally of approximately the same forecasting accuracy.

Murphy Diagrams: Murphy diagrams in Fig. 7 demonstrate that the QGAM had near best forecasts amongst the three quantile regression-based additive models though the curves were almost superimposed in many parts of the diagrams. The QGAM curve is slightly below that of PLAQR on the second Murphy diagram and also slightly below that of the AQR curve on the third Murphy diagram on some notable parts. In the first Murphy diagram, the curve for the AQR model is slightly above that of the PLAQR at low and high parametric values. From \(\theta =400\) up to \(\theta =800\) the PLAQR curve slightly is above that AQR. That is, the PLAQR model is more accurate than the AQR on \(400\le \theta \le 800\) . However, all of the Murphy diagrams had curves that were very close to each other. That is the QR-based additive models fitted had approximately the same accuracy at some degree of comparison.

Diebold–Mariano (DM) tests: The DM tests were done on the covariate stationarity assumption which was validated in Section “ Variable selection ”. The following hypotheses: \(H_0:\) The PLAQR model has the same accuracy as the AQR model. \(H_1:\) PLAQR model is less accurate than the AQR model. were tested but all p-values in Table 7 were greater than 0.05 indicating that we could not reject the null hypothesis in all five locations. This means that the PLAQR and AQR models had generally the same accuracy. We also tested the hypotheses: \(H_0:\) PLAQR model has the same accuracy as the QGAM model. \(H_1:\) PLAQR model is less accurate than the QGAM model. and all p-values were less than 0.05 (Table 7 ) indicating that we could reject the null hypothesis. It then means that the accuracy of a PLAQR model is less than that of the QGAM model. The last pair of hypotheses tested were; \(H_0:\) AQR model has the same accuracy as the QGAM model, \(H_1:\) AQR model is less accurate than the QGAM model, and all of the p-values were less than 0.05 (Table 7 ) indicating that we could also reject the null hypothesis. That is, the accuracy of an AQR model is generally less than that of the QGAM model.

Performance consistency: The forecasting performances of the models were checked separately for consistency through analysis of variance. The following assumptions were presumed valid without any loss of generality: ( 1 ) the performance scores were from random samples (random data sets used), ( 2 ) within each model set the performance scores were normal and ( 3 ) the mean performance may differ from one model to the other but the population standard deviation of the performance is the same for all models. That is, we analysed how the performances generally varied from one location to another using the following hypotheses: \(H_0:\) Model forecasting performance does not vary in all locations. \(H_1:\) Model forecasting performance varies in at least one location. The p-values obtained were all greater than 0.05 as shown in Table 8 indicating that we could not reject the null hypothesis. These results mean that we can conclude that all of the three models did not have varying forecasting performances across the locations. That is, they all had a consistent forecasting performance on solar irradiance. We can also conclude that the models were stable because location as a data variation factor did not influence the general performances of the three models.

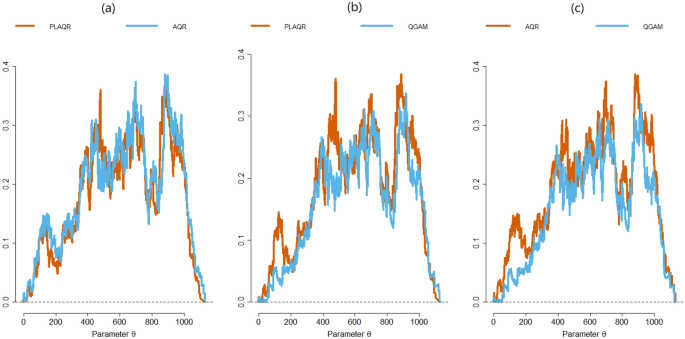
Murphy diagrams to compare the prediction accuracies of: ( a ) PLAQR and AQR models ( b ) PLAQR and QGAM models ( c ) AQR and QGAM models.

Forecasting horizon effect

The sharpness of all models was not affected by the increase in the forecasting horizon and the QGAM has been the best overall forecasting horizon as shown in Fig. 8 . Similarly, the trade-off between coverage and prediction interval width was not affected by the increase in forecasting horizon. However, the CP of the AQR model decreased with increasing forecasting horizon while that of QGAM had a turning point at \(30\%\) forecasting horizon. In contrast, the CP of the PLAQR model was constant from \(30\%\) throughout the increasing forecasting horizon. The models had approximately the same CRPS and results show that \(20\%\) is the ideal horizon when forecasting the distribution.

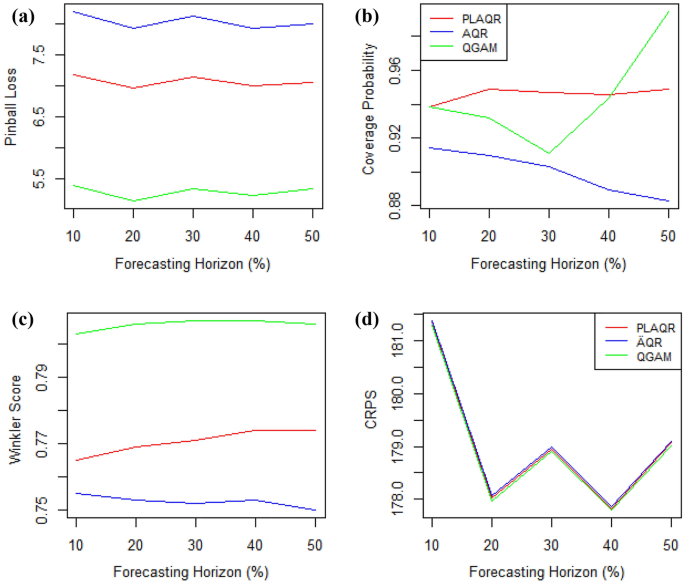
Forecasting horizon effect on model performance when considering ( a ) the pinball loss ( b ) CP ( c ) Winkler score ( d ) CRPS.

Sample sife effect

Model performances were not affected by changes in sample sizes as shown in Fig. 9 except the Winkler score. However, the movement from a sample size of 5000 to 10,000 influenced all models when considering the pinball loss, CP and Winkler scores evaluations. There is a general Winkler score improvement as the sample size increases while CP becomes approximately constant as the sample size increases from 15,000. We also note that the three models had the same CPRSs on all of the different sample sizes considered. Models’ performance on CRPS declines from the smallest sample size and then improves from the sample size of 15,000. Thus, 10,000 is a turning sample size for Pinball loss and Winkler score evaluation while 15,000 is the CRPS turning point.

Sample size effect on model performance when considering ( a ) the pinball loss ( b ) CP ( c ) Winkler score ( d ) CRPS.

Discussions and conclusions

This study introduced the QGAM framework to forecasting SI using data from five different locations in Southern Africa. A comparative investigation against the PLAQR and AQR frameworks demonstrated their appropriateness in modelling additive effects. All three non-parametric additive frameworks based on quantile regression modelling fitted the data excellently and were highly valid to model SI data from the Southern Africa region. We attribute the excellent modelling capabilities, especially the very high coefficients of determination and cross-validation correlations to the models’ ability to avoid the curse of dimensionality while retaining great flexibility in the regression function 9 . In addition, 12 concurred with 27 that the use of B-splines makes additive models very stable and flexible for large-scale interpolation. The critical forecasting performance metric when fitting a QR-based model is the pinball loss. We think that the learning rate introduced by 21 together with their replacement of the pinball loss with ELF loss function makes the QGAM framework very good and the best among the three models compared in minimising the regularised empirical risk suggested by 19 . The ELF loss function was developed as a smooth version of the pinball loss, so it led to slightly more accurate estimated quantiles. In as much as we suspected that some covariates have linear additive effects, the PLAQR framework which considers linear relationship structures was marginally outperformed by QGAM in all locations, forecasting horizons and different sample sizes except when evaluating the forecasts using the normalised Winkler score and CP. The PLAQR was the best model when evaluating the CP metric. The model uses a linear combination of B-spline basis functions to approximate the unknown nonlinear functions 8 . Probably that is why it had the highest coverage. However, all models were compared competitively very sharp, unbiased and very reliable because they had very high and approximately equal CP values. The QGAM performed the worst on the trade-off between coverage and PIW. The QGAM over- or under-estimated the SI density in fewer parts of the density plot than both the PLAQR and AQR models. Density plots of forecasts and actual GHI exhibit that QGAM predicted SI the closest. In addition, Murphy’s diagram analysis indicated that QGAM accuracy was slightly better than that of the other two non-parametric QR frameworks used to model the additive effects. Furthermore, the DM test results indicated that the QGAM framework had greater accuracy than both the PLAQR and AQR models. On the other hand, the DM test results indicated that the AQR model has a greater accuracy than the PLAQR model. We can deduce that smooth sub-optimisation of the EFL loss function within the maximum a posteriori estimation algorithm by exploiting orthogonal methods can account for the QGAM’s slightly greater accuracy than the other additive models. However, when prioritising reliability PLAQR is a recommended framework otherwise an AQR can be applied when focusing on the trade-off between coverage and PIW. The QGAM framework is recommended when focusing on the sharpness of the forecasts. Any of the three models can be used to predict the forecast distribution because they had approximately the same CRPS in all cases.

All of the models had different performances in the different locations but with no particular trend that could be established. That is, our results confirm the different model performances discovered by 18 in different regions. Change of location elevation and grid coordinates did not have any effect on model performance. However, we note that all models performed the worst in Venda when evaluating the pinball loss. Results also show that the worst performance when using CRPS was from Windhoek otherwise it cannot be deduced where the models had the best performances. Therefore, we conclude that the change of location does not influence the forecasting performance of any modelling framework. We can attribute the change in model performance as we change locations to the qualities of the data sets from the different locations. By the way, data from different ground stations is recorded using different equipment and systems though it may be in similar formats.

This study also evaluated how the change in forecasting horizon may affect model performance. Results show that the pinball loss is not affected by the increase in forecasting horizon neither is the Winkler score. The CP and CRPS were the ones affected but differently on the three models. We can deduce that 30% is the turning forecasting horizon for all of the three models when measuring reliability. The performance of the models was approximately the same when measuring how accurately they forecasted the distribution throughout the increasing forecasting horizon. However, the zig-zag pattern exhibited is quite interesting and the CRPS improvement can be wildly deduced. We would wish to investigate what happens after the \(50\%\) forecasting horizon but it is insensible to increase it beyond \(50\%\) . However, a forecasting horizon of \(20\%\) is ideal.

At last, this study investigated how the increase in sample size affects model performance. It would seem that generally, the increase does not affect the pinball loss and CP but results show that a sample size of 10,000 is ideal for measuring the pinball loss and 15,000 on CP. The best Winkler score can be obtained from the largest possible sample size while increasing it from 15,000 does not affect the models’ reliability. Model performance was also approximately the same when measuring the CRPS throughout the increasing forecasting sample size. Another interesting discovery is that CRPS had a maximum sample size of 15,000. In contrast, smaller sample sizes had better CRPS. It can be concluded that 10,000 and 15,000 sample sizes are key when modelling additive effects to SI using non-parametric QR frameworks.

Though, the QGAM framework was marginally superior on six out of the ten metrics considered in this study, the models had approximately the same metric values. The approximately equal metric values computed, small differences in the densities forecasted and the same consistency and stability results can be attributed to the same B-splines structure used by all of the models to approximate non-parametric components. Thus, except for the DM test results, other comparison investigations in this study do not indicate outright superiority of the QGAM. It is also hihghlighted that incorporating a variety of evaluation metrics in forecasting analysis enhances the robustness, comprehensiveness, and relevance of performance assessment, ultimately leading to better-informed decisions and improvements in forecasting models. However, we recommend that a future simulation study can give more conclusive information on the comparative investigation between the non-parametric quantile regression models when modelling additive effects to SI. That is, our results can not be generalised to any other locational data sets except to those extracted from the same radiometric stations of the same localities until such a simulation study is done. However, a solar power generation system may prioritise at least one of the metrics among the pinball loss, Winkler score, CRPS and CP. Our results suggest a guideline on which forecasting framework to prioritise in such situations though all of the three additive models have demonstrated to have the same forecasting accuracies. The excellent forecasting performances and consistency exhibited by all of the 3 non-parametric QR models in this study entail that the frameworks should be highly regarded when a solar power system is predicting solar irradiance for their power generation planning and management. The results suggest that including additive models compared in this study in photovoltaic power generation can help stabilise the system through improved accurate SI forecasts. It has to be noted that this study can be extended to standardising forecasts and include forecast combinations in the discussed modelling frameworks to improve the forecasts. While the study focused on modelling additive effects, modelling frameworks like random forests can be introduced to the modelling of SI in future studies.

Data availability

Most of the data used in this study are from the SAURAN website ( https://sauran.ac.za , accessed on 31 March 2023).

Sigauke, C., Chandiwana, E. & Bere, A. Spatio-temporal forecasting of global horizontal irradiance using Bayesian inference. Appl. Sci. 13 , 201. https://doi.org/10.3390/app13010201 (2023).

Article   CAS   Google Scholar  

Chandiwana, E., Sigauke, C. & Bere, A. Twenty-four-hour ahead probabilistic global horizontal irradiation forecasting using Gaussian process regression. Algorithms 14 , 177 (2021).

Article   Google Scholar  

Mutavhatsindi, T., Sigauke, C. & Mbuvha, R. Forecasting hourly global horizontal solar irradiance in South Africa. IEEE Access 8 , 198872–198885. https://doi.org/10.1109/ACCESS.2020.3034690 (2020).

Sivhugwana, K. S. & Ranganai, E. Intelligent techniques, harmonically coupled and sarima models in forecasting solar radiation data: A hybridisation approach. J. Energy South. Afr. 31 (3), 14–37. https://doi.org/10.17159/2413-3051/2020/v31i3a7754 (2020).

Davino, C., Furno, M. & Vistocco, D. Quantile Regression: Theory and Applications 1st edn. (Wiley, 2014).

Book   Google Scholar  

Koenker, R. Quantile Regression 1st edn. (Cambridge University Press, 2005). https://doi.org/10.1017/CBO9780511754098 .

Zhang, L., Lv, X. & Wang, R. Soil moisture estimation based on polarimetric decomposition and quantile regression forests. Remote Sens. 14 , 4183. https://doi.org/10.3390/rs14174183 (2022).

Article   ADS   Google Scholar  

Ravele, T., Sigauke, C. & Jhamba, L. Partially linear additive quantile regression in ultra-high dimension. Ann. Stat. 44 (1), 288–317. https://doi.org/10.1214/15-AOS1367 (2016).

Article   MathSciNet   Google Scholar  

Hoshino, T. Quantile regression estimation of partially linear additive models. J. Nonparametr. Stat. 26 (3), 509–536. https://doi.org/10.1080/10485252.2014.929675 (2014).

Maposa, D., Masache, A. & Mdlongwa, P. A quantile functions-based investigation on the characteristics of southern African solar irradiation data. Math. Comput. Appl. 28 , 86. https://doi.org/10.3390/mca28040086 (2023).

Koenker, R. Additive models for quantile regression: Model selection and confidence bandaids. Braz. J. Probab. Stat. 25 , 239–262. https://doi.org/10.1214/10-BJPS131 (2011).

Mpfumali, P., Sigauke, C., Bere, A. & Mlaudzi, S. Day ahead hourly global horizontal irradiance forecasting-application to south African data. Energies 12 , 1–28. https://doi.org/10.3390/en12183569 (2019).

Ranganai, E. & Sigauke, C. Capturing long-range dependence and harmonic phenomena in 24-hour solar irradiance forecasting. IEEE Access 8 , 172204–172218. https://doi.org/10.1109/ACCESS.2020.3024661 (2020).

Fenske, N., Kneib, T. & Hothorn, T. Identifying risk factors for severe childhood malnutrition by boosting additive quantile regression. J. Am. Stat. Assoc. 106 , 494–510. https://doi.org/10.1198/jasa.2011.ap09272 (2011).

Article   MathSciNet   CAS   Google Scholar  

Ravele, T., Sigauke, C. & Jhamba, L. Estimation of extreme quantiles of global horizontal irradiance: A comparative analysis using an extremal mixture model and a generalised additive extreme value model. Math. Stat. 10 (1), 116–133. https://doi.org/10.13189/ms.2022.100109 (2022).

Gaillard, P., Goudea, Y. & Nedellec, R. Additive models and robust aggregation for gefcom2014 probabilistic electric load and electricity price forecasting. Int. J. Forecast. 32 , 1038–1050. https://doi.org/10.1016/j.ijforecast.2015.12.001 (2016).

Tobechukwu, N. M. Quantile generalized additive model a robust alternative to generalized additive model. Int. J. Math. Res. 10 (1), 12–18 (2006).

Olivetti, L., Messori, G. & Jin, S. A quantile generalised additive approach for compound climate extremes: Pan-atlantic extremes as a case study. J. Adv. Model. Earth Syst. 1 , 1–10 (2023).

Google Scholar  

Takeuchi, I., Le, Q. V., Sears, T. D. & Smola, A. J. Nonparametric quantile estimation. J. Mach. Learn. Res. 7 , 1231–1264 (2006).

MathSciNet   Google Scholar  

Koenker, R., Ng, P. & Portnoy, S. Quantile smoothing splines. Biometrika 81 (4), 673–680 (1994).

Fasiolo, M., Wood, S. N., Zaffran, M., Nedellec, R. & Goude, Y. Fast calibrated additive quantile regression. J. Am. Stat. Assoc. 116 , 1402–1412. https://doi.org/10.1080/01621459.2020.1725521 (2021).

Yirga, A. A., Melesse, S. F., Mwambi, H. G. & Ayele, D. G. Additive quantile mixed-effects modelling with application to longitudinal cd4 count data. Sci. Rep. 11 , 11945. https://doi.org/10.1038/s41598-021-7114-9 (2021).

Bien, J. & Tibshirani, R. Package “hiernet”; version 1.9: A lasso for hierarchical interactions. CRAN (2022).

Fasiolo, M., Nedellec, R., Goude, Y., Capezza, C. & Wood, S. N. Package “mgcviz”; version 0.1.9: Visualisations for generalized additive models. CRAN (2022).

Maidman, A. Package “plaqr”; version 2.0: Partially linear additive quantile regression. CRAN (2022).

Koenker, R. et al. Package “quantreg”; version 5.95: Quantile regression. CRAN (2023).

Wood, S. N. Generalized Additive Models: An Introduction with r 2nd edn. (Chapman and Hall/CRC, 2017). https://doi.org/10.1201/9781315370279 .

Download references

Author information

These authors contributed equally: Daniel Maposa, Precious Mdlongwa, and Caston Sigauke.

Authors and Affiliations

Department of Statistics and Operations Research, National University of Science and Technology, Ascot, P.O. Box AC 939, Bulawayo, Zimbabwe

Amon Masache & Precious Mdlongwa

Department of Statistics and Operations Research, University of Limpopo, Private Bag X1106, Polokwane, Sovenga, 0727, South Africa

Daniel Maposa

Department of Mathematical and Computational Sciences, University of Venda, Venda, Thohoyandou, 0950, South Africa

Caston Sigauke

You can also search for this author in PubMed   Google Scholar

Contributions

Conceptualisation, A.M. and C.S; methodology, A.M. and C.S.; software, A.M.; validation, A.M., D.M., P.M. and C.S.; formal analysis, A.M.; investigation, A.M.; resources, A.M.; data curation, A.M.; writing-original draft preparation, A.M.; writing-review and editing, A.M., D.M., P.M, and C.S.; visualisation, A.M., D.M., P.M. and C.S; supervision, D.M., P.M. and C.S.; project administration, A.M.All authors have reviewed and agreed to the published version of the manuscript.

Corresponding author

Correspondence to Daniel Maposa .

Ethics declarations

Competing interests.

The authors declare no competing interests.

Additional information

Publisher's note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary Information

Supplementary information., rights and permissions.

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ .

Reprints and permissions

About this article

Cite this article.

Masache, A., Maposa, D., Mdlongwa, P. et al. Non-parametric quantile regression-based modelling of additive effects to solar irradiation in Southern Africa. Sci Rep 14 , 9244 (2024). https://doi.org/10.1038/s41598-024-59751-8

Download citation

Received : 30 January 2024

Accepted : 15 April 2024

Published : 22 April 2024

DOI : https://doi.org/10.1038/s41598-024-59751-8

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Additive effects
• Additive models
• Non-parametric quantile regression
• Pinball loss
• Solar irradiation

By submitting a comment you agree to abide by our Terms and Community Guidelines . If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.

Quick links

• Explore articles by subject
• Guide to authors
• Editorial policies

Sign up for the Nature Briefing: Anthropocene newsletter — what matters in anthropocene research, free to your inbox weekly.

• Math Article
• Non Parametric Test

Non-Parametric Test

Non-parametric tests are experiments that do not require the underlying population for assumptions. It does not rely on any data referring to any particular parametric group of probability distributions . Non-parametric methods are also called distribution-free tests since they do not have any underlying population.  In this article, we will discuss what a non-parametric test is, different methods, merits, demerits and examples of non-parametric testing methods.

Table of Contents:

• Non-parametric T Test
• Non-parametric Paired T-Test

Mann Whitney U Test

Wilcoxon signed-rank test, kruskal wallis test.

• Advantages and Disadvantages
• Applications

What is a Non-parametric Test?

Non-parametric tests are the mathematical methods used in statistical hypothesis testing, which do not make assumptions about the frequency distribution of variables that are to be evaluated. The non-parametric experiment is used when there are skewed data, and it comprises techniques that do not depend on data pertaining to any particular distribution.

The word non-parametric does not mean that these models do not have any parameters. The fact is, the characteristics and number of parameters are pretty flexible and not predefined. Therefore, these models are called distribution-free models.

Non-Parametric T-Test

Whenever a few assumptions in the given population are uncertain, we use non-parametric tests, which are also considered parametric counterparts. When data are not distributed normally or when they are on an ordinal level of measurement, we have to use non-parametric tests for analysis. The basic rule is to use a parametric t-test for normally distributed data and a non-parametric test for skewed data.

Non-Parametric Paired T-Test

The paired sample t-test is used to match two means scores, and these scores come from the same group. Pair samples t-test is used when variables are independent and have two levels, and those levels are repeated measures.

Non-parametric Test Methods

The four different techniques of parametric tests, such as Mann Whitney U test, the sign test, the Wilcoxon signed-rank test, and the Kruskal Wallis test are discussed here in detail. We know that the non-parametric tests are completely based on the ranks, which are assigned to the ordered data. The four different types of non-parametric test are summarized below with their uses, null hypothesis , test statistic, and the decision rule. 

Kruskal Wallis test is used to compare the continuous outcome in greater than two independent samples.

Null hypothesis, H 0 :  K Population medians are equal.

Test statistic:

If N is the total sample size, k is the number of comparison groups, R j is the sum of the ranks in the jth group and n j is the sample size in the jth group, then the test statistic, H is given by:

\(\begin{array}{l}H = \left ( \frac{12}{N(N+1)}\sum_{j=1}^{k} \frac{R_{j}^{2}}{n_{j}}\right )-3(N+1)\end{array} \)

Decision Rule: Reject the null hypothesis H 0 if H ≥ critical value

The sign test is used to compare the continuous outcome in the paired samples or the two matches samples.

Null hypothesis, H 0 : Median difference should be zero 

Test statistic: The test statistic of the sign test is the smaller of the number of positive or negative signs.

Decision Rule: Reject the null hypothesis if the smaller of number of the positive or the negative signs are less than or equal to the critical value from the table.

Mann Whitney U test is used to compare the continuous outcomes in the two independent samples. 

Null hypothesis, H 0 : The two populations should be equal.

If R 1 and R 2 are the sum of the ranks in group 1 and group 2 respectively, then the test statistic “U” is the smaller of:

\(\begin{array}{l}U_{1}= n_{1}n_{2}+\frac{n_{1}(n_{1}+1)}{2}-R_{1}\end{array} \)

\(\begin{array}{l}U_{2}= n_{1}n_{2}+\frac{n_{2}(n_{2}+1)}{2}-R_{2}\end{array} \)

Decision Rule: Reject the null hypothesis if the test statistic, U is less than or equal to critical value from the table.

Wilcoxon signed-rank test is used to compare the continuous outcome in the two matched samples or the paired samples.

Null hypothesis, H 0 : Median difference should be zero.

Test statistic: The test statistic W, is defined as the smaller of W+ or W- .

Where W+ and W- are the sums of the positive and the negative ranks of the different scores.

Decision Rule: Reject the null hypothesis if the test statistic, W is less than or equal to the critical value from the table.

Advantages and Disadvantages of Non-Parametric Test

The advantages of the non-parametric test are:

• Easily understandable
• Short calculations
• Assumption of distribution is not required
• Applicable to all types of data

The disadvantages of the non-parametric test are:

• Less efficient as compared to parametric test
• The results may or may not provide an accurate answer because they are distribution free

Applications of Non-Parametric Test

The conditions when non-parametric tests are used are listed below:

• When parametric tests are not satisfied.
• When testing the hypothesis, it does not have any distribution.
• For quick data analysis.
• When unscaled data is available.

Frequently Asked Questions on Non-Parametric Test

What is meant by a non-parametric test.

The non-parametric test is one of the methods of statistical analysis, which does not require any distribution to meet the required assumptions, that has to be analyzed. Hence, the non-parametric test is called a distribution-free test.

What is the advantage of a non-parametric test?

The advantage of nonparametric tests over the parametric test is that they do not consider any assumptions about the data.

Is Chi-square a non-parametric test?

Yes, the Chi-square test is a non-parametric test in statistics, and it is called a distribution-free test.

Mention the different types of non-parametric tests.

The different types of non-parametric test are: Kruskal Wallis Test Sign Test Mann Whitney U test Wilcoxon signed-rank test

When to use the parametric and non-parametric test?

If the mean of the data more accurately represents the centre of the distribution, and the sample size is large enough, we can use the parametric test. Whereas, if the median of the data more accurately represents the centre of the distribution, and the sample size is large, we can use non-parametric distribution.

• Share Share

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.