prime factor problem solving

Prime Factorization

Prime numbers.

A Prime Number is:

a whole number above 1 that cannot be made by multiplying other whole numbers

When it can  be made by multiplying other whole numbers it is a Composite Number , like this:

(The first few prime numbers are: 2, 3, 5, 7, 11, 13, 17, 19 and 23, and we have a prime number chart if you need more.)

"Factors" are the numbers you multiply together to get another number:

"Prime Factorization" is finding which prime numbers multiply together to make the original number.

Here are some examples:

Example: What are the prime factors of 12 ?

It is best to start working from the smallest prime number, which is 2, so let's check:

Yes, it divided exactly by 2. We have taken the first step!

But 6 is not a prime number, so we need to go further. Let's try 2 again:

Yes, that worked also. And 3 is a prime number, so we have the answer:

12 = 2 × 2 × 3

As you can see, every factor is a prime number , so the answer is right.

It is neater to show repeated numbers using  exponents :

• Without exponents:  2 × 2 × 3
• With exponents:  2 2 × 3

Example: What is the prime factorization of 147 ?

Can we divide 147 exactly by 2?

147 ÷ 2 = 73½

No we can't. The answer should be a whole number, and 73½ is not.

Let's try the next prime number, 3:

147 ÷ 3 = 49

That worked, now try factoring 49.

The next prime, 5, does not work. But 7 does, so we get:

And that is as far as we need to go, because all the factors are prime numbers.

147 = 3 × 7 × 7 = 3 × 7 2

Example: What is the prime factorization of 17 ?

Hang on ... 17 is a Prime Number .

So that is as far as we can go.

Another Method

We just did factorization by starting at the smallest prime and working upwards.

But sometimes it is easier to break a number down into any factors we can ... then work those factor down to primes.

Example: What are the prime factors of 90 ?

Break 90 into 9 × 10

• The prime factors of 9 are 3 and 3
• The prime factors of 10 are 2 and 5

So the prime factors of 90 are 3, 3, 2 and 5

90 = 2 × 3 2 × 5

Factor Tree

A "Factor Tree" can help: find any factors of the number, then the factors of those numbers, etc, until we can't factor any more.

Example: 48

48 = 8 × 6 , so we write down "8" and "6" below 48

Now we continue and factor 8 into 4 × 2

Then 4 into 2 × 2

And lastly 6 into 3 × 2

We can't factor any more, so we have found the prime factors.

Which reveals that 48 = 2 × 2 × 2 × 2 × 3

48 = 2 4 × 3

Why find Prime Factors?

A prime number can only be divided by 1 or itself, so it cannot be factored any further!

Every other whole number can be broken down into prime number factors.

This idea can be very useful when working with big numbers, such as in Cryptography.

Cryptography

Cryptography is the study of secret codes. Prime Factorization is important to people who try to make (or break) secret codes based on numbers.

That is because factoring very large numbers is very hard, and can take computers a long time to do.

And here is another thing:

There is only one (unique!) set of prime factors for any number.

Example: the prime factors of 330 are 2, 3, 5 and 11

330 = 2 × 3 × 5 × 11

There is no other possible set of prime numbers that can be multiplied to make 330.

This idea is so important it is called the Fundamental Theorem of Arithmetic .

Prime Factorization Tool

OK, we have one more method ... use our Prime Factorization Tool that can work out the prime factors for numbers up to 9007199254740991.

2.5 Prime Factorization and the Least Common Multiple

Learning objectives.

By the end of this section, you will be able to:

• Find the prime factorization of a composite number
• Find the least common multiple (LCM) of two numbers

Be Prepared 2.12

Before you get started, take this readiness quiz.

Is 810 810 divisible by 2 , 3 , 5 , 6 , or 10 ? 2 , 3 , 5 , 6 , or 10 ? If you missed this problem, review Example 2.44 .

Be Prepared 2.13

Is 127 127 prime or composite? If you missed this problem, review Example 2.47 .

Write 2 ⋅ 2 ⋅ 2 ⋅ 2 2 ⋅ 2 ⋅ 2 ⋅ 2 in exponential notation. If you missed this problem, review Example 2.5 .

Find the Prime Factorization of a Composite Number

In the previous section, we found the factors of a number. Prime numbers have only two factors, the number 1 1 and the prime number itself. Composite numbers have more than two factors, and every composite number can be written as a unique product of primes. This is called the prime factorization of a number. When we write the prime factorization of a number, we are rewriting the number as a product of primes. Finding the prime factorization of a composite number will help you later in this course.

Prime Factorization

The prime factorization of a number is the product of prime numbers that equals the number.

Manipulative Mathematics

You may want to refer to the following list of prime numbers less than 50 50 as you work through this section.

Prime Factorization Using the Factor Tree Method

One way to find the prime factorization of a number is to make a factor tree . We start by writing the number, and then writing it as the product of two factors. We write the factors below the number and connect them to the number with a small line segment—a “branch” of the factor tree.

If a factor is prime, we circle it (like a bud on a tree), and do not factor that “branch” any further. If a factor is not prime, we repeat this process, writing it as the product of two factors and adding new branches to the tree.

We continue until all the branches end with a prime. When the factor tree is complete, the circled primes give us the prime factorization.

For example, let’s find the prime factorization of 36 . 36 . We can start with any factor pair such as 3 3 and 12 . 12 . We write 3 3 and 12 12 below 36 36 with branches connecting them.

The factor 3 3 is prime, so we circle it. The factor 12 12 is composite, so we need to find its factors. Let’s use 3 3 and 4 . 4 . We write these factors on the tree under the 12 . 12 .

The factor 3 3 is prime, so we circle it. The factor 4 4 is composite, and it factors into 2 · 2 . 2 · 2 . We write these factors under the 4 . 4 . Since 2 2 is prime, we circle both 2 s . 2 s .

The prime factorization is the product of the circled primes. We generally write the prime factorization in order from least to greatest.

In cases like this, where some of the prime factors are repeated, we can write prime factorization in exponential form.

Note that we could have started our factor tree with any factor pair of 36 . 36 . We chose 12 12 and 3 , 3 , but the same result would have been the same if we had started with 2 2 and 18 , 4 18 , 4 and 9 , or 6 and 6 . 9 , or 6 and 6 .

Find the prime factorization of a composite number using the tree method.

• Step 1. Find any factor pair of the given number, and use these numbers to create two branches.
• Step 2. If a factor is prime, that branch is complete. Circle the prime.
• Step 3. If a factor is not prime, write it as the product of a factor pair and continue the process.
• Step 4. Write the composite number as the product of all the circled primes.

Example 2.48

Find the prime factorization of 48 48 using the factor tree method.

Check this on your own by multiplying all the factors together. The result should be 48 . 48 .

Try It 2.95

Find the prime factorization using the factor tree method: 80 80

Try It 2.96

Find the prime factorization using the factor tree method: 60 60

Example 2.49

Find the prime factorization of 84 using the factor tree method.

Draw a factor tree of 84 . 84 .

Try It 2.97

Find the prime factorization using the factor tree method: 126 126

Try It 2.98

Find the prime factorization using the factor tree method: 294 294

Prime Factorization Using the Ladder Method

The ladder method is another way to find the prime factors of a composite number. It leads to the same result as the factor tree method. Some people prefer the ladder method to the factor tree method, and vice versa.

To begin building the “ladder,” divide the given number by its smallest prime factor. For example, to start the ladder for 36 , 36 , we divide 36 36 by 2 , 2 , the smallest prime factor of 36 . 36 .

To add a “step” to the ladder, we continue dividing by the same prime until it no longer divides evenly.

Then we divide by the next prime; so we divide 9 9 by 3 . 3 .

We continue dividing up the ladder in this way until the quotient is prime. Since the quotient, 3 , 3 , is prime, we stop here.

Do you see why the ladder method is sometimes called stacked division?

The prime factorization is the product of all the primes on the sides and top of the ladder.

Notice that the result is the same as we obtained with the factor tree method.

Find the prime factorization of a composite number using the ladder method.

• Step 1. Divide the number by the smallest prime.
• Step 2. Continue dividing by that prime until it no longer divides evenly.
• Step 3. Divide by the next prime until it no longer divides evenly.
• Step 4. Continue until the quotient is a prime.
• Step 5. Write the composite number as the product of all the primes on the sides and top of the ladder.

Example 2.50

Find the prime factorization of 120 120 using the ladder method.

Check this yourself by multiplying the factors. The result should be 120 . 120 .

Try It 2.99

Find the prime factorization using the ladder method: 80 80

Try It 2.100

Find the prime factorization using the ladder method: 60 60

Example 2.51

Find the prime factorization of 48 48 using the ladder method.

Try It 2.101

Find the prime factorization using the ladder method. 126 126

Try It 2.102

Find the prime factorization using the ladder method. 294 294

Find the Least Common Multiple (LCM) of Two Numbers

One of the reasons we look at multiples and primes is to use these techniques to find the least common multiple of two numbers. This will be useful when we add and subtract fractions with different denominators.

Listing Multiples Method

A common multiple of two numbers is a number that is a multiple of both numbers. Suppose we want to find common multiples of 10 10 and 25 . 25 . We can list the first several multiples of each number. Then we look for multiples that are common to both lists—these are the common multiples.

We see that 50 50 and 100 100 appear in both lists. They are common multiples of 10 10 and 25 . 25 . We would find more common multiples if we continued the list of multiples for each.

The smallest number that is a multiple of two numbers is called the least common multiple (LCM). So the least LCM of 10 10 and 25 25 is 50 . 50 .

Find the least common multiple (LCM) of two numbers by listing multiples.

• Step 1. List the first several multiples of each number.
• Step 2. Look for multiples common to both lists. If there are no common multiples in the lists, write out additional multiples for each number.
• Step 3. Look for the smallest number that is common to both lists.
• Step 4. This number is the LCM.

Example 2.52

Find the LCM of 15 15 and 20 20 by listing multiples.

List the first several multiples of 15 15 and of 20 . 20 . Identify the first common multiple.

15: 15 , 30 , 45 , 60 , 75 , 90 , 105 , 120 20: 20 , 40 , 60 , 80 , 100 , 120 , 140 , 160 15: 15 , 30 , 45 , 60 , 75 , 90 , 105 , 120 20: 20 , 40 , 60 , 80 , 100 , 120 , 140 , 160

The smallest number to appear on both lists is 60 , 60 , so 60 60 is the least common multiple of 15 15 and 20 . 20 .

Notice that 120 120 is on both lists, too. It is a common multiple, but it is not the least common multiple.

Try It 2.103

Find the least common multiple (LCM) of the given numbers: 9 and 12 9 and 12

Try It 2.104

Find the least common multiple (LCM) of the given numbers: 18 and 24 18 and 24

Prime Factors Method

Another way to find the least common multiple of two numbers is to use their prime factors. We’ll use this method to find the LCM of 12 12 and 18 . 18 .

We start by finding the prime factorization of each number.

Then we write each number as a product of primes, matching primes vertically when possible.

Now we bring down the primes in each column. The LCM is the product of these factors.

Notice that the prime factors of 12 12 and the prime factors of 18 18 are included in the LCM. By matching up the common primes, each common prime factor is used only once. This ensures that 36 36 is the least common multiple.

Find the LCM using the prime factors method.

• Step 1. Find the prime factorization of each number.
• Step 2. Write each number as a product of primes, matching primes vertically when possible.
• Step 3. Bring down the primes in each column.
• Step 4. Multiply the factors to get the LCM.

Example 2.53

Find the LCM of 15 15 and 18 18 using the prime factors method.

Try It 2.105

Find the LCM using the prime factors method. 15 and 20 15 and 20

Try It 2.106

Find the LCM using the prime factors method. 15 and 35 15 and 35

Example 2.54

Find the LCM of 50 50 and 100 100 using the prime factors method.

Try It 2.107

Find the LCM using the prime factors method: 55 , 88 55 , 88

Try It 2.108

Find the LCM using the prime factors method: 60 , 72 60 , 72

ACCESS ADDITIONAL ONLINE RESOURCES

• Ex 1: Prime Factorization
• Ex 2: Prime Factorization
• Ex 3: Prime Factorization
• Ex 1: Prime Factorization Using Stacked Division
• Ex 2: Prime Factorization Using Stacked Division
• The Least Common Multiple
• Example: Determining the Least Common Multiple Using a List of Multiples
• Example: Determining the Least Common Multiple Using Prime Factorization

Section 2.5 Exercises

Practice makes perfect.

In the following exercises, find the prime factorization of each number using the factor tree method.

In the following exercises, find the prime factorization of each number using the ladder method.

In the following exercises, find the prime factorization of each number using any method.

In the following exercises, find the least common multiple (LCM) by listing multiples.

8 , 12 8 , 12

4 , 3 4 , 3

6 , 15 6 , 15

12 , 16 12 , 16

30 , 40 30 , 40

20 , 30 20 , 30

60 , 75 60 , 75

44 , 55 44 , 55

In the following exercises, find the least common multiple (LCM) by using the prime factors method.

24 , 30 24 , 30

28 , 40 28 , 40

70 , 84 70 , 84

84 , 90 84 , 90

In the following exercises, find the least common multiple (LCM) using any method.

6 , 21 6 , 21

9 , 15 9 , 15

32 , 40 32 , 40

Everyday Math

Grocery shopping Hot dogs are sold in packages of ten, but hot dog buns come in packs of eight. What is the smallest number of hot dogs and buns that can be purchased if you want to have the same number of hot dogs and buns? (Hint: it is the LCM!)

Grocery shopping Paper plates are sold in packages of 12 12 and party cups come in packs of 8 . 8 . What is the smallest number of plates and cups you can purchase if you want to have the same number of each? (Hint: it is the LCM!)

Writing Exercises

Do you prefer to find the prime factorization of a composite number by using the factor tree method or the ladder method? Why?

Do you prefer to find the LCM by listing multiples or by using the prime factors method? Why?

ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

ⓑ Overall, after looking at the checklist, do you think you are well-prepared for the next Chapter? Why or why not?

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/prealgebra-2e/pages/1-introduction

• Authors: Lynn Marecek, MaryAnne Anthony-Smith, Andrea Honeycutt Mathis
• Publisher/website: OpenStax
• Book title: Prealgebra 2e
• Publication date: Mar 11, 2020
• Location: Houston, Texas
• Book URL: https://openstax.org/books/prealgebra-2e/pages/1-introduction
• Section URL: https://openstax.org/books/prealgebra-2e/pages/2-5-prime-factorization-and-the-least-common-multiple

© Jan 23, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Prime Factorization: Definition, Methods, Examples, FAQs

What is prime factorization in math, what are factors and prime factors, how to find prime factorization of a number, solved examples on prime factorization, practice problems on prime factorization, frequently asked questions on prime factorization.

Prime factorization of a number is a way of writing a number as the product of its prime factors. Thus, the meaning of prime factorization of a number is finding prime numbers which when multiplied together give us the required number.

Example: The product prime numbers 2, 3, and 5 is 30.

Prime factorization of $30 = 2 \times 3 \times 5$

Prime Factorization Definition

Prime factorization can be defined as a way of expressing a given number as the product of its prime factors. 

If a prime number occurs more than once, we write it using exponents.

Example: Prime factorization of $18 = 2\times3\times3 = 2\times3^{2}$

Related Worksheets

A factor of a number is a number that divides the given number exactly, leaving no remainder.

Prime numbers are numbers that have only two factors, 1 and the number itself. Examples of prime numbers are: 2, 3, 5, 7, 11, 13, 17, 19, and so on.

Consider an example. The numbers 1, 2, 3, 6 are factors of the number 6.

Thus, we can say that 2 and 3 are the prime factors of 6 and express 6 as 

$6 = 2\times3$

Here, we expressed 6 as the product of its prime factors. When we write a number as a product of all its prime factors, it is called prime factorization. 

The most common methods that are used for prime factorization are:

• Prime Factorization by Factor tree method
• Prime Factorization by Division method

We will discuss these methods in detail. However, we can also find prime factors of a number by simply breaking down the number using its factors until we get prime numbers. 

Example: Find prime factorization of 48.

$42 = 8\times6$

$42 = (2\times2\times2)\times(2\times3)$

$42 = 2^{4}\times3$

Prime Factorization Methods

You can find the prime factorization of a number using various methods.

Let’s discuss the two important methods to solve prime factorization problems.

• Factor tree method
• Division method

Let us look at both the methods in detail.

Factor Tree Method

In the factor tree method, we first break down the number using the smallest prime factor of the number. The composite factors obtained in the process are further broken down until we reach the prime factors. 

The factors of the given number written in this way look like a tree. The prime numbers obtained in the end are called leaf nodes of the factor tree.

Example: Find the prime factorization of 250 using the factor tree method.

Step 1: Place the number 250 on top of the factor tree.

Step 2: Break down the given number using its smallest prime factor.

Here, $250 = 2 \times 125$

Step 3: Factorize the composite factor obtained in step 2. 

$125 = 5 \times 5$

Repeat the same step until we get all prime factors in the end. 

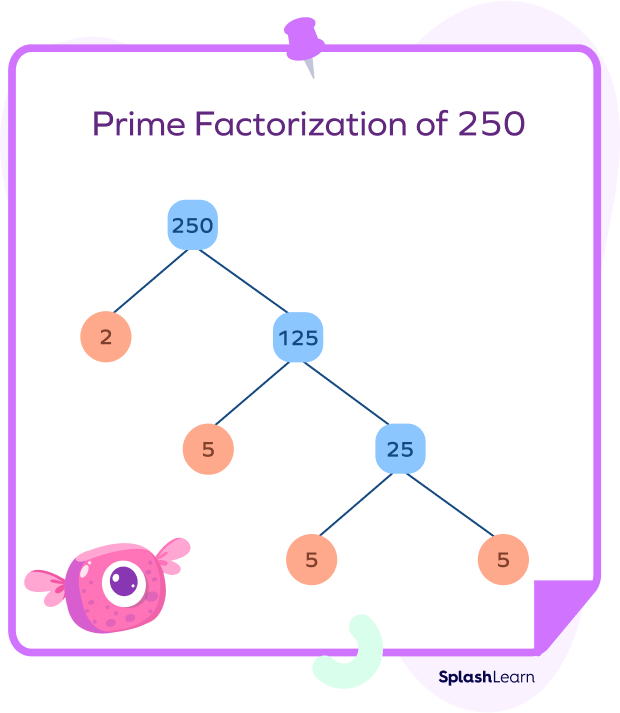
Thus, prime factorization of $250 = 2 \times 5^{3}$

Division Method

Step 1: Divide the given number by its smallest prime factor. 

Step 2: Divide the quotient obtained by its smallest prime factor.

Step 3: Repeat the process until the quotient becomes 1.

Step 4: Multiply all the prime factors.

Example: Prime factorization of 28 using division method.

Why Find Prime Factors?

As we already know that a prime number can only be divided by 1 or the number itself, so it cannot be factored any further. A composite number can be broken down using prime numbers and can be written uniquely as a product of its prime factors.

The prime numbers are the basic building blocks of any number.

We have many real-life uses of this concept while dealing with large numbers, such as in cryptography.

What Are the Applications of Prime Factorization?

• Finding square roots of perfect squares

It’s very easy to find square roots of perfect squares using prime factorization. 

Consider an example.

Prime factorization of $1225 = 5\times5\times7\times7$

$\sqrt{1225} = \sqrt{5\times5\times7\times7}$

$\sqrt{1225} = 5\times7$

$\sqrt{1225} = 35$

• Encryption or cryptography 
• Finding HCF and LCM using prime factorization
• Mental arithmetic
• Studying patterns

Finding HCF and LCM Using Prime Factorization

HCF (Highest Common Factor): The largest number of all the common factors of two numbers.

LCM (Least Common Multiple): The smallest number of all the common multiples of two numbers.

The HCF and LCM of two numbers can be calculated using the prime factorization method. It is quite useful when dealing with two or more large numbers. 

• First find the prime factorization of both the numbers. 
• HCF is the product of the smallest power of each common prime factor.
• LCM is the product of the greatest power of each prime factor.

Let us understand these points with the help of an example.

Example 1: Find the HCF and LCM of 42, 72, and 120 using prime factorization.

We will first find the prime factorization of the given numbers.

$42 = 2 \times 3 \times 7$

$72 = 2^{3} \times 3^{2}$

$120 = 2^{3} \times 3 \times 5$

HCF $=$ Product of the common prime factors with the lowest degree. 

HCF (42, 72, 120) $= 2 \times 3 = 6$

LCM = Product of the greatest powers of all prime factors.

LCM (42, 72, 120) $= 2^{3} \times 3^{2} \times 5 \times 7 = 2520$

Example 2: What is the HCF and LCM of 50 and 75?

The prime factorization of $50 = 2 \times 5^{2}$

The prime factorization of $75 = 3 × 5^{2}$

Multiply all the common prime factors with the lowest degree (power).

Here, we have only 5 as a common prime factor with the lowest power of 2.

Hence, HCF of (50, 75)$ = 5^{2} = 25$

LCM = Product of the greatest power of each prime factor.

Multiply all the prime factors with the highest degree.

Hence, LCM of (50, 75) $= 2^{1} \times  3^{1} \times 5^{2} = 150$

Prime Factorization of a Number

Take a look at the table showing prime factorization of some numbers.

Facts about Prime Factorization

• Cryptography is a branch of computer science that deals with methods of protecting important information using codes. Prime factorization plays an important role for the people who create a unique code, or encrypt the information using numbers that are not too heavy for computers to store and process quickly.
• 2 is the smallest even prime number. 2 is the only prime number that is even.
• 2 and 3 are the only consecutive prime numbers.
• 0 and 1 are neither prime nor composite.
• The only prime number that ends in 5 is 5.
• There is no largest prime number. The largest known prime number (as of February 2023) is $2^{82,589,933} \;−\; 1$, a number that has 24,862,048 digits when written in base 10. By the time you read this, it may be even larger.
• Mersenne prime: Prime number of the form $2^{n} \;−\; 1$, where n is a natural number.

In this article, we learned about factors, prime factors, prime factorization, methods of prime factorization, and how to find HCF and LCM using prime factorization. Let’s solve a few examples and practice problems for better understanding and revision!

1. Find the prime factorization of 24 using the factor tree method.

Let us look at the steps to find the prime factorization of 24 using the factor tree method:

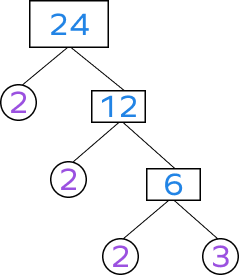
Therefore, the prime factorization of $24 = 2^{3} \times 3$.

2. Find the prime factorization of 42 using the division method.

Solution: 

Divide 42 by its smallest prime factor. Next, divide the quotient by its smallest prime factor. Repeat this process until we get 1 as a quotient.

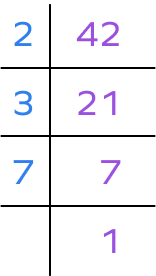
Prime factorization = Product of all prime factors

Therefore, the prime factorization of $42 = 2 \times 3 \times 7$.

3. Find the HCF of 100 and 250 using prime factorization.

To find the HCF of any number using prime factorization, we first need to find the prime factorization of both the numbers.

Prime factorization of $100 = 2^{2} \times 5^{2}$

Prime factorization of $250 = 2^{1} \times 5^{3}$

HCF (100, 250) $= 2^{1}\times 5^{2}$

Therefore, the Highest Common Factor of 100 and $250 = 50$. 

4. Find the LCM of 100 and 250 using prime factorization.

To find the LCM of any number using prime factorization, we first need to find the prime factorization of both the numbers.

LCM(100, 250) $= 2^{2} \times 5^{3}$

Therefore, the LCM of 100 and $250 = 2^{2} \times 5^{3} = 500$.

5. Write all the prime factors of 1250 using the division method.

To find the prime factors of a number, we need to find the prime factorization using one of the two methods.

Let us solve this by the division method.

Now, $\frac{1250}{2} = 625$

          $\frac{625}{5} = 125$

          $\frac{125}{5} = 25$

           $\frac{25}{5} = 5$

           $\frac{5}{5} = 1$

The prime factors of 1250 are 2 and 5. 

The prime factorization is $2 \times 5^{4}$.

Attend this quiz & Test your knowledge.

What is the prime factorization of 48?

What is the prime factorization of 15, what is the hcf of 120 and 150 using prime factorization, prime factorization is a way of expressing a given number as the ____ of its prime factors., what are the prime factors of 1000.

Is 1 a prime number?

1 is neither prime nor composite.

Is 0 prime or composite?

0 is neither prime nor composite.

How many factors does a prime number have?

Only two factors, 1 and the number itself.

Is the prime factorization of a number unique?

Yes. There is only one set of prime numbers for every whole number whose product results in the given whole number.

RELATED POSTS

• Associative Property of Multiplication – Definition With Examples
• Parentheses – Definition With Examples
• Volume of Cuboid – Definition, Formula, Derivation, Examples, FAQs
• Surface Area of Triangular Pyramid
• Power of a Power Rule: Definition, Rules, Examples, Facts, FAQs

Math & ELA | PreK To Grade 5

Kids see fun., you see real learning outcomes..

Make study-time fun with 14,000+ games & activities, 450+ lesson plans, and more—free forever.

Parents, Try for Free Teachers, Use for Free

Reset password New user? Sign up

Existing user? Log in

• Prime Factorization and Divisors

Concept Quizzes

• Prime Factorization Warmup
• Prime Factorization
• Prime Factor Trees
• Perfect Squares, Cubes and Powers
• Number of Factors / Divisors

Challenge Quizzes

• Prime Factorization and Divisors: Level 1 Challenges
• Prime Factorization and Divisors: Level 2 Challenges
• Prime Factorization and Divisors: Level 3 Challenges

Explore the properties that govern prime factorizations of even and odd numbers, perfect squares and cubes, factorials and ever larger numbers. In conjunction with prime numbers, a strong grasp of factorization serves as a guiding light for our thoughts on all number theory problems.

• Perfect Squares, Cubes, and Powers
• Perfect Numbers
• Fundamental Theorem of Arithmetic

Problem Loading...

Note Loading...

Set Loading...

• Mathematicians
• Math Lessons
• Square Roots
• Math Calculators
• Prime Factorization – Explanation & Examples

JUMP TO TOPIC

Repeated division

Factor tree, practice questions, prime factorization – explanation & examples.

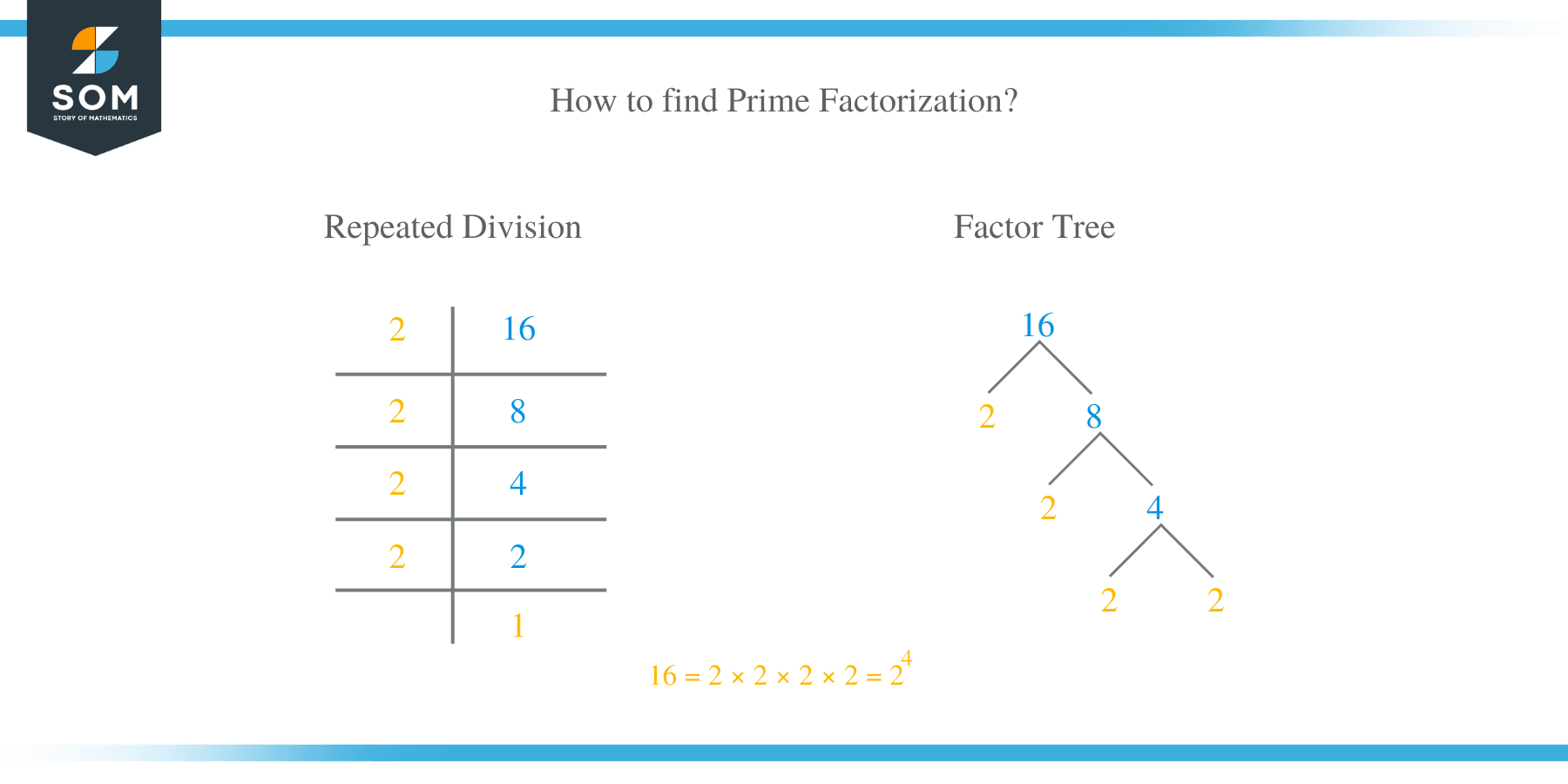
How to find Prime Factorization?

There are two methods of finding prime factors of a number. These are repeated division and factor tree.

A number is reduced by dividing it severally with prime numbers. Prime factors of number 36 are found by repeated division as shown:

The prime factors of number 36 are, therefore, 2 and 3. This can be written as 2 × 2 × 3 × 3. It is advisable to start dividing a number by the smallest prime number and proceed to bigger factors.

What are the prime factors of 16?

The best way to solve this problem is by identifying the smallest prime factor of the number, which is 2.

Divide number by 16;

Because 8 is not a prime number, proceed by dividing again by the smallest factor;

We have the prime factors of 16 highlighted in yellow, and they include: 2 x 2 x 2 x 2.

which can be written as an exponent:

Find the prime factors of 12.

Divide 12 by 2;

6 is not prime, proceed;

Therefore, 12 = 2 x 2 x 3

12 = 2 2 × 3

It is noted that, all prime factors of a number are prime.

Factorize 147.

Start by dividing 147 by the smallest prime number.

147 ÷ 2 = 73.5

Our answer isn’t an integer, try the next prime number 3.

147 ÷ 3 = 49

Yes, 3 worked, now proceed to the next prime that can divide 49.

Therefore, 147 = 3 x 7 x 7,

= 3 x 7 2 .

What is the prime factorization of 19?

Another method on how to perform factorization is to break a number down into two integers. Now find the prime factors of the integers. This technique is useful when dealing with bigger numbers.

Find the prime factors of 210.

Break down 210 into:

210 = 21 x 10

Now calculate the factors of 21 and 10

Combine the factors: 210 = 2 x 3 x 5 x 7

Previous Lesson  |  Main Page | Next Lesson

Prime Factorisation Questions

Prime factorisation questions given here with solutions will help students understand the concept of prime factorisation and how to use the concept to solve various types of problems. Students must practice these questions to score well in their examinations.

Also read: How to find prime factors?

Prime Factorisation Questions with Solutions

Now that we understand what is meant by prime factorisation, let us practice prime factorisation by solving the following questions.

Question 1: Find the prime factorisation of the following:

∴ Prime Factorisation of 284 = 2 × 2 × 71

∴ Prime factorisation of 7084 = 2 × 2 × 7 × 11 × 23.

∴ Prime factorisation of 5595 = 3 × 5 × 373.

Question 2: Find the prime factorisation of the following:

∴ Prime Factorisation of 23356 = 2 × 2 × 5839

∴ Prime Factorisation of 23356 = 2 × 3 × 31 × 269

∴ Prime Factorisation of 23356 = 11 × 317

∴ Prime Factorisation of 23356 = 2 × 2 × 2 × 2 × 2 × 3 × 3 × 5 × 13 = 2 5 × 3 2 × 5 × 13

Question 3: State ‘true’ or ‘false’ for the following:

(i) 177 is a prime number

(ii) 1 is a composite number

(iii) The prime factorisation of 252 is 2 2 × 3 3 × 7.

(iv) 5 × 33 is the prime factorisation of 165.

(i) 177 is a prime number. (False)

(ii) 1 is a composite number. (False)

(iii) The prime factorisation of 252 is 2 2 × 3 3 × 7. (True)

(iv) 5 × 33 is the prime factorisation of 165. (False)

Question 4: List the common prime factors of 256 and 156.

Prime factorisation of 256 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2

Prime factorisation of 156 = 2 × 2 × 3 × 13

The common prime factor of 256 and 156 is 2.

Question 5: List the common factors of 152 and 76.

Prime factorisation of 152 = 2 × 2 × 2 × 19

Prime factorisation of 76 = 2 × 2 × 19

The common prime factors of 152 and 76 are 2 and 19.

• HCF and LCM
• Factors and Multiples
• Prime Factorisation Calculator

Question 6: Find the highest common factor of 34, 42 and 58.

Prime factorisation of 34 = 2 × 17

Prime factorisation of 42 = 2 × 3 × 7

Prime factorisation of 58 = 2 × 29

The highest common factor of 34, 42, and 58 is 2.

Question 7: Find the lowest common multiple of 45, 75, and 125.

Prime factorisation of 45 = 3 × 3 × 5

Prime factorisation of 75 = 3 × 5 × 5

Prime factorisation of 125 = 5 × 5 × 5

Lowest common multiple of 45, 65 and 125 = 3 × 3 × 5 × 5 × 5 = 1125.

Question 8: Fill in the blank:

(i) 435 = 3 × ___ × ____.

(ii) 378 = 2 × __ × 3 × ___ × ____.

(iii) 1125 = 3 __ × 5 __ .

(i) 435 = 3 × 5 × 9.

(ii) 378 = 2 × 3 × 3 × 3 × 7.

(iii) 1125 = 3 2 × 5 3 .

Question 9: Find the prime factorisation of 118724.

The prime factorisation of 118724 is 2 × 2 × 67 × 443.

Question 10: Verify:

Prime factorisation of 284 × Prime factorisation of 456 = Prime factorisation of (284 × 456)

Prime factorisation of 284 = 2 × 2 × 71

Prime factorisation of 456 = 2 × 2 × 2 × 3 × 19

Prime factorisation of (283 × 456) = prime factorisation of 129504

= 2 × 2 × 2 × 2 × 2 × 3 × 19 × 71

Prime factorisation of 284 × Prime factorisation of 456 = Prime factorisation of (284 × 456).

Related Video on Common Factors

Practice Questions on Prime Factorisation

1. Find the prime factorisation of following:

2. Find the common prime factors of the following:

(i) 25, 65, and 55

(ii) 134 and 345

(iii) 36, 48, and 58

3. Find the lowest common multiple of the following:

(i) 34 and 45

(ii) 45, 24, and 16

(iii) 32, 16, and 18.

Keep visiting BYJU’S to get more such Maths lessons in a simple, concise and easy to understand way. Also, register at BYJU’S – The Learning App to get complete assistance for Maths preparation with video lessons, notes, tips and other study materials.

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Request OTP on Voice Call

Post My Comment

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

• Number Charts
• Multiplication
• Long division
• Basic operations
• Telling time
• Place value
• Roman numerals
• Fractions & related
• Add, subtract, multiply,   and divide fractions
• Mixed numbers vs. fractions
• Equivalent fractions
• Prime factorization & factors
• Fraction Calculator
• Decimals & Percent
• Add, subtract, multiply,   and divide decimals
• Fractions to decimals
• Percents to decimals
• Percentage of a number
• Percent word problems
• Classify triangles
• Classify quadrilaterals
• Circle worksheets
• Area & perimeter of rectangles
• Area of triangles & polygons
• Coordinate grid, including   moves & reflections
• Volume & surface area
• Pre-algebra
• Square Roots
• Order of operations
• Scientific notation
• Proportions
• Ratio word problems
• Write expressions
• Evaluate expressions
• Simplify expressions
• Linear equations
• Linear inequalities
• Graphing & slope
• Equation calculator
• Equation editor
• Elementary Math Games
• Addition and subtraction
• Math facts practice
• The four operations
• Factoring and number theory
• Geometry topics
• Middle/High School
• Statistics & Graphs
• Probability
• Trigonometry
• Logic and proof
• For all levels
• Favorite math puzzles
• Favorite challenging puzzles
• Math in real world
• Problem solving & projects
• For gifted children
• Math history
• Math games and fun websites
• Interactive math tutorials
• Math help & online tutoring
• Assessment, review & test prep
• Online math curricula

Prime factorization using a factor tree

Once you get to the primes in your "tree", they are the "leaves", and you stop factoring in that “branch”. So 24 = 2 × 2 × 2 × 3. This is the prime factorization of 24.

 Examples:

72 has lots of factors so the factoring takes many steps.

72 = 2 × 2 × 2 × 3 × 3

We could have also started by writing 72 = 2 × 36 or 72 = 4 ×18.

1. Factor the following numbers to their prime factors.

2. Factor the following numbers to their prime factors.

By using the process above (building numbers starting from primes) you can build ANY whole number there is! Can you believe that?

We can say this in another way: ALL numbers can be factored so the factors are prime numbers. That is sort of amazing! This fact is known as the fundamental theorem of arithmetic . Indeed, it is fundamental.

See 992 factored on the right. 992 = 2 × 2 × 2 × 2 × 2 × 31. For 83,283 we get 3 × 17 × 23 × 71, and 151,282 = 2 × 3 × 3 × 3 × 11 × 11 × 23.

3. Build numbers from primes.

4. Build more numbers from primes.

5. Try it on your own! Pick 3-6 primes as you wish (you can use the same prime     several times), and see what number is built from them. 

Math Mammoth Multiplication & Division 3

A self-teaching worktext for 5th grade that covers multi-digit multiplication, long division, problem solving, simple equations, ratios, divisibility, and factoring.

Download ($7.40) . Also available as a printed copy.

See more topical Math Mammoth books

• Home   |  
• About   |  
• Contact Us   |  
• Privacy   |  
• Newsletter   |  
• Shop   |  
• 🔍 Search Site
• Easter Color By Number Sheets
• Printable Easter Dot to Dot
• Easter Worksheets for kids
• Kindergarten
• All Generated Sheets
• Place Value Generated Sheets
• Addition Generated Sheets
• Subtraction Generated Sheets
• Multiplication Generated Sheets
• Division Generated Sheets
• Money Generated Sheets
• Negative Numbers Generated Sheets
• Fraction Generated Sheets
• Place Value Zones
• Number Bonds
• Addition & Subtraction
• Times Tables
• Fraction & Percent Zones
• All Calculators
• Fraction Calculators
• Percent calculators
• Area & Volume Calculators
• Age Calculator
• Height Calculator
• Roman Numeral Calculator
• Coloring Pages
• Fun Math Sheets
• Math Puzzles
• Mental Math Sheets
• Online Times Tables
• Online Addition & Subtraction
• Math Grab Packs
• All Math Quizzes
• 1st Grade Quizzes
• 2nd Grade Quizzes
• 3rd Grade Quizzes
• 4th Grade Quizzes
• 5th Grade Quizzes
• 6th Grade Math Quizzes
• Place Value
• Rounding Numbers
• Comparing Numbers
• Number Lines
• Prime Numbers
• Negative Numbers
• Roman Numerals
• Subtraction
• Add & Subtract
• Multiplication
• Fraction Worksheets
• Learning Fractions
• Fraction Printables
• Percent Worksheets & Help
• All Geometry
• 2d Shapes Worksheets
• 3d Shapes Worksheets
• Shape Properties
• Geometry Cheat Sheets
• Printable Shapes
• Coordinates
• Measurement
• Math Conversion
• Statistics Worksheets
• Bar Graph Worksheets
• Venn Diagrams
• All Word Problems
• Finding all possibilities
• Logic Problems
• Ratio Word Problems
• All UK Maths Sheets
• Year 1 Maths Worksheets
• Year 2 Maths Worksheets
• Year 3 Maths Worksheets
• Year 4 Maths Worksheets
• Year 5 Maths Worksheets
• Year 6 Maths Worksheets
• All AU Maths Sheets
• Kindergarten Maths Australia
• Year 1 Maths Australia
• Year 2 Maths Australia
• Year 3 Maths Australia
• Year 4 Maths Australia
• Year 5 Maths Australia
• Meet the Sallies
• Certificates

Prime Factorization Worksheets

Welcome to our Prime Factorization Worksheets page.

Here you will find our selection of worksheets involving finding prime factorizations for a range of numbers, and for solving prime factor problems.

We have a range of sheets at different levels of difficulty.

For full functionality of this site it is necessary to enable JavaScript.

Here are the instructions how to enable JavaScript in your web browser .

Using these factor tree worksheets will help your child to:

• practice prime factorization of a range of numbers;
• solve problems involving prime factorization;
• use and understand exponential notation.

These sheets are aimed at students from 6th grade and upwards.

We also have a link to our Prime Factorization Calculator which will quickly and easily show you all the prime factors of any number.

There is also a quick quiz at the bottom of the page where you can test your skill at prime factorization and get immediate feedback!

What is prime factorization?

To find out more about prime factorization, including how it works and to look at some worked examples, take a look at our prime factorization support page.

• What is Prime Factorization support page

Examples of Prime Factorization

Example 1) Find the prime factorization of 40.

40 is even, so we know that 2 is a factor (as well as being prime)

40 = 2 x 20.

Now we move on to the number 20.

Again 20 is even, so 2 is a factor.

20 = 2 x 10

So 40 = 2 x 20 = 2 x 2 x 10

Now we factorize 10 into 2 x 5 (both prime numbers) and we cannot go any further, as all the numbers are prime.

So 40 = 2 x 20 = 2 x 2 x 10 = 2 x 2 x 2 x 5

Our final answer is 40 = 2 x 2 x 2 x 5 = 2 3 x 5

Example 2) Find the prime factorization of 45.

45 is odd, so 2 is not a factor.

As the number ends in a 5 we know that 5 is a factor.

45 = 5 x 9.

Now we have to factorize 9.

9 = 3 x 3 (which is a prime number).

This gives us:

45 = 5 x 9 = 5 x 3 x 3

Our final answer is 45 = 3 x 3 x 5 = 3 2 x 5

Example 3) Find the prime factorization of 126.

126 is even, so 2 is a factor.

126 = 2 x 63

Now we need to factorize 63.

63 = 7 x 9.

7 is prime, but 9 is not

126 = 2 x 63 = 2 x 7 x 9 = 2 x 7 x 3 x 3

Our final answer is 126 = 2 x 3 x 3 x 7 = 2 x 3 2 x 7

All the worksheets have answers provided. The answers are given with the factors in ascending order.

The sheets get gradually harder in each section.

We have split the sheets into 3 different sections:

• Our first section involves straightforward prime factorization of different numbers.
• Our next group of sheets involves solving prime factorization riddles.
• Our final group of sheets involves finding all possibilities in our prime factorization challenges.

Prime Factorization Worksheets - 1st Section

• The two sheets just has straightforward prime factorization of a range of numbers.
• The third sheet is harder, and involves using exponential notation and looking at prime factorization from different starting points
• Prime Factorization Sheet 1
• PDF version
• Prime Factorization Sheet 2
• Prime Factorization Sheet 3

Prime Factorization Worksheets - Riddles - 2nd Section

These sheets involve solving prime factorization riddles.

There are 2 riddles on each sheet and 8 possible answers.

By correctly working out the clues in each riddle, all the incorrect answers are eliminated leaving just one correct answer.

• Prime Factorization Riddles Sheet 1
• Prime Factorization Riddles Sheet 2

Prime Factorization Worksheets - Challenges - 3rd Section

Our prime factorization challenges are a great way to stretch more able students.

The challenges involve finding all possible numbers that have certain features involving prime factors.

• Prime Factorization Challenges 1
• Prime Factorization Challenges 2

Prime Factorization Walkthrough Video

This short video walkthrough shows several problems from our Prime Factorization Worksheet 3 being solved and has been produced by the West Explains Best math channel.

If you would like some support in solving the problems on this page, check out the video!

More Recommended Math Worksheets

Take a look at some more of our worksheets similar to these.

• Factors and Multiples Worksheets

We have worksheets to help you understand more about factors and multiples.

They are aimed at a 4th/5th grade level.

• Prime Factorization Calculator

Our prime factorization calculator will help you factor any number into a product of its prime factors.

It will show the answer in exponential form as well as standard form.

You can use this calculator to check that your prime factors in your factor trees are correct.

• Factor Tree Worksheets

Using factor trees is a great visual way to understand prime factorization.

The worksheets on the link below are at an easier level to the sheets on this page and help children learn all about factor trees and prime factors.

• Greatest Common Factor Worksheets

As well as our calculator, we also have a range of greatest common factor worksheets.

These sheets have been designed for 6th and 7th grade students.

They will help students learn and practice finding the greatest common factor of numbers up to 100.

• Least Common Multiple Worksheets

We have a range of worksheets on how to find the least common multiple of two or three numbers.

The sheets vary in difficulty, and are suitable for 6th grade and up.

Sieve of Erastosthenes

The Sieve of Erastosthenes is a method for finding what is a prime numbers between 2 and any given number.

Eratosthenes was a Greek mathematician (as well as being a poet, an astronomer and musician) who lived from about 276BC to 194BC.

If you want to find out more about his sieve for finding primes, and print out some Sieve of Eratosthenes worksheets, use the link below.

• Sieve of Eratosthenes page

Want to find out more about primes?

Take a look at our Prime Number page which clearly describes what a prime numbers is and what they are not.

There are also many different questions about prime numbers answered, as well as information about the density of primes.

• What is a Prime Number

Divisibility Rules 1-10 Chart

We have a range of charts which can help you determine whether a number between 1 and 10 is a factor of a number.

• Divisibility Rules 1-10 Charts

6th Grade Mental Math Quizzes

Here you will find a range of printable mental math 6th grade quizzes for your child to enjoy.

Each worksheet tests the children on a range of math topics from number facts and mental arithmetic to geometry, fraction and measures questions.

A great way to revise topics, or use as a weekly math quiz!

• Mental Math Worksheets 6th Grade

Prime Factorization Online Quiz

Our quizzes have been created using Google Forms.

At the end of the quiz, you will get the chance to see your results by clicking 'See Score'.

This will take you to a new webpage where your results will be shown. You can print a copy of your results from this page, either as a pdf or as a paper copy.

For incorrect responses, we have added some helpful learning points to explain which answer was correct and why.

We do not collect any personal data from our quizzes, except in the 'First Name' and 'Group/Class' fields which are both optional and only used for teachers to identify students within their educational setting.

We also collect the results from the quizzes which we use to help us to develop our resources and give us insight into future resources to create.

For more information on the information we collect, please take a look at our Privacy Policy

We would be grateful for any feedback on our quizzes, please let us know using our Contact Us link, or use the Facebook Comments form at the bottom of the page.

This quick quiz tests your knowledge of prime factorization with numbers up to 120.

How to Print or Save these sheets 🖶

Need help with printing or saving? Follow these 3 steps to get your worksheets printed perfectly!

• How to Print support

Subscribe to Math Salamanders News

Sign up for our newsletter to get free math support delivered to your inbox each month. Plus, get a seasonal math grab pack included for free!

• Newsletter Signup

Return to 6th Grade Math Worksheets

Return from Prime Factorization Worksheets to Math Salamanders Homepage

Math-Salamanders.com

The Math Salamanders hope you enjoy using these free printable Math worksheets and all our other Math games and resources.

We welcome any comments about our site or worksheets on the Facebook comments box at the bottom of every page.

Solver Title

Generating PDF...

• Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Expanded Form Mean, Median & Mode
• Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Logical Sets Word Problems
• Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
• Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
• Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
• Linear Algebra Matrices Vectors
• Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
• Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
• Physics Mechanics
• Chemistry Chemical Reactions Chemical Properties
• Finance Simple Interest Compound Interest Present Value Future Value
• Economics Point of Diminishing Return
• Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
• Pre Algebra
• Two-step without parentheses
• Two-step with parentheses
• Three/four steps without parentheses
• Three/four steps with parentheses
• Multi-step without parentheses
• Multi-step with parentheses
• Prime Factorization
• Negative Factors
• Positive Factors
• Odd Factors
• Even Factors
• Biggest Factor
• Equivalent Fractions
• Add, Subtract
• Add, Subtract Like Denominators
• Add, Subtract Unlike Denominators
• Multiply with Whole Number
• Divide with Whole Number
• Mixed Numbers
• Complex Fractions
• Improper Fractions
• Long Addition
• Long Subtraction
• Long Multiplication
• Long Division
• Add/Subtract
• Multiplication
• Decimal to Fraction
• Fraction to Decimal
• Square Root
• Ratios & Proportions

Number Line

• Expanded Form
• Pre Calculus
• Linear Algebra
• Trigonometry
• Conversions

Most Used Actions

• prime\:factors\:of\:45
• prime\:factors\:of\:15
• prime\:factors\:of\:28
• prime\:factors\:of\:32

prime-factorization-calculator

• Practice, practice, practice Math can be an intimidating subject. Each new topic we learn has symbols and problems we have never seen. The unknowing...

Please add a message.

Message received. Thanks for the feedback.

Multiples, Factors and Primes Practice Questions

Click here for questions, click here for answers.

prime numbers

GCSE Revision Cards

5-a-day Workbooks

Primary Study Cards

Privacy Policy

Terms and Conditions

Corbettmaths © 2012 – 2024

• Data Science
• Courses 30% Discount

Back to Explore Page

Or search by topic

Number and algebra

• The Number System and Place Value
• Calculations and Numerical Methods
• Fractions, Decimals, Percentages, Ratio and Proportion
• Properties of Numbers
• Patterns, Sequences and Structure
• Algebraic expressions, equations and formulae
• Coordinates, Functions and Graphs

Geometry and measure

• Angles, Polygons, and Geometrical Proof
• 3D Geometry, Shape and Space
• Measuring and calculating with units
• Transformations and constructions
• Pythagoras and Trigonometry
• Vectors and Matrices

Probability and statistics

• Handling, Processing and Representing Data
• Probability

Working mathematically

• Thinking mathematically
• Mathematical mindsets
• Cross-curricular contexts
• Physical and digital manipulatives

For younger learners

• Early Years Foundation Stage

Advanced mathematics

• Decision Mathematics and Combinatorics
• Advanced Probability and Statistics

Factors, Multiples and Primes

Statement Snap

You'll need to know your number properties to win a game of Statement Snap...

Factors and Multiples Game

A game in which players take it in turns to choose a number. Can you block your opponent?

Gabriel's Problem

Gabriel multiplied together some numbers and then erased them. Can you figure out where each number was?

Factors and Multiples Puzzle

Using your knowledge of the properties of numbers, can you fill all the squares on the board?

Number Families

How many different number families can you find?

American Billions

Play the divisibility game to create numbers in which the first two digits make a number divisible by 2, the first three digits make a number divisible by 3...

Sieve of Eratosthenes

Follow this recipe for sieving numbers and see what interesting patterns emerge.

Can you select the missing digit(s) to find the largest multiple?

Multiples Sudoku

Each clue in this Sudoku is the product of the two numbers in adjacent cells.

Multiple Surprises

Sequences of multiples keep cropping up...

How Much Can We Spend?

A country has decided to have just two different coins, 3z and 5z coins. Which totals can be made? Is there a largest total that cannot be made? How do you know?

Product Sudoku

The clues for this Sudoku are the product of the numbers in adjacent squares.

Diminishing Returns

How much of the square is coloured blue? How will the pattern continue?

Alison's Quilt

Nine squares are fitted together to form a rectangle. Can you find its dimensions?

Counting Factors

Is there an efficient way to work out how many factors a large number has?

Route to Infinity

Can you describe this route to infinity? Where will the arrows take you next?

Powers of numbers behave in surprising ways. Take a look at some of these and try to explain why they are true.

Can you work out what step size to take to ensure you visit all the dots on the circle?

Funny Factorisation

Using the digits 1 to 9, the number 4396 can be written as the product of two numbers. Can you find the factors?

Differences

Can you guarantee that, for any three numbers you choose, the product of their differences will always be an even number?

Divisibility Tests

This article explains various divisibility rules and why they work. An article to read with pencil and paper handy.

Is there a relationship between the coordinates of the endpoints of a line and the number of grid squares it crosses?

Latin Numbers

Can you create a Latin Square from multiples of a six digit number?

Filling the Gaps

Which numbers can we write as a sum of square numbers?

Take Three from Five

Caroline and James pick sets of five numbers. Charlie tries to find three that add together to make a multiple of three. Can they stop him?

What is the largest number which, when divided into 1905, 2587, 3951, 7020 and 8725 in turn, leaves the same remainder each time?

Shopping Basket

The items in the shopping basket add and multiply to give the same amount. What could their prices be?

Factors, Multiple and Primes - Short Problems

A collection of short problems on factors, multiples and primes.

Xavi's T-shirt

How much can you read into a T-shirt?

Here is a Sudoku with a difference! Use information about lowest common multiples to help you solve it.

The home of mathematics education in New Zealand.

• Forgot password ?

Solve problems by finding the prime factors of numbers.

The Ministry is migrating nzmaths content to Tāhurangi.             Relevant and up-to-date teaching resources are being moved to Tāhūrangi (tahurangi.education.govt.nz).  When all identified resources have been successfully moved, this website will close. We expect this to be in June 2024.  e-ako maths, e-ako Pāngarau, and e-ako PLD 360 will continue to be available. 

For more information visit https://tahurangi.education.govt.nz/updates-to-nzmaths

Boxing Balls

investigate prime and composite numbers

Factor Trees

Going bananas.

investigate prime numbers

Going to Extraordinary Lengths

find prime numbers up to 100

explore squares, primes and cubics

Igloo Iceblocks

solve problems using prime factors

In Your Prime

explore prime numbers and factors

find prime factors of numbers

Prime Numbers

Primes and emirps.

explore prime numbers

Recurring and Terminating Decimal Fractions

Systematic prime factorisation, the sieve of eratosthenes.

• Skip to main content
• Keyboard shortcuts for audio player

Middle East

What might have caused the helicopter crash that killed iran's president.

Scott Neuman

Iranians gather at Valiasr Square in central Tehran on May 20 to mourn the deaths of President Ebrahim Raisi, Foreign Minister Hossein Amir-Abdollahian and several others in a helicopter crash the previous day. Atta Kenare/AFP via Getty Images hide caption

Iranians gather at Valiasr Square in central Tehran on May 20 to mourn the deaths of President Ebrahim Raisi, Foreign Minister Hossein Amir-Abdollahian and several others in a helicopter crash the previous day.

The crash that killed Iranian President Ebrahim Raisi and several other top officials on Sunday was the latest high-profile deadly helicopter accident in recent years.

For most people, the death of retired NBA star Kobe Bryant , his 13-year-old daughter and seven others in a helicopter crash in California four years ago comes to mind. But in 2018, Thai businessman Vichai Srivaddhanaprabha, who owned the Leicester City soccer club, died along with four others in a helicopter crash. The previous year, Troy Gentry, then part of country music act Montgomery Gentry , was also killed in a crash in New Jersey.

An investigation of the crash that killed Bryant and the others aboard a Sikorsky S-76B concluded that the pilot became disoriented as the chopper flew into a cloud bank, thinking he was climbing when in fact he was plunging into a hillside. Pilot error was also blamed in the crash that killed Gentry, while an investigation of the crash involving Vichai concluded that the Leonardo AW169 helicopter was brought down by a failure of its rear rotor mechanism.

It's impossible to say with certainty what may have caused the crash in Iran on Sunday that killed Raisi, Iranian Foreign Minister Hossein Amir-Abdollahian and the others. But one or more of the factors below may have played a part.

Could bad weather have been a factor in the fatal crash?

Early reports of the crash in Iran suggest that the helicopter was flying in a "foggy, mountainous region of the country's northwest," according to The Associated Press.

Poor weather conditions are a leading cause of helicopter, or rotor aircraft, crashes. According to an analysis presented at a 2021 forum of the American Institute of Aeronautics and Astronautics, in 28% of all fatal helicopter crashes, weather was a factor.

New Virtual Reality Tool Aims To Reduce Aviation Crashes

"Wind was involved in most incidents but more rarely involved in fatalities. Bad visibility conditions due to a combination of low illumination and clouds were responsible for most fatal weather-related accidents," the analysis says in its synopsis.

It notes that helicopters "typically operate at lower altitudes than fixed-wing aircraft and can take-off and land away from airports. Thus, helicopter pilots have decreased access to weather information due to connectivity issues or sparsity of weather coverage in those areas and at those altitudes."

In February, five Marines were killed when their CH-53E Super Stallion — the largest helicopter operated by the U.S. military — crashed into mountains outside San Diego during a storm.

Helicopters are more dangerous than planes

While directly comparing the safety records of different modes of transportation is fraught with difficulties, an analysis conducted by the travel site The Points Guy in 2019 suggests that airline flights are considerably safer than "non-scheduled helicopter flights." However, those helicopter flights still scored much better for safety than driving or riding in a car or SUV or even "general aviation," such as flights in private planes.

Because of automation, most airplanes are forgiving of a pilot's momentary distraction, but "helicopters require a lot of concentration," John Goglia, a former member of the National Transportation Safety Board, said earlier this year, speaking to PBS. "And so sometimes people will lose their focus, and [then] the consequences are severe."

This Bell 212 helicopter of the Argentine air force, seen in March 2015, is similar to the one that crashed in Iran on Sunday. Juan Mabromata/AFP via Getty Images hide caption

This Bell 212 helicopter of the Argentine air force, seen in March 2015, is similar to the one that crashed in Iran on Sunday.

The Iranian president's helicopter was an old aircraft

The helicopter that crashed in Iran was a Bell 212 , a twin-engine civilian version of the venerable "Huey" UH-1 that became ubiquitous during the Vietnam War in the 1960s and '70s.

The Aviation Safety Network , which maintains a database of accidents for various aircraft, shows that the Bell 212 and its military equivalents have experienced about 30 accidents since 2017, eight of them causing fatalities.

The Bell 212 in Iran was probably one bought in the 1970s while the Shah was still in power, prior to the country's 1979 Islamic Revolution, according to The National , the state-run English-language daily in the United Arab Emirates.

U.S. sanctions have made spare parts hard to obtain

According to the same paper, after the Shah was overthrown, Iran continued to use many U.S.-made aircraft "but faced difficulty obtaining spare parts due to American sanctions."

Iran's semiofficial Mehr News Agency in March quoted the deputy of the scientific department of knowledge-based economy development, Javad Mashayekh, as saying that the country had finally become 100% self-sufficient in supplying airplane spare parts. It did not say anything specifically about parts for helicopters.

Mashayekh was reported by Mehr News Agency as saying that previously Iran had been "highly dependent" on foreign sources for such parts and that U.S. sanctions imposed on Iran's nuclear program "caused a challenge in this regard."

In a commentary published by the Gulf International Forum, journalist Kourosh Ziabari wrote that "Iran's aviation industry has been blighted by years of neglect, underinvestment, and grueling sanctions" and that "accidents are recurrent and air transportation safety standards have steadily fallen."

Mysterious crashes have claimed the lives of politicians and rivals alike

Nothing immediate suggests sabotage as a possibility in the case of the helicopter crash in Iran, but using an aviation "accident" as a way to eliminate a national leader or political rival has been suspected in the past.

Last August, Yevgeny Prigozhin, the head of Russia's Wagner mercenary group, who led an abortive coup against the Kremlin, was killed when the private jet he was in plummeted into a field outside Moscow. Many believe the destruction of the plane was ordered by Russian President Vladimir Putin.

In April 1994, Rwandan President Juvénal Habyarimana, a Hutu, was killed when the aircraft he was in was shot down by a missile — an incident that triggered the Rwandan genocide. An inquiry did not bring charges against alleged culprits.

And in 1988, Pakistani President Muhammad Zia-ul-Haq was killed when the C-130 transport plane he was aboard suddenly crashed shortly after taking off from an airport in Pakistan's eastern city of Bahawalpur. At the time, witnesses reported seeing the plane flying erratically and then nosing down.

An official Pakistani report later concluded that "in the absence of a technical reason, the only other possible cause of the accident is the occurrence of a criminal act or sabotage."

• helicopters