null hypothesis is h0

9.1 Null and Alternative Hypotheses

The actual test begins by considering two hypotheses . They are called the null hypothesis and the alternative hypothesis . These hypotheses contain opposing viewpoints.

H 0 , the — null hypothesis: a statement of no difference between sample means or proportions or no difference between a sample mean or proportion and a population mean or proportion. In other words, the difference equals 0.

H a —, the alternative hypothesis: a claim about the population that is contradictory to H 0 and what we conclude when we reject H 0 .

Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample data.

After you have determined which hypothesis the sample supports, you make a decision. There are two options for a decision. They are reject H 0 if the sample information favors the alternative hypothesis or do not reject H 0 or decline to reject H 0 if the sample information is insufficient to reject the null hypothesis.

Mathematical Symbols Used in H 0 and H a :

H 0 always has a symbol with an equal in it. H a never has a symbol with an equal in it. The choice of symbol depends on the wording of the hypothesis test. However, be aware that many researchers use = in the null hypothesis, even with > or < as the symbol in the alternative hypothesis. This practice is acceptable because we only make the decision to reject or not reject the null hypothesis.

Example 9.1

H 0 : No more than 30 percent of the registered voters in Santa Clara County voted in the primary election. p ≤ 30 H a : More than 30 percent of the registered voters in Santa Clara County voted in the primary election. p > 30

A medical trial is conducted to test whether or not a new medicine reduces cholesterol by 25 percent. State the null and alternative hypotheses.

Example 9.2

We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). The null and alternative hypotheses are the following: H 0 : μ = 2.0 H a : μ ≠ 2.0

We want to test whether the mean height of eighth graders is 66 inches. State the null and alternative hypotheses. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

• H 0 : μ __ 66
• H a : μ __ 66

Example 9.3

We want to test if college students take fewer than five years to graduate from college, on the average. The null and alternative hypotheses are the following: H 0 : μ ≥ 5 H a : μ < 5

We want to test if it takes fewer than 45 minutes to teach a lesson plan. State the null and alternative hypotheses. Fill in the correct symbol ( =, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

• H 0 : μ __ 45
• H a : μ __ 45

Example 9.4

An article on school standards stated that about half of all students in France, Germany, and Israel take advanced placement exams and a third of the students pass. The same article stated that 6.6 percent of U.S. students take advanced placement exams and 4.4 percent pass. Test if the percentage of U.S. students who take advanced placement exams is more than 6.6 percent. State the null and alternative hypotheses. H 0 : p ≤ 0.066 H a : p > 0.066

On a state driver’s test, about 40 percent pass the test on the first try. We want to test if more than 40 percent pass on the first try. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

• H 0 : p __ 0.40
• H a : p __ 0.40

Collaborative Exercise

Bring to class a newspaper, some news magazines, and some internet articles. In groups, find articles from which your group can write null and alternative hypotheses. Discuss your hypotheses with the rest of the class.

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute Texas Education Agency (TEA). The original material is available at: https://www.texasgateway.org/book/tea-statistics . Changes were made to the original material, including updates to art, structure, and other content updates.

Access for free at https://openstax.org/books/statistics/pages/1-introduction

• Authors: Barbara Illowsky, Susan Dean
• Publisher/website: OpenStax
• Book title: Statistics
• Publication date: Mar 27, 2020
• Location: Houston, Texas
• Book URL: https://openstax.org/books/statistics/pages/1-introduction
• Section URL: https://openstax.org/books/statistics/pages/9-1-null-and-alternative-hypotheses

© Jan 23, 2024 Texas Education Agency (TEA). The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

Hypothesis Testing with One Sample

Null and Alternative Hypotheses

OpenStaxCollege

[latexpage]

The actual test begins by considering two hypotheses . They are called the null hypothesis and the alternative hypothesis . These hypotheses contain opposing viewpoints.

H 0 : The null hypothesis: It is a statement about the population that either is believed to be true or is used to put forth an argument unless it can be shown to be incorrect beyond a reasonable doubt.

H a : The alternative hypothesis: It is a claim about the population that is contradictory to H 0 and what we conclude when we reject H 0 .

Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample data.

After you have determined which hypothesis the sample supports, you make a decision. There are two options for a decision. They are “reject H 0 ” if the sample information favors the alternative hypothesis or “do not reject H 0 ” or “decline to reject H 0 ” if the sample information is insufficient to reject the null hypothesis.

Mathematical Symbols Used in H 0 and H a :

H 0 always has a symbol with an equal in it. H a never has a symbol with an equal in it. The choice of symbol depends on the wording of the hypothesis test. However, be aware that many researchers (including one of the co-authors in research work) use = in the null hypothesis, even with > or < as the symbol in the alternative hypothesis. This practice is acceptable because we only make the decision to reject or not reject the null hypothesis.

H 0 : No more than 30% of the registered voters in Santa Clara County voted in the primary election. p ≤ 30

A medical trial is conducted to test whether or not a new medicine reduces cholesterol by 25%. State the null and alternative hypotheses.

H 0 : The drug reduces cholesterol by 25%. p = 0.25

H a : The drug does not reduce cholesterol by 25%. p ≠ 0.25

We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). The null and alternative hypotheses are:

H 0 : μ = 2.0

We want to test whether the mean height of eighth graders is 66 inches. State the null and alternative hypotheses. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

• H 0 : μ = 66
• H a : μ ≠ 66

We want to test if college students take less than five years to graduate from college, on the average. The null and alternative hypotheses are:

H 0 : μ ≥ 5

We want to test if it takes fewer than 45 minutes to teach a lesson plan. State the null and alternative hypotheses. Fill in the correct symbol ( =, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

• H 0 : μ ≥ 45
• H a : μ < 45

In an issue of U. S. News and World Report , an article on school standards stated that about half of all students in France, Germany, and Israel take advanced placement exams and a third pass. The same article stated that 6.6% of U.S. students take advanced placement exams and 4.4% pass. Test if the percentage of U.S. students who take advanced placement exams is more than 6.6%. State the null and alternative hypotheses.

H 0 : p ≤ 0.066

On a state driver’s test, about 40% pass the test on the first try. We want to test if more than 40% pass on the first try. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

• H 0 : p = 0.40
• H a : p > 0.40

<!– ??? –>

Bring to class a newspaper, some news magazines, and some Internet articles . In groups, find articles from which your group can write null and alternative hypotheses. Discuss your hypotheses with the rest of the class.

Chapter Review

In a hypothesis test , sample data is evaluated in order to arrive at a decision about some type of claim. If certain conditions about the sample are satisfied, then the claim can be evaluated for a population. In a hypothesis test, we:

Formula Review

H 0 and H a are contradictory.

If α ≤ p -value, then do not reject H 0 .

If α > p -value, then reject H 0 .

α is preconceived. Its value is set before the hypothesis test starts. The p -value is calculated from the data.

You are testing that the mean speed of your cable Internet connection is more than three Megabits per second. What is the random variable? Describe in words.

The random variable is the mean Internet speed in Megabits per second.

You are testing that the mean speed of your cable Internet connection is more than three Megabits per second. State the null and alternative hypotheses.

The American family has an average of two children. What is the random variable? Describe in words.

The random variable is the mean number of children an American family has.

The mean entry level salary of an employee at a company is 💲58,000. You believe it is higher for IT professionals in the company. State the null and alternative hypotheses.

A sociologist claims the probability that a person picked at random in Times Square in New York City is visiting the area is 0.83. You want to test to see if the proportion is actually less. What is the random variable? Describe in words.

The random variable is the proportion of people picked at random in Times Square visiting the city.

A sociologist claims the probability that a person picked at random in Times Square in New York City is visiting the area is 0.83. You want to test to see if the claim is correct. State the null and alternative hypotheses.

In a population of fish, approximately 42% are female. A test is conducted to see if, in fact, the proportion is less. State the null and alternative hypotheses.

Suppose that a recent article stated that the mean time spent in jail by a first–time convicted burglar is 2.5 years. A study was then done to see if the mean time has increased in the new century. A random sample of 26 first-time convicted burglars in a recent year was picked. The mean length of time in jail from the survey was 3 years with a standard deviation of 1.8 years. Suppose that it is somehow known that the population standard deviation is 1.5. If you were conducting a hypothesis test to determine if the mean length of jail time has increased, what would the null and alternative hypotheses be? The distribution of the population is normal.

A random survey of 75 death row inmates revealed that the mean length of time on death row is 17.4 years with a standard deviation of 6.3 years. If you were conducting a hypothesis test to determine if the population mean time on death row could likely be 15 years, what would the null and alternative hypotheses be?

• H 0 : __________
• H a : __________
• H 0 : μ = 15
• H a : μ ≠ 15

The National Institute of Mental Health published an article stating that in any one-year period, approximately 9.5 percent of American adults suffer from depression or a depressive illness. Suppose that in a survey of 100 people in a certain town, seven of them suffered from depression or a depressive illness. If you were conducting a hypothesis test to determine if the true proportion of people in that town suffering from depression or a depressive illness is lower than the percent in the general adult American population, what would the null and alternative hypotheses be?

Some of the following statements refer to the null hypothesis, some to the alternate hypothesis.

State the null hypothesis, H 0 , and the alternative hypothesis. H a , in terms of the appropriate parameter ( μ or p ).

• The mean number of years Americans work before retiring is 34.
• At most 60% of Americans vote in presidential elections.
• The mean starting salary for San Jose State University graduates is at least 💲100,000 per year.
• Twenty-nine percent of high school seniors get drunk each month.
• Fewer than 5% of adults ride the bus to work in Los Angeles.
• The mean number of cars a person owns in her lifetime is not more than ten.
• About half of Americans prefer to live away from cities, given the choice.
• Europeans have a mean paid vacation each year of six weeks.
• The chance of developing breast cancer is under 11% for women.
• Private universities’ mean tuition cost is more than 💲20,000 per year.
• H 0 : μ = 34; H a : μ ≠ 34
• H 0 : p ≤ 0.60; H a : p > 0.60
• H 0 : μ ≥ 100,000; H a : μ < 100,000
• H 0 : p = 0.29; H a : p ≠ 0.29
• H 0 : p = 0.05; H a : p < 0.05
• H 0 : μ ≤ 10; H a : μ > 10
• H 0 : p = 0.50; H a : p ≠ 0.50
• H 0 : μ = 6; H a : μ ≠ 6
• H 0 : p ≥ 0.11; H a : p < 0.11
• H 0 : μ ≤ 20,000; H a : μ > 20,000

Over the past few decades, public health officials have examined the link between weight concerns and teen girls’ smoking. Researchers surveyed a group of 273 randomly selected teen girls living in Massachusetts (between 12 and 15 years old). After four years the girls were surveyed again. Sixty-three said they smoked to stay thin. Is there good evidence that more than thirty percent of the teen girls smoke to stay thin? The alternative hypothesis is:

• p < 0.30
• p > 0.30

A statistics instructor believes that fewer than 20% of Evergreen Valley College (EVC) students attended the opening night midnight showing of the latest Harry Potter movie. She surveys 84 of her students and finds that 11 attended the midnight showing. An appropriate alternative hypothesis is:

• p > 0.20
• p < 0.20

Previously, an organization reported that teenagers spent 4.5 hours per week, on average, on the phone. The organization thinks that, currently, the mean is higher. Fifteen randomly chosen teenagers were asked how many hours per week they spend on the phone. The sample mean was 4.75 hours with a sample standard deviation of 2.0. Conduct a hypothesis test. The null and alternative hypotheses are:

• H o : \(\overline{x}\) = 4.5, H a : \(\overline{x}\) > 4.5
• H o : μ ≥ 4.5, H a : μ < 4.5
• H o : μ = 4.75, H a : μ > 4.75
• H o : μ = 4.5, H a : μ > 4.5

Data from the National Institute of Mental Health. Available online at http://www.nimh.nih.gov/publicat/depression.cfm.

Null and Alternative Hypotheses Copyright © 2013 by OpenStaxCollege is licensed under a Creative Commons Attribution 4.0 International License , except where otherwise noted.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

9.1: Null and Alternative Hypotheses

• Last updated
• Save as PDF
• Page ID 23459

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

The actual test begins by considering two hypotheses . They are called the null hypothesis and the alternative hypothesis . These hypotheses contain opposing viewpoints.

\(H_0\): The null hypothesis: It is a statement of no difference between the variables—they are not related. This can often be considered the status quo and as a result if you cannot accept the null it requires some action.

\(H_a\): The alternative hypothesis: It is a claim about the population that is contradictory to \(H_0\) and what we conclude when we reject \(H_0\). This is usually what the researcher is trying to prove.

Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample data.

After you have determined which hypothesis the sample supports, you make a decision. There are two options for a decision. They are "reject \(H_0\)" if the sample information favors the alternative hypothesis or "do not reject \(H_0\)" or "decline to reject \(H_0\)" if the sample information is insufficient to reject the null hypothesis.

\(H_{0}\) always has a symbol with an equal in it. \(H_{a}\) never has a symbol with an equal in it. The choice of symbol depends on the wording of the hypothesis test. However, be aware that many researchers (including one of the co-authors in research work) use = in the null hypothesis, even with > or < as the symbol in the alternative hypothesis. This practice is acceptable because we only make the decision to reject or not reject the null hypothesis.

Example \(\PageIndex{1}\)

• \(H_{0}\): No more than 30% of the registered voters in Santa Clara County voted in the primary election. \(p \leq 30\)
• \(H_{a}\): More than 30% of the registered voters in Santa Clara County voted in the primary election. \(p > 30\)

Exercise \(\PageIndex{1}\)

A medical trial is conducted to test whether or not a new medicine reduces cholesterol by 25%. State the null and alternative hypotheses.

• \(H_{0}\): The drug reduces cholesterol by 25%. \(p = 0.25\)
• \(H_{a}\): The drug does not reduce cholesterol by 25%. \(p \neq 0.25\)

Example \(\PageIndex{2}\)

We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). The null and alternative hypotheses are:

• \(H_{0}: \mu = 2.0\)
• \(H_{a}: \mu \neq 2.0\)

Exercise \(\PageIndex{2}\)

We want to test whether the mean height of eighth graders is 66 inches. State the null and alternative hypotheses. Fill in the correct symbol \((=, \neq, \geq, <, \leq, >)\) for the null and alternative hypotheses.

• \(H_{0}: \mu \_ 66\)
• \(H_{a}: \mu \_ 66\)
• \(H_{0}: \mu = 66\)
• \(H_{a}: \mu \neq 66\)

Example \(\PageIndex{3}\)

We want to test if college students take less than five years to graduate from college, on the average. The null and alternative hypotheses are:

• \(H_{0}: \mu \geq 5\)
• \(H_{a}: \mu < 5\)

Exercise \(\PageIndex{3}\)

We want to test if it takes fewer than 45 minutes to teach a lesson plan. State the null and alternative hypotheses. Fill in the correct symbol ( =, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

• \(H_{0}: \mu \_ 45\)
• \(H_{a}: \mu \_ 45\)
• \(H_{0}: \mu \geq 45\)
• \(H_{a}: \mu < 45\)

Example \(\PageIndex{4}\)

In an issue of U. S. News and World Report , an article on school standards stated that about half of all students in France, Germany, and Israel take advanced placement exams and a third pass. The same article stated that 6.6% of U.S. students take advanced placement exams and 4.4% pass. Test if the percentage of U.S. students who take advanced placement exams is more than 6.6%. State the null and alternative hypotheses.

• \(H_{0}: p \leq 0.066\)
• \(H_{a}: p > 0.066\)

Exercise \(\PageIndex{4}\)

On a state driver’s test, about 40% pass the test on the first try. We want to test if more than 40% pass on the first try. Fill in the correct symbol (\(=, \neq, \geq, <, \leq, >\)) for the null and alternative hypotheses.

• \(H_{0}: p \_ 0.40\)
• \(H_{a}: p \_ 0.40\)
• \(H_{0}: p = 0.40\)
• \(H_{a}: p > 0.40\)

COLLABORATIVE EXERCISE

Bring to class a newspaper, some news magazines, and some Internet articles . In groups, find articles from which your group can write null and alternative hypotheses. Discuss your hypotheses with the rest of the class.

In a hypothesis test , sample data is evaluated in order to arrive at a decision about some type of claim. If certain conditions about the sample are satisfied, then the claim can be evaluated for a population. In a hypothesis test, we:

• Evaluate the null hypothesis , typically denoted with \(H_{0}\). The null is not rejected unless the hypothesis test shows otherwise. The null statement must always contain some form of equality \((=, \leq \text{or} \geq)\)
• Always write the alternative hypothesis , typically denoted with \(H_{a}\) or \(H_{1}\), using less than, greater than, or not equals symbols, i.e., \((\neq, >, \text{or} <)\).
• If we reject the null hypothesis, then we can assume there is enough evidence to support the alternative hypothesis.
• Never state that a claim is proven true or false. Keep in mind the underlying fact that hypothesis testing is based on probability laws; therefore, we can talk only in terms of non-absolute certainties.

Formula Review

\(H_{0}\) and \(H_{a}\) are contradictory.

• If \(\alpha \leq p\)-value, then do not reject \(H_{0}\).
• If\(\alpha > p\)-value, then reject \(H_{0}\).

\(\alpha\) is preconceived. Its value is set before the hypothesis test starts. The \(p\)-value is calculated from the data.References

Data from the National Institute of Mental Health. Available online at http://www.nimh.nih.gov/publicat/depression.cfm .

Module 9: Hypothesis Testing With One Sample

Null and alternative hypotheses, learning outcomes.

• Describe hypothesis testing in general and in practice

The actual test begins by considering two  hypotheses . They are called the null hypothesis and the alternative hypothesis . These hypotheses contain opposing viewpoints.

H 0 : The null hypothesis: It is a statement about the population that either is believed to be true or is used to put forth an argument unless it can be shown to be incorrect beyond a reasonable doubt.

H a : The alternative hypothesis : It is a claim about the population that is contradictory to H 0 and what we conclude when we reject H 0 .

Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample data.

After you have determined which hypothesis the sample supports, you make adecision. There are two options for a  decision . They are “reject H 0 ” if the sample information favors the alternative hypothesis or “do not reject H 0 ” or “decline to reject H 0 ” if the sample information is insufficient to reject the null hypothesis.

Mathematical Symbols Used in  H 0 and H a :

H 0 always has a symbol with an equal in it. H a never has a symbol with an equal in it. The choice of symbol depends on the wording of the hypothesis test. However, be aware that many researchers (including one of the co-authors in research work) use = in the null hypothesis, even with > or < as the symbol in the alternative hypothesis. This practice is acceptable because we only make the decision to reject or not reject the null hypothesis.

H 0 : No more than 30% of the registered voters in Santa Clara County voted in the primary election. p ≤ 30

H a : More than 30% of the registered voters in Santa Clara County voted in the primary election. p > 30

A medical trial is conducted to test whether or not a new medicine reduces cholesterol by 25%. State the null and alternative hypotheses.

H 0 : The drug reduces cholesterol by 25%. p = 0.25

H a : The drug does not reduce cholesterol by 25%. p ≠ 0.25

We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). The null and alternative hypotheses are:

H 0 : μ = 2.0

H a : μ ≠ 2.0

We want to test whether the mean height of eighth graders is 66 inches. State the null and alternative hypotheses. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses. H 0 : μ __ 66 H a : μ __ 66

• H 0 : μ = 66
• H a : μ ≠ 66

We want to test if college students take less than five years to graduate from college, on the average. The null and alternative hypotheses are:

H 0 : μ ≥ 5

H a : μ < 5

We want to test if it takes fewer than 45 minutes to teach a lesson plan. State the null and alternative hypotheses. Fill in the correct symbol ( =, ≠, ≥, <, ≤, >) for the null and alternative hypotheses. H 0 : μ __ 45 H a : μ __ 45

• H 0 : μ ≥ 45
• H a : μ < 45

In an issue of U.S. News and World Report , an article on school standards stated that about half of all students in France, Germany, and Israel take advanced placement exams and a third pass. The same article stated that 6.6% of U.S. students take advanced placement exams and 4.4% pass. Test if the percentage of U.S. students who take advanced placement exams is more than 6.6%. State the null and alternative hypotheses.

H 0 : p ≤ 0.066

H a : p > 0.066

On a state driver’s test, about 40% pass the test on the first try. We want to test if more than 40% pass on the first try. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses. H 0 : p __ 0.40 H a : p __ 0.40

• H 0 : p = 0.40
• H a : p > 0.40

Concept Review

In a  hypothesis test , sample data is evaluated in order to arrive at a decision about some type of claim. If certain conditions about the sample are satisfied, then the claim can be evaluated for a population. In a hypothesis test, we: Evaluate the null hypothesis , typically denoted with H 0 . The null is not rejected unless the hypothesis test shows otherwise. The null statement must always contain some form of equality (=, ≤ or ≥) Always write the alternative hypothesis , typically denoted with H a or H 1 , using less than, greater than, or not equals symbols, i.e., (≠, >, or <). If we reject the null hypothesis, then we can assume there is enough evidence to support the alternative hypothesis. Never state that a claim is proven true or false. Keep in mind the underlying fact that hypothesis testing is based on probability laws; therefore, we can talk only in terms of non-absolute certainties.

Formula Review

H 0 and H a are contradictory.

• OpenStax, Statistics, Null and Alternative Hypotheses. Provided by : OpenStax. Located at : http://cnx.org/contents/[email protected]:58/Introductory_Statistics . License : CC BY: Attribution
• Introductory Statistics . Authored by : Barbara Illowski, Susan Dean. Provided by : Open Stax. Located at : http://cnx.org/contents/[email protected] . License : CC BY: Attribution . License Terms : Download for free at http://cnx.org/contents/[email protected]
• Simple hypothesis testing | Probability and Statistics | Khan Academy. Authored by : Khan Academy. Located at : https://youtu.be/5D1gV37bKXY . License : All Rights Reserved . License Terms : Standard YouTube License

Have a thesis expert improve your writing

Check your thesis for plagiarism in 10 minutes, generate your apa citations for free.

• Knowledge Base
• Null and Alternative Hypotheses | Definitions & Examples

Null and Alternative Hypotheses | Definitions & Examples

Published on 5 October 2022 by Shaun Turney . Revised on 6 December 2022.

The null and alternative hypotheses are two competing claims that researchers weigh evidence for and against using a statistical test :

• Null hypothesis (H 0 ): There’s no effect in the population .
• Alternative hypothesis (H A ): There’s an effect in the population.

The effect is usually the effect of the independent variable on the dependent variable .

Table of contents

Answering your research question with hypotheses, what is a null hypothesis, what is an alternative hypothesis, differences between null and alternative hypotheses, how to write null and alternative hypotheses, frequently asked questions about null and alternative hypotheses.

The null and alternative hypotheses offer competing answers to your research question . When the research question asks “Does the independent variable affect the dependent variable?”, the null hypothesis (H 0 ) answers “No, there’s no effect in the population.” On the other hand, the alternative hypothesis (H A ) answers “Yes, there is an effect in the population.”

The null and alternative are always claims about the population. That’s because the goal of hypothesis testing is to make inferences about a population based on a sample . Often, we infer whether there’s an effect in the population by looking at differences between groups or relationships between variables in the sample.

You can use a statistical test to decide whether the evidence favors the null or alternative hypothesis. Each type of statistical test comes with a specific way of phrasing the null and alternative hypothesis. However, the hypotheses can also be phrased in a general way that applies to any test.

The null hypothesis is the claim that there’s no effect in the population.

If the sample provides enough evidence against the claim that there’s no effect in the population ( p ≤ α), then we can reject the null hypothesis . Otherwise, we fail to reject the null hypothesis.

Although “fail to reject” may sound awkward, it’s the only wording that statisticians accept. Be careful not to say you “prove” or “accept” the null hypothesis.

Null hypotheses often include phrases such as “no effect”, “no difference”, or “no relationship”. When written in mathematical terms, they always include an equality (usually =, but sometimes ≥ or ≤).

Examples of null hypotheses

The table below gives examples of research questions and null hypotheses. There’s always more than one way to answer a research question, but these null hypotheses can help you get started.

*Note that some researchers prefer to always write the null hypothesis in terms of “no effect” and “=”. It would be fine to say that daily meditation has no effect on the incidence of depression and p 1 = p 2 .

The alternative hypothesis (H A ) is the other answer to your research question . It claims that there’s an effect in the population.

Often, your alternative hypothesis is the same as your research hypothesis. In other words, it’s the claim that you expect or hope will be true.

The alternative hypothesis is the complement to the null hypothesis. Null and alternative hypotheses are exhaustive, meaning that together they cover every possible outcome. They are also mutually exclusive, meaning that only one can be true at a time.

Alternative hypotheses often include phrases such as “an effect”, “a difference”, or “a relationship”. When alternative hypotheses are written in mathematical terms, they always include an inequality (usually ≠, but sometimes > or <). As with null hypotheses, there are many acceptable ways to phrase an alternative hypothesis.

Examples of alternative hypotheses

The table below gives examples of research questions and alternative hypotheses to help you get started with formulating your own.

Null and alternative hypotheses are similar in some ways:

• They’re both answers to the research question
• They both make claims about the population
• They’re both evaluated by statistical tests.

However, there are important differences between the two types of hypotheses, summarized in the following table.

To help you write your hypotheses, you can use the template sentences below. If you know which statistical test you’re going to use, you can use the test-specific template sentences. Otherwise, you can use the general template sentences.

The only thing you need to know to use these general template sentences are your dependent and independent variables. To write your research question, null hypothesis, and alternative hypothesis, fill in the following sentences with your variables:

Does independent variable affect dependent variable ?

• Null hypothesis (H 0 ): Independent variable does not affect dependent variable .
• Alternative hypothesis (H A ): Independent variable affects dependent variable .

Test-specific

Once you know the statistical test you’ll be using, you can write your hypotheses in a more precise and mathematical way specific to the test you chose. The table below provides template sentences for common statistical tests.

Note: The template sentences above assume that you’re performing one-tailed tests . One-tailed tests are appropriate for most studies.

The null hypothesis is often abbreviated as H 0 . When the null hypothesis is written using mathematical symbols, it always includes an equality symbol (usually =, but sometimes ≥ or ≤).

The alternative hypothesis is often abbreviated as H a or H 1 . When the alternative hypothesis is written using mathematical symbols, it always includes an inequality symbol (usually ≠, but sometimes < or >).

A research hypothesis is your proposed answer to your research question. The research hypothesis usually includes an explanation (‘ x affects y because …’).

A statistical hypothesis, on the other hand, is a mathematical statement about a population parameter. Statistical hypotheses always come in pairs: the null and alternative hypotheses. In a well-designed study , the statistical hypotheses correspond logically to the research hypothesis.

Cite this Scribbr article

If you want to cite this source, you can copy and paste the citation or click the ‘Cite this Scribbr article’ button to automatically add the citation to our free Reference Generator.

Turney, S. (2022, December 06). Null and Alternative Hypotheses | Definitions & Examples. Scribbr. Retrieved 14 May 2024, from https://www.scribbr.co.uk/stats/null-and-alternative-hypothesis/

Is this article helpful?

Shaun Turney

Other students also liked, levels of measurement: nominal, ordinal, interval, ratio, the standard normal distribution | calculator, examples & uses, types of variables in research | definitions & examples.

Exploring the Null Hypothesis: Definition and Purpose

Updated: July 5, 2023 by Ken Feldman

Hypothesis testing is a branch of statistics in which, using data from a sample, an inference is made about a population parameter or a population probability distribution .

First, a hypothesis statement and assumption is made about the population parameter or probability distribution. This initial statement is called the Null Hypothesis and is denoted by H o. An alternative or alternate hypothesis (denoted Ha ), is then stated which will be the opposite of the Null Hypothesis.

The hypothesis testing process and analysis involves using sample data to determine whether or not you can be statistically confident that you can reject or fail to reject the H o. If the H o is rejected, the statistical conclusion is that the alternative or alternate hypothesis Ha is true.

Overview: What is the Null Hypothesis (Ho)? 

Hypothesis testing applies to all forms of statistical inquiry. For example, it can be used to determine whether there are differences between population parameters or an understanding about slopes of regression lines or equality of probability distributions.

In all cases, the first thing you do is state the Null and Alternate Hypotheses. The word Null in the context of hypothesis testing means “nothing” or “zero.”  

As an example, if we wanted to test whether there was a difference in two population means based on the calculations from two samples, we would state the Null Hypothesis in the form of: 

Ho: mu1 = mu2 or mu1- mu2 = 0  

In other words, there is no difference, or the difference is zero. Note that the notation is in the form of a population parameter, not a sample statistic. 

Since you are using sample data to make your inferences about the population, it’s possible you’ll make an error. In the case of the Null Hypothesis, we can make one of two errors.

•   Type 1 , or alpha error: An alpha error is when you mistakenly reject the Null and believe that something significant happened. In other words, you believe that the means of the two populations are different when they aren’t.
• Type 2, or beta error: A beta error is when you fail to reject the null when you should have.  In this case, you missed something significant and failed to take action. 

A classic example is when you get the results back from your doctor after taking a blood test. If the doctor says you have an infection when you really don’t, that is an alpha error. That is thinking that there is something significant going on when there isn’t. We also call that a false positive. The doctor rejected the null that “there was zero infection” and missed the call.

On the other hand, if the doctor told you that everything was OK when you really did have an infection, then he made a beta, or type 2, error. He failed to reject the Null Hypothesis when he should have. That is called a false negative.

The decision to reject or not to reject the Null Hypothesis is based on three numbers. 

• Alpha, which you get to choose. Alpha is the risk you are willing to assume of falsely rejecting the Null. The typical values for alpha are 1%, 5%, or 10%. Depending on the importance of the conclusion, you only want to falsely claim a difference when there is none, 1%, 5%, or 10% of the time.
• Beta, which is typically 20%. This means you’re willing to be wrong 20% of the time in failing to reject the null when you should have. 
• P-value, which is calculated from the data. The p-value is the actual risk you have in being wrong if you reject the null. You would like that to be low.  

Your decision as to what to do about the null is made by comparing the alpha value (your assumed risk) with the p-value (actual risk). If the actual risk is lower than your assumed risk, you can feel comfortable in rejecting the null and claiming something has happened. But, if the actual risk is higher than your assumed risk you will be taking a bigger risk than you want by rejecting the null.

RELATED: NULL VS. ALTERNATIVE HYPOTHESIS

3 benefits of the null hypothesis .

The stating and testing of the null hypothesis is the foundation of hypothesis testing. By doing so, you set the parameters for your statistical inference.

1. Statistical assurance of determining differences between population parameters

Just looking at the mathematical difference between the means of two samples and making a decision is woefully inadequate. By statistically testing the null hypothesis, you will have more confidence in any inferences you want to make about populations based on your samples.

2. Statistically based estimation of the probability of a population distribution

Many statistical tests require assumptions of specific distributions. Many of these tests assume that the population follows the normal distribution . If it doesn’t, the test may be invalid.  

3. Assess the strength of your conclusions as to what to do with the null hypothesis

Hypothesis testing calculations will provide some relative strength to your decisions as to whether you reject or fail to reject the null hypothesis.

Why is the Null Hypothesis important to understand?

The interpretation of the statistics relative to the null hypothesis is what’s important.

1. Properly write the null hypothesis to properly capture what you are seeking to prove

The null is always written in the same format. That is, the lack of difference or some other condition. The alternative hypothesis can be written in three formats depending on what you want to prove. 

2. Frame your statement and select an appropriate alpha risk

You don’t want to place too big of a hurdle or burden on your decision-making relative to action on the null hypothesis by selecting an alpha value that is too high or too low.

3. There are decision errors when deciding on how to respond to the Null Hypothesis

Since your decision relative to rejecting or not rejecting the null is based on statistical calculations, it is important to understand how that decision works. 

An industry example of using the Null Hypothesis 

The new director of marketing just completed the rollout of a new marketing campaign targeting the Hispanic market. Early indications showed that the campaign was successful in increasing sales in the Hispanic market. 

He came to that conclusion by comparing a sample of sales prior to the campaign and current sales after implementation of the campaign. He was anxious to proudly tell his boss how successful the campaign was. But, he decided to first check with his Lean Six Sigma Black Belt to see whether she agreed with his conclusion.

The Black Belt first asked the director his tolerance for risk of being wrong by telling the boss the campaign was successful when in fact, it wasn’t. That was the alpha value. The Director picked 5% since he was new and didn’t want to make a false claim so early in his career. He also picked 20% as his beta value.  

When the Black Belt was done analyzing the data, she found out that the p-value was 15%.  That meant if the director told the VP the campaign worked, there was a 15% chance he would be wrong and that the campaign probably needed some revising. Since he was only willing to be wrong 5% of the time, the decision was to not reject the null since his 5% assumed risk was less than the 15% actual risk.

3 best practices when thinking about the Null Hypothesis 

Using hypothesis testing to help make better data-driven decisions requires that you properly address the Null Hypothesis. 

1. Always use the proper nomenclature when stating the Null Hypothesis 

The null will always be in the form of decisions regarding the population, not the sample. 

2. The Null Hypothesis will always be written as the absence of some parameter or process characteristic

The writing of the Alternate Hypothesis can vary, so be sure you understand exactly what condition you are testing against. 

3. Pick a reasonable alpha risk so you’re not always failing to reject the Null Hypothesis

Being too cautious will lead you to make beta errors, and you’ll never learn anything about your population data. 

Frequently Asked Questions (FAQ) about the Null Hypothesis

What form should the null hypothesis be written in.

The Null Hypothesis should always be in the form of no difference or zero and always refer to the state of the population, not the sample. 

What is an alpha error? 

An alpha error, or Type 1 error, is rejecting the Null Hypothesis and claiming a significant event has occurred when, in fact, that is not true and the Null should not have been rejected.

How do I use the alpha error and p-value to decide on what decision I should make about the Null Hypothesis? 

The most common way of answering this is, “If the p-value is low (less than the alpha), the Null should be rejected. If the p-value is high (greater than the alpha) then the Null should not be rejected.”

Becoming familiar with the Null Hypothesis (Ho)

The proper writing of the Null Hypothesis is the basis for applying hypothesis testing to help you make better data-driven decisions. The format of the Null will always be in the form of zero, or the non-existence of some condition. It will always refer to a population parameter and not the sample you use to do your hypothesis testing calculations.

Be aware of the two types of errors you can make when deciding on what to do with the Null. Select reasonable risks values for your alpha and beta risks. By comparing your alpha risk with the calculated risk computed from the data, you will have sufficient information to make a wise decision as to whether you should reject the Null Hypothesis or not.

About the Author

Ken Feldman

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

• Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
• Duis aute irure dolor in reprehenderit in voluptate
• Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

6a.1 - introduction to hypothesis testing, basic terms section  .

The first step in hypothesis testing is to set up two competing hypotheses. The hypotheses are the most important aspect. If the hypotheses are incorrect, your conclusion will also be incorrect.

The two hypotheses are named the null hypothesis and the alternative hypothesis.

The goal of hypothesis testing is to see if there is enough evidence against the null hypothesis. In other words, to see if there is enough evidence to reject the null hypothesis. If there is not enough evidence, then we fail to reject the null hypothesis.

Consider the following example where we set up these hypotheses.

Example 6-1 Section  

A man, Mr. Orangejuice, goes to trial and is tried for the murder of his ex-wife. He is either guilty or innocent. Set up the null and alternative hypotheses for this example.

Putting this in a hypothesis testing framework, the hypotheses being tested are:

• The man is guilty
• The man is innocent

Let's set up the null and alternative hypotheses.

\(H_0\colon \) Mr. Orangejuice is innocent

\(H_a\colon \) Mr. Orangejuice is guilty

Remember that we assume the null hypothesis is true and try to see if we have evidence against the null. Therefore, it makes sense in this example to assume the man is innocent and test to see if there is evidence that he is guilty.

The Logic of Hypothesis Testing Section  

We want to know the answer to a research question. We determine our null and alternative hypotheses. Now it is time to make a decision.

The decision is either going to be...

• reject the null hypothesis or...
• fail to reject the null hypothesis.

Consider the following table. The table shows the decision/conclusion of the hypothesis test and the unknown "reality", or truth. We do not know if the null is true or if it is false. If the null is false and we reject it, then we made the correct decision. If the null hypothesis is true and we fail to reject it, then we made the correct decision.

So what happens when we do not make the correct decision?

When doing hypothesis testing, two types of mistakes may be made and we call them Type I error and Type II error. If we reject the null hypothesis when it is true, then we made a type I error. If the null hypothesis is false and we failed to reject it, we made another error called a Type II error.

Types of errors

The “reality”, or truth, about the null hypothesis is unknown and therefore we do not know if we have made the correct decision or if we committed an error. We can, however, define the likelihood of these events.

\(\alpha\) and \(\beta\) are probabilities of committing an error so we want these values to be low. However, we cannot decrease both. As \(\alpha\) decreases, \(\beta\) increases.

Example 6-1 Cont'd... Section  

A man, Mr. Orangejuice, goes to trial and is tried for the murder of his ex-wife. He is either guilty or not guilty. We found before that...

• \( H_0\colon \) Mr. Orangejuice is innocent
• \( H_a\colon \) Mr. Orangejuice is guilty

Interpret Type I error, \(\alpha \), Type II error, \(\beta \).

As you can see here, the Type I error (putting an innocent man in jail) is the more serious error. Ethically, it is more serious to put an innocent man in jail than to let a guilty man go free. So to minimize the probability of a type I error we would choose a smaller significance level.

Try it! Section  

An inspector has to choose between certifying a building as safe or saying that the building is not safe. There are two hypotheses:

• Building is safe
• Building is not safe

Set up the null and alternative hypotheses. Interpret Type I and Type II error.

\( H_0\colon\) Building is not safe vs \(H_a\colon \) Building is safe

Power and \(\beta \) are complements of each other. Therefore, they have an inverse relationship, i.e. as one increases, the other decreases.

What is The Null Hypothesis & When Do You Reject The Null Hypothesis

Julia Simkus

Editor at Simply Psychology

BA (Hons) Psychology, Princeton University

Julia Simkus is a graduate of Princeton University with a Bachelor of Arts in Psychology. She is currently studying for a Master's Degree in Counseling for Mental Health and Wellness in September 2023. Julia's research has been published in peer reviewed journals.

Learn about our Editorial Process

Saul Mcleod, PhD

Editor-in-Chief for Simply Psychology

BSc (Hons) Psychology, MRes, PhD, University of Manchester

Saul Mcleod, PhD., is a qualified psychology teacher with over 18 years of experience in further and higher education. He has been published in peer-reviewed journals, including the Journal of Clinical Psychology.

Olivia Guy-Evans, MSc

Associate Editor for Simply Psychology

BSc (Hons) Psychology, MSc Psychology of Education

Olivia Guy-Evans is a writer and associate editor for Simply Psychology. She has previously worked in healthcare and educational sectors.

On This Page:

A null hypothesis is a statistical concept suggesting no significant difference or relationship between measured variables. It’s the default assumption unless empirical evidence proves otherwise.

The null hypothesis states no relationship exists between the two variables being studied (i.e., one variable does not affect the other).

The null hypothesis is the statement that a researcher or an investigator wants to disprove.

Testing the null hypothesis can tell you whether your results are due to the effects of manipulating ​ the dependent variable or due to random chance. 

How to Write a Null Hypothesis

Null hypotheses (H0) start as research questions that the investigator rephrases as statements indicating no effect or relationship between the independent and dependent variables.

It is a default position that your research aims to challenge or confirm.

For example, if studying the impact of exercise on weight loss, your null hypothesis might be:

There is no significant difference in weight loss between individuals who exercise daily and those who do not.

Examples of Null Hypotheses

When do we reject the null hypothesis .

We reject the null hypothesis when the data provide strong enough evidence to conclude that it is likely incorrect. This often occurs when the p-value (probability of observing the data given the null hypothesis is true) is below a predetermined significance level.

If the collected data does not meet the expectation of the null hypothesis, a researcher can conclude that the data lacks sufficient evidence to back up the null hypothesis, and thus the null hypothesis is rejected. 

Rejecting the null hypothesis means that a relationship does exist between a set of variables and the effect is statistically significant ( p > 0.05).

If the data collected from the random sample is not statistically significance , then the null hypothesis will be accepted, and the researchers can conclude that there is no relationship between the variables. 

You need to perform a statistical test on your data in order to evaluate how consistent it is with the null hypothesis. A p-value is one statistical measurement used to validate a hypothesis against observed data.

Calculating the p-value is a critical part of null-hypothesis significance testing because it quantifies how strongly the sample data contradicts the null hypothesis.

The level of statistical significance is often expressed as a  p  -value between 0 and 1. The smaller the p-value, the stronger the evidence that you should reject the null hypothesis.

Usually, a researcher uses a confidence level of 95% or 99% (p-value of 0.05 or 0.01) as general guidelines to decide if you should reject or keep the null.

When your p-value is less than or equal to your significance level, you reject the null hypothesis.

In other words, smaller p-values are taken as stronger evidence against the null hypothesis. Conversely, when the p-value is greater than your significance level, you fail to reject the null hypothesis.

In this case, the sample data provides insufficient data to conclude that the effect exists in the population.

Because you can never know with complete certainty whether there is an effect in the population, your inferences about a population will sometimes be incorrect.

When you incorrectly reject the null hypothesis, it’s called a type I error. When you incorrectly fail to reject it, it’s called a type II error.

Why Do We Never Accept The Null Hypothesis?

The reason we do not say “accept the null” is because we are always assuming the null hypothesis is true and then conducting a study to see if there is evidence against it. And, even if we don’t find evidence against it, a null hypothesis is not accepted.

A lack of evidence only means that you haven’t proven that something exists. It does not prove that something doesn’t exist. 

It is risky to conclude that the null hypothesis is true merely because we did not find evidence to reject it. It is always possible that researchers elsewhere have disproved the null hypothesis, so we cannot accept it as true, but instead, we state that we failed to reject the null. 

One can either reject the null hypothesis, or fail to reject it, but can never accept it.

Why Do We Use The Null Hypothesis?

We can never prove with 100% certainty that a hypothesis is true; We can only collect evidence that supports a theory. However, testing a hypothesis can set the stage for rejecting or accepting this hypothesis within a certain confidence level.

The null hypothesis is useful because it can tell us whether the results of our study are due to random chance or the manipulation of a variable (with a certain level of confidence).

A null hypothesis is rejected if the measured data is significantly unlikely to have occurred and a null hypothesis is accepted if the observed outcome is consistent with the position held by the null hypothesis.

Rejecting the null hypothesis sets the stage for further experimentation to see if a relationship between two variables exists. 

Hypothesis testing is a critical part of the scientific method as it helps decide whether the results of a research study support a particular theory about a given population. Hypothesis testing is a systematic way of backing up researchers’ predictions with statistical analysis.

It helps provide sufficient statistical evidence that either favors or rejects a certain hypothesis about the population parameter. 

Purpose of a Null Hypothesis 

• The primary purpose of the null hypothesis is to disprove an assumption. 
• Whether rejected or accepted, the null hypothesis can help further progress a theory in many scientific cases.
• A null hypothesis can be used to ascertain how consistent the outcomes of multiple studies are.

Do you always need both a Null Hypothesis and an Alternative Hypothesis?

The null (H0) and alternative (Ha or H1) hypotheses are two competing claims that describe the effect of the independent variable on the dependent variable. They are mutually exclusive, which means that only one of the two hypotheses can be true. 

While the null hypothesis states that there is no effect in the population, an alternative hypothesis states that there is statistical significance between two variables. 

The goal of hypothesis testing is to make inferences about a population based on a sample. In order to undertake hypothesis testing, you must express your research hypothesis as a null and alternative hypothesis. Both hypotheses are required to cover every possible outcome of the study. 

What is the difference between a null hypothesis and an alternative hypothesis?

The alternative hypothesis is the complement to the null hypothesis. The null hypothesis states that there is no effect or no relationship between variables, while the alternative hypothesis claims that there is an effect or relationship in the population.

It is the claim that you expect or hope will be true. The null hypothesis and the alternative hypothesis are always mutually exclusive, meaning that only one can be true at a time.

What are some problems with the null hypothesis?

One major problem with the null hypothesis is that researchers typically will assume that accepting the null is a failure of the experiment. However, accepting or rejecting any hypothesis is a positive result. Even if the null is not refuted, the researchers will still learn something new.

Why can a null hypothesis not be accepted?

We can either reject or fail to reject a null hypothesis, but never accept it. If your test fails to detect an effect, this is not proof that the effect doesn’t exist. It just means that your sample did not have enough evidence to conclude that it exists.

We can’t accept a null hypothesis because a lack of evidence does not prove something that does not exist. Instead, we fail to reject it.

Failing to reject the null indicates that the sample did not provide sufficient enough evidence to conclude that an effect exists.

If the p-value is greater than the significance level, then you fail to reject the null hypothesis.

Is a null hypothesis directional or non-directional?

A hypothesis test can either contain an alternative directional hypothesis or a non-directional alternative hypothesis. A directional hypothesis is one that contains the less than (“<“) or greater than (“>”) sign.

A nondirectional hypothesis contains the not equal sign (“≠”).  However, a null hypothesis is neither directional nor non-directional.

A null hypothesis is a prediction that there will be no change, relationship, or difference between two variables.

The directional hypothesis or nondirectional hypothesis would then be considered alternative hypotheses to the null hypothesis.

Gill, J. (1999). The insignificance of null hypothesis significance testing.  Political research quarterly ,  52 (3), 647-674.

Krueger, J. (2001). Null hypothesis significance testing: On the survival of a flawed method.  American Psychologist ,  56 (1), 16.

Masson, M. E. (2011). A tutorial on a practical Bayesian alternative to null-hypothesis significance testing.  Behavior research methods ,  43 , 679-690.

Nickerson, R. S. (2000). Null hypothesis significance testing: a review of an old and continuing controversy.  Psychological methods ,  5 (2), 241.

Rozeboom, W. W. (1960). The fallacy of the null-hypothesis significance test.  Psychological bulletin ,  57 (5), 416.

Related Articles

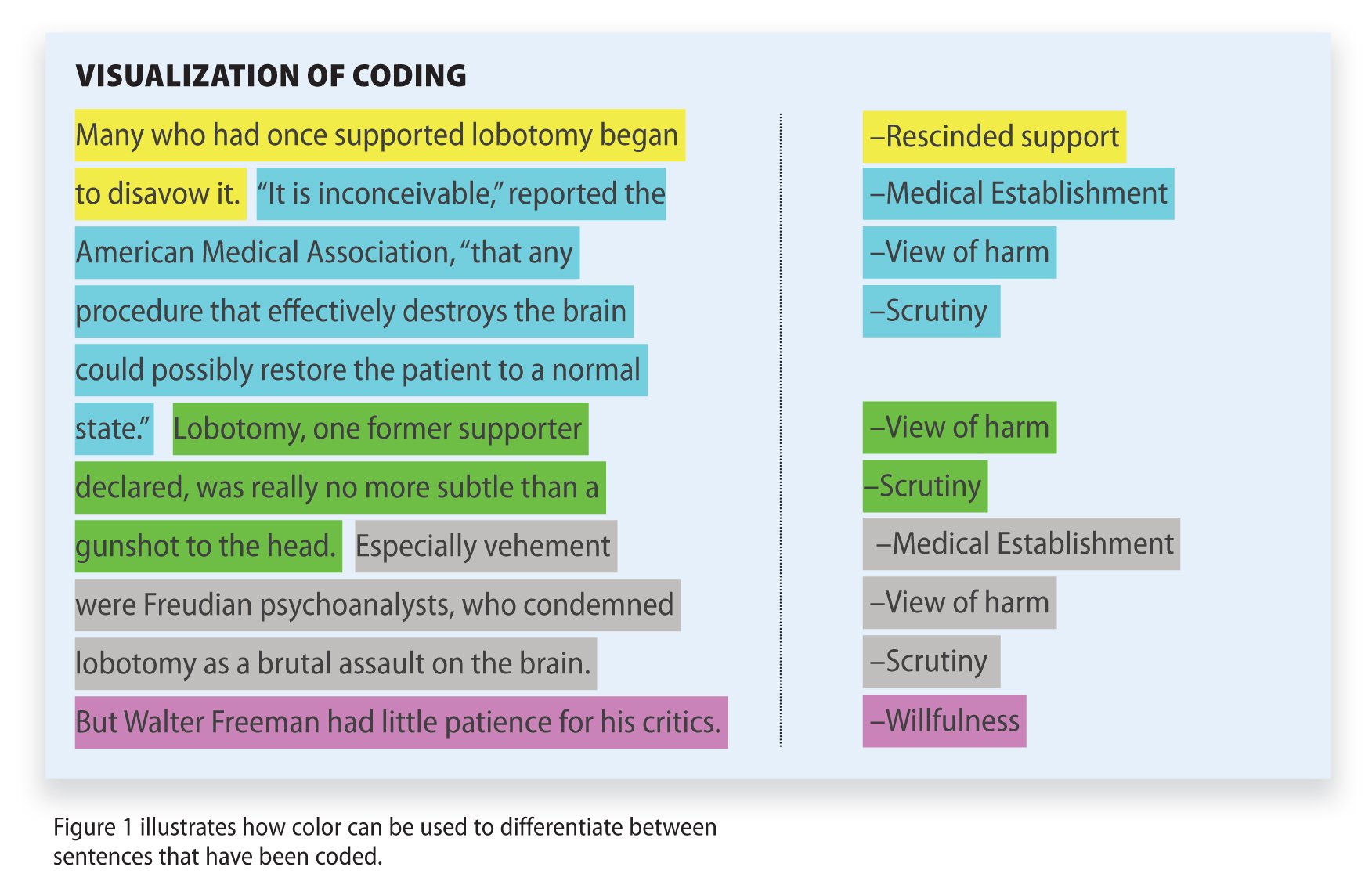
Research Methodology

Qualitative Data Coding

What Is a Focus Group?

Cross-Cultural Research Methodology In Psychology

What Is Internal Validity In Research?

Research Methodology , Statistics

What Is Face Validity In Research? Importance & How To Measure

Criterion Validity: Definition & Examples

Hypothesis Testing (cont...)

Hypothesis testing, the null and alternative hypothesis.

In order to undertake hypothesis testing you need to express your research hypothesis as a null and alternative hypothesis. The null hypothesis and alternative hypothesis are statements regarding the differences or effects that occur in the population. You will use your sample to test which statement (i.e., the null hypothesis or alternative hypothesis) is most likely (although technically, you test the evidence against the null hypothesis). So, with respect to our teaching example, the null and alternative hypothesis will reflect statements about all statistics students on graduate management courses.

The null hypothesis is essentially the "devil's advocate" position. That is, it assumes that whatever you are trying to prove did not happen ( hint: it usually states that something equals zero). For example, the two different teaching methods did not result in different exam performances (i.e., zero difference). Another example might be that there is no relationship between anxiety and athletic performance (i.e., the slope is zero). The alternative hypothesis states the opposite and is usually the hypothesis you are trying to prove (e.g., the two different teaching methods did result in different exam performances). Initially, you can state these hypotheses in more general terms (e.g., using terms like "effect", "relationship", etc.), as shown below for the teaching methods example:

Depending on how you want to "summarize" the exam performances will determine how you might want to write a more specific null and alternative hypothesis. For example, you could compare the mean exam performance of each group (i.e., the "seminar" group and the "lectures-only" group). This is what we will demonstrate here, but other options include comparing the distributions , medians , amongst other things. As such, we can state:

Now that you have identified the null and alternative hypotheses, you need to find evidence and develop a strategy for declaring your "support" for either the null or alternative hypothesis. We can do this using some statistical theory and some arbitrary cut-off points. Both these issues are dealt with next.

Significance levels

The level of statistical significance is often expressed as the so-called p -value . Depending on the statistical test you have chosen, you will calculate a probability (i.e., the p -value) of observing your sample results (or more extreme) given that the null hypothesis is true . Another way of phrasing this is to consider the probability that a difference in a mean score (or other statistic) could have arisen based on the assumption that there really is no difference. Let us consider this statement with respect to our example where we are interested in the difference in mean exam performance between two different teaching methods. If there really is no difference between the two teaching methods in the population (i.e., given that the null hypothesis is true), how likely would it be to see a difference in the mean exam performance between the two teaching methods as large as (or larger than) that which has been observed in your sample?

So, you might get a p -value such as 0.03 (i.e., p = .03). This means that there is a 3% chance of finding a difference as large as (or larger than) the one in your study given that the null hypothesis is true. However, you want to know whether this is "statistically significant". Typically, if there was a 5% or less chance (5 times in 100 or less) that the difference in the mean exam performance between the two teaching methods (or whatever statistic you are using) is as different as observed given the null hypothesis is true, you would reject the null hypothesis and accept the alternative hypothesis. Alternately, if the chance was greater than 5% (5 times in 100 or more), you would fail to reject the null hypothesis and would not accept the alternative hypothesis. As such, in this example where p = .03, we would reject the null hypothesis and accept the alternative hypothesis. We reject it because at a significance level of 0.03 (i.e., less than a 5% chance), the result we obtained could happen too frequently for us to be confident that it was the two teaching methods that had an effect on exam performance.

Whilst there is relatively little justification why a significance level of 0.05 is used rather than 0.01 or 0.10, for example, it is widely used in academic research. However, if you want to be particularly confident in your results, you can set a more stringent level of 0.01 (a 1% chance or less; 1 in 100 chance or less).

One- and two-tailed predictions

When considering whether we reject the null hypothesis and accept the alternative hypothesis, we need to consider the direction of the alternative hypothesis statement. For example, the alternative hypothesis that was stated earlier is:

The alternative hypothesis tells us two things. First, what predictions did we make about the effect of the independent variable(s) on the dependent variable(s)? Second, what was the predicted direction of this effect? Let's use our example to highlight these two points.

Sarah predicted that her teaching method (independent variable: teaching method), whereby she not only required her students to attend lectures, but also seminars, would have a positive effect (that is, increased) students' performance (dependent variable: exam marks). If an alternative hypothesis has a direction (and this is how you want to test it), the hypothesis is one-tailed. That is, it predicts direction of the effect. If the alternative hypothesis has stated that the effect was expected to be negative, this is also a one-tailed hypothesis.

Alternatively, a two-tailed prediction means that we do not make a choice over the direction that the effect of the experiment takes. Rather, it simply implies that the effect could be negative or positive. If Sarah had made a two-tailed prediction, the alternative hypothesis might have been:

In other words, we simply take out the word "positive", which implies the direction of our effect. In our example, making a two-tailed prediction may seem strange. After all, it would be logical to expect that "extra" tuition (going to seminar classes as well as lectures) would either have a positive effect on students' performance or no effect at all, but certainly not a negative effect. However, this is just our opinion (and hope) and certainly does not mean that we will get the effect we expect. Generally speaking, making a one-tail prediction (i.e., and testing for it this way) is frowned upon as it usually reflects the hope of a researcher rather than any certainty that it will happen. Notable exceptions to this rule are when there is only one possible way in which a change could occur. This can happen, for example, when biological activity/presence in measured. That is, a protein might be "dormant" and the stimulus you are using can only possibly "wake it up" (i.e., it cannot possibly reduce the activity of a "dormant" protein). In addition, for some statistical tests, one-tailed tests are not possible.

Rejecting or failing to reject the null hypothesis

Let's return finally to the question of whether we reject or fail to reject the null hypothesis.

If our statistical analysis shows that the significance level is below the cut-off value we have set (e.g., either 0.05 or 0.01), we reject the null hypothesis and accept the alternative hypothesis. Alternatively, if the significance level is above the cut-off value, we fail to reject the null hypothesis and cannot accept the alternative hypothesis. You should note that you cannot accept the null hypothesis, but only find evidence against it.

Null Hypothesis Examples

ThoughtCo / Hilary Allison

• Scientific Method
• Chemical Laws
• Periodic Table
• Projects & Experiments
• Biochemistry
• Physical Chemistry
• Medical Chemistry
• Chemistry In Everyday Life
• Famous Chemists
• Activities for Kids
• Abbreviations & Acronyms
• Weather & Climate
• Ph.D., Biomedical Sciences, University of Tennessee at Knoxville
• B.A., Physics and Mathematics, Hastings College

In statistical analysis, the null hypothesis assumes there is no meaningful relationship between two variables. Testing the null hypothesis can tell you whether your results are due to the effect of manipulating ​a dependent variable or due to chance. It's often used in conjunction with an alternative hypothesis, which assumes there is, in fact, a relationship between two variables.

The null hypothesis is among the easiest hypothesis to test using statistical analysis, making it perhaps the most valuable hypothesis for the scientific method. By evaluating a null hypothesis in addition to another hypothesis, researchers can support their conclusions with a higher level of confidence. Below are examples of how you might formulate a null hypothesis to fit certain questions.

What Is the Null Hypothesis?

The null hypothesis states there is no relationship between the measured phenomenon (the dependent variable ) and the independent variable , which is the variable an experimenter typically controls or changes. You do not​ need to believe that the null hypothesis is true to test it. On the contrary, you will likely suspect there is a relationship between a set of variables. One way to prove that this is the case is to reject the null hypothesis. Rejecting a hypothesis does not mean an experiment was "bad" or that it didn't produce results. In fact, it is often one of the first steps toward further inquiry.

To distinguish it from other hypotheses , the null hypothesis is written as ​ H 0  (which is read as “H-nought,” "H-null," or "H-zero"). A significance test is used to determine the likelihood that the results supporting the null hypothesis are not due to chance. A confidence level of 95% or 99% is common. Keep in mind, even if the confidence level is high, there is still a small chance the null hypothesis is not true, perhaps because the experimenter did not account for a critical factor or because of chance. This is one reason why it's important to repeat experiments.

Examples of the Null Hypothesis

To write a null hypothesis, first start by asking a question. Rephrase that question in a form that assumes no relationship between the variables. In other words, assume a treatment has no effect. Write your hypothesis in a way that reflects this.

Other Types of Hypotheses

In addition to the null hypothesis, the alternative hypothesis is also a staple in traditional significance tests . It's essentially the opposite of the null hypothesis because it assumes the claim in question is true. For the first item in the table above, for example, an alternative hypothesis might be "Age does have an effect on mathematical ability."

Key Takeaways

• In hypothesis testing, the null hypothesis assumes no relationship between two variables, providing a baseline for statistical analysis.
• Rejecting the null hypothesis suggests there is evidence of a relationship between variables.
• By formulating a null hypothesis, researchers can systematically test assumptions and draw more reliable conclusions from their experiments.
• Difference Between Independent and Dependent Variables
• Examples of Independent and Dependent Variables
• What Is a Hypothesis? (Science)
• Definition of a Hypothesis
• What 'Fail to Reject' Means in a Hypothesis Test
• Null Hypothesis Definition and Examples
• Scientific Method Vocabulary Terms
• Null Hypothesis and Alternative Hypothesis
• Hypothesis Test for the Difference of Two Population Proportions
• How to Conduct a Hypothesis Test
• What Is a P-Value?
• What Are the Elements of a Good Hypothesis?
• What Is the Difference Between Alpha and P-Values?
• Hypothesis Test Example
• Understanding Path Analysis
• An Example of a Hypothesis Test

• School Guide
• Mathematics
• Number System and Arithmetic
• Trigonometry
• Probability
• Mensuration
• Maths Formulas
• Integration Formulas
• Differentiation Formulas
• Trigonometry Formulas
• Algebra Formulas
• Mensuration Formula
• Statistics Formulas
• Trigonometric Table

Null Hypothesis

• Hypothesis Testing Formula
• SQLite IS NULL
• MySQL NOT NULL Constraint
• Real-life Applications of Hypothesis Testing
• Null in JavaScript
• SQL NOT NULL Constraint
• Null Cipher
• Hypothesis in Machine Learning
• Understanding Hypothesis Testing
• Difference between Null and Alternate Hypothesis
• Hypothesis Testing in R Programming
• SQL | NULL functions
• Kotlin Null Safety
• PHP | is_null() Function
• MySQL | NULLIF( ) Function
• Null-Coalescing Operator in C#
• Nullity of a Matrix

Null Hypothesis , often denoted as H 0, is a foundational concept in statistical hypothesis testing. It represents an assumption that no significant difference, effect, or relationship exists between variables within a population. It serves as a baseline assumption, positing no observed change or effect occurring. The null is t he truth or falsity of an idea in analysis.

In this article, we will discuss the null hypothesis in detail, along with some solved examples and questions on the null hypothesis.

Table of Content

What is Null Hypothesis?

Null hypothesis symbol, formula of null hypothesis, types of null hypothesis, null hypothesis examples, principle of null hypothesis, how do you find null hypothesis, null hypothesis in statistics, null hypothesis and alternative hypothesis, null hypothesis and alternative hypothesis examples, null hypothesis – practice problems.

Null Hypothesis in statistical analysis suggests the absence of statistical significance within a specific set of observed data. Hypothesis testing, using sample data, evaluates the validity of this hypothesis. Commonly denoted as H 0 or simply “null,” it plays an important role in quantitative analysis, examining theories related to markets, investment strategies, or economies to determine their validity.

Null Hypothesis Meaning

Null Hypothesis represents a default position, often suggesting no effect or difference, against which researchers compare their experimental results. The Null Hypothesis, often denoted as H 0 asserts a default assumption in statistical analysis. It posits no significant difference or effect, serving as a baseline for comparison in hypothesis testing.

The null Hypothesis is represented as H 0 , the Null Hypothesis symbolizes the absence of a measurable effect or difference in the variables under examination.

Certainly, a simple example would be asserting that the mean score of a group is equal to a specified value like stating that the average IQ of a population is 100.

The Null Hypothesis is typically formulated as a statement of equality or absence of a specific parameter in the population being studied. It provides a clear and testable prediction for comparison with the alternative hypothesis. The formulation of the Null Hypothesis typically follows a concise structure, stating the equality or absence of a specific parameter in the population.

Mean Comparison (Two-sample t-test)

H 0 : μ 1 = μ 2

This asserts that there is no significant difference between the means of two populations or groups.

Proportion Comparison

H 0 : p 1 − p 2 = 0

This suggests no significant difference in proportions between two populations or conditions.

Equality in Variance (F-test in ANOVA)

H 0 : σ 1 = σ 2

This states that there’s no significant difference in variances between groups or populations.

Independence (Chi-square Test of Independence):

H 0 : Variables are independent

This asserts that there’s no association or relationship between categorical variables.

Null Hypotheses vary including simple and composite forms, each tailored to the complexity of the research question. Understanding these types is pivotal for effective hypothesis testing.

Equality Null Hypothesis (Simple Null Hypothesis)

The Equality Null Hypothesis, also known as the Simple Null Hypothesis, is a fundamental concept in statistical hypothesis testing that assumes no difference, effect or relationship between groups, conditions or populations being compared.

Non-Inferiority Null Hypothesis

In some studies, the focus might be on demonstrating that a new treatment or method is not significantly worse than the standard or existing one.

Superiority Null Hypothesis

The concept of a superiority null hypothesis comes into play when a study aims to demonstrate that a new treatment, method, or intervention is significantly better than an existing or standard one.

Independence Null Hypothesis

In certain statistical tests, such as chi-square tests for independence, the null hypothesis assumes no association or independence between categorical variables.

Homogeneity Null Hypothesis

In tests like ANOVA (Analysis of Variance), the null hypothesis suggests that there’s no difference in population means across different groups.

• Medicine: Null Hypothesis: “No significant difference exists in blood pressure levels between patients given the experimental drug versus those given a placebo.”
• Education: Null Hypothesis: “There’s no significant variation in test scores between students using a new teaching method and those using traditional teaching.”
• Economics: Null Hypothesis: “There’s no significant change in consumer spending pre- and post-implementation of a new taxation policy.”
• Environmental Science: Null Hypothesis: “There’s no substantial difference in pollution levels before and after a water treatment plant’s establishment.”

The principle of the null hypothesis is a fundamental concept in statistical hypothesis testing. It involves making an assumption about the population parameter or the absence of an effect or relationship between variables.

In essence, the null hypothesis (H 0 ) proposes that there is no significant difference, effect, or relationship between variables. It serves as a starting point or a default assumption that there is no real change, no effect or no difference between groups or conditions.

The null hypothesis is usually formulated to be tested against an alternative hypothesis (H 1 or H [Tex]\alpha [/Tex] ) which suggests that there is an effect, difference or relationship present in the population.

Null Hypothesis Rejection

Rejecting the Null Hypothesis occurs when statistical evidence suggests a significant departure from the assumed baseline. It implies that there is enough evidence to support the alternative hypothesis, indicating a meaningful effect or difference. Null Hypothesis rejection occurs when statistical evidence suggests a deviation from the assumed baseline, prompting a reconsideration of the initial hypothesis.

Identifying the Null Hypothesis involves defining the status quotient, asserting no effect and formulating a statement suitable for statistical analysis.

When is Null Hypothesis Rejected?

The Null Hypothesis is rejected when statistical tests indicate a significant departure from the expected outcome, leading to the consideration of alternative hypotheses. It occurs when statistical evidence suggests a deviation from the assumed baseline, prompting a reconsideration of the initial hypothesis.

In statistical hypothesis testing, researchers begin by stating the null hypothesis, often based on theoretical considerations or previous research. The null hypothesis is then tested against an alternative hypothesis (Ha), which represents the researcher’s claim or the hypothesis they seek to support.

The process of hypothesis testing involves collecting sample data and using statistical methods to assess the likelihood of observing the data if the null hypothesis were true. This assessment is typically done by calculating a test statistic, which measures the difference between the observed data and what would be expected under the null hypothesis.

In the realm of hypothesis testing, the null hypothesis (H 0 ) and alternative hypothesis (H₁ or Ha) play critical roles. The null hypothesis generally assumes no difference, effect, or relationship between variables, suggesting that any observed change or effect is due to random chance. Its counterpart, the alternative hypothesis, asserts the presence of a significant difference, effect, or relationship between variables, challenging the null hypothesis. These hypotheses are formulated based on the research question and guide statistical analyses.

Difference Between Null Hypothesis and Alternative Hypothesis

The null hypothesis (H 0 ) serves as the baseline assumption in statistical testing, suggesting no significant effect, relationship, or difference within the data. It often proposes that any observed change or correlation is merely due to chance or random variation. Conversely, the alternative hypothesis (H 1 or Ha) contradicts the null hypothesis, positing the existence of a genuine effect, relationship or difference in the data. It represents the researcher’s intended focus, seeking to provide evidence against the null hypothesis and support for a specific outcome or theory. These hypotheses form the crux of hypothesis testing, guiding the assessment of data to draw conclusions about the population being studied.

Let’s envision a scenario where a researcher aims to examine the impact of a new medication on reducing blood pressure among patients. In this context:

Null Hypothesis (H 0 ): “The new medication does not produce a significant effect in reducing blood pressure levels among patients.”

Alternative Hypothesis (H 1 or Ha): “The new medication yields a significant effect in reducing blood pressure levels among patients.”

The null hypothesis implies that any observed alterations in blood pressure subsequent to the medication’s administration are a result of random fluctuations rather than a consequence of the medication itself. Conversely, the alternative hypothesis contends that the medication does indeed generate a meaningful alteration in blood pressure levels, distinct from what might naturally occur or by random chance.

People Also Read:

Mathematics Maths Formulas Probability and Statistics

Example 1: A researcher claims that the average time students spend on homework is 2 hours per night.

Null Hypothesis (H 0 ): The average time students spend on homework is equal to 2 hours per night. Data: A random sample of 30 students has an average homework time of 1.8 hours with a standard deviation of 0.5 hours. Test Statistic and Decision: Using a t-test, if the calculated t-statistic falls within the acceptance region, we fail to reject the null hypothesis. If it falls in the rejection region, we reject the null hypothesis. Conclusion: Based on the statistical analysis, we fail to reject the null hypothesis, suggesting that there is not enough evidence to dispute the claim of the average homework time being 2 hours per night.

Example 2: A company asserts that the error rate in its production process is less than 1%.

Null Hypothesis (H 0 ): The error rate in the production process is 1% or higher. Data: A sample of 500 products shows an error rate of 0.8%. Test Statistic and Decision: Using a z-test, if the calculated z-statistic falls within the acceptance region, we fail to reject the null hypothesis. If it falls in the rejection region, we reject the null hypothesis. Conclusion: The statistical analysis supports rejecting the null hypothesis, indicating that there is enough evidence to dispute the company’s claim of an error rate of 1% or higher.

Q1. A researcher claims that the average time spent by students on homework is less than 2 hours per day. Formulate the null hypothesis for this claim?

Q2. A manufacturing company states that their new machine produces widgets with a defect rate of less than 5%. Write the null hypothesis to test this claim?

Q3. An educational institute believes that their online course completion rate is at least 60%. Develop the null hypothesis to validate this assertion?

Q4. A restaurant claims that the waiting time for customers during peak hours is not more than 15 minutes. Formulate the null hypothesis for this claim?

Q5. A study suggests that the mean weight loss after following a specific diet plan for a month is more than 8 pounds. Construct the null hypothesis to evaluate this statement?

Summary – Null Hypothesis and Alternative Hypothesis

The null hypothesis (H 0 ) and alternative hypothesis (H a ) are fundamental concepts in statistical hypothesis testing. The null hypothesis represents the default assumption, stating that there is no significant effect, difference, or relationship between variables. It serves as the baseline against which the alternative hypothesis is tested. In contrast, the alternative hypothesis represents the researcher’s hypothesis or the claim to be tested, suggesting that there is a significant effect, difference, or relationship between variables. The relationship between the null and alternative hypotheses is such that they are complementary, and statistical tests are conducted to determine whether the evidence from the data is strong enough to reject the null hypothesis in favor of the alternative hypothesis. This decision is based on the strength of the evidence and the chosen level of significance. Ultimately, the choice between the null and alternative hypotheses depends on the specific research question and the direction of the effect being investigated.

FAQs on Null Hypothesis

What does null hypothesis stands for.

The null hypothesis, denoted as H 0 ​, is a fundamental concept in statistics used for hypothesis testing. It represents the statement that there is no effect or no difference, and it is the hypothesis that the researcher typically aims to provide evidence against.

How to Form a Null Hypothesis?

A null hypothesis is formed based on the assumption that there is no significant difference or effect between the groups being compared or no association between variables being tested. It often involves stating that there is no relationship, no change, or no effect in the population being studied.

When Do we reject the Null Hypothesis?

In statistical hypothesis testing, if the p-value (the probability of obtaining the observed results) is lower than the chosen significance level (commonly 0.05), we reject the null hypothesis. This suggests that the data provides enough evidence to refute the assumption made in the null hypothesis.

What is a Null Hypothesis in Research?

In research, the null hypothesis represents the default assumption or position that there is no significant difference or effect. Researchers often try to test this hypothesis by collecting data and performing statistical analyses to see if the observed results contradict the assumption.

What Are Alternative and Null Hypotheses?

The null hypothesis (H0) is the default assumption that there is no significant difference or effect. The alternative hypothesis (H1 or Ha) is the opposite, suggesting there is a significant difference, effect or relationship.

What Does it Mean to Reject the Null Hypothesis?

Rejecting the null hypothesis implies that there is enough evidence in the data to support the alternative hypothesis. In simpler terms, it suggests that there might be a significant difference, effect or relationship between the groups or variables being studied.

How to Find Null Hypothesis?

Formulating a null hypothesis often involves considering the research question and assuming that no difference or effect exists. It should be a statement that can be tested through data collection and statistical analysis, typically stating no relationship or no change between variables or groups.

How is Null Hypothesis denoted?

The null hypothesis is commonly symbolized as H 0 in statistical notation.

What is the Purpose of the Null hypothesis in Statistical Analysis?

The null hypothesis serves as a starting point for hypothesis testing, enabling researchers to assess if there’s enough evidence to reject it in favor of an alternative hypothesis.

What happens if we Reject the Null hypothesis?

Rejecting the null hypothesis implies that there is sufficient evidence to support an alternative hypothesis, suggesting a significant effect or relationship between variables.

What are Test for Null Hypothesis?

Various statistical tests, such as t-tests or chi-square tests, are employed to evaluate the validity of the Null Hypothesis in different scenarios.

Please Login to comment...

Similar reads.

• Geeks Premier League 2023
• Math-Concepts
• Geeks Premier League
• School Learning

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

Statistics Made Easy

When Do You Reject the Null Hypothesis? (3 Examples)

A hypothesis test is a formal statistical test we use to reject or fail to reject a statistical hypothesis.

We always use the following steps to perform a hypothesis test:

Step 1: State the null and alternative hypotheses.

The null hypothesis , denoted as H 0 , is the hypothesis that the sample data occurs purely from chance.

The alternative hypothesis , denoted as H A , is the hypothesis that the sample data is influenced by some non-random cause.

2. Determine a significance level to use.

Decide on a significance level. Common choices are .01, .05, and .1. 

3. Calculate the test statistic and p-value.

Use the sample data to calculate a test statistic and a corresponding p-value .

4. Reject or fail to reject the null hypothesis.

If the p-value is less than the significance level, then you reject the null hypothesis.

If the p-value is not less than the significance level, then you fail to reject the null hypothesis.

You can use the following clever line to remember this rule:

“If the p is low, the null must go.”

In other words, if the p-value is low enough then we must reject the null hypothesis.

The following examples show when to reject (or fail to reject) the null hypothesis for the most common types of hypothesis tests.

Example 1: One Sample t-test

A  one sample t-test  is used to test whether or not the mean of a population is equal to some value.

For example, suppose we want to know whether or not the mean weight of a certain species of turtle is equal to 310 pounds.

We go out and collect a simple random sample of 40 turtles with the following information:

• Sample size n = 40
• Sample mean weight  x  = 300
• Sample standard deviation s = 18.5

We can use the following steps to perform a one sample t-test:

Step 1: State the Null and Alternative Hypotheses

We will perform the one sample t-test with the following hypotheses:

• H 0 :  μ = 310 (population mean is equal to 310 pounds)
• H A :  μ ≠ 310 (population mean is not equal to 310 pounds)

We will choose to use a significance level of 0.05 .

We can plug in the numbers for the sample size, sample mean, and sample standard deviation into this One Sample t-test Calculator to calculate the test statistic and p-value:

• t test statistic: -3.4187
• two-tailed p-value: 0.0015

Since the p-value (0.0015) is less than the significance level (0.05) we reject the null hypothesis .

We conclude that there is sufficient evidence to say that the mean weight of turtles in this population is not equal to 310 pounds.

Example 2: Two Sample t-test

A  two sample t-test is used to test whether or not two population means are equal.

For example, suppose we want to know whether or not the mean weight between two different species of turtles is equal.

We go out and collect a simple random sample from each population with the following information:

• Sample size n 1 = 40
• Sample mean weight  x 1  = 300
• Sample standard deviation s 1 = 18.5
• Sample size n 2 = 38
• Sample mean weight  x 2  = 305
• Sample standard deviation s 2 = 16.7

We can use the following steps to perform a two sample t-test:

We will perform the two sample t-test with the following hypotheses:

• H 0 :  μ 1  = μ 2 (the two population means are equal)
• H 1 :  μ 1  ≠ μ 2 (the two population means are not equal)

We will choose to use a significance level of 0.10 .

We can plug in the numbers for the sample sizes, sample means, and sample standard deviations into this Two Sample t-test Calculator to calculate the test statistic and p-value:

• t test statistic: -1.2508
• two-tailed p-value: 0.2149

Since the p-value (0.2149) is not less than the significance level (0.10) we fail to reject the null hypothesis .

We do not have sufficient evidence to say that the mean weight of turtles between these two populations is different.

Example 3: Paired Samples t-test

A paired samples t-test is used to compare the means of two samples when each observation in one sample can be paired with an observation in the other sample.

For example, suppose we want to know whether or not a certain training program is able to increase the max vertical jump of college basketball players.

To test this, we may recruit a simple random sample of 20 college basketball players and measure each of their max vertical jumps. Then, we may have each player use the training program for one month and then measure their max vertical jump again at the end of the month:

We can use the following steps to perform a paired samples t-test:

We will perform the paired samples t-test with the following hypotheses:

• H 0 :  μ before = μ after (the two population means are equal)
• H 1 :  μ before ≠ μ after (the two population means are not equal)

We will choose to use a significance level of 0.01 .

We can plug in the raw data for each sample into this Paired Samples t-test Calculator to calculate the test statistic and p-value:

• t test statistic: -3.226
• two-tailed p-value: 0.0045

Since the p-value (0.0045) is less than the significance level (0.01) we reject the null hypothesis .

We have sufficient evidence to say that the mean vertical jump before and after participating in the training program is not equal.

Bonus: Decision Rule Calculator 

You can use this decision rule calculator to automatically determine whether you should reject or fail to reject a null hypothesis for a hypothesis test based on the value of the test statistic.

Featured Posts

Hey there. My name is Zach Bobbitt. I have a Masters of Science degree in Applied Statistics and I’ve worked on machine learning algorithms for professional businesses in both healthcare and retail. I’m passionate about statistics, machine learning, and data visualization and I created Statology to be a resource for both students and teachers alike.  My goal with this site is to help you learn statistics through using simple terms, plenty of real-world examples, and helpful illustrations.

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Join the Statology Community

Sign up to receive Statology's exclusive study resource: 100 practice problems with step-by-step solutions. Plus, get our latest insights, tutorials, and data analysis tips straight to your inbox!

By subscribing you accept Statology's Privacy Policy.

• Math Article

Null Hypothesis

In mathematics, Statistics deals with the study of research and surveys on the numerical data. For taking surveys, we have to define the hypothesis. Generally, there are two types of hypothesis. One is a null hypothesis, and another is an alternative hypothesis .

In probability and statistics, the null hypothesis is a comprehensive statement or default status that there is zero happening or nothing happening. For example, there is no connection among groups or no association between two measured events. It is generally assumed here that the hypothesis is true until any other proof has been brought into the light to deny the hypothesis. Let us learn more here with definition, symbol, principle, types and example, in this article.

Table of contents:

• Comparison with Alternative Hypothesis

Null Hypothesis Definition

The null hypothesis is a kind of hypothesis which explains the population parameter whose purpose is to test the validity of the given experimental data. This hypothesis is either rejected or not rejected based on the viability of the given population or sample . In other words, the null hypothesis is a hypothesis in which the sample observations results from the chance. It is said to be a statement in which the surveyors wants to examine the data. It is denoted by H 0 .

Null Hypothesis Symbol

In statistics, the null hypothesis is usually denoted by letter H with subscript ‘0’ (zero), such that H 0 . It is pronounced as H-null or H-zero or H-nought. At the same time, the alternative hypothesis expresses the observations determined by the non-random cause. It is represented by H 1 or H a .

Null Hypothesis Principle

The principle followed for null hypothesis testing is, collecting the data and determining the chances of a given set of data during the study on some random sample, assuming that the null hypothesis is true. In case if the given data does not face the expected null hypothesis, then the outcome will be quite weaker, and they conclude by saying that the given set of data does not provide strong evidence against the null hypothesis because of insufficient evidence. Finally, the researchers tend to reject that.

Null Hypothesis Formula

Here, the hypothesis test formulas are given below for reference.

The formula for the null hypothesis is:

H 0 :  p = p 0

The formula for the alternative hypothesis is:

H a = p >p 0 , < p 0 ≠ p 0

The formula for the test static is:

Remember that,  p 0  is the null hypothesis and p – hat is the sample proportion.

Also, read:

Types of Null Hypothesis

There are different types of hypothesis. They are:

Simple Hypothesis

It completely specifies the population distribution. In this method, the sampling distribution is the function of the sample size.

Composite Hypothesis

The composite hypothesis is one that does not completely specify the population distribution.

Exact Hypothesis

Exact hypothesis defines the exact value of the parameter. For example μ= 50

Inexact Hypothesis

This type of hypothesis does not define the exact value of the parameter. But it denotes a specific range or interval. For example 45< μ <60

Null Hypothesis Rejection

Sometimes the null hypothesis is rejected too. If this hypothesis is rejected means, that research could be invalid. Many researchers will neglect this hypothesis as it is merely opposite to the alternate hypothesis. It is a better practice to create a hypothesis and test it. The goal of researchers is not to reject the hypothesis. But it is evident that a perfect statistical model is always associated with the failure to reject the null hypothesis.

How do you Find the Null Hypothesis?

The null hypothesis says there is no correlation between the measured event (the dependent variable) and the independent variable. We don’t have to believe that the null hypothesis is true to test it. On the contrast, you will possibly assume that there is a connection between a set of variables ( dependent and independent).

When is Null Hypothesis Rejected?

The null hypothesis is rejected using the P-value approach. If the P-value is less than or equal to the α, there should be a rejection of the null hypothesis in favour of the alternate hypothesis. In case, if P-value is greater than α, the null hypothesis is not rejected.

Null Hypothesis and Alternative Hypothesis

Now, let us discuss the difference between the null hypothesis and the alternative hypothesis.

Null Hypothesis Examples

Here, some of the examples of the null hypothesis are given below. Go through the below ones to understand the concept of the null hypothesis in a better way.

If a medicine reduces the risk of cardiac stroke, then the null hypothesis should be “the medicine does not reduce the chance of cardiac stroke”. This testing can be performed by the administration of a drug to a certain group of people in a controlled way. If the survey shows that there is a significant change in the people, then the hypothesis is rejected.

Few more examples are:

1). Are there is 100% chance of getting affected by dengue?

Ans: There could be chances of getting affected by dengue but not 100%.

2). Do teenagers are using mobile phones more than grown-ups to access the internet?

Ans: Age has no limit on using mobile phones to access the internet.

3). Does having apple daily will not cause fever?

Ans: Having apple daily does not assure of not having fever, but increases the immunity to fight against such diseases.

4). Do the children more good in doing mathematical calculations than grown-ups?

Ans: Age has no effect on Mathematical skills.

In many common applications, the choice of the null hypothesis is not automated, but the testing and calculations may be automated. Also, the choice of the null hypothesis is completely based on previous experiences and inconsistent advice. The choice can be more complicated and based on the variety of applications and the diversity of the objectives. 

The main limitation for the choice of the null hypothesis is that the hypothesis suggested by the data is based on the reasoning which proves nothing. It means that if some hypothesis provides a summary of the data set, then there would be no value in the testing of the hypothesis on the particular set of data. 

Frequently Asked Questions on Null Hypothesis

What is meant by the null hypothesis.

In Statistics, a null hypothesis is a type of hypothesis which explains the population parameter whose purpose is to test the validity of the given experimental data.

What are the benefits of hypothesis testing?

Hypothesis testing is defined as a form of inferential statistics, which allows making conclusions from the entire population based on the sample representative.

When a null hypothesis is accepted and rejected?

The null hypothesis is either accepted or rejected in terms of the given data. If P-value is less than α, then the null hypothesis is rejected in favor of the alternative hypothesis, and if the P-value is greater than α, then the null hypothesis is accepted in favor of the alternative hypothesis.

Why is the null hypothesis important?

The importance of the null hypothesis is that it provides an approximate description of the phenomena of the given data. It allows the investigators to directly test the relational statement in a research study.

How to accept or reject the null hypothesis in the chi-square test?

If the result of the chi-square test is bigger than the critical value in the table, then the data does not fit the model, which represents the rejection of the null hypothesis.

Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!

Select the correct answer and click on the “Finish” button Check your score and answers at the end of the quiz

Visit BYJU’S for all Maths related queries and study materials

Your result is as below

Request OTP on Voice Call

• Share Share

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

Lean Six Sigma Training Certification

• Facebook Instagram Twitter LinkedIn YouTube
• (877) 497-4462

Mood’s Median Non-Parametric Hypothesis Test. A Complete Guide

May 17th, 2024

Often in stats research, teams encounter the imperative for comparing groups/samples’ central tendencies. While ANOVA frequently helps, it requires normalcy and homogeneity. When extremes or non-normality mar data, non-parametric exams better interpret. One such is Mood’s median test, which bears its discoverer’s name.

Designed by comparing medians of independent sets, it proves beneficial for exploratory or skewed information interpreters. Mood’s median examines central data proclivities without distorted normal prerequisites.

Particularly valued amid non-normalcy or outliers plaguing parametric test suppositions, it remains sturdy against aberrations.

By flagging central fixtures reliably notwithstanding abnormalities, Mood’s median grasps realities obscured to others. For teams grappling information information-defying widespread methods, it enlightens the next moves without parametric bonds.

Its sturdiness aids comprehension through hindrances to standard stats’ works, steering steady problem-solving as demands evolve. Joined insight lifts enterprises serving communities enduringly.

Key Highlights

• Mood’s median test gauges medians between independent sets or samples non-parametrically. It proves an alternative when normalcy and homogeneity fail one-way ANOVA demands.
• Stemming from chi-squared distributions, it examines normally distributed, equal medians hypotheses crosswise multitudes. Unperturbed by outliers or skews, suitability expands to non-regular figures.
• Allowing bi-sample or multi-sample examination, suppositions include detachment, continued or ordered information alongside near underlying designing forms.
• Furnishing test analytics and p-values, researchers determine if discernments distinguish significantly. Applicable where aberrations undermine orthodox techniques, it champions comprehension through unforeseen hurdles materializing.
• By flagging median divergences reliably regardless of incongruences, Mood’s median guides choice-making, and optimization cooperatively sailed.

What is Mood’s Median Test?

Mood’s median test compares groups/samples’ midpoints non-parametrically unlike parametric exams demanding specific distributions.

Not requiring normalized information lets it interpret where those prerequisites limit. It expands bi-sample median investigations to abundance.

Null proposes population-wide medians align against another differing, tested against multi-treatment, independent demographic, or non-regular set median divergences.

Keys involve:

• Examining multiple test subject brackets
• Assessing treatment effects on non-standardized figures
• Analyzing where regular assumptions constrain

While ANOVA outpaces spotting central tendency changes on normalized information, Mood’s median soundly detects divergences without such presumptions.

Proposed in ‘54 by Alexander Mood, it approximates chi-squared as repeats enlarge, providing valid conclusions minus distribution stipulations. For teams grappling with non-parametric realities, it highlights and provides choices.

Assumptions of Mood’s Median Test

Before running it, it’s important to check that the assumptions of the test are met. Violating these assumptions can lead to invalid results and conclusions. The key assumptions are:

• Random Samples : The data must be collected using random sampling from the respective populations. This ensures the representativeness of the samples.
• Independent Observations : The observations within each sample should be independent of each other. There should be no relationship between the observations that could influence the values.
• Continuous or Ordinal Data : It requires the data to be continuous (measured on an interval or ratio scale) or ordinal (ranked data).
• Similar Shape Distributions : While it does not require the distributions to be normal, the distributions should have similar shapes and spread. Dissimilar shapes can affect the validity of the results.
• No Outliers : Extreme outliers in the data can significantly influence the median values and distort the test results. It’s recommended to check for and handle any outliers before conducting the test.
• Tied Values : It can handle tied values (observations with the same value) within the samples. However, an excessive number of ties can reduce the test’s power and sensitivity.

Checking these assumptions is crucial as violations can increase the risk of Type I (false positive) or Type II (false negative) errors. Various graphical and statistical methods, such as histograms , boxplots , and normality tests , can be used to assess the assumptions.

If assumptions are violated, appropriate data transformations or non-parametric alternatives may be considered.

Hypothesis Testing in Mood’s Median Test

The Mood’s median test is a non-parametric hypothesis test that allows you to determine if the medians of two or more groups differ. It tests the null hypothesis that the medians of the groups are equal, against the alternative that at least one population median is different.

Null Hypothesis

The null hypothesis (H0) states that the medians of all groups are equal. Mathematically, this can be represented as:

H0: Median1 = Median2 = … = Mediank

Where k is the number of groups being compared.

Alternative Hypothesis

The alternative hypothesis (Ha) states that at least one median is different from the others. There are three possible alternative hypotheses:

1) Two-tailed test : At least one median differs

Ha : Not all medians are equal

2) Upper-tailed test : At least one median is larger  

Ha : At least one median is larger than the others

3) Lower-tailed test : At least one median is smaller

Ha : At least one median is smaller than the others

The choice between one-tailed or two-tailed depends on the research question.

Test Statistic

Mood’s median test uses a chi-square test statistic to evaluate the null hypothesis. The test statistic follows a chi-square distribution with k-1 degrees of freedom when the null is true.

The test statistic is calculated from the number of observations above and below the grand median in each group. Larger deviations from the expected counts indicate greater evidence against the null hypothesis of equal medians.

The p-value is the probability of observing a test statistic as extreme as the one calculated, assuming the null hypothesis is true. A small p-value (typically <0.05) indicates strong evidence against the null, allowing you to reject it.

Interpretation

If the p-value is less than the chosen significance level (e.g. 0.05), you reject the null hypothesis. This means at least one group median is statistically different from the others. Effect sizes and confidence intervals help quantify the median differences.

The test makes no assumptions about the distribution shapes, making it a robust non-parametric alternative to the one-way ANOVA when data violates normality assumptions.

Performing Mood’s Median Test

To perform it, there are several steps to follow. First, you need to state the null and alternative hypotheses. The null hypothesis (H0) is that the medians of the groups are equal, while the alternative hypothesis (Ha) is that at least one median is different.

Next, you’ll need to combine all the data points across groups and find the overall median. This combined median serves as the test criterion. 

For each group, count how many data points are greater than, less than, or equal to the combined median. These counts form the frequencies needed to calculate the test statistic.

It follows a chi-square distribution with k-1 degrees of freedom, where k is the number of groups. Calculate this test statistic based on the frequency counts and degrees of freedom.

Compare the test statistic to the critical value from the chi-square distribution for your chosen alpha level (e.g. 0.05). If the test statistic exceeds the critical value, you reject the null hypothesis. Otherwise, you fail to reject it.

Calculating the test statistic can be tedious by hand for larger sample sizes. Most statistical software like R, Python, Minitab , etc. have built-in functions to run Mood’s median test and provide the p-value directly. The p-value approach is equivalent – if p < alpha, reject H0.

It’s good practice to report the test statistic value, degrees of freedom, p-value, sample sizes, and your conclusion about the null hypothesis. Effect sizes can also provide more insight into the practical significance beyond statistical significance.

Mood’s Median Test in Statistical Software

It can be performed using various statistical software packages. While the test calculations can be done manually, using software is much more efficient, especially for larger datasets. Here are some examples of how to implement it in popular statistical programs:

Mood’s Median Test in R

In R, the mood.test() function from the RVAideMemoire package allows you to perform Mood’s median test. Here is an example:

install.packages(“RVAideMemoire”)

library(RVAideMemoire)

# Example data 

x1 <- c(42, 37, 39, 44, 36, 38)

x2 <- c(40, 39, 38, 37, 31, 43)

# Perform Mood’s test

mood.test(x1, x2)

This will output the test statistic, p-value, and other relevant metrics for Mood’s median test on the two sample vectors x1 and x2.

Mood’s Median Test in Python

For Python, the scipy.stats module provides the median_test() function to conduct the test. Here’s an example:

“`python

from scipy import stats

# Example data

x1 = [42, 37, 39, 44, 36, 38] 

x2 = [40, 39, 38, 37, 31, 43]

stats.median_test(x1, x2)

The median_test() function returns the chi-square statistic and p-value for the test.

Mood’s Median Test in Excel

Excel does not have a built-in function for this test. However, you can use add-ins or write custom VBA code to perform the test.

The Real Statistics Resource Pack provides a Mood’s Median Test data analysis tool for Excel.

Mood’s Median Test in SPSS, SAS, Minitab

Most major statistical software like SPSS , SAS, and Minitab provide the functionality to run this test, albeit through different function names and syntax. Refer to the respective documentation for implementation details.

No matter which software you use, be sure to verify the assumptions of this test before interpreting the results. Additionally, report the test statistic, p-value, sample sizes, and any other relevant metrics when presenting your findings.

Comparing Mood’s Median Test

When choosing a statistical test, it’s important to understand how Mood’s median test compares to other commonly used non-parametric tests like the Wilcoxon rank-sum test , the Kruskal-Wallis test , and the analysis of variance (ANOVA).

Mood’s Median Test vs Wilcoxon Rank-Sum Test

Both Mood’s median test and the Wilcoxon rank-sum test are non-parametric alternatives to the two-sample t-test . However, the Wilcoxon test assumes that the distributions have the same shape, while Mood’s test does not require this assumption.

Mood’s test is preferred when you cannot make the equal distribution shape assumption.

Mood’s Median Test vs Kruskal-Wallis Test

The Kruskal-Wallis test is a non-parametric alternative to one-way ANOVA for comparing more than two independent groups.

Like the Wilcoxon test, it assumes the distributions have the same shape. This test can be used when this assumption is violated, making it more robust for certain data sets.

Mood’s Median Test vs ANOVA

The key difference is that ANOVA is a parametric test that requires assumptions like normality and homogeneity of variances. The test is a non-parametric alternative when these assumptions are not met. It tests for differences in medians rather than means.

While sacrificing some statistical power compared to parametric tests when assumptions are met, this test is a robust option for non-normal data or heterogeneous variances across groups. The choice depends on whether the parametric assumptions can be reasonably satisfied.

Post-Hoc Analysis

If Mood’s median test detects a statistically significant difference among groups, post-hoc tests may be needed to determine which specific groups differ. Options include pairwise Mood’s median tests with a multiplicity adjustment.

Additional Considerations

While this is a useful non-parametric alternative to the one-way ANOVA, there are some additional points to keep in mind:

Power and Sample Size

Like other statistical tests, the power of Mood’s median test to detect an effect depends on the sample size.

With small samples, the test may not have enough power to find a significant difference even if one exists. Researchers should perform power analysis ahead of data collection to ensure adequate sample sizes.

Mood’s median test can handle tied observations within groups. However, it cannot deal with ties across different groups of medians. If there are ties across medians, the test may not be valid and an alternative like the Kruskal-Wallis test should be used instead.

If the overall test is significant, indicating differences between some of the medians, post-hoc tests are needed to determine which specific pairs of groups differ. Common post-hoc approaches include the Mann-Whitney U test or Dunn’s test .

Assumption Violations

While Mood’s test has fewer assumptions than the one-way ANOVA, the assumptions of random sampling and independence of observations still apply. Violations can increase the chance of false positives or false negatives.

Effect Size

Like other hypothesis tests, a significant p-value does not convey the degree of difference between groups. Effect sizes like the probability of superiority should be calculated and interpreted along with the p-value.

When reporting the results, good practice involves stating the test statistic value, degrees of freedom, p-value, sample sizes, medians, and effect size estimate. Graphical displays like boxplots can also aid interpretation.

Overall, Mood’s median test is a robust non-parametric tool. Still, careful checking of assumptions, appropriate sample sizing, post-hoc testing if needed, and comprehensive reporting of results is recommended for valid inference.

SixSigma.us offers both Live Virtual classes as well as Online Self-Paced training. Most option includes access to the same great Master Black Belt instructors that teach our World Class in-person sessions. Sign-up today!

Virtual Classroom Training Programs Self-Paced Online Training Programs

SixSigma.us Accreditation & Affiliations

Monthly Management Tips

• Be the first one to receive the latest updates and information from 6Sigma
• Get curated resources from industry-experts
• Gain an edge with complete guides and other exclusive materials
• Become a part of one of the largest Six Sigma community
• Unlock your path to become a Six Sigma professional

" * " indicates required fields

Miles D. Williams

Visiting Assistant Professor | Denison University

• Download My CV
• Send Me an Email
• View My LinkedIn
• Follow Me on Twitter

When the Research Hypothesis Is the Null

Posted on May 13, 2024 by Miles Williams in Methods   Statistics  

Back to Blog

What should you do if your research hypothesis is the null hypothesis? In other words, how should you approach hypothesis testing if your theory predicts no effect between two variables? I and a coauthor are working on a paper where a couple of our proposed hypotheses look like this, and we got some push-back from a reviewer about it. This prompted me to go down a rabbit hole of journal articles and message boards to see how others handle this situation. I quickly found that I waded into a contentious issue that’s connected to a bigger philosophical debate about the merits of hypothesis testing in general and whether the null hypothesis in particular as a bench-mark for hypothesis testing is even logically sound.

There’s too much to unpack with this debate for me to cover in a single blog post (and I’m sure I’d get some of the key points wrong anyway if I tried). The main issue I want to explore in this post is the practical problem of how to approach testing a null research hypothesis. From an applied perspective, this is a tricky problem that raises issues with how we calculate and interpret p-values. Thankfully, there is a sound solution for the null research hypothesis which I explore in greater detail below. It’s called a two one-sided test, and it’s easy to implement once you know what it is.

The usual approach

Most of the time when doing research, a scientist usually has a research hypothesis that goes something like X has a positive effect on Y . For example, a political scientist might propose that a get-out-the-vote (GOTV) campaign ( X ) will increase voter turnout ( Y ).

The typical approach for testing this claim might be to estimate a regression model with voter turnout as the outcome and the GOTV campaign as the explanatory variable of interest:

Y = α + β X + ε

If the parameter β > 0, this would support the hypothesis that GOTV campaigns improve voter turnout. To test this hypothesis, in practice the researcher would actually test a different hypothesis that we call the null hypothesis. This is the hypothesis that says there is no true effect of GOTV campaigns on voter turnout.

By proposing and testing the null, we now have a point of reference for calculating a measure of uncertainty—that is, the probability of observing an empirical effect of a certain magnitude or greater if the null hypothesis is true. This probability is called a p-value, and by convention if it is less than 0.05 we say that we can reject the null hypothesis.

For the hypothetical regression model proposed above, to get this p-value we’d estimate β, then calculate its standard error, and then we’d take the ratio of the former to the latter giving us what’s called a t-statistic or t-value. Under the null hypothesis, the t-value has a known distribution which makes it really easy to map any t-value to a p-value. The below figure illustrates using a hypothetical data sample of size N = 200. You can see that the t-statistic’s distribution has a distinct bell shape centered around 0. You can also see the range of t-values in blue where if we observed them in our empirical data we’d fail to reject the null hypothesis at the p < 0.05 level. Values in gray are t-values that would lead us to reject the null hypothesis at this same level.

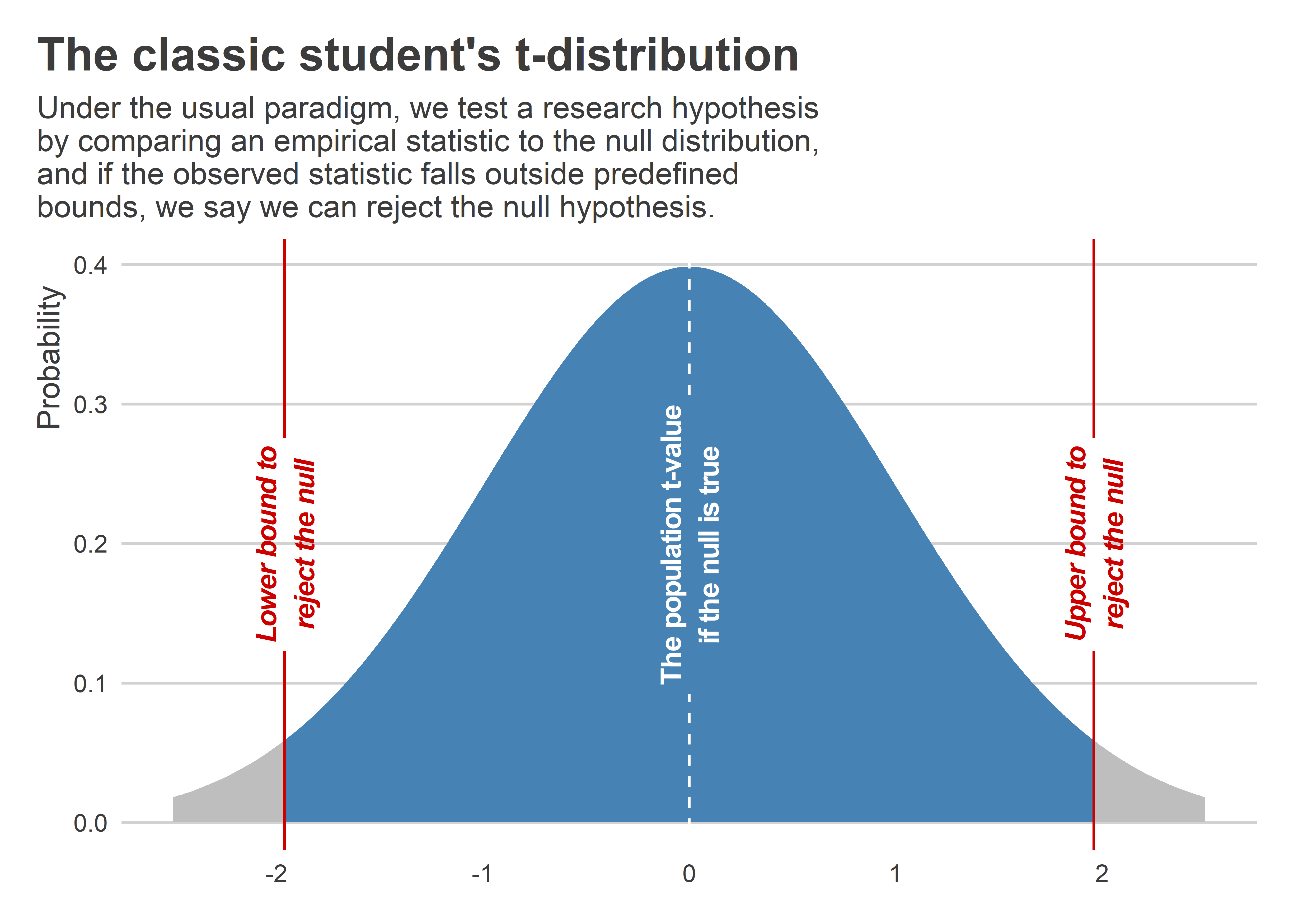
When the null is the research hypothesis we want to test

There’s nothing new or special here. If you have even a basic stats background (particularly with Frequentist statistics), the conventional approach to hypothesis testing is pretty ubiquitous. Things get more tricky when our research hypothesis is that there is no effect. Say for a certain set of theoretical reasons we think that GOTV campaigns are basically useless at increasing voter turnout. If this argument is true, then if we estimate the following regression model, we’d expect β = 0.

The problem here is that our substantive research hypothesis is also the one that we want to try to find evidence against. We could just proceed like usual and just say that if we fail to reject the null this is evidence in support of our theory, but the problem with doing this is that failure to reject the null is not the same thing as finding support for the null hypothesis.

There are a few ideas in the literature for how we should approach this instead. Many of these approaches are Bayesian, but most of my research relies on Frequentist statistics, so these approaches were a no-go for me. However, there is one really simple approach that is consistent with the Frequentist paradigm: equivalence testing . The idea is simple. Propose some absolute effect size that is of minimal interest and then test whether an observed effect is different from it. This minimum effect is called the “smallest effect size of interest” (SESOI). I read about the approach in an article by Harms and Lakens (2018) in the Journal of Clinical and Translational Research .

Say, for example, that we deemed a t-value of +/-1.96 (the usual threshold for rejecting the null hypothesis) as extreme enough to constitute good evidence of a non-zero effect. We could make the appropriate adjustments to our t-distribution to identify a new range of t-values that would allow us to reject the hypothesis that an effect is non-zero. This is illustrated in the below figure. We can now see a range of t-values in the middle where we’d have t-values such that we could reject the non-zero hypothesis at the p < 0.05 level. This distribution looks like it’s been inverted relative to the usual null distribution. The reason is that with this approach what we’re doing is conducting a pair of alternative one-tailed tests. We’re testing both the hypothesis that β / se(β) - 1.96 > 0 and β / se(β) + 1.96 < 0. In the Harms and Lakens paper cited above, they call this approach two one-sided tests or TOST (I’m guessing this is pronounced “toast”).

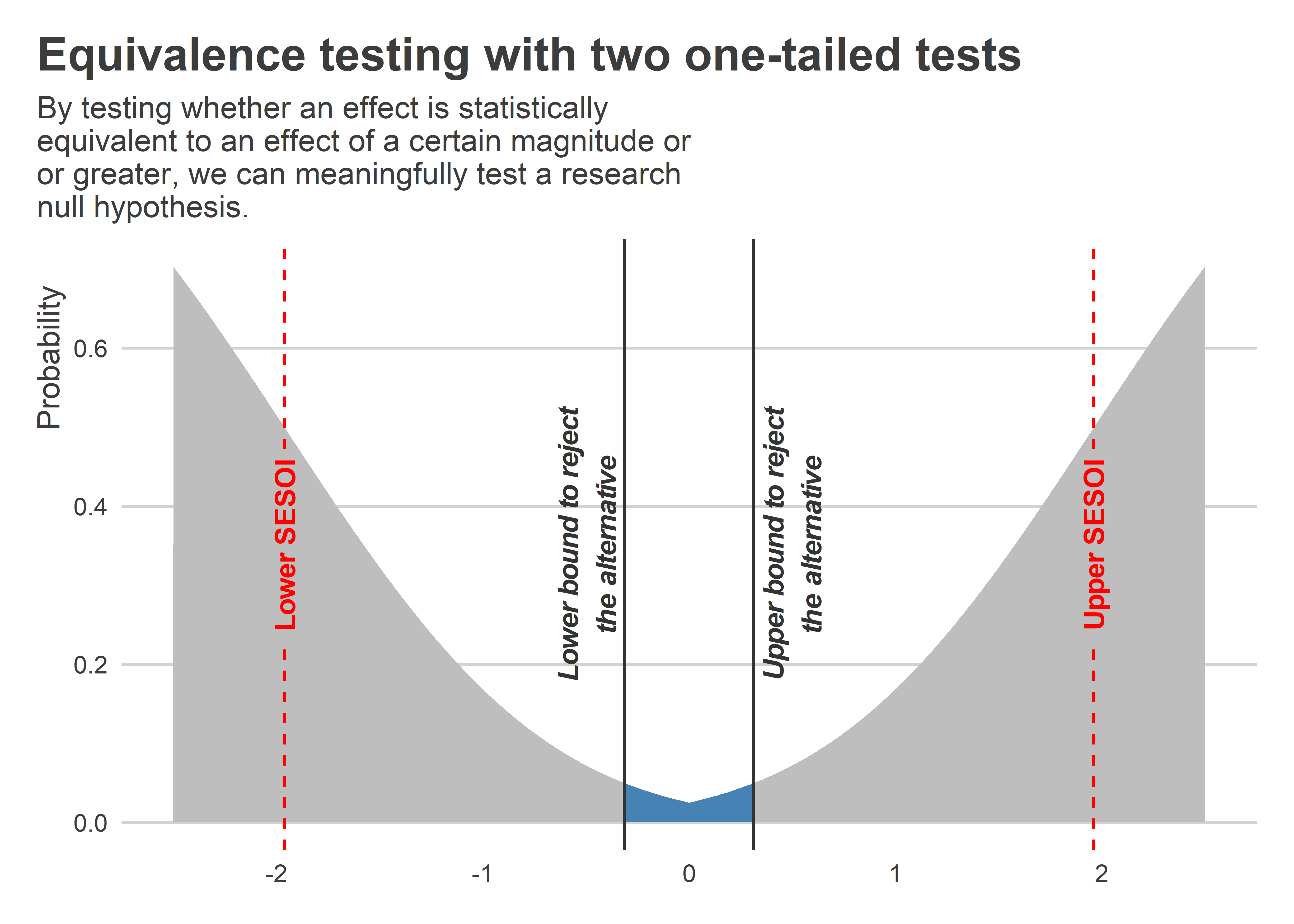
Something to pay attention to with this approach is that the observed t-statistic needs to be very small in absolute magnitude for us to reject the hypothesis of a non-zero effect. This means that the bar for testing a null research hypothesis is actually quite high. This is demonstrated using the following simulation in R. Using the {seerrr} package, I had R generate 1,000 random draws (each of size 200) for a pair of variables x and y where the former is a binary “treatment” and the latter is a random normal “outcome.” By design, there is no true causal relationship between these variables. Once I simulated the data, I then generated a set of estimates of the effect of x on y for each simulated dataset and collected the results in an object called sim_ests . I then visualized two metrics that that I calculated with the simulated results: (1) the rejection rate for the null hypothesis test and (2) the rejection rate for the two one-sided equivalence tests. As you can see, if we were to try to test a research null hypothesis the usual way, we’d expect to be able to fail to reject the null about 95% of the time. Conversely, if we were to use the two one-sided equivalence tests, we’d expect to reject the non-zero alternative hypothesis only about 25% of the time. I tested out a few additional simulations to see if a larger sample size would lead to improvements in power (not shown), but no dice.

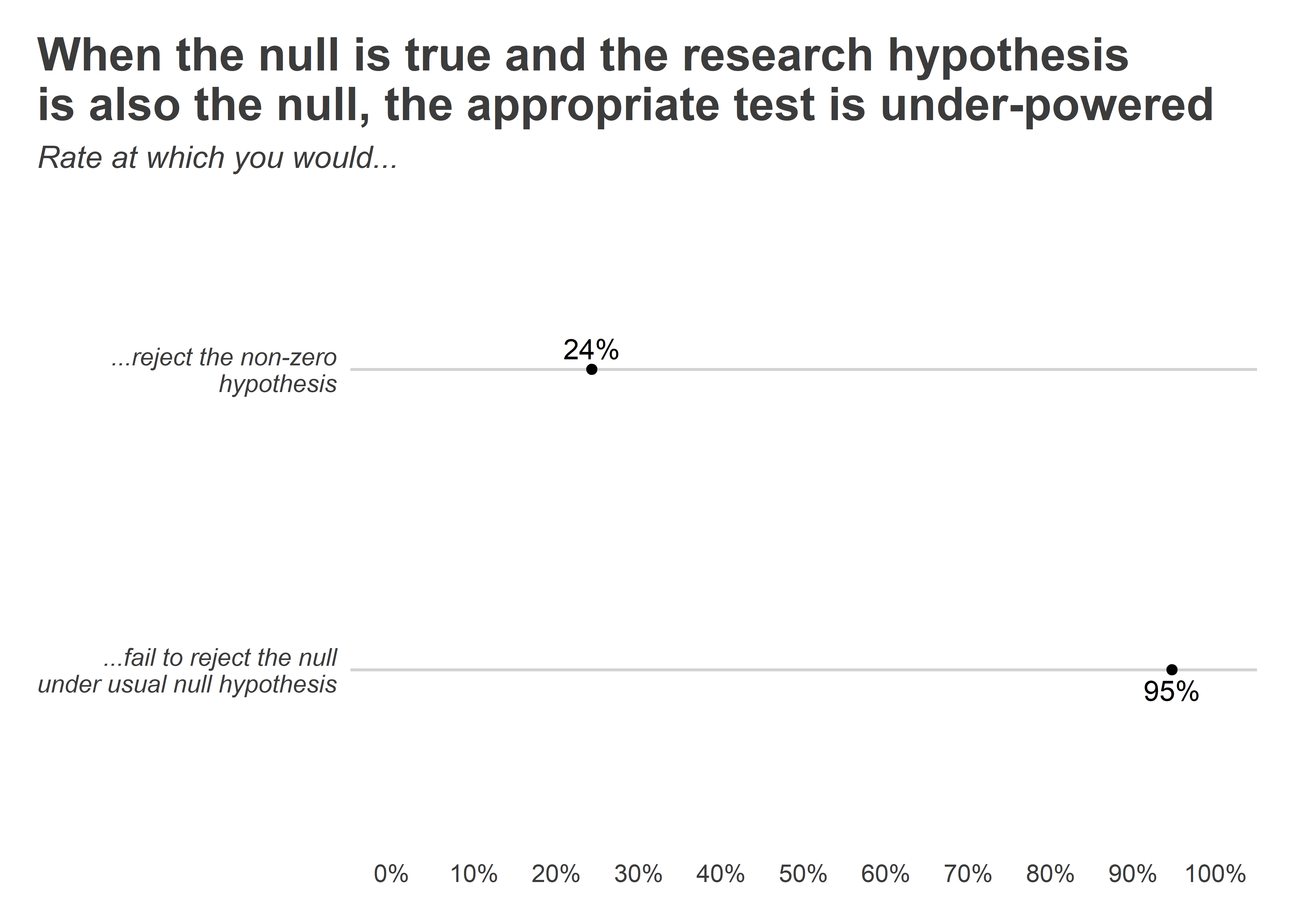
The two one-sided tests approach strikes me as a nice method when dealing with a null research hypothesis. It’s actually pretty easy to implement, too. The one downside is that this test is under-powered. If the null is true, it will only reject the alternative 25% of the time (though you could select a different non-zero alternative which would possibly give you more power). However, this isn’t all bad. The flip side of the coin is that this is a really conservative test, so if you can reject the alternative that puts you on solid rhetorical footing to show the data really do seem consistent with the null.