hypothesis testing in epidemiology

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

• Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
• Duis aute irure dolor in reprehenderit in voluptate
• Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

7.1.4 - developing and evaluating hypotheses, developing hypotheses section  .

After interviewing affected individuals, gathering data to characterize the outbreak by time, place, and person, and consulting with other health officials, a disease detective will have more focused hypotheses about the source of the disease, its mode of transmission, and the exposures which cause the disease. Hypotheses should be stated in a manner that can be tested.

Hypotheses are developed in a variety of ways. First, consider the known epidemiology for the disease: What is the agent's usual reservoir? How is it usually transmitted? What are the known risk factors? Consider all the 'usual suspects.'

Open-ended conversations with those who fell ill or even visiting homes to look for clues in refrigerators and shelves can be helpful. If the epidemic curve points to a short period of exposure, ask what events occurred around that time. If people living in a particular area have the highest attack rates, or if some groups with a particular age, sex, or other personal characteristics are at greatest risk, ask "why?". Such questions about the data should lead to hypotheses that can be tested.

Evaluating Hypotheses Section  

There are two approaches to evaluating hypotheses: comparison of the hypotheses with the established facts and analytic epidemiology , which allows testing hypotheses.

A comparison with established facts is useful when the evidence is so strong that the hypothesis does not need to be tested. A 1991 investigation of an outbreak of vitamin D intoxication in Massachusetts is a good example. All of the people affected drank milk delivered to their homes by a local dairy. Investigators hypothesized that the dairy was the source, and the milk was the vehicle of excess vitamin D. When they visited the dairy, they quickly recognized that far more than the recommended dose of vitamin D was inadvertently being added to the milk. No further analysis was necessary.

Analytic epidemiology is used when the cause is less clear. Hypotheses are tested, using a comparison group to quantify relationships between various exposures and disease. Case-control, occasionally cohort studies, are useful for this purpose.

Case-control studies Section  

As you recall from last week's lesson, in a case-control study case-patients and controls are asked about their exposures. An odds ratio is calculated to quantify the relationship between exposure and disease.

In general, the more case patients (and controls) you have, the easier it is to find an association. Often, however, an outbreak is small. For example, 4 or 5 cases may constitute an outbreak. An adequate number of potential controls is more easily located. In an outbreak of 50 or more cases, 1 control per case-patient will usually suffice. In smaller outbreaks, you might use 2, 3, or 4 controls per case-patient. More than 4 controls per case-patient are rarely worth the effort because the power of the study does not increase much when you have more than 4 controls per case-patient (we will talk more on power and sample size in epidemiologic studies later in this course!).

Testing statistical significance Section  

The final step in testing a hypothesis is to determine how likely it is that the study results could have occurred by chance alone. Is the exposure the study results suggest as the source of the outbreak related to the disease after all? The significance of the odds ratio can be assessed with a chi-square test. We will also discuss statistical tests that control for many possible factors later in the course.

Cohort studies Section  

If the outbreak occurs in a small, well-defined population a cohort study may be possible. For example, if an outbreak of gastroenteritis occurs among people who attended a particular social function, such as a banquet, and a complete list of guests is available, it is possible to ask each attendee the same set of questions about potential exposures and whether he or she had become ill with gastroenteritis.

After collecting this information from each guest, an attack rate can be calculated for people who ate a particular item (were exposed) and an attack rate for those who did not eat that item (were not exposed). For the exposed group, the attack rate is found by dividing the number of people who ate the item and became ill by the total number of people who ate that item. For those who were not exposed, the attack rate is found by dividing the number of people who did not eat the item but still became ill by the total number of people who did not eat that item.

To identify the source of the outbreak from this information, you would look for an item with:

• high attack rate among those exposed and
• a low attack rate among those not exposed (so the difference or ratio between attack rates for the two exposure groups is high); in addition
• most of the people who became ill should have consumed the item, so that the exposure could explain most, if not all, of the cases.

We will learn more about cohort studies in Week 9 of this course.

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

• View all journals
• My Account Login
• Explore content
• About the journal
• Publish with us
• Sign up for alerts
• Open access
• Published: 06 November 2020

Epidemiological hypothesis testing using a phylogeographic and phylodynamic framework

• Simon Dellicour   ORCID: orcid.org/0000-0001-9558-1052 1 , 2 ,
• Sebastian Lequime   ORCID: orcid.org/0000-0002-3140-0651 2 ,
• Bram Vrancken   ORCID: orcid.org/0000-0001-6547-5283 2 ,
• Mandev S. Gill 2 ,
• Paul Bastide   ORCID: orcid.org/0000-0002-8084-9893 2 ,
• Karthik Gangavarapu 3 ,
• Nathaniel L. Matteson 3 ,
• Yi Tan 4 , 5 ,
• Louis du Plessis   ORCID: orcid.org/0000-0003-0352-6289 6 ,
• Alexander A. Fisher 7 ,
• Martha I. Nelson 8 ,
• Marius Gilbert 1 ,
• Marc A. Suchard   ORCID: orcid.org/0000-0001-9818-479X 7 , 9 , 10 ,
• Kristian G. Andersen 3 , 11 ,
• Nathan D. Grubaugh 12 ,
• Oliver G. Pybus   ORCID: orcid.org/0000-0002-8797-2667 6 &
• Philippe Lemey   ORCID: orcid.org/0000-0003-2826-5353 2  

Nature Communications volume  11 , Article number:  5620 ( 2020 ) Cite this article

9925 Accesses

26 Citations

19 Altmetric

Metrics details

• Ecological epidemiology
• Molecular ecology
• Phylogenetics
• Viral epidemiology
• West nile virus

Computational analyses of pathogen genomes are increasingly used to unravel the dispersal history and transmission dynamics of epidemics. Here, we show how to go beyond historical reconstructions and use spatially-explicit phylogeographic and phylodynamic approaches to formally test epidemiological hypotheses. We illustrate our approach by focusing on the West Nile virus (WNV) spread in North America that has substantially impacted public, veterinary, and wildlife health. We apply an analytical workflow to a comprehensive WNV genome collection to test the impact of environmental factors on the dispersal of viral lineages and on viral population genetic diversity through time. We find that WNV lineages tend to disperse faster in areas with higher temperatures and we identify temporal variation in temperature as a main predictor of viral genetic diversity through time. By contrasting inference with simulation, we find no evidence for viral lineages to preferentially circulate within the same migratory bird flyway, suggesting a substantial role for non-migratory birds or mosquito dispersal along the longitudinal gradient.

Similar content being viewed by others

Reconstructing unseen transmission events to infer dengue dynamics from viral sequences

The evolutionary drivers and correlates of viral host jumps

Plagued by a cryptic clock: insight and issues from the global phylogeny of Yersinia pestis

Introduction.

The evolutionary analysis of rapidly evolving pathogens, particularly RNA viruses, allows us to establish the epidemiological relatedness of cases through time and space. Such transmission information can be difficult to uncover using classical epidemiological approaches. The development of spatially explicit phylogeographic models 1 , 2 , which place time-referenced phylogenies in a geographical context, can provide a detailed spatio-temporal picture of the dispersal history of viral lineages 3 . These spatially explicit reconstructions frequently serve illustrative or descriptive purposes, and remain underused for testing epidemiological hypotheses in a quantitative fashion. However, recent advances in methodology offer the ability to analyse the impact of underlying factors on the dispersal dynamics of virus lineages 4 , 5 , 6 , giving rise to the concept of landscape phylogeography 7 . Similar improvements have been made to phylodynamic analyses that use flexible coalescent models to reconstruct virus demographic history 8 , 9 ; these methods can now provide insights into epidemiological or environmental variables that might be associated with population size change 10 .

In this study, we focus on the spread of West Nile virus (WNV) across North America, which has considerably impacted public, veterinary, and wildlife health 11 . WNV is the most widely distributed encephalitic flavivirus transmitted by the bite of infected mosquitoes 12 , 13 . WNV is a single-stranded RNA virus that is maintained by an enzootic transmission cycle primarily involving Culex mosquitoes and birds 14 , 15 , 16 , 17 . Humans are incidental terminal hosts, because viremia does not reach a sufficient level for subsequent transmission to mosquitoes 17 , 18 . WNV human infections are mostly subclinical although symptoms may range from fever to meningoencephalitis and can occasionally lead to death 17 , 19 . It has been estimated that only 20–25% of infected people become symptomatic, and that <1 in 150 develops neuroinvasive disease 20 . The WNV epidemic in North America likely resulted from a single introduction to the continent 20 years ago 21 . Its persistence is likely not the result of successive reintroductions from outside of the hemisphere, but rather of local overwintering and maintenance of long-term avian and/or mosquito transmission cycles 11 . Overwintering could also be facilitated by vertical transmission of WNV from infected female mosquitos to their offspring 22 , 23 , 24 . WNV represents one of the most important vector-borne diseases in North America 15 ; there were an estimated 7 million human infections in the U.S. 25 , causing a reported 24,657 human neuroinvasive cases between 1999 to 2018, leading to 2,199 deaths ( www.cdc.gov/westnile ). In addition, WNV has had a notable impact on North American bird populations 26 , 27 , with several species 28 such as the American crow ( Corvus brachyrhynchos ) being particularly severely affected.

Since the beginning of the epidemic in North America in 1999 21 , WNV has received considerable attention from local and national health institutions and the scientific community. This had led to the sequencing of >2000 complete viral genomes collected at various times and locations across the continent. The resulting availability of virus genetic data represents a unique opportunity to better understand the evolutionary history of WNV invasion into an originally non-endemic area. Here, we take advantage of these genomic data to address epidemiological questions that are challenging to tackle with non-molecular approaches.

The overall goal of this study is to go beyond historical reconstructions and formally test epidemiological hypotheses by exploiting phylodynamic and spatially explicit phylogeographic models. We detail and apply an analytical workflow that consists of state-of-the-art methods that we further improve to test hypotheses in molecular epidemiology. We demonstrate the power of this approach by analysing a comprehensive data set of WNV genomes with the objective of unveiling the dispersal and demographic dynamics of the virus in North America. Specifically, we aim to (i) reconstruct the dispersal history of WNV on the continent, (ii) compare the dispersal dynamics of the three WNV genotypes, (iii) test the impact of environmental factors on the dispersal locations of WNV lineages, (iv) test the impact of environmental factors on the dispersal velocity of WNV lineages, (v) test the impact of migratory bird flyways on the dispersal history of WNV lineages, and (vi) test the impact of environmental factors on viral genetic diversity through time.

Reconstructing the dispersal history and dynamics of WNV lineages

To infer the dispersal history of WNV lineages in North America, we performed a spatially explicit phylogeographic analysis 1 of 801 viral genomes (Supplementary Figs.  S1 and S2 ), which is almost an order of magnitude larger than the early US-wide study by Pybus et al. 2 (104 WNV genomes). The resulting sampling presents a reasonable correspondence between West Nile fever prevalence in the human population and sampling density in most areas associated with the highest numbers of reported cases (e.g., Los Angeles, Houston, Dallas, Chicago, New York), but also some under-sampled locations (e.g., in Colorado; Supplementary Fig.  S1 ). Year-by-year visualisation of the reconstructed invasion history highlights both relatively fast and relatively slow long-distance dispersal events across the continent (Supplementary Fig.  S3 ), which is further confirmed by the comparison between the durations and geographic distances travelled by phylogeographic branches (Supplementary Fig.  S4 ). Some of these long-distance dispersal events were notably fast, with >2000 km travelled in only a couple of months (Supplementary Fig.  S4 ).

To quantify the spatial dissemination of virus lineages, we extracted the spatio-temporal information embedded in molecular clock phylogenies sampled by Bayesian phylogeographic analysis. From the resulting collection of lineage movement vectors, we estimated several key statistics of spatial dynamics (Fig.  1 ). We estimated a mean lineage dispersal velocity of ~1200 km/year, which is consistent with previous estimates 2 . We further inferred how the mean lineage dispersal velocity changed through time, and found that dispersal velocity was notably higher in the earlier years of the epidemic (Fig.  1 ). The early peak of lineage dispersal velocity around 2001 corresponds to the expansion phase of the epidemic. This is corroborated by our estimate of the maximal wavefront distance from the epidemic origin through time (Fig.  1 ). This expansion phase lasted until 2002, when WNV lineages first reached the west coast (Fig.  1 and Supplementary Fig. S3 ). From East to West, WNV lineages dispersed across various North American environmental conditions in terms of land cover, altitude, and climatic conditions (Fig.  2 ).

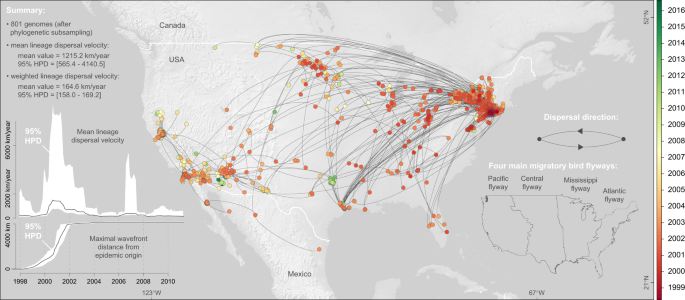
Maximum clade credibility (MCC) tree obtained by continuous phylogeographic inference based on 100 posterior trees (see the text for further details). Nodes of the tree are coloured from red (the time to the most recent common ancestor, TMRCA) to green (most recent sampling time). Older nodes are plotted on top of younger nodes, but we provide also an alternative year-by-year representation in Supplementary Fig.  S1 . In addition, this figure reports global dispersal statistics (mean lineage dispersal velocity and mean diffusion coefficient) averaged over the entire virus spread, the evolution of the mean lineage dispersal velocity through time, the evolution of the maximal wavefront distance from the origin of the epidemic, as well as the delimitations of the North American Migratory Flyways (NAMF) considered in the USA.

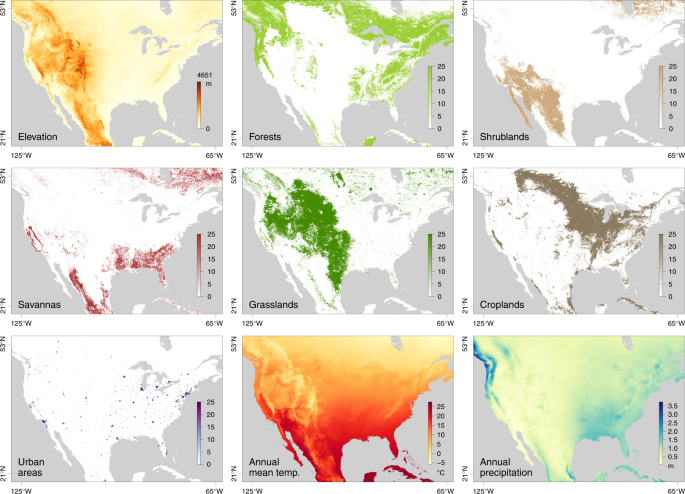
See Table S1 for the source of data for each environmental raster.

We also compared the dispersal velocity estimated for five subsets of WNV phylogenetic branches (Fig.  3 ): branches occurring during (before 2002) and after the expansion phase (after 2002), as well as branches assigned to each of the three commonly defined WNV genotypes that circulated in North America (NY99, WN02, and SW03; Supplementary Figs.  S1 – S2 ). While NY99 is the WNV genotype that initially invaded North America, WN02 and subsequently SW03 emerged as the two main co-circulating genotypes characterised by distinct amino acid substitutions 29 , 30 , 31 , 32 . We specifically compare the dispersal history and dynamics of lineages belonging to these three different genotypes in order to investigate the assumption that WNV dispersal might have been facilitated by local environmental adaptations 32 . To address this question, we performed the three landscape phylogeographic testing approaches presented below on the complete data set including all viral lineages inferred by continuous phylogeographic inference, as well as on these different subsets of lineages. We first compared the lineage dispersal velocity estimated for each subset by estimating both the mean and weighted lineage dispersal velocities. As shown in Fig.  3 and detailed in the Methods section, the weighted metric is more efficient and suitable to compare the dispersal velocity associated with different data sets, or subsets in the present situation. Posterior distributions of the weighted dispersal velocity confirmed that the lineage dispersal was much faster during the expansion phase (<2002; Fig.  3 ). Second, these estimates also indicated that SW03 is associated with a higher dispersal velocity than the dominant genotype, WN02.

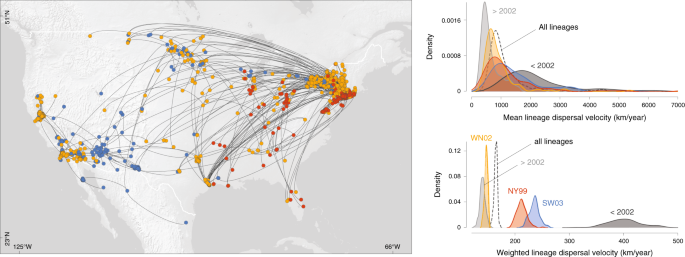
The map displays the maximum clade credibility (MCC) tree obtained by continuous phylogeographic inference with nodes coloured according to three different genotypes.

Testing the impact of environmental factors on the dispersal locations of viral lineages

To investigate the impact of environmental factors on the dispersal dynamics of WNV, we performed three different statistical tests in a landscape phylogeographic framework. First, we tested whether lineage dispersal locations tended to be associated with specific environmental conditions. In practice, we started by computing the E statistic, which measures the mean environmental values at tree node positions. These values were extracted from rasters (geo-referenced grids) that summarised the different environmental factors to be tested: elevation, main land cover variables in the study area (forests, shrublands, savannas, grasslands, croplands, urban areas; Fig.  2 ), and monthly time-series collections of climatic rasters (for temperature and precipitation; Supplementary Table  S1 ). For the time-series climatic factors, the raster used for extracting the environmental value was selected according to the time of occurrence of each tree node. The E statistic was computed for each posterior tree sampled during the phylogeographic analysis, yielding a posterior distribution of this metric (Supplementary Fig.  S5 ). To determine whether the posterior distributions for E were significantly lower or higher than expected by chance under a null dispersal model, we also computed E based on simulations, using the inferred set of tree topologies along which a new stochastic diffusion history was simulated according to the estimated diffusion parameters. The statistical support was assessed by comparing inferred and simulated distributions of E . If the inferred distribution was significantly lower than the simulated distribution of E , this provides evidence for the environmental factor to repulse viral lineages, while an inferred distribution higher than the simulated distribution of E would provide evidence for the environmental factor to attract viral lineages.

These first landscape phylogeographic tests revealed that WNV lineages (i) tended to avoid areas associated with relatively higher elevation, forest coverage, and precipitation, and (ii) tended to disperse in areas associated with relatively higher urban coverage, temperature, and shrublands (Supplementary Table  S2 ). However, when analysing each genotype separately, different trends emerged. For instance, SW03 lineages did not tend to significantly avoid (or disperse to) areas with relatively higher elevation (~600–750 m above sea level), and only SW03 lineages significantly dispersed towards areas with shrublands (Supplementary Table  S2 ). Furthermore, when only focusing on WNV lineages occurring before 2002, we did not identify any significant association between environmental values and node positions. Interestingly, this implies that we cannot associate viral dispersal during the expansion phase with specific favourable environmental conditions (Supplementary Table  S2 ). As these tests are directly based on the environmental values extracted at internal and tip node positions, their outcome can be particularly impacted by the nature of sampling. Indeed, half of the node positions, i.e., the tip node positions, are directly determined by the sampling. To assess the sensitivity of the tests to heterogeneous sampling, we also repeated these tests while only considering internal tree nodes. Since internal nodes are phylogeographically linked to tip nodes, discarding tip branches can only mitigate the direct impact of the sampling pattern on the outcome of the analysis. These additional tests provided consistent results, except for one environmental factor: while precipitation was identified as a factor repulsing viral lineages, it was not the case anymore when only considering internal tree branches, indicating that the initial result could be attributed to a sampling artefact.

Testing the impact of environmental factors on the dispersal velocity of viral lineages

In the second landscape phylogeographic test, we analysed whether the heterogeneity observed in lineage dispersal velocity could be explained by specific environmental factors that are predominant in the study area. For this purpose, we used a computational method that assesses the correlation between lineage dispersal durations and environmentally scaled distances 4 , 33 . These distances were computed on several environmental rasters (Fig.  2 and Supplementary Table  S1 ): elevation, main land cover variables in the study area (forests, shrublands, savannas, grasslands, croplands, urban areas), as well as annual mean temperature and annual precipitation. This analysis aimed to quantify the impact of each factor on virus movement by calculating a statistic, Q , that measures the correlation between lineage durations and environmentally scaled distances. Specifically, the Q statistic describes the difference in strength of the correlation when distances are scaled using the environmental raster versus when they are computed using a “null” raster (i.e., a uniform raster with a value of “1” assigned to all cells). As detailed in the Methods section, two alternative path models were used to compute these environmentally scaled distances: the least-cost path model 34 and a model based on circuit theory 35 . The Q statistic was estimated for each posterior tree sampled during the phylogeographic analysis, yielding a posterior distribution of this metric. As for the statistic E , statistical support for Q was then obtained by comparing inferred and simulated distributions of Q ; the latter was obtained by estimating Q on the same set of tree topologies, along which a new stochastic diffusion history was simulated. This simulation procedure thereby generated a null model of dispersal, and the comparison between the inferred and simulated Q distributions enabled us to approximate a Bayes factor support (see “Methods” for further details).

As summarised in Supplementary Table  S3 , we found strong support for one variable: annual temperature raster treated as a conductance factor. Using this factor, the association between lineage duration and environmentally scaled distances was significant using the path model based on circuit theory 35 . As detailed in Fig.  4 , this environmental variable better explained the heterogeneity in lineage dispersal velocity than geographic distance alone (i.e., its Q distribution was positive). Furthermore, this result received strong statistical support (Bayes factor > 20), obtained by comparing the distribution of Q values with that obtained under a null model (Fig.  4 ). We also performed these tests on each WNV genotype separately (Supplementary Table  S4 ). With these additional tests, we only found the same statistical support associated with temperature for the viral lineages belonging to the WN02 genotype. In addition, these tests based on subsets of lineages also revealed that the higher elevation was significantly associated with lower dispersal velocity of WN02 lineages.

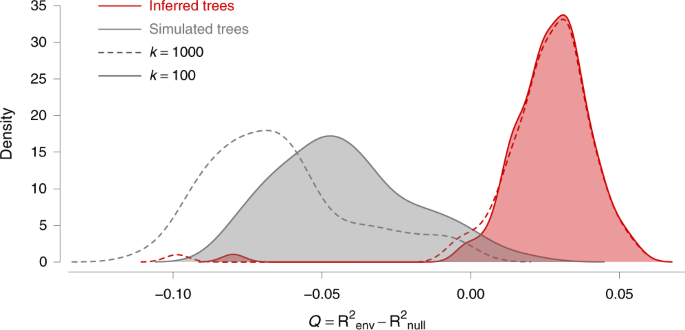
The graph displays the distribution of the correlation metric Q computed on 100 spatially annotated trees obtained by continuous phylogeographic inference (red distributions). The metric Q measures to what extent considering a heterogeneous environmental raster, increases the correlation between lineage durations and environmentally scaled distances compared to a homogeneous raster. If Q is positive and supported, it indicates that the heterogeneity in lineage dispersal velocity can be at least partially explained by the environmental factor under investigation. The graph also displays the distribution of Q values computed on the same 100 posterior trees along which we simulated a new forward-in-time diffusion process (grey distributions). These simulations are used as a null dispersal model to estimate the support associated with the inferred distribution of Q values. For both inferred and simulated trees, we report the Q distributions obtained while transforming the original environmental raster according to two different scaling parameter k values (100 and 1000; respectively full and dashed line, see the text for further details on this transformation). The annual mean temperature raster, transformed in conductance values using these two k values, is the only environmental factor for which we detect a positive distribution of Q that is also associated with a strong statistical support (Bayes factor > 20).

Testing the impact of environmental factors on the dispersal frequency of viral lineages

The third landscape phylogeography test that we performed focused on the impact of specific environmental factors on the dispersal frequency of viral lineages. Specifically, we aimed to investigate the impact of migratory bird flyways on the dispersal history of WNV. For this purpose, we first tested whether virus lineages tended to remain within the same North American Migratory Flyway (NAMF; Fig.  1 ). As in the two first testing approaches, we again compared inferred and simulated diffusion dynamics (i.e., simulation of a new stochastic diffusion process along the estimated trees). Under the null hypothesis (i.e., NAMFs have no impact on WNV dispersal history), virus lineages should not transition between flyways less often than under the null dispersal model. Our test did not reject this null hypothesis (BF < 1). As the NAMF borders are based on administrative areas (US counties), we also performed a similar test using the alternative delimitation of migratory bird flyways estimated for terrestrial bird species by La Sorte et al. 36 (Supplementary Fig.  S6 ). Again, the null hypothesis was not rejected, indicating that inferred virus lineages did not tend to remain within specific flyways more often than expected by chance. Finally, these tests were repeated on each of the five subsets of WNV lineages (<2002, >2002, NY99, WN02, SW03) and yielded the same results, i.e., no rejection of the null hypothesis stating that flyways do not constrain WNV dispersal.

Testing the impact of environmental factors on the viral genetic diversity through time

We next employed a phylodynamic approach to investigate predictors of the dynamics of viral genetic diversity through time. In particular, we used the generalised linear model (GLM) extension 10 of the skygrid coalescent model 9 , hereafter referred to as the “skygrid-GLM” approach, to statistically test for associations between estimated dynamics of virus effective population size and several covariates. Coalescent models that estimate effective population size (Ne) typically assume a single panmictic population that encompasses all individuals. As this assumption is frequently violated in practice, the estimated effective population size is sometimes interpreted as representing an estimate of the genetic diversity of the whole virus population 37 . The skygrid-GLM approach accounts for uncertainty in effective population size estimates when testing for associations with covariates; neglecting this uncertainty can lead to spurious conclusions 10 .

We first performed univariate skygrid-GLM analyses of four distinct time-varying covariates reflecting seasonal changes: monthly human WNV case counts (log-transformed), temperature, precipitation, and a greenness index. For the human case count covariate, we only detected a significant association with the viral effective population size when considering a lag period of at least one month. In addition, univariate analyses of temperature and precipitation time-series were also associated with the virus genetic diversity dynamics (i.e., the posterior GLM coefficients for these covariates had 95% credible intervals that did not include zero; Fig.  5 ). To further assess the relative importance of each covariate, we performed multivariate skygrid-GLM analyses to rank covariates based on their inclusion probabilities 38 . The first multivariate analysis involved all covariates and suggested that the lagged human case counts best explain viral population size dynamics, with an inclusion probability close to 1. However, because human case counts are known to be a consequence rather than a potential causal driver of the WNV epidemic, we performed a second multivariate analysis after having excluded this covariate. This time, the temperature time-series emerged as the covariate with the highest inclusion probability.

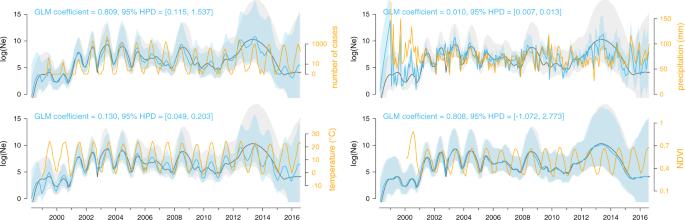
These associations were tested with a generalised linear model (GLM) extension of the coalescent model used to infer the dynamics of the viral effective population size of the virus (Ne) through time. Specifically, we here tested the following time-series variables as potential covariates (orange curves): number of human cases (log-transformed and with a negative time period of one month), mean temperature, mean precipitation, and Normalised Difference Vegetation Index (NDVI, a greenness index). Posterior mean estimates of the viral effective population size based on both sequence data and covariate data are represented by blue curves, and the corresponding blue polygon reflects the 95% HPD region. Posterior mean estimates of the viral effective population size inferred strictly from sequence data are represented by grey curves and the corresponding grey polygon reflects the 95% HPD region. A significant association between the covariate and effective population size is inferred when the 95% HPD interval of the GLM coefficient excludes zero, which is the case for the case count, temperature, and precipitation covariates.

In this study, we use spatially explicit phylogeographic and phylodynamic inference to reconstruct the dispersal history and dynamics of a continental viral spread. Through comparative analyses of lineage dispersal statistics, we highlight distinct trends within the overall spread of WNV. First, we have demonstrated that the WNV spread in North America can be divided into an initial “invasion phase” and a subsequent “maintenance phase” (see Carrington et al. 39 for similar terminology used in the context of spatial invasion of dengue viruses). The invasion phase is characterised by an increase in virus effective population size until the west coast was reached, followed by a maintenance phase associated with a more stable cyclic variation of effective population size (Fig.  5 ). In only 2–3 years, WNV rapidly spread from the east to the west coast of North America, despite the fact that the migratory flyways of its avian hosts are primarily north-south directed. This could suggest potentially important roles for non-migratory bird movements, as well as natural or human-mediated mosquito dispersal, in spreading WNV along a longitudinal gradient 40 , 41 . However, the absence of clear within flyway clustering of viral lineages could also arise when different avian migration routes intersect at southern connections. If local WNV transmission occurs at these locations, viruses could travel along different flyways when the birds make their return northward migration, as proposed by Swetnam et al. 42 . While this scenario is possible, there is insufficient data to formally investigate with our approaches. Overall, we uncover a higher lineage dispersal velocity during the invasion phase, which could reflect a consequence of increased bird immunity through time slowing down spatial dispersal. It has indeed been demonstrated that avian immunity can impact WNV transmission dynamics 43 . Second, we also reveal different dispersal velocities associated with the three WNV genotypes that have circulated in North America: viral lineages of the dominant current genotype (WN02) have spread slower than lineages of NY99 and SW03. NY99 was the main genotype during the invasion phase but has not been detected in the US since the mid 2000s. A faster dispersal associated with NY99 is thus coherent with the higher dispersal velocity identified for lineages circulating during the invasion phase. The higher dispersal velocity for SW03 compared to WN02 is in line with recently reported evidence that SW03 spread faster than WN02 in California 44 .

In the second part of the study, we illustrate the application of a phylogeographic framework for hypothesis testing that builds on previously developed models. These analytical approaches are based on a spatially explicit phylogeographic or phylodynamic (skygrid coalescent) reconstruction, and aim to assess the impact of environmental factors on the dispersal locations, velocity, and frequency of viral lineages, as well as on the overall genetic diversity of the viral population. The WNV epidemic in North America is a powerful illustration of viral invasion and emergence in a new environment 31 , making it a highly relevant case study to apply such hypothesis testing approaches. We first test the association between environmental factors and lineage dispersal locations, demonstrating that, overall, WNV lineages have preferentially circulated in specific environmental conditions (higher urban coverage, temperature, and shrublands) and tended to avoid others (higher elevation and forest coverage). Second, we have tested the association between environmental factors and lineage dispersal velocity. With these tests, we find evidence for the impact of only one environmental factor on virus lineage dispersal velocity, namely annual mean temperature. Third, we tested the impact of migratory flyways on the dispersal frequency of viral lineages among areas. Here, we formally test the hypothesis that WNV lineages are contained or preferentially circulate within the same migratory flyway and find no statistical support for this.

We have also performed these three different landscape phylogeographic tests on subsets of WNV lineages (lineages occurring during and after the invasion phase, as well as NY99, WN02, and SW03 lineages). When focusing on lineages occurring during the invasion phase (<2002), we do not identify any significant association between a particular environmental factor and the dispersal location or velocity of lineages. This result corroborates the idea that, during the early phase of the epidemic, the virus rapidly conquered the continent despite various environmental conditions, which was likely helped by large populations of susceptible hosts/vectors already present in North America 32 . These additional tests also highlight interesting differences among the three WNV genotypes. For instance, we found that the dispersal of SW03 genotype is faster than WN02 and also preferentially in shrublands and at higher temperatures. At face value, it appears that the mutations that define the SW03 genotype, NS4A-A85T and NS5-K314R 45 , may be signatures of adaptations to such specific environmental conditions. It may, however, be an artefact of the SW03 genotype being most commonly detected in mosquito species such as Cx. tarsalis and Cx. quiquefasciatus that are found in the relatively high elevation shrublands of the southwest US 44 , 46 . In this scenario, the faster dispersal velocities could result from preferentially utilising these two highly efficient WNV vectors 47 , especially when considering the warm temperatures of the southwest 48 , 49 . It is also important to note that to date, no specific phenotypic advantage has been observed for SW03 genotypes compared to WN02 genotypes 50 , 51 . Further research is needed to discern if the differences among the three WNV genotypes are due to virus-specific factors, heterogeneous sampling effort, or ecological variation.

When testing the impact of flyways on the five different subsets of lineages, we reach the same result of no preferential circulation within flyways. This overall result contrasts with previously reported phylogenetic clustering by flyways 31 , 42 . However, the clustering analysis of Di Giallonardo et al. 31 was based on a discrete phylogeographic analysis and, as recognised by the authors, it is difficult to distinguish the effect of these flyways from those of geographic distance. Here, we circumvent this issue by performing a spatial analysis that explicitly represents dispersal as a function of geographic distance. Our results are, however, not in contradiction with the already established role of migratory birds in spreading the virus 52 , 53 , but we do not find evidence that viral lineage dispersal is structured by flyway. Specifically, our test does not reject the null hypothesis of absence of clustering by flyways, which at least signals that the tested flyways do not have a discernible impact on WNV lineages circulation. Dissecting the precise involvement of migratory bird in WNV spread, thus, require additional collection of empirical data. Furthermore, our phylogeographic analysis highlights the occurrence of several fast and long-distance dispersal events along a longitudinal gradient. A potential anthropogenic contribution to such long-distance dispersal (e.g., through commercial transport) warrants further investigation.

In addition to its significant association with the dispersal locations and velocity of WNV lineages, the relevance of temperature is further demonstrated by the association between the virus genetic dynamics and several time-dependent covariates. Indeed, among the three environmental time-series we tested, temporal variation in temperature is the most important predictor of cycles in viral genetic diversity. Temperature is known to have a dramatic impact on the biology of arboviruses and their arthropod hosts 54 , including WNV. Higher temperatures have been shown to impact directly the mosquito life cycle, by accelerating larval development 11 , decreasing the interval between blood meals, and prolonging the mosquito breeding season 55 . Higher temperatures have been also associated with shorter extrinsic incubation periods, accelerating WNV transmission by the mosquito vector 56 , 57 . Interestingly, temperature has also been suggested as a variable that can increase the predictive power of WNV forecast models 58 . The impact of temperature that we reveal here on both dispersal velocity and viral genetic diversity is particularly important in the context of global warming. In addition to altering mosquito species distribution 59 , 60 , an overall temperature increase in North America could imply an increase in enzootic transmission and hence increased spill-over risk in different regions. In addition to temperature, we find evidence for an association between viral genetic diversity dynamics and the number of human cases, but only when a lag period of at least one month is added to the model (having only monthly case counts available, it was not possible to test shorter lag periods). Such lag could, at least in part, be explained by the time needed for mosquitos to become infectious and bite humans. As human case counts are in theory backdated to the date of onset of illness, incubation time in humans should not contribute to this lag.

Our study illustrates and details the utility of landscape phylogeographic and phylodynamic hypothesis tests when applied to a comprehensive data set of viral genomes sampled during an epidemic. Such spatially explicit investigations are only possible when viral genomes (whether recently collected or available on public databases such as GenBank) are associated with sufficiently precise metadata, in particular the collection date and the sampling location. The availability of precise collection dates - ideally known to the day - for isolates obtained over a sufficiently long time-span enables reliable timing of epidemic events due to the accurate calibration of molecular clock models. Further, spatially explicit phylogeographic inference is possible only when viral genomes are associated with sampling coordinates. However, geographic coordinates are frequently unknown or unreported. In practice this may not represent a limitation if a sufficiently precise descriptive sampling location is specified (e.g., a district or administrative area), as this information can be converted into geographic coordinates. The full benefits of comprehensive phylogeographic analyses of viral epidemics will be realised only when precise location and time metadata are made systematically available.

Although we use a comprehensive collection of WNV genomes in this study, it would be useful to perform analyses based on even larger data sets that cover regions under-sampled in the current study; this work is the focus of an ongoing collaborative project (westnile4k.org). While the resolution of phylogeographic analyses will always depend on the spatial granularity of available samples, they can still be powerful in elucidating the dispersal history of sampled lineages. When testing the impact of environmental factors on lineage dispersal velocity and frequency, heterogeneous sampling density will primarily affect statistical power in detecting the impact of relevant environmental factors in under- or unsampled areas 33 . However, the sampling pattern can have much more impact on the tests dedicated to the impact of environmental factors on the dispersal locations of viral lineages. As stated above, in this test, half of the environmental values will be extracted at tip node locations, which are directly determined by the sampling effort. To circumvent this issue and assess the robustness of the test regarding the sampling pattern, we here proposed to repeat the analysis after having discarded all the tip branches, which logically mitigated a potential impact of the sampling pattern on the outcome of this analysis. Furthermore, in this study, we note that heterogeneous sampling density across counties can be at least partially mitigated by performing phylogenetic subsampling (detailed in the “Methods” section). Another limitation to underline is that, contrary to the tests focusing on the impact of environmental factors on the dispersal locations and frequency, the present framework does not allow testing the impact of time-series environmental variables on the dispersal velocity of viral lineages. It would be interesting to extend that framework so that it can, e.g., test the impact of spatio-temporal variation of temperature on the dispersal velocity of WNV lineages. On the opposite, while skygrid-GLM analyses intrinsically integrate temporal variations of covariates, these tests treat the epidemic as a unique panmictic population of viruses. In addition to ignoring the actual population structure, this aspect implies the comparison of the viral effective population size with a unique environmental value per time slice and for the entire study area. To mitigate spatial heterogeneity as much as possible, we used the continuous phylogeographic reconstruction to define successive minimum convex hull polygons delimiting the study area at each time slice. These polygons were used to extract the environmental values that were then averaged to obtain a single environmental value per time slice considered in the skygrid-GLM analysis.

By placing virus lineages in a spatio-temporal context, phylogeographic inference provides information on the linkage of infections through space and time. Mapping lineage dispersal can provide a valuable source of information for epidemiological investigations and can shed light on the ecological and environmental processes that have impacted the epidemic dispersal history and transmission dynamics. When complemented with phylodynamic testing approaches, such as the skygrid-GLM approach used here, these methods offer new opportunities for epidemiological hypotheses testing. These tests can complement traditional epidemiological approaches that employ occurrence data. If coupled to real-time virus genome sequencing, landscape phylogeographic and phylodynamic testing approaches have the potential to inform epidemic control and surveillance decisions 61 .

Selection of viral sequences

We started by gathering all WNV sequences available on GenBank on the 20 th November 2017. We only selected sequences (i) of at least 10 kb, i.e., covering almost the entire viral genome (~11 kb), and (ii) associated with a sufficiently precise sampling location, i.e., at least an administrative area of level 2. Administrative areas of level 2 are hereafter abbreviated “admin-2” and correspond to US counties. Finding the most precise sampling location (admin-2, city, village, or geographic coordinates), as well as the most precise sampling date available for each sequence, required a bibliographic screening because such metadata are often missing on GenBank. The resulting alignment of 993 geo-referenced genomic sequences of at least 10 kb was made using MAFFT 62 and manually edited in AliView 63 . Based on this alignment, we performed a first phylogenetic analysis using the maximum likelihood method implemented in the programme FastTree 64 with 1000 bootstrap replicates to assess branch supports. The aim of this preliminary phylogenetic inference was solely to identify monophyletic clades of sequences sampled from the same admin-2 area associated with a bootstrap support higher than 70%. Such phylogenetic clusters of sampled sequences largely represent lineage dispersal within a specific admin-2 area. As we randomly draw geographic coordinates from an admin-2 polygon for sequences only associated with an admin-2 area of origin, keeping more than one sequence per phylogenetic cluster would not contribute any meaningful information in subsequent phylogeographic analyses 61 . Therefore, we subsampled the original alignment such that only one sequence is randomly selected per phylogenetic cluster, leading to a final alignment of 801 genomic sequences (Supplementary Fig.  S1 ). In the end, selected sequences were mostly derived from mosquitoes (~50%) and birds (~44%), with very few (~5%) from humans.

Time-scaled phylogenetic analysis

Time-scaled phylogenetic trees were inferred using BEAST 1.10.4 65 and the BEAGLE 3 library 66 to improve computational performance. The substitution process was modelled according to a GTR+Γ parametrisation 67 , branch-specific evolutionary rates were modelled according to a relaxed molecular clock with an underlying log-normal distribution 68 , and the flexible skygrid model was specified as tree prior 9 , 10 . We ran and eventually combined ten independent analyses, sampling Markov chain Monte-Carlo (MCMC) chains every 2 × 10 8 generations. Combined, the different analyses were run for >10 12 generations. For each distinct analysis, the number of sampled trees to discard as burn-in was identified using Tracer 1.7 69 . We used Tracer to inspect the convergence and mixing properties of the combined output, referred to as the “skygrid analysis” throughout the text, to ensure that estimated sampling size (ESS) values associated with estimated parameters were all >200.

Spatially explicit phylogeographic analysis

The spatially explicit phylogeographic analysis was performed using the relaxed random walk (RRW) diffusion model implemented in BEAST 1 , 2 . This model allows the inference of spatially and temporally referenced phylogenies while accommodating variation in dispersal velocity among branches 3 . Following Pybus et al. 2 , we used a gamma distribution to model the among-branch heterogeneity in diffusion velocity. Even when launching multiple analyses and using GPU resources to speed-up the analyses, poor MCMC mixing did not permit reaching an adequate sample from the posterior in a reasonable amount of time. This represents a challenging problem that is currently under further investigation 70 . To circumvent this issue, we performed 100 independent phylogeographic analyses each based on a distinct fixed tree sampled from the posterior distribution of the skygrid analysis. We ran each analysis until ESS values associated with estimated parameters were all greater than 100. We then extracted the last spatially annotated tree sampled in each of the 100 posterior distributions, which is the equivalent of randomly sampling a post-burn-in tree within each distribution. All the subsequent landscape phylogeographic testing approaches were based on the resulting distribution of the 100 spatially annotated trees. Given the computational limitations, we argue that the collection of 100 spatially annotated trees, extracted from distinct posterior distributions each based on a different fixed tree topology, represents a reasonable approach to obtain a phylogeographic reconstruction that accounts for phylogenetic uncertainty. We note that this is similar to the approach of using a set of empirical trees that is frequently employed for discrete phylogeographic inference 71 , 72 , but direct integration over such a set of trees is not appropriate for the RRW model because the proposal distribution for branch-specific scaling factors does not hold in this case. We used TreeAnnotator 1.10.4 65 to obtain the maximum clade credibility (MCC) tree representation of the spatially explicit phylogeographic reconstruction (Supplementary Fig.  S2 ).

In addition to the overall data set encompassing all lineages, we also considered five different subsets of lineages: phylogeny branches occurring before or after the end of the expansion/invasion phase (i.e., 2002; Fig.  1 ), as well as phylogeny branches assigned to each of the three WNV genotypes circulating in North America (NY99, WN02, and SW03; Supplementary Figs.  S1 – S2 ). These genotypes were identified on the basis of the WNV database published on the platform Nextstrain 32 , 73 . For the purpose of comparison, we performed all the subsequent landscape phylogeographic approaches on the overall data set but also on these five different subsets of WNV lineages.

Estimating and comparing lineage dispersal statistics

Phylogenetic branches, or “lineages”, from spatially and temporally referenced trees can be treated as conditionally independent movement vectors 2 . We used the R package “seraphim” 74 to extract the spatio-temporal information embedded within each tree and to summarise lineages as movement vectors. We further used the package “seraphim” to estimate two dispersal statistics based on the collection of such vectors: the mean lineage dispersal velocity ( v mean ) and the weighted lineage dispersal velocity ( v weighted ) 74 . While both metrics measure the dispersal velocity associated with phylogeny branches, the second version involves a weighting by branch time 75 :

where d i and t i are the geographic distance travelled (great-circle distance in km) and the time elapsed (in years) on each phylogeny branch, respectively. The weighted metric is useful for comparing branch dispersal velocity between different data sets or different subsets of the same data set. Indeed, phylogeny branches with short duration have a lower impact on the weighted lineage dispersal velocity, which results in lower‐variance estimates facilitating data set comparison 33 . On the other hand, estimating mean lineage dispersal velocity is useful when aiming to investigate the variability of lineage dispersal velocity within a distinct data set 75 . Finally, we also estimated the evolution of the maximal wavefront distance from the epidemic origin, as well as the evolution of the mean lineage dispersal velocity through time.

Generating a null dispersal model of viral lineages dispersal

To generate a null dispersal model we simulated a forward-in-time RRW diffusion process along each tree topology used for the phylogeographic analyses. These RRW simulations were performed with the “simulatorRRW1” function of the R package “seraphim” and based on the sampled precision matrix parameters estimated by the phylogeographic analyses 61 . For each tree, the RRW simulation started from the root node position inferred by the phylogeographic analysis. Furthermore, these simulations were constrained such that the simulated node positions remain within the study area, which is here defined by the minimum convex hull built around all node positions, minus non-accessible sea areas. As for the annotated trees obtained by phylogeographic inference, hereafter referred to as “inferred trees”, we extracted the spatio-temporal information embedded within their simulated counterparts, hereafter referred as “simulated trees”. As RRW diffusion processes were simulated along fixed tree topologies, each simulated tree shares a common topology with an inferred tree. Such a pair of inferred and simulated trees, thus, only differs by the geographic coordinates associated with their nodes, except for the root node position that was fixed as starting points for the RRW simulation. The distribution of 100 simulated trees served as a null dispersal model for the landscape phylogeographic testing approaches described below.

The first landscape phylogeographic testing approach consisted of testing the association between environmental conditions and dispersal locations of viral lineages. We started by simply visualising and comparing the environmental values explored by viral lineages. For each posterior tree sampled during the phylogeographic analysis, we extracted and then averaged the environmental values at the tree node positions. We then obtained, for each analysed environmental factor, a posterior distribution of mean environmental values at tree node positions for the overall data set as well as for the five subsets of WNV lineages described above. In addition to this visualisation, we also performed a formal test comparing mean environmental values extracted at node positions in inferred ( E estimated ) and simulated trees ( E simulated ). E simulated values constituted the distribution of mean environmental values explored under the null dispersal model, i.e., under a dispersal scenario that is not impacted by any underlying environmental condition. To test if a particular environmental factor e tended to attract viral lineages, we approximated the following Bayes factor (BF) support 76 :

where p e is the posterior probability that E estimated  >  E simulated , i.e., the frequency at which E estimated  >  E simulated in the samples from the posterior distribution. The prior odds is 1 because we can assume an equal prior expectation for E estimated and E simulated . To test if a particular environmental factor e tended to repulse viral lineages, BF e was approximated with p e as the posterior probability that E estimated  <  E simulated . These tests are similar to a previous approach using a null dispersal model based on randomisation of phylogeny branches 75 .

We tested several environmental factors both as factors potentially attracting or repulsing viral lineages: elevation, main land cover variables on the study area, and climatic variables. Each environmental factor was described by a raster that defines its spatial heterogeneity (see Supplementary Table  S1 for the source of each original raster file). Starting from the original categorical land cover raster with an original resolution of 0.5 arcmin (corresponding to cells ~1 km 2 ), we generated distinct land cover rasters by creating lower resolution rasters (10 arcmin) whose cell values equalled the number of occurrences of each land cover category within the 10 arcmin cells. The resolution of the other original rasters of fixed-in-time environmental factors (elevation, mean annual temperature, and annual precipitation) was also decreased to 10 arcmin for tractability, which was mostly important in the context of the second landscape phylogeographic approach detailed below. To obtain the time-series collection of temperature and precipitation rasters analysed in these first tests dedicated to the impact of environmental factors on lineage dispersal locations, we used the thin plate spline method implemented in the R package “fields” to interpolate measures obtained from the database of the US National Oceanic and Atmospheric Administration (NOAA; https://data.nodc.noaa.gov ).

The second landscape phylogeographic testing approach aimed to test the association between several environmental factors, again described by rasters (Fig.  2 ), and the dispersal velocity of WNV lineages in North America. Each environmental raster was tested as a potential conductance factor (i.e., facilitating movement) and as a resistance factor (i.e., impeding movement). In addition, for each environmental factor, we generated several distinct rasters by transforming the original raster cell values with the following formula: v t  = 1 +  k ( v o / v max ), where v t and v o are the transformed and original cell values, and v max the maximum cell value recorded in the raster. The rescaling parameter k here allows the definition and testing of different strengths of raster cell conductance or resistance, relative to the conductance/resistance of a cell with a minimum value set to “1”. For each of the three environmental factors, we tested three different values for k (i.e., k  = 10, 100, and 1000).

The following analytical procedure is adapted from a previous framework 4 and can be summarised in three distinct steps. First, we used each environmental raster to compute an environmentally scaled distance for each branch in inferred and simulated trees. These distances were computed using two different path models: (i) the least-cost path model, which uses a least-cost algorithm to determine the route taken between the starting and ending points 34 , and (ii) the Circuitscape path model, which uses circuit theory to accommodate uncertainty in the route taken 35 . Second, correlations between time elapsed on branches and environmentally scaled distances are estimated with the statistic Q defined as the difference between two coefficients of determination: (i) the coefficient of determination obtained when branch durations are regressed against environmentally scaled distances computed on the environmental raster, and (ii) the coefficient of determination obtained when branch durations are regressed against environmentally scaled distances computed on a uniform null raster. A Q statistic was estimated for each tree and we subsequently obtained two distributions of Q values, one associated with inferred trees and one associated with simulated trees. An environmental factor was only considered as potentially explanatory if both its distribution of regression coefficients and its associated distribution of Q values were positive 5 . Finally, the statistical support associated with a positive Q distribution (i.e., with at least 90% of positive values) was evaluated by comparing it with its corresponding null of distribution of Q values based on simulated trees, and formalised by approximating a BF support using formula (2), but this time defining p e as the posterior probability that Q estimated  >  Q simulated , i.e., the frequency at which Q estimated  >  Q simulated in the samples from the posterior distribution 33 .

In the third landscape phylogeographic testing approach, we investigated the impact of specific environmental factors on the dispersal frequency of viral lineages: we tested if WNV lineages tended to preferentially circulate and then remain within a distinct migratory flyway. We first performed a test based on the four North American Migratory Flyways (NAMF). Based on observed bird migration routes, these four administrative flyways (Fig.  1 ) were defined by the US Fish and Wildlife Service (USFWS; https://www.fws.gov/birds/management/ flyways.php) to facilitate management of migratory birds and their habitats. Although biologically questionable, we here used these administrative limits to discretise the study and investigate if viral lineages tended to remain within the same flyway. In practice, we analysed if viral lineages crossed NAMF borders less frequently than expected by chance, i.e., than expected in the null dispersal model in which simulated dispersal histories were not impacted by these borders. Following a procedure introduced by Dellicour et al. 61 , we computed and compared the number N of changing flyway events for each pair of inferred and simulated tree. Each “inferred” N value ( N inferred ) was thus compared to its corresponding “simulated” value ( N simulated ) by approximating a BF value using the above formula, but this time defining p e as the posterior probability that N inferred  <  N simulated , i.e., the frequency at which N inferred  <  N simulated in the samples from the posterior distribution.

To complement the first test based on an administrative flyway delimitation, we developed and performed a second test based on flyways estimated by La Sorte et al. 36 for terrestrial bird species: the Eastern, Central and Western flyways (Supplementary Fig.  S6 ). Contrary to the NAMF, these three flyways overlap with each other and are here defined by geo-referenced grids indicating the likelihood that studied species are in migration during spring or autumn (see La Sorte et al. 36 for further details). As the spring and autumn grids are relatively similar, we built an averaged raster for each flyway. For our analysis, we then generated normalised rasters obtained by dividing each raster cell by the sum of the values assigned to the same cell in the three averaged rasters (Supplementary Fig.  S6 ). Following a procedure similar to the first test based on NAMFs, we computed and compared the average difference D defined as follows:

where n is the number of branches in the tree, v i ,start the highest cell value among the three flyway normalised rasters to be associated with the position of the starting (oldest) node of tree branch i , and v i ,end the cell value extracted from the same normalised raster but associated with the position of the descendant (youngest) node of the tree branch i . D is thus a measure of the tendency of tree branches to remain within the same flyway. Each “inferred” D value ( D inferred ) is then compared to its corresponding “simulated” value ( D simulated ) by approximating a BF value using formula (2), but this time defining p e as the posterior probability that D simulated  <  D inferred , i.e., the frequency at which D simulated  <  D inferred in the samples from the posterior distribution.

Testing the impact of environmental factors on the viral diversity through time

We used the skygrid-GLM approach 9 , 10 implemented in BEAST 1.10.4 to measure the association between viral effective population size and four covariates: human case numbers, temperature, precipitation, and a greenness index. The monthly number of human cases were provided by the CDC and were considered with lag periods of one and two months (meaning that the viral effective population size was compared to case count data from one and two months later), as well as the absence of lag period. Preliminary skygrid-GLM analyses were used to determine from what lag period we obtained a significant association between viral effective population size and the number of human cases. We then used this lag period (of 1 month) in subsequent analyses. Data used to estimate the average temperature and precipitation time-series were obtained from the same database mentioned above and managed by the NOAA. For each successive month, meteorological stations were selected based on their geographic location. To estimate the average temperature/precipitation value for a specific month, we only considered meteorological stations included in the corresponding monthly minimum convex polygon obtained from the continuous phylogeographic inference. For a given month, the corresponding minimum convex hull polygon was simply defined around all the tree node positions occurring before or during that month. In order to take the uncertainty related to the phylogeographic inference into account, the construction of these minimum convex hull polygons was based on the 100 posterior trees used in the phylogeographic inference (see above). The rationale behind this approach was to base the analysis on covariate values averaged only over measures originating from areas already reached by the epidemic. Finally, the greenness index values were based on bimonthly Normalised Difference Vegetation Index (NDVI) raster files obtained from the NASA Earth Observation database (NEO; https://neo.sci.gsfc.nasa.gov ). To obtain the same level of precision and allow the co-analysis of NDVI data with human cases and climatic variables, we aggregated NDVI rasters by month. The visual comparison between covariate and skygrid curves shown in Fig.  5 indicates that this is an appropriate level of precision. Monthly NDVI values were then obtained by cropping the NDVI rasters with the series of minimum convex hull polygons introduced above, and then averaging the remaining raster cell values. While univariate skygrid-GLM analyses only involved one covariate at a time, the multivariate analyses included all the four covariates and used inclusion probabilities to assess their relative importance 38 . To allow their inclusion within the same multivariate analysis, the covariates were all log-transformed and standardised.

Reporting summary

Further information on research design is available in the  Nature Research Reporting Summary linked to this article.

Data availability

BEAST XML files of the continuous phylogeographic and skygrid-GLM analyses are available at https://github.com/sdellicour/wnv_north_america . WNV sequences analysed in the present study were available on GenBank and deposited before November 21, 2017. Accession numbers of selected genomic sequences are listed in the file “WNV_GenBank_accessions_numbers.txt” available on the GitHub repository referenced above. The source of the different raster files used in this study is provided in Supplementary Table  S1 . The administrative flyways were obtained from the US Fish and Wildlife Service (USFWS; https://www.fws.gov/birds/management/flyways.php ).

Code availability

The R script to run all the landscape phylogeographic testing analyses is available at https://github.com/sdellicour/wnv_north_america ( https://doi.org/10.5281/zenodo.4035938 ).

Lemey, P., Rambaut, A., Welch, J. J. & Suchard, M. A. Phylogeography takes a relaxed random walk in continuous space and time. Mol. Biol. Evol. 27 , 1877–1885 (2010).

Article   CAS   PubMed Central   PubMed   Google Scholar  

Pybus, O. G. et al. Unifying the spatial epidemiology and molecular evolution of emerging epidemics. Proc. Natl Acad. Sci. USA 109 , 15066–15071 (2012).

Article   ADS   CAS   PubMed   PubMed Central   Google Scholar  

Baele, G., Dellicour, S., Suchard, M. A., Lemey, P. & Vrancken, B. Recent advances in computational phylodynamics. Curr. Opin. Virol. 31 , 24–32 (2018).

Article   PubMed   Google Scholar  

Dellicour, S., Rose, R. & Pybus, O. G. Explaining the geographic spread of emerging epidemics: a framework for comparing viral phylogenies and environmental landscape data. BMC Bioinform . 17 , 1–12 (2016).

Article   CAS   Google Scholar  

Jacquot, M., Nomikou, K., Palmarini, M., Mertens, P. & Biek, R. Bluetongue virus spread in Europe is a consequence of climatic, landscape and vertebrate host factors as revealed by phylogeographic inference. Proc. R. Soc. Lond. B 284 , 20170919 (2017).

Google Scholar  

Brunker, K. et al. Landscape attributes governing local transmission of an endemic zoonosis: Rabies virus in domestic dogs. Mol. Ecol. 27 , 773–788 (2018).

Dellicour, S., Vrancken, B., Trovão, N. S., Fargette, D. & Lemey, P. On the importance of negative controls in viral landscape phylogeography. Virus Evol. 4 , vey023 (2018).

Article   PubMed Central   PubMed   Google Scholar  

Minin, V. N., Bloomquist, E. W. & Suchard, M. A. Smooth skyride through a rough skyline: Bayesian coalescent-based inference of population dynamics. Mol. Biol. Evol. 25 , 1459–1471 (2008).

Gill, M. S. et al. Improving Bayesian population dynamics inference: A coalescent-based model for multiple loci. Mol. Biol. Evol. 30 , 713–724 (2013).

Article   CAS   PubMed   Google Scholar  

Gill, M. S., Lemey, P., Bennett, S. N., Biek, R. & Suchard, M. A. Understanding past population dynamics: Bayesian coalescent-based modeling with covariates. Syst. Biol. 65 , 1041–1056 (2016).

Reisen, W. K. Ecology of West Nile virus in North America. Viruses 5 , 2079–2105 (2013).

Hayes, E. B. et al. Epidemiology and transmission dynamics of West Nile virus disease. Emerg. Infect. Dis. 11 , 1167–1173 (2005).

May, F. J., Davis, C. T., Tesh, R. B. & Barrett, A. D. T. Phylogeography of West Nile Virus: from the cradle of evolution in Africa to Eurasia, Australia, and the Americas. J. Virol. 85 , 2964–2974 (2011).

Kramer, L. D. & Bernard, K. A. West Nile virus in the western hemisphere. Curr. Opin. Infect. Dis. 14 , 519–525 (2001).

Kilpatrick, A. M., Kramer, L. D., Jones, M. J., Marra, P. P. & Daszak, P. West Nile virus epidemics in North America are driven by shifts in mosquito feeding behavior. PLoS Biol. 4 , 606–610 (2006).

Molaei, G., Andreadis, T. G., Armstrong, P. M., Anderson, J. F. & Vossbrinck, C. R. Host feeding patterns of Culex mosquitoes and West Nile virus transmission, northeastern United States. Emerg. Infect. Dis. 12 , 468–474 (2006).

Colpitts, T. M., Conway, M. J., Montgomery, R. R. & Fikrig, E. West Nile virus: biology, transmission, and human infection. Clin. Microbiol. Rev. 25 , 635–648 (2012).

Bowen, R. A. & Nemeth, N. M. Experimental infections with West Nile virus. Curr. Opin. Infect. Dis. 20 , 293–297 (2007).

Petersen, L. R. & Marfin, A. A. West Nile Virus: A primer for the clinician. Ann. Intern. Med. 137 , 173–179 (2002).

Petersen, L. R. & Fischer, M. Unpredictable and difficult to control—the adolescence of West Nile virus. N. Engl. J. Med. 367 , 1281–1284 (2012).

Lanciotti, R. S. et al. Origin of the West Nile virus responsible for an outbreak of encephalitis in the northeastern United States. Science 286 , 2333–2337 (1999).

Dohm, D. J., Sardelis, M. R. & Turell, M. J. Experimental vertical transmission of West Nile virus by Culex pipiens (Diptera: Culicidae). J. Med. Entomol. 39 , 640–644 (2002).

Goddard, L. B., Roth, A. E., Reisen, W. K. & Scott, T. W. Vertical transmission of West Nile virus by three California Culex (Diptera: Culicidae) species. J. Med. Entomol. 40 , 743–746 (2003).

Lequime, S. & Lambrechts, L. Vertical transmission of arboviruses in mosquitoes: A historical perspective. Infect. Genet. Evol. 28 , 681–690 (2014).

Ronca, S. E., Murray, K. O. & Nolan, M. S. Cumulative incidence of West Nile virus infection, continental United States, 1999–2016. Emerg. Infect. Dis. 25 , 325–327 (2019).

George, T. L. et al. Persistent impacts of West Nile virus on North American bird populations. Proc. Natl Acad. Sci. USA 112 , 14290–14294 (2015).

Kilpatrick, A. M. & Wheeler, S. S. Impact of West Nile Virus on bird populations: limited lasting effects, evidence for recovery, and gaps in our understanding of impacts on ecosystems. J. Med. Entomol. 56 , 1491–1497 (2019).

LaDeau, S. L., Kilpatrick, A. M. & Marra, P. P. West Nile virus emergence and large-scale declines of North American bird populations. Nature 447 , 710–713 (2007).

Article   ADS   CAS   PubMed   Google Scholar  

Davis, C. T. et al. Phylogenetic analysis of North American West Nile virus isolates, 2001–2004: evidence for the emergence of a dominant genotype. Virology 342 , 252–265 (2005).

Añez, G. et al. Evolutionary dynamics of West Nile virus in the United States, 1999–2011: Phylogeny, selection pressure and evolutionary time-scale analysis. PLoS Negl. Trop. Dis. 7 , e2245 (2013).

Di Giallonardo, F. et al. Fluid spatial dynamics of West Nile Virus in the United States: Rapid spread in a permissive host environment. J. Virol. 90 , 862–872 (2016).

Hadfield, J. et al. Twenty years of West Nile virus spread and evolution in the Americas visualized by Nextstrain. PLOS Pathog. 15 , e1008042 (2019).

Dellicour, S. et al. Using viral gene sequences to compare and explain the heterogeneous spatial dynamics of virus epidemics. Mol. Biol. Evol. 34 , 2563–2571 (2017).

Dijkstra, E. W. A note on two problems in connexion with graphs. Numer. Math. 1 , 269–271 (1959).

Article   MathSciNet   MATH   Google Scholar  

McRae, B. H. Isolation by resistance. Evolution 60 , 1551–1561 (2006).

La Sorte, F. A. et al. The role of atmospheric conditions in the seasonal dynamics of North American migration flyways. J. Biogeogr. 41 , 1685–1696 (2014).

Article   Google Scholar  

Holmes, E. C. & Grenfell, B. T. Discovering the phylodynamics of RNA viruses. PLoS Comput. Biol. 5 , e1000505 (2009).

Article   ADS   PubMed Central   PubMed   CAS   Google Scholar  

Faria, N. R. et al. Genomic and epidemiological monitoring of yellow fever virus transmission potential. Science 361 , 894–899 (2018).

Article   ADS   CAS   PubMed Central   PubMed   Google Scholar  

Carrington, C. V. F., Foster, J. E., Pybus, O. G., Bennett, S. N. & Holmes, E. C. Invasion and maintenance of dengue virus type 2 and Type 4 in the Americas. J. Virol. 79 , 14680–14687 (2005).

Rappole, J. H. et al. Modeling movement of West Nile virus in the western hemisphere. Vector Borne Zoonotic Dis. 6 , 128–139 (2006).

Goldberg, T. L., Anderson, T. K. & Hamer, G. L. West Nile virus may have hitched a ride across the Western United States on Culex tarsalis mosquitoes. Mol. Ecol. 19 , 1518–1519 (2010).

Swetnam, D. et al. Terrestrial bird migration and West Nile virus circulation, United States. Emerg. Infect. Dis . 24 , 12 (2018).

Kwan, J. L., Kluh, S. & Reisen, W. K. Antecedent avian immunity limits tangential transmission of West Nile virus to humans. PLoS ONE 7 , e34127 (2012).

Duggal, N. K. et al. Genotype-specific variation in West Nile virus dispersal in California. Virology 485 , 79–85 (2015).

McMullen, A. R. et al. Evolution of new genotype of West Nile virus in North America. Emerg. Infect. Dis. 17 , 785–793 (2011).

Hepp, C. M. et al. Phylogenetic analysis of West Nile Virus in Maricopa County, Arizona: evidence for dynamic behavior of strains in two major lineages in the American Southwest. PLOS ONE 13 , e0205801 (2018).

Article   PubMed Central   PubMed   CAS   Google Scholar  

Goddard, L. B., Roth, A. E., Reisen, W. K. & Scott, T. W. Vector competence of California mosquitoes for West Nile virus. Emerg. Infect. Dis. 8 , 1385–1391 (2002).

Richards, S. L., Mores, C. N., Lord, C. C. & Tabachnick, W. J. Impact of extrinsic incubation temperature and virus exposure on vector competence of Culex pipiens quinquefasciatus say (Diptera: Culicidae) for West Nile virus. Vector Borne Zoonotic Dis. 7 , 629–636 (2007).

Anderson, S. L., Richards, S. L., Tabachnick, W. J. & Smartt, C. T. Effects of West Nile virus dose and extrinsic incubation temperature on temporal progression of vector competence in Culex pipiens quinquefasciatus . J. Am. Mosq. Control Assoc. 26 , 103–107 (2010).

Worwa, G. et al. Increases in the competitive fitness of West Nile virus isolates after introduction into California. Virology 514 , 170–181 (2018).

Duggal, N. K., Langwig, K. E., Ebel, G. D. & Brault, A. C. On the fly: interactions between birds, mosquitoes, and environment that have molded west nile virus genomic structure over two decades. J. Med. Entomol. 56 , 1467–1474 (2019).

Reed, K. D., Meece, J. K., Henkel, J. S. & Shukla, S. K. Birds, migration and emerging zoonoses: West Nile virus, Lyme disease, influenza A and enteropathogens. Clin. Med. Res. 1 , 5–12 (2003).

Dusek, R. J. et al. Prevalence of West Nile virus in migratory birds during spring and fall migration. Am . J. Trop. Med. Hyg. 81 , 1151–1158 (2009).

Samuel, G. H., Adelman, Z. N. & Myles, K. M. Temperature-dependent effects on the replication and transmission of arthropod-borne viruses in their insect hosts. Curr. Opin. Insect Sci. 16 , 108–113 (2016).

Paz, S. & Semenza, J. C. Environmental drivers of West Nile fever epidemiology in Europe and Western Asia-a review. Int. J. Environ. Res. Public Health 10 , 3543–3562 (2013).

Dohm, D. J., O’Guinn, M. L. & Turell, M. J. Effect of environmental temperature on the ability of Culex pipiens (Diptera: Culicidae) to transmit West Nile virus. J. Med. Entomol. 39 , 221–225 (2002).

Kilpatrick, A. M., Meola, M. A., Moudy, R. M. & Kramer, L. D. Temperature, viral genetics, and the transmission of West Nile virus by Culex pipiens mosquitoes. PLoS Path . 4 , e1000092 (2008).

DeFelice, N. B. et al. Use of temperature to improve West Nile virus forecasts. PLoS Comput. Biol. 14 , e1006047 (2018).

Morin, C. W. & Comrie, A. C. Regional and seasonal response of a West Nile virus vector to climate change. Proc. Natl Acad. Sci. USA 110 , 15620–15625 (2013).

Samy, A. M. et al. Climate change influences on the global potential distribution of the mosquito Culex quinquefasciatus , vector of West Nile virus and lymphatic filariasis. PLoS ONE 11 , e0163863 (2016).

Dellicour, S. et al. Phylodynamic assessment of intervention strategies for the West African Ebola virus outbreak. Nat. Commun. 9 , 2222 (2018).

Katoh, K. & Standley, D. M. MAFFT multiple sequence alignment software version 7: Improvements in performance and usability. Mol. Biol. Evol. 30 , 772–780 (2013).

Larsson, A. AliView: a fast and lightweight alignment viewer and editor for large datasets. Bioinformatics 30 , 3276–3278 (2014).

Price, M. N., Dehal, P. S. & Arkin, A. P. FastTree 2–approximately maximum-likelihood trees for large alignments. PLoS ONE 5 , e9490 (2010).

Suchard, M. A. et al. Bayesian phylogenetic and phylodynamic data integration using BEAST 1.10. Virus Evol. 4 , vey016 (2018).

Ayres, D. L. et al. BEAGLE 3: Improved performance, scaling, and usability for a high-performance computing library for statistical phylogenetics. Syst. Biol ., https://doi.org/10.1093/sysbio/syz020 (2019).

Tavaré, S. Some probabilistic and statistical problems in the analysis of DNA sequences. Lectures Math. Life Sci. 17 , 57–86 (1986).

MathSciNet   MATH   Google Scholar  

Drummond, A. J., Ho, S. Y. W., Phillips, M. J. & Rambaut, A. Relaxed phylogenetics and dating with confidence. PLoS Biol. 4 , 699–710 (2006).

Rambaut, A., Drummond, A. J., Xie, D., Baele, G. & Suchard, M. A. Posterior summarization in Bayesian phylogenetics using Tracer 1.7. Syst. Biol. 67 , 901–904 (2018).

Fisher, A. A., Ji, X., Zhang, Z., Lemey, P. & Suchard, M. A. Relaxed random walks at scale. Syst. Biol ., https://doi.org/10.1093/sysbio/syaa056 (2020).

Lemey, P. et al. Unifying viral genetics and human transportation data to predict the global transmission dynamics of human influenza H3N2. PLoS Path. 10 , e1003932 (2014).

Bedford, T. et al. Global circulation patterns of seasonal influenza viruses vary with antigenic drift. Nature 523 , 217 (2015).

Hadfield, J. et al. Nextstrain: real-time tracking of pathogen evolution. Bioinformatics 34 , 4121–4123 (2018).

Dellicour, S., Rose, R., Faria, N. R., Lemey, P. & Pybus, O. G. SERAPHIM: studying environmental rasters and phylogenetically informed movements. Bioinformatics 32 , 3204–3206 (2016).

Dellicour, S. et al. Using phylogeographic approaches to analyse the dispersal history, velocity, and direction of viral lineages–application to rabies virus spread in Iran. Mol. Ecol. 28 , 4335–4350 (2019).

Suchard, M. A., Weiss, R. E. & Sinsheimer, J. S. Models for estimating Bayes factors with applications to phylogeny and tests of monophyly. Biometrics 61 , 665–673 (2005).

Article   MathSciNet   MATH   PubMed   Google Scholar  

Download references

Acknowledgements

We are grateful to Frank La Sorte for sharing their estimated flyway grids. The research leading to these results has received funding from the European Research Council under the European Union’s Horizon 2020 research and innovation programme (grant agreement no. 725422-ReservoirDOCS), from the Welcome Trust (Artic Network, project 206298/Z/17/Z), and from the European Union’s Horizon 2020 project MOOD (grant agreement no. 874850). S.D. is supported by the Fonds National de la Recherche Scientifiqu e (FNRS, Belgium) and was previously funded by the Fonds Wetenschappelijk Onderzoek (FWO, Belgium). S.L. and P.B. were funded by the Fonds Wetenschappelijk Onderzoek (FWO, Belgium). B.V. was supported by a postdoctoral grant (12U7118N) of the Research Foundation - Flanders ( Fonds voor Wetenschappelijk Onderzoek ). L.d.P. and O.G.P. are supported by the European Research Council under the European Commission Seventh Framework Programme (grant agreement no. 614725-PATHPHYLODYN) and by the Oxford Martin School. M.A.S. is partially supported by NSF grant DMS 1264153 and NIH grants R01 AI107034, U19 AI135995, and R56 AI149004. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health. P.L. acknowledges support by the Research Foundation-Flanders ( Fonds voor Wetenschappelijk Onderzoek-Vlaanderen , G066215N, G0D5117N, and G0B9317N).

Author information

Authors and affiliations.

Spatial Epidemiology Lab (SpELL), Université Libre de Bruxelles, CP160/12, 50 Avenue FD Roosevelt, 1050, Bruxelles, Belgium

Simon Dellicour & Marius Gilbert

Department of Microbiology, Immunology and Transplantation, Rega Institute, KU Leuven, Herestraat 49, 3000, Leuven, Belgium

Simon Dellicour, Sebastian Lequime, Bram Vrancken, Mandev S. Gill, Paul Bastide & Philippe Lemey

Department of Immunology and Microbiology, The Scripps Research Institute, La Jolla, CA, 92037, USA

Karthik Gangavarapu, Nathaniel L. Matteson & Kristian G. Andersen

Department of Medicine, Vanderbilt University Medical Center, Nashville, TN, USA

Infectious Diseases Group, J. Craig Venter Institute, Rockville, MD, USA

Department of Zoology, University of Oxford, Oxford, UK

Louis du Plessis & Oliver G. Pybus

Department of Biomathematics, David Geffen School of Medicine, University of California, Los Angeles, CA, USA

Alexander A. Fisher & Marc A. Suchard

Fogarty International Center, National Institutes of Health, Bethesda, MD, 20894, USA

Martha I. Nelson

Department of Biostatistics, Fielding School of Public Health, University of California, Los Angeles, CA, USA

Marc A. Suchard

Department of Human Genetics, David Geffen School of Medicine, University of California, Los Angeles, CA, USA

Scripps Research Translational Institute, La Jolla, CA, 92037, USA

Kristian G. Andersen

Department of Epidemiology of Microbial Diseases, Yale School of Public Health, New Haven, CT, 06510, USA

Nathan D. Grubaugh

You can also search for this author in PubMed   Google Scholar

Contributions

S.D., K.G.A., N.D.G., O.G.P., and P.L. designed the study. S.D., M.S.G., P.B., M.A.S., and P.L. developed the analytical framework. S.D., S.L., B.V., M.S.G., P.B., K.G., N.L.M., and Y.T. analysed the data. L.d.P., A.A.F., and M.A.S. provided statistical guidance. S.D. wrote the first draft of the manuscript. All the authors interpreted and discussed the results. S.D., S.L., M.I.N., M.G., K.G.A., N.D.G., O.G.P., and P.L. discussed the epidemiological implications. All the authors edited and approved the contents of the manuscript.

Corresponding author

Correspondence to Simon Dellicour .

Ethics declarations

Competing interests.

The authors declare no competing interests.

Additional information

Peer review information Nature Communications thanks Christine Carrington and the other, anonymous, reviewer for their contribution to the peer review of this work. Peer reviewer reports are available.

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary information, peer review file, reporting summary, rights and permissions.

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/ .

Reprints and permissions

About this article

Cite this article.

Dellicour, S., Lequime, S., Vrancken, B. et al. Epidemiological hypothesis testing using a phylogeographic and phylodynamic framework. Nat Commun 11 , 5620 (2020). https://doi.org/10.1038/s41467-020-19122-z

Download citation

Received : 11 March 2020

Accepted : 30 September 2020

Published : 06 November 2020

DOI : https://doi.org/10.1038/s41467-020-19122-z

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

This article is cited by

Integrating full and partial genome sequences to decipher the global spread of canine rabies virus.

• Andrew Holtz
• Anna Zhukova

Nature Communications (2023)

Spatial and temporal dynamics of West Nile virus between Africa and Europe

• Giulia Mencattelli
• Marie Henriette Dior Ndione
• Giovanni Savini

Phylogenetic and phylodynamic approaches to understanding and combating the early SARS-CoV-2 pandemic

• Stephen W. Attwood
• Sarah C. Hill
• Oliver G. Pybus

Nature Reviews Genetics (2022)

West Nile virus transmission potential in Portugal

• José Lourenço
• Sílvia C. Barros
• Uri Obolski

Communications Biology (2022)

Predicting the evolution of the Lassa virus endemic area and population at risk over the next decades

• Raphaëlle Klitting
• Liana E. Kafetzopoulou
• Simon Dellicour

Nature Communications (2022)

By submitting a comment you agree to abide by our Terms and Community Guidelines . If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.

Quick links

• Explore articles by subject
• Guide to authors
• Editorial policies

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Epidemiological hypothesis testing using a phylogeographic and phylodynamic framework

Affiliations.

• 1 Spatial Epidemiology Lab (SpELL), Université Libre de Bruxelles, CP160/12, 50 Avenue FD Roosevelt, 1050, Bruxelles, Belgium. [email protected].
• 2 Department of Microbiology, Immunology and Transplantation, Rega Institute, KU Leuven, Herestraat 49, 3000, Leuven, Belgium. [email protected].
• 3 Department of Microbiology, Immunology and Transplantation, Rega Institute, KU Leuven, Herestraat 49, 3000, Leuven, Belgium.
• 4 Department of Immunology and Microbiology, The Scripps Research Institute, La Jolla, CA, 92037, USA.
• 5 Department of Medicine, Vanderbilt University Medical Center, Nashville, TN, USA.
• 6 Infectious Diseases Group, J. Craig Venter Institute, Rockville, MD, USA.
• 7 Department of Zoology, University of Oxford, Oxford, UK.
• 8 Department of Biomathematics, David Geffen School of Medicine, University of California, Los Angeles, CA, USA.
• 9 Fogarty International Center, National Institutes of Health, Bethesda, MD, 20894, USA.
• 10 Spatial Epidemiology Lab (SpELL), Université Libre de Bruxelles, CP160/12, 50 Avenue FD Roosevelt, 1050, Bruxelles, Belgium.
• 11 Department of Biostatistics, Fielding School of Public Health, University of California, Los Angeles, CA, USA.
• 12 Department of Human Genetics, David Geffen School of Medicine, University of California, Los Angeles, CA, USA.
• 13 Scripps Research Translational Institute, La Jolla, CA, 92037, USA.
• 14 Department of Epidemiology of Microbial Diseases, Yale School of Public Health, New Haven, CT, 06510, USA.
• PMID: 33159066
• PMCID: PMC7648063
• DOI: 10.1038/s41467-020-19122-z

Computational analyses of pathogen genomes are increasingly used to unravel the dispersal history and transmission dynamics of epidemics. Here, we show how to go beyond historical reconstructions and use spatially-explicit phylogeographic and phylodynamic approaches to formally test epidemiological hypotheses. We illustrate our approach by focusing on the West Nile virus (WNV) spread in North America that has substantially impacted public, veterinary, and wildlife health. We apply an analytical workflow to a comprehensive WNV genome collection to test the impact of environmental factors on the dispersal of viral lineages and on viral population genetic diversity through time. We find that WNV lineages tend to disperse faster in areas with higher temperatures and we identify temporal variation in temperature as a main predictor of viral genetic diversity through time. By contrasting inference with simulation, we find no evidence for viral lineages to preferentially circulate within the same migratory bird flyway, suggesting a substantial role for non-migratory birds or mosquito dispersal along the longitudinal gradient.

Publication types

• Research Support, N.I.H., Extramural
• Research Support, Non-U.S. Gov't
• Research Support, U.S. Gov't, Non-P.H.S.
• Bird Diseases / epidemiology*
• Bird Diseases / virology
• Environment
• Genetic Variation
• Genome, Viral
• North America
• Phylogeography
• West Nile Fever / epidemiology*
• West Nile Fever / veterinary*
• West Nile Fever / virology
• West Nile virus / classification
• West Nile virus / genetics*
• West Nile virus / isolation & purification

Grants and funding

• U19 AI135995/AI/NIAID NIH HHS/United States
• R01 AI107034/AI/NIAID NIH HHS/United States
• UL1 TR001863/TR/NCATS NIH HHS/United States
• 206298/Z/17/Z/WT_/Wellcome Trust/United Kingdom
• U01 AI151812/AI/NIAID NIH HHS/United States
• R56 AI149004/AI/NIAID NIH HHS/United States

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

Hypothesis Testing

• Last updated
• Save as PDF
• Page ID 31289

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

CO-6: Apply basic concepts of probability, random variation, and commonly used statistical probability distributions.

Learning Objectives

LO 6.26: Outline the logic and process of hypothesis testing.

LO 6.27: Explain what the p-value is and how it is used to draw conclusions.

Video: Hypothesis Testing (8:43)

Introduction

We are in the middle of the part of the course that has to do with inference for one variable.

So far, we talked about point estimation and learned how interval estimation enhances it by quantifying the magnitude of the estimation error (with a certain level of confidence) in the form of the margin of error. The result is the confidence interval — an interval that, with a certain confidence, we believe captures the unknown parameter.

We are now moving to the other kind of inference, hypothesis testing . We say that hypothesis testing is “the other kind” because, unlike the inferential methods we presented so far, where the goal was estimating the unknown parameter, the idea, logic and goal of hypothesis testing are quite different.

In the first two parts of this section we will discuss the idea behind hypothesis testing, explain how it works, and introduce new terminology that emerges in this form of inference. The final two parts will be more specific and will discuss hypothesis testing for the population proportion ( p ) and the population mean ( μ, mu).

If this is your first statistics course, you will need to spend considerable time on this topic as there are many new ideas. Many students find this process and its logic difficult to understand in the beginning.

In this section, we will use the hypothesis test for a population proportion to motivate our understanding of the process. We will conduct these tests manually. For all future hypothesis test procedures, including problems involving means, we will use software to obtain the results and focus on interpreting them in the context of our scenario.

General Idea and Logic of Hypothesis Testing

The purpose of this section is to gradually build your understanding about how statistical hypothesis testing works. We start by explaining the general logic behind the process of hypothesis testing. Once we are confident that you understand this logic, we will add some more details and terminology.

To start our discussion about the idea behind statistical hypothesis testing, consider the following example:

A case of suspected cheating on an exam is brought in front of the disciplinary committee at a certain university.

There are two opposing claims in this case:

• The student’s claim: I did not cheat on the exam.
• The instructor’s claim: The student did cheat on the exam.

Adhering to the principle “innocent until proven guilty,” the committee asks the instructor for evidence to support his claim. The instructor explains that the exam had two versions, and shows the committee members that on three separate exam questions, the student used in his solution numbers that were given in the other version of the exam.

The committee members all agree that it would be extremely unlikely to get evidence like that if the student’s claim of not cheating had been true. In other words, the committee members all agree that the instructor brought forward strong enough evidence to reject the student’s claim, and conclude that the student did cheat on the exam.

What does this example have to do with statistics?

While it is true that this story seems unrelated to statistics, it captures all the elements of hypothesis testing and the logic behind it. Before you read on to understand why, it would be useful to read the example again. Please do so now.

Statistical hypothesis testing is defined as:

• Assessing evidence provided by the data against the null claim (the claim which is to be assumed true unless enough evidence exists to reject it).

Here is how the process of statistical hypothesis testing works:

• We have two claims about what is going on in the population. Let’s call them claim 1 (this will be the null claim or hypothesis) and claim 2 (this will be the alternative) . Much like the story above, where the student’s claim is challenged by the instructor’s claim, the null claim 1 is challenged by the alternative claim 2. (For us, these claims are usually about the value of population parameter(s) or about the existence or nonexistence of a relationship between two variables in the population).
• We choose a sample, collect relevant data and summarize them (this is similar to the instructor collecting evidence from the student’s exam). For statistical tests, this step will also involve checking any conditions or assumptions.
• We figure out how likely it is to observe data like the data we obtained, if claim 1 is true. (Note that the wording “how likely …” implies that this step requires some kind of probability calculation). In the story, the committee members assessed how likely it is to observe evidence such as the instructor provided, had the student’s claim of not cheating been true.
• If, after assuming claim 1 is true, we find that it would be extremely unlikely to observe data as strong as ours or stronger in favor of claim 2, then we have strong evidence against claim 1, and we reject it in favor of claim 2. Later we will see this corresponds to a small p-value.
• If, after assuming claim 1 is true, we find that observing data as strong as ours or stronger in favor of claim 2 is NOT VERY UNLIKELY , then we do not have enough evidence against claim 1, and therefore we cannot reject it in favor of claim 2. Later we will see this corresponds to a p-value which is not small.

In our story, the committee decided that it would be extremely unlikely to find the evidence that the instructor provided had the student’s claim of not cheating been true. In other words, the members felt that it is extremely unlikely that it is just a coincidence (random chance) that the student used the numbers from the other version of the exam on three separate problems. The committee members therefore decided to reject the student’s claim and concluded that the student had, indeed, cheated on the exam. (Wouldn’t you conclude the same?)

Hopefully this example helped you understand the logic behind hypothesis testing.

Interactive Applet: Reasoning of a Statistical Test

To strengthen your understanding of the process of hypothesis testing and the logic behind it, let’s look at three statistical examples.

A recent study estimated that 20% of all college students in the United States smoke. The head of Health Services at Goodheart University (GU) suspects that the proportion of smokers may be lower at GU. In hopes of confirming her claim, the head of Health Services chooses a random sample of 400 Goodheart students, and finds that 70 of them are smokers.

Let’s analyze this example using the 4 steps outlined above:

• claim 1: The proportion of smokers at Goodheart is 0.20.
• claim 2: The proportion of smokers at Goodheart is less than 0.20.

Claim 1 basically says “nothing special goes on at Goodheart University; the proportion of smokers there is no different from the proportion in the entire country.” This claim is challenged by the head of Health Services, who suspects that the proportion of smokers at Goodheart is lower.

• Choosing a sample and collecting data: A sample of n = 400 was chosen, and summarizing the data revealed that the sample proportion of smokers is p -hat = 70/400 = 0.175.While it is true that 0.175 is less than 0.20, it is not clear whether this is strong enough evidence against claim 1. We must account for sampling variation.
• Assessment of evidence: In order to assess whether the data provide strong enough evidence against claim 1, we need to ask ourselves: How surprising is it to get a sample proportion as low as p -hat = 0.175 (or lower), assuming claim 1 is true? In other words, we need to find how likely it is that in a random sample of size n = 400 taken from a population where the proportion of smokers is p = 0.20 we’ll get a sample proportion as low as p -hat = 0.175 (or lower).It turns out that the probability that we’ll get a sample proportion as low as p -hat = 0.175 (or lower) in such a sample is roughly 0.106 (do not worry about how this was calculated at this point – however, if you think about it hopefully you can see that the key is the sampling distribution of p -hat).
• Conclusion: Well, we found that if claim 1 were true there is a probability of 0.106 of observing data like that observed or more extreme. Now you have to decide …Do you think that a probability of 0.106 makes our data rare enough (surprising enough) under claim 1 so that the fact that we did observe it is enough evidence to reject claim 1? Or do you feel that a probability of 0.106 means that data like we observed are not very likely when claim 1 is true, but they are not unlikely enough to conclude that getting such data is sufficient evidence to reject claim 1. Basically, this is your decision. However, it would be nice to have some kind of guideline about what is generally considered surprising enough.

A certain prescription allergy medicine is supposed to contain an average of 245 parts per million (ppm) of a certain chemical. If the concentration is higher than 245 ppm, the drug will likely cause unpleasant side effects, and if the concentration is below 245 ppm, the drug may be ineffective. The manufacturer wants to check whether the mean concentration in a large shipment is the required 245 ppm or not. To this end, a random sample of 64 portions from the large shipment is tested, and it is found that the sample mean concentration is 250 ppm with a sample standard deviation of 12 ppm.

• Claim 1: The mean concentration in the shipment is the required 245 ppm.
• Claim 2: The mean concentration in the shipment is not the required 245 ppm.

Note that again, claim 1 basically says: “There is nothing unusual about this shipment, the mean concentration is the required 245 ppm.” This claim is challenged by the manufacturer, who wants to check whether that is, indeed, the case or not.

• Choosing a sample and collecting data: A sample of n = 64 portions is chosen and after summarizing the data it is found that the sample mean concentration is x-bar = 250 and the sample standard deviation is s = 12.Is the fact that x-bar = 250 is different from 245 strong enough evidence to reject claim 1 and conclude that the mean concentration in the whole shipment is not the required 245? In other words, do the data provide strong enough evidence to reject claim 1?
• Assessing the evidence: In order to assess whether the data provide strong enough evidence against claim 1, we need to ask ourselves the following question: If the mean concentration in the whole shipment were really the required 245 ppm (i.e., if claim 1 were true), how surprising would it be to observe a sample of 64 portions where the sample mean concentration is off by 5 ppm or more (as we did)? It turns out that it would be extremely unlikely to get such a result if the mean concentration were really the required 245. There is only a probability of 0.0007 (i.e., 7 in 10,000) of that happening. (Do not worry about how this was calculated at this point, but again, the key will be the sampling distribution.)
• Making conclusions: Here, it is pretty clear that a sample like the one we observed or more extreme is VERY rare (or extremely unlikely) if the mean concentration in the shipment were really the required 245 ppm. The fact that we did observe such a sample therefore provides strong evidence against claim 1, so we reject it and conclude with very little doubt that the mean concentration in the shipment is not the required 245 ppm.

Do you think that you’re getting it? Let’s make sure, and look at another example.

Is there a relationship between gender and combined scores (Math + Verbal) on the SAT exam?

Following a report on the College Board website, which showed that in 2003, males scored generally higher than females on the SAT exam, an educational researcher wanted to check whether this was also the case in her school district. The researcher chose random samples of 150 males and 150 females from her school district, collected data on their SAT performance and found the following:

Again, let’s see how the process of hypothesis testing works for this example:

• Claim 1: Performance on the SAT is not related to gender (males and females score the same).
• Claim 2: Performance on the SAT is related to gender – males score higher.

Note that again, claim 1 basically says: “There is nothing going on between the variables SAT and gender.” Claim 2 represents what the researcher wants to check, or suspects might actually be the case.

• Choosing a sample and collecting data: Data were collected and summarized as given above. Is the fact that the sample mean score of males (1,025) is higher than the sample mean score of females (1,010) by 15 points strong enough information to reject claim 1 and conclude that in this researcher’s school district, males score higher on the SAT than females?
• Assessment of evidence: In order to assess whether the data provide strong enough evidence against claim 1, we need to ask ourselves: If SAT scores are in fact not related to gender (claim 1 is true), how likely is it to get data like the data we observed, in which the difference between the males’ average and females’ average score is as high as 15 points or higher? It turns out that the probability of observing such a sample result if SAT score is not related to gender is approximately 0.29 (Again, do not worry about how this was calculated at this point).
• Conclusion: Here, we have an example where observing a sample like the one we observed or more extreme is definitely not surprising (roughly 30% chance) if claim 1 were true (i.e., if indeed there is no difference in SAT scores between males and females). We therefore conclude that our data does not provide enough evidence for rejecting claim 1.
• “The data provide enough evidence to reject claim 1 and accept claim 2”; or
• “The data do not provide enough evidence to reject claim 1.”

In particular, note that in the second type of conclusion we did not say: “ I accept claim 1 ,” but only “ I don’t have enough evidence to reject claim 1 .” We will come back to this issue later, but this is a good place to make you aware of this subtle difference.

Hopefully by now, you understand the logic behind the statistical hypothesis testing process. Here is a summary:

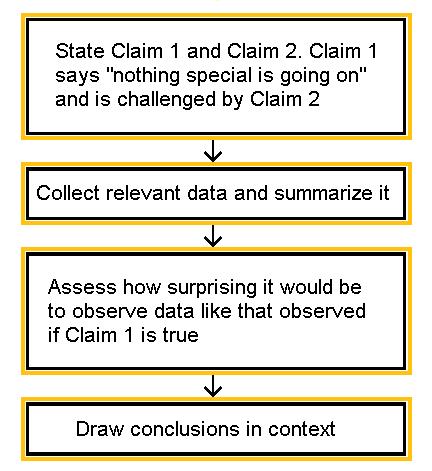
Learn by Doing: Logic of Hypothesis Testing

Did I Get This?: Logic of Hypothesis Testing

Steps in Hypothesis Testing

Video: Steps in Hypothesis Testing (16:02)

Now that we understand the general idea of how statistical hypothesis testing works, let’s go back to each of the steps and delve slightly deeper, getting more details and learning some terminology.

Hypothesis Testing Step 1: State the Hypotheses

In all three examples, our aim is to decide between two opposing points of view, Claim 1 and Claim 2. In hypothesis testing, Claim 1 is called the null hypothesis (denoted “ Ho “), and Claim 2 plays the role of the alternative hypothesis (denoted “ Ha “). As we saw in the three examples, the null hypothesis suggests nothing special is going on; in other words, there is no change from the status quo, no difference from the traditional state of affairs, no relationship. In contrast, the alternative hypothesis disagrees with this, stating that something is going on, or there is a change from the status quo, or there is a difference from the traditional state of affairs. The alternative hypothesis, Ha, usually represents what we want to check or what we suspect is really going on.

Let’s go back to our three examples and apply the new notation:

In example 1:

• Ho: The proportion of smokers at GU is 0.20.
• Ha: The proportion of smokers at GU is less than 0.20.

In example 2:

• Ho: The mean concentration in the shipment is the required 245 ppm.
• Ha: The mean concentration in the shipment is not the required 245 ppm.

In example 3:

• Ho: Performance on the SAT is not related to gender (males and females score the same).
• Ha: Performance on the SAT is related to gender – males score higher.

Learn by Doing: State the Hypotheses

Did I Get This?: State the Hypotheses

Hypothesis Testing Step 2: Collect Data, Check Conditions and Summarize Data

This step is pretty obvious. This is what inference is all about. You look at sampled data in order to draw conclusions about the entire population. In the case of hypothesis testing, based on the data, you draw conclusions about whether or not there is enough evidence to reject Ho.

There is, however, one detail that we would like to add here. In this step we collect data and summarize it. Go back and look at the second step in our three examples. Note that in order to summarize the data we used simple sample statistics such as the sample proportion ( p -hat), sample mean (x-bar) and the sample standard deviation (s).

In practice, you go a step further and use these sample statistics to summarize the data with what’s called a test statistic . We are not going to go into any details right now, but we will discuss test statistics when we go through the specific tests.

This step will also involve checking any conditions or assumptions required to use the test.

Hypothesis Testing Step 3: Assess the Evidence

As we saw, this is the step where we calculate how likely is it to get data like that observed (or more extreme) when Ho is true. In a sense, this is the heart of the process, since we draw our conclusions based on this probability.

• If this probability is very small (see example 2), then that means that it would be very surprising to get data like that observed (or more extreme) if Ho were true. The fact that we did observe such data is therefore evidence against Ho, and we should reject it.
• On the other hand, if this probability is not very small (see example 3) this means that observing data like that observed (or more extreme) is not very surprising if Ho were true. The fact that we observed such data does not provide evidence against Ho. This crucial probability, therefore, has a special name. It is called the p-value of the test.

In our three examples, the p-values were given to you (and you were reassured that you didn’t need to worry about how these were derived yet):

• Example 1: p-value = 0.106
• Example 2: p-value = 0.0007
• Example 3: p-value = 0.29

Obviously, the smaller the p-value, the more surprising it is to get data like ours (or more extreme) when Ho is true, and therefore, the stronger the evidence the data provide against Ho.

Looking at the three p-values of our three examples, we see that the data that we observed in example 2 provide the strongest evidence against the null hypothesis, followed by example 1, while the data in example 3 provides the least evidence against Ho.

• Right now we will not go into specific details about p-value calculations, but just mention that since the p-value is the probability of getting data like those observed (or more extreme) when Ho is true, it would make sense that the calculation of the p-value will be based on the data summary, which, as we mentioned, is the test statistic. Indeed, this is the case. In practice, we will mostly use software to provide the p-value for us.

Hypothesis Testing Step 4: Making Conclusions

Since our statistical conclusion is based on how small the p-value is, or in other words, how surprising our data are when Ho is true, it would be nice to have some kind of guideline or cutoff that will help determine how small the p-value must be, or how “rare” (unlikely) our data must be when Ho is true, for us to conclude that we have enough evidence to reject Ho.

This cutoff exists, and because it is so important, it has a special name. It is called the significance level of the test and is usually denoted by the Greek letter α (alpha). The most commonly used significance level is α (alpha) = 0.05 (or 5%). This means that:

• if the p-value < α (alpha) (usually 0.05), then the data we obtained is considered to be “rare (or surprising) enough” under the assumption that Ho is true, and we say that the data provide statistically significant evidence against Ho, so we reject Ho and thus accept Ha.
• if the p-value > α (alpha)(usually 0.05), then our data are not considered to be “surprising enough” under the assumption that Ho is true, and we say that our data do not provide enough evidence to reject Ho (or, equivalently, that the data do not provide enough evidence to accept Ha).

Now that we have a cutoff to use, here are the appropriate conclusions for each of our examples based upon the p-values we were given.

In Example 1:

• Using our cutoff of 0.05, we fail to reject Ho.
• Conclusion : There IS NOT enough evidence that the proportion of smokers at GU is less than 0.20
• Still we should consider: Does the evidence seen in the data provide any practical evidence towards our alternative hypothesis?

In Example 2:

• Using our cutoff of 0.05, we reject Ho.
• Conclusion : There IS enough evidence that the mean concentration in the shipment is not the required 245 ppm.

In Example 3:

• Conclusion : There IS NOT enough evidence that males score higher on average than females on the SAT.

Notice that all of the above conclusions are written in terms of the alternative hypothesis and are given in the context of the situation. In no situation have we claimed the null hypothesis is true. Be very careful of this and other issues discussed in the following comments.

• Although the significance level provides a good guideline for drawing our conclusions, it should not be treated as an incontrovertible truth. There is a lot of room for personal interpretation. What if your p-value is 0.052? You might want to stick to the rules and say “0.052 > 0.05 and therefore I don’t have enough evidence to reject Ho”, but you might decide that 0.052 is small enough for you to believe that Ho should be rejected. It should be noted that scientific journals do consider 0.05 to be the cutoff point for which any p-value below the cutoff indicates enough evidence against Ho, and any p-value above it, or even equal to it , indicates there is not enough evidence against Ho. Although a p-value between 0.05 and 0.10 is often reported as marginally statistically significant.
• It is important to draw your conclusions in context . It is never enough to say: “p-value = …, and therefore I have enough evidence to reject Ho at the 0.05 significance level.” You should always word your conclusion in terms of the data. Although we will use the terminology of “rejecting Ho” or “failing to reject Ho” – this is mostly due to the fact that we are instructing you in these concepts. In practice, this language is rarely used. We also suggest writing your conclusion in terms of the alternative hypothesis.Is there or is there not enough evidence that the alternative hypothesis is true?
• Let’s go back to the issue of the nature of the two types of conclusions that I can make.
• Either I reject Ho (when the p-value is smaller than the significance level)
• or I cannot reject Ho (when the p-value is larger than the significance level).

As we mentioned earlier, note that the second conclusion does not imply that I accept Ho, but just that I don’t have enough evidence to reject it. Saying (by mistake) “I don’t have enough evidence to reject Ho so I accept it” indicates that the data provide evidence that Ho is true, which is not necessarily the case . Consider the following slightly artificial yet effective example:

An employer claims to subscribe to an “equal opportunity” policy, not hiring men any more often than women for managerial positions. Is this credible? You’re not sure, so you want to test the following two hypotheses:

• Ho: The proportion of male managers hired is 0.5
• Ha: The proportion of male managers hired is more than 0.5

Data: You choose at random three of the new managers who were hired in the last 5 years and find that all 3 are men.

Assessing Evidence: If the proportion of male managers hired is really 0.5 (Ho is true), then the probability that the random selection of three managers will yield three males is therefore 0.5 * 0.5 * 0.5 = 0.125. This is the p-value (using the multiplication rule for independent events).

Conclusion: Using 0.05 as the significance level, you conclude that since the p-value = 0.125 > 0.05, the fact that the three randomly selected managers were all males is not enough evidence to reject the employer’s claim of subscribing to an equal opportunity policy (Ho).

However, the data (all three selected are males) definitely does NOT provide evidence to accept the employer’s claim (Ho).

Learn By Doing: Using p-values

Did I Get This?: Using p-values

Comment about wording: Another common wording in scientific journals is:

• “The results are statistically significant” – when the p-value < α (alpha).
• “The results are not statistically significant” – when the p-value > α (alpha).

Often you will see significance levels reported with additional description to indicate the degree of statistical significance. A general guideline (although not required in our course) is:

• If 0.01 ≤ p-value < 0.05, then the results are (statistically) significant .
• If 0.001 ≤ p-value < 0.01, then the results are highly statistically significant .
• If p-value < 0.001, then the results are very highly statistically significant .
• If p-value > 0.05, then the results are not statistically significant (NS).
• If 0.05 ≤ p-value < 0.10, then the results are marginally statistically significant .

Let’s summarize

We learned quite a lot about hypothesis testing. We learned the logic behind it, what the key elements are, and what types of conclusions we can and cannot draw in hypothesis testing. Here is a quick recap:

Video: Hypothesis Testing Overview (2:20)

Here are a few more activities if you need some additional practice.

Did I Get This?: Hypothesis Testing Overview

• Notice that the p-value is an example of a conditional probability . We calculate the probability of obtaining results like those of our data (or more extreme) GIVEN the null hypothesis is true. We could write P(Obtaining results like ours or more extreme | Ho is True).
• We could write P(Obtaining a test statistic as or more extreme than ours | Ho is True).
• In this case we are asking “Assuming the null hypothesis is true, how rare is it to observe something as or more extreme than what I have found in my data?”
• If after assuming the null hypothesis is true, what we have found in our data is extremely rare (small p-value), this provides evidence to reject our assumption that Ho is true in favor of Ha.
• The p-value can also be thought of as the probability, assuming the null hypothesis is true, that the result we have seen is solely due to random error (or random chance). We have already seen that statistics from samples collected from a population vary. There is random error or random chance involved when we sample from populations.

In this setting, if the p-value is very small, this implies, assuming the null hypothesis is true, that it is extremely unlikely that the results we have obtained would have happened due to random error alone, and thus our assumption (Ho) is rejected in favor of the alternative hypothesis (Ha).

• It is EXTREMELY important that you find a definition of the p-value which makes sense to you. New students often need to contemplate this idea repeatedly through a variety of examples and explanations before becoming comfortable with this idea. It is one of the two most important concepts in statistics (the other being confidence intervals).
• We infer that the alternative hypothesis is true ONLY by rejecting the null hypothesis.
• A statistically significant result is one that has a very low probability of occurring if the null hypothesis is true.
• Results which are statistically significant may or may not have practical significance and vice versa.

Error and Power

LO 6.28: Define a Type I and Type II error in general and in the context of specific scenarios.

LO 6.29: Explain the concept of the power of a statistical test including the relationship between power, sample size, and effect size.

Video: Errors and Power (12:03)

Type I and Type II Errors in Hypothesis Tests

We have not yet discussed the fact that we are not guaranteed to make the correct decision by this process of hypothesis testing. Maybe you are beginning to see that there is always some level of uncertainty in statistics.

Let’s think about what we know already and define the possible errors we can make in hypothesis testing. When we conduct a hypothesis test, we choose one of two possible conclusions based upon our data.

If the p-value is smaller than your pre-specified significance level (α, alpha), you reject the null hypothesis and either

• You have made the correct decision since the null hypothesis is false
• You have made an error ( Type I ) and rejected Ho when in fact Ho is true (your data happened to be a RARE EVENT under Ho)

If the p-value is greater than (or equal to) your chosen significance level (α, alpha), you fail to reject the null hypothesis and either

• You have made the correct decision since the null hypothesis is true
• You have made an error ( Type II ) and failed to reject Ho when in fact Ho is false (the alternative hypothesis, Ha, is true)

The following summarizes the four possible results which can be obtained from a hypothesis test. Notice the rows represent the decision made in the hypothesis test and the columns represent the (usually unknown) truth in reality.

Although the truth is unknown in practice – or we would not be conducting the test – we know it must be the case that either the null hypothesis is true or the null hypothesis is false. It is also the case that either decision we make in a hypothesis test can result in an incorrect conclusion!

A TYPE I Error occurs when we Reject Ho when, in fact, Ho is True. In this case, we mistakenly reject a true null hypothesis.

• P(TYPE I Error) = P(Reject Ho | Ho is True) = α = alpha = Significance Level

A TYPE II Error occurs when we fail to Reject Ho when, in fact, Ho is False. In this case we fail to reject a false null hypothesis.

P(TYPE II Error) = P(Fail to Reject Ho | Ho is False) = β = beta

When our significance level is 5%, we are saying that we will allow ourselves to make a Type I error less than 5% of the time. In the long run, if we repeat the process, 5% of the time we will find a p-value < 0.05 when in fact the null hypothesis was true.

In this case, our data represent a rare occurrence which is unlikely to happen but is still possible. For example, suppose we toss a coin 10 times and obtain 10 heads, this is unlikely for a fair coin but not impossible. We might conclude the coin is unfair when in fact we simply saw a very rare event for this fair coin.

Our testing procedure CONTROLS for the Type I error when we set a pre-determined value for the significance level.

Notice that these probabilities are conditional probabilities. This is one more reason why conditional probability is an important concept in statistics.

Unfortunately, calculating the probability of a Type II error requires us to know the truth about the population. In practice we can only calculate this probability using a series of “what if” calculations which depend upon the type of problem.

Comment: As you initially read through the examples below, focus on the broad concepts instead of the small details. It is not important to understand how to calculate these values yourself at this point.

• Try to understand the pictures we present. Which pictures represent an assumed null hypothesis and which represent an alternative?
• It may be useful to come back to this page (and the activities here) after you have reviewed the rest of the section on hypothesis testing and have worked a few problems yourself.

Interactive Applet: Statistical Significance

Here are two examples of using an older version of this applet. It looks slightly different but the same settings and options are available in the version above.

In both cases we will consider IQ scores.

Our null hypothesis is that the true mean is 100. Assume the standard deviation is 16 and we will specify a significance level of 5%.

In this example we will specify that the true mean is indeed 100 so that the null hypothesis is true. Most of the time (95%), when we generate a sample, we should fail to reject the null hypothesis since the null hypothesis is indeed true.

Here is one sample that results in a correct decision:

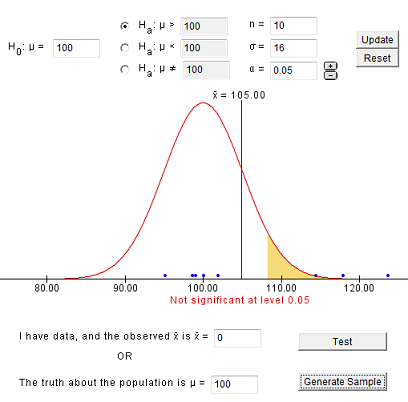
In the sample above, we obtain an x-bar of 105, which is drawn on the distribution which assumes μ (mu) = 100 (the null hypothesis is true). Notice the sample is shown as blue dots along the x-axis and the shaded region shows for which values of x-bar we would reject the null hypothesis. In other words, we would reject Ho whenever the x-bar falls in the shaded region.

Enter the same values and generate samples until you obtain a Type I error (you falsely reject the null hypothesis). You should see something like this:

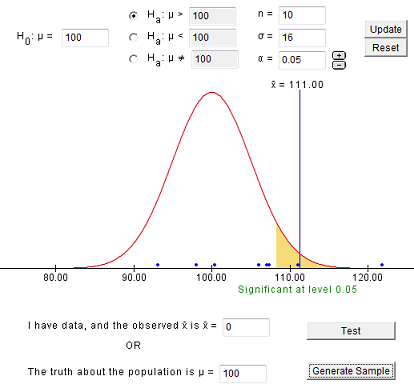
If you were to generate 100 samples, you should have around 5% where you rejected Ho. These would be samples which would result in a Type I error.

The previous example illustrates a correct decision and a Type I error when the null hypothesis is true. The next example illustrates a correct decision and Type II error when the null hypothesis is false. In this case, we must specify the true population mean.

Let’s suppose we are sampling from an honors program and that the true mean IQ for this population is 110. We do not know the probability of a Type II error without more detailed calculations.

Let’s start with a sample which results in a correct decision.

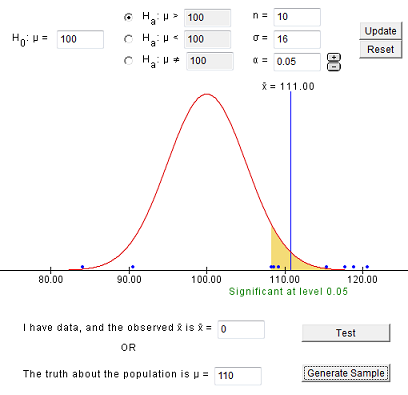
In the sample above, we obtain an x-bar of 111, which is drawn on the distribution which assumes μ (mu) = 100 (the null hypothesis is true).

Enter the same values and generate samples until you obtain a Type II error (you fail to reject the null hypothesis). You should see something like this:

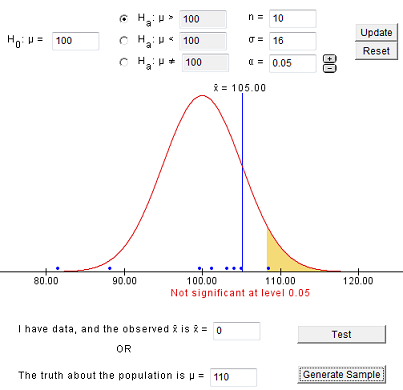
You should notice that in this case (when Ho is false), it is easier to obtain an incorrect decision (a Type II error) than it was in the case where Ho is true. If you generate 100 samples, you can approximate the probability of a Type II error.

We can find the probability of a Type II error by visualizing both the assumed distribution and the true distribution together. The image below is adapted from an applet we will use when we discuss the power of a statistical test.

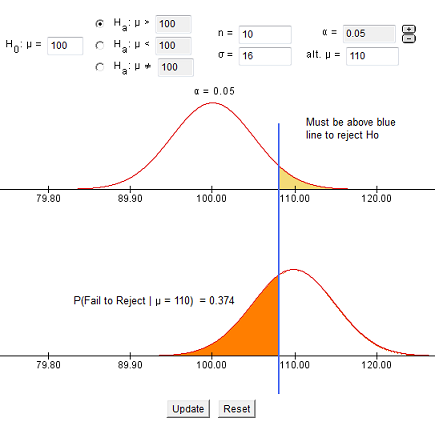
There is a 37.4% chance that, in the long run, we will make a Type II error and fail to reject the null hypothesis when in fact the true mean IQ is 110 in the population from which we sample our 10 individuals.

Can you visualize what will happen if the true population mean is really 115 or 108? When will the Type II error increase? When will it decrease? We will look at this idea again when we discuss the concept of power in hypothesis tests.

• It is important to note that there is a trade-off between the probability of a Type I and a Type II error. If we decrease the probability of one of these errors, the probability of the other will increase! The practical result of this is that if we require stronger evidence to reject the null hypothesis (smaller significance level = probability of a Type I error), we will increase the chance that we will be unable to reject the null hypothesis when in fact Ho is false (increases the probability of a Type II error).
• When α (alpha) = 0.05 we obtained a Type II error probability of 0.374 = β = beta

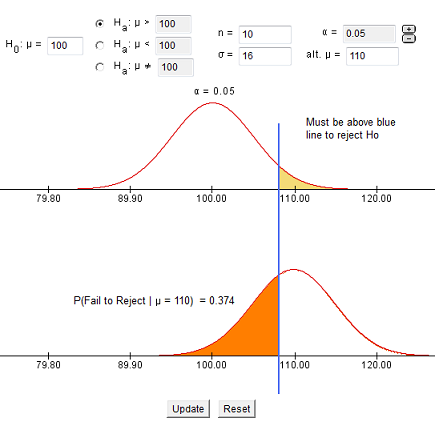
• When α (alpha) = 0.01 (smaller than before) we obtain a Type II error probability of 0.644 = β = beta (larger than before)

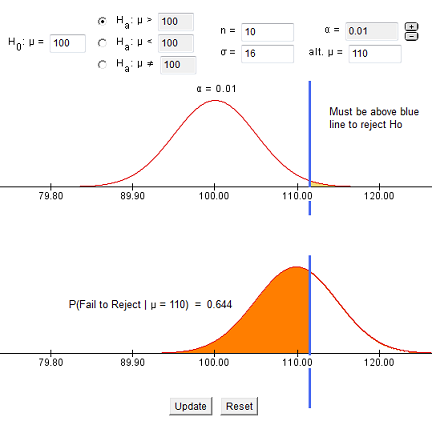
• As the blue line in the picture moves farther right, the significance level (α, alpha) is decreasing and the Type II error probability is increasing.
• As the blue line in the picture moves farther left, the significance level (α, alpha) is increasing and the Type II error probability is decreasing

Let’s return to our very first example and define these two errors in context.

• Ho = The student’s claim: I did not cheat on the exam.
• Ha = The instructor’s claim: The student did cheat on the exam.

Adhering to the principle “innocent until proven guilty,” the committee asks the instructor for evidence to support his claim.

There are four possible outcomes of this process. There are two possible correct decisions:

• The student did cheat on the exam and the instructor brings enough evidence to reject Ho and conclude the student did cheat on the exam. This is a CORRECT decision!
• The student did not cheat on the exam and the instructor fails to provide enough evidence that the student did cheat on the exam. This is a CORRECT decision!

Both the correct decisions and the possible errors are fairly easy to understand but with the errors, you must be careful to identify and define the two types correctly.

TYPE I Error: Reject Ho when Ho is True

• The student did not cheat on the exam but the instructor brings enough evidence to reject Ho and conclude the student cheated on the exam. This is a Type I Error.

TYPE II Error: Fail to Reject Ho when Ho is False

• The student did cheat on the exam but the instructor fails to provide enough evidence that the student cheated on the exam. This is a Type II Error.

In most situations, including this one, it is more “acceptable” to have a Type II error than a Type I error. Although allowing a student who cheats to go unpunished might be considered a very bad problem, punishing a student for something he or she did not do is usually considered to be a more severe error. This is one reason we control for our Type I error in the process of hypothesis testing.

Did I Get This?: Type I and Type II Errors (in context)

• The probabilities of Type I and Type II errors are closely related to the concepts of sensitivity and specificity that we discussed previously. Consider the following hypotheses:

Ho: The individual does not have diabetes (status quo, nothing special happening)

Ha: The individual does have diabetes (something is going on here)

In this setting:

When someone tests positive for diabetes we would reject the null hypothesis and conclude the person has diabetes (we may or may not be correct!).

When someone tests negative for diabetes we would fail to reject the null hypothesis so that we fail to conclude the person has diabetes (we may or may not be correct!)

Let’s take it one step further:

Sensitivity = P(Test + | Have Disease) which in this setting equals P(Reject Ho | Ho is False) = 1 – P(Fail to Reject Ho | Ho is False) = 1 – β = 1 – beta

Specificity = P(Test – | No Disease) which in this setting equals P(Fail to Reject Ho | Ho is True) = 1 – P(Reject Ho | Ho is True) = 1 – α = 1 – alpha

Notice that sensitivity and specificity relate to the probability of making a correct decision whereas α (alpha) and β (beta) relate to the probability of making an incorrect decision.

Usually α (alpha) = 0.05 so that the specificity listed above is 0.95 or 95%.

Next, we will see that the sensitivity listed above is the power of the hypothesis test!

Reasons for a Type I Error in Practice

Assuming that you have obtained a quality sample:

• The reason for a Type I error is random chance.
• When a Type I error occurs, our observed data represented a rare event which indicated evidence in favor of the alternative hypothesis even though the null hypothesis was actually true.

Reasons for a Type II Error in Practice

Again, assuming that you have obtained a quality sample, now we have a few possibilities depending upon the true difference that exists.

• The sample size is too small to detect an important difference. This is the worst case, you should have obtained a larger sample. In this situation, you may notice that the effect seen in the sample seems PRACTICALLY significant and yet the p-value is not small enough to reject the null hypothesis.
• The sample size is reasonable for the important difference but the true difference (which might be somewhat meaningful or interesting) is smaller than your test was capable of detecting. This is tolerable as you were not interested in being able to detect this difference when you began your study. In this situation, you may notice that the effect seen in the sample seems to have some potential for practical significance.
• The sample size is more than adequate, the difference that was not detected is meaningless in practice. This is not a problem at all and is in effect a “correct decision” since the difference you did not detect would have no practical meaning.
• Note: We will discuss the idea of practical significance later in more detail.

Power of a Hypothesis Test

It is often the case that we truly wish to prove the alternative hypothesis. It is reasonable that we would be interested in the probability of correctly rejecting the null hypothesis. In other words, the probability of rejecting the null hypothesis, when in fact the null hypothesis is false. This can also be thought of as the probability of being able to detect a (pre-specified) difference of interest to the researcher.

Let’s begin with a realistic example of how power can be described in a study.

In a clinical trial to study two medications for weight loss, we have an 80% chance to detect a difference in the weight loss between the two medications of 10 pounds. In other words, the power of the hypothesis test we will conduct is 80%.

In other words, if one medication comes from a population with an average weight loss of 25 pounds and the other comes from a population with an average weight loss of 15 pounds, we will have an 80% chance to detect that difference using the sample we have in our trial.

If we were to repeat this trial many times, 80% of the time we will be able to reject the null hypothesis (that there is no difference between the medications) and 20% of the time we will fail to reject the null hypothesis (and make a Type II error!).

The difference of 10 pounds in the previous example, is often called the effect size . The measure of the effect differs depending on the particular test you are conducting but is always some measure related to the true effect in the population. In this example, it is the difference between two population means.

Recall the definition of a Type II error:

Notice that P(Reject Ho | Ho is False) = 1 – P(Fail to Reject Ho | Ho is False) = 1 – β = 1- beta.

The POWER of a hypothesis test is the probability of rejecting the null hypothesis when the null hypothesis is false . This can also be stated as the probability of correctly rejecting the null hypothesis .

POWER = P(Reject Ho | Ho is False) = 1 – β = 1 – beta

Power is the test’s ability to correctly reject the null hypothesis. A test with high power has a good chance of being able to detect the difference of interest to us, if it exists .

As we mentioned on the bottom of the previous page, this can be thought of as the sensitivity of the hypothesis test if you imagine Ho = No disease and Ha = Disease.

Factors Affecting the Power of a Hypothesis Test

The power of a hypothesis test is affected by numerous quantities (similar to the margin of error in a confidence interval).

Assume that the null hypothesis is false for a given hypothesis test. All else being equal, we have the following:

• Larger samples result in a greater chance to reject the null hypothesis which means an increase in the power of the hypothesis test.
• If the effect size is larger, it will become easier for us to detect. This results in a greater chance to reject the null hypothesis which means an increase in the power of the hypothesis test. The effect size varies for each test and is usually closely related to the difference between the hypothesized value and the true value of the parameter under study.
• From the relationship between the probability of a Type I and a Type II error (as α (alpha) decreases, β (beta) increases), we can see that as α (alpha) decreases, Power = 1 – β = 1 – beta also decreases.
• There are other mathematical ways to change the power of a hypothesis test, such as changing the population standard deviation; however, these are not quantities that we can usually control so we will not discuss them here.

In practice, we specify a significance level and a desired power to detect a difference which will have practical meaning to us and this determines the sample size required for the experiment or study.

For most grants involving statistical analysis, power calculations must be completed to illustrate that the study will have a reasonable chance to detect an important effect. Otherwise, the money spent on the study could be wasted. The goal is usually to have a power close to 80%.

For example, if there is only a 5% chance to detect an important difference between two treatments in a clinical trial, this would result in a waste of time, effort, and money on the study since, when the alternative hypothesis is true, the chance a treatment effect can be found is very small.

• In order to calculate the power of a hypothesis test, we must specify the “truth.” As we mentioned previously when discussing Type II errors, in practice we can only calculate this probability using a series of “what if” calculations which depend upon the type of problem.

The following activity involves working with an interactive applet to study power more carefully.

Learn by Doing: Power of Hypothesis Tests

The following reading is an excellent discussion about Type I and Type II errors.

(Optional) Outside Reading: A Good Discussion of Power (≈ 2500 words)

We will not be asking you to perform power calculations manually. You may be asked to use online calculators and applets. Most statistical software packages offer some ability to complete power calculations. There are also many online calculators for power and sample size on the internet, for example, Russ Lenth’s power and sample-size page .

Proportions (Introduction & Step 1)

CO-4: Distinguish among different measurement scales, choose the appropriate descriptive and inferential statistical methods based on these distinctions, and interpret the results.

LO 4.33: In a given context, distinguish between situations involving a population proportion and a population mean and specify the correct null and alternative hypothesis for the scenario.

LO 4.34: Carry out a complete hypothesis test for a population proportion by hand.

Video: Proportions (Introduction & Step 1) (7:18)

Now that we understand the process of hypothesis testing and the logic behind it, we are ready to start learning about specific statistical tests (also known as significance tests).

The first test we are going to learn is the test about the population proportion (p).

This test is widely known as the “z-test for the population proportion (p).”

We will understand later where the “z-test” part is coming from.

This will be the only type of problem you will complete entirely “by-hand” in this course. Our goal is to use this example to give you the tools you need to understand how this process works. After working a few problems, you should review the earlier material again. You will likely need to review the terminology and concepts a few times before you fully understand the process.

In reality, you will often be conducting more complex statistical tests and allowing software to provide the p-value. In these settings it will be important to know what test to apply for a given situation and to be able to explain the results in context.

Review: Types of Variables

When we conduct a test about a population proportion, we are working with a categorical variable. Later in the course, after we have learned a variety of hypothesis tests, we will need to be able to identify which test is appropriate for which situation. Identifying the variable as categorical or quantitative is an important component of choosing an appropriate hypothesis test.

Learn by Doing: Review Types of Variables

One Sample Z-Test for a Population Proportion

In this part of our discussion on hypothesis testing, we will go into details that we did not go into before. More specifically, we will use this test to introduce the idea of a test statistic , and details about how p-values are calculated .

Let’s start by introducing the three examples, which will be the leading examples in our discussion. Each example is followed by a figure illustrating the information provided, as well as the question of interest.

A machine is known to produce 20% defective products, and is therefore sent for repair. After the machine is repaired, 400 products produced by the machine are chosen at random and 64 of them are found to be defective. Do the data provide enough evidence that the proportion of defective products produced by the machine (p) has been reduced as a result of the repair?

The following figure displays the information, as well as the question of interest:

The question of interest helps us formulate the null and alternative hypotheses in terms of p, the proportion of defective products produced by the machine following the repair:

• Ho: p = 0.20 (No change; the repair did not help).
• Ha: p < 0.20 (The repair was effective at reducing the proportion of defective parts).

There are rumors that students at a certain liberal arts college are more inclined to use drugs than U.S. college students in general. Suppose that in a simple random sample of 100 students from the college, 19 admitted to marijuana use. Do the data provide enough evidence to conclude that the proportion of marijuana users among the students in the college (p) is higher than the national proportion, which is 0.157? (This number is reported by the Harvard School of Public Health.)

Again, the following figure displays the information as well as the question of interest:

As before, we can formulate the null and alternative hypotheses in terms of p, the proportion of students in the college who use marijuana:

• Ho: p = 0.157 (same as among all college students in the country).
• Ha: p > 0.157 (higher than the national figure).

Polls on certain topics are conducted routinely in order to monitor changes in the public’s opinions over time. One such topic is the death penalty. In 2003 a poll estimated that 64% of U.S. adults support the death penalty for a person convicted of murder. In a more recent poll, 675 out of 1,000 U.S. adults chosen at random were in favor of the death penalty for convicted murderers. Do the results of this poll provide evidence that the proportion of U.S. adults who support the death penalty for convicted murderers (p) changed between 2003 and the later poll?

Here is a figure that displays the information, as well as the question of interest:

Again, we can formulate the null and alternative hypotheses in term of p, the proportion of U.S. adults who support the death penalty for convicted murderers.

• Ho: p = 0.64 (No change from 2003).
• Ha: p ≠ 0.64 (Some change since 2003).

Learn by Doing: Proportions (Overview)

Did I Get This?: Proportions ( Overview )

Recall that there are basically 4 steps in the process of hypothesis testing:

• STEP 1: State the appropriate null and alternative hypotheses, Ho and Ha.
• STEP 2: Obtain a random sample, collect relevant data, and check whether the data meet the conditions under which the test can be used . If the conditions are met, summarize the data using a test statistic.
• STEP 3: Find the p-value of the test.
• STEP 4: Based on the p-value, decide whether or not the results are statistically significant and draw your conclusions in context.
• Note: In practice, we should always consider the practical significance of the results as well as the statistical significance.

We are now going to go through these steps as they apply to the hypothesis testing for the population proportion p. It should be noted that even though the details will be specific to this particular test, some of the ideas that we will add apply to hypothesis testing in general.

Step 1. Stating the Hypotheses

Here again are the three set of hypotheses that are being tested in each of our three examples:

Has the proportion of defective products been reduced as a result of the repair?

Is the proportion of marijuana users in the college higher than the national figure?

Did the proportion of U.S. adults who support the death penalty change between 2003 and a later poll?

The null hypothesis always takes the form:

• Ho: p = some value

and the alternative hypothesis takes one of the following three forms:

• Ha: p < that value (like in example 1) or
• Ha: p > that value (like in example 2) or
• Ha: p ≠ that value (like in example 3).

Note that it was quite clear from the context which form of the alternative hypothesis would be appropriate. The value that is specified in the null hypothesis is called the null value , and is generally denoted by p 0 . We can say, therefore, that in general the null hypothesis about the population proportion (p) would take the form:

• Ho: p = p 0

We write Ho: p = p 0 to say that we are making the hypothesis that the population proportion has the value of p 0 . In other words, p is the unknown population proportion and p 0 is the number we think p might be for the given situation.

The alternative hypothesis takes one of the following three forms (depending on the context):

Ha: p < p 0 (one-sided)

Ha: p > p 0 (one-sided)

Ha: p ≠ p 0 (two-sided)

The first two possible forms of the alternatives (where the = sign in Ho is challenged by < or >) are called one-sided alternatives , and the third form of alternative (where the = sign in Ho is challenged by ≠) is called a two-sided alternative. To understand the intuition behind these names let’s go back to our examples.

Example 3 (death penalty) is a case where we have a two-sided alternative:

In this case, in order to reject Ho and accept Ha we will need to get a sample proportion of death penalty supporters which is very different from 0.64 in either direction, either much larger or much smaller than 0.64.

In example 2 (marijuana use) we have a one-sided alternative:

Here, in order to reject Ho and accept Ha we will need to get a sample proportion of marijuana users which is much higher than 0.157.

Similarly, in example 1 (defective products), where we are testing:

in order to reject Ho and accept Ha, we will need to get a sample proportion of defective products which is much smaller than 0.20.

Learn by Doing: State Hypotheses (Proportions)

Did I Get This?: State Hypotheses (Proportions)

Proportions (Step 2)

Video: Proportions (Step 2) (12:38)

Step 2. Collect Data, Check Conditions, and Summarize Data

After the hypotheses have been stated, the next step is to obtain a sample (on which the inference will be based), collect relevant data , and summarize them.

It is extremely important that our sample is representative of the population about which we want to draw conclusions. This is ensured when the sample is chosen at random. Beyond the practical issue of ensuring representativeness, choosing a random sample has theoretical importance that we will mention later.

In the case of hypothesis testing for the population proportion (p), we will collect data on the relevant categorical variable from the individuals in the sample and start by calculating the sample proportion p-hat (the natural quantity to calculate when the parameter of interest is p).

Let’s go back to our three examples and add this step to our figures.

As we mentioned earlier without going into details, when we summarize the data in hypothesis testing, we go a step beyond calculating the sample statistic and summarize the data with a test statistic . Every test has a test statistic, which to some degree captures the essence of the test. In fact, the p-value, which so far we have looked upon as “the king” (in the sense that everything is determined by it), is actually determined by (or derived from) the test statistic. We will now introduce the test statistic.

The test statistic is a measure of how far the sample proportion p-hat is from the null value p 0 , the value that the null hypothesis claims is the value of p. In other words, since p-hat is what the data estimates p to be, the test statistic can be viewed as a measure of the “distance” between what the data tells us about p and what the null hypothesis claims p to be.

Let’s use our examples to understand this:

The parameter of interest is p, the proportion of defective products following the repair.

The data estimate p to be p-hat = 0.16

The null hypothesis claims that p = 0.20

The data are therefore 0.04 (or 4 percentage points) below the null hypothesis value.

It is hard to evaluate whether this difference of 4% in defective products is enough evidence to say that the repair was effective at reducing the proportion of defective products, but clearly, the larger the difference, the more evidence it is against the null hypothesis. So if, for example, our sample proportion of defective products had been, say, 0.10 instead of 0.16, then I think you would all agree that cutting the proportion of defective products in half (from 20% to 10%) would be extremely strong evidence that the repair was effective at reducing the proportion of defective products.

The parameter of interest is p, the proportion of students in a college who use marijuana.

The data estimate p to be p-hat = 0.19

The null hypothesis claims that p = 0.157

The data are therefore 0.033 (or 3.3. percentage points) above the null hypothesis value.

The parameter of interest is p, the proportion of U.S. adults who support the death penalty for convicted murderers.

The data estimate p to be p-hat = 0.675

The null hypothesis claims that p = 0.64

There is a difference of 0.035 (or 3.5. percentage points) between the data and the null hypothesis value.

The problem with looking only at the difference between the sample proportion, p-hat, and the null value, p 0 is that we have not taken into account the variability of our estimator p-hat which, as we know from our study of sampling distributions, depends on the sample size.

For this reason, the test statistic cannot simply be the difference between p-hat and p 0 , but must be some form of that formula that accounts for the sample size. In other words, we need to somehow standardize the difference so that comparison between different situations will be possible. We are very close to revealing the test statistic, but before we construct it, let’s be reminded of the following two facts from probability:

Fact 1: When we take a random sample of size n from a population with population proportion p, then

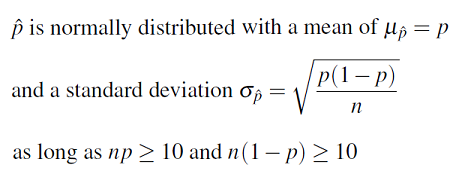
Fact 2: The z-score of any normal value (a value that comes from a normal distribution) is calculated by finding the difference between the value and the mean and then dividing that difference by the standard deviation (of the normal distribution associated with the value). The z-score represents how many standard deviations below or above the mean the value is.

Thus, our test statistic should be a measure of how far the sample proportion p-hat is from the null value p 0 relative to the variation of p-hat (as measured by the standard error of p-hat).

Recall that the standard error is the standard deviation of the sampling distribution for a given statistic. For p-hat, we know the following:

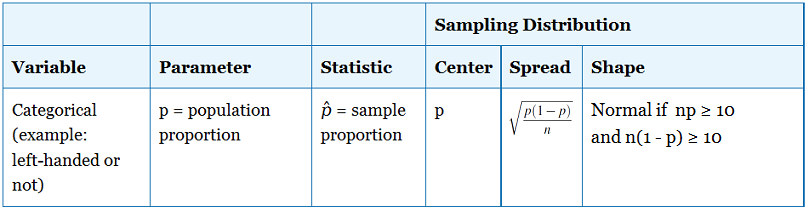
To find the p-value, we will need to determine how surprising our value is assuming the null hypothesis is true. We already have the tools needed for this process from our study of sampling distributions as represented in the table above.

If we assume the null hypothesis is true, we can specify that the center of the distribution of all possible values of p-hat from samples of size 400 would be 0.20 (our null value).

We can calculate the standard error, assuming p = 0.20 as

\(\sqrt{\dfrac{p_{0}\left(1-p_{0}\right)}{n}}=\sqrt{\dfrac{0.2(1-0.2)}{400}}=0.02\)

The following picture represents the sampling distribution of all possible values of p-hat of samples of size 400, assuming the true proportion p is 0.20 and our other requirements for the sampling distribution to be normal are met (we will review these during the next step).

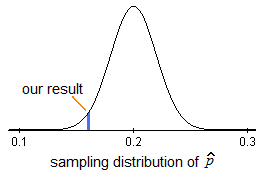
In order to calculate probabilities for the picture above, we would need to find the z-score associated with our result.

This z-score is the test statistic ! In this example, the numerator of our z-score is the difference between p-hat (0.16) and null value (0.20) which we found earlier to be -0.04. The denominator of our z-score is the standard error calculated above (0.02) and thus quickly we find the z-score, our test statistic, to be -2.

The sample proportion based upon this data is 2 standard errors below the null value.

Hopefully you now understand more about the reasons we need probability in statistics!!

Now we will formalize the definition and look at our remaining examples before moving on to the next step, which will be to determine if a normal distribution applies and calculate the p-value.

Test Statistic for Hypothesis Tests for One Proportion is:

\(z=\dfrac{\hat{p}-p_{0}}{\sqrt{\dfrac{p_{0}\left(1-p_{0}\right)}{n}}}\)

It represents the difference between the sample proportion and the null value, measured in standard deviations (standard error of p-hat).

The picture above is a representation of the sampling distribution of p-hat assuming p = p 0 . In other words, this is a model of how p-hat behaves if we are drawing random samples from a population for which Ho is true.

Notice the center of the sampling distribution is at p 0 , which is the hypothesized proportion given in the null hypothesis (Ho: p = p 0 .) We could also mark the axis in standard error units,

\(\sqrt{\dfrac{p_{0}\left(1-p_{0}\right)}{n}}\)

For example, if our null hypothesis claims that the proportion of U.S. adults supporting the death penalty is 0.64, then the sampling distribution is drawn as if the null is true. We draw a normal distribution centered at 0.64 (p 0 ) with a standard error dependent on sample size,

\(\sqrt{\dfrac{0.64(1-0.64)}{n}}\).

Important Comment:

• Note that under the assumption that Ho is true (and if the conditions for the sampling distribution to be normal are satisfied) the test statistic follows a N(0,1) (standard normal) distribution. Another way to say the same thing which is quite common is: “The null distribution of the test statistic is N(0,1).”

By “null distribution,” we mean the distribution under the assumption that Ho is true. As we’ll see and stress again later, the null distribution of the test statistic is what the calculation of the p-value is based on.

Let’s go back to our remaining two examples and find the test statistic in each case:

Since the null hypothesis is Ho: p = 0.157, the standardized (z) score of p-hat = 0.19 is

\(z=\dfrac{0.19-0.157}{\sqrt{\dfrac{0.157(1-0.157)}{100}}} \approx 0.91\)

This is the value of the test statistic for this example.

We interpret this to mean that, assuming that Ho is true, the sample proportion p-hat = 0.19 is 0.91 standard errors above the null value (0.157).

Since the null hypothesis is Ho: p = 0.64, the standardized (z) score of p-hat = 0.675 is

\(z=\dfrac{0.675-0.64}{\sqrt{\dfrac{0.64(1-0.64)}{1000}}} \approx 2.31\)

We interpret this to mean that, assuming that Ho is true, the sample proportion p-hat = 0.675 is 2.31 standard errors above the null value (0.64).

Learn by Doing: Proportions (Step 2)

Comments about the Test Statistic:

• We mentioned earlier that to some degree, the test statistic captures the essence of the test. In this case, the test statistic measures the difference between p-hat and p 0 in standard errors. This is exactly what this test is about. Get data, and look at the discrepancy between what the data estimates p to be (represented by p-hat) and what Ho claims about p (represented by p 0 ).
• You can think about this test statistic as a measure of evidence in the data against Ho. The larger the test statistic, the “further the data are from Ho” and therefore the more evidence the data provide against Ho.

Learn by Doing: Proportions (Step 2) Understanding the Test Statistic

Did I Get This?: Proportions (Step 2)

• It should now be clear why this test is commonly known as the z-test for the population proportion . The name comes from the fact that it is based on a test statistic that is a z-score.
• Recall fact 1 that we used for constructing the z-test statistic. Here is part of it again:

When we take a random sample of size n from a population with population proportion p 0 , the possible values of the sample proportion p-hat ( when certain conditions are met ) have approximately a normal distribution with a mean of p 0 … and a standard deviation of

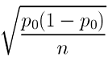
This result provides the theoretical justification for constructing the test statistic the way we did, and therefore the assumptions under which this result holds (in bold, above) are the conditions that our data need to satisfy so that we can use this test. These two conditions are:

i. The sample has to be random.

ii. The conditions under which the sampling distribution of p-hat is normal are met. In other words:

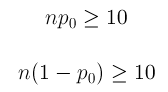
• Here we will pause to say more about condition (i.) above, the need for a random sample. In the Probability Unit we discussed sampling plans based on probability (such as a simple random sample, cluster, or stratified sampling) that produce a non-biased sample, which can be safely used in order to make inferences about a population. We noted in the Probability Unit that, in practice, other (non-random) sampling techniques are sometimes used when random sampling is not feasible. It is important though, when these techniques are used, to be aware of the type of bias that they introduce, and thus the limitations of the conclusions that can be drawn from them. For our purpose here, we will focus on one such practice, the situation in which a sample is not really chosen randomly, but in the context of the categorical variable that is being studied, the sample is regarded as random. For example, say that you are interested in the proportion of students at a certain college who suffer from seasonal allergies. For that purpose, the students in a large engineering class could be considered as a random sample, since there is nothing about being in an engineering class that makes you more or less likely to suffer from seasonal allergies. Technically, the engineering class is a convenience sample, but it is treated as a random sample in the context of this categorical variable. On the other hand, if you are interested in the proportion of students in the college who have math anxiety, then the class of engineering students clearly could not possibly be viewed as a random sample, since engineering students probably have a much lower incidence of math anxiety than the college population overall.

Learn by Doing: Proportions (Step 2) Valid or Invalid Sampling?

Let’s check the conditions in our three examples.

i. The 400 products were chosen at random.

ii. n = 400, p 0 = 0.2 and therefore:

\(n p_{0}=400(0.2)=80 \geq 10\)

\(n\left(1-p_{0}\right)=400(1-0.2)=320 \geq 10\)

i. The 100 students were chosen at random.

ii. n = 100, p 0 = 0.157 and therefore:

\begin{gathered} n p_{0}=100(0.157)=15.7 \geq 10 \\ n\left(1-p_{0}\right)=100(1-0.157)=84.3 \geq 10 \end{gathered}

i. The 1000 adults were chosen at random.

ii. n = 1000, p 0 = 0.64 and therefore:

\begin{gathered} n p_{0}=1000(0.64)=640 \geq 10 \\ n\left(1-p_{0}\right)=1000(1-0.64)=360 \geq 10 \end{gathered}

Learn by Doing: Proportions (Step 2) Verify Conditions

Checking that our data satisfy the conditions under which the test can be reliably used is a very important part of the hypothesis testing process. Be sure to consider this for every hypothesis test you conduct in this course and certainly in practice.

The Four Steps in Hypothesis Testing

With respect to the z-test, the population proportion that we are currently discussing we have:

Step 1: Completed

Step 2: Completed

Step 3: This is what we will work on next.

Proportions (Step 3)

Video: Proportions (Step 3) (14:46)

Calculators and Tables

Step 3. Finding the P-value of the Test

So far we’ve talked about the p-value at the intuitive level: understanding what it is (or what it measures) and how we use it to draw conclusions about the statistical significance of our results. We will now go more deeply into how the p-value is calculated.

It should be mentioned that eventually we will rely on technology to calculate the p-value for us (as well as the test statistic), but in order to make intelligent use of the output, it is important to first understand the details, and only then let the computer do the calculations for us. Again, our goal is to use this simple example to give you the tools you need to understand the process entirely. Let’s start.

Recall that so far we have said that the p-value is the probability of obtaining data like those observed assuming that Ho is true. Like the test statistic, the p-value is, therefore, a measure of the evidence against Ho. In the case of the test statistic, the larger it is in magnitude (positive or negative), the further p-hat is from p 0 , the more evidence we have against Ho. In the case of the p-value , it is the opposite; the smaller it is, the more unlikely it is to get data like those observed when Ho is true, the more evidence it is against Ho . One can actually draw conclusions in hypothesis testing just using the test statistic, and as we’ll see the p-value is, in a sense, just another way of looking at the test statistic. The reason that we actually take the extra step in this course and derive the p-value from the test statistic is that even though in this case (the test about the population proportion) and some other tests, the value of the test statistic has a very clear and intuitive interpretation, there are some tests where its value is not as easy to interpret. On the other hand, the p-value keeps its intuitive appeal across all statistical tests.

How is the p-value calculated?

Intuitively, the p-value is the probability of observing data like those observed assuming that Ho is true. Let’s be a bit more formal:

• Since this is a probability question about the data , it makes sense that the calculation will involve the data summary, the test statistic.
• What do we mean by “like” those observed? By “like” we mean “as extreme or even more extreme.”

Putting it all together, we get that in general:

The p-value is the probability of observing a test statistic as extreme as that observed (or even more extreme) assuming that the null hypothesis is true.

By “extreme” we mean extreme in the direction(s) of the alternative hypothesis.

Specifically , for the z-test for the population proportion:

• If the alternative hypothesis is Ha: p < p 0 (less than) , then “extreme” means small or less than , and the p-value is: The probability of observing a test statistic as small as that observed or smaller if the null hypothesis is true.
• If the alternative hypothesis is Ha: p > p 0 (greater than) , then “extreme” means large or greater than , and the p-value is: The probability of observing a test statistic as large as that observed or larger if the null hypothesis is true.
• If the alternative is Ha: p ≠ p 0 (different from) , then “extreme” means extreme in either direction either small or large (i.e., large in magnitude) or just different from , and the p-value therefore is: The probability of observing a test statistic as large in magnitude as that observed or larger if the null hypothesis is true.(Examples: If z = -2.5: p-value = probability of observing a test statistic as small as -2.5 or smaller or as large as 2.5 or larger. If z = 1.5: p-value = probability of observing a test statistic as large as 1.5 or larger, or as small as -1.5 or smaller.)

OK, hopefully that makes (some) sense. But how do we actually calculate it?

Recall the important comment from our discussion about our test statistic,

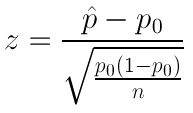
which said that when the null hypothesis is true (i.e., when p = p 0 ), the possible values of our test statistic follow a standard normal (N(0,1), denoted by Z) distribution. Therefore, the p-value calculations (which assume that Ho is true) are simply standard normal distribution calculations for the 3 possible alternative hypotheses.

Alternative Hypothesis is “Less Than”

The probability of observing a test statistic as small as that observed or smaller , assuming that the values of the test statistic follow a standard normal distribution. We will now represent this probability in symbols and also using the normal distribution.

Looking at the shaded region, you can see why this is often referred to as a left-tailed test. We shaded to the left of the test statistic, since less than is to the left.

Alternative Hypothesis is “Greater Than”

The probability of observing a test statistic as large as that observed or larger , assuming that the values of the test statistic follow a standard normal distribution. Again, we will represent this probability in symbols and using the normal distribution

Looking at the shaded region, you can see why this is often referred to as a right-tailed test. We shaded to the right of the test statistic, since greater than is to the right.

Alternative Hypothesis is “Not Equal To”

The probability of observing a test statistic which is as large in magnitude as that observed or larger, assuming that the values of the test statistic follow a standard normal distribution.

This is often referred to as a two-tailed test, since we shaded in both directions.

Next, we will apply this to our three examples. But first, work through the following activities, which should help your understanding.

Learn by Doing: Proportions (Step 3)

Did I Get This?: Proportions (Step 3)

The p-value in this case is:

• The probability of observing a test statistic as small as -2 or smaller, assuming that Ho is true.

OR (recalling what the test statistic actually means in this case),

• The probability of observing a sample proportion that is 2 standard deviations or more below the null value (p 0 = 0.20), assuming that p 0 is the true population proportion.

OR, more specifically,

• The probability of observing a sample proportion of 0.16 or lower in a random sample of size 400, when the true population proportion is p 0 =0.20

In either case, the p-value is found as shown in the following figure:

To find P(Z ≤ -2) we can either use the calculator or table we learned to use in the probability unit for normal random variables. Eventually, after we understand the details, we will use software to run the test for us and the output will give us all the information we need. The p-value that the statistical software provides for this specific example is 0.023. The p-value tells us that it is pretty unlikely (probability of 0.023) to get data like those observed (test statistic of -2 or less) assuming that Ho is true.

• The probability of observing a test statistic as large as 0.91 or larger, assuming that Ho is true.
• The probability of observing a sample proportion that is 0.91 standard deviations or more above the null value (p 0 = 0.157), assuming that p 0 is the true population proportion.
• The probability of observing a sample proportion of 0.19 or higher in a random sample of size 100, when the true population proportion is p 0 =0.157

Again, at this point we can either use the calculator or table to find that the p-value is 0.182, this is P(Z ≥ 0.91).

The p-value tells us that it is not very surprising (probability of 0.182) to get data like those observed (which yield a test statistic of 0.91 or higher) assuming that the null hypothesis is true.

• The probability of observing a test statistic as large as 2.31 (or larger) or as small as -2.31 (or smaller), assuming that Ho is true.
• The probability of observing a sample proportion that is 2.31 standard deviations or more away from the null value (p 0 = 0.64), assuming that p 0 is the true population proportion.
• The probability of observing a sample proportion as different as 0.675 is from 0.64, or even more different (i.e. as high as 0.675 or higher or as low as 0.605 or lower) in a random sample of size 1,000, when the true population proportion is p 0 = 0.64

Again, at this point we can either use the calculator or table to find that the p-value is 0.021, this is P(Z ≤ -2.31) + P(Z ≥ 2.31) = 2*P(Z ≥ |2.31|)

The p-value tells us that it is pretty unlikely (probability of 0.021) to get data like those observed (test statistic as high as 2.31 or higher or as low as -2.31 or lower) assuming that Ho is true.

• We’ve just seen that finding p-values involves probability calculations about the value of the test statistic assuming that Ho is true. In this case, when Ho is true, the values of the test statistic follow a standard normal distribution (i.e., the sampling distribution of the test statistic when the null hypothesis is true is N(0,1)). Therefore, p-values correspond to areas (probabilities) under the standard normal curve.

Similarly, in any test , p-values are found using the sampling distribution of the test statistic when the null hypothesis is true (also known as the “null distribution” of the test statistic). In this case, it was relatively easy to argue that the null distribution of our test statistic is N(0,1). As we’ll see, in other tests, other distributions come up (like the t-distribution and the F-distribution), which we will just mention briefly, and rely heavily on the output of our statistical package for obtaining the p-values.

We’ve just completed our discussion about the p-value, and how it is calculated both in general and more specifically for the z-test for the population proportion. Let’s go back to the four-step process of hypothesis testing and see what we’ve covered and what still needs to be discussed.

With respect to the z-test the population proportion:

Step 3: Completed

Step 4. This is what we will work on next.

Learn by Doing: Proportions (Step 3) Understanding P-values

Proportions (Step 4 & Summary)

Video: Proportions (Step 4 & Summary) (4:30)

Step 4. Drawing Conclusions Based on the P-Value

This last part of the four-step process of hypothesis testing is the same across all statistical tests, and actually, we’ve already said basically everything there is to say about it, but it can’t hurt to say it again.

The p-value is a measure of how much evidence the data present against Ho. The smaller the p-value, the more evidence the data present against Ho.

We already mentioned that what determines what constitutes enough evidence against Ho is the significance level (α, alpha), a cutoff point below which the p-value is considered small enough to reject Ho in favor of Ha. The most commonly used significance level is 0.05.

• Conclusion: There IS enough evidence that Ha is True
• Conclusion: There IS NOT enough evidence that Ha is True

Where instead of Ha is True , we write what this means in the words of the problem, in other words, in the context of the current scenario.

It is important to mention again that this step has essentially two sub-steps:

(i) Based on the p-value, determine whether or not the results are statistically significant (i.e., the data present enough evidence to reject Ho).

(ii) State your conclusions in the context of the problem.

Note: We always still must consider whether the results have any practical significance, particularly if they are statistically significant as a statistically significant result which has not practical use is essentially meaningless!

Let’s go back to our three examples and draw conclusions.

We found that the p-value for this test was 0.023.

Since 0.023 is small (in particular, 0.023 < 0.05), the data provide enough evidence to reject Ho.

Conclusion:

• There IS enough evidence that the proportion of defective products is less than 20% after the repair .

The following figure is the complete story of this example, and includes all the steps we went through, starting from stating the hypotheses and ending with our conclusions:

We found that the p-value for this test was 0.182.

Since .182 is not small (in particular, 0.182 > 0.05), the data do not provide enough evidence to reject Ho.

• There IS NOT enough evidence that the proportion of students at the college who use marijuana is higher than the national figure.

Here is the complete story of this example:

Learn by Doing: Learn by Doing – Proportions (Step 4)

We found that the p-value for this test was 0.021.

Since 0.021 is small (in particular, 0.021 < 0.05), the data provide enough evidence to reject Ho

• There IS enough evidence that the proportion of adults who support the death penalty for convicted murderers has changed since 2003.

Did I Get This?: Proportions (Step 4)

Many Students Wonder: Hypothesis Testing for the Population Proportion

Many students wonder why 5% is often selected as the significance level in hypothesis testing, and why 1% is the next most typical level. This is largely due to just convenience and tradition.

When Ronald Fisher (one of the founders of modern statistics) published one of his tables, he used a mathematically convenient scale that included 5% and 1%. Later, these same 5% and 1% levels were used by other people, in part just because Fisher was so highly esteemed. But mostly these are arbitrary levels.

The idea of selecting some sort of relatively small cutoff was historically important in the development of statistics; but it’s important to remember that there is really a continuous range of increasing confidence towards the alternative hypothesis, not a single all-or-nothing value. There isn’t much meaningful difference, for instance, between a p-value of .049 or .051, and it would be foolish to declare one case definitely a “real” effect and to declare the other case definitely a “random” effect. In either case, the study results were roughly 5% likely by chance if there’s no actual effect.

Whether such a p-value is sufficient for us to reject a particular null hypothesis ultimately depends on the risk of making the wrong decision, and the extent to which the hypothesized effect might contradict our prior experience or previous studies.

Let’s Summarize!!

We have now completed going through the four steps of hypothesis testing, and in particular we learned how they are applied to the z-test for the population proportion. Here is a brief summary:

Step 1: State the hypotheses

State the null hypothesis:

State the alternative hypothesis:

where the choice of the appropriate alternative (out of the three) is usually quite clear from the context of the problem. If you feel it is not clear, it is most likely a two-sided problem. Students are usually good at recognizing the “more than” and “less than” terminology but differences can sometimes be more difficult to spot, sometimes this is because you have preconceived ideas of how you think it should be! Use only the information given in the problem.

Step 2: Obtain data, check conditions, and summarize data

Obtain data from a sample and:

(i) Check whether the data satisfy the conditions which allow you to use this test.

random sample (or at least a sample that can be considered random in context)

the conditions under which the sampling distribution of p-hat is normal are met

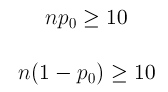
(ii) Calculate the sample proportion p-hat, and summarize the data using the test statistic:

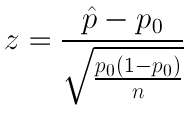
( Recall: This standardized test statistic represents how many standard deviations above or below p 0 our sample proportion p-hat is.)

Step 3: Find the p-value of the test by using the test statistic as follows

IMPORTANT FACT: In all future tests, we will rely on software to obtain the p-value.

When the alternative hypothesis is “less than” the probability of observing a test statistic as small as that observed or smaller , assuming that the values of the test statistic follow a standard normal distribution. We will now represent this probability in symbols and also using the normal distribution.

When the alternative hypothesis is “greater than” the probability of observing a test statistic as large as that observed or larger , assuming that the values of the test statistic follow a standard normal distribution. Again, we will represent this probability in symbols and using the normal distribution

When the alternative hypothesis is “not equal to” the probability of observing a test statistic which is as large in magnitude as that observed or larger, assuming that the values of the test statistic follow a standard normal distribution.

Step 4: Conclusion

Reach a conclusion first regarding the statistical significance of the results, and then determine what it means in the context of the problem.

If p-value ≤ 0.05 then WE REJECT Ho Conclusion: There IS enough evidence that Ha is True

If p-value > 0.05 then WE FAIL TO REJECT Ho Conclusion: There IS NOT enough evidence that Ha is True

Recall that: If the p-value is small (in particular, smaller than the significance level, which is usually 0.05), the results are statistically significant (in the sense that there is a statistically significant difference between what was observed in the sample and what was claimed in Ho), and so we reject Ho.

If the p-value is not small, we do not have enough statistical evidence to reject Ho, and so we continue to believe that Ho may be true. ( Remember: In hypothesis testing we never “accept” Ho ).

Finally, in practice, we should always consider the practical significance of the results as well as the statistical significance.

Learn by Doing: Z-Test for a Population Proportion

What’s next?

Before we move on to the next test, we are going to use the z-test for proportions to bring up and illustrate a few more very important issues regarding hypothesis testing. This might also be a good time to review the concepts of Type I error, Type II error, and Power before continuing on.

More about Hypothesis Testing

CO-1: Describe the roles biostatistics serves in the discipline of public health.

LO 1.11: Recognize the distinction between statistical significance and practical significance.

LO 6.30: Use a confidence interval to determine the correct conclusion to the associated two-sided hypothesis test.

Video: More about Hypothesis Testing (18:25)

The issues regarding hypothesis testing that we will discuss are:

• The effect of sample size on hypothesis testing.
• Statistical significance vs. practical importance.
• Hypothesis testing and confidence intervals—how are they related?

Let’s begin.

1. The Effect of Sample Size on Hypothesis Testing

We have already seen the effect that the sample size has on inference, when we discussed point and interval estimation for the population mean (μ, mu) and population proportion (p). Intuitively …

Larger sample sizes give us more information to pin down the true nature of the population. We can therefore expect the sample mean and sample proportion obtained from a larger sample to be closer to the population mean and proportion, respectively. As a result, for the same level of confidence, we can report a smaller margin of error, and get a narrower confidence interval. What we’ve seen, then, is that larger sample size gives a boost to how much we trust our sample results.

In hypothesis testing, larger sample sizes have a similar effect. We have also discussed that the power of our test increases when the sample size increases, all else remaining the same. This means, we have a better chance to detect the difference between the true value and the null value for larger samples.

The following two examples will illustrate that a larger sample size provides more convincing evidence (the test has greater power), and how the evidence manifests itself in hypothesis testing. Let’s go back to our example 2 (marijuana use at a certain liberal arts college).

We do not have enough evidence to conclude that the proportion of students at the college who use marijuana is higher than the national figure.

Now, let’s increase the sample size.

There are rumors that students in a certain liberal arts college are more inclined to use drugs than U.S. college students in general. Suppose that in a simple random sample of 400 students from the college, 76 admitted to marijuana use . Do the data provide enough evidence to conclude that the proportion of marijuana users among the students in the college (p) is higher than the national proportion, which is 0.157? (Reported by the Harvard School of Public Health).

Our results here are statistically significant . In other words, in example 2* the data provide enough evidence to reject Ho.

• Conclusion: There is enough evidence that the proportion of marijuana users at the college is higher than among all U.S. students.

What do we learn from this?

We see that sample results that are based on a larger sample carry more weight (have greater power).

In example 2, we saw that a sample proportion of 0.19 based on a sample of size of 100 was not enough evidence that the proportion of marijuana users in the college is higher than 0.157. Recall, from our general overview of hypothesis testing, that this conclusion (not having enough evidence to reject the null hypothesis) doesn’t mean the null hypothesis is necessarily true (so, we never “accept” the null); it only means that the particular study didn’t yield sufficient evidence to reject the null. It might be that the sample size was simply too small to detect a statistically significant difference.

However, in example 2*, we saw that when the sample proportion of 0.19 is obtained from a sample of size 400, it carries much more weight, and in particular, provides enough evidence that the proportion of marijuana users in the college is higher than 0.157 (the national figure). In this case, the sample size of 400 was large enough to detect a statistically significant difference.

The following activity will allow you to practice the ideas and terminology used in hypothesis testing when a result is not statistically significant.

Learn by Doing: Interpreting Non-significant Results

2. Statistical significance vs. practical importance.

Now, we will address the issue of statistical significance versus practical importance (which also involves issues of sample size).

The following activity will let you explore the effect of the sample size on the statistical significance of the results yourself, and more importantly will discuss issue 2: Statistical significance vs. practical importance.

Important Fact: In general, with a sufficiently large sample size you can make any result that has very little practical importance statistically significant! A large sample size alone does NOT make a “good” study!!

This suggests that when interpreting the results of a test, you should always think not only about the statistical significance of the results but also about their practical importance.

Learn by Doing: Statistical vs. Practical Significance

3. Hypothesis Testing and Confidence Intervals

The last topic we want to discuss is the relationship between hypothesis testing and confidence intervals. Even though the flavor of these two forms of inference is different (confidence intervals estimate a parameter, and hypothesis testing assesses the evidence in the data against one claim and in favor of another), there is a strong link between them.

We will explain this link (using the z-test and confidence interval for the population proportion), and then explain how confidence intervals can be used after a test has been carried out.

Recall that a confidence interval gives us a set of plausible values for the unknown population parameter. We may therefore examine a confidence interval to informally decide if a proposed value of population proportion seems plausible.

For example, if a 95% confidence interval for p, the proportion of all U.S. adults already familiar with Viagra in May 1998, was (0.61, 0.67), then it seems clear that we should be able to reject a claim that only 50% of all U.S. adults were familiar with the drug, since based on the confidence interval, 0.50 is not one of the plausible values for p.

In fact, the information provided by a confidence interval can be formally related to the information provided by a hypothesis test. ( Comment: The relationship is more straightforward for two-sided alternatives, and so we will not present results for the one-sided cases.)

Suppose we want to carry out the two-sided test:

• Ha: p ≠ p 0

using a significance level of 0.05.

An alternative way to perform this test is to find a 95% confidence interval for p and check:

• If p 0 falls outside the confidence interval, reject Ho.
• If p 0 falls inside the confidence interval, do not reject Ho.

In other words,

• If p 0 is not one of the plausible values for p, we reject Ho.
• If p 0 is a plausible value for p, we cannot reject Ho.

( Comment: Similarly, the results of a test using a significance level of 0.01 can be related to the 99% confidence interval.)

Let’s look at an example:

Recall example 3, where we wanted to know whether the proportion of U.S. adults who support the death penalty for convicted murderers has changed since 2003, when it was 0.64.

We are testing:

and as the figure reminds us, we took a sample of 1,000 U.S. adults, and the data told us that 675 supported the death penalty for convicted murderers (p-hat = 0.675).

A 95% confidence interval for p, the proportion of all U.S. adults who support the death penalty, is:

\(0.675 \pm 1.96 \sqrt{\dfrac{0.675(1-0.675)}{1000}} \approx 0.675 \pm 0.029=(0.646,0.704)\)

Since the 95% confidence interval for p does not include 0.64 as a plausible value for p, we can reject Ho and conclude (as we did before) that there is enough evidence that the proportion of U.S. adults who support the death penalty for convicted murderers has changed since 2003.

You and your roommate are arguing about whose turn it is to clean the apartment. Your roommate suggests that you settle this by tossing a coin and takes one out of a locked box he has on the shelf. Suspecting that the coin might not be fair, you decide to test it first. You toss the coin 80 times, thinking to yourself that if, indeed, the coin is fair, you should get around 40 heads. Instead you get 48 heads. You are puzzled. You are not sure whether getting 48 heads out of 80 is enough evidence to conclude that the coin is unbalanced, or whether this a result that could have happened just by chance when the coin is fair.

Statistics can help you answer this question.

Let p be the true proportion (probability) of heads. We want to test whether the coin is fair or not.

• Ho: p = 0.5 (the coin is fair).
• Ha: p ≠ 0.5 (the coin is not fair).

The data we have are that out of n = 80 tosses, we got 48 heads, or that the sample proportion of heads is p-hat = 48/80 = 0.6.

A 95% confidence interval for p, the true proportion of heads for this coin, is:

\(0.6 \pm 1.96 \sqrt{\dfrac{0.6(1-0.6)}{80}} \approx 0.6 \pm 0.11=(0.49,0.71)\)

Since in this case 0.5 is one of the plausible values for p, we cannot reject Ho. In other words, the data do not provide enough evidence to conclude that the coin is not fair.

The context of the last example is a good opportunity to bring up an important point that was discussed earlier.

Even though we use 0.05 as a cutoff to guide our decision about whether the results are statistically significant, we should not treat it as inviolable and we should always add our own judgment. Let’s look at the last example again.

It turns out that the p-value of this test is 0.0734. In other words, it is maybe not extremely unlikely, but it is quite unlikely (probability of 0.0734) that when you toss a fair coin 80 times you’ll get a sample proportion of heads of 48/80 = 0.6 (or even more extreme). It is true that using the 0.05 significance level (cutoff), 0.0734 is not considered small enough to conclude that the coin is not fair. However, if you really don’t want to clean the apartment, the p-value might be small enough for you to ask your roommate to use a different coin, or to provide one yourself!

Did I Get This?: Connection between Confidence Intervals and Hypothesis Tests

Did I Get This?: Hypothesis Tests for Proportions (Extra Practice)

Here is our final point on this subject:

When the data provide enough evidence to reject Ho, we can conclude (depending on the alternative hypothesis) that the population proportion is either less than, greater than, or not equal to the null value p 0 . However, we do not get a more informative statement about its actual value. It might be of interest, then, to follow the test with a 95% confidence interval that will give us more insight into the actual value of p.

In our example 3,

we concluded that the proportion of U.S. adults who support the death penalty for convicted murderers has changed since 2003, when it was 0.64. It is probably of interest not only to know that the proportion has changed, but also to estimate what it has changed to. We’ve calculated the 95% confidence interval for p on the previous page and found that it is (0.646, 0.704).

We can combine our conclusions from the test and the confidence interval and say:

Data provide evidence that the proportion of U.S. adults who support the death penalty for convicted murderers has changed since 2003, and we are 95% confident that it is now between 0.646 and 0.704. (i.e. between 64.6% and 70.4%).

Let’s look at our example 1 to see how a confidence interval following a test might be insightful in a different way.

Here is a summary of example 1:

We conclude that as a result of the repair, the proportion of defective products has been reduced to below 0.20 (which was the proportion prior to the repair). It is probably of great interest to the company not only to know that the proportion of defective has been reduced, but also estimate what it has been reduced to, to get a better sense of how effective the repair was. A 95% confidence interval for p in this case is:

\(0.16 \pm 1.96 \sqrt{\dfrac{0.16(1-0.16)}{400}} \approx 0.16 \pm 0.036=(0.124,0.196)\)

We can therefore say that the data provide evidence that the proportion of defective products has been reduced, and we are 95% confident that it has been reduced to somewhere between 12.4% and 19.6%. This is very useful information, since it tells us that even though the results were significant (i.e., the repair reduced the number of defective products), the repair might not have been effective enough, if it managed to reduce the number of defective products only to the range provided by the confidence interval. This, of course, ties back in to the idea of statistical significance vs. practical importance that we discussed earlier. Even though the results are statistically significant (Ho was rejected), practically speaking, the repair might still be considered ineffective.

Learn by Doing: Hypothesis Tests and Confidence Intervals

Even though this portion of the current section is about the z-test for population proportion, it is loaded with very important ideas that apply to hypothesis testing in general. We’ve already summarized the details that are specific to the z-test for proportions, so the purpose of this summary is to highlight the general ideas.

The process of hypothesis testing has four steps :

I. Stating the null and alternative hypotheses (Ho and Ha).

II. Obtaining a random sample (or at least one that can be considered random) and collecting data. Using the data:

Check that the conditions under which the test can be reliably used are met.

Summarize the data using a test statistic.

• The test statistic is a measure of the evidence in the data against Ho. The larger the test statistic is in magnitude, the more evidence the data present against Ho.

III. Finding the p-value of the test. The p-value is the probability of getting data like those observed (or even more extreme) assuming that the null hypothesis is true, and is calculated using the null distribution of the test statistic. The p-value is a measure of the evidence against Ho. The smaller the p-value, the more evidence the data present against Ho.

IV. Making conclusions.

Conclusions about the statistical significance of the results:

If the p-value is small, the data present enough evidence to reject Ho (and accept Ha).

If the p-value is not small, the data do not provide enough evidence to reject Ho.

To help guide our decision, we use the significance level as a cutoff for what is considered a small p-value. The significance cutoff is usually set at 0.05.

Conclusions should then be provided in the context of the problem.

Additional Important Ideas about Hypothesis Testing

• Results that are based on a larger sample carry more weight, and therefore as the sample size increases, results become more statistically significant.
• Even a very small and practically unimportant effect becomes statistically significant with a large enough sample size. The distinction between statistical significance and practical importance should therefore always be considered.
• Confidence intervals can be used in order to carry out two-sided tests (95% confidence for the 0.05 significance level). If the null value is not included in the confidence interval (i.e., is not one of the plausible values for the parameter), we have enough evidence to reject Ho. Otherwise, we cannot reject Ho.
• If the results are statistically significant, it might be of interest to follow up the tests with a confidence interval in order to get insight into the actual value of the parameter of interest.
• It is important to be aware that there are two types of errors in hypothesis testing ( Type I and Type II ) and that the power of a statistical test is an important measure of how likely we are to be able to detect a difference of interest to us in a particular problem.

Means (All Steps)

NOTE: Beginning on this page, the Learn By Doing and Did I Get This activities are presented as interactive PDF files. The interactivity may not work on mobile devices or with certain PDF viewers. Use an official ADOBE product such as ADOBE READER .

If you have any issues with the Learn By Doing or Did I Get This interactive PDF files, you can view all of the questions and answers presented on this page in this document:

• QUESTION/Answer (SPOILER ALERT!)

Tests About μ (mu) When σ (sigma) is Unknown – The t-test for a Population Mean

The t-distribution.

Video: Means (All Steps) (13:11)

So far we have talked about the logic behind hypothesis testing and then illustrated how this process proceeds in practice, using the z-test for the population proportion (p).

We are now moving on to discuss testing for the population mean (μ, mu), which is the parameter of interest when the variable of interest is quantitative.

A few comments about the structure of this section:

• The basic groundwork for carrying out hypothesis tests has already been laid in our general discussion and in our presentation of tests about proportions.

Therefore we can easily modify the four steps to carry out tests about means instead, without going into all of the details again.

We will use this approach for all future tests so be sure to go back to the discussion in general and for proportions to review the concepts in more detail.

• In our discussion about confidence intervals for the population mean, we made the distinction between whether the population standard deviation, σ (sigma) was known or if we needed to estimate this value using the sample standard deviation, s .

In this section, we will only discuss the second case as in most realistic settings we do not know the population standard deviation .

In this case we need to use the t- distribution instead of the standard normal distribution for the probability aspects of confidence intervals (choosing table values) and hypothesis tests (finding p-values).

• Although we will discuss some theoretical or conceptual details for some of the analyses we will learn, from this point on we will rely on software to conduct tests and calculate confidence intervals for us , while we focus on understanding which methods are used for which situations and what the results say in context.

If you are interested in more information about the z-test, where we assume the population standard deviation σ (sigma) is known, you can review the Carnegie Mellon Open Learning Statistics Course (you will need to click “ENTER COURSE”).

Like any other tests, the t- test for the population mean follows the four-step process:

• STEP 1: Stating the hypotheses H o and H a .
• STEP 2: Collecting relevant data, checking that the data satisfy the conditions which allow us to use this test, and summarizing the data using a test statistic.
• STEP 3: Finding the p-value of the test, the probability of obtaining data as extreme as those collected (or even more extreme, in the direction of the alternative hypothesis), assuming that the null hypothesis is true. In other words, how likely is it that the only reason for getting data like those observed is sampling variability (and not because H o is not true)?
• STEP 4: Drawing conclusions, assessing the statistical significance of the results based on the p-value, and stating our conclusions in context. (Do we or don’t we have evidence to reject H o and accept H a ?)
• Note: In practice, we should also always consider the practical significance of the results as well as the statistical significance.

We will now go through the four steps specifically for the t- test for the population mean and apply them to our two examples.

Only in a few cases is it reasonable to assume that the population standard deviation, σ (sigma), is known and so we will not cover hypothesis tests in this case. We discussed both cases for confidence intervals so that we could still calculate some confidence intervals by hand.

For this and all future tests we will rely on software to obtain our summary statistics, test statistics, and p-values for us.

The case where σ (sigma) is unknown is much more common in practice. What can we use to replace σ (sigma)? If you don’t know the population standard deviation, the best you can do is find the sample standard deviation, s, and use it instead of σ (sigma). (Note that this is exactly what we did when we discussed confidence intervals).

Is that it? Can we just use s instead of σ (sigma), and the rest is the same as the previous case? Unfortunately, it’s not that simple, but not very complicated either.

Here, when we use the sample standard deviation, s, as our estimate of σ (sigma) we can no longer use a normal distribution to find the cutoff for confidence intervals or the p-values for hypothesis tests.

Instead we must use the t- distribution (with n-1 degrees of freedom) to obtain the p-value for this test.

We discussed this issue for confidence intervals. We will talk more about the t- distribution after we discuss the details of this test for those who are interested in learning more.

It isn’t really necessary for us to understand this distribution but it is important that we use the correct distributions in practice via our software.

We will wait until UNIT 4B to look at how to accomplish this test in the software. For now focus on understanding the process and drawing the correct conclusions from the p-values given.

Now let’s go through the four steps in conducting the t- test for the population mean.

The null and alternative hypotheses for the t- test for the population mean (μ, mu) have exactly the same structure as the hypotheses for z-test for the population proportion (p):

The null hypothesis has the form:

• Ho: μ = μ 0 (mu = mu_zero)

(where μ 0 (mu_zero) is often called the null value)

• Ha: μ < μ 0 (mu < mu_zero) (one-sided)
• Ha: μ > μ 0 (mu > mu_zero) (one-sided)
• Ha: μ ≠ μ 0 (mu ≠ mu_zero) (two-sided)

where the choice of the appropriate alternative (out of the three) is usually quite clear from the context of the problem.

If you feel it is not clear, it is most likely a two-sided problem. Students are usually good at recognizing the “more than” and “less than” terminology but differences can sometimes be more difficult to spot, sometimes this is because you have preconceived ideas of how you think it should be! You also cannot use the information from the sample to help you determine the hypothesis. We would not know our data when we originally asked the question.

Now try it yourself. Here are a few exercises on stating the hypotheses for tests for a population mean.

Learn by Doing: State the Hypotheses for a test for a population mean

Here are a few more activities for practice.

Did I Get This?: State the Hypotheses for a test for a population mean

When setting up hypotheses, be sure to use only the information in the research question. We cannot use our sample data to help us set up our hypotheses.

For this test, it is still important to correctly choose the alternative hypothesis as “less than”, “greater than”, or “different” although generally in practice two-sample tests are used.

Obtain data from a sample:

• In this step we would obtain data from a sample. This is not something we do much of in courses but it is done very often in practice!

Check the conditions:

• Then we check the conditions under which this test (the t- test for one population mean) can be safely carried out – which are:
• The sample is random (or at least can be considered random in context).
• We are in one of the three situations marked with a green check mark in the following table (which ensure that x-bar is at least approximately normal and the test statistic using the sample standard deviation, s, is therefore a t- distribution with n-1 degrees of freedom – proving this is beyond the scope of this course):
• For large samples, we don’t need to check for normality in the population . We can rely on the sample size as the basis for the validity of using this test.
• For small samples , we need to have data from a normal population in order for the p-values and confidence intervals to be valid.

In practice, for small samples, it can be very difficult to determine if the population is normal. Here is a simulation to give you a better understanding of the difficulties.

Video: Simulations – Are Samples from a Normal Population? (4:58)

Now try it yourself with a few activities.

Learn by Doing: Checking Conditions for Hypothesis Testing for the Population Mean

• It is always a good idea to look at the data and get a sense of their pattern regardless of whether you actually need to do it in order to assess whether the conditions are met.
• This idea of looking at the data is relevant to all tests in general. In the next module—inference for relationships—conducting exploratory data analysis before inference will be an integral part of the process.

Here are a few more problems for extra practice.

Did I Get This?: Checking Conditions for Hypothesis Testing for the Population Mean

When setting up hypotheses, be sure to use only the information in the res

Calculate Test Statistic

Assuming that the conditions are met, we calculate the sample mean x-bar and the sample standard deviation, s (which estimates σ (sigma)), and summarize the data with a test statistic.

The test statistic for the t -test for the population mean is:

\(t=\dfrac{\bar{x} - \mu_0}{s/ \sqrt{n}}\)

Recall that such a standardized test statistic represents how many standard deviations above or below μ 0 (mu_zero) our sample mean x-bar is.

Therefore our test statistic is a measure of how different our data are from what is claimed in the null hypothesis. This is an idea that we mentioned in the previous test as well.

Again we will rely on the p-value to determine how unusual our data would be if the null hypothesis is true.

As we mentioned, the test statistic in the t -test for a population mean does not follow a standard normal distribution. Rather, it follows another bell-shaped distribution called the t- distribution.

We will present the details of this distribution at the end for those interested but for now we will work on the process of the test.

Here are a few important facts.

• In statistical language we say that the null distribution of our test statistic is the t- distribution with (n-1) degrees of freedom. In other words, when Ho is true (i.e., when μ = μ 0 (mu = mu_zero)), our test statistic has a t- distribution with (n-1) d.f., and this is the distribution under which we find p-values.
• For a large sample size (n), the null distribution of the test statistic is approximately Z, so whether we use t (n – 1) or Z to calculate the p-values does not make a big difference. However, software will use the t -distribution regardless of the sample size and so will we.

Although we will not calculate p-values by hand for this test, we can still easily calculate the test statistic.

Try it yourself:

Learn by Doing: Calculate the Test Statistic for a Test for a Population Mean

From this point in this course and certainly in practice we will allow the software to calculate our test statistics and we will use the p-values provided to draw our conclusions.

We will use software to obtain the p-value for this (and all future) tests but here are the images illustrating how the p-value is calculated in each of the three cases corresponding to the three choices for our alternative hypothesis.

Note that due to the symmetry of the t distribution, for a given value of the test statistic t, the p-value for the two-sided test is twice as large as the p-value of either of the one-sided tests. The same thing happens when p-values are calculated under the t distribution as when they are calculated under the Z distribution.

We will show some examples of p-values obtained from software in our examples. For now let’s continue our summary of the steps.

As usual, based on the p-value (and some significance level of choice) we assess the statistical significance of results, and draw our conclusions in context.

To review what we have said before:

If p-value ≤ 0.05 then WE REJECT Ho

If p-value > 0.05 then WE FAIL TO REJECT Ho

This step has essentially two sub-steps:

We are now ready to look at two examples.

A certain prescription medicine is supposed to contain an average of 250 parts per million (ppm) of a certain chemical. If the concentration is higher than this, the drug may cause harmful side effects; if it is lower, the drug may be ineffective.

The manufacturer runs a check to see if the mean concentration in a large shipment conforms to the target level of 250 ppm or not.

A simple random sample of 100 portions is tested, and the sample mean concentration is found to be 247 ppm with a sample standard deviation of 12 ppm.

Here is a figure that represents this example:

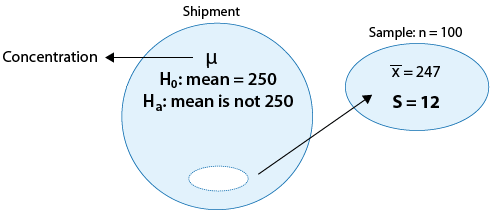
1. The hypotheses being tested are:

• Ha: μ ≠ μ 0 (mu ≠ mu_zero)
• Where μ = population mean part per million of the chemical in the entire shipment

2. The conditions that allow us to use the t-test are met since:

• The sample is random
• The sample size is large enough for the Central Limit Theorem to apply and ensure the normality of x-bar. We do not need normality of the population in order to be able to conduct this test for the population mean. We are in the 2 nd column in the table below.
• The test statistic is:

\(t=\dfrac{\bar{x}-\mu_{0}}{s / \sqrt{n}}=\dfrac{247-250}{12 / \sqrt{100}}=-2.5\)

• The data (represented by the sample mean) are 2.5 standard errors below the null value.

3. Finding the p-value.

• To find the p-value we use statistical software, and we calculate a p-value of 0.014.

4. Conclusions:

• The p-value is small (.014) indicating that at the 5% significance level, the results are significant.
• We reject the null hypothesis.
• There is enough evidence to conclude that the mean concentration in entire shipment is not the required 250 ppm.
• It is difficult to comment on the practical significance of this result without more understanding of the practical considerations of this problem.

Here is a summary:

• The 95% confidence interval for μ (mu) can be used here in the same way as for proportions to conduct the two-sided test (checking whether the null value falls inside or outside the confidence interval) or following a t- test where Ho was rejected to get insight into the value of μ (mu).
• We find the 95% confidence interval to be (244.619, 249.381) . Since 250 is not in the interval we know we would reject our null hypothesis that μ (mu) = 250. The confidence interval gives additional information. By accounting for estimation error, it estimates that the population mean is likely to be between 244.62 and 249.38. This is lower than the target concentration and that information might help determine the seriousness and appropriate course of action in this situation.

In most situations in practice we use TWO-SIDED HYPOTHESIS TESTS, followed by confidence intervals to gain more insight.

For completeness in covering one sample t-tests for a population mean, we still cover all three possible alternative hypotheses here HOWEVER, this will be the last test for which we will do so.

A research study measured the pulse rates of 57 college men and found a mean pulse rate of 70 beats per minute with a standard deviation of 9.85 beats per minute.

Researchers want to know if the mean pulse rate for all college men is different from the current standard of 72 beats per minute.

• The hypotheses being tested are:
• Ho: μ = 72
• Ha: μ ≠ 72
• Where μ = population mean heart rate among college men
• The conditions that allow us to use the t- test are met since:
• The sample is random.
• The sample size is large (n = 57) so we do not need normality of the population in order to be able to conduct this test for the population mean. We are in the 2 nd column in the table below.

\(t=\dfrac{\bar{x}-\mu}{s / \sqrt{n}}=\dfrac{70-72}{9.85 / \sqrt{57}}=-1.53\)

• The data (represented by the sample mean) are 1.53 estimated standard errors below the null value.
• Recall that in general the p-value is calculated under the null distribution of the test statistic, which, in the t- test case, is t (n-1). In our case, in which n = 57, the p-value is calculated under the t (56) distribution. Using statistical software, we find that the p-value is 0.132 .
• Here is how we calculated the p-value. http://homepage.stat.uiowa.edu/~mbognar/applets/t.html .

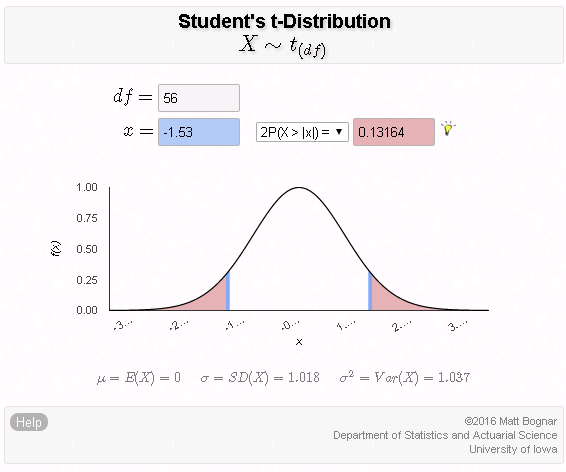
4. Making conclusions.

• The p-value (0.132) is not small, indicating that the results are not significant.
• We fail to reject the null hypothesis.
• There is not enough evidence to conclude that the mean pulse rate for all college men is different from the current standard of 72 beats per minute.
• The results from this sample do not appear to have any practical significance either with a mean pulse rate of 70, this is very similar to the hypothesized value, relative to the variation expected in pulse rates.

Now try a few yourself.

Learn by Doing: Hypothesis Testing for the Population Mean

From this point in this course and certainly in practice we will allow the software to calculate our test statistic and p-value and we will use the p-values provided to draw our conclusions.

That concludes our discussion of hypothesis tests in Unit 4A.

In the next unit we will continue to use both confidence intervals and hypothesis test to investigate the relationship between two variables in the cases we covered in Unit 1 on exploratory data analysis – we will look at Case CQ, Case CC, and Case QQ.

Before moving on, we will discuss the details about the t- distribution as a general object.

We have seen that variables can be visually modeled by many different sorts of shapes, and we call these shapes distributions. Several distributions arise so frequently that they have been given special names, and they have been studied mathematically.

So far in the course, the only one we’ve named, for continuous quantitative variables, is the normal distribution, but there are others. One of them is called the t- distribution.

The t- distribution is another bell-shaped (unimodal and symmetric) distribution, like the normal distribution; and the center of the t- distribution is standardized at zero, like the center of the standard normal distribution.

Like all distributions that are used as probability models, the normal and the t- distribution are both scaled, so the total area under each of them is 1.

So how is the t-distribution fundamentally different from the normal distribution?

• The spread .

The following picture illustrates the fundamental difference between the normal distribution and the t-distribution:

Here we have an image which illustrates the fundamental difference between the normal distribution and the t- distribution:

You can see in the picture that the t- distribution has slightly less area near the expected central value than the normal distribution does, and you can see that the t distribution has correspondingly more area in the “tails” than the normal distribution does. (It’s often said that the t- distribution has “fatter tails” or “heavier tails” than the normal distribution.)

This reflects the fact that the t- distribution has a larger spread than the normal distribution. The same total area of 1 is spread out over a slightly wider range on the t- distribution, making it a bit lower near the center compared to the normal distribution, and giving the t- distribution slightly more probability in the ‘tails’ compared to the normal distribution.

Therefore, the t- distribution ends up being the appropriate model in certain cases where there is more variability than would be predicted by the normal distribution. One of these cases is stock values, which have more variability (or “volatility,” to use the economic term) than would be predicted by the normal distribution.

There’s actually an entire family of t- distributions. They all have similar formulas (but the math is beyond the scope of this introductory course in statistics), and they all have slightly “fatter tails” than the normal distribution. But some are closer to normal than others.

The t- distributions that have higher “degrees of freedom” are closer to normal (degrees of freedom is a mathematical concept that we won’t study in this course, beyond merely mentioning it here). So, there’s a t- distribution “with one degree of freedom,” another t- distribution “with 2 degrees of freedom” which is slightly closer to normal, another t- distribution “with 3 degrees of freedom” which is a bit closer to normal than the previous ones, and so on.

The following picture illustrates this idea with just a couple of t- distributions (note that “degrees of freedom” is abbreviated “d.f.” on the picture):

The test statistic for our t-test for one population mean is a t -score which follows a t- distribution with (n – 1) degrees of freedom. Recall that each t- distribution is indexed according to “degrees of freedom.” Notice that, in the context of a test for a mean, the degrees of freedom depend on the sample size in the study.

Remember that we said that higher degrees of freedom indicate that the t- distribution is closer to normal. So in the context of a test for the mean, the larger the sample size , the higher the degrees of freedom, and the closer the t- distribution is to a normal z distribution .

As a result, in the context of a test for a mean, the effect of the t- distribution is most important for a study with a relatively small sample size .

We are now done introducing the t-distribution. What are implications of all of this?

• The null distribution of our t-test statistic is the t-distribution with (n-1) d.f. In other words, when Ho is true (i.e., when μ = μ 0 (mu = mu_zero)), our test statistic has a t-distribution with (n-1) d.f., and this is the distribution under which we find p-values.
• For a large sample size (n), the null distribution of the test statistic is approximately Z, so whether we use t(n – 1) or Z to calculate the p-values does not make a big difference.

Epidemiology & Biostatistics

• Evaluating Tests including sensitivity & specificity
• Risk Calculations
• Measures of Disease
• Hypothesis Testing and Power Analysis

Hypothesis Testing

Statistical power.

• Infection Control
• Aspects of Disease including disease prevention
• Biostatistics

There are two types of hypotheses:

• The Statistical (Null) Hypothesis is always stated as if that there is not a relationship between the variables. This might sound funny because researchers conduct studies because they think that there will be a difference or a relationship between variables. But, statistical testing starts with the assumption that there is not a relationship or difference. This is why the statistical hypothesis is called the null (none, nothing) hypotheses. For example, even though we think that a new medication will reduce the number of strokes, and we start with a research (alternative) hypothesis that Drug X is associated with a reduction in the number of strokes, the null hypothesis would be that Drug X has no relationship to the number of strokes.
• The Research (Alternative) Hypothesis states what the researcher 'thinks' or hypothesizes' will happen. For example, if a team of researchers wants to determine whether that a new medication will reduce the number of strokes, they would write a research (alternative) hypothesis such as, "The antihypertensive medication (Drug X) is associated with significantly fewer strokes when compared to the older medication (Drug Z).

There are two types of hypothesis testing errors:

• A type 1 error occurs when you incorrectly reject the null hypothesis and, thus, incorrectly accept the research (alternative) hypothesis. Since the null hypothesis states that there is no relationship between the variables or no difference between the groups, when you make a type 1 error you incorrectly reject the null hypothesis and incorrectly accept the research (alternative) hypothesis. That means that the researcher incorrectly concludes that there is a relationship or difference when there really is not one. This is important because it means that you incorrectly conclude that a new drug, treatment, or other intervention works when it really does not work. Another example of a type 1 error occurs during a jury trial, when the jury decides that the person is guilty based on the evidence provided, even though the person is not guilty and did not commit the crime.
• A type 2 error occurs when you incorrectly accept the null hypothesis and, thus, incorrectly reject the alternative hypothesis. Since the null hypothesis states that there is no relationship between the variables or no difference between the groups, when you make a type 2 error you incorrectly accept the 'no relationship/no difference' and incorrectly reject the alternative hypothesis that there is a relationship between the variables or a difference between the groups. So, you incorrectly determine that there is no relationship or difference when there really is one. This is important because it means that you incorrectly conclude that a new drug, treatment, or intervention does not work when it really does work. Another example of a type 2 error occurs during a jury trial when the jury decides that the accused person is not guilty, even though they really did commit the crime and are guilty.

It is important to note that sample size plays an important role in determining statistical significance. When the sample size is too small, there may not be enough observations to be able to determine whether there is a statistically significant difference or relationship between the variables. So, too small of a sample size increases the risk of a type 2 error and incorrectly accepting the null hypothesis when there actually is a difference or relationship present. Small sample size is a common problem in student projects, so it is important to be aware that the failure to find a statistically significant difference may be due to small sample size (lack of statistical power).

Statistical Power is the ability to discern a deviation from the null hypothesis.  In short, a researcher who wants adequate statistical power must enlist a minimal number of participants for their particular study. There are many ways to calculate the minimal number of participants. One tool is G*Power:

• G*Power Free tool to compute statistical power analyses
• << Previous: Measures of Disease
• Next: Infection Control >>
• Last Updated: Oct 10, 2022 4:02 PM
• URL: https://library.frontier.edu/epi

Descriptive Epidemiology

•   1  
• |   2  
• |   3  
• |   4  
• |   5  
• |   6  
• |   7  
• |   8  
• |   9  

Epi_Tools.XLSX

All Modules

Hypothesis Formulation – Characteristics of Person, Place, and Time

Descriptive epidemiology searches for patterns by examining characteristics of person, place, & time . These characteristics are carefully considered when a disease outbreak occurs, because they provide important clues regarding the source of the outbreak.

Hypotheses about the determinants of disease arise from considering the characteristics of person, place, and time and looking for differences, similarities, and correlations. Consider the following examples:

• Differences : if the frequency of disease differs in two circumstances, it may be caused by a factor that differs between the two circumstances. For example , there was a substantial difference in the incidence of stomach cancer in Japan & the US. There are also substantial differences in genetics and diet. Perhaps these factors are related to stomach cancer.
• Similarities : if a high frequency of disease is found in several different circumstances & one can identify a common factor, then the common factor may be responsible. Example : AIDS in IV drug users, recipients of transfusions, & hemophiliacs suggests the possibility that HIV can be transmitted via blood or blood products.
• Correlations: If the frequency of disease varies in relation to some factor, then that factor may be a cause of the disease. Example: differences in coronary heart disease vary with cigarettes consumption.

Descriptive epidemiology provides a way of organizing and analyzing data on health and disease in order to understand variations in disease frequency geographically and over time and how disease varies among people based on a host of personal characteristics (person, place, and time). Epidemiology had its origins in the desire to understand the determinants of acute infectious diseases, but its methods and applicability have expanded to include chronic diseases as well.

Descriptive Epidemiology for Infectious Disease Outbreaks

Outbreaks generally come to the attention of state or local health departments in one of two ways:

• Astute individuals (citizens, physicians, nurses, laboratory workers) will sometimes notice cases of disease occurring close together with respect to time and/or location or they will notice several individuals with unusual features of disease and report them to health authorities.
• Public health surveillance systems collect data on 'reportable diseases'. Requirements for reporting infectious diseases in Massachusetts are described in 105 CMR 300.000 ( Link to Reportable Diseases, Surveillance, and Isolation and Quarantine Requirements ).

Clues About the Source of an Outbreak of Infectious Disease

When an outbreak occurs, one of the first things that should be considered is what is known about that particular disease. How can the disease be transmitted? In what settings is it commonly found? What is the incubation period? There are many good summaries available online. For example, Massachusetts DPH provides this link to a PDF fact sheet for Hepatitis A , which provide a very succinct summary. With this background information in mind, the initial task is to begin to characterize the cases in terms of personal characteristics, location, and time (when did they become ill and where might they have been exposed given the incubation period for that disease. In sense, we are looking for the common element that explains why all of these people became ill. What do they have in common?

"Person"

Information about the cases is typically recorded in a "line listing," a grid on which information for each case is summarized with a separate column for each variable. Demographic information is always relevant, e.g., age, sex, and address, because they are often the characteristics most strongly related to exposure and to the risk of disease. In the beginning of an investigation a small number of cases will be interviewed to look for some common link. These are referred to as "hypothesis-generating interviews." Depending on the means by which the disease is generally transmitted, the investigator might also want to know about other personal characteristics, such as travel, occupation, leisure activities, use of medications, tobacco, drugs. What did these victims have in common? Where did they do their grocery shopping? What restaurants had they gone to in the past month or so? Had they traveled? Had they been exposed to other people who had been ill? Other characteristics will be more specific to the disease under investigation and the setting of the outbreak. For example, if you were investigating an outbreak of hepatitis B, you should consider the usual high-risk exposures for that infection, such as intravenous drug use, sexual contacts, and health care employment. Of course, with an outbreak of foodborne illness (such as hepatitis A), it would be important to ask many questions about possible food exposures. Where do you generally eat your meals? Do you ever eat at restaurants or obtain foods from sources outside the home? Hypothesis generating interviews may quickly reveal some commonalities that provide clues about the possible sources.

"Place"

Assessment of an outbreak by place provides information on the geographic extent of a problem and may also show clusters or patterns that provide clues to the identity and origins of the problem. A simple and useful technique for looking at geographic patterns is to plot, on a "spot map" of the area, where the affected people live, work, or may have been exposed. A spot map of cases may show clusters or patterns that reflect water supplies, wind currents, or proximity to a restaurant or grocery store.

In 1854 there was an epidemic of cholera in the Broad Street area of London. John Snow determined the residence or place of business of the victims and plotted them on a street map (the stacked black disks on the map below). He noted that the cases were clustered around the Broad Street community pump. It was also noteworthy that there were large numbers of workers in a local workhouse and a brewery, but none of these workers were affected - the workhouse and brewery each had their own well.

On a spot map within a hospital, nursing home, or other such facility, clustering usually indicates either a focal source or person-to-person spread, while the scattering of cases throughout a facility is more consistent with a common source such as a dining hall. In studying an outbreak of surgical wound infections in a hospital, we might plot cases by operating room, recovery room, and ward room to look for clustering.

• Link to more on the outbreak of cholera in the Broad Street area of London
• Link to an enlarged version of Snow's spot map

"Time"

When investigating the source of an outbreak of infectious disease, Investigators record the date of onset of disease for each of the victims and then plot the onset of new cases over time to create what is referred to as an epidemic curve . The epidemic curve for an outbreak of hepatitis A is shown in the illustration below. Begriming in late April, the number of new cases rises to a peak of twelve new cases reported on May 12, and then the number of new cases gradually drops back to zero by May 21. Knowing that the incubation period for hepatitis A averages about 28-30 days, the investigators concluded that this was a point source epidemic because the cluster of new cases all occurred within the span of a single incubation period (see explanation on the next page). This, in conjunction with other information, provided important clues that helped shape their hypotheses about the source of the outbreak.

Video Summary: Person, Place, and Time (10:42)

return to top | previous page | next page

Content ©2017. All Rights Reserved. Date last modified: May 5, 2017. Wayne W. LaMorte, MD, PhD, MPH

An official website of the United States government

The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

• Publications
• Account settings

Preview improvements coming to the PMC website in October 2024. Learn More or Try it out now .

• Advanced Search
• Journal List
• Ind Psychiatry J
• v.18(2); Jul-Dec 2009

Hypothesis testing, type I and type II errors

Amitav banerjee.

Department of Community Medicine, D. Y. Patil Medical College, Pune, India

U. B. Chitnis

S. l. jadhav, j. s. bhawalkar, s. chaudhury.

1 Department of Psychiatry, RINPAS, Kanke, Ranchi, India

Hypothesis testing is an important activity of empirical research and evidence-based medicine. A well worked up hypothesis is half the answer to the research question. For this, both knowledge of the subject derived from extensive review of the literature and working knowledge of basic statistical concepts are desirable. The present paper discusses the methods of working up a good hypothesis and statistical concepts of hypothesis testing.

Karl Popper is probably the most influential philosopher of science in the 20 th century (Wulff et al ., 1986). Many scientists, even those who do not usually read books on philosophy, are acquainted with the basic principles of his views on science. The popularity of Popper’s philosophy is due partly to the fact that it has been well explained in simple terms by, among others, the Nobel Prize winner Peter Medawar (Medawar, 1969). Popper makes the very important point that empirical scientists (those who stress on observations only as the starting point of research) put the cart in front of the horse when they claim that science proceeds from observation to theory, since there is no such thing as a pure observation which does not depend on theory. Popper states, “… the belief that we can start with pure observation alone, without anything in the nature of a theory, is absurd: As may be illustrated by the story of the man who dedicated his life to natural science, wrote down everything he could observe, and bequeathed his ‘priceless’ collection of observations to the Royal Society to be used as inductive (empirical) evidence.

STARTING POINT OF RESEARCH: HYPOTHESIS OR OBSERVATION?

The first step in the scientific process is not observation but the generation of a hypothesis which may then be tested critically by observations and experiments. Popper also makes the important claim that the goal of the scientist’s efforts is not the verification but the falsification of the initial hypothesis. It is logically impossible to verify the truth of a general law by repeated observations, but, at least in principle, it is possible to falsify such a law by a single observation. Repeated observations of white swans did not prove that all swans are white, but the observation of a single black swan sufficed to falsify that general statement (Popper, 1976).

CHARACTERISTICS OF A GOOD HYPOTHESIS

A good hypothesis must be based on a good research question. It should be simple, specific and stated in advance (Hulley et al ., 2001).

Hypothesis should be simple

A simple hypothesis contains one predictor and one outcome variable, e.g. positive family history of schizophrenia increases the risk of developing the condition in first-degree relatives. Here the single predictor variable is positive family history of schizophrenia and the outcome variable is schizophrenia. A complex hypothesis contains more than one predictor variable or more than one outcome variable, e.g., a positive family history and stressful life events are associated with an increased incidence of Alzheimer’s disease. Here there are 2 predictor variables, i.e., positive family history and stressful life events, while one outcome variable, i.e., Alzheimer’s disease. Complex hypothesis like this cannot be easily tested with a single statistical test and should always be separated into 2 or more simple hypotheses.

Hypothesis should be specific

A specific hypothesis leaves no ambiguity about the subjects and variables, or about how the test of statistical significance will be applied. It uses concise operational definitions that summarize the nature and source of the subjects and the approach to measuring variables (History of medication with tranquilizers, as measured by review of medical store records and physicians’ prescriptions in the past year, is more common in patients who attempted suicides than in controls hospitalized for other conditions). This is a long-winded sentence, but it explicitly states the nature of predictor and outcome variables, how they will be measured and the research hypothesis. Often these details may be included in the study proposal and may not be stated in the research hypothesis. However, they should be clear in the mind of the investigator while conceptualizing the study.

Hypothesis should be stated in advance

The hypothesis must be stated in writing during the proposal state. This will help to keep the research effort focused on the primary objective and create a stronger basis for interpreting the study’s results as compared to a hypothesis that emerges as a result of inspecting the data. The habit of post hoc hypothesis testing (common among researchers) is nothing but using third-degree methods on the data (data dredging), to yield at least something significant. This leads to overrating the occasional chance associations in the study.

TYPES OF HYPOTHESES

For the purpose of testing statistical significance, hypotheses are classified by the way they describe the expected difference between the study groups.

Null and alternative hypotheses

The null hypothesis states that there is no association between the predictor and outcome variables in the population (There is no difference between tranquilizer habits of patients with attempted suicides and those of age- and sex- matched “control” patients hospitalized for other diagnoses). The null hypothesis is the formal basis for testing statistical significance. By starting with the proposition that there is no association, statistical tests can estimate the probability that an observed association could be due to chance.

The proposition that there is an association — that patients with attempted suicides will report different tranquilizer habits from those of the controls — is called the alternative hypothesis. The alternative hypothesis cannot be tested directly; it is accepted by exclusion if the test of statistical significance rejects the null hypothesis.

One- and two-tailed alternative hypotheses

A one-tailed (or one-sided) hypothesis specifies the direction of the association between the predictor and outcome variables. The prediction that patients of attempted suicides will have a higher rate of use of tranquilizers than control patients is a one-tailed hypothesis. A two-tailed hypothesis states only that an association exists; it does not specify the direction. The prediction that patients with attempted suicides will have a different rate of tranquilizer use — either higher or lower than control patients — is a two-tailed hypothesis. (The word tails refers to the tail ends of the statistical distribution such as the familiar bell-shaped normal curve that is used to test a hypothesis. One tail represents a positive effect or association; the other, a negative effect.) A one-tailed hypothesis has the statistical advantage of permitting a smaller sample size as compared to that permissible by a two-tailed hypothesis. Unfortunately, one-tailed hypotheses are not always appropriate; in fact, some investigators believe that they should never be used. However, they are appropriate when only one direction for the association is important or biologically meaningful. An example is the one-sided hypothesis that a drug has a greater frequency of side effects than a placebo; the possibility that the drug has fewer side effects than the placebo is not worth testing. Whatever strategy is used, it should be stated in advance; otherwise, it would lack statistical rigor. Data dredging after it has been collected and post hoc deciding to change over to one-tailed hypothesis testing to reduce the sample size and P value are indicative of lack of scientific integrity.

STATISTICAL PRINCIPLES OF HYPOTHESIS TESTING

A hypothesis (for example, Tamiflu [oseltamivir], drug of choice in H1N1 influenza, is associated with an increased incidence of acute psychotic manifestations) is either true or false in the real world. Because the investigator cannot study all people who are at risk, he must test the hypothesis in a sample of that target population. No matter how many data a researcher collects, he can never absolutely prove (or disprove) his hypothesis. There will always be a need to draw inferences about phenomena in the population from events observed in the sample (Hulley et al ., 2001). In some ways, the investigator’s problem is similar to that faced by a judge judging a defendant [ Table 1 ]. The absolute truth whether the defendant committed the crime cannot be determined. Instead, the judge begins by presuming innocence — the defendant did not commit the crime. The judge must decide whether there is sufficient evidence to reject the presumed innocence of the defendant; the standard is known as beyond a reasonable doubt. A judge can err, however, by convicting a defendant who is innocent, or by failing to convict one who is actually guilty. In similar fashion, the investigator starts by presuming the null hypothesis, or no association between the predictor and outcome variables in the population. Based on the data collected in his sample, the investigator uses statistical tests to determine whether there is sufficient evidence to reject the null hypothesis in favor of the alternative hypothesis that there is an association in the population. The standard for these tests is shown as the level of statistical significance.

The analogy between judge’s decisions and statistical tests

TYPE I (ALSO KNOWN AS ‘α’) AND TYPE II (ALSO KNOWN AS ‘β’)ERRORS

Just like a judge’s conclusion, an investigator’s conclusion may be wrong. Sometimes, by chance alone, a sample is not representative of the population. Thus the results in the sample do not reflect reality in the population, and the random error leads to an erroneous inference. A type I error (false-positive) occurs if an investigator rejects a null hypothesis that is actually true in the population; a type II error (false-negative) occurs if the investigator fails to reject a null hypothesis that is actually false in the population. Although type I and type II errors can never be avoided entirely, the investigator can reduce their likelihood by increasing the sample size (the larger the sample, the lesser is the likelihood that it will differ substantially from the population).

False-positive and false-negative results can also occur because of bias (observer, instrument, recall, etc.). (Errors due to bias, however, are not referred to as type I and type II errors.) Such errors are troublesome, since they may be difficult to detect and cannot usually be quantified.

EFFECT SIZE

The likelihood that a study will be able to detect an association between a predictor variable and an outcome variable depends, of course, on the actual magnitude of that association in the target population. If it is large (such as 90% increase in the incidence of psychosis in people who are on Tamiflu), it will be easy to detect in the sample. Conversely, if the size of the association is small (such as 2% increase in psychosis), it will be difficult to detect in the sample. Unfortunately, the investigator often does not know the actual magnitude of the association — one of the purposes of the study is to estimate it. Instead, the investigator must choose the size of the association that he would like to be able to detect in the sample. This quantity is known as the effect size. Selecting an appropriate effect size is the most difficult aspect of sample size planning. Sometimes, the investigator can use data from other studies or pilot tests to make an informed guess about a reasonable effect size. When there are no data with which to estimate it, he can choose the smallest effect size that would be clinically meaningful, for example, a 10% increase in the incidence of psychosis. Of course, from the public health point of view, even a 1% increase in psychosis incidence would be important. Thus the choice of the effect size is always somewhat arbitrary, and considerations of feasibility are often paramount. When the number of available subjects is limited, the investigator may have to work backward to determine whether the effect size that his study will be able to detect with that number of subjects is reasonable.

α,β,AND POWER

After a study is completed, the investigator uses statistical tests to try to reject the null hypothesis in favor of its alternative (much in the same way that a prosecuting attorney tries to convince a judge to reject innocence in favor of guilt). Depending on whether the null hypothesis is true or false in the target population, and assuming that the study is free of bias, 4 situations are possible, as shown in Table 2 below. In 2 of these, the findings in the sample and reality in the population are concordant, and the investigator’s inference will be correct. In the other 2 situations, either a type I (α) or a type II (β) error has been made, and the inference will be incorrect.

Truth in the population versus the results in the study sample: The four possibilities

The investigator establishes the maximum chance of making type I and type II errors in advance of the study. The probability of committing a type I error (rejecting the null hypothesis when it is actually true) is called α (alpha) the other name for this is the level of statistical significance.

If a study of Tamiflu and psychosis is designed with α = 0.05, for example, then the investigator has set 5% as the maximum chance of incorrectly rejecting the null hypothesis (and erroneously inferring that use of Tamiflu and psychosis incidence are associated in the population). This is the level of reasonable doubt that the investigator is willing to accept when he uses statistical tests to analyze the data after the study is completed.

The probability of making a type II error (failing to reject the null hypothesis when it is actually false) is called β (beta). The quantity (1 - β) is called power, the probability of observing an effect in the sample (if one), of a specified effect size or greater exists in the population.

If β is set at 0.10, then the investigator has decided that he is willing to accept a 10% chance of missing an association of a given effect size between Tamiflu and psychosis. This represents a power of 0.90, i.e., a 90% chance of finding an association of that size. For example, suppose that there really would be a 30% increase in psychosis incidence if the entire population took Tamiflu. Then 90 times out of 100, the investigator would observe an effect of that size or larger in his study. This does not mean, however, that the investigator will be absolutely unable to detect a smaller effect; just that he will have less than 90% likelihood of doing so.

Ideally alpha and beta errors would be set at zero, eliminating the possibility of false-positive and false-negative results. In practice they are made as small as possible. Reducing them, however, usually requires increasing the sample size. Sample size planning aims at choosing a sufficient number of subjects to keep alpha and beta at acceptably low levels without making the study unnecessarily expensive or difficult.

Many studies s et al pha at 0.05 and beta at 0.20 (a power of 0.80). These are somewhat arbitrary values, and others are sometimes used; the conventional range for alpha is between 0.01 and 0.10; and for beta, between 0.05 and 0.20. In general the investigator should choose a low value of alpha when the research question makes it particularly important to avoid a type I (false-positive) error, and he should choose a low value of beta when it is especially important to avoid a type II error.

The null hypothesis acts like a punching bag: It is assumed to be true in order to shadowbox it into false with a statistical test. When the data are analyzed, such tests determine the P value, the probability of obtaining the study results by chance if the null hypothesis is true. The null hypothesis is rejected in favor of the alternative hypothesis if the P value is less than alpha, the predetermined level of statistical significance (Daniel, 2000). “Nonsignificant” results — those with P value greater than alpha — do not imply that there is no association in the population; they only mean that the association observed in the sample is small compared with what could have occurred by chance alone. For example, an investigator might find that men with family history of mental illness were twice as likely to develop schizophrenia as those with no family history, but with a P value of 0.09. This means that even if family history and schizophrenia were not associated in the population, there was a 9% chance of finding such an association due to random error in the sample. If the investigator had set the significance level at 0.05, he would have to conclude that the association in the sample was “not statistically significant.” It might be tempting for the investigator to change his mind about the level of statistical significance ex post facto and report the results “showed statistical significance at P < 10”. A better choice would be to report that the “results, although suggestive of an association, did not achieve statistical significance ( P = .09)”. This solution acknowledges that statistical significance is not an “all or none” situation.

Hypothesis testing is the sheet anchor of empirical research and in the rapidly emerging practice of evidence-based medicine. However, empirical research and, ipso facto, hypothesis testing have their limits. The empirical approach to research cannot eliminate uncertainty completely. At the best, it can quantify uncertainty. This uncertainty can be of 2 types: Type I error (falsely rejecting a null hypothesis) and type II error (falsely accepting a null hypothesis). The acceptable magnitudes of type I and type II errors are set in advance and are important for sample size calculations. Another important point to remember is that we cannot ‘prove’ or ‘disprove’ anything by hypothesis testing and statistical tests. We can only knock down or reject the null hypothesis and by default accept the alternative hypothesis. If we fail to reject the null hypothesis, we accept it by default.

Source of Support: Nil

Conflict of Interest: None declared.

• Daniel W. W. In: Biostatistics. 7th ed. New York: John Wiley and Sons, Inc; 2002. Hypothesis testing; pp. 204–294. [ Google Scholar ]
• Hulley S. B, Cummings S. R, Browner W. S, Grady D, Hearst N, Newman T. B. 2nd ed. Philadelphia: Lippincott Williams and Wilkins; 2001. Getting ready to estimate sample size: Hypothesis and underlying principles In: Designing Clinical Research-An epidemiologic approach; pp. 51–63. [ Google Scholar ]
• Medawar P. B. Philadelphia: American Philosophical Society; 1969. Induction and intuition in scientific thought. [ Google Scholar ]
• Popper K. Unended Quest. An Intellectual Autobiography. Fontana Collins; p. 42. [ Google Scholar ]
• Wulff H. R, Pedersen S. A, Rosenberg R. Oxford: Blackwell Scientific Publicatons; Empirism and Realism: A philosophical problem. In: Philosophy of Medicine. [ Google Scholar ]

Official websites use .gov

A .gov website belongs to an official government organization in the United States.

Secure .gov websites use HTTPS

A lock ( ) or https:// means you've safely connected to the .gov website. Share sensitive information only on official, secure websites.

4. Test Hypotheses Using Epidemiologic and Environmental Investigation

Once a hypothesis is generated, it should be tested to determine if the source has been correctly identified. Investigators use several methods to test their hypotheses.

Epidemiologic Investigation

Case-control studies and cohort studies are the most common type of analytic studies conducted to assist investigators in determining statistical association of exposures to ill persons. These types of studies compare information collected from ill persons with comparable well persons.

Cohort studies use well-defined groups and compare the risk of developing of illness among people who were exposed to a source with the risk of developing illness among the unexposed. In a cohort study, you are determining the risk of developing illness among the exposed.

Case-control studies compare the exposures between ill persons with exposures among well persons (called controls). Controls for a case-control study should have the same risk of exposure as the cases. In a case-control study, the comparison is the odds of illness among those exposed with those not exposed.

Using statistical tests, the investigators can determine the strength of the association to the implicated water source instead of how likely it is to have occurred by chance alone. Investigators look at many factors when interpreting results from these studies:

• Frequencies of exposure
• Strength of the statistical association
• Dose-response relationships
• Biologic /toxicological plausibility

For more information and examples on designing and conducting analytic studies in the field, please see The CDC Field Epidemiology Manual .

Information on the clinical course of illness and results of clinical laboratory testing are very important for outbreak investigations. Evaluating symptoms and sequelae across patients can guide formulation of a clinical diagnosis. Results of advance molecular diagnostics can be evaluated to compare isolates from patient and the outbreak sources (e.g., water).

Environmental Investigation

Investigating an implicated water source with an onsite environmental investigation is often important for determining the outbreak’s cause and for pinpointing which factors at the water source were responsible. This requires understanding the implicated water system, potential contamination sources, the environmental controls in effect (e.g., water disinfection), and the ways that people interact with the water source. The factors considered in this investigation will differ depending on the type of implicated water source (e.g., drinking water system, swimming pool). Environmental investigation tools for different settings and venues are available.

The investigation might include collecting water samples. Sampling strategy should include the goal of water testing and what information will be gained by evaluating water quality parameters including measurement of disinfection residuals, and/or possible detection of particular contaminants. The epidemiology of each situation will typically inform the sampling effort.

• Drinking Water
• Healthy Swimming
• Water, Sanitation, and Environmentally-related Hygiene
• Harmful Algal Blooms
• Global WASH
• WASH Surveillance
• WASH-related Emergencies and Outbreaks
• Other Uses of Water

To receive updates highlighting our recent work to prevent infectious disease, enter your email address:

Exit Notification / Disclaimer Policy

• The Centers for Disease Control and Prevention (CDC) cannot attest to the accuracy of a non-federal website.
• Linking to a non-federal website does not constitute an endorsement by CDC or any of its employees of the sponsors or the information and products presented on the website.
• You will be subject to the destination website's privacy policy when you follow the link.
• CDC is not responsible for Section 508 compliance (accessibility) on other federal or private website.

Log in using your username and password

• Search More Search for this keyword Advanced search
• Latest content
• Current issue
• BMJ Journals More You are viewing from: Google Indexer

You are here

• Online First
• Pedestrian safety on the road to net zero: cross-sectional study of collisions with electric and hybrid-electric cars in Great Britain
• Article Text
• Article info
• Citation Tools
• Rapid Responses
• Article metrics

• http://orcid.org/0000-0003-4431-8822 Phil J Edwards ,
• Siobhan Moore ,
• Craig Higgins
• London School of Hygiene & Tropical Medicine , London , UK
• Correspondence to Dr Phil J Edwards, London School of Hygiene & Tropical Medicine, London WC1E 7HT, UK; phil.edwards{at}LSHTM.ac.uk

Background Plans to phase out fossil fuel-powered internal combustion engine (ICE) vehicles and to replace these with electric and hybrid-electric (E-HE) vehicles represent a historic step to reduce air pollution and address the climate emergency. However, there are concerns that E-HE cars are more hazardous to pedestrians, due to being quieter. We investigated and compared injury risks to pedestrians from E-HE and ICE cars in urban and rural environments.

Methods We conducted a cross-sectional study of pedestrians injured by cars or taxis in Great Britain. We estimated casualty rates per 100 million miles of travel by E-HE and ICE vehicles. Numerators (pedestrians) were extracted from STATS19 datasets. Denominators (car travel) were estimated by multiplying average annual mileage (using National Travel Survey datasets) by numbers of vehicles. We used Poisson regression to investigate modifying effects of environments where collisions occurred.

Results During 2013–2017, casualty rates per 100 million miles were 5.16 (95% CI 4.92 to 5.42) for E-HE vehicles and 2.40 (95%CI 2.38 to 2.41) for ICE vehicles, indicating that collisions were twice as likely (RR 2.15; 95% CI 2.05 to 2.26) with E-HE vehicles. Poisson regression found no evidence that E-HE vehicles were more dangerous in rural environments (RR 0.91; 95% CI 0.74 to 1.11); but strong evidence that E-HE vehicles were three times more dangerous than ICE vehicles in urban environments (RR 2.97; 95% CI 2.41 to 3.7). Sensitivity analyses of missing data support main findings.

Conclusion E-HE cars pose greater risk to pedestrians than ICE cars in urban environments. This risk must be mitigated as governments phase out petrol and diesel cars.

• WOUNDS AND INJURIES
• CLIMATE CHANGE

Data availability statement

Data are available in a public, open-access repository. Numerator data (numbers of pedestrians injured in collisions) are publicly available from the Road Safety Data (STATS19) datasets ( https://www.data.gov.uk/dataset/cb7ae6f0-4be6-4935-9277-47e5ce24a11f/road-safety-data ). Denominator data (100 million miles of car travel per year) may be estimated by multiplying average annual mileage by numbers of vehicle registrations (publicly available from Department for Transport, https://www.gov.uk/government/statistical-data-sets/veh02-licensed-cars ). Average annual mileage for E-HE and ICE vehicles may be estimated separately for urban and rural environments using data that may obtained under special licence from the National Travel Survey datasets ( http://doi.org/10.5255/UKDA-Series-2000037 ).

https://doi.org/10.1136/jech-2024-221902

Statistics from Altmetric.com

Request permissions.

If you wish to reuse any or all of this article please use the link below which will take you to the Copyright Clearance Center’s RightsLink service. You will be able to get a quick price and instant permission to reuse the content in many different ways.

WHAT IS ALREADY KNOWN ON THIS TOPIC

Electric cars are quieter than cars with petrol or diesel engines and may pose a greater risk to pedestrians.

The US National Highway Transportation Safety Agency found that during 2000–2007 the odds of an electric or hybrid-electric car causing a pedestrian injury were 35% greater than a car with a petrol or diesel engine.

The UK Transport Research Laboratory found the pedestrian casualty rate per 10 000 registered electric or hybrid-electric vehicles during 2005–2007 in Great Britain was lower than the rate for petrol or diesel vehicles.

WHAT THIS STUDY ADDS

In Great Britain during 2013–2017, pedestrians were twice as likely to be hit by an electric or hybrid-electric car than by a petrol or diesel car; the risks were higher in urban areas.

HOW THIS STUDY MIGHT AFFECT RESEARCH, PRACTICE OR POLICY

The greater risk to pedestrian safety posed by electric or hybrid-electric cars needs to be mitigated as governments proceed to phase out petrol and diesel cars.

Drivers of electric or hybrid-electric cars must be cautious of pedestrians who may not hear them approaching and may step into the road thinking it is safe to do so, particularly in towns and cities.

Introduction

Many governments have set targets to reach net-zero emissions to help mitigate the harms of climate change. Short-term health benefits of reduced emissions are expected from better air quality with longer-term benefits from reduced global temperatures. 1

Transition to electric and hybrid-electric (E-HE) cars

One such target is to phase out sales of new fossil fuel-powered internal combustion engine (ICE) vehicles and replace these with E-HE vehicles. 2 3

Pedestrian safety

Road traffic injuries are the leading cause of death for children and young adults. 4 A quarter of all road traffic deaths are of pedestrians. 5 Concerns have been raised that E-HE cars may be more hazardous to pedestrians than ICE cars, due to being quieter. 6 7 It has been hypothesised that E-HE cars pose a greater risk of injury to pedestrians in urban areas where background ambient noise levels are higher. 8 However, there has been relatively little empirical research on possible impacts of E-HE cars on pedestrian road safety. A study commissioned for the US National Highway Transportation Safety Agency based on data from 16 States found that the odds of an E-HE vehicle causing a pedestrian injury were 35% greater than an ICE vehicle. 9 In contrast, a study commissioned by the UK Department for Transport found pedestrian casualty rates from collisions with E-HE vehicles during 2005–2007 were lower than for ICE vehicles. 10 Possible reasons for these conflicting results are that the two studies used different designs and estimated different measures of relative risk—the first used a case–control design and estimated an OR, whereas the second used a cross-sectional study and estimated a rate ratio. ORs will often differ from rate ratios. 11 Other reasons include differences between the USA and the UK in the amount and quality of walking infrastructure. 12

Aim and objectives

We aimed to add to the evidence base on whether E-HE cars pose a greater injury risk to pedestrians than ICE cars by analysing road traffic injury data and travel survey data in Great Britain.

We sought to improve on the previous UK study by using distance travelled instead of number of registered vehicles as the measure of exposure in estimation of collision rates.

The objectives of this study were:

To estimate pedestrian casualty rates for E-HE and ICE vehicles and to compare these by calculating a rate ratio;

To assess whether or not the evidence supports the hypothesis that casualty rate ratios vary according to urban or rural environments. 8

Study design

This study was an analysis of differences in casualty rates of pedestrians per 100 million miles of E-HE car travel and rates per 100 million miles of ICE car travel.

This study was set in Great Britain between 2013 and 2017.

Participants

The study participants were all pedestrians reported to have been injured in a collision with a car or a taxi.

The exposure was the type of propulsion of the colliding vehicle, E-HE or ICE. E-HE vehicles were treated as a single powertrain type, regardless of the mode of operation that a hybrid vehicle was in at the time of collision (hybrid vehicles typically start in electric mode and change from battery to combustion engine at higher speeds). 13

The outcome of interest was a pedestrian casualty.

Effect modification by road environment

We used the urban–rural classification 14 of the roads on which the collisions occurred to investigate whether casualty rate ratios comparing E-HE with ICE vehicles differed between rural and urban environments.

Data sources/measurement

Numerator data (numbers of pedestrians injured in collisions) were extracted from the Road Safety Data (STATS19) datasets. 15

Denominator data (100 million miles of car travel per year) were estimated by multiplying average annual mileage by numbers of vehicle registrations. 16 Average annual mileage for E-HE and ICE vehicles was estimated separately for urban and rural environments using data obtained under special licence from the National Travel Survey (NTS) datasets. 17 We estimated average annual mileage for the years 2013–2017 because the NTS variable for the vehicle fuel type did not include ‘hybrid’ prior to 2013 and data from 2018 had not been uploaded to the UK data service due to problems with the archiving process (Andrew Kelly, Database Manager, NTS, Department for Transport, 23 March 2020, personal communication). Denominators were thus available for the years 2013–2017.

Data preparation

The datasets for collisions, casualties and vehicles from the STATS19 database were merged using a unique identification number for each collision.

Statistical methods

We calculated annual casualty rates for E-HE and ICE vehicles separately and we compared these by calculating a rate ratio. We used Poisson regression models to estimate rate ratios with 95% CIs and to investigate any modifying effects of the road environment in which the collisions occurred. For this analysis, our regression model included explanatory terms for the main effects of the road environment, plus terms for the interaction between type of propulsion and the road environment. The assumptions for Poisson regression were met in our study: we modelled count data (counts of pedestrians injured), traffic collisions were independent of each other, occurring in different places over time, and never occurring simultaneously. Data preparation, management and analyses were carried out using Microsoft Access 2019 and Stata V.16. 18

Sensitivity analysis

We conducted an extreme case analysis where all missing propulsion codes were assumed to be ICE vehicles (there were over a 100 times more ICE vehicles than E-HE vehicles on the roads in Great Britain during our study period, 16 so missing propulsion is more likely to have been ICE).

The sample size for this study included all available recorded road traffic collisions in Great Britain during the study period. We estimated that for our study to have 80% power at the 5% significance level to show a difference in casualty rates of 2 per 100 miles versus 5.5 per 100 miles, we would require 481 million miles of vehicle travel in each group (E-HE and ICE); whereas to have 90% power at the 1% significance level to show this difference, 911 million miles of vehicle travel would be required in each group. Our study includes 32 000 million miles of E-HE vehicle travel and 3 000 000 million miles of ICE vehicle travel and therefore our study was sufficiently powered to detect differences in casualty rates of these magnitudes.

Between 2013 and 2017, there were 916 713 casualties from reported road traffic collisions in Great Britain. 120 197 casualties were pedestrians. Of these pedestrians, 96 285 had been hit by a car or taxi. Most pedestrians—71 666 (74%) were hit by an ICE car or taxi. 1652 (2%) casualties were hit by an E-HE car or taxi. For 22 829 (24%) casualties, the vehicle propulsion code was missing. Most collisions occurred in urban environments and a greater proportion of the collisions with E-HE vehicles occurred in an urban environment (94%) than did collisions with ICE vehicles (88%) ( figure 1 ).

• Download figure
• Open in new tab
• Download powerpoint

Flow chart of pedestrian casualties in collisions with E-HE or ICE cars or taxis from reported road traffic collisions in Great Britain 2013–2017. E-HE, electric and hybrid-electric; ICE, internal combustion engine.

Main results

During the period 2013 to 2017, the average annual casualty rates of pedestrians per 100 million miles were 5.16 (95% CI 4.92 to 5.42) for E-HE vehicles and 2.40 (95% CI 2.38 to 2.41) for ICE vehicles, which indicates that collisions with pedestrians were on average twice as likely (RR 2.15 (95% CI 2.05 to 2.26), p<0.001) with E-HE vehicles as with ICE vehicles ( table 1 ).

• View inline

Pedestrian casualties due to collisions with cars or taxis from reported road traffic collisions in Great Britain 2013–2017—by vehicle propulsion type

In our extreme case analysis, the 22 829 pedestrian casualties where vehicle propulsion was missing were all assumed to have been struck by ICE vehicles. In this case, average casualty rates of pedestrians per 100 million miles were 3.16 (95% CI 3.14 to 3.18) for ICE vehicles, which would indicate that collisions with pedestrians were on average 63% more likely (RR 1.63 (95% CI 1.56 to 1.71), p<0.001) with E-HE vehicles than with ICE vehicles ( table 2 ).

Extreme case sensitivity analysis—pedestrian casualties due to collisions with cars or taxis from reported road traffic collisions in Great Britain 2013–2017 by vehicle propulsion type where 22 829 missing vehicle propulsion codes are assumed to be ICE vehicles

Relative risks according to road environment

Casualty rates were higher in urban than rural environments ( tables 3 and 4 ).

Pedestrian casualties due to collisions with cars or taxis from reported road traffic collisions in Great Britain 2013–2017—by vehicle propulsion type in urban road environments

Pedestrian casualties due to collisions with cars or taxis from reported road traffic collisions in Great Britain 2013–2017—by vehicle propulsion type in rural road environments

Urban environments

Collisions with pedestrians in urban environments were on average over two and a half times as likely (RR 2.69 (95% CI 2.56 to 2.83, p<0.001) with E-HE vehicles as with ICE vehicles ( table 3 ).

The extreme case sensitivity analysis showed collisions with pedestrians in urban environments were more likely with E-HE vehicles (RR 2.05; 95% CI 1.95 to 2.15).

Rural environments

Collisions with pedestrians in rural environments were equally likely (RR 0.91; 95% CI 0.74 to 1.11) with E-HE vehicles as with ICE vehicles ( table 4 ).

The extreme case sensitivity analysis found evidence that collisions with pedestrians in rural environments were less likely with E-HE vehicles (RR 0.68; 95% CI 0.55 to 0.83).

Results of Poisson regression analysis

Our Poisson regression model results ( table 5 ) showed that pedestrian injury rates were on average 9.28 (95% CI 9.07 to 9.49) times greater in urban than in rural environments. There was no evidence that E-HE vehicles were more dangerous than ICE vehicles in rural environments (RR 0.91; 95% CI 0.74 to 1.11), consistent with our finding in table 4 . There was strong evidence that E-HE vehicles were on average three times more dangerous than ICE vehicles in urban environments (RR 2.97; 95% CI 2.41 to 3.67).

Results of Poisson regression analysis of annual casualty rates of pedestrians per 100 million miles by road environment and the interaction between vehicle propulsion type and environment

Statement of principal findings

This study found that in Great Britain between 2013 and 2017, casualty rates of pedestrians due to collisions with E-HE cars and taxis were higher than those due to collisions with ICE cars and taxis. Our best estimate is that such collisions are on average twice as likely, and in urban areas E-HE vehicles are on average three times more dangerous than ICE vehicles, consistent with the theory that E-HE vehicles are less audible to pedestrians in urban areas where background ambient noise levels are higher.

Strengths and weaknesses of the study

There are several limitations to this study which are discussed below.

The data used were not very recent. However, ours is the most current analysis of E-HE vehicle collisions using the STATS19 dataset.

Before we can infer that E-HE vehicles pose a greater risk to pedestrians than ICE vehicles, we must consider whether our study is free from confounding and selection bias. Confounding occurs when the exposure and outcome share a common cause. 19 Confounders in this study would be factors that may both cause a traffic collision and also cause the exposure (use of an E-HE car). Younger, less experienced drivers (ie, ages 16–24) are more likely to be involved in a road traffic collision 20 and are also more likely to own an electric car. 21 Some of the observed increased risk of electric cars may therefore be due to younger drivers preferring electric cars. This would cause positive confounding, meaning that the true relative risk of electric cars is less than we have estimated in our study. Regarding selection bias, it is known that the STATS19 dataset does not include every road traffic casualty in Great Britain, as some non-fatal casualties are not reported to the police. 22 If casualties from collisions are reported to the police differentially according to the type of vehicle propulsion, this may have biased our results; however, there is no reason to suspect that a pedestrian struck by a petrol or diesel car is any more or less likely to report the collision to the police than one struck by an electric car.

We must also address two additional concerns as ours is a cross-sectional study: The accuracy of exposure assignment (including the potential for recall bias) and the adequacy of prevalence as a proxy for incidence. 23 First, the accuracy of exposure assignment and the potential for recall bias are not issues for this study, as the exposure (type of propulsion of the colliding vehicle, E-HE or ICE), is assigned independently of the casualties by the UK Department for Transport who link the vehicle registration number (VRN) of each colliding vehicle to vehicle data held by the UK Driver Vehicle and Licensing Agency (DVLA). 10 Second, we have not used prevalence as a proxy for incidence but have estimated incidence using total distance travelled by cars as the measure of exposure.

We may therefore reasonably infer from our study results that E-HE vehicles pose a greater risk to pedestrians than ICE vehicles in urban environments, and that part of the risk may be due to younger people’s preference for E-HE cars.

A major limitation of the STATS19 road safety dataset used in this study was that it did not contain a vehicle propulsion code for all vehicles in collisions with pedestrians. We excluded these vehicles from our primary analysis (a complete case analysis) and we also conducted an extreme case sensitivity analysis. We will now argue why imputation of missing vehicle propulsion codes would not have added value to this study. Vehicle propulsion data are obtained for the STATS19 dataset by the UK Department for Transport who link the VRN of each colliding vehicle recorded in STATS19 to vehicles data held by the UK DVLA. The STATS19 data on reported collisions and casualties are collected by a Police Officer when an injury road accident is reported to them; Most police officers write details of the casualties and the vehicles involved in their notebooks for transcription onto the STATS19 form later at the Police station. 24 The VRN is one of 18 items recorded on each vehicle involved in a collision. Items may occasionally be missed due to human error during this process. Where a VRN is missing, vehicle propulsion will be missing in the STATS19 dataset. The chance that any vehicle-related item is missing will be independent of any characteristics of the casualties involved and so the vehicle propulsion codes are missing completely at random (MCAR). As the missing propulsion data are very likely MCAR, the set of pedestrians with no missing data is a random sample from the source population and hence our complete case analysis for handling the missing data gives unbiased results. The extreme case sensitivity analysis we performed shows a possible result that could occur, and it demonstrates our conclusions in urban environments are robust to the missing data. Lastly, to impute the missing data would require additional variables which are related to the likelihood of a VRN being missing. Such variables were not available and therefore we do not believe a useful multiple imputation analysis could have been performed.

Strengths and weaknesses in relation to other studies

Our study uses hundreds of millions of miles of car travel as the denominators in our estimates of annual pedestrian casualty rates which is a more accurate measure of exposure to road hazards than the number of registered vehicles, which was used as the denominator in a previous study in the UK. 10 Our results differ to this previous study which found that pedestrian casualty rates from collisions with E-HE vehicles during 2005–2007 were lower than those from ICE vehicles. Our study has updated this previous analysis and shows that casualty rates due to E-HE vehicle collisions exceed those due to ICE vehicle collisions. Similarly, our study uses a more robust measure of risk (casualty rates per miles of car travel) than that used in a US study. 9 Our study results are consistent with this US study that found that the odds of an E-HE vehicle causing a pedestrian injury were 35% greater than an ICE vehicle. Brand et al 8 hypothesised, without any supporting data, that “hybrid and electric low-noise cars cause an increase in traffic collisions involving vulnerable road users in urban areas” and recommended that “further investigations have to be done with the increase of low-noise cars to prove our hypothesis right.” 8 We believe that our study is the first to provide empirical evidence in support of this hypothesis.

Meaning of the study: possible explanations and implications for clinicians and policymakers

More pedestrians are injured in Great Britain by petrol and diesel cars than by electric cars, but compared with petrol and diesel cars, electric cars pose a greater risk to pedestrians and the risk is greater in urban environments. One plausible explanation for our results is that background ambient noise levels differ between urban and rural areas, causing electric vehicles to be less audible to pedestrians in urban areas. Such differences may impact on safety because pedestrians usually hear traffic approaching and take care to avoid any collision, which is more difficult if they do not hear electric vehicles. This is consistent with audio-testing evidence in a small study of vision-impaired participants. 10 From a Public Health perspective, our results should not discourage active forms of transport beneficial to health, such as walking and cycling, rather they can be used to ensure that any potential increased traffic injury risks are understood and safeguarded against. A better transport policy response to the climate emergency might be the provision of safe, affordable, accessible and integrated public transport systems for all. 25

Unanswered questions and future research

It will be of interest to investigate the extent to which younger drivers are involved in collisions of E-HE cars with pedestrians.

If the braking distance of electric cars is longer, 26 and electric cars are heavier than their petrol and diesel counterparts, 27 these factors may increase the risks and the severity of injuries sustained by pedestrians and require investigation.

As car manufacturers continue to develop and equip new electric cars with Collision Avoidance Systems and Autonomous Emergency Braking to ensure automatic braking in cases where pedestrians or cyclists move into the path of an oncoming car, future research can repeat the analyses presented in this study to evaluate whether the risks of E-HE cars to pedestrians in urban areas have been sufficiently mitigated.

Conclusions

E-HE vehicles pose a greater risk to pedestrians than petrol and diesel powered vehicles in urban environments. This risk needs to be mitigated as governments proceed to phase out petrol and diesel cars.

Ethics statements

Patient consent for publication.

Not applicable.

Ethics approval

This study involves human participants and was approved by the LSHTM MSc Research Ethics Committee (reference #16400). The study uses the anonymised records of people injured in road traffic collisions, data which are routinely collected by UK police forces. The participants are unknown to the investigators and could not be contacted.

Acknowledgments

We thank Rebecca Steinbach for her advice on analysis of National Travel Survey data, Jonathan Bartlett for his advice on missing data, and Ben Armstrong for his advice on Poisson regression. We are grateful to the reviewers and to Dr C Mary Schooling, Associate Editor, whose comments helped us improve the manuscript. We are grateful to Jim Edwards and Graham Try for their comments on earlier versions of this manuscript.

• H Baqui A ,
• Benfield T , et al
• Gilchrist J
• ↵ WHO factsheet on road traffic injuries . Available : https://www.who.int/news-room/fact-sheets/detail/road-traffic-injuries#:~:text=Approximately%201.19%20million%20people%20die,adults%20aged%205%E2%80%9329%20years [Accessed 14 Apr 2024 ].
• ↵ Reported road casualties great Britain, annual report . 2022 . Available : https://www.gov.uk/government/statistics/reported-road-casualties-great-britain-annual-report-2022 [Accessed 14 Apr 2024 ].
• Maryland General Assembly
• Haas P , et al
• Morgan PA ,
• Muirhead M , et al
• Greenland S
• Buehler R ,
• Alternative Fuels Data Center
• Government-Statistics
• Department for Transport
• Department for Transport. (2023
• Hernán MA ,
• Hernández-Díaz S ,
• Barriers Direct
• Savitz DA ,
• Wellenius GA
• Transport Scotland

Contributors CH and PJE developed the idea for this study and supervised SM in performing the literature search, downloading, managing and analysing the data. SM wrote the first draft of the manuscript, which was the dissertation for her MSc in Public Health. PJE prepared the first draft of the manuscript for the journal. All authors assisted in editing and refining the manuscript. The corresponding author attests that all listed authors meet authorship criteria and that no others meeting the criteria have been omitted. PJE (guarantor) accepts full responsibility for the work and the conduct of the study, had access to the data and controlled the decision to publish.

Funding This study was conducted in part fulfilment of the Masters degree in Public Health at the London School of Hygiene & Tropical Medicine. The second author was self-funded for her studies for this degree.

Competing interests None declared.

Provenance and peer review Not commissioned; externally peer reviewed.

Read the full text or download the PDF:

May 2024 EGRP Cancer Epidemiology News

Egrp cancer epidemiology news, nci-supported cancer epidemiology cohorts: past, present, and future, funding opportunities, contract opportunities, grants policy announcements, requests for information, new resources, news, blog posts, and podcasts.

The National Cancer Institute (NCI) has made substantial investments in cancer epidemiology cohorts to study both cancer etiology and survivorship. These cohorts vary in sample size and scientific scope. They have advanced knowledge across the cancer continuum by providing fundamental insights into key environmental, lifestyle, clinical, and genetic determinants of cancer and its outcomes. The Epidemiology and Genomics Research Program (EGRP) currently supports over 45 cancer epidemiology cohorts . Collectively, these survivor and etiology cohorts have enrolled over 1 million participants. Moreover, these cohorts have rich epidemiological data and biospecimens that could be leveraged by researchers worldwide to investigate novel research questions.

In the 1990s, NCI supported large-scale etiology cohorts as investigator-initiated R01s or P01s. With recognition of the rising number of cancer survivors and critical needs to ameliorate burden in survivorship, funding for survivor cohorts began in the mid-2000s to address scientific gaps. More recently, and with anticipated research needs, EGRP has enhanced its efforts to increase the diversity of the cohorts in NCI’s portfolio – in terms of the participant demographics (e.g., race/ethnicity, age, and less common cancer types) and scientific questions being addressed (e.g., emerging cancer treatments; disparities; and impact of climate change, environmental disasters, behavioral factors, and novel chemicals on cancer risk and outcomes).

In addition, EGRP has ongoing efforts to encourage grant applications that address scientific knowledge gaps in cancer etiology and cancer survivorship. New cohorts may be proposed through Building the Next Generation of Research Cohorts ( PAR-22-161 ) to initiate and build cancer epidemiology cohorts that can address critical scientific gaps concerning new or unique exposures in relation to cancer risk and/or outcomes. New cohorts proposed should seek to include understudied populations (racial/ethnic groups, rural populations, individuals living in persistent poverty areas) as the focus of the cohort, and also have plans for community engagement to establish bi-directional partnerships between researchers and community partners. This is critical to incorporate and integrate respective unique strengths and perspectives to inform research priorities in ways that are sensitive to local cultures and belief systems.

While building resources with new cohorts, NCI also seeks to leverage the existing cohort resources for hypothesis-driven studies (Research Opportunities in Established Cancer Epidemiology Cohort Studies, PAR-22-162 ). Established cohorts (defined as studies that have achieved their initial planned recruitment goal) have a wealth of exposure data, stored biospecimens, considerable follow-up time, and cancer information. Through PAR-22-162, researchers can propose studies that leverage existing cohort data and biospecimens to address novel hypotheses and address gaps in scientific knowledge (e.g., understudied populations [race/ethnicity, socioeconomic status, early-onset cancers, and geography], understudied cancers, and exposures) while supporting cohort infrastructure.

For more information about NCI-funded cancer epidemiology cohorts, visit the EGRP cohort website or contact cohort coordinators Somdat Mahabir, PhD, MPH , and Danielle Carrick, PhD, MHS . Additionally, the Cancer Epidemiology Descriptive Cohort Database (CEDCD) contains descriptive information about cohort studies in EGRP’s grants portfolio and other non-NCI funded cohorts.

• RFA-CA-24-022 , SBIR Phase IIB Bridge Awards to Accelerate the Development of Cancer-Relevant Technologies Toward Commercialization (R44, Clinical Trial Optional)
• RFA-CA-24-023 , Small Business Transition Grant For Early Career Scientists (R41/R42, Clinical Trial Not Allowed)
• PAR-24-207 , Interventions to Address Disparities in Liver Disease and Live Cancer (R01, Clinical Trials Optional)
• PAR-24-152 (R15, Clinical Trial Not Allowed)
• PAR-24-214 (R15, Clinical Trial Required)
• PA-24-175 (Parent K01, Independent Clinical Trial Required)
• PA-24-176 (Parent K01, Independent Clinical Trial Not Allowed)
• PA-24-177 (Parent K01, Independent Basic Experimental Studies with Humans Required)
• PA-24-181 (Parent K08, Independent Clinical Trial Required)
• PA-24-182 (Parent K08, Independent Clinical Trial Not Allowed)
• PA-24-183 (Parent K08, Independent Basic Experimental Studies with Humans Required)
• PA-24-193 (Parent K99/R00, Independent Clinical Trial Required)
• PA-24-194 (Parent K99/R00, Independent Clinical Trial Not Allowed)
• PA-24-195 (Parent K99/R00, Independent Basic Experimental Studies with Humans Required)
• NOT-OD-24-096 , Notice of Special Interest (NOSI): Promoting Data Reuse for Health Research
• NOT-CA-24-044 , NOSI: Administrative Supplements for the Study of the Diverse Aspects of Uterine Serous Carcinoma (Clinical Trial Not Allowed)
• NOT-CA-24-047 , NOSI: Administrative Supplement to Support the NCI Cancer Prevention-Interception Targeted Agent Discovery Program (CAP-IT) Research
• NOT-CA-24-058 , NOSI: Administrative Supplement for Natural History and Longitudinal Dynamics of Lung Nodules using the NLST dataset
• NOT-OD-24-119 , NOSI: Research Opportunities Centering the Health of Women Across the HIV Research Continuum
• NOT-CA-24-048 , Notice of Intent to Publish a Funding Opportunity Announcement for Addressing Barriers to Healthcare Transitions for Survivors of Childhood and Adolescent Cancers (R01, Clinical Trial Optional)
• Childhood Cancer Data Initiative (CCDI): Research Molecular Characterization
• NOT-OD-24-109 , Notice of Fiscal Policies in Effect for FY 2024
• NOT-OD-24-110 , Notice of Legislative Mandates in Effect for FY 2024
• NOT-OD-24-115 , Publication of the Revised NIH Grants Policy Statement (Rev. April 2024) for Fiscal Year 2024
• NOT-OD-24-118 , Continued Extension of Certain Flexibilities for Prospective Basic Experimental Studies with Human Participants
• NOT-OD-24-124 , Updates to NIH Training Grant Applications - Registration Open for June 5, 2024 Webinar
• NOT-OD-24-104 , Ruth L. Kirschstein National Research Service Award (NRSA) Stipends, Tuition/Fees and Other Budgetary Levels Effective for Fiscal Year 2024
• NOT-CA-24-046 , Seeking Input on Existing Study Populations with Multi-Cancer Detection (MCD) Test Results and Available Samples for Germline Testing (responses due by June 10, 2024)
• NOT-CA-24-051 , Seeking Input on Existing Study Populations with Germline Results and Samples Available for Multi-Cancer Detection (MCD) Assay Testing (responses due by June 17, 2024)
• NOT-OD-24-112, FDA-NIH Resource on Terminology for Clinical Research (responses due by June 24, 2024)
• NOT-OD-24-122 , The National Institutes of Health (NIH) Request for Information (RFI) on NIH-Wide Strategic Plan for Sexual and Gender Minority (SGM) Health Research (responses due by July 15, 2024)
• Informed Consent for Research Using Digital Health Technologies: Points to Consider & Sample Language
• National Standards for Cancer Survivorship Care
• LGBTQ+ Voices: Listening to Sexual and Gender Minority People Affected by Cancer
• Q&A: Learning About the Cancer Care Challenges LGBTQ+ People Face
• Analysis Identifies 50 New Genomic Regions Associated with Kidney Cancer Risk
• Increases for National Research Service Award Stipends and Childcare Subsidies
• NCI SBIR Innovation Lab: Timeline to Funding – Registering a Small Business

Stay Connected

Subscribe for updates.

Subscribe You can subscribe and unsubscribe at any time by entering your email address and selecting your preferences on the page that follows.

EGRP staff can answer questions on grant funding, policies, and research resources. If you do not know who to contact we will do our best to connect you with someone who can help you.

DSI Director Kyle Cranmer’s Work Highlighted in National Report on AI in Science

DSI Director Kyle Cranmer’s work is highlighted in a recent report from the President’s Council of Advisors on Science and Technology (PCAST) that provides recommendations about responsibly harnessing the power of AI to accelerate scientific discovery in the U.S.

Kyle’s work on simulation-based inference is referenced in a section of the report titled Revealing the Fundamental Physics of the Universe . Specifically, the report cites a 2019 paper — The Frontier of Simulation-Based Inference — authored by Kyle, Johann Brehmer, and Gilles Loupe that was published in the Proceedings of the National Academy of Sciences in 2019. Simulation-based inference harnesses the power of AI and machine learning to transform scientific practice, and the PCAST report highlights the potential for AI models to discover new laws of physics and understand the origins of our universe.

In many scientific domains, researchers create digital simulations of complex phenomena such as airflow around an airplane, infectious disease spreading through a population, or the evolution of the universe. One type of simulation is a digital simulator—a virtual representation of a real-world object or system that is sometimes called a “digital twin”. Digital twins can help scientists understand how physical systems currently function and how they might perform under different conditions. These simulators encapsulate large amounts of expert knowledge, and they often bring together teams of researchers with different types of expertise. For example, one expert might model the extreme environment near the center of a galaxy, a second expert would study how light propagates through the vast expanse of space, a third would be responsible for understanding how the light goes through the atmosphere, and a fourth would provide expertise on a telescope’s optics. The simulator can pull together this varied expertise into a coherent whole, helping scientists relate the observations to the phenomena being studied.

“You can also think of a simulator as a computational version of a hypothesis,” says Kyle. “Scientists might have two competing theories or hypotheses, and they can simulate what would happen for each of these theories.”

Testing hypotheses is a core part of the scientific method. Unfortunately, it’s not easy to test hypotheses when they are expressed as a simulator. It’s ironic, because these digital twins are detailed, accurate representations of complex, real-world phenomena. But that same complexity is what makes this work difficult.

Simulators are good at predicting what observations might look like under a single theory. Inferring which theories are preferred, based on observations, is much harder. In a complex simulation, there are many paths that could lead to the same observation, and inference requires looking at them all. Simulation-based inference uses machine learning and AI to address this complexity. AI/ML is very good at finding patterns in data, and researchers can use simulators to generate virtually unlimited synthetic data. Kyle and his colleagues figured out some clever ways to use AI/ML and the simulators together to make robust statistical statements about hypotheses.

The initial work on simulation-based inference focused on particle physics problems, but it has quickly been adopted in many other fields. It’s now popular in astrophysics and cosmology, and it is being applied to a wide range of topics including neuroscience, biology, genomics, epidemiology, genetics, social science, economics, and finance.

The report cites the potential of simulators to not only transform science, but also guide decision making:

Beyond advances in core science and engineering disciplines, AI methods promise to provide high fidelity models—“digital twins”—of the world that can help us to cut through uncertainty and complexity to predict, to plan, and to guide policymaking, where scarce data and models currently make it difficult to assess potential pathways forward.

Another part of the report addresses automated workflows, which may incorporate AI components:

Virtually every aspect of the laboratory workflow, from experimental design to data collection to data interpretation, could be partially or fully automated through AI assistance, although we view expert human supervision of such automated laboratories to be essential and highly desirable for decades to come.

This recommendation references a 2022 report from the National Academies of Sciences, Engineering and Medicine . The work done by Kyle and his team on simulation-based inference, and their work on automated workflows with AI components for particle physics, is cited in this report.

To view a full copy of the PCAST report, click here .

To view PCAST’s letter to the President and the executive summary of the report, click here .