half life problem solving

31.5 Half-Life and Activity

Learning objectives.

By the end of this section, you will be able to:

• Define half-life.
• Define dating.
• Calculate age of old objects by radioactive dating.

Unstable nuclei decay. However, some nuclides decay faster than others. For example, radium and polonium, discovered by the Curies, decay faster than uranium. This means they have shorter lifetimes, producing a greater rate of decay. In this section we explore half-life and activity, the quantitative terms for lifetime and rate of decay.

Why use a term like half-life rather than lifetime? The answer can be found by examining Figure 31.19 , which shows how the number of radioactive nuclei in a sample decreases with time. The time in which half of the original number of nuclei decay is defined as the half-life , t 1 / 2 t 1 / 2 . Half of the remaining nuclei decay in the next half-life. Further, half of that amount decays in the following half-life. Therefore, the number of radioactive nuclei decreases from N N to N / 2 N / 2 in one half-life, then to N / 4 N / 4 in the next, and to N / 8 N / 8 in the next, and so on. If N N is a large number, then many half-lives (not just two) pass before all of the nuclei decay. Nuclear decay is an example of a purely statistical process. A more precise definition of half-life is that each nucleus has a 50% chance of living for a time equal to one half-life t 1 / 2 t 1 / 2 . Thus, if N N is reasonably large, half of the original nuclei decay in a time of one half-life. If an individual nucleus makes it through that time, it still has a 50% chance of surviving through another half-life. Even if it happens to make it through hundreds of half-lives, it still has a 50% chance of surviving through one more. The probability of decay is the same no matter when you start counting. This is like random coin flipping. The chance of heads is 50%, no matter what has happened before.

There is a tremendous range in the half-lives of various nuclides, from as short as 10 − 23 10 − 23 s for the most unstable, to more than 10 16 10 16 y for the least unstable, or about 46 orders of magnitude. Nuclides with the shortest half-lives are those for which the nuclear forces are least attractive, an indication of the extent to which the nuclear force can depend on the particular combination of neutrons and protons. The concept of half-life is applicable to other subatomic particles, as will be discussed in Particle Physics . It is also applicable to the decay of excited states in atoms and nuclei. The following equation gives the quantitative relationship between the original number of nuclei present at time zero ( N 0 N 0 ) and the number ( N N ) at a later time t t :

where e = 2.71828 ... e = 2.71828 ... is the base of the natural logarithm, and λ λ is the decay constant for the nuclide. The shorter the half-life, the larger is the value of λ λ , and the faster the exponential e − λt e − λt decreases with time. The relationship between the decay constant λ λ and the half-life t 1 / 2 t 1 / 2 is

To see how the number of nuclei declines to half its original value in one half-life, let t = t 1 / 2 t = t 1 / 2 in the exponential in the equation N = N 0 e − λt N = N 0 e − λt . This gives N = N 0 e − λt = N 0 e −0.693 = 0.500 N 0 N = N 0 e − λt = N 0 e −0.693 = 0.500 N 0 . For integral numbers of half-lives, you can just divide the original number by 2 over and over again, rather than using the exponential relationship. For example, if ten half-lives have passed, we divide N N by 2 ten times. This reduces it to N / 1024 N / 1024 . For an arbitrary time, not just a multiple of the half-life, the exponential relationship must be used.

Radioactive dating is a clever use of naturally occurring radioactivity. Its most famous application is carbon-14 dating . Carbon-14 has a half-life of 5730 years and is produced in a nuclear reaction induced when solar neutrinos strike 14 N 14 N in the atmosphere. Radioactive carbon has the same chemistry as stable carbon, and so it mixes into the ecosphere, where it is consumed and becomes part of every living organism. Carbon-14 has an abundance of 1.3 parts per trillion of normal carbon. Thus, if you know the number of carbon nuclei in an object (perhaps determined by mass and Avogadro’s number), you multiply that number by 1 . 3 × 10 − 12 1 . 3 × 10 − 12 to find the number of 14 C 14 C nuclei in the object. When an organism dies, carbon exchange with the environment ceases, and 14 C 14 C is not replenished as it decays. By comparing the abundance of 14 C 14 C in an artifact, such as mummy wrappings, with the normal abundance in living tissue, it is possible to determine the artifact’s age (or time since death). Carbon-14 dating can be used for biological tissues as old as 50 or 60 thousand years, but is most accurate for younger samples, since the abundance of 14 C 14 C nuclei in them is greater. Very old biological materials contain no 14 C 14 C at all. There are instances in which the date of an artifact can be determined by other means, such as historical knowledge or tree-ring counting. These cross-references have confirmed the validity of carbon-14 dating and permitted us to calibrate the technique as well. Carbon-14 dating revolutionized parts of archaeology and is of such importance that it earned the 1960 Nobel Prize in chemistry for its developer, the American chemist Willard Libby (1908–1980).

One of the most famous cases of carbon-14 dating involves the Shroud of Turin, a long piece of fabric purported to be the burial shroud of Jesus (see Figure 31.20 ). This relic was first displayed in Turin in 1354 and was denounced as a fraud at that time by a French bishop. Its remarkable negative imprint of an apparently crucified body resembles the then-accepted image of Jesus, and so the shroud was never disregarded completely and remained controversial over the centuries. Carbon-14 dating was not performed on the shroud until 1988, when the process had been refined to the point where only a small amount of material needed to be destroyed. Samples were tested at three independent laboratories, each being given four pieces of cloth, with only one unidentified piece from the shroud, to avoid prejudice. All three laboratories found samples of the shroud contain 92% of the 14 C 14 C found in living tissues, allowing the shroud to be dated (see Example 31.4 ).

Example 31.4

How old is the shroud of turin.

Calculate the age of the Shroud of Turin given that the amount of 14 C 14 C found in it is 92% of that in living tissue.

Knowing that 92% of the 14 C 14 C remains means that N / N 0 = 0 . 92 N / N 0 = 0 . 92 . Therefore, the equation N = N 0 e − λt N = N 0 e − λt can be used to find λt λt . We also know that the half-life of 14 C 14 C is 5730 y, and so once λt λt is known, we can use the equation λ = 0 . 693 t 1 / 2 λ = 0 . 693 t 1 / 2 to find λ λ and then find t t as requested. Here, we postulate that the decrease in 14 C 14 C is solely due to nuclear decay.

Solving the equation N = N 0 e − λt N = N 0 e − λt for N / N 0 N / N 0 gives

Taking the natural logarithm of both sides of the equation yields

Rearranging to isolate t t gives

Now, the equation λ = 0 . 693 t 1 / 2 λ = 0 . 693 t 1 / 2 can be used to find λ λ for 14 C 14 C . Solving for λ λ and substituting the known half-life gives

We enter this value into the previous equation to find t t :

This dates the material in the shroud to 1988–690 = a.d. 1300. Our calculation is only accurate to two digits, so that the year is rounded to 1300. The values obtained at the three independent laboratories gave a weighted average date of a.d. 1320 ± 60 1320 ± 60 . The uncertainty is typical of carbon-14 dating and is due to the small amount of 14 C 14 C in living tissues, the amount of material available, and experimental uncertainties (reduced by having three independent measurements). It is meaningful that the date of the shroud is consistent with the first record of its existence and inconsistent with the period in which Jesus lived.

There are other forms of radioactive dating. Rocks, for example, can sometimes be dated based on the decay of 238 U 238 U . The decay series for 238 U 238 U ends with 206 Pb 206 Pb , so that the ratio of these nuclides in a rock is an indication of how long it has been since the rock solidified. The original composition of the rock, such as the absence of lead, must be known with some confidence. However, as with carbon-14 dating, the technique can be verified by a consistent body of knowledge. Since 238 U 238 U has a half-life of 4 . 5 × 10 9 4 . 5 × 10 9 y, it is useful for dating only very old materials, showing, for example, that the oldest rocks on Earth solidified about 3 . 5 × 10 9 3 . 5 × 10 9 years ago.

Activity, the Rate of Decay

What do we mean when we say a source is highly radioactive? Generally, this means the number of decays per unit time is very high. We define activity R R to be the rate of decay expressed in decays per unit time. In equation form, this is

where Δ N Δ N is the number of decays that occur in time Δ t Δ t . The SI unit for activity is one decay per second and is given the name becquerel (Bq) in honor of the discoverer of radioactivity. That is,

Activity R R is often expressed in other units, such as decays per minute or decays per year. One of the most common units for activity is the curie (Ci), defined to be the activity of 1 g of 226 Ra 226 Ra , in honor of Marie Curie’s work with radium. The definition of curie is

or 3 . 70 × 10 10 3 . 70 × 10 10 decays per second. A curie is a large unit of activity, while a becquerel is a relatively small unit. 1 MBq = 100 microcuries ( μ Ci ) 1 MBq = 100 microcuries ( μ Ci ) . In countries like Australia and New Zealand that adhere more to SI units, most radioactive sources, such as those used in medical diagnostics or in physics laboratories, are labeled in Bq or megabecquerel (MBq).

Intuitively, you would expect the activity of a source to depend on two things: the amount of the radioactive substance present, and its half-life. The greater the number of radioactive nuclei present in the sample, the more will decay per unit of time. The shorter the half-life, the more decays per unit time, for a given number of nuclei. So activity R R should be proportional to the number of radioactive nuclei, N N , and inversely proportional to their half-life, t 1 / 2 t 1 / 2 . In fact, your intuition is correct. It can be shown that the activity of a source is

where N N is the number of radioactive nuclei present, having half-life t 1 / 2 t 1 / 2 . This relationship is useful in a variety of calculations, as the next two examples illustrate.

Example 31.5

How great is the 14 c 14 c activity in living tissue.

Calculate the activity due to 14 C 14 C in 1.00 kg of carbon found in a living organism. Express the activity in units of Bq and Ci.

To find the activity R R using the equation R = 0 . 693 N t 1 / 2 R = 0 . 693 N t 1 / 2 , we must know N N and t 1 / 2 t 1 / 2 . The half-life of 14 C 14 C can be found in Appendix B , and was stated above as 5730 y. To find N N , we first find the number of 12 C 12 C nuclei in 1.00 kg of carbon using the concept of a mole. As indicated, we then multiply by 1 . 3 × 10 − 12 1 . 3 × 10 − 12 (the abundance of 14 C 14 C in a carbon sample from a living organism) to get the number of 14 C 14 C nuclei in a living organism.

One mole of carbon has a mass of 12.0 g, since it is nearly pure 12 C 12 C . (A mole has a mass in grams equal in magnitude to A A found in the periodic table.) Thus the number of carbon nuclei in a kilogram is

So the number of 14 C 14 C nuclei in 1 kg of carbon is

Now the activity R R is found using the equation R = 0 . 693 N t 1 / 2 R = 0 . 693 N t 1 / 2 .

Entering known values gives

or 7 . 89 × 10 9 7 . 89 × 10 9 decays per year. To convert this to the unit Bq, we simply convert years to seconds. Thus,

or 250 decays per second. To express R R in curies, we use the definition of a curie,

Our own bodies contain kilograms of carbon, and it is intriguing to think there are hundreds of 14 C 14 C decays per second taking place in us. Carbon-14 and other naturally occurring radioactive substances in our bodies contribute to the background radiation we receive. The small number of decays per second found for a kilogram of carbon in this example gives you some idea of how difficult it is to detect 14 C 14 C in a small sample of material. If there are 250 decays per second in a kilogram, then there are 0.25 decays per second in a gram of carbon in living tissue. To observe this, you must be able to distinguish decays from other forms of radiation, in order to reduce background noise. This becomes more difficult with an old tissue sample, since it contains less 14 C 14 C , and for samples more than 50 thousand years old, it is impossible.

Human-made (or artificial) radioactivity has been produced for decades and has many uses. Some of these include medical therapy for cancer, medical imaging and diagnostics, and food preservation by irradiation. Many applications as well as the biological effects of radiation are explored in Medical Applications of Nuclear Physics , but it is clear that radiation is hazardous. A number of tragic examples of this exist, one of the most disastrous being the meltdown and fire at the Chernobyl reactor complex in the Ukraine (see Figure 31.21 ). Several radioactive isotopes were released in huge quantities, contaminating many thousands of square kilometers and directly affecting hundreds of thousands of people. The most significant releases were of 131 I 131 I , 90 Sr 90 Sr , 137 Cs 137 Cs , 239 Pu 239 Pu , 238 U 238 U , and 235 U 235 U . Estimates are that the total amount of radiation released was about 100 million curies.

Human and Medical Applications

Example 31.6, what mass of 137 cs 137 cs escaped chernobyl.

It is estimated that the Chernobyl disaster released 6.0 MCi of 137 Cs 137 Cs into the environment. Calculate the mass of 137 Cs 137 Cs released.

We can calculate the mass released using Avogadro’s number and the concept of a mole if we can first find the number of nuclei N N released. Since the activity R R is given, and the half-life of 137 Cs 137 Cs is found in Appendix B to be 30.2 y, we can use the equation R = 0 . 693 N t 1 / 2 R = 0 . 693 N t 1 / 2 to find N N .

Solving the equation R = 0 . 693 N t 1 / 2 R = 0 . 693 N t 1 / 2 for N N gives

Entering the given values yields

Converting curies to becquerels and years to seconds, we get

One mole of a nuclide A X A X has a mass of A A grams, so that one mole of 137 Cs 137 Cs has a mass of 137 g. A mole has 6 . 02 × 10 23 6 . 02 × 10 23 nuclei. Thus the mass of 137 Cs 137 Cs released was

While 70 kg of material may not be a very large mass compared to the amount of fuel in a power plant, it is extremely radioactive, since it only has a 30-year half-life. Six megacuries (6.0 MCi) is an extraordinary amount of activity but is only a fraction of what is produced in nuclear reactors. Similar amounts of the other isotopes were also released at Chernobyl. Although the chances of such a disaster may have seemed small, the consequences were extremely severe, requiring greater caution than was used. More will be said about safe reactor design in the next chapter, but it should be noted that more recent reactors have a fundamentally safer design.

Activity R R decreases in time, going to half its original value in one half-life, then to one-fourth its original value in the next half-life, and so on. Since R = 0 . 693 N t 1 / 2 R = 0 . 693 N t 1 / 2 , the activity decreases as the number of radioactive nuclei decreases. The equation for R R as a function of time is found by combining the equations N = N 0 e − λt N = N 0 e − λt and R = 0 . 693 N t 1 / 2 R = 0 . 693 N t 1 / 2 , yielding

where R 0 R 0 is the activity at t = 0 t = 0 . This equation shows exponential decay of radioactive nuclei. For example, if a source originally has a 1.00-mCi activity, it declines to 0.500 mCi in one half-life, to 0.250 mCi in two half-lives, to 0.125 mCi in three half-lives, and so on. For times other than whole half-lives, the equation R = R 0 e − λt R = R 0 e − λt must be used to find R R .

PhET Explorations

Alpha decay.

Watch alpha particles escape from a polonium nucleus, causing radioactive alpha decay. See how random decay times relate to the half life.

Click to view content .

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/college-physics-2e/pages/1-introduction-to-science-and-the-realm-of-physics-physical-quantities-and-units

• Authors: Paul Peter Urone, Roger Hinrichs
• Publisher/website: OpenStax
• Book title: College Physics 2e
• Publication date: Jul 13, 2022
• Location: Houston, Texas
• Book URL: https://openstax.org/books/college-physics-2e/pages/1-introduction-to-science-and-the-realm-of-physics-physical-quantities-and-units
• Section URL: https://openstax.org/books/college-physics-2e/pages/31-5-half-life-and-activity

© Jan 19, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

16.1: Half-life

• Last updated
• Save as PDF
• Page ID 49052

• Thomas Tradler and Holly Carley
• CUNY New York City College of Technology via New York City College of Technology at CUNY Academic Works

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

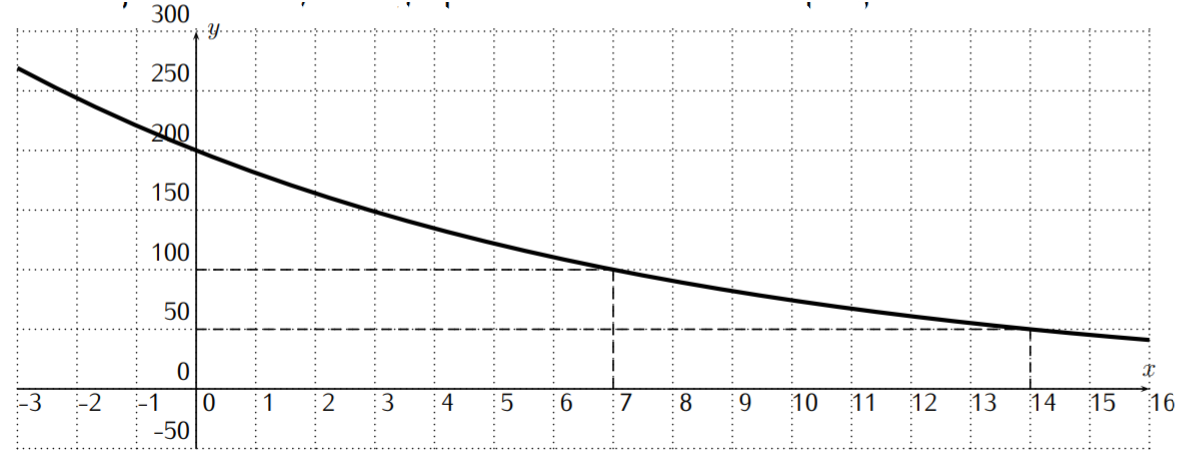
Recall from definition Rate of Growth on page that a function with rate of growth \(r\) is an exponential function \(f(x)=c\cdot b^x\) with base \(b=1+r\) . There is also another important way of determining the base of an exponential function, which is given by the notion of half-life. We start with a motivating example. Consider the function \(f(x)=200\cdot \left(\dfrac 1 2\right)^{\frac x 7}\) . We calculate the function values \(f(x)\) , for \(x=0\) , \(7\) , \(14\) , \(21\) , and \(28\) .

\[\begin{aligned} f(0)&=200\cdot \left(\dfrac 1 2\right)^{\frac 0 7}= 200 \cdot 1=200\\ f(7)&=200\cdot \left(\dfrac 1 2\right)^{\frac 7 7}= 200 \cdot \dfrac 1 2=100\\ f(14)&=200\cdot \left(\dfrac 1 2\right)^{\frac {14} 7}= 200 \cdot \dfrac 1 4=50\\ f(21)&=200\cdot \left(\dfrac 1 2\right)^{\frac {21} 7}= 200 \cdot \dfrac 1 8=25\\ f(28)&=200\cdot \left(\dfrac 1 2\right)^{\frac {28} 7}= 200 \cdot \dfrac 1 {16}=12.5\\\end{aligned} \nonumber \]

From this calculation, we can see how the function values of \(f\) behave: starting from \(f(0)=200\) , the function takes half of its value whenever \(x\) is increased by \(7\) . For this reason, we say that \(f\) has a half-life of \(7\) . (The general definition will be given below.) The graph of the function is displayed below.

We collect the ideas that are displayed in the above example in the definition and observation below.

Definition: Half-Life

Let \(f\) be an exponential function \(f(x)=c\cdot b^x\) with a domain of all real numbers, \(D=\mathbb{R}\) . Then we say that \(f\) has a half-life of \(h\) , if the base is given by

\[\label{half-life-base} \boxed{\,\, b=\left(\dfrac 1 2\right)^{\frac 1 h} \,\,}\]

Note that we can also write \(h\) in terms of \(b\) . Converting \(\ref{half-life-base}\) into a logarithmic equation gives \(\dfrac 1 h = \log_{\frac 1 2} (b)=\dfrac{\log b}{\log \frac 1 2}\) , so that \(h=\dfrac{\log \frac 1 2}{\log{b}}=\log_b\left(\dfrac 1 2\right)\) .

Let \(f\) be the exponential function given for some real constants \(c>0\) and half-life \(h>0\) , that is

\[f(x)=c\cdot \left(\left(\dfrac 1 2\right)^{\frac 1 h}\right)^x=c\cdot \left(\dfrac 1 2 \right)^{\frac x h} \nonumber \]

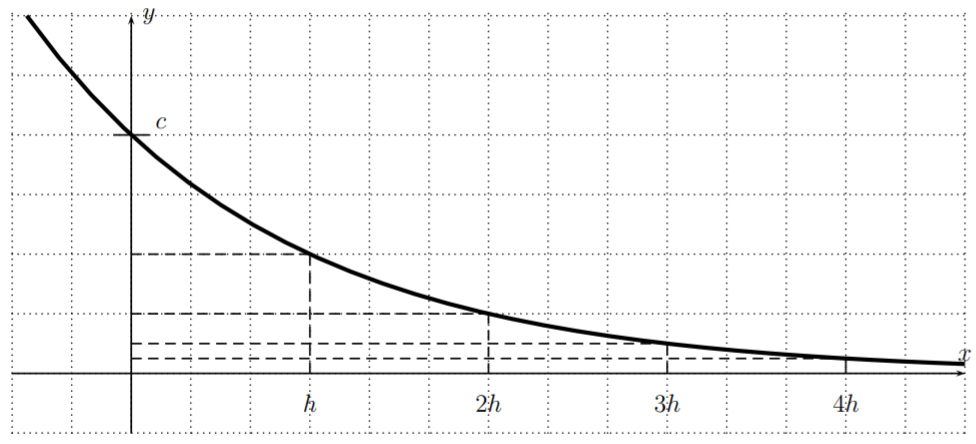
Then we can calculate \(f(x+h)\) as follows:

\[\begin{aligned} f(x+h) &= c\cdot \left(\dfrac 1 2\right)^{\frac {x+h} h}=c\cdot \left(\dfrac 1 2\right)^{\frac x h+\frac h h}=c\cdot \left(\dfrac 1 2\right)^{\frac {x} h +1} \\ &=& c\cdot \left(\dfrac 1 2\right)^{\frac {x} h}\cdot \left(\dfrac 1 2\right)^1=\dfrac 1 2 \cdot f(x) \end{aligned} \nonumber \]

To summarize, \(f\) has the following property:

\[\boxed{f(x+h)=\dfrac 1 2 f(x)} \quad\quad \text{for all }x \in \mathbb{R}.\]

The above equation shows that, whenever we add an amount of \(h\) to an input \(x\) , the effect on \(f\) is that the function value decreases by half its previous value. This is also displayed in the graph below.

We will sometimes use a different letter for the input variable. In particular, the function \(f(x)=c\cdot \left(\dfrac 1 2\right)^{\frac x h}\) is the same as the function \(f(t)=c\cdot \left(\dfrac 1 2\right)^{\frac t h}\) .

Example \(\PageIndex{1}\)

Many radioactive isotopes decay with well-known half-lives.

• Chromium-51 has a half-life of \(27.7\) days 1 . How much of \(3\) grams of chromium-51 will remain after \(90\) days?
• An isotope decays within \(20\) hours from \(5\) grams to \(2.17\) grams. Find the half-life of the isotope.
• We use the above formula \(y=c\cdot \left(\dfrac 1 2\right)^{\frac t h}\) , where \(c=3\) grams is the initial amount of chromium-51, \(h=27.7\) days is the half-life of chromium-51, and \(t=90\) days is time that the isotope decayed. Substituting these numbers into the formula for \(y\) , we obtain:

\[y=3\cdot \left(\dfrac 1 2\right)^{\frac {90}{27.7}}\approx 0.316 \nonumber \]

Therefore, after \(90\) days, \(0.316\) grams of the chromium-51 is remaining.

• We have an initial amount of \(c=5\) grams and a remaining amount of \(y=2.17\) grams after \(t=20\) hours. The half-life can be obtained as follows.

\[\begin{aligned} 2.17&=5\cdot \left(\dfrac 1 2\right)^{\frac {20} {h}}\\ \implies 0.434&= \left(\dfrac 1 2\right)^{\frac {20} {h}} \quad \text{($\div 5$)}\\ \implies \ln(0.434)&= \ln\left(0.5^{\frac {20} h}\right) \quad \text{(apply $\ln$)}\\ \implies \ln(0.434)&= \dfrac {20} h\cdot \ln\left(0.5\right)\\ \implies h&=\dfrac{{20} \cdot \ln(0.5)}{\ln(0.434)} \quad \left(\times \dfrac{h}{\ln(0.434)}\right)\\ \implies t &\approx 16.6 \end{aligned} \nonumber \]

Therefore, the half-life of the isotope is approximately \(16.6\) hours.

An important isotope is the radioisotope carbon-14. It decays with a half-life of \(5730\) years with an accuracy of \(\pm 40\) years. For definiteness we will take \(5730\) years as the half-life of carbon-14.

\[\boxed{\text{The half-life of carbon-14 is $5730$ years.}}\]

One can use the knowledge of the half-life of carbon-14 in dating organic materials via the so called carbon dating method . Carbon-14 is produced by a plant during the process of photosynthesis at a fixed level until the plant dies. Therefore by measuring the remaining amount of carbon-14 in a dead plant one can determine the date when the plant died. Furthermore, since humans and animals consume plants, the same argument can be applied to determine their (approximate) dates of death.

Example \(\PageIndex{2}\)

• A dead tree trunk has \(86\%\) of its original carbon-14. (Approximately) how many years ago did the tree die?
• A dead animal at an archeological site has lost \(41.3\%\) of its carbon-14. When did the animal die?
• Using the function \(y=c\cdot \left(\dfrac 1 2\right)^{\frac t h}\) , where \(c\) is the amount of carbon-14 that was produced by the tree until it died, \(y\) is the remaining amount to date, \(t\) is the time that has passed since the tree has died, and \(h\) is the half-life of carbon-14. Since \(86\%\) of the carbon-14 is left, we have \(y=86\%\cdot c\) . Substituting the half-life \(h=5730\) of carbon-14, we can solve for \(t\) .

\[\begin{aligned} 0.86\cdot c&=c\cdot \left(\dfrac 1 2\right)^{\frac t {5730}}\\ \implies 0.86&= \left(\dfrac 1 2\right)^{\frac t {5730}} \quad \text{($\div c$)}\\ \implies \ln(0.86)&= \ln\left(0.5^{\frac t {5730}}\right) \quad \text{(apply $\ln$)}\\ \ln(0.86)&= \dfrac t {5730}\cdot \ln\left(0.5\right)\\ \dfrac{5730}{\ln(0.5)}\cdot \ln(0.86)&=t \quad \left(\times \dfrac{5730}{\ln(0.5)}\right)\\ \implies t & \approx 1247 \end{aligned} \nonumber \]

Therefore, the tree died approximately \(1247\) years ago.

• Since \(41.3\%\) of the carbon-14 is gone, \(100\%-41.3\%=58.7\%\) is remaining. Using \(y=c\cdot \left(\dfrac 1 2\right)^{\frac{t}{h}}\) with \(y=58.7\%\cdot c\) and \(h=5730\) , we obtain

\[\begin{aligned} 0.587\cdot c&=c\cdot \left(\dfrac 1 2\right)^{\frac t {5730}}\\ \implies 0.587&= \left(\dfrac 1 2\right)^{\frac t {5730}} \quad \text{($\div c$)}\\ \implies \ln(0.587)&= \ln\left(0.5^{\dfrac t {5730}}\right) \quad \text{(apply $\ln$)}\\ \implies \ln(0.587)&= \dfrac t {5730}\cdot \ln\left(0.5\right)\\ \dfrac{5730}{\ln(0.5)}\cdot \ln(0.587)&=t \quad \left(\times \dfrac{5730}{\ln(0.5)} \right)\\ t &\approx 4404 \end{aligned} \nonumber \]

The animal died \(4404\) years ago.

• Half-lives are taken from: https://en.Wikipedia.org/wiki/List_o...fe#100_seconds

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

AP®︎/College Chemistry

Course: ap®︎/college chemistry   >   unit 5.

• First-order reactions
• Half-life of a first-order reaction

Worked example: Using the first-order integrated rate law and half-life equations

• Second-order reactions
• Zero-order reactions
• Kinetics of radioactive decay
• Concentration changes over time

Want to join the conversation?

• Upvote Button navigates to signup page
• Downvote Button navigates to signup page
• Flag Button navigates to signup page

Video transcript

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

10.3: Half-Life

• Last updated
• Save as PDF
• Page ID 155691

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Outcomes

• Define half-life as it relates to radioactive nuclides and solve half-life problems.
• Describe the general process by which radioactive dating is used to determine the age of various objects.
• Calculate the time for a sample to decay.
• Complete dosage calculations based on nuclide activity.

The rate of radioactive decay is often characterized by the half-life of a radioisotope. Half-life \(\left( t_{1/2} \right)\) is the time required for one half of the nuclei in a sample of radioactive material to decay. After each half-life has passed, one half of the radioactive nuclei will have transformed into a new nuclide (see table below). The rate of decay and the half-life do not depend on the original size of the sample. They also do not depend upon environmental factors such as temperature and pressure.

As an example, iodine-131 is a radioisotope with a half-life of 8 days. It decays by beta particle emission into xenon-131.

\[\ce{^{131}_{53}I} \rightarrow \ce{^{131}_{54}Xe} + \ce{^0_{-1}e}\]

After eight days have passed, half of the atoms of any sample of iodine-131 will have decayed, and the sample will now be \(50\%\) iodine-131 and \(50\%\) xenon-131. After another eight days pass (a total of 16 days or 2 half-lives), the sample will be \(25\%\) iodine-131 and \(75\%\) xenon-131. This continues until the entire sample of iodine-131. has completely decayed (see figure below).

Half-lives have a very wide range, from billions of years to fractions of a second. Listed below (see table below) are the half-lives of some common and important radioisotopes. Those with half-lives on the scale of hours or days are the ones most suitable for use in medical treatment.

The following example illustrates how to use the half-life of a sample to determine the amount of radioisotope that remains after a certain period of time has passed.

Example \(\PageIndex{1}\): Strontium-90

Strontium-90 has a half-life of 28.1 days. If you start with a \(5.00 \: \text{mg}\) sample of the isotope, how much remains after 140.5 days have passed?

Step 1: List the known values and plan the problem .

• Original mass \(= 5.00 \: \text{mg}\)
• \(t_{1/2} =\) 28.1 days
• Time elapsed \(=\) 140.5 days
• Final mass of \(\ce{Sr}\)-90 \(= ? \: \text{mg}\)

First, find the number of half-lives that have passed by dividing the time elapsed by the half-life. Then, reduce the amount of \(\ce{Sr}\)-90 by half, once for each half-life.

Step 2: Solve.

Number of half-lives, days, mass

0 half-lives, 0 days, \(5.00 \: \text{mg}\)

1 half-life, 28.1 days, \(2.50 \: \text{mg}\)

2 half-lives, 56.2 days, \(1.25 \: \text{mg}\)

3 half-lives, 84.3 days, \(0.613 \: \text{mg}\)

4 half-lives, 112.4 days, \(0.313 \: \text{mg}\)

5 half-lives, 140.5 days, \(0.156 \: \text{mg}\)

Step 3: Think about your result.

According to the data above, the passage of 5 half-lives means \(0.156 \: \text{mg}\) of the original \(\ce{Sr}\)-90 remains. The remaining \(4.844 \: \text{mg}\) has decayed by beta particle emission to yttrium-90.

Radioactive Dating

Radioactive dating is a process by which the approximate age of an object is determined through the use of certain radioactive nuclides . For example, carbon-14 has a half-life of 5,730 years and is used to measure the age of organic material. The ratio of carbon-14 to carbon-12 in living things remains constant while the organism is alive because fresh carbon-14 is entering the organism whenever it consumes nutrients. When the organism dies, this consumption stops, and no new carbon-14 is added to the organism. As time goes by, the ratio of carbon-14 to carbon-12 in the organism gradually declines, because carbon-14 radioactively decays while carbon-12 is stable. Analysis of this ratio allows archaeologists to estimate the age of organisms that were alive many thousands of years ago. Carbon dating is effective until about 50,000 years. The ages of many rocks and minerals are far greater than the ages of fossils. Uranium-containing minerals that have been analyzed in a similar way have allowed scientists to determine that the Earth is over 4 billion years old.

Decay Series

In many instances, the decay of an unstable radioactive nuclide simply produces another radioactive nuclide. It may take several successive steps to reach a nuclide that is stable. A decay series is a sequence of successive radioactive decays that proceeds until a stable nuclide is reached . The terms reactant and product are generally not used for nuclear reactions. Instead, the terms parent and daugher nuclide are used to to refer to the starting and ending isotopes in a decay process. The figure below shows the decay series for uranium-238.

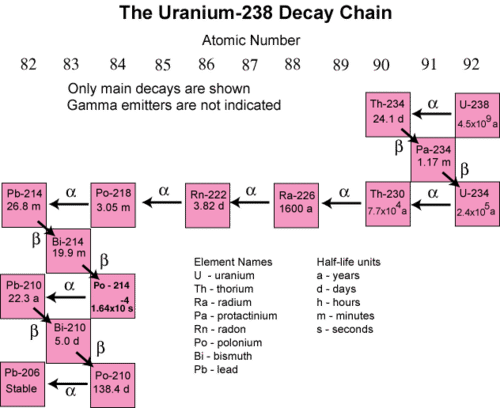
In the first step, uranium-238 decays by alpha emission to thorium-234 with a half-life of \(4.5 \times 10^9\) years. This decreases its atomic number by two. The thorium-234 rapidly decays by beta emission to protactinium-234 (\(t_{1/2} =\) 24.1 days). The atomic number increases by one. This continues for many more steps until eventually the series ends with the formation of the stable isotope lead-206.

Artificial Transmutation

As we have seen, transmutation occurs when atoms of one element spontaneously decay and are converted to atoms of another element. Artificial transmutation is the bombardment of stable nuclei with charged or uncharged particles in order to cause a nuclear reaction . The bombarding particles can be protons, neutrons, alpha particles, or larger atoms. Ernest Rutherford performed some of the earliest bombardments, including the bombardment of nitrogen gas with alpha particles to produce the unstable fluorine-18 isotope.

\[\ce{^{14}_7N} + \ce{^4_2He} \rightarrow \ce{^{18}_9F}\]

Fluorine-18 quickly decays to the stable nuclide oxygen-17 by releasing a proton.

\[\ce{^{18}_9F} \rightarrow \ce{^{17}_8O} + \ce{^1_1H}\]

When beryllium-9 is bombarded with alpha particles, carbon-12 is produced with the release of a neutron.

\[\ce{^9_4Be} + \ce{^4_2He} \rightarrow \ce{^{12}_6C} + \ce{^1_0n}\]

Transuranium Elements

Many, many radioisotopes that do not occur naturally have been generated by artificial transmutation. The elements technetium and promethium have been produced, since these elements no longer occur in nature. All of their isotopes are radioactive and have half-lives short enough that any amount of the elements that once existed have long since disappeared through natural decay. The transuranium elements are elements with atomic numbers greater than 92 . All isotopes of these elements are radioactive and none occur naturally.

Half-life calculations can be based on mass, percent remaining, or dose. Regardless of which one, the concept is still the same. Understanding the radioactivity and half-life of a sample is important for calculating the correct dose for a patient and determining the levels and duration of radioactive emission from a patient after treatment is received.

Frequently, dosages for radioactive isotopes are given the activity in volume. For example, the concentration of \(\ce{I}\)-137 is given as \(50 \: \mu \text{Ci/mL}\) (microCurie per milliliter). This relationship can be used to calculate the volume needed for a particular dose. For example, a patient needs \(125 \: \mu \text{Ci}\) of \(\ce{I}\)1-51. What volume of a \(50 \mu \text{Ci}\) per \(10 \: \text{mL}\) solution should be given?

\[125 \: \mu \text{Ci} \left( \frac{10 \: \text{mL}}{50 \: \mu \text{Ci}} \right) = 25 \: \text{mL}\]

Example \(\PageIndex{2}\)

A patient is given \(\ce{I}\)-131 to treat thyroid cancer. The patient receives \(5.50 \: \text{mL}\) of a solution containing \(50 \: \text{mCi}\) (milliCurie) in \(2 \: \text{mL}\) (assume concentration is an exact number). What does (in \(\text{mCi}\)) is given to the patient? What will be the activity in \(\text{mCi}\) after 24.21 days given that the half-life of \(\ce{I}\)-131 is 8.07 days?

The first part of the problem is to find the dose given to the patient. We are given the volume and the concentration (in units of radioactivity over volume).

\[5.50 \: \text{mL solution} \left( \frac{50 \: \text{mCi}}{2 \: \text{mL}} \right) = 138 \: \text{mCi}\]

The patient is given a does of \(138 \: \text{mCi}\).

Now, we need to find the activity after 24.21 days have passed. After one half-life (8.07 days), the sample will have half as much activity \(\left( 138/2 = 69.0 \: \text{mCi} \right)\). After two half-lives (total of 16.14 days), the sample will have half as much activity as after the first half-life \(\left( 69.0/2 = 34.5 \: \text{mCi} \right)\). After three half-lives (total of 24.21 days), the sample will have half as much activity as after the second half-life \(\left( 34.5/2 = 17.3 \: \text{mCi} \right)\). Therefore, after 24.21 days (3 half-lives), the radioactivity will be \(17.3 \: \text{mCi}\).

Contributors and Attributions

Allison Soult , Ph.D. (Department of Chemistry, University of Kentucky)

• PRO Courses Guides New Tech Help Pro Expert Videos About wikiHow Pro Upgrade Sign In
• EDIT Edit this Article
• EXPLORE Tech Help Pro About Us Random Article Quizzes Request a New Article Community Dashboard This Or That Game Popular Categories Arts and Entertainment Artwork Books Movies Computers and Electronics Computers Phone Skills Technology Hacks Health Men's Health Mental Health Women's Health Relationships Dating Love Relationship Issues Hobbies and Crafts Crafts Drawing Games Education & Communication Communication Skills Personal Development Studying Personal Care and Style Fashion Hair Care Personal Hygiene Youth Personal Care School Stuff Dating All Categories Arts and Entertainment Finance and Business Home and Garden Relationship Quizzes Cars & Other Vehicles Food and Entertaining Personal Care and Style Sports and Fitness Computers and Electronics Health Pets and Animals Travel Education & Communication Hobbies and Crafts Philosophy and Religion Work World Family Life Holidays and Traditions Relationships Youth
• Browse Articles
• Learn Something New
• Quizzes Hot
• This Or That Game
• Train Your Brain
• Explore More
• Support wikiHow
• About wikiHow
• Log in / Sign up
• Education and Communications

How to Calculate Half Life

Last Updated: May 26, 2023 References

Understanding Half-Life

Learning the half-life equation, calculating from a graph, using a calculator, example problems, calculator, practice problems, and answers, expert q&a.

This article was co-authored by Meredith Juncker, PhD and by wikiHow staff writer, Hannah Madden . Meredith Juncker is a PhD candidate in Biochemistry and Molecular Biology at Louisiana State University Health Sciences Center. Her studies are focused on proteins and neurodegenerative diseases. There are 11 references cited in this article, which can be found at the bottom of the page. This article has been viewed 1,163,173 times.

The half-life of a substance undergoing decay is the time it takes for the amount of the substance to decrease by half. It was originally used to describe the decay of radioactive elements like uranium or plutonium, but it can be used for any substance which undergoes decay along a set, or exponential, rate. You can calculate the half-life of any substance, given the rate of decay, which is the initial quantity of the substance and the quantity remaining after a measured period of time. [1] X Research source

• Elements like uranium and plutonium are most often studied with half-life in mind.

• Therefore, you can calculate the half-life for a particular element and know for certain how quickly it will break down no matter what.

• Technically, there are 2 types of carbon: carbon-14, which decays, and carbon-12, which stays constant.

• Simply replacing the variable doesn't tell us everything, though. We still have to account for the actual half-life, which is, for our purposes, a constant.

• On half-life graphs, the x-axis will usually show the timeline, while the y-axis usually shows the rate of decay.

• For example, if the starting point is 1,640, divide 1,640 / 2 to get 820.
• If you are working with a semi log  plot, meaning the count rate is not evenly spaced, you’ll have to take the logarithm of any number from the vertical axis. [11] X Research source

• If you know the half-life but you don’t know the initial quantity, you can input the half-life, the quantity that remains, and the time that has passed. As long as you know 3 of the 4 values, you’ll be able to use a half-life calculator.

• If you don’t know the half-life but you do know the decay constant and the mean lifetime, you can input those instead. Just like the initial equation, you only need to know 2 of the 3 values to get the third one.

• This is a helpful visual, and it can be useful if you don’t want to do all of the equation work.

• Check to see if the solution makes sense. Since 112 g is less than half of 300 g, at least one half-life must have elapsed. Our answer checks out.

• Substitute and evaluate.

• Remember to check your solution intuitively to see if it makes sense.

• For this particular equation, the actual length of the half-life did not play a role.

You Might Also Like

• ↑ https://chem.libretexts.org/Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Supplemental_Modules_(Physical_and_Theoretical_Chemistry)/Kinetics/Reaction_Rates/Half-lives_and_Pharmacokinetics
• ↑ https://chem.libretexts.org/Courses/Furman_University/CHM101%3A_Chemistry_and_Global_Awareness_(Gordon)/05%3A_Basics_of_Nuclear_Science/5.07%3A_Calculating_Half-Life
• ↑ https://atomic.lindahall.org/what-is-meant-by-half-life.html
• ↑ http://faculty.bard.edu/belk/math213/ExponentialDecay.pdf
• ↑ https://www.ausetute.com.au/halflife.html
• ↑ https://socratic.org/chemistry/nuclear-chemistry/nuclear-half-life-calculations
• ↑ https://www.khanacademy.org/test-prep/mcat/physical-processes/atomic-nucleus/a/decay-graphs-and-half-lives-article
• ↑ https://www.gcsescience.com/prad17-measuring-half-life.htm
• ↑ https://www.calculator.net/half-life-calculator.html
• ↑ https://www.youtube.com/watch?v=5mKrIv1lo1E&feature=youtu.be&t=163
• ↑ https://www.chemteam.info/Radioactivity/Radioactivity-Half-Life-probs1-10.html

About This Article

To find the half life of a substance, or the time it takes for a substance to decrease by half, you’ll be using a variation of the exponential decay formula. Plug in ½ for a, use the time for x, and multiply the left side by the initial quantity of the substance. Rearrange the equation so that you’re solving for what the problem asks for, whether that’s half life, mass, or another value. Plug in the values you have and solve, writing the answer in seconds, days, or years. To see the half life equation and look at examples, read on! Did this summary help you? Yes No

• Send fan mail to authors

Reader Success Stories

Georgy Komissarov

Mar 14, 2018

Did this article help you?

Feb 7, 2017

Jun 16, 2018

Christopher Emmanuel

Jan 31, 2017

Howard Farmer

Apr 19, 2017

Featured Articles

Trending Articles

Watch Articles

• Terms of Use
• Privacy Policy
• Do Not Sell or Share My Info
• Not Selling Info

wikiHow Tech Help Pro:

Develop the tech skills you need for work and life

(a) What percentage of the nuclide will have decayed after 159 days? (b) What is the half-life of the nuclide?

(a) 1/2 and 1/4 of the original amount (b) 1/9 and 1/18 of the original amount (c) 1/4 and 1/16 of the original amount (d) 1/4 and 1/8 of the original amount

U-238 ---> Pb-206

Half-Life Calculator

Table of contents

The half-life calculator is a tool that helps you understand the principles of radioactive decay. You can use it to not only learn how to calculate half-life, but also as a way of finding the initial and final quantity of a substance or its decay constant. This article will also present you with the half-life definition and the most common half-life formula.

Half-life definition

Each radioactive material contains stable and unstable nuclei. Stable nuclei don't change, but unstable nuclei undergo a type of radioactive decay , emitting alpha particles, beta particles, or gamma rays and eventually decaying into stable nuclei. Half-life is defined as the time required for half of the unstable nuclei to undergo their decay process.

Each substance has a different half-life. For example, carbon-10 has a half-life of only 19 seconds, making it impossible for this isotope to be encountered in nature. Uranium-233, on the other hand, has a half-life of about 160 000 years.

This term can also be used more generally to describe any kind of exponential decay - for example, the biological half-life of metabolites.

Half-life is a probabilistic measure - it doesn't mean that exactly half of the substance will have decayed after the time of the half-life has elapsed. Nevertheless, it is an approximation that gets very accurate when a sufficient number of nuclei are present.

🙋 One of the applications of knowing half-life is radiocarbon dating. Learn more about that by checking out our Radiocarbon dating calculator .

Half-life formula

We can determine the number of unstable nuclei remaining after time t t t using this equation:

• N ( t ) N(t) N ( t ) – Remaining quantity of a substance after time t t t has elapsed;
• N ( 0 ) N(0) N ( 0 ) – Initial quantity of this substance; and
• T T T – half-life.

It is also possible to determine the remaining quantity of a substance using a few other parameters:

• τ \tau τ – mean lifetime - the average amount of time a nucleus remains intact; and
• λ \lambda λ – decay constant (rate of decay).

All three of the parameters characterizing a substance's radioactivity are related in the following way:

How to calculate the half-life

• Determine the initial amount of a substance. For example, N ( 0 ) = 2.5  kg \small N(0) = 2.5\ \text{kg} N ( 0 ) = 2.5   kg .
• Determine the final amount of a substance - for instance, N ( t ) = 2.1  kg \small N(t) = 2.1\ \text{kg} N ( t ) = 2.1   kg .
• Measure how long it took for that amount of material to decay. In our experiment, we observed that it took 5 minutes.
• Input these values into our half-life calculator. It will compute a result for you instantaneously - in this case, the half-life is equal to 19.88  minutes \small 19.88\ \text{minutes} 19.88   minutes .
• If you are not certain that our calculator returned the correct result, you can always check it using the half-life formula.

Confused by exponential formulas? Try our exponent calculator .

Half-life is a similar concept to doubling time in biology. Check our generation time calculator to learn how exponential growth is both useful and a problem in laboratories! Also, we use a similar concept in pharmacology, and we call it the "drug half-life". Find out more about that in our drug half-life calculator .

What is half life?

Half-life is defined as the time taken by a substance to lose half of its quantity. This term should not be confused with mean lifetime , which is the average time a nucleus remains intact.

How to calculate half life?

To find half-life:

• Find the substance's decay constant.
• Divide the natural logarithm of 2 or ln(2) by the decay constant of the substance.
• Alternatively, you can multiply ln(2) by the mean lifetime.

What is the half life of radium?

The half-life of radium-218 is 25.2 x 10 -6 seconds . On the other hand, one of the most common radium isotopes is radium-226, with a half-life of 1600 years!

What is the half life of carbon?

The half-life of carbon-14 is 5730 years . This means that after 5730 years have elapsed, half of an initial quantity of carbon-14 would have disintegrated.

What is the half life of uranium?

The half-life of uranium-238 is 4.5 billion years . It is one of the three natural occurring uranium isotopes, along with uranium-235 (700 million years), and uranium-234 (246,000 years).

Initial quantity (N(0))

Half-life time (T)

Total time (t)

Remaining quantity (N(t))

Decay constant (λ)

Mean lifetime (τ)

An average length of time before an element decays.

10 half life problems and answers examples

Expert Answer(s) - 1

Tutor 5 (9 Reviews)

Chemistry Tutor

Still stuck with a Chemistry question

1. A radioisotope decays from 150 mg to 120.2 mg in 5 days. Calculate the half-life of this isotope.

          From N t = 1 2 t t 1 / 2 N o                                                                                                  

we rearrange this equation to take the form

              t 1 / 2 =  t   log 2 log N o N t

                     = 5 log 2 log 150 120 . 2

                     = 15.6482 days

2. Iodine-131 has a half-life of 8 days. What is the mass of this nuclide that remaines when 40 g of it decays in 48 hours?

We use the relalation  N t =  1 2 t t 1 / 2 N o

                                     =  0 . 5 48 8 X 40

                                     = 0.6250 g

3. A sample of Pd-100 decayed to a mass of 30 mg in 16 days. Given that the half-life of Pd is 4 days, calculate the initial mass of the sample

We are required to find  N o , when we have  N t   and t. rearranging the equation used in example 2, we obtain;

              N o =  2 t t 1 / 2   N t

                   = 2 16 4 X  30

                   = 480 g

4. Given that 50.0 g of C-14 decayed in 4 half-lives, how much of this isotope is left? C-14 Half-Life = 5730 Years.

We utilize the equation that relate amount remaining, initial mass and number of half-lives,n.

              N t =  1 2 n   X  N o

                   =  ( 1 2 ) 4   X 50

                   = 3.125 g

5. What is the half-life of an isotope that is 80 % remained after 16 days?

      % remaining= 80 100

 Therefore  N t = 80,  N o = 100, Now using the half-life equation in example 1, we have

                  t 1 / 2 =  16   log 2 log   100 80

                         = 49.7 days 

6. A certain radioisotope has a half-life of 9 days. What percentage of an initial mass of this isotope remains after 25 days?

This question requires that we calculate N t , when we have t and  t 1 / 2 ,  

                  N t =  0 . 5 t t 1 / 2 N o ,

             percentage = N t N o   x   100

                              =  0 . 5 t t 1 / 2 x 100

                              = 14.58 %

7.A radioactive source has a half-life of 80 s. How long will it take for 5/6 of the source to decay?

Fraction remaining =  1 6 , in this case  N t = 1,  N o = 6, we are required to determine t, when we have  t 1 / 2 , now from N t =  N o x  0 . 5 t t 1 / 2 ,we obtain the relation for calculating t as;

                        t =  t 1 / 2   log   N o N t log   2

                          =  80   log   1 6 log   2

                          = 206.797 seconds

8. Achaelogist dated Holy shroud using radiocarbon ( C 14 ), he found out that the amount of C 14 found in Holy shroud is 92 % of that in the living tossue (half-life of carbon-14=5730 years)

a) Calculate the decay constant for C 14  assuming that it decreases solely due to nuclear decay 

  Solution

         λ = 0 . 693 t 1 / 2

          = 0.0001 y e a r - 1

b) Calculate the age of Shroud of Turin

            N t =  N o e - λ t

              t =  1 λ ln N o N t

                = 5730 0 . 693 ln   100 72

                = 690 years

9. The activity of a radioactive source decreased from 6000  per minute to 500 counts per minute in 10 hours. Calculate the half-life of the radioactive source.

We use the equation  A t =  ( 1 2 ) t t 1 / 2   A o , where  A t is the activity in time t,  A o is the original activity

                                    500 = ( 1 2 ) 10 t 1 / 2 ×   6000

                                    t 1 / 2 =  10   log   2 log   12

                                          =  2 . 789   h o u r s

We can also use the relation  A t =  ( 1 2 ) n A o , where n is the number of half-lives

                                            A t  =  A o 2 n

                                            n =  t t 1 / 2 =  l og   A o A t log   2  

                                          t 1 / 2 =    10   log   2 log   6000 500  

                                                  = 2.789 hours

10. Calculate the percentage of the original radioisotope that remained after three half-lives elapsed

   %   r e m a i n e d =

                     = 0 . 5 3   ×   100

                     =  12 . 5   %

Get Online Tutoring or Questions answered by Experts.

You can post a question for a tutor or set up a tutoring session

Top Tutorials

Join thousands of happy students.

• Save Password
• Forget Password?

Haven't Any Account? Click here

Already Have An Account? Go For LogIn

No account yet? Register Now

Create Your Account As?

Already have an account? Login

Report your Copyright Material Concern

You need an approved tutor account in order to post an answer.

Don't have an Account? Click here

We use cookies to ensure that we give you the best experience on our website. If you continue without changing your settings, we will assume you are happy to receive all cookies

• Chemistry Concept Questions and Answers
• Half Life Questions

Half-Life Questions

Half-Life or previously known as the Half-Life Period is one of the common terminologies used in Science to describe the radioactive decay of a particular sample or element within a certain period of time.

However, this concept is also widely used to describe various types of decay processes, especially exponential and non-exponential decay. Apart from science, the term is used in medical sciences to represent the biological half-life of certain chemicals in the human body or in drugs.

Half-Life Chemistry Questions with Solutions

Q1. An isotope of caesium (Cs-137) has a half-life of 30 years. If 1.0g of Cs-137 disintegrates over a period of 90 years, how many grams of Cs-137 would remain?

b.) 0.125 g

c.) 0.00125 g

Correct Answer- (b.) 0.125 g

Q2. Selenium-83 has a half-life of 25.0 minutes. How many minutes would it take for a 10.0 mg sample to decay and only have 1.25 mg of it remain?

a.) 75 minutes

b.) 75 days

c.) 75 seconds

d.) 75 hours

Correct Answer- (a.) 75 minutes

Q3. How long does it take a 100.00g sample of As-81, with a half-life of 33 seconds, to decay to 6.25g?

a.) 122 seconds

b.) 101 seconds

c.) 132 seconds

d.) 22 seconds

Correct Answer – (c.) 132 seconds

Q4. What is the half-life of a radioactive isotope if a 500.0g sample decays to 62.5g in 24.3 hours?

a.) 8.1 hours

b.) 6.1 hours

c.) 5 hours

d.) 24 hours

Correct Answer- (a.) 8.1 hours

Q5. What is the half-life of Polonium-214 if, after 820 seconds, a 1.0g sample decays to 0.03125g?

a.) 164 minutes

b.) 164 seconds

c.) 64 seconds

d.) 160 minutes

Correct Answer- (b.) 164 seconds

Q6. The half-life of Zn-71 is 2.4 minutes. If one had 100.0 g at the beginning, how many grams would be left after 7.2 minutes have elapsed?

To begin, we’ll count the number of half-lives that have passed. This can be obtained by doing the following:

Half-life (t½) = 2.4 mins

Time (t) = 7.2 mins

Number of half-lives

n = 7.2/2.4 = 3

Thus, three half-lives have passed.

Finally, we will calculate the remaining amount. This can be obtained by doing the following:

N 0 (original amount) = 100 g

(n) = number of half-lives

Amount remaining (N) =?

N = 100 / 2 3

N = 100 / 8

As a result, the amount of Zn-71 remaining after 7.2 minutes is 12.5 g.

Q7. Pd-100 has a half-life of 3.6 days. If one had 6.02 x 10 23 atoms at the start, how many atoms would be present after 20.0 days?

Half-life = 3.6 days

Initial atoms = 6.02 ×10 23 atoms

Time = 20days

To calculate the atoms present after 20 days, we use the formula below.

Thus, the number of atoms available is 1.28 × 10 22 atoms.

Q8. Os-182 has a half-life of 21.5 hours. How many grams of a 10.0 gram sample would have decayed after exactly three half-lives?

Answer. The amount of the radioactive substance that will remain after 3- half- lives=(½) 3 × a,

where a = initial concentration of the radioactive element.

So, amount of the radioactive substance that remains aftet 3- half-lives=( ½)³x10 = 10/8= 1.25 g.

Therefore, the number of grams of the radioactive substance that decayed in 3 half-lives = (10 – 1.25) g

Q9. After 24.0 days, 2.00 milligrams of an original 128.0 milligram sample remain. What is the half-life of the sample?

Answer. The remaining decimal fraction is:

2.00 mg / 128.0 mg = 0.015625

The half-lives that must have expired to get to 0.015625?

(½) n = 0.015625

n log 0.5 = 0.015625

n = log 0.5 / 0.015625 n = 6

Calculation of the half-life:

24 days divided by 6 half-lives equals 4.00 days

Q10. A radioactive isotope decayed to 17/32 of its original mass after 60 minutes. Find the half-life of this radioisotope.

Answer. The amount that remains

17/32 = 0.53125

(1/2) n = 0.53125

n log 0.5 = log 0.53125

n = 0.91254

Half-lives that have elapsed are therefore, n = 0.9125

60 minutes divided by 0.91254 equals 65.75 minutes.

Therefore, n = 66 minutes

Q11. How long will it take for a 40 gram sample of I-131 (half-life = 8.040 days) to decay to 1/100 of its original mass?

Answer. (1/2) n = 0.01

n log 0.5 = log 0.01

6.64 x 8.040 days = 53.4 days

Therefore, it will take 53.4 days to decay to 1/100 of its original mass.

Q12. At time zero, there are 10.0 grams of W-187. If the half-life is 23.9 hours, how much will be present at the end of one day? Two days? Seven days?

24.0 hr / 23.9 hr/half-life = 1.0042 half-lives

One day = one half-life; (1/2) 1.0042 = 0.4985465 remaining = 4.98 g

Two days = two half-lives; (1/2) 2.0084 = 0.2485486 remaining = 2.48 g

Seven days = 7 half-lives; (1/2) 7.0234 = 0.0076549 remaining = 0.0765 g

Q13. 100.0 grams of an isotope with a half-life of 36.0 hours is present at time zero. How much time will have elapsed when 5.00 grams remains?

The afraction amount remaining will be-

5.00 / 100.0 = 0.05

(1/2) n = 0.05

n log 0.5 = log 0.05

n = 4.32 half-lives

36.0 hours x 4.32 = 155.6 hours

Q14. How much time will be required for a sample of H-3 to lose 75% of its radioactivity? The half-life of tritium is 12.26 years.

If you lose 75%, then 25% remains.

(1/2) n = 0.25

n = 2 (Since, (1/2) 2 = 1/4 and 1/4 = 0.25)

12.26 x 2 = 24.52 years

Therefore, 24.52 years of time will be required for a sample of H-3 to lose 75% of its radioactivity

Q15. The half-life for the radioactive decay of 14 C is 5730 years. An archaeological artifact containing wood had only 80% of the 14 C found in a living tree. Estimate the age of the sample.

Answer. Decay constant, k = 0.693/t 1/2 = 0.693/5730 years = 1/209 × 10 –4 /year

= 1846 years (approx)

Practise Questions on Half-Life

Q1. A newly prepared radioactive nuclide has a decay constant λ of 10 –6 s –1 . What is the approximate half-life of the nuclide?

d.) 1 month

Q2. If the decay constant of a radioactive nuclide is 6.93 x 10 –3 sec –1 , its half-life in minutes is:

Q3. A first-order reaction takes 40 min for 30% decomposition. Calculate t 1/2 .

Q4. What will be the time for 50% completion of a first-order reaction if it takes 72 min for 75% completion?

Q5. How much time will it take for 90% completion of a reaction if 80% of a first-order reaction was completed in 70 min?

Click the PDF to check the answers for Practice Questions. Download PDF

Recommended Videos

Zero order reaction.

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Request OTP on Voice Call

Post My Comment

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

Home of Science

• WAVES/ACOUSTICS
• THERMODYNAMICS
• ELECTROMAGNETISM
• SOLAR ENERGY
• MODERN PHYSICS
• QUESTIONS AND ANSWERS
• Privacy Policy
• Terms and Conditions

Half-life Problems And Answers Examples

By Abnurlion

On April 13, 2023

In MODERN PHYSICS

Half-life Problems And Answers Examples: Here are 18 half-life problems and answers to help you understand how to solve a question about half-life:

In 24 days, a radioactive isotope decreased in mass from 64 grams to 2 grams. What is the half-life of the radioactive material?

The half-life of the radioactive material is 4.8 days.

Explanation

We are going to apply two methods to arrive at our answer

Method 1: Conventional method

64 g to 32 g = 1 half-life

32 g to 16 g = 2 half-life

16 g to 8 g = 3 half-life

8 g to 4 g = 4 half-life

4 g to 2 g = 5 half-life

If 5 half-life is equal to 24 days. Then 1 half-life will be T

Therefore, T x 5 half-life = 1 half-life x 24 days

T = (1 half-life x 24 days) / 5 half-life = 4.8 days

Method 2: Zhepwo Method

Decay time , t = 24 days

Half-life, T = ?

Initial mass, N 1 = 64 g

Final mass, N 2 = 2 g

We will use the formula

R = N 1 / N 2 = 64 / 2 = 32

T = t / (log 2 R) = 24 / (log 2 32) = 24 / 5 = 4.8 days

Therefore, the half-life of the radioactive material is 4.8 days

The half-life of radioactive material is 6 hours. What quantity of 1 kg of the material would decay in 24 hours?

The final answer to the above question is (15/16) 0.9375 kg

We will also apply two methods to solve the above question

Method 1: Conventional Method

After 6 hours, 1/2 kg decays, and 1/2 kg will remain

Another 6 hours, 1/2 of 1/2 kg decays, 1/4 kg remains

6 hours after, 1/2 of 1/4 kg decays, 1/8 kg remains

After another 6 hours, 1/2 of 1/8 kg decays, 1/16 kg remains

Therefore, the material decayed would be:

1 kg – 1/16 kg = (15 / 16) kg = 0.9375 kg

Half-life, T = 6 hrs

Initial mass, N 1 = 1 kg

Mass of the decayed material, N d = ?

This implies that

n = t / T = 24 / 6 = 4

R = 2 n = 2 4 = 16

N d = N 1 (R – 1 / R) = 1 (16-1 / 16) = (15/16) kg

Therefore, the quantity of 1 kg of the material that would decay in 24 hours is 15/16 kilograms or 0.9375 kilograms.

A radioactive sample initially contains N atoms. After three (3) half-lives, what is the number of atoms that have disintegrated?

The final answer to the above question is (7/8) N

We will use two methods to solve the above question

First step: After 1 half-life, N/2 decay, N/2 remain

Second Step: After 2 half-life, 1/2 of N/2 decay, N/4 remain

Third step: After 3 half-life, 1/2 of N/4 decay, N/8 remains

The number of atoms disintegrated = Sum of the disintegrated atoms or fractions

This is now equal to

= N/2 + (1/2 x N/2) + (1/2 x N/4) = N/2 + N/4 + N/8 = (7/8)N

Alternatively, we can also apply the following steps to solve the problem using Zhepwo method:

Initial number of atoms, N 1 = N

Number of half-lives, n = 3

Also, the number of atoms decayed, N d = ?

R = 2 n = 2 3 = 8

N d = N 1 (R – 1 / R) = N ( 8 – 1 / 8) = N x 7/8 = (7/8)N

Therefore, the number of atoms that have disintegrated is (7/8)N

After three half-lives, the fraction of a radioactive material that has decayed is

The final answer to the above question is 7/8

We will use two methods

1 half-life implies 1/2 decays, ,1/2 remains

2 half-life shows that 1/4 decays, 1/4 remains

3 half-life, 1/8 decays, 1/8 remains

Hence, the fraction decayed = original fraction – remaining fraction = (1 – 1/8) = 7/8

Note that the original fraction is 1/1 which is equal to 1

The fraction decayed f d = ?

Disintegration ratio, R = 2 n = 2 3 = 8

f d = R – 1 / R = 8 – 1 / 8 = 7/8

Therefore, the fraction of radioactive material that has decayed is 7/8

The half-life of a radioactive element is 24 hours. Calculate the fraction of the original element that would have disintegrated in 96 hours.

The final answer to the above question is 15/16

I will apply two methods to solve the problem

After 24 hrs, 1/2 disintegrate, 1/2 remain

Another 24 hrs, 1/4 decay, 1/4 remain

Next 24 hrs, 1/8 decay, 1/8 remain

The next 24 hrs, 1/16 decay, 1/16 remain

Fraction disintegrate = sum of decayed fractions = 1/2 + 1/4 + 1/8 + 1/16 = 15/16

Half-life, T = 24 hrs

Decay time, t = 96 hrs

Fraction disintegrated, f d = ?

n = t/T = 96/24 = 4

f d = (R – 1) / R = (16 – 1) / 16 = 15/16

Therefore, the fraction of the original element that would have disintegrated in 96 hours is 15/16.

A radioactive isotope has a half-life of 20 hours. What fraction of the original radioactive nuclei will remain after 80 hours?

The final answer to the above question is 1/16

We will still use the two methods to find the answer to the problem

Let n be the original number of nuclei

After 20 hours, n/2 disintegrates and n/2 remains

The next 20 hours, 1/2 of n/2 disintegrates and n/4 remains

Next 20 hrs, 1/2 of n/4 decayed, and n/8 remains

After another 20 hrs, 1/2 of n/8 decayed, and n/16 remains

Half-life, T = 20 hrs

Decay time, t = 80 hrs

Number of half-lives, n = t/T = 80/20 = 4

Disintegration ratio, R = 2 n = 2 4 = 16

Fraction remaining, f r = 1/R = 1/16

We can also use an alternative method

T = 20, t = 80

Fraction remaining, f r = 1 / (2 t/T ) = 1 / (2 80/20 ) = 1 / 2 4 = 1 / 16

Therefore, after 80 hours. The fraction of the original number remaining would be 1/16

Two radioactive elements A and B have half-lives of 100 and 50 years respectively. Samples of A and B initially contain equal number of atoms. What is the ratio of remaining atoms of A to that of B after 200 years?

The ratio of remaining atoms of A to that of B after 200 years is 4:1

You can employ any of the two methods below to arrive at your answer:

1. Conventional Method:

When we allow n to be as the original number of the nuclei

Sample A: Half-life = 100 years

After 100 years, n/2 disintegrates and n/2 remains

Additionally, after 100 years, n/4 disintegrates and n/4 remains

Thus, after 200 years, the fraction of the original number that will remain is 1/4

Sample B: Half-life = 50 years

After 50 years, n/2 disintegrate, n/2 remain

Another 50 years, n/4 disintegrate and n/4 will remain

50 years more, n/8 will decay, n/8 remain

After 50 years, n/16 decay, n/16 remain

Therefore, after 200 years, fraction of atoms that will remain is 1/16

Ratio of A:B = 1/4 : 1/16

We will now multiply both sides by 16 to obtain:

The ratio of A:B = 4 : 1

2. Zhepwo Method

T is the Half-life for A and B which is 100 and 50 respectively

And t is the decay time for A and B which is 200 and 200 respectively

The number of half-lives n = t/T which is A = 200/100 = 2, and B = 200/50 = 4

Disintegrating ratio R = 2 n and it will give us 2 2 = 4 and 2 4 = 16

The initial number of atoms, N 1 = 1

Thus, we have A = 16 (1/4) = 4, and B = 16 (1/16) = 1

Hence we have a ratio of A:B = 4:1

A radioactive substance has a half-life of 80 days. If the initial number of atoms in the sample is 6 x 10 10 , how many atoms would remain at the end of 320 days?

The number of atoms that would remain at the end of 320 days is 3.8 x 10 9 atoms

T = 80; t = 320; and N 1 = 6 x 10 10

We will also use the formula N 2 = (N 1 / 2 t/T )

Therefore, by substituting our data into the above formula, we will have:

N 2 = (N 1 / 2 t/T ) = (6 x 10 10 ) / 2 320/80 = 6 x 10 10 / 2 4 = 6 x 10 10 / 16 = 3.8 x 10 9 atoms

A percentage of the original nuclei of a sample of a radioactive substance left after 5 half-lives is?

The percentage left is 3%

Number of hlaf-lives (n) = 5

original amount or fraction (N 1 ) = 1

Disintegrating ratio, R = 2 n = 2 5 = 32

Fraction remaining, f r = 1/R

The formula we will apply is:

Percentage of the original left = [amount left (fraction remaining) / original amount] x 100

Percentage of the original left = (f r / N 1 ) x 100 = [(1/32) / 1] x 100 = [1/32] x 100 = 3.125 = 3%

A radioactive substance of mass 768 grams has a half-life of 3 years. After how many years does this substance leave only 6 grams undecayed?

The answer is 21 years

Half-life T = 3 years

Initial mass present, N 1 = 768 g

Final mass remaining, N 2 = 6 g

Decay time, t = ?

The disintegration ratio, R = N 1 / N 2 = 768 / 6 = 128

from the formula below:

T = t / (log 2 R)

Making t subject of the formula and substituting our values, we will have:

t = T x log 2 R = 3 x log 2 128 = 3 x 7 = 21 years

An element whose half-life is 10 days is of mass 12 grams. Calculate the time during which 11.25 grams of the element would have decayed.

The final answer to this question is 40 days

Half-life, T = 10 days

Initial mass present, N 1 = 12 g

The mass of the element decayed, N d = 11.25 grams

N d = N 1 – N 2

Thus, N 2 = N 1 – N d = 12 – 11.25 = 0.75 grams

R = N 1 / N 2 = 12 / 0.75 = 16

Applying the formula T = t / (log 2 R) and making t the subject of the formula, we will have:

t = T x log 2 R = 10 x log 2 16 = 10 x 4 = 40 years

A radioactive element decreases in mass from 100g to 15g in 6 days. What is the half-life of the radioactive material?

The half-life of the radioactive element is 2.2 days

Initial mass present, N 1 = 100g

Final mass present, N 2 = 15g

Decay time, t = 6 days

Disintegration ratio, R = N 1 / N 2 = 100 / 5 = 6.67

The half-life formula T = t / (log 2 R) = 6 / log 2 6.67

Therefore, we can now say that

T = (6 x log2) / log 2 6.67 = (6 x 0.30103) / 0.824 = 2.2 days

The time it will take a certain radioactive material with a half-life of 50 days to reduce 1/32 of its original number is

The final answer to the above question is 250 days

Half-life, T = 50 days

Disintegration ratio, R = 32

Fraction remaining, f r = 1/R = 1/32

Using the formula, we will obtain

t = T x log 2 R = 50 x log 2 32 = 50 x 5 = 250 days

A radioactive substance has a half-life of 3 minutes. After 9 minutes, the count rate was observed to be 200, what was the count rate at zero time?

Note that count rate at zero time is the same as the initial count rate

9 min ===> count rate 200

6 min ===> count rate (200 x 2) = 400

3 min ===> count rate (400 x 2) = 800

0 min ===> count rate (800 x 2) = 1600

Therefore, count rate at zero time is 1600

The count rate of a radioactive material is 800 count/min. If the half-life of the material is 4 days, what would the the count rate be 16 days later?

Initial count rate = 800 count/min

Half-life = 4 days

After 4 days ==> (1/2) x 800 = 400 count/min

8 days after ==> (1/2) x 400 = 200 count/min

12 days after ==> (1/2) x 200 = 100 count/min

4 days after ==> (1/2) x 100 = 50 count/min

Therefore, the count rate 16 days later is 50 count/min

The half-life of a radioactive source is 1 minute. If a rate meter connected to the source registers 200μA at a given time, what would be its reading after 3 minutes?

A rate meter measures the count rate of radioactive of radioactive substance

Halff-life = 1 minute

1 minutes after, rate meter reads (1/2) x 200μ = 100μ

2 minutes after, rate meter reads (1/2) x 100μ = 50μ

3 minutes after, rate meter reads (1/2) x 50μ = 25μ

Therefore, rate meter reading after 3min is 25μ.

In 90 seconds, the mass of a radioactive element reduces to 1/32 of its original values. Determine the half-life of the element.

Decay time, t = 90 seconds

Fraction of initial mass remaining, F r = 1/32

Additionally, F r = 1/R

Therefore, by equating the above formulas, we will have

This implies that R = 32

Hence, Half-life (T) = t / (log 2 R) = 90 / (log 2 32) = 90 / 5 = 18 seconds

A radioactive substance has a half-life of 3 days. If a mass of 1.55 g of this substance is left after decaying for 15 days, determine the original value of the mass.

Half-life (T) = 3 days2

Decay time, t = 15 days

Final mass remaining, N 2 = 1.55 g

Therefore, n = t/T = 15/3 = 5

R = N 1 / N 2

Hence, N 1 = RN 2 = 32 x 1.55

Thus, the original mass N 1 =49.6 grams

In 90 seconds, the mass of a radioactive element reduces to 1/16 of its original value. Determine the half-life of the element.

Decay time t = 90 seconds, Fraction of mass remaining, F r = 1/16

But F r = 1/R

Therefore, 1/R = 1/16, and the value of R = 16

Half-life (T) = t / (log 2 R) = t / (log 2 16) = 90/4 = 22.5 seconds

Picture of Half-Life Formula

You may also like to read:

What is Radioactivity

University of Washington

Share this post: on Twitter on Facebook on Google+

Half-Life Formula

Powered by WordPress & Theme by Anders Norén

• Skip to content
• Skip to search
• Skip to footer

Products, Solutions, and Services

Want some help finding the Cisco products that fit your needs? You're in the right place. If you want troubleshooting help, documentation, other support, or downloads, visit our  technical support area .

Contact Cisco

• Get a call from Sales

Call Sales:

• 1-800-553-6387
• US/CAN | 5am-5pm PT
• Product / Technical Support
• Training & Certification

Products by technology

• Software-defined networking
• Cisco Silicon One
• Cloud and network management
• Interfaces and modules
• Optical networking
• See all Networking

Wireless and Mobility

• Access points
• Outdoor and industrial access points
• Controllers
• See all Wireless and Mobility

• Secure Firewall
• Secure Endpoint
• Secure Email
• Secure Access
• Multicloud Defense
• See all Security

Collaboration

• Collaboration endpoints
• Conferencing
• Cisco Contact Center
• Unified communications
• Experience Management
• See all Collaboration

Data Center

• Servers: Cisco Unified Computing System
• Cloud Networking
• Hyperconverged infrastructure
• Storage networking
• See all Data Center

• Nexus Dashboard Insights
• Network analytics
• Cisco Secure Network Analytics (Stealthwatch)

• Video endpoints
• Cisco Vision
• See all Video

Internet of Things (IoT)

• Industrial Networking
• Industrial Routers and Gateways
• Industrial Security
• Industrial Switching
• Industrial Wireless
• Industrial Connectivity Management
• Extended Enterprise
• Data Management
• See all industrial IoT

• Cisco+ (as-a-service)
• Cisco buying programs
• Cisco Nexus Dashboard
• Cisco Networking Software
• Cisco DNA Software for Wireless
• Cisco DNA Software for Switching
• Cisco DNA Software for SD-WAN and Routing
• Cisco Intersight for Compute and Cloud
• Cisco ONE for Data Center Compute and Cloud
• See all Software
• Product index

Products by business type

Service providers

Small business

Midsize business

Cisco can provide your organization with solutions for everything from networking and data center to collaboration and security. Find the options best suited to your business needs.

• By technology
• By industry
• See all solutions

CX Services

Cisco and our partners can help you transform with less risk and effort while making sure your technology delivers tangible business value.

• See all services

Design Zone: Cisco design guides by category

Data center

• See all Cisco design guides

End-of-sale and end-of-life

• End-of-sale and end-of-life products
• End-of-Life Policy
• Cisco Commerce Build & Price
• Cisco Software Central
• Cisco Feature Navigator
• See all product tools
• Cisco Mobile Apps
• Design Zone: Cisco design guides
• Cisco DevNet
• Marketplace Solutions Catalog
• Product approvals
• Product identification standard
• Product warranties
• Cisco Security Advisories
• Security Vulnerability Policy
• Visio stencils
• Local Resellers
• Technical Support