create a problem statement about hypothesis testing

Have a language expert improve your writing

Run a free plagiarism check in 10 minutes, automatically generate references for free.

• Knowledge Base
• Methodology
• How to Write a Strong Hypothesis | Guide & Examples

How to Write a Strong Hypothesis | Guide & Examples

Published on 6 May 2022 by Shona McCombes .

A hypothesis is a statement that can be tested by scientific research. If you want to test a relationship between two or more variables, you need to write hypotheses before you start your experiment or data collection.

Table of contents

What is a hypothesis, developing a hypothesis (with example), hypothesis examples, frequently asked questions about writing hypotheses.

A hypothesis states your predictions about what your research will find. It is a tentative answer to your research question that has not yet been tested. For some research projects, you might have to write several hypotheses that address different aspects of your research question.

A hypothesis is not just a guess – it should be based on existing theories and knowledge. It also has to be testable, which means you can support or refute it through scientific research methods (such as experiments, observations, and statistical analysis of data).

Variables in hypotheses

Hypotheses propose a relationship between two or more variables . An independent variable is something the researcher changes or controls. A dependent variable is something the researcher observes and measures.

In this example, the independent variable is exposure to the sun – the assumed cause . The dependent variable is the level of happiness – the assumed effect .

Prevent plagiarism, run a free check.

Step 1: ask a question.

Writing a hypothesis begins with a research question that you want to answer. The question should be focused, specific, and researchable within the constraints of your project.

Step 2: Do some preliminary research

Your initial answer to the question should be based on what is already known about the topic. Look for theories and previous studies to help you form educated assumptions about what your research will find.

At this stage, you might construct a conceptual framework to identify which variables you will study and what you think the relationships are between them. Sometimes, you’ll have to operationalise more complex constructs.

Step 3: Formulate your hypothesis

Now you should have some idea of what you expect to find. Write your initial answer to the question in a clear, concise sentence.

Step 4: Refine your hypothesis

You need to make sure your hypothesis is specific and testable. There are various ways of phrasing a hypothesis, but all the terms you use should have clear definitions, and the hypothesis should contain:

• The relevant variables
• The specific group being studied
• The predicted outcome of the experiment or analysis

Step 5: Phrase your hypothesis in three ways

To identify the variables, you can write a simple prediction in if … then form. The first part of the sentence states the independent variable and the second part states the dependent variable.

In academic research, hypotheses are more commonly phrased in terms of correlations or effects, where you directly state the predicted relationship between variables.

If you are comparing two groups, the hypothesis can state what difference you expect to find between them.

Step 6. Write a null hypothesis

If your research involves statistical hypothesis testing , you will also have to write a null hypothesis. The null hypothesis is the default position that there is no association between the variables. The null hypothesis is written as H 0 , while the alternative hypothesis is H 1 or H a .

Hypothesis testing is a formal procedure for investigating our ideas about the world using statistics. It is used by scientists to test specific predictions, called hypotheses , by calculating how likely it is that a pattern or relationship between variables could have arisen by chance.

A hypothesis is not just a guess. It should be based on existing theories and knowledge. It also has to be testable, which means you can support or refute it through scientific research methods (such as experiments, observations, and statistical analysis of data).

A research hypothesis is your proposed answer to your research question. The research hypothesis usually includes an explanation (‘ x affects y because …’).

A statistical hypothesis, on the other hand, is a mathematical statement about a population parameter. Statistical hypotheses always come in pairs: the null and alternative hypotheses. In a well-designed study , the statistical hypotheses correspond logically to the research hypothesis.

Cite this Scribbr article

If you want to cite this source, you can copy and paste the citation or click the ‘Cite this Scribbr article’ button to automatically add the citation to our free Reference Generator.

McCombes, S. (2022, May 06). How to Write a Strong Hypothesis | Guide & Examples. Scribbr. Retrieved 14 May 2024, from https://www.scribbr.co.uk/research-methods/hypothesis-writing/

Is this article helpful?

Shona McCombes

Other students also liked, operationalisation | a guide with examples, pros & cons, what is a conceptual framework | tips & examples, a quick guide to experimental design | 5 steps & examples.

• Comprehensive Learning Paths
• 150+ Hours of Videos
• Complete Access to Jupyter notebooks, Datasets, References.

Hypothesis Testing – A Deep Dive into Hypothesis Testing, The Backbone of Statistical Inference

• September 21, 2023

Explore the intricacies of hypothesis testing, a cornerstone of statistical analysis. Dive into methods, interpretations, and applications for making data-driven decisions.

In this Blog post we will learn:

• What is Hypothesis Testing?
• Steps in Hypothesis Testing 2.1. Set up Hypotheses: Null and Alternative 2.2. Choose a Significance Level (α) 2.3. Calculate a test statistic and P-Value 2.4. Make a Decision
• Example : Testing a new drug.
• Example in python

1. What is Hypothesis Testing?

In simple terms, hypothesis testing is a method used to make decisions or inferences about population parameters based on sample data. Imagine being handed a dice and asked if it’s biased. By rolling it a few times and analyzing the outcomes, you’d be engaging in the essence of hypothesis testing.

Think of hypothesis testing as the scientific method of the statistics world. Suppose you hear claims like “This new drug works wonders!” or “Our new website design boosts sales.” How do you know if these statements hold water? Enter hypothesis testing.

2. Steps in Hypothesis Testing

• Set up Hypotheses : Begin with a null hypothesis (H0) and an alternative hypothesis (Ha).
• Choose a Significance Level (α) : Typically 0.05, this is the probability of rejecting the null hypothesis when it’s actually true. Think of it as the chance of accusing an innocent person.
• Calculate Test statistic and P-Value : Gather evidence (data) and calculate a test statistic.
• p-value : This is the probability of observing the data, given that the null hypothesis is true. A small p-value (typically ≤ 0.05) suggests the data is inconsistent with the null hypothesis.
• Decision Rule : If the p-value is less than or equal to α, you reject the null hypothesis in favor of the alternative.

2.1. Set up Hypotheses: Null and Alternative

Before diving into testing, we must formulate hypotheses. The null hypothesis (H0) represents the default assumption, while the alternative hypothesis (H1) challenges it.

For instance, in drug testing, H0 : “The new drug is no better than the existing one,” H1 : “The new drug is superior .”

2.2. Choose a Significance Level (α)

When You collect and analyze data to test H0 and H1 hypotheses. Based on your analysis, you decide whether to reject the null hypothesis in favor of the alternative, or fail to reject / Accept the null hypothesis.

The significance level, often denoted by $α$, represents the probability of rejecting the null hypothesis when it is actually true.

In other words, it’s the risk you’re willing to take of making a Type I error (false positive).

Type I Error (False Positive) :

• Symbolized by the Greek letter alpha (α).
• Occurs when you incorrectly reject a true null hypothesis . In other words, you conclude that there is an effect or difference when, in reality, there isn’t.
• The probability of making a Type I error is denoted by the significance level of a test. Commonly, tests are conducted at the 0.05 significance level , which means there’s a 5% chance of making a Type I error .
• Commonly used significance levels are 0.01, 0.05, and 0.10, but the choice depends on the context of the study and the level of risk one is willing to accept.

Example : If a drug is not effective (truth), but a clinical trial incorrectly concludes that it is effective (based on the sample data), then a Type I error has occurred.

Type II Error (False Negative) :

• Symbolized by the Greek letter beta (β).
• Occurs when you accept a false null hypothesis . This means you conclude there is no effect or difference when, in reality, there is.
• The probability of making a Type II error is denoted by β. The power of a test (1 – β) represents the probability of correctly rejecting a false null hypothesis.

Example : If a drug is effective (truth), but a clinical trial incorrectly concludes that it is not effective (based on the sample data), then a Type II error has occurred.

Balancing the Errors :

In practice, there’s a trade-off between Type I and Type II errors. Reducing the risk of one typically increases the risk of the other. For example, if you want to decrease the probability of a Type I error (by setting a lower significance level), you might increase the probability of a Type II error unless you compensate by collecting more data or making other adjustments.

It’s essential to understand the consequences of both types of errors in any given context. In some situations, a Type I error might be more severe, while in others, a Type II error might be of greater concern. This understanding guides researchers in designing their experiments and choosing appropriate significance levels.

2.3. Calculate a test statistic and P-Value

Test statistic : A test statistic is a single number that helps us understand how far our sample data is from what we’d expect under a null hypothesis (a basic assumption we’re trying to test against). Generally, the larger the test statistic, the more evidence we have against our null hypothesis. It helps us decide whether the differences we observe in our data are due to random chance or if there’s an actual effect.

P-value : The P-value tells us how likely we would get our observed results (or something more extreme) if the null hypothesis were true. It’s a value between 0 and 1. – A smaller P-value (typically below 0.05) means that the observation is rare under the null hypothesis, so we might reject the null hypothesis. – A larger P-value suggests that what we observed could easily happen by random chance, so we might not reject the null hypothesis.

2.4. Make a Decision

Relationship between $α$ and P-Value

When conducting a hypothesis test:

We then calculate the p-value from our sample data and the test statistic.

Finally, we compare the p-value to our chosen $α$:

• If $p−value≤α$: We reject the null hypothesis in favor of the alternative hypothesis. The result is said to be statistically significant.
• If $p−value>α$: We fail to reject the null hypothesis. There isn’t enough statistical evidence to support the alternative hypothesis.

3. Example : Testing a new drug.

Imagine we are investigating whether a new drug is effective at treating headaches faster than drug B.

Setting Up the Experiment : You gather 100 people who suffer from headaches. Half of them (50 people) are given the new drug (let’s call this the ‘Drug Group’), and the other half are given a sugar pill, which doesn’t contain any medication.

• Set up Hypotheses : Before starting, you make a prediction:
• Null Hypothesis (H0): The new drug has no effect. Any difference in healing time between the two groups is just due to random chance.
• Alternative Hypothesis (H1): The new drug does have an effect. The difference in healing time between the two groups is significant and not just by chance.

Calculate Test statistic and P-Value : After the experiment, you analyze the data. The “test statistic” is a number that helps you understand the difference between the two groups in terms of standard units.

For instance, let’s say:

• The average healing time in the Drug Group is 2 hours.
• The average healing time in the Placebo Group is 3 hours.

The test statistic helps you understand how significant this 1-hour difference is. If the groups are large and the spread of healing times in each group is small, then this difference might be significant. But if there’s a huge variation in healing times, the 1-hour difference might not be so special.

Imagine the P-value as answering this question: “If the new drug had NO real effect, what’s the probability that I’d see a difference as extreme (or more extreme) as the one I found, just by random chance?”

For instance:

• P-value of 0.01 means there’s a 1% chance that the observed difference (or a more extreme difference) would occur if the drug had no effect. That’s pretty rare, so we might consider the drug effective.
• P-value of 0.5 means there’s a 50% chance you’d see this difference just by chance. That’s pretty high, so we might not be convinced the drug is doing much.
• If the P-value is less than ($α$) 0.05: the results are “statistically significant,” and they might reject the null hypothesis , believing the new drug has an effect.
• If the P-value is greater than ($α$) 0.05: the results are not statistically significant, and they don’t reject the null hypothesis , remaining unsure if the drug has a genuine effect.

4. Example in python

For simplicity, let’s say we’re using a t-test (common for comparing means). Let’s dive into Python:

Making a Decision : “The results are statistically significant! p-value < 0.05 , The drug seems to have an effect!” If not, we’d say, “Looks like the drug isn’t as miraculous as we thought.”

5. Conclusion

Hypothesis testing is an indispensable tool in data science, allowing us to make data-driven decisions with confidence. By understanding its principles, conducting tests properly, and considering real-world applications, you can harness the power of hypothesis testing to unlock valuable insights from your data.

More Articles

Correlation – connecting the dots, the role of correlation in data analysis, sampling and sampling distributions – a comprehensive guide on sampling and sampling distributions, law of large numbers – a deep dive into the world of statistics, central limit theorem – a deep dive into central limit theorem and its significance in statistics, skewness and kurtosis – peaks and tails, understanding data through skewness and kurtosis”, similar articles, complete introduction to linear regression in r, how to implement common statistical significance tests and find the p value, logistic regression – a complete tutorial with examples in r.

Subscribe to Machine Learning Plus for high value data science content

© Machinelearningplus. All rights reserved.

Machine Learning A-Z™: Hands-On Python & R In Data Science

Free sample videos:.

• Business Essentials
• Leadership & Management
• Credential of Leadership, Impact, and Management in Business (CLIMB)
• Entrepreneurship & Innovation
• Digital Transformation
• Finance & Accounting
• Business in Society
• For Organizations
• Support Portal
• Media Coverage
• Founding Donors
• Leadership Team

• Harvard Business School →
• HBS Online →
• Business Insights →

Business Insights

Harvard Business School Online's Business Insights Blog provides the career insights you need to achieve your goals and gain confidence in your business skills.

• Career Development
• Communication
• Decision-Making
• Earning Your MBA
• Negotiation
• News & Events
• Productivity
• Staff Spotlight
• Student Profiles
• Work-Life Balance
• AI Essentials for Business
• Alternative Investments
• Business Analytics
• Business Strategy
• Business and Climate Change
• Design Thinking and Innovation
• Digital Marketing Strategy
• Disruptive Strategy
• Economics for Managers
• Entrepreneurship Essentials
• Financial Accounting
• Global Business
• Launching Tech Ventures
• Leadership Principles
• Leadership, Ethics, and Corporate Accountability
• Leading Change and Organizational Renewal
• Leading with Finance
• Management Essentials
• Negotiation Mastery
• Organizational Leadership
• Power and Influence for Positive Impact
• Strategy Execution
• Sustainable Business Strategy
• Sustainable Investing
• Winning with Digital Platforms

A Beginner’s Guide to Hypothesis Testing in Business

• 30 Mar 2021

Becoming a more data-driven decision-maker can bring several benefits to your organization, enabling you to identify new opportunities to pursue and threats to abate. Rather than allowing subjective thinking to guide your business strategy, backing your decisions with data can empower your company to become more innovative and, ultimately, profitable.

If you’re new to data-driven decision-making, you might be wondering how data translates into business strategy. The answer lies in generating a hypothesis and verifying or rejecting it based on what various forms of data tell you.

Below is a look at hypothesis testing and the role it plays in helping businesses become more data-driven.

Access your free e-book today.

What Is Hypothesis Testing?

To understand what hypothesis testing is, it’s important first to understand what a hypothesis is.

A hypothesis or hypothesis statement seeks to explain why something has happened, or what might happen, under certain conditions. It can also be used to understand how different variables relate to each other. Hypotheses are often written as if-then statements; for example, “If this happens, then this will happen.”

Hypothesis testing , then, is a statistical means of testing an assumption stated in a hypothesis. While the specific methodology leveraged depends on the nature of the hypothesis and data available, hypothesis testing typically uses sample data to extrapolate insights about a larger population.

Hypothesis Testing in Business

When it comes to data-driven decision-making, there’s a certain amount of risk that can mislead a professional. This could be due to flawed thinking or observations, incomplete or inaccurate data , or the presence of unknown variables. The danger in this is that, if major strategic decisions are made based on flawed insights, it can lead to wasted resources, missed opportunities, and catastrophic outcomes.

The real value of hypothesis testing in business is that it allows professionals to test their theories and assumptions before putting them into action. This essentially allows an organization to verify its analysis is correct before committing resources to implement a broader strategy.

As one example, consider a company that wishes to launch a new marketing campaign to revitalize sales during a slow period. Doing so could be an incredibly expensive endeavor, depending on the campaign’s size and complexity. The company, therefore, may wish to test the campaign on a smaller scale to understand how it will perform.

In this example, the hypothesis that’s being tested would fall along the lines of: “If the company launches a new marketing campaign, then it will translate into an increase in sales.” It may even be possible to quantify how much of a lift in sales the company expects to see from the effort. Pending the results of the pilot campaign, the business would then know whether it makes sense to roll it out more broadly.

Related: 9 Fundamental Data Science Skills for Business Professionals

Key Considerations for Hypothesis Testing

1. alternative hypothesis and null hypothesis.

In hypothesis testing, the hypothesis that’s being tested is known as the alternative hypothesis . Often, it’s expressed as a correlation or statistical relationship between variables. The null hypothesis , on the other hand, is a statement that’s meant to show there’s no statistical relationship between the variables being tested. It’s typically the exact opposite of whatever is stated in the alternative hypothesis.

For example, consider a company’s leadership team that historically and reliably sees $12 million in monthly revenue. They want to understand if reducing the price of their services will attract more customers and, in turn, increase revenue.

In this case, the alternative hypothesis may take the form of a statement such as: “If we reduce the price of our flagship service by five percent, then we’ll see an increase in sales and realize revenues greater than $12 million in the next month.”

The null hypothesis, on the other hand, would indicate that revenues wouldn’t increase from the base of $12 million, or might even decrease.

Check out the video below about the difference between an alternative and a null hypothesis, and subscribe to our YouTube channel for more explainer content.

2. Significance Level and P-Value

Statistically speaking, if you were to run the same scenario 100 times, you’d likely receive somewhat different results each time. If you were to plot these results in a distribution plot, you’d see the most likely outcome is at the tallest point in the graph, with less likely outcomes falling to the right and left of that point.

With this in mind, imagine you’ve completed your hypothesis test and have your results, which indicate there may be a correlation between the variables you were testing. To understand your results' significance, you’ll need to identify a p-value for the test, which helps note how confident you are in the test results.

In statistics, the p-value depicts the probability that, assuming the null hypothesis is correct, you might still observe results that are at least as extreme as the results of your hypothesis test. The smaller the p-value, the more likely the alternative hypothesis is correct, and the greater the significance of your results.

3. One-Sided vs. Two-Sided Testing

When it’s time to test your hypothesis, it’s important to leverage the correct testing method. The two most common hypothesis testing methods are one-sided and two-sided tests , or one-tailed and two-tailed tests, respectively.

Typically, you’d leverage a one-sided test when you have a strong conviction about the direction of change you expect to see due to your hypothesis test. You’d leverage a two-sided test when you’re less confident in the direction of change.

4. Sampling

To perform hypothesis testing in the first place, you need to collect a sample of data to be analyzed. Depending on the question you’re seeking to answer or investigate, you might collect samples through surveys, observational studies, or experiments.

A survey involves asking a series of questions to a random population sample and recording self-reported responses.

Observational studies involve a researcher observing a sample population and collecting data as it occurs naturally, without intervention.

Finally, an experiment involves dividing a sample into multiple groups, one of which acts as the control group. For each non-control group, the variable being studied is manipulated to determine how the data collected differs from that of the control group.

Learn How to Perform Hypothesis Testing

Hypothesis testing is a complex process involving different moving pieces that can allow an organization to effectively leverage its data and inform strategic decisions.

If you’re interested in better understanding hypothesis testing and the role it can play within your organization, one option is to complete a course that focuses on the process. Doing so can lay the statistical and analytical foundation you need to succeed.

Do you want to learn more about hypothesis testing? Explore Business Analytics —one of our online business essentials courses —and download our Beginner’s Guide to Data & Analytics .

About the Author

Hypothesis Testing: A Comprehensive Guide to Scientific Decision-Making

In scientific research and experimentation, one needs a structured framework for answering questions, confirming results, and making decisions.

This framework, known as hypothesis testing , plays a pivotal role both in research and in various industries like healthcare, finance, and technology.

This guide will delve into the principles and processes of hypothesis testing, offering readers a holistic understanding of this fundamental aspect of scientific decision-making.

Definition of Hypothesis Testing

Hypothesis testing is a method used in statistics to decide whether a statement about a population parameter is likely to be true based on sample data.

The process involves making an initial assumption, observing data, then determining how compatible the data is with the assumption. It's a core part of many o nline certificate programs and widely used in fields requiring data analysis.

Importance of Hypothesis Testing in Research and Industry

The value of hypothesis testing goes beyond science and research. Businesses use it for making crucial decisions, such as whether a new product will succeed in the market, or if a change in strategy will lead to increased profit margins.

Similarly, in the healthcare sector, hypothesis testing helps determine if a new medication is more effective than the current standard treatment. This broad applicability underlies the significance of a problem-solving course that includes hypothesis testing.

Understanding the Basics of Hypothesis Testing

Before embarking on the journey of hypothesis testing, it's crucial to understand its fundamental elements - the Null and Alternate Hypotheses.

Explanation of Null Hypothesis

Definition Null Hypothesis

The Null Hypothesis, symbolized as H0, is a statement we test for possible rejection under the assumption that it is true. In most cases, it anticipates no effect, no difference, or no relationship between variables.

How to Formulate a Null Hypothesis

Formulating a null hypothesis requires identifying your research question, specifying your outcome variable, and expressing a statement of no effect or difference. For instance, you may hypothesize, "There is no significant difference between the performance of students who have breakfast and those who don't."

Practical Examples of Null Hypotheses

Consider a beverage company aiming to reduce its plastic use by 20% within a year. The null hypothesis might state that "There has been no decrease in the company's plastic use."

Explanation of Alternate Hypothesis

Definition Alternate Hypothesis

The alternative hypothesis, symbolized as H1, is the statement we accept when there's sufficient evidence against the null hypothesis. It anticipates an effect, a difference, or a relationship between variables.

How to Construct an Alternate Hypothesis

In constructing an alternate hypothesis, we simply state the counter of the null hypothesis. Following the above example, the alternate hypothesis would be, "There's a significant difference between the performance of students who have breakfast and those who don't."

Case Examples of Alternate Hypotheses

Referring to the beverage company example, the alternate hypothesis would state, "There has been a decrease in the company's plastic use."

Differentiating between Null and Alternate Hypotheses

While both form the crux of hypothesis testing, their roles differ significantly. The null hypothesis is the claim we test for possible rejection, while the alternate hypothesis is accepted when there's evidence against the null. However, neither proof nor disproof of either hypothesis is definitive since all statistical tests are susceptible to errors.

Understanding Errors in Hypothesis Testing

A critical aspect of hypothesis testing is the recognition and management of two types of errors: Type I and Type II errors. Understanding these errors is paramount for interpreting the results accurately and making informed decisions.

Type I Error: False Positive

A Type I error occurs when the null hypothesis is wrongly rejected when it is actually true. This is akin to a false alarm, where, for instance, a test indicates a drug is effective against a disease when it actually isn't. The probability of committing a Type I error is denoted by alpha (α), often set at 0.05 or 5%, indicating a 5% risk of rejecting the null hypothesis incorrectly.

Type II Error: False Negative

Conversely, a Type II error happens when the null hypothesis is not rejected when it is false. This can be compared to a missed detection, such as failing to identify the effectiveness of a beneficial drug. The probability of a Type II error is denoted by beta (β), and researchers strive to minimize this risk to ensure that genuine effects are detected.

Balancing the Risks: Power of the Test

The power of a statistical test is the probability that it correctly rejects a false null hypothesis, essentially avoiding a Type II error. High-powered tests are more reliable for detecting true effects. The power is influenced by the sample size, effect size, significance level, and variability within the data. Optimizing these factors can reduce the chances of both Type I and Type II errors, leading to more trustworthy conclusions.

Steps in Hypothesis Testing

Hypothesis testing involves a series of structured steps to guide researchers and professionals through the decision-making process:

Formulate Hypotheses : Clearly define the null and alternative hypotheses based on the research question or problem statement.

Choose a Significance Level (α) : Decide on the alpha level, which determines the threshold for rejecting the null hypothesis.

Select the Appropriate Test : Based on the data type and study design, choose a statistical test that aligns with the research objectives.

Collect and Analyze Data : Gather the necessary data and perform the statistical test to calculate the test statistic and p-value.

Make a Decision : Compare the p-value to the significance level. If the p-value is less than α, reject the null hypothesis in favor of the alternative. Otherwise, do not reject the null hypothesis.

Hypothesis testing is a cornerstone of scientific inquiry, providing a rigorous framework for evaluating theories, exploring relationships, and making decisions based on empirical evidence.

Whether in academia, healthcare, finance, or technology, the principles of hypothesis testing enable practitioners to draw conclusions with a defined level of confidence, navigate uncertainties, and contribute to advancements in their fields. By understanding its fundamentals, errors, and steps, professionals can apply hypothesis testing to enhance decision-making processes and achieve more reliable outcomes.

Through this exploration of hypothesis testing, it becomes clear that the method is not just a statistical tool but a comprehensive approach to answering complex questions across various domains. As researchers and industry professionals continue to harness its power, the potential for innovation and discovery remains boundless.

What is the fundamental concept and importance of hypothesis testing in scientific decision-making?

Understanding hypothesis testing.

Hypothesis testing is a cornerstone of scientific inquiry. It involves making an assumption, the hypothesis, about a population parameter. Scientists test these assumptions through experimentation and observation.

The Essence of Hypotheses

At its core, a hypothesis is a predictive statement. It usually pertains to an outcome or a relationship between variables. The hypothesis asserts a specific effect, direction, or magnitude will emerge under certain conditions.

Types of Hypotheses

There are two primary hypotheses in testing: null and alternative. The null hypothesis ( H0 ) suggests no effect or relationship exists. It represents a default position, waiting for evidence to challenge it. The alternative hypothesis ( H1 ) posits there is an effect or relationship. It states the specific condition the researcher believes is true.

Role of Evidence

Evidence plays a critical role. Researchers collect data through controlled methods. They aim to either support or refute the hypothesis. This data must be empirical and measurable, ensuring objectivity.

Decision-Making with P-Values

The p-value is a crucial concept in hypothesis testing. It is the probability of observing a test statistic as extreme as the one observed, given the null hypothesis is true. A low p-value indicates the observed data is unlikely under the null hypothesis. This typically leads to rejection of the null in favor of the alternative.

The Importance of Hypothesis Testing

Provides structure to research

Ensures consistency in methods

Allows quantification of evidence

Facilitates replication of studies

Shields from personal biases

Hypothesis testing helps map the unknown territory of scientific phenomena. It allows researchers to make informed decisions grounded in statistical evidence. This rational approach to understanding ensures that conclusions drawn from scientific work are reliable and valid.

The process also shapes the scientific method itself. It demands rigorous standards for evidence and reproducibility. Hypothesis testing thus builds a foundation on which scientific knowledge advances. It underpins the integrity of scientific disciplines. It challenges scientists to prove, disprove, and refine their understanding of the world.

Hypothesis testing is fundamental to the scientific decision-making process. It turns subjective questions into objective inquiries. It drives the pursuit of knowledge through empirical evidence. With hypothesis testing, science moves from conjecture to proven or disproven theories. It is this disciplined approach that adds credibility to scientific findings. Without it, distinguishing between chance results and true discoveries becomes impossible.

How do Type I and Type II errors relate to hypothesis testing and what are their implications on the results?

Understanding type i and type ii errors.

When delving into hypothesis testing, the concepts of Type I and Type II errors often emerge as critical elements. These errors play a paramount role in the interpretation of results. They convey the instances where our conclusions could be incorrect.

What Are Type I and Type II Errors?

Type I error occurs when we wrongly reject a true null hypothesis. We call this a false positive. It implies that the evidence suggests an effect or difference exists when it does not. In statistical terms, this is the 'alpha' (α), which defines the likelihood of a Type I error.

Type II error , in contrast, happens when we fail to reject a false null hypothesis. This error, termed a false negative, means that one overlooks an actual effect or difference. It's quantified by 'beta' (β), which gives the probability of a Type II error occurring.

Implications of Type I and Type II Errors

The implications of these errors reach far into hypothesis testing and the trustworthiness of results.

Confidence Levels : High risks of Type I errors lower confidence in findings. To mitigate this, researchers set a low alpha level, commonly 0.05. It shows a willingness to accept a 5% chance of a false positive.

Power of the Test : The risk of Type II errors correlates with the power of the test—the probability of correctly detecting an effect when it exists. A high beta value means a higher chance of missing an actual effect due to low test power.

Sample Size : Larger samples reduce both Type I and Type II error risks. They offer more accurate estimates and a clearer distinction between the null and alternative hypotheses.

Consequences : Type I errors might lead to unwarranted actions based on false positives. Type II errors could result in missed opportunities due to unrecognized truths.

Balancing Errors in Hypothesis Testing

Researchers must balance Type I and Type II errors in hypothesis testing. The balance depends on the context and potential consequences of each error.

Safety in Medicine : In drug testing, Type I errors can lead to harmful side effects if a drug isn't actually safe. Minimizing Type I errors is crucial here.

Effectiveness in Treatment : Conversely, Type II errors in medicine may miss a treatment effect. Ensuring sufficient power to detect treatment efficacy is essential.

Type I and Type II errors remind us of the limitations in hypothesis testing. No test is infallible. Decisions on alpha and beta levels depend on the stakes of potential errors.

Understanding and addressing these errors are vital. They enhance credibility in conclusions drawn from statistical testing. Proper balance ensures valuable and trustworthy research outcomes.

Can you explain the critical role of the p-value in hypothesis testing and its influence on accepting or rejecting the null hypothesis?

Understanding the p-value.

Researchers often turn to hypothesis testing to understand data. They make an initial assumption called the null hypothesis . This hypothesis suggests no effect or no difference exists. To challenge this, they use an alternative hypothesis.

The Null Hypothesis and P-value

In hypothesis testing, the p-value helps measure the strength of the results against the null hypothesis. It calculates the probability of observing data as extreme as the test results, assuming the null hypothesis is true. A low p-value indicates that the observed data would be very unlikely if the null hypothesis were true.

Significance Threshold

Scientists usually set a significance level before testing. Often, this level is 0.05 . It marks the cut-off for determining statistical significance.

If the p-value is below 0.05, the result is statistically significant.

This means the test provides enough evidence to reject the null hypothesis.

What Does Rejecting the Null Hypothesis Mean?

Rejecting the null does not prove the alternative hypothesis. It merely suggests that the data are not consistent with the null. Researchers can be more confident that an effect or difference might exist.

Misinterpretations of the P-value

A common mistake is seeing the p-value as the odds that the null hypothesis is true or false. It is not. It only assesses how compatible the data are with the null hypothesis.

Influencing Factors

Several factors influence the p-value. This includes the size of the effect and the sample size. Larger samples may detect smaller differences and result in smaller p-values.

The p-value is critical in deciding whether to accept or reject the null hypothesis. It quantifies how surprising the data are, assuming the null is true. A small p-value can lead to rejecting the null, paving the way for new scientific insights. However, it is crucial to use this tool wisely, with an understanding of its limitations and context.

He is a content producer who specializes in blog content. He has a master's degree in business administration and he lives in the Netherlands.

Unlocking Da Vinci's Problem Solving Skills

Developing Problem Solving Skills Since 1960s WSEIAC Report

The First Step in Critical Thinking & Problem Solving

What are Problem Solving Skills?

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

• Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
• Duis aute irure dolor in reprehenderit in voluptate
• Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

5.2 - writing hypotheses.

The first step in conducting a hypothesis test is to write the hypothesis statements that are going to be tested. For each test you will have a null hypothesis (\(H_0\)) and an alternative hypothesis (\(H_a\)).

When writing hypotheses there are three things that we need to know: (1) the parameter that we are testing (2) the direction of the test (non-directional, right-tailed or left-tailed), and (3) the value of the hypothesized parameter.

• At this point we can write hypotheses for a single mean (\(\mu\)), paired means(\(\mu_d\)), a single proportion (\(p\)), the difference between two independent means (\(\mu_1-\mu_2\)), the difference between two proportions (\(p_1-p_2\)), a simple linear regression slope (\(\beta\)), and a correlation (\(\rho\)). 
• The research question will give us the information necessary to determine if the test is two-tailed (e.g., "different from," "not equal to"), right-tailed (e.g., "greater than," "more than"), or left-tailed (e.g., "less than," "fewer than").
• The research question will also give us the hypothesized parameter value. This is the number that goes in the hypothesis statements (i.e., \(\mu_0\) and \(p_0\)). For the difference between two groups, regression, and correlation, this value is typically 0.

Hypotheses are always written in terms of population parameters (e.g., \(p\) and \(\mu\)).  The tables below display all of the possible hypotheses for the parameters that we have learned thus far. Note that the null hypothesis always includes the equality (i.e., =).

Statistics Made Easy

4 Examples of Hypothesis Testing in Real Life

In statistics, hypothesis tests are used to test whether or not some hypothesis about a population parameter is true.

To perform a hypothesis test in the real world, researchers will obtain a random sample from the population and perform a hypothesis test on the sample data, using a null and alternative hypothesis:

• Null Hypothesis (H 0 ): The sample data occurs purely from chance.
• Alternative Hypothesis (H A ): The sample data is influenced by some non-random cause.

If the p-value of the hypothesis test is less than some significance level (e.g. α = .05), then we can reject the null hypothesis and conclude that we have sufficient evidence to say that the alternative hypothesis is true.

The following examples provide several situations where hypothesis tests are used in the real world.

Example 1: Biology

Hypothesis tests are often used in biology to determine whether some new treatment, fertilizer, pesticide, chemical, etc. causes increased growth, stamina, immunity, etc. in plants or animals.

For example, suppose a biologist believes that a certain fertilizer will cause plants to grow more during a one-month period than they normally do, which is currently 20 inches. To test this, she applies the fertilizer to each of the plants in her laboratory for one month.

She then performs a hypothesis test using the following hypotheses:

• H 0 : μ = 20 inches (the fertilizer will have no effect on the mean plant growth)
• H A : μ > 20 inches (the fertilizer will cause mean plant growth to increase)

If the p-value of the test is less than some significance level (e.g. α = .05), then she can reject the null hypothesis and conclude that the fertilizer leads to increased plant growth.

Example 2: Clinical Trials

Hypothesis tests are often used in clinical trials to determine whether some new treatment, drug, procedure, etc. causes improved outcomes in patients.

For example, suppose a doctor believes that a new drug is able to reduce blood pressure in obese patients. To test this, he may measure the blood pressure of 40 patients before and after using the new drug for one month.

He then performs a hypothesis test using the following hypotheses:

• H 0 : μ after = μ before (the mean blood pressure is the same before and after using the drug)
• H A : μ after < μ before (the mean blood pressure is less after using the drug)

If the p-value of the test is less than some significance level (e.g. α = .05), then he can reject the null hypothesis and conclude that the new drug leads to reduced blood pressure.

Example 3: Advertising Spend

Hypothesis tests are often used in business to determine whether or not some new advertising campaign, marketing technique, etc. causes increased sales.

For example, suppose a company believes that spending more money on digital advertising leads to increased sales. To test this, the company may increase money spent on digital advertising during a two-month period and collect data to see if overall sales have increased.

They may perform a hypothesis test using the following hypotheses:

• H 0 : μ after = μ before (the mean sales is the same before and after spending more on advertising)
• H A : μ after > μ before (the mean sales increased after spending more on advertising)

If the p-value of the test is less than some significance level (e.g. α = .05), then the company can reject the null hypothesis and conclude that increased digital advertising leads to increased sales.

Example 4: Manufacturing

Hypothesis tests are also used often in manufacturing plants to determine if some new process, technique, method, etc. causes a change in the number of defective products produced.

For example, suppose a certain manufacturing plant wants to test whether or not some new method changes the number of defective widgets produced per month, which is currently 250. To test this, they may measure the mean number of defective widgets produced before and after using the new method for one month.

They can then perform a hypothesis test using the following hypotheses:

• H 0 : μ after = μ before (the mean number of defective widgets is the same before and after using the new method)
• H A : μ after ≠ μ before (the mean number of defective widgets produced is different before and after using the new method)

If the p-value of the test is less than some significance level (e.g. α = .05), then the plant can reject the null hypothesis and conclude that the new method leads to a change in the number of defective widgets produced per month.

Additional Resources

Introduction to Hypothesis Testing Introduction to the One Sample t-test Introduction to the Two Sample t-test Introduction to the Paired Samples t-test

Featured Posts

Hey there. My name is Zach Bobbitt. I have a Masters of Science degree in Applied Statistics and I’ve worked on machine learning algorithms for professional businesses in both healthcare and retail. I’m passionate about statistics, machine learning, and data visualization and I created Statology to be a resource for both students and teachers alike.  My goal with this site is to help you learn statistics through using simple terms, plenty of real-world examples, and helpful illustrations.

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Join the Statology Community

Sign up to receive Statology's exclusive study resource: 100 practice problems with step-by-step solutions. Plus, get our latest insights, tutorials, and data analysis tips straight to your inbox!

By subscribing you accept Statology's Privacy Policy.

• Product Management

How to Generate and Validate Product Hypotheses

What is a product hypothesis.

A hypothesis is a testable statement that predicts the relationship between two or more variables. In product development, we generate hypotheses to validate assumptions about customer behavior, market needs, or the potential impact of product changes. These experimental efforts help us refine the user experience and get closer to finding a product-market fit.

Product hypotheses are a key element of data-driven product development and decision-making. Testing them enables us to solve problems more efficiently and remove our own biases from the solutions we put forward.

Here’s an example: ‘If we improve the page load speed on our website (variable 1), then we will increase the number of signups by 15% (variable 2).’ So if we improve the page load speed, and the number of signups increases, then our hypothesis has been proven. If the number did not increase significantly (or not at all), then our hypothesis has been disproven.

In general, product managers are constantly creating and testing hypotheses. But in the context of new product development , hypothesis generation/testing occurs during the validation stage, right after idea screening .

Now before we go any further, let’s get one thing straight: What’s the difference between an idea and a hypothesis?

Idea vs hypothesis

Innovation expert Michael Schrage makes this distinction between hypotheses and ideas – unlike an idea, a hypothesis comes with built-in accountability. “But what’s the accountability for a good idea?” Schrage asks. “The fact that a lot of people think it’s a good idea? That’s a popularity contest.” So, not only should a hypothesis be tested, but by its very nature, it can be tested.

At Railsware, we’ve built our product development services on the careful selection, prioritization, and validation of ideas. Here’s how we distinguish between ideas and hypotheses:

Idea: A creative suggestion about how we might exploit a gap in the market, add value to an existing product, or bring attention to our product. Crucially, an idea is just a thought. It can form the basis of a hypothesis but it is not necessarily expected to be proven or disproven.

• We should get an interview with the CEO of our company published on TechCrunch.
• Why don’t we redesign our website?
• The Coupler.io team should create video tutorials on how to export data from different apps, and publish them on YouTube.
• Why not add a new ‘email templates’ feature to our Mailtrap product?

Hypothesis: A way of framing an idea or assumption so that it is testable, specific, and aligns with our wider product/team/organizational goals.

Examples: 

• If we add a new ‘email templates’ feature to Mailtrap, we’ll see an increase in active usage of our email-sending API.
• Creating relevant video tutorials and uploading them to YouTube will lead to an increase in Coupler.io signups.
• If we publish an interview with our CEO on TechCrunch, 500 people will visit our website and 10 of them will install our product.

Now, it’s worth mentioning that not all hypotheses require testing . Sometimes, the process of creating hypotheses is just an exercise in critical thinking. And the simple act of analyzing your statement tells whether you should run an experiment or not. Remember: testing isn’t mandatory, but your hypotheses should always be inherently testable.

Let’s consider the TechCrunch article example again. In that hypothesis, we expect 500 readers to visit our product website, and a 2% conversion rate of those unique visitors to product users i.e. 10 people. But is that marginal increase worth all the effort? Conducting an interview with our CEO, creating the content, and collaborating with the TechCrunch content team – all of these tasks take time (and money) to execute. And by formulating that hypothesis, we can clearly see that in this case, the drawbacks (efforts) outweigh the benefits. So, no need to test it.

In a similar vein, a hypothesis statement can be a tool to prioritize your activities based on impact. We typically use the following criteria:

• The quality of impact
• The size of the impact
• The probability of impact

This lets us organize our efforts according to their potential outcomes – not the coolness of the idea, its popularity among the team, etc.

Now that we’ve established what a product hypothesis is, let’s discuss how to create one.

Start with a problem statement

Before you jump into product hypothesis generation, we highly recommend formulating a problem statement. This is a short, concise description of the issue you are trying to solve. It helps teams stay on track as they formalize the hypothesis and design the product experiments. It can also be shared with stakeholders to ensure that everyone is on the same page.

The statement can be worded however you like, as long as it’s actionable, specific, and based on data-driven insights or research. It should clearly outline the problem or opportunity you want to address.

Here’s an example: Our bounce rate is high (more than 90%) and we are struggling to convert website visitors into actual users. How might we improve site performance to boost our conversion rate?

How to generate product hypotheses

Now let’s explore some common, everyday scenarios that lead to product hypothesis generation. For our teams here at Railsware, it’s when:

• There’s a problem with an unclear root cause e.g. a sudden drop in one part of the onboarding funnel. We identify these issues by checking our product metrics or reviewing customer complaints.
• We are running ideation sessions on how to reach our goals (increase MRR, increase the number of users invited to an account, etc.)
• We are exploring growth opportunities e.g. changing a pricing plan, making product improvements , breaking into a new market.
• We receive customer feedback. For example, some users have complained about difficulties setting up a workspace within the product. So, we build a hypothesis on how to help them with the setup.

BRIDGES framework for ideation

When we are tackling a complex problem or looking for ways to grow the product, our teams use BRIDGeS – a robust decision-making and ideation framework. BRIDGeS makes our product discovery sessions more efficient. It lets us dive deep into the context of our problem so that we can develop targeted solutions worthy of testing.

Between 2-8 stakeholders take part in a BRIDGeS session. The ideation sessions are usually led by a product manager and can include other subject matter experts such as developers, designers, data analysts, or marketing specialists. You can use a virtual whiteboard such as Figjam or Miro (see our Figma template ) to record each colored note.

In the first half of a BRIDGeS session, participants examine the Benefits, Risks, Issues, and Goals of their subject in the ‘Problem Space.’ A subject is anything that is being described or dealt with; for instance, Coupler.io’s growth opportunities. Benefits are the value that a future solution can bring, Risks are potential issues they might face, Issues are their existing problems, and Goals are what the subject hopes to gain from the future solution. Each descriptor should have a designated color.

After we have broken down the problem using each of these descriptors, we move into the Solution Space. This is where we develop solution variations based on all of the benefits/risks/issues identified in the Problem Space (see the Uber case study for an in-depth example).

In the Solution Space, we start prioritizing those solutions and deciding which ones are worthy of further exploration outside of the framework – via product hypothesis formulation and testing, for example. At the very least, after the session, we will have a list of epics and nested tasks ready to add to our product roadmap.

How to write a product hypothesis statement

Across organizations, product hypothesis statements might vary in their subject, tone, and precise wording. But some elements never change. As we mentioned earlier, a hypothesis statement must always have two or more variables and a connecting factor.

1. Identify variables

Since these components form the bulk of a hypothesis statement, let’s start with a brief definition.

First of all, variables in a hypothesis statement can be split into two camps: dependent and independent. Without getting too theoretical, we can describe the independent variable as the cause, and the dependent variable as the effect . So in the Mailtrap example we mentioned earlier, the ‘add email templates feature’ is the cause i.e. the element we want to manipulate. Meanwhile, ‘increased usage of email sending API’ is the effect i.e the element we will observe.

Independent variables can be any change you plan to make to your product. For example, tweaking some landing page copy, adding a chatbot to the homepage, or enhancing the search bar filter functionality.

Dependent variables are usually metrics. Here are a few that we often test in product development:

• Number of sign-ups
• Number of purchases
• Activation rate (activation signals differ from product to product)
• Number of specific plans purchased
• Feature usage (API activation, for example)
• Number of active users

Bear in mind that your concept or desired change can be measured with different metrics. Make sure that your variables are well-defined, and be deliberate in how you measure your concepts so that there’s no room for misinterpretation or ambiguity.

For example, in the hypothesis ‘Users drop off because they find it hard to set up a project’ variables are poorly defined. Phrases like ‘drop off’ and ‘hard to set up’ are too vague. A much better way of saying it would be: If project automation rules are pre-defined (email sequence to responsible, scheduled tickets creation), we’ll see a decrease in churn. In this example, it’s clear which dependent variable has been chosen and why.

And remember, when product managers focus on delighting users and building something of value, it’s easier to market and monetize it. That’s why at Railsware, our product hypotheses often focus on how to increase the usage of a feature or product. If users love our product(s) and know how to leverage its benefits, we can spend less time worrying about how to improve conversion rates or actively grow our revenue, and more time enhancing the user experience and nurturing our audience.

2. Make the connection

The relationship between variables should be clear and logical. If it’s not, then it doesn’t matter how well-chosen your variables are – your test results won’t be reliable.

To demonstrate this point, let’s explore a previous example again: page load speed and signups.

Through prior research, you might already know that conversion rates are 3x higher for sites that load in 1 second compared to sites that take 5 seconds to load. Since there appears to be a strong connection between load speed and signups in general, you might want to see if this is also true for your product.

Here are some common pitfalls to avoid when defining the relationship between two or more variables:

Relationship is weak. Let’s say you hypothesize that an increase in website traffic will lead to an increase in sign-ups. This is a weak connection since website visitors aren’t necessarily motivated to use your product; there are more steps involved. A better example is ‘If we change the CTA on the pricing page, then the number of signups will increase.’ This connection is much stronger and more direct.

Relationship is far-fetched. This often happens when one of the variables is founded on a vanity metric. For example, increasing the number of social media subscribers will lead to an increase in sign-ups. However, there’s no particular reason why a social media follower would be interested in using your product. Oftentimes, it’s simply your social media content that appeals to them (and your audience isn’t interested in a product).

Variables are co-dependent. Variables should always be isolated from one another. Let’s say we removed the option “Register with Google” from our app. In this case, we can expect fewer users with Google workspace accounts to register. Obviously, it’s because there’s a direct dependency between variables (no registration with Google→no users with Google workspace accounts).

3. Set validation criteria

First, build some confirmation criteria into your statement . Think in terms of percentages (e.g. increase/decrease by 5%) and choose a relevant product metric to track e.g. activation rate if your hypothesis relates to onboarding. Consider that you don’t always have to hit the bullseye for your hypothesis to be considered valid. Perhaps a 3% increase is just as acceptable as a 5% one. And it still proves that a connection between your variables exists.

Secondly, you should also make sure that your hypothesis statement is realistic . Let’s say you have a hypothesis that ‘If we show users a banner with our new feature, then feature usage will increase by 10%.’ A few questions to ask yourself are: Is 10% a reasonable increase, based on your current feature usage data? Do you have the resources to create the tests (experimenting with multiple variations, distributing on different channels: in-app, emails, blog posts)?

Null hypothesis and alternative hypothesis

In statistical research, there are two ways of stating a hypothesis: null or alternative. But this scientific method has its place in hypothesis-driven development too…

Alternative hypothesis: A statement that you intend to prove as being true by running an experiment and analyzing the results. Hint: it’s the same as the other hypothesis examples we’ve described so far.

Example: If we change the landing page copy, then the number of signups will increase.

Null hypothesis: A statement you want to disprove by running an experiment and analyzing the results. It predicts that your new feature or change to the user experience will not have the desired effect.

Example: The number of signups will not increase if we make a change to the landing page copy.

What’s the point? Well, let’s consider the phrase ‘innocent until proven guilty’ as a version of a null hypothesis. We don’t assume that there is any relationship between the ‘defendant’ and the ‘crime’ until we have proof. So, we run a test, gather data, and analyze our findings — which gives us enough proof to reject the null hypothesis and validate the alternative. All of this helps us to have more confidence in our results.

Now that you have generated your hypotheses, and created statements, it’s time to prepare your list for testing.

Prioritizing hypotheses for testing

Not all hypotheses are created equal. Some will be essential to your immediate goal of growing the product e.g. adding a new data destination for Coupler.io. Others will be based on nice-to-haves or small fixes e.g. updating graphics on the website homepage.

Prioritization helps us focus on the most impactful solutions as we are building a product roadmap or narrowing down the backlog . To determine which hypotheses are the most critical, we use the MoSCoW framework. It allows us to assign a level of urgency and importance to each product hypothesis so we can filter the best 3-5 for testing.

MoSCoW is an acronym for Must-have, Should-have, Could-have, and Won’t-have. Here’s a breakdown:

• Must-have – hypotheses that must be tested, because they are strongly linked to our immediate project goals.
• Should-have – hypotheses that are closely related to our immediate project goals, but aren’t the top priority.
• Could-have – hypotheses of nice-to-haves that can wait until later for testing. 
• Won’t-have – low-priority hypotheses that we may or may not test later on when we have more time.

How to test product hypotheses

Once you have selected a hypothesis, it’s time to test it. This will involve running one or more product experiments in order to check the validity of your claim.

The tricky part is deciding what type of experiment to run, and how many. Ultimately, this all depends on the subject of your hypothesis – whether it’s a simple copy change or a whole new feature. For instance, it’s not necessary to create a clickable prototype for a landing page redesign. In that case, a user-wide update would do.

On that note, here are some of the approaches we take to hypothesis testing at Railsware:

A/B testing

A/B or split testing involves creating two or more different versions of a webpage/feature/functionality and collecting information about how users respond to them.

Let’s say you wanted to validate a hypothesis about the placement of a search bar on your application homepage. You could design an A/B test that shows two different versions of that search bar’s placement to your users (who have been split equally into two camps: a control group and a variant group). Then, you would choose the best option based on user data. A/B tests are suitable for testing responses to user experience changes, especially if you have more than one solution to test.

Prototyping

When it comes to testing a new product design, prototyping is the method of choice for many Lean startups and organizations. It’s a cost-effective way of collecting feedback from users, fast, and it’s possible to create prototypes of individual features too. You may take this approach to hypothesis testing if you are working on rolling out a significant new change e.g adding a brand-new feature, redesigning some aspect of the user flow, etc. To control costs at this point in the new product development process , choose the right tools — think Figma for clickable walkthroughs or no-code platforms like Bubble.

Deliveroo feature prototype example

Let’s look at how feature prototyping worked for the food delivery app, Deliveroo, when their product team wanted to ‘explore personalized recommendations, better filtering and improved search’ in 2018. To begin, they created a prototype of the customer discovery feature using web design application, Framer.

One of the most important aspects of this feature prototype was that it contained live data — real restaurants, real locations. For test users, this made the hypothetical feature feel more authentic. They were seeing listings and recommendations for real restaurants in their area, which helped immerse them in the user experience, and generate more honest and specific feedback. Deliveroo was then able to implement this feedback in subsequent iterations.

Asking your users

Interviewing customers is an excellent way to validate product hypotheses. It’s a form of qualitative testing that, in our experience, produces better insights than user surveys or general user research. Sessions are typically run by product managers and involve asking  in-depth interview questions  to one customer at a time. They can be conducted in person or online (through a virtual call center , for instance) and last anywhere between 30 minutes to 1 hour.

Although CustDev interviews may require more effort to execute than other tests (the process of finding participants, devising questions, organizing interviews, and honing interview skills can be time-consuming), it’s still a highly rewarding approach. You can quickly validate assumptions by asking customers about their pain points, concerns, habits, processes they follow, and analyzing how your solution fits into all of that.

Wizard of Oz

The Wizard of Oz approach is suitable for gauging user interest in new features or functionalities. It’s done by creating a prototype of a fake or future feature and monitoring how your customers or test users interact with it.

For example, you might have a hypothesis that your number of active users will increase by 15% if you introduce a new feature. So, you design a new bare-bones page or simple button that invites users to access it. But when they click on the button, a pop-up appears with a message such as ‘coming soon.’

By measuring the frequency of those clicks, you could learn a lot about the demand for this new feature/functionality. However, while these tests can deliver fast results, they carry the risk of backfiring. Some customers may find fake features misleading, making them less likely to engage with your product in the future.

User-wide updates

One of the speediest ways to test your hypothesis is by rolling out an update for all users. It can take less time and effort to set up than other tests (depending on how big of an update it is). But due to the risk involved, you should stick to only performing these kinds of tests on small-scale hypotheses. Our teams only take this approach when we are almost certain that our hypothesis is valid.

For example, we once had an assumption that the name of one of Mailtrap ’s entities was the root cause of a low activation rate. Being an active Mailtrap customer meant that you were regularly sending test emails to a place called ‘Demo Inbox.’ We hypothesized that the name was confusing (the word ‘demo’ implied it was not the main inbox) and this was preventing new users from engaging with their accounts. So, we updated the page, changed the name to ‘My Inbox’ and added some ‘to-do’ steps for new users. We saw an increase in our activation rate almost immediately, validating our hypothesis.

Feature flags

Creating feature flags involves only releasing a new feature to a particular subset or small percentage of users. These features come with a built-in kill switch; a piece of code that can be executed or skipped, depending on who’s interacting with your product.

Since you are only showing this new feature to a selected group, feature flags are an especially low-risk method of testing your product hypothesis (compared to Wizard of Oz, for example, where you have much less control). However, they are also a little bit more complex to execute than the others — you will need to have an actual coded product for starters, as well as some technical knowledge, in order to add the modifiers ( only when… ) to your new coded feature.

Let’s revisit the landing page copy example again, this time in the context of testing.

So, for the hypothesis ‘If we change the landing page copy, then the number of signups will increase,’ there are several options for experimentation. We could share the copy with a small sample of our users, or even release a user-wide update. But A/B testing is probably the best fit for this task. Depending on our budget and goal, we could test several different pieces of copy, such as:

• The current landing page copy
• Copy that we paid a marketing agency 10 grand for
• Generic copy we wrote ourselves, or removing most of the original copy – just to see how making even a small change might affect our numbers.

Remember, every hypothesis test must have a reasonable endpoint. The exact length of the test will depend on the type of feature/functionality you are testing, the size of your user base, and how much data you need to gather. Just make sure that the experiment running time matches the hypothesis scope. For instance, there is no need to spend 8 weeks experimenting with a piece of landing page copy. That timeline is more appropriate for say, a Wizard of Oz feature.

Recording hypotheses statements and test results

Finally, it’s time to talk about where you will write down and keep track of your hypotheses. Creating a single source of truth will enable you to track all aspects of hypothesis generation and testing with ease.

At Railsware, our product managers create a document for each individual hypothesis, using tools such as Coda or Google Sheets. In that document, we record the hypothesis statement, as well as our plans, process, results, screenshots, product metrics, and assumptions.

We share this document with our team and stakeholders, to ensure transparency and invite feedback. It’s also a resource we can refer back to when we are discussing a new hypothesis — a place where we can quickly access information relating to a previous test.

Understanding test results and taking action

The other half of validating product hypotheses involves evaluating data and drawing reasonable conclusions based on what you find. We do so by analyzing our chosen product metric(s) and deciding whether there is enough data available to make a solid decision. If not, we may extend the test’s duration or run another one. Otherwise, we move forward. An experimental feature becomes a real feature, a chatbot gets implemented on the customer support page, and so on.

Something to keep in mind: the integrity of your data is tied to how well the test was executed, so here are a few points to consider when you are testing and analyzing results:

Gather and analyze data carefully. Ensure that your data is clean and up-to-date when running quantitative tests and tracking responses via analytics dashboards. If you are doing customer interviews, make sure to record the meetings (with consent) so that your notes will be as accurate as possible.

Conduct the right amount of product experiments. It can take more than one test to determine whether your hypothesis is valid or invalid. However, don’t waste too much time experimenting in the hopes of getting the result you want. Know when to accept the evidence and move on.

Choose the right audience segment. Don’t cast your net too wide. Be specific about who you want to collect data from prior to running the test. Otherwise, your test results will be misleading and you won’t learn anything new.

Watch out for bias. Avoid confirmation bias at all costs. Don’t make the mistake of including irrelevant data just because it bolsters your results. For example, if you are gathering data about how users are interacting with your product Monday-Friday, don’t include weekend data just because doing so would alter the data and ‘validate’ your hypothesis.

• Not all failed hypotheses should be treated as losses. Even if you didn’t get the outcome you were hoping for, you may still have improved your product. Let’s say you implemented SSO authentication for premium users, but unfortunately, your free users didn’t end up switching to premium plans. In this case, you still added value to the product by streamlining the login process for paying users.
• Yes, taking a hypothesis-driven approach to product development is important. But remember, you don’t have to test everything . Use common sense first. For example, if your website copy is confusing and doesn’t portray the value of the product, then you should still strive to replace it with better copy – regardless of how this affects your numbers in the short term.

Wrapping Up

The process of generating and validating product hypotheses is actually pretty straightforward once you’ve got the hang of it. All you need is a valid question or problem, a testable statement, and a method of validation. Sure, hypothesis-driven development requires more of a time commitment than just ‘giving it a go.’ But ultimately, it will help you tune the product to the wants and needs of your customers.

If you share our data-driven approach to product development and engineering, check out our services page to learn more about how we work with our clients!

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

8.4: Hypothesis Test Examples for Proportions

• Last updated
• Save as PDF
• Page ID 11533

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

• In a hypothesis test problem, you may see words such as "the level of significance is 1%." The "1%" is the preconceived or preset \(\alpha\).
• The statistician setting up the hypothesis test selects the value of α to use before collecting the sample data.
• If no level of significance is given, a common standard to use is \(\alpha = 0.05\).
• When you calculate the \(p\)-value and draw the picture, the \(p\)-value is the area in the left tail, the right tail, or split evenly between the two tails. For this reason, we call the hypothesis test left, right, or two tailed.
• The alternative hypothesis, \(H_{a}\), tells you if the test is left, right, or two-tailed. It is the key to conducting the appropriate test.
• \(H_{a}\) never has a symbol that contains an equal sign.
• Thinking about the meaning of the \(p\)-value: A data analyst (and anyone else) should have more confidence that he made the correct decision to reject the null hypothesis with a smaller \(p\)-value (for example, 0.001 as opposed to 0.04) even if using the 0.05 level for alpha. Similarly, for a large p -value such as 0.4, as opposed to a \(p\)-value of 0.056 (\(\alpha = 0.05\) is less than either number), a data analyst should have more confidence that she made the correct decision in not rejecting the null hypothesis. This makes the data analyst use judgment rather than mindlessly applying rules.

Full Hypothesis Test Examples

Example \(\PageIndex{7}\)

Joon believes that 50% of first-time brides in the United States are younger than their grooms. She performs a hypothesis test to determine if the percentage is the same or different from 50% . Joon samples 100 first-time brides and 53 reply that they are younger than their grooms. For the hypothesis test, she uses a 1% level of significance.

Set up the hypothesis test:

The 1% level of significance means that α = 0.01. This is a test of a single population proportion .

\(H_{0}: p = 0.50\)  \(H_{a}: p \neq 0.50\)

The words "is the same or different from" tell you this is a two-tailed test.

Calculate the distribution needed:

Random variable: \(P′ =\) the percent of of first-time brides who are younger than their grooms.

Distribution for the test: The problem contains no mention of a mean. The information is given in terms of percentages. Use the distribution for P′ , the estimated proportion.

\[P' - N\left(p, \sqrt{\frac{p-q}{n}}\right)\nonumber \]

\[P' - N\left(0.5, \sqrt{\frac{0.5-0.5}{100}}\right)\nonumber \]

where \(p = 0.50, q = 1−p = 0.50\), and \(n = 100\)

Calculate the p -value using the normal distribution for proportions:

\[p\text{-value} = P(p′ < 0.47 or p′ > 0.53) = 0.5485\nonumber \]

where \[x = 53, p' = \frac{x}{n} = \frac{53}{100} = 0.53\nonumber \].

Interpretation of the \(p\text{-value})\: If the null hypothesis is true, there is 0.5485 probability (54.85%) that the sample (estimated) proportion \(p'\) is 0.53 or more OR 0.47 or less (see the graph in Figure).

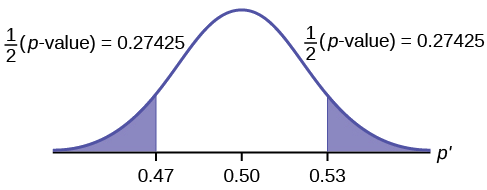
\(\mu = p = 0.50\) comes from \(H_{0}\), the null hypothesis.

\(p′ = 0.53\). Since the curve is symmetrical and the test is two-tailed, the \(p′\) for the left tail is equal to \(0.50 – 0.03 = 0.47\) where \(\mu = p = 0.50\). (0.03 is the difference between 0.53 and 0.50.)

Compare \(\alpha\) and the \(p\text{-value}\):

Since \(\alpha = 0.01\) and \(p\text{-value} = 0.5485\). \(\alpha < p\text{-value}\).

Make a decision: Since \(\alpha < p\text{-value}\), you cannot reject \(H_{0}\).

Conclusion: At the 1% level of significance, the sample data do not show sufficient evidence that the percentage of first-time brides who are younger than their grooms is different from 50%.

The \(p\text{-value}\) can easily be calculated.

Press STAT and arrow over to TESTS . Press 5:1-PropZTest . Enter .5 for \(p_{0}\), 53 for \(x\) and 100 for \(n\). Arrow down to Prop and arrow to not equals \(p_{0}\). Press ENTER . Arrow down to Calculate and press ENTER . The calculator calculates the \(p\text{-value}\) (\(p = 0.5485\)) and the test statistic (\(z\)-score). Prop not equals .5 is the alternate hypothesis. Do this set of instructions again except arrow to Draw (instead of Calculate ). Press ENTER . A shaded graph appears with \(\(z\) = 0.6\) (test statistic) and \(p = 0.5485\) (\(p\text{-value}\)). Make sure when you use Draw that no other equations are highlighted in \(Y =\) and the plots are turned off.

The Type I and Type II errors are as follows:

The Type I error is to conclude that the proportion of first-time brides who are younger than their grooms is different from 50% when, in fact, the proportion is actually 50%. (Reject the null hypothesis when the null hypothesis is true).

The Type II error is there is not enough evidence to conclude that the proportion of first time brides who are younger than their grooms differs from 50% when, in fact, the proportion does differ from 50%. (Do not reject the null hypothesis when the null hypothesis is false.)

Exercise \(\PageIndex{7}\)

A teacher believes that 85% of students in the class will want to go on a field trip to the local zoo. She performs a hypothesis test to determine if the percentage is the same or different from 85%. The teacher samples 50 students and 39 reply that they would want to go to the zoo. For the hypothesis test, use a 1% level of significance.

First, determine what type of test this is, set up the hypothesis test, find the \(p\text{-value}\), sketch the graph, and state your conclusion.

Since the problem is about percentages, this is a test of single population proportions.

• \(H_{0} : p = 0.85\)
• \(H_{a}: p \neq 0.85\)
• \(p = 0.7554\)

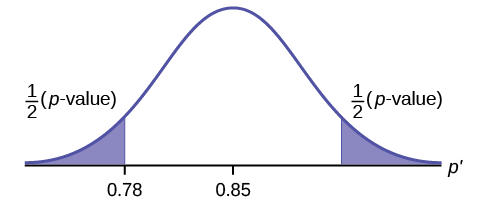
Because \(p > \alpha\), we fail to reject the null hypothesis. There is not sufficient evidence to suggest that the proportion of students that want to go to the zoo is not 85%.

Example \(\PageIndex{8}\)

Suppose a consumer group suspects that the proportion of households that have three cell phones is 30%. A cell phone company has reason to believe that the proportion is not 30%. Before they start a big advertising campaign, they conduct a hypothesis test. Their marketing people survey 150 households with the result that 43 of the households have three cell phones.

Set up the Hypothesis Test:

\(H_{0}: p = 0.30, H_{a}: p \neq 0.30\)

Determine the distribution needed:

The random variable is \(P′ =\) proportion of households that have three cell phones.

The distribution for the hypothesis test is \(P' - N\left(0.30, \sqrt{\frac{(0.30 \cdot 0.70)}{150}}\right)\)

Exercise 9.6.8.2

a. The value that helps determine the \(p\text{-value}\) is \(p′\). Calculate \(p′\).

a. \(p' = \frac{x}{n}\) where \(x\) is the number of successes and \(n\) is the total number in the sample.

\(x = 43, n = 150\)

\(p′ = 43150\)

Exercise 9.6.8.3

b. What is a success for this problem?

b. A success is having three cell phones in a household.

Exercise 9.6.8.4

c. What is the level of significance?

c. The level of significance is the preset \(\alpha\). Since \(\alpha\) is not given, assume that \(\alpha = 0.05\).

Exercise 9.6.8.5

d. Draw the graph for this problem. Draw the horizontal axis. Label and shade appropriately.

Calculate the \(p\text{-value}\).

d. \(p\text{-value} = 0.7216\)

Exercise 9.6.8.6

e. Make a decision. _____________(Reject/Do not reject) \(H_{0}\) because____________.

e. Assuming that \(\alpha = 0.05, \alpha < p\text{-value}\). The decision is do not reject \(H_{0}\) because there is not sufficient evidence to conclude that the proportion of households that have three cell phones is not 30%.

Exercise \(\PageIndex{8}\)

Marketers believe that 92% of adults in the United States own a cell phone. A cell phone manufacturer believes that number is actually lower. 200 American adults are surveyed, of which, 174 report having cell phones. Use a 5% level of significance. State the null and alternative hypothesis, find the p -value, state your conclusion, and identify the Type I and Type II errors.

• \(H_{0}: p = 0.92\)
• \(H_{a}: p < 0.92\)
• \(p\text{-value} = 0.0046\)

Because \(p < 0.05\), we reject the null hypothesis. There is sufficient evidence to conclude that fewer than 92% of American adults own cell phones.

• Type I Error: To conclude that fewer than 92% of American adults own cell phones when, in fact, 92% of American adults do own cell phones (reject the null hypothesis when the null hypothesis is true).
• Type II Error: To conclude that 92% of American adults own cell phones when, in fact, fewer than 92% of American adults own cell phones (do not reject the null hypothesis when the null hypothesis is false).

The next example is a poem written by a statistics student named Nicole Hart. The solution to the problem follows the poem. Notice that the hypothesis test is for a single population proportion. This means that the null and alternate hypotheses use the parameter \(p\). The distribution for the test is normal. The estimated proportion \(p′\) is the proportion of fleas killed to the total fleas found on Fido. This is sample information. The problem gives a preconceived \(\alpha = 0.01\), for comparison, and a 95% confidence interval computation. The poem is clever and humorous, so please enjoy it!

Example \(\PageIndex{9}\)

My dog has so many fleas,

They do not come off with ease. As for shampoo, I have tried many types Even one called Bubble Hype, Which only killed 25% of the fleas, Unfortunately I was not pleased.

I've used all kinds of soap, Until I had given up hope Until one day I saw An ad that put me in awe.

A shampoo used for dogs Called GOOD ENOUGH to Clean a Hog Guaranteed to kill more fleas.

I gave Fido a bath And after doing the math His number of fleas Started dropping by 3's! Before his shampoo I counted 42.

At the end of his bath, I redid the math And the new shampoo had killed 17 fleas. So now I was pleased.

Now it is time for you to have some fun With the level of significance being .01, You must help me figure out

Use the new shampoo or go without?

\(H_{0}: p \leq 0.25\)   \(H_{a}: p > 0.25\)

In words, CLEARLY state what your random variable \(\bar{X}\) or \(P′\) represents.

\(P′ =\) The proportion of fleas that are killed by the new shampoo

State the distribution to use for the test.

\[N\left(0.25, \sqrt{\frac{(0.25){1-0.25}}{42}}\right)\nonumber \]

Test Statistic: \(z = 2.3163\)

Calculate the \(p\text{-value}\) using the normal distribution for proportions:

\[p\text{-value} = 0.0103\nonumber \]

In one to two complete sentences, explain what the p -value means for this problem.

If the null hypothesis is true (the proportion is 0.25), then there is a 0.0103 probability that the sample (estimated) proportion is 0.4048 \(\left(\frac{17}{42}\right)\) or more.

Use the previous information to sketch a picture of this situation. CLEARLY, label and scale the horizontal axis and shade the region(s) corresponding to the \(p\text{-value}\).

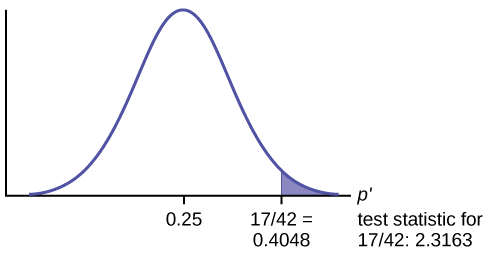
Indicate the correct decision (“reject” or “do not reject” the null hypothesis), the reason for it, and write an appropriate conclusion, using complete sentences.

Conclusion: At the 1% level of significance, the sample data do not show sufficient evidence that the percentage of fleas that are killed by the new shampoo is more than 25%.

Construct a 95% confidence interval for the true mean or proportion. Include a sketch of the graph of the situation. Label the point estimate and the lower and upper bounds of the confidence interval.

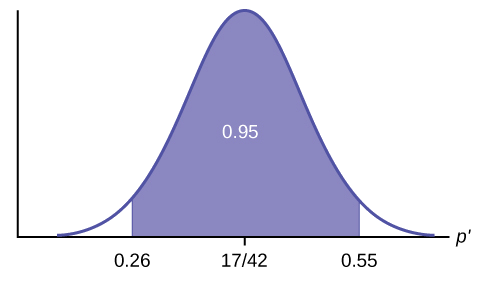
Confidence Interval: (0.26,0.55) We are 95% confident that the true population proportion p of fleas that are killed by the new shampoo is between 26% and 55%.

This test result is not very definitive since the \(p\text{-value}\) is very close to alpha. In reality, one would probably do more tests by giving the dog another bath after the fleas have had a chance to return.

Example \(\PageIndex{11}\)

In a study of 420,019 cell phone users, 172 of the subjects developed brain cancer. Test the claim that cell phone users developed brain cancer at a greater rate than that for non-cell phone users (the rate of brain cancer for non-cell phone users is 0.0340%). Since this is a critical issue, use a 0.005 significance level. Explain why the significance level should be so low in terms of a Type I error.

We will follow the four-step process.

• \(H_{0}: p \leq 0.00034\)
• \(H_{a}: p > 0.00034\)

If we commit a Type I error, we are essentially accepting a false claim. Since the claim describes cancer-causing environments, we want to minimize the chances of incorrectly identifying causes of cancer.

• We will be testing a sample proportion with \(x = 172\) and \(n = 420,019\). The sample is sufficiently large because we have \(np = 420,019(0.00034) = 142.8\), \(nq = 420,019(0.99966) = 419,876.2\), two independent outcomes, and a fixed probability of success \(p = 0.00034\). Thus we will be able to generalize our results to the population.

Figure 9.6.11.

Figure 9.6.12.

• Since the \(p\text{-value} = 0.0073\) is greater than our alpha value \(= 0.005\), we cannot reject the null. Therefore, we conclude that there is not enough evidence to support the claim of higher brain cancer rates for the cell phone users.

Example \(\PageIndex{12}\)

According to the US Census there are approximately 268,608,618 residents aged 12 and older. Statistics from the Rape, Abuse, and Incest National Network indicate that, on average, 207,754 rapes occur each year (male and female) for persons aged 12 and older. This translates into a percentage of sexual assaults of 0.078%. In Daviess County, KY, there were reported 11 rapes for a population of 37,937. Conduct an appropriate hypothesis test to determine if there is a statistically significant difference between the local sexual assault percentage and the national sexual assault percentage. Use a significance level of 0.01.

We will follow the four-step plan.

• We need to test whether the proportion of sexual assaults in Daviess County, KY is significantly different from the national average.
• \(H_{0}: p = 0.00078\)
• \(H_{a}: p \neq 0.00078\)

Figure 9.6.13.

Figure 9.6.14.

• Since the \(p\text{-value}\), \(p = 0.00063\), is less than the alpha level of 0.01, the sample data indicates that we should reject the null hypothesis. In conclusion, the sample data support the claim that the proportion of sexual assaults in Daviess County, Kentucky is different from the national average proportion.

The hypothesis test itself has an established process. This can be summarized as follows:

• Determine \(H_{0}\) and \(H_{a}\). Remember, they are contradictory.
• Determine the random variable.
• Determine the distribution for the test.
• Draw a graph, calculate the test statistic, and use the test statistic to calculate the \(p\text{-value}\). (A z -score and a t -score are examples of test statistics.)
• Compare the preconceived α with the p -value, make a decision (reject or do not reject H 0 ), and write a clear conclusion using English sentences.

Notice that in performing the hypothesis test, you use \(\alpha\) and not \(\beta\). \(\beta\) is needed to help determine the sample size of the data that is used in calculating the \(p\text{-value}\). Remember that the quantity \(1 – \beta\) is called the Power of the Test . A high power is desirable. If the power is too low, statisticians typically increase the sample size while keeping α the same.If the power is low, the null hypothesis might not be rejected when it should be.

• Data from Amit Schitai. Director of Instructional Technology and Distance Learning. LBCC.
• Data from Bloomberg Businessweek . Available online at http://www.businessweek.com/news/2011- 09-15/nyc-smoking-rate-falls-to-record-low-of-14-bloomberg-says.html.
• Data from energy.gov. Available online at http://energy.gov (accessed June 27. 2013).
• Data from Gallup®. Available online at www.gallup.com (accessed June 27, 2013).
• Data from Growing by Degrees by Allen and Seaman.
• Data from La Leche League International. Available online at www.lalecheleague.org/Law/BAFeb01.html.
• Data from the American Automobile Association. Available online at www.aaa.com (accessed June 27, 2013).
• Data from the American Library Association. Available online at www.ala.org (accessed June 27, 2013).
• Data from the Bureau of Labor Statistics. Available online at http://www.bls.gov/oes/current/oes291111.htm .
• Data from the Centers for Disease Control and Prevention. Available online at www.cdc.gov (accessed June 27, 2013)
• Data from the U.S. Census Bureau, available online at quickfacts.census.gov/qfd/states/00000.html (accessed June 27, 2013).
• Data from the United States Census Bureau. Available online at www.census.gov/hhes/socdemo/language/.
• Data from Toastmasters International. Available online at http://toastmasters.org/artisan/deta...eID=429&Page=1 .
• Data from Weather Underground. Available online at www.wunderground.com (accessed June 27, 2013).
• Federal Bureau of Investigations. “Uniform Crime Reports and Index of Crime in Daviess in the State of Kentucky enforced by Daviess County from 1985 to 2005.” Available online at http://www.disastercenter.com/kentucky/crime/3868.htm (accessed June 27, 2013).
• “Foothill-De Anza Community College District.” De Anza College, Winter 2006. Available online at research.fhda.edu/factbook/DA...t_da_2006w.pdf.
• Johansen, C., J. Boice, Jr., J. McLaughlin, J. Olsen. “Cellular Telephones and Cancer—a Nationwide Cohort Study in Denmark.” Institute of Cancer Epidemiology and the Danish Cancer Society, 93(3):203-7. Available online at http://www.ncbi.nlm.nih.gov/pubmed/11158188 (accessed June 27, 2013).
• Rape, Abuse & Incest National Network. “How often does sexual assault occur?” RAINN, 2009. Available online at www.rainn.org/get-information...sexual-assault (accessed June 27, 2013).

Contributors and Attributions

Barbara Illowsky and Susan Dean (De Anza College) with many other contributing authors. Content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/[email protected] .