case study based on coordinate geometry

• Bihar Board

SRM University

Mp board result 2024, ts inter results 2024.

• MP Board 10th Result 2024
• MP Board 12th Result 2024
• TS Board Results 2024
• NBSE Board Result 2024
• UK Board Result 2024
• Karnataka Board Result
• Shiv Khera Special
• Education News
• Web Stories
• Current Affairs
• नए भारत का नया उत्तर प्रदेश
• School & Boards
• College Admission
• Govt Jobs Alert & Prep
• GK & Aptitude
• CBSE Class 10 Study Material

CBSE Class 10 Maths Case Study Questions for Chapter 7 - Coordinate Geometry (Released By CBSE)

Cbse's question bank on case study for class 10 maths chapter 7 is available here. practice this new type of questions to score good marks in your board exam..

Case study based questions for CBSE Class 10 Maths Chapter 7 - Coordinate Geometry are provided here for students to practice this new format of questions for their Maths Board Exam 2022. All these questions are published by the Central Board of Secondary Education (CBSE) for Class 10 Maths. Students must solve these questions to familiarise themselves with the concepts and logic used in the case study. You can also check the right answer at the end of each question.

Check Case Study Questions for Class 10 Maths Chapter 7 - Coordinate Geometry

CASE STUDY 1:

In order to conduct Sports Day activities in your School, lines have been drawn with chalk powder at a distance of 1 m each, in a rectangular shaped ground ABCD, 100 flower pots have been placed at a distance of 1 m from each other along AD, as shown in given figure below. Niharika runs 1/4 th the distance AD on the 2nd line and posts a green flag. Preet runs 1/5th distance AD on the eighth line and posts a red flag.

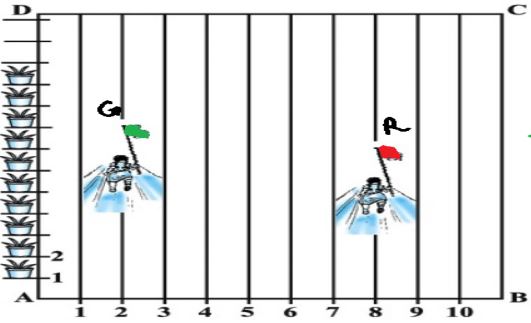
1. Find the position of green flag

b) (2,0.25)

d) (0, -25)

Answer:  a) (2,25)

2. Find the position of red flag

Answer: c) (8,20)

3. What is the distance between both the flags?

a) √41

b) √11

c) √61

d) √51

Answer: c) √61

4. If Rashmi has to post a blue flag exactly halfway between the line segment joining the two flags, where should she post her flag?

a) (5, 22.5)

d) (2.5,20)

Answer: a) (5, 22.5)

5. If Joy has to post a flag at one-fourth distance from green flag , in the line segment joining the green and red flags, then where should he post his flag?

a) (3.5,24)

b) (0.5,12.5)

c) (2.25,8.5)

Answer: a) (3.5,24)

CASE STUDY 2:

The class X students school in krishnagar have been allotted a rectangular plot of land for their gardening activity. Saplings of Gulmohar are planted on the boundary at a distance of 1 m from each other. There is triangular grassy lawn in the plot as shown in the figure. The students are to sow seeds of flowering plants on the remaining area of the plot.

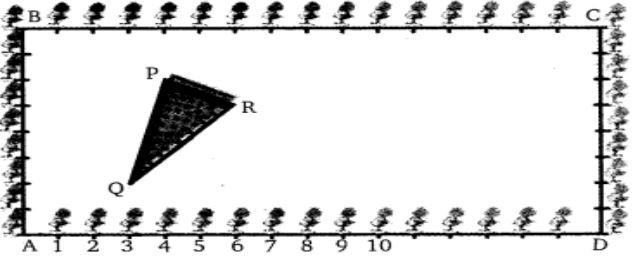
1. Taking A as origin, find the coordinates of P

Answer: a) (4,6)

2. What will be the coordinates of R, if C is the origin?

Answer: c) (10,3)

3. What will be the coordinates of Q, if C is the origin?

b) b) (-6,13)

Answer: d) (13,6)

4. Calculate the area of the triangles if A is the origin

Answer: a) 4.5

5. Calculate the area of the triangles if C is the origin

Answer: d) 4.5

Also Check:

Tips to Solve Case Study Based Questions Accurately

CBSE Class 10 Maths Best Study Material for 2021-2022

Get here latest School , CBSE and Govt Jobs notification in English and Hindi for Sarkari Naukari and Sarkari Result . Download the Jagran Josh Sarkari Naukri App . Check  Board Result 2024  for Class 10 and Class 12 like  CBSE Board Result ,  UP Board Result ,  Bihar Board Result ,  MP Board Result ,  Rajasthan Board Result  and Other States Boards.

• MP बोर्ड 2024 12th Result
• 10th MP बोर्ड रिजल्ट 2024
• MP बोर्ड 10th, 12th रिजल्ट 2024
• mpbse.nic.in 2024 रिजल्ट
• mpbse.mponline.gov.in रिजल्ट 2024
• MPBSE रिजल्ट 2024 10th, 12th
• MP बोर्ड 12वीं टॉपर लिस्ट 2024
• एमपी बोर्ड 10 वीं टॉपर लिस्ट 2024
• AP SSC Results 2024 Manabadi by Jagran Josh
• AP SSC Topper List 2024
• CBSE Study Material
• CBSE Class 10

Latest Education News

[यहां चेक करें] MP Board Result 2024 10th 12th Released LIVE: Check MPBSE HSC, HSSC Results with Roll Number and Application Number at mpbse.nic.in

mpbse.nic.in, mpresults.nic.in 2024 Result LINK Active : 10वीं में अनुष्का और 12वीं जयंत ने किया टॉप, लड़कियों ने फिर फहराया परचम

KUHS Result 2024 OUT at kuhs.ac.in; Direct Link to Download UG Marksheet

Punjab Board Class 10th Syllabus 2024-25: Download PSEB All Subject Latest Syllabus PDFs Here

UGC NET Eligibility 2024: Check Qualification and Age Limit for Assistant Professor & JRF

Personality Test: Your Thumb Shape Reveals Your Hidden Personality Traits

CBSE Class 12 Psychology Syllabus 2024-25: Download in PDF

UK Board Result 2024: Uttrakhand Board UBSE Class 10, 12 Result Date And Time at uaresults.nic.in

UK Board Result 2024 class 10: Uttrakhand Board Class 10th Result Date And Time at ubse.uk.gov.in

UK Board Result 2024 class 12: Uttrakhand Board Class 12th Result Date And Time at ubse.uk.gov.in

Find 3 differences between the pictures of a fire breathing dragon in 12 seconds!

Uttarakhand Board 10th, 12th Result 2024 Likely to Be Declared on April 29, Check Steps To Download, Other Details Here

[ऑनलाइन लिंक] MP Board 10th, 12th Result 2024 OUT Live: mpresults.nic.in पर एमपी बोर्ड 10वीं, 12वीं रिजल्ट घोषित, तुरंत एप्लीकेशन नंबर से करें चेक

MPBSE Result 2024 Out LIVE Updates: Check Madhya Pradesh Board 10th, 12th Result Online Link Active at mpbse.mponline.gov.in, mpbse.nic.in

MP Board 10th Topper List 2024: एमपी 10वीं बोर्ड रिजल्ट जारी, अनुष्का अग्रवाल ने किया टॉप, यहां मिलेगी पूरी जिलेवार लिस्ट

MP Board 10th, 12th Compartment 2024: MPBSE High School, Inter Supplementary Exam Date and Other Details

UPSC Calendar 2024, Exam Schedule for IAS, CDS, NDA, Engineering Services and Other Exams Date Sheet PDF

MP Board Compartment 2024: परीक्षा में फेल हुए छात्रों को एक और मौका, 10th, 12th कंपार्टमेंट परीक्षा के लिए 09 जून से करें आवेदन

MP Board 12th Result 2024 OUT: When, How, Where to Check MPBSE Inter Science, Arts and Commerce Stream Results etc

MP Board Result 2024 Class 10, 12 with Jagran Josh: Check MPBSE High School, Inter Results with Roll Number, School Code

• Privacy Policy
• Terms and Conditions

• Web Stories

Friday, October 1, 2021

Class 10 maths case study based questions chapter 7 coordinate geometry cbse board term 1 with answer key.

Hello students, Welcome to Maths Easy Institute.  

CASE STUDY 1:   

0 comments:

Post a comment.

Please do not enter any spam link in the comment box.

Warning: Do Not Copy!

• Blog Archives

• Best Books for IIT JEE
• Best Colleges Of India
• class 10 Case Study Based questions
• Class 10 Maths MCQ
• Class 11 Maths Case Study Questions
• Class 11 Maths MCQ
• Class 12 Math Case Study questions
• Class 12 Maths MCQ
• JEE MAIN MCQ
• Maths Strategy JEE
• News for Students

Blog Archive

• ►  April (3)
• ►  March (2)
• ►  February (1)
• ►  January (5)
• ►  December (9)
• ►  November (5)
• Case Study Questions Class 10 Maths Chapter 9 Appl...
• Class 10 Maths Case Study Based Questions Chapter ...
• Class 11 Maths MCQ Chapter 5 Complex Numbers CBSE ...
• Class 11 MCQ type Questions Chapter 2 Relations an...
• ►  September (5)
• ►  April (4)
• ►  March (3)
• ►  October (2)
• ►  September (7)
• ►  August (2)
• ►  July (4)

Class 10 Maths Chapter 7 Case Based Questions - Coordinate Geometry

Study case - 1.

The class X students of a school in Rajinder Nagar have been allotted a rectangular plot of land for their gardening activity. Sapling of Mango are planted on the boundary at the distance of 1 m from each other.

Based on the above figure, answer the following questions:

  Q4: What will be the coordinates of the vertices of ΔPQR if C is the origin? (a) (14, 3), (11, 2), (8, 6) (b) (15, 4), (12, 3), (9, 7) (c) (14, 2), (11, 1), (8, 5) (d) (15, 3), (12, 2), (9, 6) Ans:  (d) Explanation:  When C is taken as origin, we will take CB as X-axis and CD as Y-axis. Then, coordinates of points, P, Q and R are (15, 3), (12, 2)and (9, 6) respectively.

Q5: What are the coordinates of P if D is taken as the origin? (a) (−15, 5) (b) (15, 5) (c) (15, 7) (d) (15, 3) Ans:  (a) Explanation:  When D is taken as origin, we will take DA as negative X-axis and DC as positive Y-axis.   Then coordinates of point P is (−15, 5).

Case Study - 2

Based on the above information, give the answer of the following questions: 

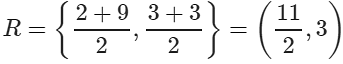
Study Case - 3

Based on the above information give the answer of the following questions:

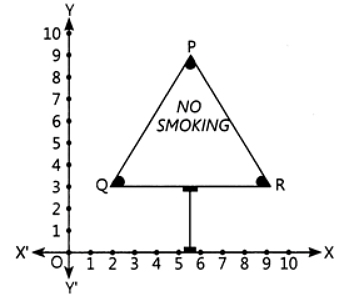
Q1: The coordinates of the point A are: (a) (4,9) (b) (5,9) (c) (92,9) (d) (4,8) Ans: (c) Explanation:  As the distance of point A is 9/2 units from the Y-axis and 9 units from the X-axis, its coordinates are x = 9/2, y = 9 or (9/2, 9)

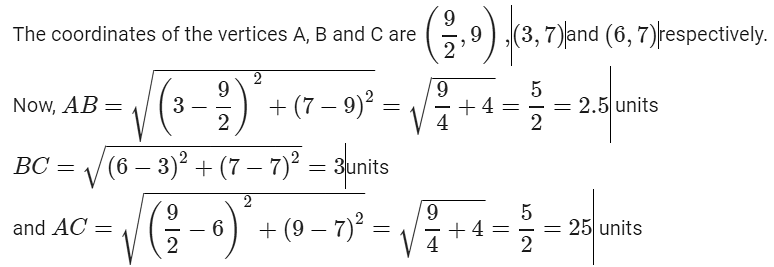
Top Courses for Class 10

Previous year questions with solutions, practice quizzes, mock tests for examination, important questions, video lectures, semester notes, past year papers, objective type questions, shortcuts and tricks, viva questions, sample paper, study material, extra questions.

Case Based Questions: Coordinate Geometry Free PDF Download

Importance of case based questions: coordinate geometry, case based questions: coordinate geometry notes, case based questions: coordinate geometry class 10, study case based questions: coordinate geometry on the app, welcome back, create your account for free.

Forgot Password

Unattempted tests, change country, practice & revise.

CBSE Case Study Questions for Class 9 Maths Coordinate Geometry Free PDF

Mere Bacchon, you must practice the CBSE Case Study Questions Class 9 Maths Coordinate Geometry  in order to fully complete your preparation . They are very very important from exam point of view. These tricky Case Study Based Questions can act as a villain in your heroic exams!

I have made sure the questions (along with the solutions) prepare you fully for the upcoming exams. To download the latest CBSE Case Study Questions , just click ‘ Download PDF ’.

CBSE Case Study Questions for Class 9 Maths Coordinate Geometry PDF

Checkout our case study questions for other chapters.

• Chapter 1 Number Systems Case Study Questions
• Chapter 2 Polynomials Case Study Questions
• Chapter 4 Linear Equations in Two Variables Case Study Questions
• Chapter 5 Euclids Geometry Case Study Questions

How should I study for my upcoming exams?

First, learn to sit for at least 2 hours at a stretch

Solve every question of NCERT by hand, without looking at the solution.

Solve NCERT Exemplar (if available)

Sit through chapter wise FULLY INVIGILATED TESTS

Practice MCQ Questions (Very Important)

Practice Assertion Reason & Case Study Based Questions

Sit through FULLY INVIGILATED TESTS involving MCQs. Assertion reason & Case Study Based Questions

After Completing everything mentioned above, Sit for atleast 6 full syllabus TESTS.

Contact Form

Privacy Policy

WorksheetsBag.com

Case Study Chapter 7 Coordinate Geometry Mathematics

Refer to Case Study Chapter 7 Coordinate Geometry Mathematics, these class 10 maths case study based questions have been designed as per the latest examination guidelines issued for the current academic year by CBSE, NCERT, KVS. Students should go through these solves case studies so that they are able to understand the pattern of questions expected in exams and get good marks.

Chapter 7 Coordinate Geometry Mathematics Case Study Based Questions

l. Read the following and answer Shaurya made a map of his locality on a coordinate plane.   

Question. The coordinates of the point which divides the line segment joining school and park internally in the ratio 3 : 2 are    (a) (–2, 2) (b) (–2, –2) (c) (2, 3) (d) (2, –2)

Question. If he considered his house as the origin, then coordinates of market are    (a) (3, –1) (b) (–3, –1) (c) (–3, 1) (d) (3, 1)

Question. The distance of his friend Kartik’s house from his house is    (a) √20 units (b) √10 units (c) 20 units (d) 10 units

Question. If you form a polygon with vertex as position of park, Shaurya’s home, railway station, post office and temple, then the polygon is    (a) Regular polygon (b) Convex Polygon (c) Concave Polygon (d) Rhombus

Question. There is a fort at a distance of 10 units from his house. If its ordinate is 6, then its abscissa is    (a) ± 2 (b) 0 (c) ± 4 (d) ± 8

ll. Read the following and answer A coach is discussing the strategy of the game with his players. The position of players is marked with ‘×’ in the figure.   

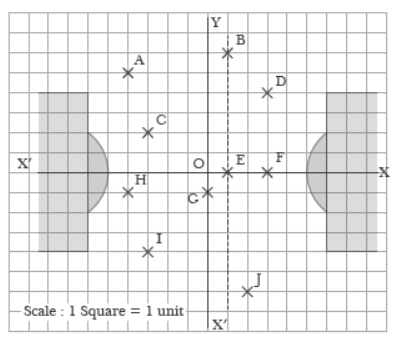
Question. The player who is 6 units from x-axis and 2 units to the right of y-axis is at position      (a) J (b) B (c) I (d) A

Question. According to sudden requirement coach of the team decided to increase one player in the 4th quadrant without increasing the total number of players, so he decided to change the position of player F in such a way that F becomes symmetric to D w.r.t x axis, then new position of F is    (a) (3, 4) (b) (3, – 4) (c) (–4, 3) (d) (4, 3)

Question. If (x, y) are the coordinates of the mid-point of the line segment joining A and H, then      (a) x = – 4, y = 2 (b) x = 2, y = 4 (c) x = –2, y = 4 (d) x = –4, y = – 2

Question. If O is taken as the origin, the point whose abscissa equal to zero is      (a) H (b) E (c) G (d) F

Question. The distance between the player C and B is      (a) 5 units  (b) 4 √2 units (c) 2 √5 units (d) 5 √2 units

lll. Read the following and answer The children of a school prepared a dance item for Republic Day parade for which they were asked to form a rectangle by standing at a fixed distance, taken as one unit. Some children, then formed a pattern inside the rectangle. 

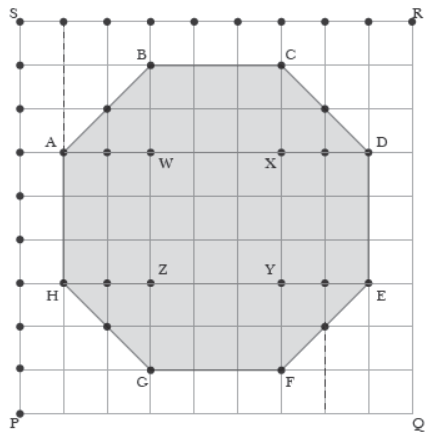
Question. The coordinate of the point that divides the line segment joining the points A and D in the ratio 2 : 3 internally are      (a) (6, 5 /19)  (b) (6, 6) (c) (6, 2) (d) (19/5 , 6)

Question. The coordinates of the point P if H is taken as the origin are      (a) (2, 3) (b) (–1, –3) (c) (–2, 3) (d) (2, –3)

Question. If a point (x, y) is equidistant from C(6, 8) and F(6, 1) then      (a) 2x – 7y + 36 = 0 (b) 144y = 63 (c) x – y = 5 (d) x + y = 5

Question. If P is considered as the origin, the coordinates of B are    (a) (8, 5) (b) (3, 8) (c) (8, 0) (d) (0, 3)

Question. The distance between the children standing at H and G is    (a) 8 units   (b) 2 units (c) 5 units (d) √8 units

lV. Read the following and answer The top of a table is shown in the figure given below: 

Question. The coordinates of the mid point of line segment joining points M and Q are    (a) (9, 3) (b) (5, 11) (c) (14, 14) (d) (7, 7)

Question. If G is taken as the origin, and x, y axis put along GF and GB, then the point denoted by coordinate (4, 2) is    (a) H (b) F (c) Q (d) R

Question. Which among the following have same ordinate ?    (a) H and A (b) T and O (c) R and M (d) N and R

Question. The coordinates of the points H and G are respectively    (a) (1, 5), (5, 1) (b) (0, 5), (5, 0) (c) (1, 5), (5, 0) (d) (5, 1), (1, 5)

Question. The distance between the points A and B is      (a) 4 units (b) 4 √2 units (c) 16 units (d) 32 units

V. Read the following and answer A rangoli design was made by Ishita using coordinate plane. 

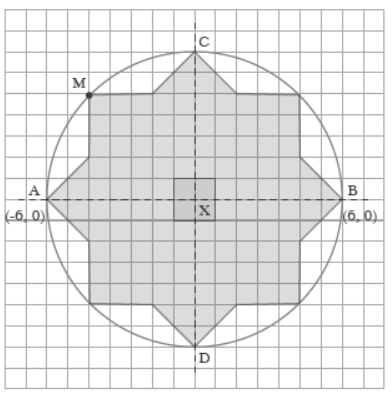
Question. PQRS is a square inside the circle where P is (–1, 1) then coordinates of R are      (a) (–1, –1) (b) (–1, 1) (c) (1, –1) (d) (1, 1)

Question. The distance of the point M on the circle from x-axis is      (a) 4 units (b) 3 units (c) 2 units (d) 5 units

Question. The coordinates of the mid point of the line segment joining PR is      (a) (1, 1) (b) (0, 0) (c) (–1, –1) (d) (1, 2)

Question. If coordinates of centre X are (0, 0) and B is a point on circle with coordinates (7, 0), then coordinate of C and D are respectively    (a) (0, 7), (0, – 7) (b) (0, –7), (0, 7) (c) (7, 7), (–7, – 7) (d) (–7, –7), (7, 7)

Question. The coordinates of the point on the circle in first quadrant whose abscissa equal to 3 is    (a) (3, 3)  (b) (3, –3) (c) (2√10, 3) (d) (3, 2 √10)

Related Posts

Worksheets Class 10 Social Science Outcomes of Democracy

Worksheets for class 10 social science civics, worksheets for class 10 mathematics real numbers.

Class 9 Maths Case Study Questions Chapter 3 Coordinate Geometry

• Post author: studyrate
• Post published:
• Post category: class 9th
• Post comments: 0 Comments

Case study Questions in Class 9 Mathematics Chapter 3  are very important to solve for your exam. Class 9 Maths Chapter 3 Case Study Questions have been prepared for the latest exam pattern. You can check your knowledge by solving  Class 9 Maths Case Study Questions  Chapter 3 Coordinate Geometry

Join our Telegram Channel, there you will get various e-books for CBSE 2024 Boards exams for Class 9th, 10th, 11th, and 12th.

In CBSE Class 9 Maths Paper, Students will have to answer some questions based on Assertion and Reason. There will be a few questions based on case studies and passage-based as well. In that, a paragraph will be given, and then the MCQ questions based on it will be asked.

Coordinate Geometry Case Study Questions With Answers

Here, we have provided case-based/passage-based questions for Class 9 Maths Chapter 3 Coordinate Geometry

Case Study/Passage-Based Questions

Answer: (d) 2 units

(ii) How far is the library from Shaguns house?

Answer: (b) 2 units

(iii) How far is the library from Alia’s house?

Answer: (d) None of these

(iv) Which of the following is true?

Answer: (b) ABC forms an isosceles triangle

Answer: (d) none of these

(ii) The distance of the bus stand from the house is

Answer: (b) 10 cm

(iii) If the grocery store and electrician’s shop lie on a line, the ratio of the distance of house from grocery store to that from electrician’s shop, is

Answer: (c) 1.2

(iv) The ratio of distances of the house from the bus stand to the food cart is

Answer: (c) 1.1

(v) The coordinates of positions of bus stand, grocery store, food cart, and electrician’s shop form a

Hope the information shed above regarding Case Study and Passage Based Questions for Class 9 Mathematics Chapter 3 Coordinate Geometry with Answers Pdf free download has been useful to an extent. If you have any other queries about CBSE Class 9 Maths Coordinate Geometry Case Study and Passage Based Questions with Answers, feel free to comment below so that we can revert back to us at the earliest possible By Team Study Rate

You Might Also Like

Class 9 science mcq questions for chapter 15 improvement in food resources with answers, class 9 maths case study questions chapter 4 linear equations in two variables, mcq questions of class 9 social science geography chapter 6 population with answers, leave a reply cancel reply.

Save my name, email, and website in this browser for the next time I comment.

• Class 6 Maths
• Class 6 Science
• Class 6 Social Science
• Class 6 English
• Class 7 Maths
• Class 7 Science
• Class 7 Social Science
• Class 7 English
• Class 8 Maths
• Class 8 Science
• Class 8 Social Science
• Class 8 English
• Class 9 Maths
• Class 9 Science
• Class 9 Social Science
• Class 9 English
• Class 10 Maths
• Class 10 Science
• Class 10 Social Science
• Class 10 English
• Class 11 Maths
• Class 11 Computer Science (Python)
• Class 11 English
• Class 12 Maths
• Class 12 English
• Class 12 Economics
• Class 12 Accountancy
• Class 12 Physics
• Class 12 Chemistry
• Class 12 Biology
• Class 12 Computer Science (Python)
• Class 12 Physical Education
• GST and Accounting Course
• Excel Course
• Tally Course
• Finance and CMA Data Course
• Payroll Course

Interesting

• Learn English
• Learn Excel
• Learn Tally
• Learn GST (Goods and Services Tax)
• Learn Accounting and Finance
• GST Tax Invoice Format
• Accounts Tax Practical
• Tally Ledger List
• GSTR 2A - JSON to Excel

Are you in school ? Do you love Teachoo?

We would love to talk to you! Please fill this form so that we can contact you

Case Based Questions (MCQ)

• NCERT Exemplar - MCQ
• Past Year MCQ
• Area of Triangle when coordinates are given
• Important Coordinate Geometry Questions

Question 2 - Case Based Questions (MCQ) - Chapter 7 Class 10 Coordinate Geometry

Last updated at April 16, 2024 by Teachoo

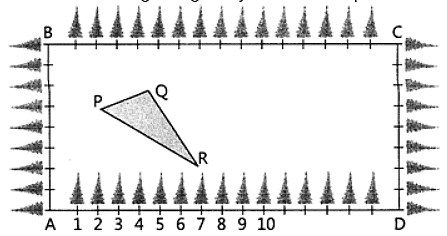
The class X students school in krishnagar have been allotted a rectangular plot of land for their gardening activity. Saplings of Gulmohar are planted on the boundary at a distance of 1 m from each other. There is triangular grassy lawn in the plot as shown in the figure. The students are to sow seeds of flowering plants on the remaining area of the plot.

This question is inspired from   Ex 7.4, 5 (Optional) - Chapter 7 Class 10 - Coordinate Geometry   Question 18 - CBSE Class 10 - Sample Paper for 2021 Board

Taking A as origin, find the coordinates of P (a) (4, 6) (b) (6, 4) (c) (0, 6) (d) (4, 0)

What will be the coordinates of R, if C is the origin? (a) (8, 6) (b) (3, 10) (c) (10, 3) (d) (0, 6)

What will be the coordinates of Q, if C is the origin? (a) (6, 13) (b) (–6, 13) (c) (–13, 6) (d) (13, 6)

Calculate the area of the triangles if A is the origin (a) 4.5 (b) 6 (c) 8 (d) 6.25

Calculate the area of the triangles if C is the origin (a) 8 (b) 5 (c) 6.25 (d) 4.5

Question The class X students school in krishnagar have been allotted a rectangular plot of land for their gardening activity. Saplings of Gulmohar are planted on the boundary at a distance of 1 m from each other. There is triangular grassy lawn in the plot as shown in the figure. The students are to sow seeds of flowering plants on the remaining area of the plot. Marking points on the image Niharika runs 1/4th of the distance AD on 2nd line So, Niharika’s x−cordinate = 2 Niharika’ y – cordinate = 1/4 × 100 = 25 ∴ Coordinates of Niharika = G (2, 25) Question 1 Taking A as origin, find the coordinates of P (a) (4, 6) (b) (6, 4) (c) (0, 6) (d) (4, 0) If A is the Origin Coordinates of point P = (4, 6) Coordinates of point Q = (3, 2) Coordinates of point R = (6, 5) So, the correct answer is (a) Question 2 What will be the coordinates of R, if C is the origin? (a) (8, 6) (b) (3, 10) (c) (10, 3) (d) (0, 6) If C is the Origin (and taking downward as positive) Coordinates of point P = (12, 2) Coordinates of point Q = (13, 6) Coordinates of point R = (10, 3) So, the correct answer is (c) Question 3 What will be the coordinates of Q, if C is the origin? (a) (6, 13) (b) (–6, 13) (c) (–13, 6) (d) (13, 6) Coordinates of point Q = (13, 6) So, the correct answer is (d) Question 4 Calculate the area of the triangles if A is the origin (a) 4.5 (b) 6 (c) 8 (d) 6.25 If A is the origin, We need to find Area of Δ PQR where P(4, 6) , Q(3, 2) and R(6, 5) Area of ∆PQR with vertices P (4, 6), Q (3, 2) & R (6, 5) Here, 𝒙_𝟏=4 , 〖 𝒚〗_𝟏=6 𝒙_𝟐=3 , 𝒚_𝟐=2 𝒙_𝟑=6 , 𝒚_𝟑=5 Now, ar (∆PQR) = 1/2 [𝑥_1 (𝑦_2−𝑦_3 )+ 𝑥_2 (𝑦_3−𝑦_1 )+𝑥_3 (𝑦_1−𝑦_2 )] = 𝟏/𝟐 [𝟒 (𝟐−𝟓)+𝟑 (𝟓−𝟔)+ 𝟔 (𝟔−𝟐)] = 1/2 [4 (−3)+3 (−1)+6 (4)] = 1/2 [−12−3+24] = 1/2 × 9 = 4.5 sq. units So, the correct answer is (a) Question 5 Calculate the area of the triangles if C is the origin (a) 8 (b) 5 (c) 6.25 (d) 4.5 If C is the origin, We need to find Area of Δ PQR where P(12, 2) , Q(13, 6) and R(10, 3) Area of ∆PQR with vertices P (12, 2), Q (13, 6) & R (10, 3) Here, 𝒙_𝟏=12 , 𝒚_𝟏=2 𝒙_𝟐=13 , 𝒚_𝟐=6 𝒙_𝟑=10 , 𝒚_𝟑=3 Now, ar (∆PQR) = 1/2 [𝑥_1 (𝑦_2−𝑦_3 )+ 𝑥_2 (𝑦_3−𝑦_1 )+𝑥_3 (𝑦_1−𝑦_2 )] = 𝟏/𝟐 [𝟏𝟐(𝟔−𝟑)+𝟏𝟑(𝟑−𝟐)+𝟏𝟎(𝟐−𝟔)] = 1/2 [12 × 3+13 × 1+10(−4)] = 1/2 [36+13−40] = 1/2 × 9 = 4.5 sq. units So, the correct answer is (d)

Davneet Singh

Davneet Singh has done his B.Tech from Indian Institute of Technology, Kanpur. He has been teaching from the past 14 years. He provides courses for Maths, Science, Social Science, Physics, Chemistry, Computer Science at Teachoo.

Hi, it looks like you're using AdBlock :(

Please login to view more pages. it's free :), solve all your doubts with teachoo black.

• Andhra Pradesh
• Chhattisgarh
• West Bengal
• Madhya Pradesh
• Maharashtra
• Jammu & Kashmir
• NCERT Books 2022-23
• NCERT Solutions
• NCERT Notes
• NCERT Exemplar Books
• NCERT Exemplar Solution
• States UT Book
• School Kits & Lab Manual
• NCERT Books 2021-22
• NCERT Books 2020-21
• NCERT Book 2019-2020
• NCERT Book 2015-2016
• RD Sharma Solution
• TS Grewal Solution
• TR Jain Solution
• Selina Solution
• Frank Solution
• ML Aggarwal Solution
• Lakhmir Singh and Manjit Kaur Solution
• I.E.Irodov solutions
• ICSE - Goyal Brothers Park
• ICSE - Dorothy M. Noronhe
• Sandeep Garg Textbook Solution
• Micheal Vaz Solution
• S.S. Krotov Solution
• Evergreen Science
• KC Sinha Solution
• ICSE - ISC Jayanti Sengupta, Oxford
• ICSE Focus on History
• ICSE GeoGraphy Voyage
• ICSE Hindi Solution
• ICSE Treasure Trove Solution
• Thomas & Finney Solution
• SL Loney Solution
• SB Mathur Solution
• P Bahadur Solution
• Narendra Awasthi Solution
• MS Chauhan Solution
• LA Sena Solution
• Integral Calculus Amit Agarwal Solution
• IA Maron Solution
• Hall & Knight Solution
• Errorless Solution
• Pradeep's KL Gogia Solution
• OP Tandon Solutions
• Sample Papers
• Previous Year Question Paper
• Value Based Questions
• CBSE Syllabus
• CBSE MCQs PDF
• Assertion & Reason
• New Revision Notes
• Revision Notes
• HOTS Question
• Marks Wise Question
• Toppers Answer Sheets
• Exam Paper Aalysis
• Concept Map
• CBSE Text Book
• Additional Practice Questions
• Vocational Book
• CBSE - Concept
• KVS NCERT CBSE Worksheets
• Formula Class Wise
• Formula Chapter Wise
• JEE Crash Course
• JEE Previous Year Paper
• Important Info
• JEE Mock Test
• JEE Sample Papers
• SRM-JEEE Mock Test
• VITEEE Mock Test
• BITSAT Mock Test
• Manipal Engineering Mock Test
• AP EAMCET Previous Year Paper
• COMEDK Previous Year Paper
• GUJCET Previous Year Paper
• KCET Previous Year Paper
• KEAM Previous Year Paper
• Manipal Previous Year Paper
• MHT CET Previous Year Paper
• WBJEE Previous Year Paper
• AMU Previous Year Paper
• TS EAMCET Previous Year Paper
• SRM-JEEE Previous Year Paper
• VITEEE Previous Year Paper
• BITSAT Previous Year Paper
• UPSEE Previous Year Paper
• CGPET Previous Year Paper
• CUSAT Previous Year Paper
• AEEE Previous Year Paper
• Crash Course
• Previous Year Paper
• NCERT Based Short Notes
• NCERT Based Tests
• NEET Sample Paper
• Previous Year Papers
• Quantitative Aptitude
• Numerical Aptitude Data Interpretation
• General Knowledge
• Mathematics
• Agriculture
• Accountancy
• Business Studies
• Political science
• Enviromental Studies
• Mass Media Communication
• Teaching Aptitude
• NAVODAYA VIDYALAYA
• SAINIK SCHOOL (AISSEE)
• Mechanical Engineering
• Electrical Engineering
• Electronics & Communication Engineering
• Civil Engineering
• Computer Science Engineering
• CBSE Board News
• Scholarship Olympiad
• School Admissions
• Entrance Exams
• All Board Updates
• Miscellaneous
• State Wise Books
• Engineering Exam

SHARING IS CARING If our Website helped you a little, then kindly spread our voice using Social Networks. Spread our word to your readers, friends, teachers, students & all those close ones who deserve to know what you know now.

• NCERT Solutions for Class 12 Maths
• NCERT Solutions for Class 10 Maths
• CBSE Syllabus 2023-24
• Social Media Channels
• Login Customize Your Notification Preferences
• Real Numbers 14 April, 2021, 6:09 pm
• Polynomials 14 April, 2021, 6:09 pm
• Pair of Equations in Two Variables 14 April, 2021, 6:09 pm
• Quadratic Equations 14 April, 2021, 6:09 pm
• Arithmetic Progressions 14 April, 2021, 6:09 pm
• Triangles 14 April, 2021, 6:09 pm
• Coordinate Geometry 14 April, 2021, 6:09 pm
• Introduction to Trigonometry 14 April, 2021, 6:09 pm
• Some Applications of Trigonometry 14 April, 2021, 6:08 pm

• Second click on the toggle icon

Provide prime members with unlimited access to all study materials in PDF format.

Allow prime members to attempt MCQ tests multiple times to enhance their learning and understanding.

Provide prime users with access to exclusive PDF study materials that are not available to regular users.

• Neet Online Test Pack

12th Standard stateboard question papers & Study material

தமிழ் subjects.

கணினி பயன்பாடுகள்

கணினி அறிவியல்

வணிகக் கணிதம் மற்றும் புள்ளியியல்.

கணினி தொழில்நுட்பம்

கணக்குப்பதிவியல்

English Subjects

Computer Science

Business Maths and Statistics

Accountancy

Computer Applications

Computer Technology

11th Standard stateboard question papers & Study material

9th Standard stateboard question papers & Study material

Social Science

சமூக அறிவியல்

6th standard stateboard question papers & study material.

10th Standard stateboard question papers & Study material

7th Standard stateboard question papers & Study material

8th Standard stateboard question papers & Study material

கணிதம் - old

12th Standard CBSE Subject Question Paper & Study Material

Introductory Micro and Macroeconomics

Business Studies

Indian Society

Physical Education

Bio Technology

Engineering Graphics

Entrepreneurship

Hindi Elective

Home Science

Legal Studies

Political Science

11th Standard CBSE Subject Question Paper & Study Material

Mathematics

Enterprenership

Applied Mathematics

10th standard cbse subject question paper & study material.

9th Standard CBSE Subject Question Paper & Study Material

8th Standard CBSE Subject Question Paper & Study Material

7th Standard CBSE Subject Question Paper & Study Material

6th Standard CBSE Subject Question Paper & Study Material

School Exams

Tamil Nadu State Board Exams

Scholarship Exams

Study Materials , News and Scholarships

Stateboard Tamil Nadu

Free Online Tests

Educational News

Scholarships

Entrance Exams India

Video Materials

9th Standard CBSE

Class 9th Maths - Coordinate Geometry Case Study Questions and Answers 2022 - 2023

Class 9th Maths - Coordinate Geometry Case Study Questions and Answers 2022 - 2023 Study Materials Sep-08 , 2022

QB365 provides a detailed and simple solution for every Possible Case Study Questions in Class 9th Maths Subject - Coordinate Geometry, CBSE. It will help Students to get more practice questions, Students can Practice these question papers in addition to score best marks.

A PHP Error was encountered

Severity: Warning

Message: in_array() expects parameter 2 to be array, null given

Filename: material/details.php

Line Number: 1436

Message: Use of undefined constant EXAM - assumed 'EXAM' (this will throw an Error in a future version of PHP)

Line Number: 1438

QB365 - Question Bank Software

Coordinate geometry case study questions with answer key.

Final Semester - June 2015

(b) What are the coordinates of C and D respectively?

(c) What is the distance between B and D?

(d) What is the distance between A and C?

(e) What are the coordinates of the point of intersection of AC and BD?

(ii) What are the coordinates of Police Station?

(iii) Distance between school and police station:

(iv) What are the coordinates of Library?

(v) In which quadrant the point (-1, 4) lies?  

(b) What are the coordinates of A and B respectively?

(c) The coordinates of point O in the sketch -2 is

(d) The point on the y-axis ( in sketch 2) which is equidistant from the points B and C is 

(e) The point on the x-axis ( in sketch 2) which is equidistant from the points C and D is

(b) What are the coordinates of R, taking A as origin?

(c) Side of lawn is :

(d) Shape of lawn is :

(e) Area of lawn is :

(ii) What are the coordinates of position 'D'?

(iii) What are the coordinates of position 'H'?

(iv) In which quadrant, the point 'C' lie?

(v) Find the perpendicular distance of the point E from the y-axis.

*****************************************

• Previous Class 9th Maths - Probability Case Study Questions and Answers 2022 - 2023
• Next Class 9th Maths - Statistics Case Study Questions and Answers 2022 - 2023

Reviews & Comments about Class 9th Maths - Coordinate Geometry Case Study Questions and Answers 2022 - 2023

Write your Comment

9th Standard CBSE Mathematics Usefull Links

• 10th Standard

Other 9th Standard CBSE Subjects

Other 9th Standard CBSE Mathematics Study material

Class 9th maths - probability case study questions and answers 2022 - 2023 click to view, class 9th maths - statistics case study questions and answers 2022 - 2023 click to view, class 9th maths - surface case study questions and answers 2022 - 2023 click to view, class 9th maths - linear equations in ... click to view, class 9th maths - coordinate geometry case ... click to view, 9th standard cbse mathematics annual exam model question 2020 click to view, 9th standard cbse mathematics public exam sample question 2020 click to view, 9th standard cbse mathematics public exam important question 2019-2020 click to view, 9th standard mathematics board exam sample question 2020 click to view, 9th standard mathematics board exam model question 2019-2020 click to view, cbse 9th mathematics - probability model question paper click to view, cbse 9th mathematics - statistics model question paper click to view, cbse 9th mathematics - surface areas and volumes model question paper click to view, cbse 9th mathematics - heron's formula model question paper click to view, cbse 9th mathematics - constructions model question paper click to view, register & get the solution for class 9th maths - coordinate geometry case study questions and answers 2022 - 2023.

CBSE Expert

CBSE Class 9 Maths Case Study Questions PDF Download

Download Class 9 Maths Case Study Questions to prepare for the upcoming CBSE Class 9 Exams 2023-24. These Case Study and Passage Based questions are published by the experts of CBSE Experts for the students of CBSE Class 9 so that they can score 100% in Exams.

Case study questions play a pivotal role in enhancing students’ problem-solving skills. By presenting real-life scenarios, these questions encourage students to think beyond textbook formulas and apply mathematical concepts to practical situations. This approach not only strengthens their understanding of mathematical concepts but also develops their analytical thinking abilities.

Table of Contents

CBSE Class 9th MATHS: Chapterwise Case Study Questions

Inboard exams, students will find the questions based on assertion and reasoning. Also, there will be a few questions based on case studies. In that, a paragraph will be given, and then the MCQ questions based on it will be asked. For Class 9 Maths Case Study Questions, there would be 5 case-based sub-part questions, wherein a student has to attempt 4 sub-part questions.

Chapterwise Case Study Questions of Class 9 Maths

• Case Study Questions for Chapter 1 Number System
• Case Study Questions for Chapter 2 Polynomials
• Case Study Questions for Chapter 3 Coordinate Geometry
• Case Study Questions for Chapter 4 Linear Equations in Two Variables
• Case Study Questions for Chapter 5 Introduction to Euclid’s Geometry
• Case Study Questions for Chapter 6 Lines and Angles
• Case Study Questions for Chapter 7 Triangles
• Case Study Questions for Chapter 8 Quadrilaterals
• Case Study Questions for Chapter 9 Areas of Parallelograms and Triangles
• Case Study Questions for Chapter 10 Circles
• Case Study Questions for Chapter 11 Constructions
• Case Study Questions for Chapter 12 Heron’s Formula
• Case Study Questions for Chapter 13 Surface Area and Volumes
• Case Study Questions for Chapter 14 Statistics
• Case Study Questions for Chapter 15 Probability

Checkout: Class 9 Science Case Study Questions

And for mathematical calculations, tap Math Calculators which are freely proposed to make use of by calculator-online.net

The above  Class 9 Maths Case Study Question s will help you to boost your scores as Case Study questions have been coming in your examinations. These CBSE Class 9 Maths Case Study Questions have been developed by experienced teachers of cbseexpert.com for the benefit of Class 10 students.

Class 9 Maths Syllabus 2023-24

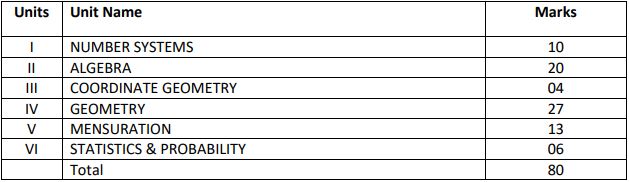
UNIT I: NUMBER SYSTEMS

1. REAL NUMBERS (18 Periods)

1. Review of representation of natural numbers, integers, and rational numbers on the number line. Rational numbers as recurring/ terminating decimals. Operations on real numbers.

2. Examples of non-recurring/non-terminating decimals. Existence of non-rational numbers (irrational numbers) such as √2, √3 and their representation on the number line. Explaining that every real number is represented by a unique point on the number line and conversely, viz. every point on the number line represents a unique real number.

3. Definition of nth root of a real number.

4. Rationalization (with precise meaning) of real numbers of the type

(and their combinations) where x and y are natural number and a and b are integers.

5. Recall of laws of exponents with integral powers. Rational exponents with positive real bases (to be done by particular cases, allowing learner to arrive at the general laws.)

UNIT II: ALGEBRA

1. POLYNOMIALS (26 Periods)

Definition of a polynomial in one variable, with examples and counter examples. Coefficients of a polynomial, terms of a polynomial and zero polynomial. Degree of a polynomial. Constant, linear, quadratic and cubic polynomials. Monomials, binomials, trinomials. Factors and multiples. Zeros of a polynomial. Motivate and State the Remainder Theorem with examples. Statement and proof of the Factor Theorem. Factorization of ax2 + bx + c, a ≠ 0 where a, b and c are real numbers, and of cubic polynomials using the Factor Theorem. Recall of algebraic expressions and identities. Verification of identities:

RELATED STORIES

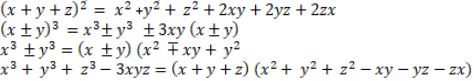
and their use in factorization of polynomials.

2. LINEAR EQUATIONS IN TWO VARIABLES (16 Periods)

Recall of linear equations in one variable. Introduction to the equation in two variables. Focus on linear equations of the type ax + by + c=0.Explain that a linear equation in two variables has infinitely many solutions and justify their being written as ordered pairs of real numbers, plotting them and showing that they lie on a line.

UNIT III: COORDINATE GEOMETRY COORDINATE GEOMETRY (7 Periods)

The Cartesian plane, coordinates of a point, names and terms associated with the coordinate plane, notations.

UNIT IV: GEOMETRY

1. INTRODUCTION TO EUCLID’S GEOMETRY (7 Periods)

History – Geometry in India and Euclid’s geometry. Euclid’s method of formalizing observed phenomenon into rigorous Mathematics with definitions, common/obvious notions, axioms/postulates and theorems. The five postulates of Euclid. Showing the relationship between axiom and theorem, for example: (Axiom)

1. Given two distinct points, there exists one and only one line through them. (Theorem)

2. (Prove) Two distinct lines cannot have more than one point in common.

2. LINES AND ANGLES (15 Periods)

1. (Motivate) If a ray stands on a line, then the sum of the two adjacent angles so formed is 180O and the converse.

2. (Prove) If two lines intersect, vertically opposite angles are equal.

3. (Motivate) Lines which are parallel to a given line are parallel.

3. TRIANGLES (22 Periods)

1. (Motivate) Two triangles are congruent if any two sides and the included angle of one triangle is equal to any two sides and the included angle of the other triangle (SAS Congruence).

2. (Prove) Two triangles are congruent if any two angles and the included side of one triangle is equal to any two angles and the included side of the other triangle (ASA Congruence).

3. (Motivate) Two triangles are congruent if the three sides of one triangle are equal to three sides of the other triangle (SSS Congruence).

4. (Motivate) Two right triangles are congruent if the hypotenuse and a side of one triangle are equal (respectively) to the hypotenuse and a side of the other triangle. (RHS Congruence)

5. (Prove) The angles opposite to equal sides of a triangle are equal.

6. (Motivate) The sides opposite to equal angles of a triangle are equal.

4. QUADRILATERALS (13 Periods)

1. (Prove) The diagonal divides a parallelogram into two congruent triangles.

2. (Motivate) In a parallelogram opposite sides are equal, and conversely.

3. (Motivate) In a parallelogram opposite angles are equal, and conversely.

4. (Motivate) A quadrilateral is a parallelogram if a pair of its opposite sides is parallel and equal.

5. (Motivate) In a parallelogram, the diagonals bisect each other and conversely.

6. (Motivate) In a triangle, the line segment joining the mid points of any two sides is parallel to the third side and in half of it and (motivate) its converse.

5. CIRCLES (17 Periods)

1. (Prove) Equal chords of a circle subtend equal angles at the center and (motivate) its converse.

2. (Motivate) The perpendicular from the center of a circle to a chord bisects the chord and conversely, the line drawn through the center of a circle to bisect a chord is perpendicular to the chord.

3. (Motivate) Equal chords of a circle (or of congruent circles) are equidistant from the center (or their respective centers) and conversely.

4. (Prove) The angle subtended by an arc at the center is double the angle subtended by it at any point on the remaining part of the circle.

5. (Motivate) Angles in the same segment of a circle are equal.

6. (Motivate) If a line segment joining two points subtends equal angle at two other points lying on the same side of the line containing the segment, the four points lie on a circle.

7. (Motivate) The sum of either of the pair of the opposite angles of a cyclic quadrilateral is 180° and its converse.

UNIT V: MENSURATION 1.

1. AREAS (5 Periods)

Area of a triangle using Heron’s formula (without proof)

2. SURFACE AREAS AND VOLUMES (17 Periods)

Surface areas and volumes of spheres (including hemispheres) and right circular cones.

UNIT VI: STATISTICS & PROBABILITY

STATISTICS (15 Periods)

 Bar graphs, histograms (with varying base lengths), and frequency polygons.

To crack case study questions, Class 9 Mathematics students need to apply their mathematical knowledge to real-life situations. They should first read the question carefully and identify the key information. They should then identify the relevant mathematical concepts that can be applied to solve the question. Once they have done this, they can start solving the Class 9 Mathematics case study question.

Benefits of Practicing CBSE Class 9 Maths Case Study Questions

Regular practice of CBSE Class 9 Maths case study questions offers several benefits to students. Some of the key advantages include:

• Deeper Understanding : Case study questions foster a deeper understanding of mathematical concepts by connecting them to real-world scenarios. This improves retention and comprehension.
• Practical Application : Students learn to apply mathematical concepts to practical situations, preparing them for real-life problem-solving beyond the classroom.
• Critical Thinking : Case study questions require students to think critically, analyze data, and devise appropriate solutions. This nurtures their critical thinking abilities, which are valuable in various academic and professional domains.
• Exam Readiness : By practicing case study questions, students become familiar with the question format and gain confidence in their problem-solving abilities. This enhances their readiness for CBSE Class 9 Maths exams.
• Holistic Development: Solving case study questions cultivates not only mathematical skills but also essential life skills like analytical thinking, decision-making, and effective communication.

Tips to Solve CBSE Class 9 Maths Case Study Questions Effectively

Solving case study questions can be challenging, but with the right approach, you can excel. Here are some tips to enhance your problem-solving skills:

• Read the case study thoroughly and understand the problem statement before attempting to solve it.
• Identify the relevant data and extract the necessary information for your solution.
• Break down complex problems into smaller, manageable parts to simplify the solution process.
• Apply the appropriate mathematical concepts and formulas, ensuring a solid understanding of their principles.
• Clearly communicate your solution approach, including the steps followed, calculations made, and reasoning behind your choices.
• Practice regularly to familiarize yourself with different types of case study questions and enhance your problem-solving speed.Class 9 Maths Case Study Questions

Remember, solving case study questions is not just about finding the correct answer but also about demonstrating a logical and systematic approach. Now, let’s explore some resources that can aid your preparation for CBSE Class 9 Maths case study questions.

Q1. Are case study questions included in the Class 9 Maths Case Study Questions syllabus?

Yes, case study questions are an integral part of the CBSE Class 9 Maths syllabus. They are designed to enhance problem-solving skills and encourage the application of mathematical concepts to real-life scenarios.

Q2. How can solving case study questions benefit students ?

Solving case study questions enhances students’ problem-solving skills, analytical thinking, and decision-making abilities. It also bridges the gap between theoretical knowledge and practical application, making mathematics more relevant and engaging.

Q3. How do case study questions help in exam preparation?

Case study questions help in exam preparation by familiarizing students with the question format, improving analytical thinking skills, and developing a systematic approach to problem-solving. Regular practice of case study questions enhances exam readiness and boosts confidence in solving such questions.

Leave a Comment Cancel reply

Save my name, email, and website in this browser for the next time I comment.

Download India's best Exam Preparation App Now.

Key Features

• Revision Notes
• Important Questions
• Previous Years Questions
• Case-Based Questions
• Assertion and Reason Questions

No thanks, I’m not interested!

myCBSEguide

• Mathematics
• CBSE Class 9 Mathematics...

CBSE Class 9 Mathematics Case Study Questions

Table of Contents

myCBSEguide App

Download the app to get CBSE Sample Papers 2023-24, NCERT Solutions (Revised), Most Important Questions, Previous Year Question Bank, Mock Tests, and Detailed Notes.

If you’re looking for a comprehensive and reliable study resource and case study questions for class 9 CBSE, myCBSEguide is the perfect door to enter. With over 10,000 study notes, solved sample papers and practice questions, it’s got everything you need to ace your exams. Plus, it’s updated regularly to keep you aligned with the latest CBSE syllabus . So why wait? Start your journey to success with myCBSEguide today!

Significance of Mathematics in Class 9

Mathematics is an important subject for students of all ages. It helps students to develop problem-solving and critical-thinking skills, and to think logically and creatively. In addition, mathematics is essential for understanding and using many other subjects, such as science, engineering, and finance.

CBSE Class 9 is an important year for students, as it is the foundation year for the Class 10 board exams. In Class 9, students learn many important concepts in mathematics that will help them to succeed in their board exams and in their future studies. Therefore, it is essential for students to understand and master the concepts taught in Class 9 Mathematics .

Case studies in Class 9 Mathematics

A case study in mathematics is a detailed analysis of a particular mathematical problem or situation. Case studies are often used to examine the relationship between theory and practice, and to explore the connections between different areas of mathematics. Often, a case study will focus on a single problem or situation and will use a variety of methods to examine it. These methods may include algebraic, geometric, and/or statistical analysis.

Example of Case study questions in Class 9 Mathematics

The Central Board of Secondary Education (CBSE) has included case study questions in the Class 9 Mathematics paper. This means that Class 9 Mathematics students will have to solve questions based on real-life scenarios. This is a departure from the usual theoretical questions that are asked in Class 9 Mathematics exams.

The following are some examples of case study questions from Class 9 Mathematics:

Class 9 Mathematics Case study question 1

There is a square park ABCD in the middle of Saket colony in Delhi. Four children Deepak, Ashok, Arjun and Deepa went to play with their balls. The colour of the ball of Ashok, Deepak,  Arjun and Deepa are red, blue, yellow and green respectively. All four children roll their ball from centre point O in the direction of   XOY, X’OY, X’OY’ and XOY’ . Their balls stopped as shown in the above image.

Answer the following questions:

Answer Key:

Class 9 Mathematics Case study question 2

• Now he told Raju to draw another line CD as in the figure
• The teacher told Ajay to mark  ∠ AOD  as 2z
• Suraj was told to mark  ∠ AOC as 4y
• Clive Made and angle  ∠ COE = 60°
• Peter marked  ∠ BOE and  ∠ BOD as y and x respectively

Now answer the following questions:

• 2y + z = 90°
• 2y + z = 180°
• 4y + 2z = 120°
• (a) 2y + z = 90°

Class 9 Mathematics Case study question 3

• (a) 31.6 m²
• (c) 513.3 m³
• (b) 422.4 m²

Class 9 Mathematics Case study question 4

How to Answer Class 9 Mathematics Case study questions

To crack case study questions, Class 9 Mathematics students need to apply their mathematical knowledge to real-life situations. They should first read the question carefully and identify the key information. They should then identify the relevant mathematical concepts that can be applied to solve the question. Once they have done this, they can start solving the Class 9 Mathematics case study question.

Students need to be careful while solving the Class 9 Mathematics case study questions. They should not make any assumptions and should always check their answers. If they are stuck on a question, they should take a break and come back to it later. With some practice, the Class 9 Mathematics students will be able to crack case study questions with ease.

Class 9 Mathematics Curriculum at Glance

At the secondary level, the curriculum focuses on improving students’ ability to use Mathematics to solve real-world problems and to study the subject as a separate discipline. Students are expected to learn how to solve issues using algebraic approaches and how to apply their understanding of simple trigonometry to height and distance problems. Experimenting with numbers and geometric forms, making hypotheses, and validating them with more observations are all part of Math learning at this level.

The suggested curriculum covers number systems, algebra, geometry, trigonometry, mensuration, statistics, graphing, and coordinate geometry, among other topics. Math should be taught through activities that include the use of concrete materials, models, patterns, charts, photographs, posters, and other visual aids.

CBSE Class 9 Mathematics (Code No. 041)

Class 9 Mathematics question paper design

The CBSE Class 9 mathematics question paper design is intended to measure students’ grasp of the subject’s fundamental ideas. The paper will put their problem-solving and analytical skills to the test. Class 9 mathematics students are advised to go through the question paper pattern thoroughly before they start preparing for their examinations. This will help them understand the paper better and enable them to score maximum marks. Refer to the given Class 9 Mathematics question paper design.

QUESTION PAPER DESIGN (CLASS 9 MATHEMATICS)

Mycbseguide: blessing in disguise.

Class 9 is an important milestone in a student’s life. It is the last year of high school and the last chance to score well in the CBSE board exams. myCBSEguide is the perfect platform for students to get started on their preparations for Class 9 Mathematics. myCBSEguide provides comprehensive study material for all subjects, including practice questions, sample papers, case study questions and mock tests. It also offers tips and tricks on how to score well in exams. myCBSEguide is the perfect door to enter for class 9 CBSE preparations.

Test Generator

Create question paper PDF and online tests with your own name & logo in minutes.

Question Bank, Mock Tests, Exam Papers, NCERT Solutions, Sample Papers, Notes

Related Posts

• Competency Based Learning in CBSE Schools
• Class 11 Physical Education Case Study Questions
• Class 11 Sociology Case Study Questions
• Class 12 Applied Mathematics Case Study Questions
• Class 11 Applied Mathematics Case Study Questions
• Class 11 Mathematics Case Study Questions
• Class 11 Biology Case Study Questions
• Class 12 Physical Education Case Study Questions

14 thoughts on “CBSE Class 9 Mathematics Case Study Questions”

This method is not easy for me

aarti and rashika are two classmates. due to exams approaching in some days both decided to study together. during revision hour both find difficulties and they solved each other’s problems. aarti explains simplification of 2+ ?2 by rationalising the denominator and rashika explains 4+ ?2 simplification of (v10-?5)(v10+ ?5) by using the identity (a – b)(a+b). based on above information, answer the following questions: 1) what is the rationalising factor of the denominator of 2+ ?2 a) 2-?2 b) 2?2 c) 2+ ?2 by rationalising the denominator of aarti got the answer d) a) 4+3?2 b) 3+?2 c) 3-?2 4+ ?2 2+ ?2 d) 2-?3 the identity applied to solve (?10-?5) (v10+ ?5) is a) (a+b)(a – b) = (a – b)² c) (a – b)(a+b) = a² – b² d) (a-b)(a+b)=2(a² + b²) ii) b) (a+b)(a – b) = (a + b

MATHS PAAGAL HAI

All questions was easy but search ? hard questions. These questions was not comparable with cbse. It was totally wastage of time.

Where is search ? bar

maths is love

Can I have more questions without downloading the app.

I love math

Hello l am Devanshu chahal and l am an entorpinior. I am started my card bord business and remanded all the existing things this all possible by math now my business is 120 crore and my business profit is 25 crore in a month. l find the worker team because my business is going well Thanks

Leave a Comment

Save my name, email, and website in this browser for the next time I comment.

A Methodological Approach and Geometry-Based Typology of Late-Gothic Net Vaults’ Rib Systems. Presented on Case Studies from Historic Hungary

• Open access
• Published: 22 April 2024

Cite this article

You have full access to this open access article

• Eszter Jobbik 1 &
• János Krähling 1  

40 Accesses

Explore all metrics

Extensive literature exists concerning the building and construction techniques of Late Gothic net vaults’ rib systems. Nonetheless, the most influential works on this subject were authored in the nineteenth and twentieth centuries—long after these structures were constructed. During this period, the accuracy of the available survey techniques limited the knowledge about these vaults’ exact geometry. Nowadays, terrestrial laser scanning allows us to gather never-before-evaluated data about them. In this article, we present a new geometry-based typology of Late Gothic net vaults’ rib systems – based on written sources and our own case studies – which challenges some premises of the literature. The typology is accompanied by a thorough explanation of our methodology for geometric analysis. We also accentuate our views on the crucial role of geometric analysis in studying building connections and genealogy.

Similar content being viewed by others

Layout, Construction and Surveying of Curvilinear Ribs in Late Gothic Vaults. The Case of Priego

The Islamic Crossed-Arch Vaults in the Mosque of Córdoba

Paula Fuentes

Algorithmic Modelling as a Key Tool for Ribbed Vault Geometry

Vincenzo Bagnolo, Raffaele Argiolas & Cristina Vanini

Avoid common mistakes on your manuscript.

Introduction

Late Gothic net vault construction and building techniques have been extensively studied. However, much of the topic’s literature dates back to the nineteenth and twentieth centuries, when original methods were obsolete and survey techniques were inadequate to reveal the exact geometry leading to developing theories on geometrically regularised plan layouts. Today's advanced surveying methods, such as terrestrial laser scanning, offer far greater precision, thus, analysing laser-scanned geometry reveals previously unexamined complex details of these structures.

In this article, we present a new geometry-based typology for Late Gothic net vault rib systems based on laser-scanned point clouds. Our typology encompasses the overall rib system geometry via interpreting its junction points in a Cartesian coordinate system and the individual ribs’ chord lengths and curvatures. Footnote 1 These enable theoretic reconstructions of original construction methods and building techniques. Our geometry-based typology and deductions can also help in understanding the genealogy and guild or master builder associations of these vaults.

In this paper, we offer theoretical geometric explanations and present examples: case studies in Hungary and Romania. During the examined period, the guilds of the Hungarian Kingdom had direct connections to Saxonian, Bohemian, and Viennese guilds (Császár 2002 ; Papp 2005 ), thus represented the forefront of Central European architecture. Furthermore, some of our case studies link to these guilds. Footnote 2

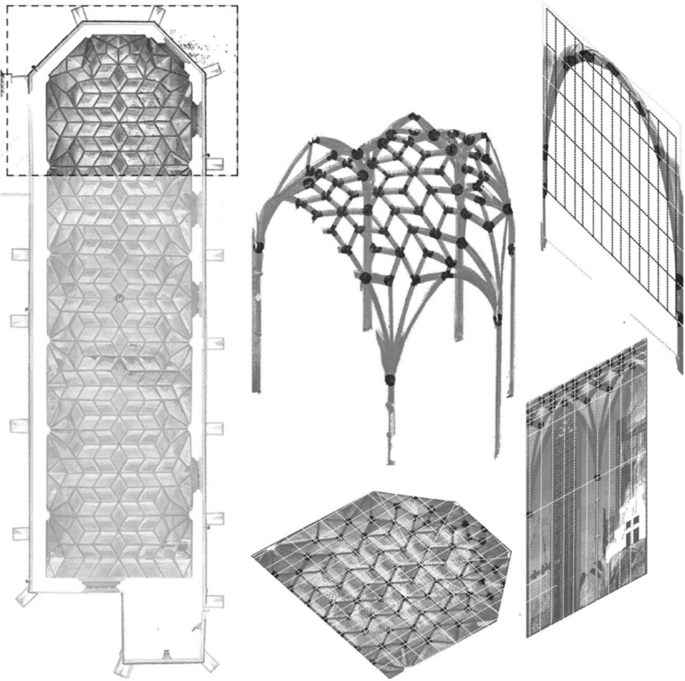
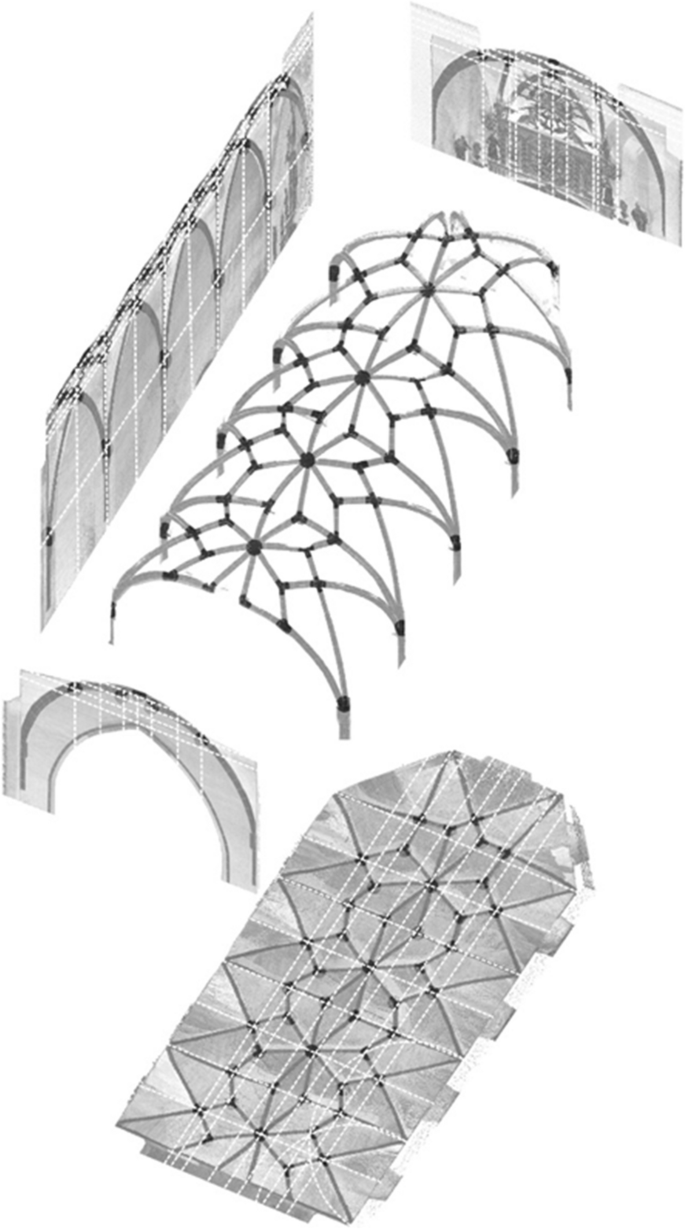
Our case studies include the nave, apse and sacristy vaults of the Franciscan church of Szeged-Alsóváros (HU), the vault of the church of Nyírbátor (HU), the nave vaults of the Church on the Hill in Sigişhoara (RO), the nave vault of the church of Bagaçiu (RO) and the stellar Footnote 3 vault of the Matthias oratorio in the Inner City Parish Church of Budapest (HU) (Fig.  1 ).

Upper row left to right: nave, apse and sacristy vaults of the church of Szeged-Alsóváros; vault of the church of Nyírbátor; lower row left to right: 1–2: vaults of the nave’s aisles in the Church on the Hill of Sigişhoara, nave vault of the church of Bagaçiu, vault of the Matthias oratorio in the Inner City Parish Church of Budapest. Image: authors

Notably, the churches in Szeged-Alsóváros and Nyírbátor are attributed to a royal guild with close ties to Late Gothic buildings in South-German regions and Vienna (Nagy 1944 ; Bálint 1966 ; Levárdy 1980 ; Papp 2005 ). The Matthias oratorio was also worked on by a royal guild (Lux 1933 ; Gerő 1956 ; Papp 2005 ; Horogszegi 2010 ). In Sigişhoara, Master Jakob Kendlinger from the Landshut guild was involved (Fabini and Fabini 1985 ; Szőke 2012 ), and supposedly workers of the same guild worked in Bagaçiu at the turn of the fifteenth and sixteenth centuries (Szőke 2012 ). There is a presumed connection between the churches in Szeged-Alsóváros and the churches with masonry ribbed vaults in South Transylvania, like Sigişhoara and Bagaçiu (Harsányi 2005 ).

Literature Framework

Main literary sources and their general evaluation.

The literature on Late Gothic net vault construction techniques is extensive, but most of it was written after the construction of these structures (Fitchen 1961 ). Although there are written and visual sources related to the geometry, Footnote 4 construction principles, and architectural details Footnote 5 from the entire Gothic period, specific records of net and stellar vault construction methods are limited and mainly date from the mid-14th to sixteenth century. Examples of such sources include the plan documentations of the Wiener Bauhütte (Böker 2005 ), the 16th-century sketchbook from Dresden (Bucher 1972 ), the drawing of Rodrigo Gil de Hontañon (Huerta 2012 ), the Manuscript Ms. 12686 of the National Library of Spain (Baño and Glera 2020 ), and the sketchbook of Master WG (Bucher 1979 ). Footnote 6

Most sources on the construction of Late Gothic vaults postdate their building times. Notably, Ranisch ( 1695 ), Hoffstadt ( 1840 ), Warth ( 1896 ), and Ungewitter ( 1901 ) are considered foundational references for analysing these structures. It is important to highlight that these books on Gothic vaulting techniques relied on survey drawings, observations, and reconstructions by their respective authors, sometimes referencing each other's work (Pliego 2012 ). However, these techniques are insufficiently detailed and consistent for a complete reproduction of the original methods (Wendland 2007 , 2012 ).

Upon examining the figures and constructions in these works, we noticed that they depict vaults’ plan layouts as regular shapes. This likely resulted from the limitations of survey methods at the time, which could not capture slight inaccuracies in structures, especially when projecting vaults’ ribs onto the plan. These approximations fail to account for cases where the plan layout was already distorted, e.g., due to previous building periods, potentially requiring adjustments of the vaulting system. Thus, the approach used in these works may not be universally applicable.

We also noticed that in each revised work, the primacy of the construction of the rib system’s plan projection is assumed and starting it from other planes is not considered. While there are known examples of 1:1 scale construction of the rib system’s plan (e.g., in the case of the Wells Cathedral (Pacey 2007 )) and numerous sources describe such a method as the general solution (Fitchen 1961 ; Pacey 2007 ), Footnote 7 net vaults with visibly irregular rib systems also exist. Therefore, we argue that this assumption should be reevaluated. Footnote 8 Our article challenges the assumption of the plan construction’s general primacy, resulting in significant findings, as presented below.

Net Vault Building Techniques in Literature

Constructing and building the rib system.

Recent research has concentrated on understanding the geometry of net vault rib systems Footnote 9 by examining the spatial positions of rib junction points. This concept can be found in’newer’ literature (Müller 1975 ; Wendland 2010 ; Huth 2020 ) and is identifiable in’classic’ sources. According to written sources, the initial step in constructing a net vault's rib system is constructing its plan. Several construction strategies may be used, including quadrate nets (e.g., Schulze's method as quoted by Müller 1975 ), rotated inscribable quadrats (Hoffstadt's XIV. A. board; Guillouёt 2019 ), triangulation, Footnote 10 and circle-based constructions (Pacey 2007 ). Some studies have even attempted to trace the genealogy and evolution of buildings based on net vault patterns (Császár 1987 –88).

Geometric descriptions in the literature for adding the vertical dimension to these systems can be categorized into surface-based approaches and linear-based approaches. Footnote 11 Thus,’surface-based approaches’ in the literature appear when net vaults are classified as deductible from cross-vaults (Warth 1896 ; Ungewitter 1901 ), from fan vaults (Warth, 1896 ; De l’Orme 1567 ), domical vault-like (Warth 1896 ; Ungewitter 1901 ; Hontañon’s sketch – as shown in Dopazo ( 2016 )) (junction points fit a spherical surface), and barrel vault-like (Warth 1896 ; Ungewitter 1901 ) (junction points fit a cylindric surface).

An example of a 'linear-based approach' in the literature is the 'longest route's principle,' initially documented in the 16th-century Dresden sketchbook (Bucher 1972 ) and Lechler's treatise (Shelby and Mark 1979 ). This principle has later appeared in works by Hoffstadt ( 1840 ), Ungewitter ( 1901 ), and Meckel ( 1933 ). According to this principle, for constructing the height of junctions, on the rib system's plan view between a given impost and a crown point, the longest possible rib-route – without turning back – must be chosen (Fig.  2 .a). Straightening this route gives the radius of a circle passing through the initial impost (Fig.  2 .b), with the centre point on a line perpendicular to the wall of the impost. By projecting the transformed positions of the junctions onto the circle, the vertical distance from the impost level Footnote 12 is determined (Fig.  2 .c). This principle not only establishes the vertical positions of the rib system but also theoretically determines the radius of the rib curvatures.

The ‘longest route’s principle’: construction steps. Image: authors

It is worth noting that most figures in the literature typically depict rib systems with outlines, using a single point to represent the position of a rib junction element. Presumably, this point is on the lower surface of the rib system, thus it can be easily positioned using temporary supporting structures (e.g., Hontañon's drawing).

The Geometry of the Individual Ribs

The widely accepted 'Prinzipalbogen' principle (Ranisch 1695 ; Hoffstadt 1840 ; Meckel 1933 ; Müller 1990 ; Tomlow 1991 ) in the literature of Late Gothic net vaults (first appearing in written sources in the sixteenth century, in Lorenz Lechler’s treatise (Shelby and Mark 1979 ) and the manuscript of Jacob von Andernach (Müller 1974 )) means that each rib in a given net vault has the same curvature. Multiple methods for determining this curvature are found in written sources, with the simplest approach using half of the diagonal (Ranisch 1695 ; Pliego 2012 ). The aim of the principle was likely to standardize ribs for prefabrication and expedite the building process (Renn et al. 2014 ; Vidal 2017 ). However, from the nineteenth century, the principle faced opposition (Lassaulx 1835, as quoted by Wendland 2012 ). Recent studies have raised doubts, but occasional findings support its existence (Voigts 2015; Jobbik and Krähling 2023a ), so it should be considered when analysing net vaults.

Net Vault Structures and Building Genealogy

Net vaults, with their diverse rib system patterns, often form the basis for theories about building genealogy, and guild associations among Late Gothic structures. These theories typically focus on the plan layout (pattern) of the rib system and overlook the three-dimensional vault geometry (Szőke 2012 ; Guzsik 2003 ), primarily due to limited possibilities until the emergence of laser scanning.

Methodology and Results

For our net vault analyses, we used point clouds generated by a Leica BLK 360 scanner, processed in Leica 360 Cyclon Register. This scanner has an accuracy of 8 mm at a 20 m distance, Footnote 13 resulting in potential 1–2 cm inaccuracies within the space dimensions of our case studies. Considering the expected accuracy of the Late Gothic building techniques, Footnote 14 we claim that these point clouds are suitable for our analyses. Footnote 15

However, inaccuracies may arise when taking manual measurements from the point cloud (e.g., measuring rib curvatures). Nonetheless, when originally forming these structures, such measurement inaccuracies also likely occurred. Thus, if such inaccuracy is acceptable in the building process, it should also be accepted in the measurements.

Examining the exact vault geometry aids in identifying unique irregularities that may offer insights into the construction process. From our experience, these irregularities, being specific to a vault, can reveal distinctive construction strategies, whereas perfect geometry can result from various methods.

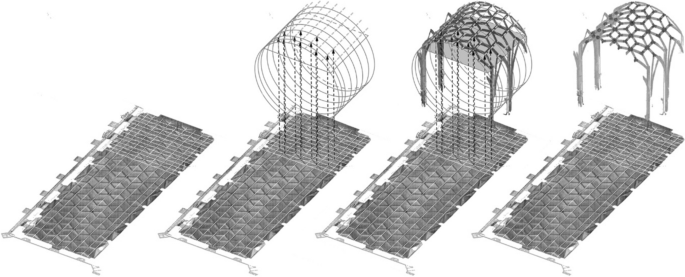
Our analysis process begins with the exact geometric description of the vaults, covering both the overall rib system geometry and the individual rib geometry. This factual description does not involve any deductions. In the second phase, we attempt to reconstruct possible original construction strategies for the vault's geometry, followed by a theoretical reconstruction of the building process and temporary supporting structures (Fig.  3 ). The deduction steps in this phase are hypotheses, representing the current state of research for the building. Future destructive wall research methods may refine, modify, or disprove them.

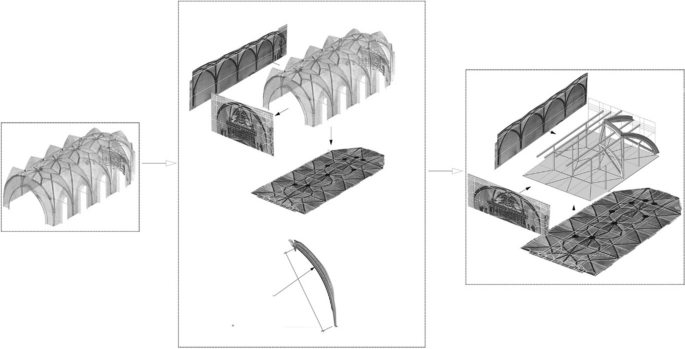
’Workflow’: point cloud, geometric description and theoretical reconstruction of the building technique. Image: authors

The Rib System’s Global Geometry

Conventionally, the examination of a net vault's rib system focuses on the spatial positioning of rib junction points, referencing the lower surface of these elements (as explained in Constructing and building the rib system ). We interpreted these coordinates using a Cartesian coordinate system with three axes: the vault's longitudinal and cross-directions, and vertical (Fig.  4 ). While the literature suggests that determining the global rib system geometry starts with plan view coordinates, we dismissed this presumption during our research due to the distorted rib system in some of our case studies. Our results appear to validate our decision (see below).

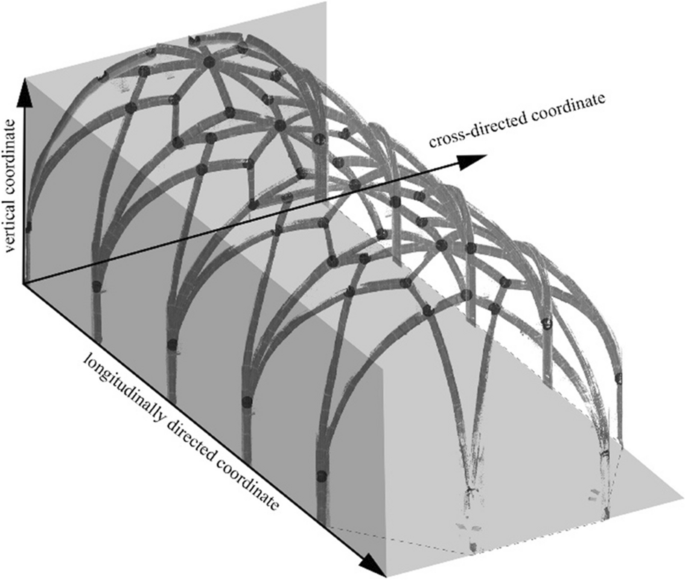
Conceptual Cartesian coordinate system to examine the spatial positions of the rib junction points. Image: authors

Examining the global geometry of the rib system, we focus on understanding the construction order of the coordinates and the underlying construction ideas (e.g., quadrate-net, triangulation, circles). Regarding the building techniques, we seek to theoretically reconstruct the nature of temporary supporting.

For the construction order of the three mentioned coordinates, four theoretical outcomes are conceivable, and so far, we have found examples of three of these (Table 1 )

First Theoretical Outcome

The first outcome occurs when the junction points' three coordinates can be independently constructed without relying on knowledge of any two other coordinates (Fig.  5 ). In such cases, the lengths necessary for the construction are generally deducible from the building's overall dimensions. This typically applies to vaults with highly regular geometry, making conclusions based solely on geometric descriptions somewhat vague: the more orderly the vault, the less specific the geometry-based conclusions.

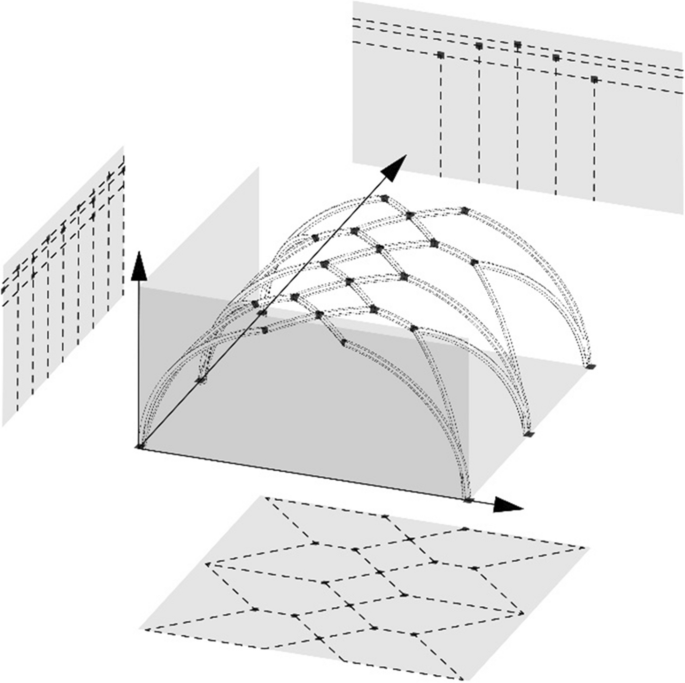
First theoretical outcome. Image: authors

Among our case studies, the Matthias oratorio's stellar vault, the net vault of the Nyírbátor Church, and the sacristy and apse vaults in Szeged-Alsóváros exemplify this method. In the Matthias oratorio, we derived both plan and vertical coordinates from the dimensions of the plan layout’s incomplete octagon by simple ratios Footnote 16 (halves, thirds) (Jobbik and Krähling 2023a ) (Fig.  6 ). In Nyírbátor, a uniform quadrate net (applicable on the plan, longitudinal and cross-sections of the vault; deductible from the plan of the church by simple ratios) helped reconstruct all three coordinates. (Jobbik and Krähling 2023b ) (Fig.  7 ). Similar results were obtained for the two vaults in Szeged-Alsóváros. (Jobbik and Budaházi) (Figs. 8 and 9 ).

The self-contained geometry of the vault of the Matthias oratorio. Image: authors

The self-contained geometry of the vault in Nyírbátor. Image: authors

The self-contained geometry of the sacristy in Szeged-Alsóváros. Image: authors

The self-contained geometry of the apse in Szeged-Alsóváros. Image: authors

In these cases, the examined parts of the building were constructed during a single building period Footnote 17 (Lux 1933 ; Gerő 1956 ; Papp 2005 ; Horogszegi 2010 ; Császár 1987 –88; Entz 1994 ), allowing for a comprehensive construction concept for the entire structure. Thus, though inaccuracies may occur during the building process, no inaccuracies from previous building periods are to be considered.

In these cases, though theoretically any plane of the visionary coordinate system could be the primary one during construction, the primacy of the plan is plausible as it is the simplest execution method, occasionally supported by empirical evidence (see above).

Second Theoretical Outcome

The second outcome comprehends the primacy of the two plan view coordinates, where knowledge of a rib junction point's position projected to the plan is necessary to construct its vertical coordinate (Fig.  10 ).

Second theoretical outcome. Image: authors

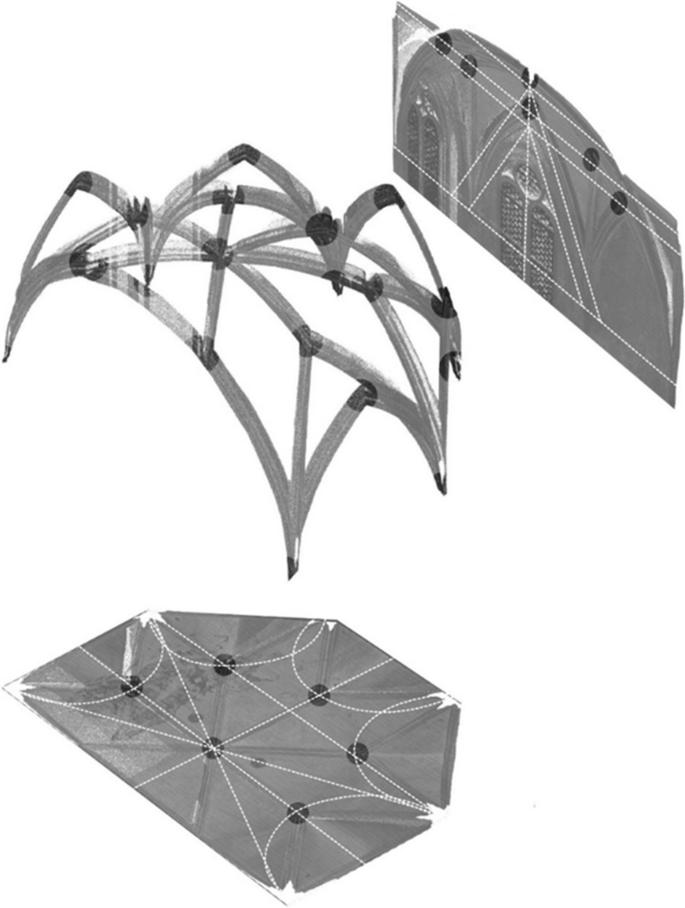
This vertical coordinate's dependence can result from various construction methods, such as the above-discussed 'surface-based approaches.' An example from our case studies is the nave vault of the Franciscan church in Szeged-Alsóváros, which exhibits a regular rib pattern, with the lower surface fitting a cylindrical surface defined by a circle-segment cross-section (Fig.  11 ). This regularity suggests a surface-based approach, as the diameter of the circle determining the cylindrical surface strongly relates to the building’s other dimensions and the geometry of the sagged southern side further supports the claim (Jobbik and Krähling 2023b ).

Theoretic reconstruction of the nave vault construction in Szeged-Alsóváros. Image: authors

Alternatively, the vertical coordinate's dependence can result from a’linear-based approach.’ A literary example is the’longest route principle,’ although such examples are absent in our case studies.

Third Theoretical Outcome

The third theoretical outcome for the construction order of the visionary Cartesian coordinate system comprehends the primacy of the cross-section over the longitudinal-direction coordinate.

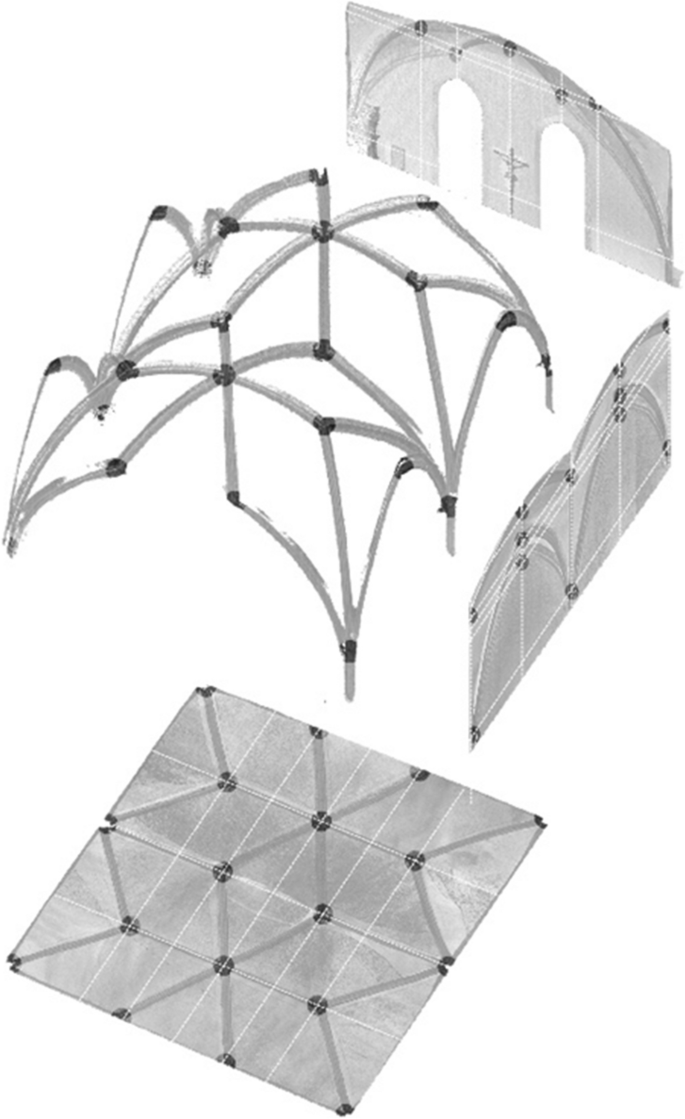
This possibility, identified in our case studies, was previously unmentioned in the literature. In the case of the nave vault of the Bagaçiu church (Jobbik and Krähling 2022 ) and the three vaults in the nave of the Church on the Hill in Sigişhoara (Jobbik and Krähling 2023c ), the plan views of the rib systems appear distorted, but the junction points' positions on the cross-sections exhibit a high degree of regularity – possibly determined by quadrate nets deducible from the nave (or aisle) width using simple ratios. This suggests that the construction of these cross-sections was the primary step.

Despite these vaults’ unorderly plan views, rib junctions consistently fall on straight lines, with only a few exceptions. These lines may not be parallel in the plan view, but they are parallel on the longitudinal sections. In the Bagaçiu vault, these lines align with the eastern side of the longitudinal wall closest to them, despite the walls not being straight or parallel to each other. In the Sigişhoara vaults, the lines also adapt to the walls (even in irregularly shaped bays near the tower). Thus, after constructing the cross-section views, the second step involves constructing the lines where junction points should fall.

In the final step, the longitudinal coordinates must be precisely defined. In both buildings, we observed highly regular chord lengths for ribs of the same type (even though these lengths show more significant standard deviations when projected onto the plan view), suggesting that using chord lengths in combination with the straight lines, defined in the second step, is a likely method for defining the longitudinal coordinates of rib junctions. If our hypothesis holds, these 'lines' might appear as temporary supporting structures during construction (Figs. 12 and 13 ).

Third theoretical outcome. Image: authors

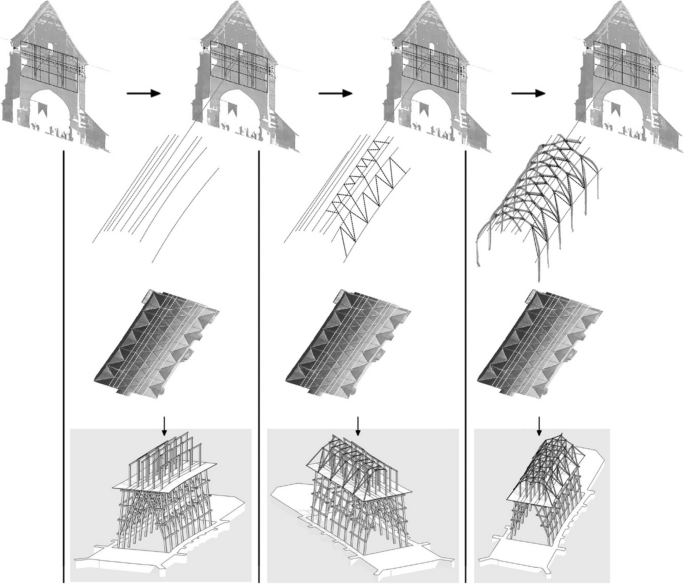
Construction steps translated into temporary supporting structures on the example of Bagaçiu. The temporary supporting structure aligns with Fitchen’s ( 1961 ) assertions. Image: authors

In both case studies, the highly irregular outline of the space to be vaulted resulted from earlier building periods (Istrate 2018 , 2021 ; Fabini 1999 ; Fabini and Fabini 1985 ). We presume that these outlines were the reason for choosing a more complex construction method. With such irregular outlines, creating a regularly constructed plan view would have been challenging, leading to anomalies either at the crown line or the imposts. Initiating the construction with the cross-section allowed for slight adjustments to the rib system's geometry at multiple points while allowing an underlying construction principle. Ultimately, this approach resulted in a more visually cohesive net vault.

While one might consider this seemingly complex construction strategy as possibly unique to South-Transylvanian Saxon churches, we do not think this is necessarily a provincial solution: In the case of Sigişhoara, the constructing guild came from Landshut, the birthplace of masonry ribbed net vaults (Fabini and Fabini 1985 ; Szőke 2012 ). Thus, classifying these monuments as provincial in the context of the fifteenth-sixteenth centuries cannot be entirely upheld.

Fourth Theoretical Outcome

The fourth theoretical outcome comprehends the primacy of the longitudinal section over the cross-direction coordinate (Fig.  14 ). While we lack real examples or descriptions in the literature, we think that if our reasoning about the use of the third theoretical outcome is accurate, this version would be a less serviceable solution to the same problem offering fewer opportunities for visual corrections. Also, creating a quadrate net on the longitudinal wall, rather than the short walls, would involve disproportionately more work.

Fourth theoretical outcome. Image: authors

Structural Solutions

Based on the geometric description of net vaults, we not only aim to reconstruct their original construction ideas but to provide theoretical reconstructions of their potential temporary supporting structures. Presumably, the geometry of the temporary supporting structure directly translates into the geometry of the rib system.

Generally, linear temporary supporting structures (Fig.  15 ) are more likely, considering both building material and workload aspects (Fitchen 1961 ), unless geometric evidence supports using an actual surface, as in the case of the Szeged-Alsóváros nave vault. (Jobbik and Krähling. 2023b ) (Fig.  16 ).

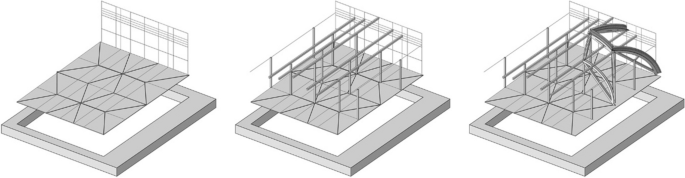
Theoretical reconstruction of a net vault’s linear temporary supporting structure. Image: authors

Theoretical reconstruction of a surface-like temporary supporting structure in the case of the nave vault in Szeged-Alsóváros. Image: authors

In the case of the third theoretical outcome (Chapter 3.1.3), the reconstructed construction method involves steps in three dimensions, not just constructions on different planes subsequently projected together. In such cases, we find it plausible that the construction of rib junctions' spatial positions and the building of temporary supporting structures were not independent steps (Fig.  13 ).

Individual Rib Geometry

Examining the individual ribs revealed their key characteristics. In certain cases, we observed that the chord lengths of the ribs were essential for completing the global geometry of the rib system (see above). Furthermore, in the example of the nave vault in Bagaçiu, we noted slight variations in the deviations from the average chord lengths, with less explicit variation in the more direct rib routes from the walls to the crown line than in the less direct routes. This suggests an order in finalizing the rib junctions' spatial positions using chord length values: the process may have started with the 'main ribs' with less variation and concluded with the 'secondary ribs,' where occasional variation was needed to connect to the well-defined rib junction points (Fig.  17 ).

Theoretical reconstruction of the construction order of the nave vault in the church of Bagaçiu, presented on the plan view. Image: authors

Regarding the individual ribs’ geometry, the other base question was whether the 'Prinzipalbogen' principle was applied in a given vault. We found clear instances where the principle was applied, such as in the vaults of the churches of Szeged-Alsóváros (Jobbik and Krähling 2023b ; Jobbik and Budaházi forthcoming), and of Nyírbátor (Jobbik and Krähling 2023b ), and the Matthias oratorio (Jobbik and Krähling 2023a ). In the case of the nave vaults of Sigişhoara and Bagaçiu, the principle does not seem to apply. Such details of vault geometry can be of great significance, particularly when considering the connection between two vault structures.

Having covered the general geometric typology of net vaults’ rib systems and their point-cloud-based identification methods, their broader implications must be discussed. While some aspects of net vault geometry have been used to identify building connections and genealogy in the literature, our research suggests that more general characteristics, such as rib patterns, may mislead researchers. Using our results from the analysis of the exact vault geometry, we compared case studies that, according to the literature, may had strong connections. In the cases of the nave vault in Szeged-Alsóváros and the vault in Nyírbátor, the claims were based on the rib system’s pattern, and an – unfounded, though deeply rooted – literary description of the same guild’s work (Nagy 1944 ; Bálint 1966 ; Levárdy 1980 ; Entz and Szalontai 1959 ; Császár 1987 –88). Similarly, written sources claimed such connection between the nave vault in Bagaçiu and those in the Church on the Hill of Sigişhoara (Roth 1905 ; Fabini and Fabini 1985 ; Szőke 2012 ).

In the case of the first pair, although the overall appearances of the vaults seem highly similar, the geometric details and reconstructed construction and building strategies differ significantly. In Nyírbátor, the rib system exhibits characteristics of the first theoretical outcome (Chapter 3.1.1), with rib junction points not fitting on a regular surface. Conversely, the rib system of the nave in Szeged-Alsóváros aligns with a cylindrical surface and can be classified in the second theoretical outcome (Chapter 3.1.1). In this case, the intricate details of the vaults' construction techniques suggest that reevaluating the connection between these buildings is worthy of scientific discussion (Jobbik and Krähling 2023b ). Worth noting is that seemingly similar results can be achieved through different methods, making the evaluation of geometric details a valuable endeavour. In the second discussed pair, as detailed in Chapter 3.1.3, a remarkable level of similarity was observed in their unique net vault constructing approach. These similarities support the potential guild connection between the churches on a geometric basis as well (Jobbik and Krähling 2023d ). Overall, laser scanning can provide valuable information that may enhance our understanding of building connections by accurately determining the vault geometry.

In our article, we conducted a comprehensive review and evaluation of the literature on net vault construction and building techniques. Challenging some deeply ingrained principles from 19th-century literature, we introduced a new theoretical outcome concerning the global geometry of net vault rib systems, which we supported with practical examples. This outcome suggests that the plan view of a rib system may not necessarily represent the initial phase of net vault construction. We also aimed to introduce a novel geometry-based typology for Late-Gothic net vaults’ rib systems and propose a point-cloud analysis method for their classification. We presented theoretical outcomes regarding the global geometry of the rib system. These four theoretical outcomes diverged from the typical literature results, including scenarios where the spatial positions of the rib junction points' three coordinates can be independently constructed; the longitudinal and cross-direction coordinates determine the vertical coordinate; the primacy of cross- and vertical coordinates over the longitudinal one; and the primacy of the longitudinal and vertical coordinates over the cross-direction (the latter remaining a theoretical concept).

To illustrate the various outcomes, we provided their geometric descriptions accompanied by case studies as examples. The broader applicability of the typology and methodology outlined in our paper stands as a significant achievement. This typology may broaden our understanding of these structures and serve as a useful addition to the’classic’ literature of the topic. Broadening our case studies in the future, the main categories of the typology may be further specified and subcategorised. Furthermore, we put forth and substantiated the thesis that assumed building connections based on the visible similarities of net vaults should be reevaluated. We contend that this revision should be grounded in the minute details of these vaults' geometry rather than their overall appearance or rib system patterns. In today's context, these intricate details can be accurately surveyed using laser scanning.

Data Availability

Not applicable.

Code Availability

Constrained by article length, the geometric correlation between the net vault's rib system and webbing is unexplored here. Extensive discussion on this matter is available in our cited articles.

At this stage of our research, we did not have any opportunities to work on Western European examples. However, our typology is purely geometry-based and is therefore applicable to net vaults in general. The case studies serve as examples.

This article primarily focuses on net vaults, which are prevalent in our case studies. However, the typology and principles presented here can also be applicable to stellar vaults: In both cases, the vault comprises a rib system with complex geometry and webbing.

Early published sources on solving geometric problems include Matthias Roriczer's booklets from 1486 and 1488, and the treatise De inquisitione capacitatis figurarumare (unknown author) (Shelby 1972 ).

E.g., the sketchbook of Villard de Honnecourt from the thirteenth century (Böker 2005 ; Fitchen 1961 ) or Lorenz Lechler’s ‘ Unterweisung ’ (Shelby 1972 ).

These sources, although originating from various parts of Europe, are equally important for our purpose of examining geometric relationships between structure and building techniques.

Wendland and Degenève ( 2017 ) presented the method with experimental archaeology as well; Lorenz Lechler (16th-century master builder) also described it in his work for his son (Shelby and Mark 1979 ).

However, it's essential to consider in each individual case whether the observed phenomenon results from subsequent distortions of the building.

The primary importance of geometric understanding of structures is also highlighted in Pottman et al. ( 2015 ).

About constructing a Medieval building based on the principles ‘ad quadratum’ and ‘ad triangulum’ see e.g., Pacey ( 2007 ).

In this article, we introduced the term ‘surface-based approach,’ where the vertical position of rib junction points is defined by projecting their position onto a specified surface. The ‘linear-based approach’ refers to constructing the vertical dimension without introducing a theoretical surface.

Here, the imposts mean the point of each rib, where the rib turns from vertically directed to curved.

https://shop.leica-geosystems.com/leica-blk/blk360/blog/blk360-frequently-asked-questions Accessed 30 October 2023.

Fehér and Halmos ( 2017 ) presents a number of discrepancies in the geometry of vault’s rib elements, some of which are due to the inaccuracy of the original work. Such discrepancies most likely occurred not only on the scale of individual elements but on the scale of the global geometry as well.

Not only our own experiences but also other research supports this claim: e.g., Vidal ( 2017 ) proved by experiential method that regardless of the deterioration, the curvature of the ribs can be found with a high probability.

It is worth noting that while we discuss ratios and proportions in this article, in some cases, the same results could stem from arithmetic considerations (Müller 1990 ).

The apse of Szeged-Alsóváros exhibits a plan alteration, where the apse polygon's outline changes at the windowsill level. Nevertheless, the walls’ upper parts and the vault represent the same period (Harsányi 2001 ; Lukács 1999 ; Levárdy 1980 ).

Bálint, Sándor. 1966. A Szeged-Alsóvárosi Templom . Budapest: Pannónia Kiadó.

Google Scholar  

Baño, Ricardo Garcia and Macarena Salcedo Glera. 2020. Geometry and Construction of the Eight-Loop Ribbed Vault. Nexus Network Journal 22: 895-913. https://doi.org/10.1007/s00004-020-00501-4

Article   Google Scholar  

Böker, Johann Josef. 2005. Architektur der Gotik: Bestandskatalog der weltgrössten Sammlung an gotischen Baurissen . Salzburg: A. Pustet.

Bucher, François. 1972. Medieval architectural design methods, 800-1560. Gesta : 37-51. https://doi.org/10.2307/766593

Bucher, Francois. 1979. Architector. The Lodge Books and Sketchbooks of Medieval Architects . New York: Abaris Books.

Császár, László. 1987-88. Későgótikus boltozattípusok Európában I. Építés- Építészettudomány 19: 93-168.

Császár, László. 2002. A Szeged-alsóvárosi ferences templom boltozatairól. In Détshy Mihály nyolcvanadik születésnapjára. Tanulmányok . ed. István Bardoly and Andrea Haris, 155–160. Budapest: Kulturális Örökségvédelmi Hivatal.

De l’Orme, Philibert. 1567. Le quatrieme livre de l’architecture de Philibert de l’Orme…, Paris: Morel.

Dopazo, Pablo Moreno. 2016. Rodrigo Gil de Hontañón and 16th Century Building Techniques: The Cimborio Vault of Archbishop Fonseca College Chapel in Salamanca (Spain). International Journal of Architectural Heritage 10(8): 1110-1124. https://doi.org/10.1080/15583058.2016.1187778

Article   MathSciNet   Google Scholar  

Entz, Géza and Szalontai Barnabás.1959. Nyírbátor , Budapest: Képzőművészeti Alap Kiadóvállalata.

Entz, Géza. 1994. Nyírbátor. Református templom . Budapest: TKM Egyesület.

Fabini, Herman. 1999., Atlas der siebenbürgisch-sächsischen Kirchenbau und Dorfkirchen . Hermannstadt: Monumenta Verlag Hermannstadt and Arbeitskreis für Siebenbürgische Landeskunde e.V. Heidelberg.

Fabini, Herman and Alida Fabini. 1985. Kirchenburgen in Siebenbürgen . Leipzig: Koehler&Amelang.

Fehér, Krisztina and Balázs Halmos. 2017. Problems of surveying profile shapes of Gothic architectural fragments. Pollack Periodica 13: 217-224.

Fitchen, John. 1961. Construction of Gothic Cathedrals. A Study of Medieval Vault Erection . Chicago: University of Chicago Press.

Gerő, László. 1956. A pesti belvárosi plébániatemplom . Budapest: Képzőművészeti Alap Kiadóvállalata.

Guillouёt, Jean-Marie. 2019. Flamboyant Architecture and Medieval Technicality (c. 1400-c. 1530) . Turnhout: Brepols.

Guzsik, Tamás. 2003. A pálos rend építészete a középkori Magyarországon, Budapest: Mikes.

Harsányi, István. 2001. A szeged-alsóvárosi ferences templom gótikus szentélye csillagboltozatának helyreállítása. Műemlékvédelem 45 (5): 294-304.

Harsányi, István. 2005. Szeged Alsóvárosi ferences templom hajó-boltozatának és falfelületeinek kutatása, építészettörténeti vonatkozások föltárása. II. kötet. A hajóboltozat felújítási munkáinak tervezését megelőző építészeti-műemléki kutatás . Available at: https://docplayer.hu/16384222-Dr-lukacs-zsuzsa-emlekere.html (Accessed 30 October 2023)

Hoffstadt, Friedrich. 1840. Gothisches ABC-Buch: Vorlegeblätter zum gothischen A-B-C-Buche… Frankfurt a. M.: Siegmund Schmerber.

Horogszegi, T. P. 2010. A belvárosi plébániatemplom építéstörténetének összefoglalása a templom korábbi kutatástörténetének tükrében. Műemlékvédelem 54(6): 373-382.

Huerta, Santiago. 2012. Technical challenges in the construction of Gothic vaults: The Gothic theory of structural design. In Bautechnik des Historismus. Von den Theorien über gotische Konstruktionen bis zu den Baustellen des 19. Jahrhunderts , ed. U. Hassler and C. Rauhut: 162–195. München: Hirmer.

Huth, Olaf. 2020. Entwurfs-und Konstruktionsprinzipien des spätgotischen Netzgewölbes der Kirche St. Peter und Paul in der Lutherstadt Eisleben . Bamberg: University of Bamberg Press.

Istrate, D. M. 2018. Voraussetzungen und Vorbedingungen für den Bau der Bergkirche in Schäßburg. Zeitschrift für Siebenbürgische Landeskunde 41: 1-16.

Istrate, D. M. 2021. Entstehung und Entwicklung der siebenbürgischen Stadtkirchen im 12–15. Jahrhunder. In Sachsgeschichte(n). Beiträge zu einer interdisziplinär verstandenen Archäologie des Mittelalters und der Neuzeit. Festschrift für Barbara Scholkmann zu ihrem 80. Geburtstag , ed. D. Ade, S. Frommer, T. Marstaller, A. K. Scholz, M. Terp-Schunter, C. Vossler-Wolf and M. Wolf: 445–464. Tübingen: Tübingen Library Publishing.

Jobbik, Eszter and Fanni Budaházi. Forthcoming 2024. Building archaeology with laser scanning: Geometry-based architectural analysis of the Franciscan Church of Szeged-Alsóváros.

Jobbik, Eszter and János Krähling. 2022. Late Mediaeval Net Vault Construction Method Rediscovered by Geometric Analysis. A Case Study of the Fortified Church of Băgaciu (Bogeschdorf). Brukenthal. Acta Musei 17: 179-202.

Jobbik, Eszter and János Krähling. 2023a. A Self-contained Stellar Vault Construction Method. The Vault of the Matthias Oratorio in the Inner City Parish Church of Budapest. Periodica Polytechnica Architecture 54(1): 73–85. https://doi.org/10.3311/PPar.21454

Jobbik, Eszter and János Krähling. 2023b. Real Net Vault or Pseudo-Ribbed Net Vault? Geometry, Construction and Building Technique of the Vault of the Reformed Church of Nyírbátor and the Nave Vault of the Franciscan Church of Szeged-Alsóváros. Építés-Építészettudomány 51: 229-256. https://doi.org/10.1556/096.2023.00100

Jobbik, Eszter and János Krähling. 2023d. Approaching building connections based on net vaults’ geometric analysis. The vaults of the Church on the Hill of Sighişoara and the church of Băgaciu. Brukenthal. Acta Musei 18(1): 49-68.

Jobbik, Eszter and János Krähling. Forthcoming 2023c. The geometric system of the nave vault of the Church on the Hill of Sighişoara. Studia Historia Artium.

Levárdy, Ferenc. 1980. Szeged, Alsóvárosi templom. Budapest: TKM Egyesület.

Lukács, Zsuzsa. 1999. Szeged. Alsóvárosi ferences templom és kolostor . Budapest: TKM Egyesület.

Lux, Kálmán. 1933. A budapesti bevárosi plébániatemplom. Tanulmányok Budapest Múltjából 2: 1-31.

Meckel, Carl Anton. 1933. Figurierte Gewölbe der deutschen Spätgotik. Architectura: Jahrbuch für Geschichte der Baukunst 1: 107-121. https://doi.org/10.11588/diglit.19241#0011

Müller, Werner. 1974. Einflüsse der österreichischen und der böhmisch-sächsischen Spätgotik in den Gewölbemustern des Jacob Facht von Andernach. Wiener Jahrbuch für Kunstgeschichte 27: 65-82.

Müller, Werner. 1975. Die Zeichnungsvorlagen für Friedrich Hoffstadts ’Gotisches A.B.C.-Buch’ und der Nachlass des Nürnberger Ratsbaumeisters Wolf Jacob Stromer (1561-1614). Wiener Jahrbuch für Kunstgechichte 28: 39-54. https://doi.org/10.7767/wjk.1975.28.1.39

Müller, Werner. 1990. Grundlagen gotischer Bautechnik. Ars sine sciencia nihil . München: Deutscher Kunstverlag.

Nagy, Zoltán. 1944. A ferencesek Szeged-alsóvárosi temploma. Magyar Építőművészet

Pacey, Arnold. 2007. Medieval architectural drawing: Geometry and Medieval Drawing . Stroud: Tempus.

Papp, Szilárd. 2005. A királyi udvar építkezései Magyarországon 1480-151 5. Budapest: Balassi.

Pliego, Elena. 2012. Georg Gottlob Ungewitters Lehrbuch der gotischen Constructionen. In Bautechnik des Historismus. Von den Theorien über gotische Konstruktionen bis zu den Baustellen des 19. Jahrhunderts , ed. U. Hassler and C. Rauhut: 217–229. München: Hirme.

Pottman, Helmut, Michael Eigensatz, Amir Vaxman and Johannes Wallner. 2015. Architectural Geometry. Computers & Graphics 47: 145-164. https://doi.org/10.1016/j.cag.2014.11.002

Ranisch, Bartel. 1695. Beschreibung aller Kirchengebäude der Stadt Dantzig… Dantzig: Raths und Gymnasii Buchdruckern.

Renn, J., W. Osthues and H. Schlimme. 2014. Wissensgeschichte der Architektur 3. Vom Mittelalter bis zur frühe Neuzeit. Berlin: Edition Open Access.

Roth, Victor. 1905. Geschichte der deutschen Baukunst in Siebenbürgen . Strassbourg: Heitz&Mündel.

Shelby, Lon R. 1972. The Geometric knowledge of mediaeval master masons. Speculum 47: 395-421.

Shelby, Lon R. and R. Mark. 1979. Late Gothic structural design in the ‘instructions’ of Lorenz Lechler. Architectura 9(2): 113-131.

Szőke, Balázs. 2012. A Wechselberger-Harperger motívum Délkelet-Erdély késő gótikus építészetében. In Tanulmányok a székelység középkori és fejedelemség kori történetéből , ed. A. Sófalvi and Zs. Visy: 201–218. Énlaka: Pro Énlaka Alapítvány and Haáz Rezső Múzeum.

Tomlow, Jos. 1991. Versuch einer (zeichnerischen) Rekonstruktion des Gewölbes im spätgotischen Kreuzgang des Klosters Hirschau. In Hirsau St. Peter und Paul 1091–1991. ed. K. Schreiner. 365–393. Stuttgart: Landesamt für Denkmalpflege im Regierungspräsidium Stuttgart.

Ungewitter, Georg Gottlob. 1901. Lehrbuch der gotischen Konstruktionen. Neue bearbeitet von K. Mohrmann . Leipzig: Chr. Herm. Tauchnitz.

Vidal, R. Maira. 2017. The evolution of the knowledge of geometry in early gothic construction: the development of the sexpartite vault in Europe. International Journal of Architectural Heritage 11(7): 1005-1025.

Viollet-le-Duc, Eugène. 1854–68. Dictionnaire raisonné de l’architecture française du XIe au XVIe siècle . Paris: Morel.

Warth, Otto. 1896. Die Konstruktionen in Stein . Leipzig: J. M. Gebhardt.

Wendland, David. 2007. Traditional vault construction without formwork: Masonry pattern and vault shape in the historical technical literature and in experimental studies. International Journal of Architectural Heritage: Conservation, Analysis, and Restoration . https://doi.org/10.1080/15583050701373803

Wendland, David. 2010. Untersuchungen zu den Entwurfs- und Konstruktionsprinzipen der spätgotischen Zellengewölbe. Ein neuer Ansatz in der Verknüpfung von geometrischen Analysen am Befund und experimenteller Archäologie. Staatliche Schlösser, Burgen und Gärten Sachsen Jahrbuch 17: 23-33.

Wendland, David and Frédéric Degenève 2017. How to order fitting components for looping ribs: Design procedures for the stone members of complex late gothic vaults. In: Building Histories: The Proceedings of the Fourth Conference of the Construction History Society. ed. J.W.P. Campbell et al., 159–170. Cambridge: Queens’ College, 2017

Wendland, David. 2012. 2012. Johann Claudius von Lassaulx' Gewölbe >aus freier Hand< - Die Wiedererfindung der gotischen Architektur und die Entwicklung der technischen Literatur. In Bautechnik des Historismus. Von den Theorien über gotische Konstruktionen bis zu den Baustellen des 19. Jahrhunderts , ed. U. Hassler and C. Rauhut, 97–117. München: Hirmer.

Download references

Acknowledgements

We are grateful to László Daragó DLA for his advice and guidance throughout the research. We are also grateful to Krisztina Fehér PhD and Fanni Budaházi for their help in handling and producing the point clouds of some of our case studies.

Open access funding provided by Budapest University of Technology and Economics.

Author information

Authors and affiliations.

Department of History of Architecture and Monument Preservation, Faculty of Architecture, Budapest University of Technology and Economics, Műegyetem Rkp. 3, H-1111, Budapest, Hungary

Eszter Jobbik & János Krähling

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Eszter Jobbik .

Ethics declarations

Conflict of interest, additional information, publisher's note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

This article is published under an open access license. Please check the 'Copyright Information' section either on this page or in the PDF for details of this license and what re-use is permitted. If your intended use exceeds what is permitted by the license or if you are unable to locate the licence and re-use information, please contact the Rights and Permissions team .

About this article

Jobbik, E., Krähling, J. A Methodological Approach and Geometry-Based Typology of Late-Gothic Net Vaults’ Rib Systems. Presented on Case Studies from Historic Hungary. Nexus Netw J (2024). https://doi.org/10.1007/s00004-024-00780-1

Download citation

Accepted : 09 April 2024

Published : 22 April 2024

DOI : https://doi.org/10.1007/s00004-024-00780-1

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Geometry-Based Typology
• Net Vault Typology
• Geometric Vault Analysis
• Late Gothic Construction Techniques
• Medieval Net Vault
• Find a journal
• Publish with us
• Track your research