assignment problem in aoa

Hungarian Method

The Hungarian method is a computational optimization technique that addresses the assignment problem in polynomial time and foreshadows following primal-dual alternatives. In 1955, Harold Kuhn used the term “Hungarian method” to honour two Hungarian mathematicians, Dénes Kőnig and Jenő Egerváry. Let’s go through the steps of the Hungarian method with the help of a solved example.

Hungarian Method to Solve Assignment Problems

The Hungarian method is a simple way to solve assignment problems. Let us first discuss the assignment problems before moving on to learning the Hungarian method.

What is an Assignment Problem?

A transportation problem is a type of assignment problem. The goal is to allocate an equal amount of resources to the same number of activities. As a result, the overall cost of allocation is minimised or the total profit is maximised.

Because available resources such as workers, machines, and other resources have varying degrees of efficiency for executing different activities, and hence the cost, profit, or loss of conducting such activities varies.

Assume we have ‘n’ jobs to do on ‘m’ machines (i.e., one job to one machine). Our goal is to assign jobs to machines for the least amount of money possible (or maximum profit). Based on the notion that each machine can accomplish each task, but at variable levels of efficiency.

Hungarian Method Steps

Check to see if the number of rows and columns are equal; if they are, the assignment problem is considered to be balanced. Then go to step 1. If it is not balanced, it should be balanced before the algorithm is applied.

Step 1 – In the given cost matrix, subtract the least cost element of each row from all the entries in that row. Make sure that each row has at least one zero.

Step 2 – In the resultant cost matrix produced in step 1, subtract the least cost element in each column from all the components in that column, ensuring that each column contains at least one zero.

Step 3 – Assign zeros

Analyse the rows one by one until you find a row with precisely one unmarked zero. Encircle this lonely unmarked zero and assign it a task. All other zeros in the column of this circular zero should be crossed out because they will not be used in any future assignments. Continue in this manner until you’ve gone through all of the rows.
Examine the columns one by one until you find one with precisely one unmarked zero. Encircle this single unmarked zero and cross any other zero in its row to make an assignment to it. Continue until you’ve gone through all of the columns.

Step 4 – Perform the Optimal Test

The present assignment is optimal if each row and column has exactly one encircled zero.
The present assignment is not optimal if at least one row or column is missing an assignment (i.e., if at least one row or column is missing one encircled zero). Continue to step 5. Subtract the least cost element from all the entries in each column of the final cost matrix created in step 1 and ensure that each column has at least one zero.

Step 5 – Draw the least number of straight lines to cover all of the zeros as follows:

(a) Highlight the rows that aren’t assigned.

(b) Label the columns with zeros in marked rows (if they haven’t already been marked).

(d) Continue with (b) and (c) until no further marking is needed.

(f) Simply draw the lines through all rows and columns that are not marked. If the number of these lines equals the order of the matrix, then the solution is optimal; otherwise, it is not.

Step 6 – Find the lowest cost factor that is not covered by the straight lines. Subtract this least-cost component from all the uncovered elements and add it to all the elements that are at the intersection of these straight lines, but leave the rest of the elements alone.

Step 7 – Continue with steps 1 – 6 until you’ve found the highest suitable assignment.

Hungarian Method Example

Use the Hungarian method to solve the given assignment problem stated in the table. The entries in the matrix represent each man’s processing time in hours.

$\begin{array}{l}\begin{bmatrix} & I & II & III & IV & V \\1 & 20 & 15 & 18 & 20 & 25 \\2 & 18 & 20 & 12 & 14 & 15 \\3 & 21 & 23 & 25 & 27 & 25 \\4 & 17 & 18 & 21 & 23 & 20 \\5 & 18 & 18 & 16 & 19 & 20 \\\end{bmatrix}\end{array} $

With 5 jobs and 5 men, the stated problem is balanced.

$\begin{array}{l}A = \begin{bmatrix}20 & 15 & 18 & 20 & 25 \\18 & 20 & 12 & 14 & 15 \\21 & 23 & 25 & 27 & 25 \\17 & 18 & 21 & 23 & 20 \\18 & 18 & 16 & 19 & 20 \\\end{bmatrix}\end{array} $

Subtract the lowest cost element in each row from all of the elements in the given cost matrix’s row. Make sure that each row has at least one zero.

$\begin{array}{l}A = \begin{bmatrix}5 & 0 & 3 & 5 & 10 \\6 & 8 & 0 & 2 & 3 \\0 & 2 & 4 & 6 & 4 \\0 & 1 & 4 & 6 & 3 \\2 & 2 & 0 & 3 & 4 \\\end{bmatrix}\end{array} $

Subtract the least cost element in each Column from all of the components in the given cost matrix’s Column. Check to see if each column has at least one zero.

$\begin{array}{l}A = \begin{bmatrix}5 & 0 & 3 & 3 & 7 \\6 & 8 & 0 & 0 & 0 \\0 & 2 & 4 & 4 & 1 \\0 & 1 & 4 & 4 & 0 \\2 & 2 & 0 & 1 & 1 \\\end{bmatrix}\end{array} $

When the zeros are assigned, we get the following:

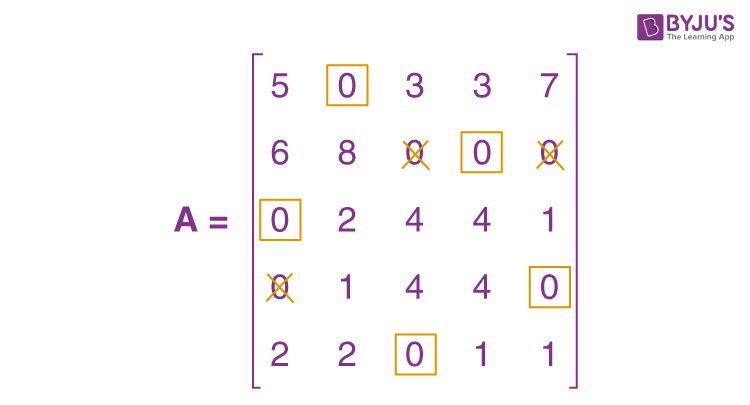
The present assignment is optimal because each row and column contain precisely one encircled zero.

Where 1 to II, 2 to IV, 3 to I, 4 to V, and 5 to III are the best assignments.

Hence, z = 15 + 14 + 21 + 20 + 16 = 86 hours is the optimal time.

Practice Question on Hungarian Method

Use the Hungarian method to solve the following assignment problem shown in table. The matrix entries represent the time it takes for each job to be processed by each machine in hours.

$\begin{array}{l}\begin{bmatrix}J/M & I & II & III & IV & V \\1 & 9 & 22 & 58 & 11 & 19 \\2 & 43 & 78 & 72 & 50 & 63 \\3 & 41 & 28 & 91 & 37 & 45 \\4 & 74 & 42 & 27 & 49 & 39 \\5 & 36 & 11 & 57 & 22 & 25 \\\end{bmatrix}\end{array} $

Stay tuned to BYJU’S – The Learning App and download the app to explore all Maths-related topics.

Frequently Asked Questions on Hungarian Method

What is hungarian method.

The Hungarian method is defined as a combinatorial optimization technique that solves the assignment problems in polynomial time and foreshadowed subsequent primal–dual approaches.

What are the steps involved in Hungarian method?

The following is a quick overview of the Hungarian method: Step 1: Subtract the row minima. Step 2: Subtract the column minimums. Step 3: Use a limited number of lines to cover all zeros. Step 4: Add some more zeros to the equation.

What is the purpose of the Hungarian method?

When workers are assigned to certain activities based on cost, the Hungarian method is beneficial for identifying minimum costs.

Register with BYJU'S & Download Free PDFs

Quadratic assignment problem

Author: Thomas Kueny, Eric Miller, Natasha Rice, Joseph Szczerba, David Wittmann (SysEn 5800 Fall 2020)

1 Introduction
2.1 Koopmans-Beckman Mathematical Formulation
2.2.1 Parameters
2.3.1 Optimization Problem
2.4 Computational Complexity
2.5 Algorithmic Discussions
2.6 Branch and Bound Procedures
2.7 Linearizations
3.1 QAP with 3 Facilities
4.1 Inter-plant Transportation Problem
4.2 The Backboard Wiring Problem
4.3 Hospital Layout
4.4 Exam Scheduling System
5 Conclusion
6 References

Introduction

The Quadratic Assignment Problem (QAP), discovered by Koopmans and Beckmann in 1957 [1] , is a mathematical optimization module created to describe the location of invisible economic activities. An NP-Complete problem, this model can be applied to many other optimization problems outside of the field of economics. It has been used to optimize backboards, inter-plant transportation, hospital transportation, exam scheduling, along with many other applications not described within this page.

Theory, Methodology, and/or Algorithmic Discussions

Koopmans-beckman mathematical formulation.

Economists Koopmans and Beckman began their investigation of the QAP to ascertain the optimal method of locating important economic resources in a given area. The Koopmans-Beckman formulation of the QAP aims to achieve the objective of assigning facilities to locations in order to minimize the overall cost. Below is the Koopmans-Beckman formulation of the QAP as described by neos-guide.org.

Quadratic Assignment Problem Formulation

$F=(F_{ij})$

Inner Product

$A,B$

Note: The true objective cost function only requires summing entries above the diagonal in the matrix comprised of elements

$F_{i,j}(X_{\phi }DX_{\phi }^{T})_{i,j}$

Since this matrix is symmetric with zeroes on the diagonal, dividing by 2 removes the double count of each element to give the correct cost value. See the Numerical Example section for an example of this note.

Optimization Problem

With all of this information, the QAP can be summarized as:

$\min _{X\in P}\langle F,XDX^{T}\rangle$

Computational Complexity

QAP belongs to the classification of problems known as NP-complete, thus being a computationally complex problem. QAP’s NP-completeness was proven by Sahni and Gonzalez in 1976, who states that of all combinatorial optimization problems, QAP is the “hardest of the hard”. [2]

Algorithmic Discussions

While an algorithm that can solve QAP in polynomial time is unlikely to exist, there are three primary methods for acquiring the optimal solution to a QAP problem:

Dynamic Program
Cutting Plane

Branch and Bound Procedures

The third method has been proven to be the most effective in solving QAP, although when n > 15, QAP begins to become virtually unsolvable.

The Branch and Bound method was first proposed by Ailsa Land and Alison Doig in 1960 and is the most commonly used tool for solving NP-hard optimization problems.

A branch-and-bound algorithm consists of a systematic enumeration of candidate solutions by means of state space search: the set of candidate solutions is thought of as forming a rooted tree with the full set at the root. The algorithm explores branches of this tree, which represent subsets of the solution set. Before one lists all of the candidate solutions of a branch, the branch is checked against upper and lower estimated bounds on the optimal solution, and the branch is eliminated if it cannot produce a better solution than the best one found so far by the algorithm.

Linearizations

The first attempts to solve the QAP eliminated the quadratic term in the objective function of

$min\sum _{i=1}^{n}\sum _{j=1}^{n}c{_{\phi (i)\phi (j)}}+\sum _{i=1}^{n}b{_{\phi (i)}}$

in order to transform the problem into a (mixed) 0-1 linear program. The objective function is usually linearized by introducing new variables and new linear (and binary) constraints. Then existing methods for (mixed) linear integer programming (MILP) can be applied. The very large number of new variables and constraints, however, usually poses an obstacle for efficiently solving the resulting linear integer programs. MILP formulations provide LP relaxations of the problem which can be used to compute lower bounds.

Numerical Example

Qap with 3 facilities.

$D={\begin{bmatrix}0&5&6\\5&0&3.6\\6&3.6&0\end{bmatrix}}$

Applications

Inter-plant transportation problem.

The QAP was first introduced by Koopmans and Beckmann to address how economic decisions could be made to optimize the transportation costs of goods between both manufacturing plants and locations. [1] Factoring in the location of each of the manufacturing plants as well as the volume of goods between locations to maximize revenue is what distinguishes this from other linear programming assignment problems like the Knapsack Problem.

The Backboard Wiring Problem

As the QAP is focused on minimizing the cost of traveling from one location to another, it is an ideal approach to determining the placement of components in many modern electronics. Leon Steinberg proposed a QAP solution to optimize the layout of elements on a blackboard by minimizing the total amount of wiring required. [4]

When defining the problem Steinberg states that we have a set of n elements

$E=\left\{E_{1},E_{2},...,E_{n}\right\}$

as well as a set of r points

$P_{1},P_{2},...,P_{r}$

In his paper he derives the below formula:

$min\sum _{1\leq i\leq j\leq n}^{}C_{ij}(d_{s(i)s(j))})$

In his paper Steinberg a backboard with a 9 by 4 array, allowing for 36 potential positions for the 34 components that needed to be placed on the backboard. For the calculation, he selected a random initial placement of s1 and chose a random family of 25 unconnected sets.

The initial placement of components is shown below:

After the initial placement of elements, it took an additional 35 iterations to get us to our final optimized backboard layout. Leading to a total of 59 iterations and a final wire length of 4,969.440.

Hospital Layout

Building new hospitals was a common event in 1977 when Alealid N Elshafei wrote his paper on "Hospital Layouts as a Quadratic Assignment Problem". [5] With the high initial cost to construct the hospital and to staff it, it is important to ensure that it is operating as efficiently as possible. Elshafei's paper was commissioned to create an optimization formula to locate clinics within a building in such a way that minimizes the total distance that a patient travels within the hospital throughout the year. When doing a study of a major hospital in Cairo he determined that the Outpatient ward was acting as a bottleneck in the hospital and focused his efforts on optimizing the 17 departments there.

Elshafei identified the following QAP to determine where clinics should be placed:

$min\sum _{i,j}\sum _{k,q}f_{ik}d_{jq}y_{ij}y_{kq}$

For the Cairo hospital with 17 clinics, and one receiving and recording room bringing us to a total of 18 facilities. By running the above optimization Elshafei was able to get the total distance per year down to 11,281,887 from a distance of 13,973,298 based on the original hospital layout.

Exam Scheduling System

The scheduling system uses matrices for Exams, Time Slots, and Rooms with the goal of reducing the rate of schedule conflicts. To accomplish this goal, the “examination with the highest cross faculty student is been prioritized in the schedule after which the examination with the highest number of cross-program is considered and finally with the highest number of repeating student, at each stage group with the highest number of student are prioritized.” [6]

$n!$

↑ 1.0 1.1 1.2 Koopmans, T., & Beckmann, M. (1957). Assignment Problems and the Location of Economic Activities. Econometrica, 25(1), 53-76. doi:10.2307/1907742
↑ 2.0 2.1 Quadratic Assignment Problem. (2020). Retrieved December 14, 2020, from https://neos-guide.org/content/quadratic-assignment-problem
↑ 3.0 3.1 3.2 Burkard, R. E., Çela, E., Pardalos, P. M., & Pitsoulis, L. S. (2013). The Quadratic Assignment Problem. https://www.opt.math.tugraz.at/~cela/papers/qap_bericht.pdf .
↑ 4.0 4.1 Leon Steinberg. The Backboard Wiring Problem: A Placement Algorithm. SIAM Review . 1961;3(1):37.
↑ 5.0 5.1 Alwalid N. Elshafei. Hospital Layout as a Quadratic Assignment Problem. Operational Research Quarterly (1970-1977) . 1977;28(1):167. doi:10.2307/300878
↑ 6.0 6.1 Muktar, D., & Ahmad, Z.M. (2014). Examination Scheduling System Based On Quadratic Assignment.

How to Solve the Assignment Problem: A Complete Guide

Table of Contents

Assignment problem is a special type of linear programming problem that deals with assigning a number of resources to an equal number of tasks in the most efficient way. The goal is to minimize the total cost of assignments while ensuring that each task is assigned to only one resource and each resource is assigned to only one task. In this blog, we will discuss the solution of the assignment problem using the Hungarian method, which is a popular algorithm for solving the problem.

Understanding the Assignment Problem

Before we dive into the solution, it is important to understand the problem itself. In the assignment problem, we have a matrix of costs, where each row represents a resource and each column represents a task. The objective is to assign each resource to a task in such a way that the total cost of assignments is minimized. However, there are certain constraints that need to be satisfied – each resource can be assigned to only one task and each task can be assigned to only one resource.

Solving the Assignment Problem

There are various methods for solving the assignment problem, including the Hungarian method, the brute force method, and the auction algorithm. Here, we will focus on the steps involved in solving the assignment problem using the Hungarian method, which is the most commonly used and efficient method.

Step 1: Set up the cost matrix

The first step in solving the assignment problem is to set up the cost matrix, which represents the cost of assigning a task to an agent. The matrix should be square and have the same number of rows and columns as the number of tasks and agents, respectively.

Step 2: Subtract the smallest element from each row and column

To simplify the calculations, we need to reduce the size of the cost matrix by subtracting the smallest element from each row and column. This step is called matrix reduction.

Step 3: Cover all zeros with the minimum number of lines

The next step is to cover all zeros in the matrix with the minimum number of horizontal and vertical lines. This step is called matrix covering.

Step 4: Test for optimality and adjust the matrix

To test for optimality, we need to calculate the minimum number of lines required to cover all zeros in the matrix. If the number of lines equals the number of rows or columns, the solution is optimal. If not, we need to adjust the matrix and repeat steps 3 and 4 until we get an optimal solution.

Step 5: Assign the tasks to the agents

The final step is to assign the tasks to the agents based on the optimal solution obtained in step 4. This will give us the most cost-effective or profit-maximizing assignment.

Solution of the Assignment Problem using the Hungarian Method

The Hungarian method is an algorithm that uses a step-by-step approach to find the optimal assignment. The algorithm consists of the following steps:

Subtract the smallest entry in each row from all the entries of the row.
Subtract the smallest entry in each column from all the entries of the column.
Draw the minimum number of lines to cover all zeros in the matrix. If the number of lines drawn is equal to the number of rows, we have an optimal solution. If not, go to step 4.
Determine the smallest entry not covered by any line. Subtract it from all uncovered entries and add it to all entries covered by two lines. Go to step 3.

The above steps are repeated until an optimal solution is obtained. The optimal solution will have all zeros covered by the minimum number of lines. The assignments can be made by selecting the rows and columns with a single zero in the final matrix.

Applications of the Assignment Problem

The assignment problem has various applications in different fields, including computer science, economics, logistics, and management. In this section, we will provide some examples of how the assignment problem is used in real-life situations.

Applications in Computer Science

The assignment problem can be used in computer science to allocate resources to different tasks, such as allocating memory to processes or assigning threads to processors.

Applications in Economics

The assignment problem can be used in economics to allocate resources to different agents, such as allocating workers to jobs or assigning projects to contractors.

Applications in Logistics

The assignment problem can be used in logistics to allocate resources to different activities, such as allocating vehicles to routes or assigning warehouses to customers.

Applications in Management

The assignment problem can be used in management to allocate resources to different projects, such as allocating employees to tasks or assigning budgets to departments.

Let’s consider the following scenario: a manager needs to assign three employees to three different tasks. Each employee has different skills, and each task requires specific skills. The manager wants to minimize the total time it takes to complete all the tasks. The skills and the time required for each task are given in the table below:

The assignment problem is to determine which employee should be assigned to which task to minimize the total time required. To solve this problem, we can use the Hungarian method, which we discussed in the previous blog.

Using the Hungarian method, we first subtract the smallest entry in each row from all the entries of the row:

Next, we subtract the smallest entry in each column from all the entries of the column:

We draw the minimum number of lines to cover all the zeros in the matrix, which in this case is three:

Since the number of lines is equal to the number of rows, we have an optimal solution. The assignments can be made by selecting the rows and columns with a single zero in the final matrix. In this case, the optimal assignments are:

Emp 1 to Task 3
Emp 2 to Task 2
Emp 3 to Task 1

This assignment results in a total time of 9 units.

I hope this example helps you better understand the assignment problem and how to solve it using the Hungarian method.

Solving the assignment problem may seem daunting, but with the right approach, it can be a straightforward process. By following the steps outlined in this guide, you can confidently tackle any assignment problem that comes your way.

How useful was this post?

Click on a star to rate it!

Average rating 0 / 5. Vote count: 0

No votes so far! Be the first to rate this post.

We are sorry that this post was not useful for you! 😔

Let us improve this post!

Tell us how we can improve this post?

Operations Research

1 Operations Research-An Overview

History of O.R.
Approach, Techniques and Tools
Phases and Processes of O.R. Study
Typical Applications of O.R
Limitations of Operations Research
Models in Operations Research
O.R. in real world

2 Linear Programming: Formulation and Graphical Method

General formulation of Linear Programming Problem
Optimisation Models
Basics of Graphic Method
Important steps to draw graph
Multiple, Unbounded Solution and Infeasible Problems
Solving Linear Programming Graphically Using Computer
Application of Linear Programming in Business and Industry

3 Linear Programming-Simplex Method

Principle of Simplex Method
Computational aspect of Simplex Method
Simplex Method with several Decision Variables
Two Phase and M-method
Multiple Solution, Unbounded Solution and Infeasible Problem
Sensitivity Analysis
Dual Linear Programming Problem

4 Transportation Problem

Basic Feasible Solution of a Transportation Problem
Modified Distribution Method
Stepping Stone Method
Unbalanced Transportation Problem
Degenerate Transportation Problem
Transhipment Problem
Maximisation in a Transportation Problem

5 Assignment Problem

Solution of the Assignment Problem
Unbalanced Assignment Problem
Problem with some Infeasible Assignments
Maximisation in an Assignment Problem
Crew Assignment Problem

6 Application of Excel Solver to Solve LPP

Building Excel model for solving LP: An Illustrative Example

7 Goal Programming

Concepts of goal programming
Goal programming model formulation
Graphical method of goal programming
The simplex method of goal programming
Using Excel Solver to Solve Goal Programming Models
Application areas of goal programming

8 Integer Programming

Some Integer Programming Formulation Techniques
Binary Representation of General Integer Variables
Unimodularity
Cutting Plane Method
Branch and Bound Method
Solver Solution

9 Dynamic Programming

Dynamic Programming Methodology: An Example
Definitions and Notations
Dynamic Programming Applications

10 Non-Linear Programming

Solution of a Non-linear Programming Problem
Convex and Concave Functions
Kuhn-Tucker Conditions for Constrained Optimisation
Quadratic Programming
Separable Programming
NLP Models with Solver

11 Introduction to game theory and its Applications

Important terms in Game Theory
Saddle points
Mixed strategies: Games without saddle points
2 x n games
Exploiting an opponent’s mistakes

12 Monte Carlo Simulation

Reasons for using simulation
Monte Carlo simulation
Limitations of simulation
Steps in the simulation process
Some practical applications of simulation
Two typical examples of hand-computed simulation
Computer simulation

13 Queueing Models

Characteristics of a queueing model
Notations and Symbols
Statistical methods in queueing
The M/M/I System
The M/M/C System
The M/Ek/I System
Decision problems in queueing

Data Structures
Linked List
Binary Tree
Binary Search Tree
Segment Tree
Disjoint Set Union
Fenwick Tree
Red-Black Tree
Advanced Data Structures

Hungarian Algorithm for Assignment Problem | Set 2 (Implementation)

Hungarian Algorithm for Assignment Problem | Set 1 (Introduction)
Implementation of Exhaustive Search Algorithm for Set Packing
Greedy Approximate Algorithm for Set Cover Problem
Introduction to Exact Cover Problem and Algorithm X
Job Assignment Problem using Branch And Bound
Prim's Algorithm (Simple Implementation for Adjacency Matrix Representation)
Introduction to Disjoint Set (Union-Find Algorithm)
Channel Assignment Problem
Java Program for Counting sets of 1s and 0s in a binary matrix
Top 20 Greedy Algorithms Interview Questions
C++ Program for Counting sets of 1s and 0s in a binary matrix
C# Program for Dijkstra's shortest path algorithm | Greedy Algo-7
Java Program for Dijkstra's shortest path algorithm | Greedy Algo-7
C / C++ Program for Dijkstra's shortest path algorithm | Greedy Algo-7
Self assignment check in assignment operator
Python Program for Dijkstra's shortest path algorithm | Greedy Algo-7
Algorithms | Dynamic Programming | Question 7
Assignment Operators in C
Assignment Operators in Programming
Merge Sort - Data Structure and Algorithms Tutorials
Must Do Coding Questions for Companies like Amazon, Microsoft, Adobe, ...
QuickSort - Data Structure and Algorithm Tutorials
Bubble Sort - Data Structure and Algorithm Tutorials
Tree Traversal Techniques - Data Structure and Algorithm Tutorials
Binary Search - Data Structure and Algorithm Tutorials
Insertion Sort - Data Structure and Algorithm Tutorials
Selection Sort – Data Structure and Algorithm Tutorials
Understanding the basics of Linked List
Breadth First Search or BFS for a Graph

Given a 2D array , arr of size N*N where arr[i][j] denotes the cost to complete the j th job by the i th worker. Any worker can be assigned to perform any job. The task is to assign the jobs such that exactly one worker can perform exactly one job in such a way that the total cost of the assignment is minimized.

Input: arr[][] = {{3, 5}, {10, 1}} Output: 4 Explanation: The optimal assignment is to assign job 1 to the 1st worker, job 2 to the 2nd worker. Hence, the optimal cost is 3 + 1 = 4. Input: arr[][] = {{2500, 4000, 3500}, {4000, 6000, 3500}, {2000, 4000, 2500}} Output: 4 Explanation: The optimal assignment is to assign job 2 to the 1st worker, job 3 to the 2nd worker and job 1 to the 3rd worker. Hence, the optimal cost is 4000 + 3500 + 2000 = 9500.

Different approaches to solve this problem are discussed in this article .

Approach: The idea is to use the Hungarian Algorithm to solve this problem. The algorithm is as follows:

For each row of the matrix, find the smallest element and subtract it from every element in its row.
Repeat the step 1 for all columns.
Cover all zeros in the matrix using the minimum number of horizontal and vertical lines.
Test for Optimality : If the minimum number of covering lines is N , an optimal assignment is possible. Else if lines are lesser than N , an optimal assignment is not found and must proceed to step 5.
Determine the smallest entry not covered by any line. Subtract this entry from each uncovered row, and then add it to each covered column. Return to step 3.

Consider an example to understand the approach:

Let the 2D array be: 2500 4000 3500 4000 6000 3500 2000 4000 2500 Step 1: Subtract minimum of every row. 2500, 3500 and 2000 are subtracted from rows 1, 2 and 3 respectively. 0 1500 1000 500 2500 0 0 2000 500 Step 2: Subtract minimum of every column. 0, 1500 and 0 are subtracted from columns 1, 2 and 3 respectively. 0 0 1000 500 1000 0 0 500 500 Step 3: Cover all zeroes with minimum number of horizontal and vertical lines. Step 4: Since we need 3 lines to cover all zeroes, the optimal assignment is found. 2500 4000 3500 4000 6000 3500 2000 4000 2500 So the optimal cost is 4000 + 3500 + 2000 = 9500

For implementing the above algorithm, the idea is to use the max_cost_assignment() function defined in the dlib library . This function is an implementation of the Hungarian algorithm (also known as the Kuhn-Munkres algorithm) which runs in O(N 3 ) time. It solves the optimal assignment problem.

Below is the implementation of the above approach:

Time Complexity: O(N 3 ) Auxiliary Space: O(N 2 )

Please Login to comment...

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

Handbook of Combinatorial Optimization pp 2741–2814 Cite as

Quadratic Assignment Problems

Rainer E. burkard 4
Reference work entry
First Online: 01 January 2013

8131 Accesses

33 Citations

This chapter introduces quadratic assignment problems (QAP) as models for finding an optimal assignment among two sets of interrelated objects. References to many applications of QAPs, like in location theory, are given. Moreover, several classical combinatorial optimization problems are identified as special cases of the QAP, like the traveling salesman problem, graph partitioning, max clique problem, minimum-weight feedback arc set problem, (FASP) and packing problems in graphs. These subproblems show that the QAP is $\mathcal{N}\mathcal{P}$ -hard.Several different formulations of the QAP are presented in detail as being basic for different solution approaches. Special emphasis is laid to the different possibilities for describing QAPs as (mixed-)integer linear programs. Moreover, QAP polyhedra are discussed.Crucial for exact solution approaches are lower bounding procedures. The paradigm of admissible transformations is introduced for describing several variants of Gilmore–Lawler type bounds. Moreover, bounds based on eigenvalues and bounds found by semidefinite programming are discussed in detail. Among exact solution methods, special emphasis is laid on branch-and-bound approaches. With respect to heuristics, not only simple construction heuristics and improvement heuristics are described, but also several metaheuristics like simulated annealing, tabu search, greedy randomized search, genetic algorithms, and ant systems are discussed. Links to available computer programs are delivered.As QAPs are $\mathcal{N}\mathcal{P}$ -hard problems, there is a special interest in polynomially solvable special cases. A comprehensive survey of results in this direction is given. Moreover, QAPs show an interesting asymptotic behavior, as the ratio of best and worst solution value tends to one in probability. This phenomenon is thoroughly discussed and implications of this strange behavior are shown.Finally, related problems are shortly treated. So, the quadratic bottleneck assignment problem is introduced and lower bounds, efficiently solvable special cases, as well as asymptotic results are reported. Moreover, cubic assignment problems, biquadratic assignment problems, and the quadratic semi-assignment problem are surveyed. An extensive bibliography provides the most important links to the literature in this field.

This is a preview of subscription content, log in via an institution .

Buying options

Available as PDF
Read on any device
Instant download
Own it forever
Available as EPUB and PDF
Durable hardcover edition
Dispatched in 3 to 5 business days
Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Author information

Authors and affiliations.

Institute of Optimization and Discrete Mathematics, Graz University of Technology, Steyrergasse 30, 8010, Graz, Austria

Rainer E. burkard

You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Rainer E. burkard .

Editor information

Editors and affiliations.

Department of Industrial and Systems Eng, University of Florida, Gainesville, Florida, USA

Panos M. Pardalos

Department of Computer Science, University of Texas, Dallas, Richardson, Texas, USA

Ding-Zhu Du

Dept. Comp. Sci. & Engineering, University of California, San Diego, La Jolla, California, USA

Ronald L. Graham

Rights and permissions

Reprints and permissions

Copyright information

About this entry

Cite this entry.

burkard, R.E. (2013). Quadratic Assignment Problems. In: Pardalos, P., Du, DZ., Graham, R. (eds) Handbook of Combinatorial Optimization. Springer, New York, NY. https://doi.org/10.1007/978-1-4419-7997-1_22

Download citation

DOI : https://doi.org/10.1007/978-1-4419-7997-1_22

Published : 26 July 2013

Publisher Name : Springer, New York, NY

Print ISBN : 978-1-4419-7996-4

Online ISBN : 978-1-4419-7997-1

eBook Packages : Mathematics and Statistics Reference Module Computer Science and Engineering

Share this entry

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

Publish with us

Policies and ethics

Find a journal
Track your research

(Stanford users can avoid this Captcha by logging in.)

Send to text email RefWorks EndNote printer

The Quadratic Assignment Problem : Theory and Algorithms

Available online.

SpringerLink

More options

Find it at other libraries via WorldCat
Contributors

Description

Creators/contributors, contents/summary.

Preface. List of Figures. List of Tables.
1. Problem Statement and Complexity Aspects.
2. Exact Algorithms and Lower Bounds.
3. Heuristics and Asymptotic Behavior.
4. QAPs on Specially Structured Matrices.
5. Two More Restricted Versions of the QAP.
6. QAPs Arising as Optimization Problems in Graphs.
7. On the Biquadratic Assignment Problem (BIQAP). References. Notation Index. Subject Index.
(source: Nielsen Book Data)

Bibliographic information

Stanford Home
Maps & Directions
Search Stanford
Emergency Info
Terms of Use
Non-Discrimination
Accessibility

IMAGES

Solved Assignment AoA and AoN 1. Single Span Bridge Project
assignment problem in analysis of algorithm aoa, design and analysis of algorithm daa in urdu hindi
Example of assignment problem in operational research
Operation Research 16: Formulation of Assignment Problem
[Solved] Please write legibly.. PROBLEM NO. 1. (AOA DIAGRAM) Given the
AOA assignment-1 2022-23

VIDEO

Congress MIM Road public show🔥👍
🎶 Karaoke song for kids with lyrics 🎤🥁
Teamfight Tactics Mobile
This Gun Sucks (Military Weapon Fail)
Anderson Paak thought Yoongi is 21 year old 😂
Twisted Towers Dustwinder Canyons Level 30 Difficulty 4

COMMENTS

Hungarian Algorithm for Assignment Problem
The Hungarian algorithm, aka Munkres assignment algorithm, utilizes the following theorem for polynomial runtime complexity (worst case O(n 3)) and guaranteed optimality: If a number is added to or subtracted from all of the entries of any one row or column of a cost matrix, then an optimal assignment for the resulting cost matrix is also an ...
PDF The Hungarian method for the assignment problem
THE HUNGARIAN METHOD FOR THE ASSIGNMENT. PROBLEM'. H. W. Kuhn. Bryn Y a w College. Assuming that numerical scores are available for the perform- ance of each of n persons on each of n jobs, the "assignment problem" is the quest for an assignment of persons to jobs so that the sum of the. n scores so obtained is as large as possible.
Hungarian Method
The Hungarian method is a computational optimization technique that addresses the assignment problem in polynomial time and foreshadows following primal-dual alternatives. In 1955, Harold Kuhn used the term "Hungarian method" to honour two Hungarian mathematicians, Dénes Kőnig and Jenő Egerváry. Let's go through the steps of the Hungarian method with the help of a solved example.
Quadratic Assignment Problem (QAP)
The Quadratic Assignment Problem (QAP) is an optimization problem that deals with assigning a set of facilities to a set of locations, considering the pairwise distances and flows between them. The problem is to find the assignment that minimizes the total cost or distance, taking into account both the distances and the flows. The distance ...
A comprehensive review of quadratic assignment problem: variants
The quadratic assignment problem (QAP) has considered one of the most significant combinatorial optimization problems due to its variant and significant applications in real life such as scheduling, production, computer manufacture, chemistry, facility location, communication, and other fields. QAP is NP-hard problem that is impossible to be solved in polynomial time when the problem size ...
The Hungarian Method for the Assignment Problem
This paper has always been one of my favorite "children," combining as it does elements of the duality of linear programming and combinatorial tools from graph theory. It may be of some interest to tell the story of its origin.
PDF Parallel Asynchronous Hungarian Methods for The Assignment Problem
An assignment is called complete (or incomplete)ifitcontains k = n (or k<n, respectively) person-object pairs. We want to ﬁnd a complete assignment with maximum total beneﬁt, assuming that there exists at least one complete assignment. The dual assignment problem is given by (see e.g. [BeT89], [PaS82], [Roc84]) minimize n j=1 p j + n i=1 π ...
PDF The Quadratic Assignment Problem
also considers problems related to the QAP, e.g. the biquadratic assignment problem, and discusses the relationship between the QAP and other well known combinatorial optimization problems, e.g. the traveling salesman problem, the graph partitioning problem, etc. The paper will appear in the Handbook of Combinatorial Optimization to be published
PDF The Dynamic Hungarian Algorithm for the Assignment Problem with
The assignment problem, also known as the maximum weighted bipartite matching problem, is a widely-studied problem applicable to many domains [2]. It can be stated as follows: given a set of workers, a set of jobs, and a set of ratings indicating how well each worker can perform each job, determine the best possible assignment of workers
PDF Chapter 2 The Hungarian Method for the Assignment Problem
the general assignment problem to a 0-1 problem. Thus, by putting the two ideas together, the Hungarian Method was born. I tested the algorithm by solving 12 by 12 problems with random 3-digit ratings by hand. I could do any such problem, with pencil and paper, in no more than 2 hours. This seemed to be much better than any other method known ...
Quadratic Assignment Problem Example
#quadraticassignmentproblem #quadratic #assignmentproblem #qapComplete Playlist of Analysis Of Algorithms (DAA):👇👇👇👇👇👇👇👇👇👇👇👇👇 https://www.youtub...
Quadratic assignment problem
The Quadratic Assignment Problem (QAP), discovered by Koopmans and Beckmann in 1957, is a mathematical optimization module created to describe the location of invisible economic activities. An NP-Complete problem, this model can be applied to many other optimization problems outside of the field of economics. It has been used to optimize ...
How to Solve the Assignment Problem: A Complete Guide
Step 1: Set up the cost matrix. The first step in solving the assignment problem is to set up the cost matrix, which represents the cost of assigning a task to an agent. The matrix should be square and have the same number of rows and columns as the number of tasks and agents, respectively.
PDF A Solution Method for the Quadratic Assignment Problem (QAP)
heuristics tends to vary with certain problem characteristics [Tat1995]. 3.1 Local Search A local search starts from some initial assignment and repeatedly tries to im-prove the current assignment by local changes. If in the neighborhood of the current assignment a better assignment is found, it replaces the current assignment and the
Hungarian Algorithm for Assignment Problem
For implementing the above algorithm, the idea is to use the max_cost_assignment() function defined in the dlib library. This function is an implementation of the Hungarian algorithm (also known as the Kuhn-Munkres algorithm) which runs in O(N 3) time. It solves the optimal assignment problem. Below is the implementation of the above approach:
The Quadratic Assignment Problem
The quadratic assignment problem (QAP) is considered one of the most difficult optimization problems to solve optimally. The QAP is a combinatorial optimization problem stated for the first time by Koopmans and Beckmann ().Early papers on the subject include Gilmore (), Pierce and Crowston (), Lawler (), and Love and Wong ().The problem is defined as follows.
assignment problem in analysis of algorithm aoa, design and ...
This tutorial explains what is assignment problem in analysis of algorithm aoa or job assignment problem in design and analysis of algorithm daa in urdu and ...
PDF The Assignment Problem and Primal-Dual Algorithms
in the assignment problem were either 0 or 1, then we could solve the assignment problem using the algorithm for the maximum cardinality bipartite matching problem: We construct a bipartite graph which has a node for every person iand every job j, and an edge from ito jif c ij = 0. A matching in this graph of size k
A survey for the quadratic assignment problem
The international literature identifies the quadratic assignment problem (QAP) as the problem of finding a minimum cost allocation of facilities into locations, taking the costs as the sum of all possible distance-flow products. The main motivation for this survey is the continuous interest in QAP, shown by a number of researchers worldwide ...
Quadratic Assignment Problem
Biquadratic Assignment Problem. A generalization of the QAP is the biquadratic assignment problem (BiQAP), which is essentially a quartic assignment problem with cost coefficients formed by the products of two four-dimensional arrays. More specifically, consider two n 4 × n 4 arrays F = ( f ijkl ) and D = ( d mpst ).
PDF the Quadratic Assignment Problem
The QAP problem was introduced by Koopmans and Beckmann in 1957 as a mathematical model for the assignment of a set of economic activities to a set of locations, with taking into account the distance and flow between the facilities and the costs of placing a facility in a specific location.
Quadratic Assignment Problems
The quadratic assignment problem (QAP) was introduced by Koopmans and Beckmann in 1957 as a mathematical model for the location of indivisible economical activities [].Consider the problem of allocating n facilities to n locations, with the cost being a function of the distance and flow between the facilities plus costs associated with placing a facility at a certain location.
The Quadratic Assignment Problem : Theory and Algorithms
The quadratic assignment problem (QAP) was introduced in 1957 by Koopmans and Beckmann to model a plant location problem. Since then the QAP has been object of numerous investigations by mathematicians, computers scientists, ope- tions researchers and practitioners. Nowadays the QAP is widely considered as a classical combinatorial optimization ...