problem solving with proportions

• PRO Courses Guides New Tech Help Pro Expert Videos About wikiHow Pro Upgrade Sign In
• EDIT Edit this Article
• EXPLORE Tech Help Pro About Us Random Article Quizzes Request a New Article Community Dashboard This Or That Game Popular Categories Arts and Entertainment Artwork Books Movies Computers and Electronics Computers Phone Skills Technology Hacks Health Men's Health Mental Health Women's Health Relationships Dating Love Relationship Issues Hobbies and Crafts Crafts Drawing Games Education & Communication Communication Skills Personal Development Studying Personal Care and Style Fashion Hair Care Personal Hygiene Youth Personal Care School Stuff Dating All Categories Arts and Entertainment Finance and Business Home and Garden Relationship Quizzes Cars & Other Vehicles Food and Entertaining Personal Care and Style Sports and Fitness Computers and Electronics Health Pets and Animals Travel Education & Communication Hobbies and Crafts Philosophy and Religion Work World Family Life Holidays and Traditions Relationships Youth
• Browse Articles
• Learn Something New
• Quizzes Hot
• This Or That Game
• Train Your Brain
• Explore More
• Support wikiHow
• About wikiHow
• Log in / Sign up
• Education and Communications
• Mathematics

How to Solve Proportions

Last Updated: March 26, 2024

This article was reviewed by Grace Imson, MA . Grace Imson is a math teacher with over 40 years of teaching experience. Grace is currently a math instructor at the City College of San Francisco and was previously in the Math Department at Saint Louis University. She has taught math at the elementary, middle, high school, and college levels. She has an MA in Education, specializing in Administration and Supervision from Saint Louis University. This article has been viewed 96,317 times.

What is the "vertical" way to solve a proportion?

How can I solve a proportion with the "horizontal" method?

How do I solve a proportion step by step by cross-multiplying?

How do you find the missing value in a proportion with a table of ratios?

• Each column in this table represents a fraction. All of the fractions in this table are equal to each other.

• The two answers are the same, which means your answer is correct.

How do you solve percent proportions?

How do you solve proportions algebraically?

• You can change the left hand side of the equation, as long as you do the same math to the right hand side.

• To get rid of the fraction on the left, multiply both sides by 27:

How do you solve a proportion with a variable on both sides?

• Warning : This is a difficult example. If you haven't learned about quadratic equations yet, you might want to skip this part.

• You can now solve this as a quadratic equation , using any method that you've learned.

Proportions Calculator, Practice Problems, and Answers

Community Q&A

• The algebraic method above works with any proportion. But for a specific proportion, there is often a faster way to use algebra to find the answer. As you learn more algebra, this will get easier. Thanks Helpful 0 Not Helpful 0

You Might Also Like

• ↑ http://www.mathvillage.info/node/72
• ↑ https://www.youtube.com/watch?v=nwsDiID7UtQ
• ↑ https://www.youtube.com/watch?v=Uo8HgcyfRFI
• ↑ https://www.purplemath.com/modules/ratio2.htm

About This Article

To solve proportions, start by taking the numerator, or top number, of the fraction you know and multiplying it with the denominator, or bottom number, of the fraction you don’t know. Next, take that number and divide it by the denominator of the fraction you know. Now you can replace x with this final number. For example, to figure out “x” in the problem 3/4 = x/8, multiply 3 x 8 to get 24, then divide 24 / 4 to get 6, or the value of x. To learn how to use proportions to determine percentages, read on! Did this summary help you? Yes No

• Send fan mail to authors

Reader Success Stories

John Almacen

Nov 10, 2022

Did this article help you?

Featured Articles

Trending Articles

Watch Articles

• Terms of Use
• Privacy Policy
• Do Not Sell or Share My Info
• Not Selling Info

wikiHow Tech Help Pro:

Develop the tech skills you need for work and life

6.5 Solve Proportions and their Applications

Learning objectives.

By the end of this section, you will be able to:

• Use the definition of proportion
• Solve proportions
• Solve applications using proportions
• Write percent equations as proportions
• Translate and solve percent proportions

Be Prepared 6.11

Before you get started, take this readiness quiz.

Simplify: 1 3 4 . 1 3 4 . If you missed this problem, review Example 4.44 .

Be Prepared 6.12

Solve: x 4 = 20 . x 4 = 20 . If you missed this problem, review Example 4.99 .

Be Prepared 6.13

Write as a rate: Sale rode his bike 24 24 miles in 2 2 hours. If you missed this problem, review Example 5.63 .

Use the Definition of Proportion

In the section on Ratios and Rates we saw some ways they are used in our daily lives. When two ratios or rates are equal, the equation relating them is called a proportion .

A proportion is an equation of the form a b = c d , a b = c d , where b ≠ 0 , d ≠ 0 . b ≠ 0 , d ≠ 0 .

The proportion states two ratios or rates are equal. The proportion is read “ a “ a is to b , b , as c c is to d ”. d ”.

The equation 1 2 = 4 8 1 2 = 4 8 is a proportion because the two fractions are equal. The proportion 1 2 = 4 8 1 2 = 4 8 is read “ 1 “ 1 is to 2 2 as 4 4 is to 8 ”. 8 ”.

If we compare quantities with units, we have to be sure we are comparing them in the right order. For example, in the proportion 20 students 1 teacher = 60 students 3 teachers 20 students 1 teacher = 60 students 3 teachers we compare the number of students to the number of teachers. We put students in the numerators and teachers in the denominators.

Example 6.40

Write each sentence as a proportion:

• ⓐ 3 3 is to 7 7 as 15 15 is to 35 . 35 .
• ⓑ 5 5 hits in 8 8 at bats is the same as 30 30 hits in 48 48 at-bats.
• ⓒ $1.50 $1.50 for 6 6 ounces is equivalent to $2.25 $2.25 for 9 9 ounces.

Try It 6.79

• ⓐ 5 5 is to 9 9 as 20 20 is to 36 . 36 .
• ⓑ 7 7 hits in 11 11 at-bats is the same as 28 28 hits in 44 44 at-bats.
• ⓒ $2.50 $2.50 for 8 8 ounces is equivalent to $3.75 $3.75 for 12 12 ounces.

Try It 6.80

• ⓐ 6 6 is to 7 7 as 36 36 is to 42 . 42 .
• ⓑ 8 8 adults for 36 36 children is the same as 12 12 adults for 54 54 children.
• ⓒ $3.75 $3.75 for 6 6 ounces is equivalent to $2.50 $2.50 for 4 4 ounces.

Look at the proportions 1 2 = 4 8 1 2 = 4 8 and 2 3 = 6 9 . 2 3 = 6 9 . From our work with equivalent fractions we know these equations are true. But how do we know if an equation is a proportion with equivalent fractions if it contains fractions with larger numbers?

To determine if a proportion is true, we find the cross products of each proportion. To find the cross products, we multiply each denominator with the opposite numerator (diagonally across the equal sign). The results are called a cross product because of the cross formed. If, and only if, the given proportion is true, that is, the two sides are equal, then the cross products of a proportion will be equal.

Cross Products of a Proportion

For any proportion of the form a b = c d , a b = c d , where b ≠ 0 , d ≠ 0 , b ≠ 0 , d ≠ 0 , its cross products are equal.

Cross products can be used to test whether a proportion is true. To test whether an equation makes a proportion, we find the cross products. If they are both equal, we have a proportion.

Example 6.41

Determine whether each equation is a proportion:

• ⓐ 4 9 = 12 28 4 9 = 12 28
• ⓑ 17.5 37.5 = 7 15 17.5 37.5 = 7 15

To determine if the equation is a proportion, we find the cross products. If they are equal, the equation is a proportion.

Since the cross products are not equal, 28 · 4 ≠ 9 · 12 , 28 · 4 ≠ 9 · 12 , the equation is not a proportion.

Since the cross products are equal, 15 · 17.5 = 37.5 · 7 , 15 · 17.5 = 37.5 · 7 , the equation is a proportion.

Try It 6.81

• ⓐ 7 9 = 54 72 7 9 = 54 72
• ⓑ 24.5 45.5 = 7 13 24.5 45.5 = 7 13

Try It 6.82

• ⓐ 8 9 = 56 73 8 9 = 56 73
• ⓑ 28.5 52.5 = 8 15 28.5 52.5 = 8 15

Solve Proportions

To solve a proportion containing a variable, we remember that the proportion is an equation. All of the techniques we have used so far to solve equations still apply. In the next example, we will solve a proportion by multiplying by the Least Common Denominator (LCD) using the Multiplication Property of Equality .

Example 6.42

Solve: x 63 = 4 7 . x 63 = 4 7 .

Try It 6.83

Solve the proportion: n 84 = 11 12 . n 84 = 11 12 .

Try It 6.84

Solve the proportion: y 96 = 13 12 . y 96 = 13 12 .

When the variable is in a denominator, we’ll use the fact that the cross products of a proportion are equal to solve the proportions.

We can find the cross products of the proportion and then set them equal. Then we solve the resulting equation using our familiar techniques.

Example 6.43

Solve: 144 a = 9 4 . 144 a = 9 4 .

Notice that the variable is in the denominator, so we will solve by finding the cross products and setting them equal.

Another method to solve this would be to multiply both sides by the LCD, 4 a . 4 a . Try it and verify that you get the same solution.

Try It 6.85

Solve the proportion: 91 b = 7 5 . 91 b = 7 5 .

Try It 6.86

Solve the proportion: 39 c = 13 8 . 39 c = 13 8 .

Example 6.44

Solve: 52 91 = −4 y . 52 91 = −4 y .

Try It 6.87

Solve the proportion: 84 98 = −6 x . 84 98 = −6 x .

Try It 6.88

Solve the proportion: −7 y = 105 135 . −7 y = 105 135 .

Solve Applications Using Proportions

The strategy for solving applications that we have used earlier in this chapter, also works for proportions, since proportions are equations. When we set up the proportion , we must make sure the units are correct—the units in the numerators match and the units in the denominators match.

Example 6.45

When pediatricians prescribe acetaminophen to children, they prescribe 5 5 milliliters (ml) of acetaminophen for every 25 25 pounds of the child’s weight. If Zoe weighs 80 80 pounds, how many milliliters of acetaminophen will her doctor prescribe?

You could also solve this proportion by setting the cross products equal.

Try It 6.89

Pediatricians prescribe 5 5 milliliters (ml) of acetaminophen for every 25 25 pounds of a child’s weight. How many milliliters of acetaminophen will the doctor prescribe for Emilia, who weighs 60 60 pounds?

Try It 6.90

For every 1 1 kilogram (kg) of a child’s weight, pediatricians prescribe 15 15 milligrams (mg) of a fever reducer. If Isabella weighs 12 12 kg, how many milligrams of the fever reducer will the pediatrician prescribe?

Example 6.46

One brand of microwave popcorn has 120 120 calories per serving. A whole bag of this popcorn has 3.5 3.5 servings. How many calories are in a whole bag of this microwave popcorn?

Try It 6.91

Marissa loves the Caramel Macchiato at the coffee shop. The 16 16 oz. medium size has 240 240 calories. How many calories will she get if she drinks the large 20 20 oz. size?

Try It 6.92

Yaneli loves Starburst candies, but wants to keep her snacks to 100 100 calories. If the candies have 160 160 calories for 8 8 pieces, how many pieces can she have in her snack?

Example 6.47

Josiah went to Mexico for spring break and changed $325 $325 dollars into Mexican pesos. At that time, the exchange rate had $1 $1 U.S. is equal to 12.54 12.54 Mexican pesos. How many Mexican pesos did he get for his trip?

Try It 6.93

Yurianna is going to Europe and wants to change $800 $800 dollars into Euros. At the current exchange rate, $1 $1 US is equal to 0.738 0.738 Euro. How many Euros will she have for her trip?

Try It 6.94

Corey and Nicole are traveling to Japan and need to exchange $600 $600 into Japanese yen. If each dollar is 94.1 94.1 yen, how many yen will they get?

Write Percent Equations As Proportions

Previously, we solved percent equations by applying the properties of equality we have used to solve equations throughout this text. Some people prefer to solve percent equations by using the proportion method. The proportion method for solving percent problems involves a percent proportion. A percent proportion is an equation where a percent is equal to an equivalent ratio.

For example, 60% = 60 100 60% = 60 100 and we can simplify 60 100 = 3 5 . 60 100 = 3 5 . Since the equation 60 100 = 3 5 60 100 = 3 5 shows a percent equal to an equivalent ratio, we call it a percent proportion . Using the vocabulary we used earlier:

Percent Proportion

The amount is to the base as the percent is to 100 . 100 .

If we restate the problem in the words of a proportion, it may be easier to set up the proportion:

We could also say:

First we will practice translating into a percent proportion. Later, we’ll solve the proportion.

Example 6.48

Translate to a proportion. What number is 75% 75% of 90 ? 90 ?

If you look for the word "of", it may help you identify the base.

Try It 6.95

Translate to a proportion: What number is 60% 60% of 105 ? 105 ?

Try It 6.96

Translate to a proportion: What number is 40% 40% of 85 ? 85 ?

Example 6.49

Translate to a proportion. 19 19 is 25% 25% of what number?

Try It 6.97

Translate to a proportion: 36 36 is 25% 25% of what number?

Try It 6.98

Translate to a proportion: 27 27 is 36% 36% of what number?

Example 6.50

Translate to a proportion. What percent of 27 27 is 9 ? 9 ?

Try It 6.99

Translate to a proportion: What percent of 52 52 is 39 ? 39 ?

Try It 6.100

Translate to a proportion: What percent of 92 92 is 23 ? 23 ?

Translate and Solve Percent Proportions

Now that we have written percent equations as proportions, we are ready to solve the equations.

Example 6.51

Translate and solve using proportions: What number is 45% 45% of 80 ? 80 ?

Try It 6.101

Translate and solve using proportions: What number is 65% 65% of 40 ? 40 ?

Try It 6.102

Translate and solve using proportions: What number is 85% 85% of 40 ? 40 ?

In the next example, the percent is more than 100 , 100 , which is more than one whole. So the unknown number will be more than the base.

Example 6.52

Translate and solve using proportions: 125% 125% of 25 25 is what number?

Try It 6.103

Translate and solve using proportions: 125% 125% of 64 64 is what number?

Try It 6.104

Translate and solve using proportions: 175% 175% of 84 84 is what number?

Percents with decimals and money are also used in proportions.

Example 6.53

Translate and solve: 6.5% 6.5% of what number is $1.56 ? $1.56 ?

Try It 6.105

Translate and solve using proportions: 8.5% 8.5% of what number is $3.23 ? $3.23 ?

Try It 6.106

Translate and solve using proportions: 7.25% 7.25% of what number is $4.64 ? $4.64 ?

Example 6.54

Translate and solve using proportions: What percent of 72 72 is 9 ? 9 ?

Try It 6.107

Translate and solve using proportions: What percent of 72 72 is 27 ? 27 ?

Try It 6.108

Translate and solve using proportions: What percent of 92 92 is 23 ? 23 ?

Section 6.5 Exercises

Practice makes perfect.

In the following exercises, write each sentence as a proportion.

4 4 is to 15 15 as 36 36 is to 135 . 135 .

7 7 is to 9 9 as 35 35 is to 45 . 45 .

12 12 is to 5 5 as 96 96 is to 40 . 40 .

15 15 is to 8 8 as 75 75 is to 40 . 40 .

5 5 wins in 7 7 games is the same as 115 115 wins in 161 161 games.

4 4 wins in 9 9 games is the same as 36 36 wins in 81 81 games.

8 8 campers to 1 1 counselor is the same as 48 48 campers to 6 6 counselors.

6 6 campers to 1 1 counselor is the same as 48 48 campers to 8 8 counselors.

$9.36 $9.36 for 18 18 ounces is the same as $2.60 $2.60 for 5 5 ounces.

$3.92 $3.92 for 8 8 ounces is the same as $1.47 $1.47 for 3 3 ounces.

$18.04 $18.04 for 11 11 pounds is the same as $4.92 $4.92 for 3 3 pounds.

$12.42 $12.42 for 27 27 pounds is the same as $5.52 $5.52 for 12 12 pounds.

In the following exercises, determine whether each equation is a proportion.

7 15 = 56 120 7 15 = 56 120

5 12 = 45 108 5 12 = 45 108

11 6 = 21 16 11 6 = 21 16

9 4 = 39 34 9 4 = 39 34

12 18 = 4.99 7.56 12 18 = 4.99 7.56

9 16 = 2.16 3.89 9 16 = 2.16 3.89

13.5 8.5 = 31.05 19.55 13.5 8.5 = 31.05 19.55

10.1 8.4 = 3.03 2.52 10.1 8.4 = 3.03 2.52

In the following exercises, solve each proportion.

x 56 = 7 8 x 56 = 7 8

n 91 = 8 13 n 91 = 8 13

49 63 = z 9 49 63 = z 9

56 72 = y 9 56 72 = y 9

5 a = 65 117 5 a = 65 117

4 b = 64 144 4 b = 64 144

98 154 = −7 p 98 154 = −7 p

72 156 = −6 q 72 156 = −6 q

a −8 = −42 48 a −8 = −42 48

b −7 = −30 42 b −7 = −30 42

2.6 3.9 = c 3 2.6 3.9 = c 3

2.7 3.6 = d 4 2.7 3.6 = d 4

2.7 j = 0.9 0.2 2.7 j = 0.9 0.2

2.8 k = 2.1 1.5 2.8 k = 2.1 1.5

1 2 1 = m 8 1 2 1 = m 8

1 3 3 = 9 n 1 3 3 = 9 n

In the following exercises, solve the proportion problem.

Pediatricians prescribe 5 5 milliliters (ml) of acetaminophen for every 25 25 pounds of a child’s weight. How many milliliters of acetaminophen will the doctor prescribe for Jocelyn, who weighs 45 45 pounds?

Brianna, who weighs 6 6 kg, just received her shots and needs a pain killer. The pain killer is prescribed for children at 15 15 milligrams (mg) for every 1 1 kilogram (kg) of the child’s weight. How many milligrams will the doctor prescribe?

At the gym, Carol takes her pulse for 10 10 sec and counts 19 19 beats. How many beats per minute is this? Has Carol met her target heart rate of 140 140 beats per minute?

Kevin wants to keep his heart rate at 160 160 beats per minute while training. During his workout he counts 27 27 beats in 10 10 seconds. How many beats per minute is this? Has Kevin met his target heart rate?

A new energy drink advertises 106 106 calories for 8 8 ounces. How many calories are in 12 12 ounces of the drink?

One 12 12 ounce can of soda has 150 150 calories. If Josiah drinks the big 32 32 ounce size from the local mini-mart, how many calories does he get?

Karen eats 1 2 1 2 cup of oatmeal that counts for 2 2 points on her weight loss program. Her husband, Joe, can have 3 3 points of oatmeal for breakfast. How much oatmeal can he have?

An oatmeal cookie recipe calls for 1 2 1 2 cup of butter to make 4 4 dozen cookies. Hilda needs to make 10 10 dozen cookies for the bake sale. How many cups of butter will she need?

Janice is traveling to Canada and will change $250 $250 US dollars into Canadian dollars. At the current exchange rate, $1 $1 US is equal to $1.01 $1.01 Canadian. How many Canadian dollars will she get for her trip?

Todd is traveling to Mexico and needs to exchange $450 $450 into Mexican pesos. If each dollar is worth 12.29 12.29 pesos, how many pesos will he get for his trip?

Steve changed $600 $600 into 480 480 Euros. How many Euros did he receive per US dollar?

Martha changed $350 $350 US into 385 385 Australian dollars. How many Australian dollars did she receive per US dollar?

At the laundromat, Lucy changed $12.00 $12.00 into quarters. How many quarters did she get?

When she arrived at a casino, Gerty changed $20 $20 into nickels. How many nickels did she get?

Jesse’s car gets 30 30 miles per gallon of gas. If Las Vegas is 285 285 miles away, how many gallons of gas are needed to get there and then home? If gas is $3.09 $3.09 per gallon, what is the total cost of the gas for the trip?

Danny wants to drive to Phoenix to see his grandfather. Phoenix is 370 370 miles from Danny’s home and his car gets 18.5 18.5 miles per gallon. How many gallons of gas will Danny need to get to and from Phoenix? If gas is $3.19 $3.19 per gallon, what is the total cost for the gas to drive to see his grandfather?

Hugh leaves early one morning to drive from his home in Chicago to go to Mount Rushmore, 812 812 miles away. After 3 3 hours, he has gone 190 190 miles. At that rate, how long will the whole drive take?

Kelly leaves her home in Seattle to drive to Spokane, a distance of 280 280 miles. After 2 2 hours, she has gone 152 152 miles. At that rate, how long will the whole drive take?

Phil wants to fertilize his lawn. Each bag of fertilizer covers about 4,000 4,000 square feet of lawn. Phil’s lawn is approximately 13,500 13,500 square feet. How many bags of fertilizer will he have to buy?

April wants to paint the exterior of her house. One gallon of paint covers about 350 350 square feet, and the exterior of the house measures approximately 2000 2000 square feet. How many gallons of paint will she have to buy?

Write Percent Equations as Proportions

In the following exercises, translate to a proportion.

What number is 35% 35% of 250 ? 250 ?

What number is 75% 75% of 920 ? 920 ?

What number is 110% 110% of 47 ? 47 ?

What number is 150% 150% of 64 ? 64 ?

45 45 is 30% 30% of what number?

25 25 is 80% 80% of what number?

90 90 is 150% 150% of what number?

77 77 is 110% 110% of what number?

What percent of 85 85 is 17 ? 17 ?

What percent of 92 92 is 46 ? 46 ?

What percent of 260 260 is 340 ? 340 ?

What percent of 180 180 is 220 ? 220 ?

In the following exercises, translate and solve using proportions.

What number is 65% 65% of 180 ? 180 ?

What number is 55% 55% of 300 ? 300 ?

18% 18% of 92 92 is what number?

22% 22% of 74 74 is what number?

175% 175% of 26 26 is what number?

250% 250% of 61 61 is what number?

What is 300% 300% of 488 ? 488 ?

What is 500% 500% of 315 ? 315 ?

17% 17% of what number is $7.65 ? $7.65 ?

19% 19% of what number is $6.46 ? $6.46 ?

$13.53 $13.53 is 8.25% 8.25% of what number?

$18.12 $18.12 is 7.55% 7.55% of what number?

What percent of 56 56 is 14 ? 14 ?

What percent of 80 80 is 28 ? 28 ?

What percent of 96 96 is 12 ? 12 ?

What percent of 120 120 is 27 ? 27 ?

Everyday Math

Mixing a concentrate Sam bought a large bottle of concentrated cleaning solution at the warehouse store. He must mix the concentrate with water to make a solution for washing his windows. The directions tell him to mix 3 3 ounces of concentrate with 5 5 ounces of water. If he puts 12 12 ounces of concentrate in a bucket, how many ounces of water should he add? How many ounces of the solution will he have altogether?

Mixing a concentrate Travis is going to wash his car. The directions on the bottle of car wash concentrate say to mix 2 2 ounces of concentrate with 15 15 ounces of water. If Travis puts 6 6 ounces of concentrate in a bucket, how much water must he mix with the concentrate?

Writing Exercises

To solve “what number is 45% 45% of 350 ” 350 ” do you prefer to use an equation like you did in the section on Decimal Operations or a proportion like you did in this section? Explain your reason.

To solve “what percent of 125 125 is 25 ” 25 ” do you prefer to use an equation like you did in the section on Decimal Operations or a proportion like you did in this section? Explain your reason.

ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

ⓑ Overall, after looking at the checklist, do you think you are well-prepared for the next Chapter? Why or why not?

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/prealgebra-2e/pages/1-introduction

• Authors: Lynn Marecek, MaryAnne Anthony-Smith, Andrea Honeycutt Mathis
• Publisher/website: OpenStax
• Book title: Prealgebra 2e
• Publication date: Mar 11, 2020
• Location: Houston, Texas
• Book URL: https://openstax.org/books/prealgebra-2e/pages/1-introduction
• Section URL: https://openstax.org/books/prealgebra-2e/pages/6-5-solve-proportions-and-their-applications

© Jan 23, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

• Pre-algebra lessons
• Pre-algebra word problems
• Algebra lessons
• Algebra word problems
• Algebra proofs
• Advanced algebra
• Geometry lessons
• Geometry word problems
• Geometry proofs
• Trigonometry lessons
• Consumer math
• Baseball math
• Math for nurses
• Statistics made easy
• High school physics
• Basic mathematics store
• SAT Math Prep
• Math skills by grade level
• Ask an expert
• Other websites
• K-12 worksheets
• Worksheets generator
• Algebra worksheets
• Geometry worksheets
• Free math problem solver
• Pre-algebra calculators
• Algebra Calculators
• Geometry Calculators
• Math puzzles
• Math tricks
• Member login

Proportion word problems

It is very important to notice that if the ratio on the left is a ratio of number of liters of water to number of lemons, you have to do the same ratio on the right before you set them equal. 

More interesting proportion word problems

Check this site if you want to solve more proportion word problems.

Ratio word problems

Recent Articles

How to divide any number by 5 in 2 seconds.

Feb 28, 24 11:07 AM

Math Trick to Square Numbers from 50 to 59

Feb 23, 24 04:46 AM

Sum of Consecutive Odd Numbers

Feb 22, 24 10:07 AM

100 Tough Algebra Word Problems. If you can solve these problems with no help, you must be a genius!

 Recommended

About me :: Privacy policy :: Disclaimer :: Donate   Careers in mathematics  

Copyright © 2008-2021. Basic-mathematics.com. All right reserved

• Number Charts
• Multiplication
• Long division
• Basic operations
• Telling time
• Place value
• Roman numerals
• Fractions & related
• Add, subtract, multiply,   and divide fractions
• Mixed numbers vs. fractions
• Equivalent fractions
• Prime factorization & factors
• Fraction Calculator
• Decimals & Percent
• Add, subtract, multiply,   and divide decimals
• Fractions to decimals
• Percents to decimals
• Percentage of a number
• Percent word problems
• Classify triangles
• Classify quadrilaterals
• Circle worksheets
• Area & perimeter of rectangles
• Area of triangles & polygons
• Coordinate grid, including   moves & reflections
• Volume & surface area
• Pre-algebra
• Square Roots
• Order of operations
• Scientific notation
• Proportions
• Ratio word problems
• Write expressions
• Evaluate expressions
• Simplify expressions
• Linear equations
• Linear inequalities
• Graphing & slope
• Equation calculator
• Equation editor
• Elementary Math Games
• Addition and subtraction
• Math facts practice
• The four operations
• Factoring and number theory
• Geometry topics
• Middle/High School
• Statistics & Graphs
• Probability
• Trigonometry
• Logic and proof
• For all levels
• Favorite math puzzles
• Favorite challenging puzzles
• Math in real world
• Problem solving & projects
• For gifted children
• Math history
• Math games and fun websites
• Interactive math tutorials
• Math help & online tutoring
• Assessment, review & test prep
• Online math curricula

Real World Algebra by Edward Zaccaro

Algebra is often taught abstractly with little or no emphasis on what algebra is or how it can be used to solve real problems. Just as English can be translated into other languages, word problems can be "translated" into the math language of algebra and easily solved. Real World Algebra explains this process in an easy to understand format using cartoons and drawings. This makes self-learning easy for both the student and any teacher who never did quite understand algebra. Includes chapters on algebra and money, algebra and geometry, algebra and physics, algebra and levers and many more. Designed for children in grades 4-9 with higher math ability and interest but could be used by older students and adults as well. Contains 22 chapters with instruction and problems at three levels of difficulty.

Proportions

Proportion says that two ratios (or fractions) are equal.

We see that 1-out-of-3 is equal to 2-out-of-6

The ratios are the same, so they are in proportion.

Example: Rope

A rope's length and weight are in proportion.

When 20m of rope weighs 1kg , then:

• 40m of that rope weighs 2kg
• 200m of that rope weighs 10kg

20 1 = 40 2

When shapes are "in proportion" their relative sizes are the same.

Example: International paper sizes (like A3, A4, A5, etc) all have the same proportions:

So any artwork or document can be resized to fit on any sheet. Very neat.

Working With Proportions

NOW, how do we use this?

Example: you want to draw the dog's head ... how long should it be?

Let us write the proportion with the help of the 10/20 ratio from above:

? 42 = 10 20

Now we solve it using a special method:

Multiply across the known corners, then divide by the third number

And we get this:

? = (42 × 10) / 20 = 420 / 20 = 21

So you should draw the head 21 long.

Using Proportions to Solve Percents

A percent is actually a ratio! Saying "25%" is actually saying "25 per 100":

25% = 25 100

We can use proportions to solve questions involving percents.

The trick is to put what we know into this form:

Part Whole = Percent 100

Example: what is 25% of 160 ?

The percent is 25, the whole is 160, and we want to find the "part":

Part 160 = 25 100

Multiply across the known corners, then divide by the third number:

Part = (160 × 25) / 100 = 4000 / 100 = 40

Answer: 25% of 160 is 40.

Note: we could have also solved this by doing the divide first, like this:

Part = 160 × (25 / 100) = 160 × 0.25 = 40

Either method works fine.

We can also find a Percent:

Example: what is $12 as a percent of $80 ?

Fill in what we know:

$12 $80 = Percent 100

Multiply across the known corners, then divide by the third number. This time the known corners are top left and bottom right:

Percent = ($12 × 100) / $80 = 1200 / 80 = 15%

Answer: $12 is 15% of $80

Or find the Whole:

Example: The sale price of a phone was $150, which was only 80% of normal price. What was the normal price?

$150 Whole = 80 100

Whole = ($150 × 100) / 80 = 15000 / 80 = 187.50

Answer: the phone's normal price was $187.50

Using Proportions to Solve Triangles

We can use proportions to solve similar triangles.

Example: How tall is the Tree?

Sam tried using a ladder, tape measure, ropes and various other things, but still couldn't work out how tall the tree was.

But then Sam has a clever idea ... similar triangles!

Sam measures a stick and its shadow (in meters), and also the shadow of the tree, and this is what he gets:

Now Sam makes a sketch of the triangles, and writes down the "Height to Length" ratio for both triangles:

Height: Shadow Length:     h 2.9 m = 2.4 m 1.3 m

h = (2.9 × 2.4) / 1.3 = 6.96 / 1.3 = 5.4 m (to nearest 0.1)

Answer: the tree is 5.4 m tall.

And he didn't even need a ladder!

The "Height" could have been at the bottom, so long as it was on the bottom for BOTH ratios, like this:

Let us try the ratio of "Shadow Length to Height":

Shadow Length: Height:     2.9 m h = 1.3 m 2.4 m

It is the same calculation as before.

A "Concrete" Example

Ratios can have more than two numbers !

For example concrete is made by mixing cement, sand, stones and water.

A typical mix of cement, sand and stones is written as a ratio, such as 1:2:6 .

We can multiply all values by the same amount and still have the same ratio.

10:20:60 is the same as 1:2:6

So when we use 10 buckets of cement, we should use 20 of sand and 60 of stones.

Example: you have just put 12 buckets of stones into a mixer, how much cement and how much sand should you add to make a 1:2:6 mix?

Let us lay it out in a table to make it clearer:

You have 12 buckets of stones but the ratio says 6.

That is OK, you simply have twice as many stones as the number in the ratio ... so you need twice as much of everything to keep the ratio.

Here is the solution:

And the ratio 2:4:12 is the same as 1:2:6 (because they show the same relative sizes)

So the answer is: add 2 buckets of Cement and 4 buckets of Sand. (You will also need water and a lot of stirring....)

Why are they the same ratio? Well, the 1:2:6 ratio says to have :

• twice as much Sand as Cement ( 1 : 2 :6)
• 6 times as much Stones as Cement ( 1 :2: 6 )

In our mix we have:

• twice as much Sand as Cement ( 2 : 4 :12)
• 6 times as much Stones as Cement ( 2 :4: 12 )

So it should be just right!

That is the good thing about ratios. You can make the amounts bigger or smaller and so long as the relative sizes are the same then the ratio is the same.

One to one maths interventions built for KS4 success

Weekly online one to one GCSE maths revision lessons now available

In order to access this I need to be confident with:

This topic is relevant for:

Here we will learn about proportion in maths, including direct and inverse proportion, real life examples, worded problems, and graphical representations. 

There are also proportion in maths worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

What is proportion?

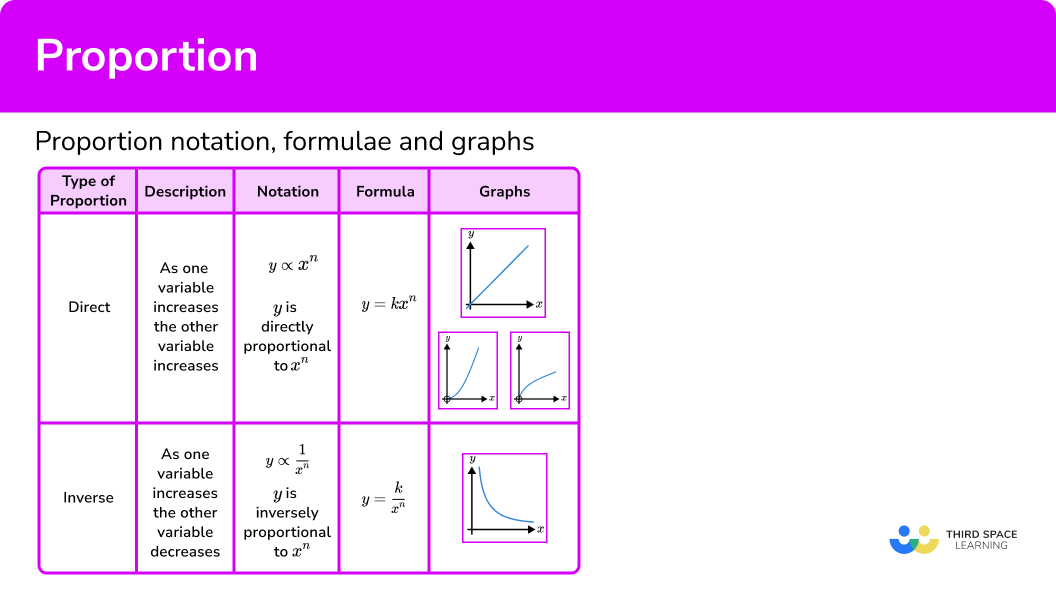
Proportion is a type of relationship between two variables linked by a constant.

There are two types of proportion, direct proportion and inverse proportion . They can also be referred to as direct variation and inverse variation.

When solving problems involving proportion it is important to know which type of proportion that you are dealing with, direct proportion or inverse proportion.

Step-by-step guide: Direct and indirect proportion

• Direct proportion

If there is a directly proportional relationship between two variables then as one variable increases, so does the other.

For example, An apple costs 60p. As the number of apples increases, so does the cost.

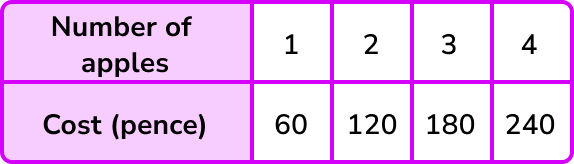
The relationship between the number of apples and the cost of the apples is directly proportional.

The constant in this example is 60.

Step-by-step guide: Direct proportion

• Inverse proportion

If there is an inversely proportional relationship between two variables then as one variable increases, the other variable decreases.

For example, 1 worker takes 30 days to paint a long fence. As the number of workers increases, the time it takes to paint the fence decreases. 

The relationship between the number of workers and the time taken to paint the fence is inversely proportional.

The constant in this example is 30.

Step-by-step guide: Inverse proportion

Solve ratio and proportion problems

Sometimes a proportion problem may also involve ratio.

For example,

A cafe sells apples and bananas in the ratio 2:3. They sell 35 pieces of fruit altogether. Apples cost 30p and bananas cost 45p. Work out the total amount of money the fruit cost.

So, first you use the ratio to work out how many apples and bananas were sold. The ratio 2:3 has 5 parts, so you divide 35 by 5 to get 7. Then you multiply each part of the ratio by 7. This means that 14 apples and 21 bananas were sold.

You can then use direct proportion to find the price of the apples and the price of the bananas.

Apples: 14\times 30=420

Bananas: 21\times 45=945

We add these together to get the total price for all the fruit.

Therefore the total price is 1365p or £13.65.

Notation for proportional relationships

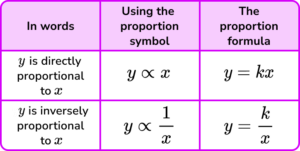
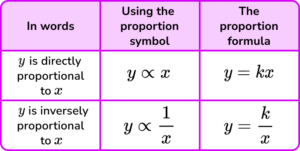
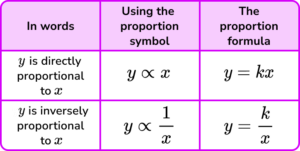
This symbol ‘\bf{\propto}’ means ‘is proportional to’.

If y is directly proportional to x you can write it as y \propto x.

If y is inversely proportional to x you can write it as y \propto \frac{1}{x}.

Proportion formulas and the constant of proportionality

Proportion is a type of relationship between two variables linked by a constant. This is known as the constant of proportionality and is usually denoted by the letter ‘k’. 

Equations of proportion:

• The direct proportion formula is, y=kx .

Step-by-step guide: Direct proportion formula

• The inverse proportion formula is, y=\frac{k}{x}.

Step-by-step guide: Inverse proportion formula

Graphs of proportional relationships

Proportional relationships can be represented graphically.

For direct proportion, as one variable increases the other variable increases.

Therefore, the graph will go up as you look from left to right. The graph can be a straight line or a curve. All direct proportion graphs must start at the origin. 

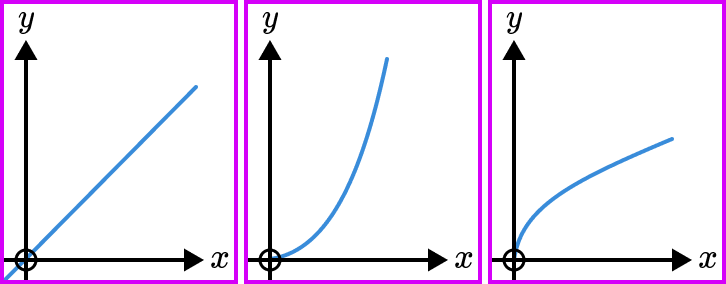
If y is directly proportional to x then the graph will be a straight line.

If y is directly proportional to a function of x such as x^{2} or \sqrt{x} then the graph will form a curve.

For inverse proportion , as one variable increases the other variable decreases.

Therefore, the graph will go down as you look from left to right. All inverse proportion graphs form a curved shape like in the example below.

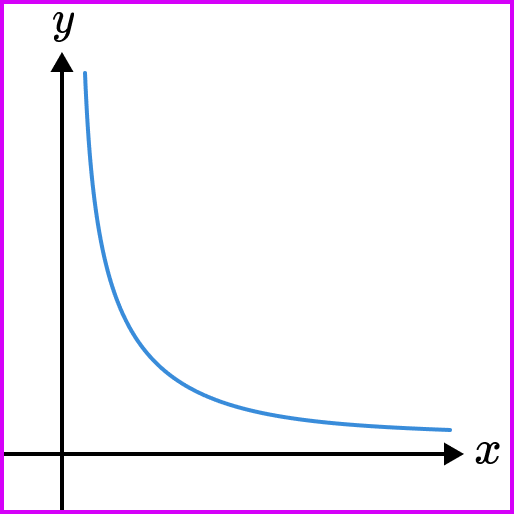
Whether y is inversely proportional to just x or a function of x it will still form a curved graph with this general shape.

Step-by-step guide: Directly proportional graph / inversely proportional graph

Types of proportion

How to use proportion in maths

In order to answer general proportion in maths problems:

• Identify if the relationship between the variables in the question is (a) directly proportional. (b) inversely proportional.
• (a) By using division, find the constant. (b) By using multiplication, find the constant.
• (a) Multiply the constant by the required value of one variable to find the answer for the other variable. (b) Divide the constant by the required value of one variable to find the answer for the other variable.

Explain how to use proportion

Proportion worksheet

Get your free proportion worksheet of 20+ questions and answers. Includes reasoning and applied questions.

Proportion examples

Example 1: worded problem.

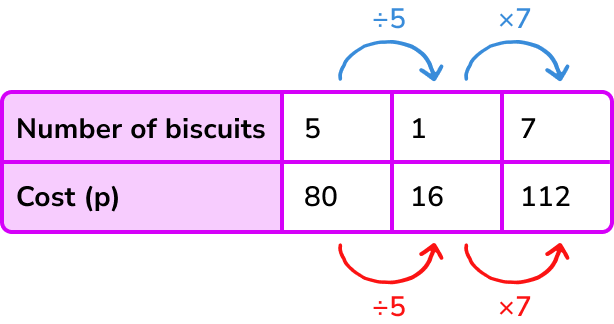
If 5 biscuits cost 80p, find the cost of 7 biscuits.

As the number of biscuits increases the cost will also increase. Therefore the variables are directly proportional.

2 (a) By using division, find the constant. (b) By using multiplication, find the constant. 

1 biscuit will cost 16p.

3 (a)  Multiply the constant by the required value of one variable to find the answer for the other variable. (b)  Divide the constant by the required value of one variable to find the answer for the other variable.

7 biscuits will cost 112p or £1.12.

You can also visualise these steps in a table.

Example 2: worded problem

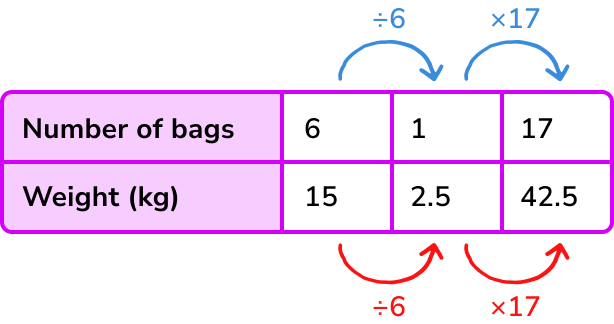
If 6 bags of flour weigh 15 \ kg, find the weight of 17 bags of flour.

Identify if the relationship between the variables in the question is (a) directly proportional.  (b) inversely proportional.

As the number of bags of flour increases the weight will also increase. Therefore the variables are directly proportional.

(a) By using division, find the constant.  (b) By using multiplication, find the constant.

1 bag of flour will weigh 2.5kg.

(a)  Multiply the constant by the required value of one variable to find the answer for the other variable. (b)  Divide the constant by the required value of one variable to find the answer for the other variable.

17 bags of flour will weigh 42.5kg.

Example 3: worded problem

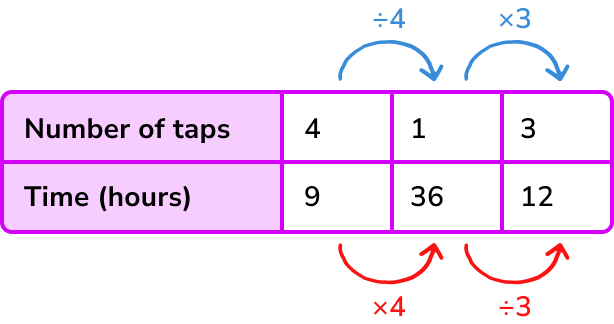
If 4 taps pumping water at a constant rate take 9 hours to fill a swimming pool, find the time it would take 3 taps pumping water at the same rate to fill the swimming pool.

As the number of taps increases the time it takes to fill the swimming pool decreases. Therefore the variables are inversely proportional.

It would take 1 tap 36 hours to fill the pool.

3 taps would take 12 hours to fill the pool.

Example 4: worded problem

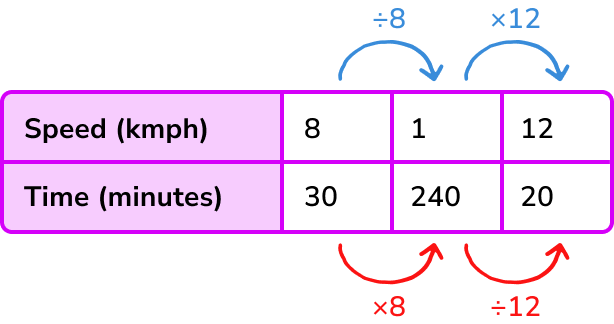
A local park has a course marked out for runners to use. One runner completes the course in 30 minutes running at a speed of 8 \ km/h.  

Another runner has a pace of 12km/h. How long will it take this runner to complete the course?

As the speed increases, the time taken to complete the course decreases. Therefore the variables are inversely proportional.

The constant for the course is 240.

If your speed was 1km/hour it would take 240 minutes.

It would take the runner 20 minutes to complete the course.

Note that this question can also be answered using the formula for speed.

Step-by-step guide: Speed distance time

Calculations with proportions

In order to answer problems involving a proportion formula:

Substitute in the given values and rearrange the resulting equation to determine the value of \textbf{k} .

Substitute the value of \textbf{k} into the formula written down in step 1.

Example 5: writing a proportion formula

y is directly proportional to x. 

When y=12, \ x=3.  

Find a formula for y in terms of x.

Identify the type of proportion and write down the appropriate formula. 

Example 6: writing a proportion formula

When a=6, \ b = 5.  

Find a formula for a in terms of b.

a = \frac{k}{b}

Common misconceptions

• Assuming worded problems reflect real life

Worded proportion problems can often imply things that are not reflective of real life. For example, It takes 3 workers 2 days to build a wall, how long does it take 4 workers to build the same wall? This question makes an assumption that all workers work the same hours each day and are equally efficient. This is not reflective of real life, but it is something we assume in order to model the situation mathematically.

• Assuming the unitary method is the only/best way to solve a proportion problem

There may be several ways to get to the correct answer for proportion questions. Some ways are more efficient than others depending on the numbers involved. You can always follow the step by step guide, however it is good practice to think independently about each question and consider other methods to develop your problem solving skills.

• Misinterpreting decimal answers

If the solution to a proportion problem is a decimal, think carefully about what this represents in the context of the question before writing your final answer.  For example, 5.3 pounds should be written as £5.30. 2.5 hours could be written as 2 hours 30 minutes.

Practice proportion questions

1. If 8 batteries cost £4.80, find the cost of 5 batteries.

This is a direct proportion problem. 

The cost of one battery would be,

The cost of 5 batteries would be,

2. If 3 paving slabs weigh 18 \ kg, find the weight of 7 slabs.

The weight of one slab would be,

The weight of 7 slabs would be,

3. If a taxi journey is shared by 4 people it costs £24 each. What does each person pay if there are only 3 people sharing the taxi for the same journey?

This is an inverse proportion problem. 

The cost of the whole taxi journey would be,

4\times 24=96 pounds.

Sharing this cost between 3 people would be,

4. If it takes 5 workers 12 hours to do a job, how long would it take 9 workers to complete the same job? Give your answer in hours and minutes.

3 hours 45 minutes

21 hours 6 minutes

6 hours 66 minutes

6 hours 40 minutes

The total time needed to complete the job would be,

5\times 12=60 hours.

Sharing this time between 9 workers would be,

Two thirds of an hour is 40 minutes, 60 \times \frac{2}{3} = 40 .

The final answer would be 6 hours 40 minutes.

5. Which of these equations indicates that y is directly proportional to x?

The correct equation will be in the form y=kx, where k is the constant of proportionality.

The correct equation will be, y=5x.

6. Which of these graphs indicates that y \propto x?

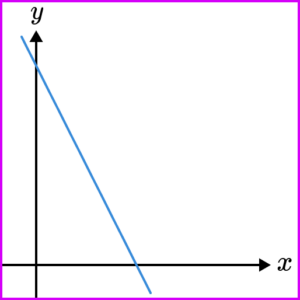
y \propto x means y is proportional to x. Therefore the graph should show that as x increases, y increases.

All direct proportion graphs go through the origin (0,0). As y is proportional to x (and not x^{2} \text{or} \sqrt{x} for example) the graph will be a straight line.

7. y is inversely proportional to x. When y=20, \ x=4. Find a formula for y in terms of x.

Start with the general formula for inverse proportion y = \frac{k}{x}.

Now substitute in the values of x and y and rearrange the resulting equation to find k.

\begin{aligned} 20 &= \frac{k}{4} \\\\ 20 \times 4 &= k \\\\ 80&=k \end{aligned} Finally, substitute this value of k into the general formula to get the final answer

Proportion GCSE questions

1. A recipe to make enough garlic bread for 5 people needs 75 \ g of butter.

Calculate the amount of butter needed to make garlic bread for 12 people.

2. y is inversely proportional to x.

Complete the table.

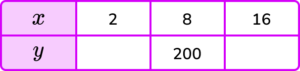
3. The graphs show different relationships between the variables x and y.

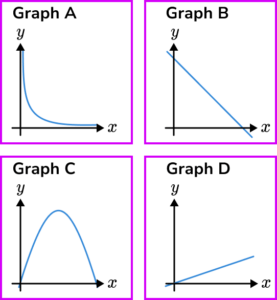
(a) Identify the graph which shows that y\propto x .

(b) Identify the graph which shows that y\propto \frac{1}{x} .

(a) Graph D

(b) Graph A

Learning checklist

You have now learned how to:

• Solve real world problems involving direct and inverse proportion
• Recognise formula and graphs for direct and inverse proportions

The next lessons are

• Compound measures
• Best buy maths

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.

Privacy Overview

• HW Guidelines
• Study Skills Quiz
• Find Local Tutors
• Demo MathHelp.com
• Join MathHelp.com

Select a Course Below

• ACCUPLACER Math
• Math Placement Test
• PRAXIS Math
• + more tests
• 5th Grade Math
• 6th Grade Math
• Pre-Algebra
• College Pre-Algebra
• Introductory Algebra
• Intermediate Algebra
• College Algebra

Proportions

Ratios Proportions Proportionality Solving Word Problems Similar Figures Sun's Rays / Parts

A ratio is one thing or value compared with or related to another thing or value; it is just a statement or an expression, and can only perhaps be simplified or reduced.

On the other hand, a proportion is two ratios which have been set equal to each other; a proportion is an equation that can be solved.

Content Continues Below

MathHelp.com

Solving Proportions

Advertisement

Solving a proportion means that we have been given an equation containing two fractions which have been set equal to each other, and we are missing one part of one of the fractions; we then need to solve for that one missing value. For instance, suppose we are given the following equation:

Verifying what we already knew, we get a solution of x  = 5 .

Often times, students are asked to solve proportions before they've learned how to solve rational equations , which can be a bit of a problem. If one hasn't yet learned about rational expressions (that is, polynomial fractions), then it will be necessary to "get by" with "cross-multiplication".

To cross-multiply , we start with an equation in which two fractions are set equal to each other. Then we take each denominator and move it aCROSS the "equals" sign and then MULTIPLY it against the other fraction's numerator. The cross-multiplication solution of the above exercise looks like this:

Then we would solve the resulting linear equation by dividing through by 2 to again arrive at x  = 5 .

Note the process in the above. We multiplied the left-hand side's denominator by the right-hand side's numerator, and then divided by the right-hand side's denominator. You may see this process explicitly applied for the solving of proportions. The method of solution would then by to cross-multiply the numbers (that is, in the direction that does not involve the variable), and then divide by the remaining number. In very informal notation, the process looks like this:

The green arrow pointing northeast (that is, from bottom left to upper right) indicates the multiplication step; the purple looping arrow that ends up pointing at the variable indicates the division step.

Solve the proportion: katex.render("\\small{ \\bm{\\color{green}{ \\dfrac{6}{13} = \\dfrac{18}{y} }}}", typed08); 6/13 = 18/ y

The variable in this proportion is in the denominator of the right-hand side's fraction, but that's okay. I can still cross-multiply and solve.

6/13 = 18/ y

(6)( y ) = (13)(18)

(6 y )/6 = 234/6

The solution of the proportion is the value of the variable, so my answer is:

If I'd done the shorthand method (shown with the green and purple arrows above), the computations would have been:

(13 × 18) ÷ 6 = 39 = y

It's harder to "show your work" using the shorthand method, but the shorthand method is easier to plug into your calculator. Use whatever method works well for you.

Solve the proportion: katex.render("\\small{ \\bm{\\color{green}{\\dfrac{5}{b} = \\dfrac{42}{35} }}}", typed10); 5/ b = 42/25

I'll cross-multiply, and then divide:

5/ b = 42/35

(5)(35) = ( b )(42)

(175)/42 = (42 b )/42

Hm... Can proportions have fractional solutions? Yes, definitely; they can! I mustn't let the only-whole-number exercises and examples mislead me into thinking that proportions must always have whole-number answers. They don't. My fractional answer is perfectly fine.

Proportions wouldn't be of much use if you only used them for reducing fractions. A more typical use would be something like the following:

The ratio of waterfowl in a given park is 16 ducks to 9 geese. Suppose that there are 192 ducks in total. How many geese are there in total?

They've asked me to solve for an unknown value, so I'll need an equation with a variable. They've given me a ratio, so my equation will be a proportion.

I'll let " G " stand for the unknown number of geese. I'll clearly label the orientation of my ratios (so I don't confuse which number stands for what), and then I'll set up my proportional equation:

I'll cross-multiply to solve for the value of G :

16 G = 1728

(16 G )/16 = (1728)/16

I labelled things clearly at the beginning, so I know that " G " stands for "the number of geese in the park". So my answer is:

"Cross-multiplying" is standard classroom language, in that it is very commonly used by students and instructors, but it is not technically a mathematical term. You might not see "cross-multiplication" mentioned in your textbook, but you will almost certainly hear it in your class or study group.

Notice how, when I was setting up my equation at the beginning of my solution above, I prefaced my proportion by writing out my ratio in words; namely:

This is not standard notation (in the sense of your textbook being likely to use it), but it can be very helpful for setting up proportions. By clearly labelling which values are represented by the numerators and denominators, respectively, you will help yourself keep track of what each number stands for; you won't mix up which number or unit goes where.

In other words, using this method will help you set up your proportions correctly. If you do not set up the ratios consistently (for instance, if, in the above example, I'd mixed up where the values for the "ducks" and the "geese" were supposed to go in the various fractions), I'd have gotten an incorrect answer. Clarity in your set-up is crucially important when working with proportions. We will return to this subject later.

URL: https://www.purplemath.com/modules/ratio2.htm

Page 1 Page 2 Page 3 Page 4 Page 5 Page 6 Page 7

Standardized Test Prep

College math, homeschool math, share this page.

• Terms of Use
• About Purplemath
• About the Author
• Tutoring from PM
• Advertising
• Linking to PM
• Site licencing

Visit Our Profiles

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Course: 7th grade   >   Unit 1

• Worked example: Solving proportions
• Solving proportions

Writing proportions example

• Writing proportions
• Proportion word problem: cookies
• Proportion word problem: hot dogs
• Proportion word problems

Want to join the conversation?

• Upvote Button navigates to signup page
• Downvote Button navigates to signup page
• Flag Button navigates to signup page

Video transcript

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

8.7: Solve Proportion and Similar Figure Applications

• Last updated
• Save as PDF
• Page ID 15179

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Objectives

By the end of this section, you will be able to:

• Solve proportions
• Solve similar figure applications

Before you get started, take this readiness quiz.

If you miss a problem, go back to the section listed and review the material.

• Solve \(\dfrac{n}{3}=30\). If you missed this problem, review Exercise 2.2.25 .
• The perimeter of a triangular window is 23 feet. The lengths of two sides are ten feet and six feet. How long is the third side? If you missed this problem, review Example 3.4.2

Solve Proportions

When two rational expressions are equal, the equation relating them is called a proportion .

Definition: PROPORTION

A proportion is an equation of the form \(\dfrac{a}{b}=\dfrac{c}{d}\), where \(b \ne 0\), \(d \ne 0\).

The proportion is read “a is to b, as c is to d"

The equation \(\dfrac{1}{2}=\dfrac{4}{8}\) is a proportion because the two fractions are equal.

The proportion \(\dfrac{1}{2}=\dfrac{4}{8}\) is read “1 is to 2 as 4 is to 8.”

Proportions are used in many applications to ‘scale up’ quantities. We’ll start with a very simple example so you can see how proportions work. Even if you can figure out the answer to the example right away, make sure you also learn to solve it using proportions.

Suppose a school principal wants to have 1 teacher for 20 students. She could use proportions to find the number of teachers for 60 students. We let x be the number of teachers for 60 students and then set up the proportion:

\[\dfrac{1\,\text{teacher}}{20\,\text{students}}=\dfrac{x\,\text{teachers}}{60\,\text{students}}\nonumber\]

We are careful to match the units of the numerators and the units of the denominators—teachers in the numerators, students in the denominators.

Since a proportion is an equation with rational expressions, we will solve proportions the same way we solved equations in Solve Rational Equations . We’ll multiply both sides of the equation by the LCD to clear the fractions and then solve the resulting equation.

Now we’ll do a few examples of solving numerical proportions without any units. Then we will solve applications using proportions.

Example \(\PageIndex{1}\)

\(\dfrac{x}{63}=\dfrac{4}{7}\).

Try It \(\PageIndex{1}\)

\(\dfrac{n}{84}=\dfrac{11}{12}\).

Try It \(\PageIndex{2}\)

\(\dfrac{y}{96}=\dfrac{13}{12}\).

Example \(\PageIndex{2}\)

\(\dfrac{144}{a}=\dfrac{9}{4}\).

Try It \(\PageIndex{3}\)

\(\dfrac{91}{b}=\dfrac{7}{5}\).

Try It \(\PageIndex{4}\)

\(\dfrac{39}{c}=\dfrac{13}{8}\).

Example \(\PageIndex{3}\)

\(\dfrac{n}{n+14}=\dfrac{5}{7}.\)

Try It \(\PageIndex{5}\)

\(\dfrac{y}{y+55}=\dfrac{3}{8}\).

Try It \(\PageIndex{6}\)

\(\dfrac{z}{z−84}=−\dfrac{1}{5}\).

Example \(\PageIndex{4}\)

\(\dfrac{p+12}{9}=\dfrac{p−12}{6}\).

Try It \(\PageIndex{7}\)

\(\dfrac{v+30}{8}=\dfrac{v+66}{12}\).

Try It \(\PageIndex{8}\)

\(\dfrac{2x+15}{9}=\dfrac{7x+3}{15}\).

To solve applications with proportions, we will follow our usual strategy for solving applications. But when we set up the proportion, we must make sure to have the units correct—the units in the numerators must match and the units in the denominators must match.

Example \(\PageIndex{5}\)

When pediatricians prescribe acetaminophen to children, they prescribe 5 milliliters (ml) of acetaminophen for every 25 pounds of the child’s weight. If Zoe weighs 80 pounds, how many milliliters of acetaminophen will her doctor prescribe?

Try It \(\PageIndex{9}\)

Pediatricians prescribe 5 milliliters (ml) of acetaminophen for every 25 pounds of a child’s weight. How many milliliters of acetaminophen will the doctor prescribe for Emilia, who weighs 60 pounds?

Try It \(\PageIndex{10}\)

For every 1 kilogram (kg) of a child’s weight, pediatricians prescribe 15 milligrams (mg) of a fever reducer. If Isabella weighs 12 kg, how many milligrams of the fever reducer will the pediatrician prescribe?

Example \(\PageIndex{6}\)

A 16-ounce iced caramel macchiato has 230 calories. How many calories are there in a 24-ounce iced caramel macchiato?

Try It \(\PageIndex{11}\)

At a fast-food restaurant, a 22-ounce chocolate shake has 850 calories. How many calories are in their 12-ounce chocolate shake? Round your answer to nearest whole number.

464 calories

Try It \(\PageIndex{12}\)

Yaneli loves Starburst candies, but wants to keep her snacks to 100 calories. If the candies have 160 calories for 8 pieces, how many pieces can she have in her snack?

Example \(\PageIndex{7}\)

Josiah went to Mexico for spring break and changed $325 dollars into Mexican pesos. At that time, the exchange rate had $1 US is equal to 12.54 Mexican pesos. How many Mexican pesos did he get for his trip?

Try It \(\PageIndex{13}\)

Yurianna is going to Europe and wants to change $800 dollars into Euros. At the current exchange rate, $1 US is equal to 0.738 Euro. How many Euros will she have for her trip?

590.4 Euros

Try It \(\PageIndex{14}\)

Corey and Nicole are traveling to Japan and need to exchange $600 into Japanese yen. If each dollar is 94.1 yen, how many yen will they get?

In the example above, we related the number of pesos to the number of dollars by using a proportion. We could say the number of pesos is proportional to the number of dollars. If two quantities are related by a proportion, we say that they are proportional.

Solve Similar Figure Applications

When you shrink or enlarge a photo on a phone or tablet, figure out a distance on a map, or use a pattern to build a bookcase or sew a dress, you are working with similar figures . If two figures have exactly the same shape, but different sizes, they are said to be similar. One is a scale model of the other. All their corresponding angles have the same measures and their corresponding sides are in the same ratio.

Definition: SIMILAR FIGURES

Two figures are similar if the measures of their corresponding angles are equal and their corresponding sides are in the same ratio.

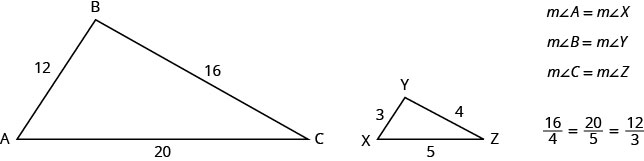
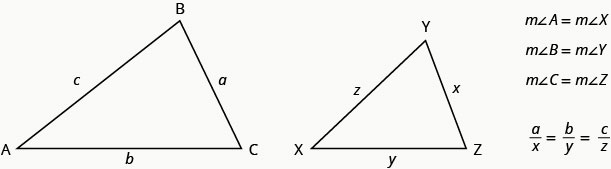
For example, the two triangles in Figure are similar. Each side of ΔABC is 4 times the length of the corresponding side of ΔXYZ.

This is summed up in the Property of Similar Triangles.

Definition: PROPERTY OF SIMILAR TRIANGLES

• If ΔABC is similar to ΔXYZ

To solve applications with similar figures we will follow the Problem-Solving Strategy for Geometry Applications we used earlier.

Definition: SOLVE GEOMETRY APPLICATIONS.

• Read the problem and make all the words and ideas are understood. Draw the figure and label it with the given information.
• Identify what we are looking for.
• Name what we are looking for by choosing a variable to represent it.
• Translate into an equation by writing the appropriate formula or model for the situation. Substitute in the given information.
• Solve the equation using good algebra techniques.
• Check the answer in the problem and make sure it makes sense.
• Answer the question with a complete sentence.

Example \(\PageIndex{8}\)

ΔABC is similar to ΔXYZ. The lengths of two sides of each triangle are given in the figure.

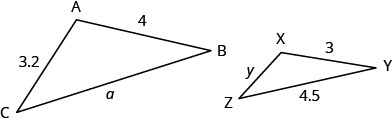
Find the length of the sides of the similar triangles.

Try It \(\PageIndex{15}\)

ΔABC is similar to ΔXYZ. The lengths of two sides of each triangle are given in the figure.

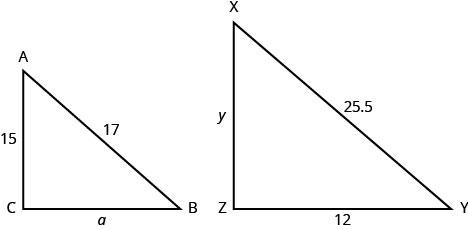
Find the length of side a

Try It \(\PageIndex{16}\)

The next example shows how similar triangles are used with maps.

Example \(\PageIndex{9}\)

On a map, San Francisco, Las Vegas, and Los Angeles form a triangle whose sides are shown in the figure below. If the actual distance from Los Angeles to Las Vegas is 270 miles find the distance from Los Angeles to San Francisco.

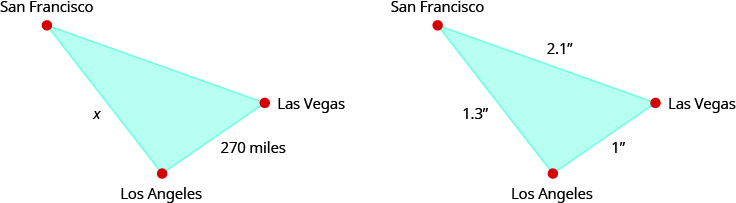
Try It \(\PageIndex{17}\)

On the map, Seattle, Portland, and Boise form a triangle whose sides are shown in the figure below. If the actual distance from Seattle to Boise is 400 miles, find the distance from Seattle to Portland.

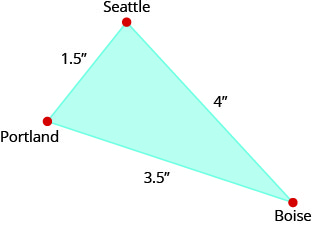
Try It \(\PageIndex{18}\)

Using the map above, find the distance from Portland to Boise.

We can use similar figures to find heights that we cannot directly measure.

Example \(\PageIndex{10}\)

Tyler is 6 feet tall. Late one afternoon, his shadow was 8 feet long. At the same time, the shadow of a tree was 24 feet long. Find the height of the tree.

Try It \(\PageIndex{19}\)

A telephone pole casts a shadow that is 50 feet long. Nearby, an 8 foot tall traffic sign casts a shadow that is 10 feet long. How tall is the telephone pole?

Try It \(\PageIndex{20}\)

A pine tree casts a shadow of 80 feet next to a 30-foot tall building which casts a 40 feet shadow. How tall is the pine tree?

Key Concepts

• Read the problem and make sure all the words and ideas are understood. Draw the figure and label it with the given information.