problem solving using addition

Problem Solving on Addition

Problem solving on addition will help us to get the idea on how to solve the basic addition statement problems.

1.  Three boys were playing cricket. Two more boys came along and played cricket with them. How many boys altogether were playing cricket?

Number of boys were playing cricket = 3

Number of boys came along and played cricket with them = 2

Therefore, total number of boys were playing cricket = 3 + 2 = 5

2.  Harry had 5 stamps. Mother gave him 4 more. How many stamps in all did Harry have?

Number of stamps Harry had = 5

Number of stamps his mother gave him = 4

Therefore, total number of stamps he have = 5 + 4 = 9

3. Rachael had 6 stamps. Father gave her 2 stamps. How many stamps does Rachael have now?

Number of stamps Rachael had = 6

Number of stamps her father gave her = 4

Therefore, total number of stamps she have now = 6 + 4 = 10

4. In a classroom, there were 2 brown tables, 1 red table and 3 green tables. How many tables were there altogether?

Number of brown tables = 2

Number of red table = 1

Number of green tables = 3

Therefore, total number of tables in a classroom = 2 + 1 + 3 = 6

5. Jack spent 5 dollars for a pen, 3 dollars for a color box, 2 dollars for a pencil box. How much did he spend altogether?

Amount of money Jack spent for a pen = $5

Amount of money he spent for a color box = $3

Amount of money he spent for a pencil box = $2

Therefore, total amount of money he spend altogether = $5 + $3 + $2 = 10

6. There were 6 yellow hats, 2 red hats and 6 blue hats. How many hats were there?

Number of yellow hats = 6

Number of red hats = 2

Number of blue hats = 6

Therefore, total number of hats were there = 6 + 2 + 6 = 14

7. Alex had 4 books on cars, 5 on airplanes and 7 on boats. How many books did he have in all?

Number of books on cars Alex had = 4

Number of books on airplanes = 5

Number of books on boats = 7

Therefore, total number of books he have in all = 4 + 5 + 7 = 16

More examples on statement problem solving on addition:

8. In a game Mary had the best score. She made 8 in her first turn, 6 in her second and 5 in her third. What was her total score?

Number of score Mary had in her first turn = 8

Number of score in her second turn = 5

Number of score in her third turn = 7

Therefore, total number of score Mary had in a game = 8 + 5 + 7 = 20

9. Sarah had 25 cards. She got 7 cards more. How many cards did she have then?

Number of cards Sarah had = 25

Number of cards she got more = 7

Therefore, total number of cards she have then = 25 + 7 = 32

10. A farmer had 45 sheep before he bought 25 more. How many sheep did he have then?

Number of sheep a farmer had = 45

Number of sheep he bought more = 25

Therefore, total number of sheep he have then = 45 + 25 = 70

Word Problems on Addition:

11. A basket had 28 mangoes in it. 14 more mangoes are kept in the basket. How many mangoes are there in the basket now?

The basket had                 2 8    mangoes

Mangoes kept in       (+)   1 4                      

Now, there are                 4 2 mangoes in all

Thus, there are 42 mangoes in the basket now.

12. Aaron scored 33 runs in the first cricket match and 29 runs in the second. How many runs did he score in all?

Aaron scored                  3 3  runs in the first match

He scored                (+)  2 9  runs in the second match

He scored                       6 2  runs in all                      

Thus, he scored 62 runs in all.

2nd Grade Math Practice

From Problem Solving on Addition to HOME PAGE

Didn't find what you were looking for? Or want to know more information about Math Only Math . Use this Google Search to find what you need.

New! Comments

• Preschool Activities
• Kindergarten Math
• 1st Grade Math
• 2nd Grade Math
• 3rd Grade Math
• 4th Grade Math
• 5th Grade Math
• 6th Grade Math
• 7th Grade Math
• 8th Grade Math
• 9th Grade Math
• 10th Grade Math
• 11 & 12 Grade Math
• Concepts of Sets
• Probability
• Boolean Algebra
• Math Coloring Pages
• Multiplication Table
• Cool Maths Games
• Math Flash Cards
• Online Math Quiz
• Math Puzzles
• Binary System
• Math Dictionary
• Conversion Chart
• Homework Sheets
• Math Problem Ans
• Free Math Answers
• Printable Math Sheet
• Funny Math Answers
• Employment Test
• Math Patterns
• Link Partners
• Privacy Policy

Recent Articles

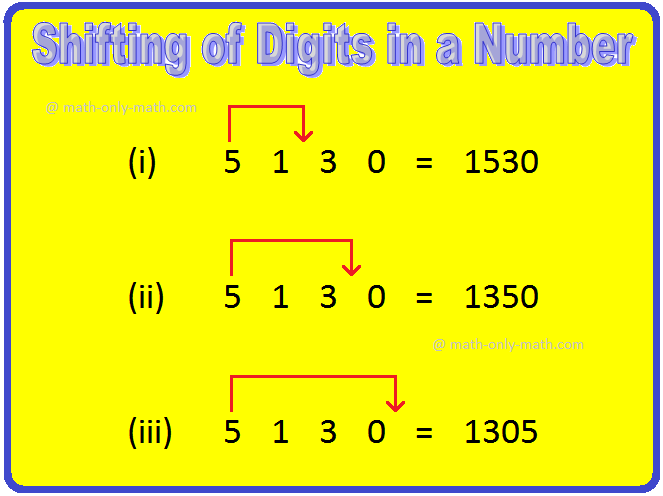
Shifting of Digits in a Number |Exchanging the Digits to Another Place

May 19, 24 06:35 PM

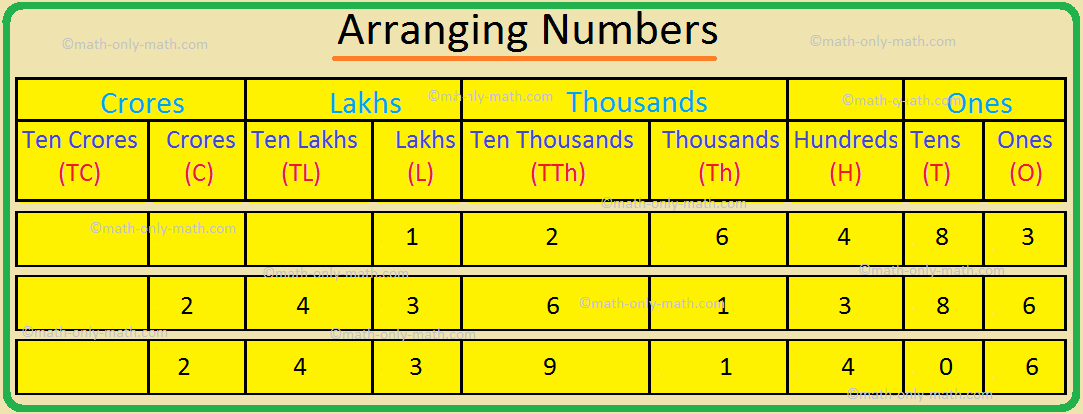
Formation of Greatest and Smallest Numbers | Arranging the Numbers

May 19, 24 03:36 PM

Formation of Numbers with the Given Digits |Making Numbers with Digits

May 19, 24 03:19 PM

Arranging Numbers | Ascending Order | Descending Order |Compare Digits

May 19, 24 02:23 PM

Comparison of Numbers | Compare Numbers Rules | Examples of Comparison

May 19, 24 01:26 PM

© and ™ math-only-math.com. All Rights Reserved. 2010 - 2024.

High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

In order to access this I need to be confident with:

Addition and subtraction

Here you will learn strategies on how to add and subtract, including using visual models, the number line, and algorithms.

Students will first learn about addition and subtraction in kindergarten, continue to add and subtract larger numbers in 2 nd and 3 rd grade, and learn the standard algorithm in 4 th grade. In 7 th grade, students learn to add and subtract with integers and then rational numbers.

What are addition and subtraction?

Addition is the operation of combining two or more numbers together. Subtraction is the operation of taking away from a number.

Students as early as pre-k have a basic, informal understanding of addition and subtraction. By the end of Kindergarten, students can operate within 10, heavily relying on models like counters or 10 frames to solve.

By the end of first grade, students should be able to add and subtract fluently within 20. As students work on repeatedly adding and subtracting with single digit numbers, they deepen their number sense around the operations by solving in different ways.

This includes beginning to build number bonds.

For example,

• Seeing 5+4 and knowing the sum is 9 without having to solve.
• Seeing 9-4 and knowing the difference is 5 without having to solve.

This aids students as they go into 2 nd and 3 rd grade and learn to add and subtract multi-digit numbers (within 1,000 ). At this level, students are still relying on number relationships, properties of operations, place value ideas, models, etc. to solve.

When adding 3- digit numbers, students may combine each place value of the addends separately.

Hundreds \hspace{1.1cm} Tens \hspace{1.2cm} Ones

200 + 100 \hspace{1cm} 30 + 40 \hspace{1cm} 5 + 9 \hspace{1cm}

= 300 \hspace{1.5cm} = 70 \hspace{1.3cm} = 14

And then add in the partial sums:

300+70+14=384

When subtracting numbers that are larger, students may use what they know about place value to solve.

The distance from 781-395 is the same as 786-400, it is just shifted up 5 on the number line.

Now solve 786-400 by taking away 4 hundreds.

786-400=386, so 781-395=386.

Once students have developed a flexible understanding of multi-digit addition and multi-digit subtraction in 2 nd grade and 3 rd grade, they learn the standard algorithm in 4 th grade.

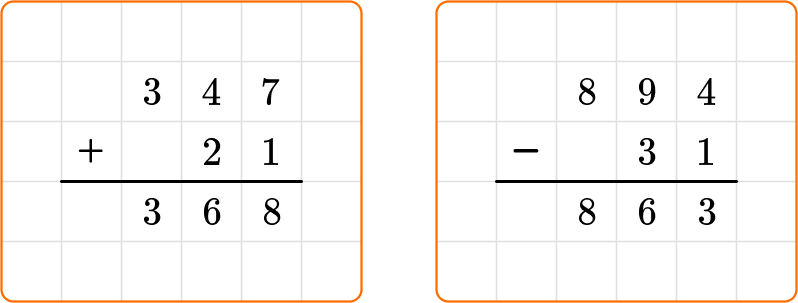
It is important to consider the place value of each digit and line up the corresponding digits in each number.

In 5 th grade and 6 th grade, students continue to add and subtract with whole numbers and apply these strategies to decimal operations.

See also: Adding and subtracting decimals

In 7 th grade, students learn to add and subtract integers and rational numbers.

You can add and subtract integers using visual models or a number line.

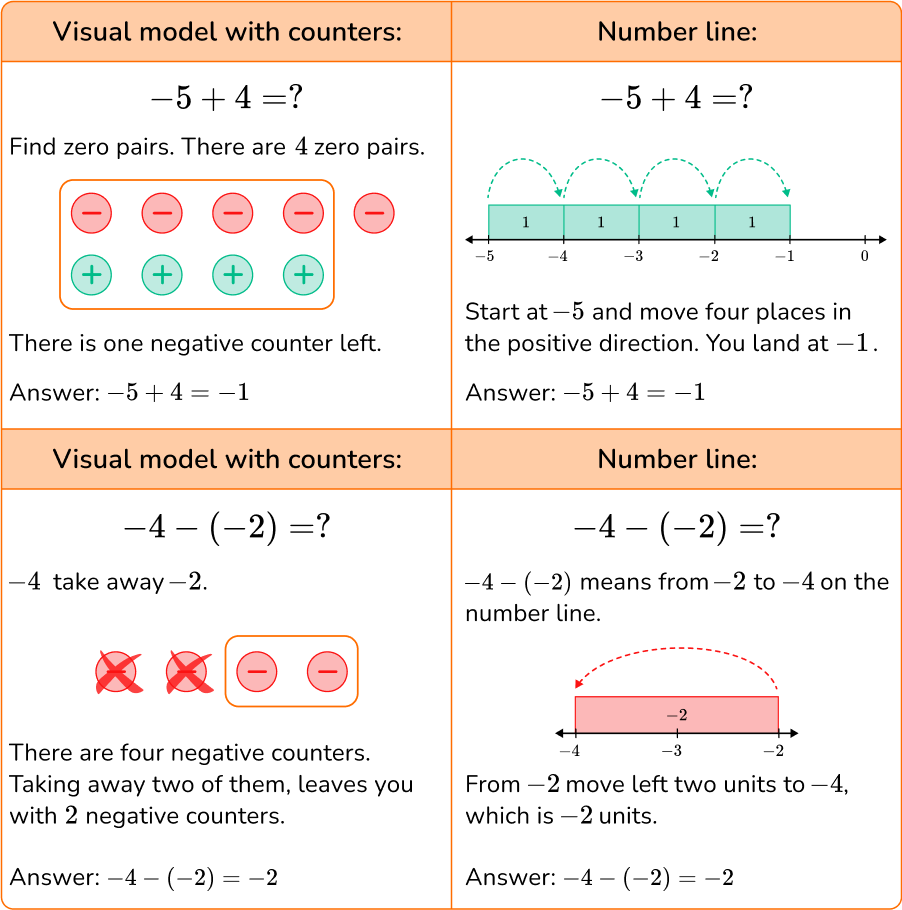
Step-by-step guide: Adding and subtracting integers

You can also add and subtract rational numbers using visual models or a number line.

[FREE] Addition and Subtraction Worksheet (Grade 2 to 7)

Use this quiz to check your grade 2, 3, 4 and 7 students’ understanding of addition and subtraction. 15+ questions with answers covering a range of 2nd, 3rd, 4th and 7th grade addition and subtraction topics to identify areas of strength and support!

Common Core State Standards

How does this apply to 2 nd grade math, 3 rd grade math, 4 th grade, and 7 th grade math?

• Kindergarten – Operations and Algebraic Thinking (K.OA.A.2) Solve addition and subtraction word problems, and add and subtract within 10, e.g., by using objects or drawings to represent the problem.
• Grade 1 – Operations and Algebraic Thinking (1.OA.C.6) Add and subtract within 20, demonstrating fluency for addition and subtraction within 10. Use strategies such as counting on; making ten (e.g., 8+6=8+2+4=10+4=14 ); decomposing a number leading to a ten (e.g., 13-4=13-3-1=10-1=9 ); using the relationship between addition and subtraction (e.g., knowing that 8+4=12, one knows 12-8=4 ); and creating equivalent but easier or known sums (e.g., adding 6+7 by creating the known equivalent 6+6+1=12+1=13 ).
• Grade 2 – Operations and Algebraic Thinking (2.OA.A.1) Use addition and subtraction within 100 to solve one- and two-step word problems involving situations of adding to, taking from, putting together, taking apart, and comparing, with unknowns in all positions, e.g., by using drawings and equations with a symbol for the unknown number to represent the problem.
• Grade 2 – Numbers and Operations in Base Ten (2.NBT.B.5) Fluently add and subtract within 100 using strategies based on place value, properties of operations, and/or the relationship between addition and subtraction.
• Grade 3 – Numbers and Operations in Base Ten (3.NBT.A.2) Fluently add and subtract within 1000 using strategies and algorithms based on place value, properties of operations, and/or the relationship between addition and subtraction.
• Grade 4 – Numbers and Operations in Base Ten (4.NBT.A.4) Fluently add and subtract multi-digit whole numbers using the standard algorithm.
• Grade 7- The Number System (7.NS.A.1) Apply and extend previous understandings of addition and subtraction to add and subtract rational numbers; represent addition and subtraction on a horizontal or vertical number line diagram.
• Grade 7- The Number System (7.NS.A.3) Solve real-world and mathematical problems involving the four operations with rational numbers.

How to add and subtract

There are a lot of ways to add and subtract. For more specific step-by-step guides, check out the individual pages linked in the “What are addition and subtraction?” section above or read through the examples below.

Addition and subtraction examples

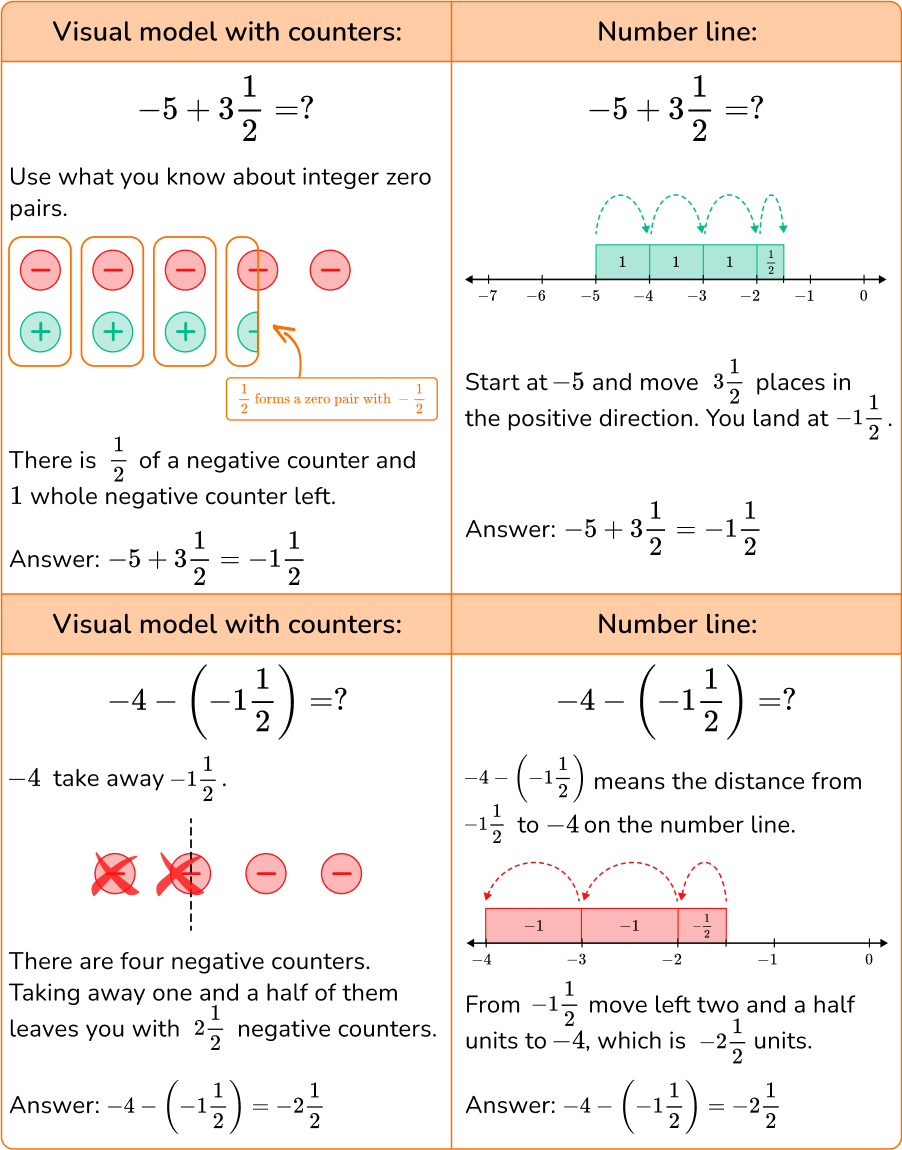
Example 1: two digit addition.

Solve 34 + 58.

Choose a strategy.

You can use a model of the tens and ones.

Combine the tens and ones.

You can create one new group of ten from 10 ones.

This leaves 9 tens and 2 ones, which is 92.

So, 34+58=92.

Example 2: three digit subtraction

Solve 340-291.

You can use a number line to count up to 340 from 291.

The difference between 291 and 340 is 49.

So, 340-291=49.

Example 3: addition with the algorithm

Add 4,297 + 381 with the algorithm.

Stack the numbers and line up the place values.

Add each column from right to left and regroup the numbers when necessary.

Write your final answer and check to make sure your answer is reasonable.

You can estimate to decide if your answer is reasonable.

4,297 rounds to 4,300.

381 rounds to 400.

4,300+400=4,700, so the answer should be close to 4,700. Since 4,678 is close, the answer is reasonable.

4,297+381=4,678

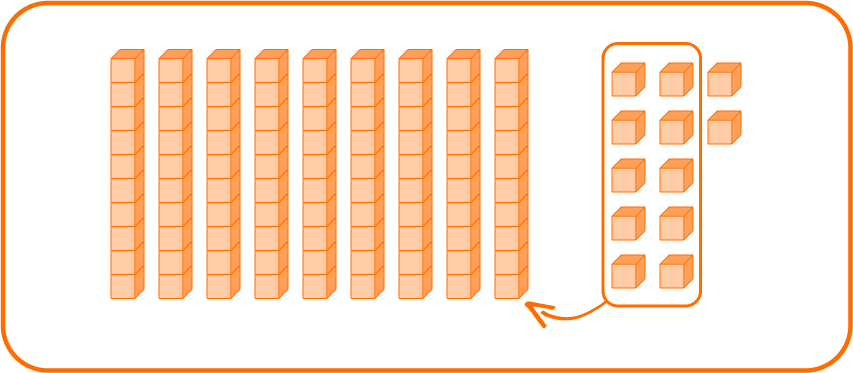
Example 4: subtraction word problem with the algorithm

After the harvest, a farmer has 2,148 pears. 213 of the pears are rotten and cannot be sold. If the farmer sells the rest, how many pears will she sell?

Write an equation that represents the word problem.

2,148 - 213 = ⬜

Subtract each column from right to left and exchange for a \bf{10} when necessary.

2,148 rounds to 2,000.

213 rounds to 200.

2,000-200=1,800, so the answer should be close to 1,800. Since 1,935 is close, the answer is reasonable.

2,148-213=1,935

Example 5: subtracting integers with models

Subtract: -4 -(-6)=?

Represent the problem with counters, identifying zero pairs with addition or adding zero pairs when necessary for subtraction.

-4 - (-6) starts with -4 and removes -6. Add 2 zero pairs in order to remove -6.

The answer is the leftover counters.

There are two positive counters left.

Example 6: adding rational numbers with the algorithm

Solve -34 \cfrac{2}{3}+\left(-567 \cfrac{3}{4}\right) .

Make sense of the calculation – relating to positive numbers when necessary.

-34 \cfrac{2}{3}+\left(-567 \cfrac{3}{4}\right) combines two negative amounts, which do not create zero pairs.

This means the answer will be even more negative. You can use the algorithm for addition to see what the total amount is.

Use an algorithm.

\begin{aligned}& 34 \frac{2}{3}+567 \frac{3}{4} \\\\ & =34 \frac{2 \times 4}{3 \times 4}+567 \frac{3 \times 3}{4 \times 3} \\\\ & =34 \frac{8}{12}+567 \frac{9}{12} \\\\ & =601 \frac{17}{12} \text { or } 602 \frac{5}{12}\end{aligned}

Decide if the final answer is positive or negative.

Adding two negative numbers results in a negative number. For example, if you started on the number line and went back 34 \cfrac{2}{3} and then you went back 567 \cfrac{3}{4} more, you are further down the negative side of the number line.

-34 \cfrac{2}{3}+\left(-567 \cfrac{3}{4}\right)=-602 \cfrac{5}{12}

Teaching tips for addition and subtraction

• Sufficient time using place value blocks, 100 s charts, grids and other interactive manipulatives should be provided to students when they are first learning to operate with any new set of numbers. The Common Core Standards intentionally allow time for students to develop an understanding of the operation, before learning how to use the algorithm.
• When students are first learning, encourage them to make connections between addition problems and subtraction problems. As students learn how to operate with any new set of numbers (whole, integer, or rational), it is crucial that they see the connection, as this opens the door to solving strategies, helps them make sense of the algorithms, and can be used to decide if an answer is reasonable. Understanding this relationship is also important for later topics like solving equations.
• When choosing printable math worksheets, look for resources that have missing numbers in all parts of the equation (start unknown, change unknown, result unknown). This helps students develop flexible ideas about the operations and can help prevent mindlessly grabbing numbers from word problems.
• Instead of giving students subtraction worksheets that have dozens of questions to solve, prioritize worksheets that allow students to solve in more than one way and that encourage them to consider the reasonableness of their answer. While there may be times that students are expected to solve in a larger quantity (for example, when learning the algorithm or completing a math review packet), the majority of student work should focus on depth not breadth.

Easy mistakes to make

• Not considering the place value of numbers when solving When using strategies to solve, students may choose a strategy they do not fully understand, causing them to misuse place value. For example, 56 + 78 Thinking that they can just add 5+6+7+8.
• Thinking subtraction always leads to a smaller number (and vice versa with addition) Students often create this false idea because subtracting a larger number from a smaller number or adding negative numbers are not addressed in elementary school. As students begin to operate with integers, it is important to consistently ask them to make sense of an equation before operating. This may be explaining the operation in their own words or using a model to show what is happening.

• Not making sense of operations with rational numbers By the time students operate with rational numbers, they will have learned many algorithms. Though algorithms can be useful, if used in a rush it is easy to make mistakes. Encourage students to think about a reasonable answer before solving. This can help them catch mistakes.

Practice addition and subtraction questions

1. Solve 39 + 46.

This leaves 8 tens and 5 ones, which is 85.

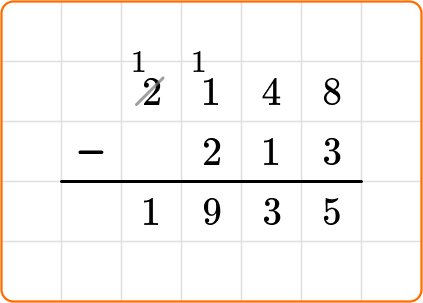
2. Solve 763-594.

You can use a number line to count up to 594 from 763.

The difference between 594 and 763 is 169.

So, 763-594=169.

3. Solve 5,621 + 3,570.

To use the standard algorithm, stack the numbers and line up the place values.

5,621 rounds to 6,000.

3,570 rounds to 4,000.

6,000+4,000=10,000, so the answer should be close to 10,000.

Since 9,191 is close, the answer is reasonable.

5,621+3,570=9,191

4. Jerome has 18,341 points in a game. Yasmine has 8,239 points in the same game. How many more points does Jerome have?

18,341-8,239 = ⬜

To solve with the standard algorithm, stack the numbers and line up the place values.

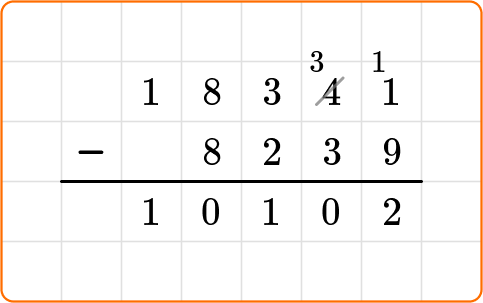
18,341 rounds to 18,000.

8,239 rounds to 8,000.

18,000-8,000=10,000, so the answer should be close to 10,000.

Since 10,102 is close, the answer is reasonable.

18,341-8,239=10,102

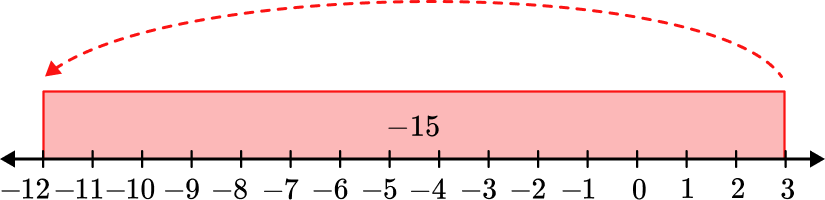
5. Subtract: -12-3= \, ?

-12-3 starts with -12 and removes 3 positives. Add 3 zero pairs in order to remove 3.

There are 15 negative counters left.

You can also think of this as the distance from 3 to -12.

6. Solve -84.4+391.02= \, ?.

-84.4 + 391.02 combines negative and positive values, which creates zero pairs. This means that -84.4+391.02=391.02-84.4, so you can use the standard algorithm to solve.

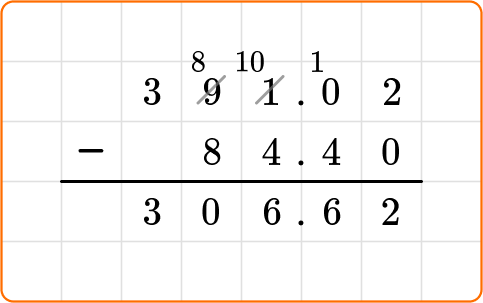
Adding a smaller negative number to a larger positive results in a positive answer.

-84.4+321.02=306.62

Addition and subtraction FAQs

Regrouping is when you are adding and have more than 10 ones, tens, hundreds, etc. and you need to regroup to create a new group of ten, hundred, etc. For example, if you add 27 + 18, you will have 3 tens and 15 ones. You regroup 10 of the ones to be a new group of ten, so you are left with 4 tens and 5 ones, or 45.

Exchanging is when you are subtracting and you do not have enough ones, tens, hundreds, etc. to take away and you need to exchange for a new group of ten, hundred, etc. For example, if you subtract 27 - 18, you start with 7 ones and need to take away 8. There are not enough, so you exchange one of the tens in 27 for ones. Then you have 1 ten and 17 ones. Now you can subtract 8 ones from 17 ones, leaving 9 ones.

In 4 th grade students learn to add and subtract fractions with common denominators. In fifth grade they learn to add and subtraction fractions with uncommon denominators. Then in 7 th grade they are expected to add and subtract negative fractions. See also: Adding and subtracting fractions

The next lessons are

• Multiplication and division
• Types of numbers
• Rounding numbers
• Adding and subtracting rational numbers
• Adding and subtracting negative numbers
• Add and subtract within 100
• Standard algorithm addition

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs .

[FREE] Common Core Practice Tests (Grades 3 to 6)

Prepare for math tests in your state with these Grade 3 to Grade 6 practice assessments for Common Core and state equivalents.

40 multiple choice questions and detailed answers to support test prep, created by US math experts covering a range of topics!

Privacy Overview

Child Login

• Kindergarten
• Number charts
• Skip Counting
• Place Value
• Number Lines
• Subtraction
• Multiplication
• Word Problems
• Comparing Numbers
• Ordering Numbers
• Odd and Even
• Prime and Composite
• Roman Numerals
• Ordinal Numbers
• In and Out Boxes
• Number System Conversions
• More Number Sense Worksheets
• Size Comparison
• Measuring Length
• Metric Unit Conversion
• Customary Unit Conversion
• Temperature
• More Measurement Worksheets
• Writing Checks
• Profit and Loss
• Simple Interest
• Compound Interest
• Tally Marks
• Mean, Median, Mode, Range
• Mean Absolute Deviation
• Stem-and-leaf Plot
• Box-and-whisker Plot
• Permutation and Combination
• Probability
• Venn Diagram
• More Statistics Worksheets
• Shapes - 2D
• Shapes - 3D
• Lines, Rays and Line Segments
• Points, Lines and Planes
• Transformation
• Quadrilateral
• Ordered Pairs
• Midpoint Formula
• Distance Formula
• Parallel, Perpendicular and Intersecting Lines
• Scale Factor
• Surface Area
• Pythagorean Theorem
• More Geometry Worksheets
• Converting between Fractions and Decimals
• Significant Figures
• Convert between Fractions, Decimals, and Percents
• Proportions
• Direct and Inverse Variation
• Order of Operations
• Squaring Numbers
• Square Roots
• Scientific Notations
• Speed, Distance, and Time
• Absolute Value
• More Pre-Algebra Worksheets
• Translating Algebraic Phrases
• Evaluating Algebraic Expressions
• Simplifying Algebraic Expressions
• Algebraic Identities
• Quadratic Equations
• Systems of Equations
• Polynomials
• Inequalities
• Sequence and Series
• Complex Numbers
• More Algebra Worksheets
• Trigonometry
• Math Workbooks
• English Language Arts
• Summer Review Packets
• Social Studies
• Holidays and Events
• Worksheets >
• Number Sense >
• Addition >

Addition Word Problem Worksheets

The addition word problem worksheets presented here involve performing addition operations with regrouping and without regrouping. Our extensive and well-researched word problem worksheets feature real-life scenarios that involve single-digit addition, two-digit addition, three-digit addition, and addition of large numbers. These pdf handouts are designed to provide ample practice for elementary school children. Free worksheets are included.

Single-digit Addition Word Problems

These printable practice worksheets involve simple addition of single-digit numbers. Read the word problems and perform addition operations to arrive at the answers.

• Download the set

Addition Word Problems: Sum up to 20

Featured in these worksheets are engaging word problems whose sums add up to 20. Addends may have a combination of single-digit and two-digit numbers.

Addition Problems: Two-digit and Single-digit

A number of real-life scenarios in the form of word problems featured in the addition worksheets here involve single digit and two-digit addends.

Two-digit Addition Problems - No Regrouping

The word problems in this section do not require regrouping or carrying. Find the answers to the word problems that feature two-digit addends.

Two-digit Addition Problems - With Regrouping

All two-digit addition word problems presented in this set of worksheets here require regrouping (carry over). Follow the place value columns to sum up the two-digit addends.

Theme based Word Problems

Presented here are worksheets with three colorful themes - Fall Season, Aquarium and Theme Park. Read the questions and solve the word problems. Answer keys are included.

Three-digit and Two-digit Addition

A total of 15 addition word problems spread over three PDF worksheets presented here require you to sum up three-digit addends with the two-digit addends.

Three-digit Addition Word Problems

Enhance your arithmetic skills. Read the word problems and sum up three-digit addends in these printable worksheets. Some problems may require regrouping. Answer key included in each worksheet.

Multi-digit Addition Word Problems: Adding Large Numbers

The word problems presented in the worksheets here feature large numbers with addends up to eight digits.

Related Worksheets

» Subtraction Word Problems

» Multiplication Word Problems

» Division Word Problems

» Math Word Problems

Become a Member

Membership Information

Privacy Policy

What's New?

Printing Help

Testimonial

Copyright © 2024 - Math Worksheets 4 Kids

This is a members-only feature!

Addition is ...

... bringing two or more numbers (or things) together to make a new total.

Example: When we add 2 and 3 we get 5 .

We can write it like this:

Write this down, with the answer, using numerals :

You should get:   4 + 3 = 7  

Have a Play

Drag the numerals to the two blue boxes see how addition works:

Swapping Places

Swapping the position of the numbers we are adding still gets the same result!

More Examples:

5 + 1 = 1 + 5 = 6

7 + 11 = 11 + 7 = 18

4 + 100 = 100 + 4 = 104

You get better at addition with practice, so we have:

Math Trainer - Addition (train your memory)

Kindergarten Worksheets (easy addition)

Addition Worksheets (normal and advanced)

Tips and Tricks

Learn more on our Addition Tips and Tricks page

Addition Table

We can also "look up" answers for simple addition using the Addition Table (but it is really best to learn to remember the answers).

Example: Find 3 + 5

• find the row starting with "3"

• move along to be under the column "5"

• and there is the number "8", so 3 + 5 = 8

Larger Numbers: Use Addition in Columns

Other names for Addition are Sum, Plus, Increase, Total

And the numbers to be added together are called the " Addends ":

Word Problems Involving Addition

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

• Pre-algebra lessons
• Pre-algebra word problems
• Algebra lessons
• Algebra word problems
• Algebra proofs
• Advanced algebra
• Geometry lessons
• Geometry word problems
• Geometry proofs
• Trigonometry lessons
• Consumer math
• Baseball math
• Math for nurses
• Statistics made easy
• High school physics
• Basic mathematics store
• SAT Math Prep
• Math skills by grade level
• Ask an expert
• Other websites
• K-12 worksheets
• Worksheets generator
• Algebra worksheets
• Geometry worksheets
• Free math problem solver
• Pre-algebra calculators
• Algebra Calculators
• Geometry Calculators
• Math puzzles
• Math tricks
• Member login

Addition word problems

 Addition word problems arise in any situations where there is a gain or an increase of something as a result of combining one or more numbers. Think of addition as combining parts to form a whole.

Consider the following situations. Problem #1: John has 800 dollars in his checking account. He received from his job a check for 1,200 dollars and deposit the amount in his checking account. How much money does he have in his checking after the deposit? Solution The fact of receiving money from his job is a gain. Therefore, we need to perform addition.

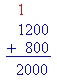
Total amount in checking account = 800 + 1200 = 2000 dollars Problem #2: Peter sells ice cream for a living. On Monday his revenue was 150 dollars. On Tuesday, his revenue was 100 dollars. Finally, on Wednesday, his revenue was 50 dollars. How much is Peter's revenue so far? Solution Peter is experiencing a gain in revenue. Therefore, we use addition.

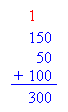
Peter's revenue = 150 + 50 + 100 = 300 dollars Problem #3: Eiffel Tower is about 1063 feet high. The Statue of Liberty along with its foundation and pedestal is about 305 feet. If you could put the Statue of Liberty on top of the Eiffel Tower, how high up in heaven will the two monuments reach? Solution The situation above is a combination of parts to form a whole. Therefore, we use addition.

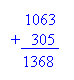
Problem #4:

Ana found a 15 dollar bill on the floor on Saturday.

Then on Sunday her parents gave her 155 dollars. How much does Ana have all together?

CLUE: Saturday~15 dollars Sunday~155 dollars

Solution: 15+155 = 170 dollars all together

Subtraction word problems

Have A Great Basic Math Word Problem?

Share it here with a very detailed solution!

Enter Your Title

Add a Picture/Graphic Caption (optional)  

Click here to upload more images (optional)

Author Information (optional)

To receive credit as the author, enter your information below.

Submit Your Contribution

• Check box to agree to these   submission guidelines .
• I am at least 16 years of age.
• I understand and accept the privacy policy .
• I understand that you will display my submission on your website.

(You can preview and edit on the next page)

What Other Visitors Have Said

Click below to see contributions from other visitors to this page...

Click here to write your own.

Recent Articles

How to divide any number by 5 in 2 seconds.

Feb 28, 24 11:07 AM

Math Trick to Square Numbers from 50 to 59

Feb 23, 24 04:46 AM

Sum of Consecutive Odd Numbers

Feb 22, 24 10:07 AM

100 Tough Algebra Word Problems. If you can solve these problems with no help, you must be a genius!

 Recommended

About me :: Privacy policy :: Disclaimer :: Donate   Careers in mathematics  

Copyright © 2008-2021. Basic-mathematics.com. All right reserved

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Course: 2nd grade   >   Unit 3

• Adding and subtracting on number line word problems
• Adding two digit numbers on a number line
• Add and subtract on the number line word problems

Multi step addition word problem

• 2-step addition word problems within 100
• Multi-step subtraction word problem
• 2-step subtraction word problems within 100

Want to join the conversation?

Video transcript.

Powerful online learning at your pace

Problem Structures for Addition & Subtraction

Quick pop quiz. How many problem structures are there for addition and subtraction problems?

If you said somewhere around 15 structures, you’re in the right ballpark. Unfortunately, students are often exposed to only the simplest structures. As teachers, we need to have an understanding of all the structures and teach them to our students in a methodical way.

This post contains affiliate links, which simply means that when you use my link and purchase a product, I receive a small commission. There is no additional cost to you, and I only link to books and products that I personally use and recommend.

“…teachers who are not aware of the variety of situations and corresponding structures may randomly offer problems to students without the proper sequencing to support students; full grasp of the meaning of the operations.” (Van de Walle et al)

The charts below were adapted from Elementary and Middle School Mathematics: Teaching Developmentally (Van de Walle et al), a phenomenal book for developing your own understanding of math.

The addition/subtraction structures are grouped into three main types: Change, Part/Part/Whole, and Comparison. For each type, there are multiple structures, depending on what information is known and unknown.

Change Problems

One of the first things you might notice is that the structures are not designated as addition or subtraction. While we typically think of  joining as addition and  separating as subtraction, you’ll see from the chart that is not always the case.  Result Unknown is the simplest and most familiar structure. You might think of these as classic addition and subtraction problems. As we move across the chart, the problems become increasingly complex, and we see that the Change Unknown and  Start Unknown structures can be interpreted as either addition or subtraction.

An appropriate way to introduce the problems is to start with the simplest,  Result Unknown , problems. Start with Join problems and allow students to practice solving just that type of problem. Help students focus on the meaning of each number in the problem, in terms of Change , Start , or Result . Drawing models is a good strategy for helping students analyze and visualize each problem. Next, introduce Separate problems, again giving them practice with just that type. Then it’s time to mix them up, so students have to determine the appropriate structure, based on the problem.

Now start to move across the chart, using the same process. Introduce the next structure (Join, Change Unknown ), practice the structure, and then mix it in with the others they already know. Keep in mind that this process takes time. If you’re a second-grade teacher, make a schedule for introducing the structures throughout the school year. Use numbers appropriate to the students’ computation skills.

Part-Part-Whole

Part-Part-Whole problems are very similar to Change. The subtle difference is that often there is no action in these problems, which makes them a little more abstract for students. The Whole Unknown structure is a very simple addition problem. In the One Part Unknown structure, we know the total and one of the parts, but we are missing the other part. This is also commonly called a Missing Addend problem. We often solve this type of problem using subtraction, but a counting-up strategy works well also. A really interesting structure is Both Parts Unknown. It’s a word problem application of knowing all the combinations for a number !

As students are introduced to more of the structures, remember that it’s just as important that they generate problems as solve them. I love an activity I call You Write the Story . Give students an equation and have them write a story to go with it and draw a model for their story.

One other note about Change and Part-Part-Whole problems, while these examples all have two addends, you can also use more than two addends to provide more of a challenge. Think: There are 425 students in the cafeteria. One hundred twenty-seven students are 5th graders, 146 are 4th graders, and the rest are 3rd graders. How many 3rd graders are in the cafeteria?

Finally, we have Comparison problems, which involve comparing two quantities–a larger quantity and a smaller one. They can also be written using either more or  fewer.  Fewer is by far more difficult for students. We want to make sure we introduce comparison subtraction using manipulatives to help students understand the structure. See this pos t for more information.

There you have it! All the structures for addition and subtraction problems. You can download your own copy of the tables showing the structures using the button below.

I look forward to hearing how you will teach these structures in your classroom, so be sure to leave a comment!

Resources for problem structures

Morrow-Leong, K., Moore, S. D., & Gojak, L. (2021). Mathematize it!: Going beyond key words to make sense of word problems , grades K-2 or grades 3-5 . Thousand Oaks, CA: Corwin.

Carpenter, Thomas P., et al. (2015) Children’s Mathematics: Cognitively Guided Instruction . Heinemann.

Similar Posts

Using Ten-Frames to Understand Numbers from 11-20

You’ve simply gotta love it when an observation lesson goes way better than you could have expected! Today I was getting ready to work with my Firsties when my AP…

The Hiding Assessment in Action

Fluency and flexibility with numbers are the hallmarks of mathematical thinking. For our students to excel in mathematics, they must understand how numbers can be composed and decomposed. That’s why…

Why Students Don’t Know Their Basic Math Facts and How to Help

If you teach 3rd grade, you know that some students come to your class not knowing their basic addition and subtraction facts. And in 4th and 5th grade, there are…

Fact Practice Your Students Will Love!

Kids are competitive. Heck, adults are competitive. Add a little competition to your fact practice activities and you’re sure to have a hit on your hands. I call this game…

Reasoning about Decimal Operations

The Common Core State Standards (CCSS) now have 5th graders computing with decimals. CCSS 5.NBT.7 reads: Add, subtract, multiply, and divide decimals to hundredths, using concrete models or drawings and…

Fact Families vs Number Bonds

For many years, primary teachers taught fact families. If you look carefully at either the CCSSM or the Texas state standards, the TEKS, you will not see fact families mentioned…

Great post! I’ve been reading the Mathematize IT: Making Sense books also.

Do you have a post for Problem Structures of multiplication and division?I saw the book, but I was hoping you had something more like this post for multiplication and division.

I follow all your posts! Thank you for helping me become a better teacher❤️

Thanks for your kind comments! I don’t have a post, but I do have a document with all the structures for all operations . Enjoy!

This is a great visual! Thanks for sharing.

Awesome blog and charts! I did notice that “amount” is misspelled in the last chart in the red boxes.

Well, yes it is! Thanks so much for calling it to my attention. I’ll get it corrected straight away.

Late to the game but I LOVE THIS!

What are your thoughts on multistep problems as it relates to these structures?

That would be another, and trickier, step! Being able to comprehend what’s happening in the problem is key. Check out this post on the 3 Reads Protocol for a great strategy for improving comprehension.

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

• Home   |  
• About   |  
• Contact Us   |  
• Privacy   |  
• Newsletter   |  
• Shop   |  
• 🔍 Search Site
• Easter Color By Number Sheets
• Printable Easter Dot to Dot
• Easter Worksheets for kids
• Kindergarten
• All Generated Sheets
• Place Value Generated Sheets
• Addition Generated Sheets
• Subtraction Generated Sheets
• Multiplication Generated Sheets
• Division Generated Sheets
• Money Generated Sheets
• Negative Numbers Generated Sheets
• Fraction Generated Sheets
• Place Value Zones
• Number Bonds
• Addition & Subtraction
• Times Tables
• Fraction & Percent Zones
• All Calculators
• Fraction Calculators
• Percent calculators
• Area & Volume Calculators
• Age Calculator
• Height Calculator
• Roman Numeral Calculator
• Coloring Pages
• Fun Math Sheets
• Math Puzzles
• Mental Math Sheets
• Online Times Tables
• Online Addition & Subtraction
• Math Grab Packs
• All Math Quizzes
• 1st Grade Quizzes
• 2nd Grade Quizzes
• 3rd Grade Quizzes
• 4th Grade Quizzes
• 5th Grade Quizzes
• 6th Grade Math Quizzes
• Place Value
• Rounding Numbers
• Comparing Numbers
• Number Lines
• Prime Numbers
• Negative Numbers
• Roman Numerals
• Subtraction
• Add & Subtract
• Multiplication
• Fraction Worksheets
• Learning Fractions
• Fraction Printables
• Percent Worksheets & Help
• All Geometry
• 2d Shapes Worksheets
• 3d Shapes Worksheets
• Shape Properties
• Geometry Cheat Sheets
• Printable Shapes
• Coordinates
• Measurement
• Math Conversion
• Statistics Worksheets
• Bar Graph Worksheets
• Venn Diagrams
• All Word Problems
• Finding all possibilities
• Logic Problems
• Ratio Word Problems
• All UK Maths Sheets
• Year 1 Maths Worksheets
• Year 2 Maths Worksheets
• Year 3 Maths Worksheets
• Year 4 Maths Worksheets
• Year 5 Maths Worksheets
• Year 6 Maths Worksheets
• All AU Maths Sheets
• Kindergarten Maths Australia
• Year 1 Maths Australia
• Year 2 Maths Australia
• Year 3 Maths Australia
• Year 4 Maths Australia
• Year 5 Maths Australia
• Meet the Sallies
• Certificates

3rd Grade Addition and Subtraction

Word problems.

Welcome to our 3rd Grade Addition and Subtraction Word Problems page. Here is our selection of free addition and subtraction word problem worksheets, which will help your child practice solving a range of addition and subtraction problems using 3-digit and 4-digit numbers.

For full functionality of this site it is necessary to enable JavaScript.

Here are the instructions how to enable JavaScript in your web browser .

Quicklinks to ...

• 3 Digit Addition & Subtraction Word Problems
• 4 Digit Addition & Subtraction Word Problems
• 2-Step Addition & Subtraction Word Problems
• Easier Addition & Subtraction Worksheets
• More related resources
• Addition & Subtraction Word Problems up to 1000 Online Quiz

3-digit and 4-digit Word Problems

Each sheet consists of a range of 5 addition and subtraction word problems with numbers up to thousands.

There is a space on each sheet for working out, so that your child can write out the problem and solve it.

We have split the worksheets up into 3-digit word problems and 4-digit word problems.

Using these sheets will help your child to:

• add and subtract numbers with 3-digit and 4-digit numbers;
• solve addition and subtraction word problems with and without regrouping.
• recognise the language used in addition and subtraction - sum, total, difference, how many more, etc.
• solve problems involving more than 1 step.

3rd Grade Addition and Subtraction Word Problems

3-digit addition and subtraction word problems.

There are two versions of each sheet.

The first version (version A) contains problems where no regrouping is needed.

The second version (version B) contains similar problems but regrouping is needed to solve them.

Answers have been provided with each sheet, along with the calculation needed to solve the problem.

The following sheets are all 1-step addition or subtraction word problems.

• 3-Digit Addition and Subtraction Word Problems Sheet 1A (no regrouping)
• PDF version
• 3-Digit Addition and Subtraction Word Problems Sheet 1B
• 3-Digit Addition and Subtraction Word Problems Sheet 2A (no regrouping)
• 3-Digit Addition and Subtraction Word Problems Sheet 2B

4-digit Addition and Subtraction Word Problems

The word problems all involve either addition or subtraction (both with and without regrouping).

• 4-Digit Addition and Subtraction Word Problems Sheet 1
• 4-Digit Addition and Subtraction Word Problems Sheet 2

Harder 2-Step Addition and Subtraction Word Problems

These problems are trickier than those above.

Each problem involved two steps to solve, and may involve just addition, just subtraction or both operators.

There are 4 problems on each sheet, and more space to work out the solutions.

• 2-Step Addition Subtraction Problems up to 3-digits Sheet 1
• 2-Step Addition Subtraction Problems up to 4-digits Sheet 1

Looking for some easier worksheets?

Take a look at our Subtraction word problems for first graders.

On this page, your child will learn to work out basic subtraction word problems with numbers to 20.

• 2nd Grade Addition and Subtraction Word Problems (up to 100)

More Recommended Math Worksheets

Take a look at some more of our worksheets similar to these.

More 3rd Grade Addition and Subtraction Worksheets

Here you will find some more of our Addition and Subtraction Worksheet generators for creating your own bespoke addition and subtraction worksheets.

• Addition Subtraction Fact Worksheets (randomly generated)
• Column Addition and Subtraction Worksheets (randomly generated)

More 3rd Grade Math Word Problems

Using the 3rd Grade Math worksheets will help your child to:

• apply their addition, subtraction, and multiplication skills;
• develop their knowledge of fractions;
• apply their knowledge of rounding and place value;
• solve a range of 'real life' problems.

These sheets involve solving one or two more challenging longer problems.

• 3rd Grade Math Problems

These sheets involve solving many 'real-life' problems involving data.

• Math Word Problems for kids 3rd Grade

These sheets involve solving 3-digit and 4-digit addition word problems.

• Addition Word Problems 3rd Grade (3- and 4-digits)

These sheets involve solving 3-digit and 4-digit subtraction problems.

• Subtraction Word Problems 3rd Grade

These sheets involve solving a range of multiplciation problems.

• Multiplication Word Problem Worksheets 3rd Grade

These sheets involve solving a range of division problems.

• Division Worksheets Grade 3 Word Problems

Addition and Subtraction Word Problems to 1000 Online Quiz

Our quizzes have been created using Google Forms.

At the end of the quiz, you will get the chance to see your results by clicking 'See Score'.

This will take you to a new webpage where your results will be shown. You can print a copy of your results from this page, either as a pdf or as a paper copy.

For incorrect responses, we have added some helpful learning points to explain which answer was correct and why.

We do not collect any personal data from our quizzes, except in the 'First Name' and 'Group/Class' fields which are both optional and only used for teachers to identify students within their educational setting.

We also collect the results from the quizzes which we use to help us to develop our resources and give us insight into future resources to create.

For more information on the information we collect, please take a look at our Privacy Policy

We would be grateful for any feedback on our quizzes, please let us know using our Contact Us link, or use the Facebook Comments form at the bottom of the page.

This quick quiz tests your knowledge and skill at solving addition and subtraction word problems within 1000.

How to Print or Save these sheets 🖶

Need help with printing or saving? Follow these 3 steps to get your worksheets printed perfectly!

• How to Print support

Subscribe to Math Salamanders News

Sign up for our newsletter to get free math support delivered to your inbox each month. Plus, get a seasonal math grab pack included for free!

• Newsletter Signup

Return to 3rd Grade Math Worksheets hub

Return to Addition Worksheets hub

Return to Subtraction Worksheets hub

Return from 3rd Grade Addition and Subtraction to Math Salamanders Home Page

Math-Salamanders.com

The Math Salamanders hope you enjoy using these free printable Math worksheets and all our other Math games and resources.

We welcome any comments about our site or worksheets on the Facebook comments box at the bottom of every page.

New! Comments

TOP OF PAGE

© 2010-2024 Math Salamanders Limited. All Rights Reserved.

• Privacy Policy
• Copyright Policy

Reading & Math for K-5

• Kindergarten
• Learning numbers
• Comparing numbers
• Place Value
• Roman numerals
• Subtraction
• Multiplication
• Order of operations
• Drills & practice
• Measurement
• Factoring & prime factors
• Proportions
• Shape & geometry
• Data & graphing
• Word problems
• Children's stories
• Leveled Stories
• Context clues
• Cause & effect
• Compare & contrast
• Fact vs. fiction
• Fact vs. opinion
• Main idea & details
• Story elements
• Conclusions & inferences
• Sounds & phonics
• Words & vocabulary
• Reading comprehension
• Early writing
• Numbers & counting
• Simple math
• Social skills
• Other activities
• Dolch sight words
• Fry sight words
• Multiple meaning words
• Prefixes & suffixes
• Vocabulary cards
• Other parts of speech
• Punctuation
• Capitalization
• Narrative writing
• Opinion writing
• Informative writing
• Cursive alphabet
• Cursive letters
• Cursive letter joins
• Cursive words
• Cursive sentences
• Cursive passages
• Grammar & Writing

Breadcrumbs

• Word Problems
• Addition (1-3 digits)

Download & Print Only $7.90

Addition word problems (1-3 digits)

Addition word problems with numbers under 1,000.

These grade 2 word problem worksheets are solved by forming addition equations involving 1, 2 or 3 digit numbers.   Sums are under 1,000.  Most questions have only 2 addends though some have 3.  

These worksheets are available to members only.

Join K5 to save time, skip ads and access more content. Learn More

More word problem worksheets

Explore all of our math word problem worksheets , from kindergarten through grade 5.

What is K5?

K5 Learning offers free worksheets , flashcards  and inexpensive  workbooks  for kids in kindergarten to grade 5. Become a member  to access additional content and skip ads.

Our members helped us give away millions of worksheets last year.

We provide free educational materials to parents and teachers in over 100 countries. If you can, please consider purchasing a membership ($24/year) to support our efforts.

Members skip ads and access exclusive features.

Learn about member benefits

This content is available to members only.

• Forgot Password?

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

4.3: Addition Algorithms

• Last updated
• Save as PDF
• Page ID 82997

• Julie Harland
• MiraCosta College

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

You will need: A Calculator, Base Blocks (Material Cards 4-15)

There is no one algorithm that everyone uses for adding numbers together. A teacher should be familiar with several methods so that the most number of students can be reached. What's important is that students understand what addition means and knows how to add numbers together one way or another. If a student figures out an algorithm that works on their own, I think that's terrific. It shows creativity and the student probably won't forget it. My hope is that more and more teachers realize many paths may lead to solving a problem correctly and that there is usually no reason to insist students work a problem in a particular way. There are many ways to solve a problem and diversity should be encouraged. This course is a little different because you are presumably interested in becoming a teacher. Therefore, it is important for you to learn as many ways as possible to work problems as well as discover some methods of your own. In this section, you will be learning a variety of algorithms for adding and should be able to work through and explain the procedures for working a problem using any of the methods presented. You will learn some new methods for addition and will be using them to add numbers in Base Ten as well as in other bases.

The DOT METHOD for adding columns of single digits

Here is a method for adding several digits together without having to keep a large running total in your head. The idea is that you only add two single digits together at a time. Any time you add and get a number over 9, you put down a dot and only keep the unit's digit in your memory. The dot stands for the ten. For instance, since 6 + 7 = 13 (which is 10 + 3), you write a dot and think 3. Think 6 + 7 = Dot 3 . In the example below, to add eight numbers together, a common approach would be to add the first two digits together, then keep adding on the next digit until all eight digits have been added. In other words, someone might think: 6 + 7 is 13, 13 + 8 is 21, 21 + 3 is 24, 24 + 5 is 29, 29 + 9 is 38, 38 + 4 is 42 and 42 + 7 is 49. Although this yields the correct answer, it's easy to lose track along the way. With the DOT METHOD shown, a dot is placed by a number if after it is added on, the sum is ten or more. At each step of the way, I've written in parentheses what number you think of after adding each digit. To start, see the eight digits to be added. Step 1: 6 + 7 = 13 so write a dot and think 3; Step 2: 3 + 8 = 11 so write a dot and think 1; Step 3: 1 + 3 = 4 so think 4; Step 4: 4 + 5 =9 so think 9; Step 5: 9 + 9 = 18 so write a dot and think 8; Step 6: 8 + 4 = 12 so write a dot and think 2; Step 7: 2 + 7 = 9 so write a 9 under the bar since all digits have been added. Count the dots (4), which stands for how many tens (40) and write in front of the 9. The answer is 49. Try it on your own now!

In the example just shown on the previous page, every single step, including what you think is shown. In reality, this is a quick algorithm and if you looked at the problem after someone did it, the work on the left is all you would see. To the right are are two more examples. Actually, each is the same sum of numbers written in a different order, which is another way to check addition! A quick check when adding only two numbers is to reverse the order and add again.

Use the dot method to add the following columns of digits shown to the right.

By the way, you could put the dots to the left or right of the digit, do whatever is most comfortable for you. If you are adding without paper and pencil, use your fingers to keep track of the dots! Instead of writing a dot, put up a finger. The beauty of this addition is you never have to keep a number higher than nine in your head!

The dot method could also be used to add several digits written in a horizontal format. The dots could be placed over the numerals. Try it on the following problems. Make up your own problems for part d and part e.

The Scratch Method

The Scratch Method is similar to the dot method. Any time you add and get a number over nine, you scratch off the last digit added. The scratch, like the dot, will represent ten. Just as in the dot method, you only keep the unit's digit in your memory or as an alternative, write the unit's digit to the right and just below the digit just scratched off. This can be done in the dot method also. I'll illustrate the steps involved by writing down the unit's digits this time. When the sum is less than ten, it is kept in your head. Parentheses will be used to denote what I am thinking in my head. The following problem is exactly the same one I did before when using the dot method. To start, see the eight digits to be added. Step 1: 6 + 7 = 13 so scratch off the 7 and write 3; Step 2: 3 + 8 = 11 so scratch off the 8 and write 1; Step 3: 1 + 3 = 4 so think 4; Step 4: 4 + 5 =9 so think 9; Step 5: 9 + 9 = 18 so scratch off the 9 and write 8; Step 6: 8 + 4 = 12 so scratch off the 4 and write 2; Step 7: 2 + 7 = 9 so write a 9 under the bar since all digits have been added. Count the scratches (4), which stands for how many tens (40) and write in front of the 9. The answer is 49. Try the problem on your own.

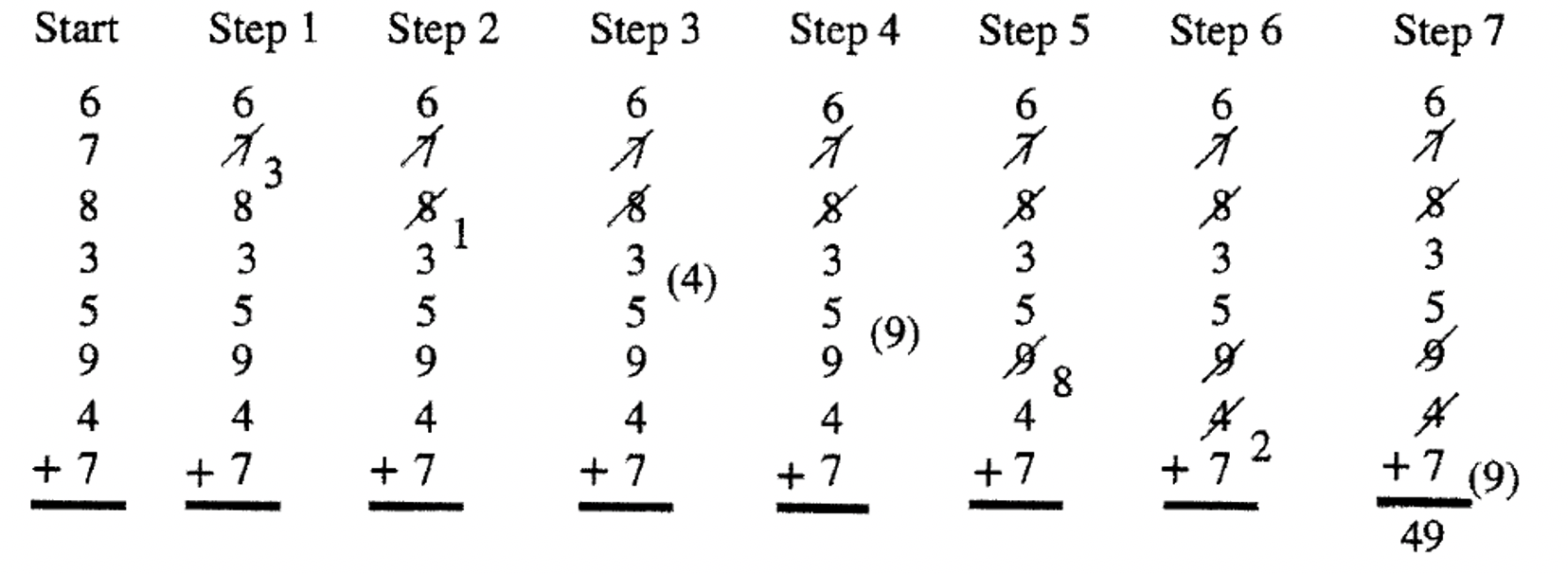
The above problem shows every single step, including what you think as you go along. If you were to look at the problem after someone did it, it would look like what you see on the left. More examples are shown on the right. Keeping the unit's digit in memory is faster than writing them down at each step. Try it both ways and ten adopt what's easiest and/or faster for you.

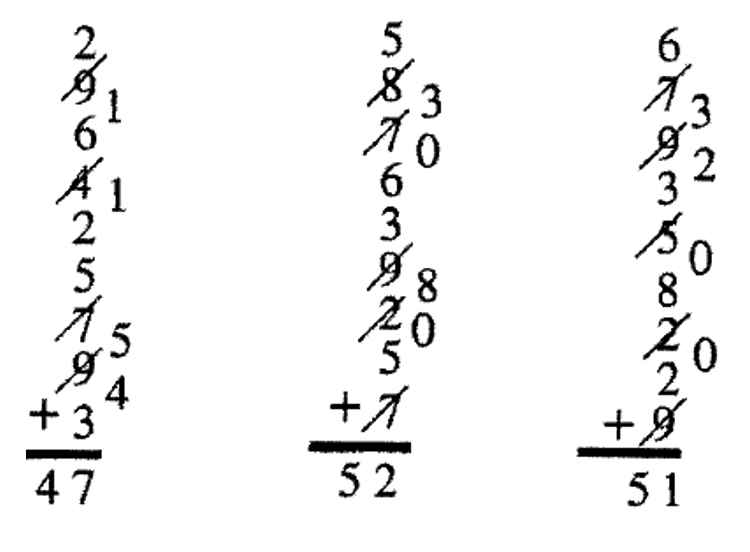
Use the scratch method to add the following columns of digits. Make up your own problem with at least 12 numbers for part e.

The Dot and Scratch Methods can be used to add numerals with more than one digit. Add one column at a time, leaving a little space between the columns for dots if you use the Dot Method. To the right is an example of adding using the Scratch method with the usual method of adding from right to left and carrying. In this case, I am keeping each unit's digit in my head as opposed to writing each digit down after each scratch. The first column has four scratches, so the 4 is carried to column 2. NOTE: Unless you practice several problems using these methods, it probably won't seem easier to add using one of these ways than whatever method you are used to using. But if you practice, you will probably become a whiz at addition and never go back to the old way!

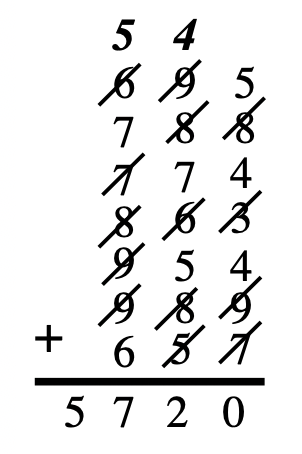
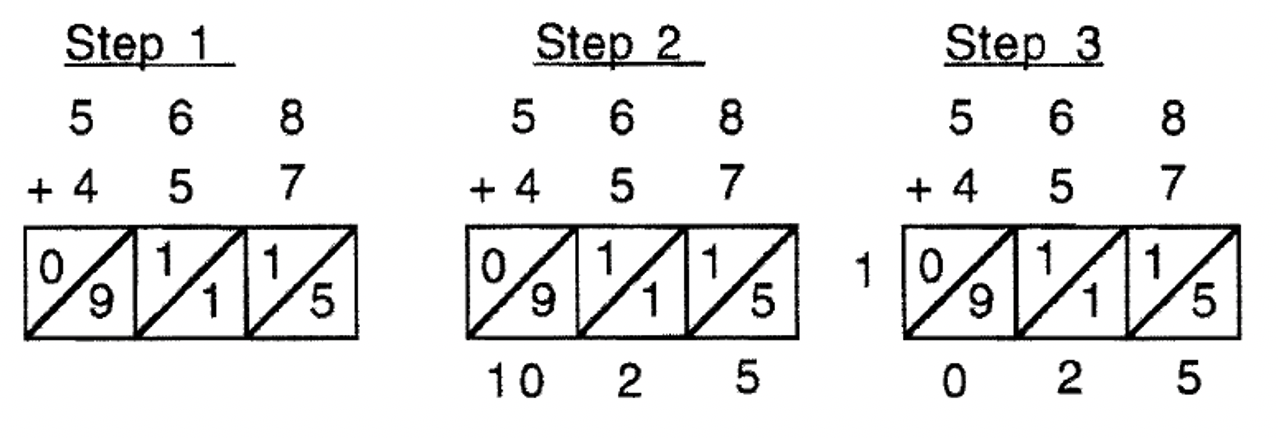
The most common addition algorithm is the Right To Left Standard Addition Algorithm , often referred to as the Standard Addition Algorithm . This is the one almost everyone grew up learning. You start on the right and add the digits. The unit's digit is put down under the line and the ten's digit is carried to the top of the next column to the left. Get out your Base Ten Blocks now to understand what is really going on.

Using Base Blocks

\[\begin{aligned} 2 \text{ flat(s) } + 4 \text{ long(s) } +6 \text{ unit(s) } \\ \underline{+ 1 \text{ flat(s) } + 7 \text{ long(s) } + 8 \text{ unit(s) }} \end{aligned} \nonumber \]

This addition problem using blocks is shown below:

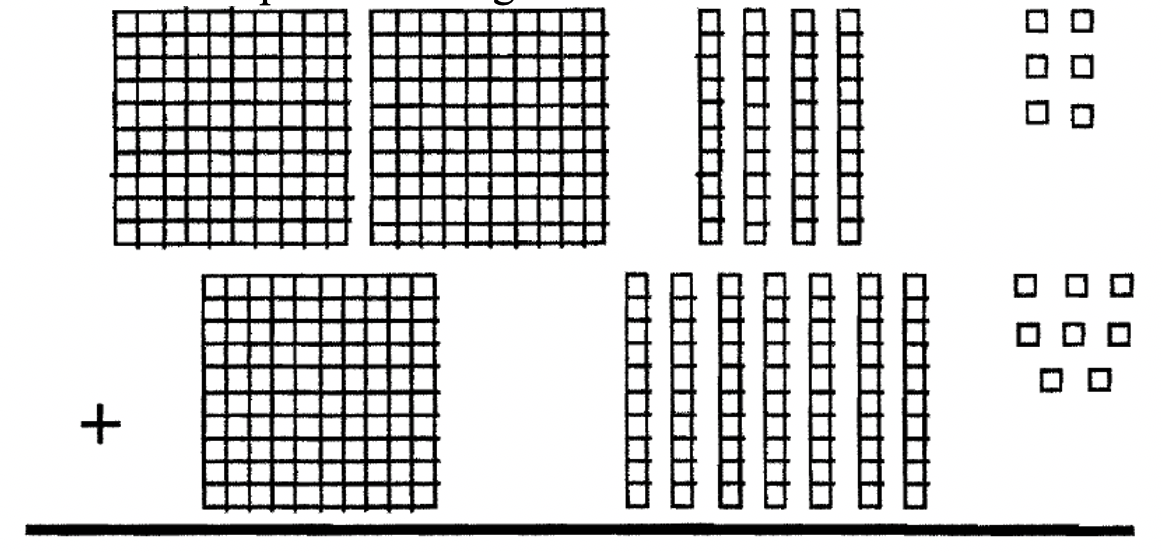
If we add, we get:

\[\begin{aligned} 2 \text{ flat(s) } + 4 \text{ long(s) } +6 \text{ unit(s) } \\ \underline{+ 1 \text{ flat(s) } + 7 \text{ long(s) } + 8 \text{ unit(s) }} \\ 3 \text{ flat(s) } +11 \text{ long(s) } +14 \text{ unit(s) } \end{aligned} \nonumber \]

Trades can now be made. Ten of the 14 units can be exchanged for a long. That leaves us with 3 flats, 12 longs and 4 units. The sum and trades are illustrated with blocks on the next page.

After trading, sum = 3 flat(s) + 12 long(s) + 4 unit(s)

After combining the blocks, the sum is shown below.

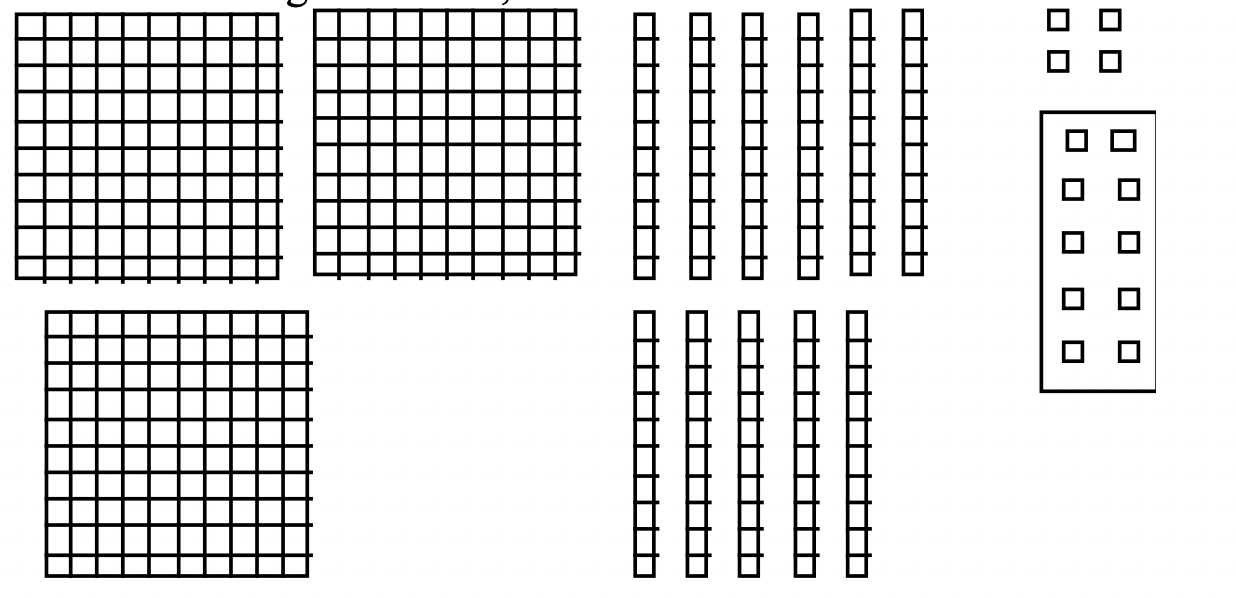
The next step is to trade in ten units for a long. I've put a box around the units to be traded above. This yields 3 flats, 12 longs and 4 units as shown below.

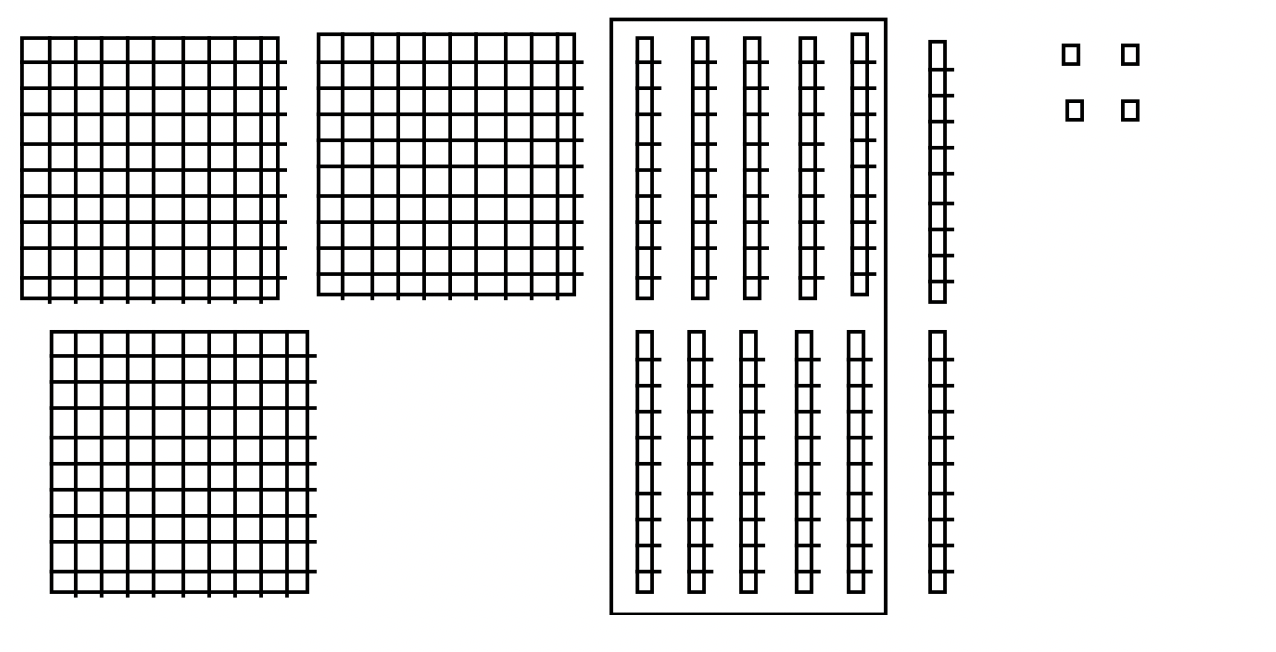
Now ten of the 12 longs can be exchanged for a flat. I've put a box around ten of the longs to be traded above. After the exchange, the sum is 4 flats, 2 longs and 4 units, which is 424. This is illustrated below.

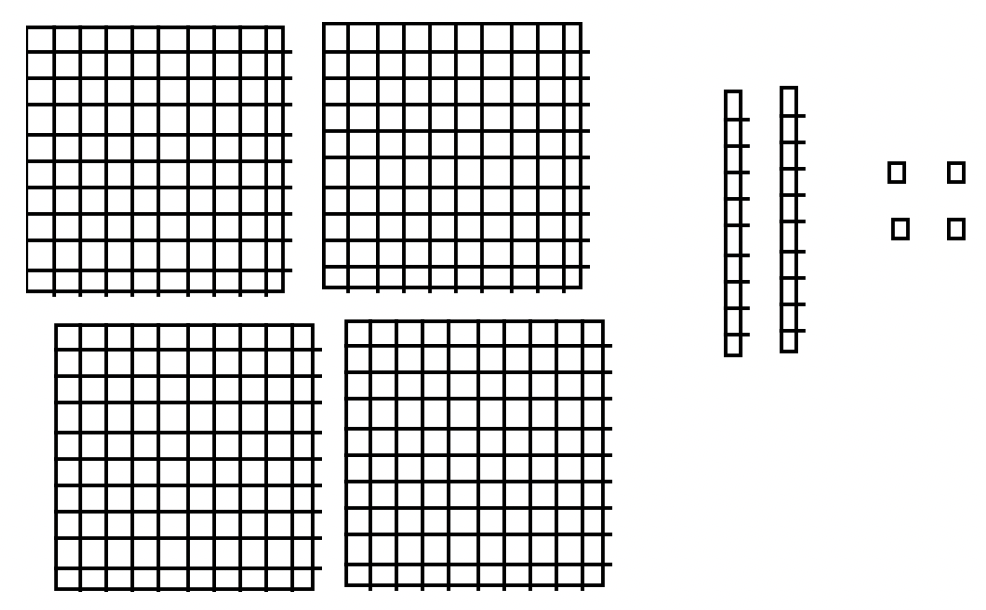
After making all traded, the final sum = 4 flat(s) + 2 long(s) + 4 unit(s)

We're in Base Ten, so the answer is 424. Therefore, 246 + 178 = 424.

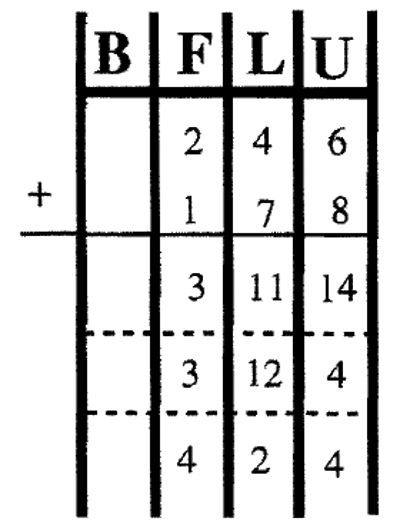
In the previous example of adding 246 + 178 using the Base Blocks, ten longs could have been exchanged for a flat at the same time that ten units were exchanged for a long. I only did one trade at a time because in the Standard Addition Algorithm, we don't combine all the blocks (or place values) at once. First, the units are added together to get 14. The 4 is written down in the unit's column and the other 10 units are written as 1 long in the next column to signify that there is another long. Now, there are 1 + 4 + 7 longs to add up, which is 12. The 2 is written down in the longs column and the other 10 units are written as 1 flat in the next column to signify that there is another flat. Finally, there are 1 + 2 + 1 flats to add up, which is 4. So the sum is 4 flats, 2 longs and 4 units, which is 424. The exchanges being made is what carrying is all about. To the right is another way of keeping track of blocks, flats, longs and units. Notice the trades being made at each step. If the largest addend has x digits, I make x + 1 columns to allow for carrying. In this problem, there are three digits for each addend, so I made four columns to allow for a possible block being made.

Now, let's perform this basic algorithm in other bases. If you are adding in Base Seven, the trick here is to recall basic addition facts in Base Seven. You need to know your addition tables. Remember \(5_{\text{seven}} + 6_{\text{seven}} = 11_{\text{ten}}\), which is \(14_{\text{seven}}\) (which is one long and four units in Base Seven). Study the examples below. To help visualize the trades, the problems are first done using a chart with the sums written in Base Ten to keep track of the units, longs, flats, etc. In exchanging blocks, the conversion to the proper unit is accomplished. Then, the same problems are done without using the charts and using the traditional carrying method –here, you add in the base given as you go along. Try these five problems on your own before going on to the next exercise.

The same examples are worked below using the traditional carrying algorithm.

Add the following. Do each problem using charts as shown in the previous examples. Use your Base Blocks to visualize the problem further.

Eventually, you should be able to do the above problems without the use of charts or manipulatives. You can always think in terms of blocks as you work them. Add the following using the traditional carrying algorithm. Practice until you feel confident and are proficient at adding without using charts or manipulatives.

Another way to add is by using expanded notation. Our first example, 246 + 178, can be written as (200 + 40 + 6) + (100 + 70 + 8). Using the commutative and associative properties, this sum can be written as (200 + 100) + (40 + 70) + (6 + 8) or 300 + 110 + 14 = 300 + (100 + 10) + (10 + 4) = (300 + 100) + (10 + 10) + 4 = 400 + 20 + 4 = 424. When written out like this, it is perhaps more clear what is really being added as opposed to doing it by rote without thinking about the place value of each digit.

6. Add by using expanded notation. Show all steps.

7. Suppose two different students add two numbers together as shown in the two problems to the right. Both have very similar methods. Explain what each student is doing and why it makes sense. Then, make up two more problems and add using one of these methods.

Below is the work of three different students doing the same addition problem. Figure out what each student is doing to get the answer before reading on.

The first student starts by adding the hundreds together (800 + 400 = 1200). Next, the tens are added together (50 + 60 = 110) and that answer is added on (1200 + 110 = 1310). Finally, the ones are added (9 + 7 = 16) and that is added on to get the answer (1310 + 16 = 1326). The second student takes the first number and adds on the hundreds of the second number (859 + 400 = 1259). Next, the tens of the second number is added on (1259 + 60 = 1319). Finally, the ones are added on (1319 + 7 = 1326). The third student starts with the first number and adds on the ones of the second digit first (859 + 7 = 866). Second, the tens digit of the second number is added on (866 + 60 = 926). Finally, the hundreds is added on (926 + 400 = 1326). Someone might be more inclined to use one of these methods if they are adding in their head.

Make up your own problem and solve using the three methods explained above. Explain the method and steps used to arrive at the correct answer.

Another method used for adding is the Left to Right Addition Algorithm . Some of the last few examples were actually employing Left to Right algorithms. In expanded notation, you could add left to right or right to left. Many people find the Left to Right Addition Algorithm easier because there is no carrying. There are a couple of ways to perform this method. Start by adding the leftmost column of digits first. As you move to the next column to the right, you add the digits. If the sum is more than 9, write the unit's digit under that column and underline the digit already put down immediately to the left. This is similar to carrying but you don't need to move up to the next column –it gets added on to the answer later . Continue until you've added the unit's digits. Then go back and add one to all the digits that are underlined. Can you understand why? The following example takes you step by step using this algorithm.

Note: Step 5 is what the problem looks like when it's done, as shown in the examples below. Study and then try the following examples on your own before going on to the next exercise.

In the Left to Right Algorithm, anytime a 9 is underlined, you must continue the underline to include the digit to the left of the nine (if there is a digit to its left). If the digit to the left is a 9, continue the underline to include the digit to its left. Keep underlining until you underline a digit that is not a nine. Then, when you go back, add 1 to the underlined number, (which will now be more than one digit). Study and then practice the following four examples on your own before attempting the next exercise.

Using this technique, the first example adds 1 to 9 to get 10. In the second example, 1 is added to 399 to get 400. In the third example, 1 is added to 9 to get 10 and 1 is added to 39 to get 40. In the fourth example, 1 is added to 99 to get 100 and 1 is added to 29 to get 30.

Exercise 10

Use the Left to Right Algorithm to add the following numbers using the above technique.

On the next page are some addition problems in other bases. The Left to Right Addition Algorithm is being used. Be careful to pay attention to the base . For example, in Base Six, any time you add and get a number higher than 5 (which is the highest digit in Base Six), you only write down the unit's digit under that column and underline the digit to its left. In Base Three, any time you add and get a number higher than 2 (which is the highest digit in Base Three), you only write down the unit's digit under that column and underline the digit to its left. In Base Twelve, any time you add and get a number higher than E (which is the highest digit in Base Twelve), you only write down the unit's digit under that column and underline the digit to its left. Make sure you understand and can do these next examples successfully on your own before going on to the next paragraph and examples.

Below are some examples where you have to do some continuous underlining similar to examples shown previously in Base Ten. Pay close attention to the base. If you underline a 5 in Base Six, you must continue underlining the digit to its left until you underline a digit less than 5! If you underline a 2 in Base Three, you must continue underlining the digit to its left until you underline a digit less than 2! If you underline an E in Base Twelve, you must continue underlining the digit to its left until you underline a digit less than E!. Study and practice the five examples below on your own before attempting the next exercise.

Exercise 11

Use the Left to Right Addition Algorithm to add the following. Pay careful attention to the Base!!!

Exercise 12

List all bases between two and thirteen in which each of the following addition problems are valid.

Exercise 13

Someone started to do each of these addition problems using the Standard Right to Left Algorithm. Figure out which base each addition problem is in and finish the computation.

Exercise 14

Someone was adding 47 + 68 in her head and said out loud, "47 + 70 = 117 and two less is 115." Explain her reasoning.

Exercise 15

Another person was adding 47 + 68 in his head and said out loud "40 + 60 is 100 and 8 + 7 is 15, so the answer is 115." Explain his reasoning.

Exercise 16

The methods in exercises 14 and 15 can be called Break-Apart Methods. You break apart one or both of the addends using the place value of the number. Mentally compute 97 + 88 and then explain the method you used.

Exercise 17

Are there any addition tricks you use? Extra credit for sharing on the Forum

Below is another addition algorithm, called the Lattice Method for Addition, used for adding two numbers together. First, add down the columns, then down the diagonals. The addition problem is 568 + 457 and the answer is 1,025. See if you can understand how to do it and understand why it works. We'll use the lattice method again when we do multiplication.

Exercise 18

Use the lattice method to compute 456 + 659. Show your work.

Exercise 19

Use the lattice method to compute the following:

Learning to estimate is a very useful skill. The idea is to convert the actual numbers in the problem to simpler numbers that are easy to compute mentally. In exercise 14, 47 + 68 is close to adding 50 + 70, which is 120. 120 is pretty close –it's within 5% of the exact answer of 115. Even if you need to know the exact answer, if you do a quick estimate, you can usually tell if you're in the ball park. Sometimes estimating is all that is really necessary. For instance, if you are shopping for groceries and have a limited amount of cash on hand to pay for them, you might want to mentally add up what you spend as you go along. The quickest way to estimate is to round. And if you want to make sure you don't go over your allotted amount, you can always just round up. Let's say you had ten items in the cart for the following amounts:

There are many ways you could choose to round and add –you could round to the nearest dollar, or up to the nearest dollar (to make sure you don't go over) or maybe to the nearest 50 cents. I am going to assume you know how to round numbers already. And you should be able to add in your head using your fingers and the Dot Method. The following are three examples of how you might get an estimate of what the grocery bill will be.

The actual sum is $31.68 which is extremely close to our rough estimate of $32 which we got rounding both to the nearest dollar and to the nearest 50 cents. If you are working with higher priced items, you might round to the nearest ten or hundred dollars, etc.

Exercise 20

Mentally estimate the cost of the grocery bill containing the following priced items. Explain how you did it. Then, compare your answer to the actual sum.

Exercise 21

Pretend you are going shopping and you buy ten items where each item is less than $10. List the actual cost of each item (make these up) and estimate the total. Then, compute the actual cost of the ten items.

Exercise 22

When do you think you might get too high or low of an estimate? Give an example.

Or search by topic

Number and algebra

• The Number System and Place Value
• Calculations and Numerical Methods
• Fractions, Decimals, Percentages, Ratio and Proportion
• Properties of Numbers
• Patterns, Sequences and Structure
• Algebraic expressions, equations and formulae
• Coordinates, Functions and Graphs

Geometry and measure

• Angles, Polygons, and Geometrical Proof
• 3D Geometry, Shape and Space
• Measuring and calculating with units
• Transformations and constructions
• Pythagoras and Trigonometry
• Vectors and Matrices

Probability and statistics

• Handling, Processing and Representing Data
• Probability

Working mathematically

• Thinking mathematically
• Mathematical mindsets
• Cross-curricular contexts
• Physical and digital manipulatives

For younger learners

• Early Years Foundation Stage

Advanced mathematics

• Decision Mathematics and Combinatorics
• Advanced Probability and Statistics

Addition and Subtraction KS2

This collection is one of our Primary Curriculum collections - tasks that are grouped by topic.

This is an adding game for two players. Can you be the first to reach the target?

Strike it Out

Use your addition and subtraction skills, combined with some strategic thinking, to beat your partner at this game.

Use these four dominoes to make a square that has the same number of dots on each side.

Always, Sometimes or Never? Number

Are these statements always true, sometimes true or never true?

First Connect Three

Add or subtract the two numbers on the spinners and try to complete a row of three. Are there some numbers that are good to aim for?

True or False?

Without doing lots of calculations, can you decide which of these number sentences are true? How do you know?

In this game for two players, the idea is to take it in turns to choose 1, 3, 5 or 7. The winner is the first to make the total 37.

Buying a Balloon

Lolla bought a balloon at the circus. She gave the clown six coins to pay for it. What could Lolla have paid for the balloon?

Build it Up

Can you find all the ways to get 15 at the top of this triangle of numbers? Many opportunities to work in different ways.

Planning a School Trip

You are organising a school trip and you need to write a letter to parents to let them know about the day. Use the cards to gather all the information you need.

Fifteen Cards

Can you use the information to find out which cards I have used?

A Mixed-up Clock

There is a clock-face where the numbers have become all mixed up. Can you find out where all the numbers have got to from these ten statements?

Super Shapes

The value of the circle changes in each of the following problems. Can you discover its value in each problem?

Domino Square

Use the 'double-3 down' dominoes to make a square so that each side has eight dots.

This challenge is a game for two players. Choose two of the numbers to multiply or divide, then mark your answer on the number line. Can you get four in a row?

Sealed Solution

Ten cards are put into five envelopes so that there are two cards in each envelope. The sum of the numbers inside it is written on each envelope. What numbers could be inside the envelopes?

Amy's Dominoes

Amy has a box containing domino pieces but she does not think it is a complete set. Which of her domino pieces are missing?

Four bags contain a large number of 1s, 3s, 5s and 7s. Can you pick any ten numbers from the bags so that their total is 37?

Six Ten Total

This challenge combines addition, multiplication, perseverance and even proof.

Twenty Divided Into Six

Katie had a pack of 20 cards numbered from 1 to 20. She arranged the cards into 6 unequal piles where each pile added to the same total. What was the total and how could this be done?

Roll These Dice

Roll two red dice and a green dice. Add the two numbers on the red dice and take away the number on the green. What are all the different possible answers?

Six Numbered Cubes

This task combines spatial awareness with addition and multiplication.

Can you go through this maze so that the numbers you pass add to exactly 100?

Finding Fifteen

Tim had nine cards each with a different number from 1 to 9 on it. How could he have put them into three piles so that the total in each pile was 15?

Choose four different digits from 1-9 and put one in each box so that the resulting four two-digit numbers add to a total of 100.

The Dice Train

This dice train has been made using specific rules. How many different trains can you make?

Dice in a Corner

How could you arrange at least two dice in a stack so that the total of the visible spots is 18?

4 by 4 Mathdokus

Can you use the clues to complete these 4 by 4 Mathematical Sudokus?

Consecutive Numbers

An investigation involving adding and subtracting sets of consecutive numbers. Lots to find out, lots to explore.

Subtraction Surprise

Try out some calculations. Are you surprised by the results?

A game for two people, or play online. Given a target number, say 23, and a range of numbers to choose from, say 1-4, players take it in turns to add to the running total to hit their target.

Three Neighbours

Take three consecutive numbers and add them together. What do you notice?