problem solving involving circumference of a circle

• Math Article
• Problems On Circles

Problems On Area And Circumference Of A Circle

Before looking at problems on a circle based on perimeter and area, we need to understand the meaning of a circle and both the properties of the circle. In geometry, a circle is a closed two-dimensional figure in which the set of all the points in the plane is equidistant from a given point called the centre. Let’s have a look the definitions of perimeter and area given below:

Perimeter Definition

Perimeter is associated with any closed figure like triangle , quadrilateral, polygons or circles. It is the measure of distance covered while going around the closed figure on its boundary.

For example, the perimeter of a square of side 2 cm = 8 cm, as we know that the square comprises 4 sides having equal lengths, thus the total distance covered will be 4×2, which will be the total length (i.e. perimeter).

Area Definition

Area means the actual space enclosed by a closed figure (or within the perimeter), and it means all the points within the closed figure and not the boundary.

Perimeter and Area of Circle Formula

Now, coming to the perimeter of a circle, as explained above, is the measure of distance going around the circle’s boundary. This distance is difficult to calculate precisely, and it is easy to visualize that the distance to go around is larger in a larger radius than a smaller radius. Hence, the perimeter is a function of the radius of a circle. In the case of the circle, we generally use the term “CIRCUMFERENCE” instead of the perimeter.

It is given by,

Circumference = 2πr

Here, r is a radius, and π is a constant defined as the ratio of circumference to the circle’s diameter.

The value of π is 22/7 or 3.1416

Also check: Circumference of a circle

The formula to find the area of a circle is given as:

Solved Problems on Circle

Let us understand the concepts related to circles along with the following questions-

To cover a distance of 10 km, a wheel rotates 5000 times. Find the radius of the wheel.

Number of rotations = 5000.

Total distance covered = 10 km

Let ‘r’ be the radius of the wheel.

Circumference of the wheel = Distance covered in 1 rotation = 2πr.

In 5000 rotations, the distance covered = 10 km = 1000000 cm.

\(\begin{array}{l}\text{Hence, in 1 rotation, the distance covered = }\frac{1000000}{5000}cm=200\: cm\end{array} \)

But this is equal to the circumference. Hence, 2πr = 200 cm

Taking the approximate value of π as 22/7, we get

r = 100 x 7/22

r = 31.82 cm approx.

The diameter of a semicircular shape is 14 cm. What will be the perimeter of this shape?

Diameter of semicircle = d = 14 cm

Radius = r = d/2 = 14/2 = 7 cm

Perimeter of semicircle = (Perimeter of circle/2) + d

= (2πr/2) + d

= (22/7) × 7 + 14

The difference between the circumference and the diameter of a circular bangle is 5 cm. Find the radius of the bangle. (Take π = 22/7)

Solution: Let the radius of the bangle be ’r’

According to the question:

Circumference – Diameter=5 cm

We know, Circumference of a circle = 2πr

Diameter of a circle = 2r

Therefore, 2πr – 2r =5 cm

2r(π-1) = 5 cm

\(\begin{array}{l}2r(\frac{22}{7}-1)=5cm\\ \\ 2r\times \frac{15}{7}=5\\ \\ r=\frac{5\times 7}{15\times 2}\\ \\ r=1.166cm\end{array} \)

The radius of bangle is 1.166 cm.

A girl wants to make a square-shaped figure from a circular wire of radius 49 cm. Determine the sides of a square.

Solution: Let the radius of the circle be ’r’.

Length of the wire=circumference of the circle= 2πr

\(\begin{array}{l}= 2\times \frac{22}{7}\times 49=2\times 22\times 7\\ \\ =308\: cm\end{array} \)

Let the side of the square be ‘s’.

Perimeter of the square = length of the wire = 4s

\(\begin{array}{l}s=\frac{308}{4}\\ \\ s=77\:cm\end{array} \)

Therefore, the sides of the square is 77 cm.

Find the area of a circular region whose radius is 21 m.

Radius of circular region = r = 21 m

Area of a circle = πr 2

= (22/7) × 21 × 21

= 22 × 3 × 21

= 1386 sq. m

Therefore, the area of the circular region is 1386 sq. m.

Video Lessons on Circles

Introduction to circles.

Parts of a Circle

Area of a Circle

All about Circles

Learn more about Surface area & volumes of the figures with BYJU’S-The learning app.

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Request OTP on Voice Call

Post My Comment

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

In order to access this I need to be confident with:

Circle math

Circumference of a circle

Here you will learn about calculating the circumference of a circle including how to calculate the circumference of a circle given the circle’s radius, diameter, or area, how to calculate the perimeter of a semi-circle, and how to calculate the radius or diameter of a circle given the circumference.

Students will first learn about circumference of a circle as part of geometry in 7 th grade.

What is the circumference of a circle?

Circumference of a circle is the distance around the circle. It can also be known as the perimeter of a circle, but circumference is a special case of perimeter.

Both describe the total length of the boundary of a two-dimensional shape, but circumference specifically refers to the perimeter of a curved figure or arc. Therefore it only applies to circles, ovals, ellipses, arcs, etc.

Circumference of a circle formula:

There is a specific relationship between the diameter of a circle and its circumference.

If you multiply the diameter of a circle by \pi , you will calculate the length of the circumference. This is true of all circles.

Therefore this formula can be used to find the circumference of any given circle:

\pi \times d

As the diameter of the circle is twice the radius, you can also use this formula:

2\times\pi \times r

Which formula you use will depend on whether you know the circle’s diameter or the circle’s radius.

For example,

What is the circumference of a circle with radius 3~{cm}?

Common Core State Standards

How does this relate to 7 th grade math?

• Grade 7 – Geometry (7.G.B.4) Know the formulas for the area and circumference of a circle and use them to solve problems; give an informal derivation of the relationship between the circumference and area of a circle.

[FREE] 2D Shape Check for Understanding Quiz (Grade 2 to 4)

Use this quiz to check your grade 2 – 4 students’ understanding of 2D shape. 10+ questions with answers covering a range of 2nd, 3rd and 4th grade 2D shape topics to identify areas of strength and support!

How to calculate the circumference of a circle

In order to calculate the circumference of a circle:

Find the radius or diameter of the circle.

Use the relevant formula to calculate the circumference of the circle.

Give your answer clearly with the correct units.

Circumference of a circle examples

Example 1: calculating the circumference of the circle given the radius.

A circle has a radius of 6~{cm}.

Calculate its circumference.

Give your answer to the nearest tenth.

The radius is given in the question.

Radius = 6~{cm}

2 Use the relevant formula to calculate the circumference of the circle.

In this question you have the radius, therefore you should use the formula,

Remember, the question asks you to round your answer to the nearest tenth.

3 Give your answer clearly with the correct units.

Remember, circumference is a measure of length; therefore, the units should not be “squared.”

Example 2: calculating the circumference of the circle given the diameter

A circle has a diameter of 10~{mm}.

In this question, the question gives you the diameter.

Diameter = 10~{mm}

\pi \times 10

Example 3: calculating the circumference of the circle, given the radius, answer in terms of 𝝅.

A circle has a radius of 8~{m}.

Give your answer in terms of \pi.

Radius = 8~{m}

2\times\pi \times 8

Remember, the question asks you to give your answer to ‘ in terms of \pi’. Therefore, you leave the answer in the form 16\pi.

Example 4: calculating the circumference of the circle given the diameter

A circle has a diameter of 420~{km}.

\pi \times 420

Remember, the question asks you to give your answer to ‘ in terms of \pi’. Therefore, you leave the answer in the form 420\pi.

Example 5: calculating the circumference of the circle given the area of a circle

A circle has an area of 21 \mathrm{~cm}^2.

Give your answer to the nearest hundredth.

The question gives you the area of the circle, but you need the radius/diameter in order to calculate the circumference.

You know that:

Area of a circle = \pi r^2

This means you can find the radius of the circle from the area.

\text {Area }=\pi r^{2}

\text {Area }=21

21=\pi r^{2} \quad Divide both sides by \pi

\cfrac{21}{\pi}=r^{2} \quad \; Square root both sides of the equation

\sqrt{\cfrac{21}{\pi}}=\sqrt{r^{2}}

2.5854 \ldots=r

Notice how you leave the answer to more decimals places than the question asks for. This is so you do not cause a rounding error later on in the question.

In this question you now have the radius, therefore you should use the formula,

2\times\pi \times 2.5854

Remember, the question asks you to round your answer to the nearest hundredth.

Example 6: calculating the perimeter of a semi-circle given the diameter

A semicircle has a diameter of 20~{m}.

Calculate its perimeter.

Diameter = 20~{m}

Remember, the question asks you to round your answer to ‘ in terms of \pi’. Therefore, you leave the answer in the form 20\pi.

This represents the circumference of a circle with a diameter of 20~{m}. The perimeter of the semi-circle is the length of the arc and the length of the diameter added together.

Length of Arc

The length of the arc is half that of the whole circle because it is a semi-circle.

Therefore, the length of the arc is 20\pi divided by 2.

Length of arc =10\pi

Length of Diameter

Given to you in the question, 20~{m}.

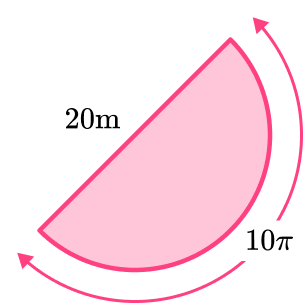
Perimeter of the circle

Length of Arc + Length of Diameter

Remember to keep it in terms of \pi as stated in the question.

Teaching tips for circumference of a circle

• Before diving into the circumference formula, ensure that students have a solid understanding of the basic concepts such as radius and diameter. Use visual aids like diagrams to illustrate these concepts and provide step by step guidance to students who need it.
• Provide practice problems that show real-life examples where understanding the circumference of a circle is important, such as measuring the distance around a circular object like a pizza, a clock, or a bicycle wheel. This helps students see the practical applications of the concept.
• Engage students with hands-on activities instead of worksheets. For example, have them measure the circumference of objects in the classroom using a string or measuring tape. This kinesthetic approach can enhance understanding.

Easy mistakes to make

• Not including the correct units When working with circumference, give the correct units; they should not be squared. For example, cm, m, km etc.
• Not rounding correctly These types of questions often involve rounding. Only round at the end of the question and ensure you are rounding to what the question specifies.
• Not giving an answer in terms of 𝝅 Sometimes the question may ask you to give the answer ‘ in terms of \pi’. This means you do not give the numerical answer that is produced when you multiply it by \pi. For example, 6 \times \pi = 6\pi (this is an answer in terms of pi) 6 \times \pi = 18.8495592… (this answer is not in terms of pi since 6 was multiplied by the value of pi)
• Misuse of a calculator Ensure you know how to correctly use the \pi button on your calculator when using one for a circumference calculation.

Related circle math lessons

• Pi r squared
• Parts of a circle
• Area of a circle
• Area and circumference of a circle

Practice circumference of a circle questions

1) A circle has a diameter of 6~{cm}. What is the circumference of the circle in terms of \pi?

2) A circle has a diameter of 6~{cm}. What is the circumference of the circle to the nearest tenth?

18.8 \mathrm{~cm} (rounded to the nearest tenth)

3) Which of these could be the circumference of a circle?

Circumference is a measure of length and this is the only answer with a measure of length (cm) as its units.

4) A circle has a radius of 1~{cm}. What is its circumference to the nearest tenth?

(rounded to the nearest tenth)

5) A circle has a radius of 1~{cm}. What is its circumference in terms of \pi?

This answer has been left in terms of \pi.

6) A circle has a diameter of 4~{cm}. What is its circumference in terms of \pi?

7) A circle has a radius of 100~{cm}. What is its circumference to the nearest whole number?

(rounded to the nearest integer)

Remember, integer means whole number.

Circumference of a circle FAQs

The circumference of a circle is found using the formula 2 \times \pi \times r or \pi \times d, where \pi is a mathematical constant with an approximate value of 3.14, r is the radius, and d is the diameter.

To find the circumference of a circle with radius r, you would use the formula 2 \times \pi \times r.

Circumference specifically applies to the distance around the outer edge of a circle while perimeter is a more general term used for any closed two-dimensional shape, including polygons with straight sides. The formulas used to calculate circumference and perimeter depend on the specific shape.

The approximate circumference of the Earth is about 40,075 kilometers ( 24,901 miles).

Pi, or mathematical constant \pi, represents the ratio of the circumference to its diameter. This relationship is expressed by the formulas 2 \times \pi \times r and \pi \times d.

The circumference of a circle is the total distance around its outer edge, while the arc length is the distance along a specific part of the circle defined by a central angle.

The next lessons are

• Angles of a circle
• Circle theorems
• Prism shape

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs .

[FREE] Common Core Practice Tests (Grades 3 to 6)

Prepare for math tests in your state with these Grade 3 to Grade 6 practice assessments for Common Core and state equivalents.

40 multiple choice questions and detailed answers to support test prep, created by US math experts covering a range of topics!

Privacy Overview

WORD PROBLEMS ON AREA AND CIRCUMFERENCE OF A CIRCLE

Problem 1 :

A cylindrical tank has radius 1.5 m. What is the circumference of its base ?

A cylindrical tank has the base which is in the shape of circle.

Circumference of base  =  2πr

radius (r)  =  1.5 m

Circumference of the base  =  2(3.14)(1.5)

=  9.42 m 2

So, circumference of the base is  9.42 m 2 .

Problem 2 :

A circular pond has diameter 8 m and needs to be fenced for the protection of children.

a) What length of fencing is required?

b) Fencing comes in 1 m lengths. How many lengths are needed?

c) What is the total cost of the fencing if each length costs $25.00?

Diameter of the circular pond  =  8 m, radius  =  4 m

(a)  Length of fencing  =  Circumference of circle

=   2 πr 

=  2(3.14) (4) 

=  25.12

So,  length of fencing is 25.12 m.

(b)  Length of each fencing  =  1 m

Number of fencing required  =  26 

(c)  Cost of each fencing  =  $25

Required cost  =  25 (26)

=  $650

So, the required cost is $650.

Problem 3 :

A car wheel has a radius of 35 cm.

a)  What is the circumference of the wheel?

b)  If the wheel rotates 100 000 times, how far does the car travel?

Radius of wheel  =  35 cm

Circumference of the wheel  =   2 πr

=  2(3.14) (35)

=  219.8

So, circumference of the circle is 220 cm.

(b)  Distance covered in  100 000 times

=  100000(220)

=  22000000 cm

100 cm  =  1 m and 1000 m  =  1 km

=  22000000/100000

=  220 km

So, distance covered by the car is 220 km.

Problem 4 :

A trundle wheel is used for measuring distances. The circumference of the wheel is exactly 1 m. Each time the wheel rotates through one complete turn a click sound is heard and a counter adds a meter to the total. What is the radius of this wheel?

Circumference of circle  =  1 m

2 πr  =  1

2(3.14) r  =  1

6.28r  =  1

r  =  1/6.28

r  =  0.159 m

100 cm  =  1 m and 1 cm  =  10 mm

r  =  159 mm

So, the required radius is 159 mm.

Problem 5 :

A circular garden plot has circumference 12.65 m. Find its radius in meters, correct to the nearest centimetre.

Circumference of circular garden  =  12.65 m

2 πr  =  12.65

2(3.14)r  =  12.65

r  =  12.65/6.28

r  =  2.01 m

So, radius of the circular garden is 2.01 m.

Problem 6 :

An irrigation sprinkler sprays water over a field. The radius of the spray is 12.6 m. What  area of the field is being watered?

Radius of the spray  =  12.6 m

Area of the field is being watered  =  Area of circle

=  πr 2

=  3.14(12.6) 2

=  3.14(158.76)

=  498.50

So, area of the field is being watered is 498.50 m 2

Problem 7 :

The rope connecting a goat to a pole is 8 m long. What area of grass can the goat eat?

Length of rope  =  8 m

Area of grass can the goat eat  =   πr 2

=  3.14(8) 2

=  200.96 

=  201 m 2

So, area of grass can the goat eat is 201 m 2 .

Problem 8 :

A circular hoop has a radius of 40 cm. Find the length of tubing needed to make the hoop.

Radius of circular hoop  =  40 cm

Length of tubing needed to make a hoop  =   2 πr

=  2(3.14)(40)

=  251.2

So, length of tubing needed is 251.2 cm.

Problem 9 :

6 identical metal discs are stamped out of an  18 cm by 12 cm sheet of copper as illustrated.  What percentage of the copper is wasted

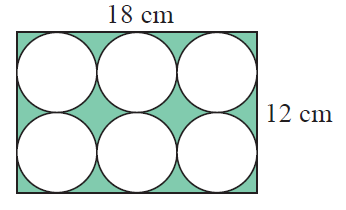
Area of 6 stamps  =  6 πr 2

3(diameter of circle)  =  18

3(2r)  =  18

r  =  18/6

r  =  3 cm

Area  =  6(3.14)(9)

Area of metal discs cut out  =  169.56 cm 2

Copper wasted  =  Area of rectangular sheet - Area of metal discs cut out

=  18 x 12 - 169.56

=  216-56.52

=  46.44

=  (46.44/216)  ⋅ 100%

=  21.5%

So, copper wasted is 21.5%.

Problem 10 :

A table-top is shaped as illustrated. A  cloth to protect the table-top from stains  and heat is cut exactly the same size as  the table-top. It is made from fabric 1.6 m  wide and costs $18.40 per metre of length.

a) What length of fabric must be purchased?

b) Calculate the cost of the fabric.

c) Find the area of the cloth.

d) Calculate the amount of fabric that is wasted.

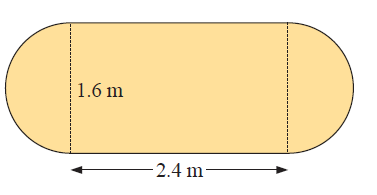
(a)  Length of fabric to be purchased  =  Side length of one side

=  2.4 + 0.8 + 0.8

=  4 m

So, length of fabric to be purchased is 4 m.

(b)  Cost of fabric  =  $18.40

Cost of fabric purchased  = 18.40(4)

=  $73.60

(c)  Area of cloth 

=  Area of rectangle in the middle + 2(Area of semicircle)

=  2.4(1.6) + 2( πr 2 /2)

=  3.84 + (3.14)(0.8) 2

=  3.84 + 2.0096

=  5.85 m 2

d) Amount of fabric wasted  =  (2.4+16) x 1.6 - 2.0096

=  6.4 - 5.85

=  0.55 m 2

Apart from the stuff given above, i f you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to   [email protected]

We always appreciate your feedback.

© All rights reserved. onlinemath4all.com

• Sat Math Practice
• SAT Math Worksheets
• PEMDAS Rule
• BODMAS rule
• GEMDAS Order of Operations
• Math Calculators
• Transformations of Functions
• Order of rotational symmetry
• Lines of symmetry
• Compound Angles
• Quantitative Aptitude Tricks
• Trigonometric ratio table
• Word Problems
• Times Table Shortcuts
• 10th CBSE solution
• PSAT Math Preparation
• Privacy Policy
• Laws of Exponents

Recent Articles

SAT Math Videos (Part 2 - No Calculator)

May 25, 24 05:35 AM

SAT Math Videos (Part 1 - No Calculator)

May 25, 24 05:07 AM

Simplifying Algebraic Expressions with Fractional Coefficients

May 17, 24 08:12 AM

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Course: 7th grade   >   Unit 9

• Finding circumference of a circle when given the area
• Area of a shaded region
• Impact of increasing the radius
• Circumference and rotations

Area and circumference of circles challenge

• Shaded areas

• Your answer should be
• an integer, like 6 ‍  
• a simplified proper fraction, like 3 / 5 ‍  
• a simplified improper fraction, like 7 / 4 ‍  
• a mixed number, like 1   3 / 4 ‍  
• an exact decimal, like 0.75 ‍  
• a multiple of pi, like 12   pi ‍   or 2 / 3   pi ‍  

Circumference Of A Circle

In these lessons, we will learn

• how pi (π) is calculated,
• the formula for the circumference of a circle,
• the diameter of the circle,
• the radius of the circle,
• the area of the circle.

Related Pages Area Of A Circle Arc Of A Circle Circles More Geometry Lessons

What Is The Circumference Of A Circle

A circle is a closed curve formed by a set of points on a plane that are the same distance from its center. The circumference of a circle is the distance around the circle. It is sometimes called the perimeter of a circle.

Formula For The Circumference Of A Circle

Calculating the circumference of a circle involves a constant called pi , with the symbol π . Pi (π) is the ratio of the circumference of a circle to its diameter. Pi is always the same number for any circle.

The value of π (pi) is approximately 3.14159265358979323846… but usually rounding to 3.142 should be sufficient. (see a mnemonic for π )

The formula for the circumference of a circle is

C = πd     (see a mnemonic for this formula )

where C is the circumference, d is the diameter and r is the radius.

The diameter of a circle is a line segment that passes through the center of the circle and has its endpoints on the circle. The radius of the circle is a line segment from the center of the circle to a point on the circle. The diameter of a circle is twice the length of its radius.

If you are given the diameter then use the formula C = πd

If you are given the radius then use the formula C = 2 πr

A fun way to remember the formulas for the circumference of a circle and the area of a circle

Pi, where does it come from? How pi can be calculated for any circle?

Find the Circumference of a Circle

The formula for the circumference of a circle is the product of pi ( π ) and the diameter or twice the product of pi ( π ) and the radius.

Example: Find the circumference of the circle with a diameter of 8 inches.

Answer: The circumference of the circle is 8 π ≈ 25.163 inches.

Example: Find the circumference of the circle with a radius of 5 inches.

Answer: The circumference of the circle is 10 π ≈ 31.42 inches.

Worksheet to calculate circumference of circle when given diameter or radius.

Worksheet to calculate circumference and area of circle when given diameter or radius.

How to find the circumference of a circle given the radius?

How to find the circumference of a circle given the radius or the diameter?

Find The Radius, Given The Circumference

From the formula C = 2 πr , we see that we can find the radius of a circle by dividing its circumference by 2 π .

The following video shows how to find the radius of a circle given its circumference. Step 1: Find the circumference and substitute. Step 2: Divide by π Step 3: Divide by 2 Step 4: Write the units

Find The Diameter, Given The Circumference

From the formula C = πd , we see that we can find the diameter of a circle by dividing its circumference by π .

Example: A circle has a circumference of 12 cm. Find the radius.

Find The Area Of Circle, Given The Circumference

To find the area of a circle when given the circumference, we first use the circumference to find the radius. Then, we use the radius to find the area of the circle.

Worksheet on problems that involve the radius, diameter, circumference and area of circle.

Worksheet 1 on word problems that involve circles.

Worksheet 2 on word problems that involve circles.

How to find the area of a circle given the circumference?

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

Circumference of Circle

The circumference of a circle is the perimeter of the circle. It is the total length of the boundary of the circle. The circumference of a circle is the product of the constant π and the diameter of the circle. A person walking across a circular park, or a circular table to be bordered requires this metric of the circumference of a circle. The circumference is a linear value and its units are the same as the units of length.

A circle is a round closed figure where all its boundary points are equidistant from a fixed point called the center. The two important metrics of a circle are the area of a circle and the circumference of a circle. Here we shall aim at understanding the formula and calculation of the circumference of a circle.

What is Circumference of a Circle?

The circumference of a circle is its boundary or the length of the complete arc of a circle . Let us understand this concept using an example. Consider a circular park shown below.

If a boy starts running from point 'A' and reaches the same point after taking one complete round of the park, a distance is covered by him. This distance or boundary is called the circumference of the park which is in the shape of a circle. The circumference is the length of the boundary.

Circumference of a Circle Definition

The circumference of a circle refers to the measure of its boundary. If we open a circle and measure the boundary just like we measure a straight line, we get the circumference of the circle in terms of units of length like centimeters, meters, or kilometers.

Now let us learn about the elements that make up circumference. These are the three most important elements of a circle.

• Center: The center of the circle is a point that is at a fixed distance from any other point from the circumference.
• Diameter: The diameter is the distance across the circle through the center, it is a line that meets the circumference at both ends and it needs to pass through the center.
• Radius: The radius of a circle is the distance from the center of a circle to any point on the circumference of the circle.

Circumference of Circle Formula

The formula for the circumference of a circle is expressed using the radius 'r' of the circle and the value of ' pi '. It is expressed as, Circumference of a circle formula = 2πr. While using this circumference formula, if we do not have the value of the radius, we can find it using the diameter. That is, if the diameter is known, it can be divided by 2 to obtain the value of the radius because of the diameter of a circle = 2 × radius. Another way to calculate the circumference of a circle is by using the formula: Circumference = π × Diameter. If we need to calculate the radius or diameter, when the circumference of a circle is given, we use the formula: Radius = Circumference/2π

How to Find the Circumference of Circle?

Although the circumference of a circle is the length of its boundary, it cannot be calculated with the help of a ruler (scale) like it is usually done for other polygons . This is because a circle is a curved figure. Therefore, to calculate the circumference of a circle, we apply a formula that uses the radius or the diameter of the circle and the value of Pi (π).

Pi is a special mathematical constant with a value approximated to 3.14159 or π = 22/7. The value of π = 22/7 is used in various formulas. It is the ratio of circumference to diameter, where C = πD. Let us consider a practical illustration to understand how to calculate the circumference of a circle with the help of the circumference formula.

Example: If the radius of the circle is 25 units, find the circumference of the circle. (Take π = 3.14)

Solution: Given, radius = 25 units

Let us write the circumference formula and then we will substitute the value of r (radius) in it.

Circumference of circle formula = 2πr

C = 2 × π × 25

C = 2 × 3.14 × 25 = 157 units

Therefore, the circumference of a circle is 157 units.

Circumference to Diameter

The circumference to diameter of a circle is a ratio used to define the standard definition of Pi (π). If you know the diameter 'd' of a circle, then you can easily find the circumference C using the relation: C = πd. So, when the circumference C is placed in a ratio with the diameter d, the answer we get is π.

Important Notes on Circumference of a Circle

• π(Pi) is a mathematical constant that is the ratio of the circumference of a circle to its diameter. It is approximated to π = 22/7or 3.14
• If the radius of a circle is extended further and touches the boundary of the circle, it becomes the diameter of a circle. Therefore, Diameter = 2 × Radius
• The circumference is the distance around a circle or the length of a circle.
• We can find the circumference of a circle using the radius or diameter.
• Circumference formula = π× Diameter; Circumference = 2πr.

☛ Related Articles

• Circumference of the Earth
• Circumference of Circles Worksheets
• Diameter to circumference calculator
• Circumference Calculator

Circumference of Circle Examples

Example 1: If the radius of a circle is 28 cm find the circumference of the circle.

Given, Radius of the circle = 28 cm. To find the circumference of the circle, we will use the circumference formula: 2πr = 2 × 22/7 × 28 = 176 cm.

Therefore, the circumference of the circle is 176 cms.

Example 2: The circumference of a wheel is 440 cm. Find its radius and diameter.

Given, the Circumference of the wheel = 440 cm

Circumference of a circle formula = 2πr

Let us substitute the known values to find the radius first.

440 = 2 × (22/7) × r

radius = 70 cm

Diameter = 2 × radius

Diameter = 2 × 70

Therefore, the radius is 70 cm, and the diameter is 140 cm.

Example 3: The perimeter of a rectangular wire is 264 m. The same wire is bent into the shape of a circle. Find the radius of the circle formed using the circumference formula.

We know that the perimeter of the rectangle = Total length of the wire used = Circumference of the circle formed.

Hence, the Circumference of the circle formed = 264 m

Circumference of the circle = 264

Let us substitute the known values to find the radius.

264 = 2 × (22/7) × r

Therefore, the radius of the circle is 42 m.

go to slide go to slide go to slide

Book a Free Trial Class

Practice Questions on Circumference of a Circle

go to slide go to slide

FAQs on Circumference of Circle

What is the circumference of a circle in geometry.

The circumference of a circle is the measure of the boundary or the length of the complete arc of a circle. The circumference of the circle is the product of π (pi) and the diameter of the circle. The circumference of a circle is a linear quantity that has the same units of length.

How to Find the Circumference of a Circle?

The circumference of a circle is calculated with the help of the circumference formula that needs the value of the radius of the circle and the value of π (pi). Circumference of a circle = 2πr, where, 'r' is the radius of the circle and π(pi) is a special mathematical constant with a value approximated to 3.14159 or π = 22/7.

How to Find the Diameter From the Circumference of a Circle?

If we need to calculate the diameter when the circumference of a circle is given, we use the formula: Circumference = π × Diameter, or, Diameter = Circumference/π

How to Find the Circumference of the Circle with the Area?

The circumference of a circle can be calculated if the area of the circle is given. Using the formula for the area of a circle the radius can be calculated. Once the radius is known, the circumference can be calculated. Area of circle = πr 2 , \(radius = \sqrt{\frac{A}{\pi}}\), and C = 2πr = 2\(\pi\sqrt{\frac{A}{\pi}}\).

What is the Unit of the Circumference of a Circle?

The circumference of the circle is a one-dimensional linear quantity and the unit of the circumference of a circle is expressed in m, inch, cm, feet, and so on. The circumference of a circle is related to other linear quantities such as the radius and diameter of the circle.

What is the Perimeter of the Circle?

The perimeter of a circle is the same as the circumference of a circle. It is the total length of the outer boundary of the circle. The perimeter or circumference of a circle is the product of the constant 'pi' and the diameter of the circle. It is expressed in linear units like m, inch, cms, feet.

What is the Value of Pi?

Pi is a constant value used for the measurement of the area and circumference of a circle or other circular figures. The symbol of pi is π and its numeric value is equal to 22/7 or 3.14. Further, these numeric values are used based on the context of the equation.

What is the Difference Between the Diameter and the Circumference of a Circle?

The diameter of the circle is the longest chord that passes through the center of the circle. The circumference of the circle is the length of the outer boundary of the circle. Both the diameter and the circumference are lengths and are expressed in linear units. The circumference of the circle is equal to the product of the diameter and the constant π (pi).

How to Find the Circumference of a Circle with Diameter?

The circumference of the circle can be calculated if the diameter is known because the relationship between the circumference and diameter of the circle is expressed as, Circumference = π × Diameter, or, diameter = Circumference/π.

Child Login

• Kindergarten
• Number charts
• Skip Counting
• Place Value
• Number Lines
• Subtraction
• Multiplication
• Word Problems
• Comparing Numbers
• Ordering Numbers
• Odd and Even
• Prime and Composite
• Roman Numerals
• Ordinal Numbers
• In and Out Boxes
• Number System Conversions
• More Number Sense Worksheets
• Size Comparison
• Measuring Length
• Metric Unit Conversion
• Customary Unit Conversion
• Temperature
• More Measurement Worksheets
• Writing Checks
• Profit and Loss
• Simple Interest
• Compound Interest
• Tally Marks
• Mean, Median, Mode, Range
• Mean Absolute Deviation
• Stem-and-leaf Plot
• Box-and-whisker Plot
• Permutation and Combination
• Probability
• Venn Diagram
• More Statistics Worksheets
• Shapes - 2D
• Shapes - 3D
• Lines, Rays and Line Segments
• Points, Lines and Planes
• Transformation
• Quadrilateral
• Ordered Pairs
• Midpoint Formula
• Distance Formula
• Parallel, Perpendicular and Intersecting Lines
• Scale Factor
• Surface Area
• Pythagorean Theorem
• More Geometry Worksheets
• Converting between Fractions and Decimals
• Significant Figures
• Convert between Fractions, Decimals, and Percents
• Proportions
• Direct and Inverse Variation
• Order of Operations
• Squaring Numbers
• Square Roots
• Scientific Notations
• Speed, Distance, and Time
• Absolute Value
• More Pre-Algebra Worksheets
• Translating Algebraic Phrases
• Evaluating Algebraic Expressions
• Simplifying Algebraic Expressions
• Algebraic Identities
• Quadratic Equations
• Systems of Equations
• Polynomials
• Inequalities
• Sequence and Series
• Complex Numbers
• More Algebra Worksheets
• Trigonometry
• Math Workbooks
• English Language Arts
• Summer Review Packets
• Social Studies
• Holidays and Events
• Worksheets >
• Geometry >
• Circle >
• Circumference and Area

Circumference and Area of a Circle Worksheets

This page is a one-stop shop for all your finding area and circumference of a circle exercises. Catering to the learning needs of students in grade 5 through grade 8, these printable worksheets practice the topic pretty much across the board: easy, moderate and hard. The job in the easy set is to calculate the area and circumference of the circles with radius ranging from 1 to 25. The moderate set requires rounding answers to tenth place with the radius of circles ranging between 25 and 100. In the hard worksheets, the radius is rendered in decimal and the task is to round your answers to two decimal places. Use pi = 3.14 wherever necessary. Explore some of these worksheets for free!

Area from Radius

Applying the formula, Area = pi * r 2 , find the area of each circle.

• Download the set

Area from Diameter

Find the radius from diameter and apply the formula to find the area of a circle.

Area from Radius or Diameter

Each printable worksheet has 9 problems on finding area of a circle with the known radius or diameter. Two simple word problems and one story problem included.

Area and Circumference: Combined Review

These are the perfect review worksheets in finding both area and circumference of the circle.

Radius or Diameter from Area

Dividing the area by pi or 3.14, you get r 2 . Taking the square root, you get radius. Solve each problem based on this technique.

Area from Circumference

Find the area from the circumference of each circle in this stock of worksheets for 7th grade students. Word problems included to understand real-life application.

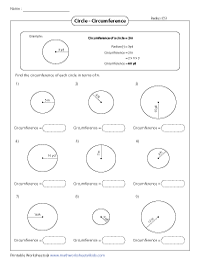
Circumference from Radius

Applying the formula, Circumference = 2 * pi * r, find the circumference of each circle.

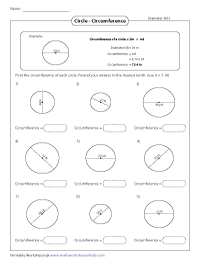
Circumference from Diameter

To find the circumference, multiply diameter with pi value. Each pdf worksheet has 9 problems.

Circumference from Radius or Diameter

Circumference of a circle worksheet contains six standard problems and two word problems.

Radius or Diameter from Circumference

Divide the circumference by pi or 3.14. You get the diameter. Answer the questions.

Circumference from Area

Each worksheet has 8 problems finding circumference from area of a circle. Simple word problems included.

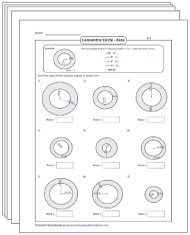
Area of an Annulus Worksheets

Imagine two circles with different radii, but the same center; can you calculate the area of the region in between? Scout around these pdf worksheets, pore over the examples, and solve similar problems on area of an annulus!

(9 Worksheets)

Related Worksheets

» Arc Length and Area of Sector

» Area of Segment

» Area of Compound Shapes

» Area of Mixed Shapes

Become a Member

Membership Information

Privacy Policy

What's New?

Printing Help

Testimonial

Copyright © 2024 - Math Worksheets 4 Kids

This is a members-only feature!

o          Circle

o          Radius

o          Diameter

o          Arc

o          Subtend

o          Sector

o          Chord

o          Secant

o          Tangent

o          Circumference

o          Know how to fundamentally define a circle

o          Identify various parts of circles

o          Calculate the area and circumference of a circle or portion thereof

Introduction to Circles

A circle is simply a figure defined by all the points that are equidistant from a given center point. Thus, we can define a circle (without a definite location) by specifying the distance from the center; alternatively, we can define a circle (with a definite location) by specifying the distance from and the location of the center. The distance from the center of the points that lie on the circle is called the radius (plural radii ) of the circle. A circle with a radius r and center point C is shown below.

Note that regardless of which point on the circle is chosen, it is always a distance r from the center point, C. Each of the line segments drawn from C to the circle is called a radius (in other words, no one segment is defined as the radius, since all such segments are equal in length). The circle itself does not show any angles or sides that we can use to determine how many degrees are in the figure (as we did with polygons), but we can see that any two radii do form an angle α , as shown below.

Using our measurement of degrees, this angle α can (unambiguously) be any value between 0° and 360°. We can also define angles with either positive or negative numbers, depending on the direction of measurement from a particular radius--a positive angle is traditionally measured in the counterclockwise direction, and a negative angle is traditionally measured in the clockwise direction, as shown below.

We can also identify other parts of a circle. Given any point P 1 on the circle, the most distant point P 2 that is also on the circle is on the exact opposite side, and these points are the length of two radii apart. The line segment that connects them passes through the center and is called the diameter of the circle.

Any two radii in the circle (which form an angle α ), such as those shown below, form an arc and a sector. The arc is the portion of the circle opposite to (or subtended by) the angle α and between the endpoints of the radii. The sector is the area enclosed by the arc and the radii. The arc A in the diagram below is shown as a bold line, and the sector S is shown as a shaded area.

Any line segment connecting two points on the circle is called a chord . Note that a diameter is a chord (the longest possible chord of a circle!). The chord D is shown below as a bold line.

Other special figures related to circles are secants and tangents. A secant is simply a line that intersects two points of the circle (a chord is a segment of a secant). A tangent is a line that intersects the circle at exactly one point. Secant E and tangent T are shown in the diagram below as bold lines.

Practice Problem : Identify each part (labeled A through E) of the circle below.

Solution : Each portion of the circle or other line can be identified by its relationship to the entire circle. Each of these figures is discussed and defined above. The shaded area A is a sector. The line (or line segment) B is a tangent (note that it intersects the circle at only one point). C is a diameter, D is a chord, and E is a radius.

Basic Characteristics of Circles

Now that we have identified some of the components of circles, we can now begin to derive some of their characteristics using the tools we have developed thus far. Some of the properties of circles require trigonometry to derive (such as the length of a chord subtended by an angle α ), but others we can derive or simply state basic formulas that we can use to solve problems. Let's start with the circumference and area of a circle. The circumference of a circle is simply the length of the boundary (that is, the perimeter) of the circle. We will simply state the formula for the circumference C of a circle in terms of the radius ( r ) or the diameter ( d ):

C = 2 πr = πd

Note that with the formula for the circumference, we introduce the number π . Because π is (most mathematicians think) an irrational number, we cannot write it out exactly in its decimal form, nor can we write it exactly as a fraction. We can, however, write a decimal estimation of π that is sufficient for our purposes.

π ≈ 3.1416

Many calculators have a built-in key for the number π (although the calculator still just uses an approximation of π ). For many calculations, an approximate π value of 3.14 yields sufficient accuracy. As it turns out, π also appears in the formula for the area of a circle. Let's write the area A in terms of the radius r .

A = πr 2

Note again that we have not really derived these formulas; we are simply stating them as fundamental facts upon which we will base the rest of our investigation of the characteristics of circles.

Practice Problem : Find the area and circumference of a circle with a diameter of 4 inches.

Solution : One of the first rules of solving these types of problems involving circles is to carefully note whether we are dealing with the radius or the diameter. In this problem, the circle is described using the diameter, which is 4 inches. The radius is thus 2 inches. Let's now calculate the area A and circumference C using the formulas given above.

A = πr 2 = π (2 in) 2 ≈ (3.14)(4 in 2 ) =12.56 in 2

C = πd = π (4 in) ≈ (3.14) (4 in) = 12.56 in

Coincidentally, the area and circumference have the same numerical values (but not the same units!). This is not generally the case, of course.

Let's take a look at the characteristics of other parts of a circle. For instance, now that we know how to calculate the circumference of a circle, we can also calculate the length of an arc (which is simply a portion of the circumference). An angle α defined by two radii subtends an arc. Let's take a look at several examples, from which we can identify a pattern. The arc K in each case is shown as a bold curve. The circumference of the circle is C .

The expressions under each example can be derived by inspection. We know that if the angle α is 90° (one-quarter of the full 360° of the circle), then the subtended arc is one-quarter of the circumference. The same reasoning applies to determining the arc length K for the other two cases as well. Thus, we can see that the arc length is related to the circumference as the angle α is related to 360°. But this is simply a ratio that we can write as follows.

Thus, the area of sector S is related to the area A according to the ratio of α to 360°. We can once again derive a formula.

Practice Problem : A central angle γ in a circle of radius 10 units forms a sector with an area of 2.62 square units. Find the measure of γ .

Solution : Let's start by drawing a diagram of the problem. This diagram need not be to scale-we can simply use it to more easily identify the parts of the circle discussed in the problem. We'll call the sector S , and we know S = 2.62 units 2 .

We can use the formula presented earlier to relate the area S of the sector to the area A of the circle.

But we also know how to calculate A using the given radius of 10 units.

A = π r 2 = π(10 units) 2 ≈ 3.14(100 units 2 ) ≈ 314 units 2

Now let's find γ .

Thus, the angle has a measure of 3°.

• Course Catalog
• Group Discounts
• Gift Certificates
• For Libraries
• CEU Verification
• Medical Terminology
• Accounting Course
• Writing Basics
• QuickBooks Training
• Proofreading Class
• Sensitivity Training
• Excel Certificate
• Teach Online
• Terms of Service
• Privacy Policy

WORD PROBLES ON CIRCUMFERENCE OF A CIRCLE

Problem 1 :

The circumference of circle whose diameter is 14 cm will be ________.

Given, diameter = 14 cm

Radius r = 14/2 = 7 cm

Circumference = 2πr

= 2 × 22/7 × 7

So, the circumference of circle whose diameter is 14 cm will be 44 cm.

Problem 2 :

What is the circumference of a circular disc of radius 14 cm?

Given, Radius r = 14 cm

= 2 × 22/7 × 14

So, the circumference of a circular disc is 88 cm.

Problem 3 :

The circumference of a circle is 31.4 cm. find the radius. (Take π = 3.14)

Given, circumference of the circle = 31.4 cm

2 × 3.14 × r = 31.4

6.28 × r = 31.4

r = 31.4/6.28

So, radius of the circle is 5 cm.

Problem 4 :

If the circumference of a circle with radius 3.5 cm is 22 cm. Find the perimeter of the semicircle. (Take π = 3.14)

Circumference = 22 cm

Radius r = 3.5 cm

Perimeter of the semicircle = πr + 2r

= r (π + 2)

= 3.5 (3.14 + 2)

= 3.5 ×5.14

So, perimeter of the semicircle is 17.99 cm.

Problem 5 :

If the circumference of a circle is 132 cm. Find the perimeter of the semicircle. (Take π = 3.14)

Circumference of a circle = 132 cm

r = 132/ (2 × 3.14)

r = 132/6.28

r = 21.01 cm

= 21.01 (3.14 + 2)

= 21.01 × 5.14

= 107.99 cm

So, perimeter of the semicircle is 108 cm.

Problem 6 :

The radii of two circles are in the ratio 2: 3. What is the ratio of their circumference?

Let the radius of two circle be 2x and 3x respectively.

Circumference of a circle = 2πr

Circumference of first circle = 2 × π × 2x

Circumference of second circle = 2 × π × 3x

Ratio of circumference of two circles = 4πx/6πx

Hence, ratio of their circumference is 2: 3.

Problem 7 :

A 44 m long wire is bent to form a circle. Find the diameter of the circle.

Given, length of the wire = 44 cm

Circumference of the circle = length of the wire = 44 cm

2 × 22/7 × r = 44

r = 44 × 7/44

Diameter = 2 × radius

Diameter = 14 cm

So, the diameter of the circle is 14 cm.

Problem 8 :

A wire is in the form of a circle of radius 35 m. It is now bent in the form of an equilateral triangle. Find the side of the triangle.

Solution : 

Given, the radius of the circle = 35 m

Circumference of circle = 2πr

= 2 × 22/7 × 35

The circumference of circle = perimeter of equilateral triangle

Let, one side of an equilateral triangle be x.

Perimeter of equilateral triangle = 3x

x = 73.33 m

So, the each side of an equilateral triangle is 73.33 m.

• Variables and Expressions
• Variables and Expressions Worksheet
• Place Value of Number
• Formation of Large Numbers
• Laws of Exponents
• Angle Bisector Theorem
• Pre Algebra
• SAT Practice Topic Wise
• Geometry Topics
• SMO Past papers
• Parallel Lines and Angles
• Properties of Quadrilaterals
• Circles and Theorems
• Transformations of 2D Shapes
• Quadratic Equations and Functions
• Composition of Functions
• Polynomials
• Fractions Decimals and Percentage
• Customary Unit and Metric Unit
• Honors Geometry
• 8th grade worksheets
• Linear Equations
• Precalculus Worksheets
• 7th Grade Math Worksheets
• Vocabulary of Triangles and Special right triangles
• 6th Grade Math Topics
• STAAR Math Practice
• Math 1 EOC Review Worksheets
• 11 Plus Math Papers
• CA Foundation Papers

Recent Articles

Finding Range of Values Inequality Problems

May 21, 24 08:51 PM

Solving Two Step Inequality Word Problems

May 21, 24 08:51 AM

Exponential Function Context and Data Modeling

May 20, 24 10:45 PM

© All rights reserved. intellectualmath.com

Appendix B: Geometry

Using the properties of circles to solve problems, learning outcomes.

• Find the circumference and area of a circular object given it’s radius
• Find the circumference and area of a circular object given it’s diameter
• Calculate the diameter of a circular object given it’s circumference

Do you remember the properties of circles from Decimals and Fractions Together? We’ll show them here again to refer to as we use them to solve applications.

Properties of Circles

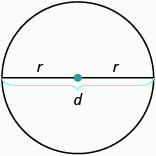
• [latex]r[/latex] is the length of the radius
• [latex]d[/latex] is the length of the diameter
• [latex]d=2r[/latex]
• Circumference is the perimeter of a circle. The formula for circumference is[latex]C=2\pi r[/latex]
• The formula for area of a circle is[latex]A=\pi {r}^{2}[/latex]

Remember, that we approximate [latex]\pi [/latex] with [latex]3.14[/latex] or [latex]\Large\frac{22}{7}[/latex] depending on whether the radius of the circle is given as a decimal or a fraction. If you use the [latex]\pi [/latex] key on your calculator to do the calculations in this section, your answers will be slightly different from the answers shown. That is because the [latex]\pi [/latex] key uses more than two decimal places.

A circular sandbox has a radius of [latex]2.5[/latex] feet. Find the 1. circumference and 2. area of the sandbox.

in the following video we show another example of how to find the area of a circle.

We usually see the formula for circumference in terms of the radius [latex]r[/latex] of the circle:

[latex]C=2\pi r[/latex]

But since the diameter of a circle is two times the radius, we could write the formula for the circumference in terms [latex]\text{of }d[/latex].

[latex]\begin{array}{cccc}& & & C=2\pi r\hfill \\ \text{Using the commutative property, we get}\hfill & & & C=\pi \cdot 2r\hfill \\ \text{Then substituting}d=2r\hfill & & & C=\pi \cdot d\hfill \\ \text{So}\hfill & & & C=\pi d\hfill \end{array}[/latex]

We will use this form of the circumference when we’re given the length of the diameter instead of the radius.

A circular table has a diameter of four feet. What is the circumference of the table?

In the next video we show two more examples of how to find the circumference of a circle given it’s diameter, or it’s radius.

Find the diameter of a circle with a circumference of [latex]47.1[/latex] centimeters.

• Question ID 146787, 146786, 146785. License : CC BY: Attribution
• Examples: Determine the Circumference of a Circle. Authored by : James Sousa (mathispower4u.com). Located at : https://youtu.be/sHtsnC2Mgnk . License : CC BY: Attribution
• Example: Determine the Area of a Circle. Authored by : James Sousa (mathispower4u.com). Located at : https://youtu.be/SIKkWLqt2mQ . License : CC BY: Attribution
• Prealgebra. Provided by : OpenStax. License : CC BY: Attribution . License Terms : Download for free at http://cnx.org/contents/[email protected]

You Can Draw It Yourself

Put a pin in a board, put a loop of string around it, and insert a pencil into the loop. Keep the string stretched and draw the circle!

Play With It

Try dragging the point to see how the radius and circumference change.

(See if you can keep a constant radius!)

Radius, Diameter and Circumference

The Radius is the distance from the center outwards.

The Diameter goes straight across the circle, through the center.

The Circumference is the distance once around the circle.

And here is the really cool thing:

When we divide the circumference by the diameter we get 3.14159265... which is the number π ( Pi )

We can say:

Circumference = π × Diameter

Example: You walk around a circle which has a diameter of 100m, how far have you walked?

Distance walked = Circumference = π × 100m

= 314m (to the nearest m)

Also note that the Diameter is twice the Radius:

Diameter = 2 × Radius

And so this is also true:

Circumference = 2 × π × Radius

In Summary:

Remembering

The length of the words may help you remember:

• Radius is the shortest word and shortest measure
• Diameter is longer
• Circumference is the longest

Circle : the set of all points on a plane that are a fixed distance from a center.

The area of a circle is π times the radius squared, which is written:

• A is the Area
• r is the radius

To help you remember think "Pie Are Squared" (even though pies are usually round) :

Example: What is the area of a circle with radius of 1.2 m ?

Or, using the Diameter:

A = ( π /4) × D 2

Area Compared to a Square

A circle has about 80% of the area of a similar-width square. The actual value is ( π /4) = 0.785398... = 78.5398...%

And something interesting for you to try: Circle Area by Lines

Because people have studied circles for thousands of years special names have come about.

Nobody wants to say "that line that starts at one side of the circle, goes through the center and ends on the other side" when they can just say "Diameter".

So here are the most common special names:

A line that "just touches" the circle as it passes by is called a Tangent .

A line that cuts the circle at two points is called a Secant .

A line segment that goes from one point to another on the circle's circumference is called a Chord .

If it passes through the center it is called a Diameter .

And a part of the circumference is called an Arc .

There are two main "slices" of a circle.

The "pizza" slice is called a Sector .

And the slice made by a chord is called a Segment .

The Quadrant is a special sector with a right angle. It has a quarter of the circle's area.

Half a circle is called a Semicircle.

Inside and Outside

A circle has an inside and an outside (of course!). But it also has an "on", because we could be right on the circle.

Example: "A" is outside the circle, "B" is inside the circle and "C" is on the circle.

A circle is a "special case" of an ellipse .

Area of a Circle Practice Questions

Click here for questions, click here for answers.

GCSE Revision Cards

5-a-day Workbooks

Primary Study Cards

Privacy Policy

Terms and Conditions

Corbettmaths © 2012 – 2024

• School Guide
• Class 10 Syllabus
• Maths Notes Class 10
• Science Notes Class 10
• History Notes Class 10
• Geography Notes Class 10
• Political Science Notes Class 10
• NCERT Soln. Class 10 Maths
• RD Sharma Soln. Class 10
• Math Formulas Class 10
• Area of a Quadrant
• Area of Square
• Surface Area of Circle Formula
• Sector of a Circle
• Area of Quadrilateral
• Secant of a Circle
• Surface Area of a Cone Formula
• Segment of a Circle
• Radius Of A Circle Calculator
• Area of Isosceles Triangle
• Area of a Circular Sector
• Area of a leaf inside a square
• Program to find area of a circle
• Area and Perimeter of a circle in PL/SQL
• Area of square Circumscribed by Circle
• Maximum area of quadrilateral
• C Program to Find Area of Circle
• JavaScript program to find area of a circle
• Area of Incircle of a Right Angled Triangle

Area of a Quarter Circle

A quarter circle is one-fourth of a full circle. It resembles a slice of pie, that is divided into four equal parts. It includes a 90° angle and a curved edge, forming a right-angled sector. Calculating the area of a quarter circle is simple and useful in various applications. This article will guide you through the steps to determine the area, making it easy to understand and apply.

Table of Content

What is a Quarter Circle?

Properties of a quarter circle, area of a quarter circle formula, derivation of the formula, calculating the area of a quarter circle, examples of area calculation, faqs on area of a quarter circle.

A quarter circle is a geometric shape that represents one-fourth of a full circle. It is formed by dividing a circle into four equal parts.

To visualize a quarter circle, imagine a pizza divided into four equal slices where the tip of each slice is at the center of the circle and the curved edge is part of the circumference. Each slice represents one-fourth of the entire pizza, so we can say that each slice is a quarter circle.

Some of the common properties of quarter circle are:

• Quater circle represents one of the four quadrants of the full circle.
• Radius of quarter circle is same as the parent circle (circle from which quarter circle is cut out).
• The two straight sides (radii) form a right angle (90°) at the center of quater circle where they meet.
• The perimeter of a quarter circle includes the length of the arc plus the lengths of the two radii.
• Quater circles shows order 4 rotational symmetry .

Formula for the area of a quarter circle with radius r is:

A = (πr 2 ) / 4

Area of a Circle : The formula for the area of a circle with radius r is given by, πr 2 .

Quarter of a Circle : Since a quarter circle is one-fourth of a full circle, the area of a quarter circle will be one-fourth of the area of a full circle.

Area of Quarter Circle = (1/4) × Area of Circle

Thus, Area of quarter = (πr 2 ) / 4.

So, the formula for the area of a quarter circle with radius r is: (πr 2 ) / 4.

We can use the formula discussed above i.e., Area of Quarter Circle = (πr 2 ) / 4

Let’s consider an example for better understanding.

Example: Find the area of Quarter Circle with radius 6 units.

Given: radius = 6 units Area of Quarter Circle = (πr 2 ) / 4 Thus, Area = (π × 6 2 ) / 4 = 36π/4 = 9π square units. Thus, the area of Quarter Circle with radius 6 unit is 9π square units.

Perimeter of a Quarter Circle

The perimeter (P) of a quarter circle consists of:

• The arc length of the quarter circle.
• The two radii that form the straight sides.

As quarter circle is one fourth of a circle, thus its arc length is also one fourth of circumference of circle.

Thus, arc length of quarter circle = 2πr/4 = πr/2

Perimeter of quarter circle = πr/2 + 2r

In conclusion, the quarter circle is a geometric object made up of a 90° angle in the middle of a circle, two straight edges, and an arc. Its area is 1/4 of a full circle’s, and the formula for it is Area = (πr 2 ) / 4. There are uses for this idea in many areas, such as planning, building, and math.

• Circumference of Circle
• Arc of Circle
• Sector of Circle

Example 1: What is the area of a quarter circle in square meters if its radius is 8 meters?

If the radius of a quarter circle is 8 meters, the area of the quarter circle can be calculated using the formula: Area = (1/4) πr 2 . Substituting the given value, we get Area = (1/4) x π x 8 2 = (1/4) x π x 64 = 16π. Therefore, the area of the quarter circle is 16π square meters.

Example 2: In a yard, there is a flower bed that is 5-feet across and made like a quarter circle. How many square feet does this flower bed cover?

The area of a quarter-circle shaped flower bed with a radius of 5 feet can be calculated similarly. Using the formula Area = (1/4) πr 2 , we get Area = (1/4) x π x 5 2 = (1/4) x π x 25 = 6.25π. Therefore, the area of the flower bed is 6.25π square feet.

Example 3: An artist is painting a picture that is 10 meters across and in the shape of a quarter circle. How big will the painting be in square meters?

For the mural with a radius of 10 meters, the area can be found using the formula Area = (1/4) πr 2 . Substituting the given value, we get Area = (1/4) πr 2 = (1/4) x π x 100 = 25π. Thus, the area of the mural is 25π square meters.

Practice Problems on Quarter Circle

Problem 1 : Find the perimeter of a quarter circle with a radius of 4 cm.

Problem 2 : A quarter circle has a radius of 7 meters. Calculate its perimeter.

Problem 3 : Determine the perimeter of a quarter circle with a radius of 10 inches.

Problem 4 : The radius of a quarter circle is 3.5 feet. What is the perimeter?

Problem 5 : Find the perimeter of a quarter circle whose radius is 8.2 meters.

What is a quarter circle?

A quarter circle is a geometric shape that forms when an arc joins the ends of two radii, creating a right angle at the center of a circle. It has an arc as its curved side and two radii as its straight sides.

How is the area of a quarter circle calculated?

The area of a quarter circle is calculated using the formula: Area = (πr 2 ) / 4, where ‘r’ is the radius of the quarter circle.

What are the properties of a quarter circle?

A quarter circle has several properties: It forms a 90-degree center angle. Its area is half that of a complete circle. It has an arc-formed curving border. It has two right-angled intersecting radii. It exhibits order 4 rotational symmetry. It finds applications in engineering, architectural design, and geometric computations.

Where is the concept of quarter circles applied?

Quarter circles are applied in various fields including engineering, architectural design, and geometric calculations involving circles and sectors.

What are some examples of calculating the area of quarter circles?

Examples include determining the area of quarter circle flower beds, murals, portions of pool bottoms, or specialty pizzas, given their respective radii or diameters.

Please Login to comment...

Similar reads.

• Maths-Class-10
• Mensuration
• Mathematics
• School Learning

Improve your Coding Skills with Practice

What kind of Experience do you want to share?