lesson 3 problem solving practice sum of angles in triangles

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

4.17: Triangle Angle Sum Theorem

• Last updated
• Save as PDF
• Page ID 4814

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

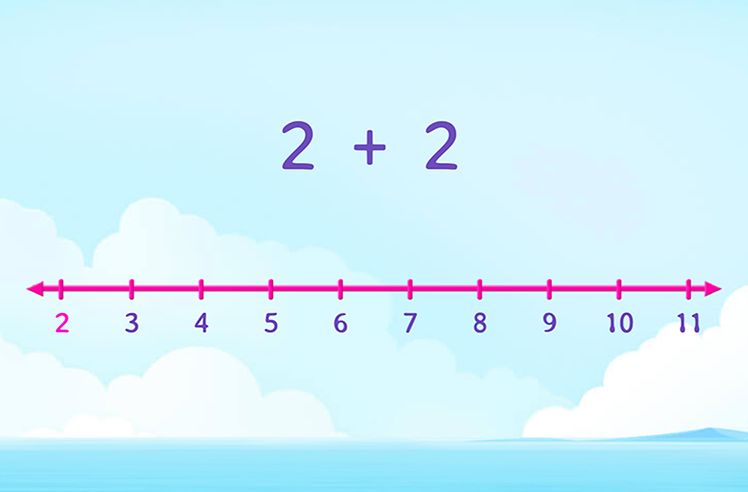
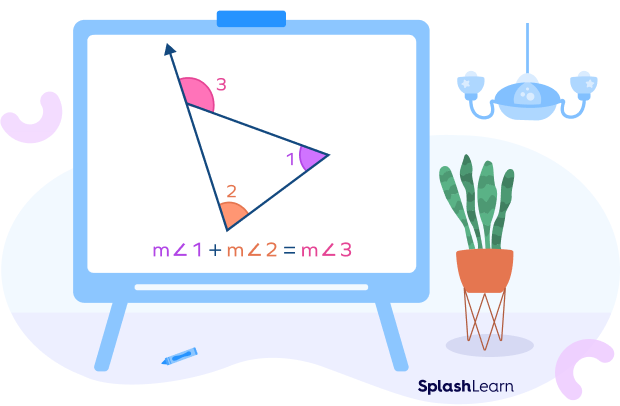
The interior angles of a triangle add to 180 degrees Use equations to find missing angle measures given the sum of 180 degrees.

Triangle Sum Theorem

The Triangle Sum Theorem says that the three interior angles of any triangle add up to \(180^{\circ}\).

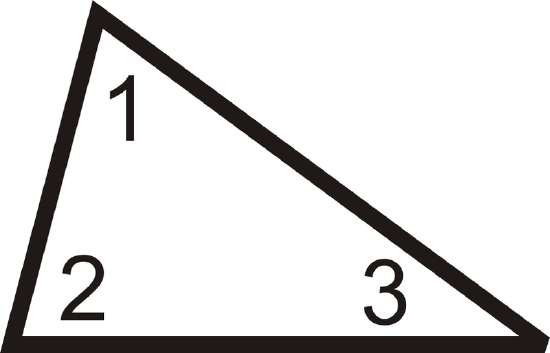
\(m\angle 1+m\angle 2+m\angle 3=180^{\circ}\).

Here is one proof of the Triangle Sum Theorem.

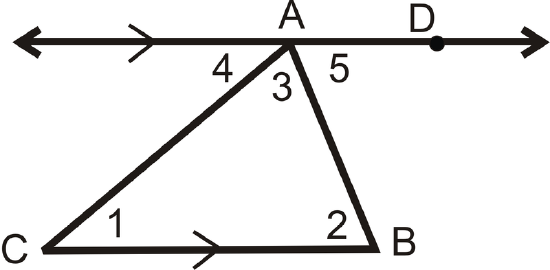
Given : \(\Delta ABC\) with \(\overleftrightarrow{AD} \parallel \overline{BC}\)

Prove : \(m\angle 1+m\angle 2+m\angle 3=180^{\circ}\)

You can use the Triangle Sum Theorem to find missing angles in triangles.

What if you knew that two of the angles in a triangle measured \(55^{\circ}\)? How could you find the measure of the third angle?

Example \(\PageIndex{1}\)

Two interior angles of a triangle measure \(50^{\circ}\) and \(70^{\circ}\). What is the third interior angle of the triangle?

\(50^{\circ}+70^{\circ}+x=180^{\circ}\).

Solve this equation and you find that the third angle is \(60^{\circ}\).

Example \(\PageIndex{2}\)

Find the value of \(x\) and the measure of each angle.

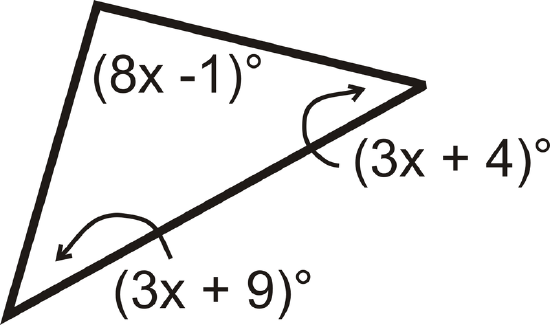
All the angles add up to \(180^{\circ}\).

\(\begin{align*} (8x−1)^{\circ}+(3x+9)^{\circ}+(3x+4)^{\circ}&=180^{\circ} \\ (14x+12)^{\circ}&=180^{\circ} \\ 14x&=168 \\ x&=12\end{align*} \)

Substitute in 12 for \(x\) to find each angle.

\([3(12)+9]^{\circ}=45^{\circ} \qquad [3(12)+4]^{\circ}=40^{\circ} \qquad [8(12)−1]^{\circ}=95^{\circ}\)

Example \(\PageIndex{3}\)

What is m\angle T?

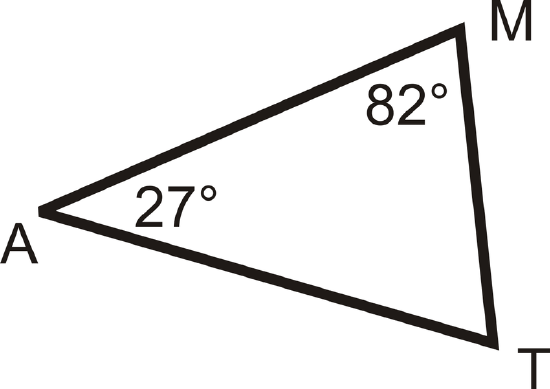
We know that the three angles in the triangle must add up to \(180^{\circ}\). To solve this problem, set up an equation and substitute in the information you know.

\(\begin{align*} m\angle M+m\angle A+m\angle T&=180^{\circ} \\ 82^{\circ}+27^{\circ}+m\angle T&=180^{\circ} \\ 109^{\circ}+m\angle T&=180^{\circ} \\ m\angle T &=71^{\circ}\end{align*}\)

Example \(\PageIndex{4}\)

What is the measure of each angle in an equiangular triangle?

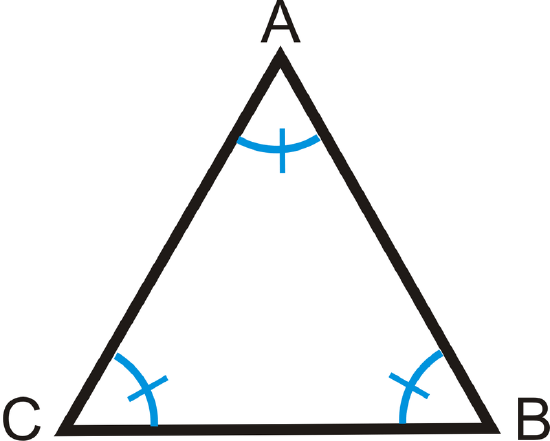
To solve, remember that \(\Delta ABC\) is an equiangular triangle, so all three angles are equal. Write an equation.

\(\begin{align*} m\angle A+m\angle B+m\angle C &=180^{\circ} \\ m\angle A+m\angle A+m\angle A&=180^{\circ} \qquad &Substitute,\: all\: angles\: are \: equal. \\ 3m\angle A&=180^{\circ} \qquad &Combine\:like \:terms. \\ m\angle A&=60^{\circ}\end{align*}\)

If \(m\angle A=60^{\circ}\), then \(m\angle B=60^{\circ}\) and \(m\angle C=60^{\circ}\).

Each angle in an equiangular triangle is \(60^{\circ}\).

Example \(\PageIndex{5}\)

Find the measure of the missing angle.

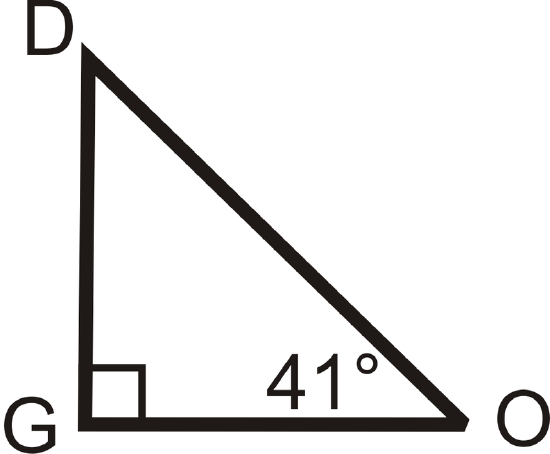
We know that \(m\angle O=41^{\circ}\) and \(m\angle G=90^{\circ}\) because it is a right angle. Set up an equation like in Example 3.

\(\begin{align*} m\angle D+m\angle O+m\angle G&=180^{\circ} \\ m\angle D+41^{\circ}+90^{\circ}&=180^{\circ} \\ m\angle D+41^{\circ}&=90^{\circ}\\ m\angle D=49^{\circ}\end{align*}\)

Determine \(m\angle 1\) in each triangle.

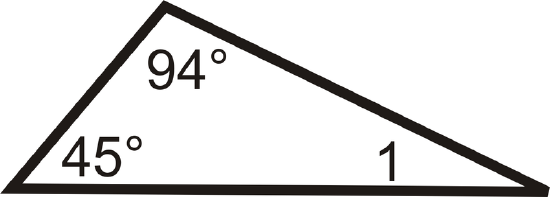
8. Two interior angles of a triangle measure \(32^{\circ}\) and \(64^{\circ}\). What is the third interior angle of the triangle?

9. Two interior angles of a triangle measure \(111^{\circ}\) and \(12^{\circ}\). What is the third interior angle of the triangle?

10. Two interior angles of a triangle measure \(2^{\circ}\) and \(157^{\circ}\). What is the third interior angle of the triangle?

Review (Answers)

To see the Review answers, open this PDF file and look for section 4.1.

Additional Resources

Interactive Element

Video: Triangle Sum Theorem Principles - Basic

Activities: Triangle Sum Theorem Discussion Questions

Study Aids: Triangle Relationships Study Guide

Practice: Triangle Angle Sum Theorem

Real World: Triangle Sum Theorem

• Number Charts
• Multiplication
• Long division
• Basic operations
• Telling time
• Place value
• Roman numerals
• Fractions & related
• Add, subtract, multiply,   and divide fractions
• Mixed numbers vs. fractions
• Equivalent fractions
• Prime factorization & factors
• Fraction Calculator
• Decimals & Percent
• Add, subtract, multiply,   and divide decimals
• Fractions to decimals
• Percents to decimals
• Percentage of a number
• Percent word problems
• Classify triangles
• Classify quadrilaterals
• Circle worksheets
• Area & perimeter of rectangles
• Area of triangles & polygons
• Coordinate grid, including   moves & reflections
• Volume & surface area
• Pre-algebra
• Square Roots
• Order of operations
• Scientific notation
• Proportions
• Ratio word problems
• Write expressions
• Evaluate expressions
• Simplify expressions
• Linear equations
• Linear inequalities
• Graphing & slope
• Equation calculator
• Equation editor
• Elementary Math Games
• Addition and subtraction
• Math facts practice
• The four operations
• Factoring and number theory
• Geometry topics
• Middle/High School
• Statistics & Graphs
• Probability
• Trigonometry
• Logic and proof
• For all levels
• Favorite math puzzles
• Favorite challenging puzzles
• Math in real world
• Problem solving & projects
• For gifted children
• Math history
• Math games and fun websites
• Interactive math tutorials
• Math help & online tutoring
• Assessment, review & test prep
• Online math curricula

Angles A and A' are corresponding angles, therefore ∠A = ∠A'.

So, the angle sum ∠A + ∠B + ∠C is equal to the angle sum ∠A' + ∠B' + ∠C'.

3. Calculate the angle marked with the question mark. Do not measure .

  4. A certain triangle has three equal angles.     What is the measure of each angle? _______°     Draw one using your protractor.     Make each of its sides 5 cm long.     This triangle has a special name.     What is it?

5. Can you draw a triangle that has     two obtuse angles?     Why or why not?

6. a. Draw a triangle with 65° and 50° angles, with         a 7.5-cm side between those two angles.          Start out by drawing the 7.5-cm side.

    b. Calculate the third angle. It is  _______°.         Then measure from your triangle to check.

    c.  Classify your triangle according to its         sides and angles:

        It is _________________________

        and _________________________.

Math Mammoth Geometry 1

A self-teaching worktext for 4th-5th grade that covers angles, triangles, quadrilaterals, cirlce, symmetry, perimeter, area, and volume. Lots of drawing exercises!

Download ($6.90) . Also available as a printed copy.

=> Learn more and see the free samples!

See more topical Math Mammoth books

Angle Sum of a Triangle

Related Topics: Lesson Plans and Worksheets for Grade 8 Lesson Plans and Worksheets for all Grades More Math Lessons for Grade 8 Common Core For Grade 8

Examples, videos, and solutions to help Grade 8 students know the Angle Sum Theorem for triangles; the sum of the interior angles of a triangle is always 180°.

Students present informal arguments to draw conclusions about the angle sum of a triangle.

New York State Common Core Math Grade 8, Module 2, Lesson 14

Worksheets for Grade 8

Student Outcomes • Students know a third informal proof of the angle sum theorem. • Students know how to find missing interior and exterior angle measures of triangles and present informal arguments to prove their answer is correct.

Lesson Summary The sum of the remote interior angles of a triangle is equal to the measure of the exterior angle.

Classwork Discussion Students will see one final informal proof of the angle sum of a triangle before moving on to working with exterior angles of triangles.

Now let’s look at what is called the exterior angle of a triangle. An exterior angle is formed when one of the sides of the triangle is extended. The interior angles are inside the triangle, so the exterior angle is outside of the triangle along the extended side.

Exercises 1 - 4 Use the diagram below to complete Exercises 1 - 4.

• Name an exterior angle and the related remote interior angles.
• Name a second exterior angle and the related remote interior angles.
• Name a third exterior angle and the related remote interior angles.
• Show that the measure of an exterior angle is equal to the sum of the related remote interior angles.

Example 1 - 4 Find the measure of angle x.

Exercise 5 - 10 5. Find the measure of angle. Present an informal argument showing that your answer is correct.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

Angle Sum Property of a Triangle: Definition, Theorem, Examples

What is the angle sum property of a triangle, triangle sum theorem proof, exterior angle theorem, solved examples on angle sum property of a triangle, practice problems on angle sum property of a triangle, frequently asked questions on angle sum property of a triangle.

The “angle sum property of a triangle theorem” (also known as the “triangle sum theorem” or “angle sum theorem”) states that the sum of the three interior angles of any triangle is always $180^{\circ}$ .

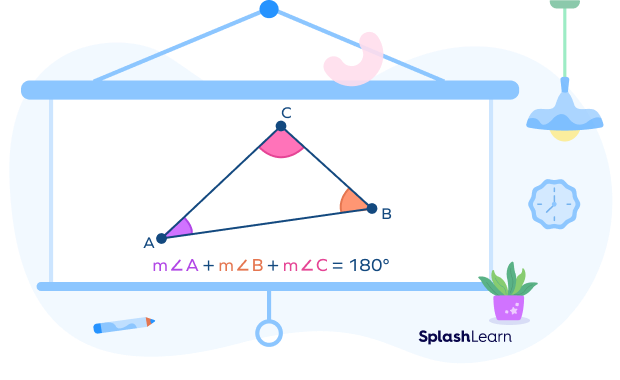
What is the angle sum theorem in geometry? In Euclidean geometry, any triangle whether it is a right triangle, an obtuse triangle, or an acute triangle all have interior angles that add up to 180 degrees .

Angle Sum Property of a Triangle Theorem

The angle sum property of a triangle theorem states that the sum of all three internal angles of a triangle is $180^{\circ}$. It is also known as the angle sum theorem or triangle sum theorem .

According to the angle sum theorem, in the above ABC, 

$m\angle A + m\angle B + m\angle C = 180^{\circ}$

Example : In PQR, $\angle P = 60^{\circ}, \angle Q = 70^{\circ}$

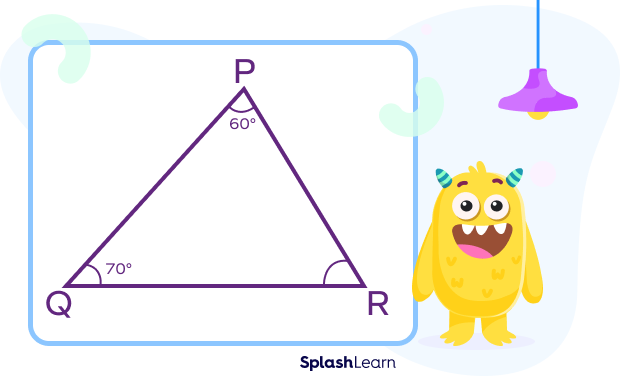
According to the angle sum theorem, in the above triangle PQR, 

$m\angle P + m\angle Q + m\angle R = 180^{\circ}$

$60^{\circ} + 70^{\circ} + m\angle R = 180^{\circ}$

$130^{\circ} + m\angle R = 180^{\circ}$

 $m\angle R = 50^{\circ}$

Related Worksheets

In the figure given below, AB, BC, and CA represent three sides of triangle ABC. A, B, and C are the three vertices. $\angle A,\; \angle B,$ and $\angle C$ are the three interior angles of $\Delta ABC$.

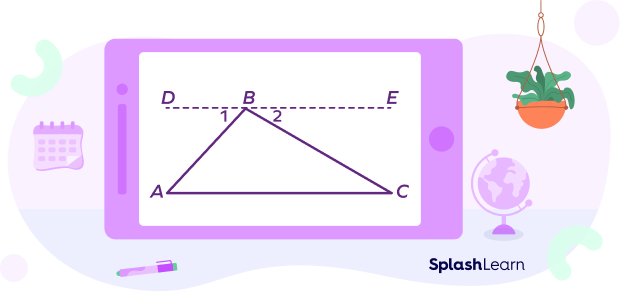
In ∆ABC, we have to prove that the sum of the angles $\angle A,\; \angle B,$ and $\angle C$ is $180^{\circ}$. 

To prove: $m\angle A + m \angle B + m\angle C = 180^{\circ}$

Construction: Draw a line DE passing through the vertex B, which is parallel to the side AC.

At point B, two angles are formed, $\angle 1$ and $\angle 2$.

Since AB is a transversal for the parallel lines DE and AC, we have 

$m\angle 1 = m\angle A$ (since the pair of alternate interior angles are equal)

Similarly, $m\angle 2 = m\angle C$.

Now, $m\angle 1,\; m\angle B,$ and $m\angle 2$ must add up to $180^{\circ}$ (angles on a straight line). 

Thus, $\angle 1 + \angle B + \angle 2 = 180^{\circ}$… (I)

Since $\angle 1 = \angle A$ and $\angle 2 = \angle C$. … (II)

Substituting equation (II) in equation (I), we get

Therefore, the sum of the three angles $\angle A,\; \angle B,$ and $\angle C$ is $180^{\circ}$. 

Hence, the triangle sum theorem was proved.

The exterior angle theorem states that “an exterior angle of a triangle is equal to the sum of its two opposite interior angles.”

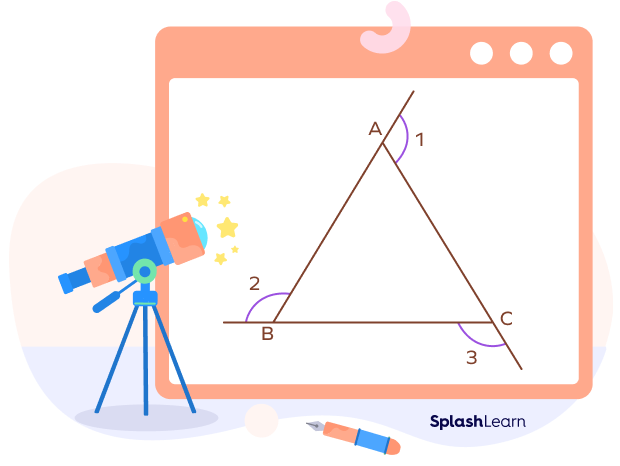
In the above triangle, $\angle A,\; \angle B,$ and $\angle C$ are the interior angles of the triangle ABC, and $\angle 1,\; \angle 2,$ and $\angle 3$ are the exterior angle.

$m\angle A + m\angle B + m\angle C = 180^{\circ}$ (angle sum property) … (I)

Also, $m\angle A + m\angle 1 = 180^{\circ}$ (linear pair angle) … (II)

From (I) and (II), we get

$m\angle A + m\angle 1 = m\angle A + m\angle B + m\angle C$

$m\angle 1 = m\angle B + m\angle C$ 

Similarly, we can derive for other two exterior angles,∠2 and ∠3 which is given by:

$m\angle 2 = m\angle A + m\angle C$

$m\angle 3 = m\angle A + m\angle B$ 

In summary: 

Facts about Angle Sum Property of a Triangle

• The theorem of angle sum property of triangles holds true for all types of triangles.
• The sum of all exterior angles of a triangle is equal to $360^{\circ}$.
• The sum of the lengths of any two sides of a triangle is always greater than the third side.
• A rectangle can be divided into two right triangles by drawing a line from one corner to the opposite corner.
• The study of the relationship between the sides and angles of triangles is known as trigonometry.
• Due to their high strength, triangle shapes are frequently utilized in construction.
• In North Carolina, there are three cities: Raleigh, Durham, and Chapel Hill, that are often referred to as the triangle.

In this article, we have learned all about the angle sum property of a triangle, exterior angle property of a triangle, proof of triangle sum theorem, and some important facts about triangles.

Let’s solve a few triangle angle sum theorem examples and practice problems.

• In a triangle, ABC, if $m\angle A = 60^{\circ},\; m\angle B = 40^{\circ}$ , then find the measure of angle $\angle C$ .

Solution: 

In $\Delta ABC,\; \angle A = 60^{\circ}$ and $\angle B = 40^{\circ}$

We know that the sum of angles in a triangle is $180^{\circ}$.

$\Rightarrow  m \angle A + \angle B + \angle C = 180^{\circ}$

$\Rightarrow  60^{\circ} + 40^{\circ} + \angle C = 180^{\circ}$

$\Rightarrow  \angle C = 180^{\circ} \;−\; ( 60^{\circ} + 40^{\circ})$

$\Rightarrow  \angle C = 180^{\circ} \;−\; 100^{\circ}$

$\therefore  \angle C = 80^{\circ}$

• One of the acute angles in a right-angled triangle is $40^{\circ}$ . Using the angle sum theorem, determine the other angle. 

Let $\Delta ABC$ be given a right-angled triangle which is right-angled at B.

$\therefore  \angle B = 90^{\circ}$

$m\angle A = 40^{\circ}$ and we have to find out $m\angle C$.

$\Rightarrow  m \angle A + m \angle B + m \angle C = 180^{\circ}$

$\Rightarrow  40^{\circ} +  90^{\circ} + m\angle C = 180^{\circ}$

$\Rightarrow  m \angle C = 180^{\circ} \;−\; (40^{\circ} + 90^{\circ})$

$\Rightarrow  m \angle C = 180^{\circ} \;−\; 130^{\circ}$

$\therefore  m \angle C = 50^{\circ}$

$\therefore m \angle A = m \angle C = 50^{\circ}$

• The measures of interior angles of a triangle are $(2x\;−\;20)^{\circ}, (3x\;−\;10)^{\circ}$ , and $2x^{\circ}$ , find the values of all three angles of the triangle.

We know that the sum of angles in a triangle is $180^{\circ}$

$\Rightarrow (2x\;−\;20)^{\circ} + (3x\;−\;10)^{\circ} + 2x^{\circ} = 180^{\circ}$

$\Rightarrow (2x\;−\;20 + 3x\;−\;10 + 2x)^{\circ} = 180^{\circ}$

$\Rightarrow 7x\;−\;30 = 180$

$\Rightarrow 7x = 180 + 30$

$\Rightarrow 7x = 210$

$\Rightarrow x = 2107= 30$

$\Rightarrow$ Angles are $40^{\circ},\; 80^{\circ}$ and $60^{\circ}$.

• Is it possible to construct a triangle with internal angles $43^{\circ},\; 49^{\circ},$ and $91^{\circ}$ ?

Given, measurements of angles $43^{\circ},\; 49^{\circ},$ and $91^{\circ}$.

Here, $43^{\circ} + 49^{\circ} + 91^{\circ} = 183^{\circ} 180^{\circ}$

We know, that, the sum of angles in a triangle is $180^{\circ}$

Hence, it is not possible to construct a triangle with measurements of angles $43^{\circ},\; 49^{\circ},$ and $91^{\circ}$.

• In the figure given below, determine the value of “x.”

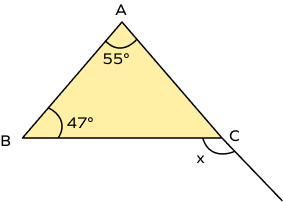
In the above figure, $\angle x$ is an exterior angle and $\angle A = 55^{\circ}$ and $\angle B = 47^{\circ}$ are given as interior angles.

According to the exterior angle property,

an exterior angle of a triangle is equal to the sum of its two interior opposite angles.

So, $\angle x = \angle A + \angle B = 55^{\circ} + 47^{\circ} = 102^{\circ}$

Hence, $x = 102^{\circ}$

Attend this quiz & Test your knowledge.

If all angles of a triangle are congruent, then each angle measures ___.

What is the sum of all interior angles of a triangle, two angles of a triangle measure $30^{\circ}$ and $60^{\circ}$. the measure of the third angle is _____..

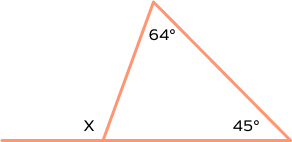
What is the sum of all exterior angles of a triangle?

What is the difference between the angle sum theorem and the exterior angle theorem?

The angle sum theorem states that the sum of all three internal angles of a triangle is 180°. Whereas the exterior angle theorem states that an exterior angle of a triangle is equal to the sum of its two interior opposite angles.

Can we define the angle sum property for a quadrilateral?

Yes, we can define the angle sum property for a quadrilateral. According to the angle sum property of a quadrilateral, the sum of all four interior angles is 360 degrees.

What is the sum of all exterior angles of a quadrilateral?

The sum of all exterior angles of any polygon is equal to $360^{\circ}$. Hence the sum of all exterior angles of a quadrilateral is also equal to $360^{\circ}$

What is the formula for the angle sum property of a triangle?

We know that the sum of angles in a triangle is $180^{\circ}$. For $\Delta ABC$, the formula for the angle sum property of a triangle is $\angle A + \angle B + \angle C = 180^{\circ}$.

What Is the angle sum theorem for any polygon?

According to the angle sum theorem for any polygon, the sum of all interior angles is equal to $(n − 2) \times 180^{\circ}$, where n is the total number of sides of the polygon.

RELATED POSTS

• Negative Slope: Definition, Graph, Solved Examples, Facts
• Milliliters to Gallons Conversion
• Square Prism – Definition, Types, Properties, Formulas, Facts, FAQs
• Perimeter of a Semicircle – Definition, Formula, Examples, Facts
• Corresponding Angles – Definition, Theorem, Types, Examples

Math & ELA | PreK To Grade 5

Kids see fun., you see real learning outcomes..

Make study-time fun with 14,000+ games & activities, 450+ lesson plans, and more—free forever.

Parents, Try for Free Teachers, Use for Free

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

8.3: Solving Triangles

• Last updated
• Save as PDF
• Page ID 41319

• Richard W. Beveridge
• Clatsop Community College

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Using information about some of the sides and angles of a triangle in order to find the unknown sides and angles is called "solving the triangle." If two sides of a triangle are known, the Pythagorean Theorem can be used to find the third side. If one of the acute angles in a right triangle is known, the other angle will be its complement with their sum being \(90^{\circ}\)

Suppose that we have a right triangle in which we know the sides, but no angles. Another situation could involve knowing the angles but just one side. How could we solve for the missing measurements in these situations?

Solving problems like these uses precalculated values of the trigonometric ratios to match the lengths with the appropriate angles and vice versa. Up until the 1980's, these values were printed in tables that were included in the back of every textbook (along with tables of logarithms), but have recently been programmed into calculators using methods that are studied in Calculus.

Most calculators have a button or function designed to find the inverse sine, inverse cosine and inverse tangent \(\left(\sin ^{-1}, \cos ^{-1}, \text {and } \tan ^{-1}\right),\) these are the functions that tell you the measure of the angle that has a sine, cosine or tangent equal to a particular value. For example, if we are given an angle \(\theta\) and know that the \(\sin \theta=\frac{1}{2}\)

Then we can find \(\sin ^{-1}\left(\frac{1}{2}\right)\) on a calculator, which should return a value of \(30^{\circ} .\) If the calculator is in radian mode, it will return a value of \(\approx 0.523598776 .\) If you divided this number by \(\pi,\) you would get \(0.1 \overline{6},\) which means that \(0.523598776 \approx \frac{\pi}{6}\) In this chapter we will work mainly in degrees. In Chapter \(2,\) when we graph the trigonometric functions we will typically use radian measure.

Solve the triangle. Round side lengths to the nearest \(100^{t h}\) and angles to the nearest \(10^{\text {th }}\) of a degree.

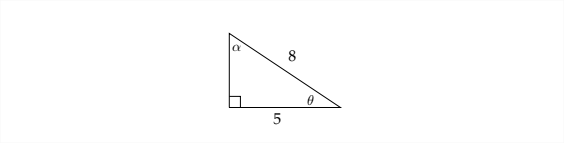
We can find the third side of the triangle by using the Pythagorean Theorem.

\[ \begin{aligned} a^{2}+5^{2} &=8^{2} \\ a^{2}+25 &=64 \end{aligned} \] \(a^{2}=39\) \[ a=\sqrt{39} \approx 6.24 \]

When solving problems of this type, I encourage people to use the most accurate values that are available in the problem. This way, there is less chance for rounding error to occur.

If we take the values for the sides that were given in the problem ( 5 and 8 ), then we can say that

\[ \begin{array}{c} \cos \theta=\frac{5}{8} \\ \theta=\cos ^{-1}\left(\frac{5}{8}\right) \\ \theta \approx 51.3^{\circ} \end{array} \]

Then \(\alpha\) would be \(90^{\circ}-51.3^{\circ}=38.7^{\circ} \approx \alpha\)

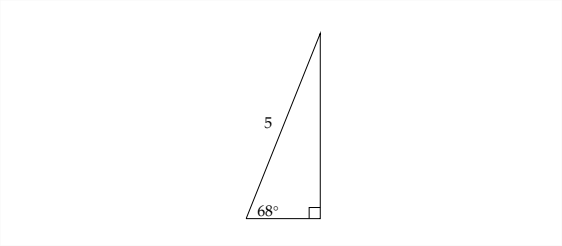
\(\cos 68^{\circ}=\frac{b}{5}\) Approximating cos \(68^{\circ}\) on a calculator: \[ \begin{array}{c} 0.3746 \approx \frac{b}{5} \\ 5 * 0.3746 \approx b \\ 1.9 \approx b \end{array} \] If we use the Pythagorean Theorem with two sides of the triangle to find the third, then we would say that: \[ \begin{array}{c} b^{2}+4.6^{2}=5^{2} \\ b^{2}+21.16=25 \\ b^{2}=3.84 \\ b=\sqrt{3.84} \approx 1.959 \approx 2.0 \end{array} \] The rounding error in this example comes from the fact that the first side we found was not exactly \(4.6 .\) If we wanted a more accurate answer that matches the answer we found using the cosine ratio, we just need more accuracy in the leg of the triangle we found. Calculating \(5 * \sin 68^{\circ} \approx 4.636\) should provide enough accuracy. \[ \begin{array}{c} b^{2}+4.636^{2}=5^{2} \\ b^{2}+21.492496=25 \\ b^{2}=3.507504 \\ b=\sqrt{3.507504} \approx 1.8728 \approx 1.9 \end{array} \]

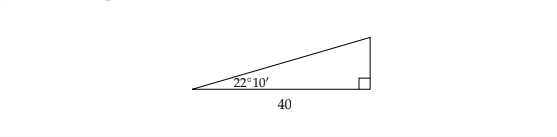
To find the other leg of the triangle, we can use the tangent ratio. \[ \tan 22.1 \overline{6}^{\circ}=\frac{a}{40} \] Approximating tan \(22.1 \overline{6}^{\circ}\) on a calculator: \[ 0.4074 \approx \frac{a}{40} \] Then, multiply on both sides by 40: \[ \begin{array}{c} 40 * 0.4074 \approx a \\ 16.3 \approx a \end{array} \] We can check this answer by the Pythagorean Theorem: \[ 16.3^{2}+40^{2}=1865.69 \] \[ \sqrt{1865.69} \approx 43.2 \]

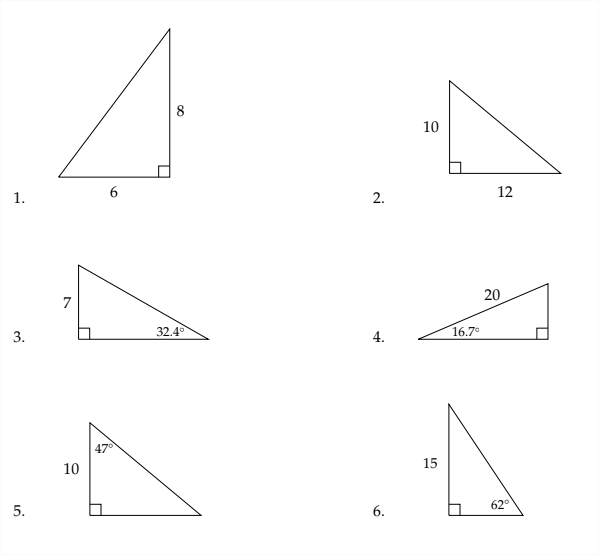
Exercises 1.3 In each problem below, solve the triangle. Round side lengths to the nearest \(100^{t h}\) and angle measures to the nearest \(10^{\text {th }}\) of a degree.

• → Resources
• → 8th Grade
• → Shapes & Angles

Triangle Sum Theorem Lesson Plan

Get the lesson materials.

Triangle Sum Theorem Guided Notes w Doodles | Graphic & Sketch Notes 8th Grade

Ever wondered how to teach the Triangle Sum Theorem in an engaging way to your 8th-grade students?

In this lesson plan, students will learn about the Triangle Sum Theorem and its real-life applications. Through artistic, interactive guided notes, check for understanding, practice coloring by code, and a maze worksheet, students will gain a comprehensive understanding of the theorem.

The lesson ends with a real-life example that explores how the Triangle Sum Theorem can be applied to solve real-world geometric problems.

• Standard : CCSS 8.G.A.5
• Topics : Shapes & Angles , Triangles & Pythagorean Theorem
• Grade : 8th Grade
• Type : Lesson Plans

Learning Objectives

After this lesson, students will be able to:

Understand the Triangle Sum Theorem and its application in solving for missing angles in triangles.

Solve for missing angles in triangles using the Triangle Sum Theorem.

Set up and solve equations to find variables representing missing angles in triangles.

Apply knowledge of the Triangle Sum Theorem to solve real-life math problems involving triangles.

Prerequisites

Before this lesson, students should be familiar with:

Understanding of angles and their measure

Knowledge of basic geometric shapes such as triangles, quadrilaterals, etc.

Colored pencils or markers

Triangle Sum Theorem Guided Notes w Doodles

Key Vocabulary

Triangle Sum Theorem

Missing Angle

Introduction

As a hook, ask students why understanding the Triangle Sum Theorem is important in real-life situations involving shapes and angles. Refer to the last page of the guided notes as well as the FAQs below for ideas.

Use the first page of the guided notes to introduce the Triangle Sum Theorem, explaining how the sum of the three interior angles of a triangle is always 180 degrees. Walk through the key points of the theorem to teach, emphasizing the relationship between the angles in a triangle. Refer to the FAQ below for a walk through on this, as well as ideas on how to respond to common student questions.

For the second page of the guided notes, continue by demonstrating how to apply the Triangle Sum Theorem to solve for missing angles in triangles. Highlight different types of triangle problems where students need to calculate the missing angles or set up equations to solve for the missing variables using the theorem. Verify student understanding by having them practice solving example problems. Refer to the FAQ below for additional support on teaching this concept effectively.

Based on student responses during the introduction, reteach concepts that students need extra help with, especially focusing on clarifying any misconceptions about the Triangle Sum Theorem. If your class has a wide range of proficiency levels, consider pulling out students for reteaching as needed while more advanced students start working on the practice exercises.

Have students practice solving problems involving the Triangle Sum Theorem using the practice worksheet provided in the resource. Students can practice using the maze activity (pg. 3) and the color by number activity (pg. 4). Walk around to answer student questions.

Fast finishers can dive into the real-life application activity for extra enrichment. You can assign it as homework for the remainder of the class.

Real-Life Application

Using the last page of the guided notes, bring the class back together, and introduce the concept of using the Triangle Sum Theorem in real life. Explain how the Triangle Sum Theorem is used to determine angles in structures like bridges, roofs, or even sports fields. Discuss how engineers and architects use this theorem to ensure the stability and integrity of their designs. Refer to the FAQ for more ideas on how to teach it!

Additional Self-Checking Digital Practice

If you’re looking for digital practice for Triangle Sum Theorem, try my Pixel Art activities in Google Sheets. Every answer is automatically checked, and correct answers unlock parts of a mystery picture. It’s incredibly fun, and a powerful tool for differentiation.

Here’s 1 activity to explore:

Triangle Sum Theorem Digital Pixel Art

What is the Triangle Sum Theorem? Open

The Triangle Sum Theorem states that the sum of the interior angles of a triangle is always equal to 180 degrees.

How can I use the Triangle Sum Theorem to find a missing angle in a triangle? Open

To find a missing angle in a triangle using the Triangle Sum Theorem:

Add the known angles in the triangle.

Subtract the sum from 180 degrees to find the missing angle.

What are the applications of the Triangle Sum Theorem in real life? Open

The Triangle Sum Theorem has various real-life applications, such as in:

Architecture and construction for designing structures.

Navigation for calculating angles and distances.

Surveying for determining land boundaries.

Can the Triangle Sum Theorem be applied to any type of triangle? Open

Yes, the Triangle Sum Theorem can be applied to any type of triangle, whether it's equilateral, isosceles, scalene, or right-angled.

How do Guided Notes and Doodles help in understanding the Triangle Sum Theorem? Open

Guided Notes and Doodles aid in understanding the Triangle Sum Theorem by:

Providing structured notes for clear explanations.

Encouraging visual learning through sketch notes and doodles.

What are some Common Core Standards related to the Triangle Sum Theorem? Open

The Common Core Standard related to the Triangle Sum Theorem is:

8.G.A.5: Use informal arguments to establish facts about the angle sum and exterior angle of triangles.

Want more ideas and freebies?

Get my free resource library with digital & print activities—plus tips over email.

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Unit 4: Triangles

About this unit.

You probably like triangles. You think they are useful. They show up a lot. What you'll see in this topic is that they are far more magical and mystical than you ever imagined!

Triangle types

• Classifying triangles (Opens a modal)
• Classifying triangles by angles (Opens a modal)
• Worked example: Classifying triangles (Opens a modal)
• Types of triangles review (Opens a modal)
• Classify triangles by angles 4 questions Practice
• Classify triangles by side lengths 4 questions Practice

Triangle angles

• Angles in a triangle sum to 180° proof (Opens a modal)
• Triangle exterior angle example (Opens a modal)
• Worked example: Triangle angles (intersecting lines) (Opens a modal)
• Worked example: Triangle angles (diagram) (Opens a modal)
• Triangle angle challenge problem (Opens a modal)
• Triangle angle challenge problem 2 (Opens a modal)
• Triangle angles review (Opens a modal)
• Find angles in triangles 7 questions Practice
• Find angles in isosceles triangles 4 questions Practice
• Finding angle measures between intersecting lines 4 questions Practice
• Finding angle measures using triangles 7 questions Practice

Triangle inequality theorem

• Triangle inequality theorem (Opens a modal)
• Triangle side length rules 4 questions Practice

Perpendicular bisectors

• Circumcenter of a triangle (Opens a modal)
• Circumcenter of a right triangle (Opens a modal)
• Three points defining a circle (Opens a modal)
• Area circumradius formula proof (Opens a modal)
• 2003 AIME II problem 7 (Opens a modal)

Angle bisectors

• Distance between a point & line (Opens a modal)
• Incenter and incircles of a triangle (Opens a modal)
• Inradius, perimeter, & area (Opens a modal)

Medians & centroids

• Triangle medians & centroids (Opens a modal)
• Triangle medians and centroids (2D proof) (Opens a modal)
• Dividing triangles with medians (Opens a modal)
• Exploring medial triangles (Opens a modal)
• Centroid & median proof (Opens a modal)
• Median, centroid example (Opens a modal)
• Proof: Triangle altitudes are concurrent (orthocenter) (Opens a modal)
• Common orthocenter and centroid (Opens a modal)

Bringing it all together

• Review of triangle properties (Opens a modal)
• Euler line (Opens a modal)
• Euler's line proof (Opens a modal)

One to one maths interventions built for KS4 success

Weekly online one to one GCSE maths revision lessons now available

In order to access this I need to be confident with:

This topic is relevant for:

Angles In A Triangle

Here is everything you need to know about angles in a triangle including what the angles in a triangle add up to, how to find missing angles, and how to use this alongside other angle facts to form and solve equations.

There are also angles in a triangle worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

What are angles in a triangle?

All triangles have interior angles that add up to 180º .

Angles in a triangle are the sum (total) of the angles at each vertex in a triangle.

We can use this fact to calculate missing angles by finding the total of the given angles and subtracting it from 180º .

This is true for all types of triangles.

• Right Angle Triangle: One 90° angle, the other two angles will have a total of 90° .
• Isosceles Triangle: Two equal sides and angles.
• Equilateral Triangle: All three angles are 60° .
• Scalene Triangle: All three angles are different.

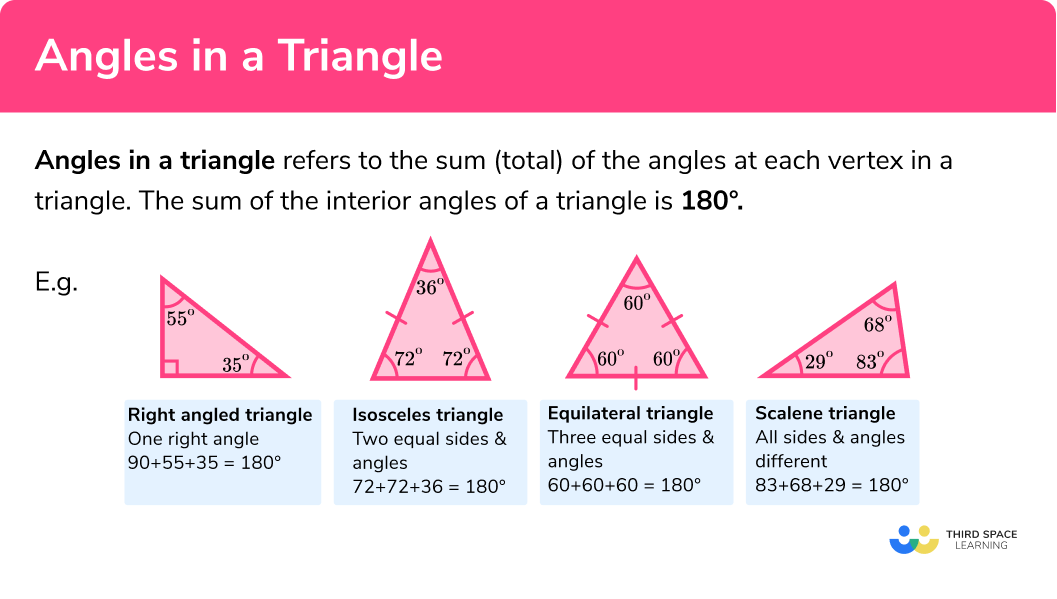
How to find a missing angle in a triangle

In order to find the missing angle in a triangle:

• Add up the other angles within the triangle.
• Subtract this total from 180º .

Explain how to find a missing angle in a triangle in 2 steps

Angles in a triangle worksheet

Get your free angles in a triangle worksheet of 20+ questions and answers. Includes reasoning and applied questions.

Related lessons on angles in polygons

Angles in a triangle  is part of our series of lessons to support revision on  angles in polygons . You may find it helpful to start with the main angles in polygons lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:

• Angles in polygons
• Interior angles of a polygon
• Exterior angles of a polygon
• Angles in a quadrilateral
• Angles in a pentagon
• Angles in a hexagon

Finding missing angles examples

Example 1: scalene triangle.

Work out the size of the angle labelled a in the following triangle.

• We are given the angles 57º and 79º . Add these together.

2 Subtract 136º from 180º .

Example 2: right angled triangle

Find the angle labelled b in the following triangle.

We are given the angles 90º and 19º . Add these together.

Subtract 109º from 180º .

Example 3: isosceles triangle

Find the angle labelled c in the following triangle.

When two sides of a triangle are equal, the angles at the ends of those sides will also be equal.

We are given the angle 64º. As this is an isosceles triangle (two equal length sides and two equal angles), the other angle at the bottom will also be 64º .

Subtract 128º from 180º .

How to find one of the two equal angles in an isosceles triangle

• Subtract the given angle from 180º .
• Divide by 2 .

Example 4: equal angles in an isosceles triangle

Find the size of the angle labelled d in the triangle below.

This is an isosceles triangle. We are given one angle and asked to find one of the remaining two angles, which we know are equal.

The other two angles in this triangle add up to 70º .

Since the other two angles in this triangle are equal, we can find d by dividing by 2 .

How to use angle facts to solve problems

Sometimes the problem will involve using other angle facts. Let’s recap some of the other angle facts we know:

• Use angle facts to fill in any possible angles.
• Use these angles to calculate missing angles in the triangle.

These steps are interchangeable and may need to be repeated for more difficult problems.

Example 5: using angles at a point

Find the size of the angle labelled e .

Here we can use the fact that angles at a point add up to 360º .

Now we know two angles within the triangle, we can find the missing angle.

Example 6: using opposite angles

This time we already know two of the angles in the triangle so we can start by finding the third angle.

We can use the fact that opposite angles are equal to find f .

Example 7: two different triangles

Find the size of the angle labelled g .

We know two of the angles in the right hand triangle and so we can calculate the third.

We can use the fact that angles on a straight line add up to 180º .

Since the sides of the triangle are equal, the left hand triangle is an isosceles triangle and the two angles at the bottom of the triangle are equal. Therefore we can work out the third angle.

How to work out angles in a triangle with algebra

We can use the fact that the angles in a triangle add up to 180º to form equations which we can then solve to find the values of the angles in the triangle.

•  Add together the expressions for each angle and simplify.
•  Put the simplified expression equal to 180º .

Solve the equation.

•  Substitute your value back in to find the angles in the triangle.

Example 8: angles involving algebra

Find the size of each angle in this triangle.

Add the expressions for each angle.

Put the simplified expression equal to 180º .

Work out the angles.

The three angles are 40º , 60º and 80º .

Example 9: angles involving algebra

Find the size of each angle in this right-angled triangle.

The three angles are 23º , 67º and 90º .

Common misconceptions

• Incorrect angle sum

Using 360º instead of 180º for the sum of the angles of the triangle.

• Equal angles in an isosceles triangle

Selecting the wrong angles when identifying the equal angles in an isosceles triangle (particularly a problem when the equal angles are not at the bottom). The angle that is different in an isosceles triangle is the one between the two sides with equal length.

Practice angles in a triangle questions

1. Find the angle labelled z in the following triangle.

2. Find the angle labelled y .

This is an isosceles triangle and the two angles at the bottom of the triangle are equal.

3. Find the angle x in the following triangle.

This is an isosceles triangle and the two angles on the right are equal.

4.  What is the size of each angle in an equilateral triangle?

All three angles in an equilateral triangle are equal so

5. Find the size of the angle labelled w in the following triangle.

The angle opposite 24^{\circ} is also 24^{\circ} since vertically opposite angles are equal.

The triangle is an isosceles triangle and the two angles on the left are the same size.

6.  Find the angle labelled v .

Looking at the left hand triangle frist, we can find the missing angle in that triangle:

We can then use the fact that angles on a straight line add up to 180^{\circ} to find the unlabelled angle in the right hand triangle:

We can then find angle v :

7. Write an equation involving u and use it to find the size of each angle in the following triangle.

Adding the expressions gives us:

Angles in a triangle GCSE questions

1. Find the size of angle x given that the exterior angle shown is 153^{\circ} .

2. (a) Calculate the size of angle ACE .

(b) Show that BCD is an isosceles triangle.

90 + 36 = 126  

            (1)

180-126=54^{\circ}  

Angle CBD :

= 180 – 117  

=63^{\circ}    

Angle BDC : 

63 + 54 = 117

180-117=63^{\circ}

Two angles equal therefore isosceles                

3. Work out the size of the smallest angle in the right angled triangle.

3x – 10 + 2x + 55 + 90 (= 5x + 135)

5x + 135 = 180

3\times 9-10=17^{\circ}   

Learning checklist:

You have now learned how to:

• Use the sum of the angles of a triangle to find missing angles
• Apply other angle facts to find missing angles in triangle problems
• Form and solve equations using the sum of the angles in a triangle

The next lessons are

• Angle rules
• Angles in parallel lines
• How to calculate volume

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.

Privacy Overview

Free Mathematics Tutorials

Grade 8 Questions on Angles with Solutions and Explanations

Detailed solutions and full explanations to grade 8 math questions on angles are presented.

More References and Links

Popular pages.

• Grade 8 Questions with Answers on Angles in Triangles
• Middle School Math (Grades 6, 7, 8, 9) - Free Questions and Problems With Answers
• Grade 8 Problems and Questions on Triangles with Answers
• Grade 8 Problems and Questions on Triangles with Solutions and Explanations
• Grade 8 Problems and Questions on Circles with Answers

Get In Touch

• Privacy Policy