hypothesis of regression test

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

13.6 Testing the Regression Coefficients

Learning objectives.

Conduct and interpret a hypothesis test on individual regression coefficients.

Previously, we learned that the population model for the multiple regression equation is

[latex]\begin{eqnarray*} y & = & \beta_0+\beta_1x_1+\beta_2x_2+\cdots+\beta_kx_k +\epsilon \end{eqnarray*}[/latex]

where [latex]x_1,x_2,\ldots,x_k[/latex] are the independent variables, [latex]\beta_0,\beta_1,\ldots,\beta_k[/latex] are the population parameters of the regression coefficients, and [latex]\epsilon[/latex] is the error variable. In multiple regression, we estimate each population regression coefficient [latex]\beta_i[/latex] with the sample regression coefficient [latex]b_i[/latex].

In the previous section, we learned how to conduct an overall model test to determine if the regression model is valid. If the outcome of the overall model test is that the model is valid, then at least one of the independent variables is related to the dependent variable—in other words, at least one of the regression coefficients [latex]\beta_i[/latex] is not zero. However, the overall model test does not tell us which independent variables are related to the dependent variable. To determine which independent variables are related to the dependent variable, we must test each of the regression coefficients.

Testing the Regression Coefficients

For an individual regression coefficient, we want to test if there is a relationship between the dependent variable [latex]y[/latex] and the independent variable [latex]x_i[/latex].

No Relationship . There is no relationship between the dependent variable [latex]y[/latex] and the independent variable [latex]x_i[/latex]. In this case, the regression coefficient [latex]\beta_i[/latex] is zero. This is the claim for the null hypothesis in an individual regression coefficient test: [latex]H_0: \beta_i=0[/latex].
Relationship. There is a relationship between the dependent variable [latex]y[/latex] and the independent variable [latex]x_i[/latex]. In this case, the regression coefficients [latex]\beta_i[/latex] is not zero. This is the claim for the alternative hypothesis in an individual regression coefficient test: [latex]H_a: \beta_i \neq 0[/latex]. We are not interested if the regression coefficient [latex]\beta_i[/latex] is positive or negative, only that it is not zero. We only need to find out if the regression coefficient is not zero to demonstrate that there is a relationship between the dependent variable and the independent variable. This makes the test on a regression coefficient a two-tailed test.

In order to conduct a hypothesis test on an individual regression coefficient [latex]\beta_i[/latex], we need to use the distribution of the sample regression coefficient [latex]b_i[/latex]:

The mean of the distribution of the sample regression coefficient is the population regression coefficient [latex]\beta_i[/latex].
The standard deviation of the distribution of the sample regression coefficient is [latex]\sigma_{b_i}[/latex]. Because we do not know the population standard deviation we must estimate [latex]\sigma_{b_i}[/latex] with the sample standard deviation [latex]s_{b_i}[/latex].
The distribution of the sample regression coefficient follows a normal distribution.

Steps to Conduct a Hypothesis Test on a Regression Coefficient

[latex]\begin{eqnarray*} H_0: & & \beta_i=0 \\ \\ \end{eqnarray*}[/latex]

[latex]\begin{eqnarray*} H_a: & & \beta_i \neq 0 \\ \\ \end{eqnarray*}[/latex]

Collect the sample information for the test and identify the significance level [latex]\alpha[/latex].

[latex]\begin{eqnarray*}t & = & \frac{b_i-\beta_i}{s_{b_i}} \\ \\ df & = & n-k-1 \\ \\ \end{eqnarray*}[/latex]

The results of the sample data are significant. There is sufficient evidence to conclude that the null hypothesis [latex]H_0[/latex] is an incorrect belief and that the alternative hypothesis [latex]H_a[/latex] is most likely correct.
The results of the sample data are not significant. There is not sufficient evidence to conclude that the alternative hypothesis [latex]H_a[/latex] may be correct.
Write down a concluding sentence specific to the context of the question.

The required [latex]t[/latex]-score and p -value for the test can be found on the regression summary table, which we learned how to generate in Excel in a previous section.

The human resources department at a large company wants to develop a model to predict an employee’s job satisfaction from the number of hours of unpaid work per week the employee does, the employee’s age, and the employee’s income. A sample of 25 employees at the company is taken and the data is recorded in the table below. The employee’s income is recorded in $1000s and the job satisfaction score is out of 10, with higher values indicating greater job satisfaction.

Previously, we found the multiple regression equation to predict the job satisfaction score from the other variables:

[latex]\begin{eqnarray*} \hat{y} & = & 4.7993-0.3818x_1+0.0046x_2+0.0233x_3 \\ \\ \hat{y} & = & \mbox{predicted job satisfaction score} \\ x_1 & = & \mbox{hours of unpaid work per week} \\ x_2 & = & \mbox{age} \\ x_3 & = & \mbox{income (\$1000s)}\end{eqnarray*}[/latex]

At the 5% significance level, test the relationship between the dependent variable “job satisfaction” and the independent variable “hours of unpaid work per week”.

Hypotheses:

[latex]\begin{eqnarray*} H_0: & & \beta_1=0 \\ H_a: & & \beta_1 \neq 0 \end{eqnarray*}[/latex]

The regression summary table generated by Excel is shown below:

The p -value for the test on the hours of unpaid work per week regression coefficient is in the bottom part of the table under the P-value column of the Hours of Unpaid Work per Week row . So the p -value=[latex]0.0082[/latex].

Conclusion:

Because p -value[latex]=0.0082 \lt 0.05=\alpha[/latex], we reject the null hypothesis in favour of the alternative hypothesis. At the 5% significance level there is enough evidence to suggest that there is a relationship between the dependent variable “job satisfaction” and the independent variable “hours of unpaid work per week.”

The null hypothesis [latex]\beta_1=0[/latex] is the claim that the regression coefficient for the independent variable [latex]x_1[/latex] is zero. That is, the null hypothesis is the claim that there is no relationship between the dependent variable and the independent variable “hours of unpaid work per week.”
The alternative hypothesis is the claim that the regression coefficient for the independent variable [latex]x_1[/latex] is not zero. The alternative hypothesis is the claim that there is a relationship between the dependent variable and the independent variable “hours of unpaid work per week.”
When conducting a test on a regression coefficient, make sure to use the correct subscript on [latex]\beta[/latex] to correspond to how the independent variables were defined in the regression model and which independent variable is being tested. Here the subscript on [latex]\beta[/latex] is 1 because the “hours of unpaid work per week” is defined as [latex]x_1[/latex] in the regression model.
The p -value for the tests on the regression coefficients are located in the bottom part of the table under the P-value column heading in the corresponding independent variable row.
Because the alternative hypothesis is a [latex]\neq[/latex], the p -value is the sum of the area in the tails of the [latex]t[/latex]-distribution. This is the value calculated out by Excel in the regression summary table.
The p -value of 0.0082 is a small probability compared to the significance level, and so is unlikely to happen assuming the null hypothesis is true. This suggests that the assumption that the null hypothesis is true is most likely incorrect, and so the conclusion of the test is to reject the null hypothesis in favour of the alternative hypothesis. In other words, the regression coefficient [latex]\beta_1[/latex] is not zero, and so there is a relationship between the dependent variable “job satisfaction” and the independent variable “hours of unpaid work per week.” This means that the independent variable “hours of unpaid work per week” is useful in predicting the dependent variable.

At the 5% significance level, test the relationship between the dependent variable “job satisfaction” and the independent variable “age”.

[latex]\begin{eqnarray*} H_0: & & \beta_2=0 \\ H_a: & & \beta_2 \neq 0 \end{eqnarray*}[/latex]

The p -value for the test on the age regression coefficient is in the bottom part of the table under the P-value column of the Age row . So the p -value=[latex]0.8439[/latex].

Because p -value[latex]=0.8439 \gt 0.05=\alpha[/latex], we do not reject the null hypothesis. At the 5% significance level there is not enough evidence to suggest that there is a relationship between the dependent variable “job satisfaction” and the independent variable “age.”

The null hypothesis [latex]\beta_2=0[/latex] is the claim that the regression coefficient for the independent variable [latex]x_2[/latex] is zero. That is, the null hypothesis is the claim that there is no relationship between the dependent variable and the independent variable “age.”
The alternative hypothesis is the claim that the regression coefficient for the independent variable [latex]x_2[/latex] is not zero. The alternative hypothesis is the claim that there is a relationship between the dependent variable and the independent variable “age.”
When conducting a test on a regression coefficient, make sure to use the correct subscript on [latex]\beta[/latex] to correspond to how the independent variables were defined in the regression model and which independent variable is being tested. Here the subscript on [latex]\beta[/latex] is 2 because “age” is defined as [latex]x_2[/latex] in the regression model.
The p -value of 0.8439 is a large probability compared to the significance level, and so is likely to happen assuming the null hypothesis is true. This suggests that the assumption that the null hypothesis is true is most likely correct, and so the conclusion of the test is to not reject the null hypothesis. In other words, the regression coefficient [latex]\beta_2[/latex] is zero, and so there is no relationship between the dependent variable “job satisfaction” and the independent variable “age.” This means that the independent variable “age” is not particularly useful in predicting the dependent variable.

At the 5% significance level, test the relationship between the dependent variable “job satisfaction” and the independent variable “income”.

[latex]\begin{eqnarray*} H_0: & & \beta_3=0 \\ H_a: & & \beta_3 \neq 0 \end{eqnarray*}[/latex]

The p -value for the test on the income regression coefficient is in the bottom part of the table under the P-value column of the Income row . So the p -value=[latex]0.0060[/latex].

Because p -value[latex]=0.0060 \lt 0.05=\alpha[/latex], we reject the null hypothesis in favour of the alternative hypothesis. At the 5% significance level there is enough evidence to suggest that there is a relationship between the dependent variable “job satisfaction” and the independent variable “income.”

The null hypothesis [latex]\beta_3=0[/latex] is the claim that the regression coefficient for the independent variable [latex]x_3[/latex] is zero. That is, the null hypothesis is the claim that there is no relationship between the dependent variable and the independent variable “income.”
The alternative hypothesis is the claim that the regression coefficient for the independent variable [latex]x_3[/latex] is not zero. The alternative hypothesis is the claim that there is a relationship between the dependent variable and the independent variable “income.”
When conducting a test on a regression coefficient, make sure to use the correct subscript on [latex]\beta[/latex] to correspond to how the independent variables were defined in the regression model and which independent variable is being tested. Here the subscript on [latex]\beta[/latex] is 3 because “income” is defined as [latex]x_3[/latex] in the regression model.
The p -value of 0.0060 is a small probability compared to the significance level, and so is unlikely to happen assuming the null hypothesis is true. This suggests that the assumption that the null hypothesis is true is most likely incorrect, and so the conclusion of the test is to reject the null hypothesis in favour of the alternative hypothesis. In other words, the regression coefficient [latex]\beta_3[/latex] is not zero, and so there is a relationship between the dependent variable “job satisfaction” and the independent variable “income.” This means that the independent variable “income” is useful in predicting the dependent variable.

Concept Review

The test on a regression coefficient determines if there is a relationship between the dependent variable and the corresponding independent variable. The p -value for the test is the sum of the area in tails of the [latex]t[/latex]-distribution. The p -value can be found on the regression summary table generated by Excel.

The hypothesis test for a regression coefficient is a well established process:

Write down the null and alternative hypotheses in terms of the regression coefficient being tested. The null hypothesis is the claim that there is no relationship between the dependent variable and independent variable. The alternative hypothesis is the claim that there is a relationship between the dependent variable and independent variable.
Collect the sample information for the test and identify the significance level.
The p -value is the sum of the area in the tails of the [latex]t[/latex]-distribution. Use the regression summary table generated by Excel to find the p -value.
Compare the p -value to the significance level and state the outcome of the test.

Linear regression - Hypothesis testing

by Marco Taboga , PhD

This lecture discusses how to perform tests of hypotheses about the coefficients of a linear regression model estimated by ordinary least squares (OLS).

Table of contents

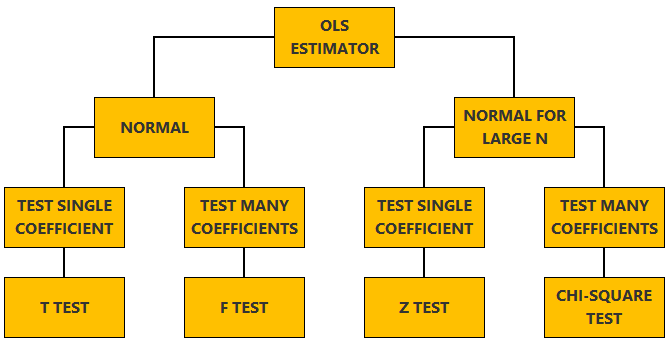
Normal vs non-normal model

The linear regression model, matrix notation, tests of hypothesis in the normal linear regression model, test of a restriction on a single coefficient (t test), test of a set of linear restrictions (f test), tests based on maximum likelihood procedures (wald, lagrange multiplier, likelihood ratio), tests of hypothesis when the ols estimator is asymptotically normal, test of a restriction on a single coefficient (z test), test of a set of linear restrictions (chi-square test), learn more about regression analysis.

The lecture is divided in two parts:

in the first part, we discuss hypothesis testing in the normal linear regression model , in which the OLS estimator of the coefficients has a normal distribution conditional on the matrix of regressors;

in the second part, we show how to carry out hypothesis tests in linear regression analyses where the hypothesis of normality holds only in large samples (i.e., the OLS estimator can be proved to be asymptotically normal).

How to choose which test to carry out after estimating a linear regression model.

We also denote:

We now explain how to derive tests about the coefficients of the normal linear regression model.

It can be proved (see the lecture about the normal linear regression model ) that the assumption of conditional normality implies that:

How the acceptance region is determined depends not only on the desired size of the test , but also on whether the test is:

one-tailed (only one of the two things, i.e., either smaller or larger, is possible).

For more details on how to determine the acceptance region, see the glossary entry on critical values .

The F test is one-tailed .

A critical value in the right tail of the F distribution is chosen so as to achieve the desired size of the test.

Then, the null hypothesis is rejected if the F statistics is larger than the critical value.

In this section we explain how to perform hypothesis tests about the coefficients of a linear regression model when the OLS estimator is asymptotically normal.

As we have shown in the lecture on the properties of the OLS estimator , in several cases (i.e., under different sets of assumptions) it can be proved that:

These two properties are used to derive the asymptotic distribution of the test statistics used in hypothesis testing.

The test can be either one-tailed or two-tailed . The same comments made for the t-test apply here.

Like the F test, also the Chi-square test is usually one-tailed .

The desired size of the test is achieved by appropriately choosing a critical value in the right tail of the Chi-square distribution.

The null is rejected if the Chi-square statistics is larger than the critical value.

Want to learn more about regression analysis? Here are some suggestions:

R squared of a linear regression ;

Gauss-Markov theorem ;

Generalized Least Squares ;

Multicollinearity ;

Dummy variables ;

Selection of linear regression models

Partitioned regression ;

Ridge regression .

How to cite

Please cite as:

Taboga, Marco (2021). "Linear regression - Hypothesis testing", Lectures on probability theory and mathematical statistics. Kindle Direct Publishing. Online appendix. https://www.statlect.com/fundamentals-of-statistics/linear-regression-hypothesis-testing.

Most of the learning materials found on this website are now available in a traditional textbook format.

F distribution
Beta distribution
Conditional probability
Central Limit Theorem
Binomial distribution
Mean square convergence
Delta method
Almost sure convergence
Mathematical tools
Fundamentals of probability
Probability distributions
Asymptotic theory
Fundamentals of statistics
About Statlect
Cookies, privacy and terms of use
Loss function
Almost sure
Type I error
Precision matrix
Integrable variable
To enhance your privacy,
we removed the social buttons,
but don't forget to share .

Prompt Library
DS/AI Trends
Stats Tools
Interview Questions
Generative AI
Machine Learning
Deep Learning

Linear regression hypothesis testing: Concepts, Examples

In relation to machine learning , linear regression is defined as a predictive modeling technique that allows us to build a model which can help predict continuous response variables as a function of a linear combination of explanatory or predictor variables. While training linear regression models, we need to rely on hypothesis testing in relation to determining the relationship between the response and predictor variables. In the case of the linear regression model, two types of hypothesis testing are done. They are T-tests and F-tests . In other words, there are two types of statistics that are used to assess whether linear regression models exist representing response and predictor variables. They are t-statistics and f-statistics. As data scientists , it is of utmost importance to determine if linear regression is the correct choice of model for our particular problem and this can be done by performing hypothesis testing related to linear regression response and predictor variables. Many times, it is found that these concepts are not very clear with a lot many data scientists. In this blog post, we will discuss linear regression and hypothesis testing related to t-statistics and f-statistics . We will also provide an example to help illustrate how these concepts work.

Table of Contents

What are linear regression models?

A linear regression model can be defined as the function approximation that represents a continuous response variable as a function of one or more predictor variables. While building a linear regression model, the goal is to identify a linear equation that best predicts or models the relationship between the response or dependent variable and one or more predictor or independent variables.

There are two different kinds of linear regression models. They are as follows:

Simple or Univariate linear regression models : These are linear regression models that are used to build a linear relationship between one response or dependent variable and one predictor or independent variable. The form of the equation that represents a simple linear regression model is Y=mX+b, where m is the coefficients of the predictor variable and b is bias. When considering the linear regression line, m represents the slope and b represents the intercept.
Multiple or Multi-variate linear regression models : These are linear regression models that are used to build a linear relationship between one response or dependent variable and more than one predictor or independent variable. The form of the equation that represents a multiple linear regression model is Y=b0+b1X1+ b2X2 + … + bnXn, where bi represents the coefficients of the ith predictor variable. In this type of linear regression model, each predictor variable has its own coefficient that is used to calculate the predicted value of the response variable.

While training linear regression models, the requirement is to determine the coefficients which can result in the best-fitted linear regression line. The learning algorithm used to find the most appropriate coefficients is known as least squares regression . In the least-squares regression method, the coefficients are calculated using the least-squares error function. The main objective of this method is to minimize or reduce the sum of squared residuals between actual and predicted response values. The sum of squared residuals is also called the residual sum of squares (RSS). The outcome of executing the least-squares regression method is coefficients that minimize the linear regression cost function .

The residual e of the ith observation is represented as the following where [latex]Y_i[/latex] is the ith observation and [latex]\hat{Y_i}[/latex] is the prediction for ith observation or the value of response variable for ith observation.

[latex]e_i = Y_i – \hat{Y_i}[/latex]

The residual sum of squares can be represented as the following:

[latex]RSS = e_1^2 + e_2^2 + e_3^2 + … + e_n^2[/latex]

The least-squares method represents the algorithm that minimizes the above term, RSS.

Once the coefficients are determined, can it be claimed that these coefficients are the most appropriate ones for linear regression? The answer is no. After all, the coefficients are only the estimates and thus, there will be standard errors associated with each of the coefficients. Recall that the standard error is used to calculate the confidence interval in which the mean value of the population parameter would exist. In other words, it represents the error of estimating a population parameter based on the sample data. The value of the standard error is calculated as the standard deviation of the sample divided by the square root of the sample size. The formula below represents the standard error of a mean.

[latex]SE(\mu) = \frac{\sigma}{\sqrt(N)}[/latex]

Thus, without analyzing aspects such as the standard error associated with the coefficients, it cannot be claimed that the linear regression coefficients are the most suitable ones without performing hypothesis testing. This is where hypothesis testing is needed . Before we get into why we need hypothesis testing with the linear regression model, let’s briefly learn about what is hypothesis testing?

Train a Multiple Linear Regression Model using R

Before getting into understanding the hypothesis testing concepts in relation to the linear regression model, let’s train a multi-variate or multiple linear regression model and print the summary output of the model which will be referred to, in the next section.

The data used for creating a multi-linear regression model is BostonHousing which can be loaded in RStudioby installing mlbench package. The code is shown below:

install.packages(“mlbench”) library(mlbench) data(“BostonHousing”)

Once the data is loaded, the code shown below can be used to create the linear regression model.

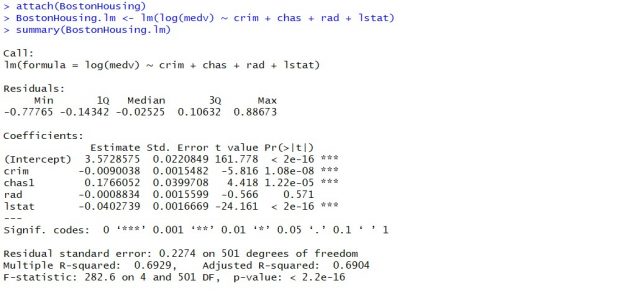
attach(BostonHousing) BostonHousing.lm <- lm(log(medv) ~ crim + chas + rad + lstat) summary(BostonHousing.lm)

Executing the above command will result in the creation of a linear regression model with the response variable as medv and predictor variables as crim, chas, rad, and lstat. The following represents the details related to the response and predictor variables:

log(medv) : Log of the median value of owner-occupied homes in USD 1000’s
crim : Per capita crime rate by town
chas : Charles River dummy variable (= 1 if tract bounds river; 0 otherwise)
rad : Index of accessibility to radial highways
lstat : Percentage of the lower status of the population

The following will be the output of the summary command that prints the details relating to the model including hypothesis testing details for coefficients (t-statistics) and the model as a whole (f-statistics)

linear regression model summary table r.png

Hypothesis tests & Linear Regression Models

Hypothesis tests are the statistical procedure that is used to test a claim or assumption about the underlying distribution of a population based on the sample data. Here are key steps of doing hypothesis tests with linear regression models:

Hypothesis formulation for T-tests: In the case of linear regression, the claim is made that there exists a relationship between response and predictor variables, and the claim is represented using the non-zero value of coefficients of predictor variables in the linear equation or regression model. This is formulated as an alternate hypothesis. Thus, the null hypothesis is set that there is no relationship between response and the predictor variables . Hence, the coefficients related to each of the predictor variables is equal to zero (0). So, if the linear regression model is Y = a0 + a1x1 + a2x2 + a3x3, then the null hypothesis for each test states that a1 = 0, a2 = 0, a3 = 0 etc. For all the predictor variables, individual hypothesis testing is done to determine whether the relationship between response and that particular predictor variable is statistically significant based on the sample data used for training the model. Thus, if there are, say, 5 features, there will be five hypothesis tests and each will have an associated null and alternate hypothesis.
Hypothesis formulation for F-test : In addition, there is a hypothesis test done around the claim that there is a linear regression model representing the response variable and all the predictor variables. The null hypothesis is that the linear regression model does not exist . This essentially means that the value of all the coefficients is equal to zero. So, if the linear regression model is Y = a0 + a1x1 + a2x2 + a3x3, then the null hypothesis states that a1 = a2 = a3 = 0.
F-statistics for testing hypothesis for linear regression model : F-test is used to test the null hypothesis that a linear regression model does not exist, representing the relationship between the response variable y and the predictor variables x1, x2, x3, x4 and x5. The null hypothesis can also be represented as x1 = x2 = x3 = x4 = x5 = 0. F-statistics is calculated as a function of sum of squares residuals for restricted regression (representing linear regression model with only intercept or bias and all the values of coefficients as zero) and sum of squares residuals for unrestricted regression (representing linear regression model). In the above diagram, note the value of f-statistics as 15.66 against the degrees of freedom as 5 and 194.
Evaluate t-statistics against the critical value/region : After calculating the value of t-statistics for each coefficient, it is now time to make a decision about whether to accept or reject the null hypothesis. In order for this decision to be made, one needs to set a significance level, which is also known as the alpha level. The significance level of 0.05 is usually set for rejecting the null hypothesis or otherwise. If the value of t-statistics fall in the critical region, the null hypothesis is rejected. Or, if the p-value comes out to be less than 0.05, the null hypothesis is rejected.
Evaluate f-statistics against the critical value/region : The value of F-statistics and the p-value is evaluated for testing the null hypothesis that the linear regression model representing response and predictor variables does not exist. If the value of f-statistics is more than the critical value at the level of significance as 0.05, the null hypothesis is rejected. This means that the linear model exists with at least one valid coefficients.
Draw conclusions : The final step of hypothesis testing is to draw a conclusion by interpreting the results in terms of the original claim or hypothesis. If the null hypothesis of one or more predictor variables is rejected, it represents the fact that the relationship between the response and the predictor variable is not statistically significant based on the evidence or the sample data we used for training the model. Similarly, if the f-statistics value lies in the critical region and the value of the p-value is less than the alpha value usually set as 0.05, one can say that there exists a linear regression model.

Why hypothesis tests for linear regression models?

The reasons why we need to do hypothesis tests in case of a linear regression model are following:

By creating the model, we are establishing a new truth (claims) about the relationship between response or dependent variable with one or more predictor or independent variables. In order to justify the truth, there are needed one or more tests. These tests can be termed as an act of testing the claim (or new truth) or in other words, hypothesis tests.
One kind of test is required to test the relationship between response and each of the predictor variables (hence, T-tests)
Another kind of test is required to test the linear regression model representation as a whole. This is called F-test.

While training linear regression models, hypothesis testing is done to determine whether the relationship between the response and each of the predictor variables is statistically significant or otherwise. The coefficients related to each of the predictor variables is determined. Then, individual hypothesis tests are done to determine whether the relationship between response and that particular predictor variable is statistically significant based on the sample data used for training the model. If at least one of the null hypotheses is rejected, it represents the fact that there exists no relationship between response and that particular predictor variable. T-statistics is used for performing the hypothesis testing because the standard deviation of the sampling distribution is unknown. The value of t-statistics is compared with the critical value from the t-distribution table in order to make a decision about whether to accept or reject the null hypothesis regarding the relationship between the response and predictor variables. If the value falls in the critical region, then the null hypothesis is rejected which means that there is no relationship between response and that predictor variable. In addition to T-tests, F-test is performed to test the null hypothesis that the linear regression model does not exist and that the value of all the coefficients is zero (0). Learn more about the linear regression and t-test in this blog – Linear regression t-test: formula, example .

Ajitesh Kumar

One response.

Very informative

ChatGPT Prompts (250+)

Generate Design Ideas for App
Expand Feature Set of App
Create a User Journey Map for App
Generate Visual Design Ideas for App
Generate a List of Competitors for App
Pricing Analytics in Banking: Strategies, Examples
How to Learn Effectively: A Holistic Approach
How to Choose Right Statistical Tests: Examples
Data Lakehouses Fundamentals & Examples
Machine Learning Lifecycle: Data to Deployment Example

Data Science / AI Trends

• Prepend any arxiv.org link with talk2 to load the paper into a responsive chat application
• Custom LLM and AI Agents (RAG) On Structured + Unstructured Data - AI Brain For Your Organization
• Guides, papers, lecture, notebooks and resources for prompt engineering
• Common tricks to make LLMs efficient and stable
• Machine learning in finance

Free Online Tools

Create Scatter Plots Online for your Excel Data
Histogram / Frequency Distribution Creation Tool
Online Pie Chart Maker Tool
Z-test vs T-test Decision Tool
Independent samples t-test calculator

Hypothesis Test for Regression Slope

This lesson describes how to conduct a hypothesis test to determine whether there is a significant linear relationship between an independent variable X and a dependent variable Y .

The test focuses on the slope of the regression line

Y = Β 0 + Β 1 X

where Β 0 is a constant, Β 1 is the slope (also called the regression coefficient), X is the value of the independent variable, and Y is the value of the dependent variable.

If we find that the slope of the regression line is significantly different from zero, we will conclude that there is a significant relationship between the independent and dependent variables.

Test Requirements

The approach described in this lesson is valid whenever the standard requirements for simple linear regression are met.

The dependent variable Y has a linear relationship to the independent variable X .
For each value of X, the probability distribution of Y has the same standard deviation σ.
The Y values are independent.
The Y values are roughly normally distributed (i.e., symmetric and unimodal ). A little skewness is ok if the sample size is large.

The test procedure consists of four steps: (1) state the hypotheses, (2) formulate an analysis plan, (3) analyze sample data, and (4) interpret results.

State the Hypotheses

If there is a significant linear relationship between the independent variable X and the dependent variable Y , the slope will not equal zero.

H o : Β 1 = 0

H a : Β 1 ≠ 0

The null hypothesis states that the slope is equal to zero, and the alternative hypothesis states that the slope is not equal to zero.

Formulate an Analysis Plan

The analysis plan describes how to use sample data to accept or reject the null hypothesis. The plan should specify the following elements.

Significance level. Often, researchers choose significance levels equal to 0.01, 0.05, or 0.10; but any value between 0 and 1 can be used.
Test method. Use a linear regression t-test (described in the next section) to determine whether the slope of the regression line differs significantly from zero.

Analyze Sample Data

Using sample data, find the standard error of the slope, the slope of the regression line, the degrees of freedom, the test statistic, and the P-value associated with the test statistic. The approach described in this section is illustrated in the sample problem at the end of this lesson.

SE = s b 1 = sqrt [ Σ(y i - ŷ i ) 2 / (n - 2) ] / sqrt [ Σ(x i - x ) 2 ]

Slope. Like the standard error, the slope of the regression line will be provided by most statistics software packages. In the hypothetical output above, the slope is equal to 35.

t = b 1 / SE

P-value. The P-value is the probability of observing a sample statistic as extreme as the test statistic. Since the test statistic is a t statistic, use the t Distribution Calculator to assess the probability associated with the test statistic. Use the degrees of freedom computed above.

Interpret Results

If the sample findings are unlikely, given the null hypothesis, the researcher rejects the null hypothesis. Typically, this involves comparing the P-value to the significance level , and rejecting the null hypothesis when the P-value is less than the significance level.

Test Your Understanding

The local utility company surveys 101 randomly selected customers. For each survey participant, the company collects the following: annual electric bill (in dollars) and home size (in square feet). Output from a regression analysis appears below.

Is there a significant linear relationship between annual bill and home size? Use a 0.05 level of significance.

The solution to this problem takes four steps: (1) state the hypotheses, (2) formulate an analysis plan, (3) analyze sample data, and (4) interpret results. We work through those steps below:

H o : The slope of the regression line is equal to zero.

H a : The slope of the regression line is not equal to zero.

Formulate an analysis plan . For this analysis, the significance level is 0.05. Using sample data, we will conduct a linear regression t-test to determine whether the slope of the regression line differs significantly from zero.

We get the slope (b 1 ) and the standard error (SE) from the regression output.

b 1 = 0.55 SE = 0.24

We compute the degrees of freedom and the t statistic, using the following equations.

DF = n - 2 = 101 - 2 = 99

t = b 1 /SE = 0.55/0.24 = 2.29

where DF is the degrees of freedom, n is the number of observations in the sample, b 1 is the slope of the regression line, and SE is the standard error of the slope.

Interpret results . Since the P-value (0.0242) is less than the significance level (0.05), we cannot accept the null hypothesis.

H 0 : β = 0 (Null hypothesis)
H A : β ≠ 0 (Alternative hypothesis)

Part of Dr. Doug Elrod 's A (Brief) Theory of Regression Talk

Remember the regression equation for predicting y from x is: y = bx + a (a is also indicated as "e" at times)

b , or the slope, is simply (r xy * S.D. y )/S.D. x a , or the intercept, is simply the value of y when x is 0:

[Why?: the point, a, where the line crosses the Y axis for X being 0 is the distance from the mean of Y predicted for the X value of 0: Remember: D y = b * D x a = D y + mean of y so:

] Example: Let's say we knew that the average UCLA student experiences a moderate level of anxiety on a 100 point scale, = 36.8, S.D. = 12.2. Also, that students average a course load of about 13 or so units, = 13.4, S.D. = 3.7. And finally, that the correlation between units taken and anxiety levels is a stunning r = .4. You might ask as you plan your schedule for next quarter, how much anxiety can I expect to experience if I take 20 units? Treat units as x and anxiety as y. Then The slope of the line predicting anxiety from units taken is (.4 * 12.2)/3.7 = (4.88)/3.7 = 1.32 The intercept is 36.8 - 1.32*13.4 = 36.8 - 17.67 = 19.13 So the predicted anxiety score when taking 20 units is: y (or anxiety) = 1.32 * (20 units) + 19.13 = 45.53

The method of least squares

The r.m.s. error for the regression line of y on x is:

The regression equation is the equation for the line that produces the least r.m.s. error or standard error of the estimate If x and y are perfectly related, that is all points lie on the regression line, the standard error of estimate is zero (the square root of 1 - 1 2 = 0), there is no deviation from the line. If x and y are not associated at all, the standard error of the estimate is the S.D. of y (the square root of 1 - 0 2 = 1) and slope is 0. So the regression line is simply a line parallel to the x axis that intercepts y at the mean of y.

Interpretation

Regression is appropriate when the relationship between two variables is linear Although we commonly think of x as causing y, this is dependent upon the research design and logic GIGO--garbage in-garbage out--you can always create regression lines predicting one variable from another. The math is the same whether or not the analysis is appropriate

Example: Calculate a regression line predicting height of the surf at Venice beach from the number of floors in the math building.

So far we have learned how to take raw data, combine it, and create statistics that allow us to describe the data in a brief summary form.

We have used statistics to describe our samples. These are called descriptive statistics. We have used our statistics to say something about the population that our samples were drawn from--this is inferential statistics. Now we are going to learn another way in which statistics can be use inferentially--hypothesis testing

At the beginning of this course, we said that an important aspect of doing research is to specify our research question

The first step in conducting research is to translate our inclinations, hunches, suspicions, beliefs into a precise question.

Example: Is this drug effective?, Does lowering the interest rate cause inflation?

The second step is to look closely at the question we have asked and assure ourselves that we know what an answer to the question would look like

Example: Is this drug effective? Do we know exactly what drug we are referring to, how big a dose, given to whom? Can we define what we mean by effective? Do we mean effective for everyone? Is it a cure? What about side effects?

Now, we are going to add one more layer to this--the third step is to translate our question into a hypothesis that we can test by using statistical methods.

Example: Is this drug effective? Does it reduce symptoms? Do people report higher average pain before they take the drug than after they have taken it for a while? Statistically, what we are saying is, perhaps, that the mean pain at time 1 is greater than the mean pain at time 2. But how much greater does it have to be?

Remember every observation is potentially made up of three components: true or expected score + bias + chance error. Things vary from being exactly the same every time we measure them for one of three possible reasons:

The true score could in fact be different from what we expect There is bias Random variation or chance

Generally, we are interested in only whether or not the true score is different. We design our studies to minimize bias as much as possible. But no matter what we do there is always random variation

This means that whenever we evaluate a change or difference between two things, we have, even with a perfect design eliminating bias, two possible causes. This is like try a solve a problem with two unknowns. If I tell you x + y = 5, you cannot tell me what x is or what y is. There are two strategies to solving this dilemma Set one of the unknowns to a value, such as 0 by use of logic Get two estimates for one of the unknowns from two different sources and divide one by the other. On average this should equal 1. Combine these two strategies

Statistical tests use these approaches to try to evaluate how much of the difference between two things can be attributed to a difference in the true score.
Now for the mind twist

To evaluate a research question, we translate the question into logical alternatives One is a mathematical statement that says there is no difference. Or essentially, all the difference that we observe is due to chance alone. This is called the null hypothesis . Null meaning nothing. And the hypothesis is that nothing is there in our data, no differences from what we expect except chance variation or chance error. Example: Does this drug reduce pain? The null hypothesis is that any change in mean levels of pain from time 1 to time 2 is simply random (explained by chance error) and the true score does not vary from time 1 to time 2. Or mathematically the truth is: 1 = 2 , in the population

Because the hypothesis does not refer to what we observe in our sample, but rather what is true in the population, the null hypothesis is typically written:

H 0 : m 1 = [some value such as 0, or any number we expect the true score to be]

There are two other possible alternatives. That pain is in fact reduced at time 2

Or mathematically: 1 < 2 in the population

That pain is in fact increased at time 2

Or mathematically: 1 > 2 in the population

Each one of these is referred to as a tail (for reasons we'll find out later). If we only predict that time 2 pain will be less that time 1 pain, then our alternative hypothesis (which is our research hypothesis) is considered one-tailed With one-tailed hypotheses, the other tail is simply added to the original null hypothesis, for the following statement: 1 � 2 If either possibility is consistent with our research hypothesis, then our statistical hypothesis that restates the research hypothesis is two-tailed or: 1 � 2

Again, our hypothesis refers to what is true in the population and so is formally written:

H 1 : m 1 � [the same value as we specified above for our null hypothesis]

Notice that if we combine the two hypotheses we have logically included all possibilities (they are mutually exclusive and exhaustive ) So if one is absolutely correct, the other must be false If one is highly unlikely to be true, the other just might possibly be true If one is perhaps correct, we have not really reduced our uncertainty at all about the other.

Because of the problems of too many unknowns, we end up only being able to evaluate the possible truth about the null hypothesis. We're not interested in the null hypothesis. But because it is related by logic to the alternative hypothesis which is a statistical restatement of our research hypothesis, if we can conclude something definitive about the null hypothesis, then we can make a judgment about the possibility of the alternative being true.

Save 10% on All AnalystPrep 2024 Study Packages with Coupon Code BLOG10 .

Payment Plans
Product List
Partnerships

Try Free Trial
Study Packages
Levels I, II & III Lifetime Package
Video Lessons
Study Notes
Practice Questions
Levels II & III Lifetime Package
About the Exam
About your Instructor
Part I Study Packages
Part I & Part II Lifetime Package
Part II Study Packages
Exams P & FM Lifetime Package
Quantitative Questions
Verbal Questions
Data Insight Questions
Live Tutoring
About your Instructors
EA Practice Questions
Data Sufficiency Questions
Integrated Reasoning Questions

Hypothesis Testing in Regression Analysis

Hypothesis testing is used to confirm if the estimated regression coefficients bear any statistical significance. Either the confidence interval approach or the t-test approach can be used in hypothesis testing. In this section, we will explore the t-test approach.

The t-test Approach

The following are the steps followed in the performance of the t-test:

Set the significance level for the test.
Formulate the null and the alternative hypotheses.

$$t=\frac{\widehat{b_1}-b_1}{s_{\widehat{b_1}}}$$

$b_1$ = True slope coefficient.

$\widehat{b_1}$ = Point estimate for $b_1$

$b_1 s_{\widehat{b_1\ }}$ = Standard error of the regression coefficient.

Compare the absolute value of the t-statistic to the critical t-value (t_c). Reject the null hypothesis if the absolute value of the t-statistic is greater than the critical t-value i.e., $t\ >\ +\ t_{critical}\ or\ t\ <\ –t_{\text{critical}}$.

Example: Hypothesis Testing of the Significance of Regression Coefficients

An analyst generates the following output from the regression analysis of inflation on unemployment:

$$\small{\begin{array}{llll}\hline{}& \textbf{Regression Statistics} &{}&{}\\ \hline{}& \text{Multiple R} & 0.8766 &{} \\ {}& \text{R Square} & 0.7684 &{} \\ {}& \text{Adjusted R Square} & 0.7394 & {}\\ {}& \text{Standard Error} & 0.0063 &{}\\ {}& \text{Observations} & 10 &{}\\ \hline {}& & & \\ \hline{} & \textbf{Coefficients} & \textbf{Standard Error} & \textbf{t-Stat}\\ \hline \text{Intercept} & 0.0710 & 0.0094 & 7.5160 \\\text{Forecast (Slope)} & -0.9041 & 0.1755 & -5.1516\\ \hline\end{array}}$$

At the 5% significant level, test the null hypothesis that the slope coefficient is significantly different from one, that is,

$$ H_{0}: b_{1} = 1\ vs. \ H_{a}: b_{1}≠1 $$

The calculated t-statistic, $\text{t}=\frac{\widehat{b_{1}}-b_1}{\widehat{S_{b_{1}}}}$ is equal to:

$$\begin{align*}\text{t}& = \frac{-0.9041-1}{0.1755}\\& = -10.85\end{align*}$$

The critical two-tail t-values from the table with $n-2=8$ degrees of freedom are:

$$\text{t}_{c}=±2.306$$

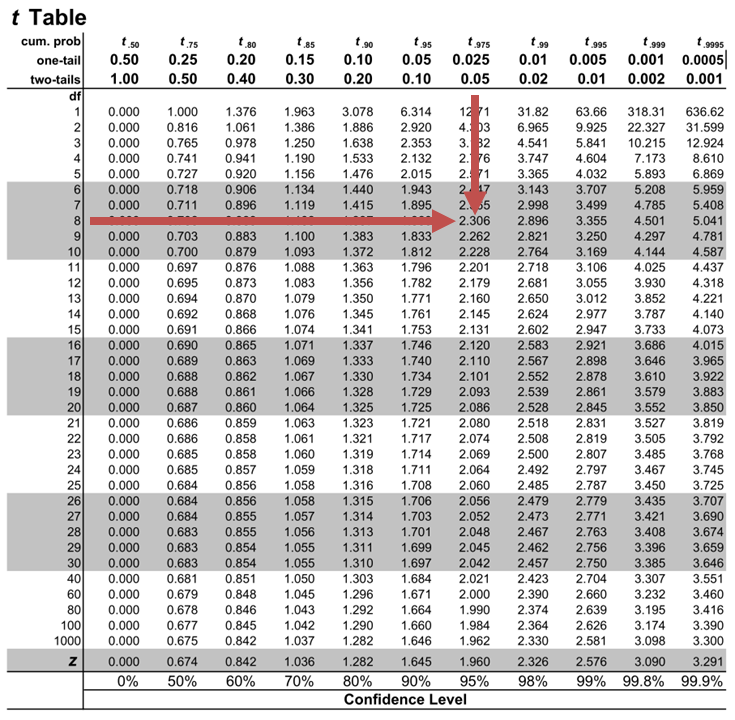
Notice that $|t|>t_{c}$ i.e., ($10.85>2.306$)

Therefore, we reject the null hypothesis and conclude that the estimated slope coefficient is statistically different from one.

Note that we used the confidence interval approach and arrived at the same conclusion.

Question Neeth Shinu, CFA, is forecasting price elasticity of supply for a certain product. Shinu uses the quantity of the product supplied for the past 5months as the dependent variable and the price per unit of the product as the independent variable. The regression results are shown below. $$\small{\begin{array}{lccccc}\hline \textbf{Regression Statistics} & & & & & \\ \hline \text{Multiple R} & 0.9971 & {}& {}&{}\\ \text{R Square} & 0.9941 & & & \\ \text{Adjusted R Square} & 0.9922 & & & & \\ \text{Standard Error} & 3.6515 & & & \\ \text{Observations} & 5 & & & \\ \hline {}& \textbf{Coefficients} & \textbf{Standard Error} & \textbf{t Stat} & \textbf{P-value}\\ \hline\text{Intercept} & -159 & 10.520 & (15.114) & 0.001\\ \text{Slope} & 0.26 & 0.012 & 22.517 & 0.000\\ \hline\end{array}}$$ Which of the following most likely reports the correct value of the t-statistic for the slope and most accurately evaluates its statistical significance with 95% confidence? A. $t=21.67$; slope is significantly different from zero. B. $t= 3.18$; slope is significantly different from zero. C. $t=22.57$; slope is not significantly different from zero. Solution The correct answer is A . The t-statistic is calculated using the formula: $$\text{t}=\frac{\widehat{b_{1}}-b_1}{\widehat{S_{b_{1}}}}$$ Where: $b_{1}$ = True slope coefficient $\widehat{b_{1}}$ = Point estimator for $b_{1}$ $\widehat{S_{b_{1}}}$ = Standard error of the regression coefficient $$\begin{align*}\text{t}&=\frac{0.26-0}{0.012}\\&=21.67\end{align*}$$ The critical two-tail t-values from the t-table with $n-2 = 3$ degrees of freedom are: $$t_{c}=±3.18$$ Notice that $|t|>t_{c}$ (i.e $21.67>3.18$). Therefore, the null hypothesis can be rejected. Further, we can conclude that the estimated slope coefficient is statistically different from zero.

Offered by AnalystPrep

Analysis of Variance (ANOVA)

Predicted value of a dependent variable, dependent and independent events.

Two or more events are independent if the occurrence of one event does... Read More

Measures of Central Tendency

Measures of central tendency are values that tend to occur at the center... Read More

Introduction to Statistics With Releva ...

Statistics refers to concepts, rules, and procedures that help us interpret data and... Read More

Probability in Terms of Odds for and a ...

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
Duis aute irure dolor in reprehenderit in voluptate
Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

6.4 - the hypothesis tests for the slopes.

At the beginning of this lesson, we translated three different research questions pertaining to heart attacks in rabbits ( Cool Hearts dataset ) into three sets of hypotheses we can test using the general linear F -statistic. The research questions and their corresponding hypotheses are:

Hypotheses 1

Is the regression model containing at least one predictor useful in predicting the size of the infarct?

$H_{0} \colon \beta_{1} = \beta_{2} = \beta_{3} = 0$
$H_{A} \colon$ At least one $\beta_{j} ≠ 0$ (for j = 1, 2, 3)

Hypotheses 2

Is the size of the infarct significantly (linearly) related to the area of the region at risk?

$H_{0} \colon \beta_{1} = 0 $
$H_{A} \colon \beta_{1} \ne 0 $

Hypotheses 3

(Primary research question) Is the size of the infarct area significantly (linearly) related to the type of treatment upon controlling for the size of the region at risk for infarction?

$H_{0} \colon \beta_{2} = \beta_{3} = 0$
$H_{A} \colon $ At least one $\beta_{j} ≠ 0$ (for j = 2, 3)

Let's test each of the hypotheses now using the general linear F -statistic:

$F^*=\left(\dfrac{SSE(R)-SSE(F)}{df_R-df_F}\right) \div \left(\dfrac{SSE(F)}{df_F}\right)$

To calculate the F -statistic for each test, we first determine the error sum of squares for the reduced and full models — SSE ( R ) and SSE ( F ), respectively. The number of error degrees of freedom associated with the reduced and full models — $df_{R}$ and $df_{F}$, respectively — is the number of observations, n , minus the number of parameters, p , in the model. That is, in general, the number of error degrees of freedom is n - p . We use statistical software, such as Minitab's F -distribution probability calculator, to determine the P -value for each test.

Testing all slope parameters equal 0 Section

To answer the research question: "Is the regression model containing at least one predictor useful in predicting the size of the infarct?" To do so, we test the hypotheses:

$H_{0} \colon \beta_{1} = \beta_{2} = \beta_{3} = 0 $
$H_{A} \colon$ At least one $\beta_{j} \ne 0 $ (for j = 1, 2, 3)

The full model

The full model is the largest possible model — that is, the model containing all of the possible predictors. In this case, the full model is:

$y_i=(\beta_0+\beta_1x_{i1}+\beta_2x_{i2}+\beta_3x_{i3})+\epsilon_i$

The error sum of squares for the full model, SSE ( F ), is just the usual error sum of squares, SSE , that appears in the analysis of variance table. Because there are 4 parameters in the full model, the number of error degrees of freedom associated with the full model is $df_{F} = n - 4$.

The reduced model

The reduced model is the model that the null hypothesis describes. Because the null hypothesis sets each of the slope parameters in the full model equal to 0, the reduced model is:

$y_i=\beta_0+\epsilon_i$

The reduced model suggests that none of the variations in the response y is explained by any of the predictors. Therefore, the error sum of squares for the reduced model, SSE ( R ), is just the total sum of squares, SSTO , that appears in the analysis of variance table. Because there is only one parameter in the reduced model, the number of error degrees of freedom associated with the reduced model is $df_{R} = n - 1 $.

Upon plugging in the above quantities, the general linear F -statistic:

$F^*=\dfrac{SSE(R)-SSE(F)}{df_R-df_F} \div \dfrac{SSE(F)}{df_F}$

becomes the usual " overall F -test ":

$F^*=\dfrac{SSR}{3} \div \dfrac{SSE}{n-4}=\dfrac{MSR}{MSE}$

That is, to test $H_{0}$ : $\beta_{1} = \beta_{2} = \beta_{3} = 0 $, we just use the overall F -test and P -value reported in the analysis of variance table:

Analysis of Variance

Regression equation.

Inf = - 0.135 + 0.613 Area - 0.2435 X2 - 0.0657 X3

There is sufficient evidence ( F = 16.43, P < 0.001) to conclude that at least one of the slope parameters is not equal to 0.

In general, to test that all of the slope parameters in a multiple linear regression model are 0, we use the overall F -test reported in the analysis of variance table.

Testing one slope parameter is 0 Section

Now let's answer the second research question: "Is the size of the infarct significantly (linearly) related to the area of the region at risk?" To do so, we test the hypotheses:

Again, the full model is the model containing all of the possible predictors:

The error sum of squares for the full model, SSE ( F ), is just the usual error sum of squares, SSE . Alternatively, because the three predictors in the model are $x_{1}$, $x_{2}$, and $x_{3}$, we can denote the error sum of squares as SSE ($x_{1}$, $x_{2}$, $x_{3}$). Again, because there are 4 parameters in the model, the number of error degrees of freedom associated with the full model is $df_{F} = n - 4 $.

Because the null hypothesis sets the first slope parameter, $\beta_{1}$, equal to 0, the reduced model is:

$y_i=(\beta_0+\beta_2x_{i2}+\beta_3x_{i3})+\epsilon_i$

Because the two predictors in the model are $x_{2}$ and $x_{3}$, we denote the error sum of squares as SSE ($x_{2}$, $x_{3}$). Because there are 3 parameters in the model, the number of error degrees of freedom associated with the reduced model is $df_{R} = n - 3$.

The general linear statistic:

simplifies to:

$F^*=\dfrac{SSR(x_1|x_2, x_3)}{1}\div \dfrac{SSE(x_1,x_2, x_3)}{n-4}=\dfrac{MSR(x_1|x_2, x_3)}{MSE(x_1,x_2, x_3)}$

Getting the numbers from the Minitab output:

we determine that the value of the F -statistic is:

$F^* = \dfrac{SSR(x_1 \vert x_2, x_3)}{1} \div \dfrac{SSE(x_1, x_2, x_3)}{28} = \dfrac{0.63742}{0.01946}=32.7554$

The P -value is the probability — if the null hypothesis were true — that we would get an F -statistic larger than 32.7554. Comparing our F -statistic to an F -distribution with 1 numerator degree of freedom and 28 denominator degrees of freedom, Minitab tells us that the probability is close to 1 that we would observe an F -statistic smaller than 32.7554:

F distribution with 1 DF in Numerator and 28 DF in denominator

Therefore, the probability that we would get an F -statistic larger than 32.7554 is close to 0. That is, the P -value is < 0.001. There is sufficient evidence ( F = 32.8, P < 0.001) to conclude that the size of the infarct is significantly related to the size of the area at risk after the other predictors x2 and x3 have been taken into account.

But wait a second! Have you been wondering why we couldn't just use the slope's t -statistic to test that the slope parameter, $\beta_{1}$, is 0? We can! Notice that the P -value ( P < 0.001) for the t -test ( t * = 5.72):

Coefficients

is the same as the P -value we obtained for the F -test. This will always be the case when we test that only one slope parameter is 0. That's because of the well-known relationship between a t -statistic and an F -statistic that has one numerator degree of freedom:

$t_{(n-p)}^{2}=F_{(1, n-p)}$

For our example, the square of the t -statistic, 5.72, equals our F -statistic (within rounding error). That is:

$t^{*2}=5.72^2=32.72=F^*$

So what have we learned in all of this discussion about the equivalence of the F -test and the t -test? In short:

Compare the output obtained when $x_{1}$ = Area is entered into the model last :

Inf = - 0.135 - 0.2435 X2 - 0.0657 X3 + 0.613 Area

to the output obtained when $x_{1}$ = Area is entered into the model first :

The t -statistic and P -value are the same regardless of the order in which $x_{1}$ = Area is entered into the model. That's because — by its equivalence to the F -test — the t -test for one slope parameter adjusts for all of the other predictors included in the model.

We can use either the F -test or the t -test to test that only one slope parameter is 0. Because the t -test results can be read right off of the Minitab output, it makes sense that it would be the test that we'll use most often.
But, we have to be careful with our interpretations! The equivalence of the t -test to the F -test has taught us something new about the t -test. The t -test is a test for the marginal significance of the $x_{1}$ predictor after the other predictors $x_{2}$ and $x_{3}$ have been taken into account. It does not test for the significance of the relationship between the response y and the predictor $x_{1}$ alone.

Testing a subset of slope parameters is 0 Section

Finally, let's answer the third — and primary — research question: "Is the size of the infarct area significantly (linearly) related to the type of treatment upon controlling for the size of the region at risk for infarction?" To do so, we test the hypotheses:

$H_{0} \colon \beta_{2} = \beta_{3} = 0 $
$H_{A} \colon$ At least one $\beta_{j} \ne 0 $ (for j = 2, 3)

Because the null hypothesis sets the second and third slope parameters, $\beta_{2}$ and $\beta_{3}$, equal to 0, the reduced model is:

$y_i=(\beta_0+\beta_1x_{i1})+\epsilon_i$

The ANOVA table for the reduced model is:

Because the only predictor in the model is $x_{1}$, we denote the error sum of squares as SSE ($x_{1}$) = 0.8793. Because there are 2 parameters in the model, the number of error degrees of freedom associated with the reduced model is $df_{R} = n - 2 = 32 – 2 = 30$.

\begin{align} F^*&=\dfrac{SSE(R)-SSE(F)}{df_R-df_F} \div\dfrac{SSE(F)}{df_F}\\&=\dfrac{0.8793-0.54491}{30-28} \div\dfrac{0.54491}{28}\\&= \dfrac{0.33439}{2} \div 0.01946\\&=8.59.\end{align}

Alternatively, we can calculate the F-statistic using a partial F-test :

\begin{align}F^*&=\dfrac{SSR(x_2, x_3|x_1)}{2}\div \dfrac{SSE(x_1,x_2, x_3)}{n-4}\\&=\dfrac{MSR(x_2, x_3|x_1)}{MSE(x_1,x_2, x_3)}.\end{align}

To conduct the test, we regress y = InfSize on $x_{1}$ = Area and $x_{2}$ and $x_{3 }$— in order (and with "Sequential sums of squares" selected under "Options"):

Inf = - 0.135 + 0.613 Area - 0.2435 X2 - 0.0657 X3

yielding SSR ($x_{2}$ | $x_{1}$) = 0.31453, SSR ($x_{3}$ | $x_{1}$, $x_{2}$) = 0.01981, and MSE = 0.54491/28 = 0.01946. Therefore, the value of the partial F -statistic is:

\begin{align} F^*&=\dfrac{SSR(x_2, x_3|x_1)}{2}\div \dfrac{SSE(x_1,x_2, x_3)}{n-4}\\&=\dfrac{0.31453+0.01981}{2}\div\dfrac{0.54491}{28}\\&= \dfrac{0.33434}{2} \div 0.01946\\&=8.59,\end{align}

which is identical (within round-off error) to the general F-statistic above. The P -value is the probability — if the null hypothesis were true — that we would observe a partial F -statistic more extreme than 8.59. The following Minitab output:

F distribution with 2 DF in Numerator and 28 DF in denominator

tells us that the probability of observing such an F -statistic that is smaller than 8.59 is 0.9988. Therefore, the probability of observing such an F -statistic that is larger than 8.59 is 1 - 0.9988 = 0.0012. The P -value is very small. There is sufficient evidence ( F = 8.59, P = 0.0012) to conclude that the type of cooling is significantly related to the extent of damage that occurs — after taking into account the size of the region at risk.

Summary of MLR Testing Section

For the simple linear regression model, there is only one slope parameter about which one can perform hypothesis tests. For the multiple linear regression model, there are three different hypothesis tests for slopes that one could conduct. They are:

Hypothesis test for testing that all of the slope parameters are 0.
Hypothesis test for testing that a subset — more than one, but not all — of the slope parameters are 0.
Hypothesis test for testing that one slope parameter is 0.

We have learned how to perform each of the above three hypothesis tests. Along the way, we also took two detours — one to learn about the " general linear F-test " and one to learn about " sequential sums of squares. " As you now know, knowledge about both is necessary for performing the three hypothesis tests.

The F -statistic and associated p -value in the ANOVA table is used for testing whether all of the slope parameters are 0. In most applications, this p -value will be small enough to reject the null hypothesis and conclude that at least one predictor is useful in the model. For example, for the rabbit heart attacks study, the F -statistic is (0.95927/(4–1)) / (0.54491/(32–4)) = 16.43 with p -value 0.000.

To test whether a subset — more than one, but not all — of the slope parameters are 0, there are two equivalent ways to calculate the F-statistic:

Use the general linear F-test formula by fitting the full model to find SSE(F) and fitting the reduced model to find SSE(R) . Then the numerator of the F-statistic is (SSE(R) – SSE(F)) / ( $df_{R}$ – $df_{F}$) .
Alternatively, use the partial F-test formula by fitting only the full model but making sure the relevant predictors are fitted last and "sequential sums of squares" have been selected. Then the numerator of the F-statistic is the sum of the relevant sequential sums of squares divided by the sum of the degrees of freedom for these sequential sums of squares. The denominator of the F -statistic is the mean squared error in the ANOVA table.

For example, for the rabbit heart attacks study, the general linear F-statistic is ((0.8793 – 0.54491) / (30 – 28)) / (0.54491 / 28) = 8.59 with p -value 0.0012. Alternatively, the partial F -statistic for testing the slope parameters for predictors $x_{2}$ and $x_{3}$ using sequential sums of squares is ((0.31453 + 0.01981) / 2) / (0.54491 / 28) = 8.59.

To test whether one slope parameter is 0, we can use an F -test as just described. Alternatively, we can use a t -test, which will have an identical p -value since in this case, the square of the t -statistic is equal to the F -statistic. For example, for the rabbit heart attacks study, the F -statistic for testing the slope parameter for the Area predictor is (0.63742/1) / (0.54491/(32–4)) = 32.75 with p -value 0.000. Alternatively, the t -statistic for testing the slope parameter for the Area predictor is 0.613 / 0.107 = 5.72 with p -value 0.000, and $5.72^{2} = 32.72$.

Incidentally, you may be wondering why we can't just do a series of individual t-tests to test whether a subset of the slope parameters is 0. For example, for the rabbit heart attacks study, we could have done the following:

Fit the model of y = InfSize on $x_{1}$ = Area and $x_{2}$ and $x_{3}$ and use an individual t-test for $x_{3}$.
If the test results indicate that we can drop $x_{3}$ then fit the model of y = InfSize on $x_{1}$ = Area and $x_{2}$ and use an individual t-test for $x_{2}$.

The problem with this approach is we're using two individual t-tests instead of one F-test, which means our chance of drawing an incorrect conclusion in our testing procedure is higher. Every time we do a hypothesis test, we can draw an incorrect conclusion by:

rejecting a true null hypothesis, i.e., make a type I error by concluding the tested predictor(s) should be retained in the model when in truth it/they should be dropped; or
failing to reject a false null hypothesis, i.e., make a type II error by concluding the tested predictor(s) should be dropped from the model when in truth it/they should be retained.

Thus, in general, the fewer tests we perform the better. In this case, this means that wherever possible using one F-test in place of multiple individual t-tests is preferable.

Hypothesis tests for the slope parameters Section

The problems in this section are designed to review the hypothesis tests for the slope parameters, as well as to give you some practice on models with a three-group qualitative variable (which we'll cover in more detail in Lesson 8). We consider tests for:

whether one slope parameter is 0 (for example, $H_{0} \colon \beta_{1} = 0 $)
whether a subset (more than one but less than all) of the slope parameters are 0 (for example, $H_{0} \colon \beta_{2} = \beta_{3} = 0 $ against the alternative $H_{A} \colon \beta_{2} \ne 0 $ or $\beta_{3} \ne 0 $ or both ≠ 0)
whether all of the slope parameters are 0 (for example, $H_{0} \colon \beta_{1} = \beta_{2} = \beta_{3}$ = 0 against the alternative $H_{A} \colon $ at least one of the $\beta_{i}$ is not 0)

(Note the correct specification of the alternative hypotheses for the last two situations.)

Sugar beets study

A group of researchers was interested in studying the effects of three different growth regulators ( treat , denoted 1, 2, and 3) on the yield of sugar beets (y = yield , in pounds). They planned to plant the beets in 30 different plots and then randomly treat 10 plots with the first growth regulator, 10 plots with the second growth regulator, and 10 plots with the third growth regulator. One problem, though, is that the amount of available nitrogen in the 30 different plots varies naturally, thereby giving a potentially unfair advantage to plots with higher levels of available nitrogen. Therefore, the researchers also measured and recorded the available nitrogen ($x_{1}$ = nit , in pounds/acre) in each plot. They are interested in comparing the mean yields of sugar beets subjected to the different growth regulators after taking into account the available nitrogen. The Sugar Beets dataset contains the data from the researcher's experiment.

Preliminary Work

The plot shows a similar positive linear trend within each treatment category, which suggests that it is reasonable to formulate a multiple regression model that would place three parallel lines through the data.

Because the qualitative variable treat distinguishes between the three treatment groups (1, 2, and 3), we need to create two indicator variables, $x_{2}$ and $x_{3}$, say, to fit a linear regression model to these data. The new indicator variables should be defined as follows:

Use Minitab's Calc >> Make Indicator Variables command to create the new indicator variables in your worksheet

Minitab creates an indicator variable for each treatment group but we can only use two, for treatment groups 1 and 2 in this case (treatment group 3 is the reference level in this case).

Then, if we assume the trend in the data can be summarized by this regression model:

$y_{i} = \beta_{0}$ + $\beta_{1}$$x_{1}$ + $\beta_{2}$$x_{2}$ + $\beta_{3}$$x_{3}$ + $\epsilon_{i}$

where $x_{1}$ = nit and $x_{2}$ and $x_{3}$ are defined as above, what is the mean response function for plots receiving treatment 3? for plots receiving treatment 1? for plots receiving treatment 2? Are the three regression lines that arise from our formulated model parallel? What does the parameter $\beta_{2}$ quantify? And, what does the parameter $\beta_{3}$ quantify?

The fitted equation from Minitab is Yield = 84.99 + 1.3088 Nit - 2.43 $x_{2}$ - 2.35 $x_{3}$, which means that the equations for each treatment group are:

Group 1: Yield = 84.99 + 1.3088 Nit - 2.43(1) = 82.56 + 1.3088 Nit
Group 2: Yield = 84.99 + 1.3088 Nit - 2.35(1) = 82.64 + 1.3088 Nit
Group 3: Yield = 84.99 + 1.3088 Nit

The three estimated regression lines are parallel since they have the same slope, 1.3088.

The regression parameter for $x_{2}$ represents the difference between the estimated intercept for treatment 1 and the estimated intercept for reference treatment 3.

The regression parameter for $x_{3}$ represents the difference between the estimated intercept for treatment 2 and the estimated intercept for reference treatment 3.

Testing whether all of the slope parameters are 0

$H_0 \colon \beta_1 = \beta_2 = \beta_3 = 0$ against the alternative $H_A \colon $ at least one of the $\beta_i$ is not 0.

$F=\dfrac{SSR(X_1,X_2,X_3)\div3}{SSE(X_1,X_2,X_3)\div(n-4)}=\dfrac{MSR(X_1,X_2,X_3)}{MSE(X_1,X_2,X_3)}$

$F = \dfrac{\frac{16039.5}{3}}{\frac{1078.0}{30-4}} = \dfrac{5346.5}{41.46} = 128.95$

Since the p -value for this F -statistic is reported as 0.000, we reject $H_{0}$ in favor of $H_{A}$ and conclude that at least one of the slope parameters is not zero, i.e., the regression model containing at least one predictor is useful in predicting the size of sugar beet yield.

Tests for whether one slope parameter is 0

$H_0 \colon \beta_1= 0$ against the alternative $H_A \colon \beta_1 \ne 0$

t -statistic = 19.60, p -value = 0.000, so we reject $H_{0}$ in favor of $H_{A}$ and conclude that the slope parameter for $x_{1}$ = nit is not zero, i.e., sugar beet yield is significantly linearly related to the available nitrogen (controlling for treatment).

$F=\dfrac{SSR(X_1|X_2,X_3)\div1}{SSE(X_1,X_2,X_3)\div(n-4)}=\dfrac{MSR(X_1|X_2,X_3)}{MSE(X_1,X_2,X_3)}$

Use the Minitab output to calculate the value of this F statistic. Does the value you obtain equal $t^{2}$, the square of the t -statistic as we might expect?

$F-statistic= \dfrac{\frac{15934.5}{1}}{\frac{1078.0}{30-4}} = \dfrac{15934.5}{41.46} = 384.32$, which is the same as $19.60^{2}$.

Because $t^{2}$ will equal the partial F -statistic whenever you test for whether one slope parameter is 0, it makes sense to just use the t -statistic and P -value that Minitab displays as a default. But, note that we've just learned something new about the meaning of the t -test in the multiple regression setting. It tests for the ("marginal") significance of the $x_{1}$ predictor after $x_{2}$ and $x_{3}$ have already been taken into account.

Tests for whether a subset of the slope parameters is 0

$H_0 \colon \beta_2=\beta_3= 0$ against the alternative $H_A \colon \beta_2 \ne 0$ or $\beta_3 \ne 0$ or both $\ne 0$.

$F=\dfrac{SSR(X_2,X_3|X_1)\div2}{SSE(X_1,X_2,X_3)\div(n-4)}=\dfrac{MSR(X_2,X_3|X_1)}{MSE(X_1,X_2,X_3)}$

$F = \dfrac{\frac{10.4+27.5}{2}}{\frac{1078.0}{30-4}} = \dfrac{18.95}{41.46} = 0.46$.

F distribution with 2 DF in Numerator and 26 DF in denominator

p-value $= 1-0.363677 = 0.636$, so we fail to reject $H_{0}$ in favor of $H_{A}$ and conclude that we cannot rule out $\beta_2 = \beta_3 = 0$, i.e., there is no significant difference in the mean yields of sugar beets subjected to the different growth regulators after taking into account the available nitrogen.

Note that the sequential mean square due to regression, MSR($X_{2}$,$X_{3}$|$X_{1}$), is obtained by dividing the sequential sum of square by its degrees of freedom (2, in this case, since two additional predictors $X_{2}$ and $X_{3}$ are considered). Use the Minitab output to calculate the value of this F statistic, and use Minitab to get the associated P -value. Answer the researcher's question at the $\alpha= 0.05$ level.

Statistics Made Easy

How to Test the Significance of a Regression Slope

Suppose we have the following dataset that shows the square feet and price of 12 different houses:

We want to know if there is a significant relationship between square feet and price.

To get an idea of what the data looks like, we first create a scatterplot with square feet on the x-axis and price on the y-axis:

We can clearly see that there is a positive correlation between square feet and price. As square feet increases, the price of the house tends to increase as well.

However, to know if there is a statistically significant relationship between square feet and price, we need to run a simple linear regression.

So, we run a simple linear regression using square feet as the predictor and price as the response and get the following output:

Whether you run a simple linear regression in Excel, SPSS, R, or some other software, you will get a similar output to the one shown above.

Recall that a simple linear regression will produce the line of best fit, which is the equation for the line that best “fits” the data on our scatterplot. This line of best fit is defined as:

ŷ = b 0 + b 1 x

where ŷ is the predicted value of the response variable, b 0 is the y-intercept, b 1 is the regression coefficient, and x is the value of the predictor variable.

The value for b 0 is given by the coefficient for the intercept, which is 47588.70.

The value for b 1 is given by the coefficient for the predictor variable Square Feet , which is 93.57.

Thus, the line of best fit in this example is ŷ = 47588.70+ 93.57x

Here is how to interpret this line of best fit:

b 0 : When the value for square feet is zero, the average expected value for price is $47,588.70. (In this case, it doesn’t really make sense to interpret the intercept, since a house can never have zero square feet)
b 1 : For each additional square foot, the average expected increase in price is $93.57.

So, now we know that for each additional square foot, the average expected increase in price is $93.57.

To find out if this increase is statistically significant, we need to conduct a hypothesis test for B 1 or construct a confidence interval for B 1 .

Note : A hypothesis test and a confidence interval will always give the same results.

Constructing a Confidence Interval for a Regression Slope

To construct a confidence interval for a regression slope, we use the following formula:

Confidence Interval = b 1 +/- (t 1-∝/2, n-2 ) * (standard error of b 1 )

b 1 is the slope coefficient given in the regression output
(t 1-∝/2, n-2 ) is the t critical value for confidence level 1-∝ with n-2 degrees of freedom where n is the total number of observations in our dataset
(standard error of b 1 ) is the standard error of b 1 given in the regression output

For our example, here is how to construct a 95% confidence interval for B 1 :

b 1 is 93.57 from the regression output.
Since we are using a 95% confidence interval, ∝ = .05 and n-2 = 12-2 = 10, thus t .975, 10 is 2.228 according to the t-distribution table
(standard error of b 1 ) is 11.45 from the regression output

Thus, our 95% confidence interval for B 1 is:

93.57 +/- (2.228) * (11.45) = (68.06 , 119.08)

This means we are 95% confident that the true average increase in price for each additional square foot is between $68.06 and $119.08.

Notice that $0 is not in this interval, so the relationship between square feet and price is statistically significant at the 95% confidence level.

Conducting a Hypothesis Test for a Regression Slope

To conduct a hypothesis test for a regression slope, we follow the standard five steps for any hypothesis test :

Step 1. State the hypotheses.

The null hypothesis (H0): B 1 = 0

The alternative hypothesis: (Ha): B 1 ≠ 0

Step 2. Determine a significance level to use.

Since we constructed a 95% confidence interval in the previous example, we will use the equivalent approach here and choose to use a .05 level of significance.

Step 3. Find the test statistic and the corresponding p-value.

In this case, the test statistic is t = coefficient of b 1 / standard error of b 1 with n-2 degrees of freedom. We can find these values from the regression output:

Using the T Score to P Value Calculator with a t score of 6.69 with 10 degrees of freedom and a two-tailed test, the p-value = 0.000 .

Step 4. Reject or fail to reject the null hypothesis.

Since the p-value is less than our significance level of .05, we reject the null hypothesis.

Step 5. Interpret the results.

Since we rejected the null hypothesis, we have sufficient evidence to say that the true average increase in price for each additional square foot is not zero.

Featured Posts

5 Regularization Techniques You Should Know

Hey there. My name is Zach Bobbitt. I have a Masters of Science degree in Applied Statistics and I’ve worked on machine learning algorithms for professional businesses in both healthcare and retail. I’m passionate about statistics, machine learning, and data visualization and I created Statology to be a resource for both students and teachers alike. My goal with this site is to help you learn statistics through using simple terms, plenty of real-world examples, and helpful illustrations.

4 Replies to “How to Test the Significance of a Regression Slope”

Thank you!:)

I am a bit confused!

The p-value is less than our alpha=0.05.

Shouldnt be the other way around that we fail to reject the H_0 hypothesis?

Why does this output change between the two examples you show? I don’t understand.

The coefficient of b1 in the first table is 93.57173

The coefficient of b1 in the second table is 92.89

Did something change or was this example not carried through the entire way through the section “Conducting a Hypothesis Test for a Regression Slope?” This is very confusing.

Hello Zach. Thank you for all of your articles on statology.org website. For the first time, I request your help about the Hypothesis Test for a Regression Slope above. I would like to know how the regression output in “Step 3. find the test statistic and the corresponding p-value” was obtained. Thank you. Elia

Join the Statology Community

Sign up to receive Statology's exclusive study resource: 100 practice problems with step-by-step solutions. Plus, get our latest insights, tutorials, and data analysis tips straight to your inbox!

By subscribing you accept Statology's Privacy Policy.

school Campus Bookshelves
menu_book Bookshelves
perm_media Learning Objects
login Login
how_to_reg Request Instructor Account
hub Instructor Commons

Margin Size

Download Page (PDF)
Download Full Book (PDF)
Periodic Table
Physics Constants
Scientific Calculator
Reference & Cite
Tools expand_more
Readability

selected template will load here

This action is not available.

15.5: Hypothesis Tests for Regression Models

Last updated
Save as PDF
Page ID 4039

Danielle Navarro
University of New South Wales

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

So far we’ve talked about what a regression model is, how the coefficients of a regression model are estimated, and how we quantify the performance of the model (the last of these, incidentally, is basically our measure of effect size). The next thing we need to talk about is hypothesis tests. There are two different (but related) kinds of hypothesis tests that we need to talk about: those in which we test whether the regression model as a whole is performing significantly better than a null model; and those in which we test whether a particular regression coefficient is significantly different from zero.

At this point, you’re probably groaning internally, thinking that I’m going to introduce a whole new collection of tests. You’re probably sick of hypothesis tests by now, and don’t want to learn any new ones. Me too. I’m so sick of hypothesis tests that I’m going to shamelessly reuse the F-test from Chapter 14 and the t-test from Chapter 13. In fact, all I’m going to do in this section is show you how those tests are imported wholesale into the regression framework.

Testing the model as a whole

Okay, suppose you’ve estimated your regression model. The first hypothesis test you might want to try is one in which the null hypothesis that there is no relationship between the predictors and the outcome, and the alternative hypothesis is that the data are distributed in exactly the way that the regression model predicts . Formally, our “null model” corresponds to the fairly trivial “regression” model in which we include 0 predictors, and only include the intercept term b 0

H 0 :Y i =b 0 +ϵ i

If our regression model has K predictors, the “alternative model” is described using the usual formula for a multiple regression model:

$H_{1}: Y_{i}=\left(\sum_{k=1}^{K} b_{k} X_{i k}\right)+b_{0}+\epsilon_{i}$

How can we test these two hypotheses against each other? The trick is to understand that just like we did with ANOVA, it’s possible to divide up the total variance SS tot into the sum of the residual variance SS res and the regression model variance SS mod . I’ll skip over the technicalities, since we covered most of them in the ANOVA chapter, and just note that:

SS mod =SS tot −SS res

And, just like we did with the ANOVA, we can convert the sums of squares in to mean squares by dividing by the degrees of freedom.

$\mathrm{MS}_{m o d}=\dfrac{\mathrm{SS}_{m o d}}{d f_{m o d}}$ $\mathrm{MS}_{r e s}=\dfrac{\mathrm{SS}_{r e s}}{d f_{r e s}}$

So, how many degrees of freedom do we have? As you might expect, the df associated with the model is closely tied to the number of predictors that we’ve included. In fact, it turns out that df mod =K. For the residuals, the total degrees of freedom is df res =N−K−1.

$\ F={MS_{mod} \over MS_{res}}$

and the degrees of freedom associated with this are K and N−K−1. This F statistic has exactly the same interpretation as the one we introduced in Chapter 14. Large F values indicate that the null hypothesis is performing poorly in comparison to the alternative hypothesis. And since we already did some tedious “do it the long way” calculations back then, I won’t waste your time repeating them. In a moment I’ll show you how to do the test in R the easy way, but first, let’s have a look at the tests for the individual regression coefficients.

Tests for individual coefficients

The F-test that we’ve just introduced is useful for checking that the model as a whole is performing better than chance. This is important: if your regression model doesn’t produce a significant result for the F-test then you probably don’t have a very good regression model (or, quite possibly, you don’t have very good data). However, while failing this test is a pretty strong indicator that the model has problems, passing the test (i.e., rejecting the null) doesn’t imply that the model is good! Why is that, you might be wondering? The answer to that can be found by looking at the coefficients for the regression.2 model:

I can’t help but notice that the estimated regression coefficient for the baby.sleep variable is tiny (0.01), relative to the value that we get for dan.sleep (-8.95). Given that these two variables are absolutely on the same scale (they’re both measured in “hours slept”), I find this suspicious. In fact, I’m beginning to suspect that it’s really only the amount of sleep that I get that matters in order to predict my grumpiness.

Once again, we can reuse a hypothesis test that we discussed earlier, this time the t-test. The test that we’re interested has a null hypothesis that the true regression coefficient is zero (b=0), which is to be tested against the alternative hypothesis that it isn’t (b≠0). That is:

H 1 : b≠0

How can we test this? Well, if the central limit theorem is kind to us, we might be able to guess that the sampling distribution of $\ \hat{b}$, the estimated regression coefficient, is a normal distribution with mean centred on b. What that would mean is that if the null hypothesis were true, then the sampling distribution of $\ \hat{b}$ has mean zero and unknown standard deviation. Assuming that we can come up with a good estimate for the standard error of the regression coefficient, SE ($\ \hat{b}$), then we’re in luck. That’s exactly the situation for which we introduced the one-sample t way back in Chapter 13. So let’s define a t-statistic like this,

$\ t = { \hat{b} \over SE(\hat{b})}$

I’ll skip over the reasons why, but our degrees of freedom in this case are df=N−K−1. Irritatingly, the estimate of the standard error of the regression coefficient, SE($\ \hat{b}$), is not as easy to calculate as the standard error of the mean that we used for the simpler t-tests in Chapter 13. In fact, the formula is somewhat ugly, and not terribly helpful to look at. For our purposes it’s sufficient to point out that the standard error of the estimated regression coefficient depends on both the predictor and outcome variables, and is somewhat sensitive to violations of the homogeneity of variance assumption (discussed shortly).

In any case, this t-statistic can be interpreted in the same way as the t-statistics that we discussed in Chapter 13. Assuming that you have a two-sided alternative (i.e., you don’t really care if b>0 or b<0), then it’s the extreme values of t (i.e., a lot less than zero or a lot greater than zero) that suggest that you should reject the null hypothesis.

Running the hypothesis tests in R

To compute all of the quantities that we have talked about so far, all you need to do is ask for a summary() of your regression model. Since I’ve been using regression.2 as my example, let’s do that:

The output that this command produces is pretty dense, but we’ve already discussed everything of interest in it, so what I’ll do is go through it line by line. The first line reminds us of what the actual regression model is:

You can see why this is handy, since it was a little while back when we actually created the regression.2 model, and so it’s nice to be reminded of what it was we were doing. The next part provides a quick summary of the residuals (i.e., the ϵi values),

which can be convenient as a quick and dirty check that the model is okay. Remember, we did assume that these residuals were normally distributed, with mean 0. In particular it’s worth quickly checking to see if the median is close to zero, and to see if the first quartile is about the same size as the third quartile. If they look badly off, there’s a good chance that the assumptions of regression are violated. These ones look pretty nice to me, so let’s move on to the interesting stuff. The next part of the R output looks at the coefficients of the regression model:

Each row in this table refers to one of the coefficients in the regression model. The first row is the intercept term, and the later ones look at each of the predictors. The columns give you all of the relevant information. The first column is the actual estimate of b (e.g., 125.96 for the intercept, and -8.9 for the dan.sleep predictor). The second column is the standard error estimate $\ \hat{\sigma_b}$. The third column gives you the t-statistic, and it’s worth noticing that in this table t= $\ \hat{b}$ /SE($\ \hat{b}$) every time. Finally, the fourth column gives you the actual p value for each of these tests. 217 The only thing that the table itself doesn’t list is the degrees of freedom used in the t-test, which is always N−K−1 and is listed immediately below, in this line:

The value of df=97 is equal to N−K−1, so that’s what we use for our t-tests. In the final part of the output we have the F-test and the R 2 values which assess the performance of the model as a whole

So in this case, the model performs significantly better than you’d expect by chance (F(2,97)=215.2, p<.001), which isn’t all that surprising: the R 2 =.812 value indicate that the regression model accounts for 81.2% of the variability in the outcome measure. However, when we look back up at the t-tests for each of the individual coefficients, we have pretty strong evidence that the baby.sleep variable has no significant effect; all the work is being done by the dan.sleep variable. Taken together, these results suggest that regression.2 is actually the wrong model for the data: you’d probably be better off dropping the baby.sleep predictor entirely. In other words, the regression.1 model that we started with is the better model.

Help | Advanced Search

Physics > Data Analysis, Statistics and Probability

Title: statistical divergences in high-dimensional hypothesis testing and a modern technique for estimating them.

Abstract: Hypothesis testing in high dimensional data is a notoriously difficult problem without direct access to competing models' likelihood functions. This paper argues that statistical divergences can be used to quantify the difference between the population distributions of observed data and competing models, justifying their use as the basis of a hypothesis test. We go on to point out how modern techniques for functional optimization let us estimate many divergences, without the need for population likelihood functions, using samples from two distributions alone. We use a physics-based example to show how the proposed two-sample test can be implemented in practice, and discuss the necessary steps required to mature the ideas presented into an experimental framework.

Submission history

Access paper:.

HTML (experimental)
Other Formats

References & Citations

INSPIRE HEP
Google Scholar
Semantic Scholar

BibTeX formatted citation

Bibliographic and Citation Tools

Code, data and media associated with this article, recommenders and search tools.

Institution

arXivLabs: experimental projects with community collaborators

arXivLabs is a framework that allows collaborators to develop and share new arXiv features directly on our website.

Both individuals and organizations that work with arXivLabs have embraced and accepted our values of openness, community, excellence, and user data privacy. arXiv is committed to these values and only works with partners that adhere to them.

Have an idea for a project that will add value for arXiv's community? Learn more about arXivLabs .

IMAGES

Mod-01 Lec-39 Hypothesis Testing in Linear Regression
Multiple Linear Regression Hypothesis Testing in Matrix Form
Linear regression
Hypothesis Tests in Multiple Linear Regression, Part 1
PPT
PPT

VIDEO

Multiple regression, hypothesis testing, model deployment
Hypothesis Testing in Simple Linear Regression
Final 08 Simple Regression &Hypothesis TestingWeek6&7&12
Regression and test of hypothesis
Hypothesis Test for Linear Regression
R6. Testing Multiple Linear Hypotheses (Econometrics in R)

COMMENTS

12.2.1: Hypothesis Test for Linear Regression
The two test statistic formulas are algebraically equal; however, the formulas are different and we use a different parameter in the hypotheses. The formula for the t-test statistic is t = b1 (MSE SSxx)√ t = b 1 ( M S E S S x x) Use the t-distribution with degrees of freedom equal to n − p − 1 n − p − 1.
13.6 Testing the Regression Coefficients
The hypothesis test for a regression coefficient is a well established process: Write down the null and alternative hypotheses in terms of the regression coefficient being tested. The null hypothesis is the claim that there is no relationship between the dependent variable and independent variable.
Linear regression
The lecture is divided in two parts: in the first part, we discuss hypothesis testing in the normal linear regression model, in which the OLS estimator of the coefficients has a normal distribution conditional on the matrix of regressors; in the second part, we show how to carry out hypothesis tests in linear regression analyses where the ...
6a.2
Below these are summarized into six such steps to conducting a test of a hypothesis. Set up the hypotheses and check conditions: Each hypothesis test includes two hypotheses about the population. One is the null hypothesis, notated as H 0, which is a statement of a particular parameter value. This hypothesis is assumed to be true until there is ...
PDF Lecture 5 Hypothesis Testing in Multiple Linear Regression
As in simple linear regression, under the null hypothesis t 0 = βˆ j seˆ(βˆ j) ∼ t n−p−1. We reject H 0 if |t 0| > t n−p−1,1−α/2. This is a partial test because βˆ j depends on all of the other predictors x i, i 6= j that are in the model. Thus, this is a test of the contribution of x j given the other predictors in the model.
PDF Chapter 9 Simple Linear Regression
218 CHAPTER 9. SIMPLE LINEAR REGRESSION 9.2 Statistical hypotheses For simple linear regression, the chief null hypothesis is H 0: β 1 = 0, and the corresponding alternative hypothesis is H 1: β 1 6= 0. If this null hypothesis is true, then, from E(Y) = β 0 + β 1x we can see that the population mean of Y is β 0 for
Hypothesis Testing
Table of contents. Step 1: State your null and alternate hypothesis. Step 2: Collect data. Step 3: Perform a statistical test. Step 4: Decide whether to reject or fail to reject your null hypothesis. Step 5: Present your findings. Other interesting articles. Frequently asked questions about hypothesis testing.
Linear regression hypothesis testing: Concepts, Examples
F-statistics for testing hypothesis for linear regression model: F-test is used to test the null hypothesis that a linear regression model does not exist, representing the relationship between the response variable y and the predictor variables x1, x2, x3, x4 and x5. The null hypothesis can also be represented as x1 = x2 = x3 = x4 = x5 = 0.
Hypothesis Test for Regression Slope
Hypothesis Test for Regression Slope. This lesson describes how to conduct a hypothesis test to determine whether there is a significant linear relationship between an independent variable X and a dependent variable Y.. The test focuses on the slope of the regression line Y = Β 0 + Β 1 X. where Β 0 is a constant, Β 1 is the slope (also called the regression coefficient), X is the value of ...
The Regression Hypothesis Test
Particular Hypotheses Tested by Linear Regression. H 0: β = 0 (Null hypothesis) H A: β ≠ 0 (Alternative hypothesis) The "true regression line" relates μ Y.X (the mean of Y for particular X) to X. In linear regression, this relationship is always a straight line, which has a slope equal to β.
Comparing Regression Lines with Hypothesis Tests
Hypothesis Tests for Comparing Regression Constants. When the constant (y intercept) differs between regression equations, the regression lines are shifted up or down on the y-axis. The scatterplot below shows how the output for Condition B is consistently higher than Condition A for any given Input. These two models have different constants.
Regression/Hypothesis testing
REGRESSION CONTINUED. Remember the regression equation for predicting y from x is: y = bx + a (a is also indicated as "e" at times) b, or the slope, is simply (r xy * S.D. y)/S.D. x. ... HYPOTHESIS TESTING. So far we have learned how to take raw data, combine it, and create statistics that allow us to describe the data in a brief summary form. ...
Hypothesis Testing in Regression Analysis
Hypothesis Testing in Regression Analysis. Hypothesis testing is used to confirm if the estimated regression coefficients bear any statistical significance. Either the confidence interval approach or the t-test approach can be used in hypothesis testing. In this section, we will explore the t-test approach.
6.4
For the multiple linear regression model, there are three different hypothesis tests for slopes that one could conduct. They are: Hypothesis test for testing that all of the slope parameters are 0. Hypothesis test for testing that a subset — more than one, but not all — of the slope parameters are 0.
How to Simplify Hypothesis Testing for Linear Regression in Python
Side note: There is another hypothesis test that is more seldom used with linear regression, which is a hypothesis regarding the intercept. It's used less since we're typically concerned with the slope of the line. The 4 Assumptions for Linear Regression Hypothesis Testing. There is a linear regression relation between Y and X
Hypothesis Testing On Linear Regression
Steps to Perform Hypothesis testing: Step 1: We start by saying that β₁ is not significant, i.e., there is no relationship between x and y, therefore slope β₁ = 0. Step 2: Typically, we set ...
Hypothesis testing in linear regression part 1
This video explains how hypothesis testing works in practice, using a particular example. Check out https://ben-lambert.com/econometrics-course-problem-sets-...
Understanding the Null Hypothesis for Linear Regression
x: The value of the predictor variable. Simple linear regression uses the following null and alternative hypotheses: H0: β1 = 0. HA: β1 ≠ 0. The null hypothesis states that the coefficient β1 is equal to zero. In other words, there is no statistically significant relationship between the predictor variable, x, and the response variable, y.
How to Test the Significance of a Regression Slope
Step 1. State the hypotheses. The null hypothesis (H0): B1 = 0. The alternative hypothesis: (Ha): B1 ≠ 0. Step 2. Determine a significance level to use. Since we constructed a 95% confidence interval in the previous example, we will use the equivalent approach here and choose to use a .05 level of significance. Step 3.
Hypothesis Testing Explained (How I Wish It Was Explained to Me)
The curse of hypothesis testing is that we will never know if we are dealing with a True or a False Positive (Negative). All we can do is fill the confusion matrix with probabilities that are acceptable given our application. To be able to do that, we must start from a hypothesis. Step 1. Defining the hypothesis
Hypothesis Testing's Role in BI Regression Analysis
In Business Intelligence (BI), regression analysis is a powerful statistical tool that helps you understand the relationship between dependent and independent variables. Hypothesis testing plays a ...
15.5: Hypothesis Tests for Regression Models
Testing the model as a whole; Tests for individual coefficients; Running the hypothesis tests in R; So far we've talked about what a regression model is, how the coefficients of a regression model are estimated, and how we quantify the performance of the model (the last of these, incidentally, is basically our measure of effect size).
Statistics and probability- Hypothesis testing of ...
With the point estimate of coefficients, wen can formulate a t statistics, in terms of the Null hypothesis of testing for specific values, and an alternative...
Linear Regression Hypothesis Testing & Inference
Hypothesis tests for regression components different from zero There are cases we might want to use the regression output to test for values of the coefficient different from zero. This is nopt given as standard output but might be a command that one can use. In the event one does not have access to this the procedure can be done as indicated below Suppose want to test H 0: β 1 ≤ τ vs. β ...
Statistical divergences in high-dimensional hypothesis testing and a
Hypothesis testing in high dimensional data is a notoriously difficult problem without direct access to competing models' likelihood functions. This paper argues that statistical divergences can be used to quantify the difference between the population distributions of observed data and competing models, justifying their use as the basis of a hypothesis test. We go on to point out how modern ...