homework 7 law of sines

Chapter 3: Laws of Sines and Cosines

Exercises: 3.2 The Law of Sines

• Use the law of sines to find a side #1-6
• Use the law of sines to find an angle #7-12
• Use the law of sines to solve an oblique triangle #13-18
• Solve problems using the law of sines #19-28
• Compute distances using the parallax #29-32
• Solve problems involving the ambiguous case #33-46

Suggested homework problems

Homework 3.2

Exercise group.

For Problems 13–18, sketch the triangle and solve. Round answers to two decimal places. 13. [latex]b = 7,~ A = 23°,~ B = 42°[/latex] 14. [latex]c = 34,~ A = 53°,~ C = 26°[/latex] 15. [latex]a = 1.8,~ c = 2.1,~ C = 44°[/latex] 16. [latex]b = 8.5,~ c = 6.8,~ B = 23°[/latex] 17. [latex]c = 75,~ A = 35°,~ B = 46°[/latex] 18. [latex]a = 94,~ B = 29°,~ C = 84°[/latex]

For Problems 19–26, sketch and label a triangle to illustrate the problem. Solve the problem. 19. Maryam wants to know the height of a cliff on the other side of a ravine. The angle of elevation from her edge of the ravine to the cliff top is [latex]84.6°{.}[/latex] When she moves [latex]30[/latex] feet back from the ravine, the angle of elevation is [latex]82.5°{.}[/latex] How tall is the cliff? 20. Amir wants to know the height of a tree in the median strip of a highway. The angle of elevation from the highway shoulder to the treetop is [latex]43.5°{.}[/latex] When he moves 10 feet farther away from the tree, the angle of elevation is [latex]37.2°{.}[/latex] How tall is the tree? 21. Delbert and Francine are [latex]10[/latex] kilometers apart, both observing a satellite that passes directly over their heads. At a moment when the satellite is between them, Francine measures its angle of elevation as [latex]84.6°{,}[/latex] and Delbert measures an angle of [latex]87°{.}[/latex] How far is the satellite from Delbert? 22. Megan rows her kayak due east. When she began, she spotted a lighthouse [latex]2000[/latex] meters in the distance at an angle of [latex]14°[/latex] south of east. After traveling for an hour, the lighthouse was at an angle of [latex]83°[/latex] south of east. How far did Megan travel, and what was her average speed? 23. Chad is hiking along a straight path but needs to detour around a large pond. He turns [latex]23°[/latex] from his path until clear of the pond, then walks back to his original path, intercepting it at an angle of [latex]29°[/latex] and at a distance of [latex]2[/latex] miles from where he had left the path. How far did Chad walk in each of the two segments of his detour, and how much farther did his detour require compared with a straight line through the pond?

• Find [latex]\angle ACB{.}[/latex]
• Find[latex]\angle CAB{,}[/latex] at the top of the antenna.
• How long is [latex]BC{,}[/latex] the distance from the bottom of the antenna to [latex]C{?}[/latex]
• How tall is the hill?

28. A billboard of California’s gubernatorial candidate Angelyne is located on the roof of a building. At a distance of [latex]180[/latex] feet from the building, the angles of elevation to the bottom and top of the billboard are, respectively, [latex]39.8°[/latex] and [latex]47.3°{.}[/latex] How tall is the billboard?

For Problems 29–32, compute the following distances in astronomical units (AUs). Then convert to kilometers, using the fact that 1 AU [latex]\approx 1.5[/latex] times [latex]10^{8}[/latex] km. 29. When observed from opposite sides of Earth’s orbit, the star Alpha Centauri has a parallax of [latex]0.76^{\prime\prime}{.}[/latex] How far from the Sun is Alpha Centauri? 30. How far from the Sun is Barnard’s Star, which has a parallax of [latex]1.1^{\prime\prime}[/latex] when observed at opposite ends of Earth’s orbit? 31. How far from the Sun is Tau Ceti, which has a parallax of [latex]0.55^{\prime\prime}[/latex] when observed from opposite ends of Earth’s orbit? 32. How far from the Sun is Sirius, which has a parallax of [latex]0.75^{\prime\prime}[/latex] when observed from opposite ends of Earth’s orbit?

• Use the definition of [latex]\sin A[/latex] to solve for [latex]a[/latex] (the length of side [latex]\overline{BC}[/latex]).
• Can you draw a triangle [latex]\triangle ABC[/latex] with [latex]\angle A = 30°[/latex] and [latex]c = 3[/latex] if [latex]a \lt \dfrac{3}{2}{?}[/latex] Why or why not?
• How many triangles are possible if [latex]\dfrac{3}{2} \lt a \lt 3{?}[/latex]
• How many triangles are possible if [latex]a \gt 3{?}[/latex]

34. In this problem we show that there are two different triangles [latex]\triangle ABC[/latex] with [latex]\angle A = 30°,~ a = 2[/latex] and [latex]c = 3{.}[/latex]

• Use a protractor to draw an angle [latex]\angle A = 30°{.}[/latex] Mark point [latex]B[/latex] on one side of the angle so that [latex]\overline{AB}[/latex] is 3 inches long.
• Locate two distinct points on the other side of the angle that are each 2 inches from point [latex]B{.}[/latex] These points are both possible locations for point [latex]C{.}[/latex]
• Use the law of sines to find two distinct possible measures for [latex]\angle C{.}[/latex]

35. In [latex]\triangle ABC, \angle A = 30°[/latex] and [latex]c = 12{.}[/latex] How many triangles are possible for each of the following lengths for side [latex]a{?}[/latex] Sketch the solutions in each case.

• [latex]a = 6[/latex]
• [latex]a = 4[/latex]
• [latex]a = 9[/latex]
• [latex]a = 15[/latex]
• Express the length of the altitude in terms of [latex]\angle A[/latex] and [latex]c{.}[/latex]
• Now suppose we keep [latex]\angle A[/latex] and side [latex]c[/latex] fixed but allow [latex]a[/latex] to vary in length. What is the smallest value [latex]a[/latex] can have and still be long enough to make a triangle?
• What are the largest and smallest values that [latex]a[/latex] can have in order to produce two distinct triangles [latex]\triangle ABC[/latex] (without changing [latex]\angle A[/latex] and side [latex]c[/latex])?

37. For the triangle in Problem 36, suppose [latex]\angle A = 40°[/latex] and [latex]c = 8{.}[/latex]

• Sketch and solve the triangle if [latex]a = 12{.}[/latex]
• Sketch and solve the triangle if [latex]a = 6{.}[/latex]
• Sketch and solve the triangle if [latex]a = 4{.}[/latex]
• For what value of [latex]a[/latex] is [latex]c[/latex] the hypotenuse of a right triangle?

38. For the figure in Problem 36, suppose [latex]\angle A = 70°[/latex] and [latex]c = 20{.}[/latex]

• For what value of [latex]a[/latex] is the triangle a right triangle?
• For what values of [latex]a[/latex] are there two solutions for the triangle?
• For what values of [latex]a[/latex] is there one obtuse solution for the triangle?
• For what value of [latex]a[/latex] is there no solution?

For Problems 39–42, find the remaining angles of the triangle. Round answers to two decimal places. (These problems involve the ambiguous case.) 39. [latex]a = 66,~ c = 43,~ \angle C = 25°[/latex] 40. [latex]b = 10,~ c = 14,~ \angle B = 20°[/latex] 41. [latex]b = 100,~ c = 80,~ \angle B = 49°[/latex] 42. [latex]b = 4.7,~ c = 6.3,~ \angle C = 54°[/latex] 43. Delbert and Francine are [latex]1000[/latex] yards apart. The angle Delbert sees between Francine and a certain tree is [latex]38°{.}[/latex] If the tree is [latex]800[/latex] yards from Francine, how far is it from Delbert? (There are two possible answers.) 44. From the lookout point on Fabrick Rock, Ann can see not only the famous “Crooked Spire” in Chesterfield, which is [latex]8[/latex] miles away, but also the red phone box in the village of Alton. Chesterfield and Alton are [latex]7[/latex] miles apart. Fabrick Rock has a plaque that shows directions to famous sites, and from the plaque Ann determines that the angle between the lines to the spire and the phone box measures [latex]19°{.}[/latex] How far is Fabrick Rock from the phone box? (There are two possible answers.) 45.

• Sketch a triangle with [latex]\angle A = 25°,~ \angle B = 35°{,}[/latex] and [latex]b = 16{.}[/latex]
• Use the law of sines to find [latex]a{.}[/latex]
• Use the law of sines to find [latex]c{.}[/latex]
• Find [latex]c[/latex] without using the law of sines. (Hint: Sketch the altitude, [latex]h{,}[/latex] from [latex]\angle C[/latex] to make two right triangles. Find [latex]h{,}[/latex] then use [latex]h[/latex] to find [latex]c[/latex].)
• Sketch a triangle with [latex]\angle A = 75°[/latex], [latex]a = 15{,}[/latex] and [latex]b = 6{.}[/latex]
• Find [latex]c[/latex] without using the law of sines.

Problems 47–48 prove the law of sines using the formula for the area of a triangle. (See Section 3.1 for the appropriate formula.) 47.

• Sketch a triangle with angles [latex]\angle A, ~\angle B[/latex] and [latex]\angle C[/latex] and opposite sides of lengths respectively [latex]a,~ b[/latex] and [latex]c{.}[/latex]
• Write the area of the triangle in terms of [latex]a,~b{,}[/latex] and angle [latex]\angle C{.}[/latex]
• Write the area of the triangle in terms of [latex]a,~c{,}[/latex] and angle [latex]\angle B{.}[/latex]
• Write the area of the triangle in terms of [latex]b

48. Equate the three different expressions from Problem 47 for the area of the triangle. Multiply through by [latex]\dfrac{2}{abc}[/latex] and simplify to deduce the law of sines. 49. Here is a method for solving certain oblique triangles by dividing them into two right triangles. In the triangle shown, we know two angles, [latex]\angle A[/latex] and [latex]\angle B{,}[/latex] and the side opposite one of them, say [latex]a{.}[/latex] We would like to find side [latex]b{.}[/latex]

• Draw the altitude [latex]h[/latex] from angle [latex]\angle C{.}[/latex]
• Write an expression for [latex]b[/latex] in terms of [latex]h[/latex] and angle [latex]\angle A{.}[/latex]
• Write an expression for [latex]h[/latex] in terms of angle [latex]\angle B{.}[/latex]
• Substitute your expression for [latex]h[/latex] into your expression for [latex]b{.}[/latex]
• [latex]a \sin A = b \sin B[/latex]
• [latex]\dfrac{a}{\sin A} = \dfrac{b}{\sin B}[/latex]
• [latex]\dfrac{a}{\sin B} = \dfrac{b}{\sin A}[/latex]

Trigonometry Copyright © 2024 by Bimal Kunwor; Donna Densmore; Jared Eusea; and Yi Zhen. All Rights Reserved.

Share This Book

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

3.1: The Law of Sines

• Last updated
• Save as PDF
• Page ID 112420

• Katherine Yoshiwara
• Los Angeles Pierce College

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

We have learned to use the trigonometric ratios to solve right triangles. But the trig ratios are only valid for the sides of right triangles. Can we find unknown sides or angles in an oblique triangle?

In this section and the next we find relationships among the sides and angles of oblique triangles. These relationships are called the Law of Sines and the Law of Cosines. To derive these new rules, we use what we already know about right triangles.

Note 3.21 Reducing a new problem to an earlier one is a frequently used technique in mathematics.

Consider the oblique triangle below. By drawing in the altitude \(h\) of the triangle, we create two right triangles, \(\triangle B C D\) and \(\triangle A B D\), as shown in the figure. Now we can write expressions in terms of \(h\) for \(\sin A\) and for \(\sin C\).

Looking at \(\triangle B C D\), we see that \(\dfrac{h}{a}=\sin C\).

Looking at \(\triangle A B D\), we see that \(\dfrac{h}{c}=\sin A\).

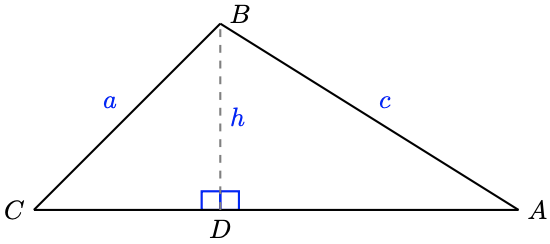
Now we solve each of these equations for \(h\):

\(\dfrac{h}{a}=\sin C \quad \text { and } \quad \dfrac{h}{c}=\sin A \quad \quad \text { Solve each equation for } \boldsymbol{h}.\)

\(h=a \sin C \quad \text{ and } \quad h=c \sin A \quad \quad \text{Equate the expressions for } \boldsymbol{h}.\)

\begin{aligned} a \sin C&=c \sin A \quad \quad \quad \text{Divide both sides by } \boldsymbol{ac}. \\ \dfrac{\sin C}{c} &= \dfrac{\sin A}{a} \end{aligned}

We have derived a relationship between the angles \(A\) and \(C\) and their opposite sides, \(a\) and \(c\). If we know any three of these quantities, we can find the fourth.

In a similar way, by drawing in the altitude from the vertex \(C\), we can show that

\(\dfrac{\sin A}{a}=\dfrac{\sin B}{b}\)

Putting both results together, we have the Law of Sines . The Law of Sines is true for any triangle, whether it is acute, right, or obtuse.

Law of Sines.

If the angles of a triangle are \(A, B\), and \(C\), and the opposite sides are respectively \(a, b\), and \(c\), then

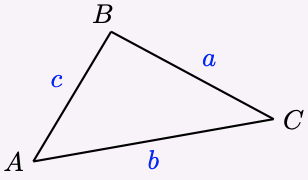
\(\dfrac{\sin A}{a}=\dfrac{\sin B}{b}=\dfrac{\sin C}{c}\)

or equivalently,

\(\dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}\)

Finding a Side

In the next example, we use the Law of Sines to find a distance.

Example 3.22

Two observers onshore sight a ship at an unknown distance from the shore. The observers are 400 yards apart at points \(A\) and \(B\), and they each measure the angle from the shoreline to the ship, as shown below. How far is the ship from the observer at \(A\)?

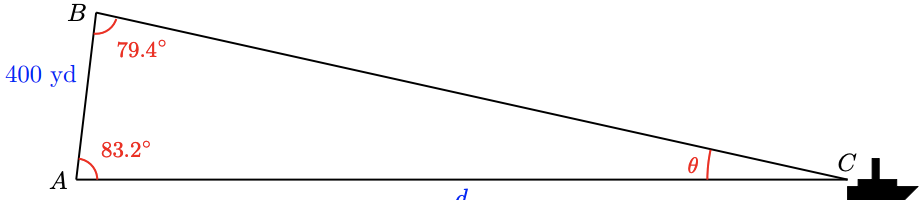
First note that \(\triangle A B C\) is not a right triangle, so we cannot use the trig ratios directly to find the sides of this triangle.

The unknown distance \(d\) is the side opposite \(\angle B=79.4^{\circ}\). In order to use the Law of Sines, we must know another angle and the side opposite that angle. We do: we know that side \(c=400\), and we can compute the angle at the ship, \(\angle C\).

\(\angle C=180^{\circ}-\left(79.4^{\circ}+83.2^{\circ}\right)=17.4^{\circ}\)

Now we apply the Law of Sines, using angles \(B\) and \(C\).

\begin{aligned} \dfrac{b}{\sin B} &= \dfrac{c}{\sin C} \quad \quad &&\text{Substitute the given values.} \\ \dfrac{d}{\sin 79.4^{\circ}} &= \dfrac{400}{\sin 17.4^{\circ}} &&\text{Evaluate sines.} \\ \dfrac{d}{0.9829} &= \dfrac{400}{0.2990} &&\text{Multiply both sides by 0.9829.} \\ d&= 1315 \end{aligned}

The ship is about 1315 yards from the observer at \(A\).

Checkpoint 3.23

Delbert and Francine are 40 feet apart on one side of a river. They make angle measurements to a pine tree on the opposite shore as shown at right. What is the distance from Francine to the pine tree?

About 114.8 feet

Solving Triangles with the Law of Sines

In order to apply the Law of Sines to find a side, we must know one angle of the triangle and its opposite side (either \(a\) and \(A\), or \(b\) and \(B\), or \(c\) and \(C\) ), and one other angle. Then we can find the side opposite that angle.

Example 3.24

In the triangle shown at right, \(A=37^{\circ}, B=54^{\circ}\), and \(a=11\).

a Find \(b\).

b Solve the triangle.

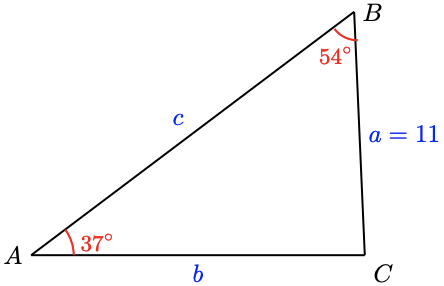
a We use the Law of Sines with \(a\) and angle \(A\) to find \(b\).

\begin{aligned} \dfrac{a}{\sin A} &= \dfrac{b}{\sin B} \quad \quad &&\text{Substitute the given values.} \\ \dfrac{11}{\sin 37^{\circ}} &= \dfrac{b}{\sin 54^{\circ}} &&\text{Multiply both sides by } \sin 54^{\circ}. \\ \dfrac{11}{\sin 37^{\circ}} \cdot \sin 54^{\circ} &= b \end{aligned}

Evaluating this expression with a calculator, we find that \(b \approx 14.79\).

b The angle \(C = 180^{\circ} - (37^{\circ} + 54^{\circ}) = 89^{\circ}\). Now we use the Law of Sines to find side \(c\). Note that it is safer to use the given side, \(a\), rather than the value we calculated for \(b\).

\begin{aligned} \dfrac{a}{\sin A} &= \dfrac{c}{\sin C} \quad \quad &&\text{Substitute the known values.} \\ \dfrac{11}{\sin 37^{\circ}} &= \dfrac{c}{\sin 89^{\circ}} &&\text{Multiply both sides by } \sin 89^{\circ}. \\ \dfrac{11}{\sin 37^{\circ}} \cdot \sin 89^{\circ} &= c \end{aligned}

so \(c \approx 18.28\).

Checkpoint 3.25

In the triangle at right, \(A=65^{\circ}, C=42^{\circ}\), and \(c=16\). Solve the triangle. (Hint: Which side will you find first?)

\(B=73^{\circ}, b=22.87, a=21.68\)

Finding an Angle

We can also use the Law of Sines to find an unknown angle of a triangle. We must know two sides of the triangle and the angle opposite one of them.

Example 3.26

In the triangle shown at right, \(B=55^{\circ}, a=5\), and \(b=11\). Solve the triangle.

We must find the three remaining parts of the triangle, \(A, C\), and \(c\). First, we use the Law of Sines to find \(\sin A\).

\begin{aligned} \dfrac{\sin A}{a} &=\dfrac{\sin B}{b} \quad \quad &&\text{Substitute the known values.} \\ \dfrac{\sin A}{5} &=\dfrac{\sin 55^{\circ}}{11} &&\text{Multiply both sides by 5. }\\ \sin A &=5 \cdot \dfrac{\sin 55^{\circ}}{11} \approx 0.3723 \end{aligned}

So \(A=\sin ^{-1}(0.3723) \approx 21.9^{\circ}\). Now we know two angles, and we can find angle \(C\).

\begin{aligned} C &=180^{\circ}-(B+A) \\ &=180^{\circ}-55^{\circ}-21.9^{\circ}=103.1^{\circ} \end{aligned}

Finally, we use the Law of Sines to find side \(c\).

\begin{aligned} \dfrac{b}{\sin B} &=\dfrac{c}{\sin C} & & \text { Substitute the known values. } \\ \dfrac{11}{\sin 55^{\circ}} &=\dfrac{c}{\sin 103.1^{\circ}} & & \text { Multiply both sides by } \sin 103.1^{\circ} \\ \dfrac{11}{\sin 55^{\circ}} \cdot \sin 103.1^{\circ} &=c & & \end{aligned}

Evaluating this expression with a calculator gives \(c \approx 13.1\).

Checkpoint 3.27

Sketch a triangle with \(C=93^{\circ}, a=7\), and \(c=11\).

a Use the Law of Sines to find another angle of the triangle.

b Solve the triangle, and label your sketch with the results.

a \(A=39.5^{\circ}\)

b \(b=8.13, B=47.5^{\circ}\)

Caution 3.28

In the last example we used the value of \(\sin A\) to find angle \(A\). But there are two angles that satisfy \(\sin A=0.3723\), one acute \(\left(21.9^{\circ}\right)\) and one obtuse \(\left(168.1^{\circ}\right)\). How did we know which one to choose?

In this case, the obtuse angle is too big to fit in the triangle, because angle \(B=55^{\circ}\). Sometimes both angles will produce (different) triangles, and sometimes only the acute angle will work. You should always check whether both angles provide solutions.

Note 3.29 Because there can be more than one solution for a triangle in which we know two sides and an angle opposite one of them, this situation is called the ambiguous case for the Law of Sines. (See Homework Problems 33-42 for more about the ambiguous case.)

Example 3.30

Find two triangles in which \(B=14.4^{\circ}, a=8\), and \(b=3\), and sketch both triangles.

\begin{aligned} &\dfrac{\sin A}{a}=\dfrac{\sin B}{b} \quad \quad &&\text{Substitute the known values.}\\ &\dfrac{\sin A}{8}=\dfrac{\sin 14.4^{\circ}}{3} &&\text{Multiply both sides by 8.}\\ &\sin A=8 \cdot \dfrac{\sin 14.4^{\circ}}{3} \approx 0.6632 \end{aligned}

There are two angles with sine \(0.6632\):

- the acute angle \(A=\sin ^{-1}(0.6632)=41.5^{\circ}\),

- or its supplement, \(A^{\prime}=180^{\circ}-41.5^{\circ}=138.5^{\circ}\).

Each of these angles produces a different solution triangle, because the angle \(C\) and side \(c\) will be different also.

- In the first case, angle \(C=180^{\circ}-\left(14.4^{\circ}+138.5^{\circ}\right)=27.1^{\circ}\), and we have the triangle shown in figure (a).

- In the second case, \(C=180^{\circ}-\left(14.4^{\circ}+41.5^{\circ}\right)=124.1^{\circ}\), which gives us the triangle shown in figure (b).

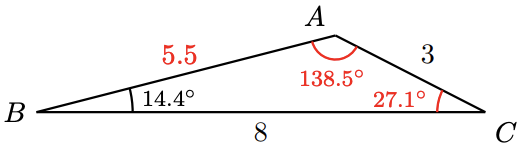
Checkpoint 3.31

Suppose that \(C=29.7^{\circ}, b=8\), and \(c=5\).

a Find two possible values for angle \(B\).

b Solve the triangle for both values of \(B\), and sketch both solutions.

a \(B=52.4^{\circ}\) or \(B=127.6^{\circ}\)

b \(A=97.9^{\circ}, a=10\)

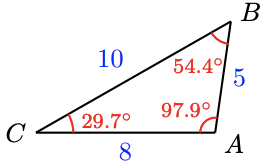
or \(A=22.7^{\circ}, a=3.9\)

Applications

In the next example, we use two triangles to solve the problem.

Example 3.32

Richard wants to measure the height of a castle controlled by hostile forces. When he is as close as he can get to the castle, the angle of elevation to the top of the wall is \(18.5^{\circ}\). He then retreats 20 yards and measures the angle of elevation again; this time it is \(15.9^{\circ}\). How tall is the castle?

Notice that \(h\) is one side of the right triangle \(ADC\). If we can find its hypotenuse, labeled \(r\) in the figure, we can use the sine ratio to find \(h\). To find \(r\), we consider a second triangle, \(ABC\), as shown below.

In this triangle, we know side \(BC = 20\) and would like to find side \(AC = r\). We can use the Law of Sines to find \(r\), but first we must calculate the other angles of the triangle.

Now, the angle opposite \(r, \angle ABC\), is the complement of \(18.5^{\circ}\), so

\[ \angle ABC = 180^{\circ} - 18.5^{\circ} = 161.5^{\circ} \nonumber\]

The angle opposite the 20-yard side, \(\angle BAC\), is

\[\angle B A C=180^{\circ}-\left(161.5^{\circ}+15.9^{\circ}\right)=2.6^{\circ} \nonumber\]

Now we can apply the Law of Sines to find \(r\). We have

\begin{aligned} \dfrac{r}{\sin 161.5^{\circ}} &=\dfrac{20}{\sin 2.6^{\circ}} \quad \quad \quad &&\text{Solve for } \mathbf{r} \\ r &=\sin 161.5^{\circ} \cdot \dfrac{20}{\sin 2.6^{\circ}} \\ & \approx 139.9 \end{aligned}

So \(r\) is about \(139.9\) yards. Finally, using the right triangle \(A D C\) and the definition of sine, we can write

\begin{aligned} \dfrac{h}{r} &=\sin 15.9^{\circ} \quad &&\text{Solve for } \boldsymbol{h}. \\ h &=r \cdot \sin 15.9^{\circ} \approx 38.33 \end{aligned}

The castle is about \(38.33\) yards tall.

Checkpoint 3.33

Solve the problem in the previous example again, but instead of finding \(r\), find the length \(A B\), and then use \(\triangle A B D\) to find \(h\).

\(A B=120.79\), the castle is about \(38.33\) yards tall.

Measuring Astronomical Distances

If you look at a nearby object and alternately close your left and right eyes, the object seems to jump in position. This apparent change occurs because your eyes are viewing the object from two different positions spaced several centimeters apart. If the object at point \(O\) is straight ahead of one eye, it appears to be at some angle \(p\) away from the line of sight of the other eye. The angle \(p\) is called the parallax of the object.

Use the figure below to see that \(p\) is also the angle between the directions to your two eyes when viewed from point \(O\). (What fact from geometry justifies this statement?)

Astronomers use parallax to determine the distance from earth to stars and other celestial objects. Two observers on Earth at a known distance apart both measure the direction to the star. The difference in angle between those two directions is the parallax.

Example 3.34

Astronomers 1000 kilometers apart observe an asteroid with a parallax of \(0.001^{\circ}\). How far is the asteroid from Earth?

We let \(x\) represent the distance to the asteroid. The asteroid and the two observers make an isosceles triangle with base \(1000 \mathrm{~km}\) and equal sides of length \(x\), as shown below.

The base angles of the triangle are both \(\frac{180^{\circ}-0.001^{\circ}}{2}=89.999^{\circ}\). By the Law of Sines,

\begin{aligned} \dfrac{x}{\sin 89.999^{\circ}} &=\dfrac{1000}{\sin 0.001^{\circ}} \quad &&\text{Solve for } \boldsymbol{x}.\\ x &=\sin 89.999^{\circ} \cdot \dfrac{1000}{\sin 0.001^{\circ}} \\ x & \approx 57,000,000 \end{aligned}

The asteroid is about 57 million kilometers from Earth (roughly one third of the distance to the Sun).

Checkpoint 3.35

Two observers 800 kilometers apart observe an object with a parallax of \(0.0005^{\circ}\). How far is the object from Earth?

About \(91,673,247\) km

Small Angles: Minutes and Seconds

To obtain the most accurate parallax measurements, the distance between the two observers should be as large as possible. But even measured from opposite sides of Earth's orbit, stars outside the solar system have parallaxes much smaller than \(0.0001^{\circ}\).

In order to handle such small angles, we divide degrees into smaller units called minutes and seconds . One minute is \(\frac{1}{60}\) of a degree, and 1 second is \(\frac{1}{60}\) of a minute, or \(\frac{1}{3600}\) of a degree. We use the following notation for minutes and seconds.

Fractions of a Degree.

• One minute: \(\quad 1^{\prime}=\dfrac{1^{\circ}}{60}\)
• One second: \(\quad 1^{\prime \prime}=\dfrac{1^{\prime}}{60}=\dfrac{1^{\circ}}{3600}\)

When describing large distances, astronomers sometimes use the distance from Earth to the Sun, about 93 million miles, as the unit of measurement. This distance is called 1 Astronomical Unit , or \(1 \mathrm{AU}\). For example, an object that is three times as far away as the Sun would be at a distance of \(3 \mathrm{AU}\).

Example 3.36

The star Wolf 359 has a parallax of \(0.85^{\prime \prime}\) when observed from opposites sides of Earth's orbit. How far away is the star?

In the figure below, the star Wolf 359 is located at point \(O\). Our Sun is located at point \(C\), halfway between the two observation points at \(A\) and \(B\). Thus, the distance between the observation points is twice the distance from the Earth to the Sun, or \(2 \mathrm{AU}\).

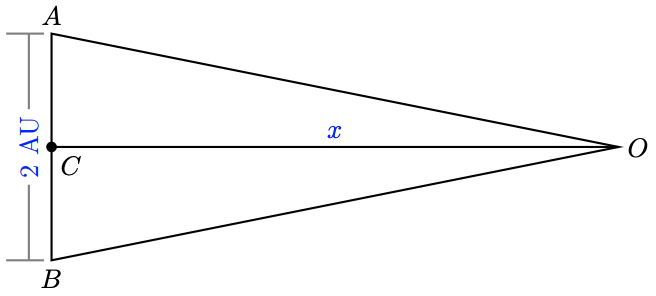
The altitude from \(O\) to side \(\overline{A B}\) forms a right triangle \(A C O\) and bisects the angle at \(O\). Thus

\(\angle A O C=\dfrac{1}{2}\left(0.85^{\prime \prime}\right)=0.425^{\prime \prime}\)

We use the definition of tangent to find

\begin{aligned} \tan 0.425^{\prime \prime} &=\dfrac{\text { opposite }}{\text { adjacent }} \\ \tan \left(0.425^{\circ} / 3600\right) &=\dfrac{1}{x} &&\text{Solve for } \boldsymbol{x}. \\ x &=\dfrac{1}{\tan 0.425^{\circ} / 3600} \approx 485,000 \end{aligned}

The star is approximately 485,000 AU from Earth, or nearly half a million times the distance from Earth to the Sun.

Checkpoint 3.37

Two observers are \(1 \mathrm{AU}\) (astronomical unit) apart. They find that the parallax to a distant star is \(1^{\prime \prime}\). What is the distance to the star, in astronomical units?

(This distance is called a parsec . In other words, a parsec is the distance at which the parallax from observations \(1 \mathrm{AU}\) apart is \(1^{\prime \prime}\). In this Exercise, you are calculating the number of astronomical units in 1 parsec.)

1 parsec \(\approx 206,265 \mathrm{AU}\)

Review the following skills you will need for this section.

Algebra Refresher 3.3

Convert to a decimal fraction.

1 5 inches = ________ foot

2 10 ounces = ________ pound

3 24 minutes = ________ hour

4 35 seconds = ________ minute

5 16 minutes = ________ degree

6 4' = ________ \({}^{\circ}\)

7 2'' = ________ \({}^{\circ}\)

8 1' 5'' = ________ \({}^{\circ}\)

1 \(0.41\bar{6}\)

2 \(0.625\)

4 \(0.58\bar{3}\)

5 \(0.2\bar{6}\)

6 \(0.0\bar{6}\)

7 \(0.000\bar{5}\)

8 \(0.0180\bar{5}\)

Section 3.2 Summary

1 If the angles of a triangle are \(A,B,\) and \(C\), and the opposite sides are respectively \(a,b\), and \(c\), then

\(\dfrac{\sin A}{a} = \dfrac{\sin B}{b} = \dfrac{\sin C}{c}\)

\(\dfrac{a}{\sin A} = \dfrac{b}{\sin B} = \dfrac{c}{\sin C}\)

2 We can use the Law of Sines to find an unknown side in an oblique triangle. We must know the angle opposite the unknown side, and another side-angle pair.

3 We can also use the Law of Sines to find an unknown angle of a triangle. We must know two sides of the triangle and the angle opposite one of them.

4 Remember that there are two angles with a given sine. When using the Law of Sines, we must check whether both angles result in possible triangles.

5 We use minutes and seconds to measure very small angles.

• One minute: \(\quad 1^{\prime} = \dfrac{1^{\circ}}{60}\)
• One second: \(\quad 1^{\prime \prime} = \dfrac{1^{\prime}}{60} = \dfrac{1^{\circ}}{3600}\)

Study Questions

1 Can we use the Law of Sines to solve a right triangle?

2 Explain why we cannot use the Law of Sines to solve the triangle with \(a = 8, b = c\) and \(C = 35^{\circ}\).

3 Francine says "I'm thinking of an angle whose sine is 0.3420 (rounded to four decimal places)." Delbert says "The angle must be \(20^{\circ}\) (rounded to the nearest degree)." Is he correct? Why or why not?

4 Sketch two possible triangles with \(A = 25^{\circ}, b = 18\), and \(a = 10\).

5 Try to sketch a triangle with \(A = 65^{\circ}, b = 18\), and \(a = 10\). What went wrong?

1 Use the Law of Sines to find a side #1-6

2 Use the Law of Sines to find an angle #7-12

3 Use the Law of Sines to solve an oblique triangle #13-18

4 Solve problems using the Law of Sines #19-28

5 Compute distances using parallax #29-32

6 Solve problems involving the ambiguous case #33-46

Homework 3.2

For Problems 1–6, use the Law of Sines to find the indicated side. Round to two decimal places.

For Problems 7–12, use the Law of Sines to find the indicated angle. Round to two decimal places.

For Problems 13–18,sketch the triangle and solve. Round answers to two decimal places.

13. \(b=7, A=23^{\circ}, B=42^{\circ}\) 14. \(c=34, A=53^{\circ}, C=26^{\circ}\) 15. \(a=1.8, c=2.1, C=44^{\circ}\) 16. \(b=8.5, c=6.8, B=23^{\circ}\) 17. \(c=75, A=35^{\circ}, B=46^{\circ}\) 18. \(a=94, B=29^{\circ}, C=84^{\circ}\)

For Problems 19–26,

a Sketch and label a triangle to illustrate the problem.

b Solve the problem.

19. Maryam wants to know the height of a cliff on the other side of a ravine. The angle of elevation from her edge of the ravine to the cliff top is \(84.6^{\circ}\). When she moves 30 feet back from the ravine, the angle of elevation is \(82.5^{\circ}\). How tall is the cliff?

20. Amir wants to know the height of a tree in the median strip of a highway. The angle of elevation from the highway shoulder to the treetop is \(43.5^{\circ}\). When he moves 10 feet farther away from the tree, the angle of elevation is \(37.2^{\circ}\) How tall is the tree?

21. Delbert and Francine are 10 kilometers apart, both observing a satellite that passes directly over their heads. At a moment when the satellite is between them, Francine measures its angle of elevation as \(84.6^{\circ}\), and Delbert measures an angle of \(87^{\circ}\). How far is the satellite from Delbert?

22. Megan rows her kayak due east. When she began, she spotted a lighthouse 2000 meters in the distance at an angle of \(14^{\circ}\) south of east. After traveling for of an hour, the lighthouse was at an angle of \(83^{\circ}\) south of east. How far did Megan travel, and what was her average speed?

23. Chad is hiking along a straight path but needs to detour around a large pond. He turns \(23^{\circ}\) from his path until clear of the pond, then walks back to his original path, intercepting it at an angle of \(29^{\circ}\) and at a distance of 2 miles from where he had left the path. How far did Chad walk in each of the two segments of his detour, and how much farther did his detour require compared with a straight line through the pond?

24. Bob is flying to Monterey but must change course to avoid a storm. He flies \(19^{\circ}\) off from his original direction until he clears the storm, then turns again to return back to his original flight path, intercepting it at an angle of \(54.9^{\circ}\) and at a distance of 50 miles from where he had left it. How much farther did his detour require compared with his original course?

25. Geologists find an outcropping from an underground rock formation that normally indicates the presence of oil. The outcropping is on a hillside, and the formation itself dips another \(17^{\circ}\) from the surface. If an oil well is placed 1000 meters downhill from the outcropping, how far will the well have to drill before it reaches the formation?

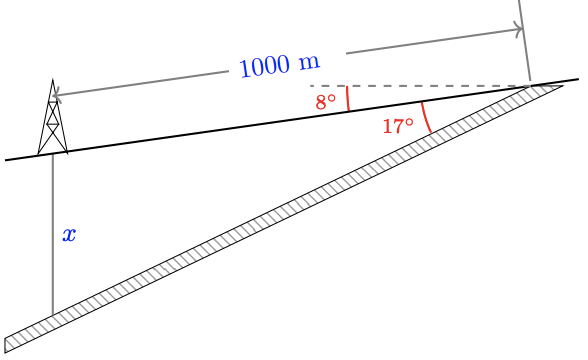
26. A proposed ski lift will rise from point near the base of the slope with an angle of \(27^{\circ}\). At a distance of 400 meters further from the slope, the angle of elevation to the top of the ski lift is \(19^{\circ}\). How long is the ski lift?

27. Thelma wants to measure the height of a hill. She first plants a 50 foot tall antenna at the hill’s peak. Then she descends the hill and finds a point where she can see the top and the bottom of the antenna. The angle of elevation to the bottom of the antenna is \(23^{\circ}\), and the angle of elevation to the top of the antenna is \(24^{\circ}\).

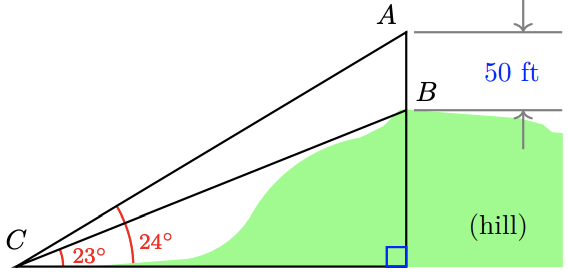
a Find \(\angle ACB\).

b Find \(\angle CAB\), at the top of the antenna.

c How long is \(BC\), the distance from the bottom of the antenna to \(C\)?

d How tall is the hill?

28. A billboard of California’s gubernatorial candidate Angelyne is located on the roof of a building. At a distance of 180 feet from the building, the angles of elevation to the bottom and top of the billboard are respectively \(39.8^{\circ}\) and \(47.3^{\circ}\). How tall is the billboard?

For Problems 29–32, compute the following distances in Astronomical Units. Then convert to kilometers, using the fact that 1 AU \(\approx 1.5 \times 108\) km.

29. When observed from opposite sides of Earth's orbit, the star Alpha Centauri has a parallax of \(0.76^{\prime \prime}\). How far from the Sun is Alpha Centauri?

30. How far from the Sun is Barnard's star, which has a parallax of \(1.1^{\prime \prime}\) when observed at opposite ends of Earth's orbit?

31. How far from the Sun is Tau Ceti, which has a parallax of \(0.55^{\prime \prime}\) when observed from opposite ends of Earth's orbit?

32. How far from the Sun is Sirius, which has a parallax of \(0.75^{\prime \prime}\) when observed from opposite ends of Earth's orbit?

Problems 33–38 consider the ambiguous case of the Law of Sines, when two sides and an angle opposite one of them are known.

33. In the right triangle \(ABC\) shown, \(\angle A = 30^{\circ}, \angle C = 90^{\circ}\), and \(c=3\) inches.

a Use the definition of \(\sin A\) to solve for \(a\) (the length of side \(\overline{B C}\)).

b Can you draw a triangle \(A B C\) with \(A=30^{\circ}\) and \(c=3\) if \(a<\frac{3}{2}\)? Why or why not?

c How many triangles are possible if \(\frac{3}{2}<a<3\)?

d How many triangles are possible if \(a>3\)?

34. In this problem we show that there are two different triangles \(A B C\) with \(A=30^{\circ}, a=2\) and \(c=3\).

a Use a protractor to draw an angle \(A=30^{\circ}\). Mark point \(B\) on one side of the angle so that \(\overline{A B}\) is 3 inches long.

b Locate two distinct points on the other side of the angle that are each 2 inches from point \(B\). These points are both possible locations for point \(C\).

c Use the Law of Sines to find two distinct possible measures for \(\angle C\).

35. In \(\triangle A B C, \angle A=30^{\circ}\) and \(c=12\). How many triangles are possible for each of the following lengths for side \(a\)? Sketch the solutions in each case.

a \(a = 6\)

b \(a = 4\)

c \(a = 9\)

d \(a = 15\)

36. Consider the triangle \(ABC\) shown below.

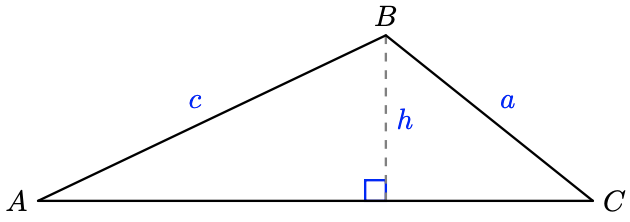
a Express the length of the altitude in terms of \(\angle A\) and \(c\).

b Now suppose we keep \(\angle A\) and side \(c\) fixed, but allow \(a\) to vary in length. What is the smallest value \(a\) can have and still be long enough to make a triangle?

c What are the largest and smallest values that \(a\) can have in order to produce two distinct triangles \(A B C\) (without changing \(\angle A\) and side \(c\))?

37. For the triangle in Problem 36, suppose \(A=40^{\circ}\) and \(c=8\).

a Sketch and solve the triangle if \(a=12\).

b Sketch and solve the triangle if \(a=6\).

c Sketch and solve the triangle if \(a=4\).

d For what value of \(a\) is \(c\) the hypotenuse of a right triangle?

38. For the figure in Problem 36, suppose \(A=70^{\circ}\) and \(c=20\).

a For what value of \(a\) is the triangle a right triangle?

b For what values of \(a\) are there two solutions for the triangle?

c For what values of \(a\) is there one obtuse solution for the triangle?

d For what value of \(a\) is there no solution?

For Problems 39–42, find the remaining angles of the triangle. Round answers to two decimal places. (These problems involve the ambiguous case.)

39. \(a=66, c=43, C=25^{\circ}\)

40. \(b=10, c=14, B=20^{\circ}\)

41. \(b=100, c=80, B=49^{\circ}\)

42. \(b=4.7, c=6.3, C=54^{\circ}\)

43. Delbert and Francine are 1000 yards apart. The angle Delbert sees between Francine and a certain tree is \(38^{\circ}\). If the tree is 800 yards from Francine, how far is it from Delbert? (There are two possible answers.)

44. From the lookout point on Fabrick Rock, Ann can see not only see the famous "Crooked Spire" in Chesterfield, which is 8 miles away, but also the red phone box in the village of Alton. Chesterfield and Alton are 7 miles apart. Fabrick Rock has a plaque that shows directions to famous sites, and from the plaque Ann determines that the angle between the lines to the spire and the phone box measures \(19^{\circ}\). How far is Fabrick Rock from the the phone box? (There are two possible answers.)

a Sketch a triangle with \(A=25^{\circ}, B=35^{\circ}\), and \(b=16\). b Use the Law of Sines to find \(a\). c Use the Law of Sines to find \(c\). d Find \(c\) without using the Law of Sines. (Hint: Sketch the altitude, \(h\), from \(C\) to make two right triangles. Find \(h\), then use \(h\) to find \(c\).)

a Sketch a triangle with \(A=75^{\circ}, a=15\), and \(b=6\).

b Use the Law of Sines to find \(c\).

c Find \(c\) without using the Law of Sines.

Problems 47–48 prove the Law of Sines using the formula for the area of a triangle. (See Section 3.1 for the appropriate formula.)

47. Sketch a triangle with angles \(A, B\) and \(C\) and opposite sides of lengths respectively \(a, b\) and \(c\).

a Write the area of the triangle in terms of \(a, b\), and angle \(C\).

b Write the area of the triangle in terms of \(a, c\), and angle \(B\).

c Write the area of the triangle in terms of \(b, c\), and angle \(A\).

48. Equate the three different expressions from Problem 47 for the area of the triangle. Multiply through by \(\frac{2}{abc}\) and simplify to deduce the Law of Sines.

49. Here is a method for solving certain oblique triangles by dividing them into two right triangles. In the triangle shown, we know two angles, \(A\) and \(B\), and the side opposite one of them, say \(a\). We would like to find side \(b\).

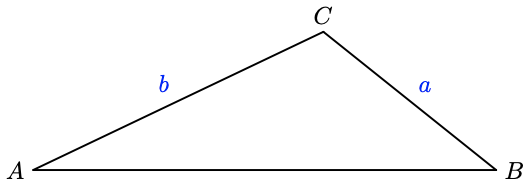
a Draw the altitude \(h\) from angle \(C\).

b Write an expression for \(b\) in terms of \(h\) and angle \(A\).

c Write an expression for \(h\) in terms of angle \(B\).

d Substitute your expression for \(h\) into your expression for \(b\).

e Which of the following is equivalent to the formula you wrote in part (d)?

i \(a \sin A=b \sin B\)

ii \(\dfrac{a}{\sin A}=\dfrac{b}{\sin B}\)

iii \(\dfrac{a}{\sin B}=\dfrac{b}{\sin A}\)

Law of Sines Worksheet

Students will practice applying the law of sines to calculate side lengths and angle measurements. This worksheet includes word problems as well as challenging bonus problems.

Example Questions

Visual Aids

Other Details

This is a 5 part worksheet:

• Part I Model Problems
• Part II Practice Problems (1-6)
• Part III Practice (harder) & Word Problems (7 - 18)
• Part IV Challenge Problems
• Part V Answer Key
• Pictures of Law of Sines (triangles, formula and more..)
• Law of Sines and Cosines Worksheets

Ultimate Math Solver (Free) Free Algebra Solver ... type anything in there!

Popular pages @ mathwarehouse.com.

The Law of Sines

The Law of Sines (or Sine Rule ) is very useful for solving triangles:

a sin A = b sin B = c sin C

It works for any triangle:

And it says that:

When we divide side a by the sine of angle A it is equal to side b divided by the sine of angle B , and also equal to side c divided by the sine of angle C

Well, let's do the calculations for a triangle I prepared earlier:

a sin A = 8 sin(62.2°) = 8 0.885... = 9.04...

b sin B = 5 sin(33.5°) = 5 0.552... = 9.06...

c sin C = 9 sin(84.3°) = 9 0.995... = 9.04...

The answers are almost the same! (They would be exactly the same if we used perfect accuracy).

So now you can see that:

Is This Magic?

Not really, look at this general triangle and imagine it is two right-angled triangles sharing the side h :

The sine of an angle is the opposite divided by the hypotenuse, so:

a sin(B) and b sin(A) both equal h , so we get:

a sin(B) = b sin(A)

Which can be rearranged to:

a sin A = b sin B

We can follow similar steps to include c/sin(C)

How Do We Use It?

Let us see an example:

Example: Calculate side "c"

Now we use our algebra skills to rearrange and solve:

Finding an Unknown Angle

In the previous example we found an unknown side ...

... but we can also use the Law of Sines to find an unknown angle .

In this case it is best to turn the fractions upside down ( sin A/a instead of a/sin A , etc):

sin A a = sin B b = sin C c

Example: Calculate angle B

Sometimes there are two answers .

There is one very tricky thing we have to look out for:

Two possible answers.

This only happens in the " Two Sides and an Angle not between " case, and even then not always, but we have to watch out for it.

Just think "could I swing that side the other way to also make a correct answer?"

Example: Calculate angle R

The first thing to notice is that this triangle has different labels: PQR instead of ABC. But that's OK. We just use P,Q and R instead of A, B and C in The Law of Sines.

But wait! There's another angle that also has a sine equal to 0.9215...

The calculator won't tell you this but sin(112.9°) is also equal to 0.9215...

So, how do we discover the value 112.9°?

Easy ... take 67.1° away from 180°, like this:

180° − 67.1° = 112.9°

So there are two possible answers for R: 67.1° and 112.9° :

Both are possible! Each one has the 39° angle, and sides of 41 and 28.

So, always check to see whether the alternative answer makes sense.

• ... sometimes it will (like above) and there are two solutions
• ... sometimes it won't (like below) and there is one solution

For example this triangle from before.

As you can see, we can try swinging the "5.5" line around, but no other solution makes sense.

So this has only one solution.

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Precalculus

Course: precalculus   >   unit 2.

• Trig word problem: stars
• General triangle word problems

Laws of sines and cosines review

Law of sines

Law of cosines, practice set 1: solving triangles using the law of sines, example 1: finding a missing side, example 2: finding a missing angle.

• Your answer should be
• an integer, like 6 ‍  
• a simplified proper fraction, like 3 / 5 ‍  
• a simplified improper fraction, like 7 / 4 ‍  
• a mixed number, like 1   3 / 4 ‍  
• an exact decimal, like 0.75 ‍  
• a multiple of pi, like 12   pi ‍   or 2 / 3   pi ‍  

Practice set 2: Solving triangles using the law of cosines

Example 1: finding an angle, example 2: finding a missing side, practice set 3: general triangle word problems, want to join the conversation.

• Upvote Button navigates to signup page
• Downvote Button navigates to signup page
• Flag Button navigates to signup page

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

4.1.1: Laws of Sines and Cosines

• Last updated
• Save as PDF
• Page ID 4154

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Solving for parts of non-right triangles using trigonometry.

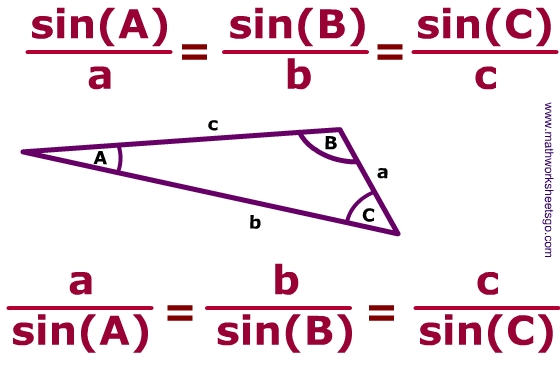
Law of Sines: If \(\Delta ABC\) has sides of length, \(a\), \(b\), and \(c\), then \(\dfrac{\sin A}{a}=\dfrac{\sin B}{b}=\dfrac{\sin C}{c}\).

Looking at a triangle, the lengths a,b, and c are opposite the angles of the same letter.

Use Law of Sines when given:

• An angle and its opposite side.
• Any two angles and one side.

Two sides and the non-included angle.

Law of Cosines: If \(\Delta ABC\) has sides of length \(a\),\(b\), and \(c\), then:

\(\begin{aligned} a^2&=b^2+c^2−2bc\cos A \\ b^2&=a^2+c^2−2ac \cos B \\ c^2&=a^2+b^2−2ab \cos C \end{aligned}\)

Even though there are three formulas, they are all very similar. First, notice that whatever angle is in the cosine, the opposite side is on the other side of the equal sign.

Use Law of Cosines when given:

• Two sides and the included angle.
• All three sides.

Using the Law of Sines

1. Solve the triangle using the Law of Sines . Round decimal answers to the nearest tenth.

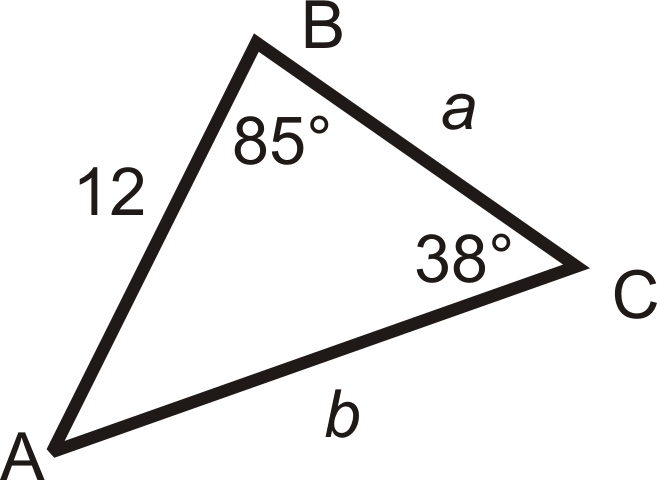
First, to find \(m\angle A\), we can use the Triangle Sum Theorem.

\(\begin{aligned} m\angle A+85^{\circ} +38^{\circ}&=180^{\circ} \\ m\angle A&=57^{\circ} \end{aligned}\)

Now, use the Law of Sines to set up ratios for \(a\) and \(b\).

\(\dfrac{\sin 57^{\circ} }{a}=\dfrac{\sin 85^{\circ} }{b}=\dfrac{\sin 38^{\circ} }{12}\)

\(\begin{aligned} \dfrac{\sin 57^{\circ}}{a} &=\dfrac{\sin 38^{\circ}}{12} & \dfrac{\sin 85^{\circ}}{b} &=\dfrac{\sin 38^{\circ}}{12} \\ a \cdot \sin 38^{\circ} &=12 \cdot \sin 57^{\circ} & b \cdot \sin 38^{\circ} &=12 \cdot \sin 85^{\circ} \\ a &=\dfrac{12 \cdot \sin 57^{\circ}}{\sin 38^{\circ}} \approx 16.4 & \quad b &=\dfrac{12 \cdot \sin 85^{\circ}}{\sin 38^{\circ}} \approx 19.4 \end{aligned}\)

2. Solve the triangle using the Law of Sines. Round decimal answers to the nearest tenth.

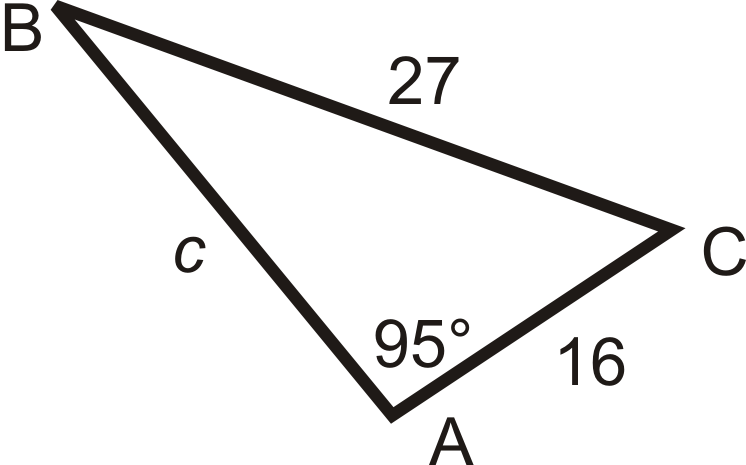
Set up the ratio for \(\angle B\) using Law of Sines.

\(\begin{aligned} \dfrac{\sin 95^{\circ} }{27}&=\dfrac{\sin B}{16} \\ 27\cdot \sin B&=16\cdot \sin 95^{\circ} \\ \sin B&=\dfrac{16\cdot \sin 95^{\circ} }{27}\rightarrow\sin ^{−1}\left(\dfrac{16\cdot \sin 95^{\circ} }{27} \right) =36.2^{\circ} \end{aligned}\)

To find \(m\angle C\) use the Triangle Sum Theorem.

\(m\angle C+95^{\circ} +36.2^{\circ} =180^{\circ} \rightarrow m\angle C=48.8^{\circ}\)

To find \(c\), use the Law of Sines again. \(\dfrac{\sin 95^{\circ} }{27}=\dfrac{\sin 48.8^{\circ} }{c}\)

\(\begin{aligned} c\cdot \sin 95^{\circ}&=27\cdot \sin 48.8^{\circ} \\ c&=27\cdot \sin 48.8^{\circ} \sin 95^{\circ} \approx 20.4 \end{aligned}\)

Using the Law of Cosines

Solve the triangle using Law of Cosines . Round your answers to the nearest hundredth.

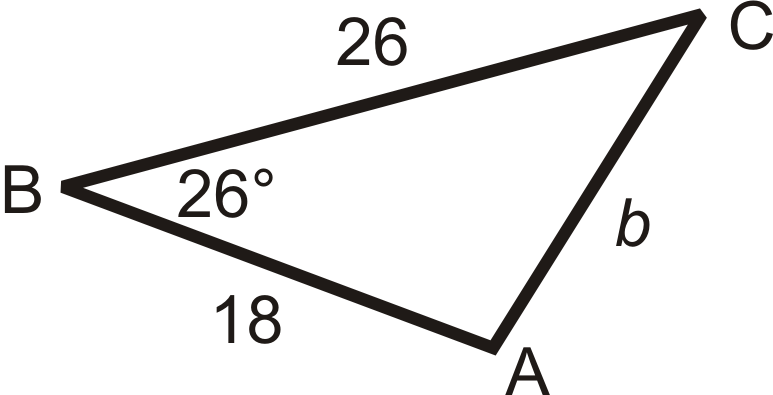
Use the second equation to solve for \(\angle B\).

\(\begin{aligned} b^2&=26^2+18^2−2(26)(18)\cos 26^{\circ} \\ b^2&=1000−936\cos 26^{\circ} \\ b^2&=158.7288 \\ b&\approx 12.60 \end{aligned}\)

To find \(m\angle A\) or \(m\angle C\), you can use either the Law of Sines or Law of Cosines . Let’s use the Law of Sines.

\(\begin{aligned} \dfrac{\sin 26^{\circ} }{12.60}&=\dfrac{\sin A}{18} \\ 12.60\cdot \sin A&=18\cdot \sin 26^{\circ} \\ \sin A&=18\cdot \sin 26^{\circ} 12.60 \end{aligned}\)

\(\sin ^{−1} \left(18\cdot \sin 26^{\circ} 12.60 \right)\approx 38.77^{\circ} \) To find \(m\angle C\), use the Triangle Sum Theorem.

\(\begin{aligned} 26^{\circ} +38.77^{\circ} +m\angle C&=180^{\circ} \\ m\angle C&=115.23^{\circ} \end{aligned}\)

Find the following angles in the triangle below. Round your answers to the nearest hundredth.

Example \(\PageIndex{1}\)

\(m\angle A\)

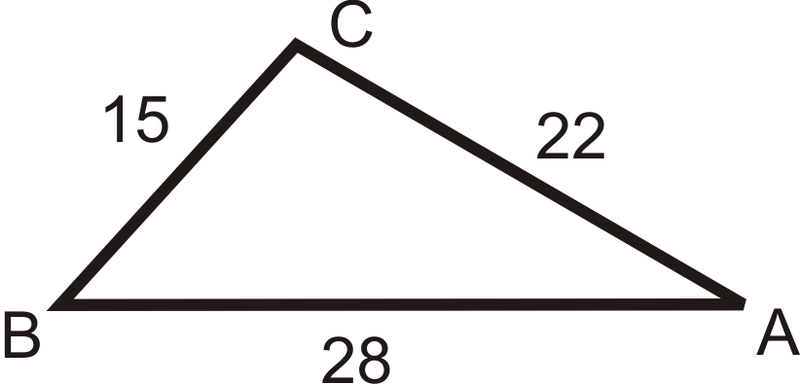
When you are given only the sides, you have to use the Law of Cosines to find one angle and then you can use the Law of Sines to find another.

\(\begin{aligned} 15^2&=22^2+28^2−2(22)(28)\cos A \\ 225&=1268−1232\cos A \\ −1043&=−1232\cos A \\ \dfrac{−1043}{−1232}&=\cos A \rightarrow \cos ^{−1}\left(\dfrac{1043}{1232}\right) \approx 32.16^{\circ}\end{aligned}\)

Example \(\PageIndex{2}\)

\(m\angle B\)

Now that we have an angle and its opposite side, we can use the Law of Sines.

\(\begin{aligned} \dfrac{\sin 32.16^{\circ} }{15} &=\dfrac{\sin B}{22} \\ 15\cdot \sin B &=22\cdot \sin 32.16^{\circ} \\ \sin B &=\dfrac{22\cdot \sin 32.16^{\circ} }{15} \end{aligned}\)

\(\sin ^{−1}\left(\dfrac{22\cdot \sin 32.16^{\circ} }{15}\right)\approx 51.32^{\circ} \).

Example \(\PageIndex{3}\)

\(m\angle C\)

To find \(m\angle C\), use the Triangle Sum Theorem.

\(\begin{aligned} 32.16^{\circ} +51.32^{\circ} +m\angle C&=180^{\circ} \\ m\angle C&=96.52^{\circ} \end{aligned}\)

Use the Law of Sines or Cosines to solve \(\Delta ABC\). If you are not given a picture, draw one. Round all decimal answers to the nearest tenth.

• \(m\angle A=74^{\circ} \), \(m\angle B=11^{\circ} \), \(BC=16\)
• \(m\angle A=64^{\circ} \), \(AB=29\), \(AC=34\)
• \(m\angle C=133^{\circ} \), \(m\angle B=25^{\circ} \),\(AB=48\)

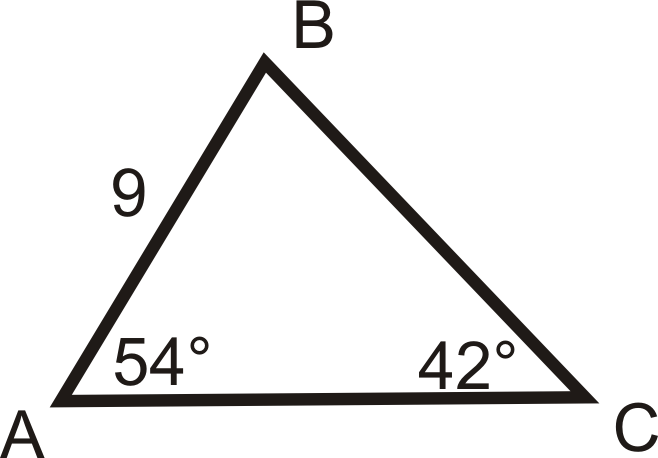
Use the Law of Sines to solve \(\Delta ABC\) below.

• \(m\angle A=20^{\circ} \), \(AB=12\), \(BC=5\)

Recall that when we learned how to prove that triangles were congruent we determined that SSA (two sides and an angle not included) did not determine a unique triangle. When we are using the Law of Sines to solve a triangle and we are given two sides and the angle not included, we may have two possible triangles. Problem 14 illustrates this.

• Let’s say we have \(\Delta ABC\) as we did in problem 13. In problem 13 you were given two sides and the not included angle. This time, you have two angles and the side between them (ASA). Solve the triangle given that \(m\angle A=20^{\circ} \), \(m\angle C=125^{\circ}\), \(AC=8.4\)
• Does the triangle that you found in problem 14 meet the requirements of the given information in problem 13? How are the two different \(m\angle C\) related? Draw the two possible triangles overlapping to visualize this relationship.

Review (Answers)

To view the Review answers, open this PDF file and look for section 8.10.

Additional Resources

Video: The Law of Sines: The Basics

Trigonometry 7th Edition

By mckeague, charles p.; turner, mark d., chapter 7 - section 7.1 - the law of sines - 7.1 problem set - page 368: 1, work step by step, update this answer.

You can help us out by revising, improving and updating this answer.

After you claim an answer you’ll have 24 hours to send in a draft. An editor will review the submission and either publish your submission or provide feedback.

10.1 Non-right Triangles: Law of Sines

Learning objectives.

In this section, you will:

• Use the Law of Sines to solve oblique triangles.
• Find the area of an oblique triangle using the sine function.
• Solve applied problems using the Law of Sines.

Suppose two radar stations located 20 miles apart each detect an aircraft between them. The angle of elevation measured by the first station is 35 degrees, whereas the angle of elevation measured by the second station is 15 degrees. How can we determine the altitude of the aircraft? We see in Figure 1 that the triangle formed by the aircraft and the two stations is not a right triangle, so we cannot use what we know about right triangles. In this section, we will find out how to solve problems involving non-right triangles .

Using the Law of Sines to Solve Oblique Triangles

In any triangle, we can draw an altitude , a perpendicular line from one vertex to the opposite side, forming two right triangles. It would be preferable, however, to have methods that we can apply directly to non-right triangles without first having to create right triangles.

Any triangle that is not a right triangle is an oblique triangle . Solving an oblique triangle means finding the measurements of all three angles and all three sides. To do so, we need to start with at least three of these values, including at least one of the sides. We will investigate three possible oblique triangle problem situations:

Knowing how to approach each of these situations enables us to solve oblique triangles without having to drop a perpendicular to form two right triangles. Instead, we can use the fact that the ratio of the measurement of one of the angles to the length of its opposite side will be equal to the other two ratios of angle measure to opposite side. Let’s see how this statement is derived by considering the triangle shown in Figure 5 .

Using the right triangle relationships, we know that sin α = h b sin α = h b and sin β = h a . sin β = h a . Solving both equations for h h gives two different expressions for h . h .

We then set the expressions equal to each other.

Similarly, we can compare the other ratios.

Collectively, these relationships are called the Law of Sines .

Note the standard way of labeling triangles: angle α α (alpha) is opposite side a ; a ; angle β β (beta) is opposite side b ; b ; and angle γ γ (gamma) is opposite side c . c . See Figure 6 .

While calculating angles and sides, be sure to carry the exact values through to the final answer. Generally, final answers are rounded to the nearest tenth, unless otherwise specified.

Law of Sines

Given a triangle with angles and opposite sides labeled as in Figure 6 , the ratio of the measurement of an angle to the length of its opposite side will be equal to the other two ratios of angle measure to opposite side. All proportions will be equal. The Law of Sines is based on proportions and is presented symbolically two ways.

To solve an oblique triangle, use any pair of applicable ratios.

Solving for Two Unknown Sides and Angle of an AAS Triangle

Solve the triangle shown in Figure 7 to the nearest tenth.

The three angles must add up to 180 degrees. From this, we can determine that

To find an unknown side, we need to know the corresponding angle and a known ratio. We know that angle α = 50° α = 50° and its corresponding side a = 10. a = 10. We can use the following proportion from the Law of Sines to find the length of c . c .

Similarly, to solve for b , b , we set up another proportion.

Therefore, the complete set of angles and sides is

Solve the triangle shown in Figure 8 to the nearest tenth.

Using The Law of Sines to Solve SSA Triangles

We can use the Law of Sines to solve any oblique triangle, but some solutions may not be straightforward. In some cases, more than one triangle may satisfy the given criteria, which we describe as an ambiguous case . Triangles classified as SSA, those in which we know the lengths of two sides and the measurement of the angle opposite one of the given sides, may result in one or two solutions, or even no solution.

Possible Outcomes for SSA Triangles

Oblique triangles in the category SSA may have four different outcomes. Figure 9 illustrates the solutions with the known sides a a and b b and known angle α . α .

Solving an Oblique SSA Triangle

Solve the triangle in Figure 10 for the missing side and find the missing angle measures to the nearest tenth.

Use the Law of Sines to find angle β β and angle γ , γ , and then side c . c . Solving for β , β , we have the proportion

However, in the diagram, angle β β appears to be an obtuse angle and may be greater than 90°. How did we get an acute angle, and how do we find the measurement of β ? β ? Let’s investigate further. Dropping a perpendicular from γ γ and viewing the triangle from a right angle perspective, we have Figure 11 . It appears that there may be a second triangle that will fit the given criteria.

The angle supplementary to β β is approximately equal to 49.9°, which means that β = 180° − 49.9° = 130.1° . β = 180° − 49.9° = 130.1° . (Remember that the sine function is positive in both the first and second quadrants.) Solving for γ , γ , we have

We can then use these measurements to solve the other triangle. Since γ ′ γ ′ is supplementary to the sum of α ′ α ′ and β ′ , β ′ , we have

Now we need to find c c and c ′ . c ′ .

To summarize, there are two triangles with an angle of 35°, an adjacent side of 8, and an opposite side of 6, as shown in Figure 12 .

However, we were looking for the values for the triangle with an obtuse angle β . β . We can see them in the first triangle (a) in Figure 12 .

Given α = 80° , a = 120 , α = 80° , a = 120 , and b = 121 , b = 121 , find the missing side and angles. If there is more than one possible solution, show both.

Solving for the Unknown Sides and Angles of a SSA Triangle

In the triangle shown in Figure 13 , solve for the unknown side and angles. Round your answers to the nearest tenth.

In choosing the pair of ratios from the Law of Sines to use, look at the information given. In this case, we know the angle γ = 85° , γ = 85° , and its corresponding side c = 12 , c = 12 , and we know side b = 9. b = 9. We will use this proportion to solve for β . β .

To find β , β , apply the inverse sine function. The inverse sine will produce a single result, but keep in mind that there may be two values for β . β . It is important to verify the result, as there may be two viable solutions, only one solution (the usual case), or no solutions.

In this case, if we subtract β β from 180°, we find that there may be a second possible solution. Thus, β = 180° − 48.3° ≈ 131.7° . β = 180° − 48.3° ≈ 131.7° . To check the solution, subtract both angles, 131.7° and 85°, from 180°. This gives

which is impossible, and so β ≈ 48.3° . β ≈ 48.3° .

To find the remaining missing values, we calculate α = 180° − 85° − 48.3° ≈ 46.7° . α = 180° − 85° − 48.3° ≈ 46.7° . Now, only side a a is needed. Use the Law of Sines to solve for a a by one of the proportions.

The complete set of solutions for the given triangle is

Given α = 80° , a = 100 , b = 10 , α = 80° , a = 100 , b = 10 , find the missing side and angles. If there is more than one possible solution, show both. Round your answers to the nearest tenth.

Finding the Triangles That Meet the Given Criteria

Find all possible triangles if one side has length 4 opposite an angle of 50°, and a second side has length 10.

Using the given information, we can solve for the angle opposite the side of length 10. See Figure 14 .

We can stop here without finding the value of α . α . Because the range of the sine function is [ − 1 , 1 ] , [ − 1 , 1 ] , it is impossible for the sine value to be 1.915. In fact, inputting sin − 1 ( 1.915 ) sin − 1 ( 1.915 ) in a graphing calculator generates an ERROR DOMAIN. Therefore, no triangles can be drawn with the provided dimensions.

Determine the number of triangles possible given a = 31 , a = 31 , b = 26 , b = 26 , β = 48° . β = 48° .

Finding the Area of an Oblique Triangle Using the Sine Function

Now that we can solve a triangle for missing values, we can use some of those values and the sine function to find the area of an oblique triangle. Recall that the area formula for a triangle is given as Area = 1 2 b h , Area = 1 2 b h , where b b is base and h h is height. For oblique triangles, we must find h h before we can use the area formula. Observing the two triangles in Figure 15 , one acute and one obtuse, we can drop a perpendicular to represent the height and then apply the trigonometric property sin α = opposite hypotenuse sin α = opposite hypotenuse to write an equation for area in oblique triangles. In the acute triangle, we have sin α = h c sin α = h c or c sin α = h . c sin α = h . However, in the obtuse triangle, we drop the perpendicular outside the triangle and extend the base b b to form a right triangle. The angle used in calculation is α ′ , α ′ , or 180 − α . 180 − α .

Area of an Oblique Triangle

The formula for the area of an oblique triangle is given by

This is equivalent to one-half of the product of two sides and the sine of their included angle.

Finding the Area of an Oblique Triangle

Find the area of a triangle with sides a = 90 , b = 52 , a = 90 , b = 52 , and angle γ = 102° . γ = 102° . Round the area to the nearest integer.

Using the formula, we have

Find the area of the triangle given β = 42° , β = 42° , a = 7.2 ft , a = 7.2 ft , c = 3.4 ft . c = 3.4 ft . Round the area to the nearest tenth.

Solving Applied Problems Using the Law of Sines

The more we study trigonometric applications, the more we discover that the applications are countless. Some are flat, diagram-type situations, but many applications in calculus, engineering, and physics involve three dimensions and motion.

Finding an Altitude

Find the altitude of the aircraft in the problem introduced at the beginning of this section, shown in Figure 16 . Round the altitude to the nearest tenth of a mile.

To find the elevation of the aircraft, we first find the distance from one station to the aircraft, such as the side a , a , and then use right triangle relationships to find the height of the aircraft, h . h .

Because the angles in the triangle add up to 180 degrees, the unknown angle must be 180°−15°−35°=130°. This angle is opposite the side of length 20, allowing us to set up a Law of Sines relationship.

The distance from one station to the aircraft is about 14.98 miles.

Now that we know a , a , we can use right triangle relationships to solve for h . h .

The aircraft is at an altitude of approximately 3.9 miles.

The diagram shown in Figure 17 represents the height of a blimp flying over a football stadium. Find the height of the blimp if the angle of elevation at the southern end zone, point A, is 70°, the angle of elevation from the northern end zone, point B , B , is 62°, and the distance between the viewing points of the two end zones is 145 yards.

Access these online resources for additional instruction and practice with trigonometric applications.

• Law of Sines: The Basics
• Law of Sines: The Ambiguous Case

10.1 Section Exercises

Describe the altitude of a triangle.

Compare right triangles and oblique triangles.

When can you use the Law of Sines to find a missing angle?

In the Law of Sines, what is the relationship between the angle in the numerator and the side in the denominator?

What type of triangle results in an ambiguous case?

For the following exercises, assume α α is opposite side a , β a , β is opposite side b , b , and γ γ is opposite side c . c . Solve each triangle, if possible. Round each answer to the nearest tenth.

α = 43° , γ = 69° , a = 20 α = 43° , γ = 69° , a = 20

α = 35° , γ = 73° , c = 20 α = 35° , γ = 73° , c = 20

α = 60° , α = 60° , β = 60° , β = 60° , γ = 60° γ = 60°

a = 4 , a = 4 , α = 60° , α = 60° , β = 100° β = 100°

b = 10 , b = 10 , β = 95° , γ = 30° β = 95° , γ = 30°

For the following exercises, use the Law of Sines to solve for the missing side for each oblique triangle. Round each answer to the nearest hundredth. Assume that angle A A is opposite side a , a , angle B B is opposite side b , b , and angle C C is opposite side c . c .

Find side b b when A = 37° , A = 37° , B = 49° , B = 49° , c = 5. c = 5.

Find side a a when A = 132° , C = 23° , b = 10. A = 132° , C = 23° , b = 10.

Find side c c when B = 37° , C = 21° , B = 37° , C = 21° , b = 23. b = 23.

For the following exercises, assume α α is opposite side a , β a , β is opposite side b , b , and γ γ is opposite side c . c . Determine whether there is no triangle, one triangle, or two triangles. Then solve each triangle, if possible. Round each answer to the nearest tenth.

α = 119° , a = 14 , b = 26 α = 119° , a = 14 , b = 26

γ = 113° , b = 10 , c = 32 γ = 113° , b = 10 , c = 32

b = 3.5 , b = 3.5 , c = 5.3 , c = 5.3 , γ = 80° γ = 80°

a = 12 , a = 12 , c = 17 , c = 17 , α = 35° α = 35°

a = 20.5 , a = 20.5 , b = 35.0 , b = 35.0 , β = 25° β = 25°

a = 7 , a = 7 , c = 9 , c = 9 , α = 43° α = 43°

a = 7 , b = 3 , β = 24° a = 7 , b = 3 , β = 24°

b = 13 , c = 5 , γ = 10° b = 13 , c = 5 , γ = 10°

a = 2.3 , c = 1.8 , γ = 28° a = 2.3 , c = 1.8 , γ = 28°

β = 119° , b = 8.2 , a = 11.3 β = 119° , b = 8.2 , a = 11.3

For the following exercises, use the Law of Sines to solve, if possible, the missing side or angle for each triangle or triangles in the ambiguous case. Round each answer to the nearest tenth.

Find angle A A when a = 24 , b = 5 , B = 22°. a = 24 , b = 5 , B = 22°.

Find angle A A when a = 13 , b = 6 , B = 20°. a = 13 , b = 6 , B = 20°.

Find angle B B when A = 12° , a = 2 , b = 9. A = 12° , a = 2 , b = 9.

For the following exercises, find the area of the triangle with the given measurements. Round each answer to the nearest tenth.

a = 5 , c = 6 , β = 35° a = 5 , c = 6 , β = 35°

b = 11 , c = 8 , α = 28° b = 11 , c = 8 , α = 28°

a = 32 , b = 24 , γ = 75° a = 32 , b = 24 , γ = 75°

a = 7.2 , b = 4.5 , γ = 43° a = 7.2 , b = 4.5 , γ = 43°

For the following exercises, find the length of side x . x . Round to the nearest tenth.

For the following exercises, find the measure of angle x , x , if possible. Round to the nearest tenth.

Notice that x x is an obtuse angle.

For the following exercise, solve the triangle. Round each answer to the nearest tenth.

For the following exercises, find the area of each triangle. Round each answer to the nearest tenth.

Find the radius of the circle in Figure 18 . Round to the nearest tenth.

Find the diameter of the circle in Figure 19 . Round to the nearest tenth.

Find m ∠ A D C m ∠ A D C in Figure 20 . Round to the nearest tenth.

Find A D A D in Figure 21 . Round to the nearest tenth.

Solve both triangles in Figure 22 . Round each answer to the nearest tenth.

Find A B A B in the parallelogram shown in Figure 23 .

Solve the triangle in Figure 24 . (Hint: Draw a perpendicular from H H to J K ). J K ). Round each answer to the nearest tenth.

Solve the triangle in Figure 25 . (Hint: Draw a perpendicular from N N to L M ). L M ). Round each answer to the nearest tenth.

In Figure 26 , A B C D A B C D is not a parallelogram. ∠ m ∠ m is obtuse. Solve both triangles. Round each answer to the nearest tenth.

Real-World Applications

A pole leans away from the sun at an angle of 7° 7° to the vertical, as shown in Figure 27 . When the elevation of the sun is 55° , 55° , the pole casts a shadow 42 feet long on the level ground. How long is the pole? Round the answer to the nearest tenth.

To determine how far a boat is from shore, two radar stations 500 feet apart find the angles out to the boat, as shown in Figure 28 . Determine the distance of the boat from station A A and the distance of the boat from shore. Round your answers to the nearest whole foot.

Figure 29 shows a satellite orbiting Earth. The satellite passes directly over two tracking stations A A and B , B , which are 69 miles apart. When the satellite is on one side of the two stations, the angles of elevation at A A and B B are measured to be 83.9° 83.9° and 86.2° , 86.2° , respectively. How far is the satellite from station A A and how high is the satellite above the ground? Round answers to the nearest whole mile.

A communications tower is located at the top of a steep hill, as shown in Figure 30 . The angle of inclination of the hill is 67° . 67° . A guy wire is to be attached to the top of the tower and to the ground, 165 meters downhill from the base of the tower. The angle formed by the guy wire and the hill is 16°. 16°. Find the length of the cable required for the guy wire to the nearest whole meter.

The roof of a house is at a 20° 20° angle. An 8-foot solar panel is to be mounted on the roof and should be angled 38° 38° relative to the horizontal for optimal results. (See Figure 31 ). How long does the vertical support holding up the back of the panel need to be? Round to the nearest tenth.

Similar to an angle of elevation, an angle of depression is the acute angle formed by a horizontal line and an observer’s line of sight to an object below the horizontal. A pilot is flying over a straight highway. He determines the angles of depression to two mileposts, 6.6 km apart, to be 37° 37° and 44° , 44° , as shown in Figure 32 . Find the distance of the plane from point A A to the nearest tenth of a kilometer.

A pilot is flying over a straight highway. He determines the angles of depression to two mileposts, 4.3 km apart, to be 32° and 56°, as shown in Figure 33 . Find the distance of the plane from point A A to the nearest tenth of a kilometer.

In order to estimate the height of a building, two students stand at a certain distance from the building at street level. From this point, they find the angle of elevation from the street to the top of the building to be 39°. They then move 300 feet closer to the building and find the angle of elevation to be 50°. Assuming that the street is level, estimate the height of the building to the nearest foot.

In order to estimate the height of a building, two students stand at a certain distance from the building at street level. From this point, they find the angle of elevation from the street to the top of the building to be 35°. They then move 250 feet closer to the building and find the angle of elevation to be 53°. Assuming that the street is level, estimate the height of the building to the nearest foot.

Points A A and B B are on opposite sides of a lake. Point C C is 97 meters from A . A . The measure of angle B A C B A C is determined to be 101°, and the measure of angle A C B A C B is determined to be 53°. What is the distance from A A to B , B , rounded to the nearest whole meter?

A man and a woman standing 3 1 2 3 1 2 miles apart spot a hot air balloon at the same time. If the angle of elevation from the man to the balloon is 27°, and the angle of elevation from the woman to the balloon is 41°, find the altitude of the balloon to the nearest foot.

Two search teams spot a stranded climber on a mountain. The first search team is 0.5 miles from the second search team, and both teams are at an altitude of 1 mile. The angle of elevation from the first search team to the stranded climber is 15°. The angle of elevation from the second search team to the climber is 22°. What is the altitude of the climber? Round to the nearest tenth of a mile.

A street light is mounted on a pole. A 6-foot-tall man is standing on the street a short distance from the pole, casting a shadow. The angle of elevation from the tip of the man’s shadow to the top of his head of 28°. A 6-foot-tall woman is standing on the same street on the opposite side of the pole from the man. The angle of elevation from the tip of her shadow to the top of her head is 28°. If the man and woman are 20 feet apart, how far is the street light from the tip of the shadow of each person? Round the distance to the nearest tenth of a foot.

Three cities, A , B , A , B , and C , C , are located so that city A A is due east of city B . B . If city C C is located 35° west of north from city B B and is 100 miles from city A A and 70 miles from city B , B , how far is city A A from city B ? B ? Round the distance to the nearest tenth of a mile.

Two streets meet at an 80° angle. At the corner, a park is being built in the shape of a triangle. Find the area of the park if, along one road, the park measures 180 feet, and along the other road, the park measures 215 feet.

Brian’s house is on a corner lot. Find the area of the front yard if the edges measure 40 and 56 feet, as shown in Figure 34 .

The Bermuda triangle is a region of the Atlantic Ocean that connects Bermuda, Florida, and Puerto Rico. Find the area of the Bermuda triangle if the distance from Florida to Bermuda is 1030 miles, the distance from Puerto Rico to Bermuda is 980 miles, and the angle created by the two distances is 62°.

A yield sign measures 30 inches on all three sides. What is the area of the sign?

Naomi bought a modern dining table whose top is in the shape of a triangle. Find the area of the table top if two of the sides measure 4 feet and 4.5 feet, and the smaller angles measure 32° and 42°, as shown in Figure 35 .

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/algebra-and-trigonometry/pages/1-introduction-to-prerequisites

• Authors: Jay Abramson
• Publisher/website: OpenStax
• Book title: Algebra and Trigonometry
• Publication date: Feb 13, 2015
• Location: Houston, Texas
• Book URL: https://openstax.org/books/algebra-and-trigonometry/pages/1-introduction-to-prerequisites
• Section URL: https://openstax.org/books/algebra-and-trigonometry/pages/10-1-non-right-triangles-law-of-sines

© Dec 8, 2021 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.