small sample size research limitations

Small Sample Research: Considerations Beyond Statistical Power

• Published: 19 August 2015
• Volume 16 , pages 1033–1036, ( 2015 )

Cite this article

• Kathleen E. Etz 1 &
• Judith A. Arroyo 2  

20k Accesses

25 Citations

Explore all metrics

Small sample research presents a challenge to current standards of design and analytic approaches and the underlying notions of what constitutes good prevention science. Yet, small sample research is critically important as the research questions posed in small samples often represent serious health concerns in vulnerable and underrepresented populations. This commentary considers the Special Section on small sample research and also highlights additional challenges that arise in small sample research not considered in the Special Section, including generalizability, determining what constitutes knowledge, and ensuring that research designs match community desires. It also points to opportunities afforded by small sample research, such as a focus on and increased understanding of context and the emphasis it may place on alternatives to the randomized clinical trial. The commentary urges the development and adoption of innovative strategies to conduct research with small samples.

Avoid common mistakes on your manuscript.

Small sample research presents a direct challenge to current standards of design and analytic approaches and the underlying notions of what constitutes good prevention science. While we can have confidence that our scientific methods have the ability to answer many research questions, we have been limited in our ability to take on research with small samples because we have not developed or adopted the means to support rigorous small sample research. This Special Section identifies some tools that can be used for small sample research. It reminds us that progress in this area will likely require expansion of our ideas of what constitutes rigor in analysis and design strategies that address the unique characteristics and accompanying challenges of small sample research. Advances will also require making room for the adoption of innovative design and statistical analysis approaches. The collection of papers makes a significant contribution to the literature and marks major development in the field.

Innovations in small sample research are particularly critical because the research questions posed in small samples often focus on serious health concerns in vulnerable populations. Individuals most at risk for or afflicted by health disparities (e.g., racial and ethnic minorities) are by definition small in number when compared to the larger, dominant society. The current state of the art in design and statistical analysis in prevention science, which is highly dependent on large samples, has severely handicapped investigation of health disparities in these smaller populations. Unless we develop research techniques suitable for small group design and expand our concepts of what design and analytic strategies provide sufficient scientific rigor, health disparities will continue to lay waste to populations that live in smaller communities or who are difficult to recruit in large numbers. Particularly when considering high-risk, low base rate behaviors such as recurrent binge drinking or chronic drug use, investigators are often limited by small populations in many health disparity groups and by small numbers of potential participants in towns, villages, and rural communities. Even in larger, urban settings, researchers may experience constraints on recruitment such as difficulty identifying a sufficiently large sample, distrust of research, lack of transportation or time outside of work hours, or language issues. Until now, small sample sizes and the lack of accepted tools for small sample research have decreased our ability to harness the power of science to research preventive solutions to health disparities. The collection of articles in this Special Section helps to address this by bringing together multiple strategies and demonstrating their strength in addressing research questions with small samples.

Small sample research issues also arise in multi-level, group-based, or community-level intervention research (Trickett et al. 2011 ). An example of this is a study that uses a media campaign and compares the efficacy of that campaign across communities. In such cases, the unit of analysis is the group, and the limited number of units that can be feasibly involved in a study makes multi-level intervention research inevitably an analysis of small samples. The increasingly recognized importance of intervening in communities at multiple levels (Frohlich and Potvin 2008 ) and the desire to understand the efficacy and effectiveness of multi-level interventions (Hawe 1994 ) increase the need to devise strategies for assessing interventions conducted with small samples.

The Special Section makes a major contribution to small sample research, identifying tools that can be used to address small sample design and analytic challenges. The articles here can be grouped into four areas: (1) identification of refinements in statistical applications and measurement that can facilitate analyses with small samples, (2) alternatives to randomized clinical trial (RCT) designs that maintain rigor while maximizing power, (3) use of qualitative and mixed methods, and (4) Bayesian analysis. The Special Section provides a range of alternative strategies to those that are currently employed with larger samples. The first and last papers in the Special Section (Fok et al. 2015 ; Henry et al. 2015a ) examine and elaborate on the contributions of these articles to the field. As this is considered elsewhere, we will focus our comments more on issues that are not already covered but that will be increasingly important as this field moves forward.

One challenge that is not addressed by the papers in this Special Section is the generalizability of small sample research findings, particularly when working with culturally distinct populations. Generalizability poses a different obstacle than those associated with design and analysis, in that it is not related to rigor or the confidence we can have in our conclusions. Rather, it limits our ability to assume the results will apply to populations other than those from whom a sample is drawn and, as such, can limit the application of the work. The need to discover prevention solutions for all people, even if they happen to be members of a small population, begs questions of the value of generalizability and of the importance ascribed to it. Further, existing research raises long-standing important questions about whether knowledge produced under highly controlled conditions can generalize to ethnoculturally diverse communities (Atkins et al. 2006 ; Beeker et al. 1998 ; Green and Glasgow 2006 ). Regardless, the inability to generalize beyond a small population can present a barrier to funding. When grant applications are reviewed, projects that are not seen as widely generalizable often receive poor ratings. Scientists conducting small sample research with culturally distinct groups are frequently stymied by how they can justify their research when it is not generalizable to large segments of the population. In some instances, the question that drives the research is that which limits generalizability. For example, research projects on cultural adaptations of established interventions are often highly specific. An adaptation that might be efficacious in one small sample might not be so in other contexts. This is particularly the case if the adaptation integrates local culture, such as preparing for winter and subsistence activities in Alaska or integrating the horse culture of the Great Plains. Even if local adaptation is not necessary, dissemination research to ascertain the efficacy and/or effectiveness of mainstream, evidence-based interventions when applied to diverse groups will be difficult to conduct if we cannot address concerns about generalizability.

It is not readily apparent how to address issues of generalizability, but it is clear that this will be challenging and will require creativity. One potential strategy is to go beyond questions of intervention efficacy to address additional research questions that have the potential to advance the field more generally. For example, Allen and colleagues’ ( 2014 ) scientific investigations extended beyond development of a prevention intervention in Alaska Native villages to identification and testing of the underlying prevention processes that were at the core of the culturally specific intervention. This isolation of the key components of the prevention process has the potential to inform and generalize across settings. The development of new statistical tools for small culturally distinct samples might also be helpful in other research contexts. Similarly, the identification of the most potent prevention processes for adaptation also might generalize. As small sample research evolves, we must remain open to how this work has the potential to be highly valuable despite recognizing that not all aspects of it will generalize and also take care to identify what can be applied generally.

While not exclusive to small sample research, additional difficulties that can arise in conducting research in some small, culturally distinct samples are the questions of what constitutes knowledge and how to include alternative forms of knowledge (e.g., indigenous ways of knowing, folk wisdom) in health research (Aikenhead and Ogawa 2007 ; Gone 2012 ). For many culturally distinct communities that turn to research to address their health challenges, the need for large samples and methods demanded by mainstream science might be incongruent with local epistemologies and cultural understandings of how the knowledge to inform prevention is generated and standards of evidence are established. Making sense of how or whether indigenous knowledge and western scientific approaches can work together is an immense challenge. The Henry, Dymnicki, Mohatt, Kelly, and Allen article in this Special Section recommends combining qualitative and quantitative methods as one way to address this conundrum. However, this strategy is not sufficient to address all of the challenges encountered by those who seek to integrate traditional knowledge into modern scientific inquiry. For culturally distinct groups who value forms of knowledge other than those generated by western science, the research team, including the community members, will need to work together to identify ways to best ensure that culturally valued knowledge is incorporated into the research endeavor. The scientific field will need to make room for approaches that stem from the integration of culturally valued knowledge.

Ensuring that the research design and methods correspond to community needs and desires can present an additional challenge. Investigations conducted with small, culturally distinct groups often use community-based participatory research (CBPR) approaches (Minkler and Wallerstein 2008 ). True CBPR mandates that community partners be equal participants in every phase of the research, including study design. From an academic researcher’s perspective, the primary obstacle for small sample research may be insufficient statistical power to conduct a classic RCT. However, for the small group partner, the primary obstacle may be the RCT design itself. Many communities will not allow a RCT because assignment of some community members to a no-treatment control condition can violate culturally based ethical principles that demand that all participants be treated equally. Particularly in communities experiencing severe health disparities, community members may want every person to receive the active intervention. While the RCT has become the gold standard because it is believed to be the most rigorous test of intervention efficacy, it is clear the RCT does not serve the needs of all communities.

While presenting challenges for current methods, it is important to note that small sample research can also expand our horizons. For example, attempts to truly comprehend culturally distinct groups will lead to a better understanding of the role of context in health outcomes. Current approaches more often attempt to control for extraneous variables rather than work to more accurately model potentially rich contextual variables. This blinds us to cultural differences between and among small groups that might contribute to outcomes and improve health. Analytical strategies that mask these nuances will fail to detect information about risk and resilience factors that could impact intervention. Multi-level intervention research (which we pointed out earlier qualifies as small sample research) that focuses on contextual changes as well as or instead of change in the individual will also inform our understanding of context, elucidating how to effectively intervene to change context to promote health outcomes. Thus, considering how prevailing methods limit our work in small samples can also expose ways that alternative methods may advance our science more broadly by enhancing both our understanding of context and how to intervene in context.

Small sample science requires us to consider alternatives to the RCT, and this consideration introduces additional opportunities. The last paper in this Special Section (Henry et al. 2015b ) notes compelling critiques of RCT. Small sample research demands we incorporate alternate strategies that may be superior in some instances regarding their efficiency in their use of available information, in contrast to the classic RCT, and may be more aligned with community desires. Alternative designs for small sample research may offer means to enhance and ensure scientific rigor without depending on RCT design (Srinivasan et al. 2015 ). It is important to consider what alternative approaches can contribute rather than adhering rigidly to the RCT.

New challenges require innovative solutions. Innovation is the foundation of scientific advances. It is one of only five National Institutes of Health grant review criteria. Despite the value to science of innovation, research grant application reviewers are often skeptical of new strategies and are reluctant to support risk taking in science. As a field, we seem accustomed to the use of certain methods and statistics, generally accepting and rarely questioning if they are the best approach. Yet, it is clear that common methods that work well with large samples are not always appropriate for small samples. Progress will demand that new approaches be well justified and also that the field supports innovation and the testing of alternative approaches. Srinivasan and colleagues ( 2015 ) further recommend that it might be necessary to offer training to grant application peer reviewers on innovative small sample research methods, thus ensuring that they are knowledgeable in this area and score grant applications appropriately. Alternative approaches need to be accepted into the repertoire of available design and assessment tools. The articles in this Special Section all highlight such innovation for small sample research.

It would be a failure of science and the imagination if newly discovered or re-discovered (i.e., Bayesian) strategies are not employed to facilitate rigorous assessment of interventions in small samples. It is imperative that the tools of science do not limit our ability to address pressing public health questions. New approaches can be used to address contemporary research questions, including providing solutions to the undue burden of disease that can and often does occur in small populations. It must be the pressing nature of the questions, not the limitations of our methods, that determines what science is undertaken (see also Srinivasan et al. 2015 ). While small sample research presents a challenge for prevailing scientific approaches, the papers in this Special Section identify ways to move this science forward with rigor. It is imperative that the field accommodates these advances, and continues to be innovative in response to the challenge of small sample research, to ensure that science can provide answers for those most in need.

Aikenhead, G. S., & Ogawa, M. (2007). Indigenous knowledge and science revisited. Cultural Studies of Science Education, 2 , 539–620.

Article   Google Scholar  

Allen, J., Mohatt, G. V., Fok, C. C. T., Henry, D., Burkett, R., & People Awakening Project. (2014). A protective factors model for alcohol abuse and suicide prevention among Alaska Native youth. American Journal of Community Psychology, 54 , 125–139.

Article   PubMed Central   PubMed   Google Scholar  

Atkins, M. S., Frazier, S. L., & Cappella, E. (2006). Hybrid research models: Natural opportunities for examining mental health in context. Clinical Psychology Review, 13 , 105–108.

Google Scholar  

Beeker, C., Guenther-Grey, C., & Raj, A. (1998). Community empowerment paradigm drift and the primary prevention of HIV/AIDS. Social Science & Medicine, 46 , 831–842.

Article   CAS   Google Scholar  

Fok, Henry, D., Allen, J. (2015). Maybe small is too small a term: Introduction to advancing small sample prevention science. Prevention Science .

Frohlich, K. L., & Potvin, L. (2008). Transcending the known in public health practice: The inequality paradox: The population approach and vulnerable populations. American Journal of Public Health, 98 , 216–221.

Gone, J. P. (2012). Indigenous traditional knowledge and substance abuse treatment outcomes: The problem of efficacy evaluation. American Journal of Drug and Alcohol Abuse, 38 , 493–497.

Article   PubMed   Google Scholar  

Green, L. W., & Glasgow, R. E. (2006). Evaluating the relevance, generalization, and applicability of research: Issues in external validation and translation methodology. Evaluation & the Health Professions, 29 , 126–153.

Hawe, P. (1994). Capturing the meaning of “community” in community intervention evaluation: Some contributions from community psychology. Health Promotion International, 9 , 199–210.

Henry, D., Dymnicki, A. B., Mohatt, N., Kelly, J. G., & Allen, J. (2015a). Clustering methods with qualitative data: A mixed methods approach for prevention research with small samples. Prevention Science . doi: 10.1007/s11121-015-0561-z .

Henry, D., Fok, C.C.T., Allen, J. (2015). Why small is too small a term: Prevention science for health disparities, culturally distinct groups, and community-level intervention. Prevention Science.

Minkler, M., & Wallerstein, N. (Eds.). (2008). Community-based participatory research for health: From process to outcomes (2nd ed.). San Francisco: Jossey-Bass.

Srinivasan, S., Moser, R. P., Willis, G., Riley, W., Alexander, M., Berrigan, D., & Kobrin, S. (2015). Small is essential: Importance of subpopulation research in cancer control. American Journal of Public Health, 105 , 371–373.

Trickett, E. J., Beehler, S., Deutsch, C., Green, L. W., Hawe, P., McLeroy, K., Miller, R. L., Rapkin, B. D., Schensul, J. J., Schulz, A. J., & Trimble, J. E. (2011). Advancing the science of community-level interventions. American Journal of Public Health, 11 , 1410–1419.

Download references

Compliance with Ethical Standards

No external funding supported this work.

Conflict of Interest

The authors declare that they have no conflict of interest.

Ethical Approval

This article does not contain any studies with human participants or animals performed by any of the authors.

Informed Consent

Because this article is a commentary, informed consent is not applicable.

Author information

Authors and affiliations.

National Institute on Drug Abuse, National Institutes of Health, 6001 Executive Blvd., Bethesda, MD, 20852, USA

Kathleen E. Etz

National Institute on Alcohol Abuse and Alcoholism, National Institutes of Health, 5635 Fishers Lane, Bethesda, MD, 20852, USA

Judith A. Arroyo

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Kathleen E. Etz .

Additional information

The opinions and conclusions here represent those of the authors and do not represent the National Institutes of Health, the National Institute on Drug Abuse, the National Institute on Alcohol Abuse and Alcoholism, or the US Government.

Rights and permissions

Reprints and permissions

About this article

Etz, K.E., Arroyo, J.A. Small Sample Research: Considerations Beyond Statistical Power. Prev Sci 16 , 1033–1036 (2015). https://doi.org/10.1007/s11121-015-0585-4

Download citation

Published : 19 August 2015

Issue Date : October 2015

DOI : https://doi.org/10.1007/s11121-015-0585-4

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Find a journal
• Publish with us
• Track your research

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

• View all journals
• Explore content
• About the journal
• Publish with us
• Sign up for alerts
• Published: 10 April 2013

Power failure: why small sample size undermines the reliability of neuroscience

• Katherine S. Button 1 , 2 ,
• John P. A. Ioannidis 3 ,
• Claire Mokrysz 1 ,
• Brian A. Nosek 4 ,
• Jonathan Flint 5 ,
• Emma S. J. Robinson 6 &
• Marcus R. Munafò 1  

Nature Reviews Neuroscience volume  14 ,  pages 365–376 ( 2013 ) Cite this article

483k Accesses

4311 Citations

1383 Altmetric

Metrics details

• Molecular neuroscience

An Erratum to this article was published on 15 April 2013

This article has been updated

Low statistical power undermines the purpose of scientific research; it reduces the chance of detecting a true effect.

Perhaps less intuitively, low power also reduces the likelihood that a statistically significant result reflects a true effect.

Empirically, we estimate the median statistical power of studies in the neurosciences is between ∼ 8% and ∼ 31%.

We discuss the consequences of such low statistical power, which include overestimates of effect size and low reproducibility of results.

There are ethical dimensions to the problem of low power; unreliable research is inefficient and wasteful.

Improving reproducibility in neuroscience is a key priority and requires attention to well-established, but often ignored, methodological principles.

We discuss how problems associated with low power can be addressed by adopting current best-practice and make clear recommendations for how to achieve this.

A study with low statistical power has a reduced chance of detecting a true effect, but it is less well appreciated that low power also reduces the likelihood that a statistically significant result reflects a true effect. Here, we show that the average statistical power of studies in the neurosciences is very low. The consequences of this include overestimates of effect size and low reproducibility of results. There are also ethical dimensions to this problem, as unreliable research is inefficient and wasteful. Improving reproducibility in neuroscience is a key priority and requires attention to well-established but often ignored methodological principles.

You have full access to this article via your institution.

Similar content being viewed by others

Dimensionality reduction beyond neural subspaces with slice tensor component analysis

Principal component analysis

Two common and distinct forms of variation in human functional brain networks

It has been claimed and demonstrated that many (and possibly most) of the conclusions drawn from biomedical research are probably false 1 . A central cause for this important problem is that researchers must publish in order to succeed, and publishing is a highly competitive enterprise, with certain kinds of findings more likely to be published than others. Research that produces novel results, statistically significant results (that is, typically p < 0.05) and seemingly 'clean' results is more likely to be published 2 , 3 . As a consequence, researchers have strong incentives to engage in research practices that make their findings publishable quickly, even if those practices reduce the likelihood that the findings reflect a true (that is, non-null) effect 4 . Such practices include using flexible study designs and flexible statistical analyses and running small studies with low statistical power 1 , 5 . A simulation of genetic association studies showed that a typical dataset would generate at least one false positive result almost 97% of the time 6 , and two efforts to replicate promising findings in biomedicine reveal replication rates of 25% or less 7 , 8 . Given that these publishing biases are pervasive across scientific practice, it is possible that false positives heavily contaminate the neuroscience literature as well, and this problem may affect at least as much, if not even more so, the most prominent journals 9 , 10 .

Here, we focus on one major aspect of the problem: low statistical power. The relationship between study power and the veracity of the resulting finding is under-appreciated. Low statistical power (because of low sample size of studies, small effects or both) negatively affects the likelihood that a nominally statistically significant finding actually reflects a true effect. We discuss the problems that arise when low-powered research designs are pervasive. In general, these problems can be divided into two categories. The first concerns problems that are mathematically expected to arise even if the research conducted is otherwise perfect: in other words, when there are no biases that tend to create statistically significant (that is, 'positive') results that are spurious. The second category concerns problems that reflect biases that tend to co-occur with studies of low power or that become worse in small, underpowered studies. We next empirically show that statistical power is typically low in the field of neuroscience by using evidence from a range of subfields within the neuroscience literature. We illustrate that low statistical power is an endemic problem in neuroscience and discuss the implications of this for interpreting the results of individual studies.

Low power in the absence of other biases

Three main problems contribute to producing unreliable findings in studies with low power, even when all other research practices are ideal. They are: the low probability of finding true effects; the low positive predictive value (PPV; see Box 1 for definitions of key statistical terms) when an effect is claimed; and an exaggerated estimate of the magnitude of the effect when a true effect is discovered. Here, we discuss these problems in more detail.

First, low power, by definition, means that the chance of discovering effects that are genuinely true is low. That is, low-powered studies produce more false negatives than high-powered studies. When studies in a given field are designed with a power of 20%, it means that if there are 100 genuine non-null effects to be discovered in that field, these studies are expected to discover only 20 of them 11 .

Second, the lower the power of a study, the lower the probability that an observed effect that passes the required threshold of claiming its discovery (that is, reaching nominal statistical significance, such as p < 0.05) actually reflects a true effect 1 , 12 . This probability is called the PPV of a claimed discovery. The formula linking the PPV to power is:

where (1 − β) is the power, β is the type II error, α is the type I error and R is the pre-study odds (that is, the odds that a probed effect is indeed non-null among the effects being probed). The formula is derived from a simple two-by-two table that tabulates the presence and non-presence of a non-null effect against significant and non-significant research findings 1 . The formula shows that, for studies with a given pre-study odds R, the lower the power and the higher the type I error, the lower the PPV. And for studies with a given pre-study odds R and a given type I error (for example, the traditional p = 0.05 threshold), the lower the power, the lower the PPV.

For example, suppose that we work in a scientific field in which one in five of the effects we test are expected to be truly non-null (that is, R = 1 / (5 − 1) = 0.25) and that we claim to have discovered an effect when we reach p < 0.05; if our studies have 20% power, then PPV = 0.20 × 0.25 / (0.20 × 0.25 + 0.05) = 0.05 / 0.10 = 0.50; that is, only half of our claims for discoveries will be correct. If our studies have 80% power, then PPV = 0.80 × 0.25 / (0.80 × 0.25 + 0.05) = 0.20 / 0.25 = 0.80; that is, 80% of our claims for discoveries will be correct.

Third, even when an underpowered study discovers a true effect, it is likely that the estimate of the magnitude of that effect provided by that study will be exaggerated. This effect inflation is often referred to as the 'winner's curse' 13 and is likely to occur whenever claims of discovery are based on thresholds of statistical significance (for example, p < 0.05) or other selection filters (for example, a Bayes factor better than a given value or a false-discovery rate below a given value). Effect inflation is worst for small, low-powered studies, which can only detect effects that happen to be large. If, for example, the true effect is medium-sized, only those small studies that, by chance, overestimate the magnitude of the effect will pass the threshold for discovery. To illustrate the winner's curse, suppose that an association truly exists with an effect size that is equivalent to an odds ratio of 1.20, and we are trying to discover it by performing a small (that is, underpowered) study. Suppose also that our study only has the power to detect an odds ratio of 1.20 on average 20% of the time. The results of any study are subject to sampling variation and random error in the measurements of the variables and outcomes of interest. Therefore, on average, our small study will find an odds ratio of 1.20 but, because of random errors, our study may in fact find an odds ratio smaller than 1.20 (for example, 1.00) or an odds ratio larger than 1.20 (for example, 1.60). Odds ratios of 1.00 or 1.20 will not reach statistical significance because of the small sample size. We can only claim the association as nominally significant in the third case, where random error creates an odds ratio of 1.60. The winner's curse means, therefore, that the 'lucky' scientist who makes the discovery in a small study is cursed by finding an inflated effect.

The winner's curse can also affect the design and conclusions of replication studies. If the original estimate of the effect is inflated (for example, an odds ratio of 1.60), then replication studies will tend to show smaller effect sizes (for example, 1.20), as findings converge on the true effect. By performing more replication studies, we should eventually arrive at the more accurate odds ratio of 1.20, but this may take time or may never happen if we only perform small studies. A common misconception is that a replication study will have sufficient power to replicate an initial finding if the sample size is similar to that in the original study 14 . However, a study that tries to replicate a significant effect that only barely achieved nominal statistical significance (that is, p ∼ 0.05) and that uses the same sample size as the original study, will only achieve ∼ 50% power, even if the original study accurately estimated the true effect size. This is illustrated in Fig. 1 . Many published studies only barely achieve nominal statistical significance 15 . This means that if researchers in a particular field determine their sample sizes by historical precedent rather than through formal power calculation, this will place an upper limit on average power within that field. As the true effect size is likely to be smaller than that indicated by the initial study — for example, because of the winner's curse — the actual power is likely to be much lower. Furthermore, even if power calculation is used to estimate the sample size that is necessary in a replication study, these calculations will be overly optimistic if they are based on estimates of the true effect size that are inflated owing to the winner's curse phenomenon. This will further hamper the replication process.

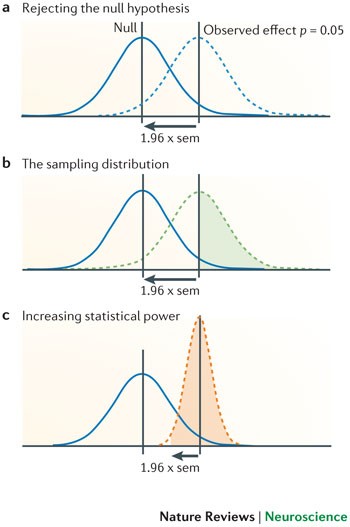
a | If a study finds evidence for an effect at p = 0.05, then the difference between the mean of the null distribution (indicated by the solid blue curve) and the mean of the observed distribution (dashed blue curve) is 1.96 × sem. b | Studies attempting to replicate an effect using the same sample size as that of the original study would have roughly the same sampling variation (that is, sem) as in the original study. Assuming, as one might in a power calculation, that the initially observed effect we are trying to replicate reflects the true effect, the potential distribution of these replication effect estimates would be similar to the distribution of the original study (dashed green curve). A study attempting to replicate a nominally significant effect ( p ∼ 0.05), which uses the same sample size as the original study, would therefore have (on average) a 50% chance of rejecting the null hypothesis (indicated by the coloured area under the green curve) and thus only 50% statistical power. c | We can increase the power of the replication study (coloured area under the orange curve) by increasing the sample size so as to reduce the sem. Powering a replication study adequately (that is, achieving a power ≥ 80%) therefore often requires a larger sample size than the original study, and a power calculation will help to decide the required size of the replication sample.

Low power in the presence of other biases

Low power is associated with several additional biases. First, low-powered studies are more likely to provide a wide range of estimates of the magnitude of an effect (which is known as 'vibration of effects' and is described below). Second, publication bias, selective data analysis and selective reporting of outcomes are more likely to affect low-powered studies. Third, small studies may be of lower quality in other aspects of their design as well. These factors can further exacerbate the low reliability of evidence obtained in studies with low statistical power.

Vibration of effects 13 refers to the situation in which a study obtains different estimates of the magnitude of the effect depending on the analytical options it implements. These options could include the statistical model, the definition of the variables of interest, the use (or not) of adjustments for certain potential confounders but not others, the use of filters to include or exclude specific observations and so on. For example, a recent analysis of 241 functional MRI (fMRI) studies showed that 223 unique analysis strategies were observed so that almost no strategy occurred more than once 16 . Results can vary markedly depending on the analysis strategy 1 . This is more often the case for small studies — here, results can change easily as a result of even minor analytical manipulations. In small studies, the range of results that can be obtained owing to vibration of effects is wider than in larger studies, because the results are more uncertain and therefore fluctuate more in response to analytical changes. Imagine, for example, dropping three observations from the analysis of a study of 12 samples because post-hoc they are considered unsatisfactory; this manipulation may not even be mentioned in the published paper, which may simply report that only nine patients were studied. A manipulation affecting only three observations could change the odds ratio from 1.00 to 1.50 in a small study but might only change it from 1.00 to 1.01 in a very large study. When investigators select the most favourable, interesting, significant or promising results among a wide spectrum of estimates of effect magnitudes, this is inevitably a biased choice.

Publication bias and selective reporting of outcomes and analyses are also more likely to affect smaller, underpowered studies 17 . Indeed, investigations into publication bias often examine whether small studies yield different results than larger ones 18 . Smaller studies more readily disappear into a file drawer than very large studies that are widely known and visible, and the results of which are eagerly anticipated (although this correlation is far from perfect). A 'negative' result in a high-powered study cannot be explained away as being due to low power 19 , 20 , and thus reviewers and editors may be more willing to publish it, whereas they more easily reject a small 'negative' study as being inconclusive or uninformative 21 . The protocols of large studies are also more likely to have been registered or otherwise made publicly available, so that deviations in the analysis plans and choice of outcomes may become obvious more easily. Small studies, conversely, are often subject to a higher level of exploration of their results and selective reporting thereof.

Third, smaller studies may have a worse design quality than larger studies. Several small studies may be opportunistic experiments, or the data collection and analysis may have been conducted with little planning. Conversely, large studies often require more funding and personnel resources. As a consequence, designs are examined more carefully before data collection, and analysis and reporting may be more structured. This relationship is not absolute — small studies are not always of low quality. Indeed, a bias in favour of small studies may occur if the small studies are meticulously designed and collect high-quality data (and therefore are forced to be small) and if large studies ignore or drop quality checks in an effort to include as large a sample as possible.

Empirical evidence from neuroscience

Any attempt to establish the average statistical power in neuroscience is hampered by the problem that the true effect sizes are not known. One solution to this problem is to use data from meta-analyses. Meta-analysis provides the best estimate of the true effect size, albeit with limitations, including the limitation that the individual studies that contribute to a meta-analysis are themselves subject to the problems described above. If anything, summary effects from meta-analyses, including power estimates calculated from meta-analysis results, may also be modestly inflated 22 .

Acknowledging this caveat, in order to estimate statistical power in neuroscience, we examined neuroscience meta-analyses published in 2011 that were retrieved using 'neuroscience' and 'meta-analysis' as search terms. Using the reported summary effects of the meta-analyses as the estimate of the true effects, we calculated the power of each individual study to detect the effect indicated by the corresponding meta-analysis.

Methods. Included in our analysis were articles published in 2011 that described at least one meta-analysis of previously published studies in neuroscience with a summary effect estimate (mean difference or odds/risk ratio) as well as study level data on group sample size and, for odds/risk ratios, the number of events in the control group.

We searched computerized databases on 2 February 2012 via Web of Science for articles published in 2011, using the key words 'neuroscience' and 'meta-analysis'. All of the articles that were identified via this electronic search were screened independently for suitability by two authors (K.S.B. and M.R.M.). Articles were excluded if no abstract was electronically available (for example, conference proceedings and commentaries) or if both authors agreed, on the basis of the abstract, that a meta-analysis had not been conducted. Full texts were obtained for the remaining articles and again independently assessed for eligibility by two authors (K.S.B. and M.R.M.) ( Fig. 2 ).

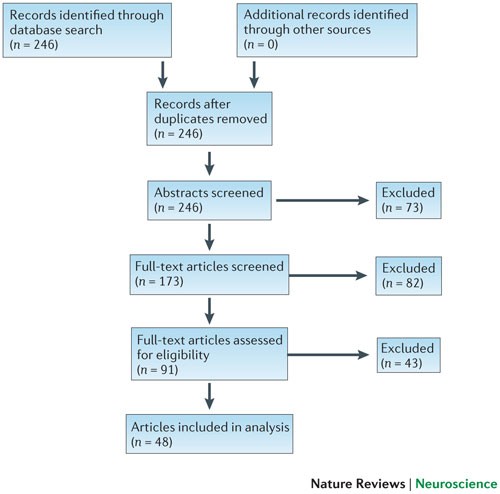
Computerized databases were searched on 2 February 2012 via Web of Science for papers published in 2011, using the key words 'neuroscience' and 'meta-analysis'. Two authors (K.S.B. and M.R.M.) independently screened all of the papers that were identified for suitability ( n = 246). Articles were excluded if no abstract was electronically available (for example, conference proceedings and commentaries) or if both authors agreed, on the basis of the abstract, that a meta-analysis had not been conducted. Full texts were obtained for the remaining articles ( n = 173) and again independently assessed for eligibility by K.S.B. and M.R.M. Articles were excluded ( n = 82) if both authors agreed, on the basis of the full text, that a meta-analysis had not been conducted. The remaining articles ( n = 91) were assessed in detail by K.S.B. and M.R.M. or C.M. Articles were excluded at this stage if they could not provide the following data for extraction for at least one meta-analysis: first author and summary effect size estimate of the meta-analysis; and first author, publication year, sample size (by groups) and number of events in the control group (for odds/risk ratios) of the contributing studies. Data extraction was performed independently by K.S.B. and M.R.M. or C.M. and verified collaboratively. In total, n = 48 articles were included in the analysis.

Data were extracted from forest plots, tables and text. Some articles reported several meta-analyses. In those cases, we included multiple meta-analyses only if they contained distinct study samples. If several meta-analyses had overlapping study samples, we selected the most comprehensive (that is, the one containing the most studies) or, if the number of studies was equal, the first analysis presented in the article. Data extraction was independently performed by K.S.B. and either M.R.M. or C.M. and verified collaboratively.

The following data were extracted for each meta-analysis: first author and summary effect size estimate of the meta-analysis; and first author, publication year, sample size (by groups), number of events in the control group (for odds/risk ratios) and nominal significance ( p < 0.05, 'yes/no') of the contributing studies. For five articles, nominal study significance was unavailable and was therefore obtained from the original studies if they were electronically available. Studies with missing data (for example, due to unclear reporting) were excluded from the analysis.

The main outcome measure of our analysis was the achieved power of each individual study to detect the estimated summary effect reported in the corresponding meta-analysis to which it contributed, assuming an α level of 5%. Power was calculated using G * Power software 23 . We then calculated the mean and median statistical power across all studies.

Results. Our search strategy identified 246 articles published in 2011, out of which 155 were excluded after an initial screening of either the abstract or the full text. Of the remaining 91 articles, 48 were eligible for inclusion in our analysis 24 , 25 , 26 , 27 , 28 , 29 , 30 , 31 , 32 , 33 , 34 , 35 , 36 , 37 , 38 , 39 , 40 , 41 , 42 , 43 , 44 , 45 , 46 , 47 , 48 , 49 , 50 , 51 , 52 , 53 , 54 , 55 , 56 , 57 , 58 , 59 , 60 , 61 , 62 , 63 , 64 , 65 , 66 , 67 , 68 , 69 , 70 , 71 , comprising data from 49 meta-analyses and 730 individual primary studies. A flow chart of the article selection process is shown in Fig. 2 , and the characteristics of included meta-analyses are described in Table 1 .

Our results indicate that the median statistical power in neuroscience is 21%. We also applied a test for an excess of statistical significance 72 . This test has recently been used to show that there is an excess significance bias in the literature of various fields, including in studies of brain volume abnormalities 73 , Alzheimer's disease genetics 70 , 74 and cancer biomarkers 75 . The test revealed that the actual number (349) of nominally significant studies in our analysis was significantly higher than the number expected (254; p < 0.0001). Importantly, these calculations assume that the summary effect size reported in each study is close to the true effect size, but it is likely that they are inflated owing to publication and other biases described above.

Interestingly, across the 49 meta-analyses included in our analysis, the average power demonstrated a clear bimodal distribution ( Fig. 3 ). Most meta-analyses comprised studies with very low average power — almost 50% of studies had an average power lower than 20%. However, seven meta-analyses comprised studies with high (>90%) average power 24 , 26 , 31 , 57 , 63 , 68 , 71 . These seven meta-analyses were all broadly neurological in focus and were based on relatively small contributing studies — four out of the seven meta-analyses did not include any study with over 80 participants. If we exclude these 'outlying' meta-analyses, the median statistical power falls to 18%.

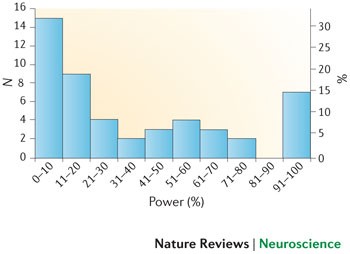
The figure shows a histogram of median study power calculated for each of the n = 49 meta-analyses included in our analysis, with the number of meta-analyses ( N ) on the left axis and percent of meta-analyses (%) on the right axis. There is a clear bimodal distribution; n = 15 (31%) of the meta-analyses comprised studies with median power of less than 11%, whereas n = 7 (14%) comprised studies with high average power in excess of 90%. Despite this bimodality, most meta-analyses comprised studies with low statistical power: n = 28 (57%) had median study power of less than 31%. The meta-analyses ( n = 7) that comprised studies with high average power in excess of 90% had their broadly neurological subject matter in common.

Small sample sizes are appropriate if the true effects being estimated are genuinely large enough to be reliably observed in such samples. However, as small studies are particularly susceptible to inflated effect size estimates and publication bias, it is difficult to be confident in the evidence for a large effect if small studies are the sole source of that evidence. Moreover, many meta-analyses show small-study effects on asymmetry tests (that is, smaller studies have larger effect sizes than larger ones) but nevertheless use random-effect calculations, and this is known to inflate the estimate of summary effects (and thus also the power estimates). Therefore, our power calculations are likely to be extremely optimistic 76 .

Empirical evidence from specific fields

One limitation of our analysis is the under-representation of meta-analyses in particular subfields of neuroscience, such as research using neuroimaging and animal models. We therefore sought additional representative meta-analyses from these fields outside our 2011 sampling frame to determine whether a similar pattern of low statistical power would be observed.

Neuroimaging studies. Most structural and volumetric MRI studies are very small and have minimal power to detect differences between compared groups (for example, healthy people versus those with mental health diseases). A cl ear excess significance bias has been demonstrated in studies of brain volume abnormalities 73 , and similar problems appear to exist in fMRI studies of the blood-oxygen-level-dependent response 77 . In order to establish the average statistical power of studies of brain volume abnormalities, we applied the same analysis as described above to data that had been previously extracted to assess the presence of an excess of significance bias 73 . Our results indicated that the median statistical power of these studies was 8% across 461 individual studies contributing to 41 separate meta-analyses, which were drawn from eight articles that were published between 2006 and 2009. Full methodological details describing how studies were identified and selected are available elsewhere 73 .

Animal model studies. Previous analyses of studies using animal models have shown that small studies consistently give more favourable (that is, 'positive') results than larger studies 78 and that study quality is inversely related to effect size 79 , 80 , 81 , 82 . In order to examine the average power in neuroscience studies using animal models, we chose a representative meta-analysis that combined data from studies investigating sex differences in water maze performance (number of studies ( k ) = 19, summary effect size Cohen's d = 0.49) and radial maze performance ( k = 21, summary effect size d = 0.69) 80 . The summary effect sizes in the two meta-analyses provide evidence for medium to large effects, with the male and female performance differing by 0.49 to 0.69 standard deviations for water maze and radial maze, respectively. Our results indicate that the median statistical power for the water maze studies and the radial maze studies to detect these medium to large effects was 18% and 31%, respectively ( Table 2 ). The average sample size in these studies was 22 animals for the water maze and 24 for the radial maze experiments. Studies of this size can only detect very large effects ( d = 1.20 for n = 22, and d = 1.26 for n = 24) with 80% power — far larger than those indicated by the meta-analyses. These animal model studies were therefore severely underpowered to detect the summary effects indicated by the meta-analyses. Furthermore, the summary effects are likely to be inflated estimates of the true effects, given the problems associated with small studies described above.

The results described in this section are based on only two meta-analyses, and we should be appropriately cautious in extrapolating from this limited evidence. Nevertheless, it is notable that the results are so consistent with those observed in other fields, such as the neuroimaging and neuroscience studies that we have described above.

Implications

Implications for the likelihood that a research finding reflects a true effect. Our results indicate that the average statistical power of studies in the field of neuroscience is probably no more than between ∼ 8% and ∼ 31%, on the basis of evidence from diverse subfields within neuro-science. If the low average power we observed across these studies is typical of the neuroscience literature as a whole, this has profound implications for the field. A major implication is that the likelihood that any nominally significant finding actually reflects a true effect is small. As explained above, the probability that a research finding reflects a true effect (PPV) decreases as statistical power decreases for any given pre-study odds (R) and a fixed type I error level. It is easy to show the impact that this is likely to have on the reliability of findings. Figure 4 shows how the PPV changes for a range of values for R and for a range of v alues for the average power in a field. For effects that are genuinely non-null, Fig. 5 shows the degree to which an effect size estimate is likely to be inflated in initial studies — owing to the winner's curse phenomenon — for a range of values for statistical power.

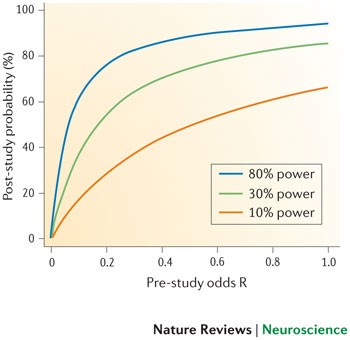
The probability that a research finding reflects a true effect — also known as the positive predictive value (PPV) — depends on both the pre-study odds of the effect being true (the ratio R of 'true effects' over 'null effects' in the scientific field) and the study's statistical power. The PPV can be calculated for given values of statistical power (1 − β), pre-study odds ratio (R) and type I error rate (α), using the formula PPV = ([1 − β] × R) / ([1− β] × R + α). The median statistical power of studies in the neuroscience field is optimistically estimated to be between ∼ 8% and ∼ 31%. The figure illustrates how low statistical power consistent with this estimated range (that is, between 10% and 30%) detrimentally affects the association between the probability that a finding reflects a true effect (PPV) and pre-study odds, assuming α = 0.05. Compared with conditions of appropriate statistical power (that is, 80%), the probability that a research finding reflects a true effect is greatly reduced for 10% and 30% power, especially if pre-study odds are low. Notably, in an exploratory research field such as much of neuroscience, the pre-study odds are often low.

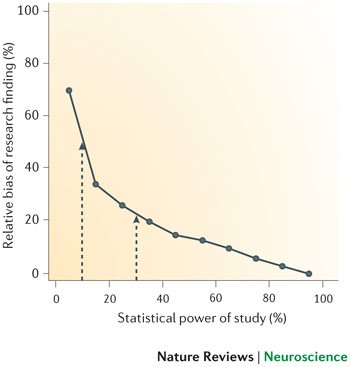
The winner's curse refers to the phenomenon that studies that find evidence of an effect often provide inflated estimates of the size of that effect. Such inflation is expected when an effect has to pass a certain threshold — such as reaching statistical significance — in order for it to have been 'discovered'. Effect inflation is worst for small, low-powered studies, which can only detect effects that happen to be large. If, for example, the true effect is medium-sized, only those small studies that, by chance, estimate the effect to be large will pass the threshold for discovery (that is, the threshold for statistical significance, which is typically set at p < 0.05). In practice, this means that research findings of small studies are biased in favour of inflated effects. By contrast, large, high-powered studies can readily detect both small and large effects and so are less biased, as both over- and underestimations of the true effect size will pass the threshold for 'discovery'. We optimistically estimate the median statistical power of studies in the neuroscience field to be between ∼ 8% and ∼ 31%. The figure shows simulations of the winner's curse (expressed on the y-axis as relative bias of research findings). These simulations suggest that initial effect estimates from studies powered between ∼ 8% and ∼ 31% are likely to be inflated by 25% to 50% (shown by the arrows in the figure). Inflated effect estimates make it difficult to determine an adequate sample size for replication studies, increasing the probability of type II errors. Figure is modified, with permission, from Ref. 103 © (2007) Cell Press.

The estimates shown in Figs 4 , 5 are likely to be optimistic, however, because they assume that statistical power and R are the only considerations in determining the probability that a research finding reflects a true effect. As we have already discussed, several other biases are also likely to reduce the probability that a research finding reflects a true effect. Moreover, the summary effect size estimates that we used to determine the statistical power of individual studies are themselves likely to be inflated owing to bias — our excess of significance test provided clear evidence for this. Therefore, the average statistical power of studies in our analysis may in fact be even lower than the 8–31% range we observed.

Ethical implications. Low average power in neuroscience studies also has ethical implications. In our analysis of animal model studies, the average sample size of 22 animals for the water maze experiments was only sufficient to detect an effect size of d = 1.26 with 80% power, and the average sample size of 24 animals for the radial maze experiments was only sufficient to detect an effect size of d = 1.20. In order to achieve 80% power to detect, in a single study, the most probable true effects as indicated by the meta-analysis, a sample size of 134 animals would be required for the water maze experiment (assuming an effect size of d = 0.49) and 68 animals for the radial maze experiment (assuming an effect size of d = 0.69); to achieve 95% power, these sample sizes would need to increase to 220 and 112, respectively. What is particularly striking, however, is the inefficiency of a continued reliance on small sample sizes. Despite the apparently large numbers of animals required to achieve acceptable statistical power in these experiments, the total numbers of animals actually used in the studies contributing to the meta-analyses were even larger: 420 for the water maze experiments and 514 for the radial maze experiments.

There is ongoing debate regarding the appropriate balance to strike between using as few animals as possible in experiments and the need to obtain robust, reliable findings. We argue that it is important to appreciate the waste associated with an underpowered study — even a study that achieves only 80% power still presents a 20% possibility that the animals have been sacrificed without the study detecting the underlying true effect. If the average power in neuroscience animal model studies is between 20–30%, as we observed in our analysis above, the ethical implications are clear.

Low power therefore has an ethical dimension — unreliable research is inefficient and wasteful. This applies to both human and animal research. The principles of the 'three Rs' in animal research (reduce, refine and replace) 83 require appropriate experimental design and statistics — both too many and too few animals present an issue as they reduce the value of research outputs. A requirement for sample size and power calculation is included in the Animal Research: Reporting In Vivo Experiments (ARRIVE) guidelines 84 , but such calculations require a clear appreciation of the expected magnitude of effects being sought.

Of course, it is also wasteful to continue data collection once it is clear that the effect being sought does not exist or is too small to be of interest. That is, studies are not just wasteful when they stop too early, they are also wasteful when they stop too late. Planned, sequential analyses are sometimes used in large clinical trials when there is considerable expense or potential harm associated with testing participants. Clinical trials may be stopped prematurely in the case of serious adverse effects, clear beneficial effects (in which case it would be unethical to continue to allocate participants to a placebo condition) or if the interim effects are so unimpressive that any prospect of a positive result with the planned sample size is extremely unlikely 85 . Within a significance testing framework, such interim analyses — and the protocol for stopping — must be planned for the assumptions of significance testing to hold. Concerns have been raised as to whether stopping trials early is ever justified given the tendency for such a practice to produce inflated effect size estimates 86 . Furthermore, the decision process around stopping is not often fully disclosed, increasing the scope for researcher degrees of freedom 86 . Alternative approaches exist. For example, within a Bayesian framework, one can monitor the Bayes factor and simply stop testing when the evidence is conclusive or when resources are expended 87 . Similarly, adopting conservative priors can substantially reduce the likelihood of claiming that an effect exists when in fact it does not 85 . At present, significance testing remains the dominant framework within neuroscience, but the flexibility of alternative (for example, Bayesian) approaches means that they should be taken seriously by the field.

Conclusions and future directions

A consequence of the remarkable growth in neuroscience over the past 50 years has been that the effects we now seek in our experiments are often smaller and more subtle than before as opposed to when mostly easily discernible 'low-hanging fruit' were targeted. At the same time, computational analysis of very large datasets is now relatively straightforward, so that an enormous number of tests can be run in a short time on the same dataset. These dramatic advances in the flexibility of research design and analysis have occurred without accompanying changes to other aspects of research design, particularly power. For example, the average sample size has not changed substantially over time 88 despite the fact that neuroscientists are likely to be pursuing smaller effects. The increase in research flexibility and the complexity of study designs 89 combined with the stability of sample size and search for increasingly subtle effects has a disquieting consequence: a dramatic increase in the likelihood that statistically significant findings are spurious. This may be at the root of the recent replication failures in the preclinical literature 8 and the correspondingly poor translation of these findings into humans 90 .

Low power is a problem in practice because of the normative publishing standards for producing novel, significant, clean results and the ubiquity of null hypothesis significance testing as the means of evaluating the truth of research findings. As we have shown, these factors result in biases that are exacerbated by low power. Ultimately, these biases reduce the reproducibility of neuroscience findings and negatively affect the validity of the accumulated findings. Unfortunately, publishing and reporting practices are unlikely to change rapidly. Nonetheless, existing scientific practices can be improved with small changes or additions that approximate key features of the idealized model 4 , 91 , 92 . We provide a summary of recommendations for future research practice in Box 2 .

Increasing disclosure. False positives occur more frequently and go unnoticed when degrees of freedom in data analysis and reporting are undisclosed 5 . Researchers can improve confidence in published reports by noting in the text: “We report how we determined our sample size, all data exclusions, all data manipulations, and all measures in the study.” 7 When such a statement is not possible, disclosure of the rationale and justification of deviations from what should be common practice (that is, reporting sample size, data exclusions, manipulations and measures) will improve readers' understanding and interpretation of the reported effects and, therefore, of what level of confidence in the reported effects is appropriate. In clinical trials, there is an increasing requirement to adhere to the Consolidated Standards of Reporting Trials ( CONSORT ), and the same is true for systematic reviews and meta-analyses, for which the Preferred Reporting Items for Systematic Reviews and Meta-Analyses ( PRISMA ) guidelines are now being adopted. A number of reporting guidelines have been produced for application to diverse study designs and tools, and an updated list is maintained by the EQUATOR Network 93 . A ten-item checklist of study quality has been developed by the Collaborative Approach to Meta-Analysis and Review of Animal Data in Experimental Stroke ( CAMARADES ), but to the best of our knowledge, this checklist is not yet widely used in primary studies.

Registration of confirmatory analysis plan. Both exploratory and confirmatory research strategies are legitimate and useful. However, presenting the result of an exploratory analysis as if it arose from a confirmatory test inflates the chance that the result is a false positive. In particular, p -values lose their diagnostic value if they are not the result of a pre-specified analysis plan for which all results are reported. Pre-registration — and, ultimately, full reporting of analysis plans — clarifies the distinction between confirmatory and exploratory analysis, encourages well-powered studies (at least in the case of confirmatory analyses) and reduces the file-drawer effect. These subsequently reduce the likelihood of false positive accumulation. The Open Science Framework ( OSF ) offers a registration mechanism for scientific research. For observational studies, it would be useful to register datasets in detail, so that one can be aware of how extensive the multiplicity and complexity of analyses can be 94 .

Improving availability of materials and data. Making research materials available will improve the quality of studies aimed at replicating and extending research findings. Making raw data available will improve data aggregation methods and confidence in reported results. There are multiple repositories for making data more widely available, such as The Dataverse Network Project and Dryad ) for data in general and others such as OpenfMRI , INDI and OASIS for neuroimaging data in particular. Also, commercial repositories (for example, figshare ) offer means for sharing data and other research materials. Finally, the OSF offers infrastructure for documenting, archiving and sharing data within collaborative teams and also making some or all of those research materials publicly available. Leading journals are increasingly adopting policies for making data, protocols and analytical codes available, at least for some types of studies. However, these policies are uncommonly adhered to 95 , and thus the ability for independent experts to repeat published analysis remains low 96 .

Incentivizing replication. Weak incentives for conducting and publishing replications are a threat to identifying false positives and accumulating precise estimates of research findings. There are many ways to alter replication incentives 97 . For example, journals could offer a submission option for registered replications of important research results (see, for example, a possible new submission format for Cortex 98 ). Groups of researchers can also collaborate on performing one or many replications to increase the total sample size (and therefore the statistical power) achieved while minimizing the labour and resource impact on any one contributor. Adoption of the gold standard of large-scale collaborative consortia and extensive replication in fields such as human genome epidemiology has transformed the reliability of the produced findings. Although previously almost all of the proposed candidate gene associations from small studies were false 99 (with some exceptions 100 ), collaborative consortia have substantially improved power, and the replicated results can be considered highly reliable. In another example, in the field of psychology, the Reproducibility Project is a collaboration of more than 100 researchers aiming to estimate the reproducibility of psychological science by replicating a large sample of studies published in 2008 in three psychology journals 92 . Each individual research study contributes just a small portion of time and effort, but the combined effect is substantial both for accumulating replications and for generating an empirical estimate of reproducibility.

Concluding remarks. Small, low-powered studies are endemic in neuroscience. Nevertheless, there are reasons to be optimistic. Some fields are confronting the problem of the poor reliability of research findings that arises from low-powered studies. For example, in genetic epidemiology sample sizes increased dramatically with the widespread understanding that the effects being sought are likely to be extremely small. This, together with an increasing requirement for strong statistical evidence and independent replication, has resulted in far more reliable results. Moreover, the pressure for emphasizing significant results is not absolute. For example, the Proteus phenomenon 101 suggests that refuting early results can be attractive in fields in which data can be produced rapidly. Nevertheless, we should not assume that science is effectively or efficiently self-correcting 102 . There is now substantial evidence that a large proportion of the evidence reported in the scientific literature may be unreliable. Acknowledging this challenge is the first step towards addressing the problematic aspects of current scientific practices and identifying effective solutions.

Box 1 | Key statistical terms

The Collaborative Approach to Meta-Analysis and Review of Animal Data from Experimental Studies ( CAMARADES ) is a collaboration that aims to reduce bias and improve the quality of methods and reporting in animal research. To this end, CAMARADES provides a resource for data sharing, aims to provide a web-based stratified meta-analysis bioinformatics engine and acts as a repository for completed reviews.

Effect size

An effect size is a standardized measure that quantifies the size of the difference between two groups or the strength of an association between two variables. As standardized measures, effect sizes allow estimates from different studies to be compared directly and also to be combined in meta-analyses.

Excess significance

Excess significance is the phenomenon whereby the published literature has an excess of statistically significant results that are due to biases in reporting. Several mechanisms contribute to reporting bias, including study publication bias, where the results of statistically non-significant ('negative') studies are left unpublished; selective outcome reporting bias, where null results are omitted; and selective analysis bias, where data are analysed with different methods that favour 'positive' results.

Fixed and random effects

A fixed-effect meta-analysis assumes that the underlying effect is the same (that is, fixed) in all studies and that any variation is due to sampling errors. By contrast, a random-effect meta-analysis does not require this assumption and allows for heterogeneity between studies. A test of heterogeneity in between-study effects is often used to test the fixed-effect assumption.

Meta-analysis

Meta-analysis refers to statistical methods for contrasting and combining results from different studies to provide more powerful estimates of the true effect size as opposed to a less precise effect size derived from a single study.

Positive predictive value

The positive predictive value (PPV) is the probability that a 'positive' research finding reflects a true effect (that is, the finding is a true positive). This probability of a research finding reflecting a true effect depends on the prior probability of it being true (before doing the study), the statistical power of the study and the level of statistical significance.

Proteus phenomenon

The Proteus phenomenon refers to the situation in which the first published study is often the most biased towards an extreme result (the winner's curse). Subsequent replication studies tend to be less biased towards the extreme, often finding evidence of smaller effects or even contradicting the findings from the initial study.

Statistical power

The statistical power of a test is the probability that it will correctly reject the null hypothesis when the null hypothesis is false (that is, the probability of not committing a type II error or making a false negative decision). The probability of committing a type II error is referred to as the false negative rate (β), and power is equal to 1 − β.

Winner's curse

The winner's curse refers to the phenomenon whereby the 'lucky' scientist who makes a discovery is cursed by finding an inflated estimate of that effect. The winner's curse occurs when thresholds, such as statistical significance, are used to determine the presence of an effect and is most severe when thresholds are stringent and studies are too small and thus have low power.

Box 2 | Recommendations for researchers

Perform an a priori power calculation

Use the existing literature to estimate the size of effect you are looking for and design your study accordingly. If time or financial constraints mean your study is underpowered, make this clear and acknowledge this limitation (or limitations) in the interpretation of your results.

Disclose methods and findings transparently

If the intended analyses produce null findings and you move on to explore your data in other ways, say so. Null findings locked in file drawers bias the literature, whereas exploratory analyses are only useful and valid if you acknowledge the caveats and limitations.

Pre-register your study protocol and analysis plan

Pre-registration clarifies whether analyses are confirmatory or exploratory, encourages well-powered studies and reduces opportunities for non-transparent data mining and selective reporting. Various mechanisms for this exist (for example, the Open Science Framework ).

Make study materials and data available

Making research materials available will improve the quality of studies aimed at replicating and extending research findings. Making raw data available will enhance opportunities for data aggregation and meta-analysis, and allow external checking of analyses and results.

Work collaboratively to increase power and replicate findings

Combining data increases the total sample size (and therefore power) while minimizing the labour and resource impact on any one contributor. Large-scale collaborative consortia in fields such as human genetic epidemiology have transformed the reliability of findings in these fields.

Change history

15 april 2013.

On page 2 of this article, the definition of R should have read: "R is the pre-study odds (that is, the odds that a probed effect is indeed non-null among the effects being probed)". This has been corrected in the online version.

Ioannidis, J. P. Why most published research findings are false. PLoS Med. 2 , e124 (2005). This study demonstrates that many (and possibly most) of the conclusions drawn from biomedical research are probably false. The reasons for this include using flexible study designs and flexible statistical analyses and running small studies with low statistical power.

Article   PubMed   PubMed Central   Google Scholar  

Fanelli, D. Negative results are disappearing from most disciplines and countries. Scientometrics 90 , 891–904 (2012).

Article   Google Scholar  

Greenwald, A. G. Consequences of prejudice against the null hypothesis. Psychol. Bull. 82 , 1–20 (1975).

Nosek, B. A., Spies, J. R. & Motyl, M. Scientific utopia: II. Restructuring incentives and practices to promote truth over publishability. Perspect. Psychol. Sci. 7 , 615–631 (2012).

Article   PubMed   Google Scholar  

Simmons, J. P., Nelson, L. D. & Simonsohn, U. False-positive psychology: undisclosed flexibility in data collection and analysis allows presenting anything as significant. Psychol. Sci. 22 , 1359–1366 (2011). This article empirically illustrates that flexible study designs and data analysis dramatically increase the possibility of obtaining a nominally significant result. However, conclusions drawn from these results are almost certainly false.

Sullivan, P. F. Spurious genetic associations. Biol. Psychiatry 61 , 1121–1126 (2007).

Article   CAS   PubMed   Google Scholar  

Begley, C. G. & Ellis, L. M. Drug development: raise standards for preclinical cancer research. Nature 483 , 531–533 (2012).

Prinz, F., Schlange, T. & Asadullah, K. Believe it or not: how much can we rely on published data on potential drug targets? Nature Rev. Drug Discov. 10 , 712 (2011).

Article   CAS   Google Scholar  

Fang, F. C. & Casadevall, A. Retracted science and the retraction index. Infect. Immun. 79 , 3855–3859 (2011).

Article   CAS   PubMed   PubMed Central   Google Scholar  

Munafo, M. R., Stothart, G. & Flint, J. Bias in genetic association studies and impact factor. Mol. Psychiatry 14 , 119–120 (2009).

Sterne, J. A. & Davey Smith, G. Sifting the evidence — what's wrong with significance tests? BMJ 322 , 226–231 (2001).

Ioannidis, J. P. A., Tarone, R. & McLaughlin, J. K. The false-positive to false-negative ratio in epidemiologic studies. Epidemiology 22 , 450–456 (2011).

Ioannidis, J. P. A. Why most discovered true associations are inflated. Epidemiology 19 , 640–648 (2008).

Tversky, A. & Kahneman, D. Belief in the law of small numbers. Psychol. Bull. 75 , 105–110 (1971).

Masicampo, E. J. & Lalande, D. R. A peculiar prevalence of p values just below .05. Q. J. Exp. Psychol. 65 , 2271–2279 (2012).

Carp, J. The secret lives of experiments: methods reporting in the fMRI literature. Neuroimage 63 , 289–300 (2012). This article reviews methods reporting and methodological choices across 241 recent fMRI studies and shows that there were nearly as many unique analytical pipelines as there were studies. In addition, many studies were underpowered to detect plausible effects.

Dwan, K. et al. Systematic review of the empirical evidence of study publication bias and outcome reporting bias. PLoS ONE 3 , e3081 (2008).

Sterne, J. A. et al. Recommendations for examining and interpreting funnel plot asymmetry in meta-analyses of randomised controlled trials. BMJ 343 , d4002 (2011).

Joy-Gaba, J. A. & Nosek, B. A. The surprisingly limited malleability of implicit racial evaluations. Soc. Psychol. 41 , 137–146 (2010).

Schmidt, K. & Nosek, B. A. Implicit (and explicit) racial attitudes barely changed during Barack Obama's presidential campaign and early presidency. J. Exp. Soc. Psychol. 46 , 308–314 (2010).

Evangelou, E., Siontis, K. C., Pfeiffer, T. & Ioannidis, J. P. Perceived information gain from randomized trials correlates with publication in high-impact factor journals. J. Clin. Epidemiol. 65 , 1274–1281 (2012).

Pereira, T. V. & Ioannidis, J. P. Statistically significant meta-analyses of clinical trials have modest credibility and inflated effects. J. Clin. Epidemiol. 64 , 1060–1069 (2011).

Faul, F., Erdfelder, E., Lang, A. G. & Buchner, A. G * Power 3: a flexible statistical power analysis program for the social, behavioral, and biomedical sciences. Behav. Res. Methods 39 , 175–191 (2007).

Babbage, D. R. et al. Meta-analysis of facial affect recognition difficulties after traumatic brain injury. Neuropsychology 25 , 277–285 (2011).

Bai, H. Meta-analysis of 5, 10-methylenetetrahydrofolate reductase gene poymorphism as a risk factor for ischemic cerebrovascular disease in a Chinese Han population. Neural Regen. Res. 6 , 277–285 (2011).

Google Scholar  

Bjorkhem-Bergman, L., Asplund, A. B. & Lindh, J. D. Metformin for weight reduction in non-diabetic patients on antipsychotic drugs: a systematic review and meta-analysis. J. Psychopharmacol. 25 , 299–305 (2011).

Bucossi, S. et al. Copper in Alzheimer's disease: a meta-analysis of serum, plasma, and cerebrospinal fluid studies. J. Alzheimers Dis. 24 , 175–185 (2011).

Chamberlain, S. R. et al. Translational approaches to frontostriatal dysfunction in attention-deficit/hyperactivity disorder using a computerized neuropsychological battery. Biol. Psychiatry 69 , 1192–1203 (2011).

Chang, W. P., Arfken, C. L., Sangal, M. P. & Boutros, N. N. Probing the relative contribution of the first and second responses to sensory gating indices: a meta-analysis. Psychophysiology 48 , 980–992 (2011).

Chang, X. L. et al. Functional parkin promoter polymorphism in Parkinson's disease: new data and meta-analysis. J. Neurol. Sci. 302 , 68–71 (2011).

Chen, C. et al. Allergy and risk of glioma: a meta-analysis. Eur. J. Neurol. 18 , 387–395 (2011).

Chung, A. K. & Chua, S. E. Effects on prolongation of Bazett's corrected QT interval of seven second-generation antipsychotics in the treatment of schizophrenia: a meta-analysis. J. Psychopharmacol. 25 , 646–666 (2011).

Domellof, E., Johansson, A. M. & Ronnqvist, L. Handedness in preterm born children: a systematic review and a meta-analysis. Neuropsychologia 49 , 2299–2310 (2011).

Etminan, N., Vergouwen, M. D., Ilodigwe, D. & Macdonald, R. L. Effect of pharmaceutical treatment on vasospasm, delayed cerebral ischemia, and clinical outcome in patients with aneurysmal subarachnoid hemorrhage: a systematic review and meta-analysis. J. Cereb. Blood Flow Metab. 31 , 1443–1451 (2011).

Feng, X. L. et al. Association of FK506 binding protein 5 ( FKBP5 ) gene rs4713916 polymorphism with mood disorders: a meta-analysis. Acta Neuropsychiatr. 23 , 12–19 (2011).

Green, M. J., Matheson, S. L., Shepherd, A., Weickert, C. S. & Carr, V. J. Brain-derived neurotrophic factor levels in schizophrenia: a systematic review with meta-analysis. Mol. Psychiatry 16 , 960–972 (2011).

Han, X. M., Wang, C. H., Sima, X. & Liu, S. Y. Interleukin-6–74G/C polymorphism and the risk of Alzheimer's disease in Caucasians: a meta-analysis. Neurosci. Lett. 504 , 4–8 (2011).

Hannestad, J., DellaGioia, N. & Bloch, M. The effect of antidepressant medication treatment on serum levels of inflammatory cytokines: a meta-analysis. Neuropsychopharmacology 36 , 2452–2459 (2011).

Hua, Y., Zhao, H., Kong, Y. & Ye, M. Association between the MTHFR gene and Alzheimer's disease: a meta-analysis. Int. J. Neurosci. 121 , 462–471 (2011).

Lindson, N. & Aveyard, P. An updated meta-analysis of nicotine preloading for smoking cessation: investigating mediators of the effect. Psychopharmacology 214 , 579–592 (2011).

Liu, H. et al. Association of 5-HTT gene polymorphisms with migraine: a systematic review and meta-analysis. J. Neurol. Sci. 305 , 57–66 (2011).

Liu, J. et al. PITX3 gene polymorphism is associated with Parkinson's disease in Chinese population. Brain Res. 1392 , 116–120 (2011).

MacKillop, J. et al. Delayed reward discounting and addictive behavior: a meta-analysis. Psychopharmacology 216 , 305–321 (2011).

Maneeton, N., Maneeton, B., Srisurapanont, M. & Martin, S. D. Bupropion for adults with attention-deficit hyperactivity disorder: meta-analysis of randomized, placebo-controlled trials. Psychiatry Clin. Neurosci. 65 , 611–617 (2011).

Ohi, K. et al. The SIGMAR1 gene is associated with a risk of schizophrenia and activation of the prefrontal cortex. Prog. Neuropsychopharmacol. Biol. Psychiatry 35 , 1309–1315 (2011).

Olabi, B. et al. Are there progressive brain changes in schizophrenia? A meta-analysis of structural magnetic resonance imaging studies. Biol. Psychiatry 70 , 88–96 (2011).

Oldershaw, A. et al. The socio-emotional processing stream in Anorexia Nervosa. Neurosci. Biobehav. Rev. 35 , 970–988 (2011).

Oliver, B. J., Kohli, E. & Kasper, L. H. Interferon therapy in relapsing-remitting multiple sclerosis: a systematic review and meta-analysis of the comparative trials. J. Neurol. Sci. 302 , 96–105 (2011).

Peerbooms, O. L. et al. Meta-analysis of MTHFR gene variants in schizophrenia, bipolar disorder and unipolar depressive disorder: evidence for a common genetic vulnerability? Brain Behav. Immun. 25 , 1530–1543 (2011).

Pizzagalli, D. A. Frontocingulate dysfunction in depression: toward biomarkers of treatment response. Neuropsychopharmacology 36 , 183–206 (2011).

Rist, P. M., Diener, H. C., Kurth, T. & Schurks, M. Migraine, migraine aura, and cervical artery dissection: a systematic review and meta-analysis. Cephalalgia 31 , 886–896 (2011).

Sexton, C. E., Kalu, U. G., Filippini, N., Mackay, C. E. & Ebmeier, K. P. A meta-analysis of diffusion tensor imaging in mild cognitive impairment and Alzheimer's disease. Neurobiol. Aging 32 , 2322.e5–2322.e18 (2011).

Shum, D., Levin, H. & Chan, R. C. Prospective memory in patients with closed head injury: a review. Neuropsychologia 49 , 2156–2165 (2011).

Sim, H. et al. Acupuncture for carpal tunnel syndrome: a systematic review of randomized controlled trials. J. Pain 12 , 307–314 (2011).

Song, F. et al. Meta-analysis of plasma amyloid-β levels in Alzheimer's disease. J. Alzheimers Dis. 26 , 365–375 (2011).

Sun, Q. L. et al. Correlation of E-selectin gene polymorphisms with risk of ischemic stroke A meta-analysis. Neural Regen. Res. 6 , 1731–1735 (2011).

CAS   Google Scholar  

Tian, Y., Kang, L. G., Wang, H. Y. & Liu, Z. Y. Meta-analysis of transcranial magnetic stimulation to treat post-stroke dysfunction. Neural Regen. Res. 6 , 1736–1741 (2011).

Trzesniak, C. et al. Adhesio interthalamica alterations in schizophrenia spectrum disorders: a systematic review and meta-analysis. Prog. Neuropsychopharmacol. Biol. Psychiatry 35 , 877–886 (2011).

Veehof, M. M., Oskam, M. J., Schreurs, K. M. & Bohlmeijer, E. T. Acceptance-based interventions for the treatment of chronic pain: a systematic review and meta-analysis. Pain 152 , 533–542 (2011).

Vergouwen, M. D., Etminan, N., Ilodigwe, D. & Macdonald, R. L. Lower incidence of cerebral infarction correlates with improved functional outcome after aneurysmal subarachnoid hemorrhage. J. Cereb. Blood Flow Metab. 31 , 1545–1553 (2011).

Vieta, E. et al. Effectiveness of psychotropic medications in the maintenance phase of bipolar disorder: a meta-analysis of randomized controlled trials. Int. J. Neuropsychopharmacol. 14 , 1029–1049 (2011).

Wisdom, N. M., Callahan, J. L. & Hawkins, K. A. The effects of apolipoprotein E on non-impaired cognitive functioning: a meta-analysis. Neurobiol. Aging 32 , 63–74 (2011).

Witteman, J., van Ijzendoorn, M. H., van de Velde, D., van Heuven, V. J. & Schiller, N. O. The nature of hemispheric specialization for linguistic and emotional prosodic perception: a meta-analysis of the lesion literature. Neuropsychologia 49 , 3722–3738 (2011).

Woon, F. & Hedges, D. W. Gender does not moderate hippocampal volume deficits in adults with posttraumatic stress disorder: a meta-analysis. Hippocampus 21 , 243–252 (2011).

Xuan, C. et al. No association between APOE ε 4 allele and multiple sclerosis susceptibility: a meta-analysis from 5472 cases and 4727 controls. J. Neurol. Sci. 308 , 110–116 (2011).

Yang, W. M., Kong, F. Y., Liu, M. & Hao, Z. L. Systematic review of risk factors for progressive ischemic stroke. Neural Regen. Res. 6 , 346–352 (2011).

Yang, Z., Li, W. J., Huang, T., Chen, J. M. & Zhang, X. Meta-analysis of Ginkgo biloba extract for the treatment of Alzheimer's disease. Neural Regen. Res. 6 , 1125–1129 (2011).

Yuan, H. et al. Meta-analysis of tau genetic polymorphism and sporadic progressive supranuclear palsy susceptibility. Neural Regen. Res. 6 , 353–359 (2011).

Zafar, S. N., Iqbal, A., Farez, M. F., Kamatkar, S. & de Moya, M. A. Intensive insulin therapy in brain injury: a meta-analysis. J. Neurotrauma 28 , 1307–1317 (2011).

Zhang, Y. G. et al. The −1082G/A polymorphism in IL-10 gene is associated with risk of Alzheimer's disease: a meta-analysis. J. Neurol. Sci. 303 , 133–138 (2011).

Zhu, Y., He, Z. Y. & Liu, H. N. Meta-analysis of the relationship between homocysteine, vitamin B(12), folate, and multiple sclerosis. J. Clin. Neurosci. 18 , 933–938 (2011).

Ioannidis, J. P. & Trikalinos, T. A. An exploratory test for an excess of significant findings. Clin. Trials 4 , 245–253 (2007). This study describes a test that evaluates whether there is an excess of significant findings in the published literature. The number of expected studies with statistically significant results is estimated and compared against the number of observed significant studies.

Ioannidis, J. P. Excess significance bias in the literature on brain volume abnormalities. Arch. Gen. Psychiatry 68 , 773–780 (2011).

Pfeiffer, T., Bertram, L. & Ioannidis, J. P. Quantifying selective reporting and the Proteus phenomenon for multiple datasets with similar bias. PLoS ONE 6 , e18362 (2011).

Tsilidis, K. K., Papatheodorou, S. I., Evangelou, E. & Ioannidis, J. P. Evaluation of excess statistical significance in meta-analyses of 98 biomarker associations with cancer risk. J. Natl Cancer Inst. 104 , 1867–1878 (2012).

Ioannidis, J. Clarifications on the application and interpretation of the test for excess significance and its extensions. J. Math. Psychol. (in the press).

David, S. P. et al. Potential reporting bias in small fMRI studies of the brain. PLoS Biol. (in the press).

Sena, E. S., van der Worp, H. B., Bath, P. M., Howells, D. W. & Macleod, M. R. Publication bias in reports of animal stroke studies leads to major overstatement of efficacy. PLoS Biol. 8 , e1000344 (2010).

Ioannidis, J. P. Extrapolating from animals to humans. Sci. Transl. Med. 4 , 151ps15 (2012).

Jonasson, Z. Meta-analysis of sex differences in rodent models of learning and memory: a review of behavioral and biological data. Neurosci. Biobehav. Rev. 28 , 811–825 (2005).

Macleod, M. R. et al. Evidence for the efficacy of NXY-059 in experimental focal cerebral ischaemia is confounded by study quality. Stroke 39 , 2824–2829 (2008).

Sena, E., van der Worp, H. B., Howells, D. & Macleod, M. How can we improve the pre-clinical development of drugs for stroke? Trends Neurosci. 30 , 433–439 (2007).

Russell, W. M. S. & Burch, R. L. The Principles of Humane Experimental Technique (Methuen, 1958).

Kilkenny, C., Browne, W. J., Cuthill, I. C., Emerson, M. & Altman, D. G. Improving bioscience research reporting: the ARRIVE guidelines for reporting animal research. PLoS Biol. 8 , e1000412 (2010).

Bassler, D., Montori, V. M., Briel, M., Glasziou, P. & Guyatt, G. Early stopping of randomized clinical trials for overt efficacy is problematic. J. Clin. Epidemiol. 61 , 241–246 (2008).

Montori, V. M. et al. Randomized trials stopped early for benefit: a systematic review. JAMA 294 , 2203–2209 (2005).

Berger, J. O. & Wolpert, R. L. The Likelihood Principle: A Review, Generalizations, and Statistical Implications (ed. Gupta, S. S.) (Institute of Mathematical Sciences, 1998).

Vesterinen, H. M. et al. Systematic survey of the design, statistical analysis, and reporting of studies published in the 2008 volume of the Journal of Cerebral Blood Flow and Metabolism . J. Cereb. Blood Flow Metab. 31 , 1064–1072 (2011).

Smith, R. A., Levine, T. R., Lachlan, K. A. & Fediuk, T. A. The high cost of complexity in experimental design and data analysis: type I and type II error rates in multiway ANOVA. Hum. Comm. Res. 28 , 515–530 (2002).

Perel, P. et al. Comparison of treatment effects between animal experiments and clinical trials: systematic review. BMJ 334 , 197 (2007).

Nosek, B. A. & Bar-Anan, Y. Scientific utopia: I. Opening scientific communication. Psychol. Inquiry 23 , 217–243 (2012).

Open-Science-Collaboration. An open, large-scale, collaborative effort to estimate the reproducibility of psychological science. Perspect. Psychol. Sci. 7 , 657–660 (2012). This article describes the Reproducibility Project — an open, large-scale, collaborative effort to systematically examine the rate and predictors of reproducibility in psychological science. This will allow the empirical rate of replication to be estimated.

Simera, I. et al. Transparent and accurate reporting increases reliability, utility, and impact of your research: reporting guidelines and the EQUATOR Network. BMC Med. 8 , 24 (2010).

Ioannidis, J. P. The importance of potential studies that have not existed and registration of observational data sets. JAMA 308 , 575–576 (2012).

Alsheikh-Ali, A. A., Qureshi, W., Al-Mallah, M. H. & Ioannidis, J. P. Public availability of published research data in high-impact journals. PLoS ONE 6 , e24357 (2011).

Ioannidis, J. P. et al. Repeatability of published microarray gene expression analyses. Nature Genet. 41 , 149–155 (2009).

Ioannidis, J. P. & Khoury, M. J. Improving validation practices in “omics” research. Science 334 , 1230–1232 (2011).

Chambers, C. D. Registered Reports : A new publishing initiative at Cortex . Cortex 49 , 609–610 (2013).

Ioannidis, J. P., Tarone, R. & McLaughlin, J. K. The false-positive to false-negative ratio in epidemiologic studies. Epidemiology 22 , 450–456 (2011).

Siontis, K. C., Patsopoulos, N. A. & Ioannidis, J. P. Replication of past candidate loci for common diseases and phenotypes in 100 genome-wide association studies. Eur. J. Hum. Genet. 18 , 832–837 (2010).

Ioannidis, J. P. & Trikalinos, T. A. Early extreme contradictory estimates may appear in published research: the Proteus phenomenon in molecular genetics research and randomized trials. J. Clin. Epidemiol. 58 , 543–549 (2005).

Ioannidis, J. Why science is not necessarily self-correcting. Perspect. Psychol. Sci. 7 , 645–654 (2012).

Zollner, S. & Pritchard, J. K. Overcoming the winner's curse: estimating penetrance parameters from case-control data. Am. J. Hum. Genet. 80 , 605–615 (2007).

Download references

Acknowledgements

M.R.M. and K.S.B. are members of the UK Centre for Tobacco Control Studies, a UK Public Health Research Centre of Excellence. Funding from British Heart Foundation, Cancer Research UK, Economic and Social Research Council, Medical Research Council and the UK National Institute for Health Research, under the auspices of the UK Clinical Research Collaboration, is gratefully acknowledged. The authors are grateful to G. Lewis for his helpful comments.

Author information

Authors and affiliations.

School of Experimental Psychology, University of Bristol, Bristol, BS8 1TU, UK

Katherine S. Button, Claire Mokrysz & Marcus R. Munafò

School of Social and Community Medicine, University of Bristol, Bristol, BS8 2BN, UK

Katherine S. Button

Stanford University School of Medicine, Stanford, 94305, California, USA

John P. A. Ioannidis

Department of Psychology, University of Virginia, Charlottesville, 22904, Virginia, USA

Brian A. Nosek

Wellcome Trust Centre for Human Genetics, University of Oxford, Oxford, OX3 7BN, UK

Jonathan Flint

School of Physiology and Pharmacology, University of Bristol, Bristol, BS8 1TD, UK

Emma S. J. Robinson

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Marcus R. Munafò .

Ethics declarations

Competing interests.

The authors declare no competing financial interests.

Related links

Further information.

Marcus R. Munafò's homepage

EQUATOR Network

The Dataverse Network Project

Rights and permissions

Reprints and permissions

About this article

Cite this article.

Button, K., Ioannidis, J., Mokrysz, C. et al. Power failure: why small sample size undermines the reliability of neuroscience. Nat Rev Neurosci 14 , 365–376 (2013). https://doi.org/10.1038/nrn3475

Download citation

Published : 10 April 2013

Issue Date : May 2013

DOI : https://doi.org/10.1038/nrn3475

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

This article is cited by

Association between hba1c and deep sternal wound infection after coronary artery bypass: a systematic review and meta-analysis.

• Haidong Luo

Journal of Cardiothoracic Surgery (2024)

Benchmark findings from a veteran electronic patient-reported outcomes evaluation from a chronic pain management telehealth program

• Jolie N. Haun
• Christopher A. Fowler
• Dustin D. French

BMC Health Services Research (2024)

Minimal clinically important difference (MCID), substantial clinical benefit (SCB), and patient-acceptable symptom state (PASS) in patients who have undergone total knee arthroplasty: a systematic review

• Filippo Migliorini
• Nicola Maffulli
• Ulf Krister Hofmann

Knee Surgery & Related Research (2024)

Exploring the steps of learning: computational modeling of initiatory-actions among individuals with attention-deficit/hyperactivity disorder

• Gili Katabi
• Nitzan Shahar

Translational Psychiatry (2024)

ezBIDS: Guided standardization of neuroimaging data interoperable with major data archives and platforms

• Daniel Levitas
• Soichi Hayashi
• Franco Pestilli

Scientific Data (2024)

Quick links

• Explore articles by subject
• Guide to authors
• Editorial policies

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

An official website of the United States government

The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

• Publications
• Account settings

Preview improvements coming to the PMC website in October 2024. Learn More or Try it out now .

• Advanced Search
• Journal List
• Biochem Med (Zagreb)
• v.31(1); 2021 Feb 15

Sample size, power and effect size revisited: simplified and practical approaches in pre-clinical, clinical and laboratory studies

Ceyhan ceran serdar.

1 Medical Biology and Genetics, Faculty of Medicine, Ankara Medipol University, Ankara, Turkey

Murat Cihan

2 Ordu University Training and Research Hospital, Ordu, Turkey

Doğan Yücel

3 Department of Medical Biochemistry, Lokman Hekim University School of Medicine, Ankara, Turkey

Muhittin A Serdar

4 Department of Medical Biochemistry, Acibadem Mehmet Ali Aydinlar University, Istanbul, Turkey

Calculating the sample size in scientific studies is one of the critical issues as regards the scientific contribution of the study. The sample size critically affects the hypothesis and the study design, and there is no straightforward way of calculating the effective sample size for reaching an accurate conclusion. Use of a statistically incorrect sample size may lead to inadequate results in both clinical and laboratory studies as well as resulting in time loss, cost, and ethical problems. This review holds two main aims. The first aim is to explain the importance of sample size and its relationship to effect size (ES) and statistical significance. The second aim is to assist researchers planning to perform sample size estimations by suggesting and elucidating available alternative software, guidelines and references that will serve different scientific purposes.

Introduction

Statistical analysis is a crucial part of a research. A scientific study must include statistical tools in the study, beginning from the planning stage. Developed in the last 20-30 years, information technology, along with evidence-based medicine, increased the spread and applicability of statistical science. Although scientists have understood the importance of statistical analysis for researchers, a significant number of researchers admit that they lack adequate knowledge about statistical concepts and principles ( 1 ). In a study by West and Ficalora, more than two-thirds of the clinicians emphasized that “the level of biostatistics education that is provided to the medical students is not sufficient” ( 2 ). As a result, it was suggested that statistical concepts were either poorly understood or not understood at all ( 3 , 4 ). Additionally, intentionally or not, researchers tend to draw conclusions that cannot be supported by the actual study data, often due to the misuse of statistics tools ( 5 ). As a result, a large number of statistical errors occur affecting the research results.

Although there are a variety of potential statistical errors that might occur in any kind of scientific research, it has been observed that the sources of error have changed due to the use of dedicated software that facilitates statistics in recent years. A summary of main statistical errors frequently encountered in scientific studies is provided below ( 6 - 13 ):

• Flawed and inadequate hypothesis;
• Improper study design;
• Lack of adequate control condition/group;
• Spectrum bias;
• Overstatement of the analysis results;
• Spurious correlations;
• Inadequate sample size;
• Circular analysis (creating bias by selecting the properties of the data retrospectively);
• Utilization of inappropriate statistical studies and fallacious bending of the analyses;
• p-hacking ( i.e. addition of new covariates post hoc to make P values significant);
• Excessive interpretation of limited or insignificant results (subjectivism);
• Confusion (intentionally or not) of correlations, relationships, and causations;
• Faulty multiple regression models;
• Confusion between P value and clinical significance; and
• Inappropriate presentation of the results and effects (erroneous tables, graphics, and figures).

Relationship among sample size, power, P value and effect size

In this review, we will concentrate on the problems associated with the relationships among sample size, power, P value, and effect size (ES). Practical suggestions will be provided whenever possible. In order to understand and interpret the sample size, power analysis, effect size, and P value, it is necessary to know how the hypothesis of the study was formed. It is best to evaluate a study for Type I and Type II errors ( Figure 1 ) through consideration of the study results in the context of its hypotheses ( 14 - 16 ).

Illustration of Type I and Type II errors.

A statistical hypothesis is the researcher’s best guess as to what the result of the experiment will show. It states, in a testable form the proposition the researcher plans to examine in a sample to be able to find out if the proposition is correct in the relevant population. There are two commonly used types of hypotheses in statistics. These are the null hypothesis (H0) and the alternative (H1) hypothesis. Essentially, the H1 is the researcher’s prediction of what will be the situation of the experimental group after the experimental treatment is applied. The H0 expresses the notion that there will be no effect from the experimental treatment.

Prior to the study, in addition to stating the hypothesis, the researcher must also select the alpha (α) level at which the hypothesis will be declared “supported”. The α represents how much risk the researcher is willing to take that the study will conclude H1 is correct when (in the full population) it is not correct (and thus, the null hypothesis is really true). In other words, alpha represents the probability of rejecting H0 when it actually is true. (Thus, the researcher has made an error by reporting that the experimental treatment makes a difference, when in fact, in the full population, that treatment has no effect.)

The most common α level chosen is 0.05, meaning the researcher is willing to take a 5% chance that a result supporting the hypothesis will be untrue in the full population. However, other alpha levels may also be appropriate in some circumstances. For pilot studies, α is often set at 0.10 or 0.20. In studies where it is especially important to avoid concluding a treatment is effective when it actually is not, the alpha may be set at a much lower value; it might be set at 0.001 or even lower. Drug studies are examples for studies that often set the alpha at 0.001 or lower because the consequences of releasing an ineffective drug can be extremely dangerous for patients.

Another probability value is called “the P value”. The P value is simply the obtained statistical probability of incorrectly accepting the alternate hypothesis. The P value is compared to the alpha value to determine if the result is “statistically significant”, meaning that with high probability the result found in the sample will also be true in the full population. If the P value is at or lower than alpha, H1 is accepted. If it is higher than alpha, the H1 is rejected and H0 is accepted instead.

There are actually two types of errors: the error of accepting H1 when it is not true in the population; this is called a Type I error; and is a false positive. The alpha defines the probability of a Type I error. Type I errors can happen for many reasons, from poor sampling that results in an experimental sample quite different from the population, to other mistakes occurring in the design stage or implementation of the research procedures. It is also possible to make an erroneous decision in the opposite direction; by incorrectly rejecting H1 and thus wrongly accepting H0. This is called a Type II error (or a false negative). The β defines the probability of a Type II error. The most common reason for this type of error is small sample size, especially when combined with moderately low or low effect sizes. Both small sample sizes and low effect sizes reduce the power in the study.

Power, which is the probability of rejecting a false null hypothesis, is calculated as 1-β (also expressed as “1 - Type II error probability”). For a Type II error of 0.15, the power is 0.85. Since reduction in the probability of committing a Type II error increases the risk of committing a Type I error (and vice versa ), a delicate balance should be established between the minimum allowed levels for Type I and Type II errors. The ideal power of a study is considered to be 0.8 (which can also be specified as 80%) ( 17 ). Sufficient sample size should be maintained to obtain a Type I error as low as 0.05 or 0.01 and a power as high as 0.8 or 0.9.

However, when power value falls below < 0.8, one cannot immediately conclude that the study is totally worthless. In parallel with this, the concept of “cost-effective sample size” has gained importance in recent years ( 18 ).

Additionally, the traditionally chosen alpha and beta error limits are generally arbitrary and are being used as a convention rather than being based on any scientific validity. Another key issue for a study is the determination, presentation and discussion of the effect size of the study, as will be discussed below in detail.

Although increasing the sample size is suggested to decrease the Type II errors, it will increase the cost of the project and delay the completion of the research activities in a foreseen period of time. In addition, it should not be forgotten that redundant samples may cause ethical problems ( 19 , 20 ).

Therefore, determination of the effective sample size is crucial to enable an efficient study with high significance, increasing the impact of the outcome. Unfortunately, information regarding sample size calculations are not often provided by clinical investigators in most diagnostic studies ( 21 , 22 ).

Calculation of the sample size

Different methods can be utilized before the onset of the study to calculate the most suitable sample size for the specific research. In addition to manual calculation, various nomograms or software can be used. The Figure 2 illustrates one of the most commonly used nomograms for sample size estimation using effect size and power ( 23 ).

Nomogram for sample size and power, for comparing two groups of equal size. Gaussian distributions assumed. Standardized difference (effect size) and aimed power values are initially selected on the nomogram. The line connecting these values cross the significance level region of the nomogram. The intercept at the appropriate significance value presents the required sample size for the study. In the above example, for effect size = 1, power = 0.8 and alpha value = 0.05, the sample size is found to be 30. (Adapted from reference 16 ).

Although manual calculation is preferred by the experts of the subject, it is a bit complicated and difficult for the researchers that are not statistics experts. In addition, considering the variety of the research types and characteristics, it should be noted that a great number of calculations will be required with too many variables ( Table 1 ) ( 16 , 24 - 30 ).

In recent years, numerous software and websites have been developed which can successfully calculate sample size in various study types. Some of the important software and websites are listed in Table 2 and are evaluated based both on the remarks stated in the literature and on our own experience, with respect to the content, ease of use, and cost ( 31 , 32 ). G-Power, R, and Piface stand out among the listed software in terms of being free-to use. G-Power is a free-to use tool that be used to calculate statistical power for many different t-tests, F-tests, χ 2 tests, z-tests and some exact tests. R is an open source programming language which can be tailored to meet individual statistical needs, by adding specific program modules called packages onto a specific base program. Piface is a java application specifically designed for sample size estimation and post-hoc power analysis. The most professional software is PASS (Power Analysis and Sample Size). With PASS, it is possible to analyse sample size and power for approximately 200 different study types. In addition, many websites provide substantial aid in calculating power and sample size, basing their methodology on scientific literature.

The sample size or the power of the study is directly related to the ES of the study. What is this important ES? The ES provides important information on how well the independent variable or variables predict the dependent variable. Low ES means that, independent variables don’t predict well because they are only slightly related to the dependent variable. Strong ES means that, independent variables are very good predictors of the dependent variable. Thus, ES is clinically important for evaluating how efficiently the clinicians can predict outcomes from the independent variables.

The scale of the ES values for different types of statistical tests conducted in different study types are presented in Table 3 .

In order to evaluate the effect of the study and indicate its clinical significance, it is very important to evaluate the effect size along with statistical significance. P value is important in the statistical evaluation of the research. While it provides information on presence/absence of an effect, it will not account for the size of the effect. For comprehensive presentation and interpretation of the studies, both effect size and statistical significance (P value) should be provided and considered.

It would be much easier to understand ES through an example. For example, assume that independent sample t-test is used to compare total cholesterol levels for two groups having normal distribution. Where X, SD and N stands for mean, standard deviation and sample size, respectively. Cohen’s d ES can be calculated as follows:

Mean (X), mmol/L Standard deviation (SD) Sample size (N)

Group 1 6.5 0.5 30

Group 2 5.2 0.8 30

Cohen d ES results represents: 0.8 large, 0.5 medium, 0.2 small effects). The result of 1.94 indicates a very large effect. Means of the two groups are remarkably different.

In the example above, the means of the two groups are largely different in a statistically significant manner. Yet, clinical importance of the effect (whether this effect is important for the patient, clinical condition, therapy type, outcome, etc .) needs to be specifically evaluated by the experts of the topic.

Power, alpha values, sample size, and ES are closely related with each other. Let us try to explain this relationship through different situations that we created using G-Power ( 33 , 34 ).

The Figure 3 shows the change of sample size depending on the ES changes (0.2, 1 and 2.5, respectively) provided that the power remains constant at 0.8. Arguably, case 3 is particularly common in pre-clinical studies, cell culture, and animal studies (usually 5-10 samples in animal studies or 3-12 samples in cell culture studies), while case 2 is more common in clinical studies. In clinical, epidemiological or meta-analysis studies, where the sample size is very large; case 1, which emphasizes the importance of smaller effects, is more commonly observed ( 33 ).

Relationship between effect size and sample size. P – power. ES - effect size. SS - sample size. The required sample size increases as the effect size decreases. In all cases, P value is set to 0.8. The sample sizes (SS) when ES is 0.2, 1, or 2.5; are 788, 34 and 8, respectively. The graphs at the bottom represent the influence of change in the sample size on the power.

In Figure 4 , case 4 exemplifies the change in power and ES values when the sample size is kept constant ( i.e. as low as 8). As can be seen here, in studies with low ES, working with few samples will mean waste of time, redundant processing, or unnecessary use of laboratory animals.

Relationship between effect size and power. Two different cases are schematized where the sample size is kept constant either at 8 or at 30. When the sample size is kept constant, the power of the study decreases as the effect size decreases. When the effect size is 2.5, even 8 samples are sufficient to obtain power = ~0.8. When the effect size is 1, increasing sample size from 8 to 30 significantly increases the power of the study. Yet, even 30 samples are not sufficient to reach a significant power value if effect size is as low as 0.2.

Likewise, case 5 exemplifies the situation where the sample size is kept constant at 30. In this case, it is important to note that when ES is 1, the power of the study will be around 0.8. Some statisticians arbitrarily regard 30 as a critical sample size. However, case 5 clearly demonstrates that it is essential not to underestimate the importance of ES, while deciding on the sample size.

Especially in recent years, where clinical significance or effectiveness of the results has outstripped the statistical significance; understanding the effect size and power has gained tremendous importance ( 35 – 38 ).

Preliminary information about the hypothesis is eminently important to calculate the sample size at intended power. Usually, this is accomplished by determining the effect size from the results of a previous study or a preliminary study. There are software available which can calculate sample size using the effect size

We now want to focus on sample size and power analysis in some of the most common research areas.

Determination of sample size in pre-clinical studies

Animal studies are the most critical studies in terms of sample size. Especially due to ethical concerns, it is vital to keep the sample size at the lowest sufficient level. It should be noted that, animal studies are radically different from human studies because many animal studies use inbred animals having extremely similar genetic background. Thus, far fewer animals are needed in the research because genetic differences that could affect the study results are kept to a minimum ( 39 , 40 ).

Consequently, alternative sample size estimation methodologies were suggested for each study type ( 41 - 44 ). If the effect size is to be determined using the results from previous or preliminary studies, sample size estimation may be performed using G-Power. In addition, Table 4 may also be used for easy estimation of the sample size ( 40 ).

In addition to sample size estimations that may be computed according to Table 4 , formulas stated in Table 1 and the websites mentioned in Table 2 may also be utilized to estimate sample size in animal studies. Relying on previous studies pose certain limitations since it may not always be possible to acquire reliable “pooled standard deviation” and “group mean” values.

Arifin et al. proposed simpler formulas ( Table 5 ) to calculate sample size in animal studies ( 45 ). In group comparison studies, it is possible to calculate the sample size as follows: N = (DF/k)+1 (Eq. 4).

Based on acceptable range of the degrees of freedom (DF), the DF in formulas are replaced with the minimum ( 10 ) and maximum ( 20 ). For example, in an experimental animal study where the use of 3 investigational drugs are tested minimum number of animals that will be required: N = (10/3)+1 = 4.3; rounded up to 5 animals / group, total sample size = 5 x 3 = 15 animals. Maximum number of animals that will be required: N = (20/3)+1 = 7.7; rounded down to 7 animals / group, total sample size = 7 x 3 = 21 animals.

In conclusion, for the recommended study, 5 to 7 animals per group will be required. In other words, a total of 15 to 21 animals will be required to keep the DF within the range of 10 to 20.

In a compilation where Ricci et al. reviewed 15 studies involving animal models, it was noted that the sample size used was 10 in average (between 6 and 18), however, no formal power analysis was reported by any of the groups. It was striking that, all studies included in the review have used parametric analysis without prior normality testing ( i.e. Shapiro-Wilk) to justify their statistical methodology ( 46 ).

It is noteworthy that, unnecessary animal use could be prevented by keeping the power at 0.8 and selecting one-tailed analysis over two-tailed analysis with an accepted 5% risk of making type I error as performed in some pharmacological studies, reducing the number of required animals by 14% ( 47 ).

Neumann et al. proposed a group-sequential design to minimize animal use without a decrease in statistical power. In this strategy, researchers started the experiments with only 30% of the animals that were initially planned to be included in the study. After an interim analysis of the results obtained with 30% of the animals, if sufficient power is not reached, another 30% is included in the study. If results from this initial 60% of the animals provide sufficient statistical power, then the rest of the animals are excused from the study. If not, the remaining animals are also included in the study. This approach was reported to save 20% of the animals in average, without leading to a decrease in statistical power ( 48 ).

Alternative sample size estimation strategies are implemented for animal testing in different countries. As an example, a local authority in southwestern Germany recommended that, in the absence of a formal sample size estimation, less than 7 animals per experimental group should be included in pilot studies and the total number of experimental animals should not exceed 100 ( 48 ).

On the other hand, it should be noted that, for a sample size of 8 to 10 animals per group, statistical significance will not be accomplished unless a large or very large ES (> 2) is expected ( 45 , 46 ). This problem remains as an important limitation for animal studies. Software like G-Power can be used for sample size estimation. In this case, results obtained from a previous or a preliminary study will be required to be used in the calculations. However, even when a previous study is available in literature, using its data for a sample size estimation will still pose an uncertainty risk unless a clearly detailed study design and data is provided in the publication. Although researchers suggested that reliability analyses could be performed by methods such as Markov Chain Monte Carlo, further research is needed in this regard ( 49 ).

The output of the joint workshop held by The National Institutes of Health (NIH), Nature Publishing Group and Science; “Principles and Guidelines for Reporting Preclinical Research” that was published in 2014, has since been acknowledged by many organizations and journals. This guide has shed significant light on studies using biological materials, involving animal studies, and handling image-based data ( 50 ).

Another important point regarding animal studies is the use of technical repetition (pseudo replication) instead of biological repetition. Technical repetition is a specific type of repetition where the same sample is measured multiple times, aiming to probe the noise associated with the measurement method or the device. Here, no matter how many times the same sample is measured, the actual sample size will remain the same. Let us assume a research group is investigating the effect of a therapeutic drug on blood glucose level. If the researchers measure the blood glucose level of 3 mice receiving the actual treatment and 3 mice receiving placebo, this would be a biological repetition. On the other hand, if the blood glucose level of a single mouse receiving the actual treatment and the blood glucose level of a single mouse receiving placebo are each measured 3 times, this would be technical repetition. Both designs will provide 6 data points to calculate P value, yet the P value obtained from the second design would be meaningless since each treatment group will only have one member ( Figure 5 ). Multiple measurements on single mice are pseudo replication; therefore do not contribute to N. No matter how ingenious, no statistical analysis method can fix incorrectly selected replicates at the post-experimental stage; replicate types should be selected accurately at the design stage. This problem is a critical limitation, especially in pre-clinical studies that conduct cell culture experiments. It is very important for critical assessment and evaluation of the published research results ( 51 ). This issue is mostly underestimated, concealed or ignored. It is striking that in some publications, the actual sample size is found to be as low as one. Experiments comparing drug treatments in a patient-derived stem cell line are specific examples for this situation. Although there may be many technical replications for such experiments and the experiment can be repeated several times, the original patient is a single biological entity. Similarly, when six metatarsals are harvested from the front paws of a single mouse and cultured as six individual cultures, another pseudo replication is practiced where the sample size is actually 1, instead of 6 ( 52 ). Lazic et al . suggested that almost half of the studies (46%) had mistaken pseudo replication (technical repeat) for genuine replication, while 32% did not provide sufficient information to enable evaluation of appropriateness of the sample size ( 53 , 54 ).

Technical vs biological repeat.

In studies providing qualitative data (such as electrophoresis, histology, chromatography, electron microscopy), the number of replications (“number of repeats” or “sample size”) should explicitly be stated.

Especially in pre-clinical studies, standard error of the mean (SEM) is frequently used instead of SD in some situations and by certain journals. The SEM is calculated by dividing the SD by the square root of the sample size (N). The SEM will indicate how variable the mean will be if the whole study is repeated many times. Whereas the SD is a measure of how scattered the scores within a set of data are. Since SD is usually higher than SEM, researchers tend to use SEM. While SEM is not a distribution criterion; there is a relation between SEM and 95% confidence interval (CI). For example, when N = 3, 95% CI is almost equal to mean ± 4 SEM, but when N ≥ 10; 95% CI equals to mean ± 2 SEM. Standard deviation and 95% CI can be used to report the statistical analysis results such as variation and precision on the same plot to demonstrate the differences between test groups ( 52 , 55 ).

Given the attrition and unexpected death risk of the laboratory animals during the study, the researchers are generally recommended to increase the sample size by 10% ( 56 ).

Sample size calculation for some genetic studies

Sample size is important for genetic studies as well. In genetic studies, calculation of allele frequencies, calculation of homozygous and heterozygous frequencies based on Hardy-Weinberg principle, natural selection, mutation, genetic drift, association, linkage, segregation, haplotype analysis are carried out by means of probability and statistical models ( 57 - 62 ). While G-Power is useful for basic statistics, substantial amount of analyses can be conducted using genetic power calculator ( http://zzz.bwh.harvard.edu/gpc/ ) ( 61 , 62 ). This calculator, which provides automated power analysis for variance components (VC) quantitative trait locus (QTL) linkage and association tests in sibships, and other common tests, is significantly effective especially for genetics studies analysing complex diseases.

Case-control association studies for single nucleotide polymorphisms (SNPs) may be facilitated using OSSE web site ( http://osse.bii.a-star.edu.sg/ ). As an example, let us assume the minor allele frequencies of an SNP in cases and controls are approximately 15% and 7% respectively. To have a power of 0.8 with 0.05 significance, the study is required to include 239 samples both for cases and controls, adding up to 578 samples in total ( Figure 6 ).

Interface of Online Sample Size Estimator (OSSE) Tool. (Available at: http://osse.bii.a-star.edu.sg/ ).

Hong and Park have proposed tables and graphics in their article for facilitating sample size estimation ( 57 ). With the assumption of 5% disease prevalence, 5% minor allele frequency and complete linkage disequilibrium (D’ = 1), the sample size in a case-control study with a single SNP marker, 1:1 case-to-control ratio, 0.8 statistical power, and 5% type I error rate can be calculated according to the genetic models of inheritance (allelic, additive, dominant, recessive, and co-dominant models) and the odd ratios of heterozygotes/rare homozygotes ( Table 6 ). As demonstrated by Hong and Park among all other types of inheritance, dominant inheritance requires the lowest sample size to achieve 0.8 statistical power. Whereas, testing a single SNP in a recessive inheritance model requires a very large sample size even with a high homozygote ratio, that is practically challenging with a limited budget ( 57 ). The Table 6 illustrates the difficulty in detecting a disease allele following a recessive mode of inheritance with moderate sample size.

Sample size and power analyses in clinical studies

In clinical research, sample size is calculated in line with the hypothesis and study design. The cross-over study design and parallel study design apply different approaches for sample size estimation. Unlike pre-clinical studies, a significant number of clinical journals necessitate sample size estimation for clinical studies.

The basic rules for sample size estimation in clinical trials are as follows ( 63 , 64 ):

• Error level (alpha): It is generally set as < 0.05. The sample size should be increased to compensate for the decrease in the effect size.
• Power must be > 0.8: The sample size should be increased to increase the power of the study. The higher the power, the lower the risk of missing an actual effect.

The relationship among clinical significance, statistical significance, power and effect size. In the example above, in order to provide a clinically significant effect, a treatment is required to trigger at least 0.5 mmol/L decreases in cholesterol levels. Four different scenarios are given for a candidate treatment, each having different mean total cholesterol change and 95% confidence interval. ES - effect size. N – number of participant. Adapted from reference 65 .

• Similarity and equivalence: The sample size required demonstrating similarity and equivalence is very low.

Sample size estimation can be performed manually using the formulas in Table 1 as well as software and websites in Table 2 (especially by G-Power). However, all of these calculations require preliminary results or previous study outputs regarding the hypothesis of interest. Sample size estimations are difficult in complex or mixed study designs. In addition: a) unplanned interim analysis, b) planned interim analysis and

• adjustments for common variables may be required for sample size estimation.

In addition, post-hoc power analysis (possible with G-Power, PASS) following the study significantly facilitates the evaluation of the results in clinical studies.

A number of high-quality journals emphasize that the statistical significance is not sufficient on its own. In fact, they would require evaluation of the results in terms of effect size and clinical effect as well as statistical significance.

In order to fully comprehend the effect size, it would be useful to know the study design in detail and evaluate the effect size with respect to the type of the statistical tests conducted as provided in Table 3 .

Hence, the sample size is one of the critical steps in planning clinical trials, and any negligence or shortcomings in its estimate may lead to rejection of an effective drug, process, or marker. Since statistical concepts have crucial roles in calculating the sample size, sufficient statistical expertise is of paramount importance for these vital studies.

Sample size, effect size and power calculation in laboratory studies

In clinical laboratories, software such as G-Power, Medcalc, Minitab, and Stata can be used for group comparisons (such as t-tests, Mann Whitney U, Wilcoxon, ANOVA, Friedman, Chi-square, etc. ), correlation analyses (Pearson, Spearman, etc .) and regression analyses.

Effect size that can be calculated according to the methods mentioned in Table 3 is important in clinical laboratories as well. However, there are additional important criteria that must be considered while investigating differences or relationships. Especially the guidelines (such as CLSI, RiliBÄK, CLIA, ISO documents) that were established according to many years of experience, and results obtained from biological variation studies provide us with essential information and critical values primarily on effect size and sometimes on sample size.

Furthermore, in addition to the statistical significance (P value interpretation), different evaluation criteria are also important for the assessment of the effect size. These include precision, accuracy, coefficient of variation (CV), standard deviation, total allowable error, bias, biological variation, and standard deviation index, etc . as recommended and elaborated by various guidelines and reference literature ( 66 - 70 ).

In this section, we will assess sample size, effect size, and power for some analysis types used in clinical laboratories.

Sample size in method and device comparisons

Sample size is a critical determinant for Linear, Passing Bablok, and Deming regression studies that are predominantly being used in method comparison studies. Sample size estimations for the Passing-Bablok and Deming method comparison studies are exemplified in Table 7 and Table 8 respectively. As seen in these tables, sample size estimations are based on slope, analytical precision (% CV), and range ratio (c) value ( 66 , 67 ). These tables might seem quite complicated for some researchers that are not familiar with statistics. Therefore, in order to further simplify sample size estimation; reference documents and guidelines have been prepared and published. As stated in CLSI EP09-A3 guideline, the general recommendation for the minimum sample size for validation studies to be conducted by the manufacturer is 100; while the minimum sample size for user-conducted verification is 40 ( 68 ). In addition, these documents clearly explain the requirements that should be considered while collecting the samples for method/device comparison studies. For instance, samples should be homogeneously dispersed covering the whole detection range. Hence, it should be kept in mind that randomly selected 40-100 sample will not be sufficient for impeccable method comparison ( 68 ).

Additionally, comparison studies might be carried out in clinical laboratories for other purposes; such as inter-device, where usage of relatively few samples is suggested to be sufficient. For method comparison studies to be conducted using patient samples; sample size estimation, and power analysis methodologies, in addition to the required number of replicates are defined in CLSI document EP31-A-IR. The critical point here is to know the values of constant difference, within-run standard deviation, and total sample standard deviation ( 69 ). While studies that compare devices having high analytical performance would suffice lower sample size; studies comparing devices with lower analytical performance would require higher sample size.

Lu et al. used maximum allowed differences for calculating sample sizes that would be required in Bland Altman comparison studies. This type of sample size estimation, which is critically important in laboratory medicine, can easily be performed using Medcalc software ( 70 ).

Sample size in lot to lot variation studies

It is acknowledged that lot-to-lot variation may influence the test results. In line with this, method comparison is also recommended to monitor the performance of the kit in use, between lot changes. To aid in the sample size estimation of these studies; CLSI has prepared the EP26-A guideline “User evaluation of between-reagent lot variation; approved guideline”, which provides a methodology like EP31-A-IR ( 71 , 72 ).

The Table 9 presents sample size and power values of a lot-to-lot variation study comparing glucose measurements at 3 different concentrations. In this example, if the difference in the glucose values measured by different lots is > 0.2 mmol/L, > 0.58 mmol/L and > 1.16 mmol/L at analyte concentrations of 2.77 mmol/L, 8.32 mmol/L and 16.65 mmol/L respectively, lots would be confirmed to be different. In a scenario where one sample is used for each concentration; if the lot-to-lot variation results obtained from each of the three different concentrations are lower than the rejection limits (meaning that the precision values for the tested lots are within the acceptance limits), then the lot variation is accepted to lie within the acceptance range. While the example for glucose measurements presented in the guideline suggests that “1 sample” would be sufficient at each analyte concentration, it should be noted that sample size might vary according to the number to devices to be tested, analytical performance results of the devices ( i.e. precision), total allowable error, etc. For different analytes and scenarios ( i.e. for occasions where one sample/concentration is not sufficient), researchers need to refer CLSI EP26-A ( 71 ).

Some researchers find CLSI EP26-A and CLSI EP31 rather complicated for estimating the sample size in lot-to-lot variation and method comparison studies (which are similar to a certain extent). They instead prefer to use the sample size (number of replicates) suggested by Mayo Laboratories. Mayo Laboratories decided that lot-to-lot variation studies may be conducted using 20 human samples where the data are analysed by Passing-Bablok regression and accepted according to the following criteria: a) slope of the regression line will lie between 0.9 and 1.1; b) R2 coefficient of determination will be > 0.95; c) the Y-intercept of the regression line will be < 50% of the lowest reportable concentration, d) difference of the means between reagent lots will be < 10% ( 73 ).

Sample size in verification studies

Acceptance limits should be defined before the verification and validation studies. These could be determined according to clinical cut-off values, biological variation, CLIA criteria, RiliBÄK criteria, criteria defined by the manufacturer, or state of the art criteria. In verification studies, the “sample size” and the “minimum proportion of the observed samples required to lie within the CI limits” are proportional. For instance, for a 50-sample study, 90% of the samples are required to lie within the CI limits for approval of the verification; while for a 200-sample study, 93% is required ( Table 10 ). In an example study whose total allowable error (TAE) is specified as 15%; 50 samples were measured. Results of the 46 samples (92% of all samples) lied within the TAE limit of 15%. Since the proportion of the samples having results within the 15% TAE limit (92% of the samples) exceeds the minimum proportion required to lie within the TAE limits (90% of the samples), the method is verified ( 74 ).

Especially in recent years, researchers tend to use CLSI EP15-A3 or alternative strategies relying on EP15-A3, for verification analyses. While the alternative strategies diverge from each other in many ways, most of them necessitate a sample size of at least 20 ( 75 - 78 ). Yet, for bias studies, especially for the ones involving External Quality Control materials, even lower sample sizes ( i.e. 10) may be observed ( 79 ). Verification still remains to be one of the critical problems for clinical laboratories. It is not possible to find a single criteria and a single verification method that fits all test methods ( i.e. immunological, chemical, chromatographical, etc. ).

While sample size for qualitative laboratory tests may vary according to the reference literature and the experimental context, CLSI EP12 recommends at least 50 positive and 50 negative samples, where 20% of the samples from each group are required to fall within cut-off value +/- 20% ( 80 , 81 ). According to the clinical microbiology validation/verification guideline Cumitech 31A, the minimum number of the samples in positive and negative groups is 100/each group for validation studies, and 10/each group for verification studies ( 82 ).

Sample size in diagnostic and prognostic studies

ROC analysis is the most important statistical analysis in diagnostic and prognostic studies. Although sample size estimation for ROC analyses might be slightly complicated; Medcalc, PASS, and Stata may be used to facilitate the estimation process. Before the actual size estimations, it is a prerequisite for the researcher to calculate potential area under the curve (AUC) using data from previous or preliminary studies. In addition, size estimation may also be calculated manually according to Table 1 , or using sensitivity (or TPF) and 1-specificity (FPF) values according to Table 11 which is adapted from CLSI EP24-A2 ( 83 , 84 ).

As is known, X-axis of the ROC curve is FPF, and Y-axis is TPF. While TPF represents sensitivity, FPF represents 1-specificity. Utilizing Table 11 , for a 0.85 sensitivity, 0.90 specificity and a maximum allowable error of 5% (L = 0.05), 196 positive and 139 negative samples are required. For the scenarios not included in this table, reader should refer to the formulas given under “diagnostic prognostic studies” subsection of Table 1 .

Standards for reporting of diagnostic accuracy studies (STARD) checklist may be followed for diagnostic studies. It is a powerful checklist whose application is explained in detail by Cohen et al. and Flaubaut et al. ( 85 , 86 ). This document suggests that, readers demand to understand the anticipated precision and power of the study and whether authors were successful in recruiting the sufficient number of participants; therefore it is critical for the authors to explain the intended sample size of their study and how it was determined. For this reason, in diagnostic and prognostic studies, sample size and power should clearly be stated.

As can be seen here, the critical parameters for sample size estimation are AUC, specificity and sensitivity, and their 95% CI values. The table 12 demonstrates the relationship of sample size with sensitivity, specificity, negative predictive value (NPV) and positive predictive value (PPV); the lower the sample size, the higher is the 95% CI values, leading to increase in type II errors ( 87 ). As can be seen here, confidence interval is narrowed as the sample size increases, leading to a decrease in type II errors.

Like all sample size calculations, preliminary information is required for sample size estimations in diagnostic and prognostic studies. Yet, variation occurs among sample size estimates that are calculated according to different reference literature or guidelines. This variation is especially prominent depending on the specific requirements of different countries and local authorities.

While sample size calculations for ROC analyses may easily be performed via Medcalc, the method explained by Hanley et al. and Delong et al. may be utilized to calculate sample size in studies comparing different ROC curves ( 88 , 89 ).

Sample size for reference interval determination

Both IFCC working groups and the CLSI guideline C28-A3c offer suggestions regarding sample size estimations in reference interval studies ( 90 - 93 ). These references mainly suggest at least 120 samples should be included for each study sub-group ( i.e., age-group, gender, race, etc. ). In addition, the guideline also states that, at least 20 samples should be studied for verification of the determined reference intervals.

Since extremes of the observed values may under/over-represent the actual percentile values of a population in nonparametric studies, care should be taken not to rely solely on the extreme values while determining the nonparametric 95% reference interval. Reed et al. suggested a minimum sample size of 120 to be used for 90% CI, 146 for 95% CI, and 210 for 99% CI (93). Linnet proposed that up to 700 samples should be obtained for results having highly skewed distributions ( 94 ). The IFCC Committee on Reference Intervals and Decision Limits working group recommends a minimum of 120 reference subjects for nonparametric methods, to obtain results within 90% CI limits ( 90 ).

Due to the inconvenience of the direct method, in addition to the challenges encountered using paediatric and geriatric samples as well as the samples obtained from complex biological fluids ( i.e. cerebrospinal fluid); indirect sample size estimations using patient results has gained significant importance in recent years. Hoffmann method, Bhattacharya method or their modified versions may be used for indirect determination of the reference intervals ( 95 - 101 ). While a specific sample size is not established, sample size between 1000 and 10.000 is recommended for each sub-group. For samples that cannot be easily acquired ( i.e. paediatric and geriatric samples, and complex biological fluids), sample sizes as low as 400 may be used for each sub-group ( 92 , 100 ).

Sample size in survey studies

The formulations given on Table 1 and the websites mentioned on Table 2 will be particularly useful for sample size estimations in survey studies which are dependent primarily on the population size ( 101 ).

Three critical aspects should be determined for sample size determination in survey studies:

• Population size
• Confidence Interval (CI) of 95% means that, when the study is repeated, with 95% probability, the same results will be obtained. Depending on the hypothesis and the study aim, confidence interval may lie between 90% and 99%. Confidence interval below 90% is not recommended.

For a given CI, sample size and ME is inversely proportional; sample size should be increased in order to obtain a narrower ME. On the contrary, for a fixed ME, CI and sample size is directly proportional; in order to obtain a higher CI, the sample size should be increased. In addition, sample size is directly proportional to the population size; higher sample size should be used for a larger population. A variation in ME causes a more drastic change in sample size than a variation in CI. As exemplified in Table 13 , for a population of 10,000 people, a survey with a 95% CI and 5% ME would require at least 370 samples. When CI is changed from 95% to 90% or 99%, the sample size which was 370 initially would change into 264 or 623 respectively. Whereas, when ME is changed from 5% to 10% or 1%; the sample size which was initially 370 would change into 96 or 4900 respectively. For other ME and CI levels, the researcher should refer to the equations and software provided on Table 1 and Table 2 .

The situation is slightly different for the survey studies to be conducted for problem detection. It would be most appropriate to perform a preliminary survey with a small sample size, followed by a power analysis, and completion of the study using the appropriate number of samples estimated based on the power analysis. While 30 is suggested as a minimum sample size for the preliminary studies, the optimal sample size can be determined using the formula suggested in Table 14 which is based on the prevalence value ( 103 ). It is unlikely to reach a sufficient power for revealing of uncommon problems (prevalence 0.02) at small sample sizes. As can be seen on the table, in the case of 0.02 prevalence, a sample size of 30 would yield a power of 0.45. In contrast, frequent problems ( i.e. prevalence 0.30) were discovered with higher power (0.83) even when the sample size was as low as 5. For situations where power and prevalence are known, effective sample size can easily be estimated using the formula in Table 1 .

Does big sample size always increase the impact of a study?

While larger sample size may provide researchers with great opportunities, it may create problems in interpretation of statistical significance and clinical impact. Especially in studies with big sample sizes, it is critically important for the researchers not to rely only on the magnitude of the regression (or correlation) coefficient, and the P value. The study results should be evaluated together with the effect size, study efficiencies ( i.e. basic research, clinical laboratory, and clinical studies) and confidence interval levels. Monte Carlo simulations could be utilized for statistical evaluations of the big data results ( 18 , 104 ).

As a result, sample size estimation is a critical step for scientific studies and may show significant differences according to research types. It is important that sample size estimation is planned ahead of the study, and may be performed through various routes:

• If a similar previous study is available, or preliminary results of the current study are present, their results may be used for sample size estimations via the websites and software mentioned in Table 1 and Table 2 . Some of these software may also be used to calculate effect size and power.
• If the magnitude of the measurand variation that is required for a substantial clinical effect is available ( i.e. significant change is 0.51 mmol/L for cholesterol, 26.5 mmol/L for creatinine, etc. ), it may be used for sample size estimation ( Figure 7 ). Presence of Total Allowable Error, constant and critical differences, biological variations, reference change value (RCV), etc. will further aid in sample size estimation process. Free software (especially G-Power) and web sites presented on Table 2 will facilitate calculations.
• If effect size can be calculated by a preliminary study, sample size estimations may be performed using the effect size ( via G-Power, Table 4 , etc. )
• In the absence of a previous study, if a preliminary study cannot be performed, an effect size may be initially estimated and be used for sample size estimations
• If none of the above is available or possible, relevant literature may be used for sample size estimation.
• For clinical laboratories, especially CLSI documents and guidelines may prove useful for sample size estimation ( Table 9,11 ​ 9,11 ).

Sample size estimations may be rather complex, requiring advanced knowledge and experience. In order to properly appreciate the concept and perform precise size estimation, one should comprehend properties of different study techniques and relevant statistics to certain extend. To assist researchers in different fields, we aimed to compile useful guidelines, references and practical software for calculating sample size and effect size in various study types. Sample size estimation and the relationship between P value and effect size are key points for comprehension and evaluation of biological studies. Evaluation of statistical significance together with the effect size is critical for both basic science, and clinical and laboratory studies. Therefore, effect size and confidence intervals should definitely be provided and its impact on the laboratory/clinical results should be discussed thoroughly.

Potential conflict of interest

None declared.

• Research article
• Open access
• Published: 21 November 2018

Characterising and justifying sample size sufficiency in interview-based studies: systematic analysis of qualitative health research over a 15-year period

• Konstantina Vasileiou   ORCID: orcid.org/0000-0001-5047-3920 1 ,
• Julie Barnett 1 ,
• Susan Thorpe 2 &
• Terry Young 3  

BMC Medical Research Methodology volume  18 , Article number:  148 ( 2018 ) Cite this article

722k Accesses

1126 Citations

172 Altmetric

Metrics details

Choosing a suitable sample size in qualitative research is an area of conceptual debate and practical uncertainty. That sample size principles, guidelines and tools have been developed to enable researchers to set, and justify the acceptability of, their sample size is an indication that the issue constitutes an important marker of the quality of qualitative research. Nevertheless, research shows that sample size sufficiency reporting is often poor, if not absent, across a range of disciplinary fields.

A systematic analysis of single-interview-per-participant designs within three health-related journals from the disciplines of psychology, sociology and medicine, over a 15-year period, was conducted to examine whether and how sample sizes were justified and how sample size was characterised and discussed by authors. Data pertinent to sample size were extracted and analysed using qualitative and quantitative analytic techniques.

Our findings demonstrate that provision of sample size justifications in qualitative health research is limited; is not contingent on the number of interviews; and relates to the journal of publication. Defence of sample size was most frequently supported across all three journals with reference to the principle of saturation and to pragmatic considerations. Qualitative sample sizes were predominantly – and often without justification – characterised as insufficient (i.e., ‘small’) and discussed in the context of study limitations. Sample size insufficiency was seen to threaten the validity and generalizability of studies’ results, with the latter being frequently conceived in nomothetic terms.

Conclusions

We recommend, firstly, that qualitative health researchers be more transparent about evaluations of their sample size sufficiency, situating these within broader and more encompassing assessments of data adequacy . Secondly, we invite researchers critically to consider how saturation parameters found in prior methodological studies and sample size community norms might best inform, and apply to, their own project and encourage that data adequacy is best appraised with reference to features that are intrinsic to the study at hand. Finally, those reviewing papers have a vital role in supporting and encouraging transparent study-specific reporting.

Peer Review reports

Sample adequacy in qualitative inquiry pertains to the appropriateness of the sample composition and size . It is an important consideration in evaluations of the quality and trustworthiness of much qualitative research [ 1 ] and is implicated – particularly for research that is situated within a post-positivist tradition and retains a degree of commitment to realist ontological premises – in appraisals of validity and generalizability [ 2 , 3 , 4 , 5 ].

Samples in qualitative research tend to be small in order to support the depth of case-oriented analysis that is fundamental to this mode of inquiry [ 5 ]. Additionally, qualitative samples are purposive, that is, selected by virtue of their capacity to provide richly-textured information, relevant to the phenomenon under investigation. As a result, purposive sampling [ 6 , 7 ] – as opposed to probability sampling employed in quantitative research – selects ‘information-rich’ cases [ 8 ]. Indeed, recent research demonstrates the greater efficiency of purposive sampling compared to random sampling in qualitative studies [ 9 ], supporting related assertions long put forward by qualitative methodologists.

Sample size in qualitative research has been the subject of enduring discussions [ 4 , 10 , 11 ]. Whilst the quantitative research community has established relatively straightforward statistics-based rules to set sample sizes precisely, the intricacies of qualitative sample size determination and assessment arise from the methodological, theoretical, epistemological, and ideological pluralism that characterises qualitative inquiry (for a discussion focused on the discipline of psychology see [ 12 ]). This mitigates against clear-cut guidelines, invariably applied. Despite these challenges, various conceptual developments have sought to address this issue, with guidance and principles [ 4 , 10 , 11 , 13 , 14 , 15 , 16 , 17 , 18 , 19 , 20 ], and more recently, an evidence-based approach to sample size determination seeks to ground the discussion empirically [ 21 , 22 , 23 , 24 , 25 , 26 , 27 , 28 , 29 , 30 , 31 , 32 , 33 , 34 , 35 ].

Focusing on single-interview-per-participant qualitative designs, the present study aims to further contribute to the dialogue of sample size in qualitative research by offering empirical evidence around justification practices associated with sample size. We next review the existing conceptual and empirical literature on sample size determination.

Sample size in qualitative research: Conceptual developments and empirical investigations

Qualitative research experts argue that there is no straightforward answer to the question of ‘how many’ and that sample size is contingent on a number of factors relating to epistemological, methodological and practical issues [ 36 ]. Sandelowski [ 4 ] recommends that qualitative sample sizes are large enough to allow the unfolding of a ‘new and richly textured understanding’ of the phenomenon under study, but small enough so that the ‘deep, case-oriented analysis’ (p. 183) of qualitative data is not precluded. Morse [ 11 ] posits that the more useable data are collected from each person, the fewer participants are needed. She invites researchers to take into account parameters, such as the scope of study, the nature of topic (i.e. complexity, accessibility), the quality of data, and the study design. Indeed, the level of structure of questions in qualitative interviewing has been found to influence the richness of data generated [ 37 ], and so, requires attention; empirical research shows that open questions, which are asked later on in the interview, tend to produce richer data [ 37 ].

Beyond such guidance, specific numerical recommendations have also been proffered, often based on experts’ experience of qualitative research. For example, Green and Thorogood [ 38 ] maintain that the experience of most qualitative researchers conducting an interview-based study with a fairly specific research question is that little new information is generated after interviewing 20 people or so belonging to one analytically relevant participant ‘category’ (pp. 102–104). Ritchie et al. [ 39 ] suggest that studies employing individual interviews conduct no more than 50 interviews so that researchers are able to manage the complexity of the analytic task. Similarly, Britten [ 40 ] notes that large interview studies will often comprise of 50 to 60 people. Experts have also offered numerical guidelines tailored to different theoretical and methodological traditions and specific research approaches, e.g. grounded theory, phenomenology [ 11 , 41 ]. More recently, a quantitative tool was proposed [ 42 ] to support a priori sample size determination based on estimates of the prevalence of themes in the population. Nevertheless, this more formulaic approach raised criticisms relating to assumptions about the conceptual [ 43 ] and ontological status of ‘themes’ [ 44 ] and the linearity ascribed to the processes of sampling, data collection and data analysis [ 45 ].

In terms of principles, Lincoln and Guba [ 17 ] proposed that sample size determination be guided by the criterion of informational redundancy , that is, sampling can be terminated when no new information is elicited by sampling more units. Following the logic of informational comprehensiveness Malterud et al. [ 18 ] introduced the concept of information power as a pragmatic guiding principle, suggesting that the more information power the sample provides, the smaller the sample size needs to be, and vice versa.

Undoubtedly, the most widely used principle for determining sample size and evaluating its sufficiency is that of saturation . The notion of saturation originates in grounded theory [ 15 ] – a qualitative methodological approach explicitly concerned with empirically-derived theory development – and is inextricably linked to theoretical sampling. Theoretical sampling describes an iterative process of data collection, data analysis and theory development whereby data collection is governed by emerging theory rather than predefined characteristics of the population. Grounded theory saturation (often called theoretical saturation) concerns the theoretical categories – as opposed to data – that are being developed and becomes evident when ‘gathering fresh data no longer sparks new theoretical insights, nor reveals new properties of your core theoretical categories’ [ 46 p. 113]. Saturation in grounded theory, therefore, does not equate to the more common focus on data repetition and moves beyond a singular focus on sample size as the justification of sampling adequacy [ 46 , 47 ]. Sample size in grounded theory cannot be determined a priori as it is contingent on the evolving theoretical categories.

Saturation – often under the terms of ‘data’ or ‘thematic’ saturation – has diffused into several qualitative communities beyond its origins in grounded theory. Alongside the expansion of its meaning, being variously equated with ‘no new data’, ‘no new themes’, and ‘no new codes’, saturation has emerged as the ‘gold standard’ in qualitative inquiry [ 2 , 26 ]. Nevertheless, and as Morse [ 48 ] asserts, whilst saturation is the most frequently invoked ‘guarantee of qualitative rigor’, ‘it is the one we know least about’ (p. 587). Certainly researchers caution that saturation is less applicable to, or appropriate for, particular types of qualitative research (e.g. conversation analysis, [ 49 ]; phenomenological research, [ 50 ]) whilst others reject the concept altogether [ 19 , 51 ].

Methodological studies in this area aim to provide guidance about saturation and develop a practical application of processes that ‘operationalise’ and evidence saturation. Guest, Bunce, and Johnson [ 26 ] analysed 60 interviews and found that saturation of themes was reached by the twelfth interview. They noted that their sample was relatively homogeneous, their research aims focused, so studies of more heterogeneous samples and with a broader scope would be likely to need a larger size to achieve saturation. Extending the enquiry to multi-site, cross-cultural research, Hagaman and Wutich [ 28 ] showed that sample sizes of 20 to 40 interviews were required to achieve data saturation of meta-themes that cut across research sites. In a theory-driven content analysis, Francis et al. [ 25 ] reached data saturation at the 17th interview for all their pre-determined theoretical constructs. The authors further proposed two main principles upon which specification of saturation be based: (a) researchers should a priori specify an initial analysis sample (e.g. 10 interviews) which will be used for the first round of analysis and (b) a stopping criterion , that is, a number of interviews (e.g. 3) that needs to be further conducted, the analysis of which will not yield any new themes or ideas. For greater transparency, Francis et al. [ 25 ] recommend that researchers present cumulative frequency graphs supporting their judgment that saturation was achieved. A comparative method for themes saturation (CoMeTS) has also been suggested [ 23 ] whereby the findings of each new interview are compared with those that have already emerged and if it does not yield any new theme, the ‘saturated terrain’ is assumed to have been established. Because the order in which interviews are analysed can influence saturation thresholds depending on the richness of the data, Constantinou et al. [ 23 ] recommend reordering and re-analysing interviews to confirm saturation. Hennink, Kaiser and Marconi’s [ 29 ] methodological study sheds further light on the problem of specifying and demonstrating saturation. Their analysis of interview data showed that code saturation (i.e. the point at which no additional issues are identified) was achieved at 9 interviews, but meaning saturation (i.e. the point at which no further dimensions, nuances, or insights of issues are identified) required 16–24 interviews. Although breadth can be achieved relatively soon, especially for high-prevalence and concrete codes, depth requires additional data, especially for codes of a more conceptual nature.

Critiquing the concept of saturation, Nelson [ 19 ] proposes five conceptual depth criteria in grounded theory projects to assess the robustness of the developing theory: (a) theoretical concepts should be supported by a wide range of evidence drawn from the data; (b) be demonstrably part of a network of inter-connected concepts; (c) demonstrate subtlety; (d) resonate with existing literature; and (e) can be successfully submitted to tests of external validity.

Other work has sought to examine practices of sample size reporting and sufficiency assessment across a range of disciplinary fields and research domains, from nutrition [ 34 ] and health education [ 32 ], to education and the health sciences [ 22 , 27 ], information systems [ 30 ], organisation and workplace studies [ 33 ], human computer interaction [ 21 ], and accounting studies [ 24 ]. Others investigated PhD qualitative studies [ 31 ] and grounded theory studies [ 35 ]. Incomplete and imprecise sample size reporting is commonly pinpointed by these investigations whilst assessment and justifications of sample size sufficiency are even more sporadic.

Sobal [ 34 ] examined the sample size of qualitative studies published in the Journal of Nutrition Education over a period of 30 years. Studies that employed individual interviews ( n  = 30) had an average sample size of 45 individuals and none of these explicitly reported whether their sample size sought and/or attained saturation. A minority of articles discussed how sample-related limitations (with the latter most often concerning the type of sample, rather than the size) limited generalizability. A further systematic analysis [ 32 ] of health education research over 20 years demonstrated that interview-based studies averaged 104 participants (range 2 to 720 interviewees). However, 40% did not report the number of participants. An examination of 83 qualitative interview studies in leading information systems journals [ 30 ] indicated little defence of sample sizes on the basis of recommendations by qualitative methodologists, prior relevant work, or the criterion of saturation. Rather, sample size seemed to correlate with factors such as the journal of publication or the region of study (US vs Europe vs Asia). These results led the authors to call for more rigor in determining and reporting sample size in qualitative information systems research and to recommend optimal sample size ranges for grounded theory (i.e. 20–30 interviews) and single case (i.e. 15–30 interviews) projects.

Similarly, fewer than 10% of articles in organisation and workplace studies provided a sample size justification relating to existing recommendations by methodologists, prior relevant work, or saturation [ 33 ], whilst only 17% of focus groups studies in health-related journals provided an explanation of sample size (i.e. number of focus groups), with saturation being the most frequently invoked argument, followed by published sample size recommendations and practical reasons [ 22 ]. The notion of saturation was also invoked by 11 out of the 51 most highly cited studies that Guetterman [ 27 ] reviewed in the fields of education and health sciences, of which six were grounded theory studies, four phenomenological and one a narrative inquiry. Finally, analysing 641 interview-based articles in accounting, Dai et al. [ 24 ] called for more rigor since a significant minority of studies did not report precise sample size.

Despite increasing attention to rigor in qualitative research (e.g. [ 52 ]) and more extensive methodological and analytical disclosures that seek to validate qualitative work [ 24 ], sample size reporting and sufficiency assessment remain inconsistent and partial, if not absent, across a range of research domains.

Objectives of the present study

The present study sought to enrich existing systematic analyses of the customs and practices of sample size reporting and justification by focusing on qualitative research relating to health. Additionally, this study attempted to expand previous empirical investigations by examining how qualitative sample sizes are characterised and discussed in academic narratives. Qualitative health research is an inter-disciplinary field that due to its affiliation with medical sciences, often faces views and positions reflective of a quantitative ethos. Thus qualitative health research constitutes an emblematic case that may help to unfold underlying philosophical and methodological differences across the scientific community that are crystallised in considerations of sample size. The present research, therefore, incorporates a comparative element on the basis of three different disciplines engaging with qualitative health research: medicine, psychology, and sociology. We chose to focus our analysis on single-per-participant-interview designs as this not only presents a popular and widespread methodological choice in qualitative health research, but also as the method where consideration of sample size – defined as the number of interviewees – is particularly salient.

Study design

A structured search for articles reporting cross-sectional, interview-based qualitative studies was carried out and eligible reports were systematically reviewed and analysed employing both quantitative and qualitative analytic techniques.

We selected journals which (a) follow a peer review process, (b) are considered high quality and influential in their field as reflected in journal metrics, and (c) are receptive to, and publish, qualitative research (Additional File  1 presents the journals’ editorial positions in relation to qualitative research and sample considerations where available). Three health-related journals were chosen, each representing a different disciplinary field; the British Medical Journal (BMJ) representing medicine, the British Journal of Health Psychology (BJHP) representing psychology, and the Sociology of Health & Illness (SHI) representing sociology.

Search strategy to identify studies

Employing the search function of each individual journal, we used the terms ‘interview*’ AND ‘qualitative’ and limited the results to articles published between 1 January 2003 and 22 September 2017 (i.e. a 15-year review period).

Eligibility criteria

To be eligible for inclusion in the review, the article had to report a cross-sectional study design. Longitudinal studies were thus excluded whilst studies conducted within a broader research programme (e.g. interview studies nested in a trial, as part of a broader ethnography, as part of a longitudinal research) were included if they reported only single-time qualitative interviews. The method of data collection had to be individual, synchronous qualitative interviews (i.e. group interviews, structured interviews and e-mail interviews over a period of time were excluded), and the data had to be analysed qualitatively (i.e. studies that quantified their qualitative data were excluded). Mixed method studies and articles reporting more than one qualitative method of data collection (e.g. individual interviews and focus groups) were excluded. Figure  1 , a PRISMA flow diagram [ 53 ], shows the number of: articles obtained from the searches and screened; papers assessed for eligibility; and articles included in the review (Additional File  2 provides the full list of articles included in the review and their unique identifying code – e.g. BMJ01, BJHP02, SHI03). One review author (KV) assessed the eligibility of all papers identified from the searches. When in doubt, discussions about retaining or excluding articles were held between KV and JB in regular meetings, and decisions were jointly made.

PRISMA flow diagram

Data extraction and analysis

A data extraction form was developed (see Additional File  3 ) recording three areas of information: (a) information about the article (e.g. authors, title, journal, year of publication etc.); (b) information about the aims of the study, the sample size and any justification for this, the participant characteristics, the sampling technique and any sample-related observations or comments made by the authors; and (c) information about the method or technique(s) of data analysis, the number of researchers involved in the analysis, the potential use of software, and any discussion around epistemological considerations. The Abstract, Methods and Discussion (and/or Conclusion) sections of each article were examined by one author (KV) who extracted all the relevant information. This was directly copied from the articles and, when appropriate, comments, notes and initial thoughts were written down.

To examine the kinds of sample size justifications provided by articles, an inductive content analysis [ 54 ] was initially conducted. On the basis of this analysis, the categories that expressed qualitatively different sample size justifications were developed.

We also extracted or coded quantitative data regarding the following aspects:

Journal and year of publication

Number of interviews

Number of participants

Presence of sample size justification(s) (Yes/No)

Presence of a particular sample size justification category (Yes/No), and

Number of sample size justifications provided

Descriptive and inferential statistical analyses were used to explore these data.

A thematic analysis [ 55 ] was then performed on all scientific narratives that discussed or commented on the sample size of the study. These narratives were evident both in papers that justified their sample size and those that did not. To identify these narratives, in addition to the methods sections, the discussion sections of the reviewed articles were also examined and relevant data were extracted and analysed.

In total, 214 articles – 21 in the BMJ, 53 in the BJHP and 140 in the SHI – were eligible for inclusion in the review. Table  1 provides basic information about the sample sizes – measured in number of interviews – of the studies reviewed across the three journals. Figure  2 depicts the number of eligible articles published each year per journal.

The publication of qualitative studies in the BMJ was significantly reduced from 2012 onwards and this appears to coincide with the initiation of the BMJ Open to which qualitative studies were possibly directed.

Pairwise comparisons following a significant Kruskal-Wallis Footnote 2 test indicated that the studies published in the BJHP had significantly ( p  < .001) smaller samples sizes than those published either in the BMJ or the SHI. Sample sizes of BMJ and SHI articles did not differ significantly from each other.

Sample size justifications: Results from the quantitative and qualitative content analysis

Ten (47.6%) of the 21 BMJ studies, 26 (49.1%) of the 53 BJHP papers and 24 (17.1%) of the 140 SHI articles provided some sort of sample size justification. As shown in Table  2 , the majority of articles which justified their sample size provided one justification (70% of articles); fourteen studies (25%) provided two distinct justifications; one study (1.7%) gave three justifications and two studies (3.3%) expressed four distinct justifications.

There was no association between the number of interviews (i.e. sample size) conducted and the provision of a justification (rpb = .054, p  = .433). Within journals, Mann-Whitney tests indicated that sample sizes of ‘justifying’ and ‘non-justifying’ articles in the BMJ and SHI did not differ significantly from each other. In the BJHP, ‘justifying’ articles ( Mean rank  = 31.3) had significantly larger sample sizes than ‘non-justifying’ studies ( Mean rank  = 22.7; U = 237.000, p  < .05).

There was a significant association between the journal a paper was published in and the provision of a justification (χ 2 (2) = 23.83, p  < .001). BJHP studies provided a sample size justification significantly more often than would be expected ( z  = 2.9); SHI studies significantly less often ( z  = − 2.4). If an article was published in the BJHP, the odds of providing a justification were 4.8 times higher than if published in the SHI. Similarly if published in the BMJ, the odds of a study justifying its sample size were 4.5 times higher than in the SHI.

The qualitative content analysis of the scientific narratives identified eleven different sample size justifications. These are described below and illustrated with excerpts from relevant articles. By way of a summary, the frequency with which these were deployed across the three journals is indicated in Table  3 .

Saturation was the most commonly invoked principle (55.4% of all justifications) deployed by studies across all three journals to justify the sufficiency of their sample size. In the BMJ, two studies claimed that they achieved data saturation (BMJ17; BMJ18) and one article referred descriptively to achieving saturation without explicitly using the term (BMJ13). Interestingly, BMJ13 included data in the analysis beyond the point of saturation in search of ‘unusual/deviant observations’ and with a view to establishing findings consistency.

Thirty three women were approached to take part in the interview study. Twenty seven agreed and 21 (aged 21–64, median 40) were interviewed before data saturation was reached (one tape failure meant that 20 interviews were available for analysis). (BMJ17). No new topics were identified following analysis of approximately two thirds of the interviews; however, all interviews were coded in order to develop a better understanding of how characteristic the views and reported behaviours were, and also to collect further examples of unusual/deviant observations. (BMJ13).

Two articles reported pre-determining their sample size with a view to achieving data saturation (BMJ08 – see extract in section In line with existing research ; BMJ15 – see extract in section Pragmatic considerations ) without further specifying if this was achieved. One paper claimed theoretical saturation (BMJ06) conceived as being when “no further recurring themes emerging from the analysis” whilst another study argued that although the analytic categories were highly saturated, it was not possible to determine whether theoretical saturation had been achieved (BMJ04). One article (BMJ18) cited a reference to support its position on saturation.

In the BJHP, six articles claimed that they achieved data saturation (BJHP21; BJHP32; BJHP39; BJHP48; BJHP49; BJHP52) and one article stated that, given their sample size and the guidelines for achieving data saturation, it anticipated that saturation would be attained (BJHP50).

Recruitment continued until data saturation was reached, defined as the point at which no new themes emerged. (BJHP48). It has previously been recommended that qualitative studies require a minimum sample size of at least 12 to reach data saturation (Clarke & Braun, 2013; Fugard & Potts, 2014; Guest, Bunce, & Johnson, 2006) Therefore, a sample of 13 was deemed sufficient for the qualitative analysis and scale of this study. (BJHP50).

Two studies argued that they achieved thematic saturation (BJHP28 – see extract in section Sample size guidelines ; BJHP31) and one (BJHP30) article, explicitly concerned with theory development and deploying theoretical sampling, claimed both theoretical and data saturation.

The final sample size was determined by thematic saturation, the point at which new data appears to no longer contribute to the findings due to repetition of themes and comments by participants (Morse, 1995). At this point, data generation was terminated. (BJHP31).

Five studies argued that they achieved (BJHP05; BJHP33; BJHP40; BJHP13 – see extract in section Pragmatic considerations ) or anticipated (BJHP46) saturation without any further specification of the term. BJHP17 referred descriptively to a state of achieved saturation without specifically using the term. Saturation of coding , but not saturation of themes, was claimed to have been reached by one article (BJHP18). Two articles explicitly stated that they did not achieve saturation; instead claiming a level of theme completeness (BJHP27) or that themes being replicated (BJHP53) were arguments for sufficiency of their sample size.

Furthermore, data collection ceased on pragmatic grounds rather than at the point when saturation point was reached. Despite this, although nuances within sub-themes were still emerging towards the end of data analysis, the themes themselves were being replicated indicating a level of completeness. (BJHP27).

Finally, one article criticised and explicitly renounced the notion of data saturation claiming that, on the contrary, the criterion of theoretical sufficiency determined its sample size (BJHP16).

According to the original Grounded Theory texts, data collection should continue until there are no new discoveries ( i.e. , ‘data saturation’; Glaser & Strauss, 1967). However, recent revisions of this process have discussed how it is rare that data collection is an exhaustive process and researchers should rely on how well their data are able to create a sufficient theoretical account or ‘theoretical sufficiency’ (Dey, 1999). For this study, it was decided that theoretical sufficiency would guide recruitment, rather than looking for data saturation. (BJHP16).

Ten out of the 20 BJHP articles that employed the argument of saturation used one or more citations relating to this principle.

In the SHI, one article (SHI01) claimed that it achieved category saturation based on authors’ judgment.

This number was not fixed in advance, but was guided by the sampling strategy and the judgement, based on the analysis of the data, of the point at which ‘category saturation’ was achieved. (SHI01).

Three articles described a state of achieved saturation without using the term or specifying what sort of saturation they had achieved (i.e. data, theoretical, thematic saturation) (SHI04; SHI13; SHI30) whilst another four articles explicitly stated that they achieved saturation (SHI100; SHI125; SHI136; SHI137). Two papers stated that they achieved data saturation (SHI73 – see extract in section Sample size guidelines ; SHI113), two claimed theoretical saturation (SHI78; SHI115) and two referred to achieving thematic saturation (SHI87; SHI139) or to saturated themes (SHI29; SHI50).

Recruitment and analysis ceased once theoretical saturation was reached in the categories described below (Lincoln and Guba 1985). (SHI115). The respondents’ quotes drawn on below were chosen as representative, and illustrate saturated themes. (SHI50).

One article stated that thematic saturation was anticipated with its sample size (SHI94). Briefly referring to the difficulty in pinpointing achievement of theoretical saturation, SHI32 (see extract in section Richness and volume of data ) defended the sufficiency of its sample size on the basis of “the high degree of consensus [that] had begun to emerge among those interviewed”, suggesting that information from interviews was being replicated. Finally, SHI112 (see extract in section Further sampling to check findings consistency ) argued that it achieved saturation of discursive patterns . Seven of the 19 SHI articles cited references to support their position on saturation (see Additional File  4 for the full list of citations used by articles to support their position on saturation across the three journals).

Overall, it is clear that the concept of saturation encompassed a wide range of variants expressed in terms such as saturation, data saturation, thematic saturation, theoretical saturation, category saturation, saturation of coding, saturation of discursive themes, theme completeness. It is noteworthy, however, that although these various claims were sometimes supported with reference to the literature, they were not evidenced in relation to the study at hand.

Pragmatic considerations

The determination of sample size on the basis of pragmatic considerations was the second most frequently invoked argument (9.6% of all justifications) appearing in all three journals. In the BMJ, one article (BMJ15) appealed to pragmatic reasons, relating to time constraints and the difficulty to access certain study populations, to justify the determination of its sample size.

On the basis of the researchers’ previous experience and the literature, [30, 31] we estimated that recruitment of 15–20 patients at each site would achieve data saturation when data from each site were analysed separately. We set a target of seven to 10 caregivers per site because of time constraints and the anticipated difficulty of accessing caregivers at some home based care services. This gave a target sample of 75–100 patients and 35–50 caregivers overall. (BMJ15).

In the BJHP, four articles mentioned pragmatic considerations relating to time or financial constraints (BJHP27 – see extract in section Saturation ; BJHP53), the participant response rate (BJHP13), and the fixed (and thus limited) size of the participant pool from which interviewees were sampled (BJHP18).

We had aimed to continue interviewing until we had reached saturation, a point whereby further data collection would yield no further themes. In practice, the number of individuals volunteering to participate dictated when recruitment into the study ceased (15 young people, 15 parents). Nonetheless, by the last few interviews, significant repetition of concepts was occurring, suggesting ample sampling. (BJHP13).

Finally, three SHI articles explained their sample size with reference to practical aspects: time constraints and project manageability (SHI56), limited availability of respondents and project resources (SHI131), and time constraints (SHI113).

The size of the sample was largely determined by the availability of respondents and resources to complete the study. Its composition reflected, as far as practicable, our interest in how contextual factors (for example, gender relations and ethnicity) mediated the illness experience. (SHI131).

Qualities of the analysis

This sample size justification (8.4% of all justifications) was mainly employed by BJHP articles and referred to an intensive, idiographic and/or latently focused analysis, i.e. that moved beyond description. More specifically, six articles defended their sample size on the basis of an intensive analysis of transcripts and/or the idiographic focus of the study/analysis. Four of these papers (BJHP02; BJHP19; BJHP24; BJHP47) adopted an Interpretative Phenomenological Analysis (IPA) approach.

The current study employed a sample of 10 in keeping with the aim of exploring each participant’s account (Smith et al. , 1999). (BJHP19).

BJHP47 explicitly renounced the notion of saturation within an IPA approach. The other two BJHP articles conducted thematic analysis (BJHP34; BJHP38). The level of analysis – i.e. latent as opposed to a more superficial descriptive analysis – was also invoked as a justification by BJHP38 alongside the argument of an intensive analysis of individual transcripts

The resulting sample size was at the lower end of the range of sample sizes employed in thematic analysis (Braun & Clarke, 2013). This was in order to enable significant reflection, dialogue, and time on each transcript and was in line with the more latent level of analysis employed, to identify underlying ideas, rather than a more superficial descriptive analysis (Braun & Clarke, 2006). (BJHP38).

Finally, one BMJ paper (BMJ21) defended its sample size with reference to the complexity of the analytic task.

We stopped recruitment when we reached 30–35 interviews, owing to the depth and duration of interviews, richness of data, and complexity of the analytical task. (BMJ21).

Meet sampling requirements

Meeting sampling requirements (7.2% of all justifications) was another argument employed by two BMJ and four SHI articles to explain their sample size. Achieving maximum variation sampling in terms of specific interviewee characteristics determined and explained the sample size of two BMJ studies (BMJ02; BMJ16 – see extract in section Meet research design requirements ).

Recruitment continued until sampling frame requirements were met for diversity in age, sex, ethnicity, frequency of attendance, and health status. (BMJ02).

Regarding the SHI articles, two papers explained their numbers on the basis of their sampling strategy (SHI01- see extract in section Saturation ; SHI23) whilst sampling requirements that would help attain sample heterogeneity in terms of a particular characteristic of interest was cited by one paper (SHI127).

The combination of matching the recruitment sites for the quantitative research and the additional purposive criteria led to 104 phase 2 interviews (Internet (OLC): 21; Internet (FTF): 20); Gyms (FTF): 23; HIV testing (FTF): 20; HIV treatment (FTF): 20.) (SHI23). Of the fifty interviews conducted, thirty were translated from Spanish into English. These thirty, from which we draw our findings, were chosen for translation based on heterogeneity in depressive symptomology and educational attainment. (SHI127).

Finally, the pre-determination of sample size on the basis of sampling requirements was stated by one article though this was not used to justify the number of interviews (SHI10).

Sample size guidelines

Five BJHP articles (BJHP28; BJHP38 – see extract in section Qualities of the analysis ; BJHP46; BJHP47; BJHP50 – see extract in section Saturation ) and one SHI paper (SHI73) relied on citing existing sample size guidelines or norms within research traditions to determine and subsequently defend their sample size (7.2% of all justifications).

Sample size guidelines suggested a range between 20 and 30 interviews to be adequate (Creswell, 1998). Interviewer and note taker agreed that thematic saturation, the point at which no new concepts emerge from subsequent interviews (Patton, 2002), was achieved following completion of 20 interviews. (BJHP28). Interviewing continued until we deemed data saturation to have been reached (the point at which no new themes were emerging). Researchers have proposed 30 as an approximate or working number of interviews at which one could expect to be reaching theoretical saturation when using a semi-structured interview approach (Morse 2000), although this can vary depending on the heterogeneity of respondents interviewed and complexity of the issues explored. (SHI73).

In line with existing research

Sample sizes of published literature in the area of the subject matter under investigation (3.5% of all justifications) were used by 2 BMJ articles as guidance and a precedent for determining and defending their own sample size (BMJ08; BMJ15 – see extract in section Pragmatic considerations ).

We drew participants from a list of prisoners who were scheduled for release each week, sampling them until we reached the target of 35 cases, with a view to achieving data saturation within the scope of the study and sufficient follow-up interviews and in line with recent studies [8–10]. (BMJ08).

Similarly, BJHP38 (see extract in section Qualities of the analysis ) claimed that its sample size was within the range of sample sizes of published studies that use its analytic approach.

Richness and volume of data

BMJ21 (see extract in section Qualities of the analysis ) and SHI32 referred to the richness, detailed nature, and volume of data collected (2.3% of all justifications) to justify the sufficiency of their sample size.

Although there were more potential interviewees from those contacted by postcode selection, it was decided to stop recruitment after the 10th interview and focus on analysis of this sample. The material collected was considerable and, given the focused nature of the study, extremely detailed. Moreover, a high degree of consensus had begun to emerge among those interviewed, and while it is always difficult to judge at what point ‘theoretical saturation’ has been reached, or how many interviews would be required to uncover exception(s), it was felt the number was sufficient to satisfy the aims of this small in-depth investigation (Strauss and Corbin 1990). (SHI32).

Meet research design requirements

Determination of sample size so that it is in line with, and serves the requirements of, the research design (2.3% of all justifications) that the study adopted was another justification used by 2 BMJ papers (BMJ16; BMJ08 – see extract in section In line with existing research ).

We aimed for diverse, maximum variation samples [20] totalling 80 respondents from different social backgrounds and ethnic groups and those bereaved due to different types of suicide and traumatic death. We could have interviewed a smaller sample at different points in time (a qualitative longitudinal study) but chose instead to seek a broad range of experiences by interviewing those bereaved many years ago and others bereaved more recently; those bereaved in different circumstances and with different relations to the deceased; and people who lived in different parts of the UK; with different support systems and coroners’ procedures (see Tables 1 and 2 for more details). (BMJ16).

Researchers’ previous experience

The researchers’ previous experience (possibly referring to experience with qualitative research) was invoked by BMJ15 (see extract in section Pragmatic considerations ) as a justification for the determination of sample size.

Nature of study

One BJHP paper argued that the sample size was appropriate for the exploratory nature of the study (BJHP38).

A sample of eight participants was deemed appropriate because of the exploratory nature of this research and the focus on identifying underlying ideas about the topic. (BJHP38).

Further sampling to check findings consistency

Finally, SHI112 argued that once it had achieved saturation of discursive patterns, further sampling was decided and conducted to check for consistency of the findings.

Within each of the age-stratified groups, interviews were randomly sampled until saturation of discursive patterns was achieved. This resulted in a sample of 67 interviews. Once this sample had been analysed, one further interview from each age-stratified group was randomly chosen to check for consistency of the findings. Using this approach it was possible to more carefully explore children’s discourse about the ‘I’, agency, relationality and power in the thematic areas, revealing the subtle discursive variations described in this article. (SHI112).

Thematic analysis of passages discussing sample size

This analysis resulted in two overarching thematic areas; the first concerned the variation in the characterisation of sample size sufficiency, and the second related to the perceived threats deriving from sample size insufficiency.

Characterisations of sample size sufficiency

The analysis showed that there were three main characterisations of the sample size in the articles that provided relevant comments and discussion: (a) the vast majority of these qualitative studies ( n  = 42) considered their sample size as ‘small’ and this was seen and discussed as a limitation; only two articles viewed their small sample size as desirable and appropriate (b) a minority of articles ( n  = 4) proclaimed that their achieved sample size was ‘sufficient’; and (c) finally, a small group of studies ( n  = 5) characterised their sample size as ‘large’. Whilst achieving a ‘large’ sample size was sometimes viewed positively because it led to richer results, there were also occasions when a large sample size was problematic rather than desirable.

‘Small’ but why and for whom?

A number of articles which characterised their sample size as ‘small’ did so against an implicit or explicit quantitative framework of reference. Interestingly, three studies that claimed to have achieved data saturation or ‘theoretical sufficiency’ with their sample size, discussed or noted as a limitation in their discussion their ‘small’ sample size, raising the question of why, or for whom, the sample size was considered small given that the qualitative criterion of saturation had been satisfied.

The current study has a number of limitations. The sample size was small (n = 11) and, however, large enough for no new themes to emerge. (BJHP39). The study has two principal limitations. The first of these relates to the small number of respondents who took part in the study. (SHI73).

Other articles appeared to accept and acknowledge that their sample was flawed because of its small size (as well as other compositional ‘deficits’ e.g. non-representativeness, biases, self-selection) or anticipated that they might be criticized for their small sample size. It seemed that the imagined audience – perhaps reviewer or reader – was one inclined to hold the tenets of quantitative research, and certainly one to whom it was important to indicate the recognition that small samples were likely to be problematic. That one’s sample might be thought small was often construed as a limitation couched in a discourse of regret or apology.

Very occasionally, the articulation of the small size as a limitation was explicitly aligned against an espoused positivist framework and quantitative research.

This study has some limitations. Firstly, the 100 incidents sample represents a small number of the total number of serious incidents that occurs every year. 26 We sent out a nationwide invitation and do not know why more people did not volunteer for the study. Our lack of epidemiological knowledge about healthcare incidents, however, means that determining an appropriate sample size continues to be difficult. (BMJ20).

Indicative of an apparent oscillation of qualitative researchers between the different requirements and protocols demarcating the quantitative and qualitative worlds, there were a few instances of articles which briefly recognised their ‘small’ sample size as a limitation, but then defended their study on more qualitative grounds, such as their ability and success at capturing the complexity of experience and delving into the idiographic, and at generating particularly rich data.

This research, while limited in size, has sought to capture some of the complexity attached to men’s attitudes and experiences concerning incomes and material circumstances. (SHI35). Our numbers are small because negotiating access to social networks was slow and labour intensive, but our methods generated exceptionally rich data. (BMJ21). This study could be criticised for using a small and unrepresentative sample. Given that older adults have been ignored in the research concerning suntanning, fair-skinned older adults are the most likely to experience skin cancer, and women privilege appearance over health when it comes to sunbathing practices, our study offers depth and richness of data in a demographic group much in need of research attention. (SHI57).

‘Good enough’ sample sizes

Only four articles expressed some degree of confidence that their achieved sample size was sufficient. For example, SHI139, in line with the justification of thematic saturation that it offered, expressed trust in its sample size sufficiency despite the poor response rate. Similarly, BJHP04, which did not provide a sample size justification, argued that it targeted a larger sample size in order to eventually recruit a sufficient number of interviewees, due to anticipated low response rate.

Twenty-three people with type I diabetes from the target population of 133 ( i.e. 17.3%) consented to participate but four did not then respond to further contacts (total N = 19). The relatively low response rate was anticipated, due to the busy life-styles of young people in the age range, the geographical constraints, and the time required to participate in a semi-structured interview, so a larger target sample allowed a sufficient number of participants to be recruited. (BJHP04).

Two other articles (BJHP35; SHI32) linked the claimed sufficiency to the scope (i.e. ‘small, in-depth investigation’), aims and nature (i.e. ‘exploratory’) of their studies, thus anchoring their numbers to the particular context of their research. Nevertheless, claims of sample size sufficiency were sometimes undermined when they were juxtaposed with an acknowledgement that a larger sample size would be more scientifically productive.

Although our sample size was sufficient for this exploratory study, a more diverse sample including participants with lower socioeconomic status and more ethnic variation would be informative. A larger sample could also ensure inclusion of a more representative range of apps operating on a wider range of platforms. (BJHP35).

‘Large’ sample sizes - Promise or peril?

Three articles (BMJ13; BJHP05; BJHP48) which all provided the justification of saturation, characterised their sample size as ‘large’ and narrated this oversufficiency in positive terms as it allowed richer data and findings and enhanced the potential for generalisation. The type of generalisation aspired to (BJHP48) was not further specified however.

This study used rich data provided by a relatively large sample of expert informants on an important but under-researched topic. (BMJ13). Qualitative research provides a unique opportunity to understand a clinical problem from the patient’s perspective. This study had a large diverse sample, recruited through a range of locations and used in-depth interviews which enhance the richness and generalizability of the results. (BJHP48).

And whilst a ‘large’ sample size was endorsed and valued by some qualitative researchers, within the psychological tradition of IPA, a ‘large’ sample size was counter-normative and therefore needed to be justified. Four BJHP studies, all adopting IPA, expressed the appropriateness or desirability of ‘small’ sample sizes (BJHP41; BJHP45) or hastened to explain why they included a larger than typical sample size (BJHP32; BJHP47). For example, BJHP32 below provides a rationale for how an IPA study can accommodate a large sample size and how this was indeed suitable for the purposes of the particular research. To strengthen the explanation for choosing a non-normative sample size, previous IPA research citing a similar sample size approach is used as a precedent.

Small scale IPA studies allow in-depth analysis which would not be possible with larger samples (Smith et al. , 2009). (BJHP41). Although IPA generally involves intense scrutiny of a small number of transcripts, it was decided to recruit a larger diverse sample as this is the first qualitative study of this population in the United Kingdom (as far as we know) and we wanted to gain an overview. Indeed, Smith, Flowers, and Larkin (2009) agree that IPA is suitable for larger groups. However, the emphasis changes from an in-depth individualistic analysis to one in which common themes from shared experiences of a group of people can be elicited and used to understand the network of relationships between themes that emerge from the interviews. This large-scale format of IPA has been used by other researchers in the field of false-positive research. Baillie, Smith, Hewison, and Mason (2000) conducted an IPA study, with 24 participants, of ultrasound screening for chromosomal abnormality; they found that this larger number of participants enabled them to produce a more refined and cohesive account. (BJHP32).

The IPA articles found in the BJHP were the only instances where a ‘small’ sample size was advocated and a ‘large’ sample size problematized and defended. These IPA studies illustrate that the characterisation of sample size sufficiency can be a function of researchers’ theoretical and epistemological commitments rather than the result of an ‘objective’ sample size assessment.

Threats from sample size insufficiency

As shown above, the majority of articles that commented on their sample size, simultaneously characterized it as small and problematic. On those occasions that authors did not simply cite their ‘small’ sample size as a study limitation but rather continued and provided an account of how and why a small sample size was problematic, two important scientific qualities of the research seemed to be threatened: the generalizability and validity of results.

Generalizability

Those who characterised their sample as ‘small’ connected this to the limited potential for generalization of the results. Other features related to the sample – often some kind of compositional particularity – were also linked to limited potential for generalisation. Though not always explicitly articulated to what form of generalisation the articles referred to (see BJHP09), generalisation was mostly conceived in nomothetic terms, that is, it concerned the potential to draw inferences from the sample to the broader study population (‘representational generalisation’ – see BJHP31) and less often to other populations or cultures.

It must be noted that samples are small and whilst in both groups the majority of those women eligible participated, generalizability cannot be assumed. (BJHP09). The study’s limitations should be acknowledged: Data are presented from interviews with a relatively small group of participants, and thus, the views are not necessarily generalizable to all patients and clinicians. In particular, patients were only recruited from secondary care services where COFP diagnoses are typically confirmed. The sample therefore is unlikely to represent the full spectrum of patients, particularly those who are not referred to, or who have been discharged from dental services. (BJHP31).

Without explicitly using the term generalisation, two SHI articles noted how their ‘small’ sample size imposed limits on ‘the extent that we can extrapolate from these participants’ accounts’ (SHI114) or to the possibility ‘to draw far-reaching conclusions from the results’ (SHI124).

Interestingly, only a minority of articles alluded to, or invoked, a type of generalisation that is aligned with qualitative research, that is, idiographic generalisation (i.e. generalisation that can be made from and about cases [ 5 ]). These articles, all published in the discipline of sociology, defended their findings in terms of the possibility of drawing logical and conceptual inferences to other contexts and of generating understanding that has the potential to advance knowledge, despite their ‘small’ size. One article (SHI139) clearly contrasted nomothetic (statistical) generalisation to idiographic generalisation, arguing that the lack of statistical generalizability does not nullify the ability of qualitative research to still be relevant beyond the sample studied.

Further, these data do not need to be statistically generalisable for us to draw inferences that may advance medicalisation analyses (Charmaz 2014). These data may be seen as an opportunity to generate further hypotheses and are a unique application of the medicalisation framework. (SHI139). Although a small-scale qualitative study related to school counselling, this analysis can be usefully regarded as a case study of the successful utilisation of mental health-related resources by adolescents. As many of the issues explored are of relevance to mental health stigma more generally, it may also provide insights into adult engagement in services. It shows how a sociological analysis, which uses positioning theory to examine how people negotiate, partially accept and simultaneously resist stigmatisation in relation to mental health concerns, can contribute to an elucidation of the social processes and narrative constructions which may maintain as well as bridge the mental health service gap. (SHI103).

Only one article (SHI30) used the term transferability to argue for the potential of wider relevance of the results which was thought to be more the product of the composition of the sample (i.e. diverse sample), rather than the sample size.

The second major concern that arose from a ‘small’ sample size pertained to the internal validity of findings (i.e. here the term is used to denote the ‘truth’ or credibility of research findings). Authors expressed uncertainty about the degree of confidence in particular aspects or patterns of their results, primarily those that concerned some form of differentiation on the basis of relevant participant characteristics.

The information source preferred seemed to vary according to parents’ education; however, the sample size is too small to draw conclusions about such patterns. (SHI80). Although our numbers were too small to demonstrate gender differences with any certainty, it does seem that the biomedical and erotic scripts may be more common in the accounts of men and the relational script more common in the accounts of women. (SHI81).

In other instances, articles expressed uncertainty about whether their results accounted for the full spectrum and variation of the phenomenon under investigation. In other words, a ‘small’ sample size (alongside compositional ‘deficits’ such as a not statistically representative sample) was seen to threaten the ‘content validity’ of the results which in turn led to constructions of the study conclusions as tentative.

Data collection ceased on pragmatic grounds rather than when no new information appeared to be obtained ( i.e. , saturation point). As such, care should be taken not to overstate the findings. Whilst the themes from the initial interviews seemed to be replicated in the later interviews, further interviews may have identified additional themes or provided more nuanced explanations. (BJHP53). …it should be acknowledged that this study was based on a small sample of self-selected couples in enduring marriages who were not broadly representative of the population. Thus, participants may not be representative of couples that experience postnatal PTSD. It is therefore unlikely that all the key themes have been identified and explored. For example, couples who were excluded from the study because the male partner declined to participate may have been experiencing greater interpersonal difficulties. (BJHP03).

In other instances, articles attempted to preserve a degree of credibility of their results, despite the recognition that the sample size was ‘small’. Clarity and sharpness of emerging themes and alignment with previous relevant work were the arguments employed to warrant the validity of the results.

This study focused on British Chinese carers of patients with affective disorders, using a qualitative methodology to synthesise the sociocultural representations of illness within this community. Despite the small sample size, clear themes emerged from the narratives that were sufficient for this exploratory investigation. (SHI98).

The present study sought to examine how qualitative sample sizes in health-related research are characterised and justified. In line with previous studies [ 22 , 30 , 33 , 34 ] the findings demonstrate that reporting of sample size sufficiency is limited; just over 50% of articles in the BMJ and BJHP and 82% in the SHI did not provide any sample size justification. Providing a sample size justification was not related to the number of interviews conducted, but it was associated with the journal that the article was published in, indicating the influence of disciplinary or publishing norms, also reported in prior research [ 30 ]. This lack of transparency about sample size sufficiency is problematic given that most qualitative researchers would agree that it is an important marker of quality [ 56 , 57 ]. Moreover, and with the rise of qualitative research in social sciences, efforts to synthesise existing evidence and assess its quality are obstructed by poor reporting [ 58 , 59 ].

When authors justified their sample size, our findings indicate that sufficiency was mostly appraised with reference to features that were intrinsic to the study, in agreement with general advice on sample size determination [ 4 , 11 , 36 ]. The principle of saturation was the most commonly invoked argument [ 22 ] accounting for 55% of all justifications. A wide range of variants of saturation was evident corroborating the proliferation of the meaning of the term [ 49 ] and reflecting different underlying conceptualisations or models of saturation [ 20 ]. Nevertheless, claims of saturation were never substantiated in relation to procedures conducted in the study itself, endorsing similar observations in the literature [ 25 , 30 , 47 ]. Claims of saturation were sometimes supported with citations of other literature, suggesting a removal of the concept away from the characteristics of the study at hand. Pragmatic considerations, such as resource constraints or participant response rate and availability, was the second most frequently used argument accounting for approximately 10% of justifications and another 23% of justifications also represented intrinsic-to-the-study characteristics (i.e. qualities of the analysis, meeting sampling or research design requirements, richness and volume of the data obtained, nature of study, further sampling to check findings consistency).

Only, 12% of mentions of sample size justification pertained to arguments that were external to the study at hand, in the form of existing sample size guidelines and prior research that sets precedents. Whilst community norms and prior research can establish useful rules of thumb for estimating sample sizes [ 60 ] – and reveal what sizes are more likely to be acceptable within research communities – researchers should avoid adopting these norms uncritically, especially when such guidelines [e.g. 30 , 35 ], might be based on research that does not provide adequate evidence of sample size sufficiency. Similarly, whilst methodological research that seeks to demonstrate the achievement of saturation is invaluable since it explicates the parameters upon which saturation is contingent and indicates when a research project is likely to require a smaller or a larger sample [e.g. 29 ], specific numbers at which saturation was achieved within these projects cannot be routinely extrapolated for other projects. We concur with existing views [ 11 , 36 ] that the consideration of the characteristics of the study at hand, such as the epistemological and theoretical approach, the nature of the phenomenon under investigation, the aims and scope of the study, the quality and richness of data, or the researcher’s experience and skills of conducting qualitative research, should be the primary guide in determining sample size and assessing its sufficiency.

Moreover, although numbers in qualitative research are not unimportant [ 61 ], sample size should not be considered alone but be embedded in the more encompassing examination of data adequacy [ 56 , 57 ]. Erickson’s [ 62 ] dimensions of ‘evidentiary adequacy’ are useful here. He explains the concept in terms of adequate amounts of evidence, adequate variety in kinds of evidence, adequate interpretive status of evidence, adequate disconfirming evidence, and adequate discrepant case analysis. All dimensions might not be relevant across all qualitative research designs, but this illustrates the thickness of the concept of data adequacy, taking it beyond sample size.

The present research also demonstrated that sample sizes were commonly seen as ‘small’ and insufficient and discussed as limitation. Often unjustified (and in two cases incongruent with their own claims of saturation) these findings imply that sample size in qualitative health research is often adversely judged (or expected to be judged) against an implicit, yet omnipresent, quasi-quantitative standpoint. Indeed there were a few instances in our data where authors appeared, possibly in response to reviewers, to resist to some sort of quantification of their results. This implicit reference point became more apparent when authors discussed the threats deriving from an insufficient sample size. Whilst the concerns about internal validity might be legitimate to the extent that qualitative research projects, which are broadly related to realism, are set to examine phenomena in sufficient breadth and depth, the concerns around generalizability revealed a conceptualisation that is not compatible with purposive sampling. The limited potential for generalisation, as a result of a small sample size, was often discussed in nomothetic, statistical terms. Only occasionally was analytic or idiographic generalisation invoked to warrant the value of the study’s findings [ 5 , 17 ].

Strengths and limitations of the present study

We note, first, the limited number of health-related journals reviewed, so that only a ‘snapshot’ of qualitative health research has been captured. Examining additional disciplines (e.g. nursing sciences) as well as inter-disciplinary journals would add to the findings of this analysis. Nevertheless, our study is the first to provide some comparative insights on the basis of disciplines that are differently attached to the legacy of positivism and analysed literature published over a lengthy period of time (15 years). Guetterman [ 27 ] also examined health-related literature but this analysis was restricted to 26 most highly cited articles published over a period of five years whilst Carlsen and Glenton’s [ 22 ] study concentrated on focus groups health research. Moreover, although it was our intention to examine sample size justification in relation to the epistemological and theoretical positions of articles, this proved to be challenging largely due to absence of relevant information, or the difficulty into discerning clearly articles’ positions [ 63 ] and classifying them under specific approaches (e.g. studies often combined elements from different theoretical and epistemological traditions). We believe that such an analysis would yield useful insights as it links the methodological issue of sample size to the broader philosophical stance of the research. Despite these limitations, the analysis of the characterisation of sample size and of the threats seen to accrue from insufficient sample size, enriches our understanding of sample size (in)sufficiency argumentation by linking it to other features of the research. As the peer-review process becomes increasingly public, future research could usefully examine how reporting around sample size sufficiency and data adequacy might be influenced by the interactions between authors and reviewers.

The past decade has seen a growing appetite in qualitative research for an evidence-based approach to sample size determination and to evaluations of the sufficiency of sample size. Despite the conceptual and methodological developments in the area, the findings of the present study confirm previous studies in concluding that appraisals of sample size sufficiency are either absent or poorly substantiated. To ensure and maintain high quality research that will encourage greater appreciation of qualitative work in health-related sciences [ 64 ], we argue that qualitative researchers should be more transparent and thorough in their evaluation of sample size as part of their appraisal of data adequacy. We would encourage the practice of appraising sample size sufficiency with close reference to the study at hand and would thus caution against responding to the growing methodological research in this area with a decontextualised application of sample size numerical guidelines, norms and principles. Although researchers might find sample size community norms serve as useful rules of thumb, we recommend methodological knowledge is used to critically consider how saturation and other parameters that affect sample size sufficiency pertain to the specifics of the particular project. Those reviewing papers have a vital role in encouraging transparent study-specific reporting. The review process should support authors to exercise nuanced judgments in decisions about sample size determination in the context of the range of factors that influence sample size sufficiency and the specifics of a particular study. In light of the growing methodological evidence in the area, transparent presentation of such evidence-based judgement is crucial and in time should surely obviate the seemingly routine practice of citing the ‘small’ size of qualitative samples among the study limitations.

A non-parametric test of difference for independent samples was performed since the variable number of interviews violated assumptions of normality according to the standardized scores of skewness and kurtosis (BMJ: z skewness = 3.23, z kurtosis = 1.52; BJHP: z skewness = 4.73, z kurtosis = 4.85; SHI: z skewness = 12.04, z kurtosis = 21.72) and the Shapiro-Wilk test of normality ( p  < .001).

Abbreviations

British Journal of Health Psychology

British Medical Journal

Interpretative Phenomenological Analysis

Sociology of Health & Illness

Spencer L, Ritchie J, Lewis J, Dillon L. Quality in qualitative evaluation: a framework for assessing research evidence. National Centre for Social Research 2003 https://www.heacademy.ac.uk/system/files/166_policy_hub_a_quality_framework.pdf Accessed 11 May 2018.

Fusch PI, Ness LR. Are we there yet? Data saturation in qualitative research Qual Rep. 2015;20(9):1408–16.

Google Scholar  

Robinson OC. Sampling in interview-based qualitative research: a theoretical and practical guide. Qual Res Psychol. 2014;11(1):25–41.

Article   Google Scholar  

Sandelowski M. Sample size in qualitative research. Res Nurs Health. 1995;18(2):179–83.

Article   CAS   Google Scholar  

Sandelowski M. One is the liveliest number: the case orientation of qualitative research. Res Nurs Health. 1996;19(6):525–9.

Luborsky MR, Rubinstein RL. Sampling in qualitative research: rationale, issues. and methods Res Aging. 1995;17(1):89–113.

Marshall MN. Sampling for qualitative research. Fam Pract. 1996;13(6):522–6.

Patton MQ. Qualitative evaluation and research methods. 2nd ed. Newbury Park, CA: Sage; 1990.

van Rijnsoever FJ. (I Can’t get no) saturation: a simulation and guidelines for sample sizes in qualitative research. PLoS One. 2017;12(7):e0181689.

Morse JM. The significance of saturation. Qual Health Res. 1995;5(2):147–9.

Morse JM. Determining sample size. Qual Health Res. 2000;10(1):3–5.

Gergen KJ, Josselson R, Freeman M. The promises of qualitative inquiry. Am Psychol. 2015;70(1):1–9.

Borsci S, Macredie RD, Barnett J, Martin J, Kuljis J, Young T. Reviewing and extending the five-user assumption: a grounded procedure for interaction evaluation. ACM Trans Comput Hum Interact. 2013;20(5):29.

Borsci S, Macredie RD, Martin JL, Young T. How many testers are needed to assure the usability of medical devices? Expert Rev Med Devices. 2014;11(5):513–25.

Glaser BG, Strauss AL. The discovery of grounded theory: strategies for qualitative research. Chicago, IL: Aldine; 1967.

Kerr C, Nixon A, Wild D. Assessing and demonstrating data saturation in qualitative inquiry supporting patient-reported outcomes research. Expert Rev Pharmacoecon Outcomes Res. 2010;10(3):269–81.

Lincoln YS, Guba EG. Naturalistic inquiry. London: Sage; 1985.

Book   Google Scholar  

Malterud K, Siersma VD, Guassora AD. Sample size in qualitative interview studies: guided by information power. Qual Health Res. 2015;26:1753–60.

Nelson J. Using conceptual depth criteria: addressing the challenge of reaching saturation in qualitative research. Qual Res. 2017;17(5):554–70.

Saunders B, Sim J, Kingstone T, Baker S, Waterfield J, Bartlam B, et al. Saturation in qualitative research: exploring its conceptualization and operationalization. Qual Quant. 2017. https://doi.org/10.1007/s11135-017-0574-8 .

Caine K. Local standards for sample size at CHI. In Proceedings of the 2016 CHI conference on human factors in computing systems. 2016;981–992. ACM.

Carlsen B, Glenton C. What about N? A methodological study of sample-size reporting in focus group studies. BMC Med Res Methodol. 2011;11(1):26.

Constantinou CS, Georgiou M, Perdikogianni M. A comparative method for themes saturation (CoMeTS) in qualitative interviews. Qual Res. 2017;17(5):571–88.

Dai NT, Free C, Gendron Y. Interview-based research in accounting 2000–2014: a review. November 2016. https://ssrn.com/abstract=2711022 or https://doi.org/10.2139/ssrn.2711022 . Accessed 17 May 2018.

Francis JJ, Johnston M, Robertson C, Glidewell L, Entwistle V, Eccles MP, et al. What is an adequate sample size? Operationalising data saturation for theory-based interview studies. Psychol Health. 2010;25(10):1229–45.

Guest G, Bunce A, Johnson L. How many interviews are enough? An experiment with data saturation and variability. Field Methods. 2006;18(1):59–82.

Guetterman TC. Descriptions of sampling practices within five approaches to qualitative research in education and the health sciences. Forum Qual Soc Res. 2015;16(2):25. http://nbn-resolving.de/urn:nbn:de:0114-fqs1502256 . Accessed 17 May 2018.

Hagaman AK, Wutich A. How many interviews are enough to identify metathemes in multisited and cross-cultural research? Another perspective on guest, bunce, and Johnson’s (2006) landmark study. Field Methods. 2017;29(1):23–41.

Hennink MM, Kaiser BN, Marconi VC. Code saturation versus meaning saturation: how many interviews are enough? Qual Health Res. 2017;27(4):591–608.

Marshall B, Cardon P, Poddar A, Fontenot R. Does sample size matter in qualitative research?: a review of qualitative interviews in IS research. J Comput Inform Syst. 2013;54(1):11–22.

Mason M. Sample size and saturation in PhD studies using qualitative interviews. Forum Qual Soc Res 2010;11(3):8. http://nbn-resolving.de/urn:nbn:de:0114-fqs100387 . Accessed 17 May 2018.

Safman RM, Sobal J. Qualitative sample extensiveness in health education research. Health Educ Behav. 2004;31(1):9–21.

Saunders MN, Townsend K. Reporting and justifying the number of interview participants in organization and workplace research. Br J Manag. 2016;27(4):836–52.

Sobal J. 2001. Sample extensiveness in qualitative nutrition education research. J Nutr Educ. 2001;33(4):184–92.

Thomson SB. 2010. Sample size and grounded theory. JOAAG. 2010;5(1). http://www.joaag.com/uploads/5_1__Research_Note_1_Thomson.pdf . Accessed 17 May 2018.

Baker SE, Edwards R. How many qualitative interviews is enough?: expert voices and early career reflections on sampling and cases in qualitative research. National Centre for Research Methods Review Paper. 2012; http://eprints.ncrm.ac.uk/2273/4/how_many_interviews.pdf . Accessed 17 May 2018.

Ogden J, Cornwell D. The role of topic, interviewee, and question in predicting rich interview data in the field of health research. Sociol Health Illn. 2010;32(7):1059–71.

Green J, Thorogood N. Qualitative methods for health research. London: Sage; 2004.

Ritchie J, Lewis J, Elam G. Designing and selecting samples. In: Ritchie J, Lewis J, editors. Qualitative research practice: a guide for social science students and researchers. London: Sage; 2003. p. 77–108.

Britten N. Qualitative research: qualitative interviews in medical research. BMJ. 1995;311(6999):251–3.

Creswell JW. Qualitative inquiry and research design: choosing among five approaches. 2nd ed. London: Sage; 2007.

Fugard AJ, Potts HW. Supporting thinking on sample sizes for thematic analyses: a quantitative tool. Int J Soc Res Methodol. 2015;18(6):669–84.

Emmel N. Themes, variables, and the limits to calculating sample size in qualitative research: a response to Fugard and Potts. Int J Soc Res Methodol. 2015;18(6):685–6.

Braun V, Clarke V. (Mis) conceptualising themes, thematic analysis, and other problems with Fugard and Potts’ (2015) sample-size tool for thematic analysis. Int J Soc Res Methodol. 2016;19(6):739–43.

Hammersley M. Sampling and thematic analysis: a response to Fugard and Potts. Int J Soc Res Methodol. 2015;18(6):687–8.

Charmaz K. Constructing grounded theory: a practical guide through qualitative analysis. London: Sage; 2006.

Bowen GA. Naturalistic inquiry and the saturation concept: a research note. Qual Res. 2008;8(1):137–52.

Morse JM. Data were saturated. Qual Health Res. 2015;25(5):587–8.

O’Reilly M, Parker N. ‘Unsatisfactory saturation’: a critical exploration of the notion of saturated sample sizes in qualitative research. Qual Res. 2013;13(2):190–7.

Manen M, Higgins I, Riet P. A conversation with max van Manen on phenomenology in its original sense. Nurs Health Sci. 2016;18(1):4–7.

Dey I. Grounding grounded theory. San Francisco, CA: Academic Press; 1999.

Hays DG, Wood C, Dahl H, Kirk-Jenkins A. Methodological rigor in journal of counseling & development qualitative research articles: a 15-year review. J Couns Dev. 2016;94(2):172–83.

Moher D, Liberati A, Tetzlaff J, Altman DG, Prisma Group. Preferred reporting items for systematic reviews and meta-analyses: the PRISMA statement. PLoS Med 2009; 6(7): e1000097.

Hsieh HF, Shannon SE. Three approaches to qualitative content analysis. Qual Health Res. 2005;15(9):1277–88.

Boyatzis RE. Transforming qualitative information: thematic analysis and code development. Thousand Oaks, CA: Sage; 1998.

Levitt HM, Motulsky SL, Wertz FJ, Morrow SL, Ponterotto JG. Recommendations for designing and reviewing qualitative research in psychology: promoting methodological integrity. Qual Psychol. 2017;4(1):2–22.

Morrow SL. Quality and trustworthiness in qualitative research in counseling psychology. J Couns Psychol. 2005;52(2):250–60.

Barroso J, Sandelowski M. Sample reporting in qualitative studies of women with HIV infection. Field Methods. 2003;15(4):386–404.

Glenton C, Carlsen B, Lewin S, Munthe-Kaas H, Colvin CJ, Tunçalp Ö, et al. Applying GRADE-CERQual to qualitative evidence synthesis findings—paper 5: how to assess adequacy of data. Implement Sci. 2018;13(Suppl 1):14.

Onwuegbuzie AJ. Leech NL. A call for qualitative power analyses. Qual Quant. 2007;41(1):105–21.

Sandelowski M. Real qualitative researchers do not count: the use of numbers in qualitative research. Res Nurs Health. 2001;24(3):230–40.

Erickson F. Qualitative methods in research on teaching. In: Wittrock M, editor. Handbook of research on teaching. 3rd ed. New York: Macmillan; 1986. p. 119–61.

Bradbury-Jones C, Taylor J, Herber O. How theory is used and articulated in qualitative research: development of a new typology. Soc Sci Med. 2014;120:135–41.

Greenhalgh T, Annandale E, Ashcroft R, Barlow J, Black N, Bleakley A, et al. An open letter to the BMJ editors on qualitative research. BMJ. 2016;i563:352.

Download references

Acknowledgments

We would like to thank Dr. Paula Smith and Katharine Lee for their comments on a previous draft of this paper as well as Natalie Ann Mitchell and Meron Teferra for assisting us with data extraction.

This research was initially conceived of and partly conducted with financial support from the Multidisciplinary Assessment of Technology Centre for Healthcare (MATCH) programme (EP/F063822/1 and EP/G012393/1). The research continued and was completed independent of any support. The funding body did not have any role in the study design, the collection, analysis and interpretation of the data, in the writing of the paper, and in the decision to submit the manuscript for publication. The views expressed are those of the authors alone.

Availability of data and materials

Supporting data can be accessed in the original publications. Additional File 2 lists all eligible studies that were included in the present analysis.

Author information

Authors and affiliations.

Department of Psychology, University of Bath, Building 10 West, Claverton Down, Bath, BA2 7AY, UK

Konstantina Vasileiou & Julie Barnett

School of Psychology, Newcastle University, Ridley Building 1, Queen Victoria Road, Newcastle upon Tyne, NE1 7RU, UK

Susan Thorpe

Department of Computer Science, Brunel University London, Wilfred Brown Building 108, Uxbridge, UB8 3PH, UK

Terry Young

You can also search for this author in PubMed   Google Scholar

Contributions

JB and TY conceived the study; KV, JB, and TY designed the study; KV identified the articles and extracted the data; KV and JB assessed eligibility of articles; KV, JB, ST, and TY contributed to the analysis of the data, discussed the findings and early drafts of the paper; KV developed the final manuscript; KV, JB, ST, and TY read and approved the manuscript.

Corresponding author

Correspondence to Konstantina Vasileiou .

Ethics declarations

Ethics approval and consent to participate.

Not applicable.

Consent for publication

Competing interests.

Terry Young is an academic who undertakes research and occasional consultancy in the areas of health technology assessment, information systems, and service design. He is unaware of any direct conflict of interest with respect to this paper. All other authors have no competing interests to declare.

Publisher’s Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Additional Files

Additional file 1:.

Editorial positions on qualitative research and sample considerations (where available). (DOCX 12 kb)

Additional File 2:

List of eligible articles included in the review ( N  = 214). (DOCX 38 kb)

Additional File 3:

Data Extraction Form. (DOCX 15 kb)

Additional File 4:

Citations used by articles to support their position on saturation. (DOCX 14 kb)

Rights and permissions

Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License ( http://creativecommons.org/licenses/by/4.0/ ), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The Creative Commons Public Domain Dedication waiver ( http://creativecommons.org/publicdomain/zero/1.0/ ) applies to the data made available in this article, unless otherwise stated.

Reprints and permissions

About this article

Cite this article.

Vasileiou, K., Barnett, J., Thorpe, S. et al. Characterising and justifying sample size sufficiency in interview-based studies: systematic analysis of qualitative health research over a 15-year period. BMC Med Res Methodol 18 , 148 (2018). https://doi.org/10.1186/s12874-018-0594-7

Download citation

Received : 22 May 2018

Accepted : 29 October 2018

Published : 21 November 2018

DOI : https://doi.org/10.1186/s12874-018-0594-7

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Sample size
• Sample size justification
• Sample size characterisation
• Data adequacy
• Qualitative health research
• Qualitative interviews
• Systematic analysis

BMC Medical Research Methodology

ISSN: 1471-2288

• General enquiries: [email protected]

Best Practices for Using Statistics on Small Sample Sizes

Put simply, this is wrong, but it’s a common misconception .

There are appropriate statistical methods to deal with small sample sizes.

Although one researcher’s “small” is another’s large, when I refer to small sample sizes I mean studies that have typically between 5 and 30 users total—a size very common in usability studies .

But user research isn’t the only field that deals with small sample sizes. Studies involving fMRIs, which cost a lot to operate, have limited sample sizes as well [pdf] as do studies using laboratory animals.

While there are equations that allow us to properly handle small “n” studies, it’s important to know that there are limitations to these smaller sample studies: you are limited to seeing big differences or big “effects.”

To put it another way, statistical analysis with small samples is like making astronomical observations with binoculars . You are limited to seeing big things: planets, stars, moons and the occasional comet.  But just because you don’t have access to a high-powered telescope doesn’t mean you cannot conduct astronomy. Galileo, in fact, discovered Jupiter’s moons with a telescope with the same power as many of today’s binoculars .

Just as with statistics, just because you don’t have a large sample size doesn’t mean you cannot use statistics. Again, the key limitation is that you are limited to detecting large differences between designs or measures.

Fortunately, in user-experience research we are often most concerned about these big differences—differences users are likely to notice, such as changes in the navigation structure or the improvement of a search results page.

Here are the procedures which we’ve tested for common, small-sample user research, and we will cover them all at the UX Boot Camp in Denver next month.

If you need to compare completion rates, task times, and rating scale data for two independent groups, there are two procedures you can use for small and large sample sizes.  The right one depends on the type of data you have: continuous or discrete-binary.

Comparing Means : If your data is generally continuous (not binary), such as task time or rating scales, use the two sample t-test . It’s been shown to be accurate for small sample sizes.

Comparing Two Proportions : If your data is binary (pass/fail, yes/no), then use the N-1 Two Proportion Test. This is a variation on the better known Chi-Square test (it is algebraically equivalent to the N-1 Chi-Square test). When expected cell counts fall below one, the Fisher Exact Test tends to perform better. The online calculator handles this for you and we discuss the procedure in Chapter 5 of Quantifying the User Experience .

Confidence Intervals

When you want to know what the plausible range is for the user population from a sample of data, you’ll want to generate a confidence interval . While the confidence interval width will be rather wide (usually 20 to 30 percentage points), the upper or lower boundary of the intervals can be very helpful in establishing how often something will occur in the total user population.

For example, if you wanted to know if users would read a sheet that said “Read this first” when installing a printer, and six out of eight users didn’t read the sheet in an installation study, you’d know that at least 40% of all users would likely do this –a substantial proportion.

There are three approaches to computing confidence intervals based on whether your data is binary, task-time or continuous.

Confidence interval around a mean : If your data is generally continuous (not binary) such as rating scales, order amounts in dollars, or the number of page views, the confidence interval is based on the t-distribution (which takes into account sample size).

Confidence interval around task-time :  Task time data is positively skewed . There is a lower boundary of 0 seconds. It’s not uncommon for some users to take 10 to 20 times longer than other users to complete the same task. To handle this skew, the time data needs to be log-transformed   and the confidence interval is computed on the log-data, then transformed back when reporting. The online calculator handles all this.

Confidence interval around a binary measure: For an accurate confidence interval around binary measures like completion rate or yes/no questions, the Adjusted Wald interval performs well for all sample sizes.

Point Estimates (The Best Averages)

The “best” estimate for reporting an average time or average completion rate for any study may vary depending on the study goals.  Keep in mind that even the “best” single estimate will still differ from the actual average, so using confidence intervals provides a better method for estimating the unknown population average.

For the best overall average for small sample sizes, we have two recommendations for task-time and completion rates, and a more general recommendation for all sample sizes for rating scales.

Completion Rate : For small-sample completion rates, there are only a few possible values for each task. For example, with five users attempting a task, the only possible outcomes are 0%, 20%, 40%, 60%, 80% and 100% success. It’s not uncommon to have 100% completion rates with five users. There’s something about reporting perfect success at this sample size that doesn’t resonate well. It sounds too good to be true.

We experimented [pdf] with several estimators with small sample sizes and found the LaPlace estimator and the simple proportion (referred to as the Maximum Likelihood Estimator) generally work well for the usability test data we examined. When you want the best estimate, the calculator will generate it based on our findings.

Rating Scales : Rating scales are a funny type of metric, in that most of them are bounded on both ends (e.g. 1 to 5, 1 to 7 or 1 to 10) unless you are Spinal Tap of course. For small and large sample sizes, we’ve found reporting the mean to be the best average over the median [pdf] . There are in fact many ways to report the scores from rating scales, including top-two boxes . The one you report depends on both the sensitivity as well as what’s used in an organization.

Average Time : One long task time can skew the arithmetic mean and make it a poor measure of the middle. In such situations, the median is a better indicator of the typical or “average” time. Unfortunately, the median tends to be less accurate and more biased than the mean when sample sizes are less than about 25. In these circumstances, the geometric mean (average of the log values transformed back) tends to be a better measure of the middle. When sample sizes get above 25, the median works fine.

You might also be interested in