problem solving involving simple interest

SIMPLE INTEREST PROBLEMS WITH SOLUTIONS

Problem 1 :

A person deposits $5,000 in a bank account which pays 6% simple interest per year. Find the value of his deposit after 4 years.

Formula for simple interest is

Substitute P = 5000, t = 4, r = 6%.

I = 5000 ⋅ 6/100 ⋅ 4

Accumulated value  = Principal + Interest

= 5000 + 1200

Problem 2 :

Glen received $2,250 loan from bank. After six months, he paid back  $2,295 and closed the loan. Find the rate of interest.

Interest = Amount - Principal

I = 2295 - 2250

Given : Time period is 6 months.

In simple interest formula, we use time period in years. But, the time period given in the question is in months.

So, let us change the given time period in years.

6 months = 6/12 year = 1 /2 years

So, the time period is 1/2 year.

Formula for simple interest :

Substitute I = 45, P = 2250, t = 1/2.

45 = 2250 ⋅ r ⋅ 1/2

45 = 1125 ⋅ r

Divide both sides by 1125.

45/1125 = r

To convert the decimal 0.04 into percentage, multiply it by 100. 

0.04 ⋅ 100% = r

Problem 3 :

A man invests $16,500 in two kinds treasury notes, which yield 7.5% and 6% annually. After two years year, he earns $2442 in interest. How much does he invest at the 6 % rate ? 

Let x be the amount invested at 6% rate.

Then, the amount invested in 7.5% account is

= 16500 - x

Given :  After two years, total interest earned in both the accounts is $2,442.

Interest at 6% rate + Interest at 7.5% rate = 2442

x  ⋅ 6/100   ⋅ 2 + (16500 - x) ⋅ 7.5/100 ⋅ 2 = 2442

x ⋅ 0.06 ⋅ 2 + (16500 - x) ⋅ 0.075 ⋅ 2 = 2442

0.12x + (16500 - x) ⋅ 0.15 = 2442

0.12x + 2475 - 0.15x = 2442

2475 - 0.03x = 2442

2475 - 2442 = 0.03x

Divide both sides by 0.03.

33/0.03 = x

Hence, the amount invested at 6% rate is $1100.

Problem 4 :

A person invested $25,200 in two accounts, which pay 5 % and 10% interest annually. The amount invested at 10% rate is 110% of the amount invested at 5% rate. After three years year, he earns $5760 in interest. How much did he invest at the 5% rate ?

Let x be the amount invested at 5% rate.

Then, the amount invested in 10% account is

= 110% of x

= 1.10  ⋅ x

Given :  After three years, total interest earned in both the accounts is $5,760.

Interest at 5% rate + Interest at 10% rate = 5760

x  ⋅ 5/100   ⋅ 3 + 1.1x ⋅ 10/100 ⋅ 3 = 5760

x ⋅ 0.05 ⋅ 3 + 1.1x ⋅ 0.1 ⋅ 3 = 5760

0.15x + 0.33x = 5760

0.48x = 5760

Divide both sides by 0.48.

x = 5760/0.48

x = 576000/48

Hence, the amount invested at 5% rate is $12000.

Problem 5 :

In simple interest, a sum of money doubles itself in 10 years. Find the number of years it will take to triple itself.

Let P be the sum of money invested.

Given : Sum of money doubles itself in 10 years.

Then, P will become 2P in 10 years.

Now we can calculate interest for ten years as given below.

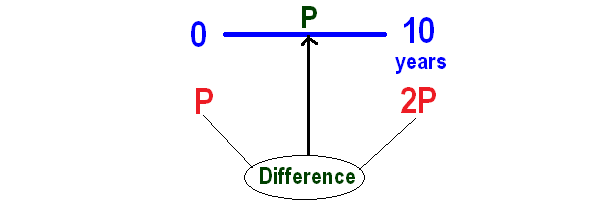
From the above calculation, P is the interest for the first 10 years.

In simple interest, interest earned will be same for every year.

So, interest earned in the next 10 years also will be P.

It has been explained below.

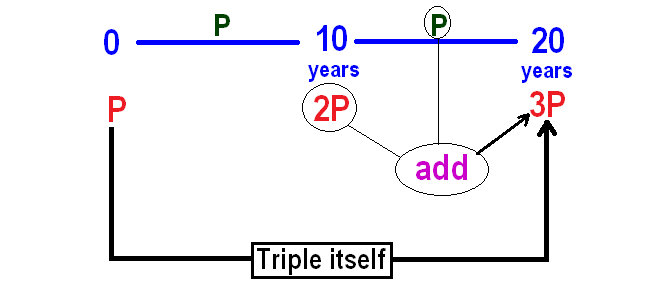
Hence, it will take 20 years for the principal to become triple itself.

Problem 6 :

In simple interest, a sum of money amounts to $ 6200 in 2 years and $ 7400 in 3 years. Find the principal.

At the end of 2 years, we get $6200

At the end of 3 years, we get $7400

From these two information, we can get the interest earned in the 3rd year as given below.

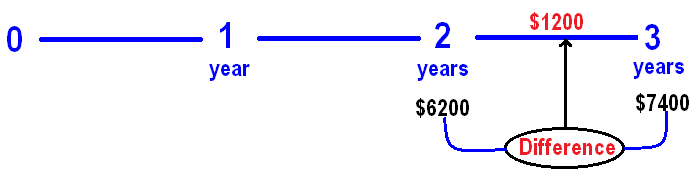
In simple interest, interest will be same for every year.

Based on this, we can calculate the principal as given below.

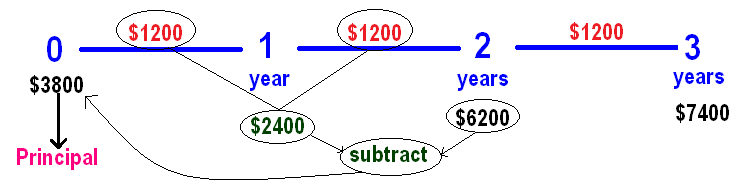
Hence, the principal is $3800.

Kindly mail your feedback to   [email protected]

We always appreciate your feedback.

© All rights reserved. onlinemath4all.com

• Sat Math Practice
• SAT Math Worksheets
• PEMDAS Rule
• BODMAS rule
• GEMDAS Order of Operations
• Math Calculators
• Transformations of Functions
• Order of rotational symmetry
• Lines of symmetry
• Compound Angles
• Quantitative Aptitude Tricks
• Trigonometric ratio table
• Word Problems
• Times Table Shortcuts
• 10th CBSE solution
• PSAT Math Preparation
• Privacy Policy
• Laws of Exponents

Recent Articles

How to Convert Between Polar and Rectangular Coordinates

Jun 08, 24 12:03 AM

SAT Math Videos (Part 1 - No Calculator)

Jun 08, 24 12:02 AM

Multiplying Matrices

Jun 07, 24 11:58 PM

• + ACCUPLACER Mathematics
• + ACT Mathematics
• + AFOQT Mathematics
• + ALEKS Tests
• + ASVAB Mathematics
• + ATI TEAS Math Tests
• + Common Core Math
• + DAT Math Tests
• + FSA Tests
• + FTCE Math
• + GED Mathematics
• + Georgia Milestones Assessment
• + GRE Quantitative Reasoning
• + HiSET Math Exam
• + HSPT Math
• + ISEE Mathematics
• + PARCC Tests
• + Praxis Math
• + PSAT Math Tests
• + PSSA Tests
• + SAT Math Tests
• + SBAC Tests
• + SIFT Math
• + SSAT Math Tests
• + STAAR Tests
• + TABE Tests
• + TASC Math
• + TSI Mathematics
• + ACT Math Worksheets
• + Accuplacer Math Worksheets
• + AFOQT Math Worksheets
• + ALEKS Math Worksheets
• + ASVAB Math Worksheets
• + ATI TEAS 6 Math Worksheets
• + FTCE General Math Worksheets
• + GED Math Worksheets
• + 3rd Grade Mathematics Worksheets
• + 4th Grade Mathematics Worksheets
• + 5th Grade Mathematics Worksheets
• + 6th Grade Math Worksheets
• + 7th Grade Mathematics Worksheets
• + 8th Grade Mathematics Worksheets
• + 9th Grade Math Worksheets
• + HiSET Math Worksheets
• + HSPT Math Worksheets
• + ISEE Middle-Level Math Worksheets
• + PERT Math Worksheets
• + Praxis Math Worksheets
• + PSAT Math Worksheets
• + SAT Math Worksheets
• + SIFT Math Worksheets
• + SSAT Middle Level Math Worksheets
• + 7th Grade STAAR Math Worksheets
• + 8th Grade STAAR Math Worksheets
• + THEA Math Worksheets
• + TABE Math Worksheets
• + TASC Math Worksheets
• + TSI Math Worksheets
• + AFOQT Math Course
• + ALEKS Math Course
• + ASVAB Math Course
• + ATI TEAS 6 Math Course
• + CHSPE Math Course
• + FTCE General Knowledge Course
• + GED Math Course
• + HiSET Math Course
• + HSPT Math Course
• + ISEE Upper Level Math Course
• + SHSAT Math Course
• + SSAT Upper-Level Math Course
• + PERT Math Course
• + Praxis Core Math Course
• + SIFT Math Course
• + 8th Grade STAAR Math Course
• + TABE Math Course
• + TASC Math Course
• + TSI Math Course
• + Number Properties Puzzles
• + Algebra Puzzles
• + Geometry Puzzles
• + Intelligent Math Puzzles
• + Ratio, Proportion & Percentages Puzzles
• + Other Math Puzzles

How to Solve Simple Interest Problems? (+FREE Worksheet!)

Learn how to solve simple interest problems using simple interest formulas.

Related Topics

• How to Find Percent of Increase and Decrease
• How to Solve Percent Problems
• How to Do Percentage Calculations
• How to Find Discount, Tax, and Tip

Step-by-step guide to solve simple interest

• Simple Interest: The charge for borrowing money or the return for lending it.
• To solve a simple interest problem, use this formula: Interest \(=\) principal \(\times\) rate \(\times\) time  \( ⇒ \color{blue}{I=p \ × \ r \ × \ t}\)  

Simple Interest – Example 1:

Find simple interest for \( $450\) investment at \(7\%\) for \(8\) years.

Use Interest formula: \(\color{ blue }{I=prt }\) \(P=$450\), \(r=7\%=\frac{7}{100}=0.07\) and \(t=8\) Then: \(I=450 \ × \ 0.07 \ × \ 8=$252\)

The Absolute Best Books to Ace Pre-Algebra to Algebra II

The Ultimate Algebra Bundle From Pre-Algebra to Algebra II

Simple interest – example 2:.

Find simple interest for \( $5,200\) investment at \(4\%\) for \(3\) years.

Use simple interest formula: \(\color{ blue }{I=prt }\) \(P=$5,200\), \(r=4\%=\frac{4}{100}=0.04\) and \(t=3\) Then: \(I=5,200 \ × \ 0.04 \ × \ 3=$624\)

Simple Interest – Example 3:

Find simple interest for \($5,000\) investment at \(3\%\) for \(4\) years.

Use simple interest formula: \(\color{ blue }{I=prt }\) \( P=$5,000, r=3\%=\frac{3}{100}=0.03\) and \(t=4\) Then: \(I= 5,000 ×0.03×4=$600\)

The Absolute Best Book to Ace the Algebra Test

Algebra I for Beginners The Ultimate Step by Step Guide to Acing Algebra I

Simple interest – example 4:.

Find simple interest for \($900\) at \(3.5\%\) for \(5\) years.

Use simple interest formula: \(\color{ blue }{I=prt }\) \( P=$900, r=3.5\%=\frac{3.5}{100}=0.035\) and \(t=5\) Then: \(I=900×0.035×5=$157.50\)

Exercises for Solving Simple Interest

Use simple interest to find the ending balance.

• \($1,300\) at \(5\%\) for \(6\) years.
• \($5,400\) at \(7.5\%\) for \(6\) months.
• \($25,600\) at \(9.2\%\) for \(5\) years.
• \($240\) interest is earned on a principal of \($1500\) at a simple interest rate of \(4\%\) interest per year. For how many years was the principal invested?
• A new car, valued at \($28,000\), depreciates at \(9\%\) per year from original price. Find the value of the car \(3\) years after purchase.
• Sara puts \($2,000\) into an investment yielding \(5\%\) annual simple interest; she left the money in for five years. How much interest does Sara get at the end of those five years?

Download Simple Interest Worksheet

• \(\color{blue}{$1,690.00}\)
• \(\color{blue}{$5,602.50}\)
• \(\color{blue}{$37,376.00}\)
• \(\color{blue}{4 \ years}\)
• \(\color{blue}{$20,440.00}\)
• \(\color{blue}{$500.00}\)

The Greatest Books for Students to Ace the Algebra

Pre-Algebra Exercise Book A Comprehensive Workbook + PreAlgebra Practice Tests

Pre-algebra in 10 days the most effective pre-algebra crash course, college algebra practice workbook the most comprehensive review of college algebra, high school algebra i a comprehensive review and step-by-step guide to mastering high school algebra 1, 10 full length clep college algebra practice tests the practice you need to ace the clep college algebra test.

by: Effortless Math Team about 5 years ago (category: Articles , Free Math Worksheets )

Effortless Math Team

Related to this article, more math articles.

• FREE ALEKS Math Practice Test
• How to Solve Absolute Values and Opposites of Rational Numbers?
• Top 10 Tips to Create a CHSPE Math Study Plan
• How to Graph Solutions to One-step and Two-step Linear Inequalities
• How to Prepare for the THEA Math Test?
• The Application of The Squeeze Theorem: Limit Problems Made Easy
• The Ultimate 6th Grade NDSA Math Course (+FREE Worksheets)
• 5th Grade NDSA Math Worksheets: FREE & Printable
• The Ultimate TABE Math Formula Cheat Sheet
• What is the Relationship Between Arcs and Central Angles?

What people say about "How to Solve Simple Interest Problems? (+FREE Worksheet!) - Effortless Math: We Help Students Learn to LOVE Mathematics"?

No one replied yet.

Leave a Reply Cancel reply

You must be logged in to post a comment.

Pre-Algebra Practice Workbook The Most Comprehensive Review of Pre-Algebra

Algebra i practice workbook the most comprehensive review of algebra 1, algebra ii practice workbook the most comprehensive review of algebra 2, algebra ii for beginners the ultimate step by step guide to acing algebra ii, pre-algebra for beginners the ultimate step by step guide to preparing for the pre-algebra test, pre-algebra tutor everything you need to help achieve an excellent score.

• ATI TEAS 6 Math
• ISEE Upper Level Math
• SSAT Upper-Level Math
• Praxis Core Math
• 8th Grade STAAR Math

Limited time only!

Save Over 45 %

It was $89.99 now it is $49.99

Login and use all of our services.

Effortless Math services are waiting for you. login faster!

Register Fast!

Password will be generated automatically and sent to your email.

After registration you can change your password if you want.

• Math Worksheets
• Math Courses
• Math Topics
• Math Puzzles
• Math eBooks
• GED Math Books
• HiSET Math Books
• ACT Math Books
• ISEE Math Books
• ACCUPLACER Books
• Premium Membership
• Youtube Videos

Effortless Math provides unofficial test prep products for a variety of tests and exams. All trademarks are property of their respective trademark owners.

• Bulk Orders
• Refund Policy

6.4 Solve Simple Interest Applications

Learning objectives.

• Use the simple interest formula
• Solve simple interest applications

Be Prepared 6.4

Before you get started, take this readiness quiz.

• Solve 0.6 y = 45 . 0.6 y = 45 . If you missed this problem, review Example 5.43 .
• Solve n 1.45 = 4.6 . n 1.45 = 4.6 . If you missed this problem, review Example 5.44 .

Use the Simple Interest Formula

Do you know that banks pay you to let them keep your money? The money you put in the bank is called the principal , P , P , and the bank pays you interest , I . I . The interest is computed as a certain percent of the principal; called the rate of interest , r . r . The rate of interest is usually expressed as a percent per year, and is calculated by using the decimal equivalent of the percent. The variable for time, t , t , represents the number of years the money is left in the account.

Simple Interest

If an amount of money, P , P , the principal, is invested for a period of t t years at an annual interest rate r , r , the amount of interest, I , I , earned is

Interest earned according to this formula is called simple interest .

The formula we use to calculate simple interest is I = P r t . I = P r t . To use the simple interest formula we substitute in the values for variables that are given, and then solve for the unknown variable. It may be helpful to organize the information by listing all four variables and filling in the given information.

Example 6.33

Find the simple interest earned after 3 3 years on $500 $500 at an interest rate of 6%. 6%.

Organize the given information in a list.

I = ? P = $500 r = 6% t = 3 years I = ? P = $500 r = 6% t = 3 years

We will use the simple interest formula to find the interest.

Try It 6.65

Find the simple interest earned after 4 4 years on $800 $800 at an interest rate of 5%. 5%.

Try It 6.66

Find the simple interest earned after 2 2 years on $700 $700 at an interest rate of 4%. 4%.

In the next example, we will use the simple interest formula to find the principal.

Example 6.34

Find the principal invested if $178 $178 interest was earned in 2 2 years at an interest rate of 4%. 4%.

I = $178 P = ? r = 4% t = 2 years I = $178 P = ? r = 4% t = 2 years

We will use the simple interest formula to find the principal.

Try It 6.67

Find the principal invested if $495 $495 interest was earned in 3 3 years at an interest rate of 6%. 6%.

Try It 6.68

Find the principal invested if $1,246 $1,246 interest was earned in 5 5 years at an interest rate of 7% . 7% .

Now we will solve for the rate of interest.

Example 6.35

Find the rate if a principal of $8,200 $8,200 earned $3,772 $3,772 interest in 4 4 years.

Organize the given information.

I = $3,772 P = $8,200 r = ? t = 4 years I = $3,772 P = $8,200 r = ? t = 4 years

We will use the simple interest formula to find the rate.

Try It 6.69

Find the rate if a principal of $5,000 $5,000 earned $1,350 $1,350 interest in 6 6 years.

Try It 6.70

Find the rate if a principal of $9,000 $9,000 earned $1,755 $1,755 interest in 3 3 years.

Solve Simple Interest Applications

Applications with simple interest usually involve either investing money or borrowing money. To solve these applications, we continue to use the same strategy for applications that we have used earlier in this chapter. The only difference is that in place of translating to get an equation, we can use the simple interest formula.

We will start by solving a simple interest application to find the interest.

Example 6.36

Nathaly deposited $12,500 $12,500 in her bank account where it will earn 4% 4% interest. How much interest will Nathaly earn in 5 5 years?

We are asked to find the Interest, I . I .

I = ? P = $12,500 r = 4% t = 5 years I = ? P = $12,500 r = 4% t = 5 years

Try It 6.71

Areli invested a principal of $950 $950 in her bank account with interest rate 3%. 3%. How much interest did she earn in 5 5 years?

Try It 6.72

Susana invested a principal of $36,000 $36,000 in her bank account with interest rate 6.5% . 6.5% . How much interest did she earn in 3 3 years?

There may be times when you know the amount of interest earned on a given principal over a certain length of time, but you don't know the rate. For instance, this might happen when family members lend or borrow money among themselves instead of dealing with a bank. In the next example, we'll show how to solve for the rate.

Example 6.37

Loren lent his brother $3,000 $3,000 to help him buy a car. In 4 years 4 years his brother paid him back the $3,000 $3,000 plus $660 $660 in interest. What was the rate of interest?

We are asked to find the rate of interest, r . r .

I = 660 P = $3,000 r = ? t = 4 years I = 660 P = $3,000 r = ? t = 4 years

Try It 6.73

Jim lent his sister $5,000 $5,000 to help her buy a house. In 3 3 years, she paid him the $5,000 , $5,000 , plus $900 $900 interest. What was the rate of interest?

Try It 6.74

Hang borrowed $7,500 $7,500 from her parents to pay her tuition. In 5 5 years, she paid them $1,500 $1,500 interest in addition to the $7,500 $7,500 she borrowed. What was the rate of interest?

There may be times when you take a loan for a large purchase and the amount of the principal is not clear. This might happen, for instance, in making a car purchase when the dealer adds the cost of a warranty to the price of the car. In the next example, we will solve a simple interest application for the principal.

Example 6.38

Eduardo noticed that his new car loan papers stated that with an interest rate of 7.5% , 7.5% , he would pay $6,596.25 $6,596.25 in interest over 5 5 years. How much did he borrow to pay for his car?

We are asked to find the principal, P . P .

I = 6,596.25 P = ? r = 7.5% t = 5 years I = 6,596.25 P = ? r = 7.5% t = 5 years

Try It 6.75

Sean's new car loan statement said he would pay $4,866.25 $4,866.25 in interest from an interest rate of 8.5% 8.5% over 5 5 years. How much did he borrow to buy his new car?

Try It 6.76

In 5 5 years, Gloria's bank account earned $2,400 $2,400 interest at 5%. 5%. How much had she deposited in the account?

In the simple interest formula, the rate of interest is given as an annual rate, the rate for one year. So the units of time must be in years. If the time is given in months, we convert it to years.

Example 6.39

Caroline got $900 $900 as graduation gifts and invested it in a 10-month 10-month certificate of deposit that earned 2.1% 2.1% interest. How much interest did this investment earn?

We are asked to find the interest, I . I .

I = ? P = $900 r = 2.1% t = 10 months I = ? P = $900 r = 2.1% t = 10 months

Try It 6.77

Adriana invested $4,500 $4,500 for 8 8 months in an account that paid 1.9% 1.9% interest. How much interest did she earn?

Try It 6.78

Milton invested $2,460 $2,460 for 20 20 months in an account that paid 3.5% 3.5% interest How much interest did he earn?

Section 6.4 Exercises

Practice makes perfect.

In the following exercises, use the simple interest formula to fill in the missing information.

In the following exercises, solve the problem using the simple interest formula.

Find the simple interest earned after 5 5 years on $600 $600 at an interest rate of 3%. 3%.

Find the simple interest earned after 4 4 years on $900 $900 at an interest rate of 6%. 6%.

Find the simple interest earned after 2 2 years on $8,950 $8,950 at an interest rate of 3.24% . 3.24% .

Find the simple interest earned after 3 3 years on $6,510 $6,510 at an interest rate of 2.85% . 2.85% .

Find the simple interest earned after 8 8 years on $15,500 $15,500 at an interest rate of 11.425% . 11.425% .

Find the simple interest earned after 6 6 years on $23,900 $23,900 at an interest rate of 12.175% . 12.175% .

Find the principal invested if $656 $656 interest was earned in 5 5 years at an interest rate of 4% . 4% .

Find the principal invested if $177 $177 interest was earned in 2 2 years at an interest rate of 3% . 3% .

Find the principal invested if $70.95 $70.95 interest was earned in 3 3 years at an interest rate of 2.75%. 2.75%.

Find the principal invested if $636.84 $636.84 interest was earned in 6 6 years at an interest rate of 4.35%. 4.35%.

Find the principal invested if $15,222.57 $15,222.57 interest was earned in 6 6 years at an interest rate of 10.28% . 10.28% .

Find the principal invested if $10,953.70 $10,953.70 interest was earned in 5 5 years at an interest rate of 11.04%. 11.04%.

Find the rate if a principal of $5,400 $5,400 earned $432 $432 interest in 2 2 years.

Find the rate if a principal of $2,600 $2,600 earned $468 $468 interest in 6 6 years.

Find the rate if a principal of $11,000 $11,000 earned $1,815 $1,815 interest in 3 3 years.

Find the rate if a principal of $8,500 $8,500 earned $3,230 $3,230 interest in 4 4 years.

Casey deposited $1,450 $1,450 in a bank account with interest rate 4%. 4%. How much interest was earned in 2 2 years?

Terrence deposited $5,720 $5,720 in a bank account with interest rate 6%. 6%. How much interest was earned in 4 4 years?

Robin deposited $31,000 $31,000 in a bank account with interest rate 5.2% . 5.2% . How much interest was earned in 3 3 years?

Carleen deposited $16,400 $16,400 in a bank account with interest rate 3.9% . 3.9% . How much interest was earned in 8 8 years?

Hilaria borrowed $8,000 $8,000 from her grandfather to pay for college. Five years later, she paid him back the $8,000 , $8,000 , plus $1,200 $1,200 interest. What was the rate of interest?

Kenneth lent his niece $1,200 $1,200 to buy a computer. Two years later, she paid him back the $1,200 , $1,200 , plus $96 $96 interest. What was the rate of interest?

Lebron lent his daughter $20,000 $20,000 to help her buy a condominium. When she sold the condominium four years later, she paid him the $20,000 , $20,000 , plus $3,000 $3,000 interest. What was the rate of interest?

Pablo borrowed $50,000 $50,000 to start a business. Three years later, he repaid the $50,000 , $50,000 , plus $9,375 $9,375 interest. What was the rate of interest?

In 10 10 years, a bank account that paid 5.25% 5.25% earned $18,375 $18,375 interest. What was the principal of the account?

In 25 25 years, a bond that paid 4.75% 4.75% earned $2,375 $2,375 interest. What was the principal of the bond?

Joshua's computer loan statement said he would pay $1,244.34 $1,244.34 in interest for a 3 3 year loan at 12.4% . 12.4% . How much did Joshua borrow to buy the computer?

Margaret's car loan statement said she would pay $7,683.20 $7,683.20 in interest for a 5 5 year loan at 9.8%. 9.8%. How much did Margaret borrow to buy the car?

Caitlin invested $8,200 $8,200 in an 18-month 18-month certificate of deposit paying 2.7% 2.7% interest. How much interest did she earn form this investment?

Diego invested $6,100 $6,100 in a 9-month 9-month certificate of deposit paying 1.8% 1.8% interest. How much interest did he earn form this investment?

Airin borrowed $3,900 $3,900 from her parents for the down payment on a car and promised to pay them back in 15 15 months at a 4% 4% rate of interest. How much interest did she owe her parents?

Yuta borrowed $840 $840 from his brother to pay for his textbooks and promised to pay him back in 5 5 months at a 6% 6% rate of interest. How much interest did Yuta owe his brother?

Everyday Math

Interest on savings Find the interest rate your local bank pays on savings accounts.

• ⓐ What is the interest rate?
• ⓑ Calculate the amount of interest you would earn on a principal of $8,000 $8,000 for 5 5 years.

Interest on a loan Find the interest rate your local bank charges for a car loan.

• ⓑ Calculate the amount of interest you would pay on a loan of $8,000 $8,000 for 5 5 years.

Writing Exercises

Why do banks pay interest on money deposited in savings accounts?

Why do banks charge interest for lending money?

ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

ⓑ On a scale of 1–10, how would you rate your mastery of this section in light of your responses on the checklist? How can you improve this?

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/prealgebra/pages/1-introduction

• Authors: Lynn Marecek, MaryAnne Anthony-Smith
• Publisher/website: OpenStax
• Book title: Prealgebra
• Publication date: Sep 25, 2015
• Location: Houston, Texas
• Book URL: https://openstax.org/books/prealgebra/pages/1-introduction
• Section URL: https://openstax.org/books/prealgebra/pages/6-4-solve-simple-interest-applications

© Feb 9, 2022 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

• HW Guidelines
• Study Skills Quiz
• Find Local Tutors
• Demo MathHelp.com
• Join MathHelp.com

Select a Course Below

• ACCUPLACER Math
• Math Placement Test
• PRAXIS Math
• + more tests
• 5th Grade Math
• 6th Grade Math
• Pre-Algebra
• College Pre-Algebra
• Introductory Algebra
• Intermediate Algebra
• College Algebra

"Investment" Word Problems

Explanation Examples

What is "interest"?

Interest is the price of money. If I borrow money from you, with a promise to pay you back later, that money is no longer available for you to use as you please. In return for the loss of your use of that money, I would pay you a certain amount (usually being a percentage of the amount that I borrowed), over and above the amount what I'd borrowed, in order to pay you for my use of your money.

Content Continues Below

MathHelp.com

Investment Word Problems

What is an "interest rate"?

An interest rate is a rate (usually expressed as a percentage) of the money borrowed, which is to be paid back over and above the borrowed amount. For instance, if I borrow $100 from you and pay you back $108 at the end of a year's time, then the interest rate "per annum" (that is, per year) is 8%.

Interest rates are almost always expressed in terms of years. If I borrowed the $100 from you and paid you back in six months, then I would owe you $104, because six months is half of a year.

What is "simple" interest?

Advertisement

Simple interest is an amount of money that is a fixed percentage of the amount borrowed, and which is added to the borrowed amount once each interest-rate period. So if I'd borrowed $100 from you and didn't pay it back until two years later, I would owe you an extra $8 for the first year and another extra $8 for the second year, for a total of $116 that I need to pay you.

In pre-algebra or beginning algebra, "investment" word problems usually involve simple annual interest — as opposed to compounded interest . Simple interest is earned on the entire investment amount for a given period of time.

This differs from compounded interest, where simple interest is earned for a smaller amount of time (for instance, for one month). Then, over the next period of time, the interest is earned on the original investment *plus* on the interest that was earned on that first time period. Then, during the third time period, interest is earned on the initial investment amount plus the interest earned during the first two periods. And so forth.

What is an example of a simple-interest situation?

One example of a simple-interest situation is getting a loan for the car you're buying. Another example would be investing in a certificate of deposit (that is, a CD ) at your bank. Mortgages and student loans can also be issued in terms of simple interest.

What is the formula for simple interest?

The formula for the simple interest I earned on the amount of an investment (that is, the "principle") P with an interest rate of r over a time period t is I  =  Prt .

In the simple-interest formula I  =  Prt , the variable I stands for the interest earned on the original investment, P stands for the amount of the original investment, r is the interest rate (expressed in decimal form), and t is the time (usually in terms of years).

The time units, in all cases, must match the interest-rate units. For instance, if you got a loan from your friendly neighborhood loan shark, where the interest rate is monthly, rather than yearly, then your time must be measured in terms of months.

When working on investment word problems, you will want to substitute all given information into the I  =  Prt equation, and then solve for whatever is left.

• You put $1000 into an investment yielding 6% annual interest; you left the money in for two years. How much interest do you get at the end of those two years?

The invested amount (that is, the principal) of my investment is P  = $1000 , the interest rate (expressed in decimal form) is r  = 0.06 per year, and the amount of time is t  = 2 . Substituting these values into the simple-interest formula, I get:

I = (1000)(0.06)(2) = 120

I will get $120 in interest.

• You invested $500 and received $650 after three years. What had been the interest rate?

For this exercise, I first need to find the amount of the interest. Since simple interest is added to the principal, and since the principal was P  = $500, then the interest is I = $650 − 500 = $150 . The time is t  = 3 . Substituting all of these values into the simple-interest formula, I get:

150 = (500)( r )(3)

150 = 1500 r

150 / 1500 = r = 0.10

Of course, I need to remember to convert this decimal to a percentage.

I was getting 10% interest.

When you have just one account, one simple situation, requiring one use of the simple-interest formula, it's pretty easy to set up and solve the exercises. The hard part comes when the exercises involve multiple investments or some other complication. But there is a trick to these that makes them fairly easy to handle. You use a simple table or grid.

• You have $50,000 to invest, and two funds into which you'd like to place those monies. The You-Risk-It Fund (Fund Y) yields 14% interest. The Extra-Dull Fund (Fund X) yields 6% interest. You'd like to earn as much as possible but, because of college financial-aid implications, you don't think you can afford to earn more than $4,500 in interest income this year. How much should you put in each fund?

The problem here comes from the fact that I'm splitting the $50,000 in principal into two smaller amounts. Here's how to handle this:

I will make a table. The top row has, as its entries, the variables in the simple-interest formula. The left-hand column labels the two funds — and, in case I need it, a "totals" row. (Not all exercises will need the "totals" row.)

I can't add rates — that's just a thing; rates can't be added — and each of the investments is for one year, so there are no "total" values for the interest rates or the years. Hence, the dashes, to remind me not to try to put anything in there.

I know the interest total that I'm aiming for, and I know the total amount that I'm investing, so I can enter "total" values for the "interest" and "investment" columns.

I know the interest rates and the time (namely, one year) for the two investments, so I can enter these values in the "rate" and "time" columns, in each fund's row.

Putting it all together, I get the following start to my set-up:

How do I fill in for those question marks? I'll start with the principal P . Let's say that I put x dollars into Fund X, and y dollars into Fund Y. Then x  +  y  =  50,000 .

But this doesn't help much, since I only know how to solve equations in one variable. However, I then notice that I can solve x  +  y = 50,000 to get y = 50,000 −  x .

THIS TECHNIQUE IS IMPORTANT! The amount left for me to put into Fund Y is (the total that I invested) less (what I've already put into Fund X), or 50,000 −  x .

Any time you have a total that is divided into two parts, you can designate one part as (one part), and the rest will be (the total) minus the (one part), because the second part is whatever is left, from the total, after (one part) is accounted for.

You will need this technique — this "how much is left" construction — in the future, so make sure you understand it now.

So now I have a variable for the Fund X part, and an expression for however much was left to go into the Fund Y part. I can add these to my table:

Now I will show you why I set up the table like this. By organizing the columns according to the interest formula, I can now multiply across (in this case, I will multiply the three right-hand columns to get expressions for I in the second column) to fill in the "interest" column.

The interest from Fund X and the interest from Fund Y will add up to $4,500 . As a result, I can add down the "interest" column, set the sum of the two interest expressions equal to the total interest, and solve the resulting equation for the value of the variable:

0.06 x + 0.14(50,000 − x ) = 4,500

0.06 x + 7,000 − 0.14 x = 4,500

7,000 − 0.08 x = 4,500

−0.08 x = −2,500

The value of x stands for the amount invested in Fund X. So the amount that is left, from the total invested, is given by 50,000 − 31,250 = 18,750 . And this (being the amount that is left after I'd put money into Fund X) is the amount that is invested in Fund Y.

I should put $31,250 into Fund X, and $18,750 into Fund Y.

Note that the answer did not involve nice, neat values like $10,000 or $35,000 . You should understand that this means that you cannot always expect to be able to use guess-n-check to find your answers. You really do need to know how to do these exercises.

URL: https://www.purplemath.com/modules/investmt.htm

Page 1 Page 2

Standardized Test Prep

College math, homeschool math, share this page.

• Terms of Use
• Privacy / Cookies
• About Purplemath
• About the Author
• Tutoring from PM
• Advertising
• Linking to PM
• Site licencing

Visit Our Profiles

MathBootCamps

Simple interest formula and examples.

Simple interest is when the interest on a loan or investment is calculated only on the amount initially invested or loaned. This is different from compound interest, where interest is calculated on on the initial amount and on any interest earned. As you will see in the examples below, the simple interest formula can be used to calculate the interest earned, the total amount, and other values depending on the problem. [adsenseWide]

Examples of finding the interest earned with the simple interest formula

In many simple interest problems, you will be finding the total interest earned over a set period, which is represented as \(I\). The formula for this is:

Let’s use an example to see how this formula works. Remember that in the formula, the principal \(P\) is the initial amount invested.

A 2-year loan of $500 is made with 4% simple interest. Find the interest earned.

Always take a moment to identify the values given in the problem. Here we are given:

• Time is 2 years: \(t = 2\)
• Initial amount is $500: \(P = 500\)
• The rate is 4%. Write this as a decimal: \(r = 0.04\)

Now apply the formula:

\(\begin{align}I &= Prt \\ &= 500(0.04)(2) \\ &= \bbox[border: 1px solid black; padding: 2px]{40}\end{align}\)

Answer : The interest earned is $40.

In this example, the time given was in years, just as in the formula. But what if you are only given a number of months? Let’s use another example to see how this might be different.

A total of $1,200 is invested at a simple interest rate of 6% for 4 months. How much interest is earned on this investment?

Before we can apply the formula, we will need to write the time of 4 months in terms of years. Since there are 12 months in a year:

\(\begin{align}t &= \dfrac{4}{12} \\ &= \dfrac{1}{3}\end{align}\)

With this adjusted to years, we can now apply the formula with \(P = 1200\) and \(r = 0.06\).

\(\begin{align}I &= Prt \\ &= 1200(0.06)\left(\dfrac{1}{3}\right) \\ &= \bbox[border: 1px solid black; padding: 2px]{24}\end{align}\)

Answer : The interest earned is $24.

If you hadn’t converted here, you would have found the interest for 4 years, which would be much higher. So, always make sure to check that the time is in years before applying the formula.

Important! The time must be in years to apply the simple interest formula. If you are given months, use a fraction to represent it as years.

Another type of problem you might run into when working with simple interest is finding the total amount owed or the total value of an investment after a given amount of time. This is known as the future value, and can be calculated in a couple of different ways.

Finding the future value for simple interest

One way to calculate the future value would be to just find the interest and then add it to the principal. The quicker method however, is to use the following formula.

You know to use this formula when you are asked questions like “what is the total amount to be repaid” or “what is the value of the investment” -anything that seems to refer to the overall total after interest is considered.

A business takes out a simple interest loan of $10,000 at a rate of 7.5%. What is the total amount the business will repay if the loan is for 8 years?

The total amount they will repay is the future value, \(A\). We are also given that:

• \(r = 0.075\)
• \(P = 10\,000\)

Using the simple interest formula for future value:

\(\begin{align}A &= P(1 + rt)\\ &= 10\,000(1 + 0.075(8)) \\ &= \bbox[border: 1px solid black; padding: 2px]{16\,000}\end{align}\)

Answer : The business will pay back a total of $16,000.

This may seem high, but remember that in the context of a loan, interest is really just a fee for borrowing the money. The larger the interest rate and the longer the time period, the more expensive the loan.

Also note that you could calculate this by first finding the interest, I = Prt = 10000(0.075(8)) = $6000, and adding it to the principal of $10000. The final answer is the same using either method.

[adsenseLargeRectangle]

Continue your study of interest

Now that you have studied the simple interest formula, you can learn the more advanced idea of compound interest. Most savings accounts, credit cards, and loans are based on compound instead of simple interest. You can review this idea here:

• Compound interest

Share this:

• Click to share on Twitter (Opens in new window)
• Click to share on Facebook (Opens in new window)

• IIT JEE Study Material

Simple Interest Problems

Simple interest is the interest calculated on the principal amount which is borrowed. While learning how simple interest is calculated, the main terms are – principal, denoted by P; rate of interest, denoted by R and time in years, denoted by T. 

The branch of commercial mathematics has one of the most important concepts, which is interest. The two types of interest are simple interest and compound interest. The idea of simple interest is based on the time value of money, which has a current value, present value and future value. If invested in a deposit, it earns an amount called interest. In this article, we will learn about simple interest, compound interest and how to solve simple interest problems.

The following example will make these terms more clear:

Malini said that she is going to buy a new refrigerator. Her father asked whether she had the money to buy it. She said to her father that she is planning to take a loan from the bank. The money she borrows is the sum borrowed or the principal. To keep this money for some time, she needs to pay some extra money to the bank. That amount is the interest. So, at the end of the year, she has to pay back the money borrowed and the interest. This is the amount denoted by A. 

Therefore, Amount = Principal + Interest. 

Interest is given in percentage for a time of one year. For example, 12% per annum or 12% p.a.

This means that for every Rs. 100 you borrow, you have to pay Rs. 12 as interest for one year. 

Example: Rajiv took a loan of Rs. 7000 from a bank at 10% as a rate of interest. Find the interest he has to pay at the end of one year.

Solution: Here, sum borrowed, P = 7000

Rate of interest, R = 10%

This means if he borrowed Rs. 100, he had to pay Rs. 10 as interest. So, for Rs. 7000, the interest he has to pay for one year is 7000×10/100 = Rs. 700.

So, at the end of the year, the amount he has to pay back = 7000 + 700 = Rs. 7700

Interest for multiple years: 

If money is borrowed for multiple years, the interest is calculated for the period of time it is kept. For example, if Rajiv returns money at the end of 2 years, he has to pay twice the interest. Rs. 700 for the first year and Rs. 700 for the second year. As the number of years increases, the interest to be paid also increases. If Rs. 100 is borrowed for 4 years at 5%, then the interest to be paid at the end of 4 years is 5 + 5 + 5 + 5 = 4 × 5 = 20. 

So, the interest paid for T years for a principal P at the rate R% is SI = PTR/100

How Simple Interest is Different from Compound Interest

The interest is calculated on the principal amount for a fixed period of time, and the rate of interest is called simple interest. It is used for a single period.

The interest calculated at the end of a certain fixed period and which adds to the principal so that interest can be earned in the next compounding period is called compound interest.

SI and CI Formulas

CI: Compound Interest

P: Principal

R: Rate of interest per annum

T: Time in years

SI: Simple Interest

Solved Examples

Example 1: An amount of Rs. 12800 was invested by Mr Rohan, dividing it into two different investment schemes, A and B, at a simple interest rate of 11% and 14%. What was the amount in plan B if the amount of interest earned in two years was Rs. 3508?

Let the sum invested in Scheme A be Rs. x and that in Scheme B be Rs.(12800 – x).

Then, [x . 14 . 2]/100 + [(12800 – x) . 11 . 2]/100 = 3508

28x – 22x = 350800 – (12800 × 22)

x = 11533.33

So, the sum invested in Scheme B = Rs. (12800 – 11533.33) = Rs. 1266.67.

Example 2: A lender claims to be lending at simple interest, but he adds the interest every 6 months in the calculation of the principal. The rate of interest charged by him is 8%. What will be the effective rate of interest?

Let the sum be Rs. 100.

Simple interest for 1 st 6 months = Rs. [100 × 8 × 1]/[100 × 2] = Rs. 4

Simple interest for last 6 months = Rs. [104 × 8 × 1]/[100 × 2] = Rs.4.16

So, amount at the end of 1 year = Rs. (100 + 4 + 4.16) = Rs. 108.16

Effective rate = (108.16 – 100) = 8.16%

Example 3: A town has a population of 20,000. The population increases by 10% per year. What will be the population after 2 years?

Here, R = 10/100

Population after 2 years will be = P[1 + (R/100)] T

= 20000[1 + (10/100)] 2

= 20000(1.1) 2

Example 4: The time required for a sum of money to amount to five times itself at 16% simple interest p.a. will be:

Let the sum of money be Rs. x and the time required to amount to five times itself be T years.

Principal amount = Rs. x

Amount after T years = Rs. 5x

So, the interest in ‘T’ year should be Rs.(5x – x) = Rs. 4x.

Using simple interest formula,

(P × T × R)/100 = SI

Where, P = Principal amount, T = Duration in years, R = Interest rate per year, SI = Simple interest

(x × T × 16)/100 = 4x

⇒ T × (16/100) = 4

⇒ T = 400/16 = 25

∴ The required time = 25 years.

Example 5:   The rate of simple interest per annum at which a sum of money doubles itself in 16⅔ years is:

Let the principal amount be P.

Now, the amount A after 16⅔  years is doubled.

Hence, amount is 2P.

I = P × R × T/100

P = principal amount

R = rate of interest

T = time in years = 16 2 / 3  = 50/3

I = simple interest

Amount A = I + P

According to question,

A = P + (P × R × T/100)

2P = P + (P × R × T/100)

P = P × R × T/100

R = 100 × 3/50

Example 6: In which year will the amount on a sum of Rs. 800 at 20% compounded half-yearly exceed Rs.1000?

Let the time taken for this amount to reach Rs. 1000 be X.

The important thing to note is that this sum is compounded half-yearly. Hence, we use the formula:

Where, A = Amount

P = Principal

r = Interest rate

m = No. of periods within a year

T = No. of years

We need to obtain T such that the RHS should be greater than the LHS:

\(\begin{array}{l}\therefore A < P\left(1 + [\frac{r}{m*100}]^{mT} \right)\end{array} \)

In this case,

m = 2 (since it is half-yearly)

Substituting these values, we have

⇒ 1.25 < (1.21) T

Now, we need to use trial and error to check for the values of T.

For T = 1, 1.25 > 1.21; hence, the condition is not satisfied.

For T = 2, 1.25 < 1.4641, hence the condition is met.

Therefore, it is the second year in which the amount would be greater than Rs. 1000.

Example 7:  In how many years will a sum of Rs. 4,000 yield a simple interest of Rs. 1,440 at 12% per annum?

We know that the formula for simple interest:

SI = [ P  ×  R  ×  T] /  100

SI = Simple Interest = 1440

P = Principal = 4000

T = Time = ?

R = Rate of Interest = 12%

Substituting the values in the formula

⇒ 1440  = [ 4000  ×  12  ×  T] /  100

⇒ 1440 = 480T

⇒ T = 1440/480 = 3 yrs

Quadratic equations

Linear equations

Frequently Asked Questions

What is the difference between simple interest and compound interest.

Simple interest is based on the principal amount of a loan. Compound interest is based on the principal amount and the interest which adds on it in every period.

Give the formula for simple interest.

Simple interest, I = PRT, where P is the principal amount, R is the rate of interest, and T is the time in years.

How to find the amount if the principal and simple interest are given?

We use the formula, amount = principal + simple interest, to find the amount.

Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!

Select the correct answer and click on the “Finish” button Check your score and answers at the end of the quiz

Visit BYJU’S for all Maths related queries and study materials

Your result is as below

Request OTP on Voice Call

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Post My Comment

Register with Aakash BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

Simple Interest Practice Questions

Click here for Questions

Click here for Answers

GCSE Revision Cards

5-a-day Workbooks

Primary Study Cards

Privacy Policy

Terms and Conditions

Corbettmaths © 2012 – 2024

Simple Interest Word Problems

These lessons, with videos, examples and step-by-step solutions, help Algebra students learn how to solve word problems that involve interest.

Related Pages Simple Interest Compound Interest More Lessons for Grade 9 Math Math Worksheets

How to solve word problems using the simple interest formula? The simple interest formula is interest = principal × rate × time or I = Prt

How to use the Simple Interest Formula?

Example: How much interest is earned in five years on $3,000 invested at an interest rate of 9% per year?

Interest Word Problems - Algebra Help How to solve simple interest word problems?

Example: Pam invested $5000. She earned 14% on part of her investment and 6% on the rest. If she earned a total of $396 for the year, how much did she invest at each rate?

Find the amount of interest earned by $8,000 invested at a 5% annual simple interest rate for 1 year.

To start a mobile dog-grooming service, a woman borrowed $2,500. If the loan was for 2 years and the amount of interest was $175, what simple interest rate was she charged?

A student borrowed some money from his father at 2% simple interest to buy a car. If he paid his father $360 in interest after 3 years, how much did he borrow?

A couple invested $6,000 of their $20,000 lottery winnings in bonds. How much do they have left to in stocks?

A college student wants to invest the $12,000 inheritance he received and use the annual interest earned to pay his tuition cost of $945. The highest rate offered by a bank is 6% annual simple interest. At this rate, he cannot earn the needed $945, so he decided to invest some of the money in a riskier, but more profitable, investment offering a 9% return. How much should he invest at each rate?

A credit union loaned out $50,000, part at an annual rate of 6% and the rest at an annual rate of 12%. The collected combined simple interest was $3600 that year. How much did the credit union loan out at each rate?

Example: Suppose $7,000 is divided into two bank accounts. One account pays 10% simple interest per year and the other pays 5%. After three years there is a total of $1451.25 in interest between the two accounts. How much was invested into each account (rounded to the nearest cent)?

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

6.1: Simple and Compound Interest

• Last updated
• Save as PDF
• Page ID 67128

• David Lippman
• Pierce College via The OpenTextBookStore

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Discussing interest starts with the principal , or amount your account starts with. This could be a starting investment, or the starting amount of a loan. Interest, in its most simple form, is calculated as a percent of the principal. For example, if you borrowed $100 from a friend and agree to repay it with 5% interest, then the amount of interest you would pay would just be 5% of 100: \(\$ 100(0.05)=\$ 5\). The total amount you would repay would be $105, the original principal plus the interest.

Simple One-time Interest

\[A=P+I=P+P r=P(1+r)\]

• \(I\) is the interest
• \(A\) is the end amount: principal plus interest
• \(P\) is the principal (starting amount)
• \(r\) is the interest rate (in decimal form. Example: \(5\% = 0.05\))

A friend asks to borrow $300 and agrees to repay it in 30 days with 3% interest. How much interest will you earn?

\(\begin{array}{ll} P=\$ 300 & \text{the principal } \\ r=0.03 & 3 \%\text{ rate} \\ I=\$ 300(0.03)=\$ 9. & \text{You will earn }\$ 9 \text{ interest.}\end{array}\)

One-time simple interest is only common for extremely short-term loans. For longer term loans, it is common for interest to be paid on a daily, monthly, quarterly, or annual basis. In that case, interest would be earned regularly. For example, bonds are essentially a loan made to the bond issuer (a company or government) by you, the bond holder. In return for the loan, the issuer agrees to pay interest, often annually. Bonds have a maturity date, at which time the issuer pays back the original bond value.

Suppose your city is building a new park, and issues bonds to raise the money to build it. You obtain a $1,000 bond that pays 5% interest annually that matures in 5 years. How much interest will you earn?

Each year, you would earn 5% interest: \(\$ 1000(0.05)=\$ 50\) in interest. So over the course of five years, you would earn a total of $250 in interest. When the bond matures, you would receive back the $1,000 you originally paid, leaving you with a total of $1,250.

We can generalize this idea of simple interest over time.

Simple Interest over Time

\(I=P r t\)

\(A=P+I=P+P r t=P(1+r t)\)

• \(r\) is the interest rate in decimal form
• \(t\) is time

The units of measurement (years, months, etc.) for the time should match the time period for the interest rate.

APR – Annual Percentage Rate

Interest rates are usually given as an annual percentage rate (APR) – the total interest that will be paid in the year. If the interest is paid in smaller time increments, the APR will be divided up.

For example, a \(6 \%\) APR paid monthly would be divided into twelve \(0.5 \%\) payments. A \(4 \%\) annual rate paid quarterly would be divided into four \(1 \%\) payments.

Example 3: Treasury Notes

Treasury Notes (T-notes) are bonds issued by the federal government to cover its expenses. Suppose you obtain a $1,000 T-note with a 4% annual rate, paid semi-annually, with a maturity in 4 years. How much interest will you earn?

Since interest is being paid semi-annually (twice a year), the 4% interest will be divided into two 2% payments.

\(\begin{array}{ll} P=\$ 1000 & \text{the principal } \\ r=0.02 & 2 \%\text{ rate} \\ t = 8 & \text{4 years = 8 half-years} \\ I=\$ 1000(0.02)(8)=\$ 160. & \text{You will earn }\$ 160 \text{ interest total over the four years.}\end{array}\)

Excercies 1

A loan company charges $30 interest for a one month loan of $500. Find the annual interest rate they are charging.

\(I=\$ 30\) of interest

\(P=\$ 500\) principal

\(r=\) unknown

\(t=1\) month

Compound Interest

With simple interest, we were assuming that we pocketed the interest when we received it. In a standard bank account, any interest we earn is automatically added to our balance, and we earn interest on that interest in future years. This reinvestment of interest is called compounding . We looked at this situation earlier, in the chapter on exponential growth.

\(A=P\left(1+\frac{r}{k}\right)^{kt}\)

\(A\) is the balance in the account after t years.

\(P\) is the starting balance of the account (also called initial deposit, or principal)

\(r\) is the annual interest rate in decimal form

\(k\) is the number of compounding periods in one year.

• If the compounding is done annually (once a year), \(k = 1\).
• If the compounding is done quarterly, \(k = 4\).
• If the compounding is done monthly, \(k = 12\).
• If the compounding is done daily, \(k = 365\).

The most important thing to remember about using this formula is that it assumes that we put money in the account once and let it sit there earning interest.

A certificate of deposit (CD) is a savings instrument that many banks offer. It usually gives a higher interest rate, but you cannot access your investment for a specified length of time. Suppose you deposit $3000 in a CD paying 6% interest, compounded monthly. How much will you have in the account after 20 years?

In this example,

\(\begin{array} {ll} P=\$ 3000 & \text{the initial deposit} \\ r = 0.06 & 6\% \text{ annual rate} \\ k = 12 & \text{12 months in 1 year} \\ t = 20 & \text{since we’re looking for how much we’ll have after 20 years} \end{array}\)

So \(A=3000\left(1+\frac{0.06}{12}\right)^{20 \times 12}=\$ 9930.61\) (round your answer to the nearest penny)

Let us compare the amount of money earned from compounding against the amount you would earn from simple interest

As you can see, over a long period of time, compounding makes a large difference in the account balance. You may recognize this as the difference between linear growth and exponential growth.

Evaluating exponents on the calculator

When we need to calculate something like \(5^3\) it is easy enough to just multiply \(5 \cdot 5 \cdot 5=125\). But when we need to calculate something like \(1.005^{240}\), it would be very tedious to calculate this by multiplying 1.005 by itself 240 times! So to make things easier, we can harness the power of our scientific calculators.

Most scientific calculators have a button for exponents. It is typically either labeled like:

\([\wedge ]\), \([y^x]\), or \([x^y]\)

To evaluate \(1.005^{240}\) we would type 1.005 \([^]\) 240, or 1.005 \([y^x]\) 240. Try it out - you should get something around 3.3102044758.

You know that you will need $40,000 for your child’s education in 18 years. If your account earns 4% compounded quarterly, how much would you need to deposit now to reach your goal?

We’re looking for \(P\).

\(\begin{array} {ll} r = 0.04 & 4\% \\ k = 4 & \text{4 quarters in 1 year} \\ t = 18 & \text{Since we know the balance in 18 years} \\ A = \$40,000 & \text{The amount we have in 18 years} \end{array}\)

In this case, we’re going to have to set up the equation, and solve for \(P\).

\[\begin{align*} 40000 &=P\left(1+\frac{0.04}{4}\right)^{18 \times 4} \\ 40000 &=P(2.0471) \\ P &=\frac{40000}{2.0471}=\$ 19539.84\end{align*}\]

So you would need to deposit $19,539.84 now to have $40,000 in 18 years.

It is important to be very careful about rounding when calculating things with exponents. In general, you want to keep as many decimals during calculations as you can. Be sure to keep at least 3 significant digits (numbers after any leading zeros). Rounding 0.00012345 to 0.000123 will usually give you a “close enough” answer, but keeping more digits is always better.

To see why not over-rounding is so important, suppose you were investing $1000 at 5% interest compounded monthly for 30 years.

\(\begin{array} {ll} P = \$1000 & \text{the initial deposit} \\ r = 0.05 & 5\% \\ k = 12 & \text{12 months in 1 year} \\ t = 30 & \text{since we’re looking for the amount after 30 years} \end{array}\)

If we first compute \(\frac{r}{k}\), we find \(\frac{0.05}{12} = 0.00416666666667\)

Here is the effect of rounding this to different values:

If you are working in a bank, of course you wouldn’t round at all. For our purposes, the answer we got by rounding to 0.00417, three significant digits, is close enough - $5 off of $4500 isn’t too bad. Certainly, keeping that fourth decimal place would not have hurt.

Using your calculator

In many cases, you can avoid rounding completely by how you enter things in your calculator. For example, in the example above, we needed to calculate

\(A=1000\left(1+\frac{0.05}{12}\right)^{12 \times 30}\)

We can quickly calculate \(12 \times 30=360\), giving \(A=1000\left(1+\frac{0.05}{12}\right)^{360}\).

Now we can use the calculator.

\(\begin{array}{|c|c|} \hline \textbf { Type this } & \textbf { Calculator shows } \\ \hline 0.05 [\div] 12 [=] & 0.00416666666667 \\ \hline [+] 11 [=] & 1.00416666666667 \\ \hline [\mathrm{y}^{\mathrm{x}}] 360 [=] & 4.46774431400613 \\ \hline [\times] 1000 [=] & 4467.74431400613 \\ \hline \hline \end{array}\)

Using your calculator continued

The previous steps were assuming you have a “one operation at a time” calculator; a more advanced calculator will often allow you to type in the entire expression to be evaluated. If you have a calculator like this, you will probably just need to enter:

1000 \([\times]\) ( 1 \([+]\) 0.05 \([\div]\) 12 ) \([\text{y}^\text{x}]\) 360 \([=]\).

Exercise \(\PageIndex{2}\)

If $70,000 are invested at 7% compounded monthly for 25 years, find the end balance.

\[A = 70,000\left(1 + \frac{0.07}{12} \right)^{12(25)} = 400,779.27 \nonumber\]  

Because of compounding throughout the year, with compound interest the actual increase in a year is more than the annual percentage rate.  If $1,000 were invested at 10%, the table below shows the value after 1 year at different compounding frequencies:

If we were to compute the actual percentage increase for the daily compounding, there was an increase of $105.16 from an original amount of $1,000, for a percentage increase of \(\frac{105.16}{1000} = 0.10516= 10.516\% \) increase.  This quantity is called the annual percentage yield (APY) .

Notice that given any starting amount, the amount after 1 year would be

\[A = P\left(1 + \frac{r}{k} \right)^k\nonumber\].

To find the total change, we would subtract the original amount, then to find the percentage change we would divide that by the original amount:

\[\frac{P\left(1 + \frac{r}{k} \right)^k - P}{P} = \left(1 + \frac{r}{k} \right)^k - 1.\nonumber \]

Definition: Annual Percentage Yield

The annual percentage yield  is the actual percent a quantity increases in one year.  It can be calculated as

\[ APY = \left(1 + \frac{r}{k} \right)^k - 1\nonumber\]

Notice this is equivalent to finding the value of $1 after 1 year, and subtracting the original dollar.

Example \(\PageIndex{7}\)

Bank \(A\) offers an account paying 1.2% compounded quarterly.  Bank \(B\) offers an account paying 1.1% compounded monthly.  Which is offering a better rate?

We can compare these rates using the annual percentage yield – the actual percent increase in a year.

Bank \(A\):  \(APY = \left(1 + \frac{0.012}{4} \right)^4 - 1 = 0.012054 = 1.2054\% \)

Bank \(B\): \(APY = \left(1 + \frac{0.011}{12} \right)^{12} - 1 = 0.011056 = 1.1056\% \)

Bank \(B\)’s monthly compounding is not enough to catch up with Bank \(A\)’s better APR.  Bank \(A\) offers a better rate.

Example \(\PageIndex{8}\)

If you invest $2000 at 6% compounded monthly, how long will it take the account to double in value?

This is a compound interest problem, since we are depositing money once and allowing it to grow.  In this problem,

\(P = \$2000\)                 the initial deposit

\(r = 0.06\)                     6% annual rate

\(k = 12\)                       12 months in 1 year

So our general equation is \(A = 2000\left( 1 + \frac{0.06}{12} \right)^{12t}\).  We also know that we want our ending amount to be double of $2000, which is $4000, so we’re looking for \(t\) so that \(A = 4000\).  To solve this, we set our equation for \(A\) equal to 4000.

\(4000 = 2000\left(1 + \frac{0.06}{12} \right)^{12t}\)                  Divide both sides by 2000

\(2 = \left(1.005 \right)^{12t}\)                                   To solve for the exponent, take the log of both sides

\(\log \left( 2 \right) = \log \left( \left(1.005 \right)^{12t} \right)\)                     Use the exponent property of logs on the right side

\(\log \left( 2 \right) = 12t\log \left( {1.005} \right)\)                       Now we can divide both sides by \(12\log(1.005)\)

\(\frac{\log \left( 2 \right)}{12\log \left(1.005 \right)} = t\)                                    Approximating this to a decimal

\(t = 11.581\)

It will take about 11.581 years for the account to double in value.  Note that your answer may come out slightly differently if you had evaluated the logs to decimals and rounded during your calculations, but your answer should be close.  For example if you rounded \(\log(2)\) to 0.301 and \(\log(1.005)\) to 0.00217, then your final answer would have been about 11.577 years.

Important Topics  of this Section

Simple interest

Compound interest

Compounding frequency

Evaluating on a calculator

Word Problems on Simple Interest

Word Problems on Simple Interest are solved here:

1.  Robert deposits $ 3000 in State Bank of India for 3 year which earn him an interest of 8%.What is the amount he gets after 1 year, 2 years and 3 years? Solution: In every $ 100, Robert gets $ 8. (Since rate is 8% → 8 for every 100) Therefore, for $ 1 he gets = $ 8/100 And for $ 2000 he gets = 3000 x 8/100  = $ 240 Simple Interest for 1 year = $ 240. Simple Interest for 2 year = $ 240 x 2  = $ 480

Simple Interest for 3 year = $ 240 x 3 = $ 720 Therefore,  Amount after 1 year = Principal (P) + Simple Interest (SI) = 3000 + 240 = $ 3240

Amount after 2 years = Principal (P) + Simple Interest (SI) = 3000 + 480 = $ 3480 Amount after 3 years = Principal (P) + Simple Interest (SI) = 3000 + 720 = $ 3720 We observe from the above example that, the Interest cannot be calculated without Principal, Rate and Time.

Therefore, we can conclude that Simple Interest (S.I.) depends upon:

(i) Principal (P) (ii) Rate (R) (iii) Time (T)

And therefore, the formula for calculating the simple interest is Simple Interest (SI) = {Principal (P) × Rate (R) × Time (T)}/100

Amount (A) = Principal (P) + Interest (I) Principal (P) = Amount (A) – Interest (I) Interest (I) = Amount (A) – Principal (P)

2. Richard deposits $ 5400 and got back an amount of $ 6000 after a year. Find the simple interest he got. Solution: Principal (P) = $ 5400, Amount (A) = $ 6000 Simple Interest (SI) = Amount (A) – Principal (P) = 6000 - 5400 = 600 Therefore, Richard got an interest of $ 600. 3. Seth invested a certain amount of money and got back an amount of $ 8400. If the bank paid an interest of $ 700, find the amount Sam invested. Solution: Amount (A) = $ 8400, Simple Interest (SI) = $ 700 Principal (P) = Amount (A) – Interest (I) = 8400 - 700 = 7700 Therefore, Seth invested $ 7700. 4. Diego deposited $ 10000 for 4 year at a rate of 6% p.a. Find the interest and amount Diego got. Solution: Principal (P) = $ 10000, Time (T) = 4 years, Rate (R) = 6% p.a. Simple Interest (SI) = {Principal (P) × Rate (R) × Time (T)}/100 = (10000 x 6 x 4)/100 = $ 2400 Amount (A) = Principal (P) + Interest (I) = 10000 + 2400 = $ 12400 The interest Diego got = $ 2400. Therefore, the amount Diego got $ 12400.

●  Simple Interest.

Word Problems on Simple Interest.

Factors Affecting Interest

In Simple Interest when the Time is given in Months and Days.

To find Principal when Time Interest and Rate are given.

To find Rate when Principal Interest and Time are given .

To find Time when Principal Interest and Rate are given.

Worksheet on Simple Interest.

Worksheet on Factors affecting Interest

5th Grade Numbers Page 5th Grade Math Problems From Word Problems on Simple Interest to HOME PAGE

Didn't find what you were looking for? Or want to know more information about Math Only Math . Use this Google Search to find what you need.

New! Comments

• Preschool Activities
• Kindergarten Math
• 1st Grade Math
• 2nd Grade Math
• 3rd Grade Math
• 4th Grade Math
• 5th Grade Math
• 6th Grade Math
• 7th Grade Math
• 8th Grade Math
• 9th Grade Math
• 10th Grade Math
• 11 & 12 Grade Math
• Concepts of Sets
• Probability
• Boolean Algebra
• Math Coloring Pages
• Multiplication Table
• Cool Maths Games
• Math Flash Cards
• Online Math Quiz
• Math Puzzles
• Binary System
• Math Dictionary
• Conversion Chart
• Homework Sheets
• Math Problem Ans
• Free Math Answers
• Printable Math Sheet
• Funny Math Answers
• Employment Test
• Math Patterns
• Link Partners
• Privacy Policy

Recent Articles

What are integers? | Negative and Positive Integers | Natural Numbers

Jun 07, 24 04:42 PM

5th Grade Factors and Multiples Worksheets | L.C.M. | H.C.F. | Answers

Jun 07, 24 02:06 PM

Math Questions Answers | Solved Math Questions and Answers | Free Math

Jun 07, 24 11:25 AM

Worksheet on Divisibility Rules | Questions on Test of Divisibility

Jun 07, 24 09:19 AM

Word Problems on H.C.F. and L.C.M. | Least Common Multiple | GCF Math

Jun 06, 24 06:27 PM

© and ™ math-only-math.com. All Rights Reserved. 2010 - 2024.

• → Resources
• → 7th Grade

Simple Interest Lesson Plan

Get the lesson materials.

Simple Interest Guided Notes with Doodles | Percents Sketch Notes Worksheets

Ever wondered how to teach simple interest in an engaging way to your seventh-grade students?

In this lesson plan, students will learn about calculating simple interest and its real-life applications. Through artistic and interactive guided notes, checks for understanding, a doodle and color by number activity, and a maze worksheet, students will gain a comprehensive understanding of simple interest.

The lesson culminates with a real-life example that explores the use of simple interest in car loans. Students will have the opportunity to read and write about how simple interest is used in this context, allowing them to see the practical application of the topic.

• Standard : CCSS 7.RP.A.3
• Topic : Percents
• Grade : 7th Grade
• Type : Lesson Plans

Learning Objectives

After this lesson, students will be able to:

Define simple interest and identify its components (principal, rate, and time)

Use the formula I = PRT to calculate simple interest, principal, or rate when given the other variables

Solve multistep percent problems involving simple interest

Apply the concept of simple interest to real-life situations, such as car loans.

Prerequisites

Before this lesson, students should be familiar with:

Basic multiplication and division of integers and decimals

Knowledge of how to solve equations using substitution and inverse operations

Colored pencils or markers

Simple Interest Guided Notes

Key Vocabulary

Simple interest

Total balance

Application

Word problem

Introduction

As a hook, ask students why understanding simple interest is important in real life financial situations. For example, you could ask them why it's important to know how much interest they will have to pay on a loan or how much they will earn in interest on a savings account. You can also refer to the last page of the guided notes and the FAQs for additional ideas.

Use the first page of the guided notes to introduce the topic of simple interest and the formula I = PRT. Explain that simple interest is the amount of money earned or paid on a principal amount over a certain period of time, and the formula allows us to calculate that amount. Walk through the key points of the formula and provide examples of how to use it to calculate simple interest. Use the first page of the guided notes to introduce the terms principal, rate, and time, and explain their role in the formula. Emphasize that the principal is the initial amount of money, the rate is the interest rate expressed as a decimal, and the time is the period over which the interest is calculated. Use the second page of the guided notes to explain the difference between calculating simple interest and total balance. Go through the word problems together.

Refer to the FAQ below for a walk-through on this, as well as ideas on how to respond to common student questions.

Based on student responses, reteach any concepts that students need extra help with. If your class has a wide range of proficiency levels, you can pull out students for reteaching, and have more advanced students begin working on the practice exercises.

Have students practice calculating simple interest and total balance using the practice sheets in the guided notes resource (page 2). Walk around to answer student questions.

Fast finishers can dive into the maze activity (page 3) and color by number activity (page 4) for extra practice. You can assign it as homework for the remainder of the class.

Real-Life Application

Bring the class back together, and introduce the concept of simple interest in real-life scenarios. Refer to the last page of the guided notes resource where students read about how simple interest is used in car loans.

Explain that simple interest is often used in financial situations such as loans, investments, and credit cards. It helps determine how much money is earned or paid for borrowing or investing a certain amount of money.

To provide a specific example, discuss the concept of car loans. Explain that when someone wants to buy a car but doesn't have enough money to pay for it upfront, they can take out a car loan from a bank or other financial institution. The bank will lend them the money to buy the car, but the borrower will have to pay back the loan over a period of time with additional interest.

Encourage students to share any personal experiences or brainstorm ideas related to loans and simple interest. This will help make the concept more relatable and engaging for them.

Additional Self-Checking Digital Practice

If you’re looking for digital practice for simple interest, try my Pixel Art activities in Google Sheets. Every answer is automatically checked, and correct answers unlock parts of a mystery picture. It’s incredibly fun, and a powerful tool for differentiation.

Here are 3 activities to explore:

Simple Interest Digital Pixel Art

Simple and Compound Interest Digital Pixel Art

Simple Interest Digital Pixel Art Activity | Word Problems with I=prt

Additional Print Practice

A fun, no-prep way to practice simple interest is Doodle Math — they’re a fresh take on color by number or color by code. It includes multiple levels of practice, perfect for a review day or sub plan.

Here are 2 activities to try:

Simple Interest | Doodle Math: Twist on Color by Number

Free Percents in Real-Life | Doodle Math: Twist on Color by Number Worksheets

What is simple interest? Open

Simple interest is the amount of money that is charged or earned on a loan or investment, based on the initial amount of money (principal), the interest rate, and the time period.

How do you calculate simple interest? Open

To calculate simple interest, you can use the formula I = PRT, where:

I is the simple interest

P is the principal (the initial amount of money)

R is the interest rate (expressed as a decimal)

T is the time period (in years)

What is the principal in simple interest? Open

The principal in simple interest refers to the initial amount of money that is borrowed or invested. It is the starting amount on which the interest is calculated.

How do you find the total balance in simple interest? Open

To find the total balance in simple interest, you need to add the principal to the simple interest. The formula is: Total balance = Principal + Simple interest.

What are multistep percent problems? Open

Multistep percent problems involve solving problems that require multiple steps and calculations to find the answer. These problems often involve using percentages in combination with other mathematical operations, such as addition, subtraction, multiplication, or division.

How can I solve multistep percent problems? Open

To solve multistep percent problems, you need to break down the problem into smaller steps and solve each step individually. Here are some strategies you can use:

Identify the given information and what you need to find.

Set up equations or formulas based on the problem.

Solve each step of the problem in the correct order.

Double-check your calculations and answer to ensure accuracy.

Can you give an example of a real-life application of simple interest? Open

Certainly! One example of a real-life application of simple interest is car loans. When someone buys a car with a loan, they usually have to pay back the borrowed money (principal) along with an additional amount of money (interest) over a certain period of time. The interest rate determines how much extra the borrower has to pay.

How can I differentiate instruction for students who may struggle with simple interest? Open

To differentiate instruction for students who may struggle with simple interest, you can:

Provide additional examples and practice problems with step-by-step guidance.

Offer extra support through one-on-one or small group instruction.

Break down the concepts into smaller, more manageable parts.

Review how to solve equations

Use visual aids, manipulatives, or hands-on activities to make the concepts more concrete.

Provide opportunities for additional practice and review to reinforce learning (tip: choose engaging activities!)

Want more ideas and freebies?

Get my free resource library with digital & print activities—plus tips over email.