h_0 hypothesis

Module 9: Hypothesis Testing With One Sample

Null and alternative hypotheses, learning outcomes.

• Describe hypothesis testing in general and in practice

The actual test begins by considering two  hypotheses . They are called the null hypothesis and the alternative hypothesis . These hypotheses contain opposing viewpoints.

H 0 : The null hypothesis: It is a statement about the population that either is believed to be true or is used to put forth an argument unless it can be shown to be incorrect beyond a reasonable doubt.

H a : The alternative hypothesis : It is a claim about the population that is contradictory to H 0 and what we conclude when we reject H 0 .

Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample data.

After you have determined which hypothesis the sample supports, you make adecision. There are two options for a  decision . They are “reject H 0 ” if the sample information favors the alternative hypothesis or “do not reject H 0 ” or “decline to reject H 0 ” if the sample information is insufficient to reject the null hypothesis.

Mathematical Symbols Used in  H 0 and H a :

H 0 always has a symbol with an equal in it. H a never has a symbol with an equal in it. The choice of symbol depends on the wording of the hypothesis test. However, be aware that many researchers (including one of the co-authors in research work) use = in the null hypothesis, even with > or < as the symbol in the alternative hypothesis. This practice is acceptable because we only make the decision to reject or not reject the null hypothesis.

H 0 : No more than 30% of the registered voters in Santa Clara County voted in the primary election. p ≤ 30

H a : More than 30% of the registered voters in Santa Clara County voted in the primary election. p > 30

A medical trial is conducted to test whether or not a new medicine reduces cholesterol by 25%. State the null and alternative hypotheses.

H 0 : The drug reduces cholesterol by 25%. p = 0.25

H a : The drug does not reduce cholesterol by 25%. p ≠ 0.25

We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). The null and alternative hypotheses are:

H 0 : μ = 2.0

H a : μ ≠ 2.0

We want to test whether the mean height of eighth graders is 66 inches. State the null and alternative hypotheses. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses. H 0 : μ __ 66 H a : μ __ 66

• H 0 : μ = 66
• H a : μ ≠ 66

We want to test if college students take less than five years to graduate from college, on the average. The null and alternative hypotheses are:

H 0 : μ ≥ 5

H a : μ < 5

We want to test if it takes fewer than 45 minutes to teach a lesson plan. State the null and alternative hypotheses. Fill in the correct symbol ( =, ≠, ≥, <, ≤, >) for the null and alternative hypotheses. H 0 : μ __ 45 H a : μ __ 45

• H 0 : μ ≥ 45
• H a : μ < 45

In an issue of U.S. News and World Report , an article on school standards stated that about half of all students in France, Germany, and Israel take advanced placement exams and a third pass. The same article stated that 6.6% of U.S. students take advanced placement exams and 4.4% pass. Test if the percentage of U.S. students who take advanced placement exams is more than 6.6%. State the null and alternative hypotheses.

H 0 : p ≤ 0.066

H a : p > 0.066

On a state driver’s test, about 40% pass the test on the first try. We want to test if more than 40% pass on the first try. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses. H 0 : p __ 0.40 H a : p __ 0.40

• H 0 : p = 0.40
• H a : p > 0.40

Concept Review

In a  hypothesis test , sample data is evaluated in order to arrive at a decision about some type of claim. If certain conditions about the sample are satisfied, then the claim can be evaluated for a population. In a hypothesis test, we: Evaluate the null hypothesis , typically denoted with H 0 . The null is not rejected unless the hypothesis test shows otherwise. The null statement must always contain some form of equality (=, ≤ or ≥) Always write the alternative hypothesis , typically denoted with H a or H 1 , using less than, greater than, or not equals symbols, i.e., (≠, >, or <). If we reject the null hypothesis, then we can assume there is enough evidence to support the alternative hypothesis. Never state that a claim is proven true or false. Keep in mind the underlying fact that hypothesis testing is based on probability laws; therefore, we can talk only in terms of non-absolute certainties.

Formula Review

H 0 and H a are contradictory.

• OpenStax, Statistics, Null and Alternative Hypotheses. Provided by : OpenStax. Located at : http://cnx.org/contents/[email protected]:58/Introductory_Statistics . License : CC BY: Attribution
• Introductory Statistics . Authored by : Barbara Illowski, Susan Dean. Provided by : Open Stax. Located at : http://cnx.org/contents/[email protected] . License : CC BY: Attribution . License Terms : Download for free at http://cnx.org/contents/[email protected]
• Simple hypothesis testing | Probability and Statistics | Khan Academy. Authored by : Khan Academy. Located at : https://youtu.be/5D1gV37bKXY . License : All Rights Reserved . License Terms : Standard YouTube License

Statistics Made Easy

5 Tips for Interpreting P-Values Correctly in Hypothesis Testing

Hypothesis testing is a critical part of statistical analysis and is often the endpoint where conclusions are drawn about larger populations based on a sample or experimental dataset. Central to this process is the p-value. Broadly, the p-value quantifies the strength of evidence against the null hypothesis. Given the importance of the p-value, it is essential to ensure its interpretation is correct. Here are five essential tips for ensuring the p-value from a hypothesis test is understood correctly. 

1. Know What the P-value Represents

First, it is essential to understand what a p-value is. In hypothesis testing, the p-value is defined as the probability of observing your data, or data more extreme, if the null hypothesis is true. As a reminder, the null hypothesis states no difference between your data and the expected population. 

For example, in a hypothesis test to see if changing a company’s logo drives more traffic to the website, a null hypothesis would state that the new traffic numbers are equal to the old traffic numbers. In this context, the p-value would be the probability that the data you observed, or data more extreme, would occur if this null hypothesis were true. 

Therefore, a smaller p-value indicates that what you observed is unlikely to have occurred if the null were true, offering evidence to reject the null hypothesis. Typically, a cut-off value of 0.05 is used where any p-value below this is considered significant evidence against the null. 

2. Understand the Directionality of Your Hypothesis

Based on the research question under exploration, there are two types of hypotheses: one-sided and two-sided. A one-sided test specifies a particular direction of effect, such as traffic to a website increasing after a design change. On the other hand, a two-sided test allows the change to be in either direction and is effective when the researcher wants to see any effect of the change. 

Either way, determining the statistical significance of a p-value is the same: if the p-value is below a threshold value, it is statistically significant. However, when calculating the p-value, it is important to ensure the correct sided calculations have been completed. 

Additionally, the interpretation of the meaning of a p-value will differ based on the directionality of the hypothesis. If a one-sided test is significant, the researchers can use the p-value to support a statistically significant increase or decrease based on the direction of the test. If a two-sided test is significant, the p-value can only be used to say that the two groups are different, but not that one is necessarily greater. 

3. Avoid Threshold Thinking

A common pitfall in interpreting p-values is falling into the threshold thinking trap. The most commonly used cut-off value for whether a calculated p-value is statistically significant is 0.05. Typically, a p-value of less than 0.05 is considered statistically significant evidence against the null hypothesis. 

However, this is just an arbitrary value. Rigid adherence to this or any other predefined cut-off value can obscure business-relevant effect sizes. For example, a hypothesis test looking at changes in traffic after a website design may find that an increase of 10,000 views is not statistically significant with a p-value of 0.055 since that value is above 0.05. However, the actual increase of 10,000 may be important to the growth of the business. 

Therefore, a p-value can be practically significant while not being statistically significant. Both types of significance and the broader context of the hypothesis test should be considered when making a final interpretation. 

4. Consider the Power of Your Study

Similarly, some study conditions can result in a non-significant p-value even if practical significance exists. Statistical power is the ability of a study to detect an effect when it truly exists. In other words, it is the probability that the null hypothesis will be rejected when it is false. 

Power is impacted by a lot of factors. These include sample size, the effect size you are looking for, and variability within the data. In the example of website traffic after a design change, if the number of visits overall is too small, there may not be enough views to have enough power to detect a difference. 

Simple ways to increase the power of a hypothesis test and increase the chances of detecting an effect are increasing the sample size, looking for a smaller effect size, changing the experiment design to control for variables that can increase variability, or adjusting the type of statistical test being run.

5. Be Aware of Multiple Comparisons

Whenever multiple p-values are calculated in a single study due to multiple comparisons, there is an increased risk of false positives. This is because each individual comparison introduces random fluctuations, and each additional comparison compounds these fluctuations. 

For example, in a hypothesis test looking at traffic before and after a website redesign, the team may be interested in making more than one comparison. This can include total visits, page views, and average time spent on the website. Since multiple comparisons are being made, there must be a correction made when interpreting the p-value. 

The Bonferroni correction is one of the most commonly used methods to account for this increased probability of false positives. In this method, the significance cut-off value, typically 0.05, is divided by the number of comparisons made. The result is used as the new significance cut-off value.  Applying this correction mitigates the risk of false positives and improves the reliability of findings from a hypothesis test. 

In conclusion, interpreting p-values requires a nuanced understanding of many statistical concepts and careful consideration of the hypothesis test’s context. By following these five tips, the interpretation of the p-value from a hypothesis test can be more accurate and reliable, leading to better data-driven decision-making.

Featured Posts

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Join the Statology Community

Sign up to receive Statology's exclusive study resource: 100 practice problems with step-by-step solutions. Plus, get our latest insights, tutorials, and data analysis tips straight to your inbox!

By subscribing you accept Statology's Privacy Policy.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

10.6: Additional Information and Full Hypothesis Test Examples

• Last updated
• Save as PDF
• Page ID 155553

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

• In a hypothesis test problem, you may see words such as "the level of significance is 1%." The "1%" is the preconceived or preset \(\alpha\).
• The statistician setting up the hypothesis test selects the value of α to use before collecting the sample data.
• If no level of significance is given, a common standard to use is \(\alpha = 0.05\).
• When you calculate the \(p\)-value and draw the picture, the \(p\)-value is the area in the left tail, the right tail, or split evenly between the two tails. For this reason, we call the hypothesis test left, right, or two tailed.
• The alternative hypothesis, \(H_{a}\), tells you if the test is left, right, or two-tailed. It is the key to conducting the appropriate test.
• \(H_{a}\) never has a symbol that contains an equal sign.
• Thinking about the meaning of the \(p\)-value: A data analyst (and anyone else) should have more confidence that he made the correct decision to reject the null hypothesis with a smaller \(p\)-value (for example, 0.001 as opposed to 0.04) even if using the 0.05 level for alpha. Similarly, for a large p -value such as 0.4, as opposed to a \(p\)-value of 0.056 (\(\alpha = 0.05\) is less than either number), a data analyst should have more confidence that she made the correct decision in not rejecting the null hypothesis. This makes the data analyst use judgment rather than mindlessly applying rules.

The following examples illustrate a left-, right-, and two-tailed test.

Example \(\PageIndex{1}\)

\(H_{0}: \mu = 5, H_{a}: \mu < 5\)

Test of a single population mean. \(H_{a}\) tells you the test is left-tailed. The picture of the \(p\)-value is as follows:

Exercise \(\PageIndex{1}\)

\(H_{0}: \mu = 10, H_{a}: \mu < 10\)

Assume the \(p\)-value is 0.0935. What type of test is this? Draw the picture of the \(p\)-value.

left-tailed test

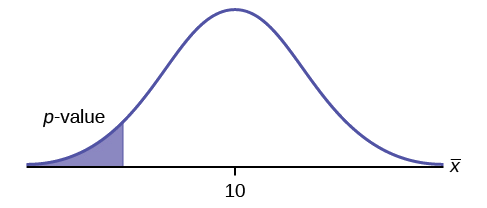
Example \(\PageIndex{2}\)

\(H_{0}: \mu \leq 0.2, H_{a}: \mu > 0.2\)

This is a test of a single population proportion. \(H_{a}\) tells you the test is right-tailed . The picture of the p -value is as follows:

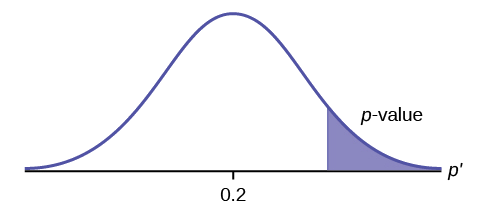
Exercise \(\PageIndex{2}\)

\(H_{0}: \mu \leq 1, H_{a}: \mu > 1\)

Assume the \(p\)-value is 0.1243. What type of test is this? Draw the picture of the \(p\)-value.

right-tailed test

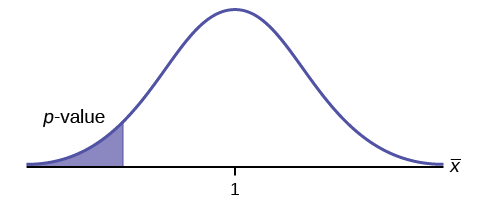
Example \(\PageIndex{3}\)

\(H_{0}: \mu = 50, H_{a}: \mu \neq 50\)

This is a test of a single population mean. \(H_{a}\) tells you the test is two-tailed . The picture of the \(p\)-value is as follows.

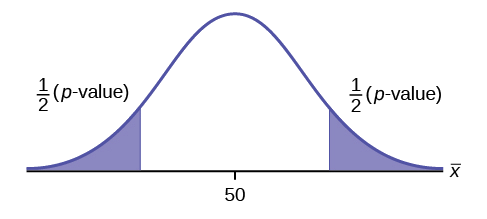
Exercise \(\PageIndex{3}\)

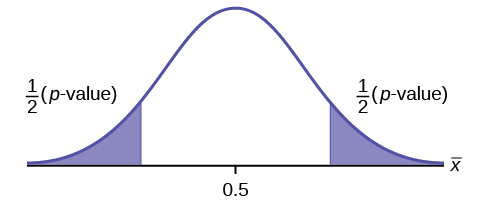
\(H_{0}: \mu = 0.5, H_{a}: \mu \neq 0.5\)

Assume the p -value is 0.2564. What type of test is this? Draw the picture of the \(p\)-value.

two-tailed test

Full Hypothesis Test Examples

Example \(\pageindex{4}\).

Jeffrey, as an eight-year old, established a mean time of 16.43 seconds for swimming the 25-yard freestyle, with a standard deviation of 0.8 seconds . His dad, Frank, thought that Jeffrey could swim the 25-yard freestyle faster using goggles. Frank bought Jeffrey a new pair of expensive goggles and timed Jeffrey for 15 25-yard freestyle swims . For the 15 swims, Jeffrey's mean time was 16 seconds. Frank thought that the goggles helped Jeffrey to swim faster than the 16.43 seconds. Conduct a hypothesis test using a preset α = 0.05. Assume that the swim times for the 25-yard freestyle are normal.

Set up the Hypothesis Test:

Since the problem is about a mean, this is a test of a single population mean .

\(H_{0}: \mu = 16.43, H_{a}: \mu < 16.43\)

For Jeffrey to swim faster, his time will be less than 16.43 seconds. The "\(<\)" tells you this is left-tailed.

Determine the distribution needed:

Random variable: \(\bar{X} =\) the mean time to swim the 25-yard freestyle.

Distribution for the test: \(\bar{X}\) is normal (population standard deviation is known: \(\sigma = 0.8\))

\(\bar{X} - N \left(\mu, \frac{\sigma_{x}}{\sqrt{n}}\right)\) Therefore, \(\bar{X} - N\left(16.43, \frac{0.8}{\sqrt{15}}\right)\)

\(\mu = 16.43\) comes from \(H_{0}\) and not the data. \(\sigma = 0.8\), and \(n = 15\).

Calculate the \(p-\text{value}\) using the normal distribution for a mean:

\(p\text{-value} = P(\bar{x} < 16) = 0.0187\) where the sample mean in the problem is given as 16.

\(p\text{-value} = 0.0187\) (This is called the actual level of significance .) The \(p-\text{value}\) is the area to the left of the sample mean is given as 16.

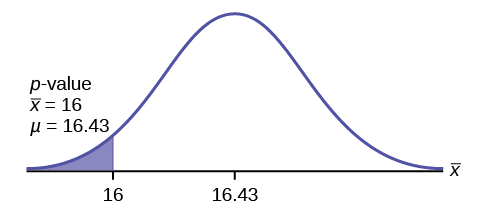
\(\mu = 16.43\) comes from \(H_{0}\). Our assumption is \(\mu = 16.43\).

Interpretation of the \(p-\text{value}\): If \(H_{0}\) is true , there is a 0.0187 probability (1.87%) that Jeffrey's mean time to swim the 25-yard freestyle is 16 seconds or less. Because a 1.87% chance is small, the mean time of 16 seconds or less is unlikely to have happened randomly. It is a rare event.

Compare \(\alpha\) and the \(p-\text{value}\):

\(\alpha = 0.05 p\text{-value} = 0.0187 \alpha > p\text{-value}\)

Make a decision: Since \(\alpha > p\text{-value}\), reject \(H_{0}\).

This means that you reject \(\mu = 16.43\). In other words, you do not think Jeffrey swims the 25-yard freestyle in 16.43 seconds but faster with the new goggles.

Conclusion: At the 5% significance level, we conclude that Jeffrey swims faster using the new goggles. The sample data show there is sufficient evidence that Jeffrey's mean time to swim the 25-yard freestyle is less than 16.43 seconds.

The p -value can easily be calculated.

Press STAT and arrow over to TESTS . Press 1:Z-Test . Arrow over to Stats and press ENTER . Arrow down and enter 16.43 for \(\mu_{0}\) (null hypothesis), .8 for σ , 16 for the sample mean, and 15 for n . Arrow down to \(\mu\) : (alternate hypothesis) and arrow over to \(< \mu_{0}\). Press ENTER . Arrow down to Calculate and press ENTER . The calculator not only calculates the p -value (\(p = 0.0187\)) but it also calculates the test statistic ( z -score) for the sample mean. \(\mu < 16.43\) is the alternative hypothesis. Do this set of instructions again except arrow to Draw (instead of Calculate ). Press ENTER . A shaded graph appears with \(z = -2.08\) (test statistic) and \(p = 0.0187\) (\(p-\text{value}\)). Make sure when you use Draw that no other equations are highlighted in \(Y =\) and the plots are turned off.

When the calculator does a \(Z\)-Test, the Z-Test function finds the p -value by doing a normal probability calculation using the central limit theorem:

\(P(\bar{X} < 16)\) 2nd DISTR normcdf (\((−10^{99},16,16.43,\frac{0.8}{\sqrt{15}})\).

The Type I and Type II errors for this problem are as follows:

The Type I error is to conclude that Jeffrey swims the 25-yard freestyle, on average, in less than 16.43 seconds when, in fact, he actually swims the 25-yard freestyle, on average, in 16.43 seconds. (Reject the null hypothesis when the null hypothesis is true.)

The Type II error is that there is not evidence to conclude that Jeffrey swims the 25-yard free-style, on average, in less than 16.43 seconds when, in fact, he actually does swim the 25-yard free-style, on average, in less than 16.43 seconds. (Do not reject the null hypothesis when the null hypothesis is false.)

Exercise \(\PageIndex{4}\)

The mean throwing distance of a football for a Marco, a high school freshman quarterback, is 40 yards, with a standard deviation of two yards. The team coach tells Marco to adjust his grip to get more distance. The coach records the distances for 20 throws. For the 20 throws, Marco’s mean distance was 45 yards. The coach thought the different grip helped Marco throw farther than 40 yards. Conduct a hypothesis test using a preset \(\alpha = 0.05\). Assume the throw distances for footballs are normal.

First, determine what type of test this is, set up the hypothesis test, find the p -value, sketch the graph, and state your conclusion.

Press STAT and arrow over to TESTS. Press 1: \(Z\)-Test. Arrow over to Stats and press ENTER. Arrow down and enter 40 for \(\mu_{0}\) (null hypothesis), 2 for \(\sigma\), 45 for the sample mean, and 20 for \(n\). Arrow down to \(\mu\): (alternative hypothesis) and set it either as \(<\), \(\neq\), or \(>\). Press ENTER. Arrow down to Calculate and press ENTER. The calculator not only calculates the p -value but it also calculates the test statistic ( z -score) for the sample mean. Select \(<\), \(\neq\), or \(>\) for the alternative hypothesis. Do this set of instructions again except arrow to Draw (instead of Calculate). Press ENTER. A shaded graph appears with test statistic and \(p\)-value. Make sure when you use Draw that no other equations are highlighted in \(Y =\) and the plots are turned off.

Since the problem is about a mean, this is a test of a single population mean.

• \(H_{0}: \mu = 40\)
• \(H_{a}: \mu > 40\)
• \(p = 0.0062\)

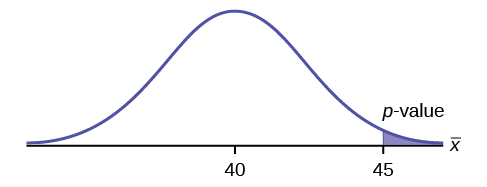
Because \(p < \alpha\), we reject the null hypothesis. There is sufficient evidence to suggest that the change in grip improved Marco’s throwing distance.

Historical Note

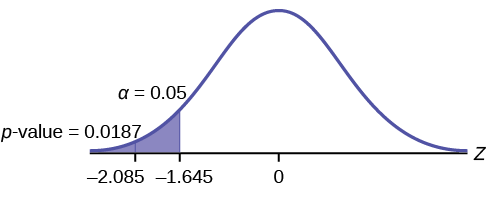
The traditional way to compare the two probabilities, \(\alpha\) and the \(p-\text{value}\), is to compare the critical value (\(z\)-score from \(\alpha\)) to the test statistic (\(z\)-score from data). The calculated test statistic for the \(p\)-value is –2.08. (From the Central Limit Theorem, the test statistic formula is \(z = \frac{\bar{x}-\mu_{x}}{\left(\frac{\sigma_{x}}{\sqrt{n}}\right)}\). For this problem, \(\bar{x} = 16\), \(\mu_{x} = 16.43\) from the null hypotheses is, \(\sigma_{x} = 0.8\), and \(n = 15\).) You can find the critical value for \(\alpha = 0.05\) in the normal table (see 15.Tables in the Table of Contents). The \(z\)-score for an area to the left equal to 0.05 is midway between –1.65 and –1.64 (0.05 is midway between 0.0505 and 0.0495). The \(z\)-score is –1.645. Since –1.645 > –2.08 (which demonstrates that \(\alpha > p-\text{value}\)), reject \(H_{0}\). Traditionally, the decision to reject or not reject was done in this way. Today, comparing the two probabilities \(\alpha\) and the \(p\)-value is very common. For this problem, the \(p-\text{value}\), 0.0187 is considerably smaller than \(\alpha = 0.05\). You can be confident about your decision to reject. The graph shows \(\alpha\), the \(p-\text{value}\), and the test statistics and the critical value.

Example \(\PageIndex{5}\)

A college football coach thought that his players could bench press a mean weight of 275 pounds . It is known that the standard deviation is 55 pounds . Three of his players thought that the mean weight was more than that amount. They asked 30 of their teammates for their estimated maximum lift on the bench press exercise. The data ranged from 205 pounds to 385 pounds. The actual different weights were (frequencies are in parentheses) 205(3); 215(3); 225(1); 241(2); 252(2); 265(2); 275(2); 313(2); 316(5); 338(2); 341(1); 345(2); 368(2); 385(1).

Conduct a hypothesis test using a 2.5% level of significance to determine if the bench press mean is more than 275 pounds.

Since the problem is about a mean weight, this is a test of a single population mean.

• \(H_{0}: \mu = 275\)
• \(H_{a}: \mu > 275\)

This is a right-tailed test.

Calculating the distribution needed:

Random variable: \(\bar{X} =\) the mean weight, in pounds, lifted by the football players.

Distribution for the test: It is normal because \(\sigma\) is known.

• \(\bar{X} - N\left(275, \frac{55}{\sqrt{30}}\right)\)
• \(\bar{x} = 286.2\) pounds (from the data).
• \(\sigma = 55\) pounds (Always use \(\sigma\) if you know it.) We assume \(\mu = 275\) pounds unless our data shows us otherwise.

Calculate the p -value using the normal distribution for a mean and using the sample mean as input (see [link] for using the data as input):

\[p\text{-value} = P(\bar{x} > 286.2) = 0.1323.\nonumber \]

Interpretation of the p -value: If \(H_{0}\) is true, then there is a 0.1331 probability (13.23%) that the football players can lift a mean weight of 286.2 pounds or more. Because a 13.23% chance is large enough, a mean weight lift of 286.2 pounds or more is not a rare event.

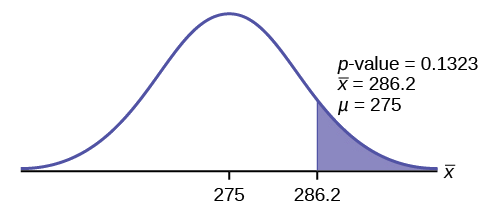
\(\alpha = 0.025 p-value = 0.1323\)

Make a decision: Since \(\alpha < p\text{-value}\), do not reject \(H_{0}\).

Conclusion: At the 2.5% level of significance, from the sample data, there is not sufficient evidence to conclude that the true mean weight lifted is more than 275 pounds.

The \(p-\text{value}\) can easily be calculated.

Put the data and frequencies into lists. Press STAT and arrow over to TESTS . Press 1:Z-Test . Arrow over to Data and press ENTER . Arrow down and enter 275 for \(\mu_{0}\), 55 for \(\sigma\), the name of the list where you put the data, and the name of the list where you put the frequencies. Arrow down to \(\mu\) : and arrow over to \(> \mu_{0}\). Press ENTER . Arrow down to Calculate and press ENTER . The calculator not only calculates the \(p-\text{value}\) (\(p = 0.1331\)), a little different from the previous calculation - in it we used the sample mean rounded to one decimal place instead of the data) but it also calculates the test statistic ( z -score) for the sample mean, the sample mean, and the sample standard deviation. \(\mu > 275\) is the alternative hypothesis. Do this set of instructions again except arrow to Draw (instead of Calculate ). Press ENTER . A shaded graph appears with \(z = 1.112\) (test statistic) and \(p = 0.1331\) (\(p-\text{value})\). Make sure when you use Draw that no other equations are highlighted in \(Y =\) and the plots are turned off.

Example \(\PageIndex{6}\)

Statistics students believe that the mean score on the first statistics test is 65. A statistics instructor thinks the mean score is higher than 65. He samples ten statistics students and obtains the scores 65 65 70 67 66 63 63 68 72 71. He performs a hypothesis test using a 5% level of significance. The data are assumed to be from a normal distribution.

Set up the hypothesis test:

A 5% level of significance means that \(\alpha = 0.05\). This is a test of a single population mean .

\(H_{0}: \mu = 65  H_{a}: \mu > 65\)

Since the instructor thinks the average score is higher, use a "\(>\)". The "\(>\)" means the test is right-tailed.

Random variable: \(\bar{X} =\) average score on the first statistics test.

Distribution for the test: If you read the problem carefully, you will notice that there is no population standard deviation given . You are only given \(n = 10\) sample data values. Notice also that the data come from a normal distribution. This means that the distribution for the test is a student's \(t\).

Use \(t_{df}\). Therefore, the distribution for the test is \(t_{9}\) where \(n = 10\) and \(df = 10 - 1 = 9\).

Calculate the \(p\)-value using the Student's \(t\)-distribution:

\(p\text{-value} = P(\bar{x} > 67) = 0.0396\) where the sample mean and sample standard deviation are calculated as 67 and 3.1972 from the data.

Interpretation of the p -value: If the null hypothesis is true, then there is a 0.0396 probability (3.96%) that the sample mean is 65 or more.

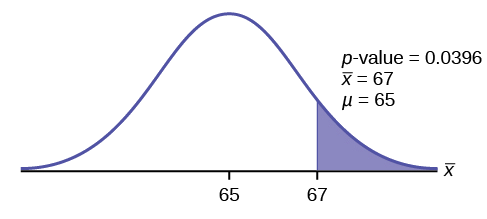
Since \(α = 0.05\) and \(p\text{-value} = 0.0396\). \(\alpha > p\text{-value}\).

This means you reject \(\mu = 65\). In other words, you believe the average test score is more than 65.

Conclusion: At a 5% level of significance, the sample data show sufficient evidence that the mean (average) test score is more than 65, just as the math instructor thinks.

The \(p\text{-value}\) can easily be calculated.

Put the data into a list. Press STAT and arrow over to TESTS . Press 2:T-Test . Arrow over to Data and press ENTER . Arrow down and enter 65 for \(\mu_{0}\), the name of the list where you put the data, and 1 for Freq: . Arrow down to \(\mu\): and arrow over to \(> \mu_{0}\). Press ENTER . Arrow down to Calculate and press ENTER . The calculator not only calculates the \(p\text{-value}\) (p = 0.0396) but it also calculates the test statistic ( t -score) for the sample mean, the sample mean, and the sample standard deviation. \(\mu > 65\) is the alternative hypothesis. Do this set of instructions again except arrow to Draw (instead of Calculate ). Press ENTER . A shaded graph appears with \(t = 1.9781\) (test statistic) and \(p = 0.0396\) (\(p\text{-value}\)). Make sure when you use Draw that no other equations are highlighted in \(Y =\) and the plots are turned off.

Exercise \(\PageIndex{6}\)

It is believed that a stock price for a particular company will grow at a rate of $5 per week with a standard deviation of $1. An investor believes the stock won’t grow as quickly. The changes in stock price is recorded for ten weeks and are as follows: $4, $3, $2, $3, $1, $7, $2, $1, $1, $2. Perform a hypothesis test using a 5% level of significance. State the null and alternative hypotheses, find the p -value, state your conclusion, and identify the Type I and Type II errors.

• \(H_{0}: \mu = 5\)
• \(H_{a}: \mu < 5\)
• \(p = 0.0082\)

Because \(p < \alpha\), we reject the null hypothesis. There is sufficient evidence to suggest that the stock price of the company grows at a rate less than $5 a week.

• Type I Error: To conclude that the stock price is growing slower than $5 a week when, in fact, the stock price is growing at $5 a week (reject the null hypothesis when the null hypothesis is true).
• Type II Error: To conclude that the stock price is growing at a rate of $5 a week when, in fact, the stock price is growing slower than $5 a week (do not reject the null hypothesis when the null hypothesis is false).

Example \(\PageIndex{7}\)

Joon believes that 50% of first-time brides in the United States are younger than their grooms. She performs a hypothesis test to determine if the percentage is the same or different from 50% . Joon samples 100 first-time brides and 53 reply that they are younger than their grooms. For the hypothesis test, she uses a 1% level of significance.

The 1% level of significance means that α = 0.01. This is a test of a single population proportion .

\(H_{0}: p = 0.50\)  \(H_{a}: p \neq 0.50\)

The words "is the same or different from" tell you this is a two-tailed test.

Calculate the distribution needed:

Random variable: \(P′ =\) the percent of of first-time brides who are younger than their grooms.

Distribution for the test: The problem contains no mention of a mean. The information is given in terms of percentages. Use the distribution for P′ , the estimated proportion.

\[P' - N\left(p, \sqrt{\frac{p-q}{n}}\right)\nonumber \]

\[P' - N\left(0.5, \sqrt{\frac{0.5-0.5}{100}}\right)\nonumber \]

where \(p = 0.50, q = 1−p = 0.50\), and \(n = 100\)

Calculate the p -value using the normal distribution for proportions:

\[p\text{-value} = P(p′ < 0.47 \space or \space p′ > 0.53) = 0.5485\nonumber \]

where \[x = 53, p' = \frac{x}{n} = \frac{53}{100} = 0.53\nonumber \].

Interpretation of the p-value: If the null hypothesis is true, there is 0.5485 probability (54.85%) that the sample (estimated) proportion \(p'\) is 0.53 or more OR 0.47 or less (see the graph in Figure).

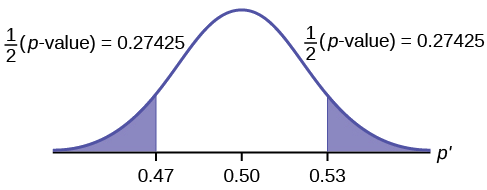
\(\mu = p = 0.50\) comes from \(H_{0}\), the null hypothesis.

\(p′ = 0.53\). Since the curve is symmetrical and the test is two-tailed, the \(p′\) for the left tail is equal to \(0.50 – 0.03 = 0.47\) where \(\mu = p = 0.50\). (0.03 is the difference between 0.53 and 0.50.)

Compare \(\alpha\) and the \(p\text{-value}\):

Since \(\alpha = 0.01\) and \(p\text{-value} = 0.5485\). \(\alpha < p\text{-value}\).

Make a decision: Since \(\alpha < p\text{-value}\), you cannot reject \(H_{0}\).

Conclusion: At the 1% level of significance, the sample data do not show sufficient evidence that the percentage of first-time brides who are younger than their grooms is different from 50%.

Press STAT and arrow over to TESTS . Press 5:1-PropZTest . Enter .5 for \(p_{0}\), 53 for \(x\) and 100 for \(n\). Arrow down to Prop and arrow to not equals \(p_{0}\). Press ENTER . Arrow down to Calculate and press ENTER . The calculator calculates the \(p\text{-value}\) (\(p = 0.5485\)) and the test statistic (\(z\)-score). Prop not equals .5 is the alternate hypothesis. Do this set of instructions again except arrow to Draw (instead of Calculate ). Press ENTER . A shaded graph appears with \(z = 0.6\) (test statistic) and \(p = 0.5485\) (\(p\text{-value}\)). Make sure when you use Draw that no other equations are highlighted in \(Y =\) and the plots are turned off.

The Type I and Type II errors are as follows:

The Type I error is to conclude that the proportion of first-time brides who are younger than their grooms is different from 50% when, in fact, the proportion is actually 50%. (Reject the null hypothesis when the null hypothesis is true).

The Type II error is there is not enough evidence to conclude that the proportion of first time brides who are younger than their grooms differs from 50% when, in fact, the proportion does differ from 50%. (Do not reject the null hypothesis when the null hypothesis is false.)

Exercise \(\PageIndex{7}\)

A teacher believes that 85% of students in the class will want to go on a field trip to the local zoo. She performs a hypothesis test to determine if the percentage is the same or different from 85%. The teacher samples 50 students and 39 reply that they would want to go to the zoo. For the hypothesis test, use a 1% level of significance.

First, determine what type of test this is, set up the hypothesis test, find the \(p\text{-value}\), sketch the graph, and state your conclusion.

Since the problem is about percentages, this is a test of single population proportions.

• \(H_{0} : p = 0.85\)
• \(H_{a}: p \neq 0.85\)
• \(p = 0.7554\)

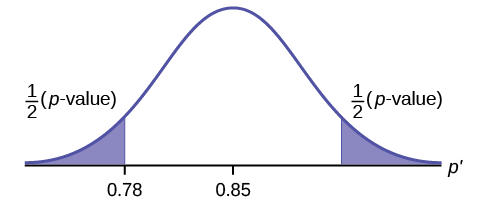
Because \(p > \alpha\), we fail to reject the null hypothesis. There is not sufficient evidence to suggest that the proportion of students that want to go to the zoo is not 85%.

Example \(\PageIndex{8}\)

Suppose a consumer group suspects that the proportion of households that have three cell phones is 30%. A cell phone company has reason to believe that the proportion is not 30%. Before they start a big advertising campaign, they conduct a hypothesis test. Their marketing people survey 150 households with the result that 43 of the households have three cell phones.

\(H_{0}: p = 0.30, H_{a}: p \neq 0.30\)

The random variable is \(P′ =\) proportion of households that have three cell phones.

The distribution for the hypothesis test is \(P' - N\left(0.30, \sqrt{\frac{(0.30 \cdot 0.70)}{150}}\right)\)

Exercise \(\PageIndex{8}\).2

a. The value that helps determine the \(p\text{-value}\) is \(p′\). Calculate \(p′\).

a. \(p' = \frac{x}{n}\) where \(x\) is the number of successes and \(n\) is the total number in the sample.

\(x = 43, n = 150\)

\(p′ = 43150\)

Exercise \(\PageIndex{8}\).3

b. What is a success for this problem?

b. A success is having three cell phones in a household.

Exercise \(\PageIndex{8}\).4

c. What is the level of significance?

c. The level of significance is the preset \(\alpha\). Since \(\alpha\) is not given, assume that \(\alpha = 0.05\).

Exercise \(\PageIndex{8}\).5

d. Draw the graph for this problem. Draw the horizontal axis. Label and shade appropriately.

Calculate the \(p\text{-value}\).

d. \(p\text{-value} = 0.7216\)

Exercise \(\PageIndex{8}\).6

e. Make a decision. _____________(Reject/Do not reject) \(H_{0}\) because____________.

e. Assuming that \(\alpha = 0.05, \alpha < p\text{-value}\). The decision is do not reject \(H_{0}\) because there is not sufficient evidence to conclude that the proportion of households that have three cell phones is not 30%.

Exercise \(\PageIndex{8}\)

Marketers believe that 92% of adults in the United States own a cell phone. A cell phone manufacturer believes that number is actually lower. 200 American adults are surveyed, of which, 174 report having cell phones. Use a 5% level of significance. State the null and alternative hypothesis, find the p -value, state your conclusion, and identify the Type I and Type II errors.

• \(H_{0}: p = 0.92\)
• \(H_{a}: p < 0.92\)
• \(p\text{-value} = 0.0046\)

Because \(p < 0.05\), we reject the null hypothesis. There is sufficient evidence to conclude that fewer than 92% of American adults own cell phones.

• Type I Error: To conclude that fewer than 92% of American adults own cell phones when, in fact, 92% of American adults do own cell phones (reject the null hypothesis when the null hypothesis is true).
• Type II Error: To conclude that 92% of American adults own cell phones when, in fact, fewer than 92% of American adults own cell phones (do not reject the null hypothesis when the null hypothesis is false).

The next example is a poem written by a statistics student named Nicole Hart. The solution to the problem follows the poem. Notice that the hypothesis test is for a single population proportion. This means that the null and alternate hypotheses use the parameter \(p\). The distribution for the test is normal. The estimated proportion \(p′\) is the proportion of fleas killed to the total fleas found on Fido. This is sample information. The problem gives a preconceived \(\alpha = 0.01\), for comparison, and a 95% confidence interval computation. The poem is clever and humorous, so please enjoy it!

Example \(\PageIndex{9}\)

My dog has so many fleas,

They do not come off with ease. As for shampoo, I have tried many types Even one called Bubble Hype, Which only killed 25% of the fleas, Unfortunately I was not pleased.

I've used all kinds of soap, Until I had given up hope Until one day I saw An ad that put me in awe.

A shampoo used for dogs Called GOOD ENOUGH to Clean a Hog Guaranteed to kill more fleas.

I gave Fido a bath And after doing the math His number of fleas Started dropping by 3's! Before his shampoo I counted 42.

At the end of his bath, I redid the math And the new shampoo had killed 17 fleas. So now I was pleased.

Now it is time for you to have some fun With the level of significance being .01, You must help me figure out

Use the new shampoo or go without?

\(H_{0}: p \leq 0.25\)   \(H_{a}: p > 0.25\)

In words, CLEARLY state what your random variable \(\bar{X}\) or \(P′\) represents.

\(P′ =\) The proportion of fleas that are killed by the new shampoo

State the distribution to use for the test.

\[N\left(0.25, \sqrt{\frac{(0.25){1-0.25}}{42}}\right)\nonumber \]

Test Statistic: \(z = 2.3163\)

Calculate the \(p\text{-value}\) using the normal distribution for proportions:

\[p\text{-value} = 0.0103\nonumber \]

In one to two complete sentences, explain what the p -value means for this problem.

If the null hypothesis is true (the proportion is 0.25), then there is a 0.0103 probability that the sample (estimated) proportion is 0.4048 \(\left(\frac{17}{42}\right)\) or more.

Use the previous information to sketch a picture of this situation. CLEARLY, label and scale the horizontal axis and shade the region(s) corresponding to the \(p\text{-value}\).

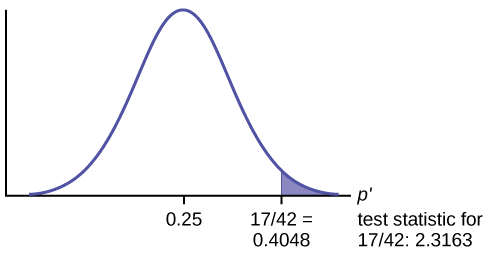
Indicate the correct decision (“reject” or “do not reject” the null hypothesis), the reason for it, and write an appropriate conclusion, using complete sentences.

Conclusion: At the 1% level of significance, the sample data do not show sufficient evidence that the percentage of fleas that are killed by the new shampoo is more than 25%.

Construct a 95% confidence interval for the true mean or proportion. Include a sketch of the graph of the situation. Label the point estimate and the lower and upper bounds of the confidence interval.

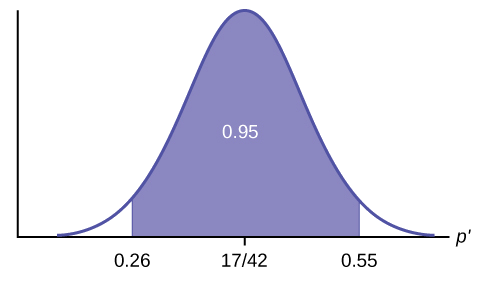
Confidence Interval: (0.26,0.55) We are 95% confident that the true population proportion p of fleas that are killed by the new shampoo is between 26% and 55%.

This test result is not very definitive since the \(p\text{-value}\) is very close to alpha. In reality, one would probably do more tests by giving the dog another bath after the fleas have had a chance to return.

Example \(\PageIndex{10}\)

The National Institute of Standards and Technology provides exact data on conductivity properties of materials. Following are conductivity measurements for 11 randomly selected pieces of a particular type of glass.

1.11; 1.07; 1.11; 1.07; 1.12; 1.08; .98; .98 1.02; .95; .95

Is there convincing evidence that the average conductivity of this type of glass is greater than one? Use a significance level of 0.05. Assume the population is normal.

Let’s follow a four-step process to answer this statistical question.

• \(H_{0}: \mu \leq 1\)
• \(H_{a}: \mu > 1\)
• Plan : We are testing a sample mean without a known population standard deviation. Therefore, we need to use a Student's-t distribution. Assume the underlying population is normal.
• Do the calculations : We will input the sample data into the TI-83 as follows.

4. State the Conclusions : Since the \(p\text{-value} (p = 0.036)\) is less than our alpha value, we will reject the null hypothesis. It is reasonable to state that the data supports the claim that the average conductivity level is greater than one.

Example \(\PageIndex{11}\)

In a study of 420,019 cell phone users, 172 of the subjects developed brain cancer. Test the claim that cell phone users developed brain cancer at a greater rate than that for non-cell phone users (the rate of brain cancer for non-cell phone users is 0.0340%). Since this is a critical issue, use a 0.005 significance level. Explain why the significance level should be so low in terms of a Type I error.

We will follow the four-step process.

• \(H_{0}: p \leq 0.00034\)
• \(H_{a}: p > 0.00034\)

If we commit a Type I error, we are essentially accepting a false claim. Since the claim describes cancer-causing environments, we want to minimize the chances of incorrectly identifying causes of cancer.

• We will be testing a sample proportion with \(x = 172\) and \(n = 420,019\). The sample is sufficiently large because we have \(np = 420,019(0.00034) = 142.8\), \(nq = 420,019(0.99966) = 419,876.2\), two independent outcomes, and a fixed probability of success \(p = 0.00034\). Thus we will be able to generalize our results to the population.

Figure \(\PageIndex{11}\).

Figure \(\PageIndex{12}\).

• Since the \(p\text{-value} = 0.0073\) is greater than our alpha value \(= 0.005\), we cannot reject the null. Therefore, we conclude that there is not enough evidence to support the claim of higher brain cancer rates for the cell phone users.

Example \(\PageIndex{12}\)

According to the US Census there are approximately 268,608,618 residents aged 12 and older. Statistics from the Rape, Abuse, and Incest National Network indicate that, on average, 207,754 rapes occur each year (male and female) for persons aged 12 and older. This translates into a percentage of sexual assaults of 0.078%. In Daviess County, KY, there were reported 11 rapes for a population of 37,937. Conduct an appropriate hypothesis test to determine if there is a statistically significant difference between the local sexual assault percentage and the national sexual assault percentage. Use a significance level of 0.01.

We will follow the four-step plan.

• We need to test whether the proportion of sexual assaults in Daviess County, KY is significantly different from the national average.
• \(H_{0}: p = 0.00078\)
• \(H_{a}: p \neq 0.00078\)

Figure \(\PageIndex{13}\).

Figure \(\PageIndex{14}\).

• Since the \(p\text{-value}\), \(p = 0.00063\), is less than the alpha level of 0.01, the sample data indicates that we should reject the null hypothesis. In conclusion, the sample data support the claim that the proportion of sexual assaults in Daviess County, Kentucky is different from the national average proportion.

The hypothesis test itself has an established process. This can be summarized as follows:

• Determine \(H_{0}\) and \(H_{a}\). Remember, they are contradictory.
• Determine the random variable.
• Determine the distribution for the test.
• Draw a graph, calculate the test statistic, and use the test statistic to calculate the \(p\text{-value}\). (A z -score and a t -score are examples of test statistics.)
• Compare the preconceived α with the p -value, make a decision (reject or do not reject H 0 ), and write a clear conclusion using English sentences.

Notice that in performing the hypothesis test, you use \(\alpha\) and not \(\beta\). \(\beta\) is needed to help determine the sample size of the data that is used in calculating the \(p\text{-value}\). Remember that the quantity \(1 – \beta\) is called the Power of the Test . A high power is desirable. If the power is too low, statisticians typically increase the sample size while keeping α the same.If the power is low, the null hypothesis might not be rejected when it should be.

Assume \(H_{0}: \mu = 9\) and \(H_{a}: \mu < 9\). Is this a left-tailed, right-tailed, or two-tailed test?

This is a left-tailed test.

Exercise \(\PageIndex{9}\)

Assume \(H_{0}: \mu \leq 6\) and \(H_{a}: \mu > 6\). Is this a left-tailed, right-tailed, or two-tailed test?

Exercise \(\PageIndex{10}\)

Assume \(H_{0}: p = 0.25\) and \(H_{a}: p \neq 0.25\). Is this a left-tailed, right-tailed, or two-tailed test?

This is a two-tailed test.

Exercise \(\PageIndex{11}\)

Draw the general graph of a left-tailed test.

Exercise \(\PageIndex{12}\)

Draw the graph of a two-tailed test.

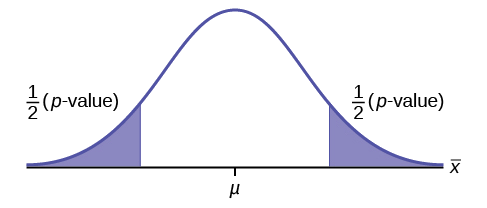
Exercise \(\PageIndex{13}\)

A bottle of water is labeled as containing 16 fluid ounces of water. You believe it is less than that. What type of test would you use?

Exercise \(\PageIndex{14}\)

Your friend claims that his mean golf score is 63. You want to show that it is higher than that. What type of test would you use?

a right-tailed test

Exercise \(\PageIndex{15}\)

A bathroom scale claims to be able to identify correctly any weight within a pound. You think that it cannot be that accurate. What type of test would you use?

Exercise \(\PageIndex{16}\)

You flip a coin and record whether it shows heads or tails. You know the probability of getting heads is 50%, but you think it is less for this particular coin. What type of test would you use?

a left-tailed test

Exercise \(\PageIndex{17}\)

If the alternative hypothesis has a not equals ( \(\neq\) ) symbol, you know to use which type of test?

Exercise \(\PageIndex{18}\)

Assume the null hypothesis states that the mean is at least 18. Is this a left-tailed, right-tailed, or two-tailed test?

Exercise \(\PageIndex{19}\)

Assume the null hypothesis states that the mean is at most 12. Is this a left-tailed, right-tailed, or two-tailed test?

Exercise \(\PageIndex{20}\)

Assume the null hypothesis states that the mean is equal to 88. The alternative hypothesis states that the mean is not equal to 88. Is this a left-tailed, right-tailed, or two-tailed test?

• Data from Amit Schitai. Director of Instructional Technology and Distance Learning. LBCC.
• Data from Bloomberg Businessweek . Available online at www.businessweek.com/news/2011- 09-15/nyc-smoking-rate-falls-to-record-low-of-14-bloomberg-says.html.
• Data from energy.gov. Available online at http://energy.gov (accessed June 27. 2013).
• Data from Gallup®. Available online at www.gallup.com (accessed June 27, 2013).
• Data from Growing by Degrees by Allen and Seaman.
• Data from La Leche League International. Available online at www.lalecheleague.org/Law/BAFeb01.html.
• Data from the American Automobile Association. Available online at www.aaa.com (accessed June 27, 2013).
• Data from the American Library Association. Available online at www.ala.org (accessed June 27, 2013).
• Data from the Bureau of Labor Statistics. Available online at http://www.bls.gov/oes/current/oes291111.htm .
• Data from the Centers for Disease Control and Prevention. Available online at www.cdc.gov (accessed June 27, 2013)
• Data from the U.S. Census Bureau, available online at quickfacts.census.gov/qfd/states/00000.html (accessed June 27, 2013).
• Data from the United States Census Bureau. Available online at www.census.gov/hhes/socdemo/language/.
• Data from Toastmasters International. Available online at http://toastmasters.org/artisan/deta...eID=429&Page=1 .
• Data from Weather Underground. Available online at www.wunderground.com (accessed June 27, 2013).
• Federal Bureau of Investigations. “Uniform Crime Reports and Index of Crime in Daviess in the State of Kentucky enforced by Daviess County from 1985 to 2005.” Available online at http://www.disastercenter.com/kentucky/crime/3868.htm (accessed June 27, 2013).
• “Foothill-De Anza Community College District.” De Anza College, Winter 2006. Available online at research.fhda.edu/factbook/DA...t_da_2006w.pdf.
• Johansen, C., J. Boice, Jr., J. McLaughlin, J. Olsen. “Cellular Telephones and Cancer—a Nationwide Cohort Study in Denmark.” Institute of Cancer Epidemiology and the Danish Cancer Society, 93(3):203-7. Available online at http://www.ncbi.nlm.nih.gov/pubmed/11158188 (accessed June 27, 2013).
• Rape, Abuse & Incest National Network. “How often does sexual assault occur?” RAINN, 2009. Available online at www.rainn.org/get-information...sexual-assault (accessed June 27, 2013).

• International

D-Day 80th anniversary in Normandy

By Joshua Berlinger, Antoinette Radford, Shania Shelton and Kyle Feldscher, CNN

These are the 11 Americans who received France's highest honor this morning in Normandy

From CNN's Emmanuel Miculita and Joshua Berlinger in Paris

French President Emmanuel Macron honored 11 American veterans with the Legion of Honor, France's highest civilian and military award.

Macron told the veterans he was honoring them "for your bravery, for your service to our freedom."

The award was created in 1802 by Napoleon.

Here are the following American veterans who were given the honor:

• Hilbert Margol 
• John Wardell
• Robert Pedigo 
• Calvin Shiner
• Edward Berthold 
• Dominick Critelli
• Bill Cassasa
• Victor Chaney 
• Raymond Glansberg
• Richard Stewart
• John Kinyon 

About 150 American veterans made the journey to Normandy to commemorate the anniversary, about two dozen of whom fought on D-Day, according to Charles Djou, the secretary of the American Battle Monuments Commission (ABMC), the independent agency responsible for managing US military cemeteries and monuments overseas.

"Placid Lassie" takes to the Normandy skies, 80 years after carrying troops into battle 

From CNN's Joseph Ataman in Arromanches-les-Bains, France

Eighty years to the day after the "Placid Lassie’" first flew in the skies above France, towing American soldiers in a glider into battle, she soared once again over Normandy. 

A troop-carrying C-47 aircraft, the Placid Lassie is one of seven World War II-era aircraft taking part in D-Day commemorations this week, kept flying by teams of volunteer pilots and mechanics. 

“It's not an airplane that looks like it. Not a replica, not something that approximates it or represents it, but this actual airplane that flew over the beaches of Normandy,” pilot Eric Zipkin said. “So there’s an extraordinary feeling of responsibility and importance.”

Most of these aircraft from the United States-based D-Day squadron, an organization that put together the Placid Lassie's trip to Normandy this year alongside several other similar aircraft.

The journey took six days, as these aircraft were built for flight during another era. They require fuel, tools and spare parts not readily available on the market today, Zipkin said.

Zipkin believes that flying these planes is one of the most important ways to bring the history of WWII to life -- second only to the stories shared by the dwindling number of living veterans.

Without modern avionics, navigation or communication equipment, flying the aircraft is a visceral and tactile experience, one that demands mastering a new way of flying, Zipkin said.

However, growing costs and the advanced age of the air frames may make this the last time the public sees such a large formation of these veteran birds in flight in Europe. 

He estimated that it costs the owners of the planes each $150,000 to $200,000 to make the journey one way.

“That's just to just just to show up. And then, of course, flying in the UK and Europe is extremely expensive, probably twice what it costs in the United States,” Zipkin said.

Tom Hanks says the US "cannot help but turn towards what is right"

From CNN's Shania Shelton

As celebrations for the  80th anniversary of D-Day are underway, actor Tom Hanks spoke with CNN's Christiane Amanpour about democracy, saying he believes the US and Western societies "cannot help but turn towards what is right."

"Our Constitution says, 'we the people of the United States, in order to form a more perfect union.' That journey to a more perfect union has missteps in it," Hanks said.

"Over the long term, however, we inevitably make progress towards, I think, a more perfect union. And how does it come about? It comes about not because of somebody's narrative of who is right or who is a victim. It comes out of the slow melding of the truth to the actual practical life that we end up living," he said.

Watch here:

Biden has delivered an emotive speech in France, drawing parallels between 1944 and now. Here's what to know

From CNN Staff

Speaking at a commemoration service marking the 80th anniversary of the D-Day landings, US President Joe Biden warned "the price of unchecked tyranny is the blood of the young and the brave."

His comments come on a day that Ukraine's fight against Russia's invasion has been a major theme and frequent parallels have been drawn by numerous leaders. In his speech, the president drew direct parallels between Nazi Germany and the threats facing Western democracies today.

"Ukrainians are fighting with extraordinary courage, suffering great losses but never backing down," Biden said.

Here's what else to know about Biden's speech:

• Tribute to veterans : At the start of the speech, Biden turned to veterans present at the commemoration and thanked them for their service.
• Biden honored "band of brothers:" Naming several veterans who made the journey back to Normandy during his speech by name.
• He acknowledged people of color and women who served in the war, noting that hundreds of thousands of people "courageously served despite unjust limitation on what they could do for their nation."
• The president acknowledged it may be the last ceremony with living veterans , which he said should inspire Americans to continue their fight against tyranny.

Biden: "Democracy is not guaranteed"

From CNN's Joshua Berlinger in Paris

US President Joe Biden acknowledged that this year's commemoration of D-Day may be the last to involve living veterans, a fact that he said must push Americans to continue the fight against tyranny.

"We're not far off from the time when the last living voices of those who fought and bled on D-Day will no longer be with us, so we have a special obligation. We cannot let what happened here be lost in the silence of the years to come," Biden said. "The fact that they were heroes here that day does not absolve us of what we have do today. Democracy is not guaranteed. Every generation must preserve it, defend it and fight for it." "In memory of those who fought here, died here and literally saved the world here, let us be worthy of their sacrifice," Biden added.

As Western allies gather for D-Day anniversary, Zelensky calls for "true unity" to prevail

From CNN's Billy Stockwell

Ukraine's President Volodymyr Zelensky has called for “true unity” to prevail as it did when allied forces rallied together to defend “Europe’s freedoms,” as D-Day anniversary commemorations took place Thursday.

Ukraine's fight against Russia's invasion has been a major theme of the D-Day commemorations on Thursday and frequent parallels have been drawn by numerous leaders.

“Allies defended Europe's freedom then, and Ukrainians do so now. Unity prevailed then, and true unity can prevail today,” he  posted  on X Thursday.

He said that he and first lady Olena Zelenska were honored to take part in today’s “special event,” adding that he wants to strengthen his country and promote unity among “all those who respect human values and life.”

“This event and day serve as a reminder of the courage and determination demonstrated in the pursuit of freedom and democracy,” he added.

"The price of unchecked tyranny is the blood of the young and the brave," Biden says

From CNN's Joshua Berlinger

US President Joe Biden ended his speech with a metaphoric call to arms against the forces of tyranny that threaten Western democracies,

"History tells us freedom is not free. If you want to know the price of freedom, come here to Normandy," Biden said from the Normandy American Cemetery and Memorial in Colleville-sur-Mer, France. "Remember, the price of unchecked tyranny is the blood of the young and the brave."

He continued:

"We're living in a time when democracy is more at risk across the world than any point since the end of World War II, since these beaches were stormed," Biden said. "In their hour of trial, the allied forces of D-Day did their duty. Now the question for us is, in our hour of trial, will we do ours?"

Biden ties D-Day to Russian invasion of Ukraine: "The struggle between a dictatorship and freedom is unending"

US President Joe Biden is using his speech to mark the 80th anniversary of D-Day to draw direct parallels between Nazi Germany and the threats facing Western democracies today -- including in eastern Europe.

"We know the dark forces that these heroes fought against 80 years ago. They never fade. Aggression and greed, the desire to dominate and control, to change borders by force. These are perennial. And the struggle between a dictatorship and freedom is unending," Biden said.

Biden mentioned Ukraine specifically, saying the country has been "invaded by a tyrant bent on domination."

The US president claimed that 350,000 Russian troops had been killed or wounded in the conflict and that nearly 1 million people had fled Russia since it launched its full-scale invasion against Ukraine in February 2022. The Kremlin has not publicly confirmed either figure.

"The United States and NATO and a coalition of more than 50 countries (are) standing strong with Ukraine. We will not walk away," Biden said. "Because if we do, Ukraine will be subjugated, and it will not end there. Ukraine's neighbors will be threatened. All of Europe will be threatened. And make no mistake, the autocrats of the world are watching closely to see what happens in Ukraine. To see if we let this illegal aggression go unchecked. We cannot let that happen. To surrender to bullies, to bow down to dictators is simply unthinkable."

Biden subtly hits out at "America First" in D-Day speech

From CNN's Josh Berlinger in Paris

US President Joe Biden appeared to hit back at former President Donald Trump's brand of "America first" isolationism in his speech marking the 80th anniversary of D-Day.

"America's unique ability to bring countries together is an undeniably source of our power. Isolationism was not the answer 80 years ago and is not the answer today," Biden said.

Please enable JavaScript for a better experience.

Lesson 27: Likelihood Ratio Tests

In this lesson, we'll learn how to apply a method for developing a hypothesis test for situations in which both the null and alternative hypotheses are composite. That's not completely accurate. The method, called the likelihood ratio test , can be used even when the hypotheses are simple, but it is most commonly used when the alternative hypothesis is composite. Throughout the lesson, we'll continue to assume that we know the the functional form of the probability density (or mass) function, but we don't know the value of one (or more) of its parameters. That is, we might know that the data come from a normal distrbution, but we don't know the mean or variance of the distribution, and hence the interest in performing a hypothesis test about the unknown parameter(s).

27.1 - A Definition and Simple Example

The title of this page is a little risky, as there are few simple examples when it comes to likelihood ratio testing! But, we'll work to make the example as simple as possible, namely by assuming again, unrealistically, that we know the population variance, but not the population mean. Before we state the definition of a likelihood ratio test, and then investigate our simple, but unrealistic, example, we first need to define some notation that we'll use throughout the lesson.

We'll assume that the probability density (or mass) function of X is \(f(x;\theta)\) where \(\theta\) represents one or more unknown parameters. Then:

• Let \(\Omega\) (greek letter "omega") denote the total possible parameter space of \(\theta\), that is, the set of all possible values of \(\theta\) as specified in totality in the null and alternative hypotheses.
• Let \(H_0 : \theta \in \omega\) denote the null hypothesis where \(\omega\) (greek letter "omega") is a subset of the parameter space \(\Omega\).
• Let \(H_A : \theta \in \omega'\) denote the alternative hypothesis where \(\omega '\) is the complement of \(\omega\) with respect to the parameter space \(\Omega\).

Let's make sure we are clear about that phrase "where \(\omega '\) is the complement of \(\omega\) with respect to the parameter space \(\Omega\)."

Example 27-1

If the total parameter space of the mean \(\mu\) is \(\Omega = {\mu: −∞ < \mu < ∞}\) and the null hypothesis is specified as \(H_0: \mu = 3\), how should we specify the alternative hypothesis so that the alternative parameter space is the complement of the null parameter space?

If the null parameter space is \(\Omega = {\mu: \mu = 3}\), then the alternative parameter space is everything that is in \(\Omega = {\mu: −∞ < \mu < ∞}\) that is not in \(\Omega\). That is, the alternative parameter space is \(\Omega ' = {\mu: \mu ≠ 3}\). And, so the alternative hypothesis is:

\(H_A : \mu \ne 3\)

In this case, we'd be interested in deriving a two-tailed test.

Example 27-2

If the alternative hypothesis is \(H_A: \mu > 3\), how should we (technically) specify the null hypothesis so that the null parameter space is the complement of the alternative parameter space?

If the alternative parameter space is (\omega ' = {\mu: \mu > 3}\), then the null parameter space is \(\omega = {\mu: \mu ≤ 3}\). And, so the null hypothesis is:

\(H_0 : \mu \le 3\)

Now, the reality is that some authors do specify the null hypothesis as such, even when they mean \(H_0: \mu = 3\). Ours don't, and so we won't. (That's why I put that "technically" in parentheses up above.) At any rate, in this case, we'd be interested in deriving a one-tailed test.

Definition. Let:

\(L(\hat{\omega})\) denote the maximum of the likelihood function with respect to \(\theta\) when \(\theta\) is in the null parameter space \(\omega\).

\(L(\hat{\Omega})\) denote the maximum of the likelihood function with respect to \(\theta\) when \(\theta\) is in the entire parameter space \(\Omega\).

Then, the likelihood ratio is the quotient:

\(\lambda = \dfrac{L(\hat{\omega})}{L(\hat{\Omega})}\)

And, to test the null hypothesis \(H_0 : \theta \in \omega\) against the alternative hypothesis \(H_A : \theta \in \omega'\), the critical region for the likelihood ratio test is the set of sample points for which:

\(\lambda = \dfrac{L(\hat{\omega})}{L(\hat{\Omega})} \le k\)

where \(0 < k < 1\), and k is selected so that the test has a desired significance level \(\alpha\).

Example 27-3

A food processing company packages honey in small glass jars. Each jar is supposed to contain 10 fluid ounces of the sweet and gooey good stuff. Previous experience suggests that the volume X , the volume in fluid ounces of a randomly selected jar of the company's honey is normally distributed with a known variance of 2. Derive the likelihood ratio test for testing, at a significance level of \(\alpha = 0.05\), the null hypothesis \(H_0: \mu = 10\) against the alternative hypothesis H_A: \mu ≠ 10\).

Because we are interested in testing the null hypothesis \(H_0: \mu = 10\) against the alternative hypothesis \(H_A: \mu ≠ 10\) for a normal mean, our total parameter space is:

\(\Omega =\left \{\mu : -\infty < \mu < \infty \right \}\)

and our null parameter space is:

\(\omega = \left \{10\right \}\)

Now, to find the likelihood ratio, as defined above, we first need to find \(L(\hat{\omega})\). Well, when the null hypothesis \(H_0: \mu = 10\) is true, the mean \(\mu\) can take on only one value, namely, \(\mu = 10\). Therefore:

\(L(\hat{\omega}) = L(10)\)

We also need to find \(L(\hat{\Omega})\) in order to define the likelihood ratio. To find it, we must find the value of \(\mu\)   that maximizes \(L(\mu)\) . Well, we did that back when we studied maximum likelihood as a method of estimation. We showed that \(\hat{\mu} = \bar{x}\) is the maximum likelihood estimate of \(\mu\) . Therefore:

\(L(\hat{\Omega}) = L(\bar{x})\)

Now, putting it all together to form the likelihood ratio, we get:

which simplifies to:

Now, let's step aside for a minute and focus just on the summation in the numerator. If we "add 0" in a special way to the quantity in parentheses:

we can show that the summation can be written as:

\(\sum_{i=1}^{n}(x_i - 10)^2 = \sum_{i=1}^{n}(x_i - \bar{x})^2 + n(\bar{x} -10)^2 \)

Therefore, the likelihood ratio becomes:

which greatly simplifies to:

\(\lambda = exp \left [-\dfrac{n}{4}(\bar{x}-10)^2 \right ]\)

Now, the likelihood ratio test tells us to reject the null hypothesis when the likelihood ratio \(\lambda\) is small, that is, when:

\(\lambda = exp\left[-\dfrac{n}{4}(\bar{x}-10)^2 \right] \le k\)

where k is chosen to ensure that, in this case, \(\alpha = 0.05\). Well, by taking the natural log of both sides of the inequality, we can show that \(\lambda ≤ k\) is equivalent to:

\( -\dfrac{n}{4}(\bar{x}-10)^2 \le \text{ln} k \)

which, by multiplying through by −4/ n , is equivalent to:

\((\bar{x}-10)^2 \ge -\dfrac{4}{n} \text{ln} k \)

which is equivalent to:

\(\dfrac{|\bar{X}-10|}{\sigma / \sqrt{n}} \ge \dfrac{\sqrt{-(4/n)\text{ln} k}}{\sigma / \sqrt{n}} =k* \)

Aha! We should recognize that quantity on the left-side of the inequality! We know that:

\(Z = \dfrac{\bar{X}-10}{\sigma / \sqrt{n}} \)

follows a standard normal distribution when \(H_0: \mu = 10\). Therefore we can determine the appropriate \(k^*\) by using the standard normal table. We have shown that the likelihood ratio test tells us to reject the null hypothesis \(H_0: \mu = 10\) in favor of the alternative hypothesis \(H_A: \mu ≠ 10\) for all sample means for which the following holds:

\(\dfrac{|\bar{X}-10|}{ \sqrt{2} / \sqrt{n}} \ge z_{0.025} = 1.96 \)

Doing so will ensure that our probability of committing a Type I error is set to \(\alpha = 0.05\), as desired.

27.2 - The T-Test For One Mean

Well, geez, now why would we be revisiting the t -test for a mean \(\mu\) when we have already studied it back in the hypothesis testing section? Well, the answer, it turns out, is that, as we'll soon see, the t -test for a mean \(\mu\) is the likelihood ratio test! Let's take a look!

Example 27-4

Suppose that a random sample \(X_1 , X_2 , \dots , X_n\) arises from a normal population with unknown mean \(\mu\) and unknown variance \(\sigma^2\). (Yes, back to the realistic situation, in which we don't know the population variance either.) Find the size \(\alpha\) likelihood ratio test for testing the null hypothesis \(H_0: \mu = \mu_0\) against the two-sided alternative hypothesis \(H_A: \mu ≠ \mu_0\) .

Our unrestricted parameter space is:

\( \Omega = \left\{ (\mu, \sigma^2) : -\infty < \mu < \infty, 0 < \sigma^2 < \infty \right\} \)

Under the null hypothesis, the mean \(\mu\) is the only parameter that is restricted. Therefore, our parameter space under the null hypothesis is:

\( \omega = \left\{(\mu, \sigma^2) : \mu =\mu_0, 0 < \sigma^2 < \infty \right\}\)

Now, first consider the case where the mean and variance are unrestricted. We showed back when we studied maximum likelihood estimation that the maximum likelihood estimates of \(\mu\) and \(\sigma^2\) are, respectively:

\(\hat{\mu} = \bar{x} \text{ and } \hat{\sigma}^2 = \dfrac{1}{n}\sum_{i=1}^{n}(x_i - \bar{x})^2 \)

Therefore, the maximum of the likelihood function for the unrestricted parameter space is:

\( L(\hat{\Omega})= \left[\dfrac{ne^{-1}}{2\pi \Sigma (x_i - \bar{x})^2} \right]^{n/2} \)

Now, under the null parameter space, the maximum likelihood estimates of \(\mu\)   and \(\sigma^2\) are, respectively:

\( \hat{\mu} = \mu_0 \text{ and } \hat{\sigma}^2 = \dfrac{1}{n}\sum_{i=1}^{n}(x_i - \mu_0)^2 \)

Therefore, the likelihood under the null hypothesis is:

\( L(\hat{\omega})= \left[\dfrac{ne^{-1}}{2\pi \Sigma (x_i - \mu_0)^2} \right]^{n/2} \)

And now taking the ratio of the two likelihoods, we get:

which reduces to:

\( \lambda = \left[ \dfrac{\sum_{i=1}^{n}(x_i - \bar{x})^2}{\sum_{i=1}^{n}(x_i - \mu_0)^2} \right] ^{n/2}\)

Focusing only on the denominator for a minute, let's do that trick again of "adding 0" in just the right away. Adding 0 to the quantity in the parentheses, we get:

\( \sum_{i=1}^{n}(x_i - \mu_0)^2 = \sum_{i=1}^{n}(x_i - \bar{x})^2 +n(\bar{x} - \mu_0)^2 \)

Then, our likelihood ratio \(\lambda\) becomes:

\( \lambda = \left[ \dfrac{\sum_{i=1}^{n}(x_i - \bar{x})^2}{\sum_{i=1}^{n}(x_i - \mu_0)^2} \right] ^{n/2} = \left[ \dfrac{\sum_{i=1}^{n}(x_i - \bar{x})^2}{ \sum_{i=1}^{n}(x_i - \bar{x})^2 +n(\bar{x} - \mu_0)^2} \right] ^{n/2} \)

which, upon dividing through numerator and denominator by \( \sum_{i=1}^{n}(x_i - \bar{x})^2 \) simplifies to:

Therefore, the likelihood ratio test's critical region, which is given by the inequality \(\lambda ≤ k\), is equivalent to:

which with some minor algebraic manipulation can be shown to be equivalent to:

So, in a nutshell, we've shown that the likelihood ratio test tells us that for this situation we should reject the null hypothesis \(H_0: \mu= \mu_0\) in favor of the alternative hypothesis \(H_A: \mu ≠ \mu_0\)   if:

\( \dfrac{(\bar{x}-\mu_0)^2 }{s^2 / n} \ge k^{*} \)

Well, okay, so I started out this page claiming that the t -test for a mean \(\mu\) is the likelihood ratio test. Is it? Well, the above critical region is equivalent to rejecting the null hypothesis if:

\( \dfrac{|\bar{x}-\mu_0| }{s / \sqrt{n}} \ge k^{**} \)

Does that look familiar? We previously learned that if \(X_1, X_2, \dots, X_n\) are normally distributed with mean \(\mu\) and variance \(\sigma^2\), then:

\( T = \dfrac{\bar{X}-\mu}{S / \sqrt{n}} \)

follows a T distribution with n − 1 degrees of freedom. So, this tells us that we should use the T distribution to choose \(k^{**}\) . That is, set:

\(k^{**} = t_{\alpha /2, n-1}\)

and we have our size \(\alpha\) t -test that ensures the probability of committing a Type I error is \(\alpha\).

It turns out... we didn't know it at the time... but every hypothesis test that we derived in the hypothesis testing section is a likelihood ratio test. Back then, we derived each test using distributional results of the relevant statistic(s), but we could have alternatively, and perhaps just as easily, derived the tests using the likelihood ratio testing method.

9.1 Null and Alternative Hypotheses

The actual test begins by considering two hypotheses . They are called the null hypothesis and the alternative hypothesis . These hypotheses contain opposing viewpoints.

H 0 , the — null hypothesis: a statement of no difference between sample means or proportions or no difference between a sample mean or proportion and a population mean or proportion. In other words, the difference equals 0.

H a —, the alternative hypothesis: a claim about the population that is contradictory to H 0 and what we conclude when we reject H 0 .

Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample data.

After you have determined which hypothesis the sample supports, you make a decision. There are two options for a decision. They are reject H 0 if the sample information favors the alternative hypothesis or do not reject H 0 or decline to reject H 0 if the sample information is insufficient to reject the null hypothesis.

Mathematical Symbols Used in H 0 and H a :

H 0 always has a symbol with an equal in it. H a never has a symbol with an equal in it. The choice of symbol depends on the wording of the hypothesis test. However, be aware that many researchers use = in the null hypothesis, even with > or < as the symbol in the alternative hypothesis. This practice is acceptable because we only make the decision to reject or not reject the null hypothesis.

Example 9.1

H 0 : No more than 30 percent of the registered voters in Santa Clara County voted in the primary election. p ≤ 30 H a : More than 30 percent of the registered voters in Santa Clara County voted in the primary election. p > 30

A medical trial is conducted to test whether or not a new medicine reduces cholesterol by 25 percent. State the null and alternative hypotheses.

Example 9.2

We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). The null and alternative hypotheses are the following: H 0 : μ = 2.0 H a : μ ≠ 2.0

We want to test whether the mean height of eighth graders is 66 inches. State the null and alternative hypotheses. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

• H 0 : μ __ 66
• H a : μ __ 66

Example 9.3

We want to test if college students take fewer than five years to graduate from college, on the average. The null and alternative hypotheses are the following: H 0 : μ ≥ 5 H a : μ < 5

We want to test if it takes fewer than 45 minutes to teach a lesson plan. State the null and alternative hypotheses. Fill in the correct symbol ( =, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

• H 0 : μ __ 45
• H a : μ __ 45

Example 9.4

An article on school standards stated that about half of all students in France, Germany, and Israel take advanced placement exams and a third of the students pass. The same article stated that 6.6 percent of U.S. students take advanced placement exams and 4.4 percent pass. Test if the percentage of U.S. students who take advanced placement exams is more than 6.6 percent. State the null and alternative hypotheses. H 0 : p ≤ 0.066 H a : p > 0.066

On a state driver’s test, about 40 percent pass the test on the first try. We want to test if more than 40 percent pass on the first try. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

• H 0 : p __ 0.40
• H a : p __ 0.40

Collaborative Exercise

Bring to class a newspaper, some news magazines, and some internet articles. In groups, find articles from which your group can write null and alternative hypotheses. Discuss your hypotheses with the rest of the class.

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute Texas Education Agency (TEA). The original material is available at: https://www.texasgateway.org/book/tea-statistics . Changes were made to the original material, including updates to art, structure, and other content updates.

Access for free at https://openstax.org/books/statistics/pages/1-introduction

• Authors: Barbara Illowsky, Susan Dean
• Publisher/website: OpenStax
• Book title: Statistics
• Publication date: Mar 27, 2020
• Location: Houston, Texas
• Book URL: https://openstax.org/books/statistics/pages/1-introduction
• Section URL: https://openstax.org/books/statistics/pages/9-1-null-and-alternative-hypotheses

© Jan 23, 2024 Texas Education Agency (TEA). The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

You are viewing this page in an unauthorized frame window.

This is a potential security issue, you are being redirected to https://nvd.nist.gov

You have JavaScript disabled. This site requires JavaScript to be enabled for complete site functionality.

Official websites use .gov A .gov website belongs to an official government organization in the United States.

Information Technology Laboratory

National vulnerability database.

• Vulnerabilities

The NVD has a new announcement page with status updates, news, and how to stay connected!

Weakness Enumeration

Change history, new cve received by nist 6/05/2024 11:15:12 am.

• Share full article

Advertisement

Supported by

N.H.L.’s Move to Salt Lake City Is Latest Sports Downsizing

Professional leagues are embracing smaller markets in their search for newer stadiums and arenas and the potential for more devoted fan bases.

By Ken Belson

Sometimes, smaller is better.

For decades, major sports leagues have tried to place teams in the country’s largest markets in the hopes of selling more tickets and sponsorships as well as satisfying broadcasters who want to reach the largest number of viewers possible.

But in recent years, leagues have embraced the charms of smaller markets. Teams have moved to cities like Oklahoma City, Las Vegas and Winnipeg, Manitoba, in search of financial incentives, newer arenas and stadiums, and more devoted fans.

In early April, the National Hockey League approved the $1.2 billion sale of the Arizona Coyotes to the tech billionaire Ryan Smith and his wife, Ashley. The team, which will be renamed, will begin play next season in the Delta Center in Salt Lake City, home of one of the Smiths’ other teams, the Utah Jazz of the National Basketball Association.

On its face, the move could be seen as a step down. Salt Lake City’s metropolitan area is less than half the size of Phoenix’s; Salt Lake City is the 29th-largest media market while Phoenix is the 11th largest. Utah has never been home to an N.H.L. team. But the league’s decision was less about the size of Salt Lake City and more about its demographics. Like Phoenix, Salt Lake City is one of the country’s fastest-growing cities. But in Utah, a thriving tech industry has attracted an influx of young workers with disposable incomes.

“People aren’t coming to Utah to just retire,” Ryan Smith said in an interview. “If you have two states that are growing fast, you would always take the youthful one for the future of prosperity.”

Leagues have been “right-sizing” their operations for years with an eye toward making money off fewer fans. The Mets were one of many baseball teams that built smaller stadiums with more exclusive clubs and suites. Citi Field, which opened in 2009, has just 42,000 seats, compared with 55,000 at the team’s previous home, Shea Stadium. Smaller arenas and stadiums are easier to fill — the sight of empty seats on television is a bad look — and teams can focus on more high-end concessions, club seats and exclusive “experiences.”

It typically takes a team several years to prepare for a relocation. But Commissioner Gary Bettman said the N.H.L. had to act quickly because the Coyotes needed stable owners and a big-league arena. The team had trouble drawing fans , and its finances were such a mess that the league temporarily took over the club a decade ago. Since arriving from Winnipeg in 1996, the Coyotes have played in an assortment of places. This past season, their home was a college arena with just 5,000 seats.

But in Salt Lake City, enthusiasm for the new team has been strong. Fans have paid deposits for more than 30,000 tickets in an arena that seats about half that number. 64 percent of those who signed up had not attended a Utah Jazz game in the past three years, Smith said. While the Coyotes were overshadowed by the N.F.L., N.B.A. and Major League Baseball teams in Phoenix, the new hockey team was already standing out in Salt Lake City, where it would compete for attention with the Jazz and two soccer teams.

“Even though the market is smaller, there may be more innovation, especially with the team being new and having some buzz around them to ride the coattails,” said Frank Hawkins, a longtime lawyer at the N.F.L. who is now a media consultant. “The other thing is you’re moving from a four-team market where your target is snowbirds who probably aren’t from hockey country.”

Salt Lake City and its surrounding counties, by contrast, already are a winter sports destination. The area boasts some of the best ski slopes in the country. The city hosted the Winter Olympics in 2002 and is trying to do so again in 2034 . Many American Olympic teams train in the area.

The broadcast media landscape is also changing. When the N.H.L. relied on broadcasters to show its games nationally over the air, networks wanted to reach the country’s largest markets so they could charge more for advertising. Similarly, cable networks like ESPN seek markets with the most cable subscribers.

But millions of households have been ditching their cable connections, undermining the sports cable networks. In response, Smith had the Jazz start its own direct-to-consumer streaming service and struck new deals with over-the-air broadcasters that reached farther than traditional cable territories.

“With vast numbers of people cutting the cord and not taking the typical cable bundle, the issue now is how many committed fans will pay extra for a streaming product versus what used to be just the pure size of the market when everyone paid whether they watched the games or not,” said Marc Ganis, a consultant on media issues to numerous sports teams.

The N.H.L. has not ruled out returning to Phoenix. Bettman spent decades trying to keep a team there, and the league believes a Phoenix franchise could still succeed with the right owner and arena.

Alex Meruelo, the owner of the Coyotes, will retain the team’s intellectual property, including its logos and records. Meruelo could reactivate the Coyotes if he finds a suitable home and pays a $1 billion expansion fee — essentially what he received for letting the team leave for Utah — to get back in the league.

The league has also considered other markets, including, reportedly, Atlanta — which has been home to an N.H.L. team twice — and Houston, which had a team in the defunct World Hockey Association.

For now, the league’s focus is on Utah, where the Smiths have just a few months to sell tickets and prepare for the franchise’s first season in a new city.

Maybe fans will “see it as a chance to kind of start from the very beginning with their family and say, ‘This is one of the things we’re going to do,’” Smith said.

Ken Belson is a Times reporter covering sports, power and money at the N.F.L. and other professional sports leagues. More about Ken Belson

Inside the World of Sports

Dive deeper into the people, issues and trends shaping professional, collegiate and amateur athletics..

The Latest in Sports Downsizing: Professional leagues are embracing smaller markets  in their search for newer stadiums and arenas and the potential for more devoted fan bases.

The History of Black Baseball Players: As the number of African American players in M.L.B. dwindles, a new exhibit at the Hall of Fame  traces 150 years of Black baseball feats, stars and obstacles.

The Dangers for Female Climbers: Women are increasingly reporting sexual harassment and abuse in the sport , including accusations against the renowned climber Nirmal Purja.

A Cricket Stadium’s Brief Life: Built in 100 days for the Cricket World Cup, a stadium on Long Island  will host nine matches before it is dismantled.

Another Fight Looms for Women: Despite gains, women still lag far behind men in the little-regulated industry of college sports. A proposed revenue-sharing deal  could create new clashes over equality.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

11.1: Testing the Hypothesis that β = 0

• Last updated
• Save as PDF
• Page ID 26113

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

The correlation coefficient, \(r\), tells us about the strength and direction of the linear relationship between \(x\) and \(y\). However, the reliability of the linear model also depends on how many observed data points are in the sample. We need to look at both the value of the correlation coefficient \(r\) and the sample size \(n\), together. We perform a hypothesis test of the "significance of the correlation coefficient" to decide whether the linear relationship in the sample data is strong enough to use to model the relationship in the population.

The sample data are used to compute \(r\), the correlation coefficient for the sample. If we had data for the entire population, we could find the population correlation coefficient. But because we have only sample data, we cannot calculate the population correlation coefficient. The sample correlation coefficient, \(r\), is our estimate of the unknown population correlation coefficient.

• The symbol for the population correlation coefficient is \(\rho\), the Greek letter "rho."
• \(\rho =\) population correlation coefficient (unknown)
• \(r =\) sample correlation coefficient (known; calculated from sample data)

The hypothesis test lets us decide whether the value of the population correlation coefficient \(\rho\) is "close to zero" or "significantly different from zero". We decide this based on the sample correlation coefficient \(r\) and the sample size \(n\).

If the test concludes that the correlation coefficient is significantly different from zero, we say that the correlation coefficient is "significant."

• Conclusion: There is sufficient evidence to conclude that there is a significant linear relationship between \(x\) and \(y\) because the correlation coefficient is significantly different from zero.
• What the conclusion means: There is a significant linear relationship between \(x\) and \(y\). We can use the regression line to model the linear relationship between \(x\) and \(y\) in the population.

If the test concludes that the correlation coefficient is not significantly different from zero (it is close to zero), we say that correlation coefficient is "not significant".

• Conclusion: "There is insufficient evidence to conclude that there is a significant linear relationship between \(x\) and \(y\) because the correlation coefficient is not significantly different from zero."
• What the conclusion means: There is not a significant linear relationship between \(x\) and \(y\). Therefore, we CANNOT use the regression line to model a linear relationship between \(x\) and \(y\) in the population.
• If \(r\) is significant and the scatter plot shows a linear trend, the line can be used to predict the value of \(y\) for values of \(x\) that are within the domain of observed \(x\) values.
• If \(r\) is not significant OR if the scatter plot does not show a linear trend, the line should not be used for prediction.
• If \(r\) is significant and if the scatter plot shows a linear trend, the line may NOT be appropriate or reliable for prediction OUTSIDE the domain of observed \(x\) values in the data.

PERFORMING THE HYPOTHESIS TEST

• Null Hypothesis: \(H_{0}: \rho = 0\)
• Alternate Hypothesis: \(H_{a}: \rho \neq 0\)

WHAT THE HYPOTHESES MEAN IN WORDS:

• Null Hypothesis \(H_{0}\) : The population correlation coefficient IS NOT significantly different from zero. There IS NOT a significant linear relationship(correlation) between \(x\) and \(y\) in the population.
• Alternate Hypothesis \(H_{a}\) : The population correlation coefficient IS significantly DIFFERENT FROM zero. There IS A SIGNIFICANT LINEAR RELATIONSHIP (correlation) between \(x\) and \(y\) in the population.

DRAWING A CONCLUSION:There are two methods of making the decision. The two methods are equivalent and give the same result.

• Method 1: Using the \(p\text{-value}\)
• Method 2: Using a table of critical values

In this chapter of this textbook, we will always use a significance level of 5%, \(\alpha = 0.05\)

Using the \(p\text{-value}\) method, you could choose any appropriate significance level you want; you are not limited to using \(\alpha = 0.05\). But the table of critical values provided in this textbook assumes that we are using a significance level of 5%, \(\alpha = 0.05\). (If we wanted to use a different significance level than 5% with the critical value method, we would need different tables of critical values that are not provided in this textbook.)

METHOD 1: Using a \(p\text{-value}\) to make a decision

To calculate the \(p\text{-value}\) using LinRegTTEST:

On the LinRegTTEST input screen, on the line prompt for \(\beta\) or \(\rho\), highlight "\(\neq 0\)"

The output screen shows the \(p\text{-value}\) on the line that reads "\(p =\)".

(Most computer statistical software can calculate the \(p\text{-value}\).)

If the \(p\text{-value}\) is less than the significance level ( \(\alpha = 0.05\) ):

• Decision: Reject the null hypothesis.
• Conclusion: "There is sufficient evidence to conclude that there is a significant linear relationship between \(x\) and \(y\) because the correlation coefficient is significantly different from zero."

If the \(p\text{-value}\) is NOT less than the significance level ( \(\alpha = 0.05\) )

• Decision: DO NOT REJECT the null hypothesis.
• Conclusion: "There is insufficient evidence to conclude that there is a significant linear relationship between \(x\) and \(y\) because the correlation coefficient is NOT significantly different from zero."

Calculation Notes:

• You will use technology to calculate the \(p\text{-value}\). The following describes the calculations to compute the test statistics and the \(p\text{-value}\):
• The \(p\text{-value}\) is calculated using a \(t\)-distribution with \(n - 2\) degrees of freedom.
• The formula for the test statistic is \(t = \frac{r\sqrt{n-2}}{\sqrt{1-r^{2}}}\). The value of the test statistic, \(t\), is shown in the computer or calculator output along with the \(p\text{-value}\). The test statistic \(t\) has the same sign as the correlation coefficient \(r\).
• The \(p\text{-value}\) is the combined area in both tails.

An alternative way to calculate the \(p\text{-value}\) ( \(p\) ) given by LinRegTTest is the command 2*tcdf(abs(t),10^99, n-2) in 2nd DISTR.

THIRD-EXAM vs FINAL-EXAM EXAMPLE: \(p\text{-value}\) method

• Consider the third exam/final exam example.
• The line of best fit is: \(\hat{y} = -173.51 + 4.83x\) with \(r = 0.6631\) and there are \(n = 11\) data points.
• Can the regression line be used for prediction? Given a third exam score ( \(x\) value), can we use the line to predict the final exam score (predicted \(y\) value)?
• \(H_{0}: \rho = 0\)
• \(H_{a}: \rho \neq 0\)
• \(\alpha = 0.05\)
• The \(p\text{-value}\) is 0.026 (from LinRegTTest on your calculator or from computer software).
• The \(p\text{-value}\), 0.026, is less than the significance level of \(\alpha = 0.05\).
• Decision: Reject the Null Hypothesis \(H_{0}\)
• Conclusion: There is sufficient evidence to conclude that there is a significant linear relationship between the third exam score (\(x\)) and the final exam score (\(y\)) because the correlation coefficient is significantly different from zero.

Because \(r\) is significant and the scatter plot shows a linear trend, the regression line can be used to predict final exam scores.

METHOD 2: Using a table of Critical Values to make a decision

The 95% Critical Values of the Sample Correlation Coefficient Table can be used to give you a good idea of whether the computed value of \(r\) is significant or not . Compare \(r\) to the appropriate critical value in the table. If \(r\) is not between the positive and negative critical values, then the correlation coefficient is significant. If \(r\) is significant, then you may want to use the line for prediction.

Example \(\PageIndex{1}\)

Suppose you computed \(r = 0.801\) using \(n = 10\) data points. \(df = n - 2 = 10 - 2 = 8\). The critical values associated with \(df = 8\) are \(-0.632\) and \(+0.632\). If \(r <\) negative critical value or \(r >\) positive critical value, then \(r\) is significant. Since \(r = 0.801\) and \(0.801 > 0.632\), \(r\) is significant and the line may be used for prediction. If you view this example on a number line, it will help you.

Exercise \(\PageIndex{1}\)

For a given line of best fit, you computed that \(r = 0.6501\) using \(n = 12\) data points and the critical value is 0.576. Can the line be used for prediction? Why or why not?

If the scatter plot looks linear then, yes, the line can be used for prediction, because \(r >\) the positive critical value.

Example \(\PageIndex{2}\)

Suppose you computed \(r = –0.624\) with 14 data points. \(df = 14 – 2 = 12\). The critical values are \(-0.532\) and \(0.532\). Since \(-0.624 < -0.532\), \(r\) is significant and the line can be used for prediction

Exercise \(\PageIndex{2}\)

For a given line of best fit, you compute that \(r = 0.5204\) using \(n = 9\) data points, and the critical value is \(0.666\). Can the line be used for prediction? Why or why not?

No, the line cannot be used for prediction, because \(r <\) the positive critical value.

Example \(\PageIndex{3}\)

Suppose you computed \(r = 0.776\) and \(n = 6\). \(df = 6 - 2 = 4\). The critical values are \(-0.811\) and \(0.811\). Since \(-0.811 < 0.776 < 0.811\), \(r\) is not significant, and the line should not be used for prediction.

Exercise \(\PageIndex{3}\)

For a given line of best fit, you compute that \(r = -0.7204\) using \(n = 8\) data points, and the critical value is \(= 0.707\). Can the line be used for prediction? Why or why not?

Yes, the line can be used for prediction, because \(r <\) the negative critical value.

THIRD-EXAM vs FINAL-EXAM EXAMPLE: critical value method

Consider the third exam/final exam example. The line of best fit is: \(\hat{y} = -173.51 + 4.83x\) with \(r = 0.6631\) and there are \(n = 11\) data points. Can the regression line be used for prediction? Given a third-exam score ( \(x\) value), can we use the line to predict the final exam score (predicted \(y\) value)?

• Use the "95% Critical Value" table for \(r\) with \(df = n - 2 = 11 - 2 = 9\).
• The critical values are \(-0.602\) and \(+0.602\)
• Since \(0.6631 > 0.602\), \(r\) is significant.
• Conclusion:There is sufficient evidence to conclude that there is a significant linear relationship between the third exam score (\(x\)) and the final exam score (\(y\)) because the correlation coefficient is significantly different from zero.

Example \(\PageIndex{4}\)

Suppose you computed the following correlation coefficients. Using the table at the end of the chapter, determine if \(r\) is significant and the line of best fit associated with each r can be used to predict a \(y\) value. If it helps, draw a number line.

• \(r = –0.567\) and the sample size, \(n\), is \(19\). The \(df = n - 2 = 17\). The critical value is \(-0.456\). \(-0.567 < -0.456\) so \(r\) is significant.
• \(r = 0.708\) and the sample size, \(n\), is \(9\). The \(df = n - 2 = 7\). The critical value is \(0.666\). \(0.708 > 0.666\) so \(r\) is significant.
• \(r = 0.134\) and the sample size, \(n\), is \(14\). The \(df = 14 - 2 = 12\). The critical value is \(0.532\). \(0.134\) is between \(-0.532\) and \(0.532\) so \(r\) is not significant.
• \(r = 0\) and the sample size, \(n\), is five. No matter what the \(dfs\) are, \(r = 0\) is between the two critical values so \(r\) is not significant.

Exercise \(\PageIndex{4}\)

For a given line of best fit, you compute that \(r = 0\) using \(n = 100\) data points. Can the line be used for prediction? Why or why not?

No, the line cannot be used for prediction no matter what the sample size is.

Assumptions in Testing the Significance of the Correlation Coefficient

Testing the significance of the correlation coefficient requires that certain assumptions about the data are satisfied. The premise of this test is that the data are a sample of observed points taken from a larger population. We have not examined the entire population because it is not possible or feasible to do so. We are examining the sample to draw a conclusion about whether the linear relationship that we see between \(x\) and \(y\) in the sample data provides strong enough evidence so that we can conclude that there is a linear relationship between \(x\) and \(y\) in the population.

The regression line equation that we calculate from the sample data gives the best-fit line for our particular sample. We want to use this best-fit line for the sample as an estimate of the best-fit line for the population. Examining the scatter plot and testing the significance of the correlation coefficient helps us determine if it is appropriate to do this.

The assumptions underlying the test of significance are:

• There is a linear relationship in the population that models the average value of \(y\) for varying values of \(x\). In other words, the expected value of \(y\) for each particular value lies on a straight line in the population. (We do not know the equation for the line for the population. Our regression line from the sample is our best estimate of this line in the population.)
• The \(y\) values for any particular \(x\) value are normally distributed about the line. This implies that there are more \(y\) values scattered closer to the line than are scattered farther away. Assumption (1) implies that these normal distributions are centered on the line: the means of these normal distributions of \(y\) values lie on the line.
• The standard deviations of the population \(y\) values about the line are equal for each value of \(x\). In other words, each of these normal distributions of \(y\) values has the same shape and spread about the line.
• The residual errors are mutually independent (no pattern).
• The data are produced from a well-designed, random sample or randomized experiment.

Linear regression is a procedure for fitting a straight line of the form \(\hat{y} = a + bx\) to data. The conditions for regression are:

• Linear In the population, there is a linear relationship that models the average value of \(y\) for different values of \(x\).
• Independent The residuals are assumed to be independent.
• Normal The \(y\) values are distributed normally for any value of \(x\).
• Equal variance The standard deviation of the \(y\) values is equal for each \(x\) value.
• Random The data are produced from a well-designed random sample or randomized experiment.

The slope \(b\) and intercept \(a\) of the least-squares line estimate the slope \(\beta\) and intercept \(\alpha\) of the population (true) regression line. To estimate the population standard deviation of \(y\), \(\sigma\), use the standard deviation of the residuals, \(s\). \(s = \sqrt{\frac{SEE}{n-2}}\). The variable \(\rho\) (rho) is the population correlation coefficient. To test the null hypothesis \(H_{0}: \rho =\) hypothesized value , use a linear regression t-test. The most common null hypothesis is \(H_{0}: \rho = 0\) which indicates there is no linear relationship between \(x\) and \(y\) in the population. The TI-83, 83+, 84, 84+ calculator function LinRegTTest can perform this test (STATS TESTS LinRegTTest).

Formula Review

Least Squares Line or Line of Best Fit:

\[\hat{y} = a + bx\]

\[a = y\text{-intercept}\]

\[b = \text{slope}\]

Standard deviation of the residuals:

\[s = \sqrt{\frac{SEE}{n-2}}\]

\[SSE = \text{sum of squared errors}\]

\[n = \text{the number of data points}\]