diagrammatic presentation of time series data is known as

List of Commerce Articles
Diagrammatic Presentation Of Data

Diagrammatic Presentation of Data

The diagrammatic presentation of data gives an immediate understanding of the real situation to be defined by the data in comparison to the tabular presentation of data or textual representations. It translates the highly complex ideas included in numbers into a more concrete and quickly understandable form pretty effectively. Diagrams may be less certain but are much more efficient than tables in displaying the data. There are many kinds of diagrams in general use. Amongst them the significant ones are the following:

(i) Geometric diagram

(ii) Frequency diagram

(iii) Arithmetic line graph

Also check: Meaning and Objective of Tabulation

Basics of Diagrammatic Presentation

Concept of Diagrammatic Presentation

It is a technique of presenting numeric data through pictograms, cartograms, bar diagrams, and pie diagrams. It is the most attractive and appealing way to represent statistical data. Diagrams help in visual comparison and they have a bird’s eye view.
Under pictograms, we use pictures to present data. For example, if we have to show the production of cars, we can draw cars. Suppose the production of cars is 40,000, we can show it by a picture having four cars, where 1 car represents 10,000 units.
Under cartograms, we make use of maps to show the geographical allocation of certain things.
Bar diagrams are rectangular and placed on the same base. Their heights represent the magnitude/value of the variable. The width of all the bars and the gaps between the two bars are kept the same.
Pie diagram is a circle that is subdivided or partitioned to show the proportion of various components of the data.
Out of the given diagrams, only one-dimensional bar diagrams and pie diagrams are there in our scope.

General Guidelines

Title: Every diagram must be given a suitable title which should be small and self-explanatory.

Size: The size of the diagram should be appropriate, i.e., neither too small nor too big.

Paper used: Diagrams are generally prepared on blank paper.

Scale: Under one-dimensional diagrams, especially bar diagrams, the y-axis is more important from the point of view of the decision of scale because we represent magnitude along this axis.

Index: When two or more variables are presented and different types of line/shading patterns are used to distinguish, an index must be given to show their details.

Selection of proper type of diagram: It is very important to select the correct type of diagram to represent data effectively.

Advantages of Diagrammatic Presentation

(1) Diagrams are attractive and impressive: The data presented in the form of diagrams can attract the attention of even a common man.

(2) Easy to remember: (a) Diagrams have a great memorising effect. (b) The picture created in mind by the diagrams last much longer than those created by figures presented through the tabular forms.

(3) Diagrams save time : (a) They present complex mass data in a simplified manner. (b) The data presented in the form of diagrams can be understood by the user very quickly.

(4) Diagrams simplify data: Diagrams are used to represent a huge mass of complex data in a simplified and intelligible form which is easy to understand.

(5) Diagrams are useful in making comparison: It becomes easier to compare two sets of data visually by presenting them through diagrams.

(6) More informative : Diagrams not only depict the characteristics of data but also bring out other hidden facts and relations which are not possible from the classified and tabulated data.

Types of One-Dimensional Diagram

One-dimensional diagram is a diagram in which only the length of the diagram is considered. It can be drawn in the form of a line or various types of bars.

The following are the types of one-dimensional diagram.

(1) Simple bar diagram

Simple bar diagram consists of a group of rectangular bars of equal width for each class or category of data.

(2) Multiple bar diagram

This diagram is used when we have to make a comparison between two or more variables like income and expenditure, import and export for different years, marks obtained in different subjects in different classes, etc.

(3) Subdivided bar diagram

This diagram is constructed by subdividing the bars in the ratio of various components.

(4) Percentage bar diagram

The subdivided bar diagram presented on a percentage basis is known as the percentage bar diagram.

(5) Broken-scale bar diagram

This diagram is used when the value of one observation is very high as compared to the other.

To gain space for the smaller bars of the series, the larger bars may be broken.

The value of each bar is written at the top of the bar.

(6) Deviation bar diagram

Deviation bars are used to represent net changes in the data like net profit, net loss, net exports, net imports, etc.

Meaning of Pie Diagram

A pie diagram is a circle that is divided into sections. The size of each section indicates the magnitude of each component as a part of the whole.

Steps involved in constructing pie diagram

Convert the given values into percentage form and multiply it with 3.6’ to get the amount of angle for each item.
Draw a circle and start the diagram at the 12 O‘clock position.
Take the highest angle first with the protector (D) and mark the lower angles successively.
Shade different angles differently to show distinction in each item.

Solved Questions

Q.1. Why is a diagrammatic presentation better than tabulation of data?

It makes the data more attractive as compared to tabulation and helps in visual comparison.

Q.2. Why do media persons prefer diagrammatic presentation of data?

Because it has an eye-catching effect and a long-lasting impact upon its readers/viewers.

Q.3. What will be the degree of an angle in the pie diagram if a family spends 50% of its income in food?

(50 ÷ 100) X 360 (Or) 50 x 3.6 = 180’

Q.4. Which bar diagram is used to show two or more characteristics of the data?

Multiple bar diagram

Q.5. Mention the sum of all the angles formed at the centre of a circle.

Q.6. Name a bar diagram where the height of all the bars is the same.

Percentage bar diagram

Q.7. Which diagram can be used to depict various components of a variable?

Subdivided bar diagram

Q.8. What is a multiple bar diagram?

A multiple bar diagram is one that shows more than one characteristic of data.

Q.9. Which bar diagram is used to represent the net changes in data?

Deviation bar diagram

Q.10. What is the other name of the subdivided bar Diagram?

Component bar diagram

The above-mentioned concept is for CBSE Class 11 Statistics for Economics – Diagrammatic Presentation of Data. For solutions and study materials, visit our website or download the app for more information and the best learning experience.

Register with BYJU'S & Download Free PDFs

Diagrammatic Representation of Data

Suppose you are interested to compare the marks of your mates in a test. How can you make the comparison interesting? It can be done by the diagrammatic representations of data. You can use a bar diagram, histograms, pie-charts etc for this. You will be able to answer questions like –

How will you find out the number of students in the various categories of marks in a certain test? What can you say about the marks obtained by the maximum students? Also, how can you compare the marks of your classmates in five other tests? Is it possible for you to remember the marks of each and every student in all subjects? No! Also, you don’t have the time to compare the marks of every student. Merely noting down the marks and doing comparisons is not interesting at all. Let us study them in detail.

Browse more Topics under Statistical Description Of Data

Introduction to Statistics
Textual and Tabular Representation of Data
Frequency Distribution
Frequency Polygon
Cumulative Frequency Graph or Ogive

Construction of a Bar Diagram

Draw two perpendicular lines intersecting each other at a point O. The vertical line is the y-axis and the horizontal is the x-axis.
Choose a suitable scale to determine the height of each bar.
On the horizontal line, draw the bars at equal distance with corresponding heights.
The space between the bars should be equal.

Properties of a Bar Diagram

Each bar or column in a bar graph is of equal width.
All bars have a common base.
The height of the bar corresponds to the value of the data.
The distance between each bar is the same.

Types of Bar Diagram

A bar graph can be either vertical or horizontal depending upon the choice of the axis as the base. The horizontal bar diagram is used for qualitative data. The vertical bar diagram is used for the quantitative data or time series data. Let us take an example of a bar graph showing the comparison of marks of a student in all subjects out of 100 marks for two tests.

With the bar graph, we can also compare the marks of students in each subject other than the marks of one student in every subject. Also, we can draw the bar graph for every student in all subjects.

We can use another way of diagrammatical representation of data. If we are working with a continuous data set or grouped dataset, we can use a histogram for the representation of data.

A histogram is similar to a bar graph except for the fact that there is no gap between the rectangular bars. The rectangular bars show the area proportional to the frequency of a variable and the width of the bars represents the class width or class interval.
Frequency means the number of times a variable is occurring or is present. It is an area graph. The heights of the rectangles are proportional to the corresponding frequencies of similar classes.

Construction of Histogram

Choose a suitable scale for both the axes to determine the height and width of each bar
On the horizontal line, draw the bars with corresponding heights
There should be no gap between two consecutive bars showing the continuity of the data
If the grouped frequencies are not continuous, the first thing to do is to make them continuous

It is done by adding the average of the difference between the lower limit of the class interval and the upper limit of the preceding class width to the upper limits of all the classes. The same quantity is subtracted from the lower limits of the classes.

Properties of Histogram

Each bar or column in a bar graph is of equal width and corresponds to the equal class interval
If the classes are of unequal width then the height of the bars will be proportional to the ration of the frequencies to the width of the classes
All bars have a common base
The height of the bar corresponds to the frequency of the data

Suppose we have a data set showing the marks obtained out of 100 by a group of 35 students in statistics. We can find the number of students in the various marks category with the help of the histogram.

A line graph is a type of chart or graph which shows information when a series of data is joined by a line. It shows the changes in the data over a period of time. In a simple line graph, we plot each pair of values of (x, y). Here, the x-axis denotes the various time point (t), and the y-axis denotes the observation based on the time.

Properties of a Line Graph

It consists of Vertical and Horizontal scales. These scales may or may not be uniform.
Data point corresponds to the change over a period of time.
The line joining these data points shows the trend of change.

Below is the line graph showing the number of buses passing through a particular street over a period of time:

Solved Examples for diagrammatic Representation of Data

Problem 1: Draw the histogram for the given data.

Solution: This grouped frequency distribution is not continuous. We need to convert it into a continuous distribution with exclusive type classes. This is done by averaging the difference of the lower limit of one class and the upper limit of the preceding class. Here, d = ½ (19 – 18) = ½ = 0.5. We add 0.5 to all the upper limits and we subtract 0.5 from all the lower limits.

The corresponding histogram is

Draw a line graph for the production of two types of crops for the given years.

Solution: The required graph is

Customize your course in 30 seconds

Which class are you in.

Statistical Description of Data

Download the App

Question and Answer forum for K12 Students

Diagrammatic Presentation of Data: Bar Diagrams, Pie Charts etc.

The compilation of this Presentation of Data Notes makes students exam preparation simpler and organised.

Diagrammatic Presentation of Data

Nowadays a lot of emphasis is laid upon exceptional presentation of data. All of this is because, when presented diagrammatically, data is easy to interpret with just a glance. In such a case we need to learn how to represent data diagrammatically via bar diagrams, pie charts, etc.

Bar Diagrams

As the name suggests, when data is presented in form of bars or rectangles, it is termed to be a bar diagram.

Features of a Bar

The rectangular box in a bar diagram is known as a bar. It represents the value of a variable.
These bars can be either vertically or horizontally arranged.
Bars are equidistant from each other.
Each bar originates from a common baseline or a common axis.
The width of bars remains the same but the height changes, according to the value of a variable, to denote the difference between their values.
Unless they are in a specific order, the convention is that bars can be arranged in an ascending or descending order.

Types of Bar Diagrams

Simple Bar Diagram These are the most basic type of bar diagrams. A simple bar diagram represents only a single set of numerical data. Generally, simple bar diagrams are used to represent time series data for a single entity.

Generally, the Y-axis contains markings which represent the range of the value of the variable whereas the X-axis contains divisions for entities like years, time periods, areas, etc.

Multiple Bar Diagram Unlike a single bar diagram, a multiple bar diagram can represent two or more sets of numerical data on the same bar diagram. Generally, these are constructed to facilitate comparison between two entities like average height and average weight, birth rates and death rates, etc.

Separate sets of numerical data are differentiated with the help of colour variation. By the same token of simple bar diagrams, multiple bar diagrams also have divisions on the Y-axis and X-axis that represent different values of the variable and entities like year, areas etc. respectively. Note that each division on X-axis has two or more bar diagrams each according to the specified number of bars.

Sub-divided or Differential Bar Diagrams Sub-divided bar diagrams are useful when we need to represent the total values and the contribution of various sections of the total simultaneously. The different sections are shaded with different colours in the same bar.

For example, such a bar diagram can be used to represent the varying levels of employment over the years in India and each bar can be divided into two sectors, the urban and rural. Again, here the Y-axis and X-axis represent the same values as in simple and multiple bar diagrams.

Percentage Bar Diagrams This is derived further from the subdivided bar diagrams. In this, each bar has the same height that represents 100 percent of the Y-axis in totality. Further, each bar is divided into sections based on percentages calculated according to the contribution of these sections.

Percentage bar diagrams are used when the values are really high. This is because using subdivided bar diagrams in such cases would not be easy and appropriate.

Deviation Bar Diagrams Lastly, the deviation bar diagrams are the most interesting of the lot. In such a type of bar diagram, there are both negative and positive values on the y-axis. The deviation bar diagrams are used to compare the net deviation of related variables with respect to time and location.

For example, it can be used to represent a bar diagram for savings (represented by positive deviations) and deficit (represented by negative deviations) over years.

Pie or Circular Diagrams

In addition to bar diagrams, pie diagrams are also widely used to pictorially represent data. In this, a circle is divided into various segments which are decided on the basis of percentages. Which means the circle is divided into sectors depending on various percentages.

These sectors are differentiated with the help of colours. Pie diagrams have an edge over bar diagrams because they can easily provide an overview and provides a better sense of the contributions of each part. The steps for the construction of a pie diagram are:

1. The first step involves finding out the respective percentages. This is done by a simple mathematical formula to find out percentages which are–

{(Parts for the respective sector)/total parts) × 100}.

For example, if in a class of 1oo students, 30 are obese, 20 are fat and 50 are slim then the percentages will be as follows: (30/100) × 100 = 30% (20/100) × 100 = 20% (50/100) × 100 = 50%

2. A circle comprises 360 degrees. The angles that each sector will span across is decided by the given formula: (Percentage value/100)×360°

3. Finally, just plot these values according to their respective angles on a circle and give appropriate markings to complete the pie chart.

Question: Which among the following is not a feature of a bar in the bar diagram? A. The width is the same but the heights are generally different B. They are rectangular in shape C. Bars should not be equidistant D. Each bar originates from a common baseline Answer: Of all the above options, option “C” is incorrect because conventionally the bars should be equidistant.

Trending Articles on Technical and Non Technical topics

Selected Reading
UPSC IAS Exams Notes
Developer's Best Practices
Questions and Answers
Effective Resume Writing
HR Interview Questions
Computer Glossary

Diagrammatic Presentation Of Data

Introduction.

The diagrammatic representation also helps in having a bird’s eye view or overall view of the differentiation of data. It is a norm to present statistical data in the form of diagrams so that it becomes easier to comprehend and understand them. Therefore, diagrammatic representation is an important tool in statistics.

What is a Diagrammatic Presentation of Data?

Diagrammatic representation refers to a representation of statistical data in the form of diagrams. The diagrams used in representing statistical data are geometrical figures, such as lines, bars, and circles. The intention of using geometrical figures in statistical presentation is to make the study more interesting and easy to understand. Diagrammatic representations are widely used in statistics, economics, and many other fields of study.

Types of Diagrammatic Presentations of Data

Various types of diagrammatic representations of data depend on the dataset and the particular statistical elements in them. Data presentation can be made in different types and forms.

These can be broadly classified into the following one-dimensional types −

Line Diagram

In a line diagram, straight lines are used to indicate various parameters. Here, a line represents the sequence of data associated with the changing of a particular variable.

Properties of Line Diagram −

The Lines are either in vertical or horizontal directions.

There may be uniform scaling but this is not mandatory.

The lines that connect the data points offer the statistical representation of data.

The following is an example of a line diagram that shows profits in Rs crore from 2002 till 2008. Profit in 2002 was Rs 5 Crore while in 2008 it was Rs 24 Crore.

diagrammatic presentation of time series data is known as

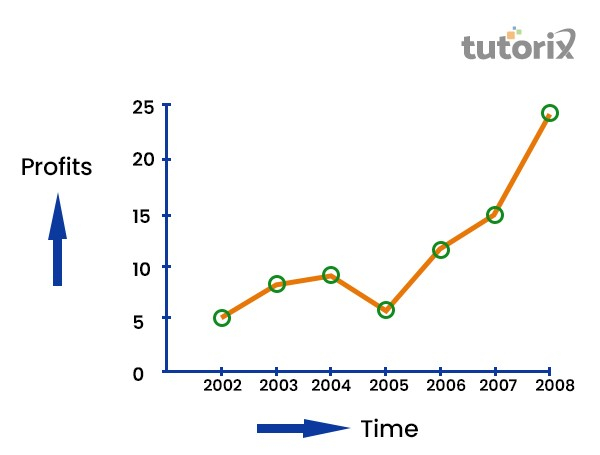
Bar Diagram

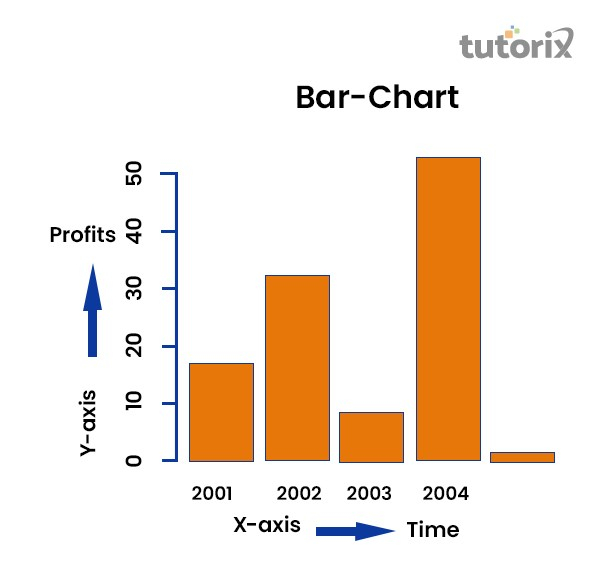
Bar diagrams have rectangular shapes of equal width that represent statistical data in a straightforward manner. Bar diagrams are one of the most widely used diagrammatic representations.

Properties of Bar Diagram −

The Bars can be vertical or horizontal in directions.

All bars in a diagram have a uniform width.

All the Bars have a common and same base.

The height or width of the Bar shows the required value.

The following is an example of a Bar Chart that has time on the X axis and profits on the Y axis.

Also known as a "circle chart" , the pie chart divides the circular statistical graphic into sectors or sections to illustrate the numerical data. Each sector in the circle denotes a proportionate part of the whole. Pie-chart works the best at the time when we want to denote the composition of something. In most cases, the pie chart replaces other diagrammatic representations, such as the bar graph, line plots, histograms, etc.

In practice, the various sections in a pie chart are derived according to their ratio to the total area of the circle. Then according to their individual contributions, sections are divided into parts derived from 360 degrees of the circle.

Advantages of Diagrammatic Presentation of Data

Easier to understand.

Pictorial representations are usually easier to understand than statistical text or representation in tabular form. One can easily understand which portion or part has more contribution toward the overall dataset. This helps in understanding the data better.

The creators of diagrams usually keep the simplicity of presentation in mind to offer more information to readers. That is why diagrams are easier to comprehend than texts and tables.

More attractive

Pictorial or diagrammatic representations of datasets are more attractive than normal representations. As colors and various other tools can be incorporated into diagrams, they become more attractive and comprehensible for the readers.

Moreover, as diagrams can be made more interactive with the help of computer graphics, they have become more acceptable and attractive currently.

Simpler presentations

Data can be presented more simply in diagrammatic form. Both extensive unstable data and smaller complex data can be represented by diagrammatic representations more easily. This helps statisticians offer more value to their findings.

Comparison is easier

When two or more data are compared, it is easier to do so in pictorial form. As diagrams clearly show the portion of data consumed, it can be easily understood from the diagrams which part of the data is consuming more area in the diagrams. This can help one to understand the real differences through pictorial comparison.

Universal acceptance

Diagrammatic representation of data is used in many fields of study, such as statistics, science, commerce, economics, etc. So, the diagrams are accepted universally and hence are used everywhere.

Moreover, since there are the same procedures for forming diagrams, the representations mean the same thing to everyone. So, there is nothing to alter when we obtain the diagrams to check the real values. It helps analysts solve problems universally.

Improvement in presentation

Diagrammatic representations improve the overall representation of data to a large extent. As the data is classified into several groups and presented in a systematic manner in diagrams, the whole presentation of data gets improved during the diagrammatic representation.

Moreover, as diagrams can be made more interactive than texts or tables, diagrammatic presentations are one step ahead in presenting the data in a simpler yet recognizable manner.

More organized and classified data

To represent data in diagrams, they must be organized and classified into comprehensive categories. This helps the data to be organized in a given fashion which makes them orderly and creates a sequence. This in turn helps realize diagrammatic data better than text forms.

Relevance Diagrammatic Presentation of Data

Diagrams are a great way of representing data because they are visually attractive and they can make large, complex datasets look simpler. The otherwise heavy data can be simply and easily represented by line and bar diagrams, and pie charts. This makes data organization simpler and neater.

Moreover, as data must be classified before representation, one must organize them according to the norms required. So, diagrammatic representations save lots of time and resources.

Diagrams also have universal acceptance and so can be used to express data in different forms. This provides the analysts and researchers flexibility to present data in any required form.

Diagrams also remove confusion and offer a simpler tactic to present data. As no special skill has to be learned to represent data in diagrams, they can be used by most to show statistical data and results of various types of research and experiments.

Therefore, diagrammatic representation has great relevance that can be used for the benefit of economists, statisticians, marketing analysts, and a lot of other professionals.

The diagrams are a central part of statistics and their importance can be known from the fact that almost all statistical researchers use them in one way or the other. The diagrammatical representations make inferring statistical data much simpler and easier. It is a much easier way to visualize and understand data in simpler forms too.

To represent data in diagrammatic form, only a simple understanding of Mathematics is required. So, no special skills are needed to use diagrams and this makes them very popular tools for the representation of data sets. Learning how to present data in diagrams, therefore, should be a priority for everyone.

Q1. Which is the simplest diagrammatic presentation of data?

Ans. The simplest diagrammatic presentation of data is a line diagram that shows data in terms of straight lines.

Q2. What are the two characteristics of bar diagrams?

Ans. Bar diagrams have uniform width and their base remains the same.

Q3. How are the sections in a pie chart formed?

Ans. In practice, the various sections in a pie chart are derived according to their ratio to the total area of the circle. Then according to their individual contributions, sections are divided into parts derived from 360 degrees of the circle.

For example, if a section requires 25% of the presentation, it will consume degrees on the chart.

The Presentation Layer of OSI Model
Explain the functions of Presentation Layer.
What is Presentation Layer?
Share Powerpoint Presentation through Facebook
What is a presentation layer?
The best presentation tools for business
Antigen Presentation: A Vital Immune Process
Importing/Exporting ABAP packages to Presentation server
Difference Between Presentation Skills and Public Speaking
Tips for Using PowerPoint Presentation More Efficiently
How to add and remove encryption for MS Powerpoint Presentation?
How to make an impressive PPT presentation for a college activity?
Figure shows a diagrammatic representation of trees in the afternoon along a sea coast.State on which side is the sea; A or B? Give reasons for your choice."
Distribution of Test Data vs. Distribution of Training Data
Characteristics of Biological Data (Genome Data Management)

Kickstart Your Career

Get certified by completing the course

To Continue Learning Please Login

Graphic Presentation of Data

First Online: 24 August 2018

Cite this chapter

Charan Singh Rayat 2

1798 Accesses

Graphic presentation is considered the preferred way of presentation of data over diagrammatic presentation as graphs are always more accurate and precise, whereas diagrams are generally used for the purpose of publicity and propaganda. Relationship between two variables can be studied by graphs. These can be drawn more easily than diagrams. Graphs are considered very useful for studying time series and frequency distribution.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Available as PDF
Read on any device
Instant download
Own it forever
Available as EPUB and PDF
Compact, lightweight edition
Dispatched in 3 to 5 business days
Free shipping worldwide - see info
Durable hardcover edition

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Author information

Authors and affiliations.

Department of Histopathology, Postgraduate Institute of Medical Education & Research, Chandigarh, India

Charan Singh Rayat

You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

Copyright information

About this chapter

Rayat, C.S. (2018). Graphic Presentation of Data. In: Statistical Methods in Medical Research. Springer, Singapore. https://doi.org/10.1007/978-981-13-0827-7_5

Download citation

DOI : https://doi.org/10.1007/978-981-13-0827-7_5

Published : 24 August 2018

Publisher Name : Springer, Singapore

Print ISBN : 978-981-13-0826-0

Online ISBN : 978-981-13-0827-7

eBook Packages : Mathematics and Statistics Mathematics and Statistics (R0)

Share this chapter

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

Publish with us

Policies and ethics

Find a journal
Track your research

school Campus Bookshelves
menu_book Bookshelves
perm_media Learning Objects
login Login
how_to_reg Request Instructor Account
hub Instructor Commons

Margin Size

Download Page (PDF)
Download Full Book (PDF)
Periodic Table
Physics Constants
Scientific Calculator
Reference & Cite
Tools expand_more
Readability

selected template will load here

This action is not available.

2: Graphical Representations of Data

Last updated
Save as PDF
Page ID 22222

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

In this chapter, you will study numerical and graphical ways to describe and display your data. This area of statistics is called "Descriptive Statistics." You will learn how to calculate, and even more importantly, how to interpret these measurements and graphs.

2.1: Introduction In this chapter, you will study numerical and graphical ways to describe and display your data. This area of statistics is called "Descriptive Statistics." You will learn how to calculate, and even more importantly, how to interpret these measurements and graphs. In this chapter, we will briefly look at stem-and-leaf plots, line graphs, and bar graphs, as well as frequency polygons, and time series graphs. Our emphasis will be on histograms and box plots.
2.2: Stem-and-Leaf Graphs (Stemplots), Line Graphs, and Bar Graphs A stem-and-leaf plot is a way to plot data and look at the distribution, where all data values within a class are visible. The advantage in a stem-and-leaf plot is that all values are listed, unlike a histogram, which gives classes of data values. A line graph is often used to represent a set of data values in which a quantity varies with time. These graphs are useful for finding trends. A bar graph is a chart that uses either horizontal or vertical bars to show comparisons among categories.
2.3: Histograms, Frequency Polygons, and Time Series Graphs A histogram is a graphic version of a frequency distribution. The graph consists of bars of equal width drawn adjacent to each other. The horizontal scale represents classes of quantitative data values and the vertical scale represents frequencies. The heights of the bars correspond to frequency values. Histograms are typically used for large, continuous, quantitative data sets. A frequency polygon can also be used when graphing large data sets with data points that repeat.
2.4: Using Excel to Create Graphs Using technology to create graphs will make the graphs faster to create, more precise, and give the ability to use larger amounts of data. This section focuses on using Excel to create graphs.
2.5: Graphs that Deceive It's common to see graphs displayed in a misleading manner in social media and other instances. This could be done purposefully to make a point, or it could be accidental. Either way, it's important to recognize these instances to ensure you are not misled.
2.E: Graphical Representations of Data (Exercises) These are homework exercises to accompany the Textmap created for "Introductory Statistics" by OpenStax.

Contributors and Attributions

Barbara Illowsky and Susan Dean (De Anza College) with many other contributing authors. Content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/[email protected] .

Graphical Representation of Data

Graphical representation of data is an attractive method of showcasing numerical data that help in analyzing and representing quantitative data visually. A graph is a kind of a chart where data are plotted as variables across the coordinate. It became easy to analyze the extent of change of one variable based on the change of other variables. Graphical representation of data is done through different mediums such as lines, plots, diagrams, etc. Let us learn more about this interesting concept of graphical representation of data, the different types, and solve a few examples.

Definition of Graphical Representation of Data

A graphical representation is a visual representation of data statistics-based results using graphs, plots, and charts. This kind of representation is more effective in understanding and comparing data than seen in a tabular form. Graphical representation helps to qualify, sort, and present data in a method that is simple to understand for a larger audience. Graphs enable in studying the cause and effect relationship between two variables through both time series and frequency distribution. The data that is obtained from different surveying is infused into a graphical representation by the use of some symbols, such as lines on a line graph, bars on a bar chart, or slices of a pie chart. This visual representation helps in clarity, comparison, and understanding of numerical data.

Representation of Data

The word data is from the Latin word Datum, which means something given. The numerical figures collected through a survey are called data and can be represented in two forms - tabular form and visual form through graphs. Once the data is collected through constant observations, it is arranged, summarized, and classified to finally represented in the form of a graph. There are two kinds of data - quantitative and qualitative. Quantitative data is more structured, continuous, and discrete with statistical data whereas qualitative is unstructured where the data cannot be analyzed.

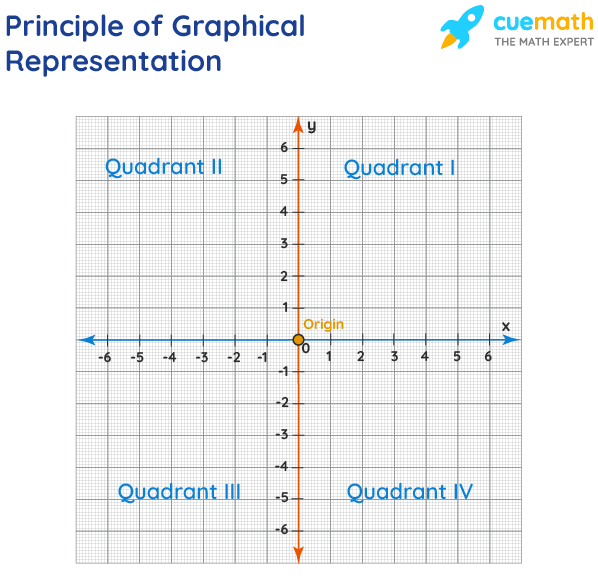
Principles of Graphical Representation of Data

The principles of graphical representation are algebraic. In a graph, there are two lines known as Axis or Coordinate axis. These are the X-axis and Y-axis. The horizontal axis is the X-axis and the vertical axis is the Y-axis. They are perpendicular to each other and intersect at O or point of Origin. On the right side of the Origin, the Xaxis has a positive value and on the left side, it has a negative value. In the same way, the upper side of the Origin Y-axis has a positive value where the down one is with a negative value. When -axis and y-axis intersect each other at the origin it divides the plane into four parts which are called Quadrant I, Quadrant II, Quadrant III, Quadrant IV. This form of representation is seen in a frequency distribution that is represented in four methods, namely Histogram, Smoothed frequency graph, Pie diagram or Pie chart, Cumulative or ogive frequency graph, and Frequency Polygon.

Principle of Graphical Representation of Data

Advantages and Disadvantages of Graphical Representation of Data

Listed below are some advantages and disadvantages of using a graphical representation of data:

It improves the way of analyzing and learning as the graphical representation makes the data easy to understand.
It can be used in almost all fields from mathematics to physics to psychology and so on.
It is easy to understand for its visual impacts.
It shows the whole and huge data in an instance.
It is mainly used in statistics to determine the mean, median, and mode for different data

The main disadvantage of graphical representation of data is that it takes a lot of effort as well as resources to find the most appropriate data and then represent it graphically.

Rules of Graphical Representation of Data

While presenting data graphically, there are certain rules that need to be followed. They are listed below:

Suitable Title: The title of the graph should be appropriate that indicate the subject of the presentation.
Measurement Unit: The measurement unit in the graph should be mentioned.
Proper Scale: A proper scale needs to be chosen to represent the data accurately.
Index: For better understanding, index the appropriate colors, shades, lines, designs in the graphs.
Data Sources: Data should be included wherever it is necessary at the bottom of the graph.
Simple: The construction of a graph should be easily understood.
Neat: The graph should be visually neat in terms of size and font to read the data accurately.

Uses of Graphical Representation of Data

The main use of a graphical representation of data is understanding and identifying the trends and patterns of the data. It helps in analyzing large quantities, comparing two or more data, making predictions, and building a firm decision. The visual display of data also helps in avoiding confusion and overlapping of any information. Graphs like line graphs and bar graphs, display two or more data clearly for easy comparison. This is important in communicating our findings to others and our understanding and analysis of the data.

Types of Graphical Representation of Data

Data is represented in different types of graphs such as plots, pies, diagrams, etc. They are as follows,

Examples on Graphical Representation of Data

Example 1 : A pie chart is divided into 3 parts with the angles measuring as 2x, 8x, and 10x respectively. Find the value of x in degrees.

We know, the sum of all angles in a pie chart would give 360º as result. ⇒ 2x + 8x + 10x = 360º ⇒ 20 x = 360º ⇒ x = 360º/20 ⇒ x = 18º Therefore, the value of x is 18º.

Example 2: Ben is trying to read the plot given below. His teacher has given him stem and leaf plot worksheets. Can you help him answer the questions? i) What is the mode of the plot? ii) What is the mean of the plot? iii) Find the range.

Solution: i) Mode is the number that appears often in the data. Leaf 4 occurs twice on the plot against stem 5.

Hence, mode = 54

ii) The sum of all data values is 12 + 14 + 21 + 25 + 28 + 32 + 34 + 36 + 50 + 53 + 54 + 54 + 62 + 65 + 67 + 83 + 88 + 89 + 91 = 958

To find the mean, we have to divide the sum by the total number of values.

Mean = Sum of all data values ÷ 19 = 958 ÷ 19 = 50.42

iii) Range = the highest value - the lowest value = 91 - 12 = 79

go to slide go to slide

Book a Free Trial Class

Practice Questions on Graphical Representation of Data

Faqs on graphical representation of data, what is graphical representation.

Graphical representation is a form of visually displaying data through various methods like graphs, diagrams, charts, and plots. It helps in sorting, visualizing, and presenting data in a clear manner through different types of graphs. Statistics mainly use graphical representation to show data.

What are the Different Types of Graphical Representation?

The different types of graphical representation of data are:

Stem and leaf plot
Scatter diagrams
Frequency Distribution

Is the Graphical Representation of Numerical Data?

Yes, these graphical representations are numerical data that has been accumulated through various surveys and observations. The method of presenting these numerical data is called a chart. There are different kinds of charts such as a pie chart, bar graph, line graph, etc, that help in clearly showcasing the data.

What is the Use of Graphical Representation of Data?

Graphical representation of data is useful in clarifying, interpreting, and analyzing data plotting points and drawing line segments , surfaces, and other geometric forms or symbols.

What are the Ways to Represent Data?

Tables, charts, and graphs are all ways of representing data, and they can be used for two broad purposes. The first is to support the collection, organization, and analysis of data as part of the process of a scientific study.

What is the Objective of Graphical Representation of Data?

The main objective of representing data graphically is to display information visually that helps in understanding the information efficiently, clearly, and accurately. This is important to communicate the findings as well as analyze the data.

DIAGRAMMATIC REPRESENTATION OF DATA

An attractive representation of statistical data is provided by charts, diagrams and pictures.

Diagrammatic representation can be used for both the educated section and uneducated section of the society. Furthermore, any hidden trend present in the given data can be noticed only in this mode of representation.

However, compared to tabulation, this is less accurate.

So if there is a priority for accuracy, we have to recommend tabulation.

We are going to consider the following types of diagrams :

1. Line diagram

2. Histogram

3. Bar diagram

4. Pie chart

Line Diagram

When the time series exhibit a wide range of fluctuations, we may think of logarithmic or ratio chart where "Log y" and not "y" is plotted against "t".

We use Multiple line chart for representing two or more related time series data expressed in the same unit and multiple – axis chart in somewhat similar situations, if the variables are expressed in different units.

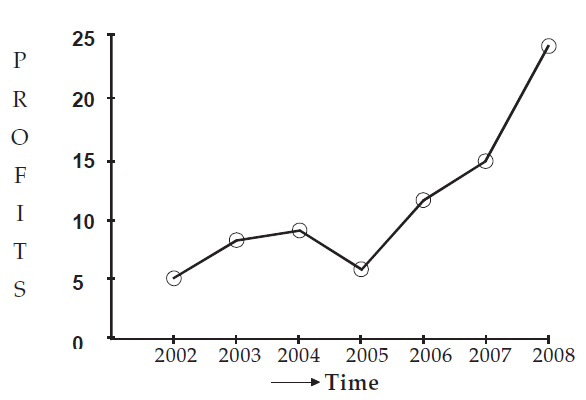
The profits in thousand of dollars of an industrial house for 2002, 2003, 2004, 2005, 2006, 2007 and 2008 are 5, 8, 9, 6, 12, 15 and 24 respectively. Represent these data using a suitable diagram.

We can represent the profits for 7 consecutive years by drawing either a line diagram as given below.

Let us consider years on horizontal axis and profits on vertical axis.

For the year 2002, the profit is 5 thousand dollars. It can be written as a point (2002, 5)

In the same manner, we can write the following points for the succeeding years.

(2003, 8), (2004, 9), (2005, 6), (2006, 12), (2007, 15) and (2008, 24)

Now, plotting all these point and joining them using ruler, we can get the line diagram.

Showing line diagram for the profit of an Industrial House during 2002 to 2008.

A two dimensional graphical representation of a continuous frequency distribution is called a histogram.

In histogram, the bars are placed continuously side by side with no gap between adjacent bars.

That is, in histogram rectangles are erected on the class intervals of the distribution. The areas of rectangle are proportional to the frequencies.

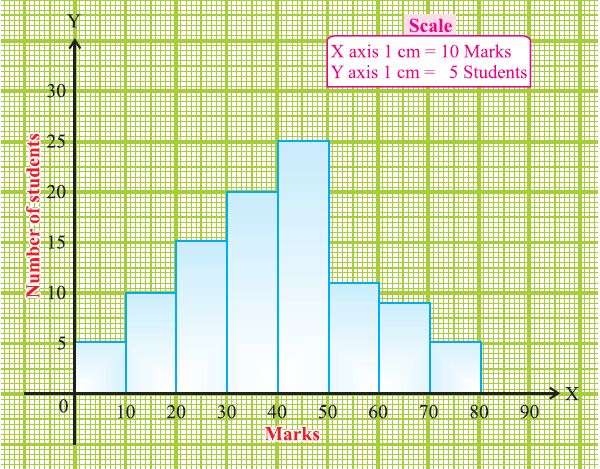
Draw a histogram for the following table which represent the marks obtained by 100 students in an examination :

The class intervals are all equal with length of 10 marks.

Let us denote these class intervals along the X-axis.

Denote the number of students along the Y-axis, with appropriate scale.

The histogram is given below.

Bar Diagram

There are two types of bar diagrams namely, Horizontal Bar diagram and Vertical bar diagram.

While horizontal bar diagram is used for qualitative data or data varying over space, the vertical bar diagram is associated with quantitative data or time series data.

Bars i.e. rectangles of equal width and usually of varying lengths are drawn either horizontally or vertically.

We consider Multiple or Grouped Bar diagrams to compare related series. Component or sub-divided Bar diagrams are applied for representing data divided into a number of components. Finally, we use Divided Bar charts or Percentage

Bar diagrams for comparing different components of a variable and also the relating of the components to the whole. For this situation, we may also use Pie chart or Pie diagram or circle diagram.

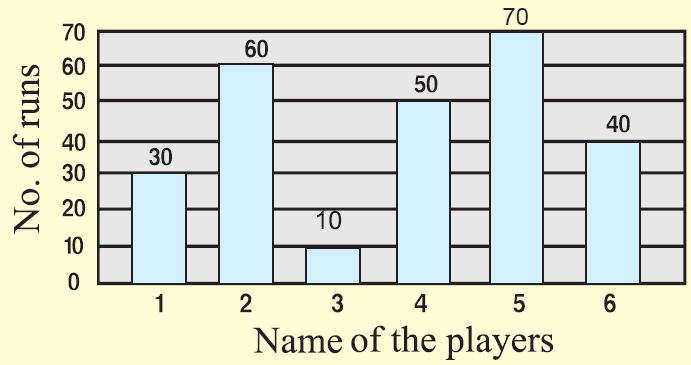
Example :

The total number of runs scored by a few players in one-day match is given.

Draw bar graph for the above data.

In a pie chart, the various observations or components are represented by the sectors of a circle and the whole circle represents the sum of the value of all the components .Clearly, the total angle of 360° at the center of the circle is divided according to the values of the components .

The central angle of a component is

= [Value of the component / Total value] x 360°

Sometimes, the value of the components are expressed in percentages. In such cases,

= [Percentage value of the component / 100] x 360°

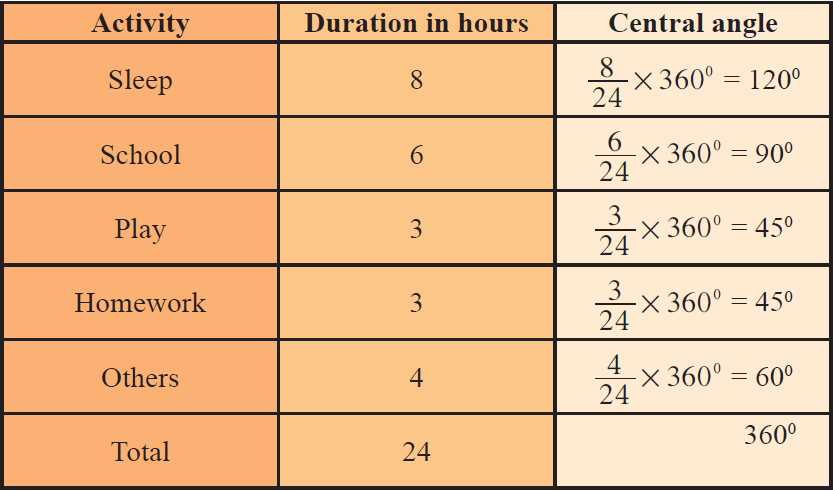
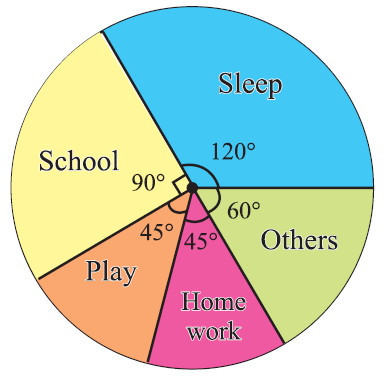
The number of hours spent by a school student on various activities on a working day, is given below. Construct a pie chart using the angle measurement.

Draw a pie chart to represent the above information.

We may calculate the central angles for various components as follows :

From the above table, clearly, we obtain the required pie chart as shown below.

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to [email protected]

We always appreciate your feedback.

Sat Math Practice
SAT Math Worksheets
PEMDAS Rule
BODMAS rule
GEMDAS Order of Operations
Math Calculators
Transformations of Functions
Order of rotational symmetry
Lines of symmetry
Compound Angles
Quantitative Aptitude Tricks
Trigonometric ratio table
Word Problems
Times Table Shortcuts
10th CBSE solution
PSAT Math Preparation
Privacy Policy
Laws of Exponents

Recent Articles

How to Convert Between Polar and Rectangular Coordinates

May 31, 24 08:11 PM

How to Convert Between Polar and Rectangular Equations

May 31, 24 08:05 PM

46 Presentation of data II – Graphical representation

Pa . Raajeswari

Graphical representation is the visual display of data using plots and charts. It is used in many academic and professional disciplines but most widely so in the fields of mathematics, medicine and sciences. Graphical representation helps to quantify, sort and present data in a method that is understandable to a large variety of audiences. A graph is the representation of data by using graphical symbols such as lines, bars, pie slices, dots etc. A graph does represent a numerical data in the form of a qualitative structure and provides important information.

Statistical surveys and experiments provides valuable information about numerical scores. For better understanding and making conclusions and interpretations, the data should be managed and organized in a systematic form.

Graphs also enable in studying both time series and frequency distribution as they give clear account and precise picture of problem. Above all graphs are also easy to understand and eye catching and can create a storing impact on memory.

General Principles of Graphic Representation:

There are some algebraic principles which apply to all types of graphic representation of data. In a graph there are two lines called coordinate axes. One is vertical known as Y axis and the other is horizontal called X axis. These two lines are perpendicular to each other. Where these two lines intersect each other is called ‘0’ or the Origin. On the X axis the distances right to the origin have positive value and distances left to the origin have negative value. On the Y axis distances above the origin have a positive value and below the origin have a negative value.

TYPES OF GRAPHICAL REPRESENTATON:

The various types of graphical representations of the data are

Circle Graph
Histogram and Frequency Polygon

1. Dot Plots

The dot plot is one of the most simplest ways of graphical representation of the statistical data. As the name itself suggests, a dot plot uses the dots. It is a graphic display which usually compares frequency within different categories. The dot plot is composed of dots that are to be plotted on a graph paper.

In the dot plot, every dot denotes a specific number of observations belonging to a data set. One dot usually represents one observation. These dots are to be marked in the form of a column for each category. In this way, the height of each column shows the corresponding frequency of some category. The dot plots are quite useful when there are small amount of data is given within the small number of categories.

2. Bar Graph

A bar graph is a very frequently used graph in statistics as well as in media. A bar graph is a type of graph which contains rectangles or rectangular bars. The lengths of these bars should be proportional to the numerical values represented by them. In bar graph, the bars may be plotted either horizontally or vertically. But a vertical bar graph (also known as column bar graph) is used more than a horizontal one.

A vertical bar graph is shown below:

Number of students went to different countries for study:

The rectangular bars are separated by some distance in order to distinguish them from one another. The bar graph shows comparison among the given categories.

Mostly, horizontal axis of the graph represents specific categories and vertical axis shows the discrete numerical values.

3.Line Graph

A line graph is a kind of graph which represents data in a way that a series of points are to be connected by segments of straight lines. In a line graph, the data points are plotted on a graph and they are joined together with straight line.

A sample line graph is illustrated in the following diagram:

The line graphs are used in the science, statistics and media. Line graphs are very easy to create. These are quite popular in comparison with other graphs since they visualize characteristics revealing data trends very clearly. A line graph gives a clear visual comparison between two variables which are represented on X-axis and Y-axis.

4.Circle Graph

A circle graph is also known as a pie graph or pie chart. It is called so since it is similar to slice of a “pie”. A pie graph is defined as a graph which contains a circle which is divided into sectors. These sectors illustrate the numerical proportion of the data.

A pie chart are shown in the following diagram:

The arc lengths of the sectors, in pie chart, are proportional to the numerical value they represent.Circle graphs are quite commonly seen in mass media as well as in business world.

5. Histogram and Frequency Polygon

The histograms and frequency polygons are very common graphs in statistics. A histogram is defined as a graphical representation of the mutually exclusive events. A histogram is quite similar to the bar graph. Both are made up of rectangular bars. The difference is that there is no gap between any two bars in the histogram. The histogram is used to represent the continuous data.

A histogram may look like the following graph:

The frequency polygon is a type of graphical representation which gives us better understanding of the shape of given distribution. Frequency polygons serve almost the similar purpose as histograms do. But the frequency polygon is quite helpful for the purpose of comparing two or more sets of data. The frequency polygons are said to be the extension of the histogram. When the midpoints of tops of the rectangular bars are joined together, the frequency polygon is made.

Few examples of graphical representation of statistical data are given below:

Example 1: Draw a dot plot for the following data.

Solution: The pie graph of the above data is:

Methods to Represent a Frequency Distribution:

Generally four methods are used to represent a frequency distribution graphically. These are Histogram, Smoothed frequency graph and Ogive or Cumulative frequency graph and pie diagram.

1. Histogram:

Histogram is a non-cumulative frequency graph, it is drawn on a natural scale in which the representative frequencies of the different class of values are represented through vertical rectangles drawn closed to each other. Measure of central tendency, mode can be easily determined with the help of this graph.

How to draw a Histogram:

Represent the class intervals of the variables along the X axis and their frequencies along the Y-axis on natural scale.

Start X axis with the lower limit of the lowest class interval. When the lower limit happens to be a distant score from the origin give a break in the X-axis n to indicate that the vertical axis has been moved in for convenience.

Now draw rectangular bars in parallel to Y axis above each of the class intervals with class units as base: The areas of rectangles must be proportional to the frequencies of the corresponding classes.

In this graph we shall take class intervals in the X axis and frequencies in the Y axis. Before plotting the graph we have to convert the class into their exact limits.

Advantages of histogram:

1. It is easy to draw and simple to understand.

2. It helps us to understand the distribution easily and quickly.

3. It is more precise than the polygene.

Limitations of histogram:

1. It is not possible to plot more than one distribution on same axes as histogram.

2. Comparison of more than one frequency distribution on the same axes is not possible.

3. It is not possible to make it smooth.

Uses of histogram:

1.Represents the data in graphic form.

2.Provides the knowledge of how the scores in the group are distributed. Whether the scores are piled up at the lower or higher end of the distribution or are evenly and regularly distributed throughout the scale.

3.Frequency Polygon. The frequency polygon is a frequency graph which is drawn by joining the coordinating points of the mid-values of the class intervals and their corresponding fre-quencies.

How to draw a frequency polygon:

Draw a horizontal line at the bottom of graph paper named ‘OX’ axis. Mark off the exact limits of the class intervals along this axis. It is better to start with i. of lowest value. When the lowest score in the distribution is a large number we cannot show it graphically if we start with the origin. Therefore put a break in the X axis to indicate that the vertical axis has been moved in for convenience. Two additional points may be added to the two extreme ends.

Draw a vertical line through the extreme end of the horizontal axis known as OY axis. Along this line mark off the units to represent the frequencies of the class intervals. The scale should be chosen in such a way that it will make the largest frequency (height) of the polygon approximately 75 percent of the width of the figure.

Plot the points at a height proportional to the frequencies directly above the point on the horizontal axis representing the mid-point of each class interval.

After plotting all the points on the graph join these points by a series of short straight lines to form the frequency polygon. In order to complete the figure two additional intervals at the high end and low end of the distribution should be included. The frequency of these two intervals will be zero.

Illustration: No. 7.3:

Draw a frequency polygon from the following data:

Advantages of frequency polygon:

2. It is possible to plot two distributions at a time on same axes.

3. Comparison of two distributions can be made through frequency polygon.

4. It is possible to make it smooth.

Limitations of frequency polygon:

1. It is less precise.

2. It is not accurate in terms of area the frequency upon each interval.

Uses of frequency polygon:

1. When two or more distributions are to be compared the frequency polygon is used.

2. It represents the data in graphic form.

3. It provides knowledge of how the scores in one or more group are distributed. Whether the scores are piled up at the lower or higher end of the distribution or are evenly and regularly distributed throughout the scale.

2. Smoothed Frequency Polygon:

When the sample is very small and the frequency distribution is irregular the polygon is very jig-jag. In order to wipe out the irregularities and “also get a better notion of how the figure might look if the data were more numerous, the frequency polygon may be smoothed.”

In this process to adjust the frequencies we take a series of ‘moving’ or ‘running’ averages. To get an adjusted or smoothed frequency we add the frequency of a class interval with the two adjacent intervals, just below and above the class interval. Then the sum is divided by 3. When these adjusted frequencies are plotted against the class intervals on a graph we get a smoothed frequency polygon.

Illustration 7.4:

Draw a smoothed frequency polygon, of the data given in the illustration No. 7.3:

Here we have to first convert the class intervals into their exact limits. Then we have to determine the adjusted or smoothed frequencies.

3. Ogive or Cumulative Frequency Polygon:

Ogive is a cumulative frequency graphs drawn on natural scale to determine the values of certain factors like median, Quartile, Percentile etc. In these graphs the exact limits of the class intervals are shown along the X-axis and the cumulative frequencies are shown along the Y-axis. Below are given the steps to draw an ogive.

Get the cumulative frequency by adding the frequencies cumulatively, from the lower end (to get a less than ogive) or from the upper end (to get a more than ogive).

Mark off the class intervals in the X-axis.

Represent the cumulative frequencies along the Y-axis beginning with zero at the base.

Put dots at each of the coordinating points of the upper limit and the corresponding frequencies.

Join all the dots with a line drawing smoothly. This will result in curve called ogive.

Illustration No. 7.5:

Draw an ogive from the data given below:

To plot this graph first we have to convert, the class intervals into their exact limits. Then we have to calculate the cumulative frequencies of the distribution.

Uses of Ogive:

1. Ogive is useful to determine the number of students below and above a particular score.

2. When the median as a measure of central tendency is wanted.

3. When the quartiles, deciles and percentiles are wanted.

4. By plotting the scores of two groups on a same scale we can compare both the groups.

4. The Pie Diagram:

Figure given below shows the distribution of elementary pupils by their academic achievement in a school. Of the total, 60% are high achievers, 25% middle achievers and 15% low achievers. The construction of this pie diagram is quite simple. There are 360 degree in the circle. Hence, 60% of 360′ or 216° are counted off as shown in the diagram; this sector represents the proportion of high achievers students.

Ninety degrees counted off for the middle achiever students (25%) and 54 degrees for low achiever students (15%). The pie-diagram is useful when one wishes to picture proportions of the total in a striking way. Numbers of degrees may be measured off “by eye” or more accurately with a protractor.

Uses of Pie diagram:

1. Pie diagram is useful when one wants to picture proportions of the total in a striking way.

2. When a population is stratified and each strata is to be presented as a percentage at that time pie diagram is used.

PURPOSE OF GRAPHICAL REPRESENTATION:

The purpose of graphical presentation of data is to provide a quick and easy-to-read picture of information that clearly shows what otherwise takes a great deal of explanation. The impact of graphical data is typically more pointed and memorable than paragraphs of written information

For example, a person making a presentation regarding sales in various states across the country establishes the point of the presentation to the audience more quickly by using a color-coded map rather than merely stating the sales figures for each state. Observers quickly determine which states are ahead and which are behind in sales, and they know where emphasis needs to be placed. Alternatively, when making a presentation on sales by age groups using a pie chart that divides the pie into various ages, the audience quickly sees the results of sales by age. This means that the audience is more likely to retain that information than if the presenter simply reads the results aloud or puts it into writing.

GENERAL RULES DISPLAYING DATA

Simpler is Better
Graphs, Tables and charts can be used together
Use clear Description, title and labels
Provide a narrative Description of the highlights
Don’t compare variables with different scales of magnitude.
A Diagram must be attractive, well proportioned,neat and pleasing to the eyes.
They should be geometrically Accurate
Size of the diagram should be proportional to paper should not be too big or too small
Different colors should be used to classify data’s.

ADVANTAGES:

Acceptability: graphical report is acceptable to the busy persons because it easily highlights about the theme of the report. This helps to avoid wastage of time.
Comparative Analysis : Information can be compared in terms of graphical representation. Â Such comparative analysis helps for quick understanding and attention.
Less cost : Information if descriptive involves huge time to present properly. It involves more money to print the information but graphical presentation can be made in short but catchy view to make the report understandable. It obviously involves less cost.
Decision Making: Business executives can view the graphs at a glance and can make decision very quickly which is hardly possible through descriptive report.
Logical Ideas: If tables, design and graphs are used to represent information then a logical sequence is created to clear the idea of the audience.
Helpful for less literate Audience: Less literate or illiterate people can understand graphical representation easily because it does not involve going through line by line of any descriptive report.
Less Effort and Time: To present any table, design, image or graphs require less effort and time. Furthermore, such presentation makes quick understanding of the information.
Less Error and Mistakes: Qualitative or informative or descriptive reports involve errors or mistakes. As graphical representations are exhibited through numerical figures, tables or graphs, it usually involves less error and mistake.
A complete Idea: Such representation creates clear and complete idea in the mind of audience. Reading hundred pages may not give any scope to make decision. But an instant view or looking at a glance obviously makes an impression inÂ Â the mind of audience regarding the topic or subject.
Use in the Notice Board: Such representation can be hanged in the notice board to quickly raise the attention of employees in any organization.

DISADVANTAGES:

Graphical representation of reports is not free from limitations. The following are the problems of graphical representation of data or reports:

Costly : Graphical representation pf reports are costly because it involves images, colors and paints. Combination of material with human efforts makes the graphical presentation expensive.
More time : Normal report involves less time to represent but graphical representation involves more time as it requires graphs and figures which are dependent to more time.
Errors and Mistakes : Since graphical representations are complex, there is- each and every chance of errors and mistake. This causes problems for better understanding to general people.
Lack of Secrecy: Graphical representation makes full presentation of information which may hamper the objective to keep something secret.
Problems to select the suitable method: Information can be presented through various graphical methods and ways. Which should be the suitable method is very hard to select.
Problem of Understanding: All may not be able to get the meaning of graphical representation because it involves various technical matters which are complex to general people.

Last of all it can be said that graphical representation does not provide proper information to general people.

CONCLUSION:

Graphical representation makes the datamore possible to easily draw; visual impression of data. Graphical representation of data enhances the understandings of the observer. It makes comparisons easy. This kind of method creates an imprint on mind for a long period of time. Well in this chapter we have discussed about the definition ,types ,advantages and disadvantages in detail with relevant examples which will have an impact in the power of understanding. I request you all to go through the various types of graphs commonly used in research studies in with reference to home science research studies to explore new ideas in the field of research.

http://shodhganga.inflibnet.ac.in/bitstream/10603/143688/2/file%202%20chapter%201 %20data%20representation%20techniques.pdf
http://www.mas.ncl.ac.uk/~ndah6/teaching/MAS1403/notes_chapter2.pdf https://www.ncbi.nlm.nih.gov/pmc/articles/PMC5453888/
http://cec.nic.in/wpresources/module/Anthropology/PaperIX/9/content/downloads/file1. pdf
https://www.kluniversity.in/arp/uploads/2096.pdf

Accountancy
Business Studies
Organisational Behaviour
Human Resource Management
Entrepreneurship
CBSE Class 11 Statistics for Economics Notes

Chapter 1: Concept of Economics and Significance of Statistics in Economics

Statistics for Economics | Functions, Importance, and Limitations

Chapter 2: Collection of Data

Data Collection & Its Methods
Sources of Data Collection | Primary and Secondary Sources
Direct Personal Investigation: Meaning, Suitability, Merits, Demerits and Precautions
Indirect Oral Investigation : Suitability, Merits, Demerits and Precautions
Difference between Direct Personal Investigation and Indirect Oral Investigation
Information from Local Source or Correspondents: Meaning, Suitability, Merits, and Demerits
Questionnaires and Schedules Method of Data Collection
Difference between Questionnaire and Schedule
Qualities of a Good Questionnaire and Types of Questionnaires
What are the Published Sources of Collecting Secondary Data?
What Precautions should be taken before using Secondary Data?
Two Important Sources of Secondary Data: Census of India and Reports & Publications of NSSO
What is National Sample Survey Organisation (NSSO)?
What is Census Method of Collecting Data?
Sample Method of Collection of Data
Methods of Sampling
Father of Indian Census
What makes a Sampling Data Reliable?
Difference between Census Method and Sampling Method of Collecting Data
What are Statistical Errors?

Chapter 3: Organisation of Data

Organization of Data
Objectives and Characteristics of Classification of Data
Classification of Data in Statistics | Meaning and Basis of Classification of Data
Concept of Variable and Raw Data
Types of Statistical Series
Difference between Frequency Array and Frequency Distribution
Types of Frequency Distribution

Chapter 4: Presentation of Data: Textual and Tabular

Textual Presentation of Data: Meaning, Suitability, and Drawbacks

Tabular Presentation of Data: Meaning, Objectives, Features and Merits

Different Types of Tables
Classification and Tabulation of Data

Chapter 5: Diagrammatic Presentation of Data

Diagrammatic Presentation of Data: Meaning , Features, Guidelines, Advantages and Disadvantages
Types of Diagrams
Bar Graph | Meaning, Types, and Examples
Pie Diagrams | Meaning, Example and Steps to Construct
Histogram | Meaning, Example, Types and Steps to Draw
Frequency Polygon | Meaning, Steps to Draw and Examples
Ogive (Cumulative Frequency Curve) and its Types
What is Arithmetic Line-Graph or Time-Series Graph?
Diagrammatic and Graphic Presentation of Data

Chapter 6: Measures of Central Tendency: Arithmetic Mean

Measures of Central Tendency in Statistics
Arithmetic Mean: Meaning, Example, Types, Merits, and Demerits
What is Simple Arithmetic Mean?
Calculation of Mean in Individual Series | Formula of Mean
Calculation of Mean in Discrete Series | Formula of Mean
Calculation of Mean in Continuous Series | Formula of Mean
Calculation of Arithmetic Mean in Special Cases
Weighted Arithmetic Mean

Chapter 7: Measures of Central Tendency: Median and Mode

Median(Measures of Central Tendency): Meaning, Formula, Merits, Demerits, and Examples
Calculation of Median for Different Types of Statistical Series
Calculation of Median in Individual Series | Formula of Median
Calculation of Median in Discrete Series | Formula of Median
Calculation of Median in Continuous Series | Formula of Median
Graphical determination of Median
Mode: Meaning, Formula, Merits, Demerits, and Examples
Calculation of Mode in Individual Series | Formula of Mode
Calculation of Mode in Discrete Series | Formula of Mode
Grouping Method of Calculating Mode in Discrete Series | Formula of Mode
Calculation of Mode in Continuous Series | Formula of Mode
Calculation of Mode in Special Cases
Calculation of Mode by Graphical Method
Mean, Median and Mode| Comparison, Relationship and Calculation

Chapter 8: Measures of Dispersion

Measures of Dispersion | Meaning, Absolute and Relative Measures of Dispersion
Range | Meaning, Coefficient of Range, Merits and Demerits, Calculation of Range
Calculation of Range and Coefficient of Range
Interquartile Range and Quartile Deviation
Partition Value | Quartiles, Deciles and Percentiles
Quartile Deviation and Coefficient of Quartile Deviation: Meaning, Formula, Calculation, and Examples
Quartile Deviation in Discrete Series | Formula, Calculation and Examples
Quartile Deviation in Continuous Series | Formula, Calculation and Examples
Mean Deviation: Coefficient of Mean Deviation, Merits, and Demerits
Calculation of Mean Deviation for different types of Statistical Series
Mean Deviation from Mean | Individual, Discrete, and Continuous Series
Mean Deviation from Median | Individual, Discrete, and Continuous Series
Standard Deviation: Meaning, Coefficient of Standard Deviation, Merits, and Demerits
Standard Deviation in Individual Series
Methods of Calculating Standard Deviation in Discrete Series
Methods of calculation of Standard Deviation in frequency distribution series
Combined Standard Deviation: Meaning, Formula, and Example
How to calculate Variance?
Coefficient of Variation: Meaning, Formula and Examples
Lorenz Curveb : Meaning, Construction, and Application

Chapter 9: Correlation

Correlation: Meaning, Significance, Types and Degree of Correlation
Methods of measurements of Correlation
Calculation of Correlation with Scattered Diagram
Spearman's Rank Correlation Coefficient
Karl Pearson's Coefficient of Correlation
Karl Pearson's Coefficient of Correlation | Methods and Examples

Chapter 10: Index Number

Index Number | Meaning, Characteristics, Uses and Limitations
Methods of Construction of Index Number
Unweighted or Simple Index Numbers: Meaning and Methods
Methods of calculating Weighted Index Numbers
Fisher's Index Number as an Ideal Method
Fisher's Method of calculating Weighted Index Number
Paasche's Method of calculating Weighted Index Number
Laspeyre's Method of calculating Weighted Index Number
Laspeyre's, Paasche's, and Fisher's Methods of Calculating Index Number
Consumer Price Index (CPI) or Cost of Living Index Number: Construction of Consumer Price Index|Difficulties and Uses of Consumer Price Index
Methods of Constructing Consumer Price Index (CPI)
Wholesale Price Index (WPI) | Meaning, Uses, Merits, and Demerits
Index Number of Industrial Production : Characteristics, Construction & Example
Inflation and Index Number

Important Formulas in Statistics for Economics

Important Formulas in Statistics for Economics | Class 11

What is Tabulation?

The systematic presentation of numerical data in rows and columns is known as Tabulation . It is designed to make presentation simpler and analysis easier. This type of presentation facilitates comparison by putting relevant information close to one another, and it helps in further statistical analysis and interpretation. One of the most important devices for presenting the data in a condensed and readily comprehensible form is tabulation. It aims to provide as much information as possible in the minimum possible space while maintaining the quality and usefulness of the data.

“Tabulation involves the orderly and systematic presentation of numerical data in a form designed to elucidate the problem under consideration.” – L.R. Connor

Objectives of Tabulation

The aim of tabulation is to summarise a large amount of numerical information into the simplest form. The following are the main objectives of tabulation:

To make complex data simpler: The main aim of tabulation is to present the classified data in a systematic way. The purpose is to condense the bulk of information (data) under investigation into a simple and meaningful form.
To save space: Tabulation tries to save space by condensing data in a meaningful form while maintaining the quality and quantity of the data.
To facilitate comparison: It also aims to facilitate quick comparison of various observations by providing the data in a tabular form.
To facilitate statistical analysis: Tabulation aims to facilitate statistical analysis because it is the stage between data classification and data presentation. Various statistical measures, including averages, dispersion, correlation, and others, are easily calculated from data that has been systematically tabulated.
To provide a reference: Since data may be easily identifiable and used when organised in tables with titles and table numbers, tabulation aims to provide a reference for future studies.

Features of a Good Table

Tabulation is a very specialised job. It requires a thorough knowledge of statistical methods, as well as abilities, experience, and common sense. A good table must have the following characteristics:

Title: The top of the table must have a title and it needs to be very appealing and attractive.
Manageable Size: The table shouldn’t be too big or too small. The size of the table should be in accordance with its objectives and the characteristics of the data. It should completely cover all significant characteristics of data.
Attractive: A table should have an appealing appearance that appeals to both the sight and the mind so that the reader can grasp it easily without any strain.
Special Emphasis: The data to be compared should be placed in the left-hand corner of columns, with their titles in bold letters.
Fit with the Objective: The table should reflect the objective of the statistical investigation.
Simplicity: To make the table easily understandable, it should be simple and compact.
Data Comparison: The data to be compared must be placed closely in the columns.
Numbered Columns and Rows: When there are several rows and columns in a table, they must be numbered for reference.
Clarity: A table should be prepared so that even a layman may make conclusions from it. The table should contain all necessary information and it must be self-explanatory.
Units: The unit designations should be written on the top of the table, below the title. For example, Height in cm, Weight in kg, Price in ₹, etc. However, if different items have different units, then they should be mentioned in the respective rows and columns.
Suitably Approximated: If the figures are large, then they should be rounded or approximated.
Scientifically Prepared: The preparation of the table should be done in a systematic and logical manner and should be free from any kind of ambiguity and overlapping.

Components of a Table

A table’s preparation is an art that requires skilled data handling. It’s crucial to understand the components of a good statistical table before constructing one. A table is created when all of these components are put together in a systematic order. In simple terms, a good table should include the following components:

1. Table Number:

Each table needs to have a number so it may be quickly identified and used as a reference.

If there are many tables, they should be numbered in a logical order.
The table number can be given at the top of the table or the beginning of the table title.
The table is also identified by its location using subscripted numbers like 1.2, 2.1, etc. For instance, Table Number 3.1 should be seen as the first table of the third chapter.

Each table should have a suitable title. A table’s contents are briefly described in the title.

The title should be simple, self-explanatory, and free from ambiguity.
A title should be brief and presented clearly, usually below the table number.
In certain cases, a long title is preferable for clarification. In these cases, a ‘Catch Title’ may be placed above the ‘Main Title’. For instance , the table’s contents might come after the firm’s name, which appears as a catch title.
Contents of Title: The title should include the following information: (i) Nature of data, or classification criteria (ii) Subject-matter (iii) Place to which the data relates (iv) Time to which the data relates (v) Source to which the data belongs (vi) Reference to the data, if available.

3. Captions or Column Headings:

A column designation is given to explain the figures in the column at the top of each column in a table. This is referred to as a “Column heading” or “Caption”.

Captions are used to describe the names or heads of vertical columns.
To save space, captions are generally placed in small letters in the middle of the columns.

4. Stubs or Row Headings:

Each row of the table needs to have a heading, similar to a caption or column heading. The headers of horizontal rows are referred to as stubs. A brief description of the row headers may also be provided at the table’s left-hand top.

5. Body of Table:

The table’s most crucial component is its body, which contains data (numerical information).

The location of any one figure or data in the table is fixed and determined by the row and column of the table.
The columns and rows in the main body’s arrangement of numerical data are arranged from top to bottom.
The size and shape of the main body should be planned in accordance with the nature of the figures and the purpose of the study.
As the body of the table summarises the facts and conclusions of the statistical investigation, it must be ensured that the table does not have irrelevant information.

6. Unit of Measurement:

If the unit of measurement of the figures in the table (real data) does not change throughout the table, it should always be provided along with the title.

However, these units must be mentioned together with stubs or captions if rows or columns have different units.
If there are large figures, they should be rounded up and the rounding method should be stated.

7. Head Notes:

If the main title does not convey enough information, a head note is included in small brackets in prominent words right below the main title.

A head-note is included to convey any relevant information.
For instance, the table frequently uses the units of measurement “in million rupees,” “in tonnes,” “in kilometres,” etc. Head notes are also known as Prefatory Notes .

8. Source Note:

A source note refers to the place where information was obtained.

In the case of secondary data, a source note is provided.
Name of the book, page number, table number, etc., from which the data were collected should all be included in the source. If there are multiple sources, each one must be listed in the source note.
If a reader wants to refer to the original data, the source note enables him to locate the data. Usually, the source note appears at the bottom of the table. For example, the source note may be: ‘Census of India, 2011’.
Importance: A source note is useful for three reasons: -> It provides credit to the source (person or group), who collected the data; -> It provides a reference to source material that may be more complete; -> It offers some insight into the reliability of the information and its source.

9. Footnotes:

The footnote is the last part of the table. The unique characteristic of the data content of the table that is not self-explanatory and has not previously been explained is mentioned in the footnote.

Footnotes are used to provide additional information that is not provided by the heading, title, stubs, caption, etc.
When there are many footnotes, they are numbered in order.
Footnotes are identified by the symbols *, @, £, etc.
In general, footnotes are used for the following reasons: (i) To highlight any exceptions to the data (ii)Any special circumstances affecting the data; and (iii)To clarify any information in the data.

Merits of Tabular Presentation of Data

The following are the merits of tabular presentation of data:

Brief and Simple Presentation: Tabular presentation is possibly the simplest method of data presentation. As a result, information is simple to understand. A significant amount of statistical data is also presented in a very brief manner.
Facilitates Comparison: By grouping the data into different classes, tabulation facilitates data comparison.
Simple Analysis: Analysing data from tables is quite simple. One can determine the data’s central tendency, dispersion, and correlation by organising the data as a table.
Highlights Characteristics of the Data: Tabulation highlights characteristics of the data. As a result of this, it is simple to remember the statistical facts.
Cost-effective: Tabular presentation is a very cost-effective way to convey data. It saves time and space.
Provides Reference: As the data provided in a tabular presentation can be used for other studies and research, it acts as a source of reference.

Please Login to comment...

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

IMAGES

What Is Time-Series Data? Definitions & Examples
(a) An example of time series measured by the 10 sensors; (b) the
Time Series
Diagrammatic and Graphic Presentation of Data
Diagrammatic presentation of data
What Is Time Series Data?

VIDEO

LIMITATIONS OF DIAGRAMMATIC PRESENTATION
Definition and examples of Time Series
Diagrammatic Representation of Data #maths #data
Class-11
11th Economics diagrammatic presentation part 1
03 Diagrammatic and Graphical Presentation of Data

COMMENTS

Diagrammatic Presentation of Data: Meaning , Features, Guidelines
Diagrammatic and graphic presentation of data means visual representation of the data. It shows a comparison between two or more sets of data and helps in the presentation of highly complex data in its simplest form. Diagrams and graphs are clear and easy to read and understand. In the diagrammatic presentation of data, bar charts, rectangles, sub-
Diagrammatic Presentation of Data: Bar Diagrams, Pie Charts etc.
Bar Diagrams. As the name suggests, when data is presented in form of bars or rectangles, it is termed to be a bar diagram. Features of a Bar. The rectangular box in a bar diagram is known as a bar. It represents the value of a variable. These bars can be either vertically or horizontally arranged. Bars are equidistant from each other.
A Thorough Guide to Time Series Analysis
A time series is a series of data points indexed (or listed or graphed) in time order. Most commonly, a time series is a sequence taken at successive equally spaced points in time. In plain language, time-series data is a dataset that tracks a sample over time and is collected regularly. Examples are commodity price, stock price, house price ...
Diagrammatic Presentation of Data
Advantages of Diagrammatic Data Presentation. Easy to understand - Diagrammatic data presentation makes it easier for a common man to understand the data. Diagrams are usually attractive and impressive and many newspapers and magazines use them frequently to explain certain facts or phenomena. Modern advertising campaigns also use diagrams.
Diagrammatic Presentation of Data
Concept of Diagrammatic Presentation. It is a technique of presenting numeric data through pictograms, cartograms, bar diagrams, and pie diagrams. It is the most attractive and appealing way to represent statistical data. Diagrams help in visual comparison and they have a bird's eye view. Under pictograms, we use pictures to present data.
Time series
Time series: random data plus trend, with best-fit line and different applied filters. In mathematics, a time series is a series of data points indexed (or listed or graphed) in time order. Most commonly, a time series is a sequence taken at successive equally spaced points in time. Thus it is a sequence of discrete-time data. Examples of time series are heights of ocean tides, counts of ...
Diagrammatic Representation of Data: Bar Diagram, Line Graphs etc.
Data point corresponds to the change over a period of time. The line joining these data points shows the trend of change. Below is the line graph showing the number of buses passing through a particular street over a period of time: Solved Examples for diagrammatic Representation of Data. Problem 1: Draw the histogram for the given data.
Diagrammatic Presentation of Data
Bars can be drawn vertically or horizontally. If the data are not in the shape of time series, the observations may be arranged in ascending or descending order to accomplish comparison. ... Such diagrams are known as "angular diagrams." ... C.S. (2018). Diagrammatic Presentation of Data. In: Statistical Methods in Medical Research ...
Data Presentation: Graphs, Frequency Tables and Histograms
Use Excel and enter the data above in your spreadsheet. Draw a time-series graph of Per capita economic growth. Comment upon the main features of the series. (b) Draw time-series graphs of the change in per capita growth, the (natural) log of growth, and the change in the ln. Comment upon the results. Print out the answers for these three ...
Diagrammatic Presentation of Data: Bar Diagrams, Pie Charts etc
Diagrammatic Presentation of Data Nowadays a lot of emphasis is laid upon exceptional presentation of data. All of this is because, when ... The rectangular box in a bar diagram is known as a bar. It represents the value of a variable. ... Generally, simple bar diagrams are used to represent time series data for a single entity.
Diagrammatic Presentation Of Data
Diagrammatic Presentation Of Data - Introduction The diagrammatic representation also helps in having a bird's eye view or overall view of the differentiation of data. ... The following is an example of a Bar Chart that has time on the X axis and profits on the Y axis. Pie Chart. Also known as a "circle chart", the pie chart divides the ...
45 Presentation of data I
A simple bar diagram is constructed for an immediate comparison. It is advisable to arrange the given data set in an ascending or descending order and plot the data variables accordingly. However, time series data are represented according to the sequencing of the time period. Construction Steps: Draw X and Y- axes on a graph paper.
Graphic Presentation of Data
Graphic presentation is considered the preferred way of presentation of data over diagrammatic presentation as graphs are always more accurate and precise, whereas diagrams are generally used for the purpose of publicity and propaganda. ... 5.4 Graphs of Time Series or Historigrams. 1. ... the graph drawn is known as "absolute historigram ...
2: Graphical Representations of Data
2.3: Histograms, Frequency Polygons, and Time Series Graphs. A histogram is a graphic version of a frequency distribution. The graph consists of bars of equal width drawn adjacent to each other. The horizontal scale represents classes of quantitative data values and the vertical scale represents frequencies. The heights of the bars correspond ...
Graphical Representation of Data
Examples on Graphical Representation of Data. Example 1: A pie chart is divided into 3 parts with the angles measuring as 2x, 8x, and 10x respectively. Find the value of x in degrees. Solution: We know, the sum of all angles in a pie chart would give 360º as result. ⇒ 2x + 8x + 10x = 360º. ⇒ 20 x = 360º.
Diagrammatic Representation of Data
Bar Diagram. There are two types of bar diagrams namely, Horizontal Bar diagram and Vertical bar diagram. While horizontal bar diagram is used for qualitative data or data varying over space, the vertical bar diagram is associated with quantitative data or time series data. Bars i.e. rectangles of equal width and usually of varying lengths are drawn either horizontally or vertically.
PDF Lesson-7 Presentation of Data
It is also known as angular diagram. Learner`s Guide. Senior Secondary Economics. (318) ... in the form of time series graph.If one of the two variables is time in days, weeks, months or years we get a time ... Polygon is a diagrammatic presentation of data which is constructed by joining the mid
4 Diagrammatic and Graphical Representation of Data I
4. Use of Diagrammatic and Graphical Presentation of the Data. Diagrammatic and Graphical presentation of the data are useful in practice due to the following reasons. These are: (1) The information that we acquire from the graphical and diagrammatic representation of the data is easy to understand even for a layman person due to its simplicity.
Statistics by Dr. B. N. Gupta (SBPD Publications)
Classification and Tabulation of Data, 9. Diagrammatic Presentation of Data, 10. Graphic Presentation of Data, 11. ... Correlation, 20. Index Number, 21. Analysis of Time Series, 22. Interpolations and Extrapolation, 23 . ... data formula four frequency distribution given gives Hence hypothesis Illustration important income Index Number ...
Presentation of data II
Presentation of data I - Diagrammatic representation 46. Presentation of data II - Graphical representation ... Graphs also enable in studying both time series and frequency distribution as they give clear account and precise picture of problem. Above all graphs are also easy to understand and eye catching and can create a storing impact on ...
Tabular Presentation of Data: Meaning, Objectives ...
As a result of this, it is simple to remember the statistical facts. Cost-effective: Tabular presentation is a very cost-effective way to convey data. It saves time and space. Provides Reference: As the data provided in a tabular presentation can be used for other studies and research, it acts as a source of reference.
Statistics for Economics Class 11 NCERT Solutions Chapter 4
Question 4. Data represented through arithmetic line graph help in understanding. (a) long term trend. (b) cyclicity in data. (c) seasonality in data. (d) All of the above. Answer: (a) Arithmetic line graph helps in understanding the trend, periodicity, etc in a long term time series data. Question 5.

Diagrammatic Presentation of Data

Basics of Diagrammatic Presentation

Advantages of Diagrammatic Presentation

Types of One-Dimensional Diagram

Meaning of Pie Diagram

Solved Questions

Leave a Comment Cancel reply

Register with BYJU'S & Download Free PDFs

Suggested Videos

Browse more Topics under Statistical Description Of Data

Construction of a Bar Diagram

Properties of a Bar Diagram

Types of Bar Diagram

Construction of Histogram

Properties of Histogram

Properties of a Line Graph

Solved Examples for diagrammatic Representation of Data

Customize your course in 30 seconds

Statistical Description of Data

Download the App

Diagrammatic Presentation of Data: Bar Diagrams, Pie Charts etc.

Diagrammatic Presentation of Data

Bar Diagrams

Types of Bar Diagrams

Pie or Circular Diagrams

Diagrammatic Presentation Of Data

What is a Diagrammatic Presentation of Data?

Types of Diagrammatic Presentations of Data

Line Diagram

Bar Diagram

Advantages of Diagrammatic Presentation of Data

More attractive

Simpler presentations

Comparison is easier

Universal acceptance

Improvement in presentation

More organized and classified data

Relevance Diagrammatic Presentation of Data

Kickstart Your Career

Graphic Presentation of Data

Cite this chapter

Access this chapter

Author information

Rights and permissions

Copyright information

About this chapter

Download citation

Share this chapter

Margin Size

2: Graphical Representations of Data

Contributors and Attributions

Graphical Representation of Data

Definition of Graphical Representation of Data

Representation of Data

Principles of Graphical Representation of Data

Advantages and Disadvantages of Graphical Representation of Data

Rules of Graphical Representation of Data

Uses of Graphical Representation of Data

Types of Graphical Representation of Data

Related Topics

Examples on Graphical Representation of Data

Practice Questions on Graphical Representation of Data

What are the Different Types of Graphical Representation?

Is the Graphical Representation of Numerical Data?

What is the Use of Graphical Representation of Data?

What are the Ways to Represent Data?

What is the Objective of Graphical Representation of Data?

DIAGRAMMATIC REPRESENTATION OF DATA

Line Diagram

Bar Diagram

Recent Articles

How to Convert Between Polar and Rectangular Coordinates

How to Convert Between Polar and Rectangular Equations

46 Presentation of data II – Graphical representation

Chapter 1: Concept of Economics and Significance of Statistics in Economics

Chapter 2: Collection of Data

Chapter 3: Organisation of Data

Chapter 4: Presentation of Data: Textual and Tabular

Tabular Presentation of Data: Meaning, Objectives, Features and Merits

Chapter 5: Diagrammatic Presentation of Data