- Bihar Board

CFA Institute
Srm university.
- Shiv Khera Special
- Education News
- Web Stories
- Current Affairs
- School & Boards
- College Admission
- Govt Jobs Alert & Prep
- GK & Aptitude
- CBSE Class 10 Study Material
CBSE Class 10 Maths Case Study Questions for Maths Chapter 5 - Arithmetic Progression (Published by CBSE)
Case study questions on cbse class 10 maths chapter 5 - arithmetic progression are provided here. these questions are published by cbse to help students prepare for their maths exam..

CBSE Class 10 Case Study Questions for Maths Chapter 5 - Arithmetic Progression are available here with answers. All the questions have been published by the CBSE board. Students must practice all these questions to prepare themselves for attempting the case study based questions with absolute correctness and obtain a high score in their Maths Exam 2021-22.
Case Study Questions for Class 10 Maths Chapter 5 - Arithmetic Progression
CASE STUDY 1:
India is competitive manufacturing location due to the low cost of manpower and strong technical and engineering capabilities contributing to higher quality production runs. The production of TV sets in a factory increases uniformly by a fixed number every year. It produced 16000 sets in 6th year and 22600 in 9th year.

Based on the above information, answer the following questions:
1. Find the production during first year.
2. Find the production during 8th year.
3. Find the production during first 3 years.
4. In which year, the production is Rs 29,200.
5. Find the difference of the production during 7th year and 4th year.
2. Production during 8th year is (a+7d) = 5000 + 2(2200) = 20400
3. Production during first 3 year = 5000 + 7200 + 9400 = 21600
4. N = 12 5.
Difference = 18200 - 11600 = 6600
CASE STUDY 2:
Your friend Veer wants to participate in a 200m race. He can currently run that distance in 51 seconds and with each day of practice it takes him 2 seconds less. He wants to do in 31 seconds.

1. Which of the following terms are in AP for the given situation
a) 51,53,55….
b) 51, 49, 47….
c) -51, -53, -55….
d) 51, 55, 59…
Answer: b) 51, 49, 47….
2. What is the minimum number of days he needs to practice till his goal is achieved
Answer: c) 11
3. Which of the following term is not in the AP of the above given situation
Answer: b) 30
4. If nth term of an AP is given by an = 2n + 3 then common difference of an AP is
Answer: a) 2
5. The value of x, for which 2x, x+ 10, 3x + 2 are three consecutive terms of an AP
Answer: a) 6
CASE STUDY 3:
Your elder brother wants to buy a car and plans to take loan from a bank for his car. He repays his total loan of Rs 1,18,000 by paying every month starting with the first instalment of Rs 1000. If he increases the instalment by Rs 100 every month , answer the following:

1. The amount paid by him in 30th installment is
Answer: a) 3900
2. The amount paid by him in the 30 installments is
Answer: b) 73500
3. What amount does he still have to pay offer 30th installment?
Answer: c) 44500
4. If total installments are 40 then amount paid in the last installment?
Answer: a) 4900
5. The ratio of the 1st installment to the last installment is
Answer: b) 10:49
Also Check:
CBSE Case Study Questions for Class 10 Maths - All Chapters
Tips to Solve Case Study Based Questions Accurately
Get here latest School , CBSE and Govt Jobs notification in English and Hindi for Sarkari Naukari and Sarkari Result . Download the Jagran Josh Sarkari Naukri App . Check Board Result 2024 for Class 10 and Class 12 like CBSE Board Result , UP Board Result , Bihar Board Result , MP Board Result , Rajasthan Board Result and Other States Boards.
- KTET Hall Ticket 2024
- APSC PRO Admit Card 2024
- BSF SI Recruitment 2024
- Kerala PSC Staff Nurse Answer Key 2024
- IITM RA Recruitment 2024
- IAS Exam Last Minute Tips 2024
- Asaduddin Owaisi vs Madhavi Latha
- Purnia Lok Sabha Election Result 2024
- Vidisha Lok Sabha Election Result 2024
- UPSC CSE Admit Card 2024
- CBSE Study Material
- CBSE Class 10
Latest Education News
Periyar University Result 2024 at periyaruniversity.ac.in; Direct Link to Download UG and PG Marksheet
Speech for World Day Against Child Labour in English
GK Quiz on Microsoft: A Quiz on Microsoft's History and Products
PM Modi Cabinet 2024: मोदी का राजतिलक, नई कैबिनेट में किसे मिला कौन-सा मंत्रालय, यहां देखें पूरी लिस्ट
SSC JE Answer Key 2024: Junior Engineer Response Sheet to Active Soon at ssc.digialm.com
TNPSC Group 4 Question Paper 2024: Download Prelims Unofficial Answer Key Paper PDF for All Sets
UP Board Class 10 Syllabus 2024-25 OUT: Download PDF for Subject-Wise Syllabus
Haryana Board Class 10 Hindi Syllabus 2024-25 with Marking Scheme and Exam Pattern; Download in PDF
साल 2024 में भारत के 10 सबसे अमीर लोगों की सूची, यहां पढ़ें
PSEB Class 9th Syllabus 2024-25: Download New Syllabus PDF
Brain Teaser IQ Test: Only The Smartest 5% Can Replace The Question Mark In 8 Seconds! (Answer Is Not 6)
HPPSC Lecturer Answer Key 2024 Out at ossc.gov.in: Here's Direct Link to Raise Objection
Sequence and Series: Formula, Definition & Concepts
KTET Hall Ticket 2024 OUT at ktet.kerala.gov.in: Download Kerala TET Admit Card Here
World Day Against Child Labour 2024 Thoughts, Slogans and Captions for School Activities
TANCET Counselling 2024 Registration Begins Today at tancet.annauniv.edu; Check Required Documents and Schedule
CBSE Class 11 Syllabus for Board Exam 2024-25: Download PDF
UP Board Class 10 Moral Sports and Physical Education Syllabus 2025: Download UPMSP 10th Moral Sports and Physical Education Syllabus 2024-25 PDF Here
JoSAA Counselling 2024: Open House Schedule Released for JEE Advanced Qualified Candidates
PSEB Class 11 Physical Education and Sports Syllabus 2024-2025: Download in PDF
Case Study Questions Class 10 Maths Arithmetic Progressions
Case study questions class 10 maths chapter 5 arithmetic progressions.
CBSE Class 10 Case Study Questions Maths Arithmetic Progressions. Term 2 Important Case Study Questions for Class 10 Board Exam Students. Here we have arranged some Important Case Base Questions for students who are searching for Paragraph Based Questions Arithmetic Progressions.
CBSE Case Study Questions Class 10 Maths Arithmetic Progressions
Case Study – 1
[ KVS Raipur 2021 – 22 ]
(ii) Find the difference in number of candies placed in 7th and 3rd rows.
(ii) 7th row=3+(7-1)X2 = 3 + 12 = 15 and 3rd row = 3+(3-1) X 2 = 7 their diff.= 8
4.) Find the production during first 3 years.
Leave a Reply Cancel reply
We have a strong team of experienced teachers who are here to solve all your exam preparation doubts, the garden party class 11 long questions for semester 2, the first war of independence class 10 mcq, factors promoting growth of nationalism, foundation of the indian national congress class 10 mcq for icse board students, case study questions class 7 maths unitary method.

Gurukul of Excellence
Classes for Physics, Chemistry and Mathematics by IITians
Join our Telegram Channel for Free PDF Download
Case Study Questions for Class 10 Maths Chapter 5 Arithmetic Progression
- Last modified on: 11 months ago
- Reading Time: 3 Minutes
Question 1:
In a flower bed, there are 43 rose plants in the first row, 41 in the second, 39 in the third and so on.
(i) If there are 11 rose plants in the last row, then number of rose required are (a) 16 (b) 15 (c) 17 (d) 10
(ii) Difference of rose plants in 7th row and 13th row is (a) 11 (b) 12 (c) 13 (d) 14
(iii) If there are x rose plants in 15 rose, then x is equal to (a) 10 (b) 12 (c) 13 (d) 15
(iv) The rose plants in 6th row is (a) 35 (b) 37 (c) 33 (d) 31
(v) The total number of rose plants in 5th and 8th row is (a) 64 (b) 54 (c) 46 (d) 45
✨ Free Quizzes, Test Series and Learning Videos for CBSE Class 10 Maths
You may also like:
Chapter 1 Real Numbers Chapter 2 Polynomials Chapter 3 Pair of Linear Equations in Two Variables C hapter 4 Quadratic Equations Chapter 5 Arithmetic Progressions Chapter 6 Triangles Chapter 7 Coordinate Geometry Chapter 8 Introduction to Trigonometry Chapter 9 Some Applications of Trigonometry Chapter 10 Circles Chapter 11 Constructions Chapter 12 Areas Related to Circles Chapter 13 Surface Areas and Volumes Chapter 14 Statistics Chapter 15 Probability
Download CBSE Books
Exam Special Series:
- Sample Question Paper for CBSE Class 10 Science (for 2024)
- Sample Question Paper for CBSE Class 10 Maths (for 2024)
- CBSE Most Repeated Questions for Class 10 Science Board Exams
- CBSE Important Diagram Based Questions Class 10 Physics Board Exams
- CBSE Important Numericals Class 10 Physics Board Exams
- CBSE Practical Based Questions for Class 10 Science Board Exams
- CBSE Important “Differentiate Between” Based Questions Class 10 Social Science
- Sample Question Papers for CBSE Class 12 Physics (for 2024)
- Sample Question Papers for CBSE Class 12 Chemistry (for 2024)
- Sample Question Papers for CBSE Class 12 Maths (for 2024)
- Sample Question Papers for CBSE Class 12 Biology (for 2024)
- CBSE Important Diagrams & Graphs Asked in Board Exams Class 12 Physics
- Master Organic Conversions CBSE Class 12 Chemistry Board Exams
- CBSE Important Numericals Class 12 Physics Board Exams
- CBSE Important Definitions Class 12 Physics Board Exams
- CBSE Important Laws & Principles Class 12 Physics Board Exams
- 10 Years CBSE Class 12 Chemistry Previous Year-Wise Solved Papers (2023-2024)
- 10 Years CBSE Class 12 Physics Previous Year-Wise Solved Papers (2023-2024)
- 10 Years CBSE Class 12 Maths Previous Year-Wise Solved Papers (2023-2024)
- 10 Years CBSE Class 12 Biology Previous Year-Wise Solved Papers (2023-2024)
- ICSE Important Numericals Class 10 Physics BOARD Exams (215 Numericals)
- ICSE Important Figure Based Questions Class 10 Physics BOARD Exams (230 Questions)
- ICSE Mole Concept and Stoichiometry Numericals Class 10 Chemistry (65 Numericals)
- ICSE Reasoning Based Questions Class 10 Chemistry BOARD Exams (150 Qs)
- ICSE Important Functions and Locations Based Questions Class 10 Biology
- ICSE Reasoning Based Questions Class 10 Biology BOARD Exams (100 Qs)
✨ Join our Online JEE Test Series for 499/- Only (Web + App) for 1 Year
✨ Join our Online NEET Test Series for 499/- Only for 1 Year
Leave a Reply Cancel reply
Join our Online Test Series for CBSE, ICSE, JEE, NEET and Other Exams

Editable Study Materials for Your Institute - CBSE, ICSE, State Boards (Maharashtra & Karnataka), JEE, NEET, FOUNDATION, OLYMPIADS, PPTs
Discover more from Gurukul of Excellence
Subscribe now to keep reading and get access to the full archive.
Type your email…
Continue reading
CBSE Expert
CBSE Class 10 Maths Case Study Questions PDF
Download Case Study Questions for Class 10 Mathematics to prepare for the upcoming CBSE Class 10 Final Exam. These Case Study and Passage Based questions are published by the experts of CBSE Experts for the students of CBSE Class 10 so that they can score 100% on Boards.

CBSE Class 10 Mathematics Exam 2024 will have a set of questions based on case studies in the form of MCQs. The CBSE Class 10 Mathematics Question Bank on Case Studies, provided in this article, can be very helpful to understand the new format of questions. Share this link with your friends.
Table of Contents
Chapterwise Case Study Questions for Class 10 Mathematics
Inboard exams, students will find the questions based on assertion and reasoning. Also, there will be a few questions based on case studies. In that, a paragraph will be given, and then the MCQ questions based on it will be asked.
The above Case studies for Class 10 Maths will help you to boost your scores as Case Study questions have been coming in your examinations. These CBSE Class 10 Mathematics Case Studies have been developed by experienced teachers of cbseexpert.com for the benefit of Class 10 students.
- Class 10th Science Case Study Questions
- Assertion and Reason Questions of Class 10th Science
- Assertion and Reason Questions of Class 10th Social Science
Class 10 Maths Syllabus 2024
Chapter-1 real numbers.
Starting with an introduction to real numbers, properties of real numbers, Euclid’s division lemma, fundamentals of arithmetic, Euclid’s division algorithm, revisiting irrational numbers, revisiting rational numbers and their decimal expansions followed by a bunch of problems for a thorough and better understanding.
Chapter-2 Polynomials
This chapter is quite important and marks securing topics in the syllabus. As this chapter is repeated almost every year, students find this a very easy and simple subject to understand. Topics like the geometrical meaning of the zeroes of a polynomial, the relationship between zeroes and coefficients of a polynomial, division algorithm for polynomials followed with exercises and solved examples for thorough understanding.
Chapter-3 Pair of Linear Equations in Two Variables
This chapter is very intriguing and the topics covered here are explained very clearly and perfectly using examples and exercises for each topic. Starting with the introduction, pair of linear equations in two variables, graphical method of solution of a pair of linear equations, algebraic methods of solving a pair of linear equations, substitution method, elimination method, cross-multiplication method, equations reducible to a pair of linear equations in two variables, etc are a few topics that are discussed in this chapter.
Chapter-4 Quadratic Equations
The Quadratic Equations chapter is a very important and high priority subject in terms of examination, and securing as well as the problems are very simple and easy. Problems like finding the value of X from a given equation, comparing and solving two equations to find X, Y values, proving the given equation is quadratic or not by knowing the highest power, from the given statement deriving the required quadratic equation, etc are few topics covered in this chapter and also an ample set of problems are provided for better practice purposes.
Chapter-5 Arithmetic Progressions
This chapter is another interesting and simpler topic where the problems here are mostly based on a single formula and the rest are derivations of the original one. Beginning with a basic brief introduction, definitions of arithmetic progressions, nth term of an AP, the sum of first n terms of an AP are a few important and priority topics covered under this chapter. Apart from that, there are many problems and exercises followed with each topic for good understanding.
Chapter-6 Triangles
This chapter Triangle is an interesting and easy chapter and students often like this very much and a securing unit as well. Here beginning with the introduction to triangles followed by other topics like similar figures, the similarity of triangles, criteria for similarity of triangles, areas of similar triangles, Pythagoras theorem, along with a page summary for revision purposes are discussed in this chapter with examples and exercises for practice purposes.
Chapter-7 Coordinate Geometry
Here starting with a general introduction, distance formula, section formula, area of the triangle are a few topics covered in this chapter followed with examples and exercises for better and thorough practice purposes.
Chapter-8 Introduction to Trigonometry
As trigonometry is a very important and vast subject, this topic is divided into two parts where one chapter is Introduction to Trigonometry and another part is Applications of Trigonometry. This Introduction to Trigonometry chapter is started with a general introduction, trigonometric ratios, trigonometric ratios of some specific angles, trigonometric ratios of complementary angles, trigonometric identities, etc are a few important topics covered in this chapter.
Chapter-9 Applications of Trigonometry
This chapter is the continuation of the previous chapter, where the various modeled applications are discussed here with examples and exercises for better understanding. Topics like heights and distances are covered here and at the end, a summary is provided with all the important and frequently used formulas used in this chapter for solving the problems.
Chapter-10 Circle
Beginning with the introduction to circles, tangent to a circle, several tangents from a point on a circle are some of the important topics covered in this chapter. This chapter being practical, there are an ample number of problems and solved examples for better understanding and practice purposes.
Chapter-11 Constructions
This chapter has more practical problems than theory-based definitions. Beginning with a general introduction to constructions, tools used, etc, the topics like division of a line segment, construction of tangents to a circle, and followed with few solved examples that help in solving the exercises provided after each topic.
Chapter-12 Areas related to Circles
This chapter problem is exclusively formula based wherein topics like perimeter and area of a circle- A Review, areas of sector and segment of a circle, areas of combinations of plane figures, and a page summary is provided just as a revision of the topics and formulas covered in the entire chapter and also there are many exercises and solved examples for practice purposes.
Chapter-13 Surface Areas and Volumes
Starting with the introduction, the surface area of a combination of solids, the volume of a combination of solids, conversion of solid from one shape to another, frustum of a cone, etc are to name a few topics explained in detail provided with a set of examples for a better comprehension of the concepts.
Chapter-14 Statistics
In this chapter starting with an introduction, topics like mean of grouped data, mode of grouped data, a median of grouped, graphical representation of cumulative frequency distribution are explained in detail with exercises for practice purposes. This chapter being a simple and easy subject, securing the marks is not difficult for students.
Chapter-15 Probability
Probability is another simple and important chapter in examination point of view and as seeking knowledge purposes as well. Beginning with an introduction to probability, an important topic called A theoretical approach is explained here. Since this chapter is one of the smallest in the syllabus and problems are also quite easy, students often like this chapter
Leave a Comment Cancel reply
Save my name, email, and website in this browser for the next time I comment.
Download India's best Exam Preparation App Now.
Key Features
- Revision Notes
- Important Questions
- Previous Years Questions
- Case-Based Questions
- Assertion and Reason Questions
No thanks, I’m not interested!
- Class 6 Maths
- Class 6 Science
- Class 6 Social Science
- Class 6 English
- Class 7 Maths
- Class 7 Science
- Class 7 Social Science
- Class 7 English
- Class 8 Maths
- Class 8 Science
- Class 8 Social Science
- Class 8 English
- Class 9 Maths
- Class 9 Science
- Class 9 Social Science
- Class 9 English
- Class 10 Maths
- Class 10 Science
- Class 10 Social Science
- Class 10 English
- Class 11 Maths
- Class 11 Computer Science (Python)
- Class 11 English
- Class 12 Maths
- Class 12 English
- Class 12 Economics
- Class 12 Accountancy
- Class 12 Physics
- Class 12 Chemistry
- Class 12 Biology
- Class 12 Computer Science (Python)
- Class 12 Physical Education
- GST and Accounting Course
- Excel Course
- Tally Course
- Finance and CMA Data Course
- Payroll Course
Interesting
- Learn English
- Learn Excel
- Learn Tally
- Learn GST (Goods and Services Tax)
- Learn Accounting and Finance
- GST Tax Invoice Format
- Accounts Tax Practical
- Tally Ledger List
- GSTR 2A - JSON to Excel
Are you in school ? Do you love Teachoo?
We would love to talk to you! Please fill this form so that we can contact you
You are learning...
Chapter 5 Class 10 Arithmetic Progressions
Click on any of the links below to start learning from Teachoo ...
Updated for new NCERT Book - 2023-24 Edition
Get solutions of all NCERT Questions with examples of Chapter 5 Class 10 Arithmetic Progressions (AP). Video of all questions are also available.
In this chapter, we will learn
- What is an AP - and what is First term (a) and Common Difference (d) of an Arithmetic Progression
- Finding n th term of an AP (a n )
- Finding n using a n formula
- Finding AP when some terms are given
- Finding n th term from the last term
- Finding Sum of n terms of an AP ( S n ) - both formulas
- Finding number of terms when Sum is given
- If n th term is given, finding S
- Some statement questions using a n and S n formulas, including optional exercise
Check out the answers to the exercises (including examples and optional) by clicking a link below, or learn from the concepts.
Serial order wise
Concept wise.
What's in it?
Hi, it looks like you're using AdBlock :(
Please login to view more pages. it's free :), solve all your doubts with teachoo black.

- Andhra Pradesh
- Chhattisgarh
- West Bengal
- Madhya Pradesh
- Maharashtra
- Jammu & Kashmir
- NCERT Books 2022-23
- NCERT Solutions
- NCERT Notes
- NCERT Exemplar Books
- NCERT Exemplar Solution
- States UT Book
- School Kits & Lab Manual
- NCERT Books 2021-22
- NCERT Books 2020-21
- NCERT Book 2019-2020
- NCERT Book 2015-2016
- RD Sharma Solution
- TS Grewal Solution
- TR Jain Solution
- Selina Solution
- Frank Solution
- Lakhmir Singh and Manjit Kaur Solution
- I.E.Irodov solutions
- ICSE - Goyal Brothers Park
- ICSE - Dorothy M. Noronhe
- Sandeep Garg Textbook Solution
- Micheal Vaz Solution
- S.S. Krotov Solution
- Evergreen Science
- KC Sinha Solution
- ICSE - ISC Jayanti Sengupta, Oxford
- ICSE Focus on History
- ICSE GeoGraphy Voyage
- ICSE Hindi Solution
- ICSE Treasure Trove Solution
- Thomas & Finney Solution
- SL Loney Solution
- SB Mathur Solution
- P Bahadur Solution
- Narendra Awasthi Solution
- MS Chauhan Solution
- LA Sena Solution
- Integral Calculus Amit Agarwal Solution
- IA Maron Solution
- Hall & Knight Solution
- Errorless Solution
- Pradeep's KL Gogia Solution
- OP Tandon Solutions
- Sample Papers
- Previous Year Question Paper
- Value Based Questions
- CBSE Syllabus
- CBSE MCQs PDF
- Assertion & Reason
- New Revision Notes
- Revision Notes
- HOTS Question
- Marks Wise Question
- Toppers Answer Sheets
- Exam Paper Aalysis
- Concept Map
- CBSE Text Book
- Additional Practice Questions
- Vocational Book
- CBSE - Concept
- KVS NCERT CBSE Worksheets
- Formula Class Wise
- Formula Chapter Wise
- JEE Crash Course
- JEE Previous Year Paper
- Important Info
- JEE Mock Test
- JEE Sample Papers
- SRM-JEEE Mock Test
- VITEEE Mock Test
- BITSAT Mock Test
- Manipal Engineering Mock Test
- AP EAMCET Previous Year Paper
- COMEDK Previous Year Paper
- GUJCET Previous Year Paper
- KCET Previous Year Paper
- KEAM Previous Year Paper
- Manipal Previous Year Paper
- MHT CET Previous Year Paper
- WBJEE Previous Year Paper
- AMU Previous Year Paper
- TS EAMCET Previous Year Paper
- SRM-JEEE Previous Year Paper
- VITEEE Previous Year Paper
- BITSAT Previous Year Paper
- UPSEE Previous Year Paper
- CGPET Previous Year Paper
- CUSAT Previous Year Paper
- AEEE Previous Year Paper
- Crash Course
- Previous Year Paper
- NCERT Based Short Notes
- NCERT Based Tests
- NEET Sample Paper
- Previous Year Papers
- Quantitative Aptitude
- Numerical Aptitude Data Interpretation
- General Knowledge
- Mathematics
- Agriculture
- Accountancy
- Business Studies
- Political science
- Enviromental Studies
- Mass Media Communication
- Teaching Aptitude
- NAVODAYA VIDYALAYA
- SAINIK SCHOOL (AISSEE)
- Mechanical Engineering
- Electrical Engineering
- Electronics & Communication Engineering
- Civil Engineering
- Computer Science Engineering
- CBSE Board News
- Scholarship Olympiad
- School Admissions
- Entrance Exams
- All Board Updates
- Miscellaneous
- State Wise Books
- Engineering Exam
Case Study on Arithmetic Progressions Class 10 Maths PDF
The passage-based questions are commonly known as case study questions. Students looking for Case Study on Arithmetic Progressions Class 10 Maths can use this page to download the PDF file.
The case study questions on Arithmetic Progressions are based on the CBSE Class 10 Maths Syllabus, and therefore, referring to the Arithmetic Progressions case study questions enable students to gain the appropriate knowledge and prepare better for the Class 10 Maths board examination. Continue reading to know how should students answer it and why it is essential to solve it, etc.
Case Study on Arithmetic Progressions Class 10 Maths with Solutions in PDF
Our experts have also kept in mind the challenges students may face while solving the case study on Arithmetic Progressions, therefore, they prepared a set of solutions along with the case study questions on Arithmetic Progressions.
The case study on Arithmetic Progressions Class 10 Maths with solutions in PDF helps students tackle questions that appear confusing or difficult to answer. The answers to the Arithmetic Progressions case study questions are very easy to grasp from the PDF - download links are given on this page.
Why Solve Arithmetic Progressions Case Study Questions on Class 10 Maths?
There are three major reasons why one should solve Arithmetic Progressions case study questions on Class 10 Maths - all those major reasons are discussed below:
- To Prepare for the Board Examination: For many years CBSE board is asking case-based questions to the Class 10 Maths students, therefore, it is important to solve Arithmetic Progressions Case study questions as it will help better prepare for the Class 10 board exam preparation.
- Develop Problem-Solving Skills: Class 10 Maths Arithmetic Progressions case study questions require students to analyze a given situation, identify the key issues, and apply relevant concepts to find out a solution. This can help CBSE Class 10 students develop their problem-solving skills, which are essential for success in any profession rather than Class 10 board exam preparation.
- Understand Real-Life Applications: Several Arithmetic Progressions Class 10 Maths Case Study questions are linked with real-life applications, therefore, solving them enables students to gain the theoretical knowledge of Arithmetic Progressions as well as real-life implications of those learnings too.
How to Answer Case Study Questions on Arithmetic Progressions?
Students can choose their own way to answer Case Study on Arithmetic Progressions Class 10 Maths, however, we believe following these three steps would help a lot in answering Class 10 Maths Arithmetic Progressions Case Study questions.
- Read Question Properly: Many make mistakes in the first step which is not reading the questions properly, therefore, it is important to read the question properly and answer questions accordingly.
- Highlight Important Points Discussed in the Clause: While reading the paragraph, highlight the important points discussed as it will help you save your time and answer Arithmetic Progressions questions quickly.
- Go Through Each Question One-By-One: Ideally, going through each question gradually is advised so, that a sync between each question and the answer can be maintained. When you are solving Arithmetic Progressions Class 10 Maths case study questions make sure you are approaching each question in a step-wise manner.
What to Know to Solve Case Study Questions on Class 10 Arithmetic Progressions?
A few essential things to know to solve Case Study Questions on Class 10 Arithmetic Progressions are -
- Basic Formulas of Arithmetic Progressions: One of the most important things to know to solve Case Study Questions on Class 10 Arithmetic Progressions is to learn about the basic formulas or revise them before solving the case-based questions on Arithmetic Progressions.
- To Think Analytically: Analytical thinkers have the ability to detect patterns and that is why it is an essential skill to learn to solve the CBSE Class 10 Maths Arithmetic Progressions case study questions.
- Strong Command of Calculations: Another important thing to do is to build a strong command of calculations especially, mental Maths calculations.
Where to Find Case Study on Arithmetic Progressions Class 10 Maths?
Use Selfstudys.com to find Case Study on Arithmetic Progressions Class 10 Maths. For ease, here is a step-wise procedure to download the Arithmetic Progressions Case Study for Class 10 Maths in PDF for free of cost.
Since you are already on this page, you can scroll to the top section of this page to get access to the Case Study on Arithmetic Progressions. To help others reach this page let them know these steps:
- Open Selfstudys.com on your computer/laptop or Smartphone
- Once the website gets loaded, click on the navigation button
- Find CBSE from the given menu
- Click on Case Study
- Choose Class 10
- Search Maths and then navigate to the Arithmetic Progressions Class 10 Maths Case Study
- NCERT Solutions for Class 12 Maths
- NCERT Solutions for Class 10 Maths
- CBSE Syllabus 2023-24
- Social Media Channels
- Login Customize Your Notification Preferences

One Last Step...

- Second click on the toggle icon

Provide prime members with unlimited access to all study materials in PDF format.
Allow prime members to attempt MCQ tests multiple times to enhance their learning and understanding.
Provide prime users with access to exclusive PDF study materials that are not available to regular users.

myCBSEguide
- Mathematics
- Case Study Class 10...
Case Study Class 10 Maths Questions
Table of Contents
myCBSEguide App
Download the app to get CBSE Sample Papers 2023-24, NCERT Solutions (Revised), Most Important Questions, Previous Year Question Bank, Mock Tests, and Detailed Notes.
Now, CBSE will ask only subjective questions in class 10 Maths case studies. But if you search over the internet or even check many books, you will get only MCQs in the class 10 Maths case study in the session 2022-23. It is not the correct pattern. Just beware of such misleading websites and books.
We advise you to visit CBSE official website ( cbseacademic.nic.in ) and go through class 10 model question papers . You will find that CBSE is asking only subjective questions under case study in class 10 Maths. We at myCBSEguide helping CBSE students for the past 15 years and are committed to providing the most authentic study material to our students.
Here, myCBSEguide is the only application that has the most relevant and updated study material for CBSE students as per the official curriculum document 2022 – 2023. You can download updated sample papers for class 10 maths .
First of all, we would like to clarify that class 10 maths case study questions are subjective and CBSE will not ask multiple-choice questions in case studies. So, you must download the myCBSEguide app to get updated model question papers having new pattern subjective case study questions for class 10 the mathematics year 2022-23.
Class 10 Maths has the following chapters.
- Real Numbers Case Study Question
- Polynomials Case Study Question
- Pair of Linear Equations in Two Variables Case Study Question
- Quadratic Equations Case Study Question
- Arithmetic Progressions Case Study Question
- Triangles Case Study Question
- Coordinate Geometry Case Study Question
- Introduction to Trigonometry Case Study Question
- Some Applications of Trigonometry Case Study Question
- Circles Case Study Question
- Area Related to Circles Case Study Question
- Surface Areas and Volumes Case Study Question
- Statistics Case Study Question
- Probability Case Study Question
Format of Maths Case-Based Questions
CBSE Class 10 Maths Case Study Questions will have one passage and four questions. As you know, CBSE has introduced Case Study Questions in class 10 and class 12 this year, the annual examination will have case-based questions in almost all major subjects. This article will help you to find sample questions based on case studies and model question papers for CBSE class 10 Board Exams.
Maths Case Study Question Paper 2023
Here is the marks distribution of the CBSE class 10 maths board exam question paper. CBSE may ask case study questions from any of the following chapters. However, Mensuration, statistics, probability and Algebra are some important chapters in this regard.
| I | NUMBER SYSTEMS | 06 |
| II | ALGEBRA | 20 |
| III | COORDINATE GEOMETRY | 06 |
| IV | GEOMETRY | 15 |
| V | TRIGONOMETRY | 12 |
| V | MENSURATION | 10 |
| VI | STATISTICS & PROBABILITY | 11 |
Case Study Question in Mathematics
Here are some examples of case study-based questions for class 10 Mathematics. To get more questions and model question papers for the 2021 examination, download myCBSEguide Mobile App .
Case Study Question – 1
In the month of April to June 2022, the exports of passenger cars from India increased by 26% in the corresponding quarter of 2021–22, as per a report. A car manufacturing company planned to produce 1800 cars in 4th year and 2600 cars in 8th year. Assuming that the production increases uniformly by a fixed number every year.
- Find the production in the 1 st year.
- Find the production in the 12 th year.
- Find the total production in first 10 years. OR In which year the total production will reach to 15000 cars?
Case Study Question – 2
In a GPS, The lines that run east-west are known as lines of latitude, and the lines running north-south are known as lines of longitude. The latitude and the longitude of a place are its coordinates and the distance formula is used to find the distance between two places. The distance between two parallel lines is approximately 150 km. A family from Uttar Pradesh planned a round trip from Lucknow (L) to Puri (P) via Bhuj (B) and Nashik (N) as shown in the given figure below.
- Find the distance between Lucknow (L) to Bhuj(B).
- If Kota (K), internally divide the line segment joining Lucknow (L) to Bhuj (B) into 3 : 2 then find the coordinate of Kota (K).
- Name the type of triangle formed by the places Lucknow (L), Nashik (N) and Puri (P) OR Find a place (point) on the longitude (y-axis) which is equidistant from the points Lucknow (L) and Puri (P).
Case Study Question – 3
- Find the distance PA.
- Find the distance PB
- Find the width AB of the river. OR Find the height BQ if the angle of the elevation from P to Q be 30 o .
Case Study Question – 4
- What is the length of the line segment joining points B and F?
- The centre ‘Z’ of the figure will be the point of intersection of the diagonals of quadrilateral WXOP. Then what are the coordinates of Z?
- What are the coordinates of the point on y axis equidistant from A and G? OR What is the area of area of Trapezium AFGH?
Case Study Question – 5
The school auditorium was to be constructed to accommodate at least 1500 people. The chairs are to be placed in concentric circular arrangement in such a way that each succeeding circular row has 10 seats more than the previous one.
- If the first circular row has 30 seats, how many seats will be there in the 10th row?
- For 1500 seats in the auditorium, how many rows need to be there? OR If 1500 seats are to be arranged in the auditorium, how many seats are still left to be put after 10 th row?
- If there were 17 rows in the auditorium, how many seats will be there in the middle row?
Case Study Question – 6
- Draw a neat labelled figure to show the above situation diagrammatically.
- What is the speed of the plane in km/hr.
More Case Study Questions
We have class 10 maths case study questions in every chapter. You can download them as PDFs from the myCBSEguide App or from our free student dashboard .
As you know CBSE has reduced the syllabus this year, you should be careful while downloading these case study questions from the internet. You may get outdated or irrelevant questions there. It will not only be a waste of time but also lead to confusion.
Here, myCBSEguide is the most authentic learning app for CBSE students that is providing you up to date study material. You can download the myCBSEguide app and get access to 100+ case study questions for class 10 Maths.
How to Solve Case-Based Questions?
Questions based on a given case study are normally taken from real-life situations. These are certainly related to the concepts provided in the textbook but the plot of the question is always based on a day-to-day life problem. There will be all subjective-type questions in the case study. You should answer the case-based questions to the point.
What are Class 10 competency-based questions?
Competency-based questions are questions that are based on real-life situations. Case study questions are a type of competency-based questions. There may be multiple ways to assess the competencies. The case study is assumed to be one of the best methods to evaluate competencies. In class 10 maths, you will find 1-2 case study questions. We advise you to read the passage carefully before answering the questions.
Case Study Questions in Maths Question Paper
CBSE has released new model question papers for annual examinations. myCBSEguide App has also created many model papers based on the new format (reduced syllabus) for the current session and uploaded them to myCBSEguide App. We advise all the students to download the myCBSEguide app and practice case study questions for class 10 maths as much as possible.
Case Studies on CBSE’s Official Website
CBSE has uploaded many case study questions on class 10 maths. You can download them from CBSE Official Website for free. Here you will find around 40-50 case study questions in PDF format for CBSE 10th class.
10 Maths Case Studies in myCBSEguide App
You can also download chapter-wise case study questions for class 10 maths from the myCBSEguide app. These class 10 case-based questions are prepared by our team of expert teachers. We have kept the new reduced syllabus in mind while creating these case-based questions. So, you will get the updated questions only.
Test Generator
Create question paper PDF and online tests with your own name & logo in minutes.
Question Bank, Mock Tests, Exam Papers, NCERT Solutions, Sample Papers, Notes
Related Posts
- CBSE Class 10 Maths Sample Paper 2020-21
- Class 12 Maths Case Study Questions
- CBSE Reduced Syllabus Class 10 (2020-21)
- Class 10 Maths Basic Sample Paper 2024
- How to Revise CBSE Class 10 Maths in 3 Days
- CBSE Practice Papers 2023
- Class 10 Maths Sample Papers 2024
- Competency Based Learning in CBSE Schools
Leave a Comment
Save my name, email, and website in this browser for the next time I comment.
- New QB365-SLMS
- NEET Materials
- JEE Materials
- Banking first yr Materials
- TNPSC Materials
- DIPLOMA COURSE Materials
- 5th Standard Materials
- 1st Standard - CVBHSS Materials
- 2nd Standard - CVBHSS Materials
- 3rd Standard - CVBHSS Materials
- 4th Standard - CVBHSS Materials
- 5th Standard - CVBHSS Materials
- 12th Standard Materials
- 11th Standard Materials
- 10th Standard Materials
- 9th Standard Materials
- 8th Standard Materials
- 7th Standard Materials
- 6th Standard Materials
- 12th Standard CBSE Materials
- 11th Standard CBSE Materials
- 10th Standard CBSE Materials
- 9th Standard CBSE Materials
- 8th Standard CBSE Materials
- 7th Standard CBSE Materials
- 6th Standard CBSE Materials
- Tamilnadu Stateboard
- Scholarship Exams
- Scholarships

CBSE 10th Standard Maths Subject Case Study Questions with Solutions
By QB365 on 20 May, 2021
QB365 Provides the updated CASE Study Questions for Class 10 , and also provide the detail solution for each and every case study questions . Case study questions are latest updated question pattern from NCERT, QB365 will helps to get more marks in Exams
Related 10th Standard CBSE Maths Materials
10th standard cbse syllabus & materials, cbse 10th social science the making of a global world chapter case study question with answers, cbse 10th social science nationalism in india chapter case study question with answers, cbse 10th social science the rise of nationalism in europe chapter case study question with answers, cbse 10th science metals and non metals chapter case study question with answers, cbse 10th science acids, bases and salts chapter case study question with answers, cbse 10th science chemical reactions and equations chapter case study question with answers, class 10th science - our environment case study questions and answers 2022 - 2023, class 10th science - magnetic effects of electric current case study questions and answers 2022 - 2023, class 10th science - electricity case study questions and answers 2022 - 2023, class 10th science - human eye and the colourful world case study questions and answers 2022 - 2023, class 10th science - light reflection and refraction case study questions and answers 2022 - 2023, class 10th science - heredity and evolution case study questions and answers 2022 - 2023, class 10th science - how do organisms reproduce case study questions and answers 2022 - 2023, class 10th science - life processes case study questions and answers 2022 - 2023, class 10th science - periodic classification of elements case study questions and answers 2022 - 2023.


Class VI to XII
Tn state board / cbse, 3000+ q&a's per subject, score high marks.

10th Standard CBSE Study Materials

10th Standard CBSE Subjects
- NCERT Solutions
- NCERT Solutions for Class 10
- NCERT Solutions for Class 10 Maths
- Chapter 5 Arithmetic Progressions
NCERT Solutions For Class 10 Maths Chapter 5 Arithmetic Progressions
Ncert solutions for class 10 maths chapter 5 – cbse free pdf download.
NCERT Solutions for Class 10 Maths Chapter 5 Arithmetic Progression is presented here for the benefit of the students preparing for the CBSE Class 10 Maths examination. It is very important for the students to get well versed with these solutions of NCERT to get a good score in the Class 10 examination. These NCERT problems are solved by the experts at BYJU’S. These solutions will help you understand and master different types of questions on arithmetic progressions. NCERT Solutions help you to attain perfection in solving different kinds of questions.
Download Exclusively Curated Chapter Notes for Class 10 Maths Chapter – 5 Arithmetic Progressions
Download most important questions for class 10 maths chapter – 5 arithmetic progressions.
- Chapter 1 Real Numbers
- Chapter 2 Polynomials
- Chapter 3 Pair of Linear Equations in Two Variables
- Chapter 4 Quadratic Equations
- Chapter 6 Triangles
- Chapter 7 Coordinate Geometry
- Chapter 8 Introduction to Trigonometry
- Chapter 9 Some Applications of Trigonometry
- Chapter 10 Circles
- Chapter 11 Constructions
- Chapter 12 Areas Related to Circles
- Chapter 13 Surface Areas and Volumes
- Chapter 14 Statistics
- Chapter 15 Probability
- Exercise 5.1
- Exercise 5.2
- Exercise 5.3
- Exercise 5.4
NCERT solutions for Class 10 Maths chapter 5 Arithmetic Progression
carouselExampleControls112

Previous Next
Access Answers of Maths NCERT solutions for Class 10 Chapter 5 – Arithmetic Progressions
Exercise 5.1 page: 99.
1. In which of the following situations, does the list of numbers involved make as arithmetic progression and why?
(i) The taxi fare after each km when the fare is Rs 15 for the first km and Rs 8 for each additional km.
We can write the given condition as;
Taxi fare for 1 km = 15
Taxi fare for first 2 kms = 15+8 = 23
Taxi fare for first 3 kms = 23+8 = 31
Taxi fare for first 4 kms = 31+8 = 39
And so on……
Thus, 15, 23, 31, 39 … forms an A.P. because every next term is 8 more than the preceding term.
(ii) The amount of air present in a cylinder when a vacuum pump removes 1/4 of the air remaining in the cylinder at a time.
Let the volume of air in a cylinder, initially, be V litres.
In each stroke, the vacuum pump removes 1/4th of air remaining in the cylinder at a time. Or we can say, after every stroke, 1-1/4 = 3/4th part of air will remain.
Therefore, volumes will be V , 3 V /4 , (3 V /4) 2 , (3 V /4) 3 …and so on
Clearly, we can see here, the adjacent terms of this series do not have the common difference between them. Therefore, this series is not an A.P.
(iii) The cost of digging a well after every metre of digging, when it costs Rs 150 for the first metre and rises by Rs 50 for each subsequent metre.
Cost of digging a well for first metre = Rs.150
Cost of digging a well for first 2 metres = Rs.150+50 = Rs.200
Cost of digging a well for first 3 metres = Rs.200+50 = Rs.250
Cost of digging a well for first 4 metres =Rs.250+50 = Rs.300
And so on..
Clearly, 150, 200, 250, 300 … forms an A.P. with a common difference of 50 between each term.
(iv) The amount of money in the account every year, when Rs 10000 is deposited at compound interest at 8% per annum.
We know that if Rs. P is deposited at r % compound interest per annum for n years, the amount of money will be:
P(1+r/100) n
Therefore, after each year, the amount of money will be;
10000(1+8/100), 10000(1+8/100) 2 , 10000(1+8/100) 3 ……
Clearly, the terms of this series do not have the common difference between them. Therefore, this is not an A.P.
2. Write first four terms of the A.P. when the first term a and the common difference are given as follows :
(i) a = 10, d = 10 (ii) a = -2, d = 0 (iii) a = 4, d = – 3 (iv) a = -1 d = 1/2 (v) a = – 1.25, d = – 0.25
(i) a = 10, d = 10
Let us consider, the Arithmetic Progression series be a 1 , a 2 , a 3 , a 4 , a 5 …
a 1 = a = 10
a 2 = a 1 + d = 10+10 = 20
a 3 = a 2 + d = 20+10 = 30
a 4 = a 3 + d = 30+10 = 40
a 5 = a 4 + d = 40+10 = 50
Therefore, the A.P. series will be 10, 20, 30, 40, 50 …
And First four terms of this A.P. will be 10, 20, 30, and 40.
(ii) a = – 2, d = 0
a 1 = a = -2
a 2 = a 1 + d = – 2+0 = – 2
a 3 = a 2 +d = – 2+0 = – 2
a 4 = a 3 + d = – 2+0 = – 2
Therefore, the A.P. series will be – 2, – 2, – 2, – 2 …
And, First four terms of this A.P. will be – 2, – 2, – 2 and – 2.
(iii) a = 4, d = – 3
a 1 = a = 4
a 2 = a 1 + d = 4-3 = 1
a 3 = a 2 + d = 1-3 = – 2
a 4 = a 3 + d = -2-3 = – 5
Therefore, the A.P. series will be 4, 1, – 2 – 5 …
And, first four terms of this A.P. will be 4, 1, – 2 and – 5.
(iv) a = – 1, d = 1/2
a 2 = a 1 + d = -1+1/2 = -1/2
a 3 = a 2 + d = -1/2+1/2 = 0
a 4 = a 3 + d = 0+1/2 = 1/2
Thus, the A.P. series will be-1, -1/2, 0, 1/2
And First four terms of this A.P. will be -1, -1/2, 0 and 1/2.
(v) a = – 1.25, d = – 0.25
a 1 = a = – 1.25
a 2 = a 1 + d = – 1.25-0.25 = – 1.50
a 3 = a 2 + d = – 1.50-0.25 = – 1.75
a 4 = a 3 + d = – 1.75-0.25 = – 2.00
Therefore, the A.P series will be 1.25, – 1.50, – 1.75, – 2.00 ……..
And first four terms of this A.P. will be – 1.25, – 1.50, – 1.75 and – 2.00.
3. For the following A.P.s, write the first term and the common difference. (i) 3, 1, – 1, – 3 … (ii) -5, – 1, 3, 7 … (iii) 1/3, 5/3, 9/3, 13/3 …. (iv) 0.6, 1.7, 2.8, 3.9 …
(i) Given series,
3, 1, – 1, – 3 …
First term, a = 3
Common difference, d = Second term – First term
⇒ 1 – 3 = -2
(ii) Given series, – 5, – 1, 3, 7 …
First term, a = -5
⇒ ( – 1)-( – 5) = – 1+5 = 4
(iii) Given series, 1/3, 5/3, 9/3, 13/3 ….
First term, a = 1/3
⇒ 5/3 – 1/3 = 4/3
(iv) Given series, 0.6, 1.7, 2.8, 3.9 …
First term, a = 0.6
⇒ 1.7 – 0.6
4. Which of the following are APs? If they form an A.P. find the common difference d and write three more terms.
(i) 2, 4, 8, 16 … (ii) 2, 5/2, 3, 7/2 …. (iii) -1.2, -3.2, -5.2, -7.2 … (iv) -10, – 6, – 2, 2 … (v) 3, 3 + √2, 3 + 2√2, 3 + 3√2 (vi) 0.2, 0.22, 0.222, 0.2222 …. (vii) 0, – 4, – 8, – 12 … (viii) -1/2, -1/2, -1/2, -1/2 …. (ix) 1, 3, 9, 27 … (x) a , 2 a , 3 a , 4 a … (xi) a , a 2 , a 3 , a 4 … (xii) √2, √8, √18, √32 … (xiii) √3, √6, √9, √12 … (xiv) 1 2 , 3 2 , 5 2 , 7 2 … (xv) 1 2 , 5 2 , 7 2 , 7 3 …
(i) Given to us,
2, 4, 8, 16 …
Here, the common difference is;
a 2 – a 1 = 4 – 2 = 2
a 3 – a 2 = 8 – 4 = 4
a 4 – a 3 = 16 – 8 = 8
Since, a n +1 – a n or the common difference is not the same every time.
Therefore, the given series are not forming an A.P.
(ii) Given, 2, 5/2, 3, 7/2 ….
a 2 – a 1 = 5/2-2 = 1/2
a 3 – a 2 = 3-5/2 = 1/2
a 4 – a 3 = 7/2-3 = 1/2
Since, a n +1 – a n or the common difference is same every time.
Therefore, d = 1/2 and the given series are in A.P.
The next three terms are;
a 5 = 7/2+1/2 = 4
a 6 = 4 +1/2 = 9/2
a 7 = 9/2 +1/2 = 5
(iii) Given, -1.2, – 3.2, -5.2, -7.2 …
a 2 – a 1 = (-3.2)-(-1.2) = -2
a 3 – a 2 = (-5.2)-(-3.2) = -2
a 4 – a 3 = (-7.2)-(-5.2) = -2
Since, a n +1 – a n or common difference is same every time.
Therefore, d = -2 and the given series are in A.P.
Hence, next three terms are;
a 5 = – 7.2-2 = -9.2
a 6 = – 9.2-2 = – 11.2
a 7 = – 11.2-2 = – 13.2
(iv) Given, -10, – 6, – 2, 2 … Here, the terms and their difference are;
a 2 – a 1 = (-6)-(-10) = 4
a 3 – a 2 = (-2)-(-6) = 4
a 4 – a 3 = (2 -(-2) = 4
Since, a n +1 – a n or the common difference is same every time.
Therefore, d = 4 and the given numbers are in A.P.
a 5 = 2+4 = 6
a 6 = 6+4 = 10
a 7 = 10+4 = 14
(v) Given, 3, 3+√2, 3+2√2, 3+3√2 Here,
a 2 – a 1 = 3+√2-3 = √2
a 3 – a 2 = (3+2√2)-(3+√2) = √2
a 4 – a 3 = (3+3√2) – (3+2√2) = √2
Therefore, d = √2 and the given series forms a A.P.
a 5 = (3+√2) +√2 = 3+4√2
a 6 = (3+4√2)+√2 = 3+5√2
a 7 = (3+5√2)+√2 = 3+6√2
(vi) 0.2, 0.22, 0.222, 0.2222 …. Here,
a 2 – a 1 = 0.22-0.2 = 0.02
a 3 – a 2 = 0.222-0.22 = 0.002
a 4 – a 3 = 0.2222-0.222 = 0.0002
Since, a n +1 – a n or the common difference is not same every time.
Therefore, and the given series doesn’t forms a A.P.
(vii) 0, -4, -8, -12 … Here,
a 2 – a 1 = (-4)-0 = -4
a 3 – a 2 = (-8)-(-4) = -4
a 4 – a 3 = (-12)-(-8) = -4
Therefore, d = -4 and the given series forms a A.P.
a 5 = -12-4 = -16
a 6 = -16-4 = -20
a 7 = -20-4 = -24
(viii) -1/2, -1/2, -1/2, -1/2 …. Here,
a 2 – a 1 = (-1/2) – (-1/2) = 0
a 3 – a 2 = (-1/2) – (-1/2) = 0
a 4 – a 3 = (-1/2) – (-1/2) = 0
Therefore, d = 0 and the given series forms a A.P.
a 5 = (-1/2)-0 = -1/2
a 6 = (-1/2)-0 = -1/2
a 7 = (-1/2)-0 = -1/2
(ix) 1, 3, 9, 27 … Here,
a 2 – a 1 = 3-1 = 2
a 3 – a 2 = 9-3 = 6
a 4 – a 3 = 27-9 = 18
Therefore, and the given series doesn’t form a A.P.
(x) a , 2 a , 3 a , 4 a …
a 2 – a 1 = 2 a – a = a
a 3 – a 2 = 3 a -2 a = a
a 4 – a 3 = 4 a -3 a = a
Therefore, d = a and the given series forms a A.P.
a 5 = 4 a + a = 5 a
a 6 = 5 a + a = 6 a
a 7 = 6 a + a = 7 a
(xi) a , a 2 , a 3 , a 4 …
a 2 – a 1 = a 2 – a = a( a -1)
a 3 – a 2 = a 3 – a 2 = a 2 ( a -1)
a 4 – a 3 = a 4 – a 3 = a 3 ( a -1)
Therefore, the given series doesn’t forms a A.P.
(xii) √2, √8, √18, √32 … Here,
a 2 – a 1 = √8-√2 = 2√2-√2 = √2
a 3 – a 2 = √18-√8 = 3√2-2√2 = √2
a 4 – a 3 = 4√2-3√2 = √2
a 5 = √32+√2 = 4√2+√2 = 5√2 = √50
a 6 = 5√2+√2 = 6√2 = √72
a 7 = 6√2+√2 = 7√2 = √98
(xiii) √3, √6, √9, √12 …
a 2 – a 1 = √6-√3 = √3×√2-√3 = √3(√2-1)
a 3 – a 2 = √9-√6 = 3-√6 = √3(√3-√2)
a 4 – a 3 = √12 – √9 = 2√3 – √3×√3 = √3(2-√3)
Therefore, the given series doesn’t form a A.P.
(xiv) 1 2 , 3 2 , 5 2 , 7 2 …
Or, 1, 9, 25, 49 …..
a 2 − a 1 = 9−1 = 8
a 3 − a 2 = 25−9 = 16
a 4 − a 3 = 49−25 = 24
(xv) 1 2 , 5 2 , 7 2 , 73 …
Or 1, 25, 49, 73 …
a 2 − a 1 = 25−1 = 24
a 3 − a 2 = 49−25 = 24
a 4 − a 3 = 73−49 = 24
Therefore, d = 24 and the given series forms a A.P.
a 5 = 73+24 = 97
a 6 = 97+24 = 121
a 7 = 121+24 = 145
Exercise 5.2 Page: 105
1. Fill in the blanks in the following table, given that a is the first term, d the common difference and a n the n th term of the A.P.

(i) Given,
First term, a = 7
Common difference, d = 3
Number of terms, n = 8,
We have to find the nth term, a n = ?
As we know, for an A.P.,
a n = a +( n −1) d
Putting the values,
=> 7+(8 −1) 3
=> 7+(7) 3
=> 7+21 = 28
Hence, a n = 28
(ii) Given,
First term, a = -18
Common difference, d = ?
Number of terms, n = 10
Nth term, a n = 0
0 = − 18 +(10−1) d
d = 18/9 = 2
Hence, common difference, d = 2
(iii) Given,
First term, a = ?
Common difference, d = -3
Number of terms, n = 18
Nth term, a n = -5
−5 = a +(18−1) (−3)
−5 = a +(17) (−3)
−5 = a −51
a = 51−5 = 46
Hence, a = 46
(iv) Given,
First term, a = -18.9
Common difference, d = 2.5
Number of terms, n = ?
Nth term, a n = 3.6
a n = a +( n −1) d
3.6 = − 18.9+( n −1)2.5
3.6 + 18.9 = ( n −1)2.5
22.5 = ( n −1)2.5
( n – 1) = 22.5/2.5
n – 1 = 9
Hence, n = 10
(v) Given,
First term, a = 3.5
Common difference, d = 0
Number of terms, n = 105
Nth term, a n = ?
a n = a +( n −1) d
a n = 3.5+(105−1) 0
a n = 3.5+104×0
Hence, a n = 3.5
2. Choose the correct choice in the following and justify: (i) 30 th term of the A.P: 10,7, 4, …, is (A) 97 (B) 77 (C) −77 (D) −87

(i) Given here,
A.P. = 10, 7, 4, …
Therefore, we can find,
First term, a = 10
Common difference, d = a 2 − a 1 = 7−10 = −3
a n = a +( n −1) d
Putting the values;
a 30 = 10+(30−1)(−3)
a 30 = 10+(29)(−3)
a 30 = 10−87 = −77
Hence, the correct answer is option C.
(ii) Given here,
A.P. = -3, -1/2, ,2 …
First term a = – 3
Common difference, d = a 2 − a 1 = (-1/2) -(-3)
⇒(-1/2) + 3 = 5/2
a 11 = -3+(11-1)(5/2)
a 11 = -3+(10)(5/2)
a 11 = -3+25
Hence, the answer is option B.
3. In the following APs find the missing term in the boxes.

(i) For the given A.P., 2,2 , 26
The first and third term are;
Therefore, putting the values here,
a 3 = 2+(3-1) d
a 2 = 2+(2-1)12
Therefore, 14 is the missing term.
(ii) For the given A.P., , 13, ,3
a 2 = 13 and
a n = a +( n −1) d
a 2 = a +(2-1) d
13 = a + d ………………. (i)
a 4 = a +(4-1) d
3 = a +3 d ………….. (ii)
On subtracting equation (i) from (ii) , we get,
– 10 = 2 d
d = – 5
From equation (i) , putting the value of d,we get
13 = a +(-5)
a 3 = 18+(3-1)(-5)
= 18+2(-5) = 18-10 = 8
Therefore, the missing terms are 18 and 8 respectively.
(iii) For the given A.P.,
a 4 = 19/2
19/2 = 5 +3d
(19/2) – 5 = 3d
a 2 = a +(2-1) d
a 2 = 5 +3/2
a 2 = 13/2
a 3 = a +(3-1) d
a 3 = 5 +2×3/2
Therefore, the missing terms are 13/2 and 8 respectively.
(iv) For the given A.P.,
a = −4 and
a n = a +( n −1) d
a 6 = a+(6−1)d
6 = − 4+5 d
a 2 = a + d = − 4+2 = −2
a 3 = a +2 d = − 4+2(2) = 0
a 4 = a +3 d = − 4+ 3(2) = 2
a 5 = a +4 d = − 4+4(2) = 4
Therefore, the missing terms are −2, 0, 2, and 4 respectively.
(v) For the given A.P.,
a 2 = a +(2−1) d
38 = a + d ……………………. (i)
a 6 = a +(6−1) d
−22 = a +5 d …………………. (ii)
On subtracting equation (i) from (ii) , we get
− 22 − 38 = 4 d
a = a 2 − d = 38 − (−15) = 53
a 3 = a + 2 d = 53 + 2 (−15) = 23
a 4 = a + 3 d = 53 + 3 (−15) = 8
a 5 = a + 4 d = 53 + 4 (−15) = −7
Therefore, the missing terms are 53, 23, 8, and −7 respectively.
4. Which term of the A.P. 3, 8, 13, 18, … is 78?
Given the A.P. series as3, 8, 13, 18, …
First term, a = 3
Common difference, d = a 2 − a 1 = 8 − 3 = 5
Let the n th term of given A.P. be 78. Now as we know,
78 = 3+( n −1)5
75 = ( n −1)5
( n −1) = 15
Hence, 16 th term of this A.P. is 78.
5. Find the number of terms in each of the following A.P.
(i) 7, 13, 19, …, 205

(i) Given, 7, 13, 19, …, 205 is the A.P
Common difference, d = a 2 − a 1 = 13 − 7 = 6
Let there are n terms in this A.P.
a n = a + ( n − 1) d
Therefore, 205 = 7 + ( n − 1) 6
198 = ( n − 1) 6
33 = ( n − 1)
Therefore, this given series has 34 terms in it.

First term, a = 18

d = (31-36)/2 = -5/2
Let there are n terms in this A.P.
a n = a+(n−1)d
-47 = 18+(n-1)(-5/2)
-47-18 = (n-1)(-5/2)
-65 = (n-1)(-5/2)
(n-1) = -130/-5
Therefore, this given A.P. has 27 terms in it.
6. Check whether -150 is a term of the A.P. 11, 8, 5, 2, …
For the given series, A.P. 11, 8, 5, 2..
First term, a = 11
Common difference, d = a 2 − a 1 = 8−11 = −3
Let −150 be the n th term of this A.P.
-150 = 11+( n -1)(-3)
-150 = 11-3 n +3
-164 = -3 n
Clearly, n is not an integer but a fraction.
Therefore, – 150 is not a term of this A.P.
7. Find the 31 st term of an A.P. whose 11 th term is 38 and the 16 th term is 73.
Given that,
11 th term, a 11 = 38
and 16 th term, a 16 = 73
We know that,
a 11 = a+(11−1)d
38 = a+10d ………………………………. (i)
In the same way,
a 16 = a +(16−1) d
73 = a +15 d ………………………………………… (ii)
On subtracting equation (i) from (ii) , we get
From equation (i) , we can write,
38 = a +10×(7)
38 − 70 = a
a 31 = a +(31−1) d
= − 32 + 30 (7)
= − 32 + 210
Hence, 31 st term is 178.
8. An A.P. consists of 50 terms of which 3 rd term is 12 and the last term is 106. Find the 29 th term.
Solution: Given that,
3 rd term, a 3 = 12
50 th term, a 50 = 106
a 3 = a +(3−1) d
12 = a +2 d ……………………………. (i)
a 50 = a +(50−1) d
106 = a +49 d …………………………. (ii)
d = 2 = common difference
From equation (i) , we can write now,
12 = a +2(2)
a = 12−4 = 8
a 29 = a +(29−1) d
a 29 = 8+(28)2
a 29 = 8+56 = 64
Therefore, 29 th term is 64.
9. If the 3 rd and the 9 th terms of an A.P. are 4 and − 8 respectively. Which term of this A.P. is zero. Solution:
3 rd term, a 3 = 4
and 9 th term, a 9 = −8
4 = a +2 d ……………………………………… (i)
a 9 = a +(9−1) d
−8 = a +8 d ………………………………………………… (ii)
On subtracting equation (i) from (ii) , we will get here,
4 = a +2(−2)
Let n th term of this A.P. be zero.
a n = a +( n −1) d
0 = 8+( n −1)(−2)
0 = 8−2 n +2
Hence, 5 th term of this A.P. is 0.
10. If 17 th term of an A.P. exceeds its 10 th term by 7. Find the common difference.
We know that, for an A.P series;
a 17 = a +(17−1) d
a 17 = a +16 d
a 10 = a +9 d
As it is given in the question,
a 17 − a 10 = 7
( a +16 d )−( a +9 d ) = 7
Therefore, the common difference is 1.
11. Which term of the A.P. 3, 15, 27, 39,.. will be 132 more than its 54 th term?
Given A.P. is 3, 15, 27, 39, …
first term, a = 3
common difference, d = a 2 − a 1 = 15 − 3 = 12
a 54 = a +(54−1) d
⇒3+(53)(12)
⇒3+636 = 639
a 54 = 639+132=771
We have to find the term of this A.P. which is 132 more than a 54, i.e.771.
Let n th term be 771.
771 = 3+( n −1)12
768 = ( n −1)12
( n −1) = 64
Therefore, 65 th term was 132 more than 54 th term.
Or another method is;
Let n th term be 132 more than 54 th term.
n = 54 + 132/2
= 54 + 11 = 65 th term
12. Two APs have the same common difference. The difference between their 100 th term is 100, what is the difference between their 1000 th terms?
Let, the first term of two APs be a 1 and a 2 respectively
And the common difference of these APs be d .
For the first A.P.,we know,
a 100 = a 1 +(100−1) d
= a 1 + 99d
a 1000 = a 1 +(1000−1) d
a 1000 = a 1 +999 d
For second A.P., we know,
a 100 = a 2 +(100−1) d
= a 2 +99 d
a 1000 = a 2 +(1000−1) d
= a 2 +999 d
Given that, difference between 100 th term of the two APs = 100
Therefore, ( a 1 +99 d ) − ( a 2 +99 d ) = 100
a 1 − a 2 = 100……………………………………………………………….. (i)
Difference between 1000 th terms of the two APs
( a 1 +999 d ) − ( a 2 +999 d ) = a 1 − a 2
From equation (i) ,
This difference, a 1 − a 2 = 100
Hence, the difference between 1000 th terms of the two A.P. will be 100.
13. How many three digit numbers are divisible by 7?
First three-digit number that is divisible by 7 are;
First number = 105
Second number = 105+7 = 112
Third number = 112+7 =119
Therefore, 105, 112, 119, …
All are three digit numbers are divisible by 7 and thus, all these are terms of an A.P. having first term as 105 and common difference as 7.
As we know, the largest possible three-digit number is 999.
When we divide 999 by 7, the remainder will be 5.
Therefore, 999-5 = 994 is the maximum possible three-digit number that is divisible by 7.
Now the series is as follows.
105, 112, 119, …, 994
Let 994 be the nth term of this A.P.
first term, a = 105
common difference, d = 7
As we know,
994 = 105+(n−1)7
889 = (n−1)7
(n−1) = 127
Therefore, 128 three-digit numbers are divisible by 7.
14. How many multiples of 4 lie between 10 and 250?
The first multiple of 4 that is greater than 10 is 12.
Next multiple will be 16.
Therefore, the series formed as;
12, 16, 20, 24, …
All these are divisible by 4 and thus, all these are terms of an A.P. with first term as 12 and common difference as 4.
When we divide 250 by 4, the remainder will be 2. Therefore, 250 − 2 = 248 is divisible by 4.
The series is as follows, now;
12, 16, 20, 24, …, 248
Let 248 be the n th term of this A.P.
first term, a = 12
common difference, d = 4
248 = 12+( n -1)×4
236/4 = n-1
Therefore, there are 60 multiples of 4 between 10 and 250.
15. For what value of n , are the n th terms of two APs 63, 65, 67, and 3, 10, 17, … equal?
Given two APs as; 63, 65, 67,… and 3, 10, 17,….
Taking first AP,
63, 65, 67, …
First term, a = 63
Common difference, d = a 2 −a 1 = 65−63 = 2
We know, n th term of this A.P. = a n = a+(n−1)d
a n = 63+( n −1)2 = 63+2 n −2
a n = 61+2 n ………………………………………. (i)
Taking second AP,
3, 10, 17, …
Common difference, d = a 2 − a 1 = 10 − 3 = 7
n th term of this A.P. = 3+( n −1)7
a n = 3+7 n −7
a n = 7 n −4 ……………………………………………………….. (ii)
Given, n th term of these A.P.s are equal to each other.
Equating both these equations, we get,
61+2 n = 7 n −4
Therefore, 13 th terms of both these A.P.s are equal to each other.
16. Determine the A.P. whose third term is 16 and the 7 th term exceeds the 5 th term by 12.
Third term, a 3 = 16
a +(3−1) d = 16
a +2 d = 16 ………………………………………. (i)
It is given that, 7 th term exceeds the 5 th term by 12.
a 7 − a 5 = 12
( a +6 d )−( a +4 d ) = 12
From equation (i), we get,
a +2(6) = 16
Therefore, A.P. will be4, 10, 16, 22, …
17. Find the 20 th term from the last term of the A.P. 3, 8, 13, …, 253.
Given A.P. is3, 8, 13, …, 253
Common difference, d= 5.
Therefore, we can write the given AP in reverse order as;
253, 248, 243, …, 13, 8, 5
Now for the new AP,
first term, a = 253
and common difference, d = 248 − 253 = −5
Therefore, using nth term formula, we get,
a 20 = a +(20−1) d
a 20 = 253+(19)(−5)
a 20 = 253−95
Therefore, 20 th term from the last term of the AP 3, 8, 13, …, 253 . is 158.
18. The sum of 4 th and 8 th terms of an A.P. is 24 and the sum of the 6 th and 10 th terms is 44. Find the first three terms of the A.P .
We know that, the nth term of the AP is;
a 4 = a +(4−1) d
a 4 = a +3 d
In the same way, we can write,
a 8 = a +7 d
a 6 = a +5 d
a 4 +a 8 = 24
a+3d+a+7d = 24
2a+10d = 24
a+5d = 12 …………………………………………………… (i)
a 6 +a 10 = 44
a +5d+a+9d = 44
2a+14d = 44
a+7d = 22 …………………………………….. (ii)
2d = 22 − 12
From equation (i) , we get,
a +5 d = 12
a +5(5) = 12
a 2 = a + d = − 13+5 = −8
a 3 = a 2 + d = − 8+5 = −3
Therefore, the first three terms of this A.P. are −13, −8, and −3.
19. Subba Rao started work in 1995 at an annual salary of Rs 5000 and received an increment of Rs 200 each year. In which year did his income reach Rs 7000?
It can be seen from the given question, that the incomes of Subba Rao increases every year by Rs.200 and hence, forms an AP.
Therefore, after 1995, the salaries of each year are;
5000, 5200, 5400, …
Here, first term, a = 5000
and common difference, d = 200
Let after n th year, his salary be Rs 7000.
Therefore, by the n th term formula of AP,
7000 = 5000+( n −1)200
200( n −1)= 2000
( n −1) = 10
Therefore, in 11th year, his salary will be Rs 7000.
20. Ramkali saved Rs 5 in the first week of a year and then increased her weekly saving by Rs 1.75. If in the n th week, her weekly savings become Rs 20.75, find n.
Given that, Ramkali saved Rs.5 in first week and then started saving each week by Rs.1.75.
First term, a = 5
and common difference, d = 1.75
Also given,
a n = 20.75
Find, n = ?
As we know, by the n th term formula,
20.75 = 5+( n -1)×1.75
15.75 = ( n -1)×1.75
( n -1) = 15.75/1.75 = 1575/175
Hence, n is 10.
Exercise 5.3 Page: 112
1. Find the sum of the following APs.
(i) 2, 7, 12 ,…., to 10 terms. (ii) − 37, − 33, − 29 ,…, to 12 terms (iii) 0.6, 1.7, 2.8 ,…….., to 100 terms (iv) 1/15, 1/12, 1/10, …… , to 11 terms
(i) Given, 2, 7, 12 ,…, to 10 terms
For this A.P.,
first term, a = 2
And common difference, d = a 2 − a 1 = 7−2 = 5
We know that, the formula for sum of nth term in AP series is,
= 5 × 49 = 245
(ii) Given, −37, −33, −29 ,…, to 12 terms
first term, a = −37
And common difference, d = a 2 − a 1
d= (−33)−(−37)
= − 33 + 37 = 4
= 6(-30) = -180
(iii) Given, 0.6, 1.7, 2.8 ,…, to 100 terms
first term, a = 0.6
Common difference, d = a 2 − a 1 = 1.7 − 0.6 = 1.1
(iv) Given, 1/15, 1/12, 1/10, …… , to 11 terms
First term, a = 1/5
Common difference, d = a 2 –a 1 = (1/12)-(1/5) = 1/60
And number of terms n = 11

= 11/2(2/15 + 10/60)
= 11/2 (9/30)
2. Find the sums given below :

First term, a = 7
n th term, a n = 84

Let 84 be the n th term of this A.P., then as per the n th term formula,
a n = a(n-1)d
84 = 7+(n – 1)×7/2
77 = (n-1)×7/2
We know that, sum of n term is;
S n = n/2 (a + l) , l = 84 S n = 23/2 (7+84)
S n = (23×91/2) = 2093/2

(ii) Given, 34 + 32 + 30 + ……….. + 10
first term, a = 34
common difference, d = a 2 −a 1 = 32−34 = −2
n th term, a n = 10
Let 10 be the n th term of this A.P., therefore,
a n = a +(n−1)d
10 = 34+(n−1)(−2)
−24 = (n −1)(−2)
We know that, sum of n terms is;
S n = n/2 (a +l) , l = 10
= 13/2 (34 + 10)
= (13×44/2) = 13 × 22
(iii) Given, (−5) + (−8) + (−11) + ………… + (−230)
First term, a = −5
nth term, a n = −230
Common difference, d = a 2 −a 1 = (−8)−(−5)
⇒d = − 8+5 = −3
Let −230 be the n th term of this A.P., and by the n th term formula we know,
a n = a +( n −1) d
−230 = − 5+( n −1)(−3)
−225 = ( n −1)(−3)
( n −1) = 75
And, Sum of n term,
S n = n /2 ( a + l )
3. In an AP (i) Given a = 5, d = 3, a n = 50, find n and S n . (ii) Given a = 7, a 13 = 35, find d and S 13 . (iii) Given a 12 = 37, d = 3, find a and S 12 . (iv) Given a 3 = 15, S 10 = 125, find d and a 10 . (v) Given d = 5, S 9 = 75, find a and a 9 . (vi) Given a = 2, d = 8, S n = 90, find n and a n . (vii) Given a = 8, a n = 62, S n = 210, find n and d . (viii) Given a n = 4, d = 2, S n = − 14, find n and a . (ix) Given a = 3, n = 8, S = 192, find d . (x) Given l = 28, S = 144 and there are total 9 terms. Find a .
(i) Given that, a = 5, d = 3, a n = 50
As we know, from the formula of the nth term in an AP,
a n = a +( n −1) d ,
Therefore, putting the given values, we get,
⇒ 50 = 5+( n -1)×3
⇒ 3( n -1) = 45
⇒ n -1 = 15
Now, sum of n terms,
S n = n /2 ( a + a n )
S n = 16/2 (5 + 50) = 440
(ii) Given that, a = 7, a 13 = 35
a n = a +( n −1) d ,
⇒ 35 = 7+(13-1) d
⇒ 12 d = 28
⇒ d = 28/12 = 2.33
Now, S n = n /2 ( a + a n )
S 13 = 13/2 (7+35) = 273
(iii) Given that, a 12 = 37, d = 3
As we know, from the formula of the n th term in an AP,
a n = a +( n −1) d ,
⇒ a 12 = a +(12−1)3
⇒ 37 = a +33
Now, sum of nth term,
S n = n /2 ( a + a n )
S n = 12 /2 (4+37)
(iv) Given that, a 3 = 15, S 10 = 125
a n = a +( n −1) d ,
15 = a +2 d ………………………….. (i)
Sum of the nth term,
125 = 5(2 a +9 d )
25 = 2 a +9 d ……………………….. (ii)
On multiplying equation (i) by (ii) , we will get;
30 = 2 a +4 d ………………………………. (iii)
By subtracting equation (iii) from (ii) , we get,
15 = a +2(−1)
a = 17 = First term
a 10 = a +(10−1) d
a 10 = 17+(9)(−1)
a 10 = 17−9 = 8
(v) Given that, d = 5, S 9 = 75
As, sum of n terms in AP is,
Therefore, the sum of first nine terms are;
25 = 3( a +20)
25 = 3 a +60
3 a = 25−60
As we know, the n th term can be written as;
a 9 = a +(9−1)(5)
= -35/3+8(5)
= (35+120/3) = 85/3
(vi) Given that, a = 2, d = 8, S n = 90
As, sum of n terms in an AP is,
⇒ 180 = n (4+8 n -8) = n (8 n -4) = 8 n 2 -4 n
⇒ 8 n 2 -4 n – 180 = 0
⇒ 2 n 2 – n -45 = 0
⇒ 2 n 2 -10 n +9 n -45 = 0
⇒ 2 n ( n -5)+9( n -5) = 0
⇒ ( n -5)(2 n +9) = 0
So, n = 5 (as n only be a positive integer)
∴ a 5 = 8+5×4 = 34
(vii) Given that, a = 8, a n = 62, S n = 210
S n = n /2 ( a + a n )
210 = n /2 (8 +62)
⇒ 35 n = 210
⇒ n = 210/35 = 6
Now, 62 = 8+5 d
⇒ 5 d = 62-8 = 54
⇒ d = 54/5 = 10.8
(viii) Given that, n th term, a n = 4, common difference, d = 2, sum of n terms, S n = −14.
4 = a +( n −1)2
4 = a +2 n −2
a +2 n = 6
a = 6 − 2 n …………………………………………. (i)
As we know, the sum of n terms is;
-14 = n /2 ( a + 4 )
−28 = n ( a +4)
−28 = n (6 −2 n +4) {From equation (i) }
−28 = n (− 2 n +10)
−28 = − 2 n 2 +10 n
2 n 2 −10 n − 28 = 0
n 2 −5 n −14 = 0
n 2 −7 n+ 2 n −14 = 0
n ( n −7)+2( n −7) = 0
( n −7)( n +2) = 0
Either n − 7 = 0 or n + 2 = 0
n = 7 or n = −2
However, n can neither be negative nor fractional.
Therefore, n = 7
From equation (i) , we get
a = 6−2(7)
(ix) Given that, first term, a = 3,
Number of terms, n = 8
And sum of n terms, S = 192
(x) Given that, l = 28, S = 144 and there are total of 9 terms.
Sum of n terms formula,
144 = 9/2( a +28)
(16)×(2) = a +28
32 = a +28
4. How many terms of the AP. 9, 17, 25 … must be taken to give a sum of 636?
Let there be n terms of the AP. 9, 17, 25 …
First term, a = 9
Common difference, d = a 2 − a 1 = 17−9 = 8
As, the sum of n terms, is;
636 = n (4 n +5)
4 n 2 +5 n −636 = 0
4 n 2 +53 n −48 n −636 = 0
n (4 n + 53)−12 (4 n + 53) = 0
(4 n +53)( n −12) = 0
Either 4 n +53 = 0 or n −12 = 0
n = (-53/4) or n = 12
n cannot be negative or fraction, therefore, n = 12 only.
5. The first term of an AP is 5, the last term is 45 and the sum is 400. Find the number of terms and the common difference.
first term, a = 5
last term, l = 45
Sum of the AP, S n = 400
As we know, the sum of AP formula is;
S n = n /2 ( a + l )
400 = n /2(5+45)
400 = n /2(50)
Number of terms, n =16
As we know, the last term of AP series can be written as;
l = a+ ( n −1) d
45 = 5 +(16 −1) d
Common difference, d = 40/15 = 8/3
6. The first and the last term of an AP are 17 and 350 respectively. If the common difference is 9, how many terms are there and what is their sum?
First term, a = 17
Last term, l = 350
Common difference, d = 9
Let there be n terms in the A.P., thus the formula for last term can be written as;
350 = 17+( n −1)9
333 = ( n −1)9
( n −1) = 37
S 38 = 38/2 (17+350)
Thus, this A.P. contains 38 terms and the sum of the terms of this A.P. is 6973.
7. Find the sum of first 22 terms of an AP in which d = 7 and 22 nd term is 149. Solution:
Given, Common difference, d = 7
22 nd term, a 22 = 149
Sum of first 22 term, S 22 = ?
By the formula of nth term,
a 22 = a +(22−1) d
149 = a +21×7
149 = a +147
a = 2 = First term
Sum of n terms,
S n = n /2( a + a n )
S 22 = 22/2 (2+149)
8. Find the sum of first 51 terms of an AP whose second and third terms are 14 and 18 respectively. Solution:
Second term, a 2 = 14
Third term, a 3 = 18
Common difference, d = a 3 − a 2 = 18−14 = 4
a 2 = a + d
a = 10 = First term
Sum of n terms;
= 51 × 220/2
9. If the sum of first 7 terms of an AP is 49 and that of 17 terms is 289, find the sum of first n terms.
S 17 = 289
We know, Sum of n terms;
7 = ( a +3 d )
a + 3 d = 7 …………………………………. (i)
289 = 17/2 (2 a +16 d )
17 = ( a +8 d )
a +8 d = 17 ………………………………. (ii)
Subtracting equation (i) from equation (ii) ,
From equation (i) , we can write it as;
a +3(2) = 7
= n /2(2+2 n -2)
= n /2(2 n )
10. Show that a 1 , a 2 … , a n , … form an AP where a n is defined as below
(i) a n = 3+4 n (ii) a n = 9−5 n Also find the sum of the first 15 terms in each case.
(i) a n = 3+4 n
a 1 = 3+4(1) = 7
a 2 = 3+4(2) = 3+8 = 11
a 3 = 3+4(3) = 3+12 = 15
a 4 = 3+4(4) = 3+16 = 19
We can see here, the common difference between the terms are;
a 2 − a 1 = 11−7 = 4
a 3 − a 2 = 15−11 = 4
a 4 − a 3 = 19−15 = 4
Hence, a k + 1 − a k is the same value every time. Therefore, this is an AP with common difference as 4 and first term as 7.
Now, we know, the sum of nth term is;
(ii) a n = 9−5 n
a 1 = 9−5×1 = 9−5 = 4
a 2 = 9−5×2 = 9−10 = −1
a 3 = 9−5×3 = 9−15 = −6
a 4 = 9−5×4 = 9−20 = −11
a 2 − a 1 = −1−4 = −5
a 3 − a 2 = −6−(−1) = −5
a 4 − a 3 = −11−(−6) = −5
Hence, a k + 1 − a k is same every time. Therefore, this is an A.P. with common difference as −5 and first term as 4.
= 15/2(8-70)
= 15/2(-62)
11. If the sum of the first n terms of an AP is 4 n − n 2 , what is the first term (that is S 1 )? What is the sum of first two terms? What is the second term? Similarly find the 3 rd , the10 th and the n th terms.
S n = 4 n − n 2
First term, a = S 1 = 4(1) − (1) 2 = 4−1 = 3
Sum of first two terms = S 2 = 4(2)−(2) 2 = 8−4 = 4
Second term, a 2 = S 2 − S 1 = 4−3 = 1
Common difference, d = a 2 − a = 1−3 = −2
N th term, a n = a +( n −1) d
= 3+( n −1)(−2)
= 3−2 n +2
Therefore, a 3 = 5−2(3) = 5-6 = −1
a 10 = 5−2(10) = 5−20 = −15
Hence, the sum of first two terms is 4. The second term is 1.
The 3 rd , the 10 th , and the n th terms are −1, −15, and 5 − 2 n respectively.
12. Find the sum of first 40 positive integers divisible by 6.
The positive integers that are divisible by 6 are 6, 12, 18, 24 ….
We can see here, that this series forms an A.P. whose first term is 6 and common difference is 6.
By the formula of sum of n terms, we know,
Therefore, putting n = 40, we get,
= 20(12+234)
13. Find the sum of first 15 multiples of 8.
The multiples of 8 are 8, 16, 24, 32…
The series is in the form of AP, having first term as 8 and common difference as 8.
Therefore, a = 8
By the formula of sum of nth term, we know,
= 15(128)/2
14. Find the sum of the odd numbers between 0 and 50.
The odd numbers between 0 and 50 are 1, 3, 5, 7, 9 … 49.
Therefore, we can see that these odd numbers are in the form of A.P.
First term, a = 1
Common difference, d = 2
Last term, l = 49
By the formula of last term, we know,
l = a +( n −1) d
49 = 1+( n −1)2
48 = 2( n − 1)
n − 1 = 24
n = 25 = Number of terms
S n = n /2( a + l )
S 25 = 25/2 (1+49)
15. A contract on construction job specifies a penalty for delay of completion beyond a certain date as follows: Rs. 200 for the first day, Rs. 250 for the second day, Rs. 300 for the third day, etc., the penalty for each succeeding day being Rs. 50 more than for the preceding day. How much money the contractor has to pay as penalty, if he has delayed the work by 30 days.
We can see, that the given penalties are in the form of A.P. having first term as 200 and common difference as 50.
Therefore, a = 200 and d = 50
Penalty that has to be paid if contractor has delayed the work by 30 days = S 30
Therefore, the contractor has to pay Rs 27750 as penalty.
16. A sum of Rs 700 is to be used to give seven cash prizes to students of a school for their overall academic performance. If each prize is Rs 20 less than its preceding prize, find the value of each of the prizes.
Let the cost of 1 st prize be Rs. P .
Cost of 2 nd prize = Rs. P − 20
And cost of 3 rd prize = Rs. P − 40
We can see that the cost of these prizes are in the form of A.P., having common difference as −20 and first term as P .
Thus, a = P and d = −20
Given that, S 7 = 700
7/2 [2 a + (7 – 1) d ] = 700

a + 3(−20) = 100
a −60 = 100
Therefore, the value of each of the prizes was Rs 160, Rs 140, Rs 120, Rs 100, Rs 80, Rs 60, and Rs 40.
17. In a school, students thought of planting trees in and around the school to reduce air pollution. It was decided that the number of trees, that each section of each class will plant, will be the same as the class, in which they are studying, e.g., a section of class I will plant 1 tree, a section of class II will plant 2 trees and so on till class XII. There are three sections of each class. How many trees will be planted by the students?
It can be observed that the number of trees planted by the students is in an AP.
1, 2, 3, 4, 5………………..12
First term, a = 1
Common difference, d = 2−1 = 1
Therefore, number of trees planted by 1 section of the classes = 78
Number of trees planted by 3 sections of the classes = 3×78 = 234
Therefore, 234 trees will be planted by the students.
18. A spiral is made up of successive semicircles, with centres alternately at A and B, starting with centre at A of radii 0.5, 1.0 cm, 1.5 cm, 2.0 cm, ……… as shown in figure. What is the total length of such a spiral made up of thirteen consecutive semicircles? (Take π = 22/7)
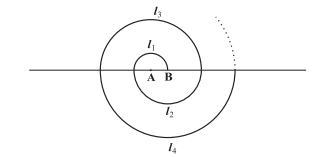
Perimeter of a semi-circle = π r
P 1 = π(0.5) = π/2 cm
P 2 = π(1) = π cm
P 3 = π(1.5) = 3π/2 cm
Where, P 1, P 2 , P 3 are the lengths of the semi-circles.
Hence we got a series here, as,
π/2, π, 3π/2, 2π, ….
P 1 = π/2 cm
P 2 = π cm
Common difference, d = P 2 – P 1 = π – π/2 = π/2
First term = P 1 = a = π/2 cm
By the sum of n term formula, we know,
Therefor, Sum of the length of 13 consecutive circles is;
=13 /2 (7π)
= 13 /2 × 7 × 22 /7
19. 200 logs are stacked in the following manner: 20 logs in the bottom row, 19 in the next row, 18 in the row next to it and so on. In how many rows are the 200 logs placed and how many logs are in the top row?

We can see that the numbers of logs in rows are in the form of an A.P.20, 19, 18…
For the given A.P.,
First term, a = 20 and common difference, d = a 2 − a 1 = 19−20 = −1
Let a total of 200 logs be placed in n rows.
Thus, S n = 200
By the sum of nth term formula,
400 = n (40− n +1)
400 = n (41- n )
400 = 41 n − n 2
n 2 −41 n + 400 = 0
n 2 −16 n −25 n +400 = 0
n ( n −16)−25( n −16) = 0
( n −16)( n −25) = 0
Either ( n −16) = 0 or n −25 = 0
n = 16 or n = 25
By the nth term formula,
a 16 = 20+(16−1)(−1)
a 16 = 20−15
Similarly, the 25 th term could be written as;
a 25 = 20+(25−1)(−1)
a 25 = 20−24
It can be seen, the number of logs in 16 th row is 5 as the numbers cannot be negative.
Therefore, 200 logs can be placed in 16 rows and the number of logs in the 16 th row is 5.
20. In a potato race, a bucket is placed at the starting point, which is 5 m from the first potato and other potatoes are placed 3 m apart in a straight line. There are ten potatoes in the line.

A competitor starts from the bucket, picks up the nearest potato, runs back with it, drops it in the bucket, runs back to pick up the next potato, runs to the bucket to drop it in, and she continues in the same way until all the potatoes are in the bucket. What is the total distance the competitor has to run? [Hint: to pick up the first potato and the second potato, the total distance (in metres) run by a competitor is 2×5+2×(5+3)]
The distances of potatoes from the bucket are 5, 8, 11, 14…, which is in the form of AP.
Given, the distance run by the competitor for collecting these potatoes are two times of the distance at which the potatoes have been kept.
Therefore, distances to be run w.r.t distances of potatoes, could be written as;
10, 16, 22, 28, 34,……….
Hence, the first term, a = 10 and d = 16−10 = 6
Therefore, the competitor will run a total distance of 370 m.
Exercise 5.4 Page: 115
1. Which term of the AP: 121, 117, 113, . . ., is its first negative term? [Hint: Find n for a n < 0]
Given the AP series is 121, 117, 113, . . .,
Thus, first term, a = 121
Common difference, d = 117-121= -4
a n = 121+(n−1)(-4)
To find the first negative term of the series, a n < 0
125-4n < 0
125 < 4n
Therefore, the first negative term of the series is 32 nd term.
2. The sum of the third and the seventh terms of an AP is 6 and their product is 8. Find the sum of first sixteen terms of the AP.
From the given statements, we can write,
a 3 + a 7 = 6 …………………………….(i)
a 3 ×a 7 = 8 ……………………………..(ii)
Third term, a 3 = a+(3 -1)d
a 3 = a + 2d………………………………(iii)
And Seventh term, a7= a+(7-1)d
a 7 = a + 6d ………………………………..(iv)
From equation (iii) and (iv), putting in equation(i), we get,
a+2d +a+6d = 6
a = 3–4d …………………………………(v)
Again putting the eq.(iii) and (iv), in eq. (ii), we get,
(a+2d)×(a+6d) = 8
Putting the value of a from equation (v), we get,
(3–4d +2d)×(3–4d+6d) = 8
(3 –2d)×(3+2d) = 8
3 2 – 2d 2 = 8
9 – 4d 2 = 8
d = 1/2 or -1/2
Now, by putting both the values of d, we get,
a = 3 – 4d = 3 – 4(1/2) = 3 – 2 = 1, when d = 1/2
a = 3 – 4d = 3 – 4(-1/2) = 3+2 = 5, when d = -1/2
We know, the sum of nth term of AP is;
So, when a = 1 and d=1/2
Then, the sum of first 16 terms are;
S 16 = 16 /2 [2 +(16-1)1/2] = 8(2+15/2) = 76
And when a = 5 and d= -1/2
S 16 = 16 /2 [2(5)+(16-1)(-1/2)] = 8(5/2)=20

Distance between the rungs of the ladder is 25cm.

Therefore, total number of rungs = 250/25 + 1 = 11
As we can see from the figure, the ladder has rungs in decreasing order from top to bottom. Thus, we can conclude now, that the rungs are decreasing in an order of AP.
And the length of the wood required for the rungs will be equal to the sum of the terms of AP series formed.
First term, a = 45
Last term, l = 25
Number of terms, n = 11
Now, as we know, sum of nth terms is equal to,
S n = n/2(a+ l )
S n = 11/2(45+25) = 11/2(70) = 385 cm
Hence, the length of the wood required for the rungs is 385cm.
4. The houses of a row are numbered consecutively from 1 to 49. Show that there is a value of x such that the sum of the numbers of the houses preceding the house numbered x is equal to the sum of the numbers of the houses following it. Find this value of x. [Hint :Sx – 1 = S49 – Sx ]
Row houses are numbers from 1,2,3,4,5…….49.
Thus we can see the houses numbered in a row are in the form of AP.
First term, a = 1
Common difference, d=1
Let us say the number of x th houses can be represented as;
Sum of number of houses beyond x house = S x-1
= x(x-1)/2 ………………………………………(i)
By the given condition, we can write,
S 49 – S x = {49/2[2(1)+(49-1)1]}–{x/2[2(1)+(x-1)1]}
= 25(49) – x(x + 1)/2 ………………………………….(ii)
As per the given condition, eq.(i) and eq(ii) are equal to each other;
x(x-1)/2 = 25(49) – x(x+1)/2
As we know, the number of houses cannot be a negative number. Hence, the value of x is 35.
5. A small terrace at a football ground comprises of 15 steps each of which is 50 m long and built of solid concrete. Each step has a rise of 1 4 m and a tread of 1 2 m. (see Fig. 5.8). Calculate the total volume of concrete required to build the terrace. [Hint : Volume of concrete required to build the first step = ¼ ×1/2 ×50 m 3 .]

As we can see from the given figure, the first step is ½ m wide, 2 nd step is 1m wide and 3 rd step is 3/2m wide. Thus we can understand that the width of step by ½ m each time when height is ¼ m. And also, given length of the steps is 50m all the time. So, the width of steps forms a series AP in such a way that;
½ , 1, 3/2, 2, ……..
Volume of steps = Volume of Cuboid
= Length × Breadth Height
Volume of concrete required to build the first step = ¼ ×1/2 ×50 = 25/4
Volume of concrete required to build the second step =¼ ×1×50 = 25/2
Volume of concrete required to build the second step = ¼ ×3/2 ×50 = 75/4
Now, we can see the volumes of concrete required to build the steps, are in AP series;
25/4 , 25/2 , 75/4 …..
Thus, applying the AP series concept,
First term, a = 25/4
Common difference, d = 25/2 – 25/4 = 25/4
S n = n/2[2a+(n-1)d] = 15/2(2×(25/4 )+(15/2 -1)25/4)
Upon solving, we get,
S n = 15/2 (100)
Hence, the total volume of concrete required to build the terrace is 750 m 3 .
This chapter comes under Unit 3 algebra, and this unit has 20 marks allotted in the examination. Students can expect an average of 3 questions from arithmetic progressions. Along with Class 10 examinations, this topic is very important from the point of competitive exams.
Sub-topics of Class 10 Chapter 5 Arithmetic Progression
5.1 Introduction
In this chapter, we shall discuss patterns which we come across in our day-to-day life, in which succeeding terms are obtained by adding a fixed number to the preceding terms. We shall also see how to find their nth terms and the sum of n consecutive terms, and use this knowledge to solve some day-to-day problems.
5.2 Arithmetic Progressions
The topic describes Arithmetic Progressions, its definition and relatable terms, along with fine examples. You will also learn about Finite Arithmetic Progressions and Infinite Arithmetic Progressions. The general form of AP is a, a + d, a + 2d, a + 3d,…
5.3 nth Term of an AP This topic discusses various methods to determine the n th term of an AP. The concepts are explained with different types of problems solving techniques and finding the n th term of an AP. The examples mentioned in the chapter will help you while solving the exercise problems.
5.4 Sum of First n Terms of an AP The topics discuss different techniques to find the sum of the first n terms of an AP. It also provides suitable examples, which show different techniques to find the sum of the first n terms of AP.
5.5 Summary It gives an overview of the entire chapter and the important topics explained in the chapter. By going through the summary part, you can cover the entire chapter in a few points, which helps in memorising the essential concepts.
List of Exercises from Class 10 Maths Chapter 5 Arithmetic progression
Exercise 5.1 – 4 questions 1 MCQ and 3 descriptive type questions Exercise 5.2 – 20 questions, 1 fill in the blanks, 2 MCQs, 7 Short answer questions and 10 Long answer questions Exercise 5.3 – 20 Questions 3 fill in the blanks, 4 daily life examples, and 13 descriptive-type questions Exercise 5.4 5 Questions- 5 Long answer questions
This NCERT Solutions for Class 10 Maths is a perfect study material that will help you solve different kinds of problems. Solving these NCERT Solutions will help you understand the topic completely and help you lay a greater foundation for future studies.
In this chapter, students will discuss patterns in succeeding terms obtained by adding a fixed number to the preceding terms. They also see how to find nth terms and the sum of n consecutive terms. Students will learn arithmetic progression effectively when they solve daily life problems.
This chapter has Arithmetic Progression Derivation of the n th term and sum of the first n terms of an A.P. and their application in solving daily life problems. This is one of the important chapters from the point of the Class 10 examination. An arithmetic progression is a very basic and important topic to study, as almost all the competitive exams will ask questions on arithmetic progression.
Key Features of NCERT Solutions for Class 10 Maths Chapter 5 Arithmetic Progressions
- Has answers to different types of questions such as MCQs and long answer questions.
- Solving this NCERT Solutions will make you well versed with important formulas.
- Acts as a basis to solve arithmetic progression problems asked in competitive examination.
- Has answers to all the exercise questions provided in the NCERT textbook
- Provides you with the necessary practice of solving questions
- You can solve different types of questions with varying difficulty levels
- Different examples taken from day to day life will help you understand the topic thoroughly.
Keep visiting BYJU’S to get complete assistance for CBSE Class 10 board exams. At BYJU’S, students can get sample papers, question papers, notes, textbooks, videos, animations and effective preparation tips, which will help you to score well in the Class 10 CBSE exams.
For more information on the study resources we provide, register with BYJU’S website or download BYJU’S Learning App for a customised learning experience.
Students can also make use of the other solutions of CBSE syllabus to understand the types of questions that would appear in the CBSE exams.
- RD Sharma Solutions for Class 10 Maths Chapter 9 Arithmetic Progressions
Frequently Asked Questions on NCERT Solutions for Class 10 Maths Chapter 5
What kind of questions are there in ncert solutions for class 10 maths chapter 5, is it necessary to learn all the topics provided in ncert solutions for class 10 maths chapter 5, are ncert solutions for class 10 maths chapter 5 sufficient to attempt all the questions that come in the cbse board exams.
Register with BYJU'S & Download Free PDFs
Register with byju's & watch live videos.
Talk to our experts
1800-120-456-456
NCERT Solutions for Class 10 Maths Chapter 5 - Arithmetic Progressions
- NCERT Solutions
- Chapter 5 Arithmetic Progressions

NCERT Solutions for Class 10 Maths Chapter 5 Arithmetic Progressions - Free PDF Download
In Maths NCERT Solutions Class 10 Chapter 5 , students will learn about the arithmetic progression. The NCERT Solutions for Class 10 Maths Chapter 5 PDF file, available for free, can help students to score good marks. Students can download this PDF file by visiting Vedantu. This file is prepared by the best academic experts in India. Every answer is written according to the guidelines set by CBSE. Further, every single step is taken to ensure that students can score good marks.
Glance of NCERT Solutions for Class 10 Maths Chapter 5 Arithmetic Progressions | Vedantu
An arithmetic progression (AP) is a sequence of numbers where the difference between consecutive terms is constant. This constant difference is called the common difference d where $(d = a_2 - a_1)$.
The first term of an AP is denoted by a and the nth term by $a_n$.
You can find nth term in the AP using the formula: $a_n = a + (n - 1)d$
The sum of the first n terms $S_n$ in an AP is calculated using the formula: $S_n = \dfrac{n}{2} [2a + (n - 1)d]$
The common difference (d) can be positive, negative, or zero.
Positive d : The sequence is increasing. (e.g., 2, 5, 8, 11, ...)
Negative d : The sequence is decreasing. (e.g., 8, 5, 2, -1, ...)
Zero d : The sequence is constant. (e.g., 4, 4, 4, 4, ...)
The graph of an AP is a straight line. The slope of this line is equal to the common difference (d).
The average of the first and last term is equal to the middle term if there are an even number of terms.
This article contains chapter notes, formula and exercises link and important questions for chapter 5 - Arithmetic Progressions.
Access Exercise Wise NCERT Solutions for Chapter 5 Maths Class 10
S. No | Current Syllabus Exercises of Class 10 Maths Chapter 5 |
1 |
|
2 |
|
3 |
|
4 |
|

Related Chapters
Exercises Ender NCERT Class 10 Maths Chapter 5 - Arithmetic Progressions
Chapter 5 of the CBSE Class 10 Term 2 syllabus includes four exercises on Arithmetic Progressions. Each exercise contains problems that aim to help students understand the concept of arithmetic progressions and their practical applications in solving various word problems.
Exercise 5.1 - This exercise contains four problems, each with multiple parts. These problems aim to introduce students to the fundamental formulas of Arithmetic Progressions. These formulas include those for finding the first and last terms, calculating the sum of an A.P., and finding an unknown term of an A.P. using the common difference, among others.
Exercise 5.2 - This is the second exercise contains 20 problems. This exercise covers several problems that involve finding the terms of an A.P. by using formulas and substituting known values of the A.P. The exercise also includes numerous word problems to help students understand how to apply A.P. formulas.
Exercise 5.3 - It contains 20 problems related to arithmetic progressions. The problems in this exercise range from very easy to difficult word problems. To solve these problems, students are advised to have a thorough understanding of all the A.P. formulas provided in the chapter.
Exercise 5.4 - It is the final exercise and contains five problems. The first two problems require students to find the first negative term of a given A.P. or the first term of a given A.P. from the sum and product of two other known terms of the same A.P. The remaining problems are word problems that involve basic applications of volume, length, and other physical measurements.
NCERT Solutions for Class 10 Maths Chapter 5 solutions PDF download
5.1 Introduction : In this chapter, we'll understand the unique number patterns and will learn how to identify them, finding specific numbers in the given sequence and also how to find the sum of all numbers in a given sequence of numbers.
5.2 Arithmetic Progression : In simple terms, Arithmetic Progression or AP can be defined as a sequence of numbers. This sequence exists in an order in which the difference between any two consecutive numbers would be constant.
For example, if 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 is a series of natural numbers. It can be said that this series is also an arithmetic progression between the difference between every two successive terms is 1. If we have a similar series of odd and even numbers, still, the difference between two successive terms will be two. This means that the odd and even number series will also be arithmetic progressions.
It should also be noted for writing NCERT Solutions for Maths Class 10 chapter 5 that we all observe examples of arithmetic progressions even in our daily lives. Some examples from the real-life of Arithmetic Progression Class 10 Maths Chapter 5 include roll numbers of students in a class, days of a week, and months in a year.
There are three different types of progressions. These different types of progressions that are mentioned in Chapter 5 Class 10 Maths NCERT book are:
Arithmetic Progression (AP)
Geometric Progression (GP)
Harmonic Progression (HP)
Before moving forward with the topic of Ch 5 Class 10 Maths, every student should know that a progression can be explained as a special type of sequence for which it is possible for one to obtain a formula for the nth term. When it comes to the subject of mathematics, then arithmetic progression is the most commonly used sequence.
There are also three other definitions of arithmetic progression that students should remember for writing Arithmetic Progression Class 10 NCERT Solutions . These definitions are:
Definition One: Arithmetic progression is a mathematical sequence in which the difference between any two consecutive terms is always a constant. It can also be abbreviated as AP
Definition Two: It is also mentioned in NCERT Solutions Class 10 Maths Chapter 5 that arithmetic progression or sequence is the sequence of numbers. In this sequence of consecutive numbers, it is possible to find the next number by adding a fixed number to the previous number in the chain
Definition Three: In Arithmetic Progression Class 10 Solutions, the common difference of the AP is the fixed number that one should add to any term of the arithmetic progression. For example, in the arithmetic progression 1, 4, 7, 10, 13, 16, 19, 22, the value of the common difference is 3
In Class 10 Maths Chapter 5 Solutions, there are three main terms. These terms are:
The common difference (d)
nth Term (an)
The num of the first n terms (Sn)
These three terms are used to represent the property of arithmetic progression. In the next section, we will look at these three properties in more detail.
The Common Difference in Arithmetic Progression
For any given series of arithmetic progression, the terms that are used are the first term, the common difference between any two terms, and the nth term. Let’s assume that a1, a2, a3, a4, …, an is an arithmetic progression.
This means that the value of the common difference ‘d’ is:
$D = a_2 - a_1 = a_3 - a_2 = … = a_1 - a_{n-1}$
Here, d is the value of the common difference. The value of d can be positive, negative, or zero.
The First Term of Arithmetic Progression
If an individual wants to write the arithmetic progression in terms of its common difference for solving, then it can be written as:
A, a + d, a + 2d, a + 3d, a + 4d, a + 5d, …, a + (n - 1) d
In this sequence, a is the first term of the progression.
The General Form of an Arithmetic Progression
In this section, students will be able to do just that. Before we proceed, a student should begin with an assumption that the arithmetic progression for class 10 maths chapter 5 solutions is $a_1, a_2, a_3, …, a_n$
Position of Terms | Representation of Terms | Values of Terms |
1 | $a_1$ | A = a + (1 - 1) d |
2 | $a_2$ | A + d = a + (2 - 1) d |
3 | $a_3$ | A + 2d = a + (3 - 1) d |
4 | $a_4$ | A + 3d = a + (4 - 1) d |
. | . | . |
. | . | . |
n | $a_n$ | A + (n - 1) d |
5.3: The nth Term of Arithmetic Progression (AP)
This formula can be used for finding the class 10 maths chapter 5 NCERT solutions in which one needs to get the value of the nth term of an arithmetic progression. The formula can be written as:
$A_n = a + (n - 1) d$
Here, a is the first term, d is the value of the common difference, n is the number of terms, and an is the nth term.
Let’s take an example. Try to find out the nth term of the following arithmetic progression 1, 2, 3, 4, 5, …, an. The total number of terms is 15.
We know that n = 15. This means that according to the formula, we can say that:
Since, a = 1, and the common difference or d = 2 - 1 = 1
Then, $a_n = 1 + (15 - 1) 1 = 1 + 14 = 15$.
The behaviour of the entire sequence will also depend on the values of the common difference. This means that if the value of the common difference is positive, then the member terms will grow towards positive infinity. And if the value of the common difference is negative, then the member terms will move towards negative infinity.
5.4 The Sum of the First n Terms of an Arithmetic Progression(AP)
One can easily calculate the sum of n terms of any known progression. For an arithmetic progression, it is possible to calculate the sum of the first n terms if the value of the first term and the total terms are known. The formula is mentioned below.
$S = \dfrac{n}{2}$
$2a+(n-1) \times d$
But what if the value of the last term of the arithmetic progression is given? In that case, students should use the formula that is mentioned below.
S = $\dfrac{n}{2}$(first term + last term)
For ease of revision, we have also summarized all the major formulas of this chapter in a table. That table is mentioned below.
General Form of AP | A, a + d, a + 2d, a + 3d, a + 4d, …, a + nd |
The nth term of AP | $A_n = a + (n - 1) \times d$ |
Sum of n terms in AP | $S =\dfrac{n}{2} (2 a + (n - 1) \times d)$ |
Sum of all terms in a finite AP with the last term as I | $\dfrac{N}{2} (a + I)$ |
Class 10 Maths NCERT Solutions Chapter 5 All Exercises
Exercise | Number of Questions | |
Exercise 5.1 Solutions | 4 Questions & Solutions | |
Exercise 5.2 Solutions | 20 Questions & Solutions | |
Exercise 5.3 Solutions | 20 Questions & Solutions | |
Exercise 5.4 Solutions | 5 Questions & Solutions | |
NCERT Solutions for Class 10 Maths Chapter on Arithmetic Progressions provided by Vedantu offer a comprehensive understanding of this fundamental concept.Students can gain a solid understanding of arithmetic progressions by concentrating on important concepts such as calculating the sum of terms, nth term, and common difference. It's important to pay close attention to the step-by-step solutions provided in the NCERT Solutions, as they help clarify concepts and reinforce problem-solving techniques.Arithmetic progressions are fundamental to more advanced mathematical ideas, hence it's important to understand them. This chapter has usually been the subject of five or six questions on previous year's exam papers . Therefore, practicing a variety of problems from NCERT Solutions and previous year papers can enhance preparation and confidence for exams.
Other Related Links
Sl. No. | Important Link for Chapter 5 Arithmetic Progressions |
1. |
|
2. |
|
3. |
|
4. |
|
5. |
|
6. |
|
Chapter-Specific NCERT Solutions for Class 10 Maths
Given below are the chapter-wise NCERT Solutions for Class 10 Maths . Go through these chapter-wise solutions to be thoroughly familiar with the concepts.
NCERT Solutions Class 10 Chapter-wise Maths PDF |
|
|
|
|
|
|
|
|
|
|
|
|
|

FAQs on NCERT Solutions for Class 10 Maths Chapter 5 - Arithmetic Progressions
1. I’m having doubts in Chapter 5 Maths NCERT. How can Vedantu help me?
If a student has any doubts, then he or she can always contact our in-house academic experts. We at Vedantu offer 24x7 query resolution services. Students can post their questions on the platform and one of our in-house experts will reply with the correct answer as soon as possible. Students can also take online classes. If there is any other way in which way we can help, you should contact us as soon as possible.
2. How can one find the sum of an arithmetic progression?
If one wants to find the sum of an arithmetic progression, then he or she must know the value of the first term, the number of terms, and the common difference that exists between each term. The following formula can be used to arrive at the final answer.
S = n / 2 (2 a + (n - 1) x d)
3. Mention the different types of progressions in mathematics.
There are three types of progressions in mathematics. These types of progressions are:
- Arithmetic progression (AP)
- Geometric progression (GP)
- Harmonic progression (HP)
4. Mention some uses of arithmetic progressions.
Arithmetic progressions can be used to generalize a set of patterns that we usually find in our daily lives.
5. What kind of questions are there in NCERT Solutions for Class 10 Maths Chapter 5?
Vedantu offers solutions for the NCERT Textbook chapter-wise in a simplified manner. Chapter 5 of Class 10 Maths is Arithmetic Progressions. This chapter includes the sequence of numbers where the difference between the two consecutive numbers is the same. This chapter also finds applications in real life such as days of the week, students’ roll numbers, etc. This chapter also includes the other two types of progressions: Geometric and Harmonic.
6. Is it necessary to learn all the topics provided in NCERT Solutions for Class 10 Maths Chapter 5?
Yes, it is very important to learn all the topics and concepts provided in NCERT Solutions for Class 10 Maths Chapter 5. As this chapter forms the foundation for higher grade Mathematics, students need to know the basic formulae and their application. Vedantu offers solutions to all the exercises of chapter 5. The students can refer them online or download them for free to refer offline from the Vedantu website or the Vedantu app.
7. How many Exercises are there in Class 10 Maths Chapter 5 AP?
Chapter 5 of Class 10 Mathematics is Arithmetic progressions. This chapter includes four exercises with similar examples. The examples give you an idea to solve the exercise problems. Vedantu provides solutions to all the exercises in a step-by-step manner. One of the advantages of referring to Vedantu Solutions is that the answers are verified by the subject-matter-experts and are given in a simplified manner.
8. Is Chapter 5 Arithmetic Progression of Class 10 Maths interesting?
Yes, Chapter 5 Arithmetic Progression of Class 10 Maths is interesting. The concepts involved in this chapter are a foundation of the concepts that appear in the higher grades. Also, these have applications in real life such as roll numbers of the students in a class, months in a year, and weeks in a day. Vedantu provides the best learning while solving problems. Not only are the solutions verified, but they are also given in a simplified step-by-step manner.
9. Is Class 10 Arithmetic Progressions of Class 10 Hard?
Maths can be a tricky subject and as the board examinations approach, most of the students have fear while giving the examinations. The only solution to this is by achieving confidence and by practising different types of problems on the same concept. Vedantu offers the previous year’s question papers that the students can refer to get an idea of the marking scheme, the difficulty level of the question paper, and important questions.
10. Is arithmetic progression important?
Yes, arithmetic progression (AP) is important because it's a fundamental concept in mathematics with wide-ranging applications in various fields.
11. What is the main purpose of arithmetic?
The main purpose of arithmetic is to help us to perform fundamental mathematical operations, such as addition, subtraction, multiplication, and division. These functions are necessary for handling daily issues, handling money, calculating amounts, and recognising trends in numerical data. Whether it's counting objects, calculating the cost of groceries, or solving complex mathematical problems, arithmetic forms the basis of mathematical understanding and problem-solving skills.
12. Who is the father of arithmetic?
Brahmagupta is known as the father of arithmetic.
13. What is the full concept of arithmetic?
The full concept of arithmetic encompasses the study of basic mathematical operations involving numbers, such as addition, subtraction, multiplication, and division. It involves understanding how these operations work and how they can be applied to solve various mathematical problems. Arithmetic is fundamental to everyday life, from counting objects to managing finances and beyond. It forms the foundation of more advanced branches of mathematics and is essential for developing strong mathematical skills. In essence, arithmetic provides the tools and techniques necessary for performing calculations and solving numerical problems in a wide range of contexts.
14. What are the real life applications of arithmetic series?
Examples of Real-Life Arithmetic Sequences
Financial Planning
Population Growth
Seating around tables
Stacking cups, chairs, bowls
NCERT Solutions for Class 10 Maths
Ncert solutions for class 10.

NCERT Solutions for Class 10 Maths Ch 5 Arithmetic Progressions


- Exercise 5.1
- Exercise 5.2
- Exercise 5.3
- Exercise 5.4
NCERT Solutions for Class 10 Maths Chapters:
How many exercises in Chapter 5 Arithmetic Progressions
What do you mean by sequence, if 9th term of an a.p. is zero, prove that its 29th term is double of its 19th term., what is common difference, contact form.
NCERT Solutions for Class 10 Maths Chapter 5 AP Arithmetic Progression
NCERT solutions for class 10 Maths chapter 5 all exercises of AP Arithmetic Progression in Hindi and English Medium updated for academic session 2024-25. Class 10 Maths solution is updated according to new textbooks published for CBSE board 2024 exams.
10th Maths Chapter 5 Exercise 5.1 Solutions
- Class 10th Maths Exercise 5.1 in English
- Class 10th Maths Exercise 5.1 in Hindi
10th Maths Chapter 5 Exercise 5.2 Solutions
- Class 10th Maths Exercise 5.2 in English
- Class 10th Maths Exercise 5.2 in Hindi
10th Maths Chapter 5 Exercise 5.3 Solutions
- Class 10th Maths Exercise 5.3 in English
- Class 10th Maths Exercise 5.3 in Hindi
10th Maths Chapter 5 Exercise 5.4 Solutions
- Class 10th Maths Exercise 5.4 in English
- Class 10th Maths Exercise 5.4 in Hindi
- Class 10th Maths Chapter 5 NCERT Book
- Class 10 Maths NCERT Solutions
- Class 10 all Subjects NCERT Solutions

| Class: 10 | Mathematics |
| Chapter 5: | Arithmetic Progression |
| Content: | Exercise Questions Solutions |
| Content Format: | Text, Images, PDF and Videos |
| Academic Session: | Year 2024-25 |
| Medium Type: | English and Hindi Medium |
Class 10 Maths Chapter 5 solutions are useful for not only for CBSE Board but UP Board, MP Board, Gujrat Board, etc. also who are using NCERT Textbooks as a course books. Uttar Pradesh Madhyamik Shiksha parishad, Prayagraj has implemented NCERT Books for Class 10 students. So, UP Board High school students can download UP Board Solutions for Class 10 Maths Chapter 5 in Hindi and English Medium here.
All the Online and Offline Apps , NCERT solutions are based on latest NCERT Books. These apps are applicable for UP Board (Higher Secondary) with CBSE Board and other boards who are using NCERT Books 2024-25 in Hindi and English medium. Download Class 10 Maths Apps based on updated NCERT Solutions for new academic session 2024-25.
NCERT Solutions for class 10 Maths chapter 5 all exercises are given to free use. NCERT Solutions 2024-25 and NCERT books are in PDF format to study online/offline by downloading in your device. Go through this page completely to know more about arithmetic series.

Extra Questions on 10th Maths Chapter 5?
What is an arithmetic progression (ap).
An arithmetic progression (AP) is a list (or pattern or series) of numbers in which each next term is obtained by adding or subtracting a fixed number to the preceding term except the first term. This fixed number is called the common difference of the AP, it may be positive, negative or zero.
What are the objective of studying Arithmetic Progression?
Objective of studying Arithmetic Progression – AP To identify arithmetic progression from a given list of numbers, to determine the general term of an arithmetic progression and to find the sum of first n terms of an arithmetic progression.
What is general form of Arithmetic Progression?
a, a + d, a + 2d, a + 3d, . . . is the general form of Arithmetic Progression where a is first term and d is common difference.
Be connected with us to get the latest update regarding to CBSE solutions, Sample Papers, board questions and all other study material related to class 10 Maths solutions of AP.
TWO MARKS QUESTIONS Find how many integers between 200 and 500 are divisible by 8. [CBSE 2017] THREE MARKS QUESTIONS 1. Find the sum of n terms of the series (4 – 1/n) + (4 – 2/n) + (4 – 3/n) + …. [CBSE 2017] 2. If the mth term of an AP is 1/n and nth term is 1/m then show that its (mn)th term is 1. [CBSE 2017] FOUR MARKS QUESTIONS 1. If the sum of first m terms of an A. P. is the same as the sum of its first n terms, show that the sum of its first (m + n) terms is zero. [CBSE 2017] 2. The ratio of the sums of first m and first n terms of an AP is m²:n². Show that the ratio of its mth and nth terms is (2m – 1):(2n – 1). [CBSE 2017]
About Arithmetic Progression – AP
a, a + d, a + 2d, a + 3d, . . . is called the general form of an AP, where a is the first term and d the common difference. If there are a finite number of terms in the AP, then it is called a finite AP. The general formula for finding nth term is given by a + (n-1)d and the sum of n terms is given by n/2[2a + (n-1)d]. The last term is denoted by l and given by a + (n-1)d.
Historical Facts!
1. Leonardo Pisano Bigollo also known as Leonardo of Pisano, Leonardo Bonacci, Leonardo Fibonacci was an Italian mathematician. He gave Fibonacci series on the basis of, how fast rabbits could breed in ideal circumstances. Fibonacci Series: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 … Here, every next term is sum of previous two terms. For the solutions of other maths chapters of class 10, click here. 2. Once, when famous mathematician Carl Friedrich Gauss (1777 – 1855) misbehaved in primary school, his teacher I.G. Buttner gave him a task to add a list of integers from 1 to 100. Gauss’s method was to realise that pairwise addition of terms from opposite ends of the list yielded identical intermediate sum: 1 + 100 = 2 + 99 = 3 + 98 = … = 50 + 51 = 101. So, here 1 + 2+ 3 + 4 + …. + 100 = the sum of 50 sums each equal to 101. Therefore, the sum is 5050. Finally he gave the answer in seconds.
How to Practice Arithmetic Progression in Class 10 Maths?
We all know the current state of education infrastructure of the country after the COVID-19 impact. We say education is evolving from Didactic methodology to concept-based education. However, it is still very expensive for most of the students to gain access. The disproportionate effects of the COVID-19 pandemic affected brilliant and average minds also. Undoubtedly, students and teachers are sailing the same boat to make the preparations effective. Some of the students are still finding ways to score 100% in the Maths board exam for 10th grade. We selected some of the suggestions that can help you to score well in Chapter 4 AP of class 10th.
Step 1: Learn class 10 Maths chpater 5 with basics and Examples before starting.
Step 2: to solve sums of 10th maths chpater 5 take help from online learning platform., step 3: class 10 maths chapter 5 needs regular homework and revision session., step 4: once go through the chapter 5 ncert 10th maths before it starts in the class., step 5: be confident with the help of regular practice in ap..

Which exercise of 10th Maths chapter 5 need less efforts?
Class 10th Maths exercise 5.2 and 5.3 are easier to solve and the scoring also. The questions given in these two exercise are based on just to formulae – nth term and sum to n terms. Most of the questions get solved just by putting the values in proper formula. So, a student can score more easily in these two exercises.
How many exercises are there in 10th Maths Chapter 5 AP?
There are 4 exercises in chapter 4 of class 10 Maths subject. Out of these exercise 5.4 is an optional exercise, which is not important for examination point of view. It is given just to practice and enhance the knowledge in arithmetic progression.
Is chapter 5 Arithmetic Progression of 10th Maths interesting?
Yes, chapter 5 of 10th Maths is very interesting chapter because you can observe Arithmetic Progressions around you at various points. Examples of AP around you: 1) The heights (in cm) of some students of a school standing in a queue in the morning assembly are 147, 148, 149, . . ., 157. 2) The cash prizes (in Rs) given by a school to the toppers of Classes I to XII are, respectively, 200, 250, 300, 350, . . ., 750.
Is there any optional exercise in chapter 5 Class 10th Math?
Yes, there is optional exercise in chapter 5 of 10th Maths. Fourth exercise (exercise 5.4) is the optional exercise. Exercise 5.4 is not an easy exercise because this exercise contains very tricky questions.
Why chapter 5 of 10th Math important?
Chapter 5 (Arithmetic Progression) of 10th Math is important because students have to study Arithmetic Progression in class 11 maths also. Arithmetic Progression(chapter 5) of 10th maths is base of Arithmetic Progression of class 11th maths.
« Chapter 4: Quadratic Equations
Chapter 6: triangles ».
Copyright 2024 by Tiwari Academy | A step towards Free Education

NCERT Solutions for Class 6, 7, 8, 9, 10, 11 and 12
NCERT Solutions for Class 10 Maths Chapter 5 Arithmetic Progressions Ex 5.1
Get Free NCERT Solutions for Class 10 Maths Chapter 5 Ex 5.1 PDF. Arithmetic Progressions Class 10 Maths NCERT Solutions are extremely helpful while doing your homework. Exercise 5.1 Class 10 Maths NCERT Solutions were prepared by Experienced LearnCBSE.in Teachers. Detailed answers of all the questions in Chapter 5 Maths Class 10 Arithmetic Progressions Exercise 5.1 provided in NCERT TextBook.
Topics and Sub Topics in Class 10 Maths Chapter 5 Arithmetic Progressions:
| 5 | Arithmetic Progressions |
| 5.1 | Introduction |
| 5.2 | Arithmetic Progressions |
| 5.3 | Nth Term Of An AP |
| 5.4 | Sum Of First N Terms Of An AP |
| 5.5 | Summary |
- Class 10 Maths Arithmetic Progressions Ex 5.1
- प्रश्नावली 5.1 का हल हिंदी में
- Class 10 Maths Arithmetic Progressions Ex 5.2
- प्रश्नावली 5.2 का हल हिंदी में
- Class 10 Maths Arithmetic Progressions Ex 5.3
- प्रश्नावली 5.3 का हल हिंदी में
- Class 10 Maths Arithmetic Progressions Ex 5.4
- प्रश्नावली 5.4 का हल हिंदी में
- Arithmetic Progressions Class 10 Extra Questions
NCERT Solutions for Class 10 Maths Chapter 5 Arithmetic Progressions Ex 5.1 are part of NCERT Solutions for Class 10 Maths . Here we have given NCERT Solutions for Class 10 Maths Chapter 5 Arithmetic Progressions Exercise 5.1
| CBSE | |
| NCERT | |
| Class 10 | |
| Maths | |
| 5 | |
| Arithmetic Progressions | |
| Ex 5.1 | |
| 4 | |
We also solved 106 questions from Chapter 9 – Arithmetic Progressions of RD Sharma Class 10 Maths Textbook.
Page No: 99


You can also download the free PDF of Ex 5.1 Class 10 Arithmetic Progressions NCERT Solutions or save the solution images and take the print out to keep it handy for your exam preparation.
Download NCERT Solutions For Class 10 Maths Chapter 5 Arithmetic Progressions PDF
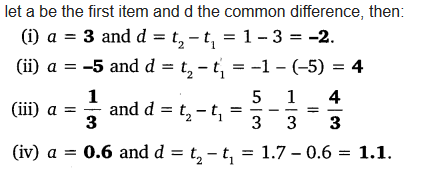
Class 10 Maths Arithmetic Progressions Mind Maps
Arithmetic progression (ap).
Consider (i) 1, 2, 3, 4, …… (ii) 3, 3, 3, 3, ….. (i) and (ii) are the sequence of numbers, each number in these sequences is called a term.
An arithmetic progression (AP) is a sequence of numbers in which each term is obtained by adding a fixed number ‘d’ to the preceeding term, except the first term. The fixed number is called the common difference. It can be positive, negative or zero. Any Arithmetic progression can be represented as : a, a + d, a + 2d, a + 3d,….. where ‘a’ is the first term and ‘d’ is the common difference. Arithmetic progressions which does not have a last term are called Infinite Arithmetic Progression. e.g.: 6, 9, 12, 15,…….
Formula for common Difference (d)
A sequence of numbers a 1 , a 2 , a 3 …. is an AP if the difference a 2 – a 1 , a 3 – a 2 , a 4 – a 3 …. gives the same value, i.e. if a k+1 – a k is the same for different values of k. The difference (a k+1 – a k ) is called common difference (d). Here a k+1 and a k are the (k + 1)th and kth terms respectively. ∴ d = a 2 – a 1 = a 3 – a 2 = a 4 – a 3
n th Term (or General Term) of an Arithmetic Progressions
In an AP, with first term ‘a’ and common difference d, the n th term(or the general term) is given by, a n = a + (n – 1)d Note that an AP can be finite or infinite according to as the number of terms are finite or infinite. If there are m terms in an AP then a m is the last term and is sometimes denoted by ‘l’.
Sum of the FIRST ‘n’ Terms of an A.P.
Arithmetic Mean Between Two Numbers
CLASS 10 MATHS CHAPTER 5 EXERCISE 5.1 AP SOLUTIONS IN HINDI

More Resources for CBSE Class 10
NCERT Solutions
Ncert solutions for class 10 maths.
- NCERT Solutions for Class 10 Science
- NCERT Solutions for Class 10 Social
- NCERT Solutions for Class 10 English
- NCERT Solutions for Class 10 Hindi
- NCERT Solutions for Class 10 Sanskrit
- NCERT Solutions for Class 10 Foundation of IT
- RD Sharma Class 10 Solutions
Formulae Handbook for Class 10 Maths and Science
- Chapter 1 Real Numbers
- Chapter 2 Polynomials
- Chapter 3 Pair of Linear Equations in Two Variables
- Chapter 4 Quadratic Equations
- Chapter 5 Arithmetic Progressions
- Chapter 6 Triangles
- Chapter 7 Coordinate Geometry
- Chapter 8 Introduction to Trigonometry
- Chapter 9 Some Applications of Trigonometry
- Chapter 10 Circles
- Chapter 11 Constructions
- Chapter 12 Areas Related to Circles
- Chapter 13 Surface Areas and Volumes
- Chapter 14 Statistics
- Chapter 15 Probability
We hope the NCERT Solutions for Class 10 Maths Chapter 5 Arithmetic Progressions Ex 5.1, help you. If you have any query regarding NCERT Solutions for Class 10 Maths Chapter 5 Arithmetic Progressions Exercise 5.1, drop a comment below and we will get back to you at the earliest.
Free Resources
Quick Resources

IMAGES
COMMENTS
Case study questions on CBSE Class 10 Maths Chapter 5 - Arithmetic Progression are provided here. These questions are published by CBSE to help students prepare for their Maths exam. By Gurmeet Kaur
Class 10 Maths Chapter 5 Case Study Questions have been prepared for the latest exam pattern. You can check your knowledge by solving case study-based questions for Class 10 Maths Chapter 5 Arithmetic Progressions. In CBSE Class 10 Maths Paper, Students will have to answer some questions based on Assertion and Reason. There will be a few ...
CBSE Board has introduced the case study questions for the ongoing academic session 2021-22. The board will ask the paper on the basis of a different exam pattern which has been introduced this year where 50% syllabus is occupied for MCQ for Term 1 exam. Selfstudys has provided below the chapter-wise questions for CBSE Class 10 Maths.
On the basis of the above information, answer any four of the following questions: (i) Find the total number of rows of candies. (ii) Find the difference in number of candies placed in 7th and 3rd rows. Answers -. (i) There is an AP: 3,5,7, a = 3 & d = 2 so apply let there are n rows sum of n terms = n/2 {2 + ( − 1)}
Case Study Questions for Class 10 Maths Chapter 5 Arithmetic Progression. Question 1: In a flower bed, there are 43 rose plants in the first row, 41 in the second, 39 in the third and so on. (i) If there are 11 rose plants in the last row, then number of rose required are. (a) 16 (b) 15 (c) 17 (d) 10. (ii) Difference of rose plants in 7th row ...
These Case Study and Passage Based questions are published by the experts of CBSE Experts for the students of CBSE Class 10 so that they can score 100% on Boards. CBSE Class 10 Mathematics Exam 2024 will have a set of questions based on case studies in the form of MCQs. The CBSE Class 10 Mathematics Question Bank on Case Studies, provided in ...
Students referring to the Class 10 Maths Case Study Questions And Answers Pdf from Selfstudys will find these features:-. Accurate answers of all the Case-based questions given in the PDF. Case Study class 10 Maths solutions are prepared by subject experts referring to the CBSE Syllabus of class 10. Free to download in Portable Document Format ...
This video explains the detailed solution and explanation of Case Study Based Questions related to Chapter 5 Arithmetic progressions.This video will give you... CBSE Exam, class 10
Case Study Based Question - Arithmetic Progressions Class 10 Maths Chapter 5 | CBSE Class 10 Maths Chapter 5 | NCERT Solutions for Class 10 Maths Chapter 5. ...
Video of all questions are also available. In this chapter, we will learn. Check out the answers to the exercises (including examples and optional) by clicking a link below, or learn from the concepts. Updated for newNCERT Book - 2023-24 EditionGet solutions of all NCERT Questions with examples of Chapter 5 Class 10 Arithmetic Progressions (AP).
The passage-based questions are commonly known as case study questions. Students looking for Case Study on Arithmetic Progressions Class 10 Maths can use this page to download the PDF file. The case study questions on Arithmetic Progressions are based on the CBSE Class 10 Maths Syllabus, and therefore, referring to the Arithmetic Progressions ...
REAL NUMBERS- CASE STUDY CASE STUDY 1. To enhance the reading skills of grade X students, the school nominates you and two of your friends to set up a class library. There are two sections- section A and section B of grade X. There are 32 students in section A and 36 students in section B. 1. What is the minimum number of books you will acquire ...
Welcome to CBSE Worldz. In this video we will be discussing CBSE class 10 Case Study Based Questions of maths Chapter 5 Arithmetic Progression for Term 2CASE...
First of all, we would like to clarify that class 10 maths case study questions are subjective and CBSE will not ask multiple-choice questions in case studies. So, you must download the myCBSEguide app to get updated model question papers having new pattern subjective case study questions for class 10 the mathematics year 2022-23.
CBSE 10th Standard Maths Subject Real Number Case Study Questions With Solution 2021 Answer Keys. Case Study Questions. (i) (d) : For a number to end in zero it must be divisible by 5, but 4 n = 22 n is never divisible by 5. So, 4 n never ends in zero for any value of n. (ii) (c) : We know that product of two rational numbers is also a rational ...
10th Standard CBSE Subjects. Maths. Science. Social Science. QB365 Provides the updated CASE Study Questions for Class 10 , and also provide the detail solution for each and every case study questions . Case study questions are latest updated question pattern from NCERT, QB365 will helps to get more marks in Exams.
List of Exercises from Class 10 Maths Chapter 5 Arithmetic progression. Exercise 5.1 - 4 questions 1 MCQ and 3 descriptive type questions. Exercise 5.2 - 20 questions, 1 fill in the blanks, 2 MCQs, 7 Short answer questions and 10 Long answer questions.
In Maths NCERT Solutions Class 10 Chapter 5, students will learn about the arithmetic progression.The NCERT Solutions for Class 10 Maths Chapter 5 PDF file, available for free, can help students to score good marks. Students can download this PDF file by visiting Vedantu. This file is prepared by the best academic experts in India. Every answer is written according to the guidelines set by CBSE.
NCERT Solutions Chapter 5 Arithmetic Progressions Class 10 Maths is given here which will be useful in completing homework on time and improving your problem solving skills. Our experts have prepared detailed solutions of every question so a student can understand them easily. As finding free and accurate NCERT Solutions for Class 10 Maths can be sometimes very challenging that is why we have ...
Step 2: To solve sums of 10th Maths chpater 5 take help from Online Learning Platform. Step 3: Class 10 Maths chapter 5 needs regular Homework and revision session. Step 4: Once go through the chapter 5 NCERT 10th Maths before it starts in the class. Step 5: Be confident with the help of regular practice in AP.
Get Free NCERT Solutions for Class 10 Maths Chapter 5 Ex 5.1 PDF. Arithmetic Progressions Class 10 Maths NCERT Solutions are extremely helpful while doing your homework or while preparing for the exam. Exercise 5.1 Class 10 Maths NCERT Solutions were prepared according to CBSE marking scheme and guidelines.
Class 10th | Maths | Chapter 3 | Exercise 3.5 Question 1,2 and 4 | KPK Board 10th class mathematics |Welcome to our comprehensive tutorial on "KPK boards Cl...