research paper using correlation analysis

Writing about Correlation

Cite this chapter.

• Lindy Woodrow 2  

1568 Accesses

Correlation analysis is another technique used to explore the relationship between variables. It is similar to regression and is the basis of other more complex statistical procedures such as factor analysis and structural equation modelling. Correlation is also widely used in establishing the reliability and validity of a questionnaire and to establish inter-rater reliability. This chapter includes the following sections:

Technical information

Bivariate correlation

Partial correlation

Reliability

Reference to correlation analysis in text sections

Using tables to report correlations

Correlation for validation

Correlation for inter-rater reliability

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

• Available as EPUB and PDF
• Read on any device
• Instant download
• Own it forever
• Compact, lightweight edition
• Dispatched in 3 to 5 business days
• Free shipping worldwide - see info
• Durable hardcover edition

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Unable to display preview.  Download preview PDF.

Further reading

Field, A. (2013). Discovering statistics using SPSS (4th ed.). London: Sage.

Google Scholar  

Lowie, W., & Seton, B. (2013). Essential statistics for Applied Linguistics . Basingstoke: Palgrave-Macmillan.

Sources of examples

Mori, Y., Sato, K., & Shimizu, H. (2007). Japanese language students’ perceptions on Kanji learning and their relationship to novel Kanji learning ability. Language Learning , 57(1), 57–85. doi: 10.1111/j.1467-9922.2007.00399.x.

Article   Google Scholar  

Nisbet, D. L., Tindal, E. R., & Arroyo, A. A. (2005). Language learning strategies and English learning proficiency of Chinese university students. Foreign Language Annals , 38(1), 100–107. doi: 10.1111/j.1944-9720.2005.tb02457.x.

Ong, J., & Zhang, L. (2012). Effects of manipulation of cognitive processes in EFL writers’ text quality. TESOL Quarterly , 47(2), 375–398. doi: 10.1002/tesq.55.

Ryan, S. (2008). The ideal L2 selves of Japanese learners of English . PhD, University of Nottingham.

Woodrow, L. J. (2006a). Academic success of international postgraduate education students and the role of English proficiency. University of Sydney Papers in TESOL , 1, 51–70.

Download references

Author information

Authors and affiliations.

University of Sydney, Australia

Lindy Woodrow

You can also search for this author in PubMed   Google Scholar

Copyright information

© 2014 Lindy Woodrow

About this chapter

Woodrow, L. (2014). Writing about Correlation. In: Writing about Quantitative Research in Applied Linguistics. Palgrave Macmillan, London. https://doi.org/10.1057/9780230369955_9

Download citation

DOI : https://doi.org/10.1057/9780230369955_9

Publisher Name : Palgrave Macmillan, London

Print ISBN : 978-0-230-36997-9

Online ISBN : 978-0-230-36995-5

eBook Packages : Palgrave Language & Linguistics Collection Education (R0)

Share this chapter

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Publish with us

Policies and ethics

• Find a journal
• Track your research

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

• View all journals
• My Account Login
• Explore content
• About the journal
• Publish with us
• Sign up for alerts
• Open access
• Published: 24 May 2021

A systematic review and meta-analysis on correlation of weather with COVID-19

• Poulami Majumder 1 &
• Partha Pratim Ray 2  

Scientific Reports volume  11 , Article number:  10746 ( 2021 ) Cite this article

8990 Accesses

29 Citations

13 Altmetric

Metrics details

• Climate sciences
• Environmental sciences
• Statistical methods
• Viral infection

This study presents a systematic review and meta-analysis over the findings of significance of correlations between weather parameters (temperature, humidity, rainfall, ultra violet radiation, wind speed) and COVID-19. The meta-analysis was performed by using ‘meta’ package in R studio. We found significant correlation between temperature (0.11 [95% CI 0.01–0.22], 0.22 [95% CI, 0.16–0.28] for fixed effect death rate and incidence, respectively), humidity (0.14 [95% CI 0.07–0.20] for fixed effect incidence) and wind speed (0.58 [95% CI 0.49–0.66] for fixed effect incidence) with the death rate and incidence of COVID-19 ( p  < 0.01). The study included 11 articles that carried extensive research work on more than 110 country-wise data set. Thus, we can show that weather can be considered as an important element regarding the correlation with COVID-19.

Similar content being viewed by others

The economic commitment of climate change

Systematic review and meta-analysis of ex-post evaluations on the effectiveness of carbon pricing

A meta-analysis on global change drivers and the risk of infectious disease

Introduction.

COVID-19 has impacted significantly over the human society in recent times 1 , 2 , 3 , 4 . More than 25 million population is already infected and over 0.8 million are already died of by the COVID-19 5 . Scientific organizations are currently involved in the development of possible vaccines to further stop the deadly spread of COVID-19 6 , 7 , 8 , 9 , 10 , 11 , 12 , 13 , 14 , 15 . Weather conditions always play important roles to the enhancement or eradication of health issues 16 , 17 , 18 , 19 . Thus, we can look for finding answer of the research question: whether weather has any correlation with COVID-19 20 .

A study 21 was conducted to find the possibility of correlation between weather parameters with COVID-19. However, the comments didn’t conform to specific answer of weather impact on COVID-19. A study was conducted to test the impact of temperature on Australia and Egypt as a case study 22 . It suggested that there is a relation between temperature and COVID-19. A systematic review was performed where advocacy was made in favour of low evidence for impact of temperature and humidity on COVID-19 23 . No meta-analysis was done in this work. Harmooshi et al. 24 investigated a generic review of 16 articles having some outcome-based impact over COVID-19. This work suggested that cool weather may affect transmissibility of COVID-19. In 25 , a prediction model was investigated for India in stating probable condition in 2020 due to COVID-19. Weather impact was found in Turkey over a 14-day long study 26 , 27 suggested that incidence of COVId-19 could lower with high temperature and high wind speed. Thus, we can see that different articles stated their own point of view via various methods while resulting into confusion.

In this paper, we present first ever meta-analysis of impacts of weather on the death and incidence on the COVID-19. Initially, we selected vital articles from digital repositories to find resourceful information. Thus, we performed a systematic review upon proper inclusion and exclusion criteria. Secondly, we used risk assessment of the included articles in this study. Thirdly, we performed evidence certainty tests of such articles to find suitability over the significant impact analysis of weather over COVID-19. We selected five weather parameter such as, temperature, humidity, rainfall, ultra violet and wind speed to find correlation with the death rate and incidence of the COVID-19. Fourthly, we performed forest and funnel plots to investigate the heterogeneity and publication bias, respectively.

Search strategy

A comprehensive literature survey was conducted while considering articles from the following digital databases such as, PubMed, Sciencedirect, IEEE Xplore, Google Scholar, and Cochrane. We used a set of combination of key words to search the articles as shown in Table 1 . One independent author (PPR) performed screening of abstract and titles of the literature against the aforementioned keyword and scope of the study. Other author (PM) did the review of final selection of the articles. Evaluation of full-texts were conducted against the inclusion and exclusion criteria.

Study selection

The work was done as per the Preferred Reporting Items for Systematic Reviews and Meta-Analyses (PRISMA) guidelines 28 . We conducted a qualitative analysis of the 11 included articles in this study based on publication year, zone or country of work, various variables used, key techniques used and remarks on the observations. Figure 1 presents the PRISMA of the meta-analysis. Inclusion of articles depends on the availability of correlation factors in the surveyed articles. We have included those studies that only discusses about the correlation between weather parameters to COVID-19. We also, seek for the relevance of performed studies in the article to prescribe some key suggestions. Further, we include those articles that are full-text published but not from the medRxiv repository for meta-analysis. We focused on the quantitative synthesis of statistical approaches used in the articles. We excluded all the articles which are published in non-indexed journals and don’t conform to the direct correlation perspective of COVID-19 with weather factors. Due to lack of minimal availability, we exclude the correlating parameters related to the pollution, air quality index (AQI), pollination, and sun light intensity as the weather parameters in this meta-analysis.

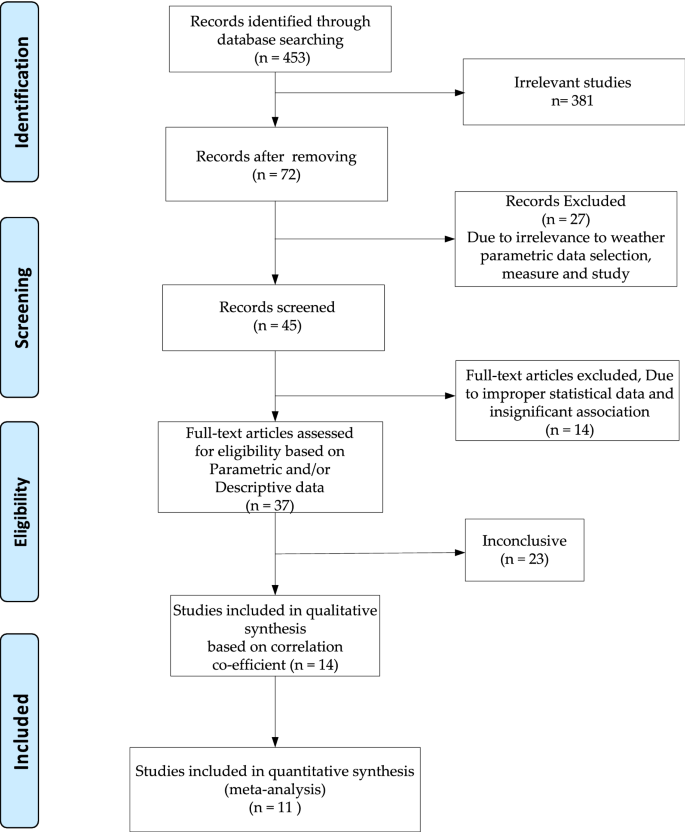
PRISMA flowchart for the study.

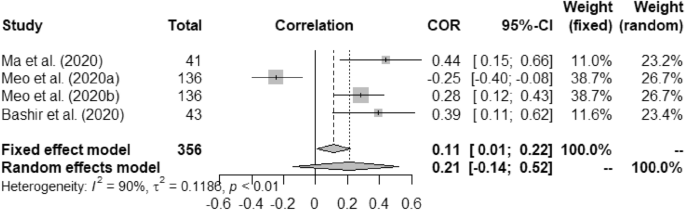
Forest plot of COVID-19 death rate with temperature.

Assessment of risk of bias

We assessed the quality of the articles selected in this study by using the Joanna Briggs Institute (JBI) tool 29 . The checklist contained eight questions such as (a) were the criteria for inclusion in the sample clearly defined, (b) were the study subjects and the setting described in detail, (c) was the exposure measured in a valid and reliable way, were objective, (d) standard criteria used for measurement of the condition, (e) were confounding factors identified, (f) were strategies to deal with confounding factors stated, (g) were the outcomes measured in a valid and reliable way and (h) was appropriate statistical analysis used. Each of the question was examined against each of the 11 articles and answer was given in ‘Yes’ and ‘No’. Overall risk was finally specified at the bottom of Table 2 with two main answers such as, ‘Low’ and ‘Moderate’. Both the authors (PPR and PM) independently evaluated risk and quality of each study and confusion was mitigated by a consensus team meeting.

Data extraction and outcome measure

Data was extracted for following variables such as, (a) temperature, (b) humidity, (c) rainfall, (d) ultra violet (UV) radiation and (e) wind speed. We considered two key COVID-19 parameters such as, (a) death rate and (b) incidence. Thus, five key weather elements were used to find association with two COVID-19 parameters for performing meta-analysis on possible weather impact on COVID-19. Solar radiation and UV radiation were assumed to be same by considering SI unit i.e. W-m -2 . We considered relative humidity out of absolute and relative humidity while performing this meta-analysis. Major characteristics of the included studies rely in the recently performed correlation assessment between the weather parameters with the incidence or death rate of COVID-19. Further, we considered the evaluation criteria as mentioned in the articles to provide the meta-analysis.

Certainty measure

The GRADE (Grading of Recommendations Assessment, Development, and Evaluation) 30 approach was used to evaluate the quality of evidence for each outcome as shown in Table 3 . We tested 7 outcomes on the correlations between (a) temperature and COVID-19 death rate, (b) humidity with COVID-19 death rate, (c) temperature with COVID-19 incidence, (d) humidity with COVID-19 incidence, (e) rainfall with COVID-19 incidence, (f) UV with COVID-19 incidence, and (g) wind speed with COVID-19 incidence. We found the impact of each of the outcomes. We also measured the evidence of certainty using  ⊕  AND/OR ◯ combination of four symbols in terms of ‘Moderate’, ‘High’, and ‘Very High’. The points in the GRADE analysis are considered as follows. Very High point is given to the correlation factor that shows the highest order significance among all the included works. Similarly, High point is given to those parametrization aspects where we notice strong evidence of measure. We give Moderate as the lowest measure to the correlating perspective having lowest of significance.

Statistical analysis

Accessed data from 11 articles were initially recorded into the excel datasheet which was later segregated into 7 different comma separated value CSV) files for feeding into the RStudio version 3.4.3 with package meta. We used metacor(cor = r, n = N, data = d, studlab = Author, sm = "ZCOR") method call to perform the fixed-effect and random effect model study. We used Fisher’s z transformed correlations to find meta-analysis. Here, r, N and d represent the CSV columns named as r, N and the CSV itself, respectively. Where, r and N (sample size) of the specific CSV stored the correlation values in ( +) and/or (-) terms and days of experiment by individual article, respectively. 95% confidence interval (CI) was measured for each of the articles. Wang et al. (2020a), Wang et al. (2020b), Meo et al. (2020a), and Meo et al. (2020b) were sub-set wise used of the Wang et al. (2020) and Meo et al. (2020) articles, respectively. Fixed and random weight of each of the article was computed. We found heterogeneity (I 2 ) and τ 2 as the level of heterogeneity and measure of dispersion of true effect sizes under the given assumptions that the true effect sizes were bell-shaped and normally distributed, respectively. We used the forest() method to derive the forest plots for seven different scenarios of correlation meta-analysis with help of the Fisher's z transformed correlations.

Study selection and characteristics

The article reporting and record keeping task was finalized on August 6, 2020. All the included papers belong to the initial to recent COVID-19 impacts i.e. December 1, 2019–June 5, 2020. Based on initial record screening, we found 453 articles. We remove 381 irrelevant articles and later moved with 72 records. Due to irrelevance to weather parametric data selection, measurement and study approaches, we excluded 27 articles. Out of 45 articles, upon full-text screening we found improper statistical data and insignificant association between weather and COVID-19, we rejected 14 articles. Rest of the 37 articles were focused on wither parametric or description statistical association study between the weather and COVID-19. However, 23 were found to be nonconclusive toward correlation between weather and COVID-19 which were later on rejected. Out of 14 articles, only 11 were finally included in this meta-analysis. All the studies discussed about some sort of correlation factor with one or more weather parameters comprising of temperature, humidity, rainfall, UV and wind speed with the COVID-19 death rate or incidence level in various parts of globe. The articles conducted studies in different zones of countries belonging to Wuhan, China, mainland China, India, USA, Japan, Jakarta, Indonesia, Australia, Canada, Iran and more than 110 countries. The article mainly used the Pearson’s correlation coefficient, cohort study, Spearman’s rank correlation logarithmic estimation, generalized additive model (GAM) and Fama–Macbeth regression statistical techniques. Out of 11 only 1 article remarked about the basic reproduction number i.e. R 0 in conjunction to the weather parameters for possible impact on the COVID-19 incidence.

Survey of articles

Table 4 presents the comparison between the articles included in this study. Wang et al. (2020a) and Wang et al. (2020b) represent a single article but two different works related to China and USA. Similarly, Meo et al. (2020) performed studies on 10 hottest and 10 coolest countries, thus two versions of citations were used into the further works such as Meo et al. (2020a) and Meo et al. (2020b) representing hot and cool countries, respectively.

Overall outcomes

Table 5 presents overall outcome from this study. Correlation between the temperature and COVID-19 death rate was measured as (a) fixed effect model: 0.11 (95% CI, 0.01–0.22) and (b) random effect model: 0.21 (95% CI − 0.14–0.52) with p  < 0.01. Similarly, humidity and COVID-19 correlation were measured as − 0.13 (95% CI, − 0.23- 0.03) and − 0.13 (95% CI, − 0.23–0.03) for fixed and random effect model, respectively against p-value at 0.53.

In case of weather and COVID-19 incidence correlation aspect, we found that temperature had 0.22 (95% CI, 0.16–0.28) and 0.23 (95% CI, 0.01–0.42) for fixed and random study, respectively. We found that humidity had positive correlation with the COVID-19 incidence at p  < 0.01. Rainfall had minimal positive correlation with COVID-19 incidence having 0.04 (95% CI, − 0.09–0.16)0.03 (95% CI, − 0.10–0.17) for fixed and random, respectively. Correlation between UV and COVID-19 incidence was measured as − 0.09 (95% CI, − 0.23–0.06) for fixed and − 0.14 (95% CI, − 0.43–0.18) for random model. Wind speed was found to have positive correlation with the incidence of COVID-19 such as, 0.58 (95% CI, 0.49–0.66) and 0.62 (95% CI, − 0.17–0.92).

Heterogeneity (I 2 ) was mostly observed with the temperature, humidity (COVID-19 incidence) and wind speed variables i.e. 90%, 96% and 98%, respectively. Complete homogeneity i.e. (I 2  = 0) was found in the humidity with the death rate of COVID-19 with zero τ 2 . I 2 of rainfall was found as 16% against the COVID-19 incidence.

Figures 2 , 3 , 4 , 5 , 6 , 7 , and 8 present the forest plots of seven different correlation aspects of weather parameters with COVID-19 death rate and incidence.

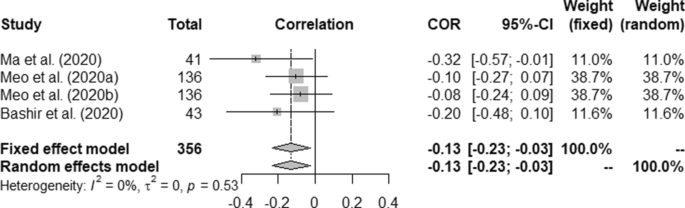
Forest plot of COVID-19 death rate with humidity.

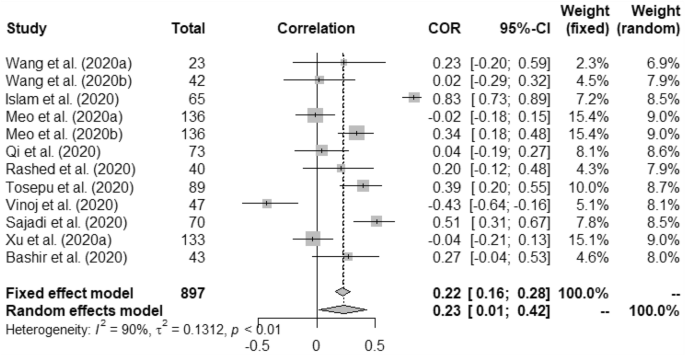
Forest plot of COVID-19 incidence with temperature.

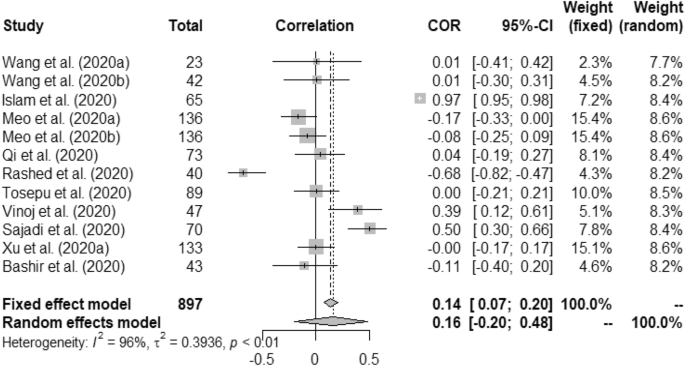
Forest plot of COVID-19 incidence with humidity.

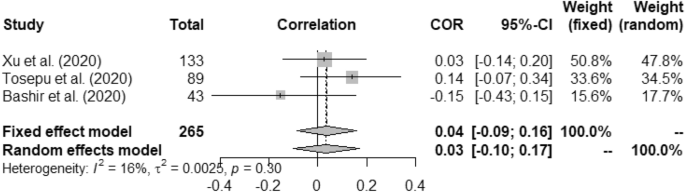
Forest plot of COVID-19 incidence with rainfall.

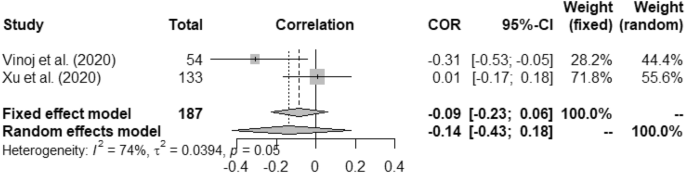
Forest plot of COVID-19 incidence with UV.

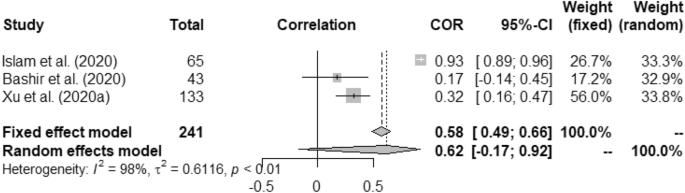
Forest plot of COVID-19 incidence with wind speed.

To best of our knowledge, herein presented systematic review and meta-analysis is the first ever work to find answer of correlation between weather on COVID-19. Our meta-analysis is the first to analyse the effect of weather on the death rate and incidence of COVID-19. Based on our meta-analysis we found correlation between weather on the COVID-19. Temperature and humidity are most crucial weather factors that are string enough to impact over the death rate and incidence of COVID-19 42 , 43 . All the articles included into this study adhere to the weather centric approaches to the COVID-19. All the articles performed their research during December, 2019 to June, 2020. Thus, a long-time duration was covered in our meta-analysis to come at genuine and effective conclusion about possibility of weather impact on COVID-19. Correlation parameters were used in this study to disseminate direct relationship between the weather and COVID-19.

Our meta-analysis included more than 110 country data regarding weather impact on the coronavirus spread and deaths. As the articles carries extensive research during initial phase and mid phase of COVID-19 in most of the countries, this meta-analysis is far more effective to provide more specific answer to correlation-related questions which were frequently asked in near past. With involvement of the JBI tools and GRADE evidence profile, presented meta-analysis serves as an indispensable literature in the current context of COVID-19 incidence.

In this meta-analysis, we assumed the correlation values to be most effective than other alternatives due to its straight forward nature of relationship measurement approach. We depended our study over the fixed and random effect models asides the heterogeneity and dispersion of true size effects. Significant forest plots were obtained for the (a) temperature versus death rate, (b) temperature versus incidence, (c) humidity versus incidence, and (d) wind speed versus incidence of COVID-19 i.e. air borne. Though, impact of UV radiation over the incidence of COVID-19 was computed but negative correlation was observed. It means that with more UV radiation lesser incidence of COVID-19 can be found. Similarly, rainfall has a positive correlation with COVID-19 incidence.

We didn’t know the exact reason why such behaviour i.e. non-significance was observed. We can hypothesize that higher rainfall increases relative humidity in air thus a greater number of cases can be seen due to COVID-19. One surprising result was found in our meta-analysis i.e. negative correlation between humidity with death rate, though its relationship to the incidence was earlier discussed to be positively correlated. We not clear about the reason behind such nature of humidity.

Our work has some limitations including availability of plentiful research on weather correlation with COVID-19. This study restricted us to conduct meta-analysis on available articles where some of them were taken from various preprint servers. Thus, risk of rejection of those articles were not accurately considered, even though we used JBI and GRADE methods. We can also say that hot countries with high average temperature and relative humidity are more prone get affected by new incidences of COVID-19 in coming days. It can be estimated that during coming winter may provide some relief to the people of world. However, more research should be conducted to better support our meta-analysis conclusions.

We found some strong correlations between weather over the incidence of COVID-19. The met-a analysis can be useful for the policy makers of the government and health incorporations to take prior decisions before the possible surge of COVID-19 cases depending on the weather forecasting mechanism. We urge the medical professionals and weather analysts to further investigate the findings of this article as the a-priori information to mitigate the COVID-19 pandemic.

COVID, T.C. and Team, R. Severe outcomes among patients with coronavirus disease 2019 (COVID-19)-United States, February 12-March 16, 2020. MMWR Morb Mortal Wkly Rep 69 (12), 343–346 (2020).

Article   Google Scholar  

Mehta, P. et al. COVID-19: consider cytokine storm syndromes and immunosuppression. Lancet (London, England) 395 (10229), 1033 (2020).

Article   CAS   Google Scholar  

Velavan, T. P. & Meyer, C. G. The COVID-19 epidemic. Tropical Med. Int. Health 25 (3), 278 (2020).

Kannan, S., Ali, P. S. S., Sheeza, A. & Hemalatha, K. COVID-19 (Novel Coronavirus 2019)-recent trends. Eur. Rev. Med. Pharmacol. Sci 24 (4), 2006–2011 (2020).

CAS   PubMed   Google Scholar  

Worldometer covid-19, Available online https://www.worldometers.info/coronavirus/ , Accessed on September 1, 2020.

Le, T. T. et al. The COVID-19 vaccine development landscape. Nat. Rev. Drug Discov. 19 (5), 305–306 (2020).

Hotez, P. J., Corry, D. B. & Bottazzi, M. E. COVID-19 vaccine design: the Janus face of immune enhancement. Nat. Rev. Immunol. 20 (6), 347–348 (2020).

Graham, B. S. Rapid COVID-19 vaccine development. Science 368 (6494), 945–946 (2020).

Corey, L., Mascola, J. R., Fauci, A. S. & Collins, F. S. A strategic approach to COVID-19 vaccine R&D. Science 368 (6494), 948–950 (2020).

Wu, S.C., 2020. Progress and Concept for COVID‐19 Vaccine Development. Biotechnology Journal.

Yamey, G. et al. Ensuring global access to COVID-19 vaccines. The Lancet 395 (10234), 1405–1406 (2020).

Lv, H., Wu, N.C. and Mok, C.K., 2020. COVID‐19 vaccines: knowing the unknown. European J. Immunol .

Koirala, A., Joo, Y.J., Khatami, A., Chiu, C. and Britton, P.N., 2020. Vaccines for COVID-19: the current state of play. Paediatric Respirat. Rev .

DeRoo, S.S., Pudalov, N.J. and Fu, L.Y., 2020. Planning for a COVID-19 Vaccination Program. JAMA .

Thunstrom, L., Ashworth, M., Finnoff, D. and Newbold, S., 2020. Hesitancy Towards a COVID-19 Vaccine and Prospects for Herd Immunity. Available at SSRN 3593098.

Kyle, C. H., Liu, J., Gallagher, M. E., Dukic, V. & Dwyer, G. Stochasticity and infectious disease dynamics: density and weather effects on a fungal insect pathogen. Am. Nat. 195 (3), 504–523 (2020).

Fujii, F., Egami, N., Inoue, M. and Koga, H., 2020. Weather condition, air pollutants, and epidemics as factors that potentially influence the development of Kawasaki disease. Sci. Total Environ , 741, p.140469.

Wang, Z.B., Ren, L., Lu, Q.B., Zhang, X.A., Miao, D., Hu, Y.Y., Dai, K., Li, H., Luo, Z.X., Fang, L.Q. and Liu, E.M., 2020. The impact of weather and air pollution on viral infection and disease outcome among pediatric pneumonia patients in Chongqing, China from 2009 to 2018: a prospective observational study. Clinical Infectious Diseases.

Passer, J.K., Danila, R.N., Laine, E.S., Como-Sabetti, K.J., Tang, W. and Searle, K.M., 2020. The association between sporadic Legionnaires' disease and weather and environmental factors, Minnesota, 2011–2018. Epidemiology & Infection, 148.

Tobías, A. & Molina, T. Is temperature reducing the transmission of COVID-19?. Environ. Res. 186 , 109553 (2020).

Yuan, S., Jiang, S. & Li, Z. L. Do humidity and temperature impact the spread of the novel coronavirus?. Front. Public Health 8 , 240 (2020).

Anis, A., 2020. The Effect of Temperature Upon Transmission of COVID-19: Australia And Egypt Case Study. Available at SSRN 3567639.

Mecenas, P., Bastos, R., Vallinoto, A. and Normando, D., 2020. Effects of temperature and humidity on the spread of COVID-19: a systematic review. medRxiv.

Harmooshi, N.N., Shirbandi, K. and Rahim, F., 2020. Environmental concern regarding the effect of humidity and temperature on 2019-nCoV survival: fact or fiction. Environmental Science and Pollution Research, pp.1–10.

Gupta, S., Raghuwanshi, G.S. and Chanda, A., 2020. Effect of weather on COVID-19 spread in the US: a prediction model for India in 2020. Science of The Total Environment, p.138860.

Şahin, M., 2020. Impact of weather on COVID-19 pandemic in Turkey. Science of The Total Environment, p.138810.

Rosario, D.K., Mutz, Y.S., Bernardes, P.C. and Conte-Junior, C.A., 2020. Relationship between COVID-19 and weather: Case study ain a tropical country. Int. J. Hyg. Environ. Health, 229, p.113587.

Chen, H. et al. Compound Kushen injection combined with platinum-based chemotherapy for stage III/IV non-small cell lung cancer: a meta-analysis of 37 RCTs following the PRISMA guidelines. J. Cancer 11 (7), 1883 (2020).

Lockwood, C., Stannard, D., Jordan, Z. and Porritt, K., 2020. The Joanna Briggs Institute clinical fellowship program: a gateway opportunity for evidence-based quality improvement and organizational culture change.

Piggott, T., Morgan, R.L., Cuello-Garcia, C.A., Santesso, N., Mustafa, R.A., Meerpohl, J.J., Schünemann, H.J. and GRADE Working Group. Grading of Recommendations Assessment, Development, and Evaluations (GRADE) notes: extremely serious, GRADE’s terminology for rating down by three levels. J. Clin. Epidemiol. 120 , 116–120 (2020).

Ma, Y., Zhao, Y., Liu, J., He, X., Wang, B., Fu, S., Yan, J., Niu, J., Zhou, J. and Luo, B., 2020. Effects of temperature variation and humidity on the death of COVID-19 in Wuhan, China. Science of The Total Environment, p.138226.

Wang, J., Tang, K., Feng, K. and Lv, W., 2020. High temperature and high humidity reduce the transmission of COVID-19. Available at SSRN 3551767.

Nazrul, I., Sharmin, S. and Mesut, E.A., 2020. Temperature, humidity, and wind speed are associated with lower Covid-19 incidence. https://www.medrxiv.org/content/medrxiv/early/2020/03/31/2020.03.27.20045658.full.pdf .

Qi, H., Xiao, S., Shi, R., Ward, M.P., Chen, Y., Tu, W., Su, Q., Wang, W., Wang, X. and Zhang, Z., 2020. COVID-19 transmission in Mainland China is associated with temperature and humidity: a time-series analysis. Science of the Total Environment, p.138778.

Meo, S. A. et al. Climate and COVID-19 pandemic: effect of heat and humidity on the incidence and mortality in world’s top ten hottest and top ten coldest countries. Eur. Rev. Med. Pharmacol. Sci. 24 (15), 8232–8238 (2020).

Rashed, E. A., Kodera, S., Gomez-Tames, J. & Hirata, A. Influence of absolute humidity, temperature and population density on COVID-19 spread and decay durations: multi-prefecture study in Japan. Int. J. Environ. Res. Public Health 17 (15), 5354 (2020).

Tosepu, R., Gunawan, J., Effendy, D.S., Lestari, H., Bahar, H. and Asfian, P., 2020. Correlation between weather and Covid-19 pandemic in Jakarta, Indonesia. Sci. Total Environ , p.138436.

Bashir, M. F. et al. Correlation between climate indicators and COVID-19 pandemic in New York 138835 (Science of The Total Environment, 2020).

Google Scholar  

Vinoj, V., Gopinath, N., Landu, K., Behera, B. and Mishra, B., 2020. The COVID-19 Spread in India and its dependence on temperature and relative humidity.

Sajadi, M.M., Habibzadeh, P., Vintzileos, A., Shokouhi, S., Miralles-Wilhelm, F. and Amoroso, A., 2020. Temperature and latitude analysis to predict potential spread and seasonality for COVID-19. Available at SSRN 3550308.

Xu, R., Rahmandad, H., Gupta, M., DiGennaro, C., Ghaffarzadegan, N., Amini, H. and Jalali, M.S., 2020. The modest impact of weather and air pollution on COVID-19 transmission. medRxiv.

Hariyanto, T. I., Kristine, E., Jillian Hardi, C. & Kurniawan, A. Efficacy of lopinavir/ritonavir compared with standard care for treatment of coronavirus disease 2019 (COVID-19): a systematic review. Infect. Disord. Drug Targets. https://doi.org/10.2174/1871526520666201029125725 (2020).

Article   PubMed   Google Scholar  

Hariyanto, T. I., Hardyson, W. & Kurniawan, A. Efficacy and safety of tocilizumab for coronavirus disease 2019 (Covid-19) patients: a systematic review and meta-analysis. Drug Res. (Stuttg). https://doi.org/10.1055/a-1336-2371 (2021).

Download references

Author information

Authors and affiliations.

Department of Biotechnology, Maulana Abul Kalam Azad University of Technology, Kolkata, India

Poulami Majumder

Department of Computer Applications, Sikkim University, Gangtok, India

Partha Pratim Ray

You can also search for this author in PubMed   Google Scholar

Contributions

P.M. gathered data and designed the experiments. P.P.R. wrote the paper and performed the analysis. All authors reviewed the manuscript.

Corresponding author

Correspondence to Partha Pratim Ray .

Ethics declarations

Competing interests.

The authors declare no competing interests.

Additional information

Publisher's note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ .

Reprints and permissions

About this article

Cite this article.

Majumder, P., Ray, P.P. A systematic review and meta-analysis on correlation of weather with COVID-19. Sci Rep 11 , 10746 (2021). https://doi.org/10.1038/s41598-021-90300-9

Download citation

Received : 17 December 2020

Accepted : 10 May 2021

Published : 24 May 2021

DOI : https://doi.org/10.1038/s41598-021-90300-9

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

This article is cited by

Association of air pollution and weather conditions during infection course with covid-19 case fatality rate in the united kingdom.

• M. Pear Hossain
• Hsiang-Yu Yuan

Scientific Reports (2024)

Bell correlations outside physics

• E. M. Pothos
• B. W. Wojciechowski

Scientific Reports (2023)

Human exposure risk assessment for infectious diseases due to temperature and air pollution: an overview of reviews

• Xuping Song

Environmental Science and Pollution Research (2023)

Assessing the impact of long-term exposure to nine outdoor air pollutants on COVID-19 spatial spread and related mortality in 107 Italian provinces

• Gaetano Perone

Scientific Reports (2022)

By submitting a comment you agree to abide by our Terms and Community Guidelines . If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.

Quick links

• Explore articles by subject
• Guide to authors
• Editorial policies

Sign up for the Nature Briefing: Anthropocene newsletter — what matters in anthropocene research, free to your inbox weekly.

Importance and use of correlational research

Affiliation.

• 1 School of Nursing and Midwifery, Trinity College Dublin, Dublin, Republic of Ireland.
• PMID: 27424963
• DOI: 10.7748/nr.2016.e1382

Background: The importance of correlational research has been reported in the literature yet few research texts discuss design in any detail.

Aim: To discuss important issues and considerations in correlational research, and suggest ways to avert potential problems during the preparation and application of the design.

Discussion: This article targets the gap identified in the literature regarding correlational research design. Specifically, it discusses the importance and purpose of correlational research, its application, analysis and interpretation with contextualisations to nursing and health research.

Conclusion: Findings from correlational research can be used to determine prevalence and relationships among variables, and to forecast events from current data and knowledge. In spite of its many uses, prudence is required when using the methodology and analysing data. To assist researchers in reducing mistakes, important issues are singled out for discussion and several options put forward for analysing data.

Implications for practice: Correlational research is widely used and this paper should be particularly useful for novice nurse researchers. Furthermore, findings generated from correlational research can be used, for example, to inform decision-making, and to improve or initiate health-related activities or change.

Keywords: correlation; correlational research; data analysis; measurement tools; nurses; nursing research; quantitative; variables.

• Nursing Research*

• SUGGESTED TOPICS
• The Magazine
• Newsletters
• Managing Yourself
• Managing Teams
• Work-life Balance
• The Big Idea
• Data & Visuals
• Reading Lists
• Case Selections
• HBR Learning
• Topic Feeds
• Account Settings
• Email Preferences

How to Use Correlation to Make Predictions

• Dean Karlan
• Michael Luca

Don’t overlook a useful pattern just because it isn’t driven by a causal relationship.

Leaders too often misinterpret empirical patterns and miss opportunities to engage in data-driven thinking. To better leverage data, leaders need to understand the types of problems data can help solve as well as the difference between those problems that can be solved with improved prediction and those that can be solved with a better understanding of causation.

Too many leaders take an incomplete approach to understanding empirical patterns, leading to costly mistakes and misinterpretations. As we have discussed before , one extremely common mistake is interpreting a misleading correlation as causal. We’ve advised countless organizations on the topic. We’ve written research papers, managerial articles, and even a book dedicated to the power of experiments and causal inference tools — a toolkit that economists have adopted and adapted over the past few decades. Yet, while we are deep believers in the causal inference toolkit, we’ve also seen the reverse problem — leaders who overlook useful patterns because they are not causal. The truth is, there are also times when a correlation is not only sufficient, but is exactly what is needed. The mistake leaders make here is failing to understand the distinction between prediction and causation. Or, more specifically, the distinction between predicting an outcome and predicting how a decision will affect an outcome.

• DK Dean Karlan is a professor at Northwestern’s Kellogg School of Management and founder of Innovations for Poverty Action.
• Michael Luca is the Lee J. Styslinger III Associate Professor of Business Administration at Harvard Business School and a coauthor (with Max H. Bazerman) of The Power of Experiments: Decision Making in a Data-Driven World (forthcoming from MIT Press).

Partner Center

• Privacy Policy

Home » Correlation Analysis – Types, Methods and Examples

Correlation Analysis – Types, Methods and Examples

Table of Contents

Correlation Analysis

Correlation analysis is a statistical method used to evaluate the strength and direction of the relationship between two or more variables . The correlation coefficient ranges from -1 to 1.

• A correlation coefficient of 1 indicates a perfect positive correlation. This means that as one variable increases, the other variable also increases.
• A correlation coefficient of -1 indicates a perfect negative correlation. This means that as one variable increases, the other variable decreases.
• A correlation coefficient of 0 means that there’s no linear relationship between the two variables.

Correlation Analysis Methodology

Conducting a correlation analysis involves a series of steps, as described below:

• Define the Problem : Identify the variables that you think might be related. The variables must be measurable on an interval or ratio scale. For example, if you’re interested in studying the relationship between the amount of time spent studying and exam scores, these would be your two variables.
• Data Collection : Collect data on the variables of interest. The data could be collected through various means such as surveys , observations , or experiments. It’s crucial to ensure that the data collected is accurate and reliable.
• Data Inspection : Check the data for any errors or anomalies such as outliers or missing values. Outliers can greatly affect the correlation coefficient, so it’s crucial to handle them appropriately.
• Choose the Appropriate Correlation Method : Select the correlation method that’s most appropriate for your data. If your data meets the assumptions for Pearson’s correlation (interval or ratio level, linear relationship, variables are normally distributed), use that. If your data is ordinal or doesn’t meet the assumptions for Pearson’s correlation, consider using Spearman’s rank correlation or Kendall’s Tau.
• Compute the Correlation Coefficient : Once you’ve selected the appropriate method, compute the correlation coefficient. This can be done using statistical software such as R, Python, or SPSS, or manually using the formulas.
• Interpret the Results : Interpret the correlation coefficient you obtained. If the correlation is close to 1 or -1, the variables are strongly correlated. If the correlation is close to 0, the variables have little to no linear relationship. Also consider the sign of the correlation coefficient: a positive sign indicates a positive relationship (as one variable increases, so does the other), while a negative sign indicates a negative relationship (as one variable increases, the other decreases).
• Check the Significance : It’s also important to test the statistical significance of the correlation. This typically involves performing a t-test. A small p-value (commonly less than 0.05) suggests that the observed correlation is statistically significant and not due to random chance.
• Report the Results : The final step is to report your findings. This should include the correlation coefficient, the significance level, and a discussion of what these findings mean in the context of your research question.

Types of Correlation Analysis

Types of Correlation Analysis are as follows:

Pearson Correlation

This is the most common type of correlation analysis. Pearson correlation measures the linear relationship between two continuous variables. It assumes that the variables are normally distributed and have equal variances. The correlation coefficient (r) ranges from -1 to +1, with -1 indicating a perfect negative linear relationship, +1 indicating a perfect positive linear relationship, and 0 indicating no linear relationship.

Spearman Rank Correlation

Spearman’s rank correlation is a non-parametric measure that assesses how well the relationship between two variables can be described using a monotonic function. In other words, it evaluates the degree to which, as one variable increases, the other variable tends to increase, without requiring that increase to be consistent.

Kendall’s Tau

Kendall’s Tau is another non-parametric correlation measure used to detect the strength of dependence between two variables. Kendall’s Tau is often used for variables measured on an ordinal scale (i.e., where values can be ranked).

Point-Biserial Correlation

This is used when you have one dichotomous and one continuous variable, and you want to test for correlations. It’s a special case of the Pearson correlation.

Phi Coefficient

This is used when both variables are dichotomous or binary (having two categories). It’s a measure of association for two binary variables.

Canonical Correlation

This measures the correlation between two multi-dimensional variables. Each variable is a combination of data sets, and the method finds the linear combination that maximizes the correlation between them.

Partial and Semi-Partial (Part) Correlations

These are used when the researcher wants to understand the relationship between two variables while controlling for the effect of one or more additional variables.

Cross-Correlation

Used mostly in time series data to measure the similarity of two series as a function of the displacement of one relative to the other.

Autocorrelation

This is the correlation of a signal with a delayed copy of itself as a function of delay. This is often used in time series analysis to help understand the trend in the data over time.

Correlation Analysis Formulas

There are several formulas for correlation analysis, each corresponding to a different type of correlation. Here are some of the most commonly used ones:

Pearson’s Correlation Coefficient (r)

Pearson’s correlation coefficient measures the linear relationship between two variables. The formula is:

   r = Σ[(xi – Xmean)(yi – Ymean)] / sqrt[(Σ(xi – Xmean)²)(Σ(yi – Ymean)²)]

• xi and yi are the values of X and Y variables.
• Xmean and Ymean are the mean values of X and Y.
• Σ denotes the sum of the values.

Spearman’s Rank Correlation Coefficient (rs)

Spearman’s correlation coefficient measures the monotonic relationship between two variables. The formula is:

   rs = 1 – (6Σd² / n(n² – 1))

• d is the difference between the ranks of corresponding variables.
• n is the number of observations.

Kendall’s Tau (τ)

Kendall’s Tau is a measure of rank correlation. The formula is:

   τ = (nc – nd) / 0.5n(n-1)

• nc is the number of concordant pairs.
• nd is the number of discordant pairs.

This correlation is a special case of Pearson’s correlation, and so, it uses the same formula as Pearson’s correlation.

Phi coefficient is a measure of association for two binary variables. It’s equivalent to Pearson’s correlation in this specific case.

Partial Correlation

The formula for partial correlation is more complex and depends on the Pearson’s correlation coefficients between the variables.

For partial correlation between X and Y given Z:

  rp(xy.z) = (rxy – rxz * ryz) / sqrt[(1 – rxz^2)(1 – ryz^2)]

• rxy, rxz, ryz are the Pearson’s correlation coefficients.

Correlation Analysis Examples

Here are a few examples of how correlation analysis could be applied in different contexts:

• Education : A researcher might want to determine if there’s a relationship between the amount of time students spend studying each week and their exam scores. The two variables would be “study time” and “exam scores”. If a positive correlation is found, it means that students who study more tend to score higher on exams.
• Healthcare : A healthcare researcher might be interested in understanding the relationship between age and cholesterol levels. If a positive correlation is found, it could mean that as people age, their cholesterol levels tend to increase.
• Economics : An economist may want to investigate if there’s a correlation between the unemployment rate and the rate of crime in a given city. If a positive correlation is found, it could suggest that as the unemployment rate increases, the crime rate also tends to increase.
• Marketing : A marketing analyst might want to analyze the correlation between advertising expenditure and sales revenue. A positive correlation would suggest that higher advertising spending is associated with higher sales revenue.
• Environmental Science : A scientist might be interested in whether there’s a relationship between the amount of CO2 emissions and average temperature increase. A positive correlation would indicate that higher CO2 emissions are associated with higher average temperatures.

Importance of Correlation Analysis

Correlation analysis plays a crucial role in many fields of study for several reasons:

• Understanding Relationships : Correlation analysis provides a statistical measure of the relationship between two or more variables. It helps in understanding how one variable may change in relation to another.
• Predicting Trends : When variables are correlated, changes in one can predict changes in another. This is particularly useful in fields like finance, weather forecasting, and technology, where forecasting trends is vital.
• Data Reduction : If two variables are highly correlated, they are conveying similar information, and you may decide to use only one of them in your analysis, reducing the dimensionality of your data.
• Testing Hypotheses : Correlation analysis can be used to test hypotheses about relationships between variables. For example, a researcher might want to test whether there’s a significant positive correlation between physical exercise and mental health.
• Determining Factors : It can help identify factors that are associated with certain behaviors or outcomes. For example, public health researchers might analyze correlations to identify risk factors for diseases.
• Model Building : Correlation is a fundamental concept in building multivariate statistical models, including regression models and structural equation models. These models often require an understanding of the inter-relationships (correlations) among multiple variables.
• Validity and Reliability Analysis : In psychometrics, correlation analysis is used to assess the validity and reliability of measurement instruments such as tests or surveys.

Applications of Correlation Analysis

Correlation analysis is used in many fields to understand and quantify the relationship between variables. Here are some of its key applications:

• Finance : In finance, correlation analysis is used to understand the relationship between different investment types or the risk and return of a portfolio. For example, if two stocks are positively correlated, they tend to move together; if they’re negatively correlated, they move in opposite directions.
• Economics : Economists use correlation analysis to understand the relationship between various economic indicators, such as GDP and unemployment rate, inflation rate and interest rates, or income and consumption patterns.
• Marketing : Correlation analysis can help marketers understand the relationship between advertising spend and sales, or the relationship between price changes and demand.
• Psychology : In psychology, correlation analysis can be used to understand the relationship between different psychological variables, such as the correlation between stress levels and sleep quality, or between self-esteem and academic performance.
• Medicine : In healthcare, correlation analysis can be used to understand the relationships between various health outcomes and potential predictors. For example, researchers might investigate the correlation between physical activity levels and heart disease, or between smoking and lung cancer.
• Environmental Science : Correlation analysis can be used to investigate the relationships between different environmental factors, such as the correlation between CO2 levels and average global temperature, or between pesticide use and biodiversity.
• Social Sciences : In fields like sociology and political science, correlation analysis can be used to investigate relationships between different social and political phenomena, such as the correlation between education levels and political participation, or between income inequality and social unrest.

Advantages and Disadvantages of Correlation Analysis

About the author.

Muhammad Hassan

Researcher, Academic Writer, Web developer

You may also like

Cluster Analysis – Types, Methods and Examples

Discriminant Analysis – Methods, Types and...

MANOVA (Multivariate Analysis of Variance) –...

Documentary Analysis – Methods, Applications and...

ANOVA (Analysis of variance) – Formulas, Types...

Graphical Methods – Types, Examples and Guide

• Open access
• Published: 27 May 2024

Association between gut microbiota and anxiety disorders: a bidirectional two-sample mendelian randomization study

• Jianbing Li 1 ,
• Changhe Fan 1 ,
• Jiaqi Wang 2 ,
• Bulang Tang 2 ,
• Jiafan Cao 2 ,
• Xianzhe Hu 2 ,
• Xuan Zhao 2 &
• Caiqin Feng 1  

BMC Psychiatry volume  24 , Article number:  398 ( 2024 ) Cite this article

144 Accesses

4 Altmetric

Metrics details

There are many articles reporting that the component of intestinal microbiota implies a link to anxiety disorders (AD), and the brain-gut axis is also a hot topic in current research. However, the specific relevance between gut microbiota and AD is uncertain. We aimed to investigate causal relationship between gut microbiota and AD by using bidirectional Mendelian randomization (MR).

Genetic instrumental variable (IV) for the gut microbiota were obtained from a genome-wide association study (GWAS) involving 18,340 participants. Summary data for AD were derived from the GWAS and included 158,565 cases and 300,995 controls. We applied the inverse variance weighted (IVW) method as the main analysis. Cochran’s Q values was computed to evaluate the heterogeneity among IVs. Sensitivity analyses including intercept of MR-Egger method and MR-PRESSO analysis were used to test the horizontal pleiotropy.

We discovered 9 potential connections between bacterial traits on genus level and AD. Utilizing the IVW method, we identified 5 bacterial genera that exhibited a direct correlation with the risk of AD: genus Eubacteriumbrachygroup , genus Coprococcus3 , genus Enterorhabdus , genus Oxalobacter , genus Ruminiclostridium6 . Additionally, we found 4 bacterial genera that exhibited a negative association with AD: genus Blautia , genus Butyricicoccus , genus Erysipelotrichaceae-UCG003 and genus Parasutterella . The associations were confirmed by the sensitivity analyses.

Our study found a causal relation between parts of the gut microbiota and AD. Further randomized controlled trials are crucial to elucidate the positive effects of probiotics on AD and their particular protection systems.

Peer Review reports

Introduction

Anxiety disorders (AD), being the prevailing mental disorders, have a substantial impact on individuals and society alike [ 1 ]. The core features of AD contain indiscriminate anxiety and fear or elusion of persistent and debilitating threats, resulting in substantial medical costs and a burdensome morbidity burden [ 1 , 2 ]. As one of the most popular mental illnesses among young individuals, AD are also the earliest-onset mental disorders [ 3 ]. Amidst the COVID-19 pandemic, there has been a significant surge in the occurrence of AD among children, adolescents, and young adults globally [ 4 ]. First-line treatments for AD include medication and psychotherapy [ 5 ]. However, medication treatments carry certain side effects and risks, such as dependence, cognitive impairment, and an increased risk of heart disease [ 6 ]. The majority of individuals suffering from AD lack access to efficacious treatment options, leaving them vulnerable to relapse [ 7 , 8 ].

Many studies have shown that the occurrence of AD is related to changes in intestinal flora [ 9 , 10 ]. In social anxiety disorder (SAD), there was an increase in the relative abundance of Anaeromassillibacillus and Gordonibacter genera, whereas healthy controls exhibited an enrichment of Parasuterella [ 11 ]. Another article found a reduction in Eubacterium rectale and Fecalibacterium , as well as an increase in Escherichia , Shigella , Fusobacterium , and Ruminococcus in patients with generalized anxiety disorder (GAD) [ 12 ]. In addition, there are numerous documents demonstrating an association between the gut microbiota and mental illness, and the modulation of the gut microbiota on the gut-brain axis has garnered significant attention, such as an elevation of Enterobacteriaceae and Desulfovibrio , and a reduction of Faecalibacterium in patients with AD [ 10 , 13 , 14 , 15 , 16 , 17 ]. In the aforementioned section, it was observed that the evidence exhibits complexities and disparities, as well as some contradictory results, potentially stemming from various confounding factors among different studies.

The previous studies examining the connection between gut microbiota and AD have predominantly relied on cross-sectional designs, which limits the ability to establish a causal relationship between these associations. Therefore, unraveling the causal mechanisms behind gut microbiota-derived AD not only enhances our understanding of their pathogenesis but also provides valuable guidance for implementing microbiota-directed interventions in clinical settings to address AD. Previous Mendelian randomization (MR) studies have primarily focused on investigating the causal relationship between oral microbiota abundance and AD, or between gut microbiota and other psychiatric disorders. A systematic MR study specifically examining the causal relationship between gut microbiota and AD is still lacking in the current literature. In light of this, it is imperative to unravel the causal link between the gut microbiota and AD.

MR is a statistical approach that infers a causal relationship with exposure to a result. It leverages genetic variations linked to the exposure as a proxy for the exposure itself, enabling the assessment of the association between the exposure and the outcome [ 18 ]. Due to the highly effective findings of large-scale genome-wide association study (GWAS) at the gut microbiota and disease level, MR analysis has been abroad used in many scenarios, such as between the oral microbiome and AD, relations between genetically determined metabolites and anxiety symptoms [ 19 , 20 ]. However, there are no specific studies on the causal relationship between gut microbiota and AD. In this research, we applied a bidirectional two-sample MR method to investigate causal relationship between the gut microbiota and AD.

Materials and methods

The assumptions and study design of mr.

MR is a methodology employed to assess causal associations between variables. In order to ensure the validity of MR analysis, 3 fundamental assumptions must be met: (i) the instrumental variable (IV) exhibits a strong link to the exposure factor, (ii) the IV remains unaffected by potential confounding factors., and (iii) the IV influences the result factor solely via the exposure factor [ 21 ]. By applying strict selection criteria, appropriate SNPs were selected as IV for conducting MR analysis on two independent samples. The main aim was to examine the causal relationship between gut microbiota and AD. Furthermore, this study adhered to the guidelines outlined in the Strengthening the Reporting of Observational Studies in Epidemiology-Mendelian Randomization (STROBE-MR) framework [ 22 ] (Fig.  1 ).

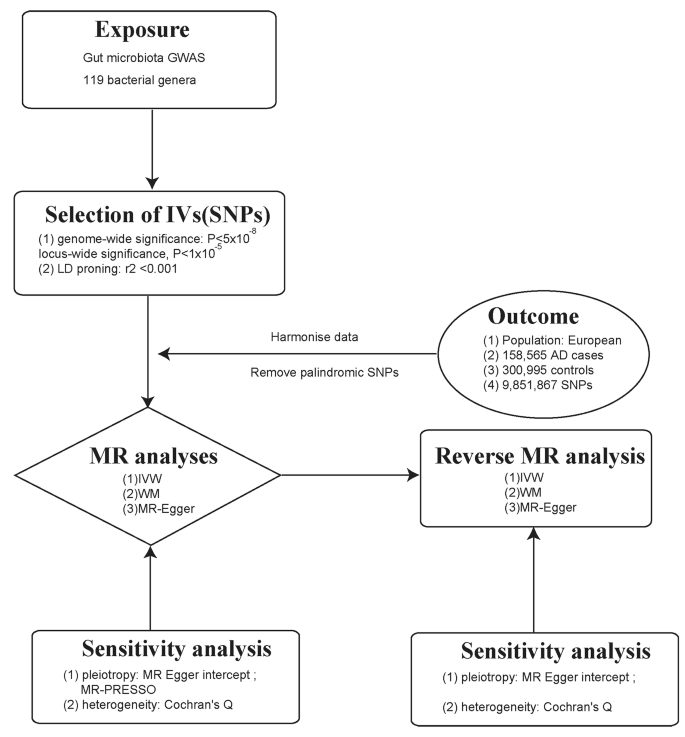
A flowchart illustrating the MR analysis process for the association between gut microbiota and AD

Data sources

The data on gut microbiota GWAS used in this study were obtained from an overall meta-analysis conducted by the MiBioGen consortium. The meta-analysis comprised a total of 18,340 individuals from 24 different groups. The alliance combines human whole-genome genotyping with fecal 16 S rRNA sequencing data to perform thorough research and analysis. The large-scale, multi-ethnic genome-wide meta-analysis provided valuable insights into the genetic influences on the gut microbiome composition [ 23 ]. The GWAS data on the gut microbiome can be integrated into MR studies to explore the causal relationship between genetic variations in the gut microbiome and phenotypic traits, providing valuable insights into the role of the microbiome in human health and disease.

As for the data on genetic variants linked to AD, they were sourced from the Medical Research Council Integrative Epidemiology Unit (MRC-IEU) consortium. The cases were defined as individuals who had sought medical attention for symptoms of nervousness, anxiety, or depression. The study population consisted of individuals of European descent, comprising both males and females, and the data were sourced from the year 2018. The dataset included a total of 158,565 cases and 300,995 controls. The diagnosis was based on self-report questionnaires. Detailed information regarding the data origins for this MR study can be found in Table  1 [ 24 , 25 ].

Selection of IV

The GWAS data of exposure contained a total of 5 taxonomic levels for 211 bacterial groups. The genus level is the smallest and most specific classification level. To accurately identify each pathogenic bacterial group, we focused our analysis only on the genus level, specifically examining 131 bacterial classifications. After excluding 12 unknown groups, a total of 119 bacterial genera were included in the study.

To fulfill the demands of MR studies, our initial step involved the SNPs that exhibited an intense association with the exposure factors. However, when employing a stringent threshold of ( P  < 5 × 10 − 8 ), we obtained a limited number of IVs. Consequently, we adjusted the threshold to ( P  < 1 × 10 − 5 ) to ensure the inclusion of more IVs, thereby enabling robust and reliable results. For the selection of IVs associated with AD in the reverse MR analysis, a heightened level of stringency was implemented by applying a P -value threshold of P  < 5 × 10 − 8 .

We utilized the F-statistic to further evaluate the instrument strength. The F-statistic was determined using the formula: F =  β 2 / SE 2 . This statistic provided an assessment of the overall instrument strength [ 26 ] (Fig.  2 ). An F-statistic exceeding 10 was considered indicative of an intense conjunction between the IV and the exposure. Besides P -value threshold, the F statistic in our analysis would provide additional information on the instrument strength beyond P -value.

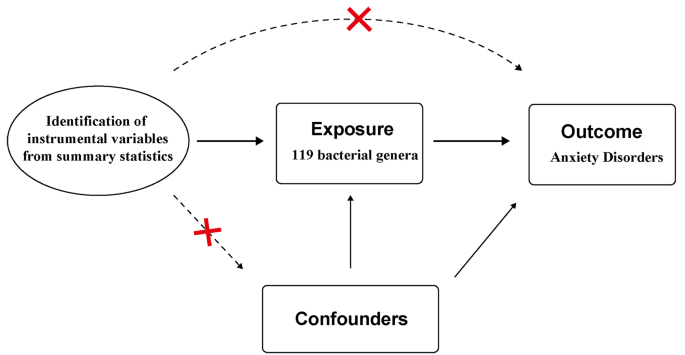
Assumptions in MR studies: a brief overview

Statistical analysis

The primary methodology employed in MR analysis is the inverse variance weighting (IVW) method. This approach utilizes a meta-analysis technique to combine the Wald estimates connected to individual single nucleotide polymorphisms (SNPs), providing comprehensive estimate of the collective impact of gut microbiota on AD. A crucial assumption in MR is the absence of horizontal pleiotropy, where the IV has a direct impact on the outcome variable solely through the exposure factor, without any influence from through alternative pathways. When this assumption is satisfied, the IVW method can provide estimates that are consistent and estimates [ 27 ]. In cases where a causal relationship ( P  < 0.05) is established by the IVW method, two alternative approaches, namely MR-Egger and the weighted median approach, are utilized to supplement an enrich the IVW results. The MR-Egger method relaxes the assumption of a zero intercept, and it can estimate causal effects, even pleiotropy was presented in IVs. The intercept in the MR-Egger method can indicate the extent of horizontal pleiotropy [ 27 ]. These additional methods provide valuable insights and strengthen the overall analysis by considering potential biases and alternative causal pathways.

The weighted median method can return unbiased causal estimate when only 50% of SNPs are valid [ 28 ]. In this study, we employed a significance threshold of P  < 0.05 to determine statistical significance, and the assessment of causality was expressed through odds ratios (OR) and 95% confidence intervals (CI). In instances where causal relationships were established, unidentified taxa were excluded, and additional sensitivity analyses were performed to guarantee the stability of the consequences. The false discovery rate (FDR) is utilized to control for multiple testing and reduce the likelihood of false positive findings. All of the aforementioned analyses were performed utilizing the TwoSampleMR package (version 0.5.7) in R (version 4.3.0), providing a robust and standardized approach to MR analysis.

According to the criteria for IV selection, a total of 1,531 SNPs were identified and selected as IV associated with gut microbiota. The F-statistics for these IVs all exceed 10, suggesting that the estimated coefficients are improbable to be influenced by the bias caused by weak instruments. Supplementary Tables 1 and 2 provides detailed information about the selected IVs. None of the SNPs were involved in more than one of the association results in Fig.  3 .

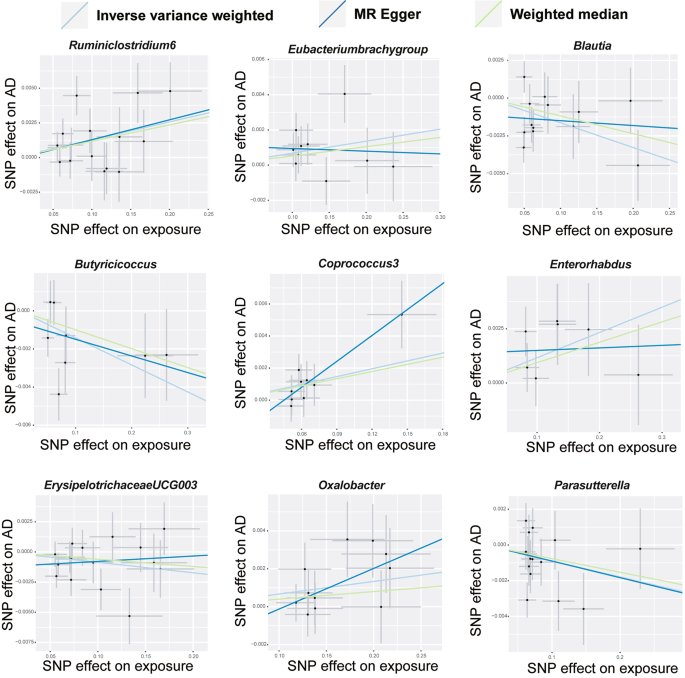
The scatter plots depict the causal relationship between gut microbiota and AD

The majority of gut microbiota showed no significant correlation with AD. However, using the IVW method, we identified 9 bacterial features that were significantly associated with the risk of AD on genus level (Supplementary Table 3 ). We used 3 methods, IVW, weighted median and MR-Egger, and defined P  < 0.05 for IVW method screening as a positive result.

Among them, 4 bacterial genera are negatively correlated with AD, indicating that a higher genetically predicted a lower risk of for AD (Fig. 4 and Supplementary Table 4 ). They are: genus Blautia (OR = 0.9838, 95% CI, 0.9725–0.9952, P  = 0.0056), genus Butyricicoccus (OR = 0.9859, 95% CI, 0.9739–0.9981, P  = 0.0233), genus ErysipelotrichaceaeUCG003 (OR = 0.9914, 95% CI, 0.9833–0.9995, P  = 0.0381) and genus Parasutterella (OR = 0.9911, 95% CI, 0.9823–0.9999, P  = 0.0478). Supplementary Table 4 shows the completed data. In sensitivity analysis, MR-Egger, weighted median demonstrated consistent results, except for genus ErysipelotrichaceaeUCG003 , where the MR-Egger trend was in the contrary direction compared to IVW and weighted median.

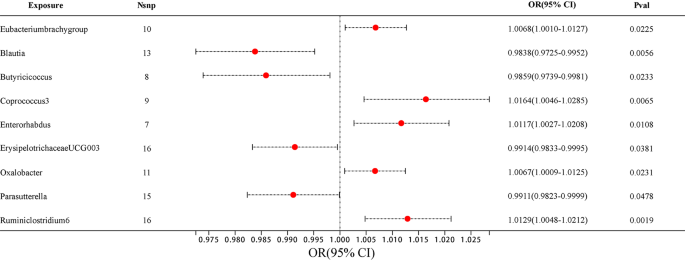
The forest plot illustrates the connections between 9 bacterial genus traits and the likelihood of developing AD

Another 5 bacterial genera showed a positive correlation with AD, genus Eubacteriumbrachygroup (OR = 1.0068, 95% CI, 1.0010–1.0127, P  = 0.0225), genus Coprococcus3 (OR = 1.0164, 95% CI, 1.0046–1.0285, P  = 0.0065), genus Enterorhabdus (OR = 1.0117, 95% CI, 1.0027–1.0208, P  = 0.0108), genus Oxalobacter (OR = 1.0067, 95% CI, 1.0009–1.0125, P  = 0.0231) and genus Ruminiclostridium6 (OR = 1.0129, 95% CI, 1.0048–1.0212, P  = 0.0019) (Fig. 4 and Supplementary Table 4 ). In the MR-Egger method, the trends of genus Eubacteriumbrachygroup are different from those of the IVW and WM methods.

In horizontal pleiotropy analysis, we used the MR-Egger method and found P -value of the MR-intercept were all greater than 0.05. In addition, further MR PRESSO analysis was conducted, ruling out the existence of horizontal pleiotropy ( P  > 0.05) (Supplementary Tables 5 and 6 ). To assess the heterogeneity of gut microbiome IVs, we employed Cochran’s Q test statistics, which revealed no heterogeneity among the gut microbiome IVs ( P  > 0.05) (Supplementary Table 7 ).

Reverse MR analyses were conducted to examine the links between the 9 bacterial genera and AD. No significant statistical relationship was observed using the IVW method: genus Eubacteriumbrachygroup (OR = 1.4058, 95% CI, 0.4060–4.8674, P  = 0.5909), genus Blautia (OR = 0.9453, 95% CI, 0.5572–1.6038, P  = 0.8348), genus Butyricicoccus (OR = 0.9834, 95% CI, 0.5704–1.6952, P  = 0.9518), genus Coprococcus3 (OR = 0.8886, 95% CI, 0.5040–1.5667, P  = 0.6831), genus Enterorhabdus (OR = 1.0383, 95% CI, 0.4168–2.5868, P  = 0.9356), genus ErysipelotrichaceaeUCG003 (OR = 0.6593, 95% CI, 0.3556–1.2221, P  = 0.1858), genus Oxalobacter (OR = 1.2849, 95% CI, 0.4021–4.1051, P  = 0.6724), genus Parasutterella (OR = 0.7245, 95% CI, 0.3713–1.4136, P  = 0.3447), genus Ruminiclostridium6 (OR = 0.7095, 95% CI, 0.3825–1.3162, P  = 0.2764) (Supplementary Tables 8 and 9 ).

In the context of this study, we used two-sample MR studies to discover the link between AD and gut microbiota. Among the 9 bacterial genus we found, 4 bacteria were negatively correlated with AD and may have a positive effect on AD, and the other 5 bacteria were positively correlated with the occurrence of AD and may promote the development of AD.

Blautia stercoris MRx0006 has been shown to alleviate social dysfunctions, monotonous behaviors, and anxiety-like behaviors relevant to autism disorders in a mouse model. MRx0006 administration at the microbial level, as observed by Paromita Sen et al., resulted in a reduction in the abundance of Alistipes putredinis, which likely underlie the observed increase in expressions of oxytocin, arginine vasopressin, and their receptors, ultimately leading to improved behavioral outcomes [ 29 ]. Butyricicoccus was also inversely associated with AD in a cross-sectional study, which is consistent with our findings [ 12 ]. Approximately 70% of individuals with autism spectrum disorder (ASD) exhibit comorbid symptoms of anxiety, and the findings from a published article confirming the decreased relative abundance of ErysipelotrichaceaeUCG003 in ASD patients further support our research results indicating a negative correlation between ErysipelotrichaceaeUCG003 and AD [ 30 ]. In a study examining SAD, the control group exhibited higher levels of the positive bacteria Parasutterella compared to the anxiety group. The term “psychobiotics” has been coined to refer to these microbes that are associated with improved mood [ 11 ]. However, in a study by Yi Zhang et al., a psychological stress model was established in C57BL/6J mice, followed by fecal microbiota transplantation using samples from stressed (S) and non-stressed (NS) mice. The results showed an increased abundance of Parasutterella in S mice and mechanistic analysis suggested its potential involvement in negative regulation of metabolism. Despite this controversial finding, our study utilized MR to reveal a negative association between Parasutterella and anxiety disorders. However, further experimental investigations are required to elucidate the underlying molecular mechanisms [ 31 ].

Five bacterial genera positively linked to anxiety may indicate that they exacerbate anxiety, but they were less reported. In a study in which consuming prebiotics altered the microbiota of healthy adults, the prebiotics reduced Eubacteriumbrachygroup but did not significantly change biomarkers of stress or mental health symptoms [ 32 ]. In previous studies on AD cases, it has been found that individuals with AD have lower levels of Coprococcus [ 33 ]. However, in our study, we observed an increasing trend in Coprococcus3 , despite belonging to the same genus. This suggests that even within the same genus, the impact of different genus may vary. In contrast to our findings, Enterorhabdus exhibited a declining pattern in a mouse model of anxiety and depression induced by social defeat [ 34 ]. This observation highlights the influence of various factors on alterations in gut microbiota, which may diverge across different species.

Nevertheless, it is crucial to acknowledge that our study has certain limitations. First, the results of this analysis are limited to European populations and may not be generalizable to other populations. Secondly, we observed that the adjusted P -values remained relatively large after multiple test adjustment. The reduced statistical power resulting from the limited sample size may also constrain our ability to detect significant associations between variables. Finally, proving the direct impact of sample types on the outcomes is challenging. However, the selection of sample types is often constrained by the availability of suitable genetic instruments and relevant data sources. The dataset we utilized does not provide specific information on the dietary habits of the individuals or their other medical conditions. Therefore, further examination and validation are needed in the future.

In summary, utilizing large-scale GWAS analysis, MR studies have disclosed a causal relationship between gut microbiota and AD. Among these, 4 bacterial genera exhibited a negative correlation, while 5 bacteria genera showed a positive correlation with AD. However, further exploration of the mechanisms linking gut microbiota to AD requires the establishment of larger GWAS databases. Several gut bacteria have been identified to reduce the occurrence of anxiety, offering promising prospects for the treatment and precaution of AD. Subsequent research should prioritize the exploration of the underlying mechanisms and the development of targeted interventions based on these findings.

Data availability

The raw data analyzed during the current study were available in public databases including IEU database(ukb-b-6991) and MiBioGen database(https://mibiogen.gcc.rug.nl). The code and data related to this study are available from the corresponding author upon reasonable request.

Abbreviations

• Anxiety disorders
• Mendelian randomization

Instrumental variable(s)

Genome-wide association study

Medical Research Council Integrative Epidemiology Unit

Inverse variance weighting

Social anxiety disorder

Generalized anxiety disorder

Strengthening the Reporting of Observational Studies in Epidemiology-Mendelian Randomization

Single nucleotide polymorphism(s)

Odds ratios

Confidence intervals

Autism spectrum disorder

Major depressive disorder

Penninx BW, Pine DS, Holmes EA, et al. Anxiety disorders[J] Lancet. 2021;397:914–27.

PubMed   PubMed Central   Google Scholar  

Bandelow B, Michaelis S. Epidemiology of anxiety disorders in the 21st century[J]. Dialogues Clin Neurosci. 2015;17:327–35.

Article   PubMed   PubMed Central   Google Scholar  

Warner EN, Ammerman RT, Glauser TA, et al. Developmental epidemiology of pediatric anxiety disorders[J]. Child Adolesc Psychiatr Clin N Am. 2023;32:511–30.

Article   PubMed   Google Scholar  

Fortuna LR, Brown IC, Lewis Woods GG, et al. The impact of COVID-19 on anxiety disorders in Youth: coping with stress, worry, and recovering from a Pandemic[J]. Child Adolesc Psychiatr Clin N Am. 2023;32:531–42.

Wehry AM, Beesdo-Baum K, Hennelly MM, et al. Assessment and treatment of anxiety disorders in children and adolescents[J]. Curr Psychiatry Rep. 2015;17:52.

Szuhany KL, Simon NM. Anxiety disorders: a review[J]. JAMA. 2022;328:2431–45.

Article   CAS   PubMed   Google Scholar  

Uher R. The global impact of anxiety disorders[J]. Lancet Psychiatry. 2023;10:239–40.

Scholten W, Ten Have M, Van Geel C, et al. Recurrence of anxiety disorders and its predictors in the general population[J]. Psychol Med. 2023;53:1334–42.

Yang B, Wei J, Ju P, et al. Effects of regulating intestinal microbiota on anxiety symptoms: a systematic review[J]. Gen Psychiatr. 2019;32:e100056.

Simpson CA, Diaz-Arteche C, Eliby D, et al. The gut microbiota in anxiety and depression - a systematic review[J]. Clin Psychol Rev. 2021;83:101943.

Butler MI, Bastiaanssen TFS, Long-Smith C, et al. The gut microbiome in social anxiety disorder: evidence of altered composition and function[J]. Translational Psychiatry. 2023;13:95.

Jiang HY, Zhang X, Yu ZH, et al. Altered gut microbiota profile in patients with generalized anxiety disorder[J]. J Psychiatr Res. 2018;104:130–6.

Socała K, Doboszewska U, Szopa A, et al. The role of microbiota-gut-brain axis in neuropsychiatric and neurological disorders[J]. Pharmacol Res. 2021;172:105840.

Nikolova VL, Smith MRB, Hall LJ, et al. Perturbations in gut microbiota composition in psychiatric disorders: a review and meta-analysis[J]. JAMA Psychiatry. 2021;78:1343–54.

Generoso JS, Giridharan VV, Lee J, et al. The role of the microbiota-gut-brain axis in neuropsychiatric disorders[J]. Braz J Psychiatry. 2021;43:293–305.

Mörkl S, Butler MI, Holl A, et al. Probiotics and the microbiota-gut-brain axis: focus on psychiatry[J]. Curr Nutr Rep. 2020;9:171–82.

Needham BD, Funabashi M, Adame MD, et al. A gut-derived metabolite alters brain activity and anxiety behaviour in mice[J]. Nature. 2022;602:647–53.

Article   CAS   PubMed   PubMed Central   Google Scholar  

Emdin CA, Khera AV, Kathiresan S. Mendelian Randomization[J] JAMA. 2017;318:1925–6.

Li C, Chen Y, Wen Y, et al. A genetic association study reveals the relationship between the oral microbiome and anxiety and depression symptoms[J]. Front Psychiatry. 2022;13:960756.

Xiao G, He Q, Liu L, et al. Causality of genetically determined metabolites on anxiety disorders: a two-sample mendelian randomization study[J]. J Transl Med. 2022;20:475.

Xie L, Zhao H, Chen W. Relationship between gut microbiota and thyroid function: a two-sample mendelian randomization study[J]. Front Endocrinol (Lausanne). 2023;14:1240752.

Skrivankova VW, Richmond RC, Woolf BR, et al. Strengthening the reporting of Observational studies in Epidemiology using mendelian randomization: the STROBE-MR Statement[J]. JAMA. 2021;326:1614–21.

Kurilshikov A, Medina-Gomez C, Bacigalupe R, et al. Large-scale association analyses identify host factors influencing human gut microbiome composition[J]. Nat Genet. 2021;53:156–65.

Lyall DM, Inskip HM, Mackay D, et al. Low birth weight and features of neuroticism and mood disorder in 83 545 participants of the UK Biobank cohort[J]. BJPsych Open. 2016;2:38–44.

Smith DJ, Nicholl BI, Cullen B, et al. Prevalence and characteristics of probable major depression and bipolar disorder within UK biobank: cross-sectional study of 172,751 participants[J]. PLoS ONE. 2013;8:e75362.

Burgess S, Thompson SG. Avoiding bias from weak instruments in mendelian randomization studies[J]. Int J Epidemiol. 2011;40:755–64.

Burgess S, Butterworth A, Thompson SG. Mendelian randomization analysis with multiple genetic variants using summarized data[J]. Genet Epidemiol. 2013;37:658–65.

Bowden J, Davey Smith G, Haycock PC, et al. Consistent estimation in mendelian randomization with some Invalid instruments using a weighted median estimator[J]. Genet Epidemiol. 2016;40:304–14.

Sen P, Sherwin E, Sandhu K, et al. The live biotherapeutic Blautia stercoris MRx0006 attenuates social deficits, repetitive behaviour, and anxiety-like behaviour in a mouse model relevant to autism[J]. Brain Behav Immun. 2022;106:115–26.

Chen Y-C, Lin H-Y, Chien Y, et al. Altered gut microbiota correlates with behavioral problems but not gastrointestinal symptoms in individuals with autism[J]. Brain Behav Immun. 2022;106:161–78.

Zhang Y, Zhang J, Wu J, et al. Implications of gut microbiota dysbiosis and fecal metabolite changes in psychologically stressed mice[J]. Front Microbiol. 2023;14:1124454.

Mysonhimer AR, Cannavale CN, Bailey MA, et al. Prebiotic consumption alters Microbiota but not biological markers of stress and inflammation or mental health symptoms in healthy adults: a randomized, controlled, crossover trial[J]. J Nutr. 2023;153:1283–96.

Chen YH, Bai J, Wu D, et al. Association between fecal microbiota and generalized anxiety disorder: severity and early treatment response[J]. J Affect Disord. 2019;259:56–66.

Zou R, Tian P, Xu M, et al. Psychobiotics as a novel strategy for alleviating anxiety and depression[J]. J Funct Foods. 2021;86:104718.

Article   Google Scholar  

Download references

Acknowledgements

We express our gratitude to the hospital action teams, staff, and participants from the participating hospitals for their valuable support in data collection. Additionally, we extend our appreciation to our collaborators for their assistance throughout the process.

Program of Guangzhou Science and Technology Program Project (No. 202102010115) and Guangdong Yiyang Healthcare Charity Foundation (No. JZ2022001-3).

Author information

Authors and affiliations.

Department of Psychiatry, Guangdong Second Provincial General Hospital, Guangzhou, 510317, PR China

Jianbing Li, Changhe Fan & Caiqin Feng

School of Pharmacy, Guangdong Pharmaceutical University, Guangzhou, 510006, China

Jiaqi Wang, Bulang Tang, Jiafan Cao, Xianzhe Hu & Xuan Zhao

You can also search for this author in PubMed   Google Scholar

Contributions

CQF designed the research framework. JBL is responsible for data and analysis methods determination as well as manuscript writing. CHF assisted in conducting the literature review. JQW was responsible for manuscript writing. BLT and JFC performed the data statistical analysis. XZH and XZ were responsible for critical revisions.

Corresponding author

Correspondence to Caiqin Feng .

Ethics declarations

Ethics approval and consent to participate.

Not applicable.

Consent for publication

Competing interests.

The authors declare no competing interests.

Additional information

Publisher’s note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Electronic supplementary material

Below is the link to the electronic supplementary material.

Supplementary Material 1

Supplementary material 2, supplementary material 3, supplementary material 4, supplementary material 5, supplementary material 6, supplementary material 7, supplementary material 8, supplementary material 9, rights and permissions.

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ . The Creative Commons Public Domain Dedication waiver ( http://creativecommons.org/publicdomain/zero/1.0/ ) applies to the data made available in this article, unless otherwise stated in a credit line to the data.

Reprints and permissions

About this article

Cite this article.

Li, J., Fan, C., Wang, J. et al. Association between gut microbiota and anxiety disorders: a bidirectional two-sample mendelian randomization study. BMC Psychiatry 24 , 398 (2024). https://doi.org/10.1186/s12888-024-05824-x

Download citation

Received : 23 December 2023

Accepted : 09 May 2024

Published : 27 May 2024

DOI : https://doi.org/10.1186/s12888-024-05824-x

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Gut microbiota
• Single nucleotide polymorphism

BMC Psychiatry

ISSN: 1471-244X

• Submission enquiries: [email protected]
• General enquiries: [email protected]

• Open access
• Published: 30 May 2024

Challenges and advantages of electronic prescribing system: a survey study and thematic analysis

• Hamid Bouraghi 1 ,
• Behzad Imani 2 ,
• Abolfazl Saeedi 3 ,
• Ali Mohammadpour 1 ,
• Soheila Saeedi 1   na1 ,
• Taleb Khodaveisi 1   na1 &
• Tooba Mehrabi 4  

BMC Health Services Research volume  24 , Article number:  689 ( 2024 ) Cite this article

Metrics details

Introduction

Electronic prescribing (e-prescribing) systems can bring many advantages and challenges. This system has been launched in Iran for more than two years. This study aimed to investigate the challenges and advantages of the e-prescribing system from the point of view of physicians.

In this survey study and thematic analysis, which was conducted in 2023, a researcher-made questionnaire was created based on the literature review and opinions of the research team members and provided to the physician. Quantitative data were analyzed using SPSS software, and qualitative data were analyzed using ATLAS.ti software. Rank and point biserial, Kendall’s tau b, and Phi were used to investigate the correlation between variables.

Eighty-four physicians participated in this study, and 71.4% preferred to use paper-based prescribing. According to the results, 53.6%, 38.1%, and 8.3% of physicians had low, medium, and high overall satisfaction with this system, respectively. There was a statistically significant correlation between the sex and overall satisfaction with the e-prescribing system ( p -value = 0.009) and the computer skill level and the prescribing methods ( P -value = 0.042). Physicians face many challenges with this system, which can be divided into five main categories: technical, patient-related, healthcare providers-related, human resources, and architectural and design issues. Also, the main advantages of the e-prescribing system were process improvement, economic efficiency, and enhanced prescribing accuracy.

The custodian and service provider organizations should upgrade the necessary information technology infrastructures, including hardware, software, and network infrastructures. Furthermore, it would be beneficial to incorporate the perspectives of end users in the system design process.

Peer Review reports

Medicine, a crucial commodity in healthcare due to its economic and strategic value, is a fundamental pillar in primary disease treatment. It constitutes significant health expenditures and budgets worldwide [ 1 ]. The prudent management of this valuable resource, through its appropriate prescription and usage, is essential. This is a key factor in ensuring the health security of communities [ 2 ]. Numerous studies indicate that errors in drug administration are prevalent. Although a significant proportion of these errors are preventable, they can leave serious complications for patients and even fatalities [ 3 ]. As the complexity of the drug prescribing process increases, resultant injuries and complications will likely escalate. Therefore, medication prescription is one of the main concerns and priorities of policymakers and trustees in the healthcare domain. In this regard, relentless endeavors are undertaken to enhance and optimize this process, and new supplementary solutions will be used as required. Employing electronic prescription (e-prescribing) systems as an alternative to manual prescription is a practical solution that can enhance and streamline this critical process [ 4 ].

In the traditional paper-based prescribing system, numerous issues arise, including illegible prescriptions, ambiguous orders, omissions, prescription forgery, and misidentification of patients. Studies indicate that these problems compromise patient safety and negatively impact the outcomes of drug treatments [ 5 , 6 ]. E-prescribing emerges as an effective and definitive solution to the inefficiencies, susceptibility to fraud, and administrative burdens associated with paper-based prescribing systems [ 7 ]. E-prescribing extends beyond merely utilizing a computer for prescription writing and storage. This technology encompasses all stages of the prescription process, including patient identification, prescription registration, prescription modification, duplication and renewal of prescriptions, and the transfer of prescriptions among stakeholders, all facilitated through specialized software and internet platforms [ 8 , 9 , 10 ].

As an information system, the e-prescribing system can integrate with other organizational systems, such as electronic health records and pharmacy information systems, within healthcare centers like hospitals [ 11 ]. Through the implementation and utilization of such a system, it is possible to overcome the problems and constraints of the traditional prescribing system due to the complexity of medical care and the increase in the number of drugs, thereby benefiting from its potential advantages. Some of the benefits of an e-prescribing system include reducing healthcare costs for stakeholders (patients, healthcare providers, insurers, and policymakers), reducing common prescribing errors, improving medication outcomes, increasing patient safety, increasing the readability and accuracy of prescriptions, enhancing coordination among stakeholders involved in the drug therapy process, and supporting clinical decision-making at the time of drug administration [ 12 , 13 , 14 ].

Despite the potential benefits of e-prescribing systems in the healthcare industry and significant investments and efforts by stakeholders to support such systems, their usage and adoption remain low, resulting in the failure of numerous implemented projects [ 11 , 12 ]. Given that e-prescribing systems are designed according to the specific needs and internal standards of each country, numerous studies have been conducted worldwide to investigate the benefits, challenges, the reasons for the failure and lack of acceptance of such systems [ 15 , 16 ].

E-prescribing systems in countries like Denmark, the United States, Finland, Sweden, and the United Kingdom are commonly tested and implemented at state, local, or regional levels. These systems cover the entire or a significant portion of the prescribing process. Variations in healthcare and insurance systems across different countries lead to diverse approaches regarding e-prescribing and its evolution. Consequently, these countries exhibit distinct starting points, implementation procedures, and technical strategies. Moreover, e-prescribing systems and models vary not only across different countries but also within the same country [ 17 ]. While meticulously developed and successfully implemented in the United States of America, England, and Germany, this system has reached significant maturity and yielded substantial advantages for the health systems of these countries. However, in other nations, especially developing countries, e-prescribing still encounters significant challenges on its path to widespread acceptance and goal achievement [ 18 , 19 , 20 , 21 ].

Recognizing that the implementation of e-prescribing is a priority for the Iran Ministry of Health and Medical Education (MOH), the Iran Food and Drug Administration (IFDA) established a multi-stakeholder working group in 2015. This group, composed of medical informatics experts, aimed to develop recommendations for effective e-prescribing implementation [ 22 ]. In Iran, adopting e-prescribing in governmental and university hospitals has been proposed as a legal requirement since 2020. The Social Security Organization, a pioneering institution in this domain, has aligned with the implementation policies of this plan and has ceased issuing treatment booklets since early 2021 [ 23 ]. The Health Insurance Organization, as another government institution, independently developed and deployed its e-prescription system across all medical education centers affiliated with universities of medical sciences in Iran. Consequently, the two primary organizations (Social Security Organization and Health Insurance Organization) have successfully implemented the e-prescribing system. Their goals include efficient management of healthcare resources, reduction of common manual prescribing errors, and enhancement of patient safety [ 24 ].

In general, medical centers in Iran employ three distinct electronic prescription systems. “Electronic Prescription (EP)” and “Dinad” serve outpatients covered by the Social Security and Health Insurance Organization, while “Shafa” caters to all inpatients. For individuals without coverage from these insurances, physicians resort to paper prescriptions [ 25 ]. Electronic prescribing was not implemented simultaneously in all provinces of Iran. It was first used on a trial basis in a few provinces and then implemented throughout the country. Although these systems have provided significant benefits to their users in Iran, they have also encountered numerous challenges. Consequently, this comprehensive study was undertaken to explore both the advantages and obstacles associated with e-prescribing systems in Iran.

This survey study and thematic analysis was conducted to examine the challenges and advantages of the e-prescribing system in Iran in 2023. This study was conducted in three main steps: literature review and questionnaire design, data collection, and data analysis.

Literature review and questionnaire design

In the first step of this research, a questionnaire was designed based on the review of similar studies and the opinions of the research team members. To design the questionnaire, various databases, including PubMed, Google Scholar, and Scopus, were searched with related terms such as “electronic prescribing,” “electronic prescribing challenges,” and “electronic prescribing advantages.” Then, the most relevant articles retrieved from these databases were examined, and relevant data were extracted from these articles. Then, focus group sessions were held with the research team. The data extracted from the articles were presented in the sessions, and based on these data and the opinions of the research team, the questionnaire was finalized. This questionnaire had three sections: (1) demographic data (2), questions related to the advantages and challenges of e-prescribing, and (3) open-ended questions related to the challenges and advantages of the e-prescribing system. A five-point Likert scale from completely agree to completely disagree was used for the questions of the second part of the questionnaire. The face and content validity of the questionnaire was checked and confirmed with the cooperation of five experts in health information management, medical informatics, and information technology who were thoroughly familiar with prescribing systems. The content validity of the questionnaire was measured using the Content Validity Index (CVI) and Content Validity Ratio (CVR). To determine CVR, the experts were asked to classify each of the questions based on the three-point Likert scale as follows:

The question is necessary

The question is useful but not necessary

The question is not necessary

Then, the following formula was used to calculate CVR:

CVR = (Ne − N/2)/ (N/2), (N: total number of experts, Ne: the number of experts who have chosen the “necessary” option.).

Based on the Lawshe table for minimum values of CVR, items with CVR equal to or greater than 0.99 were kept. To calculate the CVI, the experts determined the degree of relevance of each question on a 4-point Likert scale from not relevant to completely relevant. The following formula was used to decide about the acceptance of each question:

CVI: The number of experts who chose options 3 and 4 / the total number of experts. It was decided to reject or accept each question as follows: < 0.7 = rejected, 0.7–0.79 = revised, > 0.79 = accepted. The reliability of the questionnaire was calculated using Cronbach’s alpha and Guttman coefficient. Values greater than 0.7, 0.5–0.7, and less than 0.5 indicate high, acceptable, and low reliability of the questionnaire, respectively.

The third part of the questionnaire included open-ended questions. Two following questions were placed at the end of the questionnaire and were asked to the physicians:

In your opinion, what other advantages does this electronic prescribing system have?

In your opinion, what other challenges does this electronic prescribing system have?

Data collection

After the questionnaire was finalized, it was prepared in both paper and electronic formats. The electronic version of the questionnaire was prepared on the Porsline platform. For the survey, first, a list of physicians working in the teaching hospitals was prepared, and then we tried to get the contact numbers of the physicians as well. The questionnaire link was sent to physicians through the local social networks whose contact numbers were available, and physicians whose contact numbers were not available were referred to them in person. Many physicians refused to receive the questionnaire and answers due to lack of time. Two reminder messages were also sent to the doctors who had received the questionnaire link through social networks. In the face-to-face group, the doctors who did not have enough time to complete the questionnaire at that moment, the researcher provided the questionnaire to the physicians and coordinated with them to receive it at a later time. A total of 122 physicians agreed to participate in the study. It should be noted that to avoid missing data, it was mandatory to answer all the questions in the electronic questionnaire, and in the paper-based questionnaire, the researchers checked the questionnaire immediately, and if any fields were not completed, they asked the physicians to complete the incomplete items of the questionnaire again.

Data analysis

Descriptive statistics including mean, standard deviation, frequency median, interquartile range and percentage were used for data analysis.

The relationship of “sex,” “specialty,” “physician’s computer skills,” “age,” and “duration” with “satisfaction” was investigated. Since “satisfaction” is a qualitative ordinal variable, the Rank-biserial index was used to examine the relationship between this variable and two-level nominal variables such as “gender” and “specialty.” Kendall’s tau b index was also used to examine the relationship between “satisfaction” (ordinal variable) with rank variables such as “physician’s computer skills” and continuous quantitative variables such as “age” and “duration.” To investigate the relationship between “willingness to use paper-based or e-prescribing” with “sex,” “specialty,” “physician’s computer skills,” “age,” and “duration,” Phi, Rank-biserial, and Point-biserial were used respectively. The p -values obtained from the chi-square test were also reported to check the presence or absence of a relationship between two variables. The type I error in this study was considered 5%. Data analysis was carried out using SPSS version 26.

The answers given by 84 physicians to two open-ended questions were typed in Word.

Thematic analysis was used to analyze the open-ended questions and identify themes within qualitative data. For thematic analysis, first, the answers typed in the Word were imported into the ATLAS.ti software, and then the pattern extraction process was carried out according to the following steps:

The imported text was read several times to get familiar with the data

After familiarizing with the data, initial coding was done

After coding, the extracted codes were checked and revised many times

Similar codes were merged and grouped, and subthemes were created

Finally, the sub-themes were reviewed and linked, and the main themes were created

The designed questionnaire was given to 122 physicians, of which 84 physicians completed the questionnaires (response rate: 68.85%). Demographic characteristics of physicians are given in Table  1 . Most of the participants were general practitioners (56%) and women (53.6%). 91.7% of the physicians believed that they have medium and high computer skills and the average duration of using the e-prescribing system was 15.50 ± 8.798 months.

The results showed that the questionnaire had acceptable reliability (Cronbach’s alpha = 0.605, Guttman’s coefficient = 0.718). The mean (std. deviation), median and interquartile range of each question in the questionnaire are given in Table  2 . The questions were categorized into two sections: advantages and challenges of the e-prescribing system. The total mean score of advantages for the e-prescribing system was 2.15 and this value for challenges of this system was 2.75. Out of the advantages of this technology, the highest mean score (2.79) was related to the “E-prescribing system has reduced the possibility of wrong drug delivery due to illegible prescriptions” and the lowest (1.24) was related to the “The e-prescribing system has led to improved physician performance”. The most important challenge that physicians had with the e-prescribing system was the insufficient bandwidth with an average of 3.49. Two other challenges mentioned by physicians about this system and received a high mean score (3.43) were the challenges related to lengthening the duration of each visit and increasing the waiting time of patients.

The results of investigating the correlation between the duration of e-prescribing system use, age, sex, specialty, and the physician’s computer skills with the overall satisfaction with the e-prescribing system are reported in Table  3 . According to the results, 45 (53.6%), 32 (38.1%), and 7 (8.3%) physicians had low, medium and high overall satisfaction with this system, respectively. There was a statistically significant correlation between the sex and overall satisfaction with the e-prescribing system ( p -value = 0.009).

The results of the correlation between duration, age, sex, specialty, and the physician’s computer skills with the willingness to use paper-based prescribing or the e-prescribing system are reported in Table  4 . According to the results, 60 (71.4%) and 24 (28.6%) physicians preferred to use paper-based and e-prescribing respectively. There was a statistically significant correlation between the computer skill level and the prescribing methods ( P -value = 0.042).

The themes and sub-themes extracted from the question related to the advantages of the e-prescribing system are shown in Fig.  1 . The main themes of the e-prescribing system’s advantages were the following:

Process improvement

Economic efficiency

Enhance the accuracy of prescribing

These three themes included a total of 10 sub-themes.

Among the advantages noted for electronic prescribing, the possibility of editing prescriptions, providing different dosages of drugs, and the impossibility of manipulating prescriptions by patients or other people were mentioned more than other advantages. Also another mentioned advantage was the possibility of providing pre-prepared prescriptions for common diseases, which led to the acceleration of prescribing for these diseases.

Thematic map of concepts extracted from qualitative data related to the advantages of the e-prescribing system

Concepts related to the challenges of the e-prescribing system were categorized into five main themes as follows (Fig.  2 ):

Technical issues

Patient-related issues

Healthcare providers-related issues

Human resources challenges

Architectural and design issues

These five themes included more than 30 sub-themes.

Many challenges for electronic prescribing were mentioned in the form of given themes. One of the most important challenges mentioned by many physicians was various technical problems including network disconnection. Also, another big challenge that caused the dissatisfaction of the patients was the lack of skill of many physicians in working with computer systems, which led to the low speed of typing the drugs in the system and as a result, increased the duration of the patients’ visits. Also, many physicians did not have computer systems in their clinics, which led to the lack of electronic prescriptions and, as a result, the lack of use of insurance services for patients. Also, considering that many physicians are used to the paper prescription method, they were not willing to accept the changes and resisted these changes, as a result, they needed personnel to register the prescriptions.

Thematic map of concepts related to the challenges of the e-prescribing system

E-prescribing systems have many advantages, but they also pose certain challenges. These systems can enhance medication safety by reducing prescription errors caused by illegible handwriting or oral miscommunication. They can also improve efficiency by streamlining the prescription process, reducing the time spent on phone calls and faxes between healthcare providers and pharmacies. Furthermore, e-prescribing can provide clinicians with up-to-date information about patients’ medications and allergies, thereby improving patient care.

Although e-prescribing systems have many advantages, their implementation is not without any challenges. These include the costs associated with system implementation and maintenance, issues related to system interoperability, and the necessity for user training and technical support. Moreover, while these systems can mitigate traditional medication errors, they may also introduce new types of errors, such as those caused by user interface design or software glitches. Maximizing the benefits and minimizing the challenges associated with e-prescribing systems requires meticulous system design, comprehensive user training, and continuous system evaluation.

As demonstrated in the results section, the e-prescribing system’s mean overall benefit score was 2.15. This score suggests a moderate level of perceived benefits. It implies that while certain advantages are acknowledged, the system still needs to be improved to enhance user satisfaction and the perception of benefits. In this context, among the factors associated with the system’s benefits from the users’ perspective, the statements “Improved workflow has resulted from e-prescribing” and “The e-prescribing system has led to improved physician performance” received average scores of 1.48 and 1.24, respectively. These relatively low scores suggest that respondents of the survey or study largely disagree that the electronic system has enhanced their workflow or improved their performance. Several studies [ 11 , 12 , 26 , 27 ] have demonstrated that users do not concur that the use of prescribing systems leads to workflow improvement or performance enhancement. There are multiple possible reasons for this, including:

Usability issues: The e-prescribing system might not be user-friendly or intuitive, leading to difficulties in adoption among healthcare professionals.

Training and support: There might be a lack of adequate training and support for the users, making it challenging for them to adapt to the new system.

System limitations: The system might not be flexible enough to accommodate the diverse needs of different healthcare settings, leading to workflow inefficiencies.

Resistance to change: Healthcare professionals, like any other group, might resist changes to established routines. This resistance could affect their perception of the system’s benefits.

Among the challenges identified in the use of e-prescribing systems, the statement “Doctors have faced challenges with e-prescribing due to insufficient bandwidth” received the highest score of 3.49. According to this relatively high score, the survey or study respondents strongly agree that insufficient bandwidth has been a significant obstacle to the use of e-prescribing. This issue results in prolonged patient waiting times, leading to extended queues and a decrease in physician productivity. There are multiple factors that can cause insufficient bandwidth, such as:

Network Infrastructure: In areas with poor network infrastructure, insufficient bandwidth can significantly slow down the operation of e-prescribing systems, making it difficult for doctors to use them effectively.

System Requirements: To function optimally, e-prescribing systems may need a certain level of bandwidth. System lags or downtime could result if the available bandwidth is below this level.

Data Transfer: E-prescribing systems often need to transfer large amounts of data, including patient records, prescriptions, and other related information. Insufficient bandwidth can slow down this data transfer, affecting the system’s efficiency.

Real-time Updates: Many e-prescribing systems provide real-time updates to ensure that all users have the most current information. If there is not enough bandwidth, these updates can be delayed, resulting in potential errors or miscommunications.

Generally, as indicated by various studies [ 28 , 29 , 30 ], the implementation of e-prescribing systems requires robust hardware, sophisticated software, and a reliable network infrastructure. These elements are integral to the successful deployment and operation of such systems. According to this study, the hardware, software, and network infrastructure in Iran are not suitable for the implementation of e-prescribing systems. This inadequacy has caused increased challenges and dissatisfaction among users. Furthermore, our evaluation of physicians’ overall satisfaction with the e-prescribing system revealed that the majority, 45 (53.6%), had low satisfaction. Conversely, only a small proportion, 7 (8.3%), reported high satisfaction. Subsequently, the e-prescribing system is not widely accepted by users, with the majority (71.4%) favoring paper-based prescribing. Many other studies have indicated higher levels of user satisfaction and a greater willingness to accept and use e-prescribing systems, contrary to our study’s findings [ 31 , 32 , 33 , 34 ]. The low level of satisfaction and users’ reluctance to adopt the e-prescribing system can be attributed to various challenges and problems identified by them. Users have been greatly impacted by these issues, which range from technical difficulties to system design and architecture issues, resulting in dissatisfaction, diminished motivation, and resistance towards the system.

Although e-prescribing systems represent a novel and transformative approach in healthcare, they offer numerous benefits, including improved efficiency, reduced medication errors, and enhanced patient safety. However, our study highlights the presence of significant challenges, such as technical issues and problems related to system design and architecture, which result in low user satisfaction and hinder system adoption. The custodian and service provider organizations should upgrade the necessary information technology infrastructures, including hardware, software, and network infrastructures, to address the technical challenges. Furthermore, given that the design and architectural issues of the e-prescribing systems have resulted in user dissatisfaction and diminished motivation to use the system, identifying and addressing these problems and shortcomings in future updates is recommended. Moreover, it is important to take into account the end users’ perspectives during the system design process.

Data availability

All data generated or analyzed during this study are included within this article.

Babaie J, Elmi S. Drug prescribing in family physician program involved health care centers and hospital of Hashtrood (Iran) in 2017. Iran J Health Insurance. 2019;2(3):162–71.

Google Scholar  

Borriharn S, Kaewvichit S, Pannavalee W, Thiankhanithikun K, Kanjanarat P. A systematic review: quality indicators for assessing Drug System Management. J Health Sci. 2014:934–42.

Pirmohamed M, James S, Meakin S, Green C, Scott AK, Walley TJ, et al. Adverse drug reactions as cause of admission to hospital: prospective analysis of 18 820 patients. Bmj. 2004;329(7456):15–9.

Cresswell K, Coleman J, Slee A, Williams R, Sheikh A, Team eP. Investigating and learning lessons from early experiences of implementing ePrescribing systems into NHS hospitals: a questionnaire study. PLoS ONE. 2013;8(1):e53369.

Article   CAS   PubMed   PubMed Central   Google Scholar  

Elliott RA, Lee CY, Hussainy SY. Electronic prescribing and medication management at a residential aged care facility. Appl Clin Inf. 2016;7(01):116–27.

Article   Google Scholar  

Shawahna R, Rahman NU, Ahmad M, Debray M, Yliperttula M, Decleves X. Electronic prescribing reduces prescribing error in public hospitals. J Clin Nurs. 2011;20(21–22):3233–45.

Article   PubMed   Google Scholar  

Ahmadi M, Samadbeik M, Sadoughi F. Modeling of outpatient prescribing process in Iran: a gateway toward electronic prescribing system. Iran J Pharm Res. 2014;13(2):725.

PubMed   PubMed Central   Google Scholar  

Shi L-P, Liu C-H, Cao J-F, Lu Y, Xuan F-X, Jiang Y-T, et al. Development and application of a closed-loop medication administration system in University of Hongkong-Shenzhen Hospital. Front Nurs. 2018;5(2):105–9.

Grossman JM, Gerland A, Reed MC, Fahlman C. Physicians’ experiences using Commercial E-Prescribing systems: Physicians are optimistic about e-prescribing systems but face barriers to their adoption. Health Aff. 2007;26(Suppl2):393–404.

Bell DS, Cretin S, Marken RS, Landman AB. A conceptual framework for evaluating outpatient electronic prescribing systems based on their functional capabilities. J Am Med Inf. 2004;11(1):60–70.

Vejdani M, Varmaghani M, Meraji M, Jamali J, Hooshmand E, Vafaee-Najar A. Electronic prescription system requirements: a scoping review. BMC Med Inf Decis Mak. 2022;22(1):1–13.

Mohsin-Shaikh S, Furniss D, Blandford A, McLeod M, Ma T, Beykloo MY, et al. The impact of electronic prescribing systems on healthcare professionals’ working practices in the hospital setting: a systematic review and narrative synthesis. BMC Health Serv Res. 2019;19:1–8.

Gates PJ, Hardie R-A, Raban MZ, Li L, Westbrook JI. How effective are electronic medication systems in reducing medication error rates and associated harm among hospital inpatients? A systematic review and meta-analysis. J Am Med Inform Assoc. 2021;28(1):167–76.

Hailiye Teferi G, Wonde TE, Tadele MM, Assaye BT, Hordofa ZR, Ahmed MH, et al. Perception of physicians towards electronic prescription system and associated factors at resource limited setting 2021: Cross sectional study. PLoS ONE. 2022;17(3):e0262759.

Boonstra A. Interpretive perspectives on the acceptance of an electronic prescription system. J Inform Technol Case Application Res. 2003;5(2):27–50.

Boonstra A, Boddy D, Fischbacher M. The limited acceptance of an electronic prescription system by general practitioners: reasons and practical implications. New Technol Work Employ. 2004;19(2):128–44.

Samadbeik M, Ahmadi M, Sadoughi F, Garavand A. A copmarative review of electronic prescription systems: lessons learned from developed countries. J Res Pharm Pract. 2017;6(1):3–11.

Article   PubMed   PubMed Central   Google Scholar  

Chang H-Y, Kan HJ, Shermock KM, Alexander GC, Weiner JP, Kharrazi H. Integrating e-prescribing and pharmacy claims data for predictive modeling: comparing costs and utilization of health plan members who fill their initial medications with those who do not. J Managed Care Specialty Pharm. 2020;26(10):1282–90.

Cresswell KM, Lee L, Slee A, Coleman J, Bates DW, Sheikh A. Qualitative analysis of vendor discussions on the procurement of computerised physician order entry and clinical decision support systems in hospitals. BMJ open. 2015;5(10):e008313.

Fischer SH, Rudin RS, Shi Y, Shekelle P, Amill-Rosario A, Scanlon D, et al. Trends in the use of computerized physician order entry by health-system affiliated ambulatory clinics in the United States, 2014–2016. BMC Health Serv Res. 2020;20:1–6.

Gall W, Aly A-F, Sojer R, Spahni S, Ammenwerth E. The national e-medication approaches in Germany, Switzerland and Austria: a structured comparison. Int J Med Informatics. 2016;93:14–25.

Dehghan H, Eslami S, Ghasemi SH, Jahangiri M, Bahaadinbeigy K, Kimiafar K, et al. Development of a National Roadmap for electronic prescribing implementation. Stud Health Technol Inform. 2019;260:121–7.

PubMed   Google Scholar  

Jebraeily M, Rashidi A, Mohitmafi T, Muossazadeh R. Evaluation of Outpatient Electronic prescription system capabilities from the perspective of Physicians in Specialized Polyclinics of Urmia Social Security Organization. Payavard Salamat. 2021;14(6):557–68.

Raeesi A, Abbasi R, Khajouei R. Evaluating physicians’ perspectives on the efficiency and effectiveness of the electronic prescribing system. Int J Technol Assess Health Care. 2021;37(1):e42.

Hayavi-Haghighi MH, Davoodi S, Teshnizi SH, Jookar R. Usability evaluation of electronic prescribing systems from physicians’ perspective: a case study from southern Iran. Inf Med Unlocked. 2024;45:101460.

Williams J, Bates DW, Sheikh A. Optimising electronic prescribing in hospitals: a scoping review protocol. BMJ Health Care Inf. 2020;27(1).

Santiago BC, Bengoechea MM, Barrueta OI, Ibañez AS, Aramburu EA, Garcia EI, et al. OHP-005 advantages and disadvantages of an electronic prescribing system. Aspects to consider during pharmacist validation. Eur J Hosp Pharmacy: Sci Pract. 2013;20(Suppl 1):A137–A.

Tamblyn R, Huang A, Kawasumi Y, Bartlett G, Grad R, Jacques A, et al. The development and evaluation of an integrated electronic prescribing and drug management system for primary care. J Am Med Inform Assoc. 2006;13(2):148–59.

Elson B. Electronic prescribing in ambulatory care: a market primer and implications for managed care pharmacy. J Managed Care Pharm. 2001;7(2):115–20.

Farida S, Krisnamurti DGB, Hakim RW, Dwijayanti A, Purwaningsih EH. Implementation of electronic prescribing. eJournal Kedokteran Indonesia. 2017;5(3):16–211.

Abdel-Qader DH, Cantrill JA, Tully MP. Satisfaction predictors and attitudes towards electronic prescribing systems in three UK hospitals. Pharm World Sci. 2010;32:581–93.

Shams MEHES. Implementation of an e-prescribing service: users’ satisfaction and recommendations. Can Pharmacists J. 2011;144(4):186–91.

Bright HR, Peter J, Chandy S. Electronic prescribing system in a Teaching Hospital-user satisfaction and factors affecting successful implementation. Der Pharmacia Letter. 2019;11(2):10–24.

Jariwala KS, Holmes ER, Banahan DJ III. Adoption of and experience with e-prescribing by primary care physicians. Res Social Administrative Pharm. 2013;9(1):120–8.

Download references

Acknowledgements

This work was supported by a grant from Hamadan University of Medical Sciences Research Council (140206074578).

Author information

Soheila Saeedi and Taleb Khodaveisi contributed equally to this work.

Authors and Affiliations

Department of Health Information Technology, School of Allied Medical Sciences, Hamadan University of Medical Sciences, Shahid Fahmideh Blvd, Hamadan, Iran

Hamid Bouraghi, Ali Mohammadpour, Soheila Saeedi & Taleb Khodaveisi

Department of Operating Room, School of Paramedicine, Hamadan University of Medical Sciences, Hamadan, Iran

Behzad Imani

School of Medicine, Iran University of Medical Sciences, Tehran, Iran

Abolfazl Saeedi

Health Information Management Department, Besat Hospital, Hamadan University of Medical Sciences, Hamadan, Iran

Tooba Mehrabi

You can also search for this author in PubMed   Google Scholar

Contributions

SS, TKH and HB developed the concept for the study. SS, TM, and AS collected data. SS and TKH carried out the analysis and interpretation under the supervision of HB and BI. Finally, SS, AM, AS, and HB drafted the manuscript. All authors reviewed the content and approved it.

Corresponding authors

Correspondence to Soheila Saeedi or Taleb Khodaveisi .

Ethics declarations

Ethics approval and consent to participate.

The study was conducted in accordance with the Declaration of Helsinki and approved by a local ethics committee in Iran, namely Ethics Committee of the Hamadan University of Medical Sciences (IR.UMSHA.REC.1402.408). Verbal informed consent obtained from all the participants included in the study and was approved by the Ethics Committee of the Hamadan University of Medical Sciences.

Consent for publication

Not applicable.

Competing interests

The authors declare no competing interests.

Additional information

Publisher’s note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ . The Creative Commons Public Domain Dedication waiver ( http://creativecommons.org/publicdomain/zero/1.0/ ) applies to the data made available in this article, unless otherwise stated in a credit line to the data.

Reprints and permissions

About this article

Cite this article.

Bouraghi, H., Imani, B., Saeedi, A. et al. Challenges and advantages of electronic prescribing system: a survey study and thematic analysis. BMC Health Serv Res 24 , 689 (2024). https://doi.org/10.1186/s12913-024-11144-3

Download citation

Received : 11 December 2023

Accepted : 23 May 2024

Published : 30 May 2024

DOI : https://doi.org/10.1186/s12913-024-11144-3

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Electronic prescribing system
• Thematic analysis
• Prescription

BMC Health Services Research

ISSN: 1472-6963

• General enquiries: [email protected]

• Search Menu
• Sign in through your institution
• Supplements
• Author videos
• Advance Articles
• Author Guidelines
• Submission Site
• Open Access Options
• Why publish with CKJ?
• About the ERA
• Journals Career Network
• Editorial Board
• Advertising and Corporate Services
• Self-Archiving Policy
• The ERA Journals
• Journals on Oxford Academic
• Books on Oxford Academic

Article Contents

The basics: the correlation coefficient, the linearity of correlation, the range of observations for correlation, the non-causality of correlation, agreement between methods, conflict of interest statement.

• < Previous

Conducting correlation analysis: important limitations and pitfalls

• Article contents
• Figures & tables
• Supplementary Data

Roemer J Janse, Tiny Hoekstra, Kitty J Jager, Carmine Zoccali, Giovanni Tripepi, Friedo W Dekker, Merel van Diepen, Conducting correlation analysis: important limitations and pitfalls, Clinical Kidney Journal , Volume 14, Issue 11, November 2021, Pages 2332–2337, https://doi.org/10.1093/ckj/sfab085

• Permissions Icon Permissions

The correlation coefficient is a statistical measure often used in studies to show an association between variables or to look at the agreement between two methods. In this paper, we will discuss not only the basics of the correlation coefficient, such as its assumptions and how it is interpreted, but also important limitations when using the correlation coefficient, such as its assumption of a linear association and its sensitivity to the range of observations. We will also discuss why the coefficient is invalid when used to assess agreement of two methods aiming to measure a certain value, and discuss better alternatives, such as the intraclass coefficient and Bland–Altman’s limits of agreement. The concepts discussed in this paper are supported with examples from literature in the field of nephrology.

‘Correlation is not causation’: a saying not rarely uttered when a person infers causality from two variables occurring together, without them truly affecting each other. Yet, though causation may not always be understood correctly, correlation too is a concept in which mistakes are easily made. Nonetheless, the correlation coefficient has often been reported within the medical literature. It estimates the association between two variables (e.g. blood pressure and kidney function), or is used for the estimation of agreement between two methods of measurement that aim to measure the same variable (e.g. the Modification of Diet in Renal Disease (MDRD) formula and the Chronic Kidney Disease Epidemiology Collaboration (CKD-EPI) formula for estimating the glomerular filtration rate (eGFR)]. Despite the wide use of the correlation coefficient, limitations and pitfalls for both situations exist, of which one should be aware when drawing conclusions from correlation coefficients. In this paper, we aim to describe the correlation coefficient and its limitations, together with methods that can be applied to avoid these limitations.

Fundamentals

The correlation coefficient was described over a hundred years ago by Karl Pearson [ 1 ], taking inspiration from a similar idea of correlation from Sir Francis Galton, who developed linear regression and was the not-so-well-known half-cousin of Charles Darwin [ 2 ]. In short, the correlation coefficient, denoted with the Greek character rho ( ρ ) for the true (theoretical) population and r for a sample of the true population, aims to estimate the strength of the linear association between two variables. If we have variables X and Y that are plotted against each other in a scatter plot, the correlation coefficient indicates how well a straight line fits these data. The coefficient ranges from −1 to 1 and is dimensionless (i.e., it has no unit). Two correlations with r = −1 and r  = 1 are shown in Figure 1A and B , respectively. The values of −1 and 1 indicate that all observations can be described perfectly using a straight line, which in turn means that if X is known, Y can be determined deterministically and vice versa. Here, the minus sign indicates an inverse association: if X increases, Y decreases. Nonetheless, real-world data are often not perfectly summarized using a straight line. In a scatterplot as shown in Figure 1C , the correlation coefficient represents how well a linear association fits the data.

Different shapes of data and their correlation coefficients. ( A ) Linear association with r = −1. ( B ) A linear association with r  = 1. ( C ) A scatterplot through which a straight line could plausibly be drawn, with r  = 0.50. ( D ) A sinusoidal association with r  = 0. ( E ) A quadratic association with r  = 0. ( F ) An exponential association with r  = 0.50.

It is also possible to test the hypothesis of whether X and Y are correlated, which yields a P-value indicating the chance of finding the correlation coefficient’s observed value or any value indicating a higher degree of correlation, given that the two variables are not actually correlated. Though the correlation coefficient will not vary depending on sample size, the P-value yielded with the t -test will.

The value of the correlation coefficient is also not influenced by the units of measurement, but it is influenced by measurement error. If more error (also known as noise) is present in the variables X and Y , variability in X will be partially due to the error in X , and thus not solely explainable by Y . Moreover, the correlation coefficient is also sensitive to the range of observations, which we will discuss later in this paper.

An assumption of the Pearson correlation coefficient is that the joint distribution of the variables is normal. However, it has been shown that the correlation coefficient is quite robust with regard to this assumption, meaning that Pearson’s correlation coefficient may still be validly estimated in skewed distributions [ 3 ]. If desired, a non-parametric method is also available to estimate correlation; namely, the Spearman’s rank correlation coefficient. Instead of the actual values of observations, the Spearman’s correlation coefficient uses the rank of the observations when ordering observations from small to large, hence the ‘rank’ in its name [ 4 ]. This usage of the rank makes it robust against outliers [ 4 ].

Explained variance and interpretation

One may also translate the correlation coefficient into a measure of the explained variance (also known as R 2 ), by taking its square. The result can be interpreted as the proportion of statistical variability (i.e. variance) in one variable that can be explained by the other variable. In other words, to what degree can variable X be explained by Y and vice versa. For instance, as mentioned above, a correlation of −1 or +1 would both allow us to determine X from Y and vice versa without error, which is also shown in the coefficient of determination, which would be (−1) 2 or 1 2 = 1, indicating that 100% of variability in one variable can be explained by the other variable.

In some cases, the interpretation of the strength of correlation coefficient is based on rules of thumb, as is often the case with P-values (P-value <0.05 is statistically significant, P-value >0.05 is not statistically significant). However, such rules of thumb should not be used for correlations. Instead, the interpretation should always depend on context and purposes [ 5 ]. For instance, when studying the association of renin–angiotensin–system inhibitors (RASi) with blood pressure, patients with increased blood pressure may receive the perfect dosage of RASi until their blood pressure is exactly normal. Those with an already exactly normal blood pressure will not receive RASi. However, as the perfect dosage of RASi makes the blood pressure of the RASi users exactly normal, and thus equal to the blood pressure of the RASi non-users, no variation is left between users and non-users. Because of this, the correlation will be 0.

An important limitation of the correlation coefficient is that it assumes a linear association. This also means that any linear transformation and any scale transformation of either variable X or Y , or both, will not affect the correlation coefficient. However, variables X and Y may also have a non-linear association, which could still yield a low correlation coefficient, as seen in Figure 1D and E , even though variables X and Y are clearly related. Nonetheless, the correlation coefficient will not always return 0 in case of a non-linear association, as portrayed in Figure 1F with an exponential correlation with r  = 0.5. In short, a correlation coefficient is not a measure of the best-fitted line through the observations, but only the degree to which the observations lie on one straight line.

In general, before calculating a correlation coefficient, it is advised to inspect a scatterplot of the observations in order to assess whether the data could possibly be described with a linear association and whether calculating a correlation coefficient makes sense. For instance, the scatterplot in Figure 1C could plausibly fit a straight line, and a correlation coefficient would therefore be suitable to describe the association in the data.

An important pitfall of the correlation coefficient is that it is influenced by the range of observations. In Figure 2A , we illustrate hypothetical data with 50 observations, with r  = 0.87. Included in the figure is an ellipse that shows the variance of the full observed data, and an ellipse that shows the variance of only the 25 lowest observations. If we subsequently analyse these 25 observations independently as shown in Figure 2B , we will see that the ellipse has shortened. If we determine the correlation coefficient for Figure 2B , we will also find a substantially lower correlation: r  = 0.57.

The effect of the range of observations on the correlation coefficient, as shown with ellipses. ( A ) Set of 50 observations from hypothetical dataset X with r  = 0.87, with an illustrative ellipse showing length and width of the whole dataset, and an ellipse showing only the first 25 observations. ( B ) Set of only the 25 lowest observations from hypothetical dataset X with r  = 0.57, with an illustrative ellipse showing length and width.

The importance of the range of observations can further be illustrated using an example from a paper by Pierrat et al. [ 6 ] in which the correlation between the eGFR calculated using inulin clearance and eGFR calculated using the Cockcroft–Gault formula was studied both in adults and children. Children had a higher correlation coefficient than adults ( r  = 0.81 versus r  = 0.67), after which the authors mentioned: ‘The coefficients of correlation were even better […] in children than in adults.’ However, the range of observations in children was larger than the range of observations in adults, which in itself could explain the higher correlation coefficient observed in children. One can thus not simply conclude that the Cockcroft–Gault formula for eGFR correlates better with inulin in children than in adults. Because the range of the correlation influences the correlation coefficient, it is important to realize that correlation coefficients cannot be readily compared between groups or studies. Another consequence of this is that researchers could inflate the correlation coefficient by including additional low and high eGFR values.

Another important pitfall of the correlation coefficient is that it cannot be interpreted as causal. It is of course possible that there is a causal effect of one variable on the other, but there may also be other possible explanations that the correlation coefficient does not take into account. Take for example the phenomenon of confounding. We can study the association of prescribing angiotensin-converting enzyme (ACE)-inhibitors with a decline in kidney function. These two variables would be highly correlated, which may be due to the underlying factor albuminuria. A patient with albuminuria is more likely to receive ACE-inhibitors, but is also more likely to have a decline in kidney function. So ACE-inhibitors and a decline in kidney function are correlated not because of ACE-inhibitors causing a decline in kidney function, but because they have a shared underlying cause (also known as common cause) [ 7 ]. More reasons why associations may be biased exist, which are explained elsewhere [ 8 , 9 ].

It is however possible to adjust for such confounding effects, for example by using multivariable regression. Whereas a univariable (or ‘crude’) linear regression analysis is no different than calculating the correlation coefficient, a multivariable regression analysis allows one to adjust for possible confounder variables. Other factors need to be taken into account to estimate causal effects, but these are beyond the scope of this paper.

We have discussed the correlation coefficient and its limitations when studying the association between two variables. However, the correlation coefficient is also often incorrectly used to study the agreement between two methods that aim to estimate the same variable. Again, also here, the correlation coefficient is an invalid measure.

The correlation coefficient aims to represent to what degree a straight line fits the data. This is not the same as agreement between methods (i.e. whether X  =  Y ). If methods completely agree, all observations would fall on the line of equality (i.e. the line on which the observations would be situated if X and Y had equal values). Yet the correlation coefficient looks at the best-fitted straight line through the data, which is not per se the line of equality. As a result, any method that would consistently measure a twice as large value as the other method would still correlate perfectly with the other method. This is shown in Figure 3 , where the dashed line shows the line of equality, and the other lines portray different linear associations, all with perfect correlation, but no agreement between X and Y . These linear associations may portray a systematic difference, better known as bias, in one of the methods.

A set of linear associations, with the dashed line (- - -) showing the line of equality where X  =  Y . The equations and correlations for the other lines are shown as well, which shows that only a linear association is needed for r  = 1, and not specifically agreement.

This limitation applies to all comparisons of methods, where it is studied whether methods can be used interchangeably, and it also applies to situations where two individuals measure a value and where the results are then compared (inter-observer variation or agreement; here the individuals can be seen as the ‘methods’), and to situations where it is studied whether one method measures consistently at two different time points (also known as repeatability). Fortunately, other methods exist to compare methods [ 10 , 11 ], of which one was proposed by Bland and Altman themselves [ 12 ].

Intraclass coefficient

One valid method to assess interchangeability is the intraclass coefficient (ICC), which is a generalization of Cohen’s κ , a measure for the assessment of intra- and interobserver agreement. The ICC shows the proportion of the variability in the new method that is due to the normal variability between individuals. The measure takes into account both the correlation and the systematic difference (i.e. bias), which makes it a measure of both the consistency and agreement of two methods. Nonetheless, like the correlation coefficient, it is influenced by the range of observations. However, an important advantage of the ICC is that it allows comparison between multiple variables or observers. Similar to the ICC is the concordance correlation coefficient (CCC), though it has been stated that the CCC yields values similar to the ICC [ 13 ]. Nonetheless, the CCC may also be found in the literature [ 14 ].

The 95% limits of agreement and the Bland–Altman plot

When they published their critique on the use of the correlation coefficient for the measurement of agreement, Bland and Altman also published an alternative method to measure agreement, which they called the limits of agreement (also referred to as a Bland–Altman plot) [ 12 ]. To illustrate the method of the limits of agreement, an artificial dataset was created using the MASS package (version 7.3-53) for R version 4.0.4 (R Corps, Vienna, Austria). Two sets of observations (two observations per person) were derived from a normal distribution with a mean ( µ ) of 120 and a randomly chosen standard deviation ( σ ) between 5 and 15. The mean of 120 was chosen with the aim to have the values resemble measurements of high eGFR, where the first set of observed eGFRs was hypothetically acquired using the MDRD formula, and the second set of observed eGFRs was hypothetically acquired using the CKD-EPI formula. The observations can be found in Table 1 .

Artificial data portraying hypothetically observed MDRD measurements and CKD-EPI measurements

The 95% limits of agreement can be easily calculated using the mean of the differences ( ⁠ d ¯ ⁠ ) and the standard deviation (SD) of the differences. The upper limit (UL) of the limits of agreement would then be UL = d ¯ + 1.96 * SD and the lower limit (LL) would be LL = d ¯ - 1.96 * SD ⁠ . If we apply this to the data from Table 1 , we would find d ¯ = 0.32 and SD = 4.09. Subsequently, UL = 0.32 + 1.96 * 4.09 = 8.34 and LL = 0.32 − 1.96 * 4.09 = −7.70. Our limits of agreement are thus −7.70 to 8.34. We can now decide whether these limits of agreement are too broad. Imagine we decide that if we want to replace the MDRD formula with the CKD-EPI formula, we say that the difference may not be larger than 7 mL/min/1.73 m 2 . Thus, on the basis of these (hypothetical) data, the MDRD and CKD-EPI formulas cannot be used interchangeably in our case. It should also be noted that, as the limits of agreement are statistical parameters, they are also subject to uncertainty. The uncertainty can be determined by calculating 95% confidence intervals for the limits of agreement, on which Bland and Altman elaborate in their paper [ 12 ].

The limits of agreement are also subject to two assumptions: (i) the mean and SD of the differences should be constant over the range of observations and (ii) the differences are approximately normally distributed. To check these assumptions, two plots were proposed: the Bland–Altman plot, which is the differences plotted against the means of their measurements, and a histogram of the differences. If in the Bland–Altman plot the means and SDs of the differences appear to be equal along the x -axis, the first assumption is met. The histogram of the differences should follow the pattern of a normal distribution. We checked these assumptions by creating a Bland–Altman plot in Figure 4A and a histogram of the differences in Figure 4B . As often done, we also added the limits of agreement to the Bland–Altman plot, between which approximately 95% of datapoints are expected to be. In Figure 4A , we see that the mean of the differences appears to be equal along the x -axis; i.e., these datapoints could plausibly fit the horizontal line of the total mean across the whole x -axis. Nonetheless, the SD does not appear to be distributed equally: the means of the differences at the lower values of the x -axis are closer to the total mean (thus a lower SD) than the means of the differences at the middle values of the x -axis (thus a higher SD). Therefore, the first assumption is not met. Nonetheless, the second assumption is met, because our differences follow a normal distribution, as shown in Figure 4B . Our failure to meet the first assumption can be due to a number of reasons, for which Bland and Altman also proposed solutions [ 15 ]. For example, data may be skewed. However, in that case, log-transforming variables may be a solution [ 16 ].

Plots to check assumptions for the limits of agreement. ( A ) The Bland–Altman plot for the assumption that the mean and SD of the differences are constant over the range of observations. In our case, we see that the mean of the differences appears to be equal along the x -axis; i.e., these datapoints could plausibly fit the horizontal line of the total mean across the whole x -axis. Nonetheless, the SD does not appear to be distributed equally: the means of the differences at the lower values of the x -axis are closer to the total mean (thus a lower SD) than the means of the differences at the middle values of the x -axis (thus a higher SD). Therefore, the first assumption is not met. The limits of agreement and the mean are added as dashed (- - -) lines. ( B ) A histogram of the distribution of differences to ascertain the assumption of whether the differences are normally distributed. In our case, the observations follow a normal distribution and thus, the assumption is met.

It is often mistakenly thought that the Bland–Altman plot alone is the analysis to determine the agreement between methods, but the authors themselves spoke strongly against this [ 15 ]. We suggest that authors should both report the limits of agreement and show the Bland–Altman plot, to allow readers to assess for themselves whether they think the agreement is met.

The correlation coefficient is easy to calculate and provides a measure of the strength of linear association in the data. However, it also has important limitations and pitfalls, both when studying the association between two variables and when studying agreement between methods. These limitations and pitfalls should be taken into account when using and interpreting it. If necessary, researchers should look into alternatives to the correlation coefficient, such as regression analysis for causal research, and the ICC and the limits of agreement combined with a Bland–Altman plot when comparing methods.

None declared.

Pearson K , Henrici OMFE. VII. Mathematical contributions to the theory of evolution. III. Regression, heredity, and panmixia . Philos Trans R Soc Lond Ser A 1896 ; 187 : 253 – 318

Google Scholar

Stanton JM. Galton, Pearson, and the peas: A brief history of linear regression for statistics instructors . J Statist Educ 2001 ; 9 : doi: 10.1080/10691898.2001.11910537

Havlicek LL , Peterson NL. Effect of the violation of assumptions upon significance levels of the Pearson r . Psychol Bull 1977 ; 84 : 373 – 377

Schober P , Boer C , Schwarte LA. Correlation coefficients: appropriate use and interpretation . Anesth Analg 2018 ; 126 : 1763 – 1768

Kozak M. What is strong correlation? Teach Statist 2009 ; 31 : 85 – 86

Pierrat A , Gravier E , Saunders C et al.  . Predicting GFR in children and adults: a comparison of the Cockcroft–Gault, Schwartz, and modification of diet in renal disease formulas . Kidney Int 2003 ; 64 : 1425 – 1436

Fu EL , van Diepen M , Xu Y et al.  . Pharmacoepidemiology for nephrologists (part 2): potential biases and how to overcome them . Clin Kidney J 2021 ; 14 : 1317 – 1326

Jager KJ , Tripepi G , Chesnaye NC et al.  . Where to look for the most frequent biases? Nephrology (Carlton) 2020 ; 25 : 435 – 441

Suttorp MM , Siegerink B , Jager KJ et al.  . Graphical presentation of confounding in directed acyclic graphs . Nephrol Dial Transplant 2015 ; 30 : 1418 – 1423

van Stralen KJ , Dekker FW , Zoccali C et al. Measuring agreement, more complicated than it seems . Nephron Clin Pract 2012 ; 120 : c162 –c16 7

van Stralen KJ , Jager KJ , Zoccali C et al. Agreement between methods . Kidney Int 2008 ; 74 : 1116 – 1120

Bland JM , Altman DG. Statistical methods for assessing agreement between two methods of clinical measurement . Lancet 1986 ; 1 : 307 – 310

Carol AA , Note O. A concordance correlation coefficient to evaluate reproducibility . Biometrics 1997 ; 53 : 1503 – 1507

Pecchini P , Malberti F , Mieth M et al.  . Measuring asymmetric dimethylarginine (ADMA) in CKD: a comparison between enzyme-linked immunosorbent assay and liquid chromatography-electrospray tandem mass spectrometry . J Nephrol 2012 ; 25 : 1016 – 1022

Bland JM , Altman DG. Applying the right statistics: analyses of measurement studies . Ultrasound Obstet Gynecol 2003 ; 22 : 85 – 93

Euser AM , Dekker FW , Le Cessie S. A practical approach to Bland–Altman plots and variation coefficients for log transformed variables . J Clin Epidemiol 2008 ; 61 : 978 – 982

• correlation studies
• pearson correlation coefficient

Email alerts

Citing articles via.

• ckj Twitter
• ERA Twitter
• ERA Facebook
• ERA Instagram
• ERA LinkedIn
• ERA Youtube

Affiliations

• Online ISSN 2048-8513
• Print ISSN 2048-8505
• Copyright © 2024 European Renal Association
• About Oxford Academic
• Publish journals with us
• University press partners
• What we publish
• New features  
• Open access
• Institutional account management
• Rights and permissions
• Get help with access
• Accessibility
• Advertising
• Media enquiries
• Oxford University Press
• Oxford Languages
• University of Oxford

Oxford University Press is a department of the University of Oxford. It furthers the University's objective of excellence in research, scholarship, and education by publishing worldwide

• Copyright © 2024 Oxford University Press
• Cookie settings
• Cookie policy
• Privacy policy
• Legal notice

This Feature Is Available To Subscribers Only

Sign In or Create an Account

This PDF is available to Subscribers Only

For full access to this pdf, sign in to an existing account, or purchase an annual subscription.

An official website of the United States government

The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

• Publications
• Account settings

Preview improvements coming to the PMC website in October 2024. Learn More or Try it out now .

• Advanced Search
• Journal List
• Hum Brain Mapp
• v.41(13); 2020 Sep

A technical review of canonical correlation analysis for neuroscience applications

Xiaowei zhuang.

1 Cleveland Clinic Lou Ruvo Center for Brain Health, Las Vegas Nevada, USA

Zhengshi Yang

Dietmar cordes.

2 University of Colorado, Boulder Colorado, USA

3 Department of Brain Health, University of Nevada, Las Vegas Nevada, USA

Associated Data

There is no data or code involved in this review article.

Collecting comprehensive data sets of the same subject has become a standard in neuroscience research and uncovering multivariate relationships among collected data sets have gained significant attentions in recent years. Canonical correlation analysis (CCA) is one of the powerful multivariate tools to jointly investigate relationships among multiple data sets, which can uncover disease or environmental effects in various modalities simultaneously and characterize changes during development, aging, and disease progressions comprehensively. In the past 10 years, despite an increasing number of studies have utilized CCA in multivariate analysis, simple conventional CCA dominates these applications. Multiple CCA‐variant techniques have been proposed to improve the model performance; however, the complicated multivariate formulations and not well‐known capabilities have delayed their wide applications. Therefore, in this study, a comprehensive review of CCA and its variant techniques is provided. Detailed technical formulation with analytical and numerical solutions, current applications in neuroscience research, and advantages and limitations of each CCA‐related technique are discussed. Finally, a general guideline in how to select the most appropriate CCA‐related technique based on the properties of available data sets and particularly targeted neuroscience questions is provided.

Neuroscience applications of canonical correlation analysis (CCA) and its variants are systematically reviewed from a technical perspective. Detailed formulations, analytical and numerical solutions, current applications, and advantages and limitations of CCA and its variants are discussed. A general guideline to select the most appropriate CCA‐related technique is provided.

1. INTRODUCTION

Recently in neuroscience research, multiple types of data are usually collected from the same individual, including demographics, clinical symptoms, behavioral and neuropsychological measures, genetic information, structural and functional magnetic resonance imaging (fMRI) data, position emission tomography (PET) data, functional near‐infrared spectroscopy (fNIRS) data, and electrophysiological data. Each of these data types, termed modality here, contains multiple measurements and provides a unique view of the subject. These measurements can be the raw data (e.g., neuropsychological tests) or derived information (e.g., brain regional volume and thickness measures derived from T1‐weighted MRI).

Neuroscience research has been focused on uncovering associations between measurements from multiple modalities. Conventionally, a single measurement is selected from each modality, and their one‐to‐one univariate association is analyzed. Multiple correction is then performed to guarantee statistically meaningful results. These univariate associations have illuminated numerous findings in various neurological diseases, such as association between gray‐matter density and Mini Mental State Examination score in Alzheimer's disease (Baxter et al., 2006 ), correlation between brain network temporal dynamics and Unified Parkinson Disease Rating Scale part III motor scores in Parkinson's disease subjects (Zhuang et al., 2018 ), and relationship between imaging biomarkers and cognitive performances in fighters with repetitive head trauma (Mishra et al., 2017 ).

However, the one‐to‐one univariate association overlooks the multivariate joint relationship among multiple measurements between modalities. Furthermore, when dealing with brain imaging data, highly correlated noise further decreases the effectiveness and sensitivity of mass‐univariate voxel‐wise analysis (Cremers, Wager, & Yarkoni, 2017 ; Zhuang et al., 2017 ), and different methods of multiple corrections might lead to various statistically meaningful results. Multivariate analysis, alternatively, uncovers the joint covariate patterns among different modalities and avoids multiple correction steps, which would be more appropriate to disentangle joint relationship between modalities and guarantees full utilization of all common information.

Canonical correlation analysis (CCA) is one candidate to uncover these joint multivariate relationships among different modalities. CCA is a statistical method that finds linear combinations of two random variables so that the correlation between the combined variables is maximized (Hotelling, 1936 ). CCA can identify the source of common statistical variations among multiple modalities, without assuming any particular form of directionality, which suits neuroscience applications. In practice, CCA has been mainly implemented as a substitute for univariate general linear model (GLM) to link different modalities, and therefore, is a major and powerful tool in multimodal data fusion. Multiple CCA variants, including kernel CCA, constrained CCA, deep CCA, and multiset CCA, also have been applied in neuroscience research. However, the complicated multivariate formulations and obscure capabilities remain obstacles for CCA and its variants to being widely applied.

In this study, we review CCA applications in neuroscience research from a technical perspective to improve the understanding of the CCA technique itself and to provide neuroscience researchers with guidlines of proper CCA applications. We briefly discuss studies through December 2019 that have utilized CCA and its variants to uncover the association between multiple modalities. We explain the existing CCA method and its variants for their formulations, properties, relationships to other multivariate techniques, and advantages and limitations in neuroscience applications. We finally provide a flowchart and an experimental example to assist researchers to select the most appropriate CCA technique based on their specific applications.

2. INCLUSION/EXCLUSION OF STUDIES

Using the PubMed search engine in December 2019, we searched neuroimaging or neuroscience articles using CCA with the following string: (“canonical correlation” analysis) AND (neuroscience OR neuroimaging). This search yielded 192 articles; 11 additional articles were included based on authors' preidentification. We excluded non‐English articles, conference abstracts and duplicated studies, yielding 188 articles assessed for eligibility. We further identified 160 studies that met the following criteria: (a) primarily focused on a CCA or CCA‐variant technique and (b) with an application to neuroimaging or neuroscience modalities. Reasons for exclusion and numbers of articles meeting exclusion criteria at each stage are shown in Figure ​ Figure1 1 .

Inclusion and exclusion criteria for this review

The remaining articles were full‐text reviewed and divided into five categories based on the applied CCA technique (Figure ​ (Figure2a): 2a ): CCA ( N = 67); constrained CCA ( N = 53); nonlinear CCA ( N = 7); multiset CCA ( N = 29); and CCA‐other ( N = 7). Three articles applied constrained multiset CCA, thus are categorized into both constrained CCA and multiset CCA. Numbers of articles of every year from 1990 to 2019 are plotted in Figure ​ Figure2 2 (B).

Number of articles summarized by category (a) and year (b)

In the following sections, we present technical details (Section 3 ) and neuroscience applications for each category (Section 4 ). In Section 5 , we discuss technical differences and summarize advantages and limitations of each CCA‐related technique. We finally provide an experimental example and guidance in Section 6 to researchers who are interested in applying multivariate CCA‐related techniques in their work.

3. TECHNICAL DETAILS

Figure ​ Figure3 3 shows the detailed CCA equations (red box) and linkages between CCA and its variants. Constrained CCA (yellow boxes), nonlinear CCA (gray boxes), and multiset CCA (orange boxes) are focused, and linkages between CCA and other univariate (light green boxes) and multivariate (dark green boxes) techniques are also included. Here, we provide basic formulations and solutions of each CCA and its variants. We also discuss how CCA is mathematically linked to its variants and to other multivariate or univariate techniques. Researchers interested in further details can refer to the corresponding references.

Technical details of CCA and relationship between CCA and its variants. Background color indicates different techniques: red: conventional CCA; gray: nonlinear CCA; yellow: constrained CCA; orange: multiset CCA; green: other techniques related to CCA. CCA, canonical correlation analysis; PCA, principle component analysis; PLS, partial least square

3.1. Conventional CCA

Formulations.

CCA is designed to maximize the correlation between two latent variables y 1 ∈ R p 1 × 1 and y 2 ∈ R p 2 × 1 , which are also being referred to as modalities. Here, we denote Y k ∈ R N × p k , k = 1 , 2 as collected samples of these two variables, where N represents the number of observations (samples) and p k , k = 1, 2 represent the number of features in each variable. CCA determines the canonical coefficients u 1 ∈ R p 1 × 1 and u 2 ∈ R p 2 × 1 for Y 1 and Y 2 , respectively, by maximizing the correlation between Y 1 u 1 and Y 2 u 2 :

In Equation (1 ), ∑ 11 and ∑ 22 are the within‐set covariance matrices and ∑ 12 is the between‐set covariance matrix. The denominator in Equation (1 ) is used to normalize within‐set covariance, which guarantees that CCA is invariant to the scaling of coefficients.

Canonical coefficients u 1 and u 2 can be found by setting the partial derivative of the objective function (Equation (1 )) with respect to u 1 and u 2 to zero, respectively, leading to:

Equation (2 ) can be further reduced to a classical eigenvalue problem, if ∑ kk is invertible, as follows:

Each pair of canonical coefficients { u 1 ,  u 2 } are the eigenvectors of ∑ 11 − 1 ∑ 12 ∑ 22 − 1 ∑ 21 and ∑ 22 − 1 ∑ 21 ∑ 11 − 1 ∑ 12 , respectively with the same eigenvalue ρ 2 . Following Equation (3 ), up to M = min( p 1 ,  p 2 ) pairs of canonical coefficients can be achieved through singular value decomposition (SVD), and every pair of canonical variables Y 1 u 1 m Y 2 u 2 m , m = 1 , 2 , … , M , are uncorrelated with another pair of canonical variables. Corresponding M canonical correlation values are in descending order as ρ (1)  >  ρ (2)  > … >  ρ ( M ) .

As we stated above, one requirement for solving the CCA problem (Equation (1 )) through this eigenvalue problem (Equation (3 )) is that within‐set covariance matrices ∑ 11 and ∑ 22 must be invertible. To satisfy this requirement, the number of observations in Y 1 and Y 2 should be greater than the number of features, that is, N  >  p k , k = 1, 2. Furthermore, since the square of canonical correlation values ( ρ 2 ) are the eigenvalues of matrices ∑ 11 − 1 ∑ 12 ∑ 22 − 1 ∑ 21 and ∑ 22 − 1 ∑ 21 ∑ 11 − 1 ∑ 12 , both matrices are required to be positive definite.

Statistical inferences

Parametric inferences exist for CCA if both variables strictly follow the Gaussian distribution. The null hypothesis is that no (zero) canonical correlation exists between Y 1 and Y 2 , that is, ρ (1) = ρ (2) = … = ρ ( M ) = 0. The alternative hypothesis is that at least one canonical correlation value is nonzero. A test statistic based on Wilk's Λ is (Bartlett, 1939 ):

which follows a chi‐square distribution χ p 1 × p 2 2 with degree of freedom of p 1  ×  p 2 . It is also of interest to test if a specific canonical correlation value ( ρ ( m ) , 1 ≤  m  ≤  M ) is different from zero. In this case, the test statistic in Equation (4 ) becomes:

which follows χ p 1 − m p 2 − m 2 .

In practice, this parametric inference is not commonly used since it requires variables to strictly follow the Gaussian distribution and is sensitive to outliers (Bartlett, 1939 ). Instead, permutation‐based nonparametric statistics have been widely used in CCA applications. In general, observations of one variable are randomly shuffled ( Y 1 becomes Y 1 ^ ) while observations of the other variable are kept intact ( Y 2 remains). A new set of canonical correlation values are then computed for Y 1 ^ and Y 2 following Equation (3 ). This random shuffling is repeated multiple times, and the null distribution of canonical correlation values is generated. Statistical significance ( p ‐values) for the true canonical correlation values are finally obtained from this null distribution.

3.2. CCA variants

The conventional CCA (Equation (1 )) can be modified for different purposes. Constrained CCA penalizes canonical coefficients u 1 and u 2 to satisfy certain requirements and more specifically, to avoid overfitting and unstable results caused by insufficient observations in Y 1 or Y 2 . Kernel and deep CCA are designed to uncover nonlinear correlations between modalities by projecting the original variables to new nonlinear feature spaces. Multiset CCA is proposed to find multivariate associations among more than two modalities. In this section, we systematically review constrained CCA, nonlinear CCA, multiset CCA, and other special CCA cases.

3.2.1. Constrained CCA

Generalized constrained cca, formulation.

Constrained CCA is implemented by adding penalties to coefficients u k in Equation (1 ). Penalties can be either equality constraints or inequality constraints, and based on researcher's own considerations, penalties can be added to either u 1 or u 2 , or to both u 1 and u 2 . Therefore, in general, the constrained CCA problem can be formulated in terms of the constrained optimization problem as:

where E represents the set of equality constraints and InE represents the set of inequality constraints.

Analytical solutions usually do not exist for constrained CCA problems, and solving Equation (6 ) requires numerical solutions through iterative optimization techniques. Multiple optimization techniques can be applied, such as the Broyden–Fletcher–Goldfarb–Shanno algorithm, augmented‐Lagrangian algorithm, reduced gradient method and sequential quadratic programming. Examples and details of solving constrained CCA problems through above optimization techniques can be found in Yang, Zhuang, et al. ( 2018 ) and Zhuang et al. ( 2017 ).

Special case: L 1 ‐norm penalty and sparse CCA

The most commonly implemented penalty in constrained CCA is the L 1 ‐norm penalty added to either u 1 or u 2 , and is termed sparse CCA:

where | u i | 1  <  c i are inequality constraints.

The L 1 ‐norm penalty induces sparsity on canonical coefficients, and therefore sparse CCA can be implemented to high‐dimensional variables. When dealing with high‐dimensional variables, the within‐set covariance matrices ∑ 11 and ∑ 22 in Equation (7 ) are also high‐dimensional matrices, which are memory intensive. In addition, when the number of observations is less than the number of features, the covariance matrices cannot be estimated reliably from the sample. In these cases, within‐set covariance matrices are usually replaced by identity matrices, and sparse CCA is then equivalent to sparse PLS. Please note that researchers may still name this technique as sparse CCA even after this replacement (Witten, Tibshirani, & Hastie, 2009 ).

With known prior information about features or observations, sparse CCA can be further modified to structure sparse CCA or discriminant sparse CCA , respectively. If the known prior information is about features, such as categorizing features into different groups (Lin et al., 2014 ) or characterizing connections between features (Kim et al., 2019 ), the prior information will be implemented as an additional penalty on features, leading to structure sparse CCA . Alternatively, if the known prior information is about observations, such as diagnostic group of each subject, the prior information will be implemented as additional constraint on observations, leading to discriminant sparse CCA (Wang et al., 2019 ).

Sparse CCA, structure sparse CCA, and discriminant sparse CCA can all be considered as special cases of a generalized constrained CCA (Equation (6 )) problem with different equality and inequality constraint sets. Iterative optimization techniques used to solve the generalized constrained CCA problem are also applicable here to solve these special cases.

3.2.2. Nonlinear CCA

Both CCA and constrained CCA assume linear intervariable relationships, however, this assumption does not hold in general for all variables in real data. Nonlinear CCA uncovers the joint nonlinear relationship between different variables, which is a complementary tool to conventional CCA methods. Kernel CCA, temporal kernel CCA, and deep CCA are the foremost techniques in this category.

Kernel CCA and temporal kernel CCA

Kernel CCA uncovers the joint nonlinear relationship between two variables by mapping the original feature space in Y 1 and Y 2 on to a new feature space through a predefined kernel function . However, this new feature space is not explicitly defined. Instead, the original feature space for each observation in Y k is implicitly projected to a higher dimensional feature space Y k  →  ϕ ( Y k ) embedded in a prespecified kernel function H k ∈ R N × N , which is independent of the number of features in the projected space. After transforming u k to ϕ ( Y k ) T v k , the CCA form in Equation (1 ) in the higher dimensional feature space, namely kernel CCA can be written as:

where v 1 and v 2 are unknowns to estimate, instead of u 1 and u 2 .

Temporal kernel CCA is a kernel CCA variant that is specifically designed for two time series with temporal delays. In temporal kernel CCA, one variable, for example, Y 1 , is shifted for multiple different time points and a new variable Y ~ 1 is formed by concatenating the original Y 1 and the temporally shifted Y 1 . The new variable Y ~ 1 and the original Y 2 are then input to kernel CCA as in Equation (8 ).

Closed‐form analytical solution exists for kernel CCA (Equation (8 )). By setting the partial derivatives of the objective function in Equation (8 ) with respect to v 1 and v 2 to zero separately, kernel CCA can be converted to the following problem:

Note that the kernel CCA problem defined in Equation (9 ) always holds true when ρ = 1. To avoid this trivial solution, a penalty term needs to be introduced to the norm of original canonical coefficients u k , such that v k T H k 2 v k become v k T H k 2 v k + λ u k 2 = v k T H k 2 + λ H k v k , where λ is a regularization parameter. This regularized kernel CCA problem can be further represented as an eigenvalue problem (Hardoon, Szedmak, & Shawe‐Taylor, 2004 ):

where a closed‐form solution exists in the new feature space.

Kernel CCA requires a predefined kernel function for the feature mapping to uncover the joint nonlinear relationship between two variables. Alternatively, recent development of deep learning makes it possible to learn the feature mapping from data itself. The deep learning variant of CCA, deep CCA (Andrew, Bilmes, & Livescu, 2013 ), provides a more flexible and robust way to learn and search the nonlinear association between two variables. More specifically, deep CCA first passes the original Y 1 and Y 2 through multiple stacked layers of nonlinear transformations. Let θ 1 and θ 2 represent vectors of all parameters through all layers for Y 1 and Y 2 , respectively, deep CCA can be represented as:

Deep CCA is solved through a deep learning schema by dividing the original data into training and testing sets. θ 1 and θ 2 are optimized by following the gradient of the correlation objective as estimated on the training data (Andrew et al., 2013 ). The number of unknown parameters in deep CCA is much higher than the number of unknowns in other CCA variants; therefore, a large number of training samples (in tens of thousands) are required for deep CCA to produce meaningful results. In most studies, it is unlikely to have enough observations (e.g. subjects) as training samples for deep CCA algorithms. Instead, in neuroscience applications, treating each brain voxel as a training sample, similar to Yang et al. ( 2020 , 2019 ), would be more promising in deep CCA applications.

3.2.3. Multiset CCA

Multiset CCA extends the conventional CCA from uncovering associations between two variables to finding common patterns among more than two variables. Constraints can also be incorporated in multiset CCA for various purposes.

Multiset CCA

The most intuitive formulation of multiset CCA is to optimize canonical coefficients of all variables by maximizing pairwise canonical correlations, nameed as SUMCOR multiset CCA:

where K  > 2 is the number of variables. A new matrix ∑ ^ ∈ R K × K is defined where each element ∑ ^ i , j is a canonical correlation between two variables Y i and Y j :

and u k T ∑ kk u k , k = 1 , … , K is set to 1 for normalization.

Besides maximizing SUMCOR, Kettenring ( 1971 ) summarizes four other possible objective functions in multiset CCA optimization: (a) SSQCOR, maximizing sum of squared pairwise correlations ∑ i , j K ∑ ^ ij 2 ; (b) MAXVAR, maximizing largest eigenvalue of correlation matrix λ max ∑ ^ ; (c) MINVAR, minimizing smallest eigenvalue of correlation matrix λ min ∑ ^ ; and (d) GENVAR, minimizing the determinant of correlation matrix det ∑ ^ . In practice, SUMCOR multiset CCA is most commonly used followed by MAXVAR and SSQCOR multiset CCA.

Analytical solutions of multiset CCA are obtained by calculating the partial derivatives of the objective function with respect to each u i . Since SUMCOR and SSQCOR are linear and quadratic functions of each u i , respectively, closed‐form analytical solutions can be obtained for these two cost functions by setting the partial derivatives equal to 0, which leads to generalized eigenvalue problems. Multiset CCA with all these five objective functions can also be solved by means of the general algebraic modeling system (Brooke, Kendrick, Meeraus, & Rama, 1998 ) and NLP solver CONOPT (Drud, 1985 ).

Multiset CCA with constraints

In constrained multiset CCA, penalty terms can be added to each u i individually. Here we give examples of two commonly incorporated constraints in multiset CCA: sparse multiset CCA and multiset CCA with reference.

Formulation: Sparse multiset CCA

Similar to sparse CCA, sparse multiset CCA applies the L 1 ‐norm penalty to one or more u i in Equation (12 ), and therefore induces sparsity on canonical coefficient(s) and can be applied to high‐dimensional variables. Here, we give the equation of SUMCOR sparse multiset CCA as an example:

Formulation: Multiset CCA with reference

Multiset CCA with reference enables the discovery of multimodal associations with a specific reference variable across subjects, such as a neuropsychological measurement (Qi, Calhoun, et al., 2018 ). In multiset CCA with reference, additional constraints of correlations between each canonical variable and the reference variable ( v ref ) are added:

where λ >0 is the tuning parameter and ∙ 2 2 is the L 2 ‐norm. Therefore, multiset CCA with reference is a supervised multivariate technique that can extract common components across multiple variables that are associated with a specific prior reference.

Both Equations (14 ) and ( 15 ) can be viewed as constrained optimization problems with an objective function and multiple equality and inequality constraints. In this case, iterative optimization techniques are required to solve constrained multiset CCA problems.

3.2.4. Other CCA ‐related techniques

There are many other CCA‐related techniques developed, and here we only included three that have been applied in the neuroscience field: supervised local CCA, Bayesian CCA, and tensor CCA.

Supervised local CCA

CCA by formulation is an unsupervised technique that uncovers joint relationships between two variables. Meanwhile, CCA can become a supervised technique by (a) adding additional constraints such as CCA (multiset CCA) with reference discussed in the section “ Multiset CCA with constraints ,” or (b) directly incorporating group information into the objective function as in the supervised local CCA technique (Zhao et al., 2017 ).

Supervised local CCA is based on locally discriminant CCA (Peng, Zhang, & Zhang, 2010 ), which uses local group information to construct a between‐set covariance matrix ∑ ~ 12 , as a replacement of ∑ 12 in Equation (1 ). More specifically, ∑ ~ 12 is defined as the covariance matrix from d nearest neighboring within‐class samples ( ∑ w ) penalized by the covariance from d nearest neighboring between‐class samples ( ∑ b ) with a tuning parameter λ ,

However, this technique only considers the local group information with the global discriminating information ignored. To address this issue, Fisher discrimination information together with local group information is considered in supervised local CCA, which can be written as:

where S k denote the between‐group scatter matrices of the dataset k . If samples i and j belong to c th class, U ij is set to 1 n c , where n c denotes the number of samples in c th class; otherwise, U ij is set to 0. Supervised local CCA is usually applied sequentially with gradually decreased d (named as hierarchical supervised local CCA) to reduce the influence of the neighborhood size and improve classification performance.

Bayesian CCA

Bayesian CCA is another technique that overcomes the overfitting problem when applying CCA to variables with small sample sizes. Bayesian CCA is also proposed to complement CCA by providing a principal component analysis (PCA)‐like description of variations that are not captured by the correlated components (Klami, Virtanen, & Kaski, 2013 ). Input to CCA in Equation (1 ), Y 1 and Y 2 , can be considered as N observations of one‐dimensional random variables y 1 ∈ R p 1 × 1 and y 2 ∈ R p 2 × 1 . Using the same notations, Bayesian CCA can be formulated as a latent variable model (with latent variable z ) between y 1 and y 2 (Klami & Kaski, 2007 ; Wang, 2007 ):

where N 0 , I denotes the multivariate Gaussian distribution with mean vector 0 and identity covariance matrix I . D k are diagonal covariance matrices and indicate features in y k with independent noise. The latent variable z ∈ R q × 1 , where q represents the number of shared components, captures the shared variation between y 1 and y 2 , and can be linearly transformed back to the original space of y k through A k z , k = 1, 2. Similarly, the latent variable, where q k represents the number of variable‐specific components, captures the variable k ‐specific variation not shared between y 1 and y 2 , and can be linearly transformed back to the original space in y k by B k z k .

Browne ( 1979 ) demonstrated that Equation (18 ) was equivalent to CCA in Equation (1 ) by showing that maximum likelihood solutions to both Equations (1 ) and ( 18 ) share the same canonical coefficients with an unknown rotational transform, that is, Equation (18 ) is equivalent to conventional CCA (Equation (1 )) in the aspect that their solutions share the same subspace. However, unlike conventional CCA (Equation (1 )) that uses two variables u 1 and u 2 to project y 1 and y 2 to this subspace, Bayesian CCA maintains the shared variation between y 1 and y 2 in a single variable z .

The formulation of y k in Equation (18 ) can be rewritten as y k ∼ N A k z , B k B k T + D k , k = 1,2 after algebra operations. With Ψ k = B k B k T + D k , the model in Equation (18 ) can be transformed to

In Equation (19 ), prior knowledge of the parameters (e.g., A k and Ψ k ) are required to construct the latent variable model for Bayesian CCA. For instance, the inverse Wishart distribution as a prior for the covariance Ψ k and the automatic relevance determination (ARD; Neal, 2012 ) prior for the linear mappings A k are used when Bayesian CCA is proposed (Klami & Kaski, 2007 ; Wang, 2007 ). Since then, multiple Bayesian inference techniques have been developed, however, the early work of Bayesian CCA is limited to low‐dimensional data (not more than eight dimensions in Klami & Kaski, 2007 and Wang, 2007 ) due to the computational complexity to estimate the posterior distribution over the p k  ×  p k covariance matrices Ψ k (Klami et al., 2013 ). A group‐wise ARD prior (Klami et al., 2013 ) was recently introduced for Bayesian CCA, which automatically identifies variable‐specific and shared components. More importantly, this change made Bayesian CCA applicable for high‐dimensional data. More technical details about Bayesian CCA can be found in Klami et al. ( 2013 ).

Two‐dimensional CCA and tensor CCA for high‐dimensional variables

Variables input to CCA ( Y k ∈ R N × p k , k = 1 , 2 , … , ) are usually required to be 2D matrices with a dimension of number of observations ( N ) times number of features ( p k ) in each variable. Y k can be considered as N observations of the 1D variable y k ∈ R p k × 1 . In practice, tensor data, such as 3D images or 4D time series, are commonly involved in neuroscience applications, and these variables are required to be vectorized before inputting to CCA algorithms. This vectorization could potentially break the feature structures. In this case, to analyze 3D data, such as N samples of 2D variables ( N  ×  p 1  ×  p 2 ), without breaking the 2D feature structure, two‐dimensional CCA (2DCCA) has been proposed by Lee and Choi ( 2007 ).

Mathematically, 2DCCA maximizes the canonical correlation between two variables with N observations of 2D features: Y 1 : Y 1 n ∈ R p 11 × p 12 n = 1 … N and Y 2 : Y 2 n ∈ R p 21 × p 22 n = 1 … N . For each variable, 2DCCA searches left transforms l 1 ∈ R p 11 × 1 and l 2 ∈ R p 21 × 1 and right transforms r 1 ∈ R p 12 × 1 and r 2 ∈ R p 22 × 1 in order to maximize the correlation between l 1 T Y 1 r 1 and l 2 T Y 2 r 2 :

In Equation (20 ), for fixed l 1 and l 2 , r 1 and r 2 can be obtained with the SVD algorithm similar to the one used in conventional CCA, and l 1 and l 2 can be obtained for fixed r 1 and r 2 , alternatingly. Therefore, an iterative alternating SVD algorithm (Lee & Choi, 2007 ) has been developed to solve Equation (20 ).

Above described 2DCCA can be treated as a constrained optimization problem with low‐rank restrictions on canonical coefficients, similar restrictions are used in (Chen, Kolar, & Tsay, 2019 ), where 2DCCA has been extended to higher dimensional tensor data, termed tensor CCA. The tensor CCA (Chen et al., 2019 ) searches two rank‐one tensors u 1 = u 11 ∘ ⋯ ∘ u 1 m ∈ R p 11 × ⋯ × p 1 m and u 2 = u 21 ∘ ⋯ ∘ u 2 m ∈ R p 21 × ⋯ × p 2 m to maximize the correlation between Y 1 : Y 1 n ∈ R p 11 × ⋯ × p 1 m n = 1 … N and Y 2 : Y 2 n ∈ R p 21 × ⋯ × p 2 m n = 1 … N , where “∘” denotes outer product and u k 1 , …, u km are vectors. Chen et al. ( 2019 ) also introduced an efficient optimization algorithm to solve tensor CCA for high dimensional data sets.

Tensor CCA for multiset data

Another way to handle input variables with high‐dimensional feature spaces is to generalize conventional CCA by analyzing constructed covariance tensors (Luo, Tao, Ramamohanarao, Xu, & Wen, 2015 ). This method requires random variables to be vectorized and is similar to multiset CCA since both of them deal with more than two input modalities. The differences between tensor CCA and multiset CCA in this case lie in that tensor CCA constructs a high‐order covariance tensor for all input variables (Luo et al., 2015 ), whereas multiset CCA finds pair‐wise covariance matrices. In addition, tensor CCA (Luo et al., 2015 ) does not maximize the pairwise correlation as in multiset CCA; instead, it directly maximizes the correlation over all canonical variables,

where ʘ denotes element‐wise product and 1 ∈ R N × 1 is an all ones vector. The problem formulated in Equation (21 ) can be solved by using the alternating least square algorithm (Kroonenberg & de Leeuw, 1980 ).

3.2.5. Statistical inferences of CCA variants

Nonparametric permutation tests have been widely performed in CCA variant techniques to determine the statistical significance of each canonical correlation value and the corresponding canonical coefficients. In these permutation tests, as we described in Section 3.1 , observations of one variable are randomly shuffled ( Y 1 becomes Y 1 ^ ), while observations of the other variable are kept intact ( Y 2 remains). This random shuffling is repeated multiple times (~5,000), and the exact same CCA variant technique is applied to each shuffled data. The obtained canonical correlation values from these randomly shuffled data form the null distribution. Statistical significances ( p ‐values) of true canonical correlation values are determined by comparing true values to this null distribution.

Besides permutation tests, a null distribution can also be built by creating null data input to CCA variant techniques. The null data are usually generated based on the physical properties of input variables. For instance, when applying CCA‐variant technique to link task fMRI data and the task stimuli, the null data of task fMRI can be obtained by applying wavelet‐resampling to resting‐state fMRI data (Breakspear, Brammer, Bullmore, Das, & Williams, 2004 ; Zhuang et al., 2017 ). The null hypothesis here is that task fMRI data are not multivariately correlated with task stimuli, and the wavelet resampled resting‐state fMRI data fits the requirements of the null data in this case.

3.3. Technical differences

3.3.1. technical differences among cca ‐related techniques.

There are three prominent CCA techniques: conventional CCA shares the simplest formulation and can be easily applied to uncover multivariate linear relationships between two variables; nonlinear CCA by definition can extract multivariate nonlinear relationship between two variables through feature mapping with known predefined functions; and multiset CCA are able to find common covariated patterns among more than two variables. These three methods can be efficiently solved with closed‐form analytical solutions, which are obtained by taking the partial derivatives of the objective function with respective to each unknown, separately.

Constrained (multiset) CCA incorporates prior information about input variables into each of the three CCA methods, in terms of equality and inequality constraints on the unknowns. Prior knowledge about the data or specific hypothesis are required for its applications. Closed‐form solutions are no longer available for constrained (multiset) CCA and iterative optimization techniques are required to solve these problems.

Recently developed deep CCA is different from all other CCA‐related techniques as it learns the optimum feature mapping from the data itself through deep learning with training and testing data being specified. Machine learning and deep leaning expertise are required to solve this problem.

3.3.2. Relationship between CCA and other multivariate and univariate techniques

Relationship with other multivariate techniques.

In general, CCA can be directly rewritten in terms of the multivariate multiple regression (MVMR) model:

where u 1 and u 2 are obtained by minimizing the residual term ε ∈ R N × 1 . Since CCA is scale‐invariant, a solution to Equation (22 ) is also a solution of Equation (1 ). Furthermore, with normalization terms of u 1 T ∑ 11 u 1 = 1 and u 2 T ∑ 22 u 2 = 1 , the MVMR model is exactly equivalent to CCA, that is, maximizing the canonical correlation between Y 1 and Y 2 is equivalent to minimizing the residual term ε :

In addition, by replacing the covariance matrices ∑ 11 and ∑ 22 in the denominator in Equation (1 ) with the identity matrix I , conventional CCA is converted to partial least square (PLS), which maximizes the covariance between latent variables. If Y 1 is the same as Y 2 , the PLS will maximize the variance within a single variable, which is equivalent to PCA.

Relationship with univariate techniques

If one variable in CCA, for example, Y 1 , only has a single feature, that is, y ∈ R N × 1 , u 1 can then be defined as 1 and CCA becomes a linear regression problem:

where Y 1 is renamed as y and Y 2 is renamed as X to follow conventional notations. ε ∈ R N × 1 denotes the residual term. If both variables Y 1 and Y 2 contain only one feature, the canonical correlation between Y 1 and Y 2 becomes the Pearson's correlation between Y 1 and Y 2 as in the univariate analysis.

4. NEUROSCIENCE APPLICATIONS

4.1. cca : finding linear relationships, 4.1.1. direct application of cca, combine phenotypes and brain activities.

To date, the most common CCA application in neuroscience is to find joint multivariate linear associations between phenotypic features and neurobiological activities. Phenotypic features usually include one or more measurements from demographics, genetic information, behavioral measurements, clinical symptoms, and performances of neuropsychological tests. Neurobiological activities are generally summarized with brain structural measurements, functional activations during specific tasks, both static and dynamic resting‐state functional connectivity measurements, network topological measurements, and electrophysiological recordings (Table ​ (Table1 1 ).

CCA application

Abbreviations: CAA, canonical correlation analysis; LASSO, least absolute shrinkage and selection operator; PCA, principal component analysis.

In normal healthy subjects, using CCA, multiple studies have delineated the joint multivariate relationships between the above imaging‐derived features and nonimaging measurements, which have boosted our understandings of healthy development and healthy aging (Irimia & van Horn, 2013 ; Kuo et al., 2019 ; Shen et al., 2016 ; Tsvetanov et al., 2016 ). Furthermore, using multivariate CCA to combine imaging and nonimaging features have provided new insights to understand the joint relationship between brain activities and subjects' clinical symptoms, behavioral measurements, and performances of neuropsychological tests in various diseased populations, such as psychosis disease spectrum (Adhikari et al., 2019 ; Bai et al., 2019 ; Kottaram et al., 2019 ; Laskaris et al., 2019 ; Palaniyappan et al., 2019 ; Rodrigue et al., 2018 ; Tian et al., 2019 ; Viviano et al., 2018 ), Alzheimer's disease spectrum (Brier et al., 2016 ; Liao et al., 2010 ; McCrory & Ford, 1991 ; Zhu et al., 2016 ), neurodevelopmental diseases (Chenausky et al., 2017 ; Lin, Cocchi, et al., 2018 ; Zille et al., 2018 ), depression (Dinga et al., 2019 ), Parkinson's disease (Lin, Baumeister, Garg, and McKeown, 2018 ; Liu et al., 2018 ), multiple sclerosis (Leibach et al., 2016 ; Lin et al., 2017 ), epilepsy (Kucukboyaci et al., 2012 ) and drug addictions (Dell'Osso et al., 2014 ).

Brain activation in response to task stimuli

CCA has also been applied to detect brain activations in responses to stimuli during task‐based fMRI experiments. Compared to the most commonly general linear regression model, local neighboring voxels are considered simultaneously in CCA to determine activation status of the central voxel (Friman, Cedefamn, Lundberg, Borga, & Knutsson, 2001 ; Nandy & Cordes, 2003 ; Nandy & Cordes, 2004 ; Rydell et al., 2006 ; Shams et al., 2006 ). In addition, in task‐based electrophysiological experiments, Dmochowski et al. ( 2018 ) and de Cheveigne et al. ( 2018 ) have maximized the canonical correlation between an optimally transformed stimulus and properly filtered neural responses to delineate the stimulus–response relationship in electroencephalogram (EEG) data.

Denoising neuroscience data

Another application of CCA in neuroscience research is to remove noises from signals in the raw data. Through a blind source separation (BSS) framework, von Luhmann et al. ( 2019 ) extract comodulated canonical components between fNIRS signals and accelerometer signals, and consider those components above a canonical correlation threshold to be motion artifact. Through BSS‐CCA algorithms, multiple studies demonstrate that muscle artifact can be efficiently removed from EEG signals (Hallez et al., 2009 ; Janani et al., 2020 ; Somers & Bertrand, 2016 ; Vergult et al., 2007 ). Furthermore, Churchill et al. ( 2012 ) remove physiological noise from fMRI signals through a CCA‐based split‐half resampling framework, and Li et al. ( 2017 ) remove gradient artifacts in concurrent EEG/fMRI recordings through maximizing the temporal autocorrelations of the time series.

Canonical granger causality

CCA has also been used to determine the causal relationship among regions of interest (ROIs) in fMRI functional connectivity analysis. Instead of using the mean ROI time series directly for analysis, multiple time series are specified for each ROI and CCA searches the optimally weighted mean time series during the analysis. Sato et al. ( 2010 ) compute multiple eigen‐time series for each ROI and determine the granger causality between two ROIs by maximizing the canonical correlation between eigen‐time series at time point t and t‐1 of the two ROIs. In a more recent work, instead of using eigen‐time series of each ROI, Gulin et al. ( 2014 ) compute an optimized linear combination of signals from each ROI in CCA to enable a more accurate causality measurement.

4.1.2. Practical considerations and data reduction steps

As we stated in Section 3.1 , only if numbers of observations are more than numbers of features in both Y 1 and Y 2 , that is, N  ≫  p k , k = 1, 2, conventional CCA can produce statistically stable and meaningful results. However, in neuroscience applications, this requirement is not always fullfilled, especially when Y 1 or Y 2 represents brain activities where each brain voxel is considered a feature individually. In this case, any feature can be picked up and learned by the CCA process and directly applying Equation (1 ) to two sets will produce overfitted and unstable results. Therefore, additional data‐reduction steps applied before CCA or constraints incorporated in the CCA algorithm are necessary to avoid overfitting in CCA applications. In this section, we focus on data reduction steps applied before conventional CCA.

The most commonly used data reduction technique is the PCA method applied to Y 1 and Y 2 separately. Through orthogonal transformation, PCA converts Y 1 and Y 2 into sets of linearly uncorrelated principal components. The principal components that do not pass certain criteria are discarded, leading to dimension‐reduced variables: Y ~ 1 ∈ R N × q 1 and Y ~ 2 ∈ R N × q 2 , where N  ≫  q k , k = 1, 2. Equation (1 ) can then be applied to Y ~ 1 and Y ~ 2 . Multiple studies applied PCA to reduce data dimensions before applying CCA to find joint multivariate correlations between two high‐dimensional variables (Abrol et al., 2017 ; Churchill et al., 2012 ; Hackmack et al., 2012 ; Li et al., 2019 ; Mihalik et al., 2019 ; Ouyang et al., 2015 ; Sato et al., 2010 ; Smith et al., 2015 ; Sui et al., 2010 ; Sui et al., 2011 ; Zarnani et al., 2019 ).

In addition, the least absolute shrinkage and selection operator (LASSO) algorithm (Tibshirani, 1996 ) has also been applied prior to CCA as a feature selection step to eliminate less informative features. For instance, in delineating the association between neurophysiological measures, which are derived from transcranial magnetic stimulation and electromyographic recordings, and kinematic‐clinical‐demographic measurements in Parkinson's disease subjects, Bologna et al. ( 2018 ) first perform logistic regression with LASSO penalty to determine the most predictive features for the disease in both variables. CCA is then applied to link the most predictive features from each variable. Similarly, sparse regression techniques have also been applied before CCA to genetic data in a neurodevelopmental cohort (Zille et al., 2018 ). Furthermore, feature selection can also be implemented in PCA as done in L 1 ‐norm penalized sparse PCA (sPCA; Witten & Tibshirani, 2009 ; Yang, Zhuang, Bird, et al., 2019 ), which removes noninformative features during the dimension reduction step.

There is no single “correct” way or “gold standard” of the feature reduction step before applying CCA. Decisions should be made based on the data itself and the specific question that researchers are interested in.

4.2. Constrained CCA : Removing noninformative features and stabilizing results

The other common solution in practice for N  ≪  p k , k = 1, 2 is to incorporate constraints into the CCA algorithm directly, and consequently noninformative features can be removed and overfitting problems can be avoided (Table ​ (Table2 2 ).

Constrained CCA application

Abbreviation: CCA, canonical correlation analysis.

4.2.1. Constraints in CCA algorithms: Sparse CCA to remove noninformative features

Most studies apply the sparse CCA method (detailed in the section “ Special case: L 1 ‐norm penalty and sparse CCA ”), which maximizes canonical correlations between Y 1 and Y 2 , and suppresses noninformative features in Y 1 and Y 2 simultaneously (Badea et al., 2019 ; Lee et al., 2019 ; Moser et al., 2018 ; Pustina et al., 2018 ; Thye & Mirman, 2018 ; Vatansever et al., 2017 ; Wang et al., 2018 ; Xia et al., 2018 ). The features determined to be noninformative are assigned with zero coefficients. Therefore, sparse CCA is particularly appropriate to combine modalities with large noise or substantial noninformative features, such as voxel‐wise, regional‐wise or connectivity‐based brain features and genetic sequences (Avants et al., 2010 ; Deligianni et al., 2014 ; Du et al., 2017 ; Du, Liu, Yao, et al., 2019 ; Du, Zhang, et al., 2016 ; Duda et al., 2013 ; Gossmann et al., 2018 ; Grellmann et al., 2015 ; Jang et al., 2017 ; Kang et al., 2018 ; McMillan et al., 2014 ; Sheng et al., 2014 ; Sintini, Schwarz, Martin, et al., 2019 ; Sintini, Schwarz, Senjem, et al., 2019 ; Szefer et al., 2017 ; Wan et al., 2011 ). Rosa et al. ( 2015 ) further induce nonnegativity in the L 1 ‐norm penalty in sparse CCA to investigate multivariate similarities between the effects of two antipsychotic drugs on cerebral blood flow using collected arterial spin labeling data.

Prior knowledge about Y 1 and Y 2 might also be available in neuroscience data. With known prior information of the feature dimension, structure‐sparse CCA has been applied to associate brain activities with genetic information (Du et al., 2014 ; Du et al., 2015 ; Du, Huang, et al., 2016a ; Du, Huang, et al., 2016b ; Du, Liu, Zhang, et al., 2017 ; Kim et al., 2019 ; Lin et al., 2014 ; Liu et al., 2017 ; Yan et al., 2014 ), and to link structural and functional brain activities (Lisowska & Rekik, 2019 ; Mohammadi‐Nejad et al., 2017 ). If prior knowledge is available of the observation dimension, such as memberships of diagnostic groups, discriminant sparse CCA is applied to investigate joint relationship between brain activities and genetic information for subjects with Schizophrenia disease spectrum (Fang et al., 2016 ) or Alzheimer's disease spectrum (Wang et al., 2019 ; Yan et al., 2017 ). Longitudinal data could also be collected in neuroscience research and are useful to monitor disease progression. Temporal constrained sparse CCA has been proposed to uncover how single nucleotide polymorphisms affect brain gray matter density across multiple time points in subjects with Alzheimer's disease spectrum (Du, Liu, Zhu, et al., 2019 ; Hao, Li, Yan, et al., 2017 ).

4.2.2. Constraints in CCA algorithm: Constrained CCA to stabilize results

Multiple constraints have also been proposed in CCA applications to stabilize CCA coefficients between brain activities and clinical symptoms. For instance, to avoid overfitting between fNIRS signals during a moral judgment task and psychopathic personality inventory scores in healthy adults, Dashtestani et al. ( 2019 ) introduce a regularization parameter λ to keep the canonical coefficients small and to avoid high bias problem. Similarly, in preclinical research, Grosenick et al. ( 2019 ) uses two regularization parameters λ 1 and λ 2 to penalize the estimated covariance matrices for the resting‐state functional connectivity features and Hamilton Rating Scale for Depression clinical symptoms, respectively.

Furthermore, as we stated in Section 4.1.1 , CCA has been applied to detect brain activations in response to task stimuli during fMRI experiments. In these type of applications, Y 1 represents time series from local neighborhood that is considered simultaneously in determining the activation status of the central voxels, and Y 2 represents the task design matrix. CCA is applied to find optimized coefficients u 1 and u 2 , such that the correlation between combined local voxels and task design is maximized. In this case, even though the central voxel may be inactivated in the task, activated neighboring voxels would lead to a high canonical correlation and thus produce falsely activated status of the central voxel, which is termed assmoothing artifact (Cordes et al., 2012a ). To eliminate this artifact and to uncover real activation status, multiple constraints have been applied to u 1 to guarantee the dominant effect of the central voxel in a local neighborhood (Cordes et al., 2012b ; Dong et al., 2015 ; Friman et al., 2003 ; Zhuang et al., 2017 ; Zhuang et al., 2019 ). Yang, Zhuang, et al. ( 2018 ) further extend the constraints from two‐dimensional local neighborhood to three‐dimensional neighboring voxels.

4.3. Kernel CCA : Focusing on a nonlinear relationship between two modalities

Above CCAapplications assume joint linear relationships between two modalities; however, this assumption might not always hold in neuroscience research. Kernel CCA has been proposed to uncover the nonlinear relationship between modalities without explicitly specifying the nonlinear feature space (Equation (8 )). In human research, kernel CCA has been applied to investigate the joint nonlinear relationship between simultaneously collected fMRI and EEG data (Yang, Cao, et al., 2018 ), to uncover gene–gene co‐association in Schizophrenia subjects (Ashad Alam et al., 2019 ), and to detect brain activations in response to fMRI tasks (Hardoon et al., 2007 ; Yang, Zhuang, et al., 2018 ). In preclinical research, temporal kernel CCA has been proposed to investigate the temporal‐delayed nonlinear relationship between simultaneously recorded neural (electrophysiological recording in frequency‐time space) and hemodynamic (fMRI in voxel space) signals in monkeys (Murayama et al., 2010 ), and to investigate a nonlinear predictive relationship between EEG signals from two different brain regions in macaques (Rodu et al., 2018 ) (Table ​ (Table3 3 ).

Nonlinear Kernel CCA applications

4.4. Multiset CCA : More than two modalities

Multiset CCA has been specifically proposed to find common multivariate patterns across K modalities, with K > 2. The widest application of multiset CCA in neuroscience research is to uncover covariated patterns among demographics, clinical characteristics, behavioral measurements and multiple brain activities, including structural MRI derived measurements (gray matter, white matter, and cerebrospinal fluid densities), diffusion weighted MRI derived measurements (myelin water fraction and white matter tracts), fMRI derived measurements (static and dynamic functional connectivity, task fMRI activations, amplitude of low frequency contributions) and PET derived measurements (standardized uptake values) (Baumeister et al., 2019 ; Langers et al., 2014 ; Lerman‐Sinkoff et al., 2017 ; Lerman‐Sinkoff et al., 2019 ; Lin, Vavasour, et al., 2018 ; Lottman et al., 2018 ; Stout et al., 2018 ; Sui et al., 2013 ; Sui et al., 2015 ) (Table ​ (Table4 4 ).

Multiset CCA applications

Abbreviations: CCA, canonical correlation analysis; CSF, cerebrospinal fluid; dMRI, diffusion‐weighted MRI; EEG, electroencephalogram; GM, gray matter; MRI, magnetic resonance imaging; PET, position emission tomography; ROI, regions of interest; rsfMRI, resting‐state functional MRI; sMRI, structural MRI; Sub, subject; WM, white matter.

Multiset CCA has also been applied to group analysis, which combines data from multiple subjects within a single modality. In this type of applications, data from each subject are treated as one modality, and multiset CCA is used to uncover common patterns in fMRI data (Afshin‐Pour et al., 2012 ; Afshin‐Pour et al., 2014 ; Correa, Adali, et al., 2010 ; Varoquaux et al., 2010 ), consistent signals in electrophysiological recordings (Koskinen & Seppa, 2014 ; Lankinen et al., 2014 ; Lankinen et al., 2016 ; Lankinen et al., 2018 ; Zhang et al., 2017 ), covaried components in fNIRS data (Liu & Ayaz, 2018 ), and correlated fMRI and EEG signals (Correa, Eichele, et al., 2010 ) across multiple subjects.

Sparse multiset CCA has been applied to combine more than two variables and remove noninformative features simultaneously. Specifically, sparse multiset CCA has been applied to combine multiple brain imaging modalities with genetic information (Hao et al., 2017 ; Hu et al., 2016 ; Hu et al., 2018 ).

Multiset CCA with reference is specifically proposed as a supervised multimodal fusion technique in neuroscience research. Using neuropsychological measurements such as working memory or cognitive measurements as the reference, studies have uncovered stable covariated patterns among fractional amplitude of low frequency contribution maps derived from resting‐state fMRI, gray matter volumes derived from structural MRI and fractional anisotropy maps derived from diffusion‐weighted MRI that are linked with and can predict core cognitive deficits in schizophrenia (Qi, Calhoun, et al., 2018 ; Sui et al., 2018 ). Using genetic information as a prior reference, multiset CCA with reference has also uncovered multimodal covariated MRI biomarkers that are associated with microRNA132 in medication‐naïve major depressive patients (Qi, Yang, et al., 2018 ). Furthermore, with clinical depression rating score as guidance, Qi et al. ( 2020 ) have demonstrated that the electroconvulsive therapy Hdepressive disorder patients produces a covariated remodeling in brain structural and functional images, which is unique to an antidepressant symptom response. As a supervised technique, multiset CCA can be applied to uncover covariated patterns across multiple variables of special interest.

4.5. Other applications

CCA has also been applied in a supervised and hierarchical fashion. Zhao et al. ( 2017 ) have performed supervised local CCA with gradually varying neighborhood sizes in early autism diagnosis, and in each iteration, CCA is used to combine canonical variates from the previous step (Table ​ (Table5 5 ).

Other CCA applications

Abbreviations: CCA, canonical correlation analysis; fMRI, functional magnetic resonance imaging.

Bayesian CCA has been used to realign fMRI activation data between actors and observers during simple motor tasks to investigate whether seeing and performing an action activates similar brain areas (Smirnov et al., 2017 ). The Bayesian CCA assigns brain activations to one of three types (actor‐specific, observer‐specific and shared) via a group‐wise sparse ARD prior. Furthermore, using Bayesian CCA, Fujiwara et al. ( 2013 ) establish mappings between the stimulus and the brain by automatically extracting modules from measured fMRI data, which can be used to generate effective prediction models for encoding and decoding.

More recently, in network neuroscience, Graa and Rekik ( 2019 ) propose a multiview learning‐based data proliferator that enables the classification of imbalanced multiview representations. In their proposed approach, tensor‐CCA is used to align all original and proliferated views into a shared subspace for the target classification.

5. ADVANTAGES AND LIMITATIONS OF EACH CCA TECHNIQUE IN NEUROSCIENCE APPLICATIONS

Table ​ Table6 6 explains the advantages and limitations of each CCA and its variant techniques.

Advantages and limitations of each CCA‐related technique

Abbreviation: CCA, Canonical correlation analysis.

5.1. Canonical correlation analysis

5.1.1. advantages.

CCA can be applied easily to two variables and solved efficiently in closed‐form using algebraic methods (Equation (3 )). In CCA, the intermodality relationship is assumed to be linear and both modalities are exchangeable and treated equally. Canonical correlations are invariant to linear transforms of features in Y 1 or Y 2 . In neuroscience research, CCA uncovers the joint multivariate linear relationship between two modalities and has proven to be an effective multivariate and data‐driven analysis method.

5.1.2. Limitations

CCA assumes and uncovers only a linear intermodality relationship, which might not hold for neuroscience data. Furthermore, directly applying CCA requires sufficient observation support of the variables (detailed in Section 3.1 ). For neuroscience data, especially voxel‐wise brain imaging data, it is usually difficult to have more observations (e.g., subjects) than features (e.g., voxels). In this case, any feature in Y 1 and Y 2 can be picked up and learned by the CCA process, and directly applying CCA will produce overfitted and unstable results. ROI‐based analysis, data reduction (e.g., PCA), and feature selection (e.g., LASSO) steps are commonly applied to reduce the number of features in neuroscience data prior to CCA.

Another limitation of CCA in general is that signs of the canonical correlations and canonical coefficients are indeterminate. Solving the eigenvalue problem in Equation (3 ) will always give a positive canonical correlation value, and reversing the signs of u 1 and u 2 simultaneously will lead to the same canonical correlation value. Therefore, with CCA, we can only conclude that two modalities are linearly and multivariately correlated without determining the direction of the linear relationship.

5.2. Constrained CCA

5.2.1. advantages.

Incorporating constraints in CCA can in general avoid overfitted and unstable results in CCA. More specifically, different constraints can benefit neuroscieence research in various ways.

Sparse CCA incorporates the L 1 ‐norm penalty on the canonical coefficients u k , k = 1, 2 such that noninformative features are automatically removed by suppressing their weights. Thus, sparse CCA is suitable for high‐dimensional co‐linear data, such as whole‐brain voxel‐wise activities or genetic data. In practice, the within‐modality covariance matrices ∑ kk , k = 1, 2 are replaced with the identity matrix I in sparse CCA, since estimating ∑ kk from the high‐dimensional collinear data are both memory and time consuming. This replacement saves both computation time and physical resources, and is widely adopted in the neuroscience field.

Structure and discriminant sparse CCA removes noninformative features and incorporates prior information about the data in the algorithms simultaneously. Prior knowledge about feature structure or group assignment of each observation are required, respectively, for these two techniques. In neuroscience applications, information implanted in features can improve the performance and effectiveness of sparse CCA (Du, Liu, Zhang, et al., 2017 ) and guide the algorithm to produce more biologically meaningful results (Du, Huang, et al., 2016a ; Liu et al., 2017 ). Alternatively, with group assignments implanted in each observation, discriminant sparse CCA is able to discover group discriminant features, which can later improve the performance of supervised classification (Wang et al., 2019 ).

Other constraints are also beneficial in neuroscience research. For instance, the L 2 ‐norm penalty on canonical coefficients retains all features in the model with regularized weights, and therefore most of the variance can be maintained in a stable model (Dashtestani et al., 2019 ). In addition, when applied to task fMRI activation detection, locally constrained CCA penalizes weights on the neighboring voxels to guarantee the dominance of the central voxel and therefore, is able to reduce false positives (Cordes et al., 2012b ; Zhuang et al., 2017 ).

5.2.2. Limitations

One major limitation of constrained CCA is the requirement of expertise in optimization techniques. By having additional penalty terms on canonical coefficients or covariance matrices, analytical solutions of constrained CCA no longer exist, and, instead, iterative optimization methods are required to solve the constrained CCA problems efficiently.

The predefined constraint itself also requires prior knowledge about the data. For structure and discriminant sparse CCA, prior information about the observation domain or the feature domain is required. Furthermore, in neuroscience application, the constraint itself is usually data specific. For instance, when applying local constrained CCA to task fMRI activation detection, the predefined constraint should be strong enough to penalize neighboring voxels, but loose enough to guarantee the multivariate contribution of neighboring voxels to the central voxel. This constraint can only be selected through simulating a series of synthetic data that mimic real fMRI signals, which requires prior knowledge of the data and is time‐consuming.

5.3. Nonlinear CCA

5.3.1. advantages.

By definition, nonlinear CCA is able to uncover multivariate nonlinear relationships between two modalities, which commonly exist in neuroscience variables. For instance, during an fMRI task, collected fMRI signals are nonlinearly correlated with the task design due to the unknown hemodynamic response function; and kernel CCA can extract this multivariate nonlinear relationship and produce a localized brain activation map (Hardoon et al., 2007 ).

In general, kernel CCA first implicitly transforms the original feature space into a kernel space with a predefined kernel function. With this transform, nonlinear relationship between two modalities can be discovered. Furthermore, in the new kernel space, kernel CCA can be solved efficiently with a closed‐form analytical solution.

Temporal kernel CCA shares similar advantages with kernel CCA, with additional benefits from considering temporal delays between modalities when applied to simultaneously collected data. In neuroscience research, simultaneously collected EEG/fMRI data are a typical candidate for temporal kernel CCA, as neural activities collected by fMRI data, which are the blood oxygenated level‐dependent signals, contain temporal delays caused by the hemodynamic response function (Ogawa, Lee, Kay, & Tank, 1990 ), as compared to the simultaneously collected EEG signals.

Deep CCA, a purely data‐driven technique, can reveal unknown nonlinear relationships between variables without assuming any predefined nonlinear intermodality relationship. It has the potential to be applied to neuroscience data that contains enough samples for training a deep learning schema.

5.3.2. Limitations

For kernel CCA, a predefined kernel function needs to be selected and this selection will affect final results. This choice of kernel functions requires additional knowledge about data and the kernel function. Another major limitation of both kernel CCA and temporal kernel CCA is that it is difficult to project the kernel space ( H 1 and H 2 ) back to the original feature space ( Y 1 and Y 2 ), leading to additional difficulties in interpreting results (Hardoon et al., 2007 ). For instance, when applying kernel CCA to link fMRI task stimuli and collected BOLD signals for activation detection, the obtained high‐dimensional features cannot be mapped backwards to an individual voxel in order to assign the activation value because the feature embedded for commonly used nonlinear kernels (e.g., Gaussian kernel and power kernel) have information from multiple voxels. Therefore, kernel CCA with a general nonlinear kernel remains unsolved for fMRI activation analysis, and only linear kernels were used for constructing activation maps in fMRI.

Unlike kernel CCA, deep CCA does not require a predefined function and learns the nonlinear feature mapping from the data itself. However, in deep CCA, the number of unknown parameters significantly increases with the number of layers, which requires much more samples in the training data. In neuroscience data, it is usually difficult to have enough number of subjects as training samples for deep CCA. Furthermore, deep learning expertise is also required for selecting the appropriate deep learning structures for nonlinear feature mapping.

5.4. Multiset CCA

5.4.1. advantages.

In neuroscience research, more than two variables are commonly collected for the same set of subjects. Multiset CCA uncovers multivariate joint relationships among multiple variables, which is well defined to link all collected data in this case. Furthermore, if data from one subject are treated as one modality (or variable), multiset CCA will also discover the common patterns across subjects, which becomes a powerful data‐driven group analysis method.

Sparse multiset CCA combines more than two modalities and suppresses noninformative features simultaneously, and therefore shares the advantages and limitations with both multiset CCA and sparse CCA.

Multiset CCA with reference is the only supervised CCA technique and is proposed specifically for neuroscience applications. It discovers joint multivariate relationships among variables in response to a specific reference variable. For instance, using this method, common brain changes from structural, fMRI and diffusion MRI with respect to a specific neuropsychological measurement can be discovered.

5.4.2. Limitations

There are five possible objective functions for multiset CCA optimization, and different objective functions will lead to various results. The closed‐form analytical solution only exists for SUMCOR and SSQCOR objective functions. Optimization expertise are required to solve multiset CCA with other objective functions, and with constraints as well. Another major limitation of multiset CCA is that the number of final canonical components output from the algorithm does not represent the intersected common patterns across all modalities, or subjects. Instead, multiset CCA discovers the unified similarities among every modality pair (Levin‐Schwartz, Song, Schreier, Calhoun, & Adali, 2016 ).

5.5. Abstract

To summarize, conventional CCA uncovers joint multivariate linear relationships between two modalities and can be quickly and easily applied. In neuroscience research, due to the existing multiple modalities and nonlinear intermodality relationships, multiset CCA and nonlinear CCA have their own advantages when applied accordingly to appropriate variables. Constraints can be applied in these three methods to stabilize results, remove noninformative features, and produce supervised meaningful results. However, optimization expertise and prior knowledge about the data are required to select the appropriate constraints.

6. CHOOSING THE APPROPRIATE CCA TECHNIQUE

The first step in selecting a CCA technique is to decide what type of neuroscience application is of interest. Based on the types of combined modalities, CCA applications can be summarized into four categories (a–d): (a) finding relationship among multiple measurements; (b) detecting brain activations in response to task stimuli; (c) uncovering common patterns among multiple subjects; and (d) denoising the raw data. Table ​ Table7 7 summarizes current and potential techniques that can be applied for each application.

Current applied and potential CCA techniques for each application

After determining the application of interest, the flowchart in Figure ​ Figure4 4 provides a detailed guidance in selecting an appropriate CCA technique. Based on the number of variables ( K ) and linear or nonlinear intermodality relationships, three major applications are mostly common in neuroscience research: uncover linear relationship between two variables (dashed yellow box); find nonlinear relationship between two variables (dashed gray box) and discover covariated patterns among more than two variables (dashed orange box). Detailed choices are further made based on the number of observations and number of features within each variable, known prior knowledge about the variable, such as feature structures, and specific questions of interest for research studies.

Selecting a canonical correlation analysis (CCA)‐technique that suits your application. Three scenarios are most commonly encountered in neuroscience applications: CCA with and without constraints (dashed yellow box); nonlinear CCA (dashed gray box) and multiset CCA (dashed orange box)

Furthermore, here, we give an experimental example of CCA applications in neuroscience research.

Among many neuroscience applications, CCA is commonly used as a data fusion technique to uncover the association between two datasets. In the following, we demonstrate how to follow the guidance in Figure ​ Figure4 4 to link disease‐related pathology using fMRI and structural MRI data from cognitive normal subjects and subjects with mild cognitive impairment (MCI). As a prodromal stage of Alzheimer's disease, both functional and structural pathology are expected in MCI subjects. Yang, Zhuang, Bird, et al. ( 2019 ) used CCA to examine the disease‐related links between voxel‐wise functional information (e.g., eigenvector centrality mapping from fMRI data, X 1 ∈ R N × p 1 ) and voxel‐wise structural information (e.g., voxel‐based morphometry from T1 structural MRI data, X 2 ∈ R N × p 2 ), where N is the number of subjects, and p 1 and p 2 are the number of voxel‐wise features for fMRI and structural MRI data, respectively. Since there are only two imaging modalities in the analysis, multiset CCA is not an option for this case. Considering that deep CCA requires a large number of samples but N  ≪  p 1 or p 2 , and kernel CCA has the difficulty to project coefficients back to original voxel‐wise feature space as mentioned in Section 5.3 , a linear relationship between these two imaging modalities is considered. There are two approaches for the scenario that the number of samples is much less than the number of features.

The first approach is to perform dimension reduction before feeding data into conventional CCA as shown in Figure ​ Figure5a. 5a . Yang, Zhuang, Bird, et al. ( 2019 ) used PCA or sPCA (Witten et al., 2009 ) for dimension reduction and then fed CCA with dimension‐reduced data Y 1 and Y 2 . CCA found a set of canonical coefficients U k , k = 1, 2 and the corresponding canonical variables A k . The voxel‐wise weight coefficient can be obtained with a pseudo inverse operation. The other approach is to implement constrained CCA as shown in Figure ​ Figure5b. 5b . With the assumption that a proportion of voxels in the brain is not informative for finding the association between fMRI and structural MRI data, sparse CCA was applied with X 1 and X 2 directly without dimension reduction step (Yang, Zhuang, Bird, et al., 2019 ). The canonical coefficients U k , k = 1, 2 are in the voxel‐wise feature space, thus no operation is required to calculate voxel‐wise weight coefficients.

Example of choosing canonical correlation analysis (CCA) variants by following the guideline. Voxel‐wise functional and structural MRI information from cognitive normal subjects and subjects with mild cognitive impairment were used for data fusion analysis. (a) Schematic diagram of (sparse) principal component analysis (PCA) + CCA. The abbreviation sPCA stands for sparse PCA. (b) Schematic diagram of sparse CCA (sCCA). (c) Top panel shows the most disease‐discriminant functional and structural component and the bottom panel shows the correlation between datasets ( ρ ), the significance of the correlation derived from nonparametric permutation test ( p corr ) and the classification accuracy for each method

The voxel‐wise weight coefficients play a role in uncovering which brain regions are most relevant for finding the association between datasets. The voxel‐wise weight maps for the most significant disease‐related component in A k for (s)PCA + CCA and sparse CCA is shown in Figure ​ Figure5c. 5c . A nonparametric permutation test is applied to test the significance of the association between fMRI and structural MRI data with p values shown at the bottom of Figure ​ Figure5c. 5c . In this study, the canonical variables A k computed from sPCA + CCA have the highest classification accuracy for both fMRI and structural MRI data.

7. FUTURE DIRECTION OF CCA IN NEUROSCIENCE APPLICATIONS

Currently, when applying CCA to data with a smaller number of observations than features, either a data reduction orfeature selection step is performed as a preprocessing step, or an L 1 norm penalty is added as a constraint to remove noninformative features. Future efforts should be made toward incorporating prior information on feature structures of input variables that are more reasonable or more biological meaningful, and canonical correlation values should be computed in a one step process that includes prior information. Furthermore, applying CCA and its variant techniques to uncover joint multivariate relationships between two modalities has dominated the current CCA applications in the neuroscience field. In these applications, various techniques have been proposed to incorporate prior information within variables to boost the model performance, such as considering group‐discriminant features to strengthen group separation. However, much less effort was put to incorporate these prior information within the variables in multiset CCA. In neuroscience research, collecting multiple modalities of a single subject has become a commonplace, and with more than two variables, multiset CCA should be considered for this multimodal data‐fusion more often. Future efforts toward incorporating prior information within each variable to further improve the performance of multiset CCA could shed new lights in neuroscience research. For instance, we suggest incorporating group information in multiset CCA to extract common group‐discriminant patterns among multiple measurements derived from fMRI, or to uncover correlated group‐discriminant feature among brain imaging data and behavioral or clinical measurements. Furthermore, nonlinear relationships among multiple modalities have not been explored within multiset CCA in neuroscience research. It might be of interest to incorporate kernels in multiset CCA to uncover covariated nonlinear patterns among multiple brain imaging data, or to input each variable through multiple layers to generate “deep” features before applying multiset CCA.

In addition, future efforts are also required to statistically interpret CCA results. Currently, a parametric statistical significance of CCA model is only well defined for conventional CCA. Statistical significances of CCA variants are usually determined nonparametrically through permutation tests, which are time‐consuming and methods dependent. Furthermore, even using permutation tests, statistical significance can only be determined for each canonical correlation value, instead of canonical coefficients. Therefore, we cannot determine the statistical significance of a specific feature in the model. Identifying important features as potential biomarkers is usually an end goal in neuroscience. Therefore, developing test statistics to interpret CCA results by determining statistically important features would also benefit neuroscience research.

8. CONCLUSION

Uncovering multivariate relationships between modalities of the same subjects have gained significant attentions in neuroscience research. CCA is a powerful tool to investigate these joint associations and has been widely applied. Multiple CCA‐variant techniques have been proposed to fulfill specific analysis requirements. In this study, we reviewed CCA and its variant techniques from a technical perspective, with summarized applications in neuroscience research. Of each CCA‐related technique, detailed formulation and solution, relationship with other techniques, current applications, advantages, and limitations are provided. Selecting the most appropriate CCA‐related technique to take full advantages of available information embedded in every variable in joint multimodal research might shed new lights in our understandings of normal development, aging, and disease processes.

9. CODE AVAILABILITY

Python‐based CCA toolbox (Bilenko & Gallant, 2016 ) is available on github: http://github.com/gallantlab/pyrcca ; CCA package in R can be found in González, Déjean, Martin, and Baccini ( 2008 ). Codes for applying CCA and kernel CCA to detect task‐fMRI activations are available on github (Yang, Zhuang, et al., 2018 ; Zhuang et al., 2017 ): https://github.com/pipiyang/CCA_GUI . Bayesian CCA with group‐wise ARD prior and the relevant techniques are implemented in R CCAGFA package ( https://cran.r-project.org/web/packages/CCAGFA/index.html ).

ACKNOWLEDGMENTS

The study is supported by the National Institute of Health (grants 1R01EB014284); Institutional Development Award (IDeA) from the National Institute of General Medical Sciences of the National Institutes of Health, Grant/Award Number: 5P20GM109025; The Keep Memory Alive Foundation Young Scientist Award; A private grant from the Peter and Angela Dal Pezzo funds; A private grant from Lynn and William Weidner; A private grant from Stacie and Chuck Matthewson.

Zhuang X, Yang Z, Cordes D. A technical review of canonical correlation analysis for neuroscience applications . Hum Brain Mapp . 2020; 41 :3807–3833. 10.1002/hbm.25090 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]

Xiaowei Zhuang and Zhengshi Yang contributed equally to this manuscript.

Funding information National Institute of Health, Grant/Award Number: 1R01EB014284; Institutional Development Award (IDeA) from the National Institute of General Medical Sciences of the National Institutes of Health, Grant/Award Number: 5P20GM109025; The Keep Memory Alive Foundation Young Scientist Award; A private grant from the Peter and Angela Dal Pezzo funds; A private grant from Lynn and William Weidner; A private grant from Stacie and Chuck Matthewson

DATA AVAILABILITY STATEMENT

• Abrol, A. , Rashid, B. , Rachakonda, S. , Damaraju, E. , & Calhoun, V. D. (2017). Schizophrenia shows disrupted links between brain volume and dynamic functional connectivity . Frontiers in Neuroscience , 11 ( 624 ). 10.3389/fnins.2017.00624 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Abraham, H. D. , & Duffy, F. H. (1996). Stable quantitative EEG difference in post‐LSD visual disorder by split‐half analysis: evidence for disinhibition . Psychiatry Research , 67 , 173–187. 10.1016/0925-4927(96)02833-8 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Adhikari, B. M. , Hong, L. E. , Sampath, H. , Chiappelli, J. , Jahanshad, N. , Thompson, P. M. , … Kochunov, P. (2019). Functional network connectivity impairments and core cognitive deficits in schizophrenia . Human Brain Mapping , 40 , 4593–4605. 10.1002/hbm.24723 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Afshin‐Pour, B. , Grady, C. , & Strother, S. (2014). Evaluation of spatio‐temporal decomposition techniques for group analysis of fMRI resting state data sets . NeuroImage , 87 , 363–382. 10.1016/j.neuroimage.2013.10.062 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Afshin‐Pour, B. , Hossein‐Zadeh, G.‐A. , Strother, S. C. , & Soltanian‐Zadeh, H. (2012). Enhancing reproducibility of fMRI statistical maps using generalized canonical correlation analysis in NPAIRS framework . NeuroImage , 60 , 1970–1981. 10.1016/j.neuroimage.2012.01.137 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Andrew, G. , Arora, R. , Bilmes, J. , & Livescu, K. (2013). Deep canonical correlation analysis. In International conference on machine learning (pp. 1247–1255).
• Ashad Alam, M. , Komori, O. , Deng, H.‐W. , Calhoun, V. D. , & Wang, Y.‐P. (2019). Robust kernel canonical correlation analysis to detect gene‐gene co‐associations: A case study in genetics . Journal of Bioinformatics and Computational Biology , 17 , 1950028 10.1142/S0219720019500288 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Ashrafulla, S. , Haldar, J. P. , Joshi, A. A. , & Leahy, R. M. (2013). Canonical Granger causality between regions of interest . Neuroimage , 83 , 189–199. 10.1016/j.neuroimage.2013.06.056 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Avants, B. B. , Cook, P. A. , Ungar, L. , Gee, J. C. , & Grossman, M. (2010). Dementia induces correlated reductions in white matter integrity and cortical thickness: A multivariate neuroimaging study with sparse canonical correlation analysis . NeuroImage , 50 , 1004–1016. 10.1016/j.neuroimage.2010.01.041 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Badea, A. , Delpratt, N. A. , Anderson, R. J. , Dibb, R. , Qi, Y. , Wei, H. , … Colton, C. (2019). Multivariate MR biomarkers better predict cognitive dysfunction in mouse models of Alzheimer's disease . Magnetic Resonance Imaging , 60 , 52–67. 10.1016/j.mri.2019.03.022 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Bai, Y. , Zille, P. , Hu, W. , Calhoun, V. D. , & Wang, Y.‐P. (2019). Biomarker identification through integrating fMRI and epigenetics . IEEE Transactions on Biomedical Engineering , 67 , 1186–1196. 10.1109/TBME.2019.2932895 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Bartlett, M. S. (1939). A note on tests of significance in multivariate analysis . Mathematical Proceedings of the Cambridge Philosophical Society , 35 , 180–185. [ Google Scholar ]
• Baumeister, T. R. , Lin, S.‐J. J. , Vavasour, I. , Kolind, S. , Kosaka, B. , Li, D. K. B. B. , … McKeown, M. J. (2019). Data fusion detects consistent relations between non‐lesional white matter myelin, executive function, and clinical characteristics in multiple sclerosis . NeuroImage: Clinical , 24 , 101926 10.1016/j.nicl.2019.101926 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Baxter, L. C. , Sparks, D. L. , Johnson, S. C. , Lenoski, B. , Lopez, J. E. , Connor, D. J. , & Sabbagh, M. N. (2006). Relationship of cognitive measures and gray and white matter in Alzheimer's disease . Journal of Alzheimer's Disease , 9 , 253–260. 10.3233/JAD-2006-9304 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Bedi, G. , Carrillo, F. , Cecchi, G. A. , Slezak, D. F. , Sigman, M. , Mota, N. B. , et al. (2015). Automated analysis of free speech predicts psychosis onset in high‐risk youths . NPJ Schizophrenia , 1 , 15030. [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Bilenko, N. Y. , & Gallant, J. L. (2016). Pyrcca: Regularized kernel canonical correlation analysis in Python and its applications to neuroimaging . Frontiers in Neuroinformatics , 10 ( 49 ). 10.3389/fninf.2016.00049 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Bologna, M. , Guerra, A. , Paparella, G. , Giordo, L. , Fegatelli, D. A. , Vestri, A. R. , … Berardelli, A. (2018). Neurophysiological correlates of bradykinesia in Parkinson's disease . Brain , 141 , 2432–2444. 10.1093/brain/awy155 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Brookes, M. J. , O’Neill, G. C. , Hall, E. L. , Woolrich, M. W. , Baker, A. , Palazzo Corner, S. , et al. (2014). Measuring temporal, spectral and spatial changes in electrophysiological brain network connectivity . Neuroimage , 91 , 282–299. 10.1016/j.neuroimage.2013.12.066 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Breakspear, M. , Brammer, M. J. , Bullmore, E. T. , Das, P. , & Williams, L. M. (2004). Spatiotemporal wavelet resampling for functional neuroimaging data . Human Brain Mapping , 23 , 1–25. 10.1002/hbm.20045 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Brier, M. R. , McCarthy, J. E. , Benzinger, T. L. S. , Stern, A. , Su, Y. , Friedrichsen, K. A. , … Vlassenko, A. G. (2016). Local and distributed PiB accumulation associated with development of preclinical Alzheimer's disease . Neurobiology of Aging , 38 , 104–111. 10.1016/j.neurobiolaging.2015.10.025 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Brooke, A. , Kendrick, D. , Meeraus, A. , & Rama, R. (1998). GAMS: A user's guide (p. 1998). Washington, DC: GAMS Development Corp. [ Google Scholar ]
• Browne, M. W. (1979). The maximum‐likelihood solution in inter‐battery factor analysis . The British Journal of Mathematical and Statistical Psychology , 32 , 75–86. [ Google Scholar ]
• Chen, Y.‐L. , Kolar, M. , & Tsay, R. S. (2019). Tensor canonical correlation analysis . arXiv . Prepr arXiv190605358. [ Google Scholar ]
• Chenausky, K. , Kernbach, J. , Norton, A. , & Schlaug, G. (2017). White matter integrity and treatment‐based change in speech performance in minimally verbal children with autism spectrum disorder . Frontiers in Human Neuroscience , 11 ( 175 ). 10.3389/fnhum.2017.00175 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Churchill, N. W. , Yourganov, G. , Spring, R. , Rasmussen, P. M. , Lee, W. , Ween, J. E. , & Strother, S. C. (2012). PHYCAA: Data‐driven measurement and removal of physiological noise in BOLD fMRI . NeuroImage , 59 , 1299–1314. 10.1016/j.neuroimage.2011.08.021 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Cordes, D. , Jin, M. , Curran, T. , & Nandy, R. (2012a). The smoothing artifact of spatially constrained canonical correlation analysis in functional MRI . International Journal of Biomedical Imaging , 2012 , 1–11. 10.1155/2012/738283 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Cordes, D. , Jin, M. , Curran, T. , & Nandy, R. (2012b). Optimizing the performance of local canonical correlation analysis in fMRI using spatial constraints . Human Brain Mapping , 33 , 2611–2626. 10.1002/hbm.21388 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Correa, N. M. , Adali, T. , Li, Y. , & Calhoun, V. D. (2010). Canonical correlation analysis for data fusion and group inferences . IEEE Signal Processing Magazine , 27 , 39–50. 10.1109/MSP.2010.936725.Canonical [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Correa, N. M. , Eichele, T. , Adali, T. , Li, Y.‐O. , & Calhoun, V. D. (2010). Multi‐set canonical correlation analysis for the fusion of concurrent single trial ERP and functional MRI . NeuroImage , 50 , 1438–1445. 10.1016/j.neuroimage.2010.01.062 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Cremers, H. R. , Wager, T. D. , & Yarkoni, T. (2017). The relation between statistical power and inference in fMRI . PLoS One , 12 , 1–20. 10.1371/journal.pone.0184923 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Dashtestani, H. , Zaragoza, R. , Pirsiavash, H. , Knutson, K. M. , Kermanian, R. , Cui, J. , … Gandjbakhche, A. (2019). Canonical correlation analysis of brain prefrontal activity measured by functional near infra‐red spectroscopy (fNIRS) during a moral judgment task . Behavioural Brain Research , 359 , 73–80. 10.1016/j.bbr.2018.10.022 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• de Cheveigne, A. , Wong, D. D. E. , Di Liberto, G. M. , Hjortkjaer, J. , Slaney, M. , & Lalor, E. (2018). Decoding the auditory brain with canonical component analysis . NeuroImage , 172 , 206–216. 10.1016/j.neuroimage.2018.01.033 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Deleus, F. , & Van Hulle, M. M. (2011). Functional connectivity analysis of fMRI data based on regularized multiset canonical correlation analysis . Journal of Neuroscience Methods , 197 , 143–157. [ PubMed ] [ Google Scholar ]
• Deligianni, F. , Carmichael, D. W. , Zhang, G. H. , Clark, C. A. , & Clayden, J. D. (2016). NODDI and tensor‐based microstructural indices as predictors of functional connectivity . PLoS One , 11 , 1–17. 10.1371/journal.pone.0153404 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Deligianni, F. , Centeno, M. , Carmichael, D. W. , & Clayden, J. D. (2014). Relating resting‐state fMRI and EEG whole‐brain connectomes across frequency bands . Frontiers in Neuroscience , 8 ( 258 ). 10.3389/fnins.2014.00258 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Dell'Osso, L. , Rugani, F. , Maremmani, A. G. I. , Bertoni, S. , Pani, P. P. , & Maremmani, I. (2014). Towards a unitary perspective between post‐traumatic stress disorder and substance use disorder. Heroin use disorder as case study . Comprehensive Psychiatry , 55 , 1244–1251. 10.1016/j.comppsych.2014.03.012 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Dinga, R. , Schmaal, L. , Penninx, B. W. J. H. , van Tol, M. J. , Veltman, D. J. , van Velzen, L. , … Marquand, A. F. (2019). Evaluating the evidence for biotypes of depression: Methodological replication and extension of . NeuroImage: Clinical , 22 , 101796 10.1016/j.nicl.2019.101796 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Dmochowski, J. P. , Ki, J. J. , DeGuzman, P. , Sajda, P. , & Parra, L. C. (2018). Extracting multidimensional stimulus‐response correlations using hybrid encoding‐decoding of neural activity . NeuroImage , 180 , 134–146. 10.1016/j.neuroimage.2017.05.037 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Dong, L. , Zhang, Y. , Zhang, R. , Zhang, X. , Gong, D. , Valdes‐Sosa, P. A. , … Yao, D. (2015). Characterizing nonlinear relationships in functional imaging data using eigenspace maximal information canonical correlation analysis (emiCCA) . NeuroImage , 109 , 388–401. 10.1016/j.neuroimage.2015.01.006 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Drud, A. (1985). CONOPT: A GRG code for large sparse dynamic nonlinear optimization problems . Mathematical Programming , 31 , 153–191. [ Google Scholar ]
• Du, L. , Huang, H. , Yan, J. , Kim, S. , Risacher, S. , Inlow, M. , … Shen, L. (2016a). Structured sparse CCA for brain imaging genetics via graph OSCAR . BMC Systems Biology , 10 ( Suppl 3 ), 68 10.1186/s12918-016-0312-1 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Du, L. , Huang, H. , Yan, J. , Kim, S. , Risacher, S. L. , Inlow, M. , … Shen, L. (2016b). Structured sparse canonical correlation analysis for brain imaging genetics: An improved GraphNet method . Bioinformatics , 32 , 1544–1551. 10.1093/bioinformatics/btw033 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Du, L. , Jingwen, Y. , Kim, S. , Risacher, S. L. , Huang, H. , Inlow, M. , … Shen, L. (2014). A novel structure‐aware sparse learning algorithm for brain imaging genetics . Medical Image Computing and Computer‐Assisted Intervention , 17 , 329–336. 10.1007/978-3-319-10443-0_42 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Du, L. , Liu, K. , Yao, X. , Risacher, S. L. , Guo, L. , Saykin, A. J. , & Shen, L. (2019). Diagnosis status guided brain imaging genetics via integrated regression and sparse canonical correlation analysis . Proceedings of the IEEE International Symposium on Biomedical Imaging , 2019 , 356–359. 10.1109/ISBI.2019.8759489 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Du, L. , Liu, K. , Yao, X. , Yan, J. , Risacher, S. L. , Han, J. , … Shen, L. (2017). Pattern discovery in brain imaging genetics via SCCA modeling with a generic non‐convex penalty . Scientific Reports , 7 , 14052 10.1038/s41598-017-13930-y [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Du, L. , Liu, K. , Zhang, T. , Yao, X. , Yan, J. , Risacher, S. L. , … Shen, L. (2017). A novel SCCA approach via truncated l1‐norm and truncated group Lasso for brain imaging genetics . Bioinformatics , 34 , 278–285. 10.1093/bioinformatics/btx594 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Du, L. , Liu, K. , Zhu, L. , Yao, X. , Risacher, S. L. , Guo, L. , … Shen, L. (2019). Identifying progressive imaging genetic patterns via multi‐task sparse canonical correlation analysis: A longitudinal study of the ADNI cohort . Bioinformatics , 35 , i474–i483. 10.1093/bioinformatics/btz320 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Du, L. , Yan, J. , Kim, S. , Risacher, S. L. , Huang, H. , Inlow, M. , … Shen, L. (2015). GN‐SCCA: GraphNet based sparse canonical correlation analysis for brain imaging genetics. Brain Informatics Heal 8th Int Conf BIH 2015, London, UK, August 30‐September 2, 2015 proceedings BIH (8th 2015 London, England) 9250, 275–284. [ PMC free article ] [ PubMed ]
• Du, L. , Zhang, T. , Liu, K. , Yao, X. , Yan, J. , Risacher, S. L. , … Shen, L. (2016). Sparse canonical correlation analysis via truncated l1‐norm with application to brain imaging genetics . Proceedings IEEE International Conference on Bioinformatics and Biomedicine , 2016 , 707–711. 10.1109/BIBM.2016.7822605 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Duda, J. T. , Detre, J. A. , Kim, J. , Gee, J. C. , & Avants, B. B. (2013). Fusing functional signals by sparse canonical correlation analysis improves network reproducibility . Medical Image Computing and Computer‐Assisted Intervention , 16 , 635–642. 10.1007/978-3-642-40760-4_79 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Drysdale, A. T. , Grosenick, L. , Downar, J. , Dunlop, K. , Mansouri, F. , Meng, Y. , et al. (2017). Resting‐state connectivity biomarkers define neurophysiological subtypes of depression . Nature Medicine , 23 , 28–38. 10.1038/nm.4246 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• El‐Shabrawy, N. , Mohamed, A. S. , Youssef, A.‐B. M. , & Kadah, Y. M. (2007). Activation detection in functional MRI using model‐free technique based on CCA‐ICA analysis . In 29th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Lyon, 2007 (pp. 3430–3433) https://doi.org/10.1109/IEMBS.2007.4353068 [ PubMed ] [ Google Scholar ]
• Fang, J. , Lin, D. , Schulz, S. C. , Xu, Z. , Calhoun, V. D. , & Wang, Y.‐P. (2016). Joint sparse canonical correlation analysis for detecting differential imaging genetics modules . Bioinformatics , 32 , 3480–3488. 10.1093/bioinformatics/btw485 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Friman, O. , Borga, M. , Lundberg, P. , & Knutsson, H. (2003). Adaptive analysis of fMRI data . NeuroImage , 19 , 837–845. 10.1016/S1053-8119(03)00077-6 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Friman, O. , Cedefamn, J. , Lundberg, P. , Borga, M. , & Knutsson, H. (2001). Detection of neural activity in functional MRI using canonical correlation analysis . Magnetic Resonance in Medicine , 45 , 323–330. 10.1002/1522-2594(200102)45:2<323::AID-MRM1041>3.0.CO;2-# [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Fujiwara, Y. , Miyawaki, Y. , & Kamitani, Y. (2013). Modular encoding and decoding models derived from Bayesian canonical correlation analysis . Neural Computation , 25 , 979–1005. 10.1162/NECO_a_00423 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Gaebler, M. , Biessmann, F. , Lamke, J.‐P. , Muller, K.‐R. , Walter, H. , & Hetzer, S. (2014). Stereoscopic depth increases intersubject correlations of brain networks . NeuroImage , 100 , 427–434. 10.1016/j.neuroimage.2014.06.008 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• González, I. , Déjean, S. , Martin, P. G. P. , & Baccini, A. (2008). CCA: An R package to extend canonical correlation analysis . Journal of Statistical Software , 23 , 1–14. 10.18637/jss.v023.i12 [ CrossRef ] [ Google Scholar ]
• Gossmann, A. , Zille, P. , Calhoun, V. , & Wang, Y.‐P. (2018). FDR‐corrected sparse canonical correlation analysis with applications to imaging genomics . IEEE Transactions on Medical Imaging , 37 , 1761–1774. 10.1109/TMI.2018.2815583 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Graa, O. , & Rekik, I. (2019). Multi‐view learning‐based data proliferator for boosting classification using highly imbalanced classes . Journal of Neuroscience Methods , 327 , 108344 10.1016/j.jneumeth.2019.108344 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Grellmann, C. , Bitzer, S. , Neumann, J. , Westlye, L. T. , Andreassen, O. A. , Villringer, A. , & Horstmann, A. (2015). Comparison of variants of canonical correlation analysis and partial least squares for combined analysis of MRI and genetic data . NeuroImage , 107 , 289–310. 10.1016/j.neuroimage.2014.12.025 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Grosenick, L. , Shi, T. C. , Gunning, F. M. , Dubin, M. J. , Downar, J. , & Liston, C. (2019). Functional and Optogenetic approaches to discovering stable subtype‐specific circuit mechanisms in depression . Biological Psychiatry: Cognitive Neuroscience and Neuroimaging , 4 , 554–566. 10.1016/j.bpsc.2019.04.013 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Gulin, S. L. , Perrin, P. B. , Stevens, L. F. , Villasenor‐Cabrera, T. J. , Jimenez‐Maldonado, M. , Martinez‐Cortes, M. L. , & Arango‐Lasprilla, J. C. (2014). Health‐related quality of life and mental health outcomes in Mexican TBI caregivers . Families, Systems & Health , 32 , 53–66. 10.1037/a0032623 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Hackmack, K. , Weygandt, M. , Wuerfel, J. , Pfueller, C. F. , Bellmann‐Strobl, J. , Paul, F. , & Haynes, J.‐D. (2012). Can we overcome the “clinico‐radiological paradox” in multiple sclerosis? Journal of Neurology , 259 , 2151–2160. 10.1007/s00415-012-6475-9 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Hallez, H. , de Vos, M. , Vanrumste, B. , van Hese, P. , Assecondi, S. , van Laere, K. , … Lemahieu, I. (2009). Removing muscle and eye artifacts using blind source separation techniques in ictal EEG source imaging . Clinical Neurophysiology , 120 , 1262–1272. 10.1016/j.clinph.2009.05.010 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Hao, X. , Li, C. , Du, L. , Yao, X. , Yan, J. , Risacher, S. L. , … Zhang, D. (2017). Mining outcome‐relevant brain imaging genetic associations via three‐way sparse canonical correlation analysis in Alzheimer's disease . Scientific Reports , 7 , 44272 10.1038/srep44272 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Hao, X. , Li, C. , Yan, J. , Yao, X. , Risacher, S. L. , Saykin, A. J. , … Zhang, D. (2017). Identification of associations between genotypes and longitudinal phenotypes via temporally‐constrained group sparse canonical correlation analysis . Bioinformatics , 33 , i341–i349. 10.1093/bioinformatics/btx245 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Hardoon, D. R. , Mourão‐Miranda, J. , Brammer, M. , & Shawe‐Taylor, J. (2007). Unsupervised analysis of fMRI data using kernel canonical correlation . NeuroImage , 37 , 1250–1259. 10.1016/j.neuroimage.2007.06.017 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Hardoon, D. R. , Szedmak, S. , & Shawe‐Taylor, J. (2004). Canonical correlation analysis: An overview with application to learning methods . Neural Computation , 16 , 2639–2664. 10.1162/0899766042321814 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Hirjak, D. , Rashidi, M. , Fritze, S. , Bertolino, A. L. , Geiger, L. S. , Zang, Z. , et al. (2019). Patterns of co‐altered brain structure and function underlying neurological soft signs in schizophrenia spectrum disorders . Human Brain Mapping , 40 , 5029–5041. [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Hotelling, H. (1936). Relations between two sets of variates . Biometrika , 28 , 321–377. [ Google Scholar ]
• Hu, W. , Lin, D. , Calhoun, V. D. , & Wang, Y.‐P. (2016). Integration of SNPs‐FMRI‐methylation data with sparse multi‐CCA for schizophrenia study. Conf Proc. Annu Int Conf IEEE Eng Med Biol Soc IEEE Eng Med Biol Soc Annu Conf. 2016, 3310–3313. [ PubMed ]
• Hu, W. , Lin, D. , Cao, S. , Liu, J. , Chen, J. , Calhoun, V. D. , & Wang, Y.‐P. (2018). Adaptive sparse multiple canonical correlation analysis with application to imaging (epi)genomics study of schizophrenia . IEEE Transactions on Biomedical Engineering , 65 , 390–399. 10.1109/TBME.2017.2771483 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Irimia, A. , & van Horn, J. D. (2013). The structural, connectomic and network covariance of the human brain . NeuroImage , 66 , 489–499. 10.1016/j.neuroimage.2012.10.066 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Janani, A. S. , Grummett, T. S. , Bakhshayesh, H. , Lewis, T. W. , DeLosAngeles, D. , Whitham, E. M. , … Pope, K. J. (2020). Fast and effective removal of contamination from scalp electrical recordings . Clinical Neurophysiology , 131 , 6–24. 10.1016/j.clinph.2019.09.016 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Jang, H. , Kwon, H. , Yang, J.‐J. , Hong, J. , Kim, Y. , Kim, K. W. , … Lee, J.‐M. (2017). Correlations between gray matter and White matter degeneration in pure Alzheimer's disease, pure subcortical vascular dementia, and mixed dementia . Scientific Reports , 7 , 9541 10.1038/s41598-017-10074-x [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Ji, J. , Porjesz, B. , Begleiter, H. , & Chorlian, D. (1999). P300: the similarities and differences in the scalp distribution of visual and auditory modality . Brain Topography , 11 , 315–327. 10.1023/a:1022262721343 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• John, M. , Lencz, T. , Ferbinteanu, J. , Gallego, J. A. , & Robinson, D. G. (2017). Applications of temporal kernel canonical correlation analysis in adherence studies . Statistical Methods in Medical Research , 26 , 2437–2454. [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Kang, K. , Kwak, K. , Yoon, U. , & Lee, J.‐M. M. (2018). Lateral ventricle enlargement and cortical thinning in idiopathic normal‐pressure hydrocephalus patients . Scientific Reports , 8 , 1–9. 10.1038/s41598-018-31399-1 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Kettenring, J. R. (1971). Canonical analysis of several sets of variables . Biometrika , 58 , 433–451. 10.1093/biomet/58.3.433 [ CrossRef ] [ Google Scholar ]
• Kim, M. , Won, J. H. , Youn, J. , & Park, H. (2019). Joint‐connectivity‐based sparse canonical correlation analysis of imaging genetics for detecting biomarkers of Parkinson's disease . IEEE Transactions on Medical Imaging , 39 , 23–34. 10.1109/TMI.2019.2918839 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Klami, A. , & Kaski, S. (2007). Local dependent components. Proceedings of the 24th International Conference on Machine Learning. 425–432.
• Klami, A. , Virtanen, S. , & Kaski, S. (2013). Bayesian canonical correlation analysis . Journal of Machine Learning Research , 14 , 965–1003. [ Google Scholar ]
• Koskinen, M. , & Seppa, M. (2014). Uncovering cortical MEG responses to listened audiobook stories . NeuroImage , 100 , 263–270. 10.1016/j.neuroimage.2014.06.018 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Kottaram, A. , Johnston, L. A. , Cocchi, L. , Ganella, E. P. , Everall, I. , Pantelis, C. , … Zalesky, A. (2019). Brain network dynamics in schizophrenia: Reduced dynamism of the default mode network . Human Brain Mapping , 40 , 2212–2228. 10.1002/hbm.24519 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Kroonenberg, P. M. , & de Leeuw, J. (1980). Principal component analysis of three‐mode data by means of alternating least squares algorithms . Psychometrika , 45 , 69–97. [ Google Scholar ]
• Kucukboyaci, N. E. , Girard, H. M. , Hagler, D. J. J. , Kuperman, J. , Tecoma, E. S. , Iragui, V. J. , … McDonald, C. R. (2012). Role of frontotemporal fiber tract integrity in task‐switching performance of healthy controls and patients with temporal lobe epilepsy . Journal of the International Neuropsychological Society , 18 , 57–67. 10.1017/S1355617711001391 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Kuo, Y.‐L. L. , Kutch, J. J. , & Fisher, B. E. (2019). Relationship between interhemispheric inhibition and dexterous hand performance in musicians and non‐musicians . Scientific Reports , 9 , 1–10. 10.1038/s41598-019-47959-y [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Langers, D. R. M. , Krumbholz, K. , Bowtell, R. W. , & Hall, D. A. (2014). Neuroimaging paradigms for tonotopic mapping (I): The influence of sound stimulus type . NeuroImage , 100 , 650–662. 10.1016/j.neuroimage.2014.07.044 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Lankinen, K. , Saari, J. , Hari, R. , & Koskinen, M. (2014). Intersubject consistency of cortical MEG signals during movie viewing . NeuroImage , 92 , 217–224. 10.1016/j.neuroimage.2014.02.004 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Lankinen, K. , Saari, J. , Hlushchuk, Y. , Tikka, P. , Parkkonen, L. , Hari, R. , & Koskinen, M. (2018). Consistency and similarity of MEG‐ and fMRI‐signal time courses during movie viewing . NeuroImage , 173 , 361–369. 10.1016/j.neuroimage.2018.02.045 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Lankinen, K. , Smeds, E. , Tikka, P. , Pihko, E. , Hari, R. , & Koskinen, M. (2016). Haptic contents of a movie dynamically engage the spectator's sensorimotor cortex . Human Brain Mapping , 37 , 4061–4068. 10.1002/hbm.23295 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Laskaris, L. , Zalesky, A. , Weickert, C. S. , di Biase, M. A. , Chana, G. , Baune, B. T. , … Cropley, V. (2019). Investigation of peripheral complement factors across stages of psychosis . Schizophrenia Research , 204 , 30–37. 10.1016/j.schres.2018.11.035 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Lee, S. H. , & Choi, S. (2007). Two‐dimensional canonical correlation analysis . IEEE Signal Processing Letters , 14 ( 10 ), 735–738. [ Google Scholar ]
• Lee, W. H. , Moser, D. A. , Ing, A. , Doucet, G. E. , & Frangou, S. (2019). Behavioral and health correlates of resting‐state metastability in the human connectome project . Brain Topography , 32 , 80–86. 10.1007/s10548-018-0672-5 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Leibach, G. G. , Stern, M. , Arelis, A. A. , Islas, M. A. M. , & Barajas, B. V. R. (2016). Mental health and health‐related quality of life in multiple sclerosis caregivers in Mexico . International Journal of MS Care , 18 , 19–26. 10.7224/1537-2073.2014-094 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Leonenko, G. , Di Florio, A. , Allardyce, J. , Forty, L. , Knott, S. , Jones, L. , et al. (2018). A data‐driven investigation of relationships between bipolar psychotic symptoms and schizophrenia genome‐wide significant genetic loci . American Journal of Medical Genetics , 177 , 468–475. 10.1002/ajmg.b.32635 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Lerman‐Sinkoff, D. B. , Kandala, S. , Calhoun, V. D. , Barch, D. M. , & Mamah, D. T. (2019). Transdiagnostic multimodal neuroimaging in psychosis: Structural, resting‐state, and task magnetic resonance imaging correlates of cognitive control . Biological Psychiatry: Cognitive Neuroscience and Neuroimaging , 4 , 870–880. 10.1016/j.bpsc.2019.05.004 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Lerman‐Sinkoff, D. B. , Sui, J. , Rachakonda, S. , Kandala, S. , Calhoun, V. D. , & Barch, D. M. (2017). Multimodal neural correlates of cognitive control in the human connectome project . NeuroImage , 163 , 41–54. 10.1016/j.neuroimage.2017.08.081 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Levin‐Schwartz, Y. , Song, Y. , Schreier, P. J. , Calhoun, V. D. , & Adali, T. (2016). Sample‐poor estimation of order and common signal subspace with application to fusion of medical imaging data . NeuroImage , 134 , 486–493. 10.1016/j.neuroimage.2016.03.058 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Li, J. , Bolt, T. , Bzdok, D. , Nomi, J. S. , Yeo, B. T. T. T. , Spreng, R. N. , & Uddin, L. Q. (2019). Topography and behavioral relevance of the global signal in the human brain . Scientific Reports , 9 , 1–10. 10.1038/s41598-019-50750-8 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Li, J. , Chen, Y. , Taya, F. , Lim, J. , Wong, K. , Sun, Y. , & Bezerianos, A. (2017). A unified canonical correlation analysis‐based framework for removing gradient artifact in concurrent EEG/fMRI recording and motion artifact in walking recording from EEG signal . Medical & Biological Engineering & Computing , 55 , 1669–1681. 10.1007/s11517-017-1620-3 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Liao, J. , Zhu, Y. , Zhang, M. , Yuan, H. , Su, M.‐Y. , Yu, X. , & Wang, H. (2010). Microstructural white matter abnormalities independent of white matter lesion burden in amnestic mild cognitive impairment and early Alzheimer disease among Han Chinese elderly . Alzheimer Disease and Associated Disorders , 24 , 317–324. 10.1097/WAD.0b013e3181df1c7b [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Lin, S. J. , Baumeister, T. R. , Garg, S. & McKeown, M. J. (2018). Cognitive profiles and hub vulnerability in Parkinson's disease . Frontiers in Neurology , 9 , 482. [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Lin, D. , Calhoun, V. D. , & Wang, Y.‐P. (2014). Correspondence between fMRI and SNP data by group sparse canonical correlation analysis . Medical Image Analysis , 18 , 891–902. 10.1016/j.media.2013.10.010 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Lin, S.‐J. , Lam, J. , Beveridge, S. , Vavasour, I. , Traboulsee, A. , Li, D. K. B. , … Kosaka, B. (2017). Cognitive performance in subjects with multiple sclerosis is robustly influenced by gender in canonical‐correlation analysis . The Journal of Neuropsychiatry and Clinical Neurosciences , 29 , 119–127. 10.1176/appi.neuropsych.16040083 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Lin, S.‐J. J. , Vavasour, I. , Kosaka, B. , Li, D. K. B. B. , Traboulsee, A. , MacKay, A. , & McKeown, M. J. (2018). Education, and the balance between dynamic and stationary functional connectivity jointly support executive functions in relapsing–remitting multiple sclerosis . Human Brain Mapping , 39 , 5039–5049. 10.1002/hbm.24343 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Lisowska, A. , & Rekik, I. (2019). Joint pairing and structured mapping of convolutional brain morphological multiplexes for early dementia diagnosis . Brain Connectivity , 9 , 22–36. 10.1089/brain.2018.0578 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Liu, J. , & Calhoun, V. D. (2014). A review of multivariate analyses in imaging genetics . Frontiers in Neuroinformatics , 8 ( 29 ). 10.3389/fninf.2014.00029 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Liu, K. , Yao, X. , Yan, J. , Chasioti, D. , Risacher, S. , Nho, K. , … Shen, L. (2017). Transcriptome‐guided imaging genetic analysis via a novel sparse CCA algorithm. Graphs in Biomedical Image Analysis, Computational Anatomy and Imaging GeneticsFirst International Workshop, GRAIL 2017, 6th International Workshop, MFCA 2017, and Third International Workshop, MICGen 2017, Held in Conjunction with MICCAI 2017, Québec City, Canada, September 10–14, 2017, Proceedings 10551, 220–229. [ PMC free article ] [ PubMed ]
• Liu, L. , Wang, Q. , Adeli, E. , Zhang, L. , Zhang, H. , & Shen, D. (2018). Exploring diagnosis and imaging biomarkers of Parkinson's disease via iterative canonical correlation analysis based feature selection . Computerized Medical Imaging and Graphics , 67 , 21–29. 10.1016/j.compmedimag.2018.04.002 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Liu, Y. , & Ayaz, H. (2018). Speech recognition via fNIRS based brain signals . Frontiers in Neuroscience , 12 ( 695 ). 10.3389/fnins.2018.00695 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Lopez, E. , Steiner, A. J. , Smith, K. , Thaler, N. S. , Hardy, D. J. , Levine, A. J. , et al. (2017). Diagnostic utility of the HIV dementia scale and the international HIV dementia scale in screening for HIV‐associated neurocognitive disorders among Spanish‐speaking adults . Applied Neuropsychology Adult , 24 , 512–521. [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Lottman, K. K. , White, D. M. , Kraguljac, N. V. , Reid, M. A. , Calhoun, V. D. , Catao, F. , & Lahti, A. C. (2018). Four‐way multimodal fusion of 7 T imaging data using an mCCA+jICA model in first‐episode schizophrenia . Human Brain Mapping , 39 , 1–14. 10.1002/hbm.23906 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Luo, Y. , Tao, D. , Ramamohanarao, K. , Xu, C. , & Wen, Y. (2015). Tensor canonical correlation analysis for multi‐view dimension reduction . IEEE Transactions on Knowledge and Data Engineering , 27 , 3111–3124. [ Google Scholar ]
• McCrory, S. J. , & Ford, I. (1991). Multivariate analysis of spect images with illustrations in Alzheimer's disease . Statistics in Medicine , 10 , 1711–1718. 10.1002/sim.4780101109 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• McMillan, C. T. , Toledo, J. B. , Avants, B. B. , Cook, P. A. , Wood, E. M. , Suh, E. , … Grossman, M. (2014). Genetic and neuroanatomic associations in sporadic frontotemporal lobar degeneration . Neurobiology of Aging , 35 , 1473–1482. 10.1016/j.neurobiolaging.2013.11.029 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Mihalik, A. , Ferreira, F. S. , Rosa, M. J. , Moutoussis, M. , Ziegler, G. , Monteiro, J. M. , … Mourao‐Miranda, J. (2019). Brain‐behaviour modes of covariation in healthy and clinically depressed young people . Scientific Reports , 9 , 11536 10.1038/s41598-019-47277-3 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Mirza, M. B. , Adams, R. A. , Mathys, C. , & Friston, K. J. (2018). Human visual exploration reduces uncertainty about the sensed world . PLoS One , 13 , e0190429 10.1371/journal.pone.0190429 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Mishra, V. R. , Zhuang, X. , Sreenivasan, K. R. , Banks, S. J. S. J. , Yang, Z. , Bernick, C. , & Cordes, D. (2017). Multimodal MR imaging signatures of cognitive impairment in active professional fighters . Radiology , 285 , 555–567. 10.1148/radiol.2017162403 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Moser, D. A. , Doucet, G. E. , Lee, W. H. , Rasgon, A. , Krinsky, H. , Leibu, E. , … Frangou, S. (2018). Multivariate associations among behavioral, clinical, and multimodal imaging phenotypes in patients with psychosis . JAMA Psychiatry , 75 , 386–395. [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Mohammadi‐Nejad, A.‐R. , Hossein‐Zadeh, G.‐A. , & Soltanian‐Zadeh, H. (2017). Structured and sparse canonical correlation analysis as a brain‐wide multi‐modal data fusion approach . IEEE Transactions on Medical Imaging , 36 , 1438–1448. 10.1109/TMI.2017.2681966 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Murayama, Y. , Biessmann, F. , Meinecke, F. C. , Muller, K.‐R. , Augath, M. , Oeltermann, A. , & Logothetis, N. K. (2010). Relationship between neural and hemodynamic signals during spontaneous activity studied with temporal kernel CCA . Magnetic Resonance Imaging , 28 , 1095–1103. 10.1016/j.mri.2009.12.016 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Nandy, R. , & Cordes, D. (2004). Improving the spatial specificity of canonical correlation analysis in fMRI . Magnetic Resonance in Medicine , 52 , 947–952. 10.1002/mrm.20234 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Nandy, R. R. , & Cordes, D. (2003). Novel nonparametric approach to canonical correlation analysis with applications to low CNR functional MRI data . Magnetic Resonance in Medicine , 50 , 354–365. 10.1002/mrm.10537 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Neal, R. M. (2012). Bayesian learning for neural networks , Berlin, Germany: Springer Science & Business Media. [ Google Scholar ]
• Neumann, J. , von Cramon, D. Y. , Forstmann, B. U. , Zysset, S. , & Lohmann, G. (2006). The parcellation of cortical areas using replicator dynamics in fMRI . Neuroimage , 32 , 208–219. 10.1016/j.neuroimage.2006.02.039 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Ogawa, S. , Lee, T. M. , Kay, A. R. , & Tank, D. W. (1990). Brain magnetic resonance imaging with contrast dependent on blood oxygenation . Proceedings of the National Academy of Sciences of the United States of America , 87 , 9868–9872. 10.1073/pnas.87.24.9868 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Ouyang, X. , Chen, K. , Yao, L. , Hu, B. , Wu, X. , Ye, Q. , & Guo, X. (2015). Simultaneous changes in gray matter volume and white matter fractional anisotropy in Alzheimer's disease revealed by multimodal CCA and joint ICA . Neuroscience , 301 , 553–562. 10.1016/j.neuroscience.2015.06.031 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Palaniyappan, L. , Mota, N. B. , Oowise, S. , Balain, V. , Copelli, M. , Ribeiro, S. , & Liddle, P. F. (2019). Speech structure links the neural and socio‐behavioural correlates of psychotic disorders . Progress in Neuro‐Psychopharmacology & Biological Psychiatry , 88 , 112–120. 10.1016/j.pnpbp.2018.07.007 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Peng, Y. , Zhang, D. , & Zhang, J. (2010). A new canonical correlation analysis algorithm with local discrimination . Neural Processing Letters , 31 , 1–15. 10.1007/s11063-009-9123-3 [ CrossRef ] [ Google Scholar ]
• Pustina, D. , Avants, B. , Faseyitan, O. K. , Medaglia, J. D. , & Coslett, H. B. (2018). Improved accuracy of lesion to symptom mapping with multivariate sparse canonical correlations . Neuropsychologia , 115 , 154–166. 10.1016/j.neuropsychologia.2017.08.027 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Qi, S. , Abbott, C. C. , Narr, K. L. , Jiang, R. , Upston, J. , McClintock, S. M. , … Calhoun, V. D. (2020). Electroconvulsive therapy treatment responsive multimodal brain networks . Human Brain Mapping , 41 , 1775–1785. 10.1002/hbm.24910 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Qi, S. , Calhoun, V. D. , van Erp, T. G. M. , Bustillo, J. , Damaraju, E. , Turner, J. A. , … Sui, J. (2018). Multimodal fusion with reference: Searching for joint neuromarkers of working memory deficits in schizophrenia . IEEE Transactions on Medical Imaging , 37 , 93–105. 10.1109/TMI.2017.2725306 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Qi, S. , Yang, X. , Zhao, L. , Calhoun, V. D. , Perrone‐Bizzozero, N. , Liu, S. , … Ma, X. (2018). MicroRNA132 associated multimodal neuroimaging patterns in unmedicated major depressive disorder . Brain , 141 , 916–926. 10.1093/brain/awx366 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Rodrigue, A. L. , Mcdowell, J. E. , Tandon, N. , Keshavan, M. S. , Tamminga, C. A. , Pearlson, G. D. , … Clementz, B. A. (2018). Multivariate relationships between cognition and brain anatomy across the psychosis Spectrum . Biological Psychiatry: Cognitive Neuroscience and Neuroimaging , 3 , 992–1002. 10.1016/j.bpsc.2018.03.012 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Rodu, J. , Klein, N. , Brincat, S. L. , Miller, E. K. , & Kass, R. E. (2018). Detecting multivariate cross‐correlation between brain regions . Journal of Neurophysiology , 120 , 1962–1972. 10.1152/jn.00869.2017 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Rosa, M. J. , Mehta, M. A. , Pich, E. M. , Risterucci, C. , Zelaya, F. , Reinders, A. A. T. S. , … Marquand, A. F. (2015). Estimating multivariate similarity between neuroimaging datasets with sparse canonical correlation analysis: An application to perfusion imaging . Frontiers in Neuroscience , 9 ( 366 ). 10.3389/fnins.2015.00366 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Rydell, J. , Knutsson, H. , & Borga, M. (2006). On rotational invariance in adaptive spatial filtering of fMRI data . NeuroImage , 30 , 144–150. 10.1016/j.neuroimage.2005.09.002 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Sato, J. R. , Fujita, A. , Cardoso, E. F. , Thomaz, C. E. , Brammer, M. J. , & Amaro, E. J. (2010). Analyzing the connectivity between regions of interest: An approach based on cluster granger causality for fMRI data analysis . NeuroImage , 52 , 1444–1455. 10.1016/j.neuroimage.2010.05.022 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Shams, S.M. , Hossein‐Zadeh, G.A. , & Soltanian‐Zadeh, H. (2006). Multisubject activation detection in fMRI by testing correlation of data with a signal subspace . Magnetic Resonance Imaging , 24 , 775–784. 10.1016/j.mri.2006.03.008 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Shen, H. , Chau, D. K. P. , Su, J. , Zeng, L.L. , Jiang, W. , He, J. , … Hu, D. (2016). Brain responses to facial attractiveness induced by facial proportions: Evidence from an fMRI study . Scientific Reports , 6 , 35905 10.1038/srep35905 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Sheng, J. , Kim, S. , Yan, J. , Moore, J. , Saykin, A. , & Shen, L. (2014). Data synthesis and method evaluation for brain imaging genetics . Proceedings of the IEEE International Symposium on Biomedical Imaging , 2014 , 1202–1205. 10.1109/ISBI.2014.6868091 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Sintini, I. , Schwarz, C. G. , Martin, P. R. , Graff‐Radford, J. , Machulda, M. M. , Senjem, M. L. , … Whitwell, J. L. (2019). Regional multimodal relationships between tau, hypometabolism, atrophy, and fractional anisotropy in atypical Alzheimer's disease . Human Brain Mapping , 40 , 1618–1631. 10.1002/hbm.24473 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Sintini, I. , Schwarz, C. G. , Senjem, M. L. , Reid, R. I. , Botha, H. , Ali, F. , … Whitwell, J. L. (2019). Multimodal neuroimaging relationships in progressive supranuclear palsy . Parkinsonism & Related Disorders , 66 , 56–61. 10.1016/j.parkreldis.2019.07.001 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Smirnov, D. , Lachat, F. , Peltola, T. , Lahnakoski, J. M. , Koistinen, O.‐P. , Glerean, E. , … Nummenmaa, L. (2017). Brain‐to‐brain hyperclassification reveals action‐specific motor mapping of observed actions in humans . PLoS One , 12 , e0189508 10.1371/journal.pone.0189508 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Smith, S. M. , Nichols, T. E. , Vidaurre, D. , Winkler, A. M. , Behrens, T. E. J. , Glasser, M. F. , … Miller, K. L. (2015). A positive‐negative mode of population covariation links brain connectivity, demographics and behavior . Nature Neuroscience , 18 , 1565–1567. 10.1038/nn.4125 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Somers, B. , & Bertrand, A. (2016). Removal of eye blink artifacts in wireless EEG sensor networks using reduced‐bandwidth canonical correlation analysis . Journal of Neural Engineering , 13 , 66008 10.1088/1741-2560/13/6/066008 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Soto, J. L. P. , Lachaux, J.‐P. , Baillet, S. , & Jerbi, K. (2016). A multivariate method for estimating cross‐frequency neuronal interactions and correcting linear mixing in MEG data, using canonical correlations . Journal of Neuroscience Methods , 271 , 169–181. 10.1016/j.jneumeth.2016.07.017 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Stout, D. M. , Buchsbaum, M. S. , Spadoni, A. D. , Risbrough, V. B. , Strigo, I. A. , Matthews, S. C. , & Simmons, A. N. (2018). Multimodal canonical correlation reveals converging neural circuitry across trauma‐related disorders of affect and cognition . Neurobiology of Stress , 9 , 241–250. 10.1016/j.ynstr.2018.09.006 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Sui, J. , Adali, T. T. , Pearlson, G. , Yang, H. , Sponheim, S. R. , White, T. , … Calhoun, V. D. (2010). A CCA+ICA based model for multi‐task brain imaging data fusion and its application to schizophrenia . NeuroImage , 51 , 123–134. 10.1016/j.neuroimage.2010.01.069 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Sui, J. , Adali, T. T. , Yu, Q. , Chen, J. , & Calhoun, V. D. (2012). A review of multivariate methods for multimodal fusion of brain imaging data . Journal of Neuroscience Methods , 204 , 68–81. 10.1016/j.jneumeth.2011.10.031 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Sui, J. , He, H. , Pearlson, G. D. , Adali, T. , Kiehl, K. A. , Yu, Q. , … Calhoun, V. D. (2013). Three‐way (N‐way) fusion of brain imaging data based on mCCA+jICA and its application to discriminating schizophrenia . NeuroImage , 66 , 119–132. 10.1016/j.neuroimage.2012.10.051 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Sui, J. , Pearlson, G. , Caprihan, A. , Adali, T. , Kiehl, K. A. , Liu, J. , … Calhoun, V. D. (2011). Discriminating schizophrenia and bipolar disorder by fusing fMRI and DTI in a multimodal CCA+ joint ICA model . NeuroImage , 57 , 839–855. 10.1016/j.neuroimage.2011.05.055 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Sui, J. , Pearlson, G. D. , Du, Y. , Yu, Q. , Jones, T. R. , Chen, J. , … Calhoun, V. D. (2015). In search of multimodal neuroimaging biomarkers of cognitive deficits in schizophrenia . Biological Psychiatry , 78 , 794–804. 10.1016/j.biopsych.2015.02.017 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Sui, J. , Qi, S. , van Erp, T. G. M. M. , Bustillo, J. , Jiang, R. , Lin, D. , … Calhoun, V. D. (2018). Multimodal neuromarkers in schizophrenia via cognition‐guided MRI fusion . Nature Communications , 9 , 3028 10.1038/s41467-018-05432-w [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Szefer, E. , Lu, D. , Nathoo, F. , Beg, M. F. , & Graham, J. (2017). Multivariate association between single‐nucleotide polymorphisms in Alzgene linkage regions and structural changes in the brain: Discovery, refinement and validation . Statistical Applications in Genetics and Molecular Biology , 16 , 349–365. 10.1515/sagmb-2016-0077 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Thye, M. , & Mirman, D. (2018). Relative contributions of lesion location and lesion size to predictions of varied language deficits in post‐stroke aphasia . NeuroImage: Clinical , 20 , 1129–1138. 10.1016/j.nicl.2018.10.017 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Tian, Y. , Zalesky, A. , Bousman, C. , Everall, I. , & Pantelis, C. (2019). Insula functional connectivity in schizophrenia: Subregions, gradients, and symptoms . Biological Psychiatry: Cognitive Neuroscience and Neuroimaging , 4 , 399–408. 10.1016/j.bpsc.2018.12.003 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Tibshirani, R. (1996). Regression shrinkage and selection via the Lasso Robert Tibshirani . Journal of the Royal Statistical Society, Series B , 58 , 267–288. 10.1111/j.1467-9868.2011.00771.x [ CrossRef ] [ Google Scholar ]
• Tsvetanov, K. A. , Henson, R. N. A. , Tyler, L. K. , Razi, A. , Geerligs, L. , Ham, T. E. , & Rowe, J. B. (2016). Extrinsic and intrinsic brain network connectivity maintains cognition across the lifespan despite accelerated decay of regional brain activation . The Journal of Neuroscience , 36 , 3115–3126. 10.1523/JNEUROSCI.2733-15.2016 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Valakos, D. , Karantinos, T. , Evdokimidis, I. , Stefanis, N. C. , Avramopoulos, D. , & Smyrnis, N. (2018). Shared variance of oculomotor phenotypes in a large sample of healthy young men . Experimental Brain Research , 236 , 2399–2410. 10.1007/s00221-018-5312-5 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Varoquaux, G. , Sadaghiani, S. , Pinel, P. , Kleinschmidt, A. , Poline, J. B. , & Thirion, B. (2010). A group model for stable multi‐subject ICA on fMRI datasets . NeuroImage , 51 , 288–299. 10.1016/j.neuroimage.2010.02.010 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Vatansever, D. , Bzdok, D. , Wang, H.‐T. , Mollo, G. , Sormaz, M. , Murphy, C. , … Jefferies, E. (2017). Varieties of semantic cognition revealed through simultaneous decomposition of intrinsic brain connectivity and behaviour . NeuroImage , 158 , 1–11. 10.1016/j.neuroimage.2017.06.067 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Vergult, A. , de Clercq, W. , Palmini, A. , Vanrumste, B. , Dupont, P. , van Huffel, S. , & van Paesschen, W. (2007). Improving the interpretation of ictal scalp EEG: BSS‐CCA algorithm for muscle artifact removal . Epilepsia , 48 , 950–958. 10.1111/j.1528-1167.2007.01031.x [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Viviano, J. D. , Buchanan, R. W. , Calarco, N. , Gold, J. M. , Foussias, G. , Bhagwat, N. , … Green, M. (2018). Resting‐state connectivity biomarkers of cognitive performance and social function in individuals with schizophrenia spectrum disorder and healthy control subjects . Biological Psychiatry , 84 , 665–674. 10.1016/j.biopsych.2018.03.013 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• von Luhmann, A. , Boukouvalas, Z. , Muller, K.‐R. , & Adali, T. (2019). A new blind source separation framework for signal analysis and artifact rejection in functional near‐infrared spectroscopy . NeuroImage , 200 , 72–88. 10.1016/j.neuroimage.2019.06.021 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Wan, J. , Kim, S. , Inlow, M. , Nho, K. , Swaminathan, S. , Risacher, S. L. , … Shen, L. (2011). Hippocampal surface mapping of genetic risk factors in AD via sparse learning models . Medical Image Computing and Computer‐Assisted Intervention , 14 , 376–383. 10.1007/978-3-642-23629-7_46 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Wang, C. (2007). Variational Bayesian approach to canonical correlation analysis . IEEE Transactions on Neural Networks , 18 , 905–910. 10.1109/TNN.2007.891186 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Wang, H. T. , Poerio, G. , Murphy, C. , Bzdok, D. , Jefferies, E. , & Smallwood, J. (2018). Dimensions of experience: Exploring the heterogeneity of the wandering mind . Psychological Science , 29 , 56–71. 10.1177/0956797617728727 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Wang, M. , Shao, W. , Hao, X. , Shen, L. , & Zhang, D. (2019). Identify consistent cross‐modality imaging genetic patterns via discriminant sparse canonical correlation analysis . IEEE/ACM Transactions on Computational Biology and Bioinformatics , 1 10.1109/TCBB.2019.2944825 [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Wee, C.Y. , Tuan, T. A. , Broekman, B. F. P. , Ong, M. Y. , Chong, Y.S. , Kwek, K. , et al. (2017). Neonatal neural networks predict children behavioral profiles later in life . Human Brain Mapping , 38 , 1362–1373. 10.1002/hbm.23459 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Will, G.J. J. , Rutledge, R. B. , Moutoussis, M. , & Dolan, R. J. (2017). Neural and computational processes underlying dynamic changes in self‐esteem . Elife , 6 , 1–21. 10.7554/eLife.28098 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Witten, D. M. , Tibshirani, R. , & Hastie, T. (2009). A penalized matrix decomposition, with applications to sparse principal components and canonical correlation analysis . Biostatistics , 10 , 515–534. 10.1093/biostatistics/kxp008 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Witten, D. M. , & Tibshirani, R. J. (2009). Extensions of sparse canonical correlation analysis with applications to genomic data . Statistical Applications in Genetics and Molecular Biology , 8 , 1–27. 10.2202/1544-6115.1470 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Xia, C. H. , Ma, Z. , Ciric, R. , Gu, S. , Betzel, R. F. , Kaczkurkin, A. N. , … Satterthwaite, T. D. (2018). Linked dimensions of psychopathology and connectivity in functional brain networks . Nature Communications , 9 , 1–14. 10.1038/s41467-018-05317-y [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Yan, J. , Du, L. , Kim, S. , Risacher, S. L. , Huang, H. , Moore, J. H. , … Shen, L. (2014). Transcriptome‐guided amyloid imaging genetic analysis via a novel structured sparse learning algorithm . Bioinformatics , 30 , i564–i571. 10.1093/bioinformatics/btu465 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Yan, J. , Risacher, S. L. , Nho, K. , Saykin, A. J. , & Shen, L. I. (2017). Identification of discriminative imaging proteomics associations in Alzheimer's disease via a novel sparse correlation model . Pacific Symposium on Biocomputing , 22 , 94–104. 10.1142/9789813207813_0010 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Yang, B. , Cao, J. , Zhou, T. , Dong, L. , Zou, L. , & Xiang, J. (2018). Exploration of neural activity under cognitive reappraisal using simultaneous EEG‐fMRI data and kernel canonical correlation analysis . Computational and Mathematical Methods in Medicine , 2018 , 3018356 10.1155/2018/3018356 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Yang, Z. , Zhuang, X. , Bird, C. , Sreenivasan, K. , Mishra, V. , Banks, S. , & Cordes, D. (2019). Performing sparse regularization and dimension reduction simultaneously in multimodal data fusion . Frontiers in Neuroscience , 13 ( 878 ). 10.3389/fnins.2019.00642 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Yang, Z. , Zhuang, X. , Sreenivasan, K. , & Mishra, V. (2019). Robust Motion regression of resting‐state data using a convolutional neural network model . Frontiers in Neuroscience , 13 , 1–14. 10.3389/fnins.2019.00169 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Yang, Z. , Zhuang, X. , Sreenivasan, K. , Mishra, V. , Curran, T. , Byrd, R. , … Cordes, D. (2018). 3D spatially‐adaptive canonical correlation analysis: Local and global methods . NeuroImage , 169 , 240–255. 10.1016/j.neuroimage.2017.12.025 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Yang, Z. , Zhuang, X. , Sreenivasan, K. , Mishra, V. , Curran, T. , & Cordes, D. (2020). A robust deep neural network for denoising task‐based fMRI data: An application to working memory and episodic memory . Medical Image Analysis , 60 , 101622 10.1016/j.media.2019.101622 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Yu, Q. , Erhardt, E. B. , Sui, J. , Du, Y. , He, H. , Hjelm, D. , … Calhoun, V. D. (2015). Assessing dynamic brain graphs of time‐varying connectivity in fMRI data: Application to healthy controls and patients with schizophrenia . NeuroImage , 107 , 345–355. 10.1016/j.neuroimage.2014.12.020 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Zarnani, K. , Nichols, T. E. , Alfaro‐Almagro, F. , Fagerlund, B. , Lauritzen, M. , Rostrup, E. , & Smith, S. M. (2019). Discovering markers of healthy aging: A prospective study in a Danish male birth cohort . Aging (Albany NY) , 11 , 5943–5974. 10.18632/aging.102151 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Zhang, Q. , Borst, J. P. , Kass, R. E. , & Anderson, J. R. (2017). Inter‐subject alignment of MEG datasets in a common representational space . Human Brain Mapping , 38 , 4287–4301. 10.1002/hbm.23689 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Zhao, F. , Qiao, L. , Shi, F. , Yap, P.‐T. , & Shen, D. (2017). Feature fusion via hierarchical supervised local CCA for diagnosis of autism spectrum disorder . Brain Imaging and Behavior , 11 , 1050–1060. 10.1007/s11682-016-9587-5 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Zhu, X. , Suk, H.‐I. , Lee, S.‐W. , & Shen, D. (2016). Canonical feature selection for joint regression and multi‐class identification in Alzheimer's disease diagnosis . Brain Imaging and Behavior , 10 , 818–828. 10.1007/s11682-015-9430-4 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Zhuang, X. , Walsh, R. R. , Sreenivasan, K. , Yang, Z. , Mishra, V. , & Cordes, D. (2018). Incorporating spatial constraint in co‐activation pattern analysis to explore the dynamics of resting‐state networks: An application to Parkinson's disease . NeuroImage , 172 , 64–84. 10.1016/j.neuroimage.2018.01.019 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Zhuang, X. , Yang, Z. , Curran, T. , Byrd, R. , Nandy, R. , & Cordes, D. (2017). A family of locally constrained CCA models for detecting activation patterns in fMRI . NeuroImage , 149 , 63–84. 10.1016/j.neuroimage.2016.12.081 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Zhuang, X. , Yang, Z. , Sreenivasan, K. R. , Mishra, V. R. , Curran, T. , Nandy, R. , & Cordes, D. (2019). Multivariate group‐level analysis for task fMRI data with canonical correlation analysis . NeuroImage , 194 , 25–41. 10.1016/j.neuroimage.2019.03.030 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
• Zille, P. , Calhoun, V. D. , & Wang, Y.‐P. (2018). Enforcing co‐expression within a brain‐imaging genomics regression framework . IEEE Transactions on Medical Imaging , 37 , 2561–2571. 10.1109/TMI.2017.2721301 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]