def null hypothesis

• More from M-W
• To save this word, you'll need to log in. Log In

null hypothesis

Definition of null hypothesis

Examples of null hypothesis in a sentence.

These examples are programmatically compiled from various online sources to illustrate current usage of the word 'null hypothesis.' Any opinions expressed in the examples do not represent those of Merriam-Webster or its editors. Send us feedback about these examples.

Word History

1935, in the meaning defined above

Dictionary Entries Near null hypothesis

Nullarbor Plain

Cite this Entry

“Null hypothesis.” Merriam-Webster.com Dictionary , Merriam-Webster, https://www.merriam-webster.com/dictionary/null%20hypothesis. Accessed 15 May. 2024.

More from Merriam-Webster on null hypothesis

Britannica.com: Encyclopedia article about null hypothesis

Subscribe to America's largest dictionary and get thousands more definitions and advanced search—ad free!

Can you solve 4 words at once?

Word of the day.

See Definitions and Examples »

Get Word of the Day daily email!

Popular in Grammar & Usage

More commonly misspelled words, your vs. you're: how to use them correctly, every letter is silent, sometimes: a-z list of examples, more commonly mispronounced words, how to use em dashes (—), en dashes (–) , and hyphens (-), popular in wordplay, birds say the darndest things, the words of the week - may 10, a great big list of bread words, 10 scrabble words without any vowels, 12 more bird names that sound like insults (and sometimes are), games & quizzes.

9.1 Null and Alternative Hypotheses

The actual test begins by considering two hypotheses . They are called the null hypothesis and the alternative hypothesis . These hypotheses contain opposing viewpoints.

H 0 , the — null hypothesis: a statement of no difference between sample means or proportions or no difference between a sample mean or proportion and a population mean or proportion. In other words, the difference equals 0.

H a —, the alternative hypothesis: a claim about the population that is contradictory to H 0 and what we conclude when we reject H 0 .

Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample data.

After you have determined which hypothesis the sample supports, you make a decision. There are two options for a decision. They are reject H 0 if the sample information favors the alternative hypothesis or do not reject H 0 or decline to reject H 0 if the sample information is insufficient to reject the null hypothesis.

Mathematical Symbols Used in H 0 and H a :

H 0 always has a symbol with an equal in it. H a never has a symbol with an equal in it. The choice of symbol depends on the wording of the hypothesis test. However, be aware that many researchers use = in the null hypothesis, even with > or < as the symbol in the alternative hypothesis. This practice is acceptable because we only make the decision to reject or not reject the null hypothesis.

Example 9.1

H 0 : No more than 30 percent of the registered voters in Santa Clara County voted in the primary election. p ≤ 30 H a : More than 30 percent of the registered voters in Santa Clara County voted in the primary election. p > 30

A medical trial is conducted to test whether or not a new medicine reduces cholesterol by 25 percent. State the null and alternative hypotheses.

Example 9.2

We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). The null and alternative hypotheses are the following: H 0 : μ = 2.0 H a : μ ≠ 2.0

We want to test whether the mean height of eighth graders is 66 inches. State the null and alternative hypotheses. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

• H 0 : μ __ 66
• H a : μ __ 66

Example 9.3

We want to test if college students take fewer than five years to graduate from college, on the average. The null and alternative hypotheses are the following: H 0 : μ ≥ 5 H a : μ < 5

We want to test if it takes fewer than 45 minutes to teach a lesson plan. State the null and alternative hypotheses. Fill in the correct symbol ( =, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

• H 0 : μ __ 45
• H a : μ __ 45

Example 9.4

An article on school standards stated that about half of all students in France, Germany, and Israel take advanced placement exams and a third of the students pass. The same article stated that 6.6 percent of U.S. students take advanced placement exams and 4.4 percent pass. Test if the percentage of U.S. students who take advanced placement exams is more than 6.6 percent. State the null and alternative hypotheses. H 0 : p ≤ 0.066 H a : p > 0.066

On a state driver’s test, about 40 percent pass the test on the first try. We want to test if more than 40 percent pass on the first try. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

• H 0 : p __ 0.40
• H a : p __ 0.40

Collaborative Exercise

Bring to class a newspaper, some news magazines, and some internet articles. In groups, find articles from which your group can write null and alternative hypotheses. Discuss your hypotheses with the rest of the class.

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute Texas Education Agency (TEA). The original material is available at: https://www.texasgateway.org/book/tea-statistics . Changes were made to the original material, including updates to art, structure, and other content updates.

Access for free at https://openstax.org/books/statistics/pages/1-introduction

• Authors: Barbara Illowsky, Susan Dean
• Publisher/website: OpenStax
• Book title: Statistics
• Publication date: Mar 27, 2020
• Location: Houston, Texas
• Book URL: https://openstax.org/books/statistics/pages/1-introduction
• Section URL: https://openstax.org/books/statistics/pages/9-1-null-and-alternative-hypotheses

© Jan 23, 2024 Texas Education Agency (TEA). The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

AP®︎/College Statistics

Course: ap®︎/college statistics   >   unit 10.

• Idea behind hypothesis testing

Examples of null and alternative hypotheses

• Writing null and alternative hypotheses
• P-values and significance tests
• Comparing P-values to different significance levels
• Estimating a P-value from a simulation
• Estimating P-values from simulations
• Using P-values to make conclusions

Want to join the conversation?

• Upvote Button navigates to signup page
• Downvote Button navigates to signup page
• Flag Button navigates to signup page

Video transcript

Module 9: Hypothesis Testing With One Sample

Null and alternative hypotheses, learning outcomes.

• Describe hypothesis testing in general and in practice

The actual test begins by considering two  hypotheses . They are called the null hypothesis and the alternative hypothesis . These hypotheses contain opposing viewpoints.

H 0 : The null hypothesis: It is a statement about the population that either is believed to be true or is used to put forth an argument unless it can be shown to be incorrect beyond a reasonable doubt.

H a : The alternative hypothesis : It is a claim about the population that is contradictory to H 0 and what we conclude when we reject H 0 .

Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample data.

After you have determined which hypothesis the sample supports, you make adecision. There are two options for a  decision . They are “reject H 0 ” if the sample information favors the alternative hypothesis or “do not reject H 0 ” or “decline to reject H 0 ” if the sample information is insufficient to reject the null hypothesis.

Mathematical Symbols Used in  H 0 and H a :

H 0 always has a symbol with an equal in it. H a never has a symbol with an equal in it. The choice of symbol depends on the wording of the hypothesis test. However, be aware that many researchers (including one of the co-authors in research work) use = in the null hypothesis, even with > or < as the symbol in the alternative hypothesis. This practice is acceptable because we only make the decision to reject or not reject the null hypothesis.

H 0 : No more than 30% of the registered voters in Santa Clara County voted in the primary election. p ≤ 30

H a : More than 30% of the registered voters in Santa Clara County voted in the primary election. p > 30

A medical trial is conducted to test whether or not a new medicine reduces cholesterol by 25%. State the null and alternative hypotheses.

H 0 : The drug reduces cholesterol by 25%. p = 0.25

H a : The drug does not reduce cholesterol by 25%. p ≠ 0.25

We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). The null and alternative hypotheses are:

H 0 : μ = 2.0

H a : μ ≠ 2.0

We want to test whether the mean height of eighth graders is 66 inches. State the null and alternative hypotheses. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses. H 0 : μ __ 66 H a : μ __ 66

• H 0 : μ = 66
• H a : μ ≠ 66

We want to test if college students take less than five years to graduate from college, on the average. The null and alternative hypotheses are:

H 0 : μ ≥ 5

H a : μ < 5

We want to test if it takes fewer than 45 minutes to teach a lesson plan. State the null and alternative hypotheses. Fill in the correct symbol ( =, ≠, ≥, <, ≤, >) for the null and alternative hypotheses. H 0 : μ __ 45 H a : μ __ 45

• H 0 : μ ≥ 45
• H a : μ < 45

In an issue of U.S. News and World Report , an article on school standards stated that about half of all students in France, Germany, and Israel take advanced placement exams and a third pass. The same article stated that 6.6% of U.S. students take advanced placement exams and 4.4% pass. Test if the percentage of U.S. students who take advanced placement exams is more than 6.6%. State the null and alternative hypotheses.

H 0 : p ≤ 0.066

H a : p > 0.066

On a state driver’s test, about 40% pass the test on the first try. We want to test if more than 40% pass on the first try. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses. H 0 : p __ 0.40 H a : p __ 0.40

• H 0 : p = 0.40
• H a : p > 0.40

Concept Review

In a  hypothesis test , sample data is evaluated in order to arrive at a decision about some type of claim. If certain conditions about the sample are satisfied, then the claim can be evaluated for a population. In a hypothesis test, we: Evaluate the null hypothesis , typically denoted with H 0 . The null is not rejected unless the hypothesis test shows otherwise. The null statement must always contain some form of equality (=, ≤ or ≥) Always write the alternative hypothesis , typically denoted with H a or H 1 , using less than, greater than, or not equals symbols, i.e., (≠, >, or <). If we reject the null hypothesis, then we can assume there is enough evidence to support the alternative hypothesis. Never state that a claim is proven true or false. Keep in mind the underlying fact that hypothesis testing is based on probability laws; therefore, we can talk only in terms of non-absolute certainties.

Formula Review

H 0 and H a are contradictory.

• OpenStax, Statistics, Null and Alternative Hypotheses. Provided by : OpenStax. Located at : http://cnx.org/contents/[email protected]:58/Introductory_Statistics . License : CC BY: Attribution
• Introductory Statistics . Authored by : Barbara Illowski, Susan Dean. Provided by : Open Stax. Located at : http://cnx.org/contents/[email protected] . License : CC BY: Attribution . License Terms : Download for free at http://cnx.org/contents/[email protected]
• Simple hypothesis testing | Probability and Statistics | Khan Academy. Authored by : Khan Academy. Located at : https://youtu.be/5D1gV37bKXY . License : All Rights Reserved . License Terms : Standard YouTube License

Null Hypothesis

Null hypothesis is used to make decisions based on data and by using statistical tests. Null hypothesis is represented using H o and it states that there is no difference between the characteristics of two samples. Null hypothesis is generally a statement of no difference. The rejection of null hypothesis is equivalent to the acceptance of the alternate hypothesis.

Let us learn more about null hypotheses, tests for null hypotheses, the difference between null hypothesis and alternate hypothesis, with the help of examples, FAQs.

What Is Null Hypothesis?

Null hypothesis states that there is no significant difference between the observed characteristics across two sample sets. Null hypothesis states the observed population parameters or variables is the same across the samples. The null hypothesis states that there is no relationship between the sample parameters, the independent variable, and the dependent variable. The term null hypothesis is used in instances to mean that there is no differences in the two means, or that the difference is not so significant.

If the experimental outcome is the same as the theoretical outcome then the null hypothesis holds good. But if there are any differences in the observed parameters across the samples then the null hypothesis is rejected, and we consider an alternate hypothesis. The rejection of the null hypothesis does not mean that there were flaws in the basic experimentation, but it sets the stage for further research. Generally, the strength of the evidence is tested against the null hypothesis.

Null hypothesis and alternate hypothesis are the two approaches used across statistics. The alternate hypothesis states that there is a significant difference between the parameters across the samples. The alternate hypothesis is the inverse of null hypothesis. An important reason to reject the null hypothesis and consider the alternate hypothesis is due to experimental or sampling errors.

Tests For Null Hypothesis

The two important approaches of statistical interference of null hypothesis are significance testing and hypothesis testing. The null hypothesis is a theoretical hypothesis and is based on insufficient evidence, which requires further testing to prove if it is true or false.

Significance Testing

The aim of significance testing is to provide evidence to reject the null hypothesis. If the difference is strong enough then reject the null hypothesis and accept the alternate hypothesis. The testing is designed to test the strength of the evidence against the hypothesis. The four important steps of significance testing are as follows.

• First state the null and alternate hypotheses.
• Calculate the test statistics.
• Find the p-value.
• Test the p-value with the α and decide if the null hypothesis should be rejected or accepted.

If the p-value is lesser than the significance level α, then the null hypothesis is rejected. And if the p-value is greater than the significance level α, then the null hypothesis is accepted.

• Hypothesis Testing

Hypothesis testing takes the parameters from the sample and makes a derivation about the population. A hypothesis is an educated guess about a sample, which can be tested either through an experiment or an observation. Initially, a tentative assumption is made about the sample in the form of a null hypothesis.

There are four steps to perform hypothesis testing. They are:

• Identify the null hypothesis.
• Define the null hypothesis statement.
• Choose the test to be performed.
• Accept the null hypothesis or the alternate hypothesis.

There are often errors in the process of testing the hypothesis. The two important errors observed in hypothesis testing is as follows.

• Type - I error is rejecting the null hypothesis when the null hypothesis is actually true.
• Type - II error is accepting the null hypothesis when the null hypothesis is actually false.

Difference Between Null Hypothesis And Alternate Hypothesis

The difference between null hypothesis and alternate hypothesis can be understood through the following points.

• The opposite of the null hypothesis is the alternate hypothesis and it is the claim which is being proved by research to be true.
• The null hypothesis states that the two samples of the population are the same, and the alternate hypothesis states that there is a significant difference between the two samples of the population.
• The null hypothesis is designated as H o and the alternate hypothesis is designated as H a .
• For the null hypothesis, the same means are assumed to be equal, and we have H 0 : µ 1 = µ 2. And for the alternate hypothesis, the sample means are unequal, and we have H a : µ 1 ≠ µ 2.
• The observed population parameters and variables are the same across the samples, for a null hypothesis, but in an alternate hypothesis, there is a significant difference between the observed parameters and variables across the samples.

☛ Related Topics

The following topics help in a better understanding of the null hypothesis.

• Probability and Statistics
• Basic Statistics Formula
• Sample Space

Examples on Null Hypothesis

Example 1: A medical experiment and trial is conducted to check if a particular drug can serve as the vaccine for Covid-19, and can prevent from occurrence of Corona. Write the null hypothesis and the alternate hypothesis for this situation.

The given situation refers to a possible new drug and its effectiveness of being a vaccine for Covid-19 or not. The null hypothesis (H o ) and alternate hypothesis (H a ) for this medical experiment is as follows.

• H 0 : The use of the new drug is not helpful for the prevention of Covid-19.
• H a : The use of the new drug serves as a vaccine and helps for the prevention of Covid-19.

Example 2: The teacher has prepared a set of important questions and informs the student that preparing these questions helps in scoring more than 60% marks in the board exams. Write the null hypothesis and the alternate hypothesis for this situation.

The given situation refers to the teacher who has claimed that her important questions helps to score more than 60% marks in the board exams. The null hypothesis(H o ) and alternate hypothesis(H a ) for this situation is as follows.

• H o : The important questions given by the teacher does not really help the students to get a score of more than 60% in the board exams.
• H a : The important questions given by the teacher is helpful for the students to score more than 60% marks in the board exams.

go to slide go to slide

Book a Free Trial Class

Practice Questions on Null Hypothesis

Faqs on null hypothesis, what is null hypothesis in maths.

Null hypothesis is used in statistics and it states if there is any significant difference between the two samples. The acceptance of null hypothesis mean that there is no significant difference between the two samples. And the rejection of null hypothesis means that the two samples are different, and we need to accept the alternate hypothesis. The null hypothesis statement is represented as H 0 and the alternate hypothesis is represented as H a .

How Do You Test Null Hypothesis?

The null hypothesis is broadly tested using two methods. The null hypothesis can be tested using significance testing and hypothesis testing.Broadly the test for null hypothesis is performed across four stages. First the null hypothesis is identified, secondly the null hypothesis is defined. Next a suitable test is used to test the hypothesis, and finally either the null hypothesis or the alternate hypothesis is accepted.

How To Accept or Reject Null Hypothesis?

The null hypothesis is accepted or rejected based on the result of the hypothesis testing. The p value is found and the significance level is defined. If the p-value is lesser than the significance level α, then the null hypothesis is rejected. And if the p-value is greater than the significance level α, then the null hypothesis is accepted.

What Is the Difference Between Null Hypothesis And Alternate Hypothesis?

The null hypothesis states that there is no significant difference between the two samples, and the alternate hypothesis states that there is a significant difference between the two samples. The null hypothesis is referred using H o and the alternate hypothesis is referred using H a . As per null hypothesis the observed variables and parameters are the same across the samples, but as per alternate hypothesis there is a significant difference between the observed variables and parameters across the samples.

What Is Null Hypothesis Example?

A few quick examples of null hypothesis are as follows.

• The salary of a person is independent of his profession, is an example of null hypothesis. And the salary is dependent on the profession of a person, is an alternate hypothesis.
• The performance of the students in Maths from two different classes is a null hypothesis. And the performance of the students from each of the classes is different, is an example of alternate hypothesis.
• The nutrient content of mango and a mango milk shake is equal and it can be taken as a null hypothesis. The test to prove the different nutrient content of the two is referred to as alternate hypothesis.

Statistics Made Easy

How to Write a Null Hypothesis (5 Examples)

A hypothesis test uses sample data to determine whether or not some claim about a population parameter is true.

Whenever we perform a hypothesis test, we always write a null hypothesis and an alternative hypothesis, which take the following forms:

H 0 (Null Hypothesis): Population parameter =,  ≤, ≥ some value

H A  (Alternative Hypothesis): Population parameter <, >, ≠ some value

Note that the null hypothesis always contains the equal sign .

We interpret the hypotheses as follows:

Null hypothesis: The sample data provides no evidence to support some claim being made by an individual.

Alternative hypothesis: The sample data  does provide sufficient evidence to support the claim being made by an individual.

For example, suppose it’s assumed that the average height of a certain species of plant is 20 inches tall. However, one botanist claims the true average height is greater than 20 inches.

To test this claim, she may go out and collect a random sample of plants. She can then use this sample data to perform a hypothesis test using the following two hypotheses:

H 0 : μ ≤ 20 (the true mean height of plants is equal to or even less than 20 inches)

H A : μ > 20 (the true mean height of plants is greater than 20 inches)

If the sample data gathered by the botanist shows that the mean height of this species of plants is significantly greater than 20 inches, she can reject the null hypothesis and conclude that the mean height is greater than 20 inches.

Read through the following examples to gain a better understanding of how to write a null hypothesis in different situations.

Example 1: Weight of Turtles

A biologist wants to test whether or not the true mean weight of a certain species of turtles is 300 pounds. To test this, he goes out and measures the weight of a random sample of 40 turtles.

Here is how to write the null and alternative hypotheses for this scenario:

H 0 : μ = 300 (the true mean weight is equal to 300 pounds)

H A : μ ≠ 300 (the true mean weight is not equal to 300 pounds)

Example 2: Height of Males

It’s assumed that the mean height of males in a certain city is 68 inches. However, an independent researcher believes the true mean height is greater than 68 inches. To test this, he goes out and collects the height of 50 males in the city.

H 0 : μ ≤ 68 (the true mean height is equal to or even less than 68 inches)

H A : μ > 68 (the true mean height is greater than 68 inches)

Example 3: Graduation Rates

A university states that 80% of all students graduate on time. However, an independent researcher believes that less than 80% of all students graduate on time. To test this, she collects data on the proportion of students who graduated on time last year at the university.

H 0 : p ≥ 0.80 (the true proportion of students who graduate on time is 80% or higher)

H A : μ < 0.80 (the true proportion of students who graduate on time is less than 80%)

Example 4: Burger Weights

A food researcher wants to test whether or not the true mean weight of a burger at a certain restaurant is 7 ounces. To test this, he goes out and measures the weight of a random sample of 20 burgers from this restaurant.

H 0 : μ = 7 (the true mean weight is equal to 7 ounces)

H A : μ ≠ 7 (the true mean weight is not equal to 7 ounces)

Example 5: Citizen Support

A politician claims that less than 30% of citizens in a certain town support a certain law. To test this, he goes out and surveys 200 citizens on whether or not they support the law.

H 0 : p ≥ .30 (the true proportion of citizens who support the law is greater than or equal to 30%)

H A : μ < 0.30 (the true proportion of citizens who support the law is less than 30%)

Additional Resources

Introduction to Hypothesis Testing Introduction to Confidence Intervals An Explanation of P-Values and Statistical Significance

Featured Posts

Hey there. My name is Zach Bobbitt. I have a Masters of Science degree in Applied Statistics and I’ve worked on machine learning algorithms for professional businesses in both healthcare and retail. I’m passionate about statistics, machine learning, and data visualization and I created Statology to be a resource for both students and teachers alike.  My goal with this site is to help you learn statistics through using simple terms, plenty of real-world examples, and helpful illustrations.

2 Replies to “How to Write a Null Hypothesis (5 Examples)”

you are amazing, thank you so much

Say I am a botanist hypothesizing the average height of daisies is 20 inches, or not? Does T = (ave – 20 inches) / √ variance / (80 / 4)? … This assumes 40 real measures + 40 fake = 80 n, but that seems questionable. Please advise.

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Join the Statology Community

Sign up to receive Statology's exclusive study resource: 100 practice problems with step-by-step solutions. Plus, get our latest insights, tutorials, and data analysis tips straight to your inbox!

By subscribing you accept Statology's Privacy Policy.

• Math Article

Null Hypothesis

In mathematics, Statistics deals with the study of research and surveys on the numerical data. For taking surveys, we have to define the hypothesis. Generally, there are two types of hypothesis. One is a null hypothesis, and another is an alternative hypothesis .

In probability and statistics, the null hypothesis is a comprehensive statement or default status that there is zero happening or nothing happening. For example, there is no connection among groups or no association between two measured events. It is generally assumed here that the hypothesis is true until any other proof has been brought into the light to deny the hypothesis. Let us learn more here with definition, symbol, principle, types and example, in this article.

Table of contents:

• Comparison with Alternative Hypothesis

Null Hypothesis Definition

The null hypothesis is a kind of hypothesis which explains the population parameter whose purpose is to test the validity of the given experimental data. This hypothesis is either rejected or not rejected based on the viability of the given population or sample . In other words, the null hypothesis is a hypothesis in which the sample observations results from the chance. It is said to be a statement in which the surveyors wants to examine the data. It is denoted by H 0 .

Null Hypothesis Symbol

In statistics, the null hypothesis is usually denoted by letter H with subscript ‘0’ (zero), such that H 0 . It is pronounced as H-null or H-zero or H-nought. At the same time, the alternative hypothesis expresses the observations determined by the non-random cause. It is represented by H 1 or H a .

Null Hypothesis Principle

The principle followed for null hypothesis testing is, collecting the data and determining the chances of a given set of data during the study on some random sample, assuming that the null hypothesis is true. In case if the given data does not face the expected null hypothesis, then the outcome will be quite weaker, and they conclude by saying that the given set of data does not provide strong evidence against the null hypothesis because of insufficient evidence. Finally, the researchers tend to reject that.

Null Hypothesis Formula

Here, the hypothesis test formulas are given below for reference.

The formula for the null hypothesis is:

H 0 :  p = p 0

The formula for the alternative hypothesis is:

H a = p >p 0 , < p 0 ≠ p 0

The formula for the test static is:

Remember that,  p 0  is the null hypothesis and p – hat is the sample proportion.

Also, read:

Types of Null Hypothesis

There are different types of hypothesis. They are:

Simple Hypothesis

It completely specifies the population distribution. In this method, the sampling distribution is the function of the sample size.

Composite Hypothesis

The composite hypothesis is one that does not completely specify the population distribution.

Exact Hypothesis

Exact hypothesis defines the exact value of the parameter. For example μ= 50

Inexact Hypothesis

This type of hypothesis does not define the exact value of the parameter. But it denotes a specific range or interval. For example 45< μ <60

Null Hypothesis Rejection

Sometimes the null hypothesis is rejected too. If this hypothesis is rejected means, that research could be invalid. Many researchers will neglect this hypothesis as it is merely opposite to the alternate hypothesis. It is a better practice to create a hypothesis and test it. The goal of researchers is not to reject the hypothesis. But it is evident that a perfect statistical model is always associated with the failure to reject the null hypothesis.

How do you Find the Null Hypothesis?

The null hypothesis says there is no correlation between the measured event (the dependent variable) and the independent variable. We don’t have to believe that the null hypothesis is true to test it. On the contrast, you will possibly assume that there is a connection between a set of variables ( dependent and independent).

When is Null Hypothesis Rejected?

The null hypothesis is rejected using the P-value approach. If the P-value is less than or equal to the α, there should be a rejection of the null hypothesis in favour of the alternate hypothesis. In case, if P-value is greater than α, the null hypothesis is not rejected.

Null Hypothesis and Alternative Hypothesis

Now, let us discuss the difference between the null hypothesis and the alternative hypothesis.

Null Hypothesis Examples

Here, some of the examples of the null hypothesis are given below. Go through the below ones to understand the concept of the null hypothesis in a better way.

If a medicine reduces the risk of cardiac stroke, then the null hypothesis should be “the medicine does not reduce the chance of cardiac stroke”. This testing can be performed by the administration of a drug to a certain group of people in a controlled way. If the survey shows that there is a significant change in the people, then the hypothesis is rejected.

Few more examples are:

1). Are there is 100% chance of getting affected by dengue?

Ans: There could be chances of getting affected by dengue but not 100%.

2). Do teenagers are using mobile phones more than grown-ups to access the internet?

Ans: Age has no limit on using mobile phones to access the internet.

3). Does having apple daily will not cause fever?

Ans: Having apple daily does not assure of not having fever, but increases the immunity to fight against such diseases.

4). Do the children more good in doing mathematical calculations than grown-ups?

Ans: Age has no effect on Mathematical skills.

In many common applications, the choice of the null hypothesis is not automated, but the testing and calculations may be automated. Also, the choice of the null hypothesis is completely based on previous experiences and inconsistent advice. The choice can be more complicated and based on the variety of applications and the diversity of the objectives. 

The main limitation for the choice of the null hypothesis is that the hypothesis suggested by the data is based on the reasoning which proves nothing. It means that if some hypothesis provides a summary of the data set, then there would be no value in the testing of the hypothesis on the particular set of data. 

Frequently Asked Questions on Null Hypothesis

What is meant by the null hypothesis.

In Statistics, a null hypothesis is a type of hypothesis which explains the population parameter whose purpose is to test the validity of the given experimental data.

What are the benefits of hypothesis testing?

Hypothesis testing is defined as a form of inferential statistics, which allows making conclusions from the entire population based on the sample representative.

When a null hypothesis is accepted and rejected?

The null hypothesis is either accepted or rejected in terms of the given data. If P-value is less than α, then the null hypothesis is rejected in favor of the alternative hypothesis, and if the P-value is greater than α, then the null hypothesis is accepted in favor of the alternative hypothesis.

Why is the null hypothesis important?

The importance of the null hypothesis is that it provides an approximate description of the phenomena of the given data. It allows the investigators to directly test the relational statement in a research study.

How to accept or reject the null hypothesis in the chi-square test?

If the result of the chi-square test is bigger than the critical value in the table, then the data does not fit the model, which represents the rejection of the null hypothesis.

Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!

Select the correct answer and click on the “Finish” button Check your score and answers at the end of the quiz

Visit BYJU’S for all Maths related queries and study materials

Your result is as below

Request OTP on Voice Call

• Share Share

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

Null hypothesis

Null hypothesis n., plural: null hypotheses [nʌl haɪˈpɒθɪsɪs] Definition: a hypothesis that is valid or presumed true until invalidated by a statistical test

Table of Contents

Null Hypothesis Definition

Null hypothesis is defined as “the commonly accepted fact (such as the sky is blue) and researcher aim to reject or nullify this fact”.

More formally, we can define a null hypothesis as “a statistical theory suggesting that no statistical relationship exists between given observed variables” .

In biology , the null hypothesis is used to nullify or reject a common belief. The researcher carries out the research which is aimed at rejecting the commonly accepted belief.

What Is a Null Hypothesis?

A hypothesis is defined as a theory or an assumption that is based on inadequate evidence. It needs and requires more experiments and testing for confirmation. There are two possibilities that by doing more experiments and testing, a hypothesis can be false or true. It means it can either prove wrong or true (Blackwelder, 1982).

For example, Susie assumes that mineral water helps in the better growth and nourishment of plants over distilled water. To prove this hypothesis, she performs this experiment for almost a month. She watered some plants with mineral water and some with distilled water.

In a hypothesis when there are no statistically significant relationships among the two variables, the hypothesis is said to be a null hypothesis. The investigator is trying to disprove such a hypothesis. In the above example of plants, the null hypothesis is:

There are no statistical relationships among the forms of water that are given to plants for growth and nourishment.

Usually, an investigator tries to prove the null hypothesis wrong and tries to explain a relation and association between the two variables.

An opposite and reverse of the null hypothesis are known as the alternate hypothesis . In the example of plants the alternate hypothesis is:

There are statistical relationships among the forms of water that are given to plants for growth and nourishment.

The example below shows the difference between null vs alternative hypotheses:

Alternate Hypothesis: The world is round Null Hypothesis: The world is not round.

Copernicus and many other scientists try to prove the null hypothesis wrong and false. By their experiments and testing, they make people believe that alternate hypotheses are correct and true. If they do not prove the null hypothesis experimentally wrong then people will not believe them and never consider the alternative hypothesis true and correct.

The alternative and null hypothesis for Susie’s assumption is:

• Null Hypothesis: If one plant is watered with distilled water and the other with mineral water, then there is no difference in the growth and nourishment of these two plants.
• Alternative Hypothesis:  If one plant is watered with distilled water and the other with mineral water, then the plant with mineral water shows better growth and nourishment.

The null hypothesis suggests that there is no significant or statistical relationship. The relation can either be in a single set of variables or among two sets of variables.

Most people consider the null hypothesis true and correct. Scientists work and perform different experiments and do a variety of research so that they can prove the null hypothesis wrong or nullify it. For this purpose, they design an alternate hypothesis that they think is correct or true. The null hypothesis symbol is H 0 (it is read as H null or H zero ).

Why is it named the “Null”?

The name null is given to this hypothesis to clarify and explain that the scientists are working to prove it false i.e. to nullify the hypothesis. Sometimes it confuses the readers; they might misunderstand it and think that statement has nothing. It is blank but, actually, it is not. It is more appropriate and suitable to call it a nullifiable hypothesis instead of the null hypothesis.

Why do we need to assess it? Why not just verify an alternate one?

In science, the scientific method is used. It involves a series of different steps. Scientists perform these steps so that a hypothesis can be proved false or true. Scientists do this to confirm that there will be any limitation or inadequacy in the new hypothesis. Experiments are done by considering both alternative and null hypotheses, which makes the research safe. It gives a negative as well as a bad impact on research if a null hypothesis is not included or a part of the study. It seems like you are not taking your research seriously and not concerned about it and just want to impose your results as correct and true if the null hypothesis is not a part of the study.

Development of the Null

In statistics, firstly it is necessary to design alternate and null hypotheses from the given problem. Splitting the problem into small steps makes the pathway towards the solution easier and less challenging. how to write a null hypothesis?

Writing a null hypothesis consists of two steps:

• Firstly, initiate by asking a question.
• Secondly, restate the question in such a way that it seems there are no relationships among the variables.

In other words, assume in such a way that the treatment does not have any effect.

The usual recovery duration after knee surgery is considered almost 8 weeks.

A researcher thinks that the recovery period may get elongated if patients go to a physiotherapist for rehabilitation twice per week, instead of thrice per week, i.e. recovery duration reduces if the patient goes three times for rehabilitation instead of two times.

Step 1: Look for the problem in the hypothesis. The hypothesis either be a word or can be a statement. In the above example the hypothesis is:

“The expected recovery period in knee rehabilitation is more than 8 weeks”

Step 2: Make a mathematical statement from the hypothesis. Averages can also be represented as μ, thus the null hypothesis formula will be.

In the above equation, the hypothesis is equivalent to H1, the average is denoted by μ and > that the average is greater than eight.

Step 3: Explain what will come up if the hypothesis does not come right i.e., the rehabilitation period may not proceed more than 08 weeks.

There are two options: either the recovery will be less than or equal to 8 weeks.

H 0 : μ ≤ 8

In the above equation, the null hypothesis is equivalent to H 0 , the average is denoted by μ and ≤ represents that the average is less than or equal to eight.

What will happen if the scientist does not have any knowledge about the outcome?

Problem: An investigator investigates the post-operative impact and influence of radical exercise on patients who have operative procedures of the knee. The chances are either the exercise will improve the recovery or will make it worse. The usual time for recovery is 8 weeks.

Step 1: Make a null hypothesis i.e. the exercise does not show any effect and the recovery time remains almost 8 weeks.

H 0 : μ = 8

In the above equation, the null hypothesis is equivalent to H 0 , the average is denoted by μ, and the equal sign (=) shows that the average is equal to eight.

Step 2: Make the alternate hypothesis which is the reverse of the null hypothesis. Particularly what will happen if treatment (exercise) makes an impact?

In the above equation, the alternate hypothesis is equivalent to H1, the average is denoted by μ and not equal sign (≠) represents that the average is not equal to eight.

Significance Tests

To get a reasonable and probable clarification of statistics (data), a significance test is performed. The null hypothesis does not have data. It is a piece of information or statement which contains numerical figures about the population. The data can be in different forms like in means or proportions. It can either be the difference of proportions and means or any odd ratio.

The following table will explain the symbols:

P-value is the chief statistical final result of the significance test of the null hypothesis.

• P-value = Pr(data or data more extreme | H 0 true)
• | = “given”
• Pr = probability
• H 0 = the null hypothesis

The first stage of Null Hypothesis Significance Testing (NHST) is to form an alternate and null hypothesis. By this, the research question can be briefly explained.

Null Hypothesis = no effect of treatment, no difference, no association Alternative Hypothesis = effective treatment, difference, association

When to reject the null hypothesis?

Researchers will reject the null hypothesis if it is proven wrong after experimentation. Researchers accept null hypothesis to be true and correct until it is proven wrong or false. On the other hand, the researchers try to strengthen the alternate hypothesis. The binomial test is performed on a sample and after that, a series of tests were performed (Frick, 1995).

Step 1: Evaluate and read the research question carefully and consciously and make a null hypothesis. Verify the sample that supports the binomial proportion. If there is no difference then find out the value of the binomial parameter.

Show the null hypothesis as:

H 0 :p= the value of p if H 0 is true

To find out how much it varies from the proposed data and the value of the null hypothesis, calculate the sample proportion.

Step 2: In test statistics, find the binomial test that comes under the null hypothesis. The test must be based on precise and thorough probabilities. Also make a list of pmf that apply, when the null hypothesis proves true and correct.

When H 0 is true, X~b(n, p)

N = size of the sample

P = assume value if H 0 proves true.

Step 3: Find out the value of P. P-value is the probability of data that is under observation.

Rise or increase in the P value = Pr(X ≥ x)

X = observed number of successes

P value = Pr(X ≤ x).

Step 4: Demonstrate the findings or outcomes in a descriptive detailed way.

• Sample proportion
• The direction of difference (either increases or decreases)

Perceived Problems With the Null Hypothesis

Variable or model selection and less information in some cases are the chief important issues that affect the testing of the null hypothesis. Statistical tests of the null hypothesis are reasonably not strong. There is randomization about significance. (Gill, 1999) The main issue with the testing of the null hypothesis is that they all are wrong or false on a ground basis.

There is another problem with the a-level . This is an ignored but also a well-known problem. The value of a-level is without a theoretical basis and thus there is randomization in conventional values, most commonly 0.q, 0.5, or 0.01. If a fixed value of a is used, it will result in the formation of two categories (significant and non-significant) The issue of a randomized rejection or non-rejection is also present when there is a practical matter which is the strong point of the evidence related to a scientific matter.

The P-value has the foremost importance in the testing of null hypothesis but as an inferential tool and for interpretation, it has a problem. The P-value is the probability of getting a test statistic at least as extreme as the observed one.

The main point about the definition is: Observed results are not based on a-value

Moreover, the evidence against the null hypothesis was overstated due to unobserved results. A-value has importance more than just being a statement. It is a precise statement about the evidence from the observed results or data. Similarly, researchers found that P-values are objectionable. They do not prefer null hypotheses in testing. It is also clear that the P-value is strictly dependent on the null hypothesis. It is computer-based statistics. In some precise experiments, the null hypothesis statistics and actual sampling distribution are closely related but this does not become possible in observational studies.

Some researchers pointed out that the P-value is depending on the sample size. If the true and exact difference is small, a null hypothesis even of a large sample may get rejected. This shows the difference between biological importance and statistical significance. (Killeen, 2005)

Another issue is the fix a-level, i.e., 0.1. On the basis, if a-level a null hypothesis of a large sample may get accepted or rejected. If the size of simple is infinity and the null hypothesis is proved true there are still chances of Type I error. That is the reason this approach or method is not considered consistent and reliable. There is also another problem that the exact information about the precision and size of the estimated effect cannot be known. The only solution is to state the size of the effect and its precision.

Null Hypothesis Examples

Here are some examples:

Example 1: Hypotheses with One Sample of One Categorical Variable

Among all the population of humans, almost 10% of people prefer to do their task with their left hand i.e. left-handed. Let suppose, a researcher in the Penn States says that the population of students at the College of Arts and Architecture is mostly left-handed as compared to the general population of humans in general public society. In this case, there is only a sample and there is a comparison among the known population values to the population proportion of sample value.

• Research Question: Do artists more expected to be left-handed as compared to the common population persons in society?
• Response Variable: Sorting the student into two categories. One category has left-handed persons and the other category have right-handed persons.
• Form Null Hypothesis: Arts and Architecture college students are no more predicted to be lefty as compared to the common population persons in society (Lefty students of Arts and Architecture college population is 10% or p= 0.10)

Example 2: Hypotheses with One Sample of One Measurement Variable

A generic brand of antihistamine Diphenhydramine making medicine in the form of a capsule, having a 50mg dose. The maker of the medicines is concerned that the machine has come out of calibration and is not making more capsules with the suitable and appropriate dose.

• Research Question: Does the statistical data recommended about the mean and average dosage of the population differ from 50mg?
• Response Variable: Chemical assay used to find the appropriate dosage of the active ingredient.
• Null Hypothesis: Usually, the 50mg dosage of capsules of this trade name (population average and means dosage =50 mg).

Example 3: Hypotheses with Two Samples of One Categorical Variable

Several people choose vegetarian meals on a daily basis. Typically, the researcher thought that females like vegetarian meals more than males.

• Research Question: Does the data recommend that females (women) prefer vegetarian meals more than males (men) regularly?
• Response Variable: Cataloguing the persons into vegetarian and non-vegetarian categories. Grouping Variable: Gender
• Null Hypothesis: Gender is not linked to those who like vegetarian meals. (Population percent of women who eat vegetarian meals regularly = population percent of men who eat vegetarian meals regularly or p women = p men).

Example 4: Hypotheses with Two Samples of One Measurement Variable

Nowadays obesity and being overweight is one of the major and dangerous health issues. Research is performed to confirm that a low carbohydrates diet leads to faster weight loss than a low-fat diet.

• Research Question: Does the given data recommend that usually, a low-carbohydrate diet helps in losing weight faster as compared to a low-fat diet?
• Response Variable: Weight loss (pounds)
• Explanatory Variable: Form of diet either low carbohydrate or low fat
• Null Hypothesis: There is no significant difference when comparing the mean loss of weight of people using a low carbohydrate diet to people using a diet having low fat. (population means loss of weight on a low carbohydrate diet = population means loss of weight on a diet containing low fat).

Example 5: Hypotheses about the relationship between Two Categorical Variables

A case-control study was performed. The study contains nonsmokers, stroke patients, and controls. The subjects are of the same occupation and age and the question was asked if someone at their home or close surrounding smokes?

• Research Question: Did second-hand smoke enhance the chances of stroke?
• Variables: There are 02 diverse categories of variables. (Controls and stroke patients) (whether the smoker lives in the same house). The chances of having a stroke will be increased if a person is living with a smoker.
• Null Hypothesis: There is no significant relationship between a passive smoker and stroke or brain attack. (odds ratio between stroke and the passive smoker is equal to 1).

Example 6: Hypotheses about the relationship between Two Measurement Variables

A financial expert observes that there is somehow a positive and effective relationship between the variation in stock rate price and the quantity of stock bought by non-management employees

• Response variable- Regular alteration in price
• Explanatory Variable- Stock bought by non-management employees
• Null Hypothesis: The association and relationship between the regular stock price alteration ($) and the daily stock-buying by non-management employees ($) = 0.

Example 7: Hypotheses about comparing the relationship between Two Measurement Variables in Two Samples

• Research Question: Is the relation between the bill paid in a restaurant and the tip given to the waiter, is linear? Is this relation different for dining and family restaurants?
• Explanatory Variable- total bill amount
• Response Variable- the amount of tip
• Null Hypothesis: The relationship and association between the total bill quantity at a family or dining restaurant and the tip, is the same.

Try to answer the quiz below to check what you have learned so far about the null hypothesis.

Choose the best answer. 

Send Your Results (Optional)

• Blackwelder, W. C. (1982). “Proving the null hypothesis” in clinical trials. Controlled Clinical Trials , 3(4), 345–353.
• Frick, R. W. (1995). Accepting the null hypothesis. Memory & Cognition, 23(1), 132–138.
• Gill, J. (1999). The insignificance of null hypothesis significance testing. Political Research Quarterly , 52(3), 647–674.
• Killeen, P. R. (2005). An alternative to null-hypothesis significance tests. Psychological Science, 16(5), 345–353.

©BiologyOnline.com. Content provided and moderated by Biology Online Editors.

Last updated on June 16th, 2022

You will also like...

Geological Periods

Geological periods is a study guide that cites the different geological periods on Earth's timeline. Each has a brief ov..

The Evolutionary Development of Multicellular Organisms

Multicellular organisms evolved. The first ones were likely in the form of sponges. Multicellularity led to the evolutio..

Abiotic and Biotic Factors

This tutorial deals with the abiotic factors of the freshwater environment that determine what sort of life would be sui..

Genetic Engineering Advantages & Disadvantages

This tutorial presents the benefits and the possible adverse eventualities of genetic engineering. Know more about this ..

New Zealand’s Unique Geographical History

Explore why New Zealand has such unique flora and fauna, and learn why long periods of geographical isolation. This less..

Origins of Life on Earth

Earth was created around 4.5 billion years ago and life began not long after. Primitive life likely possessed the elemen..

Related Articles...

No related articles found

Research Hypothesis In Psychology: Types, & Examples

Saul Mcleod, PhD

Editor-in-Chief for Simply Psychology

BSc (Hons) Psychology, MRes, PhD, University of Manchester

Saul Mcleod, PhD., is a qualified psychology teacher with over 18 years of experience in further and higher education. He has been published in peer-reviewed journals, including the Journal of Clinical Psychology.

Learn about our Editorial Process

Olivia Guy-Evans, MSc

Associate Editor for Simply Psychology

BSc (Hons) Psychology, MSc Psychology of Education

Olivia Guy-Evans is a writer and associate editor for Simply Psychology. She has previously worked in healthcare and educational sectors.

On This Page:

A research hypothesis, in its plural form “hypotheses,” is a specific, testable prediction about the anticipated results of a study, established at its outset. It is a key component of the scientific method .

Hypotheses connect theory to data and guide the research process towards expanding scientific understanding

Some key points about hypotheses:

• A hypothesis expresses an expected pattern or relationship. It connects the variables under investigation.
• It is stated in clear, precise terms before any data collection or analysis occurs. This makes the hypothesis testable.
• A hypothesis must be falsifiable. It should be possible, even if unlikely in practice, to collect data that disconfirms rather than supports the hypothesis.
• Hypotheses guide research. Scientists design studies to explicitly evaluate hypotheses about how nature works.
• For a hypothesis to be valid, it must be testable against empirical evidence. The evidence can then confirm or disprove the testable predictions.
• Hypotheses are informed by background knowledge and observation, but go beyond what is already known to propose an explanation of how or why something occurs.

Predictions typically arise from a thorough knowledge of the research literature, curiosity about real-world problems or implications, and integrating this to advance theory. They build on existing literature while providing new insight.

Types of Research Hypotheses

Alternative hypothesis.

The research hypothesis is often called the alternative or experimental hypothesis in experimental research.

It typically suggests a potential relationship between two key variables: the independent variable, which the researcher manipulates, and the dependent variable, which is measured based on those changes.

The alternative hypothesis states a relationship exists between the two variables being studied (one variable affects the other).

A hypothesis is a testable statement or prediction about the relationship between two or more variables. It is a key component of the scientific method. Some key points about hypotheses:

• Important hypotheses lead to predictions that can be tested empirically. The evidence can then confirm or disprove the testable predictions.

In summary, a hypothesis is a precise, testable statement of what researchers expect to happen in a study and why. Hypotheses connect theory to data and guide the research process towards expanding scientific understanding.

An experimental hypothesis predicts what change(s) will occur in the dependent variable when the independent variable is manipulated.

It states that the results are not due to chance and are significant in supporting the theory being investigated.

The alternative hypothesis can be directional, indicating a specific direction of the effect, or non-directional, suggesting a difference without specifying its nature. It’s what researchers aim to support or demonstrate through their study.

Null Hypothesis

The null hypothesis states no relationship exists between the two variables being studied (one variable does not affect the other). There will be no changes in the dependent variable due to manipulating the independent variable.

It states results are due to chance and are not significant in supporting the idea being investigated.

The null hypothesis, positing no effect or relationship, is a foundational contrast to the research hypothesis in scientific inquiry. It establishes a baseline for statistical testing, promoting objectivity by initiating research from a neutral stance.

Many statistical methods are tailored to test the null hypothesis, determining the likelihood of observed results if no true effect exists.

This dual-hypothesis approach provides clarity, ensuring that research intentions are explicit, and fosters consistency across scientific studies, enhancing the standardization and interpretability of research outcomes.

Nondirectional Hypothesis

A non-directional hypothesis, also known as a two-tailed hypothesis, predicts that there is a difference or relationship between two variables but does not specify the direction of this relationship.

It merely indicates that a change or effect will occur without predicting which group will have higher or lower values.

For example, “There is a difference in performance between Group A and Group B” is a non-directional hypothesis.

Directional Hypothesis

A directional (one-tailed) hypothesis predicts the nature of the effect of the independent variable on the dependent variable. It predicts in which direction the change will take place. (i.e., greater, smaller, less, more)

It specifies whether one variable is greater, lesser, or different from another, rather than just indicating that there’s a difference without specifying its nature.

For example, “Exercise increases weight loss” is a directional hypothesis.

Falsifiability

The Falsification Principle, proposed by Karl Popper , is a way of demarcating science from non-science. It suggests that for a theory or hypothesis to be considered scientific, it must be testable and irrefutable.

Falsifiability emphasizes that scientific claims shouldn’t just be confirmable but should also have the potential to be proven wrong.

It means that there should exist some potential evidence or experiment that could prove the proposition false.

However many confirming instances exist for a theory, it only takes one counter observation to falsify it. For example, the hypothesis that “all swans are white,” can be falsified by observing a black swan.

For Popper, science should attempt to disprove a theory rather than attempt to continually provide evidence to support a research hypothesis.

Can a Hypothesis be Proven?

Hypotheses make probabilistic predictions. They state the expected outcome if a particular relationship exists. However, a study result supporting a hypothesis does not definitively prove it is true.

All studies have limitations. There may be unknown confounding factors or issues that limit the certainty of conclusions. Additional studies may yield different results.

In science, hypotheses can realistically only be supported with some degree of confidence, not proven. The process of science is to incrementally accumulate evidence for and against hypothesized relationships in an ongoing pursuit of better models and explanations that best fit the empirical data. But hypotheses remain open to revision and rejection if that is where the evidence leads.

• Disproving a hypothesis is definitive. Solid disconfirmatory evidence will falsify a hypothesis and require altering or discarding it based on the evidence.
• However, confirming evidence is always open to revision. Other explanations may account for the same results, and additional or contradictory evidence may emerge over time.

We can never 100% prove the alternative hypothesis. Instead, we see if we can disprove, or reject the null hypothesis.

If we reject the null hypothesis, this doesn’t mean that our alternative hypothesis is correct but does support the alternative/experimental hypothesis.

Upon analysis of the results, an alternative hypothesis can be rejected or supported, but it can never be proven to be correct. We must avoid any reference to results proving a theory as this implies 100% certainty, and there is always a chance that evidence may exist which could refute a theory.

How to Write a Hypothesis

• Identify variables . The researcher manipulates the independent variable and the dependent variable is the measured outcome.
• Operationalized the variables being investigated . Operationalization of a hypothesis refers to the process of making the variables physically measurable or testable, e.g. if you are about to study aggression, you might count the number of punches given by participants.
• Decide on a direction for your prediction . If there is evidence in the literature to support a specific effect of the independent variable on the dependent variable, write a directional (one-tailed) hypothesis. If there are limited or ambiguous findings in the literature regarding the effect of the independent variable on the dependent variable, write a non-directional (two-tailed) hypothesis.
• Make it Testable : Ensure your hypothesis can be tested through experimentation or observation. It should be possible to prove it false (principle of falsifiability).
• Clear & concise language . A strong hypothesis is concise (typically one to two sentences long), and formulated using clear and straightforward language, ensuring it’s easily understood and testable.

Consider a hypothesis many teachers might subscribe to: students work better on Monday morning than on Friday afternoon (IV=Day, DV= Standard of work).

Now, if we decide to study this by giving the same group of students a lesson on a Monday morning and a Friday afternoon and then measuring their immediate recall of the material covered in each session, we would end up with the following:

• The alternative hypothesis states that students will recall significantly more information on a Monday morning than on a Friday afternoon.
• The null hypothesis states that there will be no significant difference in the amount recalled on a Monday morning compared to a Friday afternoon. Any difference will be due to chance or confounding factors.

More Examples

• Memory : Participants exposed to classical music during study sessions will recall more items from a list than those who studied in silence.
• Social Psychology : Individuals who frequently engage in social media use will report higher levels of perceived social isolation compared to those who use it infrequently.
• Developmental Psychology : Children who engage in regular imaginative play have better problem-solving skills than those who don’t.
• Clinical Psychology : Cognitive-behavioral therapy will be more effective in reducing symptoms of anxiety over a 6-month period compared to traditional talk therapy.
• Cognitive Psychology : Individuals who multitask between various electronic devices will have shorter attention spans on focused tasks than those who single-task.
• Health Psychology : Patients who practice mindfulness meditation will experience lower levels of chronic pain compared to those who don’t meditate.
• Organizational Psychology : Employees in open-plan offices will report higher levels of stress than those in private offices.
• Behavioral Psychology : Rats rewarded with food after pressing a lever will press it more frequently than rats who receive no reward.

Related Articles

Research Methodology

What Is a Focus Group?

Cross-Cultural Research Methodology In Psychology

What Is Internal Validity In Research?

Research Methodology , Statistics

What Is Face Validity In Research? Importance & How To Measure

Criterion Validity: Definition & Examples

Convergent Validity: Definition and Examples

Exploring the Null Hypothesis: Definition and Purpose

Updated: July 5, 2023 by Ken Feldman

Hypothesis testing is a branch of statistics in which, using data from a sample, an inference is made about a population parameter or a population probability distribution .

First, a hypothesis statement and assumption is made about the population parameter or probability distribution. This initial statement is called the Null Hypothesis and is denoted by H o. An alternative or alternate hypothesis (denoted Ha ), is then stated which will be the opposite of the Null Hypothesis.

The hypothesis testing process and analysis involves using sample data to determine whether or not you can be statistically confident that you can reject or fail to reject the H o. If the H o is rejected, the statistical conclusion is that the alternative or alternate hypothesis Ha is true.

Overview: What is the Null Hypothesis (Ho)? 

Hypothesis testing applies to all forms of statistical inquiry. For example, it can be used to determine whether there are differences between population parameters or an understanding about slopes of regression lines or equality of probability distributions.

In all cases, the first thing you do is state the Null and Alternate Hypotheses. The word Null in the context of hypothesis testing means “nothing” or “zero.”  

As an example, if we wanted to test whether there was a difference in two population means based on the calculations from two samples, we would state the Null Hypothesis in the form of: 

Ho: mu1 = mu2 or mu1- mu2 = 0  

In other words, there is no difference, or the difference is zero. Note that the notation is in the form of a population parameter, not a sample statistic. 

Since you are using sample data to make your inferences about the population, it’s possible you’ll make an error. In the case of the Null Hypothesis, we can make one of two errors.

•   Type 1 , or alpha error: An alpha error is when you mistakenly reject the Null and believe that something significant happened. In other words, you believe that the means of the two populations are different when they aren’t.
• Type 2, or beta error: A beta error is when you fail to reject the null when you should have.  In this case, you missed something significant and failed to take action. 

A classic example is when you get the results back from your doctor after taking a blood test. If the doctor says you have an infection when you really don’t, that is an alpha error. That is thinking that there is something significant going on when there isn’t. We also call that a false positive. The doctor rejected the null that “there was zero infection” and missed the call.

On the other hand, if the doctor told you that everything was OK when you really did have an infection, then he made a beta, or type 2, error. He failed to reject the Null Hypothesis when he should have. That is called a false negative.

The decision to reject or not to reject the Null Hypothesis is based on three numbers. 

• Alpha, which you get to choose. Alpha is the risk you are willing to assume of falsely rejecting the Null. The typical values for alpha are 1%, 5%, or 10%. Depending on the importance of the conclusion, you only want to falsely claim a difference when there is none, 1%, 5%, or 10% of the time.
• Beta, which is typically 20%. This means you’re willing to be wrong 20% of the time in failing to reject the null when you should have. 
• P-value, which is calculated from the data. The p-value is the actual risk you have in being wrong if you reject the null. You would like that to be low.  

Your decision as to what to do about the null is made by comparing the alpha value (your assumed risk) with the p-value (actual risk). If the actual risk is lower than your assumed risk, you can feel comfortable in rejecting the null and claiming something has happened. But, if the actual risk is higher than your assumed risk you will be taking a bigger risk than you want by rejecting the null.

RELATED: NULL VS. ALTERNATIVE HYPOTHESIS

3 benefits of the null hypothesis .

The stating and testing of the null hypothesis is the foundation of hypothesis testing. By doing so, you set the parameters for your statistical inference.

1. Statistical assurance of determining differences between population parameters

Just looking at the mathematical difference between the means of two samples and making a decision is woefully inadequate. By statistically testing the null hypothesis, you will have more confidence in any inferences you want to make about populations based on your samples.

2. Statistically based estimation of the probability of a population distribution

Many statistical tests require assumptions of specific distributions. Many of these tests assume that the population follows the normal distribution . If it doesn’t, the test may be invalid.  

3. Assess the strength of your conclusions as to what to do with the null hypothesis

Hypothesis testing calculations will provide some relative strength to your decisions as to whether you reject or fail to reject the null hypothesis.

Why is the Null Hypothesis important to understand?

The interpretation of the statistics relative to the null hypothesis is what’s important.

1. Properly write the null hypothesis to properly capture what you are seeking to prove

The null is always written in the same format. That is, the lack of difference or some other condition. The alternative hypothesis can be written in three formats depending on what you want to prove. 

2. Frame your statement and select an appropriate alpha risk

You don’t want to place too big of a hurdle or burden on your decision-making relative to action on the null hypothesis by selecting an alpha value that is too high or too low.

3. There are decision errors when deciding on how to respond to the Null Hypothesis

Since your decision relative to rejecting or not rejecting the null is based on statistical calculations, it is important to understand how that decision works. 

An industry example of using the Null Hypothesis 

The new director of marketing just completed the rollout of a new marketing campaign targeting the Hispanic market. Early indications showed that the campaign was successful in increasing sales in the Hispanic market. 

He came to that conclusion by comparing a sample of sales prior to the campaign and current sales after implementation of the campaign. He was anxious to proudly tell his boss how successful the campaign was. But, he decided to first check with his Lean Six Sigma Black Belt to see whether she agreed with his conclusion.

The Black Belt first asked the director his tolerance for risk of being wrong by telling the boss the campaign was successful when in fact, it wasn’t. That was the alpha value. The Director picked 5% since he was new and didn’t want to make a false claim so early in his career. He also picked 20% as his beta value.  

When the Black Belt was done analyzing the data, she found out that the p-value was 15%.  That meant if the director told the VP the campaign worked, there was a 15% chance he would be wrong and that the campaign probably needed some revising. Since he was only willing to be wrong 5% of the time, the decision was to not reject the null since his 5% assumed risk was less than the 15% actual risk.

3 best practices when thinking about the Null Hypothesis 

Using hypothesis testing to help make better data-driven decisions requires that you properly address the Null Hypothesis. 

1. Always use the proper nomenclature when stating the Null Hypothesis 

The null will always be in the form of decisions regarding the population, not the sample. 

2. The Null Hypothesis will always be written as the absence of some parameter or process characteristic

The writing of the Alternate Hypothesis can vary, so be sure you understand exactly what condition you are testing against. 

3. Pick a reasonable alpha risk so you’re not always failing to reject the Null Hypothesis

Being too cautious will lead you to make beta errors, and you’ll never learn anything about your population data. 

Frequently Asked Questions (FAQ) about the Null Hypothesis

What form should the null hypothesis be written in.

The Null Hypothesis should always be in the form of no difference or zero and always refer to the state of the population, not the sample. 

What is an alpha error? 

An alpha error, or Type 1 error, is rejecting the Null Hypothesis and claiming a significant event has occurred when, in fact, that is not true and the Null should not have been rejected.

How do I use the alpha error and p-value to decide on what decision I should make about the Null Hypothesis? 

The most common way of answering this is, “If the p-value is low (less than the alpha), the Null should be rejected. If the p-value is high (greater than the alpha) then the Null should not be rejected.”

Becoming familiar with the Null Hypothesis (Ho)

The proper writing of the Null Hypothesis is the basis for applying hypothesis testing to help you make better data-driven decisions. The format of the Null will always be in the form of zero, or the non-existence of some condition. It will always refer to a population parameter and not the sample you use to do your hypothesis testing calculations.

Be aware of the two types of errors you can make when deciding on what to do with the Null. Select reasonable risks values for your alpha and beta risks. By comparing your alpha risk with the calculated risk computed from the data, you will have sufficient information to make a wise decision as to whether you should reject the Null Hypothesis or not.

About the Author

Ken Feldman

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

7.3: The Research Hypothesis and the Null Hypothesis

• Last updated
• Save as PDF
• Page ID 18038

• Michelle Oja
• Taft College

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Hypotheses are predictions of expected findings.

The Research Hypothesis

A research hypothesis is a mathematical way of stating a research question.  A research hypothesis names the groups (we'll start with a sample and a population), what was measured, and which we think will have a higher mean.  The last one gives the research hypothesis a direction.  In other words, a research hypothesis should include:

• The name of the groups being compared.  This is sometimes considered the IV.
• What was measured.  This is the DV.
• Which group are we predicting will have the higher mean.  

There are two types of research hypotheses related to sample means and population means:  Directional Research Hypotheses and Non-Directional Research Hypotheses

Directional Research Hypothesis

If we expect our obtained sample mean to be above or below the other group's mean (the population mean, for example), we have a directional hypothesis. There are two options:

• Symbol:       \( \displaystyle \bar{X} > \mu \)
• (The mean of the sample is greater than than the mean of the population.)
• Symbol:     \( \displaystyle \bar{X} < \mu \)
• (The mean of the sample is less than than mean of the population.)

Example \(\PageIndex{1}\)

A study by Blackwell, Trzesniewski, and Dweck (2007) measured growth mindset and how long the junior high student participants spent on their math homework.  What’s a directional hypothesis for how scoring higher on growth mindset (compared to the population of junior high students) would be related to how long students spent on their homework?  Write this out in words and symbols.

Answer in Words:            Students who scored high on growth mindset would spend more time on their homework than the population of junior high students.

Answer in Symbols:         \( \displaystyle \bar{X} > \mu \) 

Non-Directional Research Hypothesis

A non-directional hypothesis states that the means will be different, but does not specify which will be higher.  In reality, there is rarely a situation in which we actually don't want one group to be higher than the other, so we will focus on directional research hypotheses.  There is only one option for a non-directional research hypothesis: "The sample mean differs from the population mean."  These types of research hypotheses don’t give a direction, the hypothesis doesn’t say which will be higher or lower.

A non-directional research hypothesis in symbols should look like this:    \( \displaystyle \bar{X} \neq \mu \) (The mean of the sample is not equal to the mean of the population).

Exercise \(\PageIndex{1}\)

What’s a non-directional hypothesis for how scoring higher on growth mindset higher on growth mindset (compared to the population of junior high students) would be related to how long students spent on their homework (Blackwell, Trzesniewski, & Dweck, 2007)?  Write this out in words and symbols.

Answer in Words:            Students who scored high on growth mindset would spend a different amount of time on their homework than the population of junior high students.

Answer in Symbols:        \( \displaystyle \bar{X} \neq \mu \) 

See how a non-directional research hypothesis doesn't really make sense?  The big issue is not if the two groups differ, but if one group seems to improve what was measured (if having a growth mindset leads to more time spent on math homework).  This textbook will only use directional research hypotheses because researchers almost always have a predicted direction (meaning that we almost always know which group we think will score higher).

The Null Hypothesis

The hypothesis that an apparent effect is due to chance is called the null hypothesis, written \(H_0\) (“H-naught”). We usually test this through comparing an experimental group to a comparison (control) group.  This null hypothesis can be written as:

\[\mathrm{H}_{0}: \bar{X} = \mu \nonumber \]

For most of this textbook, the null hypothesis is that the means of the two groups are similar.  Much later, the null hypothesis will be that there is no relationship between the two groups.  Either way, remember that a null hypothesis is always saying that nothing is different.  

This is where descriptive statistics diverge from inferential statistics.  We know what the value of \(\overline{\mathrm{X}}\) is – it’s not a mystery or a question, it is what we observed from the sample.  What we are using inferential statistics to do is infer whether this sample's descriptive statistics probably represents the population's descriptive statistics.  This is the null hypothesis, that the two groups are similar.  

Keep in mind that the null hypothesis is typically the opposite of the research hypothesis. A research hypothesis for the ESP example is that those in my sample who say that they have ESP would get more correct answers than the population would get correct, while the null hypothesis is that the average number correct for the two groups will be similar. 

In general, the null hypothesis is the idea that nothing is going on: there is no effect of our treatment, no relation between our variables, and no difference in our sample mean from what we expected about the population mean. This is always our baseline starting assumption, and it is what we seek to reject. If we are trying to treat depression, we want to find a difference in average symptoms between our treatment and control groups. If we are trying to predict job performance, we want to find a relation between conscientiousness and evaluation scores. However, until we have evidence against it, we must use the null hypothesis as our starting point.

In sum, the null hypothesis is always : There is no difference between the groups’ means OR There is no relationship between the variables .

In the next chapter, the null hypothesis is that there’s no difference between the sample mean   and population mean.  In other words:

• There is no mean difference between the sample and population.
• The mean of the sample is the same as the mean of a specific population.
• \(\mathrm{H}_{0}: \bar{X} = \mu \nonumber \)
• We expect our sample’s mean to be same as the population mean.

Exercise \(\PageIndex{2}\)

A study by Blackwell, Trzesniewski, and Dweck (2007) measured growth mindset and how long the junior high student participants spent on their math homework.  What’s the null hypothesis for scoring higher on growth mindset (compared to the population of junior high students) and how long students spent on their homework?  Write this out in words and symbols.

Answer in Words:            Students who scored high on growth mindset would spend a similar amount of time on their homework as the population of junior high students.

Answer in Symbols:    \( \bar{X} = \mu \)

Contributors and Attributions

Foster et al.  (University of Missouri-St. Louis, Rice University, & University of Houston, Downtown Campus)

Dr. MO ( Taft College )

Null Hypothesis and Alternative Hypothesis

• Inferential Statistics
• Statistics Tutorials
• Probability & Games
• Descriptive Statistics
• Applications Of Statistics
• Math Tutorials
• Pre Algebra & Algebra
• Exponential Decay
• Worksheets By Grade
• Ph.D., Mathematics, Purdue University
• M.S., Mathematics, Purdue University
• B.A., Mathematics, Physics, and Chemistry, Anderson University

Hypothesis testing involves the careful construction of two statements: the null hypothesis and the alternative hypothesis. These hypotheses can look very similar but are actually different.

How do we know which hypothesis is the null and which one is the alternative? We will see that there are a few ways to tell the difference.

The Null Hypothesis

The null hypothesis reflects that there will be no observed effect in our experiment. In a mathematical formulation of the null hypothesis, there will typically be an equal sign. This hypothesis is denoted by H 0 .

The null hypothesis is what we attempt to find evidence against in our hypothesis test. We hope to obtain a small enough p-value that it is lower than our level of significance alpha and we are justified in rejecting the null hypothesis. If our p-value is greater than alpha, then we fail to reject the null hypothesis.

If the null hypothesis is not rejected, then we must be careful to say what this means. The thinking on this is similar to a legal verdict. Just because a person has been declared "not guilty", it does not mean that he is innocent. In the same way, just because we failed to reject a null hypothesis it does not mean that the statement is true.

For example, we may want to investigate the claim that despite what convention has told us, the mean adult body temperature is not the accepted value of 98.6 degrees Fahrenheit . The null hypothesis for an experiment to investigate this is “The mean adult body temperature for healthy individuals is 98.6 degrees Fahrenheit.” If we fail to reject the null hypothesis, then our working hypothesis remains that the average adult who is healthy has a temperature of 98.6 degrees. We do not prove that this is true.

If we are studying a new treatment, the null hypothesis is that our treatment will not change our subjects in any meaningful way. In other words, the treatment will not produce any effect in our subjects.

The Alternative Hypothesis

The alternative or experimental hypothesis reflects that there will be an observed effect for our experiment. In a mathematical formulation of the alternative hypothesis, there will typically be an inequality, or not equal to symbol. This hypothesis is denoted by either H a or by H 1 .

The alternative hypothesis is what we are attempting to demonstrate in an indirect way by the use of our hypothesis test. If the null hypothesis is rejected, then we accept the alternative hypothesis. If the null hypothesis is not rejected, then we do not accept the alternative hypothesis. Going back to the above example of mean human body temperature, the alternative hypothesis is “The average adult human body temperature is not 98.6 degrees Fahrenheit.”

If we are studying a new treatment, then the alternative hypothesis is that our treatment does, in fact, change our subjects in a meaningful and measurable way.

The following set of negations may help when you are forming your null and alternative hypotheses. Most technical papers rely on just the first formulation, even though you may see some of the others in a statistics textbook.

• Null hypothesis: “ x is equal to y .” Alternative hypothesis “ x is not equal to y .”
• Null hypothesis: “ x is at least y .” Alternative hypothesis “ x is less than y .”
• Null hypothesis: “ x is at most y .” Alternative hypothesis “ x is greater than y .”
• An Example of a Hypothesis Test
• Hypothesis Test for the Difference of Two Population Proportions
• What Is a P-Value?
• How to Conduct a Hypothesis Test
• Hypothesis Test Example
• Chi-Square Goodness of Fit Test
• What Level of Alpha Determines Statistical Significance?
• How to Do Hypothesis Tests With the Z.TEST Function in Excel
• The Difference Between Type I and Type II Errors in Hypothesis Testing
• Type I and Type II Errors in Statistics
• The Runs Test for Random Sequences
• What 'Fail to Reject' Means in a Hypothesis Test
• What Is the Difference Between Alpha and P-Values?
• An Example of Chi-Square Test for a Multinomial Experiment
• Example of a Chi-Square Goodness of Fit Test
• Null Hypothesis Definition and Examples

• Search Search Please fill out this field.
• Corporate Finance
• Financial Ratios

Null Hypothesis: What Is It and How Is It Used in Investing?

Adam Hayes, Ph.D., CFA, is a financial writer with 15+ years Wall Street experience as a derivatives trader. Besides his extensive derivative trading expertise, Adam is an expert in economics and behavioral finance. Adam received his master's in economics from The New School for Social Research and his Ph.D. from the University of Wisconsin-Madison in sociology. He is a CFA charterholder as well as holding FINRA Series 7, 55 & 63 licenses. He currently researches and teaches economic sociology and the social studies of finance at the Hebrew University in Jerusalem.

What Is a Null Hypothesis?

A null hypothesis is a type of statistical hypothesis that proposes that no statistical significance exists in a set of given observations. Hypothesis testing is used to assess the credibility of a hypothesis by using sample data. Sometimes referred to simply as the "null," it is represented as H 0 .

The null hypothesis, also known as the conjecture, is used in quantitative analysis to test theories about markets, investing strategies, or economies to decide if an idea is true or false.

Key Takeaways

• A null hypothesis is a type of conjecture in statistics that proposes that there is no difference between certain characteristics of a population or data-generating process.
• The alternative hypothesis proposes that there is a difference.
• Hypothesis testing provides a method to reject a null hypothesis within a certain confidence level.
• If you can reject the null hypothesis, it provides support for the alternative hypothesis.
• Null hypothesis testing is the basis of the principle of falsification in science.

Investopedia / Alex Dos Diaz

How a Null Hypothesis Works

A null hypothesis is a type of conjecture in statistics that proposes that there is no difference between certain characteristics of a population or data-generating process. For example, a gambler may be interested in whether a game of chance is fair. If it is fair, then the expected earnings per play come to zero for both players. If the game is not fair, then the expected earnings are positive for one player and negative for the other. To test whether the game is fair, the gambler collects earnings data from many repetitions of the game, calculates the average earnings from these data, then tests the null hypothesis that the expected earnings are not different from zero.

If the average earnings from the sample data are sufficiently far from zero, then the gambler will reject the null hypothesis and conclude the alternative hypothesis—namely, that the expected earnings per play are different from zero. If the average earnings from the sample data are near zero, then the gambler will not reject the null hypothesis, concluding instead that the difference between the average from the data and zero is explainable by chance alone.

The null hypothesis assumes that any kind of difference between the chosen characteristics that you see in a set of data is due to chance. For example, if the expected earnings for the gambling game are truly equal to zero, then any difference between the average earnings in the data and zero is due to chance.

Analysts look to reject   the null hypothesis because doing so is a strong conclusion. This requires strong evidence in the form of an observed difference that is too large to be explained solely by chance. Failing to reject the null hypothesis—that the results are explainable by chance alone—is a weak conclusion because it allows that factors other than chance may be at work but may not be strong enough for the statistical test to detect them.

A null hypothesis can only be rejected, not proven.

The Alternative Hypothesis

An important point to note is that we are testing the null hypothesis because there is an element of doubt about its validity. Whatever information that is against the stated null hypothesis is captured in the alternative (alternate) hypothesis (H1).

For the above examples, the alternative hypothesis would be:

• Students score an average that is  not  equal to seven.
• The mean annual return of the mutual fund is  not  equal to 8% per year.

In other words, the alternative hypothesis is a direct contradiction of the null hypothesis.

Examples of a Null Hypothesis

Here is a simple example: A school principal claims that students in her school score an average of seven out of 10 in exams. The null hypothesis is that the population mean is 7.0. To test this null hypothesis, we record marks of, say, 30 students (sample) from the entire student population of the school (say 300) and calculate the mean of that sample.

We can then compare the (calculated) sample mean to the (hypothesized) population mean of 7.0 and attempt to reject the null hypothesis. (The null hypothesis here—that the population mean is 7.0—cannot be proved using the sample data. It can only be rejected.)

Take another example: The annual return of a particular  mutual fund  is claimed to be 8%. Assume that a mutual fund has been in existence for 20 years. The null hypothesis is that the mean return is 8% for the mutual fund. We take a random sample of annual returns of the mutual fund for, say, five years (sample) and calculate the sample mean. We then compare the (calculated) sample mean to the (claimed) population mean (8%) to test the null hypothesis.

For the above examples, null hypotheses are:

• Example A : Students in the school score an average of seven out of 10 in exams.
• Example B: Mean annual return of the mutual fund is 8% per year.

For the purposes of determining whether to reject the null hypothesis, the null hypothesis (abbreviated H 0 ) is assumed, for the sake of argument, to be true. Then the likely range of possible values of the calculated statistic (e.g., the average score on 30 students’ tests) is determined under this presumption (e.g., the range of plausible averages might range from 6.2 to 7.8 if the population mean is 7.0). Then, if the sample average is outside of this range, the null hypothesis is rejected. Otherwise, the difference is said to be “explainable by chance alone,” being within the range that is determined by chance alone.

How Null Hypothesis Testing Is Used in Investments

As an example related to financial markets, assume Alice sees that her investment strategy produces higher average returns than simply buying and holding a stock . The null hypothesis states that there is no difference between the two average returns, and Alice is inclined to believe this until she can conclude contradictory results.

Refuting the null hypothesis would require showing statistical significance, which can be found by a variety of tests. The alternative hypothesis would state that the investment strategy has a higher average return than a traditional buy-and-hold strategy.

One tool that can determine the statistical significance of the results is the p-value. A p-value represents the probability that a difference as large or larger than the observed difference between the two average returns could occur solely by chance.

A p-value that is less than or equal to 0.05 often indicates whether there is evidence against the null hypothesis. If Alice conducts one of these tests, such as a test using the normal model, resulting in a significant difference between her returns and the buy-and-hold returns (the p-value is less than or equal to 0.05), she can then reject the null hypothesis and conclude the alternative hypothesis.

How Is the Null Hypothesis Identified?

The analyst or researcher establishes a null hypothesis based on the research question or problem that they are trying to answer. Depending on the question, the null may be identified differently. For example, if the question is simply whether an effect exists (e.g., does X influence Y?) the null hypothesis could be H 0 : X = 0. If the question is instead, is X the same as Y, the H0 would be X = Y. If it is that the effect of X on Y is positive, H0 would be X > 0. If the resulting analysis shows an effect that is statistically significantly different from zero, the null can be rejected.

How Is Null Hypothesis Used in Finance?

In finance, a null hypothesis is used in quantitative analysis. A null hypothesis tests the premise of an investing strategy, the markets, or an economy to determine if it is true or false. For instance, an analyst may want to see if two stocks, ABC and XYZ, are closely correlated. The null hypothesis would be ABC ≠ XYZ.

How Are Statistical Hypotheses Tested?

Statistical hypotheses are tested by a four-step process . The first step is for the analyst to state the two hypotheses so that only one can be right. The next step is to formulate an analysis plan, which outlines how the data will be evaluated. The third step is to carry out the plan and physically analyze the sample data. The fourth and final step is to analyze the results and either reject the null hypothesis or claim that the observed differences are explainable by chance alone.

What Is an Alternative Hypothesis?

An alternative hypothesis is a direct contradiction of a null hypothesis. This means that if one of the two hypotheses is true, the other is false.

Sage Publishing. " Chapter 8: Introduction to Hypothesis Testing ," Pages 4–7.

Sage Publishing. " Chapter 8: Introduction to Hypothesis Testing ," Page 4.

Sage Publishing. " Chapter 8: Introduction to Hypothesis Testing ," Page 7.

• Terms of Service
• Editorial Policy
• Privacy Policy
• Your Privacy Choices

• Daily Crossword
• Word Puzzle
• Word Finder
• Word of the Day
• Synonym of the Day
• Word of the Year
• Language stories
• All featured
• Gender and sexuality
• All pop culture
• Writing hub
• Grammar essentials
• Commonly confused
• All writing tips
• Pop culture
• Writing tips

Advertisement

null hypothesis

• (in the statistical testing of a hypothesis) the hypothesis to be tested.
• statistics the residual hypothesis if the alternative hypothesis tested against it fails to achieve a predetermined significance level Compare hypothesis testing alternative hypothesis

Discover More

Word history and origins.

Origin of null hypothesis 1

Compare Meanings

How does null hypothesis compare to similar and commonly confused words? Explore the most common comparisons:

• null hypothesis vs. alternative hypothesis

Example Sentences

Then they collect evidence to test whether that null hypothesis is true.

Rejecting a null hypothesis doesn’t tell an investigator anything new.

Starting in the 1930s, Fisher devised a type of significance testing to analyze the likelihood of a null hypothesis, which a researcher could propose as either an effect or no effect.

The most common analysis procedure in fMRI experiments, null hypothesis tests, require that the researcher designate a statistical threshold.

If data disprove the null hypothesis, then they can conclude an effect of noise on whales.

Miles D. Williams

Visiting Assistant Professor | Denison University

• Download My CV
• Send Me an Email
• View My LinkedIn
• Follow Me on Twitter

When the Research Hypothesis Is the Null

Posted on May 13, 2024 by Miles Williams in Methods   Statistics  

Back to Blog

What should you do if your research hypothesis is the null hypothesis? In other words, how should you approach hypothesis testing if your theory predicts no effect between two variables? I and a coauthor are working on a paper where a couple of our proposed hypotheses look like this, and we got some push-back from a reviewer about it. This prompted me to go down a rabbit hole of journal articles and message boards to see how others handle this situation. I quickly found that I waded into a contentious issue that’s connected to a bigger philosophical debate about the merits of hypothesis testing in general and whether the null hypothesis in particular as a bench-mark for hypothesis testing is even logically sound.

There’s too much to unpack with this debate for me to cover in a single blog post (and I’m sure I’d get some of the key points wrong anyway if I tried). The main issue I want to explore in this post is the practical problem of how to approach testing a null research hypothesis. From an applied perspective, this is a tricky problem that raises issues with how we calculate and interpret p-values. Thankfully, there is a sound solution for the null research hypothesis which I explore in greater detail below. It’s called a two one-sided test, and it’s easy to implement once you know what it is.

The usual approach

Most of the time when doing research, a scientist usually has a research hypothesis that goes something like X has a positive effect on Y . For example, a political scientist might propose that a get-out-the-vote (GOTV) campaign ( X ) will increase voter turnout ( Y ).

The typical approach for testing this claim might be to estimate a regression model with voter turnout as the outcome and the GOTV campaign as the explanatory variable of interest:

Y = α + β X + ε

If the parameter β > 0, this would support the hypothesis that GOTV campaigns improve voter turnout. To test this hypothesis, in practice the researcher would actually test a different hypothesis that we call the null hypothesis. This is the hypothesis that says there is no true effect of GOTV campaigns on voter turnout.

By proposing and testing the null, we now have a point of reference for calculating a measure of uncertainty—that is, the probability of observing an empirical effect of a certain magnitude or greater if the null hypothesis is true. This probability is called a p-value, and by convention if it is less than 0.05 we say that we can reject the null hypothesis.

For the hypothetical regression model proposed above, to get this p-value we’d estimate β, then calculate its standard error, and then we’d take the ratio of the former to the latter giving us what’s called a t-statistic or t-value. Under the null hypothesis, the t-value has a known distribution which makes it really easy to map any t-value to a p-value. The below figure illustrates using a hypothetical data sample of size N = 200. You can see that the t-statistic’s distribution has a distinct bell shape centered around 0. You can also see the range of t-values in blue where if we observed them in our empirical data we’d fail to reject the null hypothesis at the p < 0.05 level. Values in gray are t-values that would lead us to reject the null hypothesis at this same level.

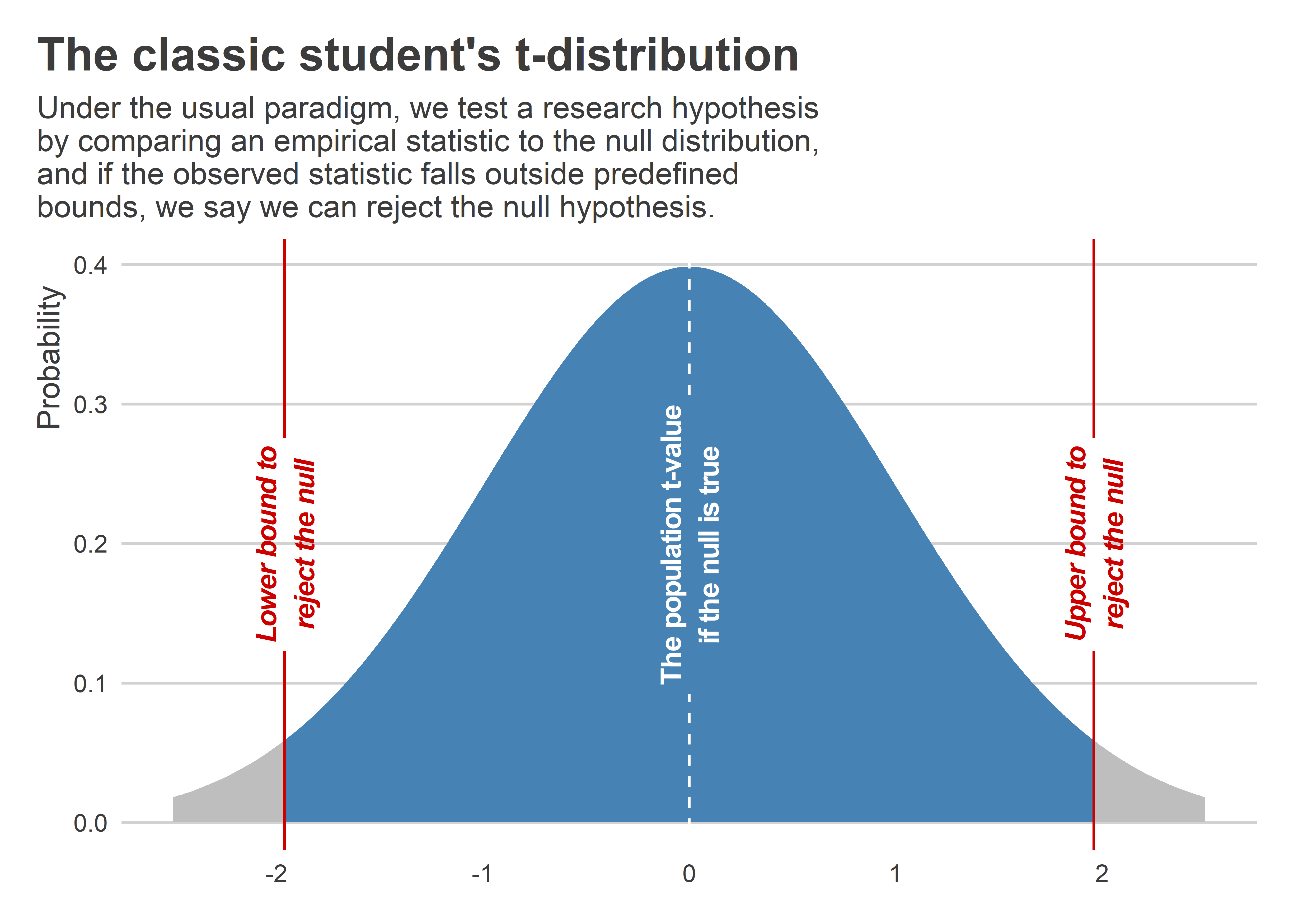
When the null is the research hypothesis we want to test

There’s nothing new or special here. If you have even a basic stats background (particularly with Frequentist statistics), the conventional approach to hypothesis testing is pretty ubiquitous. Things get more tricky when our research hypothesis is that there is no effect. Say for a certain set of theoretical reasons we think that GOTV campaigns are basically useless at increasing voter turnout. If this argument is true, then if we estimate the following regression model, we’d expect β = 0.

The problem here is that our substantive research hypothesis is also the one that we want to try to find evidence against. We could just proceed like usual and just say that if we fail to reject the null this is evidence in support of our theory, but the problem with doing this is that failure to reject the null is not the same thing as finding support for the null hypothesis.

There are a few ideas in the literature for how we should approach this instead. Many of these approaches are Bayesian, but most of my research relies on Frequentist statistics, so these approaches were a no-go for me. However, there is one really simple approach that is consistent with the Frequentist paradigm: equivalence testing . The idea is simple. Propose some absolute effect size that is of minimal interest and then test whether an observed effect is different from it. This minimum effect is called the “smallest effect size of interest” (SESOI). I read about the approach in an article by Harms and Lakens (2018) in the Journal of Clinical and Translational Research .

Say, for example, that we deemed a t-value of +/-1.96 (the usual threshold for rejecting the null hypothesis) as extreme enough to constitute good evidence of a non-zero effect. We could make the appropriate adjustments to our t-distribution to identify a new range of t-values that would allow us to reject the hypothesis that an effect is non-zero. This is illustrated in the below figure. We can now see a range of t-values in the middle where we’d have t-values such that we could reject the non-zero hypothesis at the p < 0.05 level. This distribution looks like it’s been inverted relative to the usual null distribution. The reason is that with this approach what we’re doing is conducting a pair of alternative one-tailed tests. We’re testing both the hypothesis that β / se(β) - 1.96 > 0 and β / se(β) + 1.96 < 0. In the Harms and Lakens paper cited above, they call this approach two one-sided tests or TOST (I’m guessing this is pronounced “toast”).

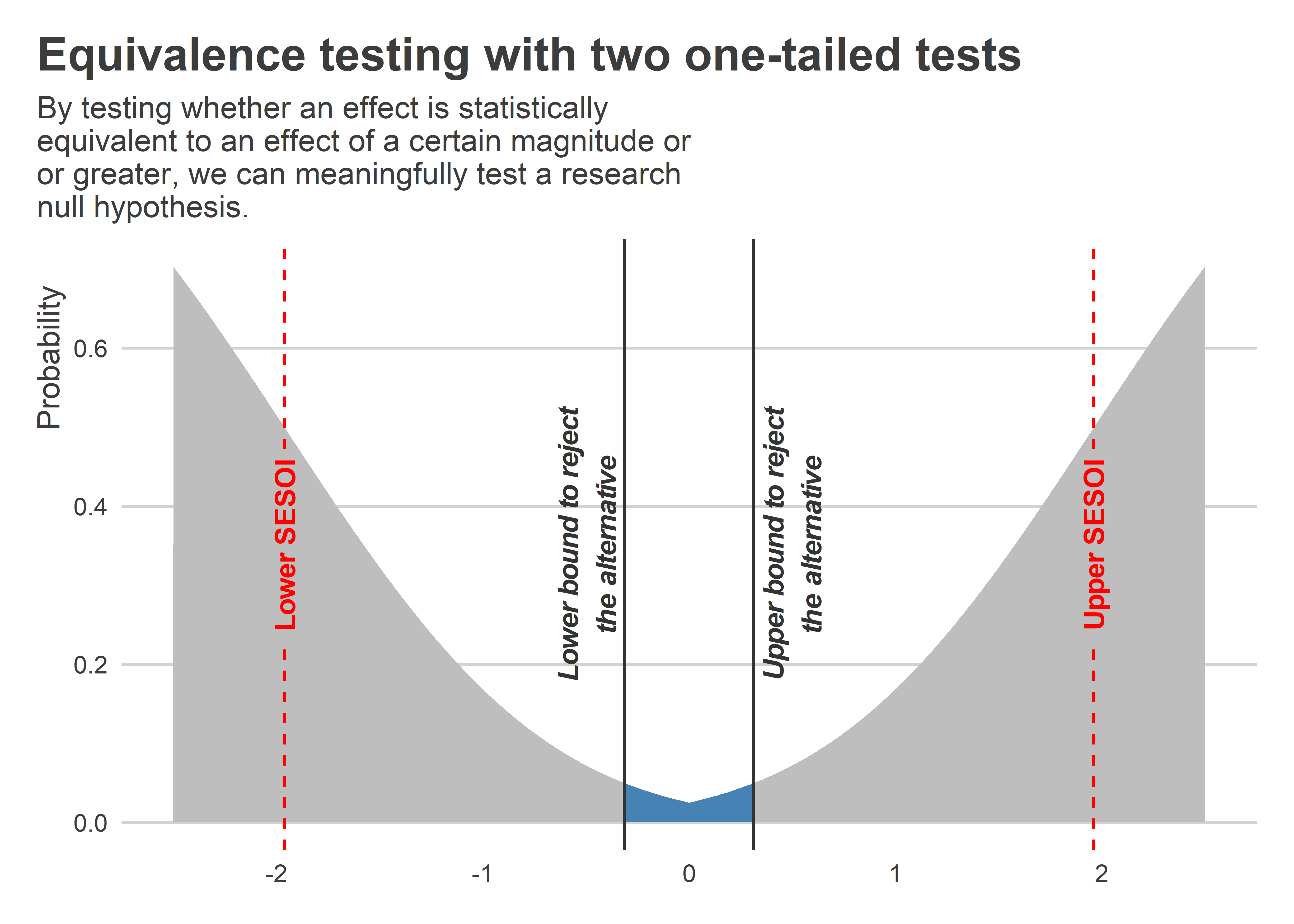
Something to pay attention to with this approach is that the observed t-statistic needs to be very small in absolute magnitude for us to reject the hypothesis of a non-zero effect. This means that the bar for testing a null research hypothesis is actually quite high. This is demonstrated using the following simulation in R. Using the {seerrr} package, I had R generate 1,000 random draws (each of size 200) for a pair of variables x and y where the former is a binary “treatment” and the latter is a random normal “outcome.” By design, there is no true causal relationship between these variables. Once I simulated the data, I then generated a set of estimates of the effect of x on y for each simulated dataset and collected the results in an object called sim_ests . I then visualized two metrics that that I calculated with the simulated results: (1) the rejection rate for the null hypothesis test and (2) the rejection rate for the two one-sided equivalence tests. As you can see, if we were to try to test a research null hypothesis the usual way, we’d expect to be able to fail to reject the null about 95% of the time. Conversely, if we were to use the two one-sided equivalence tests, we’d expect to reject the non-zero alternative hypothesis only about 25% of the time. I tested out a few additional simulations to see if a larger sample size would lead to improvements in power (not shown), but no dice.

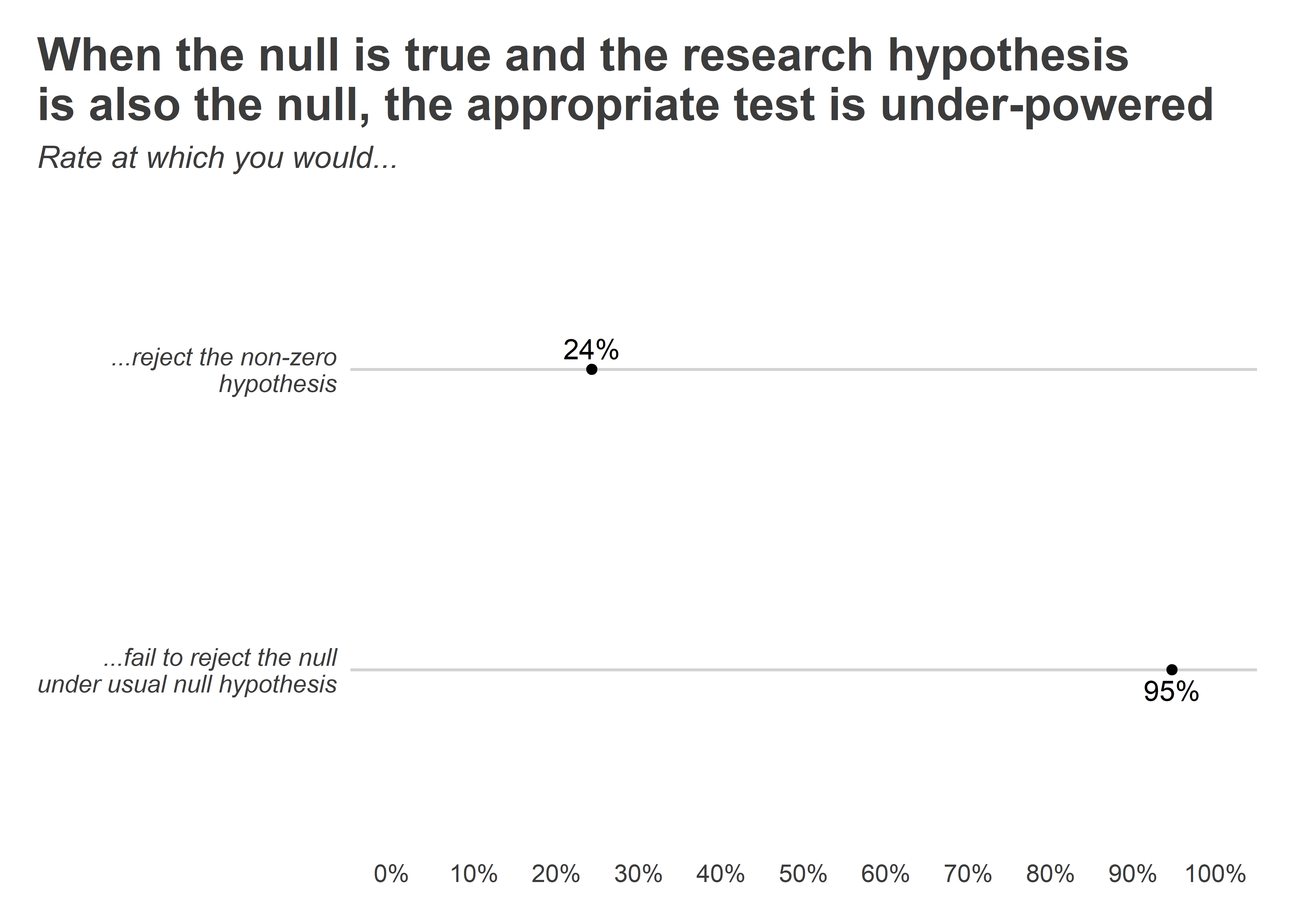
The two one-sided tests approach strikes me as a nice method when dealing with a null research hypothesis. It’s actually pretty easy to implement, too. The one downside is that this test is under-powered. If the null is true, it will only reject the alternative 25% of the time (though you could select a different non-zero alternative which would possibly give you more power). However, this isn’t all bad. The flip side of the coin is that this is a really conservative test, so if you can reject the alternative that puts you on solid rhetorical footing to show the data really do seem consistent with the null.

• School Guide
• Mathematics
• Number System and Arithmetic
• Trigonometry
• Probability
• Mensuration
• Maths Formulas
• Class 8 Maths Notes
• Class 9 Maths Notes
• Class 10 Maths Notes
• Class 11 Maths Notes
• Class 12 Maths Notes
• Alternative Dispute Resolution (ADR): Meaning, Types and FAQs
• Level of Significance-Definition, Steps and Examples
• Difference Between Hypothesis And Theory
• What is Dihybrid Cross? Examples and an Overview
• Real-life Applications of Hypothesis Testing
• T-Test in Statistics: Formula, Types and Steps
• Hypothesis Testing Formula
• Independent Sample t Test in R
• Alternate Interior Angles
• How do you define and measure your product hypothesis?
• Difference between Alternate and Alternative
• Introduction to Power Analysis in Python
• Difference between Null and Alternate Hypothesis
• Inductive Reasoning | Definition, Types, & Examples
• Python unittest - assertIn() function
• Python unittest - assertNotIsInstance() function
• Python unittest - assertIsNone() function
• Python unittest - assertIsInstance() function

Alternative Hypothesis: Definition, Types and Examples

In statistical hypothesis testing, the alternative hypothesis is an important proposition in the hypothesis test. The goal of the hypothesis test is to demonstrate that in the given condition, there is sufficient evidence supporting the credibility of the alternative hypothesis instead of the default assumption made by the null hypothesis.

Alternative Hypotheses

Both hypotheses include statements with the same purpose of providing the researcher with a basic guideline. The researcher uses the statement from each hypothesis to guide their research. In statistics, alternative hypothesis is often denoted as H a or H 1 .

Table of Content

What is a Hypothesis?

Alternative hypothesis, types of alternative hypothesis, difference between null and alternative hypothesis, formulating an alternative hypothesis, example of alternative hypothesis, application of alternative hypothesis.

“A hypothesis is a statement of a relationship between two or more variables.” It is a working statement or theory that is based on insufficient evidence.

While experimenting, researchers often make a claim, that they can test. These claims are often based on the relationship between two or more variables. “What causes what?” and “Up to what extent?” are a few of the questions that a hypothesis focuses on answering. The hypothesis can be true or false, based on complete evidence.

While there are different hypotheses, we discuss only null and alternate hypotheses. The null hypothesis, denoted H o , is the default position where variables do not have a relation with each other. That means the null hypothesis is assumed true until evidence indicates otherwise. The alternative hypothesis, denoted H 1 , on the other hand, opposes the null hypothesis. It assumes a relation between the variables and serves as evidence to reject the null hypothesis.

Example of Hypothesis:

Mean age of all college students is 20.4 years. (simple hypothesis).

An Alternative Hypothesis is a claim or a complement to the null hypothesis. If the null hypothesis predicts a statement to be true, the Alternative Hypothesis predicts it to be false. Let’s say the null hypothesis states there is no difference between height and shoe size then the alternative hypothesis will oppose the claim by stating that there is a relation.

We see that the null hypothesis assumes no relationship between the variables whereas an alternative hypothesis proposes a significant relation between variables. An alternative theory is the one tested by the researcher and if the researcher gathers enough data to support it, then the alternative hypothesis replaces the null hypothesis.

Null and alternative hypotheses are exhaustive, meaning that together they cover every possible outcome. They are also mutually exclusive, meaning that only one can be true at a time.

There are a few types of alternative hypothesis that we will see:

1. One-tailed test H 1 : A one-tailed alternative hypothesis focuses on only one region of rejection of the sampling distribution. The region of rejection can be upper or lower.

• Upper-tailed test H 1 : Population characteristic > Hypothesized value
• Lower-tailed test H 1 : Population characteristic < Hypothesized value

2. Two-tailed test H 1 : A two-tailed alternative hypothesis is concerned with both regions of rejection of the sampling distribution.

3. Non-directional test H 1 : A non-directional alternative hypothesis is not concerned with either region of rejection; rather, it is only concerned that null hypothesis is not true.

4. Point test H 1 : Point alternative hypotheses occur when the hypothesis test is framed so that the population distribution under the alternative hypothesis is a fully defined distribution, with no unknown parameters; such hypotheses are usually of no practical interest but are fundamental to theoretical considerations of statistical inference and are the basis of the Neyman–Pearson lemma.

the differences between Null Hypothesis and Alternative Hypothesis is explained in the table below:

Formulating an alternative hypothesis means identifying the relationships, effects or condition being studied. Based on the data we conclude that there is a different inference from the null-hypothesis being considered.

• Understand the null hypothesis.
• Consider the alternate hypothesis
• Choose the type of alternate hypothesis (one-tailed or two-tailed)

Alternative hypothesis must be true when the null hypothesis is false. When trying to identify the information need for alternate hypothesis statement, look for the following phrases:

• “Is it reasonable to conclude…”
• “Is there enough evidence to substantiate…”
• “Does the evidence suggest…”
• “Has there been a significant…”

When alternative hypotheses in mathematical terms, they always include an inequality ( usually ≠, but sometimes < or >) . When writing the alternate hypothesis, make sure it never includes an “=” symbol.

To help you write your hypotheses, you can use the template sentences below.

Does independent variable affect dependent variable?

• Null Hypothesis (H 0 ): Independent variable does not affect dependent variable.
• Alternative Hypothesis (H a ): Independent variable affects dependent variable.

Various examples of Alternative Hypothesis includes:

Two-Tailed Example

• Research Question : Do home games affect a team’s performance?
• Null-Hypothesis: Home games do not affect a team’s performance.
• Alternative Hypothesis: Home games have an effect on team’s performance.
• Research Question: Does sleeping less lead to depression?
• Null-Hypothesis: Sleeping less does not have an effect on depression.
• Alternative Hypothesis : Sleeping less has an effect on depression.

One-Tailed Example

• Research Question: Are candidates with experience likely to get a job?
• Null-Hypothesis: Experience does not matter in getting a job.
• Alternative Hypothesis: Candidates with work experience are more likely to receive an interview.
• Alternative Hypothesis : Teams with home advantage are more likely to win a match.

Some applications of Alternative Hypothesis includes:

• Rejecting Null-Hypothesis : A researcher performs additional research to find flaws in the null hypothesis. Following the research, which uses the alternative hypothesis as a guide, they may decide whether they have enough evidence to reject the null hypothesis.
• Guideline for Research : An alternative and null hypothesis include statements with the same purpose of providing the researcher with a basic guideline. The researcher uses the statement from each hypothesis to guide their research.
• New Theories : Alternative hypotheses can provide the opportunity to discover new theories that a researcher can use to disprove an existing theory that may not have been backed up by evidence.

We defined the relationship that exist between null-hypothesis and alternative hypothesis. While the null hypothesis is always a default assumption about our test data, the alternative hypothesis puts in all the effort to make sure the null hypothesis is disproved.

Null-hypothesis always explores new relationships between the independent variables to find potential outcomes from our test data. We should note that for every null hypothesis, one or more alternate hypotheses can be developed.

Also Check:

Mathematics Maths Formulas Branches of Mathematics

FAQs on Alternative Hypothesis

What is hypothesis.

A hypothesis is a statement of a relationship between two or more variables.” It is a working statement or theory that is based on insufficient evidence.

What is an Alternative Hypothesis?

Alternative hypothesis, denoted by H 1 , opposes the null-hypothesis. It assumes a relation between the variables and serves as an evidence to reject the null-hypothesis.

What is the Difference between Null-Hypothesis and Alternative Hypothesis?

Null hypothesis is the default claim that assumes no relationship between variables while alternative hypothesis is the opposite claim which considers statistical significance between the variables.

What is Alternative and Experimental Hypothesis?

Null hypothesis (H 0 ) states there is no effect or difference, while the alternative hypothesis (H 1 or H a ) asserts the presence of an effect, difference, or relationship between variables. In hypothesis testing, we seek evidence to either reject the null hypothesis in favor of the alternative hypothesis or fail to do so.

Please Login to comment...

Similar reads.

• Math-Statistics
• School Learning

Improve your Coding Skills with Practice

What kind of Experience do you want to share?