assignment 8 equation of a circle

High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

In order to access this I need to be confident with:

Solving equations

Distance formula

Square roots

Equation of a circle

Here you will learn about the equation of a circle, including how to recognize the equation of a circle, form an equation of a circle given its radius and center, use the equation of a circle to find its center and radius, and solve problems involving the equation of a circle.

Students will first learn about the equation of a circle as part of geometry in high school.

What is the equation of a circle?

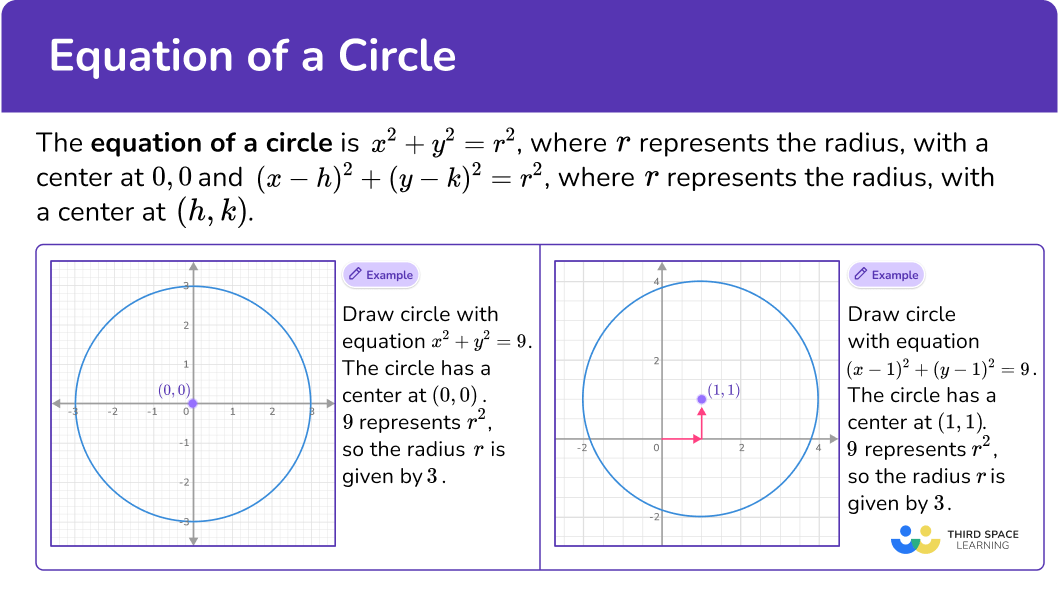
The equation of a circle is x^2+y^2=r^2, where r represents the radius, with a center at 0,0 and (x-h)^2+(y-k)^2=r^2, where r represents the radius, with a center at (h,k).

The definition of a circle is a set of all points on a plane that are a fixed distance from a center. That distance is called the radius.

To understand the equation of a circle, consider the drawing below of a circle on a set of axes with the center at the origin.

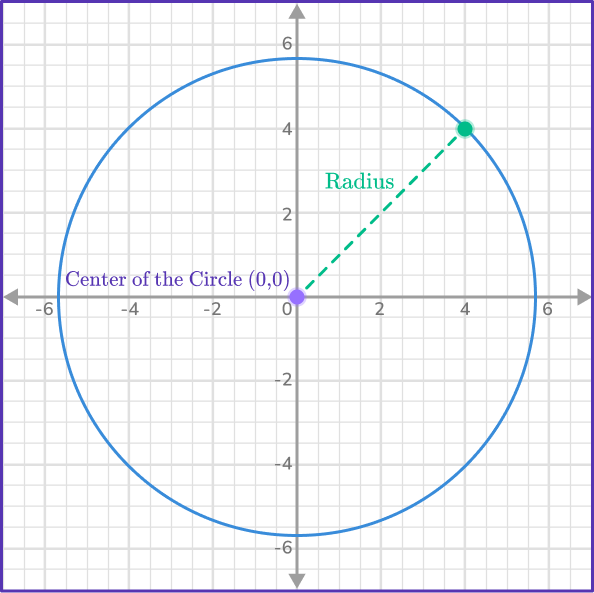
Now consider a right angled triangle created when the radius of the circle is the hypotenuse of the right triangle.

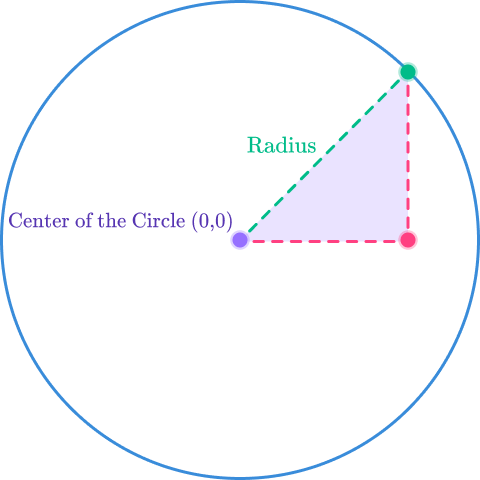
• The horizontal line is the distance to the x coordinate
• The vertical line is the distance to the y coordinate
• The hypotenuse is the distance of the radius

You can now apply Pythagoras’ theorem to the above. Therefore, the general form of the equation of a circle centered at (0,0) is:

x^2+y^2=r^2

x = x coordinate

y= y coordinate

For example,

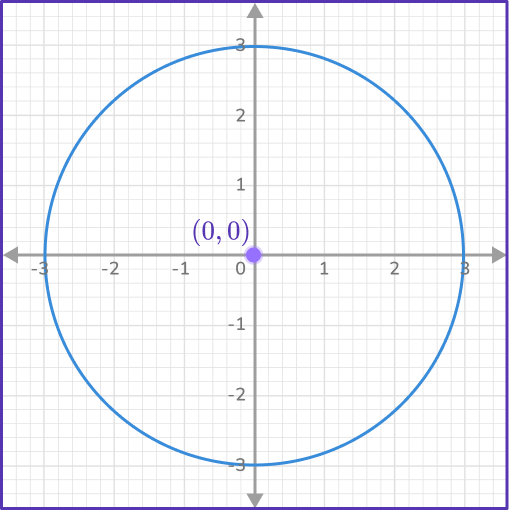
Draw circle with equation x^2+y^2=9.

The circle has a center at (0,0).

9 represents r^2, so the radius r is 3.

But what about a circle that is not centered on the origin? Let’s look at the same circle as above, but in a different position.

The radius of the circle below is still 3, but now the center is at (1,1). This means all the points on the circle have shifted up 1 and right 1.

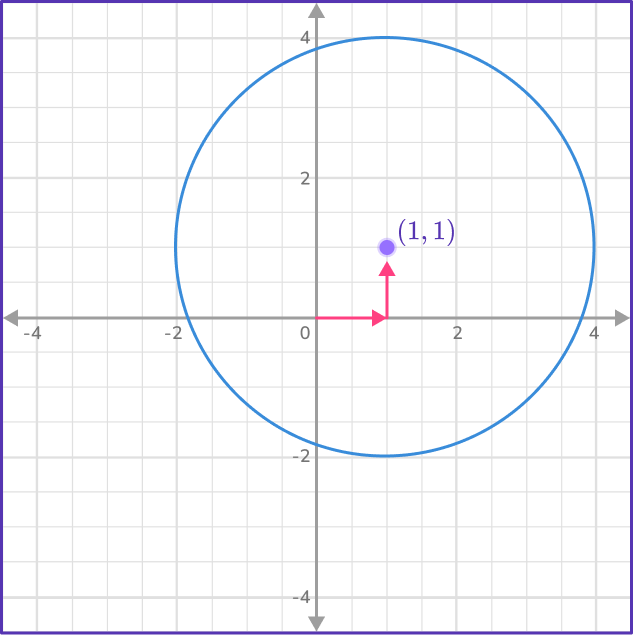
Since x^2+y^2=r^2 is true for all circles a (0,0), you can shift the circle back down to the origin.

To do that, you need to shift all the \textbf{x} coordinates left \bf{1} on the x- axis and shift all the \textbf{y} coordinates down \bf{1} on the y- axis to return this circle to the origin.

This leaves us with the equation (x-1)^2+(y-1)^2=9.

What about if this same circle was in another position?

The radius of the circle below is still 3, but now the center is at (-1,-1). This means all the points on the circle have shifted left 1 and down 1.

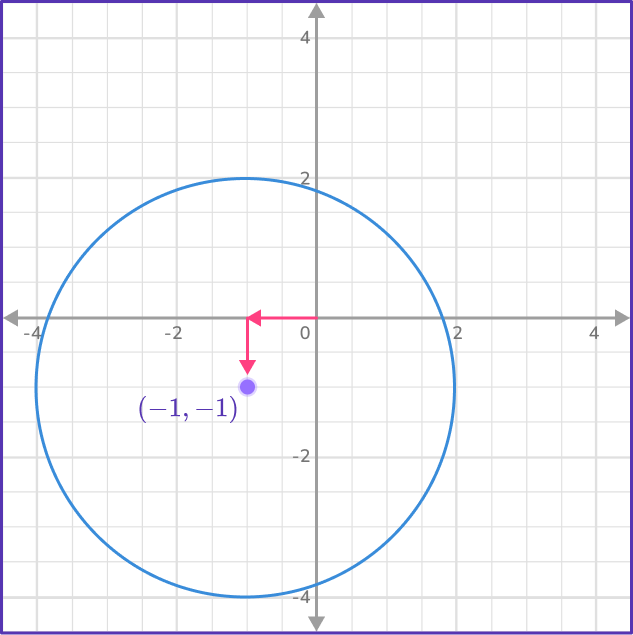
Since x^2+y^2=r^2 is true for all circles a (0,0), you need to shift all the \textbf{x} coordinates right \bf{1} and shift all the \textbf{y} coordinates up \bf{1} to return this circle to the origin. This leaves us with the equation (x+1)^2+(y+1)^2=9.

Therefore, the general form of the equation of any circle is:

(x-h)^{2}+(y-k)^{2}=r^{2}

h= x coordinate of center of the circle

k = y coordinate of center of the circle

r = radius of the circle

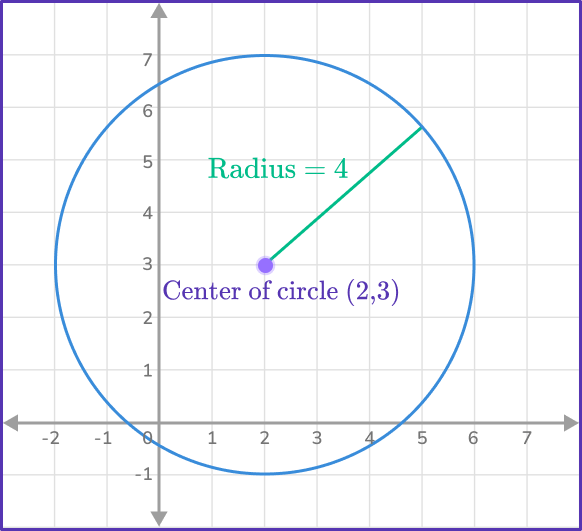
Draw the circle with equation (x-2)^2+(y-3)^2=4^2.

h = x coordinate of center = 2

k = y coordinate of center = 3

Coordinates of the center = (2,3)

r = length of radius = 4

What is the equation of the circle with a center of (2,5) and a radius of 10~{cm}?

The standard equation of a circle is (x-h)^2+(y-k)^2=r^2.

• The x -coordinate of center of the circle is 2
• The y -coordinate of the center of the circle is 5
• The radius is 10

\begin{aligned} &(x-h)^{2}+(y-k)^{2}=r^{2} \\\\ &(x-2)^{2}+(y-5)^{2}=10^{2} \\\\ &(x-2)^{2}+(y-5)^{2}=100 \end{aligned}

Common Core State Standards

How does this relate to high school math?

• Geometry – Expressing Geometric Properties with Equations (HSG.GPE.A.1) Derive the equation of a circle of given center and radius using the Pythagorean Theorem; complete the square to find the center and radius of a circle given by an equation.

[FREE] Types of Graphs Check for Understanding Quiz (Grade 5 to 8)

Use this quiz to check your grade 5 to 8 students’ understanding of type of graphs. 15+ questions with answers covering a range of 5th to 8th grade type of graphs topics to identify areas of strength and support!

How to use the equation of a circle

In order to use the equation of a circle:

Write the general equation of a circle.

State any variables you know.

Substitute any values you know into the equation.

Use the information you have to solve the problem.

Clearly state the answer.

Equation of a circle examples

Example 1: writing the equation of a circle with center at the origin.

What is the equation of the circle with a center at the origin?

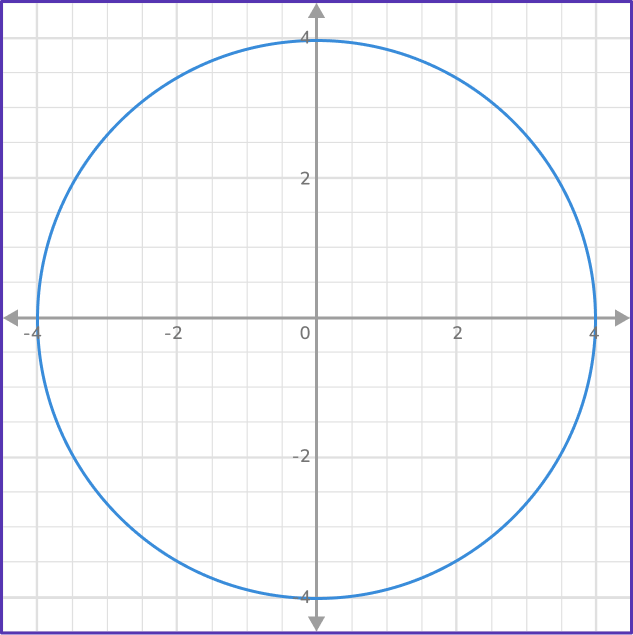
x^2+y^2=r^2 for circles at the origin.

2 State any variables you know.

The distance from the center (0,0) to the circle is 4.

Radius (r) = 4

3 Substitute any values you know into the equation.

x^2+y^2=4^2

4 Use the information you have to solve the problem.

Simplify the equation by squaring the radius.

\begin{aligned} &x^{2}+y^{2}=4^{2} \\\\ &x^{2}+y^{2}=16 \end{aligned}

5 Clearly state the answer.

The equation of the circle is: x^2+y^2=16

Example 2: finding the radius of a circle given its equation

What is the radius of the circle with the equation x^2+y^2=4?

Radius, r, is unknown.

Equation of the circle is given as x^2+y^2=4.

You do not know any variables so we are unable to substitute here.

You know that the radius squared is equal to 4, so

\begin{aligned} r^{2}&=4 \\\\ r&=\sqrt{4} \\\\ r&=2 \end{aligned}

Note: You only use the positive value as the radius’ measure of distance.

The radius is 2.

Example 3: writing the equation of a circle with center at the origin

What is the equation of a circle with a radius of \sqrt5 and a center at the origin?

Radius (r) = \sqrt5

x^{2}+y^{2}=(\sqrt{5})^{2}

\begin{aligned} &x^{2}+y^{2}=(\sqrt{5})^{2} \\\\ &x^{2}+y^{2}=5 \end{aligned}

The equation of the circle is: x^2+y^2=5

Example 4: given points – find the center of a circle

What is the equation of the circle with diameter endpoints at (-5,3) and (9,3)?

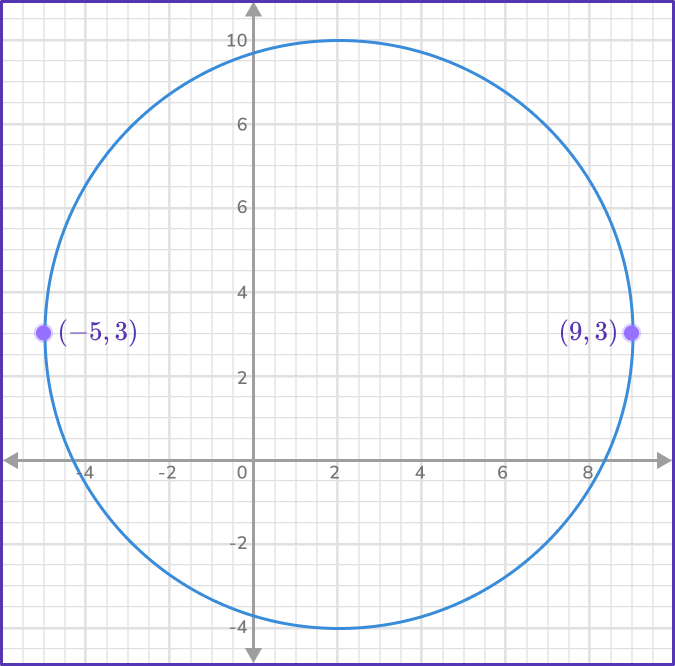
(x-h)^2+(y-k)^2=r^2, where r represents the radius, with a center at (h,k).

The distance from (-5,3) to the point (9,3) on the circle is 14. This is the diameter of the circle. The length of the radius is half the length of the diameter.

Radius (r) = 7

The center is at the midpoint of the diameter. Counting over 7 from (-5,3) shows that the center is at (2,3).

\begin{aligned} & h=2 \\\\ & k=3 \end{aligned}

(x-2)^2+(y-3)^2=7^2

\begin{aligned} & (x-2)^2+(y-3)^2=7^2 \\\\ & (x-2)^2+(y-3)^2=49 \end{aligned}

The equation of the circle is: (x-2)^2+(y-3)^2=49

Example 5: finding the center and radius of a circle given its equation

What is the center and radius of the circle with the equation

(x+2)^2+(y-5)^2=8?

The radius squared (r^2) = 8

You know that the radius squared is equal to 8, so

\begin{aligned} & r^2=8 \\\\ & r=\sqrt{8} \\\\ & r=2 \sqrt{2} \end{aligned}

The radius is 2\sqrt{2} and the center is at (-2,5).

Example 6: state the equation given the center and radius

What is the equation of a circle with a radius of \sqrt20 and a center at (4, -8)?

(x-h)^2+(y-k)^2=r^2 for circles at (h, k).

Radius (r) = \sqrt20

(x-4)^2+(y-(-8))^2=(\sqrt{20})^2

Simplify the equation.

\begin{aligned} & (x-4)^2+(y-(-8))^2=(\sqrt{20})^2 \\\\ & (x-4)^2+(y+8)^2=20 \end{aligned}

The equation of the circle is: (x-4)^2+(y+8)^2=20

Teaching tips for equation of a circle

• Be sure that students have a good understanding of coordinate geometry before asking them to graph circles and derive their equations or proofs.
• Let students use a graphing calculator to explore how changing the values for h, k and r change a circle.

Easy mistakes to make

• Forgetting the radius is squared in the equation Remember, in the equation the radius is shown as a squared value. To find the radius, you need to square root this value.
• Thinking the radius can be negative The radius cannot be negative because the radius is a length; it must always be a positive value.
• Confusing the location of the center with (x-h)^2+(y-k)^2=r^2 The equation indicates how a circle would need to shift to return to the origin. Therefore, the signs in the equation are opposite the signs in the coordinate. For example, An origin of (3, –4) would need to shift left 3 and up 4, which is (x-3)^2+(y+4)^2=r^2.
• Confusing equation of a circle with quadratic equations The equation of a circle and a quadratic equation are not the same. A quadratic equation appears on a graph as a parabola, not a circle. For example, x^2+5x+4 is a quadratic equation. This equation can be factored as (x+1)(x+4). While they share some symbol commonalities, this is NOT the same as (x-h)^2+(y-k)^2=r^2 or x^2+y^2=r^2.
• Not recognizing the equation in other forms You may need to simplify, combine like terms or balance the sides of the equation to get the standard form of the equation of a circle.

Related types of graphs lessons

• Linear graph

Practice equation of a circle questions

1) What is the equation of a circle with a radius of 4 and a center at the origin?

The equation of a circle with a center at the origin is x^2+y^2=r^2.

\begin{aligned} & x^2+y^2=r^2 \\\\ & x^2+y^2=4^2 \\\\ & x^2+y^2=16 \end{aligned}

2) What is the equation of a circle of the circle?

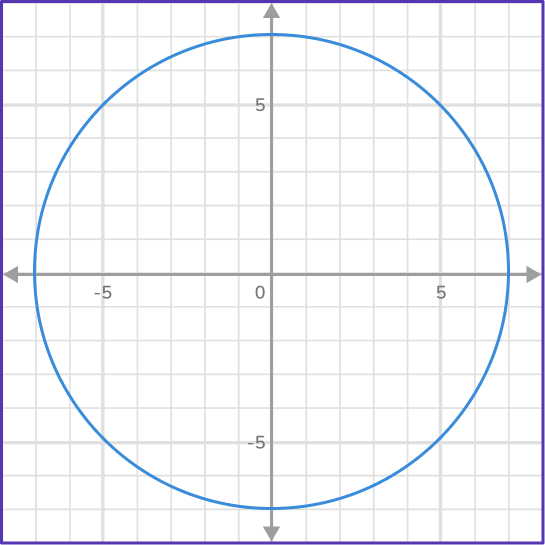
One diameter of the circle goes from (-6,0) to (6,0). This means the center is (0,0) or at the origin.

\begin{aligned} & x^2+y^2=r^2 \\\\ & x^2+y^2=6^2 \\\\ & x^2+y^2=36 \end{aligned}

3) What is the equation of a circle with a radius of \sqrt3 and a center at (-2, 3)?

The equation of a circle with a center at (h,k) is (x-h)^2+(y-k)^2=r^2.

\begin{aligned} & (x-h)^2+(y-k)^2=r^2 \\\\ & (x-(-2)^2+(y-3)^2=(\sqrt{3})^2 \\\\ & (x+2)^2+(y-3)^2=3 \end{aligned}

4) What is the radius of the circle with the equation x^2+y^2=100?

\begin{aligned} r^{2}&=100 \\\\ r&=\sqrt{100} \\\\ r&=10 \end{aligned}

5) What is the radius and the coordinates of the center of the circle with the equation \left(x-\cfrac{1}{2}\right)^2+(y+3)^2=25?

center: \left(-\cfrac{1}{2}, 3\right) and radius: 625

\left(\cfrac{1}{2},-3\right) and radius: 5

\left(-3, \cfrac{1}{2}\right) and radius: 625

1\left(-\cfrac{1}{2}, 3\right) and radius: 5

The equation of a circle with a center at (h,k) is

(x-h)^2+(y-k)^2=r^2.

\begin{aligned} & \left(x-\cfrac{1}{2}\right)^2+(y+3)^2=25 \\\\ & \left(x-\cfrac{1}{2}\right)^2+(y-(-3))^2=5^2 \\\\ & h=\cfrac{1}{2} \\\\ & k=-3 \\\\ & r=5 \end{aligned}

6) What is the equation of the circle ?

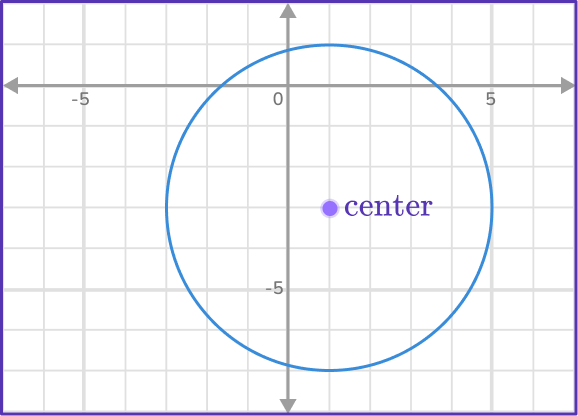
\begin{aligned} & (x-1)^2+(y-(-3))^2=4^2 \\\\ & (x-1)^2+(y+3)^2=16 \end{aligned}

Equation of a circle FAQs

The center is a fixed point inside the circle that is the same distance from all points on the circle. It can be found by finding the midpoint of any diameter.

Yes, but only if the same coefficient keeps the shape as a circle. Note also that to find the radius, the equation needs to be simplified. For example, 3 x^2+3 y^2=9 will simplify to x^2+y^2=3.

They can be used to solve real world problems and problems in geometry (for example, finding a circular conic section).

The next lessons are

• Number patterns
• Systems of equations
• Circle theorems
• Standard form

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs .

[FREE] Common Core Practice Tests (Grades 3 to 6)

Prepare for math tests in your state with these Grade 3 to Grade 6 practice assessments for Common Core and state equivalents.

40 multiple choice questions and detailed answers to support test prep, created by US math experts covering a range of topics!

Privacy Overview

Circle Equations

A circle is easy to make:

Draw a curve that is "radius" away from a central point.

All points are the same distance from the center.

In fact the definition of a circle is

Circle: The set of all points on a plane that are a fixed distance from a center.

Circle on a Graph

Let us put a circle of radius 5 on a graph:

Now let's work out exactly where all the points are.

We make a right-angled triangle:

And then use Pythagoras :

x 2 + y 2 = 5 2

There are an infinite number of those points, here are some examples:

In all cases a point on the circle follows the rule x 2 + y 2 = radius 2

We can use that idea to find a missing value

Example: x value of 2, and a radius of 5

(The ± means there are two possible values: one with + the other with − )

And here are the two points:

More General Case

Now let us put the center at (a,b)

So the circle is all the points (x,y) that are "r" away from the center (a,b) .

Now lets work out where the points are (using a right-angled triangle and Pythagoras ):

It is the same idea as before, but we need to subtract a and b :

(x−a) 2 + (y−b) 2 = r 2

And that is the "Standard Form" for the equation of a circle!

It shows all the important information at a glance: the center (a,b) and the radius r .

Example: A circle with center at (3,4) and a radius of 6:

Start with:

Put in (a,b) and r:

(x−3) 2 + (y−4) 2 = 6 2

We can then use our algebra skills to simplify and rearrange that equation, depending on what we need it for.

Try it Yourself

"general form".

But you may see a circle equation and not know it !

Because it may not be in the neat "Standard Form" above.

As an example, let us put some values to a, b and r and then expand it

And we end up with this:

x 2 + y 2 − 2x − 4y − 4 = 0

It is a circle equation, but "in disguise"!

So when you see something like that think "hmm ... that might be a circle!"

In fact we can write it in "General Form" by putting constants instead of the numbers:

x 2 + y 2 + Ax + By + C = 0

Note: General Form always has x 2 + y 2 for the first two terms .

Going From General Form to Standard Form

Now imagine we have an equation in General Form :

How can we get it into Standard Form like this?

The answer is to Complete the Square (read about that) twice ... once for x and once for y :

Example: x 2 + y 2 − 2x − 4y − 4 = 0

Now complete the square for x (take half of the −2, square it, and add to both sides):

(x 2 − 2x + (−1) 2 ) + (y 2 − 4y) = 4 + (−1) 2

And complete the square for y (take half of the −4, square it, and add to both sides):

(x 2 − 2x + (−1) 2 ) + (y 2 − 4y + (−2) 2 ) = 4 + (−1) 2 + (−2) 2

And we have it in Standard Form!

(Note: this used the a=1, b=2, r=3 example from before, so we got it right!)

Unit Circle

If we place the circle center at (0,0) and set the radius to 1 we get:

How to Plot a Circle by Hand

1. Plot the center (a,b)

2. Plot 4 points "radius" away from the center in the up, down, left and right direction

3. Sketch it in!

Example: Plot (x−4) 2 + (y−2) 2 = 25

The formula for a circle is (x−a) 2 + (y−b) 2 = r 2

So the center is at (4,2)

And r 2 is 25 , so the radius is √25 = 5

So we can plot:

• The Center: (4,2)
• Up: (4,2+5) = (4,7)
• Down: (4,2−5) = (4,−3)
• Left: (4−5,2) = (−1,2)
• Right: (4+5,2) = (9,2)

Now, just sketch in the circle the best we can!

How to Plot a Circle on the Computer

We need to rearrange the formula so we get "y=".

We should end up with two equations (top and bottom of circle) that can then be plotted.

So the center is at (4,2) , and the radius is √25 = 5

Rearrange to get "y=":

So when we plot these two equations we should have a circle:

• y = 2 + √[25 − (x−4) 2 ]
• y = 2 − √[25 − (x−4) 2 ]

Try plotting those functions on the Function Grapher .

It is also possible to use the Equation Grapher to do it all in one go.

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Digital SAT Math

Course: digital sat math   >   unit 5.

• Circle equations | Lesson
• Circle equations — Basic example
• Circle equations — Harder example

Circle equations: foundations

• (Choice A)   The center is ( 6 , − 8 ) ‍   and the radius is 1 ‍   . A The center is ( 6 , − 8 ) ‍   and the radius is 1 ‍   .
• (Choice B)   The center is ( − 6 , 8 ) ‍   and the radius is 1 ‍   . B The center is ( − 6 , 8 ) ‍   and the radius is 1 ‍   .
• (Choice C)   The center is ( − 6 , − 8 ) ‍   and the radius is 1 ‍   . C The center is ( − 6 , − 8 ) ‍   and the radius is 1 ‍   .
• (Choice D)   The center is ( 6 , 8 ) ‍   and the radius is 1 ‍   . D The center is ( 6 , 8 ) ‍   and the radius is 1 ‍   .

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

11.2: Distance and Midpoint Formulas and Circles

• Last updated
• Save as PDF
• Page ID 5188

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Objectives

By the end of this section, you will be able to:

Use the Distance Formula

Use the midpoint formula.

• Write the equation of a circle in standard form
• Graph a circle

Before you get started, take this readiness quiz.

• Find the length of the hypotenuse of a right triangle whose legs are \(12\) and \(16\) inches. If you missed this problem, review Example 2.34.
• Factor: \(x^{2}-18 x+81\). If you missed this problem, review Example 6.24.
• Solve by completing the square: \(x^{2}-12 x-12=0\). If you missed this problem, review Example 9.22.

In this chapter we will be looking at the conic sections, usually called the conics, and their properties. The conics are curves that result from a plane intersecting a double cone—two cones placed point-to-point. Each half of a double cone is called a nappe.

There are four conics—the circle , parabola , ellipse , and hyperbola . The next figure shows how the plane intersecting the double cone results in each curve.

Each of the curves has many applications that affect your daily life, from your cell phone to acoustics and navigation systems. In this section we will look at the properties of a circle.

We have used the Pythagorean Theorem to find the lengths of the sides of a right triangle. Here we will use this theorem again to find distances on the rectangular coordinate system. By finding distance on the rectangular coordinate system, we can make a connection between the geometry of a conic and algebra—which opens up a world of opportunities for application.

Our first step is to develop a formula to find distances between points on the rectangular coordinate system. We will plot the points and create a right triangle much as we did when we found slope in Graphs and Functions. We then take it one step further and use the Pythagorean Theorem to find the length of the hypotenuse of the triangle—which is the distance between the points.

Example \(\PageIndex{1}\)

Use the rectangular coordinate system to find the distance between the points \((6,4)\) and \((2,1)\).

Exercise \(\PageIndex{1}\)

Use the rectangular coordinate system to find the distance between the points \((6,1)\) and \((2,-2)\).

Exercise \(\PageIndex{2}\)

Use the rectangular coordinate system to find the distance between the points \((5,3)\) and \((-3,-3)\).

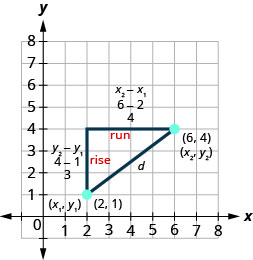
The method we used in the last example leads us to the formula to find the distance between the two points \(\left(x_{1}, y_{1}\right)\) and \(\left(x_{2}, y_{2}\right)\).

When we found the length of the horizontal leg we subtracted \(6−2\) which is \(x_{2}-x_{1}\).

When we found the length of the vertical leg we subtracted \(4−1\) which is \(y_{2}-y_{1}\).

If the triangle had been in a different position, we may have subtracted \(x_{1}-x_{2}\) or \(y_{1}-y_{2}\). The expressions \(x_{2}-x_{1}\) and \(x_{1}-x_{2}\) vary only in the sign of the resulting number. To get the positive value-since distance is positive- we can use absolute value. So to generalize we will say \(\left|x_{2}-x_{1}\right|\) and \(\left|y_{2}-y_{1}\right|\).

In the Pythagorean Theorem, we substitute the general expressions \(\left|x_{2}-x_{1}\right|\) and \(\left|y_{2}-y_{1}\right|\) rather than the numbers.

\(\begin{array}{l c}{} & {a^{2}+b^{2}=c^{2}} \\ {\text {Substitute in the values. }}&{(|x_{2}-x_{1}|)^{2}+(|y_{2}-y_{1}|)^{2}=d^{2}} \\ {\text{Squaring the expressions makes}}&{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}=d^{2}} \\ \text{them positive, so we eliminate} \\\text{the absolute value bars.}\\ {\text{Use the Square Root Property.}}&{d=\pm\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}}\\ {\text{Distance is positive, so eliminate}}&{d=\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}}\\\text{the negative value.}\end{array}\)

This is the Distance Formula we use to find the distance \(d\) between the two points \((x_{1},y_{1})\) and \((x_{2}, y_{2})\).

Definition \(\PageIndex{1}\)

Distance Formula

The distance \(d\) between the two points \((x_{1},y_{1})\) and \((x_{2}, y_{2})\) is

\(d=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)

Example \(\PageIndex{2}\)

Use the Distance Formula to find the distance between the points \((-5,-3)\) and \((7,2)\).

Write the Distance Formula.

Label the points, \(\left( \begin{array}{c}{x_{1}, y_{1}} \\ {-5,-3}\end{array}\right)\), \(\left( \begin{array}{l}{x_{2}, y_{2}} \\ {7,2}\end{array}\right)\) and substitute.

\(d=\sqrt{(7-(-5))^{2}+(2-(-3))^{2}}\)

\(d=\sqrt{12^{2}+5^{2}}\) \(d=\sqrt{144+25}\) \(d=\sqrt{169}\) \(d=13\)

Exercise \(\PageIndex{3}\)

Use the Distance Formula to find the distance between the points \((-4,-5)\) and \((5,7)\).

Exercise \(\PageIndex{4}\)

Use the Distance Formula to find the distance between the points \((-2,-5)\) and \((-14,-10)\).

Example \(\PageIndex{3}\)

Use the Distance Formula to find the distance between the points \((10,−4)\) and \((−1,5)\). Write the answer in exact form and then find the decimal approximation, rounded to the nearest tenth if needed.

Label the points, \(\left( \begin{array}{c}{x_{1}, y_{1}} \\ {10,-4}\end{array}\right)\), \(\left( \begin{array}{c}{x_{2}, y_{2}} \\ {-1,5}\end{array}\right)\) and substitute.

\(d=\sqrt{(-1-10)^{2}+(5-(-4))^{2}}\)

\(d=\sqrt{(-11)^{2}+9^{2}}\) \(d=\sqrt{121+81}\) \(d=\sqrt{202}\)

Since \(202\) is not a perfect square, we can leave the answer in exact form or find a decimal approximation.

\(d=\sqrt{202}\) or \(d \approx 14.2\)

Exercise \(\PageIndex{5}\)

Use the Distance Formula to find the distance between the points \((−4,−5)\) and \((3,4)\). Write the answer in exact form and then find the decimal approximation, rounded to the nearest tenth if needed.

\(d=\sqrt{130}, d \approx 11.4\)

Exercise \(\PageIndex{6}\)

Use the Distance Formula to find the distance between the points \((−2,−5)\) and \((−3,−4)\). Write the answer in exact form and then find the decimal approximation, rounded to the nearest tenth if needed.

\(d=\sqrt{2}, d \approx 1.4\)

It is often useful to be able to find the midpoint of a segment. For example, if you have the endpoints of the diameter of a circle, you may want to find the center of the circle which is the midpoint of the diameter. To find the midpoint of a line segment, we find the average of the \(x\)-coordinates and the average of the \(y\)-coordinates of the endpoints.

Definition \(\PageIndex{2}\)

Midpoint Formula

The midpoint of the line segment whose endpoints are the two points \(\left(x_{1}, y_{1}\right)\) and \(\left(x_{2}, y_{2}\right)\) is

\(\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\right)\)

To find the midpoint of a line segment, we find the average of the \(x\)-coordinates and the average of the \(y\)-coordinates of the endpoints.

Example \(\PageIndex{4}\)

Use the Midpoint Formula to find the midpoint of the line segments whose endpoints are \((−5,−4)\) and \((7,2)\). Plot the endpoints and the midpoint on a rectangular coordinate system.

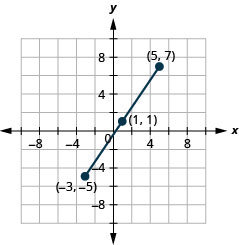
Exercise \(\PageIndex{7}\)

Use the Midpoint Formula to find the midpoint of the line segments whose endpoints are \((−3,−5)\) and \((5,7)\). Plot the endpoints and the midpoint on a rectangular coordinate system.

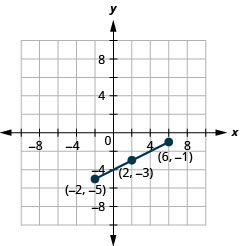
Exercise \(\PageIndex{8}\)

Use the Midpoint Formula to find the midpoint of the line segments whose endpoints are \((−2,−5)\) and \((6,−1)\). Plot the endpoints and the midpoint on a rectangular coordinate system.

Both the Distance Formula and the Midpoint Formula depend on two points, \(\left(x_{1}, y_{1}\right)\) and \(\left(x_{2}, y_{2}\right)\). It is easy to confuse which formula requires addition and which subtraction of the coordinates. If we remember where the formulas come from, is may be easier to remember the formulas.

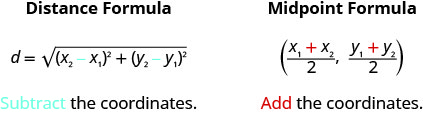
Write the Equation of a Circle in Standard Form

As we mentioned, our goal is to connect the geometry of a conic with algebra. By using the coordinate plane, we are able to do this easily.

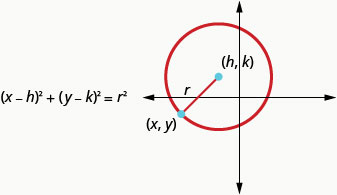
We define a circle as all points in a plane that are a fixed distance from a given point in the plane. The given point is called the center, \((h,k)\), and the fixed distance is called the radius , \(r\), of the circle.

Definition \(\PageIndex{3}\)

A circle is all points in a plane that are a fixed distance from a given point in the plane. The given point is called the center , \((h,k)\), and the fixed distance is called the radius , \(r\), of the circle.

This is the standard form of the equation of a circle with center, \((h,k)\), and radius, \(r\).

Definition \(\PageIndex{4}\)

The standard form of the equation of a circle with center, \((h,k)\), and radius, \(r\), is

Example \(\PageIndex{5}\)

Write the standard form of the equation of the circle with radius \(3\) and center \((0,0)\).

Exercise \(\PageIndex{9}\)

Write the standard form of the equation of the circle with a radius of \(6\) and center \((0,0)\).

\(x^{2}+y^{2}=36\)

Exercise \(\PageIndex{10}\)

Write the standard form of the equation of the circle with a radius of \(8\) and center \((0,0)\).

\(x^{2}+y^{2}=64\)

In the last example, the center was \((0,0)\). Notice what happened to the equation. Whenever the center is \((0,0)\), the standard form becomes \(x^{2}+y^{2}=r^{2}\).

Example \(\PageIndex{6}\)

Write the standard form of the equation of the circle with radius \(2\) and center \((−1,3)\).

Exercise \(\PageIndex{11}\)

Write the standard form of the equation of the circle with a radius of \(7\) and center \((2,−4)\).

\((x-2)^{2}+(y+4)^{2}=49\)

Exercise \(\PageIndex{12}\)

Write the standard form of the equation of the circle with a radius of \(9\) and center \((−3,−5)\).

\((x+3)^{2}+(y+5)^{2}=81\)

In the next example, the radius is not given. To calculate the radius, we use the Distance Formula with the two given points.

Example \(\PageIndex{7}\)

Write the standard form of the equation of the circle with center \((2,4)\) that also contains the point \((−2,1)\).

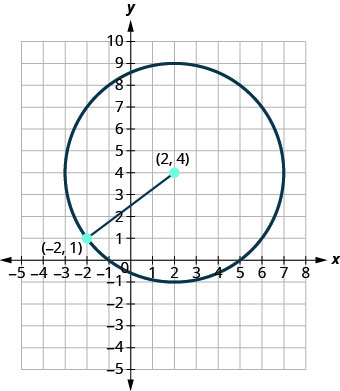
The radius is the distance from the center to any point on the circle so we can use the distance formula to calculate it. We will use the center \((2,4)\) and point \((−2,1)\)

Use the Distance Formula to find the radius.

\(r=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)

Substitute the values. \(\left( \begin{array}{l}{x_{1}, y_{1}} \\ {2,4}\end{array}\right), \left( \begin{array}{c}{x_{2}, y_{2}} \\ {-2,1}\end{array}\right)\)

\(r=\sqrt{(-2-2)^{2}+(1-4)^{2}}\)

\(r=\sqrt{(-4)^{2}+(-3)^{2}}\) \(r=\sqrt{16+9}\) \(r=\sqrt{25}\) \(r=5\)

Now that we know the radius, \(r=5\), and the center, \((2,4)\), we can use the standard form of the equation of a circle to find the equation.

Use the standard form of the equation of a circle.

\((x-h)^{2}+(y-k)^{2}=r^{2}\)

Substitute in the values.

\((x-2)^{2}+(y-4)^{2}=5^{2}\)

\((x-2)^{2}+(y-4)^{2}=25\)

Exercise \(\PageIndex{13}\)

Write the standard form of the equation of the circle with center \((2,1)\) that also contains the point \((−2,−2)\).

\((x-2)^{2}+(y-1)^{2}=25\)

Exercise \(\PageIndex{14}\)

Write the standard form of the equation of the circle with center \((7,1)\) that also contains the point \((−1,−5)\).

\((x-7)^{2}+(y-1)^{2}=100\)

Graph a Circle

Any equation of the form \((x-h)^{2}+(y-k)^{2}=r^{2}\) is the standard form of the equation of a circle with center, \((h,k)\), and radius, \(r\) . We can then graph the circle on a rectangular coordinate system.

Note that the standard form calls for subtraction from \(x\) and \(y\). In the next example, the equation has \(x+2\), so we need to rewrite the addition as subtraction of a negative.

Example \(\PageIndex{8}\)

Find the center and radius, then graph the circle: \((x+2)^{2}+(y-1)^{2}=9\).

Exercise \(\PageIndex{15}\)

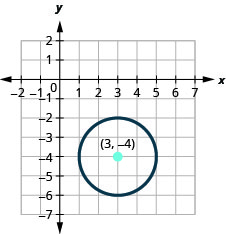
• Find the center and radius, then
• Graph the circle: \((x-3)^{2}+(y+4)^{2}=4\).
• The circle is centered at \((3,-4)\) with a radius of \(2\).

Exercise \(\PageIndex{16}\)

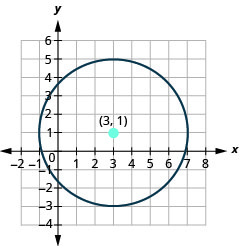
• Graph the circle: \((x-3)^{2}+(y-1)^{2}=16\).
• The circle is centered at \((3,1)\) with a radius of \(4\).

To find the center and radius, we must write the equation in standard form. In the next example, we must first get the coefficient of \(x^{2}, y^{2}\) to be one.

Example \(\PageIndex{9}\)

Find the center and radius and then graph the circle, \(4 x^{2}+4 y^{2}=64\).

Exercise \(\PageIndex{17}\)

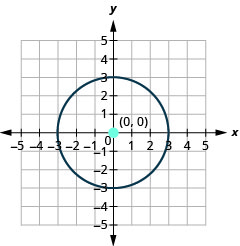
• Graph the circle: \(3 x^{2}+3 y^{2}=27\)
• The circle is centered at \((0,0)\) with a radius of \(3\).

Exercise \(\PageIndex{18}\)

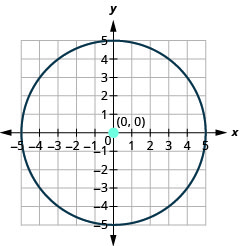
• Graph the circle: \(5 x^{2}+5 y^{2}=125\)
• The circle is centered at \((0,0)\) with a radius of \(5\).

If we expand the equation from Example 11.1.8, \((x+2)^{2}+(y-1)^{2}=9\), the equation of the circle looks very different.

\((x+2)^{2}+(y-1)^{2}=9\)

Square the binomials.

\(x^{2}+4 x+4+y^{2}-2 y+1=9\)

Arrange the terms in descending degree order, and get zero on the right

\(x^{2}+y^{2}+4 x-2 y-4=0\)

This form of the equation is called the general form of the equation of the circle .

Definition \(\PageIndex{5}\)

The general form of the equation of a circle is

\(x^{2}+y^{2}+a x+b y+c=0\)

If we are given an equation in general form, we can change it to standard form by completing the squares in both \(x\) and \(y\). Then we can graph the circle using its center and radius.

Example \(\PageIndex{10}\)

• Graph the circle: \(x^{2}+y^{2}-4 x-6 y+4=0\)

We need to rewrite this general form into standard form in order to find the center and radius.

Exercise \(\PageIndex{19}\)

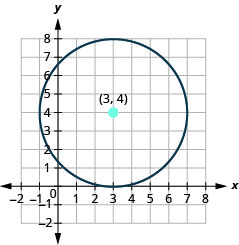
• Graph the circle: \(x^{2}+y^{2}-6 x-8 y+9=0\).
• The circle is centered at \((3,4)\) with a radius of \(4\).

Exercise \(\PageIndex{20}\)

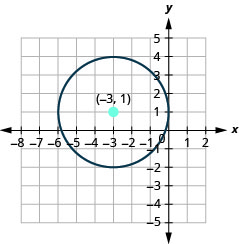
• Graph the circle: \(x^{2}+y^{2}+6 x-2 y+1=0\)
• The circle is centered at \((-3,1)\) with a radius of \(3\).

In the next example, there is a \(y\)-term and a \(y^{2}\)-term. But notice that there is no \(x\)-term, only an \(x^{2}\)-term. We have seen this before and know that it means \(h\) is \(0\). We will need to complete the square for the \(y\) terms, but not for the \(x\) terms.

Example \(\PageIndex{11}\)

• Graph the circle: \(x^{2}+y^{2}+8 y=0\)

Exercise \(\PageIndex{21}\)

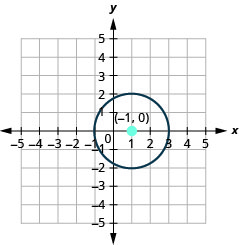
• Graph the circle: \(x^{2}+y^{2}-2 x-3=0\).
• The circle is centered at \((-1,0)\) with a radius of \(2\).

Exercise \(\PageIndex{22}\)

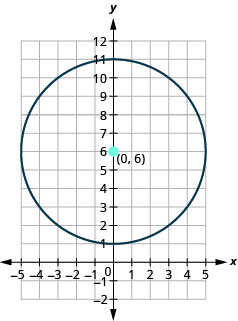
• Graph the circle: \(x^{2}+y^{2}-12 y+11=0\).
• The circle is centered at \((0,6)\) with a radius of \(5\).

Access these online resources for additional instructions and practice with using the distance and midpoint formulas, and graphing circles.

• Distance-Midpoint Formulas and Circles
• Finding the Distance and Midpoint Between Two Points
• Completing the Square to Write Equation in Standard Form of a Circle

Key Concepts

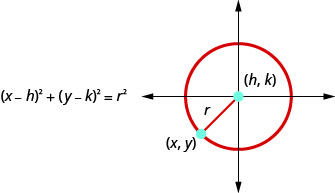
• Circle: A circle is all points in a plane that are a fixed distance from a fixed point in the plane. The given point is called the center, \((h,k)\), and the fixed distance is called the radius, \(r\), of the circle.
• Standard Form of the Equation a Circle: The standard form of the equation of a circle with center, \((h,k)\), and radius, \(r\) , is

• Math Article

Equation Of A Circle

The standard equation of a circle is given by:

(x-h) 2 + (y-k) 2 = r 2

Where (h,k) is the coordinates of center of the circle and r is the radius. 

Before deriving the equation of a circle, let us focus on what is a circle? A circle is a set of all points which are equally spaced from a fixed point in a plane. The fixed point is called the center of the circle. The distance between the center and any point on the circumference is called the radius of the circle . In this article, we are going to discuss what is an equation of a circle formula in standard form, and find the equation of a circle when the center is the origin and the center is not an origin with examples.

What is the Equation of a Circle?

A circle is a closed curve that is drawn from the fixed point called the center, in which all the points on the curve are having the same distance from the center point of the center. The equation of a circle with (h, k) center and r radius is given by:

This is the standard form of the equation. Thus, if we know the coordinates of the center of the circle and its radius as well, we can easily find its equation.

Example: Say point (1,2) is the center of the circle and radius is equal to 4 cm. Then the equation of this circle will be:

(x-1) 2 +(y-2) 2 = 4 2

(x 2 −2x+1)+(y 2 −4y+4) =16

X 2 +y 2 −2x−4y-11 = 0    

Function or Not

We know that there is a question that arises in case of circle whether being a function or not. It is clear that a circle is not a function. Because, a function is defined by each value in the domain is exactly associated with one point in the codomain, but a line that passes through the circle, intersects the line at two points on the surface.

The mathematical way to describe the circle is an equation. Here, the equation of the circle is provided in all the forms such as general form, standard form along with examples.

Equation of a Circle When the Centre is Origin

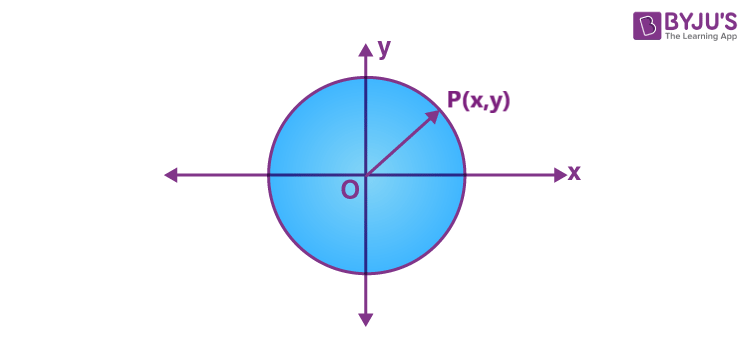
Consider an arbitrary point  P ( x ,  y )  on the circle. Let ‘ a’  be the radius of the circle which is equal to  O P .

We know that the distance between the point  ( x ,  y )  and origin  ( 0 , 0 ) can be found using the distance formula which is equal to-

√[ x 2 +  y 2 ]= a

Therefore, the equation of a circle, with the center as the origin is,

x 2 + y 2 = a 2

Where “a” is the radius of the circle.

Alternative Method

Let us derive in another way. Suppose (x,y) is a point on a circle, and the center of the circle is at origin (0,0). Now if we draw a perpendicular from point (x,y) to the x-axis, then we get a right triangle, where radius of the circle is the hypotenuse. The base of the triangle is the distance along x-axis and height is the distance along the y-axis. Thus, by applying the Pythagoras theorem here, we get:

x 2 +y 2  = radius 2

Equation of a Circle When the Centre is not an Origin

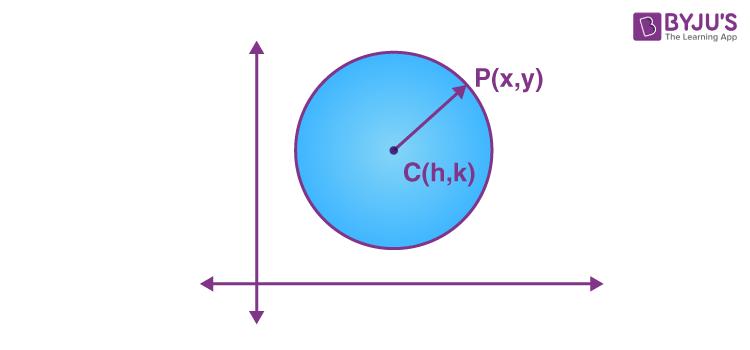
Let  C ( h ,  k )  be the centre of the circle and  P ( x ,  y )  be any point on the circle.

Therefore, the radius of a circle is CP.

By using distance formula,

(x-h) 2  + (y-k) 2 = CP 2

Let radius be ‘a’.

Therefore, the equation of the circle with center (h, k) and the radius ‘ a’  is,

(x-h) 2 +(y-k) 2 = a 2

which is called the standard form for the equation of a circle.

General form of Equation of a Circle

The general equation of any type of circle is represented by:

x 2   +   y 2   +   2 g x   +   2 f y   +   c  =  0 , for all values of  g ,  f  and  c .

Adding  g 2   +   f 2  on both sides of the equation gives,

x 2   +   2 g x   +   g 2 +   y 2   +   2 f y   +   f 2 =  g 2   +   f 2   −   c  ………………(1)

Since,  ( x + g ) 2  =  x 2 +  2 g x  +  g 2  and  ( y + f ) 2  = y 2  +  2 f y  +  f 2  substituting the values in equation (1), we have

( x + g ) 2 +  ( y + f ) 2  =  g 2  +  f 2 − c  …………….(2)

Comparing (2) with  ( x − h ) 2  +  ( y − k ) 2  =  a 2 , where  ( h ,  k )  is the center and ‘ a’  is the radius of the circle.

h = − g ,  k = − f

a 2   =  g 2 +  f 2 − c

x 2  +  y 2  +  2 g x  +  2 f y  +  c  =  0 , represents the circle with centre  ( − g , − f )  and radius equal to  a 2   =  g 2  +  f 2 −  c .

• If  g 2  +  f 2  >  c , then the radius of the circle is real.
• If  g 2  +  f 2  =  c , then the radius of the circle is zero which tells us that the circle is a point that coincides with the center. Such a type of circle is called a point circle
• g 2  +  f 2  < c , then the radius of the circle become imaginary. Therefore, it is a circle having a real center and imaginary radius.

Polar Equation of a Circle

To find the polar form of equation of a circle, replace the value of x = r cos θ and y = r sin θ, in x 2 + y 2 = a 2 .

Hence,  we get;

(r cos θ) 2 + (r sin θ) 2 = a 2

r 2 cos 2 θ + r 2 sin 2  θ = a 2

r 2 (cos 2  θ + sin 2  θ) = a 2

is the polar equation of a circle with radius a and center at the origin (0,0).

Video Lessons on Circles

Introduction to circles.

Parts of a Circle

Area of a Circle

All about Circles

Other Circle Formulas

Here are some formulas are given for circle in terms of radius.

How to Find the Equation of the Circle?

To find the equation of a circle given the radius and center of the circle, we can directly put the values in the standard form of the equation.

Here, some solved problems are given to find the equation of a circle in both cases such as when the center of a circle is origin and center is not an origin is given below.

Solved Examples

Consider a circle whose center is at the origin and radius is equal to 8 units.

Given: Centre is (0, 0), radius is 8 units.

We know that the equation of a circle when the center is origin:

x 2 +  y 2  = a 2

For the given condition, the equation of a circle is given as

x 2  +  y 2  = 8 2

x 2  +  y 2 = 64, which is the equation of a circle

Find the equation of the circle whose center is (3,5)  and the radius is 4 units.

Here, the center of the circle is not an origin.

Therefore, the general equation of the circle is,

(x-3) 2  + (y-5) 2  = 4 2

x 2  – 6x + 9 + y 2  -10y +25  = 16

x 2  +y 2  -6x -10y + 18  = 0

Equation of a circle is  x 2 + y 2 − 12 x − 16 y + 19 = 0 . Find the center and radius of the circle.

Given equation is of the form  x 2 +   y 2   +   2 g x   +   2 f y   +   c  =  0 ,

2 g  =  − 12 ,  2 f  =  − 16 , c  =  19

g  =  − 6 , f  =  − 8

Centre of the circle is  ( 6 , 8 )

Radius of the circle =  √[ ( − 6 ) 2   +   ( − 8 ) 2   −   19  ]=  √[ 100   −   19]  =

=   √81 =  9  units.

Therefore, the radius of the circle is  9 units.

Practice Questions on Equation of Circle

• Find the equation of a circle of radius 5 units, whose centre lies on the x-axis and which passes through the point (2, 3).
• Find the equation of a circle with the centre (h, k) and touching the x-axis.
• Show that the equation x 2 + y 2 – 6x + 4y – 36 = 0 represents a circle. Also, find the centre and radius of the circle.

Frequently Asked Questions on Equation of a Circle

What is the equation for a circle, what are the formulas for circles, what is the equation of a circle when the center is at the origin, if (x-4) 2 +(y+7) 2 =9 is the equation of circle, then what is the center of circle, how do we know if an equation is the equation of circle.

Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!

Select the correct answer and click on the “Finish” button Check your score and answers at the end of the quiz

Visit BYJU’S for all Maths related queries and study materials

Your result is as below

Request OTP on Voice Call

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Post My Comment

• Share Share

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

Equation of a Circle Practice Questions

Click here for questions, click here for answers, gcse revision cards.

5-a-day Workbooks

Primary Study Cards

Privacy Policy

Terms and Conditions

Corbettmaths © 2012 – 2024

• DSA with JS - Self Paced
• JS Tutorial
• JS Exercise
• JS Interview Questions
• JS Operator
• JS Projects
• JS Examples
• JS Free JS Course
• JS A to Z Guide
• JS Formatter
• JavaScript program to find area of a circle
• Find Circumference of a Circle using JavaScript
• Check if an element is present in an array using JavaScript
• How do I check if an Array includes a value in JavaScript?
• Best Way to Find an Item in an Array in JavaScript
• How to Check if a Specific Element Exists in a Set in JavaScript ?
• JavaScript Program to Find the Area of Cylinder
• How to Check if an Element Exists in an Array in JavaScript ?
• How to find if an array contains a specific string in JavaScript/jQuery ?
• Java Program to Find the Area of a Circle Given the Radius
• JavaScript Program to Return Quadrants in which a given Coordinate Lies
• Find if a point lies inside a Circle
• Count points from an array that lies inside a semi-circle
• Check if a circle lies inside another circle or not
• Find N random points within a Circle
• Find if a point lies inside, outside or on the circumcircle of three points A, B, C
• Queries on count of points lie inside a circle
• Check if a line touches or intersects a circle
• Check if a point lies inside a rectangle | Set-2

Find if a Point Lies Inside a Circle in JavaScript

A circle is a closed curve where every point on the curve is equidistant from a fixed point called the center. The problem at hand involves determining whether a given point is located inside a circle or not. Given a circle (coordinates of center and radius) and a point (coordinate), find if the point lies inside or on the circle, or not using JavaScript . 

Examples:  

These are the following approaches:

Table of Content

Using Distance Formula

Using circle equation approach.

One straightforward method to determine if a point lies inside a circle is by using the distance formula. The distance between the center of the circle (x1, y1) and the given point (x2, y2) is calculated using the formula:

Note : If the calculated distance is less than the radius of the circle, i.e. point lies inside the circle.

Example: Implementation to find if a point lies inside a Circle using Distance Formula.

Time complexity: O(1)

Space complexity: O(1)

Another approach involves using the equation of a circle. The equation of a circle with center (h, k) and radius r is:

If a point (x, y) satisfies this equation, it lies on the circle. To determine if the point lies inside the circle, we just need to check if the distance from the center (h, k) to (x, y) is less than the radius r .

Example: Implementation to find if a point lies inside a Circle using Circle Equation Approach.

Please Login to comment...

• JavaScript-DSA
• Web Technologies

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

• Technology News

Google I/O 2024: Circle to Search to arrive on 200 million Android phones by year end

Google’s Circle to Search feature on Android: Availability

How this feature will help students.