algebra formulas and problem solving

The Ultimate Guide to Algebra Formulas with Examples

If there is one thing that comes to mind when people think of algebra and mathematics, it is the  formulas.  As a branch of mathematics, the study of algebra involves many basic formulas and many advanced formulas in order to make sense of the patterns that we see in real life.

In this guide, I want to provide you with 25 algebra formulas with examples. My goal is for you to develop an understanding of the basics of algebra, so that you can start to solve any complex problems that you come across!

Whether you are looking to learn more about the quadratic formula or dig deeper into logarithm laws, this guide has you covered!

What is Algebra?

Algebra is a branch of maths that involves mathematical symbols and numbers that work together to form a mathematical expression and mathematical equations. Algebra also focuses on the rules used to rearrange algebraic expressions, solve equations, and represent relationships between real life variables.

As students advance in their studies of algebra, they start to notice letters making their way into their math courses. While this may sound confusing, letters are used as  variables  to represent unknown quantities. In algebra, we use these variables and mathematical operations such as addition, subtraction, multiplication, and division to construct  algebraic expressions and algebraic equations . 

In algebra, you will often find yourself attempting to determine the values of unknown variables using equations, specific rules, and mathematical operations. One very important rule you might know about already is that what is done to one side must be done to the other.

Algebra equations are like scales: if you change one side of the scale, it becomes out of balance. In order to balance it, you must make the same change on the other side of the scale.

Since algebra is a fundamental area of mathematics that forms the basis for many other mathematical and scientific disciplines, the importance of algebra cannot be overstated! 

What are Algebra Maths Formulas?

An algebraic equation or a “math formula” is a way of summarizing a mathematical relationship. Math formulas contain a combination of unknown values (the unknown variable x, for example), numbers, and typically, an equal sign.

While x and y tend to be the most commonly used letters, the variables that make up an algebraic equation can be any letters or mathematical symbols.

Math formulas allow us to place different values into the subject of the formula in order to see what happens. For example, if you have a formula for the surface area of a cone, you could sub in different values for the radius in order to see how the surface area changes with each. 

Mathematical formulas are very useful because they allow us to make predictions based on patterns that exist. This makes algebra formulas very  applicable to a variety of real life applications . 

For example, it is possible to use math formulas to predict how much money you will have in the future if you invest $1500 into a high interest savings account right now. A person studying social science might create a mathematical formula that predicts population growth over time. The possibilities are truly endless!

25 Algebra Formulas with Examples

The formulas of algebra range from using math basic math operations to much more complex operations. This list of algebra formulas with examples will provide you with a variety of levels of difficulty.

Let’s begin by considering one of the more basic algebraic formulas that you will encounter in your studies of elementary algebra!

The Distributive Property

One of the most common rules that you will apply in algebraic problems is the distributive property (sometimes referred to as the distributive axiom). This property states that \(z(x + y) = xz + yz\) and \(z(x – y) = xz – yz\). The final result will always be a simpler expression without brackets!

The distributive property is a common step that is taken to simplify algebraic expressions in a wide variety of mathematical applications and problems.

Below is an example of the distributive property in action!

Algebraic Identities

There are a collection of algebraic identities that can be used to expand and simplify a product of binomials. Each algebraic identity shown in the below formulas can be explained using the  Binomial Theorem .

The following algebraic identities involve trinomials that are perfect squares:

• Square of the Sum:  \((a + b)^2 = a^2 + 2ab + b^2\)
• Square of the Difference:  \((a – b)^2 = a^2 – 2ab + b^2\)
• Difference of Squares:  \(a^2 – b^2= (a + b)(a – b)\)

This quick  example of the square of the sum formula , will help you see how this formula works in practice. 

The following formulas are useful when expanding and simplifying binomials. These are especially helpful when working with a cubic equation, as these tend to be tricky to work with.

• Product of Two Binomials:  \((x + a)(x + b) = x^2 + (a + b) x + ab\)
• Cube of a Binomial (Sum):  \((a + b)^3 = a^3 + b^3 + 3ab (a + b)\)
• Cube of a Binomial (Difference):  \((a – b)^3 = a^3 – b^3 – 3ab (a – b)\)

General Form of The Quadratic Equation

The general form of the quadratic equation (also known as standard form) is the equation \(f(x) = ax^2+bx+c\). Notice that the power on x decreases on each successive term until the constant term of  c . This constant value tells us the y-intercept of the quadratic function. The general form of the quadratic equation is often considered to be the most simplified form.

The Quadratic Formula

$$x=\frac{-b \pm \sqrt{b^2-4ac}}{2a}$$

The above formula is the famous quadratic formula! While it may look complex, the quadratic formula is considered a basic algebra formula. This powerful formula allows us to determine the x-intercepts of any quadratic function (as long as it has them!). 

While the quadratic formula is helpful, many students (and teachers) prefer  factoring trinomial expressions  to solve quadratic equations in order to find their x-intercepts as it is a much faster process. Others prefer to rely on the quadratic formula as a way of avoiding factoring altogether (however, I strongly discourage this as factoring is a very useful skill that helps us write expressions in different forms!).

The values of the quadratic formula correspond to the values of a , b , and c in a quadratic trinomial.

Pythagorean Theorem

Measurement is a branch of maths that sees many applications of algebra in the real-world. I want to share a few algebra formulas with examples here that relate to measurement in the real world. One of the most famous is the Pythagorean Theorem .

$$a^2+b^2=c^2$$

This formula tells us that the square of each leg of a right triangle is equal to the sum of the hypotenuse. It is important to note that the hypotenuse is isolated on the right-hand side in the above equation. While the values of  a  and  b  are interchangeable, the hypotenuse is not!

For a quick example, of the Pythagorean Theorem in action, check out  this short example video  from my YouTube channel!

Trigonometric Ratios

Arguably some of the most important algebra formulas in mathematics, the trigonometric ratios are another set of useful algebra formulas that involve right triangles. These mathematical equations relate the side lengths of a right triangle to its angles.

• \(sin \theta = \frac{o}{h}\), where  o  is the side opposite to the angle, and  h  is the hypotenuse.
• \(cos \theta = \frac{a}{h}\), where  a  is the side adjacent to the angle, and  h  is the hypotenuse.
• \(tan \theta = \frac{o}{a}\), where  o  is the side opposite to the angle, and  a  is the side adjacent to the angle.

These ratios can be used to solve complex problems in trigonometry, a very important topic in studies of algebra and mathematics. For example, a common application is when solving  angle of elevation and depression problems .

Surface Area

When it comes to mathematical applications of algebra formulas with examples, surface area is an easy one to connect to real life. Surface area is a measurement of the amount of space that covers a three dimensional object. Mathematical problems involving surface area are everywhere, and we need a different formula for every shape that we encounter!

For example:

• Surface Area of a Rectangular Prism:  \(SA=2(lh +wh + lw)\), where  l  is the length,  w  is the width, and  h  is the height.
• Surface Area of a Cylinder:  \(SA=2 \pi rh + 2 \pi r^2\), where  r  is the radius, and  h  is the height.
• Surface Area of a Cone:  \(SA = \pi r^2 + \pi r s\), where  r  is the radius, and  s  is the slant height.
• Surface Area of a Sphere:  \(SA = 4\pi r^2\), where  r  is the radius.

Exponential Laws

The exponential laws are a useful set of rules for simplifying exponential expressions that contain different powers. Note that these laws do not work for expressions with different bases.

Some common laws of exponents are:

• Multiplying powers, add the exponents:  \(x^a \times x^b = x^{a + b}\)
• Dividing powers, subtract the exponents :  \(x^a \div x^b = x^{a – b}\)
• Power of a power:  \((x^a)^b = x^{ab}\)
• Negative exponent rule:  \(x^{-a} = \frac{1}{x^a}\)

Early in my teaching career, I wrote and performed  a cheesy exponent law song  to help my class remember these laws. Check it out!

Important Log Laws

Working with expressions in logarithmic form is a valuable skill in the study of algebra. The important log laws are similar to the exponential laws, but have their own unique set of rules that you must follow.

• Product rule for logarithms:  \(log_{a}(x \times y) = log_{a}x +  log_{a}y\)
• Quotient rule for logarithms:  \(log_{a}(x \div y) = log_{a}x –  log_{a}y\)
• Quotient rule for logarithms:  \(log_{a}(x^y) = ylog_{a}x\)
• Base change rule for logarithms with different bases:  \(log_{b}x = \frac{log_{c}x}{log_{c}b}\)

​Watch  this log laws video ​ for examples of how these important log laws can be used to simplify algebraic expressions.

Using Algebra Formulas With Examples

One important thing I have noticed in my time as a classroom teacher is that just “knowing the formulas” is not enough to guarantee success. Instead, the best thing you can do is to make sure you know  how  and  when  to use each formula. This is especially important when solving real-world algebra problems !

Algebra is more than just plugging in numbers into formulas. There is a lot of critical thought that goes into selecting and applying a specific formula over another! When it comes to using algebra formulas, practice is the key to mastery!

I hope you found this guide to algebra formulas with examples helpful as you continue your studies of algebra. While this list does not contain  every  algebraic formula, it should provide you with a good overview of just what is possible in the study of algebra.

Did you find this guide to algebra formulas with examples helpful? Share this post and subscribe to Math By The Pixel on YouTube for more helpful mathematics content!

RECOMMENDED FOR YOU

Examples of One Solution Equations, Zero, and Infinite

Linear Equations Word Problems Worksheet with Solutions

Solving Equations

What is an equation.

An equation says that two things are equal. It will have an equals sign "=" like this:

That equations says:

what is on the left (x − 2)  equals  what is on the right (4)

So an equation is like a statement " this equals that "

What is a Solution?

A Solution is a value we can put in place of a variable (such as x ) that makes the equation true .

Example: x − 2 = 4

When we put 6 in place of x we get:

which is true

So x = 6 is a solution.

How about other values for x ?

• For x=5 we get "5−2=4" which is not true , so x=5 is not a solution .
• For x=9 we get "9−2=4" which is not true , so x=9 is not a solution .

In this case x = 6 is the only solution.

You might like to practice solving some animated equations .

More Than One Solution

There can be more than one solution.

Example: (x−3)(x−2) = 0

When x is 3 we get:

(3−3)(3−2) = 0 × 1 = 0

And when x is 2 we get:

(2−3)(2−2) = (−1) × 0 = 0

which is also true

So the solutions are:

x = 3 , or x = 2

When we gather all solutions together it is called a Solution Set

The above solution set is: {2, 3}

Solutions Everywhere!

Some equations are true for all allowed values and are then called Identities

Example: sin(−θ) = −sin(θ) is one of the Trigonometric Identities

Let's try θ = 30°:

sin(−30°) = −0.5 and

−sin(30°) = −0.5

So it is true for θ = 30°

Let's try θ = 90°:

sin(−90°) = −1 and

−sin(90°) = −1

So it is also true for θ = 90°

Is it true for all values of θ ? Try some values for yourself!

How to Solve an Equation

There is no "one perfect way" to solve all equations.

A Useful Goal

But we often get success when our goal is to end up with:

x = something

In other words, we want to move everything except "x" (or whatever name the variable has) over to the right hand side.

Example: Solve 3x−6 = 9

Now we have x = something ,

and a short calculation reveals that x = 5

Like a Puzzle

In fact, solving an equation is just like solving a puzzle. And like puzzles, there are things we can (and cannot) do.

Here are some things we can do:

• Add or Subtract the same value from both sides
• Clear out any fractions by Multiplying every term by the bottom parts
• Divide every term by the same nonzero value
• Combine Like Terms
• Expanding (the opposite of factoring) may also help
• Recognizing a pattern, such as the difference of squares
• Sometimes we can apply a function to both sides (e.g. square both sides)

Example: Solve √(x/2) = 3

And the more "tricks" and techniques you learn the better you will get.

Special Equations

There are special ways of solving some types of equations. Learn how to ...

• solve Quadratic Equations
• solve Radical Equations
• solve Equations with Sine, Cosine and Tangent

Check Your Solutions

You should always check that your "solution" really is a solution.

How To Check

Take the solution(s) and put them in the original equation to see if they really work.

Example: solve for x:

2x x − 3 + 3 = 6 x − 3     (x≠3)

We have said x≠3 to avoid a division by zero.

Let's multiply through by (x − 3) :

2x + 3(x−3) = 6

Bring the 6 to the left:

2x + 3(x−3) − 6 = 0

Expand and solve:

2x + 3x − 9 − 6 = 0

5x − 15 = 0

5(x − 3) = 0

Which can be solved by having x=3

Let us check x=3 using the original question:

2 × 3 3 − 3 + 3  =   6 3 − 3

Hang On: 3 − 3 = 0 That means dividing by Zero!

And anyway, we said at the top that x≠3 , so ...

x = 3 does not actually work, and so:

There is No Solution!

That was interesting ... we thought we had found a solution, but when we looked back at the question we found it wasn't allowed!

This gives us a moral lesson:

"Solving" only gives us possible solutions, they need to be checked!

• Note down where an expression is not defined (due to a division by zero, the square root of a negative number, or some other reason)
• Show all the steps , so it can be checked later (by you or someone else)

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

1.4: Algebraic Expressions and Formulas

• Last updated
• Save as PDF
• Page ID 6229

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Objectives

• Identify the parts of an algebraic expression.
• Apply the distributive property.
• Evaluate algebraic expressions.
• Use formulas that model common applications.

Algebraic Expressions and the Distributive Property

In algebra, letters called variables are used to represent numbers. Combinations of variables and numbers along with mathematical operations form algebraic expressions 87 , or just expressions . The following are some examples of expressions with one variable, \(x\):

Terms 88 in an algebraic expression are separated by addition operators and factors 89 are separated by multiplication operators. The numerical factor of a term is called the coefficient 90 . For example, the algebraic expression \(x^{2} y^{2} + 6xy − 3\) can be thought of as \(x^{2} y^{2} + 6xy + (−3)\) and has three terms. The first term, \(x^{2} y^{2}\), represents the quantity \(1x^{2} y^{2} = 1 ⋅ x ⋅ x ⋅ y ⋅ y\) where \(1\) is the coefficient and x and y are the variables. All of the variable factors with their exponents form the variable part of a term 91 . If a term is written without a variable factor, then it is called a constant term 92 . Consider the components of \(x^{2} y^{2} + 6xy − 3\),

The third term in this expression, \(−3\), is called a constant term because it is written without a variable factor. While a variable represents an unknown quantity and may change, the constant term does not change.

Example \(\PageIndex{1}\):

List all coefficients and variable parts of each term: \(10a^{2}−5ab−b^{2}\).

We want to think of the third term in this example \(−b^{2}\) as  \(−1b^{2}\).

Answer : Coefficients: \(\{−5, −1, 10\}\); Variable parts: \(\{a^{2},  ab,  b^{2}\}\)

In our study of algebra, we will encounter a wide variety of algebraic expressions. Typically, expressions use the two most common variables, \(x\) and \(y\). However, expressions may use any letter (or symbol) for a variable, even Greek letters, such as alpha (\(\alpha\)) and beta (\(\beta\)). Some letters and symbols are reserved for constants, such as \(π ≈ 3.14159\) and \(e ≈ 2.71828\). Since there is only a limited number of letters, you will also use subscripts, \(x_{1} , x_{2} , x_{3} , x_{4} , …,\) to indicate different variables.

The properties of real numbers are important in our study of algebra because a variable is simply a letter that represents a real number. In particular, the distributive property 93 states that if given any real numbers \(a, b\) and \(c\), then,

\(\color{Cerulean}{a}\) \( ( b + c ) = \color{Cerulean}{a}\)\(b + \color{Cerulean}{a}\)\(c\)

This property is one that we apply often when simplifying algebraic expressions. To demonstrate how it will be used, we simplify \(2(5 − 3)\) in two ways, and observe the same correct result.

Certainly, if the contents of the parentheses can be simplified we should do that first. On the other hand, when the contents of parentheses cannot be simplified any further, we multiply every term within it by the factor outside of it using the distributive property. Applying the distributive property allows us to multiply and remove the parentheses.

Example \(\PageIndex{2}\):

Simplify: \(5(−2a+5b)−2c\).

Multiply only the terms grouped within the parentheses for which we are applying the distributive property.

\(=\color{Cerulean}{5}\)\(⋅(−2a)+\color{Cerulean}{5}\)\(⋅5b−2c\)

\(=−10a+25b−2c\)

Answer : \(−10a+25b−2c\)

Recall that multiplication is commutative and therefore we can write the distributive property in the following manner, \((b + c) a = ba + ca\).

Example \(\PageIndex{3}\):

Simplify:  \((3x−4y+1)⋅3\).

Multiply all terms within the parenthesis by \(3\).

\((3x−4y+1)⋅3=3x\color{Cerulean}{⋅3}\)\(−4y\color{Cerulean}{⋅3}\)\(+1\color{Cerulean}{⋅3}\)

\(=9x−12y+3\)

Answer : \(9x−12y+3\)

Terms whose variable parts have the same variables with the same exponents are called like terms 94 , or similar terms 95 . Furthermore, constant terms are considered to be like terms. If an algebraic expression contains like terms, apply the distributive property as follows:

\(5 \color{Cerulean}{x}\)\( + 7 \color{Cerulean}{x}\)\( = ( 5 + 7 ) \color{Cerulean}{x}\)\( = 12 \color{Cerulean}{x}\)

\(4 \color{Cerulean}{x ^ { 2 }}\)\( + 5 \color{Cerulean}{x ^ { 2 }}\)\( - 7 \color{Cerulean}{x ^ { 2 }}\)\( = ( 4 + 5 - 7 ) \color{Cerulean}{x ^ { 2 }}\)\( = 2 \color{Cerulean}{x ^ { 2 }}\)

In other words, if the variable parts of terms are exactly the same, then we can add or subtract the coefficients to obtain the coefficient of a single term with the same variable part. This process is called combining like terms 96 . For example,

\(12 x ^ { 2 } y ^ { 3 } + 3 x ^ { 2 } y ^ { 3 } = 15 x ^ { 2 } y ^ { 3 }\)

Notice that the variable factors and their exponents do not change. Combining like terms in this manner, so that the expression contains no other similar terms, is called simplifying the expression 97 . Use this idea to simplify algebraic expressions with multiple like terms.

Example \(\PageIndex{4}\):

\(x ^ { 2 } - 10 x + 8 + 5 x ^ { 2 } - 6 x - 1\).

Identify the like terms and add the corresponding coefficients.

\(\color{Cerulean}{\underline{1x^{2}}}\) \( - \color{OliveGreen}{\underline{\underline{10x}}}\)\( + \underline{\underline{\underline{8}}} + \color{Cerulean}{\underline{5 x ^ { 2 }}}\)\( -\color{OliveGreen}{\underline{\underline{6x}}}\)\( - \underline{\underline{\underline{1}}}\) \(\color{Cerulean}{Combine\: like\: terms.}\)

\(= 6 x ^ { 2 } - 16 x + 7\)

Answer : \(6 x ^ { 2 } - 16 x + 7\)

Example \(\PageIndex{5}\):

Simplify: \(a ^ { 2 } b ^ { 2 } - a b - 2 \left( 2 a ^ { 2 } b ^ { 2 } - 5 a b + 1 \right)\).

Distribute \(−2\) and then combine like terms.

\(\begin{aligned} a ^ { 2 } b ^ { 2 } - a b - 2 \left( 2 a ^ { 2 } b ^ { 2 } - 5 a b + 1 \right) & = a ^ { 2 } b ^ { 2 } - a b - 4 a ^ { 2 } b ^ { 2 } + 10 a b - 2 \\ & = - 3 a ^ { 2 } b ^ { 2 } + 9 a b - 2 \end{aligned}\)

Answer : \(- 3 a ^ { 2 } b ^ { 2 } + 9 a b - 2\)

Evaluating Algebraic Expressions

An algebraic expression can be thought of as a generalization of particular arithmetic operations. Performing these operations after substituting given values for variables is called evaluating 98 . In algebra, a variable represents an unknown value. However, if the problem specifically assigns a value to a variable, then you can replace that letter with the given number and evaluate using the order of operations.

Example \(\PageIndex{6}\):

• \(5x − 2\) where \(x =\frac{2}{3}\)
• \(y^{2} − y − 6\) where \(y = −4\)

To avoid common errors, it is a best practice to first replace all variables with parentheses, and then replace, or substitute 99 , the appropriate given value.

\(\begin{aligned} 5 x - 2 & = 5 (\:\: ) - 2 \\ & = 5 \left(\color{OliveGreen}{ \frac { 2 } { 3 }} \right) - 2 \\ & = \frac { 10 } { 3 } - \frac { 2 } { 1 } \cdot \color{Cerulean}{\frac { 3 } { 3 }} \\ & = \frac { 10 - 6 } { 3 } \\ & = \frac { 4 } { 3 } \end{aligned}\)

\(y ^ { 2 } - y - 6 = (\:\: ) ^ { 2 } - (\:\: ) - 6\)

\(= ( \color{OliveGreen}{- 4}\)\( ) ^ { 2 } - ( \color{OliveGreen}{- 4}\)\( ) - 6\)

\(\begin{array} { l } { = 16 + 4 - 6 } \\ { = 14 } \end{array}\)

a. \(\frac{4}{3}\)

Often algebraic expressions will involve more than one variable.

Example \(\PageIndex{7}\):

Evaluate \(a ^ { 3 } - 8 b ^ { 3 }\) where \(a = −1\) and \(b = \frac{1}{2}\).

After substituting in the appropriate values, we must take care to simplify using the correct order of operations.

\(a ^ { 3 } - 8 b ^ { 3 } = (\:\: ) ^ { 3 } - 8 (\:\: ) ^ { 3 } \color{Cerulean}{Replace\: variables\: with\: parentheses.}\)

\(= ( \color{OliveGreen}{- 1}\) \( )^{3} -8(\color{OliveGreen}{\frac{1}{2}}\)\()^{3} \color{Cerulean}{Substitute\: in\: the\: appropriate\: values.}\)

\(= - 1 - 8 \left( \frac { 1 } { 8 } \right) \color{Cerulean}{Simplify.}\)

\(\begin{array} { l } { = - 1 - 1 } \\ { = - 2 } \end{array}\)

Answer : \(-2\)

Example \(\PageIndex{8}\):

Evaluate \(\frac { x ^ { 2 } - y ^ { 2 } } { 2 x - 1 }\) where \(x = −\frac{3}{2}\) and \(y = −3\).

\(\frac { x ^ { 2 } - y ^ { 2 } } { 2 x - 1 } = \frac { (\:\: ) ^ { 2 } - ( \:\:) ^ { 2 } } { 2 ( \:\:) - 1 }\)

\(= \frac { \left( \color{OliveGreen}{- \frac { 3 } { 2 }} \right) ^ { 2 } - ( \color{OliveGreen}{- 3} \color{Black}{) ^ { 2 } }} { 2 \left( - \color{OliveGreen}{\frac { 3 } { 2 }} \right) - 1 }\)

\(= \frac { \frac { 9 } { 4 } - 9 } { - 3 - 1 }\)

At this point we have a complex fraction. Simplify the numerator and then multiply by the reciprocal of the denominator.

\(\begin{aligned} & = \frac { \frac { 9 } { 4 } - \frac { 9 } { 1 } \cdot \color{Cerulean}{\frac { 4 } { 4 } }} { - 4 } \\ & = \frac { \frac { - 27 } { 4 } } { { \frac { - 4 } { 1 } } } \\ & = \frac { - 27 } { 4 } \left( - \frac { 1 } { 4 } \right) \\ & = \frac { 27 } { 16 } \end{aligned}\)

Answer : \(\frac { 27 } { 16 }\)

The answer to the previous example can be written as a mixed number, \(\frac { 27 } { 16 } = 1 \frac { 11 } { 16 }\). Unless the original problem has mixed numbers in it, or it is an answer to a realworld application, solutions will be expressed as reduced improper fractions.

Example \(\PageIndex{9}\):

Evaluate \(\sqrt { b ^ { 2 } - 4 a c }\) where \(a = −1, b = −7\), and \(c = \frac{1}{4}\).

Substitute in the appropriate values and then simplify.

\(\sqrt { b ^ { 2 } - 4 a c } = \sqrt { ( \:\: ) ^ { 2 } - 4 ( \:\: ) \:\:(\:\:) }\)

\( = \sqrt { ( \color{OliveGreen}{- 7}\color{Black}{ ) ^ { 2 } - 4 (}\color{OliveGreen}{ - 1}\color{Black}{ ) (}\color{OliveGreen}{ \frac { 1 } { 4 }}\color{Black}{)} } \)

\(\begin{aligned} & =\sqrt { 49 + 4(\frac{1}{4}) } \\ & = \sqrt { 49 + 1 } \\ & =\sqrt{50} \\& = \sqrt { 25 \cdot 2 } \\ & = 5 \sqrt { 2 } \end{aligned}\)

Aligned : \(5 \sqrt { 2 }\)

Exercise \(\PageIndex{1}\)

Evaluate \(\frac { \sqrt { 3 \pi V h } } { \pi h }\) where \(V = 25\pi\) and \(h = 3\).

www.youtube.com/v/Y4RCMceThu4

Using Formulas

The main difference between algebra and arithmetic is the organized use of variables. This idea leads to reusable formulas 100 , which are mathematical models using algebraic expressions to describe common applications. For example, the volume of a right circular cone depends on its radius \(r\) and height \(h\) and is modeled by the formula:

\(V = \frac { 1 } { 3 } \pi r ^ { 2 } h\)

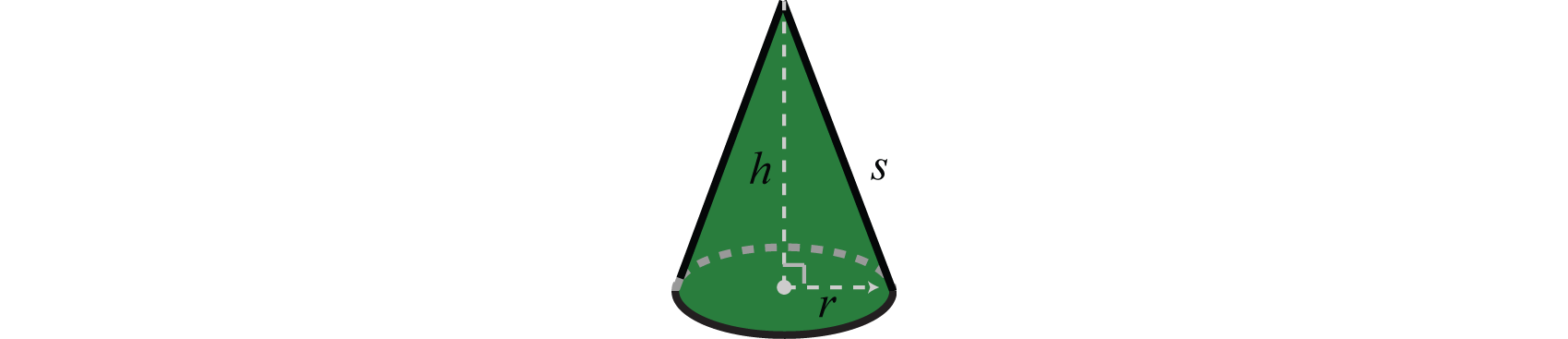
In this equation, variables and constants are used to describe the relationship between volume and the length of the base and height. If the radius of the base measures \(3\) meters and the height measures \(5\) meters, then the volume can be calculated using the formula as follows:

\(\begin{aligned} V & = \frac { 1 } { 3 } \pi r ^ { 2 } h \\ & = \frac { 1 } { 3 } \pi ( 3 m ) ^ { 2 } ( 5 m ) \\ & = \frac { 1 } {\bcancel {3}} \pi \cdot \stackrel{\color{Cerulean}{3}}{\bcancel{9}} \cdot 5 m ^ { 3 } \\ & = 15 \pi \mathrm { m } ^ { 3 } \end{aligned}\)

Using \(π ≈ 3.14\), we can approximate the volume: \(V ≈ 15 (3.14) = 47.1\) cubic meters.

A list of formulas that describe the area and perimeter of common plane figures follows. The letter P represents perimeter and is measured in linear units. The letter A represents area and is measured in square units.

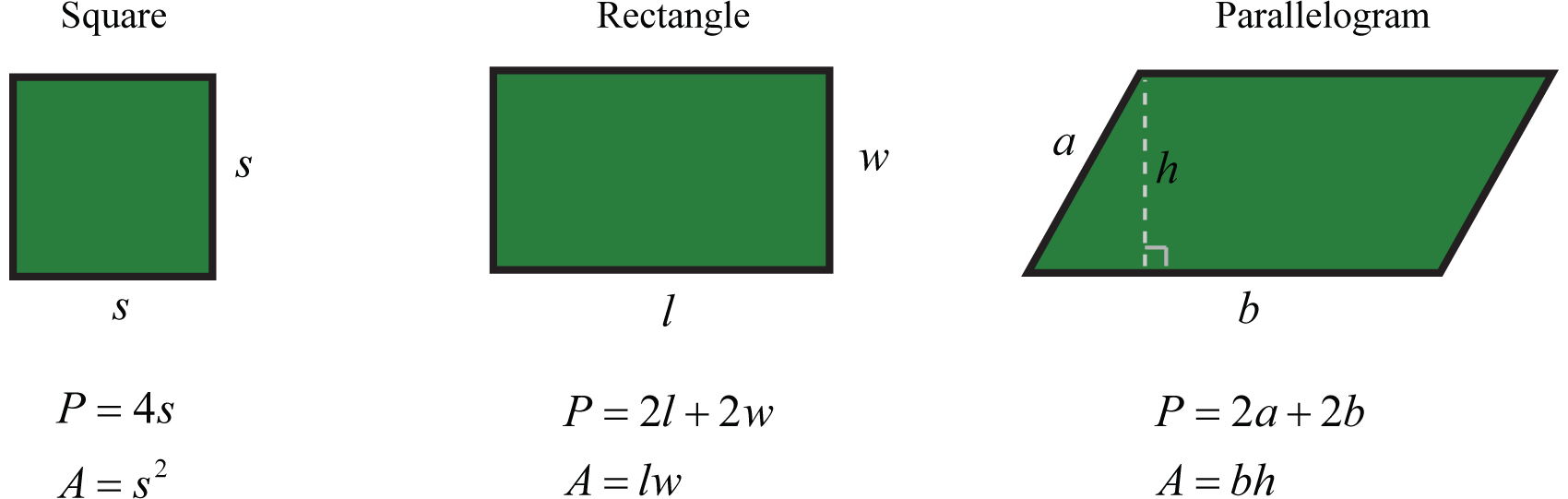
A list of formulas that describe the surface area and volume of common figures follows. Here SA represents surface area and is measured in square units. The letter V represents volume and is measured in cubic units.

Example \(\PageIndex{10}\):

The diameter of a spherical balloon is \(10\) inches. Determine the volume rounded off to the nearest hundredth.

The formula for the volume of a sphere is

\(V = \frac { 4 } { 3 } \pi r ^ { 3 }\)

This formula gives the volume in terms of the radius, \(r\). Therefore, divide the diameter by \(2\) and then substitute into the formula. Here, \(r = \frac{10}{2} = 5\) inches and we have

\(\begin{aligned} V & = \frac { 4 } { 3 } \pi r ^ { 3 } \\ & = \frac { 4 } { 3 } \pi ( 5 \mathrm { in } ) ^ { 3 } \\ & = \frac { 4 } { 3 } \pi \cdot 125 \mathrm { in } ^ { 3 } \\ & = \frac { 500 \pi } { 3 } \mathrm { in } ^ { 3 } \approx 523.60 \mathrm { in } ^ { 3 } \end{aligned}\)

Answer : The volume of the balloon is approximately \(523.60\) cubic inches.

Formulas can be found in a multitude of subjects. For example, uniform motion 101 is modeled by the formula \(D = rt\), which expresses distance \(D\), in terms of the average rate, or speed, \(r\) and the time traveled at that rate, \(t\). This formula, \(D = rt\), is used often and is read, “ distance equals rate times time .”

Example \(\PageIndex{11}\):

Jim’s road trip took \(2\:\frac{1}{2}\) hours at an average speed of \(66\) miles per hour. How far did he travel?

Substitute the appropriate values into the formula and then simplify.

\(\begin{aligned} D & = r \cdot t \\ & = ( \color{Cerulean}{66 \frac { \mathrm { mi } } { \mathrm { hr } }}\color{Black}{ ) \cdot (}\color{Cerulean}{ 2 \frac { 1 } { 2 } \mathrm { hr }}\color{Black}{)} \\ & = \frac { 66 } { 1 } \cdot \frac { 5 } { 2 } \mathrm { mi } \\ & = 33 \cdot 5 \mathrm { mi } \\ & = 165 \mathrm { mi } \end{aligned}\)

Answer : Jim traveled \(165\) miles.

Simple interest 102 \(I\) is given by the formula \(I = prt\), where \(p\) represents the principal amount invested at an annual interest rate \(r\) for \(t\) years.

Example \(\PageIndex{12}\):

Calculate the simple interest earned on a \(2\)-year investment of \($1,250\) at an annual interest rate of \(3\:\frac{3}{4} %\).

Convert \(3\:\frac{3}{4}%\) to a decimal number before using it in the formula.

\(r = 3 \frac { 3 } { 4 } \% = 3.75 \% = 0.0375\)

Use this and the fact that \(p = $1,250\) and \(t = 2\) years to calculate the simple interest.

\(\begin{aligned} I & = p r t \\ & = ( \color{Cerulean}{1,250}\color{Black}{ ) (}\color{Cerulean}{ 0.0375}\color{Black}{ ) (}\color{Cerulean}{ 2}\color{Black}{ )} \\ & = 93.75 \end{aligned}\)

Answer : The simple interest earned is \($93.75\).

Key Takeaways

• Think of algebraic expressions as generalizations of common arithmetic operations that are formed by combining numbers, variables, and mathematical operations.
• The distributive property \(a (b + c) = ab + ac\), is used when multiplying grouped algebraic expressions. Applying the distributive property allows us to remove parentheses.
• Combine like terms, or terms whose variable parts have the same variables with the same exponents, by adding or subtracting the coefficients to obtain the coefficient of a single term with the same variable part. Remember that the variable factors and their exponents do not change.
• To avoid common errors when evaluating, it is a best practice to replace all variables with parentheses and then substitute the appropriate values.
• The use of algebraic expressions allows us to create useful and reusable formulas that model common applications.

Exercise \(\PageIndex{2}\)

List all of the coefficients and variable parts of each term.

• \(−5x^{2} + x − 1\)
• \(y^{2} − 9y + 3\)
• \(5x^{2} − 3xy + y^{2}\)
• \(a^{2}b^{2} + 2ab − 4\)
• \(x^{2}y + xy^{2} − 3xy + 9\)
• \(x^{4} − x^{3} + x^{2} − x + 2\)

1. Coefficients: \(\{−5, 1, −1\}\) ; variable parts: \(\{x^{2} , x\}\)

3. Coefficients: \(\{5, −3, 1\}\) ; variable parts: \(\{x^{2} , xy, y^{2} \}\)

5. Coefficients: \(\{1, −3, 9\}\) ; variable parts: \(\{x^{2}y, xy^{2} , xy\}\)

Exercise \(\PageIndex{3}\)

• \(5 (3x − 5) \)
• \(3 (4x − 1) \)
• \(−2 (2x^{2} − 5x + 1) \)
• \(−5 (6x^{2} − 3x − 1)\)
• \(\frac{2}{3} (9y^{2} + 12y − 3)\)
• \(−\frac{3}{4} (8y^{2} + 20y + 4)\)
• \(12(\frac{1}{3} a^{2} − \frac{5}{6} a + \frac{7}{12} )\)
• \(−9 (\frac{1}{9} a^{2} − \frac{5}{3} a + 1 )\)
• \(9 (a^{2} − 2b^{2} )\)
• \(−5 (3x^{2} − y^{2} )\)
• \((5a^{2} − 3ab + b^{2} ) ⋅ 6\)
• \((a^{2}b^{2} − 9ab − 3) ⋅ 7\)
• \(− (5x^{2} − xy + y^{2} )\)
• \(− (x^{2}y^{2} − 6xy − 1)\)

1. \(15x − 25\)

3. \(−4x^{2} + 10x − 2\)

5. \(6y^{2} + 8y − 2\)

7. \(4a^{2} − 10a + 7\)

9. \(9a^{2} − 18b^{2}\)

11. \(30a^{2} − 18ab + 6b^{2}\)

13. \(−5x^{2} + xy − y^{2}\)

Exercise \(\PageIndex{4}\)

Combine like terms.

• \(18x − 5x + 3x\)
• \(30x − 50x + 10x\)
• \(3y − 4 + 2y − 12\)
• \(12y + 7 − 15y − 6\)
• \(2x^{2} − 3x + 2 + 5x^{2} − 6x + 1\)
• \(9x^{2} + 7x − 5 − 10x^{2} − 8x + 6\)
• \(\frac{3}{5} a^{2} − \frac{1}{2} + \frac{1}{3} a^{2} + \frac{4}{5}\)
• \(\frac{1}{6} a^{2} + \frac{2}{3} − \frac{4}{3} a^{2} − \frac{1}{9}\)
• \(\frac{1}{2} y^{2} + \frac{2}{3} y − 3 + \frac{3}{5} y^{2} + \frac{1}{3} y − \frac{7}{3}\)
• \(\frac{5}{6} x^{2} + \frac{1}{8} x − 1 − \frac{1}{2} x^{2} + \frac{3}{4} x − \frac{4}{5}\)
• \(a^{2}b^{2} + 5ab − 2 + 7a^{2}b^{2} − 6ab + 12\)
• \(a^{2} − 12ab + 4b^{2} − 6a^{2} + 10ab − 5b^{2}\)
• \(3x^{2}y + 12xy − 5xy^{2} + 5xy − 8x^{2}y + 2xy^{2}\)
• \(10x^{2}y + 2xy − 4xy^{2} + 2x^{2}y − 8xy + 5xy^{2}\)
• \(7m^{2}n − 9mn + mn^{2} − 6m^{2}n + mn − 2mn^{2}\)
• \(m^{2}n − 5mn + 5mn^{2} − 3m^{2}n + 5mn + 2mn^{2}\)
• \(x^{2n} − 3x^{n} + 5 + 2x^{2n} − 4x^{n} − 3\)
• \(5y^{2n} − 3y^{n} + 1 − 3y^{2n} − 2y^{n} − 1\)

3. \(5y − 16\)

5. \(7x^{2} − 9x + 3\)

7. \(\frac{14}{15}a^{2} + \frac{3}{10}\)

9. \(\frac{11}{10} y^{2} + y − \frac{16}{3}\)

11. \(8a^{2}b^{2} − ab + 10\)

13. \(−5x^{2}y + 17xy − 3xy^{2}\)

15. \(m^{2}n − 8mn − mn^{2}\)

17. \(3x^{2n} − 7x^{n} + 2\)

Exercise \(\PageIndex{5}\)

• \(5 − 2 (4x + 8)\)
• \(8 − 6 (2x − 1)\)
• \(2 (x^{2} − 7x + 1) + 3x − 7\)
• \(−5 (x^{2} + 4x − 1) + 8x^{2} − 5\)
• \(5ab − 4 (ab + 5)\)
• \(5 (7 − ab) + 2ab\)
• \(2 − a^{2} + 3 (a^{2} + 4)\)
• \(7 − 3y + 2 (y^{2} − 3y − 2)\)
• \(8x^{2} − 3x − 5 (x^{2} + 4x − 1)\)
• \(2 − 5y − 6 (y^{2} − y + 2)\)
• \(a^{2}b^{2} − 5 + 3 (a^{2}b^{2} − 3ab + 2)\)
• \(a^{2} − 3ab − 2 (a^{2} − ab + 1)\)
• \(10y^{2} + 6 − (3y^{2} + 2y + 4)\)
• \(4m^{2} − 3mn − (m^{2} − 3mn + n^{2} )\)
• \(x^{2n} − 3x^{n} + 5 (x^{2n} − x^{n} + 1)\)
• \(−3 (y^{2n} − 2y^{n} + 1) + 4y^{2n} − 5\)

1. \(−8x − 11\)

3. \(2x^{2} − 11x − 5\)

5. \(ab − 20\)

7. \(2a^{2} + 14\)

9. \(3x^{2} − 23x + 5\)

11. \(4a^{2}b^{2} − 9ab + 1\)

13. \(7y^{2} − 2y + 2\)

15. \(6x^{2n} − 8x^{n} + 5\)

Exercise \(\PageIndex{6}\)

• \(−2x + 3\) where \(x = −2\)
• \(8x − 5\) where \(x = −1\)
• \(x^{2} − x + 5\) where \(x = −5\)
• \(2x^{2} − 8x + 1\) where \(x = 3\)
• \(\frac { x ^ { 2 } - x + 2 } { 2 x - 1 }\) where \(x = -\frac{1}{2}\)
• \(\frac { 9 x ^ { 2 } + x - 2 } { 3 x - 4 }\) where \(x = -\frac{2}{3}\)
• \(( 3 y - 2 ) ( y + 5 )\) where \(y = \frac { 2 } { 3 }\)
• \((3x + 2) (5x + 1)\) where \(x = −\frac{1}{5}\)
• \((3x − 1) (x − 8)\) where \(x = −1\)
• \((7y + 5) (y + 1)\) where \(y = −2\)
• \(y^{6} − y^{3} + 2\) where \(y = −1\)
• \(y^{5} + y^{3} − 3\) where \(y = −2\)
• \(a^{2} − 5b^{2}\) where \(a = −2\) and \(b = −1\)
• \(a^{3} − 2b^{3}\) where \(a = −3\) and \(b = 2\)
• \((x − 2y) (x + 2y)\) where \(x = 2\) and \(y = −5\)
• \((4x − 3y) (x − y)\) where \(x = −4\) and \(y = −3\)
• \(a^{2} − ab + b^{2}\) where \(a = −1\) and \(b = −2\)
• \(x^{2}y^{2} − xy + 2\) where \(x = −3\) and \(y = −2\)
• \(a^{4} − b^{4}\) where \(a = −2\) and \(b = −3\)
• \(a^{6} − 2a^{3}b^{3} − b^{6}\) where \(a = 2\) and \(b = −1\)

5. \(−\frac{11}{8}\)

13. \(−1\)

15. \(−96\)

19. \(−65\)

Exercise \(\PageIndex{7}\)

Evaluate \(\sqrt { b ^ { 2 } - 4 a c }\) given the following values.

• \(a = 6, b = 1\) and \(c = −1\)
• \(a = 15, b = 4\) and \(c = −4\)
• \(a = \frac{3}{4} , b = −2\) and \(c = −4\)
• \(a = \frac{1}{2} , b = −2\) and \(c = −30\)
• \(a = 1, b = 2\) and \(c = −1\)
• \(a = 1, b = −4\) and \(c = −50\)
• \(a = 1, b = −1\) and \(c = −\frac{1}{16}\)
• \(a = −2, b = −\frac{1}{3}\) and \(c = 1\)

5. \(2\sqrt{2}\)

7. \(\frac { \sqrt { 5 } } { 2 }\)

Exercise \(\PageIndex{8}\)

Convert the following temperatures to degrees Celsius given \(C = \frac{5}{9} (F − 32)\), where F represents degrees Fahrenheit.

• \(95°\)F
• \(86°\)F
• \(32°\)F
• \(−40°\)F

1. \(35°\)C

3. \(0°\)C

Exercise \(\PageIndex{9}\)

• Calculate the perimeter and area of a rectangle with dimensions \(12\) feet by \(5\) feet.
• Calculate the perimeter and area of a rectangle with dimensions \(5\) meters by \(1\) meter.
• Calculate the surface area and volume of a sphere with radius \(6\) centimeters.
• The radius of the base of a right circular cylinder measures \(4\) inches and the height measures \(10\) inches. Calculate the surface area and volume.
• Calculate the volume of a sphere with a diameter of \(18\) centimeters.
• The diameter of the base of a right circular cone measures \(6\) inches. If the height is \(1\:\frac{1}{2}\) feet, then calculate its volume.
• Given that the height of a right circular cylinder is equal to the radius of the base, derive a formula for the surface area in terms of the radius of the base.
• Given that the area of the base of a right circular cylinder is \(25π\) square inches, find the volume if the height is \(1\) foot.
• Jose was able to drive from Tucson to Phoenix in \(2\) hours at an average speed of \(58\) mph. How far is Phoenix from Tucson?
• If a bullet train can average \(152\) mph, then how far can it travel in \(\frac{3}{4}\) of an hour?
• Margaret traveled for \(1\:\frac{3}{4}\) hour at an average speed of \(68\) miles per hour. How far did she travel?
• The trip from Flagstaff, AZ to the Grand Canyon national park took \(1\:\frac{1}{2}\) hours at an average speed of \(54\) mph. How far is the Grand Canyon national park from Flagstaff?
• Calculate the simple interest earned on a \(3\)-year investment of \($2,500\) at an annual interest rate of \(5\:\frac{1}{4} \)%.
• Calculate the simple interest earned on a \(1\)-year investment of \($5,750\) at an annual interest rate of \(2\:\frac{5}{8} \)%.
• What is the simple interest earned on a \(5\)-year investment of \($20,000\) at an annual interest rate of \(6\)%?
• What is the simple interest earned on a \(1\)-year investment of \($50,000\) at an annual interest rate of \(4.5\)%?
• The time \(t\) in seconds an object is in free fall is given by the formula \(t = \frac { \sqrt { s } } { 4 }\), where s represents the distance in feet the object has fallen. How long does it take an object to fall \(32\) feet? (Give the exact answer and the approximate answer to the nearest hundredth.)
• The current \(I\) measured in amperes, is given by the formula \(I = \sqrt { \frac { P } { R } }\), where \(P\) is the power usage measured in watts, and \(R\) is the resistance measured in ohms. If a light bulb uses \(60\) watts of power and has \(240\) ohms of resistance, then how many amperes of current are required?

1. \(P = 34\) feet; \(A = 60\) square feet

3. \(SA = 144π\) square centimeters; \(V = 288π\) cubic centimeters

5. \(972π\) cubic centimeters

7. \(SA = 4πr^{2}\)

9. \(116\) miles

11. \(119\) miles

13. \($393.75\)

15. \($6,000\)

17. \(\sqrt { 2 } \approx 1.41\) seconds

Exercise \(\PageIndex{10}\)

• Find and post a useful mathematical model. Demonstrate its use with some values.
• Research and discuss the history of the variable. What can we use if we run out of letters?
• Find and post a link to a useful resource describing the Greek alphabet.
• Given the algebraic expression \(5 − 3 (9x − 1)\), explain why we do not subtract \(5\) and \(3\) first.
• Do we need a separate distributive property for more than two terms? For example, \(a (b + c + d) = ab + ac + ad\). Explain.
• How can we check to see if we have simplified an expression correctly?

1. Answer may vary

3. Answer may vary

5. Answer may vary

87 Combinations of variables and numbers along with mathematical operations used to generalize specific arithmetic operations.

88 Components of an algebraic expression separated by addition operators.

89 Components of a term separated by multiplication operators.

90 The numerical factor of a term.

91 All the variable factors with their exponents.

92 A term written without a variable factor.

93 Given any real numbers \(a, b,\) and \(c, a (b + c) = ab + ac\) or \((b + c) a = ba + ca\).

94 Constant terms or terms whose variable parts have the same variables with the same exponents.

95 Used when referring to like terms.

96 Adding or subtracting like terms within an algebraic expression to obtain a single term with the same variable part.

97 The process of combining like terms until the expression contains no more similar terms.

98 The process of performing the operations of an algebraic expression for given values of the variables.

99 The act of replacing a variable with an equivalent quantity.

100 A reusable mathematical model using algebraic expressions to describe a common application.

101 The distance \(D\) after traveling at an average rate \(r\) for some time \(t\) can be calculated using the formula \(D = rt\).

102 Modeled by the formula \(I = prt\), where \(p\) represents the principal amount invested at an annual interest rate \(r\) for \(t\) years.

Please ensure that your password is at least 8 characters and contains each of the following:

• a special character: @$#!%*?&

Math Solver

Geogebra math solver.

Get accurate solutions and step-by-step explanations for algebra and other math problems, while enhancing your problem-solving skills!

Algebra Formulas

Algebra Formulas form the foundation of numerous topics of mathematics. Topics like equations, quadratic equations, polynomials , coordinate geometry , calculus , trigonometry , and probability , extensively depend on algebra formulas for understanding and for solving complex problems. The algebra formulas are helpful to perform complex calculations in the least time and with fewer steps. The algebraic expression formulas are used to simplify the algebraic expressions.

Based on the complexity of the math topics, the algebraic formulas have also been transformed. Topics like logarithms, indices, exponents, progressions, permutations, and combinations have their own set of algebraic formulas. Here, we shall look into the list of all algebraic formulas used across the different math topics.

Algebra Formulas - Identities

In algebra formulas , an identity is an equation that is always true regardless of the values assigned to the variables. Algebraic Identity means that the left-hand side of the equation is identical to the right-hand side of the equation, and for all values of the variables. Algebraic identities find applications in solving the values of unknown variables. Here are some most commonly used algebraic identities :

Algebraic Identities Formula

• (a + b) 2 = a 2 + 2ab + b 2
• (a - b) 2 = a 2 - 2ab + b 2
• (a + b)(a - b) = a 2 - b 2
• (x + a)(x + b) = x 2 + x(a + b) + ab

Let us look at the algebraic identity: (a + b) 2 = a 2 + 2ab + b 2 , and try to understand this identity in algebra and also in geometry. As proof of this formula, let us try to multiply algebraically the expression and try to find the formula. (a + b) 2 = (a + b) × (a + b) = a(a + b) + b(a + b) = a 2 + ab + ab + b 2 . This expression can be geometrically understood as the area of the four sub-figures of the below-given square diagram. Further, we can consolidate the proof of the identity (a + b) 2 = a 2 + 2ab + b 2 .

In the same way, by using squares and rectangles, we can prove the other algebraic identities as well.

What are Algebra Formulas?

An algebraic formula is an equation or a rule written using mathematical and algebraic symbols and terms. It is an equation that involves algebraic expressions on both sides. The algebraic formula is a short quick formula to solve complex algebraic calculations. These algebraic formulas can be derived for each maths topic, usually having an unknown variable x, and some of the common algebraic formulas can be applied to each of the maths topics.

Example: (a+b) 2 = a 2 + 2ab + b 2 is an algebraic formula and here,

• (a+b) 2 is an algebraic expression
• a 2 + 2ab + b 2 is a simplified form of an algebraic expression

Here are the algebraic formulas arranged class-wise.

• Algebraic Formulas for Class 8
• Algebraic Formulas for Class 9
• Algebraic Formulas for Class 10
• Algebraic Formulas for Class 11
• Algebraic Formulas for Class 12

Let us look at the detailed list of these formulas in the upcoming sections.

Algebra Formulas for Class 8

The algebra formulas for three variables a, b, and c and for a maximum degree of 3 can be easily derived by multiplying the expression by itself, based on the exponent value of the algebraic expression. The below formulas are for class 8.

• (a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3
• (a - b) 3 = a 3 - 3a 2 b + 3ab 2 - b 3
• a 3 + b 3 = (a + b)(a 2 - ab + b 2 )
• a 3 - b 3 = (a - b)(a 2 + ab + b 2 )
• (a + b + c) 2 = a 2 + b 2 + c 2 + 2ab + 2bc + 2ca

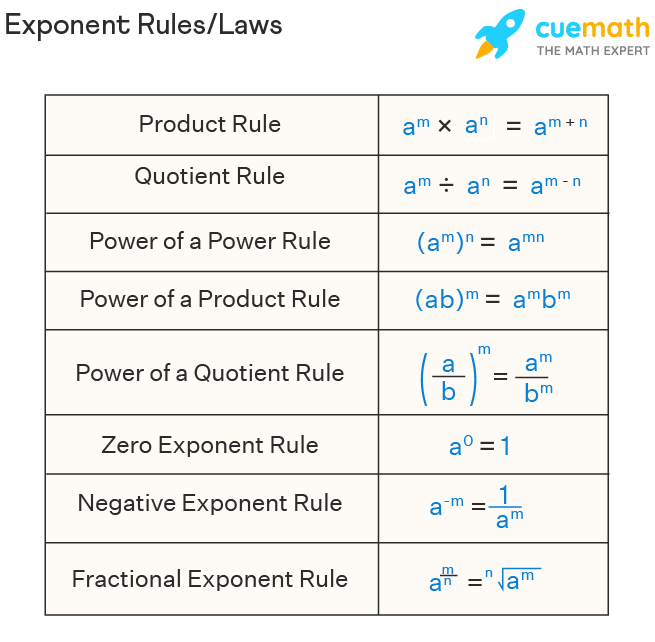
Some of the common laws of exponents with the same bases having different powers, and different bases having the same power, are useful to solve complex exponential terms. The higher exponential values can be easily solved without any expansion of the exponential terms. These exponential laws are further useful to derive some of the logarithmic laws.

• a m . a n = a m + n
• a m /a n = a m - n
• (a m ) n = a mn
• (ab) m = a m . b m
• a -m = 1/a m

Each of these laws has a specific name. Take a look at the figure below:

Algebra Formulas for Class 9

Logarithms are useful for the computation of highly complex multiplication and division calculations. The normal exponential form of 2 5 = 32 can be transformed to a logarithmic form as log 2 32 = 5. Further, the multiplication and division between two mathematic expressions can be easily transformed into addition and subtraction , after converting them to logarithmic form. The below properties of logarithms formulas are applicable in logarithmic calculations.

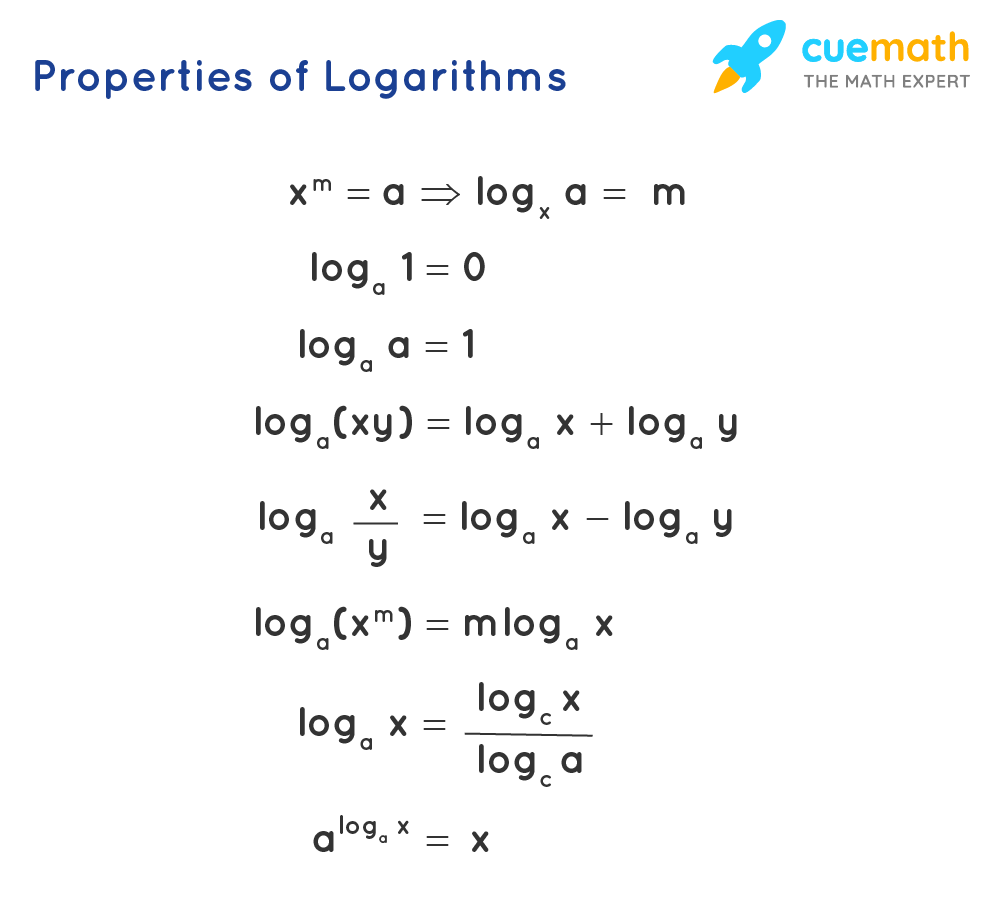
The important log algebraic formulas that we use most commonly are:

• log a (xy) = log a x + log a y
• log a (x/y) = log a x - log a y
• log a x m = m log a x
• log a a = 1
• log a 1 = 0

Algebra Formulas for Class 10

An important algebra formula introduced in class 10 is the “ quadratic formula ”. The general form of the quadratic equation is ax 2 + bx + c = 0, and there are two methods of solving this quadratic equation. The first method is to solve the quadratic equation by the algebraic method, and the second method is to solve it through the use of the quadratic formula. The below formula is helpful to quickly find the values of the variable x with the least number of steps.

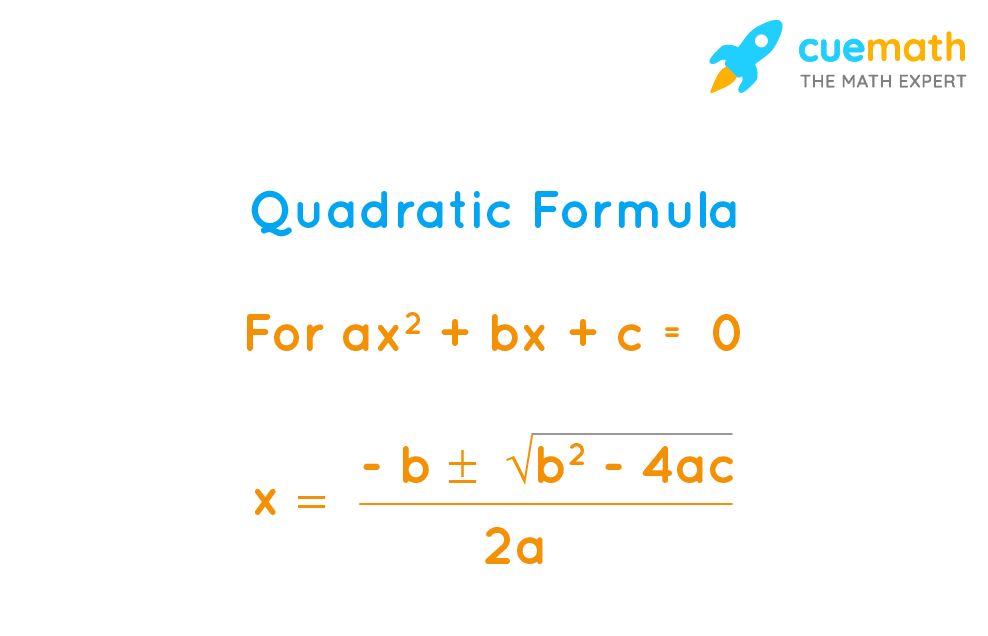
In the above expression, the value b 2 - 4ac is called the discriminant and is useful to find the nature of the roots of the given equation. Based on the value of the determinant, the three types of roots are given below.

• If b 2 - 4ac > 0, then the quadratic equation has two distinct real roots.
• If b 2 - 4ac = 0, then the quadratic equation has two equal real roots.
• If b 2 - 4ac < 0, then the quadratic equation has two imaginary roots.

Apart from this, we have a few other formulas related to progressions . Progressions include some of the basic sequences such as arithmetic sequence and geometric sequence. The arithmetic sequence is obtained by adding a constant value to the successive terms of the series. The terms of the arithmetic sequence is a, a + d, a + 2d, a + 3d, a + 4d, .... a + (n - 1)d. The geometric sequence is obtained by multiplying a constant value to the successive terms of the series. The terms of the geometric sequence are a, ar, ar 2 , ar 3 , ar 4 , .....ar n-1 . The below formulas are helpful to find the nth term and the sum of the terms of the arithmetic, and geometric sequence.

Arithmetic Sequence Formulas :

For any arithmetic sequence a, a + d, a + 2d, ...

• n th term , a n = a + (n - 1) d
• Sum of the first n terms , S n = n/2 [2a + (n - 1) d]

Geometric Sequence Formulas :

For any geometric sequence a, ar, ar 2 , ...

• n th term , a n = a r n - 1
• Sum of the first n terms , S n = a (1 - r n ) / (1 - r)
• Sum of infinite terms , S = a / (1 - r)

Algebra Formulas for Class 11

The important topics of Class 11 which have extensive use of algebraic formulas are permutations and combinations . Permutations help in finding the different arrangements of r things from the n available things, and combinations help in finding the different groups of r things from the available n things. The following formulas help in finding the permutations and combination values.

• Permutation Formulas : Factorial formula : n! = n × (n - 1) × (n - 2) × ... × 3 × 2 × 1 and nPr Formula : n P r (or) n P r = n! / (n - r)!
• Combination Formula (or) nCr Formula : n C r (or) n C r = n!/[r!(n−r)!]

Apart from the permutations and combinations, there is another important topic of “ Binomial Theorem ” as well which is used to evaluate the large exponents of algebraic expressions with two terms. Here the coefficients of the binomial terms are calculated from the formula of combinations. The below expression provides the complete formula for binomial expansion, and it can be termed the algebraic expression of the binomial theorem.

Using this binomial expansion formula , we can simplify complex expansions like (x + 2y) 7 , (3x - y) 11 , etc.

Algebra Formulas for Class 12

The vector algebra formulas that are involved in class 12 are as follows.

For any three vectors, a , b and c :

• The magnitude of a = x i +y j +z k is, | a | =√(x 2 +y 2 +z 2 ).
• The unit vector along a is a /| a |.
• The dot product is defined as: a ⋅ b = | a | | b | cos θ, where θ is the angle between the vectors a and b .
• The cross product is defined as: a × b = | a | | b | sin θ\(\hat{n}\), where θ is the angle between the vectors a and b .
• The scalar triple product of three vectors is given by [ a b c ] = a ⋅ ( b × c ) = ( a × b ) ⋅ c .

Algebra Formulas of Functions

An algebraic function is of the form y=f(x). Here, x is the input and y is the output of this function. Here, each input corresponds to exactly one output. But multiple inputs may correspond to a single output. For example: f(x) = x 2 is an algebraic function. Here, when x = 2, f(2) = 2 2 =4. Here, x = 2 is the input, and f(2) = 4 is the output of the function.

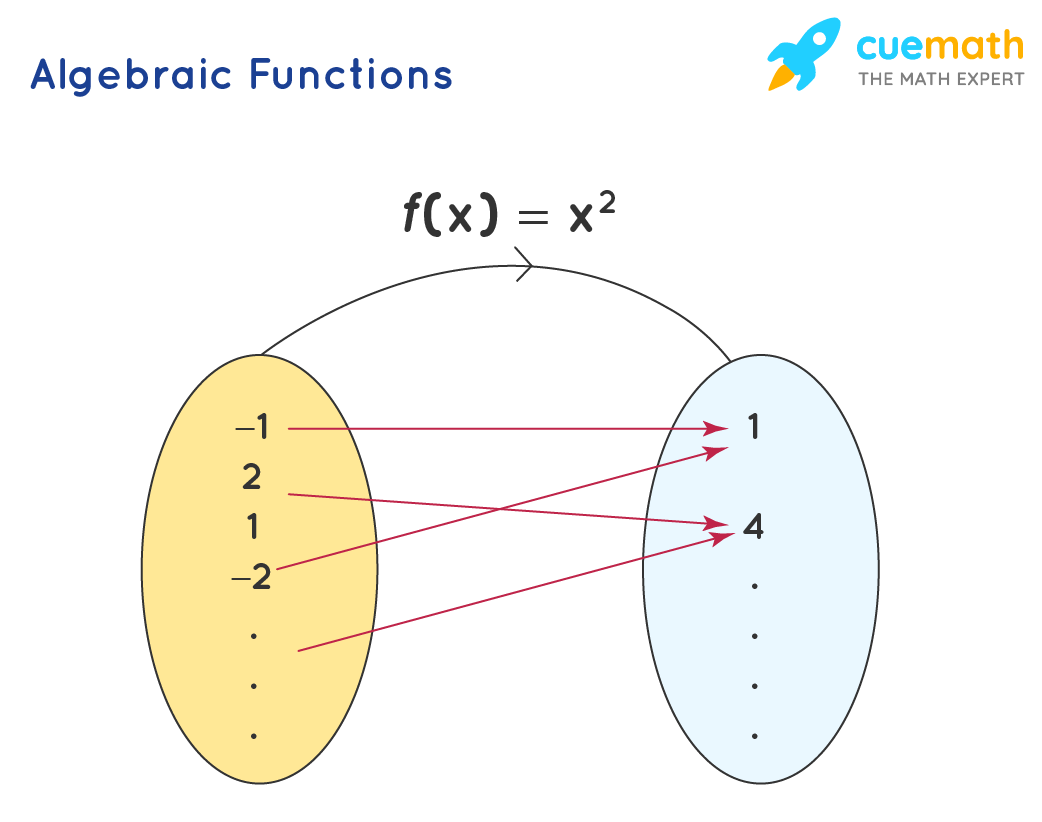
The set of all inputs of a function is known as domain and the set of all the outputs is known as the range. To know more about domain and range, click here .

Algebra Formulas of Fractions

The fractions in algebra are known as rational expressions . We can perform numerous arithmetic operations such as addition, subtraction, multiplication, and the dividing of fractions in algebra just the same way we do with fractions involving numbers. Further, it only has the unknown variables and involved the same rules of working across fractions. The below four expressions are useful for working with algebraic fractions.

• Adding Fractions : x/y + z/w = (x.w + y.z)/(y.w)
• Subtracting Fractions : x/y - z/w = (x.w - y.z)/(y.w)
• Multiplying Fractions : x/y × z/w = xz/yw
• Dividing Fractions: x/y ÷ z/w = x/y × w/z = xw/yz

Challenging Questions on Algebra Formulas:

Now having understood the concepts of algebraic expression, check out the below three questions to better practice the learned concept.

• Find the roots of the quadratic equation : x 2 +7x+12=0
• Simplify the expression: (x -9 y 3 )/(x -7 y 8 ) so that the answer has no negative exponents .
• Expand the logarithm: log x 2 y 3 z.

☛Related Articles:

• Algebraic Formula Calculator
• Algebra Calculator
• Math Formulas

Examples on Algebra Formulas

Example 1: Using algebra formulas, find (2x-3y) 2 .

Here, we use the identity (a-b) 2 = a 2 - 2ab + b 2 to expand this. Here, a= 2x and b=3y. Then we get: (2x-3y) 2 = (2x) 2 -2(2x)(3y)+(3y) 2 = 4x 2 -12xy + 9y 2 . Therefore, (2x - 3y) 2 = 4x 2 -12xy + 9y 2 .

Answer: 4x 2 -12xy + 9y 2

Example 2: Using algebra formulas (identities), evaluate 297 × 303.

The above product can be written as (300-3) × (300+3). We will find this product using the formula: (a-b)(a+b)=a 2 - b 2 Here a=300 and b=3. Then we get: (300-3) × (300+3) =300 2 - 3 2 = 90000-9 = 89991. Therefore, 297 × 303 = 89991.

Answer: 89991

Example 3: Find the roots of the quadratic equation x 2 +5x+6=0 using algebra formulas for quadratic equations.

The given equation is x 2 + 5x + 6 = 0. Comparing this with ax 2 +bx+c=0, we get: a=1; b=5; c=6. Substituting these values in the quadratic formula:

x = [−b ± √(b 2 − 4ac)] / 2(1) = [−5 ± √(5 2 − 4(1)(6))] / 2 = [−5 ± √(25 − 4(1)(6))] / 2 = [−5 ± √(25 − 24)] / 2 = [−5 ± √1] / 2 = (-5 + 1) / 2 (or) (-5 - 1) / 2 = -4/2 (or) -6/2 = -2 (or) -3

Answer: Therefore x = -2, and -3.

go to slide go to slide go to slide

Book a Free Trial Class

Practice Questions on Algebra Formulas

go to slide go to slide

FAQs on Algebra Formulas

What are all algebra formulas in math.

Here are some of the most commonly used formulas of algebra :

• a 2 - b 2 = (a - b)(a + b)
• (x + a)(x + b) = x 2 + x(a + b) + a b

Further, there are algebraic formulas for other topics of maths such as exponents, logarithms, permutations, sequences, and vector algebra. For a detailed list of formulas, scroll up this page.

How do I Learn Algebra Formulas?

Algebra formulas can be easily memorized by visualizing the formulas as squares or rectangles . Further, the understanding of the factorized forms of the formulas helps to easily learn and remember the algebraic formulas.

How to Solve Algebra Formulas?

The solving of algebra equations is aimed at equalizing the left-hand side of the expression with the right-hand side of the expression. Further, the terms can be transferred from the left to the right side of the expression, based on the formulas of algebra.

What Is The Formula For a^2 - b^2 in Algebra Formulas?

The formula for a 2 - b 2 is (a+b)(a-b)= a 2 - b 2 . It is called the difference of squares formula .

What are the Algebra Formulas for Triangular Numbers?

The algebra formula for triangular numbers is H 2 = B 2 + A 2 and it helps to relate the length of the sides of the triangle. It is applicable for a right triangle and has been derived from the Pythagoras theorem . The alphabets H represents the hypotenuse , B represents the base of the right triangle, and A represents the altitude of the triangle . Applying this same formula an example of triangular numbers is (6, 8, 10).

What is the Basis Of Algebra Formulas?

The basis of algebra formulas is that the resultant numeric value of the expressions on either side of the equals to sign is equal. Further, algebraically the terms are modified on either side to match up with the algebraic formulas.

What are Algebra Expressions?

For each of the algebra formulas, the equations with variables , powers, and arithmetic operations, and on either side of the equals to sign are called algebraic expressions/ variable expressions . In the algebraic formula (a+b)(a-b)= a 2 - b 2 , the terms on either side of the equals to sign are called algebraic expressions.

What Are the Applications of Algebraic Expressions Formulas?

The algebraic expression formulas are used to simplify complex algebraic expressions such as (3x + 4y) 2 , (a - 3b + 2c) 2 , etc. Some of these formulas are also used to factorize the polynomials .

What Are Algebraic Expressions Formulas?

The algebraic expression formulas are formulas that are used to simplify the algebraic expressions. Some important algebraic expressions formulas used for expansion are:

• (x + y) 2 = x 2 + 2xy + y 2
• (x - y) 2 = x 2 - 2xy + y 2
• (x + y) 3 = x 3 + y 3 + 3xy (x + y)
• (x - y) 3 = x 3 - y 3 - 3xy (x - y)
• (x + y + z) 2 = x 2 + y 2 + z 2 + 2xy + 2yz + 2zx

Some of the algebraic formulas used for factorization are:

• x 2 - y 2 = (x + y) (x - y)
• x 3 + y 3 = (x + y) (x 2 – xy + y 2 )
• x 3 - y 3 = (x - y) (x 2 + xy + y 2 )

How To Derive the Algebraic Expressions Formula (x + y) 3 = x 3 + y 3 + 3xy (x + y)?

We can derive this formula just by multiplying polynomials . Let us start with the left-hand side of this formula and reach the right-hand side at the end.

(x + y) 3 = (x + y) 2 (x + y)

= (x 2 + 2xy + y 2 ) (x + y)

= x 3 + 2x 2 y + xy 2 + x 2 y + 2xy 2 + y 3

= x 3 + y 3 + 3x 2 y + 3xy 2 (or)

= x 3 + y 3 + 3xy (x + y)

How to Use Algebraic Expressions Formulas While Solving Problems?

We have multiple algebraic expressions formulas and some of them have to be used according to the need while solving the problems. For example, to factorize the expression, 8x 3 + 27, we apply the a 3 + b 3 formula as follows.

a 3 + b 3 = (a + b) (a 2 - ab + b 2 )

Substitute a = 2x and b = 3 on both sides,

(2x) 3 + 3 3 = (2x + 3) ( (2x) 2 - (2x)(3) + 3 2 )

8x 3 + 27 = (2x + 3) (4x 2 - 6x + 9).

• Solve equations and inequalities
• Simplify expressions
• Factor polynomials
• Graph equations and inequalities
• Advanced solvers
• All solvers
• Arithmetics
• Determinant
• Percentages
• Scientific Notation
• Inequalities

What can QuickMath do?

QuickMath will automatically answer the most common problems in algebra, equations and calculus faced by high-school and college students.

• The algebra section allows you to expand, factor or simplify virtually any expression you choose. It also has commands for splitting fractions into partial fractions, combining several fractions into one and cancelling common factors within a fraction.
• The equations section lets you solve an equation or system of equations. You can usually find the exact answer or, if necessary, a numerical answer to almost any accuracy you require.
• The inequalities section lets you solve an inequality or a system of inequalities for a single variable. You can also plot inequalities in two variables.
• The calculus section will carry out differentiation as well as definite and indefinite integration.
• The matrices section contains commands for the arithmetic manipulation of matrices.
• The graphs section contains commands for plotting equations and inequalities.
• The numbers section has a percentages command for explaining the most common types of percentage problems and a section for dealing with scientific notation.

Math Topics

More solvers.

• Add Fractions
• Simplify Fractions

Algebra Expressions and Equations

Ai generator.

Algebra is a fundamental branch of mathematics that explores the relationships between variables and constants through expressions and equations. Algebra expressions consist of terms combined using operations like addition , subtraction , multiplication , and division , often containing variables that represent unknown values. Equations , on the other hand, set two expressions equal to each other, forming the basis for solving problems by finding the values of these variables. This field is essential in developing critical thinking and problem-solving skills, applicable in various real-world contexts from engineering to economics. Understanding how to manipulate and solve these algebraic expressions and equations is crucial for students and professionals alike

What are Algebra Expressions And Equations ?

In mathematics, particularly in algebra, the terms “expressions” and “equations” play fundamental roles and serve different functions within problem-solving contexts. Understanding each and their relationship can greatly enhance your ability to manipulate and solve algebraic problems. Here’s a breakdown:

Algebraic Expressions

An algebraic expression is a combination of variables, numbers, and operations (such as addition, subtraction, multiplication, and division). Expressions do not contain equal signs; instead, they represent values that can be simplified but not solved. For example, the expression 2x+5 combines the variable xxx with numbers through multiplication and addition. Algebraic expressions can be as simple as a single term, like 5x5x5x, or more complex with multiple terms, like 3x²−4x+7

Algebraic Equations

An algebraic equation, on the other hand, is a statement that asserts the equality of two expressions, featuring an equal sign (=). Equations are solvable, meaning you can manipulate them to find the value(s) of the variable(s) that make the equation true. For instance, the equation 2x+5=15 can be solved by finding the value of x that balances both sides of the equal sign.

Relationship and Use

Both algebraic expressions and equations are used to describe relationships between quantities and to solve problems. Expressions can be part of equations; they can be evaluated given certain values, simplified, or even transformed into equations by including an equality to another expression. Equations can be solved to find unknown values, analyzed, and applied in various practical scenarios like physics, engineering, and economics.

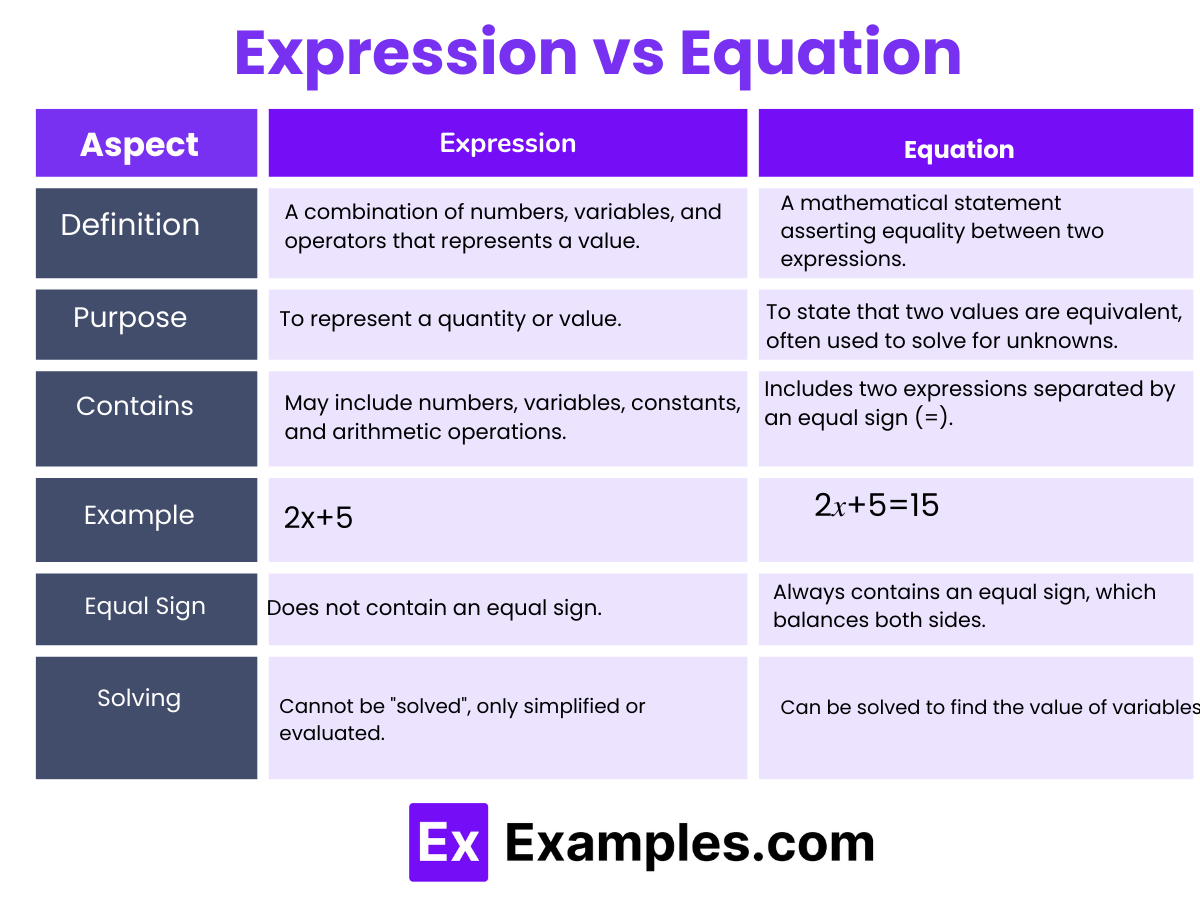
Difference between Algebraic Expression and Equation

How to Solve Algebraic Equations?

Solving algebraic equations is a systematic process that involves manipulating the equation to isolate the variable and simplify the expression. Here’s a step-by-step guide on how to approach solving algebraic equations:

Simplify Both Sides : Start by simplifying both sides of the equation. Combine like terms and simplify any algebraic expressions.

Isolate the Variable : Use addition or subtraction to move terms that contain the variable to one side of the equation and all constant terms to the other side.

Undo Multiplication or Division : If the variable is multiplied by a coefficient or divided, use the opposite operation to isolate the variable. For multiplication, divide both sides by the same number, and for division, multiply both sides.

Check for More Solutions : Some equations, like quadratic equations, may have more than one solution. Be sure to explore all potential solutions.

Verify Your Solution : Substitute the solution back into the original equation to verify that it works. This step ensures that the solution is correct and that no errors were made during the process.

Consider Special Cases : Be aware of special cases, such as no solution (when the equation simplifies to a contradiction, like 3=23) or infinite solutions (when the equation simplifies to a tautology, like 0=00).

Algebraic Expression and Equation Problem

Algebraic expressions and equations form the backbone of algebra, each serving a specific purpose in mathematical problem-solving. Understanding the distinction between them and how to handle each is crucial in mastering algebra.

Algebraic Expression

An algebraic expression is a combination of variables, numbers, and arithmetic operations (such as addition, subtraction, multiplication, and division). It does not include an equality sign, so it cannot be solved but can be simplified. Expressions are used to represent values and can be part of broader mathematical formulas or functions.

Purpose: To represent relationships or formulas involving variables without asserting equality.

Algebraic Equation

An algebraic equation , on the other hand, involves variables and numbers connected by arithmetic operations, but crucially, it includes an equality sign. This equality defines a problem that needs solving: finding the value(s) of the variables that make the equation true.

Purpose: To solve for unknown values, usually represented by variables, that satisfy the equality condition set by the equation.

Problem-Solving Approach for Algebraic Expressions and Equations

Expressions:

• Simplify : Combine like terms (terms that have the same variables raised to the same power).
• Evaluate : Substitute known values for variables if required and simplify further to find the value of the expression.
• Simplify Both Sides : Simplify each side of the equation separately by combining like terms and using the distributive property if necessary.
• Isolate the Variable : Move all terms containing the variable to one side and all constant terms to the other side using basic arithmetic operations.
• Solve for the Variable : Use inverse operations to isolate the variable completely. For instance, if the variable is multiplied by a number, divide both sides by that number.
• Check Your Solution : Substitute the solution back into the original equation to verify accuracy.

Example Problem

To illustrate, consider an equation and an expression:

• Expression: 3x+5
• Equation: 3x+5=11

For the expression, you might be asked to simplify or evaluate it for a specific value of x. For the equation, you would solve it to find the value of xxx that makes it true. Solving 3x+5=11 involves isolating x by first subtracting 5 from both sides, resulting in 3x=6, and then dividing both sides by 3 to find x=2

How to Simplify Algebraic Expressions?

Step 1: remove parentheses.

Start by expanding the expression, using the distributive property to eliminate parentheses. Multiply each term inside the parentheses by the term outside, if applicable.

Example: a(b+c)=ab+ac

Step 2: Combine Like Terms

Like terms are terms that contain the same variables raised to the same power. Add or subtract coefficients of like terms to simplify the expression.

Example: 3x+4x=7x

2y²+5−3y²+1=−y²+6

Step 3: Simplify Coefficients

If there are any coefficients that can be simplified (for example, if they are fractions), do this to make the expression cleaner.

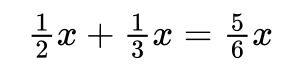
Step 4: Arrange Terms

Order the terms in a standardized form, usually from highest to lowest degree of the variable (for example, in descending powers of x). This step isn’t necessary for simplification per se, but it helps in readability and is standard practice.

Example: x²+2x−x²+3→2x+3

Step 5: Factor Out Common Factors

If there’s a common factor in all terms, factor it out. This is particularly useful if the expression is part of an equation.

Example: 4x²−8x=4x(x−2)

Step 6: Simplify Any Fractions

If the expression includes fractions, simplify them by finding the greatest common divisor for the numerator and denominator or by rationalizing the denominator if needed.

Example: 4x/8x²=1/2x

Step 7: Check for Special Products

Look for opportunities to use special products or identities (like squares of binomials or difference of squares) to further simplify the expression.

Example: x²−9=(x+3)(x−3)

What are the 5 Algebraic Expressions?

The five basic algebraic expressions include monomials (3x), binomials (3x + 4), trinomials (x² + 2x + 1), polynomials (2x³ + 3x² + x + 4), and rational expressions ((x+1)/(x-1)).

What are the 5 Types of Algebraic Expressions?

The five types of algebraic expressions are monomials, binomials, trinomials, polynomials, and rational expressions. Each type varies in the number of terms and complexity of the operations involved.

What are the 20 Algebraic Identities?

The 20 algebraic identities include essential formulas like (a + b)² = a² + 2ab + b², (a – b)² = a² – 2ab + b², and a² – b² = (a + b)(a – b), among others, used to simplify and solve equations.

What are the Four Basic Algebra Formulas?

The four basic algebra formulas are: a² – b² = (a + b)(a – b) (a + b)² = a² + 2ab + b² (a – b)² = a² – 2ab + b² (a + b)(a – b) = a² – b²

What are Basic Algebraic Expressions Examples?

Examples of basic algebraic expressions include 3x + 2, 5y – 7, x² + 4x + 4, 7a – 3b + 5, and 4x² – 9. These expressions consist of variables, constants, and operations.

What are 3 Algebraic Expressions?

Three examples of algebraic expressions are 2x + 5, 4y – 7, and x² – 3x + 2. These expressions represent different combinations of variables and constants.

How do You Write Basic Algebraic Expressions?

To write basic algebraic expressions, identify the variables, determine the constants and coefficients, and combine them using operations such as addition, subtraction, multiplication, and division. For example, 3x + 4y – 5.

How to Do an Algebra Equation?

To solve an algebra equation, combine like terms, use inverse operations to isolate the variable, simplify both sides of the equation, and check the solution. For example, to solve 2x + 3 = 7, subtract 3 and divide by 2.

How to Simplify Algebra Expressions?

To simplify algebra expressions, combine like terms, use the distributive property, reduce fractions, and simplify radicals if present. For instance, 2x + 3x simplifies to 5x.

What is an Example of an Expression and an Equation?

An example of an expression is 2x + 3, while an equation is 2x + 3 = 7. An expression shows a mathematical phrase, whereas an equation shows a mathematical statement with equality.

How to Do Algebra Easily?

To do algebra easily, understand the basics, practice regularly, break problems into smaller steps, and use algebraic rules and formulas. Use resources like textbooks, online tutorials, and practice problems to enhance skills.

How to Calculate Algebraic Expressions?

To calculate algebraic expressions, substitute the given values for variables, perform the operations according to the order of operations (PEMDAS), and simplify the result. For example, for 3x + 4 when x = 2, calculate 3(2) + 4 = 6 + 4 = 10.

What are the Terms in an Equation?

Terms in an equation are the individual components separated by addition or subtraction signs. Each term consists of constants, coefficients, and variables. For example, in the equation 3x + 5 = 11, 3x and 5 are terms.

Text prompt

• Instructive
• Professional

10 Examples of Public speaking

20 Examples of Gas lighting

Algebra Worksheets

Welcome to the Algebra worksheets page at Math-Drills.com, where unknowns are common and variables are the norm. On this page, you will find Algebra worksheets for middle school students on topics such as algebraic expressions, equations and graphing functions.

This page starts off with some missing numbers worksheets for younger students. We then get right into algebra by helping students recognize and understand the basic language related to algebra. The rest of the page covers some of the main topics you'll encounter in algebra units. Remember that by teaching students algebra, you are helping to create the future financial whizzes, engineers, and scientists that will solve all of our world's problems.

Algebra is much more interesting when things are more real. Solving linear equations is much more fun with a two pan balance, some mystery bags and a bunch of jelly beans. Algebra tiles are used by many teachers to help students understand a variety of algebra topics. And there is nothing like a set of co-ordinate axes to solve systems of linear equations.

Most Popular Algebra Worksheets this Week

Algebraic Properties, Rules and Laws Worksheets

The commutative law or commutative property states that you can change the order of the numbers in an arithmetic problem and still get the same results. In the context of arithmetic, it only works with addition or multiplication operations , but not mixed addition and multiplication. For example, 3 + 5 = 5 + 3 and 9 × 5 = 5 × 9. A fun activity that you can use in the classroom is to brainstorm non-numerical things from everyday life that are commutative and non-commutative. Putting on socks, for example, is commutative because you can put on the right sock then the left sock or you can put on the left sock then the right sock and you will end up with the same result. Putting on underwear and pants, however, is non-commutative.

• The Commutative Law Worksheets The Commutative Law of Addition (Numbers Only) The Commutative Law of Addition (Some Variables) The Commutative Law of Multiplication (Numbers Only) The Commutative Law of Multiplication (Some Variables)

The associative law or associative property allows you to change the grouping of the operations in an arithmetic problem with two or more steps without changing the result. The order of the numbers stays the same in the associative law. As with the commutative law, it applies to addition-only or multiplication-only problems. It is best thought of in the context of order of operations as it requires that parentheses must be dealt with first. An example of the associative law is: (9 + 5) + 6 = 9 + (5 + 6). In this case, it doesn't matter if you add 9 + 5 first or 5 + 6 first, you will end up with the same result. Students might think of some examples from their experience such as putting items on a tray at lunch. They could put the milk and vegetables on their tray first then the sandwich or they could start with the vegetables and sandwich then put on the milk. If their tray looks the same both times, they will have modeled the associative law. Reading a book could be argued as either associative or nonassociative as one could potentially read the final chapters first and still understand the book as well as someone who read the book the normal way.

• The Associative Law Worksheets The Associative Law of Addition (Whole Numbers Only) The Associative Law of Multiplication (Whole Numbers Only)

Inverse relationships worksheets cover a pre-algebra skill meant to help students understand the relationship between multiplication and division and the relationship between addition and subtraction.

• Inverse Mathematical Relationships with One Blank Addition and Subtraction Easy Addition and Subtraction Harder All Multiplication and Division Facts 1 to 18 in color (no blanks) Multiplication and Division Range 1 to 9 Multiplication and Division Range 5 to 12 Multiplication and Division All Inverse Relationships Range 2 to 9 Multiplication and Division All Inverse Relationships Range 5 to 12 Multiplication and Division All Inverse Relationships Range 10 to 25
• Inverse Mathematical Relationships with Two Blanks Addition and Subtraction (Sums 1-18) Addition and Subtraction Inverse Relationships with 1 Addition and Subtraction Inverse Relationships with 2 Addition and Subtraction Inverse Relationships with 3 Addition and Subtraction Inverse Relationships with 4 Addition and Subtraction Inverse Relationships with 5 Addition and Subtraction Inverse Relationships with 6 Addition and Subtraction Inverse Relationships with 7 Addition and Subtraction Inverse Relationships with 8 Addition and Subtraction Inverse Relationships with 9 Addition and Subtraction Inverse Relationships with 10 Addition and Subtraction Inverse Relationships with 11 Addition and Subtraction Inverse Relationships with 12 Addition and Subtraction Inverse Relationships with 13 Addition and Subtraction Inverse Relationships with 14 Addition and Subtraction Inverse Relationships with 15 Addition and Subtraction Inverse Relationships with 16 Addition and Subtraction Inverse Relationships with 17 Addition and Subtraction Inverse Relationships with 18

The distributive property is an important skill to have in algebra. In simple terms, it means that you can split one of the factors in multiplication into addends, multiply each addend separately, add the results, and you will end up with the same answer. It is also useful in mental math, an example of which should help illustrate the definition. Consider the question, 35 × 12. Splitting the 12 into 10 + 2 gives us an opportunity to complete the question mentally using the distributive property. First multiply 35 × 10 to get 350. Second, multiply 35 × 2 to get 70. Lastly, add 350 + 70 to get 420. In algebra, the distributive property becomes useful in cases where one cannot easily add the other factor before multiplying. For example, in the expression, 3(x + 5), x + 5 cannot be added without knowing the value of x. Instead, the distributive property can be used to multiply 3 × x and 3 × 5 to get 3x + 15.

• Distributive Property Worksheets Distributive Property (Answers do not include exponents) Distributive Property (Some answers include exponents) Distributive Property (All answers include exponents)

Students should be able to substitute known values in for an unknown(s) in an expression and evaluate the expression's value.

• Evaluating Expressions with Known Values Evaluating Expressions with One Variable, One Step and No Exponents Evaluating Expressions with One Variable and One Step Evaluating Expressions with One Variable and Two Steps Evaluating Expressions with Up to Two Variables and Two Steps Evaluating Expressions with Up to Two Variables and Three Steps Evaluating Expressions with Up to Three Variables and Four Steps Evaluating Expressions with Up to Three Variables and Five Steps

As the title says, these worksheets include only basic exponent rules questions. Each question only has two exponents to deal with; complicated mixed up terms and things that a more advanced student might work out are left alone. For example, 4 2 is (2 2 ) 2 = 2 4 , but these worksheets just leave it as 4 2 , so students can focus on learning how to multiply and divide exponents more or less in isolation.

• Exponent Rules for Multiplying, Dividing and Powers Mixed Exponent Rules (All Positive) Mixed Exponent Rules (With Negatives) Multiplying Exponents (All Positive) Multiplying Exponents (With Negatives) Multiplying the Same Exponent with Different Bases (All Positive) Multiplying the Same Exponent with Different Bases (With Negatives) Dividing Exponents with a Greater Exponent in Dividend (All Positive) Dividing Exponents with a Greater Exponent in Dividend (With Negatives) Dividing Exponents with a Greater Exponent in Divisor (All Positive) Dividing Exponents with a Greater Exponent in Divisor (With Negatives) Powers of Exponents (All Positive) Powers of Exponents (With Negatives)

Knowing the language of algebra can help to extract meaning from word problems and to situations outside of school. In these worksheets, students are challenged to convert phrases into algebraic expressions.

• Translating Algebraic Phrases into Expressions Translating Algebraic Phrases into Expressions (Simple Version) Translating Algebraic Phrases into Expressions (Complex Version)

Combining like terms is something that happens a lot in algebra. Students can be introduced to the topic and practice a bit with these worksheets. The bar is raised with the adding and subtracting versions that introduce parentheses into the expressions. For students who have a good grasp of fractions, simplifying simple algebraic fractions worksheets present a bit of a challenge over the other worksheets in this section.

• Simplifying Expressions by Combining Like Terms Simplifying Linear Expressions with 3 terms Simplifying Linear Expressions with 4 terms Simplifying Linear Expressions with 5 terms Simplifying Linear Expressions with 6 to 10 terms
• Simplifying Expressions by Combining Like Terms with Some Arithmetic Adding and simplifying linear expressions Adding and simplifying linear expressions with multipliers Adding and simplifying linear expressions with some multipliers . Subtracting and simplifying linear expressions Subtracting and simplifying linear expressions with multipliers Subtracting and simplifying linear expressions with some multipliers Mixed adding and subtracting and simplifying linear expressions Mixed adding and subtracting and simplifying linear expressions with multipliers Mixed adding and subtracting and simplifying linear expressions with some multipliers Simplify simple algebraic fractions (easier) Simplify simple algebraic fractions (harder)
• Rewriting Linear Equations Rewrite Linear Equations in Standard Form Convert Linear Equations from Standard to Slope-Intercept Form Convert Linear Equations from Slope-Intercept to Standard Form Convert Linear Equations Between Standard and Slope-Intercept Form
• Rewriting Formulas Rewriting Formulas (addition and subtraction; about one step) Rewriting Formulas (addition and subtraction; about two steps) Rewriting Formulas ( multiplication and division ; about one step)

Linear Expressions and Equations

In these worksheets, the unknown is limited to the question side of the equation which could be on the left or the right of equal sign.

• Missing Numbers in Equations with Blanks as Unknowns Missing Numbers in Equations ( All Operations ; Range 1 to 9 ; Blanks Never in Answer Position ) Missing Numbers in Equations ( All Operations ; Range 1 to 9 ; Blanks in Any Position ) Missing Numbers in Equations ( All Operations ; Range 1 to 20 ; Blanks Never in Answer Position ) Missing Numbers in Equations ( All Operations ; Range 1 to 20 ; Blanks in Any Position ) Missing Numbers in Equations ( Addition Only ; Range 1 to 9 ; Blanks Never in Answer Position ) Missing Numbers in Equations ( Addition Only ; Range 1 to 9 ; Blanks in Any Position ) Missing Numbers in Equations ( Addition Only ; Range 1 to 20 ; Blanks in Any Position ) Missing Numbers in Equations ( Subtraction Only ; Range 1 to 9 ; Blanks Never in Answer Position ) Missing Numbers in Equations ( Subtraction Only ; Range 1 to 9 ; Blanks in Any Position ) Missing Numbers in Equations ( Subtraction Only ; Range 1 to 20 ; Blanks in Any Position ) Missing Numbers in Equations ( Multiplication Only ; Range 1 to 9 ; Blanks Never in Answer Position ) Missing Numbers in Equations ( Multiplication Only ; Range 1 to 9 ; Blanks in Any Position ) Missing Numbers in Equations ( Multiplication Only ; Range 1 to 20 ; Blanks in Any Position ) Missing Numbers in Equations ( Division Only ; Range 1 to 9 ; Blanks Never in Answer Position ) Missing Numbers in Equations ( Division Only ; Range 1 to 9 ; Blanks in Any Position ) Missing Numbers in Equations ( Division Only ; Range 1 to 20 ; Blanks in Any Position )
• Missing Numbers in Equations with Symbols as Unknowns Missing Numbers in Equations ( All Operations ; Range 1 to 9 ; Symbols Never in Answer Position ) Missing Numbers in Equations ( All Operations ; Range 1 to 9 ; Symbols in Any Position ) Missing Numbers in Equations ( All Operations ; Range 1 to 20 ; Symbols Never in Answer Position ) Missing Numbers in Equations ( All Operations ; Range 1 to 20 ; Symbols in Any Position ) Missing Numbers in Equations ( Addition Only ; Range 1 to 9 ; Symbols Never in Answer Position ) Missing Numbers in Equations ( Addition Only ; Range 1 to 9 ; Symbols in Any Position ) Missing Numbers in Equations ( Addition Only ; Range 1 to 20 ; Symbols in Any Position ) Missing Numbers in Equations ( Subtraction Only ; Range 1 to 9 ; Symbols Never in Answer Position ) Missing Numbers in Equations ( Subtraction Only ; Range 1 to 9 ; Symbols in Any Position ) Missing Numbers in Equations ( Subtraction Only ; Range 1 to 20 ; Symbols in Any Position ) Missing Numbers in Equations ( Multiplication Only ; Range 1 to 9 ; Symbols Never in Answer Position ) Missing Numbers in Equations ( Multiplication Only ; Range 1 to 9 ; Symbols in Any Position ) Missing Numbers in Equations ( Multiplication Only ; Range 1 to 20 ; Symbols in Any Position ) Missing Numbers in Equations ( Division Only ; Range 1 to 9 ; Symbols Never in Answer Position ) Missing Numbers in Equations ( Division Only ; Range 1 to 9 ; Symbols in Any Position ) Missing Numbers in Equations ( Division Only ; Range 1 to 20 ; Symbols in Any Position )
• Solving Equations with Addition and Symbols as Unknowns Equalities with Addition (0 to 9) Symbol Unknowns Equalities with Addition (1 to 12) Symbol Unknowns Equalities with Addition (1 to 15) Symbol Unknowns Equalities with Addition (1 to 25) Symbol Unknowns Equalities with Addition (1 to 99) Symbol Unknowns
• Missing Numbers in Equations with Variables as Unknowns Missing Numbers in Equations ( All Operations ; Range 1 to 9 ; Variables Never in Answer Position ) Missing Numbers in Equations ( All Operations ; Range 1 to 9 ; Variables in Any Position ) Missing Numbers in Equations ( All Operations ; Range 1 to 20 ; Variables Never in Answer Position ) Missing Numbers in Equations ( All Operations ; Range 1 to 20 ; Variables in Any Position ) Missing Numbers in Equations ( Addition Only ; Range 1 to 9 ; Variables Never in Answer Position ) Missing Numbers in Equations ( Addition Only ; Range 1 to 9 ; Variables in Any Position ) Missing Numbers in Equations ( Addition Only ; Range 1 to 20 ; Variables in Any Position ) Missing Numbers in Equations ( Subtraction Only ; Range 1 to 9 ; Variables Never in Answer Position ) Missing Numbers in Equations ( Subtraction Only ; Range 1 to 9 ; Variables in Any Position ) Missing Numbers in Equations ( Subtraction Only ; Range 1 to 20 ; Variables in Any Position ) Missing Numbers in Equations ( Multiplication Only ; Range 1 to 9 ; Variables Never in Answer Position ) Missing Numbers in Equations ( Multiplication Only ; Range 1 to 9 ; Variables in Any Position ) Missing Numbers in Equations ( Multiplication Only ; Range 1 to 20 ; Variables in Any Position ) Missing Numbers in Equations ( Division Only ; Range 1 to 9 ; Variables Never in Answer Position ) Missing Numbers in Equations ( Division Only ; Range 1 to 9 ; Variables in Any Position ) Missing Numbers in Equations ( Division Only ; Range 1 to 20 ; Variables in Any Position )
• Solving Simple Linear Equations Solving Simple Linear Equations with Values from -9 to 9 (Unknown on Left Side) Solving Simple Linear Equations with Values from -99 to 99 (Unknown on Left Side) Solving Simple Linear Equations with Values from -9 to 9 (Unknown on Right or Left Side) Solving Simple Linear Equations with Values from -99 to 99 (Unknown on Right or Left Side)
• Determining Linear Equations from Slopes, y-intercepts and Points Determine a Linear Equation from the Slope and y-intercept Determine a Linear Equation from the Slope and a Point Determine a Linear Equation from Two Points Determine a Linear Equation from Two Points by Graphing

Graphing linear equations and reading existing graphs give students a visual representation that is very useful in understanding the concepts of slope and y-intercept.

• Graphing Linear Equations Graph Slope-Intercept Equations
• Determining Linear Equations from Graphs Determine the Equation from a Graph Determine the Slope from a Graph Determine the y-intercept from a Graph Determine the x-intercept from a Graph Determine the slope and y-intercept from a Graph Determine the slope and intercepts from a Graph Determine the slope, intercepts and equation from a Graph

Solving linear equations with jelly beans is a fun activity to try with students first learning algebraic concepts. Ideally, you will want some opaque bags with no mass, but since that isn't quite possible (the no mass part), there is a bit of a condition here that will actually help students understand equations better. Any bags that you use have to be balanced on the other side of the equation with empty ones.

Probably the best way to illustrate this is through an example. Let's use 3 x + 2 = 14. You may recognize the x as the unknown which is actually the number of jelly beans we put in each opaque bag. The 3 in the 3 x means that we need three bags. It's best to fill the bags with the required number of jelly beans out of view of the students, so they actually have to solve the equation.

On one side of the two-pan balance, place the three bags with x jelly beans in each one and two loose jelly beans to represent the + 2 part of the equation. On the other side of the balance, place 14 jelly beans and three empty bags which you will note are required to "balance" the equation properly. Now comes the fun part... if students remove the two loose jelly beans from one side of the equation, things become unbalanced, so they need to remove two jelly beans from the other side of the balance to keep things even. Eating the jelly beans is optional. The goal is to isolate the bags on one side of the balance without any loose jelly beans while still balancing the equation.

The last step is to divide the loose jelly beans on one side of the equation into the same number of groups as there are bags. This will probably give you a good indication of how many jelly beans there are in each bag. If not, eat some and try again. Now, we realize this won't work for every linear equation as it is hard to have negative jelly beans, but it is another teaching strategy that you can use for algebra.

Despite all appearances, equations of the type a/ x are not linear. Instead, they belong to a different kind of equations. They are good for combining them with linear equations, since they introduce the concept of valid and invalid answers for an equation (what will be later called the domain of a function). In this case, the invalid answers for equations in the form a/ x , are those that make the denominator become 0.

• Solving Linear Equations Combining Like Terms and Solving Simple Linear Equations Solving a x = c Linear Equations Solving a x = c Linear Equations including negatives Solving x /a = c Linear Equations Solving x /a = c Linear Equations including negatives Solving a/ x = c Linear Equations Solving a/ x = c Linear Equations including negatives Solving a x + b = c Linear Equations Solving a x + b = c Linear Equations including negatives Solving a x - b = c Linear Equations Solving a x - b = c Linear Equations including negatives Solving a x ± b = c Linear Equations Solving a x ± b = c Linear Equations including negatives Solving x /a ± b = c Linear Equations Solving x /a ± b = c Linear Equations including negatives Solving a/ x ± b = c Linear Equations Solving a/ x ± b = c Linear Equations including negatives Solving various a/ x ± b = c and x /a ± b = c Linear Equations Solving various a/ x ± b = c and x /a ± b = c Linear Equations including negatives Solving linear equations of all types Solving linear equations of all types including negatives

Algebra rectangles are rectangles that use linear expressions for the side measurements. With a known value (such as the perimeter), students create an algebraic equation that they can solve to determine the value of the unknown (x) and use it to determine the side lengths and area of the rectangle. The terminology in identifying the various options for worksheets use the standard equation y = mx + b where m is the coeffient of x that is generally a known value.

• Algebra Rectangles Algebra Rectangles -- Determining the Value of x, Length, Width and Area Using Algebraic Sides and the Perimeter -- m Range [1,1] Algebra Worksheet -{}- Algebra Rectangles -- Determining the Value of x, Length, Width and Area Using Algebraic Sides and the Perimeter -- m Range [2,9] Algebra Worksheet -{}- Algebra Rectangles -- Determining the Value of x, Length, Width and Area Using Algebraic Sides and the Perimeter -- m Range [2,9] or [-9,-2] Algebra Worksheet -{}- Algebra Rectangles -- Determining the Value of x, Length, Width and Area Using Algebraic Sides and the Perimeter -- m Range [2,9] or [-9,-2] -- Inverse m Possible

Linear Systems

• Solving Systems of Linear Equations Easy Linear Systems with Two Variables Easy Linear Systems with Two Variables including negative values Linear Systems with Two Variables Linear Systems with Two Variables including negative values Easy Linear Systems with Three Variables; Easy Easy Linear Systems with Three Variables including negative values Linear Systems with Three Variables Linear Systems with Three Variables including negative values
• Solving Systems of Linear Equations by Graphing Solve Linear Systems by Graphing (Solutions in first quadrant only) Solve Standard Linear Systems by Graphing Solve Slope-Intercept Linear Systems by Graphing Solve Various Linear Systems by Graphing Identify the Dependent Linear System by Graphing Identify the Inconsistent Linear System by Graphing

Quadratic Expressions and Equations

• Simplifying (Combining Like Terms) Quadratic Expressions Simplifying quadratic expressions with 5 terms Simplifying quadratic expressions with 6 terms Simplifying quadratic expressions with 7 terms Simplifying quadratic expressions with 8 terms Simplifying quadratic expressions with 9 terms Simplifying quadratic expressions with 10 terms Simplifying quadratic expressions with 5 to 10 terms
• Adding/Subtracting and Simplifying Quadratic Expressions Adding and simplifying quadratic expressions. Adding and simplifying quadratic expressions with multipliers. Adding and simplifying quadratic expressions with some multipliers. Subtracting and simplifying quadratic expressions. Subtracting and simplifying quadratic expressions with multipliers. Subtracting and simplifying quadratic expressions with some multipliers. Mixed adding and subtracting and simplifying quadratic expressions. Mixed adding and subtracting and simplifying quadratic expressions with multipliers. Mixed adding and subtracting and simplifying quadratic expressions with some multipliers.
• Multiplying Factors to Get Quadratic Expressions Multiplying Factors of Quadratics with Coefficients of 1 Multiplying Factors of Quadratics with Coefficients of 1 or -1 Multiplying Factors of Quadratics with Coefficients of 1, or 2 Multiplying Factors of Quadratics with Coefficients of 1, -1, 2 or -2 Multiplying Factors of Quadratics with Coefficients up to 9 Multiplying Factors of Quadratics with Coefficients between -9 and 9

The factoring quadratic expressions worksheets in this section provide many practice questions for students to hone their factoring strategies. If you would rather worksheets with quadratic equations, please see the next section. These worksheets come in a variety of levels with the easier ones are at the beginning. The 'a' coefficients referred to below are the coefficients of the x 2 term as in the general quadratic expression: ax 2 + bx + c. There are also worksheets in this section for calculating sum and product and for determining the operands for sum and product pairs.

• Factoring Quadratic Expressions Factoring Quadratic Expressions with Positive 'a' coefficients of 1 Factoring Quadratic Expressions with Positive or Negative 'a' coefficients of 1 Factoring Quadratic Expressions with Positive or Negative 'a' coefficients of 1 with a Common Factor Step Factoring Quadratic Expressions with Positive 'a' coefficients up to 4 Factoring Quadratic Expressions with Positive or Negative 'a' coefficients up to 4 Factoring Quadratic Expressions with Positive or Negative 'a' coefficients up to 4 with a Common Factor Step Factoring Quadratic Expressions with Positive 'a' coefficients up to 5 Factoring Quadratic Expressions with Positive or Negative 'a' coefficients up to 5 Factoring Quadratic Expressions with Positive or Negative 'a' coefficients up to 5 with a Common Factor Step Factoring Quadratic Expressions with Positive 'a' coefficients up to 9 Factoring Quadratic Expressions with Positive or Negative 'a' coefficients up to 9 Factoring Quadratic Expressions with Positive or Negative 'a' coefficients up to 9 with a Common Factor Step Factoring Quadratic Expressions with Positive 'a' coefficients up to 81 Factoring Quadratic Expressions with Positive or Negative 'a' coefficients up to 81 Factoring Quadratic Expressions with Positive or Negative 'a' coefficients up to 81 with a Common Factor Step Calculating Sum and Product (Operand Range 0 to 9 ) ✎ Calculating Sum and Product (Operand Range 1 to 9 ) ✎ Calculating Sum and Product (Operand Range 0 to 9 Including Negatives ) ✎ Calculating Sum and Product (Operand Range 1 to 9 Including Negatives ) ✎ Calculating Sum and Product (Operand Range -20 to 20 ) ✎ Calculating Sum and Product (Operand Range -99 to 99 ) ✎ Determining Operands from Sum and Product Pairs (Operand Range 0 to 9 ) ✎ Determining Operands from Sum and Product Pairs (Operand Range 1 to 9 ) ✎ Determining Operands from Sum and Product Pairs (Operand Range 0 to 12 ) ✎ Determining Operands from Sum and Product Pairs (Operand Range 1 to 12 ) ✎ Determining Operands from Sum and Product Pairs (Operand Range 0 to 9 Including Negatives ) ✎ Determining Operands from Sum and Product Pairs (Operand Range 1 to 9 Including Negatives ) ✎ Determining Operands from Sum and Product Pairs (Operand Range -20 to 20 ) ✎ Determining Operands from Sum and Product Pairs (Operand Range -99 to 99 ) ✎

Whether you use trial and error, completing the square or the general quadratic formula, these worksheets include a plethora of practice questions with answers. In the first section, the worksheets include questions where the quadratic expressions equal 0. This makes the process similar to factoring quadratic expressions, with the additional step of finding the values for x when the expression is equal to 0. In the second section, the expressions are generally equal to something other than x, so there is an additional step at the beginning to make the quadratic expression equal zero.

• Solving Quadratic Equations that Equal Zero Solving Quadratic Equations with Positive 'a' coefficients of 1 Solving Quadratic Equations with Positive or Negative 'a' coefficients of 1 Solving Quadratic Equations with Positive or Negative 'a' coefficients of 1 with a Common Factor Step Solving Quadratic Equations with Positive 'a' coefficients up to 4 Solving Quadratic Equations with Positive or Negative 'a' coefficients up to 4 Solving Quadratic Equations with Positive or Negative 'a' coefficients up to 4 with a Common Factor Step Solving Quadratic Equations with Positive 'a' coefficients up to 5 Solving Quadratic Equations with Positive or Negative 'a' coefficients up to 5 Solving Quadratic Equations with Positive or Negative 'a' coefficients up to 5 with a Common Factor Step Solving Quadratic Equations with Positive 'a' coefficients up to 9 Solving Quadratic Equations with Positive or Negative 'a' coefficients up to 9 Solving Quadratic Equations with Positive or Negative 'a' coefficients up to 9 with a Common Factor Step Solving Quadratic Equations with Positive 'a' coefficients up to 81 Solving Quadratic Equations with Positive or Negative 'a' coefficients up to 81 Solving Quadratic Equations with Positive or Negative 'a' coefficients up to 81 with a Common Factor Step
• Solving Quadratic Equations that Equal an Integer Solving Quadratic Equations for x ("a" coefficients of 1) Solving Quadratic Equations for x ("a" coefficients of 1 or -1) Solving Quadratic Equations for x ("a" coefficients up to 4) Solving Quadratic Equations for x ("a" coefficients between -4 and 4) Solving Quadratic Equations for x ("a" coefficients up to 81) Solving Quadratic Equations for x ("a" coefficients between -81 and 81)

Other Polynomial and Monomial Expressions & Equations

• Simplifying Polynomials That Involve Addition And Subtraction Addition and Subtraction; 1 variable; 3 terms Addition and Subtraction; 1 variable; 4 terms Addition and Subtraction; 2 variables; 4 terms Addition and Subtraction; 2 variables; 5 terms Addition and Subtraction; 2 variables; 6 terms
• Simplifying Polynomials That Involve Multiplication And Division Multiplication and Division; 1 variable; 3 terms Multiplication and Division; 1 variable; 4 terms Multiplication and Division; 2 variables; 4 terms Multiplication and Division; 2 variables; 5 terms
• Simplifying Polynomials That Involve Addition, Subtraction, Multiplication And Division All Operations; 1 variable; 3 terms All Operations; 1 variable; 4 terms All Operations; 2 variables; 4 terms All Operations; 2 variables; 5 terms All Operations (Challenge)
• Factoring Expressions That Do Not Include A Squared Variable Factoring Non-Quadratic Expressions with No Squares, Simple Coefficients, and Positive Multipliers Factoring Non-Quadratic Expressions with No Squares, Simple Coefficients, and Negative and Positive Multipliers Factoring Non-Quadratic Expressions with No Squares, Compound Coefficients, and Positive Multipliers Factoring Non-Quadratic Expressions with No Squares, Compound Coefficients, and Negative and Positive Multipliers
• Factoring Expressions That Always Include A Squared Variable Factoring Non-Quadratic Expressions with All Squares, Simple Coefficients, and Positive Multipliers Factoring Non-Quadratic Expressions with All Squares, Simple Coefficients, and Negative and Positive Multipliers Factoring Non-Quadratic Expressions with All Squares, Compound Coefficients, and Positive Multipliers Factoring Non-Quadratic Expressions with All Squares, Compound Coefficients, and Negative and Positive Multipliers
• Factoring Expressions That Sometimes Include Squared Variables Factoring Non-Quadratic Expressions with Some Squares, Simple Coefficients, and Positive Multipliers Factoring Non-Quadratic Expressions with Some Squares, Simple Coefficients, and Negative and Positive Multipliers Factoring Non-Quadratic Expressions with Some Squares, Compound Coefficients, and Positive Multipliers Factoring Non-Quadratic Expressions with Some Squares, Compound Coefficients, and Negative and Positive Multipliers
• Multiplying Polynomials With Two Factors Multiplying a monomial by a binomial Multiplying two binomials Multiplying a monomial by a trinomial Multiplying a binomial by a trinomial Multiplying two trinomials Multiplying two random mon/polynomials
• Multiplying Polynomials With Three Factors Multiplying a monomial by two binomials Multiplying three binomials Multiplying two binomials by a trinomial Multiplying a binomial by two trinomials Multiplying three trinomials Multiplying three random mon/polynomials

Solver Title

Generating PDF...

• Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Expanded Form Mean, Median & Mode
• Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Logical Sets Word Problems
• Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
• Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
• Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
• Linear Algebra Matrices Vectors
• Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
• Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
• Physics Mechanics
• Chemistry Chemical Reactions Chemical Properties
• Finance Simple Interest Compound Interest Present Value Future Value
• Economics Point of Diminishing Return
• Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
• Pre Algebra
• One-Step Addition
• One-Step Subtraction
• One-Step Multiplication
• One-Step Division
• One-Step Decimals
• Two-Step Integers
• Two-Step Add/Subtract
• Two-Step Multiply/Divide
• Two-Step Fractions
• Two-Step Decimals
• Multi-Step Integers
• Multi-Step with Parentheses
• Multi-Step Rational
• Multi-Step Fractions
• Multi-Step Decimals
• Solve by Factoring
• Completing the Square
• Quadratic Formula
• Biquadratic
• Logarithmic
• Exponential
• Rational Roots
• Floor/Ceiling
• Equation Given Roots
• Newton Raphson
• Substitution
• Elimination
• Cramer's Rule
• Gaussian Elimination
• System of Inequalities
• Perfect Squares
• Difference of Squares
• Difference of Cubes
• Sum of Cubes
• Polynomials
• Distributive Property
• FOIL method
• Perfect Cubes
• Binomial Expansion
• Negative Rule
• Product Rule
• Quotient Rule
• Expand Power Rule
• Fraction Exponent
• Exponent Rules
• Exponential Form
• Logarithmic Form
• Absolute Value
• Rational Number
• Powers of i
• Complex Form
• Partial Fractions
• Is Polynomial
• Leading Coefficient
• Leading Term
• Standard Form
• Complete the Square
• Synthetic Division
• Linear Factors
• Rationalize Denominator
• Rationalize Numerator
• Identify Type
• Convergence
• Interval Notation
• Pi (Product) Notation
• Boolean Algebra
• Truth Table
• Mutual Exclusive
• Cardinality
• Caretesian Product
• Age Problems
• Distance Problems
• Cost Problems
• Investment Problems
• Number Problems
• Percent Problems
• Addition/Subtraction
• Multiplication/Division
• Dice Problems
• Coin Problems
• Card Problems
• Pre Calculus
• Linear Algebra
• Trigonometry
• Conversions

Most Used Actions

Number line, algebra calculator.

The Algebra Calculator is a versatile online tool designed to simplify algebraic problem-solving for users of all levels. Here's how to make the most of it:

• Begin by typing your algebraic expression into the above input field, or scanning the problem with your camera.
• After entering the equation, click the 'Go' button to generate instant solutions.
• The calculator provides detailed step-by-step solutions, aiding in understanding the underlying concepts.
• -x+3\gt 2x+1
• (x+5)(x-5)\gt 0
• 10^{1-x}=10^4
• \sqrt{3+x}=-2
• 6+11x+6x^2+x^3=0
• factor\:x^{2}-5x+6
• simplify\:\frac{2}{3}-\frac{3}{2}+\frac{1}{4}
• x+2y=2x-5,\:x-y=3
• How do you solve algebraic expressions?
• To solve an algebraic expression, simplify the expression by combining like terms, isolate the variable on one side of the equation by using inverse operations. Then, solve the equation by finding the value of the variable that makes the equation true.
• What are the basics of algebra?
• The basics of algebra are the commutative, associative, and distributive laws.
• What are the 3 rules of algebra?
• The basic rules of algebra are the commutative, associative, and distributive laws.
• What is the golden rule of algebra?
• The golden rule of algebra states Do unto one side of the equation what you do to others. Meaning, whatever operation is being used on one side of equation, the same will be used on the other side too.
• What are the 5 basic laws of algebra?
• The basic laws of algebra are the Commutative Law For Addition, Commutative Law For Multiplication, Associative Law For Addition, Associative Law For Multiplication, and the Distributive Law.

algebra-calculator

• Middle School Math Solutions – Inequalities Calculator Next up in our Getting Started maths solutions series is help with another middle school algebra topic - solving...

Please add a message.

Message received. Thanks for the feedback.

Chapter 1: Solving Equations and Inequalities

Problem solving, learning objectives.

• Translate words into algebraic expressions and equations
• Define a process for solving word problems
• Apply the steps for solving word problems to distance, rate, and time problems
• Apply the steps for solving word problems to interest rate problems
• Evaluate a formula using substitution
• Rearrange formulas to isolate specific variables
• Identify an unknown given a formula
• Apply the steps for solving word problems to geometry problems
• Use the formula for converting between Fahrenheit and Celsius

Define a Process for Problem Solving

Word problems can be tricky. Often it takes a bit of practice to convert an English sentence into a mathematical sentence, which is one of the first steps to solving word problems. In the table below, words or phrases commonly associated with mathematical operators are categorized. Word problems often contain these or similar words, so it’s good to see what mathematical operators are associated with them.

Some examples follow:

• [latex]x\text{ is }5[/latex]  becomes [latex]x=5[/latex]
• Three more than a number becomes [latex]x+3[/latex]
• Four less than a number becomes [latex]x-4[/latex]
• Double the cost becomes [latex]2\cdot\text{ cost }[/latex]
• Groceries and gas together for the week cost $250 means [latex]\text{ groceries }+\text{ gas }=250[/latex]
• The difference of 9 and a number becomes [latex]9-x[/latex]. Notice how 9 is first in the sentence and the expression

Let’s practice translating a few more English phrases into algebraic expressions.

Translate the table into algebraic expressions:

In this example video, we show how to translate more words into mathematical expressions.

The power of algebra is how it can help you model real situations in order to answer questions about them.

Here are some steps to translate problem situations into algebraic equations you can solve. Not every word problem fits perfectly into these steps, but they will help you get started.

• Read and understand the problem.
• Determine the constants and variables in the problem.
• Translate words into algebraic expressions and equations.
• Write an equation to represent the problem.
• Solve the equation.
• Check and interpret your answer. Sometimes writing a sentence helps.

Twenty-eight less than five times a certain number is 232. What is the number?

Following the steps provided:

• Read and understand: we are looking for a number.
• Constants and variables: 28 and 232 are constants, “a certain number” is our variable because we don’t know its value, and we are asked to find it. We will call it x.
• Translate:  five times a certain number translates to [latex]5x[/latex] Twenty-eight less than five times a certain number translates to [latex]5x-28[/latex] because subtraction is built backward. is 232 translates to [latex]=232[/latex] because “is” is associated with equals.
• Write an equation:  [latex]5x-28=232[/latex]

[latex]\begin{array}{r}5x-28=232\\5x=260\\x=52\,\,\,\end{array}[/latex]

[latex]\begin{array}{r}5\left(52\right)-28=232\\5\left(52\right)=260\\260=260\end{array}[/latex].

In the video that follows, we show another example of how to translate a sentence into a mathematical expression using a problem solving method.

Another type of number problem involves consecutive numbers. Consecutive numbers are numbers that come one after the other, such as 3, 4, 5. If we are looking for several consecutive numbers it is important to first identify what they look like with variables before we set up the equation.

For example, let’s say I want to know the next consecutive integer after 4. In mathematical terms, we would add 1 to 4 to get 5. We can generalize this idea as follows: the consecutive integer of any number, x , is [latex]x+1[/latex]. If we continue this pattern we can define any number of consecutive integers from any starting point. The following table shows how to describe four consecutive integers using algebraic notation.

We apply the idea of consecutive integers to solving a word problem in the following example.

The sum of three consecutive integers is 93. What are the integers?

• Read and understand:  We are looking for three numbers, and we know they are consecutive integers.
• Constants and Variables:  93 is a constant. The first integer we will call x . Second: [latex]x+1[/latex] Third: [latex]x+2[/latex]
• Translate:  The sum of three consecutive integers translates to [latex]x+\left(x+1\right)+\left(x+2\right)[/latex], based on how we defined the first, second, and third integers. Notice how we placed parentheses around the second and third integers. This is just to make each integer more distinct. is 93 translates to [latex]=93[/latex] because is is associated with equals.
• Write an equation:  [latex]x+\left(x+1\right)+\left(x+2\right)=93[/latex]

[latex]x+x+1+x+2=93[/latex]

Combine like terms, simplify, and solve.

[latex]\begin{array}{r}x+x+1+x+2=93\\3x+3 = 93\\\underline{-3\,\,\,\,\,-3}\\3x=90\\\frac{3x}{3}=\frac{90}{3}\\x=30\end{array}[/latex]

• Check and Interpret: Okay, we have found a value for x . We were asked to find the value of three consecutive integers, so we need to do a couple more steps. Remember how we defined our variables: The first integer we will call [latex]x[/latex], [latex]x=30[/latex] Second: [latex]x+1[/latex] so [latex]30+1=31[/latex] Third: [latex]x+2[/latex] so [latex]30+2=32[/latex] The three consecutive integers whose sum is [latex]93[/latex] are [latex]30\text{, }31\text{, and }32[/latex]

There is often a well-known formula or relationship that applies to a word problem. For example, if you were to plan a road trip, you would want to know how long it would take you to reach your destination. [latex]d=rt[/latex] is a well-known relationship that associates distance traveled, the rate at which you travel, and how long the travel takes.

Distance, Rate, and Time

If you know two of the quantities in the relationship [latex]d=rt[/latex], you can easily find the third using methods for solving linear equations. For example, if you know that you will be traveling on a road with a speed limit of [latex]30\frac{\text{ miles }}{\text{ hour }}[/latex] for 2 hours, you can find the distance you would travel by multiplying rate times time or [latex]\left(30\frac{\text{ miles }}{\text{ hour }}\right)\left(2\text{ hours }\right)=60\text{ miles }[/latex].

We can generalize this idea depending on what information we are given and what we are looking for. For example, if we need to find time, we could solve the [latex]d=rt[/latex] equation for t using division:

[latex]d=rt\\\frac{d}{r}=t[/latex]

Likewise, if we want to find rate, we can isolate r using division:

[latex]d=rt\\\frac{d}{t}=r[/latex]

In the following examples you will see how this formula is applied to answer questions about ultra marathon running.

Ultra marathon running (defined as anything longer than 26.2 miles) is becoming very popular among women even though it remains a male-dominated niche sport. Ann Trason has broken twenty world records in her career. One such record was the American River 50-mile Endurance Run which begins in Sacramento, California, and ends in Auburn, California. [1] In 1993 Trason finished the run with a time of 6:09:08.  The men’s record for the same course was set in 1994 by Tom Johnson who finished the course with a time of 5:33:21. [2]

In the next examples we will use the [latex]d=rt[/latex] formula to answer the following questions about the two runners.

What was each runner’s rate for their record-setting runs?

By the time Johnson had finished, how many more miles did Trason have to run?

How much further could Johnson have run if he had run as long as Trason?

What was each runner’s time for running one mile?

To make answering the questions easier, we will round the two runners’ times to 6 hours and 5.5 hours.

Read and Understand:  We are looking for rate and we know distance and time, so we can use the idea: [latex]d=rt\\\frac{d}{t}=r[/latex]

Define and Translate: Because there are two runners, making a table to organize this information helps. Note how we keep units to help us keep track of what how all the terms are related to each other.

Write and Solve:

Trason’s rate:

[latex]\begin{array}{c}d=rt\\\\50\text{ miles }=\text{r}\left(6\text{ hours }\right)\\\frac{50\text{ miles }}{6\text{ hours }}=\frac{8.33\text{ miles }}{\text{ hour }}\end{array}[/latex].

(rounded to two decimal places)

Johnson’s rate:

[latex]\begin{array}{c}d=rt\\\\,\,\,\,\,\,\,50\text{ miles }=\text{r}\left(5.5\text{ hours }\right)\\\frac{50\text{ miles }}{6\text{ hours }}=\frac{9.1\text{ miles }}{\text{ hour }}\end{array}[/latex]

Check and Interpret:

We can fill in our table with this information.

Now that we know each runner’s rate we can answer the second question.

Here is the table we created for reference:

Read and Understand:  We are looking for how many miles Trason still had on the trail when Johnson had finished after 5.5 hours. This is a distance, and we know rate and time.

Define and Translate:  We can use the formula [latex]d=rt[/latex] again. This time the unknown is d , and the time Trason had run is 5.5 hours.

[latex]\begin{array}{l}d=rt\\\\d=8.33\frac{\text{ miles }}{\text{ hour }}\left(5.5\text{ hours }\right)\\\\d=45.82\text{ miles }\end{array}[/latex].

Have we answered the question? We were asked to find how many more miles she had to run after 5.5 hours.  What we have found is how long she had run after 5.5 hours. We need to subtract [latex]d=45.82\text{ miles }[/latex] from the total distance of the course.

[latex]50\text{ miles }-45.82\text{ miles }=1.48\text{ miles }[/latex]

The third question is similar to the second. Now that we know each runner’s rate, we can answer questions about individual distances or times.

Read and Understand:  The word further implies we are looking for a distance.

Define and Translate:  We can use the formula [latex]d=rt[/latex] again. This time the unknown is d , the time is 6 hours, and Johnson’s rate is [latex]9.1\frac{\text{ miles }}{\text{ hour }}[/latex]

[latex]\begin{array}{l}d=rt\\\\d=9.1\frac{\text{ miles }}{\text{ hour }}\left(6\text{ hours }\right)\\\\d=54.6\text{ miles }\end{array}[/latex].

Have we answered the question? We were asked to find how many more miles Johnson would have run if he had run at his rate of [latex]9.1\frac{\text{ miles }}{\text{ hour }}[/latex] for 6 hours.

Johnson would have run 54.6 miles, so that’s 4.6 more miles than than he ran for the race.

Now we will tackle the last question where we are asked to find a time for each runner.

Read and Understand:  we are looking for time, and this time our distance has changed from 50 miles to 1 mile, so we can use

Define and Translate: we can use the formula [latex]d=rt[/latex] again. This time the unknown is t , the distance is 1 mile, and we know each runner’s rate. It may help to create a new table:

We will need to divide to isolate time.

[latex]\begin{array}{c}d=rt\\\\1\text{ mile }=8.33\frac{\text{ miles }}{\text{ hour }}\left(t\text{ hours }\right)\\\\\frac{1\text{ mile }}{\frac{8.33\text{ miles }}{\text{ hour }}}=t\text{ hours }\\\\0.12\text{ hours }=t\end{array}[/latex].

0.12 hours is about 7.2 minutes, so Trason’s time for running one mile was about 7.2 minutes. WOW! She did that for 6 hours!

[latex]\begin{array}{c}d=rt\\\\1\text{ mile }=9.1\frac{\text{ miles }}{\text{ hour }}\left(t\text{ hours }\right)\\\\\frac{1\text{ mile }}{\frac{9.1\text{ miles }}{\text{ hour }}}=t\text{ hours }\\\\0.11\text{ hours }=t\end{array}[/latex].

0.11 hours is about 6.6 minutes, so Johnson’s time for running one mile was about 6.6 minutes. WOW! He did that for 5.5 hours!

Have we answered the question? We were asked to find how long it took each runner to run one mile given the rate at which they ran the whole 50-mile course.  Yes, we answered our question.

Trason’s mile time was [latex]7.2\frac{\text{minutes}}{\text{mile}}[/latex] and Johnsons’ mile time was [latex]6.6\frac{\text{minutes}}{\text{mile}}[/latex]

In the following video, we show another example of answering many rate questions given distance and time.

Simple Interest

In order to entice customers to invest their money, many banks will offer interest-bearing accounts. The accounts work like this: a customer deposits a certain amount of money (called the Principal, or P ), which then grows slowly according to the interest rate ( R , measured in percent) and the length of time ( T , usually measured in months) that the money stays in the account. The amount earned over time is called the interest ( I ), which is then given to the customer.

The simplest way to calculate interest earned on an account is through the formula [latex]\displaystyle I=P\,\cdot \,R\,\cdot \,T[/latex].

If we know any of the three amounts related to this equation, we can find the fourth. For example, if we want to find the time it will take to accrue a specific amount of interest, we can solve for T using division:

[latex]\displaystyle\begin{array}{l}\,\,\,\,\,\,\,\,\,\,\,\,I=P\,\cdot \,R\,\cdot \,T\\\\ \frac{I}{{P}\,\cdot \,R}=\frac{P\cdot\,R\,\cdot \,T}{\,P\,\cdot \,R}\\\\\,\,\,\,\,\,\,\,\,\,\,{T}=\frac{I}{\,R\,\cdot \,T}\end{array}[/latex]

Below is a table showing the result of solving for each individual variable in the formula.

In the next examples, we will show how to substitute given values into the simple interest formula, and decipher which variable to solve for.

If a customer deposits a principal of $2000 at a monthly rate of 0.7%, what is the total amount that she has after 24 months?

Substitute in the values given for the Principal, Rate, and Time.

[latex]\displaystyle\begin{array}{l}I=P\,\cdot \,R\,\cdot \,T\\I=2000\cdot 0.7\%\cdot 24\end{array}[/latex]

Rewrite 0.7% as the decimal 0.007, then multiply.

[latex]\begin{array}{l}I=2000\cdot 0.007\cdot 24\\I=336\end{array}[/latex]

Add the interest and the original principal amount to get the total amount in her account.

[latex] \displaystyle 2000+336=2336[/latex]

She has $2336 after 24 months.

The following video shows another example of finding an account balance after a given amount of time, principal invested, and a rate.

In the following example you will see why it is important to make sure the units of the interest rate match the units of time when using the simple interest formula.

Alex invests $600 at 3.25% monthly interest for 3 years. What amount of interest has Alex earned?

Read and Understand: The question asks for an amount, so we can substitute what we are given into the simple interest formula [latex]I=P\,\cdot \,R\,\cdot \,T[/latex]

Define and Translate:  we know P, R, and T so we can use substitution. R  = 0.0325, P = $600, and T = 3 years. We have to be careful! R is in months, and T is in years.  We need to change T into months because we can’t change the rate—it is set by the bank.

[latex]{T}=3\text{ years }\cdot12\frac{\text{ months }}{ year }=36\text{ months }[/latex]

Substitute the given values into the formula.

[latex]\begin{array}{l} I=P\,\cdot \,R\,\cdot \,T\\\\I=600\,\cdot \,0.035\,\cdot \,36\\\\{I}=756\end{array}[/latex]

We were asked what amount Alex earned, which is the amount provided by the formula. In the previous example we were asked the total amount in the account, which included the principal and interest earned.

Alex has earned $756.

After 10 years, Jodi’s account balance has earned $1080 in interest. The rate on the account is 0.09% monthly. What was the original amount she invested in the account?

Read and Understand: The question asks for the original amount invested, the principal. We are given a length of time in years, and an interest rate in months, and the amount of interest earned.

Define and Translate:  we know I = $1080, R = 0.009, and T = 10 years so we can use [latex]{P}=\frac{I}{{R}\,\cdot \,T}[/latex]

We also need to make sure the units on the interest rate and the length of time match, and they do not. We need to change time into months again.

[latex]{T}=10\text{ years }\cdot12\frac{\text{ months }}{ year }=120\text{ months }[/latex]

Substitute the given values into the formula

[latex]\begin{array}{l}{P}=\frac{I}{{R}\,\cdot \,T}\\\\{P}=\frac{1080}{{0.009}\,\cdot \,120}\\\\{P}=\frac{1080}{1.08}=1000\end{array}[/latex]

We were asked to find the principal given the amount of interest earned on an account.  If we substitute P = $1000 into the formula [latex]I=P\,\cdot \,R\,\cdot \,T[/latex] we get

[latex]I=1000\,\cdot \,0.009\,\cdot \,120\\I=1080[/latex]

Our solution checks out. Jodi invested $1000.

Further Applications of Linear Equations

Formulas come up in many different areas of life. We have seen the formula that relates distance, rate, and time and the formula for simple interest on an investment. In this section we will look further at formulas and see examples of formulas for dimensions of geometric shapes as well as the formula for converting temperature between Fahrenheit and Celsius.

There are many geometric shapes that have been well studied over the years. We know quite a bit about circles, rectangles, and triangles. Mathematicians have proven many formulas that describe the dimensions of geometric shapes including area, perimeter, surface area, and volume.

Perimeter is the distance around an object. For example, consider a rectangle with a length of 8 and a width of 3. There are two lengths and two widths in a rectangle (opposite sides), so we add [latex]8+8+3+3=22[/latex]. Since there are two lengths and two widths in a rectangle, you may find the perimeter of a rectangle using the formula [latex]{P}=2\left({L}\right)+2\left({W}\right)[/latex] where

In the following example, we will use the problem-solving method we developed to find an unknown width using the formula for the perimeter of a rectangle. By substituting the dimensions we know into the formula, we will be able to isolate the unknown width and find our solution.

You want to make another garden box the same size as the one you already have. You write down the dimensions of the box and go to the lumber store to buy some boards. When you get there you realize you didn’t write down the width dimension—only the perimeter and length. You want the exact dimensions so you can have the store cut the lumber for you.

Here is what you have written down:

Perimeter = 16.4 feet Length = 4.7 feet

Can you find the dimensions you need to have your boards cut at the lumber store? If so, how many boards do you need and what lengths should they be?

Read and Understand:  We know perimeter = 16.4 feet and length = 4.7 feet, and we want to find width.

Define and Translate:

Define the known and unknown dimensions:

First we will substitute the dimensions we know into the formula for perimeter:

[latex]\begin{array}{l}\,\,\,\,\,P=2{W}+2{L}\\\\16.4=2\left(w\right)+2\left(4.7\right)\end{array}[/latex]

Then we will isolate w to find the unknown width.

[latex]\begin{array}{l}16.4=2\left(w\right)+2\left(4.7\right)\\16.4=2{w}+9.4\\\underline{-9.4\,\,\,\,\,\,\,\,\,\,\,\,\,-9.4}\\\,\,\,\,\,\,\,7=2\left(w\right)\\\,\,\,\,\,\,\,\frac{7}{2}=\frac{2\left(w\right)}{2}\\\,\,\,\,3.5=w\end{array}[/latex]

Write the width as a decimal to make cutting the boards easier and replace the units on the measurement, or you won’t get the right size of board!

If we replace the width we found, [latex]w=3.5\text{ feet }[/latex] into the formula for perimeter with the dimensions we wrote down, we can check our work:

[latex]\begin{array}{l}\,\,\,\,\,{P}=2\left({L}\right)+2\left({W}\right)\\\\{16.4}=2\left({4.7}\right)+2\left({3.5}\right)\\\\{16.4}=9.4+7\\\\{16.4}=16.4\end{array}[/latex]

Our calculation for width checks out. We need to ask for 2 boards cut to 3.5 feet and 2 boards cut to 4.7 feet so we can make the new garden box.

This video shows a similar garden box problem.

We could have isolated the w in the formula for perimeter before we solved the equation, and if we were going to use the formula many times, it could save a lot of time. The next example shows how to isolate a variable in a formula before substituting known dimensions or values into the formula.

Isolate the term containing the variable, w, from the formula for the perimeter of a rectangle :  

[latex]{P}=2\left({L}\right)+2\left({W}\right)[/latex].

First, isolate the term with  w by subtracting 2 l from both sides of the equation.

[latex] \displaystyle \begin{array}{l}\,\,\,\,\,\,\,\,\,\,p\,=\,\,\,\,2l+2w\\\underline{\,\,\,\,\,-2l\,\,\,\,\,-2l\,\,\,\,\,\,\,\,\,\,\,}\\p-2l=\,\,\,\,\,\,\,\,\,\,\,\,\,2w\end{array}[/latex]

Next, clear the coefficient of w by dividing both sides of the equation by 2.

[latex]\displaystyle \begin{array}{l}\underline{p-2l}=\underline{2w}\\\,\,\,\,\,\,2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,2\\ \,\,\,\frac{p-2l}{2}\,\,=\,\,w\\\,\,\,\,\,\,\,\,\,\,\,w=\frac{p-2l}{2}\end{array}[/latex]

You can rewrite the equation so the isolated variable is on the left side.

[latex]w=\frac{p-2l}{2}[/latex]

The area of a triangle is given by [latex] A=\frac{1}{2}bh[/latex] where

A = area b = the length of the base h = the height of the triangle

Remember that when two variables or a number and a variable are sitting next to each other without a mathematical operator between them, you can assume they are being multiplied. This can seem frustrating, but you can think of it like mathematical slang. Over the years, people who use math frequently have just made that shortcut enough that it has been adopted as convention.

In the next example we will use the formula for area of a triangle to find a missing dimension, as well as use substitution to solve for the base of a triangle given the area and height.

Find the base ( b) of a triangle with an area ( A ) of 20 square feet and a height ( h) of 8 feet.

Use the formula for the area of a triangle, [latex] {A}=\frac{{1}}{{2}}{bh}[/latex] .

Substitute the given lengths into the formula and solve for  b.

[latex]\displaystyle \begin{array}{l}\,\,A=\frac{1}{2}bh\\\\20=\frac{1}{2}b\cdot 8\\\\20=\frac{8}{2}b\\\\20=4b\\\\\frac{20}{4}=\frac{4b}{4}\\\\ \,\,\,5=b\end{array}[/latex]

The base of the triangle measures 5 feet.

We can rewrite the formula in terms of b or h as we did with perimeter previously. This probably seems abstract, but it can help you develop your equation-solving skills, as well as help you get more comfortable with working with all kinds of variables, not just x .

Use the multiplication and division properties of equality to isolate the variable b .

[latex]\begin{array}{l}\,\,\,\,\,\,\,\,A=\frac{1}{2}bh\\\\\left(2\right)A=\left(2\right)\frac{1}{2}bh\\\\\,\,\,\,\,\,2A=bh\\\\\,\,\,\,\,\,\,\frac{2A}{h}=\frac{bh}{h}\\\\\,\,\,\,\,\,\,\,\frac{2A}{h}=\frac{b\cancel{h}}{\cancel{h}}\end{array}[/latex]

Write the equation with the desired variable on the left-hand side as a matter of convention:

Use the multiplication and division properties of equality to isolate the variable h .

[latex]\begin{array}{l}\,\,\,\,\,\,\,\,A=\frac{1}{2}bh\\\\\left(2\right)A=\left(2\right)\frac{1}{2}bh\\\\\,\,\,\,\,\,2A=bh\\\\\,\,\,\,\,\,\,\frac{2A}{b}=\frac{bh}{b}\\\\\,\,\,\,\,\,\,\,\frac{2A}{b}=\frac{h\cancel{b}}{\cancel{b}}\end{array}[/latex]

Temperature

Let’s look at another formula that includes parentheses and fractions, the formula for converting from the Fahrenheit temperature scale to the Celsius scale.

[latex]C=\left(F-32\right)\cdot \frac{5}{9}[/latex]

Given a temperature of [latex]12^{\circ}{C}[/latex], find the equivalent in [latex]{}^{\circ}{F}[/latex].

Substitute the given temperature in[latex]{}^{\circ}{C}[/latex] into the conversion formula:

[latex]12=\left(F-32\right)\cdot \frac{5}{9}[/latex]

Isolate the variable F to obtain the equivalent temperature.

[latex]\begin{array}{r}12=\left(F-32\right)\cdot \frac{5}{9}\\\\\left(\frac{9}{5}\right)12=F-32\,\,\,\,\,\,\,\,\,\,\,\,\,\\\\\left(\frac{108}{5}\right)12=F-32\,\,\,\,\,\,\,\,\,\,\,\,\,\\\\21.6=F-32\,\,\,\,\,\,\,\,\,\,\,\,\,\\\underline{+32\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,+32}\,\,\,\,\,\,\,\,\,\,\,\,\\\\53.6={}^{\circ}{F}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\end{array}[/latex]

As with the other formulas we have worked with, we could have isolated the variable F first, then substituted in the given temperature in Celsius.

Solve the formula shown below for converting from the Fahrenheit scale to the Celsius scale for F.

To isolate the variable F, it would be best to clear the fraction involving F first. Multiply both sides of the equation by [latex] \displaystyle \frac{9}{5}[/latex].

[latex]\begin{array}{l}\\\,\,\,\,\left(\frac{9}{5}\right)C=\left(F-32\right)\left(\frac{5}{9}\right)\left(\frac{9}{5}\right)\\\\\,\,\,\,\,\,\,\,\,\,\,\,\frac{9}{5}C=F-32\end{array}[/latex]

Add 32 to both sides.

[latex]\begin{array}{l}\frac{9}{5}\,C+32=F-32+32\\\\\frac{9}{5}\,C+32=F\end{array}[/latex]

[latex]F=\frac{9}{5}C+32[/latex]

Think About It

Express the formula for the surface area of a cylinder, [latex]s=2\pi rh+2\pi r^{2}[/latex], in terms of the height, h .

In this example, the variable h is buried pretty deeply in the formula for surface area of a cylinder. Using the order of operations, it can be isolated. Before you look at the solution, use the box below to write down what you think is the best first step to take to isolate h .

[latex]\begin{array}{r}S\,\,=2\pi rh+2\pi r^{2} \\ \underline{-2\pi r^{2}\,\,\,\,\,\,\,\,\,\,\,\,\,-2\pi r^{2}}\\S-2\pi r^{2}\,\,\,\,=\,\,\,\,2\pi rh\,\,\,\,\,\,\,\,\,\,\,\,\,\,\end{array}[/latex]

Next, isolate the variable h by dividing both sides of the equation by [latex]2\pi r[/latex].

[latex]\begin{array}{r}\frac{S-2\pi r^{2}}{2\pi r}=\frac{2\pi rh}{2\pi r} \\\\ \frac{S-2\pi r^{2}}{2\pi r}=h\,\,\,\,\,\,\,\,\,\,\end{array}[/latex]

• "Ann Trason." Wikipedia. Accessed May 05, 2016. https://en.wikipedia.org/wiki/Ann_Trason . ↵
•  "American River 50 Mile Endurance Run." Wikipedia. Accessed May 05, 2016. https://en.wikipedia.org/wiki/American_River_50_Mile_Endurance_Run . ↵
• Writing Algebraic Expressions. Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/uD_V5t-6Kzs . License : CC BY: Attribution
• Write and Solve a Linear Equations to Solve a Number Problem (1). Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/izIIqOztUyI . License : CC BY: Attribution
• Write and Solve a Linear Equations to Solve a Number Problem (Consecutive Integers). Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/S5HZy3jKodg . License : CC BY: Attribution
• Screenshot: Ann Trason Trail Running. Authored by : Lumen Learning. License : CC BY: Attribution
• Problem Solving Using Distance, Rate, Time (Running). Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/3WLp5mY1FhU . License : CC BY: Attribution
• Simple Interest - Determine Account Balance (Monthly Interest). Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/XkGgEEMR_00 . License : CC BY: Attribution
• Simple Interest - Determine Interest Balance (Monthly Interest). Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/mRV5ljj32Rg . License : CC BY: Attribution
• Simple Interest - Determine Principal Balance (Monthly Interest). Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/vbMqN6lVoOM . License : CC BY: Attribution
• Find the Width of a Rectangle Given the Perimeter / Literal Equation. Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/jlxPgKQfhQs . License : CC BY: Attribution
• Find the Base of a Triangle Given Area / Literal Equation. Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/VQZQvJ3rXYg . License : CC BY: Attribution
• Convert Celsius to Fahrenheit / Literal Equation. Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/DRydX8V-JwY . License : CC BY: Attribution
• Ann Trason. Provided by : Wikipedia. Located at : https://en.wikipedia.org/wiki/Ann_Trason . License : CC BY-SA: Attribution-ShareAlike
• American River 50 Mile Endurance Run. Provided by : Wikipedia. Located at : https://en.wikipedia.org/wiki/American_River_50_Mile_Endurance_Run . License : CC BY-SA: Attribution-ShareAlike

• Anatomy & Physiology
• Astrophysics
• Earth Science
• Environmental Science
• Organic Chemistry
• Precalculus
• Trigonometry
• English Grammar
• U.S. History
• World History

... and beyond

• Socratic Meta
• Featured Answers

• Formulas for Problem Solving

Key Questions

A few examples...

Explanation:

I will assume that you mean things like common identities and the quadratic formula . Here are just a few:

Difference of squares identity

#a^2-b^2 = (a-b)(a+b)#

Deceptively simple, but massively useful.

For example:

#a^4+b^4 = (a^2+b^2)^2 - 2a^2b^2# #color(white)(a^4+b^4) = (a^2+b^2)^2 - (sqrt(2)ab)^2# #color(white)(a^4+b^4) = ((a^2+b^2) - sqrt(2)ab)((a^2+b^2) +sqrt(2)ab)# #color(white)(a^4+b^4) = (a^2-sqrt(2)ab+b^2)(a^2+sqrt(2)ab+b^2)#

Difference of cubes identity

#a^3-b^3 = (a-b)(a^2+ab+b^2)#

Sum of cubes identity

#a^3+b^3 = (a+b)(a^2-ab+b^2)#

Quadratic formula

Very useful to know, better if you know how to derive it:

The zeros of #ax^2+bx+c# are given by:

#x = (-b+-sqrt(b^2-4ac))/(2a)#

Pythagoras theorem

If a right angled triangle has legs of length #a, b# and hypotenuse of length #c# then:

#c^2 = a^2+b^2#

This is also very useful in trigonometric form. If we have an angle #theta# in a right-angled triangle, then we call the side nearest #theta# , the #"adjacent"# side, the side opposite it the #"opposite"# side and the hypotenuse the #"hypotenuse"# .

#"hypotenuse"^2 = "adjacent"^2 + "opposite"^2#

Dividing both sides by #"hypotenuse"^2# , we get:

#1 = ("adjacent"/"hypotenuse")^2 + ("opposite"/"hypotenuse")^2#

#1 = cos^2 theta + sin^2 theta#

Then dividing both sides by #cos^2 theta# we find:

#sec^2 theta = 1 + tan^2 theta#

Binomial theorem

#(a+b)^n = sum_(k=0)^n ((n), (k)) a^(n-k) b^k#

where #((n), (k)) = (n!)/((n-k)! k!)#

#(x+1)^4 = x^4+4x^3+6x^2+4x+1#

Using Pythagoras' Theorem, we know #A^2 + B^2 = C^2#

#A^2 = 9# , #B^2 = 16 implies A^2 + B^2 = 9 + 16 = 25#

SInce #C^2 = A^2 + B^2 = 25# , you know that

#C = sqrt(C^2) = sqrt(25) = 5#

You simply find out what value goes with what part of the formula, and do this for each, and then work out the formula as normal.

What Is It?

Using a Formula is a problem-solving strategy that students can use to find answers to math problems involving geometry , percents , measurement , or algebra. To solve these problems, students must choose the appropriate formula and substitute data in the correct places of a formula. The following problem would be best solved using a formula:

If it is 46 degrees Celsius, how many degrees Fahrenheit is it?

Students can use the formula F = 1.8C + 32 to find the solution.

Why Is It Important?

Using a Formula is a problem-solving strategy that can be used for problems that involve converting units or measuring geometric objects. Also, real-world problems such as tipping in a restaurant, finding the price of a sale item, and buying enough paint for a room all involve using formulas.

How Can You Make It Happen?

Introduce a problem to students that requires them to use a formula to solve the problem. For example:

A rectangle has an area of 40 square meters. If the perimeter of the rectangle is 26 meters, what are the length and the width of the rectangle?

Understand the Problem

Demonstrate that the first step to solving the problem is understanding it. This involves identifying the key pieces of information needed to find the answer. This may require students to read the problem several times or put the problem into their own words. Here are a few formulas that students can use to solve this problem:

A = L x W 40 = L x W

2W + 2L = P 2W + 2L = 26

(Note: L and W can be interchanged in this problem.)

Choose a Strategy

The strategy of Using a Formula can be used in situations where measurements are required to find the solution.

Solve the Problem

I know 40 is a product of 2 and 20, 4 and 10, or 5 and 8.

I looked at the possible answers that would fit the formula for the area of the rectangle. Then I put the numbers into the formula for the perimeter. The numbers 5 and 8 are the two numbers that work for both formulas.

Read the problem again to be sure the question was answered.

I found the length and width of the rectangle, 5 meters and 8 meters.

Check the math to be sure it is correct.

A = L x W 40 = L x W 40 = 8 x 5 P = 2L + 2W 26 = 2L + 2W 26 + 2(8) + 2(5)

Determine if the best strategy was chosen for this problem, or if there was another way to solve the problem.

Using a formula was a good strategy to use for this problem.

The last step is explaining how you found the answer. Demonstrate how to write a paragraph describing the steps taken and how decisions were made throughout the process.

Students should explain their answer and the process they went through to solve it. It is important for students to talk or write about their thinking.

I knew the formula for area and perimeter, so I wrote down the formulas. A = L x W P = 2L + 2W I added the information I knew, which was the area and perimeter of this rectangle. 40 = L x W 26 = 2L + 2W Then I wrote down the numbers that could be the length and width if the area is 40 square meters. I know 40 is a product of 2 and 20, 4 and 10, or 5 and 8. I took those possible numbers and used them with the formula for perimeter. The numbers that did not also fit into this formula, I eliminated. I eliminated 2 and 20 as well as 4 and 10, since those numbers did not work in the perimeter formula. I was left with the numbers 8 and 5. Since they are interchangeable in this problem, I assigned the width as 5 meters and the length as 8 meters.

Guided Practice

Have students try to solve the following problem using the strategy of Using a Formula.

In an isosceles triangle, the unequal side measures half the length of one of the two equal sides. What is the perimeter if the length of the unequal side is 5 cm? What is the length of the sides if the perimeter is 80 cm?

Have students work in pairs, in groups, or individually to solve this problem. They should be able to tell or write about how they found the answer and justify their reasoning.

How Can You Stretch Students' Thinking?

Math problems requiring formulas can be simple, with few criteria needed to solve them, or they can be multidimensional, requiring charts or tables to organize students' thinking. Including more than one formula in a problem, or having multiple correct answers to a problem will help stretch this strategy.

Featured High School Resources

Related Resources

About the author.

TeacherVision Editorial Staff

The TeacherVision editorial team is comprised of teachers, experts, and content professionals dedicated to bringing you the most accurate and relevant information in the teaching space.

• Today's news
• Reviews and deals
• Climate change
• 2024 election
• Fall allergies
• Health news
• Mental health
• Sexual health
• Family health
• So mini ways
• Unapologetically
• Buying guides

Entertainment

• How to Watch
• My watchlist
• Stock market
• Biden economy
• Personal finance
• Stocks: most active
• Stocks: gainers
• Stocks: losers
• Trending tickers
• World indices
• US Treasury bonds
• Top mutual funds
• Highest open interest
• Highest implied volatility
• Currency converter
• Basic materials
• Communication services
• Consumer cyclical
• Consumer defensive
• Financial services
• Industrials
• Real estate
• Mutual funds
• Credit cards
• Balance transfer cards
• Cash back cards
• Rewards cards
• Travel cards
• Online checking
• High-yield savings
• Money market
• Home equity loan
• Personal loans
• Student loans
• Options pit
• Fantasy football
• Pro Pick 'Em
• College Pick 'Em
• Fantasy baseball
• Fantasy hockey
• Fantasy basketball
• Download the app
• Daily fantasy
• Scores and schedules
• GameChannel
• World Baseball Classic
• Premier League
• CONCACAF League
• Champions League
• Motorsports
• Horse racing
• Newsletters

New on Yahoo

• Privacy Dashboard

The Algebra Problem: How Middle School Math Became a National Flashpoint

From suburbs in the Northeast to major cities on the West Coast, a surprising subject is prompting ballot measures, lawsuits and bitter fights among parents: algebra.

Students have been required for decades to learn to solve for the variable x, and to find the slope of a line. Most complete the course in their first year of high school. But top-achievers are sometimes allowed to enroll earlier, typically in eighth grade.

The dual pathways inspire some of the most fiery debates over equity and academic opportunity in American education.

Sign up for The Morning newsletter from the New York Times

Do bias and inequality keep Black and Latino children off the fast track? Should middle schools eliminate algebra to level the playing field? What if standout pupils lose the chance to challenge themselves?

The questions are so fraught because algebra functions as a crucial crossroads in the education system.

Students who fail it are far less likely to graduate. Those who take it early can take calculus by 12th grade, giving them a potential edge when applying to elite universities and lifting them toward society’s most high-status and lucrative professions.

But racial and economic gaps in math achievement are wide in the United States, and grew wider during the pandemic. In some states, nearly 4 in 5 poor children do not meet math standards.

To close those gaps, New York City’s previous mayor, Bill de Blasio, adopted a goal embraced by many districts elsewhere. Every middle school would offer algebra, and principals could opt to enroll all of their eighth graders in the class.

San Francisco took an opposite approach: If some children could not reach algebra by middle school, no one would be allowed to take it.

The central mission in both cities was to help disadvantaged students. But solving the algebra dilemma can be more complex than solving the quadratic formula.

New York’s dream of “algebra for all” was never fully realized, and Mayor Eric Adams’ administration changed the goal to improving outcomes for ninth graders taking algebra. In San Francisco, dismantling middle-school algebra did little to end racial inequities among students in advanced math classes. After a huge public outcry, the district decided to reverse course.

“You wouldn’t think that there could be a more boring topic in the world,” said Thurston Domina, a professor at the University of North Carolina. “And yet, it’s this place of incredibly high passions.”

“Things run hot,” he said.

In some cities, disputes over algebra have been so intense that parents have sued school districts, protested outside mayors’ offices and campaigned for the ouster of school board members.

Teaching math in middle school is a challenge for educators in part because that is when the material becomes more complex, with students moving from multiplication tables to equations and abstract concepts. Students who have not mastered the basic skills can quickly become lost, and it can be difficult for them to catch up.

Many school districts have traditionally responded to divergent achievement levels by simply separating children into distinct pathways, placing some in general math classes while offering others algebra as an accelerated option. Such sorting, known as tracking, appeals to parents who want their children to reach advanced math as quickly as possible.

But tracking has cast an uncomfortable spotlight on inequality. Around a quarter of all students in the United States take algebra in middle school. But only about 12% of Black and Latino eighth graders do, compared with roughly 24% of white pupils, a federal report found.

“That’s why middle school math is this flashpoint,” said Joshua Goodman, an associate professor of education and economics at Boston University. “It’s the first moment where you potentially make it very obvious and explicit that there are knowledge gaps opening up.”

In the decades-long war over math, San Francisco has emerged as a prominent battleground.

California once required that all eighth graders take algebra. But lower-performing middle school students often struggle when forced to enroll in the class, research shows. San Francisco later stopped offering the class in eighth grade. But the ban did little to close achievement gaps in more advanced math classes, recent research has found.

As the pendulum swung, the only constant was anger. Leading Bay Area academics disparaged one another’s research. A group of parents even sued the district last spring. “Denying students the opportunity to skip ahead in math when their intellectual ability clearly allows for it greatly harms their potential for future achievement,” their lawsuit said.

The city is now back to where it began: Middle school algebra — for some, not necessarily for all — will return in August. The experience underscored how every approach carries risks.

“Schools really don’t know what to do,” said Jon R. Star, an educational psychologist at Harvard who has studied algebra education. “And it’s just leading to a lot of tension.”

In Cambridge, Massachusetts, the school district phased out middle school algebra before the pandemic. But some argued that the move had backfired: Families who could afford to simply paid for their children to take accelerated math outside school.

“It’s the worst of all possible worlds for equity,” Jacob Barandes, a Cambridge parent, said at a school board meeting.

Elsewhere, many students lack options to take the class early: One of Philadelphia’s most prestigious high schools requires students to pass algebra before enrolling, preventing many low-income children from applying because they attend middle schools that do not offer the class.

In New York, de Blasio sought to tackle the disparities when he announced a plan in 2015 to offer algebra — but not require it — in all of the city’s middle schools. More than 15,000 eighth graders did not have the class at their schools at the time.

Since then, the number of middle schools that offer algebra has risen to about 80% from 60%. But white and Asian American students still pass state algebra tests at higher rates than their peers.

The city’s schools chancellor, David Banks, also shifted the system’s algebra focus to high schools, requiring the same ninth-grade curriculum at many schools in a move that has won support and backlash from educators.

And some New York City families are still worried about middle school. A group of parent leaders in Manhattan recently asked the district to create more accelerated math options before high school, saying that many young students must seek out higher-level instruction outside the public school system.

In a vast district like New York — where some schools are filled with children from well-off families and others mainly educate homeless children — the challenge in math education can be that “incredible diversity,” said Pedro A. Noguera, the dean of the University of Southern California’s Rossier School of Education.

“You have some kids who are ready for algebra in fourth grade, and they should not be denied it,” Noguera said. “Others are still struggling with arithmetic in high school, and they need support.”

Many schools are unequipped to teach children with disparate math skills in a single classroom. Some educators lack the training they need to help students who have fallen behind, while also challenging those working at grade level or beyond.

Some schools have tried to find ways to tackle the issue on their own. KIPP charter schools in New York have added an additional half-hour of math time to many students’ schedules, to give children more time for practice and support so they can be ready for algebra by eighth grade.

At Middle School 50 in Brooklyn, where all eighth graders take algebra, teachers rewrote lesson plans for sixth- and seventh-grade students to lay the groundwork for the class.

The school’s principal, Ben Honoroff, said he expected that some students would have to retake the class in high school. But after starting a small algebra pilot program a few years ago, he came to believe that exposing children early could benefit everyone — as long as students came into it well prepared.

Looking around at the students who were not enrolling in the class, Honoroff said, “we asked, ‘Are there other kids that would excel in this?’”

“The answer was 100%, yes,” he added. “That was not something that I could live with.”

c.2024 The New York Times Company

Recommended Stories

Will biden be on the ohio ballot in november why the state’s republican governor says they’re ‘running out of time’ to make sure he is..

After missing their deadline, Ohio politicians are discussing ways to certify Biden as the 2024 Democratic nominee for president in their state.

Women in AI: Miriam Vogel stresses the need for responsible AI

To give AI-focused women academics and others their well-deserved — and overdue — time in the spotlight, TechCrunch has been publishing a series of interviews focused on remarkable women who’ve contributed to the AI revolution. Miriam Vogel is the CEO of EqualAI, a nonprofit created to reduce unconscious bias in AI and promote responsible AI governance. As a board member at the Responsible AI Institute and senior advisor to the Center for Democracy and Technology, Vogel's advised White House leadership on initiatives ranging from women, economic, regulatory and food safety policy to matters of criminal justice.

This $9 'parking garage for glasses' is a must for your spring organization spree

Never lose your specs again with a soft magnetic holder that 14,000 shoppers love.

'I can't live without this': This anti-aging eye cream has over 14,000 Amazon fans — it's on sale for just $20

Loved by over 14,000 reviewers, the Baebody formula — targets dark under-eye circles, puffiness and wrinkles.

Voters historically have short memories about the economy. Inflation might be different.

The Biden campaign is hoping voters' minds aren't fully set as it wrestles with a polling deficit and dismal economic ratings. But inflation could test those hopes.

These slimming Levi's jeans are up to 60% off for Memorial Day weekend — some styles start at just $22

Let us be your jean genie — grab this top-quality denim for a markdown before these deals go poof.

Junkyard Gem: 1999 Mitsubishi Galant GTZ

A 1999 Mitsubishi Galant GTZ-V6 sedan found in a North Carolina junkyard.

'Hides any mid-area flaws': Amazon's mega-popular casual tee is on sale for $17

Available in 42 colors and patterns, this T-shirt has more than 27,000 five-star shoppers obsessed.

I find fashion deals for a living — these are the top Memorial Day sales I've discovered at Amazon, Walmart and more

Save up to 70% on staples like flattering swimsuits, fan-favorite shorts, top-selling sneakers and a breezy cooling bra.

Angel Reese thanks Alyssa Thomas for flagrant foul: 'I got back up and I kept going and kept pushing'

Angel Reese said she wanted to get "knocked down" at the next level, and she got her wish.

'Miracle in a jar': Shoppers in their 60s and 70s say their secret to looking younger is this $9 collagen cream

4,900+ shoppers swear by this age-defying, wallet-friendly formula.

Shoppers in their 60s say this skin firming cream actually works — and it's down to $18 for Memorial Day

'My neck looks better than it has in years,' says an ecstatic Amazon customer.

The Adidas Memorial Day sale is booming — save up to 65% on the brand's popular Cloudfoam and Ultraboost sneakers

Also in the mix: leggings, T-shirts, sports bras, jackets, sandals and more.

How Americans view the economy depends on whether they rent or own

How’s the economy doing? Your answer may depend on whether you own your home.

The Fed's favored inflation gauge highlights shortened trading week: What to know this week

The Fed's preferred inflation gauge will test a stock market near record highs in a holiday-shortened trading week.

Explore more with the Garmin fenix 7 Pro Sapphire Solar Edition, now $200 off

Save $200 on the scratch-resistant, solar-powered Garmin fenix Pro Sapphire Solar Edition smart watch as part of the REI Anniversary Sale.

CD rates today, May 26, 2024 (up to 5.15% APY)

If you’re searching for today’s best CD rates, we’ve narrowed down some of the top offers. Learn more about CD rates today.

Birmingham-Southern baseball advances to DIII College World Series, as school shuts down

The Birmingham-Southern baseball team will play in the Division III College World Series as the school itself is shutting down due to financial difficulties.

AI tutors are quietly changing how kids in the US study, and the leading apps are from China

Evan, a high school sophomore from Houston, was stuck on a calculus problem. Within a few seconds, Answer AI had generated an answer alongside a step-by-step process of solving the problem. A year ago, Evan would be scouring through long YouTube videos in hopes of tackling his homework challenges.

Elon Musk is reportedly planning an xAI supercomputer to power a better version of Grok

Musk recently presented plans for a ‘gigafactory of compute’ to investors, The Information reports. This would power a future, smarter version of Grok and require at least 100,000 NVIDIA H100 GPUs.

• Share full article

Advertisement

Supported by

The Algebra Problem: How Middle School Math Became a National Flashpoint

Top students can benefit greatly by being offered the subject early. But many districts offer few Black and Latino eighth graders a chance to study it.

By Troy Closson

From suburbs in the Northeast to major cities on the West Coast, a surprising subject is prompting ballot measures, lawsuits and bitter fights among parents: algebra.

Students have been required for decades to learn to solve for the variable x, and to find the slope of a line. Most complete the course in their first year of high school. But top-achievers are sometimes allowed to enroll earlier, typically in eighth grade.

The dual pathways inspire some of the most fiery debates over equity and academic opportunity in American education.

Do bias and inequality keep Black and Latino children off the fast track? Should middle schools eliminate algebra to level the playing field? What if standout pupils lose the chance to challenge themselves?

The questions are so fraught because algebra functions as a crucial crossroads in the education system. Students who fail it are far less likely to graduate. Those who take it early can take calculus by 12th grade, giving them a potential edge when applying to elite universities and lifting them toward society’s most high-status and lucrative professions.

But racial and economic gaps in math achievement are wide in the United States, and grew wider during the pandemic. In some states, nearly four in five poor children do not meet math standards.

To close those gaps, New York City’s previous mayor, Bill de Blasio, adopted a goal embraced by many districts elsewhere. Every middle school would offer algebra, and principals could opt to enroll all of their eighth graders in the class. San Francisco took an opposite approach: If some children could not reach algebra by middle school, no one would be allowed to take it.

The central mission in both cities was to help disadvantaged students. But solving the algebra dilemma can be more complex than solving the quadratic formula.

New York’s dream of “algebra for all” was never fully realized, and Mayor Eric Adams’s administration changed the goal to improving outcomes for ninth graders taking algebra. In San Francisco, dismantling middle-school algebra did little to end racial inequities among students in advanced math classes. After a huge public outcry, the district decided to reverse course.

“You wouldn’t think that there could be a more boring topic in the world,” said Thurston Domina, a professor at the University of North Carolina. “And yet, it’s this place of incredibly high passions.”

“Things run hot,” he said.

In some cities, disputes over algebra have been so intense that parents have sued school districts, protested outside mayors’ offices and campaigned for the ouster of school board members.

Teaching math in middle school is a challenge for educators in part because that is when the material becomes more complex, with students moving from multiplication tables to equations and abstract concepts. Students who have not mastered the basic skills can quickly become lost, and it can be difficult for them to catch up.

Many school districts have traditionally responded to divergent achievement levels by simply separating children into distinct pathways, placing some in general math classes while offering others algebra as an accelerated option. Such sorting, known as tracking, appeals to parents who want their children to reach advanced math as quickly as possible.

But tracking has cast an uncomfortable spotlight on inequality. Around a quarter of all students in the United States take algebra in middle school. But only about 12 percent of Black and Latino eighth graders do, compared with roughly 24 percent of white pupils, a federal report found .

“That’s why middle school math is this flashpoint,” said Joshua Goodman, an associate professor of education and economics at Boston University. “It’s the first moment where you potentially make it very obvious and explicit that there are knowledge gaps opening up.”

In the decades-long war over math, San Francisco has emerged as a prominent battleground.

California once required that all eighth graders take algebra. But lower-performing middle school students often struggle when forced to enroll in the class, research shows. San Francisco later stopped offering the class in eighth grade. But the ban did little to close achievement gaps in more advanced math classes, recent research has found.

As the pendulum swung, the only constant was anger. Leading Bay Area academics disparaged one another’s research . A group of parents even sued the district last spring. “Denying students the opportunity to skip ahead in math when their intellectual ability clearly allows for it greatly harms their potential for future achievement,” their lawsuit said.

The city is now back to where it began: Middle school algebra — for some, not necessarily for all — will return in August. The experience underscored how every approach carries risks.

“Schools really don’t know what to do,” said Jon R. Star, an educational psychologist at Harvard who has studied algebra education. “And it’s just leading to a lot of tension.”

In Cambridge, Mass., the school district phased out middle school algebra before the pandemic. But some argued that the move had backfired: Families who could afford to simply paid for their children to take accelerated math outside of school.

“It’s the worst of all possible worlds for equity,” Jacob Barandes, a Cambridge parent, said at a school board meeting.

Elsewhere, many students lack options to take the class early: One of Philadelphia’s most prestigious high schools requires students to pass algebra before enrolling, preventing many low-income children from applying because they attend middle schools that do not offer the class.

In New York, Mr. de Blasio sought to tackle the disparities when he announced a plan in 2015 to offer algebra — but not require it — in all of the city’s middle schools. More than 15,000 eighth graders did not have the class at their schools at the time.

Since then, the number of middle schools that offer algebra has risen to about 80 percent from 60 percent. But white and Asian American students still pass state algebra tests at higher rates than their peers.

The city’s current schools chancellor, David Banks, also shifted the system’s algebra focus to high schools, requiring the same ninth-grade curriculum at many schools in a move that has won both support and backlash from educators.

And some New York City families are still worried about middle school. A group of parent leaders in Manhattan recently asked the district to create more accelerated math options before high school, saying that many young students must seek out higher-level instruction outside the public school system.

In a vast district like New York — where some schools are filled with children from well-off families and others mainly educate homeless children — the challenge in math education can be that “incredible diversity,” said Pedro A. Noguera, the dean of the University of Southern California’s Rossier School of Education.

“You have some kids who are ready for algebra in fourth grade, and they should not be denied it,” Mr. Noguera said. “Others are still struggling with arithmetic in high school, and they need support.”

Many schools are unequipped to teach children with disparate math skills in a single classroom. Some educators lack the training they need to help students who have fallen behind, while also challenging those working at grade level or beyond.

Some schools have tried to find ways to tackle the issue on their own. KIPP charter schools in New York have added an additional half-hour of math time to many students’ schedules, to give children more time for practice and support so they can be ready for algebra by eighth grade.

At Middle School 50 in Brooklyn, where all eighth graders take algebra, teachers rewrote lesson plans for sixth- and seventh-grade students to lay the groundwork for the class.

The school’s principal, Ben Honoroff, said he expected that some students would have to retake the class in high school. But after starting a small algebra pilot program a few years ago, he came to believe that exposing children early could benefit everyone — as long as students came into it well prepared.

Looking around at the students who were not enrolling in the class, Mr. Honoroff said, “we asked, ‘Are there other kids that would excel in this?’”

“The answer was 100 percent, yes,” he added. “That was not something that I could live with.”

Troy Closson reports on K-12 schools in New York City for The Times. More about Troy Closson

Along with Stanford news and stories, show me:

• Student information
• Faculty/Staff information

We want to provide announcements, events, leadership messages and resources that are relevant to you. Your selection is stored in a browser cookie which you can remove at any time using “Clear all personalization” below.

For everyone whose relationship with mathematics is distant or broken, Jo Boaler , a professor at Stanford Graduate School of Education (GSE), has ideas for repairing it. She particularly wants young people to feel comfortable with numbers from the start – to approach the subject with playfulness and curiosity, not anxiety or dread.

“Most people have only ever experienced what I call narrow mathematics – a set of procedures they need to follow, at speed,” Boaler says. “Mathematics should be flexible, conceptual, a place where we play with ideas and make connections. If we open it up and invite more creativity, more diverse thinking, we can completely transform the experience.”

Boaler, the Nomellini and Olivier Professor of Education at the GSE, is the co-founder and faculty director of Youcubed , a Stanford research center that provides resources for math learning that has reached more than 230 million students in over 140 countries. In 2013 Boaler, a former high school math teacher, produced How to Learn Math , the first massive open online course (MOOC) on mathematics education. She leads workshops and leadership summits for teachers and administrators, and her online courses have been taken by over a million users.

In her new book, Math-ish: Finding Creativity, Diversity, and Meaning in Mathematics , Boaler argues for a broad, inclusive approach to math education, offering strategies and activities for learners at any age. We spoke with her about why creativity is an important part of mathematics, the impact of representing numbers visually and physically, and how what she calls “ishing” a math problem can help students make better sense of the answer.

What do you mean by “math-ish” thinking?

It’s a way of thinking about numbers in the real world, which are usually imprecise estimates. If someone asks how old you are, how warm it is outside, how long it takes to drive to the airport – these are generally answered with what I call “ish” numbers, and that’s very different from the way we use and learn numbers in school.

In the book I share an example of a multiple-choice question from a nationwide exam where students are asked to estimate the sum of two fractions: 12/13 + 7/8. They’re given four choices for the closest answer: 1, 2, 19, or 21. Each of the fractions in the question is very close to 1, so the answer would be 2 – but the most common answer 13-year-olds gave was 19. The second most common was 21.

I’m not surprised, because when students learn fractions, they often don’t learn to think conceptually or to consider the relationship between the numerator or denominator. They learn rules about creating common denominators and adding or subtracting the numerators, without making sense of the fraction as a whole. But stepping back and judging whether a calculation is reasonable might be the most valuable mathematical skill a person can develop.

But don’t you also risk sending the message that mathematical precision isn’t important?

I’m not saying precision isn’t important. What I’m suggesting is that we ask students to estimate before they calculate, so when they come up with a precise answer, they’ll have a real sense for whether it makes sense. This also helps students learn how to move between big-picture and focused thinking, which are two different but equally important modes of reasoning.

Some people ask me, “Isn’t ‘ishing’ just estimating?” It is, but when we ask students to estimate, they often groan, thinking it’s yet another mathematical method. But when we ask them to “ish” a number, they're more willing to offer their thinking.

Ishing helps students develop a sense for numbers and shapes. It can help soften the sharp edges in mathematics, making it easier for kids to jump in and engage. It can buffer students against the dangers of perfectionism, which we know can be a damaging mindset. I think we all need a little more ish in our lives.

You also argue that mathematics should be taught in more visual ways. What do you mean by that?

For most people, mathematics is an almost entirely symbolic, numerical experience. Any visuals are usually sterile images in a textbook, showing bisecting angles, or circles divided into slices. But the way we function in life is by developing models of things in our minds. Take a stapler: Knowing what it looks like, what it feels and sounds like, how to interact with it, how it changes things – all of that contributes to our understanding of how it works.

There’s an activity we do with middle-school students where we show them an image of a 4 x 4 x 4 cm cube made up of smaller 1 cm cubes, like a Rubik’s Cube. The larger cube is dipped into a can of blue paint, and we ask the students, if they could take apart the little cubes, how many sides would be painted blue? Sometimes we give the students sugar cubes and have them physically build a larger 4 x 4 x 4 cube. This is an activity that leads into algebraic thinking.

Some years back we were interviewing students a year after they’d done that activity in our summer camp and asked what had stayed with them. One student said, “I’m in geometry class now, and I still remember that sugar cube, what it looked like and felt like.” His class had been asked to estimate the volume of their shoes, and he said he’d imagined his shoes filled with 1 cm sugar cubes in order to solve that question. He had built a mental model of a cube.

When we learn about cubes, most of us don’t get to see and manipulate them. When we learn about square roots, we don’t take squares and look at their diagonals. We just manipulate numbers.

I wonder if people consider the physical representations more appropriate for younger kids.

That’s the thing – elementary school teachers are amazing at giving kids those experiences, but it dies out in middle school, and by high school it’s all symbolic. There’s a myth that there’s a hierarchy of sophistication where you start out with visual and physical representations and then build up to the symbolic. But so much of high-level mathematical work now is visual. Here in Silicon Valley, if you look at Tesla engineers, they're drawing, they're sketching, they're building models, and nobody says that's elementary mathematics.

There’s an example in the book where you’ve asked students how they would calculate 38 x 5 in their heads, and they come up with several different ways of arriving at the same answer. The creativity is fascinating, but wouldn’t it be easier to teach students one standard method?

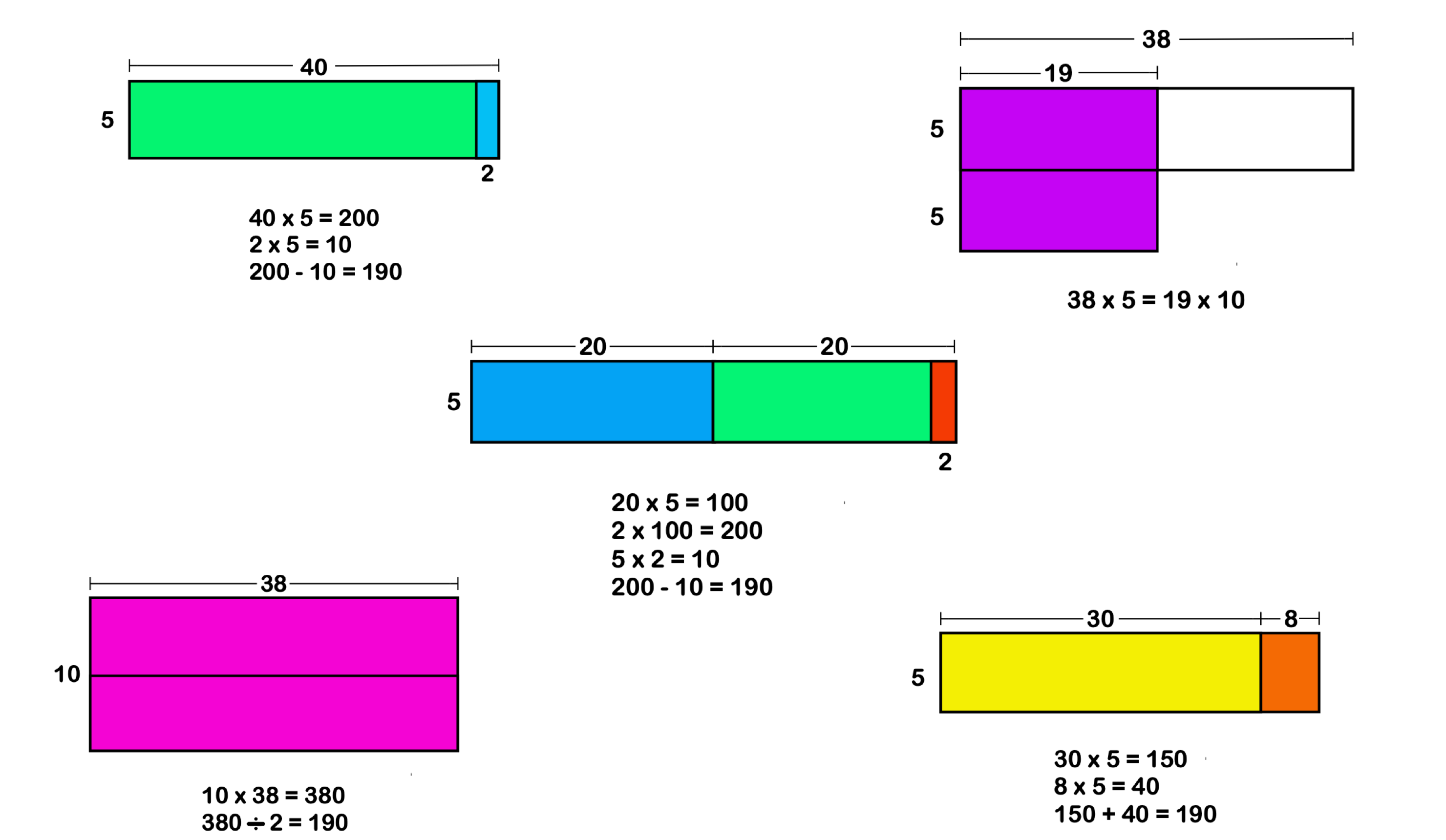
A depiction of various ways to calculate 38 x 5, numerically and visually. | Courtesy Jo Boaler

That narrow, rigid version of mathematics where there’s only one right approach is what most students experience, and it’s a big part of why people have such math trauma. It keeps them from realizing the full range and power of mathematics. When you only have students blindly memorizing math facts, they’re not developing number sense. They don’t learn how to use numbers flexibly in different situations. It also makes students who think differently believe there’s something wrong with them.

When we open mathematics to acknowledge the different ways a concept or problem can be viewed, we also open the subject to many more students. Mathematical diversity, to me, is a concept that includes both the value of diversity in people and the diverse ways we can see and learn mathematics. When we bring those forms of diversity together, it’s powerful. If we want to value different ways of thinking and problem-solving in the world, we need to embrace mathematical diversity.

The 7 Best Calculators for Going Back-to-School, Acing Tests, and Doing Accounting Work

Whether you’re aiming to ace a test or prep a career-making presentation, these tools can get you there.

Gear-obsessed editors choose every product we review. We may earn commission if you buy from a link. Why Trust Us?

Whether you’re a college student enrolled in a calculus course or a professional accountant with your own firm, having a dedicated calculator is essential to your success. These purpose-built devices allow you to perform a wide range of calculations quickly—powerful models can even tackle complicated calculus equations and graph visual representations of functions.

The Best Calculators

• Best Overall: Texas Instruments TI-84 Plus CE Graphing Calculator
• Best Budget Option: Canon LS-82Z Handheld Calculator
• Best Scientific Calculator: Casio fx-115ESPLUS2 2nd Edition Advanced Scientific Calculator
• Best for Students: Sharp EL-W516TBSL 16-Digit Advanced Scientific Calculator
• Most User-Friendly Calculator: Casio FX-9750GII Graphing Calculator

What to Consider

Capabilities.

From graphing to scientific to four-function, different types of calculators have vastly different capabilities. Be sure to choose one that serves your particular needs. Additionally, if you plan to use it for college entrance exams, make sure the model you are going to purchase is approved for use during testing.

Generally speaking, elementary and middle school students are best served by scientific calculators; high school students probably need graphing calculators; and professionals who work with numbers should look for accounting calculators.

Battery Life and Power Source

Speaking of college entrance exams, nothing could be worse than your calculator running out of power before you finish your test. Calculators are battery-powered, solar-powered, or a hybrid of both—and a few higher-end models are rechargeable. We recommend battery-powered calculators for most people, though simple four-function options can last for a while on the solar panel alone.

How We Selected

We read through a wide breadth of professional reviews to find consensus on the best calculators in a number of different categories. We also kept different coursework requirements, professional duties, and price points in mind, ensuring that our selections are useful to a wide range of people. We also made sure that the models we chose were from well-regarded companies, and considered the models we have and use around the office.

Texas Instruments TI-84 Plus CE Graphing Calculator

While the Texas Instrument TI-84 Plus is also available in a black-and-white version for slightly less money, we think the sharp backlit screen of its color edition is worth the expense—especially for college students and math professionals.

It’s a great choice for high school students, too. It comes loaded with MathPrint, which converts the equations to the same format you see in textbooks, and it’s approved for use during PSAT, SAT, and ACT college entrance exams, as well as AP exams that allow graphing calculators. It has a bunch of applications to expand the calculator’s functionality, as well as lots of images you can use for graphing.

Plus, it has a rechargeable battery that powers up with a USB cable. The TI-84 Plus is more expensive than most of the other models on this list, but it’s one of the best calculators money can buy.

Canon LS-82Z Handheld Calculator

For those whose calculating needs are minimal and for whom spending a lot on a calculator doesn’t add up (pun intended), the Canon LS-82Z four-function calculator is a great option.

Frequently priced under $10, it can handle square root functions and product dimensions, and also features a floating decimal point system. It’s dual-powered by battery and solar, so you won’t spend a lot of additional cash replacing batteries.

It doesn’t have the computing power of other models on the list, but the Canon LS-82Z is a dependable basic calculator.

Casio fx-115ESPLUS2 2nd Edition Advanced Scientific Calculator

If you’re on a budget and looking for a scientific calculator to tackle algebra, calculus, physics, or statistics problems, this Casio model is a great fit. The large four-line, 14-character display presents your formulas and results exactly as they would appear in a textbook, and a protective case keeps the unit from getting damaged in storage or during transport.

At just 3.68 ounces, it’s nice and lightweight, and the white color is an attractive aesthetic alternative to standard black calculators. For less than $20, it’s a great value, as well.

HP 12C Financial Calculator

With more than 120 different built-in functions, such as amortization, cash flow, and loan payments, this HP financial calculator makes quick work of your accounting—whether it’s personal or business-related. It’s also capable of data entry and calculations using the RPN system.

The HP 12c is compact and portable, yet its buttons are placed strategically to allow for ease of use, while its large 10-digit LCD display is easy on your eyes. Plus, it’s one of only two calculators allowed by the Chartered Financial Analyst Institute for its exam.

Casio FX-9750GII Graphing Calculator

One of our favorite graphing calculators, the Casio FX-9750GII offers a lot of machine for the money. It can handle the needs of most students all the way through college, and has an interface that most should find very user-friendly.

Meanwhile, its backlit, high-res LCD display is easy to read, and this calculator can go for over 200 hours on four AAA batteries. It lacks some of the fancy features of higher-priced models, but handles most students’ needs. Plus, it’s approved for use with most exams, including PSAT, SAT, ACT, and AP tests.

Casio CA-53W-1CR Calculator Watch

We had to include the classic Casio watch—it saved us in a pinch before smartphones and still looks just as stylish today. The simple functionality can help you split a bar tab or figure out gratuity for dinner, and it has a built-in timer and calendar (and clock, of course).

The resin armband and plastic case are highly durable and the watch is water resistant up to 100 meters. Obviously this watch won’t speed up your taxes or help you ace an SAT, but some nostalgic charm is always welcomed—especially when functional.

Sharp EL-W516TBSL 16-Digit Advanced Scientific Calculator

Students who need a scientific calculator should look no further than this Sharp 16-digit scientific calculator. Its most noticeable feature is a large, four-line screen that shows entered equations in condensed textbook form.

Powered by both solar and a battery, it offers seven different calculation modes—normal, stat, drill, complex, matrix, list, and equation. It’s capable of performing more than 600 functions and even algebra.

It comes in a nice glossy black hard case—but even better, it’s usually priced under $25, meaning it meets most students’ budgets as well.

Danny Perez is a Commerce Editor for Popular Mechanics with a focus on men's style, gear, and home goods. Recently, he was coordinator of partnership content at another product journalism outlet. Prior to that, he was a buyer for an independent men's shop in Houston, Texas, where he learned all about what makes great products great. He enjoys thrifting for 90s Broadway tees and vintage pajama sets. His spare time is occupied by watching movies and running to impress strangers on Strava.

Alex Rennie is a freelance writer who specializes in the Home Improvement, DIY, and Tool space. As a former residential and commercial carpenter, Alex uses his hands-on experience to write practical buying guides, how-to articles, and product reviews. His work has also appeared in Business Insider's Insider Picks, and before his writing career, he was a full-time carpenter living in New York City. There, he worked as part of a team designing, building, and installing large furniture pieces, as well as performing a variety of home repair and maintenance projects. Alex currently lives in Los Angeles, CA, and spends his free time exploring the beaches and mountains with his fiancé and their dog Louie.

.css-cuqpxl:before{padding-right:0.3125rem;content:'//';display:inline;} New Technology .css-xtujxj:before{padding-left:0.3125rem;content:'//';display:inline;}

The Best Memorial Day TV Sales to Shop Now

The 6 Best Shipping Label Printers

Three MIT Studies Promise Major AI Upgrades

Rebuilding the Maze

Curving Light Could Make the 6G Dream a Reality

The Best Doorbell Cameras for Surveillance

The 4 Best Smart Bird Feeders for Your Backyard

Amazon Warehouse Milwaukee Sale: Up to 42% Off

The Best Wireless Security Cameras for Your Home

The Best Amazon Gaming Week Deals

The 8 Best Outdoor Bluetooth Speakers

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Praxis Core Math

Course: praxis core math   >   unit 1.

• Algebraic properties | Lesson
• Algebraic properties | Worked example
• Solution procedures | Lesson
• Solution procedures | Worked example
• Equivalent expressions | Lesson
• Equivalent expressions | Worked example
• Creating expressions and equations | Lesson
• Creating expressions and equations | Worked example

Algebraic word problems | Lesson

• Algebraic word problems | Worked example
• Linear equations | Lesson
• Linear equations | Worked example
• Quadratic equations | Lesson
• Quadratic equations | Worked example

What are algebraic word problems?

What skills are needed.

• Translating sentences to equations
• Solving linear equations with one variable
• Evaluating algebraic expressions
• Solving problems using Venn diagrams

How do we solve algebraic word problems?

• Define a variable.
• Write an equation using the variable.
• Solve the equation.
• If the variable is not the answer to the word problem, use the variable to calculate the answer.

What's a Venn diagram?

• 7 + 10 − 13 = 4 ‍   brought both food and drinks.
• 7 − 4 = 3 ‍   brought only food.
• 10 − 4 = 6 ‍   brought only drinks.
• Your answer should be
• an integer, like 6 ‍  
• a simplified proper fraction, like 3 / 5 ‍  
• a simplified improper fraction, like 7 / 4 ‍  
• a mixed number, like 1   3 / 4 ‍  
• an exact decimal, like 0.75 ‍  
• a multiple of pi, like 12   pi ‍   or 2 / 3   pi ‍  
• (Choice A)   $ 4 ‍   A $ 4 ‍  
• (Choice B)   $ 5 ‍   B $ 5 ‍  
• (Choice C)   $ 9 ‍   C $ 9 ‍  
• (Choice D)   $ 14 ‍   D $ 14 ‍  
• (Choice E)   $ 20 ‍   E $ 20 ‍  
• (Choice A)   10 ‍   A 10 ‍  
• (Choice B)   12 ‍   B 12 ‍  
• (Choice C)   24 ‍   C 24 ‍  
• (Choice D)   30 ‍   D 30 ‍  
• (Choice E)   32 ‍   E 32 ‍  
• (Choice A)   4 ‍   A 4 ‍  
• (Choice B)   10 ‍   B 10 ‍  
• (Choice C)   14 ‍   C 14 ‍  
• (Choice D)   18 ‍   D 18 ‍  
• (Choice E)   22 ‍   E 22 ‍  

Things to remember

Want to join the conversation.

• Upvote Button navigates to signup page
• Downvote Button navigates to signup page
• Flag Button navigates to signup page

• {{subColumn.name}}

AIMS Mathematics

• {{newsColumn.name}}
• Share facebook twitter google linkedin

Caputo-Hadamard fractional boundary-value problems in $ {\mathfrak{L}}^\mathfrak{p} $-spaces

• Shayma Adil Murad 1 ,  ,  , 
• Ava Shafeeq Rafeeq 2 , 
• Thabet Abdeljawad 3,4,5,6 ,  , 
• 1. Department of Mathematics, College of Science, Univesity of Duhok, Duhok 42001, Iraq
• 2. Department of Mathematics, College of Science, Univesity of Zakho, Duhok 42001, Iraq
• 3. Department of Mathematics and Sciences, Prince Sultan Univesity, Riyadh 11586, Saudi Arabia
• 4. Department of Medical Research, China Medical Univesity, Taichung 40402, Taiwan
• 5. Department of Mathematics Kyung Hee Univesity, 26 Kyungheedae-ro, Dongdaemun-gu, Seoul 02447, Republic of Korea
• 6. Department of Mathematics and Applied Mathematics, School of Science and Technology, Sefako Makgatho Health Sciences Uni., Ga-Rankuwa, South Africa
• Received: 29 March 2024 Revised: 03 May 2024 Accepted: 10 May 2024 Published: 21 May 2024

MSC : 26A33, 34A08, 34D20, 34K20, 34B15, 34A12

• Full Text(HTML)
• Download PDF

The focal point of this investigation is the exploration of solutions for Caputo-Hadamard fractional differential equations with boundary conditions, and it follows the initial formulation of a model that is intended to address practical problems. The research emphasizes resolving the challenges associated with determining precise solutions across diverse scenarios. The application of the Burton-Kirk fixed-point theorem and the Kolmogorov compactness criterion in $ {\mathfrak{L}}^\mathfrak{p} $-spaces ensures the existence of the solution to our problem. Banach's theory is crucial for the establishment of solution uniqueness, and it is complemented by utilizing the Hölder inequality in integral analysis. Stability analyses from the Ulam-Hyers perspective provide key insights into the system's reliability. We have included practical examples, tables, and figures, thereby furnishing a comprehensive and multifaceted examination of the outcomes.

• Caputo-Hadamard fractional derivatives ,
• Ulam-Hyers stability ,
• Burton-Kirk fixed-point theorem ,
• Hölder inequality ,
• Kolmogorov compactness criterion

Citation: Shayma Adil Murad, Ava Shafeeq Rafeeq, Thabet Abdeljawad. Caputo-Hadamard fractional boundary-value problems in $ {\mathfrak{L}}^\mathfrak{p} $-spaces[J]. AIMS Mathematics, 2024, 9(7): 17464-17488. doi: 10.3934/math.2024849

Related Papers:

• This work is licensed under a Creative Commons Attribution-NonCommercial-Share Alike 4.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/4.0/ -->

Supplements

Access history.

• Corresponding authors: Email: [email protected] , [email protected] ;  Email: [email protected] , [email protected]

Reader Comments

• © 2024 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License ( http://creativecommons.org/licenses/by/4.0 )

通讯作者: 陈斌, [email protected]

沈阳化工大学材料科学与工程学院 沈阳 110142

Article views( 92 ) PDF downloads( 16 ) Cited by( 0 )

Figures and Tables

Figures( 4 )  /  Tables( 2 )

Associated material

Other articles by authors.

• Shayma Adil Murad
• Ava Shafeeq Rafeeq
• Thabet Abdeljawad

Related pages

• on Google Scholar
• Email to a friend
• Order reprints

Export File

• Figure 1. Results of $ \omega $ on $ \zeta = [1, e] $ with $ \mathfrak{p} = 2 $ for Example 2 when a) $ 1 < {\mathfrak{W}} < 2 $ and $ \; {\mathfrak{H}} = 0.3 $; b) $ {\mathfrak{W}} = 1.7 $ and $ 0 < \; {\mathfrak{H}}\leq1 $
• Figure 2. Results of $ \omega $ on $ \zeta = [1, e] $ with $ \mathfrak{p} = 3 $ for Example 2 when a) $ 1 < {\mathfrak{W}} < 2 $, $ \; {\mathfrak{H}} = 0.5 $; b) $ {\mathfrak{W}} = 1.5 $, $ 0 < \; {\mathfrak{H}}\leq1 $
• Figure 3. Results of $ \omega $ with $ \mathfrak{p} = 4 $ for Example 2 when a) $ 1 < {\mathfrak{W}} < 2 $, $ \; {\mathfrak{H}} = 0.8 $; b) $ {\mathfrak{W}} = 1.2 $, $ 0 < \; {\mathfrak{H}}\leq1 $
• Figure 4. Results of $ \omega $ with $ \mathfrak{p} = 15 $ for Example 2 when a) $ {\mathfrak{W}} = 1.2 $, $ 0 < \; {\mathfrak{H}}\leq 1 $; b) $ 1 < {\mathfrak{W}} < 2 $, $ \; {\mathfrak{H}} = 0.8 $