probability research paper pdf

An official website of the United States government

The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

• Publications
• Account settings

Preview improvements coming to the PMC website in October 2024. Learn More or Try it out now .

• Advanced Search
• Journal List
• J Thorac Dis
• v.10(2); 2018 Feb

A brief introduction to probability

Gioacchino di paola.

1 Office of Research, IRCCS ISMETT, Palermo, Italy;

Alessandro Bertani

2 Division of Thoracic Surgery and Lung Transplantation, Department for the Treatment and Study of Cardiothoracic Diseases and Cardiothoracic Transplantation, IRCCS ISMETT-UPMC, Palermo, Italy

Lavinia De Monte

Fabio tuzzolino.

The theory of probability has been debated for centuries: back in 1600, French mathematics used the rules of probability to place and win bets. Subsequently, the knowledge of probability has significantly evolved and is now an essential tool for statistics. In this paper, the basic theoretical principles of probability will be reviewed, with the aim of facilitating the comprehension of statistical inference. After a brief general introduction on probability, we will review the concept of the “probability distribution” that is a function providing the probabilities of occurrence of different possible outcomes of a categorical or continuous variable. Specific attention will be focused on normal distribution that is the most relevant distribution applied to statistical analysis.

Probability

A simple clinical vignette may help introducing the concept of probability.

In a clinical study, patients with claudicatio intermittens who received treatment “A” walked an average of 472 m, while patients who received treatment “B” walked 405 m. Given the difference of 67 m in favor of treatment “A”, is it possible to conclude that, based on this study, treatment “A” is better than treatment “B”? And, based on this assumption, should the doctor administer treatment “A” to his next patient with claudicatio intermittens?

The first question is a typical question involving the concept of statistical inference and, precisely, is: “what is the conclusion that we may draw from our study?”

The second question is a typical question about decision-making: what is the rationale for preferring a specific treatment over another, based on the information available in the study and other information coming from previous studies?

The answers to both questions may be provided with just a limited amount of uncertainty, although uncertainty may vary in different circumstances. If the degree of uncertainty is low, the conclusions will be strong and the decision based on the available knowledge (or evidence) will be almost certain. If the degree of uncertainty is high, the conclusions will be poor and the decision will not be based on evidence but will be only based on personal experience, instinct, or will be left to chance.

It is therefore very important to measure the degree of uncertainty, and the theory of probability provides us with the appropriate tools to do so. Probability may also be defined as the “logic of the possible” or the “logic of the uncertain”, because it has to deal with hypotheses that may not be associated with a completely true or false attestation, but just with a “possible” attestation. For example, “tomorrow will rain” is neither a true or false hypothesis, but it is only possible. For all the hypotheses that have to deal with uncertainty, the theory of probability will measure the degree of possibility of such hypothesis, and will assign to the hypothesis a certain value of probability ( 1 ).

Defining probability is useful to measure how likely it is that a given event will actually occur. The word “probability” actually belongs to spoken language and is used in different situations. Although the general concept of this word is very clear, a formal definition of probability is also useful for the physicians who are approaching statistics.

The most common definitions of probability are called the “frequentistic” and the “subjectivist” (or Bayesian). Both of them tend to measure probability with a quantitative ( 2 , 3 ) approach and to assign a value between 0 and 1 or, in term of percentage, any value between 0% and 100%. A value of 0 or 0% represents the absence of any probability that an event may occur. On the other side, a value of 1 or 100% means that the event will occur with complete certainty.

According to a “frequentistic” approach, probability is seen as the proportion (relative frequency) of times that a given event occurs in an infinite or very high number of attempts, performed in stable conditions. The relative frequency is the ratio between the number (k) of attempts with a favorable outcome and the overall number (n) of attempts: (k/n). For example, one should think about a clinical trial looking at complete clinical response after a certain medical treatment, and observe if the outcome is favorable (the patient recovered) or unfavorable (the patient did not recover). The relative frequency of response to the treatment is the ratio between the number of patients who recovered and the overall number of patients who received the treatment, (k/n).

On the other side, according to the subjectivist (Bayesian) approach, probability is defined as the degree of belief that an individual holds in respect to the occurrence of a certain event. The inspiring principle of the Bayesian approach is that all unknown quantities can be assigned a probability. In other words, every type of uncertainty can be represented in probabilistic terms. In this approach, probability is the expression of an evaluation of the event made by the researcher on the basis of the information available to him/her. For this reason, in order to translate the degree of belief into a number, the Bayesian approach introduces the concept of a “Bet scheme”. Probability is handled as the price that an individual feels appropriate to be paid in order to receive a value of 1 if the event occurs or a value of 0 if the event does not occur. The degree of belief that a person holds in respect to a certain event is subjective, and different individuals with similar or different information may reach different estimates of the probability of a given event.

Looking back to our previous clinical example, the probability that a patient recovers after receiving a certain treatment may be seen, according to the Bayesian approach, as a subjective estimate of the effect of the treatment. This estimate is based on the available information and may be presented as the risk that an individual may take within a fictional bet, during which patient recovery and its opposite (failed recovery) are being bet.

The debate on the definition of probability generated a basic set of axioms that may all reflect the properties of the concept of probability. The entire system of statistical probability is based on these three simple axioms of rules ( Table 1 ) ( 4 ).

There are also circumstances when information about a certain event may influence the estimate of probability of another event. For example, a physician may think that the probability for a certain disease to occur may be, generally speaking, very low. But, if the patient is exposed to a relevant risk factor for this disease, then the physician’s estimate of probability may change and he may think that the patient is more exposed to this particular disease. In this example, the probability of a certain event is modified after another separate event happens. This is the concept of “conditional probability”. Frequently, a cause-effect relationship between two events may be found under the concept of “conditional probability”.

Distribution of probability

In many situations, the events of interest have a natural interpretation in numerical terms. For example, let’s take into consideration a few typical outcome variables such as diastolic blood pressure, distance walked on a stress test, or the expenses of a family. In all these cases, it is useful to introduce a “random” variable among the results of the real, actual numbers. “Random” or “aleatory” refers to the uncertainty related to the specific value that the variable will receive in a given patient, in a given experiment, at a given time, etc.

In order to express and quantify the uncertainty of the possible values of the aleatory variable, we will introduce the concept of the distribution of probability. This is a mathematical model that is able to link every value of a variable to the probability that this value may be actually observed. Based on the scale used to measure the variable, we may distinguish between two different distributions of probability ( 5 , 6 ):

Probability distribution: discrete case and continuous case.

• “ Discrete distributions ” : the variable is measured with whole numerical values (for example, number of cigarettes in a period of time). Each probability is a number between 0 and 1. The sum of the probabilities of all the possible values is 1 ( Figure 1 ).

From a formal statistical standpoint, the distributions of probability are expressed by a mathematical formula called “function of density of probability”, called “ f(x) ” for continuous distributions or “ p(x)” for discrete distributions ( Figure 1 ). Table 2 shows the most common continuous and discrete distributions of probability.

Some theoretical distributions of probability are important because they match very closely the distribution of many variables that may be observed in the real world. Among others, the “normal” distribution is the one that has the most important role in inferential statistics, because many statistical techniques are based on this distribution. The “bell-shaped” curve of the normal distribution is able to describe very well data histograms of variables that are continuous and have a symmetrical distribution. This distribution is frequently used in medicine because many clinical variables may empirically present the typical shape of normal distribution. For example, the linear regression is based on this distribution.

In other cases, the shape of the distribution is not completely normal and there are mathematical transformations that can help the statistician to “normalize” the distribution of data ( 7 ).

The importance of the normal distribution should not minimize the role of other types of distribution, because many statistical models have been created in order to bypass the issues of non-normally distributed sets of data using different types of distributions. For example the generalized linear models can assess different types of the outcome distribution such as gamma, binomial, poisson distribution, etc.

Binary variables (dichotomous) are those variables where two only values are allowed to describe a phenomenon, defining two opposite situations (yes or not, alive or dead, etc.). The concept of probability may also apply to these variables, both as an aggregate property ((if a “representative” sample is considered and analyzed, the probability is the rate between the number of outcomes resulting in “yes” and the total number of the subjects of the sample) or an individual probability (the propensity or risk to fall into one specific category). Using this interpretation, probability for categorical variables may be described as well with a value between 0 and 1 and may be analyzed as the dependent variable in an appropriate regression model, for example the logistic regression model ( 7 ).

Take home messages

• Uncertainty characterizes every question of inference or decision in clinical research;
• Probability theories provide all the instruments and methodologies to measure these uncertain phenomena. In particular, probability may describe the proportion of times that a certain observation may occur in a large set of observations;
• In statistics, different inferential approaches are based on a probabilistic background: the frequentist (more widely used) and the Bayesan approach;
• The normal distribution has a pivotal role in clinical research because many variables present this type of distribution. Many statistical models are based on this distribution. Many alternatives are available for different type of distributions.

Acknowledgements

Conflicts of Interest: The authors have no conflicts of interest to declare.

Help | Advanced Search

Mathematics > Probability

Title: on the spielman-teng conjecture.

Abstract: Let $M$ be an $n\times n$ matrix with iid subgaussian entries with mean $0$ and variance $1$ and let $\sigma_n(M)$ denote the least singular value of $M$. We prove that \[\mathbb{P}\big( \sigma_{n}(M) \leq \varepsilon n^{-1/2} \big) = (1+o(1)) \varepsilon + e^{-\Omega(n)}\] for all $0 \leq \varepsilon \ll 1$. This resolves, up to a $1+o(1)$ factor, a seminal conjecture of Spielman and Teng.

Submission history

Access paper:.

• HTML (experimental)
• Other Formats

References & Citations

• Google Scholar
• Semantic Scholar

BibTeX formatted citation

Bibliographic and Citation Tools

Code, data and media associated with this article, recommenders and search tools.

• Institution

arXivLabs: experimental projects with community collaborators

arXivLabs is a framework that allows collaborators to develop and share new arXiv features directly on our website.

Both individuals and organizations that work with arXivLabs have embraced and accepted our values of openness, community, excellence, and user data privacy. arXiv is committed to these values and only works with partners that adhere to them.

Have an idea for a project that will add value for arXiv's community? Learn more about arXivLabs .

• Search by keyword
• Search by citation

Page 1 of 3

A generalization to the log-inverse Weibull distribution and its applications in cancer research

In this paper we consider a generalization of a log-transformed version of the inverse Weibull distribution. Several theoretical properties of the distribution are studied in detail including expressions for i...

• View Full Text

Approximations of conditional probability density functions in Lebesgue spaces via mixture of experts models

Mixture of experts (MoE) models are widely applied for conditional probability density estimation problems. We demonstrate the richness of the class of MoE models by proving denseness results in Lebesgue space...

Structural properties of generalised Planck distributions

A family of generalised Planck (GP) laws is defined and its structural properties explored. Sometimes subject to parameter restrictions, a GP law is a randomly scaled gamma law; it arises as the equilibrium la...

New class of Lindley distributions: properties and applications

A new generalized class of Lindley distribution is introduced in this paper. This new class is called the T -Lindley{ Y } class of distributions, and it is generated by using the quantile functions of uniform, expon...

Tolerance intervals in statistical software and robustness under model misspecification

A tolerance interval is a statistical interval that covers at least 100 ρ % of the population of interest with a 100(1− α ) % confidence, where ρ and α are pre-specified values in (0, 1). In many scientific fields, su...

Combining assumptions and graphical network into gene expression data analysis

Analyzing gene expression data rigorously requires taking assumptions into consideration but also relies on using information about network relations that exist among genes. Combining these different elements ...

A comparison of zero-inflated and hurdle models for modeling zero-inflated count data

Counts data with excessive zeros are frequently encountered in practice. For example, the number of health services visits often includes many zeros representing the patients with no utilization during a follo...

A general stochastic model for bivariate episodes driven by a gamma sequence

We propose a new stochastic model describing the joint distribution of ( X , N ), where N is a counting variable while X is the sum of N independent gamma random variables. We present the main properties of this gene...

A flexible multivariate model for high-dimensional correlated count data

We propose a flexible multivariate stochastic model for over-dispersed count data. Our methodology is built upon mixed Poisson random vectors ( Y 1 ,…, Y d ), where the { Y i } are conditionally independent Poisson random...

Generalized fiducial inference on the mean of zero-inflated Poisson and Poisson hurdle models

Zero-inflated and hurdle models are widely applied to count data possessing excess zeros, where they can simultaneously model the process from how the zeros were generated and potentially help mitigate the eff...

Multivariate distributions of correlated binary variables generated by pair-copulas

Correlated binary data are prevalent in a wide range of scientific disciplines, including healthcare and medicine. The generalized estimating equations (GEEs) and the multivariate probit (MP) model are two of ...

On two extensions of the canonical Feller–Spitzer distribution

We introduce two extensions of the canonical Feller–Spitzer distribution from the class of Bessel densities, which comprise two distinct stochastically decreasing one-parameter families of positive absolutely ...

A new trivariate model for stochastic episodes

We study the joint distribution of stochastic events described by ( X , Y , N ), where N has a 1-inflated (or deflated) geometric distribution and X , Y are the sum and the maximum of N exponential random variables. Mod...

A flexible univariate moving average time-series model for dispersed count data

Al-Osh and Alzaid ( 1988 ) consider a Poisson moving average (PMA) model to describe the relation among integer-valued time series data; this model, however, is constrained by the underlying equi-dispersion assumpt...

Spatio-temporal analysis of flood data from South Carolina

To investigate the relationship between flood gage height and precipitation in South Carolina from 2012 to 2016, we built a conditional autoregressive (CAR) model using a Bayesian hierarchical framework. This ...

Affine-transformation invariant clustering models

We develop a cluster process which is invariant with respect to unknown affine transformations of the feature space without knowing the number of clusters in advance. Specifically, our proposed method can iden...

Distributions associated with simultaneous multiple hypothesis testing

We develop the distribution for the number of hypotheses found to be statistically significant using the rule from Simes (Biometrika 73: 751–754, 1986) for controlling the family-wise error rate (FWER). We fin...

New families of bivariate copulas via unit weibull distortion

This paper introduces a new family of bivariate copulas constructed using a unit Weibull distortion. Existing copulas play the role of the base or initial copulas that are transformed or distorted into a new f...

Generalized logistic distribution and its regression model

A new generalized asymmetric logistic distribution is defined. In some cases, existing three parameter distributions provide poor fit to heavy tailed data sets. The proposed new distribution consists of only t...

The spherical-Dirichlet distribution

Today, data mining and gene expressions are at the forefront of modern data analysis. Here we introduce a novel probability distribution that is applicable in these fields. This paper develops the proposed sph...

Item fit statistics for Rasch analysis: can we trust them?

To compare fit statistics for the Rasch model based on estimates of unconditional or conditional response probabilities.

Exact distributions of statistics for making inferences on mixed models under the default covariance structure

At this juncture when mixed models are heavily employed in applications ranging from clinical research to business analytics, the purpose of this article is to extend the exact distributional result of Wald (A...

A new discrete pareto type (IV) model: theory, properties and applications

Discrete analogue of a continuous distribution (especially in the univariate domain) is not new in the literature. The work of discretizing continuous distributions begun with the paper by Nakagawa and Osaki (197...

Density deconvolution for generalized skew-symmetric distributions

The density deconvolution problem is considered for random variables assumed to belong to the generalized skew-symmetric (GSS) family of distributions. The approach is semiparametric in that the symmetric comp...

The unifed distribution

We introduce a new distribution with support on (0,1) called unifed. It can be used as the response distribution for a GLM and it is suitable for data aggregation. We make a comparison to the beta regression. ...

On Burr III Marshal Olkin family: development, properties, characterizations and applications

In this paper, a flexible family of distributions with unimodel, bimodal, increasing, increasing and decreasing, inverted bathtub and modified bathtub hazard rate called Burr III-Marshal Olkin-G (BIIIMO-G) fam...

The linearly decreasing stress Weibull (LDSWeibull): a new Weibull-like distribution

Motivated by an engineering pullout test applied to a steel strip embedded in earth, we show how the resulting linearly decreasing force leads naturally to a new distribution, if the force under constant stress i...

Meta analysis of binary data with excessive zeros in two-arm trials

We present a novel Bayesian approach to random effects meta analysis of binary data with excessive zeros in two-arm trials. We discuss the development of likelihood accounting for excessive zeros, the prior, a...

On ( p 1 ,…, p k )-spherical distributions

The class of ( p 1 ,…, p k )-spherical probability laws and a method of simulating random vectors following such distributions are introduced using a new stochastic vector representation. A dynamic geometric disintegra...

A new class of survival distribution for degradation processes subject to shocks

Many systems experience gradual degradation while simultaneously being exposed to a stream of random shocks of varying magnitudes that eventually cause failure when a shock exceeds the residual strength of the...

A new extended normal regression model: simulations and applications

Various applications in natural science require models more accurate than well-known distributions. In this context, several generators of distributions have been recently proposed. We introduce a new four-par...

Multiclass analysis and prediction with network structured covariates

Technological advances associated with data acquisition are leading to the production of complex structured data sets. The recent development on classification with multiclass responses makes it possible to in...

High-dimensional star-shaped distributions

Stochastic representations of star-shaped distributed random vectors having heavy or light tail density generating function g are studied for increasing dimensions along with corresponding geometric measure repre...

A unified complex noncentral Wishart type distribution inspired by massive MIMO systems

The eigenvalue distributions from a complex noncentral Wishart matrix S = X H X has been the subject of interest in various real world applications, where X is assumed to be complex matrix variate normally distribute...

Particle swarm based algorithms for finding locally and Bayesian D -optimal designs

When a model-based approach is appropriate, an optimal design can guide how to collect data judiciously for making reliable inference at minimal cost. However, finding optimal designs for a statistical model w...

Admissible Bernoulli correlations

A multivariate symmetric Bernoulli distribution has marginals that are uniform over the pair {0,1}. Consider the problem of sampling from this distribution given a prescribed correlation between each pair of v...

On p -generalized elliptical random processes

We introduce rank- k -continuous axis-aligned p -generalized elliptically contoured distributions and study their properties such as stochastic representations, moments, and density-like representations. Applying th...

Parameters of stochastic models for electroencephalogram data as biomarkers for child’s neurodevelopment after cerebral malaria

The objective of this study was to test statistical features from the electroencephalogram (EEG) recordings as predictors of neurodevelopment and cognition of Ugandan children after coma due to cerebral malari...

A new generalization of generalized half-normal distribution: properties and regression models

In this paper, a new extension of the generalized half-normal distribution is introduced and studied. We assess the performance of the maximum likelihood estimators of the parameters of the new distribution vi...

Analytical properties of generalized Gaussian distributions

The family of Generalized Gaussian (GG) distributions has received considerable attention from the engineering community, due to the flexible parametric form of its probability density function, in modeling ma...

A new Weibull- X family of distributions: properties, characterizations and applications

We propose a new family of univariate distributions generated from the Weibull random variable, called a new Weibull-X family of distributions. Two special sub-models of the proposed family are presented and t...

The transmuted geometric-quadratic hazard rate distribution: development, properties, characterizations and applications

We propose a five parameter transmuted geometric quadratic hazard rate (TG-QHR) distribution derived from mixture of quadratic hazard rate (QHR), geometric and transmuted distributions via the application of t...

A nonparametric approach for quantile regression

Quantile regression estimates conditional quantiles and has wide applications in the real world. Estimating high conditional quantiles is an important problem. The regular quantile regression (QR) method often...

Mean and variance of ratios of proportions from categories of a multinomial distribution

Ratio distribution is a probability distribution representing the ratio of two random variables, each usually having a known distribution. Currently, there are results when the random variables in the ratio fo...

The power-Cauchy negative-binomial: properties and regression

We propose and study a new compounded model to extend the half-Cauchy and power-Cauchy distributions, which offers more flexibility in modeling lifetime data. The proposed model is analytically tractable and c...

Families of distributions arising from the quantile of generalized lambda distribution

In this paper, the class of T-R { generalized lambda } families of distributions based on the quantile of generalized lambda distribution has been proposed using the T-R { Y } framework. In the development of the T - R {

Risk ratios and Scanlan’s HRX

Risk ratios are distribution function tail ratios and are widely used in health disparities research. Let A and D denote advantaged and disadvantaged populations with cdfs F ...

Joint distribution of k -tuple statistics in zero-one sequences of Markov-dependent trials

We consider a sequence of n , n ≥3, zero (0) - one (1) Markov-dependent trials. We focus on k -tuples of 1s; i.e. runs of 1s of length at least equal to a fixed integer number k , 1≤ k ≤ n . The statistics denoting the n...

Quantile regression for overdispersed count data: a hierarchical method

Generalized Poisson regression is commonly applied to overdispersed count data, and focused on modelling the conditional mean of the response. However, conditional mean regression models may be sensitive to re...

Describing the Flexibility of the Generalized Gamma and Related Distributions

The generalized gamma (GG) distribution is a widely used, flexible tool for parametric survival analysis. Many alternatives and extensions to this family have been proposed. This paper characterizes the flexib...

• ISSN: 2195-5832 (electronic)

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

• View all journals
• My Account Login
• Explore content
• About the journal
• Publish with us
• Sign up for alerts
• Open access
• Published: 17 October 2023

The impact of founder personalities on startup success

• Paul X. McCarthy 1 , 2 ,
• Xian Gong 3 ,
• Fabian Braesemann 4 , 5 ,
• Fabian Stephany 4 , 5 ,
• Marian-Andrei Rizoiu 3 &
• Margaret L. Kern 6  

Scientific Reports volume  13 , Article number:  17200 ( 2023 ) Cite this article

60k Accesses

2 Citations

305 Altmetric

Metrics details

• Human behaviour
• Information technology

An Author Correction to this article was published on 07 May 2024

This article has been updated

Startup companies solve many of today’s most challenging problems, such as the decarbonisation of the economy or the development of novel life-saving vaccines. Startups are a vital source of innovation, yet the most innovative are also the least likely to survive. The probability of success of startups has been shown to relate to several firm-level factors such as industry, location and the economy of the day. Still, attention has increasingly considered internal factors relating to the firm’s founding team, including their previous experiences and failures, their centrality in a global network of other founders and investors, as well as the team’s size. The effects of founders’ personalities on the success of new ventures are, however, mainly unknown. Here, we show that founder personality traits are a significant feature of a firm’s ultimate success. We draw upon detailed data about the success of a large-scale global sample of startups (n = 21,187). We find that the Big Five personality traits of startup founders across 30 dimensions significantly differ from that of the population at large. Key personality facets that distinguish successful entrepreneurs include a preference for variety, novelty and starting new things (openness to adventure), like being the centre of attention (lower levels of modesty) and being exuberant (higher activity levels). We do not find one ’Founder-type’ personality; instead, six different personality types appear. Our results also demonstrate the benefits of larger, personality-diverse teams in startups, which show an increased likelihood of success. The findings emphasise the role of the diversity of personality types as a novel dimension of team diversity that influences performance and success.

Similar content being viewed by others

Predicting success in the worldwide start-up network

The personality traits of self-made and inherited millionaires

The nexus of top executives’ attributes, firm strategies, and outcomes: Large firms versus SMEs

Introduction.

The success of startups is vital to economic growth and renewal, with a small number of young, high-growth firms creating a disproportionately large share of all new jobs 1 , 2 . Startups create jobs and drive economic growth, and they are also an essential vehicle for solving some of society’s most pressing challenges.

As a poignant example, six centuries ago, the German city of Mainz was abuzz as the birthplace of the world’s first moveable-type press created by Johannes Gutenberg. However, in the early part of this century, it faced several economic challenges, including rising unemployment and a significant and growing municipal debt. Then in 2008, two Turkish immigrants formed the company BioNTech in Mainz with another university research colleague. Together they pioneered new mRNA-based technologies. In 2020, BioNTech partnered with US pharmaceutical giant Pfizer to create one of only a handful of vaccines worldwide for Covid-19, saving an estimated six million lives 3 . The economic benefit to Europe and, in particular, the German city where the vaccine was developed has been significant, with windfall tax receipts to the government clearing Mainz’s €1.3bn debt and enabling tax rates to be reduced, attracting other businesses to the region as well as inspiring a whole new generation of startups 4 .

While stories such as the success of BioNTech are often retold and remembered, their success is the exception rather than the rule. The overwhelming majority of startups ultimately fail. One study of 775 startups in Canada that successfully attracted external investment found only 35% were still operating seven years later 5 .

But what determines the success of these ‘lucky few’? When assessing the success factors of startups, especially in the early-stage unproven phase, venture capitalists and other investors offer valuable insights. Three different schools of thought characterise their perspectives: first, supply-side or product investors : those who prioritise investing in firms they consider to have novel and superior products and services, investing in companies with intellectual property such as patents and trademarks. Secondly, demand-side or market-based investors : those who prioritise investing in areas of highest market interest, such as in hot areas of technology like quantum computing or recurrent or emerging large-scale social and economic challenges such as the decarbonisation of the economy. Thirdly, talent investors : those who prioritise the foundation team above the startup’s initial products or what industry or problem it is looking to address.

Investors who adopt the third perspective and prioritise talent often recognise that a good team can overcome many challenges in the lead-up to product-market fit. And while the initial products of a startup may or may not work a successful and well-functioning team has the potential to pivot to new markets and new products, even if the initial ones prove untenable. Not surprisingly, an industry ‘autopsy’ into 101 tech startup failures found 23% were due to not having the right team—the number three cause of failure ahead of running out of cash or not having a product that meets the market need 6 .

Accordingly, early entrepreneurship research was focused on the personality of founders, but the focus shifted away in the mid-1980s onwards towards more environmental factors such as venture capital financing 7 , 8 , 9 , networks 10 , location 11 and due to a range of issues and challenges identified with the early entrepreneurship personality research 12 , 13 . At the turn of the 21st century, some scholars began exploring ways to combine context and personality and reconcile entrepreneurs’ individual traits with features of their environment. In her influential work ’The Sociology of Entrepreneurship’, Patricia H. Thornton 14 discusses two perspectives on entrepreneurship: the supply-side perspective (personality theory) and the demand-side perspective (environmental approach). The supply-side perspective focuses on the individual traits of entrepreneurs. In contrast, the demand-side perspective focuses on the context in which entrepreneurship occurs, with factors such as finance, industry and geography each playing their part. In the past two decades, there has been a revival of interest and research that explores how entrepreneurs’ personality relates to the success of their ventures. This new and growing body of research includes several reviews and meta-studies, which show that personality traits play an important role in both career success and entrepreneurship 15 , 16 , 17 , 18 , 19 , that there is heterogeneity in definitions and samples used in research on entrepreneurship 16 , 18 , and that founder personality plays an important role in overall startup outcomes 17 , 19 .

Motivated by the pivotal role of the personality of founders on startup success outlined in these recent contributions, we investigate two main research questions:

Which personality features characterise founders?

Do their personalities, particularly the diversity of personality types in founder teams, play a role in startup success?

We aim to understand whether certain founder personalities and their combinations relate to startup success, defined as whether their company has been acquired, acquired another company or listed on a public stock exchange. For the quantitative analysis, we draw on a previously published methodology 20 , which matches people to their ‘ideal’ jobs based on social media-inferred personality traits.

We find that personality traits matter for startup success. In addition to firm-level factors of location, industry and company age, we show that founders’ specific Big Five personality traits, such as adventurousness and openness, are significantly more widespread among successful startups. As we find that companies with multi-founder teams are more likely to succeed, we cluster founders in six different and distinct personality groups to underline the relevance of the complementarity in personality traits among founder teams. Startups with diverse and specific combinations of founder types (e. g., an adventurous ‘Leader’, a conscientious ‘Accomplisher’, and an extroverted ‘Developer’) have significantly higher odds of success.

We organise the rest of this paper as follows. In the Section " Results ", we introduce the data used and the methods applied to relate founders’ psychological traits with their startups’ success. We introduce the natural language processing method to derive individual and team personality characteristics and the clustering technique to identify personality groups. Then, we present the result for multi-variate regression analysis that allows us to relate firm success with external and personality features. Subsequently, the Section " Discussion " mentions limitations and opportunities for future research in this domain. In the Section " Methods ", we describe the data, the variables in use, and the clustering in greater detail. Robustness checks and additional analyses can be found in the Supplementary Information.

Our analysis relies on two datasets. We infer individual personality facets via a previously published methodology 20 from Twitter user profiles. Here, we restrict our analysis to founders with a Crunchbase profile. Crunchbase is the world’s largest directory on startups. It provides information about more than one million companies, primarily focused on funding and investors. A company’s public Crunchbase profile can be considered a digital business card of an early-stage venture. As such, the founding teams tend to provide information about themselves, including their educational background or a link to their Twitter account.

We infer the personality profiles of the founding teams of early-stage ventures from their publicly available Twitter profiles, using the methodology described by Kern et al. 20 . Then, we correlate this information to data from Crunchbase to determine whether particular combinations of personality traits correspond to the success of early-stage ventures. The final dataset used in the success prediction model contains n = 21,187 startup companies (for more details on the data see the Methods section and SI section  A.5 ).

Revisions of Crunchbase as a data source for investigations on a firm and industry level confirm the platform to be a useful and valuable source of data for startups research, as comparisons with other sources at micro-level, e.g., VentureXpert or PwC, also suggest that the platform’s coverage is very comprehensive, especially for start-ups located in the United States 21 . Moreover, aggregate statistics on funding rounds by country and year are quite similar to those produced with other established sources, going to validate the use of Crunchbase as a reliable source in terms of coverage of funded ventures. For instance, Crunchbase covers about the same number of investment rounds in the analogous sectors as collected by the National Venture Capital Association 22 . However, we acknowledge that the data source might suffer from registration latency (a certain delay between the foundation of the company and its actual registration on Crunchbase) and success bias in company status (the likeliness that failed companies decide to delete their profile from the database).

The definition of startup success

The success of startups is uncertain, dependent on many factors and can be measured in various ways. Due to the likelihood of failure in startups, some large-scale studies have looked at which features predict startup survival rates 23 , and others focus on fundraising from external investors at various stages 24 . Success for startups can be measured in multiple ways, such as the amount of external investment attracted, the number of new products shipped or the annual growth in revenue. But sometimes external investments are misguided, revenue growth can be short-lived, and new products may fail to find traction.

Success in a startup is typically staged and can appear in different forms and times. For example, a startup may be seen to be successful when it finds a clear solution to a widely recognised problem, such as developing a successful vaccine. On the other hand, it could be achieving some measure of commercial success, such as rapidly accelerating sales or becoming profitable or at least cash positive. Or it could be reaching an exit for foundation investors via a trade sale, acquisition or listing of its shares for sale on a public stock exchange via an Initial Public Offering (IPO).

For our study, we focused on the startup’s extrinsic success rather than the founders’ intrinsic success per se, as its more visible, objective and measurable. A frequently considered measure of success is the attraction of external investment by venture capitalists 25 . However, this is not in and of itself a good measure of clear, incontrovertible success, particularly for early-stage ventures. This is because it reflects investors’ expectations of a startup’s success potential rather than actual business success. Similarly, we considered other measures like revenue growth 26 , liquidity events 27 , 28 , 29 , profitability 30 and social impact 31 , all of which have benefits as they capture incremental success, but each also comes with operational measurement challenges.

Therefore, we apply the success definition initially introduced by Bonaventura et al. 32 , namely that a startup is acquired, acquires another company or has an initial public offering (IPO). We consider any of these major capital liquidation events as a clear threshold signal that the company has matured from an early-stage venture to becoming or is on its way to becoming a mature company with clear and often significant business growth prospects. Together these three major liquidity events capture the primary forms of exit for external investors (an acquisition or trade sale and an IPO). For companies with a longer autonomous growth runway, acquiring another company marks a similar milestone of scale, maturity and capability.

Using multifactor analysis and a binary classification prediction model of startup success, we looked at many variables together and their relative influence on the probability of the success of startups. We looked at seven categories of factors through three lenses of firm-level factors: (1) location, (2) industry, (3) age of the startup; founder-level factors: (4) number of founders, (5) gender of founders, (6) personality characteristics of founders and; lastly team-level factors: (7) founder-team personality combinations. The model performance and relative impacts on the probability of startup success of each of these categories of founders are illustrated in more detail in section  A.6 of the Supplementary Information (in particular Extended Data Fig.  19 and Extended Data Fig.  20 ). In total, we considered over three hundred variables (n = 323) and their relative significant associations with success.

The personality of founders

Besides product-market, industry, and firm-level factors (see SI section  A.1 ), research suggests that the personalities of founders play a crucial role in startup success 19 . Therefore, we examine the personality characteristics of individual startup founders and teams of founders in relationship to their firm’s success by applying the success definition used by Bonaventura et al. 32 .

Employing established methods 33 , 34 , 35 , we inferred the personality traits across 30 dimensions (Big Five facets) of a large global sample of startup founders. The startup founders cohort was created from a subset of founders from the global startup industry directory Crunchbase, who are also active on the social media platform Twitter.

To measure the personality of the founders, we used the Big Five, a popular model of personality which includes five core traits: Openness to Experience, Conscientiousness, Extraversion, Agreeableness, and Emotional stability. Each of these traits can be further broken down into thirty distinct facets. Studies have found that the Big Five predict meaningful life outcomes, such as physical and mental health, longevity, social relationships, health-related behaviours, antisocial behaviour, and social contribution, at levels on par with intelligence and socioeconomic status 36 Using machine learning to infer personality traits by analysing the use of language and activity on social media has been shown to be more accurate than predictions of coworkers, friends and family and similar in accuracy to the judgement of spouses 37 . Further, as other research has shown, we assume that personality traits remain stable in adulthood even through significant life events 38 , 39 , 40 . Personality traits have been shown to emerge continuously from those already evident in adolescence 41 and are not significantly influenced by external life events such as becoming divorced or unemployed 42 . This suggests that the direction of any measurable effect goes from founder personalities to startup success and not vice versa.

As a first investigation to what extent personality traits might relate to entrepreneurship, we use the personality characteristics of individuals to predict whether they were an entrepreneur or an employee. We trained and tested a machine-learning random forest classifier to distinguish and classify entrepreneurs from employees and vice-versa using inferred personality vectors alone. As a result, we found we could correctly predict entrepreneurs with 77% accuracy and employees with 88% accuracy (Fig.  1 A). Thus, based on personality information alone, we correctly predict all unseen new samples with 82.5% accuracy (See SI section  A.2 for more details on this analysis, the classification modelling and prediction accuracy).

We explored in greater detail which personality features are most prominent among entrepreneurs. We found that the subdomain or facet of Adventurousness within the Big Five Domain of Openness was significant and had the largest effect size. The facet of Modesty within the Big Five Domain of Agreeableness and Activity Level within the Big Five Domain of Extraversion was the subsequent most considerable effect (Fig.  1 B). Adventurousness in the Big Five framework is defined as the preference for variety, novelty and starting new things—which are consistent with the role of a startup founder whose role, especially in the early life of the company, is to explore things that do not scale easily 43 and is about developing and testing new products, services and business models with the market.

Once we derived and tested the Big Five personality features for each entrepreneur in our data set, we examined whether there is evidence indicating that startup founders naturally cluster according to their personality features using a Hopkins test (see Extended Data Figure  6 ). We discovered clear clustering tendencies in the data compared with other renowned reference data sets known to have clusters. Then, once we established the founder data clusters, we used agglomerative hierarchical clustering. This ‘bottom-up’ clustering technique initially treats each observation as an individual cluster. Then it merges them to create a hierarchy of possible cluster schemes with differing numbers of groups (See Extended Data Fig.  7 ). And lastly, we identified the optimum number of clusters based on the outcome of four different clustering performance measurements: Davies-Bouldin Index, Silhouette coefficients, Calinski-Harabas Index and Dunn Index (see Extended Data Figure  8 ). We find that the optimum number of clusters of startup founders based on their personality features is six (labelled #0 through to #5), as shown in Fig.  1 C.

To better understand the context of different founder types, we positioned each of the six types of founders within an occupation-personality matrix established from previous research 44 . This research showed that ‘each job has its own personality’ using a substantial sample of employees across various jobs. Utilising the methodology employed in this study, we assigned labels to the cluster names #0 to #5, which correspond to the identified occupation tribes that best describe the personality facets represented by the clusters (see Extended Data Fig.  9 for an overview of these tribes, as identified by McCarthy et al. 44 ).

Utilising this approach, we identify three ’purebred’ clusters: #0, #2 and #5, whose members are dominated by a single tribe (larger than 60% of all individuals in each cluster are characterised by one tribe). Thus, these clusters represent and share personality attributes of these previously identified occupation-personality tribes 44 , which have the following known distinctive personality attributes (see also Table  1 ):

Accomplishers (#0) —Organised & outgoing. confident, down-to-earth, content, accommodating, mild-tempered & self-assured.

Leaders (#2) —Adventurous, persistent, dispassionate, assertive, self-controlled, calm under pressure, philosophical, excitement-seeking & confident.

Fighters (#5) —Spontaneous and impulsive, tough, sceptical, and uncompromising.

We labelled these clusters with the tribe names, acknowledging that labels are somewhat arbitrary, based on our best interpretation of the data (See SI section  A.3 for more details).

For the remaining three clusters #1, #3 and #4, we can see they are ‘hybrids’, meaning that the founders within them come from a mix of different tribes, with no one tribe representing more than 50% of the members of that cluster. However, the tribes with the largest share were noted as #1 Experts/Engineers, #3 Fighters, and #4 Operators.

To label these three hybrid clusters, we examined the closest occupations to the median personality features of each cluster. We selected a name that reflected the common themes of these occupations, namely:

Experts/Engineers (#1) as the closest roles included Materials Engineers and Chemical Engineers. This is consistent with this cluster’s personality footprint, which is highest in openness in the facets of imagination and intellect.

Developers (#3) as the closest roles include Application Developers and related technology roles such as Business Systems Analysts and Product Managers.

Operators (#4) as the closest roles include service, maintenance and operations functions, including Bicycle Mechanic, Mechanic and Service Manager. This is also consistent with one of the key personality traits of high conscientiousness in the facet of orderliness and high agreeableness in the facet of humility for founders in this cluster.

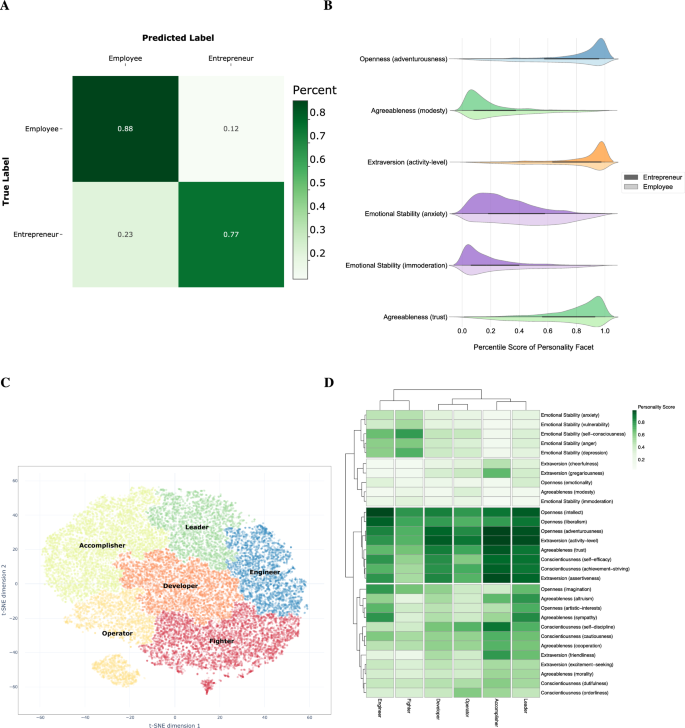
Founder-Level Factors of Startup Success. ( A ), Successful entrepreneurs differ from successful employees. They can be accurately distinguished using a classifier with personality information alone. ( B ), Successful entrepreneurs have different Big Five facet distributions, especially on adventurousness, modesty and activity level. ( C ), Founders come in six different types: Fighters, Operators, Accomplishers, Leaders, Engineers and Developers (FOALED) ( D ), Each founder Personality-Type has its distinct facet.

Together, these six different types of startup founders (Fig.  1 C) represent a framework we call the FOALED model of founder types—an acronym of Fighters, Operators, Accomplishers, Leaders, Engineers and D evelopers.

Each founder’s personality type has its distinct facet footprint (for more details, see Extended Data Figure  10 in SI section  A.3 ). Also, we observe a central core of correlated features that are high for all types of entrepreneurs, including intellect, adventurousness and activity level (Fig.  1 D).To test the robustness of the clustering of the personality facets, we compare the mean scores of the individual facets per cluster with a 20-fold resampling of the data and find that the clusters are, overall, largely robust against resampling (see Extended Data Figure  11 in SI section  A.3 for more details).

We also find that the clusters accord with the distribution of founders’ roles in their startups. For example, Accomplishers are often Chief Executive Officers, Chief Financial Officers, or Chief Operating Officers, while Fighters tend to be Chief Technical Officers, Chief Product Officers, or Chief Commercial Officers (see Extended Data Fig.  12 in SI section  A.4 for more details).

The ensemble theory of success

While founders’ individual personality traits, such as Adventurousness or Openness, show to be related to their firms’ success, we also hypothesise that the combination, or ensemble, of personality characteristics of a founding team impacts the chances of success. The logic behind this reasoning is complementarity, which is proposed by contemporary research on the functional roles of founder teams. Examples of these clear functional roles have evolved in established industries such as film and television, construction, and advertising 45 . When we subsequently explored the combinations of personality types among founders and their relationship to the probability of startup success, adjusted for a range of other factors in a multi-factorial analysis, we found significantly increased chances of success for mixed foundation teams:

Initially, we find that firms with multiple founders are more likely to succeed, as illustrated in Fig.  2 A, which shows firms with three or more founders are more than twice as likely to succeed than solo-founded startups. This finding is consistent with investors’ advice to founders and previous studies 46 . We also noted that some personality types of founders increase the probability of success more than others, as shown in SI section  A.6 (Extended Data Figures  16 and 17 ). Also, we note that gender differences play out in the distribution of personality facets: successful female founders and successful male founders show facet scores that are more similar to each other than are non-successful female founders to non-successful male founders (see Extended Data Figure  18 ).

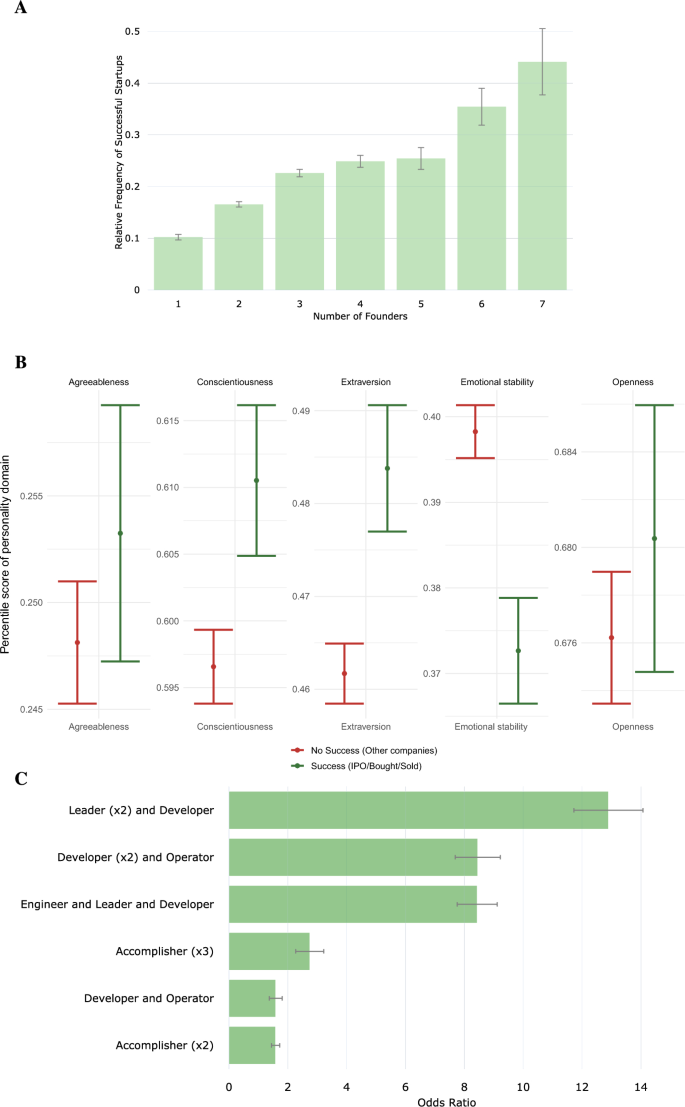
The Ensemble Theory of Team-Level Factors of Startup Success. ( A ) Having a larger founder team elevates the chances of success. This can be due to multiple reasons, e.g., a more extensive network or knowledge base but also personality diversity. ( B ) We show that joint personality combinations of founders are significantly related to higher chances of success. This is because it takes more than one founder to cover all beneficial personality traits that ‘breed’ success. ( C ) In our multifactor model, we show that firms with diverse and specific combinations of types of founders have significantly higher odds of success.

Access to more extensive networks and capital could explain the benefits of having more founders. Still, as we find here, it also offers a greater diversity of combined personalities, naturally providing a broader range of maximum traits. So, for example, one founder may be more open and adventurous, and another could be highly agreeable and trustworthy, thus, potentially complementing each other’s particular strengths associated with startup success.

The benefits of larger and more personality-diverse foundation teams can be seen in the apparent differences between successful and unsuccessful firms based on their combined Big Five personality team footprints, as illustrated in Fig.  2 B. Here, maximum values for each Big Five trait of a startup’s co-founders are mapped; stratified by successful and non-successful companies. Founder teams of successful startups tend to score higher on Openness, Conscientiousness, Extraversion, and Agreeableness.

When examining the combinations of founders with different personality types, we find that some ensembles of personalities were significantly correlated with greater chances of startup success—while controlling for other variables in the model—as shown in Fig.  2 C (for more details on the modelling, the predictive performance and the coefficient estimates of the final model, see Extended Data Figures  19 , 20 , and 21 in SI section  A.6 ).

Three combinations of trio-founder companies were more than twice as likely to succeed than other combinations, namely teams with (1) a Leader and two Developers , (2) an Operator and two Developers , and (3) an Expert/Engineer , Leader and Developer . To illustrate the potential mechanisms on how personality traits might influence the success of startups, we provide some examples of well-known, successful startup founders and their characteristic personality traits in Extended Data Figure  22 .

Startups are one of the key mechanisms for brilliant ideas to become solutions to some of the world’s most challenging economic and social problems. Examples include the Google search algorithm, disability technology startup Fingerwork’s touchscreen technology that became the basis of the Apple iPhone, or the Biontech mRNA technology that powered Pfizer’s COVID-19 vaccine.

We have shown that founders’ personalities and the combination of personalities in the founding team of a startup have a material and significant impact on its likelihood of success. We have also shown that successful startup founders’ personality traits are significantly different from those of successful employees—so much so that a simple predictor can be trained to distinguish between employees and entrepreneurs with more than 80% accuracy using personality trait data alone.

Just as occupation-personality maps derived from data can provide career guidance tools, so too can data on successful entrepreneurs’ personality traits help people decide whether becoming a founder may be a good choice for them.

We have learnt through this research that there is not one type of ideal ’entrepreneurial’ personality but six different types. Many successful startups have multiple co-founders with a combination of these different personality types.

To a large extent, founding a startup is a team sport; therefore, diversity and complementarity of personalities matter in the foundation team. It has an outsized impact on the company’s likelihood of success. While all startups are high risk, the risk becomes lower with more founders, particularly if they have distinct personality traits.

Our work demonstrates the benefits of personality diversity among the founding team of startups. Greater awareness of this novel form of diversity may help create more resilient startups capable of more significant innovation and impact.

The data-driven research approach presented here comes with certain methodological limitations. The principal data sources of this study—Crunchbase and Twitter—are extensive and comprehensive, but there are characterised by some known and likely sample biases.

Crunchbase is the principal public chronicle of venture capital funding. So, there is some likely sample bias toward: (1) Startup companies that are funded externally: self-funded or bootstrapped companies are less likely to be represented in Crunchbase; (2) technology companies, as that is Crunchbase’s roots; (3) multi-founder companies; (4) male founders: while the representation of female founders is now double that of the mid-2000s, women still represent less than 25% of the sample; (5) companies that succeed: companies that fail, especially those that fail early, are likely to be less represented in the data.

Samples were also limited to those founders who are active on Twitter, which adds additional selection biases. For example, Twitter users typically are younger, more educated and have a higher median income 47 . Another limitation of our approach is the potentially biased presentation of a person’s digital identity on social media, which is the basis for identifying personality traits. For example, recent research suggests that the language and emotional tone used by entrepreneurs in social media can be affected by events such as business failure 48 , which might complicate the personality trait inference.

In addition to sampling biases within the data, there are also significant historical biases in startup culture. For many aspects of the entrepreneurship ecosystem, women, for example, are at a disadvantage 49 . Male-founded companies have historically dominated most startup ecosystems worldwide, representing the majority of founders and the overwhelming majority of venture capital investors. As a result, startups with women have historically attracted significantly fewer funds 50 , in part due to the male bias among venture investors, although this is now changing, albeit slowly 51 .

The research presented here provides quantitative evidence for the relevance of personality types and the diversity of personalities in startups. At the same time, it brings up other questions on how personality traits are related to other factors associated with success, such as:

Will the recent growing focus on promoting and investing in female founders change the nature, composition and dynamics of startups and their personalities leading to a more diverse personality landscape in startups?

Will the growth of startups outside of the United States change what success looks like to investors and hence the role of different personality traits and their association to diverse success metrics?

Many of today’s most renowned entrepreneurs are either Baby Boomers (such as Gates, Branson, Bloomberg) or Generation Xers (such as Benioff, Cannon-Brookes, Musk). However, as we can see, personality is both a predictor and driver of success in entrepreneurship. Will generation-wide differences in personality and outlook affect startups and their success?

Moreover, the findings shown here have natural extensions and applications beyond startups, such as for new projects within large established companies. While not technically startups, many large enterprises and industries such as construction, engineering and the film industry rely on forming new project-based, cross-functional teams that are often new ventures and share many characteristics of startups.

There is also potential for extending this research in other settings in government, NGOs, and within the research community. In scientific research, for example, team diversity in terms of age, ethnicity and gender has been shown to be predictive of impact, and personality diversity may be another critical dimension 52 .

Another extension of the study could investigate the development of the language used by startup founders on social media over time. Such an extension could investigate whether the language (and inferred psychological characteristics) change as the entrepreneurs’ ventures go through major business events such as foundation, funding, or exit.

Overall, this study demonstrates, first, that startup founders have significantly different personalities than employees. Secondly, besides firm-level factors, which are known to influence firm success, we show that a range of founder-level factors, notably the character traits of its founders, significantly impact a startup’s likelihood of success. Lastly, we looked at team-level factors. We discovered in a multifactor analysis that personality-diverse teams have the most considerable impact on the probability of a startup’s success, underlining the importance of personality diversity as a relevant factor of team performance and success.

Data sources

Entrepreneurs dataset.

Data about the founders of startups were collected from Crunchbase (Table  2 ), an open reference platform for business information about private and public companies, primarily early-stage startups. It is one of the largest and most comprehensive data sets of its kind and has been used in over 100 peer-reviewed research articles about economic and managerial research.

Crunchbase contains data on over two million companies - mainly startup companies and the companies who partner with them, acquire them and invest in them, as well as profiles on well over one million individuals active in the entrepreneurial ecosystem worldwide from over 200 countries and spans. Crunchbase started in the technology startup space, and it now covers all sectors, specifically focusing on entrepreneurship, investment and high-growth companies.

While Crunchbase contains data on over one million individuals in the entrepreneurial ecosystem, some are not entrepreneurs or startup founders but play other roles, such as investors, lawyers or executives at companies that acquire startups. To create a subset of only entrepreneurs, we selected a subset of 32,732 who self-identify as founders and co-founders (by job title) and who are also publicly active on the social media platform Twitter. We also removed those who also are venture capitalists to distinguish between investors and founders.

We selected founders active on Twitter to be able to use natural language processing to infer their Big Five personality features using an open-vocabulary approach shown to be accurate in the previous research by analysing users’ unstructured text, such as Twitter posts in our case. For this project, as with previous research 20 , we employed a commercial service, IBM Watson Personality Insight, to infer personality facets. This service provides raw scores and percentile scores of Big Five Domains (Openness, Conscientiousness, Extraversion, Agreeableness and Emotional Stability) and the corresponding 30 subdomains or facets. In addition, the public content of Twitter posts was collected, and there are 32,732 profiles that each had enough Twitter posts (more than 150 words) to get relatively accurate personality scores (less than 12.7% Average Mean Absolute Error).

The entrepreneurs’ dataset is analysed in combination with other data about the companies they founded to explore questions about the nature and patterns of personality traits of entrepreneurs and the relationships between these patterns and company success.

For the multifactor analysis, we further filtered the data in several preparatory steps for the success prediction modelling (for more details, see SI section  A.5 ). In particular, we removed data points with missing values (Extended Data Fig.  13 ) and kept only companies in the data that were founded from 1990 onward to ensure consistency with previous research 32 (see Extended Data Fig.  14 ). After cleaning, filtering and pre-processing the data, we ended up with data from 25,214 founders who founded 21,187 startup companies to be used in the multifactor analysis. Of those, 3442 startups in the data were successful, 2362 in the first seven years after they were founded (see Extended Data Figure  15 for more details).

Entrepreneurs and employees dataset

To investigate whether startup founders show personality traits that are similar or different from the population at large (i. e. the entrepreneurs vs employees sub-analysis shown in Fig.  1 A and B), we filtered the entrepreneurs’ data further: we reduced the sample to those founders of companies, which attracted more than US$100k in investment to create a reference set of successful entrepreneurs (n \(=\) 4400).

To create a control group of employees who are not also entrepreneurs or very unlikely to be of have been entrepreneurs, we leveraged the fact that while some occupational titles like CEO, CTO and Public Speaker are commonly shared by founders and co-founders, some others such as Cashier , Zoologist and Detective very rarely co-occur seem to be founders or co-founders. To illustrate, many company founders also adopt regular occupation titles such as CEO or CTO. Many founders will be Founder and CEO or Co-founder and CTO. While founders are often CEOs or CTOs, the reverse is not necessarily true, as many CEOs are professional executives that were not involved in the establishment or ownership of the firm.

Using data from LinkedIn, we created an Entrepreneurial Occupation Index (EOI) based on the ratio of entrepreneurs for each of the 624 occupations used in a previous study of occupation-personality fit 44 . It was calculated based on the percentage of all people working in the occupation from LinkedIn compared to those who shared the title Founder or Co-founder (See SI section  A.2 for more details). A reference set of employees (n=6685) was then selected across the 112 different occupations with the lowest propensity for entrepreneurship (less than 0.5% EOI) from a large corpus of Twitter users with known occupations, which is also drawn from the previous occupational-personality fit study 44 .

These two data sets were used to test whether it may be possible to distinguish successful entrepreneurs from successful employees based on the different patterns of personality traits alone.

Hierarchical clustering

We applied several clustering techniques and tests to the personality vectors of the entrepreneurs’ data set to determine if there are natural clusters and, if so, how many are the optimum number.

Firstly, to determine if there is a natural typology to founder personalities, we applied the Hopkins statistic—a statistical test we used to answer whether the entrepreneurs’ dataset contains inherent clusters. It measures the clustering tendency based on the ratio of the sum of distances of real points within a sample of the entrepreneurs’ dataset to their nearest neighbours and the sum of distances of randomly selected artificial points from a simulated uniform distribution to their nearest neighbours in the real entrepreneurs’ dataset. The ratio measures the difference between the entrepreneurs’ data distribution and the simulated uniform distribution, which tests the randomness of the data. The range of Hopkins statistics is from 0 to 1. The scores are close to 0, 0.5 and 1, respectively, indicating whether the dataset is uniformly distributed, randomly distributed or highly clustered.

To cluster the founders by personality facets, we used Agglomerative Hierarchical Clustering (AHC)—a bottom-up approach that treats an individual data point as a singleton cluster and then iteratively merges pairs of clusters until all data points are included in the single big collection. Ward’s linkage method is used to choose the pair of groups for minimising the increase in the within-cluster variance after combining. AHC was widely applied to clustering analysis since a tree hierarchy output is more informative and interpretable than K-means. Dendrograms were used to visualise the hierarchy to provide the perspective of the optimal number of clusters. The heights of the dendrogram represent the distance between groups, with lower heights representing more similar groups of observations. A horizontal line through the dendrogram was drawn to distinguish the number of significantly different clusters with higher heights. However, as it is not possible to determine the optimum number of clusters from the dendrogram, we applied other clustering performance metrics to analyse the optimal number of groups.

A range of Clustering performance metrics were used to help determine the optimal number of clusters in the dataset after an apparent clustering tendency was confirmed. The following metrics were implemented to evaluate the differences between within-cluster and between-cluster distances comprehensively: Dunn Index, Calinski-Harabasz Index, Davies-Bouldin Index and Silhouette Index. The Dunn Index measures the ratio of the minimum inter-cluster separation and the maximum intra-cluster diameter. At the same time, the Calinski-Harabasz Index improves the measurement of the Dunn Index by calculating the ratio of the average sum of squared dispersion of inter-cluster and intra-cluster. The Davies-Bouldin Index simplifies the process by treating each cluster individually. It compares the sum of the average distance among intra-cluster data points to the cluster centre of two separate groups with the distance between their centre points. Finally, the Silhouette Index is the overall average of the silhouette coefficients for each sample. The coefficient measures the similarity of the data point to its cluster compared with the other groups. Higher scores of the Dunn, Calinski-Harabasz and Silhouette Index and a lower score of the Davies-Bouldin Index indicate better clustering configuration.

Classification modelling

Classification algorithms.

To obtain a comprehensive and robust conclusion in the analysis predicting whether a given set of personality traits corresponds to an entrepreneur or an employee, we explored the following classifiers: Naïve Bayes, Elastic Net regularisation, Support Vector Machine, Random Forest, Gradient Boosting and Stacked Ensemble. The Naïve Bayes classifier is a probabilistic algorithm based on Bayes’ theorem with assumptions of independent features and equiprobable classes. Compared with other more complex classifiers, it saves computing time for large datasets and performs better if the assumptions hold. However, in the real world, those assumptions are generally violated. Elastic Net regularisation combines the penalties of Lasso and Ridge to regularise the Logistic classifier. It eliminates the limitation of multicollinearity in the Lasso method and improves the limitation of feature selection in the Ridge method. Even though Elastic Net is as simple as the Naïve Bayes classifier, it is more time-consuming. The Support Vector Machine (SVM) aims to find the ideal line or hyperplane to separate successful entrepreneurs and employees in this study. The dividing line can be non-linear based on a non-linear kernel, such as the Radial Basis Function Kernel. Therefore, it performs well on high-dimensional data while the ’right’ kernel selection needs to be tuned. Random Forest (RF) and Gradient Boosting Trees (GBT) are ensembles of decision trees. All trees are trained independently and simultaneously in RF, while a new tree is trained each time and corrected by previously trained trees in GBT. RF is a more robust and straightforward model since it does not have many hyperparameters to tune. GBT optimises the objective function and learns a more accurate model since there is a successive learning and correction process. Stacked Ensemble combines all existing classifiers through a Logistic Regression. Better than bagging with only variance reduction and boosting with only bias reduction, the ensemble leverages the benefit of model diversity with both lower variance and bias. All the above classification algorithms distinguish successful entrepreneurs and employees based on the personality matrix.

Evaluation metrics

A range of evaluation metrics comprehensively explains the performance of a classification prediction. The most straightforward metric is accuracy, which measures the overall portion of correct predictions. It will mislead the performance of an imbalanced dataset. The F1 score is better than accuracy by combining precision and recall and considering the False Negatives and False Positives. Specificity measures the proportion of detecting the true negative rate that correctly identifies employees, while Positive Predictive Value (PPV) calculates the probability of accurately predicting successful entrepreneurs. Area Under the Receiver Operating Characteristic Curve (AUROC) determines the capability of the algorithm to distinguish between successful entrepreneurs and employees. A higher value means the classifier performs better on separating the classes.

Feature importance

To further understand and interpret the classifier, it is critical to identify variables with significant predictive power on the target. Feature importance of tree-based models measures Gini importance scores for all predictors, which evaluate the overall impact of the model after cutting off the specific feature. The measurements consider all interactions among features. However, it does not provide insights into the directions of impacts since the importance only indicates the ability to distinguish different classes.

Statistical analysis

T-test, Cohen’s D and two-sample Kolmogorov-Smirnov test are introduced to explore how the mean values and distributions of personality facets between entrepreneurs and employees differ. The T-test is applied to determine whether the mean of personality facets of two group samples are significantly different from one another or not. The facets with significant differences detected by the hypothesis testing are critical to separate the two groups. Cohen’s d is to measure the effect size of the results of the previous t-test, which is the ratio of the mean difference to the pooled standard deviation. A larger Cohen’s d score indicates that the mean difference is greater than the variability of the whole sample. Moreover, it is interesting to check whether the two groups’ personality facets’ probability distributions are from the same distribution through the two-sample Kolmogorov-Smirnov test. There is no assumption about the distributions, but the test is sensitive to deviations near the centre rather than the tail.

Privacy and ethics

The focus of this research is to provide high-level insights about groups of startups, founders and types of founder teams rather than on specific individuals or companies. While we used unit record data from the publicly available data of company profiles from Crunchbase , we removed all identifiers from the underlying data on individual companies and founders and generated aggregate results, which formed the basis for our analysis and conclusions.

Data availability

A dataset which includes only aggregated statistics about the success of startups and the factors that influence is released as part of this research. Underlying data for all figures and the code to reproduce them are available on GitHub: https://github.com/Braesemann/FounderPersonalities . Please contact Fabian Braesemann ( [email protected] ) in case you have any further questions.

Change history

07 may 2024.

A Correction to this paper has been published: https://doi.org/10.1038/s41598-024-61082-7

Henrekson, M. & Johansson, D. Gazelles as job creators: A survey and interpretation of the evidence. Small Bus. Econ. 35 , 227–244 (2010).

Article   Google Scholar  

Davila, A., Foster, G., He, X. & Shimizu, C. The rise and fall of startups: Creation and destruction of revenue and jobs by young companies. Aust. J. Manag. 40 , 6–35 (2015).

Which vaccine saved the most lives in 2021?: Covid-19. The Economist (Online) (2022). noteName - AstraZeneca; Pfizer Inc; BioNTech SE; Copyright - Copyright The Economist Newspaper NA, Inc. Jul 14, 2022; Last updated - 2022-11-29.

Oltermann, P. Pfizer/biontech tax windfall brings mainz an early christmas present (2021). noteName - Pfizer Inc; BioNTech SE; Copyright - Copyright Guardian News & Media Limited Dec 27, 2021; Last updated - 2021-12-28.

Grant, K. A., Croteau, M. & Aziz, O. The survival rate of startups funded by angel investors. I-INC WHITE PAPER SER.: MAR 2019 , 1–21 (2019).

Google Scholar  

Top 20 reasons start-ups fail - cb insights version (2019). noteCopyright - Copyright Newstex Oct 21, 2019; Last updated - 2022-10-25.

Hochberg, Y. V., Ljungqvist, A. & Lu, Y. Whom you know matters: Venture capital networks and investment performance. J. Financ. 62 , 251–301 (2007).

Fracassi, C., Garmaise, M. J., Kogan, S. & Natividad, G. Business microloans for us subprime borrowers. J. Financ. Quantitative Ana. 51 , 55–83 (2016).

Davila, A., Foster, G. & Gupta, M. Venture capital financing and the growth of startup firms. J. Bus. Ventur. 18 , 689–708 (2003).

Nann, S. et al. Comparing the structure of virtual entrepreneur networks with business effectiveness. Proc. Soc. Behav. Sci. 2 , 6483–6496 (2010).

Guzman, J. & Stern, S. Where is silicon valley?. Science 347 , 606–609 (2015).

Article   ADS   CAS   PubMed   Google Scholar  

Aldrich, H. E. & Wiedenmayer, G. From traits to rates: An ecological perspective on organizational foundings. 61–97 (2019).

Gartner, W. B. Who is an entrepreneur? is the wrong question. Am. J. Small Bus. 12 , 11–32 (1988).

Thornton, P. H. The sociology of entrepreneurship. Ann. Rev. Sociol. 25 , 19–46 (1999).

Eikelboom, M. E., Gelderman, C. & Semeijn, J. Sustainable innovation in public procurement: The decisive role of the individual. J. Public Procure. 18 , 190–201 (2018).

Kerr, S. P. et al. Personality traits of entrepreneurs: A review of recent literature. Found. Trends Entrep. 14 , 279–356 (2018).

Hamilton, B. H., Papageorge, N. W. & Pande, N. The right stuff? Personality and entrepreneurship. Quant. Econ. 10 , 643–691 (2019).

Salmony, F. U. & Kanbach, D. K. Personality trait differences across types of entrepreneurs: A systematic literature review. RMS 16 , 713–749 (2022).

Freiberg, B. & Matz, S. C. Founder personality and entrepreneurial outcomes: A large-scale field study of technology startups. Proc. Natl. Acad. Sci. 120 , e2215829120 (2023).

Article   CAS   PubMed   PubMed Central   Google Scholar  

Kern, M. L., McCarthy, P. X., Chakrabarty, D. & Rizoiu, M.-A. Social media-predicted personality traits and values can help match people to their ideal jobs. Proc. Natl. Acad. Sci. 116 , 26459–26464 (2019).

Article   ADS   CAS   PubMed   PubMed Central   Google Scholar  

Dalle, J.-M., Den Besten, M. & Menon, C. Using crunchbase for economic and managerial research. (2017).

Block, J. & Sandner, P. What is the effect of the financial crisis on venture capital financing? Empirical evidence from us internet start-ups. Ventur. Cap. 11 , 295–309 (2009).

Antretter, T., Blohm, I. & Grichnik, D. Predicting startup survival from digital traces: Towards a procedure for early stage investors (2018).

Dworak, D. Analysis of founder background as a predictor for start-up success in achieving successive fundraising rounds. (2022).

Hsu, D. H. Venture capitalists and cooperative start-up commercialization strategy. Manage. Sci. 52 , 204–219 (2006).

Blank, S. Why the lean start-up changes everything (2018).

Kaplan, S. N. & Lerner, J. It ain’t broke: The past, present, and future of venture capital. J. Appl. Corp. Financ. 22 , 36–47 (2010).

Hallen, B. L. & Eisenhardt, K. M. Catalyzing strategies and efficient tie formation: How entrepreneurial firms obtain investment ties. Acad. Manag. J. 55 , 35–70 (2012).

Gompers, P. A. & Lerner, J. The Venture Capital Cycle (MIT Press, 2004).

Shane, S. & Venkataraman, S. The promise of entrepreneurship as a field of research. Acad. Manag. Rev. 25 , 217–226 (2000).

Zahra, S. A. & Wright, M. Understanding the social role of entrepreneurship. J. Manage. Stud. 53 , 610–629 (2016).

Bonaventura, M. et al. Predicting success in the worldwide start-up network. Sci. Rep. 10 , 1–6 (2020).

Schwartz, H. A. et al. Personality, gender, and age in the language of social media: The open-vocabulary approach. PLoS ONE 8 , e73791 (2013).

Plank, B. & Hovy, D. Personality traits on twitter-or-how to get 1,500 personality tests in a week. In Proceedings of the 6th workshop on computational approaches to subjectivity, sentiment and social media analysis , pp 92–98 (2015).

Arnoux, P.-H. et al. 25 tweets to know you: A new model to predict personality with social media. In booktitleEleventh international AAAI conference on web and social media (2017).

Roberts, B. W., Kuncel, N. R., Shiner, R., Caspi, A. & Goldberg, L. R. The power of personality: The comparative validity of personality traits, socioeconomic status, and cognitive ability for predicting important life outcomes. Perspect. Psychol. Sci. 2 , 313–345 (2007).

Article   PubMed   PubMed Central   Google Scholar  

Youyou, W., Kosinski, M. & Stillwell, D. Computer-based personality judgments are more accurate than those made by humans. Proc. Natl. Acad. Sci. 112 , 1036–1040 (2015).

Soldz, S. & Vaillant, G. E. The big five personality traits and the life course: A 45-year longitudinal study. J. Res. Pers. 33 , 208–232 (1999).

Damian, R. I., Spengler, M., Sutu, A. & Roberts, B. W. Sixteen going on sixty-six: A longitudinal study of personality stability and change across 50 years. J. Pers. Soc. Psychol. 117 , 674 (2019).

Article   PubMed   Google Scholar  

Rantanen, J., Metsäpelto, R.-L., Feldt, T., Pulkkinen, L. & Kokko, K. Long-term stability in the big five personality traits in adulthood. Scand. J. Psychol. 48 , 511–518 (2007).

Roberts, B. W., Caspi, A. & Moffitt, T. E. The kids are alright: Growth and stability in personality development from adolescence to adulthood. J. Pers. Soc. Psychol. 81 , 670 (2001).

Article   CAS   PubMed   Google Scholar  

Cobb-Clark, D. A. & Schurer, S. The stability of big-five personality traits. Econ. Lett. 115 , 11–15 (2012).

Graham, P. Do Things that Don’t Scale (Paul Graham, 2013).

McCarthy, P. X., Kern, M. L., Gong, X., Parker, M. & Rizoiu, M.-A. Occupation-personality fit is associated with higher employee engagement and happiness. (2022).

Pratt, A. C. Advertising and creativity, a governance approach: A case study of creative agencies in London. Environ. Plan A 38 , 1883–1899 (2006).

Klotz, A. C., Hmieleski, K. M., Bradley, B. H. & Busenitz, L. W. New venture teams: A review of the literature and roadmap for future research. J. Manag. 40 , 226–255 (2014).

Duggan, M., Ellison, N. B., Lampe, C., Lenhart, A. & Madden, M. Demographics of key social networking platforms. Pew Res. Center 9 (2015).

Fisch, C. & Block, J. H. How does entrepreneurial failure change an entrepreneur’s digital identity? Evidence from twitter data. J. Bus. Ventur. 36 , 106015 (2021).

Brush, C., Edelman, L. F., Manolova, T. & Welter, F. A gendered look at entrepreneurship ecosystems. Small Bus. Econ. 53 , 393–408 (2019).

Kanze, D., Huang, L., Conley, M. A. & Higgins, E. T. We ask men to win and women not to lose: Closing the gender gap in startup funding. Acad. Manag. J. 61 , 586–614 (2018).

Fan, J. S. Startup biases. UC Davis Law Review (2022).

AlShebli, B. K., Rahwan, T. & Woon, W. L. The preeminence of ethnic diversity in scientific collaboration. Nat. Commun. 9 , 1–10 (2018).

Article   CAS   Google Scholar  

Żbikowski, K. & Antosiuk, P. A machine learning, bias-free approach for predicting business success using crunchbase data. Inf. Process. Manag. 58 , 102555 (2021).

Corea, F., Bertinetti, G. & Cervellati, E. M. Hacking the venture industry: An early-stage startups investment framework for data-driven investors. Mach. Learn. Appl. 5 , 100062 (2021).

Chapman, G. & Hottenrott, H. Founder personality and start-up subsidies. Founder Personality and Start-up Subsidies (2021).

Antoncic, B., Bratkovicregar, T., Singh, G. & DeNoble, A. F. The big five personality-entrepreneurship relationship: Evidence from slovenia. J. Small Bus. Manage. 53 , 819–841 (2015).

Download references

Acknowledgements

We thank Gary Brewer from BuiltWith ; Leni Mayo from Influx , Rachel Slattery from TeamSlatts and Daniel Petre from AirTree Ventures for their ongoing generosity and insights about startups, founders and venture investments. We also thank Tim Li from Crunchbase for advice and liaison regarding data on startups and Richard Slatter for advice and referrals in Twitter .

Author information

Authors and affiliations.

The Data Science Institute, University of Technology Sydney, Sydney, NSW, Australia

Paul X. McCarthy

School of Computer Science and Engineering, UNSW Sydney, Sydney, NSW, Australia

Faculty of Engineering and Information Technology, University of Technology Sydney, Sydney, Australia

Xian Gong & Marian-Andrei Rizoiu

Oxford Internet Institute, University of Oxford, Oxford, UK

Fabian Braesemann & Fabian Stephany

DWG Datenwissenschaftliche Gesellschaft Berlin, Berlin, Germany

Melbourne Graduate School of Education, The University of Melbourne, Parkville, VIC, Australia

Margaret L. Kern

You can also search for this author in PubMed   Google Scholar

Contributions

All authors designed research; All authors analysed data and undertook investigation; F.B. and F.S. led multi-factor analysis; P.M., X.G. and M.A.R. led the founder/employee prediction; M.L.K. led personality insights; X.G. collected and tabulated the data; X.G., F.B., and F.S. created figures; X.G. created final art, and all authors wrote the paper.

Corresponding author

Correspondence to Fabian Braesemann .

Ethics declarations

Competing interests.

The authors declare no competing interests.

Additional information

Publisher's note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

The original online version of this Article was revised: The Data Availability section in the original version of this Article was incomplete, the link to the GitHub repository was omitted. Full information regarding the corrections made can be found in the correction for this Article.

Supplementary Information

Supplementary information., rights and permissions.

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ .

Reprints and permissions

About this article

Cite this article.

McCarthy, P.X., Gong, X., Braesemann, F. et al. The impact of founder personalities on startup success. Sci Rep 13 , 17200 (2023). https://doi.org/10.1038/s41598-023-41980-y

Download citation

Received : 15 February 2023

Accepted : 04 September 2023

Published : 17 October 2023

DOI : https://doi.org/10.1038/s41598-023-41980-y

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

By submitting a comment you agree to abide by our Terms and Community Guidelines . If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.

Quick links

• Explore articles by subject
• Guide to authors
• Editorial policies

Sign up for the Nature Briefing: AI and Robotics newsletter — what matters in AI and robotics research, free to your inbox weekly.