problem solving lesson 1.9

Go Math Interactive Mimio Lesson 1.9 Problem Solving Multiplication and Division

• Mimio Ink File

Description

Questions & answers, cool corner.

• We're hiring
• Help & FAQ
• Privacy policy
• Student privacy
• Terms of service
• Tell us what you think

Technological Graphing

9.1: It Begins With Data (10 minutes)

CCSS Standards

Building On

Routines and Materials

Required Materials

• Statistical technology

The mathematical purpose of this activity is to gain familiarity with entering data into a spreadsheet and to prepare students for finding statistics using technology.

Arrange students in groups of 2. If students are using the digital version of the materials, show them how to open the GeoGebra spreadsheet app in the math tools. If students are using the print version of the materials, they can access the GeoGebra spreadsheet app at www.geogebra.org/spreadsheet . If they use a different technology, you may need to provide them with alternate instructions.

Make sure students input the data in one column, even though the data is represented in two columns in the task statement.

Student Facing

Open a spreadsheet window and enter the data so that each value is in its own cell in column A.

• How many values are in the spreadsheet? Explain your reasoning.
• If you entered the data in the order that the values are listed, the number 7 is in the cell at position A1 and the number 5 is in cell A5. List all of the cells that contain the number 13.
• In cell C1 type the word “Sum”, in C2 type “Mean”, and in C3 type “Median”. You may wish to double-click or drag the vertical line between columns C and D to allow the entire words to be seen.

Student Response

For access, consult one of our IM Certified Partners .

Activity Synthesis

The goal is to make sure that students know how to type data into a spreadsheet and to locate values in the spreadsheet by row and column. The locations will be referenced with spreadsheet functions in upcoming activities. Here are some questions for discussion.

• “What value is in cell A7?” (14)
• “What was interesting or challenging about this activity?” (I never knew that you could describe each cell in a spreadsheet using the row and column labels.)

9.2: Finding Spreadsheet Statistics (15 minutes)

Building Towards

Instructional Routines

• MLR1: Stronger and Clearer Each Time

The mathematical purpose of this activity is to calculate statistics, create data displays, and to investigate how those change when values are added or removed from the data set. Monitor for students discussing the relationship between outliers and the measure of center.

Keep students in the same groups. They will continue working using the spreadsheet they started in the previous activity.

Tell students that statistics are values that are calculated from data, such as the mean, median, or interquartile range.

Tell students that after they change the value in A1 to change the mean in the first set of questions, they should continue to use the changed value for the second set of questions rather than reset them to the values from the warm-up.

Note that GeoGebra is like any other computer program. It needs directions written in a specific way for it to execute a command. For example, if students forget to type the = symbol or don’t capitalize “Sum,” the formula won’t work. Ask students to pause after typing the formulas and ensure that cells D1, D2, and D3 display numbers for each statistic. If not, ask students to delete the contents of the cell and retype the formula, ensuring that they start with an = symbol and capitalize Sum, Mean, and Median.

Using the data from the warm-up, we can calculate a few statistics and look at the data.

• Next to the word Sum, in cell D1, type =Sum(A1:A20)
• Next to the word Mean, in cell D2, type =Mean(A1:A20)
• Next to the word Median, in cell D3, type =Median(A1:A20)
• What are the values for each of the statistics?
• Change the value in A1 to 8. How does that change the statistics?
• What value can be put into A1 to change the mean to 10.05 and the median to 9?

We can also use Geogebra to create data displays.

• Click on the letter A for the first column so that the entire column is highlighted.
• Click on the button that looks like a histogram to get a new window labeled One Variable Analysis .
• Click Analyze to see a histogram of the data.
• What does the value for n represent?
• What does the value for \(\Sigma x\) represent?
• What other statistics do you recognize?
• Adjust the slider next to the word Histogram. What changes?
• Click on the button to the right of the slider to bring in another window with more options. Then, click the box next to Set Classes Manually and set the Width to 5. What does this do to the histogram?
• Click the word Histogram and look at a box plot and dot plot of the data. When looking at the box plot, notice there is an x on the right side of box plot. This represents a data point that is considered an outlier. Click on the button to the right of the slider and uncheck the box labeled Show Outliers to include this point in the box plot. What changes? Why might you want to show outliers? Why might you want to include or exclude outliers?

The purpose of this discussion is for students to create data displays using technology and to analyze what happens to the displays and the statistics when changes are made to the data set. Here are some questions for discussion.

• What happened to the statistics when you changed the value for A1 to 8 in the spreadsheet?” (When it was changed to 8, the mean increased slightly but the median stayed the same.)
• “Why did the mean increase?” (The sum of the data increased but the number of numbers stayed the same so the mean had to increase.)
• “Why did the median stay the same?” (Changing a 7 to an 8 in the data set did not change the middle numbers, 8 and 9, in the data set).
• “What did you notice when you changed the width of the classes for the histogram?” (This changed the intervals for each bar to a width of 5 and the data was resorted into those intervals.)

Select students who were previously identified as discussing the relationship between outliers and the measures of center. Ask, “what is the relationship between outliers and the measures of center?” (When outliers are present the median is the preferred measure of center because it is less impacted by outliers than the mean.)

9.3: Making Digital Displays (10 minutes)

• MLR2: Collect and Display

The mathematical purpose of this activity is for students to create data displays and calculate statistics using technology. Students plot the survey data they collected from a statistical question in a previous lesson.

Arrange students in groups of two. Tell them that they will be using technology to create data displays and calculate statistics for data they collected from a survey question in a previous lesson.

Use the data you collected from the numerical, statistical question from a previous lesson. Use technology to create a dot plot, boxplot, and histogram for your data. Then find the mean, median, and interquartile range for the data.

Are you ready for more?

A stem and leaf plot is a table where each data point is indicated by writing the first digit(s) on the left (the stem) and the last digit(s) on the right (the leaves). Each stem is written only once and shared by all data points with the same first digit(s). For example, the values 31, 32, and 45 might be represented like:

\(\displaystyle \begin{array}{r|l l} 3 & 1 & 2\\ 4 & 5 \end{array}\) Key: 3 | 1 means 31

A class took an exam and earned the scores:

86, 73, 85, 86, 72, 94, 88, 98, 87, 86, 85, 93, 75, 64, 82, 95, 99, 76, 84, 68

Use technology to create a stem and leaf plot for this data set.

How can we see the shape of the distribution from this plot?

What information can we see from a stem and leaf plot that we cannot see from a histogram?

What do we have more control of in a histogram than in a stem and leaf plot?

Anticipated Misconceptions

Students may lose one data display when they begin to create the next one. Explain to students that it is important to copy their solutions into a more permanent place so they can refer to it later.

The goal of this activity was for students to create graphs and find statistics using technology. Here are some questions for discussion.

• “What were some challenges that you faced using technology and how did you overcome them?” (I was not sure what buttons to press to get to the spreadsheet. I checked with my partner and figured it out.)
• “What width did you use for your histogram? Why?” (I used 5 because my data set has values ranging from 1 to 42. I could have used 10 but then I would have only had 5 bars.)
• “What is the appropriate measure of center for your data set?” (The median was appropriate because my data set has a skewed distribution.)
• “Which display allows you to calculate the IQR the most easily?” (The box plot because it displays Q1 and Q3.)
• “Can you find the median using your histogram?” (No, the data is grouped into intervals, so a histogram cannot be used to find the middle value for the median.)

Lesson Synthesis

The goal of this lesson is for students to display and investigate data using technology. Here are some questions for discussion.

• “How do you create data displays using technology?” (You type the data into the spreadsheet and then click the appropriate buttons.)
• “What are some advantages of using technology to display data and calculate statistics?” (You can easily switch between different data displays and you can change the intervals on histograms without having to sort through the data again. The advantage of having the technology calculate the statistics is that I can see how the statistics change as I enter or make changes to the data.)
• “When do you think it is appropriate to use technology to display data or to calculate statistics?” (Graphing technology makes it easier to determine the shape of a distribution. I might use it to determine the most appropriate measure of center for a data set. Using technology to calculate statistics makes sense to do in most situations because statistics are calculated using algorithms that can get complicated when there are many values in the data set. The chance of making a mistake while calculating statistics by hand makes using technology a good choice.)

9.4: Cool-down - What Are These Values? (5 minutes)

Student lesson summary.

Data displays (like histograms or box plots) are very useful for quickly understanding a large amount of information, but often take a long time to construct accurately using pencil and paper. Technology can help create these displays as well as calculate useful statistics much faster than doing the same tasks by hand. Especially with very large data sets (in some experiments, millions of pieces of data are collected), technology is essential for putting the information into forms that are more easily understood.

A statistic is a quantity that is calculated from sample data as a measure of a distribution. Mean and median are examples of statistics that are measures of center. Mean absolute deviation (MAD) and interquartile range (IQR) are examples of statistics that are measures of variability. Although the interpretation must still be done by people, using the tools available can improve the accuracy and speed of doing computations and creating graphs.

• Daily Agenda
• Staying Informed

What is the "Go Math!" curriculum?

Online textbook and glossary.

• Operations and Algebraic Thinking
• Number and Operations in Base Ten
• Number and Operations—Fractions
• ​Number and Operations in Base Ten
• ​​ Number and Operations—Fractions
• ​ Measurement and Data
• Geometry Operations
• Algebraic Thinking
• ​​ Measurement and Data
• ​​ Measurement
• Data Geometry

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

9.9: Solve Geometry Applications- Volume and Surface Area (Part 1)

• Last updated
• Save as PDF
• Page ID 5010

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Objectives

• Find volume and surface area of rectangular solids
• Find volume and surface area of spheres
• Find volume and surface area of cylinders
• Find volume of cones

be prepared!

Before you get started, take this readiness quiz.

• Evaluate x 3 when x = 5. If you missed this problem, review Example 2.3.3 .
• Evaluate 2 x when x = 5. If you missed this problem, review Example 2.3.4 .
• Find the area of a circle with radius \(\dfrac{7}{2}\). If you missed this problem, review Example 5.6.12 .

In this section, we will finish our study of geometry applications. We find the volume and surface area of some three-dimensional figures. Since we will be solving applications, we will once again show our Problem-Solving Strategy for Geometry Applications.

Problem Solving Strategy for Geometry Applications

• Step 1. Read the problem and make sure you understand all the words and ideas. Draw the figure and label it with the given information.
• Step 2. Identify what you are looking for.
• Step 3. Name what you are looking for. Choose a variable to represent that quantity.
• Step 4. Translate into an equation by writing the appropriate formula or model for the situation. Substitute in the given information.
• Step 5. Solve the equation using good algebra techniques.
• Step 6. Check the answer in the problem and make sure it makes sense.
• Step 7. Answer the question with a complete sentence.

Find Volume and Surface Area of Rectangular Solids

A cheerleading coach is having the squad paint wooden crates with the school colors to stand on at the games. (See Figure \(\PageIndex{1}\)). The amount of paint needed to cover the outside of each box is the surface area , a square measure of the total area of all the sides. The amount of space inside the crate is the volume, a cubic measure.

Figure \(\PageIndex{1}\) - This wooden crate is in the shape of a rectangular solid.

Each crate is in the shape of a rectangular solid . Its dimensions are the length, width, and height. The rectangular solid shown in Figure \(\PageIndex{2}\) has length 4 units, width 2 units, and height 3 units. Can you tell how many cubic units there are altogether? Let’s look layer by layer.

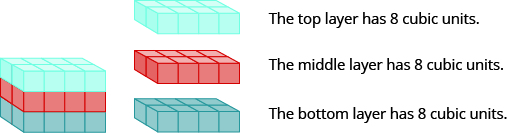
Figure \(\PageIndex{2}\) - Breaking a rectangular solid into layers makes it easier to visualize the number of cubic units it contains. This 4 by 2 by 3 rectangular solid has 24 cubic units.

Altogether there are 24 cubic units. Notice that 24 is the length × width × height.

The volume, V, of any rectangular solid is the product of the length, width, and height.

We could also write the formula for volume of a rectangular solid in terms of the area of the base. The area of the base, B, is equal to length × width.

\[B = L \cdot W\]

We can substitute B for L • W in the volume formula to get another form of the volume formula.

\[\begin{split} V &= \textcolor{red}{L \cdot W} \cdot H \\ V &= \textcolor{red}{(L \cdot W)} \cdot H \\ V &= \textcolor{red}{B} h \end{split}\]

We now have another version of the volume formula for rectangular solids. Let’s see how this works with the 4 × 2 × 3 rectangular solid we started with. See Figure \(\PageIndex{3}\).

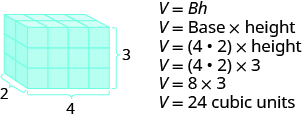
Figure \(\PageIndex{3}\)

To find the surface area of a rectangular solid, think about finding the area of each of its faces. How many faces does the rectangular solid above have? You can see three of them.

\[\begin{split} A_{front} &= L \times W \qquad A_{side} = L \times W \qquad A_{top} = L \times W \\ A_{front} &= 4 \cdot 3 \qquad \quad \; A_{side} = 2 \cdot 3 \qquad \quad \; A_{top} = 4 \cdot 2 \\ A_{front} &= 12 \qquad \qquad A_{side} = 6 \qquad \qquad \; \; A_{top} = 8 \end{split}\]

Notice for each of the three faces you see, there is an identical opposite face that does not show.

\[\begin{split} S &= (front + back)+(left\; side + right\; side) + (top + bottom) \\ S &= (2 \cdot front) + (2 \cdot left\; side) + (2 \cdot top) \\ S &= 2 \cdot 12 + 2 \cdot 6 + 2 \cdot 8 \\ S &= 24 + 12 + 16 \\ S &= 52\; sq.\; units \end{split}\]

The surface area S of the rectangular solid shown in Figure \(\PageIndex{3}\) is 52 square units.

In general, to find the surface area of a rectangular solid, remember that each face is a rectangle, so its area is the product of its length and its width (see Figure \(\PageIndex{4}\)). Find the area of each face that you see and then multiply each area by two to account for the face on the opposite side.

\[S = 2LH + 2LW + 2WH\]

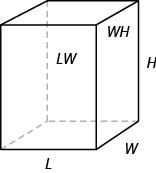
Figure \(\PageIndex{4}\) - For each face of the rectangular solid facing you, there is another face on the opposite side. There are 6 faces in all.

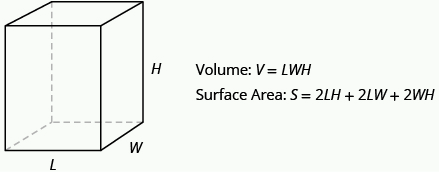
Definition: Volume and Surface Area of a Rectangular Solid

For a rectangular solid with length L, width W, and height H:

Example \(\PageIndex{1}\):

For a rectangular solid with length 14 cm, height 17 cm, and width 9 cm, find the (a) volume and (b) surface area.

Step 1 is the same for both (a) and (b), so we will show it just once.

Exercise \(\PageIndex{1}\):

Find the (a) volume and (b) surface area of rectangular solid with the: length 8 feet, width 9 feet, and height 11 feet.

Exercise \(\PageIndex{2}\):

Find the (a) volume and (b) surface area of rectangular solid with the: length 15 feet, width 12 feet, and height 8 feet.

1,440 cu. ft

Example \(\PageIndex{2}\):

A rectangular crate has a length of 30 inches, width of 25 inches, and height of 20 inches. Find its (a) volume and (b) surface area.

Exercise \(\PageIndex{3}\):

A rectangular box has length 9 feet, width 4 feet, and height 6 feet. Find its (a) volume and (b) surface area.

Exercise \(\PageIndex{4}\):

A rectangular suitcase has length 22 inches, width 14 inches, and height 9 inches. Find its (a) volume and (b) surface area.

2,772 cu. in

1,264 sq. in.

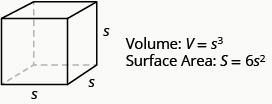
Volume and Surface Area of a Cube

A cube is a rectangular solid whose length, width, and height are equal. See Volume and Surface Area of a Cube, below. Substituting, s for the length, width and height into the formulas for volume and surface area of a rectangular solid, we get:

\[\begin{split} V &= LWH \quad \; S = 2LH + 2LW + 2WH \\ V &= s \cdot s \cdot s \quad S = 2s \cdot s + 2s \cdot s + 2s \cdot s \\ V &= s^{3} \qquad \quad S = 2s^{2} + 2s^{2} + 2s^{2} \\ &\qquad \qquad \quad \; S = 6s^{2} \end{split}\]

So for a cube, the formulas for volume and surface area are V = s 3 and S = 6s 2 .

Definition: Volume and Surface Area of a Cube

For any cube with sides of length s,

Example \(\PageIndex{3}\):

A cube is 2.5 inches on each side. Find its (a) volume and (b) surface area.

Exercise \(\PageIndex{5}\):

For a cube with side 4.5 meters, find the (a) volume and (b) surface area of the cube.

91.125 cu. m

121.5 sq. m

Exercise \(\PageIndex{6}\):

For a cube with side 7.3 yards, find the (a) volume and (b) surface area of the cube.

389.017 cu. yd.

319.74 sq. yd.

Example \(\PageIndex{4}\):

A notepad cube measures 2 inches on each side. Find its (a) volume and (b) surface area.

Exercise \(\PageIndex{7}\):

A packing box is a cube measuring 4 feet on each side. Find its (a) volume and (b) surface area.

Exercise \(\PageIndex{8}\):

A wall is made up of cube-shaped bricks. Each cube is 16 inches on each side. Find the (a) volume and (b) surface area of each cube.

4,096 cu. in.

Contributors and Attributions

Lynn Marecek (Santa Ana College) and MaryAnne Anthony-Smith (Formerly of Santa Ana College). This content is licensed under Creative Commons Attribution License v4.0 "Download for free at http://cnx.org/contents/[email protected] ."

High School Math 2012 Common-core Algebra 1 Practice And Problem Solvingworkbook Grade 8/9 1st Edition, Prentice Hall

High school math 2012 common-core algeb... 1st edition prentice hall publisher: prentice hall isbn: 9780133185614, view more textbook editions, free answers for high school math 2012 common-core algebra 1 practice and problem solvingworkbook grade 8/9, stuck on your homework.

Ask a question and get an expertly curated answer in as fast as 30 minutes.*

*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers and new subjects.

Browse All Chapters of This Textbook

More editions of this book.

Corresponding editions of this textbook are also available below:

Solver Title

Generating PDF...

• Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Expanded Form Mean, Median & Mode
• Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Logical Sets Word Problems
• Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
• Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
• Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
• Linear Algebra Matrices Vectors
• Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
• Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
• Physics Mechanics
• Chemistry Chemical Reactions Chemical Properties
• Finance Simple Interest Compound Interest Present Value Future Value
• Economics Point of Diminishing Return
• Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
• Pre Algebra
• Pre Calculus
• Linear Algebra
• Trigonometry
• Conversions

Most Used Actions

Number line.

• x^{2}-x-6=0
• -x+3\gt 2x+1
• line\:(1,\:2),\:(3,\:1)
• prove\:\tan^2(x)-\sin^2(x)=\tan^2(x)\sin^2(x)
• \frac{d}{dx}(\frac{3x+9}{2-x})
• (\sin^2(\theta))'
• \lim _{x\to 0}(x\ln (x))
• \int e^x\cos (x)dx
• \int_{0}^{\pi}\sin(x)dx
• \sum_{n=0}^{\infty}\frac{3}{2^n}
• Is there a step by step calculator for math?
• Symbolab is the best step by step calculator for a wide range of math problems, from basic arithmetic to advanced calculus and linear algebra. It shows you the solution, graph, detailed steps and explanations for each problem.
• Is there a step by step calculator for physics?
• Symbolab is the best step by step calculator for a wide range of physics problems, including mechanics, electricity and magnetism, and thermodynamics. It shows you the steps and explanations for each problem, so you can learn as you go.
• How to solve math problems step-by-step?
• To solve math problems step-by-step start by reading the problem carefully and understand what you are being asked to find. Next, identify the relevant information, define the variables, and plan a strategy for solving the problem.
• Practice Makes Perfect Learning math takes practice, lots of practice. Just like running, it takes practice and dedication. If you want...

Please add a message.

Message received. Thanks for the feedback.

5th Grade Go Math! Lessons By chapter

Mr. Math Blog

Convert Units of Length - Lesson 6.1

Convert Units of Capacity - Lesson 6.2

Convert Units of Weight and Mass - Lesson 6.3

Transform Units - Lesson 6.4

Problem Solving - Distance, Rate, and Time - Lesson 6.5

Fractions and Decimals - Lesson 2.1

Compare and order Fractions and Decimals - Lesson 2.2

Multiply Fractions - Lesson 2.3

Simplify Factors - Lesson 2.4

Model Fraction Division - Lesson 2.5

Estimate Quotients - Lesson 2.6

Dividing Fractions - Lesson 2.7

Model Mixed Number Division - Lesson 2.8

Divide Mixed Numbers - Lesson 2.9

Problem Solving - Fraction Operations - Lesson 2.10

Understanding Positive and Negative Integers - Lesson 3.1

Compare and Order Integers - Lesson 3.2

Rational Numbers and the Number Line - Lesson 3.3

Compare and Order Rational Numbers - Lesson 3.4

Absolute Value - Lesson 3.5

Compare Absolute Value - Lesson 3.6

Rational Numbers and the Coordinate Plane - Lesson 3.7

Ordered Pair Relationships - Lesson 3.8

Distance on the Coordinate Plane - Lesson 3.9

Problem Solving - The Coordinate Plane - Lesson 3.10

Solutions of Equations - Lesson 8.1

Writing Equations - Lesson 8.2

Model and Solve Addition Equations - Lesson 8.3

Solve Addition & Subtraction Equations - Lesson 8.4

Sixth Grade

     Math

Model Ratios - Lesson 4.1

Ratios and Rates - Lesson 4.2

Equivalent Ratios and the Multiplication Table - Lesson 4.3

Use Tables to Compare Ratios - Lesson 4.4

Use Equivalent Ratios - Lesson 4.5

Find Unit Rates - Lesson 4.6

Use Unit Rates - Lesson 4.7

Equivalent Ratios and Graphs - Lesson 4.8

Three Dimensional Figures and Nets - Lesson 11.1

Surface Area of Prisms - Lesson 11.3

Surface Area of Pyramids - Lesson 11.4

Volume of a Rectangular Prism - Lesson 11.6

Area of Parallelograms - Lesson 10.1

Explore Area of Triangles - Lesson 10.2

Area of Triangles - Lesson 10.3

Explore Area of Trapezoids - Lesson 10.4

Area of Trapezoids - Lesson 10.5

Area of Regular Polygons - Lesson 10.6

​Composite Figures - Lesson 10.7

Divide Multi-Digit Numbers - Lesson 1.1

Prime Factorization - Lesson 1.2

Least Common Multiple (LCM) - Lesson 1.3

Greatest Common Factor (GCF) - Lesson 1.4

Problem Solving: Apply the GCF - Lesson 1.5

Add and Subtract Decimals - Lesson 1.6

Multiply Decimals - Lesson 1.7

Divide Decimals by Whole Numbers - Lesson 1.8

Divide with Decimals - Lesson 1.9

Chapter 1 Review for Test

Please Donate, if you're a regular!

The donate link is below. Thanks so much!!

Exponents - Lesson 7.1

Evaluating Expressions Involving Exponents - Lesson 7.2

Write Algebraic Expressions - Lesson 7.3

Identify Parts of Expressions - Lesson 7.4

Evaluate Algebraic Expressions and Formulas - Lesson 7.5

Use Algebraic Expressions - Lesson 7.6

Problem Solving - Combining Like Terms - Lesson 7.7

Generate Equivalent Expressions - Lesson 7.8

Identify Equivalent Expressions - Lesson 7.9

Thanks for your donation!

​Every little bit helps me help you!  :-)

Independent and Dependent Variables - Lesson 9.1

Equations and Tables - Lesson 9.2

Model Percents - Lesson 5.1

Write Percents as Fractions and Decimals - Lesson 5.2

Write Fractions and Decimals as Percents - Lesson 5.3

Percent of a Quantity - Lesson 5.4

Problem Solving - Percents - Lesson 5.5

Find the Whole From a Percent - Lesson 5.6

• AP Calculus
• AP Statistics
• Independent Study
• Second Grade Math
• Third Grade Math
• Fourth Grade Math
• Fifth Grade Math
• Sixth Grade Math
• Sixth Grade Math (CA)
• Seventh Grade Math (CA)
• Eighth Grade Math (CA)
• Integrated Math 1
• Integrated Math 2
• Integrated Math 3
• PreCalculus
• AP Statistics Exam Prep
• Elementary Statistics
• ELM Practice
• Percents and Decimals
• Sixth Grade Math (Big Ideas)

Online Math Class

Copyright 2013. All rights reserved.

• Solve equations and inequalities
• Simplify expressions
• Factor polynomials
• Graph equations and inequalities
• Advanced solvers
• All solvers
• Arithmetics
• Determinant
• Percentages
• Scientific Notation
• Inequalities

What can QuickMath do?

QuickMath will automatically answer the most common problems in algebra, equations and calculus faced by high-school and college students.

• The algebra section allows you to expand, factor or simplify virtually any expression you choose. It also has commands for splitting fractions into partial fractions, combining several fractions into one and cancelling common factors within a fraction.
• The equations section lets you solve an equation or system of equations. You can usually find the exact answer or, if necessary, a numerical answer to almost any accuracy you require.
• The inequalities section lets you solve an inequality or a system of inequalities for a single variable. You can also plot inequalities in two variables.
• The calculus section will carry out differentiation as well as definite and indefinite integration.
• The matrices section contains commands for the arithmetic manipulation of matrices.
• The graphs section contains commands for plotting equations and inequalities.
• The numbers section has a percentages command for explaining the most common types of percentage problems and a section for dealing with scientific notation.

Math Topics

More solvers.

• Add Fractions
• Simplify Fractions

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

1.9: Solving Problems Using Percents

• Last updated
• Save as PDF
• Page ID 45768
• Lumen Learning

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Outcome

• Evaluate expressions and word problems involving percents

In this section we will solve percent questions by identifying the parts of the problem. We’ll look at a common application of percent—tips to a server at a restaurant—to see how to set up a basic percent application.

When Aolani and her friends ate dinner at a restaurant, the bill came to \(\text{\$80}\). They wanted to leave a \(20\%\) tip. What amount would the tip be?

To solve this, we want to find what amount is \(20\%\) of \(\$80\). The \(\$80\) is called the base . The percent is the given \(20\%\). The amount of the tip would be \(0.20(80)\), or \(\$16\) — see the image below. To find the amount of the tip, we multiplied the percent by the base.

A \(20\%\) tip for an \(\$80\) restaurant bill comes out to \(\$16\).

Pieces of a Percent Problem

Percent problems involve three quantities: the base amount (the whole), the percent , and the amount (a part of the whole or partial amount).

The amount is a percent of the base.

Let’s look at another example:

Jeff has a Guitar Strings coupon for \(15\%\) off any purchase of \($100\) or more. He wants to buy a used guitar that has a price tag of \($220\) on it. Jeff wonders how much money the coupon will take off the original \($220\) price. Problems involving percents will have some combination of these three quantities to work with: the percent , the amount , and the base . The percent has the percent symbol (%) or the word percent. In the problem above, \(15\%\) is the percent off the purchase price. The base is the whole amount or original amount. In the problem above, the “whole” price of the guitar is \($220\), which is the base. The amount is the unknown and what we will need to calculate.

There are thee cases: a missing amount, a missing percent or a missing base. Let’s take a look at each possibility.

Solving for the Amount

When solving for the amount in a percent problem, you will multiply the percent (as a decimal or fraction) by the base. Typically we choose the decimal value for percent.

\(\text{percent}\cdot{\text{base}}=\text{amount}\)

Find \(50\%\) of \(20\)

First identify each piece of the problem:

percent: \(50\%\) or \(.5\)

base: \(20\)

amount: unknown

Now plug them into your equation \(\text{percent}\cdot{\text{base}}=\text{amount}\)

\(.5\cdot{20}= ?\)

\(.5\cdot{20}= 10\)

Therefore, \(10\) is the amount or part that is \(50\%\) of \(20\).

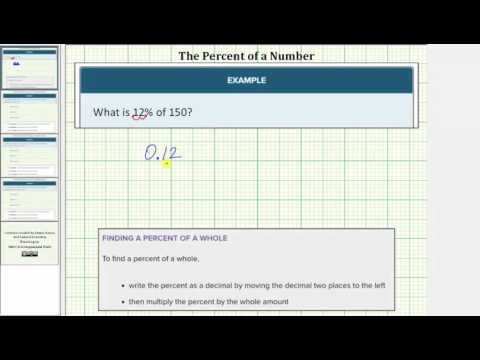
What is \(25\%\) of \(80\)?

[reveal-answer q=”813233″]Show Answer[/reveal-answer] [hidden-answer a=”813233″]

The base is \(80\) and the percent is \(25\%\), so amount \(= 80(0.25) = 20\)

[/hidden-answer]

[ohm_question]80094[/ohm_question]

A YouTube element has been excluded from this version of the text. You can view it online here: http://pb.libretexts.org/afm-2/?p=78

Solving for the Percent

When solving for the percent in a percent problem, you will divide the amount by the base. The equation above is rearranged and the percent will come back as a decimal of fraction you can report in the form asked of you.

\(\Large{\frac{\text{amount}}{\text{base}}}\normalsize=\text{percent}\)

What percent of \(320\) is \(80\)?

percent: unknown

base: \(320\)

amount: \(80\)

Now plug the values into your equation \(\Large{\frac{\text{amount}}{\text{base}}}\normalsize=\text{percent}\)

\(\large\frac{80}{320}\normalsize=?\)

\(\large\frac{80}{320}\normalsize=.25\)

Therefore, \(80\) is \(25\%\) of \(320\).

[ohm_question]80097[/ohm_question]

Solving for the Base

When solving for the base in a percent problem, you will divide the amount by the percent (as a decimal or fraction). The equation above is rearranged and you will find the base after plugging in the values.

\(\Large{\frac{\text{amount}}{\text{percent}}}\normalsize=\text{base}\)

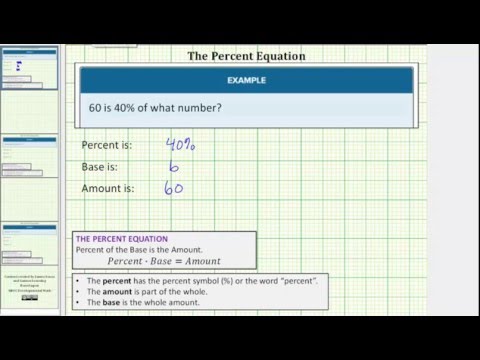
\(60\) is \(40\%\) of what number?

percent:\(40\%\) or \(.4\)

base: unknown

amount: \(60\)

Now plug the values into your equation \(\Large{\frac{\text{amount}}{\text{percent}}}\normalsize=\text{base}\)

\((60)\div(.4)=?\)

\((60)\div(.4)=150\)

Therefore, \(60\) is \(40\%\) of \(150\).

An article says that \(15\%\) of a non-profit’s donations, about \($30,000\) a year, comes from individual donors. What is the total amount of donations the non-profit receives?

[reveal-answer q=”731314″]Show Answer[/reveal-answer] [hidden-answer a=”731314″]

The percent is \(15\%\), and \($30,000\) is the amount (or part of the whole). We are looking for the base.

base = \(30000\div(.15)=$200000\)

The non-profit receives \($200000\) a year in donations

[ohm_question]157022[/ohm_question]

Here are a few more percent problems for you to try.

[ohm_question]146672[/ohm_question]

[ohm_question]146692[/ohm_question]

[ohm_question]146693[/ohm_question]

Many applications of percent occur in our daily lives, such as tips, sales tax, discount, and interest. To solve these applications we’ll translate to a basic percent equation, just like those we solved in the previous examples in this section. Once you translate the sentence into a percent equation, you know how to solve it.

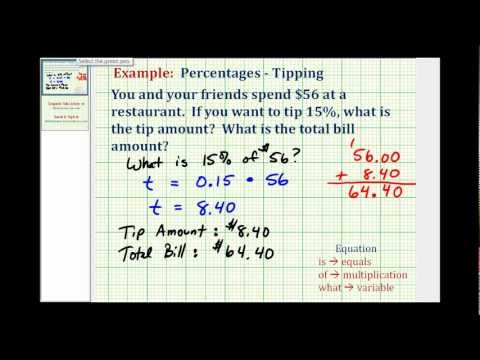
Dezohn and his girlfriend enjoyed a dinner at a restaurant, and the bill was \(\text{\$68.50}\). They want to leave an \(\text{18%}\) tip. If the tip will be \(\text{18%}\) of the total bill, how much should the tip be?

[ohm_question]146694[/ohm_question]

In the next video we show another example of finding how much tip to give based on percent.

The label on Masao’s breakfast cereal said that one serving of cereal provides \(85\) milligrams (mg) of potassium, which is \(\text{2%}\) of the recommended daily amount. What is the total recommended daily amount of potassium?

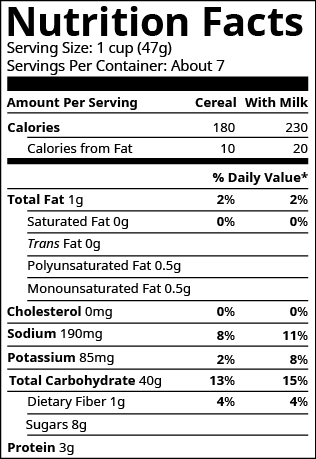
[ohm_question]146697[/ohm_question]

[ohm_question]146702[/ohm_question]

[ohm_question]146703[/ohm_question]