what is natural representation

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

AP®︎/College Art History

Course: ap®︎/college art history   >   unit 1.

• Contrapposto explained
• What is foreshortening?
• What is chiaroscuro?
• How one-point linear perspective works
• What is atmospheric perspective?
• The classical orders

Naturalism, realism, abstraction and idealization

Representational versus non-representation

Moving toward abstraction, non-representational art, idealization, naturalism and realism, want to join the conversation.

• Upvote Button navigates to signup page
• Downvote Button navigates to signup page
• Flag Button navigates to signup page

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

1.5: Representational, Abstract, and Nonrepresentational Art

• Last updated
• Save as PDF
• Page ID 71923

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Painting, sculpture, and other artforms can be divided into the categories of representational (sometimes also called figurative art although it doesn’t always contain figures), abstract and nonrepresentational art. Representational art describes artworks—particularly paintings and sculptures–that are clearly derived from real object sources, and therefore are by definition representing something with strong visual references to the real world. Most, but not all, abstract art is based on imagery from the real world. The most “extreme” form of abstract art is not connected to the visible world and is known as nonrepresentational.

• Representational art or figurative art represents objects or events in the real world, usually looking easily recognizable. For example, a painting of a cat looks very much like a cat– it’s quite obvious what the artist is depicting.
• Romanticism, Impressionism, and Expressionism contributed to the emergence of abstract art in the nineteenth century as artists became less interested in depicting things exactly like they really exist. Abstract art exists on a continuum, from somewhat realistic representational work, to work that is not based on anything visible from the real world. Even representational work is abstracted to some degree; entirely realistic art is elusive.
• Work that does not depict anything from the real world (figures, landscapes, animals, etc.) is called nonrepresentational . Nonrepresentational art may simply depict shapes, colors, lines, etc., but may also express things that are not visible– emotions or feelings for example.

This figurative or representational work from the seventeenth century depicts easily recognizable objects–ships, people, and buildings. But artistic independence was advanced during the nineteenth century, resulting in the emergence of abstract art. Three movements that contributed heavily to the development of these were Romanticism, Impressionism, and Expressionism.

Abstraction indicates a departure from reality in depiction of imagery in art. Abstraction exists along a continuum; abstract art can formally refer to compositions that are derived (or abstracted) from a figurative or other natural source. It can also refer to nonrepresentational (non-objective) art that has no derivation from figures or objects. Picasso is a well-known artist who used abstraction in many of his paintings and sculptures: figures are often simplified, distorted, exaggerated, or geometric.

Pablo Picasso, Girl Before a Mirror , 1932, MOMA Photo by Sharon Mollerus CC BY

Even art that aims for verisimilitude (accuracy and truthfulness) of the highest degree can be said to be abstract, at least theoretically, since perfect representation is likely to be exceedingly elusive. Artwork which takes liberties, altering for instance color and form in ways that are conspicuous, can be said to be partially abstract.

Delaunay’s work is a primary example of early abstract art. Nonrepresentational art is also sometimes called complete abstraction, bearing no trace of any reference to anything recognizable from the real world. In geometric abstraction, for instance, one is unlikely to find references to naturalistic entities. Figurative art and total abstraction are almost mutually exclusive. But representational (or realistic) art often contains partial abstraction. As you see, these terms are bit confusing, but do your best to understand the basic definitions of representational, abstract and nonrepresentational.

• Representational, Abstract, and Nonrepresentational Art. From Boundless Art History. Provided by : Boundless. Located at : www.boundless.com/art-history/textbooks/boundless-art-history-textbook/thinking-and-talking-about-art-1/content-42/representational-abstract-and-nonrepresentational-art-264-1615/. License : CC BY-SA: Attribution-ShareAlike

• Table of Contents
• Random Entry
• Chronological
• Editorial Information
• About the SEP
• Editorial Board
• How to Cite the SEP
• Special Characters
• Advanced Tools
• Support the SEP
• PDFs for SEP Friends
• Make a Donation
• SEPIA for Libraries
• Entry Contents

Bibliography

Academic tools.

• Friends PDF Preview
• Author and Citation Info
• Back to Top

Scientific Representation

Science provides us with representations of atoms, elementary particles, polymers, populations, pandemics, economies, rational decisions, aeroplanes, earthquakes, forest fires, irrigation systems, and the world’s climate. It’s through these representations that we learn about the world. This entry explores various different accounts of scientific representation, with a particular focus on how scientific models represent their target systems. As philosophers of science are increasingly acknowledging the importance, if not the primacy, of scientific models as representational units of science, it’s important to stress that how they represent plays a fundamental role in how we are to answer other questions in the philosophy of science (for instance in the scientific realism debate). This entry begins by disentangling “the” problem of scientific representation, and then critically evaluates the current options available in the literature.

1. Problems Concerning Scientific Representation

2. general griceanism and stipulative fiat, 3.1 similarity and er-problem, 3.2 accuracy, style, and ontology, 4.1 structures and the problem of ontology, 4.2 structuralism and the er-problem, 4.3 demarcation, accuracy, style, and target-end structure, 5.1 the ddi account, 5.2 deflationary inferentialism, 5.3 inflating inferentialism: interpretation, 6. the fiction view of models, 7.1 from art to science, 7.2 the deki account, other internet resources, related entries.

In most general terms, any representation that is the product of a scientific endeavour is a scientific representation. These representations are a heterogeneous group comprising anything from thermometer readings and flow charts to verbal descriptions, photographs, X-ray pictures, digital imagery, equations, models, and theories. How do these representations work?

The first thing that strikes the novice in the debate about scientific representation is that there seems to be little agreement about what the problem is. Different authors frame the problem of scientific representation in different ways, and eventually they examine different issues. So a discussion of scientific representation has to begin with a clarification of the problem itself. Reviewing the literature on the subject leads us to the conclusion that there is no such thing as the problem of scientific representation—in fact, there are at least five different problems concerning scientific representation (Frigg and Nguyen 2020: ch. 1). In this section we formulate these problems and articulate five conditions of adequacy that every account of scientific representation has to satisfy.

The first problem is: what turns something into a scientific representation of something else? It has become customary to phrase this problem in terms of necessary and sufficient conditions and ask: what fills the blank in “\(S\) is a scientific representation of \(T\) iff ___”, where “\(S\)” stands for the object doing the representing and “\(T\)” for “target system”, the part or aspect of the world the representation is about? [ 1 ] Let us call this the Scientific Representation Problem (or SR-Problem for short).

A number of contributors to the debate have emphasised that scientific representation is an intentional concept, depending on factors such as a user’s intentions, purposes and objectives, contextual standards of accuracy, intended audiences, and community practices (see, for instance, Boesch 2017; Giere 2010; Mäki 2011; Suárez 2004; and van Fraassen 2008). We will discuss these in detail below. At this point it needs to be emphasised that framing the problem in terms of a biconditional does not preclude such factors to be part of the analysis. The blank can be filled with a \((n+2)\)-ary relation \(C(S, T, x_1, \ldots, x_n)\) (\(C\) for “constitutes”), where \(n \ge 0\) is a natural number and the \(x_i\) are factors such as intentions and purposes.

A first important condition of adequacy on any reply to this problem is that scientific representations allow us to form hypotheses about their target systems. An X-ray picture provides information about the bones of the patient, and models allow investigators to discover features of the things models stands for. Every acceptable theory of scientific representation has to account for how reasoning conducted on representations can yield claims about their target systems. Swoyer (1991: 449) refers to this kind of representation-based thinking as “surrogative reasoning” and so we call this the Surrogative Reasoning Condition . [ 2 ] This condition distinguishes models from lexicographical and indexical representations, which do not allow for surrogative reasoning.

Unfortunately this condition does not constrain answers sufficiently because any account of representation that fills the blank in a way that satisfies the surrogative reasoning condition will almost invariably also cover other kinds of representations. Speed camera photographs give the police information about drivers breaking the law, a cardboard model of the palace instructs us about its layout and proportions, and a weather map shows you where to expect rain. These representations are therefore are likely to fall under an account of representation that explains surrogative reasoning. Hence, representations other than scientific representations also allow for surrogative reasoning, which raises the question: how do scientific representations differ from other kinds of representations that allow for surrogative reasoning? Callender and Cohen (2006: 68–69) point out that this is a version Popper’s demarcation problem, now phrased in terms of representation, and so we refer to it as the Representational Demarcation Problem .

Callender and Cohen voice scepticism about there being a solution to this problem and suggest that the distinction between scientific and non-scientific representations is circumstantial (2006: 83): scientific representations are representations that are used or developed by someone who is a scientist. Other authors do not explicitly discuss the representational demarcation problem, but stances similar to Callender and Cohen’s are implicit in any approach that analyses scientific representation alongside other kinds of representation. Elgin (2010), French (2003), Frigg (2006), Hughes (1997), Suárez (2004), and van Fraassen (2008), for instance, all draw parallels between scientific and pictorial representation, which would make little sense if pictorial and scientific representation were categorically different.

Those who reject the notion that there is an essential difference between scientific and non-scientific representation can follow a suggestion of Contessa’s (2007) and broaden the scope of the investigation. Rather than analysing scientific representation, they can analyse the broader category of epistemic representation . This category comprises scientific representations, but it also includes other representations that allow for surrogative reasoning. The task then becomes to fill the blank in “\(S\) is an epistemic representation of \(T\) iff ___”. We call this the Epistemic Representation Problem ( ER-Problem , for short), and the biconditional the ER-Scheme . So one can say that the ER-Problem is to fill the blank in the ER-Scheme.

Not all representations are of the same kind, not even if we restrict our attention to scientific representations (assuming they are found to be relevantly different to non-scientific epistemic representations). An X-ray photograph represents an ankle joint in a different way than a biomechanical model, a mercury thermometer represent the temperature of gas in a different way than statistical mechanics does, and chemical theory represents a C60 fullerene in different way that an electron-microscope image of the molecule. Even when restricting attention to the same kind of representation, there are important differences: Weizsäcker’s liquid drop model, for instance, represents the nucleus of an atom in a manner that seems to be different from the one of the shell model, and an electric circuit model represents the brain function in a different way than a neural network model. In brief, there seem to be different representational styles. This raises the question: what styles are there and how can they be characterised? [ 3 ] We call this the Problem of Style . [ 4 ] There is no expectation that a complete list of styles be provided in response. Indeed, it is unlikely that such a list can ever be drawn up, and new styles will be invented as science progresses. For this reason a response to the problem of style will always be open-ended, providing a taxonomy of what is currently available while leaving room for later additions.

Some representations are accurate; others aren’t. The quantum mechanical model is an accurate representation of the atom (at least by our current lights) but the Thomson model isn’t. On what grounds do we make such judgments? Morrison (2008: 70) reminds us that it is a task for theory of representation to identify what constitutes an accurate representation. We call this the problem of Standards of Accuracy . Providing such standards is one of the issues an account of representation has to address, which, however, is not to say that accurate representation is the sole epistemic virtue of scientific models. As Parker (2020) points out, there are numerous of considerations to take into account when evaluating a model’s adequacy for its purpose, see Downes (2021: ch. 5) for further discussion.

This problem goes hand in hand with a condition of adequacy: the Possibility of Misrepresentation . Asking what makes a representation an accurate representation ipso facto presupposes that inaccurate representations are representations too. And this is how it should be. If \(S\) does not accurately represent \(T\), then it is a misrepresentation but not a non-representation. It is therefore a general constraint on a theory of scientific representation that it has to make misrepresentation possible. [ 5 ]

A related condition concerns models that misrepresent in the sense that they lack target systems. Models of the ether, phlogiston, four-sex populations, and so on, are all deemed scientific models, but ether, phlogiston, and four-sex populations don’t exist. Such models lack (actual) target systems, and one hopes that an account of scientific representation would allow us to understand how these models work. This need not imply the claim that they are representations in the same sense as models with actual targets, and, as we discuss below, there are accounts that deny targetless models the status of being representations.

A further condition of adequacy for an account of scientific representation is that it must account for the directionality of representation. As Goodman points out (1976: 5), representations are about their targets, but (at least in general) targets are not about their representations: a photograph represents the cracks in the wing of aeroplane, but the wing does not represent the photograph. So there is an essential directionality to representations, and an account of scientific, or epistemic, representation has to identify the root of this directionality. We call this the Requirement of Directionality .

Some representations, in particular models and theories, are mathematized and their mathematical aspects are crucial to their cognitive and representational function. This forces us to reconsider a time-honoured philosophical puzzle: the applicability of mathematics in the empirical sciences. The problem can be traced back at least to Plato’s Timaeus , but its modern expression is due to Wigner who challenged us to find an explanation for the enormous usefulness of mathematics in the sciences (1960: 2). The question how a mathematized model represents its target implies the question how mathematics applies to a physical system (see Pincock 2012 for an explicit discussion of the relationship between scientific representation and the applicability of mathematics). For this reason, our fifth and final condition of adequacy is that an account of representation has to explain how mathematics is applied to the physical world. We call this the Applicability of Mathematics Condition .

In answering the above questions one invariably runs up against a further problem, the Problem of Ontology : what kinds of objects are representations? If representations are material objects the answer is straightforward: photographic plates, pieces of paper covered with ink, elliptical blocks of wood immersed in water, and so on. But not all representations are like this. As Hacking (1983: 216) puts it, some representations one holds in one’s head rather than one’s hands. The Newtonian model of the solar system, the Lotka-Volterra model of predator-prey interaction and the general theory of relativity are not things you can put on your laboratory table and look at. The problem of ontology is to come clear on our commitments and provide a list with things that we recognise—or don’t recognise—as entities performing a representational function and give an account of what they are in case these entities raise questions (what exactly do we mean by something that one holds in one’s head rather than one’s hands?). Contessa (2010), Frigg (2010a,b), Godfrey-Smith (2006), Levy (2015), Thomson-Jones (2010), Weisberg (2013), among others, have drawn attention to this problem in different ways.

In sum, a theory of scientific representation has to respond to the following issues:

• Address the Representational Demarcation Problem (the question how scientific representations differ from other kinds of representations).
• Those who demarcate scientific from non-scientific representations have to provide an answer to the Scientific Representation Problem (fill the blank in “\(S\) is a scientific representation of \(T\) iff ___”). Those who reject the representational demarcation problem can address the Epistemic Representation Problem (fill the blank in ER-Scheme: “\(S\) is an epistemic representation of \(T\) iff ___”).
• Respond to the Problem of Style (what styles are there and how can they be characterised?).
• Formulate Standards of Accuracy (how do we identify what constitutes an accurate representation?).
• Address the Problem of Ontology (what are the kind of objects that serve as representations?).

Any satisfactory answer to these five issues will have to meet the following five conditions of adequacy:

• Surrogative Reasoning (scientific representations allow us to generate hypotheses about their target systems).
• Possibility of Misrepresentation (if \(S\) does not accurately represent \(T\), then it is a misrepresentation but not a non-representation).
• Targetless Models (what are we to make of scientific representations that lack targets?).
• Requirement of Directionality (scientific representations are about their targets, but targets are not about their representations).
• Applicability of Mathematics (how does the mathematical apparatus used in some scientific representations latch onto the physical world).

Listing the problems in this way is not to say that these are separate and unrelated issues. This division is analytical, not factual. It serves to structure the discussion and to assess proposals; it does not imply that an answer to one of these questions can be dissociated from what stance we take on the other issues.

Any attempt to tackle these questions faces an immediate methodological problem. As per the problem of style, there are different kinds of representations: scientific models, theories, measurement outcomes, images, graphs, diagrams, and linguistic assertions are all scientific representations, and even within these groups there can be considerable variation. But every analysis has to start somewhere, and so the problem is where. One might adopt a universalist position, holding that the diversity of styles dissolves under analysis and at bottom all instances of scientific/epistemic representation function in the same way and are covered by the same overarching account. For such a universalist the problem loses its teeth because any starting point will lead to the same result. Those of particularist bent deny that there is such a theory. They will first divide the scientific/epistemic representations into relevant subclasses and then analyse each subclass separately.

Different authors assume different stances in this debate, and we will discuss their positions below. However, there are few, if any, thoroughgoing universalists and so a review like the current one has to discuss different cases. Unfortunately space constraints prevent us from examining all the different varieties of scientific/epistemic representation, and a selection has to be made. This invariably leads to the neglect of some kinds of representations, and the best we can do about this is to be explicit about our choices. We resolve to concentrate on scientific models, and therefore replace our variable \(S\) for the object doing the representing with the variable \(M\) for model. This is in line both with the more recent literature on scientific representation, which is predominantly concerned with scientific models, and with the prime importance that current philosophy of science attaches to models (see the SEP entry on models in science for a survey). [ 6 ]

It is, however, worth briefly mentioning some of the omissions that this brings with it. Various types of images have their place in science, and so do graphs, diagrams, and drawings. Perini (2010) and Elkins (1999) provide discussions of visual representation in science. Measurements also supply representations of processes in nature, sometimes together with the subsequent condensation of measurement results in the form of charts, curves, tables and the like (see the SEP entry on measurement in science ). Furthermore, theories represent their subject matter. At this point the vexing problem of the nature of theories rears again (see the SEP entry on the structure of scientific theories and also Portides (2017) for an extensive discussion). Proponents of the semantic view of theories construe theories as families of models, and so for them the question of how theories represent coincides with the question of how models represent. By contrast, those who regard theories as linguistic entities see theoretical representation as a special kind of linguistic representation and focus on the analysis of scientific languages, in particular the semantics of so-called theoretical terms (see the SEP entry on theoretical terms in science ).

Before delving into the discussion a common misconception needs to be dispelled. The misconception is that a representation is a mirror image, a copy, or an imitation of the thing it represents. On this view representation is ipso facto realistic representation. This is a mistake. Representations can be realistic, but they need not. And representations certainly need not be copies of the real thing, an observation exploited by Lewis Carroll and Jorge Luis Borges in their satires, Sylvie and Bruno and On Exactitude in Science respectively, about cartographers who produce maps as large as the country itself only to see them abandoned (for a discussion see Boesch 2021). Throughout this review we encounter positions that make room for non-realistic representation and hence testify to the fact that representation is a much broader notion than mirroring. [ 7 ]

Callender and Cohen (2006) give a radical answer to the demarcation problem: there is no difference between scientific representations and other kinds of representations, not even between scientific and artistic representation. Underlying this claim is a position they call “General Griceanism” (GG). The core of GG is the reductive claim that all representations owe their status as representations to a privileged core of fundamental representations. GG then comes with a practical prescription about how to proceed with the analysis of a representation:

the General Gricean view consists of two stages. First, it explains the representational powers of derivative representations in terms of those of fundamental representations; second, it offers some other story to explain representation for the fundamental bearers of content. (2006: 73)

Of these stages only the second requires serious philosophical work, and this work is done in the philosophy of mind because the fundamental form of representation is mental representation.

Scientific representation is a derivative kind of representation (2006: 71, 75) and hence falls under the first stage of the above recipe. It is reduced to mental representation by an act of stipulation. In Callender and Cohen’s own example, the salt shaker on the dinner table can represent Madagascar as long as someone stipulates that the former represents the latter, since

the representational powers of mental states are so wide-ranging that they can bring about other representational relations between arbitrary relata by dint of mere stipulation. (2006: 73–74)

So explaining any form of representation other than mental representation is a triviality—all it takes is an act of “stipulative fiat” (2006: 75). This supplies an answer to the ER-problem:

Stipulative Fiat : A scientific model \(M\) represents a target system \(T\) iff a model user stipulates that \(M\) represents \(T\).

The first problem facing Stipulative Fiat is whether or not stipulation, or the bare intentions of language users, suffice to establish representational relationships. In the philosophy of language this gets called the “Humpty Dumpty” problem. It concerns whether or not Lewis Carroll’s Humpty Dumpty could use the word “glory” to mean “a nice knockdown argument” (Donnellan 1968; MacKay 1968). (We ignore the difference between meaning and denotation here). In that context it doesn’t seem like he can, and analogous questions can be posed in the context of scientific representation: can a scientist make any model represent any target simply by stipulating that it does?

Even if stipulation were sufficient to establish some sort of representational relationship, Stipulative Fiat fails to meet the Surrogative Reasoning Condition: assuming a salt shaker represents Madagascar in virtue of someone’s stipulation that this is so, this tells us nothing about how the salt shaker could be used to learn about Madagascar in the way that scientific models are used to learn about their targets (Liu 2015: 46–47, for a related objections see Boesch 2017: 974–978, Bueno and French 2011: 871–873, Gelfert 2016: 33, Ruyant 2021: 535). And appealing to additional facts about the salt shaker (the salt shaker being to the right of the pepper mill might allow us to infer that Madagascar is to the east of Mozambique) in order to answer this objection goes beyond Stipulative Fiat . Callender and Cohen do admit some representations are more useful than others, but claim that

the questions about the utility of these representational vehicles are questions about the pragmatics of things that are representational vehicles, not questions about their representational status per se . (2006: 75)

But even if the Surrogative Reasoning Condition is relegated to the realm of “pragmatics” it seems reasonable to ask for an account of how it is met.

An important thing to note is that even if Stipulative Fiat is untenable, we needn’t give up on GG. GG only requires that there be some explanation of how derivative representations relate to fundamental representations; it does not require that this explanation be of a particular kind, much less that it consist in nothing but an act of stipulation (Toon 2010: 77–78). Ruyant (2021) has recently proposed what he calls “true Griceanism”, which differs from the original account in that it involves a non-trivial reduction of scientific representation to more fundamental representations (complex sequences mental states and purpose-directed behaviour) in a way that is also sensitive to the communal aspects of practices in which the models are embedded. This is a step into the direction indicated by Toon. More generally, as Callender and Cohen note, all that it requires is that there is a privileged class of representations and that other types of representations owe their representational capacities to their relationship with the primitive ones. So philosophers need an account of how members of this privileged class of representations represent, and how derivative representations, which includes scientific models, relate to this class. When stated like this, many recent contributors to the debate on scientific representation can be seen as falling under the umbrella of GG. Indeed, As we will see below, many of the more developed versions of the accounts of scientific representation discussed throughout this entry invoke the intentions of model users, albeit in a more complex manner than Stipulative Fiat .

3. The Similarity Conception

Similarity and representation initially appear to be two closely related concepts, and invoking the former to ground the latter has a philosophical lineage stretching back at least as far as Plato’s The Republic . [ 8 ] In its most basic guise the similarity conception of scientific representation asserts that scientific models represent their targets in virtue of being similar to them. This conception has universal aspirations in that it is taken to account for representation across a broad range of different domains. Paintings, statues, and drawings are said to represent by being similar to their subjects, and Giere proclaimed that it covers scientific models alongside “words, equations, diagrams, graphs, photographs, and, increasingly, computer-generated images” (2004: 243). So the similarity view repudiates the demarcation problem and submits that the same mechanism, namely similarity, underpins different kinds of representation in a broad variety of contexts.

The view offers an elegant account of surrogative reasoning. Similarities between model and target can be exploited to carry over insights gained in the model to the target. If the similarity between \(M\) and \(T\) is based on shared properties, then a property found in \(M\) would also have to be present in \(T\); and if the similarity holds between properties themselves, then \(T\) would have to instantiate properties similar to \(M\).

However, appeal to similarity in the context of representation leaves open whether similarity is offered as an answer to the ER-Problem or the Problem of Style, or whether it is meant to set Standards of Accuracy. Proponents of the similarity conception typically have offered little guidance on this issue. So we examine each option in turn and ask whether similarity offers a viable answer. We then turn to the question of how the similarity view deals with the Problem of Ontology.

Understood as response to the ER-Problem, the simplest similarity view is the following:

Similarity 1 : A scientific model \(M\) represents a target \(T\) iff \(M\) and \(T\) are similar.

A well-known objection to this account is that similarity has the wrong logical properties. Goodman (1976: 4–5) points out that similarity is symmetric and reflexive yet representation isn’t. If object \(A\) is similar to object \(B\), then \(B\) is similar to \(A\). But if \(A\) represents \(B\), then \(B\) need not (and in fact in most cases does not) represent \(A\). Everything is similar to itself, but most things do not represent themselves. So this account does not meet our fourth condition of adequacy for an account of scientific representation insofar as it does not provide a direction to representation.

There are accounts of similarity under which similarity is not a symmetric relation (see Tversky 1977; Weisberg 2012, 2013: ch. 8; and Poznic 2016: sec. 4.2). This raises the question of how to analyse similarity. We turn to this issue in the next subsection. However, even if we concede that similarity need not always be symmetrical, this does not solve Goodman’s problem with reflexivity; nor does it, as we will see, solve other problems of the similarity account.

The most significant problem facing Similarity 1 is that without constraints on what counts as similar, any two things can be considered similar (Aronson et al. 1995: 21; Goodman 1972: 443–444). This has the unfortunate consequence that anything represents anything else. A natural response to this difficulty is to delineate a set of relevant respects and degrees to which \(M\) and \(T\) have to be similar. This idea can be moulded into the following definition:

Similarity 2 : A scientific model \(M\) represents a target \(T\) iff \(M\) and \(T\) are similar in relevant respects and to the relevant degrees.

On this definition one is free to choose one’s respects and degrees so that unwanted similarities drop out of the picture. While this solves the last problem, it leaves the problem of logical properties untouched: similarity in relevant respects and to the relevant degrees is reflexive (and symmetrical, depending on one’s notion of similarity). Moreover, Similarity 2 faces three further problems.

Firstly, similarity, even restricted to relevant similarities, is too inclusive a concept to account for representation. In many cases neither one of a pair of similar objects represents the other. This point has been brought home in Putnam’s now-classical thought experiment due to Putnam (1981: 1–3). An ant is crawling on a patch of sand and leaves a trace that happens to resemble Winston Churchill. Has the ant produced a picture, a representation, of Churchill? Putnam’s answer is that it didn’t because the ant has never seen Churchill, had no intention to produce an image of him, was not causally connected to Churchill, and so on. Although someone else might see the trace as a depiction of Churchill, the trace itself does not represent Churchill. The fact that the trace is similar to Churchill does not suffice to establish that the trace represents him. And what is true of the trace and Churchill is true of every other pair of similar items: even relevant similarity on its own does not establish representation.

Secondly, as noted in Section 1 , allowing for the possibility of misrepresentation is a key desiderata required of any account of scientific representation. In the context of a similarity conception it would seem that a misrepresentation is one that portrays its target as having properties that are not similar in the relevant respects and to the relevant degree to the true properties of the target. But then, on Similarity 2 , \(M\) is not a representation at all. The account thus has difficulty distinguishing between misrepresentation and non-representation (Suárez 2003: 233–235).

Thirdly, there may simply be nothing to be similar to because some representations are not about an actual object. Some paintings represent elves or dragons, and some models represent phlogiston or the ether. None of these exist. This is a problem for the similarity view because models without targets cannot represent what they seem to represent because in order for two things to be similar to each other both have to exist. If there is no ether, then an ether model cannot be similar to the ether.

At least some of these problems can be resolved by taking the very act of asserting a specific similarity between a model and a target as constitutive of the scientific representation. Giere (1988: 81) suggests that models come equipped with what he calls “theoretical hypotheses”, statements asserting that model and target are similar in relevant respects and to certain degrees. He emphasises that “scientists are intentional agents with goals and purposes” (2004: 743) and proposes to build this insight explicitly into an account of representation. This involves adopting an agent-based notion of representation that focuses on “the activity of representing” (2004). Analysing representation in these terms amounts to analysing schemes like

Agents (1) intend; (2) to use model, \(M\); (3) to represent a part of the world \(W\); (4) for purposes, \(P\). So agents specify which similarities are intended and for what purpose. (2010: 274)

(see also Mäki 2009, 2011; although see Rusanen and Lappi 2012: 317 for arguments to the contrary). This leads to the following definition:

Similarity 3 : A scientific model \(M\) represents a target system \(T\) iff there is an agent \(A\) who uses \(M\) to represent a target system \(T\) by proposing a theoretical hypothesis \(H\) specifying a similarity (in certain respects and to certain degrees) between \(M\) and \(T\) for purpose \(P\).

This version of the similarity view avoids problems with misrepresentation because \(H\) being a hypothesis, there is no expectation that the assertions made in \(H\) are true. If they are, then the representation is accurate (or the representation is accurate to the extent that they hold). If they do not, then the representation is a misrepresentation. It also resolves the issue with directionality because \(H\) can be understood as introducing an asymmetry that is not present in the similarity relation. However, it fails to resolve the problem with representation without a target. If there is no ether, no hypotheses can be asserted about it, at least in any straightforward way.

Similarity 3 , by invoking an active role for the purposes and actions of scientists in constituting scientific representation, marks a significant change in emphasis for similarity-based accounts. Suárez (2003: 226–227), drawing on van Fraassen (2002) and Putnam (2002), defines “naturalistic” accounts of representation as ones where

whether or not representation obtains depends on facts about the world and does not in any way answer to the personal purposes, views or interests of enquirers.

By building the purposes of model users directly into an answer to the ER-problem, Similarity 3 is explicitly not a naturalistic account (in contrast to Similarity 1 ). The shift to users performing representational actions invites the question of it means for a scientist to perform such an action. Boesch (2019) offers an answer which draws on Anscombe’s (2000) account of intentional action: something is a “scientific, representational action” (Boesch 2019: 312) when a description of a scientist’s interaction with a model stands as an earlier description towards the final description which is some scientific aim such as explanation, predication, or theorizing.

Even though Similarity 3 resolves a number of issues that beset simpler versions, it does not seem to be a successful similarity-based solution to the ER-Problem. A closer look at Similarity 3 reveals that the role of similarity has shifted. As far as offering a solution to the ER-Problem is concerned, all the heavy lifting in Similarity 3 is done by the appeal to agents and their intentions. Giere implicitly concedes this when he observes that similarity is “the most important way, but probably not the only way” for models to function representationally (2004: 747). But if similarity is not the only way in which a model can be used as a representation, then similarity has become otiose in a reply to the ER-problem. In fact, being similar in the relevant respects to the relevant degree now plays the role either of a representational style or of a normative criterion for accurate representation, rather than constituting representation per se . We assess in the next section whether similarity offers cogent replies to the issues of style and accuracy, and we raise a further problem for any account of scientific representation that relies on the idea that models, specifically non-concrete models, are similar to their targets.

The fact that relevant properties can be delineated in different ways could potentially provide an answer to the Problem of Style. If \(M\) representing \(T\) involves the claim that \(M\) and \(T\) are similar in a certain respect, the respect chosen specifies the style of the representation; and if \(M\) and \(T\) are in fact similar in that respect (and to the specified degree), then \(M\) accurately represents \(T\) within that style. For example, if \(M\) and \(T\) are proposed to be similar with respect to their causal structure, then we might have a style of causal modelling; if \(M\) and \(T\) are proposed to be similar with respect to structural properties, then we might have a style of structural modelling; and so on and so forth.

A first step in the direction of such an understanding of styles is the explicit analysis of the notion of similarity. The standard way of cashing out what it means for an object to be similar to another object is to require that they co-instantiate properties. In fact, this is the idea that Quine (1969: 117–118) and Goodman (1972: 443) had in mind in their influential critiques of similarity. The two most prominent formal frameworks that develop this idea are the geometric and contrast accounts (see Decock and Douven 2011 for a discussion).

The geometric account, associated with Shepard (1980), assigns objects a place in a multidimensional space based on values assigned to their properties. This space is then equipped with a metric and the degree of (dis)similarity between two objects is the distance between the points representing the two objects in that space. This account is based on the strong assumptions that values can be assigned to all features relevant to similarity judgments, which is deemed unrealistic (and to the best of our knowledge no one has developed such an account in the context of scientific representation).

This problem is supposed to be overcome in Tversky’s contrast account (1977). This account defines a gradated notion of similarity based on a weighted comparison of properties. Weisberg has recently introduced this account into the philosophy of science where it serves as the starting point for his weighted feature matching account of model world-relations (for details see Weisberg 2012, 2013: ch. 8). Although the account has some advantages, questions remain whether it can capture the distinction between what Niiniluoto (1988: 272–274) calls “likeness” and “partial identity”. Two objects are alike to the extent that they co-instantiate similar properties (for example, a red phone box and a red London bus might be alike with respect to their colour, despite not instantiating the exact same shade of red). Two objects are partially identical to the extent that they co-instantiate identical properties. As Parker (2015: 273) notes, contrast based accounts of similarity like Weisberg’s have difficulties capturing the former, and this is often pertinent in the context of scientific representation where models and their targets need not co-instantiate the exact same property. Concerns of this sort have led Khosrowi (2020) to suggest that the notion of sharing features should be analysed in a pluralist manner. Sharing a feature sometimes means sharing the exact same feature; sometimes it means to share features which are sufficiently quantitatively close to one another; and sometimes it means having features which are themselves “sufficiently similar”.

A further question that remains for someone who uses the notion of similarity to answer to the Problem of Style and provide standards of accuracy in the manner under consideration here is whether it truly captures all of scientific practice. Similarity theorists are committed to the claim that whenever a scientific model represents its target system, this is established in virtue of a model user specifying a relevant similarity, and if the similarity holds, then the representational relationship is accurate. These universal aspirations require that the notion of similarity invoked capture the relationship that holds between diverse entities such as a basin-model of the San Francisco bay area, a tube map and an underground train system, and the Lotka-Volterra equations of predator-pray interaction. Whether all of these relationships can be captured in terms of similarity remains an open question. In addition, this view is commited to the idea that idealised aspects of scientific models, understood as dissimilarities between models and their targets, are misrepresenations and as such the view has difficulty capturing the positive epistemic role that such aspects can play (Nguyen 2020).

Another problem facing similarity based approaches concerns their treatment of the ontology of models. If models are supposed to be similar to their targets in the ways specified by theoretical hypotheses, then they must be the kind of things that can be so similar. For material models like the San Francisco Bay model (Weisberg 2013), ball and stick models of molecules (Toon 2011), the Phillips-Newlyn machine (Morgan and Boumans 2004), or model organisms (Ankeny and Leonelli 2021) this seems straightforward because they are of the same ontological kind as their respective targets. But many interesting scientific models are not like this: they are what Hacking aptly describes as “something you hold in your head rather than your hands” (1983: 216). Following Thomson-Jones (2012) we call such models non-concrete models . The question then is how such models can be similar to their targets. At the very least these models are “abstract” in the sense that they have no spatiotemporal location. But if so, then it remains unclear how they can instantiate the sorts of properties specified by theoretical hypotheses, since these properties are typically physical , and presumably being located in space and time is a necessary condition on instantiating such properties. For further discussion of this objection, and proposed solutions, see Teller (2001: 399), Thomson-Jones (2010; 2020), and Giere (2009), and Thomasson (2020).

4. The Structuralist Conception

The structuralist conception of model-representation originated in the so-called semantic view of theories that came to prominence in the second half of the 20 th century (see the SEP entry on the structure of scientific theories for further details). The semantic view was originally proposed as an account of theory structure rather than scientific representation. The driving idea behind the position is that scientific theories are best thought of as collections of models. This invites the questions: what are these models, and how do they represent their target systems? Most defenders of the semantic view of theories (with the notable exception of Giere, whose views on scientific representation were discussed in the previous section) take models to be structures, which represent their target systems in virtue of there being some kind of morphism (isomorphism, partial isomorphism, homomorphism, …) between the two.

This conception has two prima facie advantages. The first advantage is that it offers a straightforward answer to the ER-Problem (or SR-problem if the focus is on scientific representation), and one that accounts for surrogative reasoning: the mappings between the model and the target allow scientists to convert truths found in the model into claims about the target system. The second advantage concerns the applicability of mathematics. There is a time-honoured position in the philosophy of mathematics which sees mathematics as the study of structures; see, for instance Resnik (1997) and Shapiro (2000). It is a natural move for the scientific structuralist to adopt this point of view, which then provides a neat explanation of how mathematics is used in scientific modelling.

Almost anything from a concert hall to a kinship system can be referred to as a “structure”. So the first task for a structuralist account of representation is to articulate what notion of structure it employs. A number of different notions of structure have been discussed in the literature (for a review see Thomson-Jones 2011), but by far the most common is the notion of structure one finds in set theory and mathematical logic. A structure \(\mathcal{S}\) in that sense (sometimes “mathematical structure” or “set-theoretic structure”) is a composite entity consisting of the following: a non-empty set \(U\) of objects called the domain (or universe) of the structure and an indexed set \(R\) of relations on \(U\) (supporters of the partial structures approach, e.g., Da Costa and French (2003) and Bueno, French, and Ladyman (2002), use partial \(n\)-place relations, for which it may be undefined whether or not some \(n\)-tuples are in their extension). This definition of structure is widely used in mathematics and logic. We note, however, that in mathematical logic structures also contain a language and an interpretation function, interpreting symbols of the language in terms of \(U\) (see for instance Machover 1996 and Hodges 1997), which is absent from structures in the current context. It is convenient to write these as \(\mathcal{S}= \langle U, R \rangle\), where “\(\langle \, , \rangle\)” denotes an ordered tuple.

It is important to be clear on what we mean by “object” and “relation” in this context. As regards objects, all that matters from a structuralist point of view is that there are so and so many of them. Whether the objects are desks or planets is irrelevant. All we need are dummies or placeholders whose only property is “objecthood”. Similarly, when defining relations one disregards completely what the relation is “in itself”. Whether we talk about “being the mother of” or “standing to the left of” is of no concern in the context of a structure; all that matters is between which objects it holds. For this reason, a relation is specified purely extensionally: as a class of ordered \(n\)-tuples. The relation literally is nothing over and above this class. So a structure consists of dummy-objects between which purely extensionally defined relations hold.

The first basic posit of the structuralist theory of representation is that models are structures in this sense (the second is that models represent their targets by being suitably morphic to them; we discuss morphisms in the next subsection). Suppes has articulated this stance clearly when he declared that “the meaning of the concept of model is the same in mathematics and the empirical sciences” (1960 [1969]: 12), and many have followed suit. So we are presented with a clear answer to the Problem of Ontology: models are structures. The remaining issue is what structures themselves are. Are they Platonic entities, equivalence classes, modal constructs, or yet something else? In the context of a discussion of scientific representation one can push these questions off to the philosophy of mathematics (see the SEP entries on the philosophy of mathematics , nominalism in the philosophy of mathematics , and Platonism in the philosophy of mathematics for further details).

The most basic structuralist conception of scientific representation asserts that scientific models, understood as structures, represent their target systems in virtue of being isomorphic to them. An isomorphism between two structures \(\mathcal{S}\) and \(\mathcal{S}'\) is a bijective function from \(U\) to \(U'\) that preserves the relations on \(U\) (and inversely, the relations on \(U'\)). An isomorphism associates each object in \(U\) with an object in \(U'\) and pairs up each relation in \(R\) with a relation in \(R'\) so that a relation holds between certain objects in \(U\) iff the corresponding relation holds between the objects in \(U'\) that are associated with them. [ 9 ] Assume now that the target system \(T\) exhibits the structure \(\mathcal{S}_T\) and the model is the structure \(\mathcal{S}_M\). Then the model represents the target iff it is isomorphic to the target:

Structuralism 1 : A scientific model \(M\) represents its target \(T\) iff \(\mathcal{S}_T\) is isomorphic to \(\mathcal{S}_M\).

It bears noting that few adherents of the structuralist account of scientific representation, most closely associated with the semantic view of theories, explicitly defend this position (although see Ubbink 1960: 302). Representation was not the focus of attention in the semantic view, and the attribution of (something like) Structuralism 1 to its supporters is an extrapolation. Representation became a much-debated topic in the first decade of the 21 st century, and many proponents of the semantic view then either moved away from Structuralism 1 , or pointed out that they never held such a view. We turn to more advanced positions shortly, but to understand what motivates such positions it is helpful to understand why Structuralism 1 fails.

The first and most obvious problem is the same as with the similarity view: isomorphism is symmetrical and reflexive (and transitive) but representation isn’t. This problem could be addressed by replacing isomorphism with an alternative mapping. Bartels (2006), Lloyd (1984), and Mundy (1986) suggest homomorphism; van Fraassen (1980, 1997, 2008) and Redhead (2001) isomorphic embeddings; advocates of the partial structures approach prefer partial isomophisms (Bueno 1997; Bueno and French 2011; Da Costa and French 1990, 2003; French 2003, 2014; French and Ladyman 1999); and Swoyer (1991) introduces what he calls \(\Delta/\Psi\) morphisms. We refer to these collectively as “morphisms”. Pero and Suárez (2016) provide a comparative discussion of different morphisms.

These suggestions solve some, but not all problems. While many of these mappings are not symmetrical, they are all still reflexive. But even if these formal issues could be resolved in one way or another, a view based on structural mappings would still face other serious problems. For ease of presentation we discuss these problems in the context of the isomorphism view; mutatis mutandis other formal mappings suffer from the same difficulties. Like similarity, isomorphism is too inclusive: not all things that are isomorphic represent each other. In the case of similarity this case was brought home by Putnam’s thought experiment with the ant crawling on the beach; in the case of isomorphism a look at the history of science will do the job. Many mathematical structures were discovered and discussed long before they were used in science. Non-Euclidean geometries were studied by mathematicians long before Einstein used them in the context of spacetime theories, and Hilbert spaces were studied by mathematicians prior to their use in quantum theory. If representation was nothing over and above isomorphism, then we would have to conclude that Riemann discovered general relativity or that that Hilbert invented quantum mechanics. This does not seem correct, so it doesn’t seem like isomorphism on its own establishes scientific representation (Frigg 2002: 10).

Isomorphism is more restrictive than similarity: not everything is isomorphic to everything else. But isomorphism is still too abundant to correctly identify what a model represents. The root of the difficulties is that the same structures can be instantiated in different kinds of target systems. Certain geometrical structures are instantiated by many different systems; just think about how many spherical things we find in the world. The \(1/r^2\) law of Newtonian gravity is also the “mathematical skeleton” of Coulomb’s law of electrostatic attraction and the weakening of sound or light as a function of the distance to the source. The mathematical structure of the pendulum is also the structure of an electric circuit with a condenser and a solenoid (Kroes 1989). The same structure can be exhibited by more than one kind of target system, and so isomorphism by itself is too weak to identify a model’s target.

As we have seen in the last section, a misrepresentation is one that portrays its target as having features it doesn’t have. In the case of a structural account of representation, this means that the model portrays the target as having structural properties that it doesn’t have. However, isomorphism demands identity of structure: the structural properties of the model and the target must correspond to one another exactly. So a misrepresentation won’t be isomorphic to the target. By the lights of Structuralism 1 it therefore is not a representation at all. Like simple similarity accounts, Structuralism 1 conflates misrepresentation with non-representation (Suárez 2003: 234–235). Partial structures can avoid a mismatch due to a target relation being omitted in the model and hence go some way to shoring up the structuralist account (Bueno and French 2011: 888). It remains unclear, however, how they account for distortive representations (Pincock 2005).

Finally, like similarity accounts, Structuralism 1 has a problem with non-existent targets because no model can be isomorphic to something that doesn’t exist. If there is no ether, a model can’t be isomorphic to it. Hence models without target cannot represent what they seem to represent.

Most of these problems can be resolved by making moves similar to the ones that lead to Similarity 3 : introduce agents and hypothetical reasoning into the account of representation. Going through the motions one finds:

Structuralism 2 : A scientific model \(M\) represents a target system \(T\) iff there is an agent \(A\) who uses \(M\) to represent a target system \(T\) by proposing a theoretical hypothesis \(H\) specifying an isomorphism between \(\mathcal{S}_M\) and \(\mathcal{S}_T\).

This is in line with van Fraassen’s views on representation. He offers the following as the “Hauptstatz” of a theory of representation: “ There is no representation except in the sense that some things are used, made, or taken, to represent things as thus and so ” (2008: 23, original emphasis). Likewise, Bueno submits that “representation is an intentional act relating two objects” (2010: 94–95, original emphasis), and Bueno and French point out that using one thing to represent another thing is not only a function of (partial) isomorphism but also depends on “pragmatic” factors “having to do with the use to which we put the relevant models” (2011: 885).

As in the shift from Similarity 2 to Similarity 3 , this seems like a successful move, with many (although not all) of the aforementioned concerns being met. But, again, the role of isomorphism has shifted. The crucial ingredient is the agent’s intention and isomorphism has in fact become either a representational style or normative criterion for accurate representation. Let us now assess how well isomorphism fares as a response to these problems, and the others outlined above.

Structuralism’s stand on the Demarcation Problem is by and large an open question. Unlike similarity, which has been widely discussed across different domains, structural mappings are tied closely to the formal framework of set theory, and have been discussed only sparingly outside the context of the mathematized sciences. An exception is French (2003), who discusses isomorphism accounts in the context of pictorial representation. He considers in detail Budd’s (1993) account of pictorial representation and points out that it is based on the notion of a structural isomorphism between the structure of the surface of the painting and the structure of the relevant visual field. Therefore representation is the perceived isomorphism of structure (French 2003: 1475–1476) (this point is reaffirmed by Bueno and French (2011: 864–865); see Downes (2009: 423–425) and Isaac (2019) for critical discussions).

The Problem of Style is to identify representational styles and characterise them. A proposed structural mapping between the model and the target offers an obvious response to this challenge: one can represent a system by coming up with a model that is proposed to be appropriately morphic to it. This delivers the isomorphism-style, the homomorphism-style, the partial-isomorphism style and so on. We can call these “morphism-styles” when referring to them in general. Each of these styles also offers a clear-cut condition of accuracy: the representation is accurate if the hypothesised morphism holds; it is inaccurate if it doesn’t.

This is neat answer. The question is what status it has vis-à-vis the Problem of Style. Are morphism-styles merely a subgroup of styles or are they privileged? The former is uncontentious. However, the emphasis many structuralists place on structure preserving mappings suggests that they do not regard morphisms as merely one way among others to represent something. What they seem to have in mind is the stronger claim that a representation must be of that sort, or that morphism-styles are the only acceptable styles.

This claim seems to conflict with scientific practice in at least two respects. Firstly, many representations are inaccurate (and known to be) in some way. Some models distort, deform and twist properties of the target in ways that seem to undercut isomorphism, or indeed any of the proposed structure preserving mappings. Some models in statistical mechanics have an infinite number of particles and the Newtonian model of the solar system represents the sun as a perfect sphere where in reality it is fiery ball with no well-defined surface at all. It is at best unclear how isomorphism, partial or otherwise, or homomorphism can account for these kinds of idealisations. So it seems that styles of representation other than structure preserving mappings have to be recognised.

Secondly, the structuralist view is a rational reconstruction of scientific modelling, and as such it has some distance from the actual practice. Some philosophers have worried that this distance is too large and that the view is too far removed from the actual practice of science to be able to capture what matters to the practice of modelling (this is the thrust of many contributions to Morgan and Morrison 1999; see also Cartwright 1999). Although some models used by scientists may be best thought of as set theoretic structures, there are many where this seems to contradict how scientists actually talk about, and reason with, their models. Obvious examples include physical models like the San Francisco Bay model (Weisberg 2013), but also systems such as the idealized pendulum or imaginary populations of interbreeding animals. Such models have the strange property of being concrete-if-real and scientists talk about them as if they were real systems, despite the fact that they are obviously not (Godfrey-Smith 2006). Thomson-Jones (2010) dubs this “face value practice”, and there is a question whether structuralism can account for that practice.

There remains a final problem to be addressed in the context of structural accounts of scientific representation. Target systems are physical objects: atoms, planets, populations of rabbits, economic agents, etc. Isomorphism is a relation that holds between two structures and claiming that a set theoretic structure is isomorphic to a piece of the physical world is prima facie a category mistake. By definition, a morphism can only hold between two structures. If we are to make sense of the claim that the model is isomorphic to its target we have to assume that the target somehow exhibits a certain structure \(\mathcal{S}_T\). But what does it mean for a target system—a part of the physical world—to possess a structure, and where in the target system is the structure located?

There are two prominent suggestions in the literature. The first, originally suggested by Suppes (1962 [1969]), is that data models are the target-end structures represented by models. This approach faces a question whether we should be satisfied with an account of scientific representation that precludes phenomena being represented (see Bogen and Woodward (1988) for a discussion of the distinction between data and phenomena, and Brading and Landry (2006) for a discussion of the distinction in the context of scientific representation). Van Fraassen (2008) has addressed this problem and argues for a pragmatic resolution: in the context of use, there is no pragmatic difference between representing phenomena and data extracted from it (see Nguyen 2016 for a critical discussion). The alternative approach locates the target-end structure in the target system itself. One version of this approach sees structures as being instantiated in target systems. This view seems to be implicit in many versions of the semantic view, and it is explicitly held by authors arguing for a structuralist answer to the problem of the applicability of mathematics (Resnik 1997; Shapiro 1997). This approach faces underdetermination issues in that the same target can instantiate different structures. The issue can be seen as arising due to there being alternative descriptions of the system (Frigg 2006) or because a version of “Newman’s Objection” also bites in the current context (Newman 1928; see Ainsworth 2009 and Ketland 2004 for further discussion). A more radical version simply identifies targets with structures (Tegmark 2008). This approach is highly revisionary in particular when considering target systems like populations of breeding rabbits or economies. So the question remains for any structuralist account of scientific representation: where are the required target-end structures to be found?

5. The Inferential Conception

The core idea of the inferential conception is to analyse scientific representation in terms of the inferential function of scientific models. In the previous accounts discussed, a model’s inferential capacity dropped out of whatever it was that was supposed to answer the ER-problem (or SR-problem): proposed morphisms or similarity relations between models and their targets for example. The accounts discussed in this section reverse this order and explain scientific representation directly in terms of surrogative reasoning.

According to Hughes’ Denotation, Demonstration, and Interpretation (DDI) account of scientific representation (1997, 2010: ch. 5), models denote their targets; are such that model users can perform demonstrations on them; and interpret the results of such demonstrations in terms of the target. The last step is necessary because demonstrations establish results about the model itself, and in interpreting these results the model user draws inferences about the target from the model (1997: 333). Unfortunately Hughes has little to say about what it means to interpret a result of a demonstration on a model in terms of its target system, and so one has to retreat to an intuitive (and unanalysed) notion of drawing inferences about the target based on the model. [ 10 ]

Hughes is explicit that he is not attempting to answer the ER-problem, and that he does not offer denotation, demonstration, and interpretation as individually necessary and jointly sufficient conditions for scientific representation. He prefers the more

modest suggestion that, if we examine a theoretical model with these three activities in mind, we shall achieve some insight into the kind of representation that it provides. (1997: 339)

This is unsatisfactory because it ultimately remains unclear what allows scientists to use a model to draw inferences about the target, and it raises the question of what would have to be added to the DDI conditions to turn them into a full-fledged response to the ER-problem. If, alternatively, the conditions were taken to be necessary and sufficient, then the account would require further elaboration on what establishes the conditions.

Suárez argues that we should adopt a “deflationary or minimalist attitude and strategy” (2004: 770) when addressing the problem of scientific representation. Two different notions of deflationism are in operation in his account. The first is to abandon the aim of seeking necessary and sufficient conditions; necessary conditions will be good enough (2004: 771). The second notion is that we should seek “no deeper features to representation other than its surface features” (2004:771) or “platitudes” (Suárez and Solé 2006: 40), and that we should deny that an analysis of a concept “is the kind of analysis that will shed explanatory light on our use of the concept” (Suárez 2015: 39). Suárez intends his account of scientific representation to be deflationary in both senses, and dubs it “inferentialism”. Letting \(A\) stand for the model and \(B\) for the target, he offers the following analysis:

Inferentialism : “\(A\) represents \(B\) only if (i) the representational force of \(A\) points towards \(B\), and (ii) \(A\) allows competent and informed agents to draw specific inferences regarding \(B\)” (2004: 773).

The first condition addresses the Requirement of Directionality and ensures that \(A\) and \(B\) indeed enter into a representational relationship. On might worry that explaining representation in terms of representational force sheds little light on the matter as long as no analysis of representational force is offered. But Suárez resists attempts to explicate representational force in terms of a stronger relation, like denotation or reference, on grounds that this would violate deflationism (2015: 41). The second condition is in fact just the Surrogative Reasoning Condition, now taken as a necessary condition on scientific representation. Contessa (2007: 61) points out that it remains mysterious how these inferences are generated. An appeal to further analysis can, again, be blocked by appeal to deflationism because any attempt to explicate how inferences are drawn would go beyond “surface features”. So the tenability of Inferentialism in effect depends on the tenability of deflationism about scientific representation. Suárez (2015) defends deflationism by drawing analogies with three different deflationary theories about truth, Ramsey’s “redundancy” theory, Wright’s “abstract minimalism” and Horwich’s “use theory” (for more information of these theories see the SEP entry on the deflationary theory of truth ). An alternative defence builds on Brandom’s inferentialism in the philosophy of language (1994, 2000), a line of argument that is developed by de Donato Rodríguez and Zamora Bonilla (2009) and Kuorikoski and Lehtinen (2009).

Inferentialism provides a neat explanation of the possibility of misrepresentation because the inferences drawn about a target need not be true (Suárez 2004: 776). In as far as one accepts representational force as a cogent concept, targetless models are dealt with successfully because representational force (unlike denotation) does not require the existence of a target (2004: 772). Inferentialism repudiates the Representational Demarcation Problem and aims to offer an account of representation that also works in other domains such as painting (2004: 777). The account is ontologically non-committal because anything that has an internal structure that allows an agent to draw inferences can be a representation. Relatedly, since the account is supposed to apply to a wide variety of entities including equations and mathematical structures, the account implies that mathematics is successfully applied in the sciences, but in keeping with the spirit of deflationism no explanation is offered about how this is possible. The account does not directly address the Problem of Style.

In response to the difficulties with Inferentialism Contessa submits that “it is not clear why we should adopt a deflationary attitude from the start ” (2007: 50) and provides a “interpretational account” of scientific representation that is inspired by Suárez’s account, but without being deflationary. Contessa introduces the notion of an interpretation of a model, in terms of its target system, as a necessary and sufficient condition on epistemic representation (see also Ducheyne 2012 for a related account):

Interpretation : “A [model \(M\)] is an epistemic representation of a certain target [\(T\)] (for a certain user) if and only if the user adopts an interpretation of the [\(M\)] in terms of [\(T\)].” (Contessa 2007: 57; see also Contessa 2011: 126–127)

The leading idea of an interpretation is that the model user first identifies sets of relevant objects in the model and the target, and then pins down sets of properties and relations these objects instantiate both in the model and the target. The user then (a) takes \(M\) to denote \(T\); (b) takes every identified object in the model to denote exactly one object in the target (and every relevant object in the target has to be so denoted); (c) takes every property and relation in the model to denote a property or relation of the same type in the target (and, again, and every property and relation in the target has to be so denoted). A formal rendering of these conditions is what Contessa calls an “analytic interpretation” (see his 2007: 57–62 for details; he also includes an additional condition pertaining to functions in the model and target, which we suppress for brevity).

Interpretation offers a neat answer to the ER-problem. The account also explains the directionality of representation: interpreting a model in terms of a target does not entail interpreting a target in terms of a model. However, it has been noted that Interpretation has difficulty accounting for the possibility of misrepresentation, since it seems to require that the relevant objects, properties, and relations actually exist in the target (Shech 2015), although this objection turns on a very strict reading of Contessa’s account. This problem is solved in Díez’s (2020) “Ensemble-Plus-Standing-For” account of representation, which is based on conditions that rule out a mismatch concerning the number of objects in the collection. Contessa does not comment on the applicability of mathematics but since his account shares with the structuralist account an emphasis on relations and one-to-one model-target correspondence, Contessa can appeal to the same account of the applicability of mathematics as the structuralist. Like Suárez, Contessa takes his account to be universal and apply to non-scientific representations such as portraits and maps. But it remains unclear how Interpretation addresses the Problem of Style. As we have seen earlier, in particular visual representations fall into different categories and there is a question about how these can be classified within the interpretational framework. With respect to the Question of Ontology, Interpretation itself places few constraints on what scientific models are. All it requires is that they consist of objects, properties, relations, and functions (but see Contessa (2010) for further discussion of what he takes models to be, ontologically speaking).

A recent family of approaches analyses models by drawing an analogy between models and literary fiction. This analogy can be used in two ways, yielding two different version of the fiction view. The first is primarily motivated by ontological considerations rather than the question of scientific representation per se . Scientific discourse is rife with passages that appear to be descriptions of systems in a particular discipline, and the pages of textbooks and journals are filled with discussions of the properties and the behaviour of those systems. In mechanics, for instance, the dynamical properties of a system consisting of three spinning spheres with homogenous mass distributions are the focus of attention; in biology infinite populations are investigated; and in economics perfectly rational agents with access to perfect information exchange goods. Their surface structure notwithstanding, no one would mistake descriptions of such systems as descriptions of an actual system: we know very well that there are no such systems.

Thomson-Jones (2010: 284) refers to such a description as a “description of a missing system”. These descriptions are embedded in what he calls the “face value practice” (2010: 285) the practice of talking and thinking about these systems as if they were real. The face-value practice raises a number of questions. What account should be given of these descriptions and what sort of objects, if any, do they describe? Are we putting forward truth-evaluable claims when putting forward descriptions of missing systems?

The fiction view of models provides an answer: models are akin to places and characters in literary fiction and claims about them are true or false in the same way in which claims about these places and characters are true or false. Such a position has been recently defended explicitly by some authors (Frigg 2010a,b; Frigg and Nguyen 2021; Godfrey-Smith 2006; Salis 2021), but not without opposition (Giere 2009; Magnani 2012). It does bear noting that the analogy has been around for a while (Cartwright 1983; McCloskey 1990; Vaihinger 1911 [1924]). This leaves the thorny issue of how to analyse fictional places and characters. Here philosophers of science can draw on discussions from aesthetics to fill in the details about these questions (Friend 2007 and Salis 2013 provide useful reviews).

The second version of the fiction view explicitly focuses on representation. Most theories of representation we have encountered so far posit that there are model systems and construe scientific representation as a relation between two entities, the model system and the target system. Toon calls this the indirect view of representation (2012: 43). Indeed, Weisberg (2007) views this indirectness as the defining feature of modelling (see also Knuuttila and Loettgers 2017). This view contrasts with what Toon (2012: 43) and Levy (2015: 790) call a direct view of representation. This view does not recognise model systems instead aims to explain representation as a form of direct description. On this view, models provide an “imaginative description of real things” (Levy 2012: 741) such as actual pendula, and there is no such thing as a model system of which the pendulum description is literally true (Toon 2012: 43–44).

Both Toon (2012) and Levy (2015) articulate the direct view by drawing on Walton’s (1990) theory of make-believe. At the heart of this theory is the notion of a game of make-believe (see the SEP entry on imagination for further discussion). We play such a game if, for instance, when walking through a forest we imagine that stumps are bears and if we spot a stump we imagine that we spot a bear. In Walton’s terminology the stumps are props , and the rule that we imagine a bear when we see a stump is a principle of generation . Together a prop and principle of generation prescribe what is to be imagined. Walton considers a vast variety of different props, including statues and works of literary fiction. Toon focuses on the particular kind of game in which we are prescribed to imagine something of a real world object. A statue showing Napoleon on horseback (Toon 2012: 37) is a prop mandating us to imagine, for instance, that Napoleon has a certain physiognomy and certain facial expressions. When reading The War of the Worlds (2012: 39) we are prescribed to imagine that the dome of St Paul’s Cathedral has been attacked by aliens and now has a gaping hole on its western side.

The crucial move is to say that models are props in games of make believe. Specifically, material models are like the statue of Napoleon and theoretical models are like the text of The War of the Worlds : both prescribe, in their own way, to imagine something about a real object. A ball-and-stick model of a methane molecule prescribes us to imagine particular things about methane, and a model description describing a point mass bob bouncing on a perfectly elastic spring represents the real ball and spring system by prescribing imaginings about the real system. This provides the following answer to the ER-problem (Toon 2012: 62):

Direct Representation : \(M\) is a scientific representation of \(T\) iff \(M\) functions as prop in game of make-believe which prescribes imaginings about \(T\).

This account solves some of the problems posed in Section 1 : Direct Representation is asymmetrical, makes room for misrepresentation, and, given its roots in aesthetics, it renounces the Demarcation Problem. The view absolves the Problem of Ontology since models are either physical objects or descriptions, neither or which are problematic in this context. Toon remains silent on both the Problem of Style, and the applicability of mathematics.

Important questions remain. According to Direct Representation models prescribe us to imagine certain things about their target system. The account remains silent, however, on the relationship between what a model prescribes us to imagine and what a model user should actually infer about the target system, and so it offers no answer to the ER-problem. Levy (2015) identifies this as a gap in Toon’s account and proposes to fill it by invoking Yablo’s (2014) notion of “partial truth”, the idea being that a model user should take the imagined propositions to be partially true of their target systems. However, as Levy admits, there are other sorts of cases that don’t fit the mould, most notably distortive idealisations. These require a different treatment and it’s an open question what this treatment would be.

A further worry is how Direct Representation deals with targetless models. If there is no target system, then what does the model prescribe imaginings about? Toon is well aware of such models and suggests the following solution: if a model has no target it prescribes imaginings about a fictional character (2012: 76). This solution, however, comes with ontological costs, and one of the declared aims of the direct view was to avoid such costs by removing model systems from the picture. Levy (2015) aims to salvage ontological parsimony and proposes a radical move: there are no targetless models. If a (purported) model has no target then it is not a model. There remains a question, however, how this view can be squared with scientific practice where targetless models are not only common but also clearly acknowledged as such.

7. Representation-As

In Goodman’s (1976) account of aesthetic representation the idea is that a work of art does not just denote its subject, but moreover it represents it as being thus or so (see the SEP entry on Goodman’s aesthetics for further discussion). Elgin (2010) further developed this account and, crucially, suggested that it also applies to scientific representations. We first discuss Goodman and Elgin’s notion of representation-as and then consider a recent extension of their framework.

Many instances of epistemic representation are instances of what Goodman and Elgin call “representation-as”. Caricatures are paradigmatic examples: Churchill is represented as a bulldog and Thatcher is represented as a boxer. But the notion is more general: Holbein’s Portrait of Henry VIII represents Henry as imposing and powerful and Stoddart’s statue of David Hume represents him as thoughtful and wise. Using these representations we can learn about their targets, for example we can learn about a politician’s or philosopher’s personality. The leading idea of the views discussed in this section is that scientific representation works in much the same way. A model of the solar system represents it as consisting of perfect spheres; the logistic model of growth represents the population as reproducing at fixed intervals of time; and so on. In each instance, models can be used to attempt to learn about their targets by determining what the former represent the latter as being.

The locution of representation-as functions in the following way: an object \(X\) (e.g., a picture, statue, or model) represents a subject \(Y\) (e.g., a person or target system) as being thus or so \((Z)\). The question then is what establishes this sort of representational relationship. The answer requires introducing some of the concepts Goodman and Elgin use to develop their account of representation-as.

Goodman and Elgin draw a distinction between something being a representation of a \(Z\), and something being a \(Z\)-representation (Elgin 2010: 1–2; Goodman 1976: 21–26). A painting of a unicorn is a unicorn-representation because it shows a unicorn, but it is not a representation of a unicorn because there are no unicorns. Being a \(Z\)-representation is a one-place predicate that categorises representations according to their subject matter. Being a representation of something is established by denotation; it is a binary relation that holds between a symbol and the object which it denotes. The two can, but need not, coincide. Some dog-representations are representations of dogs, but not all are (e.g., a caricature of Churchill), and not all representations of dogs are dog-representations (e.g., a lightening bolt may represent the fastest greyhound at the races).

The next notion is exemplification : an object \(X\) exemplifies a property \(P\) iff \(X\) instantiates \(P\) and thereby refers back to \(P\) (Goodman 1976: 53). In the current context properties are to be understood in the widest possible sense. An item can exemplify one-place properties, multi-place properties (i.e., relations), higher order properties, structural properties, etc. Paradigmatic examples of this are samples. A chip of paint on a manufacturer’s sample card instantiates a certain colour and at the same time refers to that colour (Elgin 1983: 71). Notice that instantiation is necessary but insufficient for exemplification: the sample card does not exemplify being rectangular for example. When a object exemplifies a property it provides us with epistemic access to that property.

Representation-as is then established by combining these notions together: a \(Z\)-representation exemplifies properties associated with \(Z\)s, [ 11 ] and if the \(Z\)-representation additionally denotes \(Y\), then these properties can be imputed onto \(Y\) (cf. Elgin 2010: 10). This provides the following account of epistemic representation:

Representation-As : \(X\) is an epistemic representation of \(Y\) iff (i) \(X\) denotes \(Y\), (ii) \(X\) is a \(Z\)-representation exemplifying properties \(P_1, \ldots , P_n\), and (iii) \(X\) imputes \(P_1, \ldots , P_n\), or related properties, onto \(Y\).

Applying this in the scientific context, i.e., by letting \(X\) range over models and \(Y\) over target systems, we arrive at an answer to the ER-problem. Representation-As also answers the other problems introduced in Section 1 : it repudiates the demarcation problem and it explains the directionality of representation. It accounts for surrogative reasoning in terms of the properties imputed to the target. If \(Y\) possesses the imputed properties then the representation is accurate, but since the target doesn’t necessarily need to instantiate them it allows for the possibility of misrepresentation. Different styles can be accounted for by categorising representations in terms of different \(Z\)s, or in terms of the properties they exemplify. However, at least as stated, the account remains silent on the problem of ontology and the applicability of mathematics. We discuss below how to account for targetless models.

Representation-As raises a number of questions when applied in the scientific context. The first concerns the notion of a \(Z\)-representation. While it has intuitive appeal in the case of pictures, it is less clear how it works in the context of science. Phillips and Newlyn constructed an elaborate system of pipes and tanks, now know as the Phillips-Newlyn machine, to model an economy (see Morgan and Boumans 2004 and Barr 2000 for useful discussions). So the machine is an economy-representation. But what turns a system of pipes and tanks into an economy-representation?

Frigg and Nguyen (2016: 227–8) argue that in order to turn an object \(X\) into a scientific model, it must be interpreted in the appropriate way (note that they do not use “interpretation” in the way that Contessa uses it, as discussed above): properties that \(X\) has, qua object, are paired up with relevant \(Z\) properties and for quantitative properties, i.e., properties such as mass or flow, which take numerical values, there needs to a further association between the values of the \(X\) property and the values of the \(Z\) property to which it is mapped. In the case of the Phillips-Newlyn machine, for example, hydraulic properties of the machine are associated with economic properties and a rule is given specifying that a litre of water corresponds to certain amount of a model-economy’s currency (Frigg and Nguyen 2018).

The \(X\) and \(Z\) properties that are so associated need not exhaust the properties that \(X\) instantiates, nor do all possible \(Z\) properties need be associated with an \(X\) property. A scientific model can then be defined as a \(Z\)-representation, i.e., an object under an interpretation. This notion of a model explicitly does not presuppose a target system and hence makes room for targetless models. Models can then be seen as instantiating \(Z\)-properties under the relevant interpretation , which explains how the model can exemplify such properties.

The next issue is that exemplified properties are rarely exactly imputed onto target systems. According to Representation-As the imputed properties are either the ones exemplified by the \(Z\)-representation, “or related ones”. Frigg and Nguyen (2016: 228), building on Frigg (2010a: 125–135), prefer to be explicit about the relationship between the exemplified properties and the ones to be imputed onto the target. They do this by introducing a “key”, which explicitly associates the exemplified properties with properties to be imputed onto the target. For example, in the case of a London Tube map, the key associates particular colours with particular tube lines, and in the case of idealisations the key associates de-idealised properties with model-properties.

Gathering the various pieces together leads to the following account of representation (Frigg and Nguyen 2016: 229):

DEKI: Let \(M = \langle X, I \rangle\) be a model, where \(X\) is an object and \(I\) an interpretation. Let \(T\) be the target system. \(M\) represents \(T\) as \(Z\) iff all of the following conditions are satisfied:

• \(M\) denotes \(T\).
• \(M\) exemplifies \(Z\)-properties \(P_1, \ldots , P_n\).
• \(M\) comes with key \(K\) associating the set \(\{P_1, \ldots , P_n\}\) with a (possibly identical) set of properties \(\{Q_1, \ldots , Q_m\}\).
• \(M\) imputes at least one of the properties \(Q_1, \ldots , Q_m\) to \(T\).

\(M\) is a scientific representation of \(T\) iff \(M\) represents \(T\) as \(Z\) as defined in (i)–(iv).

The moniker “DEKI” highlights the account’s key features: denotation, exemplification, keying-up and imputation. DEKI answers the problems from Section 1 in much the same way as Representation-As did. However, it adds to the latter in at least three ways. Firstly, the conditions given make it clear what makes scientific models \(Z\)-representations in the first place: interpretations. Secondly, it makes explicit that the properties exemplified by the model need not be imputed exactly onto the target, and highlights the need to investigate keys specifying the relationship between properties in models and the properties that models actually impute onto their targets. Finally, it makes explicit how to account for targetless models. A scientific model that fails to denote a target system can nevertheless be a \(Z\)-representation. A model of a bridge that is never built is still a bridge-representation, which exemplifies properties related to bridges (stability and so on), despite the fact that it is not a representation of anything. However, as in the case of Representation-As questions remain with respect to the problem of ontology and the applicability of mathematics.

• Abell, Catherine, 2009, “Canny Resemblance”, Philosophical Review , 118(2): 183–223. doi:10.1215/00318108-2008-041
• Ainsworth, Peter, 2009, “Newman’s Objection”, The British Journal for the Philosophy of Science , 60(1): 135–71. doi:10.1093/bjps/axn051
• Ankeny, Rachel, & Leonelli, Sabina, 2021, Model Organisms, Cambridge: Cambridge University Press.
• Anscombe, G. E. M. 2000, Intention (2nd ed.), Cambridge, MA: Harvard University Press.
• Aronson, Jerrold L., Rom Harré, and Eileen Cornell Way, 1995, Realism Rescued: How Scientific Progress Is Possible , Chicago: Open Court.
• Bailer-Jones, Daniela M., 2003, “When Scientific Models Represent”, International Studies in the Philosophy of Science , 17(1): 59–74. doi:10.1080/02698590305238
• Bartels, Andreas, 2006, “Defending the Structural Concept of Representation”, Theoria , 21(1): 7–19.
• Barr, Nicholas, 2000, “The History of the Phillips Machine”, in, A. W. H. Phillips: Collected Works in Contemporary Perspective , Robert Leeson (ed.), 89–114, Cambridge: Cambridge University Press.
• Boesch, Brandon, 2017, “There Is a Special Problem of Scientific Representation”, Philosophy of Science , 84(5): 970–981. doi:10.1086/693989
• –––, 2019, “The Means-End Account of Scientific, Representational Actions”, Synthese , 196: 2305–2322. doi: 10.1007/s11229-017-1537-2
• –––, 2021, “Scientific Representation and Dissimilarity”, Synthese , 198: 5495–5513. doi:10.1007/s11229-019-02417-0
• Bogen, James and James Woodward, 1988, “Saving the Phenomena”, Philosophical Review , 97(3): 303–52. doi:10.2307/2185445
• Bolinska, Agnes, 2013, “Epistemic Representation, Informativeness and the Aim of Faithful Representation”, Synthese , 190(2): 219–34. doi:10.1007/s11229-012-0143-6
• –––, 2016, “Successful Visual Epistemic Representation”, Studies in History and Philosophy of Science , 56: 153–160. doi:10.1016/j.shpsa.2015.09.005
• Brading, Katherine and Elaine Landry, 2006, “Scientific Structuralism: Presentation and Representation”, Philosophy of Science , 73: 571–81.
• Brandom, Robert B., 1994, Making It Explicit: Reasoning, Representing and Discursive Commitment , Cambridge MA: Harvard University Press.
• –––, 2000, Articulating Reasons: An Introduction to Inferentialism , Cambridge MA: Harvard University Press.
• Budd, Malcolm, 1993, “How Pictures Look”, in Virtue and Taste , D. Knowles and J. Skorupski (eds.), 154–75. Oxford: Blackwell.
• Bueno, Otávio, 1997, “Empirical Adequacy: A Partial Structure Approach”, Studies in the History and Philosophy of Science , 28(4): 585–610. doi:10.1016/S0039-3681(97)00012-5
• –––, 2010, “Models and Scientific Representations”, in New Waves in Philosophy of Science , P. Magnus and J. Busch (eds.), 94–111. Basingstoke: Palgrave Macmillan.
• Bueno, Otávio and Steven French, 2011, “How Theories Represent”, The British Journal for the Philosophy of Science , 62(4): 857–94. doi:10.1093/bjps/axr010
• Bueno, Otávio, Steven French, and James Ladyman 2002, “On Representing the Relationship between the Mathematical and the Empirical”, Philosophy of Science , 69(3): 452–73. doi:10.1086/342456
• Callender, Craig and Jonathan Cohen, 2006, “There Is No Special Problem About Scientific Representation”, Theoria , 21(1): 67–84.
• Cartwright, Nancy, 1983, How the Laws of Physics Lie , Oxford: Oxford University Press.
• –––, 1999, The Dappled World: A Study of the Boundaries of Science , Cambridge: Cambridge University Press.
• Contessa, Gabriele, 2007, “Scientific Representation, Interpretation, and Surrogative Reasoning”, Philosophy of Science , 74(1): 48–68. doi:10.1086/519478
• –––, 2010, “Scientific Models and Fictional Objects”, Synthese , 172: 215–29. doi:10.1007/s11229-009-9503-2
• –––, 2011, “Scientific Models and Representation”, in The Continuum Companion to the Philosophy of Science , Steven French and Juha Saatsi (eds.), London: Continuum Press, 120–37.
• Da Costa, Newton C.A. and Steven French, 1990, “The Model-Theoretic Approach to the Philosophy of Science”, Philosophy of Science , 57(2): 248–65. doi:10.1086/289546
• –––, 2003, Science and Partial Truth: A Unitary Approach to Models and Scientific Reasoning , Oxford: Oxford University Press.
• de Donato Rodríguez, Xavier and Jesús Zamora Bonilla, 2009, “Credibility, Idealisation, and Model Building: An Inferential Approach”, Erkenntnis , 70(1): 101–18. doi:10.1007/s10670-008-9139-5
• Decock, Lieven and Igor Douven, 2011, “Similarity after Goodman”, Review of Philosophy and Psychology , 2(1): 61–75. doi:10.1007/s13164-010-0035-y
• Díez, Jose, 2020, “An Ensemble-Plus-Standing-For Account of Scientific Representation: No Need For (Unnecessary) Abstract Objects”, in Abstract Objects. For and Against , J. L. Falguera and C. Martínez-Vidal (eds.), Cham: Springer, 133–149.
• Donnellan, Keith S., 1968, “Putting Humpty Dumpty Together Again”, Philosophical Review , 77(2): 203–15. doi:10.2307/2183321
• Downes, Stephen M., 2009, “Models, Pictures, and Unified Accounts of Representation: Lessons from Aesthetics for Philosophy of Science”, Perspectives on Science , 17: 417–28.
• –––, 2021, Models and Modelling in The Sciences. A Philosophical Introduction , New York: Routledge.
• Ducheyne, Steffen, 2012, “Scientific Representations as Limiting Cases”, Erkenntnis , 76(1): 73–89. doi:10.1007/s10670-011-9309-8
• Elgin, Catherine Z., 1983, With Reference to Reference , Indianapolis: Hackett.
• –––, 2010, “Telling Instances”, in Frigg and Hunter 2010: 1–18.
• Elkins, James, 1999, The Domain of Images , Ithaca and London: Cornell University Press.
• French, Steven, 2003, “A Model-Theoretic Account of Representation (or, I Don’t Know Much About Art…But I Know It Involves Isomorphism)”, Philosophy of Science , 70(5): 1472–83. doi:10.1086/377423
• –––, 2014, The Structure of the World. Metaphysics and Representation , Oxford: Oxford University Press.
• French, Steven and James Ladyman, 1999, “Reinflating the Semantic Approach”, International Studies in the Philosophy of Science , 13(2): 103–21. doi:10.1080/02698599908573612
• Friend, Stacie, 2007, “Fictional Characters”, Philosophy Compass , 2(2): 141–56. doi:10.1111/j.1747-9991.2007.00059.x
• Frigg, Roman, 2002, “Models and Representation: Why Structures Are Not Enough”, Measurement in Physics and Economics Project Discussion Paper Series , DP MEAS 25/02. [ Frigg 2002 available online ]
• –––, 2006, “Scientific Representation and the Semantic View of Theories”, Theoria , 21(1): 49–65.
• –––, 2010a, “Fiction and Scientific Representation”, in Frigg and Hunter 2010: 97–138.
• –––, 2010b, “Models and Fiction”, Synthese , 172: 251–68. doi:10.1007/s11229-009-9505-0
• Frigg, Roman and Matthew C. Hunter (eds.), 2010, Beyond Mimesis and Convention: Representation in Art and Science , Berlin and New York: Springer.
• Frigg, Roman and James Nguyen, 2016, “The Fiction View of Models Reloaded”, The Monist , 99(3): 225–42.
• –––, 2017, “Models and Representation”, in Magnani and Bertolotti (2017): 49–102.
• –––, 2018, “The Turn of the Valve: Representing with Material Models”, European Journal for Philosophy of Science , 8(2): 205–224. doi:10.1007/s13194-017-0182-4
• –––, 2020, Modelling Nature. An Opinionated Introduction to Scientific Representation , New York: Springer.
• –––, 2021 “Seven Myths about the Fiction View of Models”, in Models and Idealizations in Science. Artifactual and Fictional Approaches , Alejandro Casini and Juan Redmond (eds.), Cham: Springer, 133–157.
• Gelfert, Axel, 2016, How To Do Science With Models: A Philosophical Primer , Cham: Springer.
• –––, forthcoming, “Models and Representation”, in Magnani and Bertolotti (eds.) forthcoming.
• Giere, Ronald N., 1988, Explaining Science: A Cognitive Approach , Chicago: Chicago University Press.
• –––, 2004, “How Models Are Used to Represent Reality”, Philosophy of Science , 71(5): 742–52. doi:10.1086/425063
• –––, 2009, “Why Scientific Models Should Not Be Regarded as Works of Fiction”, in Fictions in Science. Philosophical Essays on Modelling and Idealization , Mauricio Suárez (ed.), London: Routledge, 248–58.
• –––, 2010, “An Agent-Based Conception of Models and Scientific Representation”, Synthese , 172: 269–81. doi:10.1007/s11229-009-9506-z
• Glymour, Clark, 2013, “Theoretical Equivalence and the Semantic View of Theories”, Philosophy of Science , 80(2): 286–97. doi:10.1086/670261
• Godfrey-Smith, Peter 2006. “The Strategy of Model-Based Science”, Biology and Philosophy , 21: 725–40.
• Goodman, Nelson, 1972, “Seven Strictures on Similarity”, in Problems and Projects , Nelson Goodman (ed.), Indianapolis and New York: Bobs-Merril, 437–46.
• –––, 1976, Languages of Art , Indianapolis and Cambridge: Hackett, 2nd edition.
• Hacking, Ian, 1983, Representing and Intervening: Introductory Topics in the Philosophy of Natural Science , Cambridge: Cambridge University Press.
• Halvorson, Hans, 2012, “What Scientific Theories Could Not Be”, Philosophy of Science , 79(2): 183–206. doi:10.1086/664745
• Hartmann, Stephan, 1995, “Models as a Tool for Theory Construction: Some Strategies of Preliminary Physics”, in Theories and Models in Scientific Processes (Poznan Studies in the Philosophy of Science and the Humanities 44) , William E. Herfel, Wladiyslaw Krajewski, Ilkka Niiniluoto and Ryszard Wojcicki (eds.), Amsterdam and Atlanta: Rodopi, 49–67.
• Hodges, Wilfrid, 1997, A Shorter Model Theory , Cambridge: Cambridge University Press.
• Hughes, Richard I.G., 1997, “Models and Representation”, Philosophy of Science , 64: S325–S36. doi:10.1086/392611
• –––, 2010, The Theoretical Practises of Physics: Philosophical Essays , Oxford: Oxford University Press.
• Isaac, A. M. C., 2019, “The Allegory of Isomorphism”, AVANT. Trends in Interdisciplinary Studies , X(3): 1–23.
• Ketland, Jeffrey, 2004, “Empirical Adequacy and Ramsification”, The British Journal for the Philosophy of Science , 55(2): 287–300. doi:10.1093/bjps/55.2.287
• Khosrowi, Donal, 2020, “Getting Serious About Shared Features”, The British Journal for the Philosophy of Science , 71(2): 523–546. doi:10.1093/bjps/axy029
• Knuuttila, Tarja, 2005, “Models, Representation, and Mediation”, Philosophy of Science , 72(5): 1260–1271. doi:10.1086/508124
• –––, 2011, “Modelling and Representing: An Artefactual Approach to Model-Based Representation”, Studies in History and Philosophy of Science , 42(2): 262–71.
• Knuuttila, Tarja and Andrea Loettgers, 2017, “Modelling as Indirect Representation? The Lotka–Volterra Model Revisited”, The British Journal for the Philosophy of Science , 68(4): 1007–1036. doi: 10.1093/bjps/axv055
• Kroes, Peter, 1989, “Structural Analogies between Physical Systems”, The British Journal for the Philosophy of Science , 40(2): 145–54. doi:10.1093/bjps/40.2.145
• Kuorikoski, Jaakko and Aki Lehtinen, 2009, “Incredible Worlds, Credible Results”, Erkenntnis , 70(1): 119–131. doi:10.1007/s10670-008-9140-z
• Laurence, Stephen and Eric Margolis, 1999, “Concepts and Cognitive Science”, in Concepts: Core Readings , Stephen Laurence and Eric Margolis (eds.), Cambridge MA: MIT Press, 3–81.
• Levy, Arnon, 2012, “Models, Fictions, and Realism: Two Packages”, Philosophy of Science , 79(5): 738–48. doi:10.1086/667992
• –––, 2015, “Modeling without Models”, Philosophical Studies , 172(3): 781–98. doi:10.1007/s11098-014-0333-9
• Levy, Arnon and Peter Godfrey-Smith (eds.), 2020, The Scientific Imagination. Philosophical and Psychological Perspectives , New York: Oxford University Press
• Liu, Chuang, 2013, “Deflationism on Scientific Representation”, in EPSA Perspectives and Foundational Problems in Philosophy of Science , Vassilios Karakostas and Dennis Dieks (eds.), Springer, 93–102.
• –––, 2015, “Re-inflating the Conception of Scientific Representation”, International Studies in the Philosophy of Science , 29(1): 51–59. doi:10.1080/02698595.2014.979671
• Lloyd, Elisabeth, 1984, “A Semantic Approach to the Structure of Population Genetics”, Philosophy of Science , 51(2): 242–64. doi:10.1086/289179
• Lopes, Dominic, 2004, Understanding Pictures , Oxford: Oxford University Press.
• Lynch, Michael and Steve Woolgar, 1990, Representation in Scientific Practice , Cambridge MA: MIT Press.
• Machover, Moshe, 1996, Set Theory, Logic and Their Limitations , Cambridge: Cambridge University Press.
• MacKay, Alfred F., 1968, “Mr. Donnellan and Humpty Dumpty on Referring”, Philosophical Review , 77(2): 197–202. doi:10.2307/2183320
• Magnani, Lorenzo, 2012, “Scientific Models Are Not Fictions: Model-Based Science as Epistemic Warfare”, in Philosophy and Cognitive Science: Western and Eastern Studies , Lorenzo Magnani and Ping Li (eds.), Berlin-Heidelberg: Springer-Verlag, 1–38.
• Magnani, Lorenzo and Tommaso Bertolotti (eds.), 2017, Springer Handbook of Model-Based Science , Berlin and New York: Springer.
• Mäki, Uskali, 2009, “MISSing the World. Models as Isolations and Credible Surrogate Systems”, Erkenntnis , 70(1): 29–43. doi:10.1007/s10670-008-9135-9
• –––, 2011, “Models and the Locus of Their Truth”, Synthese , 180(1): 47–63. doi:10.1007/s11229-009-9566-0
• McCloskey, Donald, N., 1990, “Storytelling in Economics”, in Narrative in Culture. The Uses of Storytelling in the Sciences, Philosophy, and Literature , Christopher Nash (ed.), London: Routledge, 5–22.
• Morgan, Mary and Marcel Boumans, 2004, “Secrets Hidden by Two-Dimensionality: The Economy as a Hydraulic Machine”, in Models: The Third Dimension of Science , Soraya de Chadarevian and Nick Hopwood (eds.), Stanford: Standford University Press, 369–401.
• Morgan, Mary and Margaret Morrison, 1999, Models as Mediators: Perspectives on Natural and Social Science , Cambridge: Cambridge University Press
• Morrison, Margaret, 2008, “Models as Representational Structures”, in Nancy Cartwright’s Philosophy of Science , Stephan Hartmann, Carl Hoefer, and Luc Bovens (eds.), New York: Routledge, 67–90.
• Mundy, Brent, 1986, “On the General Theory of Meaningful Representation”, Synthese , 67(3): 391–437.
• Newman, M.H.A., 1928, “Mr. Russell’s ‘Causal Theory of Perception’”, Mind , 37(146): 137–48. doi:10.1093/mind/XXXVII.146.137
• Nguyen, James, 2016, “On the Pragmatic Equivalence between Representing Data and Phenomena”, Philosophy of Science , 83(2): 171–91. doi:10.1086/684959
• –––, 2020, “It's Not a Game: Accurate Representation with Toy Models”, The British Journal for the Philosophy of Science , 71(3): 1013–1041. doi:10.1093/bjps/axz010
• Niiniluoto, Ilkka, 1988, “Analogy and Similarity in Scientific Reasoning”, in Analogical Reasoning: Perspectives of Artificial Intelligence, Cognitive Science, and Philosophy , D.H. Helman (ed.), Dordrecht: Kluwer, 271–98.
• Parker, Wendy S., 2015, “Getting (Even More) Serious About Similarity”, Biology and Philosophy , 30(2): 267–76. doi:10.1007/s10539-013-9406-y
• –––, 2020, “Model Evaluation: An Adequacy-for-Purpose View”, Philosophy of Science , 87(3): 457–477. doi:10.1086/708691
• Perini, Laura, 2010, “Scientific Representation and the Semiotics of Pictures”, in New Waves in the Philosophy of Science , P.D Magnus and J. Busch (eds.), New York: Macmilan, 131–54.
• Pero, Francesca and Maricio Suárez, 2016, “Varieties of Misrepresentation and Homomorphism”, European Journal for Philosophy of Science , 6(1): 71–90. doi:10.1007/s13194-015-0125-x
• Peschard, Isabelle, 2011, “Making Sense of Modeling: Beyond Representation”, European Journal for Philosophy of Science , 1(3): 335–52. doi:10.1007/s13194-011-0032-8
• Pincock, Christopher, 2005, “Overextending Partial Structures: Idealization and Abstraction”, Philosophy of Science , 72(5): 1248–59. doi:10.1086/508123
• –––, 2012, Mathematics and Scientific Representation , Oxford: Oxford University Press.
• Portides, Demetris, 2017, “Models and Theories”, in Magnani and Bertolotti (2017): 25–48.
• Poznic, Michael, 2016, “Representation and Similarity: Suárez on Necessary and Sufficient Conditions of Scientific Representation”, Journal for General Philosophy of Science , 47(2): 331–347. doi:10.1007/s10838-015-9307-7
• –––, 2018, “Thin Versus Thick Accounts Of Scientific Representation”, Synthese , 195(8): 3433–3451. doi:10.1007/s11229-017-1374-3
• Putnam, Hilary, 1981, Reason, Truth, and History , Cambridge: Cambridge University Press.
• –––, 2002, The Collapse of the Fact-Value Distinction , Cambridge, MA: Harvard University Press.
• Quine, Willard Van Orman, 1969, Ontological Relativity and Other Essays , New York: Columbia University Press.
• Redhead, Michael, 2001, “The Intelligibility of the Universe”, in Philosophy at the New Millennium , Anthony O’Hear (ed.), Cambridge: Cambridge University Press, 73–90.
• Resnik, Michael D., 1997, Mathematics as a Science of Patterns , Oxford: Oxford University Press.
• Rusanen, Anna-Mari and Otto Lappi, 2012, “An Information Semantic Account of Scientific Models”, in EPSA Philosophy of Science: Amsterdam 2009 , Henk W. de Regt, Stephan Hartmann and Samir Okasha (eds.), Springer, 315–28.
• Ruyant, Quentin, 2021, “True Griceanism: Filling the Gaps in Callender and Cohen’s Account of Scientific Representation”, Philosophy of Science , 88(2): 533–553. doi: 10.1086/712882
• Salis, Fiora, 2013, “Fictional Entities”, in Online Companion to Problems in Analytic Philosophy , João Branquinho and Ricardo Santos (eds.), Lisbon: Centre of Philosophy, University of Lisbon. [ Salis 2013 available online ]
• –––, 2021, “The New Fiction View of Models”, The British Journal for the Philosophy of Science , 72(3): 717–742. doi: 10.1093/bjps/axz015
• Shapiro, Stewart, 1997, Philosophy of Mathematics: Structure and Ontology , Oxford: Oxford University Press.
• –––, 2000, Thinking About Mathematics , Oxford: Oxford University Press.
• Shech, Elay, 2015, “Scientific Misrepresentation and Guides to Ontology: The Need for Representational Code and Contents”, Synthese , 192(11): 3463–3485. doi:10.1007/s11229-014-0506-2.
• Shepard, Roger N., 1980, “Multidimensional Scaling, Tree-Fitting, and Clustering”, Science , 210: 390–98. doi:10.1126/science.210.4468.390
• Suárez, Mauricio, 2003, “Scientific Representation: Against Similarity and Isomorphism”, International Studies in the Philosophy of Science , 17(3): 225–44. doi:10.1080/0269859032000169442
• –––, 2004, “An Inferential Conception of Scientific Representation”, Philosophy of Science , 71(5): 767–779. doi:10.1086/421415
• –––, 2015, “Deflationary Representation, Inference, and Practice”, Studies in History and Philosophy of Science , 49: 36–47.
• Suárez, Mauricio and Albert Solé, 2006, “On the Analogy between Cognitive Representation and Truth”, Theoria , 21(1): 39–48.
• Suppes, Patrick, 1960 [1969], “A Comparison of the Meaning and Uses of Models in Mathematics and the Empirical Sciences”, reprinted in Suppes 1969: 10–23.
• –––, 1962 [1969], “Models of Data”, reprinted in Suppes 1969: 24–35.
• –––, 1969, Studies in the Methodology and Foundations of Science: Selected Papers from 1951 to 1969 , Dordrecht Reidel.
• Swoyer, Chris, 1991, “Structural Representation and Surrogative Reasoning”, Synthese , 87(3): 449–508. doi:10.1007/BF00499820
• Tegmark, Max, 2008, “The Mathematical Universe”, Foundations of Physics , 38(2): 101–50. doi:10.1007/s10701-007-9186-9
• Teller, Paul, 2001, “Twilight of the Perfect Model Model”, Erkenntnis , 55(3): 393–415. doi:10.1023/A:1013349314515
• Thomasson, Amie. L., 2020, “If Models Were Fictions, Then What Would They Be?”, in Levy and Godfrey-Smith 2021: 51–74.
• Thomson-Jones, Martin, 2010, “Missing Systems and Face Value Practice”, Synthese , 172: 283–99. doi:10.1007/s11229-009-9507-y
• –––, 2011, “Structuralism About Scientific Representation”, in Scientific Structuralism , Alisa Bokulich and Peter Bokulich (eds.), Dordrecht: Springer, 119–41.
• –––, 2012, “Modeling without Mathematics”, Philosophy of Science , 79(5): 761–72. doi:10.1086/667876
• –––, 2020, “Realism About Missing Systems”, in Levy and Godfrey-Smith 2021: 75–101.
• Toon, Adam, 2010, “Models as Make-Believe”, in Frigg and Hunter 2010: 71–96.
• –––, 2011, “Playing with Molecules”, Studies in History and Philosophy of Science , 42(4): 580–89.
• –––, 2012, Models as Make-Believe. Imagination, Fiction and Scientific Representation , Basingstoke: Palgrave Macmillan.
• Tversky, Amos, 1977, “Features of Similarity”, Psychological Review , 84(4): 327–52. doi:10.1037/0033-295X.84.4.327
• Ubbink, J.B, 1960, “Model, Description and Knowledge”, Synthese , 12(2): 302–19. doi:10.1007/BF00485108
• Vaihinger, Hans, 1911 [1924], The Philosophy of ‘as If’: A System of the Theoretical, Practical, and Religious Fictions of Mankind , 1924 English Translation, London: Kegan Paul.
• van Fraassen, Bas C., 1980, The Scientific Image , Oxford: Oxford University Press.
• –––, 1997, “Structure and Perspective: Philosophical Perplexity and Paradox”, in Logic and Scientific Methods , Marisa L. Dalla Chiara (ed.), Dordrecht: Kluwer, 511–30.
• –––, 2002, The Empirical Stance , New Haven and London: Yale University Press.
• –––, 2008, Scientific Representation: Paradoxes of Perspective , Oxford: Oxford University Press.
• Walton, Kendal L., 1990, Mimesis as Make-Believe: On the Foundations of the Representational Arts , Cambridge MA.: Harvard University Press.
• Weisberg, Michael, 2007, “Who Is a Modeler?” The British Journal for the Philosophy of Science , 58(2): 207–33. doi:10.1093/bjps/axm011
• –––, 2012, “Getting Serious about Similarity” Philosophy of Science , 59(5): 785–94. doi:10.1086/667845
• –––, 2013, Simulation and Similarity: Using Models to Understand the World , Oxford: Oxford University Press.
• Wigner, Eugene, 1960, “The Unreasonable Effectiveness of Mathematics in the Natural Sciences”, Communications on Pure and Applied Mathematics , 13: 1–14.
• Yablo, Stephen, 2014, Aboutness , Princeton: Princeton University Press.

How to cite this entry . Preview the PDF version of this entry at the Friends of the SEP Society . Look up topics and thinkers related to this entry at the Internet Philosophy Ontology Project (InPhO). Enhanced bibliography for this entry at PhilPapers , with links to its database.

• Scientific Representation , entry by Brandon Boesch (U. South Carolina), in the Internet Encyclopedia of Philosophy .

Goodman, Nelson: aesthetics | imagination | mathematics, philosophy of | mathematics, philosophy of: nominalism | mathematics, philosophy of: Platonism | measurement: in science | models in science | reference | scientific realism | scientific theories: structure of | theoretical terms in science | truth: deflationism about

Copyright © 2021 by Roman Frigg < r . p . frigg @ lse . ac . uk > James Nguyen < j . nguyen1 @ lse . ac . uk >

• Accessibility

Support SEP

Mirror sites.

View this site from another server:

• Info about mirror sites

The Stanford Encyclopedia of Philosophy is copyright © 2023 by The Metaphysics Research Lab , Department of Philosophy, Stanford University

Library of Congress Catalog Data: ISSN 1095-5054

Why Some Theoretically Possible Representations of Natural Numbers Were Historically Used and Some Were Not: An Algorithm-Based Explanation

• First Online: 19 September 2023

Cite this chapter

• Christian Servin 4 ,
• Olga Kosheleva 5 &
• Vladik Kreinovich 6  

Part of the book series: Studies in Systems, Decision and Control ((SSDC,volume 484))

138 Accesses

Historically, people have used many ways to represent natural numbers: from the original “unary” arithmetic, where each number is represented as a sequence of, e.g., cuts (4 is IIII) to modern decimal and binary systems. However, with all this variety, some seemingly reasonable ways of representing natural numbers were never used. For example, while it may seem reasonable to represent numbers as products—e.g., as products of prime numbers—such a representation was never used in history. So why some theoretically possible representations of natural numbers were historically used and some were not? In this paper, we propose an algorithm-based explanation for this different: namely, historically used representations have decidable theories—i.e., for each such representation, there is an algorithm that, given a formula, decides whether this formula is true or false, while for un-used representations, no such algorithm is possible.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

• Available as PDF
• Read on any device
• Instant download
• Own it forever
• Available as EPUB and PDF
• Durable hardcover edition
• Dispatched in 3 to 5 business days
• Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

A. Bés, Undecidable extensions of Büchi arithmetic and Cobham-Semënov theorem. J. Symb. Logic 62 (4), 1280–1296 (1997)

Article   MATH   Google Scholar  

C.B. Boyer, U.C. Merzbach, History of Mathematics (Wiley, Hoboken, New Jersey, 2011)

MATH   Google Scholar  

P. Hieronymi, C. Schulz, A strong version of Cobham’s theorem (2021). arXiv:2110.11858

A.L. Semenov, Logical theories of one-place functions on the set of natural numbers. Izvestiya: Math. 22 (3), 587–618 (1984)

Google Scholar  

R. Villemaire, The theory of \(\langle N, +, V_k, V_l\rangle \) is undecidable. Theor. Comput. Sci. 106 (2), 337–349 (1992)

Article   MathSciNet   Google Scholar  

Download references

Acknowledgements

This work was supported in part by the National Science Foundation grants 1623190 (A Model of Change for Preparing a New Generation for Professional Practice in Computer Science), and HRD-1834620 and HRD-2034030 (CAHSI Includes), and by the AT&T Fellowship in Information Technology.

It was also supported by the program of the development of the Scientific-Educational Mathematical Center of Volga Federal District No. 075-02-2020-1478, and by a grant from the Hungarian National Research, Development and Innovation Office (NRDI).

The authors are grateful to Mikhail Starchak for valuable discussions.

Author information

Authors and affiliations.

Information Technology Systems Department, El Paso Community College (EPCC), 919 Hunter Dr., El Paso, TX, 79915-1908, USA

Christian Servin

Department of Teacher Education, University of Texas at El Paso, 500 W. University El Paso, Texas, 79968, USA

Olga Kosheleva

Department of Computer Science, University of Texas at El Paso, 500 W. University El Paso, Texas, 79968, USA

Vladik Kreinovich

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Vladik Kreinovich .

Editor information

Editors and affiliations.

Department of Computer Science, University of Texas at El Paso, El Paso, TX, USA

Martine Ceberio

Rights and permissions

Reprints and permissions

Copyright information

© 2023 The Author(s), under exclusive license to Springer Nature Switzerland AG

About this chapter

Servin, C., Kosheleva, O., Kreinovich, V. (2023). Why Some Theoretically Possible Representations of Natural Numbers Were Historically Used and Some Were Not: An Algorithm-Based Explanation. In: Ceberio, M., Kreinovich, V. (eds) Uncertainty, Constraints, and Decision Making. Studies in Systems, Decision and Control, vol 484. Springer, Cham. https://doi.org/10.1007/978-3-031-36394-8_24

Download citation

DOI : https://doi.org/10.1007/978-3-031-36394-8_24

Published : 19 September 2023

Publisher Name : Springer, Cham

Print ISBN : 978-3-031-36393-1

Online ISBN : 978-3-031-36394-8

eBook Packages : Intelligent Technologies and Robotics Intelligent Technologies and Robotics (R0)

Share this chapter

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Publish with us

Policies and ethics

• Find a journal
• Track your research

• The Open University
• Guest user / Sign out
• Study with The Open University

My OpenLearn Profile

Personalise your OpenLearn profile, save your favourite content and get recognition for your learning

About this free course

Become an ou student, download this course, share this free course.

Start this free course now. Just create an account and sign in. Enrol and complete the course for a free statement of participation or digital badge if available.

2.3 Grice on natural and non-natural meaning

Ironically, the word ‘meaning’ has many different meanings. There are four occurrences of ‘mean’ (or ‘meaning’ or ‘meant’, etc.), italicised, in the following paragraph:

Roberto's instructor had been mean to put it so bluntly, but she was probably correct that his short legs meant he would never be a great dancer. He turned into the narrow alleyway, meaning to take a shortcut home. His life no longer seemed to have any meaning .

Here is the paragraph again, with each of the four occurrences of ‘mean’, ‘meant’ and ‘meaning’ replaced with an appropriate synonym.

Roberto's instructor had been cruel to put it so bluntly, but she was probably correct that his short legs were bound to result in his never being a great dancer. He turned into the narrow alleyway, intending to take a shortcut home. His life no longer seemed to have any purpose .

There is no good reason to demand of a theory of meaning that it give an account of every kind of meaning. It may turn out that there is some underlying unity to the uses of ‘mean’ (or ‘means’, ‘meant’, ‘meaning’) on display here, but that is not something on which we should insist.

In view of the plethora of meanings of 'meaning’, Grice proposes to set aside those that are not his immediate concern and to focus on understanding the nature of those that are. One kind of meaning that is left over is defined by Grice in terms of the speaker's intentions. This is a good candidate for being the kind of meaning we are interested in, i.e. the meaning utterances have that accounts for the role they play in communication. But before coming to what he says about this kind of meaning, we need to see which kinds of meaning he sets to one side as confusing distractions.

Grice begins his paper (Reading 1) by making an important distinction between two species of meaning that it is particularly easy to confuse, which he labels natural meaning and non-natural meaning . The kind of meaning he later defines in terms of speakers’ intentions is non-natural meaning. Natural meaning is the kind being attributed in claim (a):

(a) ‘Those spots on your face mean you have measles .

This claim could be true only if the italicised sub-sentence is true, i.e. only if you really do have measles. If you had spots but you didn't have measles, the spots would not mean that you had measles. They would have to have some other source. Contrast this with claim (b), which uses ‘mean’ in its non-natural sense:

(b) ’The spots in the arrangement below mean you have measles .’

This whole assertion would be true even if the italicised sub-sentence was false. That is, an assertion of (b) would still be correct even if you did not have measles. Generalising, the difference between the two kinds of meaning is this: it is consistent with something's having non-natural meaning that what it non-naturally means is false; but it is not consistent with something's having natural meaning that what it naturally means is false. (In the paper, Grice notes other differences, but this is the main one.)

Grice's purpose in making this distinction is merely to avoid confusion. He sets natural meaning (or ‘meaning n ’ as he calls it) to one side and moves on to developing a theory of non-natural meaning (‘meaning nn ’), the kind he is more interested in. His partiality has to do with the fact that examples of meaning that involve language are typically cases of meaning nn , and no one has so far come up with a good theory of meaning nn . Natural meaning, by contrast, does not really have much to do with the meaning of words or utterances, and is in any case relatively non-mysterious. ‘ X means n that p ’ can be understood as a substitute for one or other of various simple phrases, including:

X causes it to be the case that p

X is conclusive evidence for p

X is not possible unless p is true

X entails that p

Natural meaning is mentioned later in his paper, but only in order to clear up potential confusions, not because Grice is especially interested in it.

Read Part I of Grice's paper, ‘Meaning’. The original paper is not actually divided into parts; they are my addition (indicated by the square brackets) to facilitate guided reading. Grice distinguishes natural from non-natural meaning. He also rejects an attempt (by C.L. Stevenson) to define non-natural meaning in terms of natural meaning, prior to offering his own theory of non-natural meaning in the rest of the paper.

Click to view Part I ‘Meaning’ by H.P. Grice: ‘Natural meaning distinguished from non-natural meaning’ [ Tip: hold Ctrl and click a link to open it in a new tab. ( Hide tip ) ]

Which of the following claims about meaning are most plausibly interpreted as claims about natural meaning, and which are most plausibly interpreted as claims about non-natural meaning?

(i) John is sneezing. This means he has a sinus infection.

(ii) The French sentence, ‘Pierre aime les chats’, means that Pierre likes cats.

(iii) In saying what he did, John meant that he would be late.

(iv) Failure to bring an accurate map with him meant that John would be late.

(i) Natural. If John has no sinus infection, his sneezing could not possibly mean that he had a sinus infection. If it means anything, it would have to mean something else, e.g. that there is pepper in the air.

(ii) Non-natural. The sentence would mean what it does even if Pierre hates cats.

(iii) Non-natural. John's utterance (whatever it was – perhaps it was ‘I will be late’ or ‘start without me’) would have had this meaning even if he in fact ends up arriving on time.

(iv) Natural. Suppose John arrived on time. This would lead us to reject the claim that his failure to bring an accurate map meant that he would be late.

The distinction between natural and non-natural meaning is, Grice notes, not always clear cut. The same entity can sometimes have both natural and non-natural meaning. Here is an illustration:

The canyon-dweller's shout of ‘here comes an echo’ meant that we would hear an echo a few seconds later.

This is plausible on both readings of ‘meant’. But in most cases the distinction seems to be reasonably easy to apply. Let us move on, then, to Grice's theory of non-natural meaning. (Henceforth in this section, ‘meaning’ should be read as ‘non-natural meaning’ unless specified otherwise.)

Stack Exchange Network

Stack Exchange network consists of 183 Q&A communities including Stack Overflow , the largest, most trusted online community for developers to learn, share their knowledge, and build their careers.

Young's natural representation of the symmetric group

The literature on the representation theory of the symmetric group contains some terminology that I find puzzling, and I am wondering if someone here knows the full story.

One of the standard ways to construct the irreducible representations of the symmetric group is to define Specht modules . This construction produces an explicit basis for the modules. If one now writes down the representing matrices with respect to this basis, the result is often referred to as Young's natural representation .

From a modern point of view at least, this terminology seems a little strange because it attributes "the same thing" to both Specht and Young. Now one possible explanation is that when Specht and Young were working on this stuff, it didn't seem like the same thing, and it's only today that they look the same. Indeed, in Specht's paper, he writes:

Zwischen den Youngschen Arbeiten und der vorliegenden bestehen daher kaum irgendwelche Zusammenhaenge ausser den rein ausserlichen, die darauf beruhen, dass die hier verwendeten kombinatorischen Hilfsmittel haufig auch von Herrn A. Young, freilich zu ganz anderen Zwecken herangezogen werden.

My German is poor but I think this translates to:

Between Young's work and the present work there exist hardly any connections except the purely superficial one that the combinatorial tools used here are also used by Mr. A. Young, albeit for entirely different purposes.

I tried to look up Young's papers, but found them daunting, and in particular I could not immediately locate anything that looked like "Young's natural representation." Apparently I'm not the only one who is daunted by Young's papers, because here's a quote from some lecture notes of G. D. James:

The representation theory of the symmetric groups was first studied by Frobenius and Schur, and then developed in a long series of papers by Young. Although a detailed study of Young's work would undoubtedly pay dividends, anyone who has attempted this will realize just how difficult it is to read his papers. The author, for one, has never undertaken this task, and so no reference will be found here to any of Young's proofs, although it is probable that some of the techniques presented here are identical to his.

So my question is, can someone point specifically to a place in Young's papers where he discussed what we would nowadays call "Young's natural representation"? And does anyone know the history of how the term "Young's natural representation" came to have its current meaning?

• gr.group-theory
• rt.representation-theory
• ho.history-overview
• symmetric-groups

• 3 $\begingroup$ A clue appears in Garsia and McLarnan's paper ac.els-cdn.com/0001870888900606/… . They refer to QSA IV and say that Young's order on SYT appears on page 258. $\endgroup$ –  Richard Stanley Oct 10, 2018 at 13:00
• $\begingroup$ Because I always worry about linkrot, I mention that the paper that @RichardStanley references is Garsia and McLarnan - Relations between Young's natural and the Kazhdan-Lusztig representations of $\mathrm S_n$ . (Actually I see that this is also mentioned in @‍TimothyChow's summary .) $\endgroup$ –  LSpice Feb 13, 2019 at 19:03

Thanks to Richard Stanley for the pointer to Garsia and McLarnan's paper, Relations between Young's natural and the Kazhdan–Lusztig representations of $S_n$ , Advances in Math. 69 (1988), 32–92.

Young's fourth paper ("QSA IV") is:

Alfred Young, On Quantitative Substitutional Analysis (Fourth Paper), Proc. London Math. Soc. (2) 31 (1930), no. 4, 253–272.

Note that the year of publication is slightly confusing because the running head of the paper itself says "Nov. 14, 1929" but the volume of the journal was actually published in 1930. Following MathSciNet, I have given the year as 1930, but I have also seen citations of the paper that give 1929 as the year.

I have stared at QSA IV for some time but have failed to fully decipher the notation, so I hesitate to personally vouch for the claim that it describes the same matrix representation that one gets by taking (the usual basis for) Specht modules. However, in addition to Garsia and McLarnan, the book Substitional Analysis by Daniel Rutherford—which by the way is a very useful guide to Young's work—also states that QSA IV describes a recipe for (what we now call) Young's natural representation, so I believe that this claim is true.

It is understandable to me that Specht regarded his work as different from Young's. What I can say from my (limited) understanding of QSA IV is that Young did not construct anything resembling Specht modules, and that Young's recipe for constructing representing matrices came from considering the action of the symmetric group on (what we would now call) primitive idempotents.

There is an interesting remark that Garsia and McLarnan make in their paper (writing in 1988):

Very few authors today have much familiarity with Young's natural representation. The various presentations of Specht modules and the work of Garnir tend to hide the simplicity and beauty of Young's construction. … Young's natural can be constructed at once by a very simple combinatorial procedure which applies to all permutations. Moreover, the proof that the procedure is valid is actually quite short and elementary.

One reason that Young's construction of his natural representation "fell off the radar" for a while may be that the exposition in Rutherford's aforementioned book does not follow Young's construction exactly. Young derives the natural representation first and only later derives the orthogonal representation, whereas Rutherford does it the other way around, making the natural representation seem like an afterthought. In his review of Rutherford's book in the Bulletin of the American Mathematical Society , G. de B. Robinson even goes so far as to say:

[T]he natural representation appears as an anti-climax. Though reference to it had to be included, this reviewer would have preferred that it be in an appendix. The material of §§28–31 has historical and actual value, but it serves to obscure the magnitude of Young's real achievement, the orthogonal representation.

I took a quick look at Robinson's own book on the representation theory of the symmetric group and I think he does not bother at all with Young's natural representation. Anyway, it seems that for the reader who wants to understand Young's natural representation without going through Specht modules, Garsia and McLarnan's account is the most readable one.

• $\begingroup$ Rutherford’s book contains details on Young’s representation, and is reasonably easy to read. $\endgroup$ –  Dima Pasechnik Nov 17, 2018 at 2:59

Your Answer

Sign up or log in, post as a guest.

Required, but never shown

By clicking “Post Your Answer”, you agree to our terms of service and acknowledge you have read our privacy policy .

Not the answer you're looking for? Browse other questions tagged gr.group-theory rt.representation-theory ho.history-overview symmetric-groups or ask your own question .

• Featured on Meta
• Testing a new version of Stack Overflow Jobs
• What deliverables would you like to see out of a working group?

Search form

• Travel & Maps
• Our Building
• Supporting Mathematics
• Art and Oxford Mathematics
• Equality, Diversity & Inclusion
• Undergraduate Study
• Postgraduate Study
• Current Students
• Research Groups
• Case Studies
• Faculty Books
• Oxford Mathematics Alphabet
• Oxford Online Maths Club
• Oxford Maths Festival 2023
• It All Adds Up
• Problem Solving Matters
• PROMYS Europe
• Oxfordshire Maths Masterclasses
• Outreach Information
• Mailing List
• Key Contacts
• People List
• A Global Department
• Research Fellowship Programmes
• Professional Services Teams
• Conference Facilities
• Public Lectures & Events
• Departmental Seminars & Events
• Special Lectures
• Conferences
• Summer Schools
• Past Events
• Alumni Newsletters
• Info for Event Organisers & Attendees

What is Representation Theory and how is it used? Oxford Mathematics Research investigates

Oxford Mathematician Karin Erdmann  specializes in the areas of algebra known as representation theory (especially modular representation theory) and homological algebra (especially Hochschild cohomology). Here she discusses her latest work.

"Roughly speaking, representation theory investigates how algebraic systems can act on vector spaces. When the vector spaces are finite-dimensional this allows one to explicitly express the elements of the algebraic system by matrices, hence one can exploit linear algebra to study 'abstract' algebraic systems. In this way one can study symmetry, via group actions. One can also study irreversible processes. Algebras and their representations provide a natural frame for this.

An algebra is a ring which also is a vector space such that scalars commute with everything. An important construction are path algebras: Take a directed graph $Q$, which we call a quiver, and take a coefficient field $K$. Then the path algebra $KQ$ is the vector space over $K$ with basis all paths in $Q$. This becomes an algebra, where the product of two basis elements is either its concatenation if this exists, or is zero otherwise.

Algebras generalize groups, namely if we start with a group, we get naturally an algebra: take the vector space with basis labelled by the group, and extend the group multiplication to a ring structure.

When the coefficients are contained in the complex numbers, representations of groups have been studied for a long time, and have many applications. With coefficients in the integers modulo $2$, for example, the algebras and their representations are much harder to understand. For some groups, the representations have 'finite type'. These are well-understood but almost always they have 'infinite type'. With a few exceptional 'tame' cases, these are usually 'wild', that is there is no hope of a classification of the representations.

The same cases occur precisely for modulo 2 arithmetic and when the symmetry is based on dihedral or semidihedral or quaternion 2-groups. Dihedral 2-groups are symmetries of regular $n$-gons when $n$ is a power of 2. The smallest quaternion group is the famous one discovered by Hamilton.

Viewing these symmetries from groups in the wider context of algebras was used (a while ago) to classify such tame situations. Recently it was discovered that this is part of a much larger universe. Namely one can construct algebras from surface triangulations, in which the ones from the group setting occur as special cases.

One starts with a surface triangulation, and constructs from this a quiver, that is, a directed graph: Replace each edge of the triangulation by a vertex, and for each triangle

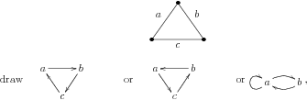
where in the last case $a=c\neq b$. At any boundary edge, draw a loop.

For example, consider triangulation of the torus with two triangles, as shown below. Then there are, up to labelling, two possible orientations of triangles and two possible quivers:

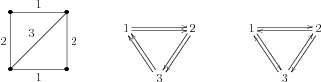
The tetrahedral triangulation of the sphere

gives rise to several quivers, depending on the orientation of each triangle, for example:

The crystal in the north wing of the Andrew Wiles Building, home of Oxford Mathematics (image drawn above) can be viewed as a triangulation of a surface with boundary. We leave drawing the quiver to the reader.

Starting with the path algebra of such a quiver, we construct algebras by imposing explicit relations, which mimic the triangulation. Although the quiver can be arbitrarily large and complicated, there is an easy description of the algebras. We call these 'weighted surface algebras.' This is joint work with A. Skowronski .

We show that these algebras place group representations in a wider context. The starting point is that (with one exception) the cohomology of a weighted surface algebra is periodic of period four, which means that these algebras generalize group algebras with quaternion symmetry.

The relations which mimic triangles can be degenerated, so that the product of two arrows around a triangle become zero in the algebra. This gives rise to many new algebras. When all such relations are degenerated, the resulting algebras are very similar to group algebras with dihedral symmetry. If we degenerate relations around some but not all triangles, we obtain algebras which share properties of group algebras with semidihedral symmetry. Work on these is in progress."

• Math Article

Natural Numbers

Natural numbers are a part of the number system which includes all the positive integers from 1 till infinity and are also used for counting purpose. It does not include zero (0). In fact, 1,2,3,4,5,6,7,8,9…., are also called counting numbers .

Natural numbers are  part of real numbers,  that include only the positive integers i.e. 1, 2, 3, 4,5,6, ………. excluding zero, fractions, decimals and negative numbers.

Note: Natural numbers do not include negative numbers or zero.

In this article, you will learn more about natural numbers with respect to their definition, comparison with whole numbers, representation in the number line, properties, etc.

Natural Number Definition

As explained in the introduction part, natural numbers are the numbers which are positive integers and includes numbers from 1 till infinity(∞). These numbers are countable and are generally used for calculation purpose.  The set of natural numbers is represented by the letter “ N ”.

N = {1,2,3,4,5,6,7,8,9,10…….}

Natural Numbers and Whole Numbers

Natural numbers include all the whole numbers excluding the number 0. In other words, all natural numbers are whole numbers, but all whole numbers are not natural numbers.

• Natural Numbers = {1,2,3,4,5,6,7,8,9,…..}
• Whole Numbers = {0,1,2,3,4,5,7,8,9,….}

Check out the difference between natural and whole numbers to know more about the differentiating properties of these two sets of numbers.

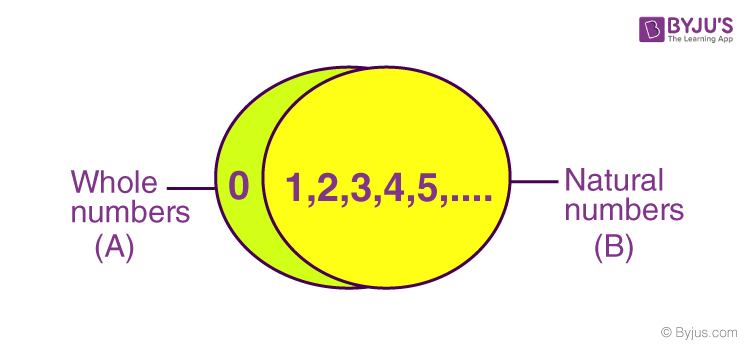
The above representation of sets shows two regions. A ∩ B i.e. intersection of natural numbers and whole numbers (1, 2, 3, 4, 5, 6, ……..) and the green region showing A-B, i.e. part of the whole number (0).

Thus, a whole number is “a part of Integers consisting of all the natural number including 0.”

Is ‘0’ a Natural Number?

The answer to this question is ‘No’. As we know already, natural numbers start with 1 to infinity and are positive integers. But when we combine 0 with a positive integer such as 10, 20, etc. it becomes a natural number. In fact, 0 is a whole number which has a null value.

Every Natural Number is a Whole Number. True or False?

Every natural number is a whole number. The statement is true because natural numbers are the positive integers that start from 1 and goes till infinity whereas whole numbers also include all the positive integers along with 0.

Representing Natural Numbers on a Number Line

Natural numbers representation on a number line is as follows:

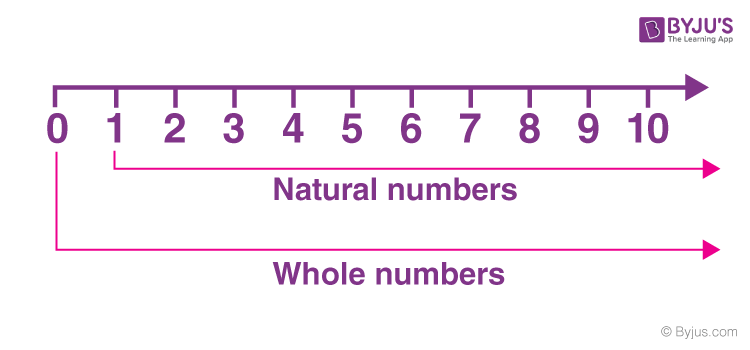
The above number line represents natural numbers and whole numbers. All the integers on the right-hand side of 0 represent the natural numbers, thus forming an infinite set of numbers. When 0 is included, these numbers become whole numbers which are also an infinite set of numbers.

Set of Natural Numbers

In a set notation, the symbol of natural number is “N” and it is represented as given below.

N = Set of all numbers starting from 1.

In Roster Form:

N = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, ………………………………}

In Set Builder Form:

N = {x : x is an integer starting from 1}

Natural Numbers Examples

The natural numbers include the positive integers (also known as non-negative integers) and a few examples include 1, 2, 3, 4, 5, 6, …∞.  In other words, natural numbers are a set of all the whole numbers excluding 0.

23, 56, 78, 999, 100202, etc. are all examples of natural numbers.

Properties of Natural Numbers

Natural numbers properties are segregated into four main properties which include:

• Closure property
• Commutative property
• Associative property
• Distributive property 

Each of these properties is explained below in detail.

Closure Property

Natural numbers are always closed under addition and multiplication. The addition and multiplication of two or more natural numbers will always yield a natural number. In the case of subtraction and division, natural numbers do not obey closure property, which means subtracting or dividing two natural numbers might not give a natural number as a result.

• Addition: 1 + 2 = 3, 3 + 4 = 7, etc. In each of these cases, the resulting number is always a natural number.
• Multiplication: 2 × 3 = 6, 5 × 4 = 20, etc. In this case also, the resultant is always a natural number.
• Subtraction: 9 – 5 = 4, 3 – 5 = -2, etc. In this case, the result may or may not be a natural number.
• Division: 10 ÷ 5 = 2, 10 ÷ 3 = 3.33, etc. In this case, also, the resultant number may or may not be a natural number.

Note: Closure property does not hold, if any of the numbers in case of multiplication and division, is not a natural number. But for addition and subtraction, if the result is a positive number, then only closure property exists.

For example: 

• -2 x 3 = -6; Not a natural number
• 6/-2 = -3; Not a natural number
• Associative Property

The associative property holds true in case of addition and multiplication of natural numbers i.e. a + ( b + c ) = ( a + b ) + c and a × ( b × c ) = ( a × b ) × c. On the other hand, for subtraction and division of natural numbers, the associative property does not hold true . An example of this is given below.

• Addition: a + ( b + c ) = ( a + b ) + c => 3 + (15 + 1 ) = 19 and (3 + 15 ) + 1 = 19.
• Multiplication: a × ( b × c ) = ( a × b ) × c => 3 × (15 × 1 ) = 45 and ( 3 × 15 ) × 1 = 45.
• Subtraction: a – ( b – c ) ≠ ( a – b ) – c => 2 – (15 – 1 ) = – 12 and ( 2 – 15 ) – 1 = – 14.
• Division: a ÷ ( b ÷ c ) ≠ ( a ÷ b ) ÷ c => 2 ÷( 3 ÷ 6 ) = 4 and ( 2 ÷ 3 ) ÷ 6 = 0.11.
• Commutative Property

For commutative property

• Addition and multiplication of natural numbers show the commutative property. For example, x + y = y + x and a × b = b × a
• Subtraction and division of natural numbers do not show the commutative property. For example, x – y ≠ y – x and x ÷ y ≠ y ÷ x
• Distributive Property
• Multiplication of natural numbers is always distributive over addition. For example, a × (b + c) = ab + ac
• Multiplication of natural numbers is also distributive over subtraction. For example, a × (b – c) = ab – ac

Read More Here:

Operations With Natural Numbers

An overview of algebraic operation with natural numbers i.e. addition, subtraction, multiplication and division, along with their respective properties are summarized in the table given below.

Video Lesson on Numbers

Solved Examples

Question 1: Sort out the natural numbers from the following list: 20, 1555, 63.99, 5/2, 60, −78, 0, −2, −3/2

Solution: Natural numbers from the above list are 20, 1555 and 60.

Question 2: What are the first 10 natural numbers?

Solution: The first 10 natural numbers on the number line are 1, 2, 3, 4, 5, 6, 7, 8, 9, 10.

Question 3: Is the number 0 a natural number?

Solution: 0 is not a natural number. It is a whole number. Natural numbers only include positive integers.

Stay tuned with BYJU’S and keep learning various other Maths topics in a simple and easily understandable way . Also, get other maths study materials, video lessons, practice questions, etc. by registering at BYJU’S.

Frequently Asked Questions on Natural Numbers

What are natural numbers.

Natural numbers are the positive integers or non-negative integers which start from 1 and ends at infinity, such as:

1,2,3,4,5,6,7,8,9,10,……,∞.

Is 0 a Natural Number?

Zero does not have a positive or negative value. Since all the natural numbers are positive integers, hence we cannot say zero is a natural number. Although zero is called a whole number.

What are the first ten Natural Numbers?

The first ten natural numbers are: 1,2,3,4,5,6,7,8,9, and 10.

What is the difference between Natural numbers and Whole numbers?

Natural numbers include only positive integers and starts from 1 till infinity. Whereas whole numbers are the combination of zero and natural numbers, as it starts from 0 and ends at infinite value.

What are the examples of Natural numbers?

The examples of natural numbers are 5, 7, 21, 24, 99, 101, etc.

Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!

Select the correct answer and click on the “Finish” button Check your score and answers at the end of the quiz

Visit BYJU’S for all Maths related queries and study materials

Your result is as below

Request OTP on Voice Call

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Post My Comment

I like your answers for my mathematics Project Work

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

Semantics - Meaning Representation in NLP

Logic and logical forms, the meaning of simple objects and events, quantifiers and the meaning of determiners, the meaning of modifiers, relative clauses, plurals, cardinality, and mass nouns, question-answering, how many and which, who and what, discourse referents, anaphora, definite reference (the), word sense disambiguation, ontological methods, statistical methods, logical forms and lambda calculus, semantic rules for context free grammars, prolog representation, semantics of a simple grammar, quantified noun phrases, semantics of filler-gap dependencies.

• Add to the lexicon an appropriate encoding for the determiner "a", so that it can be used in sentences like "terry wrote a program".  Hand-trace the application of the Prolog rules given in this section with this sentence and show the intermediate logical forms that lead to its logical form representation, exists(x, program(x) => wrote(terry, X)).
• Assuming the grammatical rules found in this section, find appropriate semantic representations for the following statements:
• Give an example of a yes-no question and a complement question to which the rules in the last section can apply.  For each example, show the intermediate steps in deriving the logical form for the question.  Assume there are sufficient definitions in the lexicon for common words, like "who", "did", and so forth.
• Look at program 4.2 on p 102 of Pereira.  Using a trace, show the intermediate steps in the parse of the sentence "every student wrote a program."

• Reference Manager
• Simple TEXT file

People also looked at

Review article, symbolic, distributed, and distributional representations for natural language processing in the era of deep learning: a survey.

• Department of Enterprise Engineering, University of Rome Tor Vergata, Rome, Italy

Natural language is inherently a discrete symbolic representation of human knowledge. Recent advances in machine learning (ML) and in natural language processing (NLP) seem to contradict the above intuition: discrete symbols are fading away, erased by vectors or tensors called distributed and distributional representations . However, there is a strict link between distributed/distributional representations and discrete symbols, being the first an approximation of the second. A clearer understanding of the strict link between distributed/distributional representations and symbols may certainly lead to radically new deep learning networks. In this paper we make a survey that aims to renew the link between symbolic representations and distributed/distributional representations. This is the right time to revitalize the area of interpreting how discrete symbols are represented inside neural networks.

1. Introduction

Natural language is inherently a discrete symbolic representation of human knowledge. Sounds are transformed in letters or ideograms and these discrete symbols are composed to obtain words. Words then form sentences and sentences form texts, discourses, dialogs, which ultimately convey knowledge, emotions, and so on. This composition of symbols in words and of words in sentences follow rules that both the hearer and the speaker know ( Chomsky, 1957 ). Hence, it seems extremely odd thinking to natural language understanding systems that are not based on discrete symbols.

Recent advances in machine learning (ML) applied to natural language processing (NLP) seem to contradict the above intuition: discrete symbols are fading away, erased by vectors or tensors called distributed and distributional representations . In ML applied to NLP, distributed representations are pushing deep learning models ( LeCun et al., 2015 ; Schmidhuber, 2015 ) toward amazing results in many high-level tasks such as image generation ( Goodfellow et al., 2014 ), image captioning ( Vinyals et al., 2015b ; Xu et al., 2015 ), machine translation ( Zou et al., 2013 ; Bahdanau et al., 2015 ), syntactic parsing ( Vinyals et al., 2015a ; Weiss et al., 2015 ) and in a variety of other NLP tasks ( Devlin et al., 2019 ). In a more traditional NLP, distributional representations are pursued as a more flexible way to represent semantics of natural language, the so-called distributional semantics (see Turney and Pantel, 2010 ). Words as well as sentences are represented as vectors or tensors of real numbers. Vectors for words are obtained observing how these words co-occur with other words in document collections. Moreover, as in traditional compositional representations, vectors for phrases ( Clark et al., 2008 ; Mitchell and Lapata, 2008 ; Baroni and Zamparelli, 2010 ; Zanzotto et al., 2010 ; Grefenstette and Sadrzadeh, 2011 ) and sentences ( Socher et al., 2011 , 2012 ; Kalchbrenner and Blunsom, 2013 ) are obtained by composing vectors for words.

The success of distributed and distributional representations over symbolic approaches is mainly due to the advent of new parallel paradigms that pushed neural networks ( Rosenblatt, 1958 ; Werbos, 1974 ) toward deep learning ( LeCun et al., 2015 ; Schmidhuber, 2015 ). Massively parallel algorithms running on Graphic Processing Units (GPUs) ( Chetlur et al., 2014 ; Cui et al., 2015 ) crunch vectors, matrices, and tensors faster than decades ago. The back-propagation algorithm can be now computed for complex and large neural networks. Symbols are not needed any more during “resoning.” Hence, discrete symbols only survive as inputs and outputs of these wonderful learning machines.

However, there is a strict link between distributed/distributional representations and symbols, being the first an approximation of the second ( Fodor and Pylyshyn, 1988 ; Plate, 1994 , 1995 ; Ferrone et al., 2015 ). The representation of the input and the output of these networks is not that far from their internal representation. The similarity and the interpretation of the internal representation is clearer in image processing ( Zeiler and Fergus, 2014a ). In fact, networks are generally interpreted visualizing how subparts represent salient subparts of target images. Both input images and subparts are tensors of real number. Hence, these networks can be examined and understood. The same does not apply to natural language processing with its discrete symbols.

A clearer understanding of the strict link between distributed/distributional representations and discrete symbols is needed ( Jacovi et al., 2018 ; Jang et al., 2018 ) to understand how neural networks treat information and to propose novel deep learning architectures. Model interpretability is becoming an important topic in machine learning in general ( Lipton, 2018 ). This clearer understanding is then the dawn of a new range of possibilities: understanding what part of the current symbolic techniques for natural language processing have a sufficient representation in deep neural networks; and, ultimately, understanding whether a more brain-like model—the neural networks—is compatible with methods for syntactic parsing or semantic processing that have been defined in these decades of studies in computational linguistics and natural language processing. There is thus a tremendous opportunity to understand whether and how symbolic representations are used and emitted in a brain model.

In this paper we make a survey that aims to draw the link between symbolic representations and distributed/distributional representations. This is the right time to revitalize the area of interpreting how symbols are represented inside neural networks. In our opinion, this survey will help to devise new deep neural networks that can exploit existing and novel symbolic models of classical natural language processing tasks.

The paper is structured as follow: first we give an introduction to the very general concept of representation, the notion of concatenative composition and the difference between local and distributed representations ( Plate, 1995 ). After that we present each techniques in detail. Afterwards, we focus on distributional representations ( Turney and Pantel, 2010 ), which we treat as a specific example of a distributed representation. Finally we discuss more in depth the general issue of compositionality, analyzing three different approaches to the problem: compositional distributional semantics ( Clark et al., 2008 ; Baroni et al., 2014 ), holographic reduced representations ( Plate, 1994 ; Neumann, 2001 ), and recurrent neural networks ( Socher et al., 2012 ; Kalchbrenner and Blunsom, 2013 ).

2. Symbolic and Distributed Representations: Interpretability and Concatenative Compositionality

Distributed representations put symbolic expressions in metric spaces where similarity among examples is used to learn regularities for specific tasks by using neural networks or other machine learning models. Given two symbolic expressions, their distributed representation should capture their similarity along specific features useful for the final task. For example, two sentences such as s 1 = “ a mouse eats some cheese” and s 2 = “ a cat swallows a mouse” can be considered similar in many different ways: (1) number of words in common; (2) realization of the pattern “ ANIMAL EATS FOOD .” The key point is to decide or to let an algorithm decide which is the best representation for a specific task.

Distributed representations are then replacing long-lasting, successful discrete symbolic representations in representing knowledge for learning machines but these representations are less human interpretable . Hence, discussing about basic, obvious properties of discrete symbolic representations is not useless as these properties may guarantee success to distributed representations similar to the one of discrete symbolic representations.

Discrete symbolic representations are human interpretable as symbols are not altered in expressions . This is one of the most important, obvious feature of these representations. Infinite sets of expressions, which are sequences of symbols, can be interpreted as these expressions are obtained by concatenating a finite set of basic symbols according to some concatenative rules. During concatenation, symbols are not altered and, then, can be recognized. By using the principle of semantic compositionality , the meaning of expressions can be obtained by combining the meaning of the parts and, hence, recursively, by combining the meaning of the finite set of basic symbols. For example, given the set of basic symbols D = { mouse, cat, a, swallows, ( , ) }, expressions like:

are totally plausible and interpretable given rules for producing natural language utterances or for producing tree structured representations in parenthetical form, respectively. This strongly depends on the fact that individual symbols can be recognized.

Distributed representations instead seem to alter symbols when applied to symbolic inputs and, thus, are less interpretable. In fact, symbols as well as expressions are represented as vectors in these metric spaces. Observing distributed representations, symbols and expressions do not immediately emerge. Moreover, these distributed representations may be transformed by using matrix multiplication or by using non-linear functions. Hence, it is generally unclear: (1) what is the relation between the initial symbols or expressions and their distributed representations and (2) how these expressions are manipulated during matrix multiplication or when applying non-linear functions. In other words, it is unclear whether symbols can be recognized in distributed representations.

Hence, a debated question is whether discrete symbolic representations and distributed representations are two very different ways of encoding knowledge because of the difference in altering symbols . The debate dates back in the late 80s. For Fodor and Pylyshyn (1988) , distributed representations in Neural Network architectures are “ only an implementation of the Classical approach” where classical approach is related to discrete symbolic representations. Whereas, for Chalmers (1992) , distributed representations give the important opportunity to reason “ holistically” about encoded knowledge. This means that decisions over some specific part of the stored knowledge can be taken without retrieving the specific part but acting on the whole representation. However, this does not solve the debated question as it is still unclear what is in a distributed representation.

To contribute to the above debated question, Gelder (1990) has formalized the property of altering symbols in expressions by defining two different notions of compositionality: concatenative compositionality and functional compositionality.

Concatenative compositionality explains how discrete symbolic representations compose symbols to obtain expressions. In fact, the mode of combination is an extended concept of juxtaposition that provides a way of linking successive symbols without altering them as these form expressions. Concatenative compositionality explains discrete symbolic representations no matter the means is used to store expressions: a piece of paper or a computer memory. Concatenation is sometime expressed with an operator like ∘, which can be used in a infix or prefix notation, that is a sort of function with arguments ∘( w 1 , ..., w n ). By using the operator for concatenation, the two above examples s 1 and t 1 can be represented as the following:

that represents a sequence with the infix notation and

that represents a tree with the prefix notation.

Functional compositionality explains compositionality in distributed representations and in semantics. In functional compositionality, the mode of combination is a function Φ that gives a reliable, general process for producing expressions given its constituents. Within this perspective, semantic compositionality is a special case of functional compositionality where the target of the composition is a way for meaning representation ( Blutner et al., 2003 ).

Local distributed representations (as referred in Plate, 1995 ) or one-hot encodings are the easiest way to visualize how functional compositionality acts on distributed representations . Local distributed representations give a first, simple encoding of discrete symbolic representations in a metric space. Given a set of symbols D , a local distributed representation maps the i -th symbol in D to the i -th base unit vector e i in ℝ n , where n is the cardinality of D . Hence, the i -th unit vector represents the i -th symbol. In functional compositionality , expressions s = w 1 … w k are represented by vectors s obtained with an eventually recursive function Φ applied to vectors e w 1 … e w k . The function f may be very simple as the sum or more complex. In case the function Φ is the sum, that is:

the derived vector is the classical bag-of-word vector space model ( Salton, 1989 ). Whereas, more complex functions f can range from different vector-to-vector operations like circular convolution in Holographic Reduced Representations ( Plate, 1995 ) to matrix multiplications plus non-linear operations in models such as in recurrent neural networks ( Hochreiter and Schmidhuber, 1997 ; Schuster and Paliwal, 1997 ) or in neural networks with attention ( Vaswani et al., 2017 ; Devlin et al., 2019 ). Example s 1 in Equation (1) can be useful to describe functional compositionality. The set D = { mouse, cat, a, swallows, eats, some, cheese, ( , ) } may be represented with the base vectors e i ∈ ℝ 9 where e 1 is the base vector for mouse , e 2 for cat , e 3 for a , e 4 for swallaws , e 5 for eats , e 6 for some , e 7 for cheese , e 8 for ( , and e 9 for ) . The additive functional composition of the expression s 1 = a cat swallows a mouse is then:

where the concatenative operator ∘ has been substituted with the sum +. Just to observe, in the additive functional composition func Σ (s 1 ) , symbols are still visible but the sequence is lost. In fact, it is difficult to reproduce the initial discrete symbolic expression. However, for example, the additive composition function gives the possibility to compare two expressions. Given the expression s 1 and s 2 = a mouse eats some cheese , the dot product between func Σ (s 1 ) and fun c ∑ ( s 2 )   = ( 1   0   1   0   1   1   1   0   0 ) T counts the common words between the two expressions. In a functional composition with a function Φ, the expression s 1 may become func Φ (s 1 ) = Φ(Φ(Φ(Φ( e 3 , e 2 ), e 4 ), e 3 ), e 1 ) by following the concatenative compositionality of the discrete symbolic expression. The same functional compositional principle can be applied to discrete symbolic trees as t 1 by producing this distributed representation Φ(Φ( e 3 , e 2 ), Φ( e 4 , Φ( e 3 , e 1 ))). Finally, in the functional composition with a generic recursive function func Φ (s 1 ) , the function Φ will be crucial to determine whether symbols can be recognized and sequence is preserved.

Distributed representations in their general form are more ambitious than distributed local representations and tend to encode basic symbols of D in vectors in ℝ d where d < < n . These vectors generally alter symbols as there is not a direct link between symbols and dimensions of the space. Given a distributed local representation e w of a symbol w , the encoder for a distributed representation is a matrix W d×n that transforms e w in y w = W d×n e w . As an example, the encoding matrix W d×n can be build by modeling words in D around three dimensions: number of vowels, number of consonants and, finally, number of non-alphabetic symbols. Given these dimensions, the matrix W 3 ×9 for the example is :

This is a simple example of a distributed representation. In a distributed representation ( Hinton et al., 1986 ; Plate, 1995 ) the informational content is distributed (hence the name) among multiple units, and at the same time each unit can contribute to the representation of multiple elements. Distributed representation has two evident advantages with respect to a distributed local representation: it is more efficient (in the example, the representation uses only 3 numbers instead of 9) and it does not treat each element as being equally different to any other. In fact, mouse and cat in this representation are more similar than mouse and a . In other words, this representation captures by construction something interesting about the set of symbols. The drawback is that symbols are altered and, hence, it may be difficult to interpret which symbol is given its distributed representation. In the example, the distributed representations for eats and some are exactly the same vector W 3 ×9 e 5 = W 3 ×9 e 6 .

Even for distributed representations in the general form, it is possible to define functional composition to represent expressions. Vectors W d×n e i should be replaced to vectors e i in the definition of functional compositionality. Equation (3) for additive functional compositionality becomes:

In the running example, the additive functional compositionality of sentence s 1 in Example 1 is:

Clearly, in this case, it is extremely difficult to derive back the discrete symbolic sequence s 1 that has generated the final distributed representation.

Hence, interpretability of distributed representations can be framed as the following question:

how much the underlying functional composition of distributed representations is concatenative ?

In fact, discrete symbolic representations are interpretable as their composition is concatenative. Then, in order to be interpretable, distributed representations, and the related functional composition, should have some concatenative properties.

Then, since a distributed representation y s of discrete symbolic expressions s are obtained by using an encoder W d×n and a composition function, assessing interpretability becomes:

• Symbol-level Interpretability - The question “Can discrete symbols be recognized?” becomes “to which degree the embedding matrix W is invertible?”

• Sequence-level Interpretability - The question “Can symbols and their relations be recognized in sequences of symbols?” becomes “how much functional composition models are concatenative?”

The two driving questions of Symbol-level Interpretability and Sequence-level Interpretability will be used to describe the presented distributed representations. In fact, we are interested in understanding whether distributed representations can be used to encode discrete symbolic structures and whether it is possible to decode the underlying discrete symbolic structure given a distributed representation. For example, it is clear that a local distributed representation is more interpretable at symbol level than the distributed representation presented in Equation (4). Yet, both representations lack in concatenative compositionality when sequences are collapsed in vectors. In fact, the sum as composition function builds bag-of-word local and distributed representation, which neglect the order of symbols in sequences. In the rest of the paper, we analyze whether other representations, such as holographic reduced representations ( Plate, 1995 ), recurrent and recursive neural networks ( Hochreiter and Schmidhuber, 1997 ; Schuster and Paliwal, 1997 ) or neural networks with attention ( Vaswani et al., 2017 ; Devlin et al., 2019 ), are instead more interpretable.

3. Strategies to Obtain Distributed Representations from Symbols

There is a wide range of techniques to transform symbolic representations in distributed representations. When combining natural language processing and machine learning, this is a major issue: transforming symbols, sequences of symbols or symbolic structures in vectors or tensors that can be used in learning machines. These techniques generally propose a function η to transform a local representation with a large number of dimensions in a distributed representation with a lower number of dimensions:

This function is often called encoder .

We propose to categorize techniques to obtain distributed representations in two broad categories, showing some degree of overlapping ( Cotterell et al., 2017 ):

• Representations derived from dimensionality reduction techniques;

• Learned representations.

In the rest of the section, we will introduce the different strategies according to the proposed categorization. Moreover, we will emphasize its degree of interpretability for each representation and its related function η by answering to two questions:

• Has a specific dimension in ℝ d a clear meaning?

• Can we decode an encoded symbolic representation? In other words, assuming a decoding function δ : ℝ d → ℝ n , how far is v ∈ ℝ n , which represents a symbolic representation, from v ′ = δ(η( v ))?

Sequence-level interpretability of the resulting representations will be analyzed in section 5.

3.1. Dimensionality Reduction With Random Projections

Random projection (RP) ( Bingham and Mannila, 2001 ; Fodor, 2002 ) is a technique based on random matrices W d ∈ ℝ d × n . Generally, the rows of the matrix W d are sampled from a Gaussian distribution with zero mean, and normalized as to have unit length ( Johnson and Lindenstrauss, 1984 ) or even less complex random vectors ( Achlioptas, 2003 ). Random projections from Gaussian distributions approximately preserves pairwise distance between points (see the Johnsonn-Lindenstrauss Lemma ; Johnson and Lindenstrauss, 1984 ), that is, for any vector x, y ∈ X :

where the approximation factor ε depends on the dimension of the projection, namely, to assure that the approximation factor is ε, the dimension k must be chosen such that:

Constraints for building the matrix W can be significantly relaxed to less complex random vectors ( Achlioptas, 2003 ). Rows of the matrix can be sampled from very simple zero-mean distributions such as:

without the need to manually ensure unit-length of the rows, and at the same time providing a significant speed up in computation due to the sparsity of the projection.

These vectors η( v ) are interpretable at symbol level as these functions can be inverted. The inverted function, that is, the decoding function, is:

and W d T W d ≈ I when W d is derived using Gaussian random vectors. Hence, distributed vectors in ℝ d can be approximately decoded back in the original symbolic representation with a degree of approximation that depends on the distance between d .

The major advantage of RP is the matrix W d can be produced à-la-carte starting from the symbols encountered so far in the encoding procedure. In fact, it is sufficient to generate new Gaussian vectors for new symbols when they appear.

3.2. Learned Representation

Learned representations differ from the dimensionality reduction techniques by the fact that: (1) encoding/decoding functions may not be linear; (2) learning can optimize functions that are different with respect to the target of Principal Component Analysis (see section 4.2); and, (3) solutions are not derived in a closed form but are obtained using optimization techniques such as stochastic gradient decent .

Learned representation can be further classified into:

• Task-independent representations learned with a standalone algorithm (as in autoencoders ; Socher et al., 2011 ; Liou et al., 2014 ) which is independent from any task, and which learns a representation that only depends from the dataset used;

• Task-dependent representations learned as the first step of another algorithm (this is called end-to-end training ), usually the first layer of a deep neural network. In this case the new representation is driven by the task.

3.2.1. Autoencoder

Autoencoders are a task independent technique to learn a distributed representation encoder η : ℝ n → ℝ d by using local representations of a set of examples ( Socher et al., 2011 ; Liou et al., 2014 ). The distributed representation encoder η is half of an autoencoder.

An autoencoder is a neural network that aims to reproduce an input vector in ℝ n as output by traversing hidden layer(s) that are in ℝ d . Given η : ℝ n → ℝ d and δ : ℝ d → ℝ n as the encoder and the decoder, respectively, an autoencoder aims to maximize the following function:

The encoding and decoding module are two neural networks, which means that they are functions depending on a set of parameters θ of the form

where the parameters of the entire model are θ, θ′ = { W, b, W ′, b ′} with W, W ′ matrices, b, b ′ vectors and s is a function that can be either a non-linearity sigmoid shaped function, or in some cases the identity function. In some variants the matrices W and W ′ are constrained to W T = W ′. This model is different with respect to PCA due to the target loss function and the use of non-linear functions.

Autoencoders have been further improved with denoising autoencoders ( Vincent et al., 2008 , 2010 ; Masci et al., 2011 ) that are a variant of autoencoders where the goal is to reconstruct the input from a corrupted version. The intuition is that higher level features should be robust with regard to small noise in the input. In particular, the input x gets corrupted via a stochastic function:

and then one minimizes again the reconstruction error, but with regard to the original (uncorrupted) input:

Usually g can be either:

• Adding Gaussian noise: g ( x ) = x + ε, where ε ~ N ( 0 , σ 𝕀 ) ;

• Masking noise: where a given a fraction ν of the components of the input gets set to 0.

For what concerns symbol-level interpretability , as for random projection, distributed representations η( v ) obtained with encoders from autoencoders and denoising autoencoders are invertible , that is decodable, as this is the nature of autoencoders.

3.2.2. Embedding Layers

Embedding layers are generally the first layers of more complex neural networks which are responsible to transform an initial local representation in the first internal distributed representation. The main difference with autoencoders is that these layers are shaped by the entire overall learning process. The learning process is generally task dependent. Hence, these first embedding layers depend on the final task.

It is argued that each layers learn a higher-level representation of its input. This is particularly visible with convolutional network ( Krizhevsky et al., 2012 ) applied to computer vision tasks. In these suggestive visualizations ( Zeiler and Fergus, 2014b ), the hidden layers are seen to correspond to abstract feature of the image, starting from simple edges (in lower layers) up to faces in the higher ones.

However, these embedding layers produce encoding functions and, thus, distributed representations that are not interpretable at symbol level. In fact, these embedding layers do not naturally provide decoders.

4. Distributional Representations as Another Side of the Coin

Distributional semantics is an important area of research in natural language processing that aims to describe meaning of words and sentences with vectorial representations (see Turney and Pantel, 2010 for a survey). These representations are called distributional representations .

It is a strange historical accident that two similar sounding names— distributed and distributional —have been given to two concepts that should not be confused for many. Maybe, this has happened because the two concepts are definitely related. We argue that distributional representation are nothing more than a subset of distributed representations, and in fact can be categorized neatly into the divisions presented in the previous section.

Distributional semantics is based on a famous slogan—“ you shall judge a word by the company it keeps” ( Firth, 1957 )—and on the distributional hypothesis ( Harris, 1954 )—words have similar meaning if used in similar contexts, that is, words with the same or similar distribution . Hence, the name distributional as well as the core hypothesis comes from a linguistic rather than computer science background.

Distributional vectors represent words by describing information related to the contexts in which they appear. Put in this way it is apparent that a distributional representation is a specific case of a distributed representation, and the different name is only an indicator of the context in which this techniques originated. Representations for sentences are generally obtained combining vectors representing words.

Hence, distributional semantics is a special case of distributed representations with a restriction on what can be used as features in vector spaces: features represent a bit of contextual information. Then, the largest body of research is on what should be used to represent contexts and how it should be taken into account. Once this is decided, large matrices X representing words in context are collected and, then, dimensionality reduction techniques are applied to have treatable and more discriminative vectors.

In the rest of the section, we present how to build matrices representing words in context, we will shortly recap on how dimensionality reduction techniques have been used in distributional semantics, and, finally, we report on word2vec ( Mikolov et al., 2013 ), which is a novel distributional semantic techniques based on deep learning.

4.1. Building Distributional Representations for Words From a Corpus

The major issue in distributional semantics is how to build distributional representations for words by observing word contexts in a collection of documents. In this section, we will describe these techniques using the example of the corpus in Table 1 .

Table 1 . A very small corpus.

A first and simple distributional semantic representations of words is given by word vs. document matrices as those typical in information retrieval ( Salton, 1989 ). Word context are represented by document indexes. Then, words are similar if these words similarly appear in documents. This is generally referred as topical similarity ( Landauer and Dumais, 1997 ) as words belonging to the same topic tend to be more similar.

A second strategy to build distributional representations for words is to build word vs. contextual feature matrices. These contextual features represent proxies for semantic attributes of modeled words ( Baroni and Lenci, 2010 ). For example, contexts of the word dog will somehow have relation with the fact that a dog has four legs, barks, eats, and so on. In this case, these vectors capture a similarity that is more related to a co-hyponymy, that is, words sharing similar attributes are similar. For example, dog is more similar to cat than to car as dog and cat share more attributes than dog and car . This is often referred as attributional similarity ( Turney, 2006 ).

A simple example of this second strategy are word-to-word matrices obtained by observing n-word windows of target words. For example, a word-to-word matrix obtained for the corpus in Table 1 by considering a 1-word window is the following:

Hence, the word cat is represented by the vector cat = (2 0 0 0 1 0) and the similarity between cat and dog is higher than the similarity between cat and mouse as the cosine similarity cos ( cat, dog ) is higher than the cosine similarity cos ( cat, mouse ).

The research on distributional semantics focuses on two aspects: (1) the best features to represent contexts; (2) the best correlation measure among target words and features.

How to represent contexts is a crucial problem in distributional semantics. This problem is strictly correlated to the classical question of feature definition and feature selection in machine learning. A wide variety of features have been tried. Contexts have been represented as set of relevant words, sets of relevant syntactic triples involving target words ( Pado and Lapata, 2007 ; Rothenhäusler and Schütze, 2009 ) and sets of labeled lexical triples ( Baroni and Lenci, 2010 ).

Finding the best correlation measure among target words and their contextual features is the other issue. Many correlation measures have been tried. The classical measures are term frequency-inverse document frequency ( tf-idf ) ( Salton, 1989 ) and point-wise mutual information ( pmi ). These, among other measures, are used to better capture the importance of contextual features for representing distributional semantic of words.

This first formulation of distributional semantics is a distributed representation that is human-interpretable . In fact, features represent contextual information which is a proxy for semantic attributes of target words ( Baroni and Lenci, 2010 ).

4.2. Compacting Distributional Representations

As distributed representations, distributional representations can undergo the process of dimensionality reduction with Principal Component Analysis and Random Indexing. This process is used for two issues. The first is the classical problem of reducing the dimensions of the representation to obtain more compact representations. The second instead want to help the representation to focus on more discriminative dimensions. This latter issue focuses on the feature selection and merging which is an important task in making these representations more effective on the final task of similarity detection.

Principal Component Analysis (PCA) is largely applied in compacting distributional representations: Latent Semantic Analysis (LSA) is a prominent example ( Landauer and Dumais, 1997 ). LSA were born in Information Retrieval with the idea of reducing word-to-document matrices. Hence, in this compact representation, word context are documents and distributional vectors of words report on the documents where words appear. This or similar matrix reduction techniques have been then applied to word-to-word matrices.

Principal Component Analysis (PCA) ( Pearson, 1901 ; Markovsky, 2011 ) is a linear method which reduces the number of dimensions by projecting ℝ n into the “ best” linear subspace of a given dimension d by using the a set of data points. The “ best” linear subspace is a subspace where dimensions maximize the variance of the data points in the set. PCA can be interpreted either as a probabilistic method or as a matrix approximation and is then usually known as truncated singular value decomposition . We are here interested in describing PCA as probabilistic method as it related to the interpretability of the related distributed representation .

As a probabilistic method, PCA finds an orthogonal projection matrix W d ∈ ℝ n × d such that the variance of the projected set of data points is maximized. The set of data points is referred as a matrix X ∈ ℝ m × n where each row x i T ∈ ℝ n is a single observation. Hence, the variance that is maximized is X ^ d = X W d T ∈ ℝ m × d .

More specifically, let's consider the first weight vector w 1 , which maps an element of the dataset x into a single number 〈 x, w 1 〉. Maximizing the variance means that w is such that:

and it can be shown that the optimal value is achieved when w is the eigenvector of X T X with largest eigenvalue. This then produces a projected dataset:

The algorithm can then compute iteratively the second and further components by first subtracting the components already computed from X :

and then proceed as before. However, it turns out that all subsequent components are related to the eigenvectors of the matrix X T X , that is, the d -th weight vector is the eigenvector of X T X with the d -th largest corresponding eigenvalue.

The encoding matrix for distributed representations derived with a PCA method is the matrix:

where w i are eigenvectors with eigenvalues decreasing with i . Hence, local representations v ∈ ℝ n are represented in distributed representations in ℝ d as:

Hence, vectors η( v ) are human-interpretable as their dimensions represent linear combinations of dimensions in the original local representation and these dimensions are ordered according to their importance in the dataset, that is, their variance. Moreover, each dimension is a linear combination of the original symbols. Then, the matrix W d reports on which combination of the original symbols is more important to distinguish data points in the set.

Moreover, vectors η( v ) are decodable . The decoding function is:

and W d T W d = I if d is the rank of the matrix X , otherwise it is a degraded approximation (for more details refer to Fodor, 2002 ; Sorzano et al., 2014 ). Hence, distributed vectors in ℝ d can be decoded back in the original symbolic representation with a degree of approximation that depends on the distance between d and the rank of the matrix X .

The compelling limit of PCA is that all the data points have to be used in order to obtain the encoding/decoding matrices. This is not feasible in two cases. First, when the model has to deal with big data. Second, when the set of symbols to be encoded in extremely large. In this latter case, local representations cannot be used to produce matrices X for applying PCA.

In Distributional Semantics, random indexing has been used to solve some issues that arise naturally with PCA when working with large vocabularies and large corpora. PCA has some scalability problems:

• The original co-occurrence matrix is very costly to obtain and store, moreover, it is only needed to be later transformed;

• Dimensionality reduction is also very costly, moreover, with the dimensions at hand it can only be done with iterative methods;

• The entire method is not incremental, if we want to add new words to our corpus we have to recompute the entire co-occurrence matrix and then re-perform the PCA step.

Random Indexing ( Sahlgren, 2005 ) solves these problems: it is an incremental method (new words can be easily added any time at low computational cost) which creates word vector of reduced dimension without the need to create the full dimensional matrix.

Interpretability of compacted distributional semantic vectors is comparable to the interpretability of distributed representations obtained with the same techniques.

4.3. Learning Representations: Word2vec

Recently, distributional hypothesis has invaded neural networks: word2vec ( Mikolov et al., 2013 ) uses contextual information to learn word vectors. Hence, we discuss this technique in the section devoted to distributional semantics .

The name word2Vec comprises two similar techniques, called skip grams and continuous bag of words (CBOW). Both methods are neural networks, the former takes input a word and try to predict its context, while the latter does the reverse process, predicting a word from the words surrounding it. With this technique there is no explicitly computed co-occurrence matrix, and neither there is an explicit association feature between pairs of words, instead, the regularities and distribution of the words are learned implicitly by the network.

We describe only CBOW because it is conceptually simpler and because the core ideas are the same in both cases. The full network is generally realized with two layers W 1 n × k and W 2 k × n plus a softmax layer to reconstruct the final vector representing the word. In the learning phase, the input and the output of the network are local representation for words. In CBOW, the network aims to predict a target word given context words. For example, given the sentence s 1 of the corpus in Table 1 , the network has to predict catches given its context (see Figure 1 ).

Figure 1 . word2vec: CBOW model.

Hence, CBOW offers an encoder W 1 n × k , that is, a linear word encoder from data where n is the size of the vocabulary and k is the size of the distributional vector. This encoder models contextual information learned by maximizing the prediction capability of the network. A nice description on how this approach is related to previous techniques is given in Goldberg and Levy (2014) .

Clearly, CBOW distributional vectors are not easily human and machine interpretable . In fact, specific dimensions of vectors have not a particular meaning and, differently from what happens for auto-encoders (see section 3.2.1), these networks are not trained to be invertible.

5. Composing Distributed Representations

In the previous sections, we described how one symbol or a bag-of-symbols can be transformed in distributed representations focusing on whether these distributed representations are interpretable . In this section, we want to investigate a second and important aspect of these representations, that is, have these representations Concatenative Compositionality as symbolic representations? And, if these representations are composed , are still interpretable ?

Concatenative Compositionality is the ability of a symbolic representation to describe sequences or structures by composing symbols with specific rules. In this process, symbols remain distinct and composing rules are clear. Hence, final sequences and structures can be used for subsequent steps as knowledge repositories.

Concatenative Compositionality is an important aspect for any representation and, then, for a distributed representation. Understanding to what extent a distributed representation has concatenative compositionality and how information can be recovered is then a critical issue. In fact, this issue has been strongly posed by Plate (1994 , 1995) who analyzed how same specific distributed representations encode structural information and how this structural information can be recovered back.

Current approaches for treating distributed/distributional representation of sequences and structures mix two aspects in one model: a “ semantic” aspect and a representational aspect. Generally, the semantic aspect is the predominant and the representational aspect is left aside. For “ semantic” aspect, we refer to the reason why distributed symbols are composed: a final task in neural network applications or the need to give a distributional semantic vector for sequences of words. This latter is the case for compositional distributional semantics ( Clark et al., 2008 ; Baroni et al., 2014 ). For the representational aspect, we refer to the fact that composed distributed representations are in fact representing structures and these representations can be decoded back in order to extract what is in these structures.

Although the “ semantic” aspect seems to be predominant in models-that-compose , the convolution conjecture ( Zanzotto et al., 2015 ) hypothesizes that the two aspects coexist and the representational aspect plays always a crucial role. According to this conjecture, structural information is preserved in any model that composes and structural information emerges back when comparing two distributed representations with dot product to determine their similarity.

Hence, given the convolution conjecture, models-that-compose produce distributed representations for structures that can be interpreted back. Interpretability is a very important feature in these models-that-compose which will drive our analysis.

In this section we will explore the issues faced with the compositionality of representations, and the main “trends”, which correspond somewhat to the categories already presented. In particular we will start from the work on compositional distributional semantics, then we revise the work on holographic reduced representations ( Plate, 1995 ; Neumann, 2001 ) and, finally, we analyze the recent approaches with recurrent and recursive neural networks. Again, these categories are not entirely disjoint, and methods presented in one class can be often interpreted to belonging into another class.

5.1. Compositional Distributional Semantics

In distributional semantics, models-that-compose have the name of compositional distributional semantics models (CDSMs) ( Mitchell and Lapata, 2010 ; Baroni et al., 2014 ) and aim to apply the principle of compositionality ( Frege, 1884 ; Montague, 1974 ) to compute distributional semantic vectors for phrases. These CDSMs produce distributional semantic vectors of phrases by composing distributional vectors of words in these phrases. These models generally exploit structured or syntactic representations of phrases to derive their distributional meaning. Hence, CDSMs aim to give a complete semantic model for distributional semantics.

As in distributional semantics for words, the aim of CDSMs is to produce similar vectors for semantically similar sentences regardless their lengths or structures. For example, words and word definitions in dictionaries should have similar vectors as discussed in Zanzotto et al. (2010) . As usual in distributional semantics, similarity is captured with dot products (or similar metrics) among distributional vectors.

The applications of these CDSMs encompass multi-document summarization, recognizing textual entailment ( Dagan et al., 2013 ) and, obviously, semantic textual similarity detection ( Agirre et al., 2013 ).

Apparently, these CDSMs are far from having concatenative compositionality , since these distributed representations that can be interpreted back. In some sense, their nature wants that resulting vectors forget how these are obtained and focus on the final distributional meaning of phrases. There is some evidence that this is not exactly the case.

The convolution conjecture ( Zanzotto et al., 2015 ) suggests that many CDSMs produce distributional vectors where structural information and vectors for individual words can be still interpreted . Hence, many CDSMs have the concatenative compositionality property and interpretable .

In the rest of this section, we will show some classes of these CDSMs and we focus on describing how these morels are interpretable.

5.1.1. Additive Models

Additive models for compositional distributional semantics are important examples of models-that-composes where semantic and representational aspects is clearly separated. Hence, these models can be highly interpretable .

These additive models have been formally captured in the general framework for two words sequences proposed by Mitchell and Lapata (2008) . The general framework for composing distributional vectors of two word sequences “ uv” is the following:

where p ∈ ℝ n is the composition vector, u and v are the vectors for the two words u and v , R is the grammatical relation linking the two words and K is any other additional knowledge used in the composition operation. In the additive model, this equation has the following form:

where A R and B R are two square matrices depending on the grammatical relation R which may be learned from data ( Guevara, 2010 ; Zanzotto et al., 2010 ).

Before investigating if these models are interpretable, let introduce a recursive formulation of additive models which can be applied to structural representations of sentences. For this purpose, we use dependency trees. A dependency tree can be defined as a tree whose nodes are words and the typed links are the relations between two words. The root of the tree represents the word that governs the meaning of the sentence. A dependency tree T is then a word if it is a final node or it has a root r T and links ( r T , R, C i ) where C i is the i-th subtree of the node r T and R is the relation that links the node r T with C i . The dependency trees of two example sentences are reported in Figure 2 . The recursive formulation is then the following:

According to the recursive definition of the additive model, the function f r ( T ) results in a linear combination of elements M s w s where M s is a product of matrices that represents the structure and w s is the distributional meaning of one word in this structure, that is:

where S ( T ) are the relevant substructures of T . In this case, S ( T ) contains the link chains. For example, the first sentence in Figure 2 has a distributed vector defined in this way:

Figure 2 . A sentence and its dependency graph.

Each term of the sum has a part that represents the structure and a part that represents the meaning, for example:

Hence, this recursive additive model for compositional semantics is a model-that-composes which, in principle, can be highly interpretable . By selecting matrices M s such that:

it is possible to recover distributional semantic vectors related to words that are in specific parts of the structure. For example, the main verb of the sample sentence in Figure 2 with a matrix A V N T , that is:

In general, matrices derived for compositional distributional semantic models ( Guevara, 2010 ; Zanzotto et al., 2010 ) do not have this property but it is possible to obtain matrices with this property by applying thee Jonson-Linderstrauss Tranform ( Johnson and Lindenstrauss, 1984 ) or similar techniques as discussed also in Zanzotto et al. (2015) .

5.1.2. Lexical Functional Compositional Distributional Semantic Models

Lexical Functional Models are compositional distributional semantic models where words are tensors and each type of word is represented by tensors of different order. Composing meaning is then composing these tensors to obtain vectors. These models have solid mathematical background linking Lambek pregroup theory, formal semantics and distributional semantics ( Coecke et al., 2010 ). Lexical Function models are concatenative compositional, yet, in the following, we will examine whether these models produce vectors that my be interpreted .

To determine whether these models produce interpretable vectors, we start from a simple Lexical Function model applied to two word sequences. This model has been largely analyzed in Baroni and Zamparelli (2010) as matrices were considered better linear models to encode adjectives .

In Lexical Functional models over two words sequences, there is one of the two words which as a tensor of order 2 (that is, a matrix) and one word that is represented by a vector. For example, adjectives are matrices and nouns are vectors ( Baroni and Zamparelli, 2010 ) in adjective-noun sequences. Hence, adjective-noun sequences like “ black cat” or “ white dog” are represented as:

where BLACK and WHITE are matrices representing the two adjectives and cat and dog are the two vectors representing the two nouns.

These two words models are partially interpretable : knowing the adjective it is possible to extract the noun but not vice-versa. In fact, if matrices for adjectives are invertible, there is the possibility of extracting which nouns has been related to particular adjectives. For example, if BLACK is invertible, the inverse matrix BLACK −1 can be used to extract the vector of cat from the vector f (black cat):

This contributes to the interpretability of this model. Moreover, if matrices for adjectives are built using Jonson-Lindestrauss Transforms ( Johnson and Lindenstrauss, 1984 ), that is matrices with the property in Equation (8), it is possible to pack different pieces of sentences in a single vector and, then, select only relevant information, for example:

On the contrary, knowing noun vectors, it is not possible to extract back adjective matrices. This is a strong limitation in term of interpretability.

Lexical Functional models for larger structures are concatenative compositional but not interpretable at all. In fact, in general these models have tensors in the middle and these tensors are the only parts that can be inverted. Hence, in general these models are not interpretable. However, using the convolution conjecture ( Zanzotto et al., 2015 ), it is possible to know whether subparts are contained in some final vectors obtained with these models.

5.2. Holographic Representations

Holographic reduced representations (HRRs) are models-that-compose expressly designed to be interpretable ( Plate, 1995 ; Neumann, 2001 ). In fact, these models encode flat structures representing assertions and these assertions should be then searched in order to recover pieces of knowledge that is in. For example, these representations have been used to encode logical propositions such as eat ( John, apple ). In this case, each atomic element has an associated vector and the vector for the compound is obtained by combining these vectors. The major concern here is to build encoding functions that can be decoded, that is, it should be possible to retrieve composing elements from final distributed vectors such as the vector of eat ( John, apple ).

In HRRs, nearly orthogonal unit vectors ( Johnson and Lindenstrauss, 1984 ) for basic symbols, circular convolution ⊗ and circular correlation ⊕ guarantees composability and interpretability . HRRs are the extension of Random Indexing (see section 3.1) to structures. Hence, symbols are represented with vectors sampled from a multivariate normal distribution N ( 0 , 1 d I d ) . The composition function is the circular convolution indicated as ⊗ and defined as:

where subscripts are modulo d . Circular convolution is commutative and bilinear. This operation can be also computed using circulant matrices :

where A ∘ and B ∘ are circulant matrices of the vectors a and b . Given the properties of vectors a and b , matrices A ∘ and B ∘ have the property in Equation (8). Hence, circular convolution is approximately invertible with the circular correlation function (⊕) defined as follows:

where again subscripts are modulo d . Circular correlation is related to inverse matrices of circulant matrices, that is B ∘ T . In the decoding with ⊕, parts of the structures can be derived in an approximated way, that is:

Hence, circular convolution ⊗ and circular correlation ⊕ allow to build interpretable representations. For example, having the vectors e, J , and a for eat , John and apple , respectively, the following encoding and decoding produces a vector that approximates the original vector for John :

The “invertibility” of these representations is important because it allow us not to consider these representations as black boxes.

However, holographic representations have severe limitations as these can encode and decode simple, flat structures. In fact, these representations are based on the circular convolution, which is a commutative function; this implies that the representation cannot keep track of composition of objects where the order matters and this phenomenon is particularly important when encoding nested structures.

Distributed trees ( Zanzotto and Dell'Arciprete, 2012 ) have shown that the principles expressed in holographic representation can be applied to encode larger structures, overcoming the problem of reliably encoding the order in which elements are composed using the shuffled circular convolution function as the composition operator. Distributed trees are encoding functions that transform trees into low-dimensional vectors that also contain the encoding of every substructures of the tree. Thus, these distributed trees are particularly attractive as they can be used to represent structures in linear learning machines which are computationally efficient.

Distributed trees and, in particular, distributed smoothed trees ( Ferrone and Zanzotto, 2014 ) represent an interesting middle way between compositional distributional semantic models and holographic representation.

5.3. Compositional Models in Neural Networks

When neural networks are applied to sequences or structured data, these networks are in fact models-that-compose . However, these models result in models-that-compose which are not interpretable. In fact, composition functions are trained on specific tasks and not on the possibility of reconstructing the structured input, unless in some rare cases ( Socher et al., 2011 ). The input of these networks are sequences or structured data where basic symbols are embedded in local representations or distributed representations obtained with word embedding (see section 4.3). The output are distributed vectors derived for specific tasks. Hence, these models-that-compose are not interpretable in our sense for their final aim and for the fact that non linear functions are adopted in the specification of the neural networks.

In this section, we revise some prominent neural network architectures that can be interpreted as models-that-compose : the recurrent neural networks ( Krizhevsky et al., 2012 ; Graves, 2013 ; Vinyals et al., 2015a ; He et al., 2016 ) and the recursive neural networks ( Socher et al., 2012 ).

5.3.1. Recurrent Neural Networks

Recurrent neural networks form a very broad family of neural networks architectures that deal with the representation (and processing) of complex objects. At its core a recurrent neural network (RNN) is a network which takes in input the current element in the sequence and processes it based on an internal state which depends on previous inputs. At the moment the most powerful network architectures are convolutional neural networks ( Krizhevsky et al., 2012 ; He et al., 2016 ) for vision related tasks and LSTM-type network for language related task ( Graves, 2013 ; Vinyals et al., 2015a ).

A recurrent neural network takes as input a sequence x = ( x 1 … x n ) and produce as output a single vector y ∈ ℝ n which is a representation of the entire sequence. At each step 1 t the network takes as input the current element x t , the previous output h t−1 and performs the following operation to produce the current output h t

where σ is a non-linear function such as the logistic function or the hyperbolic tangent and [ h t−1 x t ] denotes the concatenation of the vectors h t−1 and x t . The parameters of the model are the matrix W and the bias vector b .

Hence, a recurrent neural network is effectively a learned composition function, which dynamically depends on its current input, all of its previous inputs and also on the dataset on which is trained. However, this learned composition function is basically impossible to analyze or interpret in any way. Sometime an “intuitive” explanation is given about what the learned weights represent: with some weights representing information that must be remembered or forgotten.

Even more complex recurrent neural networks as long-short term memory (LSTM) ( Hochreiter and Schmidhuber, 1997 ) have the same problem of interpretability. LSTM are a recent and successful way for neural network to deal with longer sequences of inputs, overcoming some difficulty that RNN face in the training phase. As with RNN, LSTM network takes as input a sequence x = ( x 1 … x n ) and produce as output a single vector y ∈ ℝ n which is a representation of the entire sequence. At each step t the network takes as input the current element x t , the previous output h t−1 and performs the following operation to produce the current output h t and update the internal state c t .

where ⊙ stands for element-wise multiplication, and the parameters of the model are the matrices W f , W i , W o , W c and the bias vectors b f , b i , b o , b c .

Generally, the interpretation offered for recursive neural networks is functional or “ psychological” and not on the content of intermediate vectors. For example, an interpretation of the parameters of LSTM is the following:

• f t is the forget gate : at each step takes in consideration the new input and output computed so far to decide which information in the internal state must be forgotten (that is, set to 0);

• i t is the input gate : it decides which position in the internal state will be updated, and by how much;

• c t ~ is the proposed new internal state, which will then be updated effectively combining the previous gate;

• o t is the output gate : it decides how to modulate the internal state to produce the output

These models-that-compose have high performance on final tasks but are definitely not interpretable.

5.3.2. Recursive Neural Network

The last class of models-that-compose that we present is the class of recursive neural networks ( Socher et al., 2012 ). These networks are applied to data structures as trees and are in fact applied recursively on the structure. Generally, the aim of the network is a final task as sentiment analysis or paraphrase detection .

Recursive neural networks is then a basic block that is recursively applied on trees like the one in Figure 3 . The formal definition is the following:

where g is a component-wise sigmoid function or tanh, and W is a matrix that maps the concatenation vector ( V u U v ) to have the same dimension.

Figure 3 . A simple binary tree.

This method deals naturally with recursion: given a binary parse tree of a sentence s , the algorithm creates vectors and matrices representation for each node, starting from the terminal nodes. Words are represented by distributed representations or local representations. For example, the tree in Figure 3 is processed by the recursive network in the following way. First, the network is applied to the pair (animal,extracts) and f UV ( animal, extract ) is obtained. Then, the network is applied to the result and eat and f UV ( eat , f UV ( animal, extract )) is obtained and so on.

Recursive neural networks are not easily interpretable even if quite similar to the additive compositional distributional semantic models as those presented in section 5.1.1. In fact, the non-linear function g is the one that makes final vectors less interpretable.

5.3.3. Attention Neural Network

Attention neural networks ( Vaswani et al., 2017 ; Devlin et al., 2019 ) are an extremely successful approach for combining distributed representations of sequences of symbols. Yet, these models are very simple. In fact, these attention models are basically gigantic multi-layered perceptrons applied to distributed representations of discrete symbols. The key point is that these gigantic multi-layer percpetrons are trained on generic tasks and, then, these pre-trained models are used in specific tasks by training the last layers. From the point of view of sequence-level interpretability, these models are still under investigation as the eventual concatenative compositionality is scattered in the overall network.

6. Conclusions

In the ‘90, the hot debate on neural networks was whether or not distribute representations are only an implementation of discrete symbolic representations. The question behind this debate is in fact crucial to understand if neural networks may exploit something more that systems strictly based on discrete symbolic representations. The question is again becoming extremely relevant since natural language is by construction a discrete symbolic representations and, nowadays, deep neural networks are solving many tasks.

We made this survey to revitalize the debate. In fact, this is the right time to focus on this fundamental question. As we show, distributed representations have a the not-surprising link with discrete symbolic representations. In our opinion, by shading a light on this debate, this survey will help to devise new deep neural networks that can exploit existing and novel symbolic models of classical natural language processing tasks. We believe that a clearer understanding of the strict link between distributed/distributional representations and symbols may lead to radically new deep learning networks.

Author Contributions

All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

1. ^ we can usually think of this as a timestep, but not all applications of recurrent neural network have a temporal interpretation.

Achlioptas, D. (2003). Database-friendly random projections: Johnson-lindenstrauss with binary coins. J. Comput. Syst. Sci. 66, 671–687. doi: 10.1016/S0022-0000(03)00025-4

CrossRef Full Text | Google Scholar

Agirre, E., Cer, D., Diab, M., Gonzalez-Agirre, A., and Guo, W. (2013). “sem 2013 shared task: Semantic textual similarity,” in Second Joint Conference on Lexical and Computational Semantics (*SEM), Volume 1: Proceedings of the Main Conference and the Shared Task: Semantic Textual Similarity (Atlanta, GA: Association for Computational Linguistics), 32–43.

Google Scholar

Bahdanau, D., Cho, K., and Bengio, Y. (2015). “Neural machine translation by jointly learning to align and translate,” in Proceedings of the 3rd International Conference on Learning Representations (ICLR) .

Baroni, M., Bernardi, R., and Zamparelli, R. (2014). Frege in space: a program of compositional distributional semantics. Linguist. Issues Lang. Technol. 9, 241–346.

Baroni, M., and Lenci, A. (2010). Distributional memory: a general framework for corpus-based semantics. Comput. Linguist. 36, 673–721. doi: 10.1162/coli_a_00016

Baroni, M., and Zamparelli, R. (2010). “Nouns are vectors, adjectives are matrices: Representing adjective-noun constructions in semantic space,” in Proceedings of the 2010 Conference on Empirical Methods in Natural Language Processing (Cambridge, MA: Association for Computational Linguistics), 1183–1193.

Bingham, E., and Mannila, H. (2001). “Random projection in dimensionality reduction: applications to image and text data,” in Proceedings of the Seventh ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (San Francisco: ACM), 245–250.

Blutner, R., Hendriks, P., and de Hoop, H. (2003). “A new hypothesis on compositionality,” in Proceedings of the Joint International Conference on Cognitive Science (Sydney, NSW).

Chalmers, D. J. (1992). Syntactic Transformations on Distributed Representations. Dordrecht: Springer.

Chetlur, S., Woolley, C., Vandermersch, P., Cohen, J., Tran, J., Catanzaro, B., et al. (2014). cudnn: Efficient primitives for deep learning. arXiv (Preprint). arXiv:1410.0759 .

Chomsky, N. (1957). Aspect of Syntax Theory . Cambridge, MA: MIT Press.

Clark, S., Coecke, B., and Sadrzadeh, M. (2008). “A compositional distributional model of meaning,” in Proceedings of the Second Symposium on Quantum Interaction (QI-2008) (Oxford), 133–140.

Coecke, B., Sadrzadeh, M., and Clark, S. (2010). Mathematical foundations for a compositional distributional model of meaning. arXiv:1003.4394 .

Cotterell, R., Poliak, A., Van Durme, B., and Eisner, J. (2017). “Explaining and generalizing skip-gram through exponential family principal component analysis,” in Proceedings of the 15th Conference of the European Chapter of the Association for Computational Linguistics: Volume 2, Short Papers (Valencia: Association for Computational Linguistics), 175-181.

Cui, H., Ganger, G. R., and Gibbons, P. B. (2015). Scalable Deep Learning on Distributed GPUS with a GPU-Specialized Parameter Server. Technical report, CMU PDL Technical Report (CMU-PDL-15-107).

Dagan, I., Roth, D., Sammons, M., and Zanzotto, F. M. (2013). Recognizing Textual Entailment: Models and Applications . San Rafael, CA: Morgan & Claypool Publishers.

Devlin, J., Chang, M., Lee, K., and Toutanova, K. (2019). “BERT: pre-training of deep bidirectional transformers for language understanding,” in Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies , 4171–4186.

Ferrone, L., and Zanzotto, F. M. (2014). “Towards syntax-aware compositional distributional semantic models,” in Proceedings of COLING 2014, the 25th International Conference on Computational Linguistics: Technical Papers (Dublin: Dublin City University and Association for Computational Linguistics), 721–730.

Ferrone, L., Zanzotto, F. M., and Carreras, X. (2015). “Decoding distributed tree structures,” in Statistical Language and Speech Processing - Third International Conference, SLSP 2015 (Budapest), 73–83.

Firth, J. R. (1957). Papers in Linguistics. London: Oxford University Press.

Fodor, I. (2002). A Survey of Dimension Reduction Techniques. Technical report. Lawrence Livermore National Lab., CA, USA.

Fodor, J. A., and Pylyshyn, Z. W. (1988). Connectionism and cognitive architecture: a critical analysis. Cognition 28, 3–71.

PubMed Abstract | Google Scholar

Frege, G. (1884). Die Grundlagen der Arithmetik (The Foundations of Arithmetic): eine logisch-mathematische Untersuchung über den Begriff der Zahl . Breslau: W. Koebner.

Gelder, T. V. (1990). Compositionality: a connectionist variation on a classical theme. Cogn. Sci. 384, 355–384.

Goldberg, Y., and Levy, O. (2014). word2vec explained: deriving mikolov et al.'s negative-sampling word-embedding method. arXiv (Preprint). arXiv:1402.3722 .

Goodfellow, I., Pouget-Abadie, J., Mirza, M., Xu, B., Warde-Farley, D., Ozair, S., et al. (2014). “Generative adversarial nets,” in Advances in Neural Information Processing Systems (Montreal, QC), 2672–2680.

Graves, A. (2013). Generating sequences with recurrent neural networks. arXiv:1308.0850 .

Grefenstette, E., and Sadrzadeh, M. (2011). “Experimental support for a categorical compositional distributional model of meaning,” in Proceedings of the Conference on Empirical Methods in Natural Language Processing, EMNLP '11 (Stroudsburg, PA: Association for Computational Linguistics), 1394–1404.

Guevara, E. (2010). “A regression model of adjective-noun compositionality in distributional semantics,” in Proceedings of the 2010 Workshop on GEometrical Models of Natural Language Semantics (Uppsala: Association for Computational Linguistics), 33–37.

Harris, Z. (1954). Distributional structure. Word 10, 146–162.

He, K., Zhang, X., Ren, S., and Sun, J. (2016). Identity mappings in deep residual networks. arXiv (preprint) arXiv:1603.05027 . doi: 10.1007/978-3-319-46493-0_38

Hinton, G. E., McClelland, J. L., and Rumelhart, D. E. (1986). “Distributed representations,” in Parallel Distributed Processing: Explorations in the Microstructure of Cognition. Volume 1: Foundations , eds D. E. Rumelhart and J. L. McClelland (Cambridge, MA: MIT Press), 77–109.

Hochreiter, S., and Schmidhuber, J. (1997). Long short-term memory. Neural Comput. 9, 1735–1780.

Jacovi, A., Shalom, O. S., and Goldberg, Y. (2018). “Understanding convolutional neural networks for text classification,” in Proceedings of the 2018 EMNLP Workshop BlackboxNLP: Analyzing and Interpreting Neural Networks for NLP (Brussels), 56–65.

Jang, K.-R., Kim, S.-B., and Corp, N. (2018). “Interpretable word embedding contextualization,” in Proceedings of the 2018 EMNLP Workshop BlackboxNLP: Analyzing and Interpreting Neural Networks for NLP (Brussels), 341–343.

Johnson, W., and Lindenstrauss, J. (1984). Extensions of lipschitz mappings into a hilbert space. Contemp. Math. 26, 189–206.

Kalchbrenner, N., and Blunsom, P. (2013). “Recurrent convolutional neural networks for discourse compositionality,” in Proceedings of the 2013 Workshop on Continuous Vector Space Models and Their Compositionality (Sofia).

Krizhevsky, A., Sutskever, I., and Hinton, G. E. (2012). “Imagenet classification with deep convolutional neural networks,” in Advances in Neural Information Processing Systems (Lake Tahoe, NV), 1097–1105.

Landauer, T. K., and Dumais, S. T. (1997). A solution to plato's problem: the latent semantic analysis theory of acquisition, induction, and representation of knowledge. Psychol. Rev. 104, 211–240.

LeCun, Y., Bengio, Y., and Hinton, G. (2015). Deep learning. Nature 521, 436–444.

Liou, C.-Y., Cheng, W.-C., Liou, J.-W., and Liou, D.-R. (2014). Autoencoder for words. Neurocomputing 139, 84–96. doi: 10.1016/j.neucom.2013.09.055

Lipton, Z. C. (2018). The mythos of model interpretability. Commun. ACM 61, 36–43. doi: 10.1145/3233231

Markovsky, I. (2011). Low Rank Approximation: Algorithms, Implementation, Applications . Springer Publishing Company, Incorporated.

Masci, J., Meier, U., Cireşan, D., and Schmidhuber, J. (2011). “Stacked convolutional auto-encoders for hierarchical feature extraction,” in International Conference on Artificial Neural Networks (Springer), 52–59.

Mikolov, T., Chen, K., Corrado, G., and Dean, J. (2013). “Efficient estimation of word representations in vector space,” in Proceedings of the International Conference on Learning Representations (ICLR) .

Mitchell, J., and Lapata, M. (2008). “Vector-based models of semantic composition,” in Proceedings of ACL-08: HLT (Columbus, OH: Association for Computational Linguistics), 236–244.

Mitchell, J., and Lapata, M. (2010). Composition in distributional models of semantics. Cogn. Sci . 34, 1388–1429. doi: 10.1111/j.1551-6709.2010.01106.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Montague, R. (1974). “English as a formal language,” in Formal Philosophy: Selected Papers of Richard Montague , ed R. Thomason (New Haven: Yale University Press), 188–221.

Neumann, J. (2001). Holistic processing of hierarchical structures in connectionist networks (Ph.D. thesis). University of Edinburgh, Edinburgh.

Pado, S., and Lapata, M. (2007). Dependency-based construction of semantic space models. Comput. Linguist. 33, 161–199. doi: 10.1162/coli.2007.33.2.161

Pearson, K. (1901). Principal components analysis. Lond. Edinburgh Dublin Philos. Magn. J. 6566.

Plate, T. A. (1994). Distributed representations and nested compositional structure . Ph.D. thesis. University of Toronto, Toronto, Canada.

Plate, T. A. (1995). Holographic reduced representations. IEEE Trans. Neural Netw. 6, 623–641.

Rosenblatt, F. (1958). The perceptron: a probabilistic model for information storage and organization in the brain. Psychol. Rev. 65, 386–408.

Rothenhäusler, K., and Schütze, H. (2009). “Unsupervised classification with dependency based word spaces,” in Proceedings of the Workshop on Geometrical Models of Natural Language Semantics, GEMS '09 (Stroudsburg, PA: Association for Computational Linguistics), 17–24.

Sahlgren, M. (2005). “An introduction to random indexing,” in Proceedings of the Methods and Applications of Semantic Indexing Workshop at the 7th International Conference on Terminology and Knowledge Engineering TKE (Copenhagen).

Salton, G. (1989). Automatic Text Processing: The Transformation, Analysis and Retrieval of Information by Computer . Boston, MA: Addison-Wesley.

Schmidhuber, J. (2015). Deep learning in neural networks: an overview. Neural Netw. 61, 85–117. doi: 10.1016/j.neunet.2014.09.003

Schuster, M., and Paliwal, K. (1997). Bidirectional recurrent neural networks. Trans. Sig. Proc. 45, 2673–2681.

Socher, R., Huang, E. H., Pennington, J., Ng, A. Y., and Manning, C. D. (2011). “Dynamic pooling and unfolding recursive autoencoders for paraphrase detection,” in Advances in Neural Information Processing Systems 24 (Granada).

Socher, R., Huval, B., Manning, C. D., and Ng, A. Y. (2012). “Semantic compositionality through recursive matrix-vector spaces,” in Proceedings of the 2012 Conference on Empirical Methods in Natural Language Processing (EMNLP) (Jeju).

Sorzano, C. O. S., Vargas, J., and Montano, A. P. (2014). A survey of dimensionality reduction techniques. arXiv (Preprint). arXiv:1403.2877 .

Turney, P. D. (2006). Similarity of semantic relations. Comput. Linguist. 32, 379–416. doi: 10.1162/coli.2006.32.3.379

Turney, P. D., and Pantel, P. (2010). From frequency to meaning: vector space models of semantics. J. Artif. Intell. Res. 37, 141–188. doi: 10.1613/jair.2934

Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., et al. (2017). “Attention is all you need,” in Advances in Neural Information Processing Systems 30 , eds I. Guyon, U. V. Luxburg, S. Bengio, H. Wallach, R. Fergus, S. Vishwanathan, and R. Garnett (Long Beach, CA: Curran Associates, Inc.), 5998–6008.

Vincent, P., Larochelle, H., Bengio, Y., and Manzagol, P.-A. (2008). “Extracting and composing robust features with denoising autoencoders,” in Proceedings of the 25th International Conference on Machine learning (Helsinki: ACM), 1096–1103.

Vincent, P., Larochelle, H., Lajoie, I., Bengio, Y., and Manzagol, P.-A. (2010). Stacked denoising autoencoders: learning useful representations in a deep network with a local denoising criterion. J. Mach. Learn. Res. 11, 3371–3408.

Vinyals, O., Kaiser, L. u., Koo, T., Petrov, S., Sutskever, I., and Hinton, G. (2015a). “Grammar as a foreign language,” in Advances in Neural Information Processing Systems 28 , eds C. Cortes, N. D. Lawrence, D. D. Lee, M. Sugiyama, and R. Garnett (Montreal, QC: Curran Associates, Inc.), 2755–2763.

Vinyals, O., Toshev, A., Bengio, S., and Erhan, D. (2015b). “Show and tell: a neural image caption generator,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (Boston, MA), 3156–3164.

Weiss, D., Alberti, C., Collins, M., and Petrov, S. (2015). Structured training for neural network transition-based parsing. arXiv (Preprint). arXiv:1506.06158 . doi: 10.3115/v1/P15-1032

Werbos, P. (1974). Beyond regression: new tools for prediction and analysis in the behavioral sciences. Ph.D. Thesis, Harvard University, Cambridge.

Xu, K., Ba, J., Kiros, R., Cho, K., Courville, A., Salakhudinov, R., et al. (2015). “Show, attend and tell: neural image caption generation with visual attention,” in Proceedings of the 32nd International Conference on Machine Learning, in PMLR , Vol. 37, 2048–2057.

Zanzotto, F. M., and Dell'Arciprete, L. (2012). “Distributed tree kernels,” in Proceedings of International Conference on Machine Learning (Edinburg).

Zanzotto, F. M., Ferrone, L., and Baroni, M. (2015). When the whole is not greater than the combination of its parts: a “decompositional” look at compositional distributional semantics. Comput. Linguist. 41, 165–173. doi: 10.1162/COLI_a_00215

Zanzotto, F. M., Korkontzelos, I., Fallucchi, F., and Manandhar, S. (2010). “Estimating linear models for compositional distributional semantics,” in Proceedings of the 23rd International Conference on Computational Linguistics (COLING) (Beijing).

Zeiler, M. D., and Fergus, R. (2014a). “Visualizing and understanding convolutional networks,” in Computer Vision – ECCV 2014 , eds D. Fleet, T. Pajdla, B. Schiele, and T. Tuytelaars (Cham: Springer International Publishing), 818–833.

Zeiler, M. D., and Fergus, R. (2014b). “Visualizing and understanding convolutional networks,” in European Conference on Computer Vision (Zurich: Springer), 818–833.

Zou, W. Y., Socher, R., Cer, D. M., and Manning, C. D. (2013). “Bilingual word embeddings for phrase-based machine translation,” in EMNLP (Seattle, WA), 1393–1398.

Keywords: natural language processing (NLP), distributed representation, concatenative compositionality, deep learning (DL), compositional distributional semantic models, compositionality

Citation: Ferrone L and Zanzotto FM (2020) Symbolic, Distributed, and Distributional Representations for Natural Language Processing in the Era of Deep Learning: A Survey. Front. Robot. AI 6:153. doi: 10.3389/frobt.2019.00153

Received: 05 May 2019; Accepted: 20 December 2019; Published: 21 January 2020.

Reviewed by:

Copyright © 2020 Ferrone and Zanzotto. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY) . The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.

*Correspondence: Fabio Massimo Zanzotto, fabio.massimo.zanzotto@uniroma2.it

This article is part of the Research Topic

Language Representation and Learning in Cognitive and Artificial Intelligence Systems

Help | Advanced Search

Computer Science > Machine Learning

Title: the platonic representation hypothesis.

Abstract: We argue that representations in AI models, particularly deep networks, are converging. First, we survey many examples of convergence in the literature: over time and across multiple domains, the ways by which different neural networks represent data are becoming more aligned. Next, we demonstrate convergence across data modalities: as vision models and language models get larger, they measure distance between datapoints in a more and more alike way. We hypothesize that this convergence is driving toward a shared statistical model of reality, akin to Plato's concept of an ideal reality. We term such a representation the platonic representation and discuss several possible selective pressures toward it. Finally, we discuss the implications of these trends, their limitations, and counterexamples to our analysis.

Submission history

Access paper:.

• HTML (experimental)
• Other Formats

References & Citations

• Google Scholar
• Semantic Scholar

BibTeX formatted citation

Bibliographic and Citation Tools

Code, data and media associated with this article, recommenders and search tools.

• Institution

arXivLabs: experimental projects with community collaborators

arXivLabs is a framework that allows collaborators to develop and share new arXiv features directly on our website.

Both individuals and organizations that work with arXivLabs have embraced and accepted our values of openness, community, excellence, and user data privacy. arXiv is committed to these values and only works with partners that adhere to them.

Have an idea for a project that will add value for arXiv's community? Learn more about arXivLabs .

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

• View all journals
• Explore content
• About the journal
• Publish with us
• Sign up for alerts
• RESEARCH BRIEFINGS
• 22 May 2024

How the same brain cells can represent both the perception and memory of faces

This is a summary of: She, L. et al . Temporal multiplexing of perception and memory codes in IT cortex. Nature 629 , 861–868 (2024) .

Access options

Access Nature and 54 other Nature Portfolio journals

Get Nature+, our best-value online-access subscription

24,99 € / 30 days

cancel any time

Subscribe to this journal

Receive 51 print issues and online access

185,98 € per year

only 3,65 € per issue

Rent or buy this article

Prices vary by article type

Prices may be subject to local taxes which are calculated during checkout

doi: https://doi.org/10.1038/d41586-024-01511-9

‘Expert opinion’ and the figure are published under a CC BY 4.0 licence.

Scoville, W. B. & Milner, B. J. Neurol. Neurosurg. Psychiat. 20 , 11–21 (1957).

Article   PubMed   Google Scholar  

Hesse, J. K. & Tsao, D. Y. Nature Rev. Neurosci. 21 , 695–716 (2020).

Chang, L. & Tsao, D. Y. Cell 169 , 1013–1028 (2017).

Xiang, J.-Z. & Brown, M. W. Neuropharmacology 37 , 657–676 (1998).

Boyle, L. M., Posani, L., Irfan, S., Siegelbaum, S. A. & Fusi, S. Neuron 112 , 1358–1371 (2024).

Download references

Reprints and permissions

Related Articles

• Neuroscience

Heed lessons from past studies involving transgender people: first, do no harm

Comment 28 MAY 24

Autistic people three times more likely to develop Parkinson's-like symptoms

News 28 MAY 24

These crows have counting skills previously only seen in people

News 23 MAY 24

Seed-stashing chickadees overturn ideas about location memory

News & Views 23 MAY 24

Neural pathways for reward and relief promote fentanyl addiction

News & Views 22 MAY 24

AI networks reveal how flies find a mate

Assistant, Associate or Full Professor

The McLaughlin Research Institute and Touro University – Montana campus invite applications for open rank faculty positions.

McLaughlin Research Institute

Postdoctoral Associate- Neuroscience

Houston, Texas (US)

Baylor College of Medicine (BCM)

Call for applications- junior and senior scientists

The BORDEAUX INSTITUTE OF ONCOLOGY (BRIC U1312, https://www.bricbordeaux.com/) is seeking to recruit new junior and senior researchers

Bordeaux (Ville), Gironde (FR)

INSERM - U1312 BRIC

Postdoctoral Scholar - Organic Synthesis

Memphis, Tennessee

The University of Tennessee Health Science Center (UTHSC)

Postdoctoral Scholar - Chemical Biology

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Quick links

• Explore articles by subject
• Guide to authors
• Editorial policies

• Conferences

Representation Learning – Complete Guide for Beginner

• By Vijaysinh Lendave
• Last Updated on May 20, 2024

Representation learning is a very important aspect of machine learning which automatically discovers the feature patterns in the data. When the machine is provided with the data, it learns the representation itself without any human intervention. The goal of representation learning is to train machine learning algorithms to learn useful representations, such as those that are interpretable, incorporate latent features, or can be used for transfer learning. In this article, we will discuss the concept of representation learning along with its need and different approaches. The major points to be covered in this article are listed below.

Let’s start the discussion by understanding what is the actual need for representation learning.

Need of Representation Learning

Assume you’re developing a machine-learning algorithm to predict dog breeds based on pictures. Because image data provides all of the answers, the engineer must rely heavily on it when developing the algorithm. Each observation or feature in the data describes the qualities of the dogs. The machine learning system that predicts the outcome must comprehend how each attribute interacts with other outcomes such as Pug, Golden Retriever, and so on.

As a result, if there is any noise or irregularity in the input, the result can be drastically different, which is a risk with most machine learning algorithms. The majority of machine learning algorithms have only a basic understanding of the data. So in such cases, the solution is to provide a more abstract representation of data. It’s impossible to tell which features should be extracted for many tasks. This is where the concept of representation learning takes shape.

What is Representation Learning?

Representation learning is a class of machine learning approaches that allow a system to discover the representations required for feature detection or classification from raw data. The requirement for manual feature engineering is reduced by allowing a machine to learn the features and apply them to a given activity.

In representation learning, data is sent into the machine, and it learns the representation on its own. It is a way of determining a data representation of the features, the distance function, and the similarity function that determines how the predictive model will perform. Representation learning works by reducing high-dimensional data to low-dimensional data, making it easier to discover patterns and anomalies while also providing a better understanding of the data’s overall behaviour.

Basically, Machine learning tasks such as classification frequently demand input that is mathematically and computationally convenient to process, which motivates representation learning. Real-world data, such as photos, video, and sensor data, has resisted attempts to define certain qualities algorithmically. An approach is to examine the data for such traits or representations rather than depending on explicit techniques.

Methods of Representation Learning

We must employ representation learning to ensure that the model provides invariant and untangled outcomes in order to increase its accuracy and performance. In this section, we’ll look at how representation learning can improve the model’s performance in three different learning frameworks: supervised learning, unsupervised learning.

1. Supervised Learning

This is referred to as supervised learning when the ML or DL model maps the input X to the output Y. The computer tries to correct itself by comparing model output to ground truth, and the learning process optimizes the mapping from input to output. This process is repeated until the optimization function reaches global minima.

Even when the optimization function reaches the global minima, new data does not always perform well, resulting in overfitting. While supervised learning does not necessitate a significant amount of data to learn the mapping from input to output, it does necessitate the learned features. The prediction accuracy can improve by up to 17 percent when the learned attributes are incorporated into the supervised learning algorithm.

Using labelled input data, features are learned in supervised feature learning. Supervised neural networks, multilayer perceptrons, and (supervised) dictionary learning are some examples.

2. Unsupervised Learning

Unsupervised learning is a sort of machine learning in which the labels are ignored in favour of the observation itself. Unsupervised learning isn’t used for classification or regression; instead, it’s used to uncover underlying patterns, cluster data, denoise it, detect outliers, and decompose data, among other things.

When working with data x, we must be very careful about whatever features z we use to ensure that the patterns produced are accurate. It has been observed that having more data does not always imply having better representations. We must be careful to develop a model that is both flexible and expressive so that the extracted features can convey critical information.

Unsupervised feature learning learns features from unlabeled input data by following the methods such as Dictionary learning, independent component analysis, autoencoders, matrix factorization, and various forms of clustering are among examples.

In the next section, we will see more about these methods and workflow, how they learn the representation in detail.

Supervised Learning Algorithms

1. supervised dictionary learning.

Dictionary learning creates a set of representative elements (dictionary) from the input data, allowing each data point to be represented as a weighted sum of the representative elements. By minimizing the average representation error (across the input data) and applying L1 regularization to the weights, the dictionary items and weights may be obtained i.e., the representation of each data point has only a few nonzero weights.

For optimizing dictionary elements, supervised dictionary learning takes advantage of both the structure underlying the input data and the labels. The supervised dictionary learning technique uses dictionary learning to solve classification issues by optimizing dictionary elements, data point weights, and classifier parameters based on the input data.

A minimization problem is formulated, with the objective function consisting of the classification error, the representation error, an L1 regularization on the representing weights for each data point (to enable sparse data representation), and an L2 regularization on the parameters of the classification algorithm.

2. Multi-Layer Perceptron

The perceptron is the most basic neural unit, consisting of a succession of inputs and weights that are compared to the ground truth. A multi-layer perceptron, or MLP, is a feed-forward neural network made up of layers of perceptron units. MLP is made up of three-node layers: an input, a hidden layer, and an output layer. MLP is commonly referred to as the vanilla neural network because it is a very basic artificial neural network.

This notion serves as a foundation for hidden variables and representation learning. Our goal in this theorem is to determine the variables or required weights that can represent the underlying distribution of the entire data so that when we plug those variables or required weights into unknown data, we receive results that are almost identical to the original data. In a word, artificial neural networks (ANN) assist us in extracting meaningful patterns from a dataset.

3. Neural Networks

Neural networks are a class of learning algorithms that employ a “network” of interconnected nodes in various layers. It’s based on the animal nervous system, with nodes resembling neurons and edges resembling synapses. The network establishes computational rules for passing input data from the network’s input layer to the network’s output layer, and each edge has an associated weight.

The relationship between the input and output layers, which is parameterized by the weights, is described by a network function associated with a neural network. Various learning tasks can be achieved by minimizing a cost function over the network function (w) with correctly defined network functions.

Unsupervised Learning Algorithms

Learning Representation from unlabeled data is referred to as unsupervised feature learning. Unsupervised Representation learning frequently seeks to uncover low-dimensional features that encapsulate some structure beneath the high-dimensional input data.

1. K-Means Clustering

K-means clustering is a vector quantization approach. An n-vector set is divided into k clusters (i.e. subsets) via K-means clustering, with each vector belonging to the cluster with the closest mean. Despite the use of inferior greedy techniques, the problem is computationally NP-hard.

K-means clustering divides an unlabeled collection of inputs into k groups before obtaining centroids-based features. These characteristics can be honed in a variety of ways. The simplest method is to add k binary features to each sample, with each feature j having a value of one of the k-means learned jth centroid is closest to the sample under consideration. Cluster distances can be used as features after being processed with a radial basis function.

2. Local Linear Embedding

LLE is a nonlinear learning strategy for constructing low-dimensional neighbour-preserving representations from high-dimensional (unlabeled) input. LLE’s main goal is to reconstruct high-dimensional data using lower-dimensional points while keeping some geometric elements of the original data set’s neighbours.

There are two major steps in LLE. The first step is “neighbour-preserving,” in which each input data point Xi is reconstructed as a weighted sum of K nearest neighbour data points, with the optimal weights determined by minimizing the average squared reconstruction error (i.e., the difference between an input point and its reconstruction) while keeping the weights associated with each point equal to one.

The second stage involves “dimension reduction,” which entails searching for vectors in a lower-dimensional space that reduce the representation error while still using the optimal weights from the previous step.

The weights are optimized given fixed data in the first stage, which can be solved as a least-squares problem. Lower-dimensional points are optimized with fixed weights in the second phase, which can be solved using sparse eigenvalue decomposition.

3. Unsupervised Dictionary Mining

For optimizing dictionary elements, unsupervised dictionary learning does not use data labels and instead relies on the structure underlying the data. Sparse coding, which seeks to learn basic functions (dictionary elements) for data representation from unlabeled input data, is an example of unsupervised dictionary learning.

When the number of vocabulary items exceeds the dimension of the input data, sparse coding can be used to learn overcomplete dictionaries. K-SVD is an algorithm for learning a dictionary of elements that allows for sparse representation.

4. Deep Architectures Methods

Deep learning architectures for feature learning are inspired by the hierarchical architecture of the biological brain system, which stacks numerous layers of learning nodes. The premise of distributed representation is typically used to construct these architectures: observable data is generated by the interactions of many diverse components at several levels.

5. Restricted Boltzmann Machine (RBMs)

In multilayer learning frameworks, RBMs (restricted Boltzmann machines) are widely used as building blocks. An RBM is a bipartite undirected network having a set of binary hidden variables, visible variables, and edges connecting the hidden and visible nodes. It’s a variant of the more general Boltzmann machines, with the added constraint of no intra-node connections. In an RBM, each edge has a weight assigned to it. The connections and weights define an energy function that can be used to generate a combined distribution of visible and hidden nodes.

For unsupervised representation learning, an RBM can be thought of as a single-layer design. The visible variables, in particular, relate to the input data, whereas the hidden variables correspond to the feature detectors. Hinton’s contrastive divergence (CD) approach can be used to train the weights by maximizing the probability of visible variables.

6. Autoencoders

Deep network representations have been found to be insensitive to complex noise or data conflicts. This can be linked to the architecture to some extent. The employment of convolutional layers and max-pooling, for example, can be proven to produce transformation insensitivity.

Autoencoders are therefore neural networks that may be taught to do representation learning. Autoencoders seek to duplicate their input to their output using an encoder and a decoder. Autoencoders are typically trained via recirculation, a learning process that compares the activation of the input network to the activation of the reconstructed input.

Final Words

Unlike typical learning tasks like classification, which has the end goal of reducing misclassifications, representation learning is an intermediate goal of machine learning making it difficult to articulate a straight and obvious training target. In this post, we understood how to overcome such difficulties from scratch. From the starting, we have seen what was the actual need for this method and understood different methodologies in supervised, unsupervised, and some deep learning frameworks.

Best Face Swap AI Tools in 2024 – Remaker.ai Alternatives

Top 10 Cartoonist to Follow in 2024

The Best AI Search Engines in 2024 – Perplexity AI Alternatives

Different Types of Classification Algorithms

Top Most Important Reasons to Use Linux Operating System

Augmented Dickey-Fuller (ADF) Test In Time-Series Analysis

Bidirectional LSTM (Long-Short Term Memory) with Python Codes

Scribble Diffusion – Converts Doddles and Sketch to AI Images

Best AI Image Generator in 2024

What is Unstable Diffusion – Difference Between Stable Vs Unstable?

Difference Between NVIDIA H100 Vs A100: Which is the best GPU?

Top 10 Sentiment Analysis Dataset

Top 10 Space Observatories in India

How to Build Your First Generative AI Agent with Mistral 7B LLM

Join the forefront of data innovation at the Data Engineering Summit 2024, where industry leaders redefine technology’s future.

© Analytics India Magazine Pvt Ltd & AIM Media House LLC 2024

• Terms of use
• Privacy Policy

Subscribe to our Youtube channel and see how AI ecosystem works.

A business journal from the Wharton School of the University of Pennsylvania

Why Representation Matters in Marketing

May 28, 2024 • 4 min read.

Do TV commercials featuring diverse actors help increase sales? Wharton’s Zhenling Jiang tests this idea in her latest study on mortgage ads.

• Diversity, Equity, & Inclusion

Marketing to minority consumers has been around since the 1950s, when advertising agencies realized the untapped potential in Black consumers who were the second-largest racial group at the time. Advertising has come a long way since then, and so has the emphasis on diversity, equity, and inclusion (DEI). The result is a wider variety of ads that feature minority actors, models, and celebrities enticing minority consumers to buy. But does representation make a difference?

Research from Wharton marketing professor Zhenling Jiang determined that it does — in a big way. Her co-authored study, which examined television commercials for mortgage refinancing, found that as minority representation depicted in the ads increased from 15% to 25%, the advertising elasticity went up 14%. Advertising elasticity measures a campaign’s effectiveness in generating new sales.

Perhaps most surprisingly, the study found that ads with diverse players didn’t just increase sales among minority borrowers. There was a positive effect among white borrowers, too.

Jiang said the study sends a strong signal to brands that their genuine efforts to attract minority customers can pay off in ways they may not expect.

“When we think about DEI, we tend to think we are sacrificing something to feature more diversity. We are making a trade-off,” she said. “But it’s quite the contrary. It’s actually a nice message that they can achieve both higher sales as well as the societal goal of more inclusion and representation.”

The study , “TV Advertising Effectiveness with Racial Minority Representation: Evidence from the Mortgage Market,” was co-authored by Raphael Thomadsen , marketing professor at Washington University in St. Louis, and Donggwan Kim , who earned his doctorate at Washington University in St. Louis and joins the marketing faculty at Boston College this fall.

“We tend to think we are sacrificing something to feature more diversity. We are making a trade-off. But it’s quite the contrary.” — Zhenling Jiang

Representation and the Racial Wealth Gap

Jiang, who focuses on consumer finance topics in her research, said she chose to study mortgage refinancing ads for a very specific reason: the racial wealth gap in the U.S. With home equity as the largest contributor to household wealth, refinancing can be an important mechanism to help Black and Hispanic homeowners — two groups that haven’t always been courted by lenders.

“Mortgages are the most significant financial decision that consumers can make. If they don’t refinance when interest rates are lower, it can be very costly,” she said. “The long-standing racial disparity in the world of consumer finance makes this question more important.”

For the study, the scholars collected loan origination data from 2018 to 2021 that included information on borrower’s race and census tract-level political affiliation. They merged that with TV mortgage advertising data obtained from Kantar Media for the same time period. That data included ad spending and video files. The scholars used a double machine learning model to control for a host of variables, including image and text embeddings, lender, location, and time of year the ads ran.

To test their theory further, they conducted an experiment with participants who were randomly assigned commercials featuring minority or white families. Those who saw ads with minority families said they were more likely to apply for refinancing from that lender.

“The long-standing disparity in the world of consumer finance makes this question more important.” — Zhenling Jiang

Three Reasons Why Minority Representation Matters in Marketing

Jiang and her co-authors think there are three reasons why minority representation works so well in marketing. First, minority consumers feel a sense of connection when they see themselves portrayed in commercials, although racial homophily doesn’t explain the uptake by white consumers. Second, the depiction of minorities reflects the brand’s inclusive values, which could explain why uptake among white consumers was highest for those with liberal-leaning beliefs. Third, it’s possible that ads with diversity stand out to viewers simply because they are less common.

“I don’t have proof for this, but I believe these three things work together to have an overall effect,” Jiang said.

She said the study shows that firms don’t have to overhaul their marketing campaigns or spend a lot more money to reap the benefits. Choosing minority actors instead of white actors costs similarly. Producing different versions of the same ad can also be cost-efficient.

“If you are keeping ad spending the same and shifting the minority share, you are getting a more effective ad,” she said. “From a practical perspective, that is the lever that companies can pull to increase the minority share in ads.”

More From Knowledge at Wharton

How Can Minority Employees Be Authentic in a Corporate Workplace?

How to Succeed While Being Authentic at Work

Wholesale Prices Went Up in April. Here’s What That Means for Rate Cut Prospects

Looking for more insights.

Sign up to stay informed about our latest article releases.

• Natural Hazards Center
• Vision and Mission
• Advisory Board
• How to Contribute
• In the News
• Center Staff
• Directors 1976-Present
• Mary Fran Myers Scholarship
• Disability and Disasters Award
• Student Paper Competition
• Mary Fran Myers Gender and Disaster Award
• Press/Contact Us
• Disaster Research - News You Can Use
• Current Issue
• Issue Index
• Research Counts
• Children and Disasters
• Mass Sheltering
• The Disaster Cycle
• Equity and Inclusion
• Research to Practice Publications
• Publications Index
• Research Briefs
• Community Engagement Briefs
• Director’s Corner
• Director’s Corner Index
• Quick Response Reports
• Mitigation Matters Reports
• Weather Ready Reports
• Public Health Reports
• Legacy Publications
• Natural Hazards Observer
• Natural Hazards Informer
• Monograph Series
• Working Papers
• Our Scholarship
• Books and Monographs
• Journal Articles
• Book Chapters
• Making Mitigation Work
• CONVERGE Training Modules
• Tribal Listening Sessions
• Indigenous Sovereignty and Emergency Response
• NSF Enabling Program
• 2024 Workshop
• 2024 Researchers Meeting
• 2024 Practitioners Meeting
• Save the Dates
• Workshop History
• Past Workshops
• Quick Response Research
• Special Call: Climate and Health
• Public Health Disaster Research
• Weather Ready Research
• Mitigation Matters Research
• Current Projects and Grants
• Completed Projects and Grants
• Dissertations
• General Interest
• Upcoming Conferences
• Webinars and Training
• Documentaries
• Resource Lists
• Publication Outlets
• Book Series
• Award Opportunities
• Research Centers
• Disaster Grads Listserv

For full functionality of this site it is necessary to enable JavaScript.

Here are the instructions how to enable JavaScript in your web browser .

Emerging Praxis in Disaster Management

Thur, July 18, 8:15 to 9:45 a.m. MDT Location: Centennial E

How Duration of Event Response Shapes Disasters: Reformulating Hazard Event Types

Samantha Montano, Massachusetts Maritime Academy Amanda Savitt, Argonne National Laboratory

New Missions in Emergency Management: Insights From Oral Histories

Patrick Roberts, RAND Corporation Sally Calengor, RAND Corporation

From Prediction to Practice: Barriers to Adoption of Emergency Management Tools

Noah Hallisey, University of Rhode Island Austin Becker, University of Rhode Island Peter Stempel, Pennsylvania State University

A Conceptual Typology of Compound Hazards to Improve Theory and Practice

Logan Gerber-Chavez, Embry-Riddle Aeronautical University

Narratives and Representation in Disaster Picture Books After Japan's 3.11 Disaster

Elizabeth Maly, Tohoku University Ryo Saito, Tohoku University Julia Gerster, Tohoku University

• Computer Vision
• Federated Learning
• Reinforcement Learning
• Natural Language Processing
• New Releases
• Advisory Board Members
• 🐝 Partnership and Promotion

Niharika Singh

Niharika is a Technical consulting intern at Marktechpost. She is a third year undergraduate, currently pursuing her B.Tech from Indian Institute of Technology(IIT), Kharagpur. She is a highly enthusiastic individual with a keen interest in Machine learning, Data science and AI and an avid reader of the latest developments in these fields.

• Cognita: An Open Source Framework for Building Modular RAG Applications
• Elia: An Open Source Terminal UI for Interacting with LLMs
• Pipecat: An Open Source Framework for Voice and Multimodal Conversational AI
• Lumina-T2X: A Unified AI Framework for Text to Any Modality Generation

RELATED ARTICLES MORE FROM AUTHOR

Aaren: rethinking attention as recurrent neural network rnn for efficient sequence modeling on low-resource devices, internlm research group releases internlm2-math-plus: a series of math-focused llms in sizes 1.8b, 7b, 20b, and 8x22b with enhanced chain-of-thought, code interpretation, and lean..., inductive biases in deep learning: understanding feature representation, the rise of agentic retrieval-augmented generation (rag) in artificial intelligence ai, deep learning in healthcare: challenges, applications, and future directions, researchers at arizona state university evaluates react prompting: the role of example similarity in enhancing large language model reasoning, aaren: rethinking attention as recurrent neural network rnn for efficient sequence modeling on low-resource..., from noisy hypotheses to clean text: how denoising lm (dlm) improves speech recognition accuracy, internlm research group releases internlm2-math-plus: a series of math-focused llms in sizes 1.8b, 7b,....

• AI Magazine
• Privacy & TC
• Cookie Policy

🐝 🐝 Join the Fastest Growing AI Research Newsletter Read by Researchers from Google + NVIDIA + Meta + Stanford + MIT + Microsoft and many others...

Thank You 🙌

Privacy Overview