unit 2 homework 6 literal equations

Ms. Lartz's Classroom

Oxford prep, math teacher, unit 2: solving equations and inequalities, quick links:, unit 2 isn set up, instructions for set-up:, 1. sign up for deltamath.com. use the code 258021., 2. add pages 23-25 to your table of contents (see slideshow to the right)., 3. tape or glue inserts to pages 23-25., 4. skip page 26., 4. add inverse operations to your table of contents and head your page (27- scroll down to see the notes)., 5. complete the inverse operations insert (yellow) and put it on page 27., 5. complete the inequalities investigation (pink)., 6. add inequalities investigation to your table of contents and head your page (28)..

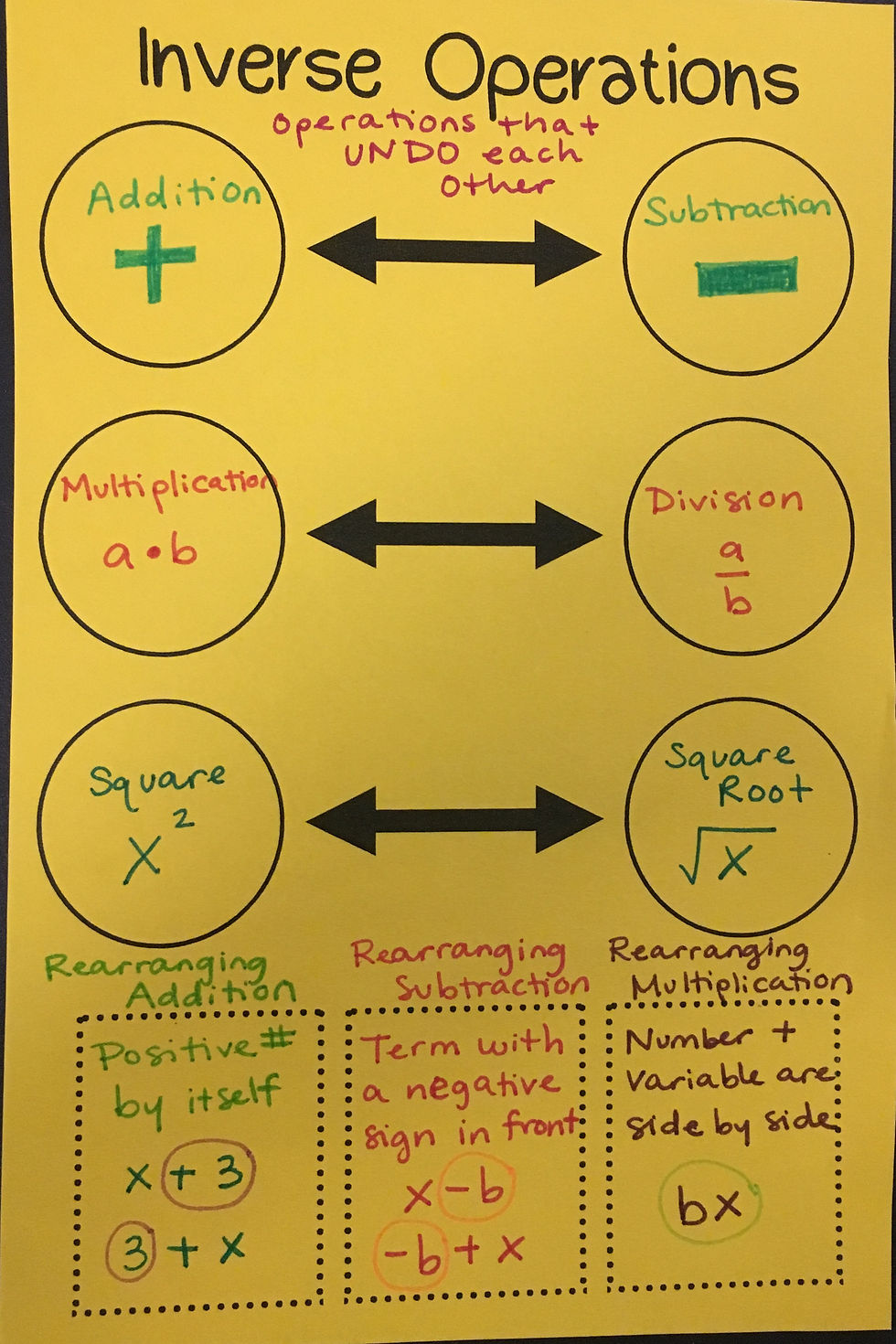
1. Inverse Operations

Delta math:,    m-linear equations: one-step equations (type 1),    m-linear equations: one-step equations (t ype 2),    m-linear equations: one-step equations (t ype 3),    m-linear equations: one-step equations (t ype 4), mathletics: ,    .

2. Inequalities Investigation

   m-inequalities: numerical inequalities (true or false).

You should complete this activity.

3. Graphing and Types of Solutions

Homework keys: pages 1-2,   page 3,    a-linear inequalities: one point inequalities from number line.

4. Solving Equations and Inequalities

Homework keys: pages 4-5 ,  page 6,   pages 8-10,   page 11,    m -inequalities : linear inequalities and number line (level 1),    a-linear inequalities: linear inequalities (level 1),    a-linear inequalities: linear inequalities (level 2),    m-linear equations: linear equations w/ distribution (lev 1),    m-linear equations: linear equations w/ distribution (lev  2), remediation work:, 1. scavenger hunt- complete your work in order based on the directions once you find your answer to the equation. you must show all your work, check your answer and graph your answer to receive credit.,           link to stations, 2. complete numbers 1-7 on this worksheet..

5. Compound Inequalities

Homework key:.

Describe your image

6. Literal Equations

Remediation: ,    a-literal equations: single step literal equations (level 1),    a -literal  equations: single step literal equations (level 2),    a -literal  equations: multi-step literal equations (level 2).

/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////

+ Unit 1: Fundamentals of Algebra

+ Unit 2: Solving Equations and Inequalities

+ Unit 3: Linear Graphs and Inequalities

+ Unit 4: Systems of Equations and Inequalities

+ Unit 5: Descriptive Statistics

+ Unit 6: Relations and Functions

+ Unit 7: Sequences and Exponential Functions

+ Unit 8: Quadratic Expressions and Equations

+ Unit 9: Quadratic Functions

+ Unit 10: Geometry

Office Hours:

Monday 7:50-8:20am

Monday 3:40-4:20pm

Tuesday 7:50-8:20am

Tuesday Lunch by Appointment

Wednesday 7:50-8:20am

Thursday 7:50-8:20am

Thursday Lunch by Appointment

Friday: Math Workshops

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

2.4: Solving Linear Equations- Part II

• Last updated
• Save as PDF
• Page ID 18336

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Objectives

• Solve general linear equations.
• Identify and solve conditional equations, identities, and contradictions.
• Clear decimals and fractions from equations.
• Solve literal equations or formulas for a given variable.

Combining Like Terms and Simplifying

Linear equations typically are not given in standard form, so solving them requires additional steps. These additional steps include simplifying expressions on each side of the equal sign using the order of operations.

Same-Side Like Terms

We will often encounter linear equations where the expressions on each side of the equal sign can be simplified. Typically, this involves combining same-side like terms. If this is the case, then it is best to simplify each side first before solving.

Example \(\PageIndex{1}\)

\(−4a+2−a=3−2\).

First, combine the like terms on each side of the equal sign.

The solution is \(\frac{1}{5}\).

Opposite-Side Like Terms

Given a linear equation in the form \(ax+b=cx+d\), we begin by combining like terms on opposite sides of the equal sign. To combine opposite-side like terms, use the addition or subtraction property of equality to effectively “move terms” from one side to the other so that they can be combined.

Example \(\PageIndex{2}\)

\(−2y−3=5y+11\).

To “move” the term \(5y\) to the left side, subtract it on both sides.

\(\begin{aligned} -2y-3&=5y+11 \\ -2y-3\color{Cerulean}{-5y}&=5y+11\color{Cerulean}{-5y} &\color{Cerulean}{Subtract\:5y\:from\:both\:sides.} \\ -7y-3&=11 \end{aligned}\)

From here, solve using the techniques developed previously.

Always check to see that the solution is correct by substituting the solution back into the original equation and simplifying to see if you obtain a true statement.

\(\begin{aligned} -2y-3&=5y+11 \\ -2(\color{OliveGreen}{-2}\color{black}{)-3}&=5(\color{OliveGreen}{-2}\color{black}{)+1} \\ 4-3&=-10+11 \\ 1&=1 \quad\color{Cerulean}{\checkmark} \end{aligned}\)

The solution is \(-2\).

General Guidelines for Solving Linear Equations

When solving linear equations, the goal is to determine what value, if any, will produce a true statement when substituted in the original equation. Do this by isolating the variable using the following steps:

Step 1 : Simplify both sides of the equation using the order of operations and combine all same-side like terms.

Step 2 : Use the appropriate properties of equality to combine opposite-side like terms with the variable term on one side of the equation and the constant term on the other.

Step 3 : Divide or multiply as needed to isolate the variable.

Step 4 : Check to see if the answer solves the original equation.

Example \(\PageIndex{3}\)

\(-\frac{1}{2}(10y-2)+3=14\)

Simplify the linear expression on the left side before solving.

\(\begin{aligned} -\frac{1}{2}(10(\color{OliveGreen}{-2}\color{black}{)-2)+3}&=14 \\ -\frac{1}{2}(-20-2)+3&=14 \\ -\frac{1}{2}(-22)+3&=14 \\ 11+3&=14 \\ 14&=14\quad\color{Cerulean}{\checkmark} \end{aligned}\)

Example \(\PageIndex{4}\)

\(5(3x+2)−2=−2(1−7x)\).

First, simplify the expressions on both sides of the equal sign.

The solution is \(−10\). The check is left as an exercise.

Exercise \(\PageIndex{1}\)

\(6−3(4x−1)=4x−7\).

Conditional Equations, Identities, and Contradictions

There are three different types of equations. Up to this point, we have been solving conditional equations. These are equations that are true for particular values. An identity is an equation that is true for all possible values of the variable. For example,

\(x=x\quad\color{Cerulean}{Identity}\)

has a solution set consisting of all real numbers, \(R\). A contradiction is an equation that is never true and thus has no solutions. For example,

\(x+1=x\quad\color{Cerulean}{Contradiction}\)

has no solution. We use the empty set, \(∅\), to indicate that there are no solutions.

If the end result of solving an equation is a true statement, like \(0 = 0\), then the equation is an identity and any real number is a solution. If solving results in a false statement, like \(0 = 1\), then the equation is a contradiction and there is no solution.

Example \(\PageIndex{5}\)

\(4(x+5)+6=2(2x+3)\).

\(\begin{aligned} 4(x+5)+6&=2(2x+3)&\color{Cerulean}{Distribute.} \\ 4x\color{OliveGreen}{+20+6}&=4x+6&\color{Cerulean}{Combine\:same-side\:like\:terms.} \\ 4x+26&=4x+6 &\color{Cerulean}{Combine\:opposite-side\:like\:terms.} \\ 4x+26\color{Cerulean}{-4x}&=4x+6\color{Cerulean}{-4x} \\ 26&=6\quad\color{red}{x} &\color{Cerulean}{False} \end{aligned}\)

\(∅\). Solving leads to a false statement; therefore, the equation is a contradiction and there is no solution.

Example \(\PageIndex{6}\)

\(3(3y+5)+5=10(y+2)−y\).

\(\begin{aligned} 3(3y+5)+5&=10(y+2)-y &\color{Cerulean}{Distribute.} \\ 9y\color{OliveGreen}{+15+5}&=10y+20-y &\color{Cerulean}{Combine\:same-side\:like\:terms.} \\ 9y+20&=9y+20 &\color{Cerulean}{Combine\:opposite-side\:like\:terms.} \\ 9y+20\color{Cerulean}{-9y}&=9y+20\color{Cerulean}{-9y} \\ 20&=20 \quad\color{Cerulean}{\checkmark} &\color{Cerulean}{True} \end{aligned}\)

\(R\). Solving leads to a true statement; therefore, the equation is an identity and any real number is a solution.

If it is hard to believe that any real number is a solution to the equation in the previous example, then choose your favorite real number, and substitute it in the equation to see that it leads to a true statement. Choose \(x=7\) and check:

Exercise \(\PageIndex{2}\)

\(−2(3x+1)−(x−3)=−7x+1\).

Clearing Decimals and Fractions

The coefficients of linear equations may be any real number, even decimals and fractions. When decimals and fractions are used, it is possible to use the multiplication property of equality to clear the coefficients in a single step. If given decimal coefficients, then multiply by an appropriate power of 10 to clear the decimals. If given fractional coefficients, then multiply both sides of the equation by the least common multiple of the denominators (LCD).

Example \(\PageIndex{7}\)

\(2.3x+2.8=−1.2x+9.8\).

Notice that all decimal coefficients are expressed with digits in the tenths place; this suggests that we can clear the decimals by multiplying both sides by \(10\). Take care to distribute \(10\) to each term on both sides of the equation.

\(\begin{aligned} \color{Cerulean}{10\cdot }\color{black}{(2.3x+2.8)} &=\color{Cerulean}{10\cdot}\color{black}{-1.2x+9.8} &\color{Cerulean}{Multiply\:both\:sides\:by\:10.} \\ \color{Cerulean}{10\cdot }\color{black}{2.3x+}\color{Cerulean}{10\cdot }\color{black}{2.8}&=\color{Cerulean}{10\cdot }\color{black}{(-1.2x)+}\color{Cerulean}{10\cdot}\color{black}{9.8} \\ 23x+28&=-12x+98 &\color{Cerulean}{Integer\:coefficients} \\ 23x+28\color{Cerulean}{+12x}&=-12x+98\color{Cerulean}{+12x} &\color{Cerulean}{Solve.} \\ 35x+28&=98 \\ 35x+28\color{Cerulean}{-28}&=98\color{Cerulean}{-28} \\ 35x&=70 \\ \frac{35x}{\color{Cerulean}{35}}&=\frac{70}{\color{Cerulean}{35}} \\ x&=2 \end{aligned}\)

The solution is \(2\).

Example \(\PageIndex{8}\)

\(\frac{1}{3}x+\frac{1}{5}=\frac{1}{5}x−1\).

Clear the fractions by multiplying both sides by the least common multiple of the given denominators. In this case, the LCM\((3, 5)=15\).

The solution is \(-9\).

It is important to know that these techniques only work for equations. Do not try to clear fractions when simplifying expressions . As a reminder

\(\begin{array}{c|c} {\underline{\color{Cerulean}{Expression}}}&{\underline{\color{Cerulean}{Equation}}} \\ {\frac{1}{2}x+\frac{5}{3}}&{\frac{1}{2}x+\frac{5}{3}=0} \end{array}\)

Solve equations and simplify expressions. If you multiply an expression by \(6\), you will change the problem. However, if you multiply both sides of an equation by 6, you obtain an equivalent equation.

\(\begin{array}{c|c} {\underline{\color{red}{Incorrect}}}&{\underline{\color{Cerulean}{Correct}}}\\{\frac{1}{2}x+\frac{5}{3}}&{\frac{1}{2}x+\frac{5}{3}=0} \\ {\neq\color{red}{6\cdot}\color{black}{\left( \frac{1}{2}x+\frac{5}{3} \right)}}&{\color{Cerulean}{6\cdot}\color{black}{\left( \frac{1}{2}x+\frac{5}{3} \right) =}\color{Cerulean}{6\cdot }\color{black}{0}} \\{=3x+10\quad\color{red}{x}}&{3x+10=10\quad\color{Cerulean}{\checkmark}} \end{array}\)

Literal Equations (Linear Formulas)

Algebra lets us solve whole classes of applications using literal equations, or formulas. Formulas often have more than one variable and describe, or model, a particular real-world problem. For example, the familiar formula \(D=rt\) describes the distance traveled in terms of the average rate and time; given any two of these quantities, we can determine the third. Using algebra, we can solve the equation for any one of the variables and derive two more formulas.

\(\begin{aligned} D&=rt \\ \frac{D}{\color{Cerulean}{r}}&=\frac{rt}{\color{Cerulean}{r}}&\color{Cerulean}{Divide\:both\:sides\:by\:r.} \\ \frac{D}{r}&=t \end{aligned}\)

If we divide both sides by \(r\), we obtain the formula \(t=Dr\). Use this formula to find the time, given the distance and the rate

\(\begin{aligned} D&=rt \\ \frac{D}{\color{Cerulean}{t}}&=\frac{rt}{\color{Cerulean}{t}}&\color{Cerulean}{Divide\:both\:sides\:by\:t.} \\ \frac{D}{t}&=r \end{aligned}\)

If we divide both sides by \(t\), we obtain the formula \(r=Dt\). Use this formula to find the rate, given the distance traveled and the time it takes to travel that distance. Using the techniques learned up to this point, we now have three equivalent formulas relating distance, average rate, and time:

\(D=rt\qquad t=\frac{D}{r}\qquad r=\frac{D}{t}\)

When given a literal equation, it is often necessary to solve for one of the variables in terms of the others. Use the properties of equality to isolate the indicated variable.

Example \(\PageIndex{9}\)

Solve for \(a\):

\(P=2a+b\).

The goal is to isolate the variable \(a\).

\(\begin{aligned} P&=2a+b \\ P\color{Cerulean}{-b}&=2a+b\color{Cerulean}{-b} &\color{Cerulean}{Subtract\:b\:from\:both\:sides.} \\ P-b&=2a \\ \frac{P-b}{\color{Cerulean}{2}}&=\frac{2a}{\color{Cerulean}{2}} &\color{Cerulean}{Divide\:both\:sides\:by\:2.} \\ \frac{P-b}{2}&=a \end{aligned}\)

\(a=\frac{P-b}{2}\)

Example \(\PageIndex{10}\)

Solve for \(y\):

\(z=\frac{x+y}{2}\).

The goal is to isolate the variable \(y\).

\(\begin{aligned} z&=\frac{x+y}{2} \\ \color{Cerulean}{2\cdot}\color{black}{z}&=\color{Cerulean}{2\cdot}\color{black}{\frac{x+y}{2}}&\color{Cerulean}{Multiply\:both\:sides\:by\:2.} \\ 2z&=x+y \\ 2z\color{Cerulean}{-x}&=x+y\color{Cerulean}{-x}&\color{Cerulean}{Subtract\:x\:from\:both\:sides.} \\ 2z-x&=y \end{aligned}\)

Exercise \(\PageIndex{3}\)

Solve for \(b\):

\(2a−3b=c\).

\(b=\frac{2a−c}{3}\)

Key Takeaways

• Solving general linear equations involves isolating the variable, with coefficient \(1\), on one side of the equal sign.
• Simplify both sides of the equation and combine all same-side like terms.
• Combine opposite-side like terms to obtain the variable term on one side of the equal sign and the constant term on the other.
• Divide or multiply as needed to isolate the variable.
• Check the answer.
• Most linear equations that you will encounter are conditional and have one solution.
• If solving a linear equation leads to a true statement like \(0 = 0\), then the equation is an identity and the solution set consists of all real numbers, \(R\).
• If solving a linear equation leads to a false statement like \(0 = 5\), then the equation is a contradiction and there is no solution, \(∅\).
• Clear fractions by multiplying both sides of a linear equation by the least common multiple of all the denominators. Distribute and multiply all terms by the LCD to obtain an equivalent equation with integer coefficients.
• Given a formula, solve for any variable using the same techniques for solving linear equations. This works because variables are simply representations of real numbers.

Exercise \(\PageIndex{4}\) Checking for Solutions

Is the given value a solution to the linear equation?

• \(2(3x+5)−6=3x−8; x=−4 \)
• \(−x+17−8x=9−x; x=−1 \)
• \(4(3x−7)−3(x+2)=−1; x=\frac{1}{3}\)
• \(−5−2(x−5)=−(x+3); x=−8 \)
• \(7−2(\frac{1}{2}x−6)=x−1; x=10 \)
• \(3x−\frac{2}{3}(9x−2)=0; x=\frac{4}{9}\)

Exercise \(\PageIndex{5}\) Solving Linear Equations

• \(4x−7=7x+5\)
• \(−5x+3=−8x−9\)
• \(3x−5=2x−17\)
• \(−2y−52=3y+13\)
• \(−4x+2=7x−20\)
• \(4x−3=6x−15\)
• \(9x−25=12x−25\)
• \(12y+15=−6y+23\)
• \(1.2x−0.7=3x+4.7\)
• \(2.1x+6.1=−1.3x+4.4\)
• \(2.02x+4.8=14.782−1.2x\)
• \(−3.6x+5.5+8.2x=6.5+4.6x\)
• \(\frac{1}{2}x−\frac{2}{3}=x+\frac{1}{5}\)
• \(\frac{1}{3}x−\frac{1}{2}=−\frac{1}{4}x−\frac{1}{3}\)
• \(−\frac{1}{10}y+\frac{2}{5}=\frac{1}{5}y+\frac{3}{10}\)
• \(x−\frac{20}{3}=\frac{5}{2}x+\frac{5}{6}\)
• \(\frac{2}{3}y+\frac{1}{2}=\frac{5}{8}y+\frac{37}{24}\)
• \(\frac{1}{3}+\frac{4}{3}x=\frac{10}{7}x+\frac{1}{3}−\frac{2}{21}x\)
• \(\frac{8}{9}−\frac{11}{18}x=\frac{7}{6}−12x\)
• \(\frac{1}{3}−9x=\frac{4}{9}+\frac{1}{2}x\)
• \(12x−5+9x=44\)
• \(10−6x−13=12\)
• \(−2+4x+9=7x+8−2x\)
• \(20x−5+12x=6−x+7\)
• \(3a+5−a=2a+7\)
• \(−7b+3=2−5b+1−2b\)
• \(7x−2+3x=4+2x−2\)
• \(−3x+8−4x+2=10\)
• \(6x+2−3x=−2x−13\)
• \(3x−0.75+0.21x=1.24x+7.13\)
• \(−x−2+4x=5+3x−7\)
• \(−2y−5=8y−6−10y\)
• \(\frac{1}{10}x−\frac{1}{3}=\frac{1}{30}−\frac{1}{15}x−\frac{7}{15}\)
• \(\frac{5}{8}−\frac{4}{3}x+\frac{1}{3}=−\frac{3}{9}x−\frac{1}{4}+\frac{1}{3}x\)

1. \(−4\)

3. \(−12\)

9. \(−3\)

11. \(3.1\)

13. \(−\frac{26}{15}\)

15. \(\frac{1}{3}\)

19. \(−\frac{5}{2}\)

21. \(\frac{7}{3}\)

23. \(−1\)

25. \(∅\)

27. \(\frac{1}{2}\)

29. \(−3\)

33. \(−\frac{3}{5}\)

Exercise \(\PageIndex{6}\) Solving Linear Equations Involving Parentheses

• \(−5(2y−3)+2=12\)
• \(3(5x+4)+5x=−8\)
• \(4−2(x−5)=−2\)
• \(10−5(3x+1)=5(x−4)\)
• \(9−(x+7)=2(x−1)\)
• \(−5(2x−1)+3=−12\)
• \(3x−2(x+1)=x+5\)
• \(5x−3(2x−1)=2(x−3)\)
• \(−6(x−1)−3x=3(x+8)\)
• \(−\frac{3}{5}(5x+10)=\frac{1}{2}(4x−12)\)
• \(3.1(2x−3)+0.5=22.2\)
• \(4.22−3.13(x−1)=5.2(2x+1)−11.38\)
• \(6(x−2)−(7x−12)=14\)
• \(−9(x−3)−3x=−3(4x+9)\)
• \(3−2(x+4)=−3(4x−5)\)
• \(12−2(2x+1)=4(x−1)\)
• \(3(x+5)−2(2x+3)=7x+9\)
• \(3(2x−1)−4(3x−2)=−5x+10\)
• \(−3(2a−3)+2=3(a+7)\)
• \(−2(5x−3)−1=5(−2x+1)\)
• \(\frac{1}{2}(2x+1)−\frac{1}{4}(8x+2)=3(x−4)\)
• \(−\frac{2}{3}(6x−3)−\frac{1}{2}=\frac{3}{2}(4x+1)\)
• \(\frac{1}{2}(3x−1)+\frac{1}{3}(2x−5)=0\)
• \(\frac{1}{3}(x−2)+\frac{1}{5}=\frac{1}{9}(3x+3)\)
• \(−2(2x−7)−(x+3)=6(x−1)\)
• \(10(3x+5)−5(4x+2)=2(5x+20)\)
• \(2(x−3)−6(2x+1)=−5(2x−4)\)
• \(5(x−2)−(4x−1)=−2(3−x)\)
• \(6(3x−2)−(12x−1)+4=0\)
• \(−3(4x−2)−(9x+3)−6x=0\)

1. \(\frac{1}{2}\)

5. \(\frac{4}{3}\)

7. \(∅\)

9. \(−\frac{3}{2}\)

13. \(−14\)

19. \(−\frac{10}{9}\)

25. \(\frac{17}{11}\)

27. \(∅\)

29. \(\frac{7}{6}\)

Exercise \(\PageIndex{7}\) Literal Equations

Solve for the indicated variable.

• Solve for \(w\): \(A=l⋅w\).
• Solve for \(a\): \(F=ma\).
• Solve for \(w\): \(P=2l+2w\).
• Solve for \(r\): \(C=2πr\).
• Solve for \(b\): \(P=a+b+c\).
• Solve for \(C\): \(F=\frac{9}{5}C+32\).
• Solve for \(h\): \(A=\frac{1}{2}bh\).
• Solve for \(t\): \(I=Prt\).
• Solve for \(y\): \(ax+by=c\).
• Solve for \(h\): \(S=2πr^{2}+2πrh\).
• Solve for \(x\): \(z=\frac{2x+y}{5}\).
• Solve for \(c\): \(a=3b−\frac{2c}{3}\).
• Solve for \(b\): \(y=mx+b\).
• Solve for \(m\): \(y=mx+b\).
• Solve for \(y\): \(3x−2y=6\).
• Solve for \(y\): \(−5x+2y=12\).
• Solve for \(y\): \(\frac{x}{3}−\frac{y}{5}=1\).
• Solve for \(y\): \(\frac{3}{4}x−\frac{1}{5}y=\frac{1}{2}\).

1. \(w=\frac{A}{l}\)

3. \(w=\frac{P−2l}{2}\)

5. \(b=P−a−c \)

7. \(h=\frac{2A}{b}\)

9. \(y=\frac{−ax+c}{b}\)

11. \(x=\frac{5z−y}{2}\)

13. \(b=y−mx\)

15. \(y=\frac{3x−6}{2}\)

17. \(y=\frac{5x−15}{3}\)

Exercise \(\PageIndex{8}\) Literal Equations

Translate the following sentences into linear equations and then solve.

• The sum of \(3x\) and \(5\) is equal to the sum of \(2x\) and \(7\).
• The sum of \(−5x\) and \(6\) is equal to the difference of \(4x\) and \(2\).
• The difference of \(5x\) and \(25\) is equal to the difference of \(3x\) and \(51\).
• The sum of \(\frac{1}{2}x\) and \(\frac{3}{4}\) is equal to \(\frac{2}{3}x\).
• A number \(n\) divided by \(5\) is equal to the sum of twice the number and \(3\).
• Negative ten times a number \(n\) is equal to the sum of three times the number and \(13\).

1. \(3x+5=2x+7\); \(x=2\)

3. \(5x−25=3x−51\); \(x=−13\)

5. \(\frac{n}{5}=2n+3\); \(n=−\frac{5}{3}\)

Exercise \(\PageIndex{9}\) Discussion Board Topics

• What is the origin of the word algebra?
• What is regarded as the main business of algebra?
• Why is solving equations such an important algebra topic?
• Post some real-world linear formulas not presented in this section.
• Research and discuss the contributions of Diophantus of Alexandria.
• Create an identity or contradiction of your own and share on the discussion board. Provide a solution and explain how you found it.

1. Answers may vary

3. Answers may vary

5. Answers may vary

REI.B.3 Algebra 1 Unit 2 Complete Lesson 6 Literal Equations

• Google Docs™

Products in this Bundle (6)

showing 1 - 5 of 6 products

Also included in

Description

Lesson includes scaffolded notes, activator, practice problems, daily quiz, daily requiz, and closing.

When I use this product in my classroom, I ask my students to watch a video of the SCAFFOLDED NOTES before class. This video can be found on my youtube channel, Hubertdollar9482.  As a warm up/activator my students correct the previous day’s google form quiz. Then I use an OPENING with different examples from the notes to review content. Next my students complete PRACTICE on the content in a google sheet that turns green when the correct answer is entered.  Finally my students complete a DAILY GRADE that contains 10 review questions and 10 questions on new content. I assign a MAKE-UP DAILY to students who were absent or did not complete the assignment before class started.

Questions & Answers

Math created by the dollar.

• We're hiring
• Help & FAQ
• Privacy policy
• Student privacy
• Terms of service
• Tell us what you think

RWM102: Algebra

Unit 2: linear equations.

We use equations everyday without realizing it. Examples include calculating the unit price to compare the price of brands in the grocery store, converting inches into feet (or centimeters into meters), estimating how much time it will take to drive to a destination at a certain speed.

In this unit, we explore formal procedures for solving equations. After reviewing basic math rules, we apply the skills we learned in Unit 1 to simplify the sides of an equation before attempting to solve it and work with equations that contain more than one variable. Because variables represent numbers, we use the same rules to find the specific variables we are looking for.

Completing this unit should take you approximately 5 hours.

Upon successful completion of this unit, you will be able to:

• determine whether a given real number is a solution of an equation;
• simplify equations using addition and multiplication properties;
• find the solution of a given linear equation with one variable;
• determine the number of solutions of a given linear equation in one variable;
• solve a literal equation for the given variable; and
• rearrange formulas to isolate a quantity of interest.

2.1: Definition of an Equation and a Solution of an Equation

We define an equation as a statement that contains a variable, which may or may not be true, depending on the value of the variable. Solving an equation means finding the possible values of the variable that make the equation true.

Read the "Define Linear Equations in One Variable" and "Solutions to Linear Equations in One Variable" sections. Then, complete exercises 1 to 5 and check your answers.

2.2: Addition/Subtraction Property of Equations

When solving algebraic equations, we need to be aware of the properties of the types of mathematical operations we are doing. The first property we explore is the addition and subtraction property of equations.

Read up to the "Solve Equations that Require Simplification" section. Pay attention to the "Solve Equations Using the Subtraction and Addition Properties of Equality" section, which gives a good example of how the two sides of an equation must be equal. After you read, complete examples 2.2 through 2.5 and check your answers.

2.3: Multiplication/Division Property of Equations

Much like in the previous section we must use the properties of multiplication and division when solving algebraic expressions involving these types of calculations.

Read up to the "Sole Equations that Require Simplification" section. Complete examples 2.13 to 2.17.

2.4: Equations of the Form x + a = b and x − a = b

Algebraic equations can be categorized based on the form and types of operations in the equation. In the next few sections, we will explore different forms of equations.

The first form is the simplest: x + a = b or x − a = b . An example of this type of equation is: 5 + x = 8.

Watch this video for examples of these types of equations.

After you watch, complete this assessment to test yourself.

2.5: Equations of the Form ax = b and x / a = b

The next general form of equations involve multiplying or dividing the variable by a coefficient. These equations are of the form ax = b or x / a = b . An example of this type of equation is: x /2 = 6.

After you watch, complete this assessment and check your answers.

2.6: Equations of the Form ax + b = c

Often types of mathematical operations are combined in an equation. For example, multiplication can be combined with addition in an equation. An example of this type of equation is: 2 x + 1 = 11. This requires a two-step process for solving the equation.

Watch this video for examples of how to solve these types of problems in a two-step process.

2.7: Equations of the Form ax + b = cx + d

This section involves solving more complicated equations where the variable appears on both sides. We can use what we learned about combining like terms to make solving these types of equations possible.

Watch these videos to see examples of how we use like terms to solve these types of equations.

2.8: Equations with Parentheses

The last general type of linear equation we can solve are those involving parentheses. For example, we can have an equation 2(4 + x ) = 12. We need to use order of operations and the distributive property to solve this type of equation.

Watch these videos to see examples of how this type of equation can be solved.

2.9: Solving Literal Equation for One of the Variables

We can use the methods we learned in the previous sections to solve literal equations, or formulas which often have more than one variable. When a literal equation has more than one variable, we can solve for the variable of interest with respect to the other variable.

For example, consider the equation 2 a + b = 10. Here, there are two variables, a and b . If we want to solve for b , we can do so with respect to a . We can subtract 2 a from both sides to obtain: 10 − 2 a = b .

Read the section on linear literal equations. Be sure to go through the examples in detail. After read, complete the exercises for literal equations and check your answers.

We can apply these concepts to known formulas, such as formulas for area of a shape or rates.

Watch these videos for real examples of using formulas. In the first video, the formula for perimeter of a rectangle is solved for the width. In the second, a formula is used to convert between Fahrenheit and Celsius.

How It Works

The experts well detail out the effect relationship between the two given subjects and underline the importance of such a relationship in your writing. Our cheap essay writer service is a lot helpful in making such a write-up a brilliant one.

I work with the same writer every time. He knows my preferences and always delivers as promised. It’s like having a 24/7 tutor who is willing to help you no matter what. My grades improved thanks to him. That’s the story.

Remember, the longer the due date, the lower the price. Place your order in advance for a discussion post with our paper writing services to save money!

Types of Paper Writing Services

Allene W. Leflore

Artikel & Berita

Write my essay for me.

I ordered a paper with a 3-day deadline. They delivered it prior to the agreed time. Offered free alterations and asked if I want them to fix something. However, everything looked perfect to me.

Calculate the price

Minimum Price

Emery Evans

How do I place an order with your paper writing service?

Finished Papers

Jalan Zamrud Raya Ruko Permata Puri 1 Blok L1 No. 10, Kecamatan Cimanggis, Kota Depok, Jawa Barat 16452

Gustavo Almeida Correia

• Kindergarten
• Greater Than Less Than
• Measurement
• Multiplication
• Place Value
• Subtraction
• Punctuation
• 1st Grade Reading
• 2nd Grade Reading
• 3rd Grade Reading
• Cursive Writing
• Alphabet Coloring
• Animals Coloring
• Birthday Coloring
• Boys Coloring
• Buildings Coloring
• Cartoons Coloring
• Christmas Coloring
• Country Flag Coloring
• Country Map Coloring
• Disney Coloring
• Fantasy Coloring
• Food Coloring
• Girls Coloring
• Holidays Coloring
• Music Coloring
• Nature Coloring
• New Year Coloring
• People Coloring
• Religious Coloring
• Sports Coloring
• Toys Coloring
• Transportation Coloring
• US Sports Team Coloring
• Valentine Day Coloring

Unit 2 Equations Inequalities Homework 6

Displaying top 8 worksheets found for - Unit 2 Equations Inequalities Homework 6 .

Some of the worksheets for this concept are Students ability to think in abstract the, Unit 2 reasoning with linear equations and inequalities, Teksstaar based lessons, Unit 6 systems of linear equations homework 9, Gina wilson 2012 unit 6 homework 9 answer key, Unit of study 5 subjectcourse 10 math length 2, Algebra 1 test unit 6 answers, Algebra 1 spencer unit 4 notes inequalities and.

Found worksheet you are looking for? To download/print, click on pop-out icon or print icon to worksheet to print or download. Worksheet will open in a new window. You can & download or print using the browser document reader options.

1. students ability to think in abstract terms. The ...

2. unit 2: reasoning with linear equations and inequalities, 3. teks/staar-based lessons, 4. unit 6 systems of linear equations homework 9, 5. gina wilson 2012 unit 6 homework 9 answer key, 6. unit of study #5 subject/course: 10 res. math length: 2 ..., 7. algebra 1 test unit 6 answers -, 8. algebra 1 spencer unit 4 notes: inequalities and ....

Margurite J. Perez

Viola V. Madsen

Finished Papers

Customer Reviews

2269 Chestnut Street, #477 San Francisco CA 94123

• Plagiarism report. .99
• High priority status .90
• Full text of sources +15%
• 1-Page summary .99
• Initial draft +20%
• Premium writer +.91

Customer Reviews