research article that used anova

An open portfolio of interoperable, industry leading products

The Dotmatics digital science platform provides the first true end-to-end solution for scientific R&D, combining an enterprise data platform with the most widely used applications for data analysis, biologics, flow cytometry, chemicals innovation, and more.

Statistical analysis and graphing software for scientists

Bioinformatics, cloning, and antibody discovery software

Plan, visualize, & document core molecular biology procedures

Electronic Lab Notebook to organize, search and share data

Proteomics software for analysis of mass spec data

Modern cytometry analysis platform

Analysis, statistics, graphing and reporting of flow cytometry data

Software to optimize designs of clinical trials

The Ultimate Guide to ANOVA

Get all of your ANOVA questions answered here

ANOVA is the go-to analysis tool for classical experimental design, which forms the backbone of scientific research.

In this article, we’ll guide you through what ANOVA is, how to determine which version to use to evaluate your particular experiment, and provide detailed examples for the most common forms of ANOVA.

This includes a (brief) discussion of crossed, nested, fixed and random factors, and covers the majority of ANOVA models that a scientist would encounter before requiring the assistance of a statistician or modeling expert.

What is ANOVA used for?

ANOVA, or (Fisher’s) analysis of variance, is a critical analytical technique for evaluating differences between three or more sample means from an experiment. As the name implies, it partitions out the variance in the response variable based on one or more explanatory factors.

As you will see there are many types of ANOVA such as one-, two-, and three-way ANOVA as well as nested and repeated measures ANOVA. The graphic below shows a simple example of an experiment that requires ANOVA in which researchers measured the levels of neutrophil extracellular traps (NETs) in plasma across patients with different viral respiratory infections.

Many researchers may not realize that, for the majority of experiments, the characteristics of the experiment that you run dictate the ANOVA that you need to use to test the results. While it’s a massive topic (with professional training needed for some of the advanced techniques), this is a practical guide covering what most researchers need to know about ANOVA.

When should I use ANOVA?

If your response variable is numeric, and you’re looking for how that number differs across several categorical groups, then ANOVA is an ideal place to start. After running an experiment, ANOVA is used to analyze whether there are differences between the mean response of one or more of these grouping factors.

ANOVA can handle a large variety of experimental factors such as repeated measures on the same experimental unit (e.g., before/during/after).

If instead of evaluating treatment differences, you want to develop a model using a set of numeric variables to predict that numeric response variable, see linear regression and t tests .

What is the difference between one-way, two-way and three-way ANOVA?

The number of “ways” in ANOVA (e.g., one-way, two-way, …) is simply the number of factors in your experiment.

Although the difference in names sounds trivial, the complexity of ANOVA increases greatly with each added factor. To use an example from agriculture, let’s say we have designed an experiment to research how different factors influence the yield of a crop.

An experiment with a single factor

In the most basic version, we want to evaluate three different fertilizers. Because we have more than two groups, we have to use ANOVA. Since there is only one factor (fertilizer), this is a one-way ANOVA. One-way ANOVA is the easiest to analyze and understand, but probably not that useful in practice, because having only one factor is a pretty simplistic experiment.

What happens when you add a second factor? 

If we have two different fields, we might want to add a second factor to see if the field itself influences growth. Within each field, we apply all three fertilizers (which is still the main interest). This is called a crossed design. In this case we have two factors, field and fertilizer, and would need a two-way ANOVA.

As you might imagine, this makes interpretation more complicated (although still very manageable) simply because more factors are involved. There is now a fertilizer effect, as well as a field effect, and there could be an interaction effect, where the fertilizer behaves differently on each field.

How about adding a third factor?

Finally, it is possible to have more than two factors in an ANOVA. In our example, perhaps you also wanted to test out different irrigation systems. You could have a three-way ANOVA due to the presence of fertilizer, field, and irrigation factors. This greatly increases the complication.

Now in addition to the three main effects (fertilizer, field and irrigation), there are three two-way interaction effects (fertilizer by field, fertilizer by irrigation, and field by irrigation), and one three-way interaction effect.

If any of the interaction effects are statistically significant, then presenting the results gets quite complicated. “Fertilizer A works better on Field B with Irrigation Method C ….”

In practice, two-way ANOVA is often as complex as many researchers want to get before consulting with a statistician. That being said, three-way ANOVAs are cumbersome, but manageable when each factor only has two levels.

What are crossed and nested factors?

In addition to increasing the difficulty with interpretation, experiments (or the resulting ANOVA) with more than one factor add another level of complexity, which is determining whether the factors are crossed or nested.

With crossed factors, every combination of levels among each factor is observed. For example, each fertilizer is applied to each field (so the fields are subdivided into three sections in this case).

With nested factors, different levels of a factor appear within another factor. An example is applying different fertilizers to each field, such as fertilizers A and B to field 1 and fertilizers C and D to field 2. See more about nested ANOVA here .

What are fixed and random factors?

Another challenging concept with two or more factors is determining whether to treat the factors as fixed or random. 

Fixed factors are used when all levels of a factor (e.g., Fertilizer A, Fertilizer B, Fertilizer C) are specified and you want to determine the effect that factor has on the mean response. 

Random factors are used when only some levels of a factor are observed (e.g., Field 1, Field 2, Field 3) out of a large or infinite possible number (e.g., all fields), but rather than specify the effect of the factor, which you can’t do because you didn’t observe all possible levels, you want to quantify the variability that’s within that factor (variability added within each field).

Many introductory courses on ANOVA only discuss fixed factors, and we will largely follow suit other than with two specific scenarios (nested factors and repeated measures). 

What are the (practical) assumptions of ANOVA?

These are one-way ANOVA assumptions, but also carryover for more complicated two-way or repeated measures ANOVA.

• Categorical treatment or factor variables - ANOVA evaluates mean differences between one or more categorical variables (such as treatment groups), which are referred to as factors or “ways.”
• Three or more groups - There must be at least three distinct groups (or levels of a categorical variable) across all factors in an ANOVA. The possibilities are endless: one factor of three different groups, two factors of two groups each (2x2), and so on. If you have fewer than three groups, you can probably get away with a simple t-test.
• Numeric Response - While the groups are categorical, the data measured in each group (i.e., the response variable) still needs to be numeric. ANOVA is fundamentally a quantitative method for measuring the differences in a numeric response between groups. If your response variable isn’t continuous, then you need a more specialized modelling framework such as logistic regression or chi-square contingency table analysis to name a few.
• Random assignment - The makeup of each experimental group should be determined by random selection.
• Normality - The distribution within each factor combination should be approximately normal, although ANOVA is fairly robust to this assumption as the sample size increases due to the central limit theorem.

What is the formula for ANOVA?

The formula to calculate ANOVA varies depending on the number of factors, assumptions about how the factors influence the model (blocking variables, fixed or random effects, nested factors, etc.), and any potential overlap or correlation between observed values (e.g., subsampling, repeated measures). 

The good news about running ANOVA in the 21st century is that statistical software handles the majority of the tedious calculations. The main thing that a researcher needs to do is select the appropriate ANOVA.

An example formula for a two-factor crossed ANOVA is:

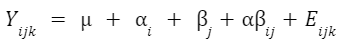
How do I know which ANOVA to use?

As statisticians, we like to imagine that you’re reading this before you’ve run your experiment. You can save a lot of headache by simplifying an experiment into a standard format (when possible) to make the analysis straightforward.

Regardless, we’ll walk you through picking the right ANOVA for your experiment and provide examples for the most popular cases. The first question is:

Do you only have a single factor of interest?

If you have only measured a single factor (e.g., fertilizer A, fertilizer B, .etc.), then use one-way ANOVA . If you have more than one, then you need to consider the following:

Are you measuring the same observational unit (e.g., subject) multiple times?

This is where repeated measures come into play and can be a really confusing question for researchers, but if this sounds like it might describe your experiment, see repeated measures ANOVA . Otherwise:

Are any of the factors nested, where the levels are different depending on the levels of another factor?

In this case, you have a nested ANOVA design. If you don’t have nested factors or repeated measures, then it becomes simple:

Do you have two categorical factors?

Then use two-way ANOVA.

Do you have three categorical factors?

Use three-way ANOVA.

Do you have variables that you recorded that aren’t categorical (such as age, weight, etc.)?

Although these are outside the scope of this guide, if you have a single continuous variable, you might be able to use ANCOVA, which allows for a continuous covariate. With multiple continuous covariates, you probably want to use a mixed model or possibly multiple linear regression.

Prism  does  offer multiple linear regression but assumes that all factors are fixed. A full “mixed model” analysis is not yet available in Prism, but is offered as options within the one- and two-way ANOVA parameters.

How do I perform ANOVA?

Once you’ve determined which ANOVA is appropriate for your experiment, use statistical software to run the calculations. Below, we provide detailed examples of one, two and three-way ANOVA models.

How do I read and interpret an ANOVA table?

Interpreting any kind of ANOVA should start with the ANOVA table in the output. These tables are what give ANOVA its name, since they partition out the variance in the response into the various factors and interaction terms. This is done by calculating the sum of squares (SS) and mean squares (MS), which can be used to determine the variance in the response that is explained by each factor.

If you have predetermined your level of significance, interpretation mostly comes down to the p-values that come from the F-tests. The null hypothesis for each factor is that there is no significant difference between groups of that factor. All of the following factors are statistically significant with a very small p-value.

One-way ANOVA Example

An example of one-way ANOVA is an experiment of cell growth in petri dishes. The response variable is a measure of their growth, and the variable of interest is treatment, which has three levels: formula A, formula B, and a control.

Classic one-way ANOVA assumes equal variances within each sample group. If that isn’t a valid assumption for your data, you have a number of alternatives .

Calculating a one-way ANOVA

Using Prism to do the analysis, we will run a one-way ANOVA and will choose 95% as our significance threshold. Since we are interested in the differences between each of the three groups, we will evaluate each and correct for multiple comparisons (more on this later!). 

For the following, we’ll assume equal variances within the treatment groups. Consider 

The first test to look at is the overall (or omnibus) F-test, with the null hypothesis that there is no significant difference between any of the treatment groups. In this case, there is a significant difference between the three groups (p<0.0001), which tells us that at least one of the groups has a statistically significant difference.

Now we can move to the heart of the issue, which is to determine which group means are statistically different. To learn more, we should graph the data and test the differences (using a multiple comparison correction).

Graphing one-way ANOVA

The easiest way to visualize the results from an ANOVA is to use a simple chart that shows all of the individual points. Rather than a bar chart, it’s best to use a plot that shows all of the data points (and means) for each group such as a scatter or violin plot.

As an example, below you can see a graph of the cell growth levels for each data point in each treatment group, along with a line to represent their mean. This can help give credence to any significant differences found, as well as show how closely groups overlap.

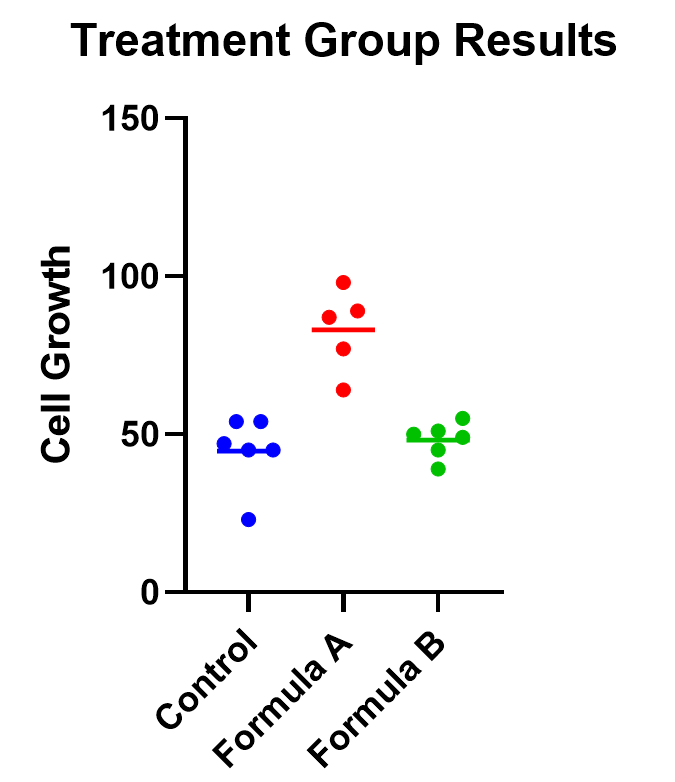
Determining statistical significance between groups

In addition to the graphic, what we really want to know is which treatment means are statistically different from each other. Because we are performing multiple tests, we’ll use a multiple comparison correction . For our example, we’ll use Tukey’s correction (although if we were only interested in the difference between each formula to the control, we could use Dunnett’s correction instead). 

In this case, the mean cell growth for Formula A is significantly  higher  than the control (p<.0001) and Formula B ( p=0.002 ), but there’s no significant difference between Formula B and the control.

Two-way ANOVA example

For two-way ANOVA, there are two factors involved. Our example will focus on a case of cell lines. Suppose we have a 2x2 design (four total groupings). There are two different treatments (serum-starved and normal culture) and two different fields. There are 19 total cell line “experimental units” being evaluated, up to 5 in each group (note that with 4 groups and 19 observational units, this study isn’t balanced). Although there are multiple units in each group, they are all completely different replicates and therefore not repeated measures of the same unit.

As with one-way ANOVA, it’s a good idea to graph the data as well as look at the ANOVA table for results.

Graphing two-way ANOVA

There are many options here. Like our one-way example, we recommend a similar graphing approach that shows all the data points themselves along with the means.

Determining statistical significance between groups in two-way ANOVA

Let’s use a two-way ANOVA with a 95% significance threshold to evaluate both factors’ effects on the response, a measure of growth.

Feel free to use our two-way ANOVA checklist as often as you need for your own analysis.

First, notice there are three sources of variation included in the model, which are interaction, treatment, and field. 

The first effect to look at is the interaction term, because if it’s significant, it changes how you interpret the main effects (e.g., treatment and field). The interaction effect calculates if the effect of a factor depends on the other factor. In this case, the significant interaction term (p<.0001) indicates that the treatment effect depends on the field type.

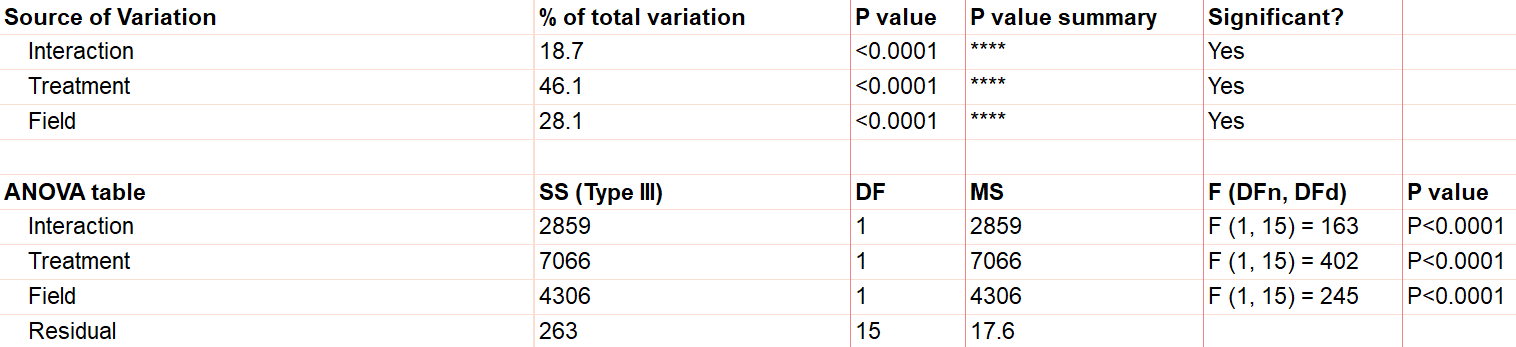
A significant interaction term muddies the interpretation, so that you no longer have the simple conclusion that “Treatment A outperforms Treatment B.” In this case, the graphic is particularly useful. It suggests that while there may be some difference between three of the groups, the precise combination of serum starved in field 2 outperformed the rest.

To confirm whether there is a statistically significant result, we would run pairwise comparisons (comparing each factor level combination with every other one) and account for multiple comparisons.

Do I need to correct for multiple comparisons for two-way ANOVA?

If you’re comparing the means for more than one combination of treatment groups, then absolutely! Here’s more information about multiple comparisons for two-way ANOVA .

Repeated measures ANOVA

So far we have focused almost exclusively on “ordinary” ANOVA and its differences depending on how many factors are involved. In all of these cases, each observation is completely unrelated to the others. Other than the combination of factors that may be the same across replicates, each replicate on its own is independent.

There is a second common branch of ANOVA known as repeated measures . In these cases, the units are related in that they are matched up in some way. Repeated measures are used to model correlation between measurements within an individual or subject. Repeated measures ANOVA is useful (and increases statistical power) when the variability within individuals is large relative to the variability among individuals.

It’s important that all levels of your repeated measures factor (usually time) are consistent. If they aren’t, you’ll need to consider running a mixed model, which is a more advanced statistical technique.

There are two common forms of repeated measures:

• You observe the same individual or subject at different time points. If you’re familiar with paired t-tests, this is an extension to that. (You can also have the same individual receive all of the treatments, which adds another level of repeated measures.)
• You have a randomized block design, where matched elements receive each treatment. For example, you split a large sample of blood taken from one person into 3 (or more) smaller samples, and each of those smaller samples gets exactly one treatment.

Repeated measures ANOVA can have any number of factors. See analysis checklists for one-way repeated measures ANOVA and two-way repeated measures ANOVA .

What does it mean to assume sphericity with repeated measures ANOVA?

Repeated measures are almost always treated as random factors, which means that the correlation structure between levels of the repeated measures needs to be defined. The assumption of sphericity means that you assume that each level of the repeated measures has the same correlation with every other level.

This is almost never the case with repeated measures over time (e.g., baseline, at treatment, 1 hour after treatment), and in those cases, we recommend not assuming sphericity. However, if you used a randomized block design, then sphericity is usually appropriate .

Example two-way ANOVA with repeated measures

Say we have two treatments (control and treatment) to evaluate using test animals. We’ll apply both treatments to each two animals (replicates) with sufficient time in between the treatments so there isn’t a crossover (or carry-over) effect. Also, we’ll measure five different time points for each treatment (baseline, at time of injection, one hour after, …). This is repeated measures because we will need to measure matching samples from the same animal under each treatment as we track how its stimulation level changes over time.

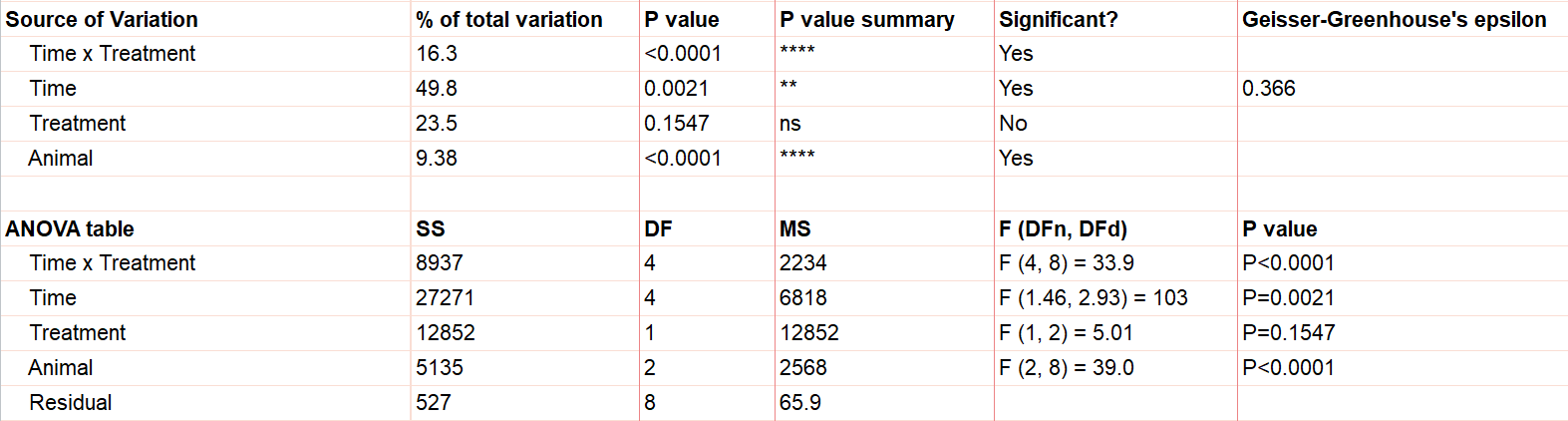
The output shows the test results from the main and interaction effects. Due to the interaction between time and treatment being significant (p<.0001), the fact that the treatment main effect isn’t significant (p=.154) isn’t noteworthy.

Graphing repeated measures ANOVA

As we’ve been saying, graphing the data is useful, and this is particularly true when the interaction term is significant. Here we get an explanation of why the interaction between treatment and time was significant, but treatment on its own was not. As soon as one hour after injection (and all time points after), treated units show a higher response level than the control even as it decreases over those 12 hours. Thus the effect of time depends on treatment. At the earlier time points, there is no difference between treatment and control.

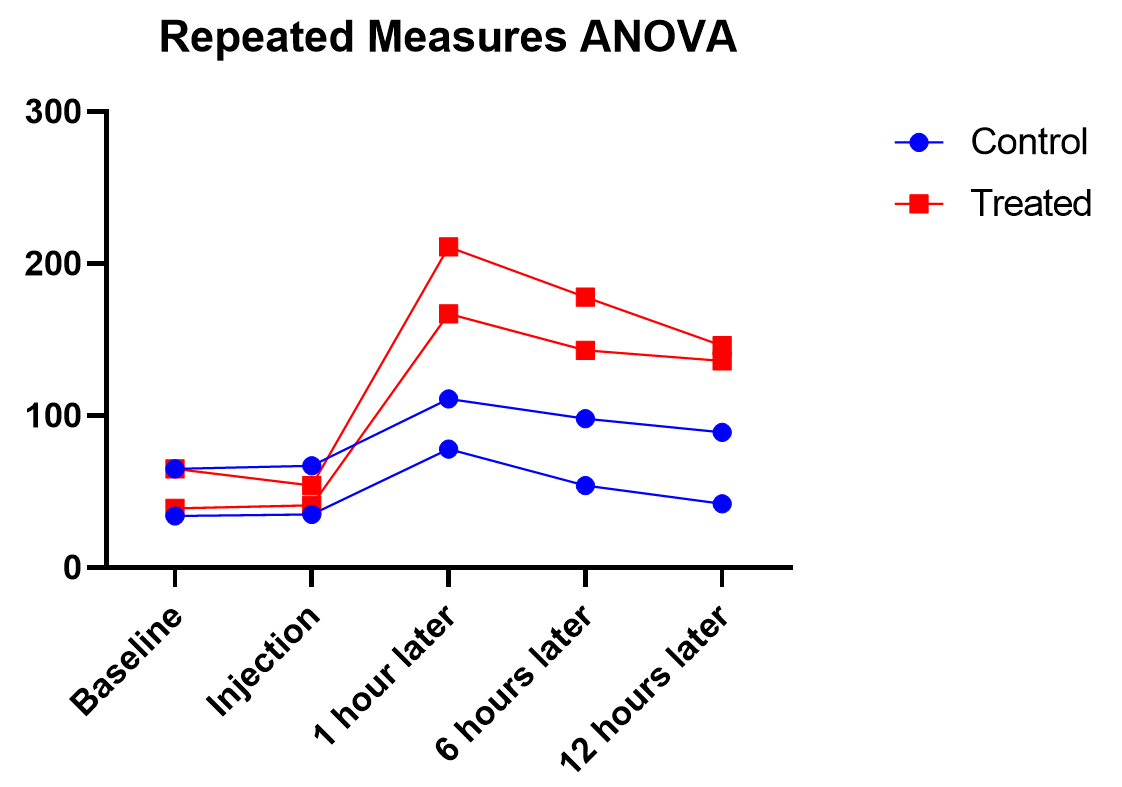
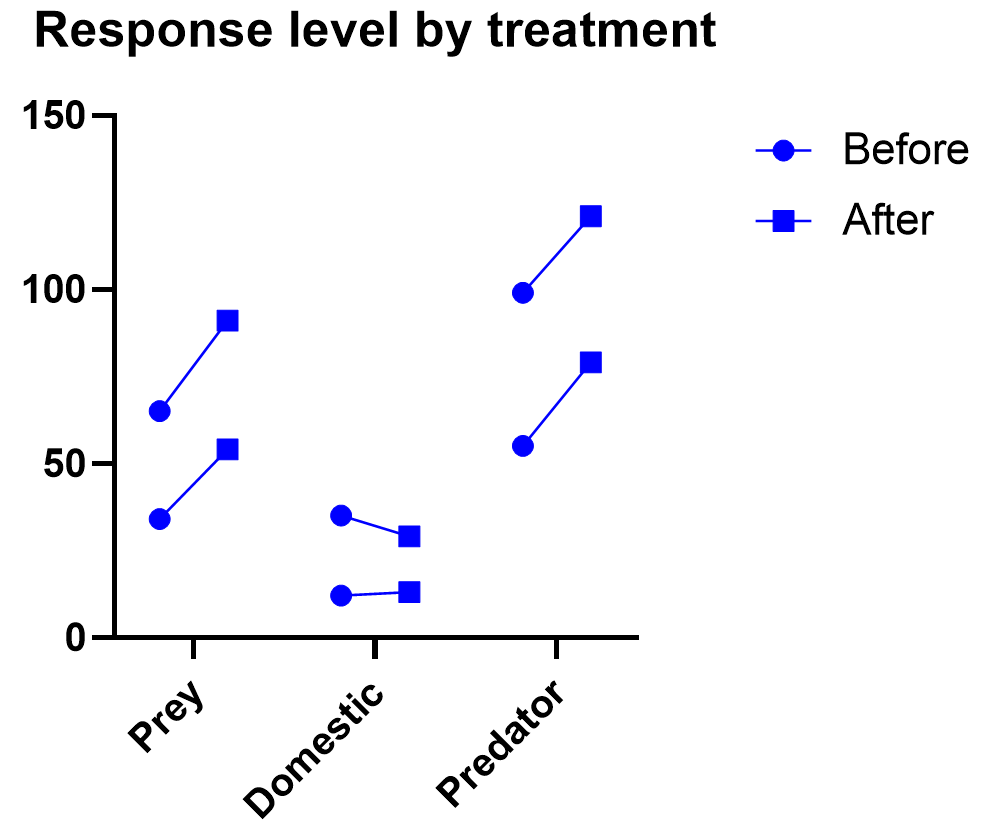
Graphing repeated measures data is an art, but a good graphic helps you understand and communicate the results. For example, it’s a completely different experiment, but here’s a great plot of another repeated measures experiment with before and after values that are measured on three different animal types.

What if I have three or more factors?

Interpreting three or more factors is very challenging and usually requires advanced training and experience . 

Just as two-way ANOVA is more complex than one-way, three-way ANOVA adds much more potential for confusion. Not only are you dealing with three different factors, you will now be testing seven hypotheses at the same time. Two-way interactions still exist here, and you may even run into a significant three-way interaction term.

It takes careful planning and advanced experimental design to be able to untangle the combinations that will be involved ( see more details here ). 

Non-parametric ANOVA alternatives

As with t-tests (or virtually any statistical method), there are alternatives to ANOVA for testing differences between three groups. ANOVA is means-focused and evaluated in comparison to an F-distribution. 

The two main non-parametric cousins to ANOVA are the Kruskal-Wallis and Friedman’s tests. Just as is true with everything else in ANOVA, it is likely that one of the two options is more appropriate for your experiment.

Kruskal-Wallis tests the difference between medians (rather than means) for 3 or more groups. It is only useful as an “ordinary ANOVA” alternative, without matched subjects like you have in repeated measures. Here are some tips for interpreting Kruskal-Wallis test results. 

Friedman’s Test is the opposite, designed as an alternative to repeated measures ANOVA with matched subjects. Here are some tips for interpreting Friedman's Test . 

What are simple, main, and interaction effects in ANOVA?

Consider the two-way ANOVA model setup that contains two different kinds of effects to evaluate:

The 𝛼 and 𝛽 factors are “main” effects, which are the isolated effect of a given factor. “Main effect” is used interchangeably with “simple effect” in some textbooks.

The interaction term is denoted as “𝛼𝛽”, and it allows for the effect of a factor to depend on the level of another factor. It can only be tested when you have replicates in your study. Otherwise, the error term is assumed to be the interaction term.

What are multiple comparisons?

When you’re doing multiple statistical tests on the same set of data, there’s a greater propensity to discover statistically significant differences that aren’t true differences. Multiple comparison corrections attempt to control for this, and in general control what is called the familywise error rate. There are a number of multiple comparison testing methods , which all have pros and cons depending on your particular experimental design and research questions.

What does the word “way” mean in one-way vs two-way ANOVA?

In statistics overall, it can be hard to keep track of factors, groups, and tails. To the untrained eye “two-way ANOVA” could mean any of these things.

The best way to think about ANOVA is in terms of factors or variables in your experiment. Suppose you have one factor in your analysis (perhaps “treatment”). You will likely see that written as a one-way ANOVA. Even if that factor has several different treatment groups, there is only one factor, and that’s what drives the name. 

Also, “way” has absolutely nothing to do with “tails” like a t-test. ANOVA relies on F tests, which can only test for equal vs unequal because they rely on squared terms. So ANOVA does not have the “one-or-two tails” question .

What is the difference between ANOVA and a t-test?

ANOVA is an extension of the t-test. If you only have two group means to compare, use a t-test. Anything more requires ANOVA.

What is the difference between ANOVA and chi-square?

Chi-square is designed for contingency tables, or counts of items within groups (e.g., type of animal). The goal is to see whether the counts in a particular sample match the counts you would expect by random chance.

ANOVA separates subjects into groups for evaluation, but there is some numeric response variable of interest (e.g., glucose level).

Can ANOVA evaluate effects on multiple response variables at the same time?

Multiple response variables makes things much more complicated than multiple factors. ANOVA (as we’ve discussed it here) can obviously handle multiple factors but it isn’t designed for tracking more than one response at a time. 

Technically, there is an expansion approach designed for this called Multivariate (or Multiple) ANOVA, or more commonly written as MANOVA. Things get complicated quickly, and in general requires advanced training.

Can ANOVA evaluate numeric factors in addition to the usual categorical factors?

It sounds like you are looking for ANCOVA (analysis of covariance). You can treat a continuous (numeric) factor as categorical, in which case you could use ANOVA, but this is a common point of confusion .

What is the definition of ANOVA?

ANOVA stands for analysis of variance, and, true to its name, it is a statistical technique that analyzes how experimental factors influence the variance in the response variable from an experiment.

What is blocking in Anova?

Blocking is an incredibly powerful and useful strategy in experimental design when you have a factor that you think will heavily influence the outcome, so you want to control for it in your experiment. Blocking affects how the randomization is done with the experiment. Usually blocking variables are nuisance variables that are important to control for but are not inherently of interest. 

A simple example is an experiment evaluating the efficacy of a medical drug and blocking by age of the subject. To do blocking, you must first gather the ages of all of the participants in the study, appropriately bin them into groups (e.g., 10-30, 30-50, etc.), and then randomly assign an equal number of treatments to the subjects within each group.

There’s an entire field of study around blocking. Some examples include having multiple blocking variables, incomplete block designs where not all treatments appear in all blocks, and balanced (or unbalanced) blocking designs where equal (or unequal) numbers of replicates appear in each block and treatment combination.

What is ANOVA in statistics?

For a one-way ANOVA test, the overall ANOVA null hypothesis is that the mean responses are equal for all treatments. The ANOVA p-value comes from an F-test.

Can I do ANOVA in R?

While Prism makes ANOVA much more straightforward, you can use open-source coding languages like R as well. Here are some examples of R code for repeated measures ANOVA, both one-way ANOVA in R and two-way ANOVA in R .

Perform your own ANOVA

Are you ready for your own Analysis of variance? Prism makes choosing the correct ANOVA model simple and transparent .

Start your 30 day free trial of Prism   and get access to:

• A step by step guide on how to perform ANOVA
• Sample data to save you time
• More tips on how Prism can help your research

With Prism, in a matter of minutes you learn how to go from entering data to performing statistical analyses and generating high-quality graphs.

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

• View all journals
• My Account Login
• Explore content
• About the journal
• Publish with us
• Sign up for alerts
• Open access
• Published: 16 March 2018

An ANOVA approach for statistical comparisons of brain networks

• Daniel Fraiman   ORCID: orcid.org/0000-0002-0482-9137 1 , 2 &
• Ricardo Fraiman 3 , 4  

Scientific Reports volume  8 , Article number:  4746 ( 2018 ) Cite this article

20k Accesses

14 Citations

3 Altmetric

Metrics details

• Data processing
• Statistical methods

The study of brain networks has developed extensively over the last couple of decades. By contrast, techniques for the statistical analysis of these networks are less developed. In this paper, we focus on the statistical comparison of brain networks in a nonparametric framework and discuss the associated detection and identification problems. We tested network differences between groups with an analysis of variance (ANOVA) test we developed specifically for networks. We also propose and analyse the behaviour of a new statistical procedure designed to identify different subnetworks. As an example, we show the application of this tool in resting-state fMRI data obtained from the Human Connectome Project. We identify, among other variables, that the amount of sleep the days before the scan is a relevant variable that must be controlled. Finally, we discuss the potential bias in neuroimaging findings that is generated by some behavioural and brain structure variables. Our method can also be applied to other kind of networks such as protein interaction networks, gene networks or social networks.

Similar content being viewed by others

Functional brain networks reflect spatial and temporal autocorrelation

Null models in network neuroscience

Telling functional networks apart using ranked network features stability

Introduction.

Understanding how individual neurons, groups of neurons and brain regions connect is a fundamental issue in neuroscience. Imaging and electrophysiology have allowed researchers to investigate this issue at different brain scales. At the macroscale, the study of brain connectivity is dominated by MRI, which is the main technique used to study how different brain regions connect and communicate. Researchers use different experimental protocols in an attempt to describe the true brain networks of individuals with disorders as well as those of healthy individuals. Understanding resting state networks is crucial for understanding modified networks, such as those involved in emotion, pain, motor learning, memory, reward processing, and cognitive development, among others. Comparing brain networks accurately can also lead to the precise early diagnosis of neuropsychiatric and neurological disorders 1 , 2 . Rigorous mathematical methods are needed to conduct such comparisons.

Currently, the two main techniques used to measure brain networks at the whole brain scale are Diffusion Tensor Imaging (DTI) and resting-state functional magnetic resonance imaging (rs-fMRI). In DTI, large white-matter fibres are measured to create a connectional neuroanatomy brain network, while in rs-fMRI, functional connections are inferred by measuring the BOLD activity at each voxel and creating a whole brain functional network based on functionally-connected voxels (i.e., those with similar behaviour). Despite technical limitations, both techniques are routinely used to provide a structural and dynamic explanation for some aspects of human brain function. These magnetic resonance neuroimages are typically analysed by applying network theory 3 , 4 , which has gained considerable attention for the analysis of brain data over the last 10 years.

The space of networks with as few as 10 nodes (brain regions) contains as many as 10 13 different networks. Thus, one can imagine the number of networks if one analyses brain network populations (e.g. healthy and unhealthy) with, say, 1000 nodes. However, most studies currently report data with few subjects, and the neuroscience community has recently begun to address this issue 5 , 6 , 7 and question the reproducibility of such findings 8 , 9 , 10 . In this work, we present a tool for comparing samples of brain networks. This study contributes to a fast-growing area of research: network statistics of network samples 11 , 12 , 13 , 14 .

We organized the paper as follows: In the Results section, we first present a discussion about the type of differences that can be observed when comparing brain networks. Second, we present the method for comparing brain networks and identifying network differences that works well even with small samples. Third, we present an example that illustrates in greater detail the concept of comparing networks. Next, we apply the method to resting-state fMRI data from the Human Connectome Project and discuss the potential biases generated by some behavioural and brain structural variables. Finally, in the Discussion section, we discuss possible improvements, the impact of sample size, and the effects of confounding variables.

Preliminars

Most studies that compare brain networks (e.g., in healthy controls vs. patients) try to identify the subnetworks, hubs, modules, etc. that are affected in the particular disease. There is a widespread belief (largely supported by data) that the brain network modifications induced by the factor studied (disease, age, sex, stimulus) are specific . This means that the factor will similarly affect the brains of different people.

On the other hand, labeled networks can be modified in many different ways while preserving the nodes, and these modifications can be categorized into three. In the first category, called here localized modifications , some particular identified links suffer changes by the factor. In the second, called unlocalized modifications , some links change, but the changed links differ among subjects. For example, the degree of interconnection of some nodes may decrease/increase by 50%, but in some individuals, this happens in the frontal lobe, in others in the right parietal lobe or the occipital lobe, and so on. In this case, the localization of the links/nodes affected by the factor can be considered random. In the third category, called here global modifications , some links (not the same across subjects) are changed, and these changes produce a global alteration of the network. For example, they can notably decrease/increase the average path length, the average degree, or the number of modules, or just produce more heterogeneous networks in a population of homogeneous ones. This last category is similar to the unlocalized modifications case, but in this case, an important global change in the network occurs.

In all cases, there are changes in the links influenced by the “factor”, while nodes are fixed. How to detect if any of these changes have occurred (hereinafter called detection) is one of the main challenges of this work. And, once their occurrence has been determined, we aim to identify where they occurred (hereinafter called identification). The difficulty lies in statistically asserting that the factor produced true modifications in the huge space of labeled networks. We aim to detect all three types of network modifications. Clearly, as is always true in statistics, more precise methods can be proposed when hypotheses regarding the data are more accurate (e.g., that the differences belong to the global modifications category). However, this last approach requires one to make many more assumptions about the brain’s behaviour. The assumptions are generally unverifiable; for this reason, we use a nonparametric approach, following the adage “less is more”, which is often very useful in statistics. For the detection problem, we developed an analysis of variance (ANOVA) test specifically for networks. As is well known, ANOVA is designed to test differences among the means of the subpopulations, and one may observe that equal means have different distributions. However, we propose a definition of means that will differ in the presence of any of the three modification categories mentioned above. As is well known, the identification stage is computationally far more complicated, and we address it partially looking at the subset of links or a subnetwork that present the highest network differences between groups.

Network Theory Framework

A network (or graph), denoted by G = ( V , E ), is an object described by a set V of nodes (vertices) and a set E   ⊂   V × V of links (edges) between them. In what follows, we consider families of networks defined over the same fixed finite set of n nodes (brain regions). A network is completely described by its adjacency matrix A   ∈  {0, 1} n  ×  n , where A ( i , j ) = 1 if and only if the link ( i , j )  ∈   E . If the matrix A is symmetric, then the graph is undirected; otherwise, we have a directed graph.

Let us suppose we are interested in studying the brain network of a given population, where most likely brain networks differ from each other to some extent. If we randomly choose a person from this population and study his/her brain network, what we obtain is a random network. This random network, G , will have a given probability of being network G 1 , another probability of being network G 2 , and so on until \({G}_{\tilde{n}}\) . Therefore, a random network is completely characterized by its probability law,

Likewise, a random variable is also completely characterized by its probability law. In this case, the most common test for comparing many subpopulations is the analysis of variance test (ANOVA). This test rejects the null hypothesis of equal means if the averages are statistically different. Here, we propose an ANOVA test designed specifically to compare networks.

To develop this test, we first need to specify the null assumption in terms of some notion of mean network and a statistic to base the test on. We only have at hand two main tools for that: the adjacency matrices of the networks and a notion of distance between networks.

The first step for comparing networks is to define a distance or metric between them. Given two networks G 1 , G 2 we consider the most classical distance, the edit distance 15 defined as

This distance corresponds to the minimum number of links that must be added and subtracted to transform G 1 into G 2 (i.e. the number of different links), and is the L 1 distance between the two matrices. We will also use equation ( 2 ) for the case of weighted networks, i.e. for matrices with A ( i , j ) taking values between 0 and 1. It is important to mention that the results presented here are still valid under other metrics 16 , 17 , 18 .

Next, we consider the average weighted network - hereinafter called the average network - defined as the network whose adjacency matrix is the average of the adjacency matrices in the sample of networks. More precisely, we consider the following definitions.

Definition 1

Given a sample of networks { G 1 , …, G l } with the same distribution

The average network \( {\mathcal M} \) that has as adjacency matrix the average of the adjacency matrices

which in terms of the population version corresponds to the mean matrix \( {\mathcal M} (i,\,j)={\mathbb{E}}({A}_{{\bf{G}}}(i,\,j))=:{p}_{ij}\) .

The average distance around a graph H is defined as

which corresponds to the mean population distance

With these definitions in mind, the natural way to define a measure of network variability is

which measures the average distance (variability) of the networks around the average weighted network.

Given m subpopulations G 1 , …, G m the null assumption for our ANOVA test will be that the means of the m subpopulations \({\tilde{{ {\mathcal M} }}}_{1},\,\ldots ,\,{\tilde{{ {\mathcal M} }}}_{m}\) are the same. The test statistic will be based on a normalized version of the sum of the differences between \({\bar{d}}_{{G}^{i}}({{ {\mathcal M} }}_{i})\) and \({\bar{d}}_{G}({{ {\mathcal M} }}_{i})\) , where \({\bar{d}}_{{G}^{i}}\) and \({\bar{d}}_{G}\) are calculated according to (4) using the i –sample and the pooled sample respectively. This is developed in more detail in the next section.

Detecting and identifying network differences

Now we address the testing problem. Let \({G}_{1}^{1},{G}_{2}^{1},\ldots ,{G}_{{n}_{1}}^{1}\) denote the networks from subpopulation 1, \({G}_{1}^{2},{G}_{2}^{2},\ldots ,{G}_{{n}_{2}}^{2}\) the ones from subpopulation 2, and so on until \({G}_{1}^{m},{G}_{2}^{m},\ldots ,{G}_{{n}_{m}}^{m}\) the networks of subpopulation m . Let G 1 , G 2 , …, G n denote, without superscript, the complete pooled sample of networks, where \(n={\sum }_{i\mathrm{=1}}^{m}{n}_{i}\) . And finally, let \({{ {\mathcal M} }}_{i}\) and σ i denote the average network and the variability of the i -subpopulation of networks. We want to test (H 0 )

that all the subpopulations have the same mean network, under the alternative that at least one subpopulation has a different mean network.

It is interesting to note that for objects that are networks, the average network ( \({ {\mathcal M} }\) ) and the variability ( σ ) are not independent summary measures. In fact, the relationship between them is given by

Therefore, the proposed test can also be considered a test for equal variability. The proposed statistic for testing the null hypothesis is:

where a is a normalization constant given in Supplementary Information  1.3 . This statistic measures the difference between the network variability of each specific subpopulation and the average distance between all the populations and the specific average network. Theorem 1 states that under the null hypothesis (items (i) and (ii)) T is asymptotically Normal(0, 1), and if H 0 is false (item (iii)) T will be smaller than some negative constant c . This specific value is obtained by the following theorem (see the Supplementary Information  1 for the proof).

. Under the null hypothesis, the T statistic fulfills (i) and (ii), while T is sensitive to the alternative hypothesis, and (iii) holds true.

\({\mathbb{E}}(T)=0\)

T is asymptotically ( K : = min { n 1 , n 2 , .., n m } → ∞) Normal(0, 1).

Under the alternative hypothesis, T will be smaller than any negative value if K is large enough (The test is consistent).

This theorem provides a procedure for testing whether two or more groups of networks are different. Although having a procedure like the one described is important, we not only want to detect network differences, we also want to identify the specific network changes or differences. We discuss this issue next.

Identification

. Let us suppose that the ANOVA test for networks rejects the null hypothesis, and now the main goal is to identify network differences. Two main objectives are discussed:

Identification of all the links that show statistical differences between groups.

Identification of a set of nodes (a subnetwork) that present the highest network differences between groups.

The identification procedure we describe below aims to eliminate the noise (links or nodes without differences between subpopulations) while keeping the signal (links or nodes with differences between subpopulations).

Given a network G = ( V , E ) and a subset of links \(\tilde{E}\subset E\) , let us generically denote \({G}_{\tilde{E}}\) the subnetwork with the same nodes but with links identified by the set \(\tilde{E}\) . The rest of the links are erased. Given a subset of nodes \(\tilde{V}\subset V\) let us denote \({G}_{\tilde{V}}\) the subnetwork that only has the nodes (with the links between them) identified by the set \(\tilde{V}\) . The T statistic for the sample of networks with only the set of \(\tilde{E}\) links is denoted by \({T}_{\tilde{E}}\) , and the T statistic computed for all the sample networks with only the nodes that belong to \(\tilde{V}\) is denoted by \({T}_{\tilde{V}}\) .

The procedure we propose for identifying all the links that show statistical differences between groups is based on the minimization for \(\tilde{E}\subset E\) of \({T}_{\tilde{E}}\) . The set of links, \(\bar{E}\) , defined by

contain all the links that show statistical differences between subpopulations. One limitation of this identification procedure is that the space E is huge (# E  = 2 n ( n −1)/2 where n is the number of nodes) and an efficient algorithm is needed to find the minimum. That is why we focus on identifying a group of nodes (or a subnetwork) expressing the largest differences.

The procedure proposed for identifying the subnetwork with the highest statistical differences between groups is similar to the previous one. It is based on the minimization of \({T}_{\tilde{V}}\) . The set of nodes, N , defined by

contains all relevant nodes. These nodes make up the subnetwork with the largest difference between groups. In this case, the complexity is smaller, since the space V is not so big (# V = 2 n  −  n  − 1).

As in other well-known statistical procedures such as cluster analysis or selection of variables in regression models, finding the size \(\tilde{j}:=\#N\) of the number of nodes in the true subnetwork is a difficult problem due to possible overestimation of noisy data. The advantage of knowing \(\tilde{j}\) is that it reduces the computational complexity for finding the minimum to an order of \({n}^{\tilde{j}}\) instead of 2 n if we have to look for all possible sizes. However, the problem in our setup is less severe than other cases since the objective function ( \({T}_{\tilde{V}}\) ) is not monotonic when the size of the space increases. To solve this problem, we suggest the following algorithm.

Let V { j } be the space of networks with j distinguishable nodes, j   ∈  {2, 3, …, n } and \(V=\mathop{\cup }\limits_{j}{V}_{\{j\}}\) . The nodes N j

define a subnetwork. In order to find the true subnetwork with differences between the groups, we now study the sequence T 2 , T 3 , …, T n . We continue with the search (increasing j ) until we find \(\tilde{j}\) fulfilling

where g is a positive function that decreases together with the sample size (in practice, a real value). \({N}_{\tilde{j}}\) are the nodes that make up the subnetwork with the largest differences among the groups or subpopulations studied.

It is important to mention that the procedures described above do not impose any assumption regarding the real connectivity differences between the populations. With additional hypotheses, the procedure can be improved. For instance, in 14 , 19 the authors proposed a methodology for the edge-identification problem that is powerful only when the real difference connection between the populations form a large unique connected component.

Examples and Applications

A relevant problem in the current neuroimaging research agenda is how to compare populations based on their brain networks. The ANOVA test presented above deals with this problem. Moreover, the ANOVA procedure allows the identification of the variables related to the brain network structure. In this section, we show an example and application of this procedure in neuroimaging (EEG, MEG, fMRI, eCoG). In the example we show the robustness of the procedures for testing and identification of different sample sizes. In the application, we analyze fMRI data to understand which variables in the dataset are dependent on the brain network structure. Identifying these variables is also very important because any fair comparison between two or more populations requires these variables be controlled (similar values).

Let us suppose we have three groups of subjects with equal sample size, K , and the brain network of each subject is studied using 16 regions (electrodes or voxels). Studies show connectivity between certain brain regions is different in certain neuropathologies, in aging, under the influence of psychedelic drugs, and more recently, in motor learning 20 , 21 . Recently, we have shown that a simple way to study connectivity is by what the physics community calls “the correlation function” 22 . This function describes the correlation between regions as a function of the distance between them. Although there exist long range connections, on average, regions (voxels or electrodes) closer to each other interact strongly, while distant ones interact more weakly. We have shown that the way in which this function decays with distance is a marker of certain diseases 23 , 24 , 25 . For example, patients with a traumatic brachial plexus lesion with root avulsions revealed a faster correlation decay as a function of distance in the primary motor cortex region corresponding to the arm 24 .

Next we present a toy model that analyses the method’s performance. In a network context, the behaviour described above can be modeled in the following way: since the probability that two regions are connected is a monotonic function of the correlation between them (i.e. on average, distant regions share fewer links than nearby regions) we decided to skip the correlations and directly model the link probability as an exponential function that decays with distance. We assume that the probability that region i is connected with j is defined as

where d ( i , j ) is the distance between regions i and j . For the alternative hypothesis, we consider that there are six frontal brain regions (see Fig.  1 Panel A) that interact with a different decay rate in each of the three subpopulations. Figure  1 panel (A) shows the 16 regions analysed on an x-y scale. Panel (B) shows the link probability function for all electrodes and for each subpopulation. As shown, there is a slight difference between the decay of the interactions between the frontal electrodes in each subpopulation ( λ 1 = 1, λ 2 = 0.8 and λ 3 = 0.6 for groups 1, 2 and 3, respectively). The aim is to determine whether the ANOVA test for networks detects the network differences that are induced by the link probability function.

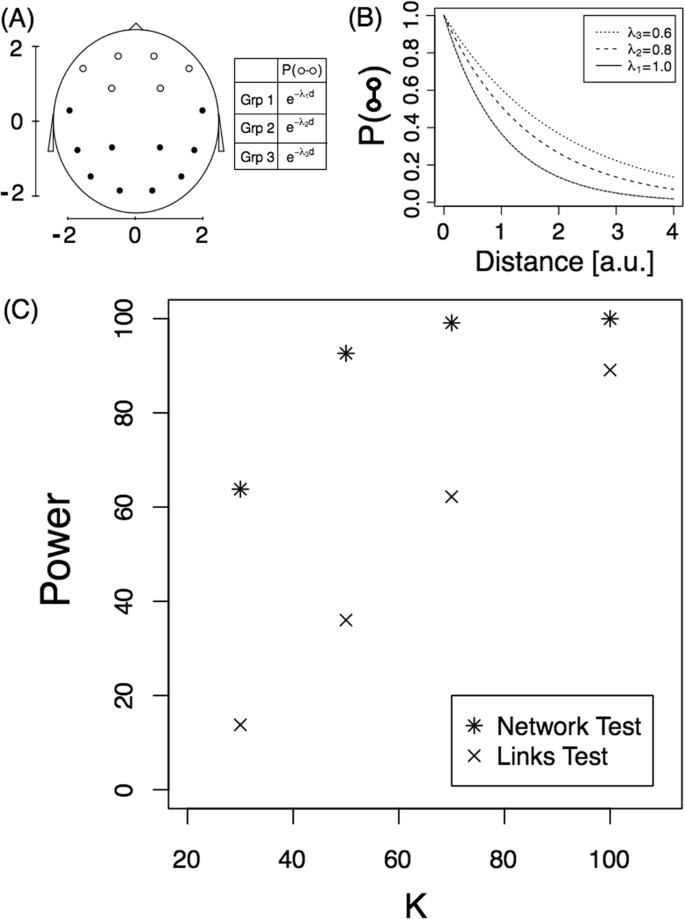
Detection problem. ( A ) Diagram of the scalp (each node represent a EEG electrode) on an x-y scale and the link probability. The three groups confirm the equation P ( ○  ↔ •) =  P (• ↔ •) =  e − d . ( B ) Link probability of frontal electrodes, P ( ○  ↔  ○ ), as a function of the distance for the three subpopulations. (C) Power of the tests as a function of sample size, K . Both tests are presented.

Here we investigated the power of the proposed test by simulating the model under different sample sizes ( K ). K networks were computed for each of the three subpopulations and the T statistic was computed for each of 10,000 replicates. The proportion of replicates with a T value smaller than −1.65 is an estimation of the power of the test for a significance level of 0.05 (unilateral hypothesis testing). Star symbols in Fig.  1C represent the power of the test for the different sample sizes. For example, for a sample size of 100, the test detects this small difference between the networks 100% of the time. As expected, the test has less power for small sample sizes, and if we change the values λ 2 and λ 3 in the model to 0.66 and 0.5, respectively, power increases. In this last case, the power changed from 64% to 96% for a sample size of 30 (see Supplementary Fig.  S1 for the complete behaviour).

To the best of our knowledge, the T statistic is the first proposal of an ANOVA test for networks. Thus, here we compare it with a naive test where each individual link is compared among the subpopulations. The procedure is as follows: for each link, we calculate a test for equal proportions between the three groups to obtain a p-value for each link. Since we are conducting multiple comparisons, we apply the Benjamini-Hochberg procedure controlling at a significance level of α = 0.05. The procedure is as follows:

1. Compute the p-value of each link comparison, pv 1 , pv 2 , …, pv m .

2. Find the j largest p-value such that \(p{v}_{(j)}\le \frac{j}{m}\alpha \mathrm{.}\)

3. Declare that the link probability is different for all links that have a p-value ≤  pv ( j ) .

This procedure detects differences in the individual links while controlling for multiple comparisons. Finally, we consider the networks as being different if at least one link (of the 15 that have real differences) was detected to have significant differences. We will call this procedure the “Links Test”. Crosses in Fig.  1C correspond to the power of this test as a function of the sample size. As can be observed, the test proposed for testing equal mean networks is much more powerful than the previous test.

Theorem 1 States that T is asymptotically (sample size → ∞) Normal(0, 1) under the Null hypothesis. Next we investigated how large the sample size must be to obtain a good approximation. Moreover, we applied Theorem 1 in the simulations above for K = {30, 50, 70, 100}, but we did not show that the approximation is valid for K = 30, for example. Here, we show that the normal approximation is valid even for K = 30 in the case of 16-node networks. We simulated 10,000 replicates of the model considering that all three groups have exactly the same probability law given by group 1, i.e. all brain connections confirm the equation \(P(i\leftrightarrow j)={e}^{-{\lambda }_{1}d(i,j)}\) for the three groups (H 0 hypothesis). The T value is computed for each replicate of sample size K = 30, and the distribution is shown in Fig.  2(A) . The histogram shows that the distribution is very close to normal. Moreover, the Kolmogorov-Smirnov test against a normal distribution did not reject the hypothesis of a normal distribution for the T statistic (p-value = 0.52). For sample sizes smaller than 30, the distribution has more variance. For example, for K = 10, the standard deviation of T is 1.1 instead of 1 (see Supplementary Fig.  S2 ). This deviation from a normal distribution can also be observed in panel B where we show the percentage of Type I errors as a function of the sample size ( K ). For sample sizes smaller than 30, this percentage is slightly greater than 5%, which is consistent with a variance greater than 1. The Links test procedure yielded a Type I error percentage smaller than 5% for small sample sizes.

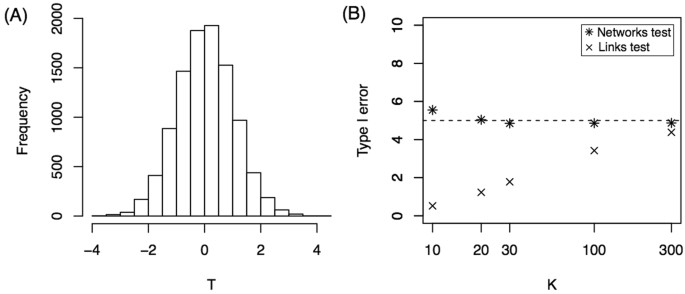
Null hypothesis. ( A ) Histogram of T statistics for K = 30. ( B ) Percentage of Type I Error as a function of sample size, K . Both tests are presented.

Finally, we applied the subnetwork identification procedure described before to this example. Fifty simulations were performed for the model with a sample size of K = 100. For each replication, the minimum statistic T j was studied as a function of the number of j nodes in the subnetwork. Figure  3A and B show two of the 50 simulation outcomes for the T j function of ( j ) number of nodes. Panel A shows that as nodes are incorporated into the subnetwork, the statistic sharply decreases to six nodes, and further incorporating nodes produces a very small decay in T j in the region between six and nine nodes. Finally, adding even more nodes results in a statistical increase. A similar behaviour is observed in the simulation shown in panel B, but the “change point” appears for a number of nodes equal to five. If we define that the number of nodes with differences, \(\tilde{j}\) , confirms

we obtain the values circled. For each of the 50 simulations, we studied the value \(\tilde{j}\) and a histogram of the results is shown in Panel C. With the criteria defined, most of the simulations (85%) result in a subnetwork of 6 nodes, as expected. Moreover, these 6 nodes correspond to the real subnetwork with differences between subpopulations (white nodes in Fig.  1A ). This was observed in 100% of simulations with \(\tilde{j}\)  = 6 (blue circles in Panel D). In the simulations where this value was 5, five of the six true nodes were identified, and five of the six nodes with differences vary between simulations (represented with grey circles in Panel D). For the simulations where \(\tilde{j}\)  = 7, all six real nodes were identified and a false node (grey circle) that changed between simulations was identified as being part of the subnetwork with differences.

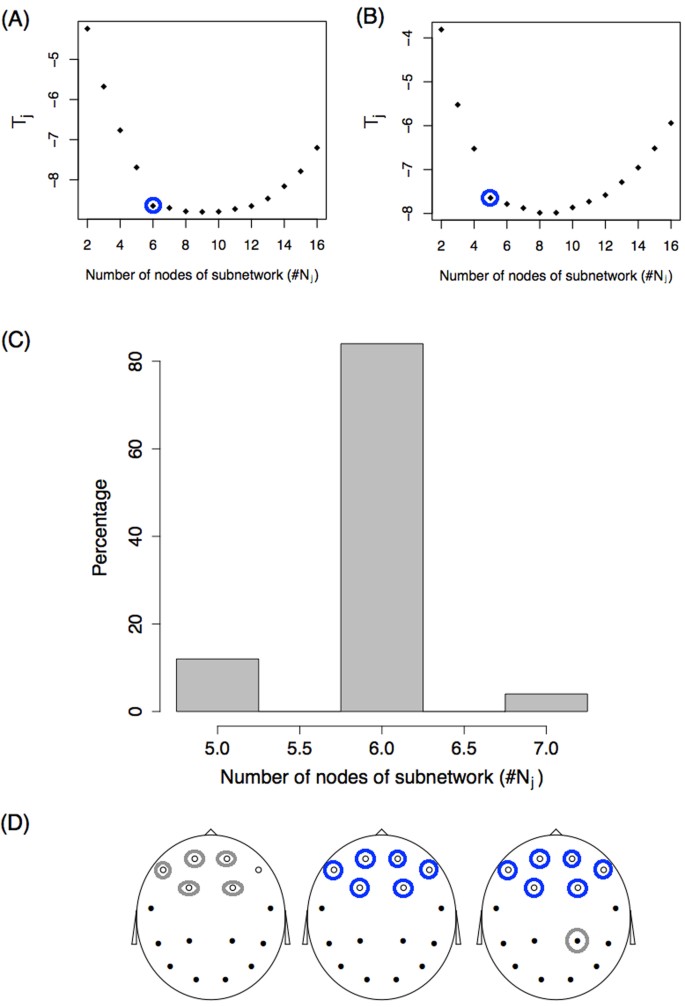
Identification problem. ( A , B ) Statistic T j as a function of the number of nodes of the subnetwork ( j ) for two simulations. Blue circles represent the value \(\tilde{j}\) following the criteria described in the text. ( C ) Histogram of the number of subnetwork nodes showing differences, \(\tilde{j}\) . ( D ) Identification of the nodes. Blue and grey circles represent the nodes identified from the set \({N}_{\tilde{j}}\) . Circled blue nodes are those identified 100% of the time. Grey circles represent nodes that are identified some of the time. On the left, grey circles alternate between the six white nodes. On the right, the grey circle alternates between the black nodes.

The identification procedure was also studied for a smaller sample size of K = 30, and in this case, the real subnetwork was identified only 28% of the time (see Suppplementary Fig.  S3 for more details). Identifying the correct subnetwork is more difficult (larger sample sizes are needed) than detecting global differences between group networks.

Resting-state fMRI functional networks

In this section, we analysed resting-state fMRI data from the 900 participants in the 2015 Human Connectome Project (HCP 26 ). We included data from the 812 healthy participants who had four complete 15-minute rs-fMRI runs, for a total of one hour of brain activity. We partitioned the 812 participants into three subgroups and studied the differences between the brain groups. Clearly, if the participants are randomly divided into groups, no brain subgroup differences are expected, but if the participants are divided in an intentional way, differences may appear. For example, if we divided the 812 by the amount of hours slept before the scan ( G 1 less than 6 hours, G 2 between 6 and 7 hours, and G 3 more than 7) it might be expected 27 , 28 to observe differences in brain connectivity on the day of the scan. Moreover, as a by-product, we obtain that this variable is an important factoring variable to be controlled before the scan. Fortunately, HCP provides interesting individual socio-demographic, behavioural and structural brain data to facilitate this analysis. Moreover, using a previous release of the HCP data (461 subjects), Smith et al . 29 , using a multivariate analysis (canonical correlation), showed that a linear combination of demographics and behavior variables highly correlates with a linear combination of functional interactions between brain parcellations (obtained by Independent Component Analysis). Our approach has the same spirit, but has some differences. In our case, the main objective is to identify variables that “explain” (that are dependent with) the individual brain network. We do not impose a linear relationship between non-imaging and imaging variables, and we study the brain network as a whole object without different “loads” in each edge. Our method does not impose any kind of linearity, and it also detects linear and non-linear dependence structures.

Data were pre-processed by HCP 30 , 31 , 32 (details can be found in 30 ), yielding the following outputs:

Group-average brain regional parcellations obtained by means of group-Independent Component Analysis (ICA 33 ). Fifteen components are described.

Subject-specific time series per ICA component.

Figure  4(A) shows three of the 15 ICA components with the specific one hour time series for a particular subject. These signals were used to construct an association matrix between pairs of ICA components per subject. This matrix represents the strength of the association between each pair of components, which can be quantified by different functional coupling metrics, such as the Pearson correlation coefficient between the signals of the component, which we adopted in the present study (panel (B)). For each of the 812 subjects, we studied functional connectivity by transforming each correlation matrix, Σ, into binary matrices or networks, G , (panel (C)). Two criteria for this transformation were used 34 , 35 , 36 : a fixed correlation threshold and a fixed number of links criterion. In the first criterion, the matrix was thresholded by a value ρ affording networks with varying numbers of links. In the second, a fixed number of link criteria were established and a specific threshold was chosen for each subject.

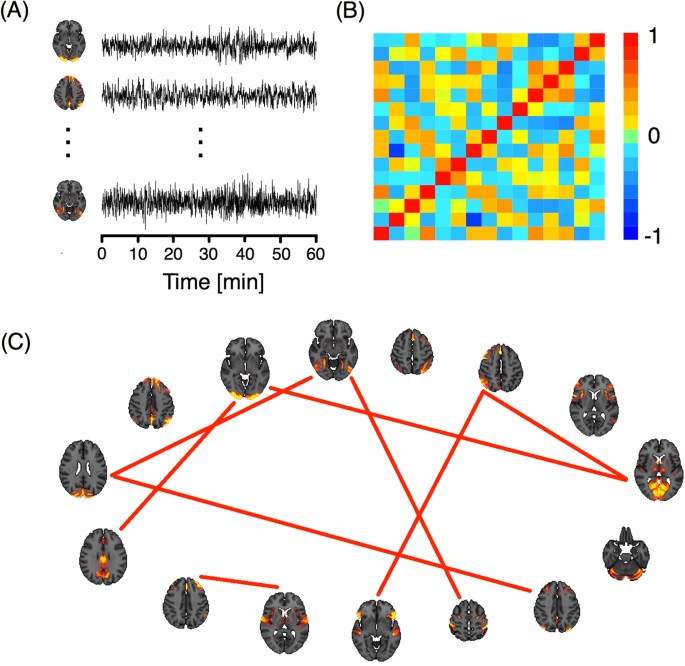
( A ) ICA components and their corresponding time series. ( B ) Correlation matrix of the time series. ( C ) Network representation. The links correspond to the nine highest correlations.

As we have already mentioned, HCP provides interesting individual socio-demographic, behavioural and structural brain data. Variables are grouped into seven main categories: alertness, motor response, cognition, emotion, personality, sensory, and brain anatomy. Volume, thickness and areas of different brain regions were computed using the T1-weighted images of each subject in Free Surfer 37 . Thus, for each subject, we obtained a brain functional network, G , and a multivariate vector X that contains this last piece of information.

The main focus of this section is to analyse the “impact” of each of these variables ( X ) on the brain networks (i.e., on brain activity). To this end, we first selected a variable such as k , X k , and grouped each subject according to his/her value into only one of three categories (Low, Medium, or High) just by placing the values in ascending and using the 33.3% percentile. In this way, we obtained three groups of subjects, each identified by its correlation matrix \({{\rm{\Sigma }}}_{1}^{L},\,\ldots ,\,{{\rm{\Sigma }}}_{{n}_{L}}^{L}\) , \({{\rm{\Sigma }}}_{1}^{M},\,\ldots ,\,{{\rm{\Sigma }}}_{{n}_{M}}^{M}\) , and \({{\rm{\Sigma }}}_{1}^{H},\,\ldots ,\,{{\rm{\Sigma }}}_{{n}_{H}}^{H}\) , or by its corresponding network (once the criteria and the parameter are chosen) \({G}_{1}^{L},\,\ldots ,\,{G}_{{n}_{L}}^{L},\,\,\,{G}_{1}^{M},\,\ldots ,\,{G}_{{n}_{M}}^{M}\) , and \({G}_{1}^{H},\,\ldots ,\,{G}_{{n}_{H}}^{H}\) . The sample size of each group ( n L , n M , and n H ) is approximately 1/3 of 812, except in cases where there were ties. Once we obtained these three sets of networks, we applied the developed test. If differences exist between all three groups, then we are confirming an interdependence between the factoring variable and the functional networks. However, we cannot yet elucidate directionality (i.e., different networks lead to different sleeping patterns or vice versa?).

After filtering the data, we identified 221 variables with 100% complete information for the 812 subjects, and 90 other variables with almost complete information, giving a total of 311 variables. We applied the network ANOVA test for each of these 311 variables and report the T statistic. Figure  5(A) shows the T statistic for the variable Thickness of the right Inferior Parietal region. All values of the T statistic are between −2 and 2 for all ρ values using the fixed correlation criterion (left panel) for constructing the networks. The same occurs when a fixed number of link criteria is used (right panel). According to Theorem 1, when there are no differences between groups, T is asymptotically normal (0, 1), and therefore a value smaller than −3 is very unlikely (p-value = 0.00135). Since all T values are between −2 and 2, we assert that Thickness of the right Inferior Parietal region is not associated with the resting-state functional interactions. In panel (B), we show the T statistic for the variable Amount of hours spent sleeping on the 30 nights prior to the scan (“During the past month, how many hours of actual sleep did you get at night? (This may be different than the number of hours you spent in bed.)”) which corresponds to the alertness category. As one can see, most T values are much lower than −3, rejecting the hypothesis of equal mean network. Importantly, this shows that the number of hours a person sleeps is associated with their brain functional networks (or brain activity). However, as explained above, we do not know whether the number of hours slept the nights before represent these individuals’ habitual sleeping patterns, complicating any effort to infer causation. In other words, six hours of sleep for an individual who habitually sleeps six hours may not produce the same network pattern as six hours in an individual who normally sleeps eight hours (and is likely tired during the scan). Alternatively, different activity observed during waking hours may “produce” different sleep behaviours. Nevertheless, we know that the amount of hours slept before the scan should be measured and controlled when scanning a subject. In Panel (C), we show that brain volumetric variables can also influence resting-state fMRI networks. In that panel, we show the T value for the variable Area of the left Middle temporal region. Significant differences for both network criteria are also observed for this variable.

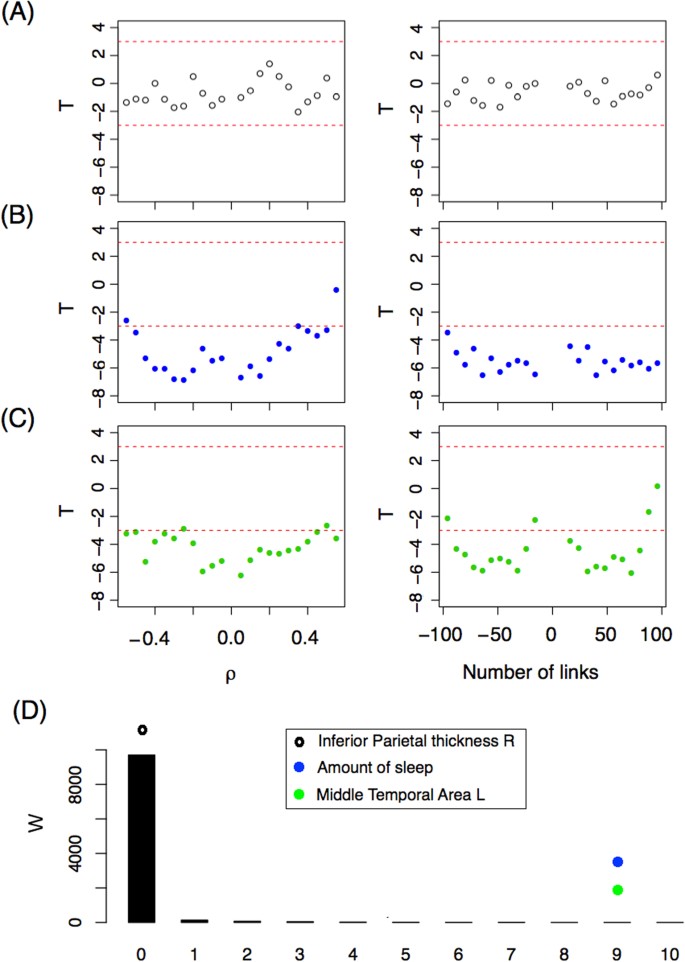
( A – C ) T –statistics as a function of (left panel) ρ and (right panel) the number of links for three variables: ( A ) Right Inferioparietal Thickness, ( B ) Number of hours slept the nights prior to the scan. ( C ) Left Middle temporal Area. ( D ) W -statistic distribution (black bars) based on a bootstrap strategy. The W -statistic of the three variables studied is depicted with dots.

Under the hypothesis of equal mean networks between groups, we expect not to obtain a T statistic less than −3 when comparing the sample networks. We tested several different thresholds and numbers of links in order to present a more robust methodology. However, in this way, we generate sets of networks that are dependent on each criterion and between criteria, similarly to what happens when studying dynamic networks with overlapping sliding windows. This makes the statistical inference more difficult. To address this problem, we decided to define a new statistic based on T , W 3 , and study its distribution using the bootstrap resampling technique. The new statistic is defined as,

where Δ is the number of values of T that are lower than −3 for the resolution (grid of thresholds) studied. The supraindex in Δ indicates the criteria (correlation threshold, ρ or number of links fixed, L ) and the subindex indicates whether it is for positive or negative parameter values ( ρ or number of links). For example, Fig.  5(C) reveals that the variable Area of the left Middle temporal confirms having \({{\rm{\Delta }}}_{+}^{\rho }=10\) , \({{\rm{\Delta }}}_{-}^{\rho }=10\) , \({{\rm{\Delta }}}_{+}^{L}=9\) , and \({{\rm{\Delta }}}_{-}^{L}=9\) , and therefore W 3 = 9. The distribution of W 3 under the null hypothesis is studied numerically. Ten thousand random resamplings of the real networks were selected and the W 3 statistic was computed for each one. Figure  5(D) shows the W empirical distribution (under the null hypothesis) with black bars. Most W 3 values are zero, as expected. In this figure, the W 3 values of the three variables described are also represented by dots. The extreme values of W 3 for the variables Amount of Sleep and Middle Temporal Area L confirm that these differences are not a matter of chance. Both variables are related to brain network connectivity.

So far we have shown, among other things, that functional networks differ between individuals who get more or fewer hours of sleep, but how do these networks differ exactly? Fig.  6(A) shows the average networks for the three groups of subjects. There are differences in connectivity strength between some of the nodes (ICA components). These differences are more evident in panel (B), which presents a weighted network Ψ with links showing the variability among the subpopulation’s average networks. This weighted network is defined as

where \(\overline{{ {\mathcal M} }}(i,\,j)=\frac{1}{3}\mathop{\sum _{s\mathrm{=1}}}\limits^{3}{{ {\mathcal M} }}^{{\rm{grp}}s}\) . The role of Ψ is to highlight the differences between the mean networks. The greatest difference is observed between nodes 1 and 11. Individuals that sleep 6.5 hours or less show the strongest connection between ICA component number 1 (which corresponds to the occipital pole and the cuneal cortex in the occipital lobe) and ICA component number 11 (which includes the middle and superior frontal gyri in the frontal lobe, the superior parietal lobule and the angular gyrus in the parietal lobe). Another important connection that differs between groups is the one between ICA components 1 and 8, which corresponds to the anterior and posterior lobes of the cerebellum. Using the subnetwork identification procedure previously described (see Fig.  6C ) we identified a 7-node subnetwork as the most significant for network differences. The nodes that make up that network are presented in panel D.

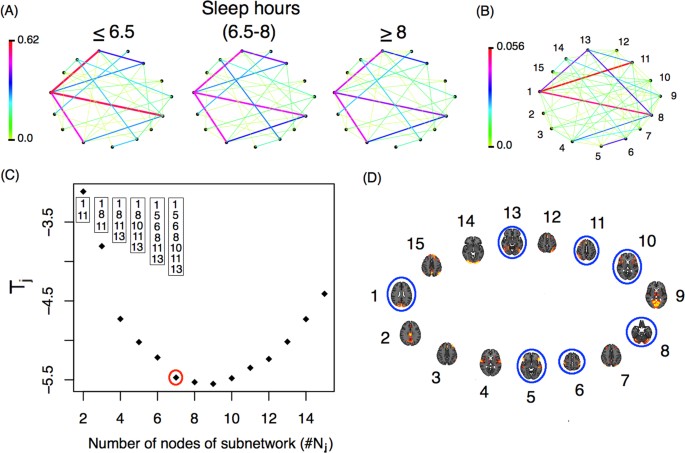
( A ) Average network for each subgroup defined by hours of sleep ( B ) Weighted network with links that represent the differences among the subpopulation mean networks. ( C ) T j -statistic as a function of the number of nodes in each subnetwork ( j ). The nodes identified by the minimum T j are presented in the boxes, while the number of nodes identified by the procedure are represented with a red circle. ( D ) Nodes from the identified subnetwork are circled in blue. The nodes identified in ( D ) correspond to those in panel ( B ).

The results described above refer to only three of the 311 variables we analysed. In terms of the remaining variables, we observed more variables that partitioned the subjects into groups presenting statistical differences between the corresponding brain networks. Two more behavioral variables were identified the variable Dimensional Change Card Sort (CardSort_AgeAdj and CardSort_Unadj) which is a measure of cognitive flexibility, and the variable motor strength (Strength_AgeAdj and Strength_Unadj). Also 20 different brain volumetric variables were identified, the complete list of these variables is shown in Suppl. Table  S1 . It is important to note that these brain volumetric variables are largely dependent on each other; for example, individuals with larger inferior-temporal areas often have a greater supratentorial volume, and so on (see Suppl. Fig.  S4 ).

We have reported only those variables for which there is very strong statistical evidence in favor of the existence of dependence between the functional networks and the “behavioral” variables, irrespectively of the threshold used to build up the networks. There are other variables that show this dependence only for some levels of the threshold parameter, but we do not report these to avoid reporting results that may not be significant. Our results complement those observed in 29 . In particular, Smith et al . report that the variable Picture Vocabulary test is the most significant. With a less restrictive criterion, this variable can also be considered significant with our methodology. In fact, the W 3 value equals 3 (see Supplementary Fig.  S5 for details), which supports the notion (see panel D in Fig.  5 ) that the variable Picture Vocabulary test is also relevant for explaining the functional networks. On the other hand, the variable we found to vary significantly ( W 3  = 9) the Amount of sleep is not reported by Smith et al . Perhaps the canonical correlation cannot find the variable because it looks for linear correlations in a high dimensional space. It is well known that non-linearities appear typically in high dimensional statistical problems (See for instance 38 ). To capture nonlinear associations, a kernel CCA method was introduced, see 39 , 40 and the references therein. By contrast, our method does not impose any kind of linearity, and detects linear as well as non-linear dependence structures. The variable “Cognitive flexibility” (Card Sort) found here was also reported in 38 . Finally, the brain volumetric variables we found to be relevant here were not analyzed in 29 .

So far, we apply the methodology presented here to analyse brain data by using only 15 brain ICA dimensions (provided by HCP). But, what is the impact of working with more ICA components? Does we identify more covariables? Fortunately, we can respond these questions since more ICA dimensions were recently made available on HCP webpage. Three new cognitive variables, Working memory , Relational processing and Self-regulation/Impulsivity were identified for higher network dimension (50 and 300 ICA dimensions, see Suppl. Table  S2 for details).

Performing statistical inference on brain networks is important in neuroimaging. In this paper, we presented a new method for comparing anatomical and functional brain networks of two or more subgroups of subjects. Two problems were studied: the detection of differences between the groups and the identification of the specific network differences. For the first problem, we developed an ANOVA test based on the distance between networks. This test performed well in terms of detecting existing differences (high statistical power). Finally, based on the statistics developed for the testing problem, we proposed a way of solving the identification problem. Next, we discuss our findings.

Based on the minimization of the T statistic, we propose a method for identifying the subnetwork that differs among the subgroups. This subnetwork is very useful. On the one hand, it allows us to understand which brain regions are involved in the specific comparison study (neurobiological interpretation), and on the other, it allows us to identify/diagnose new subjects with greater accuracy.

The relationship between the minimum T value for a fixed number of nodes as a function of the number of nodes ( T j vs. j ) is very informative. A large decrease in T j incorporating a new node into the subnetwork ( T j + 1 << T j ) means that the new node and its connections explain much of the difference between groups. A very small decrease shows that the new node explains only some of the difference because either the subgroup difference is small for the connections of the new node, or because there is a problem of overestimation.

The correct number of nodes in each subnetwork must verify

In this paper, we present ad hoc criteria in each example (a certain constant for g ( sample size )) and we do not give a general formula for g ( sample size ). We believe that this could be improved in theory, but in practice, one can propose a natural way to define the upper bound and subsequently identify the subnetwork, as we showed in the example and in the application by observing T j as a function of j . Statistical methods such as the one developed for change-point detection may be useful in solving this problem.

Sample size

What is the adequate sample size for comparing brain networks? This is typically the first question in any comparison study. Clearly, the response depends on the magnitude of the network differences between the groups and the power of the test. If the subpopulations differ greatly, then a moderate number of networks in each group is enough. On the other hand, if the differences are not very big, then a larger sample size is required to have a reasonable power of detection. The problem gets more complicated when it comes to identification. We showed in Example 1 that we obtain a good identification rate when a sample size of 100 networks is selected from each subgroup. Thus, the rate of correct identification is small for a sample size of for example 30.

Confounding variables in Neuroimaging

Humans are highly variable in their brain activity, which can be influenced, in turn, by their level of alertness, mood, motivation, health and many other factors. Even the amount of coffee drunk prior to the scan can greatly influence resting-state neural activity. What variables must be controlled to make a fair comparison between two or more groups? Certainly age, gender, and education are among those variables, and in this study we found that the amount of hours slept the nights prior to the scan is also relevant. Although this might seem pretty obvious, to the best of our knowledge, most studies do not control for this variable. Five other variables were identified, each one related with some dimensions of cognitive flexibility, self-regulation/impulsivity, relational processing, working memory or motor strength. Finally, we identified as being relevant a set of 20 highly interdependent brain volumetric variables. In principle, the role of these variables is not surprising, since comparing brain activity between individuals requires one to pre-process the images by realigning and normalizing them to a standard brain. In other words, the relevance of specific area volumes may simply be a by-product of the standardization process. However, if our finding that brain volumetric variables affect functional networks is replicated in other studies, this poses a problem for future experimental designs. Specifically, groups will not only have to be matched by variables such as age, gender and education level, but also in terms of volumetric variables, which can only be observed in the scanner. Therefore, several individuals would have to be scanned before selecting the final study groups.

In sum, a large number of subjects in each group must be tested to obtain highly reproducible findings when analysing resting-state data with network methodologies. Also, whenever possible, the same participants should be tested both as controls and as the treatment group (paired samples) in order to minimize the impact of brain volumetric variables.

Deco, G. & Kringelbach, M. L. Great expectations: using whole-brain computational connectomics for understanding neuropsychiatric disorders. Neuron 84 , 892–905 (2014).

Article   CAS   PubMed   Google Scholar  

Stephan, K. E., Iglesias, S., Heinzle, J. & Diaconescu, A. O. Translational perspectives for computational neuroimaging. Neuron 87 , 716–732 (2015).

Bullmore, E. & Sporns, O. Complex brain networks: network theoretical analysis of structural and functional systems. Nature Reviews Neuroscience 10 , 186–196 (2009).

Fornito, A., Zalesky, A. & Bullmore, E. Fundamentals of Brain Network Analysis. Elsevier .

Anonymous Focus on human brain mapping. Nat. Neurosci. 20 , 297–298 (2017).

Article   Google Scholar  

Button, K. S. et al . Power failure: why small sample size undermines the reliability of neuroscience. Nat. Rev. Neurosci. 14 , 365–376 (2013).

Poldrack, R. Scanning the horizon: towards transparent and reproducible neuroimaging research. Nat. Rev. Neurosci. 18 , 115–126 (2017).

Nichols, T. E. et al . Best Practices in Data Analysis and Sharing in Neuroimaging using MRI. Nat. Neurosci. 20 , 299–303 (2016).

Bennett, C. M. & Miller, M. B. How reliable are the results from functional magnetic resonance imaging? Annals of the New York Academy of Sciences 1191 , 133–155 (2010).

Article   ADS   PubMed   Google Scholar  

Brown, E. N. & Behrmann, M. Controversy in statistical analysis of functional magnetic resonance imaging data. Proc Natl Acad Sci USA 114 , E3368–E3369 (2017).

Article   CAS   PubMed   PubMed Central   Google Scholar  

Fraiman, D., Fraiman, N. & Fraiman, R. Non Parametric Statistics of Dynamic Networks with distinguishable nodes. Test 26 , 546?573 (2017).

Article   MATH   Google Scholar  

Cerqueira, A., Fraiman, D., Vargas, C. & Leonardi, F. A test of hypotheses for random graph distributions built from EEGdata. IEEE Transactions on Network Science and Engineering 4 , 75–82 (2017).

Article   MathSciNet   Google Scholar  

Kolar, M., Song, L., Ahmed, A. & Xing, E. Estimating Time-varying networks. Ann. Appl. Stat. Estimating Time-varying networks. 4 , 94–123 (2010).

Google Scholar  

Zalesky, A., Fornito, A. & Bullmore, E. Network-based statistic: identifying differences in brain networks. Neuroimage 53 , 1197–1207 (2010).

Article   PubMed   Google Scholar  

Sanfeliu, A. & Fu, K. A distance measure between attributed relational graphs. IEEE T. Sys. Man. Cyb. 13 , 353–363 (1983).

Schieber, T. et al . Quantification of network structural dissimilarities. Nature communications 8 , 13928 (2017).

Article   ADS   CAS   PubMed   PubMed Central   Google Scholar  

Shimada, Y., Hirata, Y., Ikeguchi, T. & Aihara, K. Graph distance for complex networks. Scientific reports 6 , 34944 (2016).

Gao, X., Xiao, B., Tao, D. & Li, X. A survey of graph edit distance. Pattern Anal Appl 13 , 113–129 (2010).

Zalesky, A., Cocchi, L., Fornito, A., Murray, M. & Bullmore, E. Connectivity differences in brain networks. Neuroimage 60 , 1055–1062 (2012).

Della-Maggiore, V., Villalta, J. I., Kovacevic, N. & McIntosh, A. R. Functional Evidence for Memory Stabilization in Sensorimotor Adaptation: A 24-h Resting-State fMRI Study. Cerebral Cortex 27 , 1748–1757 (2015).

Mawase, F., Bar-Haim, S. & Shmuelof, L. Formation of Long-Term Locomotor Memories Is Associated with Functional Connectivity Changes in the Cerebellar?Thalamic?Cortical Network. Journal of Neuroscience 37 , 349–361 (2017).

Fraiman, D. & Chialvo, D. What kind of noise is brain noise: anomalous scaling behavior of the resting brain activity fluctuations. Frontiers in Physiology 3 , 307 (2012).

Article   PubMed   PubMed Central   Google Scholar  

Garcia-Cordero, I. et al . Stroke and neurodegeneration induce different connectivity aberrations in the insula. Stroke 46 , 2673–2677 (2015).

Fraiman, D. et al . Reduced functional connectivity within the primary motor cortex of patients with brachial plexus injury. Neuroimage Clinical 12 , 277–284 (2016).

Dottori, M. et al . Towards affordable biomarkers of frontotemporal dementia: A classification study via network’s information sharing. Scientific Reports 7 , 3822 (2017).

Article   ADS   PubMed   PubMed Central   Google Scholar  

Human Connectome Project. http://www.humanconnectomeproject.org/

Kaufmann, T. et al . The brain functional connectome is robustly altered by lack of sleep. NeuroImage 127 , 324–332 (2016).

Krause, A. et al . The sleep-deprived human brain. Nature Reviews Neuroscience 18 , 404–418 (2017).

Smith, S. et al . A positive-negative mode of population covariation links brain connectivity, demographics and behavior. Nature neuroscience 18 , 1565–1567 (2015).

Human Connectome Project. WU-Minn HCP 900 Subjects Data Release: Reference Manual. 67–87 (2015).

Griffanti, L. et al . ICA-based artefact removal and accelerated fMRI acquisition for improved resting state network imaging. Neuroimage 95 , 232–247 (2014).

Smith, S. M. et al . Resting-state fMRI in the Human Connectome Project. Neuroimage 80 , 144–168 (2013).

Beckmann, C., DeLuca, M., Devlin, J. & Smith, S. Investigations into resting-state connectivity using independent component analysis. Philosophical Transactions of the Royal Society of London B: Biological Sciences 360 , 1001–1013 (2005).

Fraiman, D., Saunier, G., Martins, E. & Vargas, C. Biological Motion Coding in the Brain: Analysis of Visually Driven EEG Functional Networks. PloS One , 0084612 (2014).

Amoruso, L. et al . Brain network organization predicts style-specific expertise during Tango dance observation. Neuroimage 146 , 690–700 (2017).

van den Heuvel, M. P. et al . Proportional thresholding in resting-state fMRI functional connectivity networks and consequences for patient-control connectome studies: Issues and recommendations. Neuroimage 152 , 437–449 (2017).

Fischl, B. FreeSurfer. Neuroimage 62 , 774–781 (2012).

Buhlmann, P. & van der Geer, S. Statistics for High-Dimensional Data: Methods, Theory and Applications. Springer (2011).

Yoshida, K., Yoshimoto, J. & Doya, K. Sparse kernel canonical correlation analysis for discovery of nonlinear interactions in high-dimensional data. BMC Bioinformatics 18 , 108 (2017).

Yamanishi, Y., Vert, J. P., Nakaya, A. & Kanehisa, M. Extraction of correlated gene clusters from multiple genomic data by generalized kernel canonical correlation analysis. Bioinformatics 19 , 323–330 (2003).

Download references

Acknowledgements

We thank two anonymous reviewers for extensive comments that helped improve the manuscript significantly. Data were provided by the Human Connectome Project, WU-Minn Consortium (Principal Investigators: David Van Essen and Kamil Ugurbil; 1U54MH091657) funded by the 16 NIH Institutes and Centers that support the NIH Blueprint for Neuroscience Research; and by the McDonnell Center for Systems Neuroscience at Washington University. This paper was produced as part of the activities of FAPESP Research, Innovation and Dissemination Center for Neuromathematics (Grant No. 2013/07699-0, S. Paulo Research Foundation). This work was partially supported by PAI UdeSA.

Author information

Authors and affiliations.

Departamento de Matemática y Ciencias, Universidad de San Andrés, Buenos Aires, Argentina

Daniel Fraiman

Consejo Nacional de Investigaciones Científicas y Tecnológicas, Buenos Aires, Argentina

Centro de Matemática, Facultad de Ciencias, Universidad de la República, Montevideo, Uruguay

Ricardo Fraiman

Instituto Pasteur de Montevideo, Montevideo, Uruguay

You can also search for this author in PubMed   Google Scholar

Contributions

D.F. and R.F. conceived the research, analysed the data and wrote the manuscript.

Corresponding author

Correspondence to Daniel Fraiman .

Ethics declarations

Competing interests.

The authors declare no competing interests.

Additional information

Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Electronic supplementary material

Supplementary information, rights and permissions.

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/ .

Reprints and permissions

About this article

Cite this article.

Fraiman, D., Fraiman, R. An ANOVA approach for statistical comparisons of brain networks. Sci Rep 8 , 4746 (2018). https://doi.org/10.1038/s41598-018-23152-5

Download citation

Received : 13 November 2017

Accepted : 06 March 2018

Published : 16 March 2018

DOI : https://doi.org/10.1038/s41598-018-23152-5

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

By submitting a comment you agree to abide by our Terms and Community Guidelines . If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.

Quick links

• Explore articles by subject
• Guide to authors
• Editorial policies

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

• Hunt Library
• Ask a Librarian

Frequently Asked Questions

• 36 Circulation / Borrow / Renew
• 18 Computers / Technical Support
• 18 Document Delivery
• 9 EagleSearch
• 28 Finding Articles / Papers / Reports
• 20 Finding Books / Theses / Dissertations
• 70 How do I...
• 19 ILL (Interlibrary Loan)
• 8 Instruction / Tutorials
• 2 Library Code of Conduct
• 33 Library Services
• 4 Open Educational Resources
• 45 Research
• 3 Research Databases
• 3 Scholarly Commons
• 3 Scholarly Communication
• 5 Theses and Dissertations
• 1 Thesis Binding
• 1 University Archives
• 6 University Resources

Q. How do I find a research paper that has used ANOVA?

To find examples of scholarly research papers that have used the ANOVA analysis method, follow the steps below: 

• Go to:  the library homepage.
• In the EagleSearch box, type in the following: airlines AND ANOVA
• (See Search tips below for help composing your own searches.)
• Click on  Search

Search tips:

• AND  is used in most databases to ensure that each term is present somewhere in the search results: NextGen AND flight
• The  asterisk ( * ) is a symbol that allows for variant word endings: refuel* = refuel, refueling, refueled, etc.
• Quotes  are used to indicate that the words enclosed must be searched as a phrase: "human factors”
• OR  is used between terms to indicate that either term is acceptable: aircraft OR airplane

Options to focus and limit your results are on the left side of the search results page. These include  Scholarly & Peer-Review ,  Full Text Online ,  Publication Date , and more.  For finding articles using ANOVA be sure to limit your results to  Scholarly & Peer-Review .

For more information on this and other research methods, you may find the database Sage Research Methods useful.

If you need more specific help, please contact Ask A Librarian .

links & files

Links & files.

• How To Use Sage Research Methods
• Share on Facebook

Was this helpful? Yes 1 No 5

Need quick answers to short research questions? A librarian is ready to help.

Need in-depth research help? Email a librarian and expect a response in 1 business day.

Need to meet with a librarian? Schedule a one-on-one online meeting.

Email a Librarian

More help options.

Phone: 386-226-7656 Toll-free: 800-678-9428 Text: 386-968-8843

• Privacy Policy

Home » ANOVA (Analysis of variance) – Formulas, Types, and Examples

ANOVA (Analysis of variance) – Formulas, Types, and Examples

Table of Contents

Analysis of Variance (ANOVA)

Analysis of Variance (ANOVA) is a statistical method used to test differences between two or more means. It is similar to the t-test, but the t-test is generally used for comparing two means, while ANOVA is used when you have more than two means to compare.

ANOVA is based on comparing the variance (or variation) between the data samples to the variation within each particular sample. If the between-group variance is high and the within-group variance is low, this provides evidence that the means of the groups are significantly different.

ANOVA Terminology

When discussing ANOVA, there are several key terms to understand:

• Factor : This is another term for the independent variable in your analysis. In a one-way ANOVA, there is one factor, while in a two-way ANOVA, there are two factors.
• Levels : These are the different groups or categories within a factor. For example, if the factor is ‘diet’ the levels might be ‘low fat’, ‘medium fat’, and ‘high fat’.
• Response Variable : This is the dependent variable or the outcome that you are measuring.
• Within-group Variance : This is the variance or spread of scores within each level of your factor.
• Between-group Variance : This is the variance or spread of scores between the different levels of your factor.
• Grand Mean : This is the overall mean when you consider all the data together, regardless of the factor level.
• Treatment Sums of Squares (SS) : This represents the between-group variability. It is the sum of the squared differences between the group means and the grand mean.
• Error Sums of Squares (SS) : This represents the within-group variability. It’s the sum of the squared differences between each observation and its group mean.
• Total Sums of Squares (SS) : This is the sum of the Treatment SS and the Error SS. It represents the total variability in the data.
• Degrees of Freedom (df) : The degrees of freedom are the number of values that have the freedom to vary when computing a statistic. For example, if you have ‘n’ observations in one group, then the degrees of freedom for that group is ‘n-1’.
• Mean Square (MS) : Mean Square is the average squared deviation and is calculated by dividing the sum of squares by the corresponding degrees of freedom.
• F-Ratio : This is the test statistic for ANOVAs, and it’s the ratio of the between-group variance to the within-group variance. If the between-group variance is significantly larger than the within-group variance, the F-ratio will be large and likely significant.
• Null Hypothesis (H0) : This is the hypothesis that there is no difference between the group means.
• Alternative Hypothesis (H1) : This is the hypothesis that there is a difference between at least two of the group means.
• p-value : This is the probability of obtaining a test statistic as extreme as the one that was actually observed, assuming that the null hypothesis is true. If the p-value is less than the significance level (usually 0.05), then the null hypothesis is rejected in favor of the alternative hypothesis.
• Post-hoc tests : These are follow-up tests conducted after an ANOVA when the null hypothesis is rejected, to determine which specific groups’ means (levels) are different from each other. Examples include Tukey’s HSD, Scheffe, Bonferroni, among others.

Types of ANOVA

Types of ANOVA are as follows:

One-way (or one-factor) ANOVA

This is the simplest type of ANOVA, which involves one independent variable . For example, comparing the effect of different types of diet (vegetarian, pescatarian, omnivore) on cholesterol level.

Two-way (or two-factor) ANOVA

This involves two independent variables. This allows for testing the effect of each independent variable on the dependent variable , as well as testing if there’s an interaction effect between the independent variables on the dependent variable.

Repeated Measures ANOVA

This is used when the same subjects are measured multiple times under different conditions, or at different points in time. This type of ANOVA is often used in longitudinal studies.

Mixed Design ANOVA

This combines features of both between-subjects (independent groups) and within-subjects (repeated measures) designs. In this model, one factor is a between-subjects variable and the other is a within-subjects variable.

Multivariate Analysis of Variance (MANOVA)

This is used when there are two or more dependent variables. It tests whether changes in the independent variable(s) correspond to changes in the dependent variables.

Analysis of Covariance (ANCOVA)

This combines ANOVA and regression. ANCOVA tests whether certain factors have an effect on the outcome variable after removing the variance for which quantitative covariates (interval variables) account. This allows the comparison of one variable outcome between groups, while statistically controlling for the effect of other continuous variables that are not of primary interest.

Nested ANOVA

This model is used when the groups can be clustered into categories. For example, if you were comparing students’ performance from different classrooms and different schools, “classroom” could be nested within “school.”

ANOVA Formulas

ANOVA Formulas are as follows:

Sum of Squares Total (SST)

This represents the total variability in the data. It is the sum of the squared differences between each observation and the overall mean.

• yi represents each individual data point
• y_mean represents the grand mean (mean of all observations)

Sum of Squares Within (SSW)

This represents the variability within each group or factor level. It is the sum of the squared differences between each observation and its group mean.

• yij represents each individual data point within a group
• y_meani represents the mean of the ith group

Sum of Squares Between (SSB)

This represents the variability between the groups. It is the sum of the squared differences between the group means and the grand mean, multiplied by the number of observations in each group.

• ni represents the number of observations in each group
• y_mean represents the grand mean

Degrees of Freedom

The degrees of freedom are the number of values that have the freedom to vary when calculating a statistic.

For within groups (dfW):

For between groups (dfB):

For total (dfT):

• N represents the total number of observations
• k represents the number of groups

Mean Squares

Mean squares are the sum of squares divided by the respective degrees of freedom.

Mean Squares Between (MSB):

Mean Squares Within (MSW):

F-Statistic

The F-statistic is used to test whether the variability between the groups is significantly greater than the variability within the groups.

If the F-statistic is significantly higher than what would be expected by chance, we reject the null hypothesis that all group means are equal.

Examples of ANOVA

Examples 1:

Suppose a psychologist wants to test the effect of three different types of exercise (yoga, aerobic exercise, and weight training) on stress reduction. The dependent variable is the stress level, which can be measured using a stress rating scale.

Here are hypothetical stress ratings for a group of participants after they followed each of the exercise regimes for a period:

• Yoga: [3, 2, 2, 1, 2, 2, 3, 2, 1, 2]
• Aerobic Exercise: [2, 3, 3, 2, 3, 2, 3, 3, 2, 2]
• Weight Training: [4, 4, 5, 5, 4, 5, 4, 5, 4, 5]

The psychologist wants to determine if there is a statistically significant difference in stress levels between these different types of exercise.

To conduct the ANOVA:

1. State the hypotheses:

• Null Hypothesis (H0): There is no difference in mean stress levels between the three types of exercise.
• Alternative Hypothesis (H1): There is a difference in mean stress levels between at least two of the types of exercise.

2. Calculate the ANOVA statistics:

• Compute the Sum of Squares Between (SSB), Sum of Squares Within (SSW), and Sum of Squares Total (SST).
• Calculate the Degrees of Freedom (dfB, dfW, dfT).
• Calculate the Mean Squares Between (MSB) and Mean Squares Within (MSW).
• Compute the F-statistic (F = MSB / MSW).

3. Check the p-value associated with the calculated F-statistic.

• If the p-value is less than the chosen significance level (often 0.05), then we reject the null hypothesis in favor of the alternative hypothesis. This suggests there is a statistically significant difference in mean stress levels between the three exercise types.

4. Post-hoc tests

• If we reject the null hypothesis, we conduct a post-hoc test to determine which specific groups’ means (exercise types) are different from each other.

Examples 2:

Suppose an agricultural scientist wants to compare the yield of three varieties of wheat. The scientist randomly selects four fields for each variety and plants them. After harvest, the yield from each field is measured in bushels. Here are the hypothetical yields:

The scientist wants to know if the differences in yields are due to the different varieties or just random variation.

Here’s how to apply the one-way ANOVA to this situation:

• Null Hypothesis (H0): The means of the three populations are equal.
• Alternative Hypothesis (H1): At least one population mean is different.
• Calculate the Degrees of Freedom (dfB for between groups, dfW for within groups, dfT for total).
• If the p-value is less than the chosen significance level (often 0.05), then we reject the null hypothesis in favor of the alternative hypothesis. This would suggest there is a statistically significant difference in mean yields among the three varieties.
• If we reject the null hypothesis, we conduct a post-hoc test to determine which specific groups’ means (wheat varieties) are different from each other.

How to Conduct ANOVA

Conducting an Analysis of Variance (ANOVA) involves several steps. Here’s a general guideline on how to perform it:

• Null Hypothesis (H0): The means of all groups are equal.
• Alternative Hypothesis (H1): At least one group mean is different from the others.
• The significance level (often denoted as α) is usually set at 0.05. This implies that you are willing to accept a 5% chance that you are wrong in rejecting the null hypothesis.
• Data should be collected for each group under study. Make sure that the data meet the assumptions of an ANOVA: normality, independence, and homogeneity of variances.
• Calculate the Degrees of Freedom (df) for each sum of squares (dfB, dfW, dfT).
• Compute the Mean Squares Between (MSB) and Mean Squares Within (MSW) by dividing the sum of squares by the corresponding degrees of freedom.
• Compute the F-statistic as the ratio of MSB to MSW.
• Determine the critical F-value from the F-distribution table using dfB and dfW.
• If the calculated F-statistic is greater than the critical F-value, reject the null hypothesis.
• If the p-value associated with the calculated F-statistic is smaller than the significance level (0.05 typically), you reject the null hypothesis.
• If you rejected the null hypothesis, you can conduct post-hoc tests (like Tukey’s HSD) to determine which specific groups’ means (if you have more than two groups) are different from each other.
• Regardless of the result, report your findings in a clear, understandable manner. This typically includes reporting the test statistic, p-value, and whether the null hypothesis was rejected.

When to use ANOVA

ANOVA (Analysis of Variance) is used when you have three or more groups and you want to compare their means to see if they are significantly different from each other. It is a statistical method that is used in a variety of research scenarios. Here are some examples of when you might use ANOVA:

• Comparing Groups : If you want to compare the performance of more than two groups, for example, testing the effectiveness of different teaching methods on student performance.
• Evaluating Interactions : In a two-way or factorial ANOVA, you can test for an interaction effect. This means you are not only interested in the effect of each individual factor, but also whether the effect of one factor depends on the level of another factor.
• Repeated Measures : If you have measured the same subjects under different conditions or at different time points, you can use repeated measures ANOVA to compare the means of these repeated measures while accounting for the correlation between measures from the same subject.
• Experimental Designs : ANOVA is often used in experimental research designs when subjects are randomly assigned to different conditions and the goal is to compare the means of the conditions.

Here are the assumptions that must be met to use ANOVA:

• Normality : The data should be approximately normally distributed.
• Homogeneity of Variances : The variances of the groups you are comparing should be roughly equal. This assumption can be tested using Levene’s test or Bartlett’s test.
• Independence : The observations should be independent of each other. This assumption is met if the data is collected appropriately with no related groups (e.g., twins, matched pairs, repeated measures).

Applications of ANOVA

The Analysis of Variance (ANOVA) is a powerful statistical technique that is used widely across various fields and industries. Here are some of its key applications:

Agriculture

ANOVA is commonly used in agricultural research to compare the effectiveness of different types of fertilizers, crop varieties, or farming methods. For example, an agricultural researcher could use ANOVA to determine if there are significant differences in the yields of several varieties of wheat under the same conditions.

Manufacturing and Quality Control

ANOVA is used to determine if different manufacturing processes or machines produce different levels of product quality. For instance, an engineer might use it to test whether there are differences in the strength of a product based on the machine that produced it.

Marketing Research

Marketers often use ANOVA to test the effectiveness of different advertising strategies. For example, a marketer could use ANOVA to determine whether different marketing messages have a significant impact on consumer purchase intentions.

Healthcare and Medicine

In medical research, ANOVA can be used to compare the effectiveness of different treatments or drugs. For example, a medical researcher could use ANOVA to test whether there are significant differences in recovery times for patients who receive different types of therapy.

ANOVA is used in educational research to compare the effectiveness of different teaching methods or educational interventions. For example, an educator could use it to test whether students perform significantly differently when taught with different teaching methods.

Psychology and Social Sciences

Psychologists and social scientists use ANOVA to compare group means on various psychological and social variables. For example, a psychologist could use it to determine if there are significant differences in stress levels among individuals in different occupations.

Biology and Environmental Sciences

Biologists and environmental scientists use ANOVA to compare different biological and environmental conditions. For example, an environmental scientist could use it to determine if there are significant differences in the levels of a pollutant in different bodies of water.

Advantages of ANOVA

Here are some advantages of using ANOVA:

Comparing Multiple Groups: One of the key advantages of ANOVA is the ability to compare the means of three or more groups. This makes it more powerful and flexible than the t-test, which is limited to comparing only two groups.

Control of Type I Error: When comparing multiple groups, the chances of making a Type I error (false positive) increases. One of the strengths of ANOVA is that it controls the Type I error rate across all comparisons. This is in contrast to performing multiple pairwise t-tests which can inflate the Type I error rate.

Testing Interactions: In factorial ANOVA, you can test not only the main effect of each factor, but also the interaction effect between factors. This can provide valuable insights into how different factors or variables interact with each other.

Handling Continuous and Categorical Variables: ANOVA can handle both continuous and categorical variables . The dependent variable is continuous and the independent variables are categorical.

Robustness: ANOVA is considered robust to violations of normality assumption when group sizes are equal. This means that even if your data do not perfectly meet the normality assumption, you might still get valid results.

Provides Detailed Analysis: ANOVA provides a detailed breakdown of variances and interactions between variables which can be useful in understanding the underlying factors affecting the outcome.

Capability to Handle Complex Experimental Designs: Advanced types of ANOVA (like repeated measures ANOVA, MANOVA, etc.) can handle more complex experimental designs, including those where measurements are taken on the same subjects over time, or when you want to analyze multiple dependent variables at once.

Disadvantages of ANOVA

Some limitations or disadvantages that are important to consider:

Assumptions: ANOVA relies on several assumptions including normality (the data follows a normal distribution), independence (the observations are independent of each other), and homogeneity of variances (the variances of the groups are roughly equal). If these assumptions are violated, the results of the ANOVA may not be valid.

Sensitivity to Outliers: ANOVA can be sensitive to outliers. A single extreme value in one group can affect the sum of squares and consequently influence the F-statistic and the overall result of the test.

Dichotomous Variables: ANOVA is not suitable for dichotomous variables (variables that can take only two values, like yes/no or male/female). It is used to compare the means of groups for a continuous dependent variable.

Lack of Specificity: Although ANOVA can tell you that there is a significant difference between groups, it doesn’t tell you which specific groups are significantly different from each other. You need to carry out further post-hoc tests (like Tukey’s HSD or Bonferroni) for these pairwise comparisons.

Complexity with Multiple Factors: When dealing with multiple factors and interactions in factorial ANOVA, interpretation can become complex. The presence of interaction effects can make main effects difficult to interpret.

Requires Larger Sample Sizes: To detect an effect of a certain size, ANOVA generally requires larger sample sizes than a t-test.

Equal Group Sizes: While not always a strict requirement, ANOVA is most powerful and its assumptions are most likely to be met when groups are of equal or similar sizes.

About the author

Muhammad Hassan

Researcher, Academic Writer, Web developer

You may also like

Cluster Analysis – Types, Methods and Examples

Discriminant Analysis – Methods, Types and...

MANOVA (Multivariate Analysis of Variance) –...

Documentary Analysis – Methods, Applications and...

Graphical Methods – Types, Examples and Guide

Substantive Framework – Types, Methods and...

Click through the PLOS taxonomy to find articles in your field.

For more information about PLOS Subject Areas, click here .

Loading metrics

Open Access

Peer-reviewed

Research Article

A Hybrid One-Way ANOVA Approach for the Robust and Efficient Estimation of Differential Gene Expression with Multiple Patterns

* E-mail: [email protected]

Affiliation Institut Perubatan Molekul UKM (UMBI), University Kebangsaan Malaysia (UKM), Jalan Ya’acob Latiff, Bandar Tun Razak, Cheras 56000 Kuala Lumpur, Malaysia

Affiliations Institut Perubatan Molekul UKM (UMBI), University Kebangsaan Malaysia (UKM), Jalan Ya’acob Latiff, Bandar Tun Razak, Cheras 56000 Kuala Lumpur, Malaysia, Department of Physiology, Faculty of Medicine, Universiti Kebangsaan Malaysia, Kuala Lumpur, Malaysia

Affiliation Laboratory of Bioinformatics, Department of Statistics, University of Rajshahi, Rajshahi-6205, Bangladesh

• Mohammad Manir Hossain Mollah, 
• Rahman Jamal, 
• Norfilza Mohd Mokhtar, 
• Roslan Harun, 
• Md. Nurul Haque Mollah

• Published: September 28, 2015
• https://doi.org/10.1371/journal.pone.0138810
• Reader Comments

Identifying genes that are differentially expressed (DE) between two or more conditions with multiple patterns of expression is one of the primary objectives of gene expression data analysis. Several statistical approaches, including one-way analysis of variance (ANOVA), are used to identify DE genes. However, most of these methods provide misleading results for two or more conditions with multiple patterns of expression in the presence of outlying genes. In this paper, an attempt is made to develop a hybrid one-way ANOVA approach that unifies the robustness and efficiency of estimation using the minimum β -divergence method to overcome some problems that arise in the existing robust methods for both small- and large-sample cases with multiple patterns of expression.

The proposed method relies on a β -weight function, which produces values between 0 and 1. The β -weight function with β = 0.2 is used as a measure of outlier detection. It assigns smaller weights (≥ 0) to outlying expressions and larger weights (≤ 1) to typical expressions. The distribution of the β -weights is used to calculate the cut-off point, which is compared to the observed β -weight of an expression to determine whether that gene expression is an outlier. This weight function plays a key role in unifying the robustness and efficiency of estimation in one-way ANOVA.

Analyses of simulated gene expression profiles revealed that all eight methods (ANOVA, SAM, LIMMA, EBarrays, eLNN, KW, robust BetaEB and proposed) perform almost identically for m = 2 conditions in the absence of outliers. However, the robust BetaEB method and the proposed method exhibited considerably better performance than the other six methods in the presence of outliers. In this case, the BetaEB method exhibited slightly better performance than the proposed method for the small-sample cases, but the the proposed method exhibited much better performance than the BetaEB method for both the small- and large-sample cases in the presence of more than 50% outlying genes. The proposed method also exhibited better performance than the other methods for m > 2 conditions with multiple patterns of expression, where the BetaEB was not extended for this condition. Therefore, the proposed approach would be more suitable and reliable on average for the identification of DE genes between two or more conditions with multiple patterns of expression.

Citation: Mollah MMH, Jamal R, Mokhtar NM, Harun R, Mollah MNH (2015) A Hybrid One-Way ANOVA Approach for the Robust and Efficient Estimation of Differential Gene Expression with Multiple Patterns. PLoS ONE 10(9): e0138810. https://doi.org/10.1371/journal.pone.0138810

Editor: Ramona Natacha PENA i SUBIRÀ, University of Lleida, SPAIN

Received: January 19, 2015; Accepted: September 3, 2015; Published: September 28, 2015

Copyright: © 2015 Mollah et al. This is an open access article distributed under the terms of the Creative Commons Attribution License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited

Data Availability: The R code for implementing the proposed methodology can be downloaded at figshare.com/s/78dceda44ff511e580b706ec4b8d1f61 . Contact: [email protected].

Funding: This research was funded by a grant from the Ministry of Education under the Higher Institution Centre of Excellence (HICoE) programme (10-64-01-005).

Competing interests: The authors have declared that no competing interests exist.

1 Introduction

Microarray technology has enabled the expression levels of thousands of genes to be investigated simultaneously. However, this technology poses statistical challenges by virtue of the large number of transcripts surveyed with small sample sizes. The identification of transcripts that are differentially expressed (DE) between two or more conditions is a common task that is undertaken to reduce the dimensionality of the transcripts, as important genes belong to the reduced set of DE transcripts. Useful information regarding the regulatory network can be obtained by associating differential expressions with the genotypes of molecular markers [ 1 ]. By assigning DE genes to the list of gene sets, it is possible to obtain useful biological interpretations [ 2 , 3 ]. Furthermore, the number of DE genes that influence a certain phenotype may be large, whereas their relative proportions are typically small; therefore, identifying these DE genes from among the large number of recorded genes is challenging [ 4 – 8 ].

In general, four types of statistical procedures are used to identify DE genes: (i) classical parametric approaches, such as t-test, Ftest (ANOVA) and likelihood ratio test (LRT)-based asymptotic χ 2 -test; (ii) classical nonparametric approaches [ 8 – 11 ]; (iii) empirical Bayes (EB) parametric approaches [ 5 – 7 , 12 , 13 ]; and (iv) EB nonparametric approaches [ 14 , 15 ]. In the classical procedures, DE genes are generally detected based on p -values (significance levels) that are estimated either via permutation or based on the distribution of a test statistic, whereas in EB procedures, the posterior probability ( pp ) of differential expression is used to identify DE genes. However, most of the aforementioned algorithms are not robust against outliers [ 12 , 16 ]. Thus, they may produce misleading results in the presence of outlying transcripts or irregular patterns of expression. Several recent studies have reported that the assumption of normality does not hold for some existing microarray datasets [ 17 ]. One of the causes for this breakdown of the normality assumption may be related to the presence of outliers in the data. cDNA microarray data are often corrupted by outliers that arise because of the many steps that are involved in the experimental process, from hybridization to image analysis [ 12 , 16 ].

Some nonparametric approaches, such as KW [ 9 ], are somewhat robust against outliers between two or more conditions with multiple patterns of expression in the case of large sample sizes; however, these approaches are sensitive to outliers in the case of small sample sizes. To overcome this problem, the β -divergence-based empirical Bayes (BetaEB) approach [ 16 ] was developed for the robust identification of DE genes. This approach performs well in the presence of outlying expressions with up to 50% genes for both small- and large-sample cases. The parameters of the BetaEB approach are estimated based on the expressions of all genes. It can tolerate up to 50% outlying genes if the mean vector is initialized by the median vector. In the presence of more than 50% outlying genes, it is difficult to initialize the shifting parameters (mean vector) of this approach with the good part of the dataset. Therefore, the BetaEB approach occasionally produces misleading results. Note that more than 50% outlying genes may also occasionally occur with at least one patient/tissue sample. Moreover, this approach was not extended for the detection of DE genes in the case of more than two conditions/groups with multiple patterns of expression due to the computational complexity. Therefore, in this paper, an attempt is made to develop a hybrid approach that unifies the robustness and efficiency of estimation in one-way ANOVA using the minimum β -divergence method [ 18 – 21 ] to overcome all of the aforementioned problems that arise in the BetaEB approach. The advantage of the proposed algorithm compared to BetaEB is that it performs considerably better than the BetaEB approach for both the small- and large-sample cases in the presence of more than 50% outlying genes with 5% outlier samples for each outlying gene. The major advantage of the proposed algorithm is that it performs well in the case of multiple conditions/groups ( m > 2) for identifying DE genes with multiple patterns of expression, whereas BetaEB was not extended for multiple conditions/groups ( m > 2) due to the computational complexity. The proposed method introduces a weight function, which plays a key role in its performance. This weight function assigns smaller weights to outlying observations, thereby ensuring the robustness of the inference. Appropriate initialization of the parameters also improves the performance of the proposed method, as is also discussed in this paper.

2 Materials and Methods

2.1 Robust Multiple Comparison Test

3 Results and Discussion

We investigated the performance of the proposed method in comparison with other popular methods using both simulated and real gene expression data.

3.1 Performance Evaluation Based on Simulated Gene Expression Profiles

To investigate the performance of the proposed method in comparison with several popular existing methods, such as the classical parametric approach ANOVA (F-test), the nonparametric approaches SAM [ 10 ] and KW (Kruskal-Wallis test) and the empirical Bayes (EB) approaches LIMMA [ 13 ], EBarrays [ 5 , 24 ], eLNN [ 25 ] and BetaEB [ 16 ], in the detection of DE (important) genes, we considered gene expression profiles simulated based on classical (ANOVA) and Bayesian (EBarrays LNN) data generation models for both small- and large-sample cases with two and multiple groups/conditions in both the absence and the presence of outlying expression, as discussed in subsections 3.1.1 and 3.1.2.

3.1.1 Performance Evaluation Based on Simulated Gene Expression Profiles with m = 2 Conditions.

• PPT PowerPoint slide
• PNG larger image
• TIFF original image

https://doi.org/10.1371/journal.pone.0138810.t001

Predicted (solid curve) and simulated (histogram) observed distributions of the β weights of Eq (5) : (a) without outlying gene expressions and (b) with 5% outlying gene expressions.

https://doi.org/10.1371/journal.pone.0138810.g001

However, in the presence of 1 or 2 outlying expressions with 5%, 10% and 75% genes for the small- or large-sample or both sample cases, four methods (eLNN, KW, BetaEB and Proposed) exhibited better performance on average than the other four methods (ANOVA, SAM, EBarrays and LIMMA) because the former four methods produce larger values of TPR, AUC and pAUC and smaller values of FNR, FDR and MER compared to the other four methods. Two methods (KW and eLNN) showed slightly good performance for the large-sample case, but they were sensitive to outliers for the small-sample case. The empirical Bayes approach (BetaEB) exhibited good performance for both the small- and large-sample cases in the presence of outlying expressions with 5% and 10% genes, but it exhibited weak performance in the presence of outlying expressions in 75% genes. Thus, the robust BetaEB method and the proposed method exhibited better performance than the other six methods in presence of at most 50% outlying genes (although we provided results with 5%, 10% and 75% outlying genes only) with 5% outliers for each outlying gene. The BetaEB approach appears to be slightly better than the proposed method for the small-sample case, whereas the proposed method exhibited considerably better performance than the BetaEB method for both the small- and large-sample cases in the presence of more than 50% outlying genes. We also observed similar results when we generated gene expression profiles based on a Bayesian (EBarrays LNN) data generating model considering all aspects of the ANOVA model (Table B in S1 File ).

3.1.2 Performance Evaluation Based on Simulated Gene Expression Profiles with m ≥ 3 Conditions with Multiple Patterns.

In this study, we investigated the performance of the proposed method in comparison with only four popular methods (ANOVA, SAM, LIMMA and KW) because the robust BetaEB approach is not applicable for multiple patterns of expression because of its computational complexity. Table 2 shows that all the methods, except KW, produce almost identical values of FDR, AUC and pAUC in the absence of outlying genes for the small-sample case. KW was found to have considerably lower values of AUC and pAUC and a larger value of FDR for multiple groups/conditions (m = 4) in the small-sample case. Additionally, it exhibits greater sensitivity than the other methods (ANOVA, SAM, LIMMA and proposed) in the presence of outlying genes. However, all of the methods, including KW, perform similarly in the absence of outlying genes for the large-sample case. In this case, the performance of KW is better than that of the other three methods (ANOVA, SAM and LIMMA) in the presence of outlying genes, but it is slightly weaker than that of the proposed method. Thus, in all cases, the proposed method exhibited performance similar to that of the other approaches in the absence of outliers and better performance in the presence of outliers with lower FDR values and higher AUC and pAUC values. We also investigated the performance of the proposed method in comparison with the same four methods (ANOVA, SAM, LIMMA and KW) for m = 4 conditions with FDR and with the family-wise error rate (FWER) fixed to 1% using adjusted p -values based on the Benjamini-Hochberg (BH) and Bonferroni corrections, respectively. Tables 3 and 4 present the average TPR using p -values and adjusted p -values at the 1% level of significance for both the small- and large-sample cases, respectively. The results shown in brackets () represent the average FPR. Table 3 also shows that three methods (ANOVA, LIMMA and proposed) are strong enough to achieve higher TPR (≥ 80%) than SAM and KW using both raw p -values and adjusted p -values in the absence of outlying genes. The SAM obtains a lower TPR than the other three methods (ANOVA, LIMMA and proposed) when controlling FWER by Bonferroni corrections. The KW also shows that there are no DE genes in the absence of outlying genes for the small-sample case ( Table 3 ). As an example, from Table 3 , we observe that ANOVA, SAM, LIMMA, KW and the proposed methods obtained TPRs of 0.944 (0.012), 0.947 (0.003), 0.955 (0.009), 0.000 (0.000) and 0.944 (0.012) based on the true set of 300 DE genes in the absence of outlying genes, FPR shown in parenthesis, on average, respectively.

https://doi.org/10.1371/journal.pone.0138810.t002

https://doi.org/10.1371/journal.pone.0138810.t003

https://doi.org/10.1371/journal.pone.0138810.t004

However, in the presence of outlying genes, Tables 3 and 4 both show that most of the methods, except the proposed method, are unable to achieve high TPRs for both sample cases. Interestingly, we observed that all methods, including SAM and KW, perform well for the large-sample case in the absence of outlying genes, whereas we observed a loss of efficiency of SAM and KW for the small-sample case. The nonparametric approach KW is more efficient than the other three methods (ANOVA, SAM and LIMMA) in the presence of outliers in different proportions of genes for the large-sample case ( Table 4 ). Therefore, we observed that the proposed method performed similarly in the absence of outliers, but it exhibited the best performance in the presence of outliers compared to all other methods in all cases of both sample sizes (Tables 3 and 4 ).

The results presented in Tables 2 , 3 and 4 were calculated under the global null hypothesis ( H 0 ) of no differential gene expressions in the m = 4 conditions. However, after rejection of the global H 0 , a multiple comparison test was required to identify the pattern of differential gene expression. Tables 5 and 6 present the adjusted p -values of the multiple comparison tests for ANOVA, LIMMA, KW and the proposed method based on the datasets corresponding to the true patterns μ 1 = μ 2 ≠ μ 3 = μ 4 and μ 1 = μ 2 ≠ μ 3 ≠ μ 4 , respectively. Both tables indicate that all four methods (ANOVA, LIMMA, KW and Proposed) were successful in identifying the correct patterns of differential gene expression in the absence of outlying expressions, whereas in the presence of a few outliers (5%), the proposed method exhibited superior performance in identifying the correct patterns. For example, in the absence of outlying genes, all four methods (ANOVA, LIMMA, KW and Proposed) provided larger p -values, such as 0.9379, 1.000, 0.8808 and 0.5537, respectively ( Table 5 ), because we considered no difference between group 1 and group 2 in the pattern of a gene. Among them, the LIMMA performed better ( p -value = 1) than the other approaches in obtaining the true difference between group 1 and group 2 of the pattern. In the case of group 1 and group 3, all four methods detected the true difference between group 1 and group 3 of the pattern, but among them, the ANOVA, LIMMA and proposed methods performed better than the KW method in obtaining the true pattern. However, two (ANOVA and LIMMA) of the four methods failed to detect the true patterns in the presence of 5% outliers in the previous expression, as shown in Tables 5 and 6 , respectively. The nonparametric approach KW performed more poorly than these two methods in detecting the true patterns with larger p-values, even in the absence of outlying genes for the small-sample case, but better for the large-sample case with multiple groups in both the absence and presence of outlying genes, whereas the proposed method remained similar, as previously mentioned, to the case where outliers were absent in both sample sizes.

https://doi.org/10.1371/journal.pone.0138810.t005

https://doi.org/10.1371/journal.pone.0138810.t006

To investigate the pattern-detection performance of the proposed method in comparison to the others, we generated 300 DE genes among the 20,000 genes in the dataset for m = 4 conditions with different patterns for the sample size (n1 = n2 = n3 = n4 = 6) with a 2-fold change in expression between the groups. Then, we first applied four methods (ANOVA, LIMMA, KW and Proposed) to test the null hypothesis of no differential expression among four groups for each gene. If the test was rejected, then we applied the multiple comparison test for pattern detection of gene expression. Table 7 presents the multiple comparison results, where the values presented in the form {x, x, x, x} indicate the numbers of downregulated (DR) or upregulated (UR) differentially expressed (DE) genes estimated using ANOVA, LIMMA, KW and the proposed methods, respectively. This table also describes the true patterns of the DE genes in the various groups. We observe that all four methods exhibited nearly identical performance in the absence of outlying genes; however, in the presence of a single outlying expression in each of 10% genes, the proposed method exhibited far superior performance compared to the other methods.

https://doi.org/10.1371/journal.pone.0138810.t007

3.2 Performance Evaluation Based on Real Gene Expression Profiles

We considered three publicly available microarray gene expression datasets in the analyses presented in subsections 3.2.1, 3.2.2 and 3.2.3 to evaluate the performance of the proposed method in comparison with several popular methods, as discussed above. These three datasets are (i) the platinum spike gene expression dataset [ 27 ], (ii) the colon cancer gene expression dataset [ 28 ] and (iii) the pancreatic cancer gene expression dataset [ 29 ]. All three datasets were generated using Affymetrix technology.

3.2.1 Analysis of the Platinum Spike Gene Expression Dataset with m = 2 Conditions.

This dataset was previously analyzed in [ 4 , 27 ]. It consists of 18 spike-in samples (9 controls versus 9 test cases). We downloaded this dataset from the GEO website under the accession number GSE21344. We also downloaded the designated fold change (FC) dataset associated with the probes from www.biomedcentral.com/content/supplementary/1471-2105-11-285-s5.txt . After pre-processing (using RMA) and filtering the dataset, we obtained gene expressions with 18707 probes, among which 1944 probes are known as the designated DE genes under spiked-in fold changes of 0.25, 0.28, 0.40, 0.66, 0.83, 1.5, 1.7, 2, 3 and 3.5. In our analysis, we consider these designated DE genes as designated ‘DE gene-set’ and the rest of the genes as designated ‘EE gene-set’ for performance evaluation of the proposed method in a comparison with the other seven methods (ANOVA, SAM, eLNN, LIMMA, KW, EBarrays, BetaEB). We applied all eight methods to the dataset to identify the DE genes. We considered the estimated top 1944 genes for each method and crossed with the designated ‘DE gene-set’ to calculate the same summary statistics (TPR, TNR, FPR, FNR, FDR, MER, AUC and pAUC) for performance evaluation as used for the simulation studies. Table 8 shows that all the methods produce similar results with the original spike dataset. Although the performance of all methods appears to be similar for this dataset, the β -weight function of the proposed method detected 9% (= 1684) genes as outlying genes, where 1634 outlying genes belonged to the designated EE gene-set and the remaining 50 genes belonged to the designated DE genes. Outlier genes are indicated with a red color in S4(a)–S4(c) Fig . Both EE and DE outlying genes are distributed with respect to the interval of estimated p -values or (1-posterior probabilities), as shown in S4(d)–S4(e) Fig for each method. We observed that the proposed method detected the largest number of designated EE (233) and DE (40) outlying genes with p -values of less than 0.05. To investigate the reason for why the proposed method detected the largest number of designated EE outlying genes with p -values of less than 0.05 compared to the other approaches, we present the M-A plot based on group medians in S4F Fig . In the M-A plot, the marker (⋅) with a gray color represents all genes, the marker (°) with a green color represents designated DE genes, the marker (*) with a blue color represents designated EE outlying genes, and the marker (*) with a red color represents designated DE outlying genes. We clearly observed that some designated DE genes belong to the zero line (EE line); however, no designated EE outlying genes belong to the zero line (EE line). Therefore, the outlying 233 designated EE genes detected by the proposed method as DE genes with p -values of less than 0.05 should belong to the designated DE gene-set. Thus, the robust methods (KW, BetaEB and Proposed) did not perform better than the classical methods (ANOVA, SAM, LIMMA, eLNN and EBarrays), even for the dataset containing outlying genes. To show the outlier effects on the methods, we corrupted low label expressions of 200 designated DE genes by a single outlier larger than the maximum value of expressions. Then, we applied all methods again and evaluated the performance, as shown in Table 8 . We found that the proposed and BetaEB methods remained almost unchanged for all the summary statistics, as previously calculated in the case of the original expression, whereas all of the other methods decreased TPR, AUC, and pAUC and increased FNR, FDR and MER significantly. Thus, the application of robust methods would be better than classical methods for real gene expression data analysis.

https://doi.org/10.1371/journal.pone.0138810.t008

3.2.2 Analysis of the Colon Cancer Gene Expression Dataset with m = 2 Conditions.

This dataset has been analyzed in a previous study [ 28 ] and consists of 22 control and 40 colon cancer samples with 2000 genes. We downloaded this dataset from the website http://microarray.princeton.edu/oncology/affydata/index.html . We then directly applied three methods (KW, BetaEB and the proposed method) to this dataset, as before, to identify the DE genes. Fig 2a presents the Venn diagram of the top 100 DE genes estimated by each of the three methods (KW, BetaEB and Proposed). From this Venn diagram, it is evident that 75 DE genes are common to all three methods. The β -weight function of the proposed method identified 28% genes in the entire dataset as outliers. The outlier genes are indicated in red in S5(b)–S5(d) Fig . The proposed method identified 8 DE genes that were not detected by the other methods, of which five genes (UBE2I, R60883, PRIM1, POLD2 and REG1A) were upregulated and four genes (MUC2, ADCY2 and GLUT4) were downregulated. Six of these 8 genes were corrupted by outliers; these genes are indicated in Fig 2b by a red circle. To obtain some insights into the possible mechanisms that may be important in the development of resistance to drugs, the WebGestalt2 software package (available from http://bioinfo.vanderbilt.edu/webgestalt ) [ 30 ] was used to query two pathway databases, KEGG (Kyoto Encyclopedia of Genes and Genomes) and GO (Gene Ontology) Pathways, for these 8 DE genes, yielding many important pathways to be enriched. We identified three important genes, which were described as L21993 (ADCY2; adenylate cyclase 2 (brain)), U21090 (POLD2; polymerase (DNA directed) delta 2, accessory subunit) and X74330 (PRIM1; primase DNA, polypeptide 1 (49 kDa)), which are involved in purine metabolism, DNA replication, pyrimidine metabolism and other metabolic pathways.

Comparison of the results on the colon cancer gene expression dataset. (a) Venn diagram of the top 100 genes estimated by KW, BetaEB and the proposed method. (b) Outlying DE genes detected by the proposed method only. The results for the control group are plotted below the lines, and the results for the cancer group are plotted above the lines.

https://doi.org/10.1371/journal.pone.0138810.g002

Using the GO database, we determined that POLD2 and PRIM1 are involved in biological processes and that the genes POLD2, PRIM1, U29092 (ubiquitin-conjugating enzyme E2I (UBE2I)), ADCY2, M94132 (human mucin 2 (MUC2) mRNA sequence), and M27190 (regenerating islet-derived 1 alpha (REG1A)) are involved in molecular functions and cellular components ( S6 Fig We also investigated these 8 DE genes in the Oncomine database ( http://www.oncomine.org ). As summarized in Table C in S1 File , various independent studies have reported significant gene under-/over-expression in colon cancer tissues compared with corresponding normal tissues. We found that four independent studies have reported significant over-expression of PRIM1 ( p -value ≤ 0.0002) in colon cancer tissues compared with corresponding normal tissues. Moreover, in one of these four studies, the rank of PRIM1 over-expression was within the top 4%, whereas in the remaining studies, this over-expression was ranked in the top 6-21%, similar to other genes (Table C in S1 File ). These studies strongly suggest that these 8 genes may also be associated with colon cancer.

In our analysis, we also found some DE genes detected by other methods, such as only 5 genes by KW and 10 genes by BetaEB ( Fig 2a ). We applied all of these 15 genes to WebGestalt2 software for KEGG pathway analysis. Only five genes, X53743 (FBLN1: fibulin 1), X67699 (CD52: CD52 molecule), D38551 (RAD21: RAD21 homolog (S. pombe)), X16356 (CEACAM1: carcinoembryonic antigen-related cell adhesion molecule 1 (biliary glycoprotein)) and X07290 (ZNF3: zinc finger protein 3), were mapped using the KEGG Map in WebGestalt. We did not obtain any specific pathway for these genes, but some genes were very crucial from the previous investigations by different authors. As an example, the gene FBLN1 (fibulin 1) (detected by the KW approach only) was identified as a tumor suppressor gene whose inactivation may contribute to carcinogenesis [ 31 ]. It plays a tumor suppressive role in colorectal cancer (CRC)[ 32 ] and gastric cancer [ 33 ], among others. The gene RAD21 (detected only by the BetaEB method) is a component of the cohesion complex and is integral to chromosome segregation and error-free DNA repair. This gene expression in CRC is associated with aggressive disease, particularly in KRAS mutant tumors, and resistance to chemoradiotherapy. The gene RAD21 may be an important novel therapeutic target [ 34 ]. The gene CEACAM1 (detected only by the BetaEB method) is a tumor suppressor whose expression is known to be lost in the great majority of early adenomas and carcinomas. The loss of CEACAM1 expression is more common in neoplastic tumors than the adenomatous polyposis coli (APC) mutations [ 35 ]. Notably, these genes were also statistically significant by the proposed method with p -values ( p ) of 0.0003 < p < 0.0020, but they were not included in the top 100 genes. On the other hand, 8 DE genes of the proposed method were found by the KW and BetaEB approaches with p -values of 0.004 < p < 0.02 and posterior probabilities ( pp ) of 0.50 < pp < 1, respectively.

3.2.3 Analysis of the Pancreatic Cancer Gene Expression Dataset with m = 4 Conditions.

This dataset was used in the research reported in [ 29 ]. It consists of 24 samples, with 6 replicates in each of m = 4 conditions —circulation tumor samples (CTC), hematological cells (G), original tumor tissue (T), and non-tumor pancreatic control tissue (P) from patients and represents 8152 genes. We downloaded this dataset from the website http://www.ncbi.nlm.nih.gov/geo/query/acc.cgi?token=zbotduky//wssgujm/&acc=GSE18670 . This dataset had been pre-processed by previous users [ 29 ]. Therefore, we directly applied four methods (ANOVA, LIMMA, KW and Proposed) to this dataset to test the null hypothesis ( H 0 ) of no differential expressions among four groups for each gene. If the H 0 was rejected, we performed a pairwise comparison test for all 4 methods to identify the pattern of gene expressions. Fig 3a presents a Venn diagram of the DE genes estimated by the four methods based on pairwise comparisons of CTC vs T, CTC vs P, CTC vs G, T vs P, T vs G and G vs P, which was also the approach used in [ 29 ]. We used the Bonferroni method to adjust the p -values for ANOVA and KW and the Benjamini-Hochberg (BH) method to adjust the p -values for LIMMA and the proposed method. We used adjusted p -values at the 5% level of significance with an absolute fold change of 2 for each pairwise comparison in identifying DE genes. From this Venn diagram, it is evident that 2712 DE genes were common to all four methods in these 6 pairwise comparisons. The β -weight function of the proposed method identified 31% genes in the entire dataset as outliers. The outlier genes are indicated in red in Fig 3(b-d) . However, there exist some outliers that may not influence the classical methods. In our simulation studies, we considered some special types of outliers that influence the classical methods. For example, let us consider a true EE gene between two groups as EE = {(20, 21, 22), (21, 20, 22)} and a true DE gene between two groups as DE = {(20, 21, 22), (26, 27, 28)}, where () is used to represent the samples of expressions from a group. In the case of an EE gene, we observe that the absolute mean difference between two groups is 0, whereas in the case of a DE gene, the absolute mean difference between two groups is 6. If we corrupted the EE gene by an outlier expression as EE1 = {(20, 59*, 22), (21, 60*, 22)}, EE2 = {(20, 0*, 22), (21, 1*, 22)}, EE3 = {(20, 59*, 22), (21, 90*, 22)}, EE4 = {(20, 21, 22), (21, 60*, 22)}, we will observe that outliers (*) in EE1 and EE2 cannot influence the classical/non-robust methods, whereas outliers (*) in EE3 and EE4 can highly influence the classical/non-robust methods. Similarly, if we corrupted the previous DE gene by an outlier expression as DE1 = {(20, 21, 22), (26, 70*, 28)}, DE2 = {(20, 1*, 22), (26, 27, 28)}, DE3 = {(20, 1*, 22), (26, 70*, 28)}, DE4 = {(20, 21, 22), (26, 8*, 28)}, DE5 = {(20, 38*, 22), (26, 27, 28)}, DE6 = {(20, 29*, 22), (26, 17*, 28)}, we will observe that the assumed outliers (*) in DE1- DE3 cannot influence the classical/non-robust methods, whereas outliers (*) in DE4-DE6 can highly influence the classical/non-robust methods. The group variance/scale is 1 in both cases of original EE/DE genes, whereas the group variance/scale lies between 1 and 1565 in both cases of outlying EE/DE genes. In the current real data analysis, we found that the proposed method detected 80 DE genes that were not detected by any of the other methods. Among these 80 DE genes, 35 genes were corrupted by outliers. Among these 35 outlying genes, we considered 17 extreme outlying genes expressions for functional analysis to investigate their importance as an example. These outlying genes were then plotted above the lines with four different colors for the T, P, G and CTC groups, where the outlier samples are indicated by red circles above ( Fig 3e ). To compare all possible comparisons, only genes with significant 2-fold up/down regulation were selected (using adjusted p -values ≤ 0.05) for all methods ( Table 9 ). In this table, we observed a large number of DE genes detected by the proposed method. We searched for functional enrichment of specific pathways by these 17 DE genes using the WebGestalt gene analysis toolkit [ 30 ]. By mapping the differentially expressed gene set against the biological function annotations in the Gene Ontology database, we found significant enrichment of genes involved in the positive regulation of muscle-cell differentiation, the immune-response-regulating cell surface receptor signaling pathway, and the antigen-receptor-mediated signaling pathway, as well as genes involved in the carboxylic acid biosynthetic process ( S2 File (xls)). Using the KEGG database, we found that several probes mapped to signaling pathways, including the beta-Alanine metabolism pathway, the MAPK signaling pathway and other metabolic pathways ( Table 10 and S3 File (xls)). The pathway with the highest expression ratio in CTC was the p38 mitogen-activated protein kinase (p38 MAPK) signaling pathway, which is known to be involved in cancer cell migration. In the p38 MAPK pathway, PP2CB and MEF2C were significantly upregulated. The simulation study results in Table 7 also increase our confidence in the results of the proposed method for this real dataset because that simulated dataset was generated in accordance with the parametric properties of this real dataset.

https://doi.org/10.1371/journal.pone.0138810.t009

https://doi.org/10.1371/journal.pone.0138810.t010

(a) Venn diagram of the DE genes estimated by all four methods (ANOVA, LIMMA, KW and Proposed) based on pairwise comparisons of CTC vs T, CTC vs P, CTC vs G, T vs P, T vs G and G vs P. (b) Frequency distributions of β -weights for each expression of the 8152 genes in 24 samples. (c) Scatter plot of the smallest β -weight for each of the 8152 genes vs. the gene index, where the smallest value represents the minimum value of 24 β -weights from 24 samples for each gene. The red circles between the two gray lines represent moderate/noisy outliers, whereas the other red circles, corresponding to β -weights of less than 0.2, represent extreme outliers. (d) Plot of ordered smallest β -weights in (c) for 8152 genes. (e) The 80 DE genes detected by the proposed method only, as shown in (a). Seventeen out of 80 DE genes were detected as extreme outlying genes using the β -weight function. The results for the T, P, G and CTC groups are plotted above the lines with four different colors. The outlying samples are indicated by circles above them.

https://doi.org/10.1371/journal.pone.0138810.g003

4 Conclusion

We proposed a hybrid one-way ANOVA approach that unifies the robustness and efficiency of estimation of model parameters for the discovery of differential gene expressions with two or more conditions with multiple patterns. The proposed approach is controlled by the β -weight function of the minimum β -divergence method such that MLEs are used in the absence of outliers and minimum β -divergence estimators are used in the presence of outliers for estimating the group parameters in the ANOVA model. The proposed method produces robust and efficient results because MLEs are consistent and asymptotically efficient under a Gaussian distribution in the absence of outliers and because the minimum β -divergence estimators are highly robust and asymptotically efficient in the presence of outliers. It overcomes the problems that arise in the existing robust methods for both small- and large-sample cases with multiple patterns of gene expression. The β -weight function plays the key role in the performance of the proposed method. It can accurately and significantly detect outlying expressions.

The simulation results showed that all eight methods (ANOVA, SAM, LIMMA, EBarrays, eLNN, KW, robust BetaEB and proposed) perform almost identically for both the small- and large-sample cases with m = 2 conditions in the absence of outliers. The robust BetaEB method and the proposed method exhibited better performance than the other six methods in the presence of at most 50% outlying genes (although we provided results with 5%, 10% and 75% outlying genes only) with one or two outliers for each outlying gene. However, the BetaEB approach appears to be slightly better than the proposed method for the small-sample case, whereas the proposed method exhibited considerably better performance than the BetaEB method for both the small- and large-sample cases in the presence of more than 50% outlying genes with 5% outlier samples for each outlying gene. To investigate the performance of the proposed method in the case of multiple ( m > 2) conditions with multiple patterns of expression, four popular methods (ANOVA, SAM, LIMMA and KW) were considered based on the availability of software/extended-version of the algorithms for testing the equality multiple means. The non-parametric approach KW exhibited weak performance in a comparison of four methods (ANOVA, SAM, LIMMA and proposed) for the small-sample case with m > 2 conditions in the absence of outliers. However, the proposed method exhibited improved performance compared to the other methods for the small-sample case in the presence of outliers. The non-parametric KW method and the proposed method showed better performance in a comparison of the other three methods (ANOVA, SAM and LIMMA) for the large-sample case with m > 2 conditions in the presence of few outlying genes, where the proposed method appears to be slightly better than the KW method. The results on real gene expression datasets demonstrated that the proposed method can identify some additional outlying genes as differential expression compared to the other methods. Moreover, we found that the identified genes are reported as being important genes in different studies by other researchers. Therefore, the proposed approach would be more suitable and reliable on average for the identification of DE genes between two or more conditions with multiple patterns of expression.

Supporting Information

S1 fig. plot of fdr versus number of top de genes estimated by different methods..

(a) In the absence of outlying genes. (b) In the presence of one outlying expression in 5% genes. (c) In the presence of one outlying expression in 10% genes. (d) In the presence of one outlying expression in 75% genes.

https://doi.org/10.1371/journal.pone.0138810.s001

S2 Fig. Plot of FNR versus FPR estimated by different methods.

https://doi.org/10.1371/journal.pone.0138810.s002

S3 Fig. ROC curves produced by different methods.

https://doi.org/10.1371/journal.pone.0138810.s003

S4 Fig. Results of spike data analysis.

(a) Frequency distribution of β -weights for each expression of 18707 genes with 18 samples. (b) Scatter plot of the smallest β -weight for each of the 18707 genes vs. the gene index, where the smallest value represents the minimum value of 18 β -weights from 18 samples for each gene. The red circles between the two gray lines represent moderate/noisy outliers, whereas the remaining red circles, corresponding to β -weights of less than 0.2, represent extreme outliers. (c) Ordered plot of the smallest β -weights shown in (b) for the 18707 genes. (d) Bar plots based on the outlying designated EE genes detected by the proposed β -weight function. (e) Bar plots based on the outlying designated DE genes detected by the proposed β -weight function. (f) M-A plot based on the group medians, where red stars (⋆) are used for the 233 outlying designated EE genes detected by the proposed method with p – value < 0.05 shown in (d), and blue stars (⋆) are used for the 40 outlying designated DE genes detected by the proposed method with p – value < 0.05 shown in (e).

https://doi.org/10.1371/journal.pone.0138810.s004

S5 Fig. Results of colon cancer data analysis.

(a) Venn diagram of the top 100 genes estimated by BetaEB, KW and the proposed methods. (b) Frequency distribution of β -weights for each expression of 2000 genes with 61 samples. (c) Scatter plot of the smallest β -weight for each of the 2000 genes vs. the gene index, where the smallest value represents the minimum value of 61 β -weights from 61 samples for each gene. The red circles between the two gray lines represent moderate/noisy outliers, whereas the remaining red circles, corresponding to β -weights of less than 0.2, represent extreme outliers. (d) Ordered plot of the smallest β -weights shown in (c) for the 2000 genes.

https://doi.org/10.1371/journal.pone.0138810.s005

S6 Fig. Gene ontology (GO) categories of eight (8) genes.

This directed acyclic graph (DAG) shows the gene ontology categories of eight (8) genes, detected by the proposed method only in the colon cancer dataset, obtained using the WebGestalt database. These enriched GO categories were hierarchically organized into a DAG tree; each box in the tree lists the name of the GO category, the number of genes in that category, and the FDR-adjusted p -value (adjP) if the enrichment is significant. The categories shown in red are enriched (adjusted p -value of < 0.05), whereas those in black are non-enriched.

https://doi.org/10.1371/journal.pone.0138810.s006

S1 File. Results for simulated and real gene expression datasets.

Performance evaluations based on simulated gene expression profiles are presented in Tables A and B and real gene expression colon cancer dataset results are presented in Table C.

https://doi.org/10.1371/journal.pone.0138810.s007

S2 File. GO Pathways for 17 pancreatic cancer DE genes.

Gene Ontology analysis information.

https://doi.org/10.1371/journal.pone.0138810.s008

S3 File. KEGG Pathways for 17 pancreatic cancer DE genes.

KEGG analysis information.

https://doi.org/10.1371/journal.pone.0138810.s009

Acknowledgments

The authors thank the anonymous editors and reviewers for helpful suggestions on the manuscript.

Author Contributions

Conceived and designed the experiments: MMHM MNHM. Performed the experiments: MMHM RJ MNHM. Analyzed the data: MMHM. Contributed reagents/materials/analysis tools: RJ NMM RH. Wrote the paper: MMHM. Finalized the manuscript: RJ NMM RH MNHM. Edited and approved the final version of the manuscript: MMHM RJ NMM RH MNHM.

• View Article
• PubMed/NCBI
• Google Scholar
• 6. Newton MA, Kendziorski CM. Parametric empirical Bayes methods for microarrays. In: Parmigiani G, Garrett ES, Irizarry RA, Zeger SL, editor. The Analysis of Gene Expression Data. New York: Springer 2003: 254271.
• 22. Mood AM, Graybill FA and Boes DC. Introduction to the theory of statistics (3rd edition 1974); McGraw Hill, New York, NY.
• 23. Casella G and Berger RL. Statistical inference. Stamford, Connecticut: Thomson Learning 2002. ISBN 0-534-24312-6.
• 24. Yang M, Wang P, Sarkar D, Newton M and Kendziorski C. Parametric empirical Bayes methods for microarrays. Bioconductor.org 2009. Available: http://bioconductor.wustl.edu/bioc/vignettes/EBarrays/inst/doc/vignette.pdf .

• Announcements
• AUTHOR'S GUIDELINES

Reporting and Interpreting One-Way Analysis of Variance (ANOVA) Using a Data-Driven Example: A Practical Guide for Social Science Researchers

• Simon NTUMI University of Education, Winneba, West Africa, Ghana

One-way ( between-groups) analysis of variance (ANOVA) is a statistical tool or procedure used to analyse variation in a response variable (continuous random variable) measured under conditions defined by discrete factors (classification variables, often with nominal levels). The tool is used to detect a difference in means of 3 or more independent groups. It compares the means of the samples or groups in order to make inferences about the population means. It can be construed as an extension of the independent t-test. Given the omnibus nature of ANOVA, it appears that most researchers in social sciences and its related fields have difficulties in reporting and interpreting ANOVA results in their studies. This paper provides detailed processes and steps on how researchers can practically analyse and interpret ANOVA in their research works. The paper expounded that in applying ANOVA in analysis, a researcher must first formulate the null and in other cases alternative hypothesis. After the data have been gathered and cleaned, the researcher must test statistical assumptions to see if the data meet those assumptions. After this, the researcher must then do the necessary statistical computations and calculate the F-ratio (ANOVA result) using a software. To this end, the researcher then compares the critical value of the F-ratio with the table value or simply look at the p -value against the established alpha. If the calculated critical value is greater than the table value, the null hypothesis will be rejected and the alternative hypothesis is upheld.

• EndNote - EndNote format (Macintosh & Windows)
• ProCite - RIS format (Macintosh & Windows)
• Reference Manager - RIS format (Windows only)

The Copyright Transfer Form to ASERS Publishing (The Publisher) This form refers to the manuscript, which an author(s) was accepted for publication and was signed by all the authors. The undersigned Author(s) of the above-mentioned Paper here transfer any and all copyright-rights in and to The Paper to The Publisher. The Author(s) warrants that The Paper is based on their original work and that the undersigned has the power and authority to make and execute this assignment. It is the author's responsibility to obtain written permission to quote material that has been previously published in any form. The Publisher recognizes the retained rights noted below and grants to the above authors and employers for whom the work performed royalty-free permission to reuse their materials below. Authors may reuse all or portions of the above Paper in other works, excepting the publication of the paper in the same form. Authors may reproduce or authorize others to reproduce the above Paper for the Author's personal use or for internal company use, provided that the source and The Publisher copyright notice are mentioned, that the copies are not used in any way that implies The Publisher endorsement of a product or service of an employer, and that the copies are not offered for sale as such. Authors are permitted to grant third party requests for reprinting, republishing or other types of reuse. The Authors may make limited distribution of all or portions of the above Paper prior to publication if they inform The Publisher of the nature and extent of such limited distribution prior there to. Authors retain all proprietary rights in any process, procedure, or article of manufacture described in The Paper. This agreement becomes null and void if and only if the above paper is not accepted and published by The Publisher, or is with drawn by the author(s) before acceptance by the Publisher.

• Come and join our team! become an author
• Soon, we launch the books app stay tune!
• Online support 24/7 +4077 033 6758
• Tell Friends and get $5 a small gift for you
• Privacy Policy
• Customer Service
• Refunds Politics

Mail to: [email protected]

Phone: +40754 027 417

  International Journal of Educational Research Journal / International Journal of Educational Research / Vol. 12 No. 2 (2023) / Articles (function() { function async_load(){ var s = document.createElement('script'); s.type = 'text/javascript'; s.async = true; var theUrl = 'https://www.journalquality.info/journalquality/ratings/2405-www-ajol-info-ijer'; s.src = theUrl + ( theUrl.indexOf("?") >= 0 ? "&" : "?") + 'ref=' + encodeURIComponent(window.location.href); var embedder = document.getElementById('jpps-embedder-ajol-ijer'); embedder.parentNode.insertBefore(s, embedder); } if (window.attachEvent) window.attachEvent('onload', async_load); else window.addEventListener('load', async_load, false); })();  

Article sidebar.

Article Details

This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .

The Articles published in this Journal are published under a CC BY-NC-SA license and is subject to copyright, reserved by the Department of Educational Foundations (with Educational Psychology), University of Lagos. All works (including texts, images, graphs, tables, diagrams, photographs and statistical data) may be used for non-commercial purpose, citing appropriately the original work.

Main Article Content

Influence of witnessing domestic violence on the self concept of adolescents in lagos mainland, s.o. adeniyi, s.c. anyama, t.o. soriyan.

This study examined the impact of witnessing domestic violence on the self-concept of adolescents in Lagos mainland. This study was  limited to adolescents in public secondary schools in Mainland Local Government Area Lagos State. Descriptive survey research design  was used in the study. The respondents were one hundred and fifty (150) selected from (5) five senior secondary schools in Mainland  Local Government Area of Lagos State. Five (5) schools were selected using stratified sampling technique. Then respondents were  selected from the five schools using stratified random sampling technique based on gender and witnessing of domestic violence. The  opinions of the selected respondents were captured with the use of a researcher-developed questionnaire entitled “Witnessing Domestic  Violence Questionnaire” (WDVQ). T-test and two-way analysis of variance (ANOVA) statistical tools at 0.05 level of significance were used  in the analysis of the data. The results of the study reveal a significant influence of witnessing domestic violence on adolescents' self- concept, with gender differences playing a role. However, age and socioeconomic status do not show significant impacts. The findings underscore the serious implications of witnessing domestic violence on adolescents' social adjustment and psychological development,  emphasizing potential gender-related variations in these experiences. Implementing school-based counseling programs, community  awareness campaigns, and targeted support for affected adolescents can contribute to mitigating the adverse effects and fostering a  healthier development of their self-concept.

AJOL is a Non Profit Organisation that cannot function without donations. AJOL and the millions of African and international researchers who rely on our free services are deeply grateful for your contribution. AJOL is annually audited and was also independently assessed in 2019 by E&Y.

Your donation is guaranteed to directly contribute to Africans sharing their research output with a global readership.

• For annual AJOL Supporter contributions, please view our Supporters page.

Journal Identifiers