If you're seeing this message, it means we're having trouble loading external resources on our website.
If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.
To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Course: Algebra 1 > Unit 10
- Shifting absolute value graphs
- Shift absolute value graphs
- Scaling & reflecting absolute value functions: equation
- Scaling & reflecting absolute value functions: graph
- Scale & reflect absolute value graphs
- Graphing absolute value functions
Graph absolute value functions
- Absolute value graphs review
Advertisement
How Absolute Value Works in Equations and Graphs
- Share Content on Facebook
- Share Content on LinkedIn
- Share Content on Flipboard
- Share Content on Reddit
- Share Content via Email
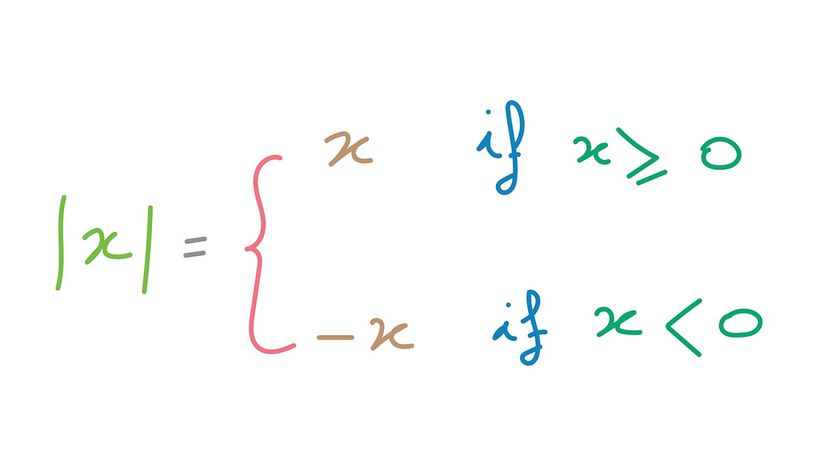
Absolute value is a mathematical concept often used in conjunction with a number line or graph to represent the relative value from zero (modulus). To illustrate this idea in a different way, the absolute value of a number can be closely related to distance in the physical world.
To illustrate this concept, regard your house as the origin point "zero," with steps toward the west as negative numbers, and steps toward the east as positive numbers. Whether you traveled a mile east or a mile west, you are an equal distance away from your home.
Walking west didn't mean you were taking a negative number of steps, and going east isn't equivalent to a positive number of steps. They have the same positive value from the origin point. Therefore, a mile in either direction has the same absolute value.
What Does an Absolute Value Symbol Look Like?
4 fundamental properties of absolute values, solving absolute value equations, absolute value function graphs.
Absolute value symbols are vertical bars on each side of a number. For instance, instead of writing "the absolute value of five," you can simply write |5|.
Now that you understand the general meaning of absolute value from the distance example above, read on to learn how you can use the following four fundamental properties to quickly identify and define a specific instance of this mathematical concept.
1. Non-negativity
An absolute value will always be a positive or non-negative value.

2. Positive-definiteness
In regards to absolute value, positive definiteness means that a number's absolute value is zero only when the number is explicitly denoted as zero |0|.
3. Multiplicativity
The absolute value of the product of two numbers is the same as the product of the absolute values because of what the negative sign becomes in an absolute value. Let's look at the following example.
The absolute value of the product of -3 and 5 is 15:
The product of |-3| and |5| is also 15:
4. Subadditivity
The concepts of subadditivity are typically illustrated in the following expression:
This means that the absolute value of the sum of two real numbers is less than or equal to the total of the absolute values of the two numbers. Let's plug in some numbers to see how this plays out in a real example:
Whether a is -2 or 2, |a| is 2. Similarly, whether b is -5 or 5, |b| is 5. Therefore:
Now let's look at the other side of that inequality: |a + b| . The expression a + b (before you take the absolute value of the expression) can play out any of the following ways:
The absolute value of the first and last examples is 7:
The same goes for the second and third examples:
Now, let's go back to the initial inequality: |a + b| ≤ |a| + |b| . No matter what values you plug into a and b, you'll find that the absolute value of the sum ( |a + b| ) is less than or equal to the sum of the absolute values ( |a| + |b| ).
First, separate the absolute value expression from the rest of the equation. Identify whether it is a positive or negative value and how it will affect the corresponding numbers. Solve the unknown and double-check your work by graphing it.
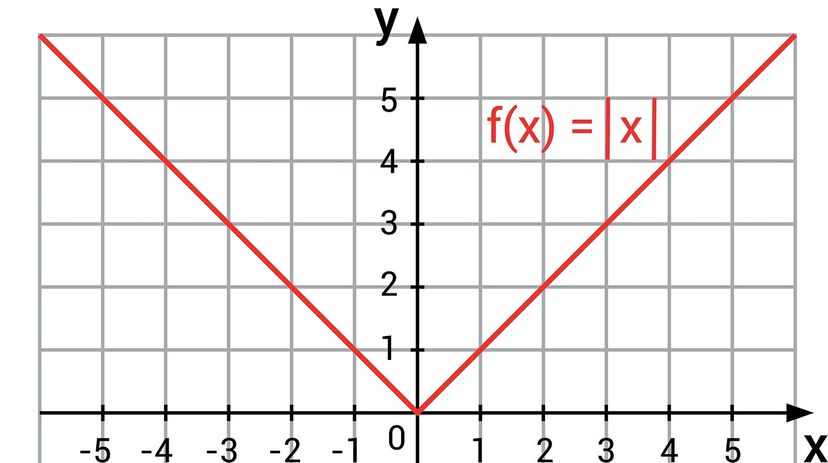
In mathematical settings it is always important to proof your work to validate your answer. The graph of the common form of the absolute value function is f(x) = |x| .
This formula can also be expressed as f(x) = x, if x ≥ 0 and -x, if x < 0 (as depicted in the image at the beginning of the article).
Jean-Robert Argand coined the term "module" in 1806 to represent the complicated absolute value. The term evolved to "modulus" 50 years later. Then, in 1841, Karl Weierstrass invented the vertical bar notation to simplify complex equations using this mathematical component.
Please copy/paste the following text to properly cite this HowStuffWorks.com article:

- school Campus Bookshelves
- menu_book Bookshelves
- perm_media Learning Objects
- login Login
- how_to_reg Request Instructor Account
- hub Instructor Commons
Margin Size
- Download Page (PDF)
- Download Full Book (PDF)
- Periodic Table
- Physics Constants
- Scientific Calculator
- Reference & Cite
- Tools expand_more
- Readability
selected template will load here
This action is not available.

1.9: Absolute Value Functions
- Last updated
- Save as PDF
- Page ID 59844

- David Arnold
- College of the Redwoods
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
- 1.9.1: Piecewise-Defined Functions In preparation for the definition of the absolute value function, it is extremely important to have a good grasp of the concept of a piecewise-defined function.
- 1.9.2: Absolute Value The absolute value of a number is a measure of its magnitude, sans (without) its sign.
- 1.9.3: Absolute Value Equations
- 1.9.4: Absolute Value Inequalities
Thumbnail: The graph of the absolute value function for real numbers. (CC BY-SA 3.0; Qef and Ævar Arnfjörð Bjarmason via Wikipedia).

IMAGES
VIDEO
COMMENTS
Study with Quizlet and memorize flashcards containing terms like Describes f(x) = lxl : graph opens up range: {y l y greater than or equal to 0} is increasing over (0, infinity) vertex at (0, 0) Does not Describe f (x) = lxl : domain: {x l x greater than or equal to 0} symmetric with respect to x-axis, The graph of the parent function f(x) = |x| is dashed and the graph of the transformed ...
Use the transformations on the function f (x) = x| to select the correct graph of f (x)= 1/3 IxI+1. Obtuse angel on (0,1) / B. Choose the function that represents the graph of the transformation of f (x) = |x| that opens down and has a vertex of (3,2) f (x) = -|x - 3| + 2. Identify the function that contains the data in the following table:
8. Find all function values f(x) f ( x) such that the distance from f(x) f ( x) to the value 8 is less than 0.03 units. Express this set of numbers using absolute value notation. For the following exercises, find the x - and y -intercepts of the graphs of each function. 9. f(x) = 4|x − 3| + 4 f ( x) = 4 | x − 3 | + 4.
The absolute value function is commonly used to measure distances between points. Applied problems, such as ranges of possible values, can also be solved using the absolute value function. The graph of the absolute value function resembles a letter V. It has a corner point at which the graph changes direction.
How To. Given an absolute value function, solve for the set of inputs where the output is positive (or negative). Set the function equal to zero, and solve for the boundary points of the solution set. Use test points or a graph to determine where the function's output is positive or negative.
The general form of an absolute value function is f (x)=a|x-h|+k. From this form, we can draw graphs. This article reviews how to draw the graphs of absolute value functions. General form of an absolute value equation: f ( x) = a | x − h | + k. The variable a tells us how far the graph stretches vertically, and whether the graph opens up or ...
The absolute value function is commonly thought of as providing the distance the number is from zero on a number line. Algebraically, for whatever the input value is, the output is the value without regard to sign. Knowing this, we can use absolute value functions to solve some kinds of real-world problems.
To solve absolute value equations, find x values that make the expression inside the absolute value positive or negative the constant. To graph absolute value functions, plot two lines for the positive and negative cases that meet at the expression's zero. The graph is v-shaped. Created by Sal Khan and CK-12 Foundation.
Downvote. Flag. Kim Seidel. 10 months ago. The standard absolute value graph y=|x| has its vertex at (0, 0). If you want to change the point to be at (3,0), that means you are making x=3. Notice, these are on opposite sides of the "=". if you need to place them on the same side of the "=", then you would have x-3=0.
3.5: Absolute Value Functions. There are a few ways to describe what is meant by the absolute value | x | of a real number x. You may have been taught that | x | is the distance from the real number x to 0 on the number line. So, for example, | 5 | = 5 and | − 5 | = 5, since each is 5 units from 0 on the number line.
Some functions include an absolute value expression. Learn all about absolute value functions and how to graph them in this free algebra lesson.
©j 7290 q1m2K 0KJu Etxa3 TSToMfytsw wayrie 0 7L sL PCx. T P LAalal R CruiBgjh ltRs X 5rOeus7eLrEvvebdB.y n OM6a QdQeb Lw 5i rt phY zIlnaf jiVnBiQtcen eA yl XgOe7bRrua f z1 m.x Worksheet by Kuta Software LLC
This lesson is about graphing an absolute value function when the expression inside the absolute value symbol is linear. It is linear if the variable "[latex]x[/latex]" has a power of [latex]1[/latex]. The graph of absolute value function has a shape of "V" or inverted "V". Absolute Value Function in Equation Form.
Graph absolute value functions. Graph g ( x) = − 5 | x + 2 | + 2 . Learn for free about math, art, computer programming, economics, physics, chemistry, biology, medicine, finance, history, and more. Khan Academy is a nonprofit with the mission of providing a free, world-class education for anyone, anywhere.
THE ABSOLUTE VALUE FUNCTION AND ITS TRANSLATIONS: Parent function: Vertical translations: Translation up k units Translation down k units Horizontal translations: Translation right h units Translation left h units Combined horizontal and vertical Reflection in x-axis Stretch Shrink Shrink/stretch with reflection Vertex form of Absolute Value
Study with Quizlet and memorize flashcards containing terms like The standard form of an absolute value function is mc002-1.jpg. Which of the following represents the vertex?, Which of the following is the graph of f(x) = |x| translated 2 units right, 2 units up, and dilated by a factor of mc018-1.jpg?, What is the range of the absolute value function below? mc009-1.jpg and more.
So far in this chapter we have been studying the behavior of linear functions. The Absolute Value Function is a piecewise-defined function made up of two linear functions. The name, Absolute Value Function, should be familiar to you from Section 1.2. In its basic form\(f(x)=\left|x\right|\) it is one of our toolkit functions.
Absolute value is a mathematical concept often used in conjunction with a number line or graph to represent the relative value from zero (modulus). To illustrate this idea in a different way, the absolute value of a number can be closely related to distance in the physical world.. To illustrate this concept, regard your house as the origin point "zero," with steps toward the west as negative ...
1.9.1: Piecewise-Defined Functions. In preparation for the definition of the absolute value function, it is extremely important to have a good grasp of the concept of a piecewise-defined function. 1.9.2: Absolute Value. The absolute value of a number is a measure of its magnitude, sans (without) its sign. 1.9.3: Absolute Value Equations.