what are the alternative hypothesis

Statistics Made Easy

What is an Alternative Hypothesis in Statistics?

Often in statistics we want to test whether or not some assumption is true about a population parameter .

For example, we might assume that the mean weight of a certain population of turtle is 300 pounds.

To determine if this assumption is true, we’ll go out and collect a sample of turtles and weigh each of them. Using this sample data, we’ll conduct a hypothesis test .

The first step in a hypothesis test is to define the null and alternative hypotheses .

These two hypotheses need to be mutually exclusive, so if one is true then the other must be false.

These two hypotheses are defined as follows:

Null hypothesis (H 0 ): The sample data is consistent with the prevailing belief about the population parameter.

Alternative hypothesis (H A ): The sample data suggests that the assumption made in the null hypothesis is not true. In other words, there is some non-random cause influencing the data.

Types of Alternative Hypotheses

There are two types of alternative hypotheses:

A one-tailed hypothesis involves making a “greater than” or “less than ” statement. For example, suppose we assume the mean height of a male in the U.S. is greater than or equal to 70 inches.

The null and alternative hypotheses in this case would be:

Null hypothesis: µ ≥ 70 inches
Alternative hypothesis: µ < 70 inches

A two-tailed hypothesis involves making an “equal to” or “not equal to” statement. For example, suppose we assume the mean height of a male in the U.S. is equal to 70 inches.

Null hypothesis: µ = 70 inches
Alternative hypothesis: µ ≠ 70 inches

Note: The “equal” sign is always included in the null hypothesis, whether it is =, ≥, or ≤.

Examples of Alternative Hypotheses

The following examples illustrate how to define the null and alternative hypotheses for different research problems.

Example 1: A biologist wants to test if the mean weight of a certain population of turtle is different from the widely-accepted mean weight of 300 pounds.

The null and alternative hypothesis for this research study would be:

Null hypothesis: µ = 300 pounds
Alternative hypothesis: µ ≠ 300 pounds

If we reject the null hypothesis, this means we have sufficient evidence from the sample data to say that the true mean weight of this population of turtles is different from 300 pounds.

Example 2: An engineer wants to test whether a new battery can produce higher mean watts than the current industry standard of 50 watts.

Null hypothesis: µ ≤ 50 watts
Alternative hypothesis: µ > 50 watts

If we reject the null hypothesis, this means we have sufficient evidence from the sample data to say that the true mean watts produced by the new battery is greater than the current industry standard of 50 watts.

Example 3: A botanist wants to know if a new gardening method produces less waste than the standard gardening method that produces 20 pounds of waste.

Null hypothesis: µ ≥ 20 pounds
Alternative hypothesis: µ < 20 pounds

If we reject the null hypothesis, this means we have sufficient evidence from the sample data to say that the true mean weight produced by this new gardening method is less than 20 pounds.

When to Reject the Null Hypothesis

Whenever we conduct a hypothesis test, we use sample data to calculate a test-statistic and a corresponding p-value.

If the p-value is less than some significance level (common choices are 0.10, 0.05, and 0.01), then we reject the null hypothesis.

This means we have sufficient evidence from the sample data to say that the assumption made by the null hypothesis is not true.

If the p-value is not less than some significance level, then we fail to reject the null hypothesis.

This means our sample data did not provide us with evidence that the assumption made by the null hypothesis was not true.

Additional Resource: An Explanation of P-Values and Statistical Significance

Featured Posts

7 Common Beginner Stats Mistakes and How to Avoid Them

Hey there. My name is Zach Bobbitt. I have a Masters of Science degree in Applied Statistics and I’ve worked on machine learning algorithms for professional businesses in both healthcare and retail. I’m passionate about statistics, machine learning, and data visualization and I created Statology to be a resource for both students and teachers alike. My goal with this site is to help you learn statistics through using simple terms, plenty of real-world examples, and helpful illustrations.

Join the Statology Community

Sign up to receive Statology's exclusive study resource: 100 practice problems with step-by-step solutions. Plus, get our latest insights, tutorials, and data analysis tips straight to your inbox!

By subscribing you accept Statology's Privacy Policy.

Module 9: Hypothesis Testing With One Sample

Null and alternative hypotheses, learning outcomes.

Describe hypothesis testing in general and in practice

The actual test begins by considering two hypotheses . They are called the null hypothesis and the alternative hypothesis . These hypotheses contain opposing viewpoints.

H 0 : The null hypothesis: It is a statement about the population that either is believed to be true or is used to put forth an argument unless it can be shown to be incorrect beyond a reasonable doubt.

H a : The alternative hypothesis : It is a claim about the population that is contradictory to H 0 and what we conclude when we reject H 0 .

After you have determined which hypothesis the sample supports, you make adecision. There are two options for a decision . They are “reject H 0 ” if the sample information favors the alternative hypothesis or “do not reject H 0 ” or “decline to reject H 0 ” if the sample information is insufficient to reject the null hypothesis.

Mathematical Symbols Used in H 0 and H a :

H 0 always has a symbol with an equal in it. H a never has a symbol with an equal in it. The choice of symbol depends on the wording of the hypothesis test. However, be aware that many researchers (including one of the co-authors in research work) use = in the null hypothesis, even with > or < as the symbol in the alternative hypothesis. This practice is acceptable because we only make the decision to reject or not reject the null hypothesis.

H 0 : No more than 30% of the registered voters in Santa Clara County voted in the primary election. p ≤ 30

H a : More than 30% of the registered voters in Santa Clara County voted in the primary election. p > 30

A medical trial is conducted to test whether or not a new medicine reduces cholesterol by 25%. State the null and alternative hypotheses.

H 0 : The drug reduces cholesterol by 25%. p = 0.25

H a : The drug does not reduce cholesterol by 25%. p ≠ 0.25

We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). The null and alternative hypotheses are:

H 0 : μ = 2.0

H a : μ ≠ 2.0

We want to test whether the mean height of eighth graders is 66 inches. State the null and alternative hypotheses. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses. H 0 : μ __ 66 H a : μ __ 66

H 0 : μ = 66
H a : μ ≠ 66

We want to test if college students take less than five years to graduate from college, on the average. The null and alternative hypotheses are:

H 0 : μ ≥ 5

H a : μ < 5

We want to test if it takes fewer than 45 minutes to teach a lesson plan. State the null and alternative hypotheses. Fill in the correct symbol ( =, ≠, ≥, <, ≤, >) for the null and alternative hypotheses. H 0 : μ __ 45 H a : μ __ 45

H 0 : μ ≥ 45
H a : μ < 45

In an issue of U.S. News and World Report , an article on school standards stated that about half of all students in France, Germany, and Israel take advanced placement exams and a third pass. The same article stated that 6.6% of U.S. students take advanced placement exams and 4.4% pass. Test if the percentage of U.S. students who take advanced placement exams is more than 6.6%. State the null and alternative hypotheses.

H 0 : p ≤ 0.066

H a : p > 0.066

On a state driver’s test, about 40% pass the test on the first try. We want to test if more than 40% pass on the first try. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses. H 0 : p __ 0.40 H a : p __ 0.40

H 0 : p = 0.40
H a : p > 0.40

Concept Review

In a hypothesis test , sample data is evaluated in order to arrive at a decision about some type of claim. If certain conditions about the sample are satisfied, then the claim can be evaluated for a population. In a hypothesis test, we: Evaluate the null hypothesis , typically denoted with H 0 . The null is not rejected unless the hypothesis test shows otherwise. The null statement must always contain some form of equality (=, ≤ or ≥) Always write the alternative hypothesis , typically denoted with H a or H 1 , using less than, greater than, or not equals symbols, i.e., (≠, >, or <). If we reject the null hypothesis, then we can assume there is enough evidence to support the alternative hypothesis. Never state that a claim is proven true or false. Keep in mind the underlying fact that hypothesis testing is based on probability laws; therefore, we can talk only in terms of non-absolute certainties.

Formula Review

H 0 and H a are contradictory.

OpenStax, Statistics, Null and Alternative Hypotheses. Provided by : OpenStax. Located at : http://cnx.org/contents/[email protected]:58/Introductory_Statistics . License : CC BY: Attribution
Introductory Statistics . Authored by : Barbara Illowski, Susan Dean. Provided by : Open Stax. Located at : http://cnx.org/contents/[email protected] . License : CC BY: Attribution . License Terms : Download for free at http://cnx.org/contents/[email protected]
Simple hypothesis testing | Probability and Statistics | Khan Academy. Authored by : Khan Academy. Located at : https://youtu.be/5D1gV37bKXY . License : All Rights Reserved . License Terms : Standard YouTube License

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

Hypothesis Testing with One Sample

Null and Alternative Hypotheses

OpenStaxCollege

[latexpage]

The actual test begins by considering two hypotheses . They are called the null hypothesis and the alternative hypothesis . These hypotheses contain opposing viewpoints.

H a : The alternative hypothesis: It is a claim about the population that is contradictory to H 0 and what we conclude when we reject H 0 .

After you have determined which hypothesis the sample supports, you make a decision. There are two options for a decision. They are “reject H 0 ” if the sample information favors the alternative hypothesis or “do not reject H 0 ” or “decline to reject H 0 ” if the sample information is insufficient to reject the null hypothesis.

Mathematical Symbols Used in H 0 and H a :

H 0 : No more than 30% of the registered voters in Santa Clara County voted in the primary election. p ≤ 30

A medical trial is conducted to test whether or not a new medicine reduces cholesterol by 25%. State the null and alternative hypotheses.

H 0 : The drug reduces cholesterol by 25%. p = 0.25

H a : The drug does not reduce cholesterol by 25%. p ≠ 0.25

We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). The null and alternative hypotheses are:

H 0 : μ = 2.0

H 0 : μ = 66
H a : μ ≠ 66

We want to test if college students take less than five years to graduate from college, on the average. The null and alternative hypotheses are:

H 0 : μ ≥ 5

H 0 : μ ≥ 45
H a : μ < 45

In an issue of U. S. News and World Report , an article on school standards stated that about half of all students in France, Germany, and Israel take advanced placement exams and a third pass. The same article stated that 6.6% of U.S. students take advanced placement exams and 4.4% pass. Test if the percentage of U.S. students who take advanced placement exams is more than 6.6%. State the null and alternative hypotheses.

H 0 : p ≤ 0.066

H 0 : p = 0.40
H a : p > 0.40

<!– ??? –>

Bring to class a newspaper, some news magazines, and some Internet articles . In groups, find articles from which your group can write null and alternative hypotheses. Discuss your hypotheses with the rest of the class.

Chapter Review

Formula Review

H 0 and H a are contradictory.

If α ≤ p -value, then do not reject H 0 .

If α > p -value, then reject H 0 .

α is preconceived. Its value is set before the hypothesis test starts. The p -value is calculated from the data.

You are testing that the mean speed of your cable Internet connection is more than three Megabits per second. What is the random variable? Describe in words.

The random variable is the mean Internet speed in Megabits per second.

You are testing that the mean speed of your cable Internet connection is more than three Megabits per second. State the null and alternative hypotheses.

The American family has an average of two children. What is the random variable? Describe in words.

The random variable is the mean number of children an American family has.

The mean entry level salary of an employee at a company is 💲58,000. You believe it is higher for IT professionals in the company. State the null and alternative hypotheses.

A sociologist claims the probability that a person picked at random in Times Square in New York City is visiting the area is 0.83. You want to test to see if the proportion is actually less. What is the random variable? Describe in words.

The random variable is the proportion of people picked at random in Times Square visiting the city.

A sociologist claims the probability that a person picked at random in Times Square in New York City is visiting the area is 0.83. You want to test to see if the claim is correct. State the null and alternative hypotheses.

In a population of fish, approximately 42% are female. A test is conducted to see if, in fact, the proportion is less. State the null and alternative hypotheses.

Suppose that a recent article stated that the mean time spent in jail by a first–time convicted burglar is 2.5 years. A study was then done to see if the mean time has increased in the new century. A random sample of 26 first-time convicted burglars in a recent year was picked. The mean length of time in jail from the survey was 3 years with a standard deviation of 1.8 years. Suppose that it is somehow known that the population standard deviation is 1.5. If you were conducting a hypothesis test to determine if the mean length of jail time has increased, what would the null and alternative hypotheses be? The distribution of the population is normal.

A random survey of 75 death row inmates revealed that the mean length of time on death row is 17.4 years with a standard deviation of 6.3 years. If you were conducting a hypothesis test to determine if the population mean time on death row could likely be 15 years, what would the null and alternative hypotheses be?

H 0 : __________
H a : __________
H 0 : μ = 15
H a : μ ≠ 15

The National Institute of Mental Health published an article stating that in any one-year period, approximately 9.5 percent of American adults suffer from depression or a depressive illness. Suppose that in a survey of 100 people in a certain town, seven of them suffered from depression or a depressive illness. If you were conducting a hypothesis test to determine if the true proportion of people in that town suffering from depression or a depressive illness is lower than the percent in the general adult American population, what would the null and alternative hypotheses be?

Some of the following statements refer to the null hypothesis, some to the alternate hypothesis.

State the null hypothesis, H 0 , and the alternative hypothesis. H a , in terms of the appropriate parameter ( μ or p ).

The mean number of years Americans work before retiring is 34.
At most 60% of Americans vote in presidential elections.
The mean starting salary for San Jose State University graduates is at least 💲100,000 per year.
Twenty-nine percent of high school seniors get drunk each month.
Fewer than 5% of adults ride the bus to work in Los Angeles.
The mean number of cars a person owns in her lifetime is not more than ten.
About half of Americans prefer to live away from cities, given the choice.
Europeans have a mean paid vacation each year of six weeks.
The chance of developing breast cancer is under 11% for women.
Private universities’ mean tuition cost is more than 💲20,000 per year.
H 0 : μ = 34; H a : μ ≠ 34
H 0 : p ≤ 0.60; H a : p > 0.60
H 0 : μ ≥ 100,000; H a : μ < 100,000
H 0 : p = 0.29; H a : p ≠ 0.29
H 0 : p = 0.05; H a : p < 0.05
H 0 : μ ≤ 10; H a : μ > 10
H 0 : p = 0.50; H a : p ≠ 0.50
H 0 : μ = 6; H a : μ ≠ 6
H 0 : p ≥ 0.11; H a : p < 0.11
H 0 : μ ≤ 20,000; H a : μ > 20,000

Over the past few decades, public health officials have examined the link between weight concerns and teen girls’ smoking. Researchers surveyed a group of 273 randomly selected teen girls living in Massachusetts (between 12 and 15 years old). After four years the girls were surveyed again. Sixty-three said they smoked to stay thin. Is there good evidence that more than thirty percent of the teen girls smoke to stay thin? The alternative hypothesis is:

p < 0.30
p > 0.30

A statistics instructor believes that fewer than 20% of Evergreen Valley College (EVC) students attended the opening night midnight showing of the latest Harry Potter movie. She surveys 84 of her students and finds that 11 attended the midnight showing. An appropriate alternative hypothesis is:

p > 0.20
p < 0.20

Previously, an organization reported that teenagers spent 4.5 hours per week, on average, on the phone. The organization thinks that, currently, the mean is higher. Fifteen randomly chosen teenagers were asked how many hours per week they spend on the phone. The sample mean was 4.75 hours with a sample standard deviation of 2.0. Conduct a hypothesis test. The null and alternative hypotheses are:

H o : $\overline{x}$ = 4.5, H a : $\overline{x}$ > 4.5
H o : μ ≥ 4.5, H a : μ < 4.5
H o : μ = 4.75, H a : μ > 4.75
H o : μ = 4.5, H a : μ > 4.5

Data from the National Institute of Mental Health. Available online at http://www.nimh.nih.gov/publicat/depression.cfm.

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

AP®︎/College Statistics

Course: ap®︎/college statistics > unit 10.

Idea behind hypothesis testing

Examples of null and alternative hypotheses

Writing null and alternative hypotheses
P-values and significance tests
Comparing P-values to different significance levels
Estimating a P-value from a simulation
Estimating P-values from simulations
Using P-values to make conclusions

Want to join the conversation?

Upvote Button navigates to signup page
Downvote Button navigates to signup page
Flag Button navigates to signup page

Video transcript

school Campus Bookshelves
menu_book Bookshelves
perm_media Learning Objects
login Login
how_to_reg Request Instructor Account
hub Instructor Commons

Margin Size

Download Page (PDF)
Download Full Book (PDF)
Periodic Table
Physics Constants
Scientific Calculator
Reference & Cite
Tools expand_more
Readability

selected template will load here

This action is not available.

7.4: The Alternative Hypothesis

Last updated
Save as PDF
Page ID 7116

Foster et al.
University of Missouri-St. Louis, Rice University, & University of Houston, Downtown Campus via University of Missouri’s Affordable and Open Access Educational Resources Initiative

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

If the null hypothesis is rejected, then we will need some other explanation, which we call the alternative hypothesis, $H_A$ or $H_1$. The alternative hypothesis is simply the reverse of the null hypothesis, and there are three options, depending on where we expect the difference to lie. Thus, our alternative hypothesis is the mathematical way of stating our research question. If we expect our obtained sample mean to be above or below the null hypothesis value, which we call a directional hypothesis, then our alternative hypothesis takes the form:

\[\mathrm{H}_{\mathrm{A}}: \mu>7.47 \quad \text { or } \quad \mathrm{H}_{\mathrm{A}}: \mu<7.47 \nonumber \]

based on the research question itself. We should only use a directional hypothesis if we have good reason, based on prior observations or research, to suspect a particular direction. When we do not know the direction, such as when we are entering a new area of research, we use a non-directional alternative:

\[\mathrm{H}_{\mathrm{A}}: \mu \neq 7.47 \nonumber \]

We will set different criteria for rejecting the null hypothesis based on the directionality (greater than, less than, or not equal to) of the alternative. To understand why, we need to see where our criteria come from and how they relate to $z$-scores and distributions.

Alternative hypothesis

by Marco Taboga , PhD

In a statistical test, observed data is used to decide whether or not to reject a restriction on the data-generating probability distribution.

The assumption that the restriction is true is called null hypothesis , while the statement that the restriction is not true is called alternative hypothesis.

A correct specification of the alternative hypothesis is essential to decide between one-tailed and two-tailed tests.

Table of contents

Mathematical setting

Choice between one-tailed and two-tailed tests, the critical region, the interpretation of the rejection, the interpretation must be coherent with the alternative hypothesis.

Power function

Accepting the alternative

More details, keep reading the glossary.

In order to fully understand the concept of alternative hypothesis, we need to remember the essential elements of a statistical inference problem:

we observe a sample drawn from an unknown probability distribution;

in principle, any valid probability distribution could have generated the sample;

however, we usually place some a priori restrictions on the set of possible data-generating distributions;

A couple of simple examples follow.

When we conduct a statistical test, we formulate a null hypothesis as a restriction on the statistical model.

The alternative hypothesis is

The alternative hypothesis is used to decide whether a test should be one-tailed or two-tailed.

The null hypothesis is rejected if the test statistic falls within a critical region that has been chosen by the statistician.

The critical region is a set of values that may comprise:

only the left tail of the distribution or only the right tail (one-tailed test);

both the left and the right tail (two-tailed test).

The choice of the critical region depends on the alternative hypothesis. Let us see why.

The interpretation is different depending on the tail of the distribution in which the test statistic falls.

The choice between a one-tailed or a two-tailed test needs to be done in such a way that the interpretation of a rejection is always coherent with the alternative hypothesis.

When we deal with the power function of a test, the term "alternative hypothesis" has a special meaning.

We conclude with a caveat about the interpretation of the outcome of a test of hypothesis.

The interpretation of a rejection of the null is controversial.

According to some statisticians, rejecting the null is equivalent to accepting the alternative.

However, others deem that rejecting the null does not necessarily imply accepting the alternative. In fact, it is possible to think of situations in which both hypotheses can be rejected. Let us see why.

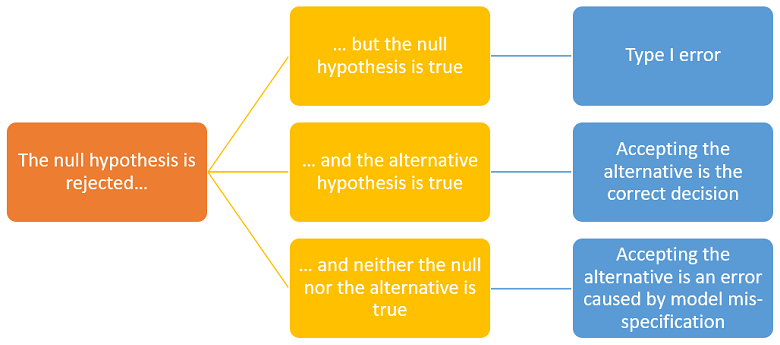
According to the conceptual framework illustrated by the images above, there are three possibilities:

the null is true;

the alternative is true;

neither the null nor the alternative is true because the true data-generating distribution has been excluded from the statistical model (we say that the model is mis-specified).

If we are in case 3, accepting the alternative after a rejection of the null is an incorrect decision. Moreover, a second test in which the alternative becomes the new null may lead us to another rejection.

There are three cases, including one case in which it is incorrect to accept the alternative hypothesis after a rejection of the null.

You can find more details about the alternative hypothesis in the lecture on Hypothesis testing .

Previous entry: Almost sure

Next entry: Binomial coefficient

How to cite

Please cite as:

Taboga, Marco (2021). "Alternative hypothesis", Lectures on probability theory and mathematical statistics. Kindle Direct Publishing. Online appendix. https://www.statlect.com/glossary/alternative-hypothesis.

Most of the learning materials found on this website are now available in a traditional textbook format.

Maximum likelihood
Binomial distribution
Beta distribution
Convergence in probability
Delta method
Exponential distribution
Chi-square distribution
Set estimation
Wishart distribution
Mathematical tools
Fundamentals of probability
Probability distributions
Asymptotic theory
Fundamentals of statistics
About Statlect
Cookies, privacy and terms of use
Precision matrix
Loss function
Integrable variable
Critical value
To enhance your privacy,
we removed the social buttons,
but don't forget to share .

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
Duis aute irure dolor in reprehenderit in voluptate
Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

5.2 - writing hypotheses.

The first step in conducting a hypothesis test is to write the hypothesis statements that are going to be tested. For each test you will have a null hypothesis ($H_0$) and an alternative hypothesis ($H_a$).

When writing hypotheses there are three things that we need to know: (1) the parameter that we are testing (2) the direction of the test (non-directional, right-tailed or left-tailed), and (3) the value of the hypothesized parameter.

At this point we can write hypotheses for a single mean ($\mu$), paired means($\mu_d$), a single proportion ($p$), the difference between two independent means ($\mu_1-\mu_2$), the difference between two proportions ($p_1-p_2$), a simple linear regression slope ($\beta$), and a correlation ($\rho$).
The research question will give us the information necessary to determine if the test is two-tailed (e.g., "different from," "not equal to"), right-tailed (e.g., "greater than," "more than"), or left-tailed (e.g., "less than," "fewer than").
The research question will also give us the hypothesized parameter value. This is the number that goes in the hypothesis statements (i.e., $\mu_0$ and $p_0$). For the difference between two groups, regression, and correlation, this value is typically 0.

Hypotheses are always written in terms of population parameters (e.g., $p$ and $\mu$). The tables below display all of the possible hypotheses for the parameters that we have learned thus far. Note that the null hypothesis always includes the equality (i.e., =).

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

8.2 Null and Alternative Hypotheses

Learning objectives.

Describe hypothesis testing in general and in practice.

A hypothesis test begins by considering two hypotheses . They are called the null hypothesis and the alternative hypothesis . These hypotheses contain opposing viewpoints and only one of these hypotheses is true. The hypothesis test determines which hypothesis is most likely true.

The null hypothesis is a claim that a population parameter equals some value. For example, [latex]H_0: \mu=5[/latex].
The alternative hypothesis is a claim that a population parameter is greater than, less than, or not equal to some value. For example, [latex]H_a: \mu>5[/latex], [latex]H_a: \mu<5[/latex], or [latex]H_a: \mu \neq 5[/latex]. The form of the alternative hypothesis depends on the wording of the hypothesis test.
An alternative notation for [latex]H_a[/latex] is [latex]H_1[/latex].

Because the null and alternative hypotheses are contradictory, we must examine evidence to decide if we have enough evidence to reject the null hypothesis or not reject the null hypothesis. The evidence is in the form of sample data. After we have determined which hypothesis the sample data supports, we make a decision. There are two options for a decision . They are “ reject [latex]H_0[/latex] ” if the sample information favors the alternative hypothesis or “ do not reject [latex]H_0[/latex] ” if the sample information is insufficient to reject the null hypothesis.

Watch this video: Simple hypothesis testing | Probability and Statistics | Khan Academy by Khan Academy [6:24]

A candidate in a local election claims that 30% of registered voters voted in a recent election. Information provided by the returning office suggests that the percentage is higher than the 30% claimed.

The parameter under study is the proportion of registered voters, so we use [latex]p[/latex] in the statements of the hypotheses. The hypotheses are

[latex]\begin{eqnarray*} \\ H_0: & & p=30\% \\ \\ H_a: & & p \gt 30\% \\ \\ \end{eqnarray*}[/latex]

The null hypothesis [latex]H_0[/latex] is the claim that the proportion of registered voters that voted equals 30%.
The alternative hypothesis [latex]H_a[/latex] is the claim that the proportion of registered voters that voted is greater than (i.e. higher) than 30%.

A medical researcher believes that a new medicine reduces cholesterol by 25%. A medical trial suggests that the percent reduction is different than claimed. State the null and alternative hypotheses.

[latex]\begin{eqnarray*} H_0: & & p=25\% \\ \\ H_a: & & p \neq 25\% \end{eqnarray*}[/latex]

We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). State the null and alternative hypotheses.

[latex]\begin{eqnarray*} H_0: & & \mu=2 \mbox{ points} \\ \\ H_a: & & \mu \neq 2 \mbox{ points} \end{eqnarray*}[/latex]

We want to test whether or not the mean height of eighth graders is 66 inches. State the null and alternative hypotheses.

[latex]\begin{eqnarray*} H_0: & & \mu=66 \mbox{ inches} \\ \\ H_a: & & \mu \neq 66 \mbox{ inches} \end{eqnarray*}[/latex]

We want to test if college students take less than five years to graduate from college, on the average. The null and alternative hypotheses are:

[latex]\begin{eqnarray*} H_0: & & \mu=5 \mbox{ years} \\ \\ H_a: & & \mu \lt 5 \mbox{ years} \end{eqnarray*}[/latex]

We want to test if it takes fewer than 45 minutes to teach a lesson plan. State the null and alternative hypotheses.

[latex]\begin{eqnarray*} H_0: & & \mu=45 \mbox{ minutes} \\ \\ H_a: & & \mu \lt 45 \mbox{ minutes} \end{eqnarray*}[/latex]

[latex]\begin{eqnarray*} H_0: & & p=6.6\% \\ \\ H_a: & & p \gt 6.6\% \end{eqnarray*}[/latex]

On a state driver’s test, about 40% pass the test on the first try. We want to test if more than 40% pass on the first try. State the null and alternative hypotheses.

[latex]\begin{eqnarray*} H_0: & & p=40\% \\ \\ H_a: & & p \gt 40\% \end{eqnarray*}[/latex]

Concept Review

In a hypothesis test , sample data is evaluated in order to arrive at a decision about some type of claim. If certain conditions about the sample are satisfied, then the claim can be evaluated for a population. In a hypothesis test, we evaluate the null hypothesis , typically denoted with [latex]H_0[/latex]. The null hypothesis is not rejected unless the hypothesis test shows otherwise. The null hypothesis always contain an equal sign ([latex]=[/latex]). Always write the alternative hypothesis , typically denoted with [latex]H_a[/latex] or [latex]H_1[/latex], using less than, greater than, or not equals symbols ([latex]\lt[/latex], [latex]\gt[/latex], [latex]\neq[/latex]). If we reject the null hypothesis, then we can assume there is enough evidence to support the alternative hypothesis. But we can never state that a claim is proven true or false. All we can conclude from the hypothesis test is which of the hypothesis is most likely true. Because the underlying facts about hypothesis testing is based on probability laws, we can talk only in terms of non-absolute certainties.

Attribution

“ 9.1 Null and Alternative Hypotheses “ in Introductory Statistics by OpenStax is licensed under a Creative Commons Attribution 4.0 International License.

Null Hypothesis and Alternative Hypothesis

Inferential Statistics
Statistics Tutorials
Probability & Games
Descriptive Statistics
Applications Of Statistics
Math Tutorials
Pre Algebra & Algebra
Exponential Decay
Worksheets By Grade
Ph.D., Mathematics, Purdue University
M.S., Mathematics, Purdue University
B.A., Mathematics, Physics, and Chemistry, Anderson University

Hypothesis testing involves the careful construction of two statements: the null hypothesis and the alternative hypothesis. These hypotheses can look very similar but are actually different.

How do we know which hypothesis is the null and which one is the alternative? We will see that there are a few ways to tell the difference.

The Null Hypothesis

The null hypothesis reflects that there will be no observed effect in our experiment. In a mathematical formulation of the null hypothesis, there will typically be an equal sign. This hypothesis is denoted by H 0 .

The null hypothesis is what we attempt to find evidence against in our hypothesis test. We hope to obtain a small enough p-value that it is lower than our level of significance alpha and we are justified in rejecting the null hypothesis. If our p-value is greater than alpha, then we fail to reject the null hypothesis.

If the null hypothesis is not rejected, then we must be careful to say what this means. The thinking on this is similar to a legal verdict. Just because a person has been declared "not guilty", it does not mean that he is innocent. In the same way, just because we failed to reject a null hypothesis it does not mean that the statement is true.

For example, we may want to investigate the claim that despite what convention has told us, the mean adult body temperature is not the accepted value of 98.6 degrees Fahrenheit . The null hypothesis for an experiment to investigate this is “The mean adult body temperature for healthy individuals is 98.6 degrees Fahrenheit.” If we fail to reject the null hypothesis, then our working hypothesis remains that the average adult who is healthy has a temperature of 98.6 degrees. We do not prove that this is true.

If we are studying a new treatment, the null hypothesis is that our treatment will not change our subjects in any meaningful way. In other words, the treatment will not produce any effect in our subjects.

The Alternative Hypothesis

The alternative or experimental hypothesis reflects that there will be an observed effect for our experiment. In a mathematical formulation of the alternative hypothesis, there will typically be an inequality, or not equal to symbol. This hypothesis is denoted by either H a or by H 1 .

The alternative hypothesis is what we are attempting to demonstrate in an indirect way by the use of our hypothesis test. If the null hypothesis is rejected, then we accept the alternative hypothesis. If the null hypothesis is not rejected, then we do not accept the alternative hypothesis. Going back to the above example of mean human body temperature, the alternative hypothesis is “The average adult human body temperature is not 98.6 degrees Fahrenheit.”

If we are studying a new treatment, then the alternative hypothesis is that our treatment does, in fact, change our subjects in a meaningful and measurable way.

The following set of negations may help when you are forming your null and alternative hypotheses. Most technical papers rely on just the first formulation, even though you may see some of the others in a statistics textbook.

Null hypothesis: “ x is equal to y .” Alternative hypothesis “ x is not equal to y .”
Null hypothesis: “ x is at least y .” Alternative hypothesis “ x is less than y .”
Null hypothesis: “ x is at most y .” Alternative hypothesis “ x is greater than y .”
Null Hypothesis Examples
An Example of a Hypothesis Test
Hypothesis Test for the Difference of Two Population Proportions
What Is a P-Value?
How to Conduct a Hypothesis Test
Hypothesis Test Example
What Level of Alpha Determines Statistical Significance?
Chi-Square Goodness of Fit Test
Maslow's Hierarchy of Needs Explained
Popular Math Terms and Definitions
The Difference Between Type I and Type II Errors in Hypothesis Testing
How to Do Hypothesis Tests With the Z.TEST Function in Excel
The Runs Test for Random Sequences
Type I and Type II Errors in Statistics
What 'Fail to Reject' Means in a Hypothesis Test
What Is the Difference Between Alpha and P-Values?

school Campus Bookshelves
menu_book Bookshelves
perm_media Learning Objects
login Login
how_to_reg Request Instructor Account
hub Instructor Commons

Margin Size

Download Page (PDF)
Download Full Book (PDF)
Periodic Table
Physics Constants
Scientific Calculator
Reference & Cite
Tools expand_more
Readability

selected template will load here

This action is not available.

10.2: Null and Alternative Hypotheses

Last updated
Save as PDF
Page ID 100392

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

The actual test begins by considering two hypotheses. They are called the null hypothesis and the alternative hypothesis. These hypotheses contain opposing viewpoints.

The null hypothesis ($H_{0}$) is a statement about the population that either is believed to be true or is used to put forth an argument unless it can be shown to be incorrect beyond a reasonable doubt.
The alternative hypothesis ($H_{a}$) is a claim about the population that is contradictory to $H_{0}$ and what we conclude when we reject $H_{0}$.

Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample data. After you have determined which hypothesis the sample supports, you make a decision. There are two options for a decision. They are "reject $H_{0}$" if the sample information favors the alternative hypothesis or "do not reject $H_{0}$" or "decline to reject $H_{0}$" if the sample information is insufficient to reject the null hypothesis.

$H_{0}$ always has a symbol with an equal in it. $H_{a}$ never has a symbol with an equal in it. The choice of symbol depends on the wording of the hypothesis test. However, be aware that many researchers (including one of the co-authors in research work) use = in the null hypothesis, even with > or < as the symbol in the alternative hypothesis. This practice is acceptable because we only make the decision to reject or not reject the null hypothesis.

Example $\PageIndex{1}$

$H_{0}$: No more than 30% of the registered voters in Santa Clara County voted in the primary election. $p \leq 30$
$H_{a}$: More than 30% of the registered voters in Santa Clara County voted in the primary election. $p > 30$

Exercise $\PageIndex{1}$

A medical trial is conducted to test whether or not a new medicine reduces cholesterol by 25%. State the null and alternative hypotheses.

$H_{0}$: The drug reduces cholesterol by 25%. $p = 0.25$
$H_{a}$: The drug does not reduce cholesterol by 25%. $p \neq 0.25$

Example $\PageIndex{2}$

We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). The null and alternative hypotheses are:

$H_{0}: \mu = 2.0$
$H_{a}: \mu \neq 2.0$

Exercise $\PageIndex{2}$

We want to test whether the mean height of eighth graders is 66 inches. State the null and alternative hypotheses. Fill in the correct symbol $(=, \neq, \geq, <, \leq, >)$ for the null and alternative hypotheses.

$H_{0}: \mu \ \_ \ 66$
$H_{a}: \mu \ \_ \ 66$
$H_{0}: \mu = 66$
$H_{a}: \mu \neq 66$

Example $\PageIndex{3}$

We want to test if college students take less than five years to graduate from college, on the average. The null and alternative hypotheses are:

$H_{0}: \mu \geq 5$
$H_{a}: \mu < 5$

Exercise $\PageIndex{3}$

$H_{0}: \mu \ \_ \ 45$
$H_{a}: \mu \ \_ \ 45$
$H_{0}: \mu \geq 45$
$H_{a}: \mu < 45$

Example $\PageIndex{4}$

In an issue of U. S. News and World Report , an article on school standards stated that about half of all students in France, Germany, and Israel take advanced placement exams and a third pass. The same article stated that 6.6% of U.S. students take advanced placement exams and 4.4% pass. Test if the percentage of U.S. students who take advanced placement exams is more than 6.6%. State the null and alternative hypotheses.

$H_{0}: p \leq 0.066$
$H_{a}: p > 0.066$

Exercise $\PageIndex{4}$

On a state driver’s test, about 40% pass the test on the first try. We want to test if more than 40% pass on the first try. Fill in the correct symbol ($=, \neq, \geq, <, \leq, >$) for the null and alternative hypotheses.

$H_{0}: p \ \_ \ 0.40$
$H_{a}: p \ \_ \ 0.40$
$H_{0}: p = 0.40$
$H_{a}: p > 0.40$

COLLABORATIVE EXERCISE

Chapter Review

Evaluate the null hypothesis , typically denoted with $H_{0}$. The null is not rejected unless the hypothesis test shows otherwise. The null statement must always contain some form of equality $(=, \leq \text{or} \geq)$
Always write the alternative hypothesis , typically denoted with $H_{a}$ or $H_{1}$, using less than, greater than, or not equals symbols, i.e., $(\neq, >, \text{or} <)$.
If we reject the null hypothesis, then we can assume there is enough evidence to support the alternative hypothesis.
Never state that a claim is proven true or false. Keep in mind the underlying fact that hypothesis testing is based on probability laws; therefore, we can talk only in terms of non-absolute certainties.

Formula Review

$H_{0}$ and $H_{a}$ are contradictory.

If $\alpha \leq p$-value, then do not reject $H_{0}$.
If$\alpha > p$-value, then reject $H_{0}$.

$\alpha$ is preconceived. Its value is set before the hypothesis test starts. The $p$-value is calculated from the data.References

Data from the National Institute of Mental Health. Available online at http://www.nimh.nih.gov/publicat/depression.cfm .

Contributors

Barbara Illowsky and Susan Dean (De Anza College) with many other contributing authors. Content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/[email protected] .

Math Article

Alternative Hypothesis

Alternative hypothesis defines there is a statistically important relationship between two variables. Whereas null hypothesis states there is no statistical relationship between the two variables. In statistics, we usually come across various kinds of hypotheses. A statistical hypothesis is supposed to be a working statement which is assumed to be logical with given data. It should be noticed that a hypothesis is neither considered true nor false.

The alternative hypothesis is a statement used in statistical inference experiment. It is contradictory to the null hypothesis and denoted by H a or H 1 . We can also say that it is simply an alternative to the null. In hypothesis testing, an alternative theory is a statement which a researcher is testing. This statement is true from the researcher’s point of view and ultimately proves to reject the null to replace it with an alternative assumption. In this hypothesis, the difference between two or more variables is predicted by the researchers, such that the pattern of data observed in the test is not due to chance.

To check the water quality of a river for one year, the researchers are doing the observation. As per the null hypothesis, there is no change in water quality in the first half of the year as compared to the second half. But in the alternative hypothesis, the quality of water is poor in the second half when observed.

Difference Between Null and Alternative Hypothesis

Basically, there are three types of the alternative hypothesis, they are;

Left-Tailed : Here, it is expected that the sample proportion (π) is less than a specified value which is denoted by π 0 , such that;

H 1 : π < π 0

Right-Tailed: It represents that the sample proportion (π) is greater than some value, denoted by π 0 .

H 1 : π > π 0

Two-Tailed: According to this hypothesis, the sample proportion (denoted by π) is not equal to a specific value which is represented by π 0 .

H 1 : π ≠ π 0

Note: The null hypothesis for all the three alternative hypotheses, would be H 1 : π = π 0 .

Register with BYJU'S & Download Free PDFs

Our websites may use cookies to personalize and enhance your experience. By continuing without changing your cookie settings, you agree to this collection. For more information, please see our University Websites Privacy Notice .

Neag School of Education

Educational Research Basics by Del Siegle

Null and alternative hypotheses.

Converting research questions to hypothesis is a simple task. Take the questions and make it a positive statement that says a relationship exists (correlation studies) or a difference exists between the groups (experiment study) and you have the alternative hypothesis. Write the statement such that a relationship does not exist or a difference does not exist and you have the null hypothesis. You can reverse the process if you have a hypothesis and wish to write a research question.

When you are comparing two groups, the groups are the independent variable. When you are testing whether something affects something else, the cause is the independent variable. The independent variable is the one you manipulate.

Teachers given higher pay will have more positive attitudes toward children than teachers given lower pay. The first step is to ask yourself “Are there two or more groups being compared?” The answer is “Yes.” What are the groups? Teachers who are given higher pay and teachers who are given lower pay. The independent variable is teacher pay. The dependent variable (the outcome) is attitude towards school.

You could also approach is another way. “Is something causing something else?” The answer is “Yes.” What is causing what? Teacher pay is causing attitude towards school. Therefore, teacher pay is the independent variable (cause) and attitude towards school is the dependent variable (outcome).

By tradition, we try to disprove (reject) the null hypothesis. We can never prove a null hypothesis, because it is impossible to prove something does not exist. We can disprove something does not exist by finding an example of it. Therefore, in research we try to disprove the null hypothesis. When we do find that a relationship (or difference) exists then we reject the null and accept the alternative. If we do not find that a relationship (or difference) exists, we fail to reject the null hypothesis (and go with it). We never say we accept the null hypothesis because it is never possible to prove something does not exist. That is why we say that we failed to reject the null hypothesis, rather than we accepted it.

Del Siegle, Ph.D. Neag School of Education – University of Connecticut [email protected] www.delsiegle.com

Alternative Hypothesis

Reference work entry
Cite this reference work entry

451 Accesses

An alternative hypothesis is the hypothesis which differs from the hypothesis being tested.

The alternative hypothesis is usually denoted by H 1 .

See hypothesis and hypothesis testing .

MATHEMATICAL ASPECTS

During the hypothesis testing of a parameter of a population , the null hypothesis is presented in the following way:

where θ is the parameter of the population that is to be estimated, and $ { \theta _0 } $ is the presumed value of this parameter. The alternative hypothesis can then take three different forms:

$ { H_1 \colon \theta > \theta_0 } $

$ { H_1 \colon \theta < \theta_0 } $

$ { H_1 \colon \theta \neq \theta_0 } $

In the first two cases, the hypothesis test is called the one-sided , whereas in the third case it is called the two-sided .

The alternative hypothesis can also take three different forms during the hypothesis testing of parameters of two populations . If the null hypothesis treats the two parameters \(...

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Available as PDF
Read on any device
Instant download
Own it forever

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Lehmann, E.I., Romann, S.P.: Testing Statistical Hypothesis, 3rd edn. Springer, New York (2005)

Google Scholar

Download references

Rights and permissions

Reprints and permissions

Copyright information

About this entry

Cite this entry.

(2008). Alternative Hypothesis. In: The Concise Encyclopedia of Statistics. Springer, New York, NY. https://doi.org/10.1007/978-0-387-32833-1_4

Download citation

DOI : https://doi.org/10.1007/978-0-387-32833-1_4

Publisher Name : Springer, New York, NY

Print ISBN : 978-0-387-31742-7

Online ISBN : 978-0-387-32833-1

eBook Packages : Mathematics and Statistics Reference Module Computer Science and Engineering

Share this entry

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

Publish with us

Policies and ethics

Find a journal
Track your research

Research Hypothesis In Psychology: Types, & Examples

Saul Mcleod, PhD

Editor-in-Chief for Simply Psychology

BSc (Hons) Psychology, MRes, PhD, University of Manchester

Saul Mcleod, PhD., is a qualified psychology teacher with over 18 years of experience in further and higher education. He has been published in peer-reviewed journals, including the Journal of Clinical Psychology.

Learn about our Editorial Process

Olivia Guy-Evans, MSc

Associate Editor for Simply Psychology

BSc (Hons) Psychology, MSc Psychology of Education

Olivia Guy-Evans is a writer and associate editor for Simply Psychology. She has previously worked in healthcare and educational sectors.

On This Page:

A research hypothesis, in its plural form “hypotheses,” is a specific, testable prediction about the anticipated results of a study, established at its outset. It is a key component of the scientific method .

Hypotheses connect theory to data and guide the research process towards expanding scientific understanding

Some key points about hypotheses:

A hypothesis expresses an expected pattern or relationship. It connects the variables under investigation.
It is stated in clear, precise terms before any data collection or analysis occurs. This makes the hypothesis testable.
A hypothesis must be falsifiable. It should be possible, even if unlikely in practice, to collect data that disconfirms rather than supports the hypothesis.
Hypotheses guide research. Scientists design studies to explicitly evaluate hypotheses about how nature works.
For a hypothesis to be valid, it must be testable against empirical evidence. The evidence can then confirm or disprove the testable predictions.
Hypotheses are informed by background knowledge and observation, but go beyond what is already known to propose an explanation of how or why something occurs.

Predictions typically arise from a thorough knowledge of the research literature, curiosity about real-world problems or implications, and integrating this to advance theory. They build on existing literature while providing new insight.

Types of Research Hypotheses

Alternative hypothesis.

The research hypothesis is often called the alternative or experimental hypothesis in experimental research.

It typically suggests a potential relationship between two key variables: the independent variable, which the researcher manipulates, and the dependent variable, which is measured based on those changes.

The alternative hypothesis states a relationship exists between the two variables being studied (one variable affects the other).

A hypothesis is a testable statement or prediction about the relationship between two or more variables. It is a key component of the scientific method. Some key points about hypotheses:

Important hypotheses lead to predictions that can be tested empirically. The evidence can then confirm or disprove the testable predictions.

In summary, a hypothesis is a precise, testable statement of what researchers expect to happen in a study and why. Hypotheses connect theory to data and guide the research process towards expanding scientific understanding.

An experimental hypothesis predicts what change(s) will occur in the dependent variable when the independent variable is manipulated.

It states that the results are not due to chance and are significant in supporting the theory being investigated.

The alternative hypothesis can be directional, indicating a specific direction of the effect, or non-directional, suggesting a difference without specifying its nature. It’s what researchers aim to support or demonstrate through their study.

Null Hypothesis

The null hypothesis states no relationship exists between the two variables being studied (one variable does not affect the other). There will be no changes in the dependent variable due to manipulating the independent variable.

It states results are due to chance and are not significant in supporting the idea being investigated.

The null hypothesis, positing no effect or relationship, is a foundational contrast to the research hypothesis in scientific inquiry. It establishes a baseline for statistical testing, promoting objectivity by initiating research from a neutral stance.

Many statistical methods are tailored to test the null hypothesis, determining the likelihood of observed results if no true effect exists.

This dual-hypothesis approach provides clarity, ensuring that research intentions are explicit, and fosters consistency across scientific studies, enhancing the standardization and interpretability of research outcomes.

Nondirectional Hypothesis

A non-directional hypothesis, also known as a two-tailed hypothesis, predicts that there is a difference or relationship between two variables but does not specify the direction of this relationship.

It merely indicates that a change or effect will occur without predicting which group will have higher or lower values.

For example, “There is a difference in performance between Group A and Group B” is a non-directional hypothesis.

Directional Hypothesis

A directional (one-tailed) hypothesis predicts the nature of the effect of the independent variable on the dependent variable. It predicts in which direction the change will take place. (i.e., greater, smaller, less, more)

It specifies whether one variable is greater, lesser, or different from another, rather than just indicating that there’s a difference without specifying its nature.

For example, “Exercise increases weight loss” is a directional hypothesis.

Falsifiability

The Falsification Principle, proposed by Karl Popper , is a way of demarcating science from non-science. It suggests that for a theory or hypothesis to be considered scientific, it must be testable and irrefutable.

Falsifiability emphasizes that scientific claims shouldn’t just be confirmable but should also have the potential to be proven wrong.

It means that there should exist some potential evidence or experiment that could prove the proposition false.

However many confirming instances exist for a theory, it only takes one counter observation to falsify it. For example, the hypothesis that “all swans are white,” can be falsified by observing a black swan.

For Popper, science should attempt to disprove a theory rather than attempt to continually provide evidence to support a research hypothesis.

Can a Hypothesis be Proven?

Hypotheses make probabilistic predictions. They state the expected outcome if a particular relationship exists. However, a study result supporting a hypothesis does not definitively prove it is true.

All studies have limitations. There may be unknown confounding factors or issues that limit the certainty of conclusions. Additional studies may yield different results.

In science, hypotheses can realistically only be supported with some degree of confidence, not proven. The process of science is to incrementally accumulate evidence for and against hypothesized relationships in an ongoing pursuit of better models and explanations that best fit the empirical data. But hypotheses remain open to revision and rejection if that is where the evidence leads.

Disproving a hypothesis is definitive. Solid disconfirmatory evidence will falsify a hypothesis and require altering or discarding it based on the evidence.
However, confirming evidence is always open to revision. Other explanations may account for the same results, and additional or contradictory evidence may emerge over time.

We can never 100% prove the alternative hypothesis. Instead, we see if we can disprove, or reject the null hypothesis.

If we reject the null hypothesis, this doesn’t mean that our alternative hypothesis is correct but does support the alternative/experimental hypothesis.

Upon analysis of the results, an alternative hypothesis can be rejected or supported, but it can never be proven to be correct. We must avoid any reference to results proving a theory as this implies 100% certainty, and there is always a chance that evidence may exist which could refute a theory.

How to Write a Hypothesis

Identify variables . The researcher manipulates the independent variable and the dependent variable is the measured outcome.
Operationalized the variables being investigated . Operationalization of a hypothesis refers to the process of making the variables physically measurable or testable, e.g. if you are about to study aggression, you might count the number of punches given by participants.
Decide on a direction for your prediction . If there is evidence in the literature to support a specific effect of the independent variable on the dependent variable, write a directional (one-tailed) hypothesis. If there are limited or ambiguous findings in the literature regarding the effect of the independent variable on the dependent variable, write a non-directional (two-tailed) hypothesis.
Make it Testable : Ensure your hypothesis can be tested through experimentation or observation. It should be possible to prove it false (principle of falsifiability).
Clear & concise language . A strong hypothesis is concise (typically one to two sentences long), and formulated using clear and straightforward language, ensuring it’s easily understood and testable.

Consider a hypothesis many teachers might subscribe to: students work better on Monday morning than on Friday afternoon (IV=Day, DV= Standard of work).

Now, if we decide to study this by giving the same group of students a lesson on a Monday morning and a Friday afternoon and then measuring their immediate recall of the material covered in each session, we would end up with the following:

The alternative hypothesis states that students will recall significantly more information on a Monday morning than on a Friday afternoon.
The null hypothesis states that there will be no significant difference in the amount recalled on a Monday morning compared to a Friday afternoon. Any difference will be due to chance or confounding factors.

More Examples

Memory : Participants exposed to classical music during study sessions will recall more items from a list than those who studied in silence.
Social Psychology : Individuals who frequently engage in social media use will report higher levels of perceived social isolation compared to those who use it infrequently.
Developmental Psychology : Children who engage in regular imaginative play have better problem-solving skills than those who don’t.
Clinical Psychology : Cognitive-behavioral therapy will be more effective in reducing symptoms of anxiety over a 6-month period compared to traditional talk therapy.
Cognitive Psychology : Individuals who multitask between various electronic devices will have shorter attention spans on focused tasks than those who single-task.
Health Psychology : Patients who practice mindfulness meditation will experience lower levels of chronic pain compared to those who don’t meditate.
Organizational Psychology : Employees in open-plan offices will report higher levels of stress than those in private offices.
Behavioral Psychology : Rats rewarded with food after pressing a lever will press it more frequently than rats who receive no reward.

Research Methodology

Qualitative Data Coding

What Is a Focus Group?

Cross-Cultural Research Methodology In Psychology

What Is Internal Validity In Research?

Research Methodology , Statistics

What Is Face Validity In Research? Importance & How To Measure

Criterion Validity: Definition & Examples

9.1 Null and Alternative Hypotheses

The actual test begins by considering two hypotheses . They are called the null hypothesis and the alternative hypothesis . These hypotheses contain opposing viewpoints.

H 0 : The null hypothesis: It is a statement of no difference between the variables—they are not related. This can often be considered the status quo and as a result if you cannot accept the null it requires some action.

H a : The alternative hypothesis: It is a claim about the population that is contradictory to H 0 and what we conclude when we reject H 0 . This is usually what the researcher is trying to prove.

After you have determined which hypothesis the sample supports, you make a decision. There are two options for a decision. They are "reject H 0 " if the sample information favors the alternative hypothesis or "do not reject H 0 " or "decline to reject H 0 " if the sample information is insufficient to reject the null hypothesis.

Mathematical Symbols Used in H 0 and H a :

Example 9.1

H 0 : No more than 30% of the registered voters in Santa Clara County voted in the primary election. p ≤ .30 H a : More than 30% of the registered voters in Santa Clara County voted in the primary election. p > 30

A medical trial is conducted to test whether or not a new medicine reduces cholesterol by 25%. State the null and alternative hypotheses.

Example 9.2

We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). The null and alternative hypotheses are: H 0 : μ = 2.0 H a : μ ≠ 2.0

H 0 : μ __ 66
H a : μ __ 66

Example 9.3

We want to test if college students take less than five years to graduate from college, on the average. The null and alternative hypotheses are: H 0 : μ ≥ 5 H a : μ < 5

H 0 : μ __ 45
H a : μ __ 45

Example 9.4

In an issue of U. S. News and World Report , an article on school standards stated that about half of all students in France, Germany, and Israel take advanced placement exams and a third pass. The same article stated that 6.6% of U.S. students take advanced placement exams and 4.4% pass. Test if the percentage of U.S. students who take advanced placement exams is more than 6.6%. State the null and alternative hypotheses. H 0 : p ≤ 0.066 H a : p > 0.066

H 0 : p __ 0.40
H a : p __ 0.40

Collaborative Exercise

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/introductory-statistics-2e/pages/1-introduction

Authors: Barbara Illowsky, Susan Dean
Publisher/website: OpenStax
Book title: Introductory Statistics 2e
Publication date: Dec 13, 2023
Location: Houston, Texas
Book URL: https://openstax.org/books/introductory-statistics-2e/pages/1-introduction
Section URL: https://openstax.org/books/introductory-statistics-2e/pages/9-1-null-and-alternative-hypotheses

© Dec 6, 2023 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

22,000-year-old artifacts could rewrite ancient human history in North America

Darrin Lowery found a collection of tools in Maryland that may date to 22,000 years ago.
That would mean humans first arrived in North America thousands of years before we thought.
Most experts believe humans first arrived in North America between 15,000 and 20,000 years ago.

North and South America were the last inhabited continents that modern humans settled thousands of years ago, but when and how they reached the Americas remains a mystery.

"We don't know who these first peoples were," Todd Braje, executive director of the University of Oregon Museum of Natural and Cultural History, told Business Insider. We don't know "where they came from, when they arrived, the technologies that they had available," he added.

For many years, archaeologists thought the first humans to set foot in the Americas did so around 13,000 years ago. But more recently, new findings have challenged that theory, pushing the timeline back even further.

Now, a recent series of discoveries on Parsons Island, Maryland, could wind back the clock yet again. And it raises some difficult questions about early human migration across North America.

Outside the mainstream

Darrin Lowery has been hunting for artifacts on Maryland islands around the Chesapeake Bay since he was 9 years old. Over 40 years later, he's amassed a large collection of tools that he believes some of the earliest Americans used.

He found nearly 300 tools on Parsons Island and says they're around 22,000 years old. That's thousands of years before many scientists think humans first journeyed to North America.

If Lowery's hypothesis is correct, it would significantly change our ideas of how and when people started arriving in this part of the world.

However, Lowery, who mainly works as an independent geologist, hasn't published his latest work in a peer-reviewed journal, making other experts skeptical of a theory that's already a bit outside the mainstream.

Lowery doesn't mind the criticism, though. "If I'm wrong, I'm fine with that," he told Business Insider. "Prove me wrong."

When did the first modern humans reach North America?

Around 13,000 years ago something significant was happening across northern North America: The glaciers that had covered part of the continent for millennia were melting.

Archaeologists thought humans needed to wait for those glaciers to melt to migrate across this region. Otherwise, the journey through what is now Canada would have been too dangerous, with little food available along the way.

So, for most of the 20th century, the theory was that the first Americans came from Asia around 13,000 years ago, crossing the now-submerged Bering land bridge that connected Siberia and present-day Alaska. Then those humans and their ancestors made their way across the areas of the Americas with fewer glaciers.

But by the second half of the 20th century, older sites were turning up, like a 14,500-year-old site in Chile, Monte Verde. If people were that far south at the time, it meant humans had to have traveled from North America to South America well before 13,000 years ago.

"It really changed everything about what we understood about when and how people arrived to the Americas," Braje said of the Chile site. One alternative theory is that people followed the less icy Pacific Coast and then started moving east.

While individual sites are often subjects of debate, the widely accepted range of humans' first arrival in the Americas is now between 20,000 to 15,000 years ago, Braje said.

Dating 22,000-year-old artifacts

Over the course of 93 visits to Parsons Island, Lowery and other volunteers found a mix of chipped-off rock flakes, a stone for hammering, and knives.

Due to erosion, most of the artifacts fell out of the embankment that once held them.

However, nine were still stuck in the bank, and three of those dated to around 22,000 years ago.

Dating ancient artifacts like this is tricky and is often the source of contention around these sites that question our understanding and timeline of ancient human history.

For instance, most dating methods require organic material and won't work on stone tools. Instead, scientists test charcoal, pollen, and other matter found near stone artifacts.

However, if a tool shifts from its original position — like if it falls out of the embankment that's holding it — it's difficult to date it reliably.

That's why only a handful of Lowery's artifacts could be tested.

Though Lowery doesn't want to publish a paper through peer review — a process he called "antiquated" — he said he did his due diligence in dating the artifacts.

He used different methods to date the still-in-place artifacts and also sent samples to independent labs for verification.

Using radiocarbon dating that measured the amount of carbon in flakes of charcoal, an independent lab estimated the artifacts' ages to be between 20,563 and 22,656 years old.

If these artifacts are as old as the lab analysis suggests, then Lowery's discovery could rewrite our understanding of ancient American human history.

The journey from Alaska to Maryland

Around 21,000 years ago, nearly all of Canada was covered in glaciers . Therefore, one of the biggest questions with Lowery's theory is how humans could have made the trek from Alaska to Maryland 22,000 years ago when there was a vast, icy landscape in between.

But Lowery said nearly 26,000 years ago, Beringian wolves traveled through a temporary corridor between ice sheets. Humans could have used the same route, he said.

"I think this is largely a misconception that ice is an impediment," Lowery said. "It's a challenge, but humans are pretty damn smart."

Lowery admitted this is just what he called "a story," but it's one some experts refuse to entertain. One archaeologist that The Washington Post spoke with refused to comment on the non-peer-reviewed paper.

For Braje, Lowery's research is reminiscent of past debates when new discoveries pushed back the timeline for the first American arrivals.

Braje didn't dismiss Lowery's ideas outright, but he thinks they need to go through the peer-review process. "I think all these ideas are valid ones that we should be talking about," he said, "but then we have to go to the scientific evidence."

"To make big claims like this takes a lot of work, a lot of evidence, a lot of enduring critique, but that's part of the scientific process," Braje said.

Watch: How 4 million fossils are excavated from La Brea Tar Pits

Main content

Search Menu
Sign in through your institution
Advance Articles
Collections
Focus Collections
Browse by cover
High-Impact Research
Author Guidelines
Quick and Simple Author Support
Focus Issues Call for Papers
Submission Site
Open Access Options
Self-Archiving Policy
Why Publish with Us?
About Plant Physiology
Editorial Board
Advertising & Corporate Services
Journals on Oxford Academic
Books on Oxford Academic

The American Society of Plant Biologists

Alternative localization of HEME OXYGENASE 1 in plant cells regulates cytosolic heme catabolism

Article contents
Figures & tables
Supplementary Data

Yingxi Chen, Kohji Nishimura, Mutsutomo Tokizawa, Yoshiharu Y Yamamoto, Yoshito Oka, Tomonao Matsushita, Kousuke Hanada, Kazumasa Shirai, Shoji Mano, Takayuki Shimizu, Tatsuru Masuda, Alternative localization of HEME OXYGENASE 1 in plant cells regulates cytosolic heme catabolism, Plant Physiology , 2024;, kiae288, https://doi.org/10.1093/plphys/kiae288

Permissions Icon Permissions

Heme, an organometallic tetrapyrrole, is widely engaged in oxygen transport, electron delivery, enzymatic reactions, and signal transduction. In plants, it is also involved in photomorphogenesis and photosynthesis. HEME OXYGENASE 1 (HO1) initiates the first committed step in heme catabolism, and it has generally been thought that this reaction takes place in chloroplasts. Here, we show that HO1 in both Arabidopsis ( Arabidopsis thaliana ) and rice ( Oryza sativa ) has 2 transcription start sites (TSSs), producing long ( HO1L ) and short ( HO1S ) transcripts. Their products localize to the chloroplast and the cytosol, respectively. During early development or de-etiolation, the HO1L / HO1S ratio gradually increases. Light perception via phytochromes (Phys) and cryptochromes elevates the HO1L / HO1S ratio in the whole seedling through the functions of ELONGATED HYPOCOTYL 5 (HY5) and HY5 HOMOLOG and through the suppression of DE-ETIOLATED 1, CONSTITUTIVE PHOTOMORPHOGENESIS 1, and PHYTOCHROME INTERACTING FACTORs. HO1L introduction complements the HO1 -deficient mutant; surprisingly, HO1S expression also restores the short hypocotyl phenotype and high pigment content and helps the mutant recover from the genomes uncoupled ( gun ) phenotype. This indicates the assembly of functional Phys within these lines. Furthermore, our findings support the hypothesis that a mobile heme signal is involved in retrograde signaling from the chloroplast. Altogether, our work clarifies the molecular mechanism of HO1 TSS regulation and highlights the presence of a cytosolic bypass for heme catabolism in plant cells.

Email alerts

Citing articles via.

Recommend to Your Librarian
Advertising & Corporate Services
Awards & Funding
Plant Science Today
Plant Biology Meeting
Meeting Management Services
Plant Science Research Weekly
Taproot: A Plantae Podcast

Affiliations

Online ISSN 1532-2548
Print ISSN 0032-0889
About Oxford Academic
Publish journals with us
University press partners
What we publish
New features
Open access
Institutional account management
Rights and permissions
Get help with access
Accessibility
Advertising
Media enquiries
Oxford University Press
Oxford Languages
University of Oxford

Oxford University Press is a department of the University of Oxford. It furthers the University's objective of excellence in research, scholarship, and education by publishing worldwide

Cookie settings
Cookie policy
Privacy policy
Legal notice

This Feature Is Available To Subscribers Only

This PDF is available to Subscribers Only

For full access to this pdf, sign in to an existing account, or purchase an annual subscription.

Titan's Massive Dunes May Be a Comet and Moon Graveyard From the Early Solar System

S aturn’s largest moon Titan has an enigmatic air fit for a Dune script. Covered in dark, ridged dunes and craters, the world is wrapped in a golden atmosphere and thought to contain a liquid ocean beneath its icy surface. Its distinct polar and desert regions have intrigued and mystified astronomers for years.

Now, in research presented at the Lunar and Planetary Science Conference this month, scientists suggest a new creation story for Titan’s characteristic ridges. These dark dunes might be a graveyard of fragments from crashed comets and small moons that collided with Titan as the solar system formed.

Titan’s dunes comprise about six million square miles of the moon, but astronomers have long questioned where they came from. Many had thought the sun’s radiation causes tiny particles to fall from the moon’s hazy atmosphere and collect on its surface, where they pile into grainy dunes. But researchers never knew for sure how these microscopic particles enlarged into sand-sized particulates, or whether the atmospheric fragments would have even stayed intact as the dunes took shape.

Instead, William Bottke , a planetary scientist at the Southwest Research Institute, and his team have proposed an alternative story that taps into various popular theories for how our solar system formed. Some four billion years ago, movements of the giant planets may have destabilized the Kuiper belt—a ring of icy space objects beyond the current orbit of Neptune—leading to an era of frequent collisions.

These planets are surrounded by moons, and this chaotic reshuffling would have caused countless comets and irregular moonlets to smash into Titan and other early planetary bodies. Space rocks would have also crashed together, breaking down into tiny particles. Bottke and his team ran simulations of this era and found that more than enough dust and particulates would have been released and scattered to form Titan’s dunes.

“Irregular satellites collisionally grind really effectively,” says Bottke to New Scientist ’s Leah Crane. “Titan gets on the order of about 10 6 kilometers cubed of material, and that’s several times more than the dunes.”

Per the team’s models, a similar amount of material would have been delivered to Jupiter’s moons Callisto and Ganymede, which might explain why they also have regions coated in dark particles today.

Because many of these smashed-comet particles have passed through Earth’s atmosphere, scientists know a lot about them—including that their size, durability and color are in line with what we know about Titan’s dunes, Bottke says to Science News ’ Nikk Ogasa.

Still, the hypothesis isn’t a slam dunk. Jani Radebaugh , a planetary scientist at Brigham Young University who was not involved in the research, tells Science News that Titan’s volcanic activity may “create a problem” for this theory, since debris from eruptions would have buried these scattered particles over time.

Radebaugh also presented research at the conference, using computer models to hypothesize that Titan’s geology may be slightly more asymmetrical than previously thought. Sand dunes likely dominate Titan’s lower latitudes, but yardangs—long, straight ridges formed by erosion—may stretch across the moon’s upper latitudes, her study suggests. This imbalance could indicate different weather conditions on different parts of the moon.

“On Titan, maybe there just isn’t sand at the high latitudes, or maybe there is material there that is more easily eroded,” Radebaugh tells New Scientist ’s Leah Crane.

Computer modeling studies like these can help scientists visualize dynamics on a world we can’t easily reach, but direct observations of the moon are on the horizon. Soon, an upcoming mission from NASA should be able to provide answers to Bottke and Radebaugh’s questions.

Announced in 2019, NASA’s Dragonfly mission is preparing for a 2028 launch to Titan, where a lander will study varied locations, searching for chemical evidence of life and clues into the world’s environmental history. Titan’s liquid reservoirs, subsurface ocean, thick atmosphere and dune fields will be explored like never before.

“Titan is unlike any other place in the solar system, and Dragonfly is like no other mission,” Thomas Zurbuchen , formerly NASA’s associate administrator for science, said in a 2019 statement announcing the mission. “Dragonfly will visit a world filled with a wide variety of organic compounds, which are the building blocks of life and could teach us about the origin of life itself.”

The darker areas across Titan's equatorial regions represent its dunes, as taken by the Cassini rover.

IMAGES

Null Hypothesis and Alternative Hypothesis
13 Different Types of Hypothesis (2024)
Alternative hypothesis
Research Hypothesis Generator
Null and Alternative Hypothesis: Symbolic Notation
Difference between Null and Alternative Hypothesis

VIDEO

Research understanding
Hypothesis Testing: the null and alternative hypotheses
Difference between null and alternative hypothesis |research methodology in tamil #sscomputerstudies
Testing of Hypothesis,Null, alternative hypothesis, type-I & -II Error etc @VATAMBEDUSRAVANKUMAR
Null Hypothesis vs Alternate Hypothesis
Null Hypothesis vs Alternate Hypothesis

COMMENTS

Null & Alternative Hypotheses
Revised on June 22, 2023. The null and alternative hypotheses are two competing claims that researchers weigh evidence for and against using a statistical test: Null hypothesis (H0): There's no effect in the population. Alternative hypothesis (Ha or H1): There's an effect in the population. The effect is usually the effect of the ...
Alternative hypothesis
The statement that is being tested against the null hypothesis is the alternative hypothesis. Alternative hypothesis is often denoted as H a or H 1. In statistical hypothesis testing, to prove the alternative hypothesis is true, it should be shown that the data is contradictory to the null hypothesis. Namely, there is sufficient evidence ...
9.1: Null and Alternative Hypotheses
The actual test begins by considering two hypotheses.They are called the null hypothesis and the alternative hypothesis.These hypotheses contain opposing viewpoints. $H_0$: The null hypothesis: It is a statement of no difference between the variables—they are not related. This can often be considered the status quo and as a result if you cannot accept the null it requires some action.
9.1 Null and Alternative Hypotheses
The actual test begins by considering two hypotheses.They are called the null hypothesis and the alternative hypothesis.These hypotheses contain opposing viewpoints. H 0, the —null hypothesis: a statement of no difference between sample means or proportions or no difference between a sample mean or proportion and a population mean or proportion. In other words, the difference equals 0.
What is an Alternative Hypothesis in Statistics?
Null hypothesis: µ ≥ 70 inches. Alternative hypothesis: µ < 70 inches. A two-tailed hypothesis involves making an "equal to" or "not equal to" statement. For example, suppose we assume the mean height of a male in the U.S. is equal to 70 inches. The null and alternative hypotheses in this case would be: Null hypothesis: µ = 70 inches.
Null and Alternative Hypotheses
The actual test begins by considering two hypotheses.They are called the null hypothesis and the alternative hypothesis.These hypotheses contain opposing viewpoints. H 0: The null hypothesis: It is a statement about the population that either is believed to be true or is used to put forth an argument unless it can be shown to be incorrect beyond a reasonable doubt.
Null and Alternative Hypotheses
H a: The alternative hypothesis: It is a claim about the population that is contradictory to H 0 and what we conclude when we reject H 0. Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample data.
Examples of null and alternative hypotheses
It is the opposite of your research hypothesis. The alternative hypothesis--that is, the research hypothesis--is the idea, phenomenon, observation that you want to prove. If you suspect that girls take longer to get ready for school than boys, then: Alternative: girls time > boys time. Null: girls time <= boys time.
8.4: The Alternative Hypothesis
The alternative hypothesis is simply the reverse of the null hypothesis, and there are three options, depending on where we expect the difference to lie. Thus, our alternative hypothesis is the mathematical way of stating our research question. If we expect our obtained sample mean to be above or below the null hypothesis value, which we call a ...
7.4: The Alternative Hypothesis
The alternative hypothesis is simply the reverse of the null hypothesis, and there are three options, depending on where we expect the difference to lie. Thus, our alternative hypothesis is the mathematical way of stating our research question. If we expect our obtained sample mean to be above or below the null hypothesis value, which we call a ...
Alternative hypothesis
The alternative hypothesis is used to decide whether a test should be one-tailed or two-tailed. The critical region. The null hypothesis is rejected if the test statistic falls within a critical region that has been chosen by the statistician. The critical region is a set of values that may comprise: ...
9.1 Null and Alternative Hypotheses
The alternative hypothesis is the contender and must win with significant evidence to overthrow the status quo. This concept is sometimes referred to the tyranny of the status quo because as we will see later, to overthrow the null hypothesis takes usually 90 or greater confidence that this is the proper decision.
Alternative hypothesis
The alternative hypothesis is one of two mutually exclusive hypotheses in a hypothesis test.The alternative hypothesis states that a population parameter does not equal a specified value. Typically, this value is the null hypothesis value associated with no effect, such as zero.If your sample contains sufficient evidence, you can reject the null hypothesis and favor the alternative hypothesis.
5.2
5.2 - Writing Hypotheses. The first step in conducting a hypothesis test is to write the hypothesis statements that are going to be tested. For each test you will have a null hypothesis (\ (H_0\)) and an alternative hypothesis (\ (H_a\)). Null Hypothesis. The statement that there is not a difference in the population (s), denoted as \ (H_0\)
8.2 Null and Alternative Hypotheses
A hypothesis test begins by considering two hypotheses. They are called the null hypothesis and the alternative hypothesis. These hypotheses contain opposing viewpoints and only one of these hypotheses is true. The hypothesis test determines which hypothesis is most likely true. The null hypothesis is denoted [latex]H_0[/latex]. It is a ...
Null Hypothesis and Alternative Hypothesis
The alternative hypothesis is what we are attempting to demonstrate in an indirect way by the use of our hypothesis test. If the null hypothesis is rejected, then we accept the alternative hypothesis. If the null hypothesis is not rejected, then we do not accept the alternative hypothesis. Going back to the above example of mean human body ...
Alternate Hypothesis in Statistics: What is it?
The Alternate Hypothesis. The alternate hypothesis is just an alternative to the null. For example, if your null is "I'm going to win up to $1,000" then your alternate is "I'm going to win $1,000 or more.". Basically, you're looking at whether there's enough change (with the alternate hypothesis) to be able to reject the null ...
10.2: Null and Alternative Hypotheses
The alternative hypothesis ( Ha H a) is a claim about the population that is contradictory to H0 H 0 and what we conclude when we reject H0 H 0. Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample ...
Alternative Hypothesis-Definition, Types and Examples
The alternative hypothesis is a statement used in statistical inference experiment. It is contradictory to the null hypothesis and denoted by H a or H 1. We can also say that it is simply an alternative to the null. In hypothesis testing, an alternative theory is a statement which a researcher is testing. This statement is true from the ...
Null and Alternative Hypotheses
Converting research questions to hypothesis is a simple task. Take the questions and make it a positive statement that says a relationship exists (correlation studies) or a difference exists between the groups (experiment study) and you have the alternative hypothesis.
Alternative Hypothesis
The alternative hypothesis will then be formulated as follows: H 1:: the values of \ ( { \theta_i (i=1,\ldots,k) } \) are not all identical. This means that only one parameter needs to have a different value to those of the other parameters in order to reject the null hypothesis and accept the alternative hypothesis.
Research Hypothesis In Psychology: Types, & Examples
Examples. A research hypothesis, in its plural form "hypotheses," is a specific, testable prediction about the anticipated results of a study, established at its outset. It is a key component of the scientific method. Hypotheses connect theory to data and guide the research process towards expanding scientific understanding.
The Job Satisfaction Paradox: Pluralistic Ignorance and the Myth of the
Hypothesis 2: A majority of workers will believe that most other workers are not at all satisfied with their job. If a minority of workers express job dissatisfaction, yet the majority perceive most others as extremely dissatisfied, it suggests the potential presence of pluralistic ignorance. ... To explore these alternative explanations, we ...
Reciprocal conversion between annual and polycarpic ...
A unified hypothesis for the evolution of diverse life-history-associated flowering behavior in the Brassicaceae Based on the above findings from four species from two genera, as well as their mutants and NILs with distinct growth habits, we propose a unified hypothesis for the regulation of flowering behavior by FLC -related MADS-box genes in ...
9.1 Null and Alternative Hypotheses
The actual test begins by considering two hypotheses.They are called the null hypothesis and the alternative hypothesis.These hypotheses contain opposing viewpoints. H 0: The null hypothesis: It is a statement of no difference between the variables—they are not related. This can often be considered the status quo and as a result if you cannot accept the null it requires some action.
22,000-Year-Old Tools Add to Debate About Humans' Arrival in Americas
Darrin Lowery. Darrin Lowery found a collection of tools in Maryland that may date to 22,000 years ago. That would mean humans first arrived in North America thousands of years before we thought ...
Alternative localization of HEME OXYGENASE 1 in plant cells regulates
Alternative localization of HO1 in the plastid or cytosol by TSS regulation This study showed that Arabidopsis HO1 is regulated by TSS selection in a light- and organ-dependent manner. HO1L and HO1S products with or without an intact TP localize to plastids and the cytosol, respectively, and either form can function in heme catabolism in plant ...
Titan's Massive Dunes May Be a Comet and Moon Graveyard From the ...
Titan's dunes comprise about six million square miles of the moon, but astronomers have long questioned where they came from. Many had thought the sun's radiation causes tiny particles to fall ...

What is an Alternative Hypothesis in Statistics?

Types of Alternative Hypotheses

Examples of Alternative Hypotheses

When to Reject the Null Hypothesis

Featured Posts

Leave a Reply Cancel reply

Join the Statology Community

Module 9: Hypothesis Testing With One Sample

Concept Review

Formula Review

Null and Alternative Hypotheses

Chapter Review

Formula Review

AP®︎/College Statistics

Examples of null and alternative hypotheses

Want to join the conversation?

Video transcript

Margin Size

7.4: The Alternative Hypothesis

Alternative hypothesis

Mathematical setting

Accepting the alternative

How to cite

User Preferences

Keyboard Shortcuts

8.2 Null and Alternative Hypotheses

Concept Review

Attribution

Null Hypothesis and Alternative Hypothesis

The Null Hypothesis

The Alternative Hypothesis

Margin Size

10.2: Null and Alternative Hypotheses

Chapter Review

Formula Review

Contributors

Alternative Hypothesis

Difference Between Null and Alternative Hypothesis

Register with BYJU'S & Download Free PDFs

Educational Research Basics by Del Siegle

Alternative Hypothesis

MATHEMATICAL ASPECTS

Access this chapter

Rights and permissions

Copyright information

About this entry

Download citation

Share this entry

Research Hypothesis In Psychology: Types, & Examples

Some key points about hypotheses:

Types of Research Hypotheses

Null Hypothesis

Nondirectional Hypothesis

Directional Hypothesis

Falsifiability

Can a Hypothesis be Proven?

How to Write a Hypothesis

More Examples

9.1 Null and Alternative Hypotheses

Example 9.1

Example 9.2

Example 9.3

Example 9.4

Collaborative Exercise

22,000-year-old artifacts could rewrite ancient human history in North America

Outside the mainstream

When did the first modern humans reach North America?

Dating 22,000-year-old artifacts

The journey from Alaska to Maryland

Watch: How 4 million fossils are excavated from La Brea Tar Pits

Alternative localization of HEME OXYGENASE 1 in plant cells regulates cytosolic heme catabolism

Email alerts

Affiliations

This Feature Is Available To Subscribers Only

Titan's Massive Dunes May Be a Comet and Moon Graveyard From the Early Solar System

IMAGES

VIDEO

COMMENTS