representation of set means

Sets in mathematics, are simply a collection of distinct objects forming a group. A set can have any group of items, be it a collection of numbers, days of a week, types of vehicles, and so on. Every item in the set is called an element of the set. Curly brackets are used while writing a set. A very simple example of a set would be like this. Set A = {1, 2, 3, 4, 5}. In set theory, there are various notations to represent elements of a set. Sets are usually represented using a roster form or a set builder form. Let us discuss each of these terms in detail.

Sets Definition

In mathematics, a set is defined as a well-defined collection of objects. Sets are named and represented using capital letters. In the set theory, the elements that a set comprises can be any kind of thing: people, letters of the alphabet, numbers, shapes, variables, etc.

Sets in Maths Examples

Some standard sets in maths are:

• Set of natural numbers , ℕ = {1, 2, 3, ...}
• Set of whole numbers , W = {0, 1, 2, 3, ...}
• Set of integers , ℤ = {..., -3, -2, -1, 0, 1, 2, 3, ...}
• Set of rational numbers , ℚ = {p/q | q is an integer and q ≠ 0}
• Set of irrational numbers , ℚ' = {x | x is not rational}
• Set of real numbers , ℝ = ℚ ∪ ℚ'

All these are infinite sets. But there can be finite sets as well. For example, the collection of even natural numbers less than 10 can be represented in the form of a set, A = {2, 4, 6, 8}, which is a finite set.

Let us use this example to understand the basic terminology associated with sets in math.

Elements of a Set

The items present in a set are called either elements or members of a set. The elements of a set are enclosed in curly brackets separated by commas. To denote that an element is contained in a set, the symbol '∈' is used. In the above example, 2 ∈ A. If an element is not a member of a set, then it is denoted using the symbol '∉'. For example, 3 ∉ A.

Cardinal Number of a Set

The cardinal number, cardinality , or order of a set denotes the total number of elements in the set. For natural even numbers less than 10, n(A) = 4. Sets are defined as a collection of unique elements. One important condition to define a set is that all the elements of a set should be related to each other and share a common property. For example, if we define a set with the elements as the names of months in a year, then we can say that all the elements of the set are the months of the year.

Representation of Sets in Set Theory

There are different set notations used for the representation of sets in set theory. They differ in the way in which the elements are listed. The three set notations used for representing sets are:

• Semantic form
• Roster form
• Set builder form

Let us understand each of these forms with an example.

Semantic Form

Semantic notation describes a statement to show what are the elements of a set. For example, a set of the first five odd numbers .

Roster Form

The most common form used to represent sets is the roster notation in which the elements of the sets are enclosed in curly brackets separated by commas. For example, Set B = {2,4,6,8,10}, which is the collection of the first five even numbers. In a roster form, the order of the elements of the set does not matter, for example, the set of the first five even numbers can also be defined as {2,6,8,10,4}. Also, if there is an endless list of elements in a set, then they are defined using a series of dots at the end of the last element. For example, infinite sets are represented as, X = {1, 2, 3, 4, 5 ...}, where X is the set of natural numbers. To sum up the notation of the roster form, please take a look at the examples below.

Finite Roster Notation of Sets : Set A = {1, 2, 3, 4, 5} (The first five natural numbers)

Infinite Roster Notation of Sets : Set B = {5, 10, 15, 20 ....} (The multiples of 5 )

Set Builder Form

The set builder notation has a certain rule or a statement that specifically describes the common feature of all the elements of a set. The set builder form uses a vertical bar in its representation, with a text describing the character of the elements of the set. For example, A = { k | k is an even number, k ≤ 20}. The statement says, all the elements of set A are even numbers that are less than or equal to 20. Sometimes a ":" is used in the place of the "|".

Visual Representation of Sets Using Venn Diagram

Venn Diagram is a pictorial representation of sets, with each set represented as a circle. The elements of a set are present inside the circles . Sometimes a rectangle encloses the circles, which represents the universal set . The Venn diagram represents how the given sets are related to each other.

Sets Symbols

Set symbols are used to define the elements of a given set. The following table shows the set theory symbols and their meaning.

Types of Sets

There are different types of sets in set theory. Some of these are singleton, finite, infinite, empty, etc.

Singleton Sets

A set that has only one element is called a singleton set or also called a unit set. Example, Set A = { k | k is an integer between 3 and 5} which is A = {4}.

Finite Sets

As the name implies, a set with a finite or countable number of elements is called a finite set . Example, Set B = {k | k is a prime number less than 20}, which is B = {2,3,5,7,11,13,17,19}

Infinite Sets

A set with an infinite number of elements is called an infinite set. Example: Set C = { Multiples of 3 }.

Empty or Null Sets

A set that does not contain any element is called an empty set or a null set. An empty set is denoted using the symbol '∅'. It is read as ' phi '. Example: Set X = { }.

If two sets have the same elements in them, then they are called equal sets . Example: A = {1,2,3} and B = {1,2,3}. Here, set A and set B are equal sets. This can be represented as A = B.

Unequal Sets

If two sets have at least one different element, then they are unequal sets. Example: A = {1,2,3} and B = {2,3,4}. Here, set A and set B are unequal sets. This can be represented as A ≠ B.

Equivalent Sets

Two sets are said to be equivalent sets when they have the same number of elements, though the elements are different. Example: A = {1,2,3,4} and B = {a,b,c,d}. Here, set A and set B are equivalent sets since n(A) = n(B)

Overlapping Sets

Two sets are said to be overlapping if at least one element from set A is present in set B. Example: A = {2,4,6} B = {4,8,10}. Here, element 4 is present in set A as well as in set B. Therefore, A and B are overlapping sets.

Disjoint Sets

Two sets are disjoint if there are no common elements in both sets. Example: A = {1,2,3,4} B = {5,6,7,8}. Here, set A and set B are disjoint sets.

Subset and Superset

For two sets A and B, if every element in set A is present in set B, then set A is a subset of set B(A ⊆ B) and in this case, B is the superset of set A(B ⊇ A). Example: Consider the sets A = {1,2,3} and B = {1,2,3,4,5,6}. Here:

• A ⊆ B, since all the elements in set A are present in set B.
• B ⊇ A denotes that set B is the superset of set A.

Universal Set

A universal set is the collection of all the elements regarding a particular subject. The universal set is denoted by the letter 'U'. Example: Let U = {The list of all road transport vehicles}. Here, a set of cars is a subset for this universal set, the set of cycles, trains are all subsets of this universal set.

Power set is the set of all subsets that a set could contain. Example: Set A = {1,2,3}. Power set of A is = {∅, {1}, {2}, {3}, {1,2}, {2,3}, {1,3}, {1,2,3}}.

Operations on Sets

Some important operations on sets in set theory include union, intersection, difference, the complement of a set, and the cartesian product of a set. A brief explanation of set operations is as follows.

Union of Sets

Union of sets, which is denoted as A U B, lists the elements in set A and set B or the elements in both set A and set B. For example, {1, 3} ∪ {1, 4} = {1, 3, 4}

Intersection of Sets

The intersection of sets which is denoted by A ∩ B lists the elements that are common to both set A and set B. For example, {1, 2} ∩ {2, 4} = {2}

Set Difference

Set difference which is denoted by A - B, lists the elements in set A that are not present in set B. For example, A = {2, 3, 4} and B = {4, 5, 6}. A - B = {2, 3}.

Set Complement

Set complement which is denoted by A', is the set of all elements in the universal set that are not present in set A. In other words, A' is denoted as U - A, which is the difference in the elements of the universal set and set A.

Cartesian Product of Sets

The cartesian product of two sets which is denoted by A × B, is the product of two non-empty sets, wherein ordered pairs of elements are obtained. For example, {1, 3} × {1, 3} = {(1, 1), (1, 3), (3, 1), (3, 3)}.

In the above figure, the shaded portions in "blue" show the set that they are labelled with.

Sets Formulas in Set Theory

Sets find their application in the field of algebra , statistics , and probability . There are some important set theory formulas in set theory as listed below.

For any two overlapping sets A and B,

• n(A U B) = n(A) + n(B) - n(A ∩ B)
• n (A ∩ B) = n(A) + n(B) - n(A U B)
• n(A) = n(A U B) + n(A ∩ B) - n(B)
• n(B) = n(A U B) + n(A ∩ B) - n(A)
• n(A - B) = n(A U B) - n(B)
• n(A - B) = n(A) - n(A ∩ B)

For any two sets A and B that are disjoint,

• n(A U B) = n(A) + n(B)
• n(A - B) = n(A)

Properties of Sets

Similar to numbers, sets also have properties like associative property, commutative property, and so on. There are six important properties of sets . Given, three sets A, B, and C, the properties for these sets are as follows.

Cuemath is one of the world's leading math learning platforms that offers LIVE 1-to-1 online math classes for grades K-12 . Our mission is to transform the way children learn math, to help them excel in school and competitive exams. Our expert tutors conduct 2 or more live classes per week, at a pace that matches the child's learning needs.

Sets Examples

Example 1: Find the elements of the sets represented as follows and write the cardinal number of each set. a) Set A is the first 8 multiples of 7 b) Set B = {a,e,i,o,u} c) Set C = {x | x are even numbers between 20 and 40}

a) Set A = {7,14,21,28,35,42,49,56}. These are the first 8 multiples of 7 .

Since there are 8 elements in the set, cardinal number n (A) = 8

b) Set B = {a,e,i,o,u}. There are five elements in the set,

Therefore, the cardinal number of set B, n(B) = 5. c) Set C = {22,24,26,28,30,32,34,36,38}. These are the even numbers between 20 and 40, which make up the elements of the set C.

Therefore, the cardinal number of set C, n(C) = 9.

Answer: (a) 8 (b) 5 (c) 9

Example 2: If Set A = {a,b,c}, Set B = {a,b,c,p,q,r}, U = {a,b,c,d,p,q,r,s}, find the following using sets formulas, a) A U B b) A ∩ B c) A' d) Is A ⊆ B? (Here 'U' is the universal set).

a) A U B = writing the elements of A and B together in one set by removing duplicates = {a,b,c,p,q,r}

b) A ∩ B = writing common elements of A and B in a set = {a,b,c}

c) A' = writing elements of U that are NOT present in A = {d,p,q,r,s}

d) A ⊆ B, (Set A is a subset of set B) since all the elements in set A are present in set B.

Answer: (a) {a,b,c,p,q,r} (b) {a,b,c} (c) {d,p,q,r,s} (d) Yes

Example 3: Express the given set in set-builder form: A = {2, 4, 6, 8, 10, 12, 14}

Solution: Given: A = {2, 4, 6, 8, 10, 12, 14}

Using sets notations, we can represent the given set A in set-builder form as,

A = {x | x is an even natural number less than 15}

Answer: A = {x | x is an even natural number less than 15}

go to slide go to slide go to slide

Book a Free Trial Class

Practice Questions on Sets

Faqs on sets, what is set in math.

Sets are a collection of distinct elements, which are enclosed in curly brackets, separated by commas. The list of items in a set is called the elements of a set. Examples are a collection of fruits, a collection of pictures. Sets are represented by the symbol { }. i.e., the elements of the set are written inside these brackets. Example: Set A = {a,b,c,d}. Here, a,b,c, and d are the elements of set A.

What are Different Sets Notations to Represent Sets?

Sets can be represented in three ways. Representing sets means a way of listing the elements of the set. They are as follows.

• Semantic Notation: The elements of a set are represented by a single statement. For example, Set A is the number of days in a week.
• Roster Notation: This form of representation of sets uses curly brackets to list the elements of the set. For example, Set A = {10,12,14,16,18}}
• Set Builder Notation: A set builder form represents the elements of a set by a common rule or a property. For example, {x | x is a prime number less than 20}

What are the Types of Sets?

Sets differ from each depending upon elements present in them. Based on this, we have the following types of sets . They are singleton sets, finite and infinite sets, empty or null sets, equal sets, unequal sets, equivalent sets, overlapping sets, disjoint sets, subsets, supersets, power sets, and universal sets.

What are the Properties of Sets in Set-Theory?

Different properties associated with sets in math are,

• Commutative Property: A U B = B U A and A ∩ B = B ∩ A
• Associative Property: (A ∩ B) ∩ C = A ∩ (B ∩ C) and (A U B) U C = A U (B U C)
• Distributive Property: A U (B ∩ C) = (A U B) ∩ (A U C) and A ∩ (B U C) = (A ∩ B) U (A ∩ C)
• Identity Property: A U ∅ = A and A ∩ U = A
• Complement Property: A U A' = U
• Idempotent Property: A ∩ A = A and A U A = A

What is the Union of Sets?

The union of two sets A and B are the elements from both set A and B, or both combined together. It is denoted using the symbol 'U'. For example, if set A = {1,2,3} and set B = {4,5,6}, then A U B = {1,2,3,4,5,6}. A U B is read as 'A union B'.

What is the Intersection of Sets?

The intersection of two sets A and B are the elements that are common to both set A and B. It is denoted using the symbol '∩'. For example, if set A = {1,2,3} and set B = {3,4,5}, then A ∩ B = {3}. A ∩ B is read as 'A intersection B'.

What are Subsets and Supersets?

If every element in a set A is present in set B, then set B is the superset of set A and set A is a subset of set B. Example: A = {1,4,5} B = {1,2,3,4,5,6}, here since all elements of set A are present in set B ⇒ A ⊆ B and B ⊇ A.

What are Universal Sets?

A universal set, denoted by the letter 'U', is the collection of all the elements in regard to a particular subject. Example: Let U = {All types of cycles}. Here, a set of cycles of a specific company is a subset of this universal set.

What Does Sets Class 11 Contain?

The sets in class 11 is an important chapter that deals with various components of set theory. It starts with definition of sets, and extends to types of sets, properties of sets, set operations, etc. It also has some real-life applications related to sets. To solve more applications related to sets class 11, click here . ☛Also Check:

• NCERT Solutions Class 11 Maths Chapter 1 Ex 1.1
• NCERT Solutions Class 11 Maths Chapter 1 Ex 1.2
• NCERT Solutions Class 11 Maths Chapter 1 Ex 1.3
• NCERT Solutions Class 11 Maths Chapter 1 Ex 1.4
• NCERT Solutions Class 11 Maths Chapter 1 Ex 1.5
• NCERT Solutions Class 11 Maths Chapter 1 Ex 1.6
• NCERT Solutions Class 11 Maths Chapter 1 Miscellaneous Exercise

What is Complement in Sets?

The complement of a set which is denoted by A', is the set of all elements in the universal set that are not present in set A. In other words, A' is denoted as U - A, which is the difference in the elements of the universal set and set A.

What is Cartesian Product in Sets?

Cartesian product of two sets, denoted by A×B, is the product of two non-empty sets, wherein ordered pairs of elements are obtained. For example, if A = {1,2} and B = {3,4}, then A×B = {(1,3), (1,4), (2,3), (2,4)}.

What is the Use of Venn Diagram in Set Theory?

Venn Diagram is a pictorial representation of the relationship between two or more sets. Circles are used to represent sets. Each circle represents a set. A rectangle that encloses the circles represents the universal set.

Set in Math – Definition, Types, Properties, Examples

What is a set, elements of a set, types of sets, solved examples, practice problems, frequently asked questions.

We commonly use the terms like ‘a complete set of novels’ or ‘a set of cutlery’ in day-to-day life. What do we mean by the term ‘set’ here? It simply defines a collection of objects or things of the same type. Sets in math are also defined in the similar context.

Set Definition

In mathematics, a set is defined as a collection of distinct, well-defined objects forming a group. There can be any number of items, be it a collection of whole numbers, months of a year, types of birds, and so on. Each item in the set is known as an element of the set. We use curly brackets while writing a set.

Consider an example of a set.

$\text{A} = \left\{1, 3, 5, 7, 9\right\}$.

It has five elements. It is a set of odd numbers less from 1 to 10.

What do we mean by ‘well-defined’ objects?

Consider an example. A collection of odd natural numbers less than 20 is defined, but a collection of brave students in a class is not defined.

We can represent a collection of odd natural numbers less than 20 in the form of a set as

$\text{B} = \left\{1, 3, 5, 7, 9, 11, 13, 15, 17, 19\right\}$. 

The number of elements in the set are denoted by n(A) where A is a set. 

Example: $\text{A} = \left\{1, 4, 9, 16, 25, 36, 49, 64, 81, 100\right\}$.

$n(A) = 10$. 

The other word used for the number of elements in the set is called its cardinality. 

Related Worksheets

Elements or members are the terms or items present in a set. They are enclosed in curly brackets and separated by commas. To represent that an element is contained in a set, we use the symbol “$\in$.” It is read as ‘belongs to.’

Suppose we have a set of even natural numbers less than 10.

$\text{A} = \left\{2, 4, 6, 8\right\}$ .

Here, $2 \in A$ but $3 \notin A$.

Representation of Sets

We represent the sets in different ways. The only difference is in the way in which the elements are listed. The different forms of representing sets are discussed below.

Roster Form

The most familiar and easy form used to represent sets is the roster form, in which the elements are enclosed in curly brackets and are separated by commas such as $\text{B} = \left\{1, 4, 9, 16, 25\right\}$, which is the collection of the square of consecutive numbers less than 30. The order of the elements does not matter and there can be an infinite number of elements in a set, which we define using a series of dots at the end of the last element. There are two types of sets in Roster Form:

Finite Roster Notation of Sets in which there are elements that can be counted, such as $\text{A} = \left\{5, 10, 15, 20, 25\right\}$ (The multiples of 5 less than 30.)

Infinite Roster Notation of Sets in which the elements can not be counted, such as $\text{B} = \left\{4, 8, 12, 16 …\right\}$ (The multiples of 4)

Set Builder Form

The set builder notation has a particular rule that describes the common feature of all the elements of a set. It uses a vertical bar in its representation along with a text describing the character of the elements, such as $\text{A} = \left\{ \text{x}\; |\; \text{x} \; \text{is a prime number}, x \le 20\right\}$. According to the statement, all the elements of the set are prime numbers less than or equal to 20. We use “:” place of the “|” sometimes. 

Let’s discuss different types of sets. 

Singleton Sets

When a set has only one element, it is known as a singleton set.

Set $\text{A} = \left\{ \text{x}\; |\; \text{x}\; \text{is a whole number between}\;12\; \text{and}\;14\right\} = \left\{13\right\}$.

Null or Empty Sets

When a set does not contain any element, it is known as a null or an empty set. It is denoted by the symbol “$\Phi$” and it is read as “phi.” 

Set $\text{B} = =$ Integers between 1 and $2 = \Phi$

Two sets are said to be equal if they have the same elements in them. Suppose there are two sets $\text{A} = \left\{1, 4, 5\right\}$ and $\text{B} = \left\{1, 4, 5\right\}$. Here, $\text{A} = \text{B}$ because each element is the same. 

Unequal Sets

Two sets are said to be unequal if they have at least one different element. Suppose we have two sets $\text{A} = \left\{1, 2, 5\right\}$ and $\text{B} = \left\{1, 2, 4\right\}$. Here, $\text{A} \neq \text{B}$ as $5 \in \text{A}$ but $5 \notin \text{B}$.  

Equivalent Sets

Equivalent sets are the two sets that have the same number of elements, even if the elements are different. Suppose we have two sets $\text{A} = \left\{10, 11, 12, 13\right\}$ and $\text{B} = \left\{January, February, March, April\right\}$. Since $n(A) = n(B)$, A and B are equivalent sets. 

Overlapping Sets

If at least one element from set A is present in set B, then the sets are said to be overlapping. Example: $\text{A} = \left\{2, 3, 6\right\} \text{B} = \left\{6, 8, 12\right\}$. 6 is present in set A and set B. So, A and B are overlapping sets.

Subset and Superset

If every element in set A is also present in set B, then set A is known as the subset of set B, which is denoted by $\text{A} \subseteq \text{B}$ and B is known as the superset of set A, which is denoted by $\text{B} \supseteq \text{A}$.

Example: $\text{A} = \left\{1, 4, 7, 10, 12\right\}\; \text{B} = \left\{1, 4, 6, 7, 8, 10, 11, 12, 13\right\}$

$\text{A} \subseteq \text{B}$, since all the elements of A are present in B.

Also, set B is the superset of set A.

Universal Set

The collection of all the elements in regard to a particular subject is known as a universal set which is denoted by the letter “U.” Suppose we have a set U as the set of all the natural numbers. So, the set of even numbers, set of odd numbers, set of prime numbers is a subset of the universal set.

Disjoint Sets

Two sets are known as disjoint sets if they have no common elements in both sets. Consider two sets – $\text{A} = \left\{5, 6, 7\right\}$ and $\text{B} = \left\{2, 3, 4\right\}$. Here, set A and set B are disjoint sets as they have no elements in common. 

The set of all subsets that a set could contain is known as the power set. Suppose we have a set $\text{A} = \left\{2, 3\right\}$. Power set of A is $= \left\{\left\{\varnothing\right\}, \left\{2\right\}, \left\{3\right\}, \left\{2,3\right\}\right\}$.

If n is the number of elements in a set, then the number of subsets $=2^{n}$.

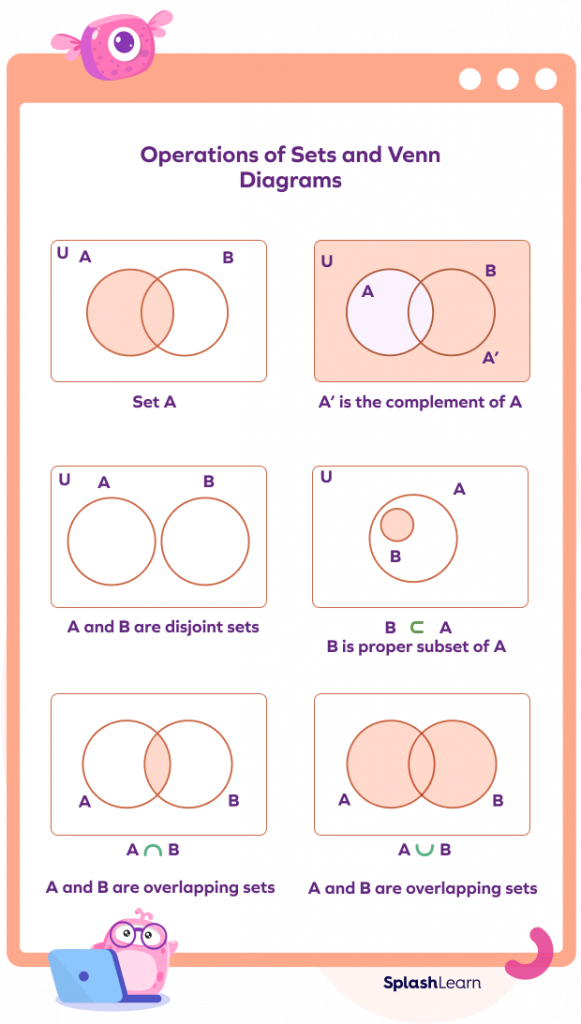
Visual Representation of Sets Using Venn Diagram

The pictorial representation of sets represented as circles is known as the Venn diagram. The elements of the sets are inside the circles. The rectangle that encloses the circles represents the universal set. The Venn diagram represents how the sets are related to each other. 

Operations on Sets

There are some operations on sets given below: 

Union of Sets

B. Suppose we have two sets $\text{A} = \left\{1, 2, 3\right\}$ and $\text{B} = \left\{3, 4, 5\right\}$

$\text{A}\; \text{U}\; \text{B} = \left\{1, 2, 3, 4, 5\right\}$

Intersection of Sets

The intersection of sets is denoted by $\text{A} \cap \text{B}$ has the elements which are common in both set A and set B. Suppose we have two sets $\text{A} = \left\{1, 3\right\}$ and $\text{B} = \left\{3, 4\right\}$

$\text{A} \cap \text{B} = {3}$

Difference of Sets

We denote the set difference by $\text{A} – \text{B}$, which has the elements in set A that are not present in set B. Suppose we have two sets, i.e.,  $\text{A} = \left\{3, 4, 5\right\}$ and $\text{B} = \left\{5, 6, 7\right\}$

$\text{A} \;–\; \text{B} = \left\{3, 4\right\}$

Complement of a Set

The complement of a set A is denoted by A’, which is the set of all elements in the universal set that are not present in set A. A’ can also be represented as $\text{U} \;–\; \text{A}$, i.e., the difference in the elements of the universal set and set A.

Suppose $\text{U} =$ Set of Natural Numbers and $\text{A} =$ Set of Prime Numbers

So, $\text{U} \;–\; \text{A} =$ Set of all Non-prime Numbers.

Sets Formulas

There are some set formulas that we can use to find the number of elements. 

For sets A and B,

• $n(A\; U\; B) = n(A) + n(B) – n(A \cap B)$
• $n(A − B) = n(A U B) − n(B)$
• $n(A − B) = n(A) − n(A \cap B)$

Properties of Sets

Here are the properties of sets:

1. How many elements are there in the set $\text{A} = \left\{ \text{x}\; : \text{x}\; \text{is a perfect square less than 30}\right\}$ ?

Solution: $\text{A} = \left\{1, 4, 9, 16, 25\right\}$

2. Arrange the set $A = \left\{ y : y^{2} = 36 ; y\; \text{is an integer}\right\}$ in roster form.

Solution: $y^{2} = 36 \Rightarrow y^{2} − 36 = 0 \Rightarrow y = \pm 6$

$\text{A} = { –\; 6, 6}$

3. Write the set $\text{B} = \left\{1, 2, 5, 10, 17\right\}$ in set builder form.

Solution: $0^{2} + 1 = 1$

$1^{2} + 1 = 2$

$2^{2} + 1 = 5$

$3^{2} + 1 = 10$

$4^{2} + 1 = 17$

So, in roaster form $\text{B} = \left\{y : y^{2} + 1, y \lt 5\right\}$ 

4. If A is a set of prime numbers and B is a set of even numbers. What will be $\text{A} \cap \text{B}$ ?

Solution: Only 2 is the number, which is a prime number as well as an even number. So,  $\text{A} \cap \text{B} = {2}$.

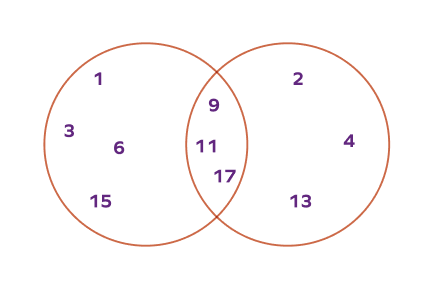
5. Draw a Venn diagram for the sets $\text{A} = \left\{1, 3, 6, 9, 11, 15, 17\right\}$ and $\text{B} = \left\{2, 4, 9, 11, 13, 17\right\}$ . 

Solution: 

What is a Set in Math

Attend this quiz & Test your knowledge.

Which of the following sets denotes $\left\{\right\}$?

If $\text{a} = \left\{\;–\; 1, 0, 2, 3, 5, 7\right\}$ and $\text{b} = \left\{0, 1, 2, 3, 5, 6\right\}$, then what is $\text{a}\; \text{u}\; \text{b}$, if $\text{p} = \left\{ \;–\; 10, \;–\; 7, \;–\; 4, \;–\; 3, \;–\; 2, \;–\; 1\right\}$ and $\text{q} = \left\{ \;–\; 9, \;–\; 8, \;–\; 7, \;–\; 6, \;–\; 4, \;–\; 2\right\}$ then __ denotes $\left\{ \;–\; 10, \;–\; 3, \;–\; 1\right\}$, how many subsets will be there if $n(a) = 3$ where a is a set, if $n(a)$ = $16,n (b) = 18$ and $n(a \cup b) = 7$, then what is the value of $n(a \cup b)$.

What are sets formula if sets are disjoint?

For disjoint sets A and B;

• $n(A U B) = n(A) + n(B)$
• $A \cap B = \varnothing$
• $n(A − B) = n(A)$

Is {0} a null set ?

No. There is one element inside the brackets. So, it is a singleton set, not a null set.

What is a Cartesian Product in sets?

Cartesian Product of Set A and B is defined as an ordered pair $(x, y)$ where $x \in A$ and $y \in B$.

How is set theory applicable in daily lives?

In real life, sets are used in bookshelves while arranging the books according to alphabetic order or genre; closets where dresses, tops, jeans are kept as a set, etc.

Does the union of two sets include the intersection of the sets?

Yes, the union of two sets includes the intersection of the sets. Union of set A and B includes the elements either in set A or in set B or in both set A and B.

RELATED POSTS

• Universal Set in Math – Definition, Symbol, Examples, Facts, FAQs
• Centimeter (CM) – Definition with Examples
• How to Convert Cm to Inches: Formula, Conversion, Examples
• Perfect Square Trinomial – Definition, Formula, Examples, FAQs
• Singleton Set: Definition, Formula, Properties, Examples, FAQs

Math & ELA | PreK To Grade 5

Kids see fun., you see real learning outcomes..

Make study-time fun with 14,000+ games & activities, 450+ lesson plans, and more—free forever.

Parents, Try for Free Teachers, Use for Free

• Introduction to Sets

Set is a collection of objects but in mathematics, the definition of the set is one of the most strange definitions. It is a way in mathematics that allows us to put similar objects together. Does mathematics have a tool that can collect families or similar mathematical objects together? A set is such an object. Want to know how? Let us see below!

Suggested Videos

Any well-defined collection of mathematical objects can form a set. These objects could be anything – from people’s names to their ages/likes /dislikes; entities from simple number system to complex scientific data; from outcomes of a single dice roll or a coin toss to such experiments repeated 100s or 1000s of times.

The ONLY condition which is to be kept in mind is that the entities or objects must be related through the same rule. For example:

• Collection of the names of the freedom fighters of India .
• Family of all natural numbers /whole numbers/ odd numbers /even numbers/rational numbers/integers/real numbers.
• A group of possible outcomes of a dice roll or a coin toss.
• Collection of crucial data gathered by ISRO from MOM.
• A collection of day/night temperatures.

And there are many more such examples that will form a collection. The important point to notice here is that the rule that defines or law through which we collect or group objects should be universal.

For example, if I say that a group of all the intelligent scientists, it will contain people who I insist are intelligent. If I ask you to form the same group, it will have different names inside it. We say that the rule “intelligent scientists” is not well-defined.

                                                     Learn Types of Sets   here.

Video on Sets

Conventions for sets.

The following are the conventions that are used here:

• Sets are usually denoted by a capital letter .
• The elements of the group are usually represented by small letters (unless specified separately.)
• If ‘ a’ is an element of ‘ A’,  or if a “belongs to” A, it is written in the conventional notion by the use of the Greek symbol ϵ (Epsilon) between them – a ϵ A.
• If b is not an element of Set A , b “does not belong to” A is written in the conventional notion by the use of the symbol ϵ (Epsilon with a line across it) between them – a ϵ A.
• Objects, elements, entities, members are all synonymous terms.

You can download Sets Cheat Sheet by clicking on the download button below

Representations of a Set

Representation of Sets and its elements is done in the following two ways.

Roster Form

In this form, all the elements are enclosed within braces {} and they are separated by commas ( , ). For example, a collection of all the numbers found on a dice N = {1, 2, 3, 4, 5, 6}. Properties of roster form: –

• The order in which the elements are listed in the Roster form for any Set is immaterial. For example, V = {a, e, i, o, u} is same as V = {u, o, e, a, i}
• The dots at the end of the last element of any Set represent its infinite form and indefinite nature. For example, group of odd natural numbers = {1, 3, 5, …}
• In this form of representation, the elements are generally not repeated. For example, the group of letters forming the word POOL = {P, O, L}

More examples for Roster form of representation are:

• A = {3, 6, 9, 12}
• F = {2, 4, 8, 16, 32}
• H = {1, 4, 9, 16, …, 100}
• L = {5, 25, 125, 625}
• Y = {1, 1, 2, 3, 5, 8, …}

Set Builder Form

In this form, all the elements possess a single common property which is NOT featured by any other element outside the Set. For example, a group of vowels in English alphabetical series.

The representation is done as follows. Let V be the collection of all English vowels, then – V = {x: x is a vowel in English alphabetical series.} Properties of Roster form: –

• Colon ( : ) is a mandatory symbol for this type of representation.
• After the colon sign, we write the common characteristic property possessed by ALL the elements belonging to that Set and enclose it within braces.
• If the Set doesn’t follow a pattern, its Set builder form cannot be written.

More examples for Set builder form of representation for a Set: –

• D = {x: x is an integer and – 3 < x < 19}
• O = {y: y is a natural number greater than 5}
• I = {f: f is a two – digit prime number less than 1000}
• R = {s: s is a natural number such that sum of its digits is 4}
• X = {m: m is a positive integer < 40}

Thus, these were some important points on Sets, what they are, how they are represented mathematically and the related properties.

                                                         Learn Operations on Sets here in detail.

Solved Examples For You

Q1: Write the statements of representation of sets for an unbiased roll for a dice.

• In Roster form – A = {1, 2, 3, 4, 5, 6}
• In Set Builder form – A = {x: x is natural number ≤ 6}

Q2: Write the statement of representation of set for a Fibonacci series in Roster form.

Solution: In Roster form, the Fibonacci series can be represented as: A = {1, 1, 2, 3, 5, 8, 13…}. Fibonacci series is a special category series that gets its next number by adding the previous two numbers .

Q. What is a set in Mathematics?

When we look at sets in Mathematics, we see it is a well-defined collection comprising of various objects. For instance, the number 2, 4 and 6 are very different from each other when we look at them separately. However, when you consider them in a collective manner, they make up a single set of size three which we write as {2, 4, 6}

Q. What is a proper set?

A proper subset of a set A is a subset of A which does not equal to A. Meaning to say if B is a proper subset of A then all elements of B are in A but A comprises a minimum of 1 element which is not present in B. For instance, if A = {5, 7, 9} then B = {5, 9}is a proper subset of A.

Q. What is an example of a set?

As a set is a collection of different objects that contain common property, an example of a set will be dog, deer, lion and mouse is all animals. So, when you consider them collectively, they are a set.

Q. What is the symbol of a set?

Sets are commonly denoted with a capital letter like A = {1, 2, 3, 4}. A set which contains no element is an empty or null set and we use { } or ∅ to denote this.

Customize your course in 30 seconds

Which class are you in.

• Venn Diagrams
• Operations on Sets
• Subsets and Supersets
• Types of Sets

One response to “Introduction to Sets”

sir can we prove all the set theorems using venn diagram ?

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Download the App

Reset password New user? Sign up

Existing user? Log in

Already have an account? Log in here.

• Joshua DeJong
• Aditya Virani
• Kristian Takvam
• Andrew Ellinor
• Jesse Nieminen
• Ashish Menon

For the computer science term, see Sets (ADT) .

A set is an unordered group of items (called elements ). For example, \(\{\text{cat}, \text{dog}, \text{fish}, \text{bird}\}\) is a set of animals, \(\{2,4,6,8,10\}\) is a set of even numbers, and \(\{a, b, c, d\}\) is a set of letters. Though sets are pretty simple data structures, they are important for understanding concepts in combinatorics, probability, and number theory.

If \(P=\{2, 5, 6, 3, 7\}\) and \(Q=\{1, 2, 3, 8, 9, 10\},\) which of the following Venn diagrams represents the relationship between the two sets?

Definition of a Set

Operations with sets, terminology.

A set is an unordered group of elements denoted by a sequence of items (separated by commas) between curly braces "\(\{\)" and "\(\}\)".

What does it mean to be unordered ? Sets are not organized in any particular way. For example, the set \(A = \{1,2,3,4,5\}\) appears to be the set of ordered numbers between 1 and 5, but this set is actually equivalent to \(B = \{2,3,1,5,4\}\). The order of elements in a set does not matter. Two sets are equal if they contain all of the same elements.

Repeated elements make no difference in a set. \(A = \{1,1,1,1\}\) is equal to \(B = \{1\}\). In fact, sets are generally not written to include repeated elements.

Which two sets are equivalent?

\(A = \{1,3,5,7,9\}\)

\(B = \{1,2,3,4,5,6\}\)

\(C = \{1,2,3,4,5\}\)

\(D = \{5,4,2,6,1,3\}\)

\(E = \{4,1,5,2,3,7\}\)

There are several useful operations one can use to combine, compare, and analyze sets.

Union: The union of two sets, denoted \( \cup\) (which is called a cup ), refers to the set of all the elements that are in at least one of the two sets. For example, \( \{1,2,3\} \cup \{3,4,5\} = \{1,2,3,4,5\}.\) In Boolean logic , union is expressed as a logical OR. Intersection: The intersection of two sets, denoted \( \cap\) (which is called a cap ), refers to the set of the elements that are in both sets. For example, \( \{1,2,3\} \cap \{3,4,5\} = \{3\}.\) In Boolean logic, intersection is expressed as a logical AND. Complement (Absolute): Denoted \( ^c\), the absolute complement refers to the set of all the elements that are not in a set. If we consider the universal set, \(U\), as the set of all integers, \( \{ 1, 2, 3 \}^c \) would represent all integers except for 1, 2, and 3. In Boolean logic, complement is expressed as a logical NOT. Complement (Relative): Relative complement, denoted \( \backslash \), refers to the set of elements that are in the first set but not in the second. For example, \( \{1,2,3\} \backslash \{3,4,5\} = \{1,2\}.\) Relative complement can also be expressed by the minus sign, and thus \(\{1,2,3\}-\{3,4,5\}=\{1,2\}.\) Symmetric Difference: Symmetric difference, denoted \( \triangle \), refers to the set of elements which are in one of the two sets but not both. For example, \( \{1,2,3\} \triangle \{3,4,5\} = \{1,2,4,5\}.\) In Boolean logic, symmetric difference is expressed as a logical XOR.

What is \( \{2,4,6\} \cup \{3,5,7\} ?\) The symbol \(\cup\) refers to the union of the two sets. Thus, \( \{2,4,6\} \cup \{3,5,7\} \) is \( \{2,3,4,5,6,7\}.\ _ \square \)

Give the answer for the following intersection:

\[\{5,3,2,6\} \cap \{7,1,6,2,8\}.\]

Give the answer for the following union:

\[ \{7,5,9\} \cup \{0,1,5\}.\]

Given the following two sets \[ \begin{align} A &= \{ 2, a^2-4a+7 \} \\ B &= \{ a+1, a^2+1, a^2-1 \}, \end{align} \] if \( A \cap B = \{4\} ,\) what is \(a?\) From \( A \cap B = \{4\}, \) we know that both sets \(A\) and \(B\) must have \(4\) as an element. Therefore, for set \(A\) we have \[ \begin{align} a^2-4a+7&=4 \\ (a-1)(a-3)&=0 \\ \Rightarrow a&= 1\text{ or }3. \end{align} \] If the value of \(a\) is 1, set \(B\) is \[ \begin{align} B &= \{a+1, a^2+1, a^2-1\} \\ &= \{1+1, 1^2+1, 1^2-1\} \\ &=\{ 2,2,0\} . \end{align} \] Then \( A \cap B = \{2\} \neq \{4\}. \) If the value of \(a\) is 3, set \(B\) is \[ \begin{align} B &= \{a+1, a^2+1, a^2-1\} \\ &= \{3+1, 3^2+1, 3^2-1\} \\ &=\{ 4,10,8\} . \end{align} \] Then \( A \cap B = \{4\}. \) Thus, the value of \(a\) that satisfies \( A \cap B = \{4\}\) is \(a=3.\ _ \square \)

What is \( \{2,4,6,8,10,12\} \triangle \{3,6,9,12,15\} ?\) The symbol \(\triangle\) denotes symmetric difference, which means the set of elements which are in one of the two sets but not both. Thus, \( \{2,4,6,8,10,12\} \triangle \{3,6,9,12,15\} \) is \( \{ 2,3,4,8,9,10,15 \} .\ _ \square \)

True or False?

\[\left|X^C \cup Y^C \cup Z^C\right| = \left|(X \cap Y \cap Z)^C\right|\]

De Morgan's laws are useful for showing equivalencies, transforming, and simplifying logical expressions.

• De Morgan's First Law: It states that the complement of the union of two sets is the intersection of their complements. For two sets \(A\) and \(B,\) \((A \cup B)^c=(A)^c\cap (B)^c.\) In Boolean logic, De Morgan's first law is expressed as \(\overline{A + B} = \overline{A} * \overline{B}.\)
• De Morgan's Second Law: It states that the complement of the intersection of two sets is the union of the complements. Specifically, \( (A \cap B)^c = A^c\cup B^c. \) In Boolean logic, De Morgan's second law is expressed as: \(\overline{A * B} = \overline{A} + \overline{B}\).

Given the following, use De Morgan's second law to determine \(A^c\cup B^c:\) \(U = \{1,2,3,4,5,6,7,8,9\},\) where \(U\) is the set of all possible values for this problem \(A=\{2,5,7,3,1\}\) \(B=\{9,8,7,5,2\}\). De Morgan's second law is \( (A \cap B)^c = A^c\cup B^c. \) Since we are looking for \(A^c\cup B^c \), we will first determine the left side of the equation, \( (A \cap B)^c\). To find \( (A \cap B)^c\), determine \( (A \cap B):\) \( (A \cap B)\) is the set of elements that are in both \(A\) and \(B,\) so \( (A \cap B) = \{2,5,7\}.\) To find \( (A \cap B)^c\), compare the elements in \( (A \cap B)\) with the elements in \(U\), and the elements in \( (A \cap B)^c\) will be the elements that are in \(U\) but not in \( (A \cap B)\). So, \( (A \cap B)^c = \{1,3,4,6,8,9\}\). We know from De Morgan's second law that \(A^c\cup B^c \) = \( (A \cap B)^c\). In other words, elements that are not in both \(A\) and \(B\) must either be missing from \(A\) or \(B\) (or both). Examine \( (A \cap B)^c = \{1,3,4,6,8,9\}\) for yourself to verify that elements in \( (A \cap B)^c\) are missing from either \(A\) or \(B\) or both. \(_\square\)

In a class of \(150\) students, \(90\%\) love singing, \(86\%\) love dancing, \(80\%\) love acting and \(74\%\) love studying. Then what is the minimum number of students who love all the mentioned activities?

Here are some important concepts and terms about sets:

Universal Set: Denoted \(U,\) a universal set is the set of all possible elements for a particular problem. For example, if a problem deals only with positive, nonzero integers, \(U = \{1,2,3,4, \dots\}\).

Empty/Null Set: Denoted by \(\{\}\) or \(\phi\), a set is said to be null or empty if it does not contain any elements. For example, if \(A\) is the set of all integers \(x\) that satisfy \(x^2=7,\) then the set \(A\) has no elements, and thus \(A=\phi.\)

Subsets : If every element of a set \(A\) is also a member of the set \(B,\) then we say that \(A\) is a subset of \(B.\) For example if \(A=\{1,2,3\}\) and \(B=\{5,4,3,2,1\},\) then \(A\) is a subset of \(B,\) or \(A \subset B.\) When two sets are equal, they are subsets of each other.

Cardinality : The cardinality of a set \(S,\) written as \(\lvert S\rvert,\) is the number of distinct elements in \(S.\) For example, if \(A\) is the set of all the letters in "Mississippi", then \(A=\{m,i,p,s\},\) and hence \(\lvert A\rvert=4.\)

Inclusion-Exclusion Principle: The inclusion-exclusion principle states that any two sets \(A\) and \(B\) satisfy \(\lvert A \cup B\rvert = \lvert A\rvert + \lvert B\rvert- \lvert A \cap B\rvert .\) In other words, to get the size of the union of sets \(A\) and \(B\), we first add (include) all the elements of \(A\), then we add (include) all the elements of \(B\), and then we remove (exclude) the elements in their intersection \(A \cap B\), since those elements were counted twice \((\)i.e. once for \(A\) and once for \(B).\) For a concrete example, let \(A=\{1,2,3,4,5\}\) and \(B=\{4,5,6,7,8\}\), which gives \(A \cap B=\{4,5\}\). Then \(\lvert A \rvert=5\), \(\lvert B \rvert=5\), and \(\lvert A \cap B \rvert=2\). By the inclusion-exclusion principle, \(\lvert A \cup B\rvert = \lvert A\rvert + \lvert B\rvert- \lvert A \cap B\rvert = 5 + 5 - 2 = 8 ,\) which we can verify directly by counting the elements of \(\lvert A \cup B\rvert =\{1,2,3,4,5,6,7,8\}.\) Note that the elements in the intersection (4 and 5) were counted once in \(A\) and once in \(B\), necessitating their exclusion.

For this problem, the universal set \(U\) is \[ U = \{ 1,2,3,4,5,6,7,8,9,10 \} ,\] and its three subsets \( A, B \) and \(C\) are as follows: \[ \begin{align} A &= \{ 1,2,3,4,5,6,7 \} \\ B &= \{ 2,6,8,9 \} \\ C &= \{ 9, 10 \}. \end{align} \] Then what is \( (A^{c} \cup B) \backslash C ?\) The symbol \(A^{c} \) means the set of all elements that are not in \(A.\) Since \( A = \{ 1,2,3,4,5,6,7 \}, \) the set \( A^{c} \) is \[ A^{c} = \{ 8,9,10\} .\] Then, \( A^{c} \cup B \) is \[ A^{c} \cup B = \{8,9,10\} \cup \{ 2,6,8,9 \} = \{ 2,6,8,9,10 \}. \] Therefore, \( (A^{c} \cup B) \backslash C \) is \[ (A^{c} \cup B) \backslash C = \{ 2,6,8,9,10 \} \backslash \{ 9, 10 \} = \{ 2,6,8 \}.\ _\square\]

Problem Loading...

Note Loading...

Set Loading...

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

5.1: Sets and Operations on Sets

• Last updated
• Save as PDF
• Page ID 7060

• Ted Sundstrom
• Grand Valley State University via ScholarWorks @Grand Valley State University

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Before beginning this section, it would be a good idea to review sets and set notation, including the roster method and set builder notation , in Section 2.3 .

PREVIEW ACTIVITY \(\PageIndex{1}\): Set Operations

In Section 2.1 , we used logical operators (conjunction, disjunction, negation) to form new statements from existing statements. In a similar manner, there are several ways to create new sets from sets that have already been defined. In fact, we will form these new sets using the logical operators of conjunction (and), disjunction (or), and negation (not). For example, if the universal set is the set of natural numbers \(N\) and

\[A = \{1, 2, 3, 4, 5, 6\} \quad \text{ and } \quad B = \{1, 3, 5, 7, 9\},\]

• The set consisting of all natural numbers that are in \(A\) and are in \(B\) is the set \(\{1, 3, 5\}\);
• The set consisting of all natural numbers that are in \(A\) or are in \(B\) is the set \(\{1, 2, 3, 4, 5, 6, 7, 9\}\); and
• The set consisting of all natural numbers that are in \(A\) and are not in \(B\) is the set \(\{2, 4, 6\}.\)

These sets are examples of some of the most common set operations, which are given in the following definitions.

Definition: intersection

Let \(A\) and \(B\) be subsets of some universal set \(U\). The intersection of \(A\) and \(B\), written \(A \cap B\) and read “\(A\) intersect \(B\),” is the set of all elements that are in both \(A\) and \(B\). That is,

\[A \cap B = \{x \in U \, | \, x \in A \text{ and } x \in B\}.\]

The union of \(A\) and \(B\), written \(A \cup B\) and read “\(A\) union \(B\),” is the set of all elements that are in \(A\) or in \(B\). That is,

\[A \cup B = \{x \in U \, | \, x \in A \text{ or } x \in B\}.\]

Definition: complement

Let \(A\) and \(B\) be subsets of some universal set \(U\). The set difference of \(A\) and \(B\), or relative complement of \(B\) with respect to \(A\), written \(A -B\) and read “\(A\) minus \(B\)” or “the complement of \(B\) with respect to \(A\),” is the set of all elements in \(A\) that are not in \(B\). That is,

\[A - B = \{x \in U \, | \, x \in A \text{ and } x \notin B\}.\]

The complement of the set \(A\), written \(A^c\) and read “the complement of \(A\),” is the set of all elements of \(U\) that are not in \(A\). That is,

\[A^c = \{x \in U \, | \, x \notin A\}.\]

For the rest of this preview activity, the universal set is \(U = \{0, 1, 2, 3, ..., 10\}\), and we will use the following subsets of \(U\):

\[A = \{0, 1, 2, 3, 9\} \quad \text{ and } \quad B = \{2, 3, 4, 5, 6\},\]

So in this case, \(A \cap B = \{x \in U \, | \, x \in A \text{ and } x \in B\} = \{2, 3\}.\) Use the roster method to specify each of the following subsets of \(U\).

• \(A \cup B\)

We can now use these sets to form even more sets. For example,

\[A \cap B^c = \{0, 1, 2, 3, 9\} \cap \{0, 1, 7, 8, 9, 10\} = \{0, 1, 9\}.\]

Use the roster method to specify each of the following subsets of \(U\).

• \(A \cup B^c\)
• \(A^c \cap B^c\)
• \(A^c \cup B^c\)
• \((A \cap B)^c\)

Preview Activity \(\PageIndex{2}\): Venn Diagrams for Two Sets

In Preview Activity \(\PageIndex{1}\), we worked with verbal and symbolic definitions of set operations. However, it is also helpful to have a visual representation of sets. Venn diagrams are used to represent sets by circles (or some other closed geometric shape) drawn inside a rectangle. The points inside the rectangle represent the universal set \(U\), and the elements of a set are represented by the points inside the circle that represents the set. For example, Figure \(\PageIndex{1}\) is a Venn diagram showing two sets.

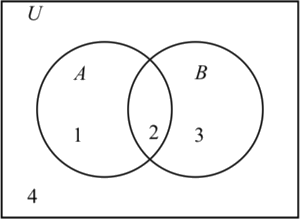
Figure \(\PageIndex{1}\) : Venn Diagram for Two Sets

In Figure \(\PageIndex{1}\), the elements of \(A\) are represented by the points inside the left circle, and the elements of \(B\) are represented by the points inside the right circle. The four distinct regions in the diagram are numbered for reference purposes only. (The numbers do not represent elements in a set.) The following table describes the four regions in the diagram.

We can use these regions to represent other sets. For example, the set \(A \cup B\) is represented by regions 1, 2, and 3 or the shaded region in Figure \(\PageIndex{2}\).

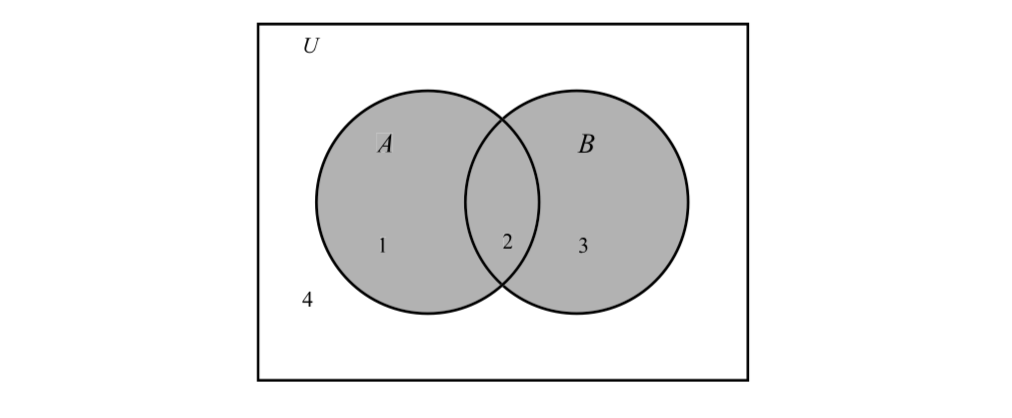
Figure \(\PageIndex{2}\): Venn Diagram for \(A \cup B\)

Let \(A\) and \(B\) be subsets of a universal set \(U\). For each of the following, draw a Venn diagram for two sets and shade the region that represent the specified set. In addition, describe the set using set builder notation.

• \(A^c \cup B\)
• \((A \cup B) - (A \cap B)\)

Set Equality, Subsets, and Proper Subsets

In Section 2.3 , we introduced some basic definitions used in set theory, what it means to say that two sets are equal and what it means to say that one set is a subset of another set. We need one more definition.

Definition: proper subset

Let \(A\) and \(B\) be two sets contained in some universal set \(U\). The set \(A\) is a proper subset of \(B\) provided that \(A \subseteq B\) and \(A \ne B\). When \(A\) is a proper subset of \(B\), we write \(A \subset B\).

One reason for the definition of proper subset is that each set is a subset of itself. That is,

If \(A\) is a set, then \(A \subseteq A\)

However, sometimes we need to indicate that a set \(X\) is a subset of \(Y\) but \(X \ne Y\). For example, if

\(X = \{1, 2\}\) and \(Y = \{0, 1, 2, 3\}.\)

then \(X \subset Y\). We know that \(X \subseteq Y\) since each element of \(X\) is an element of \(Y\), but \(X \ne Y\) since \(0 \in Y\) and \(0 \notin X\). (Also, \(3 \in Y\) and \(3 \notin X\).) Notice that the notations \(A \subset B\) and \(A \subseteq B\) are used in a manner similar to inequality notation for numbers (\(a < b\) and \(a \le b\)).

It is often very important to be able to describe precisely what it means to say that one set is not a subset of the other. In the preceding example, \(Y\) is not a subset of \(X\) since there exists an element of \(Y\) (namely, 0) that is not in \(X\).

In general, the subset relation is described with the use of a universal quantifier since \(A \subseteq B\) means that for each element \(x\) of \(U\), if \(x \in A\), then \(x \in B\). So when we negate this, we use an existential quantifier as follows:

\[\begin{array} {rcl} {A \subseteq B} &\text{means} & {(\forall x \in U)[(x \in A) \to (x \in B)].} \\ {A \not\subseteq B} &\text{means} & {\urcorner(\forall x \in U)[(x \in A) \to (x \in B)]} \\ {} & & {(\exists x \in U) \urcorner [(x \in A) \to (x \in B)]} \\ {} & & {(\exists x \in U) [(x \in A) \wedge (x \notin B)].} \end{array}\]

So we see that \(A \not\subseteq B\) means that there exists an \(x\) in \(U\) such that \(x \in A\) and \(x \notin B\).

Notice that if \(A = \emptyset\), then the conditional statement, “For each \(x \in U\), if \(x \in \emptyset\), then \(x \in B\)” must be true since the hypothesis will always be false. Another way to look at this is to consider the following statement:

\(\emptyset \not\subseteq B\) means that there exists an \(x \in \emptyset\) such that \(x \notin B\).

However, this statement must be false since there does not exist an \(x\) in \(\emptyset\). Since this is false, we must conclude that \(\emptyset \subseteq B\). Although the facts that \(\emptyset \subseteq B\) and \(B \subseteq B\) may not seem very important, we will use these facts later, and hence we summarize them in Theorem 5.1.

Theorem 5.1

For any set \(B\), \(\emptyset \subseteq B\) and \(B \subseteq B\).

In Section 2.3 , we also defined two sets to be equal when they have precisely the same elements. For example,

\(\{x \in \mathbb{R} \, | \, x^ = 4\} = \{-2, 2\}\).

If the two sets \(A\) and \(B\) are equal, then it must be true that every element of \(A\) is an element of \(B\), that is, \(A \subseteq B\), and it must be true that every element of \(B\) is an element of \(A\), this is, \(B \subseteq A\). Conversely, if \(A \subseteq B\) and \(B \subseteq A\), then \(A\) and \(B\) must have precisely the same elements. This gives us the following test for set equality:

Theorem 5.2

Let \(A\) and \(B\) be subsets of some universal set \(U\). Then \(A = B\) if and only if \(A \subseteq B\) and \(B \subseteq A\).

Progress Check 5.3: Using Set Notation

Let the universal set be \(U = \{1, 2, 3, 4, 5, 6\}\), and let

\(A = \{1, 2, 4\}\), \(B = \{1, 2, 3, 5\}\), \(C = \{x \in U \, | \, x^2 \le 2\}\).

In each of the following, fill in the blank with one or more of the symbols \(\subset\), \(\subseteq\), =, \(\ne\), \(\in\) or \(\notin\) so that the resulting statement is true. For each blank, include all symbols that result in a true statement. If none of these symbols makes a true statement, write nothing in the blank.

\[\begin{array} {rclrcl} {A} &\text{_____________} & {B\quad \quad \quad } {\emptyset} &\text{_____________}& {A} \\ {5} &\text{_____________} & {B\quad \quad \ \ \ } {\{5\}} &\text{_____________} & {B} \\ {A} &\text{_____________} & {C\quad \ \ \ \ \ \ } {\{1, 2\}} &\text{_____________} & {C} \\ {\{1, 2\}} &\text{_____________} & {A\quad \ \ \ } {\{4, 2, 1\}} &\text{_____________} & {A} \\ {6} &\text{_____________} & {A\quad \quad \quad } {B} &\text{_____________} & {\emptyset} \end{array} \nonumber\]

Add texts here. Do not delete this text first.

More about Venn Diagrams

In Preview Activity \(\PageIndex{2}\), we learned how to use Venn diagrams as a visual representation for sets, set operations, and set relationships. In that preview activity, we restricted ourselves to using two sets. We can, of course, include more than two sets in a Venn diagram. Figure \(\PageIndex{3}\) shows a general Venn diagram for three sets (including a shaded region that corresponds to \(A \cap C\)).

In this diagram, there are eight distinct regions, and each region has a unique reference number. For example, the set A is represented by the combination of regions 1, 2, 4, and 5, whereas the set C is represented by the combination of regions 4, 5, 6, and 7. This means that the set \(A \cap C\) is represented by the combination of regions 4 and 5. This is shown as the shaded region in Figure \(\PageIndex{3}\).

Finally, Venn diagrams can also be used to illustrate special relationships be- tween sets. For example, if \(A \subseteq B\), then the circle representing \(A\) should be completely contained in the circle for \(B\). So if \(A \subseteq B\), and we know nothing about

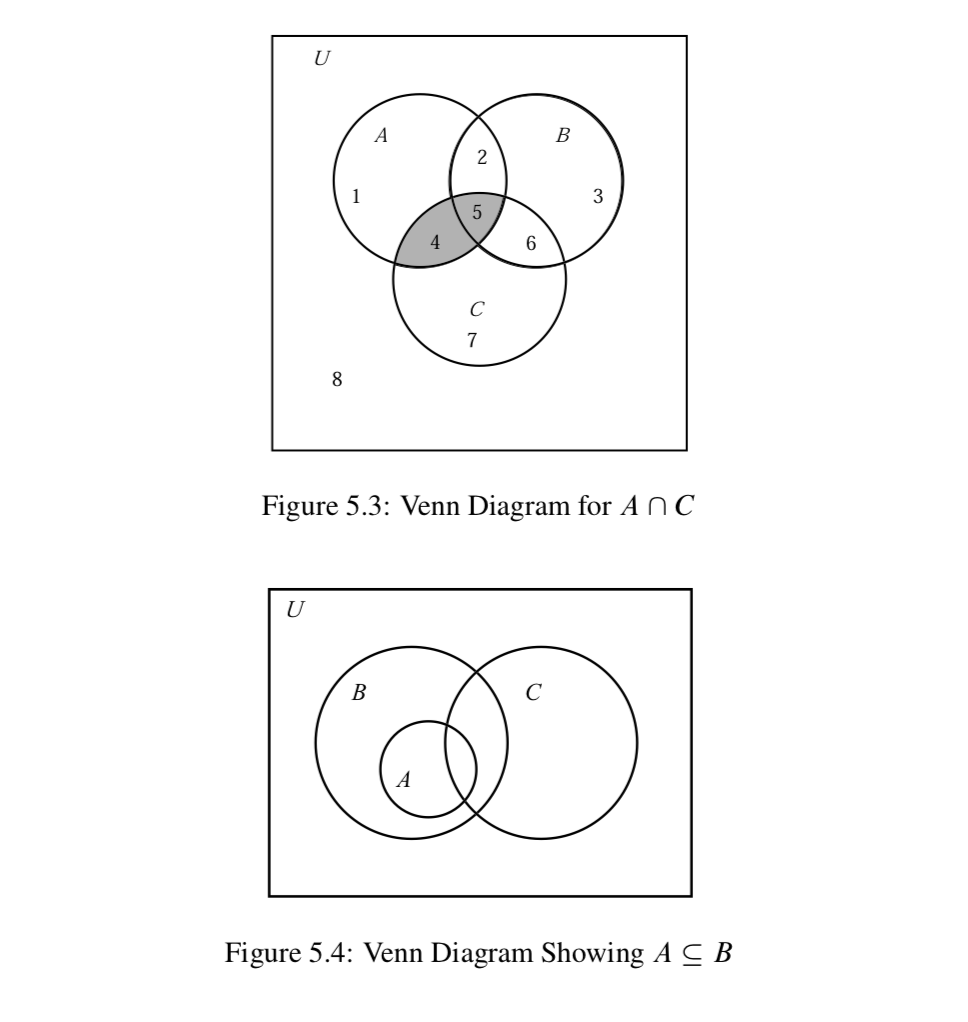
any relationship between the set \(C\) and the sets \(A\) and \(B\), we could use the Venn diagram shown in Figure \(\PageIndex{4}\).

Progress Check 5.4: Using Venn Diagrams

Let \(A\), \(B\), and \(C\) be subsets of a universal set \(U\).

• For each of the following, draw a Venn diagram for three sets and shade the region(s) that represent the specified set. (a) \((A \cap B) \cap C\) (b) \((A \cap B) \cup C\) (c) \((A^c \cup B)\) (d) \(A^c \cap (B \cup C)\)
• Draw the most general Venn diagram showing \(B \subseteq (A \cup C)\).
• Draw the most general Venn diagram showing \(A \subseteq (B^c \cup C)\).

The Power Set of a Set

The symbol 2 is used to describe a relationship between an element of the universal set and a subset of the universal set, and the symbol \(\subseteq\) is used to describe a relationship between two subsets of the universal set. For example, the number 5 is an integer, and so it is appropriate to write \(5 \in \mathbb{Z}\). It is not appropriate, however, to write \(5 \subseteq \mathbb{Z}\) since 5 is not a set. It is important to distinguish between 5 and {5}. The difference is that 5 is an integer and {5} is a set consisting of one element. Consequently, it is appropriate to write \(\{5\} \subseteq \mathbb{Z}\), but it is not appropriate to write \(\{5\} \in \mathbb{Z}\). The distinction between these two symbols (5 and {5}) is important when we discuss what is called the power set of a given set.

Definition: power set

If \(A\) is a subset of a universal set \(U\), then the set whose members are all the subsets of \(A\) is called the power set of \(A\). We denote the power set of \(A\) by \(\mathcal{P}(A)\). Symbolically, we write

\(\mathcal{P}(A) = \{X \subseteq U \, | \, X \subseteq A\}.\)

That is, \(X \in \mathcal{P}(A)\) if and only if \(X \subseteq A\).

When dealing with the power set of \(A\), we must always remember that \(\emptyset \subseteq A\) and \(A \subseteq A\). For example, if \(A = \{a, b\}\), then the subsets of \(A\) are

\[\emptyset, \{a\}, \{b\}, \{a,b\}.\]

We can write this as

\(\mathcal{P}(A) = \{\emptyset, \{a\}, \{b\}, \{a,b\}\}.\)

Now let \(B = \{a, b, c\}\). Notice that \(B = A \cup \{c\}\). We can determine the subsets of \(B\) by starting with the subsets of \(A\) in (5.1.10). We can form the other subsets of \(B\) by taking the union of each set in (5.1.10) with the set \(\{c\}\). This gives us the following subsets of \(B\).

\[\{c\}, \{a, c\}, \{b, c\}, \{a, b, c\}.\]

So the subsets of \(B\) are those sets in (5.1.10) combined with those sets in (5.1.11). That is, the subsets of \(B\) are

\[\emptyset, \{a\}, \{b\}, \{a,b\}, \{c\}, \{a, c\}, \{b, c\}, \{a, b, c\},\]

which means that

\(\mathcal{P}(B) = \{\emptyset, \{a\}, \{b\}, \{a,b\}, \{c\}, \{a, c\}, \{b, c\}, \{a, b, c\}\}.\)

Notice that we could write

\(\{a, c\} \subseteq B\) or that \(\{a, c\} \in \mathcal{P}(B)\).

Also, notice that \(A\) has two elements and \(A\) has four subsets, and \(B\) has three elements and \(B\) has eight subsets. Now, let \(n\) be a nonnegative integer. The following result can be proved using mathematical induction. (See Exercise 17).)

Theorem 5.5.

Let \(n\) be a nonnegative integer and let \(T\) be a subset of some universal set. If the set \(T\) has \(n\) elements, then the set \(T\) has \(2^n\) subsets. That is, \(\mathcal{P}(T)\) has \(2^n\) elements.

The Cardinality of a Finite Set

In our discussion of the power set, we were concerned with the number of elements in a set. In fact, the number of elements in a finite set is a distinguishing characteristic of the set, so we give it the following name.

Definition: cardinality

The number of elements in a finite set \(A\) is called the cardinality of \(A\) and is denoted by card(\(A\))

card(\(\emptyset\)) = 0;

card({\(a\), \(b\)}) = 2

card(\(\mathcal{P}(\{a, b\})\)) = 4

Theoretical Note : There is a mathematical way to distinguish between finite and infinite sets, and there is a way to define the cardinality of an infinite set. We will not concern ourselves with this at this time. More about the cardinality of finite and infinite sets is discussed in Chapter 9 .

Standard Number Systems

We can use set notation to specify and help describe our standard number systems. The starting point is the set of natural numbers , for which we use the roster method.

\(\mathbb{N} = \{1, 2, 3, 4, ...\}\)

The integers consist of the natural numbers, the negatives of the natural numbers, and zero. If we let \(\mathbb{N} ^- = \{..., -4, -3, -2, -1\}\), then we can use set union and write

\(\mathbb{Z} = \mathbb{N} ^- \cup \{0\} \cup \mathbb{N}\).

So we see that \(\mathbb{N} \subseteq \mathbb{Z}\), and in fact, \(\mathbb{N} \subset \mathbb{Z}\).

We need to use set builder notation for the set \(\mathbb{Q}\) of all rational numbers , which consists of quotients of integers.

\(\mathbb{Q} = \Big\{\dfrac{m}{n}\ |\ m, n \in \mathbb{Z} \text{and } n \ne 0\Big\}\)

Since any integer \(n\) can be written as \(n = \dfrac{n}{1}\), we see that \(\mathbb{Z} \subseteq \mathbb{Q}\).

We do not yet have the tools to give a complete description of the real numbers. We will simply say that the real numbers consist of the rational numbers and the irrational numbers . In effect, the irrational numbers are the complement of the set of rational numbers \(\mathbb{Q}\) in \(\mathbb{R}\). So we can use the notation \(\mathbb{Q} ^c = \{x \in \mathbb{R}\ |\ x \notin \mathbb{Q}\}\) and write

\(\mathbb{R} = \mathbb{Q} \cup \mathbb{Q} ^c\) and \(\mathbb{Q} \cap \mathbb{Q} ^c = \emptyset\).

A number system that we have not yet discussed is the set of complex numbers . The complex numbers, \(\mathbb{C}\), consist of all numbers of the form \(a + bi\), where \(a, b \in \mathbb{R}\) and \(i = \sqrt{-1}\) (or \(i^2 = -1\)). That is,

\(\mathbb{C} = \{a + bi\ |\ a,b \in \mathbb{R} \text{and } i = sqrt{-1}\}.\)

We can add and multiply complex numbers as follows: If \(a, b, c, d \in \mathbb{R}\), then

\[\begin{array} {rcl} {(a + bi) + (c + di)} &= & {(a + c) + (b + d)i, \text{ and}} \\ {(a + bi)(c + di)} &= & {ac + adi + bci + bdi^2} \\ {} &= & {(ac - bd) + (ad + bc)i.} \end{array}\]

Exercises for Section 5.1

• Assume the universal set is the set of real numbers. Let \(A = \{-3, -2, 2, 3\}.\) \(B = \{x \in \mathbb{R}\ |\ x^2 = 4 \text{ or } x^2 = 9\},\) \(C = \{x \in \mathbb{R}\ |\ x^2 + 2 = 0\},\) \(D = \{x \in \mathbb{R}\ |\ x > 0\}.\) Respond to each of the following questions. In each case, explain your answer. (a) Is the set \(A\) equal to the set \(B\)? (b) Is the set \(A\) a subset of the set \(B\)? (c) Is the set \(C\) equal to the set \(D\)? (d) Is the set \(C\) a subset of the set \(D\)? (e) Is the set \(A\) a subset of the set \(D\)?
• (a) Explain why the set \(\{a, b\}\) is equal to the set \(\{b, a\}\). (b) Explain why the set \(\{a, b, b, a, c\}\) is equal to the set \(\{b, c, a\}\).
• Assume that the universal set is the set of integers. Let \(A = \{-3, -2, 2, 3\}.\) \(B = \{x \in \mathbb{Z}\ |\ x^2 \le 9\},\) \(C = \{x \in \mathbb{Z}\ |\ x \ge -3\},\) \(D = \{1, 2, 3, 4\},\) In each of the following, fill in the blank with one or more of the symbols \(\subset\), \(\subseteq\), \(\not\subseteq\), \(=\), \(\ne\), \(\in\) or \(\notin\) so that the resulting statement is true. For each blank, include all symbols that result in a true statement. If none of these symbols makes a true statement, write nothing in the blank. \[\begin{array} {rclrcl} {A} &\text{_____________} & {B\quad \quad \quad \ \ \ \ \ } {\emptyset} &\text{_____________}& {A} \\ {5} &\text{_____________} & {C\quad \quad \quad \ \ } {\{5\}} &\text{_____________} & {C} \\ {A} &\text{_____________} & {C\quad \quad \ \ \ \ \ } {\{1, 2\}} &\text{_____________} & {B} \\ {\{1, 2\}} &\text{_____________} & {A\quad \quad \ \ } {\{3, 2, 1\}} &\text{_____________} & {D} \\ {4} &\text{_____________} & {B\quad \quad \quad \ \ \ \ \ } {D} &\text{_____________} & {\emptyset} \\ {\text{card} (A)} &\text{_____________} & {\text{card} (D)\quad \ } {\text{card} (A)} &\text{_____________} & {\text{card} (B)} \\ {A} &\text{_____________} & {\mathcal{P}(A)\quad \quad \quad } {A} &\text{_____________} & {\mathcal {P} (B)} \end{array}\]
• Write all of the proper subset relations that are possible using the sets of numbers \(\mathbb{N}\), \(\mathbb{Z}\), \(\mathbb{Q}\), and \(\mathbb{R}\).
• For each statement, write a brief, clear explanation of why the statement is true or why it is false. (a) The set \(\{a, b\}\) is a subset of \(\{a, c, d, e\}\). (b) The set \(\{-2, 0, 2\}\) is equal to \(\{x \in \mathbb{Z} \, | \, x\) is even and \(x^2 < 5\}.\) (c) The empty set \(\emptyset\) is a subset of \(\{1\}.\) (d) If \(A = \{a, b\}\), then the set \(\{a\}\) is a subset of \(\mathcal{P} (A)\).
• Use the definitions of set intersection, set union, and set difference to write useful negations of these definitions. That is, complete each of the following sentences (a) \(x \notin A \cap B\) if and only if ... . (b) \(x \notin A \cup B\) if and only if ... . (c) \(x \notin A - B\) if and only if ... .

Use the roster method to list all of the elements of each of the following sets. (a) \(A \cap B\) (b) \(A \cup B\) (c) \((A \cup B)^c\) (d) \(A^c \cap B^c\) (e) \((A \cup B) \cap C\) (f) \(A \cap C\) (g) \(B \cap C\) (h) \((A \cap C) \cup (B \cap C)\) (i) \(B \cap D\) (j) \((B \cap D)^c\) (k) \(A - D\) (l) \(B - D\) (m) \((A - D) \cup (B - D)\) (n) \((A \cup B) - D\)

• Let \(U = \mathbb{N}\), and let \(A =\{x \in \mathbb{N}\ |\ x \ge 7\},\) \(B =\{x \in \mathbb{N}\ |\ x \text{ is odd}\},\) \(C =\{x \in \mathbb{N}\ |\ x \text{ is a multiple of } 3\},\) \(D =\{x \in \mathbb{N}\ |\ x \text{ is even}\},\) Use the roster method to list all of the elements of each of the following sets. (a) \(A \cap B\) (b) \(A \cup B\) (c) \((A \cup B)^c\) (d) \(A^c \cap B^c\) (e) \((A \cup B) \cap C\) (f) \((A \cap C) \cup (B \cap C)\) (g) \(B \cap D\) (h) \((B \cap D)^c\) (i) \(A - D\) (j) \(B - D\) (k) \((A - D) \cup (B - D)\) (l) \((A \cup B) - D\)
• let \(P\), \(Q\), \(R\), and \(S\), be subsets of a universal set \(U\), Assume that \((P - Q) \subseteq (R \cap S)\). (a) Complete the following sentence: For each \(x \in U\), if \(x \in (P - Q)\), then ... . (b) Write a useful negation of the statement in Part (9a). (c) Write the contrapositive of the statement in Part (9a).
• Let \(U\) be the universal set. Consider the following statement: For all \(A\), \(B\), and \(C\) that are subsets of \(U\), if \(A \subseteq B\), then \(B^c \subseteq A^c\). (a) Identify three conditional statements in the given statement. (b) Write the contrapositive of this statement. (c) Write the negation of this statement.
• Let \(A\), \(B\), and \(C\) be subsets of some universal sets \(U\). Draw a Venn diagram for each of the following situations. (a) \(A \subseteq C\) (b) \(A \cap B = \emptyset\) (c) \(A \not\subseteq B\), \(B \not\subseteq A\), \(C \subseteq A\), and \(C \not\subseteq B\) (d) \(A \subseteq B\), \(C \subseteq B\), and \(A \cap C = \emptyset\)
• Let \(A\), \(B\), and \(C\) be subsets of some universal sets \(U\). For each of the following, draw a general Venn diagram for the three sets and then shade the indicated region. (a) \(A \cap B\) (b) \(A \cap C\) (c) \((A \cap B) \cup (A \cap C)\) (d) \(B \cup C\) (e) \(A \cap (B \cup C)\) (f) \((A \cap B) - C\)
• We can extend the idea of consecutive integers (See Exercise (2) in Section 3.5) to represent four consecutive integers as \(m\), \(m + 1\), \(m + 2\), and \(m + 3\), where \(m\) is an integer. There are other ways to represent four consecutive integers. For example, if \(k \in \mathbb{Z}\), then \(k - 1\), \(k\), \(k + 1\), and \(k + 2\) are four consecutive integers. (a) Prove that for each \(n \in \mathbb{Z}\), \(n\) is the sum of four consecutive integers if and only if \(n \equiv 2\) (mod 4). (b) Use set builder notation or the roster method to specify the set of integers that are the sum of four consecutive integers. (c) Specify the set of all natural numbers that can be written as the sum of four consecutive natural numbers. (d) Prove that for each \(n \in \mathbb{Z}\), \(n\) is the sum of eight consecutive integers if and only if \(n \equiv 4\) (mod 8). (e) Use set builder notation or the roster method to specify the set of integers that are the sum of eight consecutive integers. (f) Specify the set of all natural numbers can be written as the sum of eight consecutive natural numbers.
• One of the properties of real numbers is the so-called Law of Trichotomy , which states that if \(a, b \in \mathbb{R}\), then exactly one of the following is true:
• \(a < b\);
• \(a > b\). Is the following proposition concerning sets true or false? Either provide a proof that it is true or a counterexample showing it is false. If A and B are subsets of some universal set, then exactly one of the following is true:
• \(A \subseteq B\);
• \(B \subseteq A\).

Explorations and Activities

15. Intervals of Real Numbers. In previous mathematics courses, we have frequently used subsets of the real numbers called intervals. There are some common names and notations for intervals. These are given in the following table, where it is assumed that a and b are real numbers and \(a < b\).

(a) Is \((a, \, b)\) a proper subset of \((a, \, b]\)? Explain. (b) Is \([a, \, b]\) a subset of \((a, \,+ \infty)\)? Explain. (c) Use interval notation to describe i. the intersection of the interval \([-3, \, 7]\) with the interval \((5, 9];\) ii. the union of the interval \([-3, 7]\) with the interval \((5, 9];\) iii. the set difference \([-3, 7] - (5, 9].\)

(d) Write the set {\(x \in \mathbb{R} \, | \, |x| \le 0.01\)} using interval notation. (e) Write the set {\(x \in \mathbb{R} \, | \, |x| > 2\)} as the union of two intervals.

16. More Work with Intervals . For this exercise, use the interval notation described in Exercise 15. (a) Determine the intersection and union of \([2, 5]\) and \([-1, \, + \infty).\) (b) Determine the intersection and union of \([2, 5]\) and \([3.4, \, + \infty).\) (c) Determine the intersection and union of \([2, 5]\) and \([7, \, + \infty). \) Now let \(a\), \(b\) and \(c\) be real numbers with \(a < b\). (d) Explain why the intersection of \([a, \, b]\) and \([c, \, + \infty)\) is either a closed interval, a set with one element, or the empty set. (e)Explain why the union of \([a, \, b]\) and \([c, \,+ \infty)\) is either a closed ray or the union of a closed interval and a closed ray.

17. Proof of Theorem 5.5. To help with the proof by induction of Theorem 5.5, we first prove the following lemma. (The idea for the proof of this lemma was illustrated with the discussion of power set after the definition on page 222.)

Let \(A\) and \(B\) be subsets of some universal set. If \(A = B \cup \{x\}\), where \(x \notin B\), then any subset of \(A\) is either a subset of \(B\) or a set of the form \(C \cup \{x\}\), where \(C\) is a subset of \(B\).

Let \(A\) and \(B\) be subsets of some universal set, and assume that \(A = B \cup \{x\}\) where \(x \notin B\). Let \(Y\) be a subset of \(A\). We need to show that \(Y\) is a subset of \(B\) or that \(Y = C \cup \{x\}\), where \(C\) is some subset of \(B\). There are two cases to consider: (1) \(x\) is not an element of \(Y\), and (2) \(x\) is an element of \(Y\).

Case 1: Assume that \(x \notin Y\). Let \(y \in Y\). Then. \(y \in A\) and \(y \ne x\). Since

\(A = B \cup \{x\}\),

this means that \(y\) must be in \(B\). Therefore, \(Y \subseteq B\).

Case 2: Assume that \(x \in Y\). In this case, let \(C = Y - \{x\}\). Then every element of \(C\) is an element of \(B\). Hence, we can conclude that \(C \subseteq B\) and that \(Y = C \cup \{x\}\).

Cases (1) and (2) show that if \(Y \subseteq A\), then \(Y \subseteq B\) or \(Y = C \cup \{x\}\), where \(C \subseteq B\).

To begin the induction proof of Theorem 5.5, for each nonnegative integer \(n\), we let \(P(n)\) be, “If a finite set has exactly \(n\) elements, then that set has exactly \(2^n\) subsets.” (a) Verify that \(P(0)\) is true. (This is the basis step for the induction proof.) (b) Verify that \(P(1)\) and \(P(2)\) are true. (c) Now assume that \(k\) is a nonnegative integer and assume that \(P(k)\) is true. That is, assume that if a set has \(k\) elements, then that set has \(2^k\) subsets. (This is the inductive assumption for the induction proof.) Let \(T\) be a subset of the universal set with card\((T) = k + 1\), and let \(x \in T\). Then the set \(B = T - \{x\}\) has \(k\) elements. Now use the inductive assumption to determine how many subsets \(B\) has. Then use Lemma 5.6 to prove that \(T\) has twice as many subsets as \(B\). This should help complete the inductive step for the induction proof.

Set Symbols

A set is a collection of things, usually numbers. We can list each element (or "member") of a set inside curly brackets like this:

Common Symbols Used in Set Theory

Symbols save time and space when writing. Here are the most common set symbols

In the examples C = {1, 2, 3, 4} and D = {3, 4, 5}

Representation of a Set

In representation of a set the following three methods are commonly used:

(i) Statement form method

(ii) Roster or tabular form method

(iii) Rule or set builder form method

1. Statement form:

In this, well-defined description of the elements of the set is given and the same are enclosed in curly brackets.  For example:

(i) The set of odd numbers less than 7 is written as:  {odd numbers less than 7}.  (ii) A set of football players with ages between 22 years to 30 years.

(iii) A set of numbers greater than 30 and smaller than 55.

(iv) A set of students in class VII whose weights are more than your weight.

2. Roster form or tabular form:

In this, elements of the set are listed within the pair of brackets { } and are separated by commas. For example:

(i) Let N denote the set of first five natural numbers.

Therefore, N = {1, 2, 3, 4, 5}         → Roster Form (ii) The set of all vowels of the English alphabet.

Therefore, V = {a, e, i, o, u}         → Roster Form (iii) The set of all odd numbers less than 9.

Therefore, X = {1, 3, 5, 7}         → Roster Form (iv)  The set of all natural number which divide 12.

Therefore, Y = {1, 2, 3, 4, 6, 12}         → Roster Form

(v) The set of all letters in the word MATHEMATICS.

Therefore, Z = {M, A, T, H, E, I, C, S}        → Roster Form

(vi) W is the set of last four months of the year.

Therefore, W = {September, October, November, December}        → Roster Form

The order in which elements are listed is immaterial but elements must not be repeated.

3. Set builder form:

In this, a rule, or the formula or the statement is written within the pair of brackets so that the set is well defined. In the set builder form, all the elements of the set, must possess a single property to become the member of that set. In this form of representation of a set, the element of the set is described by using a symbol ‘x’ or any other variable followed by a colon The symbol ‘:‘ or ‘|‘ is used to denote such that and then we write the property possessed by the elements of the set and enclose the whole description in braces. In this, the colon stands for ‘such that’ and braces stand for ‘set of all’. For example: 

(i) Let P is a set of counting numbers greater than 12; the set P in set-builder form is written as :

                P = {x : x is a counting number and greater than 12}                                                  or                 P = {x | x is a counting number and greater than 12}

This will be read as, 'P is the set of elements x such that x is a counting number and is greater than 12'.

The symbol ':' or '|' placed between 2 x's stands for such that.

(ii) Let A denote the set of even numbers between 6 and 14. It can be written in the set builder form as;  A = {x|x is an even number, 6 < x < 14}  or  A = {x : x ∈ P, 6 < x < 14 and P is an even number}  (iii) If X = {4, 5, 6, 7} . This is expressed in roster form.  Let us express in set builder form.  X = {x : x is a natural number and 3 < x < 8}  (iv) The set A of all odd natural numbers can be written as  A = {x : x is a natural number and x = 2n + 1 for n ∈ W} 

Solved example using the three methods of representation of a set:

The set of integers lying between -2 and 3.  Statement form:  {I is a set of integers lying between -2 and 3}  Roster form:  I = {-1, 0, 1, 2}  Set builder form:  I = {x : x ∈ I, -2 < x < 3} 

● Set Theory

● Objects Form a Set

● Elements of a Set

● Properties of Sets

● Representation of a Set

● Different Notations in Sets

● Standard Sets of Numbers

● Types of Sets

● Pairs of Sets

● Subsets of a Given Set

● Operations on Sets

● Union of Sets

● Intersection of Sets

● Difference of two Sets

● Complement of a Set

● Cardinal number of a set

● Cardinal Properties of Sets

● Venn Diagrams

7th Grade Math Problems

8th Grade Math Practice From Representation of a Set to HOME PAGE

Didn't find what you were looking for? Or want to know more information about Math Only Math . Use this Google Search to find what you need.

New! Comments

• Preschool Activities
• Kindergarten Math
• 1st Grade Math
• 2nd Grade Math
• 3rd Grade Math
• 4th Grade Math
• 5th Grade Math
• 6th Grade Math
• 7th Grade Math
• 8th Grade Math
• 9th Grade Math
• 10th Grade Math
• 11 & 12 Grade Math
• Concepts of Sets
• Probability
• Boolean Algebra
• Math Coloring Pages
• Multiplication Table
• Cool Maths Games
• Math Flash Cards
• Online Math Quiz
• Math Puzzles
• Binary System
• Math Dictionary
• Conversion Chart
• Homework Sheets
• Math Problem Ans
• Free Math Answers
• Printable Math Sheet
• Funny Math Answers
• Employment Test
• Math Patterns
• Link Partners
• Privacy Policy

Recent Articles

Math Problem Answers | Solved Math Questions and Answers | Free Math

May 27, 24 06:47 PM

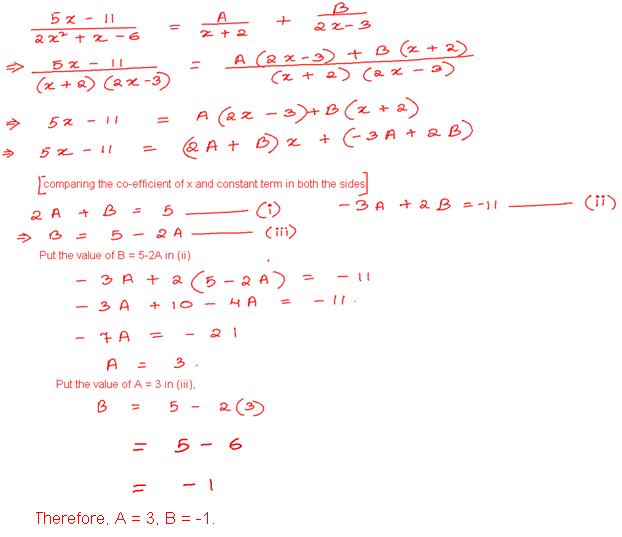
Properties of Whole Numbers | Closure Property | Commutative Property

May 27, 24 05:41 PM

Worksheet on Integers and the Number Line|Integers using a Number Line

May 27, 24 02:10 PM

Divide on a Number Line | Various Division Problems | Solved Examples

May 27, 24 11:43 AM

Multiplication using Number Lines | Multiplying on a Number Line

May 27, 24 11:28 AM

© and ™ math-only-math.com. All Rights Reserved. 2010 - 2024.

Definition and Representation of Set

Definition of a Set :

A set is a well-defined collection of distinct objects, i.e. the nature of the object is the same, or in other words the objects in a set may be anything: numbers , people, places, letters, etc. These objects are called the elements or members of the set.

Notation : A set is usually denoted by capital letters, i.e. $$A,B,C, \ldots ,X,Y,Z, \ldots $$ etc., and the elements are denoted by small letters, i.e. $$a,b,c, \ldots ,x,y,z, \ldots $$ etc.

If $$A$$ is any set and $$a$$ is the element of set $$A$$, then we write $$a \in A$$, read as $$a$$ belongs to $$A$$. If $$A$$ is any set and $$a$$ is not the element of set $$A$$, then we write $$a \notin A$$, read as $$a$$ does not belong to $$A$$.

Representation of Sets : There are three ways to represent a set.

I. Tabular Form: Listing all the elements of a set, separated by commas and enclosed within curly brackets $$\left\{ {} \right\}$$.

Example: $$A = \left\{ {1,2,3,4,5} \right\},\,\,B\left\{ {2,4,6, \cdots ,50} \right\},\,\,C\left\{ {1,3,5,7,9, \cdots } \right\}$$

II. Descriptive Form: State in words the elements of the set.

Example: $$A =$$ Set of first five natural numbers. $$B =$$ Set of positive even integers less than or equal to fifty. $$C =$$ Set of positive odd integers.

III. Set Builder Form: Writing in symbolic form the common characteristics shared by all the elements of the set.

Example: $$A = \left\{ {x:x \in \mathbb{N} \wedge x \leqslant 5} \right\}$$ N = Natural numbers $$A = \left\{ {x:x \in E \wedge 0 < y \leqslant 50} \right\}$$ E = Even numbers $$A = \left\{ {x:x \in O \wedge x > 0} \right\}$$ O = Odd numbers

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

• Trigonometry

Representation of a Set

• Math Doubts

A method of expressing a collection of well-defined objects is called the representation of a set .

Introduction

There is a purpose for introducing the concept of a set in mathematics. Hence, it is essential to express it in a special way in mathematics.

There are two different ways to express a set in mathematics.

Graphical representation

Mathematical representation.

Now, let’s understand the basic representation of a set from understandable examples.

In general, the objects are collected in closed packets. The same principle can also be used in set theory to represent the collection of well-defined objects. Therefore, a set can be represented graphically by a closed geometric shape.

There are several closed geometric shapes in geometry. Hence, a set can be represented by any one of the closed geometric shapes.

For example, a circle, a triangle, a square, or any other closed geometric shape.

There are two common problems in expressing the sets in graphical representation.

• Expressing the different sets in either a closed geometric shape or different closed geometric shapes confuse us, and it irritates us.
• It is not actually convenient for us to express a set more than once in the form of graphical representation in mathematics.

For overcoming the above two issues, the mathematical representation was introduced in set theory. In this method, we represent every set by a name and they are usually denoted by uppercase (or capital) letters.

For example, we have three sets and they are denoted by capital letters $A$, $B$ and $C$. They are called Set $A$, Set $B$ and Set $C$.

Advanced example

A set of first five natural numbers.

$1, 2, 3, 4,$ and $5$ are first five natural numbers. Display the first five natural numbers inside any closed geometrical shape for representing this set graphically.

Similarly, write the first five natural numbers with comma separation inside the curly braces.

$\Big\{\, 1, 2, 3, 4, 5 \,\Big\}$

Representation

List of the mathematical methods to learn how to express a set in different mathematical approaches.

• Pre Algebra
• Inequalities
• Quadratic Equations
• Hyperbolic functions
• Straight Lines
• Coordinate Geometry
• Differentiation
• integration

Math Questions

The math problems with solutions to learn how to solve a problem.

Learn solutions

Math Worksheets

The math worksheets with answers for your practice with examples.

Practice now

Math Videos

The math videos tutorials with visual graphics to learn every concept.

Subscribe us

Get the latest math updates from the Math Doubts by subscribing us.

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.

• Terms of Use
• Privacy policy

Copyright © 2012 - 2023 Math Doubts, All Rights Reserved

• School Guide
• Mathematics
• Number System and Arithmetic
• Trigonometry
• Probability
• Mensuration
• Maths Formulas
• Class 8 Maths Notes
• Class 9 Maths Notes
• Class 10 Maths Notes
• Class 11 Maths Notes
• Class 12 Maths Notes
• What is Set Theory? Definition, Types, Operations
• Set Theory Formulas

Representation of Set

• Representation of a Set

Set-Builder Notation

Types of set.

• Types Of Sets
• Disjoint Sets
• Finite Sets
• Universal Sets
• Subsets in Maths

Operation on Sets

• Set Operations
• Union of Sets
• Intersection of Sets
• Difference of Sets
• Complement of a Set
• Cartesian Product of Sets

Application of Set

• De Morgan's Law - Theorem, Proofs, Formula & Examples

Set-builder Notation is a type of mathematical notation used to describe sets by naming their components or highlighting the requirements that each member of the set must meet. Sets are written in the form of {y | (properties of y)}   OR {y : (properties of y)}  in the set-builder notation , where the condition that fully characterizes each member of the collection replaces the attributes of y.

The elements and properties are separated using the character ‘|’ or ‘:’ The entire set is interpreted as “the set of all elements y” such that (properties of y), while the symbols ‘|’ or ‘:’ are read as “such that.”

This article explores the set-builder notation, symbols used in set-builder notation, examples, representation of sets methods, etc.

Table of Content

What is Set-Builder Notation?

Symbols used in set-builder notation, representation of sets methods, tabular or roster form, why do we use set builder form, how to use a set builder notation, how to write a set builder notation, how to read set builder notation, set builder notation for domain and range, set builder notation examples.

A representation or notation known as “ set-builder notation ” is used to express a set that is defined by a logical formula that simplifies to be true for each element of the set. There may be one or more variables included. It also specifies a rule for the set’s constituent members.

The elements of the set are represented by a variety of symbols in the set builder form. Here is a list of some of the symbols.

• | stands for “such that” and is often inserted after the variable in the set builder form. The set condition is then written after this symbol.
• ∈ When translated as “ belongs to, ” or in other words “ is an element of “.
• The word, ∉  when translated as “ does not belong to ,” implies “ is not a part of. “
• The letter N stands for all positive integers or natural numbers .
• W stands for whole numbers .
• Z stands for integers .
• Any number that may be stated as a fraction of integers or as a rational number is represented by Q .
• Any number which is not rational is called Irrational Number and is represented by P .
• R stands for real numbers or any non-imaginary number .
• C stands for Complex Numbers .

There are two different methods to represent sets. These are:

• Tabular Form or Roster Form
• Set-Builder Form or Rule Method

Read More: Representation of Sets

The items of the set are enumerated using the roasting method’s braces{}, with commas between each piece. The element can only be written once if it appears more than once in the collection.

Examples of Roster Method

• The formula for the first five natural integers, designated as set X, is X = {6, 7, 8, 9}
• The letter combinations {D, L, H, I} make up the set A of the word DELHI.

The Roster Method is another name for this approach of defining sets. Any order may be used to list the components of the roster set. As a result, the set {A, B, C, D} may be expressed as {B, A, C, D}.

If a set’s components share a property, that property can be used to define the components. For instance, the set A = {1, 2, 3, 4, 5, 6} has a trait in common that all of its members are natural integers lower than 7. Other natural numbers do not have this characteristic. As a result, the set X may be expressed as follows:

A = {x: x is a natural number less than 7} may be translated as “A is the set of elements x such that x is a natural number less than 7.”

The set mentioned above may alternatively be expressed as A = {x: x N, x < 7}.

Another way to express set A = {the set of all natural numbers less than 7}.

In this instance, the description of a set’s common attribute is written inside brackets. This is a set-builder form or rule approach in its most basic version.

When there are many components and utilizing the roster form makes it difficult to represent the components of the set, set builder notation is employed. Let’s use an illustration to better grasp this. If you need to write a list of numbers from 1 to 8 inclusively, you may just write {1, 2, 3, 4, 5, 6, 7, 8} using the roster notation.

But when we have to list every real number, a difficulty appears. It would not be possible to use roster notation in this situation. {…, 1, 1.1, 1.01, 1.001, 1.0001, … }. However, in this case, it would be preferable to use the set-builder notation.

{x | x is a real number} OR {x | x is a rational or irrational number} is the set builder form for real numbers. Writing sets are made easier by using the set-builder notation, particularly when writing sets with an unlimited number of components. The set-builder notation may be used to express numbers like integers, real numbers, and natural numbers. Using this technique, a set containing an interval or an equation may also be represented.

A mathematical notation known as “set builder notation” lists all the requirements that each member of a set must meet in order to be included in the set. In particular, it helps to understand sets with an unlimited number of items.

There are three key parts to set builder notation:

• Typically, a variable is written in lowercase.
• “Such that” is viewed as a vertical bar separator or colon.
• logical statement of the characteristics of sets.

The three elements of set builder notation mentioned above are placed inside curly brackets as shown below:

A = { variable | attribute } OR A = { x : θ(x) }

A separator, the vertical bar is either interpreted as “such that” or a colon “:”. θ(x). For all values of x for which the predicate is true, the set being defined is represented by the symbol (x), which corresponds to the predicate (a logical statement indicating the attributes that the set contains).

Let’s go on to the next idea, writing the set-builder notation, now that we understand what that is.

To write sets in set builder notation, follow the instructions below:

• Use a lowercase letter , such as x, or any other letter, to denote the components of a set.
• As a divider, use a colon (:) or vertical bar (|) .
• Declare the property’s requirement that every member of the supplied set has items after the symbol.
• Inside the curly braces{} , type the whole description.

Think about the following illustration where set A is described as:

A = { x ∈ R | x<4 }

Where the symbol ∈ means “ member of .” The abbreviation “ R ” stands for “ real numbers. ” Because x in R can be any number less than 4, set A holds the value of x in R .

A technique for expressing set attributes that hold true for each and every element contained in the set is called set builder notation. The format of set builder notation is as follows:

A = { x | condition about x }

is to be understood as “the set of all the values of x such that the given condition about x is true for all the values of x.”

A vertical bar can be used in lieu of the colon and is interpreted in the same way.

A = { x : condition about x }

The words “such that” in the set-builder notation explanation are represented by the colon and the vertical bar, respectively.

Writing the domain and range of a function using the set builder notation is quite helpful. The set of all the values that are input into a function is the domain of the function. For example, the domain of the rational function f(x) = 2/(x-1) would include all real integers other than 1. This is due to the fact that when x = 1, the function f(x) would be undefined. As a result, the domain of this function is written as  {x ∈ R | x ≠ 1}.

The set builder notation may also be used to indicate the range of a function. The range of the function is a set of the values that a function can take and for the function f(x) = 2/(x-1) we define the range as,

y = 2/(x-1)

⇒ x – 1 = 2/y

⇒ x = 2/y + 1,

Thus we define the range of function, in the set builder notation as, {y ∈ R | y ≠ 0}.

People Also Read:

Representation of a Set Types Of Sets Operations on Sets

Example 1: Use the set-builder notation to represent the given set.

A = {2, 4, 6, 8,10}

Provided set A = {2, 4, 6, 8,10}  in the set-builder form is represented as: {x: x is an even natural number less than 12″}.

Example 2: How should x ≤ 3 or x ≥ 4 be written in set-builder notation?

In set builder notation, x ≤ 3 or x ≥ 4 may be written as: {x ∈ R | x ≤ 3 or x ≥ 4}

Example 3: Use interval notation to represent the set that contains all positive real values.

The number that is bigger than 0 would serve as the starting point for the set of positive real numbers, albeit we are unsure of the precise value of this number. Positive real numbers also exist in an unlimited number of combinations. As a result, we may express it as the interval (0, ∞).

Example 4: Decode the symbols that are presented:

(ii) -8 ∉ ℕ 

Set of natural numbers is N, while the set of rational numbers is Q. (i) 5 ∈ Q denotes that 5 is a member of a group of rational numbers. (ii) -8 ∉ N indicates that -8 does not fall under the category of natural numbers.

Summary – Set-Builder Notation

Set-builder notation is a mathematical shorthand used to define sets based on specific properties that all elements of the set share. It is particularly useful when dealing with large or complex sets where listing all elements individually would be impractical or impossible. In set-builder notation, you typically start with a variable that represents the elements of the set, followed by a vertical bar (|) or colon (:), which can be read as “such that.” After this separator, you describe the condition or rule that all elements must satisfy to be included in the set.

This method is extremely versatile and can be applied to any collection of numbers or objects that fit a certain rule, from simple sets like natural numbers under a certain value, to more complex sets involving equations or inequalities. The notation is compact and precise, making it a powerful tool for conveying a lot of information about a set in a very succinct way. Whether it’s specifying the domain and range of a function, or defining intervals of real numbers, set-builder notation simplifies the expression of mathematical ideas and ensures clarity and precision in mathematical communication.

FAQs of Set Builder Notation

Definie set-builder notation..

Set Builder Notation is a way of representing sets using logical statements. It is composed of a variable, a vertical bar (“|”) symbol, and a logical statement outlining the requirements that each member of the set must meet. The set of even numbers, for instance, may be expressed as, {x | x is an even number}

What’s the Difference between Roster Forms and Set Builder Forms?

In mathematics, there are two ways to express sets: Roster Form Set-Builder Form The roster form lists each component of a set between curly braces and commas. For instance, {1, 2, 3} The elements of the set are described by a rule or condition in the set-builder form. Consider the following example: {x | x is a positive integer less than 4} Set-builder form provides a clear, rule-based specification, whereas the roster form offers an explicit list.

What are Examples of Set Builder Notation?

We represent sets using the Set Builder Notation and some examples of sets represented using the set builder notation are, {x | x are even numbers less than 24} {x | x is an integer greater than -2 and less than 4} {x | x is a fraction where denominator is always greater than numerator}, etc.

How is Domain written in Set Builder Notation?

In set builder notation, the domain of f(x) = 1/x may be written as {x ∈ ℝ | x ≠ 0}. We can state a function’s domain as “all real numbers” if its domain is exclusively made up of real numbers. The range (-∞, ∞) can be used to represent all real numbers.

What are Real Numbers?

Rational and Irrational Numbers are combined to form a group called Real Numbers. It is represented by R.

Please Login to comment...

Similar reads.

• Maths-Class-11
• School Learning

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Class 9 (OD)

Course: class 9 (od)   >   unit 1.

• Roster form of set representation
• Set builder form and conversions to and from roster
• Subset, strict subset, and superset
• Roster form and set-builder form

• (Choice A)   Yes A Yes
• (Choice B)   No B No

• Take Action All Categories
• Lawsuits by Brand
• Search Lawsuits to Join
• Lawsuits to Join
• Pending Class Action Settlements
• Open Class Action Settlements
• Legal News All Categories
• Consumer News
• Industry & Trade
• Labor & Employment
• Medical Devices
• Pharmaceuticals
• Product Recalls
• Class Action Settlement Checks Mailed
• Closed Class Actions
• Data Breach
• Explained All Categories
• Consumer Guides
• Get Free Rebates
• I Am a Lawyer
• About Us All Categories
• Our Mission
• Vivid Vision
• Newsletter Signup
• Canada News

Mixed credit file lawsuit investigation

Meryl harris  |  may 22, 2024, category: lawsuits to join, mixed consumer credit file: who’s affected.

Does your consumer credit file include information about someone else? Have you been denied financing, jobs or housing because of these errors?

Mixed credit files occur when someone else’s information is wrongfully added to your credit file due to having similar names, addresses, birth dates, Social Security numbers or other information. 

Although these errors are often the result of simple mistakes, they can have serious consequences. If someone else’s debt, credit usage or other information is wrongfully attributed to you, you may be denied the opportunity to get certain jobs, receive financing opportunities or live in various properties. 

Due to the complexity of this issue, it can be very difficult to resolve a mixed credit file through a credit bureau’s automated dispute resolution system. You may be able to take legal action to correct your file and collect compensation for financial damages stemming from the credit mix-up.

Do you qualify?

If your credit file contains accounts and information that don’t belong to you, you may qualify to participate in this mixed-credit file investigation.

Please fill out the form on this page for more information.

Mixed credit files: causes and consequences

A mixed credit file occurs when someone else’s information is included in your credit file with a credit bureau such as TransUnion, Experian or Equifax. These digital mix-ups often occur as a result of simple errors such as similar names, birth dates, Social Security numbers, phone numbers or addresses. Similarities or errors in this information can result in multiple files being combined into a single credit file. People who have common names may be at a higher risk for having a mixed credit file.

Unfortunately, mixed credit files can have serious consequences for consumers.

A mixed credit report may result in a decreased credit score if someone else’s debt, credit utilization or hard inquiries are erroneously included in your credit history. If someone else’s debt is included in your credit report, you may be wrongfully denied lending opportunities, jobs or even housing. Having your credit judged based on someone else’s information can be a frustrating experience that is difficult to solve. 

Luckily, you have options to try to remedy this issue and take action under federal law.

Your rights under FCRA

Under the federal Fair Credit Reporting Act (FCRA), you have the right to dispute any inaccuracies on your credit report, including those stemming from mixed credit files. 

To dispute an error on your credit report, you can contact the credit reporting agency to have them correct the issue. Unfortunately, because Transunion, Experian and Equifax receive thousands of these disputes each day, they are often handled by automated processes. Although these systems effectively resolve simple disputes, they may be unequipped to handle the tangled web of a mixed credit file.

If you reach a real person within the agency, he or she may be able to remove or change information in your file to resolve the issue. However, it can be challenging to reach someone with the authority to do so, leaving some consumers frustrated.

Join a mixed credit file lawsuit investigation

You may be able to take legal action against the credit reporting agency that mixed your credit file, including requiring credit bureaus to correct your file. You may also be able to recover compensation for financial harm related to mixed-credit files, such as denied job or credit opportunities.

If your credit file contains accounts and information that don’t belong to you, you may qualify to participate in this mixed-credit file investigation. 

Please fill out the form on this page to see if you qualify for a FREE case evaluation. 

See If You Qualify

By submitting your information, you agree to receive communications from Top Class Actions and to be contacted by an attorney or law firm or their agents to discuss the details of your potential case at no charge to you if you qualify.

• Hidden Post Title
• First Name *
• Last Name *
• State * Choose a State Alabama Alaska Arizona Arkansas California Colorado Connecticut Delaware District of Columbia Florida Georgia Hawaii Idaho Illinois Indiana Iowa Kansas Kentucky Louisiana Maine Maryland Massachusetts Michigan Minnesota Mississippi Missouri Montana Nebraska Nevada New Hampshire New Jersey New Mexico New York North Carolina North Dakota Ohio Oklahoma Oregon Pennsylvania Rhode Island South Carolina South Dakota Tennessee Texas Utah Vermont Virginia Washington West Virginia Wisconsin Wyoming
• Within 6 months
• 6 – 12 months
• Describe the accounts and information on your credit reports that belong to someone else? (name of account(s) and description of wrong information) *
• I can get one / know where to request it
• What occurred after you made the disputes? (were the accounts and information verified as accurate) *
• denials for credit
• higher percentage rates
• Other damages
• Please include additional details. *

— Attorneys At Law — THE CONSUMER LAWYERS CONTRACT FOR REPRESENTATION

*IF THERE IS NO MONEY RECOVERED, I SHALL OWE NOTHING TO THE FIRM AS A FEE OR COST

FOR THEIR SERVICES*

* I WILL NEVER HAVE TO PAY THE CONSUMER LAWYERS ANY MONEY OUT OF POCKET IF MY CASE IS UNSUCCESSFUL FOR SOME REASON. THE CONSUMER LAWYERS WILL ONLY EVER GET PAID IF THEY RECOVER MONEY FOR MY CASE, IN WHICH EVENT THEY WOULD KEEP A PERCENTAGE AND RECUPERATE THE COSTS AS OUTLINED BELOW. IN OTHER WORDS, THIS PROCESS IS “RISK FREE” FOR ME AS FAR AS FINANCIAL OBLIGATIONS TO THE CONSUMER

LAWYERS GO*

If a recovery is made, I the “Client” shall be obligated to pay The Consumer Lawyers, “The Firm” a fee. This fee will be based upon a percentage of the amount recovered from the Defendant(s). Prior to any final settlement the Client will be consulted by The Firm concerning the terms and amount of settlement. The fee, as stated above, will be calculated on a contingency basis. I. CONTINGENCY I agree to pay The Firm forty-five percent (45%) of the total amount of settlement recovered on my behalf. (Total amount recovered may include amount of debt erased and money award). In the event attorneys’ fees are recovered from any adverse party pursuant to any state or federal statute, the attorneys’ fees shall be the greater of the court-awarded fee or contingency fee stated above.

II. COSTS I also acknowledge that The Firm will deduct costs from my share of the recovery after the contingency fee has been calculated. I understand and agree that I am only obligated pay costs if there is a recovery in this claim. Said costs shall include, but are not limited to, cash and non-cash expenditures for: investigator mileage to and from any initial sign up meeting, court filing fees, medical records charges, experts, mediation fees, subpoenas and deposition costs, witness fees, long-distance telephone calls, facsimiles, photocopies, postage, in-house printing, travel, parking, investigative services and all other costs necessary for proper performance of legal services, and that such costs shall bear interest at the rate of 1.5% per month. In the event that The Firm withdraws from the case, The Firm reserves the right to be reimbursed for said costs if a recovery is made by another firm. Typical costs in a case of this nature may include, for example purposes only, $405 for filing the lawsuit and $150 per Defendant for service of process. If a monetary recovery is made in my case, The Firm would deduct these costs from my portion of the settlement. If there is no recovery, or the recovery is less than the total amount of costs, I would not owe The Firm any money. III. GENERAL PROVISIONS If The Firm wishes to co-counsel with another attorney or law firm to provide legal services on my behalf, they have my authority to do so, provided any fee paid to such attorney is paid by The Firm and does not in any way increase my fees as set forth above. If The Firm does associate with co-counsel that is not already listed in Section IV below, The Firm will inform me in writing of any attorneys’ fees split(s) with such associated lawyers or law firms. I agree that preparation and trial of my lawsuit will be handled at the sole discretion of The Firm. I also agree to all reasonable requests by The Firm to aid in the investigation of this claim including responding timely to telephone calls, emails, correspondence, and requests for information and documents; assisting in discovery, disclosure, and trial preparation; cooperating in scheduling and related matters; and informing The Firm of any changes in my physical and email addresses and telephone numbers. I understand that this is a contingent fee contract and, if no recovery is made, I will not be obligated to pay attorney’s fees or costs. I agree that upon written notice, The Firm may terminate their representation under the terms of this agreement. IV. ASSOCIATION WITH LEGAFI LAW LLC I understand and consent to The Firm associating with LegaFi Law LLC (“LegaFi”) regarding the client’s FCRA case(s) (“case”) and that the legal fee described above in Section I shall be split so that 75% of any attorneys recovered shall go to The Consumer Lawyers, PLLC and 25% of any attorney fees recovered shall go to LegaFi. I understand that in no event, however, shall I incur any additional legal fees or charges by virtue of the aforesaid attorney association. The Firm and LegaFi shall assume joint legal responsibilities to me for the performance of legal services and will be available for consultation with me. It is agreed that the only person(s) represented by The Firm and LegaFi is/are the person(s) signing this agreement as set forth in the capacity below.

V. LIMITATION OF REPRESENTATION This contract applies only to the incident involving myself as Plaintiff against the entity(s), Defendant(s), discussed with The Firm and described in the intake. If the Defendant is collecting a legitimate debt, I understand that they or another entity such as the original creditor or other Debt Collector, may file a separate lawsuit or counter-claim concerning this case. I understand that The Firm advises me to obtain counsel and not try to represent myself. If I am unsure of the extent of my attorney’s representation in this matter, it is my obligation to seek clarification on this issue. Any assistance provided by The Firm in these areas or other areas is not to be considered a waiver of this provision but is recognized solely to be a courtesy extended by the lawyer. It is agreed that the only person represented by The Firm is the person or entity signing this agreement as set forth below in the capacity set forth below. Any person not signing this contract is not represented by the lawyer or law firm set forth below. VI. STATEMENT OF CLIENT’S RIGHTS The Client has, in conjunction with this Contract of Representation, also received and read the “Statement of Client’s Rights” and understands each of the rights set forth therein. The undersigned Client has signed the Statement and has received, or will be receiving, a signed copy to keep while being represented by the undersigned attorneys. VII. LIMITED POWER OF ATTORNEY FOR SETTLEMENT I give The Firm limited Power of Attorney to sign any settlement documents and/or check for settlement or a Release. (If The Firm does endorse a check for the Client, the check will be deposited in a trust account and the Client will be written a check prior to The Firm taking out their fees and costs for services). VIII. CONTACT I understand and agree that The Firm may contact me at any phone number (including mobile, cellular/wireless or similar devices) or email address I provide at any time, for any lawful purpose. The ways in which The Firm may contact me include live operator, automatic telephone dialing systems (auto-dialer), prerecorded message, text messaging systems or email. I understand that this authorization overrides any previous registrations on any federal or state Do Not Call registry(ies). Phone numbers and email addresses I provide include those I give to The Firm, those from which I contact The Firm or which is obtained through other means. I also understand and agree that The Firm may monitor/and or record any of my phone conversations with The Firm representatives. IX. MEDIA AND ADVERTISEMENT I provide my consent or The Firm, LegaFi, and their employees to publish the results of my case including, without limitation, trial verdicts, arbitration awards, settlement amounts (without disclosing the names of the parties where confidential), and/or fee awards in advertisements and other media.

X. ARBITRATION By executing this agreement you the Client, agree that, with one exception, any and all disputes between you and the Firm arising out of this agreement, our relationship with you or our performance of any past, current or future legal services, whether those services are subject of this particular agreement or otherwise, will be resolved through a binding arbitration proceeding to be conducted under the auspices of the Commercial Arbitration Rules of the American Arbitration Association in Tampa, Hillsborough County, Florida. The disputes subject to binding arbitration will include without limitation, disputes regarding attorneys’ fees or costs, and those alleging negligence, malpractice, breach of fiduciary duty, fraud or any claim based upon a statute. Both the agreement of the parties to arbitrate all disputes and the results and awards rendered through the arbitration will be final and binding on you and us and may be specifically enforced by legal proceedings. Arbitration will be the sole means of resolving such disputes, and both parties waive their rights to resolve disputes by court proceedings or any other means. The parties have agreed that judgment may be entered on the award of any court of competent jurisdiction in the state of Florida and, therefore, any award rendered shall be binding. The arbitration may not consolidate more than one person’s claims, and may not otherwise preside over any form of a representative of a class proceeding. The one exception to your agreement to arbitrate concerns ethical grievances which you may have. Nothing in this agreement limits, in any way, your right to pursue any ethical grievance against The Firm as permitted by applicable law. You understand that by agreeing to arbitration as a mechanism to resolve all potential controversies, disputes, or claims between us, you are waiving certain rights, including the right to bring an action in court, the right to a jury trial, the right to broad discovery, and the right to an appeal. You understand that in the context of arbitration, a case is decided by an arbitrator (one or more), not by a judge or a jury. You agree that, in the event of such controversy, dispute, or claim between us, the prevailing party will be entitled to recover from the losing party all costs and expenses he, she, or it incurs in bringing and prosecuting, or defending, the arbitration, including reasonable attorneys’ fees and costs. Please review this contract carefully to be certain that it accurately sets forth our agreement. In the event that you do not understand anything in this agreement, please let us know so further written explanations can be provided.

NOTICE: This Agreement contains provisions requiring arbitration of fee disputes. Before you sign this agreement you should consult with another lawyer about the advisability of making an agreement with mandatory arbitration requirements. Arbitration proceedings are ways to resolve disputes without use of the court system. By entering into agreements that require arbitration, you give up (waive) your right to go to court to resolve those disputes by a judge or jury. These are important rights that should not be given up without careful consideration.

XI. TAX CONSEQUENCES Please be aware that the attorneys and staff at The Consumer Lawyers, PLLC cannot, and will not, provide any tax advice nor can they provide information as to what tax consequences you may incur due to the receipt of any possible settlement funds. Your attorneys and their staff are not tax attorneys or tax professionals and are in no way qualified to give tax advice. If you have any tax questions related to the settlement, you should speak to a qualified tax professional so that he or she may give you a reliable assessment of what the tax consequences of any settlement agreement may be. XII. CANCELLATION I understand that this contract may be canceled by written notification to the attorneys at any time within three (3) business days of the date the contract is signed, as shown below, and if canceled, I shall not be obligated to pay any fees to the attorneys for the work performed during that time. If the attorneys have advanced funds to others in their representation of me, the attorneys are entitled to be reimbursed for such amount as they have reasonably advanced on behalf of the Client. If I discharge my attorneys for any reason after the initial three (3) days, I agree that my attorneys will be entitled to a fee based upon the percentage set forth above of any offer of settlement outstanding, or if no offer of settlement is outstanding, a reasonable fee based upon the amount of time my attorneys spent on my case. XIII. ACKNOWLEDGMENTS I acknowledge that The Firm and LegaFi have made no representations to me regarding the outcome of this matter. I acknowledge that The Firm and LegaFi have not represented me in connection with my decision to enter into this Agreement, and I have the right and am encouraged to retain separate, independent counsel for consultation in connection with this Agreement, including a review of this Agreement. By signing below, I acknowledge that this Agreement has been carefully read and reviewed and its contents understood, and that I agree to be bound by all its terms.

This Contract is entered into on _________________________________, by the below Client and The Firm.

___________________________ _____________________________ [CLIENT NAME] THE CONSUMER LAWYERS “The Client” “The Firm”

— Attorneys At Law —

STATEMENT OF CLIENT’S RIGHTS FOR CONTINGENCY FEES

Before you, the prospective client, arrange a contingent fee agreement with a lawyer, you should understand this statement of your rights as a client. This statement is not a part of the actual contract between you and your lawyer, but, as a prospective client, you should be aware of these rights. 1. There is no legal requirement that a lawyer charge a client a set fee or a percentage of money recovered in a case. You, the client, have the right to talk with your lawyer about the proposed fee and to bargain about the rate or percentage as in any other contract. If you do not reach an agreement with one lawyer, you may talk with other lawyers. 2. Any contingent fee contract must be in writing and you have three (3) business days to reconsider the contract. You may cancel the contract without any reason if you notify your lawyer in writing within three (3) business days of signing the contract. If you withdraw from the contract within the first three (3) business days, you do not owe the lawyer a fee although you may be responsible for the lawyer’s actual costs during that time. If your lawyer begins to represent you, your lawyer may not withdraw from the case without giving you notice, delivering necessary papers to you, and allowing you time to employ another lawyer. Often, your lawyer must obtain court approval before withdrawing from a case. If you discharge your lawyer without good cause after the three (3) day period, you may have to pay a fee for work the lawyer has done. 3. Before hiring a lawyer, you, the client, have the right to know about the lawyer’s education, training, and experience. If you ask, the lawyer should tell you specifically about the lawyer’s actual experience dealing with cases similar to yours. If you ask, the lawyer should provide information about special training or knowledge and give you this information in writing if you request it. 4. Before signing a contingent fee contract with you, a lawyer must advise you whether the lawyer intends to handle your case alone or whether or other lawyers will be

helping with the case. If your lawyer intends to refer the case to other lawyers, the lawyer should tell you what kind of fee sharing arrangement will be made with the other lawyers. If lawyers from different law firms will represent you, at least one (1) lawyer from each law firm must sign the contingent fee contract. 5. If your lawyer intends to refer your case to another lawyer or counsel with other lawyers, your lawyer should tell you about that at the beginning. If your lawyer takes the case and later decides to refer it to another lawyer or to associate with other lawyers, you should sign a new contract that includes the new lawyers. You, the client, also have the right to consult with each lawyer working on your case and each lawyer is legally responsible to represent your interests and is legally responsible for the acts of the other lawyers involved in the case. 6. You, the client, have the right to know in advance how you will need to pay the expenses and the legal fees at the end of the case. If you pay a deposit in advance for costs, you may ask reasonable questions about how the money will be or has been spent and how much of it remains unspent. Your lawyers should give a reasonable estimate about future necessary costs. If your lawyer agrees to lend or advance you money to prepare or research the case, you have the right to know periodically how much money your lawyer has spent on your behalf. You also have the right to decide, after consulting with your lawyer, how much money is to be spent to prepare a case. If you pay the expenses, you have the right to decide how much to spend. Your lawyer should also inform you whether the fee will be based on the gross amount recovered or on the amount recovered minus the costs. 7. You, the client, have the right to be told by your lawyer about possible adverse consequences if you lose the case. Those adverse consequences might include money that you have to pay to your lawyer for costs and liability you might have for attorney’s fees, costs, and expenses to the other side. 8. You, the client, have the right to receive and approve a closing statement at the end of the case before you pay any money. The statement must list all of the financial details of the entire case, including the amount recovered, all expenses, and a precise statement of your lawyer’s fee. Until you approve the closing statement your lawyer cannot pay any money to anyone, including you, without an appropriate order of the court. You also have the right to have every lawyer or law firm working on your case sign this closing statement. 9. You, the client, have the right to ask your lawyer at reasonable intervals how the case is progressing and to have these questions answered to the best of your lawyer’s ability. 10. You, the client, have the right to make the final decision regarding settlement of a case. Your lawyer must notify you of all offers of settlement before and after the trial. Offers during the trial must be immediately communicated and you should consult with your lawyer regarding whether to accept a settlement. However, you must make the final decision to accept or reject a settlement. 11. If at any time you, the client, believe that your lawyer has charged an excessive of illegal fee, you have the right to report the matter to The Florida Bar, the agency that oversees the practice and behavior of all lawyers in Florida. For information on how to reach The Florida Bar, call 850-561-5600 or contact the local bar association. Any disagreement

between you and your lawyer about a fee can be taken to court and you may wish to hire another lawyer to help you resolve this disagreement. Usually, fee disputes must be handled in a separate lawsuit, unless your fee contract provides for arbitration. You can rest, but may not require, that a provision for arbitration (under Chapter 682, Florida Statutes, or under the fee arbitration rule of the Rules Regulating the Florida Bar) be included in your fee contract. _____________________________ _________________________________ DATE [CLIENT]

_____________________________ _________________________________ DATE THE CONSUMER LAWYERS

• I agree to the Terms of Service
• Signature *
• Yes, sign me up!

By submitting information to Top Class Actions you agree that the information you submit, including your phone number and email address, will be shared with and used by Top Class Actions, LegaFi Law LLC (an Arizona law firm) / legafi.com / 888-4-LegaFi, Environmental Litigation Group, PC / 205-328-9200 / elglaw.com, Ron Austin Law, LLC / 504-227–8100 / ronaustinlaw.com, their agents, and their co-counsel, if any, to contact you. You understand that this authorization overrides any previous registrations on any federal or state Do Not Call registry(ies). While your communications with a lawyer may be subject to the attorney-client privilege, communications through this website may not be because Top Class Actions is not a law firm. Please do not share any confidential or privileged information through this website. Top Class Actions or the attorney(s) or their agent(s) with whom your information is shared may be ordered by a court of law to produce your information in certain legal situations. Also, you are not formally represented by a law firm unless and until a contract of representation is signed by you and the law firm. *

• I understand and agree
• Hidden Jornaya Lead ID
• Hidden Prequalified *
• Name This field is for validation purposes and should be left unchanged.

After you fill out the form, an attorney(s) or their agent(s) may contact you to discuss your legal rights.

ATTORNEY ADVERTISING

The choice of a lawyer is an important decision and should not be based solely on advertisements.

PAID ATTORNEY ADVERTISEMENT: THIS WEB PAGE IS AN ADVERTISEMENT AND THE PARTICIPATING ATTORNEY(S) ARE INCLUDED BECAUSE THEY PAY AN ADVERTISING FEE. Top Class Actions is not a law firm, lawyer referral service, or prepaid legal services plan. We do not endorse or recommend any third-party claims processing company, lawyer, or law firm who participates in the network. We do not make any representation, and have not made any judgment, as to the qualifications, expertise, or credentials of any participating lawyer or processing group. No representation is made that the quality of the legal services or claims processing to be performed is greater than the quality of legal services or claims processing performed by other lawyers or claims processing group. The information contained herein is not legal advice. Any information you submit to Top Class Actions does not create an attorney-client relationship and may not be protected by attorney-client privilege because Top Class Actions is not a law firm. Instead, your information will be forwarded to an attorney(s) or their agent(s) or a claims processing firm for the purpose of a confidential review and potential representation if you qualify. You will only be contacted by an attorney(s) or their agent(s) in response to your inquiry if your initial information appears to qualify you for representation. If you are not contacted by an attorney(s) or their agent(s) within one week, you should consult another firm since all legal claims are subject to filing deadlines. All photos on this website are stock art and do not depict clients.

We tell you about cash you can claim EVERY WEEK! Sign up for our free newsletter.

• Country * United States Canada United Kingdom Other
• State * Alabama Alaska Arizona Arkansas California Colorado Connecticut Delaware District of Columbia Florida Georgia Hawaii Idaho Illinois Indiana Iowa Kansas Kentucky Louisiana Maine Maryland Massachusetts Michigan Minnesota Mississippi Missouri Montana Nebraska Nevada New Hampshire New Jersey New Mexico New York North Carolina North Dakota Ohio Oklahoma Oregon Pennsylvania Rhode Island South Carolina South Dakota Tennessee Texas Utah Vermont Virginia Washington West Virginia Wisconsin Wyoming
• Email This field is for validation purposes and should be left unchanged.

Top Class Actions is a Proud Member of the American Bar Association

LEGAL INFORMATION IS NOT LEGAL ADVICE

This site provides information about the law and lawsuits and is designed to help users safely cope with their own legal needs. Legal information is NOT the same as legal advice - the application of law to an individual's specific circumstances. Although we go to great lengths to make sure our information is accurate and useful, we recommend you consult a lawyer if you want professional assurance that our information, and your interpretation of it, is appropriate to your particular situation. You should consider all postings or writings at TopClassActions.com by staff or others as personal opinion only and NOT the advice of a lawyer. Top Class Actions Legal Statement

©2008 – 2024 Top Class Actions® LLC

Various Trademarks held by their respective owners

Please note: Top Class Actions is not a settlement administrator or law firm. Top Class Actions is a legal news source that reports on class action lawsuits, class action settlements, drug injury lawsuits and product liability lawsuits. Top Class Actions does not process claims and we cannot advise you on the status of any class action settlement claim. You must contact the settlement administrator or your attorney for any updates regarding your claim status, claim form or questions about when payments are expected to be mailed out.

Related Posts

Patagonia class action claims company embeds hidden trackers in emails

Ally Financial class action alleges bank breached military servicemember duties

Kraft Mac & Cheese class action filed over ‘no preservatives’ label

Pedigree dog food recall issued due to potential metal contamination

Verisma Systems medical record fees $4.9M class action settlement

Audi, Volkswagen emergency brake class action settlement

Feds investigating Waymo, Zoox after dozens of safety incidents

Judge gives preliminary approval to $5.5M settlement in Apotex price-fixing MDL

Dell class action claims data breach affected 49M customers

Delta reaches $16M settlement with flight attendants in longstanding wage lawsuit

Yogi tea bags recall issued due to pesticide contamination

Supreme Court rules Consumer Financial Protection Bureau constitutionally funded

Advertisement

Supported by

There’s a New Covid Variant. What Will That Mean for Spring and Summer?

Experts are closely watching KP.2, now the leading variant.

• Share full article

By Dani Blum

For most of this year, the JN.1 variant of the coronavirus accounted for an overwhelming majority of Covid cases . But now, an offshoot variant called KP.2 is taking off. The variant, which made up just one percent of cases in the United States in mid-March, now makes up over a quarter.

KP.2 belongs to a subset of Covid variants that scientists have cheekily nicknamed “FLiRT,” drawn from the letters in the names of their mutations. They are descendants of JN.1, and KP.2 is “very, very close” to JN.1, said Dr. David Ho, a virologist at Columbia University. But Dr. Ho has conducted early lab tests in cells that suggest that slight differences in KP.2’s spike protein might make it better at evading our immune defenses and slightly more infectious than JN.1.

While cases currently don’t appear to be on the rise, researchers and physicians are closely watching whether the variant will drive a summer surge.

“I don’t think anybody’s expecting things to change abruptly, necessarily,” said Dr. Marc Sala, co-director of the Northwestern Medicine Comprehensive Covid-19 Center in Chicago. But KP.2 will most likely “be our new norm,’” he said. Here’s what to know.

The current spread of Covid

Experts said it would take several weeks to see whether KP.2 might lead to a rise in Covid cases, and noted that we have only a limited understanding of how the virus is spreading. Since the public health emergency ended , there is less robust data available on cases, and doctors said fewer people were using Covid tests.

But what we do know is reassuring: Despite the shift in variants, data from the C.D.C. suggests there are only “minimal ” levels of the virus circulating in wastewater nationally, and emergency department visits and hospitalizations fell between early March and late April.

“I don’t want to say that we already know everything about KP.2,” said Dr. Ziyad Al-Aly, the chief of research and development at the Veterans Affairs St. Louis Healthcare System. “But at this time, I’m not seeing any major indications of anything ominous.”

Protection from vaccines and past infections

Experts said that even if you had JN.1, you may still get reinfected with KP.2 — particularly if it’s been several months or longer since your last bout of Covid.

KP.2 could infect even people who got the most updated vaccine, Dr. Ho said, since that shot targets XBB.1.5, a variant that is notably different from JN.1 and its descendants. An early version of a paper released in April by researchers in Japan suggested that KP.2 might be more adept than JN.1 at infecting people who received the most recent Covid vaccine. (The research has not yet been peer-reviewed or published.) A spokesperson for the C.D.C. said the agency was continuing to monitor how vaccines perform against KP.2.

Still, the shot does provide some protection, especially against severe disease, doctors said, as do previous infections. At this point, there isn’t reason to believe that KP.2 would cause more severe illness than other strains, the C.D.C. spokesperson said. But people who are 65 and older, pregnant or immunocompromised remain at higher risk of serious complications from Covid.

Those groups, in particular, may want to get the updated vaccine if they haven’t yet, said Dr. Peter Chin-Hong, an infectious disease specialist at the University of California, San Francisco. The C.D.C. has recommended t hat people 65 and older who already received one dose of the updated vaccine get an additional shot at least four months later.

“Even though it’s the lowest level of deaths and hospitalizations we’ve seen, I’m still taking care of sick people with Covid,” he said. “And they all have one unifying theme, which is that they’re older and they didn’t get the latest shot.”

The latest on symptoms and long Covid

Doctors said that the symptoms of both KP.2 and JN.1 — which now makes up around 16 percent of cases — are most likely similar to those seen with other variants . These include sore throat, runny nose, coughing, head and body aches, fever, congestion, fatigue and in severe cases, shortness of breath. Fewer people lose their sense of taste and smell now than did at the start of the pandemic, but some people will still experience those symptoms.

Dr. Chin-Hong said that patients were often surprised that diarrhea, nausea and vomiting could be Covid symptoms as well, and that they sometimes confused those issues as signs that they had norovirus .

For many people who’ve already had Covid, a reinfection is often as mild or milder than their first case. While new cases of long Covid are less common now than they were at the start of the pandemic, repeat infections do raise the risk of developing long Covid, said Fikadu Tafesse, a virologist at Oregon Health & Science University. But researchers are still trying to determine by how much — one of many issues scientists are trying to untangle as the pandemic continues to evolve.

“That’s the nature of the virus,” Dr. Tafesse said. “It keeps mutating.”

Dani Blum is a health reporter for The Times. More about Dani Blum

Advertisement

North carolina earns national seed, set to host regional, share this article.

The North Carolina Tar Heels’ baseball program had a short stay in the 2024 ACC Baseball Championship . But the bigger focus remains on the NCAA Tournament.

When the seeds are announced on Monday, the Tar Heels already know that they are a national seed and will host a regional next weekend in Chapel Hill.

The seeds were released Sunday night with UNC landing among the top 16 national seeds. It will be the 36th appearance in the postseason tournament all time for UNC and the 13th time they have earned a national seed in program history for the Diamond Heels.

The Road to Omaha goes through Chapel Hill. #GoHeels pic.twitter.com/5E0ChVZwqL — Carolina Baseball (@DiamondHeels) May 27, 2024

With postseason play coming to the Bosh, North Carolina has a path to reach Omaha if they can advance out of the regional and then super regionals.

UNC found success in the regular season, finishing 42-13 overall and 32-2 at home. The home-field advantage could be huge for the Diamond Heels if they want to get to Omaha.

While we know the Tar Heels will host the regionals, we don’t know the other teams heading to Chapel Hill or the schedule. That will be released on Monday.

Follow us  @TarHeelsWire  on X  and like our page on  Facebook  to follow ongoing coverage of North Carolina Tar Heels news, notes and opinions.

Most Popular

Social media reacts to unc baseball earning national seed, hosting ncaa tournament regional, unc basketball 2025 recruiting class big board (summer 2024), top unc basketball recruiting target hoping to hear from another blue blood, social media reacts to unc basketball landing ven-allen lubin from the transfer portal, north carolina still a top team in early top 25 and 1 after transfer addition, unc basketball among teams that are recruiting son of former duke legend the hardest, unc basketball player slipping in latest espn 2024 nba mock draft.

Please enter an email address.

Thanks for signing up.

Please check your email for a confirmation.

Something went wrong.

• Math Article
• Set Theory Symbols

Set Theory in Maths

Set theory symbols: In Maths, the Set theory is a mathematical theory, developed to explain collections of objects . Basically, the definition states that “it is a collection of elements”. These elements could be numbers, alphabets, variables, etc. The notation and symbols for sets are based on the operations performed on them, such as the intersection of sets, the union of sets, the difference of sets, etc.

Get more: Maths symbols

You must have also heard of subset and superset, which are the counterpart of each other. The different types of sets in Mathematics set theory are explained widely with the help of Venn diagrams. Sets have turned out to be an invaluable tool for defining some of the most complicated mathematical structures. They are mostly used to define many real-life applications. Apart from this, there are also many types of sets , such as empty sets, finite and infinite sets, etc.

What is Set Theory in Maths?

As we have already discussed, in mathematics set theory, a set is a collection of different types of objects, and collectively it is called an object. For example, numbers 8, 10, 15 and 24 are 4 distinct numbers, but when we put them together, they form a set of 4 elements, such that {8, 10, 15, 24}.

In the same way, sets are defined in Maths for a different pattern of numbers or elements. Such as, sets could be a collection of odd numbers, even numbers, natural numbers, whole numbers, real or complex numbers and all the set of numbers which lies on the number line.

Set Theory in Maths – Example

Set theory in Maths has numerous applications. Let’s imagine you’re in a class of 24 students (including you). You want to know the number of males and females in your class. So you begin counting: Males: 1, 2, 3,… 12; females: 1, 2, 3,… 12 . Set theory can now be used to demonstrate this more clearly.

A = {Rahul, Leena, Akshay, Preethi,…} 

Here, the letter A represents your class.

A’s cardinality (the number of elements it contains) is 24.

I.e., |A|=24.

So there are 12 males and 12 females, right?

Let’s understand it by an example.

Now, F represents all females, while M represents all males.

F = {Leena, Preethi…} 

|F|=12  (F’s cardinality is 12)

M={Rahul, Akshay,…} 

|M|=12  (M’s cardinality is 12)

As a result, the sets are really useful for classifying things.

A famous mathematician, Georg Cantor, generated a theory of abstract sets of entities and formed it into a mathematical discipline between the years 1874 and 1897. This theory in maths is built out of his research of some definite problems about specific types of infinite sets of numbers which are real. According to Cantor, the set is a collection of definite, distinct objects or items of observation as a whole. These items are called elements or members of the set. However, he found it by a single paper based on the property of the combination of all real numbers (or real algebraic numbers).

Mathematics Set Theory Symbols

Let us see the different types of symbols used in Mathematics set theory with their meanings and examples.  Consider a Universal set (U) = {1, 2, 7, 9, 13, 15, 21, 23, 28, 30}

Basic Concepts of Set Theory

In set theory, various concepts are discussed at various levels of education. The basic concepts include representation of a set, types of sets, operations on sets (such as union, intersection), the cardinality of a set and relations, etc.  Some of the basic concepts involved in set theory are as follows:

Universal Set

A universal set is usually denoted by the capital letter ‘U’. Also, sometimes it is denoted by ε(epsilon). It is a set that contains all the elements of other sets including its own elements. 

U = {counting numbers}

U = Set of integers

Complement of Set

If A is a set, then the complement of set A will contain all the elements in the given universal set (U),  that are not in set A. It is usually denoted by A’ or A c .

A’ = = {x ∈ U : x ∉ A}

Set Builder Notation

The examples of notation of set in a set builder form are:

• If A is the set of real numbers.

A = {x: x∈R}    [x belongs to all real numbers]

• If A is a set of natural numbers

A = {x: x>0]

Applications

Set theory has many applications in mathematics and other fields. They are used in graphs, vector spaces, ring theory, and so on. All these concepts can be defined as sets satisfying specific properties (or axioms) of sets. Also, the set theory is considered as the foundation for many topics such as topology, mathematical analysis, discrete mathematics, abstract algebra, etc.

Video Lesson on What are Sets

Solved Examples

1. Let A and B be two finite sets such that n(A) = 20, n(B) = 28 and n(A ∪ B) = 36, find n(A ∩ B).

Solution: Since, n(A ∪ B) = n(A) + n(B) – n(A ∩ B). 

So, n(A ∩ B) = n(A) + n(B) – n(A ∪ B) 

= 20 + 28 – 36

= 48 – 36

2. Let A = {x : x is a natural number and a factor of 18} and B = {x : x is a natural number and less than 6}. Find A ∪ B.

Solution: Given,

A = {1, 2, 3, 6, 9, 18} 

B = {1, 2, 3, 4, 5} 

Therefore, A ∪ B = {1, 2, 3, 4, 5, 6, 9, 18}

3. Let A = {3, 5, 7}, B = {2, 3, 4, 6}. Find (A ∩ B)’.

Solution: Given, A = {3, 5, 7}, B = {2, 3, 4, 6}

A ∩ B = {3}

(A ∩ B)’ = {2, 4, 5, 6, 7} 

4. If A = {2, 3, 4, 5, 6, 7} and B = {3, 5, 7, 9, 11, 13}, then find (i) A – B and (ii) B – A.

Solution: Given, 

A = {2, 3, 4, 5, 6, 7} and B = {3, 5, 7, 9, 11, 13}

(i) A – B = {2, 4, 6}

(ii) B – A = {9, 11, 13}

Practice Questions on Set Theory Symbols

• If A = {1, 3, 5, 7} and B = {2, 3, 4, 5}, then find AUB.
• Let P = {a, e, i, o, u} and Q = {a, b, c, d, e}. Find P∩Q.
• If A = {1, 2, 3, 4, 5} and B = {2, 5, 7, 9, 11}, then find A – B.

Frequently Asked Questions Set Theory Symbols

What does ∈ mean, what does ∩ mean in math, what does ⊆ mean in math, what is the symbol for union of sets, if a = b, then what does it represent.

Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!

Select the correct answer and click on the “Finish” button Check your score and answers at the end of the quiz

Visit BYJU’S for all Maths related queries and study materials

Your result is as below

Request OTP on Voice Call

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Post My Comment

Symbol used in sets class 7

This app is really helpful for me

^ used for power . example: – 2^2=4 therefor, it means that 2 power 2 is 4

This app is very helpful 😊

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

Baby boomers are approaching 'peak burden' on the economy

• The baby-boomer "time bomb" is finally upon us, economists say.
• All boomers will be at least 65 soon, the generation's point of "peak burden" on the economy.
• Future generations can take solace in the fact that no boomer-size generations are in the making.

A time bomb has been ticking in the US.

It's the baby boomers, who as they age are approaching their "peak burden" years in regard to their drag on the economy and the resources of younger generations.

Boomers have already gotten tons of flak from younger people over the economy they've left Gen Zers, millennials, and Generation X to inherit. By the end of this year, all boomers — defined by the US Census Bureau as being born from 1946 to 1964 — will be 60 or older.

This means the youngest boomers are rapidly approaching retirement, and a bigger retirement population means more of a drag on the US economy, a burden that Barclays senior economist Jonathan Millar expects to stretch on for the next 20 years. 

"The peak burden," Millar told Business Insider, is when essentially all living baby boomers have hit retirement. "And we're getting there."

The date could fall sometime around 2029, when the youngest boomers will be 65, according to a  Census Bureau report.

A population time bomb

It isn't the boomers' fault they were born. They didn't choose to be a mammoth-size generation that's left the US with a big and probably expensive retirement-age population .

And it isn't the case that baby boomers will derail economic growth nearly as much as, say, a full-blown recession, according to Dean Baker, an economist who described the baby boomers as a " time bomb " in a 1998 paper.

"Yes, it does create strains, but the idea was just some horrible catastrophe that loomed on the horizon," he said of the public dialogue on aging boomers. "It was really just craziness."

Still, the consequences of an aging population are real — and it's expected to weigh on the US over the coming decades. Older people are just one of the many factors weighing on Japan's economy , for instance, with people over 65 making up more than 25% of the overall population.

Related stories

Baby boomers have already weighed on the US economy, and the cohort risks being a bigger drag in the coming years, Millar said.

Boomers are taking up the housing supply

Boomers are taking up a disproportionately large share of the housing supply compared with previous generations. That has been a pain for other homebuyers, as lower housing inventory has helped push up home prices .

The housing market saw its worst year of sales since 1995 in 2023 , according to the National Association of Realtors. Existing homeowners have had little incentive to downsize their homes, many of which are fully paid off or financed at ultralow rates.

"It probably means we're headed for five or six years where baby boomers contribute to very strong housing demand, and we're going to have high house prices as a result," Millar warned.

Boomers also appear to be hogging the larger homes that millennials would otherwise be flocking to as they start families. In 2022, empty-nester baby boomers owned 28% of large homes in the US, a Redfin analysis found, double the share of millennial families.

Boomers are contributing to the labor shortage

The US has more open jobs than available workers . That gap is likely to widen as more boomers leave the workforce.

As of January, the Chamber of Commerce estimated that the economy was still down about 1.7 million workers compared with before the coronavirus pandemic. The labor market, meanwhile, is staring at 9.5 million job openings.

The labor shortage could eventually spell trouble for the economy, as a low supply of workers pushes up wages, which can stoke inflation.

Boomer retirees are also still demanding goods and services in the economy. If they aren't contributing anything in labor, that demand is also inherently inflationary, Millar added.

Boomers are a risk to the stock market

Retirees, who are less tolerant of stock-market volatility, also pose a downside risk to stocks. Boomers are more likely to sell if the US economy tips into a recession. That's a problem, considering that analysis by Rosenberg Research found people 55 and older account for 80% of stock-market ownership in the US.

"Retirees don't have the luxury to buy and hold through a market downturn," the economist David Rosenberg said in a recent note. "If a downturn does materialize, demographically induced selling is a force that could exacerbate the spiral powerfully, with the effects ricocheting into consumer spending."

Boomers will drain Social Security

Finally, boomers are set to collect a large amount in Social Security payments. The Old-Age and Survivors Insurance Trust Fund is expected to be depleted in 2033, a year earlier than previously expected, the Social Security Administration said in a new report.

Politicians are averse to raising taxes or slashing spending on social programs, Millar noted, and are unlikely to let payments lapse. Instead, they'll most likely pay for the program by taking on more debt to keep funding retirees through old age.

"Any way you slice it, this is a burden on current and future generations of taxpayers," Millar added.

The silver lining is that there doesn't appear to be a baby-boomer redux in the making, Baker said. Millennials are a large generation, but after that, Gen Z and Alpha look to be much smaller, meaning there won't be a similar time bomb ticking for the economy.

"I think it's very unlikely that we're going to see another population boom like we had in the post-World War II years," Baker said. "If there's some set of events that lead to that, it's nothing I can see on the horizon."

Correction: February 5, 2024 — An earlier version of this story incorrectly described data from the National Association of Realtors. It found the housing market to have had its worst sales in 2023 since 1995, not ever.

This story was originally published in February 2024.

Watch: Millions of homes could flood the US housing market thanks to boomers

• Main content

• Grand Rapids/Muskegon
• Saginaw/Bay City
• All Michigan

Brick Elementary first school in Michigan to get national STEM certification

• Updated: May. 27, 2024, 11:05 p.m. |
• Published: May. 26, 2024, 10:27 a.m.

Scenes from the STEM Career Day event at Brick Elementary School in Ypsilanti on Wednesday, April 24, 2024. Elementary students participated in hands on activities with firefighters, engineers, the US Coast Guard, and other STEM-related professionals. Rebecca Villagracia | MLive.com

• Sophia Kalakailo | [email protected]

WASHTENAW COUNTY – An Ypsilanti-area elementary school has gained national recognition for its STEM education.

Brick Elementary School, part of Lincoln Consolidated Schools, is the first school in Michigan to secure certification from The National Institute for STEM Education, meaning Brick’s curriculum meets a high standard of quality as a STEM education center.

The school began pursuing the certification this year, gaining the stamp of approval in just seven months, Principal Cassandra Coker said. While exact numbers around student achievement aren’t available yet, she said, “the trajectory has been all positive throughout the year.”

“There’s a lot more creativity in students,” Coker said. “There’s a lot more critical thinking. The classroom discussions and the writings that students are doing have been incredible.”

To gain the title, the school had to boost its STEM effort and get five teachers STEM teaching certified through the organization, among other bench marks.

The certification comes after years of work to set a new standard for STEM education options in the Ypsilanti area. The school has had a STEM focus since 2015, according to its website .

The elementary school has previously benefited from partnerships with other local organizations such as the University of Michigan, Eastern Michigan University and Toyota Motor North America Inc., which in June awarded about $10 million over a five-year span to support technological development in southeast Michigan through its “Driving Possibilities” initiative. Brick received a $5,000 grant from Toyota to update books in the school’s library early this year, MLive previously reported .

In addition to monthly “STEM nights,” the elementary school hosted a STEM Career Day, where students could get up close to helicopters, ambulances and fire trucks and meet engineers, doctors, scientists, pilots, electricians and others.

Read More: From helicopter landings to pig lungs: Elementary students explore careers in STEM

Coker believes the national recognition will open up more resources for the school, noting that more STEM students and professionals from Eastern Michigan University, the University of Michigan and Toyota already want to get more involved and help out in the classroom.

Want more Ann Arbor-area news? Bookmark the local Ann Arbor news page , the Ypsilanti-area news page or sign up for the free “ 3@3 Ann Arbor ” daily newsletter.

Stories by Sophia Kalakailo

• Ypsilanti ranks gold in Michigan sustainability challenge
• New security cameras, safety technology could come to Lincoln schools
• ‘Illegal activity’ limits hours at Ypsilanti park’s parking lot
• ‘Creative problem solver’ tackles hoarding, homelessness, hunger near Ypsilanti

If you purchase a product or register for an account through a link on our site, we may receive compensation. By using this site, you consent to our User Agreement and agree that your clicks, interactions, and personal information may be collected, recorded, and/or stored by us and social media and other third-party partners in accordance with our Privacy Policy.

Post Office Horizon IT scandal: 80 detectives across UK set to investigate

The public inquiry into why more than 700 sub-postmasters were wrongly convicted is not expected to publish its final report until autumn 2025 - meaning any potential criminal charges may not be filed until 2026 at the earliest.

By Daniel Binns, business reporter

Tuesday 28 May 2024 08:02, UK

The criminal investigation into the Post Office scandal is to be expanded, with 80 detectives set to be involved.

The Metropolitan Police started examining possible offences, including perjury and perverting the course of justice, in January 2020.

This is now widening to forces across the UK as a public inquiry into the scandal progresses.

Please use Chrome browser for a more accessible video player

Hundreds of sub-postmasters were wrongly convicted of theft and false accounting because of a faulty IT system called Horizon.

Met Commander Stephen Clayman, who is overseeing the investigation, said officers understood the "widespread and devastating impact" of the scandal.

He added: "A team of detectives has been painstakingly working through millions of documents manually and with the help of specialist software, in parallel with the public inquiry. This is very time consuming and we cannot cut corners and risk missing evidence.

"Given the significant scale of the investigation, it has been agreed by the National Police Chiefs' Council that the next phase of the investigation will be a national policing effort, coordinated by the Met, with the pursuit of justice at its heart.

"We do not underestimate the seriousness of the task at hand and we are determined to carry out a full investigation with independence, precision and integrity."

Read more: More than £1m Post Office 'profit' may have come from victims Scotland unveils plan to exonerate sub-postmasters

The Post Office and Fujitsu - which developed the Horizon software - have been under police investigation for over four years following a referral from the Director of Public Prosecutions.

However, a final charging decision can only be made once the public inquiry reaches its conclusions - and while hearings are set to conclude later this year, a final report may only be published in late 2025.

According to The Guardian, officers have asked the government for £6.75m to fund their expanded investigation.

Be the first to get Breaking News

Install the Sky News app for free

Related Topics

• Metropolitan Police
• Post Office scandal

Here's what the Constitution's Fifth Amendment says about indictments and double jeopardy

The double jeopardy clause in the fifth amendment precludes the same state or federal court from trying the defendant twice for the same crime..

• Paul G. Summers, a lawyer, is a former appellate and senior judge, district attorney general, and the attorney general of Tennessee.

Our Constitution and amendments are the supreme law of America. The first 10 amendments, or Bill of Rights, were submitted to the state legislatures in 1789 and ratified two years later.

We now study the Fifth Amendment. This Amendment says:

“(N)o person shall be held to answer for a capital, or otherwise infamous crime, unless on a presentment or indictment of a Grand Jury, except in cases arising in the land or naval forces, or in the Militia, when in actual service in time of War or public danger; nor shall any person be subject for the same offence (sic) to be twice put in jeopardy of life or limb, nor shall be compelled in any criminal case to be a witness against himself, nor be deprived of life, liberty, or property, without due process of law; nor shall private property be taken for public use without just compensation.”

Entire books and treatises have been written about the Fifth Amendment, which also applies to the states pursuant to the Fourteenth Amendment. The Supreme Court has expanded many.  Below are some of the rights provided to all persons in accordance with the Amendment No. 5:

• Right to a presentment or indictment by a grand jury for a felony.
• Creation of a separate military justice system, for military members (e.g., UCMJ).
• Right against double jeopardy in the same jurisdiction, which bars being tried twice in a criminal case for the same offense.
• The right not to be compelled to be a witness against oneself in a criminal trial, which is commonly called “taking the Fifth” in everyday language.
• The right to be afforded “due process of law” in all criminal and civil proceedings.
• The right for “just compensation” or payment when private property is taken for public use.

Understand terms like indictment, true bill and double jeopardy

An indictment is a charge signed by a prosecutor. A presentment is a charge that is taken under consideration by a grand jury, regardless of the prosecutor’s signature. Both have to be approved by the grand jury.

If the grand jury determines “probable cause” by proper vote, it can return what is commonly called a “true bill” of indictment or presentment.

Some criminal acts could be state, federal, or both. The double jeopardy clause in the Fifth Amendment precludes the same state or federal court from trying the defendant twice for the same crime.

There may be cases where both a federal and state crime are involved.  An example would be a federally insured (FDIC) bank robbed in a Tennessee city. The defendant could be charged in federal or state court unless a law or regulation prevents it. The state and federal prosecutor usually agree on which jurisdiction handles the case. But double jeopardy does not bar prosecution in the federal and state courts for the same crimes.

The Declaration of Independence set the stage for the Constitution

Our 1776 Declaration of Independence states that people in America “…are endowed by their Creator with certain unalienable Rights, that among those are Life, Liberty and the Pursuit of Happiness….” 

That language is the initiation of the concepts of “due process of law” and “just compensation” for private property taken for public use. 

Please study our Constitution.

We shall continue with more on the Fifth Amendment. Constitutional study is time well spent.  Interpretations are that of the author.  We always encourage comments from readers.

Paul G. Summers, a lawyer, is a former appellate and senior judge, district attorney general, and the attorney general of Tennessee.  Raised in Fayette County, Judge Summers resides in Nashville and Holladay.